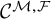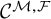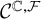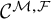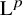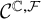1 Introduction
Understanding integrals is at the heart of many mathematical problems and often brings together challenges from both geometry and analysis. Indeed, integration is a transcendental process usually applied to functions naturally arising from basic geometric problems and, as such, having remarkable properties one aims to preserve. The present work is in the same spirit as Liouville’s theorem on elementary integrals and its recent variants by Pila and Tsimerman (see [Reference Pila and TsimermanPT22]); it concerns rich classes of functions whose parametric integrals are of a somewhat similar nature as the original functions.
To be more accurate, two types of problems may be considered in this spirit.
The first consists of describing a class of functions, possibly the smallest one, stable under parametric integration and containing a given class of functions. For instance, in the context of real o-minimal geometry, this kind of problem has been addressed for the class of semialgebraic and subanalytic functions. Indeed, in [Reference Lion and RolinLR98, Reference Comte, Lion and RolinCLR00, Reference Cluckers and MillerCM11, Reference Cluckers and MillerCM12], it has been proved that the class
![]() $\mathcal {C}$
of constructible functions (that is to say, the functions which are polynomials in globally subanalytic functions and their logarithms) forms the smallest class of real-valued functions which contains all globally subanalytic functions and which is stable under parametric integration. In [Reference KaiserKai13], a proper subclass of
$\mathcal {C}$
of constructible functions (that is to say, the functions which are polynomials in globally subanalytic functions and their logarithms) forms the smallest class of real-valued functions which contains all globally subanalytic functions and which is stable under parametric integration. In [Reference KaiserKai13], a proper subclass of
![]() $\mathcal {C}$
is introduced. This class is based on Nash functions (and their anti-derivatives) and turns out to be a small class of functions stable under parametric integration and containing the semialgebraic functions. Furthermore, this class is suitable for studying families of periods as parametric integrals in the viewpoint of [Reference Kontsevich and ZagierKZ01] (see [Reference KaiserKai23]). In a similar spirit, we fully describe here the smallest class
$\mathcal {C}$
is introduced. This class is based on Nash functions (and their anti-derivatives) and turns out to be a small class of functions stable under parametric integration and containing the semialgebraic functions. Furthermore, this class is suitable for studying families of periods as parametric integrals in the viewpoint of [Reference Kontsevich and ZagierKZ01] (see [Reference KaiserKai23]). In a similar spirit, we fully describe here the smallest class
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
of functions which contains all complex powers and complex exponentials (of module one) of globally subanalytic functions, and stable under parametric integration (a natural framework for studying families of exponential periods; see [Reference Kontsevich and ZagierKZ01, Section 4.3]).
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
of functions which contains all complex powers and complex exponentials (of module one) of globally subanalytic functions, and stable under parametric integration (a natural framework for studying families of exponential periods; see [Reference Kontsevich and ZagierKZ01, Section 4.3]).
The second type of problems, addressed here for the class
![]() $\mathcal {C}^{\mathcal {M,F}}$
, still consists of describing a class of functions containing a given class of functions and stable under parametric integration, but we additionally require our class to be stable under other analytic key operations like Fourier and Mellin transforms. A hard part of this program consists then of finding the geometric properties preserved by the parametric integration process and our analytic transformations. The challenge here comes from the fact that by the action of these analytic transformations, we leave the convenient framework of o-minimal geometry by introducing, via Mellin transforms, the (meromorphic) dependence on a complex parameter s.
$\mathcal {C}^{\mathcal {M,F}}$
, still consists of describing a class of functions containing a given class of functions and stable under parametric integration, but we additionally require our class to be stable under other analytic key operations like Fourier and Mellin transforms. A hard part of this program consists then of finding the geometric properties preserved by the parametric integration process and our analytic transformations. The challenge here comes from the fact that by the action of these analytic transformations, we leave the convenient framework of o-minimal geometry by introducing, via Mellin transforms, the (meromorphic) dependence on a complex parameter s.
Finally, let us note that several formalisms of motivic (and uniform p-adic) integration have a similar flavor and setup. Such classes can then, for example, be used to define tame classes of distributions, which are at the same time stable under Fourier transform and analytically (wave front) holonomic [Reference Aizenbud and CluckersAC20, Reference Aizenbud, Cluckers, Raibaut and ServiACRS23].
In this work, our starting point is the class
![]() $\mathcal {C}^{\mathbb {C}}$
of power-constructible functions, defined and studied in [Reference Cluckers, Comte, Rolin and ServiCCRS23], which extends
$\mathcal {C}^{\mathbb {C}}$
of power-constructible functions, defined and studied in [Reference Cluckers, Comte, Rolin and ServiCCRS23], which extends
![]() $\mathcal {C}$
by including complex powers of globally subanalytic functions. This class includes complex-valued oscillatory functions; hence, we leave the realm of o-minimality, but many tame geometric and analytic properties are preserved, such as stability under parametric integration and well-understood (convergent) power-logarithmic asymptotics. In [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18], we studied the parametric Fourier transforms of constructible functions (thus equally leaving the realm of real geometry) and described a class containing such transforms and stable under parametric integration. In [Reference Cluckers, Comte, Rolin and ServiCCRS23], we studied Mellin transforms of power-constructible functions and showed that stability under parametric integration is preserved.
$\mathcal {C}$
by including complex powers of globally subanalytic functions. This class includes complex-valued oscillatory functions; hence, we leave the realm of o-minimality, but many tame geometric and analytic properties are preserved, such as stability under parametric integration and well-understood (convergent) power-logarithmic asymptotics. In [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18], we studied the parametric Fourier transforms of constructible functions (thus equally leaving the realm of real geometry) and described a class containing such transforms and stable under parametric integration. In [Reference Cluckers, Comte, Rolin and ServiCCRS23], we studied Mellin transforms of power-constructible functions and showed that stability under parametric integration is preserved.
In the current paper, we combine the action of parametric Fourier and Mellin transforms on the class
![]() $\mathcal {C}^{\mathbb {C}}$
of power-constructible functions. We define a system
$\mathcal {C}^{\mathbb {C}}$
of power-constructible functions. We define a system
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
of
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
of
![]() $\mathbb {C}$
-algebras containing all such transforms and stable under parametric integration (see Definition 2.19 and Theorem 2.21). We describe a set of generators of a particular prepared form which allows us to prove the stability under parametric integration and deduce information about the asymptotics at infinity in a chosen variable of the functions of the class. We furthermore identify a subclass
$\mathbb {C}$
-algebras containing all such transforms and stable under parametric integration (see Definition 2.19 and Theorem 2.21). We describe a set of generators of a particular prepared form which allows us to prove the stability under parametric integration and deduce information about the asymptotics at infinity in a chosen variable of the functions of the class. We furthermore identify a subclass
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
(see Definition 2.7) of
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
(see Definition 2.7) of
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
which will turn out to be the smallest class containing
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
which will turn out to be the smallest class containing
![]() $\mathcal {C}^{\mathbb {C}}$
and stable under parametric Fourier transform and right-composition with subanalytic maps (see Theorem 2.9), and give, for the functions of this class, asymptotic expansions in the power-logarithmic scale (Theorem 7.6), in a chosen variable y and uniformly in the other variables x (which serve as parameters and range in a given globally subanalytic set). We also deduce the stability of the class
$\mathcal {C}^{\mathbb {C}}$
and stable under parametric Fourier transform and right-composition with subanalytic maps (see Theorem 2.9), and give, for the functions of this class, asymptotic expansions in the power-logarithmic scale (Theorem 7.6), in a chosen variable y and uniformly in the other variables x (which serve as parameters and range in a given globally subanalytic set). We also deduce the stability of the class
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
under taking pointwise and
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
under taking pointwise and
![]() $\text {L}^{p}$
-limits, and under the Fourier-Plancherel transform (Theorems 7.11, 8.7, 8.8).
$\text {L}^{p}$
-limits, and under the Fourier-Plancherel transform (Theorems 7.11, 8.7, 8.8).
The main geometric tools for achieving this program come from o-minimality (see [Reference van den DriesDri99]) and, more precisely, from the geometry of subanalytic sets and functions. They consist of resolution results in the form of preparation theorems, in the spirit of [Reference ParusińskiPar94], [Reference Lion and RolinLR98] or [Reference MillerMil06]. The key analytic tool (used in Section 8) we use is the theory of continuously uniformly distributed modulo one functions (c.u.d. mod 1, for short), building on [Reference WeylWey16, Reference Kuipers and NiederreiterKN74, Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18], and its uniform variants. One of the deep challenges comes from the oscillatory nature of functions in
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
and
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
and
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
, which imposes a careful study of the integration loci (see Definition 2.3 and Theorem 6.5). This is where the interaction between the theory of c.u.d. mod 1 functions and the geometry of subanalytic sets comes into play.
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
, which imposes a careful study of the integration loci (see Definition 2.3 and Theorem 6.5). This is where the interaction between the theory of c.u.d. mod 1 functions and the geometry of subanalytic sets comes into play.
The paper is organized as follows.
In Section 2, we introduce the classes
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
and
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
and
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
and state our main results (Theorems 2.9 and 2.21). The class
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
and state our main results (Theorems 2.9 and 2.21). The class
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
is a collection of functions defined on globally subanalytic sets; the class
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
is a collection of functions defined on globally subanalytic sets; the class
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
is a collection of functions that also depend on a complex parameter s, which is only allowed to range in a vertical open strip with bounded width. However, it is possible to extend a function on a given strip to a larger strip (Proposition 2.20).
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
is a collection of functions that also depend on a complex parameter s, which is only allowed to range in a vertical open strip with bounded width. However, it is possible to extend a function on a given strip to a larger strip (Proposition 2.20).
In Section 3, we choose suitable generators for
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
as an abelian group, which allow us to prove the extension result (see Section 3.2).
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
as an abelian group, which allow us to prove the extension result (see Section 3.2).
In Section 4, we identify two special types of generators, strongly integrable and monomial (see Definition 4.2), and show that their parametric integrals still belong to the class
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
(Corollary 4.6 and Proposition 4.8). In Section 4.2, we give the proof of Theorems 2.9 and 2.21, assuming Theorem 6.5, which is a precise form of Theorem 2.21 when integrating over only one variable.
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
(Corollary 4.6 and Proposition 4.8). In Section 4.2, we give the proof of Theorems 2.9 and 2.21, assuming Theorem 6.5, which is a precise form of Theorem 2.21 when integrating over only one variable.
Sections 5 and 6 are devoted to the proof of Theorem 6.5, which requires both subanalytic resolution of singularities and preparation techniques, and non-compensation results based on the theory of c.u.d. mod 1 functions.
In Section 7, we study the asymptotics of the functions in the power-logarithmic scale and prove the stability of the class
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
under pointwise limits (Theorems 7.6 and 7.11).
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
under pointwise limits (Theorems 7.6 and 7.11).
In Section 8, we prove the
![]() $\text {L}^{p}$
-completeness of the class
$\text {L}^{p}$
-completeness of the class
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
and its stability under the parametric Fourier-Plancherel transform (Theorems 8.7 and 8.8).
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
and its stability under the parametric Fourier-Plancherel transform (Theorems 8.7 and 8.8).
2 Context, definitions and main results
A subset X of
![]() $\mathbb {R}^{m}$
is globally subanalytic if it is the image under the canonical projection from
$\mathbb {R}^{m}$
is globally subanalytic if it is the image under the canonical projection from
![]() $\mathbb {R}^{m+n}$
to
$\mathbb {R}^{m+n}$
to
![]() $\mathbb {R}^{m}$
of a globally semianalytic subset of
$\mathbb {R}^{m}$
of a globally semianalytic subset of
![]() $\mathbb {R}^{m+n}$
(i.e., a subset
$\mathbb {R}^{m+n}$
(i.e., a subset
![]() $Y\subseteq \mathbb {R}^{m+n}$
such that, in a neighborhood of every point of
$Y\subseteq \mathbb {R}^{m+n}$
such that, in a neighborhood of every point of
![]() $\mathbb {P}^{1}\left (\mathbb {R}\right )^{m+n}$
, Y is described by finitely many analytic equations and inequalities). Equivalently, X is definable in the o-minimal structure
$\mathbb {P}^{1}\left (\mathbb {R}\right )^{m+n}$
, Y is described by finitely many analytic equations and inequalities). Equivalently, X is definable in the o-minimal structure
![]() $\mathbb {R}_{\text {an}}$
(see, for example, [Reference Denef and van den DriesDD88]). Thus, the logarithm
$\mathbb {R}_{\text {an}}$
(see, for example, [Reference Denef and van den DriesDD88]). Thus, the logarithm
![]() $\log :\left (0,+\infty \right )\longrightarrow \mathbb {R}$
and the power map
$\log :\left (0,+\infty \right )\longrightarrow \mathbb {R}$
and the power map
![]() $x^{y}:\left (0,+\infty \right )\times \mathbb {R}\longrightarrow \mathbb {R}$
are functions whose graph is not subanalytic, but they are definable in the o-minimal structure
$x^{y}:\left (0,+\infty \right )\times \mathbb {R}\longrightarrow \mathbb {R}$
are functions whose graph is not subanalytic, but they are definable in the o-minimal structure
![]() $\mathbb {R}_{\mathrm {an},\exp }$
(see for example [Reference van den Dries, Macintyre and MarkerDMM94]).
$\mathbb {R}_{\mathrm {an},\exp }$
(see for example [Reference van den Dries, Macintyre and MarkerDMM94]).
Throughout this paper,
![]() $X\subseteq \mathbb {R}^{m}$
will be a globally subanalytic set (from now on, just ‘subanalytic set’, for short). Denote by
$X\subseteq \mathbb {R}^{m}$
will be a globally subanalytic set (from now on, just ‘subanalytic set’, for short). Denote by
![]() $\mathcal {S}\left (X\right )$
the collection of all subanalytic functions on X (i.e., all the functions of domain X whose graph is a subanalytic set), and let
$\mathcal {S}\left (X\right )$
the collection of all subanalytic functions on X (i.e., all the functions of domain X whose graph is a subanalytic set), and let
![]() $\mathcal {S}_{+}\left (X\right )=\left \{ f\in \mathcal {S}\left (X\right ):\ f\left (X\right )\subseteq \left (0,+\infty \right )\right \} $
.
$\mathcal {S}_{+}\left (X\right )=\left \{ f\in \mathcal {S}\left (X\right ):\ f\left (X\right )\subseteq \left (0,+\infty \right )\right \} $
.
Notation 2.1. Whenever we fix, for every
![]() $m\in \mathbb {N}$
and
$m\in \mathbb {N}$
and
![]() $X\subseteq \mathbb {R}^{m}$
subanalytic, a collection
$X\subseteq \mathbb {R}^{m}$
subanalytic, a collection
![]() $\mathcal {K}\left (X\right )$
of real- or complex-valued functions defined on X, we denote by
$\mathcal {K}\left (X\right )$
of real- or complex-valued functions defined on X, we denote by
![]() $\mathcal {K}$
the system of all collections
$\mathcal {K}$
the system of all collections
![]() $\mathcal {K}\left (X\right )$
. For instance,
$\mathcal {K}\left (X\right )$
. For instance,
![]() $\mathcal {S}$
is the system of collections of all subanalytic functions defined on subanalytic sets:
$\mathcal {S}$
is the system of collections of all subanalytic functions defined on subanalytic sets:
Definition 2.2. For
![]() $X\subseteq \mathbb {R}^{m}$
subanalytic, define
$X\subseteq \mathbb {R}^{m}$
subanalytic, define
 $$ \begin{align*} \mathcal{S}_{+}^{\mathbb{C}}\left(X\right) & =\left\{ f^{\alpha}:\ f\in\mathcal{S}_{+}\left(X\right),\ \alpha\in\mathbb{C}\right\} ,\\ \log\mathcal{S}_{+}\left(X\right) & =\left\{ \log f:\ f\in\mathcal{S}_{+}\left(X\right)\right\} ,\\ \text{e}^{\text{i}\mathcal{S}}\left(X\right) & =\left\{ \text{e}^{\text{i}f}:\ f\in\mathcal{S}\left(X\right)\right\}. \end{align*} $$
$$ \begin{align*} \mathcal{S}_{+}^{\mathbb{C}}\left(X\right) & =\left\{ f^{\alpha}:\ f\in\mathcal{S}_{+}\left(X\right),\ \alpha\in\mathbb{C}\right\} ,\\ \log\mathcal{S}_{+}\left(X\right) & =\left\{ \log f:\ f\in\mathcal{S}_{+}\left(X\right)\right\} ,\\ \text{e}^{\text{i}\mathcal{S}}\left(X\right) & =\left\{ \text{e}^{\text{i}f}:\ f\in\mathcal{S}\left(X\right)\right\}. \end{align*} $$
A function defined on X and taking its values in
![]() $\mathbb {C}$
is called a complex-valued subanalytic function if its real and imaginary parts are in
$\mathbb {C}$
is called a complex-valued subanalytic function if its real and imaginary parts are in
![]() $\mathcal {S}\left (X\right )$
. For example, if
$\mathcal {S}\left (X\right )$
. For example, if
![]() $f\in \mathcal {S}\left (X\right )$
is bounded (i.e., for all
$f\in \mathcal {S}\left (X\right )$
is bounded (i.e., for all
![]() $x\in X,$
$x\in X,$
![]() $\left |f\left (x\right )\right |\leq M$
, for some
$\left |f\left (x\right )\right |\leq M$
, for some
![]() $M>0$
), then
$M>0$
), then
![]() $\text {e}^{\text {i}f}$
is a complex-valued subanalytic function. If such a bounded f is furthermore strictly positive (i.e.,
$\text {e}^{\text {i}f}$
is a complex-valued subanalytic function. If such a bounded f is furthermore strictly positive (i.e.,
![]() $f\in \mathcal {S}_{+}\left (X\right )$
) and bounded away from zero (i.e., for all
$f\in \mathcal {S}_{+}\left (X\right )$
) and bounded away from zero (i.e., for all
![]() $x\in X,\ f\left (x\right )\geq m$
, for some
$x\in X,\ f\left (x\right )\geq m$
, for some
![]() $m>0$
), then
$m>0$
), then
![]() $\log f$
is a real-valued subanalytic function and for all
$\log f$
is a real-valued subanalytic function and for all
![]() $\alpha \in \mathbb {C}$
,
$\alpha \in \mathbb {C}$
,
![]() $f^{\alpha }$
is a complex-valued subanalytic function.
$f^{\alpha }$
is a complex-valued subanalytic function.
Definition 2.3. Let
![]() $\mathcal {K}$
be a system as in Notation 2.1. For
$\mathcal {K}$
be a system as in Notation 2.1. For
![]() $h\in \mathcal {K}\left (X\times \mathbb {R}^{n}\right )$
, the integration locus of h on X is the set
$h\in \mathcal {K}\left (X\times \mathbb {R}^{n}\right )$
, the integration locus of h on X is the set
We say that
![]() $\mathcal {K}$
is stable under parametric integration if for all
$\mathcal {K}$
is stable under parametric integration if for all
![]() $h\in \mathcal {K}\left (X\times \mathbb {R}^{n}\right )$
, there exists
$h\in \mathcal {K}\left (X\times \mathbb {R}^{n}\right )$
, there exists
![]() $H\in \mathcal {K}\left (X\right )$
such that
$H\in \mathcal {K}\left (X\right )$
such that
Finally, define
![]() $\mathcal {K}\left (X\times \mathbb {R}^{n}\right )_{\text {int}}=\left \{ h\in \mathcal {K}\left (X\times \mathbb {R}^{n}\right ):\ \text {Int}\left (h;X\right )=X\right \} $
.
$\mathcal {K}\left (X\times \mathbb {R}^{n}\right )_{\text {int}}=\left \{ h\in \mathcal {K}\left (X\times \mathbb {R}^{n}\right ):\ \text {Int}\left (h;X\right )=X\right \} $
.
Thus, for example,
![]() $h\in \mathcal {K}\left (\left (X\times \mathbb {R}\right )\times \mathbb {R}\right )_{\text {int}}$
means that for all
$h\in \mathcal {K}\left (\left (X\times \mathbb {R}\right )\times \mathbb {R}\right )_{\text {int}}$
means that for all
![]() $\left (x,y\right )\in X\times \mathbb {R},\ t\longmapsto h\left (x,y,t\right )\in L^{1}\left (\mathbb {R}\right )$
, whereas
$\left (x,y\right )\in X\times \mathbb {R},\ t\longmapsto h\left (x,y,t\right )\in L^{1}\left (\mathbb {R}\right )$
, whereas
![]() $h\in \mathcal {K}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
means that for all
$h\in \mathcal {K}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
means that for all
![]() $x\in X,\ \left (y,t\right )\longmapsto h\left (x,y,t\right )\in L^{1}\left (\mathbb {R}^{2}\right )$
.
$x\in X,\ \left (y,t\right )\longmapsto h\left (x,y,t\right )\in L^{1}\left (\mathbb {R}^{2}\right )$
.
Next, we introduce the parametric Fourier transform acting on a system
![]() $\mathcal {K}$
as in Notation 2.1.
$\mathcal {K}$
as in Notation 2.1.
Definition 2.4. Let
![]() $h\in \mathcal {K}\left (X\times \mathbb {R}\right )_{\text {int}}$
. Define the parametric Fourier transform of h as the function
$h\in \mathcal {K}\left (X\times \mathbb {R}\right )_{\text {int}}$
. Define the parametric Fourier transform of h as the function
and the fixed frequency parametric Fourier transform of h as the function obtained from
![]() $\mathcal {F}\left [h\right ]$
by fixing
$\mathcal {F}\left [h\right ]$
by fixing
![]() $t=-\frac {1}{2\pi }$
; that is,
$t=-\frac {1}{2\pi }$
; that is,
Notation 2.5. The letter
![]() $\chi $
will be used for characteristic functions. Thus, if
$\chi $
will be used for characteristic functions. Thus, if
![]() $A\subseteq \mathbb {R}^{n}$
, then
$A\subseteq \mathbb {R}^{n}$
, then
![]() $\chi _{A}$
will be the characteristic function of the set A.
$\chi _{A}$
will be the characteristic function of the set A.
We will often work in restriction to subanalytic cells
![]() $A\subseteq X\times \mathbb {R}$
, for some
$A\subseteq X\times \mathbb {R}$
, for some
![]() $X\subseteq \mathbb {R}^{m}$
subanalytic. If
$X\subseteq \mathbb {R}^{m}$
subanalytic. If
![]() $x\in X$
, then
$x\in X$
, then
![]() $A_{x}$
denotes the fiber of A over x (i.e., the set
$A_{x}$
denotes the fiber of A over x (i.e., the set
![]() $\left \{ y\in \mathbb {R}:\ \left (x,y\right )\in A\right \} $
). As X serves as a space of parameters (we will never integrate with respect to the variables x ranging in X), for the questions on integration, we consider we are allowed to partition X into subanalytic cells, replace X by one of the cells of the partition and work disjointly in restriction to such a cell. In particular, we may always assume that X is itself a subanalytic cell and that all cells in
$\left \{ y\in \mathbb {R}:\ \left (x,y\right )\in A\right \} $
). As X serves as a space of parameters (we will never integrate with respect to the variables x ranging in X), for the questions on integration, we consider we are allowed to partition X into subanalytic cells, replace X by one of the cells of the partition and work disjointly in restriction to such a cell. In particular, we may always assume that X is itself a subanalytic cell and that all cells in
![]() $X\times \mathbb {R}$
project onto X. Moreover, we will always concentrate on cells A which are open over X (see [Reference Cluckers, Comte, Rolin and ServiCCRS23, Definition 3.1]), as these are the only cells whose fibers give a nonzero contribution when integrating a function defined on
$X\times \mathbb {R}$
project onto X. Moreover, we will always concentrate on cells A which are open over X (see [Reference Cluckers, Comte, Rolin and ServiCCRS23, Definition 3.1]), as these are the only cells whose fibers give a nonzero contribution when integrating a function defined on
![]() $X\times \mathbb {R}$
with respect to its last variable.
$X\times \mathbb {R}$
with respect to its last variable.
2.1 Fourier transforms of power-constructible functions
In [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18], we constructed the smallest system of
![]() $\mathbb {C}$
-algebras containing
$\mathbb {C}$
-algebras containing
![]() $\mathcal {S}\cup \text {e}^{\text {i}\mathcal {S}}$
and stable under parametric integration. Such a system contains, in particular, the parametric Fourier transforms of all subanalytic functions. The first aim of this paper is to extend such a construction to describe the smallest system
$\mathcal {S}\cup \text {e}^{\text {i}\mathcal {S}}$
and stable under parametric integration. Such a system contains, in particular, the parametric Fourier transforms of all subanalytic functions. The first aim of this paper is to extend such a construction to describe the smallest system
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
containing
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
containing
![]() $\mathcal {S}_{+}^{\mathbb {C}}\cup \text {e}^{\text {i}\mathcal {S}}$
and stable under parametric integration (see Definition 2.7 and Theorem 2.9). For this, our starting point is the system
$\mathcal {S}_{+}^{\mathbb {C}}\cup \text {e}^{\text {i}\mathcal {S}}$
and stable under parametric integration (see Definition 2.7 and Theorem 2.9). For this, our starting point is the system
![]() $\mathcal {C}^{\mathbb {C}}$
of power-constructible functions defined in [Reference Cluckers, Comte, Rolin and ServiCCRS23]. Let us recall its definition and main properties.
$\mathcal {C}^{\mathbb {C}}$
of power-constructible functions defined in [Reference Cluckers, Comte, Rolin and ServiCCRS23]. Let us recall its definition and main properties.
Theorem 2.6 [Reference Cluckers, Comte, Rolin and ServiCCRS23, Definition 2.2 and Theorem 2.4].
For
![]() $X\subseteq \mathbb {R}^{m}$
subanalytic, let
$X\subseteq \mathbb {R}^{m}$
subanalytic, let
![]() $\mathcal {C}^{\mathbb {C}}\left (X\right )$
be the
$\mathcal {C}^{\mathbb {C}}\left (X\right )$
be the
![]() $\mathbb {C}$
-algebra generated by
$\mathbb {C}$
-algebra generated by
![]() $\mathcal {S}_{+}^{\mathbb {C}}\left (X\right )\cup \log \mathcal {S}_{+}\left (X\right )$
. The system
$\mathcal {S}_{+}^{\mathbb {C}}\left (X\right )\cup \log \mathcal {S}_{+}\left (X\right )$
. The system
![]() $\mathcal {C}^{\mathbb {C}}$
of power-constructible functions is the smallest system of
$\mathcal {C}^{\mathbb {C}}$
of power-constructible functions is the smallest system of
![]() $\mathbb {C}$
-algebras containing
$\mathbb {C}$
-algebras containing
![]() $\mathcal {S}_{+}^{\mathbb {C}}$
and stable under parametric integration.
$\mathcal {S}_{+}^{\mathbb {C}}$
and stable under parametric integration.
A natural candidate for the smallest system containing
![]() $\mathcal {S}_{+}^{\mathbb {C}}\cup \text {e}^{\text {i}\mathcal {S}}$
and stable under parametric integration would be the system
$\mathcal {S}_{+}^{\mathbb {C}}\cup \text {e}^{\text {i}\mathcal {S}}$
and stable under parametric integration would be the system
![]() $\mathcal {C}^{\mathbb {C},\text {i}\mathcal {S}}$
of
$\mathcal {C}^{\mathbb {C},\text {i}\mathcal {S}}$
of
![]() $\mathbb {C}$
-algebras
$\mathbb {C}$
-algebras
![]() $\mathcal {C}^{\mathbb {C},\text {i}\mathcal {S}}\left (X\right )$
generated by
$\mathcal {C}^{\mathbb {C},\text {i}\mathcal {S}}\left (X\right )$
generated by
![]() $\mathcal {C}^{\mathbb {C}}\left (X\right )\cup \text {e}^{\text {i}\mathcal {S}}\left (X\right )$
. However, we will show (see Corollary 7.8) that such a system is not stable under parametric integration. This motivates the following definition.
$\mathcal {C}^{\mathbb {C}}\left (X\right )\cup \text {e}^{\text {i}\mathcal {S}}\left (X\right )$
. However, we will show (see Corollary 7.8) that such a system is not stable under parametric integration. This motivates the following definition.
Definition 2.7. Consider the fixed frequency parametric Fourier operator
![]() $\mathfrak {f}$
acting on
$\mathfrak {f}$
acting on
![]() $\mathcal {C}^{\mathbb {C}}$
:
$\mathcal {C}^{\mathbb {C}}$
:
Define
Remark 2.8. Notice that
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
is a
$\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
is a
![]() $\mathbb {C}$
-module and that
$\mathbb {C}$
-module and that
![]() $1=\mathfrak {f}\left [\frac {\mathrm {i}}{2}\chi _{\left [\pi ,2\pi \right ]}\right ]$
. In particular,
$1=\mathfrak {f}\left [\frac {\mathrm {i}}{2}\chi _{\left [\pi ,2\pi \right ]}\right ]$
. In particular,
![]() $\mathcal {C}^{\mathbb {C}}\left (X\right )\subseteq \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
. At this stage, it is not clear whether
$\mathcal {C}^{\mathbb {C}}\left (X\right )\subseteq \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
. At this stage, it is not clear whether
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
is a
$\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
is a
![]() $\mathbb {C}$
-algebra.
$\mathbb {C}$
-algebra.
Note also that
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
is stable under right-composition with subanalytic maps: if
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
is stable under right-composition with subanalytic maps: if
![]() $X\subseteq \mathbb {R}^{m},Y\subseteq \mathbb {R}^{n}$
are subanalytic sets,
$X\subseteq \mathbb {R}^{m},Y\subseteq \mathbb {R}^{n}$
are subanalytic sets,
![]() $G:Y\longrightarrow X$
is a subanalytic map and
$G:Y\longrightarrow X$
is a subanalytic map and
![]() $h\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
, then
$h\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
, then
![]() $h\circ G\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (Y\right )$
.
$h\circ G\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (Y\right )$
.
Our first result is the following.
Theorem 2.9. The system
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
is stable under parametric integration. It is a system of
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
is stable under parametric integration. It is a system of
![]() $\mathbb {C}$
-algebras, and indeed the smallest such system containing
$\mathbb {C}$
-algebras, and indeed the smallest such system containing
![]() $\mathcal {S}_{+}^{\mathbb {C}}\cup \mathrm {e}^{\mathrm {i}\mathcal {S}}$
and stable under parametric integration. It is also the smallest such system containing
$\mathcal {S}_{+}^{\mathbb {C}}\cup \mathrm {e}^{\mathrm {i}\mathcal {S}}$
and stable under parametric integration. It is also the smallest such system containing
![]() $\mathcal {C}^{\mathbb {C}}$
and stable under the parametric Fourier transform and right-composition with subanalytic maps.
$\mathcal {C}^{\mathbb {C}}$
and stable under the parametric Fourier transform and right-composition with subanalytic maps.
Subsequently, we derive results on asymptotic expansions, pointwise limits,
![]() $\text {L}^{p}$
-limits and the Fourier-Plancherel transform for the class
$\text {L}^{p}$
-limits and the Fourier-Plancherel transform for the class
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
. Such results are stated and proven in Sections 7 and 8.
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
. Such results are stated and proven in Sections 7 and 8.
2.2 Parametric Mellin and Fourier transforms of power-constructible functions
We now turn our attention to the Mellin transform.
Definition 2.10. Let
![]() $\Sigma \subseteq \mathbb {C}$
be an open set. For
$\Sigma \subseteq \mathbb {C}$
be an open set. For
![]() $h\in \mathcal {C}^{\mathbb {C}}\left (X\times [0,+\infty )\right )$
such that for all
$h\in \mathcal {C}^{\mathbb {C}}\left (X\times [0,+\infty )\right )$
such that for all
![]() $s\in \Sigma $
and for all
$s\in \Sigma $
and for all
![]() $x\in X$
, the function
$x\in X$
, the function
![]() $y\longmapsto y^{s-1}h\left (x,y\right )$
belongs to
$y\longmapsto y^{s-1}h\left (x,y\right )$
belongs to
![]() $L^{1}\left ([0,+\infty )\right )$
, the parametric Mellin transform of h on
$L^{1}\left ([0,+\infty )\right )$
, the parametric Mellin transform of h on
![]() $\Sigma $
is the function
$\Sigma $
is the function
 $$\begin{align*}\mathcal{M}_{\Sigma}\left[h\right]:\Sigma\times X\ni\left(s,x\right)\longmapsto\int_{0}^{+\infty}y^{s-1}h\left(x,y\right)\text{d}y. \end{align*}$$
$$\begin{align*}\mathcal{M}_{\Sigma}\left[h\right]:\Sigma\times X\ni\left(s,x\right)\longmapsto\int_{0}^{+\infty}y^{s-1}h\left(x,y\right)\text{d}y. \end{align*}$$
In [Reference Cluckers, Comte, Rolin and ServiCCRS23], we studied the parametric Mellin transforms of power-constructible functions: we constructed a system
![]() $\mathcal {C}^{\mathcal {M}}$
containing such transforms and stable under parametric integration (see Definition 2.17 and Theorem 2.18 below). The second aim of this work is to construct a system containing both the parametric Mellin transforms and the parametric Fourier transforms of power-constructible functions, and stable under parametric integration. As the Mellin transform introduces a new complex variable s, the domains of the functions we consider will be suitable subsets of
$\mathcal {C}^{\mathcal {M}}$
containing such transforms and stable under parametric integration (see Definition 2.17 and Theorem 2.18 below). The second aim of this work is to construct a system containing both the parametric Mellin transforms and the parametric Fourier transforms of power-constructible functions, and stable under parametric integration. As the Mellin transform introduces a new complex variable s, the domains of the functions we consider will be suitable subsets of
![]() $\mathbb {C}\times \mathbb {R}^{m}$
, rather than just subsets of
$\mathbb {C}\times \mathbb {R}^{m}$
, rather than just subsets of
![]() $\mathbb {R}^{m}$
. The notions of integration locus, parametric integral transform and stability under parametric integration need to be made precise in this new context, which is what we do next.
$\mathbb {R}^{m}$
. The notions of integration locus, parametric integral transform and stability under parametric integration need to be made precise in this new context, which is what we do next.
In what follows, we will consider several collections of functions defined on sets of the form
![]() $\Sigma \times X$
, where
$\Sigma \times X$
, where
![]() $\Sigma $
is a suitable subset of
$\Sigma $
is a suitable subset of
![]() $\mathbb {C}$
and X is a subanalytic subset of
$\mathbb {C}$
and X is a subanalytic subset of
![]() $\mathbb {R}^{m}$
, for some
$\mathbb {R}^{m}$
, for some
![]() $m\in \mathbb {N}$
. We will study the action of some integral operators on these collections of functions, and, more generally, the nature of the parametric integrals of such functions. Let us fix some notation.
$m\in \mathbb {N}$
. We will study the action of some integral operators on these collections of functions, and, more generally, the nature of the parametric integrals of such functions. Let us fix some notation.
Definition 2.11. An open vertical strip of bounded width in
![]() $\mathbb {C}$
is a set of the form
$\mathbb {C}$
is a set of the form
where
![]() $p,q\in \mathbb {R}$
and
$p,q\in \mathbb {R}$
and
![]() $p<q$
. For short, we will say that
$p<q$
. For short, we will say that
![]() $\Sigma $
is a strip.
$\Sigma $
is a strip.
Notation 2.12. Given a strip
![]() $\Sigma \subseteq \mathbb {C}$
and a subanalytic set
$\Sigma \subseteq \mathbb {C}$
and a subanalytic set
![]() $X\subseteq \mathbb {R}^{m}$
, let
$X\subseteq \mathbb {R}^{m}$
, let
![]() $\mathcal {D}_{\Sigma }\left (X\right )$
be a collection of complex-valued functions such that for all
$\mathcal {D}_{\Sigma }\left (X\right )$
be a collection of complex-valued functions such that for all
![]() $h\in \mathcal {D}_{\Sigma }\left (X\right )$
, there is a closed discrete set
$h\in \mathcal {D}_{\Sigma }\left (X\right )$
, there is a closed discrete set
![]() $P\subseteq \mathbb {C}$
such that the domain of h contains
$P\subseteq \mathbb {C}$
such that the domain of h contains
![]() $\left (\Sigma \setminus P\right )\times X$
(we say that h has no poles outside P). Denote by
$\left (\Sigma \setminus P\right )\times X$
(we say that h has no poles outside P). Denote by
![]() $\mathcal {D}_{\Sigma }$
the system
$\mathcal {D}_{\Sigma }$
the system
![]() $\left \{ \mathcal {D}_{\Sigma }\left (X\right ):\ X\subseteq \mathbb {R}^{m}\ \text {subanalytic, }m\in \mathbb {N}\right \} $
.
$\left \{ \mathcal {D}_{\Sigma }\left (X\right ):\ X\subseteq \mathbb {R}^{m}\ \text {subanalytic, }m\in \mathbb {N}\right \} $
.
Suppose furthermore that the collection
![]() $\left \{ \mathcal {D}_{\Sigma }:\ \Sigma \subseteq \mathbb {C}\ \text {strip}\right \} $
has the extension property: for every subanalytic set
$\left \{ \mathcal {D}_{\Sigma }:\ \Sigma \subseteq \mathbb {C}\ \text {strip}\right \} $
has the extension property: for every subanalytic set
![]() $X\subseteq \mathbb {R}^{m}$
, given any two strips
$X\subseteq \mathbb {R}^{m}$
, given any two strips
![]() $\Sigma ,\Sigma '$
such that
$\Sigma ,\Sigma '$
such that
![]() $\Sigma \subseteq \Sigma '$
and a closed discrete set
$\Sigma \subseteq \Sigma '$
and a closed discrete set
![]() $P\subseteq \mathbb {C}$
and
$P\subseteq \mathbb {C}$
and
![]() $h\in \mathcal {D}_{\Sigma }\left (X\right )$
without poles outside P, there exists
$h\in \mathcal {D}_{\Sigma }\left (X\right )$
without poles outside P, there exists
![]() $h'\in \mathcal {D}_{\Sigma '}\left (X\right )$
without poles outside P such that
$h'\in \mathcal {D}_{\Sigma '}\left (X\right )$
without poles outside P such that
![]() $h'\restriction \left (\Sigma \setminus P\right )\times X=h$
. Define
$h'\restriction \left (\Sigma \setminus P\right )\times X=h$
. Define
![]() $\mathcal {D}\left (X\right )$
as the direct limit of
$\mathcal {D}\left (X\right )$
as the direct limit of
![]() $\left \{ \mathcal {D}_{\Sigma }\left (X\right ):\ \Sigma \subseteq \mathbb {C}\ \text {strip}\right \} $
and
$\left \{ \mathcal {D}_{\Sigma }\left (X\right ):\ \Sigma \subseteq \mathbb {C}\ \text {strip}\right \} $
and
![]() $\mathcal {D}=\left \{ \mathcal {D}\left (X\right ):\ X\subseteq \mathbb {R}^{m}\text { subanalytic},\ m\in \mathbb {N}\right \} $
. For
$\mathcal {D}=\left \{ \mathcal {D}\left (X\right ):\ X\subseteq \mathbb {R}^{m}\text { subanalytic},\ m\in \mathbb {N}\right \} $
. For
![]() $h\in \mathcal {D}\left (X\right )$
and a closed discrete set
$h\in \mathcal {D}\left (X\right )$
and a closed discrete set
![]() $P\subseteq \mathbb {C}$
, we say that h has no poles outside P if this is the case for some representative of h on each strip
$P\subseteq \mathbb {C}$
, we say that h has no poles outside P if this is the case for some representative of h on each strip
![]() $\Sigma $
.
$\Sigma $
.
Definition 2.13. Given
![]() $h\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}^{n}\right )$
without poles outside some closed discrete set
$h\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}^{n}\right )$
without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
, define the integration locus of h as
$P\subseteq \mathbb {C}$
, define the integration locus of h as
and we set
 $$ \begin{align*} \mathcal{D}_{\Sigma}\left(X\times\mathbb{R}^{n}\right)_{\text{int}}= & \{h\in\mathcal{D}_{\Sigma}\left(X\times\mathbb{R}^{n}\right):\ \text{Int}\left(h;\left(\Sigma\setminus P\right)\times X\right)=\left(\Sigma\setminus P\right)\times X,\\ & \text{for some closed\ discrete }P\subseteq\mathbb{C}\}. \end{align*} $$
$$ \begin{align*} \mathcal{D}_{\Sigma}\left(X\times\mathbb{R}^{n}\right)_{\text{int}}= & \{h\in\mathcal{D}_{\Sigma}\left(X\times\mathbb{R}^{n}\right):\ \text{Int}\left(h;\left(\Sigma\setminus P\right)\times X\right)=\left(\Sigma\setminus P\right)\times X,\\ & \text{for some closed\ discrete }P\subseteq\mathbb{C}\}. \end{align*} $$
We consider the following parametric integral transforms acting on
![]() $\mathcal {D}$
, where the word generalized refers to the fact that, unlike the case of the corresponding classical transforms, we allow the operator to act on functions for which the integral transform is not everywhere defined.
$\mathcal {D}$
, where the word generalized refers to the fact that, unlike the case of the corresponding classical transforms, we allow the operator to act on functions for which the integral transform is not everywhere defined.
Definition 2.14. Let
![]() $\mathcal {D}$
be as in Notation 2.12 and
$\mathcal {D}$
be as in Notation 2.12 and
![]() $h\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}\right )$
be without poles outside some closed discrete set
$h\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}\right )$
be without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
.
$P\subseteq \mathbb {C}$
.
-
• Let
 $\chi _{+}$
be the characteristic function of the half-line
$\chi _{+}$
be the characteristic function of the half-line
 $[0,+\infty )$
and The generalized parametric Mellin transform of h is the function defined on
$[0,+\infty )$
and The generalized parametric Mellin transform of h is the function defined on $$\begin{align*}\widetilde{h}\left(s,x,y\right)=\chi_{+}\left(y\right)y^{s-1}h\left(s,x,y\right). \end{align*}$$
$$\begin{align*}\widetilde{h}\left(s,x,y\right)=\chi_{+}\left(y\right)y^{s-1}h\left(s,x,y\right). \end{align*}$$
 $\text {Int}\left (\widetilde {h};\left (\Sigma \setminus P\right )\times X\right )$
given by The integration kernel of this transform is the function
$\text {Int}\left (\widetilde {h};\left (\Sigma \setminus P\right )\times X\right )$
given by The integration kernel of this transform is the function $$\begin{align*}\mathcal{M}\left[h\right]\left(s,x\right)=\int_{0}^{+\infty}y^{s-1}h\left(s,x,y\right)\text{d}y. \end{align*}$$
$$\begin{align*}\mathcal{M}\left[h\right]\left(s,x\right)=\int_{0}^{+\infty}y^{s-1}h\left(s,x,y\right)\text{d}y. \end{align*}$$
 $\left (s,y\right )\longmapsto \chi _{+}\left (y\right )y^{s-1}$
.
$\left (s,y\right )\longmapsto \chi _{+}\left (y\right )y^{s-1}$
.
-
• The generalized parametric Fourier transform of h is the function defined on
 $\text {Int}\left (h;\left (\Sigma \setminus P\right )\times X\right )\times \mathbb {R}$
given by The integration kernel is the function
$\text {Int}\left (h;\left (\Sigma \setminus P\right )\times X\right )\times \mathbb {R}$
given by The integration kernel is the function $$\begin{align*}\mathcal{F}\left[h\right]\left(s,x,t\right)=\int_{\mathbb{R}}h\left(s,x,y\right)\text{e}^{-2\pi\text{i}ty}\text{d}y. \end{align*}$$
$$\begin{align*}\mathcal{F}\left[h\right]\left(s,x,t\right)=\int_{\mathbb{R}}h\left(s,x,y\right)\text{e}^{-2\pi\text{i}ty}\text{d}y. \end{align*}$$
 $\left (t,y\right )\longmapsto \text {e}^{-2\pi \text {i}ty}$
.
$\left (t,y\right )\longmapsto \text {e}^{-2\pi \text {i}ty}$
.
-
• The generalized fixed frequency parametric Fourier transform of h is the function defined on
 $\text {Int}\left (h;\left (\Sigma \setminus P\right )\times X\right )$
given by The integration kernel is the function
$\text {Int}\left (h;\left (\Sigma \setminus P\right )\times X\right )$
given by The integration kernel is the function $$\begin{align*}\mathfrak{f}\left[h\right]\left(s,x\right)=\mathcal{F}\left[h\right]\left(s,x,-\frac{1}{2\pi}\right)=\int_{\mathbb{R}}h\left(s,x,y\right)\,\text{e}^{\text{i}y}\text{d}y. \end{align*}$$
$$\begin{align*}\mathfrak{f}\left[h\right]\left(s,x\right)=\mathcal{F}\left[h\right]\left(s,x,-\frac{1}{2\pi}\right)=\int_{\mathbb{R}}h\left(s,x,y\right)\,\text{e}^{\text{i}y}\text{d}y. \end{align*}$$
 $y\longmapsto \text {e}^{\text {i}y}$
.
$y\longmapsto \text {e}^{\text {i}y}$
.
For each of these operators, the elements of the pairs
![]() $\left (s,x\right )$
for which the parametric transform of h is defined are called the parameters of the transform.
$\left (s,x\right )$
for which the parametric transform of h is defined are called the parameters of the transform.
Definition 2.15. Let
![]() $\mathcal {D}$
be as in Notation 2.12.
$\mathcal {D}$
be as in Notation 2.12.
-
•
 $\mathcal {D}$
is stable under the generalized parametric Mellin transform if for all
$\mathcal {D}$
is stable under the generalized parametric Mellin transform if for all
 $\Sigma $
and X, for all
$\Sigma $
and X, for all
 $h\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}\right )$
without poles outside some closed discrete set
$h\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}\right )$
without poles outside some closed discrete set
 $P\subseteq \mathbb {C}$
, there are a closed discrete set
$P\subseteq \mathbb {C}$
, there are a closed discrete set
 $P'\subseteq \mathbb {C}$
such that
$P'\subseteq \mathbb {C}$
such that
 $P\subseteq P'\subseteq \mathbb {C}$
and a function
$P\subseteq P'\subseteq \mathbb {C}$
and a function
 $H\in \mathcal {D}_{\Sigma }\left (X\right )$
without poles outside
$H\in \mathcal {D}_{\Sigma }\left (X\right )$
without poles outside
 $P'$
such that, if
$P'$
such that, if
 $\widetilde {h}\left (s,x,y\right )=\chi _{+}\left (y\right )y^{s-1}h\left (s,x,y\right )$
, then
$\widetilde {h}\left (s,x,y\right )=\chi _{+}\left (y\right )y^{s-1}h\left (s,x,y\right )$
, then  $$\begin{align*}\forall\left(s,x\right)\in\text{Int}\left(\widetilde{h};\left(\Sigma\setminus P'\right)\times X\right),\ H\left(s,x\right)=\mathcal{M}\left[h\right]\left(s,x\right). \end{align*}$$
$$\begin{align*}\forall\left(s,x\right)\in\text{Int}\left(\widetilde{h};\left(\Sigma\setminus P'\right)\times X\right),\ H\left(s,x\right)=\mathcal{M}\left[h\right]\left(s,x\right). \end{align*}$$
-
•
 $\mathcal {D}$
is stable under the generalized parametric Fourier transform if for all
$\mathcal {D}$
is stable under the generalized parametric Fourier transform if for all
 $\Sigma $
and X, for all
$\Sigma $
and X, for all
 $h\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}\right )$
without poles outside some closed discrete set
$h\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}\right )$
without poles outside some closed discrete set
 $P\subseteq \mathbb {C}$
, there are a closed discrete set
$P\subseteq \mathbb {C}$
, there are a closed discrete set
 $P'\subseteq \mathbb {C}$
such that
$P'\subseteq \mathbb {C}$
such that
 $P\subseteq P'\subseteq \mathbb {C}$
and a function
$P\subseteq P'\subseteq \mathbb {C}$
and a function
 $H\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}\right )$
without poles outside
$H\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}\right )$
without poles outside
 $P'$
such that
$P'$
such that  $$\begin{align*}\forall\left(s,x,t\right)\in\text{Int}\left(h;\left(\Sigma\setminus P'\right)\times X\right)\times\mathbb{R},\ H\left(s,x,t\right)=\mathcal{F}\left[h\right]\left(s,x,t\right). \end{align*}$$
$$\begin{align*}\forall\left(s,x,t\right)\in\text{Int}\left(h;\left(\Sigma\setminus P'\right)\times X\right)\times\mathbb{R},\ H\left(s,x,t\right)=\mathcal{F}\left[h\right]\left(s,x,t\right). \end{align*}$$
Definition 2.16. A system
![]() $\mathcal {D}$
as in Notation 2.12 is stable under parametric integration if for every strip
$\mathcal {D}$
as in Notation 2.12 is stable under parametric integration if for every strip
![]() $\Sigma \subseteq \mathbb {C}$
and every subanalytic set
$\Sigma \subseteq \mathbb {C}$
and every subanalytic set
![]() $X\subseteq \mathbb {R}^{m}$
, given
$X\subseteq \mathbb {R}^{m}$
, given
![]() $h\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}^{n}\right )$
without poles outside some closed discrete set
$h\in \mathcal {D}_{\Sigma }\left (X\times \mathbb {R}^{n}\right )$
without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
, there exists a closed discrete set
$P\subseteq \mathbb {C}$
, there exists a closed discrete set
![]() $P'\subseteq \mathbb {C}$
such that
$P'\subseteq \mathbb {C}$
such that
![]() $P\subseteq P'$
and
$P\subseteq P'$
and
![]() $P'\setminus P$
is contained in a finitely generated
$P'\setminus P$
is contained in a finitely generated
![]() $\mathbb {Z}$
-lattice, and there exists a function
$\mathbb {Z}$
-lattice, and there exists a function
![]() $H\in \mathcal {D}_{\Sigma }\left (X\right )$
without poles outside
$H\in \mathcal {D}_{\Sigma }\left (X\right )$
without poles outside
![]() $P'$
such that
$P'$
such that
The additional poles that our integral transforms will create will indeed be contained in a finitely generated
![]() $\mathbb {Z}$
-lattice.
$\mathbb {Z}$
-lattice.
2.2.1 Parametric power-constructible functions
Recall the following definitions and results from [Reference Cluckers, Comte, Rolin and ServiCCRS23].
Definition 2.17.
-
• (
 $1$
-bounded subanalytic maps) For
$1$
-bounded subanalytic maps) For
 $N\in \mathbb {N}$
, we let
$N\in \mathbb {N}$
, we let
 $\mathcal {S}_{c}^{N}\left (X\right )$
be the collection of all maps
$\mathcal {S}_{c}^{N}\left (X\right )$
be the collection of all maps
 $\psi :X\longrightarrow \mathbb {R}^{N}$
with components in
$\psi :X\longrightarrow \mathbb {R}^{N}$
with components in
 $\mathcal {S}\left (X\right )$
, such that
$\mathcal {S}\left (X\right )$
, such that
 $\overline {\psi \left (X\right )}$
is contained in the closed polydisk of
$\overline {\psi \left (X\right )}$
is contained in the closed polydisk of
 $\mathbb {R}^{N}$
centered at zero and of radius
$\mathbb {R}^{N}$
centered at zero and of radius
 $1$
. The members of the collection
$1$
. The members of the collection
 $\mathcal {S}_{c}\left (X\right )=\bigcup _{N\in \mathbb {N^{\times }}}\mathcal {S}_{c}^{N}\left (X\right )$
are called 1-bounded subanalytic maps defined on X.
$\mathcal {S}_{c}\left (X\right )=\bigcup _{N\in \mathbb {N^{\times }}}\mathcal {S}_{c}^{N}\left (X\right )$
are called 1-bounded subanalytic maps defined on X. -
• (Strongly convergent series) Let
 $\mathcal {E}$
be the field of meromorphic functions
$\mathcal {E}$
be the field of meromorphic functions
 $\xi :\mathbb {C}\longrightarrow \mathbb {P}^1(\mathbb {C})$
and denote by
$\xi :\mathbb {C}\longrightarrow \mathbb {P}^1(\mathbb {C})$
and denote by
 $D^{N}$
the closed polydisk of radius
$D^{N}$
the closed polydisk of radius
 $\frac {3}{2}$
and center
$\frac {3}{2}$
and center
 $0\in \mathbb {R}^{N}$
. Given a formal power series
$0\in \mathbb {R}^{N}$
. Given a formal power series  in N variables Z and with coefficients
in N variables Z and with coefficients
 $\xi _{I}\in \mathcal {E}$
, we say that F converges strongly if there exists a closed discrete set
$\xi _{I}\in \mathcal {E}$
, we say that F converges strongly if there exists a closed discrete set
 $P\left (F\right )\subseteq \mathbb {C}$
(called the set of poles of F) such that
$P\left (F\right )\subseteq \mathbb {C}$
(called the set of poles of F) such that -
• for every
 $s_{0}\in \mathbb {C}\setminus P\left (F\right )$
, the power series
$s_{0}\in \mathbb {C}\setminus P\left (F\right )$
, the power series  converges in a neighborhood of
converges in a neighborhood of
 $D^{N}$
(thus, F defines a function on
$D^{N}$
(thus, F defines a function on
 $\left (\mathbb {C}\setminus P\left (F\right )\right )\times D^{N}$
);
$\left (\mathbb {C}\setminus P\left (F\right )\right )\times D^{N}$
); -
• for every
 $s_{0}\in \mathbb {C}$
, there exists
$s_{0}\in \mathbb {C}$
, there exists
 $m=m\left (s_{0}\right )\in \mathbb {N}$
such that for all
$m=m\left (s_{0}\right )\in \mathbb {N}$
such that for all
 $z_{0}\in D^{N}$
, the function
$z_{0}\in D^{N}$
, the function
 $\left (s,z\right )\longmapsto \left (s-s_{0}\right )^{m}F\left (s,z\right )$
has a holomorphic extension on some complex neighborhood of
$\left (s,z\right )\longmapsto \left (s-s_{0}\right )^{m}F\left (s,z\right )$
has a holomorphic extension on some complex neighborhood of
 $\left (s_{0},z_{0}\right )$
;
$\left (s_{0},z_{0}\right )$
; -
•
 $P\left (F\right )$
is the set of all
$P\left (F\right )$
is the set of all
 $s_{0}\in \mathbb {C}$
such that the minimal such
$s_{0}\in \mathbb {C}$
such that the minimal such
 $m\left (s_{0}\right )$
is strictly positive.
$m\left (s_{0}\right )$
is strictly positive.
-
-
• (Parametric strong functions) Given a closed discrete set
 $P\subseteq \mathbb {C}$
, a function
$P\subseteq \mathbb {C}$
, a function
 $\Phi :\left (\mathbb {C}\setminus P\right )\times X\longrightarrow \mathbb {C}$
is called a parametric strong function on X if there exist a
$\Phi :\left (\mathbb {C}\setminus P\right )\times X\longrightarrow \mathbb {C}$
is called a parametric strong function on X if there exist a
 $1$
-bounded subanalytic map
$1$
-bounded subanalytic map
 $\psi \in \mathcal {S}_{c}^{N}\left (X\right )$
and a strongly convergent series
$\psi \in \mathcal {S}_{c}^{N}\left (X\right )$
and a strongly convergent series  with
with
 $P\left (F\right )\subseteq P$
such that Define
$P\left (F\right )\subseteq P$
such that Define $$\begin{align*}\forall\left(s,x\right)\in\left(\mathbb{C}\setminus P\right)\times X,\ \Phi\left(s,x\right)=F\circ\left(s,\psi\left(x\right)\right)=\sum_{I}\xi_{I}\left(s\right)\left(\psi\left(x\right)\right)^{I}. \end{align*}$$
$$\begin{align*}\forall\left(s,x\right)\in\left(\mathbb{C}\setminus P\right)\times X,\ \Phi\left(s,x\right)=F\circ\left(s,\psi\left(x\right)\right)=\sum_{I}\xi_{I}\left(s\right)\left(\psi\left(x\right)\right)^{I}. \end{align*}$$
 $\mathcal {A}\left (X\right )$
as the collection of all parametric strong functions on X. If
$\mathcal {A}\left (X\right )$
as the collection of all parametric strong functions on X. If
 $\Phi \in \mathcal {A}\left (X\right )$
has no poles outside
$\Phi \in \mathcal {A}\left (X\right )$
has no poles outside
 $P\subseteq \mathbb {C}$
, then for all
$P\subseteq \mathbb {C}$
, then for all
 $s\in \mathbb {C}\setminus P,\ x\longmapsto \Phi \left (s,x\right )$
is bounded. If, furthermore, for all
$s\in \mathbb {C}\setminus P,\ x\longmapsto \Phi \left (s,x\right )$
is bounded. If, furthermore, for all
 $s\in \mathbb {C}\setminus P,\ x\longmapsto \Phi \left (s,x\right )$
is bounded away from zero, then we call
$s\in \mathbb {C}\setminus P,\ x\longmapsto \Phi \left (s,x\right )$
is bounded away from zero, then we call
 $\Phi $
a parametric strong unit. A parametric strong function which happens not to depend on the variable s is called a subanalytic strong function, since it is indeed a subanalytic function.
$\Phi $
a parametric strong unit. A parametric strong function which happens not to depend on the variable s is called a subanalytic strong function, since it is indeed a subanalytic function.
-
• (Parametric powers) For
 $X\subseteq \mathbb {R}^{m}$
subanalytic, define the parametric powers of
$X\subseteq \mathbb {R}^{m}$
subanalytic, define the parametric powers of
 $\mathcal {S}$
on X as the functions in the collection
$\mathcal {S}$
on X as the functions in the collection  $$\begin{align*}\mathcal{P}\left(\mathcal{S}_{+}\left(X\right)\right)=\{P_{f}:\mathbb{C}\times X\longrightarrow\mathbb{C}\text{\ such\ that}\ P_{f}\left(s,x\right)=f\left(x\right)^{s},\ \text{for\ some\ }f\in\mathcal{S}_{+}\left(X\right)\}. \end{align*}$$
$$\begin{align*}\mathcal{P}\left(\mathcal{S}_{+}\left(X\right)\right)=\{P_{f}:\mathbb{C}\times X\longrightarrow\mathbb{C}\text{\ such\ that}\ P_{f}\left(s,x\right)=f\left(x\right)^{s},\ \text{for\ some\ }f\in\mathcal{S}_{+}\left(X\right)\}. \end{align*}$$
-
• (Parametric power-constructible functions) If
 $X\subseteq \mathbb {R}^{0}$
, then define
$X\subseteq \mathbb {R}^{0}$
, then define
 $\mathcal {C}^{\mathcal {M}}\left (X\right )=\mathcal {E}$
. If
$\mathcal {C}^{\mathcal {M}}\left (X\right )=\mathcal {E}$
. If
 $X\subseteq \mathbb {R}^{m}$
, with
$X\subseteq \mathbb {R}^{m}$
, with
 $m>0$
, then we let
$m>0$
, then we let
 $\mathcal {C}^{\mathcal {M}}\left (X\right )$
be the
$\mathcal {C}^{\mathcal {M}}\left (X\right )$
be the
 $\mathcal {A}\left (X\right )$
-algebra generated by
$\mathcal {A}\left (X\right )$
-algebra generated by
 $\mathcal {C}^{\mathbb {C}}\left (X\right )\cup \mathcal {P}\left (\mathcal {S}_{+}\left (X\right )\right )$
. The system
$\mathcal {C}^{\mathbb {C}}\left (X\right )\cup \mathcal {P}\left (\mathcal {S}_{+}\left (X\right )\right )$
. The system
 $\mathcal {C}^{\mathcal {M}}$
is the collection of algebras of parametric power-constructible functions. Every function
$\mathcal {C}^{\mathcal {M}}$
is the collection of algebras of parametric power-constructible functions. Every function
 $h\in \mathcal {C}^{\mathcal {M}}\left (X\right )$
can be written on
$h\in \mathcal {C}^{\mathcal {M}}\left (X\right )$
can be written on
 $\left (\mathbb {C}\setminus P\right )\times X$
(for some closed discrete
$\left (\mathbb {C}\setminus P\right )\times X$
(for some closed discrete
 $P\subseteq \mathbb {C}$
) as a closed discrete sum of generators of the form (2.1)where
$P\subseteq \mathbb {C}$
) as a closed discrete sum of generators of the form (2.1)where $$ \begin{align} \Phi\left(s,x\right)\cdot g\left(x\right)\cdot f\left(x\right)^{s}, \end{align} $$
$$ \begin{align} \Phi\left(s,x\right)\cdot g\left(x\right)\cdot f\left(x\right)^{s}, \end{align} $$
 $g\in \mathcal {C}^{\mathbb {C}}\left (X\right ),\ f\in \mathcal {S}_{+}\left (X\right )$
and
$g\in \mathcal {C}^{\mathbb {C}}\left (X\right ),\ f\in \mathcal {S}_{+}\left (X\right )$
and
 $\Phi \in \mathcal {A}\left (X\right )$
has no poles outside P. Here, the word ‘parametric’ refers to the variable
$\Phi \in \mathcal {A}\left (X\right )$
has no poles outside P. Here, the word ‘parametric’ refers to the variable
 $s\in \mathbb {C}$
seen as a new complex parameter (alongside the real parameters
$s\in \mathbb {C}$
seen as a new complex parameter (alongside the real parameters
 $x\in X$
).
$x\in X$
).
The functions in
![]() $\mathcal {C}^{\mathcal {M}}$
have a domain of the form
$\mathcal {C}^{\mathcal {M}}$
have a domain of the form
![]() $\left (\mathbb {C}\setminus P\right )\times X$
. We are interested in studying functions defined on domains of the form
$\left (\mathbb {C}\setminus P\right )\times X$
. We are interested in studying functions defined on domains of the form
![]() $\left (\Sigma \setminus P\right )\times X$
, where
$\left (\Sigma \setminus P\right )\times X$
, where
![]() $\Sigma $
is a strip. For this, we define
$\Sigma $
is a strip. For this, we define
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\right )$
as the collection of all restrictions to
$\mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\right )$
as the collection of all restrictions to
![]() $\Sigma \times X$
of functions in
$\Sigma \times X$
of functions in
![]() $\mathcal {C}^{\mathcal {M}}\left (X\right )$
and thus form the systems
$\mathcal {C}^{\mathcal {M}}\left (X\right )$
and thus form the systems
![]() $\mathcal {A},\mathcal {P}\left (\mathcal {S}_{+}\right )$
and
$\mathcal {A},\mathcal {P}\left (\mathcal {S}_{+}\right )$
and
![]() $\mathcal {C}^{\mathcal {M}}$
, proceeding as in Notation 2.12 (note that, since the functions in these collections are defined on the whole of
$\mathcal {C}^{\mathcal {M}}$
, proceeding as in Notation 2.12 (note that, since the functions in these collections are defined on the whole of
![]() $\mathbb {C}$
and not just on strips, the two definitions of
$\mathbb {C}$
and not just on strips, the two definitions of
![]() $\mathcal {C}^{\mathcal {M}}$
coincide). With this notation, we immediately derive from [Reference Cluckers, Comte, Rolin and ServiCCRS23] the following result.
$\mathcal {C}^{\mathcal {M}}$
coincide). With this notation, we immediately derive from [Reference Cluckers, Comte, Rolin and ServiCCRS23] the following result.
Theorem 2.18 [Reference Cluckers, Comte, Rolin and ServiCCRS23, Theorem 2.16 and Corollary 2.18].
The system
![]() $\mathcal {C}^{\mathcal {M}}$
is stable under parametric integration. Moreover,
$\mathcal {C}^{\mathcal {M}}$
is stable under parametric integration. Moreover,
![]() $\mathcal {C}^{\mathcal {M}}$
is the smallest system of
$\mathcal {C}^{\mathcal {M}}$
is the smallest system of
![]() $\mathcal {A}$
-algebras containing
$\mathcal {A}$
-algebras containing
![]() $\mathcal {\mathcal {C}}^{\mathbb {C}}$
and stable under the generalized parametric Mellin transform.
$\mathcal {\mathcal {C}}^{\mathbb {C}}$
and stable under the generalized parametric Mellin transform.
2.2.2 Parametric Fourier transforms of parametric power-constructible functions
Our next goal is to define a system containing both the parametric Fourier and the parametric Mellin transforms of power-constructible functions.
Definition 2.19. Let
![]() $\Sigma \subseteq \mathbb {C}$
be a strip. Consider the fixed frequency parametric Fourier operator
$\Sigma \subseteq \mathbb {C}$
be a strip. Consider the fixed frequency parametric Fourier operator
![]() $\mathfrak {f}$
acting on
$\mathfrak {f}$
acting on
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M}}$
:
$\mathcal {C}_{\Sigma }^{\mathcal {M}}$
:
If h has no poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
, then so does
$P\subseteq \mathbb {C}$
, then so does
![]() $\mathfrak {f}\left [h\right ]$
. Define
$\mathfrak {f}\left [h\right ]$
. Define
It is a
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\right )$
-module.
$\mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\right )$
-module.
We will show in Section 3 that the functions in the above collection can be extended to the whole complex plane, in the sense of Notation 2.12:
Proposition 2.20. The collection
![]() $\left \{ \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right ):\ \Sigma \ \text {strip}\right \} $
has the extension property.
$\left \{ \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right ):\ \Sigma \ \text {strip}\right \} $
has the extension property.
Thanks to the above proposition, we may define the system
Our main stability result is the following.
Theorem 2.21. The system
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
is stable under parametric integration. It is a system of
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
is stable under parametric integration. It is a system of
![]() $\mathbb {C}$
-algebras, containing
$\mathbb {C}$
-algebras, containing
![]() $\mathcal {C}^{\mathbb {C}}\cup \mathrm {e}^{\mathrm {i}\mathcal {S}}$
, and stable under generalized parametric Mellin and Fourier transforms.
$\mathcal {C}^{\mathbb {C}}\cup \mathrm {e}^{\mathrm {i}\mathcal {S}}$
, and stable under generalized parametric Mellin and Fourier transforms.
3 Generators of
 $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
and proof of the extension result
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
and proof of the extension result
3.1 Generators of
 $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
In this section, we choose a set of generators for
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
as an additive group, of a special form, which is suitable for proving Proposition 2.20 and Theorem 2.21.
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
as an additive group, of a special form, which is suitable for proving Proposition 2.20 and Theorem 2.21.
First, we recall some definitions from [Reference Cluckers, Comte, Rolin and ServiCCRS23].
Definition 3.1. Let
![]() $X\subseteq \mathbb {R}^{m}$
be a subanalytic cell and
$X\subseteq \mathbb {R}^{m}$
be a subanalytic cell and
where
![]() $a,b:X\longrightarrow \mathbb {R}$
are analytic subanalytic functions with
$a,b:X\longrightarrow \mathbb {R}$
are analytic subanalytic functions with
![]() $1\leq a\left (x\right )<b\left (x\right )\ \text {for all }x\in X$
, or b is
$1\leq a\left (x\right )<b\left (x\right )\ \text {for all }x\in X$
, or b is
![]() $\equiv +\infty $
. We say that B has bounded y-fibers if
$\equiv +\infty $
. We say that B has bounded y-fibers if
![]() $b<+\infty $
and unbounded y-fibers if
$b<+\infty $
and unbounded y-fibers if
![]() $b\equiv +\infty $
.
$b\equiv +\infty $
.
-
• A
 $1$
-bounded subanalytic map
$1$
-bounded subanalytic map
 $\psi :B\longrightarrow \mathbb {R}^{M+2}\in \mathcal {S}_{c}^{M+2}\left (B\right )$
is y-prepared if it has the form (3.2)where
$\psi :B\longrightarrow \mathbb {R}^{M+2}\in \mathcal {S}_{c}^{M+2}\left (B\right )$
is y-prepared if it has the form (3.2)where $$ \begin{align} \psi\left(x,y\right)=\left(c\left(x\right),\left(\frac{a\left(x\right)}{y}\right)^{\frac{1}{d}},\left(\frac{y}{b\left(x\right)}\right)^{\frac{1}{d}}\right), \end{align} $$
$$ \begin{align} \psi\left(x,y\right)=\left(c\left(x\right),\left(\frac{a\left(x\right)}{y}\right)^{\frac{1}{d}},\left(\frac{y}{b\left(x\right)}\right)^{\frac{1}{d}}\right), \end{align} $$
 $d\in \mathbb {N}\setminus \left \{ 0\right \} $
.If
$d\in \mathbb {N}\setminus \left \{ 0\right \} $
.If
 $b\equiv +\infty $
, then we will implicitly assume that the last component is missing, and hence,
$b\equiv +\infty $
, then we will implicitly assume that the last component is missing, and hence,
 $\psi :B\longrightarrow \mathbb {R}^{M+1}$
.
$\psi :B\longrightarrow \mathbb {R}^{M+1}$
.
-
• A subanalytic strong unit
 $U\in \mathcal {S}\left (B\right )$
is
$U\in \mathcal {S}\left (B\right )$
is
 $\psi $
-prepared if there exists a strongly convergent series
$\psi $
-prepared if there exists a strongly convergent series  such that
such that
 $U=F\circ \psi $
. If B has unbounded y-fibers, then the term
$U=F\circ \psi $
. If B has unbounded y-fibers, then the term
 $(y/b(x))^{1/d}$
does not appear in (3.2), and thus, the nested
$(y/b(x))^{1/d}$
does not appear in (3.2), and thus, the nested
 $\psi $
-prepared form of U is (3.3)where the subanalytic functions
$\psi $
-prepared form of U is (3.3)where the subanalytic functions $$ \begin{align} U\left(x,y\right)=\sum_{k}b_{k}\left(x\right)\left(\frac{a\left(x\right)}{y}\right)^{\frac{k}{d}}, \end{align} $$
$$ \begin{align} U\left(x,y\right)=\sum_{k}b_{k}\left(x\right)\left(\frac{a\left(x\right)}{y}\right)^{\frac{k}{d}}, \end{align} $$
 $b_{k}$
are bounded and
$b_{k}$
are bounded and
 $b_{0}$
does not vanish on X.
$b_{0}$
does not vanish on X.
-
• A parametric strong function
 $\Phi \in \mathcal {A}_{\Sigma }\left (B\right )$
is
$\Phi \in \mathcal {A}_{\Sigma }\left (B\right )$
is
 $\psi $
-prepared if there exists a strongly convergent series
$\psi $
-prepared if there exists a strongly convergent series  such that (3.4)If B has unbounded y-fibers, then (see [Reference Cluckers, Comte, Rolin and ServiCCRS23, Remark 3.7]) the nested
such that (3.4)If B has unbounded y-fibers, then (see [Reference Cluckers, Comte, Rolin and ServiCCRS23, Remark 3.7]) the nested $$ \begin{align} \forall\left(s,x,y\right)\in\left(\Sigma\setminus P\left(F\right)\right)\times B,\ \Phi\left(s,x,y\right)=F\circ\left(s,\psi\left(x,y\right)\right). \end{align} $$
$$ \begin{align} \forall\left(s,x,y\right)\in\left(\Sigma\setminus P\left(F\right)\right)\times B,\ \Phi\left(s,x,y\right)=F\circ\left(s,\psi\left(x,y\right)\right). \end{align} $$
 $\psi $
-prepared form of
$\psi $
-prepared form of
 $\Phi $
is (3.5)
$\Phi $
is (3.5) $$ \begin{align} & \Phi\left(s,x,y\right)=\sum_{k}\xi_{k}\left(s,x\right)\left(\frac{a\left(x\right)}{y}\right)^{\frac{k}{d}},\text{\ where}\ \xi_{k}\left(s,x\right)\in\mathcal{A}_{\Sigma}\left(X\right). \end{align} $$
$$ \begin{align} & \Phi\left(s,x,y\right)=\sum_{k}\xi_{k}\left(s,x\right)\left(\frac{a\left(x\right)}{y}\right)^{\frac{k}{d}},\text{\ where}\ \xi_{k}\left(s,x\right)\in\mathcal{A}_{\Sigma}\left(X\right). \end{align} $$
-
• A subanalytic function
 $\varphi \in \mathcal {S}\left (B\right )$
is prepared if there are
$\varphi \in \mathcal {S}\left (B\right )$
is prepared if there are
 $\omega \in \mathbb {Z}$
, an analytic function
$\omega \in \mathbb {Z}$
, an analytic function
 $\varphi _{0}\in \mathcal {S}\left (X\right )$
and a
$\varphi _{0}\in \mathcal {S}\left (X\right )$
and a
 $\psi $
-prepared subanalytic strong unit U such that (3.6)
$\psi $
-prepared subanalytic strong unit U such that (3.6) $$ \begin{align} \varphi\left(x,y\right)=\varphi_{0}\left(x\right)y^{\frac{\omega}{d}}U\left(x,y\right). \end{align} $$
$$ \begin{align} \varphi\left(x,y\right)=\varphi_{0}\left(x\right)y^{\frac{\omega}{d}}U\left(x,y\right). \end{align} $$
In order to choose suitable generators for
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
, we first need to introduce two additional classes of functions.
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
, we first need to introduce two additional classes of functions.
Definition 3.2. Let
![]() $\Sigma \subseteq \mathbb {C}$
be a strip and
$\Sigma \subseteq \mathbb {C}$
be a strip and
![]() $X\subseteq \mathbb {R}^{m}$
be a subanalytic set. Let B be as in (3.1).
$X\subseteq \mathbb {R}^{m}$
be a subanalytic set. Let B be as in (3.1).
-
• Let
 $\mathcal {C}_{\Sigma }^{\mathcal {M},\text {i}\mathcal {S}}\left (X\right )$
be the additive group generated by the functions of the form (3.7)It is a
$\mathcal {C}_{\Sigma }^{\mathcal {M},\text {i}\mathcal {S}}\left (X\right )$
be the additive group generated by the functions of the form (3.7)It is a $$ \begin{align} g\text{e}^{\text{i}\varphi}\ \ \ \left(g\in\mathcal{C}_{\Sigma}^{\mathcal{M}}\left(X\right),\varphi\in\mathcal{S}\left(X\right)\right). \end{align} $$
$$ \begin{align} g\text{e}^{\text{i}\varphi}\ \ \ \left(g\in\mathcal{C}_{\Sigma}^{\mathcal{M}}\left(X\right),\varphi\in\mathcal{S}\left(X\right)\right). \end{align} $$
 $\mathbb {C}$
-algebra.
$\mathbb {C}$
-algebra.
-
• A transcendental element is a function of the form
where $$\begin{align*}\left(\Sigma\setminus P\right)\times X\ni\left(s,x\right)\longmapsto\gamma\left(s,x\right)=\int_{\mathbb{R}}\chi_{B}\left(x,y\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\Phi\left(s,x,y\right)\text{e}^{\sigma\text{i}y}\text{d}y, \end{align*}$$
$$\begin{align*}\left(\Sigma\setminus P\right)\times X\ni\left(s,x\right)\longmapsto\gamma\left(s,x\right)=\int_{\mathbb{R}}\chi_{B}\left(x,y\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\Phi\left(s,x,y\right)\text{e}^{\sigma\text{i}y}\text{d}y, \end{align*}$$
 $\sigma \in \left \{ +,-\right \} ,\mu \in \mathbb {N},\Phi $
is a
$\sigma \in \left \{ +,-\right \} ,\mu \in \mathbb {N},\Phi $
is a
 $\psi $
-prepared parametric strong function (as in (3.4), with
$\psi $
-prepared parametric strong function (as in (3.4), with
 $\psi $
as in (3.2)) without poles outside the closed discrete set
$\psi $
as in (3.2)) without poles outside the closed discrete set
 $P\subseteq \mathbb {C}$
and
$P\subseteq \mathbb {C}$
and
 $\lambda \left (s\right )={\displaystyle \frac {\ell s+\eta }{d}}$
, for some
$\lambda \left (s\right )={\displaystyle \frac {\ell s+\eta }{d}}$
, for some
 $\ell \in \mathbb {Z},\eta \in \mathbb {C}$
and the same d appearing in (3.2). If B has unbounded y-fibers, then we require that for all
$\ell \in \mathbb {Z},\eta \in \mathbb {C}$
and the same d appearing in (3.2). If B has unbounded y-fibers, then we require that for all
 ${s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )<-1}$
.We let
${s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )<-1}$
.We let
 $\Gamma _{\Sigma }\left (X\right )$
be the collection of all transcendental elements on
$\Gamma _{\Sigma }\left (X\right )$
be the collection of all transcendental elements on
 $\Sigma \times X$
.Here, transcendental only means that such a term does not belong to
$\Sigma \times X$
.Here, transcendental only means that such a term does not belong to
 $\mathcal {C}_{\Sigma }^{\mathcal {M},\text {i}\mathcal {S}}\left (X\right )$
.
$\mathcal {C}_{\Sigma }^{\mathcal {M},\text {i}\mathcal {S}}\left (X\right )$
.
Thus, a generator (as an additive group) of the
 $\mathcal {C}_{\Sigma }^{\mathcal {M},\text {i}\mathcal {S}}\left (X\right )$
-module generated by the set
$\mathcal {C}_{\Sigma }^{\mathcal {M},\text {i}\mathcal {S}}\left (X\right )$
-module generated by the set
 $\Gamma _{\Sigma }\left (X\right )$
is a function of the form (3.8)
$\Gamma _{\Sigma }\left (X\right )$
is a function of the form (3.8) $$ \begin{align} T=g\text{e}^{\text{i}\varphi}\gamma\ \ \ \left(g\in\mathcal{C}_{\Sigma}^{\mathcal{M}}\left(X\right),\varphi\in\mathcal{S}\left(X\right),\gamma\in\Gamma_{\Sigma}\left(X\right)\right). \end{align} $$
$$ \begin{align} T=g\text{e}^{\text{i}\varphi}\gamma\ \ \ \left(g\in\mathcal{C}_{\Sigma}^{\mathcal{M}}\left(X\right),\varphi\in\mathcal{S}\left(X\right),\gamma\in\Gamma_{\Sigma}\left(X\right)\right). \end{align} $$
Notice that
![]() $1=\mathfrak {f}\left [\frac {\mathrm {i}}{2}\chi _{\left [\pi ,2\pi \right ]}\right ]\in \Gamma _{\Sigma }\left (X\right )$
. In particular, (3.7) is an instance of (3.8).
$1=\mathfrak {f}\left [\frac {\mathrm {i}}{2}\chi _{\left [\pi ,2\pi \right ]}\right ]\in \Gamma _{\Sigma }\left (X\right )$
. In particular, (3.7) is an instance of (3.8).
Lemma 3.3. Let T be a generator as in (3.8), without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
. There exists
$P\subseteq \mathbb {C}$
. There exists
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\mathrm {int}}$
without poles outside P such that
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\mathrm {int}}$
without poles outside P such that
![]() $T=\mathfrak {f}\left [h\right ]$
. In particular,
$T=\mathfrak {f}\left [h\right ]$
. In particular,
Proof. Let B be as in (3.1) and
Then,
![]() $G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\text {int}}$
and
$G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\text {int}}$
and
Thus, by a change of variables,
![]() $T=\mathfrak {f}\left [h\right ]$
with
$T=\mathfrak {f}\left [h\right ]$
with
Notice that h has no poles outside P.
Lemma 3.4. Let
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
. There are a closed discrete set
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
. There are a closed discrete set
![]() $P\subseteq \mathbb {C}$
and finitely many generators
$P\subseteq \mathbb {C}$
and finitely many generators
![]() $T_{1},\ldots ,T_{m}$
as in (3.8) such that
$T_{1},\ldots ,T_{m}$
as in (3.8) such that
![]() $h,T_{1},\ldots ,T_{m}$
have no poles outside P and
$h,T_{1},\ldots ,T_{m}$
have no poles outside P and
![]() $h=\sum T_{j}$
. In particular,
$h=\sum T_{j}$
. In particular,
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
can also be described as the
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
can also be described as the
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathrm {i}\mathcal {S}}\left (X\right )$
-module generated by the set
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathrm {i}\mathcal {S}}\left (X\right )$
-module generated by the set
![]() $\Gamma _{\Sigma }\left (X\right )$
, and the functions of the form (3.8) are generators of
$\Gamma _{\Sigma }\left (X\right )$
, and the functions of the form (3.8) are generators of
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
as an additive group.
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
as an additive group.
Recall the notation established right after Definition 3.9 in [Reference Cluckers, Comte, Rolin and ServiCCRS23].
Notation 3.5. Let
![]() $A\subseteq X\times \mathbb {R}$
be a subanalytic cell which is open over and projects onto X (see Notation 2.5), and let
$A\subseteq X\times \mathbb {R}$
be a subanalytic cell which is open over and projects onto X (see Notation 2.5), and let
![]() $\theta _{A}$
be its center, so that the set
$\theta _{A}$
be its center, so that the set
![]() $\left \{ y-\theta _{A}\left (x\right ):\ \left (x,y\right )\in A\right \} $
is contained in one of the sets
$\left \{ y-\theta _{A}\left (x\right ):\ \left (x,y\right )\in A\right \} $
is contained in one of the sets
![]() $\left (-\infty ,-1\right ),\left (-1,0\right ),\left (0,1\right ),\left (1,+\infty \right )$
, as in [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Definition 3.4]. There are unique sign conditions
$\left (-\infty ,-1\right ),\left (-1,0\right ),\left (0,1\right ),\left (1,+\infty \right )$
, as in [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Definition 3.4]. There are unique sign conditions
![]() $\sigma _{A},\tau _{A}\in \left \{ -1,1\right \} $
such that
$\sigma _{A},\tau _{A}\in \left \{ -1,1\right \} $
such that
for some analytic subanalytic functions
![]() $a_{A},b_{A}$
such that
$a_{A},b_{A}$
such that
![]() $1\leq a_{A}\left (x\right )<b_{A}\left (x\right )\leq +\infty $
. Let
$1\leq a_{A}\left (x\right )<b_{A}\left (x\right )\leq +\infty $
. Let
and
![]() $\Pi _{A}:B_{A}\longrightarrow A$
be the bijection
$\Pi _{A}:B_{A}\longrightarrow A$
be the bijection
We will still denote by
![]() $\Pi _{A}$
the map
$\Pi _{A}$
the map
![]() $\mathbb {C}\times B_{A}\ni \left (s,x,y\right )\longmapsto \left (s,\Pi _{A}\left (x,y\right )\right )\in \mathbb {C}\times A$
.
$\mathbb {C}\times B_{A}\ni \left (s,x,y\right )\longmapsto \left (s,\Pi _{A}\left (x,y\right )\right )\in \mathbb {C}\times A$
.
Remark 3.6. By [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Definition 3.4(3)], if A is a cell of the form
![]() $A=\{\left (x,y\right ):\ x\in X,\ y>f\left (x\right )\}$
with
$A=\{\left (x,y\right ):\ x\in X,\ y>f\left (x\right )\}$
with
![]() $f\in \mathcal {S}\left (X\right )$
and
$f\in \mathcal {S}\left (X\right )$
and
![]() $f\geq 1$
, then
$f\geq 1$
, then
![]() $\sigma _{A}=\tau _{A}=1$
and
$\sigma _{A}=\tau _{A}=1$
and
![]() $\theta _{A}=0$
. Hence, in this case,
$\theta _{A}=0$
. Hence, in this case,
![]() $a_{A}=f,\ b_{A}=+\infty $
and
$a_{A}=f,\ b_{A}=+\infty $
and
![]() $B_{A}=A$
.
$B_{A}=A$
.
Proof of Lemma 3.4.
Write
![]() $h=\mathfrak {f}\left [g\right ]$
, for some
$h=\mathfrak {f}\left [g\right ]$
, for some
![]() $g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\text {int}}$
and apply the parametric power-constructible Preparation Theorem [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 4.7] to g: this yields a cell-decomposition of
$g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\text {int}}$
and apply the parametric power-constructible Preparation Theorem [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 4.7] to g: this yields a cell-decomposition of
![]() $X\times \mathbb {R}$
and, by linearity of the integral, we may concentrate on a cell A which is open over X.
$X\times \mathbb {R}$
and, by linearity of the integral, we may concentrate on a cell A which is open over X.
Using Notation 3.5, if
![]() $\tau _{A}=-1$
, then the set
$\tau _{A}=-1$
, then the set
![]() $\left \{ \left |y-\theta _{A}\left (x\right )\right |:\ \left (x,y\right )\in A\right \} $
is contained in
$\left \{ \left |y-\theta _{A}\left (x\right )\right |:\ \left (x,y\right )\in A\right \} $
is contained in
![]() $\left (0,1\right )$
, so that
$\left (0,1\right )$
, so that
![]() $\left (x,y\right )\longmapsto \text {e}^{\text {i}\left (y-\theta _{A}\left (x\right )\right )}$
is a complex-valued subanalytic function. Hence, in this case, we may write
$\left (x,y\right )\longmapsto \text {e}^{\text {i}\left (y-\theta _{A}\left (x\right )\right )}$
is a complex-valued subanalytic function. Hence, in this case, we may write
As the integrand on the right-hand side is a parametric power-constructible function, by [Reference Cluckers, Comte, Rolin and ServiCCRS23, Theorem 2.16 and Remark 6.7], there are a closed discrete set
![]() $P\subseteq \mathbb {C}$
(containing the poles of g) and a parametric power-constructible function
$P\subseteq \mathbb {C}$
(containing the poles of g) and a parametric power-constructible function
![]() $G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\right )$
without poles outside P such that
$G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\right )$
without poles outside P such that
![]() $\mathfrak {f}\left [g\restriction A\right ]=\text {e}^{\text {i}\theta _{A}}G$
.
$\mathfrak {f}\left [g\restriction A\right ]=\text {e}^{\text {i}\theta _{A}}G$
.
If
![]() $\tau _{A}=1$
, then we apply the change of variables
$\tau _{A}=1$
, then we apply the change of variables
![]() $\Pi _{A}$
under the sign of integral and, using [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 4.7], we write
$\Pi _{A}$
under the sign of integral and, using [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 4.7], we write
![]() $g\circ \Pi _{A}$
as a finite sum of prepared generators as in [Reference Cluckers, Comte, Rolin and ServiCCRS23, Equation (4.8)]:
$g\circ \Pi _{A}$
as a finite sum of prepared generators as in [Reference Cluckers, Comte, Rolin and ServiCCRS23, Equation (4.8)]:
 $$ \begin{align*} \int_{A_{x}}g\restriction A\left(s,x,y\right)\text{e}^{\text{i}y}\text{d}y & =\int_{a_{A}\left(x\right)}^{b_{A}\left(x\right)}g\circ\Pi_{A}\left(s,x,y\right)\frac{\partial\Pi_{A}}{\partial y}\left(x,y\right)\text{e}^{\text{i}\left(\sigma_{A}y+\theta_{A}\left(x\right)\right)}\text{d}y\\ & =\text{e}^{\text{i}\theta_{A}\left(x\right)}\int_{a_{A}\left(x\right)}^{b_{A}\left(x\right)}\sum_{i}G_{i}\left(s,x\right)y^{\lambda_{i}\left(s\right)}\left(\log y\right)^{\mu_{i}}\Phi_{i}\left(s,x,y\right)\text{e}^{\text{i}\sigma_{A}y}\text{d}y\\ & =\sum_{i}\text{e}^{\text{i}\theta_{A}\left(x\right)}G_{i}\left(s,x\right)\gamma_{i}\left(s,x\right). \end{align*} $$
$$ \begin{align*} \int_{A_{x}}g\restriction A\left(s,x,y\right)\text{e}^{\text{i}y}\text{d}y & =\int_{a_{A}\left(x\right)}^{b_{A}\left(x\right)}g\circ\Pi_{A}\left(s,x,y\right)\frac{\partial\Pi_{A}}{\partial y}\left(x,y\right)\text{e}^{\text{i}\left(\sigma_{A}y+\theta_{A}\left(x\right)\right)}\text{d}y\\ & =\text{e}^{\text{i}\theta_{A}\left(x\right)}\int_{a_{A}\left(x\right)}^{b_{A}\left(x\right)}\sum_{i}G_{i}\left(s,x\right)y^{\lambda_{i}\left(s\right)}\left(\log y\right)^{\mu_{i}}\Phi_{i}\left(s,x,y\right)\text{e}^{\text{i}\sigma_{A}y}\text{d}y\\ & =\sum_{i}\text{e}^{\text{i}\theta_{A}\left(x\right)}G_{i}\left(s,x\right)\gamma_{i}\left(s,x\right). \end{align*} $$
Summing up, we have written h as a finite sum of generators without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
.
$P\subseteq \mathbb {C}$
.
Thus, from now on, we will refer to the functions of the form (3.8) as generators of
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
.
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
.
3.2 Proof of Proposition 2.20
Let
![]() $\Sigma ,\Sigma '\subseteq \mathbb {C}$
be strips such that
$\Sigma ,\Sigma '\subseteq \mathbb {C}$
be strips such that
![]() $\Sigma \subseteq \Sigma '$
and
$\Sigma \subseteq \Sigma '$
and
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside some closed discrete set
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
. Write h as a finite sum of generators of the form (3.8), which is possible by Lemma 3.4. The problem is that the integrands of the transcendental elements appearing in the generators are integrable on
$P\subseteq \mathbb {C}$
. Write h as a finite sum of generators of the form (3.8), which is possible by Lemma 3.4. The problem is that the integrands of the transcendental elements appearing in the generators are integrable on
![]() $\left (\Sigma \setminus P\right )\times X$
but might not be on the whole
$\left (\Sigma \setminus P\right )\times X$
but might not be on the whole
![]() $\left (\Sigma '\setminus P\right )\times X$
(the only issue here is the integrability of a power of y at
$\left (\Sigma '\setminus P\right )\times X$
(the only issue here is the integrability of a power of y at
![]() $+\infty $
, as the parametric strong functions are bounded on the whole plane
$+\infty $
, as the parametric strong functions are bounded on the whole plane
![]() $\mathbb {C}$
). In this case, we need to rewrite the transcendental elements as sums of generators on
$\mathbb {C}$
). In this case, we need to rewrite the transcendental elements as sums of generators on
![]() $\left (\Sigma '\setminus P\right )\times X$
. With this in mind, we may suppose that h itself is a transcendental element with unbounded y-fibers of the form
$\left (\Sigma '\setminus P\right )\times X$
. With this in mind, we may suppose that h itself is a transcendental element with unbounded y-fibers of the form
 $$\begin{align*}h\left(s,x\right)=\int_{a\left(x\right)}^{+\infty}y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\Phi\left(s,x,y\right)\text{e}^{\sigma\text{i}y}\text{d}y, \end{align*}$$
$$\begin{align*}h\left(s,x\right)=\int_{a\left(x\right)}^{+\infty}y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\Phi\left(s,x,y\right)\text{e}^{\sigma\text{i}y}\text{d}y, \end{align*}$$
with
![]() $a\in \mathcal {S}\left (X\right )$
such that for all
$a\in \mathcal {S}\left (X\right )$
such that for all
![]() $x\in X,\ a\left (x\right )\geq 1$
, and that the set
$x\in X,\ a\left (x\right )\geq 1$
, and that the set
![]() $S_{0}=\{s\in \Sigma ':\ \Re \left (\lambda \left (s\right )\right )<-1\}$
is a proper subset of
$S_{0}=\{s\in \Sigma ':\ \Re \left (\lambda \left (s\right )\right )<-1\}$
is a proper subset of
![]() $\Sigma '$
. It follows that the above integral is not finite on
$\Sigma '$
. It follows that the above integral is not finite on
![]() $\left (\Sigma '\setminus S_{0}\right )\times X$
. Using the strong convergence of the series defining
$\left (\Sigma '\setminus S_{0}\right )\times X$
. Using the strong convergence of the series defining
![]() $\Phi $
and (3.5), we may rewrite, for some
$\Phi $
and (3.5), we may rewrite, for some
![]() $k_{0}\geq 0$
,
$k_{0}\geq 0$
,
 $$ \begin{align*} h\left(s,x\right) & =\sum_{k\geq k_{0}}\xi_{k}^{c}\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k}{d}}\int_{a\left(x\right)}^{+\infty}y^{\frac{\ell s+\eta-k}{d}}\left(\log y\right)^{\mu}\text{e}^{\sigma\text{i}y}\text{d}y\\ & =\sum_{k\geq k_{0}}g_{k}\left(s,x\right)\int_{a\left(x\right)}^{+\infty}y^{\lambda_{k}\left(s\right)}\left(\log y\right)^{\mu}\text{e}^{\sigma\text{i}y}\text{d}y. \end{align*} $$
$$ \begin{align*} h\left(s,x\right) & =\sum_{k\geq k_{0}}\xi_{k}^{c}\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k}{d}}\int_{a\left(x\right)}^{+\infty}y^{\frac{\ell s+\eta-k}{d}}\left(\log y\right)^{\mu}\text{e}^{\sigma\text{i}y}\text{d}y\\ & =\sum_{k\geq k_{0}}g_{k}\left(s,x\right)\int_{a\left(x\right)}^{+\infty}y^{\lambda_{k}\left(s\right)}\left(\log y\right)^{\mu}\text{e}^{\sigma\text{i}y}\text{d}y. \end{align*} $$
As the real part of the exponent
![]() $\lambda _{k}\left (s\right )=(\ell s +\eta -k)/d$
decreases as k increases and as
$\lambda _{k}\left (s\right )=(\ell s +\eta -k)/d$
decreases as k increases and as
![]() $\Sigma '$
has bounded width, there are only finitely many power-log monomials which are not integrable for all
$\Sigma '$
has bounded width, there are only finitely many power-log monomials which are not integrable for all
![]() $s\in \Sigma '$
. Let us concentrate on one such critical power-log monomial and use integration by parts (where we integrate the exponential and derive the power-log monomial):
$s\in \Sigma '$
. Let us concentrate on one such critical power-log monomial and use integration by parts (where we integrate the exponential and derive the power-log monomial):
 $$ \begin{align*} \forall\left(s,x\right) & \in S_{0}\times X,\ \int_{a\left(x\right)}^{+\infty}y^{\lambda_{k}\left(s\right)}\left(\log y\right)^{\mu}\text{e}^{\sigma\text{i}y}\text{d}y\\ & =\sigma\text{i}\text{e}^{\sigma\text{i}a\left(x\right)}\left(a\left(x\right)\right)^{\lambda_{k}\left(s\right)}\left(\log\left(a\left(x\right)\right)\right)^{\mu}-\int_{a\left(x\right)}^{+\infty}y^{\lambda_{k}\left(s\right)-1}\left(\log y\right)^{\mu-1}\left(\lambda_{k}\left(s\right)\log y+\mu\right)\text{e}^{\sigma\text{i}y}\text{d}y. \end{align*} $$
$$ \begin{align*} \forall\left(s,x\right) & \in S_{0}\times X,\ \int_{a\left(x\right)}^{+\infty}y^{\lambda_{k}\left(s\right)}\left(\log y\right)^{\mu}\text{e}^{\sigma\text{i}y}\text{d}y\\ & =\sigma\text{i}\text{e}^{\sigma\text{i}a\left(x\right)}\left(a\left(x\right)\right)^{\lambda_{k}\left(s\right)}\left(\log\left(a\left(x\right)\right)\right)^{\mu}-\int_{a\left(x\right)}^{+\infty}y^{\lambda_{k}\left(s\right)-1}\left(\log y\right)^{\mu-1}\left(\lambda_{k}\left(s\right)\log y+\mu\right)\text{e}^{\sigma\text{i}y}\text{d}y. \end{align*} $$
Note that the right-hand side of the above equality is actually defined on a strictly larger set than
![]() $S_{0}\times X$
– namely, on the set
$S_{0}\times X$
– namely, on the set
![]() $S_{1}\times X$
, where
$S_{1}\times X$
, where
![]() $S_{1}=\left \{ s\in \Sigma ':\ \Re \left (\lambda _{k}\left (s\right )\right )<0\right \} $
. Since
$S_{1}=\left \{ s\in \Sigma ':\ \Re \left (\lambda _{k}\left (s\right )\right )<0\right \} $
. Since
![]() $\Sigma '$
has bounded width, there is an integer
$\Sigma '$
has bounded width, there is an integer
![]() $N_{k}\in \mathbb {N}$
such that
$N_{k}\in \mathbb {N}$
such that
![]() $\Sigma '=\left \{ s\in \Sigma ':\ \Re \left (\lambda _{k}\left (s\right )\right )<N_{k}-1\right \} $
, and if we repeat the above procedure
$\Sigma '=\left \{ s\in \Sigma ':\ \Re \left (\lambda _{k}\left (s\right )\right )<N_{k}-1\right \} $
, and if we repeat the above procedure
![]() $N_{k_{0}}$
times for each critical monomial, then we rewrite h as a sum of generators such that the transcendental elements are well defined on the whole
$N_{k_{0}}$
times for each critical monomial, then we rewrite h as a sum of generators such that the transcendental elements are well defined on the whole
![]() $\left (\Sigma '\setminus P\right )\times X$
.
$\left (\Sigma '\setminus P\right )\times X$
.
4 Strongly integrable and monomial generators
The aim of this section is to prove Theorems 2.9 and 2.21, assuming a central result, Theorem 6.5, the proof of which requires extensive work carried out in the next two sections. We start by dealing with integrals of some specific functions in our class
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
.
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
.
4.1 Special generators of
 $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
We lay the foundations for the proofs of Theorems 2.9 and 2.21 by treating some special cases to which we will reduce later (in Sections 5 and 6). More precisely, we identify two special types of generators for
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
, strongly integrable generators and monomial generators, for which we show that their parametric integrals lie in
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
, strongly integrable generators and monomial generators, for which we show that their parametric integrals lie in
![]() $\mathcal {C}^{\mathcal {M},\mathcal {F}}$
. In Section 6, Proposition 6.4 will provide a reduction to such special generators.
$\mathcal {C}^{\mathcal {M},\mathcal {F}}$
. In Section 6, Proposition 6.4 will provide a reduction to such special generators.
To illustrate the main ideas of this section, we start with two examples of explicit integration of very simple generators.
Examples 4.1. Let
![]() $\Sigma =\left \{ s:\ -2<\Re \left (s\right )<1\right \} $
and
$\Sigma =\left \{ s:\ -2<\Re \left (s\right )<1\right \} $
and
![]() $B=\left \{ \left (x,y\right ):\ x\in X,\ y>a\left (x\right )\right \} $
, for some analytic
$B=\left \{ \left (x,y\right ):\ x\in X,\ y>a\left (x\right )\right \} $
, for some analytic
![]() $a\in \mathcal {S}\left (X\right )$
such that for all
$a\in \mathcal {S}\left (X\right )$
such that for all
![]() $x\in X,\ a\left (x\right )\geq 1$
.
$x\in X,\ a\left (x\right )\geq 1$
.
-
(1) Let
 $D=\left \{ \left (x,y,t\right ):\ \left (x,y\right )\in B,\ t>\widetilde {a}\left (x,y\right )\right \} $
, for some analytic
$D=\left \{ \left (x,y,t\right ):\ \left (x,y\right )\in B,\ t>\widetilde {a}\left (x,y\right )\right \} $
, for some analytic
 $\widetilde {a}\in \mathcal {S}\left (B\right )$
such that for all
$\widetilde {a}\in \mathcal {S}\left (B\right )$
such that for all
 $\left (x,y\right )\in B,\ \widetilde {a}\left (x,y\right )\geq 1$
, and
$\left (x,y\right )\in B,\ \widetilde {a}\left (x,y\right )\geq 1$
, and
 $\Phi \in \mathcal {A}_{\Sigma }\left (D\right )$
be a parametric strong function without poles outside some closed discrete set
$\Phi \in \mathcal {A}_{\Sigma }\left (D\right )$
be a parametric strong function without poles outside some closed discrete set
 $P\subseteq \mathbb {C}$
. If then for all
$P\subseteq \mathbb {C}$
. If then for all $$\begin{align*}g\left(s,x,y,t\right)=y^{-s-3}t^{s-2}\Phi\left(s,x,y,t\right)\chi_{D}\left(x,y,t\right), \end{align*}$$
$$\begin{align*}g\left(s,x,y,t\right)=y^{-s-3}t^{s-2}\Phi\left(s,x,y,t\right)\chi_{D}\left(x,y,t\right), \end{align*}$$
 $\left (s,x,y\right )\in \left (\Sigma \setminus P\right )\times X\times \mathbb {R},\ t\longmapsto g\left (s,x,y,t\right )\in L^{1}\left (\mathbb {R}\right )$
, so
$\left (s,x,y\right )\in \left (\Sigma \setminus P\right )\times X\times \mathbb {R},\ t\longmapsto g\left (s,x,y,t\right )\in L^{1}\left (\mathbb {R}\right )$
, so
 $h=\mathfrak {f}\left [g\right ]\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
is well defined on
$h=\mathfrak {f}\left [g\right ]\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
is well defined on
 $\left (\Sigma \setminus P\right )\times X\times \mathbb {R}$
.
$\left (\Sigma \setminus P\right )\times X\times \mathbb {R}$
.
We claim that
 $g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
and that there exist a closed discrete set
$g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
and that there exist a closed discrete set
 $P'\supseteq P$
and a function
$P'\supseteq P$
and a function
 $H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
$H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
 $P'$
such that
$P'$
such that  $$\begin{align*}\forall\left(s,x\right)\in\left(\Sigma\setminus P'\right)\times X,\ H\left(s,x\right)=\int_{\mathbb{R}}h\left(s,x,y\right)\text{d}y. \end{align*}$$
$$\begin{align*}\forall\left(s,x\right)\in\left(\Sigma\setminus P'\right)\times X,\ H\left(s,x\right)=\int_{\mathbb{R}}h\left(s,x,y\right)\text{d}y. \end{align*}$$
To see this, note that, since for a fixed s,
 $(x,y,t)\mapsto \Phi (s,x,y,t)$
is bounded, there is a constant
$(x,y,t)\mapsto \Phi (s,x,y,t)$
is bounded, there is a constant
 $C=C_s>0$
such that
$C=C_s>0$
such that  $$\begin{align*}\forall\left(s,x,y\right)\in\left(\Sigma\setminus P\right)\times B,\ \int_{1}^{+\infty}t^{s-2}\left|\Phi\left(s,x,y,t\right)\right|\text{d}t<C. \end{align*}$$
$$\begin{align*}\forall\left(s,x,y\right)\in\left(\Sigma\setminus P\right)\times B,\ \int_{1}^{+\infty}t^{s-2}\left|\Phi\left(s,x,y,t\right)\right|\text{d}t<C. \end{align*}$$
It follows that
so $$\begin{align*}\forall\left(s,x,y\right)\in\left(\Sigma\setminus P\right)\times B,\ \mathfrak{f}\left[\left|g\right|\right]\leq y^{-s-3}\int_{1}^{+\infty}t^{s-2}\left|\Phi\left(s,x,y,t\right)\right|\text{d}t\leq Cy^{-s-3}, \end{align*}$$
$$\begin{align*}\forall\left(s,x,y\right)\in\left(\Sigma\setminus P\right)\times B,\ \mathfrak{f}\left[\left|g\right|\right]\leq y^{-s-3}\int_{1}^{+\infty}t^{s-2}\left|\Phi\left(s,x,y,t\right)\right|\text{d}t\leq Cy^{-s-3}, \end{align*}$$
 $y\longmapsto \mathfrak {f}\left [\left |g\right |\right ]\left (s,x,y\right )\in L^{1}\left (\mathbb {R}\right )$
, and by Tonelli’s Theorem,
$y\longmapsto \mathfrak {f}\left [\left |g\right |\right ]\left (s,x,y\right )\in L^{1}\left (\mathbb {R}\right )$
, and by Tonelli’s Theorem,
 $g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
. Hence, by Fubini’s Theorem, and the integrand
$g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
. Hence, by Fubini’s Theorem, and the integrand $$\begin{align*}\int_{\mathbb{R}}h\left(s,x,y\right)\text{d}y=\int_{\mathbb{R}}t^{s-2}\text{e}^{\text{i}t}\left[\int_{\mathbb{R}}y^{-s-3}\Phi\left(s,x,y,t\right)\chi_{D}\left(x,y,t\right)\text{d}y\right]\text{d}t, \end{align*}$$
$$\begin{align*}\int_{\mathbb{R}}h\left(s,x,y\right)\text{d}y=\int_{\mathbb{R}}t^{s-2}\text{e}^{\text{i}t}\left[\int_{\mathbb{R}}y^{-s-3}\Phi\left(s,x,y,t\right)\chi_{D}\left(x,y,t\right)\text{d}y\right]\text{d}t, \end{align*}$$
 $\tilde {g}$
in the inner integral belongs to
$\tilde {g}$
in the inner integral belongs to
 $\mathcal {C}_{\Sigma }^{\mathcal {M}}\left (D\right )$
and is integrable with respect to y. By Theorem 2.18, there are a closed discrete set
$\mathcal {C}_{\Sigma }^{\mathcal {M}}\left (D\right )$
and is integrable with respect to y. By Theorem 2.18, there are a closed discrete set
 $P'\subseteq \mathbb {C}$
containing P and a function
$P'\subseteq \mathbb {C}$
containing P and a function
 $G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )$
without poles outside
$G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )$
without poles outside
 $P'$
such that
$P'$
such that  $$\begin{align*}\forall\left(s,x\right)\in\left(\Sigma\setminus P'\right)\times X,\ G\left(s,x,t\right)=t^{s-2}\int_{\mathbb{R}}y^{-s-3}\Phi\left(s,x,y,t\right)\chi_{D}\left(x,y,t\right)\text{d}y. \end{align*}$$
$$\begin{align*}\forall\left(s,x\right)\in\left(\Sigma\setminus P'\right)\times X,\ G\left(s,x,t\right)=t^{s-2}\int_{\mathbb{R}}y^{-s-3}\Phi\left(s,x,y,t\right)\chi_{D}\left(x,y,t\right)\text{d}y. \end{align*}$$
Notice also that
 $G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\text {int}}$
and that
$G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\text {int}}$
and that
 $H=\mathfrak {f}\left [G\right ]$
proves the claim.
$H=\mathfrak {f}\left [G\right ]$
proves the claim. -
(2) Consider
 $g\left (s,x,y\right )=y^{s}\chi _{B}\left (x,y\right )\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )$
and
$g\left (s,x,y\right )=y^{s}\chi _{B}\left (x,y\right )\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )$
and
 $T\left (s,x,y\right )=g\left (s,x,y\right )\text {e}^{\text {i}y}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
. As we cannot apply the operator
$T\left (s,x,y\right )=g\left (s,x,y\right )\text {e}^{\text {i}y}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
. As we cannot apply the operator $$\begin{align*}\mathrm{Int}\left(g;\Sigma\times X\right)=\left\{ s\in\Sigma:\ \Re\left(s\right)<-1\right\} \times X\not=\Sigma\times X, \end{align*}$$
$$\begin{align*}\mathrm{Int}\left(g;\Sigma\times X\right)=\left\{ s\in\Sigma:\ \Re\left(s\right)<-1\right\} \times X\not=\Sigma\times X, \end{align*}$$
 $\mathfrak {f}$
to g in order to express the integral of T with respect to y. However, we claim that there exists a function
$\mathfrak {f}$
to g in order to express the integral of T with respect to y. However, we claim that there exists a function
 $H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
such that (4.1)
$H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
such that (4.1) $$ \begin{align} \forall\left(s,x\right)\in\mathrm{Int}\left(T;\Sigma\times X\right),\ H\left(s,x\right)=\int_{a\left(x\right)}^{+\infty}y^{s}\mathrm{e}^{\mathrm{i}y}\mathrm{d}y. \end{align} $$
$$ \begin{align} \forall\left(s,x\right)\in\mathrm{Int}\left(T;\Sigma\times X\right),\ H\left(s,x\right)=\int_{a\left(x\right)}^{+\infty}y^{s}\mathrm{e}^{\mathrm{i}y}\mathrm{d}y. \end{align} $$
To show this, let us integrate by parts
 $y^{s}\mathrm {e}^{\mathrm {i}y}$
twice, where we integrate the exponential and derive the parametric power:
$y^{s}\mathrm {e}^{\mathrm {i}y}$
twice, where we integrate the exponential and derive the parametric power:  $$ \begin{align*} \int y^{s}\mathrm{e}^{\mathrm{i}y}\mathrm{d}y & =y^{s}\frac{\mathrm{e}^{\mathrm{i}y}}{\mathrm{i}}-\frac{1}{\mathrm{i}}\int sy^{s-1}\mathrm{e}^{\mathrm{i}y}\mathrm{d}y\\ & =\mathrm{i}y^{s}\mathrm{e}^{\mathrm{i}y}+sy^{s-1}\mathrm{e}^{\mathrm{i}y}-s\left(s-1\right)\int y^{s-2}\mathrm{e}^{\mathrm{i}y}\mathrm{d}y. \end{align*} $$
$$ \begin{align*} \int y^{s}\mathrm{e}^{\mathrm{i}y}\mathrm{d}y & =y^{s}\frac{\mathrm{e}^{\mathrm{i}y}}{\mathrm{i}}-\frac{1}{\mathrm{i}}\int sy^{s-1}\mathrm{e}^{\mathrm{i}y}\mathrm{d}y\\ & =\mathrm{i}y^{s}\mathrm{e}^{\mathrm{i}y}+sy^{s-1}\mathrm{e}^{\mathrm{i}y}-s\left(s-1\right)\int y^{s-2}\mathrm{e}^{\mathrm{i}y}\mathrm{d}y. \end{align*} $$
Define
 $$\begin{align*}H\left(s,x\right)=-\mathrm{i}\left(a\left(x\right)\right)^{s}\mathrm{e}^{\mathrm{i}a\left(x\right)}-s\left(a\left(x\right)\right)^{s-1}\mathrm{e}^{\mathrm{i}a\left(x\right)}-s\left(s-1\right)\int_{a\left(x\right)}^{+\infty}y^{s-2}\mathrm{e}^{\mathrm{i}y}\mathrm{d}y. \end{align*}$$
$$\begin{align*}H\left(s,x\right)=-\mathrm{i}\left(a\left(x\right)\right)^{s}\mathrm{e}^{\mathrm{i}a\left(x\right)}-s\left(a\left(x\right)\right)^{s-1}\mathrm{e}^{\mathrm{i}a\left(x\right)}-s\left(s-1\right)\int_{a\left(x\right)}^{+\infty}y^{s-2}\mathrm{e}^{\mathrm{i}y}\mathrm{d}y. \end{align*}$$
Notice that H is well defined on
 $\Sigma \times X$
because the real part of the exponent in the integrand is always
$\Sigma \times X$
because the real part of the exponent in the integrand is always
 $<-1$
on
$<-1$
on
 $\Sigma $
, and that
$\Sigma $
, and that
 $H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
because the last term is obtained by applying the operator
$H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
because the last term is obtained by applying the operator
 $\mathfrak {f}$
to
$\mathfrak {f}$
to
 $\tilde {g}\left (s,x,y\right )=s\left (s-1\right )y^{s-2}\chi _{B}\left (s,y\right )\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\text {int}}$
. Note also that H satisfies (4.1) since
$\tilde {g}\left (s,x,y\right )=s\left (s-1\right )y^{s-2}\chi _{B}\left (s,y\right )\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\text {int}}$
. Note also that H satisfies (4.1) since
 $\mathrm {Int}\left (T;\Sigma \times X\right )=\{s\in \Sigma :\ \Re \left (s\right )<-1\}\times X,$
and on this part of the space, the exponents of the parametric powers
$\mathrm {Int}\left (T;\Sigma \times X\right )=\{s\in \Sigma :\ \Re \left (s\right )<-1\}\times X,$
and on this part of the space, the exponents of the parametric powers
 $y^{s},y^{s-1}$
have negative real part.
$y^{s},y^{s-1}$
have negative real part.
The techniques illustrated in these two examples can be generalized and used to integrate generators of
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
of a rather simple form.
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
of a rather simple form.
Recall that, by Lemma 3.3, every generator of
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
can be written as
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
can be written as
![]() $\mathfrak {f}\left [h\right ]$
, for some
$\mathfrak {f}\left [h\right ]$
, for some
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (\left (X\times \mathbb {R}\right )\times \mathbb {R}\right )_{\text {int}}$
.
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (\left (X\times \mathbb {R}\right )\times \mathbb {R}\right )_{\text {int}}$
.
Definition 4.2. Let
![]() $T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a generator.
$T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a generator.
-
• T is strongly integrable if T can be written as
 $\mathfrak {f}\left [h\right ]$
, for some
$\mathfrak {f}\left [h\right ]$
, for some
 $h\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
. If B is a cell as in (3.1), we say that T is strongly integrable on B if
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
. If B is a cell as in (3.1), we say that T is strongly integrable on B if
 $T\chi _{B}$
is strongly integrable.
$T\chi _{B}$
is strongly integrable. -
• T is monomial in (its last variable) y if T has the form
(4.2)where $$ \begin{align} T\left(s,x,y\right)=f\left(s,x\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\text{e}^{\text{i}Q\left(x,y\right)}, \end{align} $$
$$ \begin{align} T\left(s,x,y\right)=f\left(s,x\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\text{e}^{\text{i}Q\left(x,y\right)}, \end{align} $$
 $f\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right ),\mu \in \mathbb {N},\lambda \left (s\right )=\frac {\ell s+\eta }{d}$
for some
$f\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right ),\mu \in \mathbb {N},\lambda \left (s\right )=\frac {\ell s+\eta }{d}$
for some
 $\ell \in \mathbb {Z},\ \eta \in \mathbb {C},\ d\in \mathbb {N}\setminus \left \{ 0\right \} $
and
$\ell \in \mathbb {Z},\ \eta \in \mathbb {C},\ d\in \mathbb {N}\setminus \left \{ 0\right \} $
and
 $Q\in \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
is a polynomial in the variable
$Q\in \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
is a polynomial in the variable
 $y^{\frac {1}{d}}$
with coefficients subanalytic functions of x. The tuple
$y^{\frac {1}{d}}$
with coefficients subanalytic functions of x. The tuple
 $\left (d,\ell ,\eta ,\mu ,Q\right )$
is called the monomial data of T.
$\left (d,\ell ,\eta ,\mu ,Q\right )$
is called the monomial data of T.
Remark 4.3. Let
![]() $T=g\text {e}^{\text {i}\varphi }\gamma \in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a generator and write
$T=g\text {e}^{\text {i}\varphi }\gamma \in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a generator and write
![]() $\gamma $
as
$\gamma $
as
![]() $\int _{\mathbb {R}}G\left (s,x,y,t\right )\text {e}^{\text {i}t}\text {d}t$
for some appropriate
$\int _{\mathbb {R}}G\left (s,x,y,t\right )\text {e}^{\text {i}t}\text {d}t$
for some appropriate
![]() $G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (\left (X\times \mathbb {R}\right )\times \mathbb {R}\right )_{\text {int}}$
. Suppose that
$G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (\left (X\times \mathbb {R}\right )\times \mathbb {R}\right )_{\text {int}}$
. Suppose that
![]() $gG\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
. Then, T is strongly integrable. To see this, proceed as in Lemma 3.3 and write T as
$gG\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
. Then, T is strongly integrable. To see this, proceed as in Lemma 3.3 and write T as
![]() $\mathfrak {f}\left [h\right ]$
. It is clear that
$\mathfrak {f}\left [h\right ]$
. It is clear that
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
.
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
.
Our next aim is to integrate a single generator which is of either of the forms in Definition 4.2.
Proposition 4.4. Let
![]() $g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\mathrm {int}}$
be without poles outside some closed discrete set
$g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\mathrm {int}}$
be without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
and
$P\subseteq \mathbb {C}$
and
![]() $\varphi \in \mathcal {S}\left (X\times \mathbb {R}^{2}\right )$
. There exist a closed discrete set
$\varphi \in \mathcal {S}\left (X\times \mathbb {R}^{2}\right )$
. There exist a closed discrete set
![]() $P'\subseteq \mathbb {C}$
containing P and a function
$P'\subseteq \mathbb {C}$
containing P and a function
![]() $H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
$H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
![]() $P'$
such that
$P'$
such that
Moreover, the set
![]() $P'\setminus P$
is contained in a finitely generated
$P'\setminus P$
is contained in a finitely generated
![]() $\mathbb {Z}$
-lattice.
$\mathbb {Z}$
-lattice.
Proof. Up to decomposing
![]() $X\times \mathbb {R}^{2}$
into subanalytic cells, we may suppose that, on each cell A of base X and open over
$X\times \mathbb {R}^{2}$
into subanalytic cells, we may suppose that, on each cell A of base X and open over
![]() $\mathbb {R}^{m}$
, either
$\mathbb {R}^{m}$
, either
![]() $\varphi $
does not depend on
$\varphi $
does not depend on
![]() $\left (y,t\right )$
or, for one of these two variables (say, y), the function
$\left (y,t\right )$
or, for one of these two variables (say, y), the function
![]() $y\longmapsto \varphi \left (x,y,t\right )$
is
$y\longmapsto \varphi \left (x,y,t\right )$
is
![]() $C^{1}$
and strictly monotonic.
$C^{1}$
and strictly monotonic.
In the first case, we factor the exponential out of the integral, and we apply Theorem 2.18 to g. In the second case, up to applying the subanalytic change of variables
![]() $\left (x,y,t\right )\longmapsto \left (x,\varphi \left (x,y,t\right ),t\right )$
and multiplying by the Jacobian of its inverse, we may suppose that
$\left (x,y,t\right )\longmapsto \left (x,\varphi \left (x,y,t\right ),t\right )$
and multiplying by the Jacobian of its inverse, we may suppose that
![]() $\varphi \left (x,y,t\right )=y$
on A. Hence, by Fubini’s Theorem,
$\varphi \left (x,y,t\right )=y$
on A. Hence, by Fubini’s Theorem,
 $$\begin{align*}\int_{A}g\left(s,x,y,t\right)\mathrm{e}^{\mathrm{i}\varphi\left(x,y,t\right)}\text{d}y\wedge\text{d}t=\int_{\mathbb{R}}\text{e}^{\text{i}y}\left[\int_{\mathbb{R}}\chi_{A}\left(x,y,t\right)g\left(s,x,y,t\right)\text{d}t\right]\text{d}y. \end{align*}$$
$$\begin{align*}\int_{A}g\left(s,x,y,t\right)\mathrm{e}^{\mathrm{i}\varphi\left(x,y,t\right)}\text{d}y\wedge\text{d}t=\int_{\mathbb{R}}\text{e}^{\text{i}y}\left[\int_{\mathbb{R}}\chi_{A}\left(x,y,t\right)g\left(s,x,y,t\right)\text{d}t\right]\text{d}y. \end{align*}$$
Again by Theorem 2.18, applied to the integrand inside the square brackets, the right-hand side of the above equation is of the form
![]() $\mathfrak {f}\left [\tilde {g}\right ]$
, for some suitable
$\mathfrak {f}\left [\tilde {g}\right ]$
, for some suitable
![]() $\tilde {g}\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )$
without poles outside some closed discrete set
$\tilde {g}\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )$
without poles outside some closed discrete set
![]() $P'\supseteq P$
, such that
$P'\supseteq P$
, such that
![]() $P'\setminus P$
is a finitely generated
$P'\setminus P$
is a finitely generated
![]() $\mathbb {Z}$
-lattice (see Definition 2.16 and Theorem 2.18). We conclude by linearity of the integral, taking the sum over the cells of the decomposition.
$\mathbb {Z}$
-lattice (see Definition 2.16 and Theorem 2.18). We conclude by linearity of the integral, taking the sum over the cells of the decomposition.
Corollary 4.5.
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
is a
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
is a
![]() $\mathbb {C}$
-algebra.
$\mathbb {C}$
-algebra.
Proof. Is suffices to show that if
![]() $h_{1},h_{2}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
, then
$h_{1},h_{2}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
, then
![]() $h_{1}\cdot h_{2}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
. Write
$h_{1}\cdot h_{2}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
. Write
![]() $h_{i}=\mathfrak {f}\left [g_{i}\right ]$
, for some
$h_{i}=\mathfrak {f}\left [g_{i}\right ]$
, for some
![]() $g_{i}\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\text {int}}$
. By Fubini’s Theorem,
$g_{i}\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}\right )_{\text {int}}$
. By Fubini’s Theorem,
![]() $\left (s,x,y,t\right )\longmapsto g_{1}\left (s,x,y\right )\cdot g_{2}\left (s,x,t\right )\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
, so Proposition 4.4 applies.
$\left (s,x,y,t\right )\longmapsto g_{1}\left (s,x,y\right )\cdot g_{2}\left (s,x,t\right )\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
, so Proposition 4.4 applies.
Proposition 4.4 allows us to integrate strongly integrable generators.
Corollary 4.6. Let
![]() $T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a strongly integrable generator without poles outside some closed discrete set
$T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a strongly integrable generator without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
. There exist a closed discrete set
$P\subseteq \mathbb {C}$
. There exist a closed discrete set
![]() $P'\subseteq \mathbb {C}$
containing P, such that
$P'\subseteq \mathbb {C}$
containing P, such that
![]() $P'\setminus P$
is contained in a finitely generated
$P'\setminus P$
is contained in a finitely generated
![]() $\mathbb {Z}$
-lattice, and a function
$\mathbb {Z}$
-lattice, and a function
![]() $H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
$H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
![]() $P'$
, such that
$P'$
, such that
Proof. Immediate from Fubini’s Theorem and Proposition 4.4.
Next, we consider a monomial generator and interpolate its integral on a given cell by a function of the class
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}$
.
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}$
.
Lemma 4.7. Let B be a cell as in (3.1) with bounded y-fibers and let
![]() $T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a generator which is monomial in y (as in (4.2)), without poles outside some closed discrete set
$T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a generator which is monomial in y (as in (4.2)), without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
. Then, T is strongly integrable on B.
$P\subseteq \mathbb {C}$
. Then, T is strongly integrable on B.
Proof. For all
![]() $\left (s,x\right )\in \left (\Sigma \setminus P\right )\times X,\ y\longmapsto \left |T\left (s,x,y\right )\chi _{B}\left (x,y\right )\right |$
extends to a continuous function on
$\left (s,x\right )\in \left (\Sigma \setminus P\right )\times X,\ y\longmapsto \left |T\left (s,x,y\right )\chi _{B}\left (x,y\right )\right |$
extends to a continuous function on
![]() $\left [a\left (x\right ),b\left (x\right )\right ]$
. Hence, by Remark 4.3, we are done.
$\left [a\left (x\right ),b\left (x\right )\right ]$
. Hence, by Remark 4.3, we are done.
Proposition 4.8. Let B be a cell as in (3.1) with unbounded y-fibers and let
![]() $T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a generator which is monomial in y (as in (4.2)), without poles outside some closed discrete set
$T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a generator which is monomial in y (as in (4.2)), without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
. Then,
$P\subseteq \mathbb {C}$
. Then,
Moreover, there are a closed discrete set
![]() $P'\subseteq \mathbb {C}$
containing P, such that
$P'\subseteq \mathbb {C}$
containing P, such that
![]() $P'\setminus P$
is contained in a finitely generated
$P'\setminus P$
is contained in a finitely generated
![]() $\mathbb {Z}$
-lattice, and a function
$\mathbb {Z}$
-lattice, and a function
![]() $H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
$H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
![]() $P'$
, such that
$P'$
, such that
 $$\begin{align*}\forall\left(s,x\right)\in\mathrm{Int}\left(T\chi_{B};\left(\Sigma\setminus P'\right)\times X\right),\ H\left(s,x\right)=\int_{a\left(x\right)}^{+\infty}T\left(s,x,y\right)\text{d}y. \end{align*}$$
$$\begin{align*}\forall\left(s,x\right)\in\mathrm{Int}\left(T\chi_{B};\left(\Sigma\setminus P'\right)\times X\right),\ H\left(s,x\right)=\int_{a\left(x\right)}^{+\infty}T\left(s,x,y\right)\text{d}y. \end{align*}$$
Proof. The statement on the integration locus is immediate.
Write
![]() $Q\left (x,y\right )=\sum _{i\leq n}b_{i}\left (x\right )y^{\frac {i}{d}}$
. We may suppose that
$Q\left (x,y\right )=\sum _{i\leq n}b_{i}\left (x\right )y^{\frac {i}{d}}$
. We may suppose that
![]() $n>0$
because otherwise, we are done by Theorem 2.18. By o-minimality, we may suppose that for all
$n>0$
because otherwise, we are done by Theorem 2.18. By o-minimality, we may suppose that for all
![]() $x\in X,\ b_{n}\left (x\right )\not =0$
. By Lemma 4.7 and definable choice, we may suppose that for all
$x\in X,\ b_{n}\left (x\right )\not =0$
. By Lemma 4.7 and definable choice, we may suppose that for all
![]() $x\in X,\ y\longmapsto Q\left (x,y\right )$
is monotonic (say, strictly increasing) on
$x\in X,\ y\longmapsto Q\left (x,y\right )$
is monotonic (say, strictly increasing) on
![]() $\left (a\left (x\right ),+\infty \right )$
. Hence, we may write
$\left (a\left (x\right ),+\infty \right )$
. Hence, we may write
![]() $Q\left (x,y\right )=b_{n}\left (x\right )y^{\frac {n}{d}}\left (1+\varepsilon _{1}\left (x,y\right )\right )$
, where
$Q\left (x,y\right )=b_{n}\left (x\right )y^{\frac {n}{d}}\left (1+\varepsilon _{1}\left (x,y\right )\right )$
, where
![]() $\varepsilon _{1}\in \mathbb {R}\left \{ x\right \} \left [y^{-\frac {1}{d}}\right ]$
with
$\varepsilon _{1}\in \mathbb {R}\left \{ x\right \} \left [y^{-\frac {1}{d}}\right ]$
with
![]() $\varepsilon _{1}\left (x,0\right )=0$
, and the compositional inverse has the form
$\varepsilon _{1}\left (x,0\right )=0$
, and the compositional inverse has the form
![]() $\phi \left (x,z\right )=c\left (x\right )z^{\frac {d}{n}}\left (1+\varepsilon _{2}\left (x,z\right )\right )$
, for some analytic
$\phi \left (x,z\right )=c\left (x\right )z^{\frac {d}{n}}\left (1+\varepsilon _{2}\left (x,z\right )\right )$
, for some analytic
![]() $c\in \mathcal {S}\left (X\right )$
and
$c\in \mathcal {S}\left (X\right )$
and
![]() $\varepsilon _{2}\in \mathbb {R}\left \{ x,z^{-\frac {1}{n}}\right \} $
with
$\varepsilon _{2}\in \mathbb {R}\left \{ x,z^{-\frac {1}{n}}\right \} $
with
![]() $\varepsilon _{2}\left (x,0\right )=0$
. Note that
$\varepsilon _{2}\left (x,0\right )=0$
. Note that
![]() ${\displaystyle \frac {\partial \phi }{\partial z}\left (x,z\right )=\frac {d}{n}c\left (x\right )z^{\frac {d}{n}-1}\left (1+\varepsilon _{3}\left (x,z\right )\right )}$
, for some
${\displaystyle \frac {\partial \phi }{\partial z}\left (x,z\right )=\frac {d}{n}c\left (x\right )z^{\frac {d}{n}-1}\left (1+\varepsilon _{3}\left (x,z\right )\right )}$
, for some
![]() $\varepsilon _{3}\in \mathbb {R}\left \{ x,z^{-\frac {1}{n}}\right \} $
with
$\varepsilon _{3}\in \mathbb {R}\left \{ x,z^{-\frac {1}{n}}\right \} $
with
![]() $\varepsilon _{3}\left (x,0\right )=0$
. Hence, on
$\varepsilon _{3}\left (x,0\right )=0$
. Hence, on
![]() $\mathrm {Int}\left (T\chi _{B};\left (\Sigma \setminus P\right )\times X\right )$
, we may write
$\mathrm {Int}\left (T\chi _{B};\left (\Sigma \setminus P\right )\times X\right )$
, we may write
 $$\begin{align*}\int_{a\left(x\right)}^{+\infty}T\left(s,x,y\right)\text{d}y=\tilde{f}\left(s,x\right)\int_{Q\left(x,a\left(x\right)\right)}^{+\infty}z^{\tilde{\lambda}\left(s\right)}\left[\frac{d}{n}\log z+G\left(x,z\right)\right]^{\mu}u\left(s,x,z\right)\text{e}^{\text{i}z}\text{d}z, \end{align*}$$
$$\begin{align*}\int_{a\left(x\right)}^{+\infty}T\left(s,x,y\right)\text{d}y=\tilde{f}\left(s,x\right)\int_{Q\left(x,a\left(x\right)\right)}^{+\infty}z^{\tilde{\lambda}\left(s\right)}\left[\frac{d}{n}\log z+G\left(x,z\right)\right]^{\mu}u\left(s,x,z\right)\text{e}^{\text{i}z}\text{d}z, \end{align*}$$
where
![]() $\tilde {f}\left (s,x\right )=f\left (s,x\right )\frac {d}{n}\left (c\left (x\right )\right )^{\lambda \left (s\right )+1},\ \tilde {\lambda }\left (s\right )=\frac {d}{n}\lambda \left (s\right )+\frac {d}{n}-1,\ G\left (x,z\right )=\log \left (c\left (x\right )\right )+\log \left (1+\varepsilon _{2}\left (x,z\right )\right )$
and
$\tilde {f}\left (s,x\right )=f\left (s,x\right )\frac {d}{n}\left (c\left (x\right )\right )^{\lambda \left (s\right )+1},\ \tilde {\lambda }\left (s\right )=\frac {d}{n}\lambda \left (s\right )+\frac {d}{n}-1,\ G\left (x,z\right )=\log \left (c\left (x\right )\right )+\log \left (1+\varepsilon _{2}\left (x,z\right )\right )$
and
![]() $u\left (s,x,z\right )=\left (1+\varepsilon _{2}\left (x,z\right )\right )^{\lambda \left (s\right )}\left (1+\varepsilon _{3}\left (x,z\right )\right )$
is a parametric strong unit. Note that, for all
$u\left (s,x,z\right )=\left (1+\varepsilon _{2}\left (x,z\right )\right )^{\lambda \left (s\right )}\left (1+\varepsilon _{3}\left (x,z\right )\right )$
is a parametric strong unit. Note that, for all
![]() $x\in X$
, G can be expanded as a power series (with nonzero constant term) in the variable
$x\in X$
, G can be expanded as a power series (with nonzero constant term) in the variable
![]() $z^{-\frac {1}{n}}$
. By expanding the power
$z^{-\frac {1}{n}}$
. By expanding the power
![]() $\mu $
of the square bracket, we may rewrite the above integral as a finite sum of terms where the integrand has the form
$\mu $
of the square bracket, we may rewrite the above integral as a finite sum of terms where the integrand has the form
![]() $z^{\tilde {\lambda }\left (s\right )}\text {e}^{\text {i}z}\cdot \left (\log z\right )^{\nu }U_{\nu }\left (s,x,z\right )$
, for some
$z^{\tilde {\lambda }\left (s\right )}\text {e}^{\text {i}z}\cdot \left (\log z\right )^{\nu }U_{\nu }\left (s,x,z\right )$
, for some
![]() $\nu \leq \mu $
and parametric strong unit
$\nu \leq \mu $
and parametric strong unit
![]() $U_{\nu }$
which can be expanded as a series in the variable
$U_{\nu }$
which can be expanded as a series in the variable
![]() $z^{-\frac {1}{n}}$
. It follows that there are finitely many monomials in the integrand of the form
$z^{-\frac {1}{n}}$
. It follows that there are finitely many monomials in the integrand of the form
![]() $z^{\Re \left (\tilde {\lambda }\left (s\right )\right )-\frac {k}{n}}\left (\log z\right )^{\nu }$
for which the integral is not finite. Arguing as in the proof of Proposition 2.20, we find the function H in the statement by integration by parts.
$z^{\Re \left (\tilde {\lambda }\left (s\right )\right )-\frac {k}{n}}\left (\log z\right )^{\nu }$
for which the integral is not finite. Arguing as in the proof of Proposition 2.20, we find the function H in the statement by integration by parts.
4.2 Overview of the proofs of Theorems 2.9 and 2.21
The proof of Theorem 2.21, which will be completed in Section 6, is organized as follows. We show that, given
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
without poles outside some closed discrete set
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
, the domain
$P\subseteq \mathbb {C}$
, the domain
![]() $X\times \mathbb {R}$
can be partitioned into subanalytic cells such that on each cell A, up to a subanalytic change of variables, h can be written as a finite sum of generators which are either strongly integrable or monomial in the last variable (Proposition 6.4). The results of the current section provide, for each such generator
$X\times \mathbb {R}$
can be partitioned into subanalytic cells such that on each cell A, up to a subanalytic change of variables, h can be written as a finite sum of generators which are either strongly integrable or monomial in the last variable (Proposition 6.4). The results of the current section provide, for each such generator
![]() $T_{i}$
, a description of the integration locus and a function
$T_{i}$
, a description of the integration locus and a function
![]() $H_{i}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside some closed discrete set
$H_{i}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside some closed discrete set
![]() $P'\supseteq P$
, which coincides with the integral of
$P'\supseteq P$
, which coincides with the integral of
![]() $T_{i}$
on its integration locus. Next, we show that, up to possibly enlarging the closed discrete set
$T_{i}$
on its integration locus. Next, we show that, up to possibly enlarging the closed discrete set
![]() $P'$
, the integration locus of
$P'$
, the integration locus of
![]() $h\restriction A$
is the intersection of the integration loci of the generators
$h\restriction A$
is the intersection of the integration loci of the generators
![]() $T_{i}$
(this is done using a non-compensation argument proven in [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 3.4], meaning that the sum of nonintegrable terms is nonintegrable). Thus, the sum of the functions
$T_{i}$
(this is done using a non-compensation argument proven in [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 3.4], meaning that the sum of nonintegrable terms is nonintegrable). Thus, the sum of the functions
![]() $H_{i}$
interpolates the integral of
$H_{i}$
interpolates the integral of
![]() $h\restriction A$
on its integration locus (Theorem 6.5). Theorem 2.21 follows from Theorem 6.5 by Fubini’s Theorem (with an argument spelled out in detail in [Reference Cluckers, Comte, Rolin and ServiCCRS23, pp. 31-32]), which shows that we can iterate the argument above integrating with respect to one variable at the time.
$h\restriction A$
on its integration locus (Theorem 6.5). Theorem 2.21 follows from Theorem 6.5 by Fubini’s Theorem (with an argument spelled out in detail in [Reference Cluckers, Comte, Rolin and ServiCCRS23, pp. 31-32]), which shows that we can iterate the argument above integrating with respect to one variable at the time.
The proof of Theorem 2.9 is just a special case of that of Theorem 2.21, where all the functions involved happen not to depend on the variable s. In particular, that
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
is a system of
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
is a system of
![]() $\mathbb {C}$
-algebras containing
$\mathbb {C}$
-algebras containing
![]() $\text {e}^{\text {i}\mathcal {S}}$
follows from Corollary 4.5 and Lemma 3.3. It follows from stability under parametric integration and the definition of
$\text {e}^{\text {i}\mathcal {S}}$
follows from Corollary 4.5 and Lemma 3.3. It follows from stability under parametric integration and the definition of
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
that it is the smallest system of
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
that it is the smallest system of
![]() $\mathbb {C}$
-algebras containing
$\mathbb {C}$
-algebras containing
![]() $\mathcal {S}_{+}^{\mathbb {C}}\cup \mathrm {e}^{\mathrm {i}\mathcal {S}}$
and stable under parametric integration, and the smallest such system containing
$\mathcal {S}_{+}^{\mathbb {C}}\cup \mathrm {e}^{\mathrm {i}\mathcal {S}}$
and stable under parametric integration, and the smallest such system containing
![]() $\mathcal {C}^{\mathbb {C}}$
and stable under the parametric Fourier transform and right-composition with subanalytic maps.
$\mathcal {C}^{\mathbb {C}}$
and stable under the parametric Fourier transform and right-composition with subanalytic maps.
5 Preparation
With the aim of proving Proposition 6.4, in this section, we write every function of the class
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, piecewise and up to a subanalytic change of variables, as a finite sum of generators of a special prepared form which gives some information on their integration locus. This builds further (and relies) on preparation results for subanalytic functions from [Reference ParusińskiPar94, Reference ParusińskiPar01, Reference Lion and RolinLR98, Reference MillerMil06].
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, piecewise and up to a subanalytic change of variables, as a finite sum of generators of a special prepared form which gives some information on their integration locus. This builds further (and relies) on preparation results for subanalytic functions from [Reference ParusińskiPar94, Reference ParusińskiPar01, Reference Lion and RolinLR98, Reference MillerMil06].
Notation 5.1. Let
![]() $B\subseteq X\times \mathbb {R}$
be as in (3.1) Consider a cell
$B\subseteq X\times \mathbb {R}$
be as in (3.1) Consider a cell
![]() $D\subseteq B\times \mathbb {R}$
of the form
$D\subseteq B\times \mathbb {R}$
of the form
where
![]() $\widetilde {a},\widetilde {b}:B\longrightarrow \mathbb {R}$
are analytic subanalytic functions with
$\widetilde {a},\widetilde {b}:B\longrightarrow \mathbb {R}$
are analytic subanalytic functions with
![]() $1\leq \widetilde {a}\left (x,y\right )<\widetilde {b}\left (x,y\right )\ \text {for all }\left (x,y\right )\in B$
, or
$1\leq \widetilde {a}\left (x,y\right )<\widetilde {b}\left (x,y\right )\ \text {for all }\left (x,y\right )\in B$
, or
![]() $\widetilde {b}$
is
$\widetilde {b}$
is
![]() $\equiv +\infty $
. We say that D has bounded t-fibers if
$\equiv +\infty $
. We say that D has bounded t-fibers if
![]() $\widetilde {b}<+\infty $
and unbounded t-fibers if
$\widetilde {b}<+\infty $
and unbounded t-fibers if
![]() $\widetilde {b}\equiv +\infty $
.
$\widetilde {b}\equiv +\infty $
.
Suppose furthermore that
![]() $\widetilde {a},\widetilde {b},\widetilde {b}-\widetilde {a}$
have the following prepared form:
$\widetilde {a},\widetilde {b},\widetilde {b}-\widetilde {a}$
have the following prepared form:
 $$ \begin{align} \begin{aligned} & \widetilde{a}\left(x,y\right)=a_{0}\left(x\right)y^{\frac{\alpha}{d}}u_{a}\left(x,y\right), & \widetilde{b}\left(x,y\right)=b_{0}\left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right),\\ & \widetilde{b}\left(x,y\right)-\widetilde{a}\left(x,y\right)=d_{0}\left(x\right)y^{\frac{\Delta}{d}}u_{d}\left(x,y\right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \widetilde{a}\left(x,y\right)=a_{0}\left(x\right)y^{\frac{\alpha}{d}}u_{a}\left(x,y\right), & \widetilde{b}\left(x,y\right)=b_{0}\left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right),\\ & \widetilde{b}\left(x,y\right)-\widetilde{a}\left(x,y\right)=d_{0}\left(x\right)y^{\frac{\Delta}{d}}u_{d}\left(x,y\right), \end{aligned} \end{align} $$
where
![]() $\alpha ,\beta ,\Delta \in \mathbb {N},\ a_{0},b_{0},d_{0}\in \mathcal {S}\left (X\right )$
are analytic and
$\alpha ,\beta ,\Delta \in \mathbb {N},\ a_{0},b_{0},d_{0}\in \mathcal {S}\left (X\right )$
are analytic and
![]() $u_{a},u_{b},u_{d}\in \mathcal {S}\left (B\right )$
are
$u_{a},u_{b},u_{d}\in \mathcal {S}\left (B\right )$
are
![]() $\psi $
-prepared subanalytic strong units (for
$\psi $
-prepared subanalytic strong units (for
![]() $\psi $
as in (3.2)). If
$\psi $
as in (3.2)). If
![]() $\widetilde {b}=+\infty $
, we stipulate that
$\widetilde {b}=+\infty $
, we stipulate that
![]() $b_{0}=d_{0}=+\infty ,\ u_{b}=u_{d}=1$
and
$b_{0}=d_{0}=+\infty ,\ u_{b}=u_{d}=1$
and
![]() $\beta =\Delta =0$
.
$\beta =\Delta =0$
.
Define
 $$ \begin{align} \varPsi\left(x,y,t\right)=\left(\psi\left(x,y\right),\left(\frac{a_{0}\left(x\right)y^{\frac{\alpha}{d}}}{t}\right)^{\frac{1}{d}},\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{1}{d}}\right), \end{align} $$
$$ \begin{align} \varPsi\left(x,y,t\right)=\left(\psi\left(x,y\right),\left(\frac{a_{0}\left(x\right)y^{\frac{\alpha}{d}}}{t}\right)^{\frac{1}{d}},\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{1}{d}}\right), \end{align} $$
where if D has unbounded t-fibers, we omit the last component. Note that
![]() $\varPsi $
is a
$\varPsi $
is a
![]() $1$
-bounded subanalytic map on D.
$1$
-bounded subanalytic map on D.
Definition 5.2. A generator
![]() $T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
without poles outside some closed discrete set
$T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
is prepared on B if for all
$P\subseteq \mathbb {C}$
is prepared on B if for all
![]() $\left (s,x,y\right )\in \left (\Sigma \setminus P\right )\times B,$
$\left (s,x,y\right )\in \left (\Sigma \setminus P\right )\times B,$
where
![]() $g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\right ),\ \mu \in \mathbb {N},\ \varphi \in \mathcal {S}\left (B\right )$
is prepared as in (3.6) with respect to
$g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\right ),\ \mu \in \mathbb {N},\ \varphi \in \mathcal {S}\left (B\right )$
is prepared as in (3.6) with respect to
![]() $\psi $
as in (3.2),
$\psi $
as in (3.2),
![]() $\lambda \left (s\right )={\displaystyle \frac {\ell s+\eta }{d}}$
, for some
$\lambda \left (s\right )={\displaystyle \frac {\ell s+\eta }{d}}$
, for some
![]() $\ell \in \mathbb {Z},\eta \in \mathbb {C}$
and the same d appearing in (3.2), and the transcendental element
$\ell \in \mathbb {Z},\eta \in \mathbb {C}$
and the same d appearing in (3.2), and the transcendental element
![]() $\gamma \in \Gamma _{\Sigma }\left (B\right )$
has the form
$\gamma \in \Gamma _{\Sigma }\left (B\right )$
has the form
where D is as in Notation 5.1,
![]() $\sigma \in \left \{ +,-\right \} ,\ \nu \in \mathbb {N},\ \varrho \left (s\right )={\displaystyle \frac {\widetilde {\ell }s+\widetilde {\eta }}{d}}$
for some
$\sigma \in \left \{ +,-\right \} ,\ \nu \in \mathbb {N},\ \varrho \left (s\right )={\displaystyle \frac {\widetilde {\ell }s+\widetilde {\eta }}{d}}$
for some
![]() $\widetilde {\ell }\in \mathbb {Z},\widetilde {\eta }\in \mathbb {C}$
and the same d appearing in (3.2) and
$\widetilde {\ell }\in \mathbb {Z},\widetilde {\eta }\in \mathbb {C}$
and the same d appearing in (3.2) and
![]() $\Phi $
is a
$\Phi $
is a
![]() $\varPsi $
-prepared parametric strong function (with
$\varPsi $
-prepared parametric strong function (with
![]() $\varPsi $
as in (5.3)).
$\varPsi $
as in (5.3)).
Recall Notation 3.5.
Proposition 5.3 (Preparation).
Let
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
. There is a cell-decomposition of
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
. There is a cell-decomposition of
![]() $\mathbb {R}^{m+1}$
compatible with X such that for each cell A that is open over
$\mathbb {R}^{m+1}$
compatible with X such that for each cell A that is open over
![]() $\mathbb {R}^{m}$
(which we may suppose to be of the form (3.9)),
$\mathbb {R}^{m}$
(which we may suppose to be of the form (3.9)),
![]() $h\circ \Pi _{A}$
is a finite sum of prepared generators on
$h\circ \Pi _{A}$
is a finite sum of prepared generators on
![]() $B_{A}$
.
$B_{A}$
.
Proof. Write h as a sum of generators of the form (3.8) and apply [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 4.7] simultaneously to all the parametric power-constructible data appearing in the generators: this produces a cell-decomposition of
![]() $X\times \mathbb {R}^{2}$
compatible with X, and on each cell D which is open over
$X\times \mathbb {R}^{2}$
compatible with X, and on each cell D which is open over
![]() $X\times \mathbb {R}$
, a prepared form of the data with respect to the last variable t, where the coefficient functions are parametric power-constructible functions depending on the variables
$X\times \mathbb {R}$
, a prepared form of the data with respect to the last variable t, where the coefficient functions are parametric power-constructible functions depending on the variables
![]() $\left (x,y\right )\in X\times \mathbb {R}$
. Now apply [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 4.7] again simultaneously to all the coefficient functions, in order to prepare them with respect to the variable y on suitable cells
$\left (x,y\right )\in X\times \mathbb {R}$
. Now apply [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 4.7] again simultaneously to all the coefficient functions, in order to prepare them with respect to the variable y on suitable cells
![]() $B\subseteq X\times \mathbb {R}$
, thus refining the cell-decomposition. This gives the wanted result, up to trivial manipulations to adjust the definition of
$B\subseteq X\times \mathbb {R}$
, thus refining the cell-decomposition. This gives the wanted result, up to trivial manipulations to adjust the definition of
![]() $\psi $
and
$\psi $
and
![]() $\varPsi $
(see [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, pp. 1268–70] for the details).
$\varPsi $
(see [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, pp. 1268–70] for the details).
Remark 5.4. The proof of [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 4.7] (and indeed that of all preparation results based on the Subanalytic Preparation Theorem in [Reference Lion and RolinLR97]) shows that it is possible to choose the same integer d appearing in Definition 5.2 for all prepared generators on all cells. Thus, d is a data of the cell-decomposition and not of a single prepared generator on a single cell. We will hence call a d-cell-decomposition a cell-decomposition with data
![]() $d\in \mathbb {N}\setminus \left \{ 0\right \} $
, and we will say that a generator is d-prepared on one of the cells of the composition. Similar easy manipulations show that if a generator T is d-prepared on a cell of a d-cell-decomposition, then T is also
$d\in \mathbb {N}\setminus \left \{ 0\right \} $
, and we will say that a generator is d-prepared on one of the cells of the composition. Similar easy manipulations show that if a generator T is d-prepared on a cell of a d-cell-decomposition, then T is also
![]() $d^{2}$
-prepared and the decomposition can also be considered as a
$d^{2}$
-prepared and the decomposition can also be considered as a
![]() $d^{2}$
-cell-decomposition.
$d^{2}$
-cell-decomposition.
Our aim is to refine the previous preparation statement so as to write
![]() $h\circ \Pi _{A}$
as a finite sum of generators which are either strongly integrable or monomial in y.
$h\circ \Pi _{A}$
as a finite sum of generators which are either strongly integrable or monomial in y.
The first remark is that if we consider a cell A such that
![]() $B_{A}$
has bounded y-fibers, then the prepared generators which appear in
$B_{A}$
has bounded y-fibers, then the prepared generators which appear in
![]() $h\circ \Pi _{A}$
are strongly integrable.
$h\circ \Pi _{A}$
are strongly integrable.
Proposition 5.5. Suppose B as in (3.1) has bounded y-fibers and let
![]() $T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a generator which is prepared on
$T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a generator which is prepared on
![]() $B.$
Then, T is strongly integrable.
$B.$
Then, T is strongly integrable.
Proof. Let
so that
Since
![]() $\Phi $
is bounded and extends continuously to
$\Phi $
is bounded and extends continuously to
![]() $\overline {D}$
, for all
$\overline {D}$
, for all
![]() $\left (s,x\right )\in \left (\Sigma \setminus P\right )\times X,$
the function
$\left (s,x\right )\in \left (\Sigma \setminus P\right )\times X,$
the function
![]() ${y\longmapsto \int _{\mathbb {R}}\left |G\right |\text {d}t}$
extends continuously to the closed and bounded interval
${y\longmapsto \int _{\mathbb {R}}\left |G\right |\text {d}t}$
extends continuously to the closed and bounded interval
![]() $\left [a\left (x\right ),b\left (x\right )\right ]$
and is hence integrable on this interval. By Tonelli’s Theorem, for all
$\left [a\left (x\right ),b\left (x\right )\right ]$
and is hence integrable on this interval. By Tonelli’s Theorem, for all
![]() $\left (s,x\right )\in \left (\Sigma \setminus P\right )\times X,\ \left (y,t\right )\longmapsto \left |G\left (s,x,y,t\right )\right |\in L^{1}\left (\mathbb {R}^{2}\right )$
, so that
$\left (s,x\right )\in \left (\Sigma \setminus P\right )\times X,\ \left (y,t\right )\longmapsto \left |G\left (s,x,y,t\right )\right |\in L^{1}\left (\mathbb {R}^{2}\right )$
, so that
![]() $G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
and, by Remark 4.3, T is strongly integrable.
$G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
and, by Remark 4.3, T is strongly integrable.
Next, we refine the statement of Proposition 5.3 for the subclass of
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
of those functions which are naive in the last variable y (see Definition 5.6 below). On cells with unbounded y-fibers, the functions in this subclass have easily readable asymptotics in y (see Section 7) and can be written as finite sums of generators which are either strongly integrable or monomial in y.
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
of those functions which are naive in the last variable y (see Definition 5.6 below). On cells with unbounded y-fibers, the functions in this subclass have easily readable asymptotics in y (see Section 7) and can be written as finite sums of generators which are either strongly integrable or monomial in y.
Definition 5.6. Let
![]() $B\subseteq X\times \mathbb {R}$
be a subanalytic cell which is open over X. A generator
$B\subseteq X\times \mathbb {R}$
be a subanalytic cell which is open over X. A generator
![]() $T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (B\right )$
as in (3.8) is naive in y if the transcendental element
$T\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (B\right )$
as in (3.8) is naive in y if the transcendental element
![]() $\gamma $
does not depend on y. Hence,
$\gamma $
does not depend on y. Hence,
with
![]() $\gamma \in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right ),\ g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (B\right )$
and
$\gamma \in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right ),\ g\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (B\right )$
and
![]() $\varphi \in \mathcal {S}\left (B\right )$
.
$\varphi \in \mathcal {S}\left (B\right )$
.
Proposition 5.7. Let
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a finite sum of generators which are naive in y. Then, Proposition 5.3 holds for h with the additional property that the prepared generators on
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be a finite sum of generators which are naive in y. Then, Proposition 5.3 holds for h with the additional property that the prepared generators on
![]() $B_{A}$
are either monomial in y or strongly integrable.
$B_{A}$
are either monomial in y or strongly integrable.
Proof. Apply Proposition 5.3 to h: the proof shows that this produces a cell-decomposition and, for each cell A, a presentation of
![]() $h\circ \Pi _{A}$
as a finite sum of prepared generators which are themselves naive in y. By Proposition 5.5, on cells with bounded y-fibers, the generators are strongly integrable. Hence, we may concentrate on a cell
$h\circ \Pi _{A}$
as a finite sum of prepared generators which are themselves naive in y. By Proposition 5.5, on cells with bounded y-fibers, the generators are strongly integrable. Hence, we may concentrate on a cell
![]() $B=B_{A}$
of the form (3.1) with unbounded y-fibers and on a generator T which is prepared on B and naive in y. Thus, T has the form
$B=B_{A}$
of the form (3.1) with unbounded y-fibers and on a generator T which is prepared on B and naive in y. Thus, T has the form
where
![]() $f\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right ),\ \lambda \left (s\right ),\mu $
are as in Definition 5.2 and the prepared forms (with respect to
$f\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right ),\ \lambda \left (s\right ),\mu $
are as in Definition 5.2 and the prepared forms (with respect to
![]() $\psi $
as in (3.2)) of
$\psi $
as in (3.2)) of
![]() $\varphi \in \mathcal {S}\left (B\right )$
and
$\varphi \in \mathcal {S}\left (B\right )$
and
![]() $\Phi \in \mathcal {A}_{\Sigma }\left (B\right )$
are as in (3.6) and (3.5), respectively. Up to partitioning X into subanalytic cells, we may suppose that
$\Phi \in \mathcal {A}_{\Sigma }\left (B\right )$
are as in (3.6) and (3.5), respectively. Up to partitioning X into subanalytic cells, we may suppose that
![]() $\left |\varphi _{0}\right |$
is either bounded from above or bounded away from zero. If
$\left |\varphi _{0}\right |$
is either bounded from above or bounded away from zero. If
![]() $\left |\varphi _{0}\right |$
is bounded and
$\left |\varphi _{0}\right |$
is bounded and
![]() $\omega <0$
, then
$\omega <0$
, then
![]() $\text {e}^{\text {i}\varphi }$
is a complex-valued
$\text {e}^{\text {i}\varphi }$
is a complex-valued
![]() $\psi $
-prepared subanalytic strong function. If
$\psi $
-prepared subanalytic strong function. If
![]() $\omega \geq 0$
, then write
$\omega \geq 0$
, then write
where
![]() $Q\in \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
is a polynomial in the variable
$Q\in \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
is a polynomial in the variable
![]() $y^{\frac {1}{d}}$
with coefficients subanalytic functions of x and
$y^{\frac {1}{d}}$
with coefficients subanalytic functions of x and
 $$\begin{align*}\varphi_{>}\left(x,y\right)=\varphi_{0}\left(x\right)\left(a\left(x\right)\right)^{\frac{\omega}{d}}\left(\frac{a\left(x\right)}{y}\right)^{\frac{1}{d}}\sum_{k\geq0}b_{k+\omega+1}\left(x\right)\left(\frac{a\left(x\right)}{y}\right)^{\frac{k}{d}}. \end{align*}$$
$$\begin{align*}\varphi_{>}\left(x,y\right)=\varphi_{0}\left(x\right)\left(a\left(x\right)\right)^{\frac{\omega}{d}}\left(\frac{a\left(x\right)}{y}\right)^{\frac{1}{d}}\sum_{k\geq0}b_{k+\omega+1}\left(x\right)\left(\frac{a\left(x\right)}{y}\right)^{\frac{k}{d}}. \end{align*}$$
If
![]() $\left |\varphi _{0}\right |$
is bounded from above, then clearly,
$\left |\varphi _{0}\right |$
is bounded from above, then clearly,
![]() $\text {e}^{\text {i}\varphi _{>}}$
is a complex-valued
$\text {e}^{\text {i}\varphi _{>}}$
is a complex-valued
![]() $\psi $
-prepared subanalytic strong function. If
$\psi $
-prepared subanalytic strong function. If
![]() $\left |\varphi _{0}\right |$
is bounded away from zero, then we write
$\left |\varphi _{0}\right |$
is bounded away from zero, then we write
 $$\begin{align*}\varphi_{>}\left(x,y\right)=\left(a\left(x\right)\right)^{\frac{\omega}{d}}\left(\frac{a\left(x\right)\varphi_{0}\left(x\right)^{d}}{y}\right)^{\frac{1}{d}}\sum_{k\geq0}b_{k+\omega+1}\left(x\right)\varphi_{0}\left(x\right)^{-k}\left(\frac{a\left(x\right)\varphi_{0}\left(x\right)^{d}}{y}\right)^{\frac{k}{d}}. \end{align*}$$
$$\begin{align*}\varphi_{>}\left(x,y\right)=\left(a\left(x\right)\right)^{\frac{\omega}{d}}\left(\frac{a\left(x\right)\varphi_{0}\left(x\right)^{d}}{y}\right)^{\frac{1}{d}}\sum_{k\geq0}b_{k+\omega+1}\left(x\right)\varphi_{0}\left(x\right)^{-k}\left(\frac{a\left(x\right)\varphi_{0}\left(x\right)^{d}}{y}\right)^{\frac{k}{d}}. \end{align*}$$
At the price of creating a new cell with bounded y-fibers (which can be dealt with by Proposition 5.5), we may suppose that
![]() $y>a\left (x\right )\varphi _{0}\left (x\right )^{d}$
on B, so that, up to modifying the definition of
$y>a\left (x\right )\varphi _{0}\left (x\right )^{d}$
on B, so that, up to modifying the definition of
![]() $\psi $
, it is clear that
$\psi $
, it is clear that
![]() $\varphi _{>}$
is bounded on B, and hence,
$\varphi _{>}$
is bounded on B, and hence,
![]() $\text {e}^{\text {i}\varphi _{>}}$
is a complex-valued
$\text {e}^{\text {i}\varphi _{>}}$
is a complex-valued
![]() $\psi $
-prepared subanalytic strong function (we deal in the same way with the case when
$\psi $
-prepared subanalytic strong function (we deal in the same way with the case when
![]() $\left |\varphi _{0}\right |$
is bounded away from zero and
$\left |\varphi _{0}\right |$
is bounded away from zero and
![]() $\omega <0$
).
$\omega <0$
).
It follows that
![]() $\text {e}^{\text {i}\varphi _{>}}$
can be absorbed into
$\text {e}^{\text {i}\varphi _{>}}$
can be absorbed into
![]() $\Phi $
, and hence,
$\Phi $
, and hence,
where
![]() $f_{k}\left (s,x\right )=f\left (s,x\right )\xi _{k}\left (s,x\right )a\left (x\right )^{\frac {k}{d}}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
, in the notation of (3.5). Since
$f_{k}\left (s,x\right )=f\left (s,x\right )\xi _{k}\left (s,x\right )a\left (x\right )^{\frac {k}{d}}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
, in the notation of (3.5). Since
![]() $\Sigma $
has bounded width, there exists
$\Sigma $
has bounded width, there exists
![]() $k_{0}\in \mathbb {N}$
such that setting
$k_{0}\in \mathbb {N}$
such that setting
![]() $\lambda _{k}\left (s\right )=\lambda \left (s\right )-\frac {k}{d}$
, there exists
$\lambda _{k}\left (s\right )=\lambda \left (s\right )-\frac {k}{d}$
, there exists
![]() $s\in \Sigma $
such that
$s\in \Sigma $
such that
![]() $\Re \left (\lambda _{k}\left (s\right )\right )\geq -1$
if and only if
$\Re \left (\lambda _{k}\left (s\right )\right )\geq -1$
if and only if
![]() $k\leq k_{0}$
. It follows that
$k\leq k_{0}$
. It follows that
where the terms of the sum are monomial in y and R is strongly integrable.
In order to extend Proposition 5.7 to generators which are not naive in y, we need some preparatory work.
Lemma 5.8. Let T be a prepared generator (as in Definition 5.2) on a cell B with unbounded y-fibers. Suppose that either
-
(1) D has unbounded t-fibers and
 $\forall s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )<-1$
, or
$\forall s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )<-1$
, or -
(2) D has bounded t-fibers and
 $\forall s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )+\frac {\Delta }{d}<-1\text { and }\Re \left (\varrho \left (s\right )\right )\leq 0$
.
$\forall s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )+\frac {\Delta }{d}<-1\text { and }\Re \left (\varrho \left (s\right )\right )\leq 0$
.
Then, T is strongly integrable.
Proof. Suppose that T has no poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
. If we write T as in (5.4), then it suffices to prove that
$P\subseteq \mathbb {C}$
. If we write T as in (5.4), then it suffices to prove that
![]() $G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
. By Tonelli’s Theorem, it is enough to prove that for all
$G\in \mathcal {C}_{\Sigma }^{\mathcal {M}}\left (X\times \mathbb {R}^{2}\right )_{\text {int}}$
. By Tonelli’s Theorem, it is enough to prove that for all
![]() $\left (s,x\right )\in \left (\Sigma \setminus P\right )\ni X$
, the function
$\left (s,x\right )\in \left (\Sigma \setminus P\right )\ni X$
, the function
is in
![]() $L^{1}\left (\mathbb {R}\right )$
.
$L^{1}\left (\mathbb {R}\right )$
.
-
(1) Let
 $\widetilde {b}=+\infty $
. Since
$\widetilde {b}=+\infty $
. Since
 $\forall s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )<-1$
, there is a positive constant M such that
$\forall s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )<-1$
, there is a positive constant M such that  $$\begin{align*}\int_{1}^{+\infty}\left|t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi\left(s,x,y,t\right)\right|\mathrm{d}t\leq M. \end{align*}$$
$$\begin{align*}\int_{1}^{+\infty}\left|t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi\left(s,x,y,t\right)\right|\mathrm{d}t\leq M. \end{align*}$$
Therefore,
and, as $$\begin{align*}\left|f_{\left(s,x\right)}\left(y\right)\right|\leq M\left|g\left(s,x\right)\right|\chi_{B}\left(x,y\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}, \end{align*}$$
$$\begin{align*}\left|f_{\left(s,x\right)}\left(y\right)\right|\leq M\left|g\left(s,x\right)\right|\chi_{B}\left(x,y\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}, \end{align*}$$
 $\forall s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )<-1$
, we have that
$\forall s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )<-1$
, we have that
 $f_{\left (s,x\right )}\in L^{1}\left (\mathbb {R}\right )$
.
$f_{\left (s,x\right )}\in L^{1}\left (\mathbb {R}\right )$
.
-
(2) Let now
 $\widetilde {b}<+\infty $
. Since
$\widetilde {b}<+\infty $
. Since
 $\forall s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )\leq 0$
and
$\forall s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )\leq 0$
and
 $\Phi $
is bounded, there is a positive constant
$\Phi $
is bounded, there is a positive constant
 $M\left (x\right )$
such that
$M\left (x\right )$
such that  $$\begin{align*}\int_{\widetilde{a}\left(x,y\right)}^{\widetilde{b}\left(x,y\right)}\left|t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi\left(s,x,y,t\right)\right|\mathrm{d}t\leq M\left(x\right)y^{\frac{\Delta}{d}}\left(\log y\right)^{\nu}. \end{align*}$$
$$\begin{align*}\int_{\widetilde{a}\left(x,y\right)}^{\widetilde{b}\left(x,y\right)}\left|t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi\left(s,x,y,t\right)\right|\mathrm{d}t\leq M\left(x\right)y^{\frac{\Delta}{d}}\left(\log y\right)^{\nu}. \end{align*}$$
Therefore,
and, as $$\begin{align*}\left|f_{\left(s,x\right)}\left(y\right)\right|\leq M\left(x\right)\left|g\left(s,x\right)\right|\chi_{B}\left(x,y\right)y^{\lambda\left(s\right)+\frac{\Delta}{d}}\left(\log y\right)^{\mu+\nu}, \end{align*}$$
$$\begin{align*}\left|f_{\left(s,x\right)}\left(y\right)\right|\leq M\left(x\right)\left|g\left(s,x\right)\right|\chi_{B}\left(x,y\right)y^{\lambda\left(s\right)+\frac{\Delta}{d}}\left(\log y\right)^{\mu+\nu}, \end{align*}$$
 $\forall s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )+\frac {\Delta }{d}<-1$
, we have that
$\forall s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )+\frac {\Delta }{d}<-1$
, we have that
 $f_{\left (s,x\right )}\in L^{1}\left (\mathbb {R}\right )$
.
$f_{\left (s,x\right )}\in L^{1}\left (\mathbb {R}\right )$
.
Lemma 5.9. Let T be a prepared generator (as in Definition 5.2) on a cell B with unbounded y-fibers and let
![]() $k_{0}\in \mathbb {N}.$
Then, T can be rewritten as a finite sum of prepared generators which are either naive in y or such that for all
$k_{0}\in \mathbb {N}.$
Then, T can be rewritten as a finite sum of prepared generators which are either naive in y or such that for all
![]() $s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )<-k_{0}$
.
$s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )<-k_{0}$
.
Proof. Suppose that T has no poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
. Write T on B as
$P\subseteq \mathbb {C}$
. Write T on B as
where
 $$\begin{align*}\gamma\left(s,x,y\right)=\int_{\widetilde{a}\left(x,y\right)}^{\widetilde{b}\left(x,y\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi\left(s,x,y,t\right)\text{e}^{\sigma\text{i}t}\text{d}t. \end{align*}$$
$$\begin{align*}\gamma\left(s,x,y\right)=\int_{\widetilde{a}\left(x,y\right)}^{\widetilde{b}\left(x,y\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi\left(s,x,y,t\right)\text{e}^{\sigma\text{i}t}\text{d}t. \end{align*}$$
Since B has unbounded y-fibers,
![]() $\Phi $
has the following
$\Phi $
has the following
![]() $\varPsi $
-prepared nested form (see [Reference Cluckers, Comte, Rolin and ServiCCRS23, Remark 3.7]) with respect to the last three components of
$\varPsi $
-prepared nested form (see [Reference Cluckers, Comte, Rolin and ServiCCRS23, Remark 3.7]) with respect to the last three components of
![]() $\varPsi $
:
$\varPsi $
:
where
is strongly convergent and
 $$\begin{align*}\Xi\left(x,y,t\right)=\left(\left(\frac{a\left(x\right)}{y}\right)^{\frac{1}{d}},\left(\frac{a_{0}\left(x\right)y^{\frac{\alpha}{d}}}{t}\right)^{\frac{1}{d}},\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{1}{d}}\right) \end{align*}$$
$$\begin{align*}\Xi\left(x,y,t\right)=\left(\left(\frac{a\left(x\right)}{y}\right)^{\frac{1}{d}},\left(\frac{a_{0}\left(x\right)y^{\frac{\alpha}{d}}}{t}\right)^{\frac{1}{d}},\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{1}{d}}\right) \end{align*}$$
(the variable
![]() $Y_{2}$
and the last component of
$Y_{2}$
and the last component of
![]() $\Xi $
are missing if D has unbounded t-fibers).
$\Xi $
are missing if D has unbounded t-fibers).
Fix
![]() $\left (s,x,y\right )\in \left (\Sigma \setminus P\right )\times B$
and apply integration by parts to the transcendental element
$\left (s,x,y\right )\in \left (\Sigma \setminus P\right )\times B$
and apply integration by parts to the transcendental element
![]() $\gamma $
, where we integrate
$\gamma $
, where we integrate
![]() $\mathrm {e}^{\mathrm {i}\sigma t}$
and derivate
$\mathrm {e}^{\mathrm {i}\sigma t}$
and derivate
![]() $f\left (t\right ):=t^{\varrho \left (s\right )}\left (\log t\right )^{\nu }\Phi \left (s,x,y,t\right )$
. For this, write
$f\left (t\right ):=t^{\varrho \left (s\right )}\left (\log t\right )^{\nu }\Phi \left (s,x,y,t\right )$
. For this, write
where
In particular,
![]() $\widetilde {F}$
is strongly convergent and
$\widetilde {F}$
is strongly convergent and
![]() $\widetilde {\Phi }$
is a
$\widetilde {\Phi }$
is a
![]() $\varPsi $
-prepared parametric strong function. Notice that each of the terms of
$\varPsi $
-prepared parametric strong function. Notice that each of the terms of
![]() $f'\left (t\right )\frac {\mathrm {e}^{\mathrm {i}\sigma t}}{\mathrm {i}\sigma }$
gives rise to a prepared generator such that the exponent of t in the transcendental element is
$f'\left (t\right )\frac {\mathrm {e}^{\mathrm {i}\sigma t}}{\mathrm {i}\sigma }$
gives rise to a prepared generator such that the exponent of t in the transcendental element is
![]() $\varrho \left (s\right )-1$
. The other terms produced by integration by parts are of the form
$\varrho \left (s\right )-1$
. The other terms produced by integration by parts are of the form
where
![]() $\widetilde {c}$
is either
$\widetilde {c}$
is either
![]() $\widetilde {a}$
or
$\widetilde {a}$
or
![]() $\widetilde {b}$
(or the whole term is replaced by zero, if
$\widetilde {b}$
(or the whole term is replaced by zero, if
![]() $\widetilde {b}=+\infty $
, since then in this case, for all
$\widetilde {b}=+\infty $
, since then in this case, for all
![]() $s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )<-1<0$
). Now, if
$s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )<-1<0$
). Now, if
![]() $\widetilde {c}=\widetilde {b}$
, then
$\widetilde {c}=\widetilde {b}$
, then
 $$\begin{align*}\Xi\left(x,y,\widetilde{b}\left(x,y\right)\right)=\left(\left(\frac{a\left(x\right)}{y}\right)^{\frac{1}{d}},\left(\frac{a_{0}\left(x\right)y^{\frac{\alpha}{d}}}{b_{0}\left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right)}\right)^{\frac{1}{d}},\left(u_{b}\left(x,y\right)\right)^{\frac{1}{d}}\right) \end{align*}$$
$$\begin{align*}\Xi\left(x,y,\widetilde{b}\left(x,y\right)\right)=\left(\left(\frac{a\left(x\right)}{y}\right)^{\frac{1}{d}},\left(\frac{a_{0}\left(x\right)y^{\frac{\alpha}{d}}}{b_{0}\left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right)}\right)^{\frac{1}{d}},\left(u_{b}\left(x,y\right)\right)^{\frac{1}{d}}\right) \end{align*}$$
and
 $$\begin{align*}\frac{a_{0}\left(x\right)y^{\frac{\alpha}{d}}}{b_{0}\left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right)}=\left[\frac{a_{0}\left(x\right)}{b_{0}\left(x\right)a\left(x\right)^{\frac{\beta-\alpha}{d}}}\right]\left(u_{b}\left(x,y\right)\right)^{-1}\left(\frac{a\left(x\right)}{y}\right)^{\frac{\beta-\alpha}{d}}. \end{align*}$$
$$\begin{align*}\frac{a_{0}\left(x\right)y^{\frac{\alpha}{d}}}{b_{0}\left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right)}=\left[\frac{a_{0}\left(x\right)}{b_{0}\left(x\right)a\left(x\right)^{\frac{\beta-\alpha}{d}}}\right]\left(u_{b}\left(x,y\right)\right)^{-1}\left(\frac{a\left(x\right)}{y}\right)^{\frac{\beta-\alpha}{d}}. \end{align*}$$
The term between square brackets is bounded on B because all the other terms are, so we can add it to the list of functions
![]() $c\left (x\right )$
in the definition of
$c\left (x\right )$
in the definition of
![]() $\psi $
(see 3.2). The unit
$\psi $
(see 3.2). The unit
![]() $u_{b}$
is
$u_{b}$
is
![]() $\psi $
-prepared; hence,
$\psi $
-prepared; hence,
![]() $\Phi \left (s,x,y,\widetilde {b}\left (x,y\right )\right )$
is a
$\Phi \left (s,x,y,\widetilde {b}\left (x,y\right )\right )$
is a
![]() $\psi $
-prepared parametric strong function. A similar calculation shows that so is
$\psi $
-prepared parametric strong function. A similar calculation shows that so is
![]() $\Phi \left (s,x,y,\widetilde {a}\left (x,y\right )\right )$
. Thus, the terms 5.6 are generators which are naive in y and prepared with respect to
$\Phi \left (s,x,y,\widetilde {a}\left (x,y\right )\right )$
. Thus, the terms 5.6 are generators which are naive in y and prepared with respect to
![]() $\psi $
.
$\psi $
.
We iterate the process to further reduce the exponent of t: since
![]() $\Sigma $
has bounded width,
$\Sigma $
has bounded width,
![]() ${\displaystyle \sup _{s\in \Sigma }}\left (\Re \left (\varrho \left (s\right )\right )\right )\in \mathbb {R}$
. Let
${\displaystyle \sup _{s\in \Sigma }}\left (\Re \left (\varrho \left (s\right )\right )\right )\in \mathbb {R}$
. Let
 $M:={\displaystyle \left \lfloor {\displaystyle \sup _{s\in \Sigma }}\left (\Re \left (\varrho \left (s\right )\right )\right )\right \rfloor }$
. By integrating by parts
$M:={\displaystyle \left \lfloor {\displaystyle \sup _{s\in \Sigma }}\left (\Re \left (\varrho \left (s\right )\right )\right )\right \rfloor }$
. By integrating by parts
![]() $M+k_{0}+1$
times, we can rewrite T as a finite sum of generators which are either naive in y and prepared with respect to
$M+k_{0}+1$
times, we can rewrite T as a finite sum of generators which are either naive in y and prepared with respect to
![]() $\psi $
, or such that the exponent of t in the transcendental element
$\psi $
, or such that the exponent of t in the transcendental element
![]() $\gamma $
is
$\gamma $
is
![]() $\varrho \left (s\right )-M-k_{0}-1$
, whose real part is
$\varrho \left (s\right )-M-k_{0}-1$
, whose real part is
![]() $<-k_{0}$
.
$<-k_{0}$
.
Proposition 5.10. Let T be a prepared generator (as in Definition 5.2) on a cell B with unbounded y-fibers and suppose that T has no poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
. Then, there exist a closed discrete set
$P\subseteq \mathbb {C}$
. Then, there exist a closed discrete set
![]() $P'\subseteq \mathbb {C}$
containing P and such that
$P'\subseteq \mathbb {C}$
containing P and such that
![]() $P'\setminus P$
is contained in a finitely generated
$P'\setminus P$
is contained in a finitely generated
![]() $\mathbb {Z}$
-lattice, a finite partition of B into subcells and, on each subcell
$\mathbb {Z}$
-lattice, a finite partition of B into subcells and, on each subcell
![]() $B'$
which is open over X, finitely many generators
$B'$
which is open over X, finitely many generators
![]() $T_{i}$
which are either naive in y or strongly integrable on
$T_{i}$
which are either naive in y or strongly integrable on
![]() $B'$
, such that for all
$B'$
, such that for all
![]() $\left (s,x,y\right )\in \left (\Sigma \setminus P'\right )\times B',\ T\left (s,x,y\right )=\sum T_{i}\left (s,x,y,\right )$
.
$\left (s,x,y\right )\in \left (\Sigma \setminus P'\right )\times B',\ T\left (s,x,y\right )=\sum T_{i}\left (s,x,y,\right )$
.
Proof. Recall Notation 5.1. Note that
![]() $0\leq \alpha \leq \beta $
. There are three cases:
$0\leq \alpha \leq \beta $
. There are three cases:
-
(1)
 $\alpha =\beta =0$
$\alpha =\beta =0$
-
(2)
 $\alpha>0$
$\alpha>0$
-
(3)
 $\alpha =0,\beta>0$
.
$\alpha =0,\beta>0$
.
Define
![]() $C:={\displaystyle \sup _{s\in \Sigma }}\left (\Re \left (\lambda \left (s\right )\right )\right )$
.
$C:={\displaystyle \sup _{s\in \Sigma }}\left (\Re \left (\lambda \left (s\right )\right )\right )$
.
-
(1) The case
 $\beta =0$
also includes the case
$\beta =0$
also includes the case
 $\widetilde {b}\left (x,y\right )=b_{0}\left (x\right )=+\infty $
. We claim that, at the price of creating a new cell with bounded y-fibers (which can be handled using Proposition 5.5), we may suppose that for all
$\widetilde {b}\left (x,y\right )=b_{0}\left (x\right )=+\infty $
. We claim that, at the price of creating a new cell with bounded y-fibers (which can be handled using Proposition 5.5), we may suppose that for all
 $\left (x,y\right )\in B$
,
$\left (x,y\right )\in B$
, $\bullet $
$\bullet $
 $\widetilde {a}\left (x,y\right )\leq a_{0}\left (x\right )$
and
$\widetilde {a}\left (x,y\right )\leq a_{0}\left (x\right )$
and
 $b_{0}\left (x\right )\leq \widetilde {b}\left (x,y\right )$
;
$b_{0}\left (x\right )\leq \widetilde {b}\left (x,y\right )$
; $\bullet $
$\bullet $
 $\left |\widetilde {a}\left (x,y\right )-a_{0}\left (x\right )\right |\leq 1$
and
$\left |\widetilde {a}\left (x,y\right )-a_{0}\left (x\right )\right |\leq 1$
and
 $\left |\widetilde {b}\left (x,y\right )-b_{0}\left (x\right )\right |\leq 1$
.
$\left |\widetilde {b}\left (x,y\right )-b_{0}\left (x\right )\right |\leq 1$
.The proof of the claim can be found in [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, p. 1277] and only uses basic o-minimal properties of subanalytic sets and functions.
Therefore, we may write the transcendental element
 $\gamma $
as the sum of three integrals, with integration bounds, respectively,
$\gamma $
as the sum of three integrals, with integration bounds, respectively,
 $\left (\widetilde {a}\left (x,y\right ),a_{0}\left (x\right )\right )$
,
$\left (\widetilde {a}\left (x,y\right ),a_{0}\left (x\right )\right )$
,
 $\left (a_{0}\left (x\right ),b_{0}\left (x\right )\right )$
and
$\left (a_{0}\left (x\right ),b_{0}\left (x\right )\right )$
and
 $\left (b_{0}\left (x\right ),\widetilde {b}\left (x,y\right )\right )$
(if
$\left (b_{0}\left (x\right ),\widetilde {b}\left (x,y\right )\right )$
(if
 $\widetilde {b}=+\infty $
, then the second integral has
$\widetilde {b}=+\infty $
, then the second integral has
 $+\infty $
as upper integration bound and the third integral is missing). The integral with bounds
$+\infty $
as upper integration bound and the third integral is missing). The integral with bounds
 $\left (\widetilde {a}\left (x,y\right ),a_{0}\left (x\right )\right )$
can be written as (5.7)where, thanks to the claim,
$\left (\widetilde {a}\left (x,y\right ),a_{0}\left (x\right )\right )$
can be written as (5.7)where, thanks to the claim, $$ \begin{align} \mathrm{e}^{\mathrm{i}\sigma a_{0}\left(x\right)}\int_{a_{0}\left(x\right)}^{a_{0}\left(x\right)u_{a}\left(x,y\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi\left(s,x,y,t\right)\mathrm{e}^{\sigma\mathrm{i}\left(t-a_{0}\left(x\right)\right)}\text{d}t, \end{align} $$
$$ \begin{align} \mathrm{e}^{\mathrm{i}\sigma a_{0}\left(x\right)}\int_{a_{0}\left(x\right)}^{a_{0}\left(x\right)u_{a}\left(x,y\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi\left(s,x,y,t\right)\mathrm{e}^{\sigma\mathrm{i}\left(t-a_{0}\left(x\right)\right)}\text{d}t, \end{align} $$
 $\mathrm {e}^{\sigma \mathrm {i}\left (t-a_{0}\left (x\right )\right )}$
is a complex-valued subanalytic function on B. Hence, the integrand is in
$\mathrm {e}^{\sigma \mathrm {i}\left (t-a_{0}\left (x\right )\right )}$
is a complex-valued subanalytic function on B. Hence, the integrand is in
 $\mathcal {C}_{\Sigma }^{\mathcal {M}}\left (B\right )$
, and we can invoke Theorem 2.18 to obtain that the term containing (5.7) can be written, outside some closed discrete set
$\mathcal {C}_{\Sigma }^{\mathcal {M}}\left (B\right )$
, and we can invoke Theorem 2.18 to obtain that the term containing (5.7) can be written, outside some closed discrete set
 $P'$
containing P, as a generator of
$P'$
containing P, as a generator of
 $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
which is naive in y. The integral with bounds
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
which is naive in y. The integral with bounds
 $\left (b_{0}\left (x\right ),\widetilde {b}\left (x,y\right )\right )$
, if present, is handled similarly. For the integral with bounds
$\left (b_{0}\left (x\right ),\widetilde {b}\left (x,y\right )\right )$
, if present, is handled similarly. For the integral with bounds
 $\left (a_{0}\left (x\right ),b_{0}\left (x\right )\right )$
, notice that now the variable y only appears in the parametric strong function
$\left (a_{0}\left (x\right ),b_{0}\left (x\right )\right )$
, notice that now the variable y only appears in the parametric strong function
 $\Phi $
, which we can write in nested form with respect to the last component of
$\Phi $
, which we can write in nested form with respect to the last component of
 $\psi $
as (5.8)for some
$\psi $
as (5.8)for some $$ \begin{align} \sum_{k\geq0}\widetilde{\xi}_{k}\left(s,x,t\right)\left(\frac{a\left(x\right)}{y}\right)^{\frac{k}{d}}, \end{align} $$
$$ \begin{align} \sum_{k\geq0}\widetilde{\xi}_{k}\left(s,x,t\right)\left(\frac{a\left(x\right)}{y}\right)^{\frac{k}{d}}, \end{align} $$
 $\widetilde {\xi }_{k}\in \mathcal {A}_{\Sigma }\left (E\right )$
, where
$\widetilde {\xi }_{k}\in \mathcal {A}_{\Sigma }\left (E\right )$
, where
 $E=\left \{ \left (x,t\right ):\ x\in X,\ a_{0}\left (x\right )<t<b_{0}\left (x\right )\right \} $
. Let
$E=\left \{ \left (x,t\right ):\ x\in X,\ a_{0}\left (x\right )<t<b_{0}\left (x\right )\right \} $
. Let
 $k_{0}=\lceil d\left (C+1\right )\rceil +1$
, so that for all
$k_{0}=\lceil d\left (C+1\right )\rceil +1$
, so that for all
 $s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )-\frac {k_{0}}{d}<-1$
, and let
$s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )-\frac {k_{0}}{d}<-1$
, and let  $$\begin{align*}\Phi_{>k_{0}}=\Phi-\sum_{k\leq k_{0}}\widetilde{\xi}_{k}\left(s,x,t\right)\left(\frac{a\left(x\right)}{y}\right)^{\frac{k}{d}}. \end{align*}$$
$$\begin{align*}\Phi_{>k_{0}}=\Phi-\sum_{k\leq k_{0}}\widetilde{\xi}_{k}\left(s,x,t\right)\left(\frac{a\left(x\right)}{y}\right)^{\frac{k}{d}}. \end{align*}$$
Setting
write the term $$\begin{align*}f_{k}\left(s,x\right)=g\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k}{d}}\int_{a_{0}\left(x\right)}^{b_{0}\left(x\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\widetilde{\xi}_{k}\left(s,x,t\right)\mathrm{e}^{\sigma\mathrm{i}t}\text{d}t\in\mathcal{C}_{\Sigma}^{\mathcal{M},\mathcal{F}}\left(X\right), \end{align*}$$
as the following sum of generators which are naive in y,
$$\begin{align*}f_{k}\left(s,x\right)=g\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k}{d}}\int_{a_{0}\left(x\right)}^{b_{0}\left(x\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\widetilde{\xi}_{k}\left(s,x,t\right)\mathrm{e}^{\sigma\mathrm{i}t}\text{d}t\in\mathcal{C}_{\Sigma}^{\mathcal{M},\mathcal{F}}\left(X\right), \end{align*}$$
as the following sum of generators which are naive in y, $$\begin{align*}g\left(s,x\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\mathrm{e}^{\mathrm{i}\varphi\left(x,y\right)}\int_{a_{0}\left(x\right)}^{b_{0}\left(x\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\mathrm{e}^{\sigma\mathrm{i}t}\Phi\left(s,x,y,t\right)\text{d}t \end{align*}$$
plus the term
$$\begin{align*}g\left(s,x\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\mathrm{e}^{\mathrm{i}\varphi\left(x,y\right)}\int_{a_{0}\left(x\right)}^{b_{0}\left(x\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\mathrm{e}^{\sigma\mathrm{i}t}\Phi\left(s,x,y,t\right)\text{d}t \end{align*}$$
plus the term $$\begin{align*}\sum_{k\leq k_{0}}f_{k}\left(s,x\right)y^{\lambda\left(s\right)-\frac{k}{d}}\left(\log y\right)^{\mu}\mathrm{e}^{\mathrm{i}\varphi\left(x,y\right)}, \end{align*}$$
(5.9)which is strongly integrable on B by definition of
$$\begin{align*}\sum_{k\leq k_{0}}f_{k}\left(s,x\right)y^{\lambda\left(s\right)-\frac{k}{d}}\left(\log y\right)^{\mu}\mathrm{e}^{\mathrm{i}\varphi\left(x,y\right)}, \end{align*}$$
(5.9)which is strongly integrable on B by definition of $$ \begin{align} g\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k_{0}}{d}}y^{\lambda\left(s\right)-\frac{k_{0}}{d}}\left(\log y\right)^{\mu}\mathrm{e}^{\mathrm{i}\varphi\left(x,y\right)}\int_{a_{0}\left(x\right)}^{b_{0}\left(x\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi_{>k_{0}}\left(s,x,y,t\right)\mathrm{e}^{\sigma\mathrm{i}t}\text{d}t, \end{align} $$
$$ \begin{align} g\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k_{0}}{d}}y^{\lambda\left(s\right)-\frac{k_{0}}{d}}\left(\log y\right)^{\mu}\mathrm{e}^{\mathrm{i}\varphi\left(x,y\right)}\int_{a_{0}\left(x\right)}^{b_{0}\left(x\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi_{>k_{0}}\left(s,x,y,t\right)\mathrm{e}^{\sigma\mathrm{i}t}\text{d}t, \end{align} $$
 $k_{0}$
and since
$k_{0}$
and since
 $\Phi _{>k_{0}}$
is bounded.
$\Phi _{>k_{0}}$
is bounded.
-
(2) Let
 $N_{0}=\left \lceil \frac {dC+\Delta +d}{\alpha }\right \rceil +1$
. By Lemma 5.9, we may suppose that for all
$N_{0}=\left \lceil \frac {dC+\Delta +d}{\alpha }\right \rceil +1$
. By Lemma 5.9, we may suppose that for all
 $s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )<-N_{0}$
. Write
$s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )<-N_{0}$
. Write  $$\begin{align*}t^{\varrho\left(s\right)}=t^{\varrho\left(s\right)+N_{0}}\left(a_{0}\left(x\right)y^{\frac{\alpha}{d}}\right)^{-N_{0}}\left[\left(\frac{a_{0}\left(x\right)y^{\frac{\alpha}{d}}}{t}\right)^{\frac{1}{d}}\right]^{dN_{0}}. \end{align*}$$
$$\begin{align*}t^{\varrho\left(s\right)}=t^{\varrho\left(s\right)+N_{0}}\left(a_{0}\left(x\right)y^{\frac{\alpha}{d}}\right)^{-N_{0}}\left[\left(\frac{a_{0}\left(x\right)y^{\frac{\alpha}{d}}}{t}\right)^{\frac{1}{d}}\right]^{dN_{0}}. \end{align*}$$
The rightmost term in the above formula can be absorbed into
 $\Phi $
, and the central term can be factored out of the integral defining the transcendental element
$\Phi $
, and the central term can be factored out of the integral defining the transcendental element
 $\gamma $
. By the choice of
$\gamma $
. By the choice of
 $N_{0}$
, for all
$N_{0}$
, for all
 $s\in \Sigma ,$
(5.10)so by Lemma 5.8 (either of the two conditions, depending on the nature of the t-fibers of the cell D), T is strongly integrable on B.
$s\in \Sigma ,$
(5.10)so by Lemma 5.8 (either of the two conditions, depending on the nature of the t-fibers of the cell D), T is strongly integrable on B. $$ \begin{align} \Re\left(\lambda\left(s\right)\right)-\frac{N_{0}\alpha}{d}+\frac{\Delta}{d}<-1, \end{align} $$
$$ \begin{align} \Re\left(\lambda\left(s\right)\right)-\frac{N_{0}\alpha}{d}+\frac{\Delta}{d}<-1, \end{align} $$
-
(3) Let
 $N_{0}=\left \lceil \frac {dC+\Delta +d}{\beta }\right \rceil +1$
and
$N_{0}=\left \lceil \frac {dC+\Delta +d}{\beta }\right \rceil +1$
and
 $k_{0}=d\left (N_{0}-1\right )$
. By Lemma 5.9, we may suppose that for all
$k_{0}=d\left (N_{0}-1\right )$
. By Lemma 5.9, we may suppose that for all
 $s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )<-N_{0}$
. This implies, in particular, that for all
$s\in \Sigma ,\ \Re \left (\varrho \left (s\right )\right )<-N_{0}$
. This implies, in particular, that for all
 $s\in \Sigma $
, (5.11)
$s\in \Sigma $
, (5.11) $$ \begin{align} & \Re\left(\varrho\left(s\right)\right)+\frac{k_{0}}{d}<-1,\qquad\ \ \kern0.1pt\qquad \end{align} $$
(5.12)
$$ \begin{align} & \Re\left(\varrho\left(s\right)\right)+\frac{k_{0}}{d}<-1,\qquad\ \ \kern0.1pt\qquad \end{align} $$
(5.12) $$ \begin{align} & \Re\left(\varrho\left(s\right)\right)+\frac{k_{0}+1}{d}\leq0,\qquad\ \ \kern2pt\quad \end{align} $$
(5.13)
$$ \begin{align} & \Re\left(\varrho\left(s\right)\right)+\frac{k_{0}+1}{d}\leq0,\qquad\ \ \kern2pt\quad \end{align} $$
(5.13) $$ \begin{align} & \Re\left(\lambda\left(s\right)\right)-\frac{\beta\left(k_{0}+1\right)}{d^{2}}+\frac{\Delta}{d}<-1. \end{align} $$
$$ \begin{align} & \Re\left(\lambda\left(s\right)\right)-\frac{\beta\left(k_{0}+1\right)}{d^{2}}+\frac{\Delta}{d}<-1. \end{align} $$
First, we split
 $\Phi \left (s,x,y,t\right )$
into the sum of two series by separating the positive and the negative powers of t:
$\Phi \left (s,x,y,t\right )$
into the sum of two series by separating the positive and the negative powers of t:  $$\begin{align*}\Phi=\sum_{k>0}\xi_{k}^{<}\left(s,x,y\right)\left(\frac{a_{0}\left(x\right)}{t}\right)^{\frac{k}{d}}+\sum_{k\geq0}\xi_{k}^{>}\left(s,x,y\right)\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{k}{d}}. \end{align*}$$
$$\begin{align*}\Phi=\sum_{k>0}\xi_{k}^{<}\left(s,x,y\right)\left(\frac{a_{0}\left(x\right)}{t}\right)^{\frac{k}{d}}+\sum_{k\geq0}\xi_{k}^{>}\left(s,x,y\right)\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{k}{d}}. \end{align*}$$
Next, write
where $$ \begin{align*} \gamma_{\leq k_{0}}\left(s,x,y\right) & =\int_{a_{0}\left(x\right)u_{a}\left(x,y\right)}^{b_{0}\left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi_{\leq k_{0}}\left(s,x,y,t\right)\mathrm{e}^{\sigma\mathrm{i}t}\text{d}t,\\[6pt] \gamma_{>k_{0}}\left(s,x,y\right) & =\int_{a_{0}\left(x\right)u_{a}\left(x,y\right)}^{b_{0}\left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{k_{0}+1}{d}}\Phi_{>k_{0}}\left(s,x,y,t\right)\mathrm{e}^{\sigma\mathrm{i}t}\text{d}t, \end{align*} $$
$$ \begin{align*} \gamma_{\leq k_{0}}\left(s,x,y\right) & =\int_{a_{0}\left(x\right)u_{a}\left(x,y\right)}^{b_{0}\left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\Phi_{\leq k_{0}}\left(s,x,y,t\right)\mathrm{e}^{\sigma\mathrm{i}t}\text{d}t,\\[6pt] \gamma_{>k_{0}}\left(s,x,y\right) & =\int_{a_{0}\left(x\right)u_{a}\left(x,y\right)}^{b_{0}\left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right)}t^{\varrho\left(s\right)}\left(\log t\right)^{\nu}\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{k_{0}+1}{d}}\Phi_{>k_{0}}\left(s,x,y,t\right)\mathrm{e}^{\sigma\mathrm{i}t}\text{d}t, \end{align*} $$
 $$ \begin{align*} \Phi_{\leq k_{0}}= & \sum_{k>0}\xi_{k}^{<}\left(s,x,y\right)\left(\frac{a_{0}\left(x\right)}{t}\right)^{\frac{k}{d}}+\sum_{k=0}^{k_{0}}\xi_{k}^{>}\left(s,x,y\right)\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{k}{d}},\\[6pt] \Phi_{>k_{0}}= & \sum_{k\geq0}\xi_{k+k_{0}+1}^{>}\left(s,x,y\right)\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{k}{d}}. \end{align*} $$
$$ \begin{align*} \Phi_{\leq k_{0}}= & \sum_{k>0}\xi_{k}^{<}\left(s,x,y\right)\left(\frac{a_{0}\left(x\right)}{t}\right)^{\frac{k}{d}}+\sum_{k=0}^{k_{0}}\xi_{k}^{>}\left(s,x,y\right)\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{k}{d}},\\[6pt] \Phi_{>k_{0}}= & \sum_{k\geq0}\xi_{k+k_{0}+1}^{>}\left(s,x,y\right)\left(\frac{t}{b_{0}\left(x\right)y^{\frac{\beta}{d}}}\right)^{\frac{k}{d}}. \end{align*} $$
By (5.11) and linearity, we may write
 $\gamma _{\leq k_{0}}$
as the sum of two integrals with upper integration bound equal to
$\gamma _{\leq k_{0}}$
as the sum of two integrals with upper integration bound equal to
 $+\infty $
and the lower integration bounds equal to, respectively,
$+\infty $
and the lower integration bounds equal to, respectively,
 $a_{0}\left (x\right )u_{a}\left (x,y\right )$
and
$a_{0}\left (x\right )u_{a}\left (x,y\right )$
and
 $b_{0}\left (x\right )y^{\frac {\beta }{d}}u_{b}\left (x,y\right )$
. The first integral falls within the scope of the first part of this proof, whereas the second integral falls within the scope of the second part of this proof.
$b_{0}\left (x\right )y^{\frac {\beta }{d}}u_{b}\left (x,y\right )$
. The first integral falls within the scope of the first part of this proof, whereas the second integral falls within the scope of the second part of this proof.It remains to consider
(5.14) $$ \begin{align} & T_{>k_{0}}\left(s,x,y\right):=g\left(s,x\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\mathrm{e}^{\mathrm{i}\varphi\left(x,y\right)} \gamma_{>k_{0}}\left(s,x,y\right)\\ & =g\left(s,x\right)y^{\lambda\left(s\right)-\frac{\beta\left(k_{0}+1\right)}{d^{2}}}\left(\log y\right)^{\mu}\mathrm{e}^{\mathrm{i}\varphi\left(x,y\right)}\left(b_{0}\left(x\right)\right)^{-\frac{\beta\left(k_{0}+1\right)}{d^{2}}}\cdot\nonumber\\ & \cdot\int_{a_{0}\left(x\right)u_{a}\left(x,y\right)}^{b_{0} \left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right)}t^{\varrho\left(s\right)+\frac{k_{0}+1}{d}}\left(\log t\right)^{\nu}\Phi_{>k_{0}}\left(s,x,y,t\right)\mathrm{e}^{\sigma\mathrm{i}t}\text{d}t.\nonumber \end{align} $$
$$ \begin{align} & T_{>k_{0}}\left(s,x,y\right):=g\left(s,x\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\mathrm{e}^{\mathrm{i}\varphi\left(x,y\right)} \gamma_{>k_{0}}\left(s,x,y\right)\\ & =g\left(s,x\right)y^{\lambda\left(s\right)-\frac{\beta\left(k_{0}+1\right)}{d^{2}}}\left(\log y\right)^{\mu}\mathrm{e}^{\mathrm{i}\varphi\left(x,y\right)}\left(b_{0}\left(x\right)\right)^{-\frac{\beta\left(k_{0}+1\right)}{d^{2}}}\cdot\nonumber\\ & \cdot\int_{a_{0}\left(x\right)u_{a}\left(x,y\right)}^{b_{0} \left(x\right)y^{\frac{\beta}{d}}u_{b}\left(x,y\right)}t^{\varrho\left(s\right)+\frac{k_{0}+1}{d}}\left(\log t\right)^{\nu}\Phi_{>k_{0}}\left(s,x,y,t\right)\mathrm{e}^{\sigma\mathrm{i}t}\text{d}t.\nonumber \end{align} $$
By (5.12) and (5.13),
 $T_{\geq k_{0}}$
satisfies the second condition in Lemma 5.8.
$T_{\geq k_{0}}$
satisfies the second condition in Lemma 5.8.
6 Interpolation and stability under integration
In this section, we finish the proof of Theorem 2.9. For this, it suffices to consider the
![]() $1$
-dimensional case, Theorem 6.5 below (the general n-dimensional case follows from Fubini’s Theorem; see the end of Section 4.2), the proof of which requires an analysis of the integration locus.
$1$
-dimensional case, Theorem 6.5 below (the general n-dimensional case follows from Fubini’s Theorem; see the end of Section 4.2), the proof of which requires an analysis of the integration locus.
With this in mind, we adapt [Reference Cluckers, Comte, Rolin and ServiCCRS23, Definition 6.1] to the current setting.
Definition 6.1. Given
![]() $N,d\in \mathbb {N}\setminus \left \{ 0\right \} $
and
$N,d\in \mathbb {N}\setminus \left \{ 0\right \} $
and
![]() $\left \{ \left (\ell _{i},r_{i}\right ):\ 1\leq i\leq N\right \} \subseteq \mathbb {R}^{2}$
, define
$\left \{ \left (\ell _{i},r_{i}\right ):\ 1\leq i\leq N\right \} \subseteq \mathbb {R}^{2}$
, define
 $$ \begin{align*} \Xi_{i,0,-} & =\emptyset,\\ \Xi_{i,0,\circ} & =\left\{ s\in\Sigma:\ \ell_{i}\Re\left(s\right)+r_{i}+d<0\right\} \quad\left(1\leq i\leq N\right),\\ \Xi_{i,j,-} & =\left\{ s\in\Sigma:\ \ell_{i}\Re\left(s\right)+r_{i}+d=j-1\right\} \quad\left(1\leq i\leq N,\ j\in\mathbb{N}\setminus\left\{ 0\right\} \right),\\ \Xi_{i,j,\circ} & =\left\{ s\in\Sigma:\ j-1<\ell_{i}\Re\left(s\right)+r_{i}+d<j\right\} \quad\left(1\leq i\leq N,\ j\in\mathbb{N}\setminus\left\{ 0\right\} \right). \end{align*} $$
$$ \begin{align*} \Xi_{i,0,-} & =\emptyset,\\ \Xi_{i,0,\circ} & =\left\{ s\in\Sigma:\ \ell_{i}\Re\left(s\right)+r_{i}+d<0\right\} \quad\left(1\leq i\leq N\right),\\ \Xi_{i,j,-} & =\left\{ s\in\Sigma:\ \ell_{i}\Re\left(s\right)+r_{i}+d=j-1\right\} \quad\left(1\leq i\leq N,\ j\in\mathbb{N}\setminus\left\{ 0\right\} \right),\\ \Xi_{i,j,\circ} & =\left\{ s\in\Sigma:\ j-1<\ell_{i}\Re\left(s\right)+r_{i}+d<j\right\} \quad\left(1\leq i\leq N,\ j\in\mathbb{N}\setminus\left\{ 0\right\} \right). \end{align*} $$
The collection
is called the grid of denominator d and data
![]() $\left (d,\left \{ \left (\ell _{i},r_{i}\right ):\ 1\leq i\leq N\right \} \right )$
. A
$\left (d,\left \{ \left (\ell _{i},r_{i}\right ):\ 1\leq i\leq N\right \} \right )$
. A
![]() $\mathcal {G}$
-cell is a nonempty subset
$\mathcal {G}$
-cell is a nonempty subset
![]() $S\subseteq \Sigma $
such that
$S\subseteq \Sigma $
such that
Finally, given a prepared generator T as in Definition 5.2, we call the tuple
the grid data of T.
Remarks 6.2.
-
(1) Since
 $\Sigma $
has bounded width, a grid
$\Sigma $
has bounded width, a grid
 $\mathcal {G}$
induces a finite partition
$\mathcal {G}$
induces a finite partition
 $\mathcal {R}\left (\mathcal {G}\right )$
of
$\mathcal {R}\left (\mathcal {G}\right )$
of
 $\Sigma $
into
$\Sigma $
into
 $\mathcal {G}$
-cells, and each
$\mathcal {G}$
-cells, and each
 $\mathcal {G}$
-cell is either an open vertical substrip of
$\mathcal {G}$
-cell is either an open vertical substrip of
 $\Sigma $
or a vertical line.
$\Sigma $
or a vertical line. -
(2) A prepared generator T generates a grid with data the grid data of T. In this case, if T is monomial in y, then on each
 $\mathcal {G}$
-cell S, the real part of the exponent of y is either always
$\mathcal {G}$
-cell S, the real part of the exponent of y is either always
 $<-1$
or always
$<-1$
or always
 $\geq -1$
.
$\geq -1$
.
Notation 6.3. Given a subanalytic set
![]() $X\subseteq \mathbb {R}^{m}$
and functions
$X\subseteq \mathbb {R}^{m}$
and functions
![]() $Q_{1},Q_{2} \in \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
which are polynomials in
$Q_{1},Q_{2} \in \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
which are polynomials in
![]() $y^{\frac {1}{d}}$
with coefficients subanalytic functions of x, it is clearly possible to partition X into finitely many subanalytic cells such that for each cell
$y^{\frac {1}{d}}$
with coefficients subanalytic functions of x, it is clearly possible to partition X into finitely many subanalytic cells such that for each cell
![]() $X'$
, either for all
$X'$
, either for all
![]() $x\in X',\ Q_{1}\left (x,\cdot \right )$
and
$x\in X',\ Q_{1}\left (x,\cdot \right )$
and
![]() $Q_{2}\left (x,\cdot \right )$
, define the same polynomial function, or for all
$Q_{2}\left (x,\cdot \right )$
, define the same polynomial function, or for all
![]() $x\in X',\ Q_{1}\left (x,\cdot \right )$
and
$x\in X',\ Q_{1}\left (x,\cdot \right )$
and
![]() $Q_{2}\left (x,\cdot \right )$
, define different polynomial functions. In this case, we will say, respectively, that
$Q_{2}\left (x,\cdot \right )$
, define different polynomial functions. In this case, we will say, respectively, that
![]() $Q_{1}=Q_{2}$
on
$Q_{1}=Q_{2}$
on
![]() $X'$
or
$X'$
or
![]() $Q_{1}\not =Q_{2}$
on
$Q_{1}\not =Q_{2}$
on
![]() $X'$
, as functions.
$X'$
, as functions.
Proposition 6.4 (Splitting).
Let
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be without poles outside some closed discrete set
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
. There are a closed discrete set
$P\subseteq \mathbb {C}$
. There are a closed discrete set
![]() $P'\subseteq \mathbb {C}$
containing P and such that
$P'\subseteq \mathbb {C}$
containing P and such that
![]() $P'\setminus P$
is contained in a finitely generated
$P'\setminus P$
is contained in a finitely generated
![]() $\mathbb {Z}$
-lattice,
$\mathbb {Z}$
-lattice,
![]() $d\in \mathbb {N}\setminus \left \{ 0\right \} $
, finite sets
$d\in \mathbb {N}\setminus \left \{ 0\right \} $
, finite sets
![]() $J_{\mathrm {int}},J_{\mathrm {mon}}\subseteq \mathbb {N}$
and a d-cell-decomposition (see Remark 5.4) of
$J_{\mathrm {int}},J_{\mathrm {mon}}\subseteq \mathbb {N}$
and a d-cell-decomposition (see Remark 5.4) of
![]() $\mathbb {R}^{m+1}$
compatible with X such that for each cell A that is open over
$\mathbb {R}^{m+1}$
compatible with X such that for each cell A that is open over
![]() $\mathbb {R}^{m}$
(which we may suppose to be of the form (3.9)),
$\mathbb {R}^{m}$
(which we may suppose to be of the form (3.9)),
 $$ \begin{align} h\circ\Pi_{A}=\sum_{j\in J_{\mathrm{int}}}T_{j}+\sum_{j\in J_{\mathrm{mon}}}T_{j}, \end{align} $$
$$ \begin{align} h\circ\Pi_{A}=\sum_{j\in J_{\mathrm{int}}}T_{j}+\sum_{j\in J_{\mathrm{mon}}}T_{j}, \end{align} $$
where each
![]() $T_{j}$
is a d-prepared generator without poles outside
$T_{j}$
is a d-prepared generator without poles outside
![]() $P'$
(see Definition 5.2 and Remark 5.4). Moreover, using the notation in Definition 4.2,
$P'$
(see Definition 5.2 and Remark 5.4). Moreover, using the notation in Definition 4.2,
-
(1) For every
 $j\in J_{\mathrm {int}},\ T_{j}$
is strongly integrable on
$j\in J_{\mathrm {int}},\ T_{j}$
is strongly integrable on
 $B_{A}$
, and if
$B_{A}$
, and if
 $B_{A}$
has unbounded y-fibers, then, in the notation of Definition 5.2, for all
$B_{A}$
has unbounded y-fibers, then, in the notation of Definition 5.2, for all
 $s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )<-1$
.
$s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )<-1$
. -
(2) For every
 $j\in J_{\mathrm {mon}},\ T_{j}$
is monomial in y, with monomial data
$j\in J_{\mathrm {mon}},\ T_{j}$
is monomial in y, with monomial data
 $\left (d,\ell _{j},\eta _{j},\mu _{j},Q_{j}\right )$
, where
$\left (d,\ell _{j},\eta _{j},\mu _{j},Q_{j}\right )$
, where-
(a) for all
 $x\in X,\ Q_{j}\left (x,0\right )=0$
and for all
$x\in X,\ Q_{j}\left (x,0\right )=0$
and for all
 $i,j\in J_{\mathrm {mon}}$
, either
$i,j\in J_{\mathrm {mon}}$
, either
 $Q_{i}\equiv Q_{j}$
on X or
$Q_{i}\equiv Q_{j}$
on X or
 $Q_{i}\not \equiv Q_{j}$
on X (see Notation 6.3);
$Q_{i}\not \equiv Q_{j}$
on X (see Notation 6.3); -
(b) the tuples
 $\left (\ell _{j},\eta _{j},\mu _{j},Q_{j}\right )\in \mathbb {Z}\times \mathbb {C}\times \mathbb {N}\times \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
$\left (\ell _{j},\eta _{j},\mu _{j},Q_{j}\right )\in \mathbb {Z}\times \mathbb {C}\times \mathbb {N}\times \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
 $\left (j\in J_{\mathrm {mon}}\right )$
are pairwise distinct;
$\left (j\in J_{\mathrm {mon}}\right )$
are pairwise distinct; -
(c) there is a grid
 $\mathcal {G}$
such that for all
$\mathcal {G}$
such that for all
 $\mathcal {G}$
-cell S, for all
$\mathcal {G}$
-cell S, for all
 $j\in J_{\mathrm {mon}}$
, either
$j\in J_{\mathrm {mon}}$
, either
 $\Re \left (\frac {\ell _{j}s+\eta _{j}}{d}\right )<-1$
for all
$\Re \left (\frac {\ell _{j}s+\eta _{j}}{d}\right )<-1$
for all
 $s\in S$
or
$s\in S$
or
 $\Re \left (\frac {\ell _{j}s+\eta _{j}}{d}\right )\geq -1$
for all
$\Re \left (\frac {\ell _{j}s+\eta _{j}}{d}\right )\geq -1$
for all
 $s\in S$
.
$s\in S$
.
-
Proof. Apply Proposition 5.3 to h. This produces d and a d-cell-decomposition of
![]() $\mathbb {R}^{m+1}$
such that on each cell A open over X,
$\mathbb {R}^{m+1}$
such that on each cell A open over X,
![]() $h\circ \Pi _{A}$
is a finite sum of prepared generators T. Collect the grid data of all the prepared generators and generate the corresponding grid
$h\circ \Pi _{A}$
is a finite sum of prepared generators T. Collect the grid data of all the prepared generators and generate the corresponding grid
![]() $\mathcal {G}$
with denominator
$\mathcal {G}$
with denominator
![]() $d^{2}$
. For each cell A, apply Propositions 5.10 and 5.7 to each prepared generator T on
$d^{2}$
. For each cell A, apply Propositions 5.10 and 5.7 to each prepared generator T on
![]() $B_{A}$
. This produces a refinement of the d-cell-decomposition and rewrites T on each cell as a finite sum of prepared generators
$B_{A}$
. This produces a refinement of the d-cell-decomposition and rewrites T on each cell as a finite sum of prepared generators
![]() $T'$
which are either strongly integrable (and satisfying condition (1)) or monomial in y. Up to absorbing
$T'$
which are either strongly integrable (and satisfying condition (1)) or monomial in y. Up to absorbing
![]() $\text {e}^{\text {i}Q_{j}\left (x,0\right )}$
into
$\text {e}^{\text {i}Q_{j}\left (x,0\right )}$
into
![]() $f_{j}\left (s,x\right )$
and up to partitioning X into subanalytic cells, we may suppose that item (2.a) in the statement of the proposition is satisfied. Summing like terms, we may also suppose that item (2.b) is satisfied. Revisiting the proofs of Propositions 5.10 and 5.7, which are based on integration by parts of the transcendental elements and series expansion of parametric strong functions on cells with unbounded y-fibers, we see that if the exponents of y and t in the original prepared generator T are
$f_{j}\left (s,x\right )$
and up to partitioning X into subanalytic cells, we may suppose that item (2.a) in the statement of the proposition is satisfied. Summing like terms, we may also suppose that item (2.b) is satisfied. Revisiting the proofs of Propositions 5.10 and 5.7, which are based on integration by parts of the transcendental elements and series expansion of parametric strong functions on cells with unbounded y-fibers, we see that if the exponents of y and t in the original prepared generator T are
![]() $\lambda \left (s\right )$
and
$\lambda \left (s\right )$
and
![]() $\varrho \left (s\right )$
, respectively, then the exponents of y in the newly created monomial generators
$\varrho \left (s\right )$
, respectively, then the exponents of y in the newly created monomial generators
![]() $T'$
have the form
$T'$
have the form
![]() $\lambda \left (s\right )-\frac {k}{d}+\frac {\delta }{d}\left (\varrho \left (s\right )-k'\right )$
, for some
$\lambda \left (s\right )-\frac {k}{d}+\frac {\delta }{d}\left (\varrho \left (s\right )-k'\right )$
, for some
![]() $k,k'\in \mathbb {N}$
and
$k,k'\in \mathbb {N}$
and
![]() $\delta \in \left \{ 0,\alpha ,\beta \right \} $
. In particular, the grid generated by the grid data of the new monomial generators does not create any new cell. By Remark 5.4, we may rename
$\delta \in \left \{ 0,\alpha ,\beta \right \} $
. In particular, the grid generated by the grid data of the new monomial generators does not create any new cell. By Remark 5.4, we may rename
![]() $d^{2}$
as d and adapt accordingly the definitions of
$d^{2}$
as d and adapt accordingly the definitions of
![]() $\ell _{j},\eta _{j},\alpha _{j},\beta _{j}$
, so that, by Remark 6.2 (2), item (2.c) in the statement of the proposition is also satisfied.
$\ell _{j},\eta _{j},\alpha _{j},\beta _{j}$
, so that, by Remark 6.2 (2), item (2.c) in the statement of the proposition is also satisfied.
Theorem 6.5 (Interpolation and integration locus).
Let
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be without poles outside some closed discrete set
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
. There are a closed discrete set
$P\subseteq \mathbb {C}$
. There are a closed discrete set
![]() $P'\subseteq \mathbb {C}$
containing P and such that
$P'\subseteq \mathbb {C}$
containing P and such that
![]() $P'\setminus P$
is contained in a finitely generated
$P'\setminus P$
is contained in a finitely generated
![]() $\mathbb {Z}$
-lattice and a function
$\mathbb {Z}$
-lattice and a function
![]() $H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
$H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
![]() $P'$
such that
$P'$
such that
Moreover, there exists a grid
![]() $\mathcal {G}$
such that
$\mathcal {G}$
such that
 $$ \begin{align} \mathrm{Int}\left(h;\left(\Sigma\setminus P'\right)\times X\right)=\bigcup_{S\in\mathcal{\mathcal{R}\left(\mathcal{G}\right)}}\left\{ \left(s,x\right):\ s\in S\setminus P',\ \bigwedge_{j\in J_{S}}f_{j}\left(s,x\right)=0\right\} , \end{align} $$
$$ \begin{align} \mathrm{Int}\left(h;\left(\Sigma\setminus P'\right)\times X\right)=\bigcup_{S\in\mathcal{\mathcal{R}\left(\mathcal{G}\right)}}\left\{ \left(s,x\right):\ s\in S\setminus P',\ \bigwedge_{j\in J_{S}}f_{j}\left(s,x\right)=0\right\} , \end{align} $$
for a suitable finite set
![]() $J_{S}$
and suitable
$J_{S}$
and suitable
![]() $f_{j}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
$f_{j}\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
![]() $P'$
.
$P'$
.
Proof. Apply Proposition 6.4 to h: this produces a closed discrete set
![]() $P'\subseteq \mathbb {C}$
containing P and such that
$P'\subseteq \mathbb {C}$
containing P and such that
![]() $P'\setminus P$
is contained in a finitely generated
$P'\setminus P$
is contained in a finitely generated
![]() $\mathbb {Z}$
-lattice,
$\mathbb {Z}$
-lattice,
![]() $d\in \mathbb {N}\setminus \left \{ 0\right \} $
, finite sets
$d\in \mathbb {N}\setminus \left \{ 0\right \} $
, finite sets
![]() $J_{\mathrm {int}},J_{\mathrm {mon}}\subseteq \mathbb {N}$
, a grid
$J_{\mathrm {int}},J_{\mathrm {mon}}\subseteq \mathbb {N}$
, a grid
![]() $\mathcal {G}$
and a d-cell-decomposition, such that the conclusion of the proposition holds. By linearity of the integral, it suffices to prove the statement of the theorem for
$\mathcal {G}$
and a d-cell-decomposition, such that the conclusion of the proposition holds. By linearity of the integral, it suffices to prove the statement of the theorem for
![]() $h\restriction A$
, where A is a cell of the decomposition which is open over X. Recall Notation 3.5 and note that
$h\restriction A$
, where A is a cell of the decomposition which is open over X. Recall Notation 3.5 and note that
Thus, up to multiplying each
![]() $T_{j}$
in (6.1) by
$T_{j}$
in (6.1) by
![]() $\frac {\partial \Pi _{A}}{\partial y}\left (x,y\right )$
, we may write that for all
$\frac {\partial \Pi _{A}}{\partial y}\left (x,y\right )$
, we may write that for all
![]() $\left (s,x\right )\in \text {Int}\left (h\restriction A;\left (\Sigma \setminus P'\right )\times X\right ),$
$\left (s,x\right )\in \text {Int}\left (h\restriction A;\left (\Sigma \setminus P'\right )\times X\right ),$
 $$\begin{align*}\int_{A_{x}}h\left(s,x,y\right)\text{d}y=\int_{a_{A}\left(x\right)}^{b_{A}\left(x\right)}\left(\sum_{j\in J_{\mathrm{int}}}T_{j}\left(s,x,y\right)+\sum_{j\in J_{\mathrm{mon}}}T_{j}\left(s,x,y\right)\right)\text{d}y. \end{align*}$$
$$\begin{align*}\int_{A_{x}}h\left(s,x,y\right)\text{d}y=\int_{a_{A}\left(x\right)}^{b_{A}\left(x\right)}\left(\sum_{j\in J_{\mathrm{int}}}T_{j}\left(s,x,y\right)+\sum_{j\in J_{\mathrm{mon}}}T_{j}\left(s,x,y\right)\right)\text{d}y. \end{align*}$$
If
![]() $B_{A}$
has bounded y-fibers, then we are done by Proposition 5.5 and Corollary 4.6.
$B_{A}$
has bounded y-fibers, then we are done by Proposition 5.5 and Corollary 4.6.
If
![]() $B_{A}$
has unbounded y-fibers, then for all
$B_{A}$
has unbounded y-fibers, then for all
![]() $j\in J_{\text {mon}},\ T_{j}$
has the form
$j\in J_{\text {mon}},\ T_{j}$
has the form
![]() $f_{j}\left (s,x\right )y^{\lambda _{j}\left (s\right )}\left (\log y\right )^{\mu _{j}}\text {e}^{\text {i}Q_{j}\left (x,y\right )}$
, with
$f_{j}\left (s,x\right )y^{\lambda _{j}\left (s\right )}\left (\log y\right )^{\mu _{j}}\text {e}^{\text {i}Q_{j}\left (x,y\right )}$
, with
![]() $\lambda _{j}\left (s\right )=\frac {\ell _{j}s+\eta _{j}}{d}$
, and for all
$\lambda _{j}\left (s\right )=\frac {\ell _{j}s+\eta _{j}}{d}$
, and for all
![]() $\mathcal {G}$
-cell S, there is a set
$\mathcal {G}$
-cell S, there is a set
![]() $J_{S}\subseteq J_{\text {mon}}$
such that for all
$J_{S}\subseteq J_{\text {mon}}$
such that for all
![]() $j\in J_{S},\ \text {Int}\left (T_{j}\chi _{B_{A}};\left (S\setminus P'\right )\times X\right )=\left \{ \left (s,x\right )\in \left (S\setminus P'\right )\times X:\ f_{j}\left (s,x\right )=0\right \} $
, whereas for all
$j\in J_{S},\ \text {Int}\left (T_{j}\chi _{B_{A}};\left (S\setminus P'\right )\times X\right )=\left \{ \left (s,x\right )\in \left (S\setminus P'\right )\times X:\ f_{j}\left (s,x\right )=0\right \} $
, whereas for all
![]() $j\in J_{\text {mon}}\setminus J_{S},\ \text {Int}\left (T_{j}\chi _{B_{A}};\left (S\setminus P'\right )\times X\right )=\left (S\setminus P'\right )\times X$
. Thus, the set
$j\in J_{\text {mon}}\setminus J_{S},\ \text {Int}\left (T_{j}\chi _{B_{A}};\left (S\setminus P'\right )\times X\right )=\left (S\setminus P'\right )\times X$
. Thus, the set
 $$\begin{align*}E:=\bigcap_{j\in J_{\text{int}}\cup J_{\text{mon}}}\text{Int}\left(T_{j}\chi_{B_{A}};\left(\Sigma\setminus P'\right)\times X\right) \end{align*}$$
$$\begin{align*}E:=\bigcap_{j\in J_{\text{int}}\cup J_{\text{mon}}}\text{Int}\left(T_{j}\chi_{B_{A}};\left(\Sigma\setminus P'\right)\times X\right) \end{align*}$$
is of the form of the right-hand side of (6.2) and, applying either Corollary 4.6 or Proposition 4.8 to
![]() $T_{j}\chi _{B_{A}}$
and possibly enlarging
$T_{j}\chi _{B_{A}}$
and possibly enlarging
![]() $P'$
, we find
$P'$
, we find
![]() $H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
$H\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\right )$
without poles outside
![]() $P'$
which interpolates the integral of
$P'$
which interpolates the integral of
![]() $h\restriction A$
for all
$h\restriction A$
for all
![]() $\left (s,x\right )\in E$
.
$\left (s,x\right )\in E$
.
Note that
![]() $E\subseteq \mathrm {Int}\left (h\restriction A;\left (\Sigma \setminus P'\right )\times X\right )$
. It remains to show that, up to possibly enlarging
$E\subseteq \mathrm {Int}\left (h\restriction A;\left (\Sigma \setminus P'\right )\times X\right )$
. It remains to show that, up to possibly enlarging
![]() $P'$
, the set E coincides with
$P'$
, the set E coincides with
![]() $\mathrm {Int}\left (h\restriction A;\left (\Sigma \setminus P'\right )\times X\right )$
. Let
$\mathrm {Int}\left (h\restriction A;\left (\Sigma \setminus P'\right )\times X\right )$
. Let
By item (2.b) in Proposition 6.4, if
![]() $s\in \Sigma $
is such that
$s\in \Sigma $
is such that
![]() $\lambda _{i}\left (s\right )=\lambda _{j}\left (s\right )$
for some
$\lambda _{i}\left (s\right )=\lambda _{j}\left (s\right )$
for some
![]() $i\not =j$
such that
$i\not =j$
such that
![]() $\mu _{i}=\mu _{j},\ Q_{i}=Q_{j}$
, then necessarily,
$\mu _{i}=\mu _{j},\ Q_{i}=Q_{j}$
, then necessarily,
![]() $\ell _{i}\not =\ell _{j}$
, so
$\ell _{i}\not =\ell _{j}$
, so
![]() $P_{A}\setminus P'$
is finite.
$P_{A}\setminus P'$
is finite.
By definition of
![]() $P_{A}$
, if
$P_{A}$
, if
![]() $s\in \Sigma \setminus P_{A}$
and
$s\in \Sigma \setminus P_{A}$
and
![]() $i,j\in J_{\text {mon}}$
are such that
$i,j\in J_{\text {mon}}$
are such that
![]() $i\not =j,\ \mu _{i}=\mu _{j}$
and
$i\not =j,\ \mu _{i}=\mu _{j}$
and
![]() $\Re \left (\lambda _{i}\left (s\right )\right )=\Re \left (\lambda _{j}\left (s\right )\right )$
, then
$\Re \left (\lambda _{i}\left (s\right )\right )=\Re \left (\lambda _{j}\left (s\right )\right )$
, then
![]() $Q_{i}=Q_{j}\Longrightarrow \Im \left (\lambda _{i}\left (s\right )\right )\not =\Im \left (\lambda _{j}\left (s\right )\right )$
.
$Q_{i}=Q_{j}\Longrightarrow \Im \left (\lambda _{i}\left (s\right )\right )\not =\Im \left (\lambda _{j}\left (s\right )\right )$
.
Let
![]() $\left (s_{0},x_{0}\right )\in \mathrm {Int}\left (h\restriction A;\left (\Sigma \setminus P_{A}\right )\times X\right )$
and let S be the
$\left (s_{0},x_{0}\right )\in \mathrm {Int}\left (h\restriction A;\left (\Sigma \setminus P_{A}\right )\times X\right )$
and let S be the
![]() $\mathcal {G}$
-cell to which
$\mathcal {G}$
-cell to which
![]() $s_{0}$
belongs. Define
$s_{0}$
belongs. Define
Let
![]() $\left (r_{0},\nu _{0}\right )$
be the lexicographic maximum of the set
$\left (r_{0},\nu _{0}\right )$
be the lexicographic maximum of the set
![]() $\left \{ \left (\rho _{j},\mu _{j}\right ):\ j\in J_{S}\right \} $
and let
$\left \{ \left (\rho _{j},\mu _{j}\right ):\ j\in J_{S}\right \} $
and let
![]() $J_{0}=\{j\in J_{S}:\ \left (\rho _{j},\mu _{j}\right )=\left (r_{0},\nu _{0}\right )\}$
. Then,
$J_{0}=\{j\in J_{S}:\ \left (\rho _{j},\mu _{j}\right )=\left (r_{0},\nu _{0}\right )\}$
. Then,
 $$\begin{align*}\sum_{j\in J_{S}}T_{j}\left(s_{0},x_{0},y\right)=y^{r_{0}}\left(\log y\right)^{\nu_{0}}\sum_{j\in J_{0}}f_{j}\left(s_{0},x_{0}\right)y^{\text{i}\sigma_{j}}\mathrm{e}^{\mathrm{i}p_{j}\left(y\right)}+\sum_{j\in J_{S}\setminus J_{0}}f_{j}\left(s_{0},x_{0}\right)y^{\rho_{j}+\mathrm{i}\sigma_{j}}\left(\log y\right)^{\mu_{j}}\mathrm{e}^{\mathrm{i}p_{j}\left(y\right)}. \end{align*}$$
$$\begin{align*}\sum_{j\in J_{S}}T_{j}\left(s_{0},x_{0},y\right)=y^{r_{0}}\left(\log y\right)^{\nu_{0}}\sum_{j\in J_{0}}f_{j}\left(s_{0},x_{0}\right)y^{\text{i}\sigma_{j}}\mathrm{e}^{\mathrm{i}p_{j}\left(y\right)}+\sum_{j\in J_{S}\setminus J_{0}}f_{j}\left(s_{0},x_{0}\right)y^{\rho_{j}+\mathrm{i}\sigma_{j}}\left(\log y\right)^{\mu_{j}}\mathrm{e}^{\mathrm{i}p_{j}\left(y\right)}. \end{align*}$$
Since
![]() $\left (s_{0},x_{0}\right )\in \mathrm {Int}\left (h\restriction A;\left (\Sigma \setminus P_{A}\right )\times X\right )$
, it follows from [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 3.4 (1)] that
$\left (s_{0},x_{0}\right )\in \mathrm {Int}\left (h\restriction A;\left (\Sigma \setminus P_{A}\right )\times X\right )$
, it follows from [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 3.4 (1)] that
![]() $\bigwedge _{j\in J_{0}}f_{j}\left (s_{0},x_{0}\right )=0$
. By repeating this procedure with the index set
$\bigwedge _{j\in J_{0}}f_{j}\left (s_{0},x_{0}\right )=0$
. By repeating this procedure with the index set
![]() $J_{S}\setminus J_{0}$
, we end up proving that
$J_{S}\setminus J_{0}$
, we end up proving that
![]() $\left (s_{0},x_{0}\right )\in E$
.
$\left (s_{0},x_{0}\right )\in E$
.
Remark 6.6. Given
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
and a strip
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
and a strip
![]() $\Sigma '\supseteq \Sigma $
, apply Proposition 6.4 to h and consider the extension
$\Sigma '\supseteq \Sigma $
, apply Proposition 6.4 to h and consider the extension
![]() $h'$
of h to
$h'$
of h to
![]() $\Sigma '$
. The proof shows that Proposition 6.4 applies to
$\Sigma '$
. The proof shows that Proposition 6.4 applies to
![]() $h'$
with different generators
$h'$
with different generators
![]() $T_{j}'$
but with the same
$T_{j}'$
but with the same
![]() $d,\mathcal {G}$
and
$d,\mathcal {G}$
and
![]() $P'$
, by integrating by parts some of the transcendental elements appearing in the strongly integrable generators
$P'$
, by integrating by parts some of the transcendental elements appearing in the strongly integrable generators
![]() $T_{j}$
. For the same reason, Theorem 6.5 applies to
$T_{j}$
. For the same reason, Theorem 6.5 applies to
![]() $h'$
with a different H but the same
$h'$
with a different H but the same
![]() $P',\mathcal {G}$
.
$P',\mathcal {G}$
.
7 Asymptotic expansions and limits
7.1 Asymptotic expansions
In this section, we study the behavior of a function h, in
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, and, in
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, and, in
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, seen as a function of the last variable y with parameters (
$\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, seen as a function of the last variable y with parameters (
![]() $s\in \Sigma $
and)
$s\in \Sigma $
and)
![]() $x\in X$
. We are interested in ‘the germ at
$x\in X$
. We are interested in ‘the germ at
![]() $+\infty $
in y’ of h; hence, we will work in restriction to cells of the form (3.1) with unbounded y-fibers. As we are only interested in the behavior at
$+\infty $
in y’ of h; hence, we will work in restriction to cells of the form (3.1) with unbounded y-fibers. As we are only interested in the behavior at
![]() $+\infty $
in y, we will often replace the cell B by some smaller cell
$+\infty $
in y, we will often replace the cell B by some smaller cell
![]() $B'$
, still of base X and with unbounded y-fibers, but whose lower boundary function is some analytic subanalytic function
$B'$
, still of base X and with unbounded y-fibers, but whose lower boundary function is some analytic subanalytic function
![]() $a'$
which satisfies that for all
$a'$
which satisfies that for all
![]() $x\in X,\ a\left (x\right )\leq a'\left (x\right )$
. As X serves as a space of parameters, we will also often partition X into finitely many subanalytic cells and suppose, as we did in the previous sections, that X itself is one of the cells of the partition. Finally, if
$x\in X,\ a\left (x\right )\leq a'\left (x\right )$
. As X serves as a space of parameters, we will also often partition X into finitely many subanalytic cells and suppose, as we did in the previous sections, that X itself is one of the cells of the partition. Finally, if
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
has no poles outside some closed discrete set
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
has no poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
, as
$P\subseteq \mathbb {C}$
, as
![]() $\Sigma $
also serves as a space of parameters, we will often replace P by some bigger closed discrete set
$\Sigma $
also serves as a space of parameters, we will often replace P by some bigger closed discrete set
![]() $P'\subseteq \mathbb {C}$
such that
$P'\subseteq \mathbb {C}$
such that
![]() $P'\setminus P$
is contained in a finitely generated
$P'\setminus P$
is contained in a finitely generated
![]() $\mathbb {Z}$
-lattice.
$\mathbb {Z}$
-lattice.
Summing up, the sentence ‘if B is a cell of base X with unbounded y-fibers and
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
has no poles outside some closed discrete set
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
has no poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
, then, up to partitioning
$P\subseteq \mathbb {C}$
, then, up to partitioning
![]() $X,$
shrinking B and enlarging P, Property (*) holds for h’ will be used as a shorthand for the following: there are a finite partition of X into subanalytic cells
$X,$
shrinking B and enlarging P, Property (*) holds for h’ will be used as a shorthand for the following: there are a finite partition of X into subanalytic cells
![]() $X'$
and a closed discrete set
$X'$
and a closed discrete set
![]() $P'\subseteq \mathbb {C}$
such that
$P'\subseteq \mathbb {C}$
such that
![]() $P'\setminus P$
is contained in a finitely generated
$P'\setminus P$
is contained in a finitely generated
![]() $\mathbb {Z}$
-lattice, and for each cell
$\mathbb {Z}$
-lattice, and for each cell
![]() $X'$
, there is a cell
$X'$
, there is a cell
![]() $B'\subseteq B$
of base
$B'\subseteq B$
of base
![]() $X'$
and with unbounded y-fibers such that Property (*) holds for
$X'$
and with unbounded y-fibers such that Property (*) holds for
![]() $h\restriction \left (\Sigma \setminus P'\right )\times B'$
.
$h\restriction \left (\Sigma \setminus P'\right )\times B'$
.
Our first result concerns the class
![]() $\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
.
$\mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (X\times \mathbb {R}\right )$
.
Theorem 7.1. Let B be as in (3.1) with unbounded y-fibers and
![]() $h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (B\right )$
be without poles outside some closed discrete set
$h\in \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (B\right )$
be without poles outside some closed discrete set
![]() $P\subseteq \mathbb {C}$
. Up to partitioning X, shrinking B and enlarging P, there is a sequence
$P\subseteq \mathbb {C}$
. Up to partitioning X, shrinking B and enlarging P, there is a sequence
![]() $\left (T_{n}\right )_{n\in \mathbb {N}}\subseteq \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (B\right )$
of generators which are monomial in y such that
$\left (T_{n}\right )_{n\in \mathbb {N}}\subseteq \mathcal {C}_{\Sigma }^{\mathcal {M},\mathcal {F}}\left (B\right )$
of generators which are monomial in y such that
-
(1) For all
 $N\in \mathbb {N}$
, there are
$N\in \mathbb {N}$
, there are
 $j_{N}\in \mathbb {N}$
and a function
$j_{N}\in \mathbb {N}$
and a function
 $C_{N}:\left (\Sigma \setminus P\right )\times X\longrightarrow \left (0,+\infty \right )$
such that
$C_{N}:\left (\Sigma \setminus P\right )\times X\longrightarrow \left (0,+\infty \right )$
such that  $$\begin{align*}\forall\left(s,x,y\right)\in\left(\Sigma\setminus P\right)\times B,\ \left|h\left(s,x,y\right)-\sum_{j\leq j_{N}}T_{j}\left(s,x,y\right)\right|\leq C_{N}\left(s,x\right)y^{-N}. \end{align*}$$
$$\begin{align*}\forall\left(s,x,y\right)\in\left(\Sigma\setminus P\right)\times B,\ \left|h\left(s,x,y\right)-\sum_{j\leq j_{N}}T_{j}\left(s,x,y\right)\right|\leq C_{N}\left(s,x\right)y^{-N}. \end{align*}$$
-
(2) If h is a finite sum of generators which are naive in y, then we can choose the sequence
 $\left (T_{n}\right )_{n\in \mathbb {N}}$
so that the series
$\left (T_{n}\right )_{n\in \mathbb {N}}$
so that the series
 $\sum _{j\in \mathbb {N}}T_{j}$
converges absolutely to h.
$\sum _{j\in \mathbb {N}}T_{j}$
converges absolutely to h.
Proof. We first prove the two statements for a function h which is a finite sum of generators which are naive in y: write
![]() $h=\sum _{i\in I}T_{i}$
, where I is a finite index set and
$h=\sum _{i\in I}T_{i}$
, where I is a finite index set and
![]() $T_{i}$
has the form (5.5). Arguing as in the proof of Proposition 5.7 and using Remark 3.6, up to partitioning X and shrinking B, we may suppose that
$T_{i}$
has the form (5.5). Arguing as in the proof of Proposition 5.7 and using Remark 3.6, up to partitioning X and shrinking B, we may suppose that
where the
![]() $Q_{i}\in \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
satisfy items (2.a) and (2.b) of Proposition 6.4 and
$Q_{i}\in \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
satisfy items (2.a) and (2.b) of Proposition 6.4 and
![]() $\Phi _{i}$
is as in (3.5). Using the (absolutely convergent) series expansion of
$\Phi _{i}$
is as in (3.5). Using the (absolutely convergent) series expansion of
![]() $\Phi _{i}$
, we write
$\Phi _{i}$
, we write
 $$ \begin{align} h\left(s,x,y\right) & =\sum_{i\in I}f_{i}\left(s,x\right)\left(\log y\right)^{\mu_{i}}\text{e}^{\text{i}Q_{i}\left(x,y\right)}\sum_{k\in\mathbb{N}}\xi_{i,k}\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k}{d}}y^{\lambda_{i}\left(s\right)-\frac{k}{d}}\nonumber \\ & =\sum_{i\in I,k\in\mathbb{N}}f_{i,k}\left(s,x\right)y^{\lambda_{i,k}\left(s\right)}\left(\log y\right)^{\mu_{i}}\text{e}^{\text{i}Q_{i}\left(x,y\right)}, \end{align} $$
$$ \begin{align} h\left(s,x,y\right) & =\sum_{i\in I}f_{i}\left(s,x\right)\left(\log y\right)^{\mu_{i}}\text{e}^{\text{i}Q_{i}\left(x,y\right)}\sum_{k\in\mathbb{N}}\xi_{i,k}\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k}{d}}y^{\lambda_{i}\left(s\right)-\frac{k}{d}}\nonumber \\ & =\sum_{i\in I,k\in\mathbb{N}}f_{i,k}\left(s,x\right)y^{\lambda_{i,k}\left(s\right)}\left(\log y\right)^{\mu_{i}}\text{e}^{\text{i}Q_{i}\left(x,y\right)}, \end{align} $$
where
![]() $f_{i,k}\left (s,x\right )=f_{i}\left (s,x\right )\xi _{i,k}\left (s,x\right )\left (a\left (x\right )\right )^{\frac {k}{d}}$
and
$f_{i,k}\left (s,x\right )=f_{i}\left (s,x\right )\xi _{i,k}\left (s,x\right )\left (a\left (x\right )\right )^{\frac {k}{d}}$
and
![]() $\lambda _{i,k}\left (s\right )=\lambda _{i}\left (s\right )-\frac {k}{d}$
. This proves the second statement of the theorem for h.
$\lambda _{i,k}\left (s\right )=\lambda _{i}\left (s\right )-\frac {k}{d}$
. This proves the second statement of the theorem for h.
Fix
![]() $N\in \mathbb {N}$
, let
$N\in \mathbb {N}$
, let
![]() $\mu :=\max _{i\in I}\mu _{i},\ K:=\sup _{i\in I,s\in \Sigma }\left |\Re \left (\lambda _{i}\left (s\right )\right )\right |$
and choose
$\mu :=\max _{i\in I}\mu _{i},\ K:=\sup _{i\in I,s\in \Sigma }\left |\Re \left (\lambda _{i}\left (s\right )\right )\right |$
and choose
![]() $k_{0}\in \mathbb {N}$
such that
$k_{0}\in \mathbb {N}$
such that
![]() $k_{0}\geq d\left (K+N+1\right )$
. Let
$k_{0}\geq d\left (K+N+1\right )$
. Let
 $$ \begin{align*} h_{\geq k_{0}}\left(s,x,y\right) & :=h\left(s,x,y\right)-\sum_{i\in I}f_{i}\left(s,x\right)\left(\log y\right)^{\mu_{i}}\text{e}^{\text{i}Q_{i}\left(x,y\right)}\sum_{k<k_{0}}\xi_{i,k}\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k}{d}}y^{\lambda_{i}\left(s\right)-\frac{k}{d}}\\ & =\sum_{i\in I}f_{i}\left(s,x\right)y^{\lambda_{i}\left(s\right)-\frac{k_{0}}{d}}\left(\log y\right)^{\mu_{i}}\text{e}^{\text{i}Q_{i}\left(x,y\right)}\sum_{k\geq0}\xi_{i,k+k_{0}}\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k}{d}}y^{-\frac{k}{d}}. \end{align*} $$
$$ \begin{align*} h_{\geq k_{0}}\left(s,x,y\right) & :=h\left(s,x,y\right)-\sum_{i\in I}f_{i}\left(s,x\right)\left(\log y\right)^{\mu_{i}}\text{e}^{\text{i}Q_{i}\left(x,y\right)}\sum_{k<k_{0}}\xi_{i,k}\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k}{d}}y^{\lambda_{i}\left(s\right)-\frac{k}{d}}\\ & =\sum_{i\in I}f_{i}\left(s,x\right)y^{\lambda_{i}\left(s\right)-\frac{k_{0}}{d}}\left(\log y\right)^{\mu_{i}}\text{e}^{\text{i}Q_{i}\left(x,y\right)}\sum_{k\geq0}\xi_{i,k+k_{0}}\left(s,x\right)\left(a\left(x\right)\right)^{\frac{k}{d}}y^{-\frac{k}{d}}. \end{align*} $$
Setting
![]() $C_{N}\left (s,x\right )=\left (\frac {\left (\log a\left (x\right )\right )^{\mu }}{a\left (x\right )}+\frac {1}{\mathrm {e}}\right )\sum _{i\in I}\left |f_{i}\left (s,x\right )\right |\sum _{k\geq 0}\left |\xi _{i,k+k_{0}}\left (s,x\right )\right |$
, by the choice of
$C_{N}\left (s,x\right )=\left (\frac {\left (\log a\left (x\right )\right )^{\mu }}{a\left (x\right )}+\frac {1}{\mathrm {e}}\right )\sum _{i\in I}\left |f_{i}\left (s,x\right )\right |\sum _{k\geq 0}\left |\xi _{i,k+k_{0}}\left (s,x\right )\right |$
, by the choice of
![]() $k_{0}$
, we have
$k_{0}$
, we have
which proves the first statement of the theorem for h.
Suppose now that h is not a finite sum of generators which are naive in y. Apply Proposition 5.3 and Remark 3.6 to h: up to shrinking B, this writes h as a finite sum of prepared generators as in Definition 5.2. Let T be one such generator: for our aim, it is enough to show that, given
![]() $N\in \mathbb {N}$
, we can rewrite T as a finite sum of generators which are either naive in y or such that we can control their asymptotics by
$N\in \mathbb {N}$
, we can rewrite T as a finite sum of generators which are either naive in y or such that we can control their asymptotics by
![]() $y^{-N}$
. For this, we revisit the proof of Proposition 5.10 and argue according to the nature of the integration bounds in the transcendental element of T.
$y^{-N}$
. For this, we revisit the proof of Proposition 5.10 and argue according to the nature of the integration bounds in the transcendental element of T.
Recall Notation 5.1.
If
![]() $\alpha =\beta =0$
, then, up to partitioning
$\alpha =\beta =0$
, then, up to partitioning
![]() $X,$
shrinking B and enlarging P, we may rewrite T as a a finite sum of generators which are naive in y plus a term of the form (5.9), where we can expand
$X,$
shrinking B and enlarging P, we may rewrite T as a a finite sum of generators which are naive in y plus a term of the form (5.9), where we can expand
![]() $\Phi _{>k_{0}}$
as an absolutely convergent series in the variable y as in (5.8). Permuting integral and summation, we obtain that this last term can be written as an absolutely convergent series of the form (7.1). Hence, we can apply the first part of the proof to this last term.
$\Phi _{>k_{0}}$
as an absolutely convergent series in the variable y as in (5.8). Permuting integral and summation, we obtain that this last term can be written as an absolutely convergent series of the form (7.1). Hence, we can apply the first part of the proof to this last term.
If
![]() $\alpha>0$
, then chose
$\alpha>0$
, then chose
![]() $\ell _{0}\in \mathbb {N}$
such that for all
$\ell _{0}\in \mathbb {N}$
such that for all
![]() $s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )+\frac {\alpha }{d}\left (\Re \left (\varrho \left (s\right )\right )-\ell _{0}+1\right )+\frac {\Delta }{d}<-\left (N+1\right )$
. If we integrate by parts as in Lemma 5.9
$s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )+\frac {\alpha }{d}\left (\Re \left (\varrho \left (s\right )\right )-\ell _{0}+1\right )+\frac {\Delta }{d}<-\left (N+1\right )$
. If we integrate by parts as in Lemma 5.9
![]() $\ell _{0}$
times, then we create finitely many terms which are naive in y and an integral rest of the form
$\ell _{0}$
times, then we create finitely many terms which are naive in y and an integral rest of the form
 $$ \begin{align} R\left(s,x,y\right)=g\left(s,x\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\text{e}^{\text{i}\varphi\left(x,y\right)}\int_{\widetilde{a}\left(x,y\right)}^{\widetilde{b}\left(x,y\right)}t^{\varrho\left(s\right)-\ell_{0}}\left(\log t\right)^{\nu}\Phi\left(s,x,y,t\right)\text{e}^{\sigma\text{i}t}\text{d}t, \end{align} $$
$$ \begin{align} R\left(s,x,y\right)=g\left(s,x\right)y^{\lambda\left(s\right)}\left(\log y\right)^{\mu}\text{e}^{\text{i}\varphi\left(x,y\right)}\int_{\widetilde{a}\left(x,y\right)}^{\widetilde{b}\left(x,y\right)}t^{\varrho\left(s\right)-\ell_{0}}\left(\log t\right)^{\nu}\Phi\left(s,x,y,t\right)\text{e}^{\sigma\text{i}t}\text{d}t, \end{align} $$
where (5.10) is satisfied.
If
![]() $\widetilde {b}=+\infty $
, then
$\widetilde {b}=+\infty $
, then
 $$ \begin{align*} \left|R\left(s,x,y\right)\right| & \leq\widetilde{C}_{N}\left(s,x\right)y^{\Re\left(\lambda\left(s\right)\right)+\frac{\alpha}{d}\left(\Re\left(\varrho\left(s\right)\right)-\ell_{0}+1\right)}\left(\log y\right)^{\mu+\nu}\\ & \leq C_{N}\left(s,x\right)y^{-N}, \end{align*} $$
$$ \begin{align*} \left|R\left(s,x,y\right)\right| & \leq\widetilde{C}_{N}\left(s,x\right)y^{\Re\left(\lambda\left(s\right)\right)+\frac{\alpha}{d}\left(\Re\left(\varrho\left(s\right)\right)-\ell_{0}+1\right)}\left(\log y\right)^{\mu+\nu}\\ & \leq C_{N}\left(s,x\right)y^{-N}, \end{align*} $$
for suitable positive functions
![]() $\widetilde {C}_{N},C_{N}$
.
$\widetilde {C}_{N},C_{N}$
.
If
![]() $\widetilde {b}<+\infty $
, then
$\widetilde {b}<+\infty $
, then
 $$ \begin{align*} \left|R\left(s,x,y\right)\right| & \leq\widetilde{C}_{N}\left(s,x\right)y^{\Re\left(\lambda\left(s\right)\right)+\frac{\alpha}{d}\left(\Re\left(\varrho\left(s\right)\right)-\ell_{0}\right)+\frac{\Delta}{d}}\left(\log y\right)^{\mu+\nu}\\ & \leq C_{N}\left(s,x\right)y^{-N}, \end{align*} $$
$$ \begin{align*} \left|R\left(s,x,y\right)\right| & \leq\widetilde{C}_{N}\left(s,x\right)y^{\Re\left(\lambda\left(s\right)\right)+\frac{\alpha}{d}\left(\Re\left(\varrho\left(s\right)\right)-\ell_{0}\right)+\frac{\Delta}{d}}\left(\log y\right)^{\mu+\nu}\\ & \leq C_{N}\left(s,x\right)y^{-N}, \end{align*} $$
for suitable positive functions
![]() $\widetilde {C}_{N},C_{N}$
.
$\widetilde {C}_{N},C_{N}$
.
If
![]() $\alpha =0$
and
$\alpha =0$
and
![]() $\beta>0$
, then choose
$\beta>0$
, then choose
![]() $k_{0}\in \mathbb {N}$
such that for all
$k_{0}\in \mathbb {N}$
such that for all
![]() $s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )-\frac {\beta }{d}\left (\frac {k_{0}+1}{d}\right )+\frac {\Delta }{d}<-\left (N+1\right )$
and
$s\in \Sigma ,\ \Re \left (\lambda \left (s\right )\right )-\frac {\beta }{d}\left (\frac {k_{0}+1}{d}\right )+\frac {\Delta }{d}<-\left (N+1\right )$
and
![]() $\ell _{0}\in \mathbb {N}$
such that
$\ell _{0}\in \mathbb {N}$
such that
![]() $\ell _{0}>\Re \left (\varrho \left (s\right )\right )+\frac {k_{0}}{d}+1$
. Then, (5.11) and (5.12) are satisfied if we replace
$\ell _{0}>\Re \left (\varrho \left (s\right )\right )+\frac {k_{0}}{d}+1$
. Then, (5.11) and (5.12) are satisfied if we replace
![]() $\varrho \left (s\right )$
by
$\varrho \left (s\right )$
by
![]() $\varrho \left (s\right )-\ell _{0}$
. If we integrate by parts
$\varrho \left (s\right )-\ell _{0}$
. If we integrate by parts
![]() $\ell _{0}$
times, then we create finitely many terms which are naive in y and an integral rest of the form (7.2). Proceeding as in the third part of the proof of Proposition 5.10, we are left to deal with a term
$\ell _{0}$
times, then we create finitely many terms which are naive in y and an integral rest of the form (7.2). Proceeding as in the third part of the proof of Proposition 5.10, we are left to deal with a term
![]() $R_{>k_{0}}$
of the form (5.14) which satisfies
$R_{>k_{0}}$
of the form (5.14) which satisfies
 $$ \begin{align*} \left|R_{>k_{0}}\left(s,x,y\right)\right| & \leq\widetilde{C}_{N}\left(s,x\right)y^{\Re\left(\lambda\left(s\right)\right)-\frac{\beta}{d}\left(\frac{k_{0}+1}{d}\right)+\frac{\Delta}{d}}\left(\log y\right)^{\mu+\nu}\\ & \leq C_{N}\left(s,x\right)y^{-N}, \end{align*} $$
$$ \begin{align*} \left|R_{>k_{0}}\left(s,x,y\right)\right| & \leq\widetilde{C}_{N}\left(s,x\right)y^{\Re\left(\lambda\left(s\right)\right)-\frac{\beta}{d}\left(\frac{k_{0}+1}{d}\right)+\frac{\Delta}{d}}\left(\log y\right)^{\mu+\nu}\\ & \leq C_{N}\left(s,x\right)y^{-N}, \end{align*} $$
for suitable positive functions
![]() $\widetilde {C}_{N},C_{N}$
.
$\widetilde {C}_{N},C_{N}$
.
Our next goal is to concentrate on the subclass
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
and deduce from Theorem 7.1 a more precise result on the asymptotic behavior of h in y, in the sense of [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Definition 7.1] but uniformly in the variables
$\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
and deduce from Theorem 7.1 a more precise result on the asymptotic behavior of h in y, in the sense of [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Definition 7.1] but uniformly in the variables
![]() $x\in X$
.
$x\in X$
.
First, we restate and improve Theorem 7.1 for functions in the class
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
.
$\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
.
Definition 7.2. Let
![]() $\mathscr {E}\subseteq \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \left (0,+\infty \right )\right )$
be the
$\mathscr {E}\subseteq \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \left (0,+\infty \right )\right )$
be the
![]() $\mathbb {C}$
-vector space of all functions of the form
$\mathbb {C}$
-vector space of all functions of the form
 $$\begin{align*}E\left(x,y\right)=\sum_{j\in J}f_{j}\left(x\right)\text{e}^{\text{i}\zeta_{j}\left(x,y\right)}, \end{align*}$$
$$\begin{align*}E\left(x,y\right)=\sum_{j\in J}f_{j}\left(x\right)\text{e}^{\text{i}\zeta_{j}\left(x,y\right)}, \end{align*}$$
where J is a finite index set,
![]() $f_{j}\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right ),\ \zeta _{j}\left (x,y\right )=\sigma _{j}\log y+Q_{j}\left (x,y\right )$
with
$f_{j}\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right ),\ \zeta _{j}\left (x,y\right )=\sigma _{j}\log y+Q_{j}\left (x,y\right )$
with
![]() $\sigma _{j}\in \mathbb {R},\ Q_{j}\in \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
. We require, moreover, that for all
$\sigma _{j}\in \mathbb {R},\ Q_{j}\in \mathcal {S}\left (X\right )\left [y^{\frac {1}{d}}\right ]$
. We require, moreover, that for all
![]() $j\in J,\text {\ for all }x\in X,\ Q_{j}\left (x,0\right )=0,$
for all
$j\in J,\text {\ for all }x\in X,\ Q_{j}\left (x,0\right )=0,$
for all
![]() $i,j\in J$
, either
$i,j\in J$
, either
![]() $Q_{i}=Q_{j}$
on X or
$Q_{i}=Q_{j}$
on X or
![]() $Q_{i}\not =Q_{j}$
on X, and if
$Q_{i}\not =Q_{j}$
on X, and if
![]() $i\not =j$
, then for all
$i\not =j$
, then for all
![]() $x\in X$
, the functions
$x\in X$
, the functions
![]() $y\longmapsto \zeta _{i}\left (x,y\right )$
and
$y\longmapsto \zeta _{i}\left (x,y\right )$
and
![]() $y\longmapsto \zeta _{j}\left (x,y\right )$
are distinct.
$y\longmapsto \zeta _{j}\left (x,y\right )$
are distinct.
Remark 7.3. By [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 3.4 (2)], if
![]() $E\in \mathscr {E}\setminus \left \{ 0\right \} $
, then for all
$E\in \mathscr {E}\setminus \left \{ 0\right \} $
, then for all
![]() $x\in X$
, either
$x\in X$
, either
![]() $y\longmapsto E\left (x,y\right )$
is identically zero or there exist
$y\longmapsto E\left (x,y\right )$
is identically zero or there exist
![]() $\varepsilon \left (x\right )>0$
and a sequence
$\varepsilon \left (x\right )>0$
and a sequence
![]() $\left (y_{n}\right )_{n\in \mathbb {N}}$
such that
$\left (y_{n}\right )_{n\in \mathbb {N}}$
such that
![]() $\lim _{n\longrightarrow +\infty }y_{n}=+\infty $
and for all for all
$\lim _{n\longrightarrow +\infty }y_{n}=+\infty $
and for all for all
![]() $n\in \mathbb {N},\ \left |E\left (x,y_{n}\right )\right |>\varepsilon \left (x\right )$
.
$n\in \mathbb {N},\ \left |E\left (x,y_{n}\right )\right |>\varepsilon \left (x\right )$
.
Definition 7.4. A function
![]() $h\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
has a power-log asymptotic expansion with coefficients in
$h\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
has a power-log asymptotic expansion with coefficients in
![]() $\mathscr {E}$
if there are a collection
$\mathscr {E}$
if there are a collection
![]() $\left \{ E_{n}:\ n\in \mathbb {N}\right \} \subseteq \mathscr {E}$
, a sequence
$\left \{ E_{n}:\ n\in \mathbb {N}\right \} \subseteq \mathscr {E}$
, a sequence
![]() $\left (r_{n},\nu _{n}\right )_{n\in \mathbb {N}}\subseteq \mathbb {R}\times \mathbb {N}$
which is strictly decreasing with respect to the lexicographic order, a cell B as in (3.1) with unbounded y-fibers and for all
$\left (r_{n},\nu _{n}\right )_{n\in \mathbb {N}}\subseteq \mathbb {R}\times \mathbb {N}$
which is strictly decreasing with respect to the lexicographic order, a cell B as in (3.1) with unbounded y-fibers and for all
![]() $N\in \mathbb {N}$
, a function
$N\in \mathbb {N}$
, a function
![]() $C_{N}:X\longrightarrow \left (0,+\infty \right )$
such that, for all
$C_{N}:X\longrightarrow \left (0,+\infty \right )$
such that, for all
![]() $\left (x,y\right )\in B$
,
$\left (x,y\right )\in B$
,
 $$ \begin{align} \left|h\left(x,y\right)-\sum_{n<N}E_{n}\left(x,y\right)y^{r_{n}}\left(\log y\right)^{\nu_{n}}\right|\leq C_{N}\left(x\right)y^{r_{N}}\left(\log y\right)^{\nu_{N}}\!. \end{align} $$
$$ \begin{align} \left|h\left(x,y\right)-\sum_{n<N}E_{n}\left(x,y\right)y^{r_{n}}\left(\log y\right)^{\nu_{n}}\right|\leq C_{N}\left(x\right)y^{r_{N}}\left(\log y\right)^{\nu_{N}}\!. \end{align} $$
If, moreover, the series
![]() $\sum _{n\in \mathbb {N}}E_{n}\left (x,y\right )y^{r_{n}}\left (\log y\right )^{\nu _{n}}$
converges absolutely to h, then we say that h has a convergent power-log asymptotic expansion with coefficients in
$\sum _{n\in \mathbb {N}}E_{n}\left (x,y\right )y^{r_{n}}\left (\log y\right )^{\nu _{n}}$
converges absolutely to h, then we say that h has a convergent power-log asymptotic expansion with coefficients in
![]() $\mathscr {E}$
.
$\mathscr {E}$
.
Note that the sequence of real functions
![]() $\left (g_{n}\left (y\right )\right )_{n\in \mathbb {N}}=\left (y^{r_{n}}\left (\log y\right )^{\nu _{n}}\right )_{n\in \mathbb {N}}$
forms an asymptotic scale at
$\left (g_{n}\left (y\right )\right )_{n\in \mathbb {N}}=\left (y^{r_{n}}\left (\log y\right )^{\nu _{n}}\right )_{n\in \mathbb {N}}$
forms an asymptotic scale at
![]() $+\infty $
in the sense that, for all
$+\infty $
in the sense that, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\lim _{y\longrightarrow +\infty }\frac {g_{n+1}\left (y\right )}{g_{n}\left (y\right )}=0$
.
$\lim _{y\longrightarrow +\infty }\frac {g_{n+1}\left (y\right )}{g_{n}\left (y\right )}=0$
.
Recall the definition of the system
![]() $\mathcal {C}^{\mathbb {C}}$
of power-constructible functions and that of the system
$\mathcal {C}^{\mathbb {C}}$
of power-constructible functions and that of the system
![]() $\mathcal {C}^{\mathbb {C},\text {i}\mathcal {S}}$
, given in Section 2.1.
$\mathcal {C}^{\mathbb {C},\text {i}\mathcal {S}}$
, given in Section 2.1.
Definition 7.5. Let
![]() $\mathcal {C}_{\text {naive}}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be the additive group generated by the generators which are naive in y – that is, of the form
$\mathcal {C}_{\text {naive}}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
be the additive group generated by the generators which are naive in y – that is, of the form
Note that
![]() $\mathcal {C}_{\text {naive}}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
is a
$\mathcal {C}_{\text {naive}}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
is a
![]() $\mathbb {C}$
-algebra and
$\mathbb {C}$
-algebra and
Theorem 7.6. Every
![]() $h\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
has, up to partitioning X, a power-log asymptotic expansion with coefficients in
$h\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
has, up to partitioning X, a power-log asymptotic expansion with coefficients in
![]() $\mathscr {E}$
. If, moreover,
$\mathscr {E}$
. If, moreover,
![]() $h\in \mathcal {C}_{\mathrm {naive}}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, then such an asymptotic expansion is convergent.
$h\in \mathcal {C}_{\mathrm {naive}}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, then such an asymptotic expansion is convergent.
Proof. Suppose first that
![]() $h\in \mathcal {C}_{\text {naive}}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, so that, up to partitioning X and on some cell B with unbounded y-fibers, h can be written as in (7.1), where the functions
$h\in \mathcal {C}_{\text {naive}}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, so that, up to partitioning X and on some cell B with unbounded y-fibers, h can be written as in (7.1), where the functions
![]() $f_{i,k}$
only depend on the variables x and
$f_{i,k}$
only depend on the variables x and
![]() $\lambda _{i,k}=\lambda _{i}-\frac {k}{d}\in \mathbb {C}$
. Let
$\lambda _{i,k}=\lambda _{i}-\frac {k}{d}\in \mathbb {C}$
. Let
![]() $\rho _{i,k}=\Re \left (\lambda _{i}\right )-\frac {k}{d}$
,
$\rho _{i,k}=\Re \left (\lambda _{i}\right )-\frac {k}{d}$
,
![]() $\sigma _{i}=\Im \left (\lambda _{i}\right )$
and define
$\sigma _{i}=\Im \left (\lambda _{i}\right )$
and define
![]() $\zeta _{i}\left (x,y\right )=\sigma _{i}\log y+Q_{i}\left (x,y\right )$
. Hence, we can write h as the sum of the absolutely convergent series of functions
$\zeta _{i}\left (x,y\right )=\sigma _{i}\log y+Q_{i}\left (x,y\right )$
. Hence, we can write h as the sum of the absolutely convergent series of functions
The set
![]() $\left \{ \rho _{i,k}:\ i\in I,k\in \mathbb {N}\right \} $
is contained in a finitely generated
$\left \{ \rho _{i,k}:\ i\in I,k\in \mathbb {N}\right \} $
is contained in a finitely generated
![]() $\mathbb {Z}$
-lattice and, since I is finite, so is the set
$\mathbb {Z}$
-lattice and, since I is finite, so is the set
![]() $\left \{ \mu _{i}:\ i\in I\right \} $
. Hence, the set
$\left \{ \mu _{i}:\ i\in I\right \} $
. Hence, the set
is countable, and, for
![]() $\left (r,\nu \right )\in J$
, the set
$\left (r,\nu \right )\in J$
, the set
![]() $J_{\left (r,\nu \right )}=\left \{ \left (i,k\right )\in I\times \mathbb {N}:\ \rho _{i,k}=r,\ \mu _{i}=\nu \right \} $
is finite. Fix a bijection
$J_{\left (r,\nu \right )}=\left \{ \left (i,k\right )\in I\times \mathbb {N}:\ \rho _{i,k}=r,\ \mu _{i}=\nu \right \} $
is finite. Fix a bijection
which is decreasing with respect to the lexicographic order and define
 $$\begin{align*}E_{n}\left(x,y\right)=\sum_{\left(i,k\right)\in J_{\left(r_{n},\nu_{n}\right)}}f_{i,k}\left(x\right)\text{e}^{\text{i}\zeta_{i}\left(x,y\right)}. \end{align*}$$
$$\begin{align*}E_{n}\left(x,y\right)=\sum_{\left(i,k\right)\in J_{\left(r_{n},\nu_{n}\right)}}f_{i,k}\left(x\right)\text{e}^{\text{i}\zeta_{i}\left(x,y\right)}. \end{align*}$$
These are the coefficients of a convergent power-log asymptotic expansion of h in the asymptotic scale
![]() $\left \{ y^{r_{n}}\left (\log y\right )^{\nu _{n}}:\ n\in \mathbb {N}\right \} $
.
$\left \{ y^{r_{n}}\left (\log y\right )^{\nu _{n}}:\ n\in \mathbb {N}\right \} $
.
Suppose now that
![]() $h\not \in \mathcal {C}_{\text {naive}}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
. Revisiting the proof of Theorem 7.1, given
$h\not \in \mathcal {C}_{\text {naive}}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
. Revisiting the proof of Theorem 7.1, given
![]() $N\in \mathbb {N}$
, we may write h as a finite sum of generators which are either naive in y (and hence have a convergent power-log asymptotic expansion in some common asymptotic scale
$N\in \mathbb {N}$
, we may write h as a finite sum of generators which are either naive in y (and hence have a convergent power-log asymptotic expansion in some common asymptotic scale
![]() $\left (y^{r_{n}}\left (\log y\right )^{\nu _{n}}\right )_{n\in \mathbb {N}}$
with coefficients
$\left (y^{r_{n}}\left (\log y\right )^{\nu _{n}}\right )_{n\in \mathbb {N}}$
with coefficients
![]() $\left \{ E_{n}:\ n\in \mathbb {N}\right \} \subseteq \mathscr {E}$
) or whose module is bounded
$\left \{ E_{n}:\ n\in \mathbb {N}\right \} \subseteq \mathscr {E}$
) or whose module is bounded
![]() $C_{N}\left (x\right )y^{\lfloor r_{N}\rfloor -1}$
, where
$C_{N}\left (x\right )y^{\lfloor r_{N}\rfloor -1}$
, where
![]() $C_{N}$
is some positive function in
$C_{N}$
is some positive function in
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
. In particular, h has a (not necessarily convergent) power-log asymptotic expansion as in (7.3).
$\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
. In particular, h has a (not necessarily convergent) power-log asymptotic expansion as in (7.3).
Remark 7.7. Arguing as in [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Lemma 7.2] and using Remark 7.3, one sees that if h has a power-log asymptotic expansion in a certain power-log asymptotic scale and with coefficients in
![]() $\mathscr {E}$
, then its coefficients are uniquely determined. Note that the proof of Theorem 7.6 shows that the power-log asymptotic scales
$\mathscr {E}$
, then its coefficients are uniquely determined. Note that the proof of Theorem 7.6 shows that the power-log asymptotic scales
![]() $\left (y^{r_{n}}\left (\log y\right )^{\nu _{n}}\right )_{n\in \mathbb {N}}$
appearing in the asymptotic expansions of functions in
$\left (y^{r_{n}}\left (\log y\right )^{\nu _{n}}\right )_{n\in \mathbb {N}}$
appearing in the asymptotic expansions of functions in
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
have the property that the sequence
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
have the property that the sequence
![]() $\left (r_{n},\nu _{n}\right )_{n\in \mathbb {N}}$
has the same order type as
$\left (r_{n},\nu _{n}\right )_{n\in \mathbb {N}}$
has the same order type as
![]() $\omega $
. In particular, the union of two such asymptotic scales is again an asymptotic scale of the same type, so a function in
$\omega $
. In particular, the union of two such asymptotic scales is again an asymptotic scale of the same type, so a function in
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
cannot have two different asymptotic expansions in two different power-log asymptotic scales.
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
cannot have two different asymptotic expansions in two different power-log asymptotic scales.
Corollary 7.8. The systems
![]() $\mathcal {C}^{\mathbb {C},\mathrm {i}\mathcal {S}}$
and
$\mathcal {C}^{\mathbb {C},\mathrm {i}\mathcal {S}}$
and
![]() $\mathcal {C}^{\mathcal {M},\mathrm {i}\mathcal {S}}$
are not stable under parametric integration.
$\mathcal {C}^{\mathcal {M},\mathrm {i}\mathcal {S}}$
are not stable under parametric integration.
Proof. We give two examples of functions which are in
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (\mathbb {R}\right )$
but not in
$\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (\mathbb {R}\right )$
but not in
![]() $\mathcal {C}^{\mathcal {M},\text {i}\mathcal {S}}\left (\mathbb {R}\right )$
.
$\mathcal {C}^{\mathcal {M},\text {i}\mathcal {S}}\left (\mathbb {R}\right )$
.
The function
![]() $f:y\longmapsto \text {e}^{-\left |y\right |}$
belongs to
$f:y\longmapsto \text {e}^{-\left |y\right |}$
belongs to
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (\mathbb {R}\right )$
since it can be obtained as a parametric integral of a function in
$\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (\mathbb {R}\right )$
since it can be obtained as a parametric integral of a function in
![]() $\mathcal {C}^{\mathbb {C},\mathrm {i}\mathcal {S}}\left (\mathbb {R}^{2}\right )$
(it is the inverse Fourier transform of the semialgebraic function
$\mathcal {C}^{\mathbb {C},\mathrm {i}\mathcal {S}}\left (\mathbb {R}^{2}\right )$
(it is the inverse Fourier transform of the semialgebraic function
![]() $t\longmapsto \frac {2}{1+4\pi ^{2}t^{2}}$
; see, for example, [Reference Gasquet and WitomskiGW99]). If f were in
$t\longmapsto \frac {2}{1+4\pi ^{2}t^{2}}$
; see, for example, [Reference Gasquet and WitomskiGW99]). If f were in
![]() $\mathcal {C}^{\mathcal {M},\text {i}\mathcal {S}}\left (\mathbb {R}\right )$
, then it would also be in
$\mathcal {C}^{\mathcal {M},\text {i}\mathcal {S}}\left (\mathbb {R}\right )$
, then it would also be in
![]() $\mathcal {C}^{\mathbb {C},\text {i}\mathcal {S}}\left (\mathbb {R}\right )$
, and by Theorem 7.6, f would have a convergent power-log asymptotic expansion with coefficients in
$\mathcal {C}^{\mathbb {C},\text {i}\mathcal {S}}\left (\mathbb {R}\right )$
, and by Theorem 7.6, f would have a convergent power-log asymptotic expansion with coefficients in
![]() $\mathscr {E}$
. Now, arguing as in [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Example 7.4] and using Remark 7.3, one sees that no exponentially flat function can have such a convergent power-log asymptotic expansion.
$\mathscr {E}$
. Now, arguing as in [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Example 7.4] and using Remark 7.3, one sees that no exponentially flat function can have such a convergent power-log asymptotic expansion.
Now consider the function
 $$\begin{align*}\text{Si}\left(y\right)=\begin{cases} \int_{0}^{y}\frac{\text{e}^{\text{i}t}-\text{e}^{-\text{i}t}}{2\text{i}t}\text{d}t & y>0\\ 0 & y\leq0, \end{cases} \end{align*}$$
$$\begin{align*}\text{Si}\left(y\right)=\begin{cases} \int_{0}^{y}\frac{\text{e}^{\text{i}t}-\text{e}^{-\text{i}t}}{2\text{i}t}\text{d}t & y>0\\ 0 & y\leq0, \end{cases} \end{align*}$$
which is obtained as a parametric integral of a function in
![]() $\mathcal {C}^{\mathbb {C},\mathrm {i}\mathcal {S}}\left (\mathbb {R}^{2}\right )$
. It is well known that
$\mathcal {C}^{\mathbb {C},\mathrm {i}\mathcal {S}}\left (\mathbb {R}^{2}\right )$
. It is well known that
![]() $\text {Si}$
has a divergent power-log asymptotic expansion with coefficients in
$\text {Si}$
has a divergent power-log asymptotic expansion with coefficients in
![]() $\mathcal {E}$
(see [Reference Abramowitz and StegunAS65] and [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Example 7.5]). By Theorem 7.6 and Remark 7.7,
$\mathcal {E}$
(see [Reference Abramowitz and StegunAS65] and [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Example 7.5]). By Theorem 7.6 and Remark 7.7,
![]() $\text {Si}\notin \mathcal {C}^{\mathcal {M},\text {i}\mathcal {S}}\left (\mathbb {R}\right )$
.
$\text {Si}\notin \mathcal {C}^{\mathcal {M},\text {i}\mathcal {S}}\left (\mathbb {R}\right )$
.
Remark 7.9. Let
![]() $X\subseteq \mathbb {R}^{m}$
be a subanalytic open set and
$X\subseteq \mathbb {R}^{m}$
be a subanalytic open set and
![]() $K\subseteq X$
be a compact subanalytic subset. It is possible to construct a
$K\subseteq X$
be a compact subanalytic subset. It is possible to construct a
![]() $C^{\infty }$
function
$C^{\infty }$
function
![]() $\eta \in \mathcal {C}^{\mathbb {C},\mathcal {F}}(X)$
such that
$\eta \in \mathcal {C}^{\mathbb {C},\mathcal {F}}(X)$
such that
![]() $\eta \left (X\right )\subseteq \left [0,1\right ]$
and
$\eta \left (X\right )\subseteq \left [0,1\right ]$
and
![]() $\eta \equiv 1$
on a neighborhood of K in X (in particular,
$\eta \equiv 1$
on a neighborhood of K in X (in particular,
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}(X)$
contains smooth functions with compact support). One way to do this is to consider the function
$\mathcal {C}^{\mathbb {C},\mathcal {F}}(X)$
contains smooth functions with compact support). One way to do this is to consider the function
where
![]() $\|\cdot \|$
is the Euclidean norm in
$\|\cdot \|$
is the Euclidean norm in
![]() $\mathbb {R}^{m}$
and
$\mathbb {R}^{m}$
and
 $$\begin{align*}f:t\mapsto\left\{ \begin{array}{ll} \mathrm{e}^{-\frac{1}{t}} & \text{if } t>0\\ 0 & \text{if } t\leq0 \end{array}\right.. \end{align*}$$
$$\begin{align*}f:t\mapsto\left\{ \begin{array}{ll} \mathrm{e}^{-\frac{1}{t}} & \text{if } t>0\\ 0 & \text{if } t\leq0 \end{array}\right.. \end{align*}$$
Note that, considering the first example in the proof of Corollary 7.8 and using the stability under right-composition with subanalytic functions observed in Remark 2.8, we obtain that
![]() $\nu \in \mathcal {C}^{\mathbb {C},\mathcal {F}}(X)$
. We can then define
$\nu \in \mathcal {C}^{\mathbb {C},\mathcal {F}}(X)$
. We can then define
![]() $\eta $
as the convolution of
$\eta $
as the convolution of
![]() $\nu $
with the subanalytic characteristic function of a sufficiently small tubular neighborhood of K in X (see, for instance, [Reference HörmanderHör03, Theorem 1.4.1]) and thus obtain that
$\nu $
with the subanalytic characteristic function of a sufficiently small tubular neighborhood of K in X (see, for instance, [Reference HörmanderHör03, Theorem 1.4.1]) and thus obtain that
![]() $\nu \in \mathcal {C}^{\mathbb {C},\mathcal {F}}(X)$
by Theorem 2.9.
$\nu \in \mathcal {C}^{\mathbb {C},\mathcal {F}}(X)$
by Theorem 2.9.
We have at our disposal several results concerning the asymptotics at infinity of integral transforms, and in particular, of Fourier and Mellin transforms, of functions with support in
![]() $[0,+\infty )$
having an asymptotic expansions at the origin in the scale
$[0,+\infty )$
having an asymptotic expansions at the origin in the scale
![]() $\{x^{\alpha }\log ^{\beta }:\alpha ,\beta \in \mathbb {R}\}$
(see, for instance, [Reference Bleistein and HandelsmanBH86, Reference WongWon89, Reference Wong and LinWL78]). In this situation, the integral transforms have an asymptotic expansion at
$\{x^{\alpha }\log ^{\beta }:\alpha ,\beta \in \mathbb {R}\}$
(see, for instance, [Reference Bleistein and HandelsmanBH86, Reference WongWon89, Reference Wong and LinWL78]). In this situation, the integral transforms have an asymptotic expansion at
![]() $+\infty $
in the same power-log scale. However, to our knowledge, very little is known beyond this scale, in particular, with respect to asymptotic scales detecting exponentially small terms (see [Reference LombardiLom00]), a question that is relevant to the class
$+\infty $
in the same power-log scale. However, to our knowledge, very little is known beyond this scale, in particular, with respect to asymptotic scales detecting exponentially small terms (see [Reference LombardiLom00]), a question that is relevant to the class
![]() $\mathcal {C}^{\mathrm {exp}}$
of [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18] and to our class
$\mathcal {C}^{\mathrm {exp}}$
of [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18] and to our class
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
by Remark 7.9, but which seems to require new tools.
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
by Remark 7.9, but which seems to require new tools.
7.2 Pointwise limits
In this section, we prove the stability of the class
![]() $\mathbf {\mathcal {C}^{\mathbb {C},\mathcal {F}}}$
under pointwise limits.
$\mathbf {\mathcal {C}^{\mathbb {C},\mathcal {F}}}$
under pointwise limits.
Notation 7.10. For
![]() $X\subseteq {\mathbb {R}}^{m}$
and
$X\subseteq {\mathbb {R}}^{m}$
and
![]() $h\colon X\times {\mathbb {R}}\to {\mathbb {C}}$
, let
$h\colon X\times {\mathbb {R}}\to {\mathbb {C}}$
, let
Theorem 7.11. Let
![]() $h\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times {\mathbb {R}}\right )$
. There exist
$h\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times {\mathbb {R}}\right )$
. There exist
![]() $f,g\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
such that
$f,g\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\right )$
such that
and such that for all
![]() $x\in \mathrm {Lim}\left (h,X\right )$
,
$x\in \mathrm {Lim}\left (h,X\right )$
,
Proof. Apply Proposition 6.4 to h and concentrate on a cell A with unbounded y-fibers (so that, by Remark 3.6,
![]() $A=B_{A}$
and
$A=B_{A}$
and
![]() $\Pi _{A}$
is the identity map). By condition (1), the prepared generators
$\Pi _{A}$
is the identity map). By condition (1), the prepared generators
![]() $T_{j}$
which are strongly integrable tend indeed to a limit, and this limit is zero. Hence, we may suppose that
$T_{j}$
which are strongly integrable tend indeed to a limit, and this limit is zero. Hence, we may suppose that
![]() $h=\sum _{i\in I}T_{i}$
for some finite index set I, where each
$h=\sum _{i\in I}T_{i}$
for some finite index set I, where each
![]() $T_{i}$
is a monomial generator of the form
$T_{i}$
is a monomial generator of the form
where
![]() $\lambda _{i}\in \mathbb {C}$
with
$\lambda _{i}\in \mathbb {C}$
with
![]() $\Re \left (\lambda _{i}\right )\geq 0$
. Write the finite set
$\Re \left (\lambda _{i}\right )\geq 0$
. Write the finite set
as
for some
![]() $N\in \mathbb {N}$
, and suppose that
$N\in \mathbb {N}$
, and suppose that
![]() $\left (r_{0},\nu _{0}\right )>\ldots >\left (r_{N},\nu _{N}\right )$
with respect to the lexicographic order. For
$\left (r_{0},\nu _{0}\right )>\ldots >\left (r_{N},\nu _{N}\right )$
with respect to the lexicographic order. For
![]() $j=0,\ldots ,N$
, define
$j=0,\ldots ,N$
, define
Writing
![]() $\zeta _{i}\left (x,y\right )=\Im \left (\lambda _{i}\right )\log y+Q_{i}\left (x,y\right )$
and
$\zeta _{i}\left (x,y\right )=\Im \left (\lambda _{i}\right )\log y+Q_{i}\left (x,y\right )$
and
![]() $E_{j}\left (x,y\right )=\sum _{i\in J_{j}}f_{i}\left (x\right )\text {e}^{\text {i}\zeta _{i}\left (x,y\right )}$
, we obtain that
$E_{j}\left (x,y\right )=\sum _{i\in J_{j}}f_{i}\left (x\right )\text {e}^{\text {i}\zeta _{i}\left (x,y\right )}$
, we obtain that
 $$\begin{align*}h\left(x,y\right)=\sum_{j\leq N}E_{j}\left(x,y\right)y^{r_{j}}\left(\log y\right)^{\nu_{j}}. \end{align*}$$
$$\begin{align*}h\left(x,y\right)=\sum_{j\leq N}E_{j}\left(x,y\right)y^{r_{j}}\left(\log y\right)^{\nu_{j}}. \end{align*}$$
Let
![]() $x\in \mathrm {Lim}\left (h,X\right )$
. Suppose that there exists
$x\in \mathrm {Lim}\left (h,X\right )$
. Suppose that there exists
![]() $i\in J_{0}$
such that
$i\in J_{0}$
such that
![]() $f_{i}\left (x\right )=0$
. Then, by Condition (2.a) of Proposition 6.4 and by [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 3.4(2)], we have necessarily that
$f_{i}\left (x\right )=0$
. Then, by Condition (2.a) of Proposition 6.4 and by [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 3.4(2)], we have necessarily that
![]() $r_{0}=\nu _{0}=0$
. Hence, we may suppose that
$r_{0}=\nu _{0}=0$
. Hence, we may suppose that
![]() $N=0$
and
$N=0$
and
![]() $h\left (x,y\right )=\sum _{i\in J_{0}}f_{i}\left (x\right )\text {e}^{\text {i}\zeta _{i}\left (x,y\right )}$
. If there exists
$h\left (x,y\right )=\sum _{i\in J_{0}}f_{i}\left (x\right )\text {e}^{\text {i}\zeta _{i}\left (x,y\right )}$
. If there exists
![]() $i\in J_{0}$
such that either
$i\in J_{0}$
such that either
![]() $\Im \left (\lambda _{i}\right )\not =0$
or
$\Im \left (\lambda _{i}\right )\not =0$
or
![]() $Q_{i}\left (x,y\right )\not =0$
, then by [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 3.4(3)], we obtain that
$Q_{i}\left (x,y\right )\not =0$
, then by [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 3.4(3)], we obtain that
![]() $f_{i}\left (x\right )=0$
. Notice that there is at most one index
$f_{i}\left (x\right )=0$
. Notice that there is at most one index
![]() $i_{0}\in J_{0}$
such that
$i_{0}\in J_{0}$
such that
![]() $\zeta _{i_{0}}\left (x,y\right )=0$
. To conclude, we define
$\zeta _{i_{0}}\left (x,y\right )=0$
. To conclude, we define
 $$\begin{align*}f\left(x\right)=\sum_{i\in\widetilde{I}}\left|f_{i}\left(x\right)\right|{}^{2}. \end{align*}$$
$$\begin{align*}f\left(x\right)=\sum_{i\in\widetilde{I}}\left|f_{i}\left(x\right)\right|{}^{2}. \end{align*}$$
As the class
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
is clearly stable under complex conjugation, f belongs to
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
is clearly stable under complex conjugation, f belongs to
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
. Finally, define
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
. Finally, define
![]() ${g\left (x\right ){\kern-1pt}={\kern-1pt}f_{i_{0}}\left (x\right )}$
if there exists a (necessarily unique) index
${g\left (x\right ){\kern-1pt}={\kern-1pt}f_{i_{0}}\left (x\right )}$
if there exists a (necessarily unique) index
![]() $i_{0}{\kern-1pt}\in{\kern-1pt} I$
such that
$i_{0}{\kern-1pt}\in{\kern-1pt} I$
such that
![]() $\Re \left (\lambda _{i_{0}}\right ){\kern-1pt}={\kern-1pt}\mu _{i_{0}}{\kern-1pt}={\kern-1pt}0\text { and }\zeta _{i_{0}}\left (x,y\right ){\kern-1pt}={\kern-1pt}0$
, and
$\Re \left (\lambda _{i_{0}}\right ){\kern-1pt}={\kern-1pt}\mu _{i_{0}}{\kern-1pt}={\kern-1pt}0\text { and }\zeta _{i_{0}}\left (x,y\right ){\kern-1pt}={\kern-1pt}0$
, and
![]() $g=0$
otherwise.
$g=0$
otherwise.
8 The Fourier-Plancherel transform and
 $\text {L}^p$
-limits
$\text {L}^p$
-limits
We deal here with the question of parametric families of functions of
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
to provide noncompensation arguments in this framework, useful for
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
to provide noncompensation arguments in this framework, useful for
![]() $\text {L}^{p}$
-completeness and the
$\text {L}^{p}$
-completeness and the
![]() $\text {L}^{2}$
-Fourier transform, also known as the Plancherel transform, or the Fourier-Plancherel transform. In [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Section 8], this is treated in the case of the system
$\text {L}^{2}$
-Fourier transform, also known as the Plancherel transform, or the Fourier-Plancherel transform. In [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Section 8], this is treated in the case of the system
![]() $\mathcal {C}^{\mathrm {exp}}$
, which we generalize to our setting of
$\mathcal {C}^{\mathrm {exp}}$
, which we generalize to our setting of
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}$
.
$\mathcal {C}^{\mathbb {C},\mathcal {F}}$
.
We recall from [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18] what it means for a family of functions to be continuously uniformly distributed modulo 1, which extends notions from [Reference WeylWey16, Reference Kuipers and NiederreiterKN74].
Let X be a nonempty subset of
![]() $\mathbb {R}^{m}$
,
$\mathbb {R}^{m}$
,
![]() $N\in \mathbb {N}\setminus \{0\}$
and
$N\in \mathbb {N}\setminus \{0\}$
and
![]() $\rho =\left (\rho _{1},\ldots ,\rho _{N}\right ):X\times [0,+\infty )\to \mathbb {R}^{N}$
be a map. If
$\rho =\left (\rho _{1},\ldots ,\rho _{N}\right ):X\times [0,+\infty )\to \mathbb {R}^{N}$
be a map. If
![]() $I_{1},\ldots ,I_{N}\subseteq \mathbb {R}$
are bounded intervals with nonempty interior, we denote by I the box
$I_{1},\ldots ,I_{N}\subseteq \mathbb {R}$
are bounded intervals with nonempty interior, we denote by I the box
![]() $\prod _{j=1}^{N}I_{j}$
and, for
$\prod _{j=1}^{N}I_{j}$
and, for
![]() $T\ge 0$
and
$T\ge 0$
and
![]() $x\in X$
, we let
$x\in X$
, we let
where
![]() $\{\rho \left (x,t\right )\}$
denotes the vector of fractional parts
$\{\rho \left (x,t\right )\}$
denotes the vector of fractional parts
![]() $\left (\{\rho _{1}\left (x,t\right )\},\ldots ,\{\rho _{N}\left (x,t\right )\}\right )$
of the components of
$\left (\{\rho _{1}\left (x,t\right )\},\ldots ,\{\rho _{N}\left (x,t\right )\}\right )$
of the components of
![]() $\rho $
, that is to say for
$\rho $
, that is to say for
![]() $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
![]() $\{x\}=x-\lfloor x\rfloor $
.
$\{x\}=x-\lfloor x\rfloor $
.
Definition 8.1. With this notation, we say that the map
![]() $\rho $
is continuously uniformly distributed modulo
$\rho $
is continuously uniformly distributed modulo
![]() $1$
on X (abbreviated as c.u.d. mod
$1$
on X (abbreviated as c.u.d. mod
![]() $1$
on X) if for every box
$1$
on X) if for every box
![]() $I\subseteq [0,1)^{N}$
,
$I\subseteq [0,1)^{N}$
,
 $$\begin{align*}\lim_{T\to+\infty}\sup_{x\in X}\frac{\mathrm{vol}_{1}\left(W_{\rho,I,T}^{x}\right)}{T}=\mathrm{vol}_{N}\left(I\right). \end{align*}$$
$$\begin{align*}\lim_{T\to+\infty}\sup_{x\in X}\frac{\mathrm{vol}_{1}\left(W_{\rho,I,T}^{x}\right)}{T}=\mathrm{vol}_{N}\left(I\right). \end{align*}$$
We will use the c.u.d. mod 1 property in Lemma 8.5. In our context, we have to deal with sums of complex exponential functions, with phase of type
![]() $\varphi (x,y)=\sigma \log y+p(x,y)$
, where p is a polynomial in y, or more exactly in
$\varphi (x,y)=\sigma \log y+p(x,y)$
, where p is a polynomial in y, or more exactly in
![]() $y^{\frac {1}{d}}$
, for some positive integer d, and with coefficients some functions of the variable x. We cannot directly use the c.u.d. mod 1 property for those phases since
$y^{\frac {1}{d}}$
, for some positive integer d, and with coefficients some functions of the variable x. We cannot directly use the c.u.d. mod 1 property for those phases since
![]() $\log y$
is not a c.u.d. mod 1 function (although
$\log y$
is not a c.u.d. mod 1 function (although
![]() $\varphi $
turns out to be c.u.d. mod 1 when p is not constant). To overcome this technical difficulty, we compose
$\varphi $
turns out to be c.u.d. mod 1 when p is not constant). To overcome this technical difficulty, we compose
![]() $\varphi $
with
$\varphi $
with
![]() $(x,y)=(x,\mathrm {e}^{t})$
to obtain a phase of type
$(x,y)=(x,\mathrm {e}^{t})$
to obtain a phase of type
![]() $\phi (x,t)=\sigma t+p(x,\mathrm {e}^{t})$
. Now we can use the c.u.d. mod 1 property, the change of variables
$\phi (x,t)=\sigma t+p(x,\mathrm {e}^{t})$
. Now we can use the c.u.d. mod 1 property, the change of variables
![]() $y=\mathrm {e}^{t}$
being harmless in view of the conclusion of Lemma 8.5.
$y=\mathrm {e}^{t}$
being harmless in view of the conclusion of Lemma 8.5.
Proposition 8.2. Let
![]() $\ell ,p\in \mathbb {N}$
and X a compact subset of
$\ell ,p\in \mathbb {N}$
and X a compact subset of
![]() $\mathbb {R}^{m}$
. Consider a map
$\mathbb {R}^{m}$
. Consider a map
![]() $\rho =\left (\phi _{1},\cdots ,\phi _{\ell },\rho _{1},\ldots ,\rho _{p}\right ):X\times [0,+\infty )\to \mathbb {R}^{\ell +p}$
, where for each
$\rho =\left (\phi _{1},\cdots ,\phi _{\ell },\rho _{1},\ldots ,\rho _{p}\right ):X\times [0,+\infty )\to \mathbb {R}^{\ell +p}$
, where for each
![]() $i\in \{1,\ldots ,\ell \}$
, for each
$i\in \{1,\ldots ,\ell \}$
, for each
![]() $j\in \{1,\ldots ,p\}$
,
$j\in \{1,\ldots ,p\}$
,
for some continuous (nonzero) functions
![]() $g_{i}:X\to \mathbb {R}$
, positive integers d and
$g_{i}:X\to \mathbb {R}$
, positive integers d and
![]() $\delta _{i}$
, and for
$\delta _{i}$
, and for
![]() $\sigma _{j}$
real numbers. Assume that for each
$\sigma _{j}$
real numbers. Assume that for each
![]() $x\in X$
, the functions
$x\in X$
, the functions
![]() $t\mapsto \phi _{1}(x,t),\ldots ,t\mapsto \phi _{\ell }(x,t),t\mapsto \rho _{1}\left (x,t\right ),\ldots ,t\mapsto \rho _{p}\left (x,t\right )$
are linearly independent over
$t\mapsto \phi _{1}(x,t),\ldots ,t\mapsto \phi _{\ell }(x,t),t\mapsto \rho _{1}\left (x,t\right ),\ldots ,t\mapsto \rho _{p}\left (x,t\right )$
are linearly independent over
![]() $\mathbb {Q}$
. Then,
$\mathbb {Q}$
. Then,
![]() $\rho $
is c.u.d. mod
$\rho $
is c.u.d. mod
![]() $1$
on X.
$1$
on X.
Before proving the proposition, we make a remark.
Remark 8.3. In the notation of Proposition 8.2, let
![]() $\delta =\max \{\delta _{1},\ldots ,\delta _{\ell }\},$
and for each
$\delta =\max \{\delta _{1},\ldots ,\delta _{\ell }\},$
and for each
![]() $k\in \{1,\ldots ,\delta \}$
, let
$k\in \{1,\ldots ,\delta \}$
, let
![]() $I_{k}=\{i\in \{1,\ldots ,\ell \}:\delta _{i}=k\}.$
The assumption that
$I_{k}=\{i\in \{1,\ldots ,\ell \}:\delta _{i}=k\}.$
The assumption that
![]() $t\mapsto \phi _{1}(x,t),\ldots ,t\mapsto \phi _{\ell }(x,t),t\mapsto \rho _{1}\left (x,t\right ),\ldots ,t\mapsto \rho _{p}\left (x,t\right )$
are linearly independent over
$t\mapsto \phi _{1}(x,t),\ldots ,t\mapsto \phi _{\ell }(x,t),t\mapsto \rho _{1}\left (x,t\right ),\ldots ,t\mapsto \rho _{p}\left (x,t\right )$
are linearly independent over
![]() $\mathbb {Q}$
for each
$\mathbb {Q}$
for each
![]() $x\in X$
is equivalent to saying that for each
$x\in X$
is equivalent to saying that for each
![]() $k\in \{1,\ldots ,\delta \}$
and
$k\in \{1,\ldots ,\delta \}$
and
![]() $x\in X$
, the family of real numbers
$x\in X$
, the family of real numbers
![]() $\left (g_{i}\left (x\right )\right )_{i\in I_{k}}$
is linearly independent over
$\left (g_{i}\left (x\right )\right )_{i\in I_{k}}$
is linearly independent over
![]() $\mathbb {Q}$
, and that the family of real numbers
$\mathbb {Q}$
, and that the family of real numbers
![]() $(\sigma _{1},\ldots ,\sigma _{m})$
is linearly independent over
$(\sigma _{1},\ldots ,\sigma _{m})$
is linearly independent over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Proof of Proposition 8.2.
We may assume that
![]() $\ell \ge 1$
since if
$\ell \ge 1$
since if
![]() $\ell =0$
and the family of linear maps
$\ell =0$
and the family of linear maps
![]() $(t\mapsto \sigma _{1}t,\ldots ,t\mapsto \sigma _{p}t)$
is linearly independent over
$(t\mapsto \sigma _{1}t,\ldots ,t\mapsto \sigma _{p}t)$
is linearly independent over
![]() $\mathbb {Q}$
, then the map
$\mathbb {Q}$
, then the map
![]() $\rho $
is well known to be c.u.d. mod 1 (see [Reference Kuipers and NiederreiterKN74, Exercise 9.27]).
$\rho $
is well known to be c.u.d. mod 1 (see [Reference Kuipers and NiederreiterKN74, Exercise 9.27]).
Assuming
![]() $\ell \ge 1$
, the proof consists in satisfying the version in families of the criterion (8.1) (see [Reference Kuipers and NiederreiterKN74, Theorem 9.9] for the basic case, and [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Proposition 8.7] for the version in families): for any
$\ell \ge 1$
, the proof consists in satisfying the version in families of the criterion (8.1) (see [Reference Kuipers and NiederreiterKN74, Theorem 9.9] for the basic case, and [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Proposition 8.7] for the version in families): for any
![]() $h=(\alpha _{1},\ldots ,\alpha _{\ell },\beta _{1},\ldots ,\beta _{p})\in \mathbb {Z}^{\ell +p}$
,
$h=(\alpha _{1},\ldots ,\alpha _{\ell },\beta _{1},\ldots ,\beta _{p})\in \mathbb {Z}^{\ell +p}$
,
![]() $h\not =0$
,
$h\not =0$
,
 $$ \begin{align} \lim_{T\to+\infty}\dfrac{1}{T}\int_{1}^{T}\mathrm{e}^{2\pi\mathrm{i}\langle h,\rho(x,t)\rangle}\ \mathrm{d}t=0, \end{align} $$
$$ \begin{align} \lim_{T\to+\infty}\dfrac{1}{T}\int_{1}^{T}\mathrm{e}^{2\pi\mathrm{i}\langle h,\rho(x,t)\rangle}\ \mathrm{d}t=0, \end{align} $$
uniformly in
![]() $x\in X$
. We prove, in fact, that for some
$x\in X$
. We prove, in fact, that for some
![]() $T_{0}\ge 1$
,
$T_{0}\ge 1$
,
 $J(T)={\displaystyle \int _{T_{0}}^{T}\mathrm {e}^{2\pi \mathrm {i}\langle h,\rho (x,t)\rangle }\ \mathrm {d}t}$
is bounded from above by a constant not depending on
$J(T)={\displaystyle \int _{T_{0}}^{T}\mathrm {e}^{2\pi \mathrm {i}\langle h,\rho (x,t)\rangle }\ \mathrm {d}t}$
is bounded from above by a constant not depending on
![]() $x\in X$
. To do this, we follow the proof of [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 3.4]: we fix
$x\in X$
. To do this, we follow the proof of [Reference Cluckers, Comte, Rolin and ServiCCRS23, Proposition 3.4]: we fix
![]() $h\in \mathbb {Z}^{\ell +p}$
, define, in the notation of Remark 8.3,
$h\in \mathbb {Z}^{\ell +p}$
, define, in the notation of Remark 8.3,
![]() $G(x)=\sum _{i\in I_{\delta }}\alpha _{i}g_{i}(x)$
,
$G(x)=\sum _{i\in I_{\delta }}\alpha _{i}g_{i}(x)$
,
![]() $G_{k}\left (x\right )=\sum _{j\in I_{k}}\alpha _{i}g_{i}(x)$
, for
$G_{k}\left (x\right )=\sum _{j\in I_{k}}\alpha _{i}g_{i}(x)$
, for
![]() $k\in \{1,\ldots ,\delta -1\}$
, and
$k\in \{1,\ldots ,\delta -1\}$
, and
![]() $\sigma =\sum _{j=1}^{m}\beta _{j}\sigma _{j}$
, and we write
$\sigma =\sum _{j=1}^{m}\beta _{j}\sigma _{j}$
, and we write
For simplicity, we assume that
![]() $I_{k}\not =\emptyset $
, for
$I_{k}\not =\emptyset $
, for
![]() $k=1,\ldots ,\delta $
, which is harmless. Note that the continuous functions
$k=1,\ldots ,\delta $
, which is harmless. Note that the continuous functions
![]() $G_{1},\ldots ,G_{\delta -1}$
are bounded from above on X. By Remark 8.3, the function G has no zero in X since for each
$G_{1},\ldots ,G_{\delta -1}$
are bounded from above on X. By Remark 8.3, the function G has no zero in X since for each
![]() $x\in X$
, the components of
$x\in X$
, the components of
![]() $\rho $
are linearly independent over
$\rho $
are linearly independent over
![]() $\mathbb {Q}$
, and therefore, again by continuity on X,
$\mathbb {Q}$
, and therefore, again by continuity on X,
![]() $\vert G\vert $
is bounded below by a constant
$\vert G\vert $
is bounded below by a constant
![]() $C>0$
on X. It follows that we can fix
$C>0$
on X. It follows that we can fix
![]() $T_{0}$
sufficiently large so that, for each
$T_{0}$
sufficiently large so that, for each
![]() $x\in X$
,
$x\in X$
,
![]() $t\mapsto H(x,t)$
and
$t\mapsto H(x,t)$
and
![]() $t\mapsto \dfrac {\partial H}{\partial t}(x,t)$
are strictly increasing (to
$t\mapsto \dfrac {\partial H}{\partial t}(x,t)$
are strictly increasing (to
![]() $+\infty $
) on
$+\infty $
) on
![]() $[T_{0},+\infty )$
, and we can assume that for all
$[T_{0},+\infty )$
, and we can assume that for all
![]() $x\in X$
,
$x\in X$
,
![]() $\dfrac {\partial H}{\partial t}(x,T_{0})\ge 1$
.
$\dfrac {\partial H}{\partial t}(x,T_{0})\ge 1$
.
Denoting for each
![]() $x\in X$
,
$x\in X$
,
![]() $t=V(x,u)$
the inverse of
$t=V(x,u)$
the inverse of
![]() $u=H(x,t)$
, we perform the change of variables
$u=H(x,t)$
, we perform the change of variables
![]() $u=H(x,t)$
in
$u=H(x,t)$
in
![]() $J(T)$
to obtain
$J(T)$
to obtain
 $$\begin{align*}J(T)=\int_{T_{0}}^{T}\mathrm{e}^{2\pi\mathrm{i}G(x)H(x,t)}\ \mathrm{d}t=\int_{H(x,T_{0})}^{H(x,T)}\dfrac{\mathrm{e}^{2\pi\mathrm{i}G(x)u}}{\frac{\partial H}{\partial t}(x,V(x,u))}\ \mathrm{d}u. \end{align*}$$
$$\begin{align*}J(T)=\int_{T_{0}}^{T}\mathrm{e}^{2\pi\mathrm{i}G(x)H(x,t)}\ \mathrm{d}t=\int_{H(x,T_{0})}^{H(x,T)}\dfrac{\mathrm{e}^{2\pi\mathrm{i}G(x)u}}{\frac{\partial H}{\partial t}(x,V(x,u))}\ \mathrm{d}u. \end{align*}$$
Now, since
 $u\mapsto \dfrac {1}{\frac {\partial H}{\partial t}(x,V(x,u))}$
is monotonically decreasing on
$u\mapsto \dfrac {1}{\frac {\partial H}{\partial t}(x,V(x,u))}$
is monotonically decreasing on
![]() $[H(x,T_{0}),+\infty )$
, by the Second Mean Value Theorem for integrals applied to the real part of
$[H(x,T_{0}),+\infty )$
, by the Second Mean Value Theorem for integrals applied to the real part of
![]() $J(T)$
, we have
$J(T)$
, we have
 $$\begin{align*}\Re(J(T))=\dfrac{1}{\frac{\partial H}{\partial t}(x,T_{0})}\int_{H(x,T_{0})}^{\tau}\cos(2\pi G(x)u)\ \mathrm{d}u, \end{align*}$$
$$\begin{align*}\Re(J(T))=\dfrac{1}{\frac{\partial H}{\partial t}(x,T_{0})}\int_{H(x,T_{0})}^{\tau}\cos(2\pi G(x)u)\ \mathrm{d}u, \end{align*}$$
for some
![]() $\tau \in (H(x,T_{0}),H(x,T)]$
. Since
$\tau \in (H(x,T_{0}),H(x,T)]$
. Since
![]() $u\mapsto \cos \left (2\pi G(x)u\right )$
has an antiderivative with period
$u\mapsto \cos \left (2\pi G(x)u\right )$
has an antiderivative with period
![]() $\frac {1}{\left |G(x)\right |}$
, and since
$\frac {1}{\left |G(x)\right |}$
, and since
![]() $\frac {1}{\left |G(x)\right |}\leq \frac {1}{C}$
, the integral on the right side may be replaced with an integral over an interval of length at most
$\frac {1}{\left |G(x)\right |}\leq \frac {1}{C}$
, the integral on the right side may be replaced with an integral over an interval of length at most
![]() $\frac {1}{C}$
. From the fact that
$\frac {1}{C}$
. From the fact that
![]() $\dfrac {\partial H}{\partial t}(x,T_{0})\ge 1$
, for all
$\dfrac {\partial H}{\partial t}(x,T_{0})\ge 1$
, for all
![]() $x\in X$
, it follows that the real part of
$x\in X$
, it follows that the real part of
![]() $J(T)$
is uniformly bounded from above with respect to
$J(T)$
is uniformly bounded from above with respect to
![]() $x\in X$
, and so is the imaginary part of
$x\in X$
, and so is the imaginary part of
![]() $J(T)$
by the same computation.
$J(T)$
by the same computation.
We now introduce some notation for Lemma 8.4. Consider a cell
where
![]() $A_{0}$
is connected and open in
$A_{0}$
is connected and open in
![]() $\mathbb {R}^{m}$
. Let
$\mathbb {R}^{m}$
. Let
![]() $f:A\to \mathbb {C}$
be defined by
$f:A\to \mathbb {C}$
be defined by
 $$\begin{align*}f\left(x,t\right)=\sum_{j=1}^{n}f_{j}\left(x\right)\mathrm{e}^{\mathrm{i}(\sigma_{j}t+p_{j}(x,\mathrm{e}^{t}))}, \end{align*}$$
$$\begin{align*}f\left(x,t\right)=\sum_{j=1}^{n}f_{j}\left(x\right)\mathrm{e}^{\mathrm{i}(\sigma_{j}t+p_{j}(x,\mathrm{e}^{t}))}, \end{align*}$$
where
![]() $\sigma _{1},\ldots ,\sigma _{n}$
are real numbers,
$\sigma _{1},\ldots ,\sigma _{n}$
are real numbers,
![]() $\left (f_{1},\ldots ,f_{n}\right )$
is a family of (nonzero) analytic functions in
$\left (f_{1},\ldots ,f_{n}\right )$
is a family of (nonzero) analytic functions in
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (A_{0}\right )$
,
$\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (A_{0}\right )$
,
![]() $p_{1}(x,T),\ldots ,p_{n}(x,T)$
are polynomials (in
$p_{1}(x,T),\ldots ,p_{n}(x,T)$
are polynomials (in
![]() $T^{\frac {1}{d}}$
, for some positive integer d) of
$T^{\frac {1}{d}}$
, for some positive integer d) of
![]() $\mathcal {S}(A_{0})\left [T^{\frac {1}{d}}\right ]$
, with analytic coefficients in
$\mathcal {S}(A_{0})\left [T^{\frac {1}{d}}\right ]$
, with analytic coefficients in
![]() $\mathcal {S}\left (A_{0}\right )$
, and
$\mathcal {S}\left (A_{0}\right )$
, and
![]() $p_{j}\left (x,0\right )=0$
for all
$p_{j}\left (x,0\right )=0$
for all
![]() $j\in \{1,\ldots ,n\}$
and all
$j\in \{1,\ldots ,n\}$
and all
![]() $x\in A_{0}$
. We furthermore assume that for
$x\in A_{0}$
. We furthermore assume that for
![]() $j\not =j'$
in
$j\not =j'$
in
![]() $\{1,\ldots ,n\}$
,
$\{1,\ldots ,n\}$
,
![]() $\sigma _{j}t+p_{j}(x,t)\not =\sigma _{j'}t+p_{j'}(x,t)$
(as functions).
$\sigma _{j}t+p_{j}(x,t)\not =\sigma _{j'}t+p_{j'}(x,t)$
(as functions).
Lemma 8.4. In above notation, we may express f on A as
where
![]() $\rho =\left (\phi _{1},\cdots ,\phi _{\ell },\rho _{1},\ldots ,\rho _{p}\right )$
for some
$\rho =\left (\phi _{1},\cdots ,\phi _{\ell },\rho _{1},\ldots ,\rho _{p}\right )$
for some
![]() $\ell ,p\in \mathbb {N}$
, and where for each
$\ell ,p\in \mathbb {N}$
, and where for each
![]() $i\in \{1,\ldots ,\ell \}$
and for each
$i\in \{1,\ldots ,\ell \}$
and for each
![]() $j\in \{1,\ldots ,p\}$
,
$j\in \{1,\ldots ,p\}$
,
for some analytic functions
![]() $g_{i}$
in
$g_{i}$
in
![]() $\mathcal {S}\left (A_{0}\right )$
,
$\mathcal {S}\left (A_{0}\right )$
,
![]() $\delta _{i}\in \mathbb {N}$
,
$\delta _{i}\in \mathbb {N}$
,
![]() $\sigma _{j}\in \mathbb {R}$
, and where
$\sigma _{j}\in \mathbb {R}$
, and where
![]() $F\left (x,z_{1},\ldots ,z_{\ell +p}\right )$
is a Laurent polynomial in the variables
$F\left (x,z_{1},\ldots ,z_{\ell +p}\right )$
is a Laurent polynomial in the variables
![]() $\mathrm {e}^{2\pi \mathrm {i}z_{1}},\ldots ,\mathrm {e}^{2\pi \mathrm {i}z_{\ell +p}}$
with analytic coefficients in
$\mathrm {e}^{2\pi \mathrm {i}z_{1}},\ldots ,\mathrm {e}^{2\pi \mathrm {i}z_{\ell +p}}$
with analytic coefficients in
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (A_{0}\right )$
. If
$\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (A_{0}\right )$
. If
![]() $n=1$
and if
$n=1$
and if
![]() $\sigma _{1}=0$
,
$\sigma _{1}=0$
,
![]() $p_{1}=0$
, then
$p_{1}=0$
, then
![]() $\ell +p=0$
and
$\ell +p=0$
and
![]() $F\left (x\right )=f_{1}\left (x\right )$
. Otherwise, we have
$F\left (x\right )=f_{1}\left (x\right )$
. Otherwise, we have
![]() $\ell +p>0$
, and
$\ell +p>0$
, and
-
(1) there exists a set
 $A_{0}'\subseteq A_{0}$
such that
$A_{0}'\subseteq A_{0}$
such that
 $\mathrm {vol}_{m}\left (A_{0}\setminus A_{0}'\right )=0$
, and for every
$\mathrm {vol}_{m}\left (A_{0}\setminus A_{0}'\right )=0$
, and for every
 $x\in A_{0}'$
,
$x\in A_{0}'$
,
 $z\mapsto F\left (x,z\right )$
is nonconstant,
$z\mapsto F\left (x,z\right )$
is nonconstant, -
(2) for every open set
 $\Omega \subseteq A_{0}$
and every real number
$\Omega \subseteq A_{0}$
and every real number
 $\lambda <\mathrm {vol}_{m}\left (\Omega \right )$
, there exists a real number
$\lambda <\mathrm {vol}_{m}\left (\Omega \right )$
, there exists a real number
 $T_{0}$
and a compact set
$T_{0}$
and a compact set
 $K\subseteq \Omega \cap A_{0}'$
such that
$K\subseteq \Omega \cap A_{0}'$
such that
 $K\times [T_{0},+\infty )\subseteq A$
,
$K\times [T_{0},+\infty )\subseteq A$
,
 $\lambda \le \mathrm {vol}_{m}\left (K\right )\le \mathrm {vol}_{m}(\Omega )$
, and
$\lambda \le \mathrm {vol}_{m}\left (K\right )\le \mathrm {vol}_{m}(\Omega )$
, and
 $\rho \restriction {K\times [T_{0},+\infty )}$
is c.u.d. mod 1 on K.
$\rho \restriction {K\times [T_{0},+\infty )}$
is c.u.d. mod 1 on K.
Proof. The case
![]() $n=1$
,
$n=1$
,
![]() $\sigma _{1}=0$
and
$\sigma _{1}=0$
and
![]() $p_{1}=0$
being trivial, we may assume that
$p_{1}=0$
being trivial, we may assume that
![]() $\sigma _{1}\not =0$
or
$\sigma _{1}\not =0$
or
![]() $p_{1}\not =0$
. For each
$p_{1}\not =0$
. For each
![]() $j\in \{1,\ldots ,n\}$
, we write
$j\in \{1,\ldots ,n\}$
, we write
 $$\begin{align*}\sigma_{j}t+p_{j}\left(x,\mathrm{e}^{t}\right)=\sigma_{j}t+\sum_{k=1}^{D}h_{j,k}\left(x\right)\mathrm{e}^{\frac{k}{d}t} \end{align*}$$
$$\begin{align*}\sigma_{j}t+p_{j}\left(x,\mathrm{e}^{t}\right)=\sigma_{j}t+\sum_{k=1}^{D}h_{j,k}\left(x\right)\mathrm{e}^{\frac{k}{d}t} \end{align*}$$
with
![]() $D\in \mathbb {N}$
and
$D\in \mathbb {N}$
and
![]() $h_{j,k}\in \mathcal {S}\left (A_{0}\right )$
. For each
$h_{j,k}\in \mathcal {S}\left (A_{0}\right )$
. For each
![]() $k\in \{1,\ldots ,D\}$
, fix
$k\in \{1,\ldots ,D\}$
, fix
![]() $I_{k}\subseteq \{1,\ldots ,n\}$
such that
$I_{k}\subseteq \{1,\ldots ,n\}$
such that
![]() $\left (h_{i,k}\right )_{i\in I_{k}}$
is a basis of the
$\left (h_{i,k}\right )_{i\in I_{k}}$
is a basis of the
![]() $\mathbb {Q}$
-vector space generated by the family
$\mathbb {Q}$
-vector space generated by the family
![]() $\left (h_{j,k}\right )_{j\in \{1,\ldots ,n\}}$
(as functions of x), and fix
$\left (h_{j,k}\right )_{j\in \{1,\ldots ,n\}}$
(as functions of x), and fix
![]() $Q\subseteq \{1,\ldots ,n\}$
such that
$Q\subseteq \{1,\ldots ,n\}$
such that
![]() $\left (\sigma _{q}\right )_{q\in Q}$
is a basis of the
$\left (\sigma _{q}\right )_{q\in Q}$
is a basis of the
![]() $\mathbb {Q}$
-vector space generated by the family
$\mathbb {Q}$
-vector space generated by the family
![]() $\left (\sigma _{j}\right )_{j\in \{1,\ldots ,n\}}$
. We then set
$\left (\sigma _{j}\right )_{j\in \{1,\ldots ,n\}}$
. We then set
We fix a positive integer
![]() $\eta $
such that for each
$\eta $
such that for each
![]() $\left (j,k\right )\in \{1,\ldots ,n\}\times \{1,\ldots ,D\}$
,
$\left (j,k\right )\in \{1,\ldots ,n\}\times \{1,\ldots ,D\}$
,
 $$\begin{align*}h_{j,k}=\sum_{i\in I_{k}}\frac{\alpha_{j;i,k}}{\eta}h_{i,k},\ \sigma_{j}=\sum_{q\in Q}\frac{\beta_{j;q}}{\eta}\sigma_{q} \end{align*}$$
$$\begin{align*}h_{j,k}=\sum_{i\in I_{k}}\frac{\alpha_{j;i,k}}{\eta}h_{i,k},\ \sigma_{j}=\sum_{q\in Q}\frac{\beta_{j;q}}{\eta}\sigma_{q} \end{align*}$$
for unique tuples
![]() $\left (\alpha _{j;i,k}\right )_{i\in I_{k}}$
and
$\left (\alpha _{j;i,k}\right )_{i\in I_{k}}$
and
![]() $(\beta _{j;q})_{q\in L}$
of elements of
$(\beta _{j;q})_{q\in L}$
of elements of
![]() $\mathbb {Z}$
. With this notation, we have
$\mathbb {Z}$
. With this notation, we have
 $$ \begin{align*} f\left(x,t\right) & =\sum_{j=1}^{n}f_{j}\left(x\right)\mathrm{e}^{\mathrm{i}\sigma_{j}t+\mathrm{i}\sum_{k=1}^{d}h_{j,k}\left(x\right)\mathrm{e}^{\frac{k}{d}t}}\\ & =\sum_{j=1}^{n}f_{j}\left(x\right)\mathrm{e}^{\mathrm{i}\sum_{q\in Q}\frac{\beta_{j;q}}{\eta}\sigma_{q}t+\mathrm{i}\sum_{k=1}^{d}\sum_{i\in I_{k}}\frac{\alpha_{j;i,k}}{\eta}h_{i,k}\left(x\right)\mathrm{e}^{\frac{k}{d}t}}\\ & =\sum_{j=1}^{n}f_{j}\left(x\right)\prod_{q\in Q}\left(\mathrm{e}^{2\pi\mathrm{i}\rho_{q}(t)}\right)^{\beta_{j;q}}\prod_{\left(i,k\right)\in I}\left(\mathrm{e}^{2\pi\mathrm{i}\phi_{i,k}\left(x,t\right)}\right)^{\alpha_{j;i,k}}=F\left(x,\left(\phi_{i,k}\left(x,t\right)\right)_{\left(i,k\right)\in I},(\rho_{q})_{q\in Q}\right), \end{align*} $$
$$ \begin{align*} f\left(x,t\right) & =\sum_{j=1}^{n}f_{j}\left(x\right)\mathrm{e}^{\mathrm{i}\sigma_{j}t+\mathrm{i}\sum_{k=1}^{d}h_{j,k}\left(x\right)\mathrm{e}^{\frac{k}{d}t}}\\ & =\sum_{j=1}^{n}f_{j}\left(x\right)\mathrm{e}^{\mathrm{i}\sum_{q\in Q}\frac{\beta_{j;q}}{\eta}\sigma_{q}t+\mathrm{i}\sum_{k=1}^{d}\sum_{i\in I_{k}}\frac{\alpha_{j;i,k}}{\eta}h_{i,k}\left(x\right)\mathrm{e}^{\frac{k}{d}t}}\\ & =\sum_{j=1}^{n}f_{j}\left(x\right)\prod_{q\in Q}\left(\mathrm{e}^{2\pi\mathrm{i}\rho_{q}(t)}\right)^{\beta_{j;q}}\prod_{\left(i,k\right)\in I}\left(\mathrm{e}^{2\pi\mathrm{i}\phi_{i,k}\left(x,t\right)}\right)^{\alpha_{j;i,k}}=F\left(x,\left(\phi_{i,k}\left(x,t\right)\right)_{\left(i,k\right)\in I},(\rho_{q})_{q\in Q}\right), \end{align*} $$
where for each
![]() $\left (i,k\right )\in I$
,
$\left (i,k\right )\in I$
,
![]() $\phi _{i,k}\left (x,t\right )=\frac {h_{i,k}\left (x\right )}{2\pi \eta }\mathrm {e}^{\frac {k}{d}t}$
, for each
$\phi _{i,k}\left (x,t\right )=\frac {h_{i,k}\left (x\right )}{2\pi \eta }\mathrm {e}^{\frac {k}{d}t}$
, for each
![]() $q\in Q$
,
$q\in Q$
,
![]() $\rho _{q}\left (t\right )=\frac {\sigma _{q}}{2\pi \eta }t$
, and
$\rho _{q}\left (t\right )=\frac {\sigma _{q}}{2\pi \eta }t$
, and
 $$\begin{align*}F(x,(z_{i,k})_{(i,k)\in I},(z_{q})_{q\in Q})=\sum_{j=1}^{n}f_{j}\left(x\right)\prod_{q\in Q}\left(\mathrm{e}^{2\pi\mathrm{i}z_{q}}\right)^{\beta_{j;q}}\prod_{\left(i,k\right)\in I}\left(\mathrm{e}^{2\pi\mathrm{i}z_{i,k}}\right)^{\alpha_{j;i,k}}. \end{align*}$$
$$\begin{align*}F(x,(z_{i,k})_{(i,k)\in I},(z_{q})_{q\in Q})=\sum_{j=1}^{n}f_{j}\left(x\right)\prod_{q\in Q}\left(\mathrm{e}^{2\pi\mathrm{i}z_{q}}\right)^{\beta_{j;q}}\prod_{\left(i,k\right)\in I}\left(\mathrm{e}^{2\pi\mathrm{i}z_{i,k}}\right)^{\alpha_{j;i,k}}. \end{align*}$$
For each
![]() $j\in \{1,\ldots n\}$
,
$j\in \{1,\ldots n\}$
,
![]() $f_{j}$
is a nonzero analytic function on the connected and open set
$f_{j}$
is a nonzero analytic function on the connected and open set
![]() $A_{0}$
, so the set
$A_{0}$
, so the set
satisfies
![]() $\mathrm {vol}_{m}\left (A_{0}\setminus U\right )=0$
. Denote by
$\mathrm {vol}_{m}\left (A_{0}\setminus U\right )=0$
. Denote by
![]() $\mathcal {F}$
the Laurent polynomial associated to F
$\mathcal {F}$
the Laurent polynomial associated to F
 $$\begin{align*}\mathcal{F}(x,(Z_{i,k})_{(i,k)\in I},(Z_{q})_{q\in Q})=\sum_{j=1}^{n}f_{j}\left(x\right)\prod_{q\in Q}Z_{q}^{\beta_{j;q}}\prod_{\left(i,k\right)\in I}Z_{i,k}^{\alpha_{j;i,k}}. \end{align*}$$
$$\begin{align*}\mathcal{F}(x,(Z_{i,k})_{(i,k)\in I},(Z_{q})_{q\in Q})=\sum_{j=1}^{n}f_{j}\left(x\right)\prod_{q\in Q}Z_{q}^{\beta_{j;q}}\prod_{\left(i,k\right)\in I}Z_{i,k}^{\alpha_{j;i,k}}. \end{align*}$$
Note that
![]() $F(x,z)=F(x,(z_{i,k})_{(i,k)\in I},(z_{q})_{q\in Q})=\mathcal {F}(x,(\mathrm {e}^{2\pi \mathrm {i}z_{i,k}})_{(i,k)\in I},(\mathrm {e}^{2\pi \mathrm {i}z_{q}})_{q\in Q})$
.
$F(x,z)=F(x,(z_{i,k})_{(i,k)\in I},(z_{q})_{q\in Q})=\mathcal {F}(x,(\mathrm {e}^{2\pi \mathrm {i}z_{i,k}})_{(i,k)\in I},(\mathrm {e}^{2\pi \mathrm {i}z_{q}})_{q\in Q})$
.
Since we assumed
![]() $\sigma _{1}\not =0$
or
$\sigma _{1}\not =0$
or
![]() $p_{1}\not =0$
, we can always suppose
$p_{1}\not =0$
, we can always suppose
![]() $\sigma _{1}\in (\sigma _{q})_{q\in Q}$
or, for some k,
$\sigma _{1}\in (\sigma _{q})_{q\in Q}$
or, for some k,
![]() $h_{1,k}\in (h_{i,k})_{i\in I_{k}}$
, respectively. Thus,
$h_{1,k}\in (h_{i,k})_{i\in I_{k}}$
, respectively. Thus,
![]() $\mathcal {F}$
certainly contains a term of the form
$\mathcal {F}$
certainly contains a term of the form
![]() $f_{1}(x)Z_{1}$
or
$f_{1}(x)Z_{1}$
or
![]() $f_{1}(x)Z_{1,k}$
. Moreover, since for
$f_{1}(x)Z_{1,k}$
. Moreover, since for
![]() $j\not =j'$
in
$j\not =j'$
in
![]() $\{1,\ldots ,n\}$
,
$\{1,\ldots ,n\}$
,
![]() $\sigma _{j}t+p_{j}(x,t)\not =\sigma _{j'}t+p_{j'}(x,t)$
(as functions), the monomial terms in the above expression of
$\sigma _{j}t+p_{j}(x,t)\not =\sigma _{j'}t+p_{j'}(x,t)$
(as functions), the monomial terms in the above expression of
![]() $\mathcal {F}$
cannot cancel out. It follows that for each
$\mathcal {F}$
cannot cancel out. It follows that for each
![]() $x\in U$
,
$x\in U$
,
![]() $\mathcal {F}$
is not constant as a Laurent polynomial, and in particular, for each
$\mathcal {F}$
is not constant as a Laurent polynomial, and in particular, for each
![]() $x\in U$
, not constant on the real torus
$x\in U$
, not constant on the real torus
![]() $(S^{1})^{\vert Q\vert +\vert I\vert }$
. As a consequence, for each
$(S^{1})^{\vert Q\vert +\vert I\vert }$
. As a consequence, for each
![]() $x\in U$
, the trigonometric polynomial
$x\in U$
, the trigonometric polynomial
![]() $z\mapsto F\left (x,z\right )$
is not constant.
$z\mapsto F\left (x,z\right )$
is not constant.
Observe that since
![]() $\left (h_{i,k}\right )_{i\in I_{k}}$
is independent over
$\left (h_{i,k}\right )_{i\in I_{k}}$
is independent over
![]() $\mathbb {Q}$
(as functions of x), for each
$\mathbb {Q}$
(as functions of x), for each
![]() $k\in \{1,\ldots ,D\}$
and nonzero tuple
$k\in \{1,\ldots ,D\}$
and nonzero tuple
![]() $c=\left (c_{i}\right )\in \mathbb {Z}^{\vert I_{k}\vert }$
,
$c=\left (c_{i}\right )\in \mathbb {Z}^{\vert I_{k}\vert }$
,
![]() $\sum _{i\in I_{k}}c_{i}h_{i,k}$
is a nonzero analytic function on
$\sum _{i\in I_{k}}c_{i}h_{i,k}$
is a nonzero analytic function on
![]() $A_{0}$
, so the set
$A_{0}$
, so the set
![]() $\left \{ x\in U:\sum _{i\in I_{k}}c_{i}h_{i,k}\left (x\right )=0\right \} $
cannot have positive measure, and the set
$\left \{ x\in U:\sum _{i\in I_{k}}c_{i}h_{i,k}\left (x\right )=0\right \} $
cannot have positive measure, and the set
 $$\begin{align*}A_{0}':=U\setminus\left(\bigcup_{k=1}^{D}\bigcup_{c\in\mathbb{Z}^{\vert I_{k}\vert}\setminus\{0\}}\left\{ x\in U:\sum_{i\in I_{k}}c_{i}h_{i,k}\left(x\right)=0\right\} \right) \end{align*}$$
$$\begin{align*}A_{0}':=U\setminus\left(\bigcup_{k=1}^{D}\bigcup_{c\in\mathbb{Z}^{\vert I_{k}\vert}\setminus\{0\}}\left\{ x\in U:\sum_{i\in I_{k}}c_{i}h_{i,k}\left(x\right)=0\right\} \right) \end{align*}$$
satisfies
![]() $\mathrm {vol}_{m}\left (A_{0}\setminus A_{0}'\right )=0$
as well. This gives (1), for this set
$\mathrm {vol}_{m}\left (A_{0}\setminus A_{0}'\right )=0$
as well. This gives (1), for this set
![]() $A_{0}'\subset U$
.
$A_{0}'\subset U$
.
The set
![]() $A_{0}'$
is defined such that for each
$A_{0}'$
is defined such that for each
![]() $k\in \{1,\ldots ,D\}$
, for each
$k\in \{1,\ldots ,D\}$
, for each
![]() $x\in A_{0}'$
, the family of numbers
$x\in A_{0}'$
, the family of numbers
![]() $\left (h_{i,k}\left (x\right )\right )_{\left (i,k\right )\in I}$
is linearly independent over
$\left (h_{i,k}\left (x\right )\right )_{\left (i,k\right )\in I}$
is linearly independent over
![]() $\mathbb {Q}$
. By Remark 8.3, for each
$\mathbb {Q}$
. By Remark 8.3, for each
![]() $x\in A_{0}'$
, the family of functions
$x\in A_{0}'$
, the family of functions
![]() $\left (t\mapsto \phi _{i,k}\left (x,t\right )\right )_{\left (i,k\right )\in I}$
is also linearly independent over
$\left (t\mapsto \phi _{i,k}\left (x,t\right )\right )_{\left (i,k\right )\in I}$
is also linearly independent over
![]() $\mathbb {Q}$
. However, the family of functions
$\mathbb {Q}$
. However, the family of functions
![]() $\left (t\mapsto \rho _{q}\left (t\right )\right )_{q\in Q}$
is linearly independent over
$\left (t\mapsto \rho _{q}\left (t\right )\right )_{q\in Q}$
is linearly independent over
![]() $\mathbb {Q}$
, since so is the family of real numbers
$\mathbb {Q}$
, since so is the family of real numbers
![]() $(\sigma _{q})_{q\in Q}$
. In particular, for each
$(\sigma _{q})_{q\in Q}$
. In particular, for each
![]() $x\in A_{0}'$
, the family of functions
$x\in A_{0}'$
, the family of functions
![]() $t\mapsto \rho (x,t)=\left (\left (\phi _{i,k}\left (x,t\right )\right )_{\left (i,k\right )\in I},(\rho _{q}(t))_{q\in Q}\right )$
is linearly independent over
$t\mapsto \rho (x,t)=\left (\left (\phi _{i,k}\left (x,t\right )\right )_{\left (i,k\right )\in I},(\rho _{q}(t))_{q\in Q}\right )$
is linearly independent over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Given an open set
![]() $\Omega \subseteq A_{0}$
and a positive real number
$\Omega \subseteq A_{0}$
and a positive real number
![]() $\lambda $
with
$\lambda $
with
![]() $\lambda <\mathrm {vol}_{m}\left (\Omega \right )=\mathrm {vol}_{m}\left (\Omega \cap A_{0}'\right )$
, the inner regularity of the Lebesgue measure shows that we may fix a compact set
$\lambda <\mathrm {vol}_{m}\left (\Omega \right )=\mathrm {vol}_{m}\left (\Omega \cap A_{0}'\right )$
, the inner regularity of the Lebesgue measure shows that we may fix a compact set
![]() $K\subseteq \Omega \cap A_{0}'$
with
$K\subseteq \Omega \cap A_{0}'$
with
![]() $\mathrm {vol}_{m}\left (K\right )\geq \lambda $
. Since K is compact and
$\mathrm {vol}_{m}\left (K\right )\geq \lambda $
. Since K is compact and
![]() $a\left (x\right )$
is continuous, we may fix
$a\left (x\right )$
is continuous, we may fix
![]() $T_{0}$
sufficiently large so that
$T_{0}$
sufficiently large so that
![]() $K\times [T_{0},+\infty )\subseteq A$
. Proposition 8.2 then shows that the restriction of
$K\times [T_{0},+\infty )\subseteq A$
. Proposition 8.2 then shows that the restriction of
![]() $\rho $
to
$\rho $
to
![]() $K\times [T_{0},+\infty )$
is c.u.d. mod
$K\times [T_{0},+\infty )$
is c.u.d. mod
![]() $1$
on K, which completes the proof of (2).
$1$
on K, which completes the proof of (2).
Recall that
 $$\begin{align*}f\left(x,y\right)=\sum_{j=1}^{n}f_{j}\left(x\right)y^{\mathrm{i}\sigma_{j}}\mathrm{e}^{\mathrm{i}p_{j}(x,y)}, \end{align*}$$
$$\begin{align*}f\left(x,y\right)=\sum_{j=1}^{n}f_{j}\left(x\right)y^{\mathrm{i}\sigma_{j}}\mathrm{e}^{\mathrm{i}p_{j}(x,y)}, \end{align*}$$
where
![]() $\sigma _{1},\ldots ,\sigma _{n}$
are real numbers,
$\sigma _{1},\ldots ,\sigma _{n}$
are real numbers,
![]() $\left (f_{1},\ldots ,f_{n}\right )$
is a family of (nonzero) analytic functions in
$\left (f_{1},\ldots ,f_{n}\right )$
is a family of (nonzero) analytic functions in
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (A_{0}\right )$
,
$\mathcal {C}^{\mathbb {C},\mathcal {F}}\left (A_{0}\right )$
,
![]() $p_{1}(x,T),\ldots ,p_{n}(x,T)$
are polynomials (in
$p_{1}(x,T),\ldots ,p_{n}(x,T)$
are polynomials (in
![]() $T^{\frac {1}{d}}$
, for some positive integer d) of
$T^{\frac {1}{d}}$
, for some positive integer d) of
![]() $\mathcal {S}(A_{0})\left [T^{\frac {1}{d}}\right ]$
, with analytic coefficients in
$\mathcal {S}(A_{0})\left [T^{\frac {1}{d}}\right ]$
, with analytic coefficients in
![]() $\mathcal {S}\left (A_{0}\right )$
, and
$\mathcal {S}\left (A_{0}\right )$
, and
![]() $p_{j}\left (x,0\right )=0$
for all
$p_{j}\left (x,0\right )=0$
for all
![]() $j\in \{1,\ldots ,n\}$
and
$j\in \{1,\ldots ,n\}$
and
![]() $x\in A_{0}$
. Furthermore, we assume that for
$x\in A_{0}$
. Furthermore, we assume that for
![]() $j\not =j'$
in
$j\not =j'$
in
![]() $\{1,\ldots ,n\}$
,
$\{1,\ldots ,n\}$
,
![]() $\sigma _{j}+p_{j}(x,y)\not =\sigma _{j'}+p_{j'}(x,y)$
(as functions).
$\sigma _{j}+p_{j}(x,y)\not =\sigma _{j'}+p_{j'}(x,y)$
(as functions).
Lemma 8.5. In the notation above, there exist
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $\Delta>0$
, a strictly increasing sequence
$\Delta>0$
, a strictly increasing sequence
![]() $\left (y_{j}\right )_{j\in \mathbb {N}}$
in
$\left (y_{j}\right )_{j\in \mathbb {N}}$
in
![]() $\mathbb {R}$
diverging to
$\mathbb {R}$
diverging to
![]() $+\infty $
, a compact set
$+\infty $
, a compact set
![]() $K\subset A_{0}$
, and a sequence
$K\subset A_{0}$
, and a sequence
![]() $\left (X_{j}\right )_{j\in \mathbb {N}}$
of Lebesgue measurable subsets of K, with, for all
$\left (X_{j}\right )_{j\in \mathbb {N}}$
of Lebesgue measurable subsets of K, with, for all
![]() $j\in \mathbb {N}$
,
$j\in \mathbb {N}$
,
![]() $\mathrm {vol}_{m}\left (X_{j}\right )\ge \Delta $
,
$\mathrm {vol}_{m}\left (X_{j}\right )\ge \Delta $
,
![]() $X_{2j+1}\subseteq X_{2j}$
, and such that, for all
$X_{2j+1}\subseteq X_{2j}$
, and such that, for all
![]() $x_{0}\in X_{2j}$
,
$x_{0}\in X_{2j}$
,
![]() $x_{1}\in X_{2j+1}$
,
$x_{1}\in X_{2j+1}$
,
Proof. Let
![]() $\tilde {f}(x,t):=f(x,\mathrm {e}^{t})$
for any
$\tilde {f}(x,t):=f(x,\mathrm {e}^{t})$
for any
![]() $(x,t)$
such that
$(x,t)$
such that
![]() $(x,\mathrm {e}^{t})\in A$
. Then, we can apply Lemma 8.4 to
$(x,\mathrm {e}^{t})\in A$
. Then, we can apply Lemma 8.4 to
![]() $\tilde {f}$
, so that the hypothesis of [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Lemma 8.10] is satisfied by
$\tilde {f}$
, so that the hypothesis of [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Lemma 8.10] is satisfied by
![]() $\tilde {f}$
. It immediately follows that the conclusions of our lemma are satisfied by
$\tilde {f}$
. It immediately follows that the conclusions of our lemma are satisfied by
![]() $\tilde {f}$
, for a sequence of real numbers
$\tilde {f}$
, for a sequence of real numbers
![]() $(t_{j})_{j\in \mathbb {N}}$
diverging to
$(t_{j})_{j\in \mathbb {N}}$
diverging to
![]() $+\infty $
. It now suffices to set
$+\infty $
. It now suffices to set
![]() $y_{j}=\mathrm {e}^{t_{j}}$
to conclude the proof of the lemma.
$y_{j}=\mathrm {e}^{t_{j}}$
to conclude the proof of the lemma.
Definition 8.6. Let
![]() $X\subseteq \mathbb {R}^{m}$
and
$X\subseteq \mathbb {R}^{m}$
and
![]() $f\colon X\times \mathbb {R}\to \mathbb {C}$
be Lebesgue measurable, and
$f\colon X\times \mathbb {R}\to \mathbb {C}$
be Lebesgue measurable, and
![]() $p\in [1,+\infty ]$
. For each
$p\in [1,+\infty ]$
. For each
![]() $y\in \mathbb {R}$
, define
$y\in \mathbb {R}$
, define
![]() $f_{y}:X\to \mathbb {C}$
by
$f_{y}:X\to \mathbb {C}$
by
![]() $f_{y}\left (x\right )=f\left (x,y\right )$
for all
$f_{y}\left (x\right )=f\left (x,y\right )$
for all
![]() $x\in X$
. We say that the family of functions
$x\in X$
. We say that the family of functions
![]() $\left (f_{y}\right )_{y\in \mathbb {R}}$
is Cauchy in
$\left (f_{y}\right )_{y\in \mathbb {R}}$
is Cauchy in
![]() $L^{p}\left (X\right )$
as
$L^{p}\left (X\right )$
as
![]() $y\to +\infty $
if for each
$y\to +\infty $
if for each
![]() $y\in \mathbb {R}$
,
$y\in \mathbb {R}$
,
![]() $f_{y}\in L^{p}\left (X\right )$
, and for all
$f_{y}\in L^{p}\left (X\right )$
, and for all
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $y_{0}\in \mathbb {R}$
such that
$y_{0}\in \mathbb {R}$
such that
Theorem 8.7. Let
![]() $p\in [1,+\infty ]$
and
$p\in [1,+\infty ]$
and
![]() $f\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, for some subanalytic set
$f\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\left (X\times \mathbb {R}\right )$
, for some subanalytic set
![]() $X\subseteq \mathbb {R}^{m}$
, and suppose that
$X\subseteq \mathbb {R}^{m}$
, and suppose that
![]() $\left (f_{y}\right )_{y\in \mathbb {R}}$
is Cauchy in
$\left (f_{y}\right )_{y\in \mathbb {R}}$
is Cauchy in
![]() $L^{p}\left (X\right )$
as
$L^{p}\left (X\right )$
as
![]() $y\to +\infty $
. Then, there exist
$y\to +\infty $
. Then, there exist
![]() $g\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\cap L^{p}\left (X\right )$
and a subanalytic set
$g\in \mathcal {C}^{\mathbb {C},\mathcal {F}}\cap L^{p}\left (X\right )$
and a subanalytic set
![]() $X_{0}\subseteq X$
such that
$X_{0}\subseteq X$
such that
![]() $\mathrm {vol}_{m}\left (X\setminus X_{0}\right )=0$
,
$\mathrm {vol}_{m}\left (X\setminus X_{0}\right )=0$
,
and
Proof. Writing f as a sum of generators as in Theorem 7.11, we proceed as in the proof of [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Proposition 8.2], using Lemma 8.5 instead of [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Lemma 8.10].
As a direct consequence of Proposition 8.7 (see, for instance, the proof of [Reference Cluckers, Comte, Miller, Rolin and ServiCCMRS18, Theorem 8.3]), we obtain the following result.
Theorem 8.8. Let ![]() be the Fourier-Plancherel extension of the Fourier transform to
be the Fourier-Plancherel extension of the Fourier transform to
![]() $L^{2}\left (\mathbb {R}^{n}\right )$
. Then, the image of
$L^{2}\left (\mathbb {R}^{n}\right )$
. Then, the image of
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}(\mathbb {R}^{n})\cap L^{2}\left (\mathbb {R}^{n}\right )$
under
$\mathcal {C}^{\mathbb {C},\mathcal {F}}(\mathbb {R}^{n})\cap L^{2}\left (\mathbb {R}^{n}\right )$
under ![]() is
is
![]() $\mathcal {C}^{\mathbb {C},\mathcal {F}}(\mathbb {R}^{n})\cap L^{2}\left (\mathbb {R}^{n}\right )$
.
$\mathcal {C}^{\mathbb {C},\mathcal {F}}(\mathbb {R}^{n})\cap L^{2}\left (\mathbb {R}^{n}\right )$
.
Stability under parametric Fourier-Plancherel transforms is formulated and shown similarly.
Acknowledgement
The third author would like to thank the Fields Institute for Research in Mathematical Sciences for its hospitality and financial support, as part of this work was done while at its Thematic Program on Tame Geometry and Applications in 2022. The first author was partially supported by KU Leuven IF C16/23/010 and the Labex CEMPI (ANR-11-LABX-0007-01).
Competing interest
The authors have no competing interest to declare.
Financial support
The author R. C. was partially supported by KU Leuven IF C16/23/010 and the Labex CEMPI (ANR-11-LABX-0007-01).