Research Papers
A bounded growth population subjected to emigrations due to population pressure
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 571-582
-
- Article
- Export citation
On Fibonacci (or lagged Bienaymé-Galton-Watson) branching processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 583-591
-
- Article
- Export citation
On the convergence of stochastically monotone sequences of random variables and some applications
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 592-605
-
- Article
- Export citation
On the distribution of random lines
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 606-616
-
- Article
- Export citation
On the first-order bilinear time series model
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 617-627
-
- Article
- Export citation
A hide–search game
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 628-640
-
- Article
- Export citation
Dynamically optimized replacement with a Markovian renewal process
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 641-651
-
- Article
- Export citation
A characterization of the negative exponential distribution with application to reliability theory
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 652-659
-
- Article
- Export citation
Diffusion approximations for the cooperative service of voice and data messages
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 660-671
-
- Article
- Export citation
An analysis of the fixed-cycle traffic-light problem
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 672-683
-
- Article
- Export citation
Queues with paired customers
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 684-696
-
- Article
- Export citation
Another look at the two-lift problem
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 697-706
-
- Article
- Export citation
On the comparison of waiting times in tandem queues
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 707-714
-
- Article
- Export citation
Short Communications
Waveforms and velocities for models of spatial infection
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 715-720
-
- Article
- Export citation
Simpler proofs of two threshold theorems for a general stochastic epidemic
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 721-724
-
- Article
- Export citation
The determination of the age of a clone from characteristics of its geographical distribution
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 725-731
-
- Article
- Export citation
Some aspects of the non-asymptotic behaviour of a two-dimensional invasion process
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 732-737
-
- Article
- Export citation
Maintainable regions in a Markov manpower model
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 738-742
-
- Article
- Export citation
Random exchanges of information
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 743-746
-
- Article
- Export citation
Markov chains in small time intervals
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 747-751
-
- Article
- Export citation

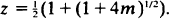 Various properties of
Various properties of 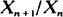 to
to  where
where