Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-16T19:04:21.479Z Has data issue: false hasContentIssue false
  • English
  • Français

Cluster categories for marked surfaces: punctured case

Part of: Homological methods Representation theory of rings and algebras Low-dimensional topology Abelian categories

Published online by Cambridge University Press:  15 June 2017

Yu Qiu  and
Yu Zhou
Yu Qiu
Affiliation:
Department of Mathematics, Chinese University of Hong Kong, Shatin, N.T., Hong Kong email [email protected]
Yu Zhou
Affiliation:
Department of Mathematical Sciences, Norwegian University of Science and Technology, N-7491, Trondheim, Norway email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

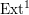We study cluster categories arising from marked surfaces (with punctures and non-empty boundaries). By constructing skewed-gentle algebras, we show that there is a bijection between tagged curves and string objects. Applications include interpreting dimensions of $\operatorname{Ext}^{1}$ as intersection numbers of tagged curves and Auslander–Reiten translation as tagged rotation. An important consequence is that the cluster(-tilting) exchange graphs of such cluster categories are connected.

Keywords

cluster categoriesintersection numberscluster exchange graphsskewed-gentle algebras

MSC classification

Primary: 16G20: Representations of quivers and partially ordered sets 18E30: Derived categories, triangulated categories 16E30: Homological functors on modules (Tor, Ext, etc.) 57M50: Geometric structures on low-dimensional manifolds
Secondary: 16G70: Auslander-Reiten sequences (almost split sequences) and Auslander-Reiten quivers
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 9 , September 2017 , pp. 1779 - 1819
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alim, M., Cecotti, S., Córdova, C., Espahbodi, S., Rastogi, A. and Vafa, C., BPS quivers and spectra of complete N = 2 quantum field theories , Comm. Math. Phys. 323 (2013), 1185–1227.CrossRefGoogle Scholar
Amiot, C., Cluster categories for algebras of global dimension 2 and quivers with potential , Ann. Inst. Fourier (Grenoble) 59 (2009), 2525–2590.Google Scholar
Assem, I., Brüstle, T., Charbonneau-Jodoin, G. and Plamondon, P. G., Gentle algebras arising from surface triangulations , Algebra Number Theory 4 (2012), 201–229.Google Scholar
Bondarenko, V. M., Representations of bundles of semichained sets and their applications , St. Petersburg Math. J. 3 (1992), 973–996.Google Scholar
Brüstle, T. and Qiu, Y., Tagged mapping class groups: Auslander–Reiten translation , Math. Z. 279 (2015), 1103–1120.Google Scholar
Brüstle, T. and Zhang, J., On the cluster category of a marked surface without punctures , Algebra Number Theory 5 (2011), 529–566.CrossRefGoogle Scholar
Buan, A. B., Marsh, R., Reineke, M., Reiten, I. and Todorov, G., Tilting theory and cluster combinatorics , Adv. Math. 204 (2006), 572–618.Google Scholar
Caldero, P., Chapoton, F. and Schiffler, R., Quivers with relations arising from clusters (A n case) , Trans. Amer. Math. Soc. 358 (2006), 1347–1364.CrossRefGoogle Scholar
Canakci, I. and Schiffler, R., Snake graph calculus and cluster algebras from surfaces , J. Algebra 382 (2013), 240–281.Google Scholar
Canakci, I. and Schiffler, R., Snake graph calculus and cluster algebras from surfaces II: Self-crossing snake graphs , Math. Z. 281 (2015), 55–102.Google Scholar
Canakci, I. and Schiffler, R., Snake graph calculus and cluster algebras from surfaces III: Band graphs and snake rings, Preprint (2015), arXiv:1506.01742.Google Scholar
Canakci, I. and Schroll, S., Extensions in Jacobian algebras and cluster categories of marked surfaces, Preprint (2014), arXiv:1408.2074.Google Scholar
Crawley-Boevey, W., Functorial filtrations II: Clans and the Gelfand problem , J. Lond. Math. Soc. (2) 40 (1989), 9–30.Google Scholar
Deng, B., On a problem of Nazarova and Roiter , Comment. Math. Helv. 75 (2000), 368–409.Google Scholar
Derksen, H., Weyman, J. and Zelevinsky, A., Quivers with potentials and their representations I: Mutations , Selecta Math. (N.S.) 14 (2008), 59–119.Google Scholar
Felikson, A., Shapiro, M. and Tumarkin, P., Skew-symmetric cluster algebras of finite mutation type , J. Eur. Math. Soc. (JEMS) 14 (2012), 1135–1180.Google Scholar
Fock, V. V. and Goncharov, A. B., Moduli spaces of local systems and higher Teichmüller theory , Publ. Math. Inst. Hautes Études Sci. 103 (2006), 1–211.CrossRefGoogle Scholar
Fock, V. V. and Goncharov, A. B., Cluster ensembles, quantization and the dilogarithm , Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 865–930.Google Scholar
Fomin, S., Shapiro, M. and Thurston, D., Cluster algebras and triangulated surfaces, part I: Cluster complexes , Acta Math. 201 (2008), 83–146.Google Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras I: Foundations , J. Amer. Math. Soc. 15 (2002), 497–529.CrossRefGoogle Scholar
Geiß, C., Maps between representations of clans , J. Algebra 218 (1999), 131–164.CrossRefGoogle Scholar
Geiß, C. and de la Peña, J. A., Auslander–Reiten components for clans , Boll. Soc. Mat. Mexicana 5 (1999), 307–326.Google Scholar
Geiß, C., Labardini-Fragoso, D. and Schröer, J., The representation type of Jacobian algebras , Adv. Math. 290 (2016), 364–452.CrossRefGoogle Scholar
Irelli, G. and Labardini-Fragoso, D., Quivers with potentials associated to triangulated surfaces, part III: Tagged triangulations and cluster monomials , Compos. Math. 148 (2012), 1833–1866.Google Scholar
Iyama, O. and Yoshino, Y., Mutations in triangulated categories and rigid Cohen–Macaulay modules , Invent. Math. 172 (2008), 117–168.Google Scholar
Keller, B., Cluster algebras and derived categories , in Derived categories in algebraic geometry, EMS Series of Congress Reports (European Mathematical Society, Zürich, 2012), 123–183.Google Scholar
Keller, B., Deformed Calabi–Yau completions , J. reine angew. Math. 2013 (2013), 125–180.Google Scholar
Keller, B. and Reiten, I., Cluster tilted algebras are Gorenstein and stably Calabi–Yau , Adv. Math. 211 (2007), 123–151.Google Scholar
Keller, B. and Yang, D., Derived equivalences from mutations of quivers with potential , Adv. Math. 226 (2011), 2118–2168.Google Scholar
Koenig, S. and Zhu, B., From triangulated categories to abelian categories: cluster tilting in a general framework , Math. Z. 258 (2008), 143–160.Google Scholar
Labardini-Fragoso, D., Quivers with potentials associated to triangulated surfaces , Proc. Lond. Math. Soc. (3) 98 (2009), 797–839.CrossRefGoogle Scholar
Labardini-Fragoso, D., Quivers with potentials associated to triangulated surfaces, Part II: Arc representations, Preprint (2009), arXiv:0909.4100.Google Scholar
Labardini-Fragoso, D., On triangulations, quivers with potentials and mutations , in Mexican mathematicians abroad: recent contributions, Contemporary Mathematics, vol. 657 (American Mathematical Society, Providence, RI, 2016), 103–127.Google Scholar
Marsh, R. J. and Palu, Y., Coloured quivers for rigid objects and partial triangulations: the unpunctured case , Proc. Lond. Math. Soc. (3) 108 (2014), 411–440.Google Scholar
Mills, M., Maximal green sequences for quivers of finite mutation type, Preprint (2016),arXiv:1606.03799.Google Scholar
Musiker, G., Schiffler, R. and Williams, L., Positivity for cluster algebras from surfaces , Adv. Math. 227 (2011), 2241–2308.Google Scholar
Musiker, G., Schiffler, R. and Williams, L., Bases for cluster algebras from surfaces , Compos. Math. 149 (2013), 217–263.Google Scholar
Musiker, G. and Williams, L., Matrix formulae and skein relations for cluster algebras from surfaces , Int. Math. Res. Not. IMRN 2013 (2012), 2891–2944.Google Scholar
Palu, Y., Cluster characters for 2-Calabi–Yau triangulated categories , Ann. Inst. Fourier (Grenoble) 58 (2008), 2221–2248.Google Scholar
Plamondon, P.-G., Cluster algebras via cluster categories with infinite dimensional morphism spaces , Compos. Math. 147 (2011), 1921–1954.CrossRefGoogle Scholar
Qiu, Y., Decorated marked surfaces: spherical twists versus braid twists , Math. Ann. 365 (2016), 595–633.Google Scholar
Qiu, Y. and Zhou, Y., Decorated marked surfaces II: Intersection numbers and dimensions of Homs, Preprint (2014), arXiv:1411.4003.Google Scholar
Schiffler, R., A geometric model for cluster categories of type D n , J. Algebraic Combin. 27 (2008), 1–21.Google Scholar
Zhang, J., Zhou, Y. and Zhu, B., Cotorsion pairs in the cluster category of a marked surface , J. Algebra 391 (2013), 209–226.Google Scholar