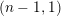1 Introduction
The theory of Coxeter groups has been developed from not only combinatorial but also geometrical aspects. One of the most fundamental and important objects associated with Coxeter groups is root systems. In the case of a finite Coxeter group, which is nothing but a finite reflection group, its roots correspond to normal vectors of hyperplanes defining Euclidean reflections. In the case of an infinite Coxeter group, if it is an affine reflection group, which is a small class of infinite Coxeter groups, then its roots also correspond to normal vectors. However, little investigation on roots has been done for the case of general infinite Coxeter groups. This paper is devoted to analyzing roots of infinite Coxeter groups whose associated bilinear forms have the signature
![]() $(n-1,1)$
. Concretely, we prove Conjecture 1.1 below for all of such Coxeter groups.
$(n-1,1)$
. Concretely, we prove Conjecture 1.1 below for all of such Coxeter groups.
Hohlweg, Labbé and Ripoll proved in 2014 that accumulation points of roots of infinite Coxeter groups lie in the projected isotropic cone
![]() $\widehat{Q}$
[Reference Hohlweg, Labbé and Ripoll6, Theorem 2.7]. In addition, they conjectured in [Reference Hohlweg, Labbé and Ripoll6, Section 3.2] that the distribution of such points can be described as some appropriate set of points. From geometrical viewpoints, as is well known in the theory of discrete groups of Möbius transformation, to study accumulation points is nothing but to study the interaction between ergodic theory and discrete groups. That has rich geometrical aspects and the theory stands as a well developed branch of mathematical researches. In order to establish that theory, the hyperbolicity of the space plays a crucial role. For the case where the associated matrices have signature
$\widehat{Q}$
[Reference Hohlweg, Labbé and Ripoll6, Theorem 2.7]. In addition, they conjectured in [Reference Hohlweg, Labbé and Ripoll6, Section 3.2] that the distribution of such points can be described as some appropriate set of points. From geometrical viewpoints, as is well known in the theory of discrete groups of Möbius transformation, to study accumulation points is nothing but to study the interaction between ergodic theory and discrete groups. That has rich geometrical aspects and the theory stands as a well developed branch of mathematical researches. In order to establish that theory, the hyperbolicity of the space plays a crucial role. For the case where the associated matrices have signature
![]() $(n-1,1)$
, Coxeter groups also have some hyperbolicity. This leads us to inspect an analogue of the theory of Kleinian groups for Coxeter groups of such class.
$(n-1,1)$
, Coxeter groups also have some hyperbolicity. This leads us to inspect an analogue of the theory of Kleinian groups for Coxeter groups of such class.
Recall that
![]() $W$
is a Coxeter group of rank
$W$
is a Coxeter group of rank
![]() $n$
with the generating set
$n$
with the generating set
![]() $S$
if
$S$
if
![]() $W$
is generated by the set
$W$
is generated by the set
![]() $S=\{s_{1},\ldots ,s_{n}\}$
subject only to the relations
$S=\{s_{1},\ldots ,s_{n}\}$
subject only to the relations
![]() $(s_{i}s_{j})^{m_{ij}}=1$
, where
$(s_{i}s_{j})^{m_{ij}}=1$
, where
![]() $m_{ij}\in \mathbb{Z}_{{>}1}\cup \{\infty \}$
for
$m_{ij}\in \mathbb{Z}_{{>}1}\cup \{\infty \}$
for
![]() $1\leqslant i<j\leqslant n$
and
$1\leqslant i<j\leqslant n$
and
![]() $m_{ii}=1$
for
$m_{ii}=1$
for
![]() $1\leqslant i\leqslant n$
. Thus,
$1\leqslant i\leqslant n$
. Thus,
![]() $m_{ij}=m_{ji}$
. We say that the pair
$m_{ij}=m_{ji}$
. We say that the pair
![]() $(W,S)$
is a Coxeter system. We refer the reader to [Reference Humphreys7] for the introduction to Coxeter groups.
$(W,S)$
is a Coxeter system. We refer the reader to [Reference Humphreys7] for the introduction to Coxeter groups.
For a Coxeter system
![]() $(W,S)$
of rank
$(W,S)$
of rank
![]() $n$
, let
$n$
, let
![]() $V$
be a real vector space with its orthonormal basis
$V$
be a real vector space with its orthonormal basis
![]() $\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FC}_{s}:s\in S\}$
. Note that by identifying
$\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FC}_{s}:s\in S\}$
. Note that by identifying
![]() $V$
with
$V$
with
![]() $\mathbb{R}^{n}$
, we treat
$\mathbb{R}^{n}$
, we treat
![]() $V$
as a Euclidean space. We define a symmetric bilinear form on
$V$
as a Euclidean space. We define a symmetric bilinear form on
![]() $V$
by setting
$V$
by setting
 $$\begin{eqnarray}\displaystyle B(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FC}_{j})\left\{\begin{array}{@{}ll@{}}=-\cos \biggl(\displaystyle \frac{\unicode[STIX]{x1D70B}}{m_{ij}}\biggr)\quad & \text{if }m_{ij}<\infty ,\\ {\leqslant}-1\quad & \text{if }m_{ij}=\infty ,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FC}_{j})\left\{\begin{array}{@{}ll@{}}=-\cos \biggl(\displaystyle \frac{\unicode[STIX]{x1D70B}}{m_{ij}}\biggr)\quad & \text{if }m_{ij}<\infty ,\\ {\leqslant}-1\quad & \text{if }m_{ij}=\infty ,\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
for
![]() $1\leqslant i\leqslant j\leqslant n$
, where
$1\leqslant i\leqslant j\leqslant n$
, where
![]() $\unicode[STIX]{x1D6FC}_{s_{i}}=\unicode[STIX]{x1D6FC}_{i}$
, and call the associated matrix
$\unicode[STIX]{x1D6FC}_{s_{i}}=\unicode[STIX]{x1D6FC}_{i}$
, and call the associated matrix
![]() $B$
the Coxeter matrix. Classically,
$B$
the Coxeter matrix. Classically,
![]() $B(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FC}_{j})=-1$
if
$B(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FC}_{j})=-1$
if
![]() $m_{ij}=\infty$
, but throughout this paper, we allow its value to be any real number less than or equal to
$m_{ij}=\infty$
, but throughout this paper, we allow its value to be any real number less than or equal to
![]() $-1$
. This definition is derived from [Reference Hohlweg, Labbé and Ripoll6] and this is available in some situations. Given
$-1$
. This definition is derived from [Reference Hohlweg, Labbé and Ripoll6] and this is available in some situations. Given
![]() $\unicode[STIX]{x1D6FC}\in V$
such that
$\unicode[STIX]{x1D6FC}\in V$
such that
![]() $B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})\not =0$
,
$B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})\not =0$
,
![]() $s_{\unicode[STIX]{x1D6FC}}$
denotes the map
$s_{\unicode[STIX]{x1D6FC}}$
denotes the map
![]() $s_{\unicode[STIX]{x1D6FC}}:V\rightarrow V$
by
$s_{\unicode[STIX]{x1D6FC}}:V\rightarrow V$
by
which is said to be a
![]() $B$
-reflection. Then
$B$
-reflection. Then
![]() $\unicode[STIX]{x1D6E5}$
satisfies that
$\unicode[STIX]{x1D6E5}$
satisfies that
(i) for all
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}$
with
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}$
with
 $\unicode[STIX]{x1D6FC}\not =\unicode[STIX]{x1D6FD}$
, one has
$\unicode[STIX]{x1D6FC}\not =\unicode[STIX]{x1D6FD}$
, one has  $$\begin{eqnarray}B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\in (-\infty ,-1]\cup \bigg\{-\text{cos}\biggl(\frac{\unicode[STIX]{x1D70B}}{k}\biggr):k\in \mathbb{Z}_{{>}1}\bigg\};\end{eqnarray}$$
$$\begin{eqnarray}B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\in (-\infty ,-1]\cup \bigg\{-\text{cos}\biggl(\frac{\unicode[STIX]{x1D70B}}{k}\biggr):k\in \mathbb{Z}_{{>}1}\bigg\};\end{eqnarray}$$
(ii) for all
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, one has
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, one has
 $B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})=1$
.
$B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC})=1$
.
Such a set
![]() $\unicode[STIX]{x1D6E5}$
is called a simple system and its elements are simple roots of
$\unicode[STIX]{x1D6E5}$
is called a simple system and its elements are simple roots of
![]() $W$
. The Coxeter group
$W$
. The Coxeter group
![]() $W$
acts on
$W$
acts on
![]() $V$
as composition of
$V$
as composition of
![]() $B$
-reflections and its generating set
$B$
-reflections and its generating set
![]() $S$
is identified with
$S$
is identified with
![]() $\{s_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\}$
. The root system
$\{s_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\}$
. The root system
![]() $\unicode[STIX]{x1D6F7}$
of
$\unicode[STIX]{x1D6F7}$
of
![]() $W$
is defined to be the orbit of
$W$
is defined to be the orbit of
![]() $\unicode[STIX]{x1D6E5}$
under the action of
$\unicode[STIX]{x1D6E5}$
under the action of
![]() $W$
and its elements are called roots of
$W$
and its elements are called roots of
![]() $W$
. The pair
$W$
. The pair
![]() $(\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6E5})$
is said to be a based root system in
$(\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6E5})$
is said to be a based root system in
![]() $(V,B)$
. We mention that
$(V,B)$
. We mention that
![]() $\unicode[STIX]{x1D6E5}$
in [Reference Hohlweg, Labbé and Ripoll6, Definition 1.2] is assumed to be positively independent, while we assume the linearly independence throughout this paper.
$\unicode[STIX]{x1D6E5}$
in [Reference Hohlweg, Labbé and Ripoll6, Definition 1.2] is assumed to be positively independent, while we assume the linearly independence throughout this paper.
Our main interest is the distribution of accumulation points of roots of an infinite Coxeter group. In the case of a finite Coxeter group, its root system
![]() $\unicode[STIX]{x1D6F7}$
is finite. When a Coxeter group is infinite,
$\unicode[STIX]{x1D6F7}$
is finite. When a Coxeter group is infinite,
![]() $\unicode[STIX]{x1D6F7}$
is also infinite. Thus the classical tools developed in the Euclidean geometry are no longer usable.
$\unicode[STIX]{x1D6F7}$
is also infinite. Thus the classical tools developed in the Euclidean geometry are no longer usable.
On the other hand, in a recent paper [Reference Hohlweg, Labbé and Ripoll6], some tools to deal with roots of infinite Coxeter groups were established as the first step of their study. Our motivation to organize this paper is to contribute further studies of the paper [Reference Hohlweg, Labbé and Ripoll6].
As is known in [Reference Hohlweg, Labbé and Ripoll6, Theorem 2.7(i)], the norm of a positive root always diverges as its depth tends to infinity. Thus, in order to investigate asymptotical behaviors of positive roots, it is needed to normalize them in the sense of a function
![]() $|\cdot |_{1}$
, which will be defined in Section 2. We also set an affine subspace
$|\cdot |_{1}$
, which will be defined in Section 2. We also set an affine subspace
![]() $V_{1}=\{x\in V:|x|_{1}=1\}$
.
$V_{1}=\{x\in V:|x|_{1}=1\}$
.
Let
and let
![]() $E$
be a set of accumulation points of normalized roots
$E$
be a set of accumulation points of normalized roots
![]() $\widehat{\unicode[STIX]{x1D70C}}$
for
$\widehat{\unicode[STIX]{x1D70C}}$
for
![]() $\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D6F7}$
, i.e., the set consisting of all the possible limits of injective sequences of normalized roots. Let
$\unicode[STIX]{x1D70C}\in \unicode[STIX]{x1D6F7}$
, i.e., the set consisting of all the possible limits of injective sequences of normalized roots. Let
![]() $w\cdot x$
denote the normalized action on
$w\cdot x$
denote the normalized action on
![]() $V_{1}$
for
$V_{1}$
for
![]() $w\in W$
and
$w\in W$
and
![]() $x\in V_{1}$
. (See Section 2.) It was proved in [Reference Hohlweg, Labbé and Ripoll6, Theorem 2.7] that
$x\in V_{1}$
. (See Section 2.) It was proved in [Reference Hohlweg, Labbé and Ripoll6, Theorem 2.7] that
![]() $E\subset \widehat{Q}$
and the following is proposed.
$E\subset \widehat{Q}$
and the following is proposed.
Conjecture 1.1. [Reference Hohlweg, Labbé and Ripoll6, Conjecture 3.9]
We say that
![]() $\unicode[STIX]{x1D6E5}_{I}\subset \unicode[STIX]{x1D6E5}$
is generating if
$\unicode[STIX]{x1D6E5}_{I}\subset \unicode[STIX]{x1D6E5}$
is generating if
![]() $\widehat{Q}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
is included in
$\widehat{Q}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
is included in
![]() $\text{conv}(\widehat{\unicode[STIX]{x1D6E5}})\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
. Let
$\text{conv}(\widehat{\unicode[STIX]{x1D6E5}})\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
. Let
![]() $E_{I}\subset E$
be the set of accumulation points of normalized roots of the parabolic subgroup associated with
$E_{I}\subset E$
be the set of accumulation points of normalized roots of the parabolic subgroup associated with
![]() $\unicode[STIX]{x1D6E5}_{I}$
. Then we have the following properties:
$\unicode[STIX]{x1D6E5}_{I}$
. Then we have the following properties:
(i) if
 $\unicode[STIX]{x1D6E5}_{I}$
is generating, then
$\unicode[STIX]{x1D6E5}_{I}$
is generating, then
 $E_{I}=\widehat{Q}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
;
$E_{I}=\widehat{Q}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
;(ii) the set
 $E$
is the topological closure of the fractal self-similar subset
$E$
is the topological closure of the fractal self-similar subset
 $F_{0}$
of
$F_{0}$
of
 $\widehat{Q}$
defined by
$\widehat{Q}$
defined by  $$\begin{eqnarray}F_{0}:=W\cdot \left(\mathop{\bigcup }_{\substack{ \unicode[STIX]{x1D6E5}_{I}\subset \unicode[STIX]{x1D6E5} \\ \unicode[STIX]{x1D6E5}_{I}~\text{is generating}}}\widehat{Q}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})\right).\end{eqnarray}$$
$$\begin{eqnarray}F_{0}:=W\cdot \left(\mathop{\bigcup }_{\substack{ \unicode[STIX]{x1D6E5}_{I}\subset \unicode[STIX]{x1D6E5} \\ \unicode[STIX]{x1D6E5}_{I}~\text{is generating}}}\widehat{Q}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})\right).\end{eqnarray}$$
In this paper, we prove the following theorem.
Theorem 1.2. For an infinite Coxeter group of rank
![]() $n$
equipped with the signature
$n$
equipped with the signature
![]() $(n-1,1)$
bilinear form, we have the following:
$(n-1,1)$
bilinear form, we have the following:
(a) When
 $\widehat{Q}\subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, we have
$\widehat{Q}\subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, we have
 $E=\widehat{Q}$
.
$E=\widehat{Q}$
.(b) When
 $\widehat{Q}\not \subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, we have
$\widehat{Q}\not \subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, we have
 $E=\widehat{Q}\setminus (\bigcup _{i=1}^{m}W\cdot D_{i})$
, where
$E=\widehat{Q}\setminus (\bigcup _{i=1}^{m}W\cdot D_{i})$
, where
 $D_{1},\ldots ,D_{m}$
are connected components of
$D_{1},\ldots ,D_{m}$
are connected components of
 $\widehat{Q}$
out of
$\widehat{Q}$
out of
 $\text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
with
$\text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
with
 $1\leqslant m\leqslant n$
.
$1\leqslant m\leqslant n$
.
Moreover, we also prove the following theorem.
Theorem 1.3. Fix
![]() $x\in E$
. Then
$x\in E$
. Then
We remark that Theorem 1.2(a) and Theorem 1.3 imply Conjecture 1.1 in the case of Coxeter matrices whose signatures are
![]() $(n-1,1)$
. For more details, see Remark 6.12.
$(n-1,1)$
. For more details, see Remark 6.12.
Remark 1.4. It is easy to calculate that each Coxeter matrix arising from a Coxeter group of rank 3 is either positive type or has the signature
![]() $(2,1)$
(cf. [Reference Humphreys7, Section 6.7]). However, for a general Coxeter group of rank
$(2,1)$
(cf. [Reference Humphreys7, Section 6.7]). However, for a general Coxeter group of rank
![]() $n$
, there exists a bilinear form whose signature is neither positive type nor
$n$
, there exists a bilinear form whose signature is neither positive type nor
![]() $(n-1,1)$
. See Example 2.2.
$(n-1,1)$
. See Example 2.2.
Remark 1.5. In [Reference Dyer, Hohlweg and Ripoll3], while revising the previous version of this paper, Dyer, Hohlweg and Ripoll also proved Theorem 1.2 and Theorem 1.3 by a different approach [Reference Dyer, Hohlweg and Ripoll3, Theorems 4.10(a) and 3.1(b)]. In fact, their approach was accomplished by using a method of so-called imaginary cones and they do not assume the linear independence of
![]() $\unicode[STIX]{x1D6E5}$
. On the other hand, in this paper, some other aspects of infinite Coxeter groups (e.g., metric on
$\unicode[STIX]{x1D6E5}$
. On the other hand, in this paper, some other aspects of infinite Coxeter groups (e.g., metric on
![]() $\widehat{Q}$
) are investigated.
$\widehat{Q}$
) are investigated.
A brief overview of this paper is as follows. First, we will prepare some lemmas and collect fundamental facts in Section 2 for the proofs of the main theorems. Next, in Section 3, we will prove Theorem 1.3. We also study the fixed points of the normalized action in Section 4. Before proving Theorem 1.2 in general case, we will show Theorem 1.2 for the case of rank 3 in Section 5. Finally, in Section 6, we will prove Theorem 1.2 for the case of an arbitrary rank. The discussion of the fixed points of the normalized action is used in the proof of Theorem 1.2 for the case of rank 3.
2 The normalized action and a metric on
 $\widehat{Q}$
$\widehat{Q}$
In this section, we prepare some notation and lemmas for proving Theorems 1.2 and 1.3. After defining
![]() $\widehat{Q}$
, we collect some fundamental results on the normalized action on
$\widehat{Q}$
, we collect some fundamental results on the normalized action on
![]() $\widehat{Q}$
and define a metric on
$\widehat{Q}$
and define a metric on
![]() $\widehat{Q}$
.
$\widehat{Q}$
.
Assumption 2.1. Unless otherwise noted, we always assume that Coxeter groups are irreducible and their Coxeter matrices have the signature
![]() $(n-1,1)$
, where
$(n-1,1)$
, where
![]() $n$
is the rank.
$n$
is the rank.
By [Reference Hohlweg, Labbé and Ripoll6, Proposition 2.14], if the based root system
![]() $(\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6E5})$
is reducible and we consider proper subsets
$(\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D6E5})$
is reducible and we consider proper subsets
![]() $\unicode[STIX]{x1D6E5}_{I},\unicode[STIX]{x1D6E5}_{J}\subsetneq \unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6E5}_{I},\unicode[STIX]{x1D6E5}_{J}\subsetneq \unicode[STIX]{x1D6E5}$
such that
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{I}\sqcup \unicode[STIX]{x1D6E5}_{J}$
with
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{I}\sqcup \unicode[STIX]{x1D6E5}_{J}$
with
![]() $B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=0$
for all
$B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=0$
for all
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{I}$
and
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{I}$
and
![]() $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}_{J}$
, then
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}_{J}$
, then
![]() $E(\unicode[STIX]{x1D6F7})=E(\unicode[STIX]{x1D6F7}_{I})\sqcup E(\unicode[STIX]{x1D6F7}_{J})$
. Hence we may restrict our study to the irreducible cases.
$E(\unicode[STIX]{x1D6F7})=E(\unicode[STIX]{x1D6F7}_{I})\sqcup E(\unicode[STIX]{x1D6F7}_{J})$
. Hence we may restrict our study to the irreducible cases.
As the following example shows, there exists a Coxeter group whose Coxeter matrix does not have the signature
![]() $(n-1,1)$
.
$(n-1,1)$
.
Example 2.2. Let
![]() $W$
be a Coxeter system of rank 4 with
$W$
be a Coxeter system of rank 4 with
![]() $S=\{s_{1},s_{2},s_{3},s_{4}\}$
and
$S=\{s_{1},s_{2},s_{3},s_{4}\}$
and
![]() $\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3},\unicode[STIX]{x1D6FC}_{4}\}$
. Let
$\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3},\unicode[STIX]{x1D6FC}_{4}\}$
. Let
where
![]() $a,b,c\in \{\cos (\unicode[STIX]{x1D70B}/k):k\in \mathbb{Z}_{{>}2}\}\cup [1,\infty )$
. It then follows from an easy computation that the signature of
$a,b,c\in \{\cos (\unicode[STIX]{x1D70B}/k):k\in \mathbb{Z}_{{>}2}\}\cup [1,\infty )$
. It then follows from an easy computation that the signature of
![]() $B$
is
$B$
is
![]() $(2,2)$
if and only if
$(2,2)$
if and only if
![]() $B$
is not positive type and three positive real numbers
$B$
is not positive type and three positive real numbers
![]() $a,b,c$
satisfy
$a,b,c$
satisfy
![]() $a^{2}+b^{2}+c^{2}-a^{2}c^{2}<1$
. (Consult, e.g., [Reference Humphreys7] for the classification of positive type.) For example, when
$a^{2}+b^{2}+c^{2}-a^{2}c^{2}<1$
. (Consult, e.g., [Reference Humphreys7] for the classification of positive type.) For example, when
![]() $(a,b,c)=(2,\frac{1}{2},2)$
, this condition is satisfied.
$(a,b,c)=(2,\frac{1}{2},2)$
, this condition is satisfied.
Thus, in the case of rank 4, there exists an infinite Coxeter group whose associated bilinear form has its signature
![]() $(2,2)$
, while each Coxeter group of rank 3 is either positive type or of type
$(2,2)$
, while each Coxeter group of rank 3 is either positive type or of type
![]() $(2,1)$
.
$(2,1)$
.
Let
and
It is known that based root system allows us to define positive roots
![]() $\unicode[STIX]{x1D6F7}^{+}:=\unicode[STIX]{x1D6F7}\cap V^{+}$
, and then
$\unicode[STIX]{x1D6F7}^{+}:=\unicode[STIX]{x1D6F7}\cap V^{+}$
, and then
![]() $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}^{+}\sqcup (-\unicode[STIX]{x1D6F7}^{+})$
(see, for instance, [Reference Bonnafé and Dyer2, Reference Krammer8]). In other words, all the roots are contained in
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}^{+}\sqcup (-\unicode[STIX]{x1D6F7}^{+})$
(see, for instance, [Reference Bonnafé and Dyer2, Reference Krammer8]). In other words, all the roots are contained in
![]() $V^{+}\cup V^{-}$
.
$V^{+}\cup V^{-}$
.
2.1 The normalized action of
 $W$
$W$
First of all, we define
![]() $\widehat{Q}$
and discuss the action of
$\widehat{Q}$
and discuss the action of
![]() $W$
on it. Let
$W$
on it. Let
We fix the vector
![]() $o\in V$
as follows. If
$o\in V$
as follows. If
![]() $B$
is of positive type, then
$B$
is of positive type, then
![]() $o=\sum _{i=1}^{n}\unicode[STIX]{x1D6FC}_{i}$
. If
$o=\sum _{i=1}^{n}\unicode[STIX]{x1D6FC}_{i}$
. If
![]() $B$
has the signature
$B$
has the signature
![]() $(n-1,1)$
, then
$(n-1,1)$
, then
![]() $o$
is the eigenvector corresponding to the negative eigenvalue of
$o$
is the eigenvector corresponding to the negative eigenvalue of
![]() $B$
whose Euclidean norm equals 1.
$B$
whose Euclidean norm equals 1.
By the following lemma, even in the case where
![]() $B$
has the signature
$B$
has the signature
![]() $(n-1,1)$
, we may assume that all coordinates of
$(n-1,1)$
, we may assume that all coordinates of
![]() $o$
are positive.
$o$
are positive.
Lemma 2.3. Let
![]() $o$
be an eigenvector for the negative eigenvalue of
$o$
be an eigenvector for the negative eigenvalue of
![]() $B$
. Then all coordinates of
$B$
. Then all coordinates of
![]() $o$
with respect to a basis
$o$
with respect to a basis
![]() $\unicode[STIX]{x1D6E5}$
have the same sign.
$\unicode[STIX]{x1D6E5}$
have the same sign.
Proof. This follows from Perron–Frobenius theorem for irreducible nonnegative matrices. Let
![]() $I$
be the identity matrix of rank
$I$
be the identity matrix of rank
![]() $n$
. Then
$n$
. Then
![]() $I-B$
is irreducible and nonnegative. Note that since
$I-B$
is irreducible and nonnegative. Note that since
![]() $I-B$
and
$I-B$
and
![]() $B$
are symmetric, all eigenvalues are real. By Perron–Frobenius theorem, we have a positive eigenvalue
$B$
are symmetric, all eigenvalues are real. By Perron–Frobenius theorem, we have a positive eigenvalue
![]() $\unicode[STIX]{x1D706}^{\prime }$
of
$\unicode[STIX]{x1D706}^{\prime }$
of
![]() $I-B$
such that
$I-B$
such that
![]() $\unicode[STIX]{x1D706}^{\prime }$
is the maximum of eigenvalues of
$\unicode[STIX]{x1D706}^{\prime }$
is the maximum of eigenvalues of
![]() $I-B$
and each entry of the corresponding eigenvector
$I-B$
and each entry of the corresponding eigenvector
![]() $u$
is positive. On the other hand, for each eigenvalue
$u$
is positive. On the other hand, for each eigenvalue
![]() $a$
of
$a$
of
![]() $B$
, there exists an eigenvalue
$B$
, there exists an eigenvalue
![]() $b$
of
$b$
of
![]() $I-B$
such that
$I-B$
such that
![]() $a=1-b$
. Let
$a=1-b$
. Let
![]() $\unicode[STIX]{x1D706}$
be the negative eigenvalue of
$\unicode[STIX]{x1D706}$
be the negative eigenvalue of
![]() $B$
. It then follows from an easy calculation that
$B$
. It then follows from an easy calculation that
![]() $\unicode[STIX]{x1D706}=1-\unicode[STIX]{x1D706}^{\prime }$
. Hence,
$\unicode[STIX]{x1D706}=1-\unicode[STIX]{x1D706}^{\prime }$
. Hence,
![]() $\mathbb{R}u=\mathbb{R}o$
. Therefore, the positivity of each entry of
$\mathbb{R}u=\mathbb{R}o$
. Therefore, the positivity of each entry of
![]() $u$
implies that the entries of
$u$
implies that the entries of
![]() $o$
are all positive or all negative.◻
$o$
are all positive or all negative.◻
Hence if we write
![]() $o$
for a linear combination
$o$
for a linear combination
![]() $o=\sum _{i=1}^{n}o_{i}\unicode[STIX]{x1D6FC}_{i}$
of
$o=\sum _{i=1}^{n}o_{i}\unicode[STIX]{x1D6FC}_{i}$
of
![]() $\unicode[STIX]{x1D6E5}$
, then
$\unicode[STIX]{x1D6E5}$
, then
![]() $o_{i}>0$
for each
$o_{i}>0$
for each
![]() $i$
. Given
$i$
. Given
![]() $v\in V$
, we define
$v\in V$
, we define
if
![]() $v=\sum _{i=1}^{n}v_{i}\unicode[STIX]{x1D6FC}_{i}$
. Note that
$v=\sum _{i=1}^{n}v_{i}\unicode[STIX]{x1D6FC}_{i}$
. Note that
![]() $|v|_{1}$
is nothing but the Euclidean inner product of
$|v|_{1}$
is nothing but the Euclidean inner product of
![]() $v$
and
$v$
and
![]() $o$
. It is obvious that
$o$
. It is obvious that
![]() $|v|_{1}>0$
for
$|v|_{1}>0$
for
![]() $v\in V^{+}\setminus \{0\}$
and
$v\in V^{+}\setminus \{0\}$
and
![]() $|v|_{1}<0$
for
$|v|_{1}<0$
for
![]() $v\in V^{-}\setminus \{0\}$
. In particular,
$v\in V^{-}\setminus \{0\}$
. In particular,
![]() $|\unicode[STIX]{x1D6FC}|_{1}>0$
for
$|\unicode[STIX]{x1D6FC}|_{1}>0$
for
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Let
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Let
![]() $V_{i}=\{v\in V~|~|v|_{1}=i\}$
, where
$V_{i}=\{v\in V~|~|v|_{1}=i\}$
, where
![]() $i=0,1$
. For
$i=0,1$
. For
![]() $v\in V\setminus V_{0}$
, we write
$v\in V\setminus V_{0}$
, we write
![]() $\widehat{v}$
for the “normalized” vector
$\widehat{v}$
for the “normalized” vector
![]() $v/|v|_{1}\in V_{1}$
. Also for a set
$v/|v|_{1}\in V_{1}$
. Also for a set
![]() $A\subset V\setminus V_{0}$
, we write
$A\subset V\setminus V_{0}$
, we write
![]() $\widehat{A}$
for the set of all
$\widehat{A}$
for the set of all
![]() $\widehat{a}$
with
$\widehat{a}$
with
![]() $a\in A$
. We notice that since
$a\in A$
. We notice that since
![]() $B(x,\unicode[STIX]{x1D6FC})=|\unicode[STIX]{x1D6FC}|_{1}B(x,\widehat{\unicode[STIX]{x1D6FC}})$
holds, the sign of
$B(x,\unicode[STIX]{x1D6FC})=|\unicode[STIX]{x1D6FC}|_{1}B(x,\widehat{\unicode[STIX]{x1D6FC}})$
holds, the sign of
![]() $B(x,\widehat{\unicode[STIX]{x1D6FC}})$
is equal to the sign of
$B(x,\widehat{\unicode[STIX]{x1D6FC}})$
is equal to the sign of
![]() $B(x,\unicode[STIX]{x1D6FC})$
for any
$B(x,\unicode[STIX]{x1D6FC})$
for any
![]() $x\in V$
and
$x\in V$
and
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
.
As noted before,
![]() $W$
acts on
$W$
acts on
![]() $V$
as composition of
$V$
as composition of
![]() $B$
-reflections. For analyzing asymptotical aspects of
$B$
-reflections. For analyzing asymptotical aspects of
![]() $W$
, we consider another action of
$W$
, we consider another action of
![]() $W$
on
$W$
on
![]() $V$
. The normalized action of
$V$
. The normalized action of
![]() $w\in W$
on
$w\in W$
on
![]() $V_{1}\setminus W(V_{0})$
is given by
$V_{1}\setminus W(V_{0})$
is given by
where
![]() $w(v)$
denotes the action of
$w(v)$
denotes the action of
![]() $w$
defined before (composition of
$w$
defined before (composition of
![]() $B$
-reflections). This action is well defined on
$B$
-reflections). This action is well defined on
![]() $V_{1}\setminus W(V_{0})$
.
$V_{1}\setminus W(V_{0})$
.
Lemma 2.4. We have
where
![]() $\mathbf{0}$
is the origin of
$\mathbf{0}$
is the origin of
![]() $\mathbb{R}^{n}$
.
$\mathbb{R}^{n}$
.
Proof. Since
![]() $Q$
is
$Q$
is
![]() $W$
-invariant, it is enough to show that
$W$
-invariant, it is enough to show that
![]() $V_{0}\cap Q=\{\mathbf{0}\}$
.
$V_{0}\cap Q=\{\mathbf{0}\}$
.
For
![]() $i=1,\ldots ,n-1$
, let
$i=1,\ldots ,n-1$
, let
![]() $p_{i}$
be an eigenvector of
$p_{i}$
be an eigenvector of
![]() $B$
with Euclidean norm 1 corresponding to each positive eigenvalue
$B$
with Euclidean norm 1 corresponding to each positive eigenvalue
![]() $\unicode[STIX]{x1D706}_{i}$
, respectively. Then, for any
$\unicode[STIX]{x1D706}_{i}$
, respectively. Then, for any
![]() $v\in V_{0}$
, we can express
$v\in V_{0}$
, we can express
![]() $v$
by a linear combination
$v$
by a linear combination
![]() $v=\sum _{i=1}^{n-1}v_{i}p_{i}+v_{n}o$
for some
$v=\sum _{i=1}^{n-1}v_{i}p_{i}+v_{n}o$
for some
![]() $v_{1},\ldots ,v_{n}\in \mathbb{R}$
with respect to an orthonormal basis
$v_{1},\ldots ,v_{n}\in \mathbb{R}$
with respect to an orthonormal basis
![]() $p_{1},\ldots ,p_{n-1},o$
for
$p_{1},\ldots ,p_{n-1},o$
for
![]() $V$
. Since
$V$
. Since
![]() $|v|_{1}=0$
, we have
$|v|_{1}=0$
, we have
![]() $v_{n}=0$
. Moreover, since
$v_{n}=0$
. Moreover, since
![]() $B$
is positive-definite in the subspace of
$B$
is positive-definite in the subspace of
![]() $V$
spanned by
$V$
spanned by
![]() $p_{1},\ldots ,p_{n-1}$
, we have
$p_{1},\ldots ,p_{n-1}$
, we have
![]() $B(v,v)=\sum _{i=1}^{n-1}\unicode[STIX]{x1D706}_{i}v_{i}^{2}\geqslant 0$
. The positivity of each
$B(v,v)=\sum _{i=1}^{n-1}\unicode[STIX]{x1D706}_{i}v_{i}^{2}\geqslant 0$
. The positivity of each
![]() $\unicode[STIX]{x1D706}_{i}$
implies that
$\unicode[STIX]{x1D706}_{i}$
implies that
![]() $B(v,v)=0$
if and only if
$B(v,v)=0$
if and only if
![]() $v=\mathbf{0}$
. This proves that
$v=\mathbf{0}$
. This proves that
![]() $V_{0}\cap Q=\{\mathbf{0}\}$
, as required.◻
$V_{0}\cap Q=\{\mathbf{0}\}$
, as required.◻
Thus,
![]() $Q\setminus \{\mathbf{0}\}$
is contained in
$Q\setminus \{\mathbf{0}\}$
is contained in
![]() $V\setminus W(V_{0})$
. This is also true in the case where
$V\setminus W(V_{0})$
. This is also true in the case where
![]() $B$
is of positive type. Let
$B$
is of positive type. Let
Then
![]() $\widehat{Q}$
coincides with the set
$\widehat{Q}$
coincides with the set
![]() $\{x\in V_{1}:B(x,x)=0\}$
, which has already appeared in Introduction. Lemma 2.4 above shows that the normalized action is also well defined on
$\{x\in V_{1}:B(x,x)=0\}$
, which has already appeared in Introduction. Lemma 2.4 above shows that the normalized action is also well defined on
![]() $\widehat{Q}\subset V_{1}\setminus W(V_{0})$
everywhere.
$\widehat{Q}\subset V_{1}\setminus W(V_{0})$
everywhere.
Moreover, we also see that
In fact, for any
![]() $\unicode[STIX]{x1D70C}\in V^{+}\cup V^{-}$
, if the Euclidean inner product of
$\unicode[STIX]{x1D70C}\in V^{+}\cup V^{-}$
, if the Euclidean inner product of
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $o$
, which coincides with
$o$
, which coincides with
![]() $|\unicode[STIX]{x1D70C}|_{1}$
, is equal to 0, then
$|\unicode[STIX]{x1D70C}|_{1}$
, is equal to 0, then
![]() $\unicode[STIX]{x1D70C}$
should be
$\unicode[STIX]{x1D70C}$
should be
![]() $\mathbf{0}$
by Lemma 2.3. Since the root system
$\mathbf{0}$
by Lemma 2.3. Since the root system
![]() $W(\unicode[STIX]{x1D6E5})$
is contained in
$W(\unicode[STIX]{x1D6E5})$
is contained in
![]() $V^{+}\cup V^{-}$
(see [Reference Hohlweg, Labbé and Ripoll6, Remark 1.3]), we obtain that
$V^{+}\cup V^{-}$
(see [Reference Hohlweg, Labbé and Ripoll6, Remark 1.3]), we obtain that
![]() $W(\unicode[STIX]{x1D6E5})\cap V_{0}=\emptyset$
, i.e.,
$W(\unicode[STIX]{x1D6E5})\cap V_{0}=\emptyset$
, i.e.,
![]() $\unicode[STIX]{x1D6E5}\cap W(V_{0})=\emptyset$
. This is also obvious in the case where
$\unicode[STIX]{x1D6E5}\cap W(V_{0})=\emptyset$
. This is also obvious in the case where
![]() $B$
is of positive type.
$B$
is of positive type.
Let
![]() $\widehat{Q_{-}}:=\{x\in V_{1}:B(x,x)<0\}$
. Then, we note that the boundary of
$\widehat{Q_{-}}:=\{x\in V_{1}:B(x,x)<0\}$
. Then, we note that the boundary of
![]() $\widehat{Q_{-}}$
with respect to the subspace topology on
$\widehat{Q_{-}}$
with respect to the subspace topology on
![]() $V_{1}$
coincides with
$V_{1}$
coincides with
![]() $\widehat{Q}$
. Since
$\widehat{Q}$
. Since
![]() $B$
is a symmetric bilinear form, we can diagonalize it by an orthogonal transformation
$B$
is a symmetric bilinear form, we can diagonalize it by an orthogonal transformation
![]() $L$
. Here we assume that
$L$
. Here we assume that
![]() $Lo=\unicode[STIX]{x1D6FC}_{n}$
. Then we see that
$Lo=\unicode[STIX]{x1D6FC}_{n}$
. Then we see that
![]() $^{t}LBL$
is equal to the diagonal matrix
$^{t}LBL$
is equal to the diagonal matrix
![]() $(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n-1},-\unicode[STIX]{x1D706}_{n})$
, denoted by
$(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n-1},-\unicode[STIX]{x1D706}_{n})$
, denoted by
![]() $A$
, where
$A$
, where
![]() $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n-1},-\unicode[STIX]{x1D706}_{n}$
are the eigenvalues of
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n-1},-\unicode[STIX]{x1D706}_{n}$
are the eigenvalues of
![]() $B$
with
$B$
with
![]() $\unicode[STIX]{x1D706}_{i}>0$
and
$\unicode[STIX]{x1D706}_{i}>0$
and
![]() $^{t}M$
means the transpose of a matrix
$^{t}M$
means the transpose of a matrix
![]() $M$
. Consider a basis
$M$
. Consider a basis
![]() $L^{-1}\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{n}\}$
. Then
$L^{-1}\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{n}\}$
. Then
![]() $\widehat{Q_{-}}=\{\sum _{i=1}^{n}v_{i}\unicode[STIX]{x1D6FD}_{i}\in V:\unicode[STIX]{x1D706}_{1}v_{1}^{2}+\cdots +\unicode[STIX]{x1D706}_{n-1}v_{n-1}^{2}-\unicode[STIX]{x1D706}_{n}v_{n}^{2}<0\}\cap V_{1}$
. From the definition of
$\widehat{Q_{-}}=\{\sum _{i=1}^{n}v_{i}\unicode[STIX]{x1D6FD}_{i}\in V:\unicode[STIX]{x1D706}_{1}v_{1}^{2}+\cdots +\unicode[STIX]{x1D706}_{n-1}v_{n-1}^{2}-\unicode[STIX]{x1D706}_{n}v_{n}^{2}<0\}\cap V_{1}$
. From the definition of
![]() $V_{1}$
, we conclude that
$V_{1}$
, we conclude that
![]() $\widehat{Q_{-}}$
is an ellipsoid and
$\widehat{Q_{-}}$
is an ellipsoid and
![]() $\widehat{Q}$
is its boundary.
$\widehat{Q}$
is its boundary.
2.2 Visibility on
 $\widehat{Q}$
$\widehat{Q}$
Next, we recall a valuable notion “visibility” from [Reference Hohlweg, Labbé and Ripoll6, Section 3] and discuss the visible points on
![]() $\widehat{Q}$
.
$\widehat{Q}$
.
Let
![]() $L(x,y)$
(resp.
$L(x,y)$
(resp.
![]() $L[x,y]$
) denote the line through
$L[x,y]$
) denote the line through
![]() $x$
and
$x$
and
![]() $y$
(resp. the segment joining
$y$
(resp. the segment joining
![]() $x$
and
$x$
and
![]() $y$
). Using this, we define a valuable idea given in [Reference Hohlweg, Labbé and Ripoll6]. That is, we say that
$y$
). Using this, we define a valuable idea given in [Reference Hohlweg, Labbé and Ripoll6]. That is, we say that
![]() $x\in \widehat{Q}$
is visible from
$x\in \widehat{Q}$
is visible from
![]() $y\in V_{1}$
if
$y\in V_{1}$
if
![]() $L[x,y]\cap \widehat{Q}=\{x\}$
. Given
$L[x,y]\cap \widehat{Q}=\{x\}$
. Given
![]() $y\in V_{1}$
, we call a curve consisting of visible points from
$y\in V_{1}$
, we call a curve consisting of visible points from
![]() $y$
in
$y$
in
![]() $\widehat{Q}$
a visible curve from
$\widehat{Q}$
a visible curve from
![]() $y$
. If there is no confusion, then we simply call it a visible curve.
$y$
. If there is no confusion, then we simply call it a visible curve.
The set of all visible points of
![]() $\widehat{Q}$
from a normalized simple root
$\widehat{Q}$
from a normalized simple root
![]() $\widehat{\unicode[STIX]{x1D6FC}}$
is said to be a visible area from
$\widehat{\unicode[STIX]{x1D6FC}}$
is said to be a visible area from
![]() $\widehat{\unicode[STIX]{x1D6FC}}$
, denoted by
$\widehat{\unicode[STIX]{x1D6FC}}$
, denoted by
![]() $V_{\unicode[STIX]{x1D6FC}}$
.
$V_{\unicode[STIX]{x1D6FC}}$
.
We recall the following proposition concerning with the notion “visible”.
Lemma 2.5. [Reference Hohlweg, Labbé and Ripoll6]
Let
![]() $x\in \widehat{Q}$
and
$x\in \widehat{Q}$
and
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
.
(i)
 $x\in V_{\unicode[STIX]{x1D6FC}}$
if and only if
$x\in V_{\unicode[STIX]{x1D6FC}}$
if and only if
 $B(\unicode[STIX]{x1D6FC},x)\geqslant 0$
.
$B(\unicode[STIX]{x1D6FC},x)\geqslant 0$
.(ii)
 $x$
and
$x$
and
 $s_{\unicode[STIX]{x1D6FC}}\cdot x$
lie on the same line
$s_{\unicode[STIX]{x1D6FC}}\cdot x$
lie on the same line
 $L(x,\unicode[STIX]{x1D6FC})$
.
$L(x,\unicode[STIX]{x1D6FC})$
.(iii)
 $x\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
if and only if
$x\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
if and only if
 $B(\unicode[STIX]{x1D6FC},x)=0$
.
$B(\unicode[STIX]{x1D6FC},x)=0$
.
The statements (i) and (ii) of Lemma 2.5 correspond to [Reference Hohlweg, Labbé and Ripoll6, Propositions 3.5(i) and 3.7(i)]. The statement (iii) of Lemma 2.5 follows from the continuity of
![]() $B$
on
$B$
on
![]() $\widehat{Q}$
and (i). Although the definition of
$\widehat{Q}$
and (i). Although the definition of
![]() $|\cdot |_{1}$
in this paper is different from that of [Reference Hohlweg, Labbé and Ripoll6], their proofs in [Reference Hohlweg, Labbé and Ripoll6] still work since
$|\cdot |_{1}$
in this paper is different from that of [Reference Hohlweg, Labbé and Ripoll6], their proofs in [Reference Hohlweg, Labbé and Ripoll6] still work since
![]() $B(x,\unicode[STIX]{x1D6FC})=|\unicode[STIX]{x1D6FC}|_{1}B(x,\widehat{\unicode[STIX]{x1D6FC}})$
and
$B(x,\unicode[STIX]{x1D6FC})=|\unicode[STIX]{x1D6FC}|_{1}B(x,\widehat{\unicode[STIX]{x1D6FC}})$
and
![]() $|\unicode[STIX]{x1D6FC}|_{1}>0$
hold for
$|\unicode[STIX]{x1D6FC}|_{1}>0$
hold for
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
.
Proposition 2.6. There is no element in
![]() $\widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
which is never visible from any normalized simple root. In other words,
$\widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
which is never visible from any normalized simple root. In other words,
![]() $\widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
is covered by
$\widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
is covered by
![]() $\{V_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\}$
.
$\{V_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\}$
.
Proof. Let
![]() $x\in \widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then
$x\in \widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then
![]() $x$
can be written like
$x$
can be written like
![]() $x=\sum _{i=1}^{n}x_{i}\widehat{\unicode[STIX]{x1D6FC}_{i}}$
, where
$x=\sum _{i=1}^{n}x_{i}\widehat{\unicode[STIX]{x1D6FC}_{i}}$
, where
![]() $x_{i}\geqslant 0$
and
$x_{i}\geqslant 0$
and
![]() $\sum _{i=1}^{n}x_{i}=1$
and
$\sum _{i=1}^{n}x_{i}=1$
and
![]() $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}$
are simple roots. Thus we have
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}$
are simple roots. Thus we have
If we suppose that
![]() $B(x,\widehat{\unicode[STIX]{x1D6FC}_{i}})<0$
for every
$B(x,\widehat{\unicode[STIX]{x1D6FC}_{i}})<0$
for every
![]() $i$
, then
$i$
, then
![]() $B(x,x)<0$
, a contradiction. Thus, there is at least one
$B(x,x)<0$
, a contradiction. Thus, there is at least one
![]() $i$
such that
$i$
such that
![]() $B(x,\unicode[STIX]{x1D6FC}_{i})\geqslant 0$
. This implies that
$B(x,\unicode[STIX]{x1D6FC}_{i})\geqslant 0$
. This implies that
![]() $x$
is visible from some normalized simple root
$x$
is visible from some normalized simple root
![]() $\widehat{\unicode[STIX]{x1D6FC}_{i}}$
from Lemma 2.5.◻
$\widehat{\unicode[STIX]{x1D6FC}_{i}}$
from Lemma 2.5.◻
In the following, we prove some lemmas for our proof of Theorem 1.2.
Lemma 2.7. For any
![]() $x\in \widehat{Q}$
and
$x\in \widehat{Q}$
and
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, one has
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, one has
![]() $B(\unicode[STIX]{x1D6FC},x)<1/(2|\unicode[STIX]{x1D6FC}|_{1})$
.
$B(\unicode[STIX]{x1D6FC},x)<1/(2|\unicode[STIX]{x1D6FC}|_{1})$
.
Proof. Suppose that
![]() $B(\unicode[STIX]{x1D6FC},x)\geqslant 1/(2|\unicode[STIX]{x1D6FC}|_{1})$
for some
$B(\unicode[STIX]{x1D6FC},x)\geqslant 1/(2|\unicode[STIX]{x1D6FC}|_{1})$
for some
![]() $x\in \widehat{Q}$
and
$x\in \widehat{Q}$
and
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Then we have
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Then we have
![]() $|s_{\unicode[STIX]{x1D6FC}}(x)|_{1}=1-2B(\unicode[STIX]{x1D6FC},x)|\unicode[STIX]{x1D6FC}|_{1}\leqslant 0$
. On the other hand, for
$|s_{\unicode[STIX]{x1D6FC}}(x)|_{1}=1-2B(\unicode[STIX]{x1D6FC},x)|\unicode[STIX]{x1D6FC}|_{1}\leqslant 0$
. On the other hand, for
![]() $y\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
, we have
$y\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
, we have
![]() $B(\unicode[STIX]{x1D6FC},y)=0$
by Lemma 2.5(iii), implying that
$B(\unicode[STIX]{x1D6FC},y)=0$
by Lemma 2.5(iii), implying that
![]() $|s_{\unicode[STIX]{x1D6FC}}(y)|_{1}=1-2B(y,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}=1>0$
. Now from the continuity of a linear map
$|s_{\unicode[STIX]{x1D6FC}}(y)|_{1}=1-2B(y,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}=1>0$
. Now from the continuity of a linear map
![]() $B(\unicode[STIX]{x1D6FC},\ast )$
, there should be
$B(\unicode[STIX]{x1D6FC},\ast )$
, there should be
![]() $z\in \widehat{Q}$
such that
$z\in \widehat{Q}$
such that
![]() $|s_{\unicode[STIX]{x1D6FC}}(z)|_{1}=0$
. However, as mentioned in Lemma 2.4,
$|s_{\unicode[STIX]{x1D6FC}}(z)|_{1}=0$
. However, as mentioned in Lemma 2.4,
![]() $W(V_{0})\cap \widehat{Q}=\emptyset$
, a contradiction.◻
$W(V_{0})\cap \widehat{Q}=\emptyset$
, a contradiction.◻
Proposition 2.8. For
![]() $x,y\in Q\setminus \{\mathbf{0}\}$
,
$x,y\in Q\setminus \{\mathbf{0}\}$
,
(a) one has
 $B(x,y)=0$
if and only if
$B(x,y)=0$
if and only if
 $\widehat{x}=\widehat{y}$
;
$\widehat{x}=\widehat{y}$
;(b) if
 $\widehat{x}\not =\widehat{y}$
, then one has
$\widehat{x}\not =\widehat{y}$
, then one has
 $B(\widehat{x},\widehat{y})<0$
;
$B(\widehat{x},\widehat{y})<0$
;(c) for any
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
and
 $x,y\in V_{\unicode[STIX]{x1D6FC}}$
, we have and the equality of this inequality holds if and only if
$x,y\in V_{\unicode[STIX]{x1D6FC}}$
, we have and the equality of this inequality holds if and only if $$\begin{eqnarray}|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,s_{\unicode[STIX]{x1D6FC}}\cdot y)|\geqslant |B(x,y)|\end{eqnarray}$$
$$\begin{eqnarray}|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,s_{\unicode[STIX]{x1D6FC}}\cdot y)|\geqslant |B(x,y)|\end{eqnarray}$$
 $x,y\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
.
$x,y\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
.
Proof. For
![]() $x,y\in Q\setminus \{\mathbf{0}\}$
with
$x,y\in Q\setminus \{\mathbf{0}\}$
with
![]() $\widehat{x}\not =\widehat{y}$
, one has
$\widehat{x}\not =\widehat{y}$
, one has
![]() $|\widehat{x}-\widehat{y}|_{1}=|\widehat{x}|_{1}-|\widehat{y}|_{1}=0$
. Thus,
$|\widehat{x}-\widehat{y}|_{1}=|\widehat{x}|_{1}-|\widehat{y}|_{1}=0$
. Thus,
![]() $\widehat{x}-\widehat{y}\in V_{0}$
. Note that
$\widehat{x}-\widehat{y}\in V_{0}$
. Note that
![]() $x\not \in V_{0}$
and
$x\not \in V_{0}$
and
![]() $y\not \in V_{0}$
by
$y\not \in V_{0}$
by
![]() $Q\cap V_{0}=\{\mathbf{0}\}$
(Lemma 2.4). Moreover, it also follows that
$Q\cap V_{0}=\{\mathbf{0}\}$
(Lemma 2.4). Moreover, it also follows that
![]() $B$
is positive-definite on
$B$
is positive-definite on
![]() $V_{0}$
. Thus, we see that
$V_{0}$
. Thus, we see that
![]() $B(\widehat{x}-\widehat{y},\widehat{x}-\widehat{y})=-2B(\widehat{x},\widehat{y})\geqslant 0$
and
$B(\widehat{x}-\widehat{y},\widehat{x}-\widehat{y})=-2B(\widehat{x},\widehat{y})\geqslant 0$
and
![]() $B(\widehat{x}-\widehat{y},\widehat{x}-\widehat{y})=0$
if and only if
$B(\widehat{x}-\widehat{y},\widehat{x}-\widehat{y})=0$
if and only if
![]() $\widehat{x}-\widehat{y}=\mathbf{0}$
. Hence, we conclude:
$\widehat{x}-\widehat{y}=\mathbf{0}$
. Hence, we conclude:
(a)
 $B(x,y)=|x|_{1}|y|_{1}B(\widehat{x},\widehat{y})=0$
if and only if
$B(x,y)=|x|_{1}|y|_{1}B(\widehat{x},\widehat{y})=0$
if and only if
 $\widehat{x}=\widehat{y}$
;
$\widehat{x}=\widehat{y}$
;(b)
 $B(\widehat{x},\widehat{y})<0$
if
$B(\widehat{x},\widehat{y})<0$
if
 $\widehat{x}\not =\widehat{y}$
.
$\widehat{x}\not =\widehat{y}$
.
In addition, thanks to Lemma 2.5 and Lemma 2.7, one has
![]() $0\leqslant B(x,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1},B(y,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}<\frac{1}{2}$
. Thus the inequality
$0\leqslant B(x,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1},B(y,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}<\frac{1}{2}$
. Thus the inequality
![]() $0<|s_{\unicode[STIX]{x1D6FC}}(x)|_{1}=$
$0<|s_{\unicode[STIX]{x1D6FC}}(x)|_{1}=$
![]() $|x-2B(x,\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D6FC}|_{1}\leqslant 1$
holds. Similarly,
$|x-2B(x,\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D6FC}|_{1}\leqslant 1$
holds. Similarly,
![]() $0<|s_{\unicode[STIX]{x1D6FC}}(y)|_{1}\leqslant 1$
. Hence
$0<|s_{\unicode[STIX]{x1D6FC}}(y)|_{1}\leqslant 1$
. Hence
In particular, since
![]() $|s_{\unicode[STIX]{x1D6FC}}(x)|_{1}=1$
if and only if we have
$|s_{\unicode[STIX]{x1D6FC}}(x)|_{1}=1$
if and only if we have
![]() $x\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
,
$x\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
,
![]() $|B(x,y)|<|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,s_{\unicode[STIX]{x1D6FC}}\cdot y)|$
holds if
$|B(x,y)|<|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,s_{\unicode[STIX]{x1D6FC}}\cdot y)|$
holds if
![]() $x\not \in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
or
$x\not \in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
or
![]() $y\not \in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
.◻
$y\not \in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
.◻
2.3 A metric on
 $\widehat{Q}$
$\widehat{Q}$
Next, we define a metric on
![]() $\widehat{Q}$
by a bilinear form
$\widehat{Q}$
by a bilinear form
![]() $B$
.
$B$
.
We first remark the following.
Remark 2.9. As in the proof of Proposition 2.8,
![]() $B$
is positive-definite on
$B$
is positive-definite on
![]() $V_{0}$
(not
$V_{0}$
(not
![]() $V$
) by
$V$
) by
![]() $Q\cap V_{0}=\{\mathbf{0}\}$
. Thus,
$Q\cap V_{0}=\{\mathbf{0}\}$
. Thus,
![]() $B(x-y,x-y)^{1/2}$
defines a metric on
$B(x-y,x-y)^{1/2}$
defines a metric on
![]() $V_{1}$
. Moreover, since
$V_{1}$
. Moreover, since
![]() $|B(x-y,x-y)|=2|B(x,y)|$
for
$|B(x-y,x-y)|=2|B(x,y)|$
for
![]() $x,y\in \widehat{Q}$
,
$x,y\in \widehat{Q}$
,
![]() $|B(\cdot ,\cdot )|^{1/2}:\widehat{Q}\times \widehat{Q}\rightarrow \mathbb{R}_{{\geqslant}0}$
defines a metric on
$|B(\cdot ,\cdot )|^{1/2}:\widehat{Q}\times \widehat{Q}\rightarrow \mathbb{R}_{{\geqslant}0}$
defines a metric on
![]() $\widehat{Q}$
. We see that
$\widehat{Q}$
. We see that
![]() $\sup _{x,y\in \widehat{Q},x\not =y}(|B(x,y)|^{1/2})/(\Vert x-y\Vert )$
is bounded, where
$\sup _{x,y\in \widehat{Q},x\not =y}(|B(x,y)|^{1/2})/(\Vert x-y\Vert )$
is bounded, where
![]() $\Vert \cdot \Vert$
denotes the Euclidean norm, because of the following:
$\Vert \cdot \Vert$
denotes the Euclidean norm, because of the following:
 $$\begin{eqnarray}\displaystyle \sup _{x,y\in \widehat{Q},x\not =y}\frac{\sqrt{2}|B(x,y)|^{1/2}}{\Vert x-y\Vert } & = & \displaystyle \sup _{x,y\in \widehat{Q},x\not =y}\frac{\sqrt{2}|\frac{1}{2}B(x-y,x-y)|^{1/2}}{\Vert x-y\Vert }\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \sup _{v\in V_{0},v\not =0}\frac{|B(v,v)|^{1/2}}{\Vert v\Vert }=\sup _{v\in V_{0},\Vert v\Vert =1}|B(v,v)|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \sup _{x,y\in \widehat{Q},x\not =y}\frac{\sqrt{2}|B(x,y)|^{1/2}}{\Vert x-y\Vert } & = & \displaystyle \sup _{x,y\in \widehat{Q},x\not =y}\frac{\sqrt{2}|\frac{1}{2}B(x-y,x-y)|^{1/2}}{\Vert x-y\Vert }\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \sup _{v\in V_{0},v\not =0}\frac{|B(v,v)|^{1/2}}{\Vert v\Vert }=\sup _{v\in V_{0},\Vert v\Vert =1}|B(v,v)|.\nonumber\end{eqnarray}$$
Since the region
![]() $\{v\in V_{0}:\Vert v\Vert =1\}$
is compact and the bilinear map
$\{v\in V_{0}:\Vert v\Vert =1\}$
is compact and the bilinear map
![]() $B(,)$
is continuous, there is
$B(,)$
is continuous, there is
![]() $u\in V$
such that
$u\in V$
such that
![]() $|B(u,u)|=\sup _{v\in V_{0},\Vert v\Vert =1}|B(v,v)|<\infty$
. Conversely, we also see that
$|B(u,u)|=\sup _{v\in V_{0},\Vert v\Vert =1}|B(v,v)|<\infty$
. Conversely, we also see that
![]() $\sup _{x,y\in \widehat{Q},x\not =y}(\Vert x-y\Vert )/(|B(x,y)|^{1/2})$
is bounded because
$\sup _{x,y\in \widehat{Q},x\not =y}(\Vert x-y\Vert )/(|B(x,y)|^{1/2})$
is bounded because
![]() $B$
is positive-definite on
$B$
is positive-definite on
![]() $V_{0}$
. These show the comparability of
$V_{0}$
. These show the comparability of
![]() $|B(\cdot ,\cdot )|^{1/2}$
and
$|B(\cdot ,\cdot )|^{1/2}$
and
![]() $\Vert \cdot \Vert$
on
$\Vert \cdot \Vert$
on
![]() $\widehat{Q}$
.
$\widehat{Q}$
.
Let
![]() $c$
be a curve in
$c$
be a curve in
![]() $\widehat{Q}$
connecting
$\widehat{Q}$
connecting
![]() $x$
and
$x$
and
![]() $y$
for
$y$
for
![]() $x,y\in \widehat{Q}$
. The length
$x,y\in \widehat{Q}$
. The length
![]() $\ell _{B}(c)$
of
$\ell _{B}(c)$
of
![]() $c$
is defined by
$c$
is defined by
where the supremum is taken over all chains
![]() $C=\{x=x_{0},x_{1},\ldots ,x_{n}=y\}$
on
$C=\{x=x_{0},x_{1},\ldots ,x_{n}=y\}$
on
![]() $c$
with unbounded
$c$
with unbounded
![]() $n$
. Given
$n$
. Given
![]() $x,y\in \widehat{Q}$
with
$x,y\in \widehat{Q}$
with
![]() $x\not =y$
, we define
$x\not =y$
, we define
Since
![]() $B$
is symmetric, the symmetry of
$B$
is symmetric, the symmetry of
![]() $d_{B}$
is trivial. Moreover, the nonnegativity of
$d_{B}$
is trivial. Moreover, the nonnegativity of
![]() $d_{B}$
is also trivial. In addition, the triangle inequality can be seen easily. Hence
$d_{B}$
is also trivial. In addition, the triangle inequality can be seen easily. Hence
![]() $d_{B}:\widehat{Q}\times \widehat{Q}\rightarrow \mathbb{R}_{{\geqslant}0}$
is a pseudometric on
$d_{B}:\widehat{Q}\times \widehat{Q}\rightarrow \mathbb{R}_{{\geqslant}0}$
is a pseudometric on
![]() $\widehat{Q}$
. The following lemma guarantees that
$\widehat{Q}$
. The following lemma guarantees that
![]() $d_{B}$
is a metric.
$d_{B}$
is a metric.
Lemma 2.10. For any
![]() $x,y\in \widehat{Q}$
, if
$x,y\in \widehat{Q}$
, if
![]() $d_{B}(x,y)=0$
, then
$d_{B}(x,y)=0$
, then
![]() $x=y$
.
$x=y$
.
Proof. When
![]() $d_{B}(x,y)=0$
, for an arbitrary
$d_{B}(x,y)=0$
, for an arbitrary
![]() $\unicode[STIX]{x1D716}>0$
, there exists a curve
$\unicode[STIX]{x1D716}>0$
, there exists a curve
![]() $c$
such that
$c$
such that
![]() $\ell _{B}(c)<\unicode[STIX]{x1D716}$
. By the definition of
$\ell _{B}(c)<\unicode[STIX]{x1D716}$
. By the definition of
![]() $\ell _{B}$
, since
$\ell _{B}$
, since
![]() $\sum _{i=1}^{m}|B(x_{i-1},x_{i})|^{1/2}<\unicode[STIX]{x1D716}$
for any chain of
$\sum _{i=1}^{m}|B(x_{i-1},x_{i})|^{1/2}<\unicode[STIX]{x1D716}$
for any chain of
![]() $c$
, one has
$c$
, one has
![]() $|B(x,y)|^{1/2}<\unicode[STIX]{x1D716}$
. This means that
$|B(x,y)|^{1/2}<\unicode[STIX]{x1D716}$
. This means that
![]() $B(x,y)=0$
. Therefore,
$B(x,y)=0$
. Therefore,
![]() $x=y$
by Proposition 2.8.◻
$x=y$
by Proposition 2.8.◻
Lemma 2.11. Let
![]() $d_{E}$
be the length metric using
$d_{E}$
be the length metric using
![]() $\Vert \cdot \Vert$
defined by the same way as
$\Vert \cdot \Vert$
defined by the same way as
![]() $d_{B}$
. Then the metric space
$d_{B}$
. Then the metric space
![]() $(\widehat{Q},d_{B})$
is homeomorphic to
$(\widehat{Q},d_{B})$
is homeomorphic to
![]() $(\widehat{Q},d_{E})$
.
$(\widehat{Q},d_{E})$
.
Proof. The discussions in Remark 2.9 imply the comparability of
![]() $d_{E}$
and
$d_{E}$
and
![]() $d_{B}$
. In fact, the (Lipschitz) continuity of
$d_{B}$
. In fact, the (Lipschitz) continuity of
![]() $\text{id}:(\widehat{Q},d_{E})\rightarrow (\widehat{Q},d_{B})$
can be proved as follows. For an arbitrary curve
$\text{id}:(\widehat{Q},d_{E})\rightarrow (\widehat{Q},d_{B})$
can be proved as follows. For an arbitrary curve
![]() $c$
in
$c$
in
![]() $\widehat{Q}$
joining
$\widehat{Q}$
joining
![]() $x$
and
$x$
and
![]() $y$
and
$y$
and
![]() $\unicode[STIX]{x1D716}>0$
, there exists a chain
$\unicode[STIX]{x1D716}>0$
, there exists a chain
![]() $C=\{x=x_{0},x_{1},\ldots ,x_{m}=y\}$
such that
$C=\{x=x_{0},x_{1},\ldots ,x_{m}=y\}$
such that
where
![]() $K=\sup _{x,y\in \widehat{Q},x\not =y}\sqrt{2}|B(x,y)|^{1/2}/\Vert x-y\Vert$
and
$K=\sup _{x,y\in \widehat{Q},x\not =y}\sqrt{2}|B(x,y)|^{1/2}/\Vert x-y\Vert$
and
![]() $\ell _{E}(c)$
is the length of
$\ell _{E}(c)$
is the length of
![]() $c$
defined by using
$c$
defined by using
![]() $\Vert \cdot \Vert$
. Thus, for any
$\Vert \cdot \Vert$
. Thus, for any
![]() $x,y\in \widehat{Q}$
and
$x,y\in \widehat{Q}$
and
![]() $\unicode[STIX]{x1D716}>0$
, we have
$\unicode[STIX]{x1D716}>0$
, we have
![]() $d_{B}(x,y)-\unicode[STIX]{x1D716}\leqslant Kd_{E}(x,y)$
. Hence,
$d_{B}(x,y)-\unicode[STIX]{x1D716}\leqslant Kd_{E}(x,y)$
. Hence,
![]() $d_{B}(x,y)\leqslant Kd_{E}(x,y)$
. Similarly, we also see the (Lipschitz) continuity of
$d_{B}(x,y)\leqslant Kd_{E}(x,y)$
. Similarly, we also see the (Lipschitz) continuity of
![]() $\text{id}:(\widehat{Q},d_{B})\rightarrow (\widehat{Q},d_{E})$
.◻
$\text{id}:(\widehat{Q},d_{B})\rightarrow (\widehat{Q},d_{E})$
.◻
Since
![]() $\widehat{Q}$
is the boundary of an ellipsoid in
$\widehat{Q}$
is the boundary of an ellipsoid in
![]() $V\cong \mathbb{R}^{n}$
,
$V\cong \mathbb{R}^{n}$
,
![]() $\widehat{Q}$
is a
$\widehat{Q}$
is a
![]() $C^{\infty }$
manifold and its topology induced from
$C^{\infty }$
manifold and its topology induced from
![]() $d_{E}$
coincides with the relative topology of
$d_{E}$
coincides with the relative topology of
![]() $V$
. Clearly,
$V$
. Clearly,
![]() $\widehat{Q}$
is compact on the relative topology of
$\widehat{Q}$
is compact on the relative topology of
![]() $V$
, so
$V$
, so
![]() $(\widehat{Q},d_{B})$
is also compact by Remark 2.9 and Lemma 2.11. The compactness of
$(\widehat{Q},d_{B})$
is also compact by Remark 2.9 and Lemma 2.11. The compactness of
![]() $(\widehat{Q},d_{B})$
also implies that
$(\widehat{Q},d_{B})$
also implies that
![]() $(\widehat{Q},d_{B})$
is a geodesic space by Hopf–Rinow theorem (see [Reference Gromov4, p. 9]). Moreover, since each normalized simple reflection is a homeomorphism on
$(\widehat{Q},d_{B})$
is a geodesic space by Hopf–Rinow theorem (see [Reference Gromov4, p. 9]). Moreover, since each normalized simple reflection is a homeomorphism on
![]() $(\widehat{Q},\Vert \cdot \Vert )$
, we obtain the following:
$(\widehat{Q},\Vert \cdot \Vert )$
, we obtain the following:
Proposition 2.12. The metric space
![]() $(\widehat{Q},d_{B})$
is a compact geodesic space. Moreover,
$(\widehat{Q},d_{B})$
is a compact geodesic space. Moreover,
![]() $W$
acts on
$W$
acts on
![]() $(\widehat{Q},d_{B})$
as a homeomorphism.
$(\widehat{Q},d_{B})$
as a homeomorphism.
Finally, we observe more precise properties of the normalized action on
![]() $(\widehat{Q},d_{B})$
.
$(\widehat{Q},d_{B})$
.
Proposition 2.13. Let
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
and
![]() $x,y\in V_{\unicode[STIX]{x1D6FC}}$
.
$x,y\in V_{\unicode[STIX]{x1D6FC}}$
.
(i) Each geodesic between
 $x$
and
$x$
and
 $y$
is contained in
$y$
is contained in
 $V_{\unicode[STIX]{x1D6FC}}$
.
$V_{\unicode[STIX]{x1D6FC}}$
.(ii) For any visible curve
 $c$
from
$c$
from
 $\widehat{\unicode[STIX]{x1D6FC}}$
, we have (1)Moreover,
$\widehat{\unicode[STIX]{x1D6FC}}$
, we have (1)Moreover, $$\begin{eqnarray}\displaystyle \ell _{B}(c)\leqslant \ell _{B}(s_{\unicode[STIX]{x1D6FC}}\cdot c). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ell _{B}(c)\leqslant \ell _{B}(s_{\unicode[STIX]{x1D6FC}}\cdot c). & & \displaystyle\end{eqnarray}$$
 $d_{B}(x,y)\leqslant d_{B}(s_{\unicode[STIX]{x1D6FC}}\cdot x,s_{\unicode[STIX]{x1D6FC}}\cdot y)$
.
$d_{B}(x,y)\leqslant d_{B}(s_{\unicode[STIX]{x1D6FC}}\cdot x,s_{\unicode[STIX]{x1D6FC}}\cdot y)$
.(iii) For any nontrivial curve
 $c$
, the equality of (1) holds if and only if
$c$
, the equality of (1) holds if and only if
 $c\subset \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
.
$c\subset \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
.
Proof. Let
![]() $c^{\prime }$
be a geodesic joining
$c^{\prime }$
be a geodesic joining
![]() $x$
and
$x$
and
![]() $y$
. Let us decompose
$y$
. Let us decompose
![]() $c^{\prime }$
into
$c^{\prime }$
into
where
![]() $c_{i}$
(
$c_{i}$
(
![]() $i\in I$
) is a visible curve from
$i\in I$
) is a visible curve from
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $c_{j}$
(
$c_{j}$
(
![]() $j\in J$
) the others. Remark that
$j\in J$
) the others. Remark that
![]() $J$
might be empty. Set
$J$
might be empty. Set
![]() $c^{\prime \prime }=\bigcup _{i\in I}c_{i}\cup \bigcup _{j\in J}s_{\unicode[STIX]{x1D6FC}}\cdot c_{j}$
. Then
$c^{\prime \prime }=\bigcup _{i\in I}c_{i}\cup \bigcup _{j\in J}s_{\unicode[STIX]{x1D6FC}}\cdot c_{j}$
. Then
![]() $c^{\prime \prime }$
is a curve joining
$c^{\prime \prime }$
is a curve joining
![]() $x$
and
$x$
and
![]() $y$
because each point of the boundary of the visible area from
$y$
because each point of the boundary of the visible area from
![]() $\unicode[STIX]{x1D6FC}$
is fixed by
$\unicode[STIX]{x1D6FC}$
is fixed by
![]() $s_{\unicode[STIX]{x1D6FC}}$
. By Proposition 2.8(c), we obtain
$s_{\unicode[STIX]{x1D6FC}}$
. By Proposition 2.8(c), we obtain
![]() $\ell _{B}(c^{\prime })>\ell _{B}(c^{\prime \prime })$
if
$\ell _{B}(c^{\prime })>\ell _{B}(c^{\prime \prime })$
if
![]() $J$
is not empty. However, since
$J$
is not empty. However, since
![]() $c^{\prime }$
is a geodesic joining
$c^{\prime }$
is a geodesic joining
![]() $x$
and
$x$
and
![]() $y$
,
$y$
,
![]() $J$
should be empty. This says that each geodesic between
$J$
should be empty. This says that each geodesic between
![]() $x$
and
$x$
and
![]() $y$
is contained in
$y$
is contained in
![]() $V_{\unicode[STIX]{x1D6FC}}$
.
$V_{\unicode[STIX]{x1D6FC}}$
.
Next, we prove (iii). If
![]() $c\subset \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
, since
$c\subset \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
, since
![]() $B(\unicode[STIX]{x1D6FC},x)=0$
for any
$B(\unicode[STIX]{x1D6FC},x)=0$
for any
![]() $x\in c$
, the equality of (1) directly follows. Assume that
$x\in c$
, the equality of (1) directly follows. Assume that
![]() $\ell _{B}(c)=\ell _{B}(s_{\unicode[STIX]{x1D6FC}}\cdot c)$
. Then for an arbitrary curve
$\ell _{B}(c)=\ell _{B}(s_{\unicode[STIX]{x1D6FC}}\cdot c)$
. Then for an arbitrary curve
![]() $c^{\prime }\subset c$
, we also have
$c^{\prime }\subset c$
, we also have
![]() $\ell _{B}(c^{\prime })=\ell _{B}(s_{\unicode[STIX]{x1D6FC}}\cdot c^{\prime })$
. Decompose
$\ell _{B}(c^{\prime })=\ell _{B}(s_{\unicode[STIX]{x1D6FC}}\cdot c^{\prime })$
. Decompose
![]() $c$
into
$c$
into
![]() $k$
curves for an arbitrary fixed
$k$
curves for an arbitrary fixed
![]() $k\in \mathbb{Z}_{{>}0}$
. Let
$k\in \mathbb{Z}_{{>}0}$
. Let
![]() $c_{1}$
be one component of such curves. For
$c_{1}$
be one component of such curves. For
![]() $0<\unicode[STIX]{x1D716}<1$
, by the definition of
$0<\unicode[STIX]{x1D716}<1$
, by the definition of
![]() $\ell _{B}$
, there exists a chain
$\ell _{B}$
, there exists a chain
![]() $\{x_{1},\ldots ,x_{m}\}$
, where
$\{x_{1},\ldots ,x_{m}\}$
, where
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{m}$
are the endpoints of
$x_{m}$
are the endpoints of
![]() $c_{1}$
, such that
$c_{1}$
, such that
Since
![]() $\ell _{B}(c_{1})=\ell _{B}(s_{\unicode[STIX]{x1D6FC}}\cdot c_{1})$
, one has
$\ell _{B}(c_{1})=\ell _{B}(s_{\unicode[STIX]{x1D6FC}}\cdot c_{1})$
, one has
 $$\begin{eqnarray}\displaystyle (1-\unicode[STIX]{x1D716})^{1/2}\ell _{B}(c_{1}) & = & \displaystyle (1-\unicode[STIX]{x1D716})^{1/2}\ell _{B}(s_{\unicode[STIX]{x1D6FC}}\cdot c_{1})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (1-\unicode[STIX]{x1D716})^{1/2}\mathop{\sum }_{i=1}^{m}|B(s_{\unicode[STIX]{x1D6FC}}\cdot x_{i-1},s_{\unicode[STIX]{x1D6FC}}\cdot x_{i})|^{1/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (1-\unicode[STIX]{x1D716})^{1/2}\ell _{B}(c_{1}) & = & \displaystyle (1-\unicode[STIX]{x1D716})^{1/2}\ell _{B}(s_{\unicode[STIX]{x1D6FC}}\cdot c_{1})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (1-\unicode[STIX]{x1D716})^{1/2}\mathop{\sum }_{i=1}^{m}|B(s_{\unicode[STIX]{x1D6FC}}\cdot x_{i-1},s_{\unicode[STIX]{x1D6FC}}\cdot x_{i})|^{1/2}.\nonumber\end{eqnarray}$$
Hence,
Now, in general, for positive real numbers
![]() $a_{1},\ldots ,a_{m}$
and
$a_{1},\ldots ,a_{m}$
and
![]() $b_{1},\ldots ,b_{m}$
, we see that
$b_{1},\ldots ,b_{m}$
, we see that
Thus, there exists some
![]() $i$
such that
$i$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{|B(x_{i-1},x_{i})|^{1/2}}{|B(s_{\unicode[STIX]{x1D6FC}}\cdot x_{i-1},s_{\unicode[STIX]{x1D6FC}}\cdot x_{i})|^{1/2}}\geqslant (1-\unicode[STIX]{x1D716})^{1/2}\Longleftrightarrow \frac{|B(x_{i-1},x_{i})|}{|B(s_{\unicode[STIX]{x1D6FC}}\cdot x_{i-1},s_{\unicode[STIX]{x1D6FC}}\cdot x_{i})|}\geqslant 1-\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & & \displaystyle \qquad \Longleftrightarrow (1-2B(x_{i-1},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1})(1-2B(x_{i},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1})\geqslant 1-\unicode[STIX]{x1D716}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{|B(x_{i-1},x_{i})|^{1/2}}{|B(s_{\unicode[STIX]{x1D6FC}}\cdot x_{i-1},s_{\unicode[STIX]{x1D6FC}}\cdot x_{i})|^{1/2}}\geqslant (1-\unicode[STIX]{x1D716})^{1/2}\Longleftrightarrow \frac{|B(x_{i-1},x_{i})|}{|B(s_{\unicode[STIX]{x1D6FC}}\cdot x_{i-1},s_{\unicode[STIX]{x1D6FC}}\cdot x_{i})|}\geqslant 1-\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & & \displaystyle \qquad \Longleftrightarrow (1-2B(x_{i-1},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1})(1-2B(x_{i},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1})\geqslant 1-\unicode[STIX]{x1D716}.\nonumber\end{eqnarray}$$
On the other hand, since
![]() $x_{i-1},x_{i}\in V_{\unicode[STIX]{x1D6FC}}$
, one has
$x_{i-1},x_{i}\in V_{\unicode[STIX]{x1D6FC}}$
, one has
![]() $1-2B(x_{i-1},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}\leqslant 1$
and
$1-2B(x_{i-1},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}\leqslant 1$
and
![]() $1-2B(x_{i},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}\leqslant 1$
. Hence
$1-2B(x_{i},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}\leqslant 1$
. Hence
![]() $1-\unicode[STIX]{x1D716}\leqslant 1-2B(x_{i-1},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}\leqslant 1$
and
$1-\unicode[STIX]{x1D716}\leqslant 1-2B(x_{i-1},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}\leqslant 1$
and
![]() $1-\unicode[STIX]{x1D716}\leqslant 1-2B(x_{i},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}\leqslant 1$
. Since
$1-\unicode[STIX]{x1D716}\leqslant 1-2B(x_{i},\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}\leqslant 1$
. Since
![]() $\unicode[STIX]{x1D716}$
is arbitrary, by taking
$\unicode[STIX]{x1D716}$
is arbitrary, by taking
![]() $\unicode[STIX]{x1D716}$
as
$\unicode[STIX]{x1D716}$
as
![]() $\unicode[STIX]{x1D716}\rightarrow 0$
, we see that
$\unicode[STIX]{x1D716}\rightarrow 0$
, we see that
![]() $x_{i-1}$
and
$x_{i-1}$
and
![]() $x_{i}$
belong to
$x_{i}$
belong to
![]() $\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
. Moreover, since
$\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
. Moreover, since
![]() $k$
is also arbitrary, by taking
$k$
is also arbitrary, by taking
![]() $k$
as
$k$
as
![]() $k\rightarrow \infty$
, we conclude that
$k\rightarrow \infty$
, we conclude that
![]() $c\subset \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
, as desired.◻
$c\subset \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
, as desired.◻
3 A proof of Theorem 1.3
In this section, we prove Theorem 1.3. First, we note that
![]() $x\in \widehat{Q}$
is fixed by the normalized action of
$x\in \widehat{Q}$
is fixed by the normalized action of
![]() $s_{\unicode[STIX]{x1D6FC}}$
for
$s_{\unicode[STIX]{x1D6FC}}$
for
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
if and only if
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
if and only if
![]() $B(x,\unicode[STIX]{x1D6FC})=0$
.
$B(x,\unicode[STIX]{x1D6FC})=0$
.
Remark 3.1. In general, each point
![]() $x\in \widehat{Q}$
fixed by every normalized action of
$x\in \widehat{Q}$
fixed by every normalized action of
![]() $s_{\unicode[STIX]{x1D6FC}}$
corresponds to an eigenvector whose eigenvalue is 0. Thus, there is no such point when
$s_{\unicode[STIX]{x1D6FC}}$
corresponds to an eigenvector whose eigenvalue is 0. Thus, there is no such point when
![]() $B$
is definite, in particular,
$B$
is definite, in particular,
![]() $B$
has the signature
$B$
has the signature
![]() $(n-1,1)$
. Hence, there is no element in
$(n-1,1)$
. Hence, there is no element in
![]() $\widehat{Q}$
which is fixed by every
$\widehat{Q}$
which is fixed by every
![]() $s_{\unicode[STIX]{x1D6FC}}$
with
$s_{\unicode[STIX]{x1D6FC}}$
with
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. In other words, we have
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. In other words, we have
![]() $\bigcap _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}=\emptyset$
.
$\bigcap _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}=\emptyset$
.
Lemma 3.2. Let
![]() $K\subset \widehat{Q}$
be a nonempty
$K\subset \widehat{Q}$
be a nonempty
![]() $W$
-invariant subset of
$W$
-invariant subset of
![]() $\widehat{Q}$
. Then for each
$\widehat{Q}$
. Then for each
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, there is
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, there is
![]() $x_{\unicode[STIX]{x1D6FC}}\in K$
such that
$x_{\unicode[STIX]{x1D6FC}}\in K$
such that
![]() $x_{\unicode[STIX]{x1D6FC}}\not =s_{\unicode[STIX]{x1D6FC}}\cdot x_{\unicode[STIX]{x1D6FC}}$
.
$x_{\unicode[STIX]{x1D6FC}}\not =s_{\unicode[STIX]{x1D6FC}}\cdot x_{\unicode[STIX]{x1D6FC}}$
.
Proof. By Remark 3.1,
![]() $K$
contains
$K$
contains
![]() $x$
with
$x$
with
![]() $x\not =s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x$
for some
$x\not =s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x$
for some
![]() $\unicode[STIX]{x1D6FC}_{0}\in \unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6FC}_{0}\in \unicode[STIX]{x1D6E5}$
.
Fix
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
arbitrarily. Since we assume that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
arbitrarily. Since we assume that
![]() $W$
is irreducible, the Coxeter graph associated with
$W$
is irreducible, the Coxeter graph associated with
![]() $W$
is connected (cf. [Reference Humphreys7, Section 2.2]). Hence there is a path from
$W$
is connected (cf. [Reference Humphreys7, Section 2.2]). Hence there is a path from
![]() $\unicode[STIX]{x1D6FC}_{0}$
to
$\unicode[STIX]{x1D6FC}_{0}$
to
![]() $\unicode[STIX]{x1D6FC}$
in the Coxeter graph, that is to say, there is a sequence of simple roots
$\unicode[STIX]{x1D6FC}$
in the Coxeter graph, that is to say, there is a sequence of simple roots
![]() $(\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})$
such that
$(\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})$
such that
![]() $\unicode[STIX]{x1D6FC}_{k}=\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}_{k}=\unicode[STIX]{x1D6FC}$
and
![]() $B(\unicode[STIX]{x1D6FC}_{i-1},\unicode[STIX]{x1D6FC}_{i})\not =0$
for
$B(\unicode[STIX]{x1D6FC}_{i-1},\unicode[STIX]{x1D6FC}_{i})\not =0$
for
![]() $i=1,\ldots ,k$
, where
$i=1,\ldots ,k$
, where
![]() $k$
is some positive integer.
$k$
is some positive integer.
For
![]() $i=0$
, by the above discussions, there is a point
$i=0$
, by the above discussions, there is a point
![]() $x_{0}\in K$
such that
$x_{0}\in K$
such that
![]() $x_{0}$
is not fixed by
$x_{0}$
is not fixed by
![]() $s_{\unicode[STIX]{x1D6FC}_{0}}$
, i.e.,
$s_{\unicode[STIX]{x1D6FC}_{0}}$
, i.e.,
![]() $x_{0}\not =s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0}$
. For
$x_{0}\not =s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0}$
. For
![]() $i=1$
, we have
$i=1$
, we have
![]() $B(\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1})\not =0$
. On the other hand, since
$B(\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1})\not =0$
. On the other hand, since
 $$\begin{eqnarray}\displaystyle B(s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0},\unicode[STIX]{x1D6FC}_{1}) & = & \displaystyle \frac{B(x_{0}-2B(x_{0},\unicode[STIX]{x1D6FC}_{0})\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1})}{|s_{\unicode[STIX]{x1D6FC}_{0}}(x_{0})|_{1}}\nonumber\\ \displaystyle & = & \displaystyle \frac{B(x_{0},\unicode[STIX]{x1D6FC}_{1})-2B(x_{0},\unicode[STIX]{x1D6FC}_{0})B(\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1})}{|s_{\unicode[STIX]{x1D6FC}_{0}}(x_{0})|_{1}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B(s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0},\unicode[STIX]{x1D6FC}_{1}) & = & \displaystyle \frac{B(x_{0}-2B(x_{0},\unicode[STIX]{x1D6FC}_{0})\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1})}{|s_{\unicode[STIX]{x1D6FC}_{0}}(x_{0})|_{1}}\nonumber\\ \displaystyle & = & \displaystyle \frac{B(x_{0},\unicode[STIX]{x1D6FC}_{1})-2B(x_{0},\unicode[STIX]{x1D6FC}_{0})B(\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1})}{|s_{\unicode[STIX]{x1D6FC}_{0}}(x_{0})|_{1}},\nonumber\end{eqnarray}$$
if
![]() $B(x_{0},\unicode[STIX]{x1D6FC}_{1})=0$
, then
$B(x_{0},\unicode[STIX]{x1D6FC}_{1})=0$
, then
![]() $B(s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0},\unicode[STIX]{x1D6FC}_{1})\not =0$
because
$B(s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0},\unicode[STIX]{x1D6FC}_{1})\not =0$
because
![]() $B(x_{0},\unicode[STIX]{x1D6FC}_{0})\not =0$
and
$B(x_{0},\unicode[STIX]{x1D6FC}_{0})\not =0$
and
![]() $B(\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1})\not =0$
. Hence either
$B(\unicode[STIX]{x1D6FC}_{0},\unicode[STIX]{x1D6FC}_{1})\not =0$
. Hence either
![]() $B(x_{0},\unicode[STIX]{x1D6FC}_{1})$
or
$B(x_{0},\unicode[STIX]{x1D6FC}_{1})$
or
![]() $B(s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0},\unicode[STIX]{x1D6FC}_{1})$
is nonzero. This means that either
$B(s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0},\unicode[STIX]{x1D6FC}_{1})$
is nonzero. This means that either
![]() $x_{0}$
or
$x_{0}$
or
![]() $s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0}$
is not fixed by
$s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0}$
is not fixed by
![]() $s_{\unicode[STIX]{x1D6FC}_{1}}$
. Let
$s_{\unicode[STIX]{x1D6FC}_{1}}$
. Let
![]() $x_{1}$
be such point. Here we remark that since
$x_{1}$
be such point. Here we remark that since
![]() $x_{0}\in K$
and
$x_{0}\in K$
and
![]() $K$
is
$K$
is
![]() $W$
-invariant, we know that
$W$
-invariant, we know that
![]() $s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0}\in K$
, so
$s_{\unicode[STIX]{x1D6FC}_{0}}\cdot x_{0}\in K$
, so
![]() $x_{1}$
belongs to
$x_{1}$
belongs to
![]() $K$
. Similarly, we obtain that either
$K$
. Similarly, we obtain that either
![]() $x_{1}$
or
$x_{1}$
or
![]() $s_{\unicode[STIX]{x1D6FC}_{1}}\cdot x_{1}$
is not fixed by
$s_{\unicode[STIX]{x1D6FC}_{1}}\cdot x_{1}$
is not fixed by
![]() $s_{\unicode[STIX]{x1D6FC}_{2}}$
. Let
$s_{\unicode[STIX]{x1D6FC}_{2}}$
. Let
![]() $x_{2}$
be such point. By repeating this consideration, we eventually obtain
$x_{2}$
be such point. By repeating this consideration, we eventually obtain
![]() $x_{k}\in K$
such that
$x_{k}\in K$
such that
![]() $x_{k}$
is not fixed by
$x_{k}$
is not fixed by
![]() $s_{\unicode[STIX]{x1D6FC}}$
, as required.◻
$s_{\unicode[STIX]{x1D6FC}}$
, as required.◻
The following proposition plays a crucial role in the proof of Theorem 1.3.
Proposition 3.3. The set
![]() $E$
of accumulation points of normalized roots is a minimal
$E$
of accumulation points of normalized roots is a minimal
![]() $W$
-invariant closed set.
$W$
-invariant closed set.
Proof. Let
![]() $K\subset \widehat{Q}$
be a
$K\subset \widehat{Q}$
be a
![]() $W$
-invariant closed subset. We may show that
$W$
-invariant closed subset. We may show that
![]() $E\subset K$
.
$E\subset K$
.
Let
Thus
![]() $K^{\prime }$
is also a
$K^{\prime }$
is also a
![]() $W$
-invariant set. In what follows, we claim the inclusion
$W$
-invariant set. In what follows, we claim the inclusion
where
![]() $\overline{K^{\prime }}$
is the closure of
$\overline{K^{\prime }}$
is the closure of
![]() $K^{\prime }$
with respect to the Euclidean topology on
$K^{\prime }$
with respect to the Euclidean topology on
![]() $V$
. Suppose, on the contrary, that
$V$
. Suppose, on the contrary, that
![]() $\overline{K^{\prime }}\cap \widehat{Q}\not \subset K$
, i.e., there is
$\overline{K^{\prime }}\cap \widehat{Q}\not \subset K$
, i.e., there is
![]() $p\in \overline{K^{\prime }}\cap \widehat{Q}$
such that
$p\in \overline{K^{\prime }}\cap \widehat{Q}$
such that
![]() $p\in \widehat{Q}\setminus K$
. Then there is an open neighborhood of
$p\in \widehat{Q}\setminus K$
. Then there is an open neighborhood of
![]() $p$
in
$p$
in
![]() $\widehat{Q}$
such that
$\widehat{Q}$
such that
![]() $U\subset \widehat{Q}\setminus K$
because
$U\subset \widehat{Q}\setminus K$
because
![]() $K$
is closed. Take a sequence
$K$
is closed. Take a sequence
![]() $\{p_{i}\}$
in
$\{p_{i}\}$
in
![]() $K^{\prime }$
converging to
$K^{\prime }$
converging to
![]() $p$
. By the definition of
$p$
. By the definition of
![]() $K^{\prime }$
, there are
$K^{\prime }$
, there are
![]() $x_{i}$
and
$x_{i}$
and
![]() $y_{i}$
in
$y_{i}$
in
![]() $K$
with
$K$
with
![]() $x_{i}\not =y_{i}$
such that
$x_{i}\not =y_{i}$
such that
![]() $p_{i}\in L(x_{i},y_{i})$
for each
$p_{i}\in L(x_{i},y_{i})$
for each
![]() $i$
. We fix such
$i$
. We fix such
![]() $x_{i}$
and
$x_{i}$
and
![]() $y_{i}$
and assume that
$y_{i}$
and assume that
![]() $x_{i}$
is visible from
$x_{i}$
is visible from
![]() $p_{i}$
and
$p_{i}$
and
![]() $y_{i}$
is not. Let
$y_{i}$
is not. Let
![]() $v_{i}=\frac{1}{2}p_{i}+\frac{1}{2}x_{i}$
. Then we have
$v_{i}=\frac{1}{2}p_{i}+\frac{1}{2}x_{i}$
. Then we have
![]() $B(v_{i},v_{i})=\frac{1}{4}(B(p_{i},p_{i})+2B(p_{i},x_{i}))$
. Since
$B(v_{i},v_{i})=\frac{1}{4}(B(p_{i},p_{i})+2B(p_{i},x_{i}))$
. Since
![]() $p_{i}$
converges to
$p_{i}$
converges to
![]() $p\in \widehat{Q}$
,
$p\in \widehat{Q}$
,
![]() $B(p_{i},p_{i})$
goes to 0. However, since
$B(p_{i},p_{i})$
goes to 0. However, since
![]() $x_{i}$
never goes to
$x_{i}$
never goes to
![]() $p$
, we have
$p$
, we have
![]() $B(p_{i},p_{i})\leqslant |B(p_{i},x_{i})|$
for sufficiently large
$B(p_{i},p_{i})\leqslant |B(p_{i},x_{i})|$
for sufficiently large
![]() $i$
. (Otherwise, by taking a subsequence
$i$
. (Otherwise, by taking a subsequence
![]() $\{p_{j_{k}}\}$
of
$\{p_{j_{k}}\}$
of
![]() $\{p_{i}\}$
with
$\{p_{i}\}$
with
![]() $B(p_{j_{k}},p_{j_{k}})>|B(p_{j_{k}},x_{j_{k}})|$
for each
$B(p_{j_{k}},p_{j_{k}})>|B(p_{j_{k}},x_{j_{k}})|$
for each
![]() $k$
, one has
$k$
, one has
![]() $0\leqslant |B(p_{j_{k}},x_{j_{k}})|<B(p_{j_{k}},p_{j_{k}})\rightarrow 0$
, which means that
$0\leqslant |B(p_{j_{k}},x_{j_{k}})|<B(p_{j_{k}},p_{j_{k}})\rightarrow 0$
, which means that
![]() $x_{j_{k}}$
goes to
$x_{j_{k}}$
goes to
![]() $p$
, a contradiction.) Moreover, since
$p$
, a contradiction.) Moreover, since
![]() $x_{i}$
never goes to
$x_{i}$
never goes to
![]() $p$
again, one has
$p$
again, one has
![]() $B(p_{i},x_{i})<0$
for sufficiently large
$B(p_{i},x_{i})<0$
for sufficiently large
![]() $i$
by Proposition 2.8. Hence, for sufficiently large
$i$
by Proposition 2.8. Hence, for sufficiently large
![]() $i$
, we have
$i$
, we have
 $$\begin{eqnarray}\displaystyle B(v_{i},v_{i}) & = & \displaystyle \frac{1}{4}(B(p_{i},p_{i})+2B(p_{i},x_{i}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{4}(|B(p_{i},x_{i})|+2B(p_{i},x_{i}))\leqslant \frac{B(p_{i},x_{i})}{4}\leqslant 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B(v_{i},v_{i}) & = & \displaystyle \frac{1}{4}(B(p_{i},p_{i})+2B(p_{i},x_{i}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{4}(|B(p_{i},x_{i})|+2B(p_{i},x_{i}))\leqslant \frac{B(p_{i},x_{i})}{4}\leqslant 0.\nonumber\end{eqnarray}$$
On the one hand, since
![]() $x_{i}$
is visible from
$x_{i}$
is visible from
![]() $p_{i}$
, each point in
$p_{i}$
, each point in
![]() $L[x_{i},p_{i}]\setminus \{x_{i},p_{i}\}$
does not belong to
$L[x_{i},p_{i}]\setminus \{x_{i},p_{i}\}$
does not belong to
![]() $\widehat{Q}\cup \widehat{Q_{-}}$
. In particular,
$\widehat{Q}\cup \widehat{Q_{-}}$
. In particular,
![]() $v_{i}\not \in \widehat{Q}\cup \widehat{Q_{-}}$
. Thus, we have
$v_{i}\not \in \widehat{Q}\cup \widehat{Q_{-}}$
. Thus, we have
![]() $B(v_{i},v_{i})>0$
for every
$B(v_{i},v_{i})>0$
for every
![]() $i$
, a contradiction. Therefore, we conclude the desired inclusion
$i$
, a contradiction. Therefore, we conclude the desired inclusion
![]() $\overline{K^{\prime }}\cap \widehat{Q}\subset K$
.
$\overline{K^{\prime }}\cap \widehat{Q}\subset K$
.
For each
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, when we take
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, when we take
![]() $x\in K$
with
$x\in K$
with
![]() $x\not =s_{\unicode[STIX]{x1D6FC}}\cdot x$
,
$x\not =s_{\unicode[STIX]{x1D6FC}}\cdot x$
,
![]() $L(x,s_{\unicode[STIX]{x1D6FC}}\cdot x)$
intersects with
$L(x,s_{\unicode[STIX]{x1D6FC}}\cdot x)$
intersects with
![]() $\unicode[STIX]{x1D6FC}$
. Since
$\unicode[STIX]{x1D6FC}$
. Since
![]() $x$
and
$x$
and
![]() $s_{\unicode[STIX]{x1D6FC}}\cdot x$
belong to
$s_{\unicode[STIX]{x1D6FC}}\cdot x$
belong to
![]() $K$
,
$K$
,
![]() $\unicode[STIX]{x1D6FC}$
belongs to
$\unicode[STIX]{x1D6FC}$
belongs to
![]() $K^{\prime }$
. By Lemma 3.2, we can take such an element of
$K^{\prime }$
. By Lemma 3.2, we can take such an element of
![]() $K$
for every
$K$
for every
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Hence
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Hence
![]() $\unicode[STIX]{x1D6E5}\subset K^{\prime }$
. Since
$\unicode[STIX]{x1D6E5}\subset K^{\prime }$
. Since
![]() $K^{\prime }$
is
$K^{\prime }$
is
![]() $W$
-invariant, we also have
$W$
-invariant, we also have
![]() $W\cdot \unicode[STIX]{x1D6E5}=\widehat{\unicode[STIX]{x1D6F7}}\subset K^{\prime }$
. Thus, the accumulation points of
$W\cdot \unicode[STIX]{x1D6E5}=\widehat{\unicode[STIX]{x1D6F7}}\subset K^{\prime }$
. Thus, the accumulation points of
![]() $W\cdot \unicode[STIX]{x1D6E5}$
, which is nothing but
$W\cdot \unicode[STIX]{x1D6E5}$
, which is nothing but
![]() $E$
, should be contained in
$E$
, should be contained in
![]() $\overline{K^{\prime }}\cap \widehat{Q}\subset K$
. Therefore, we have
$\overline{K^{\prime }}\cap \widehat{Q}\subset K$
. Therefore, we have
![]() $E\subset K$
.◻
$E\subset K$
.◻
4 Fixed points of the normalized action
For
![]() $w\in W$
, there exists a constant
$w\in W$
, there exists a constant
![]() $C\geqslant 1$
such that for any
$C\geqslant 1$
such that for any
![]() $x\in Q$
, we have
$x\in Q$
, we have
We may choose a constant
![]() $C$
such that
$C$
such that
![]() $C$
is independent of the choice of
$C$
is independent of the choice of
![]() $x$
. In fact, from
$x$
. In fact, from
![]() $Q\setminus \{\mathbf{0}\}\subset V\setminus W(V_{0})$
, we can compute
$Q\setminus \{\mathbf{0}\}\subset V\setminus W(V_{0})$
, we can compute
Since
![]() $\widehat{Q}$
is compact, there exists
$\widehat{Q}$
is compact, there exists
![]() $y^{\prime }\in \widehat{Q}$
such that
$y^{\prime }\in \widehat{Q}$
such that
![]() $||w(y^{\prime })|_{1}|=\sup _{y\in \widehat{Q}}||w(y)|_{1}|$
. Similarly, there also exists
$||w(y^{\prime })|_{1}|=\sup _{y\in \widehat{Q}}||w(y)|_{1}|$
. Similarly, there also exists
![]() $y^{\prime \prime }\in \widehat{Q}$
such that
$y^{\prime \prime }\in \widehat{Q}$
such that
![]() $||w(y^{\prime \prime })|_{1}|=\inf _{y\in \widehat{Q}}||w(y)|_{1}|$
. Let
$||w(y^{\prime \prime })|_{1}|=\inf _{y\in \widehat{Q}}||w(y)|_{1}|$
. Let
![]() $C=\max \{||w(y^{\prime })|_{1}|,1/||w(y^{\prime \prime })|_{1}|\}$
. Thus
$C=\max \{||w(y^{\prime })|_{1}|,1/||w(y^{\prime \prime })|_{1}|\}$
. Thus
![]() $C\geqslant 1$
and the inequality (2) is satisfied.
$C\geqslant 1$
and the inequality (2) is satisfied.
Lemma 4.1. For
![]() $w\in W$
with infinite order and
$w\in W$
with infinite order and
![]() $x\in \widehat{Q}$
, let
$x\in \widehat{Q}$
, let
![]() $(w^{n_{i}}\cdot x)_{n_{i}}$
be a converging subsequence of
$(w^{n_{i}}\cdot x)_{n_{i}}$
be a converging subsequence of
![]() $(w^{n}\cdot x)_{n}$
to
$(w^{n}\cdot x)_{n}$
to
![]() $y\in \widehat{Q}$
. If
$y\in \widehat{Q}$
. If
![]() $||w^{n_{i}}(x)|_{1}|\rightarrow \infty$
, then for any
$||w^{n_{i}}(x)|_{1}|\rightarrow \infty$
, then for any
![]() $k\in \mathbb{Z}$
the sequence
$k\in \mathbb{Z}$
the sequence
![]() $(w^{n_{i}+k}\cdot x)_{n_{i}}$
also converges to
$(w^{n_{i}+k}\cdot x)_{n_{i}}$
also converges to
![]() $y$
.
$y$
.
Proof. Fix
![]() $k\in \mathbb{Z}$
arbitrarily. By the remark above, we have a constant
$k\in \mathbb{Z}$
arbitrarily. By the remark above, we have a constant
![]() $C_{k}\geqslant 1$
, which depends only on
$C_{k}\geqslant 1$
, which depends only on
![]() $k$
, so that for each
$k$
, so that for each
![]() $n\in \mathbb{N}$
,
$n\in \mathbb{N}$
,
Then we see that
 $$\begin{eqnarray}\displaystyle |B(w^{n_{i}}\cdot x,w^{n_{i}+k}\cdot x)| & = & \displaystyle \frac{|B(w^{n_{i}}(x),w^{n_{i}+k}(x))|}{||w^{n_{i}}(x)|_{1}|\cdot ||w^{n_{i}+k}(x)|_{1}|}\nonumber\\ \displaystyle & = & \displaystyle \frac{|B(x,w^{k}(x))|}{||w^{n_{i}}(x)|_{1}|\cdot ||w^{n_{i}+k}(x)|_{1}|}\leqslant C_{k}\frac{|B(x,w^{k}(x))|}{||w^{n_{i}}(x)|_{1}|^{2}}\rightarrow 0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |B(w^{n_{i}}\cdot x,w^{n_{i}+k}\cdot x)| & = & \displaystyle \frac{|B(w^{n_{i}}(x),w^{n_{i}+k}(x))|}{||w^{n_{i}}(x)|_{1}|\cdot ||w^{n_{i}+k}(x)|_{1}|}\nonumber\\ \displaystyle & = & \displaystyle \frac{|B(x,w^{k}(x))|}{||w^{n_{i}}(x)|_{1}|\cdot ||w^{n_{i}+k}(x)|_{1}|}\leqslant C_{k}\frac{|B(x,w^{k}(x))|}{||w^{n_{i}}(x)|_{1}|^{2}}\rightarrow 0,\nonumber\end{eqnarray}$$
as
![]() $n_{i}\rightarrow \infty$
. By Proposition 2.8, we have the conclusion.◻
$n_{i}\rightarrow \infty$
. By Proposition 2.8, we have the conclusion.◻
For any
![]() $w\in W$
, if there is a fixed point on
$w\in W$
, if there is a fixed point on
![]() $\widehat{Q}$
of the normalized action of
$\widehat{Q}$
of the normalized action of
![]() $w$
, then such point is an eigenvector of
$w$
, then such point is an eigenvector of
![]() $w$
corresponding to a real eigenvalue.
$w$
corresponding to a real eigenvalue.
Lemma 4.2. Let
![]() $w\in W$
. Suppose that
$w\in W$
. Suppose that
![]() $w$
has distinct eigenvectors
$w$
has distinct eigenvectors
![]() $p,p^{\prime }$
lying on
$p,p^{\prime }$
lying on
![]() $\widehat{Q}$
, and let
$\widehat{Q}$
, and let
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{\prime }\in \mathbb{R}$
be corresponding eigenvalues, respectively. Then
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{\prime }\in \mathbb{R}$
be corresponding eigenvalues, respectively. Then
![]() $\unicode[STIX]{x1D706}\unicode[STIX]{x1D706}^{\prime }=1$
.
$\unicode[STIX]{x1D706}\unicode[STIX]{x1D706}^{\prime }=1$
.
Proof. We see this by calculating directly;
Since
![]() $p$
and
$p$
and
![]() $p^{\prime }$
are distinct and residing on
$p^{\prime }$
are distinct and residing on
![]() $\widehat{Q}$
, we have
$\widehat{Q}$
, we have
![]() $B(p,p^{\prime })\not =0$
by Proposition 2.8. Hence
$B(p,p^{\prime })\not =0$
by Proposition 2.8. Hence
![]() $\unicode[STIX]{x1D706}\unicode[STIX]{x1D706}^{\prime }=1$
, as required.◻
$\unicode[STIX]{x1D706}\unicode[STIX]{x1D706}^{\prime }=1$
, as required.◻
This lemma gives us the following observations about eigenvalues satisfying the condition “different from
![]() $\pm 1$
and corresponding eigenvectors are contained in
$\pm 1$
and corresponding eigenvectors are contained in
![]() $\widehat{Q}$
”.
$\widehat{Q}$
”.
∙ There are at most two such eigenvalues.
∙ The intersection of
 $Q$
(not
$Q$
(not
 $\widehat{Q}$
) and each eigenspace of such eigenvalue is one dimensional.
$\widehat{Q}$
) and each eigenspace of such eigenvalue is one dimensional.∙ If such eigenvalue exists, there are no eigenvectors in
 $\widehat{Q}$
corresponding to eigenvalues of
$\widehat{Q}$
corresponding to eigenvalues of
 $\pm 1$
.
$\pm 1$
.
Proposition 4.3. Let
![]() $w\in W$
with infinite order and take
$w\in W$
with infinite order and take
![]() $x\in \widehat{Q}$
arbitrarily. If
$x\in \widehat{Q}$
arbitrarily. If
![]() $w$
has an eigenvector
$w$
has an eigenvector
![]() $p$
in
$p$
in
![]() $\widehat{Q}$
corresponding to the eigenvalue
$\widehat{Q}$
corresponding to the eigenvalue
![]() $|\unicode[STIX]{x1D706}|>1$
, then
$|\unicode[STIX]{x1D706}|>1$
, then
![]() $(w^{n}\cdot x)_{n}$
converges to
$(w^{n}\cdot x)_{n}$
converges to
![]() $p$
. In particular,
$p$
. In particular,
![]() $p$
lies in
$p$
lies in
![]() $E$
.
$E$
.
Proof. Since
![]() $\widehat{Q}$
is compact, there exists a converging subsequence
$\widehat{Q}$
is compact, there exists a converging subsequence
![]() $(w^{n_{i}}\cdot x)_{n_{i}}$
of
$(w^{n_{i}}\cdot x)_{n_{i}}$
of
![]() $(w^{n}\cdot x)_{n}$
. Let
$(w^{n}\cdot x)_{n}$
. Let
![]() $y$
be the convergent point of the sequence above.
$y$
be the convergent point of the sequence above.
Notice that
![]() $w$
has two eigenvectors in
$w$
has two eigenvectors in
![]() $\widehat{Q}$
when
$\widehat{Q}$
when
![]() $\unicode[STIX]{x1D706}\not =\pm 1$
. In such case, we denote the other eigenvector by
$\unicode[STIX]{x1D706}\not =\pm 1$
. In such case, we denote the other eigenvector by
![]() $p^{\prime }$
and the corresponding eigenvalue by
$p^{\prime }$
and the corresponding eigenvalue by
![]() $\unicode[STIX]{x1D706}^{\prime }$
. By Lemma 4.2,
$\unicode[STIX]{x1D706}^{\prime }$
. By Lemma 4.2,
![]() $\unicode[STIX]{x1D706}\unicode[STIX]{x1D706}^{\prime }=1$
must be satisfied.
$\unicode[STIX]{x1D706}\unicode[STIX]{x1D706}^{\prime }=1$
must be satisfied.
We consider an eigenvalue
![]() $\unicode[STIX]{x1D706}^{\prime }$
with
$\unicode[STIX]{x1D706}^{\prime }$
with
![]() $|\unicode[STIX]{x1D706}^{\prime }|<1$
and the corresponding eigenvector
$|\unicode[STIX]{x1D706}^{\prime }|<1$
and the corresponding eigenvector
![]() $p^{\prime }$
. Then we have
$p^{\prime }$
. Then we have
and
![]() $|B(w^{n_{i}}\cdot x,p^{\prime })|\rightarrow |B(y,p^{\prime })|$
as
$|B(w^{n_{i}}\cdot x,p^{\prime })|\rightarrow |B(y,p^{\prime })|$
as
![]() $n_{i}\rightarrow \infty$
. Since
$n_{i}\rightarrow \infty$
. Since
![]() $|\unicode[STIX]{x1D706}^{n_{i}}|\rightarrow \infty$
, we have
$|\unicode[STIX]{x1D706}^{n_{i}}|\rightarrow \infty$
, we have
![]() $||w^{n_{i}}(x)|_{1}|\rightarrow \infty$
. Now there exists a constant
$||w^{n_{i}}(x)|_{1}|\rightarrow \infty$
. Now there exists a constant
![]() $C\geqslant 1$
so that
$C\geqslant 1$
so that
which is independent of
![]() $x$
. Therefore,
$x$
. Therefore,
 $$\begin{eqnarray}\displaystyle & & \displaystyle |B(w^{n_{i}}\cdot x,w\cdot y)|=\frac{|B(w^{n_{i}}(x),w(y))|}{||w^{n_{i}}(x)|_{1}|\cdot ||w(y)|_{1}|}=\frac{|B(w^{n_{i}-1}(x),y)|}{||w^{n_{i}}(x)|_{1}|\cdot ||w(y)|_{1}|}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,\frac{C|B(w^{n_{i}-1}(x),y)|}{||w^{n_{i}-1}(x)|_{1}|\cdot ||w(y)|_{1}|}=\frac{C}{||w(y)|_{1}|}|B(w^{n_{i}-1}\cdot x,y)|\rightarrow 0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |B(w^{n_{i}}\cdot x,w\cdot y)|=\frac{|B(w^{n_{i}}(x),w(y))|}{||w^{n_{i}}(x)|_{1}|\cdot ||w(y)|_{1}|}=\frac{|B(w^{n_{i}-1}(x),y)|}{||w^{n_{i}}(x)|_{1}|\cdot ||w(y)|_{1}|}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,\frac{C|B(w^{n_{i}-1}(x),y)|}{||w^{n_{i}-1}(x)|_{1}|\cdot ||w(y)|_{1}|}=\frac{C}{||w(y)|_{1}|}|B(w^{n_{i}-1}\cdot x,y)|\rightarrow 0,\nonumber\end{eqnarray}$$
as
![]() $n_{i}\rightarrow \infty$
by Lemma 4.1. This implies that
$n_{i}\rightarrow \infty$
by Lemma 4.1. This implies that
![]() $y=w\cdot y$
. Since we can apply this argument for each converging subsequence of
$y=w\cdot y$
. Since we can apply this argument for each converging subsequence of
![]() $(w^{n}\cdot x)_{n}$
and its convergent point, we can deduce that the convergent point, say,
$(w^{n}\cdot x)_{n}$
and its convergent point, we can deduce that the convergent point, say,
![]() $y$
, is fixed by
$y$
, is fixed by
![]() $w$
. By Lemma 4.2, we have the following two possibilities:
$w$
. By Lemma 4.2, we have the following two possibilities:
(1)
 $w$
has only one fixed point in
$w$
has only one fixed point in
 $\widehat{Q}$
;
$\widehat{Q}$
;(2)
 $w$
has two fixed points
$w$
has two fixed points
 $p,p^{\prime }$
in
$p,p^{\prime }$
in
 $\widehat{Q}$
.
$\widehat{Q}$
.
If (1), then it is obvious that
![]() $y=p$
. If (2), since
$y=p$
. If (2), since
![]() $|\unicode[STIX]{x1D706}^{-1}|<1$
and
$|\unicode[STIX]{x1D706}^{-1}|<1$
and
![]() $||w^{n_{i}}(x)|_{1}|\rightarrow \infty$
as
$||w^{n_{i}}(x)|_{1}|\rightarrow \infty$
as
![]() $n_{i}\rightarrow \infty$
, one has
$n_{i}\rightarrow \infty$
, one has
 $$\begin{eqnarray}\displaystyle |B(w^{n_{i}}\cdot x,p)| & = & \displaystyle \frac{|B(w^{n_{i}}(x),p)|}{||w^{n_{i}}(x)|_{1}|}=\frac{|B(x,w^{-n_{i}}(p))|}{||w^{n_{i}}(x)|_{1}|}\nonumber\\ \displaystyle & = & \displaystyle \frac{|\unicode[STIX]{x1D706}^{-n_{i}}|\cdot |B(x,p)|}{||w^{n_{i}}(x)|_{1}|}\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |B(w^{n_{i}}\cdot x,p)| & = & \displaystyle \frac{|B(w^{n_{i}}(x),p)|}{||w^{n_{i}}(x)|_{1}|}=\frac{|B(x,w^{-n_{i}}(p))|}{||w^{n_{i}}(x)|_{1}|}\nonumber\\ \displaystyle & = & \displaystyle \frac{|\unicode[STIX]{x1D706}^{-n_{i}}|\cdot |B(x,p)|}{||w^{n_{i}}(x)|_{1}|}\rightarrow 0.\nonumber\end{eqnarray}$$
In both cases (1) and (2), all converging subsequences of
![]() $(w^{n}\cdot x)_{n}$
converge to the same point. Thus we have the conclusion.◻
$(w^{n}\cdot x)_{n}$
converge to the same point. Thus we have the conclusion.◻
Let
![]() $w\in W$
and
$w\in W$
and
![]() $x\in \widehat{Q}$
be elements satisfying the condition in the claim of Proposition 4.3. Then we have a converging sequence
$x\in \widehat{Q}$
be elements satisfying the condition in the claim of Proposition 4.3. Then we have a converging sequence
![]() $(w^{n_{i}}\cdot x)_{n_{i}}$
to
$(w^{n_{i}}\cdot x)_{n_{i}}$
to
![]() $y\in \widehat{Q}$
so that
$y\in \widehat{Q}$
so that
![]() $|w^{n_{i}}(x)|_{1}\rightarrow \infty$
. Even in the case of
$|w^{n_{i}}(x)|_{1}\rightarrow \infty$
. Even in the case of
![]() $\unicode[STIX]{x1D706}=\pm 1$
, one has
$\unicode[STIX]{x1D706}=\pm 1$
, one has
This shows that if
![]() $||w^{n_{i}}(x)|_{1}|\rightarrow \infty$
, then
$||w^{n_{i}}(x)|_{1}|\rightarrow \infty$
, then
![]() $|B(w^{n_{i}}\cdot x,p)|$
converges to 0. This means that
$|B(w^{n_{i}}\cdot x,p)|$
converges to 0. This means that
![]() $(w^{n_{i}}\cdot x)_{n_{i}}$
converges to
$(w^{n_{i}}\cdot x)_{n_{i}}$
converges to
![]() $p$
by Proposition 2.8(a).
$p$
by Proposition 2.8(a).
Remark 4.4. In the case where
![]() $W$
is rank 3, for
$W$
is rank 3, for
![]() $\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2}\in \unicode[STIX]{x1D6E5}$
,
$\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2}\in \unicode[STIX]{x1D6E5}$
,
∙ if
 $B(\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2})<-1$
, then there exist two real eigenvalues of
$B(\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2})<-1$
, then there exist two real eigenvalues of
 $s_{\unicode[STIX]{x1D6FF}_{1}}s_{\unicode[STIX]{x1D6FF}_{2}}$
which are distinct from
$s_{\unicode[STIX]{x1D6FF}_{1}}s_{\unicode[STIX]{x1D6FF}_{2}}$
which are distinct from
 $\pm 1$
;
$\pm 1$
;∙ if
 $B(\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2})=-1$
, then an easy calculation shows that
$B(\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2})=-1$
, then an easy calculation shows that
 $||(s_{\unicode[STIX]{x1D6FF}_{1}}s_{\unicode[STIX]{x1D6FF}_{2}})^{n}(v)|_{1}|\rightarrow \infty$
for any
$||(s_{\unicode[STIX]{x1D6FF}_{1}}s_{\unicode[STIX]{x1D6FF}_{2}})^{n}(v)|_{1}|\rightarrow \infty$
for any
 $v\in \widehat{Q}\setminus \{\frac{1}{2}\unicode[STIX]{x1D6FF}_{1}+\frac{1}{2}\unicode[STIX]{x1D6FF}_{2}\}$
.
$v\in \widehat{Q}\setminus \{\frac{1}{2}\unicode[STIX]{x1D6FF}_{1}+\frac{1}{2}\unicode[STIX]{x1D6FF}_{2}\}$
.
5 A proof of Theorem 1.2: the case of rank 3
We first prove Theorem 1.2 for the case of rank 3. Since we can handle this case more combinatorially than the case of higher ranks, we concentrate on this case in this section. Before proving, we remark that the case of rank 2 is self-evident.
Remark 5.1. We consider the case of rank 2. Let
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
be two simple roots.
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
be two simple roots.
∙ If
 $B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})>-1$
, then
$B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})>-1$
, then
 $\widehat{Q}$
is empty and so is
$\widehat{Q}$
is empty and so is
 $E$
.
$E$
.∙ If
 $B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=-1$
, then
$B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=-1$
, then
 $E=L(\widehat{\unicode[STIX]{x1D6FC}},\widehat{\unicode[STIX]{x1D6FD}})\cap \widehat{Q}$
consists of one point.
$E=L(\widehat{\unicode[STIX]{x1D6FC}},\widehat{\unicode[STIX]{x1D6FD}})\cap \widehat{Q}$
consists of one point.∙ If
 $B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})<-1$
, then
$B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})<-1$
, then
 $E=L(\widehat{\unicode[STIX]{x1D6FC}},\widehat{\unicode[STIX]{x1D6FD}})\cap \widehat{Q}$
consists of two points.
$E=L(\widehat{\unicode[STIX]{x1D6FC}},\widehat{\unicode[STIX]{x1D6FD}})\cap \widehat{Q}$
consists of two points.
For more details, see [Reference Hohlweg, Labbé and Ripoll6, Example 2.1].
Let
![]() $(W,S)$
be a Coxeter system of rank 3 with
$(W,S)$
be a Coxeter system of rank 3 with
![]() $S=\{s_{\unicode[STIX]{x1D6FC}},s_{\unicode[STIX]{x1D6FD}},s_{\unicode[STIX]{x1D6FE}}\}$
and
$S=\{s_{\unicode[STIX]{x1D6FC}},s_{\unicode[STIX]{x1D6FD}},s_{\unicode[STIX]{x1D6FE}}\}$
and
![]() $\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
its simple system.
$\unicode[STIX]{x1D6E5}=\{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
its simple system.
We fix one arbitrary accumulation point
![]() $\unicode[STIX]{x1D70C}$
of orbits of normalized roots.
$\unicode[STIX]{x1D70C}$
of orbits of normalized roots.
Lemma 5.2. Let
![]() $\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
with
$\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
with
![]() $\unicode[STIX]{x1D6FF}\not =\unicode[STIX]{x1D6FF}^{\prime }$
and assume that
$\unicode[STIX]{x1D6FF}\not =\unicode[STIX]{x1D6FF}^{\prime }$
and assume that
![]() $B(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime })\geqslant -1$
. Then there exists a singleton
$B(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime })\geqslant -1$
. Then there exists a singleton
![]() $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}\subset E$
, where
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}\subset E$
, where
![]() $\unicode[STIX]{x1D6FF}^{\prime \prime }\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}\setminus \{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\}$
, such that the point in
$\unicode[STIX]{x1D6FF}^{\prime \prime }\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}\setminus \{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\}$
, such that the point in
![]() $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
is visible from
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
is visible from
![]() $\widehat{\unicode[STIX]{x1D6FF}}$
and
$\widehat{\unicode[STIX]{x1D6FF}}$
and
![]() $\widehat{\unicode[STIX]{x1D6FF}^{\prime }}$
but not visible from
$\widehat{\unicode[STIX]{x1D6FF}^{\prime }}$
but not visible from
![]() $\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
.
$\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
.
Proof. When
![]() $B(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime })=-1$
, let
$B(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime })=-1$
, let
![]() $\unicode[STIX]{x1D702}=\frac{1}{2}\unicode[STIX]{x1D6FF}+\frac{1}{2}\unicode[STIX]{x1D6FF}^{\prime }$
. Then it is easy to see that
$\unicode[STIX]{x1D702}=\frac{1}{2}\unicode[STIX]{x1D6FF}+\frac{1}{2}\unicode[STIX]{x1D6FF}^{\prime }$
. Then it is easy to see that
![]() $\widehat{\unicode[STIX]{x1D702}}=\lim _{n\rightarrow \infty }(s_{\unicode[STIX]{x1D6FF}}s_{\unicode[STIX]{x1D6FF}^{\prime }})^{n}\cdot \unicode[STIX]{x1D70C}\in E$
. Moreover, we have
$\widehat{\unicode[STIX]{x1D702}}=\lim _{n\rightarrow \infty }(s_{\unicode[STIX]{x1D6FF}}s_{\unicode[STIX]{x1D6FF}^{\prime }})^{n}\cdot \unicode[STIX]{x1D70C}\in E$
. Moreover, we have
![]() $B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FF}})=B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FF}^{\prime }})=0$
. Thus
$B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FF}})=B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FF}^{\prime }})=0$
. Thus
![]() $\widehat{\unicode[STIX]{x1D702}}$
is visible from
$\widehat{\unicode[STIX]{x1D702}}$
is visible from
![]() $\widehat{\unicode[STIX]{x1D6FF}}$
and
$\widehat{\unicode[STIX]{x1D6FF}}$
and
![]() $\widehat{\unicode[STIX]{x1D6FF}^{\prime }}$
by Lemma 2.5(i). In addition, by Remark 3.1,
$\widehat{\unicode[STIX]{x1D6FF}^{\prime }}$
by Lemma 2.5(i). In addition, by Remark 3.1,
![]() $\widehat{\unicode[STIX]{x1D702}}$
is not visible from
$\widehat{\unicode[STIX]{x1D702}}$
is not visible from
![]() $\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
. Let
$\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
. Let
![]() $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}=\{\widehat{\unicode[STIX]{x1D702}}\}$
. Then
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}=\{\widehat{\unicode[STIX]{x1D702}}\}$
. Then
![]() $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
satisfies the desired properties.
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
satisfies the desired properties.
Assume
![]() $B(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime })>-1$
. Then the order of
$B(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime })>-1$
. Then the order of
![]() $s_{\unicode[STIX]{x1D6FF}}s_{\unicode[STIX]{x1D6FF}^{\prime }}$
is finite. Let
$s_{\unicode[STIX]{x1D6FF}}s_{\unicode[STIX]{x1D6FF}^{\prime }}$
is finite. Let
![]() $m$
be a positive integer such that
$m$
be a positive integer such that
![]() $(s_{\unicode[STIX]{x1D6FC}}s_{\unicode[STIX]{x1D6FD}})^{m}=1$
. Thus the order of the parabolic subgroup
$(s_{\unicode[STIX]{x1D6FC}}s_{\unicode[STIX]{x1D6FD}})^{m}=1$
. Thus the order of the parabolic subgroup
![]() $W^{\prime }$
generated by
$W^{\prime }$
generated by
![]() $s_{\unicode[STIX]{x1D6FC}}$
and
$s_{\unicode[STIX]{x1D6FC}}$
and
![]() $s_{\unicode[STIX]{x1D6FD}}$
is
$s_{\unicode[STIX]{x1D6FD}}$
is
![]() $2m$
. Let
$2m$
. Let
![]() $T=W^{\prime }\cdot \unicode[STIX]{x1D70C}$
and let
$T=W^{\prime }\cdot \unicode[STIX]{x1D70C}$
and let
![]() $T_{\unicode[STIX]{x1D6FC}}\subset T$
(resp.
$T_{\unicode[STIX]{x1D6FC}}\subset T$
(resp.
![]() $T_{\unicode[STIX]{x1D6FD}}\subset T$
) be the set of the points in
$T_{\unicode[STIX]{x1D6FD}}\subset T$
) be the set of the points in
![]() $T$
which are visible from
$T$
which are visible from
![]() $\unicode[STIX]{x1D6FC}$
(resp.
$\unicode[STIX]{x1D6FC}$
(resp.
![]() $\unicode[STIX]{x1D6FD}$
). We prove that there is
$\unicode[STIX]{x1D6FD}$
). We prove that there is
![]() $\widehat{\unicode[STIX]{x1D702}}\in \widehat{Q}$
such that
$\widehat{\unicode[STIX]{x1D702}}\in \widehat{Q}$
such that
![]() $\{\widehat{\unicode[STIX]{x1D702}}\}$
satisfies the required property.
$\{\widehat{\unicode[STIX]{x1D702}}\}$
satisfies the required property.
Suppose that there does not exist
![]() $\widehat{\unicode[STIX]{x1D702}}$
, i.e.,
$\widehat{\unicode[STIX]{x1D702}}$
, i.e.,
![]() $T_{\unicode[STIX]{x1D6FC}}\cap T_{\unicode[STIX]{x1D6FD}}=\emptyset$
. Then
$T_{\unicode[STIX]{x1D6FC}}\cap T_{\unicode[STIX]{x1D6FD}}=\emptyset$
. Then
![]() $T_{\unicode[STIX]{x1D6FC}}$
and
$T_{\unicode[STIX]{x1D6FC}}$
and
![]() $T_{\unicode[STIX]{x1D6FD}}$
have the same cardinality. In fact,
$T_{\unicode[STIX]{x1D6FD}}$
have the same cardinality. In fact,
![]() $s_{\unicode[STIX]{x1D6FD}}:T_{\unicode[STIX]{x1D6FC}}\rightarrow T_{\unicode[STIX]{x1D6FD}}$
is well defined by
$s_{\unicode[STIX]{x1D6FD}}:T_{\unicode[STIX]{x1D6FC}}\rightarrow T_{\unicode[STIX]{x1D6FD}}$
is well defined by
![]() $T_{\unicode[STIX]{x1D6FC}}\cap T_{\unicode[STIX]{x1D6FD}}=\emptyset$
and Lemma 2.5(ii). Moreover, this is injective. Thus, one has
$T_{\unicode[STIX]{x1D6FC}}\cap T_{\unicode[STIX]{x1D6FD}}=\emptyset$
and Lemma 2.5(ii). Moreover, this is injective. Thus, one has
![]() $|T_{\unicode[STIX]{x1D6FC}}|\leqslant |T_{\unicode[STIX]{x1D6FD}}|$
. Similarly,
$|T_{\unicode[STIX]{x1D6FC}}|\leqslant |T_{\unicode[STIX]{x1D6FD}}|$
. Similarly,
![]() $|T_{\unicode[STIX]{x1D6FD}}|\leqslant |T_{\unicode[STIX]{x1D6FC}}|$
. Hence
$|T_{\unicode[STIX]{x1D6FD}}|\leqslant |T_{\unicode[STIX]{x1D6FC}}|$
. Hence
![]() $|T_{\unicode[STIX]{x1D6FC}}|=|T_{\unicode[STIX]{x1D6FD}}|$
, denoted by
$|T_{\unicode[STIX]{x1D6FC}}|=|T_{\unicode[STIX]{x1D6FD}}|$
, denoted by
![]() $m^{\prime }$
. Moreover, since
$m^{\prime }$
. Moreover, since
![]() $s_{\unicode[STIX]{x1D6FC}}:T\setminus T_{\unicode[STIX]{x1D6FC}}\rightarrow T_{\unicode[STIX]{x1D6FC}}$
is injective, one has
$s_{\unicode[STIX]{x1D6FC}}:T\setminus T_{\unicode[STIX]{x1D6FC}}\rightarrow T_{\unicode[STIX]{x1D6FC}}$
is injective, one has
![]() $|T_{\unicode[STIX]{x1D6FC}}|\geqslant |T\setminus T_{\unicode[STIX]{x1D6FC}}|=|T|-|T_{\unicode[STIX]{x1D6FC}}|$
. Thus,
$|T_{\unicode[STIX]{x1D6FC}}|\geqslant |T\setminus T_{\unicode[STIX]{x1D6FC}}|=|T|-|T_{\unicode[STIX]{x1D6FC}}|$
. Thus,
![]() $|T|\leqslant 2|T_{\unicode[STIX]{x1D6FC}}|=|T_{\unicode[STIX]{x1D6FC}}|+|T_{\unicode[STIX]{x1D6FD}}|\leqslant |T|$
. Hence
$|T|\leqslant 2|T_{\unicode[STIX]{x1D6FC}}|=|T_{\unicode[STIX]{x1D6FC}}|+|T_{\unicode[STIX]{x1D6FD}}|\leqslant |T|$
. Hence
![]() $T\setminus (T_{\unicode[STIX]{x1D6FC}}\cup T_{\unicode[STIX]{x1D6FD}})=\emptyset$
. We write
$T\setminus (T_{\unicode[STIX]{x1D6FC}}\cup T_{\unicode[STIX]{x1D6FD}})=\emptyset$
. We write
![]() $T_{\unicode[STIX]{x1D6FC}}=\{\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{m^{\prime }}\}$
and
$T_{\unicode[STIX]{x1D6FC}}=\{\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{m^{\prime }}\}$
and
![]() $T_{\unicode[STIX]{x1D6FD}}=\{\unicode[STIX]{x1D70C}_{1}^{\prime },\ldots ,\unicode[STIX]{x1D70C}_{m^{\prime }}^{\prime }\}$
. Observe that
$T_{\unicode[STIX]{x1D6FD}}=\{\unicode[STIX]{x1D70C}_{1}^{\prime },\ldots ,\unicode[STIX]{x1D70C}_{m^{\prime }}^{\prime }\}$
. Observe that
![]() $s_{\unicode[STIX]{x1D6FC}}$
and
$s_{\unicode[STIX]{x1D6FC}}$
and
![]() $s_{\unicode[STIX]{x1D6FD}}$
act on
$s_{\unicode[STIX]{x1D6FD}}$
act on
![]() $\{1,\ldots ,m^{\prime }\}$
as permutations
$\{1,\ldots ,m^{\prime }\}$
as permutations
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}:\{1,\ldots ,m^{\prime }\}\rightarrow \{1,\ldots ,m^{\prime }\}$
so that
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}:\{1,\ldots ,m^{\prime }\}\rightarrow \{1,\ldots ,m^{\prime }\}$
so that
![]() $s_{\unicode[STIX]{x1D6FD}}\cdot T_{\unicode[STIX]{x1D6FC}}=\{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}(1)}^{\prime },\ldots ,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}(m^{\prime })}^{\prime }\}$
and
$s_{\unicode[STIX]{x1D6FD}}\cdot T_{\unicode[STIX]{x1D6FC}}=\{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}(1)}^{\prime },\ldots ,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}(m^{\prime })}^{\prime }\}$
and
![]() $s_{\unicode[STIX]{x1D6FC}}\cdot T_{\unicode[STIX]{x1D6FD}}=\{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}(1)},\ldots ,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}(m^{\prime })}\}$
. In particular, we recognize that each image of the points in
$s_{\unicode[STIX]{x1D6FC}}\cdot T_{\unicode[STIX]{x1D6FD}}=\{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}(1)},\ldots ,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}(m^{\prime })}\}$
. In particular, we recognize that each image of the points in
![]() $T_{\unicode[STIX]{x1D6FD}}$
by
$T_{\unicode[STIX]{x1D6FD}}$
by
![]() $s_{\unicode[STIX]{x1D6FC}}$
must be visible from
$s_{\unicode[STIX]{x1D6FC}}$
must be visible from
![]() $\unicode[STIX]{x1D6FC}$
and vice versa. Moreover, the permutation
$\unicode[STIX]{x1D6FC}$
and vice versa. Moreover, the permutation
![]() $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}:=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}$
has order
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}:=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FD}}$
has order
![]() $m^{\prime }$
. By Proposition 2.13(i), each
$m^{\prime }$
. By Proposition 2.13(i), each
![]() $B$
-reflection extends the length of visible curves. Thus we see that
$B$
-reflection extends the length of visible curves. Thus we see that
 $$\begin{eqnarray}\displaystyle d_{B}(\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D70C}_{j}) & {\geqslant} & \displaystyle d_{B}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(i)},\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(j)})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle d_{B}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{2}(i)},\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{2}(j)})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \cdots \nonumber\\ \displaystyle & {\geqslant} & \displaystyle d_{B}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{m^{\prime }}(i)},\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{m^{\prime }}(j)})=d_{B}(\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D70C}_{j}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{B}(\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D70C}_{j}) & {\geqslant} & \displaystyle d_{B}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(i)},\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(j)})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle d_{B}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{2}(i)},\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{2}(j)})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \cdots \nonumber\\ \displaystyle & {\geqslant} & \displaystyle d_{B}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{m^{\prime }}(i)},\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{m^{\prime }}(j)})=d_{B}(\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D70C}_{j}),\nonumber\end{eqnarray}$$
for any
![]() $i,j\in \{1,2,\ldots ,m^{\prime }\}$
. Thus all the equalities of these inequalities must be satisfied. Since
$i,j\in \{1,2,\ldots ,m^{\prime }\}$
. Thus all the equalities of these inequalities must be satisfied. Since
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(i)}=s_{\unicode[STIX]{x1D6FC}}s_{\unicode[STIX]{x1D6FD}}\cdot \unicode[STIX]{x1D70C}_{i}$
,
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}(i)}=s_{\unicode[STIX]{x1D6FC}}s_{\unicode[STIX]{x1D6FD}}\cdot \unicode[STIX]{x1D70C}_{i}$
,
![]() $d_{B}(\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D70C}_{j})=d_{B}(s_{\unicode[STIX]{x1D6FD}}\cdot \unicode[STIX]{x1D70C}_{i},s_{\unicode[STIX]{x1D6FD}}\cdot \unicode[STIX]{x1D70C}_{j})$
also holds. From Proposition 2.13(iii),
$d_{B}(\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D70C}_{j})=d_{B}(s_{\unicode[STIX]{x1D6FD}}\cdot \unicode[STIX]{x1D70C}_{i},s_{\unicode[STIX]{x1D6FD}}\cdot \unicode[STIX]{x1D70C}_{j})$
also holds. From Proposition 2.13(iii),
![]() $d_{B}(\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D70C}_{j})=d_{B}(s_{\unicode[STIX]{x1D6FD}}\cdot \unicode[STIX]{x1D70C}_{i},s_{\unicode[STIX]{x1D6FD}}\cdot \unicode[STIX]{x1D70C}_{j})$
implies that
$d_{B}(\unicode[STIX]{x1D70C}_{i},\unicode[STIX]{x1D70C}_{j})=d_{B}(s_{\unicode[STIX]{x1D6FD}}\cdot \unicode[STIX]{x1D70C}_{i},s_{\unicode[STIX]{x1D6FD}}\cdot \unicode[STIX]{x1D70C}_{j})$
implies that
![]() $\unicode[STIX]{x1D70C}_{i}$
and
$\unicode[STIX]{x1D70C}_{i}$
and
![]() $\unicode[STIX]{x1D70C}_{j}$
should belong to
$\unicode[STIX]{x1D70C}_{j}$
should belong to
![]() $\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FD}}\cap T\subset T_{\unicode[STIX]{x1D6FD}}$
if
$\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FD}}\cap T\subset T_{\unicode[STIX]{x1D6FD}}$
if
![]() $\unicode[STIX]{x1D70C}_{i}\not =\unicode[STIX]{x1D70C}_{j}$
, while
$\unicode[STIX]{x1D70C}_{i}\not =\unicode[STIX]{x1D70C}_{j}$
, while
![]() $\unicode[STIX]{x1D70C}_{i}$
and
$\unicode[STIX]{x1D70C}_{i}$
and
![]() $\unicode[STIX]{x1D70C}_{j}$
belong to
$\unicode[STIX]{x1D70C}_{j}$
belong to
![]() $T_{\unicode[STIX]{x1D6FC}}$
. However, since
$T_{\unicode[STIX]{x1D6FC}}$
. However, since
![]() $T_{\unicode[STIX]{x1D6FC}}\cap T_{\unicode[STIX]{x1D6FD}}=\emptyset$
, this cannot happen. Hence,
$T_{\unicode[STIX]{x1D6FC}}\cap T_{\unicode[STIX]{x1D6FD}}=\emptyset$
, this cannot happen. Hence,
![]() $\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D70C}_{j}$
. In particular, each of
$\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D70C}_{j}$
. In particular, each of
![]() $T_{\unicode[STIX]{x1D6FC}}$
and
$T_{\unicode[STIX]{x1D6FC}}$
and
![]() $T_{\unicode[STIX]{x1D6FD}}$
consists of one element. Let
$T_{\unicode[STIX]{x1D6FD}}$
consists of one element. Let
![]() $T_{\unicode[STIX]{x1D6FC}}=\{\unicode[STIX]{x1D70C}_{1}\}$
and
$T_{\unicode[STIX]{x1D6FC}}=\{\unicode[STIX]{x1D70C}_{1}\}$
and
![]() $T_{\unicode[STIX]{x1D6FD}}=\{\unicode[STIX]{x1D70C}_{1}^{\prime }\}$
. Then four points
$T_{\unicode[STIX]{x1D6FD}}=\{\unicode[STIX]{x1D70C}_{1}^{\prime }\}$
. Then four points
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{1}^{\prime }$
and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{1}^{\prime }$
and
![]() $\unicode[STIX]{x1D6FD}$
should lie in the same line
$\unicode[STIX]{x1D6FD}$
should lie in the same line
![]() $L(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
. On the other hand, since
$L(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
. On the other hand, since
![]() $W^{\prime }$
is finite,
$W^{\prime }$
is finite,
![]() $L(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
does not intersect with
$L(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
does not intersect with
![]() $\widehat{Q}$
(see Remark 5.1), a contradiction. Hence
$\widehat{Q}$
(see Remark 5.1), a contradiction. Hence
![]() $T_{\unicode[STIX]{x1D6FC}}\cap T_{\unicode[STIX]{x1D6FD}}$
is not empty. This means that
$T_{\unicode[STIX]{x1D6FC}}\cap T_{\unicode[STIX]{x1D6FD}}$
is not empty. This means that
![]() $\widehat{\unicode[STIX]{x1D702}}$
exists in
$\widehat{\unicode[STIX]{x1D702}}$
exists in
![]() $W^{\prime }\cdot \unicode[STIX]{x1D70C}$
. Thus
$W^{\prime }\cdot \unicode[STIX]{x1D70C}$
. Thus
![]() $\widehat{\unicode[STIX]{x1D702}}\in E$
.
$\widehat{\unicode[STIX]{x1D702}}\in E$
.
Let
![]() $\widehat{\unicode[STIX]{x1D702}}=x_{\unicode[STIX]{x1D6FC}}\widehat{\unicode[STIX]{x1D6FC}}+x_{\unicode[STIX]{x1D6FD}}\widehat{\unicode[STIX]{x1D6FD}}+x_{\unicode[STIX]{x1D6FE}}\widehat{\unicode[STIX]{x1D6FE}}$
. Since
$\widehat{\unicode[STIX]{x1D702}}=x_{\unicode[STIX]{x1D6FC}}\widehat{\unicode[STIX]{x1D6FC}}+x_{\unicode[STIX]{x1D6FD}}\widehat{\unicode[STIX]{x1D6FD}}+x_{\unicode[STIX]{x1D6FE}}\widehat{\unicode[STIX]{x1D6FE}}$
. Since
![]() $\widehat{\unicode[STIX]{x1D702}}\in E\subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, we have
$\widehat{\unicode[STIX]{x1D702}}\in E\subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, we have
![]() $0\leqslant x_{\unicode[STIX]{x1D6FC}},x_{\unicode[STIX]{x1D6FD}},x_{\unicode[STIX]{x1D6FE}}\leqslant 1$
and
$0\leqslant x_{\unicode[STIX]{x1D6FC}},x_{\unicode[STIX]{x1D6FD}},x_{\unicode[STIX]{x1D6FE}}\leqslant 1$
and
![]() $x_{\unicode[STIX]{x1D6FC}}+x_{\unicode[STIX]{x1D6FD}}+x_{\unicode[STIX]{x1D6FE}}=1$
. Since
$x_{\unicode[STIX]{x1D6FC}}+x_{\unicode[STIX]{x1D6FD}}+x_{\unicode[STIX]{x1D6FE}}=1$
. Since
we have
![]() $B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FE}})<0$
or
$B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FE}})<0$
or
![]() $x_{\unicode[STIX]{x1D6FC}}B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FC}})=x_{\unicode[STIX]{x1D6FD}}B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FD}})=x_{\unicode[STIX]{x1D6FE}}B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FE}})=0$
. Suppose that the latter case happens. Since
$x_{\unicode[STIX]{x1D6FC}}B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FC}})=x_{\unicode[STIX]{x1D6FD}}B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FD}})=x_{\unicode[STIX]{x1D6FE}}B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FE}})=0$
. Suppose that the latter case happens. Since
![]() $\widehat{\unicode[STIX]{x1D702}}\not =\widehat{\unicode[STIX]{x1D6FE}}$
, (a) both of
$\widehat{\unicode[STIX]{x1D702}}\not =\widehat{\unicode[STIX]{x1D6FE}}$
, (a) both of
![]() $x_{\unicode[STIX]{x1D6FC}}$
and
$x_{\unicode[STIX]{x1D6FC}}$
and
![]() $x_{\unicode[STIX]{x1D6FD}}$
are positive, or (b) either
$x_{\unicode[STIX]{x1D6FD}}$
are positive, or (b) either
![]() $x_{\unicode[STIX]{x1D6FC}}$
or
$x_{\unicode[STIX]{x1D6FC}}$
or
![]() $x_{\unicode[STIX]{x1D6FD}}$
is 0 and the other is positive.
$x_{\unicode[STIX]{x1D6FD}}$
is 0 and the other is positive.
(a) Suppose that both of
 $x_{\unicode[STIX]{x1D6FC}}$
and
$x_{\unicode[STIX]{x1D6FC}}$
and
 $x_{\unicode[STIX]{x1D6FD}}$
are positive. If
$x_{\unicode[STIX]{x1D6FD}}$
are positive. If
 $x_{\unicode[STIX]{x1D6FE}}>0$
, then we have
$x_{\unicode[STIX]{x1D6FE}}>0$
, then we have
 $B(\widehat{\unicode[STIX]{x1D702}},\unicode[STIX]{x1D6FC})=B(\widehat{\unicode[STIX]{x1D702}},\unicode[STIX]{x1D6FD})=B(\widehat{\unicode[STIX]{x1D702}},\unicode[STIX]{x1D6FE})=0$
, a contradiction to Remark 3.1. If
$B(\widehat{\unicode[STIX]{x1D702}},\unicode[STIX]{x1D6FC})=B(\widehat{\unicode[STIX]{x1D702}},\unicode[STIX]{x1D6FD})=B(\widehat{\unicode[STIX]{x1D702}},\unicode[STIX]{x1D6FE})=0$
, a contradiction to Remark 3.1. If
 $x_{\unicode[STIX]{x1D6FE}}=0$
, then
$x_{\unicode[STIX]{x1D6FE}}=0$
, then
 $\widehat{\unicode[STIX]{x1D702}}\in E\cap \text{conv}(\{\widehat{\unicode[STIX]{x1D6FC}},\widehat{\unicode[STIX]{x1D6FD}}\})$
, a contradiction to the finiteness of
$\widehat{\unicode[STIX]{x1D702}}\in E\cap \text{conv}(\{\widehat{\unicode[STIX]{x1D6FC}},\widehat{\unicode[STIX]{x1D6FD}}\})$
, a contradiction to the finiteness of
 $W^{\prime }$
.
$W^{\prime }$
.(b) Suppose that either
 $x_{\unicode[STIX]{x1D6FC}}$
or
$x_{\unicode[STIX]{x1D6FC}}$
or
 $x_{\unicode[STIX]{x1D6FD}}$
is 0 and the other is positive, say,
$x_{\unicode[STIX]{x1D6FD}}$
is 0 and the other is positive, say,
 $x_{\unicode[STIX]{x1D6FC}}>0$
and
$x_{\unicode[STIX]{x1D6FC}}>0$
and
 $x_{\unicode[STIX]{x1D6FD}}=0$
. Then
$x_{\unicode[STIX]{x1D6FD}}=0$
. Then
 $x_{\unicode[STIX]{x1D6FE}}>0$
because of
$x_{\unicode[STIX]{x1D6FE}}>0$
because of
 $\widehat{\unicode[STIX]{x1D702}}\not =\widehat{\unicode[STIX]{x1D6FC}}$
. Thus
$\widehat{\unicode[STIX]{x1D702}}\not =\widehat{\unicode[STIX]{x1D6FC}}$
. Thus
 $\widehat{\unicode[STIX]{x1D702}}\in \text{conv}(\{\widehat{\unicode[STIX]{x1D6FC}},\widehat{\unicode[STIX]{x1D6FE}}\})$
. Since we have
$\widehat{\unicode[STIX]{x1D702}}\in \text{conv}(\{\widehat{\unicode[STIX]{x1D6FC}},\widehat{\unicode[STIX]{x1D6FE}}\})$
. Since we have $$\begin{eqnarray}B(\widehat{\unicode[STIX]{x1D702}},\unicode[STIX]{x1D6FD})=x_{\unicode[STIX]{x1D6FC}}B(\widehat{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FD})+x_{\unicode[STIX]{x1D6FE}}B(\widehat{\unicode[STIX]{x1D6FE}},\unicode[STIX]{x1D6FD})\geqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}B(\widehat{\unicode[STIX]{x1D702}},\unicode[STIX]{x1D6FD})=x_{\unicode[STIX]{x1D6FC}}B(\widehat{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D6FD})+x_{\unicode[STIX]{x1D6FE}}B(\widehat{\unicode[STIX]{x1D6FE}},\unicode[STIX]{x1D6FD})\geqslant 0,\end{eqnarray}$$
 $B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=B(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD})=0$
. This is a contradiction to our assumption “irreducible”. ◻
$B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=B(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD})=0$
. This is a contradiction to our assumption “irreducible”. ◻
If
![]() $B(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime })<-1$
, then
$B(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime })<-1$
, then
![]() $\text{conv}(\{\widehat{\unicode[STIX]{x1D6FF}},\widehat{\unicode[STIX]{x1D6FF}^{\prime }}\})$
and
$\text{conv}(\{\widehat{\unicode[STIX]{x1D6FF}},\widehat{\unicode[STIX]{x1D6FF}^{\prime }}\})$
and
![]() $\widehat{Q}$
intersect at two points (Remark 5.1) and
$\widehat{Q}$
intersect at two points (Remark 5.1) and
![]() $\text{conv}(\{\widehat{\unicode[STIX]{x1D6FF}},\widehat{\unicode[STIX]{x1D6FF}^{\prime }}\})$
separates
$\text{conv}(\{\widehat{\unicode[STIX]{x1D6FF}},\widehat{\unicode[STIX]{x1D6FF}^{\prime }}\})$
separates
![]() $\widehat{Q}$
into two components. Let
$\widehat{Q}$
into two components. Let
![]() $D$
be one of such open components with
$D$
be one of such open components with
![]() $D\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})=\emptyset$
.
$D\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})=\emptyset$
.
Lemma 5.3. Let
![]() $\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
with
$\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
with
![]() $\unicode[STIX]{x1D6FF}\not =\unicode[STIX]{x1D6FF}^{\prime }$
and assume that
$\unicode[STIX]{x1D6FF}\not =\unicode[STIX]{x1D6FF}^{\prime }$
and assume that
![]() $B(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime })<-1$
. Let
$B(\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime })<-1$
. Let
![]() $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}\subset \widehat{Q}$
be the closure of
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}\subset \widehat{Q}$
be the closure of
![]() $D$
, where
$D$
, where
![]() $\unicode[STIX]{x1D6FF}^{\prime \prime }\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}\setminus \{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\}$
and
$\unicode[STIX]{x1D6FF}^{\prime \prime }\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}\setminus \{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\}$
and
![]() $D$
is the set defined above. Then
$D$
is the set defined above. Then
![]() $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
satisfies the following:
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
satisfies the following:
∙ the end points are contained in
 $E$
;
$E$
;∙ one end point of
 $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
is visible from
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
is visible from
 $\widehat{\unicode[STIX]{x1D6FF}}$
, the other is visible from
$\widehat{\unicode[STIX]{x1D6FF}}$
, the other is visible from
 $\widehat{\unicode[STIX]{x1D6FF}^{\prime }}$
and
$\widehat{\unicode[STIX]{x1D6FF}^{\prime }}$
and
 $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
is not visible from
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
is not visible from
 $\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
.
$\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
.
Proof. The line joining a point in
![]() $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
and
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
and
![]() $\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
always crosses
$\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
always crosses
![]() $\widehat{Q}\setminus A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
. This means that
$\widehat{Q}\setminus A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
. This means that
![]() $\text{int}(A_{\unicode[STIX]{x1D6FF}^{\prime \prime }})$
is not visible from
$\text{int}(A_{\unicode[STIX]{x1D6FF}^{\prime \prime }})$
is not visible from
![]() $\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
, where
$\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
, where
![]() $\text{int}(\cdot )$
denotes the interior relative to
$\text{int}(\cdot )$
denotes the interior relative to
![]() $\widehat{Q}$
. By Remark 5.1, it follows that both two end points of
$\widehat{Q}$
. By Remark 5.1, it follows that both two end points of
![]() $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
are contained in
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
are contained in
![]() $E$
such that one end point of
$E$
such that one end point of
![]() $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
is visible from
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
is visible from
![]() $\widehat{\unicode[STIX]{x1D6FF}}$
and the other is visible from
$\widehat{\unicode[STIX]{x1D6FF}}$
and the other is visible from
![]() $\widehat{\unicode[STIX]{x1D6FF}^{\prime }}$
. Moreover, each of both two end points
$\widehat{\unicode[STIX]{x1D6FF}^{\prime }}$
. Moreover, each of both two end points
![]() $\widehat{\unicode[STIX]{x1D702}}$
is contained in
$\widehat{\unicode[STIX]{x1D702}}$
is contained in
![]() $\text{conv}(\{\widehat{\unicode[STIX]{x1D6FF}},\widehat{\unicode[STIX]{x1D6FF}^{\prime }}\})$
, so it is written like
$\text{conv}(\{\widehat{\unicode[STIX]{x1D6FF}},\widehat{\unicode[STIX]{x1D6FF}^{\prime }}\})$
, so it is written like
![]() $\widehat{\unicode[STIX]{x1D702}}=r\widehat{\unicode[STIX]{x1D6FF}}+(1-r)\widehat{\unicode[STIX]{x1D6FF}^{\prime }}$
, where
$\widehat{\unicode[STIX]{x1D702}}=r\widehat{\unicode[STIX]{x1D6FF}}+(1-r)\widehat{\unicode[STIX]{x1D6FF}^{\prime }}$
, where
![]() $0<r<1$
. Then it follows that
$0<r<1$
. Then it follows that
![]() $B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})=rB(\widehat{\unicode[STIX]{x1D6FF}},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})+(1-r)B(\widehat{\unicode[STIX]{x1D6FF}^{\prime }},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})\leqslant 0$
. Our assumption “irreducible” says that either
$B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})=rB(\widehat{\unicode[STIX]{x1D6FF}},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})+(1-r)B(\widehat{\unicode[STIX]{x1D6FF}^{\prime }},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})\leqslant 0$
. Our assumption “irreducible” says that either
![]() $B(\widehat{\unicode[STIX]{x1D6FF}},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})$
or
$B(\widehat{\unicode[STIX]{x1D6FF}},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})$
or
![]() $B(\widehat{\unicode[STIX]{x1D6FF}^{\prime }},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})$
is negative. Thus we obtain
$B(\widehat{\unicode[STIX]{x1D6FF}^{\prime }},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})$
is negative. Thus we obtain
![]() $B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})<0$
, i.e.,
$B(\widehat{\unicode[STIX]{x1D702}},\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }})<0$
, i.e.,
![]() $\widehat{\unicode[STIX]{x1D702}}$
is not visible from
$\widehat{\unicode[STIX]{x1D702}}$
is not visible from
![]() $\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
by Lemma 2.5(i). Hence
$\widehat{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
by Lemma 2.5(i). Hence
![]() $A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
satisfies the required property.◻
$A_{\unicode[STIX]{x1D6FF}^{\prime \prime }}$
satisfies the required property.◻
Now we prove the desired assertion. In the proof, we always use the relative topology of
![]() $\widehat{Q}$
.
$\widehat{Q}$
.
Proof of Theorem 1.2 in the case of rank 3.
Fix three sets
![]() $A_{\unicode[STIX]{x1D6FC}},A_{\unicode[STIX]{x1D6FD}}$
and
$A_{\unicode[STIX]{x1D6FC}},A_{\unicode[STIX]{x1D6FD}}$
and
![]() $A_{\unicode[STIX]{x1D6FE}}$
in the statements of Lemmas 5.2 and 5.3. For our proof, we introduce the following notation.
$A_{\unicode[STIX]{x1D6FE}}$
in the statements of Lemmas 5.2 and 5.3. For our proof, we introduce the following notation.
∙ Let
 $C_{\unicode[STIX]{x1D6FE}}\subset \widehat{Q}$
be the connected closed set joining end points of
$C_{\unicode[STIX]{x1D6FE}}\subset \widehat{Q}$
be the connected closed set joining end points of
 $A_{\unicode[STIX]{x1D6FC}}$
and
$A_{\unicode[STIX]{x1D6FC}}$
and
 $A_{\unicode[STIX]{x1D6FD}}$
satisfying
$A_{\unicode[STIX]{x1D6FD}}$
satisfying
 $C_{\unicode[STIX]{x1D6FE}}\subset V_{\unicode[STIX]{x1D6FE}}$
. Such a set
$C_{\unicode[STIX]{x1D6FE}}\subset V_{\unicode[STIX]{x1D6FE}}$
. Such a set
 $C_{\unicode[STIX]{x1D6FE}}$
is uniquely determined. Similarly, we also define
$C_{\unicode[STIX]{x1D6FE}}$
is uniquely determined. Similarly, we also define
 $C_{\unicode[STIX]{x1D6FC}}$
and
$C_{\unicode[STIX]{x1D6FC}}$
and
 $C_{\unicode[STIX]{x1D6FD}}$
. Note that the end points of each
$C_{\unicode[STIX]{x1D6FD}}$
. Note that the end points of each
 $C_{\unicode[STIX]{x1D6FF}}$
(
$C_{\unicode[STIX]{x1D6FF}}$
(
 $\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
) are some points in
$\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
) are some points in
 $E$
.
$E$
.
Note that we have the equality
Suppose, on the contrary, that
![]() $E\subsetneq \widehat{Q}\setminus (\bigcup _{i=1}^{m}W\cdot D_{i})$
. Since
$E\subsetneq \widehat{Q}\setminus (\bigcup _{i=1}^{m}W\cdot D_{i})$
. Since
![]() $E$
is closed, there exists a connected open set
$E$
is closed, there exists a connected open set
![]() $U_{1}\subset (\widehat{Q}\setminus (\bigcup _{i=1}^{m}W\cdot D_{i}))\setminus E$
. Note that the boundary of
$U_{1}\subset (\widehat{Q}\setminus (\bigcup _{i=1}^{m}W\cdot D_{i}))\setminus E$
. Note that the boundary of
![]() $U_{1}$
consists of two points. By taking
$U_{1}$
consists of two points. By taking
![]() $U_{1}$
as a maximal one, we may assume that
$U_{1}$
as a maximal one, we may assume that
![]() $\overline{U_{1}}\cap E$
is nonempty and consists of two points
$\overline{U_{1}}\cap E$
is nonempty and consists of two points
![]() $a_{1},b_{1}$
which are the end points of
$a_{1},b_{1}$
which are the end points of
![]() $\overline{U_{1}}$
. Since the end points of
$\overline{U_{1}}$
. Since the end points of
![]() $C_{\unicode[STIX]{x1D6FC}},C_{\unicode[STIX]{x1D6FD}}$
and
$C_{\unicode[STIX]{x1D6FC}},C_{\unicode[STIX]{x1D6FD}}$
and
![]() $C_{\unicode[STIX]{x1D6FE}}$
are contained in
$C_{\unicode[STIX]{x1D6FE}}$
are contained in
![]() $E$
,
$E$
,
![]() $\overline{U_{1}}\subset C_{\unicode[STIX]{x1D6FC}}$
or
$\overline{U_{1}}\subset C_{\unicode[STIX]{x1D6FC}}$
or
![]() $\overline{U_{1}}\subset C_{\unicode[STIX]{x1D6FD}}$
or
$\overline{U_{1}}\subset C_{\unicode[STIX]{x1D6FD}}$
or
![]() $\overline{U_{1}}\subset C_{\unicode[STIX]{x1D6FE}}$
occurs. Moreover, by
$\overline{U_{1}}\subset C_{\unicode[STIX]{x1D6FE}}$
occurs. Moreover, by
![]() $C_{\unicode[STIX]{x1D6FF}}\subset V_{\unicode[STIX]{x1D6FF}}$
for
$C_{\unicode[STIX]{x1D6FF}}\subset V_{\unicode[STIX]{x1D6FF}}$
for
![]() $\unicode[STIX]{x1D6FF}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
and Proposition 2.13(i),
$\unicode[STIX]{x1D6FF}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
and Proposition 2.13(i),
![]() $\overline{U_{1}}$
is a geodesic.
$\overline{U_{1}}$
is a geodesic.
Let, say,
![]() $\overline{U_{1}}\subset C_{\unicode[STIX]{x1D6FE}}$
. Let
$\overline{U_{1}}\subset C_{\unicode[STIX]{x1D6FE}}$
. Let
![]() $U_{2}=s_{\unicode[STIX]{x1D6FE}}\cdot U_{1}$
and let
$U_{2}=s_{\unicode[STIX]{x1D6FE}}\cdot U_{1}$
and let
![]() $a_{2}$
and
$a_{2}$
and
![]() $b_{2}$
be the end points of
$b_{2}$
be the end points of
![]() $U_{2}$
. Then
$U_{2}$
. Then
![]() $U_{2}\cap D_{i}=\emptyset$
for any
$U_{2}\cap D_{i}=\emptyset$
for any
![]() $i$
by definition of
$i$
by definition of
![]() $U_{2}=s_{\unicode[STIX]{x1D6FE}}\cdot U_{1}$
. Namely,
$U_{2}=s_{\unicode[STIX]{x1D6FE}}\cdot U_{1}$
. Namely,
![]() $U_{2}\cap A_{\unicode[STIX]{x1D6FF}}=\emptyset$
for any
$U_{2}\cap A_{\unicode[STIX]{x1D6FF}}=\emptyset$
for any
![]() $\unicode[STIX]{x1D6FF}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
. By (3) together with
$\unicode[STIX]{x1D6FF}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
. By (3) together with
![]() $U_{2}=s_{\unicode[STIX]{x1D6FE}}\cdot U_{1}\not \subset C_{\unicode[STIX]{x1D6FE}}\subset V_{\unicode[STIX]{x1D6FE}}$
,
$U_{2}=s_{\unicode[STIX]{x1D6FE}}\cdot U_{1}\not \subset C_{\unicode[STIX]{x1D6FE}}\subset V_{\unicode[STIX]{x1D6FE}}$
,
![]() $U_{2}\subset \text{int}(C_{\unicode[STIX]{x1D6FC}})$
or
$U_{2}\subset \text{int}(C_{\unicode[STIX]{x1D6FC}})$
or
![]() $U_{2}\subset \text{int}(C_{\unicode[STIX]{x1D6FD}})$
occurs. Moreover,
$U_{2}\subset \text{int}(C_{\unicode[STIX]{x1D6FD}})$
occurs. Moreover,
![]() $\overline{U_{2}}\cap E=\{a_{2},b_{2}\}$
. From Proposition 2.13(i) and (iii), we notice that
$\overline{U_{2}}\cap E=\{a_{2},b_{2}\}$
. From Proposition 2.13(i) and (iii), we notice that
![]() $\ell _{B}(U_{1})<\ell _{B}(U_{2})$
.
$\ell _{B}(U_{1})<\ell _{B}(U_{2})$
.
Similarly, for each
![]() $n\geqslant 1$
, if
$n\geqslant 1$
, if
![]() $U_{n}\subset \text{int}(C_{\unicode[STIX]{x1D6FF}})$
for some
$U_{n}\subset \text{int}(C_{\unicode[STIX]{x1D6FF}})$
for some
![]() $\unicode[STIX]{x1D6FF}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
, then let
$\unicode[STIX]{x1D6FF}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\}$
, then let
![]() $U_{n+1}=s_{\unicode[STIX]{x1D6FF}}\cdot U_{n}$
and let
$U_{n+1}=s_{\unicode[STIX]{x1D6FF}}\cdot U_{n}$
and let
![]() $a_{n+1}$
and
$a_{n+1}$
and
![]() $b_{n+1}$
be the end points of
$b_{n+1}$
be the end points of
![]() $\overline{U_{n+1}}$
. Moreover, we also have
$\overline{U_{n+1}}$
. Moreover, we also have
![]() $\ell _{B}(U_{n})<\ell _{B}(U_{n+1})$
. In particular,
$\ell _{B}(U_{n})<\ell _{B}(U_{n+1})$
. In particular,
![]() $U_{i}\not =U_{j}$
for any
$U_{i}\not =U_{j}$
for any
![]() $i$
and
$i$
and
![]() $j$
with
$j$
with
![]() $i\not =j$
. In addition,
$i\not =j$
. In addition,
![]() $\overline{U_{n}}\cap E=\{a_{n},b_{n}\}$
, where
$\overline{U_{n}}\cap E=\{a_{n},b_{n}\}$
, where
![]() $a_{n}$
and
$a_{n}$
and
![]() $b_{n}$
are the end points of
$b_{n}$
are the end points of
![]() $\overline{U_{n}}$
. If
$\overline{U_{n}}$
. If
![]() $U_{i}\cap U_{j}\not =\emptyset$
for some
$U_{i}\cap U_{j}\not =\emptyset$
for some
![]() $i$
and
$i$
and
![]() $j$
with
$j$
with
![]() $i\not =j$
, then an end point of
$i\not =j$
, then an end point of
![]() $U_{i}$
belongs to
$U_{i}$
belongs to
![]() $U_{j}$
or an end point of
$U_{j}$
or an end point of
![]() $U_{j}$
belongs to
$U_{j}$
belongs to
![]() $U_{i}$
. Since each end point of
$U_{i}$
. Since each end point of
![]() $U_{i}$
and
$U_{i}$
and
![]() $U_{j}$
is an element of
$U_{j}$
is an element of
![]() $E$
, we obtain
$E$
, we obtain
![]() $U_{i}\cap E\not =\emptyset$
or
$U_{i}\cap E\not =\emptyset$
or
![]() $U_{j}\cap E\not =\emptyset$
, a contradiction. Hence
$U_{j}\cap E\not =\emptyset$
, a contradiction. Hence
![]() $U_{i}\cap U_{j}=\emptyset$
for all
$U_{i}\cap U_{j}=\emptyset$
for all
![]() $i$
and
$i$
and
![]() $j$
with
$j$
with
![]() $i\not =j$
.
$i\not =j$
.
Now it follows that one of
![]() $C_{\unicode[STIX]{x1D6FC}}$
,
$C_{\unicode[STIX]{x1D6FC}}$
,
![]() $C_{\unicode[STIX]{x1D6FD}}$
and
$C_{\unicode[STIX]{x1D6FD}}$
and
![]() $C_{\unicode[STIX]{x1D6FE}}$
, say,
$C_{\unicode[STIX]{x1D6FE}}$
, say,
![]() $C_{\unicode[STIX]{x1D6FE}}$
, contains infinitely many open sets
$C_{\unicode[STIX]{x1D6FE}}$
, contains infinitely many open sets
![]() $U_{n}$
. Let
$U_{n}$
. Let
![]() $U_{i_{k}}\subset \text{int}(C_{\unicode[STIX]{x1D6FE}})$
for
$U_{i_{k}}\subset \text{int}(C_{\unicode[STIX]{x1D6FE}})$
for
![]() $k\geqslant 1$
, where
$k\geqslant 1$
, where
![]() $i_{1}<i_{2}<i_{3}<\cdots \,$
. Since
$i_{1}<i_{2}<i_{3}<\cdots \,$
. Since
![]() $U_{i_{k}}\cap U_{i_{k^{\prime }}}=\emptyset$
for any
$U_{i_{k}}\cap U_{i_{k^{\prime }}}=\emptyset$
for any
![]() $k\not =k^{\prime }$
, the disjoint union
$k\not =k^{\prime }$
, the disjoint union
![]() $\bigsqcup _{k=1}^{\infty }U_{i_{k}}$
is contained in
$\bigsqcup _{k=1}^{\infty }U_{i_{k}}$
is contained in
![]() $\text{int}(C_{\unicode[STIX]{x1D6FE}})$
. On the one hand, we have
$\text{int}(C_{\unicode[STIX]{x1D6FE}})$
. On the one hand, we have
![]() $\ell _{B}(C_{\unicode[STIX]{x1D6FE}})<\infty$
. On the other hand, since we have
$\ell _{B}(C_{\unicode[STIX]{x1D6FE}})<\infty$
. On the other hand, since we have
![]() $0<\ell _{B}(U_{i_{1}})<\ell _{B}(U_{i_{2}})<\cdots \,$
, we obtain that
$0<\ell _{B}(U_{i_{1}})<\ell _{B}(U_{i_{2}})<\cdots \,$
, we obtain that
![]() $\sum _{k=1}^{\infty }\ell _{B}(U_{i_{k}})=\infty$
, a contradiction.
$\sum _{k=1}^{\infty }\ell _{B}(U_{i_{k}})=\infty$
, a contradiction.
Therefore, we conclude that
![]() $E=\widehat{Q}\setminus \bigcup _{i=1}^{m}W\cdot D_{i}$
, as required.◻
$E=\widehat{Q}\setminus \bigcup _{i=1}^{m}W\cdot D_{i}$
, as required.◻
6 A proof of Theorem 1.2: the case of an arbitrary rank
Finally, in this section, we prove Theorem 1.2 for the case of an arbitrary rank.
We divide the proof of Theorem 1.2 into the following two cases:
(a)
 $\widehat{Q}\subset \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
;
$\widehat{Q}\subset \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
;(b)
 $\widehat{Q}\not \subset \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
.
$\widehat{Q}\not \subset \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
.
Here
![]() $\text{int}(\cdot )$
denotes the relative interior.
$\text{int}(\cdot )$
denotes the relative interior.
6.1 The case (a)
Since
![]() $|B(x-y,x-y)|^{1/2}$
is a metric on
$|B(x-y,x-y)|^{1/2}$
is a metric on
![]() $\widehat{Q}$
(Remark 2.9), for the proof of Theorem 1.2 in the case (a), we estimate
$\widehat{Q}$
(Remark 2.9), for the proof of Theorem 1.2 in the case (a), we estimate
![]() $|B(x,y)|$
for
$|B(x,y)|$
for
![]() $x,y\in \widehat{Q}$
.
$x,y\in \widehat{Q}$
.
Lemma 6.1. There exists a constant
![]() $C^{\prime }>0$
such that for any
$C^{\prime }>0$
such that for any
![]() $x\in \widehat{Q}$
, one has
$x\in \widehat{Q}$
, one has
![]() $B(x,\unicode[STIX]{x1D6FC})\geqslant C^{\prime }$
for some
$B(x,\unicode[STIX]{x1D6FC})\geqslant C^{\prime }$
for some
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
.
Proof. By Proposition 2.6,
![]() $\widehat{Q}$
is covered by
$\widehat{Q}$
is covered by
![]() $\{V_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\}$
. Note that
$\{V_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\}$
. Note that
![]() $V_{\unicode[STIX]{x1D6FC}}$
is a closed set. Since
$V_{\unicode[STIX]{x1D6FC}}$
is a closed set. Since
![]() $\widehat{Q}\subset \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
, for any
$\widehat{Q}\subset \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
, for any
![]() $y=\sum _{i=1}^{n}y_{i}\unicode[STIX]{x1D6FC}_{i}\in \widehat{Q}$
, one has
$y=\sum _{i=1}^{n}y_{i}\unicode[STIX]{x1D6FC}_{i}\in \widehat{Q}$
, one has
![]() $y_{i}>0$
.
$y_{i}>0$
.
Suppose that there is
![]() $x\in \widehat{Q}$
such that
$x\in \widehat{Q}$
such that
![]() $x\not \in \bigcup _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\text{int}(V_{\unicode[STIX]{x1D6FC}})$
. This means from Proposition 2.6 that
$x\not \in \bigcup _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\text{int}(V_{\unicode[STIX]{x1D6FC}})$
. This means from Proposition 2.6 that
![]() $x$
should belong to
$x$
should belong to
![]() $\bigcap _{i=1}^{k}\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}_{q_{i}}}$
for some
$\bigcap _{i=1}^{k}\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}_{q_{i}}}$
for some
![]() $\unicode[STIX]{x1D6FC}_{q_{1}},\ldots ,\unicode[STIX]{x1D6FC}_{q_{k}}\in \unicode[STIX]{x1D6E5}$
, where
$\unicode[STIX]{x1D6FC}_{q_{1}},\ldots ,\unicode[STIX]{x1D6FC}_{q_{k}}\in \unicode[STIX]{x1D6E5}$
, where
![]() $k<n$
by Lemma 3.2. Hence
$k<n$
by Lemma 3.2. Hence
![]() $B(x,\unicode[STIX]{x1D6FC}_{q_{i}})=0$
for
$B(x,\unicode[STIX]{x1D6FC}_{q_{i}})=0$
for
![]() $i=1,\ldots ,k$
by Lemma 2.5(iii). Moreover,
$i=1,\ldots ,k$
by Lemma 2.5(iii). Moreover,
![]() $B(x,\unicode[STIX]{x1D6FC}^{\prime })<0$
for all
$B(x,\unicode[STIX]{x1D6FC}^{\prime })<0$
for all
![]() $\unicode[STIX]{x1D6FC}^{\prime }\in \unicode[STIX]{x1D6E5}\setminus \{\unicode[STIX]{x1D6FC}_{q_{1}},\ldots ,\unicode[STIX]{x1D6FC}_{q_{k}}\}$
. On the other hand, when
$\unicode[STIX]{x1D6FC}^{\prime }\in \unicode[STIX]{x1D6E5}\setminus \{\unicode[STIX]{x1D6FC}_{q_{1}},\ldots ,\unicode[STIX]{x1D6FC}_{q_{k}}\}$
. On the other hand, when
![]() $x$
can be written like
$x$
can be written like
![]() $x=\sum _{i=1}^{n}x_{i}\unicode[STIX]{x1D6FC}_{i}$
, one has
$x=\sum _{i=1}^{n}x_{i}\unicode[STIX]{x1D6FC}_{i}$
, one has
![]() $B(x,x)=0$
from
$B(x,x)=0$
from
![]() $x\in Q$
, while by
$x\in Q$
, while by
![]() $x\not \in \bigcup _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\text{int}(V_{\unicode[STIX]{x1D6FC}})$
, one has
$x\not \in \bigcup _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\text{int}(V_{\unicode[STIX]{x1D6FC}})$
, one has
![]() $B(\unicode[STIX]{x1D6FC},x)=\sum _{i=1}^{n}x_{i}B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}_{i})<0$
for each
$B(\unicode[STIX]{x1D6FC},x)=\sum _{i=1}^{n}x_{i}B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}_{i})<0$
for each
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\setminus \{\unicode[STIX]{x1D6FC}_{q_{1}},\ldots ,\unicode[STIX]{x1D6FC}_{q_{k}}\}$
. In addition, one has
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\setminus \{\unicode[STIX]{x1D6FC}_{q_{1}},\ldots ,\unicode[STIX]{x1D6FC}_{q_{k}}\}$
. In addition, one has
![]() $B(\unicode[STIX]{x1D6FC},x)=0$
for each
$B(\unicode[STIX]{x1D6FC},x)=0$
for each
![]() $\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{q_{1}},\ldots ,\unicode[STIX]{x1D6FC}_{q_{k}}\}$
. Thus, we have
$\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{q_{1}},\ldots ,\unicode[STIX]{x1D6FC}_{q_{k}}\}$
. Thus, we have
where
![]() $I=\{1,\ldots ,n\}\setminus \{q_{1},\ldots ,q_{k}\}$
, a contradiction.
$I=\{1,\ldots ,n\}\setminus \{q_{1},\ldots ,q_{k}\}$
, a contradiction.
Hence
![]() $x\in \text{int}(V_{\unicode[STIX]{x1D6FC}})$
for some
$x\in \text{int}(V_{\unicode[STIX]{x1D6FC}})$
for some
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Since
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Since
![]() $B(x,\unicode[STIX]{x1D6FC})>0$
for each
$B(x,\unicode[STIX]{x1D6FC})>0$
for each
![]() $x\in \text{int}(V_{\unicode[STIX]{x1D6FC}})$
, we obtain
$x\in \text{int}(V_{\unicode[STIX]{x1D6FC}})$
, we obtain
If we set
![]() $C^{\prime }=\min _{x\in \widehat{Q}}\max _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\{B(x,\unicode[STIX]{x1D6FC})\}$
, then the assertion holds, as required.◻
$C^{\prime }=\min _{x\in \widehat{Q}}\max _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\{B(x,\unicode[STIX]{x1D6FC})\}$
, then the assertion holds, as required.◻
Remark that the constant
![]() $C^{\prime }$
appearing above depends only on
$C^{\prime }$
appearing above depends only on
![]() $B$
.
$B$
.
For
![]() $\unicode[STIX]{x1D705}>0$
and
$\unicode[STIX]{x1D705}>0$
and
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, let
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, let
![]() $U_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D705}}=\{v\in \widehat{Q}:B(\unicode[STIX]{x1D6FC},v)>\unicode[STIX]{x1D705}\}$
. We fix
$U_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D705}}=\{v\in \widehat{Q}:B(\unicode[STIX]{x1D6FC},v)>\unicode[STIX]{x1D705}\}$
. We fix
![]() $C=C^{\prime }-\unicode[STIX]{x1D716}$
for a small
$C=C^{\prime }-\unicode[STIX]{x1D716}$
for a small
![]() $\unicode[STIX]{x1D716}>0$
such as
$\unicode[STIX]{x1D716}>0$
such as
![]() $\bigcup _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}U_{\unicode[STIX]{x1D6FC}}^{C}$
covers
$\bigcup _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}U_{\unicode[STIX]{x1D6FC}}^{C}$
covers
![]() $\widehat{Q}$
. Note that Lemma 6.1 guarantees the existence of
$\widehat{Q}$
. Note that Lemma 6.1 guarantees the existence of
![]() $C$
. Let
$C$
. Let
![]() $U_{\unicode[STIX]{x1D6FC}}=U_{\unicode[STIX]{x1D6FC}}^{C}$
. By Lemma 2.5, one has
$U_{\unicode[STIX]{x1D6FC}}=U_{\unicode[STIX]{x1D6FC}}^{C}$
. By Lemma 2.5, one has
![]() $U_{\unicode[STIX]{x1D6FC}}\subset \text{int}(V_{\unicode[STIX]{x1D6FC}})$
. Thus one can rephrase Lemma 6.1 as follows.
$U_{\unicode[STIX]{x1D6FC}}\subset \text{int}(V_{\unicode[STIX]{x1D6FC}})$
. Thus one can rephrase Lemma 6.1 as follows.
Corollary 6.2. The family of the regions
![]() $\{U_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\}$
covers
$\{U_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}\}$
covers
![]() $\widehat{Q}$
.
$\widehat{Q}$
.
Let
![]() $T=\min _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}1/(1-2C|\unicode[STIX]{x1D6FC}|_{1})$
. Then
$T=\min _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}1/(1-2C|\unicode[STIX]{x1D6FC}|_{1})$
. Then
![]() $T>1$
by Lemma 2.7.
$T>1$
by Lemma 2.7.
Proposition 6.3. For an arbitrary
![]() $x\in U_{\unicode[STIX]{x1D6FC}}$
and
$x\in U_{\unicode[STIX]{x1D6FC}}$
and
![]() $y\in V_{\unicode[STIX]{x1D6FC}}$
, we have
$y\in V_{\unicode[STIX]{x1D6FC}}$
, we have
(i)
 $|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,s_{\unicode[STIX]{x1D6FC}}\cdot y)|>T|B(x,y)|$
;
$|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,s_{\unicode[STIX]{x1D6FC}}\cdot y)|>T|B(x,y)|$
;(ii)
 $|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,y)|\geqslant T|B(x,y)|$
.
$|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,y)|\geqslant T|B(x,y)|$
.
Proof. (i) By Lemma 2.7 and the definition of
![]() $C$
, one has
$C$
, one has
![]() $C<B(x,\unicode[STIX]{x1D6FC})<1/(2|\unicode[STIX]{x1D6FC}|_{1})$
. Moreover, since
$C<B(x,\unicode[STIX]{x1D6FC})<1/(2|\unicode[STIX]{x1D6FC}|_{1})$
. Moreover, since
![]() $x\in U_{\unicode[STIX]{x1D6FC}}\subset V_{1}$
and
$x\in U_{\unicode[STIX]{x1D6FC}}\subset V_{1}$
and
![]() $y\in V_{\unicode[STIX]{x1D6FC}}\subset V_{1}$
, it follows that
$y\in V_{\unicode[STIX]{x1D6FC}}\subset V_{1}$
, it follows that
and
Thus, we obtain
(ii) We have
![]() $B(x,y)\leqslant 0$
by Proposition 2.8. When
$B(x,y)\leqslant 0$
by Proposition 2.8. When
![]() $B(x,y)=0$
, the assertion is obvious. Assume that
$B(x,y)=0$
, the assertion is obvious. Assume that
![]() $B(x,y)<0$
. Since
$B(x,y)<0$
. Since
![]() $B(x,\unicode[STIX]{x1D6FC})>0$
and
$B(x,\unicode[STIX]{x1D6FC})>0$
and
![]() $B(y,\unicode[STIX]{x1D6FC})\geqslant 0$
, one has
$B(y,\unicode[STIX]{x1D6FC})\geqslant 0$
, one has
Hence
Proof of Theorem 1.2 in the case (a).
By [Reference Hohlweg, Labbé and Ripoll6, Theorem 2.7], we know
![]() $E\subset \widehat{Q}$
. What we must show is another inclusion
$E\subset \widehat{Q}$
. What we must show is another inclusion
![]() $\widehat{Q}\subset E$
.
$\widehat{Q}\subset E$
.
Fix
![]() $x\in \widehat{Q}$
. For
$x\in \widehat{Q}$
. For
![]() $x$
, we choose an element
$x$
, we choose an element
![]() $w_{x,m}=s_{\unicode[STIX]{x1D6FC}_{m}}\cdots s_{\unicode[STIX]{x1D6FC}_{1}}\in W$
of length
$w_{x,m}=s_{\unicode[STIX]{x1D6FC}_{m}}\cdots s_{\unicode[STIX]{x1D6FC}_{1}}\in W$
of length
![]() $m$
as follows:
$m$
as follows:
∙ For
 $m=1$
, write
$m=1$
, write
 $w_{x,1}=s_{\unicode[STIX]{x1D6FC}}$
for some
$w_{x,1}=s_{\unicode[STIX]{x1D6FC}}$
for some
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
such that
 $x\in U_{\unicode[STIX]{x1D6FC}}$
. There is at least one such
$x\in U_{\unicode[STIX]{x1D6FC}}$
. There is at least one such
 $\unicode[STIX]{x1D6FC}$
by Corollary 6.2.
$\unicode[STIX]{x1D6FC}$
by Corollary 6.2.∙ When we consider
 $w_{x,m-1}\cdot x$
, there exists
$w_{x,m-1}\cdot x$
, there exists
 $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}$
such that
 $w_{x,m-1}\cdot x\in U_{\unicode[STIX]{x1D6FD}}$
. We set
$w_{x,m-1}\cdot x\in U_{\unicode[STIX]{x1D6FD}}$
. We set
 $w_{x,m}=s_{\unicode[STIX]{x1D6FD}}w_{x,m-1}$
.
$w_{x,m}=s_{\unicode[STIX]{x1D6FD}}w_{x,m-1}$
.
Note that
![]() $w_{x,m}$
is not uniquely determined. Moreover, for each
$w_{x,m}$
is not uniquely determined. Moreover, for each
![]() $i$
, we have
$i$
, we have
![]() $w_{x,i}\not =1$
. Indeed, by taking
$w_{x,i}\not =1$
. Indeed, by taking
![]() $x_{i}^{\prime }\in U_{\unicode[STIX]{x1D6FC}}$
such as
$x_{i}^{\prime }\in U_{\unicode[STIX]{x1D6FC}}$
such as
![]() $w_{x,j}\cdot x_{i}^{\prime }\in U_{\unicode[STIX]{x1D6FC}_{j+1}}$
for any
$w_{x,j}\cdot x_{i}^{\prime }\in U_{\unicode[STIX]{x1D6FC}_{j+1}}$
for any
![]() $j<i$
, we have
$j<i$
, we have
![]() $|B(w_{x,i}\cdot x,w_{x,i}\cdot x_{i}^{\prime })|>|B(x,x_{i}^{\prime })|$
by the proof of Proposition 2.13.
$|B(w_{x,i}\cdot x,w_{x,i}\cdot x_{i}^{\prime })|>|B(x,x_{i}^{\prime })|$
by the proof of Proposition 2.13.
Now, one has
![]() $w_{x,m}\cdot x\in \widehat{Q}\setminus V_{\unicode[STIX]{x1D6FC}_{m}}$
. On the other hand, there exists
$w_{x,m}\cdot x\in \widehat{Q}\setminus V_{\unicode[STIX]{x1D6FC}_{m}}$
. On the other hand, there exists
![]() $y_{m}$
such that
$y_{m}$
such that
![]() $y_{m}\in E\cap (\widehat{Q}\setminus V_{\unicode[STIX]{x1D6FC}_{m}})$
. In fact, take
$y_{m}\in E\cap (\widehat{Q}\setminus V_{\unicode[STIX]{x1D6FC}_{m}})$
. In fact, take
![]() $y\in E\not =\emptyset$
. If
$y\in E\not =\emptyset$
. If
![]() $y\not \in V_{\unicode[STIX]{x1D6FC}_{m}}$
, then let
$y\not \in V_{\unicode[STIX]{x1D6FC}_{m}}$
, then let
![]() $y_{m}=y$
. If
$y_{m}=y$
. If
![]() $y\in V_{\unicode[STIX]{x1D6FC}_{m}}$
, then let
$y\in V_{\unicode[STIX]{x1D6FC}_{m}}$
, then let
![]() $y_{m}=s_{\unicode[STIX]{x1D6FC}_{m}}\cdot y$
. By definition of
$y_{m}=s_{\unicode[STIX]{x1D6FC}_{m}}\cdot y$
. By definition of
![]() $w_{x,m}$
, we see that
$w_{x,m}$
, we see that
![]() $w_{x,m-1}\cdot x\in U_{\unicode[STIX]{x1D6FC}_{m}}$
. Moreover,
$w_{x,m-1}\cdot x\in U_{\unicode[STIX]{x1D6FC}_{m}}$
. Moreover,
![]() $s_{\unicode[STIX]{x1D6FC}_{m}}\cdot y_{m}\in V_{\unicode[STIX]{x1D6FC}_{m}}$
. If we set
$s_{\unicode[STIX]{x1D6FC}_{m}}\cdot y_{m}\in V_{\unicode[STIX]{x1D6FC}_{m}}$
. If we set
![]() $y_{m-1}=s_{\unicode[STIX]{x1D6FC}_{m}}\cdot y_{m}$
, then
$y_{m-1}=s_{\unicode[STIX]{x1D6FC}_{m}}\cdot y_{m}$
, then
![]() $y_{m-1}\in E$
. By Proposition 6.3(i), we see that
$y_{m-1}\in E$
. By Proposition 6.3(i), we see that
Let
By Proposition 6.3(ii) if
![]() $y_{m-2}=y_{m-1}$
and Proposition 6.3(i) if
$y_{m-2}=y_{m-1}$
and Proposition 6.3(i) if
![]() $y_{m-2}=s_{\unicode[STIX]{x1D6FC}_{m-1}}\cdot y_{m-1}$
, we obtain that
$y_{m-2}=s_{\unicode[STIX]{x1D6FC}_{m-1}}\cdot y_{m-1}$
, we obtain that
By repeating this estimation, we conclude that
Let
![]() $M=\max _{u,v\in \widehat{Q}}|B(u,v)|$
. Then
$M=\max _{u,v\in \widehat{Q}}|B(u,v)|$
. Then
![]() $M$
is finite by the compactness of
$M$
is finite by the compactness of
![]() $\widehat{Q}$
. Moreover, we have
$\widehat{Q}$
. Moreover, we have
![]() $M>0$
and
$M>0$
and
By taking a large
![]() $m$
, one can find
$m$
, one can find
![]() $y_{0}\in E$
such that
$y_{0}\in E$
such that
![]() $|B(x,y_{0})|$
is arbitrarily small. Therefore, we obtain that
$|B(x,y_{0})|$
is arbitrarily small. Therefore, we obtain that
![]() $x\in E$
, as desired.◻
$x\in E$
, as desired.◻
6.2 The case (b)
We prove the case (b) by induction on the rank of Coxeter groups. The following remark guarantees that we can use the induction for the proof.
Remark 6.4. For an arbitrary
![]() $\unicode[STIX]{x1D6E5}_{I}\subset \unicode[STIX]{x1D6E5}$
, let
$\unicode[STIX]{x1D6E5}_{I}\subset \unicode[STIX]{x1D6E5}$
, let
![]() $W_{I}$
be a parabolic subgroup of
$W_{I}$
be a parabolic subgroup of
![]() $W$
for
$W$
for
![]() $\unicode[STIX]{x1D6E5}_{I}$
and let
$\unicode[STIX]{x1D6E5}_{I}$
and let
![]() $B_{I}$
be the bilinear form associated to
$B_{I}$
be the bilinear form associated to
![]() $W_{I}$
. Then the signature of
$W_{I}$
. Then the signature of
![]() $B_{I}$
is
$B_{I}$
is
![]() $(m,0)$
or
$(m,0)$
or
![]() $(m-1,0)$
or
$(m-1,0)$
or
![]() $(m-1,1)$
, where
$(m-1,1)$
, where
![]() $m=|\unicode[STIX]{x1D6E5}_{I}|$
. In fact, since
$m=|\unicode[STIX]{x1D6E5}_{I}|$
. In fact, since
![]() $B_{I}$
is a principal submatrix of
$B_{I}$
is a principal submatrix of
![]() $B$
, the eigenvalues of
$B$
, the eigenvalues of
![]() $B_{I}$
interlace those of
$B_{I}$
interlace those of
![]() $B$
by [Reference Haemers5, Corollary 2.2].
$B$
by [Reference Haemers5, Corollary 2.2].
For
![]() $v\in \text{span}(\unicode[STIX]{x1D6E5}_{I})$
, we define
$v\in \text{span}(\unicode[STIX]{x1D6E5}_{I})$
, we define
![]() $|v|_{1}^{I}$
from
$|v|_{1}^{I}$
from
![]() $B_{I}$
in the same manner as
$B_{I}$
in the same manner as
![]() $B$
in
$B$
in
![]() $V$
and consider
$V$
and consider
![]() $\text{span}(\unicode[STIX]{x1D6E5}_{I})_{1}=\{v\in \text{span}(\unicode[STIX]{x1D6E5}_{I}):|v|_{1}^{I}=1\}$
. Then there exists a map
$\text{span}(\unicode[STIX]{x1D6E5}_{I})_{1}=\{v\in \text{span}(\unicode[STIX]{x1D6E5}_{I}):|v|_{1}^{I}=1\}$
. Then there exists a map
![]() $\unicode[STIX]{x1D719}_{I}$
from
$\unicode[STIX]{x1D719}_{I}$
from
![]() $\text{span}(\unicode[STIX]{x1D6E5}_{I})_{1}$
to
$\text{span}(\unicode[STIX]{x1D6E5}_{I})_{1}$
to
![]() $V_{1}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
which is just the normalization
$V_{1}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
which is just the normalization
![]() $\widehat{\cdot }$
restricted to
$\widehat{\cdot }$
restricted to
![]() $\text{span}(\unicode[STIX]{x1D6E5}_{I})_{1}$
. This is actually a homeomorphism. Via the map
$\text{span}(\unicode[STIX]{x1D6E5}_{I})_{1}$
. This is actually a homeomorphism. Via the map
![]() $\unicode[STIX]{x1D719}_{I}$
, we can identify the sets
$\unicode[STIX]{x1D719}_{I}$
, we can identify the sets
![]() $E\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
and
$E\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
and
![]() $\widehat{Q}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
with the corresponding sets defined by using
$\widehat{Q}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})$
with the corresponding sets defined by using
![]() $|\cdot |_{1}^{I}$
.
$|\cdot |_{1}^{I}$
.
We divide the case (b) into the following two cases:
(b-1)
 $\widehat{Q}\not \subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
;
$\widehat{Q}\not \subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
;(b-2)
 $\widehat{Q}\subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
and
$\widehat{Q}\subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
and
 $\widehat{Q}\cap \unicode[STIX]{x2202}\text{conv}(\widehat{\unicode[STIX]{x1D6E5}})\not =\emptyset$
.
$\widehat{Q}\cap \unicode[STIX]{x2202}\text{conv}(\widehat{\unicode[STIX]{x1D6E5}})\not =\emptyset$
.
For
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, let
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, let
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6E5}\setminus \{\unicode[STIX]{x1D6FC}\}$
,
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6E5}\setminus \{\unicode[STIX]{x1D6FC}\}$
,
![]() $S_{\unicode[STIX]{x1D6FC}}=S\setminus \{s_{\unicode[STIX]{x1D6FC}}\}$
and let
$S_{\unicode[STIX]{x1D6FC}}=S\setminus \{s_{\unicode[STIX]{x1D6FC}}\}$
and let
![]() $W_{\unicode[STIX]{x1D6FC}}$
denote the parabolic subgroup of
$W_{\unicode[STIX]{x1D6FC}}$
denote the parabolic subgroup of
![]() $W$
generated by
$W$
generated by
![]() $S_{\unicode[STIX]{x1D6FC}}$
. When
$S_{\unicode[STIX]{x1D6FC}}$
. When
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{j}$
, we denote
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{j}$
, we denote
![]() $\unicode[STIX]{x1D6E5}_{j}$
,
$\unicode[STIX]{x1D6E5}_{j}$
,
![]() $S_{j}$
and
$S_{j}$
and
![]() $W_{j}$
instead of
$W_{j}$
instead of
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}_{j}}$
,
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}_{j}}$
,
![]() $S_{\unicode[STIX]{x1D6FC}_{j}}$
and
$S_{\unicode[STIX]{x1D6FC}_{j}}$
and
![]() $W_{\unicode[STIX]{x1D6FC}_{j}}$
, respectively.
$W_{\unicode[STIX]{x1D6FC}_{j}}$
, respectively.
Now we see that
![]() $\widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})\not =\emptyset$
. In fact, we have
$\widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})\not =\emptyset$
. In fact, we have
![]() $B(o,o)<0$
and
$B(o,o)<0$
and
![]() $B(\widehat{\unicode[STIX]{x1D6FC}},\widehat{\unicode[STIX]{x1D6FC}})>0$
for all
$B(\widehat{\unicode[STIX]{x1D6FC}},\widehat{\unicode[STIX]{x1D6FC}})>0$
for all
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Moreover, since
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Moreover, since
![]() $\widehat{Q}$
is connected, our assumption
$\widehat{Q}$
is connected, our assumption
![]() $\widehat{Q}\not \subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
implies that
$\widehat{Q}\not \subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
implies that
![]() $\widehat{Q}\cap \unicode[STIX]{x2202}\text{conv}(\widehat{\unicode[STIX]{x1D6E5}})\not =\emptyset$
. Since
$\widehat{Q}\cap \unicode[STIX]{x2202}\text{conv}(\widehat{\unicode[STIX]{x1D6E5}})\not =\emptyset$
. Since
![]() $\unicode[STIX]{x2202}\text{conv}(\widehat{\unicode[STIX]{x1D6E5}})=\bigcup _{j=1}^{n}\text{conv}(\widehat{\unicode[STIX]{x1D6E5}_{j}})$
, one has
$\unicode[STIX]{x2202}\text{conv}(\widehat{\unicode[STIX]{x1D6E5}})=\bigcup _{j=1}^{n}\text{conv}(\widehat{\unicode[STIX]{x1D6E5}_{j}})$
, one has
![]() $\widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}_{j}})\not =\emptyset$
for some
$\widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}_{j}})\not =\emptyset$
for some
![]() $j$
’s.
$j$
’s.
For
![]() $j=1,\ldots ,n$
, let
$j=1,\ldots ,n$
, let
![]() $A_{j}=\text{conv}(\widehat{\unicode[STIX]{x1D6E5}_{j}})$
and
$A_{j}=\text{conv}(\widehat{\unicode[STIX]{x1D6E5}_{j}})$
and
![]() $H_{j}=\text{span}(\widehat{\unicode[STIX]{x1D6E5}_{j}})$
.
$H_{j}=\text{span}(\widehat{\unicode[STIX]{x1D6E5}_{j}})$
.
Lemma 6.5. Assume
![]() $\widehat{Q}\not \subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then for a component
$\widehat{Q}\not \subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then for a component
![]() $D$
of
$D$
of
![]() $\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, we have the following:
$\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, we have the following:
(i)
 $\unicode[STIX]{x2202}(W\cdot D)$
is
$\unicode[STIX]{x2202}(W\cdot D)$
is
 $W$
-invariant, i.e.,
$W$
-invariant, i.e.,
 $W\cdot \unicode[STIX]{x2202}(W\cdot D)=\unicode[STIX]{x2202}(W\cdot D)$
;
$W\cdot \unicode[STIX]{x2202}(W\cdot D)=\unicode[STIX]{x2202}(W\cdot D)$
;(ii)
 $\unicode[STIX]{x2202}D=\widehat{Q}\cap \bigcup _{\unicode[STIX]{x2202}D\cap A_{j}\not =\emptyset }A_{j}$
.
$\unicode[STIX]{x2202}D=\widehat{Q}\cap \bigcup _{\unicode[STIX]{x2202}D\cap A_{j}\not =\emptyset }A_{j}$
.
Proof. (i) Let
![]() $y\in W\cdot \unicode[STIX]{x2202}(W\cdot D)$
. Then
$y\in W\cdot \unicode[STIX]{x2202}(W\cdot D)$
. Then
![]() $y=w\cdot z$
for some
$y=w\cdot z$
for some
![]() $w\in W$
and
$w\in W$
and
![]() $z\in \unicode[STIX]{x2202}(W\cdot D)$
. Since
$z\in \unicode[STIX]{x2202}(W\cdot D)$
. Since
![]() $W$
acts on
$W$
acts on
![]() $\widehat{Q}$
as homeomorphisms, any neighborhood of
$\widehat{Q}$
as homeomorphisms, any neighborhood of
![]() $y$
can be expressed as an image by
$y$
can be expressed as an image by
![]() $w$
of some neighborhood of
$w$
of some neighborhood of
![]() $z$
. Let
$z$
. Let
![]() $O$
be a neighborhood of
$O$
be a neighborhood of
![]() $y$
in
$y$
in
![]() $\widehat{Q}$
. Since
$\widehat{Q}$
. Since
![]() $w^{-1}\cdot y=z$
is contained in
$w^{-1}\cdot y=z$
is contained in
![]() $\unicode[STIX]{x2202}(W\cdot D)$
, one has
$\unicode[STIX]{x2202}(W\cdot D)$
, one has
![]() $w^{-1}\cdot O\cap W\cdot D\not =\emptyset$
and
$w^{-1}\cdot O\cap W\cdot D\not =\emptyset$
and
![]() $w^{-1}\cdot O\cap (\widehat{Q}\setminus W\cdot D)\not =\emptyset$
. Since
$w^{-1}\cdot O\cap (\widehat{Q}\setminus W\cdot D)\not =\emptyset$
. Since
![]() $W\cdot D$
and
$W\cdot D$
and
![]() $\widehat{Q}\setminus W\cdot D$
are
$\widehat{Q}\setminus W\cdot D$
are
![]() $W$
-invariant, one has
$W$
-invariant, one has
![]() $w\cdot (w^{-1}\cdot O\cap W\cdot D)=O\cap W\cdot D\not =\emptyset$
and
$w\cdot (w^{-1}\cdot O\cap W\cdot D)=O\cap W\cdot D\not =\emptyset$
and
![]() $w\cdot (w^{-1}\cdot O\cap (\widehat{Q}\setminus W\cdot D))=O\cap (\widehat{Q}\setminus W\cdot D)\not =\emptyset$
. Thus
$w\cdot (w^{-1}\cdot O\cap (\widehat{Q}\setminus W\cdot D))=O\cap (\widehat{Q}\setminus W\cdot D)\not =\emptyset$
. Thus
![]() $y$
should belong to
$y$
should belong to
![]() $\unicode[STIX]{x2202}(W\cdot D)$
. Hence
$\unicode[STIX]{x2202}(W\cdot D)$
. Hence
![]() $W\cdot \unicode[STIX]{x2202}(W\cdot D)\subset \unicode[STIX]{x2202}(W\cdot D)$
. On the other hand, the reverse inclusion is obvious. Thus
$W\cdot \unicode[STIX]{x2202}(W\cdot D)\subset \unicode[STIX]{x2202}(W\cdot D)$
. On the other hand, the reverse inclusion is obvious. Thus
![]() $\unicode[STIX]{x2202}(W\cdot D)$
is
$\unicode[STIX]{x2202}(W\cdot D)$
is
![]() $W$
-invariant.
$W$
-invariant.
(ii) After some reordering of indices
![]() $1,\ldots ,n$
, we assume that
$1,\ldots ,n$
, we assume that
![]() $\unicode[STIX]{x2202}D\cap A_{j}\not =\emptyset$
if and only if
$\unicode[STIX]{x2202}D\cap A_{j}\not =\emptyset$
if and only if
![]() $1\leqslant j\leqslant k$
for some
$1\leqslant j\leqslant k$
for some
![]() $k$
. The inclusion
$k$
. The inclusion
![]() $\unicode[STIX]{x2202}D\subset \widehat{Q}\cap \bigcup _{j=1}^{k}A_{j}$
is obvious. Moreover, since
$\unicode[STIX]{x2202}D\subset \widehat{Q}\cap \bigcup _{j=1}^{k}A_{j}$
is obvious. Moreover, since
![]() $\{v\in A_{j}:B(v,v)\leqslant 0\}$
is convex, a point in a segment joining two points of
$\{v\in A_{j}:B(v,v)\leqslant 0\}$
is convex, a point in a segment joining two points of
![]() $\{v\in A_{j}:B(v,v)\leqslant 0\}$
is also a point in this set. This implies that
$\{v\in A_{j}:B(v,v)\leqslant 0\}$
is also a point in this set. This implies that
![]() $\{v\in A_{j}:B(v,v)\leqslant 0\}$
consists of a single component, i.e.,
$\{v\in A_{j}:B(v,v)\leqslant 0\}$
consists of a single component, i.e.,
![]() $A_{j}$
does not intersect with any component except for
$A_{j}$
does not intersect with any component except for
![]() $D$
. Thus, we obtain
$D$
. Thus, we obtain
![]() $\widehat{Q}\cap A_{j}\subset \unicode[STIX]{x2202}D$
for each
$\widehat{Q}\cap A_{j}\subset \unicode[STIX]{x2202}D$
for each
![]() $j=1,\ldots ,k$
. Hence one has
$j=1,\ldots ,k$
. Hence one has
![]() $\unicode[STIX]{x2202}D=\widehat{Q}\cap \bigcup _{j=1}^{k}A_{j}$
, as required.◻
$\unicode[STIX]{x2202}D=\widehat{Q}\cap \bigcup _{j=1}^{k}A_{j}$
, as required.◻
Let
![]() $D_{1},\ldots ,D_{m}$
denote the connected components of
$D_{1},\ldots ,D_{m}$
denote the connected components of
![]() $\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then each
$\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then each
![]() $D_{i}$
is an open set with respect to the relative topology of
$D_{i}$
is an open set with respect to the relative topology of
![]() $\widehat{Q}$
.
$\widehat{Q}$
.
Proposition 6.6. Assume
![]() $\widehat{Q}\not \subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then one has
$\widehat{Q}\not \subset \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then one has
![]() $E=\bigcup _{i=1}^{m}\unicode[STIX]{x2202}(W\cdot D_{i})=\unicode[STIX]{x2202}\bigcup _{i=1}^{m}W\cdot D_{i}$
.
$E=\bigcup _{i=1}^{m}\unicode[STIX]{x2202}(W\cdot D_{i})=\unicode[STIX]{x2202}\bigcup _{i=1}^{m}W\cdot D_{i}$
.
Proof. Fix an open component
![]() $D$
of
$D$
of
![]() $\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, i.e., let
$\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, i.e., let
![]() $D=D_{j}$
for some
$D=D_{j}$
for some
![]() $1\leqslant j\leqslant m$
. By Lemma 6.5(i), we know that
$1\leqslant j\leqslant m$
. By Lemma 6.5(i), we know that
![]() $\unicode[STIX]{x2202}(W\cdot D)$
is closed and
$\unicode[STIX]{x2202}(W\cdot D)$
is closed and
![]() $W$
-invariant. Hence, by Proposition 3.3, in order to prove
$W$
-invariant. Hence, by Proposition 3.3, in order to prove
![]() $\unicode[STIX]{x2202}(W\cdot D)=\bigcup _{i=1}^{m}\unicode[STIX]{x2202}(W\cdot D_{i})=E$
, it suffices to show that
$\unicode[STIX]{x2202}(W\cdot D)=\bigcup _{i=1}^{m}\unicode[STIX]{x2202}(W\cdot D_{i})=E$
, it suffices to show that
![]() $\unicode[STIX]{x2202}(W\cdot D)$
is contained in
$\unicode[STIX]{x2202}(W\cdot D)$
is contained in
![]() $E$
.
$E$
.
As in the proof of Lemma 6.5, we assume that
![]() $\unicode[STIX]{x2202}D\cap A_{j}\not =\emptyset$
if and only if
$\unicode[STIX]{x2202}D\cap A_{j}\not =\emptyset$
if and only if
![]() $1\leqslant j\leqslant k$
for some
$1\leqslant j\leqslant k$
for some
![]() $k$
. Let
$k$
. Let
![]() $\widehat{Q_{j}}=\{\widehat{v}:v\in H_{j},B_{j}(v,v)=0\}\subset \widehat{Q}$
, where
$\widehat{Q_{j}}=\{\widehat{v}:v\in H_{j},B_{j}(v,v)=0\}\subset \widehat{Q}$
, where
![]() $B_{j}$
is the Coxeter matrix associated with
$B_{j}$
is the Coxeter matrix associated with
![]() $W_{j}$
. (Note that
$W_{j}$
. (Note that
![]() $B_{j}$
is a principal submatrix of
$B_{j}$
is a principal submatrix of
![]() $B$
.) Then
$B$
.) Then
![]() $\widehat{Q}\cap H_{j}=\widehat{Q_{j}}$
and
$\widehat{Q}\cap H_{j}=\widehat{Q_{j}}$
and
![]() $D\cap H_{j}=\widehat{Q_{j}}\setminus A_{j}$
for each
$D\cap H_{j}=\widehat{Q_{j}}\setminus A_{j}$
for each
![]() $1\leqslant j\leqslant k$
. (Note that
$1\leqslant j\leqslant k$
. (Note that
![]() $\widehat{Q_{j}}\setminus A_{j}$
might be nonempty. In fact, if, for distinct
$\widehat{Q_{j}}\setminus A_{j}$
might be nonempty. In fact, if, for distinct
![]() $i,j$
, the parabolic subgroup generated by
$i,j$
, the parabolic subgroup generated by
![]() $S\setminus \{s_{\unicode[STIX]{x1D6FC}_{i}},s_{\unicode[STIX]{x1D6FC}_{j}}\}$
is infinite, then
$S\setminus \{s_{\unicode[STIX]{x1D6FC}_{i}},s_{\unicode[STIX]{x1D6FC}_{j}}\}$
is infinite, then
![]() $D\cap H_{i}\not =\emptyset$
and
$D\cap H_{i}\not =\emptyset$
and
![]() $D\cap H_{j}\not =\emptyset$
.) By the inductive hypothesis and Remark 6.4, one has
$D\cap H_{j}\not =\emptyset$
.) By the inductive hypothesis and Remark 6.4, one has
where
![]() $E_{j}$
is the accumulation set of normalized roots of
$E_{j}$
is the accumulation set of normalized roots of
![]() $W_{j}$
.
$W_{j}$
.
Let
![]() $x\in \unicode[STIX]{x2202}(W\cdot D)$
. Suppose that
$x\in \unicode[STIX]{x2202}(W\cdot D)$
. Suppose that
![]() $x\not \in E$
. Since
$x\not \in E$
. Since
![]() $E$
is a closed set, there exists an open neighborhood
$E$
is a closed set, there exists an open neighborhood
![]() $U$
of
$U$
of
![]() $x$
in
$x$
in
![]() $\widehat{Q}$
such that
$\widehat{Q}$
such that
![]() $U\cap E=\emptyset$
. Moreover, since
$U\cap E=\emptyset$
. Moreover, since
![]() $\unicode[STIX]{x2202}(W\cdot D)\subset W\cdot \unicode[STIX]{x2202}D$
, one has
$\unicode[STIX]{x2202}(W\cdot D)\subset W\cdot \unicode[STIX]{x2202}D$
, one has
![]() $w\cdot x\in \unicode[STIX]{x2202}D=\widehat{Q}\cap \bigcup _{j=1}^{k}A_{j}$
for some
$w\cdot x\in \unicode[STIX]{x2202}D=\widehat{Q}\cap \bigcup _{j=1}^{k}A_{j}$
for some
![]() $w\in W$
. Thus
$w\in W$
. Thus
![]() $w\cdot x\in \widehat{Q}\cap A_{j}$
for some
$w\cdot x\in \widehat{Q}\cap A_{j}$
for some
![]() $j\in \{1,\ldots ,k\}$
. Since
$j\in \{1,\ldots ,k\}$
. Since
![]() $(w\cdot U)\cap E_{j}\subset (w\cdot U)\cap E=\emptyset$
, we have
$(w\cdot U)\cap E_{j}\subset (w\cdot U)\cap E=\emptyset$
, we have
![]() $(w\cdot U)\cap E_{j}=\emptyset$
. Hence, by the inductive hypothesis (4) and the equality
$(w\cdot U)\cap E_{j}=\emptyset$
. Hence, by the inductive hypothesis (4) and the equality
![]() $\widehat{Q}\cap H_{j}=\widehat{Q_{j}}$
, we have
$\widehat{Q}\cap H_{j}=\widehat{Q_{j}}$
, we have
![]() $(w\cdot U)\cap A_{j}\subset W_{j}\cdot (\widehat{Q_{j}}\setminus A_{j})$
, i.e., there exists
$(w\cdot U)\cap A_{j}\subset W_{j}\cdot (\widehat{Q_{j}}\setminus A_{j})$
, i.e., there exists
![]() $w^{\prime }\in W_{j}$
such that
$w^{\prime }\in W_{j}$
such that
![]() $w^{\prime }\cdot ((w\cdot U)\cap A_{j})\subset \widehat{Q_{j}}\setminus A_{j}=D\cap H_{j}\subset D$
. Since
$w^{\prime }\cdot ((w\cdot U)\cap A_{j})\subset \widehat{Q_{j}}\setminus A_{j}=D\cap H_{j}\subset D$
. Since
![]() $w\cdot x\in w\cdot U\cap A_{j}$
and
$w\cdot x\in w\cdot U\cap A_{j}$
and
![]() $W_{j}\cdot (\widehat{Q}\setminus A_{j})\subset W\cdot D$
by
$W_{j}\cdot (\widehat{Q}\setminus A_{j})\subset W\cdot D$
by
![]() $D\cap H_{j}=\widehat{Q_{j}}\setminus A_{j}$
, we have
$D\cap H_{j}=\widehat{Q_{j}}\setminus A_{j}$
, we have
![]() $w\cdot x\in W\cdot D$
and therefore
$w\cdot x\in W\cdot D$
and therefore
![]() $x\in W\cdot D$
, but this contradicts the assumption
$x\in W\cdot D$
, but this contradicts the assumption
![]() $x\in \unicode[STIX]{x2202}(W\cdot D)$
since
$x\in \unicode[STIX]{x2202}(W\cdot D)$
since
![]() $W\cdot D$
is now open. Therefore,
$W\cdot D$
is now open. Therefore,
![]() $x\in E$
, i.e.,
$x\in E$
, i.e.,
Finally, by Lemma 6.7 below, we also have
![]() $\bigcup _{i=1}^{m}\unicode[STIX]{x2202}(W\cdot D_{i})=\unicode[STIX]{x2202}\bigcup _{i=1}^{m}$
$\bigcup _{i=1}^{m}\unicode[STIX]{x2202}(W\cdot D_{i})=\unicode[STIX]{x2202}\bigcup _{i=1}^{m}$
![]() $W\cdot D_{i}$
.◻
$W\cdot D_{i}$
.◻
Lemma 6.7. Let
![]() $D$
and
$D$
and
![]() $D^{\prime }$
be different components of
$D^{\prime }$
be different components of
![]() $\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then
$\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then
For the proof of Lemma 6.7, we prepare two lemmas.
Lemma 6.8. Let
![]() $D$
be a component of
$D$
be a component of
![]() $\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then a set
$\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Then a set
is nonempty.
Note that for each point
![]() $x\in V_{1}$
, we can write
$x\in V_{1}$
, we can write
![]() $x=\sum _{i=1}^{n}x_{i}\widehat{\unicode[STIX]{x1D6FC}_{i}}$
. Then every point
$x=\sum _{i=1}^{n}x_{i}\widehat{\unicode[STIX]{x1D6FC}_{i}}$
. Then every point
![]() $x=\sum _{i=1}^{n}x_{i}\widehat{\unicode[STIX]{x1D6FC}_{i}}$
in a component
$x=\sum _{i=1}^{n}x_{i}\widehat{\unicode[STIX]{x1D6FC}_{i}}$
in a component
![]() $D$
of
$D$
of
![]() $\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
has at least one index
$\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
has at least one index
![]() $j$
such that
$j$
such that
![]() $x_{j}<0$
. Let
$x_{j}<0$
. Let
![]() $J_{D}\subset \{1,\ldots ,n\}$
denote the set of such indices. Conversely, if
$J_{D}\subset \{1,\ldots ,n\}$
denote the set of such indices. Conversely, if
![]() $x_{j}<0$
for some
$x_{j}<0$
for some
![]() $j$
, then there exists a component
$j$
, then there exists a component
![]() $D$
in
$D$
in
![]() $\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. By the convexity of
$\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. By the convexity of
![]() $\widehat{Q_{-}}$
, such a component is uniquely determined for
$\widehat{Q_{-}}$
, such a component is uniquely determined for
![]() $j$
. Hence, for different components
$j$
. Hence, for different components
![]() $D$
and
$D$
and
![]() $D^{\prime }$
, we have
$D^{\prime }$
, we have
![]() $J_{D}\cap J_{D^{\prime }}=\emptyset$
.
$J_{D}\cap J_{D^{\prime }}=\emptyset$
.
Proof of Lemma 6.8.
Take
![]() $j\in J_{D}$
. For
$j\in J_{D}$
. For
![]() $t\in \mathbb{R}$
, let
$t\in \mathbb{R}$
, let
![]() $H(t)$
be an affine subspace in
$H(t)$
be an affine subspace in
![]() $V_{1}$
which is parallel to
$V_{1}$
which is parallel to
![]() $H_{j}$
whose
$H_{j}$
whose
![]() $j$
th coordinate is equal to
$j$
th coordinate is equal to
![]() $t$
, i.e.,
$t$
, i.e.,
![]() $H(t)=\{x\in V_{1}:x=\sum _{i=1}^{n}x_{i}\widehat{\unicode[STIX]{x1D6FC}_{i}},x_{j}=t\}$
. Note that
$H(t)=\{x\in V_{1}:x=\sum _{i=1}^{n}x_{i}\widehat{\unicode[STIX]{x1D6FC}_{i}},x_{j}=t\}$
. Note that
![]() $H_{j}=H(0)$
and
$H_{j}=H(0)$
and
![]() $\widehat{\unicode[STIX]{x1D6FC}_{j}}\in H(1)$
. Since
$\widehat{\unicode[STIX]{x1D6FC}_{j}}\in H(1)$
. Since
![]() $H(0)$
intersects with
$H(0)$
intersects with
![]() $\widehat{Q_{-}}$
, there is
$\widehat{Q_{-}}$
, there is
![]() $t_{0}<0$
such that
$t_{0}<0$
such that
![]() $H(t_{0})$
is tangent to
$H(t_{0})$
is tangent to
![]() $\widehat{Q}$
. Such a tangent point is unique on
$\widehat{Q}$
. Such a tangent point is unique on
![]() $H(t_{0})$
. Let
$H(t_{0})$
. Let
![]() $x\in H(t_{0})\cap \widehat{Q}$
be the tangent point. Then each segment connecting
$x\in H(t_{0})\cap \widehat{Q}$
be the tangent point. Then each segment connecting
![]() $x$
and
$x$
and
![]() $\widehat{\unicode[STIX]{x1D6FC}}$
(
$\widehat{\unicode[STIX]{x1D6FC}}$
(
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
) should intersect with
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
) should intersect with
![]() $\widehat{Q_{-}}$
. This implies that
$\widehat{Q_{-}}$
. This implies that
![]() $x$
is not visible from
$x$
is not visible from
![]() $\widehat{\unicode[STIX]{x1D6FC}}$
. Hence, by Lemma 2.5(i), we have
$\widehat{\unicode[STIX]{x1D6FC}}$
. Hence, by Lemma 2.5(i), we have
![]() $B(x,\unicode[STIX]{x1D6FC})<0$
for any
$B(x,\unicode[STIX]{x1D6FC})<0$
for any
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Moreover, since the
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Moreover, since the
![]() $j$
th coordinate of
$j$
th coordinate of
![]() $x$
is negative, we have
$x$
is negative, we have
![]() $x\in D$
and thus,
$x\in D$
and thus,
![]() $x\in K_{D}$
.◻
$x\in K_{D}$
.◻
Lemma 6.9. Let
![]() $D$
be a component of
$D$
be a component of
![]() $\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Assume that
$\widehat{Q}\setminus \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
. Assume that
![]() $\ell (ws_{\unicode[STIX]{x1D6FC}})>\ell (w)$
for
$\ell (ws_{\unicode[STIX]{x1D6FC}})>\ell (w)$
for
![]() $w\in W$
and
$w\in W$
and
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, where
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, where
![]() $\ell$
denotes the word length on
$\ell$
denotes the word length on
![]() $(W,S)$
. For any
$(W,S)$
. For any
![]() $x\in K_{D}$
and
$x\in K_{D}$
and
![]() $i\in \{1,\ldots ,n\}$
, if
$i\in \{1,\ldots ,n\}$
, if
![]() $(w\cdot x)_{i}>0$
then
$(w\cdot x)_{i}>0$
then
![]() $(ws_{\unicode[STIX]{x1D6FC}}\cdot x)_{i}>0$
, where
$(ws_{\unicode[STIX]{x1D6FC}}\cdot x)_{i}>0$
, where
![]() $y_{i}$
denotes the
$y_{i}$
denotes the
![]() $i$
th coordinate of
$i$
th coordinate of
![]() $y$
when we write
$y$
when we write
![]() $y=\sum _{i=1}^{n}y_{i}\widehat{\unicode[STIX]{x1D6FC}_{i}}$
for
$y=\sum _{i=1}^{n}y_{i}\widehat{\unicode[STIX]{x1D6FC}_{i}}$
for
![]() $y\in V_{1}$
.
$y\in V_{1}$
.
Proof. First, we claim that
![]() $|w(x)|_{1}>0$
for any
$|w(x)|_{1}>0$
for any
![]() $w\in W$
by induction on
$w\in W$
by induction on
![]() $\ell (w)$
. Clearly,
$\ell (w)$
. Clearly,
![]() $|x|_{1}=1$
by
$|x|_{1}=1$
by
![]() $x\in V_{1}$
. Now, [Reference Björner and Brenti1, Proposition 4.2.5(i)] says that for all
$x\in V_{1}$
. Now, [Reference Björner and Brenti1, Proposition 4.2.5(i)] says that for all
![]() $w^{\prime }\in W$
and
$w^{\prime }\in W$
and
![]() $s\in S$
, if
$s\in S$
, if
![]() $\ell (w^{\prime }s)>\ell (w^{\prime })$
then
$\ell (w^{\prime }s)>\ell (w^{\prime })$
then
![]() $w^{\prime }(\unicode[STIX]{x1D6FC}_{s})_{i}>0$
for any
$w^{\prime }(\unicode[STIX]{x1D6FC}_{s})_{i}>0$
for any
![]() $i$
. From this fact together with
$i$
. From this fact together with
![]() $B(x,\unicode[STIX]{x1D6FD})<0$
for any
$B(x,\unicode[STIX]{x1D6FD})<0$
for any
![]() $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}$
, we obtain that
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}$
, we obtain that
![]() $|w^{\prime }(s(x))|_{1}=|w^{\prime }(x)|_{1}-2B(x,\unicode[STIX]{x1D6FC}_{s})|w^{\prime }(\unicode[STIX]{x1D6FC}_{s})|_{1}>0$
by the inductive hypothesis.
$|w^{\prime }(s(x))|_{1}=|w^{\prime }(x)|_{1}-2B(x,\unicode[STIX]{x1D6FC}_{s})|w^{\prime }(\unicode[STIX]{x1D6FC}_{s})|_{1}>0$
by the inductive hypothesis.
Thus the sign of
![]() $(w\cdot x)_{i}$
is equal to the sign of
$(w\cdot x)_{i}$
is equal to the sign of
![]() $w(x)_{i}$
. Note that a reflection
$w(x)_{i}$
. Note that a reflection
![]() $s_{\unicode[STIX]{x1D6FC}}\in S$
changes the value of the
$s_{\unicode[STIX]{x1D6FC}}\in S$
changes the value of the
![]() $i$
th coordinate if and only if
$i$
th coordinate if and only if
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}$
. Let
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}$
. Let
![]() $\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FC}_{i}$
. Then the sign of the
$\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FC}_{i}$
. Then the sign of the
![]() $i$
th coordinate is preserved. Let
$i$
th coordinate is preserved. Let
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}$
. Since
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}$
. Since
![]() $-2B(x,\unicode[STIX]{x1D6FC})>0$
, if
$-2B(x,\unicode[STIX]{x1D6FC})>0$
, if
![]() $w(x)_{i}>0$
, then one has
$w(x)_{i}>0$
, then one has
![]() $w(s_{\unicode[STIX]{x1D6FC}}(x))_{i}>0$
by [Reference Björner and Brenti1, Proposition 4.2.5(i)] again.◻
$w(s_{\unicode[STIX]{x1D6FC}}(x))_{i}>0$
by [Reference Björner and Brenti1, Proposition 4.2.5(i)] again.◻
Note that for any
![]() $w\in W$
, there exists a reduced expression
$w\in W$
, there exists a reduced expression
![]() $w=s_{1}s_{2}\cdots s_{q}$
, where
$w=s_{1}s_{2}\cdots s_{q}$
, where
![]() $s_{i}\in S$
, such that
$s_{i}\in S$
, such that
![]() $\ell (s_{1}\cdots s_{i})>\ell (s_{1}\cdots s_{i-1})$
for any
$\ell (s_{1}\cdots s_{i})>\ell (s_{1}\cdots s_{i-1})$
for any
![]() $i=1,\ldots ,q$
. It follows from this fact and Lemma 6.9 that for any
$i=1,\ldots ,q$
. It follows from this fact and Lemma 6.9 that for any
![]() $x\in K_{D}$
, if
$x\in K_{D}$
, if
![]() $x_{j}>0$
, then
$x_{j}>0$
, then
![]() $(w\cdot x)_{j}>0$
.
$(w\cdot x)_{j}>0$
.
Proof of Lemma 6.7.
Suppose that there exists
![]() $w\in W$
such that
$w\in W$
such that
![]() $w\cdot D\cap D^{\prime }\neq 0$
. Let
$w\cdot D\cap D^{\prime }\neq 0$
. Let
![]() $C$
(resp.
$C$
(resp.
![]() $C^{\prime }$
) be the component of
$C^{\prime }$
) be the component of
![]() $W\cdot D$
(resp.
$W\cdot D$
(resp.
![]() $W\cdot D^{\prime }$
) with
$W\cdot D^{\prime }$
) with
![]() $w\cdot D\subset C$
(resp.
$w\cdot D\subset C$
(resp.
![]() $D^{\prime }\subset C^{\prime }$
). Since
$D^{\prime }\subset C^{\prime }$
). Since
![]() $C\cap C^{\prime }\neq \emptyset$
, we see that
$C\cap C^{\prime }\neq \emptyset$
, we see that
![]() $C=C^{\prime }$
. This shows that
$C=C^{\prime }$
. This shows that
![]() $D^{\prime }\subset W\cdot D$
. Thus, for
$D^{\prime }\subset W\cdot D$
. Thus, for
![]() $x^{\prime }\in K_{D^{\prime }}\subset D^{\prime }$
, there exist
$x^{\prime }\in K_{D^{\prime }}\subset D^{\prime }$
, there exist
![]() $x\in D$
and
$x\in D$
and
![]() $w\in W$
so that
$w\in W$
so that
![]() $x^{\prime }=w\cdot x$
, namely,
$x^{\prime }=w\cdot x$
, namely,
![]() $x=w^{-1}\cdot x^{\prime }$
. Let
$x=w^{-1}\cdot x^{\prime }$
. Let
![]() $j\in J_{D}$
. On the one hand, one has
$j\in J_{D}$
. On the one hand, one has
![]() $x_{j}<0$
by definition of
$x_{j}<0$
by definition of
![]() $J_{D}$
. On the other hand, one also has
$J_{D}$
. On the other hand, one also has
![]() $(w^{-1}\cdot x^{\prime })_{j}>0$
by Lemma 6.9 and
$(w^{-1}\cdot x^{\prime })_{j}>0$
by Lemma 6.9 and
![]() $j\not \in J_{D^{\prime }}$
, a contradiction.◻
$j\not \in J_{D^{\prime }}$
, a contradiction.◻
Lemma 6.10. For a
![]() $W$
-invariant set
$W$
-invariant set
![]() $G\subset \widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
with nonempty interior, there exists
$G\subset \widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
with nonempty interior, there exists
![]() $x\in \text{int}(G)$
such that for any
$x\in \text{int}(G)$
such that for any
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
we have the following:
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
we have the following:
where
![]() $x_{\unicode[STIX]{x1D6FC}}$
denotes the
$x_{\unicode[STIX]{x1D6FC}}$
denotes the
![]() $\unicode[STIX]{x1D6FC}$
th coordinate of
$\unicode[STIX]{x1D6FC}$
th coordinate of
![]() $x$
.
$x$
.
Proof. By our assumption, there exist
![]() $x\in \overline{G}$
and
$x\in \overline{G}$
and
![]() $y\in \unicode[STIX]{x2202}G$
such that
$y\in \unicode[STIX]{x2202}G$
such that
![]() $|B(x,y)|=\max _{v\in \overline{G}}\min _{u\in \unicode[STIX]{x2202}G}|B(u,v)|>0$
. Then
$|B(x,y)|=\max _{v\in \overline{G}}\min _{u\in \unicode[STIX]{x2202}G}|B(u,v)|>0$
. Then
![]() $x$
should belong to
$x$
should belong to
![]() $\text{int}(G)$
from Proposition 2.8(a). By Proposition 2.6, there is
$\text{int}(G)$
from Proposition 2.8(a). By Proposition 2.6, there is
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
such that
![]() $x\in V_{\unicode[STIX]{x1D6FC}}$
.
$x\in V_{\unicode[STIX]{x1D6FC}}$
.
Suppose that
![]() $y\notin V_{\unicode[STIX]{x1D6FC}}$
. Then
$y\notin V_{\unicode[STIX]{x1D6FC}}$
. Then
![]() $s_{\unicode[STIX]{x1D6FC}}\cdot y\in \unicode[STIX]{x2202}G\cap \text{int}(V_{\unicode[STIX]{x1D6FC}})$
. Let
$s_{\unicode[STIX]{x1D6FC}}\cdot y\in \unicode[STIX]{x2202}G\cap \text{int}(V_{\unicode[STIX]{x1D6FC}})$
. Let
![]() $z:=s_{\unicode[STIX]{x1D6FC}}\cdot y$
. Then one has
$z:=s_{\unicode[STIX]{x1D6FC}}\cdot y$
. Then one has
![]() $0\leqslant B(x,\unicode[STIX]{x1D6FC})$
,
$0\leqslant B(x,\unicode[STIX]{x1D6FC})$
,
![]() $0<B(z,\unicode[STIX]{x1D6FC})<1/(2|\unicode[STIX]{x1D6FC}|_{1})$
and
$0<B(z,\unicode[STIX]{x1D6FC})<1/(2|\unicode[STIX]{x1D6FC}|_{1})$
and
![]() $B(x,z)<0$
by Lemmas 2.5, 2.7 and Proposition 2.8, respectively. Thus
$B(x,z)<0$
by Lemmas 2.5, 2.7 and Proposition 2.8, respectively. Thus
![]() $0<1-2B(z,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}<1$
. Hence we see that
$0<1-2B(z,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}<1$
. Hence we see that
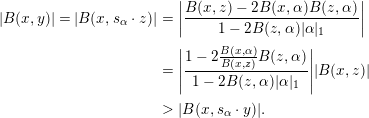 $$\begin{eqnarray}\displaystyle |B(x,y)|=|B(x,s_{\unicode[STIX]{x1D6FC}}\cdot z)| & = & \displaystyle \biggl|\frac{B(x,z)-2B(x,\unicode[STIX]{x1D6FC})B(z,\unicode[STIX]{x1D6FC})}{1-2B(z,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}}\biggr|\nonumber\\ \displaystyle & = & \displaystyle \left|\frac{1-2\frac{B(x,\unicode[STIX]{x1D6FC})}{B(x,z)}B(z,\unicode[STIX]{x1D6FC})}{1-2B(z,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}}\right||B(x,z)|\nonumber\\ \displaystyle & {>} & \displaystyle |B(x,s_{\unicode[STIX]{x1D6FC}}\cdot y)|.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |B(x,y)|=|B(x,s_{\unicode[STIX]{x1D6FC}}\cdot z)| & = & \displaystyle \biggl|\frac{B(x,z)-2B(x,\unicode[STIX]{x1D6FC})B(z,\unicode[STIX]{x1D6FC})}{1-2B(z,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}}\biggr|\nonumber\\ \displaystyle & = & \displaystyle \left|\frac{1-2\frac{B(x,\unicode[STIX]{x1D6FC})}{B(x,z)}B(z,\unicode[STIX]{x1D6FC})}{1-2B(z,\unicode[STIX]{x1D6FC})|\unicode[STIX]{x1D6FC}|_{1}}\right||B(x,z)|\nonumber\\ \displaystyle & {>} & \displaystyle |B(x,s_{\unicode[STIX]{x1D6FC}}\cdot y)|.\end{eqnarray}$$
However, this is a contradiction to
![]() $|B(x,y)|=\min _{u\in \unicode[STIX]{x2202}G}|B(x,u)|$
. Hence,
$|B(x,y)|=\min _{u\in \unicode[STIX]{x2202}G}|B(x,u)|$
. Hence,
![]() $y$
should belong to
$y$
should belong to
![]() $V_{\unicode[STIX]{x1D6FC}}$
.
$V_{\unicode[STIX]{x1D6FC}}$
.
Moreover, suppose that
![]() $x\notin \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
. Since
$x\notin \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
. Since
![]() $G$
and
$G$
and
![]() $\unicode[STIX]{x2202}G$
are
$\unicode[STIX]{x2202}G$
are
![]() $W$
-invariant, one has
$W$
-invariant, one has
![]() $s_{\unicode[STIX]{x1D6FC}}\cdot x\in G$
and
$s_{\unicode[STIX]{x1D6FC}}\cdot x\in G$
and
![]() $s_{\unicode[STIX]{x1D6FC}}\cdot y\in \unicode[STIX]{x2202}G$
. Since
$s_{\unicode[STIX]{x1D6FC}}\cdot y\in \unicode[STIX]{x2202}G$
. Since
![]() $|B(x,y)|<|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,s_{\unicode[STIX]{x1D6FC}}\cdot y)|$
by Proposition 2.8(c), from the maximality of
$|B(x,y)|<|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,s_{\unicode[STIX]{x1D6FC}}\cdot y)|$
by Proposition 2.8(c), from the maximality of
![]() $|B(x,y)|$
, there is
$|B(x,y)|$
, there is
![]() $z^{\prime }\in \unicode[STIX]{x2202}G\setminus \{s_{\unicode[STIX]{x1D6FC}}\cdot y\}$
such that
$z^{\prime }\in \unicode[STIX]{x2202}G\setminus \{s_{\unicode[STIX]{x1D6FC}}\cdot y\}$
such that
![]() $|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,z^{\prime })|=\min _{u\in \unicode[STIX]{x2202}G}|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,u)|\leqslant |B(x,y)|$
. If
$|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,z^{\prime })|=\min _{u\in \unicode[STIX]{x2202}G}|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,u)|\leqslant |B(x,y)|$
. If
![]() $z^{\prime }\in V_{\unicode[STIX]{x1D6FC}}$
, then we obtain that
$z^{\prime }\in V_{\unicode[STIX]{x1D6FC}}$
, then we obtain that
![]() $|B(x,z^{\prime })|<|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,z^{\prime })|$
by the similar calculation to (6). If
$|B(x,z^{\prime })|<|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,z^{\prime })|$
by the similar calculation to (6). If
![]() $z^{\prime }\not \in V_{\unicode[STIX]{x1D6FC}}$
, then we have
$z^{\prime }\not \in V_{\unicode[STIX]{x1D6FC}}$
, then we have
![]() $|B(x,s_{\unicode[STIX]{x1D6FC}}\cdot z^{\prime })|<|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,z^{\prime })|$
by Proposition 2.8(c). In both cases, we have a contradiction to the choice of
$|B(x,s_{\unicode[STIX]{x1D6FC}}\cdot z^{\prime })|<|B(s_{\unicode[STIX]{x1D6FC}}\cdot x,z^{\prime })|$
by Proposition 2.8(c). In both cases, we have a contradiction to the choice of
![]() $y$
, i.e.,
$y$
, i.e.,
![]() $|B(x,y)|=\min _{u\in \unicode[STIX]{x2202}G}|B(x,u)|$
. Hence,
$|B(x,y)|=\min _{u\in \unicode[STIX]{x2202}G}|B(x,u)|$
. Hence,
![]() $x$
should belong to
$x$
should belong to
![]() $\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
.
$\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
.
Therefore, for each
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, if
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, if
![]() $x\in V_{\unicode[STIX]{x1D6FC}}$
, then
$x\in V_{\unicode[STIX]{x1D6FC}}$
, then
![]() $x\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
. This implies that
$x\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
. This implies that
![]() $B(x,\widehat{\unicode[STIX]{x1D6FC}})=0$
if
$B(x,\widehat{\unicode[STIX]{x1D6FC}})=0$
if
![]() $x\in V_{\unicode[STIX]{x1D6FC}}$
. Moreover, since
$x\in V_{\unicode[STIX]{x1D6FC}}$
. Moreover, since
![]() $x\in \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
,
$x\in \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
,
![]() $x$
can be written like
$x$
can be written like
![]() $x=\sum _{\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}}x_{\unicode[STIX]{x1D6FF}}\widehat{\unicode[STIX]{x1D6FF}}$
, with
$x=\sum _{\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}}x_{\unicode[STIX]{x1D6FF}}\widehat{\unicode[STIX]{x1D6FF}}$
, with
![]() $x_{\unicode[STIX]{x1D6FF}}\geqslant 0$
for each
$x_{\unicode[STIX]{x1D6FF}}\geqslant 0$
for each
![]() $\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
. On the other hand, we have
$\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
. On the other hand, we have
 $$\begin{eqnarray}0=B(x,x)=B\left(x,\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}}x_{\unicode[STIX]{x1D6FF}}\widehat{\unicode[STIX]{x1D6FF}}\right)=\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}:x\notin V_{\unicode[STIX]{x1D6FD}}\}}x_{\unicode[STIX]{x1D6FF}}B(x,\widehat{\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$
$$\begin{eqnarray}0=B(x,x)=B\left(x,\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}}x_{\unicode[STIX]{x1D6FF}}\widehat{\unicode[STIX]{x1D6FF}}\right)=\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E5}:x\notin V_{\unicode[STIX]{x1D6FD}}\}}x_{\unicode[STIX]{x1D6FF}}B(x,\widehat{\unicode[STIX]{x1D6FF}}).\end{eqnarray}$$
Since
![]() $B(x,\widehat{\unicode[STIX]{x1D6FF}})<0$
for each
$B(x,\widehat{\unicode[STIX]{x1D6FF}})<0$
for each
![]() $\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
such that
![]() $x\notin V_{\unicode[STIX]{x1D6FF}}$
by Lemma 2.5, we have
$x\notin V_{\unicode[STIX]{x1D6FF}}$
by Lemma 2.5, we have
![]() $x_{\unicode[STIX]{x1D6FF}}=0$
for such
$x_{\unicode[STIX]{x1D6FF}}=0$
for such
![]() $\unicode[STIX]{x1D6FF}$
.◻
$\unicode[STIX]{x1D6FF}$
.◻
Proposition 6.11. For a
![]() $W$
-invariant subset
$W$
-invariant subset
![]() $K\subset \widehat{Q}$
, if
$K\subset \widehat{Q}$
, if
![]() $\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))\neq \emptyset$
and
$\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))\neq \emptyset$
and
![]() $\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))\subset K$
, then
$\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))\subset K$
, then
![]() $\overline{K}=\widehat{Q}$
.
$\overline{K}=\widehat{Q}$
.
Proof. Let
![]() $G=\widehat{Q}\setminus K$
. If
$G=\widehat{Q}\setminus K$
. If
![]() $G$
has no interior then we have the conclusion. Thus it suffices to consider the case where
$G$
has no interior then we have the conclusion. Thus it suffices to consider the case where
![]() $G$
has interior points. Note that
$G$
has interior points. Note that
![]() $G$
is
$G$
is
![]() $W$
-invariant.
$W$
-invariant.
Since
![]() $G\subset \widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, by Lemma 6.10, there exists
$G\subset \widehat{Q}\cap \text{conv}(\widehat{\unicode[STIX]{x1D6E5}})$
, by Lemma 6.10, there exists
![]() $x\in \text{int}(G)$
which satisfies that if
$x\in \text{int}(G)$
which satisfies that if
![]() $x\not \in V_{\unicode[STIX]{x1D6FC}}$
the
$x\not \in V_{\unicode[STIX]{x1D6FC}}$
the
![]() $\unicode[STIX]{x1D6FC}$
th coordinate of
$\unicode[STIX]{x1D6FC}$
th coordinate of
![]() $x$
equals
$x$
equals
![]() $0$
, otherwise,
$0$
, otherwise,
![]() $x\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
. However, the assumption
$x\in \unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
. However, the assumption
![]() $\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))\subset K$
actually implies that
$\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))\subset K$
actually implies that
![]() $G\subset \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
. Hence
$G\subset \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
. Hence
![]() $x_{\unicode[STIX]{x1D6FC}}\neq 0$
for all
$x_{\unicode[STIX]{x1D6FC}}\neq 0$
for all
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Thus
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Thus
![]() $x$
should belong to
$x$
should belong to
![]() $\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
for all
$\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D6FC}}$
for all
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. This contradicts to Remark 3.1.◻
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. This contradicts to Remark 3.1.◻
Proof of Theorem 1.2 in the case (b).
Recall that
![]() $\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))\neq \emptyset$
in this case.
$\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))\neq \emptyset$
in this case.
(b-1) We set
 $K=\bigcup _{i=1}^{m}\overline{W\cdot D_{i}}$
. Then
$K=\bigcup _{i=1}^{m}\overline{W\cdot D_{i}}$
. Then
 $K$
obviously contains
$K$
obviously contains
 $\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
and is
$\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
and is
 $W$
-invariant. Therefore we have
$W$
-invariant. Therefore we have
 $\overline{K}=K=\widehat{Q}$
by applying Proposition 6.11 to
$\overline{K}=K=\widehat{Q}$
by applying Proposition 6.11 to
 $K$
. In addition, Proposition 6.6 says that
$K$
. In addition, Proposition 6.6 says that
 $E=\unicode[STIX]{x2202}K$
. Thus the conclusion follows.
$E=\unicode[STIX]{x2202}K$
. Thus the conclusion follows.(b-2) Let
 $K^{\prime }=\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
and consider
$K^{\prime }=\widehat{Q}\setminus \text{int}(\text{conv}(\widehat{\unicode[STIX]{x1D6E5}}))$
and consider
 $K=W\cdot K^{\prime }$
. Then we can also apply Proposition 6.11 to this
$K=W\cdot K^{\prime }$
. Then we can also apply Proposition 6.11 to this
 $K$
and we get
$K$
and we get
 $\overline{K}=\widehat{Q}$
.
$\overline{K}=\widehat{Q}$
.In this case, for each
 $x\in K^{\prime }$
, there is
$x\in K^{\prime }$
, there is
 $j\in \{1,\ldots ,n\}$
such that
$j\in \{1,\ldots ,n\}$
such that
 $x\in \widehat{Q}\cap A_{j}$
. By the inductive hypothesis,
$x\in \widehat{Q}\cap A_{j}$
. By the inductive hypothesis,
 $x$
is the accumulation point of normalized roots of
$x$
is the accumulation point of normalized roots of
 $W_{j}$
. Thus
$W_{j}$
. Thus
 $K^{\prime }\subset E$
. Since
$K^{\prime }\subset E$
. Since
 $E$
is a minimal
$E$
is a minimal
 $W$
-invariant subset of
$W$
-invariant subset of
 $\widehat{Q}$
by Proposition 3.3, we have
$\widehat{Q}$
by Proposition 3.3, we have
 $\overline{K}=E$
. Hence we are done. ◻
$\overline{K}=E$
. Hence we are done. ◻
Finally, we conclude this paper with the following remark.
Remark 6.12. We see that Theorems 1.2(a) and 1.3 imply Conjecture 1.1.
∙ We first discuss Conjecture 1.1(i). For a Coxeter group
 $W$
of rank
$W$
of rank
 $n$
whose Coxeter matrix is of type
$n$
whose Coxeter matrix is of type
 $(n-1,1)$
, as mentioned in Remark 6.4, every bilinear form associated with a parabolic subgroup of rank
$(n-1,1)$
, as mentioned in Remark 6.4, every bilinear form associated with a parabolic subgroup of rank
 $m$
is of positive type or has the signature
$m$
is of positive type or has the signature
 $(m-1,1)$
.
$(m-1,1)$
.If
 $\unicode[STIX]{x1D6E5}_{I}$
is generating, then we can apply Theorem 1.2(a) to
$\unicode[STIX]{x1D6E5}_{I}$
is generating, then we can apply Theorem 1.2(a) to
 $W_{I}$
. By using the correspondence induced from
$W_{I}$
. By using the correspondence induced from
 $\unicode[STIX]{x1D719}_{I}$
, which is defined in Remark 6.4, we obtain the conclusion.
$\unicode[STIX]{x1D719}_{I}$
, which is defined in Remark 6.4, we obtain the conclusion.∙ For Conjecture 1.1(ii), from the definition of “generating” and Theorem 1.2(a), it follows that
 $\overline{F_{0}}$
is contained in
$\overline{F_{0}}$
is contained in
 $E$
. Moreover, when we take
$E$
. Moreover, when we take
 $x\in \widehat{Q}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})=E_{I}\subset E$
, where
$x\in \widehat{Q}\cap \text{span}(\unicode[STIX]{x1D6E5}_{I})=E_{I}\subset E$
, where
 $\unicode[STIX]{x1D6E5}_{I}$
is generating, it is obvious that
$\unicode[STIX]{x1D6E5}_{I}$
is generating, it is obvious that
 $\overline{W\cdot x}\subset \overline{F_{0}}$
. Furthermore, by Theorem 1.3, we know that
$\overline{W\cdot x}\subset \overline{F_{0}}$
. Furthermore, by Theorem 1.3, we know that
 $E=\overline{W\cdot x}$
. Hence, Therefore, we conclude that
$E=\overline{W\cdot x}$
. Hence, Therefore, we conclude that $$\begin{eqnarray}E=\overline{W\cdot x}\subset \overline{F_{0}}\subset E.\end{eqnarray}$$
$$\begin{eqnarray}E=\overline{W\cdot x}\subset \overline{F_{0}}\subset E.\end{eqnarray}$$
 $E=\overline{F_{0}}$
.
$E=\overline{F_{0}}$
.
Acknowledgments
The authors would like to be grateful to Yohei Komori and Hideki Miyachi for their helpful advices and instructive discussions on Theorem 1.2 and also thank Yuriko Umemoto for having useful seminars on Coxeter groups together, which are the origin of this work. The authors also would like to express a lot of thanks to Matthew Dyer, Christophe Hohlweg and Vivien Ripoll for giving several helpful comments and fruitful suggestions on this paper. The authors also would like to thank to the anonymous referee for a lot of helpful comments.