1. INTRODUCTION
A primary factor influencing geolocation resolution is the particular topology of the network of points available for triangulation. The celestial navigator keeps a wary eye on the advancing cloud bank for this reason, while the designer of surveillance aircraft maximises the field of view by placing sensors along the full length of the aircraft (Grabbe and Hamschin, Reference Grabbe and Hamschin2013).
Fix algorithms work with the translational/orientational distribution of Lines Of Position (LOPs) derived from the triangulation network (Wax, Reference Wax1983). Hence in looking to quantitatively establish connections between topology and algorithm accuracy, it is the LOP distribution which provides the natural focus for investigation. An example of such a connection is the derivation from the LOP distribution of an elliptical form for the equal probability contours in the region of a fix (Daniels, Reference Daniels1951; Holland, Reference Holland1981), the contrasting axes of this “error ellipse” in effect reflecting the degree of azimuthal anisotropy inherent to the triangulation network. From the perspective of algorithm development, the availability in this sense of a parametric characterisation of azimuthal coverage clearly presents useful scope for optimisation tuning.
Here we point out an alternative scalar characterisation of azimuthal anisotropy which is more low-level than the error ellipse, in the sense that it is a property of the LOP distribution alone. In contrast to the error ellipse, it does not depend on the particular choice of fix algorithm. While to our knowledge this scalar, which we denote Q, has not previously been introduced in geolocation literature, it has a well-established counterpart in the nematic order parameter which features in the statistical physics literature on orientational order, particularly as applied to rod-like molecules (de Gennes and Prost, Reference de Gennes and Prost1995). The term “nematic” comes from the Greek for “thread”, and refers to ordering about a preferential alignment axis known as the director. As we substantiate the analogy between lines of position and rods, it is appropriate for us to retain this existing nematic/director nomenclature.
In the following we first revisit the basic least-squares method of geolocation in order to incorporate Q and express its relation to fix error. We then present a small simulation study demonstrating its practical deployment. Terminology and the simulation are drawn from the specific context of celestial navigation, but the discussion applies generally to other types of LOP.
2. LEAST SQUARES METHOD OF GEOLOCATION
Consider n lines of position in the (x, y) plane, each described by the form
where a is the altitude intercept and Z is the azimuth of the observed celestial body. The least-squares result for the fix (DeWit, Reference DeWit1974), in the form in which it appears in recent editions of the Nautical Almanac, is
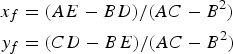 $$\eqalign{ x_{f} &= (AE - BD)/(AC - B^{2}) \cr y_{f} &=(CD - BE)/(AC - B^{2})}$$
$$\eqalign{ x_{f} &= (AE - BD)/(AC - B^{2}) \cr y_{f} &=(CD - BE)/(AC - B^{2})}$$
where
![]() $A = \langle \cos^{2} Z \rangle$
,
$A = \langle \cos^{2} Z \rangle$
,
![]() $B = \langle \sin Z \cos Z \rangle$
,
$B = \langle \sin Z \cos Z \rangle$
,
![]() $C = \langle \sin^{2} Z \rangle$
,
$C = \langle \sin^{2} Z \rangle$
,
![]() $D = \langle a \cos^{2} Z \rangle$
,
$D = \langle a \cos^{2} Z \rangle$
,
![]() $E = \langle a \sin Z \rangle$
; the angled brackets denoting distribution moments
$E = \langle a \sin Z \rangle$
; the angled brackets denoting distribution moments
![]() $n^{-1} \sum\limits_{n} [\ldots]$
.
$n^{-1} \sum\limits_{n} [\ldots]$
.
In order to introduce the new parameter Q we recast Equations (2) firstly by eliminating the moment B, which we can achieve by rotating the coordinate system appropriately about the origin. Let Z
0 be the requisite rotation defined in the clockwise direction. In the rotated (primed) frame of reference we have then
![]() $B^{\prime} = \langle \sin (Z - Z_{0}) \cos (Z - Z_{0}) \rangle = 0$
, which with the help of standard trigonometrical identities is solved to yield
$B^{\prime} = \langle \sin (Z - Z_{0}) \cos (Z - Z_{0}) \rangle = 0$
, which with the help of standard trigonometrical identities is solved to yield
In the nomenclature of orientational statistical mechanics, Z 0 is the nematic director; that is, the alignment axis which exists whenever the azimuthal distribution of intercepts is not perfectly isotropic. The degree of alignment along this axis is expressed by the nematic moment
The arctan degeneracy of Equation (3) is removed by requiring that Q be positive, ranging from 0 (isotropic) to 1 (maximally anisotropic, i.e., all intercepts aligned parallel to the director).
Noting
![]() $A^{\prime} = (1 + Q)/2$
and
$A^{\prime} = (1 + Q)/2$
and
![]() $C^{\prime} = (1 - Q)/2$
, we have now for the fix coordinates in the director frame of reference
$C^{\prime} = (1 - Q)/2$
, we have now for the fix coordinates in the director frame of reference
 $$\eqalign{ {x}_{f}^{\prime} &= 2E^{\prime} /(1 - Q) \cr {y}_{f}^{\prime} &= 2D^{\prime} /(1 + Q). }$$
$$\eqalign{ {x}_{f}^{\prime} &= 2E^{\prime} /(1 - Q) \cr {y}_{f}^{\prime} &= 2D^{\prime} /(1 + Q). }$$
The choice of (x, y) origin is arbitrary thus far; it may for example be an initial guess at the true position. However, consider the figurative case where the origin corresponds exactly to the true position. This is instructive because Equations (5) are then equivalently the fix error for a sample drawn from the distribution of intercepts f(a) about the true position. With the assumption that this distribution is normal,
![]() $f(a) = {\cal N} (0, \sigma_{a}^{2})$
, the root mean square integration of Equations (5) determines effective resolution length scales for the fix, i.e., the axes of the error ellipse, respectively perpendicular (⊥) and parallel (∥) to the director
$f(a) = {\cal N} (0, \sigma_{a}^{2})$
, the root mean square integration of Equations (5) determines effective resolution length scales for the fix, i.e., the axes of the error ellipse, respectively perpendicular (⊥) and parallel (∥) to the director
 $$\eqalign{ \Delta_{\bot} &= \sigma_{a} \sqrt{{2/n \over 1-Q}} \cr \Delta_{\parallel} &= \sigma_{a} \sqrt{{2/n \over 1+Q}}, }$$
$$\eqalign{ \Delta_{\bot} &= \sigma_{a} \sqrt{{2/n \over 1-Q}} \cr \Delta_{\parallel} &= \sigma_{a} \sqrt{{2/n \over 1+Q}}, }$$
subject to the usual large-n proviso of the central limit theorem.
With increasing anisotropy Q, the fix evidently tends to improve along the director, while deteriorating along the perpendicular. Overall, the fix resolution deteriorates as
 $$\Delta = \sqrt{\Delta_{\bot}^{2} + \Delta_{\parallel}^{2}} =\sigma_{a} \sqrt{{4/n \over 1-Q^{2}}}.$$
$$\Delta = \sqrt{\Delta_{\bot}^{2} + \Delta_{\parallel}^{2}} =\sigma_{a} \sqrt{{4/n \over 1-Q^{2}}}.$$
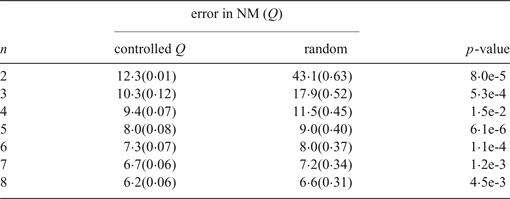
3. SIMULATION
Table 1 presents celestial navigational simulation results illustrating how this formulation can be usefully put to work. The general trend is of course that the error decreases with the number of celestial bodies contributing to the fix. This applies if the n are chosen at random. However, a statistically significant improvement is achieved if some method of Q-control is introduced. In our simulation, the method is to randomly generate 30 sets of n, selecting that set for which n is lowest.
Table 1. Simulated dependence of celestial fix error on number of sights, for a sextant accuracy of 10 arc minutes (i.e. standard deviation of the stochastically generated altitude measurement error). Consistently with Equation (7) the fix improves if the sighted bodies are collectively subject to selection for isotropic azimuthal coverage (low Q). Each entry is averaged over 1,000 runs to ensure the improvement is statistically significant (p-values calculated from Student's t-distribution with unequal variances).
It is worthwhile noting that we might follow much the same strategy using the error ellipse eccentricity ϵ in place of Q, by virtue of the mapping
It must be stressed however that this correspondence is specific to the present choice of fix algorithm. For other choices (see e.g. Gustafsson and Gunnarsson (Reference Gustafsson and Gunnarsson2005) for a review) it is often the case that the error ellipse requires a numerical solution, obscuring analytical insight into its relation to the LOP distribution. As a general measure of azimuthal coverage, Q holds the upper hand in that it is always the same function of the LOP azimuth distribution defined by Equation (4).
4. SUMMARY
We have shown how the nematic order parameter Q of statistical physics emerges as an ancillary statistic for geolocation fix determination. While our presentation focus here has been on the simplest two-dimensional least-squares algorithm, and by way of practical example, on celestial sight reduction, we anticipate that since Q is not tied to the choice of algorithm per se, the general idea might usefully be extended to the wider ecosystem of sensor/emitter technologies and their associated algorithms.



