No CrossRef data available.
Article contents
ON 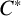 $\mathbf{\mathit{C}}^{*}$-ALGEBRAS WHICH DETECT NUCLEARITY
$\mathbf{\mathit{C}}^{*}$-ALGEBRAS WHICH DETECT NUCLEARITY
Published online by Cambridge University Press: 05 May 2022
Abstract
A
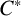 $C^{*}$
-algebra A is said to detect nuclearity if, whenever a
$C^{*}$
-algebra A is said to detect nuclearity if, whenever a
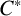 $C^{*}$
-algebra B satisfies
$C^{*}$
-algebra B satisfies
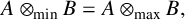 $A\otimes _{\mathrm{min}} B = A\otimes _{\mathrm{max}} B,$
it follows that B is nuclear. In this note, we survey the main results associated with this topic and present the background and tools necessary for proving the main results. In particular, we show that the
$A\otimes _{\mathrm{min}} B = A\otimes _{\mathrm{max}} B,$
it follows that B is nuclear. In this note, we survey the main results associated with this topic and present the background and tools necessary for proving the main results. In particular, we show that the
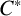 $C^{*}$
-algebra
$C^{*}$
-algebra
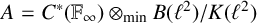 $A = C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2})$
detects nuclearity. This result is known to experts, but has never appeared in the literature.
$A = C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2})$
detects nuclearity. This result is known to experts, but has never appeared in the literature.
Keywords
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 125 - 133
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.



