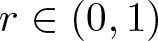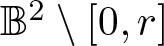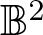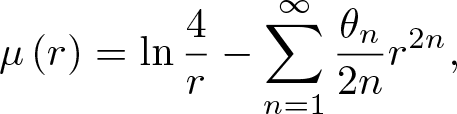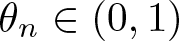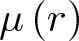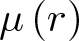1. Introduction
For 
$r\in(0,1)$, the complete elliptic integral of the first and second kinds are defined by
\begin{equation*}
\mathcal{K}\equiv \mathcal{K}\left( r\right) =\int_{0}^{\pi /2}\frac{1}{
\sqrt{1-r^{2}\sin ^{2}t}}\text{d}t, \\
\end{equation*}
\begin{equation*}
\mathcal{E}\equiv \mathcal{E}\left( r\right) =\int_{0}^{\pi /2}\sqrt{
1-r^{2}\sin ^{2}t}\text{d}t.
\end{equation*}They have the Gaussian hypergeometric series representations:
\begin{align*}
\mathcal{K}\left( r\right)=\frac{\pi }{2}F\left( \frac{1}{2},\frac{1}{2}
;1;r^{2}\right) =\frac{\pi }{2}\sum_{n=0}^{\infty }W_{n}^{2}r^{2n},
\end{align*}
\begin{align*}
\mathcal{E}\left( r\right)=\frac{\pi }{2}F\left( -\frac{1}{2},\frac{1}{2}
;1;r^{2}\right) =\frac{\pi }{2}\sum_{n=0}^{\infty }\frac{W_{n}^{2}}{1-2n}
r^{2n},
\end{align*}where
\begin{equation}
W_{n}=\frac{\left( 1/2\right) _{n}}{n!}=\frac{\Gamma \left( n+1/2\right) }{
\Gamma \left( 1/2\right) \Gamma \left( n+1\right) }
\end{equation} is the Wallis ratio. The complete elliptic integral of the first kind 
$
\mathcal{K}\left( r\right) $ satisfies Landen identities
\begin{equation}
\mathcal{K}\left( \frac{2\sqrt{r}}{1+r}\right) =\left( 1+r\right) \mathcal{K}
\left( r\right) \text{\ and \ }\mathcal{K}\left( \frac{1-r}{1+r}\right) =
\frac{1+r}{2}\mathcal{K}\left( r^{\prime}\right) ,
\end{equation}and the asymptotic formula
\begin{equation}
\mathcal{K}\left( r\right) \sim \ln \frac{4}{r^{\prime}}\text{\ as }
r\rightarrow 1^{-},
\end{equation} where and in what follows 
$r^{\prime}=\sqrt{1-r^{2}}$ (see [Reference Byrd and Friedman14]).
As usual, let 
$\mathbb{C}$ be the complex plane and 
$\mathbb{B}^2$ (
$
\overline{\mathbb{B}^2}$) be open (closed) the unit disk in 
$\mathbb{C}$, and let 
$\mu(r)$ be the modulus of the Grötzsch (extremely) ring 
$
\mathbb{B}^2\setminus[0,r]$ for 
$r\in(0,1)$. Then,
\begin{equation}
\mu \left( r\right) =\frac{\pi }{2}\frac{\mathcal{K}\left( r^{\prime
}\right) }{\mathcal{K}\left( r\right) }
\end{equation} (see [Reference Anderson, Vamanamurthy and Vuorinen6, Reference Lehto and Virtanen16]). Using the Möbius transformation, the Grötzsch ring can be mapped onto 
${{\mathbb{C}}}
\setminus \left(\overline{\mathbb{B}^2}\cup [s,+\infty)\right)$, with 
$
s=1/r\in(1,+\infty)$, which has the conformal capacity
\begin{equation}
\gamma \left( s\right) =\frac{2\pi }{\mu \left( 1/s\right) } .
\end{equation} As is well known, the special function 
$\mu(r)$ plays an important role in conformal and quasiconformal mappings, and many conformal invariants and quasiconformal distortion functions can be expressed by it (see [Reference Anderson, Qiu and Vuorinen3, Reference Anderson, Vamanamurthy and Vuorinen5, Reference Anderson, Vamanamurthy and Vuorinen6, Reference Lehto and Virtanen16]). For example, for 
$K\geq1$, the Hersch–Pfluger distortion function 
$\varphi_{K}(r)$, which occurs in the Schwarz Lemma for K-quasiconformal mappings, is defined by
\begin{equation*}
\varphi_{K}(r)=\mu^{-1}\left(\displaystyle\frac{\mu(r)}{K}\right).
\end{equation*}The function
\begin{equation*}
\lambda(K)=\left(\frac{\varphi_{K}(1/\sqrt{2})}{\varphi_{1/K}(1/\sqrt{2})}
\right)^2
\end{equation*} gives the maximal value of boundary linear distortion for a K-quasiconformal automorphism of the upper half plane with fixed 
$\infty$.
Now, let us return to equation (1.4). By equations (1.2) and (1.3), it is easy to check that 
$\mu \left( r\right) $ satisfies
\begin{equation*}
\mu \left( r\right) \mu \left( r^{\prime}\right) =\frac{\pi ^{2}}{4}\text{,
\ }\mu \left( r\right) \mu \left( \frac{1-r}{1+r}\right) =\frac{\pi ^{2}}{2}
\text{, \ }\mu \left( r\right) =2\mu \left( \frac{2\sqrt{r}}{1+r}\right) ,
\end{equation*}and the asymptotic formula
\begin{equation}
\mu \left( r\right) \sim \ln \frac{4}{r}\text{\ as }r\rightarrow 0^{+}\text{
\ and \ }\mu \left( 1^{-}\right) =0\text{.}
\end{equation} Moreover, 
$\mu \left( r\right) $ has the derivative formula
\begin{equation}
\mu ^{\prime}\left( r\right) =-\frac{\pi ^{2}}{4}\frac{1}{rr^{\prime 2}
\mathcal{K}^{2}\left( r\right) }
\end{equation} (see [Reference Anderson, Vamanamurthy and Vuorinen4]). It was proved in [Reference Anderson, Vamanamurthy and Vuorinen4, Theorem 4.3] that 
$\mu \left( r\right) $ has the following properties:
P1 The function
$\mu \left( r\right) $ is strictly decreasing, has exactly one inflection point on $\left( 0,1\right) $ and satisfies $\mu ^{\prime}\left( 0^{+}\right) =-\infty =\mu ^{\prime}\left(
1^{-}\right) $.P2 The function
$1/\mu \left( r\right) $ is strictly increasing and has exactly one inflection point on $\left( 0,1\right) $.P3 The function
$g_{1}(r)=\mu \left( r\right) +\ln r$ is strictly decreasing and concave on $\left( 0,1\right)$ and satisfies $g_{1}^{\prime}(0^{+})=0$, $g_{1}^{\prime}\left( 1^{-}\right) =-\infty $.P4 The function
$g_{2}(r)=\mu \left( r\right) +\ln \left(
r/r^{\prime}\right) $ is strictly increasing and convex on $\left(
0,1\right)$ and satisfies $g_{2}^{\prime}(0^{+})=0$, $g_{2}^{\prime
}\left( 1^{-}\right) =\infty $.P5 The function
$\mu \left( r\right) /\ln \left( 1/r\right) $ is strictly increasing but is neither convex nor concave on $\left(
0,1\right) $.P6 The function
$\mu \left( r\right) /\ln \left( 4/r\right) $ is strictly decreasing and concave on $\left( 0,1\right) $.
It was shown in [Reference Anderson, Vamanamurthy and Vuorinen6, Theorem 5.13(4) and Theorem 5.17] that 
$
\mu \left( r\right) $ also satisfies the following monotonicity and convexity/concavity properties:
P7 The function
$\mu \left( 1/s\right) /\ln s$ is decreasing and convex on $\left( 1,\infty \right) $.P8 The function
$\mu \left( 1/s\right) /\ln \left( 4s\right)
$ is increasing and concave on $\left( 1,\infty \right) $.P9 The function
$g_{3}(r)=\mu \left( r\right) +\ln \left(
r/\left( 1+r^{\prime}\right) \right) $ is strictly decreasing and concave from $\left( 0,1\right) $ onto $\left( 0,\ln 2\right) $.
Alzer and Richards [Reference Alzer and Richards1] proved that
P10 The function
$\alpha \mapsto \mu \left( r^{\alpha
}\right) /\alpha $ is decreasing and log-convex on $\left( 0,\infty \right) $.
They further made the following
Conjecture 1.1.
The function 
$\alpha \mapsto \mu \left( r^{\alpha }\right) /\alpha $ is completely monotonic on 
$\left( 0,\infty \right) $.
It is worth mentioning that there are two famous infinite-product formulas
\begin{align*}
\exp(\mu(r)+\ln{r})=&4\sqrt{r^{\prime}}\prod_{n=1}^{\infty}\left(\frac{a_{n}
}{b_{n}}\right)^{3/2^{n+1}},\\
\exp(\mu(r)+\ln{r})=&\prod_{n=1}^{\infty}\left(1+\frac{b_{n}}{a_{n}}\right)^{2^{-n}}
\end{align*} for 
$r\in(0,1)$, where
\begin{equation*}
a_{0}=1,\quad b_{0}=r^{\prime},\quad a_{n}=\frac{a_{n-1}+b_{n-1}}{2},\quad
b_{n}=\sqrt{a_{n-1}b_{n-1}}.
\end{equation*} The first identity was due to Jacobi (see [Reference Borwein and Borwein13, Formula (2.5.15), p. 52]), and the second one was given by Qiu and Vuorinen in [Reference Qiu and Vuorinen20]. For more other properties of 
$\mu \left( r\right)$ and its generalization, the readers can refer to the literature [Reference Anderson, Qiu, Vamanamurthy and Vuorinen2, Reference Balasubramaniana, Ponnusamy and Vuorinen8, Reference Qiu and Vuorinen19, Reference Wang, Qiu, Zhang and Chu26–Reference Wang, Chu and Chu28, Reference Wang, Li and Chu30, Reference Zhang, Wang and Chu37, Reference Zhang38].
The first aim of this paper is to present the power series representation of 
$\ln \left( 4/r\right) -\mu \left( r\right) $ and then show that the coefficients of the power series are all positive. More precisely, we shall prove the following theorem.
Theorem 1.1. Let 
$r\in \left( 0,1\right) $. Then,
\begin{equation}
\mu \left( r\right) =\ln \frac{4}{r}-\sum_{n=1}^{\infty }\frac{\theta _{n}}{
2n}r^{2n},
\end{equation} with 
$\theta _{0}=1$, and for 
$n\geq 1$,
\begin{equation*}
\theta _{n}=\sum_{k=1}^{n}\left( a_{k-1}-a_{k}\right) \theta _{n-k},
\end{equation*} where 
$a_{n}=\sum_{k=0}^{n}\left( W_{k}^{2}W_{n-k}^{2}\right) $ and Wn is defined by equation (1.1). Moreover, 
$\theta _{n}\in \left( 0,1\right)$ for every 
$n\in \mathbb{N}$.
Remark 1.1. Since 
$\mu \left( 1^{-}\right) =0$, it follows from equation (1.8) that
\begin{equation*}
\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}=\ln 4.
\end{equation*}Then, equation (1.8) can be written as
\begin{equation}
\mu \left( r\right) =-\ln r+\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}\left(
1-r^{2n}\right) .
\end{equation} Taking 
$r=1/\sqrt{2}$ in equation (1.8), we have
\begin{equation*}
\sum_{n=1}^{\infty }\frac{\theta _{n}}{n\times 2^{n}}=5\ln 2-\pi .
\end{equation*}A function f is called absolutely monotonic on an interval I if it has non-negative derivatives of all orders on I, that is,
\begin{equation*}
f^{\left( n\right) }\left( x\right) \geq 0
\end{equation*} for 
$x\in I$ and every 
$n\geq 0$ (see [Reference Widder31]). Clearly, if f(x) is a power series converging on 
$(0,r)$ 
$(r \gt 0)$, then f(x) is absolutely monotonic on 
$(0,r)$ if and only if all coefficients of f(x) are non-negative.
A function f is said to be completely monotonic on an interval I if f has the derivative of any order on I and satisfies
\begin{equation*}
\left( -1\right) ^{n}f^{\left( n\right) }\left( x\right) \geq 0
\end{equation*} for 
$x\in I$ and every 
$n\geq 0$ (see [Reference Bernstein11, Reference Widder31]). A positive function f is called logarithmically completely monotonic on an interval I, if 
$-\left( \ln f\right) ^{\prime}$ is completely monotonic on I, see [Reference Atanassov and Tsoukrovski7, Reference Berg10, Reference Qi and Chen18].
Recently, some monotonicity and convexity or concavity involving the complete elliptic integrals have been extended to the high-order monotonicity, including absolute monotonicity and completely monotonicity, see, for example, [Reference Barnard, Pearce and Richards9, Reference Richards21, Reference Tian and Yang24, Reference Tian and Yang25, Reference Wang, Chu, Li and Chu29, Reference Yang and Tian33, Reference Yang and Tian34, Reference Yang36]. These remind us to consider the higher-order monotonicity of the special combinations of 
$\mu \left(
r\right)$ (or 
$\gamma \left( s\right)$) and the elementary functions.
The second aim of this paper is to establish absolutely monotonicity and completely monotonicity results involving 
$\mu \left( r\right) $ and 
$\gamma
\left( s\right) $ using Theorem 1.1, which extend those properties listed above and give an answer to Conjecture 1.1. To be more special, Theorem 1.2 extends Properties P1–P4, Theorems 1.3 and 1.5 are the extensions of Properties P7–P9 and Theorem 1.6 solves Conjecture 1.1.
Theorem 1.2. The function 
$\mu \left( r\right) $ satisfies
(i) for every
$m\in \mathbb{N}_{0}$, $\mu ^{\left( 2m+1\right)}\left(
r\right) \lt 0$ for $r\in \left( 0,1\right) $;(ii) the function
$-\left[ \mu \left( r\right) +\ln r\right]^{\prime}$ is absolutely monotonic on $\left( 0,1\right) $;(iii) the function
$\left[\ln \left( 4/r\right)-\mu \left( r\right)\right]/r^{2}$ is absolutely monotonic on $\left(0,1\right)$;(iv) the function
$\mu\left(r\right)+\ln\left( r/r^{\prime}\right)$ is absolutely monotonic on $\left(0,1\right) $.
Theorem 1.3. The function 
$-{\left[ \mu \left( r\right) +\ln \left( r/\left(
1+r^{\prime}\right) \right) \right]}^{\prime}$ is absolutely monotonic on 
$\left(0,1\right) $.
Theorem 1.4. Let 
$r\in(0,1)$ and θn be defined in Theorem 1.1. Then,
\begin{equation}
\exp \left( -2\mu \left( r\right) \right) =\frac{1}{16}\sum_{n=1}^{\infty
}\nu _{n}r^{2n},
\end{equation} where 
$\nu _{1}=1$, 
$\nu _{2}=1/2$ and 
$\nu _{3}=21/64$, and for 
$n\geq 2$,
\begin{equation}
\nu _{n}=\frac{1}{n-1}\sum_{k=1}^{n-1}\theta _{k}\nu _{n-k},
\end{equation} which satisfies 
$\nu _{n}\in (0,1]$ for all 
$n\geq 1$. Consequently, the function 
$r\mapsto \exp \left(-2\mu \left( r\right) \right) $ is absolutely monotonic on 
$\left( 0,1\right) $.
Remark 1.2. Taking 
$r=1/\sqrt{2}$ and 
$r\rightarrow 1^{-}$ in equation (1.10), we obtain two identities
\begin{equation*}
\sum_{n=1}^{\infty }\frac{\nu _{n}}{2^{n+4}}=\text{e}^{-\pi }\text{\ and \ }
\sum_{n=1}^{\infty }\nu _{n}=16.
\end{equation*}Theorem 1.5. The functions
\begin{equation*}
s\mapsto \frac{d[\mu\left(1/s\right)]}{\text{d}s}, \
s\mapsto \frac{\mu \left( 1/s\right)}{\ln s},\
s\mapsto 1-\frac{\mu\left(1/s\right)}{\ln \left( 4s\right) }\text{\ and \ }
s\mapsto \frac{\text{d}[\mu(1/s)/\ln(4s)]}{\text{d}s}
\end{equation*} are completely monotonic on 
$\left( 1,\infty \right) $. Consequently, the functions
\begin{equation*}
s\mapsto \frac{1}{\mu \left( 1/s\right) }\text{\ and \ }s\mapsto \frac{\ln
\left( 4s\right) }{\mu \left( 1/s\right) }
\end{equation*} are logarithmically completely monotonic on 
$\left( 1,\infty \right) $.
Combining Theorem 1.5 and equation (1.5), we obtain
Corollary 1.1. The functions 
$s\mapsto \gamma \left( s\right) $ and 
$
s\mapsto \gamma \left( s\right) \ln \left( 4s\right) $ are logarithmically completely monotonic on 
$\left( 1,\infty \right) $.
Theorem 1.6. For each 
$r\in(0,1)$, the function 
$\alpha \mapsto \mu \left( r^{\alpha }\right)
/\alpha $ is completely monotonic on 
$\left( 0,\infty \right) $.
The rest of this paper is organized as follows. In the next section, we present several lemmas which are needed to prove Theorems 1.1 and 1.3. The proof of Theorem 1.1 is given at the beginning of 
$\S$ 3 by use of Lemmas 2.1 and 2.2, and then the absolute monotonicity and (logarithmically) complete monotonicity results including Theorems 1.2–1.6, and the extensions of Properties P5 and P6, are also proved subsequently. As applications of main results, several sharp bounds for 
$\mu(r)$ are established in 
$\S$ 4.
2. Lemmas
To prove main results, we need the following important lemmas.
Lemma 2.1. Let
\begin{align}
\mathcal{K}^{2} &=\frac{\pi ^{2}}{4}\sum_{n=0}^{\infty }a_{n}r^{2n},
\end{align}
\begin{align}
\mathcal{E}^{2} &=\frac{\pi ^{2}}{4}\sum_{n=0}^{\infty }b_{n}r^{2n},
\end{align}
\begin{align}
\mathcal{KE} &=\frac{\pi ^{2}}{4}\sum_{n=0}^{\infty }c_{n}r^{2n}.
\end{align}Then, the coefficients an, bn and cn satisfy
(i)
$a_{0}=1$, $a_{1}=1/2$ and for $n\geq 2$,
(2.4)\begin{equation}
a_{n}=\frac{1}{2}\frac{\left( 2n-1\right) \left( 2n^{2}-2n+1\right) }{n^{3}}
a_{n-1}-\frac{\left( n-1\right) ^{3}}{n^{3}}a_{n-2};
\end{equation}(ii)
$b_{0}=1$, $b_{1}=-1/2$ and for $n\geq 2$,
(2.5)\begin{equation}
b_{n}=\frac{1}{2}\frac{4n^{3}-12n^{2}+10n-3}{n^{3}}b_{n-1}-\frac{\left(
n-1\right) \left( n-2\right) \left( n-3\right) }{n^{3}}b_{n-2};
\end{equation}(iii)
$c_{0}=1$, $c_{1}=0$, $c_{2}=1/32$ and for $n\geq 3$,
(2.6)\begin{equation}
c_{n}=\frac{1}{2}\frac{\left( n-1\right) \left( 4n^{3}-12n^{2}+10n-3\right)
}{n^{3}\left( n-2\right) }c_{n-1}-\frac{\left( n-1\right) ^{2}\left(
n-2\right) }{n^{3}}c_{n-2}.
\end{equation}
Proof. Differentiating and using the derivative formulas
\begin{equation}
\frac{\text{d}\mathcal{K}}{\text{d}r}=\frac{\mathcal{E}-r^{\prime ^{2}}\mathcal{K}}{
rr^{\prime ^{2}}}\text{\ \ and \ \ }\frac{\text{d}\mathcal{E}}{\text{d}r}=\frac{\mathcal{E
}-\mathcal{K}}{r}
\end{equation}yield
\begin{align*}
\left( \mathcal{K}^{2}\right) ^{\prime} &=2\mathcal{K}\frac{\mathcal{E}
-r^{\prime ^{2}}\mathcal{K}}{rr^{\prime ^{2}}}=2\frac{\mathcal{KE}-r^{\prime
^{2}}\mathcal{K}^{2}}{rr^{\prime ^{2}}}, \\
\left( \mathcal{E}^{2}\right) ^{\prime} &=2\mathcal{E}\frac{\mathcal{E}-
\mathcal{K}}{r}=2\frac{\mathcal{E}^{2}-\mathcal{KE}}{r}, \\
\left( \mathcal{KE}\right) ^{\prime} &=\frac{\mathcal{E}-r^{\prime ^{2}}
\mathcal{K}}{rr^{\prime ^{2}}}\mathcal{E}+\mathcal{K}\frac{\mathcal{E}-
\mathcal{K}}{r}=\frac{\mathcal{E}^{2}-r^{\prime ^{2}}\mathcal{K}^{2}}{
rr^{\prime ^{2}}}.
\end{align*}Substituting equations (2.1) (2.2) and (2.3) into the above three relations and arranging lead to
\begin{align*}
\sum_{n=1}^{\infty }2na_{n}r^{2n-1} &=2\frac{\sum_{n=0}^{\infty
}c_{n}r^{2n}-\left( 1-r^{2}\right) \sum_{n=0}^{\infty }a_{n}r^{2n}}{r\left(
1-r^{2}\right) }, \\
\sum_{n=1}^{\infty }2nb_{n}r^{2n-1} &=\frac{2}{r}\left( \sum_{n=0}^{\infty
}b_{n}r^{2n}-\sum_{n=0}^{\infty }c_{n}r^{2n}\right) , \\
\sum_{n=1}^{\infty }2nc_{n}r^{2n-1} &=\frac{\sum_{n=0}^{\infty
}b_{n}r^{2n}-\left( 1-r^{2}\right) \sum_{n=0}^{\infty }a_{n}r^{2n}}{r\left(
1-r^{2}\right) },
\end{align*}which can be simplified to
\begin{align*}
\sum_{n=1}^{\infty }\left[ na_{n}-\left( n-1\right) a_{n-1}\right] r^{2n}
&=c_{0}-a_{0}+\sum_{n=1}^{\infty }\left( c_{n}-a_{n}+a_{n-1}\right) r^{2n},
\\
\sum_{n=1}^{\infty }nb_{n}r^{2n} &=\sum_{n=0}^{\infty }\left(
b_{n}-c_{n}\right) r^{2n}, \\
\sum_{n=1}^{\infty }\left[ 2nc_{n}-2\left( n-1\right) c_{n-1}\right] r^{2n}
&=b_{0}-a_{0}+\sum_{n=1}^{\infty }\left( b_{n}-a_{n}+a_{n-1}\right) r^{2n}.
\end{align*} Comparing coefficients of 
$r^{2n}$ gives 
$a_{0}=b_{0}=c_{0}$, and for 
$n\geq
1 $,
\begin{equation}
\left\{
\begin{array}{l}
na_{n}-\left( n-1\right) a_{n-1}=c_{n}-a_{n}+a_{n-1}, \\
nb_{n}=b_{n}-c_{n}, \\
2nc_{n}-2\left( n-1\right) c_{n-1}=b_{n}-a_{n}+a_{n-1}.
\end{array}
\right.
\end{equation} Solving the recurrence equations gives 
$a_{1}=a_{0}/2$, 
$b_{1}=-a_{0}/2$, 
$
c_{1}=0$ and the desired recurrence relations for 
$n\geq 2$. Finally, it is clear that 
$a_{0}=b_{0}=c_{0}=1$, which yields that 
$a_{1}=1/2$, 
$b_{1}=-1/2$, 
$c_{1}=0$. This completes the proof.
Lemma 2.2. Let an be as in Lemma 2.1. The following statements are valid:
(i) The sequence
$\left\{a_{n}\right\} _{n\geq 0}$ is decreasing.(ii) The sequence
$\left\{\left( n+1\right) a_{n}\right\} _{n\geq 0}$ is increasing or equivalently $a_{n}/a_{n-1}\geq n/\left( n+1\right) $ for $
n\geq 1$.(iii) Let Wn be defined by equation (1.1).The sequence
$\left\{a_{n}/W_{n}\right\} _{n\geq 0}$ is decreasing or equivalently $a_{n}/a_{n-1}\leq \left( 2n-1\right) /\left( 2n\right) $ for $n\geq 1$.
(i) We write equation (2.4) as
\begin{equation*}
a_{n}-a_{n-1}=\frac{\left( n-1\right) ^{3}}{n^{3}}\left(
a_{n-1}-a_{n-2}\right) -\frac{1}{2}\frac{2n-1}{n^{3}}a_{n-1}.
\end{equation*}Since
$a_{n}=\sum_{k=0}^{n}W_{k}^{2}W_{n-k}^{2} \gt 0$ for all $n\geq 0$, we have
\begin{equation*}
n^{3}\left( a_{n}-a_{n-1}\right) \lt \left( n-1\right) ^{3}\left(
a_{n-1}-a_{n-2}\right)
\end{equation*}for
$n\geq 2$, which implies that
\begin{equation*}
n^{3}\left( a_{n}-a_{n-1}\right) \lt a_{1}-a_{0}=-\frac{1}{2} \lt 0
\end{equation*}for
$n\geq 2$, and then, the first statement follows.(ii) We write equation (2.4) as
\begin{equation*}
a_{n}-\frac{n}{n+1}a_{n-1}=\frac{\left( n-1\right) ^{2}}{n^{2}}\left(
a_{n-1}-\frac{n-1}{n}a_{n-2}\right) +\frac{1}{2}\frac{n-1}{n^{3}\left(
n+1\right) }a_{n-1}.
\end{equation*}Since
$a_{n} \gt 0$ for all $n\geq 0$, we have
\begin{equation*}
n^{2}\left( a_{n}-\frac{n}{n+1}a_{n-1}\right) \gt \left( n-1\right) ^{2}\left(
a_{n-1}-\frac{n-1}{n}a_{n-2}\right)
\end{equation*}for
$n\geq 2$, which yields
\begin{equation*}
n^{2}\left( a_{n}-\frac{n}{n+1}a_{n-1}\right) \gt 1^{2}\left( a_{1}-\frac{1}{2}
a_{0}\right) =0,
\end{equation*}as well as
$\left( n+1\right) a_{n} \gt na_{n-1}$ for $n\geq 2$. Due to $
2a_{1}=a_{0}=1$, we find that $\left( n+1\right) a_{n}\geq na_{n-1}$ for all $n\geq 1$, which proves the second statement.(iii) We write equation (2.4) as
\begin{align*}
a_{n}-\frac{2n-1}{2n}a_{n-1}=&\frac{\left( n-1\right) ^{3}}{n^{3}}\frac{2n-2
}{2n-3}\left( a_{n-1}-\frac{2n-3}{2n-2}a_{n-2}\right) \\
&-\frac{1}{2}\frac{\left( n-1\right) ^{2}}{n^{3}\left( 2n-3\right) }a_{n-1}.
\end{align*}Since
$a_{n} \gt 0$ for all $n\geq 0$, we have $\alpha _{n} \lt \beta _{n}\alpha
_{n-1}$ for $n\geq 2$, where
\begin{equation*}
\alpha _{n}=a_{n}-\frac{2n-1}{2n}a_{n-1}\text{ and }\beta _{n}=\frac{\left(
n-1\right) ^{3}}{n^{3}}\frac{2n-2}{2n-3},
\end{equation*}with
$\alpha _{1}=a_{1}-a_{0}/2=0$ and $\alpha _{2}=a_{2}-3a_{1}/4=-1/32 \lt 0$. Then,
\begin{equation*}
\alpha _{n} \lt \beta _{n}\beta _{n-1}\cdot \cdot \cdot \beta _{2}\alpha _{1}=0
\end{equation*}for
$n\geq 2$. In view of $W_{n}/W_{n-1}=\left( 2n-1\right) /\left(
2n\right) $, the inequality $\alpha _{n} \lt 0$ implies that $
a_{n}/W_{n} \lt a_{n-1}/W_{n-1}$ for $n\geq 2$, that is, the sequence $\left\{
a_{n}/W_{n}\right\} _{n\geq 1}$ is decreasing. Since $\alpha _{1}=0$, so is $
\left\{a_{n}/W_{n}\right\} _{n\geq 0}$. This completes the proof.
Lemma 2.3. Let Wn be defined by equation (1.1). Then
\begin{equation}
s_{n}=\sum_{k=0}^{n}\frac{W_{k}}{2k-1}a_{n-k} \gt 0
\end{equation} for 
$n\geq 1$.
Proof. Note that
\begin{align*}
r^{\prime} &=\sqrt{1-r^{2}}=-\sum_{n=0}^{\infty }\frac{W_{n}}{2n-1}r^{2n},
\\
\frac{1}{r^{\prime}} &=\frac{1}{\sqrt{1-r^{2}}}=\sum_{n=0}^{\infty
}W_{n}r^{2n}.
\end{align*}Then,
\begin{equation*}
r^{\prime}\mathcal{K}^{2}=-\frac{\pi ^{2}}{4}\sum_{n=0}^{\infty }\left(
\sum_{k=0}^{n}\frac{W_{k}}{2k-1}a_{n-k}\right) r^{2n}=-\frac{\pi ^{2}}{4}
\sum_{n=0}^{\infty }s_{n}r^{2n}.
\end{equation*}Differentiation yields
\begin{equation*}
\left( r^{\prime}\mathcal{K}^{2}\right)^{\prime}=r^{\prime}2\mathcal{K}
\frac{\mathcal{E}-r^{\prime ^{2}}\mathcal{K}}{rr^{\prime ^{2}}}-\frac{r}{
r^{\prime}}\mathcal{K}^{2}=\frac{2\mathcal{KE}-2\mathcal{K}^{2}+r^{2}
\mathcal{K}^{2}}{rr^{\prime}},
\end{equation*}which can be expanded in power series as
\begin{align*}
\left( r^{\prime}\mathcal{K}^{2}\right)^{\prime} &=\frac{\pi ^{2}}{4}\frac{
1}{r}\sum_{n=0}^{\infty }W_{n}r^{2n}\sum_{n=1}^{\infty }\left(
2c_{n}-2a_{n}+a_{n-1}\right) r^{2n} \\
&=\frac{\pi ^{2}}{4}\sum_{n=1}^{\infty }\left( \sum_{k=1}^{n}\left(
2c_{k}-2a_{k}+a_{k-1}\right) W_{n-k}\right) r^{2n-1}.
\end{align*}On the other hand, we have
\begin{equation*}
\left(r^{\prime}\mathcal{K}^{2}\right)^{\prime}=-\frac{\pi ^{2}}{4}
\sum_{n=1}^{\infty }2ns_{n}r^{2n-1}.
\end{equation*} Comparing coefficients of 
$r^{2n-1}$ gives
\begin{equation*}
2ns_{n}=-\sum_{k=1}^{n}\left( 2c_{k}-2a_{k}+a_{k-1}\right) W_{n-k}
\end{equation*} for 
$n\geq 1$.
If we prove that 
$\left( 2c_{k}-2a_{k}+a_{k-1}\right) \lt 0$ for 
$k\geq 1$, then 
$s_{n} \gt 0$ for 
$n\geq 1$, and the proof is done. The first relation of (2.19) implies that 
$c_{n}=\left( n+1\right) a_{n}-na_{n-1}$. It follows from Lemma 2.2 (iii) that
\begin{equation*}
2c_{k}-2a_{k}+a_{k-1}=2ka_{k}-\left( 2k-1\right) a_{k-1}\leq 0
\end{equation*} for 
$k\geq 1$. This completes the proof.
Remark 2.1. The above lemma implies that 
$-\left( r^{\prime}\mathcal{K}^{2}\right)
^{\prime}$ is absolutely monotonic on 
$\left( 0,1\right) $, which extends the result in [Reference Anderson, Vamanamurthy and Vuorinen4, Theorem 2.2(3)].
To observe the complete monotonicity involving 
$\mu\left( r\right)$ in 
$\S$ 3, we need the following lemma.
Lemma 2.4. ([Reference Miller and Samko17, Theorem 2])
Let f(x) be completely monotonic, and let h(x) be non-negative with a completely monotonic derivative. Then, 
$f\left(
h(x)\right) $ is also completely monotonic.
Remark 2.2. By Lemma 2.4, we immediately find that, if 
$
h\left( x\right) \gt 0$ and 
$h^{\prime}(x)$ is completely monotonic, then 
$
1/h\left( x\right) $ is also completely monotonic. Since
\begin{equation*}
\left[ \ln h\left( x\right) \right] ^{\prime}=\frac{1}{h\left( x\right) }
\times h^{\prime}\left( x\right),
\end{equation*} 
$\left[\ln h\left( x\right)\right] ^{\prime}$, as well as 
$1/h\left( x\right)$, is logarithmically completely monotonic (see also [Reference Chen, Qi and Srivastava15, Theorem 3]).
3. Proofs of main results
We are now in a position to prove main results.
Proof of Theorem 1.1
(i) We first prove that
(3.1)\begin{equation}
\frac{1}{r^{\prime 2}\mathcal{K}^{2}\left( r\right) }=\frac{4}{\pi ^{2}}
\sum_{n=0}^{\infty }\theta _{n}r^{2n},
\end{equation}where
(3.2)\begin{equation}
\theta _{0}=1\text{\ and \ }\theta _{n}=\sum_{k=1}^{n}\left(
a_{k-1}-a_{k}\right) \theta _{n-k}\text{ for }n\geq 1\text{.}
\end{equation}In fact, since
$\left( 4/\pi ^{2}\right) \mathcal{K}^{2}\left( r\right)
=\sum_{n=0}^{\infty }a_{n}r^{2n}$, we have
\begin{equation*}
\frac{4}{\pi ^{2}}r^{\prime 2}\mathcal{K}^{2}\left( r\right)
=\sum_{n=0}^{\infty }a_{n}r^{2n}-\sum_{n=1}^{\infty
}a_{n-1}r^{2n}=1+\sum_{n=1}^{\infty }\left( a_{n}-a_{n-1}\right) r^{2n}.
\end{equation*}By the Cauchy product formula,
\begin{equation*}
1=\sum_{n=0}^{\infty }\left( \sum_{k=0}^{n}a_{k}^{\ast }\theta _{n-k}\right)
r^{2n},
\end{equation*}where
$a_{0}^{\ast }=1$ and $a_{k}^{\ast }=a_{k}-a_{k-1}$ for $k\geq 1$. Comparing coefficients of $r^{2n}$ yields that $a_{0}^{\ast }\theta _{0}=1$ and
\begin{equation*}
\sum_{k=0}^{n}a_{k}^{\ast }\theta _{n-k}=0\text{ for }n\geq 1,
\end{equation*}which gives
$\theta _{0}=1$ and
\begin{equation*}
\theta _{n}=-\sum_{k=1}^{n}a_{k}^{\ast }\theta _{n-k}=\sum_{k=1}^{n}\left(
a_{k-1}-a_{k}\right) \theta _{n-k}\text{.}
\end{equation*}By means of this recurrence relation, it is easy to verify that
\begin{equation*}
\theta _{1}=\frac{1}{2}\text{, \ }\theta _{2}=\frac{13}{32}\text{, \ }\theta
_{3}=\frac{23}{64}\text{, \ }\theta _{4}=\frac{2701}{8192}.
\end{equation*}(ii) We next prove
$\theta _{n}\in \left( 0,1\right) $ for $n\geq 1$. From the above recurrence formula, it is immediate to get that $\theta
_{1}=\left( a_{0}-a_{1}\right) \theta _{0}=1/2$. Suppose that $\theta _{k} \gt 0$ for $0\leq k\leq n$. By Lemma 2.2, we see that $
a_{k-1}-a_{k} \gt 0$ for all $k\geq 1$. Then,
\begin{equation*}
\theta _{n+1}=\sum_{k=1}^{n+1}\left( a_{k-1}-a_{k}\right) \theta _{n+1-k} \gt 0.
\end{equation*}By induction, we conclude that
$\theta _{n} \gt 0$ for all $n\geq 0$. On the other hand, we have shown that $\theta _{0}=1$, $\theta _{1}=1/2$. Suppose that $\theta _{k}\leq 1$ for $0\leq k\leq n-1$. Then,
\begin{equation*}
\theta _{n}=\sum_{k=1}^{n}\left( a_{k-1}-a_{k}\right) \theta _{n-k}\leq
\sum_{k=1}^{n}\left( a_{k-1}-a_{k}\right) =a_{0}-a_{n}=1-a_{n} \lt 1.
\end{equation*}(iii) Finally, by the formula in equations (1.7) and (3.1), we have
\begin{equation*}
\mu ^{\prime}\left( r\right) =-\frac{\pi ^{2}}{4}\frac{1}{rr^{\prime 2}
\mathcal{K}\left( r\right) ^{2}}=-\sum_{n=0}^{\infty }\theta _{n}r^{2n-1}=-
\frac{1}{r}-\sum_{n=1}^{\infty }\theta _{n}r^{2n-1},
\end{equation*}which implies that
\begin{equation*}
\left[ \mu \left( r\right) -\ln \left( 4/r\right) \right] ^{\prime
}=-\sum_{n=1}^{\infty }\theta _{n}r^{2n-1}.
\end{equation*}Since
$\lim_{r\rightarrow 0^{+}}\left[ \mu \left( r\right) -\ln \left(
4/r\right) \right] =0$, an integration yields
\begin{equation*}
\int_{0}^{r}\left[ \mu \left( t\right) -\ln \left( 4/t\right) \right]
^{\prime}\text{d}t=-\int_{0}^{r}\sum_{n=1}^{\infty }\theta _{n}t^{2n-1}\text{d}t,
\end{equation*}which implies the power series representation equation (1.8). This completes the proof.
From the above proof, we make the following conjecture.
Conjecture 3.1.
The sequence 
$\{\theta_{n}\}_{n\geq 0}$ is strictly decreasing.
Proof of Theorem 1.2
(i) Using the series representation equation (1.8) and differentiating give
\begin{equation*}
\mu ^{\left( 2m+1\right) }\left( r\right)=-\frac{\left( 2m\right) !}{r^{2m+1}
}-\sum_{n=1}^{\infty }\left( \prod_{k=1}^{2m}\left( 2n-k\right) \right)
\theta _{n}r^{2n-2m-1} \lt 0
\end{equation*}for
$r\in \left( 0,1\right) $.(ii) By equation (1.9) we see that
\begin{equation*}
-\left[ \mu \left( r\right) +\ln r\right] ^{\prime}=\sum_{n=1}^{\infty
}\theta _{n}r^{2n-1},
\end{equation*}which is obviously absolutely monotonic on
$\left(0,1\right) $.(iii) We write (1.8) in the form of
\begin{equation*}
\frac{1}{r^{2}}\left[ \ln \frac{4}{r}-\mu \left( r\right) \right]
=\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}r^{2n-2},
\end{equation*}which is obviously absolutely monotonic on
$\left( 0,1\right) $.(iv) Expanding in power series for
$\mu \left( r\right) +\ln \left(
r/r^{\prime}\right) $ gives
\begin{align*}
\mu \left( r\right) +\ln \left( r/r^{\prime}\right) &=\ln
4-\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}r^{2n}+\frac{1}{2}
\sum_{n=1}^{\infty }\frac{1}{n}r^{2n} \\
&=\ln 4+\sum_{n=1}^{\infty }\frac{1-\theta _{n}}{2n}r^{2n},
\end{align*}which is absolutely monotonic on
$\left( 0,1\right) $ due to $\theta_{n}\in
\left( 0,1\right) $ for $n\geq 1$. This completes the proof.
Proof of Theorem 1.3
Since
\begin{equation*}
\frac{\text{d}}{\text{d}r}\ln \left( 1+r^{\prime}\right) =\frac{1}{r}\left( 1-\frac{1}{
\sqrt{1-r^{2}}}\right) =-\sum_{n=1}^{\infty }W_{n}r^{2n-1},
\end{equation*}we have
\begin{align*}
-\left[ \mu \left( r\right) +\ln \left( r/\left( 1+r^{\prime}\right)
\right) \right] ^{\prime} &=-\left[ \mu \left( r\right) +\ln r\right]
^{\prime}+\left[ \ln \left( 1+r^{\prime}\right) \right] ^{\prime} \\
&=\sum_{n=1}^{\infty }\theta _{n}r^{2n-1}-\sum_{n=1}^{\infty
}W_{n}r^{2n-1}=\sum_{n=1}^{\infty }\left( \theta _{n}-W_{n}\right) r^{2n-1}.
\end{align*} If we prove that 
$\theta _{n}\geq W_{n}$ for 
$n\geq 1$, the required result follows. Clearly, 
$\theta _{1}=1/2=W_{1}$, 
$\theta
_{2}=13/32 \gt W_{2}=3/8 $. Suppose that 
$\theta _{k}\geq W_{k}$ for 
$1\leq
k\leq n-1$. We prove that 
$\theta _{n} \gt W_{n}$. In fact, we have
\begin{equation*}
\theta _{n}-W_{n}=\sum_{k=1}^{n}\left( a_{k-1}-a_{k}\right) \theta
_{n-k}-W_{n} \gt \sum_{k=1}^{n}\left( a_{k-1}-a_{k}\right)
W_{n-k}-W_{n}=s_{n}^{\ast }\text{.}
\end{equation*} We next check that 
$s_{n}^{\ast }=s_{n}$, which is defined in equation (2.9). Since 
$a_{0}=1$, 
$s_{n}^{\ast }$ can be changed to
\begin{align*}
s_{n}^{\ast } &=\sum_{k=1}^{n}a_{k-1}W_{n-k}-\sum_{k=1}^{n}a_{k}W_{n-k}-W_{n}
\\
&=\sum_{k=0}^{n-1}\left( \frac{n-k}{n-k-1/2}-1\right) W_{n-k}a_{k}-a_{n} \\
&=\sum_{k=0}^{n-1}\frac{W_{n-k}}{2\left( n-k\right) -1}a_{k}-a_{n}=
\sum_{k=0}^{n}\frac{W_{n-k}}{2\left( n-k\right) -1}a_{k},
\end{align*} which, by a shift of indexes, equals to sn, and by Lemma 2.3, 
$
s_{n}^* \gt 0$. This completes the proof.
Remark 3.1. From the above proof, we see that 
$W_{n}\leq \theta _{n}\leq 1$ for all 
$
n\geq 0$ and
\begin{equation}
\mu \left( r\right) +\ln \left( \frac{r}{1+r^{\prime}}\right) =\ln
2-\sum_{n=2}^{\infty }\frac{\theta _{n}-W_{n}}{2n}r^{2n}.
\end{equation}Proof of Theorem 1.4.
Using the series representation equation (1.8) we have
\begin{align*}
\exp \left( -2\mu \left( r\right) \right)&=\exp \left( -2\ln \frac{4}{r}
+2\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}r^{2n}\right) . \\
&=\frac{r^{2}}{16}\exp \left( \sum_{n=1}^{\infty }\frac{\theta _{n}}{n}
r^{2n}\right) =\frac{1}{16}\sum_{n=1}^{\infty }\nu _{n}r^{2n}.
\end{align*}Then,
\begin{equation}
\exp \left( \sum_{n=1}^{\infty }\frac{\theta _{n}}{n}r^{2n}\right)
=\sum_{n=0}^{\infty }\nu _{n+1}r^{2n}.
\end{equation}Differentiation yields
\begin{equation*}
\sum_{n=1}^{\infty }2\theta _{n}r^{2n-1}\exp \left( \sum_{n=1}^{\infty }
\frac{\theta _{n}}{n}r^{2n}\right) =\sum_{n=1}^{\infty }2n\nu _{n+1}r^{2n-1}.
\end{equation*}Substituting equation (3.4) into the above equality and dividing by 2r give
\begin{equation*}
\left( \sum_{n=0}^{\infty }\theta _{n+1}r^{2n}\right) \left(
\sum_{n=0}^{\infty }\nu _{n+1}r^{2n}\right) =\sum_{n=0}^{\infty }\left(
n+1\right) \nu _{n+2}r^{2n}.
\end{equation*} Using Cauchy product formula and comparing coefficients of 
$r^{2n}$ lead to
\begin{equation*}
\left( n+1\right) \nu _{n+2}=\sum_{k=0}^{n}\theta _{k+1}\nu _{n+1-k},
\end{equation*} which implies equation (1.11). Taking r = 0 in equation (3.4) yields 
$\nu _{1}=1$. The values of ν 2 and ν 3 are obtained by equation (3.4).
Since 
$\theta _{n}\in \left( 0,1\right) $ for 
$n\geq 1$ and 
$\nu _{1}=1$, 
$
\nu _{2}=1/2$, it follows from equation (3.4) and by induction that 
$\nu
_{n}\in (0,1]$ for all 
$n\geq 1$. Consequently, the function 
$r\mapsto \exp
\left( -2\mu \left( r\right) \right) $ is absolutely monotonic on 
$\left(
0,1\right) $. This completes the proof.
Theorem 3.1. The functions
\begin{equation*}
t\mapsto \left[ \mu \left( e^{-t}\right) \right] ^{\prime}\text{, \ }
t\mapsto \frac{\mu \left( e^{-t}\right) }{t}\text{, \ }t\mapsto 1-\frac{\mu
\left( e^{-t}\right) }{t+\ln 4}\text{\ and }t\mapsto \left[ \frac{\mu
\left( e^{-t}\right) }{t+\ln 4}\right] ^{\prime}
\end{equation*} are completely monotonic on 
$\left( 0,\infty \right) $. Consequently, the functions
\begin{equation*}
t\mapsto \frac{1}{\mu \left( e^{-t}\right) }\text{\ and \ }t\mapsto \frac{
t+\ln 4}{\mu \left( e^{-t}\right) }
\end{equation*} are logarithmically completely monotonic on 
$\left( 0,\infty \right) $.
Proof. By equation (1.9), we see that
\begin{align*}
\mu \left( \text{e}^{-t}\right)&=t+\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}\left(
1-\text{e}^{-2nt}\right) , \\
\frac{\mu \left( \text{e}^{-t}\right) }{t}&=1+\sum_{n=1}^{\infty }\theta _{n}\frac{
1-\text{e}^{-2nt}}{2nt}.
\end{align*}(i) Differentiation yields
\begin{equation*}
\left[ \mu \left( \text{e}^{-t}\right) \right] ^{\prime}=1+\sum_{n=1}^{\infty
}\theta _{n}\text{e}^{-2nt}=\sum_{n=0}^{\infty }\theta _{n}\text{e}^{-2nt},
\end{equation*}which is clearly positive and completely monotonic on
$\left( 0,\infty
\right) $.(ii) Since
\begin{equation*}
\frac{1-\text{e}^{-2nt}}{2nt}=\int_{0}^{1}\text{e}^{-2nxt}\text{d}x
\end{equation*}is completely monotonic in t on
$\left( 0,\infty \right) $, so is $\mu
\left( \text{e}^{-t}\right) /t$.(iii) By equation (1.8), we see that
\begin{equation*}
\mu \left( \text{e}^{-t}\right) =t+\ln 4-\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}
\text{e}^{-2nt},
\end{equation*}which implies that
\begin{equation*}
\frac{\mu \left( \text{e}^{-t}\right) }{t+\ln 4}=1-\sum_{n=1}^{\infty }\frac{\theta
_{n}}{2n}\left(\frac{\text{e}^{-2nt}}{t+\ln 4}\right).
\end{equation*}Since
$\text{e}^{-2nt}$ and $1/\left( t+\ln 4\right) $ are both completely monotonic on $\left( 0,\infty \right) $, so is $1-\mu \left( \text{e}^{-t}\right)
/\left( t+\ln 4\right) $ and $\left[ \mu \left( \text{e}^{-t}\right) /\left( t+\ln
4\right) \right] ^{\prime}$.(iv) Finally, the logarithmically complete monotonicity of the latter two functions follows from Remark 2.2. This completes the proof.
Proof of Theorem 1.5
Let 
$t=t\left( s\right) =\ln s$, s > 1. Then, 
$t\left( s\right) \gt 0$ and 
$
t^{\prime}\left( s\right) =1/s$ is completely monotonic on 
$\left( 1,\infty
\right) $. Using Theorem 3.1 and Lemma 2.4, the desired results follow.
Remark 3.2. Recall that an infinitely differentiable function 
$f:I\rightarrow \lbrack
0,\infty )$ is called a Bernstein function on an interval I if f ʹ is completely monotonic on I (see [Reference Schilling, Song and Vondra\u cek22, Definition 3.1]). Theorem 3.1 shows that 
$\mu \left( \text{e}^{-t}\right) \gt 0$ and 
$\left[ \mu \left( \text{e}^{-t}\right)
\right] ^{\prime}$ is completely monotonic on 
$\left( 0,\infty \right)$, so that the function 
$t\mapsto \mu \left( \text{e}^{-t}\right) $ is a Bernstein function on 
$\left( 0,\infty \right) $. Similarly, 
$t\mapsto \mu \left( \text{e}^{-t}\right)
/\left( t+\ln 4\right) $ is so. Also, Theorem 1.5 leads to the conclusion that the functions 
$s\mapsto \mu \left( 1/s\right) $ and 
$s\mapsto \mu
\left( 1/s\right) /\ln \left( 4s\right) $ are both Bernstein functions on 
$
\left( 1,\infty \right) $.
Remark 3.3. Teichumüller extremely ring 
$\mathbb{C}\setminus[-1,0]\cup[t,+\infty)(t \gt 0)$ has conformal capacity 
$\tau(t)=\pi/\mu(1/\sqrt{1+t})$ (see [Reference Anderson, Vamanamurthy and Vuorinen6]). Since 
$s\left( t\right) =\sqrt{t+1}$ satisfies that 
$s\left( t\right) \gt 0$ and 
$s^{\prime}\left( t\right) $ is completely monotonic on 
$\left(
0,\infty \right) $, using Lemma 2.4 and Theorem 1.5, we conclude that the functions 
$t\mapsto \tau \left( t\right) $ and 
$t\mapsto \tau \left(
t\right) \ln \left( 4\sqrt{t+1}\right) $ are logarithmically completely monotonic on 
$\left( 0,\infty \right) $, which extends the properties of 
$\tau \left( t\right) $ given in [Reference Anderson, Vamanamurthy and Vuorinen6, Exercises 5.19 (8), (9)].
Proof of Theorem 1.6
Using equation (1.9), we have
\begin{equation*}
\frac{\mu \left( r^{\alpha }\right) }{\alpha }=-\ln r+\sum_{n=1}^{\infty
}\theta _{n}\frac{1-r^{2\alpha n}}{2\alpha n}=\left( -\ln r\right) \left[
1+\sum_{n=1}^{\infty }\theta _{n}\frac{1-r^{2\alpha n}}{-2\alpha n\ln r}
\right].
\end{equation*}Since
\begin{equation*}
\frac{1-r^{2\alpha n}}{-2\alpha n\ln r}=\int_{0}^{1}r^{2\alpha
nx}\text{d}x=\int_{0}^{1}e^{-2\alpha nx\ln \left( 1/r\right) }\text{d}x
\end{equation*} is completely monotonic in α on 
$\left( 0,\infty \right) $, so is 
$
\alpha \mapsto \mu \left( r^{\alpha }\right) /\alpha $. This completes the proof.
The following two theorems extend Properties P5 and P6 listed in the first section in this paper.
Theorem 3.2. Let 
$r\in \left( 0,1\right) $. Then
\begin{align*}
\left[ \frac{\mu \left( r\right) }{\ln \left( 4/r\right) }\right] ^{\left(
m\right) } & \lt 0\text{\ for\ }m=1,2,3, \\
\left[ \frac{\mu \left( \sqrt{r}\right) }{\ln \left( 4/\sqrt{r}\right) }
\right] ^{\left( m\right) } & \lt 0\text{\ for }m=1,2.
\end{align*}(i) Using series representation equation (1.8), we have
(3.5)\begin{equation}
\frac{\mu \left( r\right) }{\ln \left( 4/r\right) }=1-\sum_{n=1}^{\infty }
\frac{\theta _{n}}{2n}\frac{r^{2n}}{\ln \left( 4/r\right) }.
\end{equation}Differentiation yields
\begin{align*}
\left[ \frac{\mu \left( r\right) }{\ln \left( 4/r\right) }\right] ^{\prime}
&=-\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}\frac{r^{2n-1}}{\ln \left(
4/r\right) }\left( 2n+\frac{1}{\ln \left( 4/r\right) }\right) \lt 0, \\
\left[ \frac{\mu \left( r\right) }{\ln \left( 4/r\right) }\right] ^{\prime
\prime } &=-\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}\frac{r^{2n-2}}{\ln
\left( 4/r\right) }\left( 2n\left( 2n-1\right) +\frac{4n-1}{\ln \left(
4/r\right) }+\frac{2}{\ln ^{2}\left( 4/r\right) }\right) \lt 0.
\end{align*}Since
$r^{2n-2}$ for $n\geq 1$ and $1/\ln \left( 4/r\right) $ is positive and increasing, the function
\begin{equation*}
r\mapsto \frac{r^{2n-2}}{\ln \left( 4/r\right) }\left( 2n\left( 2n-1\right) +
\frac{4n-1}{\ln \left( 4/r\right) }+\frac{2}{\ln ^{2}\left( 4/r\right) }
\right)
\end{equation*}is also positive and increasing, which means that
$\left[ \mu \left(
r\right) /\ln \left( 4/r\right) \right] ^{\prime \prime }$ is decreasing on $
\left( 0,1\right) $.(ii) By equation (3.5), we have
\begin{equation*}
\frac{\mu \left( \sqrt{r}\right) }{\ln \left( 4/\sqrt{r}\right) }
=1-\sum_{n=1}^{\infty }\frac{\theta _{n}}{n}\frac{r^{n}}{\ln \left(
16/r\right) }.
\end{equation*}Differentiation yields
\begin{equation*}
\left[ \frac{\mu \left( \sqrt{r}\right) }{\ln \left( 4/\sqrt{r}\right) }
\right] ^{\prime}=-\sum_{n=1}^{\infty }\frac{\theta _{n}}{n}\frac{r^{n-1}}{
\ln \left( 16/r\right) }\left( n+\frac{1}{\ln \left( 16/r\right) }\right) \lt 0.
\end{equation*}Since
$r^{n-1}$ for $n\geq 1$ and $1/\ln \left( 16/r\right) $ is positive and increasing, the function
\begin{equation*}
r\mapsto \frac{r^{n-1}}{\ln \left( 16/r\right) }\left( n+\frac{1}{\ln \left(
16/r\right) }\right)
\end{equation*}is also positive and increasing, which means that
$\left[ \mu \left( \sqrt{r}
\right) /\ln \left( 4/\sqrt{r}\right) \right] ^{\prime}$ is decreasing on $
\left(0,1\right) $. This completes the proof.
Theorem 3.3. Let 
$r\in \left( 0,1\right) $. Then,
\begin{equation*}
\left[\frac{\mu \left( r\right) }{\ln \left( 1/r\right) }\right]^{\left(m\right)} \gt 0\text{\ and \ }
\left[ \frac{\mu \left( \sqrt{r}\right) }{\ln \left( 1/\sqrt{r}\right) }\right] ^{\left( m\right) } \gt 0
\end{equation*} for 
$r\in \left( 0,1\right) $ and 
$m=1,3$.
Proof. Using equation (1.9), we have
\begin{align*}
\frac{\mu \left( r\right) }{\ln \left( 1/r\right) } &=1-\sum_{n=1}^{\infty }
\frac{\theta _{n}}{2n}\frac{1-r^{2n}}{\ln r}, \\
\frac{\mu \left( \sqrt{r}\right) }{\ln \left( 1/\sqrt{r}\right) }
&=1-\sum_{n=1}^{\infty }\frac{\theta _{n}}{n}\frac{1-r^{n}}{\ln r}.
\end{align*} Let 
$\eta _{k}\left( r\right) =\left( 1-r^{k}\right) /\ln r$, 
$k\in \mathbb{N
}$. Differentiation yields
\begin{equation*}
\eta _{k}^{\prime}\left( r\right) =-\frac{r^{k-1}}{\ln ^{2}r}\left( k\ln
r-1+r^{-k}\right) ,
\end{equation*}
\begin{align*}
-\frac{\ln ^{4}r}{r^{k-3}}\eta _{k}^{\prime \prime \prime}\left( r\right)
=&2\left( \ln ^{2}r+3\ln r+3\right) r^{-k}+k\left( k-1\right) \left(
k-2\right) \ln ^{3}r \\
&-\left( 3k^{2}-6k+2\right) \ln ^{2}r+6\left( k-1\right) \ln r-6:=\xi \left(
r\right) .
\end{align*} From the known inequality 
$x-1-\ln x \gt 0$ for x > 1, it follows that 
$\eta
_{k}^{\prime}\left( r\right) \lt 0$ for 
$r\in \left( 0,1\right) $. To prove that 
$\eta_{k}^{\prime \prime \prime }(r) \lt 0$ for 
$r\in \left( 0,1\right) $, it suffices to prove that 
$\xi \left( e^{-t}\right) \gt 0$ for t > 0. Expanding in power series yields
\begin{align*}
\xi \left( \text{e}^{-t}\right)=&2\left( t^{2}-3t+3\right) \text{e}^{kt}-k\left(
k-1\right) \left( k-2\right) t^{3} \\
&-\left( 3k^{2}-6k+2\right) t^{2}-6\left( k-1\right) t-6 \\
=&2\sum_{j=4}^{\infty }\frac{j\left( j-1\right) -3jk+3k^{2}}{j!}
k^{j-2}t^{j} \gt 0,
\end{align*}where the inequality holds due to
\begin{equation*}
j\left( j-1\right)-3jk+3k^{2}=3\left( k-\frac{j}{2}\right)^{2}+\frac{1}{4}
j\left(j-4\right) \gt 0
\end{equation*} for 
$k\in \mathbb{N}$ and 
$j\geq 4$. It is deduced that
\begin{align*}
\left[ \frac{\mu \left( r\right) }{\ln \left( 1/r\right) }\right] ^{\left(
m\right) }=&-\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}\eta _{2n}^{\left(
m\right) }\left( r\right) \gt 0, \\
\left[ \frac{\mu \left( \sqrt{r}\right) }{\ln \left( 1/\sqrt{r}\right) }
\right] ^{\left( m\right) }=&-\sum_{n=1}^{\infty }\frac{\theta _{n}}{n}\eta
_{n}^{\left( m\right) }\left( r\right) \gt 0
\end{align*} for 
$r\in \left( 0,1\right) $ and 
$m=1,3$. This completes the proof.
4. Inequalities for the modulus of the Grötzsch ring
Using those higher-order monotonicity given in the above sections, we can deduce some functional inequalities and bounds for 
$\mu\left(r\right) $. By Theorem 1.3 (iii), we see that the function
\begin{equation*}
r\mapsto \phi _{1}\left( r\right) =\frac{1}{r^{2n}}\left[ \ln \frac{4}{r}
-\mu \left( r\right) -\sum_{k=1}^{n-1}\frac{\theta _{k}}{2k}r^{2k}\right]
\end{equation*} is increasing on 
$\left( 0,1\right) $ with 
$\phi _{1}\left( 0^{+}\right)
=\theta _{n}/\left( 2n\right) $ and 
$\phi _{1}\left( 1^{-}\right) =\ln
4-\sum_{k=1}^{n-1}\theta _{k}/\left( 2k\right) $. Then, we have the following
Corollary 4.1. Let θn be given in Theorem 1.1. The double inequality
\begin{equation*}
\ln \frac{4}{r}-\sum_{k=1}^{n-1}\frac{\theta _{k}}{2k}r^{2k}-\alpha
_{1}r^{2n} \lt \mu \left( r\right) \lt \ln \frac{4}{r}-\sum_{k=1}^{n-1}\frac{\theta
_{k}}{2k}r^{2k}-\beta _{1}r^{2n}
\end{equation*} holds for 
$r\in \left( 0,1\right) $ with the optimal constants
\begin{equation*}
\alpha _{1}=\ln 4-\sum_{k=1}^{n-1}\frac{\theta _{k}}{2k}\text{\ and \ }
\beta _{1}=\frac{\theta _{n}}{2n}.
\end{equation*}In particular, for n = 2, we have
\begin{equation*}
\ln \frac{4}{r}-\frac{1}{4}r^{2}-\left( \ln 4-\frac{1}{4}\right) r^{4} \lt \mu
\left( r\right) \lt \ln \frac{4}{r}-\frac{1}{4}r^{2}-\frac{13}{128}r^{4}
\end{equation*} for 
$r\in \left( 0,1\right) $.
Theorem 1.3 and equation (3.3) imply that the function
\begin{equation*}
r\mapsto \phi _{2}\left( r\right) =\frac{1}{r^{4}}\left[ \mu \left( r\right)
+\ln \left( \frac{r}{1+r^{\prime}}\right) -\ln 2\right]
\end{equation*} is decreasing on 
$\left( 0,1\right) $, with
\begin{align}
\phi _{2}\left( 1^{-}\right)&=-\ln 2=-\beta _{22},
\end{align}
\begin{align}
\phi _{2}\left( \frac{1}{\sqrt{2}}\right)&=2\pi -4\ln \left( \sqrt{2}
+1\right) -4\ln 2=-\beta _{21},
\end{align}
\begin{align}
\phi _{2}\left( 0^{+}\right)&=-\frac{\theta _{2}-W_{2}}{4}=-\frac{1}{4}
\left( \frac{13}{32}-\frac{3}{8}\right) =-\frac{1}{128}=-\alpha _{2}.
\end{align}Then, we have
Corollary 4.2. The double inequalities
\begin{equation*}
-\ln \left( \frac{r}{1+r^{\prime}}\right) +\ln 2-\beta _{22}r^{4} \lt \mu
\left( r\right) \lt -\ln \left( \frac{r}{1+r^{\prime}}\right) +\ln 2-\alpha
_{2}r^{4}
\end{equation*} for 
$r\in \left( 0,1\right) $ and
\begin{equation*}
-\ln \left( \frac{r}{1+r^{\prime}}\right) +\ln 2-\beta _{21}r^{4} \lt \mu
\left( r\right) \lt -\ln \left( \frac{r}{1+r^{\prime}}\right) +\ln 2-\alpha
_{2}r^{4}
\end{equation*} for 
$r\in \left( 0,1/\sqrt{2}\right) $ hold, where the constants α 2, β 21 and β 22 given in equations (4.1)–(4.3) are the best possible.
The following lemma was proved in [Reference Tian and Yang24, Lemma 4].
Lemma 4.1. Let the function h be defined on 
$\mathbb{R}$ which has the derivative of all orders. If 
$h^{\left( 2k+1\right) }\left( x\right) \gt \left( \lt \right) 0$ for 
$x\in \mathbb{R}$ and 
$k\in \mathbb{N}$, then the function
\begin{equation*}
\phi \left( x\right) =\frac{h\left( 2c-x\right) -h\left( x\right) }{2c-2x}
\text{ if }x\neq c\text{\ and \ }\phi \left( c\right) =h^{\prime}\left(
c\right)
\end{equation*} satisfies that 
$\phi ^{\left( 2k-2\right) }\left( x\right) $ is strictly convex (concave) on 
$\mathbb{R}$ and is decreasing (increasing) on 
$\left(
-\infty ,c\right) $ and increasing (decreasing) on 
$\left( c,\infty \right) $. Furthermore, if 
$h^{\prime}\left( x\right) $ is absolutely monotonic on 
$
\mathbb{R}$, then 
$\phi \left( x\right) $ is completely monotonic on 
$\left(
-\infty ,c\right) $ and absolutely monotonic on 
$\left( c,\infty \right) $.
Applying Lemma 4.1 and our main theorems, we can obtain some higher-order monotonicity results involving 
$\mu \left( r\right) $ and establish several inequalities for 
$\mu \left( r\right) $. For example, by Theorem 1.3 and Lemma 4.1, we see that the function
\begin{equation*}
\phi _{3}\left( x\right) =\frac{\mu \left( \sqrt{x}\right) -\mu \left( \sqrt{
1-x}\right) }{2x-1}\text{ if }x\neq \frac{1}{2}\text{ and }\phi _{3}\left(
\frac{1}{2}\right) =\left[ \mu \left( \sqrt{x}\right) \right]
_{x=1/2}^{\prime}
\end{equation*} satisfies that 
$\phi _{3}^{\left( 2k-2\right) }\left( x\right) $ is strictly concave on 
$\left( 0,1\right) $ and is increasing on 
$\left( 0,1/2\right) $ and decreasing on 
$\left( 1/2,1\right) $. Since
\begin{equation*}
\left[ \mu \left( \sqrt{x}\right) \right] ^{\prime}=-\frac{\pi ^{2}}{8}
\frac{1}{x\left( 1-x\right) \mathcal{K}^{2}\left( \sqrt{x}\right) }\text{\
and \ }\mathcal{K}\left( \frac{1}{\sqrt{2}}\right) =\frac{\Gamma ^{2}\left(
1/4\right) }{4\sqrt{\pi }},
\end{equation*}we have
\begin{equation*}
\phi _{3}\left( \frac{1}{2}\right) =-\frac{2}{\pi }\Gamma ^{4}\left( \frac{3
}{4}\right) .
\end{equation*} Setting 
$x=r^{2}$. Then, the inequality
\begin{equation*}
\frac{\mu \left( r\right) -\mu \left( r^{\prime}\right) }{2r^{2}-1} \lt -\frac{2
}{\pi }\Gamma ^{4}\left( \frac{3}{4}\right) =-\alpha _{3}
\end{equation*} holds for 
$r\in \left( 0,1\right) $. This, by 
$\mu \left( r\right) \mu
\left( r^{\prime}\right) =\pi ^{2}/4$, gives the following corollary.
Corollary 4.3. The function
\begin{equation*}
r\mapsto \frac{\mu \left( r\right) -\mu \left( r^{\prime}\right) }{2r^{2}-1}
\end{equation*} is increasing on 
$\left( 0,1/\sqrt{2}\right) $ and decreasing on 
$\left( 1/
\sqrt{2},1\right) $. Therefore, the inequality
\begin{equation*}
\mu \left( r\right) \gt \sqrt{\alpha _{3}^{2}\left( r^{2}-\frac{1}{2}\right)
^{2}+\frac{\pi ^{2}}{4}}-\alpha _{3}\left( r^{2}-\frac{1}{2}\right)
\end{equation*} holds for 
$r\in \left( 0,1/\sqrt{2}\right) $. It is reversed for 
$r\in
\left( 1/\sqrt{2},1\right) $.
We have shown in Theorem 3.2 that 
$\phi _{4}\left( x\right) =\mu
\left( \sqrt{x}\right) /\ln \left( 4/\sqrt{x}\right) $ is concave on 
$\left(
0,1\right) $. Then,
\begin{equation*}
\phi _{5}\left( x\right) =\phi _{4}\left( x\right) +\phi _{4}\left(
1-x\right)
\end{equation*} is also concave on 
$\left( 0,1\right)$, with 
$\phi _{5}^{\prime}\left(
1/2\right) =0$, which means that 
$\phi _{5}\left( x\right) $ is increasing on 
$\left( 0,1/2\right) $ and decreasing on 
$\left( 1/2,1\right) $. Consequently,
\begin{equation*}
1=\phi _{5}\left( 0^{+}\right) \lt \phi _{5}\left( x\right) \leq \phi
_{5}\left( \frac{1}{2}\right)=\frac{2\pi }{5\ln 2}
\end{equation*} for 
$x\in \left( 0,1\right) $. Substituting 
$x=r^{2}$ gives the following corollary.
Corollary 4.4. The double inequality
\begin{equation*}
1 \lt \frac{\mu \left( r\right) }{\ln \left( 4/r\right) }+\frac{\mu \left(
r^{\prime}\right) }{\ln \left( 4/r^{\prime}\right) } \lt \frac{2\pi }{5\ln 2}
\end{equation*} holds for 
$r\in \left( 0,1\right) $, where both bounds are sharp.
We establish functional inequalities by Theorem 3.1.
Corollary 4.5. The double inequality
\begin{equation*}
\frac{4\ln r_{1}\ln r_{2}}{\left( \ln r_{1}+\ln r_{2}\right) ^{2}} \lt \frac{\mu
\left( r_{1}\right) \mu \left( r_{2}\right) }{\mu ^{2}\left( \sqrt{r_{1}r_{2}
}\right) } \lt \frac{\ln \left( 4/r_{1}\right) \ln \left( 4/r_{2}\right) }{\ln
^{2}\left( 4/\sqrt{r_{1}r_{2}}\right) }
\end{equation*} holds for 
$r_{1},r_{2}\in \left( 0,1\right) $ with 
$r_{1}\neq r_{2}$.
Proof. Note that a completely monotonic function is log-convex. By Theorem 3.1, the functions 
$\mu \left( \text{e}^{-t}\right) /t$ and 
$\mu \left(
\text{e}^{-t}\right) /\left( t+\ln 4\right) $ are log-convex and log-concave on 
$
\left( 0,\infty \right) $, respectively. Then, for t 1, 
$t_{2}\in \left(
0,\infty \right) $ with 
$t_{1}\neq t_{2}$, the inequalities
\begin{align*}
\left[ \frac{\mu \left( \text{e}^{-\left( t_{1}+t_{2}\right) /2}\right) }{\left(
t_{1}+t_{2}\right) /2}\right] ^{2} \lt &\frac{\mu \left( \text{e}^{-t_{1}}\right) }{
t_{1}}\frac{\mu \left( \text{e}^{-t_{2}}\right) }{t_{2}}, \\
\left[\frac{\mu \left( \text{e}^{-t_{1}}\right) }{t_{1}+\ln 4}\right]\left[\frac{\mu \left(
\text{e}^{-t_{2}}\right) }{t_{2}+\ln 4}\right] \lt &\left[ \frac{\mu \left( \text{e}^{-\left(
t_{1}+t_{2}\right) /2}\right) }{\left( t_{1}+t_{2}\right) /2+\ln 4}\right]
^{2}
\end{align*} hold. Making a change of variables 
$t_{i}=-\ln r_{i}$, 
$i=1,2$, and arranging give the required double inequality. This completes the proof.
Remark 4.1. Taking 
$\left( r_{1},r_{2}\right) =\left( r,r^{\prime}\right) $ in the above corollary, we derive that
\begin{equation*}
\frac{\pi }{2}\frac{\ln \left( 4/\sqrt{rr^{\prime}}\right) }{\sqrt{\ln
\left( 4/r\right) \ln \left( 4/r^{\prime}\right) }} \lt \mu \left( \sqrt{
rr^{\prime}}\right) \lt -\frac{\pi }{4}\frac{\ln \left( rr^{\prime}\right) }{
\sqrt{\ln r\ln r^{\prime}}}
\end{equation*} for 
$r\in \left( 0,1\right) $, with 
$r\neq 1/\sqrt{2}$.
Finally, as another application of Lemmas 2.1 and 2.2, we prove that the ratio 
$\phi _{6}\left( r\right) /\mu \left( r\right) $ is decreasing on 
$\left( 0,1\right) $, where
\begin{equation*}
\phi _{6}\left( r\right) =\ln \frac{4}{\sqrt{\rho }}, \quad \rho \equiv \rho \left( r\right) =-\ln \left( 1-r^{2}\right) .
\end{equation*}To this end, we also need other two tools. The first tool is the monotonicity rule of a ratio of two power series ([Reference Biernacki and Krzyz12, Reference Yang, Chu and Wang32]), which states that
Lemma 4.2. Let 
$A\left( t\right) =\sum_{n=0}^{\infty }a_{n}t^{n}$ and 
$
B\left( t\right) =\sum_{n=0}^{\infty }b_{n}t^{n}$ be two real power series converging on 
$\left( -r,r\right) $ (r > 0) with 
$b_{n} \gt 0$ for all n. If the sequence 
$\{a_{n}/b_{n}\}_{n\geq 0}\ $is increasing (decreasing), then so is the ratio 
$A\left( t\right) /B\left( t\right) $ on 
$\left( 0,r\right)$.
The second tool is an auxiliary function 
$H_{f,g}$ presented first in [Reference Yang35], which was called Yang’s H-function in [Reference Tian, Ha and Xing23] by Tian et al. For 
$-\infty \leq a \lt b\leq \infty $, let f and g be differentiable on (a, b) and 
$g^{\prime}\neq 0$ on (a, b). Then, the function 
$H_{f,g}$ is defined by
\begin{equation*}
H_{f,g}=\frac{f^{\prime}}{g^{\prime}}g-f.
\end{equation*}If f and g are twice differentiable on (a, b), then
\begin{align*}
\left( \frac{f}{g}\right) ^{\prime}=&\frac{g^{\prime}}{g^{2}}\left( \frac{
f^{\prime}}{g^{\prime}}g-f\right) =\frac{g^{\prime}}{g^{2}}H_{f,g}, \\
H_{f,g}^{\prime}=&\left( \frac{f^{\prime}}{g^{\prime}}\right) ^{\prime}g.
\end{align*}Theorem 4.1. The function 
$r\mapsto \phi _{6}\left( r\right) /\mu
\left( r\right) $ is decreasing on 
$\left( 0,1\right) $. Therefore, the double inequality
\begin{equation}
\beta _{4}\ln \frac{4}{\sqrt{\rho }} \lt \mu \left( r\right) \lt \alpha _{4}\ln
\frac{4}{\sqrt{\rho }}
\end{equation} holds for 
$r\in \left( 0,1/\sqrt{2}\right) $ with the best constants
\begin{equation*}
\beta _{4}=1\text{\ and \ }\alpha _{4}=\frac{\pi }{4\ln 2-\ln \left( \ln
2\right) }=1.000\,793\,54\cdots\text{.}
\end{equation*} While 
$r\in \left( 1/\sqrt{2},1\right) $, the double inequality
\begin{equation*}
\frac{\pi ^{2}}{\alpha _{4}}\frac{1}{2\left[3\ln 2-\ln \left( -\ln r\right)\right] } \lt \mu
\left( r\right) \lt \frac{\pi ^{2}}{\beta _{4}}\frac{1}{2\left[3\ln 2-\ln \left( -\ln r\right)\right] }
\end{equation*}holds.
Proof. First, we show that 
$\phi _{6}^{\prime}\left( r\right) /\mu
^{\prime}\left( r\right) $ is increasing on 
$\left( 0,1\right) $. Since
\begin{equation*}
\mu ^{\prime}\left( r\right) =-\frac{\pi ^{2}}{4}\frac{1}{rr^{\prime 2}
\mathcal{K}^{2}\left( r\right) }\text{\ and \ }\phi _{6}^{\prime}\left(
r\right) =-\frac{r}{r^{\prime 2}}\frac{1}{\rho },
\end{equation*}we have
\begin{equation*}
\frac{\phi _{6}^{\prime}\left( r\right) }{\mu ^{\prime}\left( r\right) }=
\frac{\left( 4/\pi ^{2}\right) \mathcal{K}\left( r\right) ^{2}}{\rho /r^{2}}=
\frac{\sum_{n=0}^{\infty }a_{n}r^{2n}}{\sum_{n=0}^{\infty }\left( n+1\right)
^{-1}r^{2n}}.
\end{equation*} As shown in Lemma 2.2 (ii), the sequence 
$\left\{\left( n+1\right)
a_{n}\right\} _{n\geq 0}$ is increasing. It follows from Lemma 4.2 that the function 
$\phi _{6}^{\prime}\left( r\right) /\mu ^{\prime}\left(
r\right) $ is increasing on 
$\left( 0,1\right) $.
Second, we show that
\begin{equation*}
H_{\phi _{6},\mu }\left( r\right) =\frac{\phi _{6}^{\prime}\left( r\right)
}{\mu ^{\prime}\left( r\right) }\mu \left( r\right) -\phi _{6}\left(
r\right) \gt 0
\end{equation*} for 
$r\in \left( 0,1\right) $. Since 
$H_{\phi _{6},\mu }^{\prime}=\left(
\phi _{6}^{\prime}/\mu ^{\prime}\right)^{\prime}\mu $, we see that 
$H_{\phi_{6},\mu }^{\prime} \gt 0$ for all 
$r\in(0,1)$, that is, 
$H_{\phi _{6},\mu }$ is increasing on 
$\left( 0,1\right) $. If we prove 
$H_{\phi _{6},\mu }\left( 0^{+}\right)
=0$, then 
$H_{\phi _{6},\mu }\left( r\right) \gt H_{\phi _{6},\mu }\left(
0^{+}\right) =0$. Due to
\begin{equation*}
\frac{\phi _{6}^{\prime}\left( r\right) }{\mu ^{\prime}\left( r\right) }
\rightarrow 1\text{\ and \ }\mu \left( r\right) \sim \ln \left( 4/r\right)
\text{, \ as }r\rightarrow 0^{+},
\end{equation*}it is obtained that
\begin{equation*}
H_{\phi _{6},\mu }\left( r\right) \sim \ln \left( 4/r\right) -\ln \frac{4}{
\sqrt{\rho }}=\frac{1}{2}\ln \frac{-\ln \left( 1-r^{2}\right) }{r^{2}}
\rightarrow 0\text{, \ as }r\rightarrow 0^{+}.
\end{equation*} Third, since 
$\mathfrak{\mu }^{\prime}\left( r\right) \lt 0$, it follows that
\begin{equation*}
\left[ \frac{\phi _{6}\left( r\right) }{\mu \left( r\right) }\right]
^{\prime}=\frac{\mathfrak{\mu }^{\prime}\left( r\right) }{\mathfrak{\mu }
^{2}\left( r\right) }H_{\phi _{6},\mu }\left( r\right) \lt 0
\end{equation*} for 
$r\in \left( 0,1\right) $.
Finally, the first double inequality follows from the decreasing property of the ratio 
$\phi _{6}\left( r\right) /\mu \left( r\right) $ on 
$
\left( 0,1/\sqrt{2}\right) $; the second one follows from the first double inequality and 
$\mu \left( r\right) \mu \left( r^{\prime}\right) =\pi
^{2}/4 $.
This completes the proof.
(1) It was proved in [Reference Anderson, Vamanamurthy and Vuorinen6, Theorem 5.54] that the function
$r\mapsto \mu \left( r\right) -\phi _{6}\left( r\right) $ is increasing from $\left( 0,1\right) $ onto $\left( \ln 4,\infty \right) $. Now, we can give a new proof of this by using Theorem 4.1. In fact, the increasing property of $r\mapsto \phi _{6}^{\prime}\left(
r\right) /\mu ^{\prime}\left( r\right) $ on $\left( 0,1\right) $ yields that
\begin{equation*}
\frac{\phi _{6}^{\prime}\left( r\right) }{\mu ^{\prime}\left( r\right) } \gt \lim_{r\rightarrow 0^{+}}\frac{\phi _{6}^{\prime}\left( r\right) }{\mu
^{\prime}\left( r\right) }=1
\end{equation*}for
$r\in \left( 0,1\right) $. This together with $\mu ^{\prime}\left(
r\right) \lt 0$ implies that
\begin{equation*}
\left[ \mu \left( r\right) -\phi _{6}\left( r\right) \right] ^{\prime}=\mu
^{\prime}\left( r\right) \left[ 1-\frac{\phi _{6}^{\prime}\left( r\right)
}{\mu ^{\prime}\left( r\right) }\right] \gt 0
\end{equation*}for
$r\in \left( 0,1\right)$.(2) Rewrite equation (4.4) as
\begin{equation*}
0 \lt \frac{\mu \left( r\right) -\ln \left( 4/\sqrt{\rho }\right) }{\mu \left(
r\right) } \lt 1-\frac{4\ln 2-\ln \left( \ln 2\right) }{\pi }=0.000\,792\,913\cdots
\end{equation*}for
$r\in \left( 0,1/\sqrt{2}\right)$. This shows that $\ln \left( 4/\sqrt{
\rho }\right) $ is a very accurate estimation of $\mu \left( r\right) $ on $
\left( 0,1/\sqrt{2}\right) $.
5. Conclusions
In this paper, we proved that 
$\mu \left( r\right) =\ln \left( 4/r\right)
-\sum_{n=1}^{\infty }\left[ \theta _{n}/\left( 2n\right) \right] r^{2n}$, with 
$\theta _{n}\in \left( 0,1\right) $ for every 
$n\in \mathbb{N}$ by the recursion method. Thereout, we further showed some elegant results, for example,
(i) the functions
$r\mapsto -\left[ \mu \left( r\right) +\ln r\right]
^{\prime}$, $r\mapsto \mu \left( r\right) +\ln \left( r/r^{\prime}\right) $, $r\mapsto -[ \mu ( r) +\ln ( r/( 1+r^{\prime}) )] ^{\prime}$ and $r\mapsto \exp \left( -2\mu \left(
r\right) \right) $ are absolutely monotonic on $\left( 0,1\right) $;(ii) the functions
$t\mapsto \mu \left( \text{e}^{-t}\right) /t$ and $t\mapsto
1-\mu \left( e^{-t}\right) /\left( t+\ln 4\right) $ are completely monotonic on $\left( 0,1\right) $;(iii) the functions
$t\mapsto 1/\mu \left( \text{e}^{-t}\right) $ and $t\mapsto
( t+\ln 4) /\mu ( \text{e}^{-t}) $ are logarithmically completely monotonic on $\left( 0,\infty \right) $;(iv) the functions
$s\mapsto \gamma \left( s\right) $ and $s\mapsto \gamma
\left( s\right) \ln \left( 4s\right) $ are logarithmically completely monotonic on $\left( 1,\infty \right) $;(v) the function
$\alpha \mapsto \mu \left( r^{\alpha }\right) /\alpha $ is completely monotonic on $\left( 0,\infty \right) $.
As applications, several sharp bounds and functional inequalities for 
$\mu \left( r\right)$ were derived, and they are new. In particular, we proved that the double inequality
\begin{equation*}
\ln \frac{4}{r}-\sum_{k=1}^{n-1}\frac{\theta _{k}}{2k}r^{2k}-\alpha
_{1}r^{2n} \lt \mu \left( r\right) \lt \ln \frac{4}{r}-\sum_{k=1}^{n-1}\frac{\theta
_{k}}{2k}r^{2k}-\beta _{1}r^{2n}
\end{equation*} holds for all 
$r\in\left(0,1\right) $ with the best possible constants
\begin{equation*}
\alpha _{1}=\ln 4-\sum_{k=1}^{n-1}\frac{\theta _{k}}{2k}\text{\ and \ }
\beta _{1}=\frac{\theta _{n}}{2n}.
\end{equation*} Here, 
$\theta _{n}=\sum_{k=1}^{n}\left( a_{k-1}-a_{k}\right) \theta_{n-k}$, 
$a_{n}=\sum_{k=0}^{n}\left( W_{k}^{2}W_{n-k}^{2}\right) $ and Wn is the Wallis ratio defined by equation (1.1). Using the above formula of θn, we can calculate the value of θn for any fixed 
$n\in \mathbb{N}$. For example,
\begin{align*}
&\theta_{1}=\frac{1}{2},\quad \theta_{2}=\frac{13}{23},\quad \theta_{3}=\frac{23}{64},\quad \theta_{4}=\frac{2701}{8192},\quad \theta_{5}=\frac{5057}{16384}, \quad \theta_{6}=\frac{76715}{262144},\\
&\theta_{7}=\frac{146749}{5242288},\quad \theta_{8}=\frac{1446447449}{536870912},\quad \theta_{9}=\frac{279805685}{1073741824},\quad \theta_{10}=\frac{4346533901}{17179869184}.
\end{align*}Besides, we also showed that the double inequality
\begin{equation*}
\beta _{4}\ln \frac{4}{\sqrt{-\ln(1-r^2)}} \lt \mu \left( r\right) \lt \alpha _{4}\ln
\frac{4}{\sqrt{-\ln(1-r^2)}}
\end{equation*} holds for 
$r\in \left( 0,1/\sqrt{2}\right) $ with the best constants
\begin{equation*}
\beta _{4}=1\text{\ and \ }\alpha _{4}=\frac{\pi }{4\ln 2-\ln \left( \ln
2\right) }=1.000\,793\,54\cdots\text{.}
\end{equation*}Funding Statement
This research was supported by the Natural Science Foundation of China under Grant no. 11701176 and Zhejiang Provincial Natural Science Foundation of China under Grant no. LY24A010011.
