1 Introduction
In the celebrated paper [Reference BlochBlo86], Bloch defined the higher Chow groups
![]() ${\mathrm {CH}}^p(X,q)$
for a variety X, which are generalizations of the classical Chow groups. They are identified with the motivic cohomology when X is smooth. Higher Chow groups appear in many aspects of algebraic geometry and number theory and are related to many important problems. However, their structures are still mysterious for many varieties when the codimension p is greater than 1. In general, it is not easy to construct nontrivial higher Chow cycles (cf. [Reference FlachFla92, Reference MildenhallMil92, Reference SpießSpi99]).
${\mathrm {CH}}^p(X,q)$
for a variety X, which are generalizations of the classical Chow groups. They are identified with the motivic cohomology when X is smooth. Higher Chow groups appear in many aspects of algebraic geometry and number theory and are related to many important problems. However, their structures are still mysterious for many varieties when the codimension p is greater than 1. In general, it is not easy to construct nontrivial higher Chow cycles (cf. [Reference FlachFla92, Reference MildenhallMil92, Reference SpießSpi99]).
We study
![]() ${\mathrm {CH}}^2(X,1)$
for a certain type of Kummer surfaces X. A cycle
${\mathrm {CH}}^2(X,1)$
for a certain type of Kummer surfaces X. A cycle
![]() ${\xi \in {\mathrm {CH}}^2(X,1)}$
is called indecomposable if it is not contained in the image of the map
${\xi \in {\mathrm {CH}}^2(X,1)}$
is called indecomposable if it is not contained in the image of the map
induced by the intersection product. The image of this map is called the decomposable part: this is an easily accessible part. The cokernel of this map is called the indecomposable part and is denoted by
![]() ${\mathrm {CH}}^2(X,1)_{\mathrm {ind}}$
. We are interested in the size of
${\mathrm {CH}}^2(X,1)_{\mathrm {ind}}$
. We are interested in the size of
![]() ${\mathrm {CH}}^2(X,1)_{\mathrm {ind}}$
. Explicit constructions of nontrivial elements of
${\mathrm {CH}}^2(X,1)_{\mathrm {ind}}$
. Explicit constructions of nontrivial elements of
![]() ${\mathrm {CH}}^2(X,1)_{\mathrm {ind}}$
for
${\mathrm {CH}}^2(X,1)_{\mathrm {ind}}$
for
![]() $K3$
surfaces X were initiated by Müller–Stach [Reference Müller-StachMS97]. Since then, further examples have been constructed (see [Reference Chen, Doran, Kerr and LewisCDKL16, Reference Chen and LewisCL05, Reference CollinoCol99, Reference del Angel and Müller-StachdAMS02, Reference KerrKer13, Reference SasakiSas21]).
$K3$
surfaces X were initiated by Müller–Stach [Reference Müller-StachMS97]. Since then, further examples have been constructed (see [Reference Chen, Doran, Kerr and LewisCDKL16, Reference Chen and LewisCL05, Reference CollinoCol99, Reference del Angel and Müller-StachdAMS02, Reference KerrKer13, Reference SasakiSas21]).
In this paper, we study a two-dimensional family of Kummer surfaces
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
associated with products of elliptic curves. We construct a collection of families of higher Chow cycles on
$\widetilde {{\mathcal {X}}}\rightarrow T$
associated with products of elliptic curves. We construct a collection of families of higher Chow cycles on
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
. They generate a subgroup
$\widetilde {{\mathcal {X}}}\rightarrow T$
. They generate a subgroup
![]() $\Xi _t$
of
$\Xi _t$
of
![]() ${\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{{\mathrm {ind}}}$
for every
${\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{{\mathrm {ind}}}$
for every
![]() $t\in T$
. Our main result is the following.
$t\in T$
. Our main result is the following.
Theorem 1.1 (Theorem 7.1) For a very generalFootnote
1
![]() $t\in T$
, we have
$t\in T$
, we have
![]() ${\mathrm {rank}\:} \Xi _t \ge 18$
. In particular,
${\mathrm {rank}\:} \Xi _t \ge 18$
. In particular,
![]() ${\mathrm {rank}\:} {\mathrm {CH}}^2({\mathcal {X}}_t,1)_{\mathrm {ind}} \ge 18$
.
${\mathrm {rank}\:} {\mathrm {CH}}^2({\mathcal {X}}_t,1)_{\mathrm {ind}} \ge 18$
.
Our construction uses the realization of the Kummer surfaces as the desingularized double coverings of
![]() ${\mathbb {P}}^1\times {\mathbb {P}}^1$
, and our construction of higher Chow cycles uses special types of
${\mathbb {P}}^1\times {\mathbb {P}}^1$
, and our construction of higher Chow cycles uses special types of
![]() $(1,1)$
-curves on
$(1,1)$
-curves on
![]() ${\mathbb {P}}^1\times {\mathbb {P}}^1$
. This is similar to the construction of higher Chow cycles on abelian surfaces in [Reference SreekantanSre14]. The fact that
${\mathbb {P}}^1\times {\mathbb {P}}^1$
. This is similar to the construction of higher Chow cycles on abelian surfaces in [Reference SreekantanSre14]. The fact that
![]() ${\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{\mathrm {ind}} \neq 0$
already follows from the result of Section 6 of [Reference Chen, Doran, Kerr and LewisCDKL16] because our family is a base change of the family considered there. Our novelty here is the rank estimate
${\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{\mathrm {ind}} \neq 0$
already follows from the result of Section 6 of [Reference Chen, Doran, Kerr and LewisCDKL16] because our family is a base change of the family considered there. Our novelty here is the rank estimate
![]() ${{\mathrm {rank}\:} {\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{\mathrm {ind}}\ge 18}$
. To produce many indecomposable cycles, we use a group action on the family as we will explain below.
${{\mathrm {rank}\:} {\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{\mathrm {ind}}\ge 18}$
. To produce many indecomposable cycles, we use a group action on the family as we will explain below.
A standard way to detect indecomposability is to use the transcendental regulator map

where the first map is the Beilinson regulator map and the last is the natural projection. It is known that the map r factors through
![]() ${\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{\mathrm {ind}}$
. For a family
${\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{\mathrm {ind}}$
. For a family
![]() $\{\xi _t\}_{t\in T}$
of higher Chow cycles on
$\{\xi _t\}_{t\in T}$
of higher Chow cycles on
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
, their transcendental regulators give rise to a certain type of normal function
$\widetilde {{\mathcal {X}}}\rightarrow T$
, their transcendental regulators give rise to a certain type of normal function
![]() $\nu _{\mathrm {tr}}(\xi )=\{r(\xi _t)\}_{t\in T}$
. If we take the pairing of
$\nu _{\mathrm {tr}}(\xi )=\{r(\xi _t)\}_{t\in T}$
. If we take the pairing of
![]() $\nu _{{\mathrm {tr}}}(\xi )$
with a relative 2-form
$\nu _{{\mathrm {tr}}}(\xi )$
with a relative 2-form
![]() $\omega $
on
$\omega $
on
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
, this gives a multivalued holomorphic function on T.
$\widetilde {{\mathcal {X}}}\rightarrow T$
, this gives a multivalued holomorphic function on T.
Our construction begins with an initial cycle family
![]() $\xi _1-\xi _0$
(see Section 4 for the definition). For this cycle family, the above multivalued function is given by the improper integral
$\xi _1-\xi _0$
(see Section 4 for the definition). For this cycle family, the above multivalued function is given by the improper integral
 $$ \begin{align} {\mathcal{L}} (a,b) = 2\int_{\triangle}\frac{dxdy}{\sqrt{x(1-x)(1-ax)}\sqrt{y(1-y)(1-by)}}, \end{align} $$
$$ \begin{align} {\mathcal{L}} (a,b) = 2\int_{\triangle}\frac{dxdy}{\sqrt{x(1-x)(1-ax)}\sqrt{y(1-y)(1-by)}}, \end{align} $$
where
![]() $\triangle =\{(x,y)\in {\mathbb {R}}^2\::\: 0<y<x<1\}$
. The integral (1) is similar to the integral representation of Appell’s hypergeometric functions (though the boundary
$\triangle =\{(x,y)\in {\mathbb {R}}^2\::\: 0<y<x<1\}$
. The integral (1) is similar to the integral representation of Appell’s hypergeometric functions (though the boundary
![]() $\partial \triangle $
is not necessarily contained in the branching locus of the integrand). What is important to us is that
$\partial \triangle $
is not necessarily contained in the branching locus of the integrand). What is important to us is that
![]() ${\mathcal {L}}$
satisfies the following system of inhomogeneous differential equations:
${\mathcal {L}}$
satisfies the following system of inhomogeneous differential equations:
 $$ \begin{align} \left\{ \begin{aligned} a(1-a) \frac{\partial^2{\mathcal{L}}}{\partial a^2} +(1-2a)\frac{\partial{\mathcal{L}}}{\partial a} -\frac{1}{4}{\mathcal{L}} &= \frac{2}{a-b}\left(\frac{\sqrt{1-b}}{\sqrt{1-a}}-1\right), \\ b(1-b) \frac{\partial^2{\mathcal{L}}}{\partial b^2} +(1-2b)\frac{\partial{\mathcal{L}}}{\partial b} -\frac{1}{4}{\mathcal{L}} &= \frac{2}{a-b}\left(1-\frac{\sqrt{1-a}}{\sqrt{1-b}}\right). \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} a(1-a) \frac{\partial^2{\mathcal{L}}}{\partial a^2} +(1-2a)\frac{\partial{\mathcal{L}}}{\partial a} -\frac{1}{4}{\mathcal{L}} &= \frac{2}{a-b}\left(\frac{\sqrt{1-b}}{\sqrt{1-a}}-1\right), \\ b(1-b) \frac{\partial^2{\mathcal{L}}}{\partial b^2} +(1-2b)\frac{\partial{\mathcal{L}}}{\partial b} -\frac{1}{4}{\mathcal{L}} &= \frac{2}{a-b}\left(1-\frac{\sqrt{1-a}}{\sqrt{1-b}}\right). \end{aligned} \right. \end{align} $$
We denote the differential operators appearing in the left-hand side of (2) by
![]() ${\mathscr {D}}_1$
and
${\mathscr {D}}_1$
and
![]() ${\mathscr {D}}_2$
, respectively. Note that they are the Gauss hypergeometric differential operators of type
${\mathscr {D}}_2$
, respectively. Note that they are the Gauss hypergeometric differential operators of type
![]() $\left (\frac {1}{2},\frac {1}{2},1\right )$
. Since the periods of
$\left (\frac {1}{2},\frac {1}{2},1\right )$
. Since the periods of
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
are annihilated by
$\widetilde {{\mathcal {X}}}\rightarrow T$
are annihilated by
![]() ${\mathscr {D}}=({\mathscr {D}}_1,{\mathscr {D}}_2)$
,
${\mathscr {D}}=({\mathscr {D}}_1,{\mathscr {D}}_2)$
,
![]() ${\mathscr {D}}$
is called a Picard–Fuchs differential operator on
${\mathscr {D}}$
is called a Picard–Fuchs differential operator on
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
. From the differential equations (2), we see that the image of
$\widetilde {{\mathcal {X}}}\rightarrow T$
. From the differential equations (2), we see that the image of
![]() $(\xi _1)_t-(\xi _0)_t$
under the transcendental regulator is nontrivial for very general t.
$(\xi _1)_t-(\xi _0)_t$
under the transcendental regulator is nontrivial for very general t.
The second part of our construction is to produce more cycles from
![]() $\xi _1-\xi _0$
by using a group action on
$\xi _1-\xi _0$
by using a group action on
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
. For our purpose, automorphisms which act trivially on T are not sufficient. We consider a finite group
$\widetilde {{\mathcal {X}}}\rightarrow T$
. For our purpose, automorphisms which act trivially on T are not sufficient. We consider a finite group
![]() $G_{{\mathcal {X}}}$
(isomorphic to a
$G_{{\mathcal {X}}}$
(isomorphic to a
![]() ${\mathbb {Z}}/2$
-extension of
${\mathbb {Z}}/2$
-extension of
![]() $(\mathfrak {S}_4\times _{\mathfrak {S}_3} \mathfrak {S}_4)^2$
) which acts on the total space
$(\mathfrak {S}_4\times _{\mathfrak {S}_3} \mathfrak {S}_4)^2$
) which acts on the total space
![]() $\widetilde {{\mathcal {X}}}$
and also on the base T. By letting
$\widetilde {{\mathcal {X}}}$
and also on the base T. By letting
![]() $G_{{\mathcal {X}}}$
act on
$G_{{\mathcal {X}}}$
act on
![]() $\xi _1-\xi _0$
, we obtain the subgroup
$\xi _1-\xi _0$
, we obtain the subgroup
![]() $\Xi _t$
of
$\Xi _t$
of
![]() ${\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{{\mathrm {ind}}}$
. To show that
${\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{{\mathrm {ind}}}$
. To show that
![]() $\Xi _t$
has rank
$\Xi _t$
has rank
![]() $\ge 18$
, we consider the
$\ge 18$
, we consider the
![]() $G_{{\mathcal {X}}}$
-action on the normal function of
$G_{{\mathcal {X}}}$
-action on the normal function of
![]() $\xi _1-\xi _0$
and the differential equations (2) it satisfies. This is the second main calculation in this paper.
$\xi _1-\xi _0$
and the differential equations (2) it satisfies. This is the second main calculation in this paper.
Inhomogeneous Picard–Fuchs differential equations arising from normal functions are studied recently (e.g., [Reference del Angel and Müller-StachdAMS08]). The differential equations (2) is a
![]() ${\mathbb {Q}}(0)$
-extension of the exterior tensor product of the two Gauss hypergeometric differential equations. Hence, this is an example where the normal function can be expressed by a variant of hypergeometric functions. In [Reference Asakura and OtsuboAO21], Asakura and Otsubo constructed a family of varieties and cycles whose normal functions are expressed by the generalized hypergeometric function
${\mathbb {Q}}(0)$
-extension of the exterior tensor product of the two Gauss hypergeometric differential equations. Hence, this is an example where the normal function can be expressed by a variant of hypergeometric functions. In [Reference Asakura and OtsuboAO21], Asakura and Otsubo constructed a family of varieties and cycles whose normal functions are expressed by the generalized hypergeometric function
![]() ${}_3F_2$
. Our cycles give an analogous example.
${}_3F_2$
. Our cycles give an analogous example.
1.1 Outline of the paper
This paper is divided into two parts. Part 1 is devoted to the construction of the initial cycle family
![]() $\xi _1-\xi _0$
and the computation of its normal function. In Section 2, we recall basic facts about higher Chow cycles and the regulator map. In Sections 3 and 4, we define the family of Kummer surfaces and higher Chow cycles. In Section 5, we compute the normal function of
$\xi _1-\xi _0$
and the computation of its normal function. In Section 2, we recall basic facts about higher Chow cycles and the regulator map. In Sections 3 and 4, we define the family of Kummer surfaces and higher Chow cycles. In Section 5, we compute the normal function of
![]() $\xi _1-\xi _0$
and deduce the indecomposability. Part 2 is devoted to the construction and calculation of the group action. In Section 6, we construct the finite group action on the Kummer family. In Section 7, we construct more higher Chow cycles using the group action and calculate the images of their normal functions under the Picard–Fuchs differential operator. This calculation is based on the transformation formula proved in Section 8.
$\xi _1-\xi _0$
and deduce the indecomposability. Part 2 is devoted to the construction and calculation of the group action. In Section 6, we construct the finite group action on the Kummer family. In Section 7, we construct more higher Chow cycles using the group action and calculate the images of their normal functions under the Picard–Fuchs differential operator. This calculation is based on the transformation formula proved in Section 8.
1.2 List of notations
We summarize the frequently used notations in this paper. Usually,
![]() $\widetilde {(-)}$
indicates a blow-up. The subscript
$\widetilde {(-)}$
indicates a blow-up. The subscript
![]() $0$
(e.g.,
$0$
(e.g.,
![]() $T_0$
) means an initial space; when it is taken out (e.g.,
$T_0$
) means an initial space; when it is taken out (e.g.,
![]() $T\rightarrow T_0$
), this means taking an étale cover or an étale base change (e.g.,
$T\rightarrow T_0$
), this means taking an étale cover or an étale base change (e.g.,
![]() $\widetilde {{\mathcal {X}}}\rightarrow \widetilde {{\mathcal {X}}}_0$
).
$\widetilde {{\mathcal {X}}}\rightarrow \widetilde {{\mathcal {X}}}_0$
).

2 Preliminaries
2.1 Higher Chow cycles of type (2,1)
For a smooth variety X over
![]() ${\mathbb {C}}$
, let
${\mathbb {C}}$
, let
![]() ${\mathrm {CH}}^p(X,q)$
be the higher Chow group defined by Bloch. In this paper, we treat the case
${\mathrm {CH}}^p(X,q)$
be the higher Chow group defined by Bloch. In this paper, we treat the case
![]() $(p,q)=(2,1)$
. In this case, the following fact is well-known (see, e.g., [Reference Müller-StachMS98, Corollary 5.3]).
$(p,q)=(2,1)$
. In this case, the following fact is well-known (see, e.g., [Reference Müller-StachMS98, Corollary 5.3]).
Proposition 2.1 The higher Chow group
![]() $\mathrm {CH}^2(X,1)$
is isomorphic to the middle homology group of the following complex:
$\mathrm {CH}^2(X,1)$
is isomorphic to the middle homology group of the following complex:
Here,
![]() $X^{(r)}$
denotes the set of closed subvarieties of X of codimension r. The map T denotes the tame symbol map from the Milnor
$X^{(r)}$
denotes the set of closed subvarieties of X of codimension r. The map T denotes the tame symbol map from the Milnor
![]() $K_2$
-group of the function field
$K_2$
-group of the function field
![]() ${\mathbb {C}}(X)$
.
${\mathbb {C}}(X)$
.
Therefore, a higher Chow cycle in
![]() $\mathrm {CH}^2(X,1)$
is represented by a formal sum
$\mathrm {CH}^2(X,1)$
is represented by a formal sum
where
![]() $C_j$
are prime divisors on X and
$C_j$
are prime divisors on X and
![]() $f_j\in {\mathbb {C}}(C_j)^\times $
are nonzero rational functions on them such that
$f_j\in {\mathbb {C}}(C_j)^\times $
are nonzero rational functions on them such that
![]() $\sum _j {\mathrm {div}}_{C_j}(f_j) = 0$
as codimension two cycles on X.
$\sum _j {\mathrm {div}}_{C_j}(f_j) = 0$
as codimension two cycles on X.
A decomposable cycle in
![]() $\mathrm {CH}^2(X,1)$
is an element of the image of the group homomorphism
$\mathrm {CH}^2(X,1)$
is an element of the image of the group homomorphism
induced by the intersection product. Let C be a prime divisor on X, and let
![]() $[C]\in \mathrm {Pic}(X)$
be the class corresponding to C. The image of
$[C]\in \mathrm {Pic}(X)$
be the class corresponding to C. The image of
![]() $[C]\otimes \alpha $
under (4) is represented by
$[C]\otimes \alpha $
under (4) is represented by
![]() $(C,\alpha |_C)$
in the presentation (3). The cokernel of (4) is denoted by
$(C,\alpha |_C)$
in the presentation (3). The cokernel of (4) is denoted by
![]() $\mathrm {CH}^2(X,1)_{\mathrm {ind}}$
. For
$\mathrm {CH}^2(X,1)_{\mathrm {ind}}$
. For
![]() $\xi \in {\mathrm {CH}}^2(X,1)$
,
$\xi \in {\mathrm {CH}}^2(X,1)$
,
![]() $\xi _{{\mathrm {ind}}}$
denotes its image in
$\xi _{{\mathrm {ind}}}$
denotes its image in
![]() $\mathrm {CH}^2(X,1)_{\mathrm {ind}}$
. A cycle
$\mathrm {CH}^2(X,1)_{\mathrm {ind}}$
. A cycle
![]() $\xi $
is called indecomposable if
$\xi $
is called indecomposable if
![]() $\xi _{{\mathrm {ind}} }\neq 0$
.
$\xi _{{\mathrm {ind}} }\neq 0$
.
2.2 The regulator map
By the canonical identification of
![]() $\mathrm {CH}^2(X,1)$
with the motivic cohomology
$\mathrm {CH}^2(X,1)$
with the motivic cohomology
![]() $H^3_M(X,{\mathbb {Z}}(2))$
, there exists the map
$H^3_M(X,{\mathbb {Z}}(2))$
, there exists the map
 $$ \begin{align} \mathrm{reg}: \mathrm{CH}^2(X,1) \longrightarrow H^3_{\mathcal D}(X, {\mathbb{Z}}(2)) = \frac{H^2(X,{\mathbb{C}})}{F^2H^2(X,{\mathbb{C}})+H^2(X,{\mathbb{Z}}(2))} \end{align} $$
$$ \begin{align} \mathrm{reg}: \mathrm{CH}^2(X,1) \longrightarrow H^3_{\mathcal D}(X, {\mathbb{Z}}(2)) = \frac{H^2(X,{\mathbb{C}})}{F^2H^2(X,{\mathbb{C}})+H^2(X,{\mathbb{Z}}(2))} \end{align} $$
called the regulator map. The target
![]() $H^3_{\mathcal D}(X, {\mathbb {Z}}(2))$
denotes the Deligne cohomology of X. This map can be regarded as the Abel–Jacobi map for
$H^3_{\mathcal D}(X, {\mathbb {Z}}(2))$
denotes the Deligne cohomology of X. This map can be regarded as the Abel–Jacobi map for
![]() ${\mathrm {CH}}^2(X,1)$
. We recall an explicit formula for (5) following [Reference LevineLev88, pp. 458–459].
${\mathrm {CH}}^2(X,1)$
. We recall an explicit formula for (5) following [Reference LevineLev88, pp. 458–459].
Let X be a
![]() $K3$
surface over
$K3$
surface over
![]() ${\mathbb {C}}$
. By the Poincaré duality, the Deligne cohomology of X is isomorphic to the generalized complex torus
${\mathbb {C}}$
. By the Poincaré duality, the Deligne cohomology of X is isomorphic to the generalized complex torus
 $$ \begin{align} H^3_{\mathcal{D}}(X, {\mathbb{Z}}(2)) \simeq \frac{(F^1H^2(X,{\mathbb{C}}))^\vee}{H_2(X,{\mathbb{Z}})}, \end{align} $$
$$ \begin{align} H^3_{\mathcal{D}}(X, {\mathbb{Z}}(2)) \simeq \frac{(F^1H^2(X,{\mathbb{C}}))^\vee}{H_2(X,{\mathbb{Z}})}, \end{align} $$
where
![]() $(F^1H^2(X,{\mathbb {C}}))^\vee $
is the dual
$(F^1H^2(X,{\mathbb {C}}))^\vee $
is the dual
![]() ${\mathbb {C}}$
-vector space of
${\mathbb {C}}$
-vector space of
![]() $F^1H^2(X,{\mathbb {C}})$
and we regard
$F^1H^2(X,{\mathbb {C}})$
and we regard
![]() $H_2(X,{\mathbb {Z}})$
as a subgroup of
$H_2(X,{\mathbb {Z}})$
as a subgroup of
![]() $(F^1H^2(X,{\mathbb {C}}))^\vee $
by the integration. Under the isomorphism (6), the image of the cycle
$(F^1H^2(X,{\mathbb {C}}))^\vee $
by the integration. Under the isomorphism (6), the image of the cycle
![]() $\xi $
represented by a formal sum
$\xi $
represented by a formal sum
![]() $\sum _j (C_j, f_j)$
under the regulator map is described as follows.
$\sum _j (C_j, f_j)$
under the regulator map is described as follows.
Let
![]() $D_j$
be the normalization of the closed curve
$D_j$
be the normalization of the closed curve
![]() $C_j$
on X. Let
$C_j$
on X. Let
![]() $\mu _j: D_j\rightarrow X$
denote the composition of
$\mu _j: D_j\rightarrow X$
denote the composition of
![]() $D_j\rightarrow C_j$
and
$D_j\rightarrow C_j$
and
![]() $C_j\rightarrow X$
. We will define a topological 1-chain
$C_j\rightarrow X$
. We will define a topological 1-chain
![]() $\gamma _j$
on
$\gamma _j$
on
![]() $D_j$
. If
$D_j$
. If
![]() $f_j$
is constant, we define
$f_j$
is constant, we define
![]() $\gamma _j = 0$
. If
$\gamma _j = 0$
. If
![]() $f_j$
is not constant, we regard
$f_j$
is not constant, we regard
![]() $f_j$
as a finite morphism from
$f_j$
as a finite morphism from
![]() $D_j$
to
$D_j$
to
![]() ${\mathbb {P}}^1$
. Then we define
${\mathbb {P}}^1$
. Then we define
![]() $\gamma _j = f_j^{-1}([\infty , 0]),$
where
$\gamma _j = f_j^{-1}([\infty , 0]),$
where
![]() $[\infty , 0]$
is a path on
$[\infty , 0]$
is a path on
![]() ${\mathbb {P}}^1$
from
${\mathbb {P}}^1$
from
![]() $\infty $
to
$\infty $
to
![]() $0$
along the positive real axis. By the condition,
$0$
along the positive real axis. By the condition,
![]() $\sum _j {\mathrm {div}}_{C_j}(f_j) = 0$
,
$\sum _j {\mathrm {div}}_{C_j}(f_j) = 0$
,
![]() $\gamma = \sum _j (\mu _j)_*\gamma _j$
is a topological 1-cycle on X. Since
$\gamma = \sum _j (\mu _j)_*\gamma _j$
is a topological 1-cycle on X. Since
![]() $H_1(X, {\mathbb {Z}}) = 0$
, there exists a 2-chain
$H_1(X, {\mathbb {Z}}) = 0$
, there exists a 2-chain
![]() $\Gamma $
on X such that
$\Gamma $
on X such that
![]() $\partial \Gamma = \gamma $
. In this paper,
$\partial \Gamma = \gamma $
. In this paper,
![]() $\gamma $
and
$\gamma $
and
![]() $\Gamma $
are called the 1-cycle associated with
$\Gamma $
are called the 1-cycle associated with
![]() $\xi $
and a 2-chain associated with
$\xi $
and a 2-chain associated with
![]() $\xi $
, respectively. Then the image of
$\xi $
, respectively. Then the image of
![]() $\xi $
under the regulator map is represented by the pairing
$\xi $
under the regulator map is represented by the pairing
 $$ \begin{align*} \langle \mathrm{reg}(\xi), [\omega]\rangle = \displaystyle\int_\Gamma\omega + \sum_j\dfrac{1}{2\pi\sqrt{-1}}\displaystyle\int_{D_j-\gamma_j}\log (f_j)\mu_j^*\omega\quad ([\omega]\in F^1H^2(X,{\mathbb{C}})). \end{align*} $$
$$ \begin{align*} \langle \mathrm{reg}(\xi), [\omega]\rangle = \displaystyle\int_\Gamma\omega + \sum_j\dfrac{1}{2\pi\sqrt{-1}}\displaystyle\int_{D_j-\gamma_j}\log (f_j)\mu_j^*\omega\quad ([\omega]\in F^1H^2(X,{\mathbb{C}})). \end{align*} $$
Here,
![]() $\log (f_j)$
is the pull-back of the logarithmic function on
$\log (f_j)$
is the pull-back of the logarithmic function on
![]() ${\mathbb {P}}^1-[\infty ,0]$
by
${\mathbb {P}}^1-[\infty ,0]$
by
![]() $f_j$
.
$f_j$
.
In this paper, we use the following variant of the regulator map.
Definition 2.2 The transcendental regulator map is the composite of the regulator map 5 and the projection induced by
![]() $H^{2,0}(X) \hookrightarrow F^1H^2(X,{\mathbb {C}})$
:
$H^{2,0}(X) \hookrightarrow F^1H^2(X,{\mathbb {C}})$
:

We denote this map by r.
By taking the pairing with a nonzero holomorphic 2-form
![]() $\omega $
on X, we have an isomorphism
$\omega $
on X, we have an isomorphism
![]() $H^{2,0}(X)^\vee /H_2(X,{\mathbb {Z}}) \simeq {\mathbb {C}}/{\mathcal {P}}(\omega ),$
where
$H^{2,0}(X)^\vee /H_2(X,{\mathbb {Z}}) \simeq {\mathbb {C}}/{\mathcal {P}}(\omega ),$
where
![]() ${\mathcal {P}}(\omega )$
is the subgroup of
${\mathcal {P}}(\omega )$
is the subgroup of
![]() ${\mathbb {C}}$
defined by
${\mathbb {C}}$
defined by
i.e.,
![]() ${\mathcal {P}}(\omega )$
is the set of periods of X with respect to
${\mathcal {P}}(\omega )$
is the set of periods of X with respect to
![]() $\omega $
. By the above formula, the image of
$\omega $
. By the above formula, the image of
![]() $\xi \in {\mathrm {CH}}^2(X,1)$
under the transcendental regulator map is
$\xi \in {\mathrm {CH}}^2(X,1)$
under the transcendental regulator map is
where
![]() $\Gamma $
is a 2-chain associated with
$\Gamma $
is a 2-chain associated with
![]() $\xi $
. If
$\xi $
. If
![]() $\xi $
is decomposable,
$\xi $
is decomposable,
![]() $r(\xi ) = 0$
. This implies the following.
$r(\xi ) = 0$
. This implies the following.
Proposition 2.3 If
![]() $r(\xi )\neq 0$
, we have
$r(\xi )\neq 0$
, we have
![]() $\xi _{{\mathrm {ind}}}\neq 0$
. In other words, the transcendental regulator map factors through
$\xi _{{\mathrm {ind}}}\neq 0$
. In other words, the transcendental regulator map factors through
![]() ${\mathrm {CH}}^2(X,1)_{{\mathrm {ind}}}$
.
${\mathrm {CH}}^2(X,1)_{{\mathrm {ind}}}$
.
2.3 A relative setting
Since it is difficult to prove non-vanishingness of an element of
![]() $H^{2,0}(X)^\vee /H_2(X,{\mathbb {Z}})$
, we use its relative version. Let
$H^{2,0}(X)^\vee /H_2(X,{\mathbb {Z}})$
, we use its relative version. Let
![]() $\pi :{\mathcal {X}}\rightarrow S$
be an algebraic family of
$\pi :{\mathcal {X}}\rightarrow S$
be an algebraic family of
![]() $K3$
surfaces over a variety S. We define sheaves
$K3$
surfaces over a variety S. We define sheaves
![]() ${\mathcal {P}}$
and
${\mathcal {P}}$
and
![]() ${\mathcal {Q}}$
of abelian groups on S by
${\mathcal {Q}}$
of abelian groups on S by
 $$ \begin{align*} \begin{aligned} {\mathcal{P}} &= \mathrm{Im}(R^2\pi_*\underline{{\mathbb{Z}}}_ {{\mathcal{X}}}\rightarrow \mathcal{H}om_{{\mathcal{O}}^{{\mathrm{an}}}_{S}}(\pi_*\Omega^2_{{\mathcal{X}}/S}, {\mathcal{O}}^{\mathrm{an}}_{S})), \\ {\mathcal{Q}} &= \mathrm{Coker}(R^2\pi_*\underline{{\mathbb{Z}}}_ {{\mathcal{X}}}\rightarrow \mathcal{H}om_{{\mathcal{O}}^{{\mathrm{an}}}_{S}}(\pi_*\Omega^2_{{\mathcal{X}}/S}, {\mathcal{O}}^{\mathrm{an}}_{S})), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} {\mathcal{P}} &= \mathrm{Im}(R^2\pi_*\underline{{\mathbb{Z}}}_ {{\mathcal{X}}}\rightarrow \mathcal{H}om_{{\mathcal{O}}^{{\mathrm{an}}}_{S}}(\pi_*\Omega^2_{{\mathcal{X}}/S}, {\mathcal{O}}^{\mathrm{an}}_{S})), \\ {\mathcal{Q}} &= \mathrm{Coker}(R^2\pi_*\underline{{\mathbb{Z}}}_ {{\mathcal{X}}}\rightarrow \mathcal{H}om_{{\mathcal{O}}^{{\mathrm{an}}}_{S}}(\pi_*\Omega^2_{{\mathcal{X}}/S}, {\mathcal{O}}^{\mathrm{an}}_{S})), \end{aligned} \end{align*} $$
where
![]() $\underline {{\mathbb {Z}}}_{{\mathcal {X}}}$
is the constant sheaf on
$\underline {{\mathbb {Z}}}_{{\mathcal {X}}}$
is the constant sheaf on
![]() ${\mathcal {X}}$
and
${\mathcal {X}}$
and
![]() ${\mathcal {O}}^{\mathrm {an}}_{S}$
is the sheaf of holomorphic functions on S. Note that
${\mathcal {O}}^{\mathrm {an}}_{S}$
is the sheaf of holomorphic functions on S. Note that
![]() ${\mathcal {P}}$
is a local system on S.
${\mathcal {P}}$
is a local system on S.
By considering the pairing with a nonzero relative 2-form
![]() $\omega \in \Gamma ({\mathcal {X}},\Omega ^2_{{\mathcal {X}}/S})$
, we have an isomorphism
$\omega \in \Gamma ({\mathcal {X}},\Omega ^2_{{\mathcal {X}}/S})$
, we have an isomorphism
![]() $\mathcal {H}om_{{\mathcal {O}}^{{\mathrm {an}}}_{S}}(\pi _*\Omega ^2_{{\mathcal {X}}/S}, {\mathcal {O}}^{\mathrm {an}}_{S})\simeq {\mathcal {O}}^{\mathrm {an}}_{S}$
. Hence,
$\mathcal {H}om_{{\mathcal {O}}^{{\mathrm {an}}}_{S}}(\pi _*\Omega ^2_{{\mathcal {X}}/S}, {\mathcal {O}}^{\mathrm {an}}_{S})\simeq {\mathcal {O}}^{\mathrm {an}}_{S}$
. Hence,
![]() ${\mathcal {P}}$
is isomorphic to the subsheaf
${\mathcal {P}}$
is isomorphic to the subsheaf
![]() ${\mathcal {P}}_\omega $
of
${\mathcal {P}}_\omega $
of
![]() ${\mathcal {O}}^{\mathrm {an}}_{S}$
generated by period functions with respect to
${\mathcal {O}}^{\mathrm {an}}_{S}$
generated by period functions with respect to
![]() $\omega $
and
$\omega $
and
![]() ${\mathcal {Q}}$
is isomorphic to
${\mathcal {Q}}$
is isomorphic to
![]() ${\mathcal {Q}}_\omega = {\mathcal {O}}^{\mathrm {an}}_{S}/{\mathcal {P}}_\omega $
. For a local section
${\mathcal {Q}}_\omega = {\mathcal {O}}^{\mathrm {an}}_{S}/{\mathcal {P}}_\omega $
. For a local section
![]() $\varphi $
of
$\varphi $
of
![]() ${\mathcal {O}}^{\mathrm {an}}_{S}$
, its image in
${\mathcal {O}}^{\mathrm {an}}_{S}$
, its image in
![]() ${\mathcal {Q}}_\omega $
is denoted by
${\mathcal {Q}}_\omega $
is denoted by
![]() $[\varphi ]$
.
$[\varphi ]$
.
For each
![]() $s\in S$
, there exists the evaluation map
$s\in S$
, there exists the evaluation map
Under the isomorphisms
![]() ${\mathcal {Q}}\simeq {\mathcal {Q}}_{\omega }$
and
${\mathcal {Q}}\simeq {\mathcal {Q}}_{\omega }$
and
![]() $H^{2,0}({\mathcal {X}}_s)^\vee /H_2({\mathcal {X}}_s,{\mathbb {Z}})\simeq {\mathbb {C}}/{\mathcal {P}}(\omega _s)$
induced by
$H^{2,0}({\mathcal {X}}_s)^\vee /H_2({\mathcal {X}}_s,{\mathbb {Z}})\simeq {\mathbb {C}}/{\mathcal {P}}(\omega _s)$
induced by
![]() $\omega $
and
$\omega $
and
![]() $\omega _s$
, the evaluation map coincides with the map
$\omega _s$
, the evaluation map coincides with the map
where
![]() $f(s)\in {\mathbb {C}}$
denotes the value of the holomorphic function f at s. The following elementary lemma is crucial for the result.
$f(s)\in {\mathbb {C}}$
denotes the value of the holomorphic function f at s. The following elementary lemma is crucial for the result.
Lemma 2.4 For a nonzero element
![]() $\nu \in \Gamma (S,{\mathcal {Q}})$
, we have
$\nu \in \Gamma (S,{\mathcal {Q}})$
, we have
![]() ${\mathrm {ev}}_s(\nu )\neq 0$
for very general
${\mathrm {ev}}_s(\nu )\neq 0$
for very general
![]() $s\in S$
.
$s\in S$
.
Proof Since the question is local, we can shrink S in the sense of the classical topology. By fixing a relative 2-form
![]() $\omega \in \Gamma ({\mathcal {X}},\Omega _{{\mathcal {X}}/S}^2)$
, we have the isomorphism
$\omega \in \Gamma ({\mathcal {X}},\Omega _{{\mathcal {X}}/S}^2)$
, we have the isomorphism
![]() ${{\mathcal {Q}} \simeq {\mathcal {O}}_S^{\mathrm {an}}/{\mathcal {P}}_\omega} $
. We may assume that there exist a holomorphic function
${{\mathcal {Q}} \simeq {\mathcal {O}}_S^{\mathrm {an}}/{\mathcal {P}}_\omega} $
. We may assume that there exist a holomorphic function
![]() $\varphi \in {\mathcal {O}}_S^{{\mathrm {an}}}(S)$
such that
$\varphi \in {\mathcal {O}}_S^{{\mathrm {an}}}(S)$
such that
![]() $\nu = [\varphi ]$
and a free basis
$\nu = [\varphi ]$
and a free basis
![]() $f_1,f_2,\dots ,f_r$
of
$f_1,f_2,\dots ,f_r$
of
![]() ${\mathcal {P}}_\omega (S)$
.
${\mathcal {P}}_\omega (S)$
.
For each
![]() $\underline {c} = (c_i) \in {\mathbb {Z}}^r$
, we define the holomorphic function
$\underline {c} = (c_i) \in {\mathbb {Z}}^r$
, we define the holomorphic function
![]() $F_{\underline {c}}$
by
$F_{\underline {c}}$
by
 $$ \begin{align*} F_{\underline{c}} = \varphi - \sum_{i=1}^r c_if_i. \end{align*} $$
$$ \begin{align*} F_{\underline{c}} = \varphi - \sum_{i=1}^r c_if_i. \end{align*} $$
Since
![]() $\nu = [\varphi ]$
is nonzero in
$\nu = [\varphi ]$
is nonzero in
![]() ${\mathcal {Q}}_\omega (S)$
,
${\mathcal {Q}}_\omega (S)$
,
![]() $F_{\underline {c}}$
is a nonzero holomorphic function for each
$F_{\underline {c}}$
is a nonzero holomorphic function for each
![]() $\underline {c} \in {\mathbb {Z}}^r$
. Consider the countable family
$\underline {c} \in {\mathbb {Z}}^r$
. Consider the countable family
![]() $\{F_{\underline {c}}\}_{\underline {c}\in {\mathbb {Z}}^r}$
of the holomorphic functions. Then outside of the zeros of the functions in this family,
$\{F_{\underline {c}}\}_{\underline {c}\in {\mathbb {Z}}^r}$
of the holomorphic functions. Then outside of the zeros of the functions in this family,
![]() $\varphi (s)\not \in {\mathcal {P}}(\omega _s) = \langle f_1(s),f_2(s),\dots , f_r(s) \rangle _{\mathbb {Z}}$
. Hence
$\varphi (s)\not \in {\mathcal {P}}(\omega _s) = \langle f_1(s),f_2(s),\dots , f_r(s) \rangle _{\mathbb {Z}}$
. Hence
![]() ${\mathrm {ev}}_s(\nu )\neq 0$
.
${\mathrm {ev}}_s(\nu )\neq 0$
.
The following corollary is also used in technical propositions.
Corollary 2.5 If local sections
![]() $\nu , \nu '$
of
$\nu , \nu '$
of
![]() ${\mathcal {Q}}$
on an open subset U satisfy
${\mathcal {Q}}$
on an open subset U satisfy
![]() ${\mathrm {ev}}_s(\nu ) = {\mathrm {ev}}_s(\nu ')$
for any
${\mathrm {ev}}_s(\nu ) = {\mathrm {ev}}_s(\nu ')$
for any
![]() $s\in U$
, we have
$s\in U$
, we have
![]() $\nu =\nu '$
.
$\nu =\nu '$
.
Finally, we consider the regulator map in the relative setting. Suppose that we have irreducible divisors
![]() ${\mathcal {C}}_j$
on
${\mathcal {C}}_j$
on
![]() ${\mathcal {X}}$
which are smooth over S and nonzero rational functions
${\mathcal {X}}$
which are smooth over S and nonzero rational functions
![]() $f_j$
on
$f_j$
on
![]() ${\mathcal {C}}_j$
whose zeros and poles are also smooth over S. Assume that they satisfy the condition
${\mathcal {C}}_j$
whose zeros and poles are also smooth over S. Assume that they satisfy the condition
![]() $\sum _j{\mathrm {div}}_{({\mathcal {C}}_j)_s}((f_j)_s) = 0$
for each
$\sum _j{\mathrm {div}}_{({\mathcal {C}}_j)_s}((f_j)_s) = 0$
for each
![]() $s\in S$
. Then we have a family of higher Chow cycles
$s\in S$
. Then we have a family of higher Chow cycles
![]() $\xi = \{\xi _s\}_{s\in S}$
such that
$\xi = \{\xi _s\}_{s\in S}$
such that
![]() $\xi _s\in {\mathrm {CH}}^2({\mathcal {X}}_s,1)$
is represented by the formal sum
$\xi _s\in {\mathrm {CH}}^2({\mathcal {X}}_s,1)$
is represented by the formal sum
![]() $\sum _{j}(({\mathcal {C}}_j)_s,(f_j)_s)$
. A family of higher Chow cycles constructed in this way is called an algebraic family of higher Chow cycles in this paper.
$\sum _{j}(({\mathcal {C}}_j)_s,(f_j)_s)$
. A family of higher Chow cycles constructed in this way is called an algebraic family of higher Chow cycles in this paper.
Remark 2.6 In the above situation, let
![]() $\xi $
be the higher Chow cycle on the total space
$\xi $
be the higher Chow cycle on the total space
![]() ${\mathcal {X}}$
defined by the formal sum
${\mathcal {X}}$
defined by the formal sum
![]() $\sum _j({\mathcal {C}}_j,f_j)$
. For each
$\sum _j({\mathcal {C}}_j,f_j)$
. For each
![]() $s\in S$
,
$s\in S$
,
![]() $\xi _s \in {\mathrm {CH}}^2({\mathcal {X}}_s,1)$
is the pull-back of
$\xi _s \in {\mathrm {CH}}^2({\mathcal {X}}_s,1)$
is the pull-back of
![]() $\xi $
by
$\xi $
by
![]() ${\mathcal {X}}_s\hookrightarrow {\mathcal {X}}$
. Hence, we can regard an algebraic family of higher Chow cycle as a higher Chow cycle of the total space
${\mathcal {X}}_s\hookrightarrow {\mathcal {X}}$
. Hence, we can regard an algebraic family of higher Chow cycle as a higher Chow cycle of the total space
![]() ${\mathcal {X}}$
.
${\mathcal {X}}$
.
If we shrink S in the sense of the classical topology, there exists a
![]() $C^\infty $
-family of topological 2-chains
$C^\infty $
-family of topological 2-chains
![]() $\{\Gamma _s\}_{s\in S}$
such that
$\{\Gamma _s\}_{s\in S}$
such that
![]() $\Gamma _s$
is a 2-chain associated with
$\Gamma _s$
is a 2-chain associated with
![]() $\xi _s$
. If we fix a relative 2-form
$\xi _s$
. If we fix a relative 2-form
![]() $\omega $
, the function
$\omega $
, the function
is holomorphic (cf. [Reference Chen and LewisCL05, Proposition 4.1]). Hence, we can define the element
![]() ${\nu _{\mathrm {tr}}(\xi ) \in \Gamma (S,{\mathcal {Q}})}$
such that
${\nu _{\mathrm {tr}}(\xi ) \in \Gamma (S,{\mathcal {Q}})}$
such that
for every
![]() $s\in S$
. This
$s\in S$
. This
![]() $\nu _{\mathrm {tr}}(\xi )$
can be regarded as a part of the normal function associated with
$\nu _{\mathrm {tr}}(\xi )$
can be regarded as a part of the normal function associated with
![]() $\xi $
.
$\xi $
.
By combining Proposition 2.3 and Lemma 2.4, we have the following.
Proposition 2.7 Let
![]() ${\mathcal {X}}\rightarrow S$
be an algebraic family of
${\mathcal {X}}\rightarrow S$
be an algebraic family of
![]() $K3$
surfaces, and let
$K3$
surfaces, and let
![]() $\xi = \{\xi _s\}_{s\in S}$
be an algebraic family of higher Chow cycles. Suppose
$\xi = \{\xi _s\}_{s\in S}$
be an algebraic family of higher Chow cycles. Suppose
![]() $\nu _{\mathrm {tr}}(\xi )\neq 0$
. Then for very general
$\nu _{\mathrm {tr}}(\xi )\neq 0$
. Then for very general
![]() $s\in S$
, we have
$s\in S$
, we have
![]() $(\xi _s)_{{\mathrm {ind}}} \neq 0$
.
$(\xi _s)_{{\mathrm {ind}}} \neq 0$
.
3 The family of Kummer surfaces
In this section, we define the family of Kummer surfaces. This is the famous family, and our main purpose is to fix the notation. Let
![]() $S_0 = {\mathbb {P}}^1-\{0,1,\infty \}$
and
$S_0 = {\mathbb {P}}^1-\{0,1,\infty \}$
and
![]() $A_0= {\mathbb {C}}\left [c,\frac {1}{c(c-1)}\right ]$
be the coordinate ring of
$A_0= {\mathbb {C}}\left [c,\frac {1}{c(c-1)}\right ]$
be the coordinate ring of
![]() $S_0$
. Let
$S_0$
. Let
![]() ${\mathcal {E}}\rightarrow S_0$
be the Legendre family of elliptic curves over
${\mathcal {E}}\rightarrow S_0$
be the Legendre family of elliptic curves over
![]() $S_0$
. The fiber of
$S_0$
. The fiber of
![]() ${\mathcal {E}} \rightarrow S_0$
over
${\mathcal {E}} \rightarrow S_0$
over
![]() $c\in S_0$
is the elliptic curve
$c\in S_0$
is the elliptic curve
We have the natural
![]() $S_0$
-morphism
$S_0$
-morphism
![]() ${\mathcal {E}} \rightarrow {\mathbb {P}}^1\times S_0$
defined by
${\mathcal {E}} \rightarrow {\mathbb {P}}^1\times S_0$
defined by
![]() $(x,y)\mapsto x$
. Let
$(x,y)\mapsto x$
. Let
![]() $\Sigma $
denote the set of 2-torsion sections of
$\Sigma $
denote the set of 2-torsion sections of
![]() ${\mathcal {E}}\rightarrow S_0$
. The set
${\mathcal {E}}\rightarrow S_0$
. The set
![]() $\Sigma $
consists of four sections corresponding to
$\Sigma $
consists of four sections corresponding to
![]() $x=0,1,1/c,\infty $
. We use the same symbol
$x=0,1,1/c,\infty $
. We use the same symbol
![]() $\Sigma $
for its image under
$\Sigma $
for its image under
![]() ${\mathcal {E}}\rightarrow {\mathbb {P}}^1\times S_0$
.
${\mathcal {E}}\rightarrow {\mathbb {P}}^1\times S_0$
.
Next, we define the family of Kummer surfaces and related families. Let
![]() $T_0$
be the (Zariski) open set of
$T_0$
be the (Zariski) open set of
![]() $S_0\times S_0$
defined by
$S_0\times S_0$
defined by
and
![]() $B_0$
be the coordinate ring of
$B_0$
be the coordinate ring of
![]() $T_0$
. We will define the following families of varieties over
$T_0$
. We will define the following families of varieties over
![]() $T_0$
.
$T_0$
.

Let
![]() ${\mathcal {Y}}_0={\mathbb {P}}^1\times {\mathbb {P}}^1\times T_0$
. We use x (resp. y) for coordinates of the first (resp. second)
${\mathcal {Y}}_0={\mathbb {P}}^1\times {\mathbb {P}}^1\times T_0$
. We use x (resp. y) for coordinates of the first (resp. second)
![]() ${\mathbb {P}}^1$
of
${\mathbb {P}}^1$
of
![]() ${\mathcal {Y}}_0$
. We define the family of abelian surfaces
${\mathcal {Y}}_0$
. We define the family of abelian surfaces
![]() ${\mathcal {A}}_0\rightarrow T_0$
by the restriction of
${\mathcal {A}}_0\rightarrow T_0$
by the restriction of
![]() ${\mathcal {E}} \times {\mathcal {E}} \rightarrow S_0\times S_0$
to
${\mathcal {E}} \times {\mathcal {E}} \rightarrow S_0\times S_0$
to
![]() $T_0$
. The fiber of
$T_0$
. The fiber of
![]() ${\mathcal {A}}_0\rightarrow T_0$
over
${\mathcal {A}}_0\rightarrow T_0$
over
![]() $(a,b)\in T_0$
corresponds to the product of elliptic curves
$(a,b)\in T_0$
corresponds to the product of elliptic curves
![]() ${\mathcal {E}}_a\times {\mathcal {E}}_b$
. We have the natural
${\mathcal {E}}_a\times {\mathcal {E}}_b$
. We have the natural
![]() $T_0$
-morphism
$T_0$
-morphism
![]() ${\mathcal {A}}_0\rightarrow {\mathcal {Y}}_0$
induced by the direct product of
${\mathcal {A}}_0\rightarrow {\mathcal {Y}}_0$
induced by the direct product of
![]() $S_0$
-morphism
$S_0$
-morphism
![]() ${\mathcal {E}} \rightarrow {\mathbb {P}}^1\times S_0$
. The map
${\mathcal {E}} \rightarrow {\mathbb {P}}^1\times S_0$
. The map
![]() ${\mathcal {A}}_0\rightarrow {\mathcal {Y}}_0$
is a 4:1 cover. Let
${\mathcal {A}}_0\rightarrow {\mathcal {Y}}_0$
is a 4:1 cover. Let
![]() ${\iota : {\mathcal {A}}_0\rightarrow {\mathcal {A}}_0}$
be the map of taking inverses and we define
${\iota : {\mathcal {A}}_0\rightarrow {\mathcal {A}}_0}$
be the map of taking inverses and we define
![]() ${\mathcal {X}}_0$
as the quotient of
${\mathcal {X}}_0$
as the quotient of
![]() ${\mathcal {A}}_0$
by
${\mathcal {A}}_0$
by
![]() $\iota $
. Then the morphism
$\iota $
. Then the morphism
![]() ${\mathcal {A}}_0\rightarrow {\mathcal {Y}}_0$
factors
${\mathcal {A}}_0\rightarrow {\mathcal {Y}}_0$
factors
![]() ${\mathcal {X}}_0$
.
${\mathcal {X}}_0$
.
We define
![]() $\Sigma ^2$
as the set of 2-torsion sections of
$\Sigma ^2$
as the set of 2-torsion sections of
![]() ${\mathcal {A}}_0 \rightarrow T_0$
. The set
${\mathcal {A}}_0 \rightarrow T_0$
. The set
![]() $\Sigma ^2$
consists of 16 sections corresponding to
$\Sigma ^2$
consists of 16 sections corresponding to
![]() $\Sigma \times \Sigma $
. We use the same symbol
$\Sigma \times \Sigma $
. We use the same symbol
![]() $\Sigma ^2$
for its images in
$\Sigma ^2$
for its images in
![]() ${\mathcal {X}}_0$
and
${\mathcal {X}}_0$
and
![]() ${\mathcal {Y}}_0$
. Using the coordinates x and y, the set
${\mathcal {Y}}_0$
. Using the coordinates x and y, the set
![]() $\Sigma ^2$
can be described as 16 points
$\Sigma ^2$
can be described as 16 points
Let
![]() $\widetilde {{\mathcal {A}}}_0, \widetilde {{\mathcal {X}}}_0$
, and
$\widetilde {{\mathcal {A}}}_0, \widetilde {{\mathcal {X}}}_0$
, and
![]() $\widetilde {{\mathcal {Y}}}_0$
be the blowing-ups of
$\widetilde {{\mathcal {Y}}}_0$
be the blowing-ups of
![]() ${\mathcal {A}}_0$
,
${\mathcal {A}}_0$
,
![]() ${\mathcal {X}}_0$
, and
${\mathcal {X}}_0$
, and
![]() ${\mathcal {Y}}_0$
along
${\mathcal {Y}}_0$
along
![]() $\Sigma ^2$
. The universality of the blowing-up induces the maps
$\Sigma ^2$
. The universality of the blowing-up induces the maps
![]() $\widetilde {{\mathcal {A}}}_0\rightarrow \widetilde {{\mathcal {X}}}_0\rightarrow \widetilde {{\mathcal {Y}}}_0$
. Since
$\widetilde {{\mathcal {A}}}_0\rightarrow \widetilde {{\mathcal {X}}}_0\rightarrow \widetilde {{\mathcal {Y}}}_0$
. Since
![]() $\widetilde {{\mathcal {X}}}_0\rightarrow {\mathcal {X}}_0$
is the minimal resolution of singularities,
$\widetilde {{\mathcal {X}}}_0\rightarrow {\mathcal {X}}_0$
is the minimal resolution of singularities,
![]() $\widetilde {{\mathcal {X}}}_0\rightarrow T_0$
is the family of Kummer surfaces. At
$\widetilde {{\mathcal {X}}}_0\rightarrow T_0$
is the family of Kummer surfaces. At
![]() $t=(a,b)\in T_0$
, the fiber
$t=(a,b)\in T_0$
, the fiber
![]() $\widetilde {{\mathcal {X}}}_t$
is the Kummer surface
$\widetilde {{\mathcal {X}}}_t$
is the Kummer surface
![]() ${\mathrm {Km}}({\mathcal {E}}_a\times {\mathcal {E}}_b)$
associated with
${\mathrm {Km}}({\mathcal {E}}_a\times {\mathcal {E}}_b)$
associated with
![]() ${\mathcal {E}}_a\times {\mathcal {E}}_b$
. For
${\mathcal {E}}_a\times {\mathcal {E}}_b$
. For
![]() $\sigma \in \Sigma ^2$
,
$\sigma \in \Sigma ^2$
,
![]() $Q_{\sigma }$
denotes the exceptional divisor over
$Q_{\sigma }$
denotes the exceptional divisor over
![]() $\sigma \in \Sigma ^2$
. The configuration of
$\sigma \in \Sigma ^2$
. The configuration of
![]() $Q_\sigma $
on
$Q_\sigma $
on
![]() $\widetilde {{\mathcal {X}}}_0$
is described in Figure 1.
$\widetilde {{\mathcal {X}}}_0$
is described in Figure 1.

Figure 1: The exceptional divisors
![]() $Q_\sigma $
on
$Q_\sigma $
on
![]() $\widetilde {{\mathcal {X}}}_0$
.
$\widetilde {{\mathcal {X}}}_0$
.
Finally, we define local charts on
![]() ${\mathcal {Y}}_0$
and
${\mathcal {Y}}_0$
and
![]() $\widetilde {{\mathcal {X}}}_0$
. Let
$\widetilde {{\mathcal {X}}}_0$
. Let
![]() $U={\mathrm {Spec}\,} B_0[x,y]\subset {\mathcal {Y}}_0$
be the affine open subset which is the complement of the divisors
$U={\mathrm {Spec}\,} B_0[x,y]\subset {\mathcal {Y}}_0$
be the affine open subset which is the complement of the divisors
![]() $x=\infty $
and
$x=\infty $
and
![]() $y=\infty $
. The inverse image of U by
$y=\infty $
. The inverse image of U by
![]() $\widetilde {{\mathcal {X}}}_0\rightarrow {\mathcal {Y}}_0$
is covered by two open affine subschemes
$\widetilde {{\mathcal {X}}}_0\rightarrow {\mathcal {Y}}_0$
is covered by two open affine subschemes
![]() $V={\mathrm {Spec}\,} B_0[x,y,v]/(v^2f(x)-g(y))$
and
$V={\mathrm {Spec}\,} B_0[x,y,v]/(v^2f(x)-g(y))$
and
![]() $W={\mathrm {Spec}\,} B_0[x,y,w]/(w^2g(y)-f(x)),$
where
$W={\mathrm {Spec}\,} B_0[x,y,w]/(w^2g(y)-f(x)),$
where
![]() $f(x)=x(1-x)(1-ax)$
and
$f(x)=x(1-x)(1-ax)$
and
![]() $g(y)=y(1-y)(1-by)$
. These two subsets are glued by the relation
$g(y)=y(1-y)(1-by)$
. These two subsets are glued by the relation
![]() $v = 1/w$
.
$v = 1/w$
.
4 Construction of initial higher Chow cycles
In this section, we construct families
![]() $\xi _0, \xi _1$
, and
$\xi _0, \xi _1$
, and
![]() $\xi _{\infty }$
of higher Chow cycles on a base change
$\xi _{\infty }$
of higher Chow cycles on a base change
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
of
$\widetilde {{\mathcal {X}}}\rightarrow T$
of
![]() $\widetilde {{\mathcal {X}}}_0\rightarrow T_0$
.
$\widetilde {{\mathcal {X}}}_0\rightarrow T_0$
.
4.1 Construction of higher Chow cycles at fibers
First, we explain the construction at each fiber over
![]() $t=(a,b)\in T_0$
. Let
$t=(a,b)\in T_0$
. Let
![]() ${\mathcal {D}} \subset {\mathbb {P}}^1\times {\mathbb {P}}^1=({\mathcal {Y}}_0)_t$
be the diagonal curve. Since
${\mathcal {D}} \subset {\mathbb {P}}^1\times {\mathbb {P}}^1=({\mathcal {Y}}_0)_t$
be the diagonal curve. Since
![]() $a\neq b$
,
$a\neq b$
,
![]() ${\mathcal {D}} $
intersects with the branching locus of
${\mathcal {D}} $
intersects with the branching locus of
![]() $({\mathcal {X}}_0)_t\rightarrow ({\mathcal {Y}}_0)_t$
as Figure 2.
$({\mathcal {X}}_0)_t\rightarrow ({\mathcal {Y}}_0)_t$
as Figure 2.
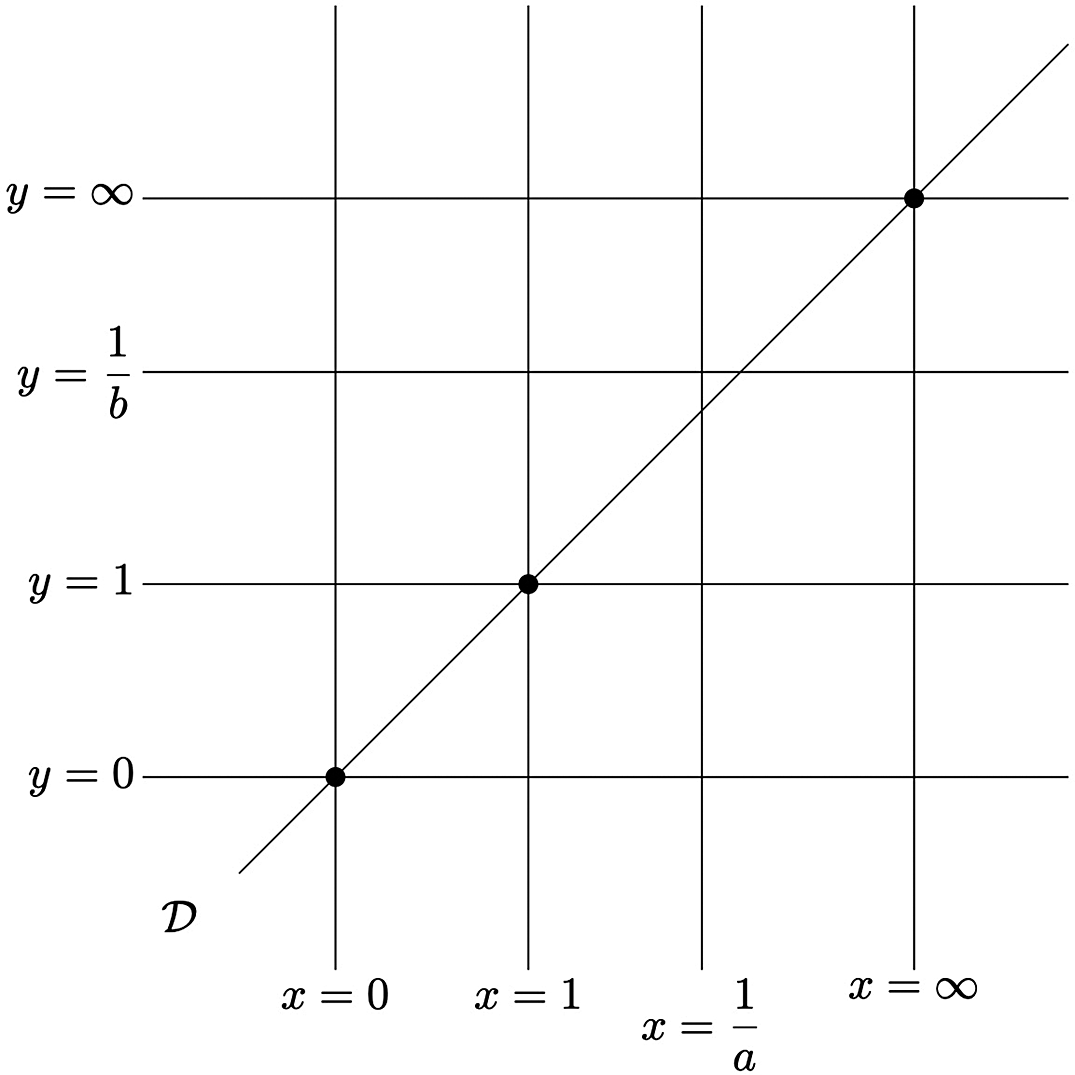
Figure 2: The diagonal curve
![]() ${\mathcal {D}}$
and the branching locus.
${\mathcal {D}}$
and the branching locus.
Let
![]() ${\mathcal {C}} \subset ({\mathcal {X}}_0)_t$
be the pull-back of
${\mathcal {C}} \subset ({\mathcal {X}}_0)_t$
be the pull-back of
![]() ${\mathcal {D}}$
by
${\mathcal {D}}$
by
![]() $({\mathcal {X}}_0)_t\rightarrow ({\mathcal {Y}}_0)_t$
, and let
$({\mathcal {X}}_0)_t\rightarrow ({\mathcal {Y}}_0)_t$
, and let
![]() $\widetilde {{\mathcal {C}}}$
be the strict transform of
$\widetilde {{\mathcal {C}}}$
be the strict transform of
![]() ${\mathcal {C}}$
by the blowing-up
${\mathcal {C}}$
by the blowing-up
![]() $(\widetilde {{\mathcal {X}}}_0)_t\rightarrow ({\mathcal {X}}_0)_t$
. Then we see that
$(\widetilde {{\mathcal {X}}}_0)_t\rightarrow ({\mathcal {X}}_0)_t$
. Then we see that
![]() $\widetilde {{\mathcal {C}}}$
is smooth and
$\widetilde {{\mathcal {C}}}$
is smooth and
![]() $\widetilde {{\mathcal {C}}} \rightarrow {\mathcal {D}} $
is a double covering ramified at two points. Hence,
$\widetilde {{\mathcal {C}}} \rightarrow {\mathcal {D}} $
is a double covering ramified at two points. Hence,
![]() $\widetilde {{\mathcal {C}}}$
is isomorphic to
$\widetilde {{\mathcal {C}}}$
is isomorphic to
![]() ${\mathbb {P}}^1$
. Furthermore, for each
${\mathbb {P}}^1$
. Furthermore, for each
![]() $\bullet \in \{0,1,\infty \}$
,
$\bullet \in \{0,1,\infty \}$
,
![]() $\widetilde {{\mathcal {C}}} $
intersects with
$\widetilde {{\mathcal {C}}} $
intersects with
![]() $Q_{(\bullet ,\bullet )}$
at two points
$Q_{(\bullet ,\bullet )}$
at two points
![]() $p_{\bullet }^+$
and
$p_{\bullet }^+$
and
![]() $p_{\bullet }^-$
(cf. Figure 3).
$p_{\bullet }^-$
(cf. Figure 3).

Figure 3: The intersections of
![]() $\widetilde {{\mathcal {C}}}$
,
$\widetilde {{\mathcal {C}}}$
,
![]() $Q_{(0,0)}$
,
$Q_{(0,0)}$
,
![]() $Q_{(1,1)}$
, and
$Q_{(1,1)}$
, and
![]() $Q_{(\infty ,\infty )}$
.
$Q_{(\infty ,\infty )}$
.
Hence, we can find rational functions
![]() $\psi _0, \psi _1,\psi _\infty \in {\mathbb {C}}(\widetilde {{\mathcal {C}}})$
and
$\psi _0, \psi _1,\psi _\infty \in {\mathbb {C}}(\widetilde {{\mathcal {C}}})$
and
![]() $\varphi _{\bullet } \in {\mathbb {C}}(Q_{(\bullet , \bullet )}) (\bullet = 0,1,\infty \})$
which satisfy the following relations:
$\varphi _{\bullet } \in {\mathbb {C}}(Q_{(\bullet , \bullet )}) (\bullet = 0,1,\infty \})$
which satisfy the following relations:
 $$ \begin{align} \begin{aligned} {\mathrm{div}}_{\widetilde{{\mathcal{C}}}}(\psi_0) &= p_{0}^- - p_{0}^+ = - {\mathrm{div}}_{Q_{(0,0)}}(\varphi_0), \\{\mathrm{div}}_{\widetilde{{\mathcal{C}}}}(\psi_1) &= p_{1}^- - p_{1}^+ = - {\mathrm{div}}_{Q_{(1,1)}}(\varphi_1), \\{\mathrm{div}}_{\widetilde{{\mathcal{C}}}}(\psi_\infty) &= p_\infty^- - p_\infty^+ = - {\mathrm{div}}_{Q_{(\infty,\infty)}}(\varphi_\infty). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {\mathrm{div}}_{\widetilde{{\mathcal{C}}}}(\psi_0) &= p_{0}^- - p_{0}^+ = - {\mathrm{div}}_{Q_{(0,0)}}(\varphi_0), \\{\mathrm{div}}_{\widetilde{{\mathcal{C}}}}(\psi_1) &= p_{1}^- - p_{1}^+ = - {\mathrm{div}}_{Q_{(1,1)}}(\varphi_1), \\{\mathrm{div}}_{\widetilde{{\mathcal{C}}}}(\psi_\infty) &= p_\infty^- - p_\infty^+ = - {\mathrm{div}}_{Q_{(\infty,\infty)}}(\varphi_\infty). \end{aligned} \end{align} $$
We define
![]() $(\xi _0)_t,(\xi _1)_t,(\xi _\infty )_t\in {\mathrm {CH}}^2((\widetilde {{\mathcal {X}}}_0)_t,1)$
by the formal sums
$(\xi _0)_t,(\xi _1)_t,(\xi _\infty )_t\in {\mathrm {CH}}^2((\widetilde {{\mathcal {X}}}_0)_t,1)$
by the formal sums
 $$ \begin{align} \begin{aligned} (\xi_0)_t &= (\widetilde{{\mathcal{C}}}, \psi_0) + (Q_{(0,0)},\varphi_0), \\(\xi_1)_t &= (\widetilde{{\mathcal{C}}}, \psi_1) + (Q_{(1,1)},\varphi_1), \\(\xi_\infty)_t &= (\widetilde{{\mathcal{C}}}, \psi_\infty) + (Q_{(\infty,\infty)},\varphi_\infty). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\xi_0)_t &= (\widetilde{{\mathcal{C}}}, \psi_0) + (Q_{(0,0)},\varphi_0), \\(\xi_1)_t &= (\widetilde{{\mathcal{C}}}, \psi_1) + (Q_{(1,1)},\varphi_1), \\(\xi_\infty)_t &= (\widetilde{{\mathcal{C}}}, \psi_\infty) + (Q_{(\infty,\infty)},\varphi_\infty). \end{aligned} \end{align} $$
4.2 Construction of families of higher Chow cycles
To get families of higher Chow cycles, it is enough to construct rational functions
![]() $\varphi _\bullet $
and
$\varphi _\bullet $
and
![]() $\psi _\bullet $
on the family. However, the intersection points
$\psi _\bullet $
on the family. However, the intersection points
![]() $p_{1}^+$
and
$p_{1}^+$
and
![]() $ p_{1}^-$
(resp.
$ p_{1}^-$
(resp.
![]() $p_{\infty }^+$
and
$p_{\infty }^+$
and
![]() $ p_{\infty }^-$
) interchange by the monodromy of
$ p_{\infty }^-$
) interchange by the monodromy of
![]() $T_0$
. Hence, it is impossible to construct such rational functions for
$T_0$
. Hence, it is impossible to construct such rational functions for
![]() $\bullet = 1,\infty $
. Thus, it is necessary to take a finite étale base change of
$\bullet = 1,\infty $
. Thus, it is necessary to take a finite étale base change of
![]() $T_0$
to define the families of cycles.
$T_0$
to define the families of cycles.
Let
![]() $B = B_0[\sqrt {a},\sqrt {b},\sqrt {1-a},\sqrt {1-b}]$
and
$B = B_0[\sqrt {a},\sqrt {b},\sqrt {1-a},\sqrt {1-b}]$
and
![]() $T\rightarrow T_0$
be the finite étale cover corresponding to
$T\rightarrow T_0$
be the finite étale cover corresponding to
![]() $B_0\rightarrow B$
. The base changes of
$B_0\rightarrow B$
. The base changes of
![]() ${\mathcal {Y}}_0,{\mathcal {X}}_0,{\mathcal {A}}_0, \widetilde {{\mathcal {Y}}}_0, \widetilde {{\mathcal {X}}}_0$
, and
${\mathcal {Y}}_0,{\mathcal {X}}_0,{\mathcal {A}}_0, \widetilde {{\mathcal {Y}}}_0, \widetilde {{\mathcal {X}}}_0$
, and
![]() $\widetilde {{\mathcal {A}}}_0$
by
$\widetilde {{\mathcal {A}}}_0$
by
![]() $T\rightarrow T_0$
are denoted by
$T\rightarrow T_0$
are denoted by
![]() ${\mathcal {Y}},{\mathcal {X}},{\mathcal {A}}, \widetilde {{\mathcal {Y}}}, \widetilde {{\mathcal {X}}}$
, and
${\mathcal {Y}},{\mathcal {X}},{\mathcal {A}}, \widetilde {{\mathcal {Y}}}, \widetilde {{\mathcal {X}}}$
, and
![]() $\widetilde {{\mathcal {A}}}$
, respectively.
$\widetilde {{\mathcal {A}}}$
, respectively.
Let
![]() ${\mathcal {D}}\subset {\mathcal {Y}}$
be the closed subscheme defined by the local equation
${\mathcal {D}}\subset {\mathcal {Y}}$
be the closed subscheme defined by the local equation
![]() $x=y$
, let
$x=y$
, let
![]() ${\mathcal {C}}$
be its pull-back by
${\mathcal {C}}$
be its pull-back by
![]() ${\mathcal {X}}\rightarrow {\mathcal {Y}}$
, and let
${\mathcal {X}}\rightarrow {\mathcal {Y}}$
, and let
![]() $\widetilde {{\mathcal {C}}}$
be its strict transform by the blowing up
$\widetilde {{\mathcal {C}}}$
be its strict transform by the blowing up
![]() $\widetilde {{\mathcal {X}}}\rightarrow {\mathcal {X}}$
. On the local chart V,
$\widetilde {{\mathcal {X}}}\rightarrow {\mathcal {X}}$
. On the local chart V,
![]() $\widetilde {{\mathcal {C}}}\hookrightarrow \widetilde {{\mathcal {X}}}$
is described by the following ring homomorphism:
$\widetilde {{\mathcal {C}}}\hookrightarrow \widetilde {{\mathcal {X}}}$
is described by the following ring homomorphism:
By this description, we see that
![]() $Q_{(0,0)}$
and
$Q_{(0,0)}$
and
![]() $\widetilde {{\mathcal {C}}}$
intersect at
$\widetilde {{\mathcal {C}}}$
intersect at
![]() $(x,y,v) = (0,0,\pm 1)$
, and
$(x,y,v) = (0,0,\pm 1)$
, and
![]() $Q_{(1,1)}$
and
$Q_{(1,1)}$
and
![]() $\widetilde {{\mathcal {C}}}$
intersect at
$\widetilde {{\mathcal {C}}}$
intersect at
![]() $(x,y,v) = \left (1,1,\pm \sqrt {1-b}/\sqrt {1-a}\right )$
. By the local computation on another local chart containing
$(x,y,v) = \left (1,1,\pm \sqrt {1-b}/\sqrt {1-a}\right )$
. By the local computation on another local chart containing
![]() $(\infty ,\infty )\in \Sigma ^2$
,
$(\infty ,\infty )\in \Sigma ^2$
,
![]() $Q_{(\infty ,\infty )}$
and
$Q_{(\infty ,\infty )}$
and
![]() $\widetilde {{\mathcal {C}}}$
intersect at
$\widetilde {{\mathcal {C}}}$
intersect at
![]() $(\xi ,\eta ,v')=\left (0,0,\pm \sqrt {b}/\sqrt {a}\right )$
, where local coordinates
$(\xi ,\eta ,v')=\left (0,0,\pm \sqrt {b}/\sqrt {a}\right )$
, where local coordinates
![]() $\xi ,\eta $
, and
$\xi ,\eta $
, and
![]() $v'$
are defined by
$v'$
are defined by
![]() $\xi =1/x$
,
$\xi =1/x$
,
![]() $\eta =1/y,$
and
$\eta =1/y,$
and
![]() $v' = x^2v/y^2$
. Hence, we can define rational functions
$v' = x^2v/y^2$
. Hence, we can define rational functions
![]() $\psi _\bullet \in {\mathbb {C}}(\widetilde {{\mathcal {C}}})$
and
$\psi _\bullet \in {\mathbb {C}}(\widetilde {{\mathcal {C}}})$
and
![]() $\varphi _{\bullet }\in {\mathbb {C}}(Q_{(\bullet ,\bullet )})\: (\bullet \in \{0,1,\infty \})$
by the following equations:
$\varphi _{\bullet }\in {\mathbb {C}}(Q_{(\bullet ,\bullet )})\: (\bullet \in \{0,1,\infty \})$
by the following equations:
 $$ \begin{align*} \begin{aligned} & \psi_0 = (v+1)\cdot(v-1)^{-1}, && \varphi_0 = (v-1)\cdot(v + 1)^{-1}, \\ & \psi_1 = \left(v + \frac{\sqrt{1-b}}{\sqrt{1-a}}\right)\cdot\left(v - \frac{\sqrt{1-b}}{\sqrt{1-a}}\right)^{-1}, && \varphi_1 = \left(v-\frac{\sqrt{1-b}}{\sqrt{1-a}}\right)\cdot\left(v+\frac{\sqrt{1-b}}{\sqrt{1-a}}\right)^{-1}, \\ & \psi_\infty = \left(v' + \frac{\sqrt{b}}{\sqrt{a}}\right)\cdot\left(v' - \frac{\sqrt{b}}{\sqrt{a}}\right)^{-1}, && \varphi_\infty =\left(v'- \frac{\sqrt{b}}{\sqrt{a}}\right)\cdot\left(v'+ \frac{\sqrt{b}}{\sqrt{a}}\right)^{-1}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \psi_0 = (v+1)\cdot(v-1)^{-1}, && \varphi_0 = (v-1)\cdot(v + 1)^{-1}, \\ & \psi_1 = \left(v + \frac{\sqrt{1-b}}{\sqrt{1-a}}\right)\cdot\left(v - \frac{\sqrt{1-b}}{\sqrt{1-a}}\right)^{-1}, && \varphi_1 = \left(v-\frac{\sqrt{1-b}}{\sqrt{1-a}}\right)\cdot\left(v+\frac{\sqrt{1-b}}{\sqrt{1-a}}\right)^{-1}, \\ & \psi_\infty = \left(v' + \frac{\sqrt{b}}{\sqrt{a}}\right)\cdot\left(v' - \frac{\sqrt{b}}{\sqrt{a}}\right)^{-1}, && \varphi_\infty =\left(v'- \frac{\sqrt{b}}{\sqrt{a}}\right)\cdot\left(v'+ \frac{\sqrt{b}}{\sqrt{a}}\right)^{-1}. \end{aligned} \end{align*} $$
They satisfy the relations in (8) and we define algebraic families of higher Chow cycles
![]() $\xi _0 = \left \{(\xi _0)_t\right \}_{t\in T}, \xi _1 = \left \{(\xi _1)_t\right \}_{t\in T}$
and
$\xi _0 = \left \{(\xi _0)_t\right \}_{t\in T}, \xi _1 = \left \{(\xi _1)_t\right \}_{t\in T}$
and
![]() $\xi _{\infty } =\left \{(\xi _\infty )_t\right \}_{t\in T}$
by the equations (9).
$\xi _{\infty } =\left \{(\xi _\infty )_t\right \}_{t\in T}$
by the equations (9).
5 Computation of the regulator
In this section, we compute the image of
![]() $(\xi _1)_t-(\xi _0)_t$
under the regulator map and prove its indecomposability. Our main result is the following.
$(\xi _1)_t-(\xi _0)_t$
under the regulator map and prove its indecomposability. Our main result is the following.
Theorem 5.1 For very general
![]() $t\in T$
,
$t\in T$
,
![]() $(\xi _1)_{t}-(\xi _0)_{t}$
is an indecomposable cycle.
$(\xi _1)_{t}-(\xi _0)_{t}$
is an indecomposable cycle.
The main ingredients of the proof is the following two propositions.
Proposition 5.2 Let
![]() $\omega $
be the relative 2-form
$\omega $
be the relative 2-form
![]() $\frac {dx\wedge dy}{vf(x)}$
on the family
$\frac {dx\wedge dy}{vf(x)}$
on the family
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
and
$\widetilde {{\mathcal {X}}}\rightarrow T$
and
![]() ${\mathscr {D}}_1,{\mathscr {D}}_2: {\mathcal {O}}_{T}^{\mathrm {an}} \rightarrow {\mathcal {O}}_{T}^{\mathrm {an}}$
be the differential operators defined by
${\mathscr {D}}_1,{\mathscr {D}}_2: {\mathcal {O}}_{T}^{\mathrm {an}} \rightarrow {\mathcal {O}}_{T}^{\mathrm {an}}$
be the differential operators defined by
 $$ \begin{align*} \begin{aligned} &{\mathscr{D}}_1 = a(1-a) \frac{\partial^2}{\partial a^2} +(1-2a)\frac{\partial }{\partial a} -\frac{1}{4}, \\ &{\mathscr{D}}_2 = b(1-b) \frac{\partial^2}{\partial b^2} +(1-2b)\frac{\partial }{\partial b} -\frac{1}{4}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &{\mathscr{D}}_1 = a(1-a) \frac{\partial^2}{\partial a^2} +(1-2a)\frac{\partial }{\partial a} -\frac{1}{4}, \\ &{\mathscr{D}}_2 = b(1-b) \frac{\partial^2}{\partial b^2} +(1-2b)\frac{\partial }{\partial b} -\frac{1}{4}. \end{aligned} \end{align*} $$
Let
 ${\mathscr {D}} = \begin {pmatrix} {\mathscr {D}}_1 \\ {\mathscr {D}}_2\end {pmatrix}:{\mathcal {O}}_{T}^{\mathrm {an}} \rightarrow \left ({\mathcal {O}}_{T}^{\mathrm {an}}\right )^{\oplus 2}$
. Then for any local section f of
${\mathscr {D}} = \begin {pmatrix} {\mathscr {D}}_1 \\ {\mathscr {D}}_2\end {pmatrix}:{\mathcal {O}}_{T}^{\mathrm {an}} \rightarrow \left ({\mathcal {O}}_{T}^{\mathrm {an}}\right )^{\oplus 2}$
. Then for any local section f of
![]() ${\mathcal {P}}_{\omega }\subset {\mathcal {O}}_{T}^{\mathrm {an}}$
, we have
${\mathcal {P}}_{\omega }\subset {\mathcal {O}}_{T}^{\mathrm {an}}$
, we have
![]() ${\mathscr {D}}(f)=0$
. In particular,
${\mathscr {D}}(f)=0$
. In particular,
![]() ${\mathscr {D}}$
factors the sheaf
${\mathscr {D}}$
factors the sheaf
![]() ${\mathcal {Q}}_{\omega }$
. We use the same symbol
${\mathcal {Q}}_{\omega }$
. We use the same symbol
![]() ${\mathscr {D}}$
for the induced morphisms
${\mathscr {D}}$
for the induced morphisms
![]() ${\mathcal {Q}}_\omega \rightarrow \left ({\mathcal {O}}_{T}^{\mathrm {an}}\right )^{\oplus 2}$
and
${\mathcal {Q}}_\omega \rightarrow \left ({\mathcal {O}}_{T}^{\mathrm {an}}\right )^{\oplus 2}$
and
![]() ${\mathcal {Q}}\simeq {\mathcal {Q}}_\omega \rightarrow \left ({\mathcal {O}}_{T}^{\mathrm {an}}\right )^{\oplus 2}$
.
${\mathcal {Q}}\simeq {\mathcal {Q}}_\omega \rightarrow \left ({\mathcal {O}}_{T}^{\mathrm {an}}\right )^{\oplus 2}$
.
Recall that
![]() ${\mathcal {P}}_\omega $
is the local system consisting of period functions with respect to
${\mathcal {P}}_\omega $
is the local system consisting of period functions with respect to
![]() $\omega $
and
$\omega $
and
![]() ${\mathcal {Q}}_\omega $
is the quotient of
${\mathcal {Q}}_\omega $
is the quotient of
![]() ${\mathcal {O}}_{T}^{\mathrm {an}}$
by
${\mathcal {O}}_{T}^{\mathrm {an}}$
by
![]() ${\mathcal {P}}_\omega $
. The differential operator
${\mathcal {P}}_\omega $
. The differential operator
![]() ${\mathscr {D}}$
is called a Picard–Fuchs differential operator because it annihilates all period functions with respect to
${\mathscr {D}}$
is called a Picard–Fuchs differential operator because it annihilates all period functions with respect to
![]() $\omega $
.
$\omega $
.
By Proposition 2.7, to prove Theorem 5.1, it is enough to show
![]() $\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)$
is nonzero. Then by the Proposition 5.2, it is enough to show
$\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)$
is nonzero. Then by the Proposition 5.2, it is enough to show
![]() ${\mathscr {D}}(\nu _{{\mathrm {tr}}}(\xi _1-\xi _0))$
is nonzero. To prove this, we will find an explicit multivalued function which represents
${\mathscr {D}}(\nu _{{\mathrm {tr}}}(\xi _1-\xi _0))$
is nonzero. To prove this, we will find an explicit multivalued function which represents
![]() ${\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)}$
.
${\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)}$
.
For
![]() $(a,b)\in T_0$
such that
$(a,b)\in T_0$
such that
![]() $a,b\in {\mathbb {R}}_{<0}$
, let
$a,b\in {\mathbb {R}}_{<0}$
, let
![]() ${\mathcal {L}}(a,b)$
be the improper integral
${\mathcal {L}}(a,b)$
be the improper integral
 $$ \begin{align} {\mathcal{L}}(a,b)=2\int_{\triangle}\frac{dxdy}{\sqrt{x(1-x)(1-ax)}\sqrt{y(1-y)(1-by)}}, \end{align} $$
$$ \begin{align} {\mathcal{L}}(a,b)=2\int_{\triangle}\frac{dxdy}{\sqrt{x(1-x)(1-ax)}\sqrt{y(1-y)(1-by)}}, \end{align} $$
where
![]() $\triangle =\{(x,y)\in {\mathbb {R}}^2\::\: 0<y<x<1\}$
. This integral converges and defines a local holomorphic function around
$\triangle =\{(x,y)\in {\mathbb {R}}^2\::\: 0<y<x<1\}$
. This integral converges and defines a local holomorphic function around
![]() $(a,b)$
. There exists a lift
$(a,b)$
. There exists a lift
![]() ${\mathcal {L}}$
of
${\mathcal {L}}$
of
![]() ${\mathcal {L}}(a,b)$
by
${\mathcal {L}}(a,b)$
by
![]() $T\rightarrow T_0$
which satisfies the the following properties.
$T\rightarrow T_0$
which satisfies the the following properties.
Proposition 5.3
-
(1) For any
 $t\in T$
,
$t\in T$
,
 ${\mathcal {L}}$
can be analytically continued to an open neighborhood of t.
${\mathcal {L}}$
can be analytically continued to an open neighborhood of t. -
(2) The multivalued holomorphic function
 ${\mathcal {L}}$
represents
${\mathcal {L}}$
represents
 $\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)$
under the isomorphism
$\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)$
under the isomorphism
 ${\mathcal {Q}}_\omega \simeq {\mathcal {Q}}$
induced by the relative 2-form
${\mathcal {Q}}_\omega \simeq {\mathcal {Q}}$
induced by the relative 2-form
 $\omega $
in Proposition 5.2. In particular, for any
$\omega $
in Proposition 5.2. In particular, for any
 $t\in T$
, we have (11)where
$t\in T$
, we have (11)where $$ \begin{align} \langle r((\xi_1)_t-(\xi_0)_t), [\omega_t]\rangle \equiv {\mathcal{L}}(t) \quad\mod {\mathcal{P}}(\omega_t), \end{align} $$
$$ \begin{align} \langle r((\xi_1)_t-(\xi_0)_t), [\omega_t]\rangle \equiv {\mathcal{L}}(t) \quad\mod {\mathcal{P}}(\omega_t), \end{align} $$
 $\omega _t$
is the pull-back of
$\omega _t$
is the pull-back of
 $\omega $
at
$\omega $
at
 $\widetilde {{\mathcal {X}}}_t$
.
$\widetilde {{\mathcal {X}}}_t$
.
-
(3) The multivalued holomorphic function
 ${\mathcal {L}}$
satisfies the following system of the differential equations: (12)In particular,
${\mathcal {L}}$
satisfies the following system of the differential equations: (12)In particular, $$ \begin{align} {\mathscr{D}}({\mathcal{L}})= \frac{2}{a-b} \begin{pmatrix} \frac{\sqrt{1-b}}{\sqrt{1-a}}-1\\[1.5ex] 1-\frac{\sqrt{1-a}}{\sqrt{1-b}} \end{pmatrix}. \end{align} $$
$$ \begin{align} {\mathscr{D}}({\mathcal{L}})= \frac{2}{a-b} \begin{pmatrix} \frac{\sqrt{1-b}}{\sqrt{1-a}}-1\\[1.5ex] 1-\frac{\sqrt{1-a}}{\sqrt{1-b}} \end{pmatrix}. \end{align} $$
 ${\mathscr {D}}(\nu _{{\mathrm {tr}}}(\xi _1-\xi _0))$
coincides with the right-hand side of (12).
${\mathscr {D}}(\nu _{{\mathrm {tr}}}(\xi _1-\xi _0))$
coincides with the right-hand side of (12).
Thus, we have
![]() $\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)\neq 0$
and this implies Theorem 5.1 by Proposition 2.7. We will prove Propositions 5.2 and 5.3 in this section.
$\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)\neq 0$
and this implies Theorem 5.1 by Proposition 2.7. We will prove Propositions 5.2 and 5.3 in this section.
5.1 The Picard–Fuchs differential operator
For
![]() $c\in {\mathbb {C}}-{\mathbb {R}}_{\ge 0}$
, we consider the following improper integrals:
$c\in {\mathbb {C}}-{\mathbb {R}}_{\ge 0}$
, we consider the following improper integrals:
 $$ \begin{align*} P_1(c)=\int_0^1\frac{dx}{\sqrt{x(1-x)(1-c x)}},\quad P_2(c)=\int_1^\infty\frac{dx}{\sqrt{x(1-x)(1-c x)}}. \end{align*} $$
$$ \begin{align*} P_1(c)=\int_0^1\frac{dx}{\sqrt{x(1-x)(1-c x)}},\quad P_2(c)=\int_1^\infty\frac{dx}{\sqrt{x(1-x)(1-c x)}}. \end{align*} $$
As is well-known (see, e.g., [Reference Whittaker and WatsonWW62, p. 253]), these integrals converge and give linearly independent solutions of the hypergeometric differential equation
For any
![]() $c\in S_0$
, they can be analytically continued to a neighborhood of c and we use the same notation for the resulting multivalued functions.
$c\in S_0$
, they can be analytically continued to a neighborhood of c and we use the same notation for the resulting multivalued functions.
Let
![]() $\theta $
be the relative 1-form
$\theta $
be the relative 1-form
![]() $\frac {dx}{y}$
on the Legendre family of elliptic curves
$\frac {dx}{y}$
on the Legendre family of elliptic curves
![]() ${\mathcal {E}}\rightarrow S_0$
. For
${\mathcal {E}}\rightarrow S_0$
. For
![]() $c\in {\mathbb {C}}-{\mathbb {R}}_{\ge 0}$
, let
$c\in {\mathbb {C}}-{\mathbb {R}}_{\ge 0}$
, let
![]() $\gamma _+,\gamma _-$
(resp.
$\gamma _+,\gamma _-$
(resp.
![]() $\delta _+,\delta _-$
) be lifts of paths
$\delta _+,\delta _-$
) be lifts of paths
![]() $[0,1]$
and
$[0,1]$
and
![]() $[1,\infty ]$
on
$[1,\infty ]$
on
![]() ${\mathbb {P}}^1$
by
${\mathbb {P}}^1$
by
![]() ${\mathcal {E}}_c \rightarrow {\mathbb {P}}^1$
. Let
${\mathcal {E}}_c \rightarrow {\mathbb {P}}^1$
. Let
![]() $\theta _c$
be the pull-back of
$\theta _c$
be the pull-back of
![]() $\theta $
at
$\theta $
at
![]() ${\mathcal {E}}_c$
. Then we have
${\mathcal {E}}_c$
. Then we have
and they coincide with
![]() $\pm P_1(c)$
and
$\pm P_1(c)$
and
![]() $\pm P_2(c)$
, respectively. Since
$\pm P_2(c)$
, respectively. Since
![]() $[\gamma _+]-[\gamma _-]$
and
$[\gamma _+]-[\gamma _-]$
and
![]() $[\delta _+]-[\delta _-]$
are generators of
$[\delta _+]-[\delta _-]$
are generators of
![]() $H_1({\mathcal {E}}_c,{\mathbb {Z}})$
(see, e.g., [Reference Carlson, Müller-Stach and PetersCMP02, p. 10]),
$H_1({\mathcal {E}}_c,{\mathbb {Z}})$
(see, e.g., [Reference Carlson, Müller-Stach and PetersCMP02, p. 10]),
![]() $2P_1$
and
$2P_1$
and
![]() $2P_2$
are local basis of the period functions of
$2P_2$
are local basis of the period functions of
![]() ${\mathcal {E}}\rightarrow S_0$
with respect to
${\mathcal {E}}\rightarrow S_0$
with respect to
![]() $\theta $
. In particular, hypergeometric differential equation (13) is a Picard–Fuchs differential equation of
$\theta $
. In particular, hypergeometric differential equation (13) is a Picard–Fuchs differential equation of
![]() ${\mathcal {E}}\rightarrow S_0$
.
${\mathcal {E}}\rightarrow S_0$
.
Next, we will find a Picard–Fuchs differential operator of
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
. Recall that we have T-morphisms
$\widetilde {{\mathcal {X}}}\rightarrow T$
. Recall that we have T-morphisms
We name the morphisms p and
![]() $\pi $
as above. We have the relative 2-form
$\pi $
as above. We have the relative 2-form
![]() $pr_1^*(\theta )\wedge pr_2^*(\theta )$
on
$pr_1^*(\theta )\wedge pr_2^*(\theta )$
on
![]() ${\mathcal {A}}\rightarrow T$
, where
${\mathcal {A}}\rightarrow T$
, where
![]() $pr_i$
is the morphism
$pr_i$
is the morphism
![]() ${\mathcal {A}}\rightarrow {\mathcal {A}}_0 \hookrightarrow {\mathcal {E}}\times {\mathcal {E}} \xrightarrow {pr_i} {\mathcal {E}}$
. Then its pull-back by p is stable under the covering transformation of
${\mathcal {A}}\rightarrow {\mathcal {A}}_0 \hookrightarrow {\mathcal {E}}\times {\mathcal {E}} \xrightarrow {pr_i} {\mathcal {E}}$
. Then its pull-back by p is stable under the covering transformation of
![]() $\pi $
, so it descends to
$\pi $
, so it descends to
![]() $\widetilde {{\mathcal {X}}}$
. We denote the resulting 2-form on
$\widetilde {{\mathcal {X}}}$
. We denote the resulting 2-form on
![]() $\widetilde {{\mathcal {X}}}$
by
$\widetilde {{\mathcal {X}}}$
by
![]() $\omega $
. The relative 2-form
$\omega $
. The relative 2-form
![]() $\omega $
is described as
$\omega $
is described as
![]() $\frac {dx\wedge dy}{vf(x)}$
and
$\frac {dx\wedge dy}{vf(x)}$
and
![]() $\frac {dx\wedge dy}{wg(y)}$
on the local charts V and W. Then we have the following.
$\frac {dx\wedge dy}{wg(y)}$
on the local charts V and W. Then we have the following.
Proposition 5.4 The four local holomorphic functions
![]() $2P_i(a)P_j(b) \:\: (i,j\in \{1,2\})$
are a local basis for the local system
$2P_i(a)P_j(b) \:\: (i,j\in \{1,2\})$
are a local basis for the local system
![]() ${\mathcal {P}}_{\omega }\subset {\mathcal {O}}_{T}^{\mathrm {an}}$
generated by period functions of
${\mathcal {P}}_{\omega }\subset {\mathcal {O}}_{T}^{\mathrm {an}}$
generated by period functions of
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
with respect to
$\widetilde {{\mathcal {X}}}\rightarrow T$
with respect to
![]() $\omega $
.
$\omega $
.
Proof By the Künneth formula, we see that
![]() $4P_i(a)P_j(b) \:\: (i,j\in \{1,2\})$
is a local basis for the local system generated by period functions of
$4P_i(a)P_j(b) \:\: (i,j\in \{1,2\})$
is a local basis for the local system generated by period functions of
![]() ${\mathcal {A}}\rightarrow T$
with respect to
${\mathcal {A}}\rightarrow T$
with respect to
![]() $pr_1^*(\theta )\wedge pr_2^*(\theta )$
. For
$pr_1^*(\theta )\wedge pr_2^*(\theta )$
. For
![]() $t\in T$
, let
$t\in T$
, let
![]() $\phi $
be the morphism of Hodge structures defined by
$\phi $
be the morphism of Hodge structures defined by
where
![]() $\pi _!$
is the Gysin morphism induced by
$\pi _!$
is the Gysin morphism induced by
![]() $\pi $
. Since the mapping degree of
$\pi $
. Since the mapping degree of
![]() $\pi $
is 2,
$\pi $
is 2,
![]() $\pi _!\circ \pi ^*: H^2(\widetilde {{\mathcal {X}}}_t)\rightarrow H^2(\widetilde {{\mathcal {X}}}_t)$
equals multiplication by 2 (cf. [Reference Voisin and SchnepsVoi02, Remark 7.29]). Since
$\pi _!\circ \pi ^*: H^2(\widetilde {{\mathcal {X}}}_t)\rightarrow H^2(\widetilde {{\mathcal {X}}}_t)$
equals multiplication by 2 (cf. [Reference Voisin and SchnepsVoi02, Remark 7.29]). Since
![]() $\pi ^*(\omega ) = p^*\left (pr_1^*(\theta )\wedge pr_2^*(\theta )\right )$
, we have the relation
$\pi ^*(\omega ) = p^*\left (pr_1^*(\theta )\wedge pr_2^*(\theta )\right )$
, we have the relation
Let
![]() $\phi ^\vee : H_2(\widetilde {{\mathcal {X}}}_t) \rightarrow H_2({\mathcal {A}}_t)$
be the dual of
$\phi ^\vee : H_2(\widetilde {{\mathcal {X}}}_t) \rightarrow H_2({\mathcal {A}}_t)$
be the dual of
![]() $\phi $
. For any
$\phi $
. For any
![]() $[\Gamma ]\in H_2(\widetilde {{\mathcal {X}}}_t,{\mathbb {Z}})$
and
$[\Gamma ]\in H_2(\widetilde {{\mathcal {X}}}_t,{\mathbb {Z}})$
and
![]() $[\Gamma ']\in H_2({\mathcal {A}}_t,{\mathbb {Z}})$
such that
$[\Gamma ']\in H_2({\mathcal {A}}_t,{\mathbb {Z}})$
such that
![]() $\phi ^\vee ([\Gamma ]) = [\Gamma ']$
, we have
$\phi ^\vee ([\Gamma ]) = [\Gamma ']$
, we have
by (14). Since the right-hand side is a linear combination of
![]() $2P_i(a)P_j(b)$
, we see that any period function of
$2P_i(a)P_j(b)$
, we see that any period function of
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
with respect to
$\widetilde {{\mathcal {X}}}\rightarrow T$
with respect to
![]() $\omega $
is a linear combination of
$\omega $
is a linear combination of
![]() $2P_i(a)P_j(b)$
. Furthermore, since
$2P_i(a)P_j(b)$
. Furthermore, since
![]() $\phi $
is injective and its cokernel has no torsion (cf. [Reference Barth, Hulek, Peters and Van de VenBHPV04], Chapter VIII, Proposition 5.1, and Corollary 5.6),
$\phi $
is injective and its cokernel has no torsion (cf. [Reference Barth, Hulek, Peters and Van de VenBHPV04], Chapter VIII, Proposition 5.1, and Corollary 5.6),
![]() $\phi ^\vee $
is surjective. Thus,
$\phi ^\vee $
is surjective. Thus,
![]() $2P_i(a)P_j(b)$
itself is a period function for
$2P_i(a)P_j(b)$
itself is a period function for
![]() $i,j\in \{1,2\}$
and we have the result.
$i,j\in \{1,2\}$
and we have the result.
Now we can prove Proposition 5.2.
Proof of Proposition 5.2
Let
![]() $f\in {\mathcal {P}}_\omega \subset {\mathcal {O}}_T^{\mathrm {an}}$
be any local section. Then f is a linear combination of
$f\in {\mathcal {P}}_\omega \subset {\mathcal {O}}_T^{\mathrm {an}}$
be any local section. Then f is a linear combination of
![]() $2P_i(a)P_j(b)$
by Proposition 5.4. Since
$2P_i(a)P_j(b)$
by Proposition 5.4. Since
![]() $P_i(c)$
are solutions of (13), both of the differential operators
$P_i(c)$
are solutions of (13), both of the differential operators
![]() ${\mathscr {D}}_1$
and
${\mathscr {D}}_1$
and
![]() ${\mathscr {D}}_2$
annihilate
${\mathscr {D}}_2$
annihilate
![]() $2P_i(a)P_j(b)$
. Hence, we have the result.
$2P_i(a)P_j(b)$
. Hence, we have the result.
5.2 Calculation of the regulator
For a while, we fix
![]() $t_0\in T$
such thatFootnote
2
$t_0\in T$
such thatFootnote
2
![]() $\sqrt {1-a}$
,
$\sqrt {1-a}$
,
![]() $\sqrt {1-b}\in {\mathbb {R}}_{>0}$
. Our first goal is to compute the image of
$\sqrt {1-b}\in {\mathbb {R}}_{>0}$
. Our first goal is to compute the image of
![]() $(\xi _1)_t-(\xi _0)_t$
under the transcendental regulator map locally around
$(\xi _1)_t-(\xi _0)_t$
under the transcendental regulator map locally around
![]() $t_0$
. For the computation, we construct a 2-chain and use (7). In the calculation, we replace a 2-chain associated with
$t_0$
. For the computation, we construct a 2-chain and use (7). In the calculation, we replace a 2-chain associated with
![]() $(\xi _1)_t-(\xi _0)_t$
with another 2-chain to make the computation easier.
$(\xi _1)_t-(\xi _0)_t$
with another 2-chain to make the computation easier.
Let
![]() $\xi $
be a higher Chow cycle on a
$\xi $
be a higher Chow cycle on a
![]() $K3$
surface X, and let
$K3$
surface X, and let
![]() $\gamma $
be the topological 1-cycle associated with
$\gamma $
be the topological 1-cycle associated with
![]() $\xi $
. A topological 2-chain
$\xi $
. A topological 2-chain
![]() $\Gamma '$
is called a 2-chain associated with
$\Gamma '$
is called a 2-chain associated with
![]() $\xi $
in a weak sense if there exists a finite family of curves
$\xi $
in a weak sense if there exists a finite family of curves
![]() $\{E_k\}_{k}$
on X and a topological 2-chain
$\{E_k\}_{k}$
on X and a topological 2-chain
![]() $\Gamma _k$
on each
$\Gamma _k$
on each
![]() $E_k$
such that
$E_k$
such that
Let
![]() $\Gamma $
be a 2-chain associated with
$\Gamma $
be a 2-chain associated with
![]() $\xi $
. If
$\xi $
. If
![]() $\Gamma '$
is a 2-chain associated with
$\Gamma '$
is a 2-chain associated with
![]() $\xi $
in a weak sense,
$\xi $
in a weak sense,
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma '+\sum _{k}\Gamma _k$
coincide up to topological 2-cycles. Since the pull-back of a holomorphic 2-form
$\Gamma '+\sum _{k}\Gamma _k$
coincide up to topological 2-cycles. Since the pull-back of a holomorphic 2-form
![]() $\omega $
on
$\omega $
on
![]() $E_k$
vanishes, we have
$E_k$
vanishes, we have
Hence, we can also use
![]() $\Gamma '$
for the computation of the transcendental regulator map.
$\Gamma '$
for the computation of the transcendental regulator map.
We will construct a desired 2-chain. For t which is sufficiently close to
![]() $t_0$
, let
$t_0$
, let
![]() $\triangle _+$
and
$\triangle _+$
and
![]() $\triangle _-$
be the images of the following maps:
$\triangle _-$
be the images of the following maps:

Note that since t is sufficiently close to
![]() $t_0$
, we may assume the function
$t_0$
, we may assume the function
![]() $\sqrt {1-ax}$
(resp.
$\sqrt {1-ax}$
(resp.
![]() $\sqrt {1-by}$
) do not ramify on
$\sqrt {1-by}$
) do not ramify on
![]() $\triangle $
and we can fix the branch of it so that it takes a value
$\triangle $
and we can fix the branch of it so that it takes a value
![]() $1$
and
$1$
and
![]() $\sqrt {1-a}$
at
$\sqrt {1-a}$
at
![]() $x=0,1$
(resp.
$x=0,1$
(resp.
![]() $1$
and
$1$
and
![]() $\sqrt {1-b}$
at
$\sqrt {1-b}$
at
![]() $y=0,1$
).
$y=0,1$
).
We define
![]() $K_+$
and
$K_+$
and
![]() $K_-$
as the closures of
$K_-$
as the closures of
![]() $\triangle _+$
and
$\triangle _+$
and
![]() $\triangle _-$
, respectively. Let
$\triangle _-$
, respectively. Let
![]() $\gamma $
be a path
$\gamma $
be a path
![]() $[0,1]$
on
$[0,1]$
on
![]() ${\mathbb {P}}^1$
reparameterized so that
${\mathbb {P}}^1$
reparameterized so that
![]() $\gamma (s) = s^2$
(resp.
$\gamma (s) = s^2$
(resp.
![]() $1-\gamma (s) = (1-s)^2$
) on a neighborhood of
$1-\gamma (s) = (1-s)^2$
) on a neighborhood of
![]() $0$
(resp.
$0$
(resp.
![]() $1$
). Then if we replace x and y in the target in (16) by
$1$
). Then if we replace x and y in the target in (16) by
![]() $\gamma (x)$
and
$\gamma (x)$
and
![]() $\gamma (y)$
, respectively, (16) can be extended to a map from a compact-oriented manifold with corners, so
$\gamma (y)$
, respectively, (16) can be extended to a map from a compact-oriented manifold with corners, so
![]() $K_+$
and
$K_+$
and
![]() $K_-$
are
$K_-$
are
![]() $C^\infty $
-chains.
$C^\infty $
-chains.
Proposition 5.5 For any t which is sufficiently close to
![]() $t_0$
, we have
$t_0$
, we have
To prove this, we should examine the boundaries of
![]() $K_+$
and
$K_+$
and
![]() $K_-$
. Recall that we have the following morphisms.
$K_-$
. Recall that we have the following morphisms.
We regard
![]() $\triangle =\{(x,y)\in {\mathbb {R}}^2:0<y<x<1\}$
as a subset of
$\triangle =\{(x,y)\in {\mathbb {R}}^2:0<y<x<1\}$
as a subset of
![]() ${\mathcal {Y}}_t={\mathbb {P}}^1\times {\mathbb {P}}^1$
. Let K be the closure of the inverse image of
${\mathcal {Y}}_t={\mathbb {P}}^1\times {\mathbb {P}}^1$
. Let K be the closure of the inverse image of
![]() $\triangle $
by
$\triangle $
by
![]() $\widetilde {{\mathcal {Y}}}_t\rightarrow {\mathcal {Y}}_t$
(see Figure 4). We define paths
$\widetilde {{\mathcal {Y}}}_t\rightarrow {\mathcal {Y}}_t$
(see Figure 4). We define paths
![]() $\gamma _c,\gamma _{11},\gamma _{y},\gamma _{10}, \gamma _x,$
and
$\gamma _c,\gamma _{11},\gamma _{y},\gamma _{10}, \gamma _x,$
and
![]() $\gamma _{00}$
on the boundary
$\gamma _{00}$
on the boundary
![]() $\partial K$
as in Figure 4.
$\partial K$
as in Figure 4.
Figure 4: The 2-chain K and its boundary.

Figure 5: The 2-chains
![]() $K_+$
and
$K_+$
and
![]() $K_-$
and their boundaries.
$K_-$
and their boundaries.
Then
![]() $\widetilde {{\mathcal {X}}}_t\rightarrow \widetilde {{\mathcal {Y}}}_t$
induces the homeomorphism
$\widetilde {{\mathcal {X}}}_t\rightarrow \widetilde {{\mathcal {Y}}}_t$
induces the homeomorphism
![]() $K_+\xrightarrow {\sim } K$
and
$K_+\xrightarrow {\sim } K$
and
![]() $K_-\xrightarrow {\sim } K$
(see Figure 5). Here, the bold line in the figure denotes the branching locus of
$K_-\xrightarrow {\sim } K$
(see Figure 5). Here, the bold line in the figure denotes the branching locus of
![]() $\widetilde {{\mathcal {X}}}_t\rightarrow \widetilde {{\mathcal {Y}}}_t$
. We define paths
$\widetilde {{\mathcal {X}}}_t\rightarrow \widetilde {{\mathcal {Y}}}_t$
. We define paths
![]() $\gamma _{c,\pm }, \gamma _{11,\pm }, \gamma _y,\gamma _{10,\pm },\gamma _x,$
and
$\gamma _{c,\pm }, \gamma _{11,\pm }, \gamma _y,\gamma _{10,\pm },\gamma _x,$
and
![]() $\gamma _{00,\pm }$
on
$\gamma _{00,\pm }$
on
![]() $\partial K_+$
and
$\partial K_+$
and
![]() $\partial K_-$
as in Figure 5. They satisfy the following properties:
$\partial K_-$
as in Figure 5. They satisfy the following properties:
-
(1) The paths
 $\gamma _{c,+}$
and
$\gamma _{c,+}$
and
 $\gamma _{c,-}$
are the lifts of
$\gamma _{c,-}$
are the lifts of
 $\gamma _c$
. Since
$\gamma _c$
. Since
 $\gamma _c$
is on the strict transformation of
$\gamma _c$
is on the strict transformation of
 ${\mathcal {D}}$
, they are on the curve
${\mathcal {D}}$
, they are on the curve
 $\widetilde {{\mathcal {C}}}$
.
$\widetilde {{\mathcal {C}}}$
. -
(2) Furthermore, since t is close to
 $t_0$
,
$t_0$
,
 $\gamma _{c,+}$
(resp.
$\gamma _{c,+}$
(resp.
 $\gamma _{c,-}$
) is a path from
$\gamma _{c,-}$
) is a path from
 $(1,1,\sqrt {1-b}/\sqrt {1-a})$
to
$(1,1,\sqrt {1-b}/\sqrt {1-a})$
to
 $(0,0,1)$
(resp.
$(0,0,1)$
(resp.
 $(1,1,-\sqrt {1-b}/\sqrt {1-a})$
to
$(1,1,-\sqrt {1-b}/\sqrt {1-a})$
to
 $(0,0,-1)$
).
$(0,0,-1)$
). -
(3) The paths
 $\gamma _{00,+},\gamma _{10,+}$
, and
$\gamma _{00,+},\gamma _{10,+}$
, and
 $\gamma _{11,+}$
(resp.
$\gamma _{11,+}$
(resp.
 $\gamma _{00,-},\gamma _{10,-}$
, and
$\gamma _{00,-},\gamma _{10,-}$
, and
 $\gamma _{11,-}$
) are the lifts of
$\gamma _{11,-}$
) are the lifts of
 $\gamma _{00},\gamma _{10}$
, and
$\gamma _{00},\gamma _{10}$
, and
 $\gamma _{11}$
and they are on the exceptional curves
$\gamma _{11}$
and they are on the exceptional curves
 $Q_{(0,0)}, Q_{(1,0)}$
, and
$Q_{(0,0)}, Q_{(1,0)}$
, and
 $Q_{(1,1)}$
, respectively.
$Q_{(1,1)}$
, respectively. -
(4) Since
 $\gamma _x$
and
$\gamma _x$
and
 $\gamma _y$
on
$\gamma _y$
on
 $\partial K$
is contained in the branching locus of
$\partial K$
is contained in the branching locus of
 $\widetilde {{\mathcal {X}}}_t\rightarrow \widetilde {{\mathcal {Y}}}_t$
, there exist the unique lifts of them and their lifts are contained in
$\widetilde {{\mathcal {X}}}_t\rightarrow \widetilde {{\mathcal {Y}}}_t$
, there exist the unique lifts of them and their lifts are contained in
 $\partial K_+\cap \partial K_-$
.
$\partial K_+\cap \partial K_-$
.
Then we can prove Proposition 5.5.
Proof of Proposition 5.5
It is enough to show that
![]() $K_+-K_-$
is a 2-chain associated with
$K_+-K_-$
is a 2-chain associated with
![]() $(\xi _1)_t-(\xi _0)_t$
in a weak sense. Note that
$(\xi _1)_t-(\xi _0)_t$
in a weak sense. Note that
![]() $(\xi _1)_t-(\xi _0)_t$
is represented by the formal sum
$(\xi _1)_t-(\xi _0)_t$
is represented by the formal sum
Let
![]() $\widetilde {\gamma }_c$
(resp.
$\widetilde {\gamma }_c$
(resp.
![]() $\widetilde {\gamma }_{00}$
,
$\widetilde {\gamma }_{00}$
,
![]() $\widetilde {\gamma }_{11}$
) be the 1-chain on
$\widetilde {\gamma }_{11}$
) be the 1-chain on
![]() $\widetilde {{\mathcal {C}}}$
(resp.
$\widetilde {{\mathcal {C}}}$
(resp.
![]() $Q_{(0,0)}$
,
$Q_{(0,0)}$
,
![]() $Q_{(1,1)}$
) defined by the pull-back of
$Q_{(1,1)}$
) defined by the pull-back of
![]() $[\infty ,0]$
on
$[\infty ,0]$
on
![]() ${\mathbb {P}}^1$
by the rational function
${\mathbb {P}}^1$
by the rational function
![]() $\psi _0^{-1}\psi _1$
(resp.
$\psi _0^{-1}\psi _1$
(resp.
![]() $\varphi _0^{-1}$
,
$\varphi _0^{-1}$
,
![]() $\varphi _1$
). Then
$\varphi _1$
). Then
![]() $\widetilde {\gamma }_c+\widetilde {\gamma }_{00}+\widetilde {\gamma }_{11}$
is the 1-cycle associated with
$\widetilde {\gamma }_c+\widetilde {\gamma }_{00}+\widetilde {\gamma }_{11}$
is the 1-cycle associated with
![]() $\xi $
. By Figure 5, we have
$\xi $
. By Figure 5, we have
Hence, we should show that the 1-chains
![]() $(\gamma _{c,+}-\gamma _{c,-}-\widetilde {\gamma }_c)$
,
$(\gamma _{c,+}-\gamma _{c,-}-\widetilde {\gamma }_c)$
,
![]() $(\gamma _{00,+}-\gamma _{00,-}-\widetilde {\gamma }_{00})$
,
$(\gamma _{00,+}-\gamma _{00,-}-\widetilde {\gamma }_{00})$
,
![]() $(\gamma _{10,+} -\gamma _{10,-}),$
and
$(\gamma _{10,+} -\gamma _{10,-}),$
and
![]() $(\gamma _{11,+}-\gamma _{11,-}-\widetilde {\gamma }_{11})$
are 1-boundaries on the curves
$(\gamma _{11,+}-\gamma _{11,-}-\widetilde {\gamma }_{11})$
are 1-boundaries on the curves
![]() $\widetilde {{\mathcal {C}}},Q_{(0,0)}, Q_{(1,0)}$
, and
$\widetilde {{\mathcal {C}}},Q_{(0,0)}, Q_{(1,0)}$
, and
![]() $Q_{(1,1)}$
, respectively. Since
$Q_{(1,1)}$
, respectively. Since
![]() $\widetilde {{\mathcal {C}}},Q_{(0,0)},Q_{(1,0)}$
and
$\widetilde {{\mathcal {C}}},Q_{(0,0)},Q_{(1,0)}$
and
![]() $Q_{(1,1)}$
are isomorphic to
$Q_{(1,1)}$
are isomorphic to
![]() ${\mathbb {P}}^1$
and
${\mathbb {P}}^1$
and
![]() $H_1({\mathbb {P}}^1)=0$
, it is enough to show that they are 1-cycles. By Figure 5, we have the following relations:
$H_1({\mathbb {P}}^1)=0$
, it is enough to show that they are 1-cycles. By Figure 5, we have the following relations:
 $$ \begin{align*} \begin{aligned} &\partial(\gamma_{c,+}-\gamma_{c,-}) ={\mathrm{div}}_{\widetilde{{\mathcal{C}}}}(\psi_0^{-1}\psi_1) = \partial\widetilde{\gamma}_c,&&\partial(\gamma_{00,+}-\gamma_{00,-}) = {\mathrm{div}}_{Q_{(0,0)}}(\varphi_0^{-1}) = \partial\widetilde{\gamma}_{00,}\\ &\partial(\gamma_{11,+}-\gamma_{11,-}) = {\mathrm{div}}_{Q_{(1,1)}}(\varphi_1) = \partial\widetilde{\gamma}_{11},&& \partial(\gamma_{10,+} -\gamma_{10,-})=0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\partial(\gamma_{c,+}-\gamma_{c,-}) ={\mathrm{div}}_{\widetilde{{\mathcal{C}}}}(\psi_0^{-1}\psi_1) = \partial\widetilde{\gamma}_c,&&\partial(\gamma_{00,+}-\gamma_{00,-}) = {\mathrm{div}}_{Q_{(0,0)}}(\varphi_0^{-1}) = \partial\widetilde{\gamma}_{00,}\\ &\partial(\gamma_{11,+}-\gamma_{11,-}) = {\mathrm{div}}_{Q_{(1,1)}}(\varphi_1) = \partial\widetilde{\gamma}_{11},&& \partial(\gamma_{10,+} -\gamma_{10,-})=0. \end{aligned} \end{align*} $$
Hence, they are 1-cycles and we confirm that
![]() $K_+-K_-$
is a 2-chain associated with
$K_+-K_-$
is a 2-chain associated with
![]() $(\xi _1)_t-(\xi _0)_t$
in a weak sense.
$(\xi _1)_t-(\xi _0)_t$
in a weak sense.
Let
![]() ${\mathcal {L}}$
be the local holomorphic function
${\mathcal {L}}$
be the local holomorphic function
which is defined around
![]() $t_0$
. Using the local description of
$t_0$
. Using the local description of
![]() $\omega _t$
, we see that
$\omega _t$
, we see that
 $$ \begin{align*} \int_{K_+}\omega_t=-\int_{K_-}\omega_t = \int_{\triangle}\frac{dxdy}{\sqrt{x(1-x)(1-ax)}\sqrt{y(1-y)(1-by)}}. \end{align*} $$
$$ \begin{align*} \int_{K_+}\omega_t=-\int_{K_-}\omega_t = \int_{\triangle}\frac{dxdy}{\sqrt{x(1-x)(1-ax)}\sqrt{y(1-y)(1-by)}}. \end{align*} $$
Hence,
![]() ${\mathcal {L}}(t)$
is a lift of
${\mathcal {L}}(t)$
is a lift of
![]() ${\mathcal {L}}(a,b)$
in (10). Then we can prove Proposition 5.3.
${\mathcal {L}}(a,b)$
in (10). Then we can prove Proposition 5.3.
Proof of Proposition 5.3
We will prove (1) and (2) simultaneously. Let
![]() $\{U_i\}_i$
be a good open cover of T such that for each i, there exists a local holomorphic function
$\{U_i\}_i$
be a good open cover of T such that for each i, there exists a local holomorphic function
![]() $\varphi _i$
on
$\varphi _i$
on
![]() $U_i$
which represents
$U_i$
which represents
![]() $\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)|_{U_i}$
. To prove (1) and (2), it is enough to show that
$\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)|_{U_i}$
. To prove (1) and (2), it is enough to show that
![]() ${\mathcal {L}}$
have an analytic continuation on each
${\mathcal {L}}$
have an analytic continuation on each
![]() $U_i$
and the resulting function coincides with
$U_i$
and the resulting function coincides with
![]() $\varphi _i$
up to an elements in
$\varphi _i$
up to an elements in
![]() ${\mathcal {P}}_\omega (U_i)$
.
${\mathcal {P}}_\omega (U_i)$
.
By Proposition 5.5, the equation (11) holds for any point t of an open neighborhood
![]() $U_0$
of
$U_0$
of
![]() $t_0$
. Since the left-hand side of (11) corresponds to
$t_0$
. Since the left-hand side of (11) corresponds to
![]() $\langle {\mathrm {ev}}_t(\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)),[\omega _t]\rangle $
, we see that
$\langle {\mathrm {ev}}_t(\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)),[\omega _t]\rangle $
, we see that
![]() $[{\mathcal {L}}]$
corresponds to
$[{\mathcal {L}}]$
corresponds to
![]() $\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)|_{U_0}$
by Corollary 2.5. Thus if
$\nu _{{\mathrm {tr}}}(\xi _1-\xi _0)|_{U_0}$
by Corollary 2.5. Thus if
![]() $U_i\cap U_0\neq \emptyset $
, we have
$U_i\cap U_0\neq \emptyset $
, we have
![]() $[\varphi _i]|_{U_i\cap U_0} = [{\mathcal {L}}]|_{U_i\cap U_0}$
, so
$[\varphi _i]|_{U_i\cap U_0} = [{\mathcal {L}}]|_{U_i\cap U_0}$
, so
![]() ${\mathcal {L}}-\varphi _i \in {\mathcal {P}}_\omega (U_i\cap U_0)$
. Let
${\mathcal {L}}-\varphi _i \in {\mathcal {P}}_\omega (U_i\cap U_0)$
. Let
![]() $p_i$
be the restriction of
$p_i$
be the restriction of
![]() ${{\mathcal {L}}-\varphi _i}$
on
${{\mathcal {L}}-\varphi _i}$
on
![]() $U_i\cap U_0$
. Then we can extend
$U_i\cap U_0$
. Then we can extend
![]() $p_i$
on
$p_i$
on
![]() $U_i$
. The function
$U_i$
. The function
![]() $\varphi _i + p_i$
is a desired analytic continuation of
$\varphi _i + p_i$
is a desired analytic continuation of
![]() ${\mathcal {L}}$
on
${\mathcal {L}}$
on
![]() $U_i$
. For a general
$U_i$
. For a general
![]() $U_i$
, take a finite family
$U_i$
, take a finite family
![]() $U_{i_1},\dots , U_{i_n}=U_i$
such that
$U_{i_1},\dots , U_{i_n}=U_i$
such that
![]() $U_0\cap U_{i_1}\neq \emptyset $
and
$U_0\cap U_{i_1}\neq \emptyset $
and
![]() $U_{i_{k-1}}\cap U_{i_{k}}\neq \emptyset $
for
$U_{i_{k-1}}\cap U_{i_{k}}\neq \emptyset $
for
![]() $k = 2,\dots ,n$
and repeat the above process.
$k = 2,\dots ,n$
and repeat the above process.
Next, we will prove (3). We will compute
![]() ${\mathscr {D}}_1({\mathcal {L}})$
. It is enough to calculate it on a neighborhood of
${\mathscr {D}}_1({\mathcal {L}})$
. It is enough to calculate it on a neighborhood of
![]() $t_0$
. Hence, we may assume
$t_0$
. Hence, we may assume
![]() ${\mathcal {L}}$
is given by (17).
${\mathcal {L}}$
is given by (17).
Let
![]() $H(a,x)$
be a local holomorphic function defined by
$H(a,x)$
be a local holomorphic function defined by
![]() $H(a,x) =-\frac {\sqrt {x(1-x)}}{2\sqrt {1-ax}^3}$
. We can check that
$H(a,x) =-\frac {\sqrt {x(1-x)}}{2\sqrt {1-ax}^3}$
. We can check that
 $$ \begin{align*} {\mathscr{D}}_1 \left(\frac{1}{\sqrt{x(1-x)(1-ax)}}\right) = \frac{\partial H(a,x)}{\partial x}. \end{align*} $$
$$ \begin{align*} {\mathscr{D}}_1 \left(\frac{1}{\sqrt{x(1-x)(1-ax)}}\right) = \frac{\partial H(a,x)}{\partial x}. \end{align*} $$
Then by Stokes’ theorem,Footnote 3 we have
 $$ \begin{align*} \begin{aligned} &{\mathscr{D}}_1\left(\frac{1}{2}{\mathcal{L}}\right) = {\mathscr{D}}_1\left( \int_{K_+}\frac{dxdy}{\sqrt{x(1-x)(1-ax)}\sqrt{y(1-y)(1-by)}}\right) \\ &= \int_{K_+} d\left(\frac{H(a,x)dy}{\sqrt{y(1-y)(1-by)}}\right) = \int_{\partial K_+} \frac{H(a,x)dy}{\sqrt{y(1-y)(1-by)}}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &{\mathscr{D}}_1\left(\frac{1}{2}{\mathcal{L}}\right) = {\mathscr{D}}_1\left( \int_{K_+}\frac{dxdy}{\sqrt{x(1-x)(1-ax)}\sqrt{y(1-y)(1-by)}}\right) \\ &= \int_{K_+} d\left(\frac{H(a,x)dy}{\sqrt{y(1-y)(1-by)}}\right) = \int_{\partial K_+} \frac{H(a,x)dy}{\sqrt{y(1-y)(1-by)}}, \end{aligned} \end{align*} $$
and since the 1-form
![]() $\frac {H(a,x)dy}{\sqrt {y(1-y)(1-by)}}$
vanishes on
$\frac {H(a,x)dy}{\sqrt {y(1-y)(1-by)}}$
vanishes on
![]() $\partial K_+$
except
$\partial K_+$
except
![]() $\gamma _{c,+}$
, we have
$\gamma _{c,+}$
, we have
 $$ \begin{align*} =\frac{1}{2}\int_0^1 \frac{dz}{(1-bz)^{\frac{1}{2}}(1-az)^{\frac{3}{2}}} =\frac{1}{a-b} \int_1^{\frac{\sqrt{1-b}}{\sqrt{1-a}}} du = \frac{1}{a-b}\cdot\left(\frac{\sqrt{1-b}}{\sqrt{1-a}}-1\right). \end{align*} $$
$$ \begin{align*} =\frac{1}{2}\int_0^1 \frac{dz}{(1-bz)^{\frac{1}{2}}(1-az)^{\frac{3}{2}}} =\frac{1}{a-b} \int_1^{\frac{\sqrt{1-b}}{\sqrt{1-a}}} du = \frac{1}{a-b}\cdot\left(\frac{\sqrt{1-b}}{\sqrt{1-a}}-1\right). \end{align*} $$
Here, we use the coordinate transform
![]() $u= \frac {\sqrt {1-bz}}{\sqrt {1-az}}$
. We can compute
$u= \frac {\sqrt {1-bz}}{\sqrt {1-az}}$
. We can compute
![]() ${\mathscr {D}}_2({\mathcal {L}})$
similarly.
${\mathscr {D}}_2({\mathcal {L}})$
similarly.
6 The group action on the Kummer family
In this section, we construct a group action on
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
. To produce many higher Chow cycles, it is not enough to consider only automorphisms which are trivial on T. We will consider automorphisms of the following type.
$\widetilde {{\mathcal {X}}}\rightarrow T$
. To produce many higher Chow cycles, it is not enough to consider only automorphisms which are trivial on T. We will consider automorphisms of the following type.
Definition 6.1 Let
![]() $X\rightarrow S$
be a family of algebraic varieties. The automorphism group
$X\rightarrow S$
be a family of algebraic varieties. The automorphism group
![]() ${\mathrm {Aut}}(X\rightarrow S)$
of
${\mathrm {Aut}}(X\rightarrow S)$
of
![]() $X\rightarrow S$
consists of a pair
$X\rightarrow S$
consists of a pair
![]() $(g,h)$
with
$(g,h)$
with
![]() $g\in {\mathrm {Aut}}(X)$
and
$g\in {\mathrm {Aut}}(X)$
and
![]() $h\in {\mathrm {Aut}}(S)$
such that the following diagram commutes.
$h\in {\mathrm {Aut}}(S)$
such that the following diagram commutes.

We say that a group G acts on a family of varieties
![]() $X\rightarrow S$
if we have a group homomorphism
$X\rightarrow S$
if we have a group homomorphism
![]() $G\rightarrow {\mathrm {Aut}}(X\rightarrow S)$
.
$G\rightarrow {\mathrm {Aut}}(X\rightarrow S)$
.
The main result of this section is as follows.
Proposition 6.2 There exists a
![]() $G_{{\mathcal {X}}}$
-action on
$G_{{\mathcal {X}}}$
-action on
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
, where
$\widetilde {{\mathcal {X}}}\rightarrow T$
, where
![]() $G_{{\mathcal {X}}}$
is a
$G_{{\mathcal {X}}}$
is a
![]() ${\mathbb {Z}}/2$
-extension of
${\mathbb {Z}}/2$
-extension of
![]() $(\mathfrak {S}_4\times _{\mathfrak {S}_3} \mathfrak {S}_4)^2$
.
$(\mathfrak {S}_4\times _{\mathfrak {S}_3} \mathfrak {S}_4)^2$
.
We use the following conventions for group actions.
-
(1) In this paper, we consider left group actions unless specified otherwise.
-
(2) Suppose a group G acts on a set M. The group G stabilizes a subset
 $M'$
of M if we have
$M'$
of M if we have
 $g\cdot m\in M'$
for any
$g\cdot m\in M'$
for any
 $g\in G$
and
$g\in G$
and
 $m\in M'$
.
$m\in M'$
. -
(3) For a
 ${\mathbb {C}}$
-scheme X,
${\mathbb {C}}$
-scheme X,
 ${\mathrm {Aut}}(X)$
denotes the
${\mathrm {Aut}}(X)$
denotes the
 ${\mathbb {C}}$
-automorphism group of X. For
${\mathbb {C}}$
-automorphism group of X. For
 ${\rho \in {\mathrm {Aut}}(X)}$
,
${\rho \in {\mathrm {Aut}}(X)}$
,
 $\rho ^\sharp $
denotes the morphism of sheaves
$\rho ^\sharp $
denotes the morphism of sheaves
 ${\mathcal {O}}_X\rightarrow \rho _*{\mathcal {O}}_X$
.
${\mathcal {O}}_X\rightarrow \rho _*{\mathcal {O}}_X$
. -
(4) For
 $n\in {\mathbb {Z}}_{>1}$
,
$n\in {\mathbb {Z}}_{>1}$
,
 $\mu _n$
denotes the group of nth roots of unity.
$\mu _n$
denotes the group of nth roots of unity. -
(5) For
 $n\in {\mathbb {Z}}_{\ge 1}$
,
$n\in {\mathbb {Z}}_{\ge 1}$
,
 $\mathfrak {S}_n$
denotes the symmetric group of degree n. For a set M,
$\mathfrak {S}_n$
denotes the symmetric group of degree n. For a set M,
 $\mathfrak {S}(M)$
denotes the symmetric group of M. The sign character is denoted by
$\mathfrak {S}(M)$
denotes the symmetric group of M. The sign character is denoted by
 ${\mathrm {sgn}}: \mathfrak {S}(M)\rightarrow \mu _2$
.
${\mathrm {sgn}}: \mathfrak {S}(M)\rightarrow \mu _2$
.
Before the construction of the
![]() $G_{{\mathcal {X}}}$
-action on
$G_{{\mathcal {X}}}$
-action on
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
, we recall some formal properties of finite group actions on schemes in Section 6.1.
$\widetilde {{\mathcal {X}}}\rightarrow T$
, we recall some formal properties of finite group actions on schemes in Section 6.1.
6.1 Generalities
A scheme with a group action
![]() $(S,H,\varphi )$
is a triplet consisting of a
$(S,H,\varphi )$
is a triplet consisting of a
![]() ${\mathbb {C}}$
-scheme S, a group H and a group homomorphism
${\mathbb {C}}$
-scheme S, a group H and a group homomorphism
![]() $\varphi : H\rightarrow {\mathrm {Aut}}(S)$
. We usually omit
$\varphi : H\rightarrow {\mathrm {Aut}}(S)$
. We usually omit
![]() $\varphi $
from the notation and write
$\varphi $
from the notation and write
![]() $(S,H)$
. A morphism
$(S,H)$
. A morphism
![]() $(X,G)\rightarrow (S,H)$
between two such objects is a pair of a morphism
$(X,G)\rightarrow (S,H)$
between two such objects is a pair of a morphism
![]() $X\rightarrow S$
of varieties and a group homomorphism
$X\rightarrow S$
of varieties and a group homomorphism
![]() $G\rightarrow H$
satisfying the usual compatibility condition.
$G\rightarrow H$
satisfying the usual compatibility condition.
In Section 6.2, we use the following fiber product construction. Suppose we have two morphisms
![]() $(\pi ,\psi ): (X,G)\rightarrow (S,H)$
and
$(\pi ,\psi ): (X,G)\rightarrow (S,H)$
and
![]() $(f,\varphi ):(S',H')\rightarrow (S,H)$
. Recall that the fiber product of G and
$(f,\varphi ):(S',H')\rightarrow (S,H)$
. Recall that the fiber product of G and
![]() $H'$
over H is defined by
$H'$
over H is defined by
Then we define the fiber product of
![]() $(X,G)$
and
$(X,G)$
and
![]() $(S',H')$
over
$(S',H')$
over
![]() $(S,H)$
by
$(S,H)$
by
This is indeed the fiber product in the category of schemes with group actions.
Let
![]() $(X,G)$
be a scheme with a group action. Then we have the natural right G-action on
$(X,G)$
be a scheme with a group action. Then we have the natural right G-action on
![]() $\Gamma (X,{\mathcal {O}}_X^\times )$
. A 1-cocycle on
$\Gamma (X,{\mathcal {O}}_X^\times )$
. A 1-cocycle on
![]() $\Gamma (X,{\mathcal {O}}_X^\times )$
is a map
$\Gamma (X,{\mathcal {O}}_X^\times )$
is a map
![]() $\chi : G\rightarrow \Gamma (X,{\mathcal {O}}_X^\times )$
satisfying
$\chi : G\rightarrow \Gamma (X,{\mathcal {O}}_X^\times )$
satisfying
for any
![]() $g,h\in G$
. Here,
$g,h\in G$
. Here,
![]() $h^\sharp : {\mathcal {O}}_X\rightarrow h_*{\mathcal {O}}_{X}$
is the natural morphism induced by
$h^\sharp : {\mathcal {O}}_X\rightarrow h_*{\mathcal {O}}_{X}$
is the natural morphism induced by
![]() ${h:X\rightarrow X}$
.
${h:X\rightarrow X}$
.
Let
![]() ${\mathscr {L}}$
be a G-linearized line bundle on X. The G-linearization is the same as a collection
${\mathscr {L}}$
be a G-linearized line bundle on X. The G-linearization is the same as a collection
![]() $(\Phi _{g}: g^*{\mathscr {L}}\xrightarrow {\sim } {\mathscr {L}})_{g\in G}$
of isomorphisms satisfying the relation
$(\Phi _{g}: g^*{\mathscr {L}}\xrightarrow {\sim } {\mathscr {L}})_{g\in G}$
of isomorphisms satisfying the relation
![]() $\Phi _{h}\circ h^*(\Phi _g) = \Phi _{gh}$
for
$\Phi _{h}\circ h^*(\Phi _g) = \Phi _{gh}$
for
![]() $g,h\in G$
. We can construct a 1-cocycle as follows. Let s be a global section of
$g,h\in G$
. We can construct a 1-cocycle as follows. Let s be a global section of
![]() ${\mathscr {L}}$
such that
${\mathscr {L}}$
such that
![]() ${\mathrm {div}}(s)$
is stable under the G-action. Then there exists the unique 1-cocycle
${\mathrm {div}}(s)$
is stable under the G-action. Then there exists the unique 1-cocycle
![]() $\chi :G\rightarrow \Gamma (X,{\mathcal {O}}_X^\times )$
such that
$\chi :G\rightarrow \Gamma (X,{\mathcal {O}}_X^\times )$
such that
Finally, we prove liftability of a group action by a cyclic covers. For a line bundle
![]() ${\mathscr {L}}$
and a section
${\mathscr {L}}$
and a section
![]() $s\in \Gamma (X,{\mathscr {L}}^{\otimes (-m)})$
, the cyclic covering
$s\in \Gamma (X,{\mathscr {L}}^{\otimes (-m)})$
, the cyclic covering
![]() $Y\rightarrow X$
associated with
$Y\rightarrow X$
associated with
![]() $({\mathscr {L}},s)$
is defined as the relative spectrum of the
$({\mathscr {L}},s)$
is defined as the relative spectrum of the
![]() ${\mathcal {O}}_X$
-algebra
${\mathcal {O}}_X$
-algebra
![]() $\bigoplus _{i=0}^{m-1}{\mathscr {L}}^{\otimes i}$
(cf. [Reference Barth, Hulek, Peters and Van de VenBHPV04, p. 54]). The branching locus of
$\bigoplus _{i=0}^{m-1}{\mathscr {L}}^{\otimes i}$
(cf. [Reference Barth, Hulek, Peters and Van de VenBHPV04, p. 54]). The branching locus of
![]() $Y\rightarrow X$
coincides with
$Y\rightarrow X$
coincides with
![]() ${\mathrm {div}}(s)$
.
${\mathrm {div}}(s)$
.
Proposition 6.3 Let
![]() $\pi :Y\rightarrow X$
be the degree m cyclic covering associated with
$\pi :Y\rightarrow X$
be the degree m cyclic covering associated with
![]() $({\mathscr {L}},s)$
. Suppose a group G acts on X and a G-linearization
$({\mathscr {L}},s)$
. Suppose a group G acts on X and a G-linearization
![]() $(\Phi _g)_{g\in G}$
of
$(\Phi _g)_{g\in G}$
of
![]() ${\mathscr {L}}$
are given. Assume that there exists a 1-cocycle
${\mathscr {L}}$
are given. Assume that there exists a 1-cocycle
![]() $\chi :G\rightarrow \Gamma (X,{\mathcal {O}}_X^\times )$
such that
$\chi :G\rightarrow \Gamma (X,{\mathcal {O}}_X^\times )$
such that
for any
![]() $g\in G$
. Then there exists a G-action on Y such that
$g\in G$
. Then there exists a G-action on Y such that
![]() $\pi $
is G-equivariant.
$\pi $
is G-equivariant.
Proof For
![]() $g\in G$
, we define an automorphism
$g\in G$
, we define an automorphism
![]() $\tilde {g}: Y\rightarrow Y$
as follows.
$\tilde {g}: Y\rightarrow Y$
as follows.
-
1. Let
 $Y_1$
be the cyclic covering associated with
$Y_1$
be the cyclic covering associated with
 $(g^*{\mathscr {L}}, g^*(s))$
. Then
$(g^*{\mathscr {L}}, g^*(s))$
. Then
 $Y_1$
is the fiber product of
$Y_1$
is the fiber product of
 $Y\rightarrow X$
and
$Y\rightarrow X$
and
 $X\xrightarrow {\:g\:} X$
. Since g is an isomorphism,
$X\xrightarrow {\:g\:} X$
. Since g is an isomorphism,
 $Y_1\rightarrow Y$
is an isomorphism as well.
$Y_1\rightarrow Y$
is an isomorphism as well. -
2. Let
 $Y_2$
be the cyclic covering associated with
$Y_2$
be the cyclic covering associated with
 $({\mathscr {L}},\chi (g)^{-m}\cdot s)$
. Then we have the isomorphism
$({\mathscr {L}},\chi (g)^{-m}\cdot s)$
. Then we have the isomorphism
 $Y_2\simeq Y_1$
over X induced by
$Y_2\simeq Y_1$
over X induced by
 $\Phi _g$
.
$\Phi _g$
. -
3. We have the
 ${\mathcal {O}}_X$
-module automorphism on
${\mathcal {O}}_X$
-module automorphism on
 ${\mathscr {L}}$
defined by the multiplication of
${\mathscr {L}}$
defined by the multiplication of
 $\chi (g)^{-1}$
. This automorphism induces an isomorphism
$\chi (g)^{-1}$
. This automorphism induces an isomorphism
 $Y\simeq Y_2$
over X.
$Y\simeq Y_2$
over X.
Composing these isomorphisms, we get an automorphism
![]() $\tilde {g}\in {\mathrm {Aut}}(Y)$
.
$\tilde {g}\in {\mathrm {Aut}}(Y)$
.

We can show that
![]() $G\rightarrow {\mathrm {Aut}}(Y);g\mapsto \tilde {g}$
is a group homomorphism by the condition on
$G\rightarrow {\mathrm {Aut}}(Y);g\mapsto \tilde {g}$
is a group homomorphism by the condition on
![]() $(\Phi _{g})_{g\in G}$
and the property of the 1-cocycles. Hence, we can construct a G-action on Y and
$(\Phi _{g})_{g\in G}$
and the property of the 1-cocycles. Hence, we can construct a G-action on Y and
![]() $\pi $
is G-equivariant by the construction.
$\pi $
is G-equivariant by the construction.
6.2 Construction of the groups and their actions
In this section, we will construct a group action on
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
by four steps.
$\widetilde {{\mathcal {X}}}\rightarrow T$
by four steps.
-
1. We construct a
 $\mathfrak {S}(\Sigma )$
-action on
$\mathfrak {S}(\Sigma )$
-action on
 ${\mathbb {P}}^1\times S_0\rightarrow S_0$
. By taking its direct product, we have a
${\mathbb {P}}^1\times S_0\rightarrow S_0$
. By taking its direct product, we have a
 $G_{{\mathcal {Y}}_0}(=\mathfrak {S}(\Sigma )^2)$
-action on
$G_{{\mathcal {Y}}_0}(=\mathfrak {S}(\Sigma )^2)$
-action on
 ${\mathcal {Y}}_0\rightarrow T_0$
which stabilizes
${\mathcal {Y}}_0\rightarrow T_0$
which stabilizes
 $\Sigma ^2$
.
$\Sigma ^2$
. -
2. By taking the fiber product of the
 $G_{{\mathcal {Y}}_0}$
-action on
$G_{{\mathcal {Y}}_0}$
-action on
 ${\mathcal {Y}}_0\rightarrow T_0$
and a
${\mathcal {Y}}_0\rightarrow T_0$
and a
 $G_{T}(=\mathfrak {S}_4^2)$
-action on
$G_{T}(=\mathfrak {S}_4^2)$
-action on
 $T\rightarrow T_0$
, we have a
$T\rightarrow T_0$
, we have a
 $G_{{\mathcal {Y}}}$
-action on
$G_{{\mathcal {Y}}}$
-action on
 ${\mathcal {Y}}\rightarrow T$
.
${\mathcal {Y}}\rightarrow T$
. -
3. By considering a
 $\mu _2$
-extension
$\mu _2$
-extension
 $G_{{\mathcal {X}}}$
of
$G_{{\mathcal {X}}}$
of
 $G_{{\mathcal {Y}}}$
, we can construct a
$G_{{\mathcal {Y}}}$
, we can construct a
 $G_{{\mathcal {X}}}$
-action on
$G_{{\mathcal {X}}}$
-action on
 ${\mathcal {X}} \rightarrow T$
by applying Proposition 6.3.
${\mathcal {X}} \rightarrow T$
by applying Proposition 6.3. -
4. We lift the
 $G_{{\mathcal {X}}}$
-action on
$G_{{\mathcal {X}}}$
-action on
 ${\mathcal {X}}\rightarrow T$
to
${\mathcal {X}}\rightarrow T$
to
 $\widetilde {{\mathcal {X}}}\rightarrow T$
.
$\widetilde {{\mathcal {X}}}\rightarrow T$
.
Throughout in this section, we identify
![]() ${\mathrm {Aut}}(S_0) = \mathfrak {S}(\{0,1,\infty \}) (\simeq \mathfrak {S}_3)$
.
${\mathrm {Aut}}(S_0) = \mathfrak {S}(\{0,1,\infty \}) (\simeq \mathfrak {S}_3)$
.
Proposition 6.4 There exists a
![]() $\mathfrak {S}_4$
-action on
$\mathfrak {S}_4$
-action on
![]() ${\mathbb {P}}^1\times S_0\rightarrow S_0$
satisfying the following properties.
${\mathbb {P}}^1\times S_0\rightarrow S_0$
satisfying the following properties.
-
(1) The natural map
 $\mathfrak {S}_4\rightarrow {\mathrm {Aut}}(S_0)=\mathfrak {S}(\{0,1,\infty \})$
is surjective. For
$\mathfrak {S}_4\rightarrow {\mathrm {Aut}}(S_0)=\mathfrak {S}(\{0,1,\infty \})$
is surjective. For
 $\rho \in \mathfrak {S}_4$
, its image in
$\rho \in \mathfrak {S}_4$
, its image in
 $\mathfrak {S}(\{0,1,\infty \})$
is denoted by
$\mathfrak {S}(\{0,1,\infty \})$
is denoted by
 $\underline {\rho }$
.
$\underline {\rho }$
. -
(2) For
 $\rho \in \mathfrak {S}_4$
and
$\rho \in \mathfrak {S}_4$
and
 $\sigma \in \Sigma $
, we have
$\sigma \in \Sigma $
, we have
 $\rho \circ \sigma \circ \underline {\rho }^{-1}\in \Sigma $
. Moreover, the following map induces an isomorphism of groups. (20)
$\rho \circ \sigma \circ \underline {\rho }^{-1}\in \Sigma $
. Moreover, the following map induces an isomorphism of groups. (20)
Since another group which is isomorphic to
![]() $\mathfrak {S}_4$
appears elsewhere, hereafter we denote this group by
$\mathfrak {S}_4$
appears elsewhere, hereafter we denote this group by
![]() $\mathfrak {S}(\Sigma )$
.
$\mathfrak {S}(\Sigma )$
.
Proof Consider the following contravariant functor from the category of varieties to the category of sets.

For each
![]() $(Y\rightarrow X;p_1,p_2,p_3,p_4)$
, by considering the cross-ratio of
$(Y\rightarrow X;p_1,p_2,p_3,p_4)$
, by considering the cross-ratio of
![]() $p_1(x)$
,
$p_1(x)$
,
![]() $p_2(x)$
,
$p_2(x)$
,
![]() $p_3(x)$
,
$p_3(x)$
,
![]() $p_4(x)\in {\mathbb {P}}^1$
at
$p_4(x)\in {\mathbb {P}}^1$
at
![]() $x\in X$
, we have the morphism
$x\in X$
, we have the morphism
![]() $X\rightarrow S_0$
. Then we can check that
$X\rightarrow S_0$
. Then we can check that
![]() $S_0$
represents this functor and
$S_0$
represents this functor and
![]() $({\mathbb {P}}^1\times S_0\rightarrow S_0;0,1,\infty ,1/c)$
is the universal element. For each
$({\mathbb {P}}^1\times S_0\rightarrow S_0;0,1,\infty ,1/c)$
is the universal element. For each
![]() $\rho \in \mathfrak {S}_4$
,
$\rho \in \mathfrak {S}_4$
,
![]() $\rho $
induces a natural automorphism on this functor. Combining with the fact that an automorphism on
$\rho $
induces a natural automorphism on this functor. Combining with the fact that an automorphism on
![]() ${\mathbb {P}}^1$
which stabilizes four points is identity, this induces a
${\mathbb {P}}^1$
which stabilizes four points is identity, this induces a
![]() $\mathfrak {S}_4$
-action on
$\mathfrak {S}_4$
-action on
![]() ${\mathbb {P}}^1\times S_0\rightarrow S_0$
. The property (2) is clear from this construction. The property (1) follows from the property of the cross-ratio.
${\mathbb {P}}^1\times S_0\rightarrow S_0$
. The property (2) is clear from this construction. The property (1) follows from the property of the cross-ratio.
We need an explicit description of the
![]() $\mathfrak {S}(\Sigma )$
-action on
$\mathfrak {S}(\Sigma )$
-action on
![]() ${\mathbb {P}}^1\times S_0$
for Step 3. We summarize them on Table 1. In the table, for each
${\mathbb {P}}^1\times S_0$
for Step 3. We summarize them on Table 1. In the table, for each
![]() $\rho \in \mathfrak {S}(\Sigma )$
, the image of c under
$\rho \in \mathfrak {S}(\Sigma )$
, the image of c under
![]() $\underline {\rho }^\sharp :{\mathcal {O}}_{S_0}\rightarrow \underline {\rho }_*{\mathcal {O}}_{S_0}$
and the image of the local coordinate z on
$\underline {\rho }^\sharp :{\mathcal {O}}_{S_0}\rightarrow \underline {\rho }_*{\mathcal {O}}_{S_0}$
and the image of the local coordinate z on
![]() ${\mathbb {P}}^1$
under
${\mathbb {P}}^1$
under
![]() $\rho ^\sharp : {\mathcal {O}}_{{\mathbb {P}}^1\times S_0}\rightarrow \rho _*{\mathcal {O}}_{{\mathbb {P}}^1\times S_0}$
are given.
$\rho ^\sharp : {\mathcal {O}}_{{\mathbb {P}}^1\times S_0}\rightarrow \rho _*{\mathcal {O}}_{{\mathbb {P}}^1\times S_0}$
are given.
Table 1: The
![]() $\mathfrak {S}(\Sigma )$
-action on
$\mathfrak {S}(\Sigma )$
-action on
![]() ${\mathbb {P}}^1\times S_0.$
${\mathbb {P}}^1\times S_0.$

From Proposition 6.4, we have a morphism
![]() $({\mathbb {P}}^1\times S_0,\mathfrak {S}(\Sigma ))\rightarrow (S_0,\mathfrak {S}(\{0,1,\infty \}))$
. By taking the direct product, we have the morphism
$({\mathbb {P}}^1\times S_0,\mathfrak {S}(\Sigma ))\rightarrow (S_0,\mathfrak {S}(\{0,1,\infty \}))$
. By taking the direct product, we have the morphism
We denote the group
![]() $\mathfrak {S}(\Sigma )\times \mathfrak {S}(\Sigma )$
(resp.
$\mathfrak {S}(\Sigma )\times \mathfrak {S}(\Sigma )$
(resp.
![]() $\mathfrak {S}(\{0,1,\infty \}) \times \mathfrak {S}(\{0,1,\infty \})$
) by
$\mathfrak {S}(\{0,1,\infty \}) \times \mathfrak {S}(\{0,1,\infty \})$
) by
![]() $G_{{\mathcal {Y}}_0}$
(resp.
$G_{{\mathcal {Y}}_0}$
(resp.
![]() $G_{T_0}$
). Since
$G_{T_0}$
). Since
![]() $T_0\subset S_0\times S_0$
is stable under the
$T_0\subset S_0\times S_0$
is stable under the
![]() $G_{T_0}$
-action, (21) induces a morphism
$G_{T_0}$
-action, (21) induces a morphism
![]() $({\mathcal {Y}}_0,G_{{\mathcal {Y}}_0})\rightarrow (T_0,G_{T_0})$
. Furthermore, by the property (2) of Proposition 6.4, we see that
$({\mathcal {Y}}_0,G_{{\mathcal {Y}}_0})\rightarrow (T_0,G_{T_0})$
. Furthermore, by the property (2) of Proposition 6.4, we see that
![]() $\Sigma ^2\subset {\mathcal {Y}}_0$
is stable under the
$\Sigma ^2\subset {\mathcal {Y}}_0$
is stable under the
![]() $G_{{\mathcal {Y}}_0}$
-action on
$G_{{\mathcal {Y}}_0}$
-action on
![]() ${\mathcal {Y}}_0$
. We finish Step 1.
${\mathcal {Y}}_0$
. We finish Step 1.
Next, we will construct a group action on T. Recall that T is a finite étale cover of
![]() $T_0$
corresponding to
$T_0$
corresponding to
![]() $B_0 \rightarrow B_0[\sqrt {a},\sqrt {b},\sqrt {1-a},\sqrt {1-b}]$
.
$B_0 \rightarrow B_0[\sqrt {a},\sqrt {b},\sqrt {1-a},\sqrt {1-b}]$
.
Proposition 6.5 Let
![]() $S'={\mathrm {Spec}\,} A_0[\sqrt {c},\sqrt {1-c}]$
. Then there exists a
$S'={\mathrm {Spec}\,} A_0[\sqrt {c},\sqrt {1-c}]$
. Then there exists a
![]() $\mathfrak {S}_4$
-action on
$\mathfrak {S}_4$
-action on
![]() ${S'\rightarrow S_0}$
such that the natural map
${S'\rightarrow S_0}$
such that the natural map
![]() $\mathfrak {S}_4\rightarrow {\mathrm {Aut}}(S_0)=\mathfrak {S}(\{0,1,\infty \})$
is surjective.
$\mathfrak {S}_4\rightarrow {\mathrm {Aut}}(S_0)=\mathfrak {S}(\{0,1,\infty \})$
is surjective.
Proof We have the following ring isomorphism:
Using the ring isomorphism (22), we can check directly that for each
![]() $\rho \in {\mathrm {Aut}}(S_0)$
, there exists a lift of
$\rho \in {\mathrm {Aut}}(S_0)$
, there exists a lift of
![]() $\rho $
in
$\rho $
in
![]() ${\mathrm {Aut}}(S')$
. Moreover, the
${\mathrm {Aut}}(S')$
. Moreover, the
![]() $S_0$
-automorphism group of
$S_0$
-automorphism group of
![]() $S'$
is isomorphic to
$S'$
is isomorphic to
![]() $\mu _2\times \mu _2$
. Thus we have the following exact sequence of groups:
$\mu _2\times \mu _2$
. Thus we have the following exact sequence of groups:
To prove the proposition, we should show that
![]() ${\mathrm {Aut}}(S'\rightarrow S_0)$
is isomorphic to
${\mathrm {Aut}}(S'\rightarrow S_0)$
is isomorphic to
![]() $\mathfrak {S}_4$
. We will construct an
$\mathfrak {S}_4$
. We will construct an
![]() ${\mathrm {Aut}}(S'\rightarrow S_0)$
-action on a set of cardinality
${\mathrm {Aut}}(S'\rightarrow S_0)$
-action on a set of cardinality
![]() $4$
. By the ring isomorphism (22), we have
$4$
. By the ring isomorphism (22), we have
![]() $S' \simeq {\mathbb {P}}^1-\{0,\infty ,\pm 1, \pm \sqrt {-1}\}$
. Thus,
$S' \simeq {\mathbb {P}}^1-\{0,\infty ,\pm 1, \pm \sqrt {-1}\}$
. Thus,
![]() ${\mathrm {Aut}}(S'\rightarrow S_0)$
acts on the set
${\mathrm {Aut}}(S'\rightarrow S_0)$
acts on the set
![]() $\{0,\infty ,\pm 1, \pm \sqrt {-1}\}$
. Let F be the set
$\{0,\infty ,\pm 1, \pm \sqrt {-1}\}$
. Let F be the set
 $$ \begin{align*} F = \left\{ \begin{aligned} &\{\{1,\sqrt{-1},\infty\},\{-1,-\sqrt{-1},0\}\}, && \{\{-1,\sqrt{-1},\infty\},\{1,-\sqrt{-1},0\}\} \\ &\{\{1,-\sqrt{-1},\infty\},\{-1,\sqrt{-1},0\}\}, &&\{\{-1,-\sqrt{-1},\infty\},\{1,\sqrt{-1},0\}\} \end{aligned} \right\}. \end{align*} $$
$$ \begin{align*} F = \left\{ \begin{aligned} &\{\{1,\sqrt{-1},\infty\},\{-1,-\sqrt{-1},0\}\}, && \{\{-1,\sqrt{-1},\infty\},\{1,-\sqrt{-1},0\}\} \\ &\{\{1,-\sqrt{-1},\infty\},\{-1,\sqrt{-1},0\}\}, &&\{\{-1,-\sqrt{-1},\infty\},\{1,\sqrt{-1},0\}\} \end{aligned} \right\}. \end{align*} $$
If we plot
![]() $\pm 1, \pm \sqrt {-1},0,\infty $
on the Riemann sphere, they are the vertexes of the regular octahedron. Then F is the set of pairs of opposite faces of the octahedron. We can check that
$\pm 1, \pm \sqrt {-1},0,\infty $
on the Riemann sphere, they are the vertexes of the regular octahedron. Then F is the set of pairs of opposite faces of the octahedron. We can check that
![]() ${\mathrm {Aut}}(S'\rightarrow S_0)$
acts on F and the group homomorphism
${\mathrm {Aut}}(S'\rightarrow S_0)$
acts on F and the group homomorphism
![]() ${\mathrm {Aut}}(S'\rightarrow S_0)\rightarrow \mathfrak {S}(F)$
is surjective. By the exact sequence above, the orders of
${\mathrm {Aut}}(S'\rightarrow S_0)\rightarrow \mathfrak {S}(F)$
is surjective. By the exact sequence above, the orders of
![]() ${\mathrm {Aut}}(S'\rightarrow S_0)$
and
${\mathrm {Aut}}(S'\rightarrow S_0)$
and
![]() $\mathfrak {S}(F)$
coincide. Thus
$\mathfrak {S}(F)$
coincide. Thus
![]() ${\mathrm {Aut}}(S'\rightarrow S_0)\simeq \mathfrak {S}(F)$
.
${\mathrm {Aut}}(S'\rightarrow S_0)\simeq \mathfrak {S}(F)$
.
From Proposition 6.5, we have a morphism
![]() $(S',\mathfrak {S}_4)\rightarrow (S_0,\mathfrak {S}(\{0,1,\infty \}))$
. By taking its direct product, we have
$(S',\mathfrak {S}_4)\rightarrow (S_0,\mathfrak {S}(\{0,1,\infty \}))$
. By taking its direct product, we have
We denote the group
![]() $\mathfrak {S}_4\times \mathfrak {S}_4$
by
$\mathfrak {S}_4\times \mathfrak {S}_4$
by
![]() $G_{T}$
. Since T is a fiber product of
$G_{T}$
. Since T is a fiber product of
![]() $T_0$
and
$T_0$
and
![]() $S'\times S'$
over
$S'\times S'$
over
![]() $S_0\times S_0$
, this induces a morphism
$S_0\times S_0$
, this induces a morphism
![]() $(T,G_{T})\rightarrow (T_0,G_{T_0})$
.
$(T,G_{T})\rightarrow (T_0,G_{T_0})$
.
We have already constructed the morphisms
![]() $({\mathcal {Y}}_0,G_{{\mathcal {Y}}_0})\rightarrow (T_0,G_{T_0})$
and
$({\mathcal {Y}}_0,G_{{\mathcal {Y}}_0})\rightarrow (T_0,G_{T_0})$
and
![]() $(T,G_{T})\rightarrow (T_0,G_{T_0})$
. Then the group
$(T,G_{T})\rightarrow (T_0,G_{T_0})$
. Then the group
acts on
![]() ${\mathcal {Y}} = {\mathcal {Y}}_0\times _{T_0} T$
by (18). We denote this group by
${\mathcal {Y}} = {\mathcal {Y}}_0\times _{T_0} T$
by (18). We denote this group by
![]() $G_{\mathcal {Y}}$
. Thus, we have the morphism
$G_{\mathcal {Y}}$
. Thus, we have the morphism
![]() $({\mathcal {Y}},G_{\mathcal {Y}})\rightarrow (T,G_{T})$
. We often denote an element of
$({\mathcal {Y}},G_{\mathcal {Y}})\rightarrow (T,G_{T})$
. We often denote an element of
![]() $G_{\mathcal {Y}}$
by a 3-tuple
$G_{\mathcal {Y}}$
by a 3-tuple
such that
![]() $\tau \in G_{T}$
and
$\tau \in G_{T}$
and
![]() $(\rho _1,\rho _2)\in G_{{\mathcal {Y}}_0}$
have the same image in
$(\rho _1,\rho _2)\in G_{{\mathcal {Y}}_0}$
have the same image in
![]() $G_{T_0}=\mathfrak {S}(\{0,1,\infty \})^2$
. We finish Step 2.
$G_{T_0}=\mathfrak {S}(\{0,1,\infty \})^2$
. We finish Step 2.
We will lift this group action to the double cover
![]() ${\mathcal {X}}\rightarrow {\mathcal {Y}}$
. Let
${\mathcal {X}}\rightarrow {\mathcal {Y}}$
. Let
![]() ${\mathscr {L}}$
be the line bundle on
${\mathscr {L}}$
be the line bundle on
![]() ${\mathcal {Y}}$
defined by
${\mathcal {Y}}$
defined by
where
![]() $pr_i$
is a morphism
$pr_i$
is a morphism
![]() ${\mathcal {Y}}\rightarrow {\mathcal {Y}}_0 \hookrightarrow ({\mathbb {P}}^1\times S_0)\times ({\mathbb {P}}^1\times S_0) \xrightarrow {pr_i} {\mathbb {P}}^1\times S_0$
. Let s be the section of
${\mathcal {Y}}\rightarrow {\mathcal {Y}}_0 \hookrightarrow ({\mathbb {P}}^1\times S_0)\times ({\mathbb {P}}^1\times S_0) \xrightarrow {pr_i} {\mathbb {P}}^1\times S_0$
. Let s be the section of
![]() ${\mathscr {L}}^{\otimes (-2)}$
defined by
${\mathscr {L}}^{\otimes (-2)}$
defined by
We have the natural
![]() $G_{{\mathcal {Y}}}$
-linearization
$G_{{\mathcal {Y}}}$
-linearization
![]() $(\Phi _\rho )_{\rho \in G_{{\mathcal {Y}}}}$
of
$(\Phi _\rho )_{\rho \in G_{{\mathcal {Y}}}}$
of
![]() ${\mathscr {L}}$
since it is constructed from sheaves of differentials.
${\mathscr {L}}$
since it is constructed from sheaves of differentials.
The morphism
![]() ${\mathcal {X}}\rightarrow {\mathcal {Y}}$
is the double covering associated with
${\mathcal {X}}\rightarrow {\mathcal {Y}}$
is the double covering associated with
![]() $({\mathscr {L}},s)$
. Since
$({\mathscr {L}},s)$
. Since
![]() ${\mathrm {div}}(s)$
is equal to the branching locus of
${\mathrm {div}}(s)$
is equal to the branching locus of
![]() ${\mathcal {X}}\rightarrow {\mathcal {Y}}$
,
${\mathcal {X}}\rightarrow {\mathcal {Y}}$
,
![]() ${\mathrm {div}}(s)$
is stable under the
${\mathrm {div}}(s)$
is stable under the
![]() $G_{{\mathcal {Y}}}$
-action. Hence, we have the 1-cocycle
$G_{{\mathcal {Y}}}$
-action. Hence, we have the 1-cocycle
![]() $\eta : G_{{\mathcal {Y}}}\rightarrow \Gamma ({\mathcal {Y}},{\mathcal {O}}_{{\mathcal {Y}}}^\times ) = B^\times $
such that
$\eta : G_{{\mathcal {Y}}}\rightarrow \Gamma ({\mathcal {Y}},{\mathcal {O}}_{{\mathcal {Y}}}^\times ) = B^\times $
such that
for any
![]() $\rho \in G_{{\mathcal {Y}}}$
. We can compute
$\rho \in G_{{\mathcal {Y}}}$
. We can compute
![]() $\eta $
as follows.
$\eta $
as follows.
Proposition 6.6 For
![]() $\rho = (\rho _1,\rho _2,\tau )\in G_{{\mathcal {Y}}}$
,
$\rho = (\rho _1,\rho _2,\tau )\in G_{{\mathcal {Y}}}$
,
![]() $\eta (\rho )$
is determined by
$\eta (\rho )$
is determined by
![]() $\underline {\rho }_1, \underline {\rho }_2 \in \mathfrak {S}(\{0,1,\infty \})$
and calculated by the following formula:
$\underline {\rho }_1, \underline {\rho }_2 \in \mathfrak {S}(\{0,1,\infty \})$
and calculated by the following formula:
where
![]() $\eta _1(\underline {\rho }_1), \eta _2(\underline {\rho }_2)\in B^\times $
are given by the following table.
$\eta _1(\underline {\rho }_1), \eta _2(\underline {\rho }_2)\in B^\times $
are given by the following table.

Proof By the definition of the
![]() $G_{{\mathcal {Y}}}$
-linearization on
$G_{{\mathcal {Y}}}$
-linearization on
![]() ${\mathscr {L}}$
, we have
${\mathscr {L}}$
, we have
 $$ \begin{align*} \Phi_{\rho}(\rho^*(dx\otimes dy)) = \left(\frac{\partial }{\partial x}\rho_1^\sharp(x)\right)\left(\frac{\partial }{\partial y}\rho_2^\sharp(y)\right)\cdot (dx\otimes dy). \end{align*} $$
$$ \begin{align*} \Phi_{\rho}(\rho^*(dx\otimes dy)) = \left(\frac{\partial }{\partial x}\rho_1^\sharp(x)\right)\left(\frac{\partial }{\partial y}\rho_2^\sharp(y)\right)\cdot (dx\otimes dy). \end{align*} $$
Using Table 1, we can compute
![]() $\eta $
for each
$\eta $
for each
![]() $\rho _1,\rho _2\in \mathfrak {S}(\Sigma )$
and we get the result.
$\rho _1,\rho _2\in \mathfrak {S}(\Sigma )$
and we get the result.
To apply Proposition 6.3, we should construct a “square root” of the 1-cocycle
![]() $\eta $
. We define coboundary 1-cocycles
$\eta $
. We define coboundary 1-cocycles
![]() $\phi _1,\phi _2:G_{T}\rightarrow B^\times $
by
$\phi _1,\phi _2:G_{T}\rightarrow B^\times $
by
 $$ \begin{align*} \phi_1(\tau) = \tau^\sharp\left(\frac{\sqrt{a}\sqrt{1-a}}{a^2-a+1}\right)\cdot \left(\frac{\sqrt{a}\sqrt{1-a}}{a^2-a+1}\right)^{-1},\:\phi_2(\tau) = \tau^\sharp\left(\frac{\sqrt{b}\sqrt{1-b}}{b^2-b+1}\right)\cdot \left(\frac{\sqrt{b}\sqrt{1-b}}{b^2-b+1}\right)^{-1} \end{align*} $$
$$ \begin{align*} \phi_1(\tau) = \tau^\sharp\left(\frac{\sqrt{a}\sqrt{1-a}}{a^2-a+1}\right)\cdot \left(\frac{\sqrt{a}\sqrt{1-a}}{a^2-a+1}\right)^{-1},\:\phi_2(\tau) = \tau^\sharp\left(\frac{\sqrt{b}\sqrt{1-b}}{b^2-b+1}\right)\cdot \left(\frac{\sqrt{b}\sqrt{1-b}}{b^2-b+1}\right)^{-1} \end{align*} $$
for
![]() $\tau \in G_{T}$
. Then we can check that for any
$\tau \in G_{T}$
. Then we can check that for any
![]() $\rho =(\rho _1,\rho _2,\tau )\in G_{{\mathcal {Y}}}$
,
$\rho =(\rho _1,\rho _2,\tau )\in G_{{\mathcal {Y}}}$
,
holds for
![]() $i=1,2$
. Hence,
$i=1,2$
. Hence,
![]() $\phi _1\cdot \phi _2$
coincides with a square root of
$\phi _1\cdot \phi _2$
coincides with a square root of
![]() $\eta $
up to sign. To get a square root of sign, we enlarge the group
$\eta $
up to sign. To get a square root of sign, we enlarge the group
![]() $G_{{\mathcal {Y}}}$
as follows.
$G_{{\mathcal {Y}}}$
as follows.
We define the group
![]() $G_{{\mathcal {X}}}$
as the fiber product
$G_{{\mathcal {X}}}$
as the fiber product
![]() $G_{{\mathcal {Y}}}\times _{\mu _2} \mu _4$
, where the group homomorphisms
$G_{{\mathcal {Y}}}\times _{\mu _2} \mu _4$
, where the group homomorphisms
![]() $G_{{\mathcal {Y}}}\rightarrow \mu _2$
and
$G_{{\mathcal {Y}}}\rightarrow \mu _2$
and
![]() $\mu _4\rightarrow \mu _2$
is given by
$\mu _4\rightarrow \mu _2$
is given by
 $$ \begin{align*} \begin{aligned} &G_{{\mathcal{Y}}} \rightarrow \mu_2; && (\rho_1,\rho_2,\tau) \mapsto {\mathrm{sgn}}(\underline{\rho}_1){\mathrm{sgn}}(\underline{\rho}_2), \\ &\mu_4 \rightarrow \mu_2; && \zeta \mapsto \zeta^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &G_{{\mathcal{Y}}} \rightarrow \mu_2; && (\rho_1,\rho_2,\tau) \mapsto {\mathrm{sgn}}(\underline{\rho}_1){\mathrm{sgn}}(\underline{\rho}_2), \\ &\mu_4 \rightarrow \mu_2; && \zeta \mapsto \zeta^2. \end{aligned} \end{align*} $$
We denote an element of
![]() $G_{{\mathcal {X}}}$
by a 4-tuple
$G_{{\mathcal {X}}}$
by a 4-tuple
The group
![]() $G_{{\mathcal {X}}}$
acts on
$G_{{\mathcal {X}}}$
acts on
![]() ${\mathcal {Y}}$
through the surjection
${\mathcal {Y}}$
through the surjection
![]() $G_{{\mathcal {X}}}\twoheadrightarrow G_{{\mathcal {Y}}}$
. For
$G_{{\mathcal {X}}}\twoheadrightarrow G_{{\mathcal {Y}}}$
. For
![]() $\rho = (\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
, we define
$\rho = (\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
, we define
Then by (24),
![]() $\chi :G_{{\mathcal {X}}}\rightarrow \Gamma ({\mathcal {Y}},{\mathcal {O}}_{{\mathcal {Y}}}^\times )$
is a 1-cocycle satisfying the relation
$\chi :G_{{\mathcal {X}}}\rightarrow \Gamma ({\mathcal {Y}},{\mathcal {O}}_{{\mathcal {Y}}}^\times )$
is a 1-cocycle satisfying the relation
Hence, we have the following result.
Proposition 6.7 There exists a
![]() $G_{{\mathcal {X}}}$
-action on
$G_{{\mathcal {X}}}$
-action on
![]() ${\mathcal {X}}$
such that the morphism
${\mathcal {X}}$
such that the morphism
![]() ${\mathcal {X}}\rightarrow {\mathcal {Y}}$
is
${\mathcal {X}}\rightarrow {\mathcal {Y}}$
is
![]() $G_{{\mathcal {X}}}$
-equivariant.
$G_{{\mathcal {X}}}$
-equivariant.
Proof The
![]() $G_{{\mathcal {Y}}}$
-linearization
$G_{{\mathcal {Y}}}$
-linearization
![]() $(\Phi _\rho )_{\rho \in G_{{\mathcal {Y}}}}$
of
$(\Phi _\rho )_{\rho \in G_{{\mathcal {Y}}}}$
of
![]() ${\mathscr {L}}$
induces the natural
${\mathscr {L}}$
induces the natural
![]() $G_{{\mathcal {X}}}$
-linearization of
$G_{{\mathcal {X}}}$
-linearization of
![]() ${\mathscr {L}}$
. This linearization satisfies the equation
${\mathscr {L}}$
. This linearization satisfies the equation
Hence, by applying Proposition 6.3, we have the result.
Thus, we have the morphism
![]() $({\mathcal {X}},G_{{\mathcal {X}}})\rightarrow (T,G_{T})$
. We finish Step 3.
$({\mathcal {X}},G_{{\mathcal {X}}})\rightarrow (T,G_{T})$
. We finish Step 3.
Recall that the set
![]() $\Sigma ^2$
on
$\Sigma ^2$
on
![]() ${\mathcal {Y}}_0$
is stable under the
${\mathcal {Y}}_0$
is stable under the
![]() $G_{{\mathcal {Y}}_0}$
-action. Then its base change
$G_{{\mathcal {Y}}_0}$
-action. Then its base change
![]() $\Sigma ^2$
on
$\Sigma ^2$
on
![]() ${\mathcal {Y}}$
is also stable under the
${\mathcal {Y}}$
is also stable under the
![]() $G_{{\mathcal {Y}}}$
-action. Since
$G_{{\mathcal {Y}}}$
-action. Since
![]() $\Sigma ^2\subset {\mathcal {Y}}$
is contained in the branching locus of
$\Sigma ^2\subset {\mathcal {Y}}$
is contained in the branching locus of
![]() ${\mathcal {X}}\rightarrow {\mathcal {Y}}$
and
${\mathcal {X}}\rightarrow {\mathcal {Y}}$
and
![]() ${\mathcal {X}}\rightarrow {\mathcal {Y}}$
is
${\mathcal {X}}\rightarrow {\mathcal {Y}}$
is
![]() $G_{{\mathcal {X}}}$
-equivariant,
$G_{{\mathcal {X}}}$
-equivariant,
![]() $\Sigma ^2$
on
$\Sigma ^2$
on
![]() ${\mathcal {X}}$
is also
${\mathcal {X}}$
is also
![]() $G_{{\mathcal {X}}}$
-stable. Then by the universality of the blowing-up, for any
$G_{{\mathcal {X}}}$
-stable. Then by the universality of the blowing-up, for any
![]() $\rho \in G_{{\mathcal {X}}}$
, there exists the unique lift
$\rho \in G_{{\mathcal {X}}}$
, there exists the unique lift
![]() $\widetilde {\rho }\in {\mathrm {Aut}}(\widetilde {{\mathcal {X}}})$
of
$\widetilde {\rho }\in {\mathrm {Aut}}(\widetilde {{\mathcal {X}}})$
of
![]() $\rho $
. By the uniqueness,
$\rho $
. By the uniqueness,
![]() $G_{{\mathcal {X}}}\rightarrow {\mathrm {Aut}}(\widetilde {{\mathcal {X}}});\rho \mapsto \widetilde {\rho }$
defines a
$G_{{\mathcal {X}}}\rightarrow {\mathrm {Aut}}(\widetilde {{\mathcal {X}}});\rho \mapsto \widetilde {\rho }$
defines a
![]() $G_{{\mathcal {X}}}$
-action on
$G_{{\mathcal {X}}}$
-action on
![]() $\widetilde {{\mathcal {X}}}$
. We finish Step 4.
$\widetilde {{\mathcal {X}}}$
. We finish Step 4.
Finally, we can prove the main result of this section.
Proof of Proposition 6.2
We have the morphisms
By composing these morphisms, we have the
![]() $G_{{\mathcal {X}}}$
-action on the family
$G_{{\mathcal {X}}}$
-action on the family
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
.
$\widetilde {{\mathcal {X}}}\rightarrow T$
.
At the end of this section, we see an explicit description of the
![]() $G_{{\mathcal {X}}}$
-action on
$G_{{\mathcal {X}}}$
-action on
![]() $\widetilde {{\mathcal {X}}}$
using the local coordinates
$\widetilde {{\mathcal {X}}}$
using the local coordinates
![]() $x,y,v$
on V. Let
$x,y,v$
on V. Let
![]() $\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
. Since
$\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
. Since
![]() $\widetilde {{\mathcal {X}}}\rightarrow {\mathcal {Y}}$
is
$\widetilde {{\mathcal {X}}}\rightarrow {\mathcal {Y}}$
is
![]() $G_{{\mathcal {X}}}$
-equivariant, we see that
$G_{{\mathcal {X}}}$
-equivariant, we see that
Locally on
![]() $U\subset {\mathcal {Y}}$
, the morphism
$U\subset {\mathcal {Y}}$
, the morphism
![]() ${\mathcal {X}}\rightarrow {\mathcal {Y}}$
is described by the ring homomorphism
${\mathcal {X}}\rightarrow {\mathcal {Y}}$
is described by the ring homomorphism
where u corresponds to the local section
![]() $(dx\otimes dy)$
of
$(dx\otimes dy)$
of
![]() ${\mathscr {L}}$
. By the construction of the
${\mathscr {L}}$
. By the construction of the
![]() $G_{{\mathcal {X}}}$
-action, the local coordinate u transforms
$G_{{\mathcal {X}}}$
-action, the local coordinate u transforms
Since
![]() $u=vf(x)$
, by the formula
$u=vf(x)$
, by the formula
![]() $\rho _1^\sharp (f(x))=\eta _1(\underline {\rho }_1)^{-1}\left (\frac {\partial }{\partial x}\rho _1^\sharp (x)\right )^2f(x)$
, v transforms as follows:
$\rho _1^\sharp (f(x))=\eta _1(\underline {\rho }_1)^{-1}\left (\frac {\partial }{\partial x}\rho _1^\sharp (x)\right )^2f(x)$
, v transforms as follows:
 $$ \begin{align*} v\mapsto \frac{\eta_1(\underline{\rho}_1)}{\chi(\rho)}\frac{\frac{\partial}{\partial y}(\rho_2^\sharp(y))}{\frac{\partial}{\partial x}(\rho_1^\sharp(x))}v. \end{align*} $$
$$ \begin{align*} v\mapsto \frac{\eta_1(\underline{\rho}_1)}{\chi(\rho)}\frac{\frac{\partial}{\partial y}(\rho_2^\sharp(y))}{\frac{\partial}{\partial x}(\rho_1^\sharp(x))}v. \end{align*} $$
7 The group action on the higher Chow cycles
In this section, we prove the main result in this paper by using some technical propositions which is proved Section 8.
7.1 The group action on the higher Chow cycles
First, we produce more families of higher Chow cycles from
![]() $\xi _0,\xi _1$
and
$\xi _0,\xi _1$
and
![]() $\xi _\infty $
by using the group action. For
$\xi _\infty $
by using the group action. For
![]() $t\in T$
,
$t\in T$
,
![]() $\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
induces the isomorphism
$\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
induces the isomorphism
![]() $\rho _t:\widetilde {{\mathcal {X}}}_t\rightarrow \widetilde {{\mathcal {X}}}_{\tau (t)}$
such that
$\rho _t:\widetilde {{\mathcal {X}}}_t\rightarrow \widetilde {{\mathcal {X}}}_{\tau (t)}$
such that

commutes. The morphism
![]() $\rho _t$
induces a map
$\rho _t$
induces a map
![]() $\rho _t^*:{\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_{\tau (t)},1)\rightarrow {\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)$
. For an algebraic family of higher Chow cycles
$\rho _t^*:{\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_{\tau (t)},1)\rightarrow {\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)$
. For an algebraic family of higher Chow cycles
![]() $\xi =\{\xi _t\}_{t\in T}$
on
$\xi =\{\xi _t\}_{t\in T}$
on
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
, we define the algebraic family
$\widetilde {{\mathcal {X}}}\rightarrow T$
, we define the algebraic family
![]() $\rho ^*\xi $
of higher Chow cycles by
$\rho ^*\xi $
of higher Chow cycles by
![]() $\rho ^*\xi = \{\rho _t^*(\xi _{\tau (t)})\}_{t\in T}$
.
$\rho ^*\xi = \{\rho _t^*(\xi _{\tau (t)})\}_{t\in T}$
.
In particular, we have defined families of higher Chow cycles
![]() $\rho ^*\xi _0, \rho ^*\xi _1$
and
$\rho ^*\xi _0, \rho ^*\xi _1$
and
![]() $\rho ^*\xi _\infty $
for
$\rho ^*\xi _\infty $
for
![]() $\rho \in G_{{\mathcal {X}}}$
. For each
$\rho \in G_{{\mathcal {X}}}$
. For each
![]() $t\in T$
, we define the subgroup
$t\in T$
, we define the subgroup
![]() $\Xi _t$
of
$\Xi _t$
of
![]() ${\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{{\mathrm {ind}}}$
by
${\mathrm {CH}}^2(\widetilde {{\mathcal {X}}}_t,1)_{{\mathrm {ind}}}$
by
Then we can state the main theorem.
Theorem 7.1 For a very general
![]() $t\in T$
, we have
$t\in T$
, we have
![]() ${\mathrm {rank}\:} \Xi _t \ge 18$
. In particular,
${\mathrm {rank}\:} \Xi _t \ge 18$
. In particular,
![]() ${\mathrm {rank}\:} {\mathrm {CH}}^2({\mathcal {X}}_t,1)_{\mathrm {ind}} \ge 18$
.
${\mathrm {rank}\:} {\mathrm {CH}}^2({\mathcal {X}}_t,1)_{\mathrm {ind}} \ge 18$
.
To be more specific, 18 linearly independent cycles in
![]() $\Xi _t$
are given as follows. Let
$\Xi _t$
are given as follows. Let
![]() $\rho ^1,\rho ^2,\dots ,\rho ^6\in G_{{\mathcal {X}}}$
be lifts of
$\rho ^1,\rho ^2,\dots ,\rho ^6\in G_{{\mathcal {X}}}$
be lifts of
![]() $({\mathrm {id}},{\mathrm {id}})$
,
$({\mathrm {id}},{\mathrm {id}})$
,
![]() $({\mathrm {id}},(0\:\:1))$
,
$({\mathrm {id}},(0\:\:1))$
,
![]() $({\mathrm {id}},(1\:\:\infty ))$
,
$({\mathrm {id}},(1\:\:\infty ))$
,
![]() $({\mathrm {id}},(0\:\:1\:\:\infty ))$
,
$({\mathrm {id}},(0\:\:1\:\:\infty ))$
,
![]() $({\mathrm {id}}, (0\:\:\infty ))$
and
$({\mathrm {id}}, (0\:\:\infty ))$
and
![]() $({\mathrm {id}}, (0\:\:\infty \:\:1))\in G_{{\mathcal {Y}}_0}$
by
$({\mathrm {id}}, (0\:\:\infty \:\:1))\in G_{{\mathcal {Y}}_0}$
by
![]() $G_{{\mathcal {X}}}\twoheadrightarrow G_{{\mathcal {Y}}_0}=\mathfrak {S}(\Sigma )^2$
, respectively. Then we will show that
$G_{{\mathcal {X}}}\twoheadrightarrow G_{{\mathcal {Y}}_0}=\mathfrak {S}(\Sigma )^2$
, respectively. Then we will show that
![]() $(((\rho ^i)^*\xi _{\bullet })_t)_{\mathrm {ind}} \:\:(i=1,2,\dots ,6,\bullet = 0,1,\infty )$
are linearly independent in
$(((\rho ^i)^*\xi _{\bullet })_t)_{\mathrm {ind}} \:\:(i=1,2,\dots ,6,\bullet = 0,1,\infty )$
are linearly independent in
![]() $\Xi _t$
for very general
$\Xi _t$
for very general
![]() $t\in T$
. The key of the proof is to compute
$t\in T$
. The key of the proof is to compute
![]() ${\mathscr {D}}(\nu _{{\mathrm {tr}}}((\rho ^i)^*\xi _{\bullet }))$
for each
${\mathscr {D}}(\nu _{{\mathrm {tr}}}((\rho ^i)^*\xi _{\bullet }))$
for each
![]() $i=1,2,\dots ,6$
and
$i=1,2,\dots ,6$
and
![]() $\bullet = 0,1,\infty $
.
$\bullet = 0,1,\infty $
.
Before proceeding to the proof, we explain geometric constructions of cycles in
![]() $\Xi _t$
. For
$\Xi _t$
. For
![]() $\rho = (\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
, let
$\rho = (\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
, let
![]() ${\mathcal {D}}_{\rho }$
be the
${\mathcal {D}}_{\rho }$
be the
![]() $(1,1)$
-curve on
$(1,1)$
-curve on
![]() ${\mathbb {P}}^1\times {\mathbb {P}}^1$
which passes through
${\mathbb {P}}^1\times {\mathbb {P}}^1$
which passes through
![]() $(\rho _1^{-1}(0),\rho _2^{-1}(0))$
,
$(\rho _1^{-1}(0),\rho _2^{-1}(0))$
,
![]() $(\rho _1^{-1}(1),\rho _2^{-1}(1))$
and
$(\rho _1^{-1}(1),\rho _2^{-1}(1))$
and
![]() $(\rho _1^{-1}(\infty ),\rho _2^{-1}(\infty )) \in \Sigma ^2$
. The local equation of
$(\rho _1^{-1}(\infty ),\rho _2^{-1}(\infty )) \in \Sigma ^2$
. The local equation of
![]() ${\mathcal {D}}_{\rho }$
is given by
${\mathcal {D}}_{\rho }$
is given by
![]() $\rho _1^\sharp (x) = \rho _2^\sharp (y)$
. Let
$\rho _1^\sharp (x) = \rho _2^\sharp (y)$
. Let
![]() ${\mathcal {C}}_{\rho }\subset {\mathcal {X}}_t$
be its pull-back by
${\mathcal {C}}_{\rho }\subset {\mathcal {X}}_t$
be its pull-back by
![]() ${\mathcal {X}}_t\rightarrow {\mathcal {Y}}_t ={\mathbb {P}}^1\times {\mathbb {P}}^1$
and
${\mathcal {X}}_t\rightarrow {\mathcal {Y}}_t ={\mathbb {P}}^1\times {\mathbb {P}}^1$
and
![]() $\widetilde {{\mathcal {C}}}_{\rho }\subset \widetilde {{\mathcal {X}}}_t$
be the strict transform of
$\widetilde {{\mathcal {C}}}_{\rho }\subset \widetilde {{\mathcal {X}}}_t$
be the strict transform of
![]() ${\mathcal {C}}_{\rho }$
. By definition,
${\mathcal {C}}_{\rho }$
. By definition,
![]() ${\mathcal {D}}_{\rho }$
coincides with the inverse image of
${\mathcal {D}}_{\rho }$
coincides with the inverse image of
![]() ${\mathcal {D}}$
by
${\mathcal {D}}$
by
![]() $\rho $
, so we have
$\rho $
, so we have
![]() $\widetilde {{\mathcal {C}}}_{\rho } =\rho ^{-1}_t(\widetilde {{\mathcal {C}}})$
. Moreover, by considering the
$\widetilde {{\mathcal {C}}}_{\rho } =\rho ^{-1}_t(\widetilde {{\mathcal {C}}})$
. Moreover, by considering the
![]() $G_{{\mathcal {X}}}$
-action on
$G_{{\mathcal {X}}}$
-action on
![]() $\Sigma ^2$
, we have
$\Sigma ^2$
, we have
![]() $Q_{(\rho _1^{-1}(\bullet ), \rho _2^{-1}(\bullet ))}=\rho _t^{-1}(Q_{(\bullet ,\bullet )})$
for
$Q_{(\rho _1^{-1}(\bullet ), \rho _2^{-1}(\bullet ))}=\rho _t^{-1}(Q_{(\bullet ,\bullet )})$
for
![]() $\bullet = 0,1,\infty $
. Thus we see that
$\bullet = 0,1,\infty $
. Thus we see that
![]() $(\rho ^*\xi _\bullet )_t=\rho _t^*((\xi _{\bullet })_{\tau (t)})\:\:(\bullet \in \{0,1,\infty \})$
is represented by the formal sum
$(\rho ^*\xi _\bullet )_t=\rho _t^*((\xi _{\bullet })_{\tau (t)})\:\:(\bullet \in \{0,1,\infty \})$
is represented by the formal sum
For example, for
![]() $\rho ^1,\rho ^2,\dots ,\rho ^6\in G_{{\mathcal {X}}}$
defined above,
$\rho ^1,\rho ^2,\dots ,\rho ^6\in G_{{\mathcal {X}}}$
defined above,
![]() ${\mathcal {D}}_{\rho ^1},{\mathcal {D}}_{\rho ^2},\dots ,{\mathcal {D}}_{\rho ^6}$
are graphs of rational functions
${\mathcal {D}}_{\rho ^1},{\mathcal {D}}_{\rho ^2},\dots ,{\mathcal {D}}_{\rho ^6}$
are graphs of rational functions
![]() $z,1-z,z/(1-z),1/(1-z),1/z,$
and
$z,1-z,z/(1-z),1/(1-z),1/z,$
and
![]() $(z-1)/z$
on
$(z-1)/z$
on
![]() ${\mathbb {P}}^1$
, respectively. Hence,
${\mathbb {P}}^1$
, respectively. Hence,
![]() $((\rho ^i)^*\xi _{\bullet })_t$
are higher Chow cycles made from such graphs.
$((\rho ^i)^*\xi _{\bullet })_t$
are higher Chow cycles made from such graphs.
Remark 7.2 The idea of the construction of higher Chow cycles from the curve
![]() ${\mathcal {D}}_{\rho }$
is of Terasoma. The referee pointed out that the explicit 18 cycles made from the graphs of six rational functions on
${\mathcal {D}}_{\rho }$
is of Terasoma. The referee pointed out that the explicit 18 cycles made from the graphs of six rational functions on
![]() ${\mathbb {P}}^1$
are enough for the rank estimate.
${\mathbb {P}}^1$
are enough for the rank estimate.
7.2 Proof of the main theorem
We define subgroups
![]() $N^{\mathrm {can}}$
and N of
$N^{\mathrm {can}}$
and N of
![]() $\Gamma (T,{\mathcal {Q}})$
as follows:
$\Gamma (T,{\mathcal {Q}})$
as follows:
 $$ \begin{align*} \begin{aligned} &N^{\mathrm{can}} = \langle \nu_{\mathrm{tr}}(\xi_0),\nu_{\mathrm{tr}}(\xi_1),\nu_{{\mathrm{tr}}}(\xi_\infty)\rangle_{\mathbb{Z,}} \\ &N = \langle \nu_{{\mathrm{tr}}}(\rho^*\xi_\bullet): \rho\in G_{{\mathcal{X}}}, \bullet \in \{0,1,\infty\}\rangle_{\mathbb{Z}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &N^{\mathrm{can}} = \langle \nu_{\mathrm{tr}}(\xi_0),\nu_{\mathrm{tr}}(\xi_1),\nu_{{\mathrm{tr}}}(\xi_\infty)\rangle_{\mathbb{Z,}} \\ &N = \langle \nu_{{\mathrm{tr}}}(\rho^*\xi_\bullet): \rho\in G_{{\mathcal{X}}}, \bullet \in \{0,1,\infty\}\rangle_{\mathbb{Z}}. \end{aligned} \end{align*} $$
By Proposition 2.3, the transcendental regulator map induces a surjective map
![]() $\Xi _t\twoheadrightarrow {\mathrm {ev}}_t(N)$
for each
$\Xi _t\twoheadrightarrow {\mathrm {ev}}_t(N)$
for each
![]() $t\in T$
. Hence, to prove Theorem 7.1, we have to examine the rank of N. To get a rank estimate for N, we use the following proposition, whose proof will be given in the next section.
$t\in T$
. Hence, to prove Theorem 7.1, we have to examine the rank of N. To get a rank estimate for N, we use the following proposition, whose proof will be given in the next section.
Proposition 7.3 For
![]() $\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
, let
$\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
, let
![]() $\Theta _{\rho }: \tau ^*({\mathcal {O}}_T^{\mathrm {an}})^{\oplus 2}\rightarrow ({\mathcal {O}}_T^{\mathrm {an}})^{\oplus 2}$
be the morphism defined by
$\Theta _{\rho }: \tau ^*({\mathcal {O}}_T^{\mathrm {an}})^{\oplus 2}\rightarrow ({\mathcal {O}}_T^{\mathrm {an}})^{\oplus 2}$
be the morphism defined by

where
![]() $\tau ^\sharp :\tau ^*{\mathcal {O}}_T^{\mathrm {an}}\rightarrow {\mathcal {O}}_T^{\mathrm {an}}; \varphi \mapsto \varphi \circ \tau $
. Let
$\tau ^\sharp :\tau ^*{\mathcal {O}}_T^{\mathrm {an}}\rightarrow {\mathcal {O}}_T^{\mathrm {an}}; \varphi \mapsto \varphi \circ \tau $
. Let
![]() $\xi $
be an algebraic family of higher Chow cycles on
$\xi $
be an algebraic family of higher Chow cycles on
![]() $\widetilde {{\mathcal {X}}}\rightarrow T$
. Then we have
$\widetilde {{\mathcal {X}}}\rightarrow T$
. Then we have
where
![]() ${\mathscr {D}}:{\mathcal {Q}}\simeq {\mathcal {Q}}_\omega \rightarrow ({\mathcal {O}}_T^{{\mathrm {an}}})^{\oplus 2}$
is the Picard–Fuchs differential operator defined in Proposition 5.2.
${\mathscr {D}}:{\mathcal {Q}}\simeq {\mathcal {Q}}_\omega \rightarrow ({\mathcal {O}}_T^{{\mathrm {an}}})^{\oplus 2}$
is the Picard–Fuchs differential operator defined in Proposition 5.2.
Thanks to this proposition, we can compute
![]() ${\mathscr {D}}(N)$
explicitly and we get the desired rank estimate for N. First, we compute
${\mathscr {D}}(N)$
explicitly and we get the desired rank estimate for N. First, we compute
![]() ${\mathscr {D}}(N^{\mathrm {can}})$
.
${\mathscr {D}}(N^{\mathrm {can}})$
.
Proposition 7.4 The images of
![]() $\nu _{\mathrm {tr}}(\xi _0),\nu _{\mathrm {tr}}(\xi _1),\nu _{\mathrm {tr}}(\xi _\infty )$
under the Picard–Fuchs differential operator
$\nu _{\mathrm {tr}}(\xi _0),\nu _{\mathrm {tr}}(\xi _1),\nu _{\mathrm {tr}}(\xi _\infty )$
under the Picard–Fuchs differential operator
![]() ${\mathscr {D}}$
are as follows:
${\mathscr {D}}$
are as follows:
 $$ \begin{align*} {\mathscr{D}}(\nu_{\mathrm{tr}}(\xi_0)) = \frac{2}{a-b} \begin{pmatrix} 1 \\[1.5ex] -1 \end{pmatrix} ,\:\: {\mathscr{D}}(\nu_{\mathrm{tr}}(\xi_1))= \frac{2}{a-b} \begin{pmatrix} \frac{\sqrt{1-b}}{\sqrt{1-a}}\\[1.5ex] -\frac{\sqrt{1-a}}{\sqrt{1-b}} \end{pmatrix} ,\:\: {\mathscr{D}}(\nu_{\mathrm{tr}}(\xi_\infty)) = \frac{2}{a-b} \begin{pmatrix} \frac{\sqrt{b}}{\sqrt{a}} \\[1.5ex] -\frac{\sqrt{a}}{\sqrt{b}} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} {\mathscr{D}}(\nu_{\mathrm{tr}}(\xi_0)) = \frac{2}{a-b} \begin{pmatrix} 1 \\[1.5ex] -1 \end{pmatrix} ,\:\: {\mathscr{D}}(\nu_{\mathrm{tr}}(\xi_1))= \frac{2}{a-b} \begin{pmatrix} \frac{\sqrt{1-b}}{\sqrt{1-a}}\\[1.5ex] -\frac{\sqrt{1-a}}{\sqrt{1-b}} \end{pmatrix} ,\:\: {\mathscr{D}}(\nu_{\mathrm{tr}}(\xi_\infty)) = \frac{2}{a-b} \begin{pmatrix} \frac{\sqrt{b}}{\sqrt{a}} \\[1.5ex] -\frac{\sqrt{a}}{\sqrt{b}} \end{pmatrix}. \end{align*} $$
In particular,
![]() ${\mathrm {rank}\:} N^{\mathrm {can}} = 3$
.
${\mathrm {rank}\:} N^{\mathrm {can}} = 3$
.
Proof The key for the proof is to find
![]() $\rho ^a,\rho ^b\in G_{{\mathcal {X}}}$
such that
$\rho ^a,\rho ^b\in G_{{\mathcal {X}}}$
such that
We consider the following elements.
-
(a)
 $\rho ^a = ({\mathrm {id}},{\mathrm {id}},\tau ^a,1),$
where
$\rho ^a = ({\mathrm {id}},{\mathrm {id}},\tau ^a,1),$
where
 $\tau ^a\in G_T$
satisfies
$\tau ^a\in G_T$
satisfies
 $(\tau ^a)^\sharp \left (\sqrt {a}\right )=\sqrt {a}$
,
$(\tau ^a)^\sharp \left (\sqrt {a}\right )=\sqrt {a}$
,
 $(\tau ^a)^\sharp \left (\sqrt {1-a}\right )=-\sqrt {1-a}$
,
$(\tau ^a)^\sharp \left (\sqrt {1-a}\right )=-\sqrt {1-a}$
,
 $(\tau ^a)^\sharp \left (\sqrt {b}\right )=\sqrt {b}$
, and
$(\tau ^a)^\sharp \left (\sqrt {b}\right )=\sqrt {b}$
, and
 $(\tau ^a)^\sharp \left (\sqrt {1-b}\right )=\sqrt {1-b}$
. Then we have
$(\tau ^a)^\sharp \left (\sqrt {1-b}\right )=\sqrt {1-b}$
. Then we have
 $\phi _1(\tau ^a) = -1$
and
$\phi _1(\tau ^a) = -1$
and
 $\phi _2(\tau ^b)=1$
.
$\phi _2(\tau ^b)=1$
. -
(b)
 $\rho ^b = ((1\:\:\:\infty ),(1\:\:\:\infty ),\tau ^b,1),$
where
$\rho ^b = ((1\:\:\:\infty ),(1\:\:\:\infty ),\tau ^b,1),$
where
 $\tau ^b\in G_T$
satisfies
$\tau ^b\in G_T$
satisfies
 $(\tau ^b)^\sharp \left (\sqrt {a}\right )=\sqrt {1-a}$
,
$(\tau ^b)^\sharp \left (\sqrt {a}\right )=\sqrt {1-a}$
,
 $(\tau ^b)^\sharp \left (\sqrt {1-a}\right )=\sqrt {a}$
,
$(\tau ^b)^\sharp \left (\sqrt {1-a}\right )=\sqrt {a}$
,
 $(\tau ^b)^\sharp \left (\sqrt {b}\right )=\sqrt {1-b}$
, and
$(\tau ^b)^\sharp \left (\sqrt {b}\right )=\sqrt {1-b}$
, and
 $(\tau ^b)^\sharp \left (\sqrt {1-b}\right )=\sqrt {b}$
. Then we have
$(\tau ^b)^\sharp \left (\sqrt {1-b}\right )=\sqrt {b}$
. Then we have
 $\phi _1(\tau ^b)=1$
and
$\phi _1(\tau ^b)=1$
and
 $\phi _2(\tau ^b)=1$
.
$\phi _2(\tau ^b)=1$
.
These elements stabilize the curve
![]() $\widetilde {{\mathcal {C}}}$
. By the local description of the
$\widetilde {{\mathcal {C}}}$
. By the local description of the
![]() $G_{{\mathcal {X}}}$
-action in the end of Section 6, we see that these elements satisfy (27).
$G_{{\mathcal {X}}}$
-action in the end of Section 6, we see that these elements satisfy (27).
By Proposition 7.3 and (27), we can compute
![]() ${\mathscr {D}}(\nu _{\mathrm {tr}}(\xi _0+\xi _1))$
and
${\mathscr {D}}(\nu _{\mathrm {tr}}(\xi _0+\xi _1))$
and
![]() ${\mathscr {D}}(\nu _{\mathrm {tr}}(\xi _0-\xi _\infty ))$
from Proposition 5.3 as follows:
${\mathscr {D}}(\nu _{\mathrm {tr}}(\xi _0-\xi _\infty ))$
from Proposition 5.3 as follows:
 $$ \begin{align*} \begin{aligned} &{\mathscr{D}}(\nu_{\mathrm{tr}}(\xi_0+\xi_1)) =\Theta_{\rho^a}\left({\mathscr{D}}(\nu_{tr}(\xi_1-\xi_0))\right) = \frac{2}{a-b} \begin{pmatrix} 1+ \frac{\sqrt{1-b}}{\sqrt{1-a}} \\[1.5ex] -1-\frac{\sqrt{1-a}}{\sqrt{1-b}} \end{pmatrix}, \\ &{\mathscr{D}}(\nu_{\mathrm{tr}}(\xi_0-\xi_\infty))= \Theta_{\rho^b}\left({\mathscr{D}}(\nu_{tr}(\xi_1-\xi_0))\right) = \frac{2}{(1-a)-(1-b)} \begin{pmatrix} \frac{\sqrt{b}}{\sqrt{a}}-1 \\[1.5ex] 1-\frac{\sqrt{a}}{\sqrt{b}} \end{pmatrix}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &{\mathscr{D}}(\nu_{\mathrm{tr}}(\xi_0+\xi_1)) =\Theta_{\rho^a}\left({\mathscr{D}}(\nu_{tr}(\xi_1-\xi_0))\right) = \frac{2}{a-b} \begin{pmatrix} 1+ \frac{\sqrt{1-b}}{\sqrt{1-a}} \\[1.5ex] -1-\frac{\sqrt{1-a}}{\sqrt{1-b}} \end{pmatrix}, \\ &{\mathscr{D}}(\nu_{\mathrm{tr}}(\xi_0-\xi_\infty))= \Theta_{\rho^b}\left({\mathscr{D}}(\nu_{tr}(\xi_1-\xi_0))\right) = \frac{2}{(1-a)-(1-b)} \begin{pmatrix} \frac{\sqrt{b}}{\sqrt{a}}-1 \\[1.5ex] 1-\frac{\sqrt{a}}{\sqrt{b}} \end{pmatrix}. \end{aligned} \end{align*} $$
Hence, the images of
![]() $\nu _{\mathrm {tr}}(\xi _0),\nu _{\mathrm {tr}}(\xi _1),$
and
$\nu _{\mathrm {tr}}(\xi _0),\nu _{\mathrm {tr}}(\xi _1),$
and
![]() $\nu _{\mathrm {tr}}(\xi _\infty )$
under the Picard–Fuchs differential operator are as in the statement. Since they are linearly independent over
$\nu _{\mathrm {tr}}(\xi _\infty )$
under the Picard–Fuchs differential operator are as in the statement. Since they are linearly independent over
![]() ${\mathbb {Q}}$
, the latter part follows from these expressions.
${\mathbb {Q}}$
, the latter part follows from these expressions.
Next, we give an estimate for the rank of N. The proof below was simplified by advice from Terasoma. Furthermore, Sreekantan pointed out an error in the Table 2 in the previous version of this paper.
Table 2: The images
![]() $\nu _{\mathrm {tr}}((\rho ^i)^*\xi _\bullet )$
under the Picard–Fuchs differential operator
$\nu _{\mathrm {tr}}((\rho ^i)^*\xi _\bullet )$
under the Picard–Fuchs differential operator
![]() ${\mathscr {D.}}$
${\mathscr {D.}}$
Proposition 7.5
![]() ${\mathrm {Rank}\:} N\ge 18$
.
${\mathrm {Rank}\:} N\ge 18$
.
Proof Let
![]() $\rho ^1,\rho ^2,\dots ,\rho ^6 \in G_{{\mathcal {X}}}$
be elements defined after Theorem 7.1. Using Propositions 7.3 and 7.4, we can compute
$\rho ^1,\rho ^2,\dots ,\rho ^6 \in G_{{\mathcal {X}}}$
be elements defined after Theorem 7.1. Using Propositions 7.3 and 7.4, we can compute
![]() ${\mathscr {D}}(\nu _{\mathrm {tr}}((\rho ^i)^*\xi _\bullet ))$
for
${\mathscr {D}}(\nu _{\mathrm {tr}}((\rho ^i)^*\xi _\bullet ))$
for
![]() $i = 1,\dots , 6$
and
$i = 1,\dots , 6$
and
![]() $\bullet = 0,1,\infty $
as Table 2. Note that this table contains the ambiguity of signs because we do not fix the
$\bullet = 0,1,\infty $
as Table 2. Note that this table contains the ambiguity of signs because we do not fix the
![]() $G_{T}$
-components of
$G_{T}$
-components of
![]() $\rho ^i$
.
$\rho ^i$
.
We will show that the vectors in Table 2 are linearly independent over
![]() ${\mathbb {Q}}$
. It is enough to show that the first components of these vectors are linearly independent over
${\mathbb {Q}}$
. It is enough to show that the first components of these vectors are linearly independent over
![]() ${\mathbb {C}}$
. Note that the first components of these vectors are expressed by
${\mathbb {C}}$
. Note that the first components of these vectors are expressed by
where
![]() $\zeta \in \mu _4$
,
$\zeta \in \mu _4$
,
![]() $F_1$
is either
$F_1$
is either
and
![]() $F_2$
is either
$F_2$
is either
 $$ \begin{align} 1,\:\dfrac{\sqrt{b}}{\sqrt{a}},\:\dfrac{\sqrt{1-b}}{\sqrt{1-a}},\:\dfrac{\sqrt{1-b}}{\sqrt{a}},\:\dfrac{\sqrt{b}}{\sqrt{1-a}},\:\dfrac{1}{\sqrt{1-a}},\: \sqrt{1-b},\:\dfrac{1}{\sqrt{a}}\text{ or }\sqrt{b} \in {\mathrm{Frac}}(B). \end{align} $$
$$ \begin{align} 1,\:\dfrac{\sqrt{b}}{\sqrt{a}},\:\dfrac{\sqrt{1-b}}{\sqrt{1-a}},\:\dfrac{\sqrt{1-b}}{\sqrt{a}},\:\dfrac{\sqrt{b}}{\sqrt{1-a}},\:\dfrac{1}{\sqrt{1-a}},\: \sqrt{1-b},\:\dfrac{1}{\sqrt{a}}\text{ or }\sqrt{b} \in {\mathrm{Frac}}(B). \end{align} $$
Since elements in (28) are linearly independent over
![]() ${\mathbb {C}}$
and elements in (29) are linearly independent over
${\mathbb {C}}$
and elements in (29) are linearly independent over
![]() ${\mathrm {Frac}}(B_0)$
, their products are linearly independent over
${\mathrm {Frac}}(B_0)$
, their products are linearly independent over
![]() ${\mathbb {C}}$
. Hence, we have the result.
${\mathbb {C}}$
. Hence, we have the result.
Then we can prove the main theorem as follows.
Proof of Theorem 7.1
Since N is countable, by Lemma 2.4,
![]() $N\twoheadrightarrow {\mathrm {ev}}_t(N)$
is bijective for very general
$N\twoheadrightarrow {\mathrm {ev}}_t(N)$
is bijective for very general
![]() $t\in T$
. By Proposition 7.5,
$t\in T$
. By Proposition 7.5,
![]() ${\mathrm {rank}\:} {\mathrm {ev}}_t(N)\ge 18$
for such t. Since
${\mathrm {rank}\:} {\mathrm {ev}}_t(N)\ge 18$
for such t. Since
![]() ${\mathrm {ev}}_t(\nu _{{\mathrm {tr}}}(\rho ^*\xi _\bullet ))=r((\rho ^*\xi _\bullet )_t)$
,
${\mathrm {ev}}_t(\nu _{{\mathrm {tr}}}(\rho ^*\xi _\bullet ))=r((\rho ^*\xi _\bullet )_t)$
,
![]() ${\mathrm {ev}}_t(N)$
is generated by the images of
${\mathrm {ev}}_t(N)$
is generated by the images of
![]() $(\rho ^*\xi _\bullet )_t\:(\rho \in G_{{\mathcal {X}}},\bullet \in \{ 0,1,\infty \})$
under the transcendental regulator map. By Proposition 2.3, the transcendental regulator map induces the surjective map
$(\rho ^*\xi _\bullet )_t\:(\rho \in G_{{\mathcal {X}}},\bullet \in \{ 0,1,\infty \})$
under the transcendental regulator map. By Proposition 2.3, the transcendental regulator map induces the surjective map
![]() $\Xi _t\twoheadrightarrow {\mathrm {ev}}_t(N)$
. Hence, we have
$\Xi _t\twoheadrightarrow {\mathrm {ev}}_t(N)$
. Hence, we have
![]() ${\mathrm {rank}\:} \Xi _t \ge {\mathrm {rank}\:} {\mathrm {ev}}_t(N)\ge 18$
for very general
${\mathrm {rank}\:} \Xi _t \ge {\mathrm {rank}\:} {\mathrm {ev}}_t(N)\ge 18$
for very general
![]() $t\in T$
.
$t\in T$
.
7.3 Precise rank of N
Proposition 7.6
![]() ${\mathrm {rank}\:} N = 18$
.
${\mathrm {rank}\:} N = 18$
.
To prove this, we use the following proposition which we prove in Section 8.
Proposition 7.7
-
(1) For
 $\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
, let
$\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
, let
 $\Psi _{\rho }:\tau ^*{\mathcal {O}}_T^{\mathrm {an}} \rightarrow {\mathcal {O}}_T^{\mathrm {an}}$
be the
$\Psi _{\rho }:\tau ^*{\mathcal {O}}_T^{\mathrm {an}} \rightarrow {\mathcal {O}}_T^{\mathrm {an}}$
be the
 ${\mathcal {O}}_T^{\mathrm {an}}$
-module isomorphism defined by Then
${\mathcal {O}}_T^{\mathrm {an}}$
-module isomorphism defined by Then
 $(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
defines a
$(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
defines a
 $G_{{\mathcal {X}}}$
-linearization on
$G_{{\mathcal {X}}}$
-linearization on
 ${\mathcal {O}}_T^{\mathrm {an}}$
. Furthermore,
${\mathcal {O}}_T^{\mathrm {an}}$
. Furthermore,
 $(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
induces a
$(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
induces a
 $G_{{\mathcal {X}}}$
-linearization on
$G_{{\mathcal {X}}}$
-linearization on
 ${\mathcal {Q}}_\omega = {\mathcal {O}}_T^{\mathrm {an}}/{\mathcal {P}}_\omega $
. Under the isomorphism
${\mathcal {Q}}_\omega = {\mathcal {O}}_T^{\mathrm {an}}/{\mathcal {P}}_\omega $
. Under the isomorphism
 ${\mathcal {Q}}_\omega \simeq {\mathcal {Q}}$
,
${\mathcal {Q}}_\omega \simeq {\mathcal {Q}}$
,
 $(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
defines a
$(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
defines a
 $G_{{\mathcal {X}}}$
-linearization on
$G_{{\mathcal {X}}}$
-linearization on
 ${\mathcal {Q}}$
.
${\mathcal {Q}}$
.
-
(2) Let
 $\xi $
be an algebraic family of higher Chow cycles on
$\xi $
be an algebraic family of higher Chow cycles on
 $\widetilde {{\mathcal {X}}}\rightarrow T$
. For any
$\widetilde {{\mathcal {X}}}\rightarrow T$
. For any
 $\rho \in G_{{\mathcal {X}}}$
, we have
$\rho \in G_{{\mathcal {X}}}$
, we have  $$ \begin{align*} \nu_{{\mathrm{tr}}}(\rho^*\xi) = \Psi_{\rho}(\nu_{{\mathrm{tr}}}(\xi)). \end{align*} $$
$$ \begin{align*} \nu_{{\mathrm{tr}}}(\rho^*\xi) = \Psi_{\rho}(\nu_{{\mathrm{tr}}}(\xi)). \end{align*} $$
The following proof of Proposition 7.6 was simplified by the advice from T. Saito.
Proof of Proposition 7.6
It is enough to prove
![]() ${\mathrm {rank}\:} N \le 18$
. By the
${\mathrm {rank}\:} N \le 18$
. By the
![]() $G_{{\mathcal {X}}}$
-linearization
$G_{{\mathcal {X}}}$
-linearization
![]() $(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
of
$(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
of
![]() ${\mathcal {Q}}$
, N becomes a right
${\mathcal {Q}}$
, N becomes a right
![]() $G_{{\mathcal {X}}}$
-module.
$G_{{\mathcal {X}}}$
-module.
We consider the following two subgroups H and I of
![]() $G_{{\mathcal {X}}}$
. We define the normal subgroup H by
$G_{{\mathcal {X}}}$
. We define the normal subgroup H by
![]() ${\mathrm {Ker}}(G_{{\mathcal {X}}}\rightarrow G_{T})$
. By the definition of
${\mathrm {Ker}}(G_{{\mathcal {X}}}\rightarrow G_{T})$
. By the definition of
![]() $\Psi _{\rho }$
, H acts on N as
$\Psi _{\rho }$
, H acts on N as
![]() $\pm 1$
. Next, we define the subgroup I of
$\pm 1$
. Next, we define the subgroup I of
![]() $G_{{\mathcal {X}}}$
by
$G_{{\mathcal {X}}}$
by
where we regard
![]() $\mathfrak {S}(\{0,1,\infty \})$
as a subgroup of
$\mathfrak {S}(\{0,1,\infty \})$
as a subgroup of
![]() $\mathfrak {S}(\Sigma )$
by
$\mathfrak {S}(\Sigma )$
by
![]() $\{0,1,\infty \}\subset \Sigma $
. By definition, I stabilizes the subset
$\{0,1,\infty \}\subset \Sigma $
. By definition, I stabilizes the subset
![]() $\{(0,0),(1,1),(\infty ,\infty )\}$
of
$\{(0,0),(1,1),(\infty ,\infty )\}$
of
![]() $\Sigma ^2$
on
$\Sigma ^2$
on
![]() ${\mathcal {Y}}$
. Thus
${\mathcal {Y}}$
. Thus
![]() $\widetilde {{\mathcal {C}}}$
is stable under the I-action. Hence, for
$\widetilde {{\mathcal {C}}}$
is stable under the I-action. Hence, for
![]() $\bullet = 0,1,\infty $
and
$\bullet = 0,1,\infty $
and
![]() $\rho \in I$
,
$\rho \in I$
,
![]() $(\rho ^*\xi _\bullet )_t$
coincides with either
$(\rho ^*\xi _\bullet )_t$
coincides with either
![]() $\pm (\xi _0)_t,\pm (\xi _1)_t$
, or
$\pm (\xi _0)_t,\pm (\xi _1)_t$
, or
![]() $\pm (\xi _\infty )_t$
up to decomposable cycles (see (26)). By Proposition 2.3,
$\pm (\xi _\infty )_t$
up to decomposable cycles (see (26)). By Proposition 2.3,
![]() $\nu _{\mathrm {tr}}(\xi )$
is determined by
$\nu _{\mathrm {tr}}(\xi )$
is determined by
![]() $\xi _{\mathrm {ind}}$
, therefore
$\xi _{\mathrm {ind}}$
, therefore
![]() $\nu _{\mathrm {tr}}(\rho ^*\xi _\bullet )$
coincides with either
$\nu _{\mathrm {tr}}(\rho ^*\xi _\bullet )$
coincides with either
![]() $\pm \nu _{\mathrm {tr}}(\xi _0),\pm \nu _{\mathrm {tr}}(\xi _1)$
or
$\pm \nu _{\mathrm {tr}}(\xi _0),\pm \nu _{\mathrm {tr}}(\xi _1)$
or
![]() $\pm \nu _{{\mathrm {tr}}}(\xi _\infty )$
. This implies that
$\pm \nu _{{\mathrm {tr}}}(\xi _\infty )$
. This implies that
![]() $N^{\mathrm {can}}$
is an I-submodule of N.
$N^{\mathrm {can}}$
is an I-submodule of N.
Therefore
![]() $N^{\mathrm {can}}$
is a
$N^{\mathrm {can}}$
is a
![]() $H I$
-submodule of N. Then
$H I$
-submodule of N. Then
![]() $N^{\mathrm {can}} \hookrightarrow N$
induces the following
$N^{\mathrm {can}} \hookrightarrow N$
induces the following
![]() $G_{{\mathcal {X}}}$
-module homomorphism:
$G_{{\mathcal {X}}}$
-module homomorphism:
where
![]() $\mathrm {Ind}_{H I }^{G_{{\mathcal {X}}}} N^{\mathrm {can}}$
is the induced representation. Since the
$\mathrm {Ind}_{H I }^{G_{{\mathcal {X}}}} N^{\mathrm {can}}$
is the induced representation. Since the
![]() $G_{{\mathcal {X}}}$
-module N is generated by
$G_{{\mathcal {X}}}$
-module N is generated by
![]() $N^{\mathrm {can}}$
, the map (30) is surjective. Then we have
$N^{\mathrm {can}}$
, the map (30) is surjective. Then we have
Hence it is enough to show
![]() $ |G_{{\mathcal {X}}}/H I| = 6$
. First, we show
$ |G_{{\mathcal {X}}}/H I| = 6$
. First, we show
![]() $H \cap I = \{{\mathrm {id}}\}$
. Let
$H \cap I = \{{\mathrm {id}}\}$
. Let
![]() $\rho =(\rho _1,\rho _2,\tau ,\zeta )\in H\cap I$
. Then we have
$\rho =(\rho _1,\rho _2,\tau ,\zeta )\in H\cap I$
. Then we have
![]() $\rho _1=\rho _2\in \mathfrak {S}(\{0,1,\infty \})$
,
$\rho _1=\rho _2\in \mathfrak {S}(\{0,1,\infty \})$
,
![]() $\tau = {\mathrm {id}}$
and
$\tau = {\mathrm {id}}$
and
![]() $\zeta = 1$
. Furthermore, the image of
$\zeta = 1$
. Furthermore, the image of
![]() $(\rho _1,\rho _2)\in G_{{\mathcal {Y}}_0}$
under
$(\rho _1,\rho _2)\in G_{{\mathcal {Y}}_0}$
under
![]() $G_{{\mathcal {Y}}_0}\rightarrow G_{T_0}$
is
$G_{{\mathcal {Y}}_0}\rightarrow G_{T_0}$
is
![]() $({\mathrm {id}},{\mathrm {id}})$
by the condition of the fiber product. Since
$({\mathrm {id}},{\mathrm {id}})$
by the condition of the fiber product. Since
![]() $\mathfrak {S}(\{0,1,\infty \})\hookrightarrow \mathfrak {S}(\Sigma )\twoheadrightarrow {\mathrm {Aut}}(S_0)$
is the isomorphism, we see that
$\mathfrak {S}(\{0,1,\infty \})\hookrightarrow \mathfrak {S}(\Sigma )\twoheadrightarrow {\mathrm {Aut}}(S_0)$
is the isomorphism, we see that
![]() $(\rho _1,\rho _2)=({\mathrm {id}},{\mathrm {id}})$
. Hence
$(\rho _1,\rho _2)=({\mathrm {id}},{\mathrm {id}})$
. Hence
![]() $\rho ={\mathrm {id}}$
. Second, we calculate
$\rho ={\mathrm {id}}$
. Second, we calculate
![]() $|G_{{\mathcal {X}}}|$
and
$|G_{{\mathcal {X}}}|$
and
![]() $|H|$
. We have that
$|H|$
. We have that
![]() $|G_{{\mathcal {X}}}| = 2\cdot |G_{{\mathcal {Y}}}| = 2\cdot |\mathfrak {S}_4\times _{\mathfrak {S}_3}\mathfrak {S}_4|^2 = 2^{11}\cdot 3^2$
. By
$|G_{{\mathcal {X}}}| = 2\cdot |G_{{\mathcal {Y}}}| = 2\cdot |\mathfrak {S}_4\times _{\mathfrak {S}_3}\mathfrak {S}_4|^2 = 2^{11}\cdot 3^2$
. By
![]() $|G_{T}| = |\mathfrak {S}_4^2| = 2^6\cdot 3^2$
and the fact that
$|G_{T}| = |\mathfrak {S}_4^2| = 2^6\cdot 3^2$
and the fact that
![]() $G_{{\mathcal {X}}}\rightarrow G_{T}$
is surjective,
$G_{{\mathcal {X}}}\rightarrow G_{T}$
is surjective,
![]() $|H| =|G_{{\mathcal {X}}}|/|G_T| =2^5$
. Third, we calculate
$|H| =|G_{{\mathcal {X}}}|/|G_T| =2^5$
. Third, we calculate
![]() $|I|$
. For each
$|I|$
. For each
![]() $\rho \in \mathfrak {S}(\{0,1,\infty \})$
, the number of elements in
$\rho \in \mathfrak {S}(\{0,1,\infty \})$
, the number of elements in
![]() $G_{{\mathcal {X}}}$
of the form
$G_{{\mathcal {X}}}$
of the form
![]() $(\rho ,\rho ,*,1)$
equals to the cardinality of
$(\rho ,\rho ,*,1)$
equals to the cardinality of
![]() ${\mathrm {Ker}}(G_{T}\rightarrow G_{T_0})$
, i.e.,
${\mathrm {Ker}}(G_{T}\rightarrow G_{T_0})$
, i.e.,
![]() $2^4$
. Hence
$2^4$
. Hence
![]() $|I|=2^4\cdot |\mathfrak {S}(\{0,1,\infty \})| = 2^5\cdot 3$
. To sum up these results, we have
$|I|=2^4\cdot |\mathfrak {S}(\{0,1,\infty \})| = 2^5\cdot 3$
. To sum up these results, we have
 $$ \begin{align*} |G_{{\mathcal{X}}}/H I| = \frac{|G_{{\mathcal{X}}}|}{|H I|} = \frac{|G_{{\mathcal{X}}}|}{|H|\cdot |I|} = 6.\\[-41pt] \end{align*} $$
$$ \begin{align*} |G_{{\mathcal{X}}}/H I| = \frac{|G_{{\mathcal{X}}}|}{|H I|} = \frac{|G_{{\mathcal{X}}}|}{|H|\cdot |I|} = 6.\\[-41pt] \end{align*} $$
8 The group action on the Picard–Fuchs differential operator
In this section, we prove Propositions 7.3 and 7.7 and complete the proof of the main theorem. They are proved by examining the
![]() $G_{{\mathcal {X}}}$
-actions on the periods and the Picard–Fuchs differential operator.
$G_{{\mathcal {X}}}$
-actions on the periods and the Picard–Fuchs differential operator.
8.1 The group action on periods
First, we prove Proposition 7.7. By the property of 1-cocycles, we see that
![]() $(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
defines a
$(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
defines a
![]() $G_{{\mathcal {X}}}$
-linearization on
$G_{{\mathcal {X}}}$
-linearization on
![]() ${\mathcal {O}}_T^{\mathrm {an}}$
. To prove that this induces the
${\mathcal {O}}_T^{\mathrm {an}}$
. To prove that this induces the
![]() $G_{{\mathcal {X}}}$
-linearization on
$G_{{\mathcal {X}}}$
-linearization on
![]() ${\mathcal {Q}}_\omega $
, we should prove that
${\mathcal {Q}}_\omega $
, we should prove that
![]() $\Psi _{\rho }$
preserves the subsheaf
$\Psi _{\rho }$
preserves the subsheaf
![]() ${\mathcal {P}}_\omega $
which is the local system consisting of period function with respect to
${\mathcal {P}}_\omega $
which is the local system consisting of period function with respect to
![]() $\omega $
.
$\omega $
.
Let
![]() $\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
. By the local description of the
$\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
. By the local description of the
![]() $G_{{\mathcal {X}}}$
-action on
$G_{{\mathcal {X}}}$
-action on
![]() $\widetilde {{\mathcal {X}}}$
, we can check that
$\widetilde {{\mathcal {X}}}$
, we can check that
![]() $\rho ^*\omega = \chi (\rho )\cdot \omega $
. Pulling-back this relation at
$\rho ^*\omega = \chi (\rho )\cdot \omega $
. Pulling-back this relation at
![]() $\tau (t)\in T$
, we have
$\tau (t)\in T$
, we have
Here,
![]() $\rho _t:\widetilde {{\mathcal {X}}}_t\rightarrow \widetilde {{\mathcal {X}}}_{\tau (t)}$
is the isomorphism in the diagram (25) and
$\rho _t:\widetilde {{\mathcal {X}}}_t\rightarrow \widetilde {{\mathcal {X}}}_{\tau (t)}$
is the isomorphism in the diagram (25) and
![]() $\chi (\rho ^{-1})(\tau (t))\in {\mathbb {C}}$
is the value of
$\chi (\rho ^{-1})(\tau (t))\in {\mathbb {C}}$
is the value of
![]() $\chi (\rho ^{-1})\in B$
at
$\chi (\rho ^{-1})\in B$
at
![]() $\tau (t)$
. From the equation (31), for any 2-chain
$\tau (t)$
. From the equation (31), for any 2-chain
![]() $\Gamma _{\tau (t)}$
on
$\Gamma _{\tau (t)}$
on
![]() $\widetilde {{\mathcal {X}}}_{\tau (t)}$
, we have
$\widetilde {{\mathcal {X}}}_{\tau (t)}$
, we have
 $$ \begin{align} \begin{aligned} \int_{\rho_t^{-1}(\Gamma_{\tau(t)})}\omega_t &= \int_{\Gamma_{\tau(t)}}(\rho^{-1}_t)^*(\omega_t) = \chi(\rho^{-1})(\tau(t))\cdot \int_{\Gamma_{\tau(t)}}\omega_{\tau(t)} \\ &= \tau^\sharp\left(\chi(\rho^{-1})\right)(t)\cdot \int_{\Gamma_{\tau(t)}}\omega_{\tau(t)} = \chi(\rho)(t)^{-1}\cdot \int_{\Gamma_{\tau(t)}}\omega_{\tau(t),} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \int_{\rho_t^{-1}(\Gamma_{\tau(t)})}\omega_t &= \int_{\Gamma_{\tau(t)}}(\rho^{-1}_t)^*(\omega_t) = \chi(\rho^{-1})(\tau(t))\cdot \int_{\Gamma_{\tau(t)}}\omega_{\tau(t)} \\ &= \tau^\sharp\left(\chi(\rho^{-1})\right)(t)\cdot \int_{\Gamma_{\tau(t)}}\omega_{\tau(t)} = \chi(\rho)(t)^{-1}\cdot \int_{\Gamma_{\tau(t)}}\omega_{\tau(t),} \end{aligned} \end{align} $$
where the last equality follows from the property of 1-cocycles. This is the key for the proof of Proposition 7.7.
Proof of Proposition 7.7
We prove (1). We prove that
![]() $\Psi _{\rho }(\tau ^*{\mathcal {P}}_\omega ) = {\mathcal {P}}_{\omega }$
. Since
$\Psi _{\rho }(\tau ^*{\mathcal {P}}_\omega ) = {\mathcal {P}}_{\omega }$
. Since
![]() $\rho ^*(\Psi _{\rho ^{-1}})=\Psi _{\rho }^{-1}$
, it is enough to show only
$\rho ^*(\Psi _{\rho ^{-1}})=\Psi _{\rho }^{-1}$
, it is enough to show only
![]() $(\subset )$
. Let
$(\subset )$
. Let
![]() $U'$
be an open subset of T in the classical topology and
$U'$
be an open subset of T in the classical topology and
![]() $\varphi \in \tau ^*{\mathcal {P}}_\omega (U')={\mathcal {P}}_\omega (\tau (U'))$
. Then there exists a
$\varphi \in \tau ^*{\mathcal {P}}_\omega (U')={\mathcal {P}}_\omega (\tau (U'))$
. Then there exists a
![]() $C^\infty $
-family of 2-cycles
$C^\infty $
-family of 2-cycles
![]() $\{\Gamma _t\}_{t\in \tau (U)}$
such that
$\{\Gamma _t\}_{t\in \tau (U)}$
such that
![]() $\varphi (t) = \int _{\Gamma _t}\omega _t$
. For any
$\varphi (t) = \int _{\Gamma _t}\omega _t$
. For any
![]() $t\in U'$
, we have
$t\in U'$
, we have
Hence, we have
![]() $\Psi _{\rho }(\varphi )\in {\mathcal {P}}_\omega (U')$
. Thus,
$\Psi _{\rho }(\varphi )\in {\mathcal {P}}_\omega (U')$
. Thus,
![]() $(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
induces the
$(\Psi _{\rho })_{\rho \in G_{{\mathcal {X}}}}$
induces the
![]() $G_{{\mathcal {X}}}$
-linearization on
$G_{{\mathcal {X}}}$
-linearization on
![]() ${\mathcal {Q}}_\omega = {\mathcal {O}}_T^{\mathrm {an}}/{\mathcal {P}}_\omega $
.
${\mathcal {Q}}_\omega = {\mathcal {O}}_T^{\mathrm {an}}/{\mathcal {P}}_\omega $
.
Next, we prove (2). By Corollary 2.5, it is enough to show that
for any
![]() $t\in T$
. We take a neighborhood
$t\in T$
. We take a neighborhood
![]() $U'$
of
$U'$
of
![]() $\tau (t)$
and a
$\tau (t)$
and a
![]() $C^\infty $
-family of 2-chains
$C^\infty $
-family of 2-chains
![]() $\{\Gamma _{t'}\}_{t'\in U'}$
such that
$\{\Gamma _{t'}\}_{t'\in U'}$
such that
![]() $\Gamma _{t'}$
is a 2-chain associated with
$\Gamma _{t'}$
is a 2-chain associated with
![]() $\xi _{t'}$
. We will compute the right-hand side of (33). Under the isomorphism
$\xi _{t'}$
. We will compute the right-hand side of (33). Under the isomorphism
![]() ${\mathcal {Q}}\xrightarrow {\sim }{\mathcal {Q}}_\omega $
,
${\mathcal {Q}}\xrightarrow {\sim }{\mathcal {Q}}_\omega $
,
![]() $\Psi _{\rho }(\nu _{\mathrm {tr}}(\xi ))$
is represented by the local holomorphic function
$\Psi _{\rho }(\nu _{\mathrm {tr}}(\xi ))$
is represented by the local holomorphic function
The right-hand side of (33) is represented by the value of this function at t. That is,
On the other hand, the left-hand side of (33) is
![]() $\langle r((\rho ^*\xi )_t), [\omega _t]\rangle = \langle r(\rho _t^*(\xi _{\tau (t)})), [\omega _t]\rangle $
. Since
$\langle r((\rho ^*\xi )_t), [\omega _t]\rangle = \langle r(\rho _t^*(\xi _{\tau (t)})), [\omega _t]\rangle $
. Since
![]() $\rho _t^{-1}(\Gamma _{\tau (t)})$
is a 2-chain associated with
$\rho _t^{-1}(\Gamma _{\tau (t)})$
is a 2-chain associated with
![]() $\rho _t^*(\xi _{\tau (t)})$
, the left-hand side of (33) also coincides with (34). Hence we have the result.
$\rho _t^*(\xi _{\tau (t)})$
, the left-hand side of (33) also coincides with (34). Hence we have the result.
8.2 The group action on the Picard–Fuchs operator
Next, we will investigate the
![]() $G_{{\mathcal {X}}}$
-action on the differential operator
$G_{{\mathcal {X}}}$
-action on the differential operator
![]() ${\mathscr {D}}$
. For
${\mathscr {D}}$
. For
![]() $\tau \in G_{T}$
, we define differential operators
$\tau \in G_{T}$
, we define differential operators
![]() ${\mathscr {D}}^{\tau }_1,{\mathscr {D}}^{\tau }_2:{\mathcal {O}}_T^{\mathrm {an}} \rightarrow {\mathcal {O}}_T^{\mathrm {an}}$
as follows:
${\mathscr {D}}^{\tau }_1,{\mathscr {D}}^{\tau }_2:{\mathcal {O}}_T^{\mathrm {an}} \rightarrow {\mathcal {O}}_T^{\mathrm {an}}$
as follows:
 $$ \begin{align*} \begin{aligned} &{\mathscr{D}}^{\tau}_1 = a'(1-a') \frac{\partial^2}{(\partial a')^2} +(1-2a')\frac{\partial}{\partial a'} -\frac{1}{4}, \\ &{\mathscr{D}}^{\tau}_2 = b'(1-b') \frac{\partial^2}{(\partial b')^2} +(1-2b')\frac{\partial}{\partial b'} -\frac{1}{4}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &{\mathscr{D}}^{\tau}_1 = a'(1-a') \frac{\partial^2}{(\partial a')^2} +(1-2a')\frac{\partial}{\partial a'} -\frac{1}{4}, \\ &{\mathscr{D}}^{\tau}_2 = b'(1-b') \frac{\partial^2}{(\partial b')^2} +(1-2b')\frac{\partial}{\partial b'} -\frac{1}{4}, \end{aligned} \end{align*} $$
where
![]() $a'=\tau ^\sharp (a)$
and
$a'=\tau ^\sharp (a)$
and
![]() $b'=\tau ^\sharp (b)$
. By definition,
$b'=\tau ^\sharp (b)$
. By definition,
holds for any local section
![]() $\varphi $
of
$\varphi $
of
![]() ${\mathcal {O}}_T^{\mathrm {an}}$
. We have the following transformation formulas.
${\mathcal {O}}_T^{\mathrm {an}}$
. We have the following transformation formulas.
Proposition 8.1 For
![]() $\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
, we have the following relations in the ring of differential operators on
$\rho =(\rho _1,\rho _2,\tau ,\zeta )\in G_{{\mathcal {X}}}$
, we have the following relations in the ring of differential operators on
![]() ${\mathcal {O}}_T^{\mathrm {an}}$
:
${\mathcal {O}}_T^{\mathrm {an}}$
:
 $$ \begin{align*} \begin{aligned} &{\mathscr{D}}_1\cdot \chi(\rho)^{-1} = \chi(\rho)^{-1}\cdot \phi_1(\tau)^{-2}\cdot {\mathscr{D}}^\tau_1, \\ &{\mathscr{D}}_2\cdot \chi(\rho)^{-1} = \chi(\rho)^{-1}\cdot \phi_2(\tau)^{-2}\cdot {\mathscr{D}}^\tau_2, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &{\mathscr{D}}_1\cdot \chi(\rho)^{-1} = \chi(\rho)^{-1}\cdot \phi_1(\tau)^{-2}\cdot {\mathscr{D}}^\tau_1, \\ &{\mathscr{D}}_2\cdot \chi(\rho)^{-1} = \chi(\rho)^{-1}\cdot \phi_2(\tau)^{-2}\cdot {\mathscr{D}}^\tau_2, \end{aligned} \end{align*} $$
where we regard
![]() $\chi (\rho ),\phi _1(\tau )$
and
$\chi (\rho ),\phi _1(\tau )$
and
![]() $\phi _2(\tau )$
as differential operators by multiplication.
$\phi _2(\tau )$
as differential operators by multiplication.
Proof We prove the first equation. The second equation is proved similarly. Since
![]() $\chi (\rho ) = \zeta \phi _1(\tau )\phi _2(\tau )$
and
$\chi (\rho ) = \zeta \phi _1(\tau )\phi _2(\tau )$
and
![]() $\zeta \phi _2(\tau )$
commutes with
$\zeta \phi _2(\tau )$
commutes with
![]() ${\mathscr {D}}_1$
, it is enough to show that
${\mathscr {D}}_1$
, it is enough to show that
Let
![]() $\tau = (\tau _1,\tau _2)\in G_{T}=\mathfrak {S}_4^2$
. We denote the image of
$\tau = (\tau _1,\tau _2)\in G_{T}=\mathfrak {S}_4^2$
. We denote the image of
![]() $\tau _1$
under
$\tau _1$
under
![]() $\mathfrak {S}_4\rightarrow {\mathrm {Aut}}(S_0)=\mathfrak {S}(\{0,1,\infty \})$
by
$\mathfrak {S}_4\rightarrow {\mathrm {Aut}}(S_0)=\mathfrak {S}(\{0,1,\infty \})$
by
![]() $\underline {\tau }_1$
. By (24) and the table in Proposition 6.6,
$\underline {\tau }_1$
. By (24) and the table in Proposition 6.6,
![]() $\phi _1(\tau )$
is determined by
$\phi _1(\tau )$
is determined by
![]() $\underline {\tau }_1$
up to sign and coincides with either
$\underline {\tau }_1$
up to sign and coincides with either
![]() $\pm 1, \pm \sqrt {-1}\sqrt {1-a}$
or
$\pm 1, \pm \sqrt {-1}\sqrt {1-a}$
or
![]() $\pm \sqrt {-1}\sqrt {a}$
. Using
$\pm \sqrt {-1}\sqrt {a}$
. Using
![]() $\frac {\partial }{\partial a}\cdot a^\lambda = \lambda a^{\lambda -1}+a^{\lambda }\frac {\partial }{\partial a}$
and
$\frac {\partial }{\partial a}\cdot a^\lambda = \lambda a^{\lambda -1}+a^{\lambda }\frac {\partial }{\partial a}$
and
![]() $\frac {\partial }{\partial a}\cdot (1-a)^\lambda = -\lambda (1-a)^{\lambda -1}+(1-a)^{\lambda }\frac {\partial }{\partial a}$
, we can compute the left-hand side of (36) as follows:
$\frac {\partial }{\partial a}\cdot (1-a)^\lambda = -\lambda (1-a)^{\lambda -1}+(1-a)^{\lambda }\frac {\partial }{\partial a}$
, we can compute the left-hand side of (36) as follows:
 $$ \begin{align} \begin{aligned} &a(1-a)\dfrac{\partial^2}{\partial a^2} + (1-2a)\dfrac{\partial}{\partial a} -\dfrac{1}{4} && (\underline{\tau}_1 = {\mathrm{id}}, (0\:\:1)), \\ &-a(1-a)^2\frac{\partial^2}{\partial a^2}-(1-a)^2\frac{\partial}{\partial a} -\frac{1}{4} && (\underline{\tau}_1 = (1\:\;\infty), (0\:\:1\:\:\infty)), \\ &-a^2(1-a)\frac{\partial^2}{\partial a^2}+a^2\frac{\partial}{\partial a}-\frac{1}{4} && (\underline{\tau}_1 = (0\:\:\infty), (0\:\:\infty\:\;1)). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &a(1-a)\dfrac{\partial^2}{\partial a^2} + (1-2a)\dfrac{\partial}{\partial a} -\dfrac{1}{4} && (\underline{\tau}_1 = {\mathrm{id}}, (0\:\:1)), \\ &-a(1-a)^2\frac{\partial^2}{\partial a^2}-(1-a)^2\frac{\partial}{\partial a} -\frac{1}{4} && (\underline{\tau}_1 = (1\:\;\infty), (0\:\:1\:\:\infty)), \\ &-a^2(1-a)\frac{\partial^2}{\partial a^2}+a^2\frac{\partial}{\partial a}-\frac{1}{4} && (\underline{\tau}_1 = (0\:\:\infty), (0\:\:\infty\:\;1)). \end{aligned} \end{align} $$
On the other hand,
![]() ${\mathscr {D}}_1^\tau $
is also determined by
${\mathscr {D}}_1^\tau $
is also determined by
![]() $\underline {\tau }_1\in {\mathrm {Aut}}(S_0)=\mathfrak {S}(\{0,1,\infty \})$
by definition. We can check (36) holds for each
$\underline {\tau }_1\in {\mathrm {Aut}}(S_0)=\mathfrak {S}(\{0,1,\infty \})$
by definition. We can check (36) holds for each
![]() $\underline {\tau }_1$
. For example, when
$\underline {\tau }_1$
. For example, when
![]() $\underline {\tau }_1 = (1\:\:\infty )$
, the differential operator
$\underline {\tau }_1 = (1\:\:\infty )$
, the differential operator
![]() ${\mathscr {D}}_1^\tau $
is computed as follows: since
${\mathscr {D}}_1^\tau $
is computed as follows: since
![]() $a' = \frac {a}{a-1}$
, we have
$a' = \frac {a}{a-1}$
, we have
 $$ \begin{align*} \begin{aligned} &\frac{\partial}{\partial a'} = \frac{\partial a}{\partial a'}\cdot \frac{\partial }{\partial a} = -\frac{1}{(a'-1)^2}\cdot \frac{\partial}{\partial a} = -(a-1)^2\cdot \frac{\partial }{\partial a} \\ &\frac{\partial^2}{(\partial a')^2}= \left(-(a-1)^2\cdot \frac{\partial}{\partial a}\right)^2 = (a-1)^4\frac{\partial^2}{\partial a^2}+2(a-1)^3\frac{\partial }{\partial a}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\frac{\partial}{\partial a'} = \frac{\partial a}{\partial a'}\cdot \frac{\partial }{\partial a} = -\frac{1}{(a'-1)^2}\cdot \frac{\partial}{\partial a} = -(a-1)^2\cdot \frac{\partial }{\partial a} \\ &\frac{\partial^2}{(\partial a')^2}= \left(-(a-1)^2\cdot \frac{\partial}{\partial a}\right)^2 = (a-1)^4\frac{\partial^2}{\partial a^2}+2(a-1)^3\frac{\partial }{\partial a}. \end{aligned} \end{align*} $$
By substituting
![]() $a',\frac {\partial }{\partial a'}, \frac {\partial ^2}{(\partial a')^2}$
in
$a',\frac {\partial }{\partial a'}, \frac {\partial ^2}{(\partial a')^2}$
in
![]() ${\mathscr {D}}_1^{\tau }$
by them, we can confirm that
${\mathscr {D}}_1^{\tau }$
by them, we can confirm that
![]() ${\mathscr {D}}_1^\tau $
coincides with the second differential operator in (37).
${\mathscr {D}}_1^\tau $
coincides with the second differential operator in (37).
Finally, we prove Proposition 7.3.
Proof of Proposition 7.3
By Proposition 8.1, for a local section
![]() $\varphi $
of
$\varphi $
of
![]() ${\mathcal {O}}_T^{\mathrm {an}}$
, we have
${\mathcal {O}}_T^{\mathrm {an}}$
, we have
 $$ \begin{align*} \begin{aligned} {\mathscr{D}}_1\left(\Psi_{\rho}(\varphi)\right) &= {\mathscr{D}}_1\left(\chi(\rho)^{-1}\cdot \tau^\sharp(\varphi)\right) = \chi(\rho)^{-1}\cdot \phi_1(\tau)^{-2}\cdot {\mathscr{D}}_1^\tau(\tau^\sharp(\varphi)) \\ &\underset{({eqn35}{35})}{=} \chi(\rho)^{-1}\cdot \phi_1(\tau)^{-2}\cdot \tau^\sharp({\mathscr{D}}_1(\varphi)), \\ {\mathscr{D}}_2\left(\Psi_{\rho}(\varphi)\right) &= \chi(\rho)^{-1}\cdot \phi_2(\tau)^{-2}\cdot \tau^\sharp({\mathscr{D}}_2(\varphi)). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} {\mathscr{D}}_1\left(\Psi_{\rho}(\varphi)\right) &= {\mathscr{D}}_1\left(\chi(\rho)^{-1}\cdot \tau^\sharp(\varphi)\right) = \chi(\rho)^{-1}\cdot \phi_1(\tau)^{-2}\cdot {\mathscr{D}}_1^\tau(\tau^\sharp(\varphi)) \\ &\underset{({eqn35}{35})}{=} \chi(\rho)^{-1}\cdot \phi_1(\tau)^{-2}\cdot \tau^\sharp({\mathscr{D}}_1(\varphi)), \\ {\mathscr{D}}_2\left(\Psi_{\rho}(\varphi)\right) &= \chi(\rho)^{-1}\cdot \phi_2(\tau)^{-2}\cdot \tau^\sharp({\mathscr{D}}_2(\varphi)). \end{aligned} \end{align*} $$
In particular, we have
![]() ${\mathscr {D}}(\Psi _{\rho }(\varphi )) = \Theta _{\rho }({\mathscr {D}}(\varphi ))$
. Then by Proposition 7.7, we have
${\mathscr {D}}(\Psi _{\rho }(\varphi )) = \Theta _{\rho }({\mathscr {D}}(\varphi ))$
. Then by Proposition 7.7, we have
Acknowledgments
The author expresses his sincere gratitude to his supervisor Professor Tomohide Terasoma, who lead the author to this subject. The ideas of construction of higher Chow cycles were taught by him. Furthermore, he read the draft of this paper carefully and gave many valuable comments which simplifies the arguments in this paper. He also thanks Professor Shuji Saito and Professor Takeshi Saito sincerely, who gave the author many helpful comments on this paper. The author is very grateful to the referee for a lot of helpful advices for improving the exposition of the paper.