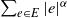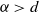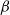Upper large deviations for power-weighted edge lengths in spatial random networks

Abstract

We study the large-volume asymptotics of the sum of power-weighted edge lengths $\sum_{e \in E}|e|^\alpha$ in Poisson-based spatial random networks. In the regime $\alpha > d$, we provide a set of sufficient conditions under which the upper-large-deviation asymptotics are characterized by a condensation phenomenon, meaning that the excess is caused by a negligible portion of Poisson points. Moreover, the rate function can be expressed through a concrete optimization problem. This framework encompasses in particular directed, bidirected, and undirected variants of the k-nearest-neighbor graph, as well as suitable $\beta$-skeletons.

1. Introduction

Many real-world networks are not merely a collection of nodes and edges but live in an ambient Euclidean space. Thanks to seminal research efforts on laws of large numbers and central limit theorems, we now have good understanding of how characteristics computed from stochastic models for geometric networks behave on average in large sampling windows, and how they fluctuate around the mean [16, 17]. However, when envisioning such models to be used in security-critical applications, it is essential to understand also the behavior during rare events. The theory of large deviations is designed to deal with such questions. Its achievement is to reduce the understanding of rare events to the solution of deterministic optimization problems.

On a very general level, one can think of two radically different causes for a rare event that we refer to as homogenization and condensation, respectively. In the case of homogenization, small but consistent deviations throughout the sampling window add up to yield a macroscopic deviation of the considered quantity. On the other hand, in the case of condensation, there is a small isolated structure with the property that its configuration is so extraordinary that it is alone responsible for a deviation that is visible on the macroscopic level. We stress that condensation effects are not by any means restricted to spatial random networks but also play an important role in Erdös–Rényi graphs, branching processes, mathematical biology, and statistical physics [1, 2, 4, 9, 10]. In the classical setting of sums of random variables, this effect is typical for heavy-tailed models.

For network functionals with finite exponential moments, which includes the power-weighted edge lengths for a wide range of graphs in the case that the power is strictly smaller than the dimension, the homogenization can be made rigorous under very general near-additivity and stabilization conditions [19, 20]. However, on the side of condensation, the research is far less well-developed. Recently, a breakthrough has been achieved by describing the large deviations of seeing too many edges in the Gilbert graph [7] based on a Poisson point process in $\mathbb R^d $ . Loosely speaking, these additional edges are induced by a clique obtained from putting a large number of points in a small spatial domain.

In this work, we illustrate that condensation phenomena in upper large deviations are not restricted to the Gilbert graph but occur for a broad class of spatial random networks, including most prominently the k-nearest-neighbor graph (kNN). To that end, we study the upper large deviations of the sum of power-weighted edge lengths, i.e., $\sum_e |e|^\alpha $ , where the sum is taken over all network edges in a growing sampling window and $\alpha$ denotes the power considered. This is a fundamental characteristic for spatial random networks, which has already been studied in detail for the Gilbert graph and the directed spanning forest [5, 18].

Speaking of the kNN, for $k = 1 $ and very large $\alpha $ , the excess weight is induced by a single large edge. Although this is no longer the case for general $k\ge 1 $ and $\alpha > d$ , we show that the condensate can still be described in terms of a specific spatial optimization problem. Besides k -nearest-neighbor graphs, our framework also encompasses circle-based $\beta $ -skeletons in two dimensions.

The idea of the proof is to adapt and refine a three-step strategy that has already been successfully implemented to understand the onset of condensation phenomena in other contexts [6, 7]. First, the proportion of nodes making a very large contribution to the power-weighted edge lengths is negligible. We identify these nodes as the condensate. Second, the contribution from nodes outside of the condensate sharply concentrates around the mean. Finally, analyzing the most likely way that the condensate can cause the excess weight leads to the spatial optimization problem mentioned earlier.

The rest of the article is organized as follows. Section 2 contains precise statements of and conditions for our main results on the upper large deviations of the power-weighted edge lengths. Here, we also describe in detail the spatial optimization problem that determines the shape of the condensate. In Sections 3 and 4, the theorems connecting the upper large deviations to the optimization problem are applied to the directed, bidirected, and undirected versions of the kNN, as well as to two-dimensional circle-based $\beta $ -skeletons for $\beta>1 $ . Lastly, Sections 5 and 6 deal with the proofs of our results.

2. Model and main results

To assist the reader, we start by loosely collecting some of the most important notation here. Let $d\ge1$ be the dimension. By $|x|$ we denote the Euclidean norm of $x\in\mathbb R^d$ . For $e=(x, y)\in(\mathbb R^d)^2$ , we set $|e| \;:\!=\; |x-y|$ , which is interpreted as the length of an edge between x and y. Given three points $x,y,z\in\mathbb R^d$ , we denote the absolute value of the angle of the triangle spanned by x, y, and z at the point y by $\angle xyz$ . Further, $B_r (x) \;:\!=\; \{y \in\mathbb R^d \,:\, |y - x|\le r\} $ denotes the Euclidean ball with radius $r>0 $ centered at $x \in \mathbb R^d$ , and for a Borel set $C\subseteq\mathbb R^d$ we will use $|C|$ to denote the d-dimensional Lebesgue measure of C. The symbol $\partial$ refers to the boundary operator that can be applied to a subset of $\mathbb R^d$ . The ceiling function $\lceil\cdot\rceil$ and floor function $\lfloor\cdot\rfloor$ will appear and are given by $\lceil t\rceil \;:\!=\; \min\{m\in\mathbb Z\,:\, m\ge t\}$ and $\lfloor t\rfloor \;:\!=\; \max\{m\in\mathbb Z\,:\, m\le t\}$ for $t\in\mathbb R$ . By $\textbf{N}$ and $\textbf{N}_0$ , we denote the space of all locally finite subsets of $\mathbb R^d$ , where elements of the latter must additionally contain the origin $0 \in \mathbb R^d $ . For a configuration $\varphi\in\textbf{N}$ and a set $C\subseteq\mathbb R^d$ , by $\varphi(C)$ we mean $\#(\varphi\cap C)$ , the number of points in $\varphi$ that are within C. Throughout the paper, $Q_n \;:\!=\; [{-}n/2,n/2]^d$ , $n\ge 1$ , represents a cubical observation window.

In the following we describe the general graphs that we study. For $\varphi\in\textbf{N}$ , the pair $G(\varphi) \;:\!=\; (\varphi, E)$ represents a directed graph, along with a set of edges $E\;:\!=\; E(\varphi)\subseteq\{(x,y)\,:\, x\neq y\in\varphi\}$ on the vertex set $\varphi$ . In particular, we stress that the edges are drawn according to some general construction rule that does not depend on the specific point configuration, and the edge set is determined once we fix $\varphi$ and does not require any randomness. For $\varphi\in\textbf{N}_0$ , we let

(1) \begin{equation}\mathcal{E} (\varphi) \;:\!=\; \{z\in \varphi \,:\, (0,z)\in E (\varphi)\}\end{equation}

denote the set of out-neighbors of the origin and

(2) \begin{equation}E_0 (\varphi) \;:\!=\;\mathcal{E} (\varphi) \cup \{ x \in \varphi\,:\, 0 \in \mathcal{E} (\varphi-x) + x\}\end{equation}

all out- and in-neighbors of 0. Whenever convenient, we use $\mathcal{E}_x(\psi) \;:\!=\; \mathcal{E}(\psi-x) + x$ for the out-neighbors of $x\in\psi\in\textbf{N}$ instead.

In this work, we study the upper large deviations of the sum of $\alpha $ -power-weighted edge lengths in the box $Q_n $ for $\alpha > d $ . For $\varphi\in\textbf{N}$ , that is the quantity

\begin{align*}H_{n,\textsf{dir}} ^{ (\alpha)} (G (\varphi)) \;:\!=\; \frac1{n^d} \sum_{\substack{e = (x, y)\in E\\ x\in \varphi \cap Q_n} } |e|^\alpha = \frac1{n^d} \sum_{\substack{z \in\mathcal{E} (\varphi - x)\\ x \in \varphi \cap Q_n }} |z|^\alpha.\end{align*}

Hence, by defining the score function $\xi^{ (\alpha)} _\textsf{dir} (\psi) \;:\!=\;\sum_{z\in\mathcal{E} (\psi)} |z|^\alpha $ for $\psi \in\textbf{N}_0$ , we can also express $H_{n, \textsf{dir}} ^{ (\alpha)} (G (\varphi)) $ as

(3) \begin{equation}H_{n,\textsf{dir}} ^{ (\alpha)} (G (\varphi)) = \frac1{n^d} \sum_{x \in \varphi \cap Q_n} \xi^{ (\alpha)} _\textsf{dir} (\varphi- x).\end{equation}

If we represent the nodes of a directed graph by a Poisson point process $X \subseteq \mathbb R^d $ with intensity 1, then G(X) plugged into the representation in (3) embeds our problem in the setting of general limit results in stochastic geometry, where a score is assigned to each $x\in X $ encoding the contribution to the total power-weighted edge lengths.

Moreover, we note that a directed graph naturally gives rise to two further spatial networks, namely an undirected network, where an edge is put between two nodes x, y if there is a directed edge from x to y or a directed edge from y to x, and a bidirected network, where an edge is put between x, y if there is a directed edge from x to y and a directed edge from y to x; see [16, Section 2.3]. To extend our results to these networks as well, we henceforth work with a score function $\xi^{ (\alpha)} $ that, for $\varphi\in\textbf{N}_0$ , may take one of the following three forms:

\begin{align*}\xi^{ (\alpha)} (\varphi) \;:\!=\; \begin{cases} \xi^{ (\alpha)} _\textsf{dir} (\varphi)\;:\!=\; \sum_{x\in\mathcal{E} (\varphi)} |x|^\alpha; \\[5pt] \xi^{ (\alpha)} _\textsf{undir} (\varphi) \;:\!=\;\sum_{x\in\mathcal{E} (\varphi)} \frac12 |x|^\alpha + \frac12|x|^\alpha\mathbb{1}\{0\not\in\mathcal{E} (\varphi-x)\} ;\\[5pt] \xi^{ (\alpha)} _\textsf{bidir} (\varphi) \;:\!=\; \sum_{x\in\mathcal{E} (\varphi)} \frac12|x|^\alpha\mathbb{1}\{0\in\mathcal{E} (\varphi-x)\}.\end{cases} \end{align*}

In words, the definition of $\xi_\textsf{undir}^{(\alpha)}$ means that if x is an out-neighbor of 0 but not an in-neighbor, then the edge length $|x|$ contributes fully to the score at 0, whereas it is not considered for the score at x.

We proceed by denoting the corresponding functional for $\varphi\in\textbf{N}$ by

(4) \begin{equation}H_n^{ (\alpha)} (\varphi) \;:\!=\;\frac1{n^d} \sum_{x\in \varphi\cap Q_n} \xi^{ (\alpha)} (\varphi-x),\end{equation}

and if we plug in the Poisson point process X for the random point configuration in (4), we abbreviate the result as

(5) \begin{equation}H_n \;:\!=\; H_n^{ (\alpha)} (X).\end{equation}

In order to describe the large-deviation asymptotics for the upper tails of $H_n $ , we require that the graph and the score function satisfy some additional properties. Our conditions are designed with the (un-/bidirected) kNN and a version of the $\beta $ -skeleton in mind as prototypical examples; see Section 3. It will become apparent that some of the conditions are substantially more delicate than the ones appearing for weak laws of large numbers or central limit theorems on Poisson functionals [15, 16]. This is because for many of the spatial random networks satisfying weak laws of large numbers or central limit theorems, such as Delaunay tessellations (DTs), Gabriel graphs (GGs), and relative neighborhood graphs (RNGs), the upper large deviations will be markedly different from those of the kNN. In all of these graphs, the excess in the large deviation tail may be determined by configurations with a growing number of nodes. For instance, the DT, GG, and RNG can, with significantly high probability, exhibit a large total sum of power-weighted edge lengths by having more than a negligible proportion of edges almost parallel to each other. Nevertheless, we have decided to present our results in a general framework for two reasons. First, we can pinpoint precisely the requirements that are not satisfied by the standard examples mentioned earlier. Second, if one aims to establish upper-large-deviation asymptotics for a specific class of networks, the conditions give a clear view of the points at which additional arguments will be needed to prove the desired result.

We next state the conditions rigorously, then provide a detailed discussion to explain more precisely their meaning and impact. We have not attempted to aggressively minimize the number of conditions, because in doing so we would risk making our statements less accessible. The conditions are the following:

1. 1. $\mathcal{E} $ is scale-invariant: $\tau\mathcal{E} (\varphi)=\mathcal{E} (\tau\varphi) $ for all $\varphi\in\textbf{N}_0 $ and $\tau>0 $ .

2. 2. Adding a new point affects only a bounded number of nodes: there exists $c_\textsf{FIN} > 0$ such that for every $y\in\mathbb R^d $ and $\varphi\in\textbf{N} $ ,

   (FIN) \begin{equation} \#\big\{x\in \varphi \,:\, \mathcal{E} (\varphi-x) \neq\mathcal{E} ( (\varphi-x)\cup\{y-x\} )\big\} \le c_\textsf{FIN}. \end{equation}

3. 3. $\mathcal{E} $ has bounded large-edge density: there exists $c_\textsf{FIN2} \geq 1 $ such that for all $M>0 $ and $\varphi\in\textbf{N} $ ,

   (FIN2) \begin{equation} \#\big\{x\in \varphi\cap B_M (0)\,:\,\max_{y\in\mathcal{E} (\varphi-x)} |y| >M\big\} \le c_\textsf{FIN2}. \end{equation}

4. 4. Proceeding in the vein of [16], we introduce a stabilization condition for G. This condition is based on a collection of cones $S_i $ , $i\le I_d$ , with apex 0 whose union covers the whole space and which do not have parts of their lateral boundary parallel to any coordinate axis of $\mathbb R^d$ . Then, for a constant $c_\textsf{STA} > 0$ and $\varphi \in \textbf{N}_0$ , we put

   \begin{align*}\mathcal{S}_i (\varphi) \;:\!=\; c_\textsf{STA}\inf\{r>0\,:\,\varphi (S_i\cap B_r (0)) \ge c_\textsf{STA} \}.\end{align*}
   We say that G is stabilizing if there exists $c_\textsf{STA} \ge 1 $ such that for every $\eta\in\textbf{N}_0 $ there exists $\textbf{N}_0\ni\theta\subseteq\eta $ such that (i) $\theta \subseteq\cup_{i \le I_d} \big (S_i\cap B_{\mathcal{S}_i (\eta)} (0)\big) =:\mathcal{B} $ , (ii) $\#\theta\le I_d c_\textsf{STA}$ , and (iii)
   (STA) \begin{equation} E_0 (\eta) = E_0 (\psi\cup\mathcal{A}) \quad \text{for all $\psi\subseteq\eta \cap \mathcal{B} $ with $\psi\supseteq\theta $ and all finite $\mathcal{A} \subseteq \mathbb R^d \setminus \mathcal{B} $},\end{equation}
   where $E_0(\!\cdot\!)$ , the set of in- and out-neighbors of the origin, was defined in (2).

5. 5. For every $m \ge 1 $ , there exists a subset $N_m\subseteq\textbf{N} $ of finite configurations consisting of precisely m elements which is a zero-set with respect to the dm -dimensional Lebesgue measure, and which has the property that for $\varphi\in\textbf{N}\setminus N_m$ consisting of m elements, the set of out-neighbors $\mathcal{E} $ is continuous. Setting $\mathcal{N}\;:\!=\; \cup_{m \ge 1} N_m $ , this means that for a finite $\varphi\in\textbf{N}\setminus \mathcal{N} $ , there exists $\delta>0 $ such that for every $x,y\in\varphi $ and every sequence $ (z_w)_{w\in\varphi} \subseteq B_\delta (0) $ ,

   (CON) \begin{equation} y+z_y\in \mathcal{E}_{x+z_x} (\{w + z_w\,:\, w\in\varphi\})\quad\text{if and only if} \quad y\in\mathcal{E}_x (\varphi). \end{equation}
   This assumption excludes finite configurations for which the graph is sensitive to small shifts of single or multiple nodes.

6. 6. There exists $c_\textsf{INF} > 0 $ with the following property: let $\psi\in\textbf{N}_0 $ with $\#\psi\ge c_\textsf{INF} $ and $\theta\in\textbf{N} $ . We demand that

   (INF) \begin{align} \tag{\textbf{INF}} \begin{split} &\mathcal{E} (\psi)\subseteq\mathcal{E} (\psi\cup\theta)\quad\text{if and only if} \quad\mathcal{E} (\psi)\subseteq\mathcal{E} (\psi\cup\{y\} )\text{ for all } y\in\theta. \end{split}\end{align}
   In words, if the configuration $\theta $ is such that no edges are removed by adding an element from $\theta $ to $\varphi $ , then adding the entire set $\theta $ also does not remove any edges (and vice versa).

Each of these properties stays true if we increase $c_\textsf{FIN}$ , $c_\textsf{FIN2}$ , or $c_\textsf{STA} $ . Thus, we can set

\begin{align*}c_\textsf{max} \;:\!=\;\max\{c_\textsf{DEG},c_\textsf{FIN}, c_\textsf{FIN2},c_\textsf{STA},c_\textsf{INF} \} \end{align*}

and use it instead, where $c_\textsf{DEG}$ represents a bound on the maximal node degree that is deduced in Item 4 below.

We now provide more detailed explanations for the conditions and their necessity:

1. 1. The scale-invariance is a fundamental ingredient for controlling the asymptotic behavior of long edges. This condition is satisfied by a variety of spatial networks, such as the DT, the GG, and the RNG.

2. 2-3 The condition ( FIN ) is violated by the DT, the GG, and the RNG. Moreover, if a graph does not fulfill the condition ( FIN2 ), then configurations may be possible with many points having very large edge lengths. The RNG does not satisfy ( FIN2 ) (and, therefore, neither do the DT and the GG). In this case, it is possible to have many nearby points with large combined edge lengths, by having two layers of points almost parallel to each other, as we elaborated in the paragraph after Equation (5).

3. 4 In contrast to the stabilization conditions in [11, 16], we use a very specific class of stabilization regions $\mathcal{B}$ based on cones. Nevertheless, it is still encompassed by more examples of spatial networks (such as RNG). Our variant of the stabilization condition allows not only for arbitrary modifications of the configuration outside the stabilization region $\mathcal{B}$ , but also for the addition of points from the original configuration $\eta$ within $\mathcal{B}$ . Our stabilization condition ( STA ) implies an alternative weaker version that is encompassed by even more examples of spatial networks (such as DT and GG), which is closer to the notion of stabilizing appearing in [11, 16]. Namely, keeping the notation $\mathcal{S}_i$ from ( STA ) and all assumptions made there, we can define a stabilization radius

   (6) \begin{align} \mathcal{R} \,:\, \textbf{N}_0\rightarrow [0,\infty],\ \varphi\mapsto \max_{i\le I_d} \mathcal{S}_i (\varphi), \end{align}
   so that for all finite $\mathcal{A} \subseteq \mathbb R^d \setminus B_{\mathcal{R}(X^*)}(0)$ , setting $X^*=X\cup\{0\}$ , we have
   (7) \begin{equation}E_0(X^*) = E_0\Big(\Big(X^* \cap B_{\mathcal{R}(X^*)}(0)\Big) \cup \mathcal{A}\Big).\end{equation}
   Defining stabilization by demanding the existence of an almost surely finite random variable, the stabilization radius $\mathcal{R}(X^*)$ , such that (7) is fulfilled is very similar to stabilization as it occurs in [11, 16].

   Additionally, ( STA ) yields a bound on the maximal node degree. In particular, when choosing $c_\textsf{DEG} = I_d c_\textsf{STA}$ , we see that $\# E_0(\varphi)\le c_\textsf{DEG}$ for all $\varphi\in\textbf{N}_0$ . The implied uniformly bounded node degree helps to limit the number of edges that can contribute substantially to the power-weighted sum of edge lengths.

   The requirement that the lateral boundaries of the cones must not be parallel to any of the axes is of a technical nature and necessary in the proof of Lemma 10. There we use a weak law of large numbers for Poisson functionals from [16, Theorem 2.1] which does not allow for points to be considered in the functional without their own scores contributing to the total sum. This can cause issues if we desire to compute probabilities which involve cones containing only a limited number of nodes up until a certain radius, if the respective apex of the cone is close to the boundary of the observation window, as happens in the proof of Lemma 10. Here, we imagine that there might be some room to improve ( STA ) and drop the requirement about the lateral boundaries of the cones. For instance, one could try to be more lenient in a weak law of large numbers and also allow the consideration of points whose scores do not contribute. Another option would be to try to make use of the fact that [16, Theorem 2.1] allows for inhomogeneity of the points in some finer arguments. However, it is not clear whether there are interesting examples of graphs that fulfill all the other conditions but do not allow for lateral boundaries of the cones that are not parallel to any of the axes in ( STA ).

4. 5. In the theory of large deviations, it is common to make continuity assumptions in order to obtain asymptotically matching upper and lower bounds for the probability of rare events. For instance, for the kNNs we want to avoid configurations where two distinct pairs of points have the same distance.

5. 6. The bound $c_\textsf{INF} $ is necessary to ensure that the optimization problem introduced later that determines the rate of the large deviations is indeed meaningful. In the simplest case, we would like to avoid situations in which there is a region such that adding a single point anywhere in it does not interfere with any existing edges, but adding a second point to the region suddenly deletes one of the original edges. This could happen, for example, in the directed kNN with $k=2$ if the initial configuration consists of fewer than three points.

Before introducing the deterministic optimization problem connected with the upper tails, we illustrate in Figure 1 how the upper large deviations of $H_n $ feature a condensate for the nearest-neighbor graph. There appears to be one large edge that carries the entire excess weight.

Figure 1. Two configurations that result in a typical sum (left) and an exceptionally large sum (right) of $\alpha $ -power-weighted edge lengths with $\alpha =15 $ . In each configuration, the three vertices inside an observation window with the most distant nearest neighbor are highlighted.

The rate function in the large-volume asymptotics will be given as a solution of an optimization problem. To make this precise, we define the influence zone

(8) \begin{equation}A (\varphi,\psi)\;:\!=\;\big\{y\in\mathbb R^d \,:\, \mathcal{E}_x (\psi)\not\subseteq \mathcal{E}_x ( (\psi\cup\{y\} )) \text{ for some } x\in\varphi \cup\cup_{z\in\varphi} \mathcal{E}_z (\psi)\big\}\end{equation}

for configurations $\varphi\subseteq\psi\in\textbf{N} $ . Loosely speaking, the cost of observing a certain configuration $\psi$ in the large-volume limit comes from the requirement that the influence zone may not contain any additional Poisson points. For instance, in the case of the kNN, the influence zone describes the region of points such that adding another Poisson point would change one of the k nearest neighbors either of an element of $\varphi$ , or of a point that is itself one of the k nearest neighbors of some element of $\varphi$ .

To be able to apply ( CON ) in Section 5.2, we set $D (\varphi)\;:\!=\;\{y\in\mathbb R^d\,:\,\varphi\cup\{y\} \in N_{\#\varphi+1} \} $ for a finite $\varphi\in\textbf{N}\setminus\mathcal{N} $ as well as $D^{\prime}_{\!m} \;:\!=\; \{\psi\in\textbf{N}\,:\,\#\psi=m,|D (\psi)|>0\} $ for $m\in\mathbb N $ . Letting $N^{\prime}_{\!m}\;:\!=\; N_m\cup D^{\prime}_{\!m} $ and $\mathcal{N}^{\prime}\;:\!=\;\cup_{m\ge1} N^{\prime}_{\!m} \supseteq \mathcal{N}$ , we then define the set of admissible configurations over which we optimize. These are configurations whose total contributed power-weighted edge lengths exceed 1, i.e.,

(9) \begin{equation}B\;:\!=\; \Bigg\{ (\varphi,\psi) \,:\, \varphi\subseteq\psi\in\textbf{N}\setminus\mathcal{N}^{\prime},\, c_{\textsf{INF}} \le \#\psi< \infty, \,\sum_{x\in\varphi} \xi^{ (\alpha)} (\psi - x) \geq 1\Bigg\}.\end{equation}

The most likely realizations in the large-deviation asymptotics are then the result of a delicate trade-off. We search for configurations that lead to a small influence zone A but simultaneously exhibit edges that are long enough to be in the admissible set B.

Now we can state the main theorem, where $\mu_\alpha \;:\!=\; \mathbb E[\xi^{ (\alpha)} (X\cup\{0\} )] $ denotes the expected edge length contribution of one vertex.

Theorem 1. (Upper large deviations.) Let $\alpha > d $ and $r > 0 $ . Let the directed edge set $\mathcal{E} $ be scale-invariant and satisfy ( FIN ), ( FIN2 ), ( STA ), ( CON ), and ( INF ). Then

(10) \begin{equation}\lim_{n \uparrow \infty} \frac1{n^{d^2/\alpha}} \log\mathbb P (H_n > \mu_\alpha + r) =-\inf_{ (\varphi,\psi)\in B} |A (\varphi,\psi)| r^{d/\alpha}.\end{equation}

The statement of Theorem 1 indicates the necessity of a power larger than the dimension. The usual speed for large deviations caused by homogenization in the situation of functionals of this type of spatial random network is $n^d$ . If, for $\alpha<d$ , the equality in (10) were still satisfied, then we would have a faster speed than in a homogenization regime, which is not very reasonable and already gives a hint as to why our arguments require $\alpha>d$ .

Next, we are going to assert that if the optimization problem has a strictly positive solution, then with high probability, only a negligible proportion of nodes is responsible for the entire excess when conditioned on the unlikely event. In some cases, we can prove a sharper statement in the sense that only finitely many points carry the excess weight. To make this precise, we introduce additional notation. For configurations $\varphi\subseteq\psi\in\textbf{N} $ , we will consider the order statistics of $\xi^{ (\alpha)} (\psi-x) ,\, x\in\varphi$ . That is, we let $Z^{ (i)} (\varphi,\psi) $ denote the i th-largest element among $\{\xi^{ (\alpha)} (\psi-x)\} _{x \in \varphi} $ . In the case $\varphi = X\cap Q_n $ and $\psi = X $ , we abbreviate $Z_n^{ (i)} \;:\!=\; Z^{ (i)} (X\cap Q_n,X) $ for $i\ge 1 $ . Besides that, recall the definition of the floor function $\lfloor t\rfloor \;:\!=\; \max\{m\in\mathbb Z\,:\, m\le t\}$ for $t\in\mathbb R$ . In Theorem 2 we add a further condition, demanding that the volume of the influence zone does not become arbitrarily small even if we are using many nodes.

Theorem 2. (Condensation conditioned on rare event.) Under the same conditions as in Theorem 1 and the additional assumption that $\inf_{ (\varphi,\psi)\in B} |A (\varphi,\psi)| > 0 $ , the following hold:

1. (a) Let $\varepsilon\in (0, (1-d/\alpha)/ (2\alpha)) $ and $\delta>0 $ . Then

   \begin{align*}\mathbb P\!\left(\Big| (rn^d)^{-1} {\sum_{i\le \lfloor n^{d^2/\alpha-\varepsilon} \rfloor} Z_n^{ (i)}} - 1\Big| > \delta\,\bigg|\, H_n>\mu_\alpha + r\right)\overset{n\uparrow\infty} {\longrightarrow} 0. \end{align*}

2. (b) Additionally, assume there exists $m_0 \ge 1 $ such that for every $\delta\in (0,1) $ ,

   (11) \begin{equation} \inf_{ (\varphi,\psi)\in B} |A (\varphi,\psi)| <\inf_{ (\varphi,\psi)\in B,\, \sum_{i\le m_0} Z^{ (i)} (\varphi,\psi) < 1-\delta} |A (\varphi,\psi)|. \end{equation}
   Then, for every $\delta>0 $ ,
   \begin{align*}\mathbb P\Bigg (\Big| (rn^d)^{-1} {\sum_{i\le m_0} Z_n^{ (i)}} -1\Big| > \delta\, \bigg|\, H_n>\mu_\alpha + r\Bigg)\overset{n\uparrow\infty} {\longrightarrow} 0. \end{align*}

The condition (11) implies that any optimal configuration consists of at most $m_0$ nodes. As will be shown in Section 4.1, the nearest-neighbor graph (NNG) for large $\alpha $ is an example of a graph satisfying (11).

Remark 1. Theorem 1 can also be applied if, instead of X, we consider a Poisson process Y with intensity $n^{-\beta d} $ for some $\beta < 1 $ . Scaling Y by $n^{-\beta} $ yields a Poisson process with intensity 1, and the window becomes $Q_{n^{1 -\beta}} $ . The mean is given as $\mathbb E\big[\xi^{ (\alpha)} \big( (n^{-\beta} Y)\cup\{0\} \big)\big] =n^{-\alpha\beta} \mu_\alpha, $ finally yielding upper tails of the form

\begin{align*} &\lim_{n \uparrow\infty} \frac1{n^{ (1-\beta)d^2/\alpha}} \log\mathbb P\bigg (\frac1{n^{d+\beta (\alpha-d)}} \sum_{x\in Y\cap Q_n} \xi^{ (\alpha)} (Y-x) > \mu_\alpha + r\bigg) \\[5pt] &=\lim_{n \uparrow\infty} \frac1{n^{ (1-\beta)d^2/\alpha}} \log\mathbb P\bigg (\frac1{n^{d-\beta d}} \sum_{x\in X\cap Q_{n^{1- \beta}} } \xi^{ (\alpha)} (X-x) > \mu_\alpha +r\bigg) = -\inf_{ (\varphi,\psi)\in B} |A (\varphi,\psi)|r^{d/\alpha}, \end{align*}

where in the last line we applied Theorem 1 with $n^{\prime}=n^{1-\beta} $ .

Remark 2. Another interesting graph to examine in terms of a condensation phenomenon is the directed spanning forest (DSF). Very loosely speaking, this graph draws an edge from a node to the closest other node that has a higher value in the dth coordinate; see [8]. This graph does not satisfy the condition ( FIN ) required for the upper large deviations and condensation. Furthermore, in the given form of the DSF, this would be one of the few common examples where ( STA ) is violated because of the lateral boundary part. Nevertheless, we suspect the total power-weighted edge lengths for $\alpha>d$ for the DSF to admit upper large deviations with a condensate that might even involve the same optimization problem as appears in Theorem 1. One would need a more generous concentration bound that does not rely on ( FIN ) to prove Lemma 7, and as pointed out in the explanation of ( STA ), we are also confident that it is possible, with finer arguments, to drop the lateral boundary condition from ( STA ). Here, this issue could even be avoided if the search process of the DSF for the closest point were not parallel to one of the axes.

Remark 3. We limit ourselves to the study of the functional representing power-weighted edge lengths of spatial random networks in terms of its upper large deviations. Even the consideration of this functional for a power larger than the dimension restricts the class of admissible graphs heavily. Nevertheless, we believe that there may be room to improve this and, on top of the graph, to generalize the functional as well. An idea would be to consider functional–graph combinations that, for a node to have a large score, would require a relatively large region to contain no points or only a limited number of points. This would include the total sum of power-weighted edge lengths for the kNN and $\beta$ -skeleton. Apart from the functional we have studied, an example that would fit this description could be the sum of power-weighted circumradii of the simplices in the DT. However, if, as in this specific example, we study condensation phenomena for functionals that we apply to the DT, we would run into other issues that were described in the explanations of our conditions.

3. Applications of Theorem 1

We verify that the (un-/bidirected) kNN and suitable $\beta $ -skeletons satisfy the conditions in Theorem 1.

3.1. k-nearest-neighbor graphs

In the kNN, a directed edge is drawn from each node to the $k\ge1 $ points that are closest in Euclidean distance. As explained in Section 2, this definition gives rise to undirected and bidirected kNNs. For $j\le k $ , we define the distance from the origin to the jth closest point in a configuration by

\begin{align*}\mathcal{D}_j \,:\, \textbf{N}_0 \rightarrow [0,\infty),\ \varphi \mapsto \inf\{r>0\,:\, \varphi(B_r(0)) \ge j+1\}.\end{align*}

This leads to the set of the k nearest neighbors of the origin,

(12) \begin{equation}\mathcal{E}\,:\, \textbf{N}_0 \rightarrow \textbf{N},\ \varphi \mapsto \{x\in\varphi\cap B_{\mathcal{D}_k(\varphi)}(0)\}\setminus\{0\}.\end{equation}

We will use the lexicographical order to determine the k nearest neighbors of a node in case more than k neighbors are potential candidates. In the following, we quickly verify the conditions in Theorem 1:

1. 1. $\mathcal{E}$ defined as in (12) is scale-invariant.

2. 2. The bounded node degree [22, Lemma 8.4] entails ( FIN ) with $c_\textsf{FIN}=c_\textsf{DEG} $ , since all nodes that are affected by adding a new vertex to the configuration must be part of an edge with the new vertex.

3. 3. Let $\varphi\in\textbf{N}$ and $M>0$ be arbitrary. For ease of presentation, we consider $k=1$ first. Each vertex $x\in\varphi\cap B_M(0)$ incident to an edge longer than M defines a ball of radius at least M, centered at x, that does not contain any other vertices in its interior. Hence, scaling the radii by 1/2 gives rise to a family of balls that are pairwise disjoint, each having radius at least $M/2$ . Thus, the number of nodes within $B_M(0)$ that are incident to an edge larger than M is at most $|B_{2M}(0)|/|B_{M/2}(0)|=4^d$ .

   Now, let $k \ge 2$ be general and set $\varphi^{\prime}=\varphi$ . Starting with a node

   \begin{align*}x\in\mathop{\textrm{arg max}}_{z\in\varphi^{\prime}\cap B_M(0)} \{|y|\,:\, y\in\mathcal{E}(\varphi-z)\text{ and }|y|>M\},\end{align*}
   we delete all points in $\varphi^{\prime}$ that are within the interior of $B_{\mathcal{D}_k(\varphi-x)}(x)\setminus\{x\}$ , which are at most $k-1$ , and mark x as already dealt with. We repeat this procedure recursively, ignoring nodes in the index of the ${\textrm{arg max}}$ that are already marked, until all nodes in $\varphi^{\prime}\cap B_M(0)$ are either marked or not associated with an edge of length exceeding M. Then, by the same arguments as in the case $k = 1$ , the interiors of the balls $B_{\mathcal{D}_1(\varphi^{\prime}-x)/2}(x)$ are pairwise disjoint for $x\in\{z\in\varphi^{\prime}\cap B_M(0)\,:\, |y|>M \text{ for some }y\in\mathcal{E}(\varphi-z)\}$ , and
   \begin{align*}\#\{z\in\varphi^{\prime}\cap B_M(0)\,:\, |y|>M \text{ for some }y\in\mathcal{E}(\varphi-z)\}\end{align*}
   is bounded by $4^d$ . Moreover, for every marked node left in the thinned configuration $\varphi^{\prime}\cap B_M(0)$ , we have deleted at most $k-1$ nodes from $\varphi$ , and thus we deduce that the total number of nodes in $\varphi\cap B_M(0)$ incident to an edge of length exceeding M is at most $c_\textsf{FIN2}\;:\!=\; k4^d$ , which yields ( FIN2 ).

4. 4. Considering only the undirected kNN, from [15, Lemma 6.1] it follows that we can find a collection of cones such that $\mathcal{R} $ can be used as stabilization radius in the weaker sense of ( STA ) with $c_\textsf{STA} \;:\!=\; k+1 $ . Now, for $\varphi\in\textbf{N}_0$ , let $P_i$ denote the set of the $c_\textsf{STA}$ closest points to the origin in $\varphi\cap (S_i\setminus\{0\})$ . If the intersection does not contain $c_\textsf{STA}$ points, then let $P_i=\varphi\cap S_i\setminus\{0\}$ ; if there are more than $c_\textsf{STA}$ candidates, let the lexicographical order decide which of the farthest-away candidates to include in $P_i$ , and put $\theta\;:\!=\;\{x\in P_i\,:\, i\in\{1,\dots,I_d\}\}$ . Then [22, Lemma 8.4], which asserts that the undirected kNN has bounded node degree, and its proof imply that we can choose the cones in such a way that for this choice of $\theta$ , the condition ( STA ) is satisfied. Further, because ( STA ) only incorporates $\mathcal{E}$ , the condition ( STA ) follows for the undirected, bidirected, and directed kNN.

5. 5. The continuity condition ( CON ) is satisfied with

   \begin{align*}N_m & \;:\!=\; \{\varphi\in\textbf{N}\,:\, \#\varphi=m \text{ and }|w-x|=|y-z|>0 \text{ for some } w,x,y,z\in\varphi \text{ with }\{w,x\}\\[5pt] & \neq\{y,z\}\}\end{align*}
   as the set of configurations containing m nodes, where there are pairs of nodes with equal distances.

6. 6. We choose $c_\textsf{INF}\;:\!=\; k+1 $ to ensure that each node has k neighbors. Then ( INF ) is satisfied, since for $\varphi\in\textbf{N}_0 $ with $\#\varphi\ge c_\textsf{INF} $ , a node in the set $\mathcal{E}(\varphi) $ only vanishes when a vertex is added within the interior of the ball $B_{\mathcal{D}_k(\varphi)}(0) $ . Adding more vertices can only cause more differences.

3.2. $\beta $ -skeletons

$\beta $ -skeletons are geometric graphs that are popular in applications in pattern recognition [12] and machine learning [21]. The two-dimensional $\beta $ -skeleton, $\beta > 1$ , has an edge between two nodes x and y if there is no vertex that has an angle, generated by the two lines to x and y, that is larger than $\gamma\;:\!=\;\arcsin(\beta^{-1}) $ . In other words, there is an edge if the union C(x,y) of the two disks with radius $\beta|x-y|/2 $ and having x and y on their boundary does not contain any other vertices; see Figure 2. This construction rule determines the set of neighbors $\mathcal{E} $ . Note that this definition also makes sense for $\beta = 1$ , leading to a spatial network known as the Gabriel graph.

Figure 2. Illustration of an edge in the $\beta $ -skeleton and a random simulation of the $\beta $ -skeleton with $\beta=1.2$ .

Although the $\beta$ -skeleton can also be defined in higher dimensions, we henceforth restrict our attention to the two-dimensional $\beta $ -skeleton, for two reasons. First, the two-dimensional case already covers the vast majority of applications of $\beta $ -skeletons. Second, as we will see below, even in the two-dimensional case, the verification of the condition ( FIN ) requires delicate geometric arguments. Although we believe an extension to higher dimension is possible, this would entail an even more tedious geometric analysis. Since the focus of our article is on presenting novel probabilistic aspects of large deviations in a geometric context, it would not be appropriate to devote several pages of trigonometry arguments to the verification of the conditions in three and higher dimensions.

We now verify that the $\beta$ -skeletons satisfy the conditions of Theorem 1. To that end, we state an auxiliary result capturing the stabilization properties of $\beta$ -skeletons needed for the condition ( STA ). Since the $\beta$ -skeleton is intrinsically an undirected graph, we henceforth consider all appearing edges as undirected in order to make the presentation more accessible.

Lemma 1. (Stabilization for $\beta$ -skeletons.) For $\beta> 1 $ , there is a collection of cones $(S_i)_{1\le i\le I_2} $ satisfying the requirements of ( STA ) with $c_\textsf{STA} = 2$ .

Proof. We choose the cones $S_i$ , $i \le I_2 $ , sufficiently thin and not axes-parallel so that for any $r>0 $ , the angle generated by starting from the origin, proceeding to any point in $S_i\cap B_r(0) $ , and ending at any point in $S_i\cap \partial B_r(0)$ exceeds $\gamma $ . Now, if $x \in \varphi$ is the closest point to 0 contained in $S_i$ , then $\angle 0xy > \gamma$ for every $y \in S_i$ with $|y| \ge |x|$ and $x\neq y$ . Thus, there cannot be an edge between the origin and y.

To construct $\theta$ , we first let $P_i$ denote the point closest to the origin in $\varphi \cap (S_i\setminus\{0\})$ , if the intersection is non-empty (resolving potential ties by choosing the lexicographic minimum). Then we put $\theta \;:\!=\; \{P_i \,:\, \varphi \cap S_i \ne\emptyset\}\cup\{0\}$ .

Leveraging Lemma 1, we now verify the conditions 1 and 4–6. The application of Theorem 2 for the $\beta $ -skeleton is verified in Section 4 below.

1. 1. $\mathcal{E} $ for the $\beta $ -skeleton, where $\beta>1 $ , is scale-invariant.

2. 4. This is the content of Lemma 1.

3. 5. The continuity condition ( CON ) is satisfied with

   \begin{align*}N_m \;:\!=\; \{\varphi\in\textbf{N}\,:\, \#\varphi=m \text{ and }\varphi\cap \partial C(x, y) \ne \{x, y\}\text{ for some } x,y\in\varphi \}\end{align*}
   as the set of configurations containing m nodes, where there are two nodes that have a vertex on the boundary of the union of disks illustrated in Figure 2.

4. 6. To remove a $\beta $ -skeleton edge e, only one node in C(e) is sufficient. Hence, $c_\textsf{INF}=1 $ .

In the rest of this section, we verify conditions ( FIN ) and ( FIN2 ).

For $e_1, e_2\in\mathbb R^2 $ and the edge $e \,:\!=\, (e_1, e_2)$ with $|e_1-e_2|\ge a>0 $ , we define the point between $e_1 $ and $e_2 $ that has distance a from $e_1 $ by $h_a(e) \;:\!=\; e_1+(e_2-e_1)a/|e| $ . Further, let M(e) be a point at distance $\beta|e|/2 $ to both $e_1 $ and $e_2 $ . In other words, M(e) represents the center of one of the two disks whose union comprises C(e); see Figure 2. In some cases, we will need to make a specific choice between one of the two options, and then we will state this clearly. Finally, let $\Delta_{M(e)}(e) $ be the triangle formed by M(e) and e.

Lemma 2. (Disjoint regions for $\beta $ -skeletons.) Let $e_1, e_2, f_1, f_2 \in \mathbb R^2$ be pairwise distinct, and assume that $e = \{e_1, e_2\}, f = \{f_1, f_2\} \in E(\{e_1, e_2, f_1, f_2\}) $ . Then the following hold:

1. (i) f does not intersect $\Delta_{M(e)}(e)$ ;

2. (ii) there exists a constant $c_\textsf{disj} = c_\textsf{disj}(\beta) \in(0,1/2) $ such that if $|e| \wedge |f| \ge a $ for some $a>0 $ , then

   \begin{align*}B_{c_\textsf{disj}a}(h_m(e)) \cap B_{c_\textsf{disj}a}(h_{m^{\prime}}(f)) = \emptyset\end{align*}
   for all $m\in[a/2,|e|-a/2] $ and $m^{\prime}\in[a/2,|f|-a/2] $ .

We postpone the proof of Lemma 2 to the end of this section, and elucidate how to verify the condition ( FIN2 ). First, instead of bounding the number of nodes in $B_M(0)$ incident to a long edge, we may bound the number of disjoint long edges with one endpoint in $B_M(0)$ . Then, we apply Lemma 2 for every pair of such disjoint edges e and f with $a \;:\!=\; M$ , $m \in\{a/2,|e|-a/2\}$ , and $m^{\prime}\in\{a/2,|f|-a/2\}$ , depending on which choice of m and m’ makes the points $h_m(e)$ and $h_{m^{\prime}}(f)$ closer to $B_M(0)$ . Hence, having $k \ge 1$ disjoint long edges with an endpoint in $B_M(0)$ leads to k disjoint disks with radius $c_\textsf{disj}M$ that are contained entirely within $B_{2M}(0)$ . Thus, the number of such edges is at most $|B_{2M}(0)|/|B_{c_\textsf{disj}M}(0)| = |B_2(0)|/|B_{c_\textsf{disj}}(0)|$ .

Finally, we verify the condition ( FIN ). To achieve this goal, note that the number of edges that can arise from $y \in \mathbb R^2$ is limited by the bound on the node degree. Hence, it remains to consider the number of edges removed by adding the point y. In particular, the number of disjoint edges removed is sufficient. Here, a key observation is that if e, f are disjoint edges with $y \in C(e) \cap C(f)$ , then this implies a very particular relative configuration for e and f. More precisely, the edges e and f do not intersect, and the triangle $\Delta_y(e)$ does not contain an endpoint of f and vice versa. Hence, if we consider the cones $S_y(e)$ and $S_y(f)$ with apex y obtained by extending these triangles, then there are only three options: (i) $S_y(e) \cap S_y(f) = \{y\}$ , (ii) $S_y(e) \subseteq S_y(f)$ , or (iii) $S_y(f) \subseteq S_y(e)$ . In the latter cases, we say that e and f are related. Since the angle at the apex of each of these cones is at least $\gamma$ , the number of equivalence classes of related edges is at most $2\pi /\gamma$ .

Hence, to complete the proof of the condition ( FIN ) it suffices to bound the number of elements in each equivalence class. For this step, we need two further results. To state them, we set $\tau \;:\!=\; \arccos(\beta^{-1})$ .

Lemma 3. (Exclusion of short edges.) Let $e_1, e_2, f_1, f_2 \in \mathbb R^2$ be pairwise distinct, and assume that $e \;:\!=\; \{e_1, e_2\}, f \;:\!=\; \{f_1, f_2\} \in E(\{e_1, e_2, f_1, f_2\})$ and that $|f| \le \tan(\tau) |e|$ . Furthermore, let $y \in C(e)$ be such that f crosses $\Delta_y(e) $ between e and y. Then $y \in \Delta_{M(f)}(f). $

The configuration in Lemma 3 is sketched in Figure 3. Next, for $\varphi\in\textbf{N} $ , $y\in\mathbb R^2 $ , and $e \in E(\varphi)$ with $y \in C(e)$ , we define

(13) \begin{equation} E_\textsf{REC}(\varphi,y, e) \;:\!=\; \{f\in E(\varphi) \,:\, S_y(e) \subseteq S_y(f) \text{ and }y \in C(f)\} \end{equation}

as the set of recorded edges.

Figure 3. Illustration of the statement of Lemma 3, including the inserted node relevant for ( FIN ). The extended line between $f_1 $ and M(f) is tangent to the disk segment.

Lemma 4. (Size bound for recorded set.) There exists $c_\textsf{edges} = c_\textsf{edges}(\beta)>0 $ such that for any $\varphi\in\textbf{N}$ , $e \in E(\varphi)$ , and $y\in\mathbb R^2 $ with $y \in C(e)$ , we have $\#E_\textsf{REC}(\varphi,y, e) \le c_\textsf{edges}$ .

Note that once Lemma 4 is established, the condition ( FIN ) is verified, since then the total number of deleted edges is at most $c_\textsf{edges}2\pi/\gamma$ . Hence, it remains to prove the auxiliary results Lemmas 2, 3, and 4.

Proof of Lemma 2.

Part (i). In the setting of Lemma 2, assume that f intersects $\Delta_{M(e)}(e) $ and note that the nodes $f_1 $ and $f_2 $ have to be outside C(e) for e to exist. But since f intersects $\Delta_{M(e)}(e) $ , at least one of $e_1 $ and $e_2 $ is in $B_{|f|/2}(h_{|f|/2}(f)) $ . Therefore, f would not exist in the GG, and thus also not in the $\beta$ -skeleton. Hence, $\Delta_{M(e)}(e) $ cannot intersect f.

Part (ii). Repeating the above argument for the second choice of M(e) yields a rhombus with centroid $h_{|e|/2}(e) $ that cannot be intersected by other edges. However, since the side lengths of this rhombus are of order $|e|>a $ , there exists a constant $c_\textsf{disj} = c_\textsf{disj}(\beta)\in(0,1/2) $ such that any disk with center between $h_{a/2}(e) $ and $h_{|e|-a/2}(e)$ and radius $c_\textsf{disj}a $ also has distance of more than $c_\textsf{disj}a $ to the boundary of the rhombus (and similarly for e replaced by f). Since the rhombus linked to any edge cannot be intersected by another edge, it follows that the disk associated with e and the disk associated with f are disjoint.

Proof of Lemma 3. Since e is an edge in the $\beta$ -skeleton, the nodes $f_1 , f_2 $ lie outside the interior of C(e). We first consider the case where $f_1, f_2$ are contained in the boundary of C(e), and the segments $[M(f), f_1]$ , $[M(f), f_2]$ are tangent to C(e). Then $\Delta_{M(f)}(f)\cap C(e) $ yields a full circular segment of $B_{\beta|e|/2}(M(e))$ so that $y \in \Delta_{M(f)}(f)$ . We assert that if $[M(f), f_1]$ and $[M(f), f_2]$ are tangent to C(e), then $|f|=\tan(\tau)|e|$ . Since $y \in \Delta_{M(f)}(f)$ will remain true if we shorten $|f|$ , this will conclude the proof of the lemma.

To prove that $|f| = \tan(\tau)|e|$ , note that the tangency implies that $M(e)f_1M(f)$ is a right triangle. Thus,

\begin{align*} \frac{|f_1-M(f)|}{|f_1 - M(e)|}= \frac{|f_1-M(f)|}{\beta|e|/2} = \tan(\tau).\end{align*}

Next, $f_1M(f) h_{|f|/2}(f) $ also defines a right triangle so that ${|f|}/{(2|f_1-M(f)|)} = \cos(\tau) = \beta^{-1}.$ Finally, combining these two relations yields the asserted $|f| = \tan(\tau)|e|.$

Proof of Lemma 4. First, we note that $E_\textsf{REC}(\varphi,y, e)$ contains at most one edge that is shorter than $\tan(\tau)|e|$ . Indeed, suppose that $f \ne f^{\prime}$ are two such edges with $S_y(f) \subseteq S_y(f^{\prime})$ . Now, from Lemma 2(i), we know that f ^′ cannot intersect $\Delta_{M(f)}(f) $ and therefore also not $\Delta_y(e)\cap\Delta_y(f) $ .

This contradicts Lemma 3.

Hence, it suffices to bound the number of $f \in E_\textsf{REC}(\varphi,y, e)$ with $|f| \ge \tan(\tau)|e|$ . To achieve this goal, let $f^{(1)},\dots,f^{(c)}\in E_\textsf{REC}(\varphi,y,e)$ be disjoint edges, each of length at least $\tan(\tau)|e|$ . Note that none of these edges can intersect. Furthermore, for the edge e to exist, the edges $f^{(1)},\dots,f^{(c)} $ must also fully cross the disk segment C(e), as drawn in Figure 3.

Then, for all $i \le c$ , the edge $f^{(i)}$ crosses the cone $S_y(e)$ somewhere since $S_y(e)\subseteq S_y(f^{(i)})$ . In particular, $f^{(i)}$ has to cross the triangle $\Delta_y(e)$ . If that were not the case and $f^{(i)}$ were to cross $S_y(e)\setminus \Delta_y(e)$ , then $e_1,e_2\in \Delta_y(f^{(i)})\subseteq C(f)$ , which would contradict the existence of the edge $f^{(i)}$ . It is impossible for $f^{(i)}$ to cross both $S_y(e)\setminus \Delta_y(e)$ and $\Delta_y(e)$ , because then it would have to intersect e.

Then, by Lemma 2, each $f^{(i)}$ generates a disk with radius $c_\textsf{disj}\tan(\tau)|e| $ whose center has to be within distance $\tan(\tau)|e| $ of C(e), disjoint from the disks created by other edges longer than $\tan(\tau)|e| $ . Thus, the total number of long edges that can cross $\Delta_y(e) $ is bounded by

\begin{equation*} \frac{2|B_{2\tan(\tau)|e|+\beta|e|/2}(M(e))|}{\pi(c_\textsf{disj}\tan(\tau)|e|)^2}=\frac{2|B_{2\tan(\tau)+\beta/2}(0)|}{\pi c_\textsf{disj}^2\tan(\tau)^2} =: c_\textsf{edges}(\beta)-1, \end{equation*}

thereby concluding the proof.

4. Applications of Theorem 2(a)–(b)

In this section, we verify the conditions of Theorem 2(a) for the graphs from Section 3. We also apply Theorem 2(b) to the NNG. To ease the overall presentation, we start with the latter.

4.1. Theorem 2(b) for the NNG

We start with an auxiliary result simplifying the definition of the influence zone for the NNG. Loosely speaking, we can ignore the constraints on the out-neighbors of $\varphi$ and can concentrate on the areas influencing the nearest neighbors of points in $\varphi$ itself.

Lemma 5. (Influence zone for the NNG.) It holds that

\begin{align*}\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)| = \inf_{(\varphi,\psi)\in B} |\cup_{x\in\varphi} B_{\mathcal{D}_1(\psi-x)} (x)|.\end{align*}

Remark 4. An adaptation of the proof of Lemma 5 shows that it remains true if on both sides we replace B by $\{(\varphi,\psi)\in B\,:\,\sum_{i\le m_0} Z^{(i)}(\varphi,\psi) < 1-\delta\}$ . The proof can be replicated without significant alterations.

Next, we further examine the geometric interpretation of the optimization problem.

Lemma 6. (One single large ball is the unique optimal solution for the NNG and $\alpha\gg d$ .) There exists $\alpha_0 > d$ such that the configuration $(\{{0}\},\{{0},(1,0\dots,0)\})$ solves the optimization problem for all $\alpha\ge\alpha_0$ . In particular,

(14) \begin{equation}\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)| = |B_1(0)| = \kappa_d.\end{equation}

Moreover, for every $\delta>0$ there exists $\varepsilon>0$ such that $|\cup_{x\in\varphi} B_{\mathcal{D}_1(\psi-x)}(x)| \ge (1+\varepsilon)\kappa_d$ holds for all $(\varphi,\psi)\in B$ with $\max_{x\in\varphi}\mathcal{D}^{(\alpha)}_1(\psi-x) < 1-\delta$ .

Hence, to verify the application of Theorem 2(b) for the NNG, only the proofs of Lemmas 5 and 6 are necessary.

Proof of Lemma 5. First, by the definition of A in the case of the NNG, we have that

\begin{align*}|A(\varphi,\psi)| = |\underbrace{\cup_{x\in\varphi} \big(B_{\mathcal{D}_1(\psi-x)} (x)\cup\cup_{z\in\mathcal{E}_x(\psi)} B_{\mathcal{D}_1(\psi-z)}(z)\big)}_{=: K(\varphi,\psi)}|\end{align*}

for all $(\varphi,\psi)\in B$ , since in the NNG an edge can only be deleted if an additional node is put within the open ball with radius given by $\mathcal{D}_1(\!\cdot\!)$ , centered at a vertex in $\psi$ . This implies $\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)| \ge \inf_{(\varphi,\psi)\in B} |\cup_{x\in\varphi} B_{\mathcal{D}_1(\psi-x)} (x)|$ .

For the other direction, let $\varepsilon>0$ and $(\varphi,\psi)\in B$ be arbitrary. Now, for $\delta>0$ , we introduce an extended configuration $\theta_{\delta}\supseteq\psi$ by adding a further point to $B_\delta(x)\setminus\{x\}$ for all $x\in\cup_{z\in\varphi} (\mathcal{E}_z(X))\setminus\varphi$ . Hence,

\begin{align*}\underbrace{|\cup_{x\in\varphi} B_{\mathcal{D}_1(\psi-x)-\delta} (x)|}_{\overset{\delta\downarrow 0}{\longrightarrow} |\cup_{x\in\varphi} B_{\mathcal{D}_1(\psi-x)} (x)|} \le |K(\varphi,\theta_{\delta})| \le \underbrace{|\cup_{x\in\varphi} \big(B_{\mathcal{D}_1(\psi-x)} (x)\cup\cup_{z\in\mathcal{E}_x(\theta_{\delta})} B_{\delta}(z)\big)|}_{\overset{\delta\downarrow 0}{\longrightarrow} |\cup_{x\in\varphi} B_{\mathcal{D}_1(\psi-x)} (x)|},\end{align*}

where the convergences follow because the chosen configurations are finite. Thus, we can choose $\delta$ small enough for $\big||K(\varphi,\theta_{\delta})|-|\cup_{x\in\varphi} B_{\mathcal{D}_1(\psi-x)} (x)|\big| \le \varepsilon$ . Scaling all the configurations with $1+\varepsilon$ gives that $\sum_{x\in(1+\varepsilon)\varphi} \xi^{(\alpha)}((1+\varepsilon)\psi-x) \ge 1+\varepsilon$ . Note that owing to the finiteness of the configurations in B, we can let $\delta$ be small enough so that we still have $\sum_{x\in(1+\varepsilon)\varphi} \xi^{(\alpha)}((1+\varepsilon)\theta_{\delta}-x) \ge 1$ , which implies that $((1+\varepsilon)\varphi,(1+\varepsilon)\theta_{\delta})\in B$ . Thus,

\begin{align*} |\cup_{x\in\varphi} B_{\mathcal{D}_1(\psi-x)} (x)| \ge |K(\varphi,\theta_{\delta})| - \varepsilon & = (1 + \varepsilon)^{-d}|K((1+\varepsilon)\varphi,(1+\varepsilon)\theta_{\delta})| - \varepsilon \\[5pt] & \quad \ge (1 + \varepsilon)^{-d}\hspace{-.4cm}\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)| -\varepsilon.\end{align*}

Since $\varepsilon > 0$ was arbitrary, we conclude the proof.

Proof of Lemma 6. Throughout the proof we rely on the interpretation of the optimization problem in Lemma 5. We set $M\;:\!=\; c_\textsf{max}+1$ and let $(\varphi,\psi)\in B$ . Then we represent $\varphi$ as $\varphi = \{x_1, \dots, x_m\}$ such that $D_1 \ge D_2 \ge \cdots \ge D_m$ , where $D_i \;:\!=\; \mathcal{D}_1(\psi-x_i)$ . Next, we define the normalized $\alpha$ -weighted distances by $\gamma_i \;:\!=\; {D_i^\alpha}/(\sum_{j \le m}D_j^\alpha)$ , emphasizing that $D_i\ge \gamma_i^{1/\alpha}$ because the denominator is at least 1. For the first part of the lemma, we will distinguish between the two cases that the maximal nearest-neighbor distance of a configuration is either large or small.

Case 1: $\boldsymbol{\gamma_1 \le 1/M}$ . Note that by ( FIN ), each point in $\mathbb R^d$ is contained in at most $c_\textsf{max}$ balls $B_{D_i}(x_i)$ , $i \le m$ . Thus,

(15) \begin{equation} |\cup_{i \le m} B_{D_i}(x_i)| \ge \frac1{c_\textsf{max}}\sum_{i\le m} |B_{D_i}(x_i)| = \frac{\kappa_d}{c_\textsf{max}} \sum_{i \le m} D_i^d \ge \frac{\kappa_d}{c_\textsf{max}} \sum_{i\le m}\gamma_i^{d/\alpha}.\end{equation}

Now we formally modify the weights $\{\gamma_i\}_{i \le m}$ to decrease this sum. More precisely, we can decrease the values of $\gamma_l$ for $l\in\{M+1,\dots, m\}$ and simultaneously increase some of $\gamma_1,\dots,\gamma_M$ until they are all equal to $1/M$ , while keeping $\sum_{i \le m}\gamma_i =1$ . Since concavity implies that $y^{d/\alpha}+z^{d/\alpha}\ge (y+z)^{d/\alpha}$ for $y,z\ge 0$ , we deduce that this weight modification only decreases the sum of the $d/\alpha$ -weighted values of the $\gamma_i$ compared to (15). Thus,

(16) \begin{equation} \frac{\kappa_d}{c_\textsf{max}} \sum_{i \le m} \gamma_i^{d/\alpha} \ge \frac{\kappa_d}{c_\textsf{max}} \sum_{i \le M} M^{-d/\alpha} = \frac{\kappa_d}{c_\textsf{max}} M^{1-d/\alpha} > \kappa_d = |B_1(0)|,\end{equation}

for $\alpha$ sufficiently large, depending only on $c_\textsf{max}$ and d.

Case 2: $\boldsymbol{\gamma_1 > 1/M}$ . First, we decompose the volume of the union of balls as

\begin{align*}|\cup_{i \le m} B_{D_i}(x_i)| = |B_{D_1}(x_1)| + |\cup_{i=2}^{m} \big(B_{D_i}(x_i)\setminus B_{D_1}(x_1)\big)|.\end{align*}

Now note that in the NNG, the balls $B_{D_i}(x_i)$ and $B_{D_1}(x_1)$ cannot fully overlap, since $x_i$ cannot be in the interior of $B_{D_1}(x_1)$ and vice versa. Even after subtracting $B_{D_1}(x_1)$ , the volume of the remaining shape is still larger than half of its original volume. Thus, by concavity,

\begin{align*}|\cup_{i \le m} B_{D_i}(x_i)| - \kappa_d\gamma_1^{d/\alpha}\ge \frac1{c_\textsf{max}}\sum_{i=2}^{m} \big|B_{D_i}(x_i)\setminus B_{D_1}(x_1)\big| & \ge \frac{\kappa_d}{2c_\textsf{max}}\sum_{i=2}^{m} \gamma_i^{d/\alpha}\\[5pt] & \ge \frac{\kappa_d}{2c_\textsf{max}} (1-\gamma_1)^{d/\alpha}.\end{align*}

Next, since the minimum of a concave function is attained at the boundary,

(17) \begin{equation}\kappa_d \gamma_1^{d/\alpha} + \frac{\kappa_d}{2c_\textsf{max}} (1-\gamma_1)^{d/\alpha} \ge \kappa_d\min\!\bigg\{1,M^{-d/\alpha} + \frac1{2c_\textsf{max}} (1-1/M)^{d/\alpha}\bigg\} \ge \kappa_d\end{equation}

for $\alpha$ sufficiently large depending on $c_\textsf{max}$ and d. We summarize the requirement that $\alpha$ was supposed to be sufficiently large by writing $\alpha\ge \alpha_0$ with $\alpha_0$ depending on $c_\textsf{max}$ and d. Finally, we point out that the configurations $(\{{0}\},\{{0},(1,0,\dots,0)\})$ are in B since $c_\textsf{INF}=2$ for the NNG and it yields the influence zone that is a ball with radius 1 when using the interpretation of the optimization problem for the NNG derived in Lemma 5. Thus, the volume of the unit ball can indeed be approached by the infimum, which gives the first part of Lemma 6.

For the second part, fix $\delta>0$ and let the configurations $(\varphi,\psi)\in B$ satisfy $\gamma_1 < 1-\delta$ . We repeat the case distinction that we conducted in the first part; without any adjustments, (15) and (16) show that if $\gamma_1 \le 1/M$ , there exists an $\varepsilon_1>0$ depending on $c_\textsf{max}$ and d such that

\begin{align*}|\cup_{i \le m} B_{D_i}(x_i)| \ge (1+\varepsilon_1)\kappa_d\end{align*}

for $\alpha\ge\alpha_0$ . In the case that $1/M \le \gamma_1 < 1-\delta$ , we can perform a similar calculation as the one that led to (17); then, by concavity, as well as by the fact that the sum of strictly concave functions is again strictly concave, we arrive at

\begin{align*}|\cup_{i\le m} B_{D_i}(x_i)| &\ge \kappa_d \gamma_1^{d/\alpha} + \frac{\kappa_d}{2c_\textsf{max}} (1-\gamma_1)^{d/\alpha} \\[5pt] &\ge \kappa_d\min\!\Bigg\{ (1-\delta)^{d/\alpha} + \frac{\delta^{d/\alpha}}{2c_\textsf{max}} , M^{-d/\alpha} + \frac{1}{2c_\textsf{max}} (1-1/M)^{d/\alpha}\Bigg\} \ge (1+\varepsilon_2)\kappa_d\end{align*}

for an $\varepsilon_2>0$ depending on $\delta$ , $c_\textsf{max}$ , and d if $\alpha\ge\alpha_0$ . Taking $\varepsilon=\min\{\varepsilon_1,\varepsilon_2\}$ concludes the proof.

A slightly altered version of the proof of Lemma 6 would also work for the undirected NNG. One would have to approximate $(\{0\},\{0,(1,0,\dots,0)\})$ by putting an additional point close to $(1,0,\dots,0)$ to guarantee that the score of the origin is equal to 1. There are some reasons why the bidirected version does not admit $\kappa_d$ as solution of its optimization problem for large $\alpha$ . First, Lemma 5 no longer holds for the bidirected NNG. Another reason is that for $(\{0\},\{0,(1,0,\dots,0)\})$ , the value of the score function is $\xi^{(\alpha)}(\psi)\le 1/2 < 1$ and cannot be approximated with elements of B that yield a score of approximately 1 for the origin while maintaining an influence zone with volume about $\kappa_d$ .

4.2. Theorem 2(a) for the (un-/bidirected) kNN and the $\beta$ -skeleton

Recall that we need to prove that the optimization problems of the graphs described in Section 3 admit strictly positive solutions. Consider any of those graphs and let $(\varphi,\psi)\in B$ . Note that this implies that

(18) \begin{equation}\sum_{x\in\varphi}\sum_{y\in\mathcal{E}(\psi-x)} \underbrace{|x-y|^\alpha}_{=:\lambda_{x,y}} \ge \sum_{x\in\varphi} \mathcal{E}(\psi-x) \ge 1,\end{equation}

by the definitions of $\mathcal{E}$ and B that we recall from (1) and (9). First, we derive a lower bound for $|A(\varphi,\psi)|$ in terms of a volume of a union of suitable balls. This will be done separately for the (un-/bidirected) kNN and the $\beta$ -skeletons. After that we can consider both cases simultaneously.

(un-/bidirected) kNN: First, since $\#\psi\ge c_\textsf{INF}=k+1$ , we know that for any $x\in\varphi$ , the addition of a node within the interior of $B_{\mathcal{D}_k(\psi)}(x)$ would delete a vertex in $\{y\,:\, y\in\mathcal{E}(\psi-x)\}$ . The influence zone prohibits such nodes, from which we deduce that $|A(\varphi,\psi)| \ge |\cup_xB_{\mathcal{D}_k(\psi)}(x)| = |\cup_x\cup_y B_{\lambda_{x,y}^{1/\alpha}} (x)|$ . We intentionally let the balls after the equals sign overlap to avoid being forced to distinguish between the (un-/bidirected) kNN and $\beta$ -skeleton below.

$\boldsymbol\beta$ -skeleton: For $x\in\varphi$ and $y\in\mathcal{E}(\psi-x)$ , define $h(x,y) \;:\!=\; (x + y)/2$ as the midpoint between x and y. The $\beta$ -skeleton for $\beta>1$ is a subgraph of the GG. Therefore, any node placed in the ball $B_{\lambda_{x,y}^{1/\alpha}/2}(h(x,y))$ would remove the edge between x and y. Thus, $|A(\varphi,\psi)| \ge |\cup_x\cup_y B_{\lambda_{x,y}^{1/\alpha}/2} (h(x,y))|.$

Now, let us enumerate the $\lambda_{x,y}$ in decreasing order, i.e., $\lambda_1\ge \lambda_2 \ge \cdots$ . Furthermore, we set $\gamma_i = \lambda_i/(\sum_j \lambda_j)$ , implying that $ \lambda_i\ge \gamma_i$ by (18). Because of ( FIN ) and the bound on the maximal node degree, every point $y\in\mathbb R^d$ is contained in at most $(c_\textsf{max}+1)^2$ of these balls. Thus,

\begin{align*}|A(\varphi,\psi)| \ge \sum_i \frac1{(c_\textsf{max}+1)^2} |B_{\lambda_i^{1/\alpha}/2} (0)| \ge \sum_i \frac1{2^d(c_\textsf{max}+1)^2} |B_{\gamma_i^{1/\alpha}} (0)| = \sum_i \frac{\kappa_d\gamma_i^{d/\alpha}}{2^d(c_\textsf{max}+1)^2}.\end{align*}

Now, as in the proof of Lemma 6, we use concavity to arrive at

\begin{align*}\sum_i \frac{\kappa_d\gamma_i^{d/\alpha}}{2^d(c_\textsf{max}+1)^2} \ge \frac{\kappa_d}{2^d(c_\textsf{max}+1)^2} \bigg(\sum_i \gamma_i\bigg)^{d/\alpha} = \frac{\kappa_d}{2^d(c_\textsf{max}+1)^2} > 0.\end{align*}

Thus, Theorem 1(a) becomes applicable.

5. Proof of Theorem 1

The proof of Theorem 1 is split up into the upper bound (Section 5.1) and the lower bound (Section 5.2).

5.1. Upper bound

We will follow the strategy that has already been successfully applied in [6], and divide the contributions to $H_n$ into those coming from small and those coming from large scores. These are then treated separately by the lemmas below, whose proofs are given after the proof of the upper bound of Theorem 1. For convenience, we let

(19) \begin{equation}\mathcal{R}_n(X) \;:\!=\; \max_{x\in X\cap Q_n}\mathcal{R}(X-x)\end{equation}

denote the maximal stabilization radius in the sampling window; cf. (6). We start by bounding summands with small contributions through a Poisson functional concentration inequality from [3] to verify that these cannot contribute substantially to the excess.

Lemma 7. (Upper bound for contribution of small summands.) Let $\varepsilon \in (0,1)$ and $a\in (0,(1-d/\alpha)/2)$ . Then

(20) \begin{equation}\limsup_{n\uparrow\infty} \frac1{n^{d^2/\alpha}}\log\mathbb P\bigg(\frac1{n^d}\!\sum_{x\in X\cap Q_n}\! \xi^{(\alpha)}(X-x)\mathbb{1}\{\xi^{(\alpha)}(X-x) < n^a\} > \mu_\alpha + \varepsilon r,\mathcal{R}_n(X) \leq n\!\bigg) = -\infty.\end{equation}

Next we use a concentration result for binomial random variables from [14, Lemma 1.1] to bound the number

(21) \begin{equation}J_n^{(a)}(X)\;:\!=\; \#\mathcal{J}_n^{(a)}(X)\;:\!=\;\#\{x\in X\cap Q_n \,:\, \xi^{(\alpha)}(X-x)\ge n^a\}\end{equation}

of $x\in X\cap Q_n$ that have a score of at least $n^a$ .

Lemma 8. (Upper bound for number of large summands.) Let $a\in (0,1)$ and $\varepsilon \in (0,ad/\alpha)$ . Then

(22) \begin{equation}\limsup_{n\uparrow\infty} \frac1{n^{d^2/\alpha}}\log\mathbb P\big(J_n^{(a)}(X) > n^{d^2/\alpha-\varepsilon}\big) = -\infty.\end{equation}

Furthermore, we bound the probability that a small number of Poisson points carry a lot of the excess weight.

Lemma 9. (Upper bound for condensation probability.) Let $m,n\ge1$ and $\tau>0$ . Then

(23) \begin{align}\begin{split}&\mathbb P\!\left(\sum_{x\in\mathcal{J}_n^{(a)}(X)} \xi^{(\alpha)}(X-x) \ge \tau, J_n^{(a)} \le m, \mathcal{R}_{3n}(X) \le n\right) \\[5pt] &\le (I_d c_\textsf{max} + 1)^4 m^2 (5n)^{d 2 (I_d c_\textsf{max} + 1)^2 m} \exp\!\bigg({-}\tau^{d/\alpha} \inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|\bigg).\end{split}\end{align}

Before proving these lemmas, we apply them to get the upper bound.

Proof of the upper bound of Theorem 1. Let $a\in (0,(1-d/\alpha)/2)$ and $\varepsilon\in(0,ad/\alpha)$ . Then

(24) \begin{align}&\mathbb P\Bigg(\sum_{x\in X\cap Q_n} \xi^{(\alpha)}(X-x) > \mu_\alpha n^d + rn^d\Bigg) \nonumber \\[5pt] &\le \mathbb P\Bigg(\sum_{x\in X\cap Q_n} \xi^{(\alpha)}(X-x)\mathbb{1}\{\xi^{(\alpha)}(X-x) < n^a\} - \mu_\alpha n^d > \varepsilon rn^d\Bigg) \nonumber \\[5pt] &\quad + \mathbb P\Bigg(\sum_{x\in X\cap Q_n} \xi^{(\alpha)}(X-x)\mathbb{1}\{\xi^{(\alpha)}(X-x) \ge n^a\} \ge (1-\varepsilon)rn^d\Bigg) \nonumber \\[5pt] &\le \mathbb P\Bigg(\frac1{n^d}\sum_{x\in X\cap Q_n} \xi^{(\alpha)}(X-x)\mathbb{1}\{\xi^{(\alpha)}(X-x) < n^a\} > \mu_\alpha + \varepsilon r,\mathcal{R}_n(X) \le n\Bigg) \nonumber \\[5pt] & \quad + \mathbb P\Big(J_n^{(a)}(X) > n^{d^2/\alpha-\varepsilon}\Big) \nonumber \\[5pt] &\quad + 2\mathbb P(\mathcal{R}_{3n}(X) > n) + \mathbb P\!\left(\sum_{x\in\mathcal{J}_n^{(a)} (X)}\! \xi^{(\alpha)}(X-x) \ge (1-\varepsilon)rn^d, J_n^{(a)}(X)\le n^{d^2/\alpha-\varepsilon}, \mathcal{R}_{3n}(X) \le n\!\right)\!. \end{align}

From Lemmas 7 and 8 we know that with our choices of a and $\varepsilon$ , the first two summands after the last inequality of (24) do not play a role in large-volume asymptotics. Moreover, with the help of Markov’s inequality and Mecke’s formula [13, Theorem 4.4], we get that

(25) \begin{align}\begin{split}\mathbb P(\mathcal{R}_{3n}(X) > n) &= \mathbb P(\#\{x\in X\cap Q_{3n}\,:\, \mathcal{R}(X-x) > n\} \ge 1) \le \mathbb E[\#\{x\in X\cap Q_{3n}\,:\, \mathcal{R}(X-x) > n\}] \\[5pt] &= \mathbb E\Bigg[\sum_{x\in X\cap Q_{3n}} \mathbb{1}\{\mathcal{R}(X-x) > n\}\Bigg] = \int_{ Q_{3n}} \mathbb P(\mathcal{R}((X\cup\{x\})-x) \ge n)dx \\[5pt] &\le \int_{ Q_{3n}} \sum_{i\le I_d} \mathbb P(\mathcal{S}_i((X\cup\{x\})-x) \ge n)dx.\end{split}\end{align}

From here, owing to the characteristics of ( STA ), it is implied that for each $i\le I_d$ and $r>0$ it holds that

\begin{align*}|S_i\cap B_r(0)| \ge r^d \underbrace{\min_{j\le I_d} |S_j\cap B_1(0)|}_{ =: c_\textsf{cones}},\end{align*}

and by applying a Poisson concentration bound [14, Lemma 1.2] for a large enough n, we can continue our computations for each $i\le I_d$ and $x\in Q_{3n}$ with

\begin{align*}\mathbb P(\mathcal{S}_i((X\cup\{x\})-x) \ge n) &\le \mathbb P\big(X(S_i\cap B_{n/c_\textsf{STA}}(0)) \le c_\textsf{STA}\big) \\[5pt] &\le \exp\!\bigg({-}c_\textsf{cones} \bigg(\frac{n}{c_\textsf{STA}}\bigg)^d + c_\textsf{STA} - c_\textsf{STA}\log\!\bigg(\frac{c_\textsf{STA}^{d+1}}{c_\textsf{cones} n^d}\bigg)\bigg),\end{align*}

where we recall that if X is interpreted as a Poisson random measure, we can denote the random number of points in a Borel set by $X(\!\cdot\!)$ . Therefore, continuing from (25), we arrive at

(26) \begin{equation}\frac1{n^{d^2/\alpha}}\log \mathbb P(\mathcal{R}_{3n}(X) > n) \le - \frac{c_\textsf{cones}}{c_\textsf{STA}^d} n^{d(1-d/\alpha)} + \frac{c_\textsf{STA}}{n^{d^2/\alpha}} - \frac1{n^{d^2/\alpha}}\log\!\bigg(\frac{c_\textsf{STA}^{d+1}}{c_\textsf{cones} n^d}\bigg) \overset{n\uparrow\infty}{\longrightarrow} -\infty.\end{equation}

Thus, it remains to consider the fourth summand after the last inequality of (24). Here, Lemma 9 yields

\begin{align*} &\limsup_{n \uparrow \infty}\frac1{n^{d^2/\alpha}} \log\mathbb P\!\left(\sum_{x\in\mathcal{J}_n^{(a)} (X)} \xi^{(\alpha)}(X-x) \ge (1-\varepsilon)rn^d, J_n^{(a)}(X)\le n^{d^2/\alpha-\varepsilon}, \mathcal{R}_{3n}(X) \le n\right) \\[5pt] &\le -((1-\varepsilon)r)^{d/\alpha} \inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|.\end{align*}

In brief, we arrive at

\begin{align*}\limsup_{n \uparrow \infty}\frac1{n^{d^2/\alpha}}\log\mathbb P(H_n > \mu_\alpha + r) \le -((1-\varepsilon)r)^{d/\alpha} \inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|.\end{align*}

Letting $\varepsilon\downarrow 0$ concludes the proof of the upper bound.

In the rest of this subsection, we will prove Lemmas 7, 8, and 9. The essential ingredient for the proof of Lemma 7 is a concentration bound from [3, Corollary 3.3(i)].

Proof of Lemma 7. We start by introducing some of the notation from [3]. For the Poisson process X, we define the functional

(27) \begin{equation}F_n^{(\alpha)}(X) \;:\!=\; \sum_{x\in X\cap Q_n} \xi^{(\alpha)}(X\cap Q_{3n}-x)\mathbb{1}\{\xi^{(\alpha)}(X\cap Q_{3n}-x) < n^a\}.\end{equation}

Before we can apply the concentration bound, we need to find a link between the typical value $n^d \mu_\alpha$ and the expectation of the functional defined in (27). We can find the connection using the fact that, because of ( STA ), under the event $\{\mathcal{R}_n(X) \leq n\}$ , this functional is equal to the one considered in Lemma 7:

\begin{align*}n^d\mu_\alpha &\ge \mathbb E\Bigg[\sum_{x\in X\cap Q_n}\xi^{(\alpha)}(X-x)\mathbb{1}_{\{\xi^{(\alpha)}(X-x) < n^a\}}\Bigg]\\ & \ge \mathbb E\Bigg[\sum_{x\in X\cap Q_n}\xi^{(\alpha)}(X-x)\mathbb{1}_{\{\xi^{(\alpha)}(X-x) < n^a\}}\mathbb{1}_{\{\mathcal{R}_n(X) \le n\}}\Bigg] \\[5pt] &= \mathbb E\Bigg[\sum_{x\in X\cap Q_n}\xi^{(\alpha)}(X\cap Q_{3n}-x)\mathbb{1}{\{\xi^{(\alpha)}(X\cap Q_{3n}-x) < n^a, \, \mathcal{R}_n(X) \le n\}}\Bigg] \\[5pt] &= \mathbb E\Bigg[\sum_{x\in X\cap Q_n}\xi^{(\alpha)}(X\cap Q_{3n}-x)\mathbb{1}{\{\xi^{(\alpha)}(X\cap Q_{3n}-x) < n^a\}}(1-\mathbb{1}{\{\mathcal{R}_n(X) > n\}})\Bigg] \\[5pt] &= \mathbb E[F_n^{(\alpha)}(X)] - \mathbb E\Bigg[\sum_{x\in X\cap Q_n}\xi^{(\alpha)}(X\cap Q_{3n}-x)\mathbb{1}{\{\xi^{(\alpha)}(X\cap Q_{3n}-x) < n^a,\,\mathcal{R}_n(X) > n\}}\Bigg] \\[5pt] &\ge \mathbb E[F_n^{(\alpha)}(X)] - \mathbb E[X(Q_n)n^a\mathbb{1}{\{\mathcal{R}_n(X) > n\}}].\end{align*}

Subsequently, the Cauchy–Schwarz inequality yields

\begin{align*}& n^d\mu_\alpha \ge \mathbb E[F_n^{(\alpha)}(X)] - \sqrt{\mathbb E[X(Q_n)^2 n^{2a}] \mathbb E[\mathbb{1}_{\{\mathcal{R}_n(X) > n\}}]} \\[5pt] & \quad = \mathbb E[F_n^{(\alpha)}(X)] - \sqrt{(n^{2d}+n^d)n^{2a} \mathbb P(\mathcal{R}_n(X)>n)}.\end{align*}

As argued in (26), the factor $\mathbb P(\mathcal{R}_n(X)>n)$ decays exponentially with n, and consequently we can assume that n is large enough to guarantee that $n^d\mu_\alpha \ge \mathbb E[F_n^{(\alpha)}(X)] - \varepsilon$ . Therefore,

(28) \begin{align}\begin{split}&\mathbb P\Bigg(\sum_{x\in X\cap Q_n} \xi^{(\alpha)}(X-x)\mathbb{1}_{\{\xi^{(\alpha)}(X-x) < n^a\}} > n^d\mu_\alpha + n^d\varepsilon r,\mathcal{R}_n(X) \leq n\Bigg)\\[5pt] & \le \mathbb P\big(F_n^{(\alpha)}(X) > n^d\mu_\alpha +n^d\varepsilon r\big) \\[5pt] &\le \mathbb P(F_n^{(\alpha)}(X) > \mathbb E[F_n^{(\alpha)}(X)] + n^d\varepsilon r - \varepsilon).\end{split}\end{align}

Furthermore, we need the difference operator $D_y$ , $y \in \mathbb R^d$ , defined by $D_yF_n^{(\alpha)}(X) \;:\!=\; F_n^{(\alpha)}(X\cup\{y\}) - F_n^{(\alpha)}(X).$ For $\beta\ge0$ , we now set

(29) \begin{equation}V_\beta^+(F_n^{(\alpha)}(X)) \;:\!=\; \int_{\mathbb R^d} \big(D_yF_n^{(\alpha)}(X)\mathbb{1}_{\{D_yF_n^{(\alpha)}(X) \le \beta\}}\big)^2 dy + \sum_{x\in X} \Big(D_xF_n^{(\alpha)}(X\setminus\{x\})\mathbb{1}_{\{D_xF_n^{(\alpha)}(X\setminus\{x\}) > \beta\}}\Big)^2.\end{equation}

To apply [3, Corollary 3.3(i)], we need to find an almost sure upper bound for $V_\beta^+(F_n^{(\alpha)})$ . Points outside of $Q_{3n}$ do not affect the functional. Thus, choosing $y\in\mathbb R^d\setminus Q_{3n}$ in the difference operator has no effect and yields $D_yF_n^{(\alpha)}(X) = 0$ . Moreover, by ( FIN ), adding a point to any configuration can only affect the outgoing edges of $c_\textsf{max}$ nodes, and the degree of each node is bounded by $c_\textsf{max}$ as well. Hence, $\sup_{y \in Q_{3n}}|D_yF_n^{(\alpha)}(X)| \le(c_\textsf{max}+1)^2 n^a =: \beta$ , and by the same reasoning, $\sup_{x \in X}|D_xF_n^{(\alpha)}(X\setminus\{x\})| \le \beta$ . Thus, we bound (29) by

\begin{align*}V_\beta^+(F_n^{(\alpha)}(X)) \le \int_{Q_{3n}} (c_\textsf{max}+1)^4 n^{2a} dy = ((c_\textsf{max}+1)^2 n^a)^2(3n)^d.\end{align*}

Then, by applying [3, Corollary 3.3(i)], we have

\begin{align*}& \mathbb P(F_n^{(\alpha)}(X) > \mathbb E [F_n^{(\alpha)}(X)] + n^d\varepsilon r - \varepsilon)\\[5pt] \quad & \le \exp\!\Bigg({-}\frac{n^d\varepsilon r - \varepsilon}{2|\beta|}\log\!\Bigg(1+\frac{|\beta|(n^d\varepsilon r - \varepsilon)}{((c_\textsf{max}+1)^2 n^a)^2(3n)^d}\Big)\Bigg) \\[5pt] & \quad = \exp\!\Bigg({-}\frac{n^d\varepsilon r - \varepsilon}{2(c_\textsf{max}+1)^2 n^a}\log\!\Bigg(1+\frac{(c_\textsf{max}+1)^2 n^a (n^d\varepsilon r - \varepsilon)}{(c_\textsf{max}+1)^4 n^{2a}(3n)^d}\Bigg)\Bigg) \\[5pt] & \quad = \exp\!\Bigg({-}\frac{n^{d-a}(\varepsilon r - \varepsilon/n^d)}{2(c_\textsf{max}+1)^2}\log\!\Bigg(1+\frac{n^{-a}(\varepsilon r - \varepsilon/n^d)}{(c_\textsf{max}+1)^2 3^d}\Bigg)\Bigg)\end{align*}

if $n^d\varepsilon r - \varepsilon \ge 0$ . Finally, with the help of (28), we obtain

\begin{align*}\limsup_{n\uparrow\infty} \frac1{n^{d^2/\alpha}} \log \mathbb P\Bigg(\sum_{x\in X\cap Q_n} \xi^{(\alpha)}(X-x)\mathbb{1}_{\{\xi^{(\alpha)}(X-x) < n^a\}} > n^d\mu_\alpha +n^d\varepsilon r, \mathcal{R}_n(X) \le n\Bigg) = - \infty\end{align*}

for $a\in(0,(1-d/\alpha)/2)$ .

Proof of Lemma 8. Let $a\in(0,1)$ . We divide $Q_n$ into a grid consisting of $\lfloor n^{1-a/\alpha}\rfloor^d$ smaller boxes with side length $l_n \;:\!=\; n/\lfloor n^{1-a/\alpha}\rfloor$ . The set of all of these cubes is

\begin{align*}\mathcal{Q} \;:\!=\; \big\{Q \,:\, Q = l_n z + [{-}n/2,-n/2+l_n]^d, z\in\{0,\dots,\lfloor n^{1-a/\alpha}\rfloor - 1\}^d\big\}.\end{align*}

Furthermore, we label each box in such a way that between two boxes of the same label there are always two boxes with a different label. For instance, we can label the boxes according to elements of the set $\mathcal{L} = \{0,1,2\}^d$ , thus using $\#\mathcal{L} = 3^d$ different labels; see Figure 4. For $m\in \mathcal{L}$ , we denote the set of label-m cubes by

\begin{align*}\mathcal{Q}^{(m)} & \;:\!=\; \big\{Q \,:\, Q = l_n z + [{-}n/2,-n/2+l_n]^d,\\[5pt] z & =(z_1,\dots,z_d)\in\{0,\dots,\lfloor n^{1-a/\alpha}\rfloor - 1\}^d \text{ with } z_i\bmod 3 = m_i\big\},\end{align*}

so that $\#\mathcal{Q}^{(m)} = \lfloor n^{1-a/\alpha}\rfloor^d/3^d + o( n^{1-a/\alpha}) =: K_n.$

Figure 4. Labeling of the boxes in three dimensions, where 27 labels are sufficient, and two dimensions, where 9 are sufficient.

Setting $P_n\;:\!=\; (n^a/c_\textsf{max})^{1/\alpha}$ , we start bounding the probabilities under consideration using the bounded node degree:

(30) \begin{align}\begin{split}\mathbb P(J_n^{(a)}(X) > n^{d^2/\alpha-\varepsilon}) &\le \mathbb P\Big(\xi^{(\alpha)}(X-x) > n^a \text{ for all }x\text{ in some }\varphi\subseteq X\cap Q_n\text{ with }\#\varphi\ge n^{d^2/\alpha-\varepsilon}\Big) \\[5pt] &\le \mathbb P\bigg(\max_{y\in\mathcal{E}(X-x)} |y| > P_n \text{ for all }x\text{ in some }\varphi\subseteq X\cap Q_n\text{ with }\#\varphi\ge n^{d^2/\alpha-\varepsilon}\bigg).\end{split}\end{align}

We now thin out the configuration consisting of all x as in the previous line, as follows. Starting with any point $x\in\varphi$ , we omit all points of $\varphi$ that are at distance at most $P_n$ to x. According to ( FIN2 ) with $M=P_n$ , this operation removes at most $c_\textsf{max}-1$ points. Repeating iteratively for the other points of $\varphi$ yields a configuration $\varphi$ that contains at least $N_n \;:\!=\; n^{d^2/\alpha-\varepsilon}/c_\textsf{max}$ nodes satisfying $\max_{y\in\mathcal{E}(X-x)} |y| > P_n$ and $|x-y| > P_n$ for all $x,y\in\varphi$ with $x\ne y$ . Thus, we can continue in (30) with

(31) \begin{align}\begin{split}&\mathbb P\bigg(\max_{y\in\mathcal{E}(X-x)} |y| > P_n \text{ for all }x\text{ in some }\varphi\subseteq X\cap Q_n\text{ with }\#\varphi\ge n^{d^2/\alpha-\varepsilon}\bigg) \\[5pt] &\le \mathbb P\bigg(\max_{y\in\mathcal{E}(X-x)} |y| > P_n \text{ and } |x-y| > P_n \text{ for all }x\ne y\text{ in some }\varphi\subseteq X\cap Q_n\text{ with }\#\varphi\ge N_n \bigg).\end{split}\end{align}

Next, we note that in a ball of radius $\sqrt dl_n$ , only a limited number of points can be placed so that all of their mutual distances are larger than $P_n$ . For large n, this number is bounded by the number of balls with radius $(n^a/c_\textsf{max})^{1/\alpha}/2$ that fit in a ball with radius $4\sqrt d n^{a/\alpha}$ in such a way that none of the smaller balls overlap. The ratio between the volume of $B_{4\sqrt d n^{a/\alpha}}(0)$ and the volume of $B_{(n^a/c_\textsf{max})^{1/\alpha}/2}(0)$ yields the bound $8^d c_\textsf{max}^{d/\alpha} d^{d/2}$ for n large. Thus, after setting $M_n \;:\!=\; N_n/(8^d c_\textsf{max}^{d/\alpha + 1} d^{d/2})$ , we can use this argument to proceed in (31) and estimate, for n sufficiently large,

(32) \begin{align}\begin{split}&\mathbb P\bigg(\max_{y\in\mathcal{E}(X-x)} |y| > P_n \text{ and } |x-y| > P_n \text{ for all }x\ne y\text{ in some }\varphi\subseteq X\cap Q_n\text{ with }\#\varphi\ge N_n \bigg) \\[5pt] &\le \mathbb P\bigg(\max_{y\in\mathcal{E}(X-x)} |y| > P_n \text{ and } |x-y| > \sqrt{d} l_n \text{ for all }x\ne y\text{ in some }\varphi\subseteq X\cap Q_n\text{ with }\#\varphi\ge M_n \bigg).\end{split}\end{align}

In the event on the right-hand side of (32), each hypercube $Q\in\mathcal{Q}$ contains at most one node that has an edge larger than $P_n$ . Furthermore, if $\max_{y\in\mathcal{E}(X-x)} |y| > P_n$ holds for an $x\in X$ , then ( STA ) gives that $\mathcal{R}(X-x) > P_n$ . Thus, by a union bound, we arrive at

(33) \begin{align}&\mathbb P\bigg(\max_{y\in\mathcal{E}(X-x)} |y| > P_n \text{ and } |x-y| > \sqrt{d} l_n \text{ for all }x\ne y\text{ in some }\varphi\subseteq X\cap Q_n\text{ with }\#\varphi\ge M_n \bigg)\nonumber \\[5pt] &\le \sum_{m\in \mathcal{L}} \mathbb P\bigg(\#\{Q\in \mathcal{Q}^{(m)} \,:\, \max_{y\in\mathcal{E}(X-x)} |y| > P_n \text{ for some } x\in Q\cap X\} \ge M_n/3^d\bigg) \\[5pt] &\le \sum_{m\in \mathcal{L}} \mathbb P\bigg(\#\{Q\in \mathcal{Q}^{(m)} \,:\, \mathcal{R}(X-x) \ge P_n \text{ for some } x\in Q\cap X\} \ge M_n/3^d\bigg).\nonumber \end{align}

Through a calculation performed in the same fashion as in (26), we get

\begin{align*}\mathbb P\bigg(\max_{x \in Q \cap X}\mathcal{R}(X-x) \ge P_n \bigg) \le \int_Q\mathbb P\big(\mathcal{R}(X\cup\{x\}-x) \ge (n^a/c_\textsf{max})^{1/\alpha}\big)dx \le l_n^ d e^{-cn^{ad/\alpha}}\end{align*}

for n large enough and a value $c>0$ . Next, note that $l_n\ge P_n$ . Thus, for a fixed $m\in\mathcal{L}$ , the events of finding a Poisson point with a stabilization radius exceeding $P_n$ in a box Q are independent for different choices of $Q \in \mathcal{Q}^{(m)}$ . Therefore, a binomial concentration bound [14, Lemma 1.1] gives that for each $m\in \mathcal{L}$ ,

(34) \begin{align}\begin{split} &\mathbb P\big(\#\{Q\in \mathcal{Q}^{(m)} \,:\, \max_{x \in Q \cap X}\mathcal{R}(X-x) \ge P_n \} \ge M_n/3^d\big) \\[5pt] &\le \exp\!\bigg({-}\frac{M_n}{3^d 2} \log\!\bigg(\frac{M_n/3^d}{K_n l_n^d e^{-cn^{ad/\alpha}}}\bigg)\bigg),\end{split}\end{align}

assuming n is sufficiently large. Now, note that

(35) \begin{equation}\lim_{n\uparrow\infty} -\frac1{n^{d^2/\alpha}}\frac{M_n}{3^d 2}\log\!\bigg(\frac{M_n/3^d}{K_n l_n^ d e^{-cn^{ad/\alpha}}}\bigg) = -\infty\end{equation}

holds if $\varepsilon\in (0,ad/\alpha)$ . Finally, combining (30), (31), (32), (33), (34), and (35) yields the desired result.

Proof of Lemma 9. Let $m\ge1$ and $\tau>0$ , and let us assume that we are under the event that we would like to bound in Lemma 9. Note that by (7), under $\{\mathcal{R}_{3n}(X) \le n\}$ we have that $\mathcal{E}(X-x) = \mathcal{E}(X\cap Q_{5n}-x)$ for all $x\in X\cap Q_{3n}$ . Under the event $\{J_n^{(a)}(X) \le m\}$ , we choose $\varphi=\mathcal{J}_n^a(X)$ and $\psi^{\prime}=\cup_{x\in\varphi}\mathcal{E}_x(X)$ . From ( STA ), we obtain configurations $\theta_x$ , $x\in\varphi\cup\psi^{\prime}$ , with $\mathcal{E}(X-x)=\mathcal{E}(\theta_x-x)$ and $\#\theta_x\le I_d c_\textsf{STA}$ . The condition ( STA ) also implies that $\mathcal{E}(X-x)=\mathcal{E}(\psi-x)$ for every $x\in\varphi\cup\psi^{\prime}$ where $\psi \;:\!=\; \varphi\cup\psi^{\prime}\cup_{x\in\varphi\cup\psi^{\prime}} \theta_x$ . Note that, thanks to the bound on the stabilization radius, the set $\psi$ is entirely contained in $Q_{5n}$ . Moreover, the bounded node degree implies that

(36) \begin{equation}\#\psi \le \#\varphi + \#\psi^{\prime} + (\#\varphi + \#\psi^{\prime}) I_d c_\textsf{STA} \le (I_d c_\textsf{STA} + 1) (c_\textsf{max} + 1) m \le (I_d c_\textsf{max} + 1)^2 m.\end{equation}

Below, in the case that $\#\psi<c_\textsf{INF}$ , we add $c_\textsf{INF}-\#\psi$ points in $X\cap Q_{5n}$ to $\psi$ to be able to apply ( INF ). To justify that $X(Q_{5n}) \ge c_\textsf{INF}-\#\psi$ can be assumed here, we remark that under $\big\{\!\sum_{x\in\mathcal{J}_n^{(a)}(X)} \xi^{(\alpha)}(X-x) \ge \tau, \mathcal{R}_{3n}(X) \le n\big\}$ , it must hold that $X(Q_{5n})\ge c_\textsf{INF}$ . The reason for this is that the fact that $\xi^{(\alpha)}(X-x) > 0$ for some $x\in X\cap Q_n$ implies that $X\cap Q_n$ cannot be empty, and $\mathcal{R}_{3n}(X) \le n$ implies that there have to be at least $I_d (c_\textsf{max}-1)$ other Poisson points within distance n of any point in $Q_n$ . Thus, we even get that $X(Q_{5n})\ge I_d(c_\textsf{max}-1) + 1 \ge c_\textsf{INF}$ , which concludes this argument. Next, using (36) together with $\mathcal{E}(X-x)=\mathcal{E}(\psi-x)$ and ( INF ), we obtain that

\begin{align*}&\mathbb P\Bigg(\sum_{x\in\mathcal{J}_n^{(a)}(X)} \xi^{(\alpha)}(X-x) \ge \tau, J_n^{(a)}(X) \le m, \mathcal{R}_{3n}(X) \le n\Bigg) \\[5pt] &\le\mathbb P\Bigg(\sum_{x\in\varphi} \xi^{(\alpha)}(\psi-x) \ge \tau, \text{ for some }\varphi\subseteq X\cap Q_n, \#\varphi \le m \text{ and } \varphi\subseteq\psi\subseteq X\cap Q_{5n}, \\[5pt] &\qquad\quad c_\textsf{INF} \le \#\psi\le (I_d c_\textsf{max} + 1)^2 m, \mathcal{E}(\psi-x)=\mathcal{E}(X-x) \text{ for all } x\in\varphi \cup \cup_{z\in\varphi} \mathcal{E}_z(\psi)\Bigg) \\[5pt] &\le\mathbb P\Bigg(\sum_{x\in\varphi} \xi^{(\alpha)}(\psi-x) \ge \tau, \text{ for some }\varphi\subseteq X\cap Q_n, \#\varphi \le m \text{ and } \varphi\subseteq\psi\subseteq X\cap Q_{5n}, \\[5pt] &\qquad\quad c_\textsf{INF} \le \#\psi\le (I_d c_\textsf{max} + 1)^2 m, \mathcal{E}(\psi-x)\subseteq\mathcal{E}((\psi\cup\{y\}-x) \text{ for all } y\in X \text{ and } \\[5pt] &\qquad\quad x\in\varphi \cup \cup_{z\in\varphi}\mathcal{E}_z(\psi)\Bigg) \\[5pt] &=\mathbb P\Bigg(\sum_{x\in\varphi} \xi^{(\alpha)}(\psi-x) \ge \tau, \text{ for some }\varphi\subseteq X\cap Q_n, \#\varphi \le m \text{ and } \varphi\subseteq\psi\subseteq X\cap Q_{5n}, \\[5pt] &\qquad\quad c_\textsf{INF} \le \#\psi\le (I_d c_\textsf{max} + 1)^2 m, X\cap A(\varphi,\psi) = \emptyset\Bigg) =: (\star).\end{align*}

We remind the reader of the sets $D^{\prime}_{l}$ , $l\in\mathbb N$ , and $\mathcal{N}^{\prime}$ that were defined in Section 2, before Equation (9). Note that by the assumptions in ( CON ),

\begin{align*}0=|N_{l+1}| = \int_{\{(x_1,\dots,x_l)\in\mathbb R^{dl}:\text{ pw.~distinct}\}} |D(\{x_1,\dots,x_l\})| d(x_1,\dots,x_l),\end{align*}

which implies that $|D^{\prime}_{l}|=0$ , and thus $\mathcal{N}^{\prime}$ is a zero-set. In the following, let $\textbf{x}=(x_1,\dots,x_{l_1})$ and $\textbf{y}=(y_1,\dots,y_{l_2})$ represent $\varphi$ and $\psi\setminus\varphi$ , respectively. We will abuse notation and allow $\textbf{x}$ and $\textbf{y}$ to be treated as sets. A combination of the union bound, Markov’s inequality, and Mecke’s formula yields

\begin{align*}(\star) &\le \sum_{0\le l_1,l_2\le (I_d c_\textsf{max} + 1)^2 m} \int_{Q_{5n}^{l_2}}\int_{Q_{5n}^{l_1}} \mathbb P\bigg(\sum_{x\in\textbf{x}} \xi^{(\alpha)}(\textbf{x}\cup\textbf{y}-x) \ge \tau,\#\textbf{y} \ge c_\textsf{INF}, X\cap A(\textbf{x},\textbf{x}\cup\textbf{y})=\emptyset\bigg) d\textbf{x} d\textbf{y} \\[5pt] &= \sum_{0\le l_1,l_2\le (I_d c_\textsf{max} + 1)^2 m} \int_{Q_{5n}^{l_2}}\int_{Q_{5n}^{l_1}} \mathbb{1}_{\{\sum_{x\in\textbf{x}} \xi^{(\alpha)}(\textbf{x}\cup\textbf{y}-x) \ge \tau\}} \mathbb{1}_{\{\textbf{x}\cup\textbf{y}\not\in\mathcal{N}^{\prime},\,\#\textbf{y} \ge c_\textsf{INF}\}} \exp\!({-}|A(\textbf{x},\textbf{x}\cup\textbf{y})|) d\textbf{x} d\textbf{y} \\[5pt] &\le (I_d c_\textsf{max} + 1)^4 m^2 (5n)^{d 2 (I_d c_\textsf{max} + 1)^2 m}\exp\!\Big({-}\tau^{d/\alpha}\inf_{(\textbf{x},\textbf{x}\cup\textbf{y})\in B} |A(\textbf{x},\textbf{x}\cup\textbf{y})|\Big),\end{align*}

from which the assertion follows.

5.2. Lower bound

First, if $\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|=\infty$ then there is nothing to prove. Thus, throughout the proof of the lower bound we assume that $\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|<\infty$ . Recall that $\lceil\cdot\rceil$ denotes the ceiling function, given by $\lceil t\rceil \;:\!=\; \min\{m\in\mathbb Z\,:\, m\ge t\}$ for $t\in\mathbb R$ . The rough idea for the proof of the lower bound is to use separated boxes

\begin{align*}W_n \;:\!=\; \big[0,\underbrace{\lceil n-n^{d/\alpha}\log n- (\log n)^2\rceil}_{=: b_n}\big]^d\end{align*}

and $U_n \;:\!=\; [n-n^{d/\alpha}\log n, n]^d$ and place the configuration responsible for the excess weight entirely in $U_n$ while letting $W_n$ be responsible for the typical value. The separation is achieved by conditioning on points being close to the boundary of $W_n$ . In particular, we introduce a smaller box

\begin{align*}W_n^{2-} \;:\!=\; \big[2(\log n)^2, b_n - 2(\log n)^2\big]\end{align*}

inside of $W_n$ and condition on a certain number of points lying in $W_n\setminus W_n^{2-}$ . This is realized by covering that volume with layers of boxes with side lengths between $\log n$ and $2\log n$ , preferably hypercubes with length $\log n$ as pointed out in Figure 5. Hence, each box has a volume between $(\log n)^d$ and $(2\log n)^d$ .

Figure 5. Sketch of $U_n$ , $W_n$ , $W_n^-$ , and $W_n^{2-}$ .

Hence, for sufficiently large n we need at most

(37) \begin{equation}\left\lceil \frac{b_n^d-(b_n - 4(\log n)^2)^d}{(\log n)^d}\right\rceil \le \left\lceil\frac{n^{d-1}}{(\log n)^{d-3}}\right\rceil\end{equation}

additional boxes to cover the space $W_n\setminus W_n^{2-}$ entirely. We denote these boxes by $(Q^{\prime}_{i})_i$ and define the event

\begin{align*}E_n^\textsf{good} \;:\!=\; \big\{X(Q^{\prime}_{i}) \in [c_\textsf{max},(\log n)^{2d}) \text{ for all } i\big\}\end{align*}

that will generate independence between the functional of Poisson points in $W_n$ and Poisson points in $U_n$ . In addition, we introduce the abbreviation

\begin{align*}H_n (A,B) \;:\!=\; \frac1{n^d}\sum_{x\in X\cap A} \xi^{(\alpha)}(X\cap B-x)\end{align*}

for $A,B\subseteq\mathbb R^d$ . For $\varepsilon < \mu_\alpha$ , we also define the event

(38) \begin{equation}G_{1,n} \;:\!=\; \{H_n(W_n,W_n) > \mu_\alpha - \varepsilon/2\} \cap E_n^\textsf{good}.\end{equation}

The next lemma gives a lower bound for the probability of this event.

Lemma 10. (Lower bound for $\mathbb P(G_{1, n})$ .) It holds that $\liminf_{n\uparrow\infty} {n^{-d^2/\alpha}} \log \mathbb P(G_{1,n}) \ge 0.$

We now focus our attention on what happens within $U_n$ . We will rescale a configuration so that it is responsible for the entire excess weight and so that there is also enough flexibility to embed the points in open balls to get a configuration that can be attained with positive probability. For the chosen $\varepsilon$ , we will use

\begin{align*}\tau_n \;:\!=\; ((r+\varepsilon) (1+\varepsilon) n^d)^{1/\alpha}\end{align*}

as the parameter for the rescaling. The following lemma will be used to find the proper configuration within $U_n$ to rescale.

Lemma 11. (Approximation of optimal configurations.) Let $\varepsilon > 0$ and $(\varphi, \psi) \in B$ . Then there exists $\delta \in (0,1)$ such that the following inequalities hold:

1. (a)

   \begin{align*}|\underbrace{\bigcup_{(z_y)_{y\in\psi}\subseteq B_\delta(0)} A(\{x+z_x \,:\, x\in\varphi\},\{y+z_y \,:\, y\in\psi\})}_{=: A_{\delta}(\varphi,\psi)}| \le |A(\varphi, \psi)| + \varepsilon\end{align*}
   and

2. (b)

   \begin{align*}\inf_{(z_x)_{x\in\psi} \subseteq B_\delta(0)} \sum_{x\in\varphi} \xi^{(\alpha)}(\{y+z_y \,:\, y\in\psi\}-(x+z_x)) > 1/(1+\varepsilon).\end{align*}

We insert another lemma to deal with the diameter of the influence zone.

Lemma 12. (Diameter of bounded influence zone.) Let $(\varphi,\psi)\in B$ with $|A(\varphi,\psi)| < \infty$ . Then there is $\delta \in (0, 1)$ such that $\textrm{diam}(A_\delta(\varphi,\psi))<\infty$ .

Note that, if we pick $(\varphi,\psi)\in B$ such that $|A(\varphi,\psi)|<\infty$ , then, for $\delta $ small enough, by Lemma 12 the diameter of $\tau_nA_{\delta}(\varphi,\psi)$ is of order $n^{d/\alpha}$ , while $U_n$ has side length $n^{d/\alpha}\log n$ . This means we can choose n large enough for $U_n$ to contain a shifted copy of $\tau_n A_{\delta}(\varphi,\psi)$ . Thus, from now on we can assume that $\tau_nA_{\delta}(\varphi,\psi)$ , as well as $\cup_{x\in\tau_n\psi} B_1(x)$ , is entirely contained in $U_n$ if $|A(\varphi,\psi)|<\infty$ .

We set

\begin{align*}A_{\delta, n}^- \;:\!=\; \tau_nA_{\delta}(\varphi,\psi) \setminus \bigcup_{x\in\tau_n\psi} B_1(x),\end{align*}

and similarly to (38), we define the event

(39) \begin{equation}G_{2,n}(\delta) \;:\!=\; \big\{X(B_1(x)) = 1 \text{ for all } x\in\tau_n\psi, X(A_{\delta, n}^-) = 0\big\}.\end{equation}

A bound for its probability is given in the following lemma.

Lemma 13. (Lower bound for $\mathbb P(G_{2, n}(\delta))$ .) Let $\delta \in (0, 1)$ and $(\varphi, \psi) \in B$ . Then

\begin{align*}\liminf_{n\uparrow\infty} \frac1{n^{d^2/\alpha}} \log \mathbb P(G_{2,n}(\delta)) \ge -\big( |A(\varphi,\psi)|+\varepsilon\big)(r+\varepsilon)^{d/\alpha}(1+\varepsilon)^{d/\alpha}.\end{align*}

Now we can give the proof of the lower bound.

Proof of the lower bound of Theorem 1. First, fix two configurations $(\varphi, \psi) \in B$ such that $|A(\varphi, \psi)| \le \inf_{(\varphi^{\prime},\psi^{\prime})\in B} |A(\varphi^{\prime},\psi^{\prime})| + \varepsilon$ . Because $\inf_{(\varphi^{\prime},\psi^{\prime})\in B} |A(\varphi^{\prime},\psi^{\prime})|<\infty$ was assumed at the start of this section, $|A(\varphi,\psi)|<\infty$ also has to be satisfied. Now, let $\delta>0$ be such that (a) and (b) from Lemma 11 are satisfied. Under the event $\cap_{x\in\tau_n\varphi} \{X(B_1(x))=1\}$ , we can find $(z_x)_{x\in\tau_n\psi} \subseteq B_1(0)$ such that $\{x+z_x\} = X\cap B_1(x)$ for each $x\in\tau_n\psi$ . Furthermore, if n is so large that $\tau_n \delta \ge 1$ , then under $\{X(\tau_nA_{\delta}^-)=0\}$ it is guaranteed by ( INF ) that for each $x+z_x\in\{y+z_y \,:\, y\in\tau_n\varphi\}\cup\cup_{w\in\tau_n\varphi} (\mathcal{E}_{w+z_w}(\{y+z_y \,:\, y\in\tau_n\psi\}))$ ,

(40) \begin{equation}\mathcal{E}(X-(x+z_x)) \supseteq \mathcal{E}(\{y+z_y \,:\, y\in\tau_n\psi\}-(x+z_x)).\end{equation}

Then, also if $\tau_n \delta \ge 1$ , Lemma 11(b) and (40) give that

(41) \begin{equation}\sum_{x\in\tau_n\psi} \xi^{(\alpha)}(X-(x+z_x)) \ge \sum_{x\in\tau_n\varphi} \xi^{(\alpha)}(\{y+z_y \,:\, y\in\tau_n\psi\}-(x+z_x)) > \tau_n^\alpha/(1+\varepsilon) = (r+\varepsilon)n^d.\end{equation}

Note that the index set in the sum before the first inequality in (41) contains more points than the one after it. The reason for this is that when a point is added outside of the influence zone of $(\tau_n\varphi,\tau_n\psi)$ , our framework for graphs does not exclude new edges from being created between two already existing nodes in $\tau_n\psi$ . While it is admittedly hard to come up with an actual example of a graph for which the following is possible, it might potentially happen that when the points from $X\setminus(\tau_n\psi)$ are added to $\tau_n\psi$ , an additional edge arises from a point in $\tau_n\psi\setminus(\tau_n\varphi)$ to a point in $\tau_n\varphi$ . In an undirected graph this could have the effect that the power-weighted edge lengths of some outgoing edges from points in $\tau_n\varphi$ are only taken into account with the factor $1/2$ on the left-hand side of the first inequality in (41), while being considered with their full weight on the right-hand side of it. Summing over all points in $\tau_n\psi$ lets us avoid this issue.

As the remark after Lemma 12 suggets, we can assume that all of the occurring sets and configurations are contained in $U_n$ , from which point (41) implies that $G_{2,n}(\delta) \subseteq \{H_n(U_n,\mathbb R^d) > r + \varepsilon\}.$

We now define the set $W_n^- \;:\!=\; \big[(\log n)^2, b_n - (\log n)^2\big]$ and assert that under the event $G_{1, n}$ from (38), we have

(42) \begin{align}H_n(W_n\setminus W^-_n, W_n) < \varepsilon/2\end{align}

for all large n. Once (42) is established, we can conclude the proof of the lower bound of Theorem 1. Indeed, under $E_n^\textsf{good}$ each box in $W_n\setminus W_n^-$ contains at least $c_\textsf{max}$ Poisson points, and therefore, if n is chosen large, then each of the cones around an $x\in X\cap W_n^-$ has to contain $c_\textsf{max}$ Poisson points before the base of the cone leaves $W_n$ , which more formally means that $\cup_{i \le I_d} \big ((S_i+x)\cap B_{\mathcal{S}_i (X-x)} (x)\big) \subseteq W_n$ . Thus, under $E_n^\textsf{good}$ , again by ( STA ), we get that $\xi^{(\alpha)}(X\cap W_n-x) = \xi^{(\alpha)}(X-x)$ for all points $x\in X\cap W^-_n$ if n is sufficiently large. In other words, the layer of boxes containing points would not admit the score of points in $W_n^-$ being influenced by any points outside of $W_n$ . With (42) we get that under $G_{1,n}$ ,

\begin{align*}H_n\big(W_n,\mathbb R^d\big) \ge H_n\big(W^-_n,\mathbb R^d\big) = H_n\big(W^-_n, W_n\big) = H_n\big(W_n, W_n\big) - H_n\big(W_n\setminus W^-_n, W_n\big)> \mu_\alpha - \varepsilon.\end{align*}

In addition, $G_{1, n}$ and $G_{2,n}(\delta)$ are independent for large n. Next, shifting the coordinate system shows that $\mathbb P(H_n > \mu_\alpha + r) = \mathbb P\big(H_n([0,n]^d,\mathbb R^d) > \mu_\alpha + r\big).$ Hence,

\begin{align*}\mathbb P\big(H_n > \mu_\alpha + r\big) &\ge \mathbb P\big(H_n\big(U_n,\mathbb R^d\big) > r + \varepsilon, H_n\big(W_n,\mathbb R^d\big) > \mu_\alpha - \varepsilon\big)\\[5pt] &\ge \mathbb P\big(G_{2,n}(\delta), G_{1,n}\big)\\[5pt] &= \mathbb P\big(G_{2,n}(\delta)\big) \mathbb P\big(G_{1,n}\big).\end{align*}

Using Lemmas 10 and 13, it follows that

(43) \begin{equation}\liminf_{n\uparrow\infty} \frac1{n^{d^2/\alpha}} \log \mathbb P(H_n > \mu_\alpha + r) \ge -\bigg(\!\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|+\varepsilon\bigg)(r+\varepsilon)^{d/\alpha},\end{equation}

and letting $\varepsilon\downarrow 0$ gives the asserted result.

It remains to prove (42) under the event $G_{1, n}$ . To that end, we recall that

\begin{align*}H_n(W_n\setminus W_n^-,W_n) = \frac1{n^d} \sum_{x\in X\cap (W_n\setminus W^-_n)} \xi^{(\alpha)}(X\cap W_n - x).\end{align*}

Henceforth, we bound the summands on the right-hand side separately in the cases where $\textrm{dist}(x,\partial W_n)\ge c\log n$ and where $\textrm{dist}(x,\partial W_n)< c\log n$ for a suitable $c > 0$ .

First, consider the case $\textrm{dist}(x,\partial W_n)\ge c\log n$ . If we cut off the cone $S_i + x$ at a distance $c\log n$ for large enough c, then it still contains one of the boxes $Q^{\prime}_j$ . By definition of the event $E_n^\textsf{good}$ , each of these boxes contains at least $c_\textsf{max}$ nodes. Therefore, $\mathcal{S}_i(X\cap W_n-x)$ is of order $\log n$ for all $1\le i\le I_d$ .

Now, consider the case that $\textrm{dist}(x,\partial W_n) < c\log n$ . If a cone that arises from x does not intersect $W_n$ anymore after a distance from the apex of order $\log n$ , then it contains Poisson points of $X\cap W_n$ only up until a distance of order $\log n$ . Since, by ( STA ), none of the lateral boundaries of any cone are parallel to an axis of the coordinate system, we obtain that otherwise the cone envelopes a whole box $Q^{\prime}_j$ after a distance from the apex of order $\log n$ . Then $\mathcal{S}_i(X\cap W_n-x)$ is of order $\log n$ as argued for above. Hence, after n is chosen sufficiently large, ( STA ) yields a finite configuration $\theta_x$ with $\theta_x\subseteq B_{(\log n)^2}(x)\cap W_n$ satisfying that $\mathcal{E}(X\cap W_n-x)=\mathcal{E}(\theta_x-x)$ . Together with the bounded node degree, we have for n large

\begin{align*} n^dH_n(W_n\setminus W_n^-,W_n) &\le \hspace{-.5cm} \sum_{\substack{x\in X\cap (W_n\setminus W^-_n)\\ y\in\mathcal{E}(\theta_x -x)}} \hspace{-.5cm}|y| \\[5pt] &\le X(W_n\setminus W^-_n) c_\textsf{max} (\log n)^{2\alpha} \\[5pt] &\le (\log n)^{2d}\left\lceil\frac{n^{d-1}}{(\log n)^{d-3}}\right\rceil c_\textsf{max} (\log n)^{2\alpha},\end{align*}

where the final inequality follows from (37), the upper bound on the number of Poisson points in each box $Q^{\prime}_{i}$ . Hence, we can choose n sufficiently large to ensure that $H_n(W_n\setminus W_n^-,W_n)<\varepsilon/2$ .

The key ingredient to prove Lemma 10 is a weak law of large numbers for Poisson functionals from [16].

Proof of Lemma 10. We consider separately each of the two events whose intersection forms $G_{1,n}$ . For $E_n^{\textsf{good}}$ we use a Poisson bound from [14, Lemma 1.2] and calculate, for n sufficiently large,

(44) \begin{align}\mathbb P\big(E_n^\textsf{good}\Big) &= 1-\mathbb P\big(X(Q^{\prime}_{i}) < c_\textsf{max} \text{ or } X(Q^{\prime}_{i}) \ge (\log n)^{2d} \text{ for some } i\big) \nonumber\\[5pt] &\ge 1-\left\lceil\frac{n^{d-1}}{(\log n)^{d-3}}\right\rceil \Bigg(e^{-(\log n)^d} \sum_{i \le c_\textsf{max}-1} \frac{(2\log n)^{di}}{i!} + e^{-\frac12(\log n)^{2d}\log\!\big(\frac{(\log n)^{2d}}{(2\log n)^d}\big)}\Bigg) \nonumber\\[5pt] &\ge 1-n^{d-1}\Big(e^{-(\log n)^d} (\log n)^{d c_\textsf{max}+2} + e^{-\frac12(\log n)^{2d}}\Big).\end{align}

Next, we deal with $\{H_n(W_n,W_n) > \mu_\alpha - \varepsilon/2\}$ . Under the condition that $X(W_n) = b_n^d$ , we can deduce

\begin{align*}\big(H_n(W_n,W_n)\ \big|\ X(W_n) = b_n^d\big) &\overset d= \frac{b_n^d}{n^d} \frac1{b_n^d} \sum_{i \le b_n^d} \xi^{(\alpha)}\big(\{X_1^{(n)},\dots,X_{b_n^d}^{(n)}\} - X_i^{(n)}\big) \\[2pt] &\overset d= \frac{b_n^d}{n^d} \frac1{b_n^d} \sum_{i \le b_n^d} \xi^{(\alpha)}\big(b_n\{\widehat X_1,\dots,\widehat X_{b_n^d}\} - b_n\widehat X_i\big)\end{align*}

for $X_1^{(n)}, X_2^{(n)},\dots$ being independent and identically distributed (i.i.d.) uniform random variables on $W_n$ and $\widehat X_1,\widehat X_2,\dots$ being i.i.d. uniform random variables on $[0,1]^d$ . In order to apply [16, Theorem 2.1], we need to check the moment condition, i.e., that for $p>2$ ,

(45) \begin{equation}\sup_{n\ge 1} \mathbb E\big[\xi^{(\alpha)}\big(b_n\big\{\widehat X_1,\dots, \widehat X_{b_n^d}\big\}- b_n\widehat X_1\big)^p\big] <\infty.\end{equation}

We can use the bound on the node degree to get

(46) \begin{align}\begin{split}&\mathbb E\big[\xi^{(\alpha)}\big(b_n\big\{\widehat X_1,\dots, \widehat X_{b_n^d}\big\}- b_n\widehat X_1\big)^p\big] = \int_0^\infty \mathbb P\big(\xi^{(\alpha)}\big(b_n\big\{\widehat X_1,\dots, \widehat X_{b_n^d}\big\}- b_n\widehat X_1\big)^p > s\big)ds \\[2pt] &\le \int_0^\infty \mathbb P\big(|y| > \big(s^{1/p}/c_\textsf{max}\big)^{1/\alpha} \text{ for some }y\in \mathcal{E}\big(b_n\big\{\widehat X_1,\dots, \widehat X_{b_n^d}\big\}- b_n\widehat X_1\big)\big)ds.\end{split}\end{align}

Next, from ( STA ) we can deduce that, for every $s>0$ , if $b_n \widehat X_1$ has an out-neighbor among $b_n\big\{\widehat X_2,\dots, \widehat X_{b_n^d}\big\}$ that is farther away than $\big(s^{1/p}/c_\textsf{max}\big)^{1/\alpha}$ , then one of the cones arising from $b_n \widehat X_1$ has to extend until at least a distance of $\big(s^{1/p}/c_\textsf{max}\big)^{1/\alpha}$ from its apex before it contains $c_\textsf{STA}$ vertices. More precisely, there has to be an $i\le I_d$ such that $\mathcal{S}_i\big(b_n\big\{\widehat X_1,\dots, \widehat X_{b_n^d}\big\}- b_n\widehat X_1\big) > \big(s^{1/p}/c_\textsf{max}\big)^{1/\alpha}$ . Additionally, the intersection of $W_n$ and $\big(S_i + b_n \widehat X_1\big)\setminus B_{\big(s^{1/p}/c_\textsf{max}\big)^{1/\alpha}}\big(b_n \widehat X_1\big)$ cannot be empty, since the aforementioned out-neighbor has to be within $W_n$ . Therefore, under the event from the last line of (46), it is implied by the definition of $\mathcal{S}_i(\!\cdot\!)$ that for some $i \le I_d$ it holds that $b_n\big\{\widehat X_1,\dots, \widehat X_{b_n^d}\big\}\cap\big(S_i+b_n\widehat X_1\big)\cap B_{\big(s^{1/p}/c_\textsf{max}\big)^{1/\alpha}}\big(b_n\widehat X_1\big)$ contains at most $c_\textsf{max}$ points, while $W_n\cap \big(S_i+b_n\widehat X_1\big)\setminus B_{\big(s^{1/p}/c_\textsf{max}\big)^{1/\alpha}}\big(b_n\widehat X_1\big)\neq\emptyset$ . With these arguments we arrive at

(47) \begin{align}\begin{split}&\int_0^\infty \mathbb P\big(|y| > \big(s^{1/p}/c_\textsf{max}\big)^{1/\alpha} \text{ for some }y\in \mathcal{E}\big(b_n\big\{\widehat X_1,\dots, \widehat X_{b_n^d}\big\}- b_n\widehat X_1\big)\big)ds \\[2pt] &\le \sum_{i \le I_d} \int_0^\infty \mathbb P\big(\#\big(b_n\big\{\widehat X_1,\dots, \widehat X_{b_n^d}\big\}\cap\big(S_i+b_n\widehat X_1\big)\cap B_{\big(s^{1/p}/c_\textsf{max}\big)^{1/\alpha}}\big(b_n\widehat X_1\big)\big) \le c_\textsf{max} \\[2pt] &\qquad\qquad\qquad\ \text{and } W_n\cap \big(S_i+b_n\widehat X_1\big)\setminus B_{\big(s^{1/p}/c_\textsf{max}\big)^{1/\alpha}}\big(b_n\widehat X_1\big) \ne\emptyset \big)ds.\end{split}\end{align}

Furthermore, since the cones do not have lateral boundaries parallel to any axes, under the event after the last inequality in (47), the volume of the set $W_n\cap (S_i+b_n\widehat X_1)\cap B_{(s^{1/p}/c_\textsf{max})^{1/\alpha}}(b_n\widehat X_1)$ is of order $s^{d/(p\alpha)}$ and therefore at least $c s^{d/(p\alpha)}$ for all i, where $c>0$ depends only on the layout of the cones, $\alpha$ , and $c_\textsf{max}$ . Thus, by the independence of $\widehat X_2,\dots,\widehat X_{b_n^d}$ , when conditioned on $\widehat X_1$ , we can bound the probability of the event after the last inequality in (47) by the probability of a binomial random variable consisting of $b_n^d-1$ trials with success probability

\begin{align*} & \mathbb P(b_n \widehat X_2 \in (S_i+b_n\widehat X_1)\cap B_{(s^{1/p}/c_\textsf{max})^{1/\alpha}}(b_n\widehat X_1) \mid\, W_n\cap (S_i+b_n\widehat X_1)\setminus B_{(s^{1/p}/c_\textsf{max})^{1/\alpha}}(b_n\widehat X_1) \ne\emptyset)\\[5pt] & \ge cs^{d/(p\alpha)}/b_n^d\end{align*}

realizing a value of at most $c_\textsf{max}-1$ . Thus, by a binomial concentration bound [14, Lemma 1.1],

\begin{align*}&\mathbb E\big[\xi^{(\alpha)}(b_n\{\widehat X_1,\dots, \widehat X_{b_n^d}\}- b_n\widehat X_1)^p\big] \\[5pt] &\le I_d \int_0^\infty \mathbb P\big(\textsf{Bin}\big(b_n^d-1, c s^{d/(p\alpha)} / b_n^d\big) \le c_\textsf{max}-1\big)ds \\[5pt] & \le I_d \int_0^\infty \mathbb P\big(\textsf{Bin}(b_n^d, c s^{d/(p\alpha)} / b_n^d) \le c_\textsf{max}\big)ds \\[5pt] &\le I_d (c_\textsf{max}/c)^{p\alpha/d} + I_d \int_{(c_\textsf{max}/c)^{p\alpha/d}}^\infty \mathbb P\big(\text{Bin}(b_n^d, c s^{d/(p\alpha)} / b_n^d) \le c_\textsf{max}\big)ds \\[5pt] &\le I_d (c_\textsf{max}/c)^{p\alpha/d} +I_d \int_{(c_\textsf{max}/c)^{p\alpha/d}}^\infty \exp\!\big({-}c s^{d/(p\alpha)} (1- \tfrac{c_\textsf{max}}{c s^{d/(p\alpha)}} + \tfrac{c_\textsf{max}}{c s^{d/(p\alpha)}} \log(\tfrac{c_\textsf{max}}{c s^{d/(p\alpha)}})\big)ds < \infty.\end{align*}

In particular, the bound does not depend on n. Therefore, the moment condition (45) is satisfied. Now, [16, Theorem 2.1] gives

\begin{align*}\frac1{b_n^d} \sum_{i=1}^{b_n^d} \xi^{(\alpha)}\big(b_n\big\{\widehat X_1,\dots,\widehat X_{b_n^d}\big\} - b_n\widehat X_i\big) \overset{P}{\longrightarrow} \mu_\alpha,\end{align*}

and since $b_n^d/n^d \overset{n\uparrow\infty}{\longrightarrow} 1$ , it follows that

(48) \begin{equation}\lim_{n\uparrow\infty} \mathbb P\big(H_n(W_n,W_n) > \mu_\alpha - \varepsilon/2\, |\, X(W_n) = b_n^d\big) = 1.\end{equation}

Now we can use the union bound to arrive at

\begin{align*}\mathbb P(G_{1,n}) &\ge \mathbb P\big(H_n(W_n,W_n) > \mu_\alpha - \varepsilon/2\big) + \mathbb P\big(E_n^\textsf{good}\big) - 1 \\[5pt] &\ge \mathbb P\big(H_n(W_n,W_n) > \mu_\alpha - \varepsilon/2\, |\, X(W_n) = b_n^d\big) \mathbb P(X(W_n) = b_n^d) + \mathbb P\big(E_n^\textsf{good}\big) - 1\\[5pt] &\ge \mathbb P\big(H_n(W_n,W_n) > \mu_\alpha - \varepsilon/2\, |\, X(W_n) = b_n^d\big) \frac{\exp\left({-}\frac1{12 b_n^d}\right)}{\sqrt{2\pi b_n^d}} + \mathbb P\big(E_n^\textsf{good}\big) - 1,\end{align*}

where in the last line we used [14, Lemma 1.3]. By (48) we can assume n large enough so that

\begin{align*}\mathbb P\big((H_n(W_n,W_n) > \mu_\alpha - \varepsilon/2\, |\, X(W_n) = b_n^d\big) \ge 1/2.\end{align*}

Hence, combining this with (44), we get that

\begin{align*}\mathbb P(G_{1,n}) \ge \frac12\frac{\exp\left({-}\frac1{12b_n^d}\right)}{\sqrt{2\pi b_n^d}} - n^{d-1}\big(e^{-(\log n)^d} (\log n)^{d c_\textsf{max}+2} + e^{-\frac12(\log n)^{2d}}\big),\end{align*}

as asserted.

We continue with the proof of Lemma 11.

Proof of Lemma 11. First, we show that

(49) \begin{equation}\bigcap_{\delta>0}\underbrace{\bigcup_{(z_y)_{y\in\psi}\subseteq B_\delta(0)} A(\{x+z_x \,:\, x\in\varphi\},\{x+z_x \,:\, x\in\psi\})}_{=: A_\delta(\varphi,\psi)} \subseteq A(\varphi,\psi) \cup D(\psi),\end{equation}

where we recall that $D(\psi) = \{y \in \mathbb R^d \,:\, \varphi \cup\{y\} \in N_{\#\varphi +1}\}$ . The subset relation in (49) holds because if we let $y\in\cap_{\delta>0} A_\delta(\varphi,\psi)\setminus D(\psi)$ , then for every $\delta\in(0,1)$ there exists a family $(z_w)_{w\in\psi}\subseteq B_\delta(0)$ such that $y\in A(\{w+z_w \,:\, w\in\varphi\},\{w+z_w \,:\, w\in\psi\})$ . Hence,

\begin{align*}\mathcal{E}_{x+z_x}(\{w+z_w \,:\, w\in\psi\}) \not\subseteq \mathcal{E}_{x+z_x}(\{w+z_w \,:\, w\in\psi\}\cup\{y\})\end{align*}

for some

\begin{align*}x+z_x\in\{w+z_w \,:\, w\in\varphi\}\cup\cup_{v+z_v\in\{w+z_w \,:\, w\in\varphi\}} (\mathcal{E}_{v+z_v}(\{w+z_w \,:\, w\in\psi\})).\end{align*}

Since $y\not\in D(\psi)$ , we can apply ( CON ) to both sides, choosing $\delta$ sufficiently small, which gives $\mathcal{E}_x(\psi) \not\subseteq \mathcal{E}_x(\psi\cup\{y\})$ for some $x\in\varphi\cup\cup_{v\in\varphi} (\mathcal{E}_v(\psi))$ and therefore $y\in A(\varphi,\psi)$ . Since $|D(\psi)|=0$ , we deduce from (49) that for $\delta$ sufficiently small we have $|A_\delta(\varphi,\psi)|\leq |A(\varphi,\psi)| + \varepsilon.$

To prove Part (b), note that since $\psi$ is finite, we can use ( CON ) and find $\delta\in(0,1)$ small enough so that for all choices of $(z_x)_{x\in\psi} \subseteq B_\delta(0)$ we have

(50) \begin{equation}\{w - z_w \,:\, w\in\mathcal{E}_{x+z_x}(\{y+z_y \,:\, y\in\psi\})\} = \mathcal{E}_x(\psi).\end{equation}

This means the graph looks the same despite some small noise of at most $\delta$ for every node. But the finiteness of the configuration combined with (50) guarantees that for $\delta$ sufficiently small,

\begin{align*}\inf_{(z_x)_{x\in\psi} \subseteq B_\delta(0)} \sum_{x\in\varphi} \xi^{(\alpha)}(\{y+z_y \,:\, y\in\psi\}-(x+z_x)) > 1/(1+\varepsilon).\end{align*}

What follows is the proof of Lemma 12.

Proof of Lemma 12. Let $(\varphi,\psi)\in B$ be such that $|A(\varphi,\psi)|<\infty$ . The key step is to construct a finite set of points $\theta \subseteq \mathbb R^d$ and a scalar $R > 0$ such that, for all $x\in\eta\;:\!=\;\varphi \cup\cup_{z\in\varphi} (\mathcal{E}_z (\psi))$ and $(z_y)_{y\in\psi}\subseteq B_\delta(0)$ , we have (i) $\mathcal{R}\big((\{y+z_y\,:\, y\in\psi\} \cup \theta) - (x + z_x)\big) \le R$ , and (ii)

(51) \begin{align} \mathcal{E}\big(\{y+z_y\,:\, y\in\psi\}-(x+z_x)\big)\subseteq\mathcal{E}\big((\{y+z_y\,:\, y\in\psi\}\cup\theta )-(x+z_x)\big).\end{align}

Once $\theta$ is constructed, we assert that $A_\delta(\varphi, \psi) \subseteq \bigcup_{x \in \eta} B_{R + 1}(x)$ . Indeed, for any $v \in \mathbb R^d\setminus \bigcup_{x \in \eta} B_{R + 1}(x)$ , the definition of the stabilization radius implies that

(52) \begin{equation} \mathcal{E}\big((\{y+z_y\,:\, y\in\psi\}\cup\theta)-(x+z_x)\big) = \mathcal{E}\big((\{y+z_y\,:\, y\in\psi\}\cup\theta\cup\{v\})-(x+z_x)\big).\end{equation}

Hence, combining (51), (52), and ( STA ) gives that

\begin{align*} \mathcal{E}\big(\{y+z_y\,:\, y\in\psi\}-(x+z_x)\big) \subseteq \mathcal{E}\big((\{y+z_y\,:\, y\in\psi\}\cup\{v\})-(x+z_x)\big),\end{align*}

thereby proving the assertion that $v \not\in A_\delta(\varphi, \psi)$ .

It remains to prove the existence of $R > 0$ and $\theta \subseteq \mathbb R^d$ . To that end, first note that $|T_i(x,\delta)| = \infty$ for all $i \le I_d$ and $x\in\mathbb R^d$ , where $T_i(x,\delta)\;:\!=\; \cap_{y\in B_\delta(x)} (S_i+y)$ . Since $|A_\delta(\varphi,\psi)|<\infty$ , by Lemma 11(a), if $\delta$ is chosen appropriately, it follows that for every $x\in \eta$ and $i\le I_d$ there are distinct $w_{x,i}^{(1)},\dots,w_{x,i}^{(c_\textsf{STA})}\in T_i(x,\delta)\setminus A_\delta(\varphi,\psi)$ . Then, defining $\theta\;:\!=\; \{w_{x,i}^{(j)} \,:\, x\in\eta, i \le I_d, j \le c_\textsf{STA}\}$ , we note that ( INF ) implies the property (51). Now, set

\begin{align*}R\;:\!=\; \max_{\substack{x\in\eta, \, z\in B_\delta(x)\\ i\le I_d, j\le c_\textsf{STA}}} c_\textsf{STA}|z-w_{x,i}^{(j)}| \le \max_{\substack{x\in\eta\\ i \le I_d, j\le c_\textsf{STA}}} c_\textsf{STA} |x-w_{x,i}^{(j)}|+c_\textsf{STA} \delta,\end{align*}

and note that the finiteness of the configurations in B implies that $R < \infty$ . Then the definition of the stabilization radius yields $\mathcal{R}\big((\{y+z_y\,:\, y\in\psi\} \cup \theta) - (x + z_x)\big) \le R$ , as asserted.

Finally, we show Lemma 13.

Proof of Lemma 13. Let $(\varphi,\psi)\in B$ and $\delta\in(0,1)$ be given according to the setting of Lemma 11. First note that $B_1(x) \subseteq B_{\tau_n \delta}(x)$ for sufficiently large $n\ge 1$ . Moreover, the events $\{X(B_1(x)) = 1 \text{ for all } x\in\tau_n\psi\}$ and $\{X(A_{\delta, n}^-) = 0\}$ are independent. Thus, we can examine them separately and start with the first one. We assume that n is chosen large enough so that all of the balls around points in $\tau_n\psi$ are disjoint. Therefore,

\begin{align*}\mathbb P\big(X(B_1 (x)) = 1 \text{ for all } x\in\tau_n\psi\big) = \prod_{x\in\tau_n\psi}\mathbb P\big(X(B_1 (x)) = 1\big) = \kappa_d ^{\#\psi} e^{-\#\psi \kappa_d}.\end{align*}

For the second event, Lemma 11(a) yields

\begin{align*}\mathbb P\big(X(A_{\delta, n}^-) = 0\big) \ge \mathbb P\big(X(\tau_nA_{\delta}(\varphi,\psi)) = 0\big) \ge \exp\!\big({-}\big( |A(\varphi,\psi)|+\varepsilon\big)\tau_n^d\big).\end{align*}

All of this combined shows that for large enough n,

\begin{align*} \frac1{n^{d^2/\alpha}} \log \mathbb P(G_{2,n}(\delta)) &\ge \frac1{n^{d^2/\alpha}} \log\!\Big( \kappa_d^{\#\psi} e^{-\#\psi \kappa_d}\Big) - \Big(\!\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|+\varepsilon\Big)((r+\varepsilon)(1+\varepsilon))^{d/\alpha} \\[5pt] &\overset{n\uparrow\infty}{\longrightarrow} - \Big(\!\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|+\varepsilon\Big)((r+\varepsilon)(1+\varepsilon))^{d/\alpha},\end{align*}

as asserted.

6. Proof of Theorem 2

The proof of Theorem 2 consists mainly of a refinement of the steps in the proofs of Theorem 1 and Lemma 9.

Proof of Theorem 2(a). To begin with, let $\delta\in (0,1)$ , and for $\varepsilon\in(0,(1-d/\alpha)/(2\alpha))$ , set $h_{n,\varepsilon} \;:\!=\; \lfloor n^{d^2/\alpha-\varepsilon}\rfloor$ . Putting $H^{\prime}_{n} \;:\!=\; n^{-d}\sum_{i \le h_{n,\varepsilon}} Z_n^{(i)}$ , we will look separately at the numerator and the denominator of

\begin{align*}\mathbb P\big(H^{\prime}_{n} < r(1-\delta)\, \big|\, H_n > \mu_\alpha + r\big) = \frac{\mathbb P(H^{\prime}_{n} < r(1-\delta), H_n > \mu_\alpha + r)}{\mathbb P(H_n > \mu_\alpha + r)}\end{align*}

and prove that this ratio tends to zero. To start with the numerator, recall how Lemma 9 was used in the proof of Theorem 1. The event $\{H_n>\mu_\alpha+r\}$ was split up into small and large contributions. Instead of $\varepsilon$ , here we use an arbitrary $\tilde\varepsilon < (1-d/\alpha)/(2\alpha) \wedge \delta$ to divide the term $\mu_\alpha n^d+rn^d$ . Then, since $\tilde\varepsilon<\delta$ , we have

\begin{align*}\big\{H^{\prime}_{n} < r(1-\delta)\big\} \cap \bigg\{\sum_{x\in\mathcal{J}_n^{(a)}(X)} \xi^{(\alpha)}(X-x) \ge rn^d(1-\tilde\varepsilon), J_n^{(a)}(X) \le h_{n,\varepsilon}\bigg\} = \emptyset.\end{align*}

Using this, Lemma 7, and Lemma 8 similarly as in the proof of Theorem 1 gives that

(53) \begin{equation}\limsup_{n\uparrow\infty} \frac1{n^{d^2/\alpha}} \log\mathbb P\big(H^{\prime}_{n} < r(1-\delta),H_n > \mu_\alpha + r\big) =-\infty.\end{equation}

For the denominator, after additionally assuming that $\tilde\varepsilon < \mu_\alpha$ , we deduce from (43) that

(54) \begin{equation} \mathbb P(H_n > \mu_\alpha + r) \geq \exp\!({-}\gamma(\tilde \varepsilon)n^{d^2/\alpha} + o(n^{d^2/\alpha})),\end{equation}

where $\gamma(\tilde \varepsilon) \;:\!=\; (\!\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|+\tilde\varepsilon\big)(r+\tilde\varepsilon)^{d/\alpha}$ . Together, (53) and (54) imply that for any $c>0$ , if n is chosen large enough, then we have that

\begin{align*} \mathbb P\big(H^{\prime}_{n} < r(1-\delta)\, \big|\, H_n > \mu_\alpha + r\big) &\leq \frac{\exp\!({-}cn^{d^2/\alpha} + o(n^{d^2/\alpha}))}{\exp\!({-}\gamma(\tilde \varepsilon)n^{d^2/\alpha} + o(n^{d^2/\alpha}))},\end{align*}

which indeed converges to 0 when we let n go to infinity, provided that $c > \gamma(\tilde\varepsilon)$ .

Next, we prove that the statement about the other side holds, i.e.,

\begin{align*}\mathbb P\big(H^{\prime}_{n} > r(1+\delta)\, \big|\, H_n > \mu_\alpha + r\big) \overset{n\uparrow\infty}{\longrightarrow} 0.\end{align*}

To that end, we note that the proof of Lemma 9 extends without any changes to the case where we replace $\mathcal{J}_n^{(a)}(X)$ by the set of nodes with the $h_{n, \varepsilon}$ largest scores. Then, applying this result with $\tau =rn^d(1+\delta) $ and $m =h_{n,\varepsilon}$ yields

\begin{align*}&\mathbb P\big(H^{\prime}_{n} > r(1+\delta), \mathcal{R}_{3n} \le n\big) \\[5pt] &\leq ((I_d c_\textsf{max} + 1)^2 h_{n,\varepsilon})^2 (5n)^{d 2 (I_d c_\textsf{max} + 1)^2 h_{n,\varepsilon}}\exp\!\Big({-} (rn^d(1+\delta))^{d/\alpha} \inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|\Big) \\[5pt] &= \exp\!\Big({-} (rn^d(1+\delta))^{d/\alpha} \inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)| + o(n^{d^2/\alpha})\Big).\end{align*}

Proceeding similarly to the proof of Theorem 1, we get the bound for the numerator and can estimate

\begin{align*}\mathbb P\big(H^{\prime}_{n} > r(1+\delta)\, \big|\, H_n > \mu_\alpha + r\big) \leq \frac{\exp\!\big({-} (rn^d(1+\delta))^{d/\alpha} \inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)| + o(n^{d^2/\alpha})\big)}{\exp\!({-}\gamma(\tilde\varepsilon)n^{d^2/\alpha} + o(n^{d^2/\alpha}))}.\end{align*}

Now, choosing $\tilde\varepsilon$ small enough so that the bound for the numerator converges to 0 faster than the bound for the denominator gives the claimed convergence. Thus,

\begin{align*}\mathbb P\big(|{H^{\prime}_{n}}/r - 1| > \delta\, \big|\, H_n > \mu_\alpha + r\big) \overset{n\uparrow\infty}{\longrightarrow} 0,\end{align*}

as asserted.

Showing Part (b) mainly requires repeating the steps of Part (a). Nevertheless, it is a bit more challenging since we need to replicate Lemma 9 in a slightly extended form that incorporates the additional bound for the sum of the largest scores within the sample space.

Proof of Theorem 2(b). Let $m_0>0$ satisfy (11). Let $\delta, \varepsilon > 0$ be chosen as in the proof of Part (a). This time, let $\tilde\varepsilon < (1-d/\alpha)/(2\alpha)\wedge \delta/2$ be arbitrary, and define $H^{\prime}_{n} \;:\!=\; n^{-d}\sum_{i=1}^{m_0} Z_n^{(i)}$ and $H^{\prime}(\varphi, \psi) \;:\!=\; \sum_{i=1}^{m_0} Z^{(i)}(\varphi, \psi)$ . As in the proof of Lemma 9, we can show that

(55) \begin{align}&\mathbb P\Bigg(H^{\prime}_{n} < (1-\tilde\varepsilon)r\tfrac{1-\delta}{1-\delta/2}, \sum_{x\in\mathcal{J}_n^{(a)}(X)} \xi^{(\alpha)}(X-x) \geq (1-\tilde\varepsilon)rn^d, J_n^{(a)}\le \lfloor n^{d^2/\alpha-\varepsilon}\rfloor, \mathcal{R}_{3n}(X) \leq n\Bigg)\nonumber \\[5pt] &\leq k_{n,\varepsilon} \exp\!\bigg({-}((1-\tilde\varepsilon)rn^d)^{d/\alpha}\inf_{(\varphi,\psi)\in B,\, H^{\prime}(\varphi,\psi) < (1-\delta)/(1-\delta/2)} |A(\varphi,\psi)|\bigg),\end{align}

where

\begin{align*}k_{n,\varepsilon} \;:\!=\; (I_d c_\textsf{max} + 1)^4 \lfloor n^{d^2/\alpha-\varepsilon}\rfloor^2 (5n)^{d 2 (I_d c_\textsf{max} + 1)^2 \lfloor n^{d^2/\alpha-\varepsilon}\rfloor} \in e^{o(n^{d^2/\alpha})}.\end{align*}

Furthermore, repeating the arguments from the proof of Theorem 1 as we did to get (53), but replacing Lemma 9 with (55), we arrive at

(56) \begin{align}\begin{split}& \mathbb P\big(H^{\prime}_{n} < r(1-\delta), H_n > \mu_\alpha + r\big) \le \mathbb P\big(H^{\prime}_{n} < (1-\tilde\varepsilon)r\tfrac{1-\delta}{1-\delta/2}, H_n > \mu_\alpha + r \big) \\[5pt] &\le \exp\!\Big({-}((1-\tilde\varepsilon) rn^d)^{d/\alpha} \inf_{(\varphi,\psi)\in B,\, H^{\prime}(\varphi, \psi) < (1-\delta)/(1-\delta/2)} |A(\varphi,\psi)| + o(n^{d^2/\alpha})\Big),\end{split}\end{align}

which is sufficient for dealing with the numerator.

For the denominator, we can reuse the inequality stated in (54) with the assumption $\tilde\varepsilon <\mu_\alpha$ . Next, because of (11) applied to $\delta^{\prime} = 1-(1-\delta)/(1-\delta/2)$ , we can require $\tilde\varepsilon$ to be small enough to ensure that

(57) \begin{equation}((1-\tilde\varepsilon) r)^{d/\alpha} \inf_{(\varphi,\psi)\in B,\, H^{\prime}(\varphi, \psi) < 1-\delta^{\prime}} |A(\varphi,\psi)| > \Big(\!\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|+\tilde\varepsilon\Big)((r+\tilde\varepsilon))^{d/\alpha}.\end{equation}

We proceed by plugging (54) and (56) into the fraction that arises from the conditional probability and get

\begin{align*}& \mathbb P\big(H^{\prime}_{n} < r(1-\delta)\, \big|\, H_n > \mu_\alpha + r\big) \\[5pt] &\le \frac{\exp\!\big({-}(1-\tilde\varepsilon)^{d/\alpha} r^{d/\alpha}n^{d^2/\alpha} \inf_{(\varphi,\psi)\in B,\, H^{\prime}(\varphi, \psi) < 1-\delta^{\prime}} |A(\varphi,\psi)|+o(n^{d^2/\alpha})\big)}{\exp\!\big({-}(\!\inf_{(\varphi,\psi)\in B} |A(\varphi,\psi)|+\tilde\varepsilon)(r+\tilde\varepsilon)^{d/\alpha}n^{d^2/\alpha} + o(n^{d^2/\alpha})\big)},\end{align*}

which converges to 0 by the assumed relationship of the coefficients in (57).

The assertion on the upper tails, i.e., $\mathbb P\big(H^{\prime}_{n} > r(1+\delta)\, \big|\, H_n > \mu_\alpha + r\big) \overset{n\uparrow\infty}{\longrightarrow} 0$ , follows analogously to Part (a).