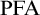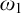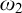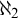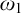1 Introduction
By the well-known work of Baumgartner, Malitz, and Reinhardt [Reference Baumgartner, Malitz and Reinhardt2], under Martin’s axiom at
![]() $\aleph _1$
, all trees of height and size
$\aleph _1$
, all trees of height and size
![]() $\omega _1$
without cofinal branches are special. Unfortunately, the straightforward generalisations of
$\omega _1$
without cofinal branches are special. Unfortunately, the straightforward generalisations of
![]() $\mathrm{MA}$
were not thus far capable of specialising
$\mathrm{MA}$
were not thus far capable of specialising
![]() $\omega _2$
-Aronszajn trees (see [Reference Baumgartner1, Reference Shelah19, Reference Shelah and Stanley20]). The different behaviour of the specialising problem beyond
$\omega _2$
-Aronszajn trees (see [Reference Baumgartner1, Reference Shelah19, Reference Shelah and Stanley20]). The different behaviour of the specialising problem beyond
![]() $\omega _1$
arises from two interconnected factors: the weakness of the current technology of forcing iterations and the nature of trees of height at least
$\omega _1$
arises from two interconnected factors: the weakness of the current technology of forcing iterations and the nature of trees of height at least
![]() $\omega _2$
. Thus, the question of finding a legitimate higher version of Martin’s axiom, under which every
$\omega _2$
. Thus, the question of finding a legitimate higher version of Martin’s axiom, under which every
![]() $\omega _2$
-Aronszajn tree is special seems challenging (we will say more about this). However, there are still many intriguing results in this research direction. For example, Laver and Shelah [Reference Laver and Shelah12] showed, assuming the consistency of a weakly compact cardinal, that the
$\omega _2$
-Aronszajn tree is special seems challenging (we will say more about this). However, there are still many intriguing results in this research direction. For example, Laver and Shelah [Reference Laver and Shelah12] showed, assuming the consistency of a weakly compact cardinal, that the
![]() $\omega _2$
-Suslin Hypothesis is consistent with the Continuum Hypothesis (in fact, they showed that it is consistent that there are
$\omega _2$
-Suslin Hypothesis is consistent with the Continuum Hypothesis (in fact, they showed that it is consistent that there are
![]() $\omega _2$
-Aronszajn trees and all of them are special). This result was extended by Golshani and Hayut in [Reference Golshani and Hayut7], where they proved that, modulo the consistency of large cardinals, it is consistent that for every regular cardinal
$\omega _2$
-Aronszajn trees and all of them are special). This result was extended by Golshani and Hayut in [Reference Golshani and Hayut7], where they proved that, modulo the consistency of large cardinals, it is consistent that for every regular cardinal
![]() $\kappa $
, there are
$\kappa $
, there are
![]() $\kappa ^{+}$
-Aronszajn trees and all of them are special. A more relevant result, where wide trees were involved, was obtained by Golshani and Shelah in [Reference Golshani and Shelah8], that is for a prescribed regular cardinal
$\kappa ^{+}$
-Aronszajn trees and all of them are special. A more relevant result, where wide trees were involved, was obtained by Golshani and Shelah in [Reference Golshani and Shelah8], that is for a prescribed regular cardinal
![]() $\kappa $
, it is consistent that every tree of height and size
$\kappa $
, it is consistent that every tree of height and size
![]() $\kappa ^+$
(with a small number of branches) is weakly special (i.e., there is a colouring with
$\kappa ^+$
(with a small number of branches) is weakly special (i.e., there is a colouring with
![]() $\kappa $
colours so that if
$\kappa $
colours so that if
![]() $s<t,u$
have the same colour, then t and u are comparable). The affinity between these and other similar results is that they rely upon the original technique of Laver and Shelah [Reference Laver and Shelah12]. Although the main difficulty in proving an iteration theorem for countably closed and
$s<t,u$
have the same colour, then t and u are comparable). The affinity between these and other similar results is that they rely upon the original technique of Laver and Shelah [Reference Laver and Shelah12]. Although the main difficulty in proving an iteration theorem for countably closed and
![]() $\aleph _2$
-c.c forcings is the preservation of
$\aleph _2$
-c.c forcings is the preservation of
![]() $\aleph _2$
, it was surmountable by Laver–Shelah’s argument due to the particular features of the iterands. The attempts to overcome the difficulty and find a higher analogue of
$\aleph _2$
, it was surmountable by Laver–Shelah’s argument due to the particular features of the iterands. The attempts to overcome the difficulty and find a higher analogue of
![]() $\mathrm{MA}$
have been generally devoted to countably closed forcings until Neeman’s discovery [Reference Neeman17] of generalised side conditions. His technology allows us to examine the connection between the specialisation problem and generalised forms of Martin’s axiom, and ask if we still need to consider countably closed forcings in this context. If the consistency of a higher analogue of
$\mathrm{MA}$
have been generally devoted to countably closed forcings until Neeman’s discovery [Reference Neeman17] of generalised side conditions. His technology allows us to examine the connection between the specialisation problem and generalised forms of Martin’s axiom, and ask if we still need to consider countably closed forcings in this context. If the consistency of a higher analogue of
![]() $\mathrm{PFA}$
is achievable, it is then natural to speculate whether such a forcing axiom can imply that all trees in an appropriate subclass of trees of height and size
$\mathrm{PFA}$
is achievable, it is then natural to speculate whether such a forcing axiom can imply that all trees in an appropriate subclass of trees of height and size
![]() $\omega _2$
are special. As an early application of his method, Neeman [Reference Neeman18] attempted to (partially) specialise trees of height
$\omega _2$
are special. As an early application of his method, Neeman [Reference Neeman18] attempted to (partially) specialise trees of height
![]() $\omega _2$
with finite conditions. To achieve this, he attaches the partial specialising functions to the sequences of models as side conditions. He then demonstrates that the resulting construction belongs to an iterable class which also includes a forcing notion for adding a nonspecial
$\omega _2$
with finite conditions. To achieve this, he attaches the partial specialising functions to the sequences of models as side conditions. He then demonstrates that the resulting construction belongs to an iterable class which also includes a forcing notion for adding a nonspecial
![]() $\omega _2$
-Aronszajn tree.
$\omega _2$
-Aronszajn tree.
The second factor mentioned above may also lead one to recast the program of finding a generalised
![]() $\mathrm{MA}$
for the problem of special
$\mathrm{MA}$
for the problem of special
![]() $\omega _2$
-Aronszajn trees, as such trees intrinsically involve a particular compactness phenomenon. One can use some forms of the square principle to construct trees without cofinal branches that cannot be special, even in transitive outer models with the same cardinals. The basic idea goes back to Laver (see [Reference Shelah and Stanley21]) who isolated the concept of an ascending path through a tree and showed that an
$\omega _2$
-Aronszajn trees, as such trees intrinsically involve a particular compactness phenomenon. One can use some forms of the square principle to construct trees without cofinal branches that cannot be special, even in transitive outer models with the same cardinals. The basic idea goes back to Laver (see [Reference Shelah and Stanley21]) who isolated the concept of an ascending path through a tree and showed that an
![]() $\omega _2$
-Aronszajn tree with an ascending path is non-special even in any transitive outer model that computes the relevant cardinals correctly. However, the earliest example of a non-special
$\omega _2$
-Aronszajn tree with an ascending path is non-special even in any transitive outer model that computes the relevant cardinals correctly. However, the earliest example of a non-special
![]() $\omega _2$
-Aronszajn tree was constructed by Baumgartner using
$\omega _2$
-Aronszajn tree was constructed by Baumgartner using
![]() $\square _{\omega _1},$
which was also independently discovered and generalised by Shelah and Stanley [Reference Shelah and Stanley21]. They showed that
$\square _{\omega _1},$
which was also independently discovered and generalised by Shelah and Stanley [Reference Shelah and Stanley21]. They showed that
![]() $\square _{\lambda }$
implies the existence of non-specialisable
$\square _{\lambda }$
implies the existence of non-specialisable
![]() $\lambda ^+$
-Aronszajn trees. The connection between square-like principles and ascending paths through trees or tree-like systems has been studied by several people, just to mention a few: Baumgartner (as mentioned above), Brodsky and Rinot [Reference Brodsky and Rinot3], Devlin [Reference Devlin6], Cummings [Reference Cummings5], Lambie-Hanson [Reference Lambie-Hanson10], Lambie-Hanson and Lücke [Reference Lambie-Hanson and Lücke11], Laver and Shelah [Reference Laver and Shelah12], Lücke [Reference Lücke13], Neeman [Reference Neeman18], Shelah and Stanley [Reference Shelah and Stanley21], and Todorčević [Reference Todorčević22].
$\lambda ^+$
-Aronszajn trees. The connection between square-like principles and ascending paths through trees or tree-like systems has been studied by several people, just to mention a few: Baumgartner (as mentioned above), Brodsky and Rinot [Reference Brodsky and Rinot3], Devlin [Reference Devlin6], Cummings [Reference Cummings5], Lambie-Hanson [Reference Lambie-Hanson10], Lambie-Hanson and Lücke [Reference Lambie-Hanson and Lücke11], Laver and Shelah [Reference Laver and Shelah12], Lücke [Reference Lücke13], Neeman [Reference Neeman18], Shelah and Stanley [Reference Shelah and Stanley21], and Todorčević [Reference Todorčević22].
To see why specialising a tree of height beyond
![]() $\omega _1$
is subtly different from that of a tree of height
$\omega _1$
is subtly different from that of a tree of height
![]() $\omega _1$
, let us first recall that the standard forcing to specialises a tree T of height
$\omega _1$
, let us first recall that the standard forcing to specialises a tree T of height
![]() $\kappa ^+$
uses partial specialising functions of size less than
$\kappa ^+$
uses partial specialising functions of size less than
![]() $\kappa $
, and let us denote this forcing by
$\kappa $
, and let us denote this forcing by
![]() $\mathbb S_{\kappa }(T)$
. For a cardinal
$\mathbb S_{\kappa }(T)$
. For a cardinal
![]() $\lambda \leq \kappa $
,
$\lambda \leq \kappa $
,
![]() $\mathbb S_\lambda (T)$
is defined naturally. Lücke [Reference Lücke13] studied the chain condition of
$\mathbb S_\lambda (T)$
is defined naturally. Lücke [Reference Lücke13] studied the chain condition of
![]() $\mathbb S_\lambda (T)$
, and complete the bridge between the notion of an ascending path and the chain condition of
$\mathbb S_\lambda (T)$
, and complete the bridge between the notion of an ascending path and the chain condition of
![]() $\mathbb S_\lambda (T)$
. Under some cardinal arithmetic assumptions, he showed that the nonexistence of a weak form of ascending paths
Footnote
1
of width less than
$\mathbb S_\lambda (T)$
. Under some cardinal arithmetic assumptions, he showed that the nonexistence of a weak form of ascending paths
Footnote
1
of width less than
![]() $\lambda $
through T is equivalent to the
$\lambda $
through T is equivalent to the
![]() $\kappa ^+$
-chain condition of
$\kappa ^+$
-chain condition of
![]() $\mathbb S_{\lambda }(T)$
. Note that it is easily seen that
$\mathbb S_{\lambda }(T)$
. Note that it is easily seen that
![]() $\mathbb S_{\lambda }(T)$
collapses
$\mathbb S_{\lambda }(T)$
collapses
![]() $\kappa ^+$
if T has a cofinal branch. Observe that also by Baumgartner–Malitz–Reinhardt [Reference Baumgartner, Malitz and Reinhardt2], if T is of height
$\kappa ^+$
if T has a cofinal branch. Observe that also by Baumgartner–Malitz–Reinhardt [Reference Baumgartner, Malitz and Reinhardt2], if T is of height
![]() $\omega _1$
without cofinal branches, then
$\omega _1$
without cofinal branches, then
![]() $\mathbb S_{\omega }(T)$
has the countable chain condition, as the existence of a cofinal branch through such tree is equivalent to the existence of a (weak) ascending path of finite length. It is also not hard to see that if
$\mathbb S_{\omega }(T)$
has the countable chain condition, as the existence of a cofinal branch through such tree is equivalent to the existence of a (weak) ascending path of finite length. It is also not hard to see that if
![]() $\kappa =\omega _1$
and the
$\kappa =\omega _1$
and the
![]() $\mathrm{CH}$
fails, then
$\mathrm{CH}$
fails, then
![]() $\mathbb S_{\omega _1}(T)$
collapses the continuum onto
$\mathbb S_{\omega _1}(T)$
collapses the continuum onto
![]() $\omega _1$
. Thus not only the
$\omega _1$
. Thus not only the
![]() $\mathrm{CH}$
is necessary for preserving
$\mathrm{CH}$
is necessary for preserving
![]() $\aleph _2$
, but also by Lücke’s result, the lack of cofinal branches through T is not enough to ensure that
$\aleph _2$
, but also by Lücke’s result, the lack of cofinal branches through T is not enough to ensure that
![]() $\mathbb S_{\omega _1}(T)$
preserves
$\mathbb S_{\omega _1}(T)$
preserves
![]() $\aleph _2$
. On the other hand, if T is of height
$\aleph _2$
. On the other hand, if T is of height
![]() $\omega _2$
and has no cofinal branches, then
$\omega _2$
and has no cofinal branches, then
![]() $\mathbb S_{\omega }(T)$
has the
$\mathbb S_{\omega }(T)$
has the
![]() $\aleph _2$
-chain condition, but then the question is how to preserve
$\aleph _2$
-chain condition, but then the question is how to preserve
![]() $\omega _1$
?
$\omega _1$
?
Therefore, the behaviour of the continuum function and the existence of ascending paths of width
![]() $\omega $
can prevent us from specialising trees of height
$\omega $
can prevent us from specialising trees of height
![]() $\omega _2$
merely with countable conditions. Lücke [Reference Lücke13] asked the following questions:
$\omega _2$
merely with countable conditions. Lücke [Reference Lücke13] asked the following questions:
-
(1) Assume
 $\mathrm{PFA}$
. Is every tree of height
$\mathrm{PFA}$
. Is every tree of height
 $\omega _2$
without cofinal branches specialisable?
$\omega _2$
without cofinal branches specialisable? -
(2) If T is a tree of height
 $\kappa ^+$
, for an uncountable regular cardinal
$\kappa ^+$
, for an uncountable regular cardinal
 $\kappa $
without ascending paths of width less than
$\kappa $
without ascending paths of width less than
 $\kappa $
, is then T specialisable?
$\kappa $
, is then T specialisable?
Let us end our discussion with a couple of general questions: Do we still need to consider the specialisation of all
![]() $\omega _2$
-Aronszajn trees in the context of generalised Martin’s axiom? If looking for a generalised
$\omega _2$
-Aronszajn trees in the context of generalised Martin’s axiom? If looking for a generalised
![]() $\mathrm{MA}$
, do we want to have some kinds of compactness at
$\mathrm{MA}$
, do we want to have some kinds of compactness at
![]() $\aleph _2$
or not?
$\aleph _2$
or not?
In this paper, we prove the following theorem.
Theorem 1.1. Assume
![]() $\mathrm{PFA}$
. Every tree of height
$\mathrm{PFA}$
. Every tree of height
![]() $\omega _2$
without cofinal branches is specialisable via a proper and
$\omega _2$
without cofinal branches is specialisable via a proper and
![]() $\aleph _2$
-preserving forcing with finite conditions. Moreover, the forcing has the
$\aleph _2$
-preserving forcing with finite conditions. Moreover, the forcing has the
![]() $\omega _1$
-approximation property.
$\omega _1$
-approximation property.
This theorem answers Lücke’s first question in the affirmative.Footnote
2
Given a tree T of height
![]() $\omega _2$
with no cofinal branches, we shall use internally club
$\omega _2$
with no cofinal branches, we shall use internally club
![]() $\omega _1$
-guessing models to construct a proper forcing notion
$\omega _1$
-guessing models to construct a proper forcing notion
![]() $\mathbb P_T$
similar to Neeman’s in [Reference Neeman18], so that forcing with
$\mathbb P_T$
similar to Neeman’s in [Reference Neeman18], so that forcing with
![]() $\mathbb P_T$
specialises T. Notice that the existence of sufficiently many
$\mathbb P_T$
specialises T. Notice that the existence of sufficiently many
![]() $\omega _1$
-guessing models of size
$\omega _1$
-guessing models of size
![]() $\omega _1$
implies the failure of certain versions of the square principle. It is also worth mentioning that by an observation due to Lücke, the existence of sufficiently many
$\omega _1$
implies the failure of certain versions of the square principle. It is also worth mentioning that by an observation due to Lücke, the existence of sufficiently many
![]() $\omega _1$
-guessing models of size
$\omega _1$
-guessing models of size
![]() $\aleph _1$
(and hence under
$\aleph _1$
(and hence under
![]() $\mathrm{PFA}$
) no tree of height
$\mathrm{PFA}$
) no tree of height
![]() $\omega _2$
without cofinal branches contains an ascending path of width
$\omega _2$
without cofinal branches contains an ascending path of width
![]() $\omega $
. Interestingly, we will not use this fact, as the presence of guessing models in our side conditions suffices. By a theorem due to Viale and Weiß [Reference Viale and Weiß25], under
$\omega $
. Interestingly, we will not use this fact, as the presence of guessing models in our side conditions suffices. By a theorem due to Viale and Weiß [Reference Viale and Weiß25], under
![]() $\mathrm{PFA}$
, there are stationarily many internally club guessing models, and by a theorem due to Cox and Krueger [Reference Cox and Krueger4], this consequence of
$\mathrm{PFA}$
, there are stationarily many internally club guessing models, and by a theorem due to Cox and Krueger [Reference Cox and Krueger4], this consequence of
![]() $\mathrm{PFA}$
is consistent with arbitrarily large continuum. Thus essentially, the fact that
$\mathrm{PFA}$
is consistent with arbitrarily large continuum. Thus essentially, the fact that
![]() $2^{\aleph _0}=\aleph _2$
holds under
$2^{\aleph _0}=\aleph _2$
holds under
![]() $\mathrm{PFA}$
does not play a role in our result and proofs.
$\mathrm{PFA}$
does not play a role in our result and proofs.
We shall also answer the second question above consistently in the affirmative, for trees of height
![]() $\kappa ^{++}$
without cofinal branches, in our forthcoming paper [Reference Mohammadpour16], which in particular includes a proof of the following theorem.
$\kappa ^{++}$
without cofinal branches, in our forthcoming paper [Reference Mohammadpour16], which in particular includes a proof of the following theorem.
Theorem 1.2 [Reference Mohammadpour16].
Assume
![]() $\kappa $
is a regular cardinal, and that
$\kappa $
is a regular cardinal, and that
![]() $\lambda>\kappa $
is a supercompact cardinal. Then in generic extensions by some
$\lambda>\kappa $
is a supercompact cardinal. Then in generic extensions by some
![]() $<\!\kappa $
-closed forcing notion,
$<\!\kappa $
-closed forcing notion,
![]() $\kappa ^{<\kappa }=\kappa $
,
$\kappa ^{<\kappa }=\kappa $
,
![]() $2^{\kappa }=\lambda =\kappa ^{++}$
, and every tree of height
$2^{\kappa }=\lambda =\kappa ^{++}$
, and every tree of height
![]() $\kappa ^{++}$
without cofinal branches is specialisable via some
$\kappa ^{++}$
without cofinal branches is specialisable via some
![]() $<\!\kappa $
-closed forcing which preserves
$<\!\kappa $
-closed forcing which preserves
![]() $\kappa ^+$
and
$\kappa ^+$
and
![]() $\kappa ^{++}$
.
$\kappa ^{++}$
.
Our paper includes four additional sections. We give the preliminaries in Section 2. Section 3 is devoted to the introduction and the basic properties of forcing with pure side conditions. We shall introduce our main forcing and state its basic properties in Section 4. Finally, we establish our main result in Section 5.
2 Preliminaries
We shall follow standard conventions and notation, but let us recall some of the most important ones. In this paper, by
![]() $p\leq q$
in a forcing ordering
$p\leq q$
in a forcing ordering
![]() $\leq $
, we mean p is stronger than q; for a cardinal
$\leq $
, we mean p is stronger than q; for a cardinal
![]() $\theta $
,
$\theta $
,
![]() $H_\theta $
denotes the collection of sets whose hereditary size is less than
$H_\theta $
denotes the collection of sets whose hereditary size is less than
![]() $\theta $
; for a set X, we let
$\theta $
; for a set X, we let
![]() $\mathcal P(X)$
denote the power-set of X, and if
$\mathcal P(X)$
denote the power-set of X, and if
![]() $\kappa $
is a cardinal, we let
$\kappa $
is a cardinal, we let
![]() $\mathcal P_\kappa (X):= \{A\in \mathcal P(X):|A|<\kappa \}$
; recall that a set
$\mathcal P_\kappa (X):= \{A\in \mathcal P(X):|A|<\kappa \}$
; recall that a set
![]() $\mathcal S\subseteq \mathcal P_\kappa (H_\theta )$
is stationary, if for every function
$\mathcal S\subseteq \mathcal P_\kappa (H_\theta )$
is stationary, if for every function
![]() $F:\mathcal P_{\aleph _0}(H_\theta )\rightarrow \mathcal P_\kappa (H_\theta )$
, there is
$F:\mathcal P_{\aleph _0}(H_\theta )\rightarrow \mathcal P_\kappa (H_\theta )$
, there is
![]() $M\prec H_\theta $
in
$M\prec H_\theta $
in
![]() $\mathcal S$
with
$\mathcal S$
with
![]() $M\cap \kappa \in \kappa $
such that M is closed under F.
$M\cap \kappa \in \kappa $
such that M is closed under F.
2.1 Trees
Let us recall the definition of a tree and some related concepts.
Definition 2.1. A tree is a partially ordered set
![]() $(T,<_T)$
such that for every
$(T,<_T)$
such that for every
![]() $t\in T$
,
$t\in T$
,
![]() $b_t:= \{s\in T: s<_T t\}$
is well ordered with respect to
$b_t:= \{s\in T: s<_T t\}$
is well ordered with respect to
![]() $<_T$
.
$<_T$
.
Definition 2.2. Suppose
![]() $T=(T,<_T)$
is a tree.
$T=(T,<_T)$
is a tree.
-
(1) For every
 $t\in T$
, the height of t, denoted by
$t\in T$
, the height of t, denoted by
 ${\mathrm {ht}}_T(t)$
, is the order type of
${\mathrm {ht}}_T(t)$
, is the order type of
 $b_t$
.
$b_t$
. -
(2) The height of T, denoted by
 ${\mathrm {ht}}(T)$
, is
${\mathrm {ht}}(T)$
, is
 ${\mathrm {sup}}\{{\mathrm {ht}}_T(t)+1:t\in T\}$
.
${\mathrm {sup}}\{{\mathrm {ht}}_T(t)+1:t\in T\}$
. -
(3) For every
 $\alpha \leq {\mathrm {ht}}(T)$
,
$\alpha \leq {\mathrm {ht}}(T)$
,
 $T_{\alpha }$
denotes the set of nodes of height
$T_{\alpha }$
denotes the set of nodes of height
 $\alpha $
.
$\alpha $
.
 $T_{\leq \alpha }$
and
$T_{\leq \alpha }$
and
 $T_{<\alpha }$
have the obvious meanings. In particular,
$T_{<\alpha }$
have the obvious meanings. In particular,
 $T=T_{<{\mathrm {ht}}(T)}$
and
$T=T_{<{\mathrm {ht}}(T)}$
and
 $T_{{\mathrm {ht}}(T)}=\varnothing $
.
$T_{{\mathrm {ht}}(T)}=\varnothing $
. -
(4) A set
 $b\subseteq T$
is called a branch through T if
$b\subseteq T$
is called a branch through T if
 $(b,<_T)$
is a downward-closed and linearly ordered set. A branch is a cofinal branch if its order type is the height of T.
$(b,<_T)$
is a downward-closed and linearly ordered set. A branch is a cofinal branch if its order type is the height of T. -
(5) T is called Hausdorff if for every limit ordinal
 $\alpha (\alpha =0$
is allowed
$\alpha (\alpha =0$
is allowed
 $)$
, and every
$)$
, and every
 $t\neq s$
in
$t\neq s$
in
 $T_\alpha $
, we have
$T_\alpha $
, we have
 $b_t\neq b_s$
.
$b_t\neq b_s$
. -
(6) For every
 $t\in T$
, we let
$t\in T$
, we let
 $\overline {b}_t$
denotes
$\overline {b}_t$
denotes
 $\{s\in T: s\leq _T t\}$
.
$\{s\in T: s\leq _T t\}$
.
Observe that a Hausdorff tree is rooted, i.e., it has a unique minimal point.
Definition 2.3. Suppose
![]() $\kappa $
is an infinite cardinal. A tree
$\kappa $
is an infinite cardinal. A tree
![]() $(T,<_T)$
of height
$(T,<_T)$
of height
![]() $\kappa ^+$
is called special if there is a specialising function
$\kappa ^+$
is called special if there is a specialising function
![]() $f:T\rightarrow \kappa $
, i.e., if
$f:T\rightarrow \kappa $
, i.e., if
![]() $s<_T t$
, then
$s<_T t$
, then
![]() $f(s)\neq f(t)$
.
$f(s)\neq f(t)$
.
Definition 2.4. Suppose that
![]() $\lambda \leq \kappa $
are infinite regular cardinals. Assume that T is a tree of height
$\lambda \leq \kappa $
are infinite regular cardinals. Assume that T is a tree of height
![]() $\kappa ^+$
. Let
$\kappa ^+$
. Let
![]() $\mathbb S_{\lambda }(T)$
denote the forcing notion consisting of partial specialising functions, of size less than
$\mathbb S_{\lambda }(T)$
denote the forcing notion consisting of partial specialising functions, of size less than
![]() $\lambda $
, ordered by reversed inclusion, that is
$\lambda $
, ordered by reversed inclusion, that is
![]() $f\in \mathbb S_{\lambda }(T)$
is a partial function from T to
$f\in \mathbb S_{\lambda }(T)$
is a partial function from T to
![]() $\kappa $
such that if
$\kappa $
such that if
![]() $s,t\in {\mathrm {dom}}(f)$
are comparable in T, then
$s,t\in {\mathrm {dom}}(f)$
are comparable in T, then
![]() $f(t)\neq f(s)$
.
$f(t)\neq f(s)$
.
Lemma 2.5. In order to specialise a tree
![]() $T ($
of height
$T ($
of height
![]() $\kappa ^+$
, for some infinite cardinal
$\kappa ^+$
, for some infinite cardinal
![]() $\kappa )$
, one may assume, without loss of generality, that T is a Hausdorff tree.
$\kappa )$
, one may assume, without loss of generality, that T is a Hausdorff tree.
Proof Recall that a function
![]() $f:T_1\rightarrow T_2$
between two trees is called a weak embedding if f respects the strict orders. It is easily seen that if
$f:T_1\rightarrow T_2$
between two trees is called a weak embedding if f respects the strict orders. It is easily seen that if
![]() $T_1$
weakly embeds into
$T_1$
weakly embeds into
![]() $T_2$
and
$T_2$
and
![]() $T_2$
is special, then
$T_2$
is special, then
![]() $T_1$
is special, as the inverse image of an antichain in
$T_1$
is special, as the inverse image of an antichain in
![]() $T_2$
under a weak embedding is an antichain in
$T_2$
under a weak embedding is an antichain in
![]() $T_1$
. Thus to prove the lemma, it is enough to show that there is a weak embedding from T into a Hausdorff tree
$T_1$
. Thus to prove the lemma, it is enough to show that there is a weak embedding from T into a Hausdorff tree
![]() $T^*$
of the same height as T.
$T^*$
of the same height as T.
Let
![]() $T^*$
be the set of all non cofinal branches through T. Then,
$T^*$
be the set of all non cofinal branches through T. Then,
![]() $(T^*,\subset )$
is a tree of the same height as T. Note that
$(T^*,\subset )$
is a tree of the same height as T. Note that
![]() $\varnothing $
is the root of
$\varnothing $
is the root of
![]() $T^*$
. Moreover, if
$T^*$
. Moreover, if
![]() $a\in T^*$
, then the order type of
$a\in T^*$
, then the order type of
![]() $(a,<_T)$
is exactly
$(a,<_T)$
is exactly
![]() ${\mathrm {ht}}_{T^*}(a)$
. Suppose that
${\mathrm {ht}}_{T^*}(a)$
. Suppose that
![]() $\alpha $
is a nonzero limit ordinal and
$\alpha $
is a nonzero limit ordinal and
![]() $a, a'\in T^*_\alpha $
with
$a, a'\in T^*_\alpha $
with
![]() $b_a=b_{a'}$
. We claim that
$b_a=b_{a'}$
. We claim that
![]() $a=a'$
. Let
$a=a'$
. Let
![]() $t\in a$
. Since the order type of a is a limit ordinal, there is
$t\in a$
. Since the order type of a is a limit ordinal, there is
![]() $s\in a$
with
$s\in a$
with
![]() $t<_T s$
. Let
$t<_T s$
. Let
![]() $x=\{u\in T: u<_T s\}$
. Now
$x=\{u\in T: u<_T s\}$
. Now
![]() $x <_{T^*}a$
. Thus
$x <_{T^*}a$
. Thus
![]() $x\in b_{a}=b_{a'}$
. Then
$x\in b_{a}=b_{a'}$
. Then
![]() $t\in x\subseteq a'$
. So we have
$t\in x\subseteq a'$
. So we have
![]() $a\subseteq a'$
. Similarly, we have
$a\subseteq a'$
. Similarly, we have
![]() $a'\subseteq a$
, and therefore,
$a'\subseteq a$
, and therefore,
![]() $a=a'$
. Now, let
$a=a'$
. Now, let
![]() $f:T\rightarrow T^*$
be defined by
$f:T\rightarrow T^*$
be defined by
![]() $f(t)=b_t$
. If
$f(t)=b_t$
. If
![]() $s<t$
, then
$s<t$
, then
![]() $b_s$
is a proper subset of
$b_s$
is a proper subset of
![]() $b_t$
, and hence f is a weak embedding.
$b_t$
, and hence f is a weak embedding.
2.2 Strong properness and the approximation property
Recall that if
![]() $M\prec H_\theta $
contains a forcing
$M\prec H_\theta $
contains a forcing
![]() $\mathbb P$
, then a condition
$\mathbb P$
, then a condition
![]() $p\in \mathbb P$
is called
$p\in \mathbb P$
is called
![]() $(M,\mathbb P)$
-generic if for every dense subset D of
$(M,\mathbb P)$
-generic if for every dense subset D of
![]() $\mathbb P$
in M,
$\mathbb P$
in M,
![]() $D\cap M$
is pre-dense below p.
$D\cap M$
is pre-dense below p.
Definition 2.6. Assume that
![]() $\mathbb P$
is a forcing, and
$\mathbb P$
is a forcing, and
![]() $\theta $
is a sufficiently large regular cardinal. Suppose
$\theta $
is a sufficiently large regular cardinal. Suppose
![]() $\mathcal S\subseteq \mathcal P_\kappa (H_\theta )$
consists of elementary submodels. Then,
$\mathcal S\subseteq \mathcal P_\kappa (H_\theta )$
consists of elementary submodels. Then,
![]() $\mathbb P$
is said to be proper for
$\mathbb P$
is said to be proper for
![]() $\mathcal S$
, if for every
$\mathcal S$
, if for every
![]() $M\in \mathcal S$
and every
$M\in \mathcal S$
and every
![]() $p\in \mathbb P\cap M$
, there is an
$p\in \mathbb P\cap M$
, there is an
![]() $(M,\mathbb P)$
-generic condition
$(M,\mathbb P)$
-generic condition
![]() $q\leq p$
.
$q\leq p$
.
Lemma 2.7. Let
![]() $\kappa $
be a regular cardinal. Assume that
$\kappa $
be a regular cardinal. Assume that
![]() $\mathbb P$
is a forcing, and
$\mathbb P$
is a forcing, and
![]() $\theta>\kappa $
is a sufficiently large regular cardinal. Suppose
$\theta>\kappa $
is a sufficiently large regular cardinal. Suppose
![]() $\mathcal S\subseteq \mathcal P_\kappa (H_\theta )$
is a stationary set of elementary submodels. If
$\mathcal S\subseteq \mathcal P_\kappa (H_\theta )$
is a stationary set of elementary submodels. If
![]() $\mathbb P$
is proper for
$\mathbb P$
is proper for
![]() $\mathcal S$
, then
$\mathcal S$
, then
![]() $\mathbb P$
preserves the regularity of
$\mathbb P$
preserves the regularity of
![]() $\kappa $
.
$\kappa $
.
Proof Let
![]() $\gamma <\kappa $
be an ordinal. Assume towards a contraction that some
$\gamma <\kappa $
be an ordinal. Assume towards a contraction that some
![]() $p\in \mathbb P$
forces that
$p\in \mathbb P$
forces that
![]() $\dot {f}$
is an unbounded function from
$\dot {f}$
is an unbounded function from
![]() $\gamma $
into
$\gamma $
into
![]() $\kappa $
. Pick
$\kappa $
. Pick
![]() $M\in \mathcal S$
such that
$M\in \mathcal S$
such that
![]() $\gamma ,\kappa ,p,\dot {f}\in M$
. Let
$\gamma ,\kappa ,p,\dot {f}\in M$
. Let
![]() $q\leq p$
be an
$q\leq p$
be an
![]() $(M,\mathbb P)$
-generic condition. Note that
$(M,\mathbb P)$
-generic condition. Note that
![]() $\gamma \subseteq M$
and
$\gamma \subseteq M$
and
![]() $M\cap \kappa \in \kappa $
. By our assumption, we can find a condition
$M\cap \kappa \in \kappa $
. By our assumption, we can find a condition
![]() $q'\leq q$
, and ordinal
$q'\leq q$
, and ordinal
![]() $\zeta <\gamma $
and an ordinal
$\zeta <\gamma $
and an ordinal
![]() $\delta \geq M\cap \kappa $
such that,
$\delta \geq M\cap \kappa $
such that,
![]() $q'\Vdash " \dot {f}(\zeta )=\delta ."$
Set
$q'\Vdash " \dot {f}(\zeta )=\delta ."$
Set
Then D is a dense subset of
![]() $\mathbb P$
and belongs to M. Since q is
$\mathbb P$
and belongs to M. Since q is
![]() $(M,\mathbb P)$
-generic, there is
$(M,\mathbb P)$
-generic, there is
![]() $r\in D\cap M$
such that
$r\in D\cap M$
such that
![]() $r|| q'$
. Thus r is compatible with p, and hence, by elementarity, there is
$r|| q'$
. Thus r is compatible with p, and hence, by elementarity, there is
![]() $\delta '\in M$
such that
$\delta '\in M$
such that
![]() $r\Vdash "\delta '= \dot {f}(\zeta )."$
Now if s is a common extension of
$r\Vdash "\delta '= \dot {f}(\zeta )."$
Now if s is a common extension of
![]() $q'$
and r, we have
$q'$
and r, we have
![]() $s\Vdash "\delta '=\delta ."$
Thus
$s\Vdash "\delta '=\delta ."$
Thus
![]() $\delta '=\delta \in M\cap \kappa $
, a contradiction!
$\delta '=\delta \in M\cap \kappa $
, a contradiction!
Let us now recall the following closely related definitions from [Reference Hamkins9, Reference Mitchell14], respectively.
Definition 2.8 (Strong properness).
Suppose
![]() $\mathbb P$
is a forcing notion.
$\mathbb P$
is a forcing notion.
-
(1) Let X be a set. A condition
 $p\in \mathbb P$
is said to be strongly
$p\in \mathbb P$
is said to be strongly
 $(X,\mathbb P)$
-generic, if for every
$(X,\mathbb P)$
-generic, if for every
 $q\leq p$
, there is some
$q\leq p$
, there is some
 $q\! \upharpoonright \!_X\in X\cap \mathbb P$
such that every condition
$q\! \upharpoonright \!_X\in X\cap \mathbb P$
such that every condition
 $r\in \mathbb P\cap X$
extending
$r\in \mathbb P\cap X$
extending
 $q\! \upharpoonright \!_X$
is compatible with q.
$q\! \upharpoonright \!_X$
is compatible with q. -
(2) For a collection of sets
 $\mathcal S$
, we say
$\mathcal S$
, we say
 $\mathbb P$
is strongly proper for
$\mathbb P$
is strongly proper for
 $\mathcal S$
, if for every
$\mathcal S$
, if for every
 $X\in \mathcal S$
and every
$X\in \mathcal S$
and every
 $p\in \mathbb P\cap X$
, there is a strongly
$p\in \mathbb P\cap X$
, there is a strongly
 $(X,\mathbb P)$
-generic condition extending p.
$(X,\mathbb P)$
-generic condition extending p.
Remark 2.9. It is easily seen that if p is strongly
![]() $(X,\mathbb P)$
-generic and
$(X,\mathbb P)$
-generic and
![]() $M\prec H_\theta $
is such that
$M\prec H_\theta $
is such that
![]() $M\cap \mathbb P=X\cap \mathbb P$
, then p is strongly
$M\cap \mathbb P=X\cap \mathbb P$
, then p is strongly
![]() $(M,\mathbb P)$
-generic, and hence
$(M,\mathbb P)$
-generic, and hence
![]() $(M,\mathbb P)$
-generic. It turns out that if a forcing notion is strongly proper for some stationary set
$(M,\mathbb P)$
-generic. It turns out that if a forcing notion is strongly proper for some stationary set
![]() $\mathcal S\subseteq \mathcal P_{\kappa }(H_\theta )$
, then
$\mathcal S\subseteq \mathcal P_{\kappa }(H_\theta )$
, then
![]() $\mathbb P$
is
$\mathbb P$
is
![]() $\mathcal S$
-proper, and hence it preserves
$\mathcal S$
-proper, and hence it preserves
![]() $\kappa $
, by Lemma 2.7.
$\kappa $
, by Lemma 2.7.
Definition 2.10 (
 $\kappa $
-approximation property).
$\kappa $
-approximation property).
Suppose
![]() $\kappa $
is an uncountable regular cardinal. A forcing notion
$\kappa $
is an uncountable regular cardinal. A forcing notion
![]() $\mathbb P$
has the
$\mathbb P$
has the
![]() $\kappa $
-approximation property, if for every V-generic filter G, and every
$\kappa $
-approximation property, if for every V-generic filter G, and every
![]() $A\in V[G]$
with
$A\in V[G]$
with
![]() $A\subseteq V$
, the following are equivalent.
$A\subseteq V$
, the following are equivalent.
-
(1)
 $A\in V$
.
$A\in V$
. -
(2) For every
 $a\in V$
with
$a\in V$
with
 $|a|^V<\kappa $
, we have
$|a|^V<\kappa $
, we have
 $a\cap A\in V$
.
$a\cap A\in V$
.
Note that it is well-known that if a forcing notion is strongly proper for sufficiently many models in
![]() $\mathcal P_\kappa (H_\theta )$
, then it has the
$\mathcal P_\kappa (H_\theta )$
, then it has the
![]() $\kappa $
-approximation property (see [Reference Mitchell15]).
$\kappa $
-approximation property (see [Reference Mitchell15]).
2.3 Guessing models
For a set M, we say that a set
![]() $x\subseteq M$
is bounded in M if there is
$x\subseteq M$
is bounded in M if there is
![]() $y\in M$
such that
$y\in M$
such that
![]() $x\subseteq y$
. Recall that an elementary submodel M of
$x\subseteq y$
. Recall that an elementary submodel M of
![]() $H_\theta $
is called an internally club model (or
$H_\theta $
is called an internally club model (or
![]() $\mathrm{IC}$
-model for short) if it is the union of a continuous
$\mathrm{IC}$
-model for short) if it is the union of a continuous
![]() $\in $
-sequence
$\in $
-sequence
![]() $\langle M_\alpha :\alpha <\omega _1\rangle $
of countable elementary submodels of
$\langle M_\alpha :\alpha <\omega _1\rangle $
of countable elementary submodels of
![]() $H_\theta $
.
$H_\theta $
.
Notation 2.11. For a model
![]() $M\prec H_\theta $
, let
$M\prec H_\theta $
, let
![]() $\kappa _M=\min \{\alpha \in M\cap \theta : \alpha \nsubseteq M\}$
. Let
$\kappa _M=\min \{\alpha \in M\cap \theta : \alpha \nsubseteq M\}$
. Let
![]() $\kappa _M$
be undefined if the above supremum does not exist.
$\kappa _M$
be undefined if the above supremum does not exist.
Definition 2.12. Suppose M is a set. A set x is guessed in M if there is some
![]() $x^*\in M$
such that
$x^*\in M$
such that
![]() $x^*\cap M=x\cap M$
.
$x^*\cap M=x\cap M$
.
We now recall the definition of a guessing model from [Reference Viale and Weiß25].
Definition 2.13 (
 $\gamma $
-guessing model).
$\gamma $
-guessing model).
Assume that
![]() $\theta $
is an uncountable regular cardinal. Let
$\theta $
is an uncountable regular cardinal. Let
![]() $M\prec H_\theta $
. Suppose that
$M\prec H_\theta $
. Suppose that
![]() $\gamma \in M$
is a regular cardinal with
$\gamma \in M$
is a regular cardinal with
![]() $\gamma \leq \kappa _M$
. Then M is said to be a
$\gamma \leq \kappa _M$
. Then M is said to be a
![]() $\gamma $
-guessing model if the following are equivalent for any x which is bounded in M.
$\gamma $
-guessing model if the following are equivalent for any x which is bounded in M.
-
(1) x is
 $\gamma $
-approximated in M, i.e.,
$\gamma $
-approximated in M, i.e.,
 $x\cap a \in M$
, for all
$x\cap a \in M$
, for all
 $a\in M$
of size less than
$a\in M$
of size less than
 $\gamma $
.
$\gamma $
. -
(2) x is guessed in M.
Definition 2.14 (
 ${\mathrm {GM}}^*(\omega _2)$
).
${\mathrm {GM}}^*(\omega _2)$
).
The principle
![]() ${\mathrm {GM}}^*(\omega _2)$
states that for every sufficiently large regular cardinal
${\mathrm {GM}}^*(\omega _2)$
states that for every sufficiently large regular cardinal
![]() $\theta $
, the set of
$\theta $
, the set of
![]() $\omega _1$
-guessing elementary
$\omega _1$
-guessing elementary
![]() $\mathrm{IC}$
-submodels of
$\mathrm{IC}$
-submodels of
![]() $H_\theta $
is stationary in
$H_\theta $
is stationary in
![]() $\mathcal P_{\omega _2}(H_\theta )$
.
$\mathcal P_{\omega _2}(H_\theta )$
.
The above principle is slightly stronger than Weiß’s
![]() $\mathrm{ISP}(\omega _2)$
(see [Reference Weiß26, Reference Weiß27] for more information on
$\mathrm{ISP}(\omega _2)$
(see [Reference Weiß26, Reference Weiß27] for more information on
![]() $\mathrm{ISP}(\omega _2)$
), which is also equivalent to the principle
$\mathrm{ISP}(\omega _2)$
), which is also equivalent to the principle
![]() ${\mathrm {GM}}(\omega _2)$
that states for every sufficiently large regular cardinal
${\mathrm {GM}}(\omega _2)$
that states for every sufficiently large regular cardinal
![]() $\theta $
, the set of
$\theta $
, the set of
![]() $\omega _1$
-guessing elementary submodels of
$\omega _1$
-guessing elementary submodels of
![]() $H_\theta $
is stationary in
$H_\theta $
is stationary in
![]() $\mathcal P_{\omega _2}(H_\theta )$
.
$\mathcal P_{\omega _2}(H_\theta )$
.
Proposition 2.15 (Viale–Weiß [Reference Viale and Weiß25]).
![]() $\mathrm{PFA}$
implies
$\mathrm{PFA}$
implies
![]() ${\mathrm {GM}}^*(\omega _2)$
.
${\mathrm {GM}}^*(\omega _2)$
.
Proof The proposition above was mentioned without proof in [Reference Viale and Weiß25]. A sketch of a proof can be found in [Reference Viale24, Theorem 4.4].
The following lemma plays a crucial role in our later proofs.
Lemma 2.16. Suppose
![]() $\theta $
is an uncountable regular cardinal. Assume that
$\theta $
is an uncountable regular cardinal. Assume that
![]() $M\prec H_\theta $
is countable. Let
$M\prec H_\theta $
is countable. Let
![]() $Z\in M$
a set. Suppose that
$Z\in M$
a set. Suppose that
![]() $z\mapsto f_z$
is a function on
$z\mapsto f_z$
is a function on
![]() $\mathcal P_{\omega _1}(Z)$
in M, where for each
$\mathcal P_{\omega _1}(Z)$
in M, where for each
![]() $z\in \mathcal P_{\omega _1}(Z)$
,
$z\in \mathcal P_{\omega _1}(Z)$
,
![]() $f_z$
is a
$f_z$
is a
![]() $\{0,1\}$
-valued function with
$\{0,1\}$
-valued function with
![]() $z\subseteq {\mathrm {dom}}(f_z)$
. Assume that
$z\subseteq {\mathrm {dom}}(f_z)$
. Assume that
![]() $f:Z\cap M\rightarrow 2$
is a function that is not guessed in M. Suppose that
$f:Z\cap M\rightarrow 2$
is a function that is not guessed in M. Suppose that
![]() $B\in M$
is a cofinal subset of
$B\in M$
is a cofinal subset of
![]() $\mathcal P_{\omega _1}(Z)$
. Then there is
$\mathcal P_{\omega _1}(Z)$
. Then there is
![]() $B^*\in M$
cofinal in B such that for every
$B^*\in M$
cofinal in B such that for every
![]() $z\in B^*$
,
$z\in B^*$
,
![]() $f_z\nsubseteq f$
.
$f_z\nsubseteq f$
.
Proof For each
![]() $\zeta \in Z$
, and
$\zeta \in Z$
, and
![]() $\epsilon =0,1$
, let
$\epsilon =0,1$
, let
Notice that the sequence
belongs to M. We are done if there is some
![]() $\zeta \in Z$
such that both
$\zeta \in Z$
such that both
![]() $A_\zeta ^0$
and
$A_\zeta ^0$
and
![]() $A_\zeta ^1$
are cofinal in B, as then by elementarity one can find such
$A_\zeta ^1$
are cofinal in B, as then by elementarity one can find such
![]() $\zeta \in M\cap Z$
, and then pick
$\zeta \in M\cap Z$
, and then pick
![]() $A_\zeta ^{1-f(\zeta )}$
. Therefore, let us assume that for every
$A_\zeta ^{1-f(\zeta )}$
. Therefore, let us assume that for every
![]() $\zeta \in Z$
, there is an
$\zeta \in Z$
, there is an
![]() $\epsilon \in \{0,1\}$
, which is necessarily unique, such that
$\epsilon \in \{0,1\}$
, which is necessarily unique, such that
![]() $A_\zeta ^\epsilon $
is cofinal in B. Now, define h on
$A_\zeta ^\epsilon $
is cofinal in B. Now, define h on
![]() $ Z$
by letting
$ Z$
by letting
![]() $h(\zeta )$
be
$h(\zeta )$
be
![]() $\epsilon $
if and only if
$\epsilon $
if and only if
![]() $A_\zeta ^\epsilon $
is cofinal is B. Clearly h is in M, but then
$A_\zeta ^\epsilon $
is cofinal is B. Clearly h is in M, but then
![]() $h\! \upharpoonright \!_{M}\neq f$
since f is not guessed in M. Thus, there exists
$h\! \upharpoonright \!_{M}\neq f$
since f is not guessed in M. Thus, there exists
![]() $\zeta \in M\cap Z$
such that
$\zeta \in M\cap Z$
such that
![]() $h(\zeta )\neq f(\zeta )$
, but it then implies that
$h(\zeta )\neq f(\zeta )$
, but it then implies that
![]() $A_\zeta ^{1-f(\zeta )}$
is cofinal in B and belongs to M. Let
$A_\zeta ^{1-f(\zeta )}$
is cofinal in B and belongs to M. Let
![]() $B^*$
be
$B^*$
be
![]() $A_\zeta ^{1-f(\zeta )}$
. Now if
$A_\zeta ^{1-f(\zeta )}$
. Now if
![]() $z\in B^*$
,
$z\in B^*$
,
![]() $f_z\nsubseteq f$
.
$f_z\nsubseteq f$
.
3 Pure side conditions
This section is devoted to the forcing with pure side conditions. Such a forcing notion, as well as a finite-support iteration of proper forcings with side conditions, was introduced by Neeman in [Reference Neeman17]. However, we cannot use Neeman forcing directly, since we shall work with non-transitive models. Instead, we follow Veličković’s presentation [Reference Veličković and Venturi23] of Neeman forcing with finite
![]() $\in $
-chains of models of two types, where both types of models are non-transitive. We shall sketch some proofs of the necessary facts in this section, and we encourage the reader to consult [Reference Veličković and Venturi23] for more details.
$\in $
-chains of models of two types, where both types of models are non-transitive. We shall sketch some proofs of the necessary facts in this section, and we encourage the reader to consult [Reference Veličković and Venturi23] for more details.
Fix an uncountable regular cardinal
![]() $\theta $
, and let
$\theta $
, and let
![]() $x\in H_\theta $
be arbitrary. We let
$x\in H_\theta $
be arbitrary. We let
![]() $\mathcal {E}^0:= \mathcal E^0(x)$
denote the collection of all countable elementary submodels of
$\mathcal {E}^0:= \mathcal E^0(x)$
denote the collection of all countable elementary submodels of
![]() $(H_{\theta },\in ,x)$
, and let
$(H_{\theta },\in ,x)$
, and let
![]() $\mathcal {E}^1:= \mathcal E^1(x)$
denote a collection of elementary
$\mathcal {E}^1:= \mathcal E^1(x)$
denote a collection of elementary
![]() $\mathrm{IC}$
-submodels of
$\mathrm{IC}$
-submodels of
![]() $(H_{\theta },\in ,x)$
. Note that for every
$(H_{\theta },\in ,x)$
. Note that for every
![]() $N\in \mathcal E^1$
and every
$N\in \mathcal E^1$
and every
![]() $M\in \mathcal E^0$
, if
$M\in \mathcal E^0$
, if
![]() $N\in M$
, then
$N\in M$
, then
![]() $N\cap M\in \mathcal E^0\cap N$
.
$N\cap M\in \mathcal E^0\cap N$
.
Definition 3.1. Assume that
![]() $\mathcal M\subseteq \mathcal {E}^0\cup \mathcal {E}^1$
.
$\mathcal M\subseteq \mathcal {E}^0\cup \mathcal {E}^1$
.
-
(1) Suppose that
 $M,N\in \mathcal M$
. We say M is below N in
$M,N\in \mathcal M$
. We say M is below N in
 $\mathcal M$
, or equivalently N is above M in
$\mathcal M$
, or equivalently N is above M in
 $\mathcal M$
, and denote this by
$\mathcal M$
, and denote this by
 $M\in ^* N$
if there is a finite set
$M\in ^* N$
if there is a finite set
 $\{M_i:i\leq n\}\subseteq \mathcal M$
such that
$\{M_i:i\leq n\}\subseteq \mathcal M$
such that
 $M=M_0\in \dots \in M_n=N$
.
$M=M_0\in \dots \in M_n=N$
. -
(2) We say
 $\mathcal M$
is an
$\mathcal M$
is an
 $\in $
-chain, if for every distinct
$\in $
-chain, if for every distinct
 $M,N\in \mathcal M$
, either
$M,N\in \mathcal M$
, either
 $M\in ^* N$
in
$M\in ^* N$
in
 $\mathcal M$
or
$\mathcal M$
or
 $N\in ^* M$
in
$N\in ^* M$
in
 $\mathcal M$
.
$\mathcal M$
. -
(3) We say
 $\mathcal M$
is closed under intersections if for every
$\mathcal M$
is closed under intersections if for every
 $M\in \mathcal M\cap \mathcal {E}^0 $
, and every
$M\in \mathcal M\cap \mathcal {E}^0 $
, and every
 $N\in M\cap \mathcal M$
,
$N\in M\cap \mathcal M$
,
 $N\cap M$
belongs to
$N\cap M$
belongs to
 $\mathcal M$
.
$\mathcal M$
. -
(4) If
 $M,N\in \mathcal M\cup \{\varnothing , H_\theta \}$
, then by
$M,N\in \mathcal M\cup \{\varnothing , H_\theta \}$
, then by
 $(M,N)_{\mathcal {M}}$
, and intervals of other types, we mean that the interval is considered in the linearly ordered structure
$(M,N)_{\mathcal {M}}$
, and intervals of other types, we mean that the interval is considered in the linearly ordered structure
 $(\mathcal M,\in ^*)$
, e.g.,
$(\mathcal M,\in ^*)$
, e.g.,
 $(M,N)_{\mathcal M}=\{P\in \mathcal M: M\in ^* P\in ^* N\}$
.
$(M,N)_{\mathcal M}=\{P\in \mathcal M: M\in ^* P\in ^* N\}$
.
It is easily seen that if
![]() $M\in ^* N$
holds in an
$M\in ^* N$
holds in an
![]() $\in $
-chain
$\in $
-chain
![]() $\mathcal M$
, and that
$\mathcal M$
, and that
![]() $N\in \mathcal E^1$
, then
$N\in \mathcal E^1$
, then
![]() $M\in N$
. We simply write
$M\in N$
. We simply write
![]() $M\in ^* N$
, whenever
$M\in ^* N$
, whenever
![]() $\mathcal M$
is clear from the context.
$\mathcal M$
is clear from the context.
Remark 3.2. If
![]() $M,N\in \mathcal E^0$
, then
$M,N\in \mathcal E^0$
, then
![]() $M\subseteq N$
if and only if there is no
$M\subseteq N$
if and only if there is no
![]() $P\in \mathcal E^1\cap \mathcal M$
with
$P\in \mathcal E^1\cap \mathcal M$
with
![]() $P\cap N \in ^* M\in ^* P\in N$
.
$P\cap N \in ^* M\in ^* P\in N$
.
Definition 3.3 (Forcing with pure side conditions).
We let
![]() $\mathbb M(\mathcal {E}^0,\mathcal {E}^1)$
denote the collection of
$\mathbb M(\mathcal {E}^0,\mathcal {E}^1)$
denote the collection of
![]() $\in $
-chains
$\in $
-chains
![]() $p=\mathcal M_p\subseteq \mathcal {E}^0\cup \mathcal {E}^1$
which are closed under intersections. We consider
$p=\mathcal M_p\subseteq \mathcal {E}^0\cup \mathcal {E}^1$
which are closed under intersections. We consider
![]() $\mathbb M(\mathcal {E}^0,\mathcal {E}^1)$
as a notion of forcing ordered by reversed inclusion.
$\mathbb M(\mathcal {E}^0,\mathcal {E}^1)$
as a notion of forcing ordered by reversed inclusion.
We simply denote
![]() $\mathbb M(\mathcal {E}^0,\mathcal {E}^1)$
by
$\mathbb M(\mathcal {E}^0,\mathcal {E}^1)$
by
![]() $\mathbb M$
whenever there are no confusions. For a condition
$\mathbb M$
whenever there are no confusions. For a condition
![]() $p\in \mathbb M$
, we let also
$p\in \mathbb M$
, we let also
![]() $\mathcal {E}^0_p$
and
$\mathcal {E}^0_p$
and
![]() $\mathcal {E}^1_p$
denote
$\mathcal {E}^1_p$
denote
![]() $\mathcal M_p\cap \mathcal {E}^0$
and
$\mathcal M_p\cap \mathcal {E}^0$
and
![]() $\mathcal M_p\cap \mathcal {E}^1$
, respectively. If
$\mathcal M_p\cap \mathcal {E}^1$
, respectively. If
![]() $p=(\mathcal M_p,\dots )$
is a condition in a forcing notion with
$p=(\mathcal M_p,\dots )$
is a condition in a forcing notion with
![]() $\mathcal M_p\in \mathbb M$
, we denote the interval
$\mathcal M_p\in \mathbb M$
, we denote the interval
![]() $(M,N)_{\mathcal M_p}$
by
$(M,N)_{\mathcal M_p}$
by
![]() $(M,N)_p$
; such an agreement applies to other types of intervals as well.
$(M,N)_p$
; such an agreement applies to other types of intervals as well.
Definition 3.4. Let
![]() $M\in \mathcal {E}^0\cup \mathcal {E}^1$
, and suppose that
$M\in \mathcal {E}^0\cup \mathcal {E}^1$
, and suppose that
![]() $p\in \mathbb M\cap M$
. We let
$p\in \mathbb M\cap M$
. We let
![]() $p^M$
denote the closure of
$p^M$
denote the closure of
![]() $\mathcal M\cup \{M\}$
under intersections.
$\mathcal M\cup \{M\}$
under intersections.
The following is easy and we leave the proof to the reader.
Fact 3.5 [Reference Veličković and Venturi23, Lemma 1.8].
Let
![]() $M\in \mathcal {E}^0\cup \mathcal {E}^1$
, and suppose that
$M\in \mathcal {E}^0\cup \mathcal {E}^1$
, and suppose that
![]() $p\in \mathbb M\cap M$
.
$p\in \mathbb M\cap M$
.
-
(1) If
 $M\in \mathcal {E}^1$
, then
$M\in \mathcal {E}^1$
, then
 $p^M=\mathcal M\cup \{M\}$
.
$p^M=\mathcal M\cup \{M\}$
. -
(2) If
 $M\in \mathcal {E}^0$
, then
$M\in \mathcal {E}^0$
, then
 $p^M=\mathcal M\cup \{M\}\cup \{N\cap M: N\in \mathcal {E}^1_p\}$
.
$p^M=\mathcal M\cup \{M\}\cup \{N\cap M: N\in \mathcal {E}^1_p\}$
. -
(3)
 $p^M$
is a condition in
$p^M$
is a condition in
 $\mathbb M$
and extends p.
$\mathbb M$
and extends p.
Definition 3.6. For a condition
![]() $p\in \mathbb M$
and a model
$p\in \mathbb M$
and a model
![]() $M\in \mathcal M_p$
, let
$M\in \mathcal M_p$
, let
![]() $p\! \upharpoonright \!_M:= \mathcal M_p\cap M$
.
$p\! \upharpoonright \!_M:= \mathcal M_p\cap M$
.
Notice that
![]() $p\! \upharpoonright \!_M$
is in M, as it is a finite subset of M. If M is in
$p\! \upharpoonright \!_M$
is in M, as it is a finite subset of M. If M is in
![]() $\mathcal {E}^1$
, then
$\mathcal {E}^1$
, then
![]() $p\! \upharpoonright \!_M$
is the interval
$p\! \upharpoonright \!_M$
is the interval
![]() $(\varnothing ,M)_p$
that is an
$(\varnothing ,M)_p$
that is an
![]() $\in $
-chain, but if M is countable, then it is a union of intervals.
$\in $
-chain, but if M is countable, then it is a union of intervals.
Fact 3.7 [Reference Veličković and Venturi23, Fact 1.7].
Suppose that
![]() $p\in \mathbb M$
. Assume that
$p\in \mathbb M$
. Assume that
![]() $M\in \mathcal M_p$
is countable. Then
$M\in \mathcal M_p$
is countable. Then
Proof Let
![]() $P\in \mathcal M_{p}\! \upharpoonright \!_M$
. Thus
$P\in \mathcal M_{p}\! \upharpoonright \!_M$
. Thus
![]() $P\in M$
, which in turn implies that P does not belong to the interval
$P\in M$
, which in turn implies that P does not belong to the interval
![]() $[M,H_\theta )_p$
. Now, let
$[M,H_\theta )_p$
. Now, let
![]() $N\in \mathcal E^1_p\cap M$
. If
$N\in \mathcal E^1_p\cap M$
. If
![]() $N\in ^* P$
or
$N\in ^* P$
or
![]() $N=P$
, then P does not belong to the interval
$N=P$
, then P does not belong to the interval
![]() $[N\cap M,N)_p$
. Suppose
$[N\cap M,N)_p$
. Suppose
![]() $P\in ^* N$
, then
$P\in ^* N$
, then
![]() $P\in N$
, and hence
$P\in N$
, and hence
![]() $P\in N\cap M$
, which in turn implies that
$P\in N\cap M$
, which in turn implies that
![]() $P\notin [N\cap M,N)_p$
. Therefore, the LHS is a subset of RHS. To see the other direction, suppose P does not belong to any interval as described in the above equation. In particular,
$P\notin [N\cap M,N)_p$
. Therefore, the LHS is a subset of RHS. To see the other direction, suppose P does not belong to any interval as described in the above equation. In particular,
![]() $P\in ^* M$
. Now, if
$P\in ^* M$
. Now, if
![]() $P\notin M$
, it then means there are some models in
$P\notin M$
, it then means there are some models in
![]() $\mathcal E^1_p\cap (P,M)_p$
. Let N be the least such model. Then,
$\mathcal E^1_p\cap (P,M)_p$
. Let N be the least such model. Then,
![]() $N\cap M\in ^* P$
, since otherwise by the minimality of N, we have
$N\cap M\in ^* P$
, since otherwise by the minimality of N, we have
![]() $P\in N\cap M\subseteq M$
. Thus P belongs to
$P\in N\cap M\subseteq M$
. Thus P belongs to
![]() $[N\cap M,N)_p$
, which is a contradiction.
$[N\cap M,N)_p$
, which is a contradiction.
It is not hard to see that
![]() $p\! \upharpoonright \!_M$
is an
$p\! \upharpoonright \!_M$
is an
![]() $\in $
-chain. Now, the following is immediate.
$\in $
-chain. Now, the following is immediate.
Fact 3.8. For every condition
![]() $p\in \mathbb M$
and
$p\in \mathbb M$
and
![]() $M\in \mathcal M_p$
,
$M\in \mathcal M_p$
,
![]() $p\! \upharpoonright \!_M$
is a condition and
$p\! \upharpoonright \!_M$
is a condition and
![]() $p\leq p\! \upharpoonright \!_M$
.
$p\leq p\! \upharpoonright \!_M$
.
Thus we also have
![]() $\mathcal M_{{p}\upharpoonright _M}=\mathcal M_p\! \upharpoonright \!_M$
! This notational equality will be useful later.
$\mathcal M_{{p}\upharpoonright _M}=\mathcal M_p\! \upharpoonright \!_M$
! This notational equality will be useful later.
Fact 3.9 [Reference Veličković and Venturi23, Fact 1.12].
Suppose that
![]() $p\in \mathbb M$
and
$p\in \mathbb M$
and
![]() $M\in \mathcal {E}^1_p$
. Then every condition
$M\in \mathcal {E}^1_p$
. Then every condition
![]() $q\in M$
extending
$q\in M$
extending
![]() $p\! \upharpoonright \!_M$
is compatible with p.
$p\! \upharpoonright \!_M$
is compatible with p.
Proof Let
![]() $\mathcal M_r=\mathcal M_p\cup \mathcal M_q$
. It is easy to see that
$\mathcal M_r=\mathcal M_p\cup \mathcal M_q$
. It is easy to see that
![]() $\mathcal M_r$
is closed under intersections. To see that it is an
$\mathcal M_r$
is closed under intersections. To see that it is an
![]() $\in $
-chain, suppose that
$\in $
-chain, suppose that
![]() $P\in \mathcal M_p\setminus \mathcal M_q$
and
$P\in \mathcal M_p\setminus \mathcal M_q$
and
![]() $Q\in \mathcal M_q\setminus \mathcal M_p$
. If
$Q\in \mathcal M_q\setminus \mathcal M_p$
. If
![]() $P\neq M$
, we then have
$P\neq M$
, we then have
![]() $Q\in M\in ^* P$
, and if
$Q\in M\in ^* P$
, and if
![]() $P=M$
, then obviously
$P=M$
, then obviously
![]() $Q\in M$
. It is clear that
$Q\in M$
. It is clear that
![]() $r\leq p,q$
.
$r\leq p,q$
.
Remark 3.10. The above condition is the greatest lower bound of p and q, and denoted by
![]() $p\land q$
. Notice that
$p\land q$
. Notice that
Fact 3.11.
![]() $\mathbb M$
is strongly proper for
$\mathbb M$
is strongly proper for
![]() $\mathcal {E}^1$
, and hence if
$\mathcal {E}^1$
, and hence if
![]() $\mathcal {E}^1$
is stationary, then
$\mathcal {E}^1$
is stationary, then
![]() $\mathbb M$
preserves
$\mathbb M$
preserves
![]() $\aleph _2$
.
$\aleph _2$
.
Proof Suppose that
![]() $M\in \mathcal E^1$
. If
$M\in \mathcal E^1$
. If
![]() $p\in M\cap \mathbb M$
, then by Fact 3.5,
$p\in M\cap \mathbb M$
, then by Fact 3.5,
![]() $p^M$
is a condition extending p. Let
$p^M$
is a condition extending p. Let
![]() $q\leq p^M$
, then
$q\leq p^M$
, then
![]() $M\in \mathcal M_q$
. By Fact 3.8,
$M\in \mathcal M_q$
. By Fact 3.8,
![]() $q\! \upharpoonright \!_M$
is a condition in
$q\! \upharpoonright \!_M$
is a condition in
![]() $M\cap \mathbb M$
. Now if
$M\cap \mathbb M$
. Now if
![]() $r\in M\cap \mathbb M$
extends
$r\in M\cap \mathbb M$
extends
![]() $q\! \upharpoonright \!_M$
, then q is compatible with r by Fact 3.9. Thus q is strongly
$q\! \upharpoonright \!_M$
, then q is compatible with r by Fact 3.9. Thus q is strongly
![]() $(M,\mathbb M)$
-generic. By Lemma 2.7 and Remark 2.9,
$(M,\mathbb M)$
-generic. By Lemma 2.7 and Remark 2.9,
![]() $\mathbb P$
perseveres
$\mathbb P$
perseveres
![]() $\aleph _2$
.
$\aleph _2$
.
Lemma 3.12 [Reference Veličković and Venturi23, Lemma 1.12].
Suppose that
![]() $p\in \mathbb M$
. Let
$p\in \mathbb M$
. Let
![]() $M\in \mathcal {E}^0_p$
. Then every condition
$M\in \mathcal {E}^0_p$
. Then every condition
![]() $q\in M$
extending
$q\in M$
extending
![]() $p\! \upharpoonright \!_M$
is compatible with q. In fact, the closure of
$p\! \upharpoonright \!_M$
is compatible with q. In fact, the closure of
![]() $\mathcal M_p\cup \mathcal M_q$
is a condition in
$\mathcal M_p\cup \mathcal M_q$
is a condition in
![]() $\mathbb M$
, which is also the greatest lower bound of p and q.
$\mathbb M$
, which is also the greatest lower bound of p and q.
Remark 3.13. As before we again denote the above common extension by
![]() $p\land q$
. Notice that
$p\land q$
. Notice that
The following is similar to Fact 3.11 in light of Lemma 3.12.
Fact 3.14.
![]() $\mathbb M$
is strongly proper for
$\mathbb M$
is strongly proper for
![]() $\mathcal {E}^0$
.
$\mathcal {E}^0$
.
4 The forcing construction
In this section, we first present the phenomenon of overlapping that was introduced by Neeman in his paper [Reference Neeman18] regarding (partial) specialisation of trees of height and size
![]() $\omega _2$
. Neeman’s strategy is to attach
$\omega _2$
. Neeman’s strategy is to attach
![]() $\mathbb S_{\omega }(T)$
to side conditions consisting of models of two types: countable and transitive, where he also requires several constraints describing the interaction of the working parts, which are elements of
$\mathbb S_{\omega }(T)$
to side conditions consisting of models of two types: countable and transitive, where he also requires several constraints describing the interaction of the working parts, which are elements of
![]() $\mathbb S_{\omega }(T)$
, and the models as side conditions. He then analyses this interaction. Our approach is similar to Neeman’s, and we still need to require one of the fundamental constraints, though our forcing is simpler than Neeman’s. His definition of overlapping reads as follows: A model M overlaps a node
$\mathbb S_{\omega }(T)$
, and the models as side conditions. He then analyses this interaction. Our approach is similar to Neeman’s, and we still need to require one of the fundamental constraints, though our forcing is simpler than Neeman’s. His definition of overlapping reads as follows: A model M overlaps a node
![]() $t\in T\setminus M$
, if there is no non-cofinal branch
$t\in T\setminus M$
, if there is no non-cofinal branch
![]() $b\in M$
with
$b\in M$
with
![]() $t\in b$
. Our terminology is different from Neeman’s; we say a node
$t\in b$
. Our terminology is different from Neeman’s; we say a node
![]() $t\in T$
is guessed in M if t belongs to some (non-cofinal) branch
$t\in T$
is guessed in M if t belongs to some (non-cofinal) branch
![]() $b\in M$
.
$b\in M$
.
Throughout this section, we fix a Hausdorff tree
![]() $(T,<_T)$
of height
$(T,<_T)$
of height
![]() $\omega _2$
without cofinal branches. We also fix a regular cardinal
$\omega _2$
without cofinal branches. We also fix a regular cardinal
![]() $\theta $
such that
$\theta $
such that
![]() $\mathcal P(T)\in H_{\theta }$
. We let
$\mathcal P(T)\in H_{\theta }$
. We let
![]() $\mathcal {E}^0:= \mathcal E^0(T)$
and
$\mathcal {E}^0:= \mathcal E^0(T)$
and
![]() $\mathcal {E}^1:= \mathcal E^1(T)$
consist, respectively, of countable elementary submodels, and
$\mathcal {E}^1:= \mathcal E^1(T)$
consist, respectively, of countable elementary submodels, and
![]() $\omega _1$
-guessing elementary
$\omega _1$
-guessing elementary
![]() $\mathrm{IC}$
-submodels of
$\mathrm{IC}$
-submodels of
![]() $(H_\theta ,\in ,T)$
. We reserve the symbols
$(H_\theta ,\in ,T)$
. We reserve the symbols
![]() $p,q,r$
for forcing conditions, and
$p,q,r$
for forcing conditions, and
![]() $s,t,u$
for nodes in T.
$s,t,u$
for nodes in T.
4.1 Overlaps between models and nodes
Convention 4.1. A branch through T is called a T-branch.
Definition 4.2. Suppose that
![]() $t\in T$
and
$t\in T$
and
![]() $M\in \mathcal {E}^0\cup \mathcal {E}^1$
. We abuse language and say t is guessed in M if and only if there is a T-branch
$M\in \mathcal {E}^0\cup \mathcal {E}^1$
. We abuse language and say t is guessed in M if and only if there is a T-branch
![]() $b\in M$
with
$b\in M$
with
![]() $t\in b$
.
$t\in b$
.
Thus every
![]() $t\in M$
is already guessed in M, and that no node t with
$t\in M$
is already guessed in M, and that no node t with
![]() ${\mathrm {ht}}(t)\geq {\mathrm {sup}}(M\cap \omega _2)$
is guessed in M, since M has no cofinal branches. We shall often use the following without mentioning.
${\mathrm {ht}}(t)\geq {\mathrm {sup}}(M\cap \omega _2)$
is guessed in M, since M has no cofinal branches. We shall often use the following without mentioning.
Lemma 4.3. Suppose that
![]() $t\in T$
and
$t\in T$
and
![]() $M\in \mathcal {E}^0\cup \mathcal {E}^1$
. If there is
$M\in \mathcal {E}^0\cup \mathcal {E}^1$
. If there is
![]() $s\in M$
with
$s\in M$
with
![]() $t\leq _T s$
, then t is guessed in M.
$t\leq _T s$
, then t is guessed in M.
Proof Pick
![]() $s\in T\cap M$
with
$s\in T\cap M$
with
![]() $t\leq _T s$
. Then
$t\leq _T s$
. Then
![]() $\bar {b}_s\in M$
is a T-branch and
$\bar {b}_s\in M$
is a T-branch and
![]() $t\in \bar {b}_s$
.
$t\in \bar {b}_s$
.
Notation 4.4. Assume that
![]() $t\in T$
and
$t\in T$
and
![]() $M\in \mathcal {E}^0\cup \mathcal {E}^1$
. Then
$M\in \mathcal {E}^0\cup \mathcal {E}^1$
. Then
-
•
 $\eta _M(t)$
denotes
$\eta _M(t)$
denotes
 ${\mathrm {sup}}\{{\mathrm {ht}}(s): s\in T\cap M \text { and } s\leq _T t \}$
.
${\mathrm {sup}}\{{\mathrm {ht}}(s): s\in T\cap M \text { and } s\leq _T t \}$
. -
•
 $O_M(t)$
denotes the unique node
$O_M(t)$
denotes the unique node
 $s\in T_{\eta _M(t)}$
such that
$s\in T_{\eta _M(t)}$
such that
 $s\leq _T t$
.
$s\leq _T t$
. -
•
 $b_M(t)$
denotes
$b_M(t)$
denotes
 $b_{O_M(t)}$
.
$b_{O_M(t)}$
.
Observe that
![]() $O_M(t)$
is always well-defined as T is a rooted tree belonging to every model in
$O_M(t)$
is always well-defined as T is a rooted tree belonging to every model in
![]() $\mathcal {E}^0\cup \mathcal {E}^1$
. By definition, we have
$\mathcal {E}^0\cup \mathcal {E}^1$
. By definition, we have
![]() $\eta _M(t)\leq {\mathrm {sup}}(M\cap \omega _2)$
. In our analysis, we shall focus on
$\eta _M(t)\leq {\mathrm {sup}}(M\cap \omega _2)$
. In our analysis, we shall focus on
![]() $O_M(t)$
rather than t itself. It would be useful to have this intuition that if
$O_M(t)$
rather than t itself. It would be useful to have this intuition that if
![]() $t\notin M$
, then the node
$t\notin M$
, then the node
![]() $O_M(t)$
is where
$O_M(t)$
is where
![]() $b_t$
detaches from M. We shall see that if
$b_t$
detaches from M. We shall see that if
![]() $M\in \mathcal {E}^1$
, then not only
$M\in \mathcal {E}^1$
, then not only
![]() $\eta _M(t)$
is less than
$\eta _M(t)$
is less than
![]() $M\cap \omega _2$
, but also if its cofinality is uncountable, then
$M\cap \omega _2$
, but also if its cofinality is uncountable, then
![]() $O_M(t)$
is in M. Moreover, if
$O_M(t)$
is in M. Moreover, if
![]() $M\in \mathcal E^1$
, then t is guessed in M if and only if
$M\in \mathcal E^1$
, then t is guessed in M if and only if
![]() $t=O_M(t)\in M$
. The situation is different for countable models, as if
$t=O_M(t)\in M$
. The situation is different for countable models, as if
![]() $M\in \mathcal E^0$
and
$M\in \mathcal E^0$
and
![]() $t\in M$
is of uncountable height in T, then one can find some
$t\in M$
is of uncountable height in T, then one can find some
![]() $s\in b_t\setminus M$
. Such an s is necessarily guessed in M though it does not belong to M.
$s\in b_t\setminus M$
. Such an s is necessarily guessed in M though it does not belong to M.
Lemma 4.5. Suppose that
![]() $t\in T$
and
$t\in T$
and
![]() $M\in \mathcal {E}^0\cup \mathcal {E}^1$
.
$M\in \mathcal {E}^0\cup \mathcal {E}^1$
.
-
(1) If t is guessed in M and
 $\eta _M(t)\in M$
, then
$\eta _M(t)\in M$
, then
 $t\in M$
.
$t\in M$
. -
(2) If t is guessed in M, but
 $\eta _M(t)\notin M$
, then
$\eta _M(t)\notin M$
, then
 ${\mathrm {ht}}(t)\leq {\mathrm {min}}(M\cap \omega _2\setminus \eta _M(t))$
.
${\mathrm {ht}}(t)\leq {\mathrm {min}}(M\cap \omega _2\setminus \eta _M(t))$
.
Proof Of course, the first item follows from the proof of the second one, but we prefer to give independent proofs.
-
(1) Assume that
 $b\in M$
is a T-branch containing t. Pick
$b\in M$
is a T-branch containing t. Pick
 $s\in b\cap M$
of height
$s\in b\cap M$
of height
 $\eta _M(t)$
, which is possible as
$\eta _M(t)$
, which is possible as
 $t\in b$
implies that the order-type of b is at least
$t\in b$
implies that the order-type of b is at least
 $\eta _M(t)+1$
. Thus
$\eta _M(t)+1$
. Thus
 $s\leq _T t$
. On the other hand, if
$s\leq _T t$
. On the other hand, if
 $s<_T t$
, then there is
$s<_T t$
, then there is
 $u\in b\cap M$
of height
$u\in b\cap M$
of height
 $\eta _M(t)+1$
, but then
$\eta _M(t)+1$
, but then
 $u\leq _T t$
, which is impossible by the definition of
$u\leq _T t$
, which is impossible by the definition of
 $\eta _M(t)$
. Thus
$\eta _M(t)$
. Thus
 $t=s\in M$
.
$t=s\in M$
. -
(2) We may assume that M is in
 $\mathcal E^0$
as otherwise it is trivial. One easily observes that
$\mathcal E^0$
as otherwise it is trivial. One easily observes that
 $\eta _M(t)$
is below
$\eta _M(t)$
is below
 ${\mathrm {sup}}(M\cap \omega _2)$
since T does not have cofinal branches. Now
${\mathrm {sup}}(M\cap \omega _2)$
since T does not have cofinal branches. Now
 $\eta ^*:= {\mathrm {min}}(M\cap \omega _2\setminus \eta _M(t))$
is an ordinal below
$\eta ^*:= {\mathrm {min}}(M\cap \omega _2\setminus \eta _M(t))$
is an ordinal below
 $\omega _2$
, but above
$\omega _2$
, but above
 $\eta _M(t)$
. Let
$\eta _M(t)$
. Let
 $b\in M$
be a branch containing t. Assume towards a contradiction that
$b\in M$
be a branch containing t. Assume towards a contradiction that
 ${\mathrm {ht}}(t)>\eta ^*$
, then there is some node
${\mathrm {ht}}(t)>\eta ^*$
, then there is some node
 $s\in b$
of height
$s\in b$
of height
 $\eta ^*$
, and thus
$\eta ^*$
, and thus
 $s<_T t$
. It then follows that
$s<_T t$
. It then follows that
 $\eta _M(t)\geq \eta ^*>\eta _M(t)$
, a contradiction.
$\eta _M(t)\geq \eta ^*>\eta _M(t)$
, a contradiction.
The following is too easy, and we leave the proof to the reader.
Lemma 4.6. Suppose that
![]() $t\in T$
and
$t\in T$
and
![]() $M\in \mathcal {E}^0\cup \mathcal {E}^1$
. If
$M\in \mathcal {E}^0\cup \mathcal {E}^1$
. If
![]() $\eta _M(t)$
is a successor ordinal, then
$\eta _M(t)$
is a successor ordinal, then
![]() $O_M(t)$
is in M.
$O_M(t)$
is in M.
In general, if the supremum in the definition of
![]() $\eta _M(t)$
is attained by an element in
$\eta _M(t)$
is attained by an element in
![]() $T\cap M$
, then that element is
$T\cap M$
, then that element is
![]() $O_M(t)$
, which belongs to M. The above lemma essentially means that it does happen if
$O_M(t)$
, which belongs to M. The above lemma essentially means that it does happen if
![]() $\eta _M(t)$
is a successor ordinal. We now turn our attention to the situation where the overlaps are more complicated as
$\eta _M(t)$
is a successor ordinal. We now turn our attention to the situation where the overlaps are more complicated as
![]() $\eta _M(t)$
is a limit ordinal.
$\eta _M(t)$
is a limit ordinal.
Lemma 4.7. Suppose that
![]() $t\in T$
and
$t\in T$
and
![]() $M\in \mathcal {E}^1$
. If
$M\in \mathcal {E}^1$
. If
![]() ${\mathrm {cof}}(\eta _M(t))$
is not countable, then
${\mathrm {cof}}(\eta _M(t))$
is not countable, then
![]() $O_M(t)\in M$
.
$O_M(t)\in M$
.
Proof By Lemma 4.6, we may assume that
![]() $\eta _M(t)$
is a limit ordinal, and thus of cofinality
$\eta _M(t)$
is a limit ordinal, and thus of cofinality
![]() $\omega _1$
. Let
$\omega _1$
. Let
![]() $\eta =\eta _M(t)$
. Since M is of size
$\eta =\eta _M(t)$
. Since M is of size
![]() $\aleph _1$
and
$\aleph _1$
and
![]() $\omega _1\subseteq M$
, we have
$\omega _1\subseteq M$
, we have
![]() $b_M(t)\subseteq M$
. For every countable
$b_M(t)\subseteq M$
. For every countable
![]() $a\in M$
, the height of nodes in
$a\in M$
, the height of nodes in
![]() $a\cap b_M(t)$
is bounded below
$a\cap b_M(t)$
is bounded below
![]() $\eta $
due to the fact that
$\eta $
due to the fact that
![]() $\eta _M(t)$
has uncountable cofinality. Thus it is easily seen that
$\eta _M(t)$
has uncountable cofinality. Thus it is easily seen that
![]() $b_M(t)$
is countably approximated in M. Since M is an
$b_M(t)$
is countably approximated in M. Since M is an
![]() $\omega _1$
-guessing model, there is
$\omega _1$
-guessing model, there is
![]() $b\in M$
such that
$b\in M$
such that
![]() $b\cap M=b_M(t)$
. By elementarity, b is a T-branch, and hence it is of size
$b\cap M=b_M(t)$
. By elementarity, b is a T-branch, and hence it is of size
![]() $\aleph _1$
(in particular,
$\aleph _1$
(in particular,
![]() $\eta <M\cap \omega _2$
.) Thus
$\eta <M\cap \omega _2$
.) Thus
![]() $b\subseteq M$
, which in turn implies that
$b\subseteq M$
, which in turn implies that
![]() $b_M(t)=b\in M$
. But then
$b_M(t)=b\in M$
. But then
![]() $O_M(t)\in M$
as it can be read off from
$O_M(t)\in M$
as it can be read off from
![]() $b_M(t)$
due to the fact that T is Hausdorff.
$b_M(t)$
due to the fact that T is Hausdorff.
Corollary 4.8. Suppose that
![]() $t\in T$
and
$t\in T$
and
![]() $M\in \mathcal {E}^1$
. Then
$M\in \mathcal {E}^1$
. Then
![]() $\eta _M(t)$
is in M.
$\eta _M(t)$
is in M.
Proof By definition
![]() $\eta _M(t)\leq M\cap \omega _2$
. Since M is an
$\eta _M(t)\leq M\cap \omega _2$
. Since M is an
![]() $\mathrm{IC}$
-model with
$\mathrm{IC}$
-model with
![]() $\omega _1\subseteq M$
, the ordinal
$\omega _1\subseteq M$
, the ordinal
![]() $M\cap \omega _2$
is of uncountable cofinality. If
$M\cap \omega _2$
is of uncountable cofinality. If
![]() $\eta _M(t)= M\cap \omega _2$
, then by Lemma 4.7,
$\eta _M(t)= M\cap \omega _2$
, then by Lemma 4.7,
![]() $O_M(t)\in M$
. This is a contradiction, as
$O_M(t)\in M$
. This is a contradiction, as
![]() $M\cap \omega _2=\eta _M(t)={\mathrm {ht}}(O_M(t))\in M$
! Thus
$M\cap \omega _2=\eta _M(t)={\mathrm {ht}}(O_M(t))\in M$
! Thus
![]() $\eta _M(t)<M\cap \omega _2$
, and hence
$\eta _M(t)<M\cap \omega _2$
, and hence
![]() $\eta _M(t)\in M$
.
$\eta _M(t)\in M$
.
The following is key for us.
Lemma 4.9. Assume that
![]() $N\in \mathcal {E}^1$
and
$N\in \mathcal {E}^1$
and
![]() $M\in \mathcal {E}^0$
with
$M\in \mathcal {E}^0$
with
![]() $N\in M$
. Let
$N\in M$
. Let
![]() $t\in T\cap N$
. If t is guessed in M, then t is guessed in
$t\in T\cap N$
. If t is guessed in M, then t is guessed in
![]() $N\cap M$
.
$N\cap M$
.
Proof Let
![]() $b\in M$
be a T-branch containing t. Let
$b\in M$
be a T-branch containing t. Let
![]() $\gamma ={\mathrm {sup}}\{{\mathrm {ht}}(s):s\in N\cap b\}$
. Then
$\gamma ={\mathrm {sup}}\{{\mathrm {ht}}(s):s\in N\cap b\}$
. Then
![]() $\gamma $
exists as
$\gamma $
exists as
![]() $t\in N$
and
$t\in N$
and
![]() ${\mathrm {ht}}(t)\leq \gamma $
. Note that
${\mathrm {ht}}(t)\leq \gamma $
. Note that
![]() $\gamma \in M\cap \omega _2$
by elementarity. Observe that if
$\gamma \in M\cap \omega _2$
by elementarity. Observe that if
![]() $\gamma ={\mathrm {ht}}(s)$
, for some
$\gamma ={\mathrm {ht}}(s)$
, for some
![]() $s\in N\cap b$
, then by elementarity,
$s\in N\cap b$
, then by elementarity,
![]() $s\in N\cap M$
. We then have
$s\in N\cap M$
. We then have
![]() $t\in \overline {b}_s\in N\cap M$
. Thus let us assume that the supremum
$t\in \overline {b}_s\in N\cap M$
. Thus let us assume that the supremum
![]() $\gamma $
is not obtained by any element of
$\gamma $
is not obtained by any element of
![]() $N\cap b$
. In particular,
$N\cap b$
. In particular,
![]() ${\mathrm {ht}}(t)<\gamma $
and the cofinality of
${\mathrm {ht}}(t)<\gamma $
and the cofinality of
![]() $\gamma $
is either
$\gamma $
is either
![]() $\omega $
or
$\omega $
or
![]() $\omega _1$
. We consider two cases:
$\omega _1$
. We consider two cases:
Case 1:
![]() ${\mathrm {cof}}(\gamma )=\omega $
.
${\mathrm {cof}}(\gamma )=\omega $
.
By elementarity, there is a strictly
![]() $<_T$
-increasing sequence
$<_T$
-increasing sequence
![]() $\langle s_n: n\in \omega \rangle \in M$
of nodes in
$\langle s_n: n\in \omega \rangle \in M$
of nodes in
![]() $b\cap N$
such that
$b\cap N$
such that
![]() $\sup \{{\mathrm {ht}}(s_n):n\in \omega \}=\gamma $
. Since we assumed
$\sup \{{\mathrm {ht}}(s_n):n\in \omega \}=\gamma $
. Since we assumed
![]() ${\mathrm {ht}}(t)<\gamma $
, there is n such that
${\mathrm {ht}}(t)<\gamma $
, there is n such that
![]() $t\leq _T s_n$
. Note that
$t\leq _T s_n$
. Note that
![]() $s_n\in N\cap M$
, and hence
$s_n\in N\cap M$
, and hence
![]() $t\in \overline {b}_{s_n}\in N\cap M$
. Therefore, t is guessed in
$t\in \overline {b}_{s_n}\in N\cap M$
. Therefore, t is guessed in
![]() $N\cap M$
.
$N\cap M$
.
Case 2:
![]() ${\mathrm {cof}}(\gamma )=\omega _1$
.
${\mathrm {cof}}(\gamma )=\omega _1$
.
We claim that
![]() $ b\cap T_{\leq \gamma }$
is guessed in N. To see this, observe that
$ b\cap T_{\leq \gamma }$
is guessed in N. To see this, observe that
![]() $ b\cap T_{\leq \gamma }$
is
$ b\cap T_{\leq \gamma }$
is
![]() $\omega _1$
-approximated in N, since if
$\omega _1$
-approximated in N, since if
![]() $a\in N$
is a countable set, then there is
$a\in N$
is a countable set, then there is
![]() $s\in N\cap b\cap T_{\leq \gamma }$
such that
$s\in N\cap b\cap T_{\leq \gamma }$
such that
![]() $a\cap b\cap T_{\leq \gamma }= a\cap b_s$
(as the cofinality of
$a\cap b\cap T_{\leq \gamma }= a\cap b_s$
(as the cofinality of
![]() $\gamma $
is
$\gamma $
is
![]() $\omega _1$
.) But
$\omega _1$
.) But
![]() $a\cap b_s\in N$
. As N is an
$a\cap b_s\in N$
. As N is an
![]() $\omega _1$
-guessing model, we have
$\omega _1$
-guessing model, we have
![]() $ b\cap T_{\leq \gamma }$
is guessed in N. By the elementarity of M, there is
$ b\cap T_{\leq \gamma }$
is guessed in N. By the elementarity of M, there is
![]() $b^*\in N\cap M$
such that
$b^*\in N\cap M$
such that
![]() $b^*\cap N=b\cap T_{\leq \gamma }\cap N $
. Now
$b^*\cap N=b\cap T_{\leq \gamma }\cap N $
. Now
![]() $t\in N\cap b\cap T_{\leq \gamma }=b^*\cap N$
. Notice that, by elementarity,
$t\in N\cap b\cap T_{\leq \gamma }=b^*\cap N$
. Notice that, by elementarity,
![]() $b^*$
is a T-branch. Thus
$b^*$
is a T-branch. Thus
![]() $b^*\in N\cap M$
witnesses that t is guessed in
$b^*\in N\cap M$
witnesses that t is guessed in
![]() $N\cap M$
.
$N\cap M$
.
Lemma 4.10. Assume that
![]() $N\in \mathcal {E}^1$
and
$N\in \mathcal {E}^1$
and
![]() $M\in \mathcal {E}^0$
with
$M\in \mathcal {E}^0$
with
![]() $N\in M$
. Let
$N\in M$
. Let
![]() $t\in T\cap N$
. Then
$t\in T\cap N$
. Then
![]() $\eta _{N\cap M}(t)=\eta _M(t)$
, and hence
$\eta _{N\cap M}(t)=\eta _M(t)$
, and hence
![]() $O_{N\cap M}(t)=O_M(t)$
.
$O_{N\cap M}(t)=O_M(t)$
.
Proof Since
![]() $N\cap M\subseteq M$
,
$N\cap M\subseteq M$
,
![]() $\eta _{N\cap M}(t)\leq \eta _M(t)$
. Assume towards a contradiction that the equality fails. Thus, there is some
$\eta _{N\cap M}(t)\leq \eta _M(t)$
. Assume towards a contradiction that the equality fails. Thus, there is some
![]() $s\in M$
whose height is above
$s\in M$
whose height is above
![]() $\eta _{N\cap M}(t)$
such that
$\eta _{N\cap M}(t)$
such that
![]() $s\leq _T O_M(t)\leq _T t$
. Then
$s\leq _T O_M(t)\leq _T t$
. Then
![]() $s\in N$
as
$s\in N$
as
![]() $\omega _1\cup \{t\}\subseteq N$
. Therefore,
$\omega _1\cup \{t\}\subseteq N$
. Therefore,
![]() $s\in N\cap M$
, and hence
$s\in N\cap M$
, and hence
![]() ${\mathrm {ht}}(s)\leq \eta _{N\cap M}(t)$
, a contradiction. Since both
${\mathrm {ht}}(s)\leq \eta _{N\cap M}(t)$
, a contradiction. Since both
![]() $O_{N\cap M}(t)$
and
$O_{N\cap M}(t)$
and
![]() $O_M(t)$
are below t and of the same height, they are equal.
$O_M(t)$
are below t and of the same height, they are equal.
4.2 The forcing construction and its basic properties
We are now ready to define our forcing notion
![]() $\mathbb P_T$
to specialise T in generic extensions.
$\mathbb P_T$
to specialise T in generic extensions.
Definition 4.11 (
 $\mathbb P_T$
).
$\mathbb P_T$
).
A condition in
![]() $\mathbb P_T$
is a pair
$\mathbb P_T$
is a pair
![]() $p=(\mathcal M_p,f_p)$
satisfying the following items.
$p=(\mathcal M_p,f_p)$
satisfying the following items.
-
(1)
 $\mathcal M_p\in \mathbb M:= \mathbb M(\mathcal E^0,\mathcal E^1)$
.
$\mathcal M_p\in \mathbb M:= \mathbb M(\mathcal E^0,\mathcal E^1)$
. -
(2)
 $f_p\in \mathbb S_{\omega }(T)$
.
$f_p\in \mathbb S_{\omega }(T)$
. -
(3) For every
 $M\in \mathcal {E}^0_p$
, if
$M\in \mathcal {E}^0_p$
, if
 $t\in {\mathrm {dom}}(f_p)\cap M$
, then
$t\in {\mathrm {dom}}(f_p)\cap M$
, then
 $f_p(t)\in M$
.
$f_p(t)\in M$
. -
(4) For every
 $M\in \mathcal {E}^0_p$
and every
$M\in \mathcal {E}^0_p$
and every
 $t\in {\mathrm {dom}}(f_p)$
with
$t\in {\mathrm {dom}}(f_p)$
with
 $f_p(t)\in M$
, if t is guessed in M, then
$f_p(t)\in M$
, if t is guessed in M, then
 $t\in M$
.
$t\in M$
.
We say p is stronger than q if and only if the following are satisfied.
-
(1)
 $\mathcal M_p\supseteq \mathcal M_q$
.
$\mathcal M_p\supseteq \mathcal M_q$
. -
(2)
 $f_p\supseteq f_q$
.
$f_p\supseteq f_q$
.
Given a condition p in
![]() $\mathbb P_T$
and a model
$\mathbb P_T$
and a model
![]() $M\in \mathcal {E}^0\cup \mathcal {E}^1$
containing p, we define an extension of p that will turn later to be generic for the relevant models.
$M\in \mathcal {E}^0\cup \mathcal {E}^1$
containing p, we define an extension of p that will turn later to be generic for the relevant models.
Definition 4.12. Suppose that
![]() $M\in \mathcal {E}^0\cup \mathcal {E}^1$
and
$M\in \mathcal {E}^0\cup \mathcal {E}^1$
and
![]() $p\in M\cap \mathbb P_T$
. We let
$p\in M\cap \mathbb P_T$
. We let
![]() $p^M$
be defined by
$p^M$
be defined by
![]() $(\mathcal M^M_p,f_p)$
.
$(\mathcal M^M_p,f_p)$
.
Recall that
![]() $\mathcal M_p^M$
is the closure of
$\mathcal M_p^M$
is the closure of
![]() $\mathcal M_p\cup \{M\}$
under intersections (see Fact 3.5).
$\mathcal M_p\cup \{M\}$
under intersections (see Fact 3.5).
Proposition 4.13. Suppose that
![]() $M\in \mathcal {E}^0\cup \mathcal {E}^1$
and
$M\in \mathcal {E}^0\cup \mathcal {E}^1$
and
![]() $p\in M\cap \mathbb P_T$
. Then
$p\in M\cap \mathbb P_T$
. Then
![]() $p^M$
is a condition extending p such that
$p^M$
is a condition extending p such that
![]() $M\in \mathcal M_{p^M}$
.
$M\in \mathcal M_{p^M}$
.
Proof We check Definition 4.11 item by item. Item 1 is essentially Fact 3.5. Item 2 is obvious of course. To see Items 3 and 4 hold true, let
![]() $N\in \mathcal {E}^0_{p^M}$
. We may assume that
$N\in \mathcal {E}^0_{p^M}$
. We may assume that
![]() $N\notin \mathcal M_p$
. Therefore, the only interesting case is
$N\notin \mathcal M_p$
. Therefore, the only interesting case is
![]() $M\in \mathcal E^0$
and
$M\in \mathcal E^0$
and
![]() $N=P\cap M$
, for some
$N=P\cap M$
, for some
![]() $P\in \mathcal {E}^1_p$
. Thus fix such models.
$P\in \mathcal {E}^1_p$
. Thus fix such models.
Item 3: Let
![]() $t\in {\mathrm {dom}}(f_{p^M})\cap N$
. We have
$t\in {\mathrm {dom}}(f_{p^M})\cap N$
. We have
![]() $f_p(t)\in M$
, as
$f_p(t)\in M$
, as
![]() $p\in M$
, and also we have
$p\in M$
, and also we have
![]() $f_p(t)\in P$
, as
$f_p(t)\in P$
, as
![]() $\omega _1\subseteq P$
. Thus
$\omega _1\subseteq P$
. Thus
![]() $f_p(t)\in P\cap M=N$
.
$f_p(t)\in P\cap M=N$
.
Item 4: Let
![]() $t\in {\mathrm {dom}}(f_p)$
be such that
$t\in {\mathrm {dom}}(f_p)$
be such that
![]() $f_p(t)\in N$
. If there is a T-branch
$f_p(t)\in N$
. If there is a T-branch
![]() $b\in N$
with
$b\in N$
with
![]() $t\in b$
, then
$t\in b$
, then
![]() $t\in P$
(since
$t\in P$
(since
![]() $b\subseteq P$
), and hence
$b\subseteq P$
), and hence
![]() $t\in P\cap M=N$
.
$t\in P\cap M=N$
.
Finally, by the construction of
![]() $p^M$
, we have
$p^M$
, we have
![]() $M\in \mathcal M_{p^M}$
, and by Fact 3.5,
$M\in \mathcal M_{p^M}$
, and by Fact 3.5,
![]() $p^M\leq p$
.
$p^M\leq p$
.
We now define the restriction of a condition to a model in the side conditions coordinate.
Definition 4.14 (Restriction).
Suppose that
![]() $p\in \mathbb P_T$
and
$p\in \mathbb P_T$
and
![]() $M\in \mathcal M_p$
. We let the restriction of p to M be
$M\in \mathcal M_p$
. We let the restriction of p to M be
![]() $p\! \upharpoonright \!_M=(\mathcal {M}_{p\upharpoonright _M},f_p\! \upharpoonright \!_M)$
, where
$p\! \upharpoonright \!_M=(\mathcal {M}_{p\upharpoonright _M},f_p\! \upharpoonright \!_M)$
, where
![]() $f_p\! \upharpoonright \!_M$
is the restriction of the function
$f_p\! \upharpoonright \!_M$
is the restriction of the function
![]() $f_p$
to
$f_p$
to
![]() ${\mathrm {dom}}(f_p)\cap M$
.
${\mathrm {dom}}(f_p)\cap M$
.
Recall that
![]() $\mathcal {M}_{p\upharpoonright _M}=\mathcal M_p\cap M$
. Observe that if M is in
$\mathcal {M}_{p\upharpoonright _M}=\mathcal M_p\cap M$
. Observe that if M is in
![]() $\mathcal E^0$
, then by Item 3 of Definition 4.11,
$\mathcal E^0$
, then by Item 3 of Definition 4.11,
![]() $f_{p\upharpoonright _M}=f_p\cap M$
. This is trivial for models in
$f_{p\upharpoonright _M}=f_p\cap M$
. This is trivial for models in
![]() $\mathcal E^1$
.
$\mathcal E^1$
.
Proposition 4.15. Suppose that
![]() $p\in \mathbb P_T$
and
$p\in \mathbb P_T$
and
![]() $M\in \mathcal M_p$
. Then
$M\in \mathcal M_p$
. Then
![]() $p\! \upharpoonright \!_M\in \mathbb P_T\cap M$
and
$p\! \upharpoonright \!_M\in \mathbb P_T\cap M$
and
![]() $p\leq p\! \upharpoonright \!_M$
.
$p\leq p\! \upharpoonright \!_M$
.
Proof We check Definition 4.11 item by item. By Fact 3.8,
![]() $\mathcal M_{p\upharpoonright _M}$
is an
$\mathcal M_{p\upharpoonright _M}$
is an
![]() $\in $
-chain and closed under intersections, and hence it is in
$\in $
-chain and closed under intersections, and hence it is in
![]() $\mathbb M$
. By Item 3 of Definition 4.11,
$\mathbb M$
. By Item 3 of Definition 4.11,
![]() $f_p\cap M$
is in
$f_p\cap M$
is in
![]() $\mathbb S_{\omega }(T)$
. Observe that M contains
$\mathbb S_{\omega }(T)$
. Observe that M contains
![]() $p\! \upharpoonright \!_M$
, as it is a finite subset of M. Items 3 and 4 remain valid since all models in
$p\! \upharpoonright \!_M$
, as it is a finite subset of M. Items 3 and 4 remain valid since all models in
![]() $\mathcal M_{p\upharpoonright _M}$
and all nodes in
$\mathcal M_{p\upharpoonright _M}$
and all nodes in
![]() ${\mathrm {dom}}(f_{p\upharpoonright _M})$
are, respectively, in
${\mathrm {dom}}(f_{p\upharpoonright _M})$
are, respectively, in
![]() $\mathcal M_p$
and
$\mathcal M_p$
and
![]() ${\mathrm {dom}}(f_p)$
. It is easy to see that p extends
${\mathrm {dom}}(f_p)$
. It is easy to see that p extends
![]() $p\! \upharpoonright \!_M$
.
$p\! \upharpoonright \!_M$
.
Notation 4.16. For a condition
![]() $p\in \mathbb P_T$
, a model
$p\in \mathbb P_T$
, a model
![]() $M\in \mathcal M_p$
, and a condition
$M\in \mathcal M_p$
, and a condition
![]() $q\in M\cap \mathbb P_T$
with
$q\in M\cap \mathbb P_T$
with
![]() $q\leq p\! \upharpoonright \!_M$
, we let
$q\leq p\! \upharpoonright \!_M$
, we let
![]() $p\land q$
denote the pair
$p\land q$
denote the pair
![]() $(\mathcal M_p\land \mathcal M_q, f_p\cup f_q)$
.
$(\mathcal M_p\land \mathcal M_q, f_p\cup f_q)$
.
Note that
![]() $p\land q$
is not necessarily a condition; however we shall use it as a pair of objects. Notice that
$p\land q$
is not necessarily a condition; however we shall use it as a pair of objects. Notice that
![]() $\mathcal M_{p\land q}$
is the closure of
$\mathcal M_{p\land q}$
is the closure of
![]() $\mathcal M_p\cup \mathcal M_q$
under intersections, and belongs to
$\mathcal M_p\cup \mathcal M_q$
under intersections, and belongs to
![]() $\mathbb M$
(see Remark 3.10 and Remark 3.13) and that also
$\mathbb M$
(see Remark 3.10 and Remark 3.13) and that also
![]() $f_{p\land q}$
is a well-defined function due to the fact that p satisfies Item 3 of Definition 4.11.
$f_{p\land q}$
is a well-defined function due to the fact that p satisfies Item 3 of Definition 4.11.
Lemma 4.17. Suppose p is a condition in
![]() $\mathbb P_T$
and M is a model in
$\mathbb P_T$
and M is a model in
![]() $\mathcal M_p$
. Assume that
$\mathcal M_p$
. Assume that
![]() $q\in M\cap \mathbb P_T$
extends
$q\in M\cap \mathbb P_T$
extends
![]() $p\! \upharpoonright \!_M$
. Then
$p\! \upharpoonright \!_M$
. Then
![]() $p\land q$
satisfies Item 3 of Definition 4.11.
$p\land q$
satisfies Item 3 of Definition 4.11.
Proof Fix
![]() $N\in \mathcal E^0_{p\land q}$
and
$N\in \mathcal E^0_{p\land q}$
and
![]() $t\in {\mathrm {dom}}(f_p)\cup {\mathrm {dom}}(f_q)$
. Assume that t is in N. We shall show that
$t\in {\mathrm {dom}}(f_p)\cup {\mathrm {dom}}(f_q)$
. Assume that t is in N. We shall show that
![]() $f_{p\land q}(t)\in N$
. We split the proof into two cases.
$f_{p\land q}(t)\in N$
. We split the proof into two cases.
Case 1: M is in
![]() $\mathcal {E}^1$
.
$\mathcal {E}^1$
.
In this case,
![]() $\mathcal M_{p\land q}=\mathcal M_p\cup \mathcal M_q$
, by Remark 3.10. If
$\mathcal M_{p\land q}=\mathcal M_p\cup \mathcal M_q$
, by Remark 3.10. If
![]() $N\in \mathcal M_q$
, then
$N\in \mathcal M_q$
, then
![]() $t\in N\subseteq M$
, and hence
$t\in N\subseteq M$
, and hence
![]() $t\in {\mathrm {dom}}(f_q)$
. Thus
$t\in {\mathrm {dom}}(f_q)$
. Thus
![]() $f_{p\land q}(t)=f_q(t)\in N$
. Now suppose that
$f_{p\land q}(t)=f_q(t)\in N$
. Now suppose that
![]() $N\in \mathcal M_p\setminus \mathcal M_q$
. We may assume
$N\in \mathcal M_p\setminus \mathcal M_q$
. We may assume
![]() $t\in {\mathrm {dom}}(f_q)$
. Therefore, in
$t\in {\mathrm {dom}}(f_q)$
. Therefore, in
![]() $\mathcal M_p$
, we have
$\mathcal M_p$
, we have
![]() $M\in ^* N$
, which in turn implies that there is
$M\in ^* N$
, which in turn implies that there is
![]() $M'\in \mathcal {E}^1_p$
such that
$M'\in \mathcal {E}^1_p$
such that
![]() $M\subseteq M'\in N$
and
$M\subseteq M'\in N$
and
![]() $M'\cap N\in M$
. Then,
$M'\cap N\in M$
. Then,
![]() $M'\cap N\in \mathcal M_q$
and
$M'\cap N\in \mathcal M_q$
and
![]() $t\in M'\cap N$
. As q is a condition, we have
$t\in M'\cap N$
. As q is a condition, we have
![]() $f_{p\land q}(t)=f_q(t)\in M'\cap N\subseteq N$
.
$f_{p\land q}(t)=f_q(t)\in M'\cap N\subseteq N$
.
Case 2: M is in
![]() $\mathcal {E}^0$
.
$\mathcal {E}^0$
.
Observe that it is enough to assume
![]() $N\in \mathcal M_p\cup \mathcal M_q$
: if
$N\in \mathcal M_p\cup \mathcal M_q$
: if
![]() $N\in \mathcal M_p\land \mathcal M_q$
, then
$N\in \mathcal M_p\land \mathcal M_q$
, then
![]() $N=P\cap N'$
, for some
$N=P\cap N'$
, for some
![]() $P'\in \mathcal M_p\cup \mathcal M_q$
, and some
$P'\in \mathcal M_p\cup \mathcal M_q$
, and some
![]() $N'\in \mathcal M_p\cup \mathcal M_q$
. By our assumption,
$N'\in \mathcal M_p\cup \mathcal M_q$
. By our assumption,
![]() $f_{p\land q}(t)$
belongs to
$f_{p\land q}(t)$
belongs to
![]() $N'$
, and hence,
$N'$
, and hence,
![]() $f_{p\land q}(t)\in P'\cap N'=N$
, as
$f_{p\land q}(t)\in P'\cap N'=N$
, as
![]() $\omega _1\subseteq P'$
.
$\omega _1\subseteq P'$
.
As in the previous case, we may assume
![]() $t\in {\mathrm {dom}}(f_q)$
and
$t\in {\mathrm {dom}}(f_q)$
and
![]() $N\in \mathcal M_p\setminus \mathcal M_q$
. Let us first assume that
$N\in \mathcal M_p\setminus \mathcal M_q$
. Let us first assume that
![]() $N\in ^* M$
. Suppose that N is the minimal counter-example with the above properties. Thus there is
$N\in ^* M$
. Suppose that N is the minimal counter-example with the above properties. Thus there is
![]() $P\in \mathcal {E}^1_p\cap M$
such that
$P\in \mathcal {E}^1_p\cap M$
such that
![]() $N\in [P\cap M,P)_p$
. Now
$N\in [P\cap M,P)_p$
. Now
![]() $P\cap M\nsubseteq N$
, as otherwise
$P\cap M\nsubseteq N$
, as otherwise
![]() $f_q(t)\in N$
, since
$f_q(t)\in N$
, since
![]() $t\in P\in \mathcal M_q$
and
$t\in P\in \mathcal M_q$
and
![]() $f_q(t)\in P\cap M$
. Therefore, there is some
$f_q(t)\in P\cap M$
. Therefore, there is some
![]() $Q\in N$
such that
$Q\in N$
such that
![]() $Q\cap N\in ^* P\cap M\in Q$
. Notice that
$Q\cap N\in ^* P\cap M\in Q$
. Notice that
![]() $t\in P$
, and hence
$t\in P$
, and hence
![]() $t\in P\cap M\subseteq Q$
. Thus
$t\in P\cap M\subseteq Q$
. Thus
![]() $t\in Q\cap N$
. Now
$t\in Q\cap N$
. Now
![]() $Q\cap N$
is also a counter-example to our claim, since
$Q\cap N$
is also a counter-example to our claim, since
![]() $t\in Q\cap N\subseteq N$
,
$t\in Q\cap N\subseteq N$
,
![]() $Q\cap N\in \mathcal M_p\setminus \mathcal M_q$
(as otherwise, we would have
$Q\cap N\in \mathcal M_p\setminus \mathcal M_q$
(as otherwise, we would have
![]() $f_q(t)\in Q\cap N\subseteq N$
), and
$f_q(t)\in Q\cap N\subseteq N$
), and
![]() $Q\cap N\in ^* M$
. This contradicts our minimality assumption.
$Q\cap N\in ^* M$
. This contradicts our minimality assumption.
Two cases remain. The case
![]() $N=M$
is trivial, and thus we only need to assume that
$N=M$
is trivial, and thus we only need to assume that
![]() $M\in ^* N$
. If
$M\in ^* N$
. If
![]() $M\subseteq N$
, then
$M\subseteq N$
, then
![]() $f_q(t)\in N$
. And if
$f_q(t)\in N$
. And if
![]() $M\nsubseteq N$
, then there is some
$M\nsubseteq N$
, then there is some
![]() $P\in \mathcal {E}^1_p$
such that
$P\in \mathcal {E}^1_p$
such that
![]() $P\cap N\in ^* M\in P\in N$
(see Remark 3.2). Notice that
$P\cap N\in ^* M\in P\in N$
(see Remark 3.2). Notice that
![]() $t\in P\cap N$
. Thus by the previous paragraph,
$t\in P\cap N$
. Thus by the previous paragraph,
![]() $f_q(t)\in P\cap N\subseteq N$
.
$f_q(t)\in P\cap N\subseteq N$
.
4.3 Preserving
 $\aleph _2$
$\aleph _2$
In this subsection, we prove that
![]() $\mathbb P_T$
preserves the regularity of
$\mathbb P_T$
preserves the regularity of
![]() $\aleph _2$
. With a similar idea, we shall establish the properness of
$\aleph _2$
. With a similar idea, we shall establish the properness of
![]() $\mathbb P_T$
in the subsequent subsection.
$\mathbb P_T$
in the subsequent subsection.
Lemma 4.18. Suppose p is a condition in
![]() $\mathbb P_T$
and that
$\mathbb P_T$
and that
![]() $M\in \mathcal {E}^1_p$
. Assume that
$M\in \mathcal {E}^1_p$
. Assume that
![]() $q\in M$
is a condition extending
$q\in M$
is a condition extending
![]() $p\! \upharpoonright \!_M$
. Then
$p\! \upharpoonright \!_M$
. Then
![]() $p\land q$
satisfies Item 4 of Definition 4.11.
$p\land q$
satisfies Item 4 of Definition 4.11.
Proof Set
![]() $r=p\land q$
. Notice that
$r=p\land q$
. Notice that
![]() $f_r$
is well-defined as a function. Now fix
$f_r$
is well-defined as a function. Now fix
![]() $t\in {\mathrm {dom}}(f_r)$
and
$t\in {\mathrm {dom}}(f_r)$
and
![]() $N\in \mathcal E^0\cap \mathcal M_r$
so that
$N\in \mathcal E^0\cap \mathcal M_r$
so that
![]() $f_r(t)\in N$
. We shall show that if t is guessed in N, then
$f_r(t)\in N$
. We shall show that if t is guessed in N, then
![]() $t\in N$
. Notice that by Remark 3.10, we have
$t\in N$
. Notice that by Remark 3.10, we have
![]() $\mathcal M_r=\mathcal M_p\cup \mathcal M_q$
. We shall consider the nontrivial cases:
$\mathcal M_r=\mathcal M_p\cup \mathcal M_q$
. We shall consider the nontrivial cases:
Case 1:
![]() $t\in {\mathrm {dom}}(f_p)$
and
$t\in {\mathrm {dom}}(f_p)$
and
![]() $N\in \mathcal M_q\setminus \mathcal M_p$
.
$N\in \mathcal M_q\setminus \mathcal M_p$
.
Assume that t is guessed in N. Thus there is a T-branch
![]() $b\in N\subseteq M$
with
$b\in N\subseteq M$
with
![]() $t\in b$
. As b is of size
$t\in b$
. As b is of size
![]() $\leq \!\aleph _1$
and
$\leq \!\aleph _1$
and
![]() $\omega _1\subseteq M$
, we have
$\omega _1\subseteq M$
, we have
![]() $t\in b\subseteq M$
. Thus
$t\in b\subseteq M$
. Thus
![]() $t\in M$
, which in turn implies that
$t\in M$
, which in turn implies that
![]() $t\in {\mathrm {dom}}(f_q)$
and
$t\in {\mathrm {dom}}(f_q)$
and
![]() $f_q(t)=f_p(t)=f_r(t)\in N$
. But then
$f_q(t)=f_p(t)=f_r(t)\in N$
. But then
![]() $t\in N$
, as q is a condition.
$t\in N$
, as q is a condition.
Case 2:
![]() $t\in {\mathrm {dom}}(f_q)\setminus {\mathrm {dom}}(f_p)$
and
$t\in {\mathrm {dom}}(f_q)\setminus {\mathrm {dom}}(f_p)$
and
![]() $N\in \mathcal M_p\setminus \mathcal M_q$
.
$N\in \mathcal M_p\setminus \mathcal M_q$
.
In this situation, N is not in M since
![]() $\mathcal M_q\supseteq \mathcal M_p\cap M$
, and hence there is some
$\mathcal M_q\supseteq \mathcal M_p\cap M$
, and hence there is some
![]() $M'\in \mathcal E^1_p$
with
$M'\in \mathcal E^1_p$
with
![]() $M\subseteq M'\in N$
such that
$M\subseteq M'\in N$
such that
![]() $M'\cap N\in M$
. Note that
$M'\cap N\in M$
. Note that
![]() $t\in M'$
. Assume that t is guessed in N. By Lemma 4.9, t is guessed in
$t\in M'$
. Assume that t is guessed in N. By Lemma 4.9, t is guessed in
![]() $M'\cap N$
. On the one hand,
$M'\cap N$
. On the one hand,
![]() $f_q(t)=f_r(t) $
belongs to
$f_q(t)=f_r(t) $
belongs to
![]() $ M'\cap N$
, and that
$ M'\cap N$
, and that
![]() $M'\cap N\in M\cap \mathcal M_p\subseteq \mathcal M_q$
. Since q is a condition, we have
$M'\cap N\in M\cap \mathcal M_p\subseteq \mathcal M_q$
. Since q is a condition, we have
![]() $t\in M'\cap N\subseteq N$
.
$t\in M'\cap N\subseteq N$
.
Thus far, we have shown that
![]() $p\land q$
satisfies all items in Definition 4.11, possibly except Item 2. We shall show that under appropriate circumstances,
$p\land q$
satisfies all items in Definition 4.11, possibly except Item 2. We shall show that under appropriate circumstances,
![]() $p\land q$
is indeed a condition. We now prepare the ground for this.
$p\land q$
is indeed a condition. We now prepare the ground for this.
Definition 4.19. For a condition
![]() $p\in \mathbb P_T$
and a model
$p\in \mathbb P_T$
and a model
![]() $M\in \mathcal {E}^1_p$
, we let
$M\in \mathcal {E}^1_p$
, we let
Definition 4.20 (M-support).
Suppose p is a condition in
![]() $\mathbb P_T$
and that
$\mathbb P_T$
and that
![]() $M\in \mathcal {E}^1_p$
. We say that a function
$M\in \mathcal {E}^1_p$
. We say that a function
![]() $\sigma :\mathscr {D}(p,M)\rightarrow T\cap M$
is an M-support for p if the following hold, for every
$\sigma :\mathscr {D}(p,M)\rightarrow T\cap M$
is an M-support for p if the following hold, for every
![]() $t\in {\mathrm {dom}}(\sigma )$
.
$t\in {\mathrm {dom}}(\sigma )$
.
-
(1) If
 $O_M(t)\in M$
, then
$O_M(t)\in M$
, then
 $\sigma (t)=O_M(t)$
.
$\sigma (t)=O_M(t)$
. -
(2) If
 $O_M(t)\notin M$
, then
$O_M(t)\notin M$
, then
 $\sigma (t)<_T O_M(t)$
is such that there is no node in
$\sigma (t)<_T O_M(t)$
is such that there is no node in
 ${\mathrm {dom}}(f_p)$
whose height belongs to the interval
${\mathrm {dom}}(f_p)$
whose height belongs to the interval
 $\big [{\mathrm {ht}}(\sigma (t)),\eta _M(t)\big )$
.
$\big [{\mathrm {ht}}(\sigma (t)),\eta _M(t)\big )$
.
Lemma 4.21. Suppose p is a condition in
![]() $\mathbb P_T$
. Assume that
$\mathbb P_T$
. Assume that
![]() $M\in \mathcal {E}^1_p$
. Then, there is an M-support
$M\in \mathcal {E}^1_p$
. Then, there is an M-support
![]() $\sigma $
for p.
$\sigma $
for p.
Proof Fix
![]() $p\in \mathbb P_T$
. It is enough to define
$p\in \mathbb P_T$
. It is enough to define
![]() $\sigma $
for
$\sigma $
for
![]() $t\in \mathscr D(p,M) $
with
$t\in \mathscr D(p,M) $
with
![]() $O_M(t)\notin M$
. Thus fix such a t. Notice that
$O_M(t)\notin M$
. Thus fix such a t. Notice that
![]() ${\mathrm {dom}}(f_p)$
is finite, and that, by Lemma 4.6,
${\mathrm {dom}}(f_p)$
is finite, and that, by Lemma 4.6,
![]() $\eta _M(t)$
is a limit ordinal. Thus one may easily find a node
$\eta _M(t)$
is a limit ordinal. Thus one may easily find a node
![]() $\sigma (t)$
with the above properties.
$\sigma (t)$
with the above properties.
Definition 4.22 (M-reflection).
Suppose that
![]() $p\in \mathbb P_T$
and
$p\in \mathbb P_T$
and
![]() $M\in \mathcal {E}^1_p$
. A condition q is called an
$M\in \mathcal {E}^1_p$
. A condition q is called an
![]() $(M,\sigma )$
-reflection of p, where
$(M,\sigma )$
-reflection of p, where
![]() $\sigma $
is an M-support for p, if the following properties are satisfied.
$\sigma $
is an M-support for p, if the following properties are satisfied.
-
(1)
 $q\leq p\! \upharpoonright \!_M$
.
$q\leq p\! \upharpoonright \!_M$
. -
(2) For every
 $t\in {\mathrm {dom}}(\sigma )$
, the following hold:
$t\in {\mathrm {dom}}(\sigma )$
, the following hold:-
(a) There is no node in
 ${\mathrm {dom}}(f_q)$
whose height is the interval
${\mathrm {dom}}(f_q)$
whose height is the interval
 $\big [{\mathrm {ht}}(\sigma (t)),\eta _M(t)\big )$
.
$\big [{\mathrm {ht}}(\sigma (t)),\eta _M(t)\big )$
. -
(b) For every
 $s\in {\mathrm {dom}}(f_q)$
, if
$s\in {\mathrm {dom}}(f_q)$
, if
 $s<_T \sigma (t)$
, then
$s<_T \sigma (t)$
, then
 $f_q(s)\neq f_p(t)$
.
$f_q(s)\neq f_p(t)$
.
-
Let
![]() $R_p(M,\sigma )$
be the set of
$R_p(M,\sigma )$
be the set of
![]() $(M,\sigma )$
-reflections of p with support
$(M,\sigma )$
-reflections of p with support
![]() $\sigma $
.
$\sigma $
.
Remark 4.23. Notice that if
![]() $M^*\prec H_{\theta ^*}$
, for some sufficiently large regular cardinal
$M^*\prec H_{\theta ^*}$
, for some sufficiently large regular cardinal
![]() $\theta ^*$
, which contains T and
$\theta ^*$
, which contains T and
![]() $H_{\theta }$
, and that p is a condition in
$H_{\theta }$
, and that p is a condition in
![]() $\mathbb P_T$
with
$\mathbb P_T$
with
![]() $M:= M^*\cap H_{\theta }\in \mathcal {E}^1_p $
, then
$M:= M^*\cap H_{\theta }\in \mathcal {E}^1_p $
, then
![]() $R_p(M,\sigma )\in M^*$
, whenever
$R_p(M,\sigma )\in M^*$
, whenever
![]() $\sigma $
is an M-support for p.
$\sigma $
is an M-support for p.
Lemma 4.24. Let
![]() $p\in \mathbb P_T$
. Assume that
$p\in \mathbb P_T$
. Assume that
![]() $M\in \mathcal {E}^1_p$
, and let
$M\in \mathcal {E}^1_p$
, and let
![]() $\sigma $
be an M-support for p. Then
$\sigma $
be an M-support for p. Then
![]() $p\in R_p(M,\sigma )$
.
$p\in R_p(M,\sigma )$
.
Proof We check the items in Definition 4.22. Item 1 is essentially Proposition 4.15. Item 2a follows from the definition of
![]() $\sigma $
. Item 2b follows from the fact that p is a condition, and that
$\sigma $
. Item 2b follows from the fact that p is a condition, and that
![]() $\sigma (t)<_T t$
.
$\sigma (t)<_T t$
.
Lemma 4.25. Suppose p is a condition in
![]() $\mathbb P_T$
. Let
$\mathbb P_T$
. Let
![]() $M\in \mathcal {E}^1_p$
, and let
$M\in \mathcal {E}^1_p$
, and let
![]() $q\in M$
be an
$q\in M$
be an
![]() $(M,\sigma )$
-reflection of p, for some M-support
$(M,\sigma )$
-reflection of p, for some M-support
![]() $\sigma $
for p. Let
$\sigma $
for p. Let
![]() $r=p\land q$
. Then
$r=p\land q$
. Then
![]() $f_r\in B_{\omega }(T)$
.
$f_r\in B_{\omega }(T)$
.
Proof Since
![]() $q\leq p\! \upharpoonright \!_M$
,
$q\leq p\! \upharpoonright \!_M$
,
![]() $f_r$
is well-defined as a function. We shall show that it satisfies the specialising property. To do this, we only discuss the nontrivial case by considering two arbitrary comparable nodes
$f_r$
is well-defined as a function. We shall show that it satisfies the specialising property. To do this, we only discuss the nontrivial case by considering two arbitrary comparable nodes
![]() $t\in {\mathrm {dom}}(f_p)\setminus {\mathrm {dom}}(f_q)$
and
$t\in {\mathrm {dom}}(f_p)\setminus {\mathrm {dom}}(f_q)$
and
![]() $s\in {\mathrm {dom}}(f_q)\setminus {\mathrm {dom}}(f_p)$
. We claim that
$s\in {\mathrm {dom}}(f_q)\setminus {\mathrm {dom}}(f_p)$
. We claim that
![]() $f_r(t)\neq f_r(s)$
. Observe that
$f_r(t)\neq f_r(s)$
. Observe that
![]() $s\in M$
. The fact that
$s\in M$
. The fact that
![]() $M\cap \omega _2$
is an ordinal imply that if
$M\cap \omega _2$
is an ordinal imply that if
![]() $t\leq _T s$
, then
$t\leq _T s$
, then
![]() $t\in M$
, which is a contradiction as
$t\in M$
, which is a contradiction as
![]() $t\notin {\mathrm {dom}}(f_q)$
. Thus, the only possibility is
$t\notin {\mathrm {dom}}(f_q)$
. Thus, the only possibility is
![]() $s<_T t$
. Since
$s<_T t$
. Since
![]() $q\in R_p(M,\sigma )\cap M$
, the height of s is not in the interval
$q\in R_p(M,\sigma )\cap M$
, the height of s is not in the interval
![]() $\big [{\mathrm {ht}}(\sigma (t)),\eta _M(t)\big )$
. Thus
$\big [{\mathrm {ht}}(\sigma (t)),\eta _M(t)\big )$
. Thus
![]() $s<_T\sigma (t)$
. Then Item 2b of Definition 4.22 implies that
$s<_T\sigma (t)$
. Then Item 2b of Definition 4.22 implies that
![]() $f_q(s)\neq f_p(t)$
. Therefore,
$f_q(s)\neq f_p(t)$
. Therefore,
![]() $f_r(t)\neq f_r(s)$
.
$f_r(t)\neq f_r(s)$
.
We have now all the necessary tools to prove the preservation of
![]() $\aleph _2$
by
$\aleph _2$
by
![]() $\mathbb P_T$
.
$\mathbb P_T$
.
Lemma 4.26. Suppose p is a condition in
![]() $\mathbb P_T$
. Assume that
$\mathbb P_T$
. Assume that
![]() $\theta ^*$
is a sufficiently large regular cardinal, and that
$\theta ^*$
is a sufficiently large regular cardinal, and that
![]() $M^*\prec H_{\theta ^*}$
contains the relevant objects. Suppose that
$M^*\prec H_{\theta ^*}$
contains the relevant objects. Suppose that
![]() $M:= M^*\cap H_{\theta }$
is in
$M:= M^*\cap H_{\theta }$
is in
![]() $\mathcal {E}^1_p$
. Then, p is
$\mathcal {E}^1_p$
. Then, p is
![]() $(M^*,\mathbb P_T)$
-generic.
$(M^*,\mathbb P_T)$
-generic.
Proof Fix
![]() $p'\leq p$
. Then
$p'\leq p$
. Then
![]() $M\in \mathcal M_{p'}$
. Thus we may assume that
$M\in \mathcal M_{p'}$
. Thus we may assume that
![]() $p=p'$
. Let
$p=p'$
. Let
![]() $D\in M^*$
be a dense subset of
$D\in M^*$
be a dense subset of
![]() $\mathbb P_T$
. We may also assume that
$\mathbb P_T$
. We may also assume that
![]() $p\in D$
. By Lemmas 4.21 and 4.24, there exists an M-support of p, say
$p\in D$
. By Lemmas 4.21 and 4.24, there exists an M-support of p, say
![]() $\sigma $
, such that
$\sigma $
, such that
![]() $p\in R_p(M,\sigma )$
. Notice that
$p\in R_p(M,\sigma )$
. Notice that
![]() $R_p(M,\sigma )$
is in
$R_p(M,\sigma )$
is in
![]() $M^*$
. Thus by elementarity, there is some
$M^*$
. Thus by elementarity, there is some
![]() $q\in D\cap R_p(M,\sigma )\cap M$
. Set
$q\in D\cap R_p(M,\sigma )\cap M$
. Set
![]() $r=p\land q$
. Now, Fact 3.9 and Lemmas 4.17, 4.18, and 4.25 imply that r satisfies Items 1–4 of Definition 4.11, respectively. It is clear that
$r=p\land q$
. Now, Fact 3.9 and Lemmas 4.17, 4.18, and 4.25 imply that r satisfies Items 1–4 of Definition 4.11, respectively. It is clear that
![]() $p\land q$
extends both p and q.
$p\land q$
extends both p and q.
Corollary 4.27. Assume
![]() ${\mathrm {GM}}^*(\omega _2)$
. Then
${\mathrm {GM}}^*(\omega _2)$
. Then
![]() $\mathbb P_T$
preserves
$\mathbb P_T$
preserves
![]() $\aleph _2$
.
$\aleph _2$
.
Proof Let
![]() $\theta ^*$
be a sufficiently large regular cardinal. By Lemma 2.7, it is enough to show that for stationary many models M in
$\theta ^*$
be a sufficiently large regular cardinal. By Lemma 2.7, it is enough to show that for stationary many models M in
![]() $H_{\theta ^*}$
, of size
$H_{\theta ^*}$
, of size
![]() $\aleph _1$
, every condition in M can be extended to an
$\aleph _1$
, every condition in M can be extended to an
![]() $(M,\mathbb P_T)$
-generic condition. Let
$(M,\mathbb P_T)$
-generic condition. Let
By
![]() ${\mathrm {GM}}^*(\omega _2)$
,
${\mathrm {GM}}^*(\omega _2)$
,
![]() $\mathcal S$
is stationary in
$\mathcal S$
is stationary in
![]() $\mathcal P_{\omega _2}(H_{\theta ^*})$
. Now let
$\mathcal P_{\omega _2}(H_{\theta ^*})$
. Now let
![]() $M^*\in \mathcal S$
and
$M^*\in \mathcal S$
and
![]() $p\in \mathbb P_T\cap M^*$
. Set
$p\in \mathbb P_T\cap M^*$
. Set
![]() $M=M^*\cap H_\theta $
. By Proposition 4.13,
$M=M^*\cap H_\theta $
. By Proposition 4.13,
![]() $p^M$
is a condition with
$p^M$
is a condition with
![]() $p^M\leq p$
, and by Lemma 4.26 it is
$p^M\leq p$
, and by Lemma 4.26 it is
![]() $(M^*,\mathbb P_T)$
-generic.
$(M^*,\mathbb P_T)$
-generic.
4.4 Properness
This subsection is devoted to the proof of the properness of
![]() $\mathbb P_T$
. We will closely follow our strategy in the previous subsection. Notice that our notation and definition related to models in
$\mathbb P_T$
. We will closely follow our strategy in the previous subsection. Notice that our notation and definition related to models in
![]() $\mathcal E^0$
are similar to the ones we used for the preservation of
$\mathcal E^0$
are similar to the ones we used for the preservation of
![]() $\aleph _2$
, but hopefully there will be no confusion, since these two parts are completely independent.
$\aleph _2$
, but hopefully there will be no confusion, since these two parts are completely independent.
Lemma 4.28. Suppose p is a condition in
![]() $\mathbb P_T$
and that
$\mathbb P_T$
and that
![]() $M\in \mathcal {E}^0_p$
. Assume that
$M\in \mathcal {E}^0_p$
. Assume that
![]() $q\in M$
is a condition extending
$q\in M$
is a condition extending
![]() $p\! \upharpoonright \!_M$
. Then
$p\! \upharpoonright \!_M$
. Then
![]() $p\land q$
satisfies Item 4 of Definition 4.11.
$p\land q$
satisfies Item 4 of Definition 4.11.
Proof Set
![]() $r=p\land q$
. Notice that
$r=p\land q$
. Notice that
![]() $f_r$
is well-defined as a function. Fix
$f_r$
is well-defined as a function. Fix
![]() $t\in {\mathrm {dom}}(f_r)$
and
$t\in {\mathrm {dom}}(f_r)$
and
![]() $N\in \mathcal E^0\cap \mathcal M_r$
so that t is guessed in N and
$N\in \mathcal E^0\cap \mathcal M_r$
so that t is guessed in N and
![]() $f_r(t)\in N$
. We shall show that
$f_r(t)\in N$
. We shall show that
![]() $t\in N$
. As in Lemma 4.18, we shall study the nontrivial cases, and thus we may assume that either
$t\in N$
. As in Lemma 4.18, we shall study the nontrivial cases, and thus we may assume that either
![]() $t\in {\mathrm {dom}}(f_q)$
and
$t\in {\mathrm {dom}}(f_q)$
and
![]() $N\notin \mathcal M_q$
, or
$N\notin \mathcal M_q$
, or
![]() $t\in {\mathrm {dom}}(f_p)$
and
$t\in {\mathrm {dom}}(f_p)$
and
![]() $N\notin \mathcal M_p$
. Since M is in
$N\notin \mathcal M_p$
. Since M is in
![]() $\mathcal {E}^0$
, the proof consists of three cases as
$\mathcal {E}^0$
, the proof consists of three cases as
![]() $\mathcal M_r\setminus (\mathcal M_p\cup \mathcal M_q)$
may be nonempty. Recall that by Remark 3.13,
$\mathcal M_r\setminus (\mathcal M_p\cup \mathcal M_q)$
may be nonempty. Recall that by Remark 3.13,
![]() $\mathcal M_r$
is the union of
$\mathcal M_r$
is the union of
![]() $\mathcal M_p\cup \mathcal M_q$
and the set of models of the form
$\mathcal M_p\cup \mathcal M_q$
and the set of models of the form
![]() $P\cap Q$
, where
$P\cap Q$
, where
![]() $P\in Q$
are in
$P\in Q$
are in
![]() $\mathcal E^1_q$
and
$\mathcal E^1_q$
and
![]() $\mathcal E^0_p$
, respectively.
$\mathcal E^0_p$
, respectively.
Case 1:
![]() $t\in {\mathrm {dom}}(f_q)$
and
$t\in {\mathrm {dom}}(f_q)$
and
![]() $N\in \mathcal M_p\setminus \mathcal M_q$
.
$N\in \mathcal M_p\setminus \mathcal M_q$
.
In this situation, we have
![]() $N\in (P\cap M,P]_p$
for some
$N\in (P\cap M,P]_p$
for some
![]() $P\in (\mathcal {E}^1_p\cap M)\cup \{H_\theta \}$
. Since t is guessed in
$P\in (\mathcal {E}^1_p\cap M)\cup \{H_\theta \}$
. Since t is guessed in
![]() $N\subseteq P$
and
$N\subseteq P$
and
![]() $\omega _1\subseteq P$
, we have
$\omega _1\subseteq P$
, we have
![]() $t\in P$
. Assume towards a contraction that
$t\in P$
. Assume towards a contraction that
![]() $t\notin N$
. We may assume that N is the least model in
$t\notin N$
. We may assume that N is the least model in
![]() $\mathcal M_p$
with the above properties. This implies that
$\mathcal M_p$
with the above properties. This implies that
![]() $P\cap M\nsubseteq N$
, since
$P\cap M\nsubseteq N$
, since
![]() $t\in P\cap M$
. Therefore, by Remark 3.2, there is a model
$t\in P\cap M$
. Therefore, by Remark 3.2, there is a model
![]() $Q\in \mathcal E^1_p$
such that
$Q\in \mathcal E^1_p$
such that
![]() $P\cap M\in Q\in N\in P$
and
$P\cap M\in Q\in N\in P$
and
![]() $Q\cap N\in ^* P\cap M$
. Observe that
$Q\cap N\in ^* P\cap M$
. Observe that
![]() $t\in Q$
. By Lemma 4.9, t is guessed in
$t\in Q$
. By Lemma 4.9, t is guessed in
![]() $Q\cap N$
. On the other hand
$Q\cap N$
. On the other hand
![]() $f_q(t)\in Q\cap N$
. Since
$f_q(t)\in Q\cap N$
. Since
![]() $t\notin Q\cap N$
, our minimality assumption implies that
$t\notin Q\cap N$
, our minimality assumption implies that
![]() $Q\cap N$
is in
$Q\cap N$
is in
![]() $\mathcal M_q$
, but then since q is a condition, t is an element of
$\mathcal M_q$
, but then since q is a condition, t is an element of
![]() $Q\cap N\subseteq N$
, a contradiction!
$Q\cap N\subseteq N$
, a contradiction!
Case 2:
![]() $t\in {\mathrm {dom}}(f_p)$
and
$t\in {\mathrm {dom}}(f_p)$
and
![]() $N\in \mathcal M_q$
.
$N\in \mathcal M_q$
.
We have
![]() $f_p(t)\in N\subseteq M$
. Observe that t is also guessed in M, since
$f_p(t)\in N\subseteq M$
. Observe that t is also guessed in M, since
![]() $N\subseteq M$
. As p is a condition, Item 4 of Definition 4.11 implies that
$N\subseteq M$
. As p is a condition, Item 4 of Definition 4.11 implies that
![]() $t\in M\cap {\mathrm {dom}}(f_p)\subseteq {\mathrm {dom}}(f_q)$
. On the other hand, q is a condition and
$t\in M\cap {\mathrm {dom}}(f_p)\subseteq {\mathrm {dom}}(f_q)$
. On the other hand, q is a condition and
![]() $N\in \mathcal M_q$
, and hence, by Item 4 of Definition 4.11,
$N\in \mathcal M_q$
, and hence, by Item 4 of Definition 4.11,
![]() $t\in N$
.
$t\in N$
.
Case 3:
![]() $t\in {\mathrm {dom}}(f_r)$
and
$t\in {\mathrm {dom}}(f_r)$
and
![]() $N\in \mathcal M_r\setminus (\mathcal M_p\cup \mathcal M_q)$
.
$N\in \mathcal M_r\setminus (\mathcal M_p\cup \mathcal M_q)$
.
There are
![]() $P\in \mathcal E^1_q$
and
$P\in \mathcal E^1_q$
and
![]() $Q\in \mathcal E^0_p$
with
$Q\in \mathcal E^0_p$
with
![]() $P\in Q$
such that
$P\in Q$
such that
![]() $N=P\cap Q$
. Let
$N=P\cap Q$
. Let
![]() $b\in N$
be a T-branch with
$b\in N$
be a T-branch with
![]() $t\in b$
. Then t is guessed in Q, as
$t\in b$
. Then t is guessed in Q, as
![]() $b\in Q$
. We have also
$b\in Q$
. We have also
![]() $f_p(t)\in Q$
. Thus by the two previous cases,
$f_p(t)\in Q$
. Thus by the two previous cases,
![]() $t\in Q$
. On the other hand,
$t\in Q$
. On the other hand,
![]() $b\in P$
and
$b\in P$
and
![]() $b\subseteq P$
, as T has no cofinal branches, and
$b\subseteq P$
, as T has no cofinal branches, and
![]() $P\cap \omega _2$
is an ordinal. Thus
$P\cap \omega _2$
is an ordinal. Thus
![]() $t\in P$
. Therefore,
$t\in P$
. Therefore,
![]() $t\in P\cap Q=N$
.
$t\in P\cap Q=N$
.
Notation 4.29. Assume that p is a condition in
![]() $\mathbb P_T$
, and that
$\mathbb P_T$
, and that
![]() $M\in \mathcal E^0_p$
.
$M\in \mathcal E^0_p$
.
-
(1) We let
 $\mathscr {D}(p,M)$
denote the set of
$\mathscr {D}(p,M)$
denote the set of
 $t\in {\mathrm {dom}}(f\kern-4pt_p)$
such that
$t\in {\mathrm {dom}}(f\kern-4pt_p)$
such that
 $t\notin M$
, but
$t\notin M$
, but
 $f\kern-4pt_p(t)\in M$
.
$f\kern-4pt_p(t)\in M$
. -
(2)
 $\mathscr {O}(p,M):= \{t\in \mathscr {D}(p,M): O_M(t) \text { is not guessed in } M \text { and } \eta _M(t)\notin M \}$
.
$\mathscr {O}(p,M):= \{t\in \mathscr {D}(p,M): O_M(t) \text { is not guessed in } M \text { and } \eta _M(t)\notin M \}$
.
Definition 4.30 (M-support).
Suppose p is a condition in
![]() $\mathbb P_T$
and
$\mathbb P_T$
and
![]() $M\in \mathcal {E}^0_p$
. We say a function
$M\in \mathcal {E}^0_p$
. We say a function
![]() $\sigma :\mathscr {D}(p,M)\rightarrow M$
is an M-support for p if the following hold, for every
$\sigma :\mathscr {D}(p,M)\rightarrow M$
is an M-support for p if the following hold, for every
![]() $t\in {\mathrm {dom}}(\sigma )$
.
$t\in {\mathrm {dom}}(\sigma )$
.
-
(1) If
 $O_M(t)$
is guessed in M, then
$O_M(t)$
is guessed in M, then
 $\sigma (t)\in M$
is such that
$\sigma (t)\in M$
is such that
 $M\cap \sigma (t)= M\cap b_M(t)$
.
$M\cap \sigma (t)= M\cap b_M(t)$
. -
(2) If
 $O_M(t)$
is not guessed in M, then
$O_M(t)$
is not guessed in M, then
 $\sigma (t)\subseteq b_M(t)$
is a T-branch in M such that no node in
$\sigma (t)\subseteq b_M(t)$
is a T-branch in M such that no node in
 ${\mathrm {dom}}(f\kern-4pt_p)$
has height in the interval
${\mathrm {dom}}(f\kern-4pt_p)$
has height in the interval
 $\big [{\mathrm {ht}}(\sup (\sigma (t))),\eta _M(t)\big )$
.
$\big [{\mathrm {ht}}(\sup (\sigma (t))),\eta _M(t)\big )$
.
Note that if
![]() $t\in {\mathrm {dom}}(\sigma )$
and
$t\in {\mathrm {dom}}(\sigma )$
and
![]() $O_M(t)$
is guessed in M, then by elementarity,
$O_M(t)$
is guessed in M, then by elementarity,
![]() $\sigma (t)$
is a T-branch, in fact it is a cofinal branch through
$\sigma (t)$
is a T-branch, in fact it is a cofinal branch through
![]() $ T_{<\eta ^*_M(t)}$
, where
$ T_{<\eta ^*_M(t)}$
, where
![]() $\eta ^*_M(t)={\mathrm {min}}(M\cap \omega _2\setminus \eta _M(t))$
. Moreover,
$\eta ^*_M(t)={\mathrm {min}}(M\cap \omega _2\setminus \eta _M(t))$
. Moreover,
![]() $\sigma (t)$
is unique.
$\sigma (t)$
is unique.
Lemma 4.31. Let
![]() $p\in \mathbb P_T$
, and let
$p\in \mathbb P_T$
, and let
![]() $M\in \mathcal E^0_p$
. Then, there is an M-support for p.
$M\in \mathcal E^0_p$
. Then, there is an M-support for p.
Proof Suppose that
![]() $t\in \mathscr {D}(p,M)$
. If
$t\in \mathscr {D}(p,M)$
. If
![]() $O_M(t)$
is guessed in M, then there is a T-branch
$O_M(t)$
is guessed in M, then there is a T-branch
![]() $b\in M$
such that
$b\in M$
such that
![]() $O_M(t)\in b$
. Let
$O_M(t)\in b$
. Let
![]() $\eta ^*_M(t)={\mathrm {min}}(M\cap \omega _2\setminus \eta _M(t))$
, and set
$\eta ^*_M(t)={\mathrm {min}}(M\cap \omega _2\setminus \eta _M(t))$
, and set
![]() $\sigma (t):= b\cap T_{<\eta ^*_M(t)}$
. It is easily seen that
$\sigma (t):= b\cap T_{<\eta ^*_M(t)}$
. It is easily seen that
![]() $M\cap \sigma (t)=M\cap b_M(t).$
$M\cap \sigma (t)=M\cap b_M(t).$
If
![]() $O_M(t)$
is not guessed in M, then
$O_M(t)$
is not guessed in M, then
![]() $\eta _M(t)$
is a limit ordinal by Lemma 4.6. Since
$\eta _M(t)$
is a limit ordinal by Lemma 4.6. Since
![]() ${\mathrm {dom}}(f\kern-4pt_p)$
is finite, there is a sequence of nodes in M cofinal in
${\mathrm {dom}}(f\kern-4pt_p)$
is finite, there is a sequence of nodes in M cofinal in
![]() $O_M(t)$
. Thus one can find an ordinal
$O_M(t)$
. Thus one can find an ordinal
![]() $\gamma \in M$
, such that there is no node in
$\gamma \in M$
, such that there is no node in
![]() ${\mathrm {dom}}(f\kern-4pt_p)$
whose height is in the interval
${\mathrm {dom}}(f\kern-4pt_p)$
whose height is in the interval
![]() $[\gamma ,\eta _M(t))$
. Choose a node s of height
$[\gamma ,\eta _M(t))$
. Choose a node s of height
![]() $\gamma $
below
$\gamma $
below
![]() $O_M(t)$
and set
$O_M(t)$
and set
![]() $\sigma (t):= \overline {b}_{s}$
. We have
$\sigma (t):= \overline {b}_{s}$
. We have
![]() $s\in M$
, since
$s\in M$
, since
![]() $\gamma \in M$
. Thus
$\gamma \in M$
. Thus
![]() $\sigma (t)\in M$
. Observe that
$\sigma (t)\in M$
. Observe that
![]() ${\mathrm {ht}}(\sup (\sigma (t)))= {\mathrm {ht}}(s)=\gamma $
.
${\mathrm {ht}}(\sup (\sigma (t)))= {\mathrm {ht}}(s)=\gamma $
.
Definition 4.32 (M-reflection).
Suppose p is a condition in
![]() $\mathbb P_T$
. Assume that
$\mathbb P_T$
. Assume that
![]() $M\in \mathcal {E}^0_p$
. Let
$M\in \mathcal {E}^0_p$
. Let
![]() $\sigma $
be an M-support for p. A condition q is called an
$\sigma $
be an M-support for p. A condition q is called an
![]() $(M,\sigma )$
-reflection of p if the following properties are satisfied.
$(M,\sigma )$
-reflection of p if the following properties are satisfied.
-
(1)
 $q\leq p\! \upharpoonright \!_M$
.
$q\leq p\! \upharpoonright \!_M$
. -
(2) The following hold for every
 $t\in {\mathrm {dom}}(\sigma )$
.
$t\in {\mathrm {dom}}(\sigma )$
.-
(a) If
 $\eta _M(t)\in M$
, then there is no node in
$\eta _M(t)\in M$
, then there is no node in
 ${\mathrm {dom}}(f_q)$
whose height belongs to the interval
${\mathrm {dom}}(f_q)$
whose height belongs to the interval
 $\big [{\mathrm {ht}}(\sup (\sigma (t))),\eta _M(t)\big )$
.
$\big [{\mathrm {ht}}(\sup (\sigma (t))),\eta _M(t)\big )$
. -
(b) For every
 $s\in {\mathrm {dom}}(f_q)$
with
$s\in {\mathrm {dom}}(f_q)$
with
 $s\in \sigma (t)$
,
$s\in \sigma (t)$
,
 $f_q(s)\neq f\kern-4pt_p(t)$
.
$f_q(s)\neq f\kern-4pt_p(t)$
.
-
Let
![]() $R_p(M,\sigma )$
denote the set of
$R_p(M,\sigma )$
denote the set of
![]() $(M,\sigma )$
-reflections of p.
$(M,\sigma )$
-reflections of p.
Notice that as before, if
![]() $M^*\prec H_{\theta ^*}$
, for some sufficiently large regular cardinal
$M^*\prec H_{\theta ^*}$
, for some sufficiently large regular cardinal
![]() $\theta ^*$
which contains T and
$\theta ^*$
which contains T and
![]() $H_\theta $
, and p is a condition in
$H_\theta $
, and p is a condition in
![]() $\mathbb P_T$
with
$\mathbb P_T$
with
![]() $M:= M^*\cap H_{\theta }\in \mathcal {E}^0_p $
, then
$M:= M^*\cap H_{\theta }\in \mathcal {E}^0_p $
, then
![]() $R_p(M,\sigma )\in M^*$
, whenever
$R_p(M,\sigma )\in M^*$
, whenever
![]() $\sigma $
is an M-support for p.
$\sigma $
is an M-support for p.
Lemma 4.33. Suppose p is a condition in
![]() $\mathbb P_T$
, and that
$\mathbb P_T$
, and that
![]() $M\in \mathcal {E}^0_p$
. Let
$M\in \mathcal {E}^0_p$
. Let
![]() $\sigma $
be an M-support set for p. Then
$\sigma $
be an M-support set for p. Then
![]() $p\in R_p(M,\sigma )$
.
$p\in R_p(M,\sigma )$
.
Proof Let us check the items in Definition 4.32. Item 1 is essentially Proposition 4.15. To verify Item 2, let us fix
![]() $t\in {\mathrm {dom}}(\sigma )$
.
$t\in {\mathrm {dom}}(\sigma )$
.
Item 2a: Assume that
![]() $\eta _M(t)\in M$
. If
$\eta _M(t)\in M$
. If
![]() $O_M(t)$
is not guessed in M, then by the Item 2 of Definition 4.30, there is no node in
$O_M(t)$
is not guessed in M, then by the Item 2 of Definition 4.30, there is no node in
![]() ${\mathrm {dom}}(f\kern-4pt_p)$
with height in the interval
${\mathrm {dom}}(f\kern-4pt_p)$
with height in the interval
![]() $\big [{\mathrm {ht}}(\sup (\sigma (t))),\eta _M(t)\big )$
. Thus let us assume that
$\big [{\mathrm {ht}}(\sup (\sigma (t))),\eta _M(t)\big )$
. Thus let us assume that
![]() $O_M(t)$
is guessed in M. We show that
$O_M(t)$
is guessed in M. We show that
![]() $\sigma (t)=b_M(t)$
, which in turn implies that the interval
$\sigma (t)=b_M(t)$
, which in turn implies that the interval
![]() $\big [{\mathrm {ht}}(\sup (\sigma (t))),\eta _M(t)\big )$
is empty. To show that
$\big [{\mathrm {ht}}(\sup (\sigma (t))),\eta _M(t)\big )$
is empty. To show that
![]() $\sigma (t)=b_M(t)$
, it is enough to show that
$\sigma (t)=b_M(t)$
, it is enough to show that
![]() $b_M(t)\in M$
. Suppose
$b_M(t)\in M$
. Suppose
![]() $b\in M$
is a T-branch with
$b\in M$
is a T-branch with
![]() $O_M(t)\in b$
. Then the order type of b is at least
$O_M(t)\in b$
. Then the order type of b is at least
![]() $\eta _M(t)+1$
and
$\eta _M(t)+1$
and
![]() $O_M(t)$
is the
$O_M(t)$
is the
![]() $\eta _M(t)$
-th element of b. Since
$\eta _M(t)$
-th element of b. Since
![]() $\eta _M(t)\in M$
, we have
$\eta _M(t)\in M$
, we have
![]() $O_M(t)\in M$
, and hence
$O_M(t)\in M$
, and hence
![]() $b_M(t)\in M$
.
$b_M(t)\in M$
.
Item 2b: Suppose that
![]() $s\in \sigma (t)$
and
$s\in \sigma (t)$
and
![]() $f\kern-4pt_p(s)=f\kern-4pt_p(t)$
. Then s is guessed in M. As
$f\kern-4pt_p(s)=f\kern-4pt_p(t)$
. Then s is guessed in M. As
![]() $f\kern-4pt_p(t)\in M$
and p is a condition, we have
$f\kern-4pt_p(t)\in M$
and p is a condition, we have
![]() $s\in M$
. This implies that
$s\in M$
. This implies that
![]() $s\leq _T O_M(t)\leq _T t$
. Since p is a condition, we
$s\leq _T O_M(t)\leq _T t$
. Since p is a condition, we
![]() $t=s\in M$
, which is a contradiction (as
$t=s\in M$
, which is a contradiction (as
![]() $t\notin M$
)!
$t\notin M$
)!
Lemma 4.34. Suppose
![]() $p\in \mathbb P_T$
, and that
$p\in \mathbb P_T$
, and that
![]() $M\in \mathcal {E}^0_p$
. Assume that
$M\in \mathcal {E}^0_p$
. Assume that
![]() $q\in M\cap R_p(M,\sigma )$
. Let
$q\in M\cap R_p(M,\sigma )$
. Let
![]() $r:= p\land q$
. Then
$r:= p\land q$
. Then
![]() $r'=(\mathcal M_r, f_r\setminus \{(t,f\kern-4pt_p(t)): t\notin \mathscr {O}(p,M)\})$
is a condition.
$r'=(\mathcal M_r, f_r\setminus \{(t,f\kern-4pt_p(t)): t\notin \mathscr {O}(p,M)\})$
is a condition.
Proof Lemmas 3.12, 4.17, and 4.28 imply that
![]() $r'$
satisfies Items 1, 3, and 4 of Definition 4.11, respectively. Therefore, it remains to show that the well-defined function
$r'$
satisfies Items 1, 3, and 4 of Definition 4.11, respectively. Therefore, it remains to show that the well-defined function
![]() $f_{r'}:= f_r\setminus \{(t,f\kern-4pt_p(t)): t\notin \mathscr {O}(p,M)\}$
is a condition in
$f_{r'}:= f_r\setminus \{(t,f\kern-4pt_p(t)): t\notin \mathscr {O}(p,M)\}$
is a condition in
![]() $\mathbb S_{\omega }(T)$
. To see this, let
$\mathbb S_{\omega }(T)$
. To see this, let
![]() $s\in {\mathrm {dom}}(f_q)\setminus {\mathrm {dom}}(f\kern-4pt_p)$
and
$s\in {\mathrm {dom}}(f_q)\setminus {\mathrm {dom}}(f\kern-4pt_p)$
and
![]() $t\in {\mathrm {dom}}(f_{r'})\setminus {\mathrm {dom}}(f_q)$
. Assume that s and t are comparable in T, we shall show that
$t\in {\mathrm {dom}}(f_{r'})\setminus {\mathrm {dom}}(f_q)$
. Assume that s and t are comparable in T, we shall show that
![]() $f_q(s)\neq f\kern-4pt_p(t)$
. We may assume that
$f_q(s)\neq f\kern-4pt_p(t)$
. We may assume that
![]() $f\kern-4pt_p(t)\in M$
. Thus
$f\kern-4pt_p(t)\in M$
. Thus
![]() $t<_T s$
is impossible, as otherwise t is guessed in M, and hence
$t<_T s$
is impossible, as otherwise t is guessed in M, and hence
![]() $t\in M$
, which is a contradiction! Consequently, the only possible case is
$t\in M$
, which is a contradiction! Consequently, the only possible case is
![]() $s<_T t$
. In this case,
$s<_T t$
. In this case,
![]() $s<_T O_M(t)$
. We claim that
$s<_T O_M(t)$
. We claim that
![]() $s\in \sigma (t)$
. This is clear if
$s\in \sigma (t)$
. This is clear if
![]() $O_M(t)$
is guessed in M. If
$O_M(t)$
is guessed in M. If
![]() $O_M(t)$
is not guessed in M, then
$O_M(t)$
is not guessed in M, then
![]() $\eta _M(t)\in M$
as
$\eta _M(t)\in M$
as
![]() $t\notin \mathscr O(p,M)$
. Therefore, by Item 2a of Definition 4.32, the height of s avoids the interval
$t\notin \mathscr O(p,M)$
. Therefore, by Item 2a of Definition 4.32, the height of s avoids the interval
![]() $\big [{\mathrm {ht}}(\sup (\sigma (t))),\eta _M(t)\big )$
. Thus
$\big [{\mathrm {ht}}(\sup (\sigma (t))),\eta _M(t)\big )$
. Thus
![]() $s<_T \sup (\sigma (t))$
, and hence
$s<_T \sup (\sigma (t))$
, and hence
![]() $s\in \sigma (t)$
. In either case,
$s\in \sigma (t)$
. In either case,
![]() $s\in \sigma (t)$
, but then Item 2b of Definition 4.32 implies that
$s\in \sigma (t)$
, but then Item 2b of Definition 4.32 implies that
![]() $f\kern-4pt_p(t)\neq f_q(s)$
.
$f\kern-4pt_p(t)\neq f_q(s)$
.
Proposition 4.35. Suppose that
![]() $p\in \mathbb P_T$
. Let
$p\in \mathbb P_T$
. Let
![]() $\theta ^*$
be a sufficiently large regular cardinal. Assume that
$\theta ^*$
be a sufficiently large regular cardinal. Assume that
![]() $M^*\prec H_{\theta ^*}$
is countable and contains T and
$M^*\prec H_{\theta ^*}$
is countable and contains T and
![]() $\theta $
. If
$\theta $
. If
![]() $M:= M^*\cap H_{\theta }\in \mathcal M_p$
. Then p is
$M:= M^*\cap H_{\theta }\in \mathcal M_p$
. Then p is
![]() $(M^*,\mathbb P_T)$
-generic.
$(M^*,\mathbb P_T)$
-generic.
Proof Assume that
![]() $p'\leq p$
. Since
$p'\leq p$
. Since
![]() $M\in \mathcal M_{p'}$
, we may assume without loss of generality that
$M\in \mathcal M_{p'}$
, we may assume without loss of generality that
![]() $p'=p$
. Let
$p'=p$
. Let
![]() $D\in M^*$
be a dense subset of
$D\in M^*$
be a dense subset of
![]() $\mathbb P_T$
. We may also assume, without loss of generality, that
$\mathbb P_T$
. We may also assume, without loss of generality, that
![]() $p\in D$
. Since
$p\in D$
. Since
![]() $M^*$
is fixed throughout proof, we simply denote
$M^*$
is fixed throughout proof, we simply denote
![]() $\eta _M(t)$
by
$\eta _M(t)$
by
![]() $\eta _t$
. By Lemmas 4.31 and 4.33, there is an M-support
$\eta _t$
. By Lemmas 4.31 and 4.33, there is an M-support
![]() $\sigma $
for p so that
$\sigma $
for p so that
![]() $p\in R_p(M,\sigma )$
. Observe that
$p\in R_p(M,\sigma )$
. Observe that
![]() $R_p(M,\sigma )\in M^*$
. Let
$R_p(M,\sigma )\in M^*$
. Let
![]() $\langle t_i: i< m\rangle $
enumerate
$\langle t_i: i< m\rangle $
enumerate
![]() $\mathscr {O}(p,M)$
so that
$\mathscr {O}(p,M)$
so that
![]() $\eta _{t_i}\leq \eta _{t_{i+1}}$
, for every
$\eta _{t_i}\leq \eta _{t_{i+1}}$
, for every
![]() $i<m-1$
. Let
$i<m-1$
. Let
![]() $\langle \eta _i: i< m'\rangle $
be the strictly increasing enumeration of
$\langle \eta _i: i< m'\rangle $
be the strictly increasing enumeration of
![]() $\{ \eta _{t_i}:i< m\}$
. To reduce the amount of notation, we may assume that
$\{ \eta _{t_i}:i< m\}$
. To reduce the amount of notation, we may assume that
![]() $m=m'$
. For every
$m=m'$
. For every
![]() $i< m$
, set
$i< m$
, set
Notice that
![]() $\eta _i^*<\eta _{i+1}$
, for every
$\eta _i^*<\eta _{i+1}$
, for every
![]() $i<m-1$
. For every
$i<m-1$
. For every
![]() $i<m$
, we let also
$i<m$
, we let also
![]() $\hat {t_i}$
denote
$\hat {t_i}$
denote
![]() $\sup (\sigma (t_i))$
. Note that
$\sup (\sigma (t_i))$
. Note that
![]() $\hat {t_i}$
exists, as
$\hat {t_i}$
exists, as
![]() $t_i\in \mathscr {O}(p,M)$
. Let us call a map
$t_i\in \mathscr {O}(p,M)$
. Let us call a map
![]() $ x\mapsto p_x$
from
$ x\mapsto p_x$
from
![]() $\mathcal P_{\omega _1}(T)$
into
$\mathcal P_{\omega _1}(T)$
into
![]() $ \mathbb P_T$
, a T-assignment if the following properties are satisfied for every
$ \mathbb P_T$
, a T-assignment if the following properties are satisfied for every
![]() $x\in \mathcal P_{\omega _1}(T)$
.
$x\in \mathcal P_{\omega _1}(T)$
.
-
(1)
 $p_x\in R_p(M,\sigma )\cap D$
.
$p_x\in R_p(M,\sigma )\cap D$
. -
(2)
 $ |{\mathrm {dom}}(f_{p_x})|=|{\mathrm {dom}}(f\kern-4pt_p)|$
.
$ |{\mathrm {dom}}(f_{p_x})|=|{\mathrm {dom}}(f\kern-4pt_p)|$
. -
(3) For every
 $s\in {\mathrm {dom}}(f_{p_x})$
and every
$s\in {\mathrm {dom}}(f_{p_x})$
and every
 $i< m$
, if
$i< m$
, if
 ${\mathrm {ht}}(s)\in \big [{\mathrm {ht}}(\hat {t}_i),\eta ^*_i\big )$
, then
${\mathrm {ht}}(s)\in \big [{\mathrm {ht}}(\hat {t}_i),\eta ^*_i\big )$
, then  $$ \begin{align*}{\mathrm{sup}}\{{\mathrm{ht}}(u): u\in x\cap T_{< \eta^*_{i}}\}<{\mathrm{ht}}(s).\end{align*} $$
$$ \begin{align*}{\mathrm{sup}}\{{\mathrm{ht}}(u): u\in x\cap T_{< \eta^*_{i}}\}<{\mathrm{ht}}(s).\end{align*} $$
We first show that there are T-assignments in
![]() $M^*$
.
$M^*$
.
Claim 4.36. There is a T-assignment in
![]() $M^*$
.
$M^*$
.
Proof We observe that all the parameters in the above properties are in
![]() $M^*$
. By elementarity and the Axiom of Choice, it is enough to show that for every
$M^*$
. By elementarity and the Axiom of Choice, it is enough to show that for every
![]() $x\in M^*$
, there is such
$x\in M^*$
, there is such
![]() $p_x\in H_{\theta ^*}$
. Thus fix
$p_x\in H_{\theta ^*}$
. Thus fix
![]() $x\in M^*$
. We claim that p is such a witness. The first item is clear by Lemma 4.33 and that the second one is trivial. To see the third one holds true, fix
$x\in M^*$
. We claim that p is such a witness. The first item is clear by Lemma 4.33 and that the second one is trivial. To see the third one holds true, fix
![]() $i<m$
and observe that
$i<m$
and observe that
-
•
 $\{{\mathrm {ht}}(u): u\in x\cap T_{< \eta ^*_{i}}\}$
is bounded below
$\{{\mathrm {ht}}(u): u\in x\cap T_{< \eta ^*_{i}}\}$
is bounded below
 $\eta _i$
(as the cofinality of
$\eta _i$
(as the cofinality of
 $\eta ^*_i$
is uncountable, x is countable and
$\eta ^*_i$
is uncountable, x is countable and
 $M\cap \eta ^*_i=M\cap \eta _i$
) and
$M\cap \eta ^*_i=M\cap \eta _i$
) and -
• there is no node in
 ${\mathrm {dom}}(f\kern-4pt_p)$
whose height lies in the interval
${\mathrm {dom}}(f\kern-4pt_p)$
whose height lies in the interval
 $\big [{\mathrm {ht}}(\hat {t}_i),\eta _i\big )$
(by the construction of
$\big [{\mathrm {ht}}(\hat {t}_i),\eta _i\big )$
(by the construction of
 $\sigma (t_i)$
, see Item 2 of Definition 4.30).
$\sigma (t_i)$
, see Item 2 of Definition 4.30).
Thus if
![]() $s\in {\mathrm {dom}}(f\kern-4pt_p)$
is of height at least
$s\in {\mathrm {dom}}(f\kern-4pt_p)$
is of height at least
![]() ${\mathrm {ht}}(\hat {t}_i)$
, then
${\mathrm {ht}}(\hat {t}_i)$
, then
![]() ${\mathrm {ht}}(s)\geq \eta _i$
, and thus
${\mathrm {ht}}(s)\geq \eta _i$
, and thus
Fix a T-assignment
![]() $x\mapsto p_x$
in
$x\mapsto p_x$
in
![]() $M^*$
. We shall show that there is a set
$M^*$
. We shall show that there is a set
![]() $B^*\in M^*$
cofinal in
$B^*\in M^*$
cofinal in
![]() $\mathcal P_{\omega _1}(T)$
such that for every
$\mathcal P_{\omega _1}(T)$
such that for every
![]() $x\in M^*\cap B^*$
,
$x\in M^*\cap B^*$
,
![]() $p_x$
and p are compatible. Let
$p_x$
and p are compatible. Let
![]() $n:= |{\mathrm {dom}}(f\kern-4pt_p)|$
. For each
$n:= |{\mathrm {dom}}(f\kern-4pt_p)|$
. For each
![]() $x\in \mathcal P_{\omega _1}(T)$
, fix an enumeration of
$x\in \mathcal P_{\omega _1}(T)$
, fix an enumeration of
![]() ${\mathrm {dom}}(f_{p_x})$
, say
${\mathrm {dom}}(f_{p_x})$
, say
![]() $\langle t^x_j: j< n\rangle $
. For every
$\langle t^x_j: j< n\rangle $
. For every
![]() $B\subseteq \mathcal P_{\omega _1}(T)$
, let
$B\subseteq \mathcal P_{\omega _1}(T)$
, let
Note that if
![]() $B\in M^*$
, then
$B\in M^*$
, then
![]() $B(i,j)\in M^*$
.
$B(i,j)\in M^*$
.
Claim 4.37. Let
![]() $i< m$
and
$i< m$
and
![]() $j< n$
. Suppose that
$j< n$
. Suppose that
![]() $B\in M^*$
is an unbounded subset of
$B\in M^*$
is an unbounded subset of
![]() $\mathcal P_{\omega _1}(T)$
. Assume that
$\mathcal P_{\omega _1}(T)$
. Assume that
![]() $B(i,j)$
is cofinal in B. Then, there is a cofinal subset
$B(i,j)$
is cofinal in B. Then, there is a cofinal subset
![]() $B_{i,j}$
of
$B_{i,j}$
of
![]() $B(i,j)$
in
$B(i,j)$
in
![]() $M^*$
such that for every
$M^*$
such that for every
![]() $x\in M^*\cap B_{i,j}$
,
$x\in M^*\cap B_{i,j}$
,
![]() $t^x_j\nless _T O_M(t_i)$
.
$t^x_j\nless _T O_M(t_i)$
.
Proof Let
![]() $\Psi _i$
be the characteristic function of
$\Psi _i$
be the characteristic function of
![]() $b_M(t_i)$
on T. Note that
$b_M(t_i)$
on T. Note that
![]() $\Psi _i$
is not guessed in M. For every
$\Psi _i$
is not guessed in M. For every
![]() $x\subseteq T$
, we let
$x\subseteq T$
, we let
![]() $\psi ^x_j:x\rightarrow 2$
be defined by
$\psi ^x_j:x\rightarrow 2$
be defined by
![]() $\psi ^x_j(s)=1$
if and only if
$\psi ^x_j(s)=1$
if and only if
![]() $s<_T t^x_j$
. Now consider the mapping
$s<_T t^x_j$
. Now consider the mapping
![]() $x\mapsto \psi ^x_j$
. Since
$x\mapsto \psi ^x_j$
. Since
![]() $\Psi _i$
is not guessed in M, Lemma 2.16 implies that there is a set
$\Psi _i$
is not guessed in M, Lemma 2.16 implies that there is a set
![]() $B_{i,j}\in M^*$
cofinal in
$B_{i,j}\in M^*$
cofinal in
![]() $B(i,j)$
such that for every
$B(i,j)$
such that for every
![]() $x\in B_{i,j}$
,
$x\in B_{i,j}$
,
![]() $\psi ^x_j\nsubseteq \Psi _i$
.
$\psi ^x_j\nsubseteq \Psi _i$
.
Assume towards a contradiction that there is
![]() $x\in M^*\cap B_{i,j}$
with
$x\in M^*\cap B_{i,j}$
with
![]() $t^x_j<_T O_M(t_i)$
. Then
$t^x_j<_T O_M(t_i)$
. Then
![]() $t^x_j\in M\cap T_{<\eta _i}$
, and for every
$t^x_j\in M\cap T_{<\eta _i}$
, and for every
![]() $s\in x$
of height at least
$s\in x$
of height at least
![]() $\eta ^*_i$
, we have
$\eta ^*_i$
, we have
![]() $\psi ^x_j(s)=0=\Psi _i(s)$
. Thus
$\psi ^x_j(s)=0=\Psi _i(s)$
. Thus
![]() $\psi ^x_j\nsubseteq \Psi _i$
implies that there is some
$\psi ^x_j\nsubseteq \Psi _i$
implies that there is some
![]() $s\in T_{<\eta ^*_i}\cap M$
such that
$s\in T_{<\eta ^*_i}\cap M$
such that
![]() $\psi ^x_j(s)\neq \Psi _i(s)$
. Since
$\psi ^x_j(s)\neq \Psi _i(s)$
. Since
![]() $x\in B(i,j)$
, we have
$x\in B(i,j)$
, we have
![]() ${\mathrm {ht}}(t^x_j)\in \big [{\mathrm {ht}}(\hat {t}_i),\eta ^*_i\big )$
. On the other hand, by Item 3 in the definition of a T-assignment, we have
${\mathrm {ht}}(t^x_j)\in \big [{\mathrm {ht}}(\hat {t}_i),\eta ^*_i\big )$
. On the other hand, by Item 3 in the definition of a T-assignment, we have
![]() ${\mathrm {ht}}(s)<{\mathrm {ht}}(t^x_j)$
. Thus
${\mathrm {ht}}(s)<{\mathrm {ht}}(t^x_j)$
. Thus
![]() $s<_T t^x_j$
if and only if
$s<_T t^x_j$
if and only if
![]() $s\nless _T O_M(t_i)$
, which contradicts
$s\nless _T O_M(t_i)$
, which contradicts
![]() $t^x_j<_T O_M(t_i)$
.
$t^x_j<_T O_M(t_i)$
.
Returning to our main proof, let e be a bijection between
![]() $mn$
and
$mn$
and
![]() $m\times n$
. For every
$m\times n$
. For every
![]() $k<mn$
, set
$k<mn$
, set
![]() $e(k):= (e_0(k),e_1(k))$
. We build a descending sequence
$e(k):= (e_0(k),e_1(k))$
. We build a descending sequence
![]() $\langle B_k:{-}1\!\leq k<mn\rangle $
of cofinal subsets of
$\langle B_k:{-}1\!\leq k<mn\rangle $
of cofinal subsets of
![]() $ P_{\omega _1}(T)$
with
$ P_{\omega _1}(T)$
with
![]() $B_k\in M^*$
as follows. Let also
$B_k\in M^*$
as follows. Let also
![]() $B_{-1}:= \mathcal P_{\omega _1}(T)$
. Suppose that
$B_{-1}:= \mathcal P_{\omega _1}(T)$
. Suppose that
![]() $B_k$
, for
$B_k$
, for
![]() $k\geq {-}1$
, is constructed. Set
$k\geq {-}1$
, is constructed. Set
![]() $C^k:= B_k(e_0(k),e_1(k))$
and ask the following question:
$C^k:= B_k(e_0(k),e_1(k))$
and ask the following question:
-
• Is
 $C^k$
cofinal in
$C^k$
cofinal in
 $B_k$
?
$B_k$
?
Then proceed as follows:
-
• If the answer to the above question is YES, then apply Claim 4.37 to
 $C^k$
,
$C^k$
,
 $e_0(k+1)$
and
$e_0(k+1)$
and
 $e_1(k+1)$
to obtain
$e_1(k+1)$
to obtain
 $ C^k_{e_0(k+1),e_1(k+1)}\in M^*$
as in the claim, and then set
$ C^k_{e_0(k+1),e_1(k+1)}\in M^*$
as in the claim, and then set
 $B_{k+1}:= C^k_{e_0(k+1),e_1(k+1)}$
.
$B_{k+1}:= C^k_{e_0(k+1),e_1(k+1)}$
. -
• If the answer to the above question is NO, then let
 $B_{k+1}=B_k\setminus C^k$
.
$B_{k+1}=B_k\setminus C^k$
.
It is clear that
![]() $\langle B_k: {-}1\!\leq k< mn\rangle $
is descending and each
$\langle B_k: {-}1\!\leq k< mn\rangle $
is descending and each
![]() $B_k$
is in
$B_k$
is in
![]() $M^*$
. Set
$M^*$
. Set
![]() $B^*:= B_{mn-1}$
. Note that if
$B^*:= B_{mn-1}$
. Note that if
![]() $x\in C^k_{e_0(k+1),e_1(k+1)}$
, then
$x\in C^k_{e_0(k+1),e_1(k+1)}$
, then
![]() $t^x_{e_1(k+1)}\nless _T O_M(t_{e_0(k+1)})$
, by Claim 4.37.
$t^x_{e_1(k+1)}\nless _T O_M(t_{e_0(k+1)})$
, by Claim 4.37.
Claim 4.38. For every
![]() $x\in B^*\cap M^*$
,
$x\in B^*\cap M^*$
,
![]() $p_x$
and p are compatible.
$p_x$
and p are compatible.
Proof Fix
![]() $x\in B^*\cap M^*$
. Then
$x\in B^*\cap M^*$
. Then
![]() $p_x\in M^*\cap D$
. Let
$p_x\in M^*\cap D$
. Let
![]() $r=p_x\land p$
. We claim that r is a condition. By Lemma 4.34, we only need to check if there are comparable
$r=p_x\land p$
. We claim that r is a condition. By Lemma 4.34, we only need to check if there are comparable
![]() $s\in {\mathrm {dom}}(f_{p_x})\setminus {\mathrm {dom}}(f\kern-4pt_p)$
and
$s\in {\mathrm {dom}}(f_{p_x})\setminus {\mathrm {dom}}(f\kern-4pt_p)$
and
![]() $t\in \mathscr {O}(p,M)$
such that
$t\in \mathscr {O}(p,M)$
such that
![]() $f_{p_x}(s)=f\kern-4pt_p(t)$
. We shall see that it does not happen. Thus assume towards a contradiction that there are such t and s. Then
$f_{p_x}(s)=f\kern-4pt_p(t)$
. We shall see that it does not happen. Thus assume towards a contradiction that there are such t and s. Then
![]() $t=t_i$
and
$t=t_i$
and
![]() $s=t^x_j$
, for some
$s=t^x_j$
, for some
![]() $i< m$
and
$i< m$
and
![]() $j< n$
. Note that
$j< n$
. Note that
![]() $f_{p_x}(s),t^x_j\in M$
, as
$f_{p_x}(s),t^x_j\in M$
, as
![]() $x\in M^*$
. Observe that if
$x\in M^*$
. Observe that if
![]() $t_i\leq _T t^x_j$
, then
$t_i\leq _T t^x_j$
, then
![]() $t_i$
is guessed in M, and hence it belongs to M by Item 4 of Definition 4.11, which is a contradiction. Thus
$t_i$
is guessed in M, and hence it belongs to M by Item 4 of Definition 4.11, which is a contradiction. Thus
![]() $t^x_j<_T t_i$
, which in turn implies that
$t^x_j<_T t_i$
, which in turn implies that
![]() $t^x_j\in b_M(t_i)$
(recall that
$t^x_j\in b_M(t_i)$
(recall that
![]() $O_M(t_i)$
is not guessed in M.) Since
$O_M(t_i)$
is not guessed in M.) Since
![]() $f_{p_x}(s)=f\kern-4pt_p(t)$
and
$f_{p_x}(s)=f\kern-4pt_p(t)$
and
![]() $p_x\in R_p(M,\sigma )$
, Item 2b in Definition 4.32 implies that
$p_x\in R_p(M,\sigma )$
, Item 2b in Definition 4.32 implies that
![]() ${\mathrm {ht}}(t^x_j)\nless {\mathrm {ht}}(\hat {t}_i)$
. Thus
${\mathrm {ht}}(t^x_j)\nless {\mathrm {ht}}(\hat {t}_i)$
. Thus
![]() ${\mathrm {ht}}(t^x_j)\geq {\mathrm {ht}}(\hat {t}_i)$
. Let
${\mathrm {ht}}(t^x_j)\geq {\mathrm {ht}}(\hat {t}_i)$
. Let
![]() $k\geq 0$
be such that
$k\geq 0$
be such that
![]() $e(k)=(i,j)$
. Since
$e(k)=(i,j)$
. Since
![]() $x\in B^*\subseteq B_k\subseteq B_{k-1}$
and that
$x\in B^*\subseteq B_k\subseteq B_{k-1}$
and that
![]() ${\mathrm {ht}}(t^x_j)\geq {\mathrm {ht}}(\hat {t}_i)$
, we have
${\mathrm {ht}}(t^x_j)\geq {\mathrm {ht}}(\hat {t}_i)$
, we have
![]() $B_k=C^{k-1}_{i,j}$
, but then
$B_k=C^{k-1}_{i,j}$
, but then
![]() $t^x_j\nless _T O_M(t_i)$
by Claim 4.37, which is a contradiction since
$t^x_j\nless _T O_M(t_i)$
by Claim 4.37, which is a contradiction since
![]() $t^x_j\in b_M(t_i)$
implies that
$t^x_j\in b_M(t_i)$
implies that
![]() $t^x_j<_T O_M(t_i)$
.
$t^x_j<_T O_M(t_i)$
.
Remark 4.39. Note that to find the cofinal set
![]() $B^*$
in the above proof, we could start with any set which is cofinal in
$B^*$
in the above proof, we could start with any set which is cofinal in
![]() $\mathcal P_{\omega _1}(T)$
.
$\mathcal P_{\omega _1}(T)$
.
Corollary 4.40.
![]() $\mathbb P_T$
is proper.
$\mathbb P_T$
is proper.
Proof Let
![]() $\theta ^*$
be a sufficiently large regular cardinal. Assume that
$\theta ^*$
be a sufficiently large regular cardinal. Assume that
![]() $M^*\prec H_{\theta ^*}$
is countable and contains
$M^*\prec H_{\theta ^*}$
is countable and contains
![]() $H_\theta ,T, \mathcal E^0$
, and
$H_\theta ,T, \mathcal E^0$
, and
![]() $\mathcal E^1$
. Set
$\mathcal E^1$
. Set
![]() $M=M^*\cap H_{\theta }$
, and let
$M=M^*\cap H_{\theta }$
, and let
![]() $p\in M^*$
be a condition. Notice that the set of such models is a club in
$p\in M^*$
be a condition. Notice that the set of such models is a club in
![]() $\mathcal P_{\omega _1}(H_{\theta ^*})$
. By Proposition 4.13,
$\mathcal P_{\omega _1}(H_{\theta ^*})$
. By Proposition 4.13,
![]() $p^M$
is a condition with
$p^M$
is a condition with
![]() $p^M\leq p$
such that
$p^M\leq p$
such that
![]() $M\in \mathcal M_{p^M}$
. Now, Proposition 4.35 guarantees that
$M\in \mathcal M_{p^M}$
. Now, Proposition 4.35 guarantees that
![]() $p^M$
is
$p^M$
is
![]() $(M^*,\mathbb P_T)$
-generic. Thus
$(M^*,\mathbb P_T)$
-generic. Thus
![]() $\mathbb P_T$
is proper.
$\mathbb P_T$
is proper.
We shall use the above strategy and Lemma 2.16 to show that
![]() $\mathbb P_T$
has the
$\mathbb P_T$
has the
![]() $\omega _1$
-approximation property.
$\omega _1$
-approximation property.
Proposition 4.41.
![]() $\mathbb P_T$
has the
$\mathbb P_T$
has the
![]() $\omega _1$
-approximation property.
$\omega _1$
-approximation property.
Proof Assume towards a contradiction that
![]() $\dot A$
is a
$\dot A$
is a
![]() $\mathbb P_T$
-name such that for some
$\mathbb P_T$
-name such that for some
![]() $p\in \mathbb P_T$
and some
$p\in \mathbb P_T$
and some
![]() $X\in V$
, we have
$X\in V$
, we have
-
•
 $p\Vdash "\dot {A}\subseteq \check {X},"$
$p\Vdash "\dot {A}\subseteq \check {X},"$
-
•
 $p\Vdash "\dot {A}\notin V,"$
and
$p\Vdash "\dot {A}\notin V,"$
and -
•
 $p\Vdash "\dot {A} \mbox { is countable approximated in } V,"$
i.e., for every countable set
$p\Vdash "\dot {A} \mbox { is countable approximated in } V,"$
i.e., for every countable set
 $a\in V$
,
$a\in V$
,
 $p\Vdash "\dot {A}\cap \check {a}\in V."$
$p\Vdash "\dot {A}\cap \check {a}\in V."$
Without loss of generality, we may work with a
![]() $\mathbb P_T$
-name for the characteristic function of
$\mathbb P_T$
-name for the characteristic function of
![]() $\dot {A}$
, say
$\dot {A}$
, say
![]() $\dot {f}$
. We may also, without loss of generality, assume that either
$\dot {f}$
. We may also, without loss of generality, assume that either
![]() $T\subseteq X$
or
$T\subseteq X$
or
![]() $X\subseteq T$
. To see this, observe that by passing to an isomorphic copy of T, we may assume that the underlying set of T is
$X\subseteq T$
. To see this, observe that by passing to an isomorphic copy of T, we may assume that the underlying set of T is
![]() $|T|$
. On the other hand, using a bijection between X and
$|T|$
. On the other hand, using a bijection between X and
![]() $|X|$
, we can assume that the domain of
$|X|$
, we can assume that the domain of
![]() $\dot f$
is forced to be
$\dot f$
is forced to be
![]() $|X|$
. As
$|X|$
. As
![]() $|X|$
and
$|X|$
and
![]() $|T|$
are comparable, we may assume that either
$|T|$
are comparable, we may assume that either
![]() $T\subseteq X$
or
$T\subseteq X$
or
![]() $X\subseteq T$
.
$X\subseteq T$
.
Let us assume that
![]() $T\subseteq X$
, the other case is proved similarly. Let
$T\subseteq X$
, the other case is proved similarly. Let
![]() $\theta ^*$
be a sufficiently large regular cardinal. Let
$\theta ^*$
be a sufficiently large regular cardinal. Let
![]() $M^*\prec H_{\theta ^*}$
be a countable model containing all the relevant objects, including p. Set
$M^*\prec H_{\theta ^*}$
be a countable model containing all the relevant objects, including p. Set
![]() $M=M^*\cap H_\theta $
. We can extend
$M=M^*\cap H_\theta $
. We can extend
![]() $ p^M$
to a condition q such that q decides
$ p^M$
to a condition q such that q decides
![]() $\dot {f}\! \upharpoonright \!_{M^*}$
, i.e., for some function
$\dot {f}\! \upharpoonright \!_{M^*}$
, i.e., for some function
![]() $g:M^*\cap X\rightarrow 2$
in V,
$g:M^*\cap X\rightarrow 2$
in V,
![]() $q\Vdash "\dot {f}\! \upharpoonright \!_{M^*}=\check {g}."$
$q\Vdash "\dot {f}\! \upharpoonright \!_{M^*}=\check {g}."$
Claim 4.42.
g is not guessed in
![]() $M^*$
.
$M^*$
.
Proof Suppose that g is guessed in
![]() $M^*$
. Let
$M^*$
. Let
![]() $g^*\in M^*$
be such that
$g^*\in M^*$
be such that
![]() $g^*\cap M^*=g$
. Set
$g^*\cap M^*=g$
. Set
Obviously
![]() $D\in M^*$
. We use elementarity to show that D is dense in
$D\in M^*$
. We use elementarity to show that D is dense in
![]() $\mathbb P_T$
. Thus let
$\mathbb P_T$
. Thus let
![]() $r\in M^*\cap \mathbb P_T$
. We may assume that r is compatible with p. Thus, there is
$r\in M^*\cap \mathbb P_T$
. We may assume that r is compatible with p. Thus, there is
![]() $s\in M\cap \mathbb P_T$
such that
$s\in M\cap \mathbb P_T$
such that
![]() $s\leq p,r$
. Since
$s\leq p,r$
. Since
![]() $p\Vdash "\dot {f}\notin V,"$
there is
$p\Vdash "\dot {f}\notin V,"$
there is
![]() $x\in M^*\cap X$
and there is
$x\in M^*\cap X$
and there is
![]() $s'\leq s$
in
$s'\leq s$
in
![]() $M^*$
such that
$M^*$
such that
![]() $s'\Vdash "g^*(x)\neq \dot {f}(x)."$
Thus
$s'\Vdash "g^*(x)\neq \dot {f}(x)."$
Thus
![]() $s'\in D\cap M$
.
$s'\in D\cap M$
.
On the other hand, by Proposition 4.35, q is
![]() $(M^*,\mathbb P_T)$
-generic. Thus, there is
$(M^*,\mathbb P_T)$
-generic. Thus, there is
![]() $u\in D\cap M^*$
such that
$u\in D\cap M^*$
such that
![]() $u||q$
. But then
$u||q$
. But then
![]() $u||p$
, and thus there is
$u||p$
, and thus there is
![]() $x\in M^*\cap X$
such that
$x\in M^*\cap X$
such that
![]() $u\Vdash "g^*(x)\neq \dot {f}(x)."$
This is impossible, as
$u\Vdash "g^*(x)\neq \dot {f}(x)."$
This is impossible, as
![]() $q\Vdash g^*(x)=g(x)=\dot {f}(x)$
.
$q\Vdash g^*(x)=g(x)=\dot {f}(x)$
.
Fix an M-support set
![]() $\sigma $
for q. As in the proof of Proposition 4.35, we can find, in
$\sigma $
for q. As in the proof of Proposition 4.35, we can find, in
![]() $M^*$
, a function
$M^*$
, a function
![]() $x\mapsto (q_x,g_x)$
on
$x\mapsto (q_x,g_x)$
on
![]() $\mathcal P_{\omega _1}(X)$
such that:
$\mathcal P_{\omega _1}(X)$
such that:
-
(1)
 $q_x\in R_p(M,\sigma )$
.
$q_x\in R_p(M,\sigma )$
. -
(2)
 $ |{\mathrm {dom}}(f_{q_x})|=|{\mathrm {dom}}(f_q)|$
.
$ |{\mathrm {dom}}(f_{q_x})|=|{\mathrm {dom}}(f_q)|$
. -
(3) For every
 $s\in {\mathrm {dom}}(f_{q_x})$
and every
$s\in {\mathrm {dom}}(f_{q_x})$
and every
 $i< m$
, if
$i< m$
, if
 ${\mathrm {ht}}(s)\in \big [{\mathrm {ht}}(\hat {t}_i),\eta ^*_i\big )$
, then
${\mathrm {ht}}(s)\in \big [{\mathrm {ht}}(\hat {t}_i),\eta ^*_i\big )$
, then  $$ \begin{align*}{\mathrm{sup}}\{{\mathrm{ht}}(u): u\in x\cap T_{< \eta^*_{i}}\}<{\mathrm{ht}}(s).\end{align*} $$
$$ \begin{align*}{\mathrm{sup}}\{{\mathrm{ht}}(u): u\in x\cap T_{< \eta^*_{i}}\}<{\mathrm{ht}}(s).\end{align*} $$
-
(4)
 $g_x:{\mathrm {dom}}(g_x)\rightarrow 2$
is a function with countable domain containing x as a subset.
$g_x:{\mathrm {dom}}(g_x)\rightarrow 2$
is a function with countable domain containing x as a subset. -
(5)
 $q_x\Vdash g_x\! \upharpoonright \!_x=\dot {f}\! \upharpoonright \!_x$
.
$q_x\Vdash g_x\! \upharpoonright \!_x=\dot {f}\! \upharpoonright \!_x$
.
Here,
![]() $\eta _i$
,
$\eta _i$
,
![]() $\eta ^*_i$
, and
$\eta ^*_i$
, and
![]() $\hat {t}_i$
are as in the proof of Proposition 4.35. Note that to find an assignment in
$\hat {t}_i$
are as in the proof of Proposition 4.35. Note that to find an assignment in
![]() $M^*$
, observe that if
$M^*$
, observe that if
![]() $x\in M^*$
, then
$x\in M^*$
, then
![]() $x\subseteq {\mathrm {dom}}(g)$
, and thus we can use
$x\subseteq {\mathrm {dom}}(g)$
, and thus we can use
![]() $(q,g)$
as a witness. Since we assumed
$(q,g)$
as a witness. Since we assumed
![]() $T\subseteq X$
and by the above claim g is not guessed in
$T\subseteq X$
and by the above claim g is not guessed in
![]() $M^*$
, we first apply Lemma 2.16 to find a set
$M^*$
, we first apply Lemma 2.16 to find a set
![]() $B\in M^*$
, cofinal in
$B\in M^*$
, cofinal in
![]() $\mathcal P_{\omega _1}(X)$
, such that for every
$\mathcal P_{\omega _1}(X)$
, such that for every
![]() $x\in B$
,
$x\in B$
,
![]() $g_x\nsubseteq g$
. Now let C be the restriction of B to T, i.e.,
$g_x\nsubseteq g$
. Now let C be the restriction of B to T, i.e.,
![]() $C=\{x\cap T:x\in B\}$
. Then C is cofinal in
$C=\{x\cap T:x\in B\}$
. Then C is cofinal in
![]() $\mathcal P_{\omega _1}(T)$
. Using the Axiom of Choice, for each
$\mathcal P_{\omega _1}(T)$
. Using the Axiom of Choice, for each
![]() $c\in C$
, pick
$c\in C$
, pick
![]() $x_c\in B$
such that
$x_c\in B$
such that
![]() $x_c\cap T=c$
. Fix such a choice function
$x_c\cap T=c$
. Fix such a choice function
![]() $c\mapsto x_c$
in
$c\mapsto x_c$
in
![]() $M^*$
and consider the assignment
$M^*$
and consider the assignment
![]() $c\mapsto q_{x_c}$
. By the above properties,
$c\mapsto q_{x_c}$
. By the above properties,
![]() $c\mapsto q_c=q_{x_c}$
is a T-assignment in
$c\mapsto q_c=q_{x_c}$
is a T-assignment in
![]() $M^*$
. Thus, as in Proposition 4.35, there is some
$M^*$
. Thus, as in Proposition 4.35, there is some
![]() $c\in C\cap M^*$
such that
$c\in C\cap M^*$
such that
![]() $q_{c}$
is compatible with q. There exists
$q_{c}$
is compatible with q. There exists
![]() $x\in B\cap M^*$
with
$x\in B\cap M^*$
with
![]() $x_c=c$
, but this is a contradiction, as
$x_c=c$
, but this is a contradiction, as
![]() $g_x\nsubseteq g$
implies that
$g_x\nsubseteq g$
implies that
![]() $q_{x_c}=q_c$
is not compatible with q!
$q_{x_c}=q_c$
is not compatible with q!
Lemma 4.43. Suppose that
![]() $p\in \mathbb P_T$
and
$p\in \mathbb P_T$
and
![]() $t\in T$
. Then there is some
$t\in T$
. Then there is some
![]() $q\leq p$
such that
$q\leq p$
such that
![]() $t\in {\mathrm {dom}}(f_q)$
.
$t\in {\mathrm {dom}}(f_q)$
.
Proof Assume that t is not in
![]() ${\mathrm{dom}}(f\kern-4pt_p)$
. If t is not in any model belonging to
${\mathrm{dom}}(f\kern-4pt_p)$
. If t is not in any model belonging to
![]() $\mathcal E^0_p$
, then pick
$\mathcal E^0_p$
, then pick
![]() $\nu $
below
$\nu $
below
![]() $\omega _1$
and different from the values of
$\omega _1$
and different from the values of
![]() $f\kern-4pt_p$
such that
$f\kern-4pt_p$
such that
and then set
![]() $q=(\mathcal M_p, f\kern-4pt_p\cup \{(t,\nu )\})$
. Then Item 1 of Definition 4.11 is easily fulfilled, Item 2 holds true as
$q=(\mathcal M_p, f\kern-4pt_p\cup \{(t,\nu )\})$
. Then Item 1 of Definition 4.11 is easily fulfilled, Item 2 holds true as
![]() $\nu \notin {\mathrm {rang}}(f\kern-4pt_p)$
. Item 3 is obvious as t does not belong to any model in
$\nu \notin {\mathrm {rang}}(f\kern-4pt_p)$
. Item 3 is obvious as t does not belong to any model in
![]() $\mathcal M_q=\mathcal M_p$
. Finally, Item 4 is fulfilled, since
$\mathcal M_q=\mathcal M_p$
. Finally, Item 4 is fulfilled, since
![]() $f_q(t)=\nu $
belongs to no model in
$f_q(t)=\nu $
belongs to no model in
![]() $\mathcal E^0_q=\mathcal E^0_p$
.
$\mathcal E^0_q=\mathcal E^0_p$
.
Now assume that there are some models in
![]() $\mathcal E^0_p$
containing t. Let M be the least countable model in
$\mathcal E^0_p$
containing t. Let M be the least countable model in
![]() $\mathcal M_p$
with
$\mathcal M_p$
with
![]() $t\in M$
. Let
$t\in M$
. Let
![]() $\nu \in M\cap \omega _1\setminus {\mathrm {ran}}(f\kern-4pt_p)$
be such that
$\nu \in M\cap \omega _1\setminus {\mathrm {ran}}(f\kern-4pt_p)$
be such that
Set
![]() $q=(\mathcal M_{}, f\kern-4pt_p\cup \{(t,\nu )\})$
. We claim that q is a condition. As in the previous case, Items 1 and 2 of Definition 4.11 hold true, and thus we only need to check Items 3 and 4.
$q=(\mathcal M_{}, f\kern-4pt_p\cup \{(t,\nu )\})$
. We claim that q is a condition. As in the previous case, Items 1 and 2 of Definition 4.11 hold true, and thus we only need to check Items 3 and 4.
Item 3: Assume that
![]() $N\in \mathcal {E}^0_p$
contains t. By the minimality of M,
$N\in \mathcal {E}^0_p$
contains t. By the minimality of M,
![]() $M\in ^* N$
. We claim that
$M\in ^* N$
. We claim that
![]() $M\subseteq N$
. Suppose this is not the case. Thus there is some
$M\subseteq N$
. Suppose this is not the case. Thus there is some
![]() $P\in \mathcal {E}^1_p$
such that
$P\in \mathcal {E}^1_p$
such that
![]() $P\cap N\in ^* M\in P\in N$
, but then
$P\cap N\in ^* M\in P\in N$
, but then
![]() $t\in P\cap N$
, which contradicts the minimality of M. Thus
$t\in P\cap N$
, which contradicts the minimality of M. Thus
![]() $M\subseteq N$
, and hence
$M\subseteq N$
, and hence
![]() $\nu \in M\subseteq N$
.
$\nu \in M\subseteq N$
.
Item 4: Suppose that
![]() $N\in \mathcal {E}^0_p$
is such that
$N\in \mathcal {E}^0_p$
is such that
![]() $\nu \in N$
and t is guessed in N. We shall show that
$\nu \in N$
and t is guessed in N. We shall show that
![]() $M\subseteq N$
, and hence
$M\subseteq N$
, and hence
![]() $t\in N$
. We first show that
$t\in N$
. We first show that
![]() $N\in ^* M$
is impossible. To see this, observe that
$N\in ^* M$
is impossible. To see this, observe that
![]() $N\notin M$
by our choice of
$N\notin M$
by our choice of
![]() $\nu $
. Thus if
$\nu $
. Thus if
![]() $N\in ^* M$
, then there is some
$N\in ^* M$
, then there is some
![]() $P\in \mathcal {E}^1_p\cap M$
such that
$P\in \mathcal {E}^1_p\cap M$
such that
![]() $N\in [P\cap M,P)_p$
. Now t belongs to P as it is guessed in
$N\in [P\cap M,P)_p$
. Now t belongs to P as it is guessed in
![]() $N\subseteq P$
, and thus
$N\subseteq P$
, and thus
![]() $t\in P\cap M$
, which contradicts the minimality of M.
$t\in P\cap M$
, which contradicts the minimality of M.
Now if
![]() $M\nsubseteq N$
, there is
$M\nsubseteq N$
, there is
![]() $P\in \mathcal M_p$
such that
$P\in \mathcal M_p$
such that
![]() $P\cap N\in ^* M\in P\in N$
. Then since
$P\cap N\in ^* M\in P\in N$
. Then since
![]() $t\in P$
is guessed in N, by Lemma 4.9, t is guessed in
$t\in P$
is guessed in N, by Lemma 4.9, t is guessed in
![]() $P\cap N$
. Notice that
$P\cap N$
. Notice that
![]() $\nu \in P\cap N\in ^* M $
, which is a contradiction as
$\nu \in P\cap N\in ^* M $
, which is a contradiction as
![]() $P\cap N\in ^* M$
, as is was shown in the previous paragraph.
$P\cap N\in ^* M$
, as is was shown in the previous paragraph.
Remark 4.44. Notice that
![]() $\mathbb P_T$
forces
$\mathbb P_T$
forces
![]() $|H_{\theta }|=|T|=\aleph _2$
.
$|H_{\theta }|=|T|=\aleph _2$
.
5 Conclusion
In this section, we prove our main theorem.
Theorem 5.1. Assume that
![]() ${\mathrm {GM}}^*(\omega _2)$
holds. Then, every tree of height
${\mathrm {GM}}^*(\omega _2)$
holds. Then, every tree of height
![]() $\omega _2$
without cofinal branches is specialisable via a proper and
$\omega _2$
without cofinal branches is specialisable via a proper and
![]() $\aleph _2$
-preserving forcing with finite conditions. Moreover, the forcing has the
$\aleph _2$
-preserving forcing with finite conditions. Moreover, the forcing has the
![]() $\omega _1$
-approximation property.
$\omega _1$
-approximation property.
Proof By Lemma 2.5, we may also assume that T is a Hausdorff tree. By Corollaries 4.27 and 4.40,
![]() $\mathbb P_T$
preserves
$\mathbb P_T$
preserves
![]() $\aleph _1$
and
$\aleph _1$
and
![]() $\aleph _2$
, respectively. Let
$\aleph _2$
, respectively. Let
![]() $G\subseteq \mathbb P_T$
be V-generic filter, and set
$G\subseteq \mathbb P_T$
be V-generic filter, and set
By Lemma 4.43,
![]() $f_G:T\rightarrow \omega _1$
is a total function on T. It is clear that
$f_G:T\rightarrow \omega _1$
is a total function on T. It is clear that
![]() $f_G$
is a specialising function on T.
$f_G$
is a specialising function on T.
Since
![]() $\mathrm{PFA}$
implies
$\mathrm{PFA}$
implies
![]() ${\mathrm {GM}}^*(\omega _2)$
by Proposition 2.15, we obtain the following corollary.
${\mathrm {GM}}^*(\omega _2)$
by Proposition 2.15, we obtain the following corollary.
Corollary 5.2. Assume
![]() $\mathrm{PFA}$
. Suppose T is a tree of height
$\mathrm{PFA}$
. Suppose T is a tree of height
![]() $\omega _2$
without cofinal branches. Then there is a proper and
$\omega _2$
without cofinal branches. Then there is a proper and
![]() $\aleph _2$
-preserving forcing with the
$\aleph _2$
-preserving forcing with the
![]() $\omega _1$
-approximation property such that T is special in generic extensions by
$\omega _1$
-approximation property such that T is special in generic extensions by
![]() $\mathbb P_T$
.
$\mathbb P_T$
.
Acknowledgements
The author’s research was supported through the project M 3024 by the Austrian Science Fund (FWF). The author acknowledges TU Wien Bibliothek for financial support through its Open Access Funding Program. The author is grateful to M. Golshani and B. Veličković for the fruitful conversations about the contents of this paper. The author would like to extend his thanks to the referee for their careful reading and constructive comments that significantly improved the readability of this manuscript.