Article contents
TIGHT UNIVERSAL SUMS OF m-GONAL NUMBERS
Published online by Cambridge University Press: 13 July 2022
Abstract
For a positive integer n, let
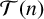 $\mathcal T(n)$
denote the set of all integers greater than or equal to n. A sum of generalised m-gonal numbers g is called tight
$\mathcal T(n)$
denote the set of all integers greater than or equal to n. A sum of generalised m-gonal numbers g is called tight
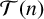 $\mathcal T(n)$
-universal if the set of all nonzero integers represented by g is equal to
$\mathcal T(n)$
-universal if the set of all nonzero integers represented by g is equal to
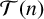 $\mathcal T(n)$
. We prove the existence of a minimal tight
$\mathcal T(n)$
. We prove the existence of a minimal tight
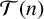 $\mathcal T(n)$
-universality criterion set for a sum of generalised m-gonal numbers for any pair
$\mathcal T(n)$
-universality criterion set for a sum of generalised m-gonal numbers for any pair
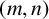 $(m,n)$
. To achieve this, we introduce an algorithm giving all candidates for tight
$(m,n)$
. To achieve this, we introduce an algorithm giving all candidates for tight
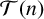 $\mathcal T(n)$
-universal sums of generalised m-gonal numbers. Furthermore, we provide some experimental results on the classification of tight
$\mathcal T(n)$
-universal sums of generalised m-gonal numbers. Furthermore, we provide some experimental results on the classification of tight
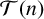 $\mathcal T(n)$
-universal sums of generalised m-gonal numbers.
$\mathcal T(n)$
-universal sums of generalised m-gonal numbers.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 40 - 52
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The research of the first author was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2019R1F1A1064037). The research of the second author was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2021R1C1C2010133).
References
- 1
- Cited by



