I. INTRODUCTION
There is a recent surge in research activities around the idea of the so-called “deep neural networks” or simply DNN. This is in part triggered by the paper “dimensionality reduction” published in Science by Hinton and Salakhutdinov [Reference Hinton and Salakhutdinov1] and subsequent applications of the related ideas in various problems (e.g. [Reference Hinton2,Reference Krizhevsky, Sutskever and Hinton3]). Many impressive results have been reported in various areas. In many classes of machine learning, this is considered a topic of crucial importance, not to mention its popularity.
While neural networks have enjoyed cycles of interest (this most recent wave may be the third or the fourth), concrete and impressive advances now abound indeed. As a technical item, DNN therefore without a doubt is an important classroom topic and several tutorial articles and related learning resources are available ([Reference Hinton and Salakhutdinov1–Reference LeCun, Bengio and Hinton8] and online information at http://deeplearning.net/). Nevertheless, streams of questions never subside from students or researchers and there appears to be a frustrating tendency among the learners to treat DNN simply as a black box (since computer code from various sources is openly available). This is an awkward and alarming situation in education.
This paper is thus written with the attempt to help students or readers better understand DNN so as to be able to take advantage of the advances in their problems in a proper manner. In particular, it is written from a developmental perspective with a comprehensive view, from the very basic but oft-neglected principle of statistical pattern recognition and decision theory, through the stages of problems that may be encountered during system design, to key ideas that led to the new advance. Individual topics in this paper may be well known, but our attempt is to thread and position them to form a landscape, which brings out the developmental logic. This paper also aims to serve as a learning guide with important references that are deemed helpful in reaching an insightful understanding of the subject.
This paper compiles materials and concepts related to DNN, starting with the foundation of statistical pattern recognition. The material in the paper about DNN is not meant to be exhaustive but pedagogical. Moreover, it addresses deep neural networks but not deep learning; the latter may be broader than neural networks. Such a distinction is necessary in placing the right focus on the subject matter although toward the end (Section VIII) we do provide an example that makes suggestions on the possible extent of deep learning that may go beyond statistical pattern recognition.
A deep neural net obviously has its root in artificial neural networks (ANN) and to understand DNN, it is very helpful to understand ANN first, at least the relevant parts. Therefore, a brief exposition of ANN relevant to the development of DNN is provided as an important review of the background knowledge.
The paper is organized as follows. In Section II, the foundation of statistical pattern recognition based on Bayes’ optimal decision theory is reviewed, to establish the core problems in designing a pattern recognition system. We discuss how these core problems are traditionally dealt with and the shortcomings thereof. The reinforced insights from the review will bring out the often-overlooked key principles that underlie the development of DNN. In Section III, we review relevant models of the ANNs and point out the traditional hindrance that had prevented ANN from being widely adopted for pattern recognition tasks, in spite of the massive amount of research in the late 1980s and early 1990s. The discussion is particularly important as a backdrop for the development of DNN in explaining how ideas behind DNN attempt to overcome these past hindrances. We then come back to the issue of statistical modeling in Section IV with a focus placed on modeling of data of large dimensionality. We relate the concept of a Markov random field (MRF) to the mechanism of a restricted Boltzmann machine (RBM) and point out what an RBM can achieve as a statistical model for binary data of large dimensions. In Section V, we explore the capabilities and properties of an RBM in its original design. We then explain why it is a good idea to stack up several RBMs in reference to the revisited design principles of statistical pattern recognition. In Section VI, we provide further supporting views on the roles of dimensionality reduction algorithms, and how RBMs can also serve to produce the so-called distributive representations of the input, moving a step closer to satisfying the need in statistical pattern recognition, namely matching statistical models to the representations of the input. We reach the idea of Deep Belief Networks (DBN) in Section VII, which is the focal point in the aforementioned developmental landscape of DNN for pattern recognition. In Section VIII, we make an excursion to problems that may be beyond the approach of statistical pattern recognition, in hopes of stimulating more thoughts on the so-called data science, particularly to raise the question if statistics equals data science. In Section IX, we examine reported experimental results of DNN and offer interpretations as to what DNN's strengths and weaknesses may be. We summarize the key points in this commentary and pedagogical article in Section X.
II. STATISTICAL PATTERN RECOGNITION
We first establish the foundation of pattern recognition as a technical area for the development of algorithms, such as DNN, which have attracted attention in pattern recognition applications. Although pattern recognition techniques have been used in a wide range of problems, we review its elementary formulation here for generality.
Pattern recognition problems share a common theme: Given a set of observed data,
![]() $\{x_{i}\}_{i=1}^{N} $
, with known corresponding class labels
$\{x_{i}\}_{i=1}^{N} $
, with known corresponding class labels
![]() $\{c_{i}\}_{i=1}^{N}$
as reference (sometimes called the ground truth),
$\{c_{i}\}_{i=1}^{N}$
as reference (sometimes called the ground truth),
![]() $c_{i} \in \{1,2,\ldots,M\} = N_{M}$
, determine the class label of an unlabeled observation, x, so as to satisfy a certain performance criterion. (Note that the dimensionality of x is arbitrary here; when necessary, a boldface will mean a vector.) In most applications, one wants to see if the determined class label is identical to the ground truth, which is assumed available during formal system evaluation.
$c_{i} \in \{1,2,\ldots,M\} = N_{M}$
, determine the class label of an unlabeled observation, x, so as to satisfy a certain performance criterion. (Note that the dimensionality of x is arbitrary here; when necessary, a boldface will mean a vector.) In most applications, one wants to see if the determined class label is identical to the ground truth, which is assumed available during formal system evaluation.
Beyond the above shared theme, variations exist among various problem formulations and approaches, primarily around the implied statistical rigor. In some problems, the evaluation set consists of a collection of the so-called test tokens and the system evaluation is based on the error rate, defined as the ratio of wrong decisions over the size of the evaluation set. Many evaluation competitions, such as those sponsored by National Institute of Standards and Technology (NIST), are of this nature. Although the evaluation may involve validation in some statistical sense, this type of problem formulation does not directly address the “expected performance” of the system; systems are compared pretty much on the reported (empirical) error rate calculated on the provided evaluation set, without explicitly involving data distributions or assumptions thereof. In other words, the predicted performance of the system upon all future observations is beyond the scope of these most prevalent practices.
Statistical pattern recognition is motivated by the pursuit of “expected performance” and is based on Bayes’ optimal decision theory. Assume that each class of the observed data is governed by a probability density (or mass) function, denoted by p(X|C=c), c∈N
M
, where X denotes the random observation as a variable with the associated class variable C, which has a prior probability mass function of P(C=c), c∈N
M
. Suppose we are given a cost matrix E,
![]() ${\bf E}=[e_{ij}]_{\,i,j\in N_{M}}$
, where e
ij
is the cost of labeling a class i observation as class j. The a posteriori probability
${\bf E}=[e_{ij}]_{\,i,j\in N_{M}}$
, where e
ij
is the cost of labeling a class i observation as class j. The a posteriori probability
![]() $P(C = c\vert X = x)$
is the probability that the (realized) observation x is a class c event. (We shall at times use a short hand notation,
$P(C = c\vert X = x)$
is the probability that the (realized) observation x is a class c event. (We shall at times use a short hand notation,
![]() $P(C = c\vert X = x) = P(c\vert x)$
.) Then, the cost of making a decision C=i is given as [Reference Duda, Hart and Stork9],
$P(C = c\vert X = x) = P(c\vert x)$
.) Then, the cost of making a decision C=i is given as [Reference Duda, Hart and Stork9],
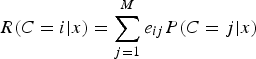 $$R(C = i\vert x) = \sum_{j = 1}^M e_{ij} P(C = j\vert x)$$
$$R(C = i\vert x) = \sum_{j = 1}^M e_{ij} P(C = j\vert x)$$
and the expected performance, in terms of the incurred decision cost, is
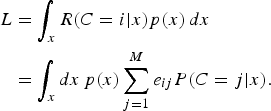 $$\eqalign{L &= \int_x {R(C = i\vert x)p(x)\,dx} \cr &= \int_x dx\,p(x)\sum_{j = 1}^M e_{ij} P(C = j \vert x).}$$
$$\eqalign{L &= \int_x {R(C = i\vert x)p(x)\,dx} \cr &= \int_x dx\,p(x)\sum_{j = 1}^M e_{ij} P(C = j \vert x).}$$
L is thus called the expected cost. If the cost function is of the usual 0–1 type, i.e. e
ii
=0 and
![]() $e_{ij} = 1, \forall i\ne j$
, then the individual cost of (1) becomes
$e_{ij} = 1, \forall i\ne j$
, then the individual cost of (1) becomes
 $$R(C = i\vert x) = \sum_{j = 1,j\ne i}^M P(C = j\vert x) = 1 - P(C = i \vert x) $$
$$R(C = i\vert x) = \sum_{j = 1,j\ne i}^M P(C = j\vert x) = 1 - P(C = i \vert x) $$
and the expected cost is reduced to
 $$\eqalign{L &= \int_x dx\,p(x)\sum_{j = 1,j\ne i}^M P(C = j\vert x) \cr &= \int_x dx\,p(x)[1 - P(C = i\vert x)].} $$
$$\eqalign{L &= \int_x dx\,p(x)\sum_{j = 1,j\ne i}^M P(C = j\vert x) \cr &= \int_x dx\,p(x)[1 - P(C = i\vert x)].} $$
The expected cost is minimized by instituting the decision policy of labeling x to accomplish
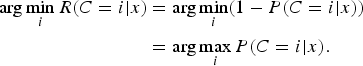 $$\eqalign{\arg \min_i R(C = i\vert x) &= \arg \min_i (1 - P (C = i\vert x)) \cr &= \arg \max_i P(C = i\vert x).}$$
$$\eqalign{\arg \min_i R(C = i\vert x) &= \arg \min_i (1 - P (C = i\vert x)) \cr &= \arg \max_i P(C = i\vert x).}$$
This is the well-known maximum a posteriori (MAP) decision and the achieved minimum cost is also called Bayes minimum cost (or risk) [Reference Duda, Hart and Stork9]. This is the foundation of statistical pattern recognition.
Note that in Bayes' optimal decision theory, the distributions that govern the observed data, the class conditional as well as the class prior, are all assumed to be available to the system designer to implement the decision rule. In practice, this is far from reality and all knowledge about the probabilistic behavior of the data must be learned from the given data and the corresponding labels, i.e. both
![]() $\{x_{i} \}_{i=1}^{N} $
and
$\{x_{i} \}_{i=1}^{N} $
and
![]() $\{c_{i} \}_{i=1}^{N} $
. This is why the pattern recognition problem is often viewed as a distribution estimation problem. There are a number of issues with this age-old practice that need to be re-brought to light as we venture into new advances if we want to adhere to the rigor of statistical pattern recognition.
$\{c_{i} \}_{i=1}^{N} $
. This is why the pattern recognition problem is often viewed as a distribution estimation problem. There are a number of issues with this age-old practice that need to be re-brought to light as we venture into new advances if we want to adhere to the rigor of statistical pattern recognition.
The first issue is the choice of the distribution for the given data, before the required parameters are estimated from the data. Most of the time, a functional form of the data distribution is assumed, e.g. a multivariate Gaussian or other distributions that the system designer feels comfortable with. With the assumed distribution, then, all the required parameters that define the distribution function are then estimated from the given data using various criteria and techniques. The validity of the form of the distribution function (typically the same form is chosen and shared among all classes of data, perhaps to simplify the implementation) is rarely rigorously examined. One must note that if the chosen form deviates from the true one, the aforementioned Bayes minimum cost becomes unattainable, although it is very difficult to obtain an expression or a bound for the degradation from the optimal performance. The second issue is somewhat related to the first but is spawned by the explicit concern of the functional expressions of the class boundaries. In the case of MAP, the recognition system is specified by the parameters that define the distributions (to implement the MAP policy), which in turn define the class boundaries (through comparison of a posteriori probabilities). In light of the potential mismatch between the true data distribution and the chosen distribution, some researchers have advocated for the use of explicit class boundaries, particularly when the class confusion is being examined at a locality of the data space. The third issue, rarely addressed in pattern recognition, is the potential sampling bias or contamination in the given data set. Sampling bias is a topic very much in the minds of statisticians, but it is not, conventionally, in those of the practitioners in computational pattern recognition. Most of the data-related attention from practitioners of pattern recognition focuses on the quantity, rather than quality, of the data; data are given by the authority or clientele who wants the problem solved. All these issues, and more, have made the problem of pattern recognition worthy of intensive research.
While all of these are important, although sometimes illusive, issues, it is helpful in the current discussion to construct some controlled experiments to demonstrate Bayes' optimal decision theory as applied to pattern recognition. A toy problem involving two classes of data is constructed as follows. First, the probability density functions of the two classes are specified, respectively, as two-mixture bivariate Gaussians, the contours of which are plotted in Fig. 1(a), where each class is signified by the color of the label located near the means. Specifically, the probability density function (pdf) for each class takes the form
where we have used the shorthand notation
![]() ${\cal N}(x;\mu, \sigma^{2})$
for a Gaussian pdf and k is the class identity. This two-class problem is obviously linearly inseparable. In each run of the experiment, random observations, 1000 for each class, are generated according to the specified distributions. One quarter of the data are retained for test and evaluation purposes and the rest are used for training.
${\cal N}(x;\mu, \sigma^{2})$
for a Gaussian pdf and k is the class identity. This two-class problem is obviously linearly inseparable. In each run of the experiment, random observations, 1000 for each class, are generated according to the specified distributions. One quarter of the data are retained for test and evaluation purposes and the rest are used for training.

Fig. 1. A two-class toy problem of pattern recognition in a 2D. (a) Contour of pdf of the two classes of data. (b) A scatter plot of the data, overlaid by support vectors and the class boundary selected by a linear SVM. (c) A scatter plot of the data, overlaid by support vectors and the class boundary selected by an RBF SVM.
A number of recognizers are evaluated, as characterized by the implied models:
-
(1) the original pdf;
-
(2) the original pdf but only the maximum of the mixture components is used in decision;
-
(3) the k-nearest neighbor (k-NN) non-parametric model with k=1;
-
(4) a generic linear support vector machine (SVM);
-
(5) an SVM with radial basis function (RBF) kernels;
-
(6) two-mixture bivariate Gaussian pdfs estimated from the training data; and
-
(7) the estimated Gaussian mixture pdfs as in (6) but only the maximum of the mixture component is used in the decision.
Obviously, other than the SVM recognizers (4 and 5), these are differentiated by the probability models that are used in the system. Probability models used in (6) offer an opportunity for us to see how a minor deviation in the model parameters would affect the recognition performance. For (2) and (7), we mean instead of summing the two calculated pdf values on an observation, the larger of the two is used in the decision process. Figures 2(b) and 2(c) show an example of the dataset in color scatter plots during one run of the experiment, together with the class boundaries as obtained by a linear SVM (4) and an SVM with RBF (5), respectively. The black circles in the scatter plots represent the support vectors selected by the corresponding SVMs as a result of the supervised training. The SVM recognizer can be considered as using non-parametric models represented by the support vectors, which are optimized with the aim of defining the class boundaries to minimize the structured error (see [Reference Cortes and Vapnik10]), while the k-NN recognizer also makes use of non-parametric models defined by the given labeled data, focusing on local discrimination, although without optimization with respect to some explicit form of recognition error measure.

Fig. 2. A conventional pattern recognition system versus an alternative. (a) A conventional pattern recognition system. (b) An alternative pattern recognition system; boundaries between blocks may not be clearly defined.
The recognition error rates of the above recognizers are tabulated in Table 1 for comparison. These error rates are obtained by averaging the evaluation results over 600 runs of the same experiment. Also listed in the table is the number of parameters used in each recognizer. For the SVM-linear recognizer, the separating line, defined by two parameters, is obtained with about 600 (varies in different runs) two-dimensional (2D) vectors (due to the linear-inseparability) and thus we include “~1200” in the parentheses under “{#} param”. The number of support vectors in “SVM–RBF” is in the vicinity of 250 and thus roughly 500 parameters. We also experimented with estimated models (similar to 6 above) with four-mixture components and the results are very close to those reported above for (6).
Table 1. Comparison of performance for the toy two-class problem.

The above controlled experiment clearly shows that if the chosen distributions are as close to the true distributions as possible, even with estimated parameter values (rather than the true values), a distribution based recognition usually proves best-performing and most efficient in terms of the required number of parameters. The results pertaining to (2) and (7) using the local maximum likelihood are surprisingly competitive. This, while a reflection of the scatter of mixture means, i.e. μ ik s of each class, may have a positive implication in the development of distributed representations that will be discussed in later sections.
However, in real problems, the match between the statistical behavior of the data and the chosen model form is usually not readily guaranteed. To overcome this issue, some transformation of the data becomes necessary. In other words, one tries to take advantage of a transformation function,
![]() $x^{\prime} = f(x)$
, such that
$x^{\prime} = f(x)$
, such that
![]() $p({X}^{\prime} \vert C)\cong p({X}^{\prime} \vert C, \theta_{c})$
; that is, the distribution of X′ can be quite accurately represented by
$p({X}^{\prime} \vert C)\cong p({X}^{\prime} \vert C, \theta_{c})$
; that is, the distribution of X′ can be quite accurately represented by
![]() $p({X}^{\prime} \vert C,\theta_{c})$
, parameterized by θ
c
. More specifically, we may not be able to model p(X| C) accurately, but we hope to do a good job in modeling
$p({X}^{\prime} \vert C,\theta_{c})$
, parameterized by θ
c
. More specifically, we may not be able to model p(X| C) accurately, but we hope to do a good job in modeling
![]() $p(X^{\prime} \vert C)$
, even though
$p(X^{\prime} \vert C)$
, even though
![]() $p(X^{\prime} \vert C)$
can be derived (in theory but not in practice) from
$p(X^{\prime} \vert C)$
can be derived (in theory but not in practice) from
![]() $p(X^{\prime} \vert C)$
. This is a very important pattern recognition system design principle. This principle is also upheld in other extensions and further improvements of pattern recognition techniques, such as discriminative training [Reference Juang and Katagiri11]. The core question is what this function looks like and how to find it. We shall call this the “bridge function”. In some cases, a multiplicity of functions may be needed and used.
$p(X^{\prime} \vert C)$
. This is a very important pattern recognition system design principle. This principle is also upheld in other extensions and further improvements of pattern recognition techniques, such as discriminative training [Reference Juang and Katagiri11]. The core question is what this function looks like and how to find it. We shall call this the “bridge function”. In some cases, a multiplicity of functions may be needed and used.
In the traditional pattern recognition paradigm, the process which transforms the raw observation data into a representation to be followed by the implementation of a decision policy is called “feature extraction.” Figure 2(a) illustrates the process in a conventional pattern recognition system design.
The objectives of feature extraction are multi-faceted. One motivation comes from the empirical observation that data, be it from measurement or survey, will inevitably contain fluctuations or uncertainties that cannot be reasonably or accurately accounted for and thus it is advantageous to separate these components out if possible. This would be in the realm of data reduction, dimension reduction, factor analysis, or principal component analysis (PCA), to name a few. Another objective of feature extraction is motivated by the availability of independent knowledge (often from the so-called domain experts) which foretells what matters in discriminating one class from another. For example, to distinguish a square from a triangle of an arbitrary size, one should not be looking for the perimeter of the shape because the perimeter length depends on the size; instead, it is more effective to compare the number of line segments (the feature), which is independent of the size. Traditionally, the choice of feature is NOT determined by how appropriate it is for statistical modeling but by the judgment of the system designer, who may try to follow the advice of domain experts or simply use some tools expediently. (Not often asked are important questions like: Is the statistical distribution of the feature easy to estimate? How complete is the set of feature in describing the classes without incurring additional ambiguity?) This is a loose-end in most of the conventionally pattern recognition system design.
Figure 2(b) depicts an alternative design philosophy, in that it contemplates on the possibility of replacing the conventional feature extraction by a data-driven transformation with the goal of producing a set of internal representations that will ultimately contribute to the accuracy in class identity retrieval in the final stage. In other words, the alternative paradigm is to seek a bridge function, whose sole purpose is to transform the observed data into a representation that projects ease, consistency and accuracy when it comes to statistical modeling for optimal decision. This bridge function is data driven, both in terms of the computational structure and the defining parameter values, to avoid undue a priori constraints; this is particularly important for patterns of high dimensionality as it is in general difficult to determine the salient feature of the patterns by human experts or the system designer. In the figure, the blocks are adjoined to signify the possibility of a gradual integration. As will be discussed later, this perspective is considered to be responsible for the recent advances in DNN. The unfulfilling side of this approach is that the data-driven bridge function may turn the otherwise intuitive observations into something hard to explain and interpret – the bridge function becomes a blackbox.
Another often-hidden issue is worthy of mentioning here. Bayes' optimal decision theory is the foundation of statistical pattern recognition, built upon the knowledge of probability distributions of the information source and the realized observations. It is nevertheless NOT the only approach and in fact, it may not always lead to the best result. A probability distribution is defined in a probability space, which exists in a regular manifold where the observations are made. The theory of probability and probability distribution sometimes fails to address the inner structure of the data. Some data may look random in one manifold but otherwise highly structured in another. In Section VIII, we will see an example that goes beyond the paradigm of statistical pattern recognition. The term “deep learning” should ideally encompass the notion of topology and manifold.
III. ARTIFICIAL NEURAL NETWORKS
Scientists have long been interested in understanding how the brain works and in mimicking the functionality of the brain with artificial means. The advent of electronic computers and computational theory in the early to mid-20th century brought in a new prospect of the interest in that computational logic was introduced as a viable model of the brain. Many models of neurons and their connections have been proposed, some aiming at physiological/biological mimicry and others focusing on the functionality. An entry level introduction to neural models of the human brain can be found, e.g. in [Reference Rumelhart and McClelland12–Reference Haykin16]. Here we build our narrative toward the so-called ANN.
A brain comprises a large number of neurons that are interconnected. Figure 3(a) is a depiction of connected neurons as a model of the brain. Each neuron receives neural signals from other neurons that are connected to it via the mechanism of synapse. Depending on the collective strength of the incoming signals, the neuron may be “activated”, meaning it further sends out a signal (a neural pulse) to other neurons, resulting in the transmission of neural activities. A neuron can thus be considered as a computational unit, the most prevalent model of which is the so-called McCulloch–Pitt neuron [Reference McCulloch and Pitts14]. Figure 3(b) shows a model of the McCulloch–Pitt neuron. The signals coming from other connecting neurons are denoted by
![]() $\{x_{i} \}_{i = 1}^{n}$
, each of which is multiplied by a synaptic weight w
i
to aggregate at the receiving neuron as
$\{x_{i} \}_{i = 1}^{n}$
, each of which is multiplied by a synaptic weight w
i
to aggregate at the receiving neuron as
![]() $y = \sum\nolimits_{i=1}^{n} w_{i} x_{i}$
. An activation threshold, denoted as b, is applied at the neuron, and when y>b, the neuron is activated to send out a neural pulse. The threshold is usually not a hard one; it is typically executed as a sigmoid function. Thus, the output y of a McCullough–Pitt neuron is totally characterized by:
$y = \sum\nolimits_{i=1}^{n} w_{i} x_{i}$
. An activation threshold, denoted as b, is applied at the neuron, and when y>b, the neuron is activated to send out a neural pulse. The threshold is usually not a hard one; it is typically executed as a sigmoid function. Thus, the output y of a McCullough–Pitt neuron is totally characterized by:

Fig. 3. An illustration of basic neural networks consisting of interconnected neurons (a) Neural networks. (b) Computational model of a McCulloch–Pitts neuron.
 $$\eqalign{ y &= \sigma \left(\sum_{i = 1}^n w_i x_i -b \right), \quad \hbox{where} \cr &\sigma (x) = \hbox{sgm}(x) = (1 + e^{-x})^{-1}.} $$
$$\eqalign{ y &= \sigma \left(\sum_{i = 1}^n w_i x_i -b \right), \quad \hbox{where} \cr &\sigma (x) = \hbox{sgm}(x) = (1 + e^{-x})^{-1}.} $$
While it is possible to draw rough parallels between a McCulloch–Pitts neuron and a true neuron, some may choose to focus on its computational logic and call it Threshold Logic Unit, or Linear Threshold Unit. (The original 1943 paper of McCulloch and Pitts [Reference McCulloch and Pitts14] has the title of “A logical calculus of the ideas immanent in nervous activity” with a clear emphasis on threshold logic.)
Among the many uses of the neural network model, two most prevalent ones are emulations of the brain memory (retrieval of memory by association) and the cognitive capability (decision making by weighing the provided evidence). The first is related to the idea of associative memory [Reference Hopfield17,Reference Kohonen18] using recurrent neural networks (RNNs) and the second gave rise to Perceptron [Reference Rosenblatt19], Adalines [Reference Widrow and Hoff20], and their variants [Reference Haykin16].
A) Recurrent neural networks
The Hopfield network proposed by John Hopfield in 1982 [Reference Hopfield17] is considered a pioneering model of a RNN. A Hopfield net consists of a number of, say n, binary McCulloch–Pitts threshold units (or nodes), each assuming one of two values, say 0 and 1, and the interconnectivity between each pair of neurons, defined by the corresponding synaptic weight. Figure 4(a) depicts a three-node (3 units) Hopfield net.

Fig. 4. Two equivalent depictions of a three-node Hopfield network. (a) A three-node Hopfield net. (b) A three-node Hopfield net with explicit synchronous delay and recurrence.
The synaptic weight in a Hopfield net is symmetric; i.e. the connectivity between unit i and j is undirected and has the property that w
ij
=w
ji
. Furthermore, w
ij
=0, if i=j. The synaptic weights and the network configuration do not change. The network operates as follows. At the onset, t=0, a bit pattern
![]() ${\bf x}^{(0)} = [x_{1}^{(0)}, x_{2}^{(0)}, \ldots, x_{n}^{(0)}]$
is applied as input, where the subscript of the element denotes the index of the corresponding unit. At the next time epoch (assuming synchronous update), the state of network becomes
${\bf x}^{(0)} = [x_{1}^{(0)}, x_{2}^{(0)}, \ldots, x_{n}^{(0)}]$
is applied as input, where the subscript of the element denotes the index of the corresponding unit. At the next time epoch (assuming synchronous update), the state of network becomes
![]() ${\bf x}^{(t)} \to {\bf x}^{(t + 1)}$
according to
${\bf x}^{(t)} \to {\bf x}^{(t + 1)}$
according to
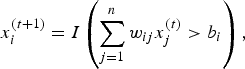 $$x_i^{(t + 1)} = I\left(\sum_{j = 1}^n w_{ij} x_j^{(t)} \gt b_i \right), $$
$$x_i^{(t + 1)} = I\left(\sum_{j = 1}^n w_{ij} x_j^{(t)} \gt b_i \right), $$
where I denotes the indicator function, which produces a value of 1 if the argument is true and 0 otherwise and b i is the threshold for the ith neuron. Figure 4(b) includes a time delay element to account for this temporal process. We also call x (t) the network state at time t. Each network state has an “energy” level, E:
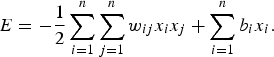 $$E = - {1 \over 2}\sum_{i = 1}^n \sum_{j = 1}^n w_{ij} x_i x_j + \sum_{i = 1}^n b_i x_i. $$
$$E = - {1 \over 2}\sum_{i = 1}^n \sum_{j = 1}^n w_{ij} x_i x_j + \sum_{i = 1}^n b_i x_i. $$
The network state eventually converges to a bit pattern which is determined by the input at onset and the set of synaptic weights, W=[w
ij
]. The converged pattern corresponds to a local minimum energy state and is considered the retrieved memory in response to the input applied at t=0. The evolutionary nature of the operation gives the network the name “recurrent neural networks”. In a study by Posner co-workers [Reference McEliece, Posner, Rodemich and Venkatesh21], it is found that for an n-node Hopfield net, the number of bit patterns that can be stored and retrieved is about or below
![]() $n(4\log n)^{-1}$
a, which, to be noted, is not very efficient.
$n(4\log n)^{-1}$
a, which, to be noted, is not very efficient.
In the above, it is implied that the synaptic states of all neurons in the network are synchronously processed and updated; some call this “fully parallel” processing. The opposite of the fully parallel case is the strictly sequential mode, in which one neuron is being updated at a time sequentially. Other modes of the temporal response, between the above two extremes, in terms of synchrony in neural activation, are possible, leading to other forms of recurrent nets. Furthermore, when RNNs are used for time-varying input (as opposed to a fixed input applied only once at the beginning as in the current discussion), the system behaves differently (much like the transient versus the steady-state analysis in system theory). The convergence properties of a recurrent neural network depends on the processing mode and [Reference Bruck22] provides an introductory guide to the analysis of convergence. Here, we focus on the general behavior of an RNN as an associative memory.
The synaptic weights that “remember” the stored patterns are typically trained by the Hebbian rule [Reference Hebb15] aiming at reducing the system energy (i.e. the minimum entropy principle in thermodynamics). To explore more about the Hopfield network, consult [Reference Hopfield17]. Other types of associative memory using computational networks include Kohonen's self-organizing map and learning vector quantizers [Reference Kohonen18].
Another RNN very relevant to the current discussion is the Boltzmann machine (BM) [Reference Ackley, Hinton and Sejnowski23]. Like the Hopfield net, a BM is also a recurrent network, although it differs from the Hopfield net in its association with the statistical regularity of the input patterns that are used to train the net (to obtain the synaptic weights). It is also called a stochastic recurrent neural network. It acquires this ability by incorporating in the network system additional units or nodes that are separate from those that accept external input. These additional units are called “hidden units” as opposed to those visible units which accept external input. Figure 5(a) depicts a BM.

Fig. 5. BMs. (a) A BM. (b) A RBM.
The energy state of a BM has the same expression as a Hopfield net, Equation (7). The name “Boltzmann” has its origin in “Boltzmann probability distribution” which relates the energy of a physical system with a probability measure of the particles in the system,
![]() $p \propto e^{-E/kT}$
, where k is the Boltzmann constant and T the thermodynamic temperature of the system. Again, assume that the machine has n nodes all together. We examine the energy change due to the change of state of a single node, say changing the jth node from 0 to 1. Obviously,
$p \propto e^{-E/kT}$
, where k is the Boltzmann constant and T the thermodynamic temperature of the system. Again, assume that the machine has n nodes all together. We examine the energy change due to the change of state of a single node, say changing the jth node from 0 to 1. Obviously,
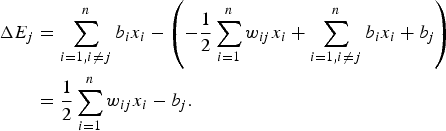 $$\eqalign{\Delta E_j &= \sum_{i = 1, i \ne j}^n b_i x_i - \left(- {1 \over 2} \sum_{i = 1}^n w_{ij} x_i + \sum_{i = 1, i \ne j}^n b_i x_i + b_j \right) \cr &= {1 \over 2} \sum_{i = 1}^n w_{ij} x_i -b_j.} $$
$$\eqalign{\Delta E_j &= \sum_{i = 1, i \ne j}^n b_i x_i - \left(- {1 \over 2} \sum_{i = 1}^n w_{ij} x_i + \sum_{i = 1, i \ne j}^n b_i x_i + b_j \right) \cr &= {1 \over 2} \sum_{i = 1}^n w_{ij} x_i -b_j.} $$
As a result,
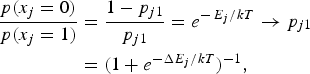 $$\eqalign{{p(x_j = 0) \over p(x_j = 1)} & = {1 - p_{j1} \over p_{j1}} = e^{-\,E_j /kT} \to p_{j1} \cr &= \lpar 1 + e^{-\Delta E_j /kT} \rpar ^{-1},} $$
$$\eqalign{{p(x_j = 0) \over p(x_j = 1)} & = {1 - p_{j1} \over p_{j1}} = e^{-\,E_j /kT} \to p_{j1} \cr &= \lpar 1 + e^{-\Delta E_j /kT} \rpar ^{-1},} $$
which is also the sigmoidal output of neuron j subject to the adjustment of the scale factors, 1/2, and kT. Equations (8) and (9) validate the notion of a stochastic RNN and the goal of decreasing the system energy during training is tantamount to maximizing the likelihood (given the training sample for the system to remember as the most likely patterns). The states that have locally minimum energy in the Hopfield net are now those with locally maximum probabilities, which can be computed by the converged values of the neurons. The hidden units can thus be viewed as providing interpolation for the data distribution estimate as well as increasing the number of local probability peaks, akin to increasing the capacity of the recurrent neural network (at the expense of the addition of hidden units). Also, when the input is only partial, meaning not all the input nodes receive input, the machine would still produce an equilibrium output after convergence. The output can be interpreted as the most likely system state associated with the partial input. This can be considered a form of imputation by correlation or association – imputing the missing value in the input by using the value that has the highest correlation with the given available input.
There had been attempts to use RNNs to perform class identification tasks. Consider a BM with an observation vector x as input. The vector may be augmented as
![]() ${\bf x}^{\prime} = [{\bf x},c]$
, where c denotes the class that x belongs to. The machine can be trained with these augmented (labeled) vectors and when an observation without label is given as input (as a partial input), the converged output will contain the result at the node designated for the (estimated) class label. In other words, this application is tantamount to treating classification as a mere task of memory recall. While the idea is as palatable as it appears, it was rarely shown to be practically effective. One may thus suspect if indeed a classification task calls for more than memory recall.
${\bf x}^{\prime} = [{\bf x},c]$
, where c denotes the class that x belongs to. The machine can be trained with these augmented (labeled) vectors and when an observation without label is given as input (as a partial input), the converged output will contain the result at the node designated for the (estimated) class label. In other words, this application is tantamount to treating classification as a mere task of memory recall. While the idea is as palatable as it appears, it was rarely shown to be practically effective. One may thus suspect if indeed a classification task calls for more than memory recall.
A variation of the BM, called RBM [Reference Smolensky, Rumelhart and McLelland24], turns out to be more useful than the original BM in machine learning applications. An RBM is a BM in which the interconnections between visible units and those between invisible units are no longer allowed, as depicted in Fig. 5(b). The energy function of an RBM has thus a reduced form from (7):
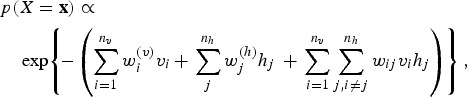 $$\eqalign{&p(X = {\bf x}) \propto \cr &\quad \exp \!\left\{\!-\left(\sum_{i = 1}^{n_v} w_i^{(v)} v_i \,{+}\, \sum_j^{n_h} w_j^{(h)} h_j \,+ \, \sum_{i = 1}^{n_v} \sum_{j,i\ne j}^{n_h} w_{ij} v_i h_j \right) \right\},} $$
$$\eqalign{&p(X = {\bf x}) \propto \cr &\quad \exp \!\left\{\!-\left(\sum_{i = 1}^{n_v} w_i^{(v)} v_i \,{+}\, \sum_j^{n_h} w_j^{(h)} h_j \,+ \, \sum_{i = 1}^{n_v} \sum_{j,i\ne j}^{n_h} w_{ij} v_i h_j \right) \right\},} $$
where the nodes of the network have been explicitly separated into two distinct groups, one pertaining to those nodes where external input is applied, the so-called visible nodes denoted by
![]() $\{v_{i}\}_{i = 1}^{n_{v}}$
, and the other the hidden nodes, denoted by
$\{v_{i}\}_{i = 1}^{n_{v}}$
, and the other the hidden nodes, denoted by
![]() $\{h_{i}\}_{i = 1}^{n_{h}}$
, which serve as internal latent variables. The notation x thus encompasses both v and h.
$\{h_{i}\}_{i = 1}^{n_{h}}$
, which serve as internal latent variables. The notation x thus encompasses both v and h.
What does this simple condition imply and what effects does it bring to its applications? We shall postpone the discussion after we introduce the concept of MRF and the Gibbs distribution. Keep in mind that a RBM is still an RNN.
B) Feedforward Neural Networks (FNN)
As mentioned, RNNs are not effective in class identification tasks. A more prevalent study of the cognitive capability of an ANN is the Perceptron, which was proposed by Rosenblatt in 1957 [Reference Rosenblatt19,Reference Olazaran25].Footnote
1
A perceptron is a linear binary classifier function g(x),
![]() ${\bf x} = [x_{1},x_{2}, \ldots, x_{n}]$
, defined as
${\bf x} = [x_{1},x_{2}, \ldots, x_{n}]$
, defined as
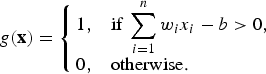 $$g({\bf x}) = \left\{\matrix{1, \hfill &\hbox{if} \displaystyle\;\sum_{i = 1}^n w_i x_i -b \gt 0, \hfill \cr 0, \hfill &\hbox{otherwise.} \hfill}\right. $$
$$g({\bf x}) = \left\{\matrix{1, \hfill &\hbox{if} \displaystyle\;\sum_{i = 1}^n w_i x_i -b \gt 0, \hfill \cr 0, \hfill &\hbox{otherwise.} \hfill}\right. $$
This nonlinear function is basically identical to the McCulloch–Pitts neuron as a computational element (with a hard sigmoid function, just like the original threshold logic of McCulloch and Pitts). While McCulloch and Pitts focused on the calculus of threshold logic, Rosenblatt, more than a decade after McCulloch and Pitts [Reference McCulloch and Pitts14], described ways to “learn” the synaptic weights and showed how to use it in cognitive applications. Obviously, a binary classifier is not particularly interesting and several ideas had been proposed to generalize the Perceptron to deal with multi-class problems. As said previously, we do not aim at exhaustive exposition here; rather, we focus on one stream of thought that is consistent with the subsequent development of understanding around DNN.
Recall the pattern recognition problem, which is an essential form of the cognitive function, where a set of known class labels
![]() $\{c_{i} \}_{i = 1}^{n}$
is provided along with the observation data
$\{c_{i} \}_{i = 1}^{n}$
is provided along with the observation data
![]() $\{{\bf x}_{i}\}_{i = 1}^n$
. The objective is thus to find a function
$\{{\bf x}_{i}\}_{i = 1}^n$
. The objective is thus to find a function
![]() $g:{\bf x} \to c \in N_M$
that satisfies some performance judgment. To take advantage of the Perceptron with binary output (recall the McCulloch–Pitts neuron which can only fire or not fire at the output), the most straightforward choice is to stack up M of these two-class Perceptrons side by side, each sharing the same input as depicted in Fig. 6, where each x is a 4D vector and M=3, since c∈N
3. It is easy to see the binary output mapping; e.g.
$g:{\bf x} \to c \in N_M$
that satisfies some performance judgment. To take advantage of the Perceptron with binary output (recall the McCulloch–Pitts neuron which can only fire or not fire at the output), the most straightforward choice is to stack up M of these two-class Perceptrons side by side, each sharing the same input as depicted in Fig. 6, where each x is a 4D vector and M=3, since c∈N
3. It is easy to see the binary output mapping; e.g.
![]() $c = 2 \to (0\;1\;0)$
, the second output node would be activated.
$c = 2 \to (0\;1\;0)$
, the second output node would be activated.

Fig. 6. Multi-layer FNNs (a) A single-layer multi-class (M=3) Perceptron (b) Multi-layer FNN.
This gave rise to the name Feedforward Neural Networks or simply FNN. One can interpret an FNN or a multi-class Perceptron as a structure that learns the best synaptic weights from examples to approximate a target function, which in the example maps a vector to a discrete or natural number. Note that although an FNN looks the same as an RBM, it has directed synaptic weights and does not invoke the concept of recurrence to converge over time to a locally equilibrium low-energy state (or high probability state).
The function approximation capability of a single-layer multi-class Perceptron was soon to be found rather limiting and the development of Perceptron in the 1960s stalled due to a number of reasons, which are beyond the scope of the current discussion. The interest on FNNs was revived in the late 1970s and early 1980s after the work of Paul Werbos [Reference Werbos26,Reference Werbos27] became better known in the pattern recognition community. In his 1974 thesis, Werbos proposed the so-called error backpropagation (often contracted to “backprop”) algorithm to adjust the parameters of a stacked system that aims at approximating a function, of which the aforementioned pattern recognition function is an example. That led to the widespread adoption of multilayer FNNs as the preferred form of the brain model to carry out cognitive functions, particularly, in terms of identifying the class membership of an observation or object. A large number of works were published in the 1980s; notably, it was shown [Reference Funahashi28,Reference Hornik, Stinchcombe and White29] that without constraint on the number of the hidden units, the structure can be “trained” to approximate any function with arbitrary accuracy. Several further enhancements of the backpropagation algorithm were also proposed (e.g. [Reference Juang and Katagiri30]).
Although the multi-layer FNN has received widespread validation in terms of its cognitive capabilities, at least theoretically, it was rarely used in large problems, which may demand a very large network. The determination of the number of layers and the number of hidden units to match a given problem is in general difficult and often compounded by the required amount of labeled data; the larger the network, the more data would be needed for reliable “training” of the network. The backpropagation algorithm is slow in convergence and for a large network trained on a large dataset, its slowness becomes a limiting factor. A very serious drawback of the backpropagation algorithm was found in the tradeoff consideration of the network depth (more layers) versus the width (more hidden units). There is a desire to use more layers to curtail the growth of hidden units so as to keep the total number of units within reach (to take advantage of the increasing coverage of nonlinearity over the domain of the input). When the network is very deep, nevertheless, the propagated error becomes less effective as it moves away from the output layer, thereby reducing its significance in changing the behavior (via the synaptic weights) of the network. This drawback turns out to be the bottleneck of FNN for it to be an effective recognizer. Interpreted in the context of the bridge function, the influence of the output error is ineffective in transforming the input, during the first few layers of processing, into a representation suitable for classification function mapping, carried out in the last few layers of the network.
C) Sectional remarks
Many studies about FNN and RNN in the 1980s and 1990s were about the utility of these neural processing models in search of their capability of emulating the human brain for intelligent tasks, of which memory and decision are the major two. After extensive explorations, a general consensus emerges in that FNN is associated with the task of making intelligent decisions while RNN with memory retrieval. (Other proposals with much added sophistication and variation in network structures for unique tasks do exist. For example, there are numerous investigations of expanded structures of RNN [Reference Kosko31,Reference Giles, Miller, Chen, Chen, Sun and Lee32] to cope with a stream of dynamic input, rather than responding to a static pattern. The term “recurrence” thus has varying meanings which are to be considered separately.) This empirical opinion of dichotomizing the two tasks, memory retrieval and intelligent decision making, is in retrospect limiting. It turns out, if we are not bogged down to the far-fetched goal of emulating the human brain, much is to be gained by staying on finding the maximum utility of the neural nets as a powerful computational structure for constructing a data-driven function. In pursuit of the latter, FNN and RNN need not be viewed as two entirely orthogonal constructs; the question is if they can be built and combined to complement each other toward a common objective.
The insights about Bayes optimal decision theory based on statistical models and the need for some bridge function suggest that the stochastic RNN, namely the BM, may have something to offer because the state of BM carries some information about the probabilistic behavior of the data, on which the network is trained. Obviously, to materialize this speculation, a more detailed analysis of BM and/or RBM and how they may be used to represent statistical models is necessary. This is done in the next section.
IV. MULTIVARIATE DISTRIBUTION AND MRF
Earlier in Section II, we state that the Bayes decision theory to achieve minimum error probability requires us to choose, as best as we can, a probability measure that matches the data. This of course imposes a demand on the system designer (us) to have as many choices of the probability measure as possible; even then, we cannot be sure if the data indeed has a distribution that is a member of the set of distributions we can work with. This is practically a lot more difficult than one realizes – practitioners tend to only work with easy ones, such as a multivariate Gaussian distributions or a mixture of multivariate Gaussian distributions. Often we fail to ascertain the appropriateness of the chosen measure – rarely if any, we hear designers launch distribution tests before settling on the choice of distribution and performing system training.
Another aspect of the difficulty in working with probability measures arises when the data dimensionality is very high, as in image or speech recognition (dimension reduction notwithstanding). When the dimensionality is high, even the simple ones like multivariate Gaussian become hard to handle. Here, we bring in a limited expansion of the choices, namely, the Gibbs measure or the MRF, to demonstrate a possible direction of development to cope with the difficulty. In spite of the different roots, the two are essentially the same as is established by the Hammersley–Clifford theorem [Reference Hammersley and Clifford33,Reference Spitzer34] for strictly positive measures (zero measure events are of little interest to us).
A MRF [Reference Lafferty and Mccallum35] consists of a set of (say n) multivariate random variables,
![]() $X = \{X_{i} \}_{i = 1}^{n}$
, whose joint probability measure has a Markovian property, specified by an undirected graph G=(S, U), where S is the set of vertices or nodes,
$X = \{X_{i} \}_{i = 1}^{n}$
, whose joint probability measure has a Markovian property, specified by an undirected graph G=(S, U), where S is the set of vertices or nodes,
![]() $S = \{s_{i}\}_{i = 1}^n$
, each corresponding to a random variable indexed from 1 to n, and U is the set of edges that specify the connections among the n nodes. An edge (i, j) that exists in U means the ith node and the jth node are connected in the graph G; otherwise, the connection is broken. Various Markovian properties can be invoked or assumed in defining an MRF and the most common form is to factorize the measure based on a “clique” system,
$S = \{s_{i}\}_{i = 1}^n$
, each corresponding to a random variable indexed from 1 to n, and U is the set of edges that specify the connections among the n nodes. An edge (i, j) that exists in U means the ith node and the jth node are connected in the graph G; otherwise, the connection is broken. Various Markovian properties can be invoked or assumed in defining an MRF and the most common form is to factorize the measure based on a “clique” system,
![]() $Q=\{Q_{i} \}_{i = 1}^n$
, where Q
i
denotes the set of nodes that are connected to the ith node:
$Q=\{Q_{i} \}_{i = 1}^n$
, where Q
i
denotes the set of nodes that are connected to the ith node:
and
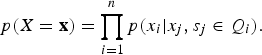 $$p(X = {\bf x}) = \prod_{i = 1}^n p(x_i \vert x_j, s_j \in Q_i). $$
$$p(X = {\bf x}) = \prod_{i = 1}^n p(x_i \vert x_j, s_j \in Q_i). $$
In many applications, the clique system is based on “vicinity” or “neighborhood”, meaning only the adjacent random variables, in time or in space, and affects the conditional probability of (13). For example,
![]() $Q_{i} = \{s_{j}; d(i,j) \lt d_{u} \},$
where d is the distance between two points (nodes) and d
u
defines the bound of neighborhood. (It is then easy to see how this reduces to the usual Markov chain if the index of the vertices corresponds to that of a sequence.) Another way to represent the clique system is through a connected graph, resulting in the so-called graphical model [Reference Jordan36]. A popular MRF model takes the following form for the “local” probability
$Q_{i} = \{s_{j}; d(i,j) \lt d_{u} \},$
where d is the distance between two points (nodes) and d
u
defines the bound of neighborhood. (It is then easy to see how this reduces to the usual Markov chain if the index of the vertices corresponds to that of a sequence.) Another way to represent the clique system is through a connected graph, resulting in the so-called graphical model [Reference Jordan36]. A popular MRF model takes the following form for the “local” probability
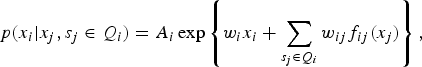 $$p(x_i \vert x_j, s_j \in Q_i) = A_i \exp \left\{w_i x_i + \sum_{s_j \in Q_i} w_{ij} f_{ij} (x_j) \right\}, $$
$$p(x_i \vert x_j, s_j \in Q_i) = A_i \exp \left\{w_i x_i + \sum_{s_j \in Q_i} w_{ij} f_{ij} (x_j) \right\}, $$
where A
i
is the normalizing factor and in the simplest case,
![]() $f_{ij}(x_{j}) = x_{i} x_{j}$
, resulting in
$f_{ij}(x_{j}) = x_{i} x_{j}$
, resulting in
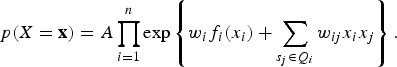 $$p(X = {\bf x}) = A \prod\limits_{i = 1}^n \exp \left\{w_i f_i (x_i) + \sum_{s_j \in Q_i} w_{ij} x_i x_j \right\}. $$
$$p(X = {\bf x}) = A \prod\limits_{i = 1}^n \exp \left\{w_i f_i (x_i) + \sum_{s_j \in Q_i} w_{ij} x_i x_j \right\}. $$
It is illuminating to look at a Gauss-MRF in reference to the regular multivariate Gaussian distribution. For ease in visualization, we assume the Gaussian random variables have 0 mean and the joint pdf is thus
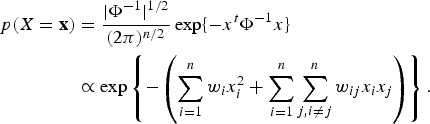 $$\eqalign{p(X = {\bf x}) & = {\vert \Phi^{-1} \vert ^{1/2} \over (2\pi)^{n/2}} \exp \lcub -x^t \Phi^{-1}x \rcub \cr &\propto \exp \left\{-\left(\sum_{i = 1}^n w_i x_i^2 + \sum_{i = 1}^n \sum_{j,i\ne j}^n w_{ij} x_i x_j \right) \right\}.} $$
$$\eqalign{p(X = {\bf x}) & = {\vert \Phi^{-1} \vert ^{1/2} \over (2\pi)^{n/2}} \exp \lcub -x^t \Phi^{-1}x \rcub \cr &\propto \exp \left\{-\left(\sum_{i = 1}^n w_i x_i^2 + \sum_{i = 1}^n \sum_{j,i\ne j}^n w_{ij} x_i x_j \right) \right\}.} $$
Comparing (16) and (17), we see
![]() $f_{i} (x_{i}) = x_{i}^{2}$
and the multipliers {w
ij
} are elements of the precision matrix W, i.e. the inverse of the covariance matrix Φ. The clique or neighborhood system specifies the existence of correlation between any pair of random variables and reduces the double summation in (16) to only those correlated pairs. It can be shown that if nodes i and j are not connected, i.e.
$f_{i} (x_{i}) = x_{i}^{2}$
and the multipliers {w
ij
} are elements of the precision matrix W, i.e. the inverse of the covariance matrix Φ. The clique or neighborhood system specifies the existence of correlation between any pair of random variables and reduces the double summation in (16) to only those correlated pairs. It can be shown that if nodes i and j are not connected, i.e.
![]() $(i,j) \notin U$
, w
ij
=0 then [Reference Rue and Held37].
$(i,j) \notin U$
, w
ij
=0 then [Reference Rue and Held37].
For a binary system,
![]() $X = \{X_{i} \}_{i=1}^{n}$
are multivariate Bernoulli and [Reference Dai, Ding and Wahba38] offers a rather rigorous treatment. Here, a quick and dilettantish view is to use the fact that x
i
∈{0, 1} and therefore
$X = \{X_{i} \}_{i=1}^{n}$
are multivariate Bernoulli and [Reference Dai, Ding and Wahba38] offers a rather rigorous treatment. Here, a quick and dilettantish view is to use the fact that x
i
∈{0, 1} and therefore
![]() $f_{i} (x_{i} ) = x_{i}$
, which can be substituted back into (16) resulting in
$f_{i} (x_{i} ) = x_{i}$
, which can be substituted back into (16) resulting in
 $$p(X = {\bf x}) \propto \exp \left\{-\left(\sum_{i = 1}^n w_i x_i + \sum_{i = 1}^n \sum_{j,i\ne j}^n w_{ij} x_i x_j \right) \right\}. $$
$$p(X = {\bf x}) \propto \exp \left\{-\left(\sum_{i = 1}^n w_i x_i + \sum_{i = 1}^n \sum_{j,i\ne j}^n w_{ij} x_i x_j \right) \right\}. $$
It is seen that the exponent contains important terms that are in the core of the McCulloch–Pitts neuron and the energy functions of (10), (17), and (18) show a rather explicit relationship between MRF and RBM. Hence, an MRF is a general statistical model defined over a possibly arbitrary clique system, while an RBM is capable of efficiently implementing the model provided that the clique system is linear (in parameter) as shown in (18). (The measure of (18) is sometimes said to be log–linear.)
A network can involve mixed nodes, some operating on real unbounded values such as Gaussian random variables while some on bounded values such as the Bernoulli for binary variables. The energy function of (17) and (18) can be combined to form the so-called Gaussian–Bernoulli RBM [Reference Cho, Raiko and Ilin39]:
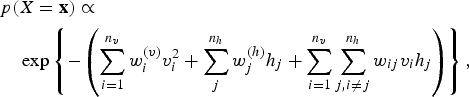 $$\eqalign{&p(X = {\bf x})\propto \cr &\quad \exp \left\{ -\left(\sum_{i = 1}^{n_v} w_i^{(v)} v_i^2 + \sum_j^{n_h} w_j^{(h)} h_j + \sum_{i=1}^{n_v} \sum_{j,i\ne j}^{n_h} w_{ij} v_i h_j \right) \right\},} $$
$$\eqalign{&p(X = {\bf x})\propto \cr &\quad \exp \left\{ -\left(\sum_{i = 1}^{n_v} w_i^{(v)} v_i^2 + \sum_j^{n_h} w_j^{(h)} h_j + \sum_{i=1}^{n_v} \sum_{j,i\ne j}^{n_h} w_{ij} v_i h_j \right) \right\},} $$
where the random variable
![]() ${\bf x} = [{\bf v},{\bf h}] = [\{v_{i} \},\{h_{j} \}]$
encompasses the states of both the visible and the invisible nodes of an RBM. The model of (19) is obviously very closely related to the RBM energy function of (10), which was introduced for a network of binary nodes.
${\bf x} = [{\bf v},{\bf h}] = [\{v_{i} \},\{h_{j} \}]$
encompasses the states of both the visible and the invisible nodes of an RBM. The model of (19) is obviously very closely related to the RBM energy function of (10), which was introduced for a network of binary nodes.
It is important to note that the clique system helps to reduce the complexity of the distribution and often is assumed and instituted by the designer, much like assuming a finite-order Markov chain to analyze the fluctuation in the S&P500 stock index. No one can ascertain that the index is indeed following a finite-order Markov chain; it is just that a certain model is assumed to facilitate the analysis, the results of which are always subject to interpretation. Once a clique system is instituted, those inter-nodal relationships not included in U are forever lost. In the usual neighborhood-based approach, the MRF model would not be able to account for those so-called “long-span” (in time or in space) relationships. Therefore, if one is concerned about loss of modeling accuracy because of undue a priori constraints, an alternative is to include the connections in U also as part of the learning process, i.e. a data-driven approach (let the data determine). In this context, an MRF (as a modeling tool) in conventional practices may have a pre-specified set of connections among nodes, while an RBM would learn the connections from data. This is an important point to remember and will be elaborated in later sections.
Equations (16)–(19) establish the equivalence between minimization of the system energy (7) and (8) and the usual maximum likelihood method in statistical estimation theory. That is, given a set of data
![]() $\{{\bf x}_{i} \}_{i = 1}^n$
, whose collective statistical properties are encapsulated in the probability measure,
$\{{\bf x}_{i} \}_{i = 1}^n$
, whose collective statistical properties are encapsulated in the probability measure,
![]() $p(X = {\bf x}) = p({\bf x};W)$
, where W is chosen to achieve
$p(X = {\bf x}) = p({\bf x};W)$
, where W is chosen to achieve
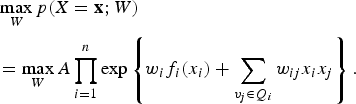 $$\eqalign{&\max_W p(X = {\bf x};W) \cr &= \max_W A \prod_{i = 1}^n \exp \left\{w_i f_i (x_i) + \sum_{v_j \in Q_i} w_{ij} x_i x_j \right\}.} $$
$$\eqalign{&\max_W p(X = {\bf x};W) \cr &= \max_W A \prod_{i = 1}^n \exp \left\{w_i f_i (x_i) + \sum_{v_j \in Q_i} w_{ij} x_i x_j \right\}.} $$
Techniques such as the EM algorithm for maximum likelihood and its various variants can be related or contrasted to those (e.g. contrastive divergence [Reference Hinton40]) used in training the RBM. Papers that address the training techniques and their statistical significance are widely available (e.g. [Reference Carreira-Perpinan and Hinton41] and references therein). Readers are encouraged to establish these relationships as exercises.
The upshot here is as follows. An RBM can be properly trained to produce a set of synaptic interconnection weights for the recurrent neural networks to approximate an unknown probability distribution (taking the form of (20) which is related to an MRF and has its root in multivariate Gaussian when the weights are properly related to the precision matrix), evaluation of which for an arbitrary input can be computed directly from the state of the nodes of the network. The hidden nodes thus contain pivotal values in the computation of probability of an input and also can be regarded as a transformed set of feature or parameters that well represent the input by projecting its key probabilistic characteristics into a form suitable for later processing.
V. WHAT DOES AN RBM DO?
We have explained the role of an RBM as a stochastic recurrent network, as opposed to the original Hopfield net which functions as a deterministic associative memory. To fix the idea of a stochastic recurrent neural net, we provide two sets of actual computational examples here, one set showing how an RBM functions as an RNN to retrieve the stored memory and the other how an RBM functions as a generative probabilistic model. The latter is helpful in realizing the potential of an RBM as an effective data-driven statistical modeling tool.
Let (k+l) denote the configuration of an RBM, where k is the number of visible nodes, i.e. n v in (19) (or the dimensionality of the input vector) and l is that of hidden nodes, i.e. n h . In the first set of examples, each RBM has a configuration of (2+8) and is trained on a set of input vectors using a generic contrastive divergence algorithm [Reference Hinton40]. The first RBM is a Gaussian–Bernoulli type with a model specified by (19) and is trained on vectors drawn from an independent 0-mean Gaussian bivariate with unity variance. This can be considered as training a (2+8) RBM to remember a single point, namely (0, 0), in the 2D space, with the possible contamination of 0-mean unit-variance noise in the input. Once the RBM training converges, two sets of vectors are applied as input to the network. The first set has the same statistical property as the training set, i.e. 0-mean unit-variance independent Gaussian bivariate vectors (purple color in Fig. 7(b)) and the second set consists of independent uniformly distributed vector within the square of ±5, a scatter plot of which is shown in Fig. 7(a). Figures 7(c)–7(e) show the converged state of the visible nodes at the end of the 1st, 3rd, and 5th recurrent epoch. (Panel (b) is a zoomed-in version of (c) to show the two colored sets.) All these input vectors converge to a point extremely close to the recorded location of (0, 0).

Fig. 7. Convergence of a (2×8) RBM trained to memorize a single point. (a) uniformly distributed random points used to test the RBM; (b) enlarged (c) to show the output of the RBM after epoch 1 in response to (1) 0-mean 1-var noise (purple color) and (2) uniform-distributed random point set of (a); (c)–(e) RBM output at epoch 1, 3, and 5.
Another RBM is trained on random vectors drawn from independent Gaussian bivariate
![]() ${\cal N} ((2,2),(1,1))$
and
${\cal N} ((2,2),(1,1))$
and
![]() ${\cal N} ((-2, -2),(1,1))$
as shown in Fig. 8(a). This is equivalent to a two-point memory, targeting (2, 2) and (−2, −2) with 0-mean 1-variance additive noise contamination. Similar to the previous case, the trained network received two sets of inputs, one with the same distribution as that the network is trained on (red) and the other the independent uniform bivariate (purple) as before. Figure 8(b)–8(e) show the converged state of the visible nodes at the end of the 1st, 3rd, 5th, and 7th recurrent epoch. This time the converged memory points are still clearly seen although they no longer coincide with the original points of (2, 2) and (−2, −2). Furthermore, some of the uniform bivariate vectors only produce, in the converged visible nodes, points between the two “attractor” states; these are considered spurious states of the network. To see how individual vectors from the uniform bivariate distribution converge to a point, we plot the trajectory of movement from the initial input vector (starting point) to the converged state (ending point) in Fig. 8(f). Points near the line that separates the two original clusters (dotted line in (a)) may only converge to a point on the line that connects the two cluster centers (in reference to those converged points shown in (e), Epoch 7). If the two clusters represent two classes, the RBM is seen to perform some sort of data/dimension reduction (from 2D to 1D) while retaining a similar separability as the original 2D observations.
${\cal N} ((-2, -2),(1,1))$
as shown in Fig. 8(a). This is equivalent to a two-point memory, targeting (2, 2) and (−2, −2) with 0-mean 1-variance additive noise contamination. Similar to the previous case, the trained network received two sets of inputs, one with the same distribution as that the network is trained on (red) and the other the independent uniform bivariate (purple) as before. Figure 8(b)–8(e) show the converged state of the visible nodes at the end of the 1st, 3rd, 5th, and 7th recurrent epoch. This time the converged memory points are still clearly seen although they no longer coincide with the original points of (2, 2) and (−2, −2). Furthermore, some of the uniform bivariate vectors only produce, in the converged visible nodes, points between the two “attractor” states; these are considered spurious states of the network. To see how individual vectors from the uniform bivariate distribution converge to a point, we plot the trajectory of movement from the initial input vector (starting point) to the converged state (ending point) in Fig. 8(f). Points near the line that separates the two original clusters (dotted line in (a)) may only converge to a point on the line that connects the two cluster centers (in reference to those converged points shown in (e), Epoch 7). If the two clusters represent two classes, the RBM is seen to perform some sort of data/dimension reduction (from 2D to 1D) while retaining a similar separability as the original 2D observations.

Fig. 8. Convergence of a (2×8) RBM trained to memorize two points (2, 2) and (−2,−2). (a) random points used to train the RBM; (b)–(e) RBM output at epoch 1, 3, 5, and 7 showing convergence in response to two sets of input; (f) trajectories of convergence for uniformly distributed points as input.
Now the number of clusters is increased to four as shown in Fig. 9(a) and the same toy experiment is repeated resulting in plots shown in Figs 9(b)–9(d). A similar data reduction effect is seen, although the implied manifold on which the converged points lie becomes more sophisticated.

Fig. 9. Convergence of a (2×8) RBM trained to memorize four points. (a) random points from four bivariate Gaussian distributions used to train the RBM; (b)–(d) RBM output at epoch 1, 3, and 5, showing convergence in response to two sets of input (uniform and Gaussian mixtures).
In the second set of examples, the familiar hand-written digit set of MNIST [42] is used. A hand-written digit in MNIST is an image of 28×28 (784) pixels. The example will demonstrate the ability of an RBM to function as an effective model for MRF for observations of high dimensionality. Note that the data in this example has a dimensionality of 784, while that it was 2 in the previous example. Figure 10 shows a collection of 100 images of the digit 2 (they are stacked together without separating grids in the figure). An RBM is trained on 500 images of the digit 2. The RBM is of type Bernoulli–Bernoulli and has the configuration (784, 2000). Figure 11 shows the effect of recurrent processing by such an RBM upon presentation of various inputs. First, part (a) of the figure shows the result of progressive epochs (from left, the original image, to right, 1st to 6th epochs) of recurrence in response to different digits, from 0 to 9. The RBM, as an RNN, is producing in the converged result the pixel values according to the corresponding correlation between the input image and those used in training the RBM. For the digit 2, the RBM retains very well the digit obviously. For digit 0 which is a closed circle in the input, an opening appears in the converged result due to the fact that a digit 2 would not normally show a closed connection on the left of writing stroke (see Fig. 10 of example of the digit 2). Similar observations of retention of the correlation (similar to matched filtering) can be made for other digits. Part (b) of the figure shows the converged state of the RBM in response to 36 random bit patterns of size 28×28. It can be seen that these converged visible node states share very similar values. At the bottom of parts (b) and (c), the states of the visible nodes in sequence of progressive epochs in response to a random image pattern (the leftmost) is shown.

Fig. 10. Examples of MNIST dataset, digit 2.

Fig. 11. (a) Output of an RBM trained on digit 2, in response to all digits (0–9) as input; progressive epochs toward convergence are shown from left to right; (b) converged output of the same RBM in response to random patterns as input; (c) a random pattern as input and outputs at six successive epochs.
It is interesting to further probe the effect of the RBM in response to “noisy” input. This time, random Gaussian noise of two different variance values, 0.04 and 1, respectively, are added to those image pixels of various digits. Figure 12(a) (low-noise) and (b) (high-noise) display the corresponding results in progressive epochs from left to right as in Fig. 12(a). The rightmost in each row is the converged output. As expected, noise has caused change, commensurate with the level of noise, in the output. However, it is important to take note of the changes, particularly for the high-noise case part (b), during the first few epochs. The effect of noise suppression of some sort by the RBM is clearly seen; this is typical of an associative memory that an RNN like the Hopfield net would behave. At the end of 2nd or 3rd epoch, the resultant images seem to have a good tradeoff between the amount of noise suppression and the introduced distortion (due to correlation with the RBM, which was trained on the digit 2). For recognition purposes, the original images seem to be too noisy for reliable identification but after a couple of recurrent epochs before the final convergence, the representation of the original image appears to be more appropriate as they retain more of the characteristics of the inputs. This may have spawned some innovative ideas behind DNN, namely, turning an RNN into an FNN before convergence and taking advantage of its noise suppression capability. We shall elaborate the idea in a later section.

Fig. 12. RBM trained on digit 2 responds to noisy input from all digits: (a) low noise (high signal-to-noise ratio (SNR)); (b) high noise (low SNR).
VI. LATENT VARIABLE MODEL AND MIXTURE MODEL
In Section IV, we discuss how an RBM is related to a MRF and has the potential of fulfilling the role of a data-driven statistical modeling structure. In Section V, we show how an RBM as an RNN can regularize an input vector/pattern, which may inherently contain uncertainties, noise or only partial information, and produce a converged output, which presents itself as the most likely vector/pattern behind the raw input according to the network weights.
In this section, we elaborate on the potential of an RBM in coping with modeling difficulties that may arise when the data dimensionality is high. In relating the RBM model to an MRF, the states of all visible and invisible nodes collectively define the distribution model; the implied dimensionality of data is the sum of the number of visible nodes and that of the invisible ones. The introduction of hidden nodes, with the conditional independent assumption, provides a data-driven selection of the correlation structure, i.e. the network connections or the equivalent of the clique system of an MRF. That circumvents the undesirable and undue constraints, often resulted from an arbitrary a priori definition of what the clique system should look like. The introduction of hidden nodes also contributes to the functionality of an RBM as a ready candidate for the aforementioned bridge function (Section II) in many applications, image recognition in particular. In this section, we discuss additional relevant problems that the RBM and its implied statistical models may be configured to address, eventually toward the possibility of serving as an effective “bridge function” for the problem of statistical pattern recognition.
Expressions (17)–(19) show the possibility of multivariate Gaussian models with reduced complexity. When the data are of high dimensionality, such reductions are necessary although care must be taken to ensure the effectiveness of the resulting models. Take the handwritten digit data as an example. Each image is of dimension 28×28 or 784 when put in a vector form. A 784-dimensional Gaussian multivariate has a covariance matrix with
![]() $785\times 392=307\,720$
second moment terms. How many such 784-dimensional vectors (i.e. the number of samples of a handwritten digit) must be available for a reasonable estimation of this many parameters? It is exorbitant if we go with traditional rules of thumb in setting up an estimation task. (It is interesting to note that the MNIST dataset widely used in evaluating many pattern recognition systems contains no more than 100 K patterns for each digit. A sample size of 100 K sounds a lot. But is it sufficient for the estimation of a covariance matrix with over 307 K terms?)
$785\times 392=307\,720$
second moment terms. How many such 784-dimensional vectors (i.e. the number of samples of a handwritten digit) must be available for a reasonable estimation of this many parameters? It is exorbitant if we go with traditional rules of thumb in setting up an estimation task. (It is interesting to note that the MNIST dataset widely used in evaluating many pattern recognition systems contains no more than 100 K patterns for each digit. A sample size of 100 K sounds a lot. But is it sufficient for the estimation of a covariance matrix with over 307 K terms?)
For most applications, fortunately, it can be argued that in real world random observations of large dimensionality, not all pairs of dimensions are significantly correlated. However, we may not be able to prejudge which pairs of the variables have significant correlations that must be accounted for. Resorting to the independence assumption (using a diagonal covariance matrix) would quickly lead to oversimplification of the data model and will not solve the problem at hand. For imagery data, use of an MRF model with its clique system defined by proximity and neighborhood appears to make a lot of sense. The clique system certainly makes the correlation structure easier to handle as it reduces the correlation structure to an often small subset, implied in the clique (or neighborhood) system. One nevertheless may argue that complexity reduction with the neighborhood clique system may fail to account for important correlations that span over some distances. Keep in mind that we need a probabilistic model that characterizes the statistical behavior of the data well for the purpose of pattern recognition.
A technique that has often been suggested for “dimensionality reduction” (and for probability density function approximation) is the so-called latent variable model
and assume that
meaning the data are conditionally independent given h. We also assume that same is true for h given v. Conditional independence does simplify the model as explain below. We suggest that readers keep the clique system in the backdrop and contemplate on other alternatives for reducing the complexity.
Here we are interested in a particular form of the latent variable model, in which the latent variables are introduced with the following assumed relationships:
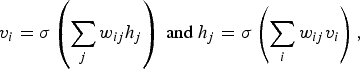 $$v_i =\sigma \left(\sum_j w_{ij} h_j \right)\;\hbox{and}\;h_j = \sigma \left(\sum_i w_{ij} v_i \right), $$
$$v_i =\sigma \left(\sum_j w_{ij} h_j \right)\;\hbox{and}\;h_j = \sigma \left(\sum_i w_{ij} v_i \right), $$
where the function σ is the usual sigmoid to be consistent with the notion of an RBM, although the function is not essential in visualizing the multivariate relationship here. Let us interpret this latent variable model in the context of a Gaussian multivariate. Suppose the data dimensionality is N and the number of latent variables is M. This is equivalent to a multivariate model involving N+M random variables. For a Gaussian multivariate model, there would be
![]() $(N + M)(N + M - 1)/2$
second moment coefficients. With the conditional independence assumptions (both ways) and the relationship of (23), only NM parameters are necessary, eliminating
$(N + M)(N + M - 1)/2$
second moment coefficients. With the conditional independence assumptions (both ways) and the relationship of (23), only NM parameters are necessary, eliminating
![]() $(N^{2} + M^{2} - N - M)/2$
parameters. Again with the concatenated data of v and h envisioned as Gaussian multivariate, these parameters {w
ij
} can be interpreted as the non-zero elements of the precision matrix, which is the inverse of the covariance matrix.
$(N^{2} + M^{2} - N - M)/2$
parameters. Again with the concatenated data of v and h envisioned as Gaussian multivariate, these parameters {w
ij
} can be interpreted as the non-zero elements of the precision matrix, which is the inverse of the covariance matrix.
Let us refocus on the modeling of the original data v of dimensionality N. It is interesting to discuss the data modeling scenario in reference to two extremes: (a) the full multivariate model with N(N−1)/2 covariance coefficients, and (b) the independent model with only N variance parameters. The full model of (a) does not have an inherently imposed limitation in structure and is certainly capable of achieving good modeling quality, PROVIDED there is sufficient data to support parameter estimation, a very tall order given the large dimensionality. The model with the independence assumption does not take statistical relationship among data dimensions into account and will not be able to achieve highly accurate data modeling in general. Two popular choices can be employed in between the two extremes: a mixture of independent models and the latent variable model. The two share some common mixture roots as seen in equation (21). The difference is often in the interpretation and the customary practice. In the traditional mixture model, the constituent models are often chosen, although not required, to be independent models. If M is interpreted as the number of latent variables, usually M≪N, the model can be seen as somewhere between the aforementioned two extremes; it has a better modeling power than the single independent model but does not naively incur the level of complexity as the full covariance model. If we associate h with the hidden nodes of an RBM, then the RBM implements a mixture density model with p(h) being the mixture weights. If h is Bernoulli, then p(h) can be computed by (9) and is equal to the activation state of the node itself.
What happens if M>N? Certainly, the situation would deviate from the original motivation behind the latent variable model, but the interpretation of a mixture model can continue. A simple illustration is helpful in visualizing the situation. Let X be a 1D random variable with pdf as depicted in Fig. 13 (black line). As shown, p(X=x) can be decomposed in various ways, two of which are shown in different color (blue and red) in the figure. The blue one with more (i.e. larger M) mixture components obviously places more emphasis on local distributions (i.e. mean values of the components spread out distributively); the relationship between the mixture weights and the data locality would grow stronger, although the concern of insufficient data support for estimating the local mixture parameters also deepens (e.g. in the case of a large number of mixtures, some may not be supported by any data). The concern notwithstanding (see below on imputation) the idea of using h (the states of the hidden nodes or the mixture weights) as a transformed and distributed representation of the data, effectively as a result of the “bridge function,” emerges promisingly. In Section II, we have also observed the surprising effectiveness of local likelihood for class decisions. In this section, we stay in the realm of statistical modeling; we discuss transformed representation in the next section.

Fig. 13. Fitting mixture densities to data distribution.
VII. DEEP BELIEF NETWORK
We have suggested the idea of taking advantage of the behavior of an RNN, in that a noisy input or a partial input will converge to a “stored” memory state with an intended and desired regularity, and coupling it with a FNN for its functional approximation capability (e.g. mapping an arbitrary input into a discrete class label). How can this be best accomplished? Earlier we have stated that the best recognition performance is to be achieved when the observation can be transformed into a representation (hopefully without loss of discriminability), the distribution of which can be accurately established (both in form and in value of the defining parameters). Given these two structures, RNN and FNN (or MLP, used interchangeably here), what design choices are available?
If an RNN is used in its traditional manner, meaning an RNN is trained to perform a transformation from an input to the converged state as output, then the coupling with the latter MLP may be “abrupt”; i.e. an RNN hands the converged result as new feature over to the MLP, which performs the decision function. This “hand-over” lays all the decision performance responsibilities on the MLP, whose pros and cons (such as the diminishing gradient problem [Reference Hochreiter43,Reference Bengio44]) would remain the same as usual. The feature produced by the (single) RNN might already be better than the original input, but one may not be sure if the new feature is going to lead to the best result (modeling and recognition decision) possible. A natural contemplation is then: if an RNN has the ability to reduce noise, which interferes with statistical modeling, and to impute possibly missing information, would not a stack of RNNs perform even better? Such a contemplation gives rise to the so-called DBN.
A DBN has the same structure of an MLP. Nevertheless, each pair of layers, from the input layer up, are first trained like an RBM without supervision. These RBMs aim at capturing the relevant statistical models for the intermediate input at each layer and are successively trained one pair at a time and stacked together afterwards. Once stacked up, a final layer is added to interface with the “desired output” and additional training, the so-called “fine-tuning”, is conducted in a supervised manner with the usual error back-propagation method, instead of the contrastive divergence algorithm for estimating the implied statistical model for the data. In essence, thus, those layers of pre-trained RBMs are used to implement the aforementioned “bridge function” to produce a representation for function approximation, which is by definition a supervised process, by the later FNNs. It is interesting that the principle of statistical pattern recognition, namely matching the data representation with probabilistic models as reviewed in Section II, is age-old, but its realization in layers of neural networks through a soft division between the task of representation transformation and that of statistical modeling for optimal decision is surprisingly new.
Depending on the supply of the “desired output” in the supervised training, a DBN can be trained as, for example, an autoencoder [Reference Bourlard and Kamp45,Reference Bengio46], where the desired output is in the same domain as the input (e.g. a clean, noise-free version of the noisy observation), or as an MLP for a classification or recognition task with the true class labels as the target outputs. Recently, a number of attempts have been reported in using a DBN/autoencoder for speech signal enhancements (e.g. [Reference Xu, Du, Dai and Lee47,Reference Seltzer, Yu and Wang48]).
A DBN is thus essentially an MLP with the following properties. Layers that are close to the input layer have connection weights that retain the original behaviors of the corresponding RBMs, meaning to produce output that contains fewer irrelevant or less likely components, and are less affected by the supervised training because of the diminishing gradient phenomenon of the back-prop algorithm. In other words, they attempt to reduce extraneous uncertainty such as noise contamination in the observation and regularize the input by producing the most likely (probable) representation according to the generative model embedded in the trained networks, so as to match the function approximation design in those layers close to the output.
Another developmental paradigm behind the DBN design is to unroll an RBM, as a traditional RNN, into an MLP, and train the resultant MLP with back-prop in a supervised manner after setting up the desired output. Note that the original RBM is an RNN, which takes a few processing epochs (assuming a full parallel mode) to converge to its proper memory state. Each epoch thus involves a pair of layers and Fig. 14 shows an example of the unrolled MLP from the corresponding RBM. The weight matrices, W and its transpose W′, are alternately used in successive layers of the unrolled MLP. Without further supervised training, the output would be the converged memory state. The activation patterns of those neurons in the intermediate layers would be the result of the corresponding recurrence at certain epochs. Once a new desired output is supplied and the back-prop is employed to complete the supervised training, the resultant multilayer structure can be considered as a gradual merging, layer by layer, of a stack of RBMs with an MLP. The intermediate representations, or feature, would gradually emerge in preparation for the last (possible a few) layers of the feed-forward networks to accomplish the assigned recognition task.

Fig. 14. Unrolling of an RBM.
This explains the key difference between a DNN and an MLP, even though their structures may look identical at a superficial glance.
Unrolling an RBM from an RNN to a FNN also unravels a number of possibilities in terms of how such a structure can be used in some tasks. There are two sets of such possibilities, one being in the complexity and the other in the objective for the final supervised training. For the former, we can consider each pair of visible and hidden layers as an RBM, which is trained as such. Then, the hidden layer can be treated as the visible layer in the next pair of visible and hidden layers, and so on until one exhausts its capacity for handling the complexity (e.g. due to computational as well as data constraints). The width (size) of the next hidden layer is up to the designer and it does not have to fall back to the width of the previous visible layer. This stacking of RBMs is the basis of the notion of a DBN. The latter, the objective of the final supervised training, gives rise to the notion of a deep autoencoder, which is discussed below.
A) Deep autoencoder and PCA
An autoencoder is an MLP that is trained with the input itself as the desired output. Consider an MLP with one single hidden (intermediate) layer as shown in Fig. 5(b). Let M be the number of neurons of the hidden layer. Typically, an autoencoder has M<N, the dimension of the input vector (and the output vector). The weight matrix W is then of dimension N×M. When trained with the back-propagation algorithm, the optimization objective can be written as:
If we take away the nonlinearity function, σ, the objective function is minimized when the weight matrix is associated with the top M eigenvalues of the system, M<N. One thus can envision an autoencoder as one that performs a function closely related to PCA. With the flexibility that there could be many layers, those synaptic units of the layer with the least number of units then hold the (generalized) principal components or forms an encoded representation. This layer divides the whole stack into two parts. In the terminology of data compression, the part on the input side can be considered as the encoder and the part on the output side is then the decoder, which uses the coded representation to reconstruct the output.
Recognizing the usual weaknesses of the error backpropagation algorithm, Hinton suggests building an autoencoder by stacking a number of RBMs together, with the same motivation as discussed in the previous section, each trained first as a generative model with the contrastive divergence algorithm, followed by the back-prop algorithm. A new term called deep autoencoder thus emerges. In [Reference Hinton and Salakhutdinov1], Hinton demonstrate the performance of a DBN autoencoder in terms of its ability to reduce the data dimensionality in comparison with a traditional PCA. This comparison can also be viewed as a comparison between an MLP-autoencoder and a DBN-autoencoder, the nonlinearity notwithstanding.
The upshot of a deep autoencoder, as claimed by Hinton in [Reference Hinton and Salakhutdinov1], is that it implements a form of PCA better than a traditional PCA because its construct (and how it is trained) can circumvent the shortcomings of an MLP-based autoencoder which has been studied in the 1990s [Reference Bourlard and Kamp45].
B) Distributive representation
The interpretation of an autoencoder constructed from a stack of RBMs, i.e. a DBN, as a means for data reduction closely related to PCA, is justified only when the size of the intermediate representation has a reduced dimension (i.e. M<N). When this is not true, the view of data reduction needs to be generalized to the so-called distributive representation. This is similar to the previous discussion of the latent variable model versus the general mixture model. An input vector can be transformed into another representation with increased dimensionality to aid statistical modeling for pattern recognition.
In Section VI, we discussed the role of RBM in terms of the statistical model that it projects itself into. Such a model can be interpreted as a latent variable model or as a mixture model. In the former, an input to an RBM is projected onto those directions along the principal components (of reduced dimensionality), while in the mixture model, an input is projected onto a space, in which the coordinates are measured as the probabilities evaluated along the mixture components. The resultant probability vector can be considered a distributed representation of the input, with respect to the mixture model embedded in the RBM. Studies of this type of representation as well as other popular kernel transformations are abundant and not particularly elaborated in this paper. As pointed out, the one with more (i.e. larger M) mixture components obviously places more emphasis on local distributions with the concern of insufficient data support for estimating the local mixture parameters during model training. We address this issue from the perspectives of imputation and interpolation.
In statistics, imputation refers to the process of replacing missing data values with properly justified substitutes so as to avoid complicated inconsistencies in the overall data analysis. Imputation can be viewed as a form of interpolation. If
![]() $x = \{x_{i} \}_{i = 1}^{n}$
is a sequence and say x
k
is missing, one can seek a proper interpolation technique to find ~x
k
as the substitute. The substitute is required to possess some properties consistent with the rest of the data. For example, if the sequence is a sampled version of a bandlimited signal with a sample missing (say erroneously set to the value zero), a reasonable proposal would be to use an ideal lowpass filter (equivalent to using a sinc function for interpolation) to find the output and then use the output at the missing instance as the substitute value. There are advantages in doing so. For one, the quality of the autocorrelation estimate would certainly be improved. Thus, in the same vein, imputation augments the dataset according to some prior constraints and can potentially lead to a better characterization of the data statistics. Gibbs sampling [Reference Hinton40,Reference Geman and Geman49], a crucial component in the contrastive divergence algorithm, or similar variations of the Metropolis–Hastings algorithm [Reference Metropolis, Rosenbluth, Rosenbluth, Teller and Teller50], offer a form of imputation and alleviates the concern of insufficient data support mentioned above. The general discussion on learning with missing data is beyond the scope of this article.
$x = \{x_{i} \}_{i = 1}^{n}$
is a sequence and say x
k
is missing, one can seek a proper interpolation technique to find ~x
k
as the substitute. The substitute is required to possess some properties consistent with the rest of the data. For example, if the sequence is a sampled version of a bandlimited signal with a sample missing (say erroneously set to the value zero), a reasonable proposal would be to use an ideal lowpass filter (equivalent to using a sinc function for interpolation) to find the output and then use the output at the missing instance as the substitute value. There are advantages in doing so. For one, the quality of the autocorrelation estimate would certainly be improved. Thus, in the same vein, imputation augments the dataset according to some prior constraints and can potentially lead to a better characterization of the data statistics. Gibbs sampling [Reference Hinton40,Reference Geman and Geman49], a crucial component in the contrastive divergence algorithm, or similar variations of the Metropolis–Hastings algorithm [Reference Metropolis, Rosenbluth, Rosenbluth, Teller and Teller50], offer a form of imputation and alleviates the concern of insufficient data support mentioned above. The general discussion on learning with missing data is beyond the scope of this article.
Another interpretation of distributed representation can be borrowed from the technique of Kriging, which is a technique used in spatial prediction. It attempts to predict the value of a spatial function at a point of interest by a weighted average of the known values of the function in the area, most likely and conveniently in the vicinity of the point. The problem stems from geo explorations. Suppose in an area of interest, several boreholes have been dug and ores are found in some of them. Let these known results be denoted by
![]() $\{p({\bf x}_{i})\}_{i}$
, where p is the value of the function (e.g. density of the ore deposit) and {x
i
} are the locations of the boreholes. Kriging aims at predicting the value of p at new locations x before digging new boreholes. Classical Kriging involves the assumption of a Gaussian process and is also known as Wiener–Kolmogorov prediction. Details of the technique and the properties of the predictor can be found in [Reference Cressie51]. Here, we draw an analogy with the RBM to explain the idea of distributed representation. Suppose instead of predicting the distribution of the ore, the known values are binary, representing the simple result whether the ore finding is positive or negative at each known location. Then, it is possible to use these known binary values to “optimally” predict if it is likely to find ore at an arbitrary location in the area, based on the technique and the assumed statistical model. These new values, calculated as properly interpolated and smoothed results from the known values, can be viewed as a distributed representation of the ore distribution in the area, with reduced statistical fluctuations (similar to model-based smoothing). Indeed, this has been observed in the digit pattern examples in Section V.
$\{p({\bf x}_{i})\}_{i}$
, where p is the value of the function (e.g. density of the ore deposit) and {x
i
} are the locations of the boreholes. Kriging aims at predicting the value of p at new locations x before digging new boreholes. Classical Kriging involves the assumption of a Gaussian process and is also known as Wiener–Kolmogorov prediction. Details of the technique and the properties of the predictor can be found in [Reference Cressie51]. Here, we draw an analogy with the RBM to explain the idea of distributed representation. Suppose instead of predicting the distribution of the ore, the known values are binary, representing the simple result whether the ore finding is positive or negative at each known location. Then, it is possible to use these known binary values to “optimally” predict if it is likely to find ore at an arbitrary location in the area, based on the technique and the assumed statistical model. These new values, calculated as properly interpolated and smoothed results from the known values, can be viewed as a distributed representation of the ore distribution in the area, with reduced statistical fluctuations (similar to model-based smoothing). Indeed, this has been observed in the digit pattern examples in Section V.
A summarizing remark with the interpretation of the core distribution associated with an area is that the borehole results, realized at known locations, can be reasonably replaced by a new set of interpolated values, possibly denser and more in quantity without actual digging, to characterize or identify the area with the potential benefits of reduced inconsistencies (in the context of the assumed model).
VIII. MANIFOLDS AND PROBABILITY SPACE
Earlier in Section II, we have alerted readers that the statistical approach to pattern recognition, namely the optimality of the underpinning Bayes decision theory, has exceptions where it fails to deliver the best performance. In particular, as alluded to in the introduction on the differentiation between DNN and deep learning, the inherent structure of data and the manifold that the data resides in are not yet within the learning capability of DNN. The following example, although contrived, is one such case that offers a glimpse into what may be construed as the potential of “deep learning”, something that is beyond the current “DNN.”
Consider the following dataset
![]() $c \in C = \{C1, C2\}: C1 = \{.04, 0.10, 0.16, 0.25, 0.31, 0.46, 0.61\}$
and
$c \in C = \{C1, C2\}: C1 = \{.04, 0.10, 0.16, 0.25, 0.31, 0.46, 0.61\}$
and
![]() $\hbox{C}2 = \{.05, 0.09, 0.15, 0.18, 0.35, 0.45, 0.6\}$
, each constituting a class. These are obviously 1D data. If we look at their individual means and variances, they are very close, implying a large overlapping area under the (assumed) distribution functions. Figure 15(a) shows some possible distribution fits (some bad ones!) to the given data. A simple statistical pattern recognizer will have a hard time recognizing the two classes. And since they are 1D data, no dimensional correlation can be exploited as in PCA. Now suppose we transform the data into a 2D representation according to the following:
$\hbox{C}2 = \{.05, 0.09, 0.15, 0.18, 0.35, 0.45, 0.6\}$
, each constituting a class. These are obviously 1D data. If we look at their individual means and variances, they are very close, implying a large overlapping area under the (assumed) distribution functions. Figure 15(a) shows some possible distribution fits (some bad ones!) to the given data. A simple statistical pattern recognizer will have a hard time recognizing the two classes. And since they are 1D data, no dimensional correlation can be exploited as in PCA. Now suppose we transform the data into a 2D representation according to the following:

Fig. 15. Illustration of data in a manifold. (a) Two classes of data fitted by two Gaussian pdfs. (b) Scatter plot of the transformed representations.
Then C1 becomes R1={(0, 1), (0, 1), (0, 1), (1, 1), (1, 1), (0, 1), (0, 1)} and C2 becomes R2={(1, 2), (1, 0), (1, 0), (0, 0), (1, 2), (1, 0), (0, 0)}. The transformed dataset now has five clusters in a 2D space, {(0, 1), (1, 1)} from R1 and {(0, 0), (1, 0), and (1, 2)} from R2. This is shown in Fig. 15(b).
If one continues to follow the statistical model approach for making classification decisions, the transformed representation in R would be quite appropriate. As a matter of fact, the first class of data consists of integers that satisfy c=(3n+1)/100, and the second class, c=(2n+1)/100 or c=3n/100, where n is an arbitrary positive integer. (The factor 100 is only to produce the appearance of decimal numbers, here in the range of 0<c<1. If larger n is involved, this factor can be scaled up accordingly to maintain the range of the decimal numbers. The data are scattered with a Gaussian looking distribution due to normal, rather than uniform, sampling.) In the transformed space, the same five clusters remain for any extended datasets, although overlaps do exist, amounting to 1/8 in probability. That is far less than a statistical pattern recognition system using naïve 1D distribution models as implied in Fig. 15(a).
It is often difficult to foresee if the data should be examined with a particular manifold in mind. We often start with a space in which Riemann and Lebesgue integrals are easily interpreted. The interesting problem area of manifold learning at the moment is still in its infancy. While the caution stated in this section is well warranted, we shall defer further discussion on the subject of manifold learning.
IX. WHAT SOME EXPERIMENTAL RESULTS MAY TELL US
DNN has been shown successful in a number of pattern recognition tasks, of which automatic speech recognition is an important one. In [Reference Hinton2], a series of experiments have been reported with the conclusion that DNN offers substantial performance improvements over the prevalent method of hidden Markov modeling (HMM) with mixture densities [Reference Rabiner and Juang52,Reference Rabiner53]. While the overall progress is in general impressive, some careful discussion of the results may be also helpful in truly evaluating what the DNN has to offer.
The speech recognition system described in [Reference Hinton2] is what may be called a hybrid HMM–DNN. (For the general background of a speech recognition system, the reader is referred to [Reference Rabiner and Juang54].) With the HMM, the sequential relationship between successive speech signals/frames is modeled as an N-state Markov chain and the signal observation in each state is then governed by a probability density function, briefly called “in-state probability.” The DNN in an HMM–DNN according to [Reference Hinton2] is trained to compute the in-state probability, which is conventionally computed with a (Gaussian) mixture density model. Traditionally with mixture density models, the evaluation of probability is carried out on a single frame basis. Let
![]() ${\bf X} = ({\bf x}_{1}, {\bf x}_{2}, \ldots, {\bf x}_{t}, \ldots, {\bf x}_{T})$
be a sequence of observation vectors/frames that represent a speech signal. The probability of the sequence evaluated on a hidden Markov model, under the hypothesis that it is generated in association of the state sequence of
${\bf X} = ({\bf x}_{1}, {\bf x}_{2}, \ldots, {\bf x}_{t}, \ldots, {\bf x}_{T})$
be a sequence of observation vectors/frames that represent a speech signal. The probability of the sequence evaluated on a hidden Markov model, under the hypothesis that it is generated in association of the state sequence of
![]() ${\bf q} = (q_{0}, q_{1},{\ldots},q_{T})$
, is given as
${\bf q} = (q_{0}, q_{1},{\ldots},q_{T})$
, is given as
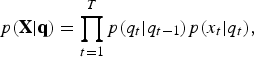 $$p({\bf X} \vert {\bf q}) = \prod_{t = 1}^T p(q_t \vert q_{t - 1}) p(x_t \vert q_t), $$
$$p({\bf X} \vert {\bf q}) = \prod_{t = 1}^T p(q_t \vert q_{t - 1}) p(x_t \vert q_t), $$
where
![]() $p(x_{t} \vert q_{t})$
is a mixture density and
$p(x_{t} \vert q_{t})$
is a mixture density and
![]() $p(q_{t} \vert q_{t - 1})$
is the transition probability from state q
t−1 to q
t
. In an HMM–DNN, such an in-state probability is calculated by the trained DNN, in lieu of the mixture model.
$p(q_{t} \vert q_{t - 1})$
is the transition probability from state q
t−1 to q
t
. In an HMM–DNN, such an in-state probability is calculated by the trained DNN, in lieu of the mixture model.
Table 2, taken from [Reference Hinton2], provides a comparison of the system performance measured in “word error rate” (WER) for various systems and training conditions. Readers should consult [Reference Hinton2] for detailed conditions under which a wide range of evaluations were conducted. We summarize here the key points in the result for discussion. They are: (a) speaker independent HMM–GMM (Gaussian mixture) model with 40 independent Gaussian multivariate (39 dimensions) pdfs within each state trained on 309 h of speech; (b) HMM using FNN with one hidden layer of 4634 units in lieu of the GMMs, with likelihood computed on each single frame of input; (c) same as (b) but with an expanded input consisting of additional five frames on each side of the “current” frame, i.e. each input vector being a block of 11 frames/vectors in model training as well as in likelihood evaluation; (d) similar to (c) but with seven hidden layers, each having 2048 units; and (e) HMM–GMM as in (a) except now with 72 mixture components (increased from 40), trained on 2000 h of speech, and with speaker adaption. (We have left out two original rows of results as they contain additional level of sophistication, non-essential to the present discussion.)
Table 2. Performance evaluation for various modeling techniques and systems [Reference Hinton2].

Much of the interpretation of the results can be found in [Reference Hinton2]. We point out three observations here. First, a major improvement in performance comes from the expanded input dimensions (from (b) to (c)). That advantage is carried through and further realized when DNN with many additional hidden layers are used (from (c) to (d)). Second, the modeling performance of neural networks may not be competitive with traditional mixture models (compare (a) and (b)), but neural networks with a data-driven correlation structure, as discussed earlier, are readily employable when the input dimensionality is large (compare (a) and (c)). When many adjacent frames of speech vectors are considered simultaneously for modeling and likelihood calculation, it is like treating the speech modeling problem as an image modeling problem (recall the MRF model). Third, when there is sufficient data to match the complexity of the traditional HMM–GMM model, its performance can be tuned up competitively (compare (d) and (e)). Figure 16 illustrates the difference in processing a single frame at a time using a simple FNN versus many frames at a time with a DNN.

Fig. 16. An illustration of simultaneous processing of K frames of speech.
The crux of these insights is further confirmed by other researchers, e.g. [Reference Pan, Liu, Wang, Hu and Jiang55]. Table 3 below, duplicated from Table 2 of [Reference Pan, Liu, Wang, Hu and Jiang55], shows the relevant results. The task in the experiment is pertaining to Mandarin speech transcription (called the Mandarin PSC). In Table 3(a), the WERs for three systems, all based on the conventional single frame processing, are listed. NN-1 refers to an FNN with a single hidden layer, equivalent to (b) of Table 2 and DNN-6 has six hidden layers, similar to (d). Adding hidden layers does substantially improve the WER, and the traditional system is rather competitive, best among the three compared. The WERs of DNN-6 as a function of the number of simultaneous frames in a processing block are given in Table 3(b). It appears to indicate a saddle point at K=11, which is consistent with the result of [Reference Hinton2].
Table 3. (a) WER for three systems with single frame modeling; (b) WER of DNN-6 as a function of the size (K) of the processing block in no. of frames [Reference Pan, Liu, Wang, Hu and Jiang55].
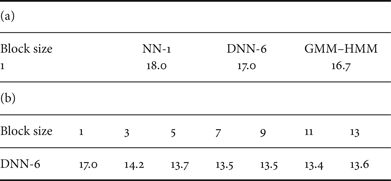
Some check on the dimensionality issue is warranted. A typical frame-level speech feature vector has a dimensionality of 39. When K frames are modeled simultaneously, each observation vector consists of 39K dimensions. For K=11, this is equal to 429. A Gaussian multivariate of this dimensionality has 91 806 second-order moment terms. It is prohibitively exorbitant to produce reliable estimates of the model parameters. (See Section VI for discussion of model complexity.)
The result suggests a few important insights:
-
• A DNN is an effective modeling tool for data of high dimensionality due to its ability to capture the dimensional correlations through the automatically learned precision matrix structure; it is considered a useful solution to problems where conventional models may fail due to complexity concerns (in terms of reliable statistical estimation);
-
• A DNN, when used as a probability model, is nevertheless only an approximation, accuracy of which may not compete with traditional models in problems where the data distribution can be reasonably observed and tested.
A pattern recognition system designer may use these suggested insights as guidelines in their system development.
X. OVERALL REMARKS & SUMMARY
A DNN has the structure of a conventional multilayer perceptron (MLP) or multi-layer FNN, which has long existed for decades. An MLP/FNN was proposed as a computational structure to solve problems in function approximation, of which an obvious application is in the area of pattern recognition and intelligent decision. While promising, an MLP/FNN also has been known to have difficulties in dealing with real-world problems, particularly those of a large scale. A DNN, nevertheless, embraces several clever engineering practices to overcome the issues of an FNN, which the conventional MLP was overtrusted to handle. A key developmental differentiation is the explicit intent of using statistical models (sometimes called generative models) in DNN to regularize the input, a task that can be well handled by one or a multiplicity of restrictive BMs. Regularization here casually means reducing the noise of interference that cannot be accounted for with the implied network structure (or model), or reducing the dimensionality of the input data to retain the saliency of the representation in order to ease the later task of functional approximation. A conventional MLP trained with the popular error backpropagation algorithm does not automatically come with these goals or benefits.
A DNN design starts with the training of an RBM, which is a stochastic recurrent network and aims at capturing the statistical regularities in the data (e.g. pairs of dimensions that have significant correlation). It can accomplish this because the statistical model represented by an RBM can (and most often do) take the form of an MRF and it “finds” the clique system of an MRF directly from data rather than pre-specified by the designer. When the number of hidden nodes is smaller than the input dimensionality, an RBM performs data/dimensionality reduction and regularization as noted above. When the number of hidden nodes exceeds that of the input dimensionality, an additional benefit of the RBM is the possibility of a transformed representation, the so-called distributive representation, of the data, which combines the notions of probability and geometric locality in a new manifold projected from the mixture density model implied by the hidden nodes in various layers.
A DNN has typically several such layers of RBM, trained one after another (thus deep), which are then stacked up to form a multilayer FNN. This multilayer network can then be further “fine-tuned” in a supervised fashion according to the supplied desired output to perform various tasks. When such a network is trained to approximate the input itself at the final output, after layers of processing, reduction, regularization, and possibly expansion, one obtains an autoencoder, in which the states of nodes at a certain intermediate layer can be considered an encoded (and compressed if reduction is involved) representation of the input. If the desired output is the class label of the input (through direct index mapping or after a final softmax operation to identify the node associated with the maximum output), it becomes an MLP although it differs from the traditional MLP in that those layers close to the input perform statistical regularization and transformation according to the RBM model. Use of MLP, particularly those layers close to the (decision) output, as an effective implementation of the decision function, remains as usual.
As noted in the very beginning, the Bayes optimal decision theory is at the core of pattern recognition system design, the issue of manifold notwithstanding (Section VIII). It teaches the principle of matching the data representation with probabilistic models for decision making in pattern identification. It is somewhat surprising that its realization in the context of ANNs through a soft division (or rather a soft integration) between the task of representation transformation (i.e. use of RBMs as the “bridge function” to prepare the data for identification) and that of statistical modeling for decision function implementation is only recent. It bespeaks the importance of cross- fertilization.
ACKNOWLEDGEMENT
The author would like to thank Prof. Mark Clements of Georgia Institute of Technology and Prof. Jiang Hui of York University for their reading of an earlier manuscript of this article.
Biing-Hwang (Fred) Juang is the Motorola Foundation Chair Professor and a Georgia Research Alliance Eminent Scholar at Georgia Institute of Technology, which he joined in 2002. He received a Ph.D. degree from the University of California, Santa Barbara. He had conducted research work at Speech Communications Research Laboratory (SCRL) and Signal Technology, Inc. (STI) in the late 1970s on a number of Government-sponsored research projects. He joined Bell Laboratories (Bell Labs) in 1982 as a Member of Technical Staff and was the Director of Acoustics and Speech Research (1996–2001). He became the Director of Multimedia Technologies Research at Avaya Labs (a spin-off of Bell Labs) in 2001. Professor Juang has published extensively, including the book “Fundamentals of Speech Recognition”, co-authored with L.R. Rabiner, and holds nearly two dozen patents. He received the Technical Achievement Award from the IEEE Signal Processing Society in 1998. He served as the Editor-in-Chief of the IEEE Transactions on Speech and Audio Processing from 1996 to 2002. He was elected an IEEE Fellow (1991), a Bell Labs Fellow (1999), a member of the US National Academy of Engineering (2004), and an Academician of the Academia Sinica (2006). He was named recipient of the IEEE Field Award in Audio, Speech, and Acoustics, the J.L. Flanagan Medal, and a Charter Fellow of the National Academy of Inventors (NAI), in 2014.





















