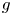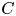1 Introduction
Improving confinement in fusion plasmas is crucial in order to achieve viable fusion power plants. In tokamaks, cross-field transport is mainly driven by turbulence, with a wide range of instabilities that can tap energy out of the gradients to drive it. These instabilities can be distinguished based on their properties, in terms of fluctuation amplitude, cross-phase and nonlinear behaviour. Dominant contributions to cross-field transport in an L-mode edge are likely caused by micro-instabilities at the ion scale (Liewer Reference Liewer1985). Those can be organized in two main classes of instabilities. First, the interchange, which requires an inhomogeneous magnetic field, such as the resistive ballooning modes (RBM), which bears analogy with the Rayleigh–Bénard instability in neutral fluids. Then, the drift-wave instability (DW), that results from a non-adiabatic electron response, which manifests itself as a finite phase shift between density and electric potential fluctuations (Hasegawa & Wakatani Reference Hasegawa and Wakatani1983), whose wave dynamics is similar to Rossby waves in the atmosphere. While the interchange tends to favour structures with zero parallel wave vectors $k_\parallel \approx 0$![]() , the DW requires non-vanishing $k_\parallel \neq 0$
, the DW requires non-vanishing $k_\parallel \neq 0$![]() . Both RBM and DW have been found to be dominant in a broad range of tokamak edge conditions (Bonanomi et al. Reference Bonanomi, Angioni, Crandall, Di Siena, Maggi and Schneider2019).
. Both RBM and DW have been found to be dominant in a broad range of tokamak edge conditions (Bonanomi et al. Reference Bonanomi, Angioni, Crandall, Di Siena, Maggi and Schneider2019).
In tokamaks, turbulent structures develop a strong anisotropy due to the strong magnetic field with variations primarily in the direction perpendicular to the magnetic field. In turn, turbulence is often considered as a quasi-two-dimensional problem, similarly to planetary atmospheres (Boffetta & Ecke Reference Boffetta and Ecke2012). In neutral fluids obeying the Navier–Stokes equations, turbulence in two dimensions presents a dual-cascade picture, with a forward cascade of enstrophy accompanied by an inverse cascade of energy (Kraichnan Reference Kraichnan1971). This singular behaviour arises due to the fact that, in such fluids, two-dimensional (2-D) turbulence is characterized by two nonlinear inviscid invariants, energy and enstrophy, while only the former is conserved in three dimensions. This leads to a self-organization of micro-turbulence at large scales into minimum enstrophy states through a mechanism of selective decay. In the case of turbulence with large background inhomogeneities, this leads to the generation of large-scale motions named zonal flows (ZFs). In planetary atmospheres, these flows exhibit an azimuthal symmetry and have long been considered important contributors to large-scale circulation (Rossby Reference Rossby1947). In magnetic fusion devices, ZFs are poloidally and toroidally symmetric, varying only across magnetic surfaces. Note that in magnetic fusion plasmas, the two-dimensional state does not necessarily mean that enstrophy is conserved. As a consequence, inverse energy cascade is not always active. However, this does not preclude the excitation of ZFs, which are usually generated by non-local interactions in the Fourier space: a non-vanishing flux-surface-averaged Reynolds stress is driven by the nonlinear coupling of small-scale fluctuations. While electric Reynolds stress, i.e. coupling of electric velocity fluctuations $\varPi _{E} = \langle \tilde {v}_{E_y} \tilde {v}_{E_x} \rangle$![]() , with $\boldsymbol {v_E} = \boldsymbol {E}\times \boldsymbol {B}/B^2$
, with $\boldsymbol {v_E} = \boldsymbol {E}\times \boldsymbol {B}/B^2$![]() the electric drift depending on the electric field E and magnetic field B, has long been deemed central in the generation processes (Diamond & Kim Reference Diamond and Kim1991), the diamagnetic component, $\varPi _* = \langle \tilde {v}_{E_y} \tilde {v}_{\rm ix}^* \rangle$
the electric drift depending on the electric field E and magnetic field B, has long been deemed central in the generation processes (Diamond & Kim Reference Diamond and Kim1991), the diamagnetic component, $\varPi _* = \langle \tilde {v}_{E_y} \tilde {v}_{\rm ix}^* \rangle$![]() , through the diamagnetic velocity, $\boldsymbol {v_\star } = \boldsymbol {B}\times \pmb {\nabla } p/(enB^2)$
, through the diamagnetic velocity, $\boldsymbol {v_\star } = \boldsymbol {B}\times \pmb {\nabla } p/(enB^2)$![]() with p is the plasma pressure, now also appears as an important mechanism for the dynamics (Smolyakov, Diamond & Medvedev Reference Smolyakov, Diamond and Medvedev2000; Hallatschek Reference Hallatschek2004; McDevitt et al. Reference McDevitt, Diamond, Gürcan and Hahm2010; Sarazin et al. Reference Sarazin, Dif-Pradalier, Garbet, Ghendrih, Berger, Gillot, Grandgirard, Obrejan, Varennes and Vermare2021; Dif-Pradalier et al. Reference Dif-Pradalier, Ghendrih, Sarazin, Caschera, Clairet, Camenen, Donnel, Garbet, Grandgirard and Munschy2022).
with p is the plasma pressure, now also appears as an important mechanism for the dynamics (Smolyakov, Diamond & Medvedev Reference Smolyakov, Diamond and Medvedev2000; Hallatschek Reference Hallatschek2004; McDevitt et al. Reference McDevitt, Diamond, Gürcan and Hahm2010; Sarazin et al. Reference Sarazin, Dif-Pradalier, Garbet, Ghendrih, Berger, Gillot, Grandgirard, Obrejan, Varennes and Vermare2021; Dif-Pradalier et al. Reference Dif-Pradalier, Ghendrih, Sarazin, Caschera, Clairet, Camenen, Donnel, Garbet, Grandgirard and Munschy2022).
Turbulence-generated ZFs are crucial for the self-regulation of turbulent transport. Through their back reaction to turbulence, and their involvement in the ensuing predator–prey dynamics, they play a dominant role in its saturation (Lin et al. Reference Lin, Hahm, Lee, Tang and White1998). They act as a sink for turbulent energy, and constitute, together with the mean background flow, the flow shear that decorrelates radially elongated eddies (Biglari, Diamond & Terry Reference Biglari, Diamond and Terry1990; Terry Reference Terry2000). Detailed reviews of the physics and formation of ZFs as well as their role on self-regulating turbulent transport can be found in literature (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005; Gürcan & Diamond Reference Gürcan and Diamond2015). Zonal flows are also regulators of linear instability mechanisms (Sugama & Wakatani Reference Sugama and Wakatani1991) and have been put forward as a possible mechanism to explain density limits in tokamaks (Hajjar, Diamond & Malkov Reference Hajjar, Diamond and Malkov2018). However, the experimental measurement of ZFs and the Reynolds stress remains a challenge, and sophisticated methods of data analysis are usually required to infer their existence, both for ZFs (Fujisawa Reference Fujisawa2008; Pedrosa et al. Reference Pedrosa, Silva, Hidalgo, Carreras, Orozco and Carralero2008) and for the role of the Reynolds stress (Tynan et al. Reference Tynan, Holland, Yu, James, Nishijima, Shimada and Taheri2006).
Additionally, ZFs organize naturally into staircases, which are persistent radially localized sheared layers associated with corrugations in radial gradients of density or pressure (Kosuga, Diamond & Gürcan Reference Kosuga, Diamond and Gürcan2013; Dif-Pradalier et al. Reference Dif-Pradalier, Hornung, Ghendrih, Sarazin, Clairet, Vermare, Diamond, Abiteboul, Cartier-Michaud and Ehrlacher2015, Reference Dif-Pradalier, Hornung, Garbet, Ghendrih, Grandgirard, Latu and Sarazin2017). Staircases are also quite difficult to observe experimentally: the flow pattern has to be sufficiently stable and large scale so that a diagnostic system can resolve its radial structure (Hillesheim et al. Reference Hillesheim, Delabie, Meyer, Maggi, Meneses and Poli2016; Hornung et al. Reference Hornung, Dif-Pradalier, Clairet, Sarazin, Sabot, Hennequin and Verdoolaege2016; Liu et al. Reference Liu, Chen, Ke, McKee, Yan, Fang, Yang, Gao, Tan and Tynan2021). Thus, identifying regimes where staircases are likely to occur, and providing signatures of the turbulence–flow interactions that can be used to identify them, would be extremely useful to guide experimental observations.
A significant effort has been devoted to studying the generation and impact of ZFs on turbulent transport, both analytically and in direct numerical simulations using both gyrokinetic simulations as well as fluid models (Scott Reference Scott2005b). Reduced models are also common in the study of turbulence/ZF interactions. They allow large parameter scans on confinement times while resolving turbulence scales. Also, they are useful tools for understanding the key physics mechanisms that are often confounded with other effects in first principle simulations. Among those, the pioneering work of Hasegawa-Mima (Hasegawa & Mima Reference Hasegawa and Mima1978), who developed a turbulence model for drift waves, and the work of Hasegawa–Wakatani (Wakatani & Hasegawa Reference Wakatani and Hasegawa1984) that expanded it to include an intrinsic instability, named the collisional drift wave (CDW), due to the non-adiabatic response of electron density fluctuations, can be cited. In the latter, the finite phase shift is caused by parallel electron–ion collisions and the instability is controlled by the adiabaticity parameter $C$![]() that scales as the square of the parallel wave vector divided by the electron–ion collision frequency. Since then, many models have been built on the same principle, (Camargo, Biskamp & Scott Reference Camargo, Biskamp and Scott1995; Numata, Ball & Dewar Reference Numata, Ball and Dewar2007; Majda, Qi & Cerfon Reference Majda, Qi and Cerfon2018). Note that these models usually evolve the electron density together with the vorticity and often assume cold ions. Therefore, the role of the diamagnetic drift in the Reynolds stress is overlooked. Some reduced models have also been dedicated to the interchange instability (Benkadda, Garbet & Verga Reference Benkadda, Garbet and Verga1994; Sarazin & Ghendrih Reference Sarazin and Ghendrih1998) with some including the diamagnetic contribution to the Reynolds stress (Ivanov et al. Reference Ivanov, Schekochihin, Dorland, Field and Parra2020). In these models, the linear instability is controlled by the mean curvature of the magnetic field, $g$
that scales as the square of the parallel wave vector divided by the electron–ion collision frequency. Since then, many models have been built on the same principle, (Camargo, Biskamp & Scott Reference Camargo, Biskamp and Scott1995; Numata, Ball & Dewar Reference Numata, Ball and Dewar2007; Majda, Qi & Cerfon Reference Majda, Qi and Cerfon2018). Note that these models usually evolve the electron density together with the vorticity and often assume cold ions. Therefore, the role of the diamagnetic drift in the Reynolds stress is overlooked. Some reduced models have also been dedicated to the interchange instability (Benkadda, Garbet & Verga Reference Benkadda, Garbet and Verga1994; Sarazin & Ghendrih Reference Sarazin and Ghendrih1998) with some including the diamagnetic contribution to the Reynolds stress (Ivanov et al. Reference Ivanov, Schekochihin, Dorland, Field and Parra2020). In these models, the linear instability is controlled by the mean curvature of the magnetic field, $g$![]() that scales with the Larmor radius divided by the major radius of the tokamak. A few include both interchange and drift waves (Scott Reference Scott2005a; Ghendrih et al. Reference Ghendrih2022).
that scales with the Larmor radius divided by the major radius of the tokamak. A few include both interchange and drift waves (Scott Reference Scott2005a; Ghendrih et al. Reference Ghendrih2022).
Many of these reduced models are formulated in a gradient-driven form, meaning that a constant pressure gradient is imposed throughout the simulation domain. In addition, one usually assumes a scale separation between the background gradients and the turbulence. While this has the advantage of providing a simpler local linear structure, it lacks crucial mechanisms for turbulence saturation. Indeed, three main saturation mechanisms can be identified: nonlinear mode–mode coupling, leading to the transfer of energy from linearly unstable to linearly stable modes, nonlinear transfer of turbulent energy to large-scale flows (ZFs) that do not contribute to transport and/or profile relaxation as a result of turbulent fluxes. The second and third mechanisms are either neglected or present at reduced magnitude (see § 5.2) because of the scale separation assumption in a local formulation. These non-local interactions indeed pose a challenge, because both micro-scale turbulence and large-scale profiles and flows have to be described self-consistently. This means that the simulations require good spatial and temporal resolution over extended spatial domains as well as over long times, which comes with numerical costs. In the edge of tokamaks, especially just inside the last closed flux surface, multi-scale interactions are of particular importance. Large gradients are usually present – even more so when the plasma is in H-mode – together with large radial electric fields, which requires a proper description of the interactions between equilibrium profiles, flows and turbulence. Flux-driven models are able to capture this dynamics, with the profiles evolving self-consistently as a balance between the sources and transport.
Here, we present a minimal flux-driven model of tokamak edge turbulence, called Tokam1D, with self-generated flows and profile interactions, featuring simple versions of both interchange (which is an analogue of the RBM instability in the framework of the model) and CDW instabilities, and a constant ion temperature in order to include the diamagnetic component of the Reynolds stress. Since the present version does not account for electromagnetic effects, it is restricted to L-mode regimes only (cf. § 2). The model is reduced to one dimension (radial) by retaining a single parallel and poloidal wavenumber for the fluctuations – possibly the linearly most unstable one. By doing so, nonlinear mode–mode couplings are discarded in the dynamics of the fluctuations, hence also possible energy and enstrophy cascades. Yet, nonlinear terms are retained in the dynamics of the density and poloidal flow equilibrium profiles via the particle turbulent flux and the Reynolds stresses. Turbulence saturation is therefore governed by profile relaxation and the generation of ZFs. The compressibility terms in the density equation are also included and prove important for the stabilization of interchange at large scale. The two instability parameters: the adiabatic parameter C and the magnetic inhomogeneity g, are found to have a destabilizing or stabilizing role depending on the regime. Also, they govern the phase shift between the density and electrostatic potential fluctuations, hence the strength of the turbulent transport at prescribed fluctuation amplitude. Finally, turbulence self-organization is studied in the CDW instability regime at $g=0$![]() (the study of the competition and/or synergy between CDW and interchange turbulence self-organization will be addressed in a forthcoming paper). It is shown that having a flux-driven model greatly influences the radial flow structure and the energy partition of the system. In particular, the ‘ZF energy collapse’ previously observed when $C$
(the study of the competition and/or synergy between CDW and interchange turbulence self-organization will be addressed in a forthcoming paper). It is shown that having a flux-driven model greatly influences the radial flow structure and the energy partition of the system. In particular, the ‘ZF energy collapse’ previously observed when $C$![]() is lowered (Numata et al. Reference Numata, Ball and Dewar2007) is not recovered. Although the same trend is observed, the transition appears to be more gradual.
is lowered (Numata et al. Reference Numata, Ball and Dewar2007) is not recovered. Although the same trend is observed, the transition appears to be more gradual.
The paper is organized as follows. In § 2, the model is derived together with its energetic properties. In § 3, the linear analysis of CDW and interchange instabilities is performed and the importance of the compressibility terms is highlighted. The remainder of the paper restricts the analysis of the nonlinear regime to $g=0$![]() cases, featuring only CDW turbulence. In § 4, the generation of flows is studied in the CDW regime. Zonal flows are shown to act as a reservoir for turbulence energy, even more so at large $C$
cases, featuring only CDW turbulence. In § 4, the generation of flows is studied in the CDW regime. Zonal flows are shown to act as a reservoir for turbulence energy, even more so at large $C$![]() . Finally, in § 5, flow radial structure is studied. The role of the phase during a staircase nucleation is emphasized and the importance of profile relaxation is pointed out.
. Finally, in § 5, flow radial structure is studied. The role of the phase during a staircase nucleation is emphasized and the importance of profile relaxation is pointed out.
2 Tokam1D: a reduced flux-driven interchange–CDW model
The governing fluid equations of the model rely on a certain number of simplifications that are detailed below. Their derivation proceeds in the standard systematic way (see e.g. Scott Reference Scott1997; Beyer et al. Reference Beyer, Benkadda, Garbet and Diamond2000; Chôné et al. Reference Chôné, Beyer, Sarazin, Fuhr, Bourdelle and Benkadda2014) by considering the adiabatic regime where the time and spatial scales of the plasma dynamics are much larger than those of the cyclotron motion, namely the gyro-frequency and the sound Larmor radius $\rho _s$![]() . In this framework, velocity drifts retained up to the second order in the small expanding parameter, typically the ratio between $\rho _s$
. In this framework, velocity drifts retained up to the second order in the small expanding parameter, typically the ratio between $\rho _s$![]() and the gradient length $R$
and the gradient length $R$![]() (also the tokamak major radius) of the magnetic field $\rho _\star \sim \rho _s/R \ll 1$
(also the tokamak major radius) of the magnetic field $\rho _\star \sim \rho _s/R \ll 1$![]() . These velocities are the electric and diamagnetic drifts at first order, and the ion polarization drift at second order. Other finite Larmor radius effects than the polarization drift are not retained.
. These velocities are the electric and diamagnetic drifts at first order, and the ion polarization drift at second order. Other finite Larmor radius effects than the polarization drift are not retained.
We consider a magnetized plasma of constant (in time and spatially uniform) ion $T_i$![]() and electron $T_e$
and electron $T_e$![]() temperatures (with $\tau = T_i / T_e$
temperatures (with $\tau = T_i / T_e$![]() ) in a stationary magnetic field $\boldsymbol {B}$
) in a stationary magnetic field $\boldsymbol {B}$![]() . We focus on the tokamak edge, just inside the last closed flux surface. The plasma is assumed to be in L-mode so that one can neglect electromagnetic effects. Indeed, when approaching the H-mode, the pressure gradient length $L_p$
. We focus on the tokamak edge, just inside the last closed flux surface. The plasma is assumed to be in L-mode so that one can neglect electromagnetic effects. Indeed, when approaching the H-mode, the pressure gradient length $L_p$![]() decreases strongly, so that the effective beta parameter $\beta _{{\rm eff}} = (qR/L_p)^2 \beta$
decreases strongly, so that the effective beta parameter $\beta _{{\rm eff}} = (qR/L_p)^2 \beta$![]() – with $\beta = 2\mu _0 p/B^2$
– with $\beta = 2\mu _0 p/B^2$![]() the ratio of plasma pressure to magnetic pressure, $q$
the ratio of plasma pressure to magnetic pressure, $q$![]() the safety factor and $R$
the safety factor and $R$![]() the major radius – can exceed unity. In this case, as early noticed in Catto et al. (Reference Catto, Elnadi, Liu and Rosenbluth1974) and further detailed in Scott (Reference Scott1997), magnetic induction can no longer be ignored since it controls the linear response of the parallel current to parallel gradients in the three state variables (electric field, density and electron temperature). The geometry can be approximated as cylindrical, using Cartesian coordinates as if the toroidal axis were unwrapped onto a Cartesian plane, with the unit vectors ($\boldsymbol {e}_x, \boldsymbol {e}_y, \boldsymbol {e}_\parallel$
the major radius – can exceed unity. In this case, as early noticed in Catto et al. (Reference Catto, Elnadi, Liu and Rosenbluth1974) and further detailed in Scott (Reference Scott1997), magnetic induction can no longer be ignored since it controls the linear response of the parallel current to parallel gradients in the three state variables (electric field, density and electron temperature). The geometry can be approximated as cylindrical, using Cartesian coordinates as if the toroidal axis were unwrapped onto a Cartesian plane, with the unit vectors ($\boldsymbol {e}_x, \boldsymbol {e}_y, \boldsymbol {e}_\parallel$![]() ), where $x$
), where $x$![]() is the radial, $y$
is the radial, $y$![]() is the poloidal (now vertical) and $z$
is the poloidal (now vertical) and $z$![]() is the parallel (along the field line) direction.
is the parallel (along the field line) direction.
The magnetic field magnitude decreases as the inverse of the major radius, $\boldsymbol {B}(R) = ({B_0 R_0}/{R}) \boldsymbol {e}_\parallel$![]() . Considering that later on the system will be reduced to one dimension by keeping only one mode for the fluctuations (§ 2.5), terms that are linked to the magnetic inhomogeneity such as compressibility terms (divergence of the electric drift and diamagnetic flux) can be written as
. Considering that later on the system will be reduced to one dimension by keeping only one mode for the fluctuations (§ 2.5), terms that are linked to the magnetic inhomogeneity such as compressibility terms (divergence of the electric drift and diamagnetic flux) can be written as
with $h=n$![]() the density or $h=\varPhi$
the density or $h=\varPhi$![]() the electrostatic potential. Note that both the curvature and the amplitude variation lead to the magnetic inhomogeneity. Note that, while the first term on the right-hand side relates to Ampere–Maxwell's law, which is small for tokamaks at low $\beta$
the electrostatic potential. Note that both the curvature and the amplitude variation lead to the magnetic inhomogeneity. Note that, while the first term on the right-hand side relates to Ampere–Maxwell's law, which is small for tokamaks at low $\beta$![]() , the second term comes from the variation of $\boldsymbol {B}$
, the second term comes from the variation of $\boldsymbol {B}$![]() along the major radius of the tokamak and should be kept. We call this term linked to the inhomogeneity of $\boldsymbol {B}$
along the major radius of the tokamak and should be kept. We call this term linked to the inhomogeneity of $\boldsymbol {B}$![]() as $g$
as $g$![]() , the ‘curvature term’
, the ‘curvature term’
It controls the interchange instability. In the framework of the model, this instability is analogous to the more familiar RBM, which have already received much attention in the electrostatic (Guzdar et al. Reference Guzdar, Drake, McCarthy, Hassam and Liu1993; Beyer et al. Reference Beyer, Benkadda, Garbet and Diamond2000; Chôné et al. Reference Chôné, Beyer, Sarazin, Fuhr, Bourdelle and Benkadda2014) and electromagnetic (Scott Reference Scott1997; Dominici et al. Reference Dominici, Fuhr, Bourdelle, Beyer, Garbet, Sarazin and Falchetto2019) regimes. More recently, their interplay with drift-wave turbulence at the edge of tokamak plasmas has been investigated with the GBS code (Giacomin & Ricci Reference Giacomin and Ricci2022).
Tokam1D then considers the flux-driven dynamics of the density and vorticity in a 1-D radial plasma. It can be derived from the electron continuity and charge balance equations where the $E\times B$![]() , diamagnetic and polarization drifts are considered. A generalized Ohm's law closes the system by relating the parallel current to the electric field and the electron pressure gradient.
, diamagnetic and polarization drifts are considered. A generalized Ohm's law closes the system by relating the parallel current to the electric field and the electron pressure gradient.
First, the model is derived in three dimensions. Then, it is reduced to one dimension by keeping only one fluctuating mode for the poloidal ($\boldsymbol {e}_y$![]() ) and parallel $(\boldsymbol {e}_\parallel )$
) and parallel $(\boldsymbol {e}_\parallel )$![]() directions. Its assumptions and limitations are discussed. Finally, an energy principle is calculated and energy channels for the profile, flows and turbulence are clarified.
directions. Its assumptions and limitations are discussed. Finally, an energy principle is calculated and energy channels for the profile, flows and turbulence are clarified.
2.1 Electron continuity equation
The particle conservation equation, (2.3), evolves the electron density $n$![]() taking into account the $E\times B$
taking into account the $E\times B$![]() and diamagnetic drifts, $\boldsymbol {v}_E$
and diamagnetic drifts, $\boldsymbol {v}_E$![]() and $\boldsymbol {v}_\star$
and $\boldsymbol {v}_\star$![]() , the electron parallel current $\boldsymbol {j}_{\parallel,e}$
, the electron parallel current $\boldsymbol {j}_{\parallel,e}$![]() and the source of particles $S_n$
and the source of particles $S_n$![]() . The polarization drift $\boldsymbol {v}_{{\rm pol}}$
. The polarization drift $\boldsymbol {v}_{{\rm pol}}$![]() , proportional to the mass of the species, is neglected for the electrons
, proportional to the mass of the species, is neglected for the electrons
Owing to the large inertia of the ions, the total parallel current is approximated by the electron parallel current: $j_{\parallel e} = - e n v_{\parallel e} \approx j_{\parallel }$![]() . The compressibility terms, $\pmb {\nabla } \boldsymbol {\cdot } \boldsymbol {v}_E$
. The compressibility terms, $\pmb {\nabla } \boldsymbol {\cdot } \boldsymbol {v}_E$![]() and $\pmb {\nabla } \boldsymbol {\cdot } (n \boldsymbol {v_{\star e}})$
and $\pmb {\nabla } \boldsymbol {\cdot } (n \boldsymbol {v_{\star e}})$![]() are kept as derived from (2.1). They are crucial in the linear behaviour of the instabilities as they stabilize the interchange instability at large scale, see § 3. Also, they will prove essential in the energy budget equation § 2.6 and in the nonlinear analysis. In this framework, (2.3) reads as follows:
are kept as derived from (2.1). They are crucial in the linear behaviour of the instabilities as they stabilize the interchange instability at large scale, see § 3. Also, they will prove essential in the energy budget equation § 2.6 and in the nonlinear analysis. In this framework, (2.3) reads as follows:
With $n_0$![]() a constant reference density used for normalization and $\varPhi$
a constant reference density used for normalization and $\varPhi$![]() the electric potential. The advection of density due to the electric drift is contained in Poisson brackets $\{\varPhi,n\} = (\boldsymbol {\nabla } \varPhi \times \boldsymbol {\nabla } n) \boldsymbol {\cdot } \boldsymbol {e}_\parallel$
the electric potential. The advection of density due to the electric drift is contained in Poisson brackets $\{\varPhi,n\} = (\boldsymbol {\nabla } \varPhi \times \boldsymbol {\nabla } n) \boldsymbol {\cdot } \boldsymbol {e}_\parallel$![]() .
.
2.2 Charge conservation equation
With the quasi-neutrality assumption, charge conservation reduces to $\pmb {\nabla } \boldsymbol {\cdot } \boldsymbol {j} = 0$![]() . Taking both the diamagnetic current $\boldsymbol {j}_\star = (en \boldsymbol {v}_{\star i} - en \boldsymbol {v}_{\star e})$
. Taking both the diamagnetic current $\boldsymbol {j}_\star = (en \boldsymbol {v}_{\star i} - en \boldsymbol {v}_{\star e})$![]() and the polarization current $\boldsymbol {j}_{{\rm pol}} = en \boldsymbol {v}_{\rm pol}$
and the polarization current $\boldsymbol {j}_{{\rm pol}} = en \boldsymbol {v}_{\rm pol}$![]() into account, it takes the form
into account, it takes the form
Divergence of diamagnetic current can be written directly as
with $\tau = T_i/T_e$![]() the temperature ratio. The polarization current can be computed from the ion polarization drift, which can be written as
the temperature ratio. The polarization current can be computed from the ion polarization drift, which can be written as
where the parallel advection has been neglected assuming that the parallel gradient length remains small as compared with the transverse ones. This expression of the drift results from the partial cancellation of the advection by the diamagnetic velocity with the anisotropic part of the pressure tensor, which is usually referred to as the diamagnetic cancellation (Hinton & Horton Reference Hinton and Horton1971; Smolyakov Reference Smolyakov1998). Finally, the Boussinesq approximation is used for the polarization current, allowing us to commute the density with the divergence and avoid dealing with time derivatives of different quantities. To keep track of the origin of this density term, we name it $n_\varOmega$![]() hereafter
hereafter

The Boussinesq assumption is considered valid whenever the density gradient length is large with respect to that of the electric potential and is routinely used in fluid models to simplify computation. Note that, depending on the model, the choice is made to commute either a constant density $n_\varOmega =n_0$![]() , such as in Tamain et al. (Reference Tamain, Bufferand, Ciraolo, Colin, Galassi, Ghendrih, Schwander and Serre2016), Dudson & Leddy (Reference Dudson and Leddy2017) and Stegmeir et al. (Reference Stegmeir, Coster, Ross, Maj, Lackner and Poli2018), or to commute the full density $n_\varOmega =n$
, such as in Tamain et al. (Reference Tamain, Bufferand, Ciraolo, Colin, Galassi, Ghendrih, Schwander and Serre2016), Dudson & Leddy (Reference Dudson and Leddy2017) and Stegmeir et al. (Reference Stegmeir, Coster, Ross, Maj, Lackner and Poli2018), or to commute the full density $n_\varOmega =n$![]() (Yu, Krasheninnikov & Guzdar Reference Yu, Krasheninnikov and Guzdar2006; Angus & Umansky Reference Angus and Umansky2014; Ghendrih et al. Reference Ghendrih2022). Although it is usually considered correct in the core, its validity is debated for simulations including the scrape-off layer as the density fluctuations tend to be larger relative to the background density; see dedicated contributions (Yu et al. Reference Yu, Krasheninnikov and Guzdar2006; Angus & Umansky Reference Angus and Umansky2014; Ross, Stegmeir & Coster Reference Ross, Stegmeir and Coster2018). The validity of the Boussinesq assumption can be verified at the end of the simulation by comparing $\boldsymbol {\nabla }_\perp n \boldsymbol {\cdot }\boldsymbol {\nabla }_\perp (\varPhi + \tau \ln (n/n_0))$
(Yu, Krasheninnikov & Guzdar Reference Yu, Krasheninnikov and Guzdar2006; Angus & Umansky Reference Angus and Umansky2014; Ghendrih et al. Reference Ghendrih2022). Although it is usually considered correct in the core, its validity is debated for simulations including the scrape-off layer as the density fluctuations tend to be larger relative to the background density; see dedicated contributions (Yu et al. Reference Yu, Krasheninnikov and Guzdar2006; Angus & Umansky Reference Angus and Umansky2014; Ross, Stegmeir & Coster Reference Ross, Stegmeir and Coster2018). The validity of the Boussinesq assumption can be verified at the end of the simulation by comparing $\boldsymbol {\nabla }_\perp n \boldsymbol {\cdot }\boldsymbol {\nabla }_\perp (\varPhi + \tau \ln (n/n_0))$![]() and $n \nabla _\perp ^2 (\varPhi + \tau \ln (n/n_0))$
and $n \nabla _\perp ^2 (\varPhi + \tau \ln (n/n_0))$![]() . In the simulations performed, the mismatch proved to be of a few per cent. Also, the magnetic field is assumed to commute with the $\boldsymbol {\nabla }$
. In the simulations performed, the mismatch proved to be of a few per cent. Also, the magnetic field is assumed to commute with the $\boldsymbol {\nabla }$![]() operator. It is acceptable as the $B$
operator. It is acceptable as the $B$![]() field is large and decays as $1/R$
field is large and decays as $1/R$![]() , which is on much larger scales than the density and electric potential inhomogeneities. Equation (2.5) then reads as follows:
, which is on much larger scales than the density and electric potential inhomogeneities. Equation (2.5) then reads as follows:

where $\boldsymbol {\nabla }_{\perp,i} \{ . , \boldsymbol {\nabla }_{\perp,i} (.) \}$![]() represents Poisson brackets that can be developed assuming Einstein's notation, $\partial _x \{ ., \partial _x (.) \} + \partial _y \{ ., \partial _y (.) \}$
represents Poisson brackets that can be developed assuming Einstein's notation, $\partial _x \{ ., \partial _x (.) \} + \partial _y \{ ., \partial _y (.) \}$![]() . Here, the generalized vorticity is defined as follows:
. Here, the generalized vorticity is defined as follows:
With $\nabla _\perp ^2 = (\partial _x^2 + \partial _y^2)$![]() the perpendicular Laplacian.
the perpendicular Laplacian.
2.3 Ohm's law
Finally, Ohm's law is derived using the electron parallel momentum conservation equation
Due to the small electron inertia, the first term proportional to $m_e$![]() drops. In this case, the generalized Ohm's law reduces to a balance between parallel current, parallel Coulomb force and parallel pressure. One is left with an explicit relationship between the parallel current on the one hand, and density and electric potential on the other
drops. In this case, the generalized Ohm's law reduces to a balance between parallel current, parallel Coulomb force and parallel pressure. One is left with an explicit relationship between the parallel current on the one hand, and density and electric potential on the other
The parallel current depends on the electron–ion collision frequency that itself depends directly on the density and temperature: $\nu _{\rm ei} \propto n/T_e^{3/2}$![]() . The temperature is taken constant in the present model but the density has to be made explicit so that we can deal with the pre-factor as a constant. Then, we define $\nu _{{\rm ei},0} = \nu _{\rm ei} n_0 /n_\nu$
. The temperature is taken constant in the present model but the density has to be made explicit so that we can deal with the pre-factor as a constant. Then, we define $\nu _{{\rm ei},0} = \nu _{\rm ei} n_0 /n_\nu$![]() , the electron–ion collision frequency taken at reference density $n_0$
, the electron–ion collision frequency taken at reference density $n_0$![]() with the density labelled $n_\nu$
with the density labelled $n_\nu$![]() to keep track of its origin.
to keep track of its origin.
In this case, the divergence of the parallel current reads as follows:
The parallel current is then introduced into the electron density and charge conservation equations to close the system.
2.4 Three-dimensional model
The 3-D system of equations then involves the logarithm of the electron density $N=\ln {n / n_0}$![]() and the generalized vorticity $\varOmega = \nabla _\perp ^2 (\phi + \tau N)$
and the generalized vorticity $\varOmega = \nabla _\perp ^2 (\phi + \tau N)$![]() with the electric potential normalized to the electron temperature $\phi = e\varPhi /T_e$
with the electric potential normalized to the electron temperature $\phi = e\varPhi /T_e$![]() . The dimensionless three-dimensional system can be written as follows:
. The dimensionless three-dimensional system can be written as follows:
Regarding normalizations, time is normalized to the ion cyclotron frequency $\omega _{\rm cs} = (e B)/m_i$![]() and the lengths to the sound Larmor radius $\rho _s = (m_i c_s)/(eB)$
and the lengths to the sound Larmor radius $\rho _s = (m_i c_s)/(eB)$![]() with $c_s = \sqrt {T_e/m_i}$
with $c_s = \sqrt {T_e/m_i}$![]() . The magnetic curvature parameter is defined as $g = (2\rho _s)/R$
. The magnetic curvature parameter is defined as $g = (2\rho _s)/R$![]() , with $R$
, with $R$![]() the major radius of the tokamak. The parallel conductivity is considered constant and is defined as the electron cyclotron frequency to the electron–ion collision frequency taken at $n_0$
the major radius of the tokamak. The parallel conductivity is considered constant and is defined as the electron cyclotron frequency to the electron–ion collision frequency taken at $n_0$![]() , $\sigma _0 = \omega _{\rm ce}/\nu _{{\rm ei},0}$
, $\sigma _0 = \omega _{\rm ce}/\nu _{{\rm ei},0}$![]() . The system is flux driven with a source of particles $S_N$
. The system is flux driven with a source of particles $S_N$![]() and the damping of small scales is ensured by the diffusive terms $D$
and the damping of small scales is ensured by the diffusive terms $D$![]() and $\nu$
and $\nu$![]() .
.
As a last remark, note that (2.14)–(2.15) derive from (2.3) and (2.9) divided by $n$![]() and $n_\varOmega$
and $n_\varOmega$![]() , respectively. When doing so, the density dependencies of the parallel current terms should read $(n_0/n_\nu ) \sigma _0$
, respectively. When doing so, the density dependencies of the parallel current terms should read $(n_0/n_\nu ) \sigma _0$![]() in (2.14) and $(n_0/n_\nu ) (n/n_\varOmega ) \sigma _0$
in (2.14) and $(n_0/n_\nu ) (n/n_\varOmega ) \sigma _0$![]() in (2.15). The simplifications done in (2.14)–(2.15) are then to replace $(n_0/n_\nu )$
in (2.15). The simplifications done in (2.14)–(2.15) are then to replace $(n_0/n_\nu )$![]() and $(n/n_\varOmega )$
and $(n/n_\varOmega )$![]() by one. This amounts to performing the Boussinesq approximation with the total density $n_\varOmega =n$
by one. This amounts to performing the Boussinesq approximation with the total density $n_\varOmega =n$![]() , and to neglect the density dependence of the collision frequency $n_\nu =n_0$
, and to neglect the density dependence of the collision frequency $n_\nu =n_0$![]() .Footnote 1 The latter dependency may be revealed to be particularly important when looking for plasma bifurcations as density increases, such as the density limit. Its effect will be investigated in a forthcoming paper. For the time being, the normalized parallel conductivity is taken as constant and equal to $\sigma _0$
.Footnote 1 The latter dependency may be revealed to be particularly important when looking for plasma bifurcations as density increases, such as the density limit. Its effect will be investigated in a forthcoming paper. For the time being, the normalized parallel conductivity is taken as constant and equal to $\sigma _0$![]() .
.
2.5 Semi-spectral formulation: from three dimensions to one dimension
In order to keep track of the nonlinear dynamics while dealing with a more tractable system, each field is decomposed into a flux-surface-averaged and a fluctuating component (2.16). In the spirit of previous similar models (Sarazin et al. Reference Sarazin, Garbet, Ghendrih and Benkadda2000; Benkadda et al. Reference Benkadda, Beyer, Bian, Figarella, Garcia, Garbet, Ghendrih, Sarazin and Diamond2001; Bian et al. Reference Bian, Benkadda, Garcia, Paulsen and Garbet2003), the fluctuating components are Fourier transformed and projected onto a single parallel and poloidal wave vector $(k_\parallel, k_y)$![]() , so that $(\boldsymbol {\nabla }_\parallel, \partial _y) \longrightarrow {\rm i} ( k_\parallel, k_y)$
, so that $(\boldsymbol {\nabla }_\parallel, \partial _y) \longrightarrow {\rm i} ( k_\parallel, k_y)$![]() . Here, c.c. stands for the complex conjugate
. Here, c.c. stands for the complex conjugate
As a caveat, note that the ‘eq’ subscript should not be misunderstood. Here, what is meant by ‘equilibrium’ only refers to the flux-surface average of the considered quantity. This zonal component is not at all assumed to represent any steady state of the system. When discussing $N_{\rm eq}$![]() and $\phi _{\rm eq}$
and $\phi _{\rm eq}$![]() in the remainder of this article, we shall loosely refer to them as equilibrium quantities, bearing in mind the caveats mentioned above.
in the remainder of this article, we shall loosely refer to them as equilibrium quantities, bearing in mind the caveats mentioned above.
The implications of this choice call for further discussion. In particular, retaining a single poloidal wavenumber $k_y$![]() implies that, in the time evolution of the fluctuating modes $N_k$
implies that, in the time evolution of the fluctuating modes $N_k$![]() and $\phi _k$
and $\phi _k$![]() , the model cannot consider the nonlinear terms that arise due to mode–mode coupling. Indeed, these terms involve other modes $k_y^\prime \neq k_y$
, the model cannot consider the nonlinear terms that arise due to mode–mode coupling. Indeed, these terms involve other modes $k_y^\prime \neq k_y$![]() which are by essence outside the model. One of the consequences is that possible energy (and enstrophy) cascade processes cannot be accounted for. Three important remarks can be made at this point:
which are by essence outside the model. One of the consequences is that possible energy (and enstrophy) cascade processes cannot be accounted for. Three important remarks can be made at this point:
(i) A refinement of the model would consist in adding a nonlinear saturation mechanism to the fluctuations of the form $\partial _t N_k = \dots -D_{\rm NL} \lvert N_k \rvert ^2 N_k$
 with $D_{\rm NL}$
with $D_{\rm NL}$ some positive coefficient (Sarazin et al. Reference Sarazin, Garbet, Ghendrih and Benkadda2000). It would account for part of the physics contained in the missing nonlinear interactions, namely nonlinear energy transfer into dissipative scales as one of the routes towards turbulence saturation. We have performed a number of simulations with such a term present, and found that the resulting dynamics was qualitatively analogous to simulations with stronger diffusion. So as to keep the number of free parameters to a minimum, we therefore decided not to include such a nonlinearity in the present study.
some positive coefficient (Sarazin et al. Reference Sarazin, Garbet, Ghendrih and Benkadda2000). It would account for part of the physics contained in the missing nonlinear interactions, namely nonlinear energy transfer into dissipative scales as one of the routes towards turbulence saturation. We have performed a number of simulations with such a term present, and found that the resulting dynamics was qualitatively analogous to simulations with stronger diffusion. So as to keep the number of free parameters to a minimum, we therefore decided not to include such a nonlinearity in the present study.(ii) Even with $D_{\rm NL}=0$
 , the model still retains important nonlinearities. The main ones are the turbulent flux and the Reynolds stresses that govern respectively the time evolution of the equilibrium density $N_{\rm eq}$
, the model still retains important nonlinearities. The main ones are the turbulent flux and the Reynolds stresses that govern respectively the time evolution of the equilibrium density $N_{\rm eq}$ and poloidal flow $V_{\rm eq}$
and poloidal flow $V_{\rm eq}$ profiles (see (2.17)–(2.18) and (2.21)–(2.22)). Note also that, since these radial profiles enter the time dynamics of the fluctuating modes, they result in nonlinear couplings between different radial wave vectors $k_x$
profiles (see (2.17)–(2.18) and (2.21)–(2.22)). Note also that, since these radial profiles enter the time dynamics of the fluctuating modes, they result in nonlinear couplings between different radial wave vectors $k_x$ (cf. all terms in (2.19)–(2.20) of the form $F(A_{\rm eq}) G(B_k)$
(cf. all terms in (2.19)–(2.20) of the form $F(A_{\rm eq}) G(B_k)$ , where $F$
, where $F$ and $G$
and $G$ stand for linear operators and $A,B \in \{N, V, \varOmega \}$
stand for linear operators and $A,B \in \{N, V, \varOmega \}$ ). This latter point is not explicit in the equations since they are not written in the Fourier space in $k_x$
). This latter point is not explicit in the equations since they are not written in the Fourier space in $k_x$ but in the configuration space $x$
but in the configuration space $x$ .
.(iii) In the absence of an ad hoc nonlinear term in the dynamics of the fluctuating fields (i.e. when taking $D_{\rm NL}=0$
 ), turbulence saturation in Tokam1D therefore relies mainly on two mechanisms: (a) nonlinear transfer of turbulent energy to large-scale flows (ZFs) that do not contribute to transport and (b) the relaxation of mean profiles – as a result of turbulent fluxes – leading to a reduction of the turbulence drive (lower gradients, i.e. thermodynamic forces). The last one is often overlooked since it is absent from gradient-driven models. We argue these two mechanisms play a key role close to marginal stability. As a matter of fact, this regime is likely to be relevant in fusion reactor plasmas. Indeed, given the expected large volume of reactor devices, they will likely be weakly driven – low power density – so that the strong efficiency of turbulent transport – as attested by the stiffness of the experimental temperature profiles in tokamak plasmas (see e.g. Ryter et al. Reference Ryter, Leuterer, Pereverzev, Fahrbach, Stober and Suttrop2000) – should maintain the gradients close to marginality. Note that, since all the modes are kept along the $x$
), turbulence saturation in Tokam1D therefore relies mainly on two mechanisms: (a) nonlinear transfer of turbulent energy to large-scale flows (ZFs) that do not contribute to transport and (b) the relaxation of mean profiles – as a result of turbulent fluxes – leading to a reduction of the turbulence drive (lower gradients, i.e. thermodynamic forces). The last one is often overlooked since it is absent from gradient-driven models. We argue these two mechanisms play a key role close to marginal stability. As a matter of fact, this regime is likely to be relevant in fusion reactor plasmas. Indeed, given the expected large volume of reactor devices, they will likely be weakly driven – low power density – so that the strong efficiency of turbulent transport – as attested by the stiffness of the experimental temperature profiles in tokamak plasmas (see e.g. Ryter et al. Reference Ryter, Leuterer, Pereverzev, Fahrbach, Stober and Suttrop2000) – should maintain the gradients close to marginality. Note that, since all the modes are kept along the $x$ direction, ZFs can further contribute to turbulence saturation through wave coupling: (I) through turbulence vortex shearing, they can lead to the generation of large $k_x$
direction, ZFs can further contribute to turbulence saturation through wave coupling: (I) through turbulence vortex shearing, they can lead to the generation of large $k_x$ wave vectors which are linearly stable (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005); also, (II) they can mediate energy transfer to damped eigenmodes, as highlighted e.g. in Hatch et al. (Reference Hatch, Terry, Jenko, Merz and Nevins2011). Lastly, (III) they can also trap waves (Garbet et al. Reference Garbet, Panico, Varennes, Gillot, Dif-Pradalier, Sarazin, Grandgirard, Ghendrih and Vermare2021), further leading to the possible filamentation of distribution functions in the velocity space and the subsequent collisional dissipation.
wave vectors which are linearly stable (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005); also, (II) they can mediate energy transfer to damped eigenmodes, as highlighted e.g. in Hatch et al. (Reference Hatch, Terry, Jenko, Merz and Nevins2011). Lastly, (III) they can also trap waves (Garbet et al. Reference Garbet, Panico, Varennes, Gillot, Dif-Pradalier, Sarazin, Grandgirard, Ghendrih and Vermare2021), further leading to the possible filamentation of distribution functions in the velocity space and the subsequent collisional dissipation.
The final system of equations involves 4 fields. Two real fields for the equilibrium components (2.17), (2.18), and two complex fields for the fluctuating parts (2.19), (2.20). It is solved using a fourth-order Runge–Kutta scheme in time and centred fourth-order finite differences in the radial direction. Note that the dissipation terms are treated to the second order in the present version of the code, equally limiting the order of the scheme. Appendix D details the numerical scheme and the successful verification tests. Different values for the diffusion and viscosity can be chosen for the equilibrium $(D_0, \nu _0)$![]() and the fluctuations $(D_1, \nu _1)$
and the fluctuations $(D_1, \nu _1)$![]()

with $\varOmega _k = (\partial _x^2-k_y^2) (\phi _k + \tau N_k)$![]() . The adiabaticity parameter is defined as $C = \sigma _0 k_\parallel ^2$
. The adiabaticity parameter is defined as $C = \sigma _0 k_\parallel ^2$![]() . It is equivalent to the $C_1$
. It is equivalent to the $C_1$![]() parameter initially derived by Wakatani & Hasegawa (Reference Wakatani and Hasegawa1984). Typically, the parallel wavenumber is estimated considering a connection length, $L_q = 2 {\rm \pi}q R$
parameter initially derived by Wakatani & Hasegawa (Reference Wakatani and Hasegawa1984). Typically, the parallel wavenumber is estimated considering a connection length, $L_q = 2 {\rm \pi}q R$![]() , which gives $k_\parallel = 2 {\rm \pi}/ L_q = 1/(q R)$
, which gives $k_\parallel = 2 {\rm \pi}/ L_q = 1/(q R)$![]() . Taking a typical edge plasma of the WEST tokamak, major radius $R = 2.5$
. Taking a typical edge plasma of the WEST tokamak, major radius $R = 2.5$![]() m, minor radius $a = 0.5$
m, minor radius $a = 0.5$![]() m, magnetic field at separatrix $B_{\rm sep} \approx 3\ {\rm T}$
m, magnetic field at separatrix $B_{\rm sep} \approx 3\ {\rm T}$![]() and considering a density of $n_0 = 10^{-19}\ {\rm m}^{-3}$
and considering a density of $n_0 = 10^{-19}\ {\rm m}^{-3}$![]() , a temperature of $T_e \approx 70\ {\rm eV}$
, a temperature of $T_e \approx 70\ {\rm eV}$![]() and a safety factor $q_{95} = 5$
and a safety factor $q_{95} = 5$![]() , the main parameters of the model can be estimated. Their typical values are given in table 1.
, the main parameters of the model can be estimated. Their typical values are given in table 1.
Table 1. Main parameters of the model and their typical values for the WEST tokamak.

It appears from the parameter dependencies that the strong variation of density and temperature profiles at the edge of tokamak plasmas translates into a wide range of $g$![]() and $C$
and $C$![]() values. Nevertheless, one has to keep in mind that (2.12) assumes a large electron–ion collision frequency as compared with the electron inertial term. Therefore, the model loses its validity if $T_e$
values. Nevertheless, one has to keep in mind that (2.12) assumes a large electron–ion collision frequency as compared with the electron inertial term. Therefore, the model loses its validity if $T_e$![]() is too large or $n$
is too large or $n$![]() too small. Also, $C$
too small. Also, $C$![]() decreases with increasing density. This density dependence, although not retained in the current version of Tokam1D, is deemed important for the turbulence-flows energy partition, as highlighted in § 4.2. Finally, we can note that $g=2\rho _s/R=2\rho _\star a/R$
decreases with increasing density. This density dependence, although not retained in the current version of Tokam1D, is deemed important for the turbulence-flows energy partition, as highlighted in § 4.2. Finally, we can note that $g=2\rho _s/R=2\rho _\star a/R$![]() , with $\rho _\star =\rho _s/a$
, with $\rho _\star =\rho _s/a$![]() . It follows that $g$
. It follows that $g$![]() is expected to increase for smaller aspect ratio machines operating at the same temperature and magnetic field.
is expected to increase for smaller aspect ratio machines operating at the same temperature and magnetic field.
The turbulent particle flux results from the advection of density by the radial $E\times B$![]() drift
drift
With $^*$![]() denoting the complex conjugate and $\Delta \varphi = \varphi _k^N - \varphi _k^\phi$
denoting the complex conjugate and $\Delta \varphi = \varphi _k^N - \varphi _k^\phi$![]() the cross-phase between density and electric potential fluctuations defined as the difference between the phases of the density, $N_k = \lvert N_k \rvert {\rm e}^{{\rm i} \varphi _k^N}$
the cross-phase between density and electric potential fluctuations defined as the difference between the phases of the density, $N_k = \lvert N_k \rvert {\rm e}^{{\rm i} \varphi _k^N}$![]() and of the electrostatic potential. This quantity can be estimated through a linear analysis, see § 3.
and of the electrostatic potential. This quantity can be estimated through a linear analysis, see § 3.
The equilibrium flow $V_{\rm eq} = \partial _x \phi _{\rm eq}$![]() is generated by the Reynolds stress, which is the sum of two components: $E\times B$
is generated by the Reynolds stress, which is the sum of two components: $E\times B$![]() and diamagnetic (Smolyakov et al. Reference Smolyakov, Diamond and Medvedev2000; Sarazin et al. Reference Sarazin, Dif-Pradalier, Garbet, Ghendrih, Berger, Gillot, Grandgirard, Obrejan, Varennes and Vermare2021)
and diamagnetic (Smolyakov et al. Reference Smolyakov, Diamond and Medvedev2000; Sarazin et al. Reference Sarazin, Dif-Pradalier, Garbet, Ghendrih, Berger, Gillot, Grandgirard, Obrejan, Varennes and Vermare2021)
Finally, a friction $\mu$![]() is added to the equilibrium velocity equation in order to account for neoclassical damping of the poloidal flow. The code allows for the friction to be estimated through neoclassical assumptions such as in Gianakon, Kruger & Hegna (Reference Gianakon, Kruger and Hegna2002), but we kept it constant in this study. Additionally, the code allows for a relaxation of the poloidal flow towards the radial force balance equilibrium, $\partial _t V_{\rm eq} = \dots - \mu (V_{\rm eq} - V_{\rm eq}^{\rm FB})$
is added to the equilibrium velocity equation in order to account for neoclassical damping of the poloidal flow. The code allows for the friction to be estimated through neoclassical assumptions such as in Gianakon, Kruger & Hegna (Reference Gianakon, Kruger and Hegna2002), but we kept it constant in this study. Additionally, the code allows for a relaxation of the poloidal flow towards the radial force balance equilibrium, $\partial _t V_{\rm eq} = \dots - \mu (V_{\rm eq} - V_{\rm eq}^{\rm FB})$![]() , as prescribed in Chôné et al. (Reference Chôné, Beyer, Sarazin, Fuhr, Bourdelle and Benkadda2015). If the toroidal rotation is neglected, the force balanced $E\times B$
, as prescribed in Chôné et al. (Reference Chôné, Beyer, Sarazin, Fuhr, Bourdelle and Benkadda2015). If the toroidal rotation is neglected, the force balanced $E\times B$![]() velocity reads $V_{\rm eq}^{\rm FB} = v_{\theta } - \partial _x p_i / n$
velocity reads $V_{\rm eq}^{\rm FB} = v_{\theta } - \partial _x p_i / n$![]() , with $p_i$
, with $p_i$![]() the ion pressure and $v_{\theta } = K(\nu _\star, \epsilon ) {\boldsymbol {\nabla }_r T_i}/{e B}$
the ion pressure and $v_{\theta } = K(\nu _\star, \epsilon ) {\boldsymbol {\nabla }_r T_i}/{e B}$![]() if one assumes that the poloidal velocity is governed by neoclassical theory. Here, $\nu _\star$
if one assumes that the poloidal velocity is governed by neoclassical theory. Here, $\nu _\star$![]() accounts for the collisionality and $\epsilon$
accounts for the collisionality and $\epsilon$![]() for the inverse aspect ratio. In the case of Tokam1D, due to the isothermal assumption, the velocity from radial force balance would reduce to $V_{\rm eq}^{\rm FB} = - \tau \partial _x N_{\rm eq}$
for the inverse aspect ratio. In the case of Tokam1D, due to the isothermal assumption, the velocity from radial force balance would reduce to $V_{\rm eq}^{\rm FB} = - \tau \partial _x N_{\rm eq}$![]() . The coupling of the $E\times B$
. The coupling of the $E\times B$![]() flow to the density gradient through radial force balance has already been shown to be able to trigger and sustain edge transport barriers in resistive ballooning mode turbulence simulations (Gianakon et al. Reference Gianakon, Kruger and Hegna2002; Chôné et al. Reference Chôné, Beyer, Sarazin, Fuhr, Bourdelle and Benkadda2015; Giacomin & Ricci Reference Giacomin and Ricci2020). Since our present study aims primarily at investigating how turbulence self-organizes in the presence of self-generated flows, we have decided to drop this radial force balance self-consistency in our study. In this framework, the mean radial electric field in the Tokam1D simulations reported here is only set by the balance between the Reynolds force and the flow damping terms controlled by the friction $\mu$
flow to the density gradient through radial force balance has already been shown to be able to trigger and sustain edge transport barriers in resistive ballooning mode turbulence simulations (Gianakon et al. Reference Gianakon, Kruger and Hegna2002; Chôné et al. Reference Chôné, Beyer, Sarazin, Fuhr, Bourdelle and Benkadda2015; Giacomin & Ricci Reference Giacomin and Ricci2020). Since our present study aims primarily at investigating how turbulence self-organizes in the presence of self-generated flows, we have decided to drop this radial force balance self-consistency in our study. In this framework, the mean radial electric field in the Tokam1D simulations reported here is only set by the balance between the Reynolds force and the flow damping terms controlled by the friction $\mu$![]() and viscosity $\nu _0$
and viscosity $\nu _0$![]() coefficients. As a consequence, in particular, the present simulations cannot address possible transitions towards improved confinement regimes such as the H-mode, which has long been known to be associated with a strong modification of the mean radial electric field in the vicinity of the separatrix, in response to the steepening of the pressure profile (Groebner, Burrell & Seraydarian Reference Groebner, Burrell and Seraydarian1990). The impact of the radial force balance will be addressed in a future dedicated work.
coefficients. As a consequence, in particular, the present simulations cannot address possible transitions towards improved confinement regimes such as the H-mode, which has long been known to be associated with a strong modification of the mean radial electric field in the vicinity of the separatrix, in response to the steepening of the pressure profile (Groebner, Burrell & Seraydarian Reference Groebner, Burrell and Seraydarian1990). The impact of the radial force balance will be addressed in a future dedicated work.
2.6 Energetics
Here, we consider the energetics of the system of (2.14), (2.15), which provides a consistency check in order to prevent the appearance of spurious instabilities. Also, partitioning the energy into distinct channels gives insight into the energy transfer between turbulence, flows and profiles in the nonlinear regime. As it should, the model obeys an energy conservation principle, which states that energy is conserved in the absence of a source (particle source $S_N$![]() here) and sinks (due to dissipative and viscous terms). In other words, linear and nonlinear energy transfer terms are conservative.
here) and sinks (due to dissipative and viscous terms). In other words, linear and nonlinear energy transfer terms are conservative.
To formulate the energy balance equation, we multiply (2.14) and (2.15) by $(1+\tau ) N$![]() and $(\phi + \tau N)$
and $(\phi + \tau N)$![]() , respectively. After integrating by parts, and summing the two equations, the interchange terms, proportional to the $g$
, respectively. After integrating by parts, and summing the two equations, the interchange terms, proportional to the $g$![]() parameter, are found to vanish. Such a cancellation requires us to keep compressibility terms in the density continuity equation. The drift-wave terms can be reorganized in the form of a parallel current $j_\parallel = \sigma n \boldsymbol {\nabla }_\parallel (N-\phi )$
parameter, are found to vanish. Such a cancellation requires us to keep compressibility terms in the density continuity equation. The drift-wave terms can be reorganized in the form of a parallel current $j_\parallel = \sigma n \boldsymbol {\nabla }_\parallel (N-\phi )$![]() . The conservation of energy then takes the following form:
. The conservation of energy then takes the following form:
With $\mathcal {E}_{\rm tot}$![]() the total energy, $P_\mathcal {E}$
the total energy, $P_\mathcal {E}$![]() the production term and $D_\mathcal {E}$
the production term and $D_\mathcal {E}$![]() the dissipation term
the dissipation term
With $\int {\rm d}\mathcal {V}$![]() being the integration on the whole volume $(x,y,z)$
being the integration on the whole volume $(x,y,z)$![]() . It can be verified that the advection terms, linked to Poisson brackets, vanish upon integration. The production term involves the source of particles injected in the system. The dissipation term contains the parallel plasma resistivity, the dissipation and the viscosity. The total energy $E_{\rm tot}$
. It can be verified that the advection terms, linked to Poisson brackets, vanish upon integration. The production term involves the source of particles injected in the system. The dissipation term contains the parallel plasma resistivity, the dissipation and the viscosity. The total energy $E_{\rm tot}$![]() involves two terms. The second one scales like the kinetic energy associated with both electric and diamagnetic drifts, while the first one involves both electron and ion pressures. Notice its somewhat peculiar structure already found in Scott (Reference Scott1997), neither proportional to $(1+\tau ^2)N^2$
involves two terms. The second one scales like the kinetic energy associated with both electric and diamagnetic drifts, while the first one involves both electron and ion pressures. Notice its somewhat peculiar structure already found in Scott (Reference Scott1997), neither proportional to $(1+\tau ^2)N^2$![]() nor to $(1+\tau )^2 N^2$
nor to $(1+\tau )^2 N^2$![]() . Note that the final result, ensuring that the sum is strictly negative, directly results from $\sigma$
. Note that the final result, ensuring that the sum is strictly negative, directly results from $\sigma$![]() depending only on radial direction and time. Therefore, if one chooses to include a non-constant electron–ion collision frequency in the model, it is necessary to consider a flux-surface-averaged quantity.
depending only on radial direction and time. Therefore, if one chooses to include a non-constant electron–ion collision frequency in the model, it is necessary to consider a flux-surface-averaged quantity.
The energy conservation terms can be decomposed in equilibrium and fluctuating components, following the same method used to derive (2.17), (2.18), (2.19) and (2.20). Noticing that linear terms vanish after the volume integration, the pressure energy can be restricted to
The factor 2 in front of $\lvert N_k \rvert ^2$![]() comes from the definition of (2.16). The generalized vorticity energy reads
comes from the definition of (2.16). The generalized vorticity energy reads

The total energy can then be organized into different channels: the equilibrium profiles of density (2.29) and velocity (2.30) on the one hand, and in between fluctuating components on the other hand. The latter can be split into electron and ion (terms proportional to $\tau$![]() ) components but for the sake of simplicity, only a turbulent energy that takes all the fluctuations into account (2.31) is considered. Finally, a term corresponding to the interaction between the density and the flows is also obtained (2.32). Its role is still unclear; it remains small in all simulations
) components but for the sake of simplicity, only a turbulent energy that takes all the fluctuations into account (2.31) is considered. Finally, a term corresponding to the interaction between the density and the flows is also obtained (2.32). Its role is still unclear; it remains small in all simulations

The total energy $E_{\rm tot}$![]() , whose volume integral evolves according to (2.24)–(2.26), can then be recast as
, whose volume integral evolves according to (2.24)–(2.26), can then be recast as
It allows one to study the transfer of energy between the density, flows and turbulence. The dynamics between the flow and turbulence energies typically follows a predator–prey behaviour. First, the energy of turbulence increases, until ZFs are created and pump out energy from turbulence. This well-established behaviour has been studied in specific models such as in Malkov & Diamond (Reference Malkov and Diamond2001) and in experiments (Schmitz et al. Reference Schmitz, Zeng, Rhodes, Hillesheim, Doyle, Groebner, Peebles, Burrell and Wang2012). It will be shown that the energy ratio between flows and turbulence greatly changes when scanning the $(g,C)$![]() parameters of the model: some domains in the parameter space are characterized by large flow to turbulence energy ratio.
parameters of the model: some domains in the parameter space are characterized by large flow to turbulence energy ratio.
3 Linear behaviour of interchange–CDW instabilities
In the absence of any ad hoc nonlinear dissipative coefficient, i.e. for $D_{\rm NL}=0$![]() , (2.19)–(2.20) are already in their linear form: they do not involve any coupling of the chosen wave vectors at $k_y$
, (2.19)–(2.20) are already in their linear form: they do not involve any coupling of the chosen wave vectors at $k_y$![]() and $k_\parallel$
and $k_\parallel$![]() with other wave vectors. To derive the linear dispersion relation, the last step consists in assuming a scale separation between equilibrium and fluctuation radial scales, the former evolving on larger spatial and temporal scales. As a result, equilibrium gradients – and possibly higher-order derivatives of $N_{\rm eq}$
with other wave vectors. To derive the linear dispersion relation, the last step consists in assuming a scale separation between equilibrium and fluctuation radial scales, the former evolving on larger spatial and temporal scales. As a result, equilibrium gradients – and possibly higher-order derivatives of $N_{\rm eq}$![]() and $V_{\rm eq}$
and $V_{\rm eq}$![]() – can be considered constant on the scale of the fluctuations. These derivatives are then considered as prescribed parameters, and each radial Fourier mode $k_x$
– can be considered constant on the scale of the fluctuations. These derivatives are then considered as prescribed parameters, and each radial Fourier mode $k_x$![]() of the fluctuations is then independent from the others. The analytical calculations are performed in Fourier space
of the fluctuations is then independent from the others. The analytical calculations are performed in Fourier space
In this case, each Fourier mode is an eigenmode of the linear system. For the sake of simplicity and because the weight of high-order derivatives is expected to be small within the scale separation assumption, all derivatives higher than one are neglected in the analysis (in particular, $N_{\rm eq}^{\prime \prime }$![]() and $N_{\rm eq}^{\prime \prime \prime }$
and $N_{\rm eq}^{\prime \prime \prime }$![]() are assumed to be vanishingly small, with the prime denoting the derivative along $x$
are assumed to be vanishingly small, with the prime denoting the derivative along $x$![]() ). The derivative of the velocity terms, $V_{\rm eq}'$
). The derivative of the velocity terms, $V_{\rm eq}'$![]() and $V_{\rm eq}''$
and $V_{\rm eq}''$![]() are also neglected. We introduce the electron diamagnetic frequency $\omega _{*e} = - k_y N_{\rm eq}'$
are also neglected. We introduce the electron diamagnetic frequency $\omega _{*e} = - k_y N_{\rm eq}'$![]() . The equilibrium velocity leads to a Doppler shift on the frequency, therefore we solve for $\bar {\omega } = \omega - k_y V_{\rm eq}$
. The equilibrium velocity leads to a Doppler shift on the frequency, therefore we solve for $\bar {\omega } = \omega - k_y V_{\rm eq}$![]() . The determinant then reads
. The determinant then reads
With the following notations:
The linear growth rate and frequency are solutions of $D(k, \bar {\omega }) = 0$![]() . The linear phase shift between density and electric potential fluctuations corresponds to the phase of the complex response function $F(k, \bar {\omega }) = N_k/\phi _k$
. The linear phase shift between density and electric potential fluctuations corresponds to the phase of the complex response function $F(k, \bar {\omega }) = N_k/\phi _k$![]()
The turbulent particle flux scales like the sine of the cross-phase $\Delta \varphi _k$![]() . Its linear expression is given by
. Its linear expression is given by
The growth rate, frequency and phase are studied as a function of the three plasma parameters, $g$![]() , $C$
, $C$![]() and $\tau$
and $\tau$![]() by performing parameter scans. First, the interchange and CDW cases will be studied, then the general dispersion relation is considered with a particular focus on the compressibility terms.
by performing parameter scans. First, the interchange and CDW cases will be studied, then the general dispersion relation is considered with a particular focus on the compressibility terms.
3.1 Specific cases: interchange only or CDW only
Setting $\tau = C = 0$![]() eliminates the drift instability, leaving only the interchange. Consider no dissipation $D=\nu =0$
eliminates the drift instability, leaving only the interchange. Consider no dissipation $D=\nu =0$![]() for simplicity. The dispersion relation then reduces to
for simplicity. The dispersion relation then reduces to
The instability develops above the density gradient threshold
In particular, the instability disappears for negative density gradients, recovering the asymmetric nature of the interchange instability with respect to the magnetic field inhomogeneity (Liewer Reference Liewer1985). Also, the largest scales (small $k_\perp$![]() ) are found to be destabilized first. Interestingly, the instability threshold increases with $g$
) are found to be destabilized first. Interestingly, the instability threshold increases with $g$![]() . This effect results from the compressibility terms, as will be discussed in the following.
. This effect results from the compressibility terms, as will be discussed in the following.
Then, let us consider the purely drift instability case, with finite $C$![]() and $\tau$
and $\tau$![]() but with $g=0$
but with $g=0$![]() , assuming the same simplifications. The dispersion relation then reads as follows:
, assuming the same simplifications. The dispersion relation then reads as follows:
In the cold ion limit, $\tau = 0$![]() , one is left with the Hasegawa–Wakatani system (Wakatani & Hasegawa Reference Wakatani and Hasegawa1984), for which two limits can be distinguished. The case $C \to 0$
, one is left with the Hasegawa–Wakatani system (Wakatani & Hasegawa Reference Wakatani and Hasegawa1984), for which two limits can be distinguished. The case $C \to 0$![]() corresponds to the hydrodynamic, highly collisional, regime while $C \to + \infty$
corresponds to the hydrodynamic, highly collisional, regime while $C \to + \infty$![]() corresponds to the adiabatic regime. Keeping only the leading-order terms, the solution in the hydrodynamic case reads
corresponds to the adiabatic regime. Keeping only the leading-order terms, the solution in the hydrodynamic case reads

One effectively recovers the resistive drift instability, mostly unstable at large scales ($k_\perp \approx 0$![]() ), with the instability growth rate increasing with both the density gradient and the adiabaticity parameter. It exhibits no threshold in the absence of dissipation coefficients, and the instability develops whatever the sign of the density gradient. In the collisionless regime $C\to +\infty$
), with the instability growth rate increasing with both the density gradient and the adiabaticity parameter. It exhibits no threshold in the absence of dissipation coefficients, and the instability develops whatever the sign of the density gradient. In the collisionless regime $C\to +\infty$![]() , the system reduces to the Hasegawa–Mima equation and one is left with stable drift waves
, the system reduces to the Hasegawa–Mima equation and one is left with stable drift waves
where $\bar {\omega }_+$![]() corresponds to the Doppler shifted drift-wave frequency as given in Hasegawa & Mima (Reference Hasegawa and Mima1978). The system is stable and oscillates at the drift frequency. Also notice that, as expected, the turbulent flux (2.21) is strictly zero in this case since the phase shift $\Delta \varphi$
corresponds to the Doppler shifted drift-wave frequency as given in Hasegawa & Mima (Reference Hasegawa and Mima1978). The system is stable and oscillates at the drift frequency. Also notice that, as expected, the turbulent flux (2.21) is strictly zero in this case since the phase shift $\Delta \varphi$![]() between density and electric potential fluctuations vanishes.
between density and electric potential fluctuations vanishes.
It appears from the asymptotic analysis that the drift-wave instability is stable at both small and large $C$![]() . The interchange instability exhibits a threshold in density gradient and is then stabilized at very large $g$
. The interchange instability exhibits a threshold in density gradient and is then stabilized at very large $g$![]() , as further detailed in the following sections.
, as further detailed in the following sections.
Also, the two instabilities ($C=0, g=0$![]() ) can be distinguished from their linear cross-phase. On the one hand, interchange displays a much larger sine of the cross-phase, typically close to $\Delta \varphi _k \approx {\rm \pi}/2$
) can be distinguished from their linear cross-phase. On the one hand, interchange displays a much larger sine of the cross-phase, typically close to $\Delta \varphi _k \approx {\rm \pi}/2$![]() . This is verified taking $C=0$
. This is verified taking $C=0$![]() and neglecting the compressibility terms in both (3.9) and (3.7). One is left with $F(k, \bar {\omega })=\bar {\omega }/\omega _{*e}$
and neglecting the compressibility terms in both (3.9) and (3.7). One is left with $F(k, \bar {\omega })=\bar {\omega }/\omega _{*e}$![]() with $\bar {\omega } = {\rm i} \left ( gk_y\omega _{*e}/k_\perp ^2 \right )^{1/2}$
with $\bar {\omega } = {\rm i} \left ( gk_y\omega _{*e}/k_\perp ^2 \right )^{1/2}$![]() . Then, the phase relation is purely imaginary and the corresponding cross-phase reads $\sin \Delta \varphi _k = -1$
. Then, the phase relation is purely imaginary and the corresponding cross-phase reads $\sin \Delta \varphi _k = -1$![]() . On the other hand, the drift-wave instability exhibits a lower cross-phase which further decreases as $C$
. On the other hand, the drift-wave instability exhibits a lower cross-phase which further decreases as $C$![]() increases. At large $C$
increases. At large $C$![]() , the adiabatic regime forces $N_k \sim \phi _k$
, the adiabatic regime forces $N_k \sim \phi _k$![]() . It leads to a vanishing phase shift $\sin \Delta \varphi = 0$
. It leads to a vanishing phase shift $\sin \Delta \varphi = 0$![]() implying a vanishing quasi-linear transport. Taking the limit at large $C$
implying a vanishing quasi-linear transport. Taking the limit at large $C$![]() one can replace $\bar {\omega }$
one can replace $\bar {\omega }$![]() with the drift-wave solution in (3.7). This leads to ${\rm Im}\,F(k, \bar {\omega }) = 0$
with the drift-wave solution in (3.7). This leads to ${\rm Im}\,F(k, \bar {\omega }) = 0$![]() and thus $\sin \Delta \varphi _k = 0$
and thus $\sin \Delta \varphi _k = 0$![]() . At low $C$
. At low $C$![]() using (3.12), the phase relation at leading order reads $F(k,\bar {\omega }) \approx - (1+{\rm i}) (C/2k_\perp ^2\omega _{*e})^{1/2}$
using (3.12), the phase relation at leading order reads $F(k,\bar {\omega }) \approx - (1+{\rm i}) (C/2k_\perp ^2\omega _{*e})^{1/2}$![]() , which implies $\sin \Delta \varphi _k = -1/\sqrt {2}$
, which implies $\sin \Delta \varphi _k = -1/\sqrt {2}$![]() .
.
3.2 General case: coupling CDW and interchange instabilities
Both CDW and interchange instabilities are expected to coexist in the edge of tokamak plasmas. Understanding their coupling is therefore essential. While drift waves are stabilized at both small and large $C$![]() , we show that the interchange instability does not take over in these regimes in the Tokam1D model. Indeed, interchange is also stabilized as the adiabaticity parameter is increased. Recall that the sine of the cross-phase gives an indication of the efficiency of the transport. Thus, predicting its linear value together with the growth rate helps us understand which regimes are expected to yield stronger transport. Finally, we analyse the role of the compressibility terms in the general case, and show that they stabilize the largest scale at very large $g$
, we show that the interchange instability does not take over in these regimes in the Tokam1D model. Indeed, interchange is also stabilized as the adiabaticity parameter is increased. Recall that the sine of the cross-phase gives an indication of the efficiency of the transport. Thus, predicting its linear value together with the growth rate helps us understand which regimes are expected to yield stronger transport. Finally, we analyse the role of the compressibility terms in the general case, and show that they stabilize the largest scale at very large $g$![]() . The role of $\tau$
. The role of $\tau$![]() is considered in Appendix A. We show that it can be stabilizing or destabilizing depending on the instability at play. Also, it is shown that having a single $k_y$
is considered in Appendix A. We show that it can be stabilizing or destabilizing depending on the instability at play. Also, it is shown that having a single $k_y$![]() is detrimental to the study of $\tau$
is detrimental to the study of $\tau$![]() . Therefore, the choice is made to keep $\tau =1$
. Therefore, the choice is made to keep $\tau =1$![]() for the rest of the study.
for the rest of the study.
In the following, the dispersion relation is solved for different cases with fixed equilibrium parameters. Whenever used, the density gradient is fixed to $-N_{\rm eq}'= \rho _s/L_N = 1/100$![]() , $L_N$
, $L_N$![]() being the gradient length. The diffusion parameters are set to $D_1=\nu _1=10^{-2}$
being the gradient length. The diffusion parameters are set to $D_1=\nu _1=10^{-2}$![]() . The size of the radial domain is $L_x = 400$
. The size of the radial domain is $L_x = 400$![]() (this constrains $\min (k_x)$
(this constrains $\min (k_x)$![]() ). The radial wavenumber is defined as $k_{x} = m ({2 {\rm \pi}}/{L_x})$
). The radial wavenumber is defined as $k_{x} = m ({2 {\rm \pi}}/{L_x})$![]() , with $m$
, with $m$![]() the radial mode number and $L_x$
the radial mode number and $L_x$![]() the size of the simulation domain.
the size of the simulation domain.
The growth rate is plotted as a function of $k_x$![]() and $k_y$
and $k_y$![]() for $C=10^{-3}$
for $C=10^{-3}$![]() and $g=2 \times 10^{-3}$
and $g=2 \times 10^{-3}$![]() in figure 1(a). The white contour corresponds to the linear threshold $\gamma (k_x,k_y)=0$
in figure 1(a). The white contour corresponds to the linear threshold $\gamma (k_x,k_y)=0$![]() with these parameters. The white crosses note the positions of the maxima for positive and negative poloidal wavenumbers. In figure 1(b), the effect of $C$
with these parameters. The white crosses note the positions of the maxima for positive and negative poloidal wavenumbers. In figure 1(b), the effect of $C$![]() and $g$
and $g$![]() on the growth rate is explored. Here, the wavenumbers are fixed: $(k_x, k_y) = (0.06, 0.3)$
on the growth rate is explored. Here, the wavenumbers are fixed: $(k_x, k_y) = (0.06, 0.3)$![]() . Three cases are shown: a CDW only case with $g=0$
. Three cases are shown: a CDW only case with $g=0$![]() , an interchange only with $C=0$
, an interchange only with $C=0$![]() and a case ‘both’ with $g=C$
and a case ‘both’ with $g=C$![]() .
.

Figure 1. (a) Growth rate without equilibrium flows as a function of $k_x$![]() and $k_y$
and $k_y$![]() for $g=2 \times 10^{-3}$
for $g=2 \times 10^{-3}$![]() , $C=10^{-3}$
, $C=10^{-3}$![]() . White crosses correspond to maxima in positive and negative $k_y$
. White crosses correspond to maxima in positive and negative $k_y$![]() . White contour denotes the threshold $\gamma (k_x,k_y)=0$
. White contour denotes the threshold $\gamma (k_x,k_y)=0$![]() . (b) Growth rate for the case collisional drift waves (CDW) $g=0$
. (b) Growth rate for the case collisional drift waves (CDW) $g=0$![]() , interchange (inter) $C=0$
, interchange (inter) $C=0$![]() and coupled CDW–inter $C=g$
and coupled CDW–inter $C=g$![]() , as a function of $C$
, as a function of $C$![]() and $g$
and $g$![]() for $k_x=2{\rm \pi} /400$
for $k_x=2{\rm \pi} /400$![]() and $k_y=0.3$
and $k_y=0.3$![]() . Both figures are computed considering: $1/L_N=1/100$
. Both figures are computed considering: $1/L_N=1/100$![]() , $D_1=\nu _1=10^{-2}$
, $D_1=\nu _1=10^{-2}$![]() .
.
In figure 1(a), the growth rate is maximum for the largest radial scale achievable for the system: $k_x = 2{\rm \pi} /L_x$![]() , and finite poloidal scale: $k_y \sim 0.35$
, and finite poloidal scale: $k_y \sim 0.35$![]() . Note that in practice the solution $k_x=0$
. Note that in practice the solution $k_x=0$![]() , although given by the linear analysis, would corresponds to a constant fluctuation along $x$
, although given by the linear analysis, would corresponds to a constant fluctuation along $x$![]() direction which is imposed to zero by the Dirichlet boundary condition on both boundaries. The growth rate displays a symmetric pattern for positive and negative poloidal and radial wavenumbers. Also, it decays like $-k_\perp ^2$
direction which is imposed to zero by the Dirichlet boundary condition on both boundaries. The growth rate displays a symmetric pattern for positive and negative poloidal and radial wavenumbers. Also, it decays like $-k_\perp ^2$![]() due to small-scale dissipation governed by the $D$
due to small-scale dissipation governed by the $D$![]() and $\nu$
and $\nu$![]() coefficients. In figure 1(b), the growth rate of the $(k_x=2{\rm \pi} /400, k_y=0.3)$
coefficients. In figure 1(b), the growth rate of the $(k_x=2{\rm \pi} /400, k_y=0.3)$![]() mode is plotted as a function of the $g$
mode is plotted as a function of the $g$![]() and $C$
and $C$![]() parameters. The case interchange only leads to a larger growth rate, with $\gamma$
parameters. The case interchange only leads to a larger growth rate, with $\gamma$![]() increasing rapidly with $g$
increasing rapidly with $g$![]() . It is abruptly stabilized at $g=10^{-2}$
. It is abruptly stabilized at $g=10^{-2}$![]() due to compressibility terms. The CDW are found to be stable, as expected, in both small and large $C$
due to compressibility terms. The CDW are found to be stable, as expected, in both small and large $C$![]() limits. For the chosen equilibrium parameters, the CDW only case ($g=0$
limits. For the chosen equilibrium parameters, the CDW only case ($g=0$![]() ) exhibits a smaller growth rate as compared with interchange. When both instabilities are taken into account, the growth rate stays relatively small. The CDW then proves to have a stabilizing effect on the interchange instability when $C=g$
) exhibits a smaller growth rate as compared with interchange. When both instabilities are taken into account, the growth rate stays relatively small. The CDW then proves to have a stabilizing effect on the interchange instability when $C=g$![]() with the growth rate being barely above the pure drift-wave case.
with the growth rate being barely above the pure drift-wave case.
A more thorough analysis is provided by studying the full parameter space $(C,g)$![]() while scanning the values of $k_x$
while scanning the values of $k_x$![]() and $k_y$
and $k_y$![]() . The radial and poloidal wavenumbers of interest here are those that maximize the growth rate. The result is shown in figure 2 as a function of $C$
. The radial and poloidal wavenumbers of interest here are those that maximize the growth rate. The result is shown in figure 2 as a function of $C$![]() and $g$
and $g$![]() . The white contour corresponds to the threshold $\gamma (g,C)=0$
. The white contour corresponds to the threshold $\gamma (g,C)=0$![]() . This figure displays the growth rate $\gamma$
. This figure displays the growth rate $\gamma$![]() , the absolute value of the sine of the cross-phase $\lvert \sin \Delta \varphi \rvert$
, the absolute value of the sine of the cross-phase $\lvert \sin \Delta \varphi \rvert$![]() and $k_y$
and $k_y$![]() corresponding to the maximum growth rate. The radial wavenumber that maximizes $\gamma$
corresponding to the maximum growth rate. The radial wavenumber that maximizes $\gamma$![]() is always equal to $k_x = 2{\rm \pi} /L_x$
is always equal to $k_x = 2{\rm \pi} /L_x$![]() .
.

Figure 2. Linear analysis of the system without equilibrium flows as a function of $C$![]() and $g$
and $g$![]() for a fixed density gradient. (a) Growth rate $\gamma$
for a fixed density gradient. (a) Growth rate $\gamma$![]() . (b) Sine of the cross-phase between density and electric potential fluctuations. (c) Poloidal wavenumber $k_y$
. (b) Sine of the cross-phase between density and electric potential fluctuations. (c) Poloidal wavenumber $k_y$![]() corresponding to the maximum growth rate. The radial and poloidal wavenumbers $(k_x, k_y)$
corresponding to the maximum growth rate. The radial and poloidal wavenumbers $(k_x, k_y)$![]() are chosen such that the growth rate is maximal.
are chosen such that the growth rate is maximal.
The growth rate governed by the two coupled instabilities, in figure 2(a), is maximal at large $g$![]() and small $C$
and small $C$![]() : the interchange instability alone leads to a larger growth rate. The drift $C$
: the interchange instability alone leads to a larger growth rate. The drift $C$![]() parameter acts as a stabilization to the interchange instability. At large $g$
parameter acts as a stabilization to the interchange instability. At large $g$![]() , the growth rate is always negative whatever the value of $C$
, the growth rate is always negative whatever the value of $C$![]() . This is due to the compressibility terms and will be detailed in the next section.
. This is due to the compressibility terms and will be detailed in the next section.
In figure 2(b), the sine of the cross-phase is maximal for interchange dominated cases, at large $g$![]() for a fixed $C$
for a fixed $C$![]() , consistently with the analytical developments performed in § 3.1. Indeed, the case interchange only is expected to yield $\sin \Delta \varphi = -1$
, consistently with the analytical developments performed in § 3.1. Indeed, the case interchange only is expected to yield $\sin \Delta \varphi = -1$![]() when the compressibility terms are neglected. In the case of figure 2(b), the compressibility terms do not seem to change this behaviour. The cross-phase decreases with $C$
when the compressibility terms are neglected. In the case of figure 2(b), the compressibility terms do not seem to change this behaviour. The cross-phase decreases with $C$![]() at fixed $g$
at fixed $g$![]() . That is also expected from the asymptotic analysis performed earlier. The growth rate is negative at high $C$
. That is also expected from the asymptotic analysis performed earlier. The growth rate is negative at high $C$![]() whatever the value of $g$
whatever the value of $g$![]() . In other word, drift waves dominate at large $C$
. In other word, drift waves dominate at large $C$![]() while interchange takes over at low $C$
while interchange takes over at low $C$![]() . Finally, the most unstable poloidal wavenumber varies from $0.15$
. Finally, the most unstable poloidal wavenumber varies from $0.15$![]() to $0.4$
to $0.4$![]() in the studied parameter domain. The variation remains marginal considering $g$
in the studied parameter domain. The variation remains marginal considering $g$![]() and $C$
and $C$![]() are changed over two decades each.
are changed over two decades each.
Remember that Tokam1D considers a constant and unique poloidal wavenumber $k_y$![]() ($k_y = 0.3$
($k_y = 0.3$![]() in the simulations). In turn, this can lead to spurious effects such as the stabilization of the interchange instability at very large gradients. Indeed, since the instability shifts towards higher values of $k_y$
in the simulations). In turn, this can lead to spurious effects such as the stabilization of the interchange instability at very large gradients. Indeed, since the instability shifts towards higher values of $k_y$![]() as the gradient increases, the retained $k_y$
as the gradient increases, the retained $k_y$![]() may become linearly stable while larger $k_y$
may become linearly stable while larger $k_y$![]() modes get excited. In such regimes, Tokam1D will then consider the system as linearly stable while it is actually still unstable, but at smaller scale (larger $k_y$
modes get excited. In such regimes, Tokam1D will then consider the system as linearly stable while it is actually still unstable, but at smaller scale (larger $k_y$![]() ). However, note that, for physics-relevant parameters, the stabilization does not occur as the density profile stays close to marginality. Moreover, the density starts from a flat profile and slowly builds up with the source. Therefore, there is little chance that the profile suddenly stiffens to reach stabilization. Also, we note that taking a single $k_y$
). However, note that, for physics-relevant parameters, the stabilization does not occur as the density profile stays close to marginality. Moreover, the density starts from a flat profile and slowly builds up with the source. Therefore, there is little chance that the profile suddenly stiffens to reach stabilization. Also, we note that taking a single $k_y$![]() leads to a stabilization of the interchange instability at very low values of $C$
leads to a stabilization of the interchange instability at very low values of $C$![]() and $g$
and $g$![]() , $C<10^{-7}$
, $C<10^{-7}$![]() and $g<10^{-5}$
and $g<10^{-5}$![]() , which is out of the scanned parameter space. Other than these specific cases, we expect the role of $k_y$
, which is out of the scanned parameter space. Other than these specific cases, we expect the role of $k_y$![]() to be marginal on the linear results, and no strong qualitative changes have been observed. A possible upgrade of the reduced model Tokam1D would consist in considering a non-constant poloidal wave vector $k_y$
to be marginal on the linear results, and no strong qualitative changes have been observed. A possible upgrade of the reduced model Tokam1D would consist in considering a non-constant poloidal wave vector $k_y$![]() , that would depend on the equilibrium gradients. Such a refinement has not been retained in the present study.
, that would depend on the equilibrium gradients. Such a refinement has not been retained in the present study.
3.3 Compressibility terms stabilize interchange instability at large scales
The compressibility terms, due to the divergence of the electric velocity and diamagnetic flux in the particle balance equation (2.3), involve the magnetic curvature $g \partial _y ( \phi - N)$![]() (2.14). Those terms stabilize the interchange instability at large scales. Taking the same case as in figure 2 and turning off the compressibility terms, one obtains the growth rate of figure 3(a). In that case the interchange instability is not stabilized and the growth rate diverges with $g$
(2.14). Those terms stabilize the interchange instability at large scales. Taking the same case as in figure 2 and turning off the compressibility terms, one obtains the growth rate of figure 3(a). In that case the interchange instability is not stabilized and the growth rate diverges with $g$![]() . Additionally, one can look for the minimum gradient needed to destabilize the system figure 3(b). Similarly, due to compressibility terms, this critical gradient increases at large magnetic curvature. Note that there is a threshold for both cases at low $g$
. Additionally, one can look for the minimum gradient needed to destabilize the system figure 3(b). Similarly, due to compressibility terms, this critical gradient increases at large magnetic curvature. Note that there is a threshold for both cases at low $g$![]() due to the dissipation terms $D$
due to the dissipation terms $D$![]() and $\nu$
and $\nu$![]() .
.

Figure 3. (a) Growth rate computed using parameters of figure 2 without the compressibility terms. (b) First density gradient $R/L_n$![]() to destabilize the system as a function of $g$
to destabilize the system as a function of $g$![]() . The red and blue shaded regions correspond to the stable parts of the red and blue curves, respectively.
. The red and blue shaded regions correspond to the stable parts of the red and blue curves, respectively.
The stabilization due to compressibility terms can be obtained analytically. A simplified system with, $C=0$![]() , $\tau =0$
, $\tau =0$![]() and no dissipation or viscosity $D=\nu =0$
and no dissipation or viscosity $D=\nu =0$![]() leads to the interchange instability. In order to distinguish the compressibility terms coming from the diamagnetic and $E\times B$
leads to the interchange instability. In order to distinguish the compressibility terms coming from the diamagnetic and $E\times B$![]() terms, the interchange parameter is written as $g_\star$
terms, the interchange parameter is written as $g_\star$![]() and $g_E$
and $g_E$![]() , respectively, even though both are actually equal to $g$
, respectively, even though both are actually equal to $g$![]() as they come from the same curvature term. The threshold can be written as
as they come from the same curvature term. The threshold can be written as
where it seems that the interchange instability threshold is linearly proportional to compressibility. In the absence of compressibility terms and without dissipation or viscosity, there is no threshold and $\omega _{*e}^{\rm crit}=0$![]() .
.
4 Nonlinear regime: ZF generation
The linear properties of the system change with the parameters $C$![]() and $g$
and $g$![]() . Moreover, turbulence self-organization and saturation mechanisms are fundamentally different depending on the type and intensity of the system's forcing. The objective here is to characterize the self-organization by analysing the generation of ZFs and staircases as a function of $C$
. Moreover, turbulence self-organization and saturation mechanisms are fundamentally different depending on the type and intensity of the system's forcing. The objective here is to characterize the self-organization by analysing the generation of ZFs and staircases as a function of $C$![]() and forcing. The choice is made to restrict ourselves to the $g=0$
and forcing. The choice is made to restrict ourselves to the $g=0$![]() cases to simplify the analysis. The interplay between CDW and interchange turbulence, requiring finite $g$
cases to simplify the analysis. The interplay between CDW and interchange turbulence, requiring finite $g$![]() values, will be thoroughly investigated in a future contribution. First, the generation of ZFs is analysed in terms of the ratio of the ZF to turbulence energy and Reynolds stress. Then, the generation of a staircase is studied.
values, will be thoroughly investigated in a future contribution. First, the generation of ZFs is analysed in terms of the ratio of the ZF to turbulence energy and Reynolds stress. Then, the generation of a staircase is studied.
We analyse a set of flux-driven simulations in the drift-wave regime, at $g=0$![]() and $C$
and $C$![]() ranging from $3\times 10^{-4}$
ranging from $3\times 10^{-4}$![]() to $8\times 10^{-1}$
to $8\times 10^{-1}$![]() . Simulations are performed on $L_x=400$
. Simulations are performed on $L_x=400$![]() $\rho _s$
$\rho _s$![]() using a grid of $N_x = 1024$
using a grid of $N_x = 1024$![]() radial points and using time steps ${d}t_{\rm num} = 0.1$
radial points and using time steps ${d}t_{\rm num} = 0.1$![]() . The dissipation coefficients are constant, $D=\nu =10^{-2}$
. The dissipation coefficients are constant, $D=\nu =10^{-2}$![]() and the equilibrium velocity friction is set to $\mu = 10^{-4}$
and the equilibrium velocity friction is set to $\mu = 10^{-4}$![]() . The poloidal wavenumber and the ion to electron temperature ratios are chosen constant for every simulation at $k_y = 0.3$
. The poloidal wavenumber and the ion to electron temperature ratios are chosen constant for every simulation at $k_y = 0.3$![]() and $\tau =1$
and $\tau =1$![]() . Finally, Neumann boundary conditions with vanishing gradients are used for the density at $x=0$
. Finally, Neumann boundary conditions with vanishing gradients are used for the density at $x=0$![]() and for the velocity at both ends. The density is taken equal to $N_{\rm eq} = 0.1$
and for the velocity at both ends. The density is taken equal to $N_{\rm eq} = 0.1$![]() at $x=L_x$
at $x=L_x$![]() and the fluctuations are set to zero at the boundaries. Simulations are run until the particle confinement time, $\tau _p$
and the fluctuations are set to zero at the boundaries. Simulations are run until the particle confinement time, $\tau _p$![]() , reaches a statistical steady state. It is computed from the density profile and the source
, reaches a statistical steady state. It is computed from the density profile and the source

The source is chosen to be a Gaussian, with the maximum located at the left boundary of the simulation domain. The amplitude is adjusted for each simulation, such that the ‘target profile’ is $6$![]() times the critical gradient for each value of $C$
times the critical gradient for each value of $C$![]() . The target profile is defined as the gradient in the absence of turbulence such that the dissipative flux of particles equals the integral of the particle source. The diffusive gradient is shown figure 4 together with the critical gradient for each value of $C$
. The target profile is defined as the gradient in the absence of turbulence such that the dissipative flux of particles equals the integral of the particle source. The diffusive gradient is shown figure 4 together with the critical gradient for each value of $C$![]() . Constraining the source with the critical gradient ensures that the steady-state gradient will be above but not too far from the threshold. Proceeding this way, the distance to marginality can be controlled. The steady-state gradient is shown in the same figure. Due to the flux-driven characteristics, the simulations now evolve in a 2-D space where different gradients are accessible for each value of $C$
. Constraining the source with the critical gradient ensures that the steady-state gradient will be above but not too far from the threshold. Proceeding this way, the distance to marginality can be controlled. The steady-state gradient is shown in the same figure. Due to the flux-driven characteristics, the simulations now evolve in a 2-D space where different gradients are accessible for each value of $C$![]() depending on forcing and dissipation.
depending on forcing and dissipation.

Figure 4. Absolute critical density gradient indicating the instability threshold, corresponding diffusive gradient ($\lvert \partial _x N_{\rm eq}^{\rm diff} \rvert = 6 \lvert \partial _x N_{\rm eq}^{\rm crit} \rvert$![]() ) and steady-state gradient as a function of the adiabatic parameter $C$
) and steady-state gradient as a function of the adiabatic parameter $C$![]() .
.
As shown in figure 4, the critical gradient increases with $C$![]() . To keep the target profile at a constant relative distance to the critical gradient the source amplitude is increased from $S_N (0) = 1.5\times 10^{-5}$
. To keep the target profile at a constant relative distance to the critical gradient the source amplitude is increased from $S_N (0) = 1.5\times 10^{-5}$![]() at $C=2\times 10^{-4}$
at $C=2\times 10^{-4}$![]() to $S_N (0) = 4.3\times 10^{-4}$
to $S_N (0) = 4.3\times 10^{-4}$![]() at $C=8\times 10^{-1}$
at $C=8\times 10^{-1}$![]() . The poloidal wavenumber corresponding to the maximum growth rate stays close to the chosen value $k_y = 0.3$
. The poloidal wavenumber corresponding to the maximum growth rate stays close to the chosen value $k_y = 0.3$![]() for the considered values of $C$
for the considered values of $C$![]() .Footnote 2 The steady-state gradient moves closer to the diffusive gradient as $C$
.Footnote 2 The steady-state gradient moves closer to the diffusive gradient as $C$![]() increases. This results from the fact that the contribution of turbulence to the total flux is reduced: the system is better confined at large $C$
increases. This results from the fact that the contribution of turbulence to the total flux is reduced: the system is better confined at large $C$![]() .
.
It should be emphasized that the variation of $C$![]() only is not enough to conclude on the transition from a hydrodynamic to an adiabatic regime. Instead, one considers the transition to the adiabatic regime when $C/\kappa$
only is not enough to conclude on the transition from a hydrodynamic to an adiabatic regime. Instead, one considers the transition to the adiabatic regime when $C/\kappa$![]() is large, with $\kappa =\partial _x N_{\rm eq}$
is large, with $\kappa =\partial _x N_{\rm eq}$![]() the logarithmic derivative (Özgür Reference Özgür2024). For flux-driven simulations, the density gradient evolves together with the adiabaticity parameter. In particular, the density gradient increases with $C$
the logarithmic derivative (Özgür Reference Özgür2024). For flux-driven simulations, the density gradient evolves together with the adiabaticity parameter. In particular, the density gradient increases with $C$![]() , resulting in a smoother evolution of $C/\kappa$
, resulting in a smoother evolution of $C/\kappa$![]() . In the simulations performed, for $C$
. In the simulations performed, for $C$![]() scanned from $3\times 10^{-4}$
scanned from $3\times 10^{-4}$![]() to $8\times 10^{-1}$
to $8\times 10^{-1}$![]() , the corresponding $C/\kappa$
, the corresponding $C/\kappa$![]() evolves from $10^{-2}$
evolves from $10^{-2}$![]() to $8 \times 10^{-1}$
to $8 \times 10^{-1}$![]() . However, this calculation is performed using the root-mean-square value of the density gradient and does not take into account possible corrugations due to staircase generation. It is not obvious whether one should take into account only the large-scale gradients or also include small-scale structures in the adiabaticity estimation. Therefore, $C$
. However, this calculation is performed using the root-mean-square value of the density gradient and does not take into account possible corrugations due to staircase generation. It is not obvious whether one should take into account only the large-scale gradients or also include small-scale structures in the adiabaticity estimation. Therefore, $C$![]() alone is used as the control parameter in the following sections and the gradient is indicated wherever deemed necessary.
alone is used as the control parameter in the following sections and the gradient is indicated wherever deemed necessary.
4.1 Rich dynamics and flow patterns
In the present model, ZFs are generated nonlinearly by the Reynolds stresses. The action of these sheared flows on the fluctuations then regulates turbulence and therefore the transport. In fact, it is not the amplitude of these flows but whether or not they organize into well-defined sheared layers, leading to corrugations of density or pressure profiles, called staircases, that is the determining factor. It may critically impact the resulting turbulence saturation and therefore the overall quality of confinement. A strong shear may be expected to tilt and elongate turbulent structures, leading to their decorrelation, provided that the shear persists longer than the lifetime of the turbulent structure.
In figure 5 are presented four different velocity patterns as a function of time and radial coordinate $x$![]() for $C=8 \times 10^{-4}$
for $C=8 \times 10^{-4}$![]() , $10^{-2}$
, $10^{-2}$![]() , $5 \times 10^{-2}$
, $5 \times 10^{-2}$![]() and $5 \times 10^{-1}$
and $5 \times 10^{-1}$![]() . Each case is taken when the profiles have reached steady state and is plotted for $1.2\times 10^{4}$
. Each case is taken when the profiles have reached steady state and is plotted for $1.2\times 10^{4}$![]() time steps, corresponding to $1.2\times 10^{5}$
time steps, corresponding to $1.2\times 10^{5}$![]() cyclotron periods $\omega _{\rm cs}^{-1}$
cyclotron periods $\omega _{\rm cs}^{-1}$![]() . Note that the scale of the colour bars is different for each case.
. Note that the scale of the colour bars is different for each case.

Figure 5. Four examples of equilibrium velocity $V_{\rm eq} = - \langle E_r \rangle$![]() at equilibrium $(\tau > \tau _p)$
at equilibrium $(\tau > \tau _p)$![]() . Panels show (a) $C=8 \times 10^{-4}$
. Panels show (a) $C=8 \times 10^{-4}$![]() , (b) $C=10^{-2}$
, (b) $C=10^{-2}$![]() , (c) $C=5 \times 10^{-2}$
, (c) $C=5 \times 10^{-2}$![]() , (d) $C=5 \times 10^{-1}$
, (d) $C=5 \times 10^{-1}$![]() .
.
In all simulations, ZFs are active and prove crucial to mitigating turbulence. When the flows are artificially switched off by removing the Reynolds stress drive, a large, system-size radial mode develops. In those cases, the system enters a quasi-periodic regime where a large density gradient builds up and relaxes through a strong transport event. An example of this regime is given in Appendix B. When flows are present, they can be radially structured and stable, as in figure 5(d) or intermittent as in figure 5(c). For the other cases (a,b) the system exhibits intermediate structuration with meandering, splitting and merging events. An example of splitting appears in case (a) at $x=100$![]() with a fork-like pattern of the flow. Merging occurs in case (b) at $x\approx 220$
with a fork-like pattern of the flow. Merging occurs in case (b) at $x\approx 220$![]() . The radial structure of the flow also depends on damping. An example is shown in Appendix C, for the case of figure 5(b), where greater flow time stability is obtained when the dissipation coefficients on fluctuations $D_1$
. The radial structure of the flow also depends on damping. An example is shown in Appendix C, for the case of figure 5(b), where greater flow time stability is obtained when the dissipation coefficients on fluctuations $D_1$![]() and $\nu _1$
and $\nu _1$![]() are increased.
are increased.
The dynamics depends on the adiabaticity parameter: at low $C$![]() , the system develops smooth structures that evolve slowly. When $C$
, the system develops smooth structures that evolve slowly. When $C$![]() increases, the dynamics of turbulence and flows is faster. Moreover, diagonal stripes are visible for cases (b,c), associated with ballistic transport events of particles called avalanches. It is known that staircases can act as micro-barriers for these avalanches, efficiently limiting their radial extension (Kosuga et al. Reference Kosuga, Diamond, Dif-Pradalier and Gürcan2014). In general, the flows can either stop the avalanches or, if the avalanches are strong enough, they can travel through the shear layer, perturbing it in the process. In the observed cases, when the flows are radially structured, they always manage to recover their radial structure after an avalanche. Importantly, it is found that the radial size of the ZF is an emergent property independent of the box size $L_x$
increases, the dynamics of turbulence and flows is faster. Moreover, diagonal stripes are visible for cases (b,c), associated with ballistic transport events of particles called avalanches. It is known that staircases can act as micro-barriers for these avalanches, efficiently limiting their radial extension (Kosuga et al. Reference Kosuga, Diamond, Dif-Pradalier and Gürcan2014). In general, the flows can either stop the avalanches or, if the avalanches are strong enough, they can travel through the shear layer, perturbing it in the process. In the observed cases, when the flows are radially structured, they always manage to recover their radial structure after an avalanche. Importantly, it is found that the radial size of the ZF is an emergent property independent of the box size $L_x$![]() . For simulations performed at very low $L_x \approx 10$
. For simulations performed at very low $L_x \approx 10$![]() , a single ZF can fill up all of the simulation domain.
, a single ZF can fill up all of the simulation domain.
In the confined region of tokamak plasmas, one expects an additional radial electric field that exists alongside this turbulence-driven flow (remember that $V_{\rm eq} \sim - \langle E_r \rangle$![]() in dimensionless variables). Indeed, the radial force balance relates the mean $E_r$
in dimensionless variables). Indeed, the radial force balance relates the mean $E_r$![]() to the ion pressure gradient and the Lorentz force. This physics is ignored in the present version of Tokam1D, the focus being on the self-regulation of turbulence by self-generated ZFs. Therefore, the flows here are mostly sinusoidal and symmetric around zero.
to the ion pressure gradient and the Lorentz force. This physics is ignored in the present version of Tokam1D, the focus being on the self-regulation of turbulence by self-generated ZFs. Therefore, the flows here are mostly sinusoidal and symmetric around zero.
The diagonal stripes are also visible in the amplitude of the density fluctuations. Figure 6(a) shows the amplitude of the density fluctuations for $C=10^{-2}$![]() , corresponding to the flows in figure 5(b). Density fluctuations are propagating both in and outward at similar speed. The associated turbulent particle flux is always positive, resulting in an outward transport. For the case shown, the typical avalanche length is comparable to the radial size of the velocity structures. The right-hand side features the form of the turbulence in the $(x,y)$
, corresponding to the flows in figure 5(b). Density fluctuations are propagating both in and outward at similar speed. The associated turbulent particle flux is always positive, resulting in an outward transport. For the case shown, the typical avalanche length is comparable to the radial size of the velocity structures. The right-hand side features the form of the turbulence in the $(x,y)$![]() plane for $t=6.03\times 10^6$
plane for $t=6.03\times 10^6$![]() . It is computed using the complex density fluctuation field and the definition (2.16). On top of the density fluctuation is shown the equilibrium velocity after being coarse grained on a few time and radial points. The tilt of the turbulent structures in the $(x,y)$
. It is computed using the complex density fluctuation field and the definition (2.16). On top of the density fluctuation is shown the equilibrium velocity after being coarse grained on a few time and radial points. The tilt of the turbulent structures in the $(x,y)$![]() plane corresponds to the velocity direction, indicating that flows are efficiently elongating turbulent structures in the poloidal direction. Noticeably, the phase of the fluctuations can exhibit quasi-profile discontinuities, as visible e.g. at $x\sim 160$
plane corresponds to the velocity direction, indicating that flows are efficiently elongating turbulent structures in the poloidal direction. Noticeably, the phase of the fluctuations can exhibit quasi-profile discontinuities, as visible e.g. at $x\sim 160$![]() .
.

Figure 6. Density fluctuation for case $C=10^{-2}$![]() . (a) Amplitude of the Fourier component $N_k$
. (a) Amplitude of the Fourier component $N_k$![]() as a function of time and space, the white line notes the snapshot for which is plotted the fluctuation field. (b) Two-dimensional fluctuating density field $\tilde {N}(x,y,t) = N_k(x, t) \exp ({\rm i}k_yy) + \text {c.c.}$
as a function of time and space, the white line notes the snapshot for which is plotted the fluctuation field. (b) Two-dimensional fluctuating density field $\tilde {N}(x,y,t) = N_k(x, t) \exp ({\rm i}k_yy) + \text {c.c.}$![]() taken at $z=0$
taken at $z=0$![]() (cf. (2.16)) for $t=6.03\times 10^6$
(cf. (2.16)) for $t=6.03\times 10^6$![]() . The black line shows the equilibrium velocity around the same time snapshot.
. The black line shows the equilibrium velocity around the same time snapshot.
4.2 Transition from turbulence to flow dominated regime at large $C$
Zonal flows act as a repository for the energy of the system. The more energy is stored inside the ZFs, the less is available for turbulence to generate transport. Numata et al. have shown that there was a collapse of relative energy stored in the flows at low $C$![]() (Numata et al. Reference Numata, Ball and Dewar2007). Here, we show that, in flux-driven regimes, the density gradient also adapts to the presence of flows and turbulence. Therefore, the transition from a turbulence dominated regime to a flow dominated regime is much smoother. This is in agreement with previous work (Numata et al. Reference Numata, Ball and Dewar2007), provided one accounts for the gradient evolution together with the flows.
(Numata et al. Reference Numata, Ball and Dewar2007). Here, we show that, in flux-driven regimes, the density gradient also adapts to the presence of flows and turbulence. Therefore, the transition from a turbulence dominated regime to a flow dominated regime is much smoother. This is in agreement with previous work (Numata et al. Reference Numata, Ball and Dewar2007), provided one accounts for the gradient evolution together with the flows.
Using the energy channels defined (2.29)–(2.32), we can evaluate whether the free energy is captured by turbulence or is stored in the flows. Flows and turbulence energy $E_{\rm Veq}$![]() and $E_{\rm turb}$
and $E_{\rm turb}$![]() are coarse grained on a few turbulence auto-correlation times. Then, the root-mean-square (r.m.s.) radial profiles are computed
are coarse grained on a few turbulence auto-correlation times. Then, the root-mean-square (r.m.s.) radial profiles are computed
with $\langle \ldots \rangle _t$![]() a time average. To get a single value per simulation, the radial average of the energy partition is performed, $\langle E_{\rm Veq}^{\rm rms} / (E_{\rm Veq}^{\rm rms} + E_{\rm turb}^{\rm rms}) \rangle _x$
a time average. To get a single value per simulation, the radial average of the energy partition is performed, $\langle E_{\rm Veq}^{\rm rms} / (E_{\rm Veq}^{\rm rms} + E_{\rm turb}^{\rm rms}) \rangle _x$![]() . The flow and turbulence energy channels are shown in figure 7(b) as a function of $C$
. The flow and turbulence energy channels are shown in figure 7(b) as a function of $C$![]() and their partition ratio is shown in figure 7(a). The colour of the points corresponds to the steady-state density gradient, already shown in figure 4.
and their partition ratio is shown in figure 7(a). The colour of the points corresponds to the steady-state density gradient, already shown in figure 4.

Figure 7. (a) Flow to turbulence energy partition ratio as a function of $C$![]() with the colour indicating the absolute value of the density gradient in log scale. Error bars represent the standard deviation of the r.m.s. profiles. (b) Corresponding normalized flow and turbulence energies.
with the colour indicating the absolute value of the density gradient in log scale. Error bars represent the standard deviation of the r.m.s. profiles. (b) Corresponding normalized flow and turbulence energies.
The flow to turbulence energy partition ratio increases with the adiabaticity parameter; see figure 7(a). At low $C$![]() the system is dominated by turbulence with approximately $0.001\,\%$
the system is dominated by turbulence with approximately $0.001\,\%$![]() of the energy stored in the flows. In the adiabatic regime, at large $C$
of the energy stored in the flows. In the adiabatic regime, at large $C$![]() , flows account for $80\,\%$
, flows account for $80\,\%$![]() of the total energy. Consistently, the density gradient increases with $C$
of the total energy. Consistently, the density gradient increases with $C$![]() . It is illuminating to look at each channel separately. In figure 7(b) the turbulence and velocity channels computed using (4.2) and divided by the total energy are shown. Most of the energy variation is carried by turbulence: it evolves from $3\times 10^{-4}$
. It is illuminating to look at each channel separately. In figure 7(b) the turbulence and velocity channels computed using (4.2) and divided by the total energy are shown. Most of the energy variation is carried by turbulence: it evolves from $3\times 10^{-4}$![]() of the total energy at low $C$
of the total energy at low $C$![]() to $4 \times 10^{-6}$
to $4 \times 10^{-6}$![]() at large $C$
at large $C$![]() .
.
On the basis of these observations, we focus on the expected impact of density on the ZF and turbulence dynamics. Although taken constant in the present simulations, the adiabaticity parameter $C=(k_\parallel \rho _s)^2 \omega _{\rm cs}/\nu _{\rm ei}$![]() should actually scale like $1/N_{\rm eq}$
should actually scale like $1/N_{\rm eq}$![]() . High density plasmas are then characterized by small $C$
. High density plasmas are then characterized by small $C$![]() values (assuming constant $k_\parallel \rho _s$
values (assuming constant $k_\parallel \rho _s$![]() ). In this case, on the basis of figure 7(a), one expects a low ZF to turbulence energy ratio. This suggests that the turbulent transport should increase when density increases or respectively when $C$
). In this case, on the basis of figure 7(a), one expects a low ZF to turbulence energy ratio. This suggests that the turbulent transport should increase when density increases or respectively when $C$![]() decreases. The trend is qualitatively similar to results in Numata et al. (Reference Numata, Ball and Dewar2007) but not quantitatively. More precisely, the ZF magnitude decreases rather monotonically at large density (collisionality) and does not exhibit the collapse reported in Numata et al. (Reference Numata, Ball and Dewar2007). The difference results from the self-consistent evolution of $N_{\rm eq}$
decreases. The trend is qualitatively similar to results in Numata et al. (Reference Numata, Ball and Dewar2007) but not quantitatively. More precisely, the ZF magnitude decreases rather monotonically at large density (collisionality) and does not exhibit the collapse reported in Numata et al. (Reference Numata, Ball and Dewar2007). The difference results from the self-consistent evolution of $N_{\rm eq}$![]() in flux-driven simulations. In the absence of nonlinear mode–mode coupling , the system has two ways to saturate turbulence: by profile relaxation (transport) and ZF generation. In low $C$
in flux-driven simulations. In the absence of nonlinear mode–mode coupling , the system has two ways to saturate turbulence: by profile relaxation (transport) and ZF generation. In low $C$![]() cases, for which the energy stored in ZFs is minimal, the former mechanism is favoured. The richness of the saturation channels permitted by flux-driven simulations thus leads to a less abrupt transition of the system. It should be noted that figure 7(a) is consistent with the ZF collapse reported in Numata et al. (Reference Numata, Ball and Dewar2007) provided one also moves from one density gradient to another when decreasing $C$
cases, for which the energy stored in ZFs is minimal, the former mechanism is favoured. The richness of the saturation channels permitted by flux-driven simulations thus leads to a less abrupt transition of the system. It should be noted that figure 7(a) is consistent with the ZF collapse reported in Numata et al. (Reference Numata, Ball and Dewar2007) provided one also moves from one density gradient to another when decreasing $C$![]() (green and red curves in figure 5 of Numata et al. Reference Numata, Ball and Dewar2007). A steep increase of ZF energy has also been found in gyrofluid modified Hasegawa–Wakatani simulations including warm ions (Grander, Locker & Kendl Reference Grander, Locker and Kendl2024). In this latter contribution, mode–mode interactions are retained, leading to a self-consistent turbulent cascade, but the background density gradient is imposed, limiting the liberty of the system to explore the $(C, \partial _x N_{\rm eq})$
(green and red curves in figure 5 of Numata et al. Reference Numata, Ball and Dewar2007). A steep increase of ZF energy has also been found in gyrofluid modified Hasegawa–Wakatani simulations including warm ions (Grander, Locker & Kendl Reference Grander, Locker and Kendl2024). In this latter contribution, mode–mode interactions are retained, leading to a self-consistent turbulent cascade, but the background density gradient is imposed, limiting the liberty of the system to explore the $(C, \partial _x N_{\rm eq})$![]() parameter space.
parameter space.
A few experiments have reported the strong reduction of ZFs – or proxies for ZFs – when approaching the density limit in L-mode tokamak plasmas (Xu et al. Reference Xu, Carralero, Hidalgo, Jachmich, Manz, Martines, van Milligen, Pedrosa, Ramisch and Shesterikov2011; Hong et al. Reference Hong, Tynan, Diamond, Nie, Guo, Long, Ke, Wu, Yuan and Xu2017; Long et al. Reference Long, Diamond, Xu, Ke, Nie, Li, Wang, Xu and Duan2019). In this context, the ZF collapse at large density in gradient-driven simulations of Hasegawa–Wakatani turbulence (Numata et al. Reference Numata, Ball and Dewar2007) has recently been put forward as a possible explanation for these observations (Hajjar et al. Reference Hajjar, Diamond and Malkov2018; Singh & Diamond Reference Singh and Diamond2022). Our simulations suggest, however, that, in the flux-driven regime relevant to tokamak plasmas, this reduction of ZFs could be much more gradual. Although not discarding the physics as a possible explanation for the issue of density limit in the L-mode, these new results advocate for a renewed exploration of the link between ZF reduction and density limit in a self-consistent flux-driven regime. Whether these findings may explain the reason why ZFs are found to play a secondary role in the density limit mechanism reported in Giacomin et al. (Reference Giacomin, Pau, Ricci, Sauter and Eich2022) remains an interesting yet open question. Last, note that the above analysis has only focused on the impact of density on the adiabaticity parameter, $C$![]() , that governs the transition from the adiabatic to the hydrodynamic regime in Hasegawa-Wakatani turbulence. However, increasing density also increases the friction coefficient acting on the poloidal flow, hence on ZFs ($\mu$
, that governs the transition from the adiabatic to the hydrodynamic regime in Hasegawa-Wakatani turbulence. However, increasing density also increases the friction coefficient acting on the poloidal flow, hence on ZFs ($\mu$![]() parameter in (2.18)). Gianakon et al. (Reference Gianakon, Kruger and Hegna2002) provide a heuristic expression for this neoclassical coefficient. This density dependency has already been proven to be key to the modelling of Low to High (L-H) confinement bifurcations in flux-driven simulations of resistive ballooning turbulence (Chôné et al. Reference Chôné, Beyer, Sarazin, Fuhr, Bourdelle and Benkadda2014, Reference Chôné, Beyer, Sarazin, Fuhr, Bourdelle and Benkadda2015). This improvement of the model is left for future work.
parameter in (2.18)). Gianakon et al. (Reference Gianakon, Kruger and Hegna2002) provide a heuristic expression for this neoclassical coefficient. This density dependency has already been proven to be key to the modelling of Low to High (L-H) confinement bifurcations in flux-driven simulations of resistive ballooning turbulence (Chôné et al. Reference Chôné, Beyer, Sarazin, Fuhr, Bourdelle and Benkadda2014, Reference Chôné, Beyer, Sarazin, Fuhr, Bourdelle and Benkadda2015). This improvement of the model is left for future work.
5 Staircase dynamics
The amplitude and the energy of the ZFs and hence the zonal to total energy ratio are large at large $C$![]() . However, the radial structure does not depend directly on $C$
. However, the radial structure does not depend directly on $C$![]() as structures are observed at both small and large $C$
as structures are observed at both small and large $C$![]() values. Here, we focus on the formation of staircases and on the importance of the feedback loop between the density gradient and flows, still in the CDW turbulence regime at $g=0$
values. Here, we focus on the formation of staircases and on the importance of the feedback loop between the density gradient and flows, still in the CDW turbulence regime at $g=0$![]() . In particular, we observe that the staircases disappear when we break this feedback loop.
. In particular, we observe that the staircases disappear when we break this feedback loop.
5.1 Staircase nucleation
Staircases are robust structures. We have found that they always manage to recover after a perturbation. Here, we look at the nucleation of a staircase when restarting a steady-state simulation after having smoothed out the corrugation in $N_{\rm eq}$![]() and $V_{\rm eq}$
and $V_{\rm eq}$![]() and damped out the fluctuations $N_k$
and damped out the fluctuations $N_k$![]() , $\varOmega _k$
, $\varOmega _k$![]() . The system then has no memory of the past structures. The chosen simulation corresponds to $C=5 \times 10^{-4}$
. The system then has no memory of the past structures. The chosen simulation corresponds to $C=5 \times 10^{-4}$![]() , with the steady-state flows shown figure 5(a). The nucleation of the flow pattern is shown in figure 8(a) together with the dynamics of the density profile in figure 8(b). The black rectangle indicates the time window of the nucleation process which is studied in the following.
, with the steady-state flows shown figure 5(a). The nucleation of the flow pattern is shown in figure 8(a) together with the dynamics of the density profile in figure 8(b). The black rectangle indicates the time window of the nucleation process which is studied in the following.

Figure 8. (a) Equilibrium velocity after being smoothed out at $t=3 \times 10^4$![]() . Nucleation is indicated with dotted lines. (b) Evolution of the equilibrium density as compared with its value at the restart: $N_{\rm eq} - N_{\rm eq}(t=3 \times 10^4)$
. Nucleation is indicated with dotted lines. (b) Evolution of the equilibrium density as compared with its value at the restart: $N_{\rm eq} - N_{\rm eq}(t=3 \times 10^4)$![]() .
.
Upon restart, at $t=3\times 10^4$![]() in figure 8, the equilibrium density gradient is above the linear threshold. Therefore, instability and flows appear directly in the whole domain after a short growth time. Qualitatively, a similar staircase structure is recovered. However, there are approximately $7$
in figure 8, the equilibrium density gradient is above the linear threshold. Therefore, instability and flows appear directly in the whole domain after a short growth time. Qualitatively, a similar staircase structure is recovered. However, there are approximately $7$![]() structures in figure 8, as compared with the initial $9$
structures in figure 8, as compared with the initial $9$![]() structures.
structures.
Focusing on the nucleation of a particular staircase step located at $x=123$![]() , which is indicated with a vertical dashed line, the time evolution of the flows and Reynolds stress at this location are shown in figure 9.
, which is indicated with a vertical dashed line, the time evolution of the flows and Reynolds stress at this location are shown in figure 9.

Figure 9. Energy of the equilibrium flow, total Reynolds stress and its components as a function of time for $x=123$![]() .
.
An exponential growth of both electric and diamagnetic components of the Reynolds stress is observed. The flows result from a secondary instability (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005) and are governed by the Reynolds stress components. For this simulation, both components of the Reynolds stress are important for the generation of the flows, with the diamagnetic one being slightly larger at initial times.
The dynamics of the phase is essential in the generation of both components. Bearing in mind that fluctuations can be decomposed into amplitude and phase, $\phi _k = \lvert \phi _k \rvert {\rm e}^{{\rm i}\varphi _k^{\phi }}$![]() , the electric component of the Reynolds stress can be recast as
, the electric component of the Reynolds stress can be recast as
The ZF dynamics is governed by the divergence of the Reynolds stress. The separate roles of the phase and of the amplitude clearly appear when computing the logarithmic derivative of $\varPi _E$![]()

The value of $\varPi _E$![]() is displayed in figure 10(a) together with its decomposition. The Reynolds force is detailed in figure 10(b).
is displayed in figure 10(a) together with its decomposition. The Reynolds force is detailed in figure 10(b).

Figure 10. Electric Reynolds stress decomposition as a function of time for $x=123$![]() . (a) Reynolds stress. (b) Logarithmic derivative of the Reynolds stress, relating to the Reynolds force. The phase jumps have been removed by ‘unwrapping’ the phase in the post-processing.
. (a) Reynolds stress. (b) Logarithmic derivative of the Reynolds stress, relating to the Reynolds force. The phase jumps have been removed by ‘unwrapping’ the phase in the post-processing.
In figure 10(a), it appears that both the amplitude and the phase are important for $\varPi _E$![]() growth. When computing the Reynolds force, see figure 10(b), the phase itself dominates the dynamics. The key role of the phase was already pointed out in Guo & Diamond (Reference Guo and Diamond2016) and in Sarazin et al. (Reference Sarazin, Dif-Pradalier, Garbet, Ghendrih, Berger, Gillot, Grandgirard, Obrejan, Varennes and Vermare2021). It shows that it is essential for a reduced model to retain the complete fluctuations as both amplitude and phase play a role in the generation of flows.
growth. When computing the Reynolds force, see figure 10(b), the phase itself dominates the dynamics. The key role of the phase was already pointed out in Guo & Diamond (Reference Guo and Diamond2016) and in Sarazin et al. (Reference Sarazin, Dif-Pradalier, Garbet, Ghendrih, Berger, Gillot, Grandgirard, Obrejan, Varennes and Vermare2021). It shows that it is essential for a reduced model to retain the complete fluctuations as both amplitude and phase play a role in the generation of flows.
The diamagnetic component of the Reynolds stress, (2.22), can be decomposed in the same way. Considering the conjugate of density fluctuations as $N_k^* = \lvert N_k \rvert {\rm e}^{-{\rm i} \varphi _k^N}$![]() , the tensor reads
, the tensor reads

With $\Delta \varphi = \varphi _k^{\phi } - \varphi _k^{N}$![]() the cross-phase between the density and electric potential fluctuations. The first term on the right-hand side is proportional to the electrostatic component of the Reynolds stress while the second relates to the turbulent flux of particles. It writes
the cross-phase between the density and electric potential fluctuations. The first term on the right-hand side is proportional to the electrostatic component of the Reynolds stress while the second relates to the turbulent flux of particles. It writes
The correlation between these two components of the total Reynolds stress ultimately depends on the relative weight of the second term with respect to the first. If it is negligible, then the two tensors appear correlated. In this case, the sign of the phase coupling ($\cos \Delta \varphi$![]() ) then determines whether $\varPi _\star$
) then determines whether $\varPi _\star$![]() and $\varPi _E$
and $\varPi _E$![]() are in or out of phase. For CDW turbulence, the two tensors appear correlated and in phase ($\mathcal {C}(\varPi _e, \varPi _\star )\approx 0.7$
are in or out of phase. For CDW turbulence, the two tensors appear correlated and in phase ($\mathcal {C}(\varPi _e, \varPi _\star )\approx 0.7$![]() for $C=3\times 10^{-4}$
for $C=3\times 10^{-4}$![]() ), which is even stronger at large $C$
), which is even stronger at large $C$![]() ($\mathcal {C}(\varPi _e, \varPi _\star )\approx 0.98$
($\mathcal {C}(\varPi _e, \varPi _\star )\approx 0.98$![]() for $C=8\times 10^{-1}$
for $C=8\times 10^{-1}$![]() ). This is expected, since the phase between density and electrostatic potential fluctuations decreases approaching the adiabatic limit. The diamagnetic contribution is also larger than the electrostatic contribution with $\varPi _\star > 1.5 \varPi _E$
). This is expected, since the phase between density and electrostatic potential fluctuations decreases approaching the adiabatic limit. The diamagnetic contribution is also larger than the electrostatic contribution with $\varPi _\star > 1.5 \varPi _E$![]() for $C<10^{-2}$
for $C<10^{-2}$![]() , then slowly decreases towards $\varPi _\star \approx 1.1 \varPi _E$
, then slowly decreases towards $\varPi _\star \approx 1.1 \varPi _E$![]() at large $C$
at large $C$![]() . As a matter of fact, turbulence in the CDW regime is carried mostly by density fluctuations, which results in $\lvert N_k\rvert / \lvert \phi _k \rvert >1$
. As a matter of fact, turbulence in the CDW regime is carried mostly by density fluctuations, which results in $\lvert N_k\rvert / \lvert \phi _k \rvert >1$![]() .
.
5.2 Profile relaxation crucial to self-organization
Profile relaxation is an important saturation mechanism for the turbulence in tokamaks. It is thus crucial to allow this mechanism for studying turbulence saturation and turbulence–ZF interactions in these systems. In order to assess the importance of this mechanism, in this section we artificially prevent any profile relaxation by fixing the density gradient and perform a restart of a steady-state flux-driven (FD) simulation in a gradient-driven (GD) framework. Note that the flux-surface-averaged density gradient does not evolve in time at all in these restarted simulations. This is in marked contrast with the more common GD simulations of the Hasegawa–Wakatani system that one can find in the published literature (see e.g. Majda et al. Reference Majda, Qi and Cerfon2018). Indeed, in these latter cases, the density fluctuations contain a zonal component ($k_y=0$![]() ) whose time evolving gradient adds up algebraically to the one (constant in time) set by the background density. Yet, a restoring force prevents this back reaction from balancing the initial gradient – and therefore to annihilate it – so that the self-consistent dynamics of the system gets frustrated. Another difference with respect to more standard simulations – apart from the absence of nonlinear mode–mode coupling in Tokam1D (cf. § 2.5) – is that fluctuations are not assumed to be periodic in $x$
) whose time evolving gradient adds up algebraically to the one (constant in time) set by the background density. Yet, a restoring force prevents this back reaction from balancing the initial gradient – and therefore to annihilate it – so that the self-consistent dynamics of the system gets frustrated. Another difference with respect to more standard simulations – apart from the absence of nonlinear mode–mode coupling in Tokam1D (cf. § 2.5) – is that fluctuations are not assumed to be periodic in $x$![]() in Tokam1D.
in Tokam1D.
We choose the case $C=5\times 10^{-4}$![]() and continue the simulation while fixing the gradient. The density profile has been smoothed so that the corrugations are removed, as exemplified in figure 11(b). In figure 11(a), the equilibrium velocity $V_{\rm eq}$
and continue the simulation while fixing the gradient. The density profile has been smoothed so that the corrugations are removed, as exemplified in figure 11(b). In figure 11(a), the equilibrium velocity $V_{\rm eq}$![]() and the density fluctuation amplitude $\lvert N_k \rvert$
and the density fluctuation amplitude $\lvert N_k \rvert$![]() are shown as a function of space and time. The first half of the simulation is the steady-state FD simulation. At $t=3\times 10^4$
are shown as a function of space and time. The first half of the simulation is the steady-state FD simulation. At $t=3\times 10^4$![]() , the equilibrium density profile is smoothed using a Savitzky–Golay filter of order $3$
, the equilibrium density profile is smoothed using a Savitzky–Golay filter of order $3$![]() on a 301 point window size. The second half of the simulation corresponds to the GD regime using the smoothed density profile.
on a 301 point window size. The second half of the simulation corresponds to the GD regime using the smoothed density profile.

Figure 11. (a) Equilibrium velocity from GD restart of steady-state simulation at $C=5 \times 10^{-4}$![]() : switch from FD to GD is made at $t=3 \times 10^4$
: switch from FD to GD is made at $t=3 \times 10^4$![]() . (b) Density gradient and its radial derivative before and after the GD restart. The density profile before the restart is taken at $t=2.9 \times 10^4$
. (b) Density gradient and its radial derivative before and after the GD restart. The density profile before the restart is taken at $t=2.9 \times 10^4$![]() .
.
Figure 11(a) shows that the flows exhibit roughly the same amplitude in both FD and GD settings. However, their radial structure is very different. The chosen case is radially structured in the steady-state FD case, while no clear layering emerges in the GD case. The flow layers are still present just after the restart but this configuration cannot be sustained in the GD regime. These observations suggest that the system – at least in the regimes explored – must be able to store energy in the density (pressure) profile in addition to the flows in order to develop well-localized flow layers. In other words, the staircase structure requires two critical ingredients: localized shear flow layers in association with large density (pressure) gradients, which appear to reinforce each other. The loss of one of these ingredients prevents the appearance of the whole structure. In the GD regime, the density gradient is frozen in time so that this mechanism is absent. This symbiotic relationship between flow layers and pressure corrugations appears to be instrumental in the staircase dynamics.Footnote 3 The electrostatic potential fluctuations, plotted in figure 12(a), exhibit a slightly larger magnitude in the GD regime as compared with the FD regime. Also, their dynamics looks similar to that of the equilibrium flow in the GD regime, from $t = 3\times 10^4$![]() onwards. In particular, the radial distance of propagation of avalanches is much larger in the GD regime, sometimes reaching the system size.
onwards. In particular, the radial distance of propagation of avalanches is much larger in the GD regime, sometimes reaching the system size.

Figure 12. (a) Electric potential fluctuations for the GD restart of the steady-state simulation $C=8$![]() $10^{-4}$
$10^{-4}$![]() . (b) Radial derivative of electric potential fluctuation phase.
. (b) Radial derivative of electric potential fluctuation phase.
The presence of avalanches in itself may appear surprising. Indeed, avalanches are often understood, by analogy with sandpiles, as resulting from a domino-like effect (Diamond & Hahm Reference Diamond and Hahm1995): a localized strong flux tends to flatten the profile locally and steepens it on both sides due to conservation laws. The strong gradients on both sides then lead to strong local fluxes, further leading to local flattening. The process can repeat over long distances, resulting in the formation of voids and bumps that propagate radially up and down hill, respectively. Local profile relaxation then appears to be key to the whole dynamics. In GD simulations where the density gradient is frozen in time, this mechanism is absent and cannot therefore explain the existence of avalanches on $V_{\rm eq}$![]() . Interestingly, it appears that the electric potential fluctuations magnitude $|\phi _k|$
. Interestingly, it appears that the electric potential fluctuations magnitude $|\phi _k|$![]() and phase gradient $\partial _x\varphi _k^\phi$
and phase gradient $\partial _x\varphi _k^\phi$![]() exhibit an avalanche dynamics, as can be seen in figure 12. They both govern the electric component of the Reynolds stress, (5.1). It is so far unclear whether one or the other – or both – is the main drive for the dynamics of $V_{\rm eq}$
exhibit an avalanche dynamics, as can be seen in figure 12. They both govern the electric component of the Reynolds stress, (5.1). It is so far unclear whether one or the other – or both – is the main drive for the dynamics of $V_{\rm eq}$![]() , the other quantity being slaved to it via the back reaction of the flow shear. Note that both terms, the phase gradient and the fluctuation magnitude, are contributors to the turbulent energy. Therefore, discriminating one scenario with respect to the other is not obvious solely from an energetics standpoint. This remains an open issue for future works.
, the other quantity being slaved to it via the back reaction of the flow shear. Note that both terms, the phase gradient and the fluctuation magnitude, are contributors to the turbulent energy. Therefore, discriminating one scenario with respect to the other is not obvious solely from an energetics standpoint. This remains an open issue for future works.
6 Conclusion
The primary goal of this paper was to understand how turbulence and ZFs interact in a flux-driven formulation, resulting in a redistribution of the turbulent energy and its effect on turbulent transport. In order to achieve this, a reduced, nonlinear model, called Tokam1D, that captures the dynamics of the two key instabilities, namely the CDW and the interchange (or RBM in three dimensions) is proposed. The model, which includes both an electric and a diamagnetic Reynolds stress nonlinearities, is derived in some detail, first in a general form, and then the underlying assumptions leading to the reduction are clearly presented. It was noted that the total energy can be defined for the full flux-driven system, and shown to be conserved. A linear study shows that both instabilities are well captured by this model, showing that, with a given value of viscosity, the drift instability is saturated at both large and small values of the adiabaticity parameter $C$![]() , while the interchange exhibits a threshold in density gradient but is stabilized at very large $g$
, while the interchange exhibits a threshold in density gradient but is stabilized at very large $g$![]() due to the effect of compressibility terms.
due to the effect of compressibility terms.
These two instabilities are possibly the key players in the physics of turbulent transport at the tokamak edge, especially in density limited and $L$![]() -mode plasmas, and the reduced model allows a detailed study of the competition and the interaction between, on the one hand, the two instabilities, and on the other hand, the ZFs and the underlying turbulence, while allowing a self-consistent evolution of both the density and the poloidal flow profiles.
-mode plasmas, and the reduced model allows a detailed study of the competition and the interaction between, on the one hand, the two instabilities, and on the other hand, the ZFs and the underlying turbulence, while allowing a self-consistent evolution of both the density and the poloidal flow profiles.
Unlike GD simulations that impose a constant pressure gradient, the FD Tokam1D model enables self-consistent evolution of equilibrium profiles. This allows for a more natural representation of how turbulence interacts with background profiles, leading to more realistic saturation mechanisms, including profile relaxation, sometimes through avalanching and flow self-organization, which leads to self-organized criticality. It makes the dynamics primarily near marginal, even if it was initially far from it, possibly linked to the experimental phenomenon of profile stiffness (Mantica et al. Reference Mantica, Strintzi, Tala, Giroud, Johnson, Leggate, Lerche, Loarer, Peeters and Salmi2009).
Being a reduced 1-D model, where the fluctuation dynamics is mainly linearized and projected onto a fixed poloidal $k_{y}$![]() and parallel $k_{\parallel }$
and parallel $k_{\parallel }$![]() mode, the model focuses mainly on the interplay with ZFs and profile relaxation due to its FD nature. One can further add a nonlinear saturation term to account for mode–mode coupling, but in the absence of this proxy for nonlinear coupling, the primary saturation mechanism is that of the density profile relaxation – in the spirit of quasilinear theory – and the storage of turbulent energy in equilibrium poloidal flows. These two mechanisms play important roles in weakly forced systems that remain close to marginality.
mode, the model focuses mainly on the interplay with ZFs and profile relaxation due to its FD nature. One can further add a nonlinear saturation term to account for mode–mode coupling, but in the absence of this proxy for nonlinear coupling, the primary saturation mechanism is that of the density profile relaxation – in the spirit of quasilinear theory – and the storage of turbulent energy in equilibrium poloidal flows. These two mechanisms play important roles in weakly forced systems that remain close to marginality.
One of the issues that is considered in some detail in this paper is the dynamics and structuring of the equilibrium flow $V_{\rm eq}$![]() at vanishing $g$
at vanishing $g$![]() , which corresponds to the Hasegawa–Wakatani limit, where the effects of magnetic field inhomogeneity are neglected. We have scanned the so-called adiabaticity parameter $C$
, which corresponds to the Hasegawa–Wakatani limit, where the effects of magnetic field inhomogeneity are neglected. We have scanned the so-called adiabaticity parameter $C$![]() to study its impact on flow self-organization in this regime. The scans are usually performed with adapted magnitudes of the particle source, so that the steady-state equilibrium density gradient remains close to the linear threshold regardless of the $C$
to study its impact on flow self-organization in this regime. The scans are usually performed with adapted magnitudes of the particle source, so that the steady-state equilibrium density gradient remains close to the linear threshold regardless of the $C$![]() value (cf. figure 4). Note that, even though the role of the competition between CDW and interchange in ZF formation will be explored in a future work, several key results have already emerged from the current analysis.
value (cf. figure 4). Note that, even though the role of the competition between CDW and interchange in ZF formation will be explored in a future work, several key results have already emerged from the current analysis.
First, unlike previous numerical observations based on fixed gradient simulations that reported a sharp collapse of the ZFs at low $C$![]() , with a threshold that is proportional to the fixed gradient parameter, our results show that the energy stored in ZFs decreases smoothly as the adiabaticity parameter $C$
, with a threshold that is proportional to the fixed gradient parameter, our results show that the energy stored in ZFs decreases smoothly as the adiabaticity parameter $C$![]() is reduced. In our FD model, the absence of such a collapse can be attributed to the simultaneous adjustment of the equilibrium density profile, which provides a self-organized distribution of local gradients and therefore a distribution of local thresholds for the $C$
is reduced. In our FD model, the absence of such a collapse can be attributed to the simultaneous adjustment of the equilibrium density profile, which provides a self-organized distribution of local gradients and therefore a distribution of local thresholds for the $C$![]() parameter to compete against. This underscores the importance of self-consistent profile evolution in FD models and suggests that such models may provide a more accurate representation of tokamak edge turbulence compared with their GD counterparts. It was also observed that the electric and diamagnetic components of the Reynolds stress are large and organized in such a way that they add up at large $C$
parameter to compete against. This underscores the importance of self-consistent profile evolution in FD models and suggests that such models may provide a more accurate representation of tokamak edge turbulence compared with their GD counterparts. It was also observed that the electric and diamagnetic components of the Reynolds stress are large and organized in such a way that they add up at large $C$![]() . Unfortunately, since our model also suppresses fluctuation–fluctuation interactions, the standard dual-cascade picture of 2-D turbulence cannot be activated for any value of $C$
. Unfortunately, since our model also suppresses fluctuation–fluctuation interactions, the standard dual-cascade picture of 2-D turbulence cannot be activated for any value of $C$![]() , it is difficult to disentangle the two effects. Our results provide a clear opportunity for a 2-D FD model to resolve this issue.
, it is difficult to disentangle the two effects. Our results provide a clear opportunity for a 2-D FD model to resolve this issue.
Second, we observe that the ZFs organize themselves into staircases at both small and large $C$![]() values. The steps in these staircases can be characterized by well localized flow layers, that act as micro (particle) transport barriers leading to increased density gradients. These structures are well known in the study of plasma turbulence, and they were previously observed in FD gyrokinetic simulations of ion temperature gradient-driven turbulence (Dif-Pradalier et al. Reference Dif-Pradalier, Hornung, Garbet, Ghendrih, Grandgirard, Latu and Sarazin2017), however, the dynamics observed in our simulations – such as meandering, merging and splitting of staircase layers – underlines the complex, non-trivial dynamics of these structures.
values. The steps in these staircases can be characterized by well localized flow layers, that act as micro (particle) transport barriers leading to increased density gradients. These structures are well known in the study of plasma turbulence, and they were previously observed in FD gyrokinetic simulations of ion temperature gradient-driven turbulence (Dif-Pradalier et al. Reference Dif-Pradalier, Hornung, Garbet, Ghendrih, Grandgirard, Latu and Sarazin2017), however, the dynamics observed in our simulations – such as meandering, merging and splitting of staircase layers – underlines the complex, non-trivial dynamics of these structures.
Third, the staircases are found to be robust and to recover after a natural – or artificial – perturbation. This suggests that staircases may survive in the presence of additional physics, and mechanisms that our model lacks and therefore they may have relevance even in realistic conditions of a tokamak edge turbulence.
Finally, one of the key findings of this study is the numerical observation of the role that the phase dynamics plays in the formation of staircases. The cross-phase between density and potential fluctuations coincides with the localization and strength of the steps of the staircase, underlining the importance of properly retaining the phase dynamics in turbulence models. Importantly, the ability of ZFs to develop radial structures – i.e. well-organized steady layers that are localized radially – looks bound to the capacity of the system to store energy in the mean density (pressure) profile: in other words, the staircase pattern of the pressure profile does not appear to be the mere consequence, a simple signature of the sheared layers, but more critically a key ingredient of their generation and sustainment. These observations could be used in order to interpret and direct experimental efforts to identify these structures in real tokamak plasmas, where they are very difficult to observe.
In conclusion, this study has introduced Tokam1D, as a reduced model of turbulence capable of capturing essential aspects of FD turbulence in tokamak edge plasmas, demonstrating the key role of ZFs in regulating turbulent transport and underlining the importance of self-consistent profile evolution in FD simulations, offering new insights that could guide both theoretical and experimental efforts to better understand and control turbulence in fusion plasmas. Future work will extend this analysis to include the interplay between CDW and interchange instabilities and explore the implications for confinement and transport in more complex plasma regimes.
Acknowledgements
The authors would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programme ‘Anti-diffusive dynamics: from sub-cellular to astrophysical scales’, where work on this paper was undertaken. This work was supported by EPSRC grant EP/R014604/1. G.D.P., Y.S. and O.P. acknowledge that this work was partially supported by a grant from the Simons Foundation.
Editor Paolo Ricci thanks the referees for their advice in evaluating this article.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, partially funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 – EUROfusion). The French contribution to this work has been partially funded by the Research Federation Fusion par Confinement Magnétique (FRFCM). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union, the European Commission or SERI. Neither the European Union nor the European Commission nor FRFCM can be held responsible for them.
This work was supported by the EUROfusion Theory and Advanced Simulation Coordination (E-TASC) initiative under the TSVV (Theory, Simulation, Verification, and Validation) ‘Physics of the L-H Transition and Pedestals’ (2021–2025).
Declaration of interests
The authors report no conflict of interest.
Data availability
The data that support the findings of this study are available upon reasonable request.
Appendix A. Dual role of ion to electron temperature ratio
The role of the ion to electron temperature ratio, $\tau =T_i/T_e$![]() , in the linear instabilities is studied in the framework of Tokam1D. A more complete contribution about the role of $\tau$
, in the linear instabilities is studied in the framework of Tokam1D. A more complete contribution about the role of $\tau$![]() can be found in Casati et al. (Reference Casati, Bourdelle, Garbet and Imbeaux2008) for Ion Temperature Gradient (ITG) and Trapped Electron Mode (TEM) instabilities. The case of Tokam1D is peculiar: a single poloidal wavenumber $k_y$
can be found in Casati et al. (Reference Casati, Bourdelle, Garbet and Imbeaux2008) for Ion Temperature Gradient (ITG) and Trapped Electron Mode (TEM) instabilities. The case of Tokam1D is peculiar: a single poloidal wavenumber $k_y$![]() is chosen. Therefore, in the following we will treat both the case $k_y=cte$
is chosen. Therefore, in the following we will treat both the case $k_y=cte$![]() and the case where $k_x$
and the case where $k_x$![]() and $k_y$
and $k_y$![]() are chosen such that they maximize the growth rate, dubbed $k_y (\gamma _{\max })$
are chosen such that they maximize the growth rate, dubbed $k_y (\gamma _{\max })$![]() . We will show that $\tau$
. We will show that $\tau$![]() can be either stabilizing or destabilizing depending on the instability at play. Also, it will appear that fixing a single $k_y$
can be either stabilizing or destabilizing depending on the instability at play. Also, it will appear that fixing a single $k_y$![]() can lead to very different results as compared with the full 2-D case.
can lead to very different results as compared with the full 2-D case.
First, let us study the case with both CDW and interchange instabilities. In figure 13(a), we plot the growth rate as a function of $\tau$![]() for $4$
for $4$![]() different density gradients. The interchange parameter is fixed at $g=2 \times 10^{-3}$
different density gradients. The interchange parameter is fixed at $g=2 \times 10^{-3}$![]() and the adiabatic parameter at $C=10^{-3}$
and the adiabatic parameter at $C=10^{-3}$![]() . The growth rate is shown for the case $k_y=0.3$
. The growth rate is shown for the case $k_y=0.3$![]() in full lines and $k_y(\gamma _{\max })$
in full lines and $k_y(\gamma _{\max })$![]() in dotted lines. In figure 13(b), the value of $k_y$
in dotted lines. In figure 13(b), the value of $k_y$![]() leading to the maximal $\gamma$
leading to the maximal $\gamma$![]() is indicated for each $\tau$
is indicated for each $\tau$![]() and gradient. The horizontal dotted line indicates $k_y=0.3$
and gradient. The horizontal dotted line indicates $k_y=0.3$![]() , as chosen for Tokam1D.
, as chosen for Tokam1D.

Figure 13. (a) Growth rate as a function of $\tau$![]() for different density gradients, $C=10^{-3}$
for different density gradients, $C=10^{-3}$![]() , $g=2 \times 10^{-3}$
, $g=2 \times 10^{-3}$![]() . The case at fixed $k_y$
. The case at fixed $k_y$![]() is indicated by full lines. (b) $k_y$
is indicated by full lines. (b) $k_y$![]() corresponding to the maximum growth rate (dotted lines in a). Here, $D_1=\nu _1=10^{-2}$
corresponding to the maximum growth rate (dotted lines in a). Here, $D_1=\nu _1=10^{-2}$![]() .
.
For small $\tau$![]() , the effect on the growth rate is limited. The most prominent effect is visible for small density gradients where the growth rate increases from $\gamma \approx 0$
, the effect on the growth rate is limited. The most prominent effect is visible for small density gradients where the growth rate increases from $\gamma \approx 0$![]() at $\tau =10^{-3}$
at $\tau =10^{-3}$![]() to $\gamma =2.5 \times 10^{-3}$
to $\gamma =2.5 \times 10^{-3}$![]() at $\tau \approx 6$
at $\tau \approx 6$![]() . At larger $\tau$
. At larger $\tau$![]() , there is a large discrepancy between the cases at fixed $k_y$
, there is a large discrepancy between the cases at fixed $k_y$![]() , and the cases $k_y(\gamma _{\max })$
, and the cases $k_y(\gamma _{\max })$![]() . When several $k_y$
. When several $k_y$![]() are allowed, $\tau$
are allowed, $\tau$![]() appears to be destabilizing whereas it is stabilizing in the fixed $k_y$
appears to be destabilizing whereas it is stabilizing in the fixed $k_y$![]() case. This is a result of the ion to electron temperature ratio shifting the $k_y$
case. This is a result of the ion to electron temperature ratio shifting the $k_y$![]() value of maximum growth rate from $k_y \approx 0.35$
value of maximum growth rate from $k_y \approx 0.35$![]() to $k_y \approx 0.1$
to $k_y \approx 0.1$![]() , see figure 13(b). This highlights that Tokam1D is not suited to studying the role of large ion to electron temperature ratios in the linear and nonlinear dynamics since it requires several $k_y$
, see figure 13(b). This highlights that Tokam1D is not suited to studying the role of large ion to electron temperature ratios in the linear and nonlinear dynamics since it requires several $k_y$![]() to be described. For $\tau =1$
to be described. For $\tau =1$![]() , the growth rates for the case at fixed $k_y$
, the growth rates for the case at fixed $k_y$![]() and $k_y(\gamma _{\max })$
and $k_y(\gamma _{\max })$![]() have been observed to be similar for most of the tested equilibrium parameters. It is considered relevant.
have been observed to be similar for most of the tested equilibrium parameters. It is considered relevant.
The parameter $\tau$![]() is stabilizing as it tends towards infinity. What happens between $\tau =1$
is stabilizing as it tends towards infinity. What happens between $\tau =1$![]() and $\tau \longrightarrow +\infty$
and $\tau \longrightarrow +\infty$![]() depends on the instability at play. Displaying the same analysis as in figure 13, for the case interchange only and CDW only, one obtains the result of figure 14.
depends on the instability at play. Displaying the same analysis as in figure 13, for the case interchange only and CDW only, one obtains the result of figure 14.

Figure 14. (a) Growth rate as a function of $\tau$![]() for different density gradients, $C=10^{-3}$
for different density gradients, $C=10^{-3}$![]() , $g=0$
, $g=0$![]() . (b) Same as (a) with $C=0$
. (b) Same as (a) with $C=0$![]() and $g=2 \times 10^{-3}$
and $g=2 \times 10^{-3}$![]() . Here, $D_1=\nu _1=10^{-2}$
. Here, $D_1=\nu _1=10^{-2}$![]() .
.
For both CDW and interchange instabilities, $\tau$![]() is slightly destabilizing when small. Note that it can be enough to destabilize the system; see the case of drift waves at $1/L_N=10^{-2}$
is slightly destabilizing when small. Note that it can be enough to destabilize the system; see the case of drift waves at $1/L_N=10^{-2}$![]() which display a positive growth rate at $\tau =3$
which display a positive growth rate at $\tau =3$![]() . When larger, $\tau$
. When larger, $\tau$![]() is always stabilizing for the Tokam1D case at fixed $k_y$
is always stabilizing for the Tokam1D case at fixed $k_y$![]() but can be stabilizing or destabilizing depending on the instability at play for the general $k_y (\gamma _{\max })$
but can be stabilizing or destabilizing depending on the instability at play for the general $k_y (\gamma _{\max })$![]() case. At large $\tau$
case. At large $\tau$![]() , for the CDW case, in figure 14(a) $\tau$
, for the CDW case, in figure 14(a) $\tau$![]() is stabilizing. For interchange, $\tau$
is stabilizing. For interchange, $\tau$![]() appears as destabilizing for the general case and stabilizing for the fixed $k_y$
appears as destabilizing for the general case and stabilizing for the fixed $k_y$![]() case. The behaviour of the general case with coupled instabilities displayed figure 13 then depends on which instability is dominant.
case. The behaviour of the general case with coupled instabilities displayed figure 13 then depends on which instability is dominant.
We can conclude that $\tau$![]() exerts a dual effect on both the instabilities, depending on the dominant instability, density gradient and value of $\tau$
exerts a dual effect on both the instabilities, depending on the dominant instability, density gradient and value of $\tau$![]() . More importantly, it is made clear that Tokam1D is not suited to the study of large $\tau$
. More importantly, it is made clear that Tokam1D is not suited to the study of large $\tau$![]() since the growth rate exhibits a maximum at a poloidal wavenumber that significantly evolves with $\tau$
since the growth rate exhibits a maximum at a poloidal wavenumber that significantly evolves with $\tau$![]() .
.
Appendix B. Artificially switching off ZFs
It has now been clear that ZFs play a role in stabilizing the turbulence for more than 20 years (Lin et al. Reference Lin, Hahm, Lee, Tang and White1998). Here, we show that they are essential, even in the case where they are shown to be very small. We take a case with a low flow to turbulence energy ratio, at $C=2\times 10^{-4}$![]() and $g=10^{-4}$
and $g=10^{-4}$![]() . In this simulation, the flows account for ${\approx }0.1$
. In this simulation, the flows account for ${\approx }0.1$![]() % of the turbulence energy. We show that by artificially suppressing them, the simulation diverges and a large radial mode fills the simulation box. The results are shown in figure 15.
% of the turbulence energy. We show that by artificially suppressing them, the simulation diverges and a large radial mode fills the simulation box. The results are shown in figure 15.

Figure 15. Turbulent flux $\varGamma _{\rm turb}$![]() as a function of time and radius. The ZFs are artificially switched off at $T=3\times 10^{4}$
as a function of time and radius. The ZFs are artificially switched off at $T=3\times 10^{4}$![]() .
.
A large relaxation mode occurs when the ZFs are switched off due to the gradient being large. The profile relaxes until it gets below the linear threshold. Then the system enters a periodic state where the gradient builds up, a large radial mode appears and the profile gets relaxed.
Appendix C. Larger dissipation leads to more structured flows
What leads to the radial structure of the flows? In the presented simulations, structured flows can appear both at low and large $C$![]() , with no clear dependence on linear properties or turbulence parameters. Flows are shown to lose their structure when switching from FD to GD simulations. The source and dissipation also appear as key players when it comes to the radial structure.
, with no clear dependence on linear properties or turbulence parameters. Flows are shown to lose their structure when switching from FD to GD simulations. The source and dissipation also appear as key players when it comes to the radial structure.
We take the case $C=10^{-2}$![]() , shown figure 5(b), and we vary the dissipation coefficients in the fluctuation equations while keeping the source constant. Doing so, the linear threshold is modified as it depends directly on the dissipation. Since the source is kept constant, the distance to the linear threshold is also modified. Two cases are performed, at $D_1=\nu _1=2\times 10^{-2}$
, shown figure 5(b), and we vary the dissipation coefficients in the fluctuation equations while keeping the source constant. Doing so, the linear threshold is modified as it depends directly on the dissipation. Since the source is kept constant, the distance to the linear threshold is also modified. Two cases are performed, at $D_1=\nu _1=2\times 10^{-2}$![]() and $D_1=\nu _1 = 5\times 10^{-3}$
and $D_1=\nu _1 = 5\times 10^{-3}$![]() . The results in terms of flows and density fluctuations are shown figure 16.
. The results in terms of flows and density fluctuations are shown figure 16.

Figure 16. Variation of fluctuation dissipation coefficient $D_1$![]() and $\nu _1$
and $\nu _1$![]() . Panels show (a,c) $D_1=\nu _1=5\times 10^{-3}$
. Panels show (a,c) $D_1=\nu _1=5\times 10^{-3}$![]() , (b,d) $D_1=\nu _1=2\times 10^{-2}$
, (b,d) $D_1=\nu _1=2\times 10^{-2}$![]() . The equilibrium velocity is displayed in (a,b) while the density fluctuation amplitude is shown in (c,d).
. The equilibrium velocity is displayed in (a,b) while the density fluctuation amplitude is shown in (c,d).
In figures 16(a) and 16(b) are shown the equilibrium flows for both cases. Both ZFs have similar amplitude, with the latter being more structured and stable in time. In figures 16(c) and 16(d) are displayed the corresponding density fluctuation amplitudes. The low dissipation case leads to larger fluctuations. The size of the turbulent structures does not seem to vary much in between the two cases.
It is apparent that a larger dissipation leads to more stable flow structures. The distance to the linear threshold seems to play a role, case $D_1=\nu _1=2\times 10^{-2}$![]() evolves very close to its linear threshold, with its gradient being only $1.1$
evolves very close to its linear threshold, with its gradient being only $1.1$![]() times the linear threshold. Case $D_1=\nu _1=5\times 10^{-3}$
times the linear threshold. Case $D_1=\nu _1=5\times 10^{-3}$![]() stands far from threshold with its gradient being $2.6$
stands far from threshold with its gradient being $2.6$![]() times the linear threshold. The underlying linear characteristics of the system are similar, for the high dissipation case $\omega =0.02$
times the linear threshold. The underlying linear characteristics of the system are similar, for the high dissipation case $\omega =0.02$![]() , $\gamma =0.005$
, $\gamma =0.005$![]() and $\sin \Delta \varphi = -0.35$
and $\sin \Delta \varphi = -0.35$![]() . For the low dissipation case, $\omega =0.017$
. For the low dissipation case, $\omega =0.017$![]() , $\gamma =0.0044$
, $\gamma =0.0044$![]() and $\sin \Delta \varphi = -0.3$
and $\sin \Delta \varphi = -0.3$![]() . However, it should be noted that these characteristics are computed with the smoothed steady-state gradient and do not take into account the corrugations. Possibly, the bifurcation occurs as a result of small-scale effects. The link between corrugation, radial structure and stiffness of the system (in terms of variation of turbulent flux with density gradient) should also be explored.
. However, it should be noted that these characteristics are computed with the smoothed steady-state gradient and do not take into account the corrugations. Possibly, the bifurcation occurs as a result of small-scale effects. The link between corrugation, radial structure and stiffness of the system (in terms of variation of turbulent flux with density gradient) should also be explored.
Appendix D. Numerical implementation and verification
The 1-D radial system of equations is written in FORTRAN90 and solved using a fourth-order Runge–Kutta scheme in time and centred fourth-order finite differences in space. The dissipation terms are treated to the second order using the semi-implicit Crank–Nicolson scheme. A basic sketch of the workflow used in Tokam1D is given in figure 17. The numerical scheme is symmetric. Dissipation is applied $2$![]() times on $\Delta t/2$
times on $\Delta t/2$![]() , before and after the equation evolution. The arrays are saved every $X_d = 2 \,{{\rm d}\kern0.7pt x}$
, before and after the equation evolution. The arrays are saved every $X_d = 2 \,{{\rm d}\kern0.7pt x}$![]() and $T_d = 100 \,{\rm d}t$
and $T_d = 100 \,{\rm d}t$![]() points into HDF5 files. Neumann boundary conditions with vanishing gradients are used for the density at $x=0$
points into HDF5 files. Neumann boundary conditions with vanishing gradients are used for the density at $x=0$![]() and for the velocity at both ends. Dirichlet is used for the density imposed as $N_{\rm eq}=0.1$
and for the velocity at both ends. Dirichlet is used for the density imposed as $N_{\rm eq}=0.1$![]() at $x=L_x$
at $x=L_x$![]() and the fluctuations set to zero at both boundaries. Finally, at the end of a restart, a file is written containing arrays, parameters and boundary conditions to the maximum accuracy. A subsequent simulation can then restart from this file.
and the fluctuations set to zero at both boundaries. Finally, at the end of a restart, a file is written containing arrays, parameters and boundary conditions to the maximum accuracy. A subsequent simulation can then restart from this file.

Figure 17. Tokam1D numerical workflow.
The time step, ${\rm d}t$![]() , needs to be small with respect to the typical time involved in the system. In the present case, it should be compared with the growth rate $\gamma$
, needs to be small with respect to the typical time involved in the system. In the present case, it should be compared with the growth rate $\gamma$![]() and the real frequency $\omega$
and the real frequency $\omega$![]() of the instabilities. One needs to ensure that $\gamma \,{\rm d}t \ll 1$
of the instabilities. One needs to ensure that $\gamma \,{\rm d}t \ll 1$![]() and $\omega \,{\rm d}t \ll 1$
and $\omega \,{\rm d}t \ll 1$![]() . As shown in figure 2, these inequalities are well fulfilled since the growth rate and frequencies are, respectively, of the order of $10^{-3}$
. As shown in figure 2, these inequalities are well fulfilled since the growth rate and frequencies are, respectively, of the order of $10^{-3}$![]() and $10^{-2}$
and $10^{-2}$![]() for typical values of the parameters. When the equilibrium density profile is corrugated, it can locally develop large gradients, leading to larger values of $\gamma$
for typical values of the parameters. When the equilibrium density profile is corrugated, it can locally develop large gradients, leading to larger values of $\gamma$![]() . The conservative choice ${\rm d}t=0.1$
. The conservative choice ${\rm d}t=0.1$![]() then leaves a comfortable margin to ensure proper convergence even in these large $\gamma$
then leaves a comfortable margin to ensure proper convergence even in these large $\gamma$![]() regions.
regions.
In addition, one can compute the Courant–Friedrichs–Lewy (CFL) condition of numerical stability:
Here, $v_{\max }$![]() is the maximum characteristic speed of waves or information propagation in the simulation. In the reported simulations, the grid step size is ${{\rm d}\kern0.7pt x} = 400/1024$
is the maximum characteristic speed of waves or information propagation in the simulation. In the reported simulations, the grid step size is ${{\rm d}\kern0.7pt x} = 400/1024$![]() $\rho _s$
$\rho _s$![]() and the time step is $\omega _{\rm cs} \,{\rm d}t=0.1$
and the time step is $\omega _{\rm cs} \,{\rm d}t=0.1$![]() , where $\rho _s$
, where $\rho _s$![]() is the sound Larmor radius and $\omega _{cs}$
is the sound Larmor radius and $\omega _{cs}$![]() the ion cyclotron pulsation. The condition leads to $v_{\max } < 4$
the ion cyclotron pulsation. The condition leads to $v_{\max } < 4$![]() $\rho _{rm cs} \omega _{\rm cs} \approx 4 v_{\rm th}$
$\rho _{rm cs} \omega _{\rm cs} \approx 4 v_{\rm th}$![]() , where $v_{\rm th}$
, where $v_{\rm th}$![]() is the thermal velocity of the particles. In the framework of this reduced fluid model, we deal with drift velocities of the order of $\rho _\star v_{\rm th} \ll v_{\rm th}$
is the thermal velocity of the particles. In the framework of this reduced fluid model, we deal with drift velocities of the order of $\rho _\star v_{\rm th} \ll v_{\rm th}$![]() , where $\rho _\star = \rho _s/a \ll 1$
, where $\rho _\star = \rho _s/a \ll 1$![]() is the sound Larmor radius normalized by the minor radius of the tokamak. It results in the CFL condition being well fulfilled with the time step $\omega _{\rm cs} \,{\rm d}t=0.1$
is the sound Larmor radius normalized by the minor radius of the tokamak. It results in the CFL condition being well fulfilled with the time step $\omega _{\rm cs} \,{\rm d}t=0.1$![]() . Tests with smaller and larger time steps have shown that the simulations were actually well converged. For post-processing purposes, data are saved every $100\,{\rm d}t$
. Tests with smaller and larger time steps have shown that the simulations were actually well converged. For post-processing purposes, data are saved every $100\,{\rm d}t$![]() . The compromise is to have a sufficiently small diagnostic time step so that physical quantities exhibit a continuous dynamics, while not saving an unnecessarily large amount of data. The actual retained value ensures that the physical processes of interest are well captured even after this coarse graining in time.
. The compromise is to have a sufficiently small diagnostic time step so that physical quantities exhibit a continuous dynamics, while not saving an unnecessarily large amount of data. The actual retained value ensures that the physical processes of interest are well captured even after this coarse graining in time.
The model is first verified in the linear regime during the exponential growth of the fluctuations. With this aim, simulations are initialized with single modes $k_x = m_k 2 {\rm \pi}/L_x$![]() , with $m_k$
, with $m_k$![]() the radial mode number and $L_x$
the radial mode number and $L_x$![]() the radial size of the simulation. When scanning the launched modes $m_k$
the radial size of the simulation. When scanning the launched modes $m_k$![]() , one can check whether the exponential growth is in agreement with the linear prediction. These tests have been performed by launching GD simulations with no flows and parameters $(C,g, \tau ) = (4 \times 10^{-3}, 10^{-3}, 1)$
, one can check whether the exponential growth is in agreement with the linear prediction. These tests have been performed by launching GD simulations with no flows and parameters $(C,g, \tau ) = (4 \times 10^{-3}, 10^{-3}, 1)$![]() . A total of $9$
. A total of $9$![]() simulations are launched, with modes $m_k = 1,3,5,7,9,11,15,30,60$
simulations are launched, with modes $m_k = 1,3,5,7,9,11,15,30,60$![]() . The resulting growth rate is successfully compared with the linear prediction in figure 18.
. The resulting growth rate is successfully compared with the linear prediction in figure 18.

Figure 18. Agreement of the fluctuations’ exponential growth between simulation and linear analysis. Performed for case $(C,g, \tau ) = (4 \times 10^{-3}, 10^{-3}, 1)$![]() . Initial density profile gradient length $L_N = 50$
. Initial density profile gradient length $L_N = 50$![]() .
.
The nonlinear saturated regime of the simulations is also verified to be well resolved. Typical $k_x$![]() spectra of the fluctuations are shown to span several orders of magnitude, as shown in figure 19.
spectra of the fluctuations are shown to span several orders of magnitude, as shown in figure 19.

Figure 19. Fluctuation $k_x$![]() -spectra for the fluctuations of density $N_k$
-spectra for the fluctuations of density $N_k$![]() , electric potential $\phi _k$
, electric potential $\phi _k$![]() and vorticity $\varOmega _k$
and vorticity $\varOmega _k$![]() . Performed for the case $C=3 \times 10^{-3}$
. Performed for the case $C=3 \times 10^{-3}$![]() at statistical steady state.
at statistical steady state.