QuantiVA: quantitative verification of autonomous driving

Abstract

We present a practical verification method for safety analysis of the autonomous driving system (ADS). The main idea is to build a surrogate model that quantitatively depicts the behavior of an ADS in the specified traffic scenario. The safety properties proved in the resulting surrogate model apply to the original ADS with a probabilistic guarantee. Given the complexity of a traffic scenario in autonomous driving, our approach further partitions the parameter space of a traffic scenario for the ADS into safe sub-spaces with varying levels of guarantees and unsafe sub-spaces with confirmed counter-examples. Innovatively, the partitioning is based on a branching algorithm that features explainable AI methods. We demonstrate the utility of the proposed approach by evaluating safety properties on the state-of-the-art ADS Interfuser, with a variety of simulated traffic scenarios, and we show that our approach and existing ADS testing work complement each other. We certify five safe scenarios from the verification results and find out three sneaky behavior discrepancies in Interfuser which can hardly be detected by safety testing approaches.

Introduction

Autonomous driving systems (ADS) are anticipated to revolutionize road traffic by enhancing efficiency and safety. However, ensuring the safety of such AI-enabled systems is a critical challenge. An ADS relies on a variety of sensors, algorithms and hardware components that must work together to ensure safe and efficient driving. However, each of these components can fail or malfunction, leading to incorrect or unexpected behaviors. Additionally, environmental factors such as weather, traffic and road conditions can also affect the performance of the system. Another challenge in the reliability of autonomous driving is ensuring that the system can handle corner cases. Corner cases refer to rare scenarios that the system may encounter but are crucial for its safety, such as unexpected behavior by other drivers, pedestrian crossings, or sudden changes in road conditions. Ensuring that the system can handle these scenarios requires a rigorous testing process that covers a wide range of possible scenarios and corner cases.

ADS evaluation

The ADS evaluation encompasses both component-level and system-level assessments, using various metrics to gauge the performance and behavior of the system or its components and determine whether they meet the specified design requirements. Common component-level metrics include accuracy, precision, recall and Intersection over Union, while system-level metrics often focus on passenger experience, robustness and system latency. Public datasets are essential to ADS evaluation, with widely used datasets like nuScenes (Caesar et al. 2020), KITTI (Geiger, Lenz, and Urtasun 2012), CityScapes (Cordts et al. 2016) and ApolloScape (Huang et al. 2018) serving as valuable benchmarks. Although real-world datasets can address some evaluation needs, certain metrics – such as system latency and passenger experience – necessitate real-world road testing for more comprehensive analysis. While ADS evaluations provide a solid understanding of a system’s or component’s overall performance, their static nature limits the ability to explore corner cases, which are crucial for thorough safety assessment.

Safety assessment

Testing is a critical approach to evaluating and improving the safety of ADS. However, conducting thorough real-world testing of an ADS is impractical due to the significant resources required to build scenarios and simulate real traffic. To address this challenge, driving simulators such as CARLA (Dosovitskiy et al. 2017) and BeamNG (BeamNG GmbH 2022) have been developed, which enable testing in virtual simulated environments and significantly reduce testing costs. Various testing approaches have been developed based on these simulators to generate test cases and analyze different traffic scenarios (Fremont et al. 2019). Search-based testing approaches (Abdessalem, Nejati, et al. 2018; Arcaini, Zhang, and Ishikawa 2021; Calò et al. 2020; Borg et al. 2021; Gambi, Mueller, and Fraser 2019; Gambi, Müller, and Fraser 2019; Tian et al. 2022; Haq, Shin, and Briand 2022) are widely used for the rigorous testing of ADS. These approaches are designed to achieve comprehensive testing of the system by exploring the search space to identify different scenarios in which the system may fail. One of the main approaches is the use of meta-heuristic search techniques such as genetic algorithms and particle swarm optimization. These methods can efficiently search for optimal test cases based on various criteria, such as coverage, fault detection and diversity. Another approach is model-based testing (Abdessalem et al. 2016; Haq, Shin, and Briand 2022), where a model of the ADS is used to generate test cases. These models can be crafted using techniques such as finite-state machines, Petri nets, or hybrid systems. The generated test cases can then be used to validate the system’s behavior under different conditions. These testing approaches have identified numerous unsafe testing cases, they offer minimal safety guarantees for ADS.

Verification

In contrast to traditional testing approaches, formal verification aims to provide a mathematical proof of a given property of a system. This involves formally modeling the system and specifying the desired property in a formal language. In the context of ADS, they can be modeled as Neural Network Controlled Systems (NNCS), which combine neural networks with control systems to enable autonomous decision-making and control. Previous works have explored safety verification of NNCS based on reachability analysis. These methods utilize techniques such as activation function reduction (Ivanov et al. 2019), abstract interpretation (Tran et al. 2020) and function approximation (Ivanov et al. 2020; Ivanov et al. 2021; Huang et al. 2019; Fan et al. 2020; Huang et al. 2022). However, these white-box methods have limitations when applied to large systems like ADS. They often suffer from inefficiency due to the complexity of the neural network models. Therefore, there is a need for more efficient verification techniques that can handle the scale and complexity of ADS.

In this paper, we propose a formal verification framework for ensuring safety properties of ADS. To illustrate our methodology more vividly, we describe it and perform experiments in the context of self-driving cars, but it is applicable to a wide range of autonomous systems (such as drones) and can be extended to them without major modifications. Unlike traditional reachability analysis methods, our approach provides quantified certificates of safety properties in a more efficient and general black-box manner. To specify safety properties, we adopt the concept of fitness functions. Inspired by previous work on learning linear models from deep neural networks (Li et al. 2022), we learn a fully connected neural network (FNN) model that approximates the fitness function. Unlike testing-based approaches, the learned FNN model can be proven to be probably approximately correct (PAC), which was not achievable with prior ADS testing methods. This allows us to verify the safety property of a given ADS under various traffic scenarios with a PAC guarantee. For example, with 99.9% confidence, the ADS is collision-free with a probability of at least 99% in an emergency braking scenario. A traffic scenario can include parameters such as vehicle velocity, weather conditions and more.

The core idea of our approach is to learn a surrogate model that approximates the fitness function of the ADS with a measurable difference gap. If the surrogate model is proven to be safe, we can derive a probabilistic guarantee on the safety property for the ADS in the same scenario. In cases where the surrogate model fails to meet the safety property, we further explore its parameter space by dividing the entire space into cells based on specified parameters. We then analyze the quantified level of safety in each of these cells. This allows us to provide a quantitative verification framework that includes the formal specification of safety properties, the learned surrogate model with its probabilistic guarantee, and the analysis of safe and unsafe regions. Overall, our approach provides a more efficient and rigorous method for verifying the safety of ADS in various traffic scenarios, considering a wide range of parameters.

Our approach demonstrates significant effectiveness and advantages in verifying ADS. Firstly, compared to traditional verification methods, our approach offers a more efficient verification process. By learning a surrogate model that approximates the original ADS fitness function, we can provide probabilistic guarantees of ADS safety in a shorter timeframe. This enables us to verify the safety of ADS in a wider range of traffic scenarios, encompassing various parameters and conditions. Secondly, our approach provides quantified safety proofs. By learning the surrogate model of the fitness function, we can derive safety probabilities of ADS in different traffic scenarios. This quantified proof allows for a more accurate assessment of ADS safety and provides decision-makers with more reliable evidence. Furthermore, our approach is black-box, requiring no knowledge of the internal structure and implementation details of ADS. This makes our method more versatile and applicable to different types of ADS. Whether the ADS is based on deep learning or other technologies, our approach can effectively verify its safety. Lastly, our approach also enables analysis of safe and unsafe regions. By partitioning the parameter space into different cells, we can further analyze the safety levels within each cell. This analysis helps us better understand the behavior of ADS under different parameter combinations and provides guidance for improving the design and implementation of ADS.

The contributions of this paper are threefold:

• We propose a noval verification framework for ensuring the scenario-specific safety of ADS with a probabilistic guarantee. To our best knowledge, it is the first of its kind designed specifically for complex ADSs, providing an efficient and reliable approach for verifying ADS safety in various traffic scenarios.

• Our framework provide a new technique to perform quantitative analysis of configuration parameters for ADS. It helps identify potentially unsafe regions in the configuration space that require attention and improvement.

• We apply our verification approach and configuration space exploration method to a state-of-the-art ADS in five different traffic scenarios. The results validate the potential of learning-based verification techniques and provide evidence for the applicability of the framework in practical ADS.

Background

ADSs

An ADS is designed to assist or replace human drivers in real traffic scenarios. The level of automation of an ADS can be categorized into six levels, ranging from L0 to L5, as defined by the SAE standard. The ultimate goal is to achieve a Level 5 ADS, which can independently handle all driving tasks without any human intervention.

A modern ADS consists of various components, including sensors, perception module, prediction module, planning module and control module. The sensors collect data from the surrounding environment, while the perception module processes this data to understand the current traffic situation. The prediction module anticipates the future behavior of other road users, and the planning module generates a safe and efficient trajectory for the vehicle. Finally, the control module translates the planned trajectory into control signals to execute the desired actions.

Ensuring on-road safety properties in different traffic scenarios, such as collision-free, route completion, speed limitation, lane keeping, etc., is of paramount importance for ADS. Especially, collision-free is the key requirement among these properties, which evaluates the general safety by judging whether a collision occurs.

CARLA & scenario runner

We utilize the high-fidelity simulator CARLA, which is built on Unreal Engine 4, to generate realistic traffic scenarios for our research. CARLA offers real-time simulation capabilities for sensors, dynamic physics and traffic environments. It also provides an extensive library of traffic blueprints, including pedestrians, vehicles and street signs, making it a popular choice for developing modern ADSs such as Transfuser (Chitta et al. 2022) and LAV (Chen and Krähenbühl 2022).

In our study, we employ the Scenario Runner tool provided by CARLA to construct various traffic scenarios within the simulator. The Scenario Runner utilizes a behavior tree structure to encode the logic of each scenario. This tree consists of non-leaf control nodes (such as Select, Sequence and Parallel) and leaf nodes representing specific behaviors. By executing the scenario based on the state of its behavior tree, we can simulate and analyze the interactions and decision-making processes of the ADS in different traffic situations.

By leveraging the capabilities of CARLA and the Scenario Runner, we can create a diverse range of realistic traffic scenarios to evaluate the performance and safety of ADSs. This allows us to gain valuable insights and make informed improvements to enhance the reliability and effectiveness of these systems in real-world driving conditions.

PAC-model learning

PAC-model learning was first proposed in Li et al. (2022) to verify local robustness properties of deep neural networks. The key idea behind PAC-model learning is to train a simplified model using a subset of the original training data. This subset is carefully selected to cover the critical regions of the input space where the DNN is most sensitive to adversarial perturbations. The learned model can provide robustness guarantees for the DNN’s performance.

We state the PAC-model learning technique in a more generalized way. Let $\rho :$ $\to {\mathbb R}$ be a real-valued function with the domain $\subset {{\mathbb R}^m}$ a closed set. The purpose of PAC-model learning is to learn a model $f\left( {\theta ;\beta } \right) \in {\cal F}$ whose difference from $\rho \left( \theta \right)$ is uniformly bounded by a constant $\lambda $ as small as possible, where ${\cal F}$ is a parametric function space with parameter $\beta \in {{\mathbb R}^n}$ . Given a set of samples ${{\rm{\Theta }}_{{\rm{sample}}}}$ i.i.d from a probability distribution ${\mathbb P}$ on , the problem is reduced to an optimization problem

(1) $$\matrix{ {} \hfill & {\mathop {{\rm{min}}}\limits_{\lambda, \beta } \lambda } \hfill \cr {{\rm{s}}.{\rm{t}}.{\rm{\;\;}}} \hfill & {\left| {f\left( {\theta ;\beta } \right) - \rho \left( \theta \right)} \right| \le \lambda, {\rm{\;\;}}\forall \theta \in {{\rm{\Theta }}_{{\rm{sample}}}}.} \hfill \cr } $$

In general, the solution of (1) does not necessarily bound $\rho $ within $\lambda $ . However, the following lemma shows, the optimal solution of (1) does probably approximately correctly, if the number of samples in ${{\rm{\Theta }}_{{\rm{sample}}}}$ reaches a threshold.

Lemma 1 ((Campi, Garatti, and Prandini 2009)) Let $\varepsilon $ and $\eta $ be the pre-defined error rate and the significance level, respectively. If (1) is feasible and has an optimal solution $\left( {{\lambda ^*},{\beta ^*}} \right)$ , and $\left| {{\Theta _{sample}}} \right| = K$ with

(2) $$\epsilon \ge {2 \over K}\left( {{\rm{ln}}{1 \over \eta } + n + 1} \right),$$

then with confidence at least $1 - \eta $ , the optimal ${\lambda ^*}$ satisfies all the constraints in but only at most a fraction of probability measure $\varepsilon $ , i.e., ${\mathbb P}(\left| {f\left( {\theta ;{\beta ^{\rm{*}}}} \right) - \rho \left( \theta \right)} \right| \gt {\lambda ^{\rm{*}}}) \le \epsilon $ .t

In Li et al. (2022), the component-based learning technique is proposed to handle the situations when it is difficult to solve (1). The idea is to first learn a function $f\left( \theta \right)$ without the PAC guarantee and then estimate the margin $\lambda $ with the PAC guarantee. In this situation, the problem is reduced to the optimation problem

(3) $$\matrix{ {} \hfill & {\mathop {{\rm{min}}}\limits_{\lambda \in {\mathbb R}} \lambda } \hfill \cr {{\rm{s}}.{\rm{t}}.{\rm{\;\;}}} \hfill & {\left| {f\left( \theta \right) - \rho \left( \theta \right)} \right| \le \lambda, {\rm{\;\;}}\forall \theta \in {{\rm{\Theta }}_{{\rm{sample}}}},} \hfill \cr } $$

and the number of samples $K$ should satisfy

(4) $$\epsilon \ge {2 \over K}\left( {{\rm{ln}}{1 \over \eta } + 1} \right)$$

to establish the PAC guarantee, according to Lemma 1.

After obtaining the PAC model $f$ with a margin $\lambda $ , we can derive properties of the black-box function $\rho $ based on $f$ and $\lambda $ . These derived properties hold for $\rho $ with the same PAC guarantee. In the following section, we will demonstrate how to formally model autonomous driving scenarios and specify safety properties within these scenarios. PAC-model learning will play a crucial role in verifying these safety properties in autonomous driving scenarios.

Scenario driven safety verification

In this section, we introduce the verification framework (see Figure 1) in detail.  We first formalize the autonomous driving scenario (Section “Formalism of autonomous driving scenarios”). Then, we propose a model learning-based verification approach starting from Section “Safety verification with PAC guarantee.” When the verification cannot conclude the safety property, in Section “Configuration space exploration,” techniques are also proposed to partition the configuration space into safe/unsafe regions.

Figure 1. The verification framework. We learn a surrogate model and verify the property on it. The surrogate model is iteratively refined by incremental sampling. The whole procedure is recursive by dividing the configuration space.

Formalism of autonomous driving scenarios

An autonomous driving scenario comprises an autonomous driving agent ${\rm{ego}}$ and other NPC agents in the simulator environment. Let $\theta = \left( {{\theta _1}, \ldots .,{\theta _m}} \right) \in {[0,1]^m}$ be a configuration which consists of $m$ normalized parameters defining the scenario. Denoted by $\subseteq {[0,1]^m}$ a configuration space which represents a certain range of configurations.

Denote by ${s_t} \in S$ the status at step $t$ of all agents in the virtual world, including locations, speeds, accelerations, etc. The simulator generates the next state ${s_{t + 1}}$ according to the current state ${s_t}$ as well as the actions of both ego and NPCs at step $t$ . We call a sequence of states ${s_0},{s_1}, \ldots, {s_{{t_ \bot }}}$ a simulation generated by the simulator, where ${s_0}$ is the initial state and ${s_{{t_ \bot }}}$ is the final state satisfying some terminating conditions.

With the assumption that the behavior of the simulator and NPCs is deterministic, the simulation ${s_0},{s_1}, \ldots, {s_{{t_ \bot }}}$ is uniquely determined by the configuration $\theta $ and the behavior of ${\rm{ego}}$ . Therefore, for a fixed ${\rm{ego}}$ , i.e., an ADS need to be verified, each state ${s_t}$ in a simulation can be considered as a function ${s_t}\left( \theta \right)$ . It is important to note that the assumption of the determinacy here does not imply that the behavior or simulation environment is entirely fixed. Instead, they are varying with the aforementioned parameters. This assumption is made to establish a unified probability space by eliminating other sources of randomness.

Safety properties

We are interested in the safety requirement of critical scenarios. In traffic scenarios, many safety properties can be described as a physical quantity (such as velocity, distance, angle, etc.) always satisfying a certain threshold during the entire driving process. In autonomous driving scenarios, we define a function $\omega $ to measure such physical quantity at a given state, and the safety properties can be defined as follows.

Definition 1 (Safety Property) For a given configuration $\theta \in$ , a quantitative measure $\omega :S \to {\mathbb R}$ and a threshold $\tau \in {\mathbb R}$ , the state sequence ${s_0},{s_1}, \ldots, {s_{{t_ \bot }}}$ is safe if

(5) $$\forall t \in \left\{ {0,1, \ldots, {t_ \bot }} \right\}{\rm{\;\;}}\omega \left( {{s_t}\left( \theta \right)} \right) \ge \tau .$$

We introduce a fitness function $\rho \left( \theta \right) = {\rm{mi}}{{\rm{n}}_{0 \le i \le {t_ \bot }}}\left[ 0 \right]\omega \left( {{s_i}\left( \theta \right)} \right)$ , and the property can be equivalently rewritten as $\rho \left( \theta \right) \ge \tau $ . For instance, we can use the distance between two vehicles as the quantitative measure $\omega $ , and the collision-free property requires that the distance is no smaller than a safe threshold $\tau \gt 0$ .

We illustrate a scenario – Emergency Braking in Figure 2. The safety property is to guarantee the safe distance of $\tau = 0.2$ (m) between two vehicles. The problem is how to verify that an ADS meets the safe requirement defined by Equation (5), as a scenario can be initialized with all possible configuration values.

Figure 2. Scenario (i) Emergency Braking: the ego drives along the road while the leading NPC brakes. The configuration $\theta \in $ consists of several parameters such as NPC’s velocity, deceleration, trigger distance, etc. A function $\omega $ measures the distance between the two vehicles.

Safety verification with PAC guarantee

In general, checking a safety property is challenging because the fitness function $\rho \left( \theta \right)$ relies on the behavior models and the simulator, which cannot be explicitly expressed. Additionally, both the simulator and the ADS often operate as black boxes, further complicating the analysis. To address this challenge, we propose analyzing safety properties at two different levels: PAC-model safety and PAC safety. PAC-model safety involves constructing a surrogate model that approximates the behavior of the original ADS. This surrogate model is trained using PAC learning techniques, which provide a probabilistic guarantee of its performance. By analyzing the surrogate model, we can assess the safety properties of the original ADS with a certain level of confidence. On the other hand, PAC safety is a statistical method that directly analyzes the sample behaviors of the ADS. This approach involves collecting a set of sample behaviors and performing statistical analysis to evaluate the safety properties. While this method does not rely on a surrogate model, it still provides insights into the safety performance of the ADS.

PAC-model safety

We use a surrogate model $f$ to approximate the original fitness function $\rho $ . An illustrative example is in Figure 3 for assisting the following discussion. By extracting $K$ samples in , solving the absolute distance $\lambda $ between the surrogate model $f$ and the original fitness function $\rho $ can be reduced to the optimization problem (3). As stated in Section “PAC-model learning,” when there are sufficient samples, i.e., Equation (4) holds, the optimal absolute distance ${\lambda ^{\rm{*}}}$ we obtain satisfies the PAC guarantee ${\mathbb P}(\left| {f\left( \theta \right) - \rho \left( \theta \right)} \right| \gt {\lambda ^{\rm{*}}}) \le \epsilon $ with confidence at least $1 - \eta $ . Intuitively, the PAC model $f$ can effectively approximate the fitness function $\rho $ by given enough samples. The surrogate model in this paper adopts an FNN with the ReLU activation function, whose well-defined mathematical structure with piecewise linearity allows it to be effectively verified within a certain model size. Meanwhile, compared to simpler models (e.g., affine function), it is more expressive to model the nonlinearity characteristics of the fitness function.

Figure 3. We show the fitness function $\rho $ and the learned surrogate model $f$ w.r.t. ${\theta _1}$ (NPC’s initial velocity), by fixing other parameters. Here, $\rho $ is bounded by $f \pm {\lambda ^{\rm{*}}}$ with PAC guarantee. Note that there exist velocity values that makes the lower bound smaller than threshold $\tau $ (at bottom right corner), which violates Equation (6), i.e., the ADS may break the collision-free property.

Once obtaining the absolute distance evaluation ${\lambda ^{\rm{*}}}$ , we can utilize neural network verification tools such as DeepPoly (Singh et al. 2019) and MILP (Dutta et al. 2019) to determine whether it holds that

Here, $f\left( \theta \right) - {\lambda ^{\rm{*}}}$ serves as a probabilistic lower bound of the fitness function $\rho $ of the original model, and $\tau $ represents the threshold for safety requirements. By verifying that Equation (6) holds, we can conclude that the ADS satisfies PAC-model safety with an error rate of $\varepsilon $ and a significance level of $\eta $ . This verification process allows us to ensure that the ADS meets the required safety standards and provides a level of confidence in its performance.

PAC-model safety refers to the existence of a PAC model $f$ as the surrogate model that, when combined with the induced probability lower bound from the absolute distance estimation ${\lambda ^{\rm{*}}}$ , still guarantees safety. In other words, if we can construct a PAC model and verify the system’s safety using this model and the probability lower bound from the margin, we can trust that the system will also be safe in practical operation. By using PAC-model safety, we can validate and test ADSs in practical scenarios to ensure their safety under various conditions. This approach helps us better understand and assess the performance and reliability of ADSs, providing guidance for further improvement and optimization of the system.

PAC safety

If there is no sample in ${{\rm{\Theta }}_{{\rm{sample}}}}$ that violates the safety property, i.e., $\rho \left( \theta \right) \ge \tau $ for all $\theta \in {{\rm{\Theta }}_{{\rm{sample}}}}$ , but the probabilistic lower bound $f\left( \theta \right) - {\lambda ^{\rm{*}}}$ proves unsafe on ${\rm{\Theta }}$ , we may further lower the requirements and say that it satisfies a weaker property – PAC safety, i.e., ${\mathbb P}\left( {\rho \left( \theta \right) \ge \tau } \right) \ge 1 - \varepsilon $ with confidence at least $1 - \eta $ .

PAC safety is an statistical relaxation and extension of the strict safety. Compared to PAC-model safety, it is much weaker since it essentially only focuses on the input samples but mostly ignores the behavioral nature of the original model. For a detailed comparison, please refer to Section 2 & 5 of Li et al. (2022). Here we infer PAC safety instantly via the samples used in the verification for PAC-model safety, since by Lemma 1, the number of the samples is sufficient for estimating a constant lower bound of $\rho \left( \theta \right)$ (Anderson and Sojoudi 2023).

Surrogate model learning

As mentioned above, we adopt model learning to approximate, with the PAC guarantee in Lemma 1, the original fitness function $\rho $ . The effectiveness of the verification procedure relies heavily on the precision of the surrogate model, which is indicated by the absolute distance evaluation ${\lambda ^{\rm{*}}}$ . To obtain a small ${\lambda ^{\rm{*}}}$ , the surrogate model is trained iteratively. After each training iteration, we calculate ${\lambda ^{\rm{*}}}$ and verify whether it is PAC-model safe at this stage. If not, it means that the surrogate model $f$ is not sufficiently trained, and we need to perform incremental sampling to improve its accuracy. We propose the following three methods for incremental sampling:

1. • Uniform sampling: In order to improve the diversity of the database, we sample extra configurations uniformly. These new configurations (denoted by ${{\rm{\Theta }}_{{\rm{in}}{{\rm{c}}_{\rm{u}}}}}$ ) are randomly selected from the configuration space , following a uniform distribution. This helps to explore undiscovered areas of the configuration space.

2. • Deviated sampling: We examine the predictions of the current surrogate model and identify the configurations with the most deviated predictions, indicating the areas where the surrogate model is most inaccurate. We then sample additional configurations (denoted by ${{\rm{\Theta }}_{{\rm{in}}{{\rm{c}}_{\rm{d}}}}}$ ) in the neighborhood of these deviated samples (denoted by ${{\rm{\Theta }}_{{\rm{devi}}}}$ ) to refine the learned model. The size of such neibourhood is bounded by a constant $a$ . In our settings, we sample one additional sample near each deviated configuration ${\theta _{{\rm{devi}}}}$ uniformly from the interval $\left( {{\theta _{{\rm{devi}}}} - a,{\theta _{{\rm{devi}}}} + a} \right)$ .

3. • Surrogate-assisted sampling: We can exploit the surrogate model to generate extreme configurations that potentially maximize or minimize the predictions. These extreme configurations (denoted by ${{\rm{\Theta }}_{{\rm{sa}}}}$ ) are more likely to be over-fitted or adversarial examples. We achieve this by utilizing adversarial attacks like PGD (Goodfellow, Shlens, and Szegedy 2015). We generate the extreme configurations using the PGD attack for both optimization directions (maximization and minimization). The generated configurations are obtained by perturbing the original configurations in the direction that maximizes or minimizes the surrogate model’s predictions.

The configurations obtained through incremental sampling are added to the current training set, and the surrogate model is re-trained in the next iteration. If PAC-model safety is not proven after a certain number of iterations, it indicates that incremental sampling alone cannot significantly improve the accuracy of the surrogate model $f$ . In such cases, we employ a strategy of splitting the configuration space , and the verification procedure will proceed along different branches.

Explanation based branching

When the surrogate model is not precise enough or adversarial examples have been found, the ADS cannot prove PAC-model safe. In such situations, we employ a strategy of splitting the configuration space into smaller blocks to refine our surrogate model and improve the verification results. To determine the branching parameter for the splitting, we utilize explanation methods. Explanation methods are techniques that can quantify the importance of different parameters for a specific prediction. They provide insights into which parameters have the most significant influence on the predictions and help us understand the underlying relationships between parameters and output predictions. By analyzing the explanation results, we can gain a better understanding of the critical factors that affect the safety of the ADS.

In our implementation, we utilize the SHAP values (Lundberg and Lee 2017) as the explanation tool. SHAP values provide a measure of the contribution of each input feature to the output of a model. In our case, the scenario configurations in our settings are relatively low-dimensional, which makes SHAP values a suitable choice for feature importance analysis. The SHAP values, denoted as ${\rm{S}}{{\rm{V}}_i}\left( \theta \right)$ ( $i = 1,2, \ldots, m$ ), represent the contribution of the $i$ -th entry in the input configuration $\theta $ . By calculating the absolute mean of the SHAP values over the samples, we can determine the most important parameter, denoted as ${i^{\rm{*}}}$ , which has the highest absolute mean of SHAP values:

$${i^{\rm{*}}} = {\rm{arg\;}}\mathop {{\rm{max}}}\limits_i \mathop \sum \limits_{\theta \in {\rm{\Theta }}} \left| {{\rm{S}}{{\rm{V}}_i}\left( \theta \right)} \right|.$$

Then we accordingly bisect the current configuration space , denoted by ${\rm{Bisec}}{{\rm{t}}_{{i^{\rm{*}}}}}\:$ (), into two sub-spaces ′ and ″ by evenly splitting the range of the ${i^{\rm{*}}}$ -th entry.

This bisection process allows us to focus on refining the surrogate model in specific regions of the configuration space that are deemed to be more critical for safety. By iteratively refining the model and exploring different branches, we can improve the accuracy of the surrogate model in those areas, ultimately enhancing the precision of the verification procedure.

Main algorithm

Algorithm 1 QuantiVA

We name our verification method QuantiVA. We present the main algorithm of QuantiVA in Algorithm 1. Given a safety property $\rho \left( \theta \right) \ge \tau $ with the configuration space , we maintain a sample set ${\rm{\Theta }} \subset$ as the sample legacy for surrogate model learning. At the beginning, we ensure that ${\rm{\Theta }}$ has sufficient samples by sampling a configuration set ${{\rm{\Theta }}_0}$ and add it to ${\rm{\Theta }}$ (Line 2–3).

Now we start the iterative surrogate model learning. In each iteration, we first learn an FNN $f$ with the current set ${\rm{\Theta }}$ of samples (Line 5) and evaluate the absolute distance evaluation ${\lambda ^{\rm{*}}}$ with the PAC guarantee (Line 6–7). If PAC-model safety is proved, the algorithm terminates and return the result (Line 8–9), or otherwise it executes incremental sampling introduced in Section “Surrogate model learning” and adds these samples to ${\rm{\Theta }}$ for the next learning iteration, until the number of iterations reaches a threshold ${n_{{\rm{iter}}}}$ (Line 10–12).

Throughout the iterative surrogate model learning, we cannot prove PAC-model safety, so we have to split the current configuration space if the current branching depth $d$ is still not $0$ . We calculate the mean absolute SHAP values of each input dimension and choose the one with the largest to bisect into two sub-spaces ′ and ″ (Line 13–16). Now we divide the verification problem into two branches, and the output of this verification procedure is the union of the verification results of these two branches, initialized with the configuration space ′ and ″, the sample legacy ${\rm{\Theta }} \cap$ ′ and ${\rm{\Theta }} \cap $ ″, respectively, and the max branching depth both $d - 1$ (Line 17–18). For the branches where PAC-model safety cannot be proved and the max branching depth $d = 0$ , we output the current verification result (Line 19–22).

The output of Algorithm 1 is a set of pairs $($ $$_j,{P_j})$$ which indicates the safety level on each block. The blocks with the verification result NOT PAC-model safe must be in the branching depth $d = 0$ , so these potentially risky sub-spaces are the most fine-grained. That is to say, our verification of a safety property on a set of parametric scenarios is not simply a binary answer of being safe or not, but a detailed analysis report on which sub-spaces are highly likely to be safe (PAC-model safe), which have potential risks (PAC safe) and which are indeed unsafe with counter-examples (unsafe). These potentially risky blocks are small enough so that we may find valuable insights in why they are risky and how we improve them.

Configuration space exploration

Since an ADS is a complex combination of many components and algorithms, it is hard for them to behave safely in the whole configuration space. When the verification result is not PAC-model safe, it is meaningful to further analyze the relationship between the unsafe behavior and the parameters, which will provide an important reference for improving the system. Thus, based on the parameters we care about, which we call the associated parameters, we divide the configuration space into cells, and in a quantitative way, an indicator $\rho \in \left[ {0, + \infty } \right)$ can be computed to express how unsafe the model is within each cell.

With two associated parameters ${\theta _1} \in \left[ {{a_1},{b_1}} \right]$ and ${\theta _2} \in \left[ {{a_2},{b_2}} \right]$ , we can evenly split the two-dimensional parameter space into an $l$ -by- $l$ grid where each rectangle has the size ${{{b_1} - {a_1}} \over l} \times {{{b_2} - {a_2}} \over l}$ . Namely, the whole configuration space is divided into ${l^2}$ cells, denoted by $ = \mathop \cup \nolimits_{i,j = 0, \ldots, l - 1}$ $_{i,j}$ .

For a cell $_{i,j}$ , we define the quantitative unsafe indicatort

The quantitative unsafe indicator ${\rho _{i,j}}$ can be computed by MILP. Intuitively, each $\tau - {\rho _{i,j}}$ indicates the maximal threshold such that the surrogate model is safe with all $\theta \in$ $_{i,j}$ . The region $_{{\rm{safe}}} = \mathop \cup \nolimits_{{\rho _{i,j}} = 0}$ $_{i,j}$ is an under-approximation of the configuration region where the surrogate is safe, and a larger ${\rho _{i,j}}$ implies that the ADS is more prone to unsafe behavior in such scenarios within the corresponding configuration region. In this work, we focus on the analysis for pairs of two associated parameters since the results can be easily visualized by heat map. It is straightforward to generalize this analysis to more associated parameters.

Experiments

In this section, we evaluate QuantiVA with the state-of-the-art ADS Interfuser (Shao et al. 2023). ¹ We report the experiment results for answering the following five research questions.

• RQ1: Can QuantiVA effectively quantify the safety of an ADS in critical scenarios?

• RQ2: Can QuantiVA reveal abnormal behaviors of an ADS?

• RQ3: What are the insights from the explanations by QuantiVA?

• RQ4: What is efficiency and scalability of QuantiVA?

• RQ5: What is the relation between QuantiVA safety verification and existing testing approach for autonomous driving?

Setup

QuantiVA is implemented based on python 3.7.8 with Gurobi (Gurobi Optimization, LLC 2023) as the MILP solver. We use CARLA 0.9.10.1 to run Interfuser and build our traffic scenarios. All the experiments are conducted on two servers with AMD EYPC 7543 CPU, 128G RAM and 4 Nvidia RTX 3090. The detailed settings of our experiments are described as follows.

Safety requirement

Here, we consider the safety property of collision-free. Note that it is relevant more complex among kinds of safety properties aforementioned, since it usually involves the relationship of more than one agents. We require a safe road distance ( $0.2$ m) between the ego and the NPCs in various scenarios. Namely, we define the fitness function $\rho \left( \theta \right)$ as the minimum distance between the ego and the NPCs at every step of the simulations and require $\rho \left( \theta \right) \ge 0.2$ to hold.

Scenarios & parameters

By Scenario Runner, we build five traffic scenarios for the property, shown in Figure 2 and Figure 4. Four of them have two variants each at different locations, labeled with “Case #1” and “Case #2.” These scenarios are based on key scenarios mentioned in industry standards (Sun et al. 2022) and government documents (NHTSA 2007). There are totally 12 parameters to determine the scenarios: besides the parameters as detailed in Table 1, there are also 8 weather parameters in each scenario, including cloudness, fog density, precipitation, precipitation deposits, sun altitude angle, sun azimuth angle, wetness and wind intensity.

Figure 4. (ii) Follow Pedestrian: The ego car keeps a safe distance with the pedestrian in front. (iii) Cut-in with Obstacle: An NPC car in front of a van tries to cut into the road where the ego car drives along. (iv) Pedestrian Crossing: A pedestrian crosses the road while the ego car enters the junction. (v) Through Redlight: The ego car encounters a NPC car running the red light when crossing the junctions.

Table 1. The physical value corresponding to the range of parameters in the safety property for each scenario

Simulation

We set CARLA to the synchronous mode when conducting our scenario simulation. The time step we set is 0.05 seconds (each simulation step will forward the simulation 0.05 seconds). We build route scenarios defined by the Scenario Runner. These scenarios spawn the ego vehicle at a given spot and instruct the vehicle to reach a pre-defined position. The termination of such route scenario is either the autonomous vehicle reaching the goal or a time-out triggered. In our experiments, the time-out is set as $10$ minutes.

QuantiVA settings

For each scenario, an initial sample database was given before running QuantiVA. The total number requirement of initial samples is $1000$ in our experiments. We add extra samples if the given database doesn’t meet the requirement. The surrogate model is a 2-layer FNN with 50 neurons in each hidden layer. The error rate $\varepsilon $ and the significance level $\eta $ of the model are $0.01$ and $0.001$ respectively. The model is trained in $6$ iterations of refinement by increasing $80$ uniform samples, $10$ surrogate-assisted samples ( $5$ for each direction) and $20$ deviated samples after each iteration. The initial max branching depth is set as $d = 2$ .

Verification results

We first apply QuantiVA to evaluate the safety property on the five traffic scenarios. We start the verification on the whole configuration space and then branching the space according to the SHAP value. The execution paths of the verification form a tree, each of whose node corresponds to a configuration (sub)space that needs to be verified. The result is depicted in Figure 5, in which we additionally record the absolute difference evaluation $\lambda $ of the model and the number of adversarial examples found in the verification procedure.

Figure 5. Verification result for each scenario formed as a tree according to the branching paths. Each $\lambda $ and $\# {\rm{adv}}$ indicate the absolute distance between the surrogate model and the fitness function and the number of the adversarial examples found in such (sub)space, respectively.

The verification shows that the ADS is PAC-model/PAC safe in the scenarios (i) Emergency Braking, (ii) Follow Pedestrian and (iv.2) Pedestrian Crossing #2: It is verified to be PAC-model safe in the scenarios (i.2) & (ii.2) with the whole configuration space; Especially, it further satisfies PAC-model safe in the scenarios (i.1) & (ii.1) with the sub-spaces of ${\rm{SUN}} - {\rm{ALT}} \ge 0.5$ and ${\rm{SUN}} - {\rm{ALT}} \ge 0.5 \wedge {\rm{VELOCITY}} \le 0.5$ , respectively. In the rest scenarios, the ADS is verified to be unsafe since adversarial examples are found in the verification procedure. We also find it seems to be more dangerous in the scenarios (iii.1) Cut-in #1 & (v.1) Through Redlight, where the number of adversarial examples is enormous.

Note that we utilize the SHAP values to guide the branching in QuantiVA. The branching can help to reduce the absolute distance ${\lambda ^{\rm{*}}}$ between the surrogate model and the ground truth. For instance, in scenario (i.1) Emergency Braking #1, the distance decreases from $8.21$ to $1.32$ after branching on the condition ${\rm{SUN}} - {\rm{ALT}} \ge 0.5$ . As mentioned before, we can infer stronger safe property under smaller distance. Moreover, such branching can divide the configuration space into sub-spaces with different safety levels. In the scenario (iv.1) Pedestrian Crossing #1, it is branched into two sub-spaces containing $591/2933$ and $144/2933$ adversarial samples, respectively. It is evident that the second sub-space is safer than the first one.

Answer RQ1: QuantiVA adeptly identifies safe scenarios and validates safety properties across varying levels. It proficiently discerns the safer sub-space from the hazardous counterpart.

Abnormal behaviors

From the verification results, we have observed that the absolute distance $\lambda $ is anomalously large in some scenarios. Such occurrences prompt us to review these scenarios and analyze the behavior of the ADS. We have successfully identified outliers in the samples and traced some abnormal behaviors of Interfuser.

1. • Unexpected Stop: The autonomous vehicle halts in the middle of the road, which occurs in scenarios (i.1) Emergency Braking #1, (ii.1) Follow Pedestrian #1, and (iv.2) Pedestrian Crossing #2.

2. • Repetitive Braking: The autonomous vehicle repeatedly brakes immediately after moving forward. This occurs in scenario (iv.2) Pedestrian Crossing #2.

These abnormal behaviors violate the logic of normal driving, making the behavior of autonomous vehicles more difficult to predict, and consequently increase the absolute distance between the surrogate model and the ground truth. We closely scrutinize the intermediate output of Interfuser in these abnormal scenarios and identify the root causes of these behaviors:

1. • Crude Redlight Logic: Interfuser halts the vehicle immediately if it senses a red light, even if the vehicle is unreasonably far from the junction. This is because Interfuser cannot accurately predict the distance between the vehicle and the junction. As a result, unexpected stops occur in scenarios (i.1) Emergency Braking #1 and (ii.1) Follow Pedestrian #1.

2. • Mistaken Detection: Interfuser can produce mistaken detections of traffic lights, leading to incorrect decisions. In scenario (iv.2) Pedestrian Crossing #2, it detects a nonexistent red light and triggers braking. Coupled with the crude redlight logic, this causes the vehicle to stop in the middle of the road.

3. • Redundant Stopline Response: Interfuser can detect the stopline multiple times and engage in unnecessary braking. This triggers the repetitive braking in scenario (iv.2) Pedestrian Crossing #2.

It is difficult to detect these underlying defects through testing since they actually make the ADS more conservative and, as a result, appear to be more “safe.” QuantiVA proposes a surrogate model and further evaluates the absolute distance ${\lambda ^{\rm{*}}}$ between the surrogate model and the ground truth, where a large distance indicates a poorly learned model. Since the traffic scenarios we verify belong to the same category, the operation and outcome of an ADS should be similar and can be learned easily. Such a poorly learned model becomes an indicator of abnormal behavior in the ADS.

Answer RQ2: QuantiVA facilitates the revelation of behavioral discrepancies within the ADS. The absolute distance between the surrogate model and the ground truth serves as an indicator of such abnormal behavior.

Insights from explanation

The SHAP values of the top-3 important parameters for each scenario are visualized in Figure 6, from which we can get more explanations about the ADS as well as our verification results. The pattern of SHAP values for most parameters is spindle-shaped. This situation can be roughly understood as the influence of the parameters on the fitness function is close to a normal distribution, which is reasonable and common. However, we note that effect of a small number of parameters presents a bimodal shape showing two peaks concurrently at where SHAP values are positive and negative. For example, we consider the sun altitude angle (SUN-ALT) in #1 of scenario (i), whose SHAP implies its influence on the fitness function is polarized, either extreme positive or extreme negative. Here we can draw two insights: (1) we might be able to obtained more accurate sub-models if we divide the configuration space at this parameter. In fact, our verification results confirmed this. (2) We find a negative correlation of SUN-ALT with the value of the fitness function, which implies that the safe distance is more likely to be violated during the day, but satisfied at night – this counter-intuitive phenomenon may point to incorrect behavior or potential flaws of the ADS (see Section “Abnormal behaviors” for detailed analysis).

Figure 6. The visualization of SHAP values for the surrogate model learned for the whole configuration space in each scenario (i.e., corresponding to the root of each tree in the verification results).

As described above, we obtain explanations from the SHAP values. For more insights, the exploration of the configuration space is further conducted. For the scenario of pedestrian crossing #1, we focus on three associated parameters FOG-DENS, PREC-DEP and SUN-ALT, which are the top-3 important parameters according to the SHAP values. The analysis result is illustrated in Figure 7.

Figure 7. By heatmap, the results of parameter space exploration are illustrated for the Pedestrian Crossing #1. The grid marked with brighter color implies that the ADS is more likely to violate the safety property with the parameters in it.

From the figure (a) and (b), we find that the ADS is more likely to violate the safe distance when FOG-DENS is small. Similarly, from the figure (c), we also find that the large SUN-ALT may lead to unsafe behavior. These two conclusions are counter-intuitive, but consistent with the verification results (see the number of the adversarial examples in iv.1 of Figure 5). The underlying reason may be that the decision-making of the ADS in foggy weather is more conservative, as well as in dark environments.

The figure (d) demonstrates the exploration result in the sub-space of ${\rm{FOG}} - {\rm{DENS}} \ge 0.5$ , from which we find that the safety of ADS is almost independent of FOG-DENS but highly negatively correlated with PREC-DEP. It is also consistent with the verification results – 8 versus 227 adversarial examples in the two rightmost leaf nodes of the corresponding tree in Figure 5. More interestingly, the figure (d) exhibits a completely different pattern than that in the whole configuration space, i.e., the figure (a). It implies that the behavior of the ADS in different configuration sub-spaces may vary greatly, which further illustrates the necessity of dividing the space during surrogate model learning.

Answer RQ3: The embedded SHAP value within QuantiVA can be harnessed to yield deeper insights into ADS behavior in specific scenarios. Also, exploring the configuration space can provide further quantitative analysis of safety properties.

Efficiency

We investigate the efficiency of QuantiVA in this section. We measure the time consumed by different phases of QuantiVA individually and list the times in Table 2. It is evident that the sampling process accounts for a significant proportion of the total time. In our experiments, the average sampling time across all scenarios is $389.68$ hours, which takes about 99.98% of the total average time. This demonstrates that the learning, verification and explanation of the surrogate model are relatively lightweight compared to the sampling process. Considering that extensive sampling effort is also unavoidable in testing approaches, combining QuantiVA with testing shows promise. For instance, testing approaches can generate additional samples for training the surrogate model in verification. Meanwhile, QuantiVA can serve as a criterion to assess whether the tested scenario is safe enough and can be skipped.

Table 2. The time consumed of each phase of the verification procedures

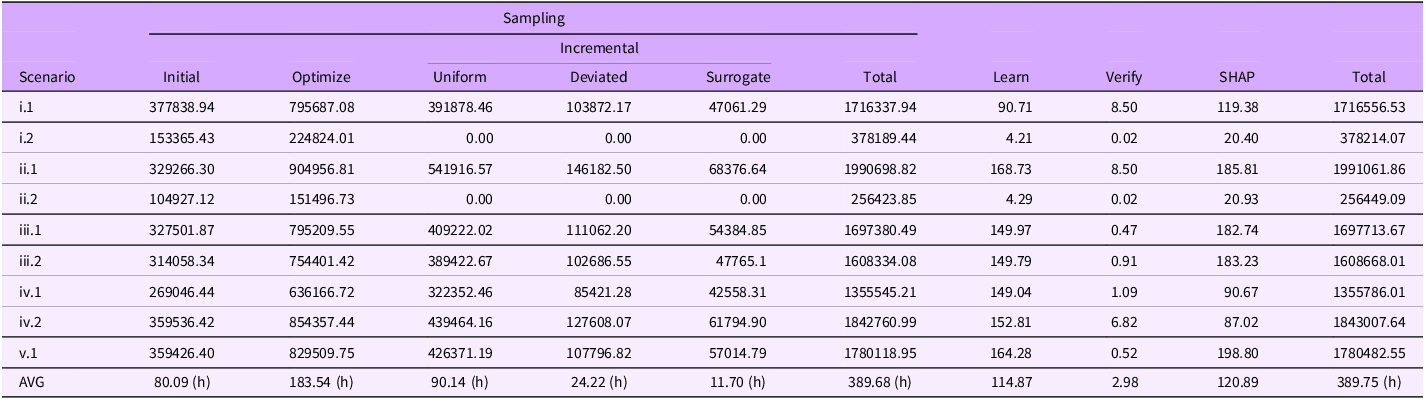
We also record the time taken by three incremental sampling approaches, namely uniform, deviated and surrogate-assisted sampling. The average time to sample by these approaches is $2.34$ , $2.51$ and $2.43$ minutes, respectively. Compared to uniform sampling, the deviated and surrogate-assisted sampling do not require significantly more time, but obtain the configurations where the surrogate model is potentially under-fitting. As a result, these two strategies can efficiently improve the accuracy of our surrogate model.

Answer RQ4: Learning, verification and explanation in QuantiVA are remarkably lightweight. The predominant time consumption arises from inevitable sampling, prompting us to consider synergizing QuantiVA with testing approaches.

Testing

We have verified that the scenarios (i) Emergency Braking and (ii) Follow Pedestrian are at least PAC safe. To validate our findings, we try to evaluate the safety in these scenarios by genetic algorithms. Genetic algorithms are widely used in prior ADS testing methods (Tian et al. 2022; Haq, Shin, and Briand 2022). We implement a genetic algorithm tester with uniform crossover and elitism. We mutate the parameters with probability $0.2$ and save top $10{\rm{\% }}$ configurations for elitism. The size of the population is $100$ . The time budget of the genetic algorithm is $14$ days. We report the testing results in Table. 3.

Table 3. The testing results for the scenario i and ii, where we show the number of generations, the minimum population fitness and the number of the adversarial examples found in the genetic testing

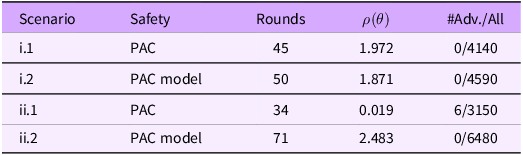
The testing results report no adversarial example in the scenarios where the ADS is verified to be PAC-model safe. For the scenarios (i.1) and (ii.1), there is also no adversarial example found in the former, but 6 in the latter. Note that the sampling in genetic algorithm is not uniform, but tends to search for the samples that violate the safety property, which somehow implies the rate of the parameters causing unsafe behavior in scenarios (ii.1) is indeed less than ${6 \over {3150}}$ , this confirms the correctness of the PAC safety (with $\varepsilon = 0.01$ ) we have verified in this scenarios.

Furthermore, by checking these adversarial examples, we observe that none of them belongs to the configuration sub-space ( ${\rm{SUN}} - {\rm{ALT}} \ge 0.5 \wedge {\rm{VELOCITY}} \le 0.5$ ) verified to be PAC-model safe (recall Figure 5). This situation is consistent with our verification results and shows that PAC-model safety is indeed a higher-level safety property compared to PAC safety.

Answer RQ5: The safety guarantee endorsed by QuantiVA aligns with the genetic testing outcomes, thereby underscoring the promising potential of integrating QuantiVA with testing approaches.

Case study on comprehensive scenario

In previous experiments, the scenarios we used were derived from critical situations outlined in standards or documentation. These scenarios were typically highly abstract and focused on isolated elements, meaning they involved fewer traffic components. In this case study, we utilize a comprehensive scenario with more complex traffic situations to demonstrate the performance of our verification framework in a denser and more intricate environment.

As shown in Figure 8, we created a multi-lane scenario with heavy traffic. This scenario includes two pedestrians walking on the sidewalk, two vehicles and a motorcycle driving near the ego vehicle. Additionally, a vehicle in front of the ego vehicle is changing lanes to the left. The two vehicles and the motorcycle are controlled by an autonomous system with a “god view” (i.e., it has access to map-level information such as the positions of surrounding vehicles). Meanwhile, the control of the tested vehicle is subject to intermittent jitters, affecting both the throttle and steering. In addition to the parameters aforementioned, such as the distance between the two vehicles and the speed of the NPCs, this scenario also includes the magnitude of the jitters, with throttle variations ranging from $0$ % to $40$ % and steering disturbances ranging from $ - 10$ % to $10$ %.

Figure 8. A comprehensive scenario under more complex traffic situations, which involves various traffic participants and intermittent jitters of the ego vehicle.

In this more complex scenario, the sampling time increased compared to simpler ones, with the average time per sample rising approximately from $2$ minutes to $3$ minutes. This increase is due to the larger number of scene elements and more intricate behaviors, resulting in a longer overall verification process. However, the rise in complexity is not exponential, and no dimensionality explosion occurs. QuantiVA remains efficient in evaluating the safety of the scenario through sampling.

Moreover, even in this more challenging setting, the neural network-based surrogate model successfully approximated the behavior of the autonomous system under test. Using this surrogate model, our incremental sampling algorithm identified $43$ corner cases. Shapley value-based interpretability analysis revealed that the most critical factor affecting safety was the distance to the lane-changing vehicle, followed by its speed. Finally, despite the increased complexity of the scenario, the verification algorithm we designed – based on DeepPoly and MILP – maintained high verification efficiency without a significant increase in the size of the surrogate model.

Related work

We discuss more results on testing, verification and probabilistic approaches. Search-based testing is studied in Dreossi et al. (2019), Sun et al. (2022), Zhong, Kaiser, and Ray (2023), Abdessalem, Nejati, et al. (2018), Arcaini, Zhang, and Ishikawa (2021), Calò et al. (2020), Borg et al. (2021), Gambi, Mueller, and Fraser (2019), Gambi, Müller, and Fraser (2019), Tian et al. (2022), Haq, Shin, and Briand (2022), Abdessalem, Panichella, et al. (2018), Klück et al. (2019), Li et al. (2020), Arcaini, Zhang, and Ishikawa (2021), Gladisch et al. (2019), Ishikawa (2020), and Luo et al. (2022). These approaches utilize optimization methods like genetic algorithm and evolution algorithm to search scenario configurations that introduce abnormal ADS behaviors. Such testing approaches cannot give safety guarantee if no violations are found through the testing trails, while QuantiVA is a good complement which can reuse the testing samples and give safety guarantee of different levels. In Tao et al. (2019), Li, Tao, and Wotawa (2020), Klück et al. (2018), Gambi, Huynh, and Fraser (2019a), Chandrasekaran et al. (2021), Zhou et al. (2020), Zhang and Cai (2023), Nguyen, Huber, and Gambi (2021), and Gambi, Huynh, and Fraser (2019b), domain knowledge is leveraged to assist the corner case discovery. Metamorphic testing approaches (Zhang et al. 2018; Tian et al. 2018; Han and Zhou 2020; Valle 2021; Deng et al. 2021) exploit the metamorphic relations to find potential dangerous cases, e.g., weather and time should not affect the control of the autonomous vehicle. QuantiVA follows such ideas and goes deeper to the influence on the behavior regarding the parameters. Runtime verification methods (Zapridou, Bartocci, and Katsaros 2020; Balakrishnan et al. 2021; An et al. 2020; Alotaibi and Zedan 2010; Bogomolov et al. 2022) monitor the ADS status and alarm the abnormal status to avoid disastrous outcome. Compared with QuantiVA, they only observe the status during execution and cannot provide global safety guarantee. Besides, components of ADS are formally verified in Xu et al. (2019), Zhang et al. (2022), Ivanov et al. (2019), Tran et al. (2020), Ivanov et al. (2020), Ivanov et al. (2021), Huang et al. (2019), Fan et al. (2020), and Huang et al. (2022). These methods work on a subset of a ADS, limited in evaluating the ADS behaviors as a whole. We note that QuantiVA is a probabilistic verification approach, and similar works include (Li et al. 2022; Anderson and Sojoudi 2023; Cardelli et al. 2019; Mangal, Nori, and Orso 2019; Webb et al. 2019; Weng et al. 2019). Our approach integrates multiple safety level and can give a more comprehensive safety assessment.

Limitations

While we believe our work have made a step forward in verifying ADS at the system-level, there are still some limitations that warrant discussion here.

One key limitation of QuantiVA is its efficacy, which can vary based on the system’s complexity and the dimensionality of the parameter space. When dealing with highly complex scenarios or resource-intensive ADSs, the sampling time may increase significantly, potentially extending the overall verification process.

Another significant limitation lies in the gap between simulation environments and real-world autonomous driving scenarios. At present, our method cannot be directly applied to real-world settings due to the challenges of modeling real-world environments solely through parameters. Furthermore, performing uniform sampling in real-world conditions is difficult, if not impossible, making the direct deployment of this framework impractical in real-world applications.

Lastly, our approach relies on black-box methods, which approximate the behavior of ADSs in various scenarios using surrogate models. However, if the surrogate model fails to sufficiently capture the original system’s behavior – due to limited expressiveness or insufficient sampling and learning – the entire verification framework may be unable to provide an accurate assessment, reducing the reliability of its results.

In terms of future work, managing intricate systems with expansive parameter spaces could be addressed by exploring lightweight pre-branching techniques to mitigate complexity. Additionally, the development of high-fidelity simulators is crucial to bridging the simulation-reality gap. Recent advancements in real traffic scenario simulation, such as those utilizing neural radiance fields [?], offer a promising direction toward achieving high-fidelity simulations. For surrogate models, we plan to investigate more expressive models – such as behavior trees – to approximate the behavior of ADS and scenario elements.

Conclusion

We introduce QuantiVA, a novel approach to verify safety properties of ADS at the scenario level. A safety property is formally specified by a fitness function with scenario configurations. A surrogate model is learned for approximating this fitness function, and the safety property verified on the surrogate model can be inherited to the ADS with specified confidence and error rate. By introducing a divide-and-conquer design to configuration space splitting, QuantiVA gives fine-grained analysis on which sub-spaces are potentially risky or even unsafe. The experiments validate the utility of our approach with promising results and vivid examples.