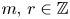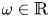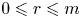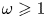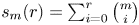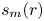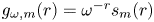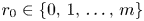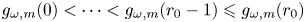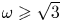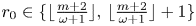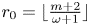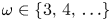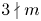1. Introduction
Given a real number $\omega \geqslant 1$![]() and integers $m,\,r$
and integers $m,\,r$![]() satisfying $0\leqslant r\leqslant m$
satisfying $0\leqslant r\leqslant m$![]() , set
, set

where the binomial coefficient $\binom{m}{i}$![]() equals $\prod _{k=1}^i\frac {m-k+1}{k}$
equals $\prod _{k=1}^i\frac {m-k+1}{k}$![]() for $i>0$
for $i>0$![]() and $\binom{m}{0}=1$
and $\binom{m}{0}=1$![]() . The weighted binomial sum $g_{\omega,m}(r)$
. The weighted binomial sum $g_{\omega,m}(r)$![]() and the partial binomial sum $s_m(r)=g_{1,m}(r)$
and the partial binomial sum $s_m(r)=g_{1,m}(r)$![]() appear in many formulas and inequalities, e.g. the cumulative distribution function $2^{-m}s_m(r)$
appear in many formulas and inequalities, e.g. the cumulative distribution function $2^{-m}s_m(r)$![]() of a binomial random variable with $p=q=\tfrac {1}{2}$
of a binomial random variable with $p=q=\tfrac {1}{2}$![]() as in remark 5.3, and the Gilbert–Varshamov bound [Reference Ling and Xing6, Theorem 5.2.6] for a code $C\subseteq \{0,\,1\}^n$
as in remark 5.3, and the Gilbert–Varshamov bound [Reference Ling and Xing6, Theorem 5.2.6] for a code $C\subseteq \{0,\,1\}^n$![]() . Partial sums of binomial coefficients are found in probability theory, coding theory, group theory, and elsewhere. As $s_m(r)$
. Partial sums of binomial coefficients are found in probability theory, coding theory, group theory, and elsewhere. As $s_m(r)$![]() cannot be computed exactly for most values of $r$
cannot be computed exactly for most values of $r$![]() , it is desirable for certain applications to find simple sharp upper and lower bounds for $s_m(r)$
, it is desirable for certain applications to find simple sharp upper and lower bounds for $s_m(r)$![]() . Our interest in bounding $2^{-r}s_m(r)$
. Our interest in bounding $2^{-r}s_m(r)$![]() was piqued in [Reference Glasby and Paseman4] by an application to Reed–Muller codes $\textrm{RM}(m,\,r)$
was piqued in [Reference Glasby and Paseman4] by an application to Reed–Muller codes $\textrm{RM}(m,\,r)$![]() , which are linear codes of dimension $s_m(r)$
, which are linear codes of dimension $s_m(r)$![]() .
.
Our main result is a generalized continued fraction $a_0 + \mathcal{K}_{i=1}^{r} \frac {b_i}{a_i}$![]() (using Gauss’ Kettenbruch notation) for $Q:=\frac {(r+1)}{s_m(r)}\binom{m}{r+1}$
(using Gauss’ Kettenbruch notation) for $Q:=\frac {(r+1)}{s_m(r)}\binom{m}{r+1}$![]() . From this we derive useful approximations to $Q,\, 2+\frac {Q}{r+1}$
. From this we derive useful approximations to $Q,\, 2+\frac {Q}{r+1}$![]() , and $s_m(r)$
, and $s_m(r)$![]() , and with these find a maximizing input $r_0$
, and with these find a maximizing input $r_0$![]() for $g_{\omega,m}(r)$
for $g_{\omega,m}(r)$![]() .
.
The $j$![]() th tail of the generalized continued fraction $\mathcal{K}_{i=1}^{r} \frac {b_i}{a_i}$
th tail of the generalized continued fraction $\mathcal{K}_{i=1}^{r} \frac {b_i}{a_i}$![]() is denoted by ${\mathcal {T}}_j$
is denoted by ${\mathcal {T}}_j$![]() where
where

If ${\mathcal {T}}_j=\frac {B_j}{A_j}$![]() , then ${\mathcal {T}}_j=\frac {b_j}{a_j+{\mathcal {T}}_{j+1}}$
, then ${\mathcal {T}}_j=\frac {b_j}{a_j+{\mathcal {T}}_{j+1}}$![]() shows $b_jA_j-a_jB_j={\mathcal {T}}_{j+1}B_j$
shows $b_jA_j-a_jB_j={\mathcal {T}}_{j+1}B_j$![]() . By convention we set ${\mathcal {T}}_{r+1}=0$
. By convention we set ${\mathcal {T}}_{r+1}=0$![]() .
.
It follows from $\binom{m}{r-i}=\binom{m}{r}\prod _{k=1}^i\frac {r-k+1}{m-r+k}$![]() that $x^i\binom{m}{r}\leqslant \binom{m}{r-i}\le y^i\binom{m}{r}$
that $x^i\binom{m}{r}\leqslant \binom{m}{r-i}\le y^i\binom{m}{r}$![]() for $0\leqslant i\leqslant r$
for $0\leqslant i\leqslant r$![]() where $x:=\frac {1}{m}$
where $x:=\frac {1}{m}$![]() and $y:=\frac {r}{m-r+1}$
and $y:=\frac {r}{m-r+1}$![]() . Hence $\frac {1-x^{r+1}}{1-x}\binom{m}{r}\leqslant s_m(r)\leqslant \frac {1-y^{r+1}}{1-y}\binom{m}{r}$
. Hence $\frac {1-x^{r+1}}{1-x}\binom{m}{r}\leqslant s_m(r)\leqslant \frac {1-y^{r+1}}{1-y}\binom{m}{r}$![]() . These bounds are close if $\frac {r}{m}$
. These bounds are close if $\frac {r}{m}$![]() is near 0. If $\frac {r}{m}$
is near 0. If $\frac {r}{m}$![]() is near $\tfrac {1}{2}$
is near $\tfrac {1}{2}$![]() then better approximations involve the Berry–Esseen inequality [Reference Nagaev and Chebotarev7] to estimate the binomial cumulative distribution function $2^{-m}s_m(r)$
then better approximations involve the Berry–Esseen inequality [Reference Nagaev and Chebotarev7] to estimate the binomial cumulative distribution function $2^{-m}s_m(r)$![]() . The cumulative distribution function $\Phi (x)=\frac {1}{\sqrt {2\pi }}\int _{-\infty }^xe^{-t^2/2}\,dt$
. The cumulative distribution function $\Phi (x)=\frac {1}{\sqrt {2\pi }}\int _{-\infty }^xe^{-t^2/2}\,dt$![]() is used in remark 5.3 to show that $|2^{-m}s_m(r)-\Phi (\frac {2r-m}{\sqrt {m}})|\leqslant \frac {0.4215}{\sqrt {m}}$
is used in remark 5.3 to show that $|2^{-m}s_m(r)-\Phi (\frac {2r-m}{\sqrt {m}})|\leqslant \frac {0.4215}{\sqrt {m}}$![]() for $0\leqslant r\leqslant m$
for $0\leqslant r\leqslant m$![]() and $m\ne 0$
and $m\ne 0$![]() . Each binomial $\binom{m}{i}$
. Each binomial $\binom{m}{i}$![]() can be estimated using Stirling's approximation as in [Reference Stănică10, p. 2]: $\binom{m}{i}=\frac {C_i^m}{\sqrt {2\pi p(1-p)m}}\left (1+O\left (\frac {1}{m}\right )\right )$
can be estimated using Stirling's approximation as in [Reference Stănică10, p. 2]: $\binom{m}{i}=\frac {C_i^m}{\sqrt {2\pi p(1-p)m}}\left (1+O\left (\frac {1}{m}\right )\right )$![]() where $C_i=\frac {1}{p^p(1-p)^{1-p}}$
where $C_i=\frac {1}{p^p(1-p)^{1-p}}$![]() and $p=p_i=i/m$
and $p=p_i=i/m$![]() . However, the sum $\sum _{i=0}^r\binom{m}{i}$
. However, the sum $\sum _{i=0}^r\binom{m}{i}$![]() of binomials is harder to approximate. The preprint [Reference Worsch11] discusses different approximations to $s_m(r)$
of binomials is harder to approximate. The preprint [Reference Worsch11] discusses different approximations to $s_m(r)$![]() .
.
Sums of binomial coefficients modulo prime powers, where $i$![]() lies in a congruence class, can be studied using number theory, see [Reference Granville5, p. 257]. Theorem 1.1 below shows how to find excellent rational approximations to $s_m(r)$
lies in a congruence class, can be studied using number theory, see [Reference Granville5, p. 257]. Theorem 1.1 below shows how to find excellent rational approximations to $s_m(r)$![]() via generalized continued fractions.
via generalized continued fractions.
Theorem 1.1 Fix $r,\,m\in {\mathbb {Z}}$![]() where $0\leqslant r\leqslant m$
where $0\leqslant r\leqslant m$![]() and recall that $s_m(r)=\sum _{i=0}^r\binom{m}{i}$
and recall that $s_m(r)=\sum _{i=0}^r\binom{m}{i}$![]() .
.
(a) If $b_i=2i(r+1-i)$
 , $a_i=m-2r+3i$
, $a_i=m-2r+3i$ for $0\leqslant i\leqslant r$
for $0\leqslant i\leqslant r$ , then
\[ Q:=\frac{(r+1)\binom{m}{r+1}}{s_m(r)}=a_0+{\vcenter{\hbox{ $\mathcal{K}$}}}_{i=1}^{r} \frac{b_i}{a_i}. \]
, then
\[ Q:=\frac{(r+1)\binom{m}{r+1}}{s_m(r)}=a_0+{\vcenter{\hbox{ $\mathcal{K}$}}}_{i=1}^{r} \frac{b_i}{a_i}. \]
(b) If $1\leqslant j\leqslant r$
 , then ${\mathcal {T}}_j=R_j/R_{j-1}>0$
, then ${\mathcal {T}}_j=R_j/R_{j-1}>0$ where the sum $R_j:= 2^j j!\sum _{k=0}^{r-j}\binom{r-k}{j}\binom{m}{k}$
where the sum $R_j:= 2^j j!\sum _{k=0}^{r-j}\binom{r-k}{j}\binom{m}{k}$ satisfies $b_j R_{j-1} - a_j R_j = R_{j+1}$
satisfies $b_j R_{j-1} - a_j R_j = R_{j+1}$ . Also, $(m-r)\binom{m}{r}-a_0R_0=R_1$
. Also, $(m-r)\binom{m}{r}-a_0R_0=R_1$ .
.
Since $s_m(m)=2^m$![]() , it follows that $s_m(m-r)=2^m-s_m(r-1)$
, it follows that $s_m(m-r)=2^m-s_m(r-1)$![]() so we focus on values of $r$
so we focus on values of $r$![]() satisfying $0\leqslant r\leqslant \lfloor \frac {m}{2}\rfloor$
satisfying $0\leqslant r\leqslant \lfloor \frac {m}{2}\rfloor$![]() . Theorem 1.1 allows us to find a sequence of successively sharper upper and lower bounds for $Q$
. Theorem 1.1 allows us to find a sequence of successively sharper upper and lower bounds for $Q$![]() (which can be made arbitrarily tight), the coarsest being $m-2r\leqslant Q\leqslant m-2r+\frac {2r}{m-2r+3}$
(which can be made arbitrarily tight), the coarsest being $m-2r\leqslant Q\leqslant m-2r+\frac {2r}{m-2r+3}$![]() for $1\leqslant r<\frac {m+3}{2}$
for $1\leqslant r<\frac {m+3}{2}$![]() , see proposition 2.3 and corollary 2.4.
, see proposition 2.3 and corollary 2.4.
The fact that the tails ${\mathcal {T}}_1,\,\ldots,\,{\mathcal {T}}_r$![]() are all positive is unexpected as $b_i/a_i$
are all positive is unexpected as $b_i/a_i$![]() is negative if $\frac {m+3i}{2}< r$
is negative if $\frac {m+3i}{2}< r$![]() . This fact is crucial for approximating ${\mathcal {T}}_1=\mathcal{K}_{i=1}^{r} \frac {b_i}{a_i}$
. This fact is crucial for approximating ${\mathcal {T}}_1=\mathcal{K}_{i=1}^{r} \frac {b_i}{a_i}$![]() , see theorem 1.3. Theorem 1.1 implies that ${\mathcal {T}}_1{\mathcal {T}}_2\cdots {\mathcal {T}}_r=R_r/R_0$
, see theorem 1.3. Theorem 1.1 implies that ${\mathcal {T}}_1{\mathcal {T}}_2\cdots {\mathcal {T}}_r=R_r/R_0$![]() . Since $R_0=s_m(r)$
. Since $R_0=s_m(r)$![]() , $R_r=2^rr!$
, $R_r=2^rr!$![]() , ${\mathcal {T}}_j=\frac {b_j}{a_j+{\mathcal {T}}_{j+1}}$
, ${\mathcal {T}}_j=\frac {b_j}{a_j+{\mathcal {T}}_{j+1}}$![]() and $\prod _{j=1}^rb_j=2^r(r!)^2$
and $\prod _{j=1}^rb_j=2^r(r!)^2$![]() , the surprising factorizations below follow c.f. remark 2.1.
, the surprising factorizations below follow c.f. remark 2.1.
Corollary 1.2 We have $s_m(r)\prod _{j=1}^r{\mathcal {T}}_j=2^rr!$![]() and $r!s_m(r)=\prod _{j=1}^r(a_j+{\mathcal {T}}_{j+1})$
and $r!s_m(r)=\prod _{j=1}^r(a_j+{\mathcal {T}}_{j+1})$![]() .
.
Suppose that $\omega >1$![]() and write $g(r)=g_{\omega,m}(r)$
and write $g(r)=g_{\omega,m}(r)$![]() . We extend the domain of $g(r)$
. We extend the domain of $g(r)$![]() by setting $g(-1)=0$
by setting $g(-1)=0$![]() and $g(m+1)=\frac {g(m)}{\omega }$
and $g(m+1)=\frac {g(m)}{\omega }$![]() in keeping with (1.1). It is easy to prove that $g(r)$
in keeping with (1.1). It is easy to prove that $g(r)$![]() is a unimodal function c.f. [Reference Byun and Poznanović2, § 2]. Hence there exists some $r_0\in \{0,\,1,\,\ldots,\,m\}$
is a unimodal function c.f. [Reference Byun and Poznanović2, § 2]. Hence there exists some $r_0\in \{0,\,1,\,\ldots,\,m\}$![]() that satisfies
that satisfies
As $g(-1)< g(0)=1$![]() and $\left (\frac {2}{\omega }\right )^m=g(m)>g(m+1)=\frac {2^m}{\omega ^{m+1}}$
and $\left (\frac {2}{\omega }\right )^m=g(m)>g(m+1)=\frac {2^m}{\omega ^{m+1}}$![]() , both chains of inequalities are non-empty. The chains of inequalities (1.3) serve to define $r_0$
, both chains of inequalities are non-empty. The chains of inequalities (1.3) serve to define $r_0$![]() .
.
We use theorem 1.1 to show that $r_0$![]() is commonly close to $r':=\lfloor \frac {m+2}{\omega +1}\rfloor$
is commonly close to $r':=\lfloor \frac {m+2}{\omega +1}\rfloor$![]() . We always have $r'\leqslant r_0$
. We always have $r'\leqslant r_0$![]() (by lemma 3.3) and though $r_0-r'$
(by lemma 3.3) and though $r_0-r'$![]() approaches $\frac {m}{2}$
approaches $\frac {m}{2}$![]() as $\omega$
as $\omega$![]() approaches 1 (see remark 4.4), if $\omega \geqslant \sqrt {3}$
approaches 1 (see remark 4.4), if $\omega \geqslant \sqrt {3}$![]() then $0\leqslant r_0 - r'\leqslant 1$
then $0\leqslant r_0 - r'\leqslant 1$![]() by the next theorem.
by the next theorem.
Theorem 1.3 If $\omega \geqslant \sqrt {3}$![]() , $m\in \{0,\,1,\,\ldots \}$
, $m\in \{0,\,1,\,\ldots \}$![]() and $r':=\lfloor \frac {m+2}{\omega +1}\rfloor$
and $r':=\lfloor \frac {m+2}{\omega +1}\rfloor$![]() , then $r_0\in \{r',\,r'+1\}$
, then $r_0\in \{r',\,r'+1\}$![]() , that is
, that is
Sharp bounds for $Q$![]() seem powerful: they enable short and elementary proofs of results that previously required substantial effort. For example, our proof in [Reference Glasby and Paseman4, Theorem 1.1] for $\omega =2$
seem powerful: they enable short and elementary proofs of results that previously required substantial effort. For example, our proof in [Reference Glasby and Paseman4, Theorem 1.1] for $\omega =2$![]() of the formula $r_0=\lfloor \frac {m}{3}\rfloor +1$
of the formula $r_0=\lfloor \frac {m}{3}\rfloor +1$![]() involved a lengthy argument, and our first proof of theorem 1.4 below involved a delicate induction. By this theorem there is a unique maximum, namely $r_0=r'=\lfloor \frac {m+2}{\omega +1}\rfloor$
involved a lengthy argument, and our first proof of theorem 1.4 below involved a delicate induction. By this theorem there is a unique maximum, namely $r_0=r'=\lfloor \frac {m+2}{\omega +1}\rfloor$![]() when $\omega \in \{3,\,4,\,5,\,\ldots \}$
when $\omega \in \{3,\,4,\,5,\,\ldots \}$![]() and $\omega \ne m+1$
and $\omega \ne m+1$![]() , c.f. remark 4.2. In particular, strict inequality $g_{\omega,m}(r'-1)< g_{\omega,m}(r')$
, c.f. remark 4.2. In particular, strict inequality $g_{\omega,m}(r'-1)< g_{\omega,m}(r')$![]() holds.
holds.
Theorem 1.4 Suppose that $\omega \in \{3,\,4,\,5,\,\ldots \}$![]() and $r'=\lfloor \frac {m+2}{\omega +1}\rfloor$
and $r'=\lfloor \frac {m+2}{\omega +1}\rfloor$![]() . Then
. Then
with equality if and only if $\omega =m+1$![]() .
.
Our motivation was to analyse $g_{\omega,m}(r)$![]() by using estimates for $Q$
by using estimates for $Q$![]() given by the generalized continued fraction in theorem 1.1. This gives tighter estimates than the method involving partial sums used in [Reference Glasby and Paseman4]. The plots of $y=g_{\omega,m}(r)$
given by the generalized continued fraction in theorem 1.1. This gives tighter estimates than the method involving partial sums used in [Reference Glasby and Paseman4]. The plots of $y=g_{\omega,m}(r)$![]() for $0\leqslant r\leqslant m$
for $0\leqslant r\leqslant m$![]() are highly asymmetrical if $\omega -1$
are highly asymmetrical if $\omega -1$![]() and $m$
and $m$![]() are small. However, if $m$
are small. However, if $m$![]() is large the plots exhibit an ‘approximate symmetry’ about the vertical line $r=r_0$
is large the plots exhibit an ‘approximate symmetry’ about the vertical line $r=r_0$![]() (see figure 1). Our observation that $r_0$
(see figure 1). Our observation that $r_0$![]() is close to $r'$
is close to $r'$![]() for many choices of $\omega$
for many choices of $\omega$![]() was the starting point of our research.
was the starting point of our research.

Figure 1. Plots of $y=g_{\omega,24}(r)$![]() for $0\leqslant r\leqslant 24$
for $0\leqslant r\leqslant 24$![]() with $\omega \in \{1,\,\frac 32,\,2,\,3\}$
with $\omega \in \{1,\,\frac 32,\,2,\,3\}$![]() , and $y=g_{3,12}(r)$
, and $y=g_{3,12}(r)$![]()
Byun and Poznanović [Reference Byun and Poznanović2, Theorem 1.1] compute the maximizing input, call it $r^*$![]() , for the function $f_{m,a}(r):=(1+a)^{-r}\sum _{i=0}^r\binom{m}{i}a^i$
, for the function $f_{m,a}(r):=(1+a)^{-r}\sum _{i=0}^r\binom{m}{i}a^i$![]() where $a\in \{1,\,2,\,\ldots \}$
where $a\in \{1,\,2,\,\ldots \}$![]() . Their function equals $g_{\omega,m}(r)$
. Their function equals $g_{\omega,m}(r)$![]() only when $\omega =1+a=2$
only when $\omega =1+a=2$![]() . Some of their results and methods are similar to those in [Reference Glasby and Paseman4] which studied the case $\omega =2$
. Some of their results and methods are similar to those in [Reference Glasby and Paseman4] which studied the case $\omega =2$![]() . They prove that $r^*=\lfloor \frac {a(m+1)+2}{2a+1}\rfloor$
. They prove that $r^*=\lfloor \frac {a(m+1)+2}{2a+1}\rfloor$![]() provided $m\not \in \{3,\,2a+4,\,4a+5\}$
provided $m\not \in \{3,\,2a+4,\,4a+5\}$![]() or $(a,\,m)\ne (1,\,12)$
or $(a,\,m)\ne (1,\,12)$![]() when $r^*=\lfloor \frac {a(m+1)+2}{2a+1}\rfloor -1$
when $r^*=\lfloor \frac {a(m+1)+2}{2a+1}\rfloor -1$![]() .
.
In Section 2 we prove theorem 1.1 and record approximations to our generalized continued fraction expansion. When $m$![]() is large, the plots of $y=g_{\omega,m}(r)$
is large, the plots of $y=g_{\omega,m}(r)$![]() are reminiscent of a normal distribution with mean $\mu \approx \frac {m}{\omega +1}$
are reminiscent of a normal distribution with mean $\mu \approx \frac {m}{\omega +1}$![]() . Section 3 proves key lemmas for estimating $r_0$
. Section 3 proves key lemmas for estimating $r_0$![]() , and applies theorem 1.1 to prove theorem 1.4. Non-integral values of $\omega$
, and applies theorem 1.1 to prove theorem 1.4. Non-integral values of $\omega$![]() are considered in Section 4 where theorem 1.3 is proved. In Section 5 we estimate the maximum height $g(r_0)$
are considered in Section 4 where theorem 1.3 is proved. In Section 5 we estimate the maximum height $g(r_0)$![]() using elementary methods and estimations, see lemma 5.1. A ‘statistical’ approximation to $s_m(r)$
using elementary methods and estimations, see lemma 5.1. A ‘statistical’ approximation to $s_m(r)$![]() is given in remark 5.3, and it is compared in remark 5.4 to the ‘generalized continued fraction approximations’ of $s_m(r)$
is given in remark 5.3, and it is compared in remark 5.4 to the ‘generalized continued fraction approximations’ of $s_m(r)$![]() in proposition 2.3.
in proposition 2.3.
2. Generalized continued fraction formulas
In this section we prove theorem 1.1, namely that $Q:=\frac {r+1}{s_m(r)}\binom{m}{r+1}=a_0+{\mathcal {T}}_1$![]() where ${\mathcal {T}}_1=\mathcal{K}_{i=1}^r\frac {b_i}{a_i}$
where ${\mathcal {T}}_1=\mathcal{K}_{i=1}^r\frac {b_i}{a_i}$![]() . The equality $s_m(r)=\frac {r+1}{a_0+{\mathcal {T}}_1}\binom{m}{r+1}$
. The equality $s_m(r)=\frac {r+1}{a_0+{\mathcal {T}}_1}\binom{m}{r+1}$![]() is noted in corollary 2.2.
is noted in corollary 2.2.
A version of theorem 1.1(a) was announced in the SCS2022 Poster room, created to run concurrently with vICM 2022, see [Reference Paseman9].
Proof Proof of theorem 1.1
Set $R_{-1}=Q\,s_m(r)=(r+1)\binom{m}{r+1}=(m-r)\binom{m}{r}$![]() and
and

Clearly $R_0=s_m(r)$![]() , $R_{r+1}=0$
, $R_{r+1}=0$![]() and $R_j>0$
and $R_j>0$![]() for $0\leqslant j\leqslant r$
for $0\leqslant j\leqslant r$![]() . We will prove in the following paragraph that the quantities $R_j$
. We will prove in the following paragraph that the quantities $R_j$![]() , $a_j=m-2r+3j$
, $a_j=m-2r+3j$![]() , and $b_j=2j(r+1-j)$
, and $b_j=2j(r+1-j)$![]() satisfy the following $r+1$
satisfy the following $r+1$![]() equations, where the first equation (2.1) is atypical:
equations, where the first equation (2.1) is atypical:
Assuming (2.2) is true, we prove by induction that ${\mathcal {T}}_{j}=R_{j}/R_{j-1}$![]() holds for $r+1\geqslant j\geqslant 1$
holds for $r+1\geqslant j\geqslant 1$![]() . This is clear for $j=r+1$
. This is clear for $j=r+1$![]() since ${\mathcal {T}}_{r+1}=R_{r+1}=0$
since ${\mathcal {T}}_{r+1}=R_{r+1}=0$![]() . Suppose that $1\leqslant j\leqslant r$
. Suppose that $1\leqslant j\leqslant r$![]() and ${\mathcal {T}}_{j+1}=R_{j+1}/R_{j}$
and ${\mathcal {T}}_{j+1}=R_{j+1}/R_{j}$![]() holds. We show that ${\mathcal {T}}_{j}=R_{j}/R_{j-1}$
holds. We show that ${\mathcal {T}}_{j}=R_{j}/R_{j-1}$![]() holds. Using (2.2) and $R_j>0$
holds. Using (2.2) and $R_j>0$![]() we have $b_jR_{j-1}/R_j-a_j=R_{j+1}/R_j={\mathcal {T}}_{j+1}$
we have $b_jR_{j-1}/R_j-a_j=R_{j+1}/R_j={\mathcal {T}}_{j+1}$![]() . Hence $R_j/R_{j-1}=b_j/(a_j+{\mathcal {T}}_{j+1})={\mathcal {T}}_j$
. Hence $R_j/R_{j-1}=b_j/(a_j+{\mathcal {T}}_{j+1})={\mathcal {T}}_j$![]() , completing the induction. Equation (2.1) gives $Q=R_{-1}/R_0=a_0+R_1/R_{0}=a_0+{\mathcal {T}}_1$
, completing the induction. Equation (2.1) gives $Q=R_{-1}/R_0=a_0+R_1/R_{0}=a_0+{\mathcal {T}}_1$![]() as claimed. Since $R_j>0$
as claimed. Since $R_j>0$![]() for $0\leqslant j\leqslant r$
for $0\leqslant j\leqslant r$![]() , we have ${\mathcal {T}}_{j}=R_{j}/R_{j-1}>0$
, we have ${\mathcal {T}}_{j}=R_{j}/R_{j-1}>0$![]() for $1\leqslant j\leqslant r$
for $1\leqslant j\leqslant r$![]() . This proves the first half of theorem 1.1(b), and the recurrence ${\mathcal {T}}_j=b_j/(a_j+{\mathcal {T}}_{j+1})$
. This proves the first half of theorem 1.1(b), and the recurrence ${\mathcal {T}}_j=b_j/(a_j+{\mathcal {T}}_{j+1})$![]() for $1\leqslant j\leqslant r$
for $1\leqslant j\leqslant r$![]() , proves part (a).
, proves part (a).
We now show that (2.1) holds. The identity $R_0=2^00!\sum _{k=0}^r\binom{m}{k}=s_m(r)$![]() gives
gives

As $(i+1)\binom{m}{i+1}=(m-i)\binom{m}{i}$![]() , we get $R_{-1}-a_0R_0=2\sum _{k=0}^{r-1}\binom{r-k}{1}\binom{m}{k}=R_1$
, we get $R_{-1}-a_0R_0=2\sum _{k=0}^{r-1}\binom{r-k}{1}\binom{m}{k}=R_1$![]() .
.
We next show that (2.2) holds. In order to simplify our calculations, we divide by $C_{j}:= 2^j j!$![]() . Using $(j+1)\binom{r-k}{j+1}=(r-k-j)\binom{r-k}{j}$
. Using $(j+1)\binom{r-k}{j+1}=(r-k-j)\binom{r-k}{j}$![]() gives
gives

noting that the term with $k=r-j+1$![]() in the first sum is zero as $\binom{j-1}{j}=0$
in the first sum is zero as $\binom{j-1}{j}=0$![]() . Using the abbreviation $L=\sum _{k=0}^{r-j}(k-2r+3j)\binom{r-k}{j}\binom{m}{k}$
. Using the abbreviation $L=\sum _{k=0}^{r-j}(k-2r+3j)\binom{r-k}{j}\binom{m}{k}$![]() and using the identity $j\binom{r-k}{j}=(r+1-j-k)\binom{r-k}{j-1}$
and using the identity $j\binom{r-k}{j}=(r+1-j-k)\binom{r-k}{j-1}$![]() gives
gives

However, $k\binom{m}{k}=(m-k+1)\binom{m}{k-1}$![]() , and therefore,
, and therefore,

Thus

Hence $\frac {R_{j+1}}{C_{j}}=\frac {b_{j}R_{j-1}}{C_{j}}-\frac {a_{j}R_{j}}{C_{j}}$![]() for $1\leqslant j\leqslant r$
for $1\leqslant j\leqslant r$![]() . When $j=r$
. When $j=r$![]() , our convention gives $R_{r+1}=0$
, our convention gives $R_{r+1}=0$![]() . This proves part (b) and completes the proof of part (a).
. This proves part (b) and completes the proof of part (a).
Remark 2.1 View $m$![]() as an indeterminant, so that $r!s_m(r)$
as an indeterminant, so that $r!s_m(r)$![]() is a polynomial in $m$
is a polynomial in $m$![]() over ${\mathbb {Z}}$
over ${\mathbb {Z}}$![]() of degree $r$
of degree $r$![]() . The factorization $r!s_m(r)=\prod _{j=1}^r(a_j+{\mathcal {T}}_{j+1})$
. The factorization $r!s_m(r)=\prod _{j=1}^r(a_j+{\mathcal {T}}_{j+1})$![]() in corollary 1.2 involves the rational functions $a_j+{\mathcal {T}}_{j+1}$
in corollary 1.2 involves the rational functions $a_j+{\mathcal {T}}_{j+1}$![]() . However, theorem 1.1(b) gives ${\mathcal {T}}_{j+1}=\frac {R_{j+1}}{R_{j}}$
. However, theorem 1.1(b) gives ${\mathcal {T}}_{j+1}=\frac {R_{j+1}}{R_{j}}$![]() , so that $a_j+{\mathcal {T}}_{j+1}=\frac {a_{j}R_{j}+R_{j+1}}{R_j}=\frac {b_{j}R_{j-1}}{R_j}$
, so that $a_j+{\mathcal {T}}_{j+1}=\frac {a_{j}R_{j}+R_{j+1}}{R_j}=\frac {b_{j}R_{j-1}}{R_j}$![]() . This determines the numerator and denominator of the rational function $a_j+{\mathcal {T}}_{j+1}$
. This determines the numerator and denominator of the rational function $a_j+{\mathcal {T}}_{j+1}$![]() , and explains why we have $\prod _{j=1}^r(a_j+{\mathcal {T}}_{j+1})= \frac {R_0}{R_r}\prod _{j=1}^rb_{j}=r!s_m(r)$
, and explains why we have $\prod _{j=1}^r(a_j+{\mathcal {T}}_{j+1})= \frac {R_0}{R_r}\prod _{j=1}^rb_{j}=r!s_m(r)$![]() . This is different from, but reminiscent of, the ratio $p_{j+1}/p_j$
. This is different from, but reminiscent of, the ratio $p_{j+1}/p_j$![]() described on p. 26 of [Reference Olds8]. $\diamond$
described on p. 26 of [Reference Olds8]. $\diamond$![]()
Corollary 2.2 If $r,\,m\in {\mathbb {Z}}$![]() and $0< r< m$
and $0< r< m$![]() , then
, then

If $r=0$![]() , then $s_m(r)=\frac {(r+1)\binom{m}{r+1}}{m-2r+{\mathcal {T}}_1}$
, then $s_m(r)=\frac {(r+1)\binom{m}{r+1}}{m-2r+{\mathcal {T}}_1}$![]() is true, but ${\mathcal {T}}_1=\mathcal{K}_{i=1}^r\frac {2i(r+1-i)}{m-2r+3i}=0$
is true, but ${\mathcal {T}}_1=\mathcal{K}_{i=1}^r\frac {2i(r+1-i)}{m-2r+3i}=0$![]() .
.
We will need some additional tools such as proposition 2.3 and corollary 2.4 below in order to prove theorem 1.3.
Since $s_m(m-r)=2^m-s_m(r-1)$![]() approximating $s_m(r)$
approximating $s_m(r)$![]() for $0\leqslant r\leqslant m$
for $0\leqslant r\leqslant m$![]() reduces to approximating $s_m(r)$
reduces to approximating $s_m(r)$![]() for $0\leqslant r\leqslant \lfloor \frac {m}{2}\rfloor$
for $0\leqslant r\leqslant \lfloor \frac {m}{2}\rfloor$![]() . Hence the hypothesis $r<\frac {m+3}{2}$
. Hence the hypothesis $r<\frac {m+3}{2}$![]() in proposition 2.3 and corollary 2.4 is not too restrictive. Proposition 2.3 generalizes [Reference Olds8, Theorem 3.3].
in proposition 2.3 and corollary 2.4 is not too restrictive. Proposition 2.3 generalizes [Reference Olds8, Theorem 3.3].
Let ${\mathcal {H}}_j:=\mathcal{K}_{i=1}^j\frac {b_i}{a_i}$![]() denote the $j$
denote the $j$![]() th head of the fraction $\mathcal{K}_{i=1}^r\frac {b_i}{a_i}$
th head of the fraction $\mathcal{K}_{i=1}^r\frac {b_i}{a_i}$![]() , where ${\mathcal {H}}_0=0$
, where ${\mathcal {H}}_0=0$![]() .
.
Proposition 2.3 Let $b_i=2i(r+1-i)$![]() and $a_i=m-2r+3i$
and $a_i=m-2r+3i$![]() for $0\leqslant i\leqslant r$
for $0\leqslant i\leqslant r$![]() . If $r<\frac {m+3}{2}$
. If $r<\frac {m+3}{2}$![]() , then $a_0+{\mathcal {H}}_r=\frac {(r+1)\binom{m}{r+1}}{s_m(r)}$
, then $a_0+{\mathcal {H}}_r=\frac {(r+1)\binom{m}{r+1}}{s_m(r)}$![]() can be approximated using the following chain of inequalities
can be approximated using the following chain of inequalities
Proof. Note that $r$![]() equals either $2\lfloor r/2\rfloor$
equals either $2\lfloor r/2\rfloor$![]() or $2\lfloor (r-1)/2\rfloor +1$
or $2\lfloor (r-1)/2\rfloor +1$![]() , depending on its parity.
, depending on its parity.
We showed in the proof of theorem 1.1 that $\frac {(r+1)\binom{m}{r+1}}{s_m(r)}=a_0+{\mathcal {H}}_r=a_0+\mathcal{K}_{i=1}^r\frac {b_i}{a_i}$![]() . Since $r<\frac {m+3}{2}$
. Since $r<\frac {m+3}{2}$![]() , we have $a_i>0$
, we have $a_i>0$![]() and $b_i>0$
and $b_i>0$![]() for $1\leqslant i\leqslant r$
for $1\leqslant i\leqslant r$![]() and hence $\frac {b_i}{a_i}>0$
and hence $\frac {b_i}{a_i}>0$![]() . A straightforward induction (which we omit) depending on the parity of $r$
. A straightforward induction (which we omit) depending on the parity of $r$![]() proves that ${\mathcal {H}}_0<{\mathcal {H}}_2<\cdots <{\mathcal {H}}_{2\lfloor r/2\rfloor }<{\mathcal {H}}_{2\lfloor (r-1)/2\rfloor +1}<\cdots <{\mathcal {H}}_3<{\mathcal {H}}_1$
proves that ${\mathcal {H}}_0<{\mathcal {H}}_2<\cdots <{\mathcal {H}}_{2\lfloor r/2\rfloor }<{\mathcal {H}}_{2\lfloor (r-1)/2\rfloor +1}<\cdots <{\mathcal {H}}_3<{\mathcal {H}}_1$![]() . For example, if $r=3$
. For example, if $r=3$![]() , then
, then

proves ${\mathcal {H}}_0<{\mathcal {H}}_2<{\mathcal {H}}_3<{\mathcal {H}}_1$![]() as the tails are positive. Adding $a_0$
as the tails are positive. Adding $a_0$![]() proves the claim.
proves the claim.
In asking whether $g_{\omega,m}(r)$![]() is a unimodal function, it is natural to consider the ratio $g_{\omega,m}(r+1)/g_{\omega,m}(r)$
is a unimodal function, it is natural to consider the ratio $g_{\omega,m}(r+1)/g_{\omega,m}(r)$![]() of successive terms. This suggests defining
of successive terms. This suggests defining
We will prove in lemma 3.1 that $t(r)$![]() is a strictly decreasing function that determines when $g_{\omega,m}(r)$
is a strictly decreasing function that determines when $g_{\omega,m}(r)$![]() is increasing or decreasing, and $t_{m}(r_0-1)\geqslant \omega >t_{m}(r_0)$
is increasing or decreasing, and $t_{m}(r_0-1)\geqslant \omega >t_{m}(r_0)$![]() determines $r_0$
determines $r_0$![]() .
.
Corollary 2.4 We have $m-2r\leqslant \frac {(r+1)\binom{m}{r+1}}{s_m(r)}$![]() for $r\geqslant 0$
for $r\geqslant 0$![]() , and
, and
Hence $\frac {m+2}{r+1}\leqslant t_m(r)+1$![]() for $r\geqslant 0$
for $r\geqslant 0$![]() , and
, and
Also $\frac {m+2}{r+1}< t_m(r)+1$![]() for $r>0$
for $r>0$![]() , and the above upper bound is strict for $1< r<\frac {m+3}{2}$
, and the above upper bound is strict for $1< r<\frac {m+3}{2}$![]() .
.
Proof. We proved $Q=\frac {(r+1)\binom{m}{r}}{s_m(r)}=(m-2r)+\mathcal{K}_{i=1}^r\frac {2i(r+1-i)}{m-2r+3i}$![]() in theorem 1.1. Hence $m-2r=\frac {(r+1)\binom{m}{r+1}}{s_m(r)}$
in theorem 1.1. Hence $m-2r=\frac {(r+1)\binom{m}{r+1}}{s_m(r)}$![]() if $r=0$
if $r=0$![]() and $m-2r<\frac {(r+1)\binom{m}{r+1}}{s_m(r)}$
and $m-2r<\frac {(r+1)\binom{m}{r+1}}{s_m(r)}$![]() if $1\leqslant r<\frac {m+3}{2}$
if $1\leqslant r<\frac {m+3}{2}$![]() by proposition 2.3. Clearly $m-2r<0\le \frac {(r+1)\binom{m}{r+1}}{s_m(r)}$
by proposition 2.3. Clearly $m-2r<0\le \frac {(r+1)\binom{m}{r+1}}{s_m(r)}$![]() if $\frac {m+3}{2}\le r\le m$
if $\frac {m+3}{2}\le r\le m$![]() . Similarly $\frac {(r+1)\binom{m}{r+1}}{s_m(r)}= m-2r+\frac {2r}{m-2r+3}$
. Similarly $\frac {(r+1)\binom{m}{r+1}}{s_m(r)}= m-2r+\frac {2r}{m-2r+3}$![]() if $r=0,\,1$
if $r=0,\,1$![]() , and again proposition 2.3 shows that ${\frac {(r+1)\binom{m}{r+1}}{s_m(r)}< m-2r+\frac {2r}{m-2r+3}}$
, and again proposition 2.3 shows that ${\frac {(r+1)\binom{m}{r+1}}{s_m(r)}< m-2r+\frac {2r}{m-2r+3}}$![]() if $1< r<\frac {m+3}{2}$
if $1< r<\frac {m+3}{2}$![]() . The remaining inequalities (and equalities) follow similarly since $t_m(r)+1=2+\frac {\binom{m}{r+1}}{s_m(r)}$
. The remaining inequalities (and equalities) follow similarly since $t_m(r)+1=2+\frac {\binom{m}{r+1}}{s_m(r)}$![]() and $2+\frac {m-2r}{r+1}=\frac {m+2}{r+1}$
and $2+\frac {m-2r}{r+1}=\frac {m+2}{r+1}$![]() .
.
3. Estimating the maximizing input $r_0$
Fix $\omega >1$![]() . In this section we consider the function $g(r)=g_{\omega,m}(r)$
. In this section we consider the function $g(r)=g_{\omega,m}(r)$![]() given by (1.1). As seen in table 1, it is easy to compute $g(r)$
given by (1.1). As seen in table 1, it is easy to compute $g(r)$![]() if $r$
if $r$![]() is near $0$
is near $0$![]() or $m$
or $m$![]() . For $m$
. For $m$![]() large and $r$
large and $r$![]() near $0$
near $0$![]() , we have ‘sub-exponential’ growth $g(r)\approx \frac {m^r}{r!\omega ^r}$
, we have ‘sub-exponential’ growth $g(r)\approx \frac {m^r}{r!\omega ^r}$![]() . Similarly for $r$
. Similarly for $r$![]() near $m$
near $m$![]() , we have exponential decay $g(r)\approx \frac {2^m}{\omega ^r}$
, we have exponential decay $g(r)\approx \frac {2^m}{\omega ^r}$![]() . The middle values require more thought.
. The middle values require more thought.
Table 1. Values of $g_{w,m}(r)$![]()

On the other hand, the plots $y=g(r)$![]() , $0\leqslant r\leqslant m$
, $0\leqslant r\leqslant m$![]() , exhibit a remarkable visual symmetry when $m$
, exhibit a remarkable visual symmetry when $m$![]() is large. The relation $s_m(m-r)=2^m-s_m(r-1)$
is large. The relation $s_m(m-r)=2^m-s_m(r-1)$![]() and the distorting scale factor of $\omega ^{-r}$
and the distorting scale factor of $\omega ^{-r}$![]() shape the plots. The examples in figure 1 show an approximate left–right symmetry about a maximizing input $r\approx \frac {m}{\omega +1}$
shape the plots. The examples in figure 1 show an approximate left–right symmetry about a maximizing input $r\approx \frac {m}{\omega +1}$![]() . It surprised the authors that in many cases there exists a simple exact formula for the maximizing input (it is usually unique as corollary 3.2 suggests). In figure 1 we have used different scale factors for the $y$
. It surprised the authors that in many cases there exists a simple exact formula for the maximizing input (it is usually unique as corollary 3.2 suggests). In figure 1 we have used different scale factors for the $y$![]() -axes. The maximum value of $g_{\omega,m}(r)$
-axes. The maximum value of $g_{\omega,m}(r)$![]() varies considerably as $\omega$
varies considerably as $\omega$![]() varies (c.f. lemma 5.1), so we scaled the maxima (rounded to the nearest integer) to the same height.
varies (c.f. lemma 5.1), so we scaled the maxima (rounded to the nearest integer) to the same height.
Lemma 3.1 Recall that $g(r)=\omega ^{-r} s_m(r)$![]() by (1.1) and $t(r)=\frac {s_m(r+1)}{s_m(r)}$
by (1.1) and $t(r)=\frac {s_m(r+1)}{s_m(r)}$![]() by (2.3).
by (2.3).
(a) $t(r-1)>t(r)>\frac {m-r}{r+1}$
 for $0\leqslant r\leqslant m$
for $0\leqslant r\leqslant m$ where $t(-1):=\infty$
where $t(-1):=\infty$ ;
;(b) $g(r)< g(r+1)$
 if and only if $t(r)>\omega$
if and only if $t(r)>\omega$ ;
;(c) $g(r)\leqslant g(r+1)$
 if and only if $t(r)\geqslant \omega$
if and only if $t(r)\geqslant \omega$ ;
;(d) $g(r)> g(r+1)$
 if and only if $\omega > t(r)$
if and only if $\omega > t(r)$ ;
;(e) $g(r)\geqslant g(r+1)$
 if and only if $\omega \geqslant t(r)$
if and only if $\omega \geqslant t(r)$ ;
;(f) if $\omega >1$
 then some $r_0\in \{0,\,\ldots,\,m\}$
then some $r_0\in \{0,\,\ldots,\,m\}$ satisfies $t(r_0-1)\geqslant \omega > t(r_0)$
satisfies $t(r_0-1)\geqslant \omega > t(r_0)$ , and this condition is equivalent to
\[ g(0)<\cdots < g(r_0-1)\leqslant g(r_0) \quad {\rm and}\quad g(r_0)>\cdots >g(m). \]
, and this condition is equivalent to
\[ g(0)<\cdots < g(r_0-1)\leqslant g(r_0) \quad {\rm and}\quad g(r_0)>\cdots >g(m). \]
Proof. (a) We prove, using induction on $r$![]() , that $t(r-1)>t(r)>\binom{m}{r+1}/\binom{m}{r}$
, that $t(r-1)>t(r)>\binom{m}{r+1}/\binom{m}{r}$![]() holds for $0\leqslant r\leqslant m$
holds for $0\leqslant r\leqslant m$![]() . These inequalities are clear for $r=0$
. These inequalities are clear for $r=0$![]() as $\infty >m+1>m$
as $\infty >m+1>m$![]() . For real numbers $\alpha,\,\beta,\,\gamma,\,\delta >0$
. For real numbers $\alpha,\,\beta,\,\gamma,\,\delta >0$![]() , we have $\alpha \delta -\beta \gamma >0$
, we have $\alpha \delta -\beta \gamma >0$![]() if and only if $\frac {\alpha }{\beta }>\frac {\alpha +\gamma }{\beta +\delta }>\frac {\gamma }{\delta }$
if and only if $\frac {\alpha }{\beta }>\frac {\alpha +\gamma }{\beta +\delta }>\frac {\gamma }{\delta }$![]() ; that is, the mediant $\frac {\alpha +\gamma }{\beta +\delta }$
; that is, the mediant $\frac {\alpha +\gamma }{\beta +\delta }$![]() of $\frac {\alpha }{\beta }$
of $\frac {\alpha }{\beta }$![]() and $\frac {\gamma }{\delta }$
and $\frac {\gamma }{\delta }$![]() lies strictly between $\frac {\alpha }{\beta }$
lies strictly between $\frac {\alpha }{\beta }$![]() and $\frac {\gamma }{\delta }$
and $\frac {\gamma }{\delta }$![]() . If $0< r\leqslant m$
. If $0< r\leqslant m$![]() , then by induction
, then by induction

Applying the ‘mediant sum’ to $t(r-1)=\frac {s_m(r)}{s_m(r-1)}>\frac {\binom{m}{r+1}}{\binom{m}{r}}$![]() gives
gives

Therefore $t(r-1)>t(r)>\binom{m}{r+1}/\binom{m}{r}=\frac {m-r}{r+1}$![]() completing the induction, and proving (a).
completing the induction, and proving (a).
(b,c,d,e) The following are equivalent: $g(r)< g(r+1)$![]() ; $\omega s_m(r)< s_m(r+1)$
; $\omega s_m(r)< s_m(r+1)$![]() ; and $\omega < t(r)$
; and $\omega < t(r)$![]() . The other claims are proved similarly by replacing < with $\leqslant$
. The other claims are proved similarly by replacing < with $\leqslant$![]() , >, $\geqslant$
, >, $\geqslant$![]() .
.
(f) Observe that $t(m)=\frac {s_m(m+1)}{s_m(m)}=\frac {2^m}{2^m}=1$![]() . By part (a), the function $y=t(r)$
. By part (a), the function $y=t(r)$![]() is decreasing for $-1\leqslant r\leqslant m$
is decreasing for $-1\leqslant r\leqslant m$![]() . Since $\omega >1$
. Since $\omega >1$![]() , there exists an integer $r_0\in \{0,\,\ldots,\,m\}$
, there exists an integer $r_0\in \{0,\,\ldots,\,m\}$![]() such that $\infty =t(-1)>\cdots >t(r_0-1)\geqslant \omega > t(r_0)>\cdots > t(m)=1$
such that $\infty =t(-1)>\cdots >t(r_0-1)\geqslant \omega > t(r_0)>\cdots > t(m)=1$![]() . By parts (b,c,d,e) an equivalent condition is $g(0)<\cdots < g(r_0-1)\leqslant g(r_0)$
. By parts (b,c,d,e) an equivalent condition is $g(0)<\cdots < g(r_0-1)\leqslant g(r_0)$![]() and $g(r_0)>\cdots >g(m)$
and $g(r_0)>\cdots >g(m)$![]() .
.
The following is an immediate corollary of lemma 3.1(f).
Corollary 3.2 If $t(r_0-1)>\omega$![]() , then the function $g(r)$
, then the function $g(r)$![]() in (1.1) has a unique maximum at $r_0$
in (1.1) has a unique maximum at $r_0$![]() . If $t(r_0-1)=\omega$
. If $t(r_0-1)=\omega$![]() , then $g(r)$
, then $g(r)$![]() has two equal maxima, one at $r_0-1$
has two equal maxima, one at $r_0-1$![]() and one at $r_0$
and one at $r_0$![]() .
.
As an application of theorem 1.1 we show that the largest maximizing input $r_0$![]() for $g_{\omega,m}(r)$
for $g_{\omega,m}(r)$![]() satisfies $\lfloor \frac {m+2}{\omega +1}\rfloor \leqslant r_0$
satisfies $\lfloor \frac {m+2}{\omega +1}\rfloor \leqslant r_0$![]() . There are at most two maximizing inputs by corollary 3.2.
. There are at most two maximizing inputs by corollary 3.2.
Lemma 3.3 Suppose that $\omega >1$![]() and $m\in {\mathbb {Z}}$
and $m\in {\mathbb {Z}}$![]() , $m\geqslant 0$
, $m\geqslant 0$![]() . If $r':=\lfloor \frac {m+2}{\omega +1}\rfloor$
. If $r':=\lfloor \frac {m+2}{\omega +1}\rfloor$![]() , then
, then
if $r'>1$![]() or $\omega \ne m+1$
or $\omega \ne m+1$![]() .
.
Proof. The result is clear when $r'=0$![]() . If $r'=1$
. If $r'=1$![]() , then $r'\leqslant \frac {m+2}{\omega +1}$
, then $r'\leqslant \frac {m+2}{\omega +1}$![]() gives $\omega \leqslant m+1$
gives $\omega \leqslant m+1$![]() or $g(0)\leqslant g(1)$
or $g(0)\leqslant g(1)$![]() . Hence $g(0)< g(1)$
. Hence $g(0)< g(1)$![]() if $\omega \ne m+1$
if $\omega \ne m+1$![]() . Suppose that $r'>1$
. Suppose that $r'>1$![]() . By lemma 3.1(c,f) the chain $g(0)<\dots < g(r')$
. By lemma 3.1(c,f) the chain $g(0)<\dots < g(r')$![]() is equivalent to $g(r'-1)< g(r')$
is equivalent to $g(r'-1)< g(r')$![]() , that is $t(r'-1)> \omega$
, that is $t(r'-1)> \omega$![]() . However, $t(r'-1)+1>\frac {m+2}{r'}$
. However, $t(r'-1)+1>\frac {m+2}{r'}$![]() by corollary 2.4 and $r'\leqslant \frac {m+2}{\omega +1}$
by corollary 2.4 and $r'\leqslant \frac {m+2}{\omega +1}$![]() implies $\frac {m+2}{r'}\geqslant \omega +1$
implies $\frac {m+2}{r'}\geqslant \omega +1$![]() . Hence $t(r'-1)+1>\omega +1$
. Hence $t(r'-1)+1>\omega +1$![]() , so that $t(r'-1)> \omega$
, so that $t(r'-1)> \omega$![]() as desired.
as desired.
Proof Proof of theorem 1.4
Suppose that $\omega \in \{3,\,4,\,\ldots \}$![]() . Then $g(0)<\dots < g(r'-1)\leqslant g(r')$
. Then $g(0)<\dots < g(r'-1)\leqslant g(r')$![]() by lemma 3.3 with strictness when $\omega \ne m+1$
by lemma 3.3 with strictness when $\omega \ne m+1$![]() . If $\omega =m+1$
. If $\omega =m+1$![]() , then $r'=\lfloor \frac {m+2}{\omega +1}\rfloor =1$
, then $r'=\lfloor \frac {m+2}{\omega +1}\rfloor =1$![]() and $g(0)=g(1)$
and $g(0)=g(1)$![]() as claimed. It remains to show that $g(r')>g(r'+1)>\cdots >g(m)$
as claimed. It remains to show that $g(r')>g(r'+1)>\cdots >g(m)$![]() . However, we need only prove that $g(r')> g(r'+1)$
. However, we need only prove that $g(r')> g(r'+1)$![]() by lemma 3.1(f), or equivalently $\omega > t(r')$
by lemma 3.1(f), or equivalently $\omega > t(r')$![]() by lemma 3.1(d).
by lemma 3.1(d).
Clearly $\omega \geqslant 3$![]() implies $r'\leqslant \frac {m+2}{\omega +1}\leqslant \frac {m+2}{4}$
implies $r'\leqslant \frac {m+2}{\omega +1}\leqslant \frac {m+2}{4}$![]() . As $0\leqslant r'<\frac {m+3}{2}$
. As $0\leqslant r'<\frac {m+3}{2}$![]() , corollary 2.4 gives
, corollary 2.4 gives
Hence $\omega +1> t(r')+1$![]() holds if $\omega +1> \frac {m+2}{r'+1}+\frac {2r'}{(r'+1)(m-2r'+3)}$
holds if $\omega +1> \frac {m+2}{r'+1}+\frac {2r'}{(r'+1)(m-2r'+3)}$![]() . Since $\omega +1$
. Since $\omega +1$![]() is an integer, we have $m+2=r'(\omega +1)+c$
is an integer, we have $m+2=r'(\omega +1)+c$![]() where $0\leqslant c\leqslant \omega$
where $0\leqslant c\leqslant \omega$![]() . It follows from $0\leqslant r'\leqslant \frac {m+2}{4}$
. It follows from $0\leqslant r'\leqslant \frac {m+2}{4}$![]() that $\frac {2r'}{m-2r'+3}<1$
that $\frac {2r'}{m-2r'+3}<1$![]() . This inequality and $m+2\leqslant r'(\omega +1)+\omega$
. This inequality and $m+2\leqslant r'(\omega +1)+\omega$![]() gives
gives
Thus $\omega +1>\frac {m+2}{r'+1}+\frac {2r'}{(r'+1)(m-2r'+3)}\geqslant t(r')+1$![]() , so $\omega >t(r')$
, so $\omega >t(r')$![]() as required.
as required.
Remark 3.4 The proof of theorem 1.4 can be adapted to the case $\omega =2$![]() . If $m+2=3r'+c$
. If $m+2=3r'+c$![]() where $c\leqslant \omega -1=1$
where $c\leqslant \omega -1=1$![]() , then $\frac {2r'}{m-2r'+3}=\frac {2r'}{r'+c+1}<2$
, then $\frac {2r'}{m-2r'+3}=\frac {2r'}{r'+c+1}<2$![]() , and if $c=\omega =2$
, and if $c=\omega =2$![]() , then a sharper ${\mathcal {H}}_2$
, then a sharper ${\mathcal {H}}_2$![]() -bound must be used. This leads to a much shorter proof than [Reference Glasby and Paseman4, Theorem 1.1]. $\diamond$
-bound must be used. This leads to a much shorter proof than [Reference Glasby and Paseman4, Theorem 1.1]. $\diamond$![]()
4. Non-integral values of $\omega$
In this section, we prove that the maximum value of $g(r)$![]() is $g(r')$
is $g(r')$![]() or $g(r'+1)$
or $g(r'+1)$![]() if $\omega \geqslant \sqrt {3}$
if $\omega \geqslant \sqrt {3}$![]() . Before proving this result (theorem 1.3), we shall prove two preliminary lemmas.
. Before proving this result (theorem 1.3), we shall prove two preliminary lemmas.
Lemma 4.1 Suppose that $\omega >1$![]() and $r':=\lfloor \frac {m+2}{\omega +1}\rfloor$
and $r':=\lfloor \frac {m+2}{\omega +1}\rfloor$![]() . If $\frac {m+2}{r'+1}\geqslant \sqrt {3}+1$
. If $\frac {m+2}{r'+1}\geqslant \sqrt {3}+1$![]() , then
, then
Proof. It suffices, by lemma 3.1(f) and lemma 3.3 to prove that $g(r'+1)>g(r'+2)$![]() . The strategy is to show $\omega >t(r'+1)$
. The strategy is to show $\omega >t(r'+1)$![]() , that is $\omega +1>t(r'+1)+1$
, that is $\omega +1>t(r'+1)+1$![]() . However, $\omega +1>\frac {m+2}{r'+1}$
. However, $\omega +1>\frac {m+2}{r'+1}$![]() , so it suffices to prove that $\frac {m+2}{r'+1}\geqslant t(r'+1)+1$
, so it suffices to prove that $\frac {m+2}{r'+1}\geqslant t(r'+1)+1$![]() . Since $r'+1\leqslant \frac {m+2}{\sqrt {3}+1}<\frac {m+2}{2}$
. Since $r'+1\leqslant \frac {m+2}{\sqrt {3}+1}<\frac {m+2}{2}$![]() , we can use corollary 2.4 and just prove that $\frac {m+2}{r'+1}\geqslant \frac {m+2}{r'+2}+\frac {2r'+2}{(r'+2)(m-2r'+1)}$
, we can use corollary 2.4 and just prove that $\frac {m+2}{r'+1}\geqslant \frac {m+2}{r'+2}+\frac {2r'+2}{(r'+2)(m-2r'+1)}$![]() . This inequality is equivalent to $\frac {m+2}{r'+1}\geqslant \frac {2r'+2}{m-2r'+1}$
. This inequality is equivalent to $\frac {m+2}{r'+1}\geqslant \frac {2r'+2}{m-2r'+1}$![]() . However, $\frac {m+2}{r'+1}\geqslant \sqrt {3}+1$
. However, $\frac {m+2}{r'+1}\geqslant \sqrt {3}+1$![]() , so we need only show that $\sqrt {3}+1\geqslant \frac {2(r'+1)}{m-2r'+1}$
, so we need only show that $\sqrt {3}+1\geqslant \frac {2(r'+1)}{m-2r'+1}$![]() , or equivalently $m-2r'+1\geqslant (\sqrt {3}-1)(r'+1)$
, or equivalently $m-2r'+1\geqslant (\sqrt {3}-1)(r'+1)$![]() . This is true since $\frac {m+2}{r'+1}\geqslant \sqrt {3}+1$
. This is true since $\frac {m+2}{r'+1}\geqslant \sqrt {3}+1$![]() implies $m-2r'+1\geqslant (\sqrt {3}-1)r'+\sqrt {3}>(\sqrt {3}-1)(r'+1)$
implies $m-2r'+1\geqslant (\sqrt {3}-1)r'+\sqrt {3}>(\sqrt {3}-1)(r'+1)$![]() .
.
Remark 4.2 The strict inequality $g(r'-1)< g(r')$![]() holds by lemma 3.3 if $r'>1$
holds by lemma 3.3 if $r'>1$![]() or $\omega \ne m+1$
or $\omega \ne m+1$![]() . It holds vacuously for $r'=0$
. It holds vacuously for $r'=0$![]() . Hence adding the additional hypothesis that $\omega \ne m+1$
. Hence adding the additional hypothesis that $\omega \ne m+1$![]() if $r'=1$
if $r'=1$![]() to lemma 4.1 (and theorem 1.3), we may conclude that the inequality $g(r'-1)\leqslant g(r')$
to lemma 4.1 (and theorem 1.3), we may conclude that the inequality $g(r'-1)\leqslant g(r')$![]() is strict.
is strict.
Remark 4.3 In lemma 4.1, the maximum can occur at $r'+1$![]() . If $\omega =2.5$
. If $\omega =2.5$![]() and $m=8$
and $m=8$![]() , then $r'=\lfloor \frac {10}{3.5}\rfloor =2$
, then $r'=\lfloor \frac {10}{3.5}\rfloor =2$![]() and $\frac {m+2}{r'+1}=\frac {10}{3}\geqslant \sqrt {3}+1$
and $\frac {m+2}{r'+1}=\frac {10}{3}\geqslant \sqrt {3}+1$![]() however $g_{2.5,8}(2)=\frac {740}{125}< \frac {744}{125}=g_{2.5,8}(3)$
however $g_{2.5,8}(2)=\frac {740}{125}< \frac {744}{125}=g_{2.5,8}(3)$![]() . $\diamond$
. $\diamond$![]()
Remark 4.4 The gap between $r'$![]() and the largest maximizing input $r_0$
and the largest maximizing input $r_0$![]() can be arbitrarily large if $\omega$
can be arbitrarily large if $\omega$![]() is close to 1. For $\omega >1$
is close to 1. For $\omega >1$![]() , we have $r'=\lfloor \frac {m+2}{\omega +1}\rfloor <\frac {m+2}{2}$
, we have $r'=\lfloor \frac {m+2}{\omega +1}\rfloor <\frac {m+2}{2}$![]() . If $1<\omega \leqslant \frac {1}{1-2^{-m}}$
. If $1<\omega \leqslant \frac {1}{1-2^{-m}}$![]() , then $g(m-1)\leqslant g(m)$
, then $g(m-1)\leqslant g(m)$![]() , so $r_0=m$
, so $r_0=m$![]() . Hence $r_0-r'>\frac {m-2}{2}$
. Hence $r_0-r'>\frac {m-2}{2}$![]() .
.
Remark 4.5 Since $r'\leqslant \lfloor \frac {m+2}{\omega +1}\rfloor < r'+1$![]() , we see that $r'+1\approx \frac {m+2}{\omega +1}$
, we see that $r'+1\approx \frac {m+2}{\omega +1}$![]() , so that $\frac {m+2}{r'+1}\approx \omega +1$
, so that $\frac {m+2}{r'+1}\approx \omega +1$![]() . Thus lemma 4.1 suggests that if $\omega \gtrsim \sqrt {3}$
. Thus lemma 4.1 suggests that if $\omega \gtrsim \sqrt {3}$![]() , then $g_{\omega,m}(r)$
, then $g_{\omega,m}(r)$![]() may have a maximum at $r'$
may have a maximum at $r'$![]() or $r'+1$
or $r'+1$![]() . This heuristic reasoning is made rigorous in theorem 1.3. $\diamond$
. This heuristic reasoning is made rigorous in theorem 1.3. $\diamond$![]()
Remark 4.6 Theorem 1.1 can be rephrased as $t_m(r)=\frac {s_m(r+1)}{s_m(r)}=\frac {m-r+1}{r+1}+\frac {{\mathcal {K}}_m(r)}{r+1}$![]() where
where

The following lemma repeatedly uses the expression $\omega >t_m(r+1)$![]() . This is equivalent to $\omega >\frac {m-r}{r+2}+\frac {{\mathcal {K}}_m(r+1)}{r+2}$
. This is equivalent to $\omega >\frac {m-r}{r+2}+\frac {{\mathcal {K}}_m(r+1)}{r+2}$![]() , that is $(\omega +1)(r+2)>m+2+{\mathcal {K}}_m(r+1)$
, that is $(\omega +1)(r+2)>m+2+{\mathcal {K}}_m(r+1)$![]() . $\diamond$
. $\diamond$![]()
Lemma 4.7 Let $m\in \{0,\,1,\,\ldots \}$![]() and $r'=\lfloor \frac {m+2}{\omega +1}\rfloor$
and $r'=\lfloor \frac {m+2}{\omega +1}\rfloor$![]() . If any of the following three conditions are met, then $g_{\omega,m}(r'+1)>\cdots >g_{\omega,m}(m)$
. If any of the following three conditions are met, then $g_{\omega,m}(r'+1)>\cdots >g_{\omega,m}(m)$![]() holds: (a) $\omega \geqslant 2$
holds: (a) $\omega \geqslant 2$![]() , or (b) $\omega \geqslant \frac {1+\sqrt {97}}{6}$
, or (b) $\omega \geqslant \frac {1+\sqrt {97}}{6}$![]() and $r'\ne 2$
and $r'\ne 2$![]() , or (c) $\omega \geqslant \sqrt {3}$
, or (c) $\omega \geqslant \sqrt {3}$![]() and $r'\not \in \{2,\,3\}$
and $r'\not \in \{2,\,3\}$![]() .
.
Proof. The conclusion $g_{\omega,m}(r'+1)>\cdots >g_{\omega,m}(m)$![]() holds trivially if $r'+1\geqslant m$
holds trivially if $r'+1\geqslant m$![]() . Suppose henceforth that $r'+1< m$
. Suppose henceforth that $r'+1< m$![]() . Except for the excluded values of $r',\,\omega$
. Except for the excluded values of $r',\,\omega$![]() , we will prove that $g_{\omega,m}(r'+1)>g_{\omega,m}(r'+2)$
, we will prove that $g_{\omega,m}(r'+1)>g_{\omega,m}(r'+2)$![]() holds, as this implies $g_{\omega,m}(r'+1)>\cdots >g_{\omega,m}(m)$
holds, as this implies $g_{\omega,m}(r'+1)>\cdots >g_{\omega,m}(m)$![]() by lemma 3.1(f). Hence we must prove that $\omega >t_m(r'+1)$
by lemma 3.1(f). Hence we must prove that $\omega >t_m(r'+1)$![]() by lemma 3.1(d).
by lemma 3.1(d).
Recall that $r'\leqslant \frac {m+2}{\omega +1}< r'+1$![]() . If $r'=0$
. If $r'=0$![]() , then $m+2<\omega +1$
, then $m+2<\omega +1$![]() , that is $\omega >m+1>t(1)$
, that is $\omega >m+1>t(1)$![]() as desired. Suppose now that $r'=1$
as desired. Suppose now that $r'=1$![]() . There is nothing to prove if $m=r'+1=2$
. There is nothing to prove if $m=r'+1=2$![]() . Assume that $m>2$
. Assume that $m>2$![]() . Since $m+2<2(\omega +1)$
. Since $m+2<2(\omega +1)$![]() , we have $2< m<2\omega$
, we have $2< m<2\omega$![]() . The last line of remark 4.6 and (4.1) give the desired inequality:
. The last line of remark 4.6 and (4.1) give the desired inequality:

In summary, $g_{\omega,m}(r'+1)>\cdots >g_{\omega,m}(m)$![]() holds for all $\omega >1$
holds for all $\omega >1$![]() if $r'\in \{0,\,1\}$
if $r'\in \{0,\,1\}$![]() .
.
We next prove $g_{\omega,m}(r'+1)>g_{\omega,m}(r'+2)$![]() , or equivalently $\omega >t_m(r'+1)$
, or equivalently $\omega >t_m(r'+1)$![]() for $r'$
for $r'$![]() large enough, depending on $\omega$
large enough, depending on $\omega$![]() . We must prove that $(\omega +1)(r'+2)>m+2+\mathcal{K}_m(r'+1)$
. We must prove that $(\omega +1)(r'+2)>m+2+\mathcal{K}_m(r'+1)$![]() by remark 4.6. Writing $m+2=(\omega +1)(r'+\varepsilon )$
by remark 4.6. Writing $m+2=(\omega +1)(r'+\varepsilon )$![]() where $0\leqslant \varepsilon <1$
where $0\leqslant \varepsilon <1$![]() , our goal, therefore, is to show $(\omega +1)(2-\varepsilon )>{\mathcal {K}}_m(r'+1)$
, our goal, therefore, is to show $(\omega +1)(2-\varepsilon )>{\mathcal {K}}_m(r'+1)$![]() . Using (4.1) gives
. Using (4.1) gives
where ${\mathcal {T}}>0$![]() by theorem 1.1 as $r'>0$
by theorem 1.1 as $r'>0$![]() . Rewriting the denominator using
. Rewriting the denominator using
our goal $(\omega +1)(2-\varepsilon )>{\mathcal {K}}_m(r'+1)$![]() becomes
becomes
Dividing by $(2-\varepsilon )(r'+1)$![]() and rearranging gives
and rearranging gives
This inequality may be written $(\omega ^2-1)+\lambda >\frac {2}{2-\varepsilon }+\mu (1-\varepsilon )$![]() where $\lambda =\frac {(\omega +1)(1+{\mathcal {T}})}{r'+1}>0$
where $\lambda =\frac {(\omega +1)(1+{\mathcal {T}})}{r'+1}>0$![]() and $\mu =\frac {(\omega +1)^2}{r'+1}>0$
and $\mu =\frac {(\omega +1)^2}{r'+1}>0$![]() . We view $f(\varepsilon ):=\frac {2}{2-\varepsilon }+\mu (1-\varepsilon )$
. We view $f(\varepsilon ):=\frac {2}{2-\varepsilon }+\mu (1-\varepsilon )$![]() as a function of a real variable $\varepsilon$
as a function of a real variable $\varepsilon$![]() where $0\leqslant \varepsilon <1$
where $0\leqslant \varepsilon <1$![]() . However, $f(\varepsilon )$
. However, $f(\varepsilon )$![]() is concave as the second derivative $f''(\varepsilon )=\frac {4}{(2-\varepsilon )^3}$
is concave as the second derivative $f''(\varepsilon )=\frac {4}{(2-\varepsilon )^3}$![]() is positive for $0\leqslant \varepsilon <1$
is positive for $0\leqslant \varepsilon <1$![]() . Hence the maximum value occurs at an end point: either $f(0)=1+\mu$
. Hence the maximum value occurs at an end point: either $f(0)=1+\mu$![]() or $f(1)=2$
or $f(1)=2$![]() . Therefore, it suffices to prove that $(\omega ^2-1)+\lambda >\max \{2,\,1+\mu \}$
. Therefore, it suffices to prove that $(\omega ^2-1)+\lambda >\max \{2,\,1+\mu \}$![]() .
.
If $2\geqslant 1+\mu$![]() , then the desired bound $(\omega ^2-3)+\lambda >0$
, then the desired bound $(\omega ^2-3)+\lambda >0$![]() holds as $\omega \geqslant \sqrt {3}$
holds as $\omega \geqslant \sqrt {3}$![]() . Suppose now that $2<1+\mu$
. Suppose now that $2<1+\mu$![]() . We must show $(\omega ^2-1)+\lambda >1+\mu$
. We must show $(\omega ^2-1)+\lambda >1+\mu$![]() , that is $\omega ^2-2>\mu -\lambda =\frac {(\omega +1)(\omega -{\mathcal {T}})}{r'+1}$
, that is $\omega ^2-2>\mu -\lambda =\frac {(\omega +1)(\omega -{\mathcal {T}})}{r'+1}$![]() . Since ${\mathcal {T}}>0$
. Since ${\mathcal {T}}>0$![]() , a stronger inequality (that implies this) is $\omega ^2-2\geqslant \frac {(\omega +1)\omega }{r'+1}$
, a stronger inequality (that implies this) is $\omega ^2-2\geqslant \frac {(\omega +1)\omega }{r'+1}$![]() . The (equivalent) quadratic inequality $r'\omega ^2-\omega -2(r'+1)\geqslant 0$
. The (equivalent) quadratic inequality $r'\omega ^2-\omega -2(r'+1)\geqslant 0$![]() in $\omega$
in $\omega$![]() is true provided $\omega \geqslant \frac {1+\sqrt {1+8r'(r'+1)}}{2r'}$
is true provided $\omega \geqslant \frac {1+\sqrt {1+8r'(r'+1)}}{2r'}$![]() . This says $\omega \geqslant 2$
. This says $\omega \geqslant 2$![]() if $r'=2$
if $r'=2$![]() , and $\omega \geqslant \frac {1+\sqrt {97}}{6}$
, and $\omega \geqslant \frac {1+\sqrt {97}}{6}$![]() if $r'=3$
if $r'=3$![]() . If $r'\geqslant 4$
. If $r'\geqslant 4$![]() , we have
, we have

The conclusion now follows from the fact that $2>\frac {1+\sqrt {97}}{6} >\sqrt {3}$![]() .
.
Proof Proof of theorem 1.3
By lemma 4.1 it suffices to show that $g(r'+1)>g(r'+2)$![]() holds when $r'+1< m$
holds when $r'+1< m$![]() and $\omega \geqslant \sqrt {3}$
and $\omega \geqslant \sqrt {3}$![]() . By lemma 4.7(a), we can assume that $\sqrt {3}\leqslant \omega <2$
. By lemma 4.7(a), we can assume that $\sqrt {3}\leqslant \omega <2$![]() and $r'\in \{2,\,3\}$
and $r'\in \{2,\,3\}$![]() . For these choices of $\omega$
. For these choices of $\omega$![]() and $r'$
and $r'$![]() , we must show that $\omega >t_m(r'+1)$
, we must show that $\omega >t_m(r'+1)$![]() by lemma 3.1 for all permissible choices of $m$
by lemma 3.1 for all permissible choices of $m$![]() . Since $(\omega +1)r'\leqslant m+2<(\omega +1)(r'+1)$
. Since $(\omega +1)r'\leqslant m+2<(\omega +1)(r'+1)$![]() , when $r'=2$
, when $r'=2$![]() we have $5<2(\sqrt {3}+1)\leqslant m+2<9$
we have $5<2(\sqrt {3}+1)\leqslant m+2<9$![]() so that $4\leqslant m\leqslant 6$
so that $4\leqslant m\leqslant 6$![]() . However, $t_m(3)$
. However, $t_m(3)$![]() equals $\tfrac {16}{15},\,\tfrac {31}{26},\,\tfrac {19}{14}$
equals $\tfrac {16}{15},\,\tfrac {31}{26},\,\tfrac {19}{14}$![]() for these values of $m$
for these values of $m$![]() . Thus $\sqrt {3}>t_m(3)$
. Thus $\sqrt {3}>t_m(3)$![]() holds as desired. Similarly, if $r'=3$
holds as desired. Similarly, if $r'=3$![]() , then $8<3(\sqrt {3}+1)\leqslant m+2<12$
, then $8<3(\sqrt {3}+1)\leqslant m+2<12$![]() so that $7\leqslant m\leqslant 9$
so that $7\leqslant m\leqslant 9$![]() . In this case $t_m(4)$
. In this case $t_m(4)$![]() equals $\tfrac {40}{33},\,\tfrac {219}{163},\,\tfrac {191}{128}$
equals $\tfrac {40}{33},\,\tfrac {219}{163},\,\tfrac {191}{128}$![]() for these values of $m$
for these values of $m$![]() . In each case $\sqrt {3}>t_m(4)$
. In each case $\sqrt {3}>t_m(4)$![]() , so the proof is complete.
, so the proof is complete.
Remark 4.8 We place remark 4.4 in context. The conclusion of theorem 1.3 remains true for values of $\omega$![]() smaller than $\sqrt {3}$
smaller than $\sqrt {3}$![]() and not ‘too close to 1’ and $m$
and not ‘too close to 1’ and $m$![]() is ‘sufficiently large’. Indeed, by adapting the proof of lemma 4.7 we can show there exists a sufficiently large integer $d$
is ‘sufficiently large’. Indeed, by adapting the proof of lemma 4.7 we can show there exists a sufficiently large integer $d$![]() such that $m > d^4$
such that $m > d^4$![]() and $\omega > 1 + \frac {1}{d}$
and $\omega > 1 + \frac {1}{d}$![]() implies $g(r'+d) > g(r'+d+1)$
implies $g(r'+d) > g(r'+d+1)$![]() . This shows that $r' \leqslant r_0 \leqslant r' +d$
. This shows that $r' \leqslant r_0 \leqslant r' +d$![]() , so $r_0-r'\leqslant d$
, so $r_0-r'\leqslant d$![]() . We omit the technical proof of this fact. $\diamond$
. We omit the technical proof of this fact. $\diamond$![]()
Remark 4.9 The sequence, $a_0+{\mathcal {H}}_1,\,\ldots,\,a_0+{\mathcal {H}}_r$![]() terminates at $\frac {r+1}{s_m(r)}\binom{m}{r+1}$
terminates at $\frac {r+1}{s_m(r)}\binom{m}{r+1}$![]() by theorem 1.1. We will not comment here on how quickly the alternating sequence in proposition 2.3 converges when $r<\frac {m+3}{2}$
by theorem 1.1. We will not comment here on how quickly the alternating sequence in proposition 2.3 converges when $r<\frac {m+3}{2}$![]() . If $r=m$
. If $r=m$![]() , then $a_0=-m$
, then $a_0=-m$![]() and $\frac {m+1}{s_m(m+1)}\binom{m}{m+1}=0$
and $\frac {m+1}{s_m(m+1)}\binom{m}{m+1}=0$![]() , so theorem 1.1 gives the curious identity ${\mathcal {H}}_m=\mathcal{K}_{i=1}^m\frac {2i(m+1-i)}{3i-m}=m$
, so theorem 1.1 gives the curious identity ${\mathcal {H}}_m=\mathcal{K}_{i=1}^m\frac {2i(m+1-i)}{3i-m}=m$![]() . If $\omega$
. If $\omega$![]() is less than $\sqrt {3}$
is less than $\sqrt {3}$![]() and ‘not too close to 1’, then we believe that $r_0$
and ‘not too close to 1’, then we believe that $r_0$![]() is approximately $\lfloor \frac {m+2}{\omega +1}+ \frac {2}{\omega ^2 -1}\rfloor$
is approximately $\lfloor \frac {m+2}{\omega +1}+ \frac {2}{\omega ^2 -1}\rfloor$![]() , c.f. remark 4.8.
, c.f. remark 4.8.
5. Estimating the maximum value of $g_{\omega,m}(r)$
In this section we relate the size of the maximum value $g_{\omega,m}(r_0)$![]() to the size of the binomial coefficient $\binom{m}{r_0}$
to the size of the binomial coefficient $\binom{m}{r_0}$![]() . In the case that we know a formula for a maximizing input $r_0$
. In the case that we know a formula for a maximizing input $r_0$![]() , we can readily estimate $g_{\omega,m}(r_0)$
, we can readily estimate $g_{\omega,m}(r_0)$![]() using approximations, such as [Reference Stănică10], for binomial coefficients.
using approximations, such as [Reference Stănică10], for binomial coefficients.
Lemma 5.1 The maximum value $g_{\omega,m}(r_0)$![]() of $g_{\omega,m}(r)$
of $g_{\omega,m}(r)$![]() , $0\leqslant r\leqslant m$
, $0\leqslant r\leqslant m$![]() , satisfies
, satisfies
Proof. Since $g(r_0)$![]() is a maximum value, we have $g(r_0-1)\leqslant g(r_0)$
is a maximum value, we have $g(r_0-1)\leqslant g(r_0)$![]() . This is equivalent to $(\omega -1)s_m(r_0-1)\leqslant \binom{m}{r_0}$
. This is equivalent to $(\omega -1)s_m(r_0-1)\leqslant \binom{m}{r_0}$![]() as $s_m(r_0)=s_m(r_0-1)+\binom{m}{r_0}$
as $s_m(r_0)=s_m(r_0-1)+\binom{m}{r_0}$![]() . Adding $(\omega -1)\binom{m}{r_0}$
. Adding $(\omega -1)\binom{m}{r_0}$![]() to both sides gives the equivalent inequality $(\omega -1) s_m(r_0)\leqslant \omega \binom{m}{r_0}$
to both sides gives the equivalent inequality $(\omega -1) s_m(r_0)\leqslant \omega \binom{m}{r_0}$![]() . This proves the upper bound.
. This proves the upper bound.
Similar reasoning shows that the following are equivalent: (a) $g(r_0)> g(r_0+1)$![]() ; (b) $(\omega -1)s_m(r_0)> \binom{m}{r_0+1}$
; (b) $(\omega -1)s_m(r_0)> \binom{m}{r_0+1}$![]() ; and (c) $g_{\omega,m}(r_0)>\frac {1}{(\omega -1)\omega ^{r_0}}\binom{m}{r_0+1}$
; and (c) $g_{\omega,m}(r_0)>\frac {1}{(\omega -1)\omega ^{r_0}}\binom{m}{r_0+1}$![]() .
.
In theorem 1.3 the maximizing input $r_0$![]() satisfies $r_0=r'+d$
satisfies $r_0=r'+d$![]() where $d\in \{0,\,1\}$
where $d\in \{0,\,1\}$![]() . In such cases when $r_0$
. In such cases when $r_0$![]() and $d$
and $d$![]() are known, we can bound the maximum $g_{\omega,m}(r_0)$
are known, we can bound the maximum $g_{\omega,m}(r_0)$![]() as follows.
as follows.
Corollary 5.2 Set $r' := \lfloor \frac {m+2}{\omega +1}\rfloor$![]() and $k := m+2 - (\omega +1)r'$
and $k := m+2 - (\omega +1)r'$![]() . Suppose that $r_0 = r'+d$
. Suppose that $r_0 = r'+d$![]() and $G=\frac {1}{(\omega -1)\omega ^{r_0-1}}\binom{m}{r_0}$
and $G=\frac {1}{(\omega -1)\omega ^{r_0-1}}\binom{m}{r_0}$![]() . Then
. Then
Proof. By lemma 3.3, $r_0 = r'+d$![]() where $d\in \{0,\,1,\,\ldots \}$
where $d\in \{0,\,1,\,\ldots \}$![]() . Since $r' = \lfloor \frac {m+2}{\omega +1}\rfloor$
. Since $r' = \lfloor \frac {m+2}{\omega +1}\rfloor$![]() , we have $m+2 = (\omega +1)r'+k$
, we have $m+2 = (\omega +1)r'+k$![]() where $0\leqslant k< \omega +1$
where $0\leqslant k< \omega +1$![]() . The result follows from lemma 5.1 and $m = (\omega +1)(r_0-d)+k-2$
. The result follows from lemma 5.1 and $m = (\omega +1)(r_0-d)+k-2$![]() as $\binom{m}{r_0+1}=\frac {m-r_0}{r_0+1}\binom{m}{r_0}$
as $\binom{m}{r_0+1}=\frac {m-r_0}{r_0+1}\binom{m}{r_0}$![]() and $\frac {m-r_0}{r_0+1}$
and $\frac {m-r_0}{r_0+1}$![]() equals
equals

The following remark is an application of the Chernoff bound, c.f. [Reference Worsch11, Section 4]. Unlike theorem 1.1, it requires the cumulative distribution function $\Phi (x)$![]() , which is a non-elementary integral, to approximate $s_m(r)$
, which is a non-elementary integral, to approximate $s_m(r)$![]() . It seems to give better approximations only for values of $r$
. It seems to give better approximations only for values of $r$![]() near $\frac {m}{2}$
near $\frac {m}{2}$![]() , see remark 5.4.
, see remark 5.4.
Remark 5.3 We show how the Berry–Esseen inequality for a sum of binomial random variables can be used to approximate $s_m(r)$![]() . Let $B_1,\,\ldots,\,B_m$
. Let $B_1,\,\ldots,\,B_m$![]() be independent identically distributed binomial variables with a parameter $p$
be independent identically distributed binomial variables with a parameter $p$![]() where $0< p<1$
where $0< p<1$![]() , so that $P(B_i=1)=p$
, so that $P(B_i=1)=p$![]() and $P(B_i=0)=q:= 1-p$
and $P(B_i=0)=q:= 1-p$![]() . Let $X_i:= B_i-p$
. Let $X_i:= B_i-p$![]() and $X:=\frac {1}{\sqrt {mpq}}(\sum _{i=1}^m X_i)$
and $X:=\frac {1}{\sqrt {mpq}}(\sum _{i=1}^m X_i)$![]() . Then
. Then
Hence $E(X)=\frac {1}{\sqrt {mpq}}(\sum _{i=1}^m E(X_i))=0$![]() and $E(X^2)=\frac {1}{mpq}(\sum _{i=1}^m E(X_i^2))=1$
and $E(X^2)=\frac {1}{mpq}(\sum _{i=1}^m E(X_i^2))=1$![]() . By [Reference Nagaev and Chebotarev7, Theorem 2] the Berry–Esseen inequality applied to $X$
. By [Reference Nagaev and Chebotarev7, Theorem 2] the Berry–Esseen inequality applied to $X$![]() states that
states that

where the constant $C:= 0.4215$![]() is close to the lower bound $C_0=\frac {10+\sqrt {3}}{6\sqrt {2\pi }}=0.4097\cdots$
is close to the lower bound $C_0=\frac {10+\sqrt {3}}{6\sqrt {2\pi }}=0.4097\cdots$![]() and $\Phi (x)=\frac {1}{\sqrt {2\pi }}\int _{-\infty }^x e^{-t^2/2}\,dt=\frac {1}{2}\left (1+{\rm erf}\left (\frac {x}{\sqrt {2}}\right )\right )$
and $\Phi (x)=\frac {1}{\sqrt {2\pi }}\int _{-\infty }^x e^{-t^2/2}\,dt=\frac {1}{2}\left (1+{\rm erf}\left (\frac {x}{\sqrt {2}}\right )\right )$![]() is the cumulative distribution function for standard normal distribution.
is the cumulative distribution function for standard normal distribution.
Writing $B=\sum _{i=1}^mB_i$![]() we have $P(B\leqslant b)=\sum _{i=0}^{\lfloor b\rfloor }\binom{m}{i}p^iq^{m-i}$
we have $P(B\leqslant b)=\sum _{i=0}^{\lfloor b\rfloor }\binom{m}{i}p^iq^{m-i}$![]() for $b\in {\mathbb {R}}$
for $b\in {\mathbb {R}}$![]() . Thus $X=\frac {B-mp}{\sqrt {mpq}}$
. Thus $X=\frac {B-mp}{\sqrt {mpq}}$![]() and $x=\frac {b-mp}{\sqrt {mpq}}$
and $x=\frac {b-mp}{\sqrt {mpq}}$![]() satisfy
satisfy
Setting $p=q=\tfrac {1}{2}$![]() , and taking $b=r\in \{0,\,1,\,\ldots,\,m\}$
, and taking $b=r\in \{0,\,1,\,\ldots,\,m\}$![]() shows
shows
Remark 5.4 Let $a_0+{\mathcal {H}}_k$![]() be the generalized continued fraction approximation to $\frac {(r+1)\binom{m}{r+1}}{s_m(r)}$
be the generalized continued fraction approximation to $\frac {(r+1)\binom{m}{r+1}}{s_m(r)}$![]() suggested by theorem 1.1, where ${\mathcal {H}}_k:=\mathcal{K}_{i=1}^k\frac {b_i}{a_i}$
suggested by theorem 1.1, where ${\mathcal {H}}_k:=\mathcal{K}_{i=1}^k\frac {b_i}{a_i}$![]() , and $k$
, and $k$![]() is the depth of the generalized continued fraction. We compare the following two quantities:
is the depth of the generalized continued fraction. We compare the following two quantities:

The sign of $e_{m,r,k}$![]() is governed by the parity of $k$
is governed by the parity of $k$![]() by proposition 2.3. We shall assume that $r\leqslant \frac {m}{2}$
by proposition 2.3. We shall assume that $r\leqslant \frac {m}{2}$![]() . As $\frac {2^m}{s_m(r)}$
. As $\frac {2^m}{s_m(r)}$![]() ranges from $2^m$
ranges from $2^m$![]() to about 2 as $r$
to about 2 as $r$![]() ranges from 0 to $\lfloor \frac {m}{2}\rfloor$
ranges from 0 to $\lfloor \frac {m}{2}\rfloor$![]() , it is clear that the upper bound for $E_{m,r}$
, it is clear that the upper bound for $E_{m,r}$![]() will be huge unless $r$
will be huge unless $r$![]() satisfies $\frac {m-\varepsilon }{2}\le r\le \frac {m}{2}$
satisfies $\frac {m-\varepsilon }{2}\le r\le \frac {m}{2}$![]() where $\varepsilon$
where $\varepsilon$![]() is ‘small’ compared to $m$
is ‘small’ compared to $m$![]() . By contrast, the computer code [Reference Glasby3] verifies that the same is true for $E_{m,r}$
. By contrast, the computer code [Reference Glasby3] verifies that the same is true for $E_{m,r}$![]() , and shows that $|e_{m,r,k}|$
, and shows that $|e_{m,r,k}|$![]() is small, even when $k$
is small, even when $k$![]() is tiny, when $0\le r<\frac {m-\varepsilon }{2}$
is tiny, when $0\le r<\frac {m-\varepsilon }{2}$![]() , see table 2. Hence the ‘generalized continued fraction’ approximation to $s_m(r)$
, see table 2. Hence the ‘generalized continued fraction’ approximation to $s_m(r)$![]() is complementary to the ‘statistical’ approximation, as shown in table 2. The reader can extend table 2 by running the code [Reference Glasby3] written in the Magma [Reference Bosma, Cannon and Playoust1] language, using the online calculator http://magma.maths.usyd.edu.au/calc/, for example.
is complementary to the ‘statistical’ approximation, as shown in table 2. The reader can extend table 2 by running the code [Reference Glasby3] written in the Magma [Reference Bosma, Cannon and Playoust1] language, using the online calculator http://magma.maths.usyd.edu.au/calc/, for example.
Table 2. Upper bounds for $|e_{m,r,k}|$![]() and $E_{m,r}$
and $E_{m,r}$![]() for $m=10^4$
for $m=10^4$![]()

Acknowledgements
SPG received support from the Australian Research Council Discovery Project Grant DP190100450. GRP thanks his family, and SPG thanks his mother.