1. Introduction
The development of finger-like structures in porous media and in confined geometries such as Hele-Shaw cells is a well-known phenomenon that has been observed experimentally in a variety of flow configurations. For example, instabilities that develop into finger-like structures occur in shear-stress-dominated flows when a viscous fluid is displaced by a less viscous one, and in extensional-stress-dominated flows when a shear-thinning fluid is extruded.
In the former case involving shear-dominated flows, fingering originates from the Saffman–Taylor instability (Saffman & Taylor Reference Saffman and Taylor1958), which occurs at the displacement front. There is a jump in dynamic pressure gradient across this moving front, with its magnitude being greater in the more viscous, displaced fluid than in the less viscous, displacing fluid. Therefore, any protrusion of the invading fluid finds itself in an environment of higher pressure gradient and, having itself less resistance to flow than the ambient, advances further, ultimately forming an extended finger. The Saffman–Taylor instability involves the coupled dynamics of two regions of fluid separated by an interface, whose pressure gradients are determined by transverse viscous shear stresses. It has been widely studied in the context of two-dimensional, planar fronts (Bensimon et al. Reference Bensimon, Kadanoff, Liang, Shraiman and Tang1986; Saffman Reference Saffman1986) and axisymmetric, radial fronts (Paterson Reference Paterson1981, Reference Paterson1985). The Saffman–Taylor instability also features in complex fluids (Wilson Reference Wilson1990; Lemaire et al. Reference Lemaire, Levitz, Daccord and Van Damme1991; Kondic, Palffy-Muhoray & Shelley Reference Kondic, Palffy-Muhoray and Shelley1996; Kondic, Shelley & Palffy-Muhoray Reference Kondic, Shelley and Palffy-Muhoray1998; Coussot Reference Coussot1999; Lindner, Bonn & Meunier Reference Lindner, Bonn and Meunier2000a; Lindner, Coussot & Bonn Reference Lindner, Coussot and Bonn2000b; Fast et al. Reference Fast, Kondic, Shelley and Palffy-Muhoray2001; Azaiez & Singh Reference Azaiez and Singh2002; Lindner et al. Reference Lindner, Bonn, Poiré, Amar and Meunier2002; Tordjeman Reference Tordjeman2007; Mora & Manna Reference Mora and Manna2009; Fadoul & Coussot Reference Fadoul and Coussot2019; Ball, Balmforth & Dufresne Reference Ball, Balmforth and Dufresne2021; Abedi et al. Reference Abedi, Berghe, Fonseca, Rodrigues, Oliveira and de Souza Mendes2022; Dufresne Reference Dufresne2022; Dufresne, Ball & Balmforth Reference Dufresne, Ball and Balmforth2023).
It has been noted that, in a Hele-Shaw cell, a thin film of the ambient fluid can be left behind, separating the intruding fluid from the cell walls. Studies of the effect of the thin film have been undertaken (Tabeling, Zocchi & Libchaber Reference Tabeling, Zocchi and Libchaber1987; Tanveer Reference Tanveer1990, Reference Tanveer2000; Dauck Reference Dauck2020) in which it has been shown to modify the instability rather than determine it. Nevertheless, these studies indicate how ambient fluid can be left behind, which could have the potential to lubricate the intruding fluid, resulting in the reduction of shear stress.
The Saffman–Taylor, frontal instability does not occur when the displacing fluid is more viscous than its environment. However, an entirely different fingering instability can occur when a shear-thinning fluid is extruded radially, regardless of its environment, if its dynamics is dominated by extensional stresses rather than shear stresses. Sayag & Worster (Reference Sayag and Worster2019b) explained such instabilities using a two-dimensional, linear stability analysis. The driving mechanism of instability is the relief of hoop stresses, stresses induced as rings of fluid stretch circumferentially while flowing radially outwards. That mechanism exists even for Newtonian fluids but is stabilised at both long and short wavelengths by horizontal (in the plane of the flow) shear stresses. The stabilisation of short wavelengths is weakened in shear-thinning fluids, allowing instability if the fluid is sufficiently shear thinning.
The analysis of Sayag & Worster (Reference Sayag and Worster2019b) was motivated by experiments in which shear-thinning fluids flowed radially outwards, floating on a layer of denser, relatively inviscid fluid (Pegler & Worster Reference Pegler and Worster2012; Sayag & Worster Reference Sayag and Worster2019a). In those experiments, the extensionally dominated region began at a dynamic grounding line, where the intruding fluid first detached from a rigid base to form a floating layer, which also thinned under the action of gravity. The overall dynamics of the experimental system was therefore much more complicated than the idealised stability analysis (Sayag & Worster Reference Sayag and Worster2019b). Our study began with the aim of developing an experimental set-up closer to the idealised system. In short, to develop a Hele-Shaw cell with negligible wall stress so that the thickness of the shear-thinning fluid layer would be controlled, and its dynamics determined by extensional stresses and in-plane shear stresses rather than by transverse shear stresses. We achieved our goal by having the viscous, shear-thinning fluid intrude an ambient fluid that is sufficiently viscous to maintain a lubricating layer separating the intruding fluid from the walls of the cell, whilst having a sufficiently low viscosity to render the effective wall stress negligible. Specifically, we used a solution of xanthan gum intruding into water. An added advantage of this system is that the two fluids have almost the same density, so the intruding fluid is neutrally buoyant and gravity can be neglected.
Initially, we injected xanthan gum solutions into a water-filled, parallel-sided Hele-Shaw cell. We found that over most of the flow the xanthan gum either displaced the water completely, or there was such a thin film of water left behind that it was not sufficiently lubricating. However, there was a relatively narrow annulus behind the leading edge of the xanthan gum in which there was a lubricating water film. Fractures formed in this region similar to those seen in experiments using Carbopol injected radially into a water-filled Hele-Shaw cell (Ball et al. Reference Ball, Balmforth and Dufresne2021). Those authors conducted further studies (Ball & Balmforth Reference Ball and Balmforth2021; Ball et al. Reference Ball, Balmforth, Dufresne and Morris2022) and argued against the mechanism proposed by Sayag & Worster (Reference Sayag and Worster2019b), suggesting instead that the fracturing resulted from a reduction in the fracture energy of the suspension when placed in contact with water. Whatever the mechanism, whether it be the release of hoop stresses or the reduction of fracture energy, it was clear that the fractures in our experiments were not as extended as the fingers observed by Sayag & Worster (Reference Sayag and Worster2019a).
To extend the region of lubrication, we inserted disks at the top and bottom of the Hele-Shaw cell from between which the xanthan gum solution was injected, so that there was a pre-determined initial thickness to the lubricating films of water. With this device, branches formed with troughs extending most of the way back to the edge of the inserted disks, having similar character to the fingers observed by Sayag & Worster (Reference Sayag and Worster2019a). We repeated a few of these experiments using rapeseed oil as the ambient fluid. These experiments also exhibited extended fingers, albeit their troughs were rounded by surface tension, which suggests that the mechanism of instability leading to this fingering was fluid mechanical rather than chemical fracturing. We proceeded to focus on using water as the lubricating fluid as the density difference between xanthan gum and water is negligible, thus eliminating the effect of buoyancy, and conducted a systematic investigation of the number of branches formed as we varied the flow rate and the radius of injection.
In § 2, we derive some theoretical estimates for the viscosity of the intruding fluid to rule out a Saffman–Taylor mechanism for instability in our experiments and to determine the minimum thickness needed for the lubricating films for extensional stresses to dominate transverse shear stresses. We describe our experimental set-up and the series of experiments that we conducted in § 3, where we also provide an analysis of the results. Discussions are presented in § 4 and conclusions are given in § 5.
2. Theoretical estimates
Consider an axisymmetric configuration in which a shear-thinning fluid initially occupies the region between two disks ![]() $-h< z< h$,
$-h< z< h$, ![]() $r< r_G$, while a Newtonian fluid of a similar density occupies
$r< r_G$, while a Newtonian fluid of a similar density occupies ![]() $-H< z< H$,
$-H< z< H$, ![]() $r>r_G$, with
$r>r_G$, with ![]() $h< H$, in cylindrical polar coordinates
$h< H$, in cylindrical polar coordinates ![]() $(r,\theta,z)$. From time
$(r,\theta,z)$. From time ![]() $t=0$, flow is initiated by supplying more of the shear-thinning fluid at a constant flux
$t=0$, flow is initiated by supplying more of the shear-thinning fluid at a constant flux ![]() $Q_0$ from
$Q_0$ from ![]() $r=0$, as illustrated in figure 1. For
$r=0$, as illustrated in figure 1. For ![]() $r< r_G$, the shear-thinning fluid is in contact with both disks, while for
$r< r_G$, the shear-thinning fluid is in contact with both disks, while for ![]() $r>r_G$, a layered fluid structure develops in which the shear-thinning fluid is bounded by two lubricating layers of Newtonian fluid.
$r>r_G$, a layered fluid structure develops in which the shear-thinning fluid is bounded by two lubricating layers of Newtonian fluid.

Figure 1. Side view of the axisymmetric injection of a shear-thinning fluid that fills the gap of size ![]() $2 h$ between two disks completely for
$2 h$ between two disks completely for ![]() $r< r_G$, and is confined between two lubricating layers of Newtonian fluid in the region
$r< r_G$, and is confined between two lubricating layers of Newtonian fluid in the region ![]() $r>r_G$, where
$r>r_G$, where ![]() $r_G$ is the radius of the disks.
$r_G$ is the radius of the disks.
2.1. Viscosity of the intruding fluid
We want to rule out the Saffman–Taylor mechanism of instability by ensuring that the viscosity of the intruding fluid is everywhere greater than the ambient fluid. In the region between the two disks, ![]() $r< r_G$, the flow is axisymmetric and in contact with both the top and bottom solid boundaries where the no-slip condition applies. Denote the velocity component in the
$r< r_G$, the flow is axisymmetric and in contact with both the top and bottom solid boundaries where the no-slip condition applies. Denote the velocity component in the ![]() $r$ direction by
$r$ direction by ![]() $u_r(r,z)$, the pressure by
$u_r(r,z)$, the pressure by ![]() $p(r)$ and the viscosity by
$p(r)$ and the viscosity by ![]() $\mu (r,z)$. In this region, we can neglect the velocity component in the
$\mu (r,z)$. In this region, we can neglect the velocity component in the ![]() $z$ direction. We use a power-law model to describe the shear-thinning fluid with dynamic viscosity
$z$ direction. We use a power-law model to describe the shear-thinning fluid with dynamic viscosity
where the consistency factor ![]() $m$ and the constant
$m$ and the constant ![]() $n$ are properties of the fluid,
$n$ are properties of the fluid,
 \begin{equation} e_{II} = \frac{1}{2} e_{i j} e_{i j} =\frac{1}{2} \left[ \left(\frac{\partial u_r}{\partial r} \right)^2 + \left(\frac{u_r}{r} \right)^2 +\frac{1}{2} \left(\frac{\partial u_r}{\partial z} \right)^2 \right], \end{equation}
\begin{equation} e_{II} = \frac{1}{2} e_{i j} e_{i j} =\frac{1}{2} \left[ \left(\frac{\partial u_r}{\partial r} \right)^2 + \left(\frac{u_r}{r} \right)^2 +\frac{1}{2} \left(\frac{\partial u_r}{\partial z} \right)^2 \right], \end{equation}
and ![]() $e_{i j}$ is the rate-of-strain tensor. Values of
$e_{i j}$ is the rate-of-strain tensor. Values of ![]() $n$ in the range
$n$ in the range ![]() $0< n<1$ correspond to fluids that are shear-thickening,
$0< n<1$ correspond to fluids that are shear-thickening, ![]() $n=1$ pertains to Newtonian fluids and
$n=1$ pertains to Newtonian fluids and ![]() $n>1$ corresponds to fluids that are shear-thinning.
$n>1$ corresponds to fluids that are shear-thinning.
In the region between the two disks, ![]() $r< r_G$, sufficiently far from the source, we approximate the flow using the thin-film-flow equation
$r< r_G$, sufficiently far from the source, we approximate the flow using the thin-film-flow equation
where ![]() $G(r)>0$ is a function of
$G(r)>0$ is a function of ![]() $r$ only. Within this approximation, where
$r$ only. Within this approximation, where ![]() $z \ll r$, (2.1) becomes
$z \ll r$, (2.1) becomes
 \begin{equation} \mu(r,z) = 2^{1-1/n } m\left|\frac{\partial u_r}{\partial z}\right|^{1/n -1}. \end{equation}
\begin{equation} \mu(r,z) = 2^{1-1/n } m\left|\frac{\partial u_r}{\partial z}\right|^{1/n -1}. \end{equation}
Global conservation of mass dictates that, for ![]() $0< r< r_G$,
$0< r< r_G$,
is the depth-averaged radial velocity. In (2.5), we have exploited the fact that, ![]() $u_r(r, z)$ is an even function of
$u_r(r, z)$ is an even function of ![]() $z$.
$z$.
Solving (2.3) with symmetry and no-slip conditions
in the top half ![]() $0 \leq z \leq h$, where
$0 \leq z \leq h$, where ![]() ${\partial u_r}/{\partial z} \leq 0$, leads to
${\partial u_r}/{\partial z} \leq 0$, leads to
We use this velocity field in the conservation condition (2.5) to obtain
Therefore, for ![]() $0< r< r_G$,
$0< r< r_G$, ![]() $-h \leq z \leq h$, we have
$-h \leq z \leq h$, we have
 \begin{equation} u_r (r,z)= \frac{n+2}{n+1} \frac{Q_0 }{4 {\rm \pi}r h } \left[ 1-\left(\frac{|z|}{h}\right)^{n+1} \right] \end{equation}
\begin{equation} u_r (r,z)= \frac{n+2}{n+1} \frac{Q_0 }{4 {\rm \pi}r h } \left[ 1-\left(\frac{|z|}{h}\right)^{n+1} \right] \end{equation}and
 \begin{equation} \mu(r,z) = m \left( \frac{8 {\rm \pi}h^{2} r}{(n+2)Q_0}\right)^{1-1/n} \left(\frac{h}{|z|} \right)^{n-1}. \end{equation}
\begin{equation} \mu(r,z) = m \left( \frac{8 {\rm \pi}h^{2} r}{(n+2)Q_0}\right)^{1-1/n} \left(\frac{h}{|z|} \right)^{n-1}. \end{equation}As expected, the viscosity takes on its minimum value
 \begin{equation} \mu_{min}(r) = m \left( \frac{8 {\rm \pi}h^{2} r}{(n+2)Q_0}\right)^{1-1/n} \end{equation}
\begin{equation} \mu_{min}(r) = m \left( \frac{8 {\rm \pi}h^{2} r}{(n+2)Q_0}\right)^{1-1/n} \end{equation}
at the walls, ![]() $z = \pm h$, where the shear is greatest.
$z = \pm h$, where the shear is greatest.
Our estimate for the viscosity (2.10), based on shear-dominated dynamics, tends to infinity as ![]() $z \rightarrow 0$, where there is no shear. In this central region, the viscosity is determined by both radial and azimuthal extension. In a purely extensional flow with no vertical shear, the radial component of the velocity is
$z \rightarrow 0$, where there is no shear. In this central region, the viscosity is determined by both radial and azimuthal extension. In a purely extensional flow with no vertical shear, the radial component of the velocity is
which is equivalent to the depth-averaged radial velocity, (2.5). In this case,
 \begin{equation} e_{II} =\frac{1}{2} \left[ \left(\frac{\partial u_r}{\partial r} \right)^2 + \left(\frac{u_r}{r} \right)^2 \right] = \left( \frac{Q_0}{4 {\rm \pi}h r^2}\right)^2, \end{equation}
\begin{equation} e_{II} =\frac{1}{2} \left[ \left(\frac{\partial u_r}{\partial r} \right)^2 + \left(\frac{u_r}{r} \right)^2 \right] = \left( \frac{Q_0}{4 {\rm \pi}h r^2}\right)^2, \end{equation}with corresponding viscosity
 \begin{equation} \mu^*(r) = m \left( \frac{4 {\rm \pi}h r^2}{Q_0}\right)^{1-1/n} =\mu_{min}(r) \left[ \frac{(n+2) r}{2 h}\right]^{1-1/n}. \end{equation}
\begin{equation} \mu^*(r) = m \left( \frac{4 {\rm \pi}h r^2}{Q_0}\right)^{1-1/n} =\mu_{min}(r) \left[ \frac{(n+2) r}{2 h}\right]^{1-1/n}. \end{equation}
Provided the radius of the disks ![]() $r_G >2h/(n+2)$, which is the case for all of our experiments, the lowest viscosity that the intruding fluid has adjacent to the ambient fluid is
$r_G >2h/(n+2)$, which is the case for all of our experiments, the lowest viscosity that the intruding fluid has adjacent to the ambient fluid is ![]() $\mu _{min}(r_G)$, attained at the surface of the disks just before the fluid exits the gap between them.
$\mu _{min}(r_G)$, attained at the surface of the disks just before the fluid exits the gap between them.
In practice, the constants ![]() $m$ and
$m$ and ![]() $n$ are determined from a log–log plot of shear viscosity versus shear rate over a range of shear rates, from data generated by a rheometer. In our experiments, we used a xanthan gum solution and lubricating fluids that were either water or rapeseed oil. In Appendix A, § A.1, we estimate these values for the xanthan gum solution used in our experiments. This leads to values for
$n$ are determined from a log–log plot of shear viscosity versus shear rate over a range of shear rates, from data generated by a rheometer. In our experiments, we used a xanthan gum solution and lubricating fluids that were either water or rapeseed oil. In Appendix A, § A.1, we estimate these values for the xanthan gum solution used in our experiments. This leads to values for ![]() $\mu _{min}(r_G)$ in the range 1–26 Pa s, which is well above the viscosity of the lubricating fluids, water and rapeseed oil, which have viscosities of 0.001 Pa s and 0.066 Pa s, respectively. We can therefore conclude that the viscosity of the shear-thinning fluid just before it exits the disks is everywhere greater than the viscosity of either of the lubricating fluids, and so any interfacial instabilities that do form are not of Saffman–Taylor type.
$\mu _{min}(r_G)$ in the range 1–26 Pa s, which is well above the viscosity of the lubricating fluids, water and rapeseed oil, which have viscosities of 0.001 Pa s and 0.066 Pa s, respectively. We can therefore conclude that the viscosity of the shear-thinning fluid just before it exits the disks is everywhere greater than the viscosity of either of the lubricating fluids, and so any interfacial instabilities that do form are not of Saffman–Taylor type.
2.2. Lubrication
In this section, we establish the conditions under which extensional stresses dominate over shear stresses in the shear-thinning fluid layer within the lubricated region. Our experiments indicated that the lubrication layers started to thin near to the disks at later times. However, we can ensure that, for early times, we begin with effective pre-formed lubrication layers close to the disks, separating the shear-thinning fluid from the cell walls. Near to the disks, we approximate the viscosity of the shear-thinning fluid by (2.14), and assume the velocity ![]() $u_r = u_r(r,z)$ is a function of
$u_r = u_r(r,z)$ is a function of ![]() $r$ and
$r$ and ![]() $z$ only.
$z$ only.
At the interfaces between the two fluids, there is continuity of velocity and shear stress,
where ![]() $\mu _L$ and
$\mu _L$ and ![]() $U_r$ are the dynamic viscosity and the radial velocity of the Newtonian fluid in the lubricating layers, respectively. The initial thicknesses of the shear-thinning fluid layer and each lubricating layer are approximately
$U_r$ are the dynamic viscosity and the radial velocity of the Newtonian fluid in the lubricating layers, respectively. The initial thicknesses of the shear-thinning fluid layer and each lubricating layer are approximately ![]() $2 h$ and
$2 h$ and ![]() $H-h$, respectively. Let
$H-h$, respectively. Let ![]() $U^*$ be the characteristic radial speed. From (2.15), we deduce that the magnitude of the shear stress is
$U^*$ be the characteristic radial speed. From (2.15), we deduce that the magnitude of the shear stress is
which is negligible in comparison with the extensional stress
provided
 \begin{equation} H-h \gg \frac{\mu_L}{m} \left(\frac{Q_0}{4 {\rm \pi}h} \right)^{1-1/n} \frac{1}{r^{1-2/n}}. \end{equation}
\begin{equation} H-h \gg \frac{\mu_L}{m} \left(\frac{Q_0}{4 {\rm \pi}h} \right)^{1-1/n} \frac{1}{r^{1-2/n}}. \end{equation}
From (2.18), we see that for ![]() $n>2$, thicker lubrication layers are required when
$n>2$, thicker lubrication layers are required when ![]() $r$ is small and when the flux
$r$ is small and when the flux ![]() $Q_0$ and ambient viscosity
$Q_0$ and ambient viscosity ![]() $\mu _L$ are large. In Appendix A, § A.3, we evaluate (2.18) at
$\mu _L$ are large. In Appendix A, § A.3, we evaluate (2.18) at ![]() $r=r_G$, where the shear-thinning fluid emerges from between the two disks, to estimate sufficient thicknesses for the disks. Using our experimental parameters, we find that for effective lubrication to occur across the entire range of our experiments, we require
$r=r_G$, where the shear-thinning fluid emerges from between the two disks, to estimate sufficient thicknesses for the disks. Using our experimental parameters, we find that for effective lubrication to occur across the entire range of our experiments, we require
for water-lubricated layers, and
for rapeseed oil-lubricated layers. These results are useful estimates to ensure that each experiment starts with effective pre-formed lubrication layers. We shall see later, however, that the lubrication layers thin over time and become less effective.
3. Experimental results
In all of our experiments, we used the shear-thinning fluid xanthan gum and created a 1 % (by mass) solution. To make 1 litre of this solution, 10 g of xanthan powder was first mixed thoroughly with 20 g of vegetable oil which was then added to 970 g of warm water. An electric mixer was used to combine this solution until it was smooth and devoid of lumps. The solution was left for approximately 48 hours before being used in the experiments to allow the solution to undergo full hydration and cool to room temperature, resulting in a smooth mixture free of bubbles and clumps. The density of the xanthan gum was measured and found to be approximately ![]() $1 \pm 0.01$ g cm
$1 \pm 0.01$ g cm![]() $^{-3}$, with negligible difference to that of the tap water used for the experiments. Further properties of the xanthan gum mixture are discussed in Appendix A.
$^{-3}$, with negligible difference to that of the tap water used for the experiments. Further properties of the xanthan gum mixture are discussed in Appendix A.
3.1. Experiments without pre-formed lubrication layers
Our initial experimental set-up consisted of: a square tray with each side of length 66 cm with side walls of height 4 cm; a perspex sheet which formed the bottom of the tray with a hole of diameter 1.2 cm located at the centre; a second square perspex sheet with each side of length 50 cm; and plate spacers of 4 mm thick placed at each corner which separated the top perspex sheet from the tray. The top perspex sheet was clamped down at two opposite edges to minimise any plate deflection. The top and bottom perspex sheets were 15 mm thick. Xanthan gum was injected into the space between the two plates through the hole located on the lower perspex sheet using a peristaltic pump, with fluxes in the range ![]() $0.14\ {\rm ml}\ {\rm s}^{-1}$ to
$0.14\ {\rm ml}\ {\rm s}^{-1}$ to ![]() $2.8\ {\rm ml}\ {\rm s}^{-1}$. When the gap between the two plates contained only air i.e. a dry Hele-Shaw cell, the xanthan gum displaced the air and filled the gap completely, and the flow spread axisymmetrically as shown in figure 2(a).
$2.8\ {\rm ml}\ {\rm s}^{-1}$. When the gap between the two plates contained only air i.e. a dry Hele-Shaw cell, the xanthan gum displaced the air and filled the gap completely, and the flow spread axisymmetrically as shown in figure 2(a).

Figure 2. Sample photographs viewed from above for three different experiments without pre-formed lubrication layers where (a) xanthan gum is injected into an air-filled gap; (b) xanthan gum is injected into a water-filled gap; and (c) xanthan gum is injected into an oil-filled gap. In each photograph, the circular rings are at 5 cm intervals.
In the lubricated Hele-Shaw cell experiments, we ensured that we started with an initially circular xanthan gum profile by first injecting it into the air-filled gap, until the leading edge reached a radius of approximately 5 cm. The xanthan gum displaced the air, filling the gap entirely in this region for the range of fluxes considered. The lubricating fluid was then carefully poured into the tray at the edges, until the remaining air in the gap between the two plates was replaced by the lubricant. Once this process was complete, the peristaltic pump was restarted at the chosen flux and subsequent injection of the xanthan gum began. When water was used as the lubricating fluid, the initially circular leading edge became jagged, consisting of rectangular and triangular protrusions, as shown in figure 2(b). We also performed a number of experiments where rapeseed oil was used as the lubricating fluid. Here, we saw that the protrusions at the leading edge were larger in magnitude, and much smoother and less jagged. An example of such an experiment is shown in figure 2(c).
The structural differences in the protrusions may be due to a number of factors. In particular, because xanthan gum and rapeseed oil are immiscible, it is likely that surface tension is responsible for the much smoother leading edges, whereas xanthan gum is a water-based solution and surface tension at the xanthan gum–water interface is negligible, resulting in rougher, more jagged edges. Nevertheless, it is clear from these experiments that the intruding flow is unstable given lubricating ambient fluids of significantly different chemistry. We hypothesise that the instability leading to these protrusions is dynamical rather than chemical. Given that the rapeseed oil has a density of approximately 0.9 g cm![]() $^{-3}$, which is significantly less dense than xanthan gum, we chose to use water for the experiments that followed, which is more convenient experimentally and reduces the effect of buoyancy significantly.
$^{-3}$, which is significantly less dense than xanthan gum, we chose to use water for the experiments that followed, which is more convenient experimentally and reduces the effect of buoyancy significantly.
Four such experiments for different fluxes showed that the protrusions do not grow significantly in size over the duration of each experiment. They remained within an annular region near to the leading edge of the xanthan gum, and migrated with the flow. In other words, there was no clear branch-like structure in these experiments, the type of which we were aiming to reproduce, as observed in the studies of Sayag & Worster (Reference Sayag and Worster2019a). We also saw that the xanthan gum started to displace the water completely outside of the initial 5 cm radius, an observation which was confirmed when the top plate was removed at the end of an experiment and xanthan gum was found to be in contact with it. We postulated that the absence of clear branch-like structures was a result of the diminishing effectiveness of the lubrication layers which occurred over the bulk of the flow where the xanthan gum was in contact with the cell walls. In the small annular region in which the protrusions were embedded, the xanthan gum remained separated from the cell walls. Our rather small estimate from (2.19) of the required thickness for effective lubricating layers indicated that the outer annular region, where the xanthan gum was separated from the cells walls, was most likely sufficiently lubricated, and extensional stresses dominated. However, in the grounded region where the shear-thinning fluid was in contact with both the top and bottom plates, the thickness of the lubrication layers tended to zero, and shear stresses dominated. The observation that the instabilities occurred only within the lubricated region was the motivation behind the design of the next set of experiments which included pre-formed lubrication layers.
3.2. Experiments with pre-formed lubrication layers
We altered our initial experimental set-up by placing a disk at the centre of the top perspex plate, and another disk of the same dimensions, but with a hole in the centre through which fluid could be injected, on the lower plate. The disks, each having a radius of 5.5 cm and thicknesses of either 1 mm or 2 mm, created pre-formed lubrication layers initially having approximately the same thickness as that of the disks, by ensuring that when the leading edge of the xanthan gum exceeded the radius of the disks, the xanthan gum layer was confined to the space between the two lubricating water layers.
We conducted two sets of experiments with disks of radius 5.5 cm. In the first set, larger plate spacings of 8 mm were used and each disk had a thickness of 2 mm, so that the xanthan gum was confined to a 4 mm gap in the disk region and the lubricating layers were initially 2 mm thick. In the second set, we halved the thickness of the disks to 1 mm, and used smaller plate spacings of only 6 mm, to maintain a 4-mm-thick xanthan gum layer between the two disks, and lubricating layers that were initially 1 mm thick. Although selecting disks of either 1 mm or 2 mm thick greatly exceeds the requirement for effective lubrication as estimated by (2.19), we chose these larger thicknesses to account for the thinning of the lubrication layers over time, an effect for which we had clear observational evidence. The purpose of the second set of experiments, where disks of 1 mm were used, was to observe this effect in more detail.
We first injected xanthan gum into the narrow 4 mm air-filled gap between the two disks until the radius of the leading edge of the current reached approximately 5 cm which was just less than the radius of the disks. The xanthan gum once again displaced the air and filled the gap completely, while spreading axisymmetrically, creating an initially circular profile. Water was then added at the edges of the tray until the remaining air in the gap between the two plates was completely ejected. The peristaltic pump was restarted at time ![]() $t=0$ at some chosen flux ranging from
$t=0$ at some chosen flux ranging from ![]() $0.14\ {\rm ml}\ {\rm s}^{-1}$ to
$0.14\ {\rm ml}\ {\rm s}^{-1}$ to ![]() $2.8\ {\rm ml}\ {\rm s}^{-1}$.
$2.8\ {\rm ml}\ {\rm s}^{-1}$.
3.2.1. 2 mm lubrication layers
We varied the flux and recorded the results of 14 experiments with lubrication layers initially 2 mm thick. In each experiment, at early times, small tears in the outer annular region of the xanthan gum were observed. Some of the tears may have formed before the leading edge of the xanthan gum exited the disks but no definite conclusion regarding this could be made. At later times, some of these tears grew in size, resulting in the formation of branches in the lubricated region beyond the disks. The branches were rather rectangular with straight edges, whilst some triangular-shaped branches were observed at lower fluxes. This is in contrast with the experiments without the disks where the protrusions did not grow much in size, and here a proper branch-like structure was observed with the troughs of the branches located near to the edge of the disks.
A series of photographs of one such experiment, where ![]() $Q_0=0.56\ {\rm ml}\ {\rm s}^{-1}$, is shown in figure 3. For early times, shown in panel (a), tears can be clearly seen in the outer edge of the xanthan gum, with some of these tears leading to the formation of branch-like structures, as shown in panel (b). Four clear branches emerged at approximately
$Q_0=0.56\ {\rm ml}\ {\rm s}^{-1}$, is shown in figure 3. For early times, shown in panel (a), tears can be clearly seen in the outer edge of the xanthan gum, with some of these tears leading to the formation of branch-like structures, as shown in panel (b). Four clear branches emerged at approximately ![]() $t=60$ s and the branches continued to grow and propagate radially up until approximately
$t=60$ s and the branches continued to grow and propagate radially up until approximately ![]() $t=180$ s, at which point we started to see the troughs migrating radially outwards away from the disks. Some of the branches also started to rotate and develop vertical creases, as shown in panel (c). Visual observations suggested that by this stage, the lubrication layers were no longer effective, which was evidenced by finding xanthan gum in contact with the top plate once it was removed.
$t=180$ s, at which point we started to see the troughs migrating radially outwards away from the disks. Some of the branches also started to rotate and develop vertical creases, as shown in panel (c). Visual observations suggested that by this stage, the lubrication layers were no longer effective, which was evidenced by finding xanthan gum in contact with the top plate once it was removed.

Figure 3. Sample photographs viewed from above where xanthan gum is injected at a constant flux ![]() $Q_0 = 0.56\ {\rm ml}\ {\rm s}^{-1}$ into a Hele-Shaw cell, using disks of radius 5.5 cm and pre-formed lubrication layers of 2 mm, at times (a)
$Q_0 = 0.56\ {\rm ml}\ {\rm s}^{-1}$ into a Hele-Shaw cell, using disks of radius 5.5 cm and pre-formed lubrication layers of 2 mm, at times (a) ![]() $t=38$ s; (b);
$t=38$ s; (b); ![]() $t=150$ s; and (c)
$t=150$ s; and (c) ![]() $t=258$ s.
$t=258$ s.
In figure 4, sample photographs of three experiments with different fluxes are shown. In the low-flux experiment, shown in panel (a), 10 branches developed, both rectangular and triangular in shape. In the intermediate-flux experiment, shown in panel (b), three rectangular branches formed. In both of these experiments, the troughs remained near to the edge of the disks until much later times, when they were swept radially outwards. In the high-flux experiment, shown in panel (c), we saw that counting branches was not always a straightforward exercise. Here, we defined a branch as a protruding section where the troughs were located very near to the edge of the disks and where clear tearing or fracturing behaviour was observed at the troughs. For illustrative purposes, the edge of the disks have been highlighted, and the two troughs, which are located near to the edge of the disks, and at which fracturing behaviour occurred, are labelled. Based on this reasoning, in figure 4(c), we counted two branches.

Figure 4. Sample photographs viewed from above for three different experiments using disks of radius 5.5 cm and pre-formed lubrication layers of 2 mm, where (a) the output flux is ![]() $0.14\ {\rm ml}\ {\rm s}^{-1}$; (b) the output flux is
$0.14\ {\rm ml}\ {\rm s}^{-1}$; (b) the output flux is ![]() $0.84\ {\rm ml}\ {\rm s}^{-1}$; and (c) the output flux is
$0.84\ {\rm ml}\ {\rm s}^{-1}$; and (c) the output flux is ![]() $2.45\ {\rm ml}\ {\rm s}^{-1}$.
$2.45\ {\rm ml}\ {\rm s}^{-1}$.
3.2.2. 1 mm lubrication layers
In each of the experiments carried out with the 2 mm lubrication layers, we saw that at later times the branches started to thicken both width-wise and vertically, and become ‘stuck’, restricting radial motion significantly. When the top plate was removed, xanthan gum was found to be in contact with it in regions outside of where the disks were located, i.e. in the initially lubricated region. In this set-up, the initial thicknesses of the lubrication layers were halved and we highlighted the branches by instead dying the water and leaving the xanthan gum its natural off-white colour. According to the estimate for the thickness required for effective pre-formed lubrication layers, (2.19), halving the thickness of the lubrication layers from 2 mm to 1 mm would have little effect. However, decreasing the thickness of the pre-formed lubrication layers, which then thin further over time, allowed us to observe the impact of the increase in shear stresses on the development of the branch-like structures.
We performed 12 experiments in which the flux was varied over the range ![]() $0.14\ {\rm ml}\ {\rm s}^{-1} \leq Q_0 \leq 2.8\ {\rm ml}\ {\rm s}^{-1}$. Images taken from three such experiments are shown in figure 5. We counted 10 branches in the low-flux experiment, shown in panel (a), 5 in the intermediate-flux experiment, shown in panel (b), and two in the high-flux experiment, shown in panel (c). In general, we saw that the water lubrication layers continued to be effective at early times and the radial progression of the branches was only marginally impacted, with significant effects only noticeable at later times, as was the case where thicker lubrication layers were used. In fact, the number of branches that initially emerged from between the disks were similar to those recorded in § 3.2.1, where larger lubrication layers were used. However, there were noticeable differences between the two sets of experiments. Supplementary movies are available at https://doi.org/10.1017/jfm.2024.1169 for two experiments, both with an output flux of
$0.14\ {\rm ml}\ {\rm s}^{-1} \leq Q_0 \leq 2.8\ {\rm ml}\ {\rm s}^{-1}$. Images taken from three such experiments are shown in figure 5. We counted 10 branches in the low-flux experiment, shown in panel (a), 5 in the intermediate-flux experiment, shown in panel (b), and two in the high-flux experiment, shown in panel (c). In general, we saw that the water lubrication layers continued to be effective at early times and the radial progression of the branches was only marginally impacted, with significant effects only noticeable at later times, as was the case where thicker lubrication layers were used. In fact, the number of branches that initially emerged from between the disks were similar to those recorded in § 3.2.1, where larger lubrication layers were used. However, there were noticeable differences between the two sets of experiments. Supplementary movies are available at https://doi.org/10.1017/jfm.2024.1169 for two experiments, both with an output flux of ![]() $0.56\ {\rm ml}\ {\rm s}^{-1}$. The duration of each experiment was approximately 360 s in real time. In the experiment using disks of 2 mm, four clear branches emerge in the early stage, and the radial progression of the branches is impacted by thinning of the lubrication layers at approximately
$0.56\ {\rm ml}\ {\rm s}^{-1}$. The duration of each experiment was approximately 360 s in real time. In the experiment using disks of 2 mm, four clear branches emerge in the early stage, and the radial progression of the branches is impacted by thinning of the lubrication layers at approximately ![]() $t=180$ s, where we see some of the branches beginning to bend and the troughs starting to migrate radially outwards. In the experiment using disks of 1 mm, where five clear branches formed, the effects of the thinning of the lubrication layers is noticed earlier, at
$t=180$ s, where we see some of the branches beginning to bend and the troughs starting to migrate radially outwards. In the experiment using disks of 1 mm, where five clear branches formed, the effects of the thinning of the lubrication layers is noticed earlier, at ![]() $t=148$ s. At the end of both experiments, we see that in the experiment using the 1 mm disks, the branch-like structure is far more indistinct compared with the other experiment.
$t=148$ s. At the end of both experiments, we see that in the experiment using the 1 mm disks, the branch-like structure is far more indistinct compared with the other experiment.

Figure 5. Sample photographs viewed from above for three different experiments using disks of radius 5.5 cm and pre-formed lubrication layers of 1 mm, where (a) the output flux is ![]() $0.14\ {\rm ml}\ {\rm s}^{-1}$; (b) the output flux is
$0.14\ {\rm ml}\ {\rm s}^{-1}$; (b) the output flux is ![]() $0.56\ {\rm ml}\ {\rm s}^{-1}$; and (c) the output flux is
$0.56\ {\rm ml}\ {\rm s}^{-1}$; and (c) the output flux is ![]() $2.8\ {\rm ml}\ {\rm s}^{-1}$.
$2.8\ {\rm ml}\ {\rm s}^{-1}$.
3.2.3. Combined results
To compare the results across the two sets of experiments, we counted the number of fully developed branches that emerged from the region between the disks which reached a steady number, before the troughs were swept radially outwards. A plot of branch number versus flux is shown in figure 6. We saw that, in general, the number of branches decreased with increasing flux, with a much more pronounced decrease for fluxes in the range ![]() $0\ {\rm ml}\ {\rm s}^{-1}< Q_0 < 0.5\ {\rm ml}\ {\rm s}^{-1}$, and a relatively gradual decrease for
$0\ {\rm ml}\ {\rm s}^{-1}< Q_0 < 0.5\ {\rm ml}\ {\rm s}^{-1}$, and a relatively gradual decrease for ![]() $Q_0>1\ {\rm ml}\ {\rm s}^{-1}$. Our branch-counting method suggested that over the range of fluxes we considered and, in particular, the high-end region where
$Q_0>1\ {\rm ml}\ {\rm s}^{-1}$. Our branch-counting method suggested that over the range of fluxes we considered and, in particular, the high-end region where ![]() $Q_0> 2\ {\rm ml}\ {\rm s}^{-1}$, we did not see an experiment where fewer than two branches were observed. However, it was also in these high-flux experiments where we noticed significant thinning of the lubrication layers, leading to rather early radial migration of the troughs away from the edge of the disks. We also saw that at a fixed flux, there was a difference of at most one branch between each set of experiments. This result is as expected. There was no experimental evidence to suggest that the formation of the branch-like structures was impacted by the actual thickness of the lubrication layers, while they are sufficiently lubricating. At early times, thinner lubrication layers would still be effective and we would not expect major deviations in the number of branches that emerge.
$Q_0> 2\ {\rm ml}\ {\rm s}^{-1}$, we did not see an experiment where fewer than two branches were observed. However, it was also in these high-flux experiments where we noticed significant thinning of the lubrication layers, leading to rather early radial migration of the troughs away from the edge of the disks. We also saw that at a fixed flux, there was a difference of at most one branch between each set of experiments. This result is as expected. There was no experimental evidence to suggest that the formation of the branch-like structures was impacted by the actual thickness of the lubrication layers, while they are sufficiently lubricating. At early times, thinner lubrication layers would still be effective and we would not expect major deviations in the number of branches that emerge.
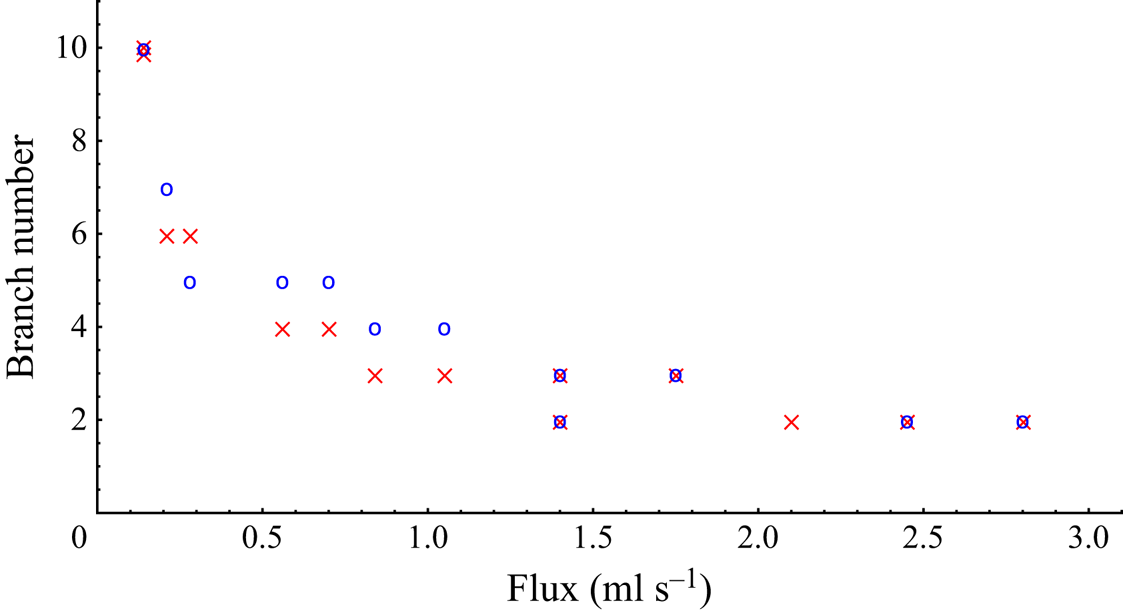
Figure 6. Branch number plotted against flux for the experimental set-ups using disks of radius ![]() $5.5$ cm, where the data points
$5.5$ cm, where the data points ![]() $\times$ (red) and
$\times$ (red) and ![]() $\circ$ (blue) correspond to 2 and 1 mm lubrication layers, respectively. The number of branches decreases with increasing flux, and between the two sets of experiments, there is a difference of at most one branch at a given flux. Repeated experiments are offset slightly.
$\circ$ (blue) correspond to 2 and 1 mm lubrication layers, respectively. The number of branches decreases with increasing flux, and between the two sets of experiments, there is a difference of at most one branch at a given flux. Repeated experiments are offset slightly.
In all of the experiments, at the stage where we saw the clear emergence of branch-like structures, the troughs of the branches where fracturing or tearing behaviour was observed were located near to the edge of the disks. Heuristically, given the instability mechanism suggested by Sayag & Worster (Reference Sayag and Worster2019b) involving the relief of hoop stresses associated with radial strain, we might expect the instability to be related to the strain rate. At the edge of the disks, the magnitude of the azimuthal strain rate is approximately
The strain rate takes on smaller values at lower fluxes, where it was seen experimentally that a higher number of branches formed. At a fixed flux, increasing ![]() $r_G$, which corresponds experimentally to using disks of a larger radius, also decreases the strain rate, and so we might expect a larger number of branches to form. We tested this hypothesis in the next set of experiments where we considered the same range of fluxes, but increased the radius of the disks from 5.5 cm to 8 cm.
$r_G$, which corresponds experimentally to using disks of a larger radius, also decreases the strain rate, and so we might expect a larger number of branches to form. We tested this hypothesis in the next set of experiments where we considered the same range of fluxes, but increased the radius of the disks from 5.5 cm to 8 cm.
3.3. Effect of strain rate on branch number
We ran 15 experiments in which disks of radius 8 cm and 2 mm thick were used instead of the disks with a smaller radius of 5.5 cm in a cell of total thickness 8 mm so that the thickness of the xanthan gum as it emerges from the gap between the disks was again 4 mm. Theoretically, from (2.18), we could select lubrication layers less than 2 mm thick and still satisfy the requirement for effective lubrication.
In figure 7, sample photographs are shown for three experiments with different fluxes. For the low-flux experiment with ![]() $Q_0=0.14\ {\rm ml}\ {\rm s}^{-1}$, shown in panel (a), a total of 17 branches formed, whereas with the smaller disks at the same flux we had seen only 10 branches. For
$Q_0=0.14\ {\rm ml}\ {\rm s}^{-1}$, shown in panel (a), a total of 17 branches formed, whereas with the smaller disks at the same flux we had seen only 10 branches. For ![]() $Q_0=0.28\ {\rm ml}\ {\rm s}^{-1}$, 15 branches formed whereas only five or six branches had been counted in the corresponding experiments with the smaller disks. As we moved to higher fluxes, we saw that the difference in branch number between the sets of experiments started to reduce. At
$Q_0=0.28\ {\rm ml}\ {\rm s}^{-1}$, 15 branches formed whereas only five or six branches had been counted in the corresponding experiments with the smaller disks. As we moved to higher fluxes, we saw that the difference in branch number between the sets of experiments started to reduce. At ![]() $Q_0=1.75\ {\rm ml}\ {\rm s}^{-1}$, we saw four branches, which was only one branch more than the experiments with the smaller disks at the same flux.
$Q_0=1.75\ {\rm ml}\ {\rm s}^{-1}$, we saw four branches, which was only one branch more than the experiments with the smaller disks at the same flux.

Figure 7. Sample photographs viewed from above for three different experiments using disks of radius 8 cm and pre-formed lubrication layers of 2 mm, where (a) the output flux is ![]() $0.14\ {\rm ml}\ {\rm s}^{-1}$; (b) the output flux is
$0.14\ {\rm ml}\ {\rm s}^{-1}$; (b) the output flux is ![]() $0.28\ {\rm ml}\ {\rm s}^{-1}$; and (c) the output flux is
$0.28\ {\rm ml}\ {\rm s}^{-1}$; and (c) the output flux is ![]() $1.75\ {\rm ml}\ {\rm s}^{-1}$.
$1.75\ {\rm ml}\ {\rm s}^{-1}$.
In figure 8(a), branch number is plotted against flux for all three sets of experiments, using disks of radius 5.5 cm and either 1 mm or 2 mm thick, and disks of radius 8 cm and 2 mm thick. It is seen that, in general, the branch number is greater at a given flux in the experiments using the disks of the larger radius, with the most noticeable differences occurring at lower fluxes. For higher fluxes, for all three sets of experiments, the branch number appeared to converge to two, provided that lubrication remained effective. There was one experiment, with ![]() $Q_0=2.8\ {\rm ml}\ {\rm s}^{-1}$ where lubrication was ineffective, caused by early rapid thinning, resulting in an ill-defined branch structure, in close resemblance to the experiments without disks.
$Q_0=2.8\ {\rm ml}\ {\rm s}^{-1}$ where lubrication was ineffective, caused by early rapid thinning, resulting in an ill-defined branch structure, in close resemblance to the experiments without disks.

Figure 8. Branch number plotted against (a) the output flux and (b) the magnitude of the strain rate ![]() $E$ defined by (3.1) evaluated as the fluid emerged from between the two disks. The data points
$E$ defined by (3.1) evaluated as the fluid emerged from between the two disks. The data points ![]() $\circ$ (blue) and
$\circ$ (blue) and ![]() $\times$ (red) correspond to the two sets of experiments where disks of radius 5.5 cm and thicknesses of 2 and 1 mm were used, respectively, and
$\times$ (red) correspond to the two sets of experiments where disks of radius 5.5 cm and thicknesses of 2 and 1 mm were used, respectively, and ![]() $\square$ (black) corresponds to the set of experiments where disks of radius 8 cm and 2 mm thickness were used. In panel (b), the data points collapsed onto the curve
$\square$ (black) corresponds to the set of experiments where disks of radius 8 cm and 2 mm thickness were used. In panel (b), the data points collapsed onto the curve ![]() $A E^b$ with
$A E^b$ with ![]() $A \approx 0.26$,
$A \approx 0.26$, ![]() $b \approx -0.58$, as shown using a log–log plot in the inset. Repeated experiments are offset slightly.
$b \approx -0.58$, as shown using a log–log plot in the inset. Repeated experiments are offset slightly.
Exploring the hypothesis mentioned above, we also plotted the branch number against the magnitude of the strain rate ![]() $E$ defined by (3.1) in figure 8. Here, we saw that the data collapsed onto a single universal curve. Empirically, we found the data could be fitted well with a simple power law of the form
$E$ defined by (3.1) in figure 8. Here, we saw that the data collapsed onto a single universal curve. Empirically, we found the data could be fitted well with a simple power law of the form ![]() $A E^b$ with
$A E^b$ with ![]() $A \approx 0.26$,
$A \approx 0.26$, ![]() $b \approx - 0.58$. These empirical results are suggestive that tearing occurs at a critical strain rate, an idea that deserves analysis in future studies.
$b \approx - 0.58$. These empirical results are suggestive that tearing occurs at a critical strain rate, an idea that deserves analysis in future studies.
4. Discussion
The primary result of our experimental study is an empirical relationship between the number of branches formed, provided the cell is sufficiently lubricated, and the strain rate at the radius of extrusion. Here, we speculate on that relationship using a scaling analysis and provide additional evidence regarding lubrication.
In our experiments, we measured significant differences depending on the radius ![]() $r_G$ where the extruded fluid first becomes lubricated (figure 8a), but little if any difference, within experimental error, depending on the initial thickness of the lubricating layers (figure 6). We also anticipate that, in the lubricated region on which we are focusing, there is negligible shear across the extruded layer and so the thickness of the layer should not affect the dynamics of the flow. With these ideas in mind, we consider that the dynamics of the flow is essentially two-dimensional. In two dimensions, the external parameters of our system are the flux
$r_G$ where the extruded fluid first becomes lubricated (figure 8a), but little if any difference, within experimental error, depending on the initial thickness of the lubricating layers (figure 6). We also anticipate that, in the lubricated region on which we are focusing, there is negligible shear across the extruded layer and so the thickness of the layer should not affect the dynamics of the flow. With these ideas in mind, we consider that the dynamics of the flow is essentially two-dimensional. In two dimensions, the external parameters of our system are the flux ![]() $Q_0/2h$ with dimensions
$Q_0/2h$ with dimensions ![]() $L^2 T^{-1}$, and the radius of extrusion
$L^2 T^{-1}$, and the radius of extrusion ![]() $r_G$ with dimension
$r_G$ with dimension ![]() $L$, where
$L$, where ![]() $L$ and
$L$ and ![]() $T$ are length and time scales, respectively. For a power-law fluid, the only dimensional physical parameter is the consistency
$T$ are length and time scales, respectively. For a power-law fluid, the only dimensional physical parameter is the consistency ![]() $m$, with dimensions
$m$, with dimensions ![]() $M L^{-1}T^{1/n -2}$, where
$M L^{-1}T^{1/n -2}$, where ![]() $M$ is a mass scale. There is no dimensionless grouping that can be formed from these parameters, which means that (excluding additional physics) the wavenumber must depend on
$M$ is a mass scale. There is no dimensionless grouping that can be formed from these parameters, which means that (excluding additional physics) the wavenumber must depend on ![]() $Q t/hr_G^2$, where
$Q t/hr_G^2$, where ![]() $t$ is the time elapsed since the start of the experiment. This is consistent with Sayag & Worster (Reference Sayag and Worster2019b) (see their (5.1) for example). Those authors also found that the number of branches decreased as the flow rate was increased (in agreement with our findings) and, in their experiments, that the wavenumber decreased with time. For a steady state to be reached, which seemed to be the case in our experiments, there needs to be a characteristic time scale determined by the physical parameters of the system. One possibility is to recognise that xanthan gum has a yield stress
$t$ is the time elapsed since the start of the experiment. This is consistent with Sayag & Worster (Reference Sayag and Worster2019b) (see their (5.1) for example). Those authors also found that the number of branches decreased as the flow rate was increased (in agreement with our findings) and, in their experiments, that the wavenumber decreased with time. For a steady state to be reached, which seemed to be the case in our experiments, there needs to be a characteristic time scale determined by the physical parameters of the system. One possibility is to recognise that xanthan gum has a yield stress ![]() $\sigma$ and may be better modelled as a Herschel–Bulkley fluid (see Appendix A, figure 11). In that case, there is a characteristic time scale
$\sigma$ and may be better modelled as a Herschel–Bulkley fluid (see Appendix A, figure 11). In that case, there is a characteristic time scale ![]() $(m/\sigma )^n$ and we can define a dimensionless flow rate
$(m/\sigma )^n$ and we can define a dimensionless flow rate
where ![]() $E$ is the strain rate defined by (3.1). On scaling grounds, the steady wavenumber should then be a function of this unique dimensionless grouping, which is consistent with our experimental findings.
$E$ is the strain rate defined by (3.1). On scaling grounds, the steady wavenumber should then be a function of this unique dimensionless grouping, which is consistent with our experimental findings.
Our experiments have shown that provided lubrication is effective at early times in an experiment where branches begin to develop, the branch number is independent of the thickness of the lubrication layers. However, we found that the lubrication layers thinned over time, becoming less efficient. At higher fluxes, particularly in the set of experiments using 1 mm lubrication layers, it was clear that the xanthan gum started to displace the water completely in regions beyond the two disks at earlier times. In figure 9(a), an image from an experiment using a flux of ![]() $1.4\ {\rm ml}\ {\rm s}^{-1}$ is displayed. In the upper half of the image, one large structure is shown. The patches with the lighter colour indicated that the xanthan gum had displaced the water layer in that region. We can compare this structure to the experiments described in § 3.1 without the presence of pre-formed lubrication layers, where the fractures at the leading edge did not develop into fully formed branches (figure 2b). In the lower half of the image, we see two branches that continued to propagate freely, and only at much later times did we see a reduction in their radial movement. This is a very interesting experiment in that it supports two observations: branches will develop and propagate radially in extensional-stress dominated regions, whereas when shear stresses are significant, the leading edge will simply become jagged rather than forming fully developed branches. In figure 9(b), a high-flux experiment with
$1.4\ {\rm ml}\ {\rm s}^{-1}$ is displayed. In the upper half of the image, one large structure is shown. The patches with the lighter colour indicated that the xanthan gum had displaced the water layer in that region. We can compare this structure to the experiments described in § 3.1 without the presence of pre-formed lubrication layers, where the fractures at the leading edge did not develop into fully formed branches (figure 2b). In the lower half of the image, we see two branches that continued to propagate freely, and only at much later times did we see a reduction in their radial movement. This is a very interesting experiment in that it supports two observations: branches will develop and propagate radially in extensional-stress dominated regions, whereas when shear stresses are significant, the leading edge will simply become jagged rather than forming fully developed branches. In figure 9(b), a high-flux experiment with ![]() $Q_0=2.8\ {\rm ml}\ {\rm s}^{-1}$ is shown, and it is clearly seen that the xanthan gum displaced the water lubrication layers completely in regions beyond the disks, and the branch-like structure disappeared.
$Q_0=2.8\ {\rm ml}\ {\rm s}^{-1}$ is shown, and it is clearly seen that the xanthan gum displaced the water lubrication layers completely in regions beyond the disks, and the branch-like structure disappeared.

Figure 9. Sample photographs viewed from above for three different experiments using disks of radius 5.5 cm and pre-formed lubrication layers of 1 mm where (a) the output flux is ![]() $1.4\ {\rm ml}\ {\rm s}^{-1}$; (b) the output flux is
$1.4\ {\rm ml}\ {\rm s}^{-1}$; (b) the output flux is ![]() $2.8\ {\rm ml}\ {\rm s}^{-1}$; and (c) a branch of an experiment using a flux of
$2.8\ {\rm ml}\ {\rm s}^{-1}$; and (c) a branch of an experiment using a flux of ![]() $1.05\ {\rm ml}\ {\rm s}^{-1}$ is shown. Note the vertical striations, indicating out-of-plane folds in the extruded fluid.
$1.05\ {\rm ml}\ {\rm s}^{-1}$ is shown. Note the vertical striations, indicating out-of-plane folds in the extruded fluid.
A further observation that could be explored in future studies is shown in figure 9(c), where a close up of one of the branches reveals buckles, indicating vertical motion out of the plane of the main flow.
5. Conclusions
We have demonstrated the onset of branch-forming instabilities of radially extruded shear-thinning fluids in extensional-stress-dominated regions of a lubricated Hele-Shaw cell. In our experiments, the shear-thinning fluid, xanthan gum, was injected at a constant flux into the space between two plates where it displaced a less viscous Newtonian fluid, which was either water or rapeseed oil. Water proved to be a more convenient choice, as water and xanthan gum have similar densities, reducing the effects of buoyancy. Pre-formed lubrication layers were incorporated into the experimental design and used to create an extensional-stress-dominated region by reducing the shear stress imposed by the confining walls of the cell. Experiments both with and without pre-formed lubrication layers were run.
We studied the effect of lubrication on the resulting instabilities that emerged from an initially circular region of xanthan gum. Without pre-formed lubrication layers, shear stresses dominated over the bulk of the flow, where it remained stable. However, within a small annular region at the leading edge where the xanthan gum was separated from the cell walls, fracturing behaviour was observed, and as a result the leading edge became jagged, displaying small cracks and tears. In the experiments with pre-formed lubrication layers, tears and fractures were seen at the leading edge of the xanthan gum, with some of these evolving to form branch-like structures within the lubricated region. Fracturing or tearing behaviour was observed at the troughs of the branches. Over time, the lubrication layers started to thin, hindering the radial progression of the branches. A plot of branch number against the azimuthal strain rate at the distance at which the branches emerge, showed a collapse of the data onto a universal, power-law curve with the number of branches decreasing with strain rate.
We have demonstrated that quasi-two-dimensional, extensionally dominated flows can be achieved in the laboratory, which offers up interesting possibilities for future work, exploring crack propagation, for example. The duration of our experiments was limited due to thinning of the lubricating layers of ambient fluid. Understanding this thinning and extending the duration of an experiment could be useful topics for further investigation.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2024.1169.
Acknowledgements
We thank M. Hallworth and S. Dalziel, University of Cambridge, for assisting with the experimental set-up that was used, and the anonymous referees for their valuable comments and constructive input.
Funding
A.J.H. is indebted to the Royal Society for funding her research as a Newton International Fellow (grant number 202518).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Properties of xanthan gum
A.1. Estimates for  $\mu _{min}$
$\mu _{min}$
To estimate the viscosity of the extruded fluid we used in our experiments, a 1 % solution of xanthan gum, we approximated its rheology as that of a simple power-law fluid. Data of viscosity versus shear rate measured using a shear-flow rheometer are shown on log–log axes in figure 10. We see (black-dotted line) that our solution conformed very closely to power-law behaviour for shear rates between ![]() $0.1\text { and }5~{\rm s}^{-1}$. From the graph in this range, we obtained the estimates
$0.1\text { and }5~{\rm s}^{-1}$. From the graph in this range, we obtained the estimates
Over the full range of data (red-dotted line), we can estimate an approximate power law with
but it is clear that there are deviations from power-law behaviour for shear rates lower than approximately ![]() $0.1\ {\rm s}^{-1}$. These results are broadly consistent with Sayag & Worster (Reference Sayag and Worster2013), who also used a 1 % xanthan solution and found
$0.1\ {\rm s}^{-1}$. These results are broadly consistent with Sayag & Worster (Reference Sayag and Worster2013), who also used a 1 % xanthan solution and found ![]() $n = 11.4$ for shear rates above 0.1 s
$n = 11.4$ for shear rates above 0.1 s![]() $^{-1}$ and
$^{-1}$ and ![]() $n=5.4$ for shear rates lower than 0.1 s
$n=5.4$ for shear rates lower than 0.1 s![]() $^{-1}$.
$^{-1}$.
For our experimental parameters ![]() $0.14 \le Q_0 \le 2.4\ {\rm cm}^3\ {\rm s}^{-1}$,
$0.14 \le Q_0 \le 2.4\ {\rm cm}^3\ {\rm s}^{-1}$, ![]() $r_G = 5.5$ cm or
$r_G = 5.5$ cm or ![]() $r_G = 8$ cm, and
$r_G = 8$ cm, and ![]() $h = 0.2$ cm, we can estimate the minimum viscosity of the fluid extruded from between the disks
$h = 0.2$ cm, we can estimate the minimum viscosity of the fluid extruded from between the disks ![]() $\mu _{min}$, using (2.11) and (A1), to be between 1 and 26 Pa s for the full range of our experiments, which is well above the viscosities of water and rapeseed oil, which are 0.001 Pa s and 0.066 Pa s, respectively. We can use this range of viscosities to infer from figure 10 that the corresponding shear rates at the disks as the xanthan gum exited was in the range
$\mu _{min}$, using (2.11) and (A1), to be between 1 and 26 Pa s for the full range of our experiments, which is well above the viscosities of water and rapeseed oil, which are 0.001 Pa s and 0.066 Pa s, respectively. We can use this range of viscosities to infer from figure 10 that the corresponding shear rates at the disks as the xanthan gum exited was in the range ![]() $0.15\unicode{x2013}5\ {\rm s}^{-1}$, so it is consistent to have used (A1) in our determinations. Note that, using (A2) to estimate
$0.15\unicode{x2013}5\ {\rm s}^{-1}$, so it is consistent to have used (A1) in our determinations. Note that, using (A2) to estimate ![]() $\mu _{min}$ from (2.11) gives the range 2–35 Pa s, which is not very different from the estimates using (A1).
$\mu _{min}$ from (2.11) gives the range 2–35 Pa s, which is not very different from the estimates using (A1).
A.2. Rheology of branched structures
Once the radial flow had become unstable and branches formed, the branches themselves had very low shear and extension rates, so they had very high viscosity, behaving essentially rigidly. It was hinted at in figure 10 but can be seen more clearly in figure 11 that the rheology changes below a shear rate of approximately ![]() $0.1\ {\rm s}^{-1}$. The rheometer indicated a yield stress of approximately 4 Pa, as shown in figure 11. There is strange behaviour indicated for shear stresses between 4 and 10 Pa, but overall, it appears as though the solution of xanthan gum may be more closely modelled as a Herschel–Bulkley fluid than as a pure power-law fluid.
$0.1\ {\rm s}^{-1}$. The rheometer indicated a yield stress of approximately 4 Pa, as shown in figure 11. There is strange behaviour indicated for shear stresses between 4 and 10 Pa, but overall, it appears as though the solution of xanthan gum may be more closely modelled as a Herschel–Bulkley fluid than as a pure power-law fluid.

Figure 11. Shear stress (Pa) versus shear rate (s![]() $^{-1}$) indicating the presence of a yield stress of approximately 4 Pa.
$^{-1}$) indicating the presence of a yield stress of approximately 4 Pa.
A.3. Estimates for the size of the lubrication layers
We focused on obtaining the largest estimate for the size of the lubrication layers to be effective at reducing shear stress, across the experimental and model parameters. This was done to ensure that all of our experiments had effective pre-formed lubrication layers. We saw that thicker lubrication layers are required when ![]() $r$ is small and when
$r$ is small and when ![]() $Q_0$ is large, so we used the parameter values
$Q_0$ is large, so we used the parameter values ![]() $r_G=5.5$ cm and
$r_G=5.5$ cm and ![]() $Q_0 = 2.8\ {\rm cm}^3\ {\rm s}^{-1}$. Substituting these values, as well as those for
$Q_0 = 2.8\ {\rm cm}^3\ {\rm s}^{-1}$. Substituting these values, as well as those for ![]() $m$ and
$m$ and ![]() $n$, as given in (A1), into (2.18) gives
$n$, as given in (A1), into (2.18) gives ![]() $H-h \gg 0.0005$ mm for water-lubricating layers, and
$H-h \gg 0.0005$ mm for water-lubricating layers, and ![]() $H-h \gg 0.03$ mm for rapeseed oil-lubricating layers.
$H-h \gg 0.03$ mm for rapeseed oil-lubricating layers.


















































