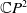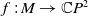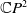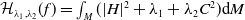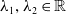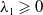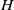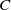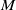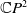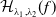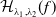1. Introduction
Helfrich functional dates back to Helfrich’s seminal work [Reference Helfrich7], which proposed the functional model of the elastic lipid bilayer or membrane. Let
![]() $f\;:\;M \rightarrow \mathbb{R}^{3}$
be a smooth immersed surface in
$f\;:\;M \rightarrow \mathbb{R}^{3}$
be a smooth immersed surface in
![]() $\mathbb{R}^{3}$
, the Helfrich functional (see [Reference Deckelnick, Doemeland and Grunau5]) is given by:
$\mathbb{R}^{3}$
, the Helfrich functional (see [Reference Deckelnick, Doemeland and Grunau5]) is given by:
where
![]() $H$
denotes the mean curvature vector of surface,
$H$
denotes the mean curvature vector of surface,
![]() $K$
is the Gaussian curvature,
$K$
is the Gaussian curvature,
![]() $\textrm{d} M$
is the area measure of the induced metric,
$\textrm{d} M$
is the area measure of the induced metric,
![]() $\gamma \in \mathbb{R}$
is a constant bending rigidity,
$\gamma \in \mathbb{R}$
is a constant bending rigidity,
![]() $\lambda \geqslant 0$
is the weight factor of the area functional, and
$\lambda \geqslant 0$
is the weight factor of the area functional, and
![]() $c_{0}\in \mathbb{R}$
is a given spontaneous curvature caused by asymmetry between the two layers of the membrane. The functional with zero spontaneous curvature can be considered as a weighted sum of the Willmore functional and the area, which represent the bending energy and the surface energy, respectively. The critical surfaces of the first variation of
$c_{0}\in \mathbb{R}$
is a given spontaneous curvature caused by asymmetry between the two layers of the membrane. The functional with zero spontaneous curvature can be considered as a weighted sum of the Willmore functional and the area, which represent the bending energy and the surface energy, respectively. The critical surfaces of the first variation of
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
are called Helfrich surfaces. In recent years, many important researches have been developed in the study of the functional in geometry. Examples include the existence and regularity of solutions for Helfrich immersion from surfaces into
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
are called Helfrich surfaces. In recent years, many important researches have been developed in the study of the functional in geometry. Examples include the existence and regularity of solutions for Helfrich immersion from surfaces into
![]() $\mathbb{R}^{3}$
(see, for instance, [Reference Choksi and Veneroni3, Reference Deckelnick, Doemeland and Grunau5, Reference Eichmann6, Reference Mondino and Scharrer13, Reference Tu16]), the classification ([Reference Bernard, Wheeler and Wheeler1, Reference McCoy and Wheeler15]) of Helfrich surfaces in
$\mathbb{R}^{3}$
(see, for instance, [Reference Choksi and Veneroni3, Reference Deckelnick, Doemeland and Grunau5, Reference Eichmann6, Reference Mondino and Scharrer13, Reference Tu16]), the classification ([Reference Bernard, Wheeler and Wheeler1, Reference McCoy and Wheeler15]) of Helfrich surfaces in
![]() $\mathbb{R}^{3}$
.
$\mathbb{R}^{3}$
.
It is well know that the Willmore functional is conformal invariant and has been a field of active research since the work of Willmore [Reference Willmore17]. And many of the techniques developed have played important roles in geomotry. Despite this, the functional for a immersed surface in complex manifolds is relatively less discussed. As noted in [Reference Castro and Urbano2], Castro and Urbano proved the Whitney sphere is the only Willmore Lagrangian surface of genus zero in
![]() $\mathbb{C}^{2}$
. Hu and Li [Reference Hu and Li9] considered higher-dimensional case, and they proved Whitney spheres are Willmore submanifolds of
$\mathbb{C}^{2}$
. Hu and Li [Reference Hu and Li9] considered higher-dimensional case, and they proved Whitney spheres are Willmore submanifolds of
![]() $\mathbb{C}^{n}$
if and only if
$\mathbb{C}^{n}$
if and only if
![]() $n = 2$
and constructed examples of Willmore Lagrangian spheres in
$n = 2$
and constructed examples of Willmore Lagrangian spheres in
![]() $\mathbb{C}^{n}$
for all
$\mathbb{C}^{n}$
for all
![]() $n \geq 2$
. Immersions from surfaces into the complex projective plane
$n \geq 2$
. Immersions from surfaces into the complex projective plane
![]() $\mathbb{C}P^{2}$
are also considered. In [Reference Hu and Li8], Hu and Li calculate the Euler–Lagrangian equation of the Willmore functional for an
$\mathbb{C}P^{2}$
are also considered. In [Reference Hu and Li8], Hu and Li calculate the Euler–Lagrangian equation of the Willmore functional for an
![]() $n$
-dimensional submanifold in an
$n$
-dimensional submanifold in an
![]() $(n + p)$
-dimensional Riemannian manifold. As a corollary, the authors have given the Euler–Lagrangian equation of the Willmore functional for an immersed surface in complex projective plane
$(n + p)$
-dimensional Riemannian manifold. As a corollary, the authors have given the Euler–Lagrangian equation of the Willmore functional for an immersed surface in complex projective plane
![]() $\mathbb{C}P^{2}$
. In [Reference Montiel and Urbano14], Montiel and Urbano studied the Willmore functional for compact surface
$\mathbb{C}P^{2}$
. In [Reference Montiel and Urbano14], Montiel and Urbano studied the Willmore functional for compact surface
![]() $M$
in
$M$
in
![]() $\mathbb{C}P^{2}$
. In this case, the Willmore functional is given by:
$\mathbb{C}P^{2}$
. In this case, the Willmore functional is given by:
where
![]() $C$
denotes the Kähler function of
$C$
denotes the Kähler function of
![]() $M$
in
$M$
in
![]() $\mathbb{C}P^{2}$
. The authors decomposed
$\mathbb{C}P^{2}$
. The authors decomposed
![]() $W$
into two global conformal invariants:
$W$
into two global conformal invariants:
They proved that
![]() $W^{-}\geqslant 4\pi \mu -2\int |C|\textrm{d} M$
, where
$W^{-}\geqslant 4\pi \mu -2\int |C|\textrm{d} M$
, where
![]() $\mu$
denotes the maximum multiplicity of the immersion. The equality holds if and only if
$\mu$
denotes the maximum multiplicity of the immersion. The equality holds if and only if
![]() $\mu =1$
and
$\mu =1$
and
![]() $M$
is either the complex projective line or totally geodesic real projective plane, or
$M$
is either the complex projective line or totally geodesic real projective plane, or
![]() $\mu =2$
and
$\mu =2$
and
![]() $M$
is the Lagrangian Whitney sphere. Moreover, Montiel and Urbano obtained
$M$
is the Lagrangian Whitney sphere. Moreover, Montiel and Urbano obtained
![]() $W^{-}\geqslant 8\pi ^{2}/3\sqrt{3}$
for all homogeneous tori in
$W^{-}\geqslant 8\pi ^{2}/3\sqrt{3}$
for all homogeneous tori in
![]() $\mathbb{C}P^{2}$
and conjectured that the Clifford torus attains the minimum of
$\mathbb{C}P^{2}$
and conjectured that the Clifford torus attains the minimum of
![]() $W^{-}$
among all Lagrangian tori in
$W^{-}$
among all Lagrangian tori in
![]() $\mathbb{C}P^{2}$
. In this regard, Ma, Mironov, and Zuo [Reference Ma, Mironov and Zuo11] studied a family of Hamiltonian-minimal Lagrangian tori and proved Montiel–Urbano’s conjecture is valid. For arbitrary Lagrangian tori, the conjecture remains open.
$\mathbb{C}P^{2}$
. In this regard, Ma, Mironov, and Zuo [Reference Ma, Mironov and Zuo11] studied a family of Hamiltonian-minimal Lagrangian tori and proved Montiel–Urbano’s conjecture is valid. For arbitrary Lagrangian tori, the conjecture remains open.
In this paper, we will focus on the Helfrich functional for surfaces in the complex projective plane
![]() $\mathbb{C}P^{2}$
(with holomorphic sectional curvature 4). Let
$\mathbb{C}P^{2}$
(with holomorphic sectional curvature 4). Let
![]() $f\;:\; M\rightarrow \mathbb{C}P^{2}$
be an isometric immersion of a compact surface in
$f\;:\; M\rightarrow \mathbb{C}P^{2}$
be an isometric immersion of a compact surface in
![]() $\mathbb{C}P^{2}$
. For simplicity, we assume that the spontaneous curvature
$\mathbb{C}P^{2}$
. For simplicity, we assume that the spontaneous curvature
![]() $c_{0}=0$
. The Helfrich functional is defined by:
$c_{0}=0$
. The Helfrich functional is defined by:
where
![]() $\lambda _{1}, \,\lambda _{2}\in \mathbb{R}$
and
$\lambda _{1}, \,\lambda _{2}\in \mathbb{R}$
and
![]() $\lambda _{1}\geqslant 0$
. When
$\lambda _{1}\geqslant 0$
. When
![]() $\lambda _{1}=1, \lambda _{2}=3$
, the functional reduces to Willmore functioal
$\lambda _{1}=1, \lambda _{2}=3$
, the functional reduces to Willmore functioal
![]() $W$
. When
$W$
. When
![]() $\lambda _{1}=0, \lambda _{2}=6$
, the functional reduces to
$\lambda _{1}=0, \lambda _{2}=6$
, the functional reduces to
![]() $W^{+}$
and when
$W^{+}$
and when
![]() $\lambda _{1}=2, \lambda _{2}=0$
, reduces to
$\lambda _{1}=2, \lambda _{2}=0$
, reduces to
![]() $W^{-}$
. We first give the Euler–Lagrange equation of Helfrich functional
$W^{-}$
. We first give the Euler–Lagrange equation of Helfrich functional
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
. This can also be derived by Hu–Li’s result (See [Reference Hu and Li8]).
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
. This can also be derived by Hu–Li’s result (See [Reference Hu and Li8]).
Let
![]() $\{e_{A}\}_{1\leq A\leq 4}$
be a local orthonormal frame on
$\{e_{A}\}_{1\leq A\leq 4}$
be a local orthonormal frame on
![]() $\mathbb{C}P^{2}$
such that when restricts to
$\mathbb{C}P^{2}$
such that when restricts to
![]() $M$
,
$M$
,
![]() $\{e_{1}, e_{2}\}$
is a local orthonormal basis for
$\{e_{1}, e_{2}\}$
is a local orthonormal basis for
![]() $TM$
. Then the Kähler function
$TM$
. Then the Kähler function
![]() $C$
on
$C$
on
![]() $M$
can be given by
$M$
can be given by
![]() $C=\langle Je_{1},e_{2}\rangle$
. Without loss of generality, we assume that
$C=\langle Je_{1},e_{2}\rangle$
. Without loss of generality, we assume that
![]() $\{e_{A}\}$
satisfy
$\{e_{A}\}$
satisfy
 \begin{equation} \begin{cases} Je_{1}=C\ e_{2}+\sqrt{1-C^{2}}\,e_{4},\ Je_{2}=-C\,e_{1}-\sqrt{1-C^{2}}\,e_{3},\\[9pt] Je_{3}=-C\,e_{4}+\sqrt{1-C^{2}}\,e_{2},\ Je_{4}=C\,e_{3}-\sqrt{1-C^{2}}\,e_{1}. \end{cases} \end{equation}
\begin{equation} \begin{cases} Je_{1}=C\ e_{2}+\sqrt{1-C^{2}}\,e_{4},\ Je_{2}=-C\,e_{1}-\sqrt{1-C^{2}}\,e_{3},\\[9pt] Je_{3}=-C\,e_{4}+\sqrt{1-C^{2}}\,e_{2},\ Je_{4}=C\,e_{3}-\sqrt{1-C^{2}}\,e_{1}. \end{cases} \end{equation}
Then, we have
Theorem 1.1.
Let
![]() $f\;:\; M\rightarrow \mathbb{C}P^{2}$
be an isometric immersion of a compact surface in the complex projective plane
$f\;:\; M\rightarrow \mathbb{C}P^{2}$
be an isometric immersion of a compact surface in the complex projective plane
![]() $\mathbb{C}P^{2}$
. Then,
$\mathbb{C}P^{2}$
. Then,
![]() $M$
is a Helfrich surface if and only if
$M$
is a Helfrich surface if and only if
 \begin{equation*} \begin {cases} \triangle ^{\perp }H^{3}+(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{3}+ \sum \limits _{\beta ij}h_{ij}^{3}h_{ij}^{\beta }H^{\beta }-2\lambda _{2}\sqrt {1-C^{2}}C_{,1}=0,\\[12pt] \triangle ^{\perp }H^{4}+(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{4}+ \sum \limits _{\beta ij}h_{ij}^{4}h_{ij}^{\beta }H^{\beta }-2\lambda _{2}\sqrt {1-C^{2}}C_{,2}=0, \end {cases} \end{equation*}
\begin{equation*} \begin {cases} \triangle ^{\perp }H^{3}+(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{3}+ \sum \limits _{\beta ij}h_{ij}^{3}h_{ij}^{\beta }H^{\beta }-2\lambda _{2}\sqrt {1-C^{2}}C_{,1}=0,\\[12pt] \triangle ^{\perp }H^{4}+(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{4}+ \sum \limits _{\beta ij}h_{ij}^{4}h_{ij}^{\beta }H^{\beta }-2\lambda _{2}\sqrt {1-C^{2}}C_{,2}=0, \end {cases} \end{equation*}
where
![]() $C$
denotes the Kähler function of
$C$
denotes the Kähler function of
![]() $M$
in
$M$
in
![]() $\mathbb{C}P^{2}$
,
$\mathbb{C}P^{2}$
,
![]() $C_{,i}\,(1\leq i\leq 2)$
denote the first covariant derivatives of
$C_{,i}\,(1\leq i\leq 2)$
denote the first covariant derivatives of
![]() $C$
, and
$C$
, and
![]() $H^{\beta }\,(3\leq \beta \leq 4)$
are the coefficient of the mean curvature vector
$H^{\beta }\,(3\leq \beta \leq 4)$
are the coefficient of the mean curvature vector
![]() $H$
of
$H$
of
![]() $M$
.
$M$
.
It follows from the above Euler–Lagrange equation that every minimal surfaces with constant Kähler angle is Helfrich surface. In particular, the complex curve and Lagrangian minimal surface in
![]() $\mathbb{C}P^{2}$
are Helfrich surfaces.
$\mathbb{C}P^{2}$
are Helfrich surfaces.
We, on the other hand, will focus on the homogeneous tori in
![]() $\mathbb{C}P^{2}$
. We are going to show the homogeneous Helfrich tori in
$\mathbb{C}P^{2}$
. We are going to show the homogeneous Helfrich tori in
![]() $\mathbb{C}P^{2}$
and compute the Helfrich energy for the homogenous tori, thereby determining the energy minimizers within this class of surfaces.
$\mathbb{C}P^{2}$
and compute the Helfrich energy for the homogenous tori, thereby determining the energy minimizers within this class of surfaces.
Theorem 1.2.
Let
![]() $T_{r_{1},r_{2},r_{3}}$
be a homogeneous torus in
$T_{r_{1},r_{2},r_{3}}$
be a homogeneous torus in
![]() $\mathbb{C}P^{2}$
. Then,
$\mathbb{C}P^{2}$
. Then,
![]() $T_{r_{1},r_{2},r_{3}}$
is a Helfrich surface if and only if
$T_{r_{1},r_{2},r_{3}}$
is a Helfrich surface if and only if
-
1. When
 $0\leqslant \lambda _{1}\leqslant \frac{5}{2}$
,
$0\leqslant \lambda _{1}\leqslant \frac{5}{2}$
,
 $T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}.$
$T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}.$
-
2. When
 $\lambda _{1}\gt \frac{5}{2}$
,
$\lambda _{1}\gt \frac{5}{2}$
,
 $T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
or
$T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
or
 $T_{r_{1},r_{2},r_{3}}=T_{\sqrt{\frac{1}{4\lambda _{1}-9}}, \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}$
.
$T_{r_{1},r_{2},r_{3}}=T_{\sqrt{\frac{1}{4\lambda _{1}-9}}, \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}$
.
Theorem 1.3.
Let
![]() $T_{r_{1},r_{2},r_{3}}$
be a homogeneous torus in
$T_{r_{1},r_{2},r_{3}}$
be a homogeneous torus in
![]() $\mathbb{C}P^{2}$
. Then,
$\mathbb{C}P^{2}$
. Then,
-
1. When
 $0\leqslant \lambda _{1}\leqslant 3$
,with equality holding if and only if
$0\leqslant \lambda _{1}\leqslant 3$
,with equality holding if and only if \begin{equation*}\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac {4\lambda _{1}\pi ^{2}}{3\sqrt {3}}\end{equation*}
\begin{equation*}\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac {4\lambda _{1}\pi ^{2}}{3\sqrt {3}}\end{equation*}
 $T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
.
$T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
.
-
2. When
 $\lambda _{1}\gt 3$
,with equality holding if and only if
$\lambda _{1}\gt 3$
,with equality holding if and only if \begin{equation*}\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac {(4\lambda _{1}-8)\pi ^{2}}{\sqrt {4\lambda _{1}-9}}\end{equation*}
\begin{equation*}\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac {(4\lambda _{1}-8)\pi ^{2}}{\sqrt {4\lambda _{1}-9}}\end{equation*}
 $T_{r_{1},r_{2},r_{3}}=T_{\sqrt{\frac{1}{4\lambda _{1}-9}}, \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}$
.
$T_{r_{1},r_{2},r_{3}}=T_{\sqrt{\frac{1}{4\lambda _{1}-9}}, \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}$
.
The arrangement of this paper is as follows. In Section 2, we recall the basic theory of surfaces in
![]() $\mathbb{C}P^{2}$
. In Section 3, we calculate the Euler–Lagrangian equation of the critical surfaces of
$\mathbb{C}P^{2}$
. In Section 3, we calculate the Euler–Lagrangian equation of the critical surfaces of
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
. Then, in Section 4, we consider the homogeneous tori in
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
. Then, in Section 4, we consider the homogeneous tori in
![]() $\mathbb{C}P^{2}$
and give the proof of Theorems 1.2 and 1.3.
$\mathbb{C}P^{2}$
and give the proof of Theorems 1.2 and 1.3.
2. Preliminaries
In this section, we will review the moving frame method for surfaces in
![]() $\mathbb{C}P^{2}$
following Chern and Wolfson (for more details, see [Reference Chern and Wolfson4]). In the paper, we will adopt the following ranges of indices:
$\mathbb{C}P^{2}$
following Chern and Wolfson (for more details, see [Reference Chern and Wolfson4]). In the paper, we will adopt the following ranges of indices:
Let
![]() $\langle,\rangle$
be the hermitian product in
$\langle,\rangle$
be the hermitian product in
![]() $\mathbb{C}^{3}$
, that is,
$\mathbb{C}^{3}$
, that is,
for any
![]() $Z,W\in \mathbb{C}^{3}$
, where
$Z,W\in \mathbb{C}^{3}$
, where
![]() $\overline{W}$
denotes the conjugate of
$\overline{W}$
denotes the conjugate of
![]() $W$
. Let
$W$
. Let
![]() $\mathbb{C}P^{2}$
be the complex projective plane with its canonical Fubini–Study metric of constant holomorphic sectional curvature 4. Then,
$\mathbb{C}P^{2}$
be the complex projective plane with its canonical Fubini–Study metric of constant holomorphic sectional curvature 4. Then,
where
![]() $\Pi \;:\; S^{5}\rightarrow \mathbb{C}P^{2}$
is the Hopf projection. We denote
$\Pi \;:\; S^{5}\rightarrow \mathbb{C}P^{2}$
is the Hopf projection. We denote
![]() $g$
by its Fubini–Study metric and
$g$
by its Fubini–Study metric and
![]() $J$
by its complex structure induced by
$J$
by its complex structure induced by
![]() $\mathbb{C}^{3}$
on
$\mathbb{C}^{3}$
on
![]() $\mathbb{C}P^{2}$
. Then,
$\mathbb{C}P^{2}$
. Then,
The Kähler form
![]() $\Omega$
on
$\Omega$
on
![]() $\mathbb{C}P^{2}$
is defined by:
$\mathbb{C}P^{2}$
is defined by:
Let
![]() $\{Z_{0},Z_{1},Z_{2}\}$
be a unitary frames in
$\{Z_{0},Z_{1},Z_{2}\}$
be a unitary frames in
![]() $\mathbb{C}^{3}$
. Then, we have
$\mathbb{C}^{3}$
. Then, we have
where
![]() $\psi _{a\overline{b}}=\overline{\psi _{\overline{a}b}}$
is connection 1-form and satisfies structure equation:
$\psi _{a\overline{b}}=\overline{\psi _{\overline{a}b}}$
is connection 1-form and satisfies structure equation:
Moreover, the Fubini–Study metric (2.1) can be written as:
On the other hand, let
![]() $\{\varsigma _{i}\}$
be a unitary frames in
$\{\varsigma _{i}\}$
be a unitary frames in
![]() $\mathbb{C}P^{2}$
with dual frames
$\mathbb{C}P^{2}$
with dual frames
![]() $\{\omega _{i}\}$
, the structure equation of
$\{\omega _{i}\}$
, the structure equation of
![]() $\mathbb{C}P^{2}$
can be written as:
$\mathbb{C}P^{2}$
can be written as:
with
![]() $\{\omega _{i\overline{j}}\}$
being the unitary connection forms with respect to
$\{\omega _{i\overline{j}}\}$
being the unitary connection forms with respect to
![]() $\{\omega _{i}\}$
. We have then
$\{\omega _{i}\}$
. We have then
Combining with (2.5) and (2.7) and (2.4) and (2.6), we get
Let
![]() $f\;:\; M\rightarrow \mathbb{C}P^{2}$
be an isometric immersion of a compact surface
$f\;:\; M\rightarrow \mathbb{C}P^{2}$
be an isometric immersion of a compact surface
![]() $M$
in the complex projective plane
$M$
in the complex projective plane
![]() $\mathbb{C}P^{2}$
. The Kähler function
$\mathbb{C}P^{2}$
. The Kähler function
![]() $C$
on
$C$
on
![]() $M$
is defined by:
$M$
is defined by:
where
![]() $\textrm{d} M$
is the area form on
$\textrm{d} M$
is the area form on
![]() $M$
. The surface
$M$
. The surface
![]() $f$
is holomorphic, anti-holomorphic, or Lagrangian, respectively, depending on
$f$
is holomorphic, anti-holomorphic, or Lagrangian, respectively, depending on
![]() $C\equiv 1,-1$
, or
$C\equiv 1,-1$
, or
![]() $0$
. Now, we consider
$0$
. Now, we consider
![]() $M\subset \mathbb{C}P^{2}$
first from the Riemannian geometry version and then from the complex version due to Chern and Wolfson [Reference Chern and Wolfson4].
$M\subset \mathbb{C}P^{2}$
first from the Riemannian geometry version and then from the complex version due to Chern and Wolfson [Reference Chern and Wolfson4].
Let us choose a (new) local orthonormal frame
![]() $\{e_{A}\}$
of
$\{e_{A}\}$
of
![]() $\mathbb{C}P^{2}$
with its dual
$\mathbb{C}P^{2}$
with its dual
![]() $\{\theta _{A}\}$
such that restricting to
$\{\theta _{A}\}$
such that restricting to
![]() $M$
,
$M$
,
![]() $\{e_{i}\}$
is a local orthonormal basis of
$\{e_{i}\}$
is a local orthonormal basis of
![]() $TM$
. Then, we have restricted to
$TM$
. Then, we have restricted to
![]() $M$
$M$
The second fundamental form
![]() $II$
and the mean curvature vector
$II$
and the mean curvature vector
![]() $H$
are defined by:
$H$
are defined by:
Let
![]() $\overline{\nabla }$
be the Riemannian connection of
$\overline{\nabla }$
be the Riemannian connection of
![]() $\mathbb{C}P^{2}$
, and let
$\mathbb{C}P^{2}$
, and let
![]() $\nabla$
and
$\nabla$
and
![]() $\nabla ^{\perp }$
be the induced connection and normal connection of
$\nabla ^{\perp }$
be the induced connection and normal connection of
![]() $M$
, respectively. The covariant derivative and Laplacian of
$M$
, respectively. The covariant derivative and Laplacian of
![]() $H$
on the normal bundle of
$H$
on the normal bundle of
![]() $M$
are, respectively, defined as:
$M$
are, respectively, defined as:
Let
![]() $\overline{R}_{ABCD}$
be the Riemannian curvature tensor of
$\overline{R}_{ABCD}$
be the Riemannian curvature tensor of
![]() $\mathbb{C}P^{2}$
, we have then
$\mathbb{C}P^{2}$
, we have then
 \begin{equation} \begin{aligned} \overline{R}_{ABCD} &=g(e_{A},e_{C})g(e_{B},e_{D})-g(e_{A},e_{D})g(e_{B},e_{C}) +g(Je_{A},e_{C})g(Je_{B},e_{D})\\[5pt] &\quad -g(Je_{A},e_{D})g(Je_{B},e_{C})+2g(Je_{A},e_{B})g(Je_{C},e_{D}). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \overline{R}_{ABCD} &=g(e_{A},e_{C})g(e_{B},e_{D})-g(e_{A},e_{D})g(e_{B},e_{C}) +g(Je_{A},e_{C})g(Je_{B},e_{D})\\[5pt] &\quad -g(Je_{A},e_{D})g(Je_{B},e_{C})+2g(Je_{A},e_{B})g(Je_{C},e_{D}). \end{aligned} \end{equation}
Now, let us recall the complex version of the geometry of
![]() $M$
which is due to Chern and Wolfson [Reference Chern and Wolfson4]. Set
$M$
which is due to Chern and Wolfson [Reference Chern and Wolfson4]. Set
![]() $\phi =\theta _{1}+i\theta _{2}$
. It defines a complex structure on
$\phi =\theta _{1}+i\theta _{2}$
. It defines a complex structure on
![]() $M$
. The induced metric on
$M$
. The induced metric on
![]() $M$
is of the form:
$M$
is of the form:
Then after a normalization of
![]() $\{\varsigma _i\}$
if necessary ([Reference Chern and Wolfson4, p. 66]), we can assume that there exist complex-valued smooth functions
$\{\varsigma _i\}$
if necessary ([Reference Chern and Wolfson4, p. 66]), we can assume that there exist complex-valued smooth functions
![]() $s,t$
which satisfy
$s,t$
which satisfy
![]() $|s|^{2}+|t|^{2}=1$
such that
$|s|^{2}+|t|^{2}=1$
such that
In particular, setting
![]() $|s|=\cos \dfrac{\alpha }{2}, \,|t|=\sin \dfrac{\alpha }{2}$
, one has then
$|s|=\cos \dfrac{\alpha }{2}, \,|t|=\sin \dfrac{\alpha }{2}$
, one has then
![]() $C=\cos \alpha$
with
$C=\cos \alpha$
with
![]() $0\leq \alpha \leq \pi$
. Now we have, along
$0\leq \alpha \leq \pi$
. Now we have, along
![]() $M$
,
$M$
,
Taking exterior derivative of the first term of (2.15), we get
Set
then the complex-valued second fundamental forms can be given by:
Lemma 2.1.
The coefficients
![]() $a,\,b,\,c$
of the complex-valued second fundamental forms
$a,\,b,\,c$
of the complex-valued second fundamental forms
![]() $II^{\mathbb{C}}$
satisfy
$II^{\mathbb{C}}$
satisfy
 \begin{equation} \begin{aligned} &\textit{Re}(a+c)+\textit{Re}(2b)=h_{11}^{3}, \,\textit{Im}(c-a)=h_{12}^{3}, \,\textit{Re}(2b)-\textit{Re}(a+c)=h_{22}^{3},\\[5pt] &\textit{Im}(a+c)+\textit{Im}(2b)=h_{11}^{4},\,\textit{Re}(a-c)=h_{12}^{4},\,\textit{Im}(2b)-\textit{Im}(a+c)=h_{22}^{4}, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &\textit{Re}(a+c)+\textit{Re}(2b)=h_{11}^{3}, \,\textit{Im}(c-a)=h_{12}^{3}, \,\textit{Re}(2b)-\textit{Re}(a+c)=h_{22}^{3},\\[5pt] &\textit{Im}(a+c)+\textit{Im}(2b)=h_{11}^{4},\,\textit{Re}(a-c)=h_{12}^{4},\,\textit{Im}(2b)-\textit{Im}(a+c)=h_{22}^{4}, \end{aligned} \end{equation}
where
![]() $\text{Re}$
and
$\text{Re}$
and
![]() $\text{Im}$
denote, respectively, the real and imaginary parts.
$\text{Im}$
denote, respectively, the real and imaginary parts.
Proof. Taking exterior derivative of the second term of (2.15), we get
 \begin{equation*} \begin {aligned} &d(\theta _{3}+i\theta _{4})\\[5pt] =&-\frac {1}{2}\left(\frac {h_{11}^{3}-h_{22}^{3}+2h_{12}^{4} +i(h_{11}^{4}-h_{22}^{4}-2h_{12}^{3})}{4}\phi +\frac {h_{11}^{3}+h_{22}^{3}+i(h_{11}^{4}+h_{22}^{4})}{4}\overline {\phi }\right)\wedge \phi \\[5pt] &-\frac {1}{2}\left(\frac {h_{11}^{3}+h_{22}^{3}+i(h_{11}^{4}+h_{22}^{4})}{4}\phi +\frac {h_{11}^{3}-h_{22}^{3}-2h_{12}^{4} +i(h_{11}^{4}-h_{22}^{4}+2h_{12}^{3})}{4}\overline {\phi }\right)\wedge \overline {\phi }. \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} &d(\theta _{3}+i\theta _{4})\\[5pt] =&-\frac {1}{2}\left(\frac {h_{11}^{3}-h_{22}^{3}+2h_{12}^{4} +i(h_{11}^{4}-h_{22}^{4}-2h_{12}^{3})}{4}\phi +\frac {h_{11}^{3}+h_{22}^{3}+i(h_{11}^{4}+h_{22}^{4})}{4}\overline {\phi }\right)\wedge \phi \\[5pt] &-\frac {1}{2}\left(\frac {h_{11}^{3}+h_{22}^{3}+i(h_{11}^{4}+h_{22}^{4})}{4}\phi +\frac {h_{11}^{3}-h_{22}^{3}-2h_{12}^{4} +i(h_{11}^{4}-h_{22}^{4}+2h_{12}^{3})}{4}\overline {\phi }\right)\wedge \overline {\phi }. \end {aligned} \end{equation*}
Then from (2.15), (2.16), (2.17), and (2.18), we have that
 \begin{equation*} \begin {aligned} &a=\frac {h_{11}^{3}-h_{22}^{3}+2h_{12}^{4} +i(h_{11}^{4}-h_{22}^{4}-2h_{12}^{3})}{4},\\[5pt] &b=\frac {h_{11}^{3}+h_{22}^{3}+i(h_{11}^{4}+h_{22}^{4})}{4},\\[5pt] &c=\frac {h_{11}^{3}-h_{22}^{3}-2h_{12}^{4} +i(h_{11}^{4}-h_{22}^{4}+2h_{12}^{3})}{4}, \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} &a=\frac {h_{11}^{3}-h_{22}^{3}+2h_{12}^{4} +i(h_{11}^{4}-h_{22}^{4}-2h_{12}^{3})}{4},\\[5pt] &b=\frac {h_{11}^{3}+h_{22}^{3}+i(h_{11}^{4}+h_{22}^{4})}{4},\\[5pt] &c=\frac {h_{11}^{3}-h_{22}^{3}-2h_{12}^{4} +i(h_{11}^{4}-h_{22}^{4}+2h_{12}^{3})}{4}, \end {aligned} \end{equation*}
and (2.20) follows.
Remark 2.2.
Note that we can re-choose the unitary coframe
![]() $\{\omega _{1},\omega _{2}\}$
such that
$\{\omega _{1},\omega _{2}\}$
such that
The Kähler angle
![]() $\alpha$
is smooth at the points with
$\alpha$
is smooth at the points with
![]() $0\lt \alpha \lt \pi$
. At the points
$0\lt \alpha \lt \pi$
. At the points
![]() $\alpha =0$
or
$\alpha =0$
or
![]() $\pi$
,
$\pi$
,
![]() $\alpha$
could be only continuous. Moreover, under the assumption of (2.21), we can obtain by (2.13) that
$\alpha$
could be only continuous. Moreover, under the assumption of (2.21), we can obtain by (2.13) that
 \begin{equation*} \left \{\begin {split}\omega _1&=\cos \frac {\alpha }{2}\theta _{1}+\sin \frac {\alpha }{2}\theta _{3} +i\!\left(\!\cos \frac {\alpha }{2}\theta _{2}+\sin \frac {\alpha }{2}\theta _{4}\right),\\[5pt] \omega _2&=\sin \frac {\alpha }{2}\theta _{1}-\cos \frac {\alpha }{2}\theta _{3} +i\!\left(\!-\!\sin \frac {\alpha }{2}\theta _{2}+\cos \frac {\alpha }{2}\theta _{4}\right), \end {split}\right. \end{equation*}
\begin{equation*} \left \{\begin {split}\omega _1&=\cos \frac {\alpha }{2}\theta _{1}+\sin \frac {\alpha }{2}\theta _{3} +i\!\left(\!\cos \frac {\alpha }{2}\theta _{2}+\sin \frac {\alpha }{2}\theta _{4}\right),\\[5pt] \omega _2&=\sin \frac {\alpha }{2}\theta _{1}-\cos \frac {\alpha }{2}\theta _{3} +i\!\left(\!-\!\sin \frac {\alpha }{2}\theta _{2}+\cos \frac {\alpha }{2}\theta _{4}\right), \end {split}\right. \end{equation*}
and hence
 \begin{equation*} \left \{\begin {split}\varsigma _1&=\frac {1}{2}\left(\!\cos \frac {\alpha }{2}e_{1}+\sin \frac {\alpha }{2}e_{3} -i\!\left(\!\cos \frac {\alpha }{2}e_{2}+\sin \frac {\alpha }{2}e_{4}\right)\right),\\[5pt] \varsigma _2&=\frac {1}{2}\left(\!\sin \frac {\alpha }{2}e_{1}-\cos \frac {\alpha }{2}e_{3} -i\!\left(\!-\!\sin \frac {\alpha }{2}e_{2}+\cos \frac {\alpha }{2}e_{4}\right)\right). \end {split}\right .\end{equation*}
\begin{equation*} \left \{\begin {split}\varsigma _1&=\frac {1}{2}\left(\!\cos \frac {\alpha }{2}e_{1}+\sin \frac {\alpha }{2}e_{3} -i\!\left(\!\cos \frac {\alpha }{2}e_{2}+\sin \frac {\alpha }{2}e_{4}\right)\right),\\[5pt] \varsigma _2&=\frac {1}{2}\left(\!\sin \frac {\alpha }{2}e_{1}-\cos \frac {\alpha }{2}e_{3} -i\!\left(\!-\!\sin \frac {\alpha }{2}e_{2}+\cos \frac {\alpha }{2}e_{4}\right)\right). \end {split}\right .\end{equation*}
So, we have
from which we get
 \begin{equation*} \left \{\begin {split}Je_{1}&=C e_{2}+\sqrt {1-C^{2}} e_{4},\ Je_{2}=-C e_{1}-\sqrt {1-C^{2}} e_{3},\\[5pt] Je_{3}&=-C e_{4}+\sqrt {1-C^{2}} e_{2},\ Je_{4}=C e_{3}-\sqrt {1-C^{2}} e_{1}. \end {split}\right .\end{equation*}
\begin{equation*} \left \{\begin {split}Je_{1}&=C e_{2}+\sqrt {1-C^{2}} e_{4},\ Je_{2}=-C e_{1}-\sqrt {1-C^{2}} e_{3},\\[5pt] Je_{3}&=-C e_{4}+\sqrt {1-C^{2}} e_{2},\ Je_{4}=C e_{3}-\sqrt {1-C^{2}} e_{1}. \end {split}\right .\end{equation*}
3. Euler–Lagrange equation of Helfrich functional
Let
![]() $f(p,t)\;:\; M\times (\!-\!\epsilon,\epsilon )\rightarrow \mathbb{C}P^{2}$
be a variation of
$f(p,t)\;:\; M\times (\!-\!\epsilon,\epsilon )\rightarrow \mathbb{C}P^{2}$
be a variation of
![]() $M$
with
$M$
with
![]() $f_{0}(p)=f(p)$
. Here, we denote by
$f_{0}(p)=f(p)$
. Here, we denote by
![]() $f_t(p)=f(p,t)\;:\;M\rightarrow \mathbb{C}P^{2}$
for
$f_t(p)=f(p,t)\;:\;M\rightarrow \mathbb{C}P^{2}$
for
![]() $t\in (\!-\!\epsilon,\epsilon )$
. Let
$t\in (\!-\!\epsilon,\epsilon )$
. Let
![]() $\{x_{1},x_{2},t\}$
be a local coordinate system around the point
$\{x_{1},x_{2},t\}$
be a local coordinate system around the point
![]() $(p,0)$
such that
$(p,0)$
such that
![]() $\{\textrm{d} f\!\left(\dfrac{\partial }{\partial x_{1}}\right),\textrm{d} f\!\left(\dfrac{\partial }{\partial x_{2}}\right)\}|_p$
is an orthonormal basis of
$\{\textrm{d} f\!\left(\dfrac{\partial }{\partial x_{1}}\right),\textrm{d} f\!\left(\dfrac{\partial }{\partial x_{2}}\right)\}|_p$
is an orthonormal basis of
![]() $T_{p}M$
. Set
$T_{p}M$
. Set
![]() $\bar V=\textrm{d} f_{t}\!\left(\dfrac{\partial }{\partial t}\right), X_{i}=\textrm{d} f_{t}\!\left(\frac{\partial }{\partial x_{i}}\right)$
. Then, we have the induced metric of
$\bar V=\textrm{d} f_{t}\!\left(\dfrac{\partial }{\partial t}\right), X_{i}=\textrm{d} f_{t}\!\left(\frac{\partial }{\partial x_{i}}\right)$
. Then, we have the induced metric of
![]() $ f_{t}$
and its area form as follows:
$ f_{t}$
and its area form as follows:
Then
![]() $(g_0)_{ij}(p)=g_{ij}(p)\delta _{ij}$
. Set
$(g_0)_{ij}(p)=g_{ij}(p)\delta _{ij}$
. Set
![]() $\tilde e_{i}=\textrm{d} f_{t}|_{t=0} \left(\dfrac{\partial }{\partial x_{i}}\right)$
and
$\tilde e_{i}=\textrm{d} f_{t}|_{t=0} \left(\dfrac{\partial }{\partial x_{i}}\right)$
and
![]() $V=\textrm{d} f_{t}|_{t=0}\left(\dfrac{\partial }{\partial t}\right)=V^{\top }+V^{\perp }$
with
$V=\textrm{d} f_{t}|_{t=0}\left(\dfrac{\partial }{\partial t}\right)=V^{\top }+V^{\perp }$
with
![]() $V^{\top }\in \Gamma (TM)$
and
$V^{\top }\in \Gamma (TM)$
and
![]() $V^{\perp }\in \Gamma (T^{\perp }M)$
.
$V^{\perp }\in \Gamma (T^{\perp }M)$
.
We first consider
![]() $\dfrac{\partial (\sqrt{G_{t}})}{\partial t}|_{t=0}$
and
$\dfrac{\partial (\sqrt{G_{t}})}{\partial t}|_{t=0}$
and
![]() $\dfrac{\partial |H|^{2}}{\partial t}|_{t=0}$
. It is well known that
$\dfrac{\partial |H|^{2}}{\partial t}|_{t=0}$
. It is well known that
Now we consider
![]() $\dfrac{\partial |H|^{2}}{\partial t}|_{t=0}$
. It follows the definition of the mean curvature vector that
$\dfrac{\partial |H|^{2}}{\partial t}|_{t=0}$
. It follows the definition of the mean curvature vector that
where
![]() $((g_{t})^{ij})$
denotes the inverse matrix of
$((g_{t})^{ij})$
denotes the inverse matrix of
![]() $((g_{t})_{ij})$
. Thus, we have at the point
$((g_{t})_{ij})$
. Thus, we have at the point
![]() $p$
that
$p$
that
Differentiating the formula
![]() $\sum \limits _{j}g^{ij}g_{jk}=\delta _{ik}$
and using the fact that
$\sum \limits _{j}g^{ij}g_{jk}=\delta _{ik}$
and using the fact that
![]() $\left[\dfrac{\partial }{\partial t}, \dfrac{\partial }{\partial x_{i}}\right]=0$
, we get
$\left[\dfrac{\partial }{\partial t}, \dfrac{\partial }{\partial x_{i}}\right]=0$
, we get
 \begin{equation} \begin{aligned} \frac{\partial (g_{t})^{ij}}{\partial t}|_{t=0} &=-\frac{\partial (g_{t})_{ij}}{\partial t}|_{t=0} =-\overline{\nabla }_{V}g(\tilde e_i,\tilde e_{j})\\[5pt] &=-\overline{\nabla }_{V^{\top }}g(\tilde e_i,\tilde e_{j}) +(\overline{\nabla }_{\tilde e_i}V^{\bot },\tilde e_{j}) +( \tilde e_i,\overline{\nabla }_{\tilde e_{j}}V^{\bot }))\\[5pt] &=-\nabla _{V^{\top }}g(\tilde e_i,\tilde e_{j}) +2g(h(\tilde e_i,\tilde e_{j}),V^{\bot }). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \frac{\partial (g_{t})^{ij}}{\partial t}|_{t=0} &=-\frac{\partial (g_{t})_{ij}}{\partial t}|_{t=0} =-\overline{\nabla }_{V}g(\tilde e_i,\tilde e_{j})\\[5pt] &=-\overline{\nabla }_{V^{\top }}g(\tilde e_i,\tilde e_{j}) +(\overline{\nabla }_{\tilde e_i}V^{\bot },\tilde e_{j}) +( \tilde e_i,\overline{\nabla }_{\tilde e_{j}}V^{\bot }))\\[5pt] &=-\nabla _{V^{\top }}g(\tilde e_i,\tilde e_{j}) +2g(h(\tilde e_i,\tilde e_{j}),V^{\bot }). \end{aligned} \end{equation}
Also, we have
 \begin{equation} \begin{aligned} \delta _{ij}\frac{\partial h(X_{i},X_{j})}{\partial t}|_{t=0} &=\overline{\nabla }_{V}(\overline{\nabla }_{\tilde e_i}\tilde e_i -\nabla _{\tilde e_i}\tilde e_i)\\[5pt] &=\overline{\nabla }_{V^{\top }}\overline{\nabla }_{\tilde e_i}\tilde e_i -\overline{\nabla }_{V^{\top }}\nabla _{\tilde e_i}\tilde e_i\\[5pt] & \quad +\overline{\nabla }_{\tilde e_i}\overline{\nabla }_{\tilde e_i}V^{\bot } +\overline{R}(V^{\bot },\tilde e_i)\tilde e_i-\overline{\nabla }_{V^{\bot }}\nabla _{\tilde e_i}\tilde e_i. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \delta _{ij}\frac{\partial h(X_{i},X_{j})}{\partial t}|_{t=0} &=\overline{\nabla }_{V}(\overline{\nabla }_{\tilde e_i}\tilde e_i -\nabla _{\tilde e_i}\tilde e_i)\\[5pt] &=\overline{\nabla }_{V^{\top }}\overline{\nabla }_{\tilde e_i}\tilde e_i -\overline{\nabla }_{V^{\top }}\nabla _{\tilde e_i}\tilde e_i\\[5pt] & \quad +\overline{\nabla }_{\tilde e_i}\overline{\nabla }_{\tilde e_i}V^{\bot } +\overline{R}(V^{\bot },\tilde e_i)\tilde e_i-\overline{\nabla }_{V^{\bot }}\nabla _{\tilde e_i}\tilde e_i. \end{aligned} \end{equation}
Since
![]() $\dfrac{\partial |H|^{2}}{\partial t}=g\left(H,2\dfrac{\partial H}{\partial t}\right)$
, we only need to know the normal part of (3.4). So, by a direct computation we have
$\dfrac{\partial |H|^{2}}{\partial t}=g\left(H,2\dfrac{\partial H}{\partial t}\right)$
, we only need to know the normal part of (3.4). So, by a direct computation we have
 \begin{equation} \begin{aligned} \left(\sum \limits _{i}(\overline{\nabla }_{V^{\top }}\overline{\nabla }_{\tilde e_i}\tilde e_i -\overline{\nabla }_{V^{\top }}\nabla _{\tilde e_i}\tilde e_i)\right)^{\bot } =\left(\sum \limits _{i}\overline{\nabla }_{V^{\top }}h(\tilde e_i,\tilde e_i)\right)^{\bot } =2\nabla _{V^{\top }}^{\bot }H, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \left(\sum \limits _{i}(\overline{\nabla }_{V^{\top }}\overline{\nabla }_{\tilde e_i}\tilde e_i -\overline{\nabla }_{V^{\top }}\nabla _{\tilde e_i}\tilde e_i)\right)^{\bot } =\left(\sum \limits _{i}\overline{\nabla }_{V^{\top }}h(\tilde e_i,\tilde e_i)\right)^{\bot } =2\nabla _{V^{\top }}^{\bot }H, \end{aligned} \end{equation}
 \begin{equation} \begin{aligned} &\left(\sum \limits _{i}(\overline{\nabla }_{\tilde e_i}\overline{\nabla }_{\tilde e_i}V^{\bot } +\overline{R}(V^{\bot },\tilde e_i)\tilde e_i-\overline{\nabla }_{V^{\bot }}\nabla _{\tilde e_i}\tilde e_i)\right)^{\bot }\\[5pt] &=\sum \limits _{i}(\!-\!h(\tilde e_i,A_{V^{\bot }}(\tilde e_i)) +\nabla _{\tilde e_i}^{\bot }\nabla _{\tilde e_i}^{\bot }V^{\bot } +(\overline{R}(V^{\bot },\tilde e_i)\tilde e_i)^{\bot } -\nabla _{\nabla _{\tilde e_i}\tilde e_i}^{\bot }V^{\bot })\\[5pt] &=\triangle ^{\bot }V^{\bot }+\sum \limits _{i}(\!-\!g(h(\tilde e_i,\tilde e_{j}),V^{\bot })h(\tilde e_i,\tilde e_{j}) +(\overline{R}(V^{\bot },\tilde e_i)\tilde e_i)^{\bot }). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &\left(\sum \limits _{i}(\overline{\nabla }_{\tilde e_i}\overline{\nabla }_{\tilde e_i}V^{\bot } +\overline{R}(V^{\bot },\tilde e_i)\tilde e_i-\overline{\nabla }_{V^{\bot }}\nabla _{\tilde e_i}\tilde e_i)\right)^{\bot }\\[5pt] &=\sum \limits _{i}(\!-\!h(\tilde e_i,A_{V^{\bot }}(\tilde e_i)) +\nabla _{\tilde e_i}^{\bot }\nabla _{\tilde e_i}^{\bot }V^{\bot } +(\overline{R}(V^{\bot },\tilde e_i)\tilde e_i)^{\bot } -\nabla _{\nabla _{\tilde e_i}\tilde e_i}^{\bot }V^{\bot })\\[5pt] &=\triangle ^{\bot }V^{\bot }+\sum \limits _{i}(\!-\!g(h(\tilde e_i,\tilde e_{j}),V^{\bot })h(\tilde e_i,\tilde e_{j}) +(\overline{R}(V^{\bot },\tilde e_i)\tilde e_i)^{\bot }). \end{aligned} \end{equation}
Here, we used the fact that
![]() $(\overline{\nabla }_{V^{\bot }}\nabla _{\tilde e_i}\tilde e_i)^{\bot } =\nabla _{\nabla _{\tilde e_i}\tilde e_i}^{\bot }V^{\bot }$
. Finally, substituting (3.3) and (3.4) into (3.2) and using (3.5), (3.6), and (2.11), we obtain at the point
$(\overline{\nabla }_{V^{\bot }}\nabla _{\tilde e_i}\tilde e_i)^{\bot } =\nabla _{\nabla _{\tilde e_i}\tilde e_i}^{\bot }V^{\bot }$
. Finally, substituting (3.3) and (3.4) into (3.2) and using (3.5), (3.6), and (2.11), we obtain at the point
![]() $p$
that
$p$
that
 \begin{align} \frac{\partial |H|^{2}}{\partial t}|_{t=0} &=g\!\left(H,2\frac{\partial H}{\partial t}\right) \nonumber \\[5pt] &=\sum \limits _{\alpha }\Big (H^{\alpha }\triangle ^{\bot }V^{\alpha } +V^{\alpha }(5-3C^{2})H^{\alpha } +\sum \limits _{ij\beta }V^{\alpha }H^{\beta }h_{ij}^{\alpha }h_{ij}^{\beta } \nonumber \\[5pt] & \quad -\sum \limits _{ijk}H^{\alpha }h_{ij}^{\alpha }V^{k}\nabla _{\tilde e_{k}}g_{ij}\Big ) +\sum \limits _{i}V^{i}\nabla _{\tilde e_i}|H|^{2}. \nonumber \\[5pt] &=\sum \limits _{\alpha }\left (H^{\alpha }\triangle ^{\bot }V^{\alpha } +V^{\alpha }(5-3C^{2})H^{\alpha } +\sum \limits _{ij\beta }V^{\alpha }H^{\beta }h_{ij}^{\alpha }h_{ij}^{\beta }\right) +\sum \limits _{i}V^{i}\nabla _{\tilde e_i}|H|^{2}. \end{align}
\begin{align} \frac{\partial |H|^{2}}{\partial t}|_{t=0} &=g\!\left(H,2\frac{\partial H}{\partial t}\right) \nonumber \\[5pt] &=\sum \limits _{\alpha }\Big (H^{\alpha }\triangle ^{\bot }V^{\alpha } +V^{\alpha }(5-3C^{2})H^{\alpha } +\sum \limits _{ij\beta }V^{\alpha }H^{\beta }h_{ij}^{\alpha }h_{ij}^{\beta } \nonumber \\[5pt] & \quad -\sum \limits _{ijk}H^{\alpha }h_{ij}^{\alpha }V^{k}\nabla _{\tilde e_{k}}g_{ij}\Big ) +\sum \limits _{i}V^{i}\nabla _{\tilde e_i}|H|^{2}. \nonumber \\[5pt] &=\sum \limits _{\alpha }\left (H^{\alpha }\triangle ^{\bot }V^{\alpha } +V^{\alpha }(5-3C^{2})H^{\alpha } +\sum \limits _{ij\beta }V^{\alpha }H^{\beta }h_{ij}^{\alpha }h_{ij}^{\beta }\right) +\sum \limits _{i}V^{i}\nabla _{\tilde e_i}|H|^{2}. \end{align}
Here, we used
Next, we consider
![]() $\dfrac{\partial (C_{t})^2}{\partial t}|_{t=0}$
. First for an oriented orthonormal basis
$\dfrac{\partial (C_{t})^2}{\partial t}|_{t=0}$
. First for an oriented orthonormal basis
![]() $\{e_1, e_2\}$
of
$\{e_1, e_2\}$
of
![]() $TM$
, set
$TM$
, set
It is direct to check that
![]() $X_{V}$
is independent of the choice
$X_{V}$
is independent of the choice
![]() $\{e_{1},e_{2}\}$
, and hence it defines a smooth vector field on
$\{e_{1},e_{2}\}$
, and hence it defines a smooth vector field on
![]() $M$
with
$M$
with
The definition of the Kähler function means that
So we get, at the point
![]() $p$
,
$p$
,
Since
![]() $[\tilde e_1,\tilde e_2]|_p=0$
and
$[\tilde e_1,\tilde e_2]|_p=0$
and
![]() $[V,\tilde e_i]|_p=0$
for
$[V,\tilde e_i]|_p=0$
for
![]() $1\leq i\leq 2$
, we have at the point
$1\leq i\leq 2$
, we have at the point
![]() $p$
that
$p$
that
 \begin{equation} \begin{aligned} \frac{\partial \Omega (X_{1},X_{2})}{\partial t}|_{t=0} &=\Omega (\overline{\nabla }_{\tilde e_{1}}V,\tilde e_{2})+\Omega (\tilde e_{1},\overline{\nabla }_{\tilde e_{2}}V)\\[5pt] &=\overline{\nabla }_{\tilde e_{1}}\Omega (V,\tilde e_{2})-\Omega (V,\overline{\nabla }_{\tilde e_{1}}\tilde e_{2}) +\overline{\nabla }_{\tilde e_{2}}\Omega (\tilde e_{1},V)-\Omega (\overline{\nabla }_{\tilde e_{2}}\tilde e_{1},V)\\[5pt] &=\nabla _{\tilde e_{1}}\Omega (V,\tilde e_{2})+\nabla _{\tilde e_{2}}\Omega (\tilde e_{1},V)=\text{div}(X_V). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \frac{\partial \Omega (X_{1},X_{2})}{\partial t}|_{t=0} &=\Omega (\overline{\nabla }_{\tilde e_{1}}V,\tilde e_{2})+\Omega (\tilde e_{1},\overline{\nabla }_{\tilde e_{2}}V)\\[5pt] &=\overline{\nabla }_{\tilde e_{1}}\Omega (V,\tilde e_{2})-\Omega (V,\overline{\nabla }_{\tilde e_{1}}\tilde e_{2}) +\overline{\nabla }_{\tilde e_{2}}\Omega (\tilde e_{1},V)-\Omega (\overline{\nabla }_{\tilde e_{2}}\tilde e_{1},V)\\[5pt] &=\nabla _{\tilde e_{1}}\Omega (V,\tilde e_{2})+\nabla _{\tilde e_{2}}\Omega (\tilde e_{1},V)=\text{div}(X_V). \end{aligned} \end{equation}
Substituting (3.1) and (3.10) into (3.9), we obtain at the point
![]() $p$
that
$p$
that
Noting that the right sides of (3.7) and (3.11) are independent of the coordinates and hence valid at any point of
![]() $M$
. Thus, from (3.1), (3.7), and (3.11), we get
$M$
. Thus, from (3.1), (3.7), and (3.11), we get
 \begin{equation} \begin{aligned} \frac{d}{dt}|_{t=0}(\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)) &=\int _{M}\frac{\partial }{\partial t}(|H|^{2}+\lambda _{1}+\lambda _{2} C^{2})|_{t=0}\textrm{d} M +\int _{M}(|H|^{2}+\lambda _{1}+\lambda _{2} C^{2})\frac{\partial (\textrm{d} M)}{\partial t}|_{t=0}\\[5pt] &=\int _{M}\bigg (\sum \limits _{\alpha }\bigg (H^{\alpha }\triangle ^{\perp }V^{\alpha } +[(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{\alpha } +\sum \limits _{\beta ij}h_{ij}^{\alpha }h_{ij}^{\beta }H^{\beta }]V^{\alpha }\bigg )\\[5pt] &\quad +\sum \limits _{i}V^{i}\nabla _{\tilde e_i}|H|^{2} +2\lambda _{2}C\,\text{div}X_{V}+(\lambda _{1}+\lambda _{2}C^{2}+|H|^{2})\text{div}V_{\top }\bigg )\textrm{d} M. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \frac{d}{dt}|_{t=0}(\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)) &=\int _{M}\frac{\partial }{\partial t}(|H|^{2}+\lambda _{1}+\lambda _{2} C^{2})|_{t=0}\textrm{d} M +\int _{M}(|H|^{2}+\lambda _{1}+\lambda _{2} C^{2})\frac{\partial (\textrm{d} M)}{\partial t}|_{t=0}\\[5pt] &=\int _{M}\bigg (\sum \limits _{\alpha }\bigg (H^{\alpha }\triangle ^{\perp }V^{\alpha } +[(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{\alpha } +\sum \limits _{\beta ij}h_{ij}^{\alpha }h_{ij}^{\beta }H^{\beta }]V^{\alpha }\bigg )\\[5pt] &\quad +\sum \limits _{i}V^{i}\nabla _{\tilde e_i}|H|^{2} +2\lambda _{2}C\,\text{div}X_{V}+(\lambda _{1}+\lambda _{2}C^{2}+|H|^{2})\text{div}V_{\top }\bigg )\textrm{d} M. \end{aligned} \end{equation}
Furthermore, it follows from the divergence theorem that
Substituting (3.13)–(3.16) into (3.12) and noting
 \begin{align} \nabla _{e_{1}}C \cdot \Omega (V^{\perp },e_{2})+\nabla _{e_{2}}C \cdot \Omega (e_{1},V^{\perp }) &=-\nabla _{e_{1}}C\cdot \langle Je_{2}, V^{\perp }\rangle +\nabla _{e_{2}}C \cdot \langle Je_{1},V^{\perp }\rangle \nonumber \\[5pt] &=\sqrt{1-C^{2}}\langle (\nabla _{e_{1}}C\,e_{3}+\nabla _{e_{2}}C\,e_{4}),V\rangle, \end{align}
\begin{align} \nabla _{e_{1}}C \cdot \Omega (V^{\perp },e_{2})+\nabla _{e_{2}}C \cdot \Omega (e_{1},V^{\perp }) &=-\nabla _{e_{1}}C\cdot \langle Je_{2}, V^{\perp }\rangle +\nabla _{e_{2}}C \cdot \langle Je_{1},V^{\perp }\rangle \nonumber \\[5pt] &=\sqrt{1-C^{2}}\langle (\nabla _{e_{1}}C\,e_{3}+\nabla _{e_{2}}C\,e_{4}),V\rangle, \end{align}
we obtain that
 \begin{align*} \frac {d}{dt}|_{t=0}(\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)) &=\int _{M}\bigg (\sum \limits _{\alpha }V^{\alpha }[\triangle ^{\perp } H^{\alpha } +(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{\alpha }\nonumber \\[5pt] &\quad +\sum \limits _{\beta ij}h_{ij}^{\alpha }h_{ij}^{\beta }H^{\beta }] -2\lambda _{2}\sqrt {1-C^{2}}(C_{,1}V^{3}+C_{,2}V^{4})\bigg )\textrm {d} M, \end{align*}
\begin{align*} \frac {d}{dt}|_{t=0}(\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)) &=\int _{M}\bigg (\sum \limits _{\alpha }V^{\alpha }[\triangle ^{\perp } H^{\alpha } +(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{\alpha }\nonumber \\[5pt] &\quad +\sum \limits _{\beta ij}h_{ij}^{\alpha }h_{ij}^{\beta }H^{\beta }] -2\lambda _{2}\sqrt {1-C^{2}}(C_{,1}V^{3}+C_{,2}V^{4})\bigg )\textrm {d} M, \end{align*}
where
![]() $C_{,i}\,(1\leq i\leq 2)$
denote the first covariant derivatives of
$C_{,i}\,(1\leq i\leq 2)$
denote the first covariant derivatives of
![]() $C$
. This implies that the Euler–Lagrange equation of
$C$
. This implies that the Euler–Lagrange equation of
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
is
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
is
 \begin{equation} \begin{cases} \triangle ^{\perp }H^{3}+(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{3}+ \sum \limits _{\beta ij}H^{\beta }h_{ij}^{\beta }h_{ij}^{3}-2\lambda _{2}\sqrt{1-C^{2}}C_{,1}=0,\\[12pt] \triangle ^{\perp }H^{4}+(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{4}+ \sum \limits _{\beta ij}H^{\beta }h_{ij}^{\beta }h_{ij}^{4}-2\lambda _{2}\sqrt{1-C^{2}}C_{,2}=0. \end{cases} \end{equation}
\begin{equation} \begin{cases} \triangle ^{\perp }H^{3}+(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{3}+ \sum \limits _{\beta ij}H^{\beta }h_{ij}^{\beta }h_{ij}^{3}-2\lambda _{2}\sqrt{1-C^{2}}C_{,1}=0,\\[12pt] \triangle ^{\perp }H^{4}+(5-2\lambda _{1}-(3-2\lambda _{2})C^{2}-2|H|^{2})H^{4}+ \sum \limits _{\beta ij}H^{\beta }h_{ij}^{\beta }h_{ij}^{4}-2\lambda _{2}\sqrt{1-C^{2}}C_{,2}=0. \end{cases} \end{equation}
This gives the proof of Theorem 1.1.
Remark 3.1.
When
![]() $\lambda _{2}=0$
, the function reduces to
$\lambda _{2}=0$
, the function reduces to
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)=\int _{M}(|H|^{2}+\lambda _{1})\textrm{d} M$
. In this situation, if
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)=\int _{M}(|H|^{2}+\lambda _{1})\textrm{d} M$
. In this situation, if
![]() $M$
is minimal, we obtain from (3.18) that
$M$
is minimal, we obtain from (3.18) that
![]() $M$
is Helfrich surface.
$M$
is Helfrich surface.
Remark 3.2.
When
![]() $C=constant$
, that is,
$C=constant$
, that is,
![]() $M$
has constant Kähler angle. If
$M$
has constant Kähler angle. If
![]() $M$
is minimal, then
$M$
is minimal, then
![]() $M$
is Helfrich surface.
$M$
is Helfrich surface.
Combing this we have
Corollary 3.3.
The complex curves and Lagrangian minimal surfaces in complex projective plane
![]() $\mathbb{C}P^{2}$
are Helfrich surfaces.
$\mathbb{C}P^{2}$
are Helfrich surfaces.
Corollary 3.4.
Let
![]() $f\;:\; M\rightarrow \mathbb{C}P^{2}$
be an isometric immersion of a compact surface in
$f\;:\; M\rightarrow \mathbb{C}P^{2}$
be an isometric immersion of a compact surface in
![]() $\mathbb{C}P^{2}$
. If
$\mathbb{C}P^{2}$
. If
![]() $M$
is a Helfrich surface for any
$M$
is a Helfrich surface for any
![]() $\lambda _{1},\lambda _{2}$
. Then
$\lambda _{1},\lambda _{2}$
. Then
![]() $M$
is minimal.
$M$
is minimal.
4. Homogeneous tori in
 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$
In this section, we consider the homogeneous tori in
![]() $\mathbb{C}P^{2}$
.
$\mathbb{C}P^{2}$
.
4.1. The geometry of homogeneous tori
The definition of the homogeneous torus in
![]() $\mathbb{C}P^{2}$
is given by the image of the Hopf projection:
$\mathbb{C}P^{2}$
is given by the image of the Hopf projection:
for positive numbers
![]() $r_{1}, r_{2}, r_{3}$
that satisfy
$r_{1}, r_{2}, r_{3}$
that satisfy
![]() $r_{1}^{2}+r_{2}^{2}+r_{3}^{2}=1$
. In this case, we also call
$r_{1}^{2}+r_{2}^{2}+r_{3}^{2}=1$
. In this case, we also call
![]() $T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
the Clifford torus. We note that Ma, Mironov, and Zuo in [Reference Ma, Mironov and Zuo11] gave a basis of the period module for the homogeneous tori. Here, we discuss the conformal structure of the homogeneous tori for completeness.
$T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
the Clifford torus. We note that Ma, Mironov, and Zuo in [Reference Ma, Mironov and Zuo11] gave a basis of the period module for the homogeneous tori. Here, we discuss the conformal structure of the homogeneous tori for completeness.
Taking into account the definition of
![]() $T_{r_{1},r_{2},r_{3}}$
, we assume that the homogeneous coordinate of
$T_{r_{1},r_{2},r_{3}}$
, we assume that the homogeneous coordinate of
![]() $T_{r_{1},r_{2},r_{3}}$
is
$T_{r_{1},r_{2},r_{3}}$
is
where
![]() $\varphi,\,\psi \in \mathbb{R}$
. Then we have from (2.1) that
$\varphi,\,\psi \in \mathbb{R}$
. Then we have from (2.1) that
Lemma 4.1.
The induced metric of
![]() $T_{r_{1},r_{2},r_{3}}$
in
$T_{r_{1},r_{2},r_{3}}$
in
![]() $\mathbb{C}P^{2}$
is
$\mathbb{C}P^{2}$
is
Setting
 \begin{equation} \begin{cases} u=\frac{\sqrt{1-r_{2}^{2}}}{r_{3}}\varphi -\frac{r_{3}}{\sqrt{1-r_{2}^{2}}}\psi,\\[12pt] v=\frac{r_{1}}{r_{2}\sqrt{1-r_{2}^{2}}}\psi, \end{cases} \hbox{i.e. } \begin{cases} \varphi =\frac{r_{3}}{\sqrt{1-r_{2}^{2}}}u+\frac{r_{2}^{2}r_{3}}{r_{1}\sqrt{1-r_{2}^{2}}}v,\\[12pt] \psi =\frac{r_{2}\sqrt{1-r_{2}^{2}}}{r_{1}}\psi. \end{cases} \end{equation}
\begin{equation} \begin{cases} u=\frac{\sqrt{1-r_{2}^{2}}}{r_{3}}\varphi -\frac{r_{3}}{\sqrt{1-r_{2}^{2}}}\psi,\\[12pt] v=\frac{r_{1}}{r_{2}\sqrt{1-r_{2}^{2}}}\psi, \end{cases} \hbox{i.e. } \begin{cases} \varphi =\frac{r_{3}}{\sqrt{1-r_{2}^{2}}}u+\frac{r_{2}^{2}r_{3}}{r_{1}\sqrt{1-r_{2}^{2}}}v,\\[12pt] \psi =\frac{r_{2}\sqrt{1-r_{2}^{2}}}{r_{1}}\psi. \end{cases} \end{equation}
Then
and hence
![]() $z=u+iv$
gives a complex coordinate of
$z=u+iv$
gives a complex coordinate of
![]() $T_{r_{1},r_{2},r_{3}}$
. Also, from (4.2) we get a basis
$T_{r_{1},r_{2},r_{3}}$
. Also, from (4.2) we get a basis
![]() $(\omega _{1}, \omega _{2})$
of the period module for
$(\omega _{1}, \omega _{2})$
of the period module for
![]() $T_{r_{1},r_{2},r_{3}}$
with
$T_{r_{1},r_{2},r_{3}}$
with
So without loss of generality, we assume
![]() $r_{3}\geqslant r_{1}\geqslant r_{2}$
,
$r_{3}\geqslant r_{1}\geqslant r_{2}$
,
![]() $k=\frac{r_{3}}{r_{1}}$
, then
$k=\frac{r_{3}}{r_{1}}$
, then
gives the module space for
![]() $T_{r_{1},r_{2},r_{3}}$
(see the shaded part of Figure 1).
$T_{r_{1},r_{2},r_{3}}$
(see the shaded part of Figure 1).

Figure 1.
![]() $\tau$
-plane.
$\tau$
-plane.
In particular, for Clifford torus
![]() $T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
,
$T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
,
![]() $\tau =\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}$
.
$\tau =\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}$
.
Now, we are going to consider the second fundamental forms of
![]() $T_{r_{1},r_{2},r_{3}}$
in
$T_{r_{1},r_{2},r_{3}}$
in
![]() $\mathbb{C}P^{2}$
.
$\mathbb{C}P^{2}$
.
Lemma 4.2.
The second fundamental forms of
![]() $T_{r_{1},r_{2},r_{3}}$
satisfy
$T_{r_{1},r_{2},r_{3}}$
satisfy
 \begin{equation} \left ( \begin{array}{c@{\quad}c} h_{11}^{3}&h_{12}^{3}\\[5pt] h_{21}^{3}&h_{22}^{3} \end{array} \right ) = \left ( \begin{array}{c@{\quad}c} 0 & \frac{-r_{2}}{\sqrt{1-r_{2}^{2}}}\\[12pt] \frac{-r_{2}}{\sqrt{1-r_{2}^{2}}}&\frac{r_{1}^{2}-r_{3}^{2}}{r_{1}r_{3}\sqrt{1-r_{2}^{2}}} \end{array} \right ), \end{equation}
\begin{equation} \left ( \begin{array}{c@{\quad}c} h_{11}^{3}&h_{12}^{3}\\[5pt] h_{21}^{3}&h_{22}^{3} \end{array} \right ) = \left ( \begin{array}{c@{\quad}c} 0 & \frac{-r_{2}}{\sqrt{1-r_{2}^{2}}}\\[12pt] \frac{-r_{2}}{\sqrt{1-r_{2}^{2}}}&\frac{r_{1}^{2}-r_{3}^{2}}{r_{1}r_{3}\sqrt{1-r_{2}^{2}}} \end{array} \right ), \end{equation}
 \begin{equation} \left ( \begin{array}{c@{\quad}c} h_{11}^{4}&h_{12}^{4}\\[5pt] h_{21}^{4}&h_{22}^{4} \end{array} \right ) = \left ( \begin{array}{c@{\quad}c} \frac{2r_{2}^{2}-1}{r_{2}\sqrt{1-r_{2}^{2}}} & 0\\[12pt] 0&\frac{r_{2}}{\sqrt{1-r_{2}^{2}}} \end{array} \right ). \end{equation}
\begin{equation} \left ( \begin{array}{c@{\quad}c} h_{11}^{4}&h_{12}^{4}\\[5pt] h_{21}^{4}&h_{22}^{4} \end{array} \right ) = \left ( \begin{array}{c@{\quad}c} \frac{2r_{2}^{2}-1}{r_{2}\sqrt{1-r_{2}^{2}}} & 0\\[12pt] 0&\frac{r_{2}}{\sqrt{1-r_{2}^{2}}} \end{array} \right ). \end{equation}
Proof. Set
![]() $\phi =r_{2}r_{3}(\textrm{d} u+i\textrm{d} v)$
, then the induced metric of
$\phi =r_{2}r_{3}(\textrm{d} u+i\textrm{d} v)$
, then the induced metric of
![]() $T_{r_{1},r_{2},r_{3}}$
can be written as:
$T_{r_{1},r_{2},r_{3}}$
can be written as:
Let
![]() $\{Z_{0},Z_{1},Z_{2}\}$
be a unitary frames in
$\{Z_{0},Z_{1},Z_{2}\}$
be a unitary frames in
![]() $\mathbb{C}^{3}$
. Then
$\mathbb{C}^{3}$
. Then
![]() $\textrm{d} Z_{0}=\sum \limits _{a}\psi _{0\overline{a}}Z_{a}$
with
$\textrm{d} Z_{0}=\sum \limits _{a}\psi _{0\overline{a}}Z_{a}$
with
![]() $\psi _{a\overline{b}}=\overline{\psi _{\overline{a}b}}$
. From this, we get
$\psi _{a\overline{b}}=\overline{\psi _{\overline{a}b}}$
. From this, we get
 \begin{align} \psi _{0\overline{1}}Z_{1}+\psi _{0\overline{2}}Z_{2} &=\textrm{d} Z_{0}-\psi _{0\overline{0}}Z_{0} \nonumber \\[5pt] &=\textrm{d} Z_{0}-h(dZ_{0},Z_{0})Z_{0} \nonumber \\[5pt] &=\left(\frac{-r_{3}-ir_{1}r_{2}}{2\sqrt{1-r_{2}^{2}}},\frac{i\sqrt{1-r_{2}^{2}}e^{i\varphi }}{2}, \frac{(r_{1}-ir_{2}r_{3})e^{i\psi }}{2\sqrt{1-r_{2}^{2}}}\right)\phi \nonumber \\[5pt] &\quad +\left(\frac{r_{3}-ir_{1}r_{2}}{2\sqrt{1-r_{2}^{2}}},\frac{i\sqrt{1-r_{2}^{2}}e^{i\varphi }}{2}, \frac{(\!-\!r_{1}-ir_{2}r_{3})e^{i\psi }}{2\sqrt{1-r_{2}^{2}}}\right)\overline{\phi }. \end{align}
\begin{align} \psi _{0\overline{1}}Z_{1}+\psi _{0\overline{2}}Z_{2} &=\textrm{d} Z_{0}-\psi _{0\overline{0}}Z_{0} \nonumber \\[5pt] &=\textrm{d} Z_{0}-h(dZ_{0},Z_{0})Z_{0} \nonumber \\[5pt] &=\left(\frac{-r_{3}-ir_{1}r_{2}}{2\sqrt{1-r_{2}^{2}}},\frac{i\sqrt{1-r_{2}^{2}}e^{i\varphi }}{2}, \frac{(r_{1}-ir_{2}r_{3})e^{i\psi }}{2\sqrt{1-r_{2}^{2}}}\right)\phi \nonumber \\[5pt] &\quad +\left(\frac{r_{3}-ir_{1}r_{2}}{2\sqrt{1-r_{2}^{2}}},\frac{i\sqrt{1-r_{2}^{2}}e^{i\varphi }}{2}, \frac{(\!-\!r_{1}-ir_{2}r_{3})e^{i\psi }}{2\sqrt{1-r_{2}^{2}}}\right)\overline{\phi }. \end{align}
And hence we obtain from
![]() $|Z_{1}|=|Z_{2}|=1$
that
$|Z_{1}|=|Z_{2}|=1$
that
 \begin{equation} \begin{aligned} Z_{1}=\left(\frac{-r_{3}-ir_{1}r_{2}}{\sqrt{2(1-r_{2}^{2})}},\frac{i\sqrt{1-r_{2}^{2}}e^{i\varphi }}{\sqrt{2}}, \frac{(r_{1}-ir_{2}r_{3})e^{i\psi }}{\sqrt{2(1-r_{2}^{2}})}\right),\\[5pt] Z_{2}=\left(\frac{r_{3}-ir_{1}r_{2}}{\sqrt{2(1-r_{2}^{2}})},\frac{i\sqrt{1-r_{2}^{2}}e^{i\varphi }}{\sqrt{2}}, \frac{(\!-\!r_{1}-ir_{2}r_{3})e^{i\psi }}{\sqrt{2(1-r_{2}^{2})}}\right). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} Z_{1}=\left(\frac{-r_{3}-ir_{1}r_{2}}{\sqrt{2(1-r_{2}^{2})}},\frac{i\sqrt{1-r_{2}^{2}}e^{i\varphi }}{\sqrt{2}}, \frac{(r_{1}-ir_{2}r_{3})e^{i\psi }}{\sqrt{2(1-r_{2}^{2}})}\right),\\[5pt] Z_{2}=\left(\frac{r_{3}-ir_{1}r_{2}}{\sqrt{2(1-r_{2}^{2}})},\frac{i\sqrt{1-r_{2}^{2}}e^{i\varphi }}{\sqrt{2}}, \frac{(\!-\!r_{1}-ir_{2}r_{3})e^{i\psi }}{\sqrt{2(1-r_{2}^{2})}}\right). \end{aligned} \end{equation}
Let
![]() $\{\omega _{i}\}$
be an unitary coframe in
$\{\omega _{i}\}$
be an unitary coframe in
![]() $\mathbb{C}P^{2}$
such that restricting to
$\mathbb{C}P^{2}$
such that restricting to
![]() $M$
$M$
Then from (2.8) and (4.5), we have
Now, using the fact
![]() $\psi _{a\overline{b}}=\langle dZ_{a},Z_{b}\rangle$
, then from (2.9) we get
$\psi _{a\overline{b}}=\langle dZ_{a},Z_{b}\rangle$
, then from (2.9) we get
and so
 \begin{equation*} \begin {aligned} s\overline {t}(\omega _{1\overline {1}} +\omega _{2\overline {2}})&=\left(\frac {2r_{3}^{2}+r_{2}^{2}-1}{4r_{1}r_{3}\sqrt {(1-r_{2}^{2})}} +\frac {i(3r_{2}^{2}-1)}{4r_{2}\sqrt {1-r_{2}^{2}}}\right)\phi \\[5pt] &\quad +\left(\frac {-(2r_{3}^{2}+r_{2}^{2}-1)}{4r_{1}r_{3}\sqrt {(1-r_{2}^{2})}} +\frac {i(3r_{2}^{2}-1)}{4r_{2}\sqrt {1-r_{2}^{2}}}\right)\overline {\phi }, \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} s\overline {t}(\omega _{1\overline {1}} +\omega _{2\overline {2}})&=\left(\frac {2r_{3}^{2}+r_{2}^{2}-1}{4r_{1}r_{3}\sqrt {(1-r_{2}^{2})}} +\frac {i(3r_{2}^{2}-1)}{4r_{2}\sqrt {1-r_{2}^{2}}}\right)\phi \\[5pt] &\quad +\left(\frac {-(2r_{3}^{2}+r_{2}^{2}-1)}{4r_{1}r_{3}\sqrt {(1-r_{2}^{2})}} +\frac {i(3r_{2}^{2}-1)}{4r_{2}\sqrt {1-r_{2}^{2}}}\right)\overline {\phi }, \end {aligned} \end{equation*}
 \begin{equation*} \begin {aligned} \omega _{1\overline {2}} &=\left(\frac {-(2r_{3}^{2}+r_{2}^{2}-1)}{4r_{1}r_{3}\sqrt {(1-r_{2}^{2})}} +\frac {i(3r_{2}^{2}-1)}{4r_{2}\sqrt {1-r_{2}^{2}}}\right)\phi \\[5pt] &\quad +\left(\frac {2r_{3}^{2}+r_{2}^{2}-1}{4r_{1}r_{3}\sqrt {(1-r_{2}^{2})}} -\frac {i(r_{2}^{2}+1)}{4r_{2}\sqrt {1-r_{2}^{2}}}\right)\overline {\phi }. \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} \omega _{1\overline {2}} &=\left(\frac {-(2r_{3}^{2}+r_{2}^{2}-1)}{4r_{1}r_{3}\sqrt {(1-r_{2}^{2})}} +\frac {i(3r_{2}^{2}-1)}{4r_{2}\sqrt {1-r_{2}^{2}}}\right)\phi \\[5pt] &\quad +\left(\frac {2r_{3}^{2}+r_{2}^{2}-1}{4r_{1}r_{3}\sqrt {(1-r_{2}^{2})}} -\frac {i(r_{2}^{2}+1)}{4r_{2}\sqrt {1-r_{2}^{2}}}\right)\overline {\phi }. \end {aligned} \end{equation*}
Thus, we obtain from (2.17) and (2.18) that the coefficients of the complex-valued second fundamental forms (see (2.19)) of
![]() $T_{r_{1},r_{2},r_{3}}$
are
$T_{r_{1},r_{2},r_{3}}$
are
 \begin{equation} \begin{cases} a=\dfrac{r_{3}^{2}-r_{1}^{2}}{4r_{1}r_{3}\sqrt{1-r_{2}^{2}}} +\dfrac{i(3r_{2}^{2}-1)}{4r_{2}\sqrt{1-r_{2}^{2}}},\\[16pt] b=\dfrac{r_{1}^{2}-r_{3}^{2}}{4r_{1}r_{3}\sqrt{1-r_{2}^{2}}} +\dfrac{i(3r_{2}^{2}-1)}{4r_{2}\sqrt{1-r_{2}^{2}}},\\[16pt] c=\dfrac{r_{3}^{2}-r_{1}^{2}}{4r_{1}r_{3}\sqrt{1-r_{2}^{2}}} -\dfrac{i(r_{2}^{2}+1)}{4r_{2}\sqrt{1-r_{2}^{2}}}. \end{cases} \end{equation}
\begin{equation} \begin{cases} a=\dfrac{r_{3}^{2}-r_{1}^{2}}{4r_{1}r_{3}\sqrt{1-r_{2}^{2}}} +\dfrac{i(3r_{2}^{2}-1)}{4r_{2}\sqrt{1-r_{2}^{2}}},\\[16pt] b=\dfrac{r_{1}^{2}-r_{3}^{2}}{4r_{1}r_{3}\sqrt{1-r_{2}^{2}}} +\dfrac{i(3r_{2}^{2}-1)}{4r_{2}\sqrt{1-r_{2}^{2}}},\\[16pt] c=\dfrac{r_{3}^{2}-r_{1}^{2}}{4r_{1}r_{3}\sqrt{1-r_{2}^{2}}} -\dfrac{i(r_{2}^{2}+1)}{4r_{2}\sqrt{1-r_{2}^{2}}}. \end{cases} \end{equation}
Using Lemma 2.1, (4.3) and (4.4) follow directly.
Remark 4.3.
The above proof shows that
![]() $s=t=\dfrac{\sqrt{2}}{2}$
, that is,
$s=t=\dfrac{\sqrt{2}}{2}$
, that is,
![]() $\cos \alpha =\dfrac{\sqrt{2}}{2}$
and the Kähler function
$\cos \alpha =\dfrac{\sqrt{2}}{2}$
and the Kähler function
![]() $C=\cos \alpha =0$
, which also implies that the homogeneous torus in
$C=\cos \alpha =0$
, which also implies that the homogeneous torus in
![]() $\mathbb{C}P^{2}$
is Lagrangian.
$\mathbb{C}P^{2}$
is Lagrangian.
Now we discuss the classification the homogeneous Helfrich tori in
![]() $\mathbb{C}P^{2}$
.
$\mathbb{C}P^{2}$
.
Theorem 4.4.
![]() $T_{r_{1},r_{2},r_{3}}$
is a Helfrich surface if and only if
$T_{r_{1},r_{2},r_{3}}$
is a Helfrich surface if and only if
-
1. When
 $0\leqslant \lambda _{1}\leqslant \dfrac{5}{2}$
,
$0\leqslant \lambda _{1}\leqslant \dfrac{5}{2}$
,
 $T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}.$
$T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}.$
-
2. When
 $\lambda _{1}\gt \dfrac{5}{2}$
,
$\lambda _{1}\gt \dfrac{5}{2}$
,
 $T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
or
$T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
or
 $T_{r_{1},r_{2},r_{3}}=T_{\sqrt{\frac{1}{4\lambda _{1}-9}}, \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}$
.
$T_{r_{1},r_{2},r_{3}}=T_{\sqrt{\frac{1}{4\lambda _{1}-9}}, \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}$
.
Proof. By Lemma 4.2, we get the coefficients of the mean curvature of
![]() $T_{r_{1},r_{2},r_{3}}$
as follows:
$T_{r_{1},r_{2},r_{3}}$
as follows:
And hence the norm square of the mean curvature is
Thus, substituting (4.10) and (4.11) into the Euler–Lagrange equation (3.18) and using the fact
![]() $C=\cos \alpha \equiv 0$
, we get that
$C=\cos \alpha \equiv 0$
, we get that
 \begin{equation*} \begin {cases} \left \{\left (12-4\lambda _{1}+(4\lambda _{1}-8)r_{2}^{2}\right ) r_{1}^{2}r_{2}^{2}r_{3}^{2}+2r_{2}^{2}(r_{1}^{4}+r_{3}^{4}) -(1-r_{1}^{2})(1-r_{2}^{2})^{2}(1-r_{3}^{2})\right \}(r_{1}^{2}-r_{3}^{2})=0,\\[5pt] \left \{\left (10-4\lambda _{1}+(4\lambda _{1}-8)r_{2}^{2}\right ) r_{1}^{2}r_{2}^{2}r_{3}^{2}+2r_{1}^{2}r_{3}^{2} -(1-r_{1}^{2})(1-r_{2}^{2})^{2}(1-r_{3}^{2})\right \}(3r_{2}^{2}-1) +2r_{2}^{4}(r_{1}^{2}-r_{3}^{2})=0,\\[5pt] r_{1}^{2}+r_{2}^{2}+r_{3}^{2}=1. \end {cases} \end{equation*}
\begin{equation*} \begin {cases} \left \{\left (12-4\lambda _{1}+(4\lambda _{1}-8)r_{2}^{2}\right ) r_{1}^{2}r_{2}^{2}r_{3}^{2}+2r_{2}^{2}(r_{1}^{4}+r_{3}^{4}) -(1-r_{1}^{2})(1-r_{2}^{2})^{2}(1-r_{3}^{2})\right \}(r_{1}^{2}-r_{3}^{2})=0,\\[5pt] \left \{\left (10-4\lambda _{1}+(4\lambda _{1}-8)r_{2}^{2}\right ) r_{1}^{2}r_{2}^{2}r_{3}^{2}+2r_{1}^{2}r_{3}^{2} -(1-r_{1}^{2})(1-r_{2}^{2})^{2}(1-r_{3}^{2})\right \}(3r_{2}^{2}-1) +2r_{2}^{4}(r_{1}^{2}-r_{3}^{2})=0,\\[5pt] r_{1}^{2}+r_{2}^{2}+r_{3}^{2}=1. \end {cases} \end{equation*}
By solving the equation above, we obtain
-
1. When
 $0\leqslant \lambda _{1}\leqslant \dfrac{5}{2}$
,
$0\leqslant \lambda _{1}\leqslant \dfrac{5}{2}$
,
 $T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}.$
$T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}.$
-
2. When
 $\lambda _{1}\gt \dfrac{5}{2}$
,
$\lambda _{1}\gt \dfrac{5}{2}$
,
 $T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}} \,\text{or} \,T_{r_{1},r_{2},r_{3}}=T_{\sqrt{\frac{1}{4\lambda _{1}-9}}, \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}.$
$T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}} \,\text{or} \,T_{r_{1},r_{2},r_{3}}=T_{\sqrt{\frac{1}{4\lambda _{1}-9}}, \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}.$
4.2. The Helfrich energy of homogeneous tori
Proposition 4.5.
The Helfrich energy of
![]() $T_{r_{1},r_{2},r_{3}}$
is
$T_{r_{1},r_{2},r_{3}}$
is
 \begin{equation} \begin{aligned} \mathcal{H}_{\lambda _{1},\lambda _{2}}(f) &=\int _{M}(|H|^{2}+\lambda _{1}+\lambda _{2} C^{2})\textrm{d} M\\[5pt] &=\frac{((1-r_{1}^{2})(1-r_{2}^{2})(1-r_{3}^{2}) +(4\lambda _{1}-8)r_{1}^{2}r_{2}^{2}r_{3}^{2})\pi ^{2}}{r_{1}r_{2}r_{3}}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \mathcal{H}_{\lambda _{1},\lambda _{2}}(f) &=\int _{M}(|H|^{2}+\lambda _{1}+\lambda _{2} C^{2})\textrm{d} M\\[5pt] &=\frac{((1-r_{1}^{2})(1-r_{2}^{2})(1-r_{3}^{2}) +(4\lambda _{1}-8)r_{1}^{2}r_{2}^{2}r_{3}^{2})\pi ^{2}}{r_{1}r_{2}r_{3}}. \end{aligned} \end{equation}
Proof. From Lemma 4.1, we have
![]() $\textrm{d} T_{r_{1},r_{2},r_{3}}=r_{1}r_{2}r_{3}\textrm{d}\varphi \textrm{d}\psi$
. By using of (4.11), (4.12) follows directly.
$\textrm{d} T_{r_{1},r_{2},r_{3}}=r_{1}r_{2}r_{3}\textrm{d}\varphi \textrm{d}\psi$
. By using of (4.11), (4.12) follows directly.
Now we consider the lower bound of
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
for
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
for
![]() $T_{r_{1},r_{2},r_{3}}$
.
$T_{r_{1},r_{2},r_{3}}$
.
Theorem 4.6.
The Helfrich energy of
![]() $T_{r_{1},r_{2},r_{3}}$
satisfies
$T_{r_{1},r_{2},r_{3}}$
satisfies
-
1. When
 $0\leqslant \lambda _{1}\leqslant 3$
,and the equality holds if and only if
$0\leqslant \lambda _{1}\leqslant 3$
,and the equality holds if and only if \begin{equation*}\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac {4\lambda _{1}\pi ^{2}}{3\sqrt {3}},\end{equation*}
\begin{equation*}\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac {4\lambda _{1}\pi ^{2}}{3\sqrt {3}},\end{equation*}
 $r_{1}=r_{2}=r_{3}=\dfrac{\sqrt{3}}{3}$
.
$r_{1}=r_{2}=r_{3}=\dfrac{\sqrt{3}}{3}$
.
-
2. When
 $\lambda _{1}\gt 3$
,and the equality holds if and only if
$\lambda _{1}\gt 3$
,and the equality holds if and only if \begin{equation*}\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac {(4\lambda _{1}-8)\pi ^{2}}{\sqrt {4\lambda _{1}-9}},\end{equation*}
\begin{equation*}\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac {(4\lambda _{1}-8)\pi ^{2}}{\sqrt {4\lambda _{1}-9}},\end{equation*}
 $r_{1}=\sqrt{\dfrac{1}{4\lambda _{1}-9}},\,r_{2}=r_{3} =\sqrt{\dfrac{2\lambda _{1}-5}{4\lambda _{1}-9}}.$
$r_{1}=\sqrt{\dfrac{1}{4\lambda _{1}-9}},\,r_{2}=r_{3} =\sqrt{\dfrac{2\lambda _{1}-5}{4\lambda _{1}-9}}.$
Proof. Computing the extreme value of (4.12) under the constraint
![]() $r_{1}^{2}+r_{2}^{2}+r_{3}^{2}=1$
yields
$r_{1}^{2}+r_{2}^{2}+r_{3}^{2}=1$
yields
 \begin{equation*} \begin {cases} (4\lambda _{1}-8)(r_{1}^{2}-r_{2}^{2})r_{1}^{2}r_{2}^{2}r_{3}^{2} +(1+r_{1}^{2})(1-r_{2}^{2})(1-r_{3}^{2})r_{2}^{2} -(1-r_{1}^{2})(1+r_{2}^{2})(1-r_{3}^{2})r_{1}^{2}=0,\\[5pt] (4\lambda _{1}-8)(r_{1}^{2}-r_{3}^{2})r_{1}^{2}r_{2}^{2}r_{3}^{2} +(1+r_{1}^{2})(1-r_{2}^{2})(1-r_{3}^{2})r_{3}^{2} -(1-r_{1}^{2})(1-r_{2}^{2})(1+r_{3}^{2})r_{1}^{2}=0,\\[5pt] r_{1}^{2}+r_{2}^{2}+r_{3}^{2}=1. \end {cases} \end{equation*}
\begin{equation*} \begin {cases} (4\lambda _{1}-8)(r_{1}^{2}-r_{2}^{2})r_{1}^{2}r_{2}^{2}r_{3}^{2} +(1+r_{1}^{2})(1-r_{2}^{2})(1-r_{3}^{2})r_{2}^{2} -(1-r_{1}^{2})(1+r_{2}^{2})(1-r_{3}^{2})r_{1}^{2}=0,\\[5pt] (4\lambda _{1}-8)(r_{1}^{2}-r_{3}^{2})r_{1}^{2}r_{2}^{2}r_{3}^{2} +(1+r_{1}^{2})(1-r_{2}^{2})(1-r_{3}^{2})r_{3}^{2} -(1-r_{1}^{2})(1-r_{2}^{2})(1+r_{3}^{2})r_{1}^{2}=0,\\[5pt] r_{1}^{2}+r_{2}^{2}+r_{3}^{2}=1. \end {cases} \end{equation*}
A straightforward calculation shows that
-
1. When
 $0\leqslant \lambda _{1}\leqslant \dfrac{5}{2}$
,
$0\leqslant \lambda _{1}\leqslant \dfrac{5}{2}$
, \begin{equation*}T_{r_{1},r_{2},r_{3}}=T_{\frac {\sqrt {3}}{3},\frac {\sqrt {3}}{3},\frac {\sqrt {3}}{3}}, \,\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)=\frac {4\lambda _{1}\pi ^{2}}{3\sqrt {3}}.\end{equation*}
\begin{equation*}T_{r_{1},r_{2},r_{3}}=T_{\frac {\sqrt {3}}{3},\frac {\sqrt {3}}{3},\frac {\sqrt {3}}{3}}, \,\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)=\frac {4\lambda _{1}\pi ^{2}}{3\sqrt {3}}.\end{equation*}
-
2. When
 $\lambda _{1}\gt \dfrac{5}{2}$
,or
$\lambda _{1}\gt \dfrac{5}{2}$
,or \begin{equation*}T_{r_{1},r_{2},r_{3}}=T_{\frac {\sqrt {3}}{3},\frac {\sqrt {3}}{3},\frac {\sqrt {3}}{3}}, \,\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)=\frac {4\lambda _{1}\pi ^{2}}{3\sqrt {3}},\end{equation*}
\begin{equation*}T_{r_{1},r_{2},r_{3}}=T_{\frac {\sqrt {3}}{3},\frac {\sqrt {3}}{3},\frac {\sqrt {3}}{3}}, \,\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)=\frac {4\lambda _{1}\pi ^{2}}{3\sqrt {3}},\end{equation*}
 \begin{equation*}T_{r_{1},r_{2},r_{3}}=T_{\sqrt {\frac {1}{4\lambda _{1}-9}}, \sqrt {\frac {2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt {\frac {2\lambda _{1}-5}{4\lambda _{1}-9}}}, \,\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)=\frac {(4\lambda _{1}-8)\pi ^{2}}{\sqrt {4\lambda _{1}-9}}.\end{equation*}
\begin{equation*}T_{r_{1},r_{2},r_{3}}=T_{\sqrt {\frac {1}{4\lambda _{1}-9}}, \sqrt {\frac {2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt {\frac {2\lambda _{1}-5}{4\lambda _{1}-9}}}, \,\mathcal {H}_{\lambda _{1},\lambda _{2}}(f)=\frac {(4\lambda _{1}-8)\pi ^{2}}{\sqrt {4\lambda _{1}-9}}.\end{equation*}
For the case of
![]() $0\leqslant \lambda _{1}\leqslant \dfrac{5}{2}$
, it is obvious that
$0\leqslant \lambda _{1}\leqslant \dfrac{5}{2}$
, it is obvious that
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \dfrac{4\lambda _{1}\pi ^{2}}{3\sqrt{3}}$
and equality holds if and only if
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \dfrac{4\lambda _{1}\pi ^{2}}{3\sqrt{3}}$
and equality holds if and only if
![]() $T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
. In the second case, if
$T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
. In the second case, if
![]() $\dfrac{5}{2}\lt \lambda _{1}\leqslant 3$
, since
$\dfrac{5}{2}\lt \lambda _{1}\leqslant 3$
, since
![]() $\dfrac{4\lambda _{1}\pi ^{2}}{3\sqrt{3}} \leqslant \dfrac{(4\lambda _{1}-8)\pi ^{2}}{\sqrt{4\lambda _{1}-9}}$
, we have that
$\dfrac{4\lambda _{1}\pi ^{2}}{3\sqrt{3}} \leqslant \dfrac{(4\lambda _{1}-8)\pi ^{2}}{\sqrt{4\lambda _{1}-9}}$
, we have that
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac{4\lambda _{1}\pi ^{2}}{3\sqrt{3}}$
and equality holds if and only if
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac{4\lambda _{1}\pi ^{2}}{3\sqrt{3}}$
and equality holds if and only if
![]() $T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
. If
$T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
. If
![]() $\lambda _{1}\gt 3$
,
$\lambda _{1}\gt 3$
,
![]() $\dfrac{4\lambda _{1}\pi ^{2}}{3\sqrt{3}} \gt \dfrac{(4\lambda _{1}-8)\pi ^{2}}{\sqrt{4\lambda _{1}-9}}$
, and hence
$\dfrac{4\lambda _{1}\pi ^{2}}{3\sqrt{3}} \gt \dfrac{(4\lambda _{1}-8)\pi ^{2}}{\sqrt{4\lambda _{1}-9}}$
, and hence
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac{(4\lambda _{1}-8)\pi ^{2}}{\sqrt{4\lambda _{1}-9}}$
, the equality holds if and only if
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \frac{(4\lambda _{1}-8)\pi ^{2}}{\sqrt{4\lambda _{1}-9}}$
, the equality holds if and only if
![]() $T_{r_{1},r_{2},r_{3}}=T_{\sqrt{\frac{1}{4\lambda _{1}-9}}, \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}$
.
$T_{r_{1},r_{2},r_{3}}=T_{\sqrt{\frac{1}{4\lambda _{1}-9}}, \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}$
.
Remark 4.7.
For the case of
![]() $\lambda _{1}=3$
in the above proof,
$\lambda _{1}=3$
in the above proof,
![]() $T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}} =T_{\sqrt{\frac{1}{4\lambda _{1}-9}}. \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}$
, This implies that
$T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}} =T_{\sqrt{\frac{1}{4\lambda _{1}-9}}. \sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}},\sqrt{\frac{2\lambda _{1}-5}{4\lambda _{1}-9}}}$
, This implies that
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \dfrac{4\lambda _{1}\pi ^{2}}{3\sqrt{3}}$
, and equality holds if and only if
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)\geqslant \dfrac{4\lambda _{1}\pi ^{2}}{3\sqrt{3}}$
, and equality holds if and only if
![]() $T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
.
$T_{r_{1},r_{2},r_{3}}=T_{\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}}$
.
Remark 4.8.
In [Reference Montiel and Urbano14], Montiel and Urbano introduced the conformal invariants
![]() $W^{-}(F)$
and
$W^{-}(F)$
and
![]() $W^{+}(F)$
for compact surfaces in
$W^{+}(F)$
for compact surfaces in
![]() $\mathbb{C}P^{2}$
. In view of the Helfrich functional
$\mathbb{C}P^{2}$
. In view of the Helfrich functional
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
, we have
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$
, we have
-
1. When
 $\lambda _{1}=2, \lambda _{2}=0$
,
$\lambda _{1}=2, \lambda _{2}=0$
,
 $\mathcal{H}_{2,0}(F)=W^{-}(F)=\int _{M}(|H|^{2}+2)\textrm{d} M$
;
$\mathcal{H}_{2,0}(F)=W^{-}(F)=\int _{M}(|H|^{2}+2)\textrm{d} M$
; -
2. When
 $\lambda _{1}=0, \lambda _{2}=6$
,
$\lambda _{1}=0, \lambda _{2}=6$
,
 $\mathcal{H}_{0,6}(F)=W^{+}(F)=\int _{M}(|H|^{2}+6C^{2})\textrm{d} M$
;
$\mathcal{H}_{0,6}(F)=W^{+}(F)=\int _{M}(|H|^{2}+6C^{2})\textrm{d} M$
; -
3. When
 $\lambda _{1}=1, \,\lambda _{2}=3$
,
$\lambda _{1}=1, \,\lambda _{2}=3$
,
 $\mathcal{H}_{1,3}(F)=W(F)=\int _{M}(|H|^{2}+1+3C^{2})\textrm{d} M$
, that is, the Willmore functional.
$\mathcal{H}_{1,3}(F)=W(F)=\int _{M}(|H|^{2}+1+3C^{2})\textrm{d} M$
, that is, the Willmore functional.
Thus, by using the Euler–Lagrange equation of
![]() $\mathcal{H}_{\lambda _{1},\lambda _{2}}(F)$
, we have the following corollary.
$\mathcal{H}_{\lambda _{1},\lambda _{2}}(F)$
, we have the following corollary.
Corollary 4.9. ([Reference Hu and Li8]) The Euler–Lagrange equation of
![]() $W(F)$
is
$W(F)$
is
 \begin{equation*} \begin {cases} \triangle ^{\perp }H^{3}+(3+3C^{2}-2|H|^{2})H^{3}+ \sum \limits _{\beta, i,j}h_{ij}^{3}h_{ij}^{\beta }H^{\beta }-6\sqrt {1-C^{2}}C_{,1}=0,\\[12pt] \triangle ^{\perp }H^{4}+(3+3C^{2}-2|H|^{2})H^{4}+ \sum \limits _{\beta, i,j}h_{ij}^{4}h_{ij}^{\beta }H^{\beta }-6\sqrt {1-C^{2}}C_{,2}=0. \end {cases} \end{equation*}
\begin{equation*} \begin {cases} \triangle ^{\perp }H^{3}+(3+3C^{2}-2|H|^{2})H^{3}+ \sum \limits _{\beta, i,j}h_{ij}^{3}h_{ij}^{\beta }H^{\beta }-6\sqrt {1-C^{2}}C_{,1}=0,\\[12pt] \triangle ^{\perp }H^{4}+(3+3C^{2}-2|H|^{2})H^{4}+ \sum \limits _{\beta, i,j}h_{ij}^{4}h_{ij}^{\beta }H^{\beta }-6\sqrt {1-C^{2}}C_{,2}=0. \end {cases} \end{equation*}
Corollary 4.10. ([Reference Hu and Li8]) The Euler–Lagrange equation of
![]() $W^{-}(F)$
is
$W^{-}(F)$
is
Corollary 4.11.
The Euler–Lagrange equation of
![]() $W^{+}(F)$
is
$W^{+}(F)$
is
 \begin{equation*} \begin {cases} \triangle ^{\perp }H^{3}+(5+9C^{2}-2|H|^{2})H^{3}+ \sum \limits _{\beta, i,j}h_{ij}^{3}h_{ij}^{\beta }H^{\beta }-12\sqrt {1-C^{2}}C_{,1}=0,\\[12pt] \triangle ^{\perp }H^{4}+(3+3C^{2}-2|H|^{2})H^{4}+ \sum \limits _{\beta, i,j}h_{ij}^{4}h_{ij}^{\beta }H^{\beta }-12\sqrt {1-C^{2}}C_{,2}=0. \end {cases} \end{equation*}
\begin{equation*} \begin {cases} \triangle ^{\perp }H^{3}+(5+9C^{2}-2|H|^{2})H^{3}+ \sum \limits _{\beta, i,j}h_{ij}^{3}h_{ij}^{\beta }H^{\beta }-12\sqrt {1-C^{2}}C_{,1}=0,\\[12pt] \triangle ^{\perp }H^{4}+(3+3C^{2}-2|H|^{2})H^{4}+ \sum \limits _{\beta, i,j}h_{ij}^{4}h_{ij}^{\beta }H^{\beta }-12\sqrt {1-C^{2}}C_{,2}=0. \end {cases} \end{equation*}
Let us consider the homogeneous tori
![]() $T_{r_{1},r_{2},r_{3}}$
in
$T_{r_{1},r_{2},r_{3}}$
in
![]() $\mathbb{C}P^{2}$
, then it follows from Theorems 4.4 and 4.6 that
$\mathbb{C}P^{2}$
, then it follows from Theorems 4.4 and 4.6 that
Corollary 4.12.
![]() $T_{r_{1},r_{2},r_{3}}$
is a critical surface for
$T_{r_{1},r_{2},r_{3}}$
is a critical surface for
![]() $W(F),\,W^{-}(F)$
, or
$W(F),\,W^{-}(F)$
, or
![]() $W^{+}(F)$
if and only if it is the Cliford torus
$W^{+}(F)$
if and only if it is the Cliford torus
![]() $T_{\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}}$
.
$T_{\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}}$
.
Corollary 4.13.
Considering the homogeneous tori
![]() $T_{r_{1},r_{2},r_{3}}$
in
$T_{r_{1},r_{2},r_{3}}$
in
![]() $\mathbb{C}P^{2}$
. Then
$\mathbb{C}P^{2}$
. Then
![]() $W^{-}(F)\geqslant \dfrac{8\pi ^{2}}{3\sqrt{3}}$
(see also [Reference Montiel and Urbano14]) and
$W^{-}(F)\geqslant \dfrac{8\pi ^{2}}{3\sqrt{3}}$
(see also [Reference Montiel and Urbano14]) and
![]() $W^{+}(F)\geqslant 0$
, and the equalities hold if and only if
$W^{+}(F)\geqslant 0$
, and the equalities hold if and only if
![]() $T_{r_{1},r_{2},r_{3}}$
is the Cliford torus
$T_{r_{1},r_{2},r_{3}}$
is the Cliford torus
![]() $T_{\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}}$
.
$T_{\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}}$
.