A two-dimensional numerical study of film boiling over an elliptical cylinder in the mixed regime under aiding and orthogonal saturated liquid flow configurations

Abstract

Saturated film boiling over an elliptical heater is investigated in the mixed regime considering both aiding and orthogonal liquid flow configurations relative to gravity. A computational framework developed for phase change problems on unstructured grids based on a coupled level set and volume of fluid interface capturing method is used to characterize interface evolution and vapour wake dynamics alongside quantifying heat transfer at low values of the Froude number (Fr). The influence of hydrodynamic and thermal conditions along with cross-flow direction for a fixed heater geometry manifests in the form of varied wake profiles with the quasi-steady nature of film boiling lost as Fr increases. Additionally, while the heater aspect ratio affects the rate of vapour infusion into the wake, the heater orientation significantly affects the film boiling behaviour. With horizontal cross-flow, higher angles of incidence entail a lower influence of flow inertia while augmenting buoyancy-driven vapour removal leading to enhanced heat transfer compared to aiding flow under certain cases, and adding a further dimension to the interplay between buoyancy and inertia. Similarly an anomalous impairment of heat transfer with an increase in cross-flow velocity arises from a competing influence of buoyancy and drag as an artefact of heater and cross-flow configurations. The mutual coupling of liquid and vapour wakes is also discussed in detail under such conditions. Finally, a shape factor $(\psi )$ is proposed to comprehensively predict the heat transfer in conjunction with correlations for a circular heater, and determined based on the effect of the elliptical geometry in the mixed regime.

1. Introduction

Film boiling is encountered in numerous applications such as metal quenching, cryogenics, superconducting devices and nuclear reactor accident analysis. Thus despite the low heat transfer rates observed post heater dryout, the study of hydrodynamics and heat transfer in film boiling with regard to different geometries and operating conditions is essential. Further, the low heat transfer rates present a limiting case of boiling heat transfer, and estimating these becomes crucial from design considerations. Pioneered by some early works for a flat heater geometry (Son & Dhir 1997; Juric & Tryggvason 1998; Welch & Wilson 2000), direct numerical simulations have gained traction in recent years as an important means to study boiling flows. These involve solving the transport mechanisms directly across the phase interface without resorting to any empiricism. As a result, significant insights can be obtained while alleviating issues such as measurements at small spatiotemporal scales in boiling experiments, and major simplifying assumptions often employed in various theoretical analysis carried out until the present.

Owing to the importance of the flat plate geometry coupled with a relative ease in its computational treatment, many of the earlier numerical models focused on horizontal film boiling. Nonetheless, a circular wire is often the optimal geometric choice as a boiling heater, and also presents itself as an important baseline case for understanding film boiling physics over different complex geometries encountered across practical applications. Despite this only a few direct numerical simulations (Esmaeeli & Tryggvason 2004; Son & Dhir 2008; Tsui et al. 2014; Singh & Premachandran 2018a) have been performed over a cylinder in the context of pool film boiling, with external forced convection film boiling receiving considerably less attention. This can be partly attributed to numerical challenges associated with geometric considerations in the framework of nonlinear phase change simulations. However, recent efforts have been directed towards accurate interface capturing on unstructured grids for two-phase flows (Balcázar et al. 2016) including phase change (Singh & Premachandran 2018a) that have enabled important film boiling results to be obtained in a wider geometrical ambit (Singh & Premachandran 2018b, 2019, 2020). Further, an ellipse represents the simplest deviation from a circular body as a non-canonical form with features such as aspect ratio $(\varGamma )$ and angle of incidence $(\theta )$ offering possibilities to study the interfacial dynamics and heat transfer for external flow film boiling in a comprehensive manner. It can also be noted that many important aspects including wake characteristics even for single-phase flow over an ellipse have been brought to the fore only in recent studies (Paul et al. 2016; Rao et al. 2017) as compared with an extensive effort dedicated towards understanding flow over a circular cylinder. Additionally, the interfacial dynamics in film boiling is prominently governed by Rayleigh–Taylor and Kelvin–Helmholtz instabilities, which can result in the heat transfer behaviour being counter-intuitive to that expected for single phase flows under certain conditions, as shown in some previous studies (Singh & Premachandran 2019, 2020) by the present authors. Thus the aim of the present work is to study the flow and heat transfer characteristics in saturated film boiling over an ellipse in the mixed regime (Singh & Premachandran 2018b) under different liquid cross-flow configurations, with a suitable computational framework for boiling flows. To the best of authors’ knowledge, this has not been attempted previously, and thus would help in gaining interesting insights.

The significance of mixed regime stems from the often overlooked aspect pertaining to the effect of gravity in flow film boiling over a bluff body, which cannot be neglected under certain conditions. The relative importance of buoyancy and flow inertia is characterized by the Froude number, $Fr=U^{2}/gD$, where $U$ is the liquid cross-flow velocity and $D$ is the characteristic dimension. Still, most of the experimental studies for forced convection film boiling over a circular cylinder focused only on the inertia dominated regime. At the same time, the challenges associated with the analytical treatment of the problem become more pronounced under comparable influence of buoyancy and inertia leading to almost all prior theoretical studies neglecting the effect of gravity. The mixed regime of film boiling over a circular cylinder has been explicitly identified only in the studies of Bromley, LeRoy & Robbers (1953) and Ito, Nishikawa & Shigechi (1981). However, these studies differed in the prediction for the onset of the mixed regime in terms of the Froude number. Also, no conclusive heat transfer results were provided by either study in the mixed regime thereby leaving a discernible gap in the literature. Bromley et al. (1953) proposed semiempirical heat transfer correlations only for pool film boiling and purely forced convection film boiling. Ito et al. (1981) noted that a similarity solution in the mixed regime was not possible and used an integral method for the two-phase boundary layer in their analysis. They also established a definitive relationship between the Nusselt number and other non-dimensional parameters only in the buoyancy or inertia dominated regimes, while noting anomalous heat transfer behaviour when both the forces were comparable. Here it can be mentioned that the aforementioned gaps can be suitably addressed through computations of film boiling. As such, the present authors performed direct numerical simulations in the mixed regime of saturated film boiling over a horizontal circular cylinder under different liquid flow configurations in recent studies (Singh & Premachandran 2018b, 2019), where the effect of different film boiling parameters was analysed and all the relevant aspects discussed in detail. It was shown that a complex interplay of buoyancy and inertia governed the interfacial dynamics and heat transfer in the mixed regime, in addition to surface tension, vapour properties and wall superheat. A comprehensive heat transfer correlation was proposed for upward cross-flow (Singh & Premachandran 2018b), while a reduction factor (Singh & Premachandran 2019) as a function of the Froude number was proposed to quantify the heat transfer with horizontal cross-flow of liquid.

With regard to an elliptical cylinder, only a few analytical studies have been performed in the purview of natural convection film boiling. Nakayama & Koyama (1986) theoretically studied heat transfer in saturated pool film boiling over arbitrary geometries using an integral formulation for two-phase boundary layer. They considered the inertial and convective effects in the film along with interfacial shear, while not incorporating surface tension in their analysis. Amongst the results for several different geometries, only local heat transfer variation with two different aspect ratios of an ellipse was presented. Subsequently, the effect of surface tension was considered in their analytical model by Yang & Hsu (1997), who studied the problem with the major axis of the isothermal elliptical cylinder oriented along gravity. They presented the mean heat transfer results with variation in several different parameters such as wall superheat, surface tension, liquid viscosity and eccentricity of the ellipse. The vapour flow adjacent to the heater surface can become turbulent at high Grashof number values as noted by Sarma et al. (2001) for a horizontal cylinder. As such Hu, Wang & Chen (2008) analytically studied turbulent film boiling over an ellipse under free convection considering radiation effects. Despite these analyses determining some important aspects, it can be seen that a pertinent gap exists in the literature even for natural convection film boiling physics over elliptical cylinders, in contrast to many experimental, theoretical and numerical investigations performed for circular cylinders. Noting this, Sadeghi, Shadloo & Hooman (2016) numerically studied bubble dynamics and heat transfer in saturated pool film boiling over an elliptical tube with different aspect ratios using the volume of fluid method. Additionally, they proposed a correlation for Nusselt number involving a polynomial expression for aspect ratio of the ellipse. Furthermore, to the best of authors’ knowledge, no prior detailed investigation has focused on ascertaining film boiling behaviour with a forced flow of liquid over an elliptical tube. This entails a critical gap in the literature regarding interesting interfacial dynamics and heat transfer that can be observed under such conditions, and forms an important aspect of the present work.

Significant mathematical difficulties are associated with the analytical prediction of interfacial behaviour including vapour flow separation and wake dynamics in flow film boiling over bluff bodies under different operating conditions. This is the case even for circular cylinders, especially when the effect of gravity is considerable in addition to flow inertia. Kaul & Witte (1987) predicted vapour wake profiles over a cylinder using cavitation theory from purely inertial considerations. As such their model was observed to deviate significantly from experimental data where the effect of gravity was notable. Direct numerical simulations can aid in gaining detailed insights about such aspects of film boiling dynamics, while also alleviating major simplifying assumptions employed in various theoretical studies. A direct consequence of the difficulty in obtaining wake profiles is a substantial gap in the understanding of vapour wake heat transfer, which has been neglected in most classical film boiling analyses for a cylinder. Such studies have modelled the heat transfer based on the front stagnation region only leading to discrepancies from empirical data in several studies (Bromley et al. 1953; Witte & Orozco 1984; Chou, Sankaran & Witte 1995). The wake heat transfer can thus be significant under certain conditions, especially for an elliptical cylinder with different angles of incidence to the liquid flow. This is directly accounted for in the present simulations as also other often overlooked aspects in forced convection film boiling analyses such as inertial and convective effects in the vapour film, surface tension, and mutual interaction of the liquid and vapour wakes. While the liquid flow expectedly drives the vapour wake evolution, the vapour wake structure itself can cause the liquid pressure field to deviate from the potential flow assumption, which has been employed in previous analyses again primarily owing to unknown wake profiles. Hence, it can be deduced from the aforementioned discussion that direct numerical simulations present a significant and unique opportunity to understand film boiling physics over an ellipse in the mixed regime.

The aim of the present work is thus to numerically investigate the mixed regime of saturated film boiling over an elliptical cylinder under different geometric conditions defined by the aspect ratio $(\varGamma )$ and angle of incidence $(\theta )$ to the flow. Additionally, the present study considers both upward and horizontal cross-flow of liquid as shown in the problem schematic in figure 1. The cross-flow direction has been shown to be non-trivial in the mixed regime in recent studies for a circular cylinder by the authors (Singh & Premachandran 2018b, 2019), with markedly different interface evolution, vapour wake structure and heat transfer obtained for different orientations. Direct numerical simulations have been performed for the liquid flow Reynolds number varying in the range $10 \leq Re_{l} \leq 170$, which along with other relevant parameters ascribe to the mixed regime of the Froude number. To this effect, a computational framework developed by the present authors for phase change problems on two-dimensional unstructured grids based on the coupled level set and volume of fluid (CLSVOF) interface capturing algorithm (Singh & Premachandran 2018a) is used. The problem formulation and numerical methodology have been presented in § 2. The interface morphology and heat transfer as determined under the effect of cross-flow velocity as well as orientation, and wall superheat along with the geometrical parameters of the ellipse is discussed in detail in §§ 3.1–3.3. The mutual interaction of liquid and vapour wakes in the mixed regime is discussed in § 3.4. Based on the simulation results, a correlation for heat transfer is presented in terms of a shape factor $(\psi )$ for elliptical cylinders in § 3.5. Finally, the key conclusions from the present study are summarized in § 4.

Figure 1. Problem schematic for the mixed regime of saturated film boiling over an elliptical cylinder: ($a$) upward cross-flow and ($b$) horizontal cross-flow.

Lack of any prior investigation with regard to the above aspects lays the foundation for the present work. Through this work, some completely new inferences on film boiling physics in liquid cross-flow over bluff bodies will be outlined that are counter-intuitive to our previous understanding of the phenomenon, and would be difficult to readily ascertain from experiments or analytical models. As such, the observations from the present simulations could also serve as reference for real applications or future empirical studies that may be required to further the relevant body of research. The present analysis is envisaged to plug a major gap towards the understanding of flow film boiling in the mixed regime with a non-canonical heater profile.

2. Methodology

2.1. Governing equations and CLSVOF method

The mass, momentum and energy conservation equations are solved in a single fluid formulation for both the phases while suitably accounting for the property variations across the liquid–vapour interface, surface tension and phase change. An in-house numerical framework developed by the present authors (Singh & Premachandran 2018a) for phase change problems on two-dimensional unstructured grids is employed to perform the simulations. The solver is based on the CLSVOF method and has been parallelized using OpenMP to utilize multiple cores on a shared memory system and reduce the computational time. It has been validated in detail against a number of benchmark problems (Singh & Premachandran 2018a), and also adopted in some recent studies (Singh & Premachandran 2018b, 2019, 2020) to obtain important results and physical insights for film boiling. For the sake of completeness, the salient features of the numerical method are presented succinctly along with the governing equations in this section.

Apart from the unsteady interfacial dynamics, the flow is considered to be laminar and incompressible. The continuity equation in any single phase region is given as

(2.1)\begin{equation} \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{v} = 0, \end{equation}

where $\boldsymbol {v}$ represents the fluid velocity vector. However, for a two-phase computational cell, with its boundary denoted as $S_c$ and having a part of the interface $S_{int}(t)$ between the two phases, the continuity equation is modified as (Welch & Wilson 2000)

(2.2)\begin{equation} \int_{S_c}\boldsymbol{v}\boldsymbol{\cdot}\boldsymbol{n}\,\mathrm{d}S + \int_{S_{int}(t)}\Vert\boldsymbol{v}-\boldsymbol{v}_{int}\Vert\boldsymbol{\cdot}\boldsymbol{n}\,\mathrm{d}S = 0, \end{equation}

where $\Vert \cdot \Vert$ represents the jump in the variable across the phase interface. The interface with the unit normal $\boldsymbol {n}$ pointing into the liquid phase moves with a velocity $\boldsymbol {v}_{int}$. Further, the mass and energy jump conditions at the phase interface are given as

(2.3)\begin{gather} \Vert \rho\left(\boldsymbol{v}-\boldsymbol{v}_{int}\right)\Vert\boldsymbol{\cdot}\boldsymbol{n} = 0, \end{gather}

(2.4)\begin{gather} \dot{m}h_{lv}=\Vert\boldsymbol{q}_{int}^{''}\Vert\boldsymbol{\cdot}\boldsymbol{n}, \end{gather}

where $\rho$ is the fluid density, $\dot {m}$ represents the mass flux across the phase interface, $h_{lv}$ is the latent heat of vaporization and $\boldsymbol {q}_{int}^{''}$ denotes the heat flux vector at the interface. By incorporating these jump conditions, the continuity equation for the two-phase cells in a boiling flow is written as (Welch & Wilson 2000)

(2.5)\begin{equation} \int_{S_c}\boldsymbol{v}\boldsymbol{\cdot}\boldsymbol{n}\,\mathrm{d}S + \int_{S_{int}(t)}\left(\frac{1}{\rho_{l}}-\frac{1}{\rho_{v}}\right)\frac{\Vert\boldsymbol{q}_{int}^{''}\Vert\boldsymbol{\cdot}\boldsymbol{n}}{h_{lv}}\,\mathrm{d}S = 0, \end{equation}

where the subscripts l and v denote liquid and vapour phases, respectively.

The Navier–Stokes equations in the conservative form are written as

(2.6)\begin{equation} \frac{ \partial \left( \rho\boldsymbol{v}\right) }{ \partial t} + \boldsymbol{\nabla}\boldsymbol{\cdot}\left(\rho\boldsymbol{v}\boldsymbol{v}\right) = -\boldsymbol{\nabla} P + \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{\tau} + \rho\boldsymbol{g} + \boldsymbol{f}_{st}, \end{equation}

for the entire flow field. Here $P$ denotes the pressure field, $\boldsymbol {\tau } = \mu (\boldsymbol {\nabla }\boldsymbol {v} + \boldsymbol {\nabla }\boldsymbol {v}^{T})$ is the deviatoric stress tensor for a Newtonian fluid and $\boldsymbol {g}$ represents the acceleration due to gravity. Here $\boldsymbol {f}_{st}$ is the surface tension force per unit volume that acts only in the interfacial region and is treated as a body force following the continuum surface force model of Brackbill, Kothe & Zemach (1992). Neglecting any variations in the surface tension coefficient $\sigma$, it is expressed as $\boldsymbol {f}_{st}= \sigma \kappa \boldsymbol {n}\delta$, where $\delta$ is a delta function centred at the interface and $\kappa$ is the interfacial curvature.

The temperature field ($T$) is determined by solving the energy equation only in the vapour phase as

(2.7)\begin{equation} \rho c_p\left(\frac{ \partial T}{ \partial t} + \boldsymbol{v}\boldsymbol{\cdot}\boldsymbol{\nabla} T\right) = \boldsymbol{\nabla}\boldsymbol{\cdot}\left(k\boldsymbol{\nabla} T\right). \end{equation}

This follows directly from the fact that saturated boiling is investigated in the present study with the liquid and the interface temperature considered to be constant at the saturation temperature (Son & Dhir 1998; Welch & Wilson 2000). The properties appearing in (2.6) and (2.7) can be identified as dynamic viscosity ($\mu$), specific heat ($c_p$) and thermal conductivity ($k$).

Upon calculation of the instantaneous velocity and temperature fields, the CLSVOF algorithm that incorporates accurate geometric procedures for interface advection and reconstruction is invoked to capture the interface on the Eulerian finite volume grid. The colour function or the volume fraction $F$, with a value of zero in the liquid, is advected in space at each time step as

(2.8)\begin{equation} \frac{ \partial F}{ \partial t} + \boldsymbol{\nabla}\boldsymbol{\cdot}\left(\boldsymbol{v} F\right) = F_{mt}. \end{equation}

The above equation, where $F_{mt}$ denotes the rate of generation of volume fraction due to mass transfer at the interface, is solved in an unsplit manner using the edge matched flux polygon advection (EMFPA) algorithm proposed by López et al. (2004). Within the EMFPA algorithm, the cell vertex velocities are directly used to construct the flux polygons, while a scaling factor derived from cell face velocities is used to correct the advected flux through each face. The level set ($\phi$) advection equation (Son & Dhir 1998) is written as

(2.9)\begin{equation} \frac{ \partial \phi}{ \partial t} + \left(\boldsymbol{v}_{int}\boldsymbol{\cdot}\phi\right) = 0, \end{equation}

where $\boldsymbol {v}_{int} = \boldsymbol {v} + \boldsymbol {v}_{mt}$ is the sum of cell fluid velocity and interfacial velocity due to mass transfer. A total variational diminishing (TVD) scheme for unstructured grids (Darwish & Moukalled 2003) along with a Min-Mod flux limiter function is used to solve (2.9). The interface normal is subsequently calculated as

(2.10)\begin{equation} \boldsymbol{n} = \frac{\boldsymbol{\nabla}\phi}{\vert\boldsymbol{\nabla}\phi\vert}. \end{equation}

Upon calculation of the interface normal and the volume fraction, a piecewise linear interface is geometrically reconstructed in each two-phase cell using an analytical procedure for volume reinforcement by López & Hernández (2008). For the level set field to remain a signed distance function, it is geometrically reinitialized using the reconstructed phase interface at the end of each time step. The reinitialization procedure on unstructured grids has been described in a previous study by the present authors (Singh & Premachandran 2018b).

The smoothed Heaviside function, $H(\phi )$ is employed to prevent any numerical instability arising from discontinuous properties at the liquid–vapour interface. The calculation procedure for $H(\phi )$ with a varying grid size across the domain is outlined in previous studies (Singh & Premachandran 2018b, 2019). As such any fluid property $\chi$ is calculated as follows:

(2.11)\begin{equation} \chi = \chi_v + \left(\chi_l - \chi_v\right) H\left(\phi\right). \end{equation}

Further, the present algorithm uses the gradient of the Heaviside function to ascertain the term $\boldsymbol {n}\delta$ appearing in the expression for surface tension force, which is eventually determined as

(2.12)\begin{equation} \boldsymbol{f}_{st}=\sigma\kappa\boldsymbol{\nabla} H. \end{equation}

The interfacial curvature is calculated as

(2.13)\begin{equation} \kappa = -\boldsymbol{\nabla}\boldsymbol{\cdot}\left(\frac{\boldsymbol{\nabla}\phi}{\vert\boldsymbol{\nabla}\phi\vert}\right). \end{equation}

The gradients of $\phi$ and $H(\phi )$ are calculated using the multidimensional Taylor series expansion based second-order accurate scheme (Lehnhäuser & Schäfer 2002) for unstructured grids.

The heat flux at the phase interface is calculated to determine the interfacial mass transfer as

(2.14)\begin{equation} \Vert\boldsymbol{q}_{int}^{''}\Vert\boldsymbol{\cdot}\boldsymbol{n} = k_v \left(\frac{T_v - T_{int}}{\Delta n}\right) - k_l \left(\frac{T_{int} - T_l}{\Delta n}\right), \end{equation}

where $T_v$ and $T_l$ are the temperatures of the vapour and liquid phases at a normal distance $\Delta n$ from the interface. In the present study under saturation conditions, the heat flux is calculated only in the vapour phase.

The finite volume method is used to solve the governing equations on collocated unstructured grids. The SIMPLE algorithm (Patankar 1980) is invoked for pressure and velocity coupling while the convective terms in the momentum and energy equations are discretized using a second-order upwind scheme (Mathur & Murthy 1997) for unstructured grids. The time integration is performed using the Euler explicit scheme. Based on the smallest grid size in the computational domain encountered near the heated elliptical cylinder, time step restrictions are imposed on account of Courant–Friedrichs–Lewy (CFL) condition, gravity, viscosity and the explicit treatment of the surface tension force (Singh & Premachandran 2018b, 2019).

2.2. Problem formulation

2.2.1. Computational domain and boundary conditions

The layout of the computational domain for both the flow orientations considered in this study is presented in figure 2 along with the boundary conditions. The heated elliptical cylinder has an aspect ratio $\varGamma = b/a$, where $a$ and $b$ denote its semimajor and semiminor axis, respectively, as also shown in figure 1. It is situated in a cross-flow of saturated liquid with the free stream flow aiding buoyancy for the case of upward cross-flow (figure 2$a$), while being orthogonal to the gravity field for horizontal cross-flow configuration (figure 2$b$). The flow inlet is situated 20$b$ upstream of the cylinder where the liquid enters with a uniform velocity $U$ at a temperature $T_{sat}$. The velocity $U$ is determined based on the liquid flow Reynolds number ($Re_l$) considered in the simulations. At the outlet section normal to the free stream situated at a distance of 40$b$ downstream of the elliptical cylinder, Neumann boundary conditions are prescribed for all the variables, while the Dirichlet boundary condition is specified for pressure. With $u$ and $v$ representing the velocity components in the $x$ and $y$ directions, respectively, and in accordance with the layout shown in figure 2, the Neumann boundary conditions are expressed as $\partial u / \partial y = \partial v / \partial y = \partial T / \partial y = 0$ for upward cross-flow, and $\partial u / \partial x = \partial v / \partial x = \partial T / \partial x = 0$ for horizontal cross-flow.

Figure 2. Computational domain with boundary conditions: ($a$) upward cross-flow and ($b$) horizontal cross-flow.

For upward flow configuration, symmetry boundary conditions $(u=0, \partial v / \partial x = 0)$ are prescribed at the domain boundaries aligned to the free stream direction and positioned on either side at a distance of 20$b$ from the central heater axis. This leads to a blockage ratio of 0.05 at $\theta =0^{\circ }$, which is in line with the previous studies for a circular cylinder pertaining to film boiling in the mixed regime (Singh & Premachandran 2018b) and single phase forced and mixed convection (Sarkar, Dalal & Biswas 2011). Even for other angles and all aspect ratios considered in the present work, the blockage broadly conforms to the study performed by Jackson (1987) for different bodies including elliptical cylinders, and mitigates any significant confinement effect on the flow field. Similarly for horizontal cross-flow, the bottom boundary at 20$b$ distance from the heater axis is considered as a free-slip boundary $( \partial u / \partial y = 0,v=0)$. However, at the top boundary located at a larger distance of 30$b$ from the heater axis, symmetry condition is prescribed only up to a distance of 20$b$ from the inlet, while the remaining portion is considered to be a free outlet as shown in figure 2($b$). This is done to ensure that vapour bubbles can freely move out of the domain even from the top boundary, which can be expected at the low $Re_l$ values used in this study, and thus prevent any unphysical behaviour to arise in the domain. A similar choice of boundary condition has been followed in previous studies for a circular cylinder (Singh & Premachandran 2019) and two-phase mixing layer (Ling et al. 2019). Thus bubbles can freely move out even under buoyancy dominated conditions, with the domain size being much larger than considered by Sadeghi et al. (2016) for natural convection film boiling over an ellipse.

The surface of the elliptical cylinder is considered to be isothermal in the present simulations where the temperature is specified as $T_w = T_{sat} + \Delta T$. Here $\Delta T$ is the wall superheat. Further, no-slip conditions ($u=0, v=0$) are prescribed for the velocity components. At the commencement of each simulation, a thin vapour film is initialized over the heater surface blanketing it from the surrounding liquid. The thickness of the vapour layer is specified uniformly as 0.1 times the minor axis, where a linear temperature distribution is initially specified with temperature varying from $T_w$ at the wall to $T_{sat}$ at the phase interface. The simulations are subsequently run for a long time such that multiple ebullition cycles are established while being governed by the hydrodynamics of the case being investigated, thereby ensuring that the initial conditions do not affect the interface evolution and heat transfer.

2.2.2. Fluid properties and physical parameters

Water at near-critical conditions is considered as the boiling fluid for the present simulations with constant properties assumed in each phase corresponding to saturation conditions. The corresponding liquid and vapour properties (Singh & Premachandran 2018a) are presented in table 1, with the reduced pressure $p / p_c=0.99$, and $p_c$ denoting the critical pressure. Low values of the liquid cross-flow Reynolds number $(Re_l=\rho _{l}UD/\mu _l)$ in the range 10–170 are considered such that film boiling occurs in the mixed regime where the flow inertia is accompanied by a significant effect of buoyancy. The selected values of $Re_l$ also conform to the critical limits reported for flow transition to a three-dimensional nature in single phase flow over an ellipse with different aspect ratios (Thompson et al. 2014; Paul et al. 2016), which is necessary with regard to the present two-dimensional numerical model and different angles of incidence investigated including $\theta =90^{\circ }$. At this stage it is important to define the characteristic geometric dimension $D$ used to calculate the various non-dimensional parameters in this study. While this is simply the diameter for a circular cylinder ($\varGamma =1$), it is considered as the length presented by the elliptical body normal to the flow and given as (Jackson 1987)

(2.15)\begin{equation} D= 2b\cos\theta\left(1+\left(\frac{a}{b}\right)^{2}\tan^{2}\theta\right)^{{1}/{2}}. \end{equation}

Table 1. Liquid and vapour properties for water at near-critical conditions $(p_{sat} = 21.9\ \mathrm {MPa}, T_{sat} = 646\ \mathrm {K}).$ $\left (\sigma =0.07\ \mathrm {mN}\,\mathrm {m}^{-1}, h_{lv}=276.4\ \mathrm {kJ}\,\mathrm {kg}^{-1}.\right )$

A careful choice of the fluid properties and the free stream velocity magnitudes thus determined lead to low values of the Froude number, with $\sqrt {Fr}\leq 2$ in almost all the simulations involving different aspect ratios and orientations of the elliptical cylinder. This ascertains a combined influence of buoyancy and inertia on the film boiling behaviour, for which other relevant parameters are the Grashof number ($Gr$) and the vapour Prandtl number ($Pr_v$). While the Grashof number is defined as $Gr=\rho _v(\rho _l-\rho _v)gD^{3}/{\mu _v}^{2}$ and varies with the elliptical geometry, the vapour Prandtl number given as $Pr_v=\mu _v c_{pv}/k_v$ has a fixed value of 21.18 based on the fluid properties. Further, the aspect ratio ($\varGamma$) and the angle of incidence ($\theta$) for the elliptical cylinder are varied in a wide range to gain interesting insights regarding interface evolution and heat transfer for both upward and horizontal liquid cross-flow orientations in a comprehensive manner. In all the simulations, the minor axis of the ellipse is fixed with respect to the characteristic capillary length scale $\lambda _o$ such that $2b/\lambda _o=1$ or $b/\lambda _o=0.5$. Here, the capillary length scale is defined as $\lambda _o = \sqrt {\sigma / (\rho _l - \rho _v)g}$. The values of $\varGamma$ along with $b/\lambda _o$ considered in this study primarily result in conditions where surface tension also governs the hydrodynamics, in addition to a competing influence of buoyancy and inertia, and is duly considered in the simulations. This can also be ascertained by specifically calculating the Bond number, which can be defined as $Bo=(\rho _l-\rho _v)ga^{2}/\sigma$ (Yang & Hsu 1997). Additionally, the effect of wall superheat ($\Delta T$) is also studied in detail, which is specified in non-dimensional terms throughout the study as $Ja_v/Pr_v$, with $Ja_v=c_{pv} \Delta T/h_{lv}$ representing the Jacob number. The values of the various parameters considered in the present simulations are summarized in table 2. Corresponding to the conditions in the present simulations and a circular geometry, the radiation contribution to the total heat transfer coefficient has been shown to be quite small in previous studies by the present authors (Singh & Premachandran 2018b, 2019) when considering a well-polished heater surface. Thus radiation heat transfer is safely neglected in the present study also.

Table 2. Range of different parameters considered in the study. Other fixed parameters are $Pr_v=21.18$ and $2b/\lambda _o=1.$ Results for $\varGamma =1$ have been adopted from Singh & Premachandran (2018b, 2019).

A summary of the simulation runs in this study is as follows. Firstly, corresponding to $\varGamma =0.6$ and $\theta =0^{\circ }$, four different values of $Re_l$, viz., 10, 50, 100 and 170 are considered to study the effect of free stream velocity, while the non-dimensional wall superheat, $Ja_v/Pr_v$, is varied from 0.3 to 1.2 in increments of 0.3 at each $Re_l$. Subsequently, two other aspect ratios, viz., $\varGamma = 0.4$ and 0.8 are considered with similar variation in $Re_l$ but fixed values of $\theta =0^{0}$ and $Ja_v/Pr_v=0.6$. Finally, the effect of heater orientation is investigated by considering three different values of $\theta$, viz., $30^{\circ }, 60^{\circ }$ and $90^{\circ }$ corresponding to each heater aspect ratio. This set of simulations is extended to two levels of wall superheat, $Ja_v/Pr_v=0.6$ and 1.2, and different $Re_l$ values in the range 10–170. All the cases specified above have been investigated for both upward and horizontal cross-flow of saturated liquid. This results in a total of 118 simulations as a part of this study while a comparison with circular heater geometry ($\varGamma = 1$) (Singh & Premachandran 2018b, 2019) under similar conditions is also included in the analysis.

An important part of the present study is the quantification of heat transfer, which is done in terms of the Nusselt number. The local Nusselt number ($Nu$) is calculated using the temperature gradient normal to the heater wall as

(2.16)\begin{equation} Nu =\left. \frac{D}{\left(T_w - T_{sat}\right)}\frac{ \partial T}{ \partial n} \right\vert_w. \end{equation}

The space-averaged Nusselt number ($\overline {Nu}$) is calculated by integrating the local $Nu$ values over the surface of the elliptical cylinder as

(2.17)\begin{equation} \overline{Nu} =\frac{1}{S}\int_S Nu \,\mathrm{d}S. \end{equation}

The time–space averaged Nusselt number ($\overline {Nu_T}$), referred to simply as the time-averaged Nusselt number in the subsequent text, is calculated by averaging over a time period $T$ as

(2.18)\begin{equation} \overline{Nu_T} =\frac{1}{T}\int_0^{T} \overline{Nu}\,\mathrm{d} t. \end{equation}

2.2.3. Validation of the numerical model

The present numerical framework based on the CLSVOF interface capturing method has been extensively validated qualitatively as well as quantitatively in an earlier work (Singh & Premachandran 2018a) for both structured and unstructured grids. A number of standard advection test cases, two-phase flow problems and phase change problems including film boiling and condensation were considered to establish the accuracy of interface advection and reconstruction, surface tension and phase change calculations.

Subsequently, the numerical solver has been employed to study the mixed regime of film boiling over a circular heater geometry with upward and horizontal cross-flow (Singh & Premachandran 2018b, 2019) configurations, and a comprehensive heat transfer model has been developed based on the simulation results. The model predictions have further been compared with some of the available empirical data in the mixed regime of saturated film boiling for upward cross-flow corresponding to benzene at atmospheric conditions (Bromley et al. 1953) and water at 294 kPa (Liu & Fukuda 2008). The values of $D/\lambda _o$ for the two sets of data are calculated as 6.05 and 2.1, respectively. The comparison is presented in table 3 showing a deviation within ${\pm }10\,\%$ in most of the cases, which is an excellent agreement for boiling data. It can be noted that the convective heat transfer has been compared in table 3 with the property values calculated at the average film temperature to match the experimental conditions. At the same time, the interfacial dynamics has not been presented in the aforementioned empirical studies. With regard to horizontal cross-flow configuration, it was shown by means of a reduction factor that for conditions approaching natural convection or purely inertial film boiling regime the results were similar to the established results for upward cross-flow, thereby enforcing the validity of the simulations. Additionally the present solver has been used to obtain important results for a wavy horizontal heater (Singh & Premachandran 2020), where validation against an available Nusselt number correlation for a flat heater has been presented. For the present problem, while a direct comparison is limited by the availability of empirical data for film boiling over an ellipse in the mixed regime, to the best of authors’ knowledge, the above discussion lends substantial credence to the use of the present numerical method to perform the simulations.

Table 3. Comparison of heat transfer predictions in upward cross-flow ($\varGamma =1$; Singh & Premachandran (2018b)) obtained using the present numerical method with the literature for different conditions in the mixed regime.

2.2.4. Grid convergence study

The computational domain in the present simulations is discretized using quadrangular cells, and the grid layout is depicted in figure 3($a$) for upward cross-flow configuration. A non-uniform mesh is used to achieve the desired level of refinement in different parts of the domain such as near the heater wall and downstream of the heater. A similar mesh layout is also employed in the domain for horizontal cross-flow, with the mesh also refined diagonally across the domain where the vapour is expected to move with orthogonal flow and gravity fields. The grid size is finest adjacent to the elliptical heater to capture the thin vapour film as can be seen in the close-up view shown in figure 3($b$). Further, the grid is stretched along the major axis to accommodate a decrease in the aspect ratio of the ellipse for different simulations.

Figure 3. Finite volume mesh used for the computations (shown here for upward cross-flow): ($a$) full domain and ($b$) close-up view near the elliptical cylinder.

The grid convergence for mixed regime of film boiling over a circular cylinder ($\varGamma =1$) has been presented in previous studies by the present authors (Singh & Premachandran 2018b, 2019). Nonetheless, it is established for the elliptical geometry by considering three different meshes, as presented here for upward cross-flow. The relevant details such as number of cells in the entire domain ($N_{cell}$) and on the ellipse surface ($E_{cell}$) are presented in table 3. While there is grid stretching along the major axis, the grid size adjacent to the heater wall for the three meshes is maintained to be nearly 0.02, 0.01 and 0.005 times the minor axis, respectively, as listed in table 4. Corresponding to $\varGamma =0.6$, $\theta =0^{\circ }$ and $Ja_v/Pr_v=0.6$, the time-averaged Nusselt number ($\overline {Nu_T}$) values obtained with each mesh for two different $Re_l$ values, viz., 50 and 170 are included in table 4, while the time period of the periodic ebullition cycle ($t_c$) is also listed alongside for $Re_l=50$. Additionally, for both values of $Re_l$, the interface morphology at $t=0.125\ \textrm {s}$ is compared with regard to different grids in figure 4. From these results, it can be inferred that the mesh M2 presents an optimum resolution with regard to computational cost and grid independence, which is selected for the subsequent computations. For horizontal cross-flow, a mesh with $N_{cell}=74\,265$ and $E_{cell}=228$ is suitably employed for the simulations. Concomitantly, it is confirmed that the mesh selected for each flow configuration is able to resolve the thin vapour film near the heater wall for the various cases considered in the present study.

Figure 4. Interface morphology obtained with upward liquid cross-flow at time $t = 0.125\ \textrm {s}$ corresponding to different grids and parameters mentioned in table 3: ($a$) $Re_l=50$ and ($b$) $Re_l=170$.

Table 4. Grid independence study (upward cross-flow, $\varGamma =0.6$, $\theta =0^{\circ }$, $Ja_v/Pr_v=0.6$).

3. Results and discussion

With a careful choice of different parameters that are coupled on account of fluid properties, flow velocity and elliptical heater geometry, mixed regime of film boiling is ascertained in the present computations entailing a significant effect of buoyancy in addition to flow inertia. With regard to interface evolution and heat transfer as influenced by various hydrodynamic, thermal and geometric parameters, a detailed investigation is presented in §§ 3.1–3.3, considering aiding as well as orthogonal configurations of gravity and flow fields under saturation conditions. Subsequently, the vapour and liquid wake dynamics is discussed in § 3.4 while highlighting their mutual interaction. Finally, a shape factor ($\psi$) based on the geometrical parameters of the elliptical heater is conceived and determined in § 3.5 to correlate the heat transfer quantified through the present simulations.

3.1. Effect of liquid cross-flow velocity, orientation and wall superheat

Four different values of $Re_l$, viz., 10, 50, 100 and 170 are considered to study the effect of free stream velocity in both upward and horizontal cross-flow of saturated liquid. The major axis of the elliptical heater is aligned to the flow direction ($\theta =0^{\circ }$) in these simulations while the aspect ratio is fixed as $\varGamma =0.6$. Correspondingly, the square root of the Froude number is calculated as 0.12, 0.6, 1.2 and 2.04, respectively, for different $Re_l$ that signifies a successively growing influence of flow inertia. The non-dimensional wall superheat, $Ja_v/Pr_v$ , is varied from 0.3 to 1.2 at each $Re_l$, and is an important parameter affecting the interfacial dynamics by controlling the rate of vapour generation that is subsequently infused into the vapour wake.

The effect of different upward cross-flow velocities on the interface evolution at $Ja_v/Pr_v=0.6$ is presented in figure 5. A periodic ebullition is observed at $Re_l=10$ as shown in figure 5($a$), involving various stages such as bubble growth at the top of the heater, necking and pinch-off, recoil of the remaining vapour mass, and subsequent undulations leading to the next bubble formation and release cycle. Such a quasi-steady nature is characteristic of natural convection film boiling where bubble removal is governed by Rayleigh–Taylor instability. This is expected to be the case with a dominant effect of buoyancy at a low value of Fr. A similar interface evolution is also seen at $Re_l=50$ from figure 5($b$). However, an increase in the bubble release frequency is observed that indicates an additional effect of flow inertia on vapour removal, although being quite subtle with respect to the interface morphology. At $Re_l=100$, the influence of inertia becomes more prominent with the vapour wake dynamics visibly affected by the liquid flow, as shown in figure 5($c$). A combined effect of inertia and buoyancy results in a larger pinch-off distance ($t=0.74\ \textrm {s}$) along with a thinner film at the bottom of the cylinder. Further, a loss of the periodic nature of film boiling can be seen accompanied by a random detachment of bubbles from the vapour wake. Upon further increase in flow velocity at $Re_l=170$, a thin film is wrapped around the bottom half of the cylinder, and a steady and thick vapour wake along with a trailing column is formed behind the elliptical cylinder. Further, small bubbles are observed to release from the top of the vapour mass. While such a steady interface morphology indicates a suppression of vortex shedding at the $Re_l$ value under consideration, it is also inherently different from that observed for a circular cylinder ($\varGamma =1$) under similar conditions (Singh & Premachandran 2018b). This shows the effect of elliptical geometry in the present configuration on vapour removal in terms of accentuating the rate at which kinetic energy of the vapour is carried into the wake.

Figure 5. Interface evolution with different upward liquid cross-flow velocities over an elliptical cylinder $(b / \lambda _o = 0.5,\varGamma =0.6)$ for water $(p / p_c = 0.99)$ at $Ja_v / Pr_v = 0.6$ and $\theta =0^{\circ }$: ($a$) $Re_l = 10$ ($\sqrt {Fr} = 0.12$), ($b$) $Re_l = 50$ ($\sqrt {Fr}= 0.6$), ($c$) $Re_l = 100$ ($\sqrt {Fr}=1.2$) and ($d$) $Re_l = 170$ ($\sqrt {Fr} = 2.04$).

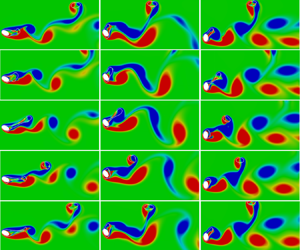
Figure 6 shows the effect of free stream velocity on interface evolution in horizontal cross-flow at $Ja_v/Pr_v =0.6$. From figure 6($a$) at $Re_l=10$, similar phases of interface evolution are observed as for upward cross-flow with buoyancy predominantly determining the vapour morphology. However, a much thicker film can be seen in the bottom portion of the cylinder, which can be attributed to a constriction in the vapour removal due to buoyancy, and is discussed in § 3.2. This also leads to a much lower bubble release frequency compared with upward flow orientation. Nonetheless, the voluminous vapour mass at the top of the elliptical heater is observed to be slightly deflected sideways even with a minimal effect of liquid flow. At $Re_l=50$, the effect of flow inertia can be clearly visualized from figure 6($b$) with the bubbles releasing from the top right-hand portion of the heater at a higher frequency, while the role of buoyancy is verified from the periodic nature of ebullition. Such a competing effect of inertia and buoyancy causes a recirculation in the vapour film leading to a vapour bulge at the bottom of the heater, as analysed in an earlier study for $\varGamma =1$ (Singh & Premachandran 2019). However, with the present aspect ratio of 0.6, the bulge is more prominent as compared with a circular cylinder due to the ellipse orientation blocking vapour passage against a significant influence of buoyancy at $\sqrt {Fr}=0.6$. At $Re_l=100$, the vapour wake shifts entirely to the rear of the elliptical cylinder as shown in figure 6($c$). While the vapour wake shows a slight tendency to rise even with a weak effect of gravity, the overall vapour morphology along with a random detachment of bubbles from the tail end of the wake indicates that the aperiodic interface evolution is primarily governed by flow inertia in contrast to Rayleigh–Taylor instability at lower velocities. Upon further increase in cross-flow velocity, it is seen from figure 6($d$) at $Re_l=170$ that the vapour wake is again formed at the cylinder rear with the front stagnation region covered with a thin and steady film. However, an interesting build-up of the instability is observed in distinct phases, as also marked in Figure 6($d$). Initially, the instability evolves from the top rear portion of the cylinder (phase I) with small bubbles detached from the end, which characterizes a smaller effect of gravity being overcome by the dominant liquid flow. Further, the ellipse orientation along the flow causes a rapid infusion of vapour into the wake leading to a thick vapour mass in the entire rear portion of the heater (phase II). Subsequently the effect of Kelvin–Helmholtz instability on the interface becomes pronouncedly visible (phase III), which eventually leads to tearing of the vapour sheet behind the ellipse (phase IV). Such interesting interfacial features indicate a significant effect of the bluff-body geometry on film boiling behaviour along with relative strengths of buoyancy and flow inertia in the mixed regime.

Figure 6. Interface evolution with different horizontal liquid cross-flow velocities over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ for water $(p/p_c =0.99)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a$) $Re_l = 10$ ($\sqrt {Fr} = 0.12$), ($b$) $Re_l = 50$ ($\sqrt {Fr}= 0.6$), ($c$) $Re_l = 100$ ($\sqrt {Fr}=1.2$) and ($d$) $Re_l = 170$ ($\sqrt {Fr} = 2.04$).

The non-dimensional parameter $Ja_v/Pr_v$ is varied from 0.3 to 1.2 in the present simulations to assess the effect of wall superheat on the interfacial dynamics. With upward cross-flow of liquid, a periodic ebullition cycle is observed at $Re_l=10$ for all the wall superheats, as discussed previously for $Ja_v/Pr_v =0.6$. At subsequently larger values of $Re_l$, stable vapour columns are formed due to enhanced vapour generation at elevated wall superheats, with small bubbles releasing from their tail end. However, with the aiding influence of cross-flow velocity on carrying the vapour into the wake, such vapour jets are observed at successively lower degrees of superheat as $Re_l$ increases. This is clearly depicted in figure 7 for $Re_l=50$ and 100, and also seen from figure 5($d$) for $Re_l=170$. Additionally, a lesser portion of the heater wall is wrapped with a thin film as the liquid cross-flow velocity increases leading to a thicker wake behind the heater, as seen prominently for $Re_l=170$ in figure 5($d$). Such an observation is analogous to the case of a circular cylinder with regard to vapour flow separation (Singh & Premachandran 2018b). With horizontal cross-flow orientation, periodic bubble release is observed for $Re_l=10$ and 50 at different values of $Ja_v/Pr_v$. However, the orthogonal gravity and flow fields do not support formation of stable columns at any of the wall superheats investigated in this study. Further, the interfacial dynamics at a lower non-dimensional superheat of 0.3 corresponding to $Re_l=170$ is shown in figure 8 for both the cross-flow orientations. For upward liquid flow, a transient vapour wake with random detachment of bubbles is observed from figure 8($a$), in contrast to a steady wake with a trailing column formed at $Ja_v/Pr_v =0.6$ and beyond. Similarly from figure 8($b$) for horizontal cross-flow, the interface is seen to evolve in a considerably different manner when compared with $Ja_v/Pr_v =0.6$, with the instability evolution essentially restricted to phase I described with respect to figure 6($d$). The subsequent phases are eliminated on account of reduced vapour generation at a lower superheat. The above discussion highlights the role of wall superheat as a major factor affecting the film boiling dynamics in the mixed regime that affects the evolution rate leading to a change in the interface morphology altogether under certain conditions.

Figure 7. Interface morphology showing formation of vapour columns in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $\theta =0^{\circ }$ and elevated wall superheats: ($a$) $Re_l=50, Ja_v/Pr_v =1.2$ and ($b$) $Re_l=100, Ja_v/Pr_v =0.9$.

Figure 8. Interface evolution over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ for water $(p/p_c =0.99)$ at $Re_l=170, Ja_v/Pr_v =0.3$ and $\theta =0^{\circ }$: ($a$) upward cross-flow and ($b$) horizontal cross-flow. (For interface evolution at $Ja_v/Pr_v =0.6$, one may refer to figures 5 and 6.)

The heat transfer is quantified by means of the Nusselt number and the corresponding values for the present set of simulations are shown in figure 9. The space-averaged Nusselt number variation with upward cross-flow at $Ja_v/Pr_v =0.6$ and 1.2 is plotted in figures 9($a$) and 9($b$), respectively. At $Ja_v/Pr_v =0.6$, a quasi-steady variation is obtained concomitant to periodic ebullition under Rayleigh–Taylor instability for $Re_l=10$ and 50. An increase in the ebullition frequency is seen at $Re_l=50$, depicting considerable effect of flow inertia at a low magnitude of Froude number. The transient Nusselt number variation at $Re_l=100$ corresponds to the aperiodic interface evolution presented previously. At the same time, a steady vapour structure near the elliptical heater comprising of a thin film and thick vapour wake leads to a constant Nusselt number for $Re_l=170$. Further, a decrease in bubble release period with superheat is evident from the Nusselt number distribution shown in figure 9($b$) at $Ja_v/Pr_v =1.2$ and $Re_l=10$. At all subsequent $Re_l$ values, stable vapour columns are formed with the particular conditions aided by the elliptical heater orientation as discussed earlier, resulting in the Nusselt number remaining constant with time. Corresponding to horizontal liquid flow and similar levels of wall superheat, the space-averaged Nusselt number distribution is shown in figures 9($c$) and 9($d$). A quite low bubble release frequency is observed at $Re_l=10$ compared with upflow due to the major axis of the elliptical heater oriented normal to the direction of buoyancy, which is the dominant factor controlling vapour removal at such low value of $Re_l$. Nonetheless, an increase in the frequency is observed with cross-flow velocity as well as wall superheat. For $Re_l=100$, the Nusselt number variation is in accordance with the random interface evolution. A steady vapour region near the wall along with the wake fluctuations primarily confined away from the wall, as presented in figure 6($d$) at $Ja_v/Pr_v =0.6$, results in a constant Nusselt number for $Re_l=170$.

Figure 9. Nusselt number with different liquid flow velocities and wall superheats for water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $\theta =0^{\circ }$. Corresponding to ($a{,}b$) upward and ($c{,}d$) horizontal cross-flow; the temporal variation of space-averaged Nusselt number at various $Re_l$ is shown for ($a{,}c$) $Ja_v/Pr_v =0.6$ and ($b{,}d$) $Ja_v/Pr_v =1.2$. Time-averaged values of the Nusselt number for all the parameters considered are shown in panel ($e$).

Figure 9($e$) shows the time-averaged Nusselt number values obtained with various parameters in the present set of simulations. For both the liquid flow orientations, an increase in Nusselt number with $Re_l$ is observed that depicts an appreciable influence of flow inertia on heat transfer even at low cross-flow velocities, thereby marking the onset of the mixed regime. On the other hand, the wall superheat is observed to weakly affect the heat transfer especially at low cross-flow velocities, where an augmentation of the bubble release frequency is largely offset by a thicker film near the heater wall at elevated superheats. Even at higher $Re_l$ values, the Nusselt number is almost invariant once a steady vapour region is formed near the wall at a particular degree of superheat. Furthermore, the heat transfer with upward liquid flow directly aiding buoyancy in the mixed regime is higher as compared with horizontal cross-flow configuration, except at $Re_l=170$. A high magnitude of Froude number $(\sqrt {Fr}=2.04)$ corresponding to $Re_l=170$ implies film boiling occurring in the purely inertial regime, where the liquid flow inertia drives the interfacial dynamics. As such, the flow direction becomes trivial leading to same magnitude of the Nusselt number for both cross-flow directions. A similar coincidence of heat transfer magnitude would have been expected for $Re_l=10$, with conditions approaching natural convection film boiling due to minimal effect of liquid flow. However, the relative orientation of the elliptical heater and gravity differs in both cases as the angle of incidence $(\theta =0^{\circ })$ is defined with respect to the flow direction, which leads to significantly lower Nusselt number values with horizontal cross-flow at $Re_l=10$. Incidentally, the Nusselt number values at $Re_l=10$ with upward cross-flow are slightly higher than those obtained at even $Re_l=50$ with horizontal cross-flow for all superheats, thereby highlighting the effect of elliptical geometry in aiding vapour removal and improving the heat transfer. Consequently, the effect of important geometrical parameters on film boiling characteristics in the mixed regime is investigated in the next sections.

3.2. Effect of aspect ratio $(\varGamma )$

The aspect ratio is an important parameter that affects the front stagnation region of the elliptical heater for a fixed orientation, which is a critical zone for film boiling heat transfer and vapour generation. As such, the vapour removal passage is altered with a change in the aspect ratio thereby affecting the rate of vapour infusion into the wake, interface morphology and associated heat transfer rates. While important results for $\varGamma =0.6$ have been presented in § 3.1, two other aspect ratios, viz., $\varGamma =0.4$ and 0.8 are considered here to investigate the film boiling behaviour at a fixed value of $\theta =0^{\circ }$. The analysis also includes a comparison with circular heater geometry ($\varGamma =1$) (Singh & Premachandran 2018b, 2019) under similar conditions. The non-dimensional wall superheat is fixed at 0.6 in the simulations. Similar to the previous section, four different magnitudes of $Re_l$ in the range 10–170 are considered with both upward and horizontal liquid cross-flow configurations. Since the characteristic dimension normal to the flow remains the same for different aspect ratios with $\theta =0^{\circ }$, the Froude number magnitude at each $Re_l$ also remains unchanged ($\sqrt {Fr}=0.12\text {--}2.04$). This assumes importance from the view of determining the sole effect of $\varGamma$ on interface evolution and heat transfer under similar hydrodynamic and thermal conditions.

Figure 10 shows the interface evolution for $\varGamma =0.4$ and 0.8 at several $Re_l$ values in upward cross-flow corresponding to $Ja_v/Pr_v =0.6$. For $\varGamma =0.4$, quasi-steady film boiling is observed at $Re_l=10$ similar to $\varGamma =0.6$, and is not presented here. At $Re_l=50$, the bubble pinch-off after vapour growth occurs at a relatively larger distance from the heater wall, as shown in figure 10($a$) ($t=0.97\ \textrm {s}$). This is accompanied by a limited recoil of the remaining vapour mass on account of surface tension, resulting in the vapour undulations confined to only a small top portion of the heater. A major portion of the heater wall thus remains blanketed by a thin vapour film. Such a behaviour is ascribed to the combined action of buoyancy and inertia along the elongated elliptical profile, and also leads to a certain loss of the periodic nature of ebullition. Further, the effect of lower aspect ratio is also seen with the formation of a stable vapour column at $Re_l=100$ itself for the present wall superheat in contrast to $\varGamma =0.6$. At $Re_l=170$, figure 10($c$) shows a thin vapour column to be preceded by a thicker wake that reinforces the argument regarding vapour flow separation occurring earlier at increased cross-flow velocities, irrespective of the aspect ratio. At the same time, the thickness of the wake is lower as compared with $\varGamma =0.6$ due to the heater profile, which indicates a delayed vapour wake separation at lower aspect ratios. For $\varGamma =0.8$, the interface evolution is essentially similar to $\varGamma =0.6$ up to $Re_l=100$, with the bubble release becoming transient at $Re_l=100$ due to flow inertia as shown in figure 10($d$). With further increase in cross-flow velocity at $Re_l=170$, a long vapour sheet is seen to form behind the heater from figure 10($e$). While bubbles are detached randomly from the top of the sheet, the sheet itself is torn at some instants ($t=0.535\ \textrm {s}$) due to an interaction with the liquid flow. The behaviour, though quite different from a steady vapour region formed at lower aspect ratios, is characteristically similar to that observed for a circular cylinder (Singh & Premachandran 2018b).

Figure 10. Interface evolution with different heater aspect ratios and $Re_l$ (mentioned alongside each case) in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a\text {--}c$) $\varGamma =0.4$ and ($d{,}e$) $\varGamma =0.8$. (For interface evolution at $\varGamma =0.6$ with the same non-dimensional wall superheat, one may refer to figure 5.)

With horizontal cross-flow, the bubble release is periodic at $Re_l=10$ and 50 for $\varGamma =0.4$ as well as 0.8 accompanied by the formation of a thick film below the heater, as seen from figures 11($a$) and 11($b$) at $Re_l=10$. A similar observation was earlier made for $\varGamma =0.6$ from figure 6($a$). Further, the interface morphology at $Re_l=170$ is presented in figures 11($c$) and 11($d$) corresponding to $\varGamma =0.4$ and 0.8, respectively. For $\varGamma =0.4$, the instability evolves in a similar manner as described in figure 6($d$) for $\varGamma =0.6$. However, in comparison, the growth of the vapour wake is much more rapid while no tearing of the vapour sheet due to Kelvin–Helmholtz instability is observed behind the ellipse. This can directly be attributed to the enhanced rate at which the vapour kinetic energy is carried into the wake due to the lower heater aspect ratio coupled with its orientation along the strong flow inertia. On the other hand, for a higher aspect ratio of 0.8, the interface evolution is limited to the phase prior to vapour wake growth. Overall, it is observed that varied wake profiles can result for an elliptical heater in the mixed regime solely based on geometric considerations. This renders the mathematical prediction of wake profiles to be quite difficult, with several other factors including an interplay of buoyancy and inertia and the cross-flow orientation significantly affecting the vapour wake dynamics.

Figure 11. Interface evolution with different heater aspect ratios for ($a{,}b$) $Re_l=10$ and ($c{,}d$) $Re_l=170$ in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a{,}c$) $\varGamma =0.4$ and ($b{,}d$) $\varGamma =0.8$. (For interface evolution at $\varGamma =0.6$ with the same non-dimensional wall superheat, one may refer to figure 6.)

Furthermore, the thick vapour film formed beneath the heater with horizontal cross-flow at a low $Re_l$ value of 10 is shown in figure 12 for different aspect ratios, along with the vapour temperature distribution. While the vapour removal occurs mainly due to buoyancy under these conditions, the orientation of the major axis normal to gravity offers a constriction to the vapour passage towards the top region of the cylinder. The blockage is more severe at a lower aspect ratio of 0.4 where the situation resembles a downward facing surface with the stagnation points forming the edges of such a surface. The situation subsequently eases out as $\varGamma$ increases allowing a smaller escape route for the vapour. A higher temperature is observed adjacent to the heater wall with a thicker vapour film that is detrimental to the heat transfer rates obtained, as already seen for $\varGamma =0.6$ earlier, and further discussed for other aspect ratios.

Figure 12. Instantaneous temperature distribution and interface morphology in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Re_l=10, Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$, showing the effect of heater aspect ratio on vapour removal, thereby affecting film thickness around the cylinder and heat transfer: ($a$) $\varGamma =0.4$, ($b$) $\varGamma =0.6$ and ($c$) $\varGamma =0.8$.

The temporal variation of space-averaged Nusselt number in upward cross-flow at $\varGamma =0.4$ and 0.8 is plotted in figures 13($a$) and 13($b$), respectively, for different $Re_l$. The Nusselt number distribution follows from the nature of ebullition and wake dynamics for each case. For $\varGamma =0.4$, a loss of periodic ebullition can be observed at $Re_l=50$ with vapour recoil affecting only a small upper portion of the heater. A constant Nusselt number is obtained at $Re_l=100$ and 170 due to formation of stable vapour jets even at a low wall superheat, which is an artefact of the heater geometry. On the other hand, no such stable vapour structures are formed for $\varGamma =0.8$ as confirmed from figure 13($b$). Even at $Re_l=170$, the vapour sheet formed behind the elliptical heater is unstable due to rigorous interaction with the liquid flow, as seen previously, resulting in a transient Nusselt number variation. Further, the frequency of periodic bubble release at $Re_l=10$ is much lower as compared with $\varGamma =0.4$. Additionally, it is also observed that the variation of space-averaged Nusselt number from minimum to maximum value is lower for $\varGamma =0.4$ with enhanced vapour infusion into the wake, which limits the vapour undulations post recoil to a small region near the heater wall. With horizontal cross-flow, the space-averaged Nusselt number variation is presented in figures 13($c$) and 13($d$). Here an opposite trend compared with upward flow is notable regarding the bubble release frequency at lower $Re_l$ values, which is shown to increase with the aspect ratio. This is due to the heater profile blocking upward vapour passage with buoyancy more severely at a lower aspect ratio, as discussed in figure 12. An increase in flow inertia, though, alleviates such an effect to an extent, affecting the interface morphology for all the aspect ratios. However, at $Re_l=170$, the Nusselt number is constant for $\varGamma =0.4$ due to a thick and stable vapour wake behind the heater, while very rapid fluctuations are seen corresponding to $\varGamma =0.8$ which are characteristic of vortex shedding behind the heater affecting the vapour morphology. While such fluctuations are also observed for a circular heater (Singh & Premachandran 2019) at the present wall superheat, the absence of these at lower values of $\varGamma$ indicates a mutual interaction of vapour and liquid wakes, with the vapour dynamics also affecting the liquid flow characteristics.

Figure 13. Nusselt number with different heater aspect ratios for water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$. The temporal variation of space-averaged Nusselt number at various $Re_l$ is shown for ($a{,}c$) $\varGamma =0.4$ and ($b{,}d$) $\varGamma =0.8$, corresponding to both ($a{,}b$) upward and ($c{,}d$) horizontal cross-flow. Time-averaged values of the Nusselt number for all the parameters considered are shown in panel ($e$). (For space-averaged Nusselt number at $\varGamma =0.6$, one may refer to figure 9.)

The time-averaged Nusselt number values obtained with the present set of parameters are shown in figure 13($e$). From the observations up until this stage in the present work, it can be deduced that the film boiling behaviour in the mixed regime for a given thermal condition of the heater wall is determined primarily by the geometric configuration of the bluff body and a combined influence of buoyancy and flow inertia as per the cross-flow direction. With upward cross-flow, both these factors aid in efficient vapour removal from the heater without any hindrance caused to the vapour flow by the geometric orientation. As such, a minimal variation is seen in the Nusselt number at $Re_l=10$ with bubble release occurring primarily due to buoyancy in a periodic manner. As the effect of flow inertia increases with $Re_l$, a rise in the Nusselt number is seen corresponding to all aspect ratios. However, for $\varGamma =0.4$, the geometric profile of the heater is the dominant factor governing vapour removal even at low $Re_l$ values, which has been discussed previously with regard to figures 10($a$) and 13($a$). As a result, the increase in Nusselt number with flow inertia is not as steep as observed for increasingly higher aspect ratios. As $\varGamma$ increases, the influence of geometry gradually diminishes, while an increase in cross-flow velocity substantially increases the Nusselt number with the formation of a thin stable film over a larger area of the heater wall. This explains the increase in heat transfer with aspect ratio observed at higher $Re_l$ values in figure 13($e$). With horizontal cross-flow, the heater orientation causes a constriction to vapour flow under buoyancy that is accentuated at lower values of $\varGamma$, as described earlier. Thus at a low $Re_l$ value of 10, the heat transfer rate is observed to be considerably smaller than in upward cross-flow for $\varGamma =0.4$. As $\varGamma$ increases, the blockage to vapour passage eases out leading to a linear increase in the Nusselt number. Eventually, the Nusselt number magnitude at $\varGamma =1$ is almost the same as obtained with upward cross-flow, which indeed should be the case with conditions close to pool boiling. Similarly at $Re_l=170$, the Nusselt number is almost independent of the cross-flow orientation due to a predominant effect of inertia ($\sqrt {Fr}=2.04$) driving film boiling dynamics. At the same time, the Nusselt number at intermediate values of $Re_l$ is higher for upward cross-flow, with a comparable influence of buoyancy and inertia aiding each other in the mixed regime.

3.3. Effect of angle of incidence $(\theta )$

From the previous results, it has been established that the geometrical configuration of the elliptical heater coupled with other film boiling parameters in the mixed regime determines the overall interface dynamics and heat transfer. However, the simulations up until this stage have been performed considering the major axis of the ellipse to be aligned along the free stream flow ($\theta =0^{\circ }$). As such, an investigation with different angles of incidence becomes imperative to comprehensively assess the effect of heater geometry on the film boiling behaviour. To this effect, three different values of $\theta$, viz., $30^{\circ }, 60^{\circ }$ and $90^{\circ }$ are considered here corresponding to different heater aspect ratios. The investigation has also been extended to different wall superheats and $Re_l$ values (10–170) as presented subsequently for both liquid cross-flow orientations. However, for each geometric configuration, the magnitude of $Re_l$ is carefully selected to conform to the critical limits reported for flow transition to a three-dimensional nature in single phase flow (Thompson et al. 2014; Paul et al. 2016). Corresponding to the various conditions, the magnitude of the Froude number varies as $\sqrt {Fr}=0.086\text {--}1.86$, which again ascertains a significant influence of buoyancy in addition to flow inertia.

The interface evolution in upward liquid cross-flow with different angles of incidence is presented in figure 14 for two different aspect ratios at $Re_l=100$ and $Ja_v/Pr_v =0.6$. For $\varGamma =0.4$, a thin vapour column was observed at $\theta =0^{\circ }$ previously under similar conditions. However, a discrete bubble release in a periodic manner at subsequently higher angles of incidence is shown in figure 14($a$–$c$). The periodic ebullition indicates that even at a high $Re_l$ value of 100 the effect of flow inertia is overshadowed by buoyancy for these heater orientations. This is, however, conceivable due to a reduction in the magnitude of the Froude number as $\theta$ increases for a given aspect ratio. Nonetheless, the bubble pinch-off occurs at a larger distance from the wall for $\theta =30^{\circ }$. It is also observed that the vapour film is relatively thin over the portion of the heater directly facing the liquid flow. This leads to a much thinner vapour region below the heater at $\theta =90^{\circ }$ when compared with a similar configuration with regard to vapour removal for horizontal cross-flow (figure 12). The constriction to vapour flow is, though, still evident from a visibly thick film due to which buoyancy cannot easily overcome surface tension, leading to severe undulations at the top of the heater during the bubble growth phase ($t=0.63\ \textrm {s}$ and 0.65 s). For $\varGamma =0.6$, the Froude number again reduces with $\theta$, but the magnitude is higher than $\varGamma =0.4$ for each case. As such the random bubble release at $\theta =0^{\circ }$ (figure 5$c$) gradually attains a quasi-steady nature with the effect of flow inertia perceivable up to $\theta =60^{\circ }$ (for instance, $t=0.66\ \textrm {s}$ and 0.7 s in figure 14$e$). The ebullition becomes essentially periodic at $\theta =90^{\circ }$, where no undulations are observed during bubble growth unlike $\varGamma =0.4$ along with a thin film in the bottom region of the heater since the vapour passage becomes easier for a higher aspect ratio.

Figure 14. Interface evolution with different angles of incidence for ($a\text {--}c$) $\varGamma =0.4$ and ($d\text {--}f$) $\varGamma =0.6$ in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Re_l=100$ and $Ja_v/Pr_v =0.6$: ($a{,}d$) $\theta =30^{\circ }$, ($b{,}e$) $\theta =60^{\circ }$ and ($c,\kern0.05em f$) $\theta =90^{\circ }$. (For interface evolution at $\theta =0^{\circ }$ with the same non-dimensional wall superheat, one may refer to figures 5 and 10.)

For $\varGamma =0.8$ at $Re_l=100$ and $Ja_v/Pr_v =0.6$, the interface evolution occurs under a slightly enhanced influence of flow inertia for various angles of incidence, and is not presented in figure 14. Instead, the interface morphology obtained with different values of $Re_l$ at $\theta =60^{\circ }$ is shown in figure 15 with upward cross-flow. A periodic film boiling cycle at $Re_l=50$ is replaced by an increasingly transient interfacial dynamics as $Re_l$ increases. Such a characteristic behaviour with variation in cross-flow velocity is observed at all angles of incidence with $\varGamma =0.8$. While the periodic ebullition occurs in a similar manner at different values of $\theta$, a certain difference in the vapour profiles at higher $Re_l$ values is observed compared with $\theta =0^{\circ }$ (figure 10), especially with regard to the vapour sheet formed behind the heater at $Re_l=170$. Nonetheless, the heater orientation has a smaller influence on vapour morphology, in contrast to a substantial change in the ebullition process observed at lower aspect ratios under a given set of conditions. Further, simulations have also been performed considering a higher non-dimensional superheat of 1.2 at $Re_l=100$ for various values of $\varGamma$ and $\theta$. Stable vapour columns are formed in almost all these cases, which have been depicted for $\theta =60^{\circ }$ in figure 16. It is seen that as $\varGamma$ increases, a larger proportion of the heater area is covered by the vapour wake behind the heater.

Figure 15. Interface evolution for ($a$) $Re_l=50$, ($b$) $Re_l=100$ and ($c$) $Re_l=170$ in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.8)$ at $\theta =60^{\circ }$ and $Ja_v/Pr_v =0.6$. (For interface evolution at $\theta =0^{\circ }$ and $\varGamma =0.8$, one may refer to figure 10.)

Figure 16. Vapour column formation for ($a$) $\varGamma =0.4$, ($b$) $\varGamma =0.6$ and ($c$) $\varGamma =0.8$ in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Re_l=100, \theta =60^{\circ }$ and $Ja_v/Pr_v =1.2$.

The space-averaged Nusselt number distribution at $Re_l=100$ and $Ja_v/Pr_v =0.6$ with upward cross-flow is plotted in figure 17($a$–$c$) for different values of $\varGamma$ and $\theta$. For $\varGamma =0.4$, a completely periodic Nusselt number variation concomitant with the interface evolution is obtained at all angles other than $\theta =0^{\circ }$ for which the Nusselt number is constant due to the formation of a stable vapour column. The frequency of periodic ebullition is observed to decrease with an increase in $\theta$ as the heater orientation offers an increasing resistance to the vapour flow. Further, the undulations observed during the vapour growth phase at $\theta =90^{\circ }$ are also evident from the oscillating Nusselt number variation during each cycle. The effect of flow inertia indicated by a loss in periodicity can be seen at larger heater inclinations with an increase in the aspect ratio. Additionally, as a larger portion of the heater wall is affected by the vapour dynamics during an ebullition cycle for higher values of $\theta$, the corresponding variation in the Nusselt number from minimum to maximum value is observed to increase for all the aspect ratios. The time-averaged Nusselt number values for the various cases investigated with $\varGamma =0.8$ are shown in figure 17($d$). While there is a significant rise in heat transfer as $Re_l$ increases, the comparative influence of heater orientation on the Nusselt number is quite low, with any appreciable increase observed only at higher $Re_l$ values. However, this is not the case at lower aspect ratios for which the time-averaged Nusselt number values corresponding to different $\theta$ and $Re_l$ at $Ja_v/Pr_v =0.6$ are presented in figure 17($e$). In general, the Nusselt number is shown to increase with $\theta$ for all the aspect ratios except $\varGamma =1$, where the definition of $\theta$ is trivial. The increase is significant at $\varGamma =0.4$, while the effect diminishes gradually at subsequently higher values of $\varGamma$ corresponding to both $Re_l$ magnitudes. This in turn leads to a trend (barring a few anomalies that are discussed next) where the Nusselt number decreases with aspect ratio for $\theta =30^{\circ }$ and beyond, and is in contrast to the observation at $\theta =0^{\circ }$. However, a closer investigation of the data reveals that an increase in Nusselt number with $\theta$ for a given aspect ratio is not commensurate to a corresponding increase in the characteristic dimension normal to the flow ($D$), thereby leading to a reduction in heat transfer as $\theta$ increases. This essentially translates into an increase in heat transfer coefficient with $\varGamma$ at all angles of incidence, which is directly reflected in the plot for $\theta =0^{\circ }$ with $D$ being constant for all the aspect ratios. The aforementioned discussion is also directly in line with the results for a circular cylinder (Singh & Premachandran 2018b), where an increase in the characteristic dimension relative to the capillary length scale ($\lambda _o$) has a detrimental effect on heat transfer.

Figure 17. Nusselt number showing the effect of angle of incidence on heat transfer in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$. Space-averaged Nusselt number variation at $Ja_v/Pr_v =0.6$, $Re_l=100$ and different values of $\theta$ is shown for ($a$) $\varGamma =0.4$, ($b$) $\varGamma =0.6$ and ($c$) $\varGamma =0.8$. Time-averaged values of the Nusselt number for various parameters considered are shown in panels ($d\text {--}f$).

Further, some differences are observed with regard to the Nusselt number trend outlined in the preceding text, which can be traced to the specific interface morphologies. One such observation relates to especially low values of Nusselt number obtained at $Re_l=50$ with $\theta =90^{\circ }$ for all values of $\varGamma$. This is due to a much thicker vapour film formed beneath the heater at $Re_l=50$ compared with $Re_l=100$, as shown in figure 18. While such a thick film is an artefact of a constriction to vapour flow due to the heater orientation, the action of liquid flow at a higher $Re_l$ value of 100 is able to effectively squeeze out the vapour from the underside of the heater directly facing the flow. However, this is not the case at $Re_l=50$ leading to a severe impairment in heat transfer. Additionally, a slightly thicker film even for $Re_l=100$ at a lower aspect ratio of 0.4 leads to a quite low value of Nusselt number at the said conditions in figure 17(e). Furthermore, the variation of time-averaged Nusselt number with heater geometry as described above is also verified from similar trends observed at an enhanced non-dimensional wall superheat of 1.2 and $Re_l=100$, as shown in figure 17($\,f$).

Figure 18. Interface morphology en route bubble pinch-off in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Ja_v/Pr_v =0.6$ and $\theta =90^{\circ }$, showing the effect of angle of incidence in conjunction with $Re_l$ on film thickness around the cylinder: ($a$) $\varGamma =0.4$ and ($b$) $\varGamma =0.6$.

The effect of heater orientation relative to free stream flow on the film boiling dynamics is further discussed considering horizontal cross-flow configuration. Figure 19 shows the interface evolution with different angles of incidence for two different aspect ratios at $Re_l=100$ and $Ja_v/Pr_v =0.6$. For $\varGamma =0.4$, the interface dynamics obtained from an earlier investigation at $\theta =0^{\circ }$ is transient in nature with the vapour wake lying entirely behind the heater under the influence of cross-flow. The ebullition becomes increasingly periodic at subsequently higher values of $\theta$ as seen from figure 19($a$–$c$), with a reduction in the magnitude of the Froude number similar to upward cross-flow. While a decrease in Froude number implies a more pronounced effect of buoyancy, the vapour flow due to buoyancy is restricted to varying degrees with different heater orientations leading to an accumulation of vapour on the underside of the heater directly facing the flow. Under such conditions in the mixed regime, a competing effect of buoyancy and inertia forces causes a recirculation in the vapour film leading to a vapour bulge or thick film region. The extent and location of such a recirculation near the heater wall is observed to vary with heater orientation, and is further presented by plotting streamlines in figure 20. For $\theta =0^{\circ }$, the recirculation is confined to the thick vapour wake formed behind the heater under a dominant effect of flow inertia at a higher Froude number, and is indicative of a direct effect of the bluff body rather than arising from an interplay of buoyancy and inertia. However, there is an increased effect of buoyancy at $\theta =30^{\circ }$, while the vapour removal under buoyancy is severely restricted due to the heater orientation. This leads to a vapour bulge in the lower region of the cylinder side facing the flow as shown in figure 20($b$). At $\theta =60^{\circ }$, the vapour can escape more easily from the underside of the heater with buoyancy leading to a thinner and more uniform recirculation region as highlighted in figure 20($c$). Further, the constriction to buoyancy-driven vapour removal is completely absent at $\theta =90^{\circ }$, while the horizontal liquid flow has a further squeezing effect on the vapour side directly facing the flow as also described previously for upward cross-flow. Such a concerted action of buoyancy and inertia leads to a much thinner vapour film near the heater wall. Additionally, the effect of instantaneous vapour wake profiles on the liquid flow is also visualized from figure 20 that indicates a coupling of the vapour and liquid wake behaviour under the present conditions.

Figure 19. Interface evolution with different angles of incidence for ($a\text {--}c$) $\varGamma =0.4$ and ($d\text {--}f$) $\varGamma =0.6$ in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Re_l=100$ and $Ja_v/Pr_v =0.6$: ($a{,}d$) $\theta =30^{\circ }$, ($b{,}e$) $\theta =60^{\circ }$ and ($c,\kern0.05em f$) $\theta =90^{\circ }$. (For interface evolution at $\theta =0^{\circ }$ with $\varGamma =0.6$ and same non-dimensional wall superheat, one may refer to figure 6.)

Figure 20. Instantaneous view of streamlines near an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.4)$ with different angles of incidence in horizontal cross-flow of water $(p/p_c =0.99)$ at $Re_l=100$ and $Ja_v/Pr_v =0.6$: ($a$) $\theta =0^{\circ }$, ($b$) $\theta =30^{\circ }$, ($c$) $\theta =60^{\circ }$ and ($d$) $\theta =90^{\circ }$. All of the above views correspond to the time instant, $t = 0.7\ \textrm {s}$.

The interface evolution at the aforementioned conditions with a lower heater aspect ratio of 0.6 is presented in figure 19($d$–$\,f$). As with $\varGamma =0.4$, film boiling becomes increasingly periodic at higher values of $\theta$. However, an enhanced effect of flow inertia persists up until higher heater inclinations, with relatively higher Froude number magnitudes at a higher aspect ratio. As such, an elongated vapour wake can be seen at $\theta =30^{\circ }$ along with a quite small vapour bulge beneath the heater. Although the recirculation region becomes more prominent for $\theta =60^{\circ }$ with increased buoyancy effect, it is still confined to the lower portion of the heater with the oncoming liquid flow in contrast to $\varGamma =0.4$. Such a thick vapour region near the wall was previously observed for $\theta =0^{\circ }$ only at a lower $Re_l$ value of 50 (figure 6$b$). At $\theta =90^{\circ }$, the recirculation again disappears on account of heater orientation being favourable to buoyancy, and a much thinner vapour film is observed as compared with $\varGamma =0.4$. The overall results put forth the significance of the Froude number as the major parameter governing film boiling behaviour in the mixed regime. Additionally, under such an interplay of buoyancy and inertia forces for both the cross-flow directions, their relative effects are determined by the orientation of the elliptical heater showing a coupled effect of geometry and hydrodynamics on the interface evolution. This adds a further degree of complexity compared with a circular heater, where the heater orientation is inconsequential.

In figure 21, the interface evolution at a higher aspect ratio of 0.8 is presented for two different cross-flow velocities and wall superheats at $\theta =60^{\circ }$. At $Re_l=100$ and $Ja_v/Pr_v =0.6$, the bubble release is periodic as compared with a random vapour release obtained at $\theta =0^{\circ }$ previously. The vapour bulge beneath the heater is, however, much smaller than observed at lower aspect ratios showing a lesser constriction to buoyancy governed vapour passage. With increase in $Re_l$ to 170, a random bubble release is again observed with the vapour wake concentrated in an upward region behind the heater as shown in figure 21($b$). At the same time, an increase in wall superheat at $Re_l=100$ also leads to a significant change in the vapour morphology due to enhanced vapour generation. As such, an elongated wake covering the entire rear portion of the heater is observed. The characteristic nature of these changes with $Re_l$ and $Ja_v/Pr_v$, though, is along expected lines, and in consonance with the discussion in previous sections at $\theta =0^{\circ }$.

Figure 21. Interface evolution in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.8)$ at $\theta =60^{\circ }$: ($a$) $Re_l=100, Ja_v/Pr_v =0.6$, ($b$) $Re_l=170, Ja_v/Pr_v =0.6$ and ($c$) $Re_l=100, Ja_v/Pr_v =1.2$.

The temporal variation of space-averaged Nusselt number with horizontal cross-flow at $Re_l=100$ and $Ja_v/Pr_v =0.6$ is plotted in figure 22($a$–$c$) for different values of $\varGamma$ and $\theta$. The Nusselt number distribution is concomitant with the interface evolution described in previous paragraphs for the various cases. However, amongst the cases with periodic ebullition, no noticeable change in bubble release frequency is observed for $\varGamma =0.4$ and also for $\varGamma =0.8$ at a later time. In fact, the frequency is seen to increase with angle at $\varGamma =0.6$ which is in stark contrast to the observation with upward cross-flow. This can, however, be attributed to the opposing effects of heater orientation in aiding or opposing buoyancy-driven vapour removal with regard to the two cross-flow orientations, which have already been discussed in detail. The time-averaged Nusselt number values for the various cases investigated with $\varGamma =0.8$ are shown in figure 22($d$), while the values obtained at other aspect ratios for different conditions are presented in figures 22($e$) and 22($\,f$). The trends, with slight differences, can be broadly related to the discussion for upward cross-flow. However, two major instances of peculiar behaviour can be observed from these results. The first relates to a higher heat transfer compared with upward liquid flow (figure 17) for a few cases at higher angles of incidence. While such an observation is completely counter-intuitive with buoyancy aiding flow inertia in liquid upflow, it stems from the prominent role of heater orientation on the interfacial dynamics. For upward cross-flow, an increase in the angle of incidence has a detrimental effect on vapour removal due to buoyancy, as well as liquid flow. However, with horizontal cross-flow, while higher values of $\theta$ entail a lower influence of flow inertia with a reduction in Froude number, the buoyancy-driven vapour removal is simultaneously enhanced leading to higher heat transfer rates compared with upflow under certain conditions. Thus an additional degree to the interplay between buoyancy and inertia is imposed by the heater orientation that already depends substantially on the Froude number as well as the cross-flow orientation, thereby establishing a strong coupling between the angle of incidence and Froude number.

Figure 22. Nusselt number showing the effect of angle of incidence on heat transfer in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$. Space-averaged Nusselt number variation at $Ja_v/Pr_v =0.6, Re_l=100$ and different values of $\theta$ is shown for ($a$) $\varGamma =0.4$, ($b$) $\varGamma =0.6$ and ($c$) $\varGamma =0.8$. Time-averaged values of the Nusselt number for various parameters considered are shown in panels ($d\text {--}f$).

Another major anomaly that can be observed from the results concerns a reduction in heat transfer with increase in $Re_l$ under a given set of conditions, as seen at $\theta =60^{\circ }$ and $90^{\circ }$ with $Re_l=10$ and 50 for $\varGamma =0.8$, and a few other cases in figure 22($e$). This is directly a consequence of the cross-flow orientation since such an observation does not relate to any of the results for upward cross-flow, and is explained further in figure 23. The interface morphology prior to bubble pinch-off at $\varGamma =0.8$ and $Ja_v/Pr_v =0.6$ is shown for $Re_l=10$ and 50 in figure 23($a$), with a fixed heater orientation of $60^{\circ }$. At $Re_l=50$, a recirculation zone near the heater wall is clearly evident from figure 23($c$) that forms with an interplay of buoyancy and inertia, as has been described previously for various conditions. On the other hand, at $Re_l=10$ the effect of buoyancy is much stronger along with the heater geometry not offering any major resistance to the vapour flow. As such, the vapour smoothly flows over the ellipse driven strongly by the buoyancy force, as seen from the streamlines in figure 23($b$). For $Re_l=50$, the recirculation leads to a thick film with a higher temperature in the affected zone near the wall, which causes the impairment in heat transfer observed in figure 22($d$). Further, such an effect is dependent on several parameters including heater geometry as shown previously, thereby affecting the heat transfer to different extents under various conditions.

Figure 23. ($a$) Interface morphology prior to bubble pinch-off for $Re_l=10$ and 50 in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.8)$ at $Ja_v/Pr_v =0.6$ and $\theta =60^{\circ }$. Comparison of instantaneous temperature distribution in the vapour film and streamlines near the cylinder is shown for ($b$) $Re_l=10$ and ($c$) $Re_l=50$.

At this stage, it is prudent to briefly discuss the two-dimensional nature of the present film boiling simulations. With no prior study performed for film boiling over an ellipse with liquid cross-flow, the qualitative as well as quantitative insights obtained from the present two-dimensional simulations form an important first step towards plugging a discernible gap existing in the literature. While the operating conditions correspond to the mixed regime with low magnitudes of the Froude number, these have also been selected while considering the limitation of the current study being two-dimensional. At system pressures near-critical conditions, the interfacial dynamics in film boiling is closer to a two-dimensional situation (Son & Dhir 1998). Additionally, low values of $Re_l$ are employed as discussed in the beginning of this section. Furthermore, several studies (Panzarella, Davis & Bankoff 2000; Aursand, Davis & Ytrehus 2018) have relied on two-dimensional models to obtain significant insights pertaining to nonlinear dynamics and thermocapillary effects in horizontal pool film boiling, where the physics is inherently three-dimensional. Based on the aforementioned considerations, it is expected that the observations from the present study are not just limited to two-dimensional scenarios, and the physical insights would very well apply to real problems. For instance, the recirculation mechanism identified as impairing the heat transfer, results from the competing influence of buoyancy and inertia along the circumferential direction of the elliptical heater, which would exist in the mixed regime even when velocity along the longitudinal axis is present for three-dimensional cases. At the same time, the location and extent of the recirculation may vary depending on the film boiling conditions including any three-dimensional effects. Such an observation from the present study assumes a greater significance considering that the effect in the thin vapour film would be quite difficult to ascertain from experiments. Similar arguments can be applied to other aspects of interface evolution and vapour wake dynamics presented in this work, even if exact quantitative predictions can be better obtained from three-dimensional simulations or experiments that are missing from the literature as yet.

Another major feature of the present work is the quantification of heat transfer under different conditions in the mixed regime. In this regard, the results with upward cross-flow for $\varGamma =1$ have been shown to be in close agreement with available experimental data, thereby ensuring the validity of the present simulations. Additionally, the two-dimensional simulations offer much more flexibility to account for the influence of various parameters on the film boiling behaviour at a reasonable computational cost. This has been a major consideration in some previous film boiling studies (Esmaeeli & Tryggvason 2004) relying on two-dimensional simulations to obtain parametric heat transfer data that is in reasonable agreement with empirical results.

3.4. Liquid and vapour wake dynamics in the mixed regime

Based on the results obtained in the previous sections, it is overall observed that the interfacial dynamics and associated heat transfer in the mixed regime of film boiling over an ellipse are determined by a coupled effect and complex interplay of several parameters, including a prominent effect of the geometrical configuration of the heater as well as the cross-flow orientation. This results in substantially varying film boiling characteristics including wake profiles as shown for various conditions investigated in the present study. A closer examination of the interplay of buoyancy and inertia at different conditions in the mixed regime, that forms the central theme of the present work, is presented in this section. Further, the mutual interaction of liquid and vapour wakes for different cases is also discussed.

To assess the comparative influence of buoyancy and inertia for a fixed heater geometry, fast Fourier transform (FFT) analysis of the space-averaged Nusselt number in upward liquid cross-flow with different Reynolds number is presented in figure 24, corresponding to $Ja_v/Pr_v =0.3, \varGamma =0.6$ and $\theta =0^{\circ }$. Here, the amplitude is normalized with respect to the dominant frequency observed in each case, and the typical interface morphology is also shown alongside. A dominant frequency is observed at $f_1=3.91\ \textrm {Hz}$ from figure 24($a$) for $Re_l=10$, and is followed by several superharmonics that are exact multiples of $f_1$. Further, $f_1$ corresponds to the frequency of the periodic ebullition driven primarily by buoyancy at such a low value of $Re_l$ (and $Fr$). This indicates that the bubble release occurring under Rayleigh–Taylor instability governs the heat transfer over the elliptical heater. At $Re_l=50$, an almost similar nature of the FFT plot is observed. However, a higher magnitude of the dominant frequency (5.48 Hz) points to an additional effect of flow inertia in aiding bubble release that eventually determines the heat transfer. The effect of inertia is not directly discernible from the interface morphology, which evolves almost identically to $Re_l=10$. At $Re_l=100$, while a dominant peak can be identified from figure 24($c$), it is saddled between several subharmonics and superharmonics. This characterizes a loss of the quasi-steady nature of ebullition under an enhanced influence of flow inertia. Upon further increase in $Re_l$ to 170, multiple frequencies with comparable magnitude are observed on account of random bubble release, with $\sqrt {Fr}=2.04$ implying film boiling occurring in the purely inertial regime. The deductions from the present analysis are in line with those for a circular cylinder (Singh & Premachandran 2018b) under similar conditions, which can be expected for the same characteristic dimension resulting from the present configuration of the elliptical heater.

Figure 24. Normalized FFT analysis of the space-averaged Nusselt number with different Reynolds numbers in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $Ja_v/Pr_v =0.3$ and $\theta =0^{\circ }$: ($a$) $Re_l=10$ ($\sqrt {Fr}=0.12$), ($b$) $Re_l=50$ ($\sqrt {Fr}=0.6$), ($c$) $Re_l=100$ ($\sqrt {Fr}=1.2$) and ($d$) $Re_l=170$ ($\sqrt {Fr}=2.04$).

Further, FFT analysis of the space-averaged Nusselt number in horizontal cross-flow with different angles of incidence and $\varGamma =0.6$ is presented in figure 25, corresponding to $Ja_v/Pr_v =0.6$ and $Re_l=100$. While multiple frequencies at $\theta =0^{\circ }$ and $30^{\circ }$ indicate a random and transient nature of interfacial dynamics, a periodic ebullition governs the heat transfer at higher angles of incidence as evidenced from clearly demarcated peak frequencies in the FFT plots. Such a behaviour can be ascribed to a more prominent effect of buoyancy due to a reduction in the magnitude of Froude number with an increase in $\theta$, as has been described earlier in § 3.3. It can, however, be noted from the interface morphologies presented alongside that the liquid flow does affect the interface evolution at $\theta =60^{\circ }$ and $90^{\circ }$ for a higher $Re_l$ value of 100, as seen from the vapour bulge near the wall and diagonal nature of bubble release. However, there is a pronounced effect of buoyancy along with the heater orientation aiding buoyancy-driven at these angles of incidence, which curtails the randomness arising out of the effect of flow inertia and leads to a periodic ebullition that eventually governs the heat transfer. As such, the magnitude of the dominant frequency is also observed to become higher as $\theta$ increases from $60^{\circ }$ to $90^{\circ }$. Furthermore, the analysis from figures 24 and 25 establishes the Froude number as a key parameter dictating heat transfer in the mixed regime, irrespective of the cross-flow orientation or geometric configuration of the elliptical heater.

Figure 25. Normalized FFT analysis of the space-averaged Nusselt number with different angles of incidence in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $Ja_v/Pr_v =0.6$ and $Re_l=100$: ($a$) $\theta =0^{\circ }$, ($b$) $\theta =30^{\circ }$, ($c$) $\theta =60^{\circ }$ and ($d$) $\theta =90^{\circ }$.

To take a closer look at the mutual interaction of liquid and vapour wakes in the mixed regime of film boiling over an elliptical heater, instantaneous contours of the non-dimensional vorticity are plotted for different conditions along with the vapour morphology. The vorticity $\varOmega$ is non-dimensionalized as $\omega =\varOmega D/U$. Figure 26 shows the contours of $\omega$ obtained in upward liquid cross-flow for different Reynolds number values with $Ja_v/Pr_v =0.6, \varGamma =0.6$ and $\theta =0^{\circ }$. From figure 26($a$) at $Re_l=50$, a strong pair of counter-rotating vortices can be seen in the saturated liquid behind the growing vapour mass ($t=0.625\ \textrm {s}$). With further growth of the vapour at the top of the heater, these extend as asymmetric vorticity patches in the liquid wake. However, as the bubble pinch-off stage is reached ($t=0.705\ \textrm {s}$), the vorticity around the liquid–vapour interface becomes substantially higher in comparison. This indicates a significant effect of buoyancy in addition to a relatively smaller effect of flow inertia, with bubble release primarily occurring under Rayleigh–Taylor instability. In a previous study for single phase flow over an ellipse (Paul, Prakash & Vengadesan 2014), it has been established that the critical Reynolds number beyond which the steady flow bifurcates into unsteady vortex shedding is approximately 87.5, for $\varGamma =0.6$ and $\theta =0^{\circ }$ as per the current configuration. From figure 26($b$) for $Re_l=100$, it is observed that asymmetric vorticity patches extend from near the wall along the length of the vapour wake, while vortex shedding starts only beyond the bubble mass. Eventually the bubble detaches and rises ($t=0.76\ \textrm {s}$) preventing vortex shedding to fully establish in the liquid flow region. Thus, while the interface evolves under a prominent influence of liquid flow inertia, the above observation reveals an inherent effect of the vapour wake dynamics itself on the liquid wake characteristics. This is further seen in a more pronounced manner at $Re_l=170$, where bifurcation of the liquid flow into characteristic vortex shedding is altogether prevented with the formation of a steady vapour wake behind the heater. Subsequently, the contours of $\omega$ for the same set of parameters in horizontal cross-flow are plotted in figure 27. Since the detached bubbles do not move directly in line with the free stream flow due to orthogonal gravity and flow fields, a more continuous vortex street is established beyond the vapour wake at $Re_l=100$ compared with upward cross-flow. At $Re_l=170$, a voluminous vapour wake is formed behind the heater, with the different stages of interface evolution and effect of Kelvin–Helmholtz instability described earlier in figure 6($d$). The thick vapour wake again affects the liquid wake nature, even though vortex shedding can be observed beyond the vapour region at several instants. Interestingly the value of $Re_l=50$ is much below the critical Reynolds number with the present heater geometry as mentioned earlier. Still vortices can be seen emanating from the tip of the vapour wake as well as adjacent to the film beneath the heater wall, thereby showing the effect of vapour wake profile on the liquid flow in addition to the bluff-body geometry. Additionally, a long vorticity patch along with a smaller vortex is observed in the trail of the rising bubble, which is eventually shed as a vortex along the liquid flow ($t=0.8\ \textrm {s}$).

Figure 26. Instantaneous non-dimensional vorticity contours with different $Re_l$ in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a$) $Re_l=50$, ($b$) $Re_l=100$ and ($c$) $Re_l=170$.

Figure 27. Instantaneous non-dimensional vorticity contours with different $Re_l$ in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a$) $Re_l=50$, ($b$) $Re_l=100$ and ($c$) $Re_l=170$.

Further, the non-dimensional vorticity contours are plotted for similar conditions but different aspect ratios of the elliptical heater in figure 28. For $\varGamma =0.4$ and $\theta =0^{\circ }$, the $Re_l$ values considered in the present study are much lower than the corresponding magnitude of the critical Reynolds number (Paul et al. 2014). Thus the steady vapour region formed behind the heater for both the cross-flow orientations and particular $Re_l$, although resulting from an accentuated rate of vapour infusion due to a lower aspect ratio, also broadly conforms to the liquid flow behaviour expected under the present conditions as shown in figures 28($a$) and 28($c$). For $\varGamma =0.8$, a more rigorous effect of the liquid flow on the vapour wake is observed, especially with horizontal cross-flow at $Re_l=170$. As shown in figure 28($d$), the vapour wake fluctuations and bubble detachment are primarily governed by the alternate vortex shedding process, while the small bubbles are carried along the typical alleyway in unsteady flow behind the cylinder. The current analysis is also extended to different orientations of the elliptical heater in figure 29, where the contours of $\omega$ are plotted in horizontal liquid cross-flow for different values of $\theta$ with $Re_l=100, Ja_v/Pr_v =0.6$ and $\varGamma =0.6$. The intensity of vortex shedding is observed to increase with an increase in $\theta$, with the vortex street behind the heater becoming quite dense for $\theta =90^{\circ }$. While this follows directly as an influence of the bluff-body configuration, the vapour wake during bubble growth phase has a wider span along the vertical direction due to buoyancy-driven vapour removal becoming more prominent at higher angles of incidence. Since the vortices originate from the tips of the vapour region as also discussed earlier, the span of the vorticity field in the saturated liquid becomes wider at $\theta =60^{\circ }$ and $90^{\circ }$ compared with $\theta =30^{\circ }$.

Figure 28. Instantaneous non-dimensional vorticity contours for ($a{,}b$) upward ($Re_l=100$) and ($c{,}d$) horizontal ($Re_l=170$) cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a{,}c$) $\varGamma =0.4$ and ($b{,}d$) $\varGamma =0.8$. (For contours at $\varGamma =0.6$ with similar conditions, one may refer to figures 26 and 27.)

Figure 29. Instantaneous non-dimensional vorticity contours in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5, \varGamma =0.6)$ at $Ja_v/Pr_v =0.6$ and $Re_l=100$: ($a$) $\theta =30^{\circ }$, ($b$) $\theta =60^{\circ }$ and ($c$) $\theta =90^{\circ }$. (For contours at $\theta =0^{\circ }$ with similar conditions, one may refer to figure 27.)

The aforementioned discussion characterizes a mutual interaction of the liquid and vapour wakes under different conditions in the investigated mixed regime of film boiling over an ellipse, which is quite significant considering that a discernible gap regarding the same exists even in classical film boiling studies for a circular cylinder. Here, it can be mentioned that the qualitative nature of these results established for the first time is not expected to change for three-dimensional cases. Simultaneously, two-dimensional simulations allow characterization of the mutual wake interaction under the influence of various parameters at a much lower computational cost. While the veracity of the above analysis based on vorticity contours can be exactly established only through future three-dimensional simulations or experiments, the present observations can also serve as an important reference for such studies. As such, the present analysis assumes a greater significance in the absence of any prior empirical or three-dimensional data, as also discussed towards the end of § 3.3.

3.5. Shape factor ($\psi$): correlation for heat transfer

With the extensive set of simulations performed in the present study, a correlation for the time-averaged Nusselt number (subsequently referred to as $Nu$) is arrived at in this section to comprehensively predict the heat transfer in the mixed regime of film boiling over an elliptical heater. It can be noted that a heat transfer correlation for saturated film boiling over a circular heater geometry has been proposed in an earlier study by the present authors (Singh & Premachandran 2018b) under similar conditions in the mixed regime with upward liquid cross-flow. Subsequently in another study (Singh & Premachandran 2019), a reduction factor as a function of the Froude number was proposed to quantify the heat transfer with horizontal cross-flow of liquid over a circular cylinder. These correlations comprehensively account for the various hydrodynamic, thermal and geometric parameters that are observed to affect the film boiling heat transfer. An attempt is made to quantify the heat transfer in the present case while avoiding an altogether new formulation, considering that the interfacial dynamics results from an interplay of similar parameters in addition to the elliptical geometry. To this effect, a shape factor ($\psi$) is conceived as a function of the geometrical parameters of the ellipse such that

(3.1)\begin{equation} Nu_e=\psi Nu_c, \end{equation}

where the subscripts $e$ and $c$ denote elliptical ($\varGamma <1$) and circular ($\varGamma =1$) heater geometries, respectively. Further, it has been shown previously that the Nusselt number increases with the aspect ratio of the heater for $\theta =0^{\circ }$, while broadly showing a decreasing trend with $\varGamma$ for other values of $\theta$. Thus the Nusselt number can be directly related to the elliptical geometry based on a parameter $\varGamma ^{'}$ which is defined as

(3.2)\begin{equation} \varGamma^{'}=\varGamma + \frac{\theta}{\varGamma}. \end{equation}

It should be mentioned that the unit of $\theta$ is radians in (3.2). For upward cross-flow, the heater orientation has a consistent effect on vapour removal due to buoyancy as well as flow inertia. As such, the shape factor is suitably determined by fitting a polynomial to the simulation data. However, a coupled effect of heater orientation and the Froude number is observed with horizontal cross-flow, as has been discussed previously in § 3.3. Under these conditions, a close fit based on the simulation results is obtained with the inclusion of an additional logarithmic function in the functional form of the shape factor. Eventually, the expression for the shape factor is obtained as

(3.3)\begin{equation} \psi (\varGamma,\theta,Fr)=\left(1+\delta_h\gamma\left(\varGamma^{'},Fr\right)\right)\left(-0.045\varGamma^{'2}+0.2\varGamma^{'}+0.825\right), \end{equation}

where

(3.4)\begin{equation} \gamma\left(\varGamma^{'},Fr\right)=-0.08x_1+0.065x_2+0.1x_1 x_2+0.2x_1^{3}+0.08x_1 x_2^{2}, \end{equation}

with $x_1=ln(\varGamma ^{'})$, $x_2=ln(\sqrt {Fr})$, and $\delta _h$ being unity for horizontal cross-flow and zero for upward cross-flow. It must be carefully noted that the Nusselt number calculated using the above expression relates only to the convective heat transfer, since the radiation contribution in the present study is negligible as already mentioned in § 2.2.2. Further, the shape factor is strictly derived for the mixed regime only, while a detailed analysis would be required to characterize the same in the purely inertial regime of forced convection film boiling. The parity plot for the time-averaged Nusselt number obtained from the present simulations and predicted using (3.1)–(3.4) is shown in figure 30. The maximum deviation from the plot is observed to be within $\pm 12\,\%$ for all data points, which is quite a reasonable fit for boiling data.

Figure 30. Parity plot for the time-averaged Nusselt number obtained from the present simulations and the proposed correlation in terms of the shape factor ($\psi$).

4. Conclusions

Saturated film boiling over an elliptical cylinder has been computationally investigated under conditions entailing a combined influence of buoyancy and flow inertia. The simulations have been performed using a numerical framework for phase change problems on unstructured grids based on a CLSVOF interface capturing algorithm. Both aiding and orthogonal liquid flow configurations relative to gravity are considered, where the mixed regime is ascertained by low magnitudes of the Froude number ($\sqrt {Fr}\le 2$) resulting from a careful choice of various coupled parameters. The film boiling behaviour in terms of interfacial dynamics, vapour wake profiles and heat transfer along with a mutual interaction of liquid and vapour wakes is characterized, as influenced by various hydrodynamic, thermal and geometric parameters.

For a fixed geometric configuration of the elliptical heater, a significant variation is observed in the interface evolution with liquid cross-flow velocity due to a change in the relative influence of buoyancy and flow inertia. The quasi-steady nature of ebullition is gradually lost with successively higher influence of flow inertia while the bubble release becomes increasingly random. The cross-flow orientation relative to gravity is shown to further affect the nature of interplay between buoyancy and inertia leading to varied vapour wake profiles. The wall superheat while affecting the rate of evolution process, also leads to an altogether change in the interface morphology and wake dynamics under different conditions in the mixed regime. The influence of flow inertia even at low cross-flow velocities is evident from the heat transfer behaviour in the mixed regime, with lower magnitudes observed in horizontal liquid cross-flow.

With the major axis of the elliptical heater aligned along the free stream flow, the vapour infusion into the wake is accentuated at lower aspect ratios. For upward cross-flow, this leads to formation of stable vapour jets at lower velocities and wall superheats, while affecting the stages of instability growth behind the heater in horizontal cross-flow at elevated flow inertia. Additionally, a thick vapour film is formed beneath the heater in horizontal cross-flow at low Froude numbers due to a constriction in the vapour removal with buoyancy. The constriction that leads to an impairment of heat transfer eases out with an increase in the heater aspect ratio. Subsequently, investigations with different angles of incidence reveal a substantial influence of heater orientation on the film boiling characteristics in the mixed regime. For upward cross-flow, the angle of incidence has a monotonic influence on vapour removal due to buoyancy as well as liquid flow. However, with orthogonal gravity and flow fields, while higher heater inclinations entail a lower influence of flow inertia with a reduction in Froude number, the buoyancy-driven vapour removal is simultaneously enhanced. This results in higher heat transfer as compared with liquid upflow for some cases. The heater orientation thus adds an additional degree to the interplay between buoyancy and inertia that already depends substantially on the Froude number as well as the cross-flow orientation. An additional artefact of cross-flow direction is a recirculation in the vapour film that causes an anomalous impairment of heat transfer with an increase in $Re_l$. The extent and location of this phenomenon again depends on the heater orientation as well as the comparative influence of buoyancy and inertia, showcasing a strong coupling between the angle of incidence and Froude number.

The interplay of buoyancy and inertia is closely characterized through FFT analysis of the space-averaged Nusselt number for different conditions. A detailed and lucid explanation regarding the coupling of the liquid and vapour wake behaviour is also presented by means of dimensionless vorticity contours. The vortex shedding in the liquid region is strongly affected by the vapour wake profiles leading to its appearance or suppression compared with single phase flows, while the heater orientation affects the intensity and span of the vorticity field in the saturated liquid. Eventually a shape factor ($\psi$) is proposed that depends majorly on the elliptical geometry but also accounts for its coupling with Froude number in horizontal cross-flow. This is used in conjunction with correlations for a circular heater encompassing all relevant film boiling parameters to predict the heat transfer comprehensively under the conditions investigated in the present study.

The present investigation establishes several critical results based on a two-dimensional numerical model. Three-dimensional simulations or experiments would be required in future to obtain a more quantitative prediction of interfacial dynamics in film boiling over an elliptical heater with liquid cross-flow. Such studies, which are completely missing from the literature as yet, can also be used to recalibrate the heat transfer correlation developed from the present simulations in case such a need arises.