1. Introduction
Turbulent boundary layers (TBLs) with embedded large-scale streamwise vortices represent an important class of three-dimensional wall-bounded flows due to their common occurrence. Vortices occur naturally in flow situations such as Görtler vortices on concave plates (Görtler Reference Görtler1955) or horseshoe vortices at the base of a blunt object in contact with a boundary layer (Baker Reference Baker1979, Reference Baker1980). Streamwise vortices can also be intentionally introduced to boundary layers, via the use of vortex generators, often in order to delay or avoid separation under adverse pressure gradient conditions. This is done by exchanging momentum between the near-wall boundary layer and the free stream flow. This energises the near-wall flow, providing a delay in the onset of separation. Due to the large energy losses that can be caused by separation of a boundary layer, delaying its onset can considerably reduce the drag of the body. For this reason, vortex generators are prevalent in aerodynamic designs such as in aircraft (Bragg & Gregorek Reference Bragg and Gregorek1987), automotive (Aider, Beaudoin & Wesfreid Reference Aider, Beaudoin and Wesfreid2010), motorsport (Pegrum Reference Pegrum2007) and wind turbine blade (Gao et al. Reference Gao, Zhang, Liu and Han2015) design, and have also found practical use in the enhancement of heat transfer (Torii & Yanagihara Reference Torii and Yanagihara1997).
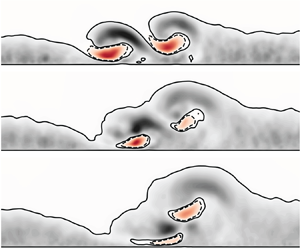
Vortex generation devices generally introduce vortices in pairs, leading to three main flow configurations of interest: co-rotating, counter-rotating with a common flow upwards, and counter-rotating with a common flow downwards (Lögdberg, Fransson & Alfredsson Reference Lögdberg, Fransson and Alfredsson2009), as shown in figure 1. Due to the interaction with the wall, common flow upward vortex pairs tend to leave the boundary layer (Mehta & Bradshaw Reference Mehta and Bradshaw1988), while common flow downward vortex pairs are held within the boundary layer for a longer period downstream of the generator (Pauley & Eaton Reference Pauley and Eaton1988). The use of vortex generators in complex flow applications, for example those found on the wings or diffusers of both aircraft and land vehicles, can lead to uncertainty or variation in the yaw alignment of the vortex generators. This skewed flow to the vortex generators can lead to an imbalance in strength between the pair of vortices that are designed to be of equal strength. Assessing the interaction of unbalanced vortex pairs is important in order to understand both the performance and robustness of vortex generators in their application. The wide variance possible in the set-up and configuration of vortex generators makes it difficult to assess which variables are important for increasing the effectiveness of the vortices at delaying the onset of separation.

Figure 1. Diagram showing three configurations of vortex pairs and their naming.
Early work on the effect of vortex generating devices by Taylor (Reference Taylor1947) looked at rows of aerofoils mounted within a boundary layer. This was followed by a study by Spangenberg & Schubauerand (Reference Spangenberg and Schubauerand1960), who compared the effect of the addition of vortex generators to varying adverse pressure gradient boundary layers. They concluded that the increased mixing introduced by the vortex generators had an effect comparable to reducing the pressure gradient. Pearcy (Reference Pearcy1961) investigated different vortex pair configurations – common flow down, common flow up, and co-rotating vortices – and focused on the design of the vortex generators. The study also tracked the movement of the vortices produced by a common flow down vortex generator design, showing that the vortices initially dipped towards the wall before being held at a constant height within the boundary layer. The dynamics of a common flow up vortex pair was presented by Mehta & Bradshaw (Reference Mehta and Bradshaw1988), showing that the vortices were lifted out of the boundary layer before settling at a height of approximately twice the boundary layer thickness, above the wall. The boundary layer thickness, denoted ![]() $\delta$, is defined as the height above the surface at which the velocity has reached
$\delta$, is defined as the height above the surface at which the velocity has reached ![]() $99\,\%$ of the free stream velocity.
$99\,\%$ of the free stream velocity.
The evolution of both the mean velocity and the Reynolds stresses of a single vortex interacting with a turbulent boundary layer were investigated by Westphal, Pauley & Eaton (Reference Westphal, Pauley and Eaton1987). This was extended by Pauley & Eaton (Reference Pauley and Eaton1988) to include pairs and arrays of longitudinal vortices embedded within a turbulent boundary layer. A range of blade angles and separation distances were investigated for the common flow down vortex pair case as well as presenting results for common flow up and co-rotating vortices. They found that the rate of spreading of the vorticity was increased by the presence of nearby vortices.
In their work on the design of vortex generator devices, Wendt (Reference Wendt2001) investigated the initial circulation and peak vorticity generated from different geometries. Among other parameters, it was found that the strength of the vortex produced was proportional to the angle of the blade compared to the flow direction. A further optimisation study performed by Godard & Stanislas (Reference Godard and Stanislas2006) found that counter-rotating vortex pairs performed better than co-rotating pairs, indicated by a larger increase in the skin friction at the wall, and defined an optimal angle of the vortex generator to the incoming flow direction under the given conditions. The experimental work of Lögdberg et al. (Reference Lögdberg, Fransson and Alfredsson2009) looked at different configurations of counter-rotating vortices and the effect that yaw had on the vortex development. They found that adjusting the yaw angle between ![]() $0^{\circ }$ and
$0^{\circ }$ and ![]() $20^{\circ }$ led to a linear increase in the strength of one vortex and a linear decrease in the other, with the total circulation remaining broadly constant. It was found that this also had an effect on the vortex paths with both vortices moving in the direction of the now stronger vortex, and the weaker vortex staying closer to the wall.
$20^{\circ }$ led to a linear increase in the strength of one vortex and a linear decrease in the other, with the total circulation remaining broadly constant. It was found that this also had an effect on the vortex paths with both vortices moving in the direction of the now stronger vortex, and the weaker vortex staying closer to the wall.
Early numerical studies, including those by Liandrat, Aupoix & Cousteix (Reference Liandrat, Aupoix and Cousteix1987), Sankaran & Russell (Reference Sankaran and Russell1990) and Kim & Patel (Reference Kim and Patel1994), employed a variety of Reynolds-averaged Navier–Stokes (RANS) models for the computation of longitudinal vortices embedded in a turbulent boundary layer. Mean flow field predictions were found, in general, to be quite reasonable around and away from the vortex core. Numerical predictions at the vortex core were less favourable when using standard linear eddy viscosity models, with axial velocity and vorticity both being significantly lower than expected. This was due to both excessive numerical diffusion and over-prediction of turbulence kinetic energy in this region. Guohua & Guanghua (Reference Guohua and Guanghua1998), and more recently Spalart et al. (Reference Spalart, Shur, Strelets and Travin2015), applied a series of nonlinear eddy viscosity models to similar flows, the latter with a specific curvature correction term included to reduce the turbulence generation in the vortex core. While these modifications helped to improve predictions, they did not achieve sufficient reduction in the levels of turbulence at the core needed to ensure the persistence of the vortex. Second moment closure methods, based on modelling the transport of the Reynolds stress components individually, have been shown to improve the representation of the turbulence statistics, such as the study of wingtip vortices by Craft et al. (Reference Craft, Gerasimov, Launder and Robinson2006), and the application to three-dimensional boundary layer flows by Billard, Revell & Craft (Reference Billard, Revell and Craft2012). Esmaili & Piomelli (Reference Esmaili and Piomelli1992) and then Liu, Piomelli & Spalart (Reference Liu, Piomelli and Spalart1996) used large eddy simulations (LES) to replicate the common flow down vortex pair case of Pauley & Eaton (Reference Pauley and Eaton1988). They reproduced the effect of the vortex generators by superimposing a Batchelor vortex pair over a recycled and rescaled turbulent boundary layer. They found that they were able to better match the mean velocity with a reduction in the peak streamwise vorticity matching far closer to that found in the experimental cases. They were also able to accurately match the turbulence statistics in the vicinity of the vortex core. Off-design conditions of vortex generators were also investigated by Baldacchino et al. (Reference Baldacchino, Ferreira, Ragni and Van Bussel2016) using a point vortex model. Whilst exploring the parameter space of asymmetric vortex pairs, they found that two regimes existed, defined as translating and orbital trajectories. However, this model did not include viscous diffusion or high Reynolds number effects.
While nonlinear RANS and stress-transport models bring improvement to the prediction of these flows, the use of scale-resolving methods is expected to be required to accurately predict the interaction of the vortices and the boundary layer. The practical compromise of hybrid RANS-LES (HRL) methods is therefore appealing, as demonstrated in their application to aerospace flows in various applied aerospace cases considered in Haase, Braza & Revell (Reference Haase, Braza and Revell2009). Of the various HRL approaches developed in the past two decades, one of the more promising candidates is embedded/zonal simulation, whereby a RANS model is used away from the region of interest, and LES are employed where improved accuracy is required. The two approaches can be bridged by the use of synthetic turbulence approximations (see e.g. Holgate et al. Reference Holgate, Skillen, Craft and Revell2019, for a recent review). In the present work, we begin by demonstrating the capability of an efficient scale-resolving framework based on use of synthetic turbulence and wall-modelled LES. In this regard, we are motivated by the work of Liu et al. (Reference Liu, Piomelli and Spalart1996) and seek to validate the present methodology with their work using rescaling methods. In doing so, we also compare our work to experimental data of flow in the wake of vortex generation devices, demonstrating that the present framework avoids the need to resolve directly the geometry of these devices. The framework is used in order to provide an accurate representation of the downstream interaction between the vortex pairs and the boundary layer, whilst remaining computationally efficient and flexible enough to explore configurations with varying vortex strength, positioning and rotation direction. Our second objective is to build on previous experimental and modelling work on embedded vortices in a zero pressure gradient (ZPG) turbulent boundary layer, to provide further physical insight using a combination of wall data, the impact on the mean boundary layer, and a detailed analysis of turbulence quantities. The resulting data and discussion will provide insight into the current performance and future improvement of both RANS and reduced-order models relevant for industrial development of vortex generators.
In the following, § 2 describes the numerical methods employed and the framework used to introduce vortices into the turbulent boundary layer. In § 3, the method is applied to a ZPG turbulent boundary layer with no vortices, before we present in § 4.1 our results validating the method with a common flow down vortex pair compared to experimental results. Further analysis of counter-rotating and co-rotating vortices is presented in § 4.2. The method is then extended to provide analysis of cases including skewed vortex generators and variation in separation distance in § 4.3, before conclusions are drawn in § 5.
2. Methodology
2.1. Governing equations
The present approach comprises a RANS computation of the full boundary layer domain used as a precursor calculation and a smaller LES domain situated within. This allows for the scale resolving LES to be used where it is required in predicting the interaction between the multiple vortices and the turbulent boundary layer, with the inlet conditions supplied from the precursor RANS calculation and a vortex model. Figure 2 shows the set-up of the two domains.

Figure 2. Diagram showing the set-up of the RANS domain and LES domain for the base case of a ZPG turbulent boundary layer.
In the LES region, the filtered Navier–Stokes equations are solved. These are given by
where the vector ![]() ${\boldsymbol{x}}_i$ comprises
${\boldsymbol{x}}_i$ comprises ![]() ${x}_1 = {x}$,
${x}_1 = {x}$, ![]() ${x}_2 = {y}$ and
${x}_2 = {y}$ and ![]() ${x}_3 = z$, being the streamwise, wall-normal and spanwise directions, respectively. Correspondingly,
${x}_3 = z$, being the streamwise, wall-normal and spanwise directions, respectively. Correspondingly, ![]() ${\boldsymbol{u}}_i = ({u}, {v}, {w})$ is the velocity vector field, with the subscript
${\boldsymbol{u}}_i = ({u}, {v}, {w})$ is the velocity vector field, with the subscript ![]() $i$ denoting the direction. Also,
$i$ denoting the direction. Also, ![]() $p$ is the pressure field,
$p$ is the pressure field, ![]() $\rho$ is the fluid density, and
$\rho$ is the fluid density, and ![]() $\nu$ is the kinematic viscosity of the fluid. The angle brackets denote a filtering operation, and the turbulence stress terms
$\nu$ is the kinematic viscosity of the fluid. The angle brackets denote a filtering operation, and the turbulence stress terms ![]() $\langle \boldsymbol{u}_i \boldsymbol{u}_j\rangle$ comprise both the resolved term and the effect of the sub-grid scales, which are modelled using a sub-grid scale (SGS) model. When presenting results, an overbar represents time averaging, and a dash represents the remaining fluctuating part of the field.
$\langle \boldsymbol{u}_i \boldsymbol{u}_j\rangle$ comprise both the resolved term and the effect of the sub-grid scales, which are modelled using a sub-grid scale (SGS) model. When presenting results, an overbar represents time averaging, and a dash represents the remaining fluctuating part of the field.
In order to relax the grid requirements needed to complete wall-resolved LES (WRLES), a hybrid RANS-LES model was used. By using the improved delayed detached eddy simulation (IDDES) implementation of Shur et al. (Reference Shur, Spalart, Strelets and Travin2008) in the configuration designed for wall-modelled LES (WMLES), the grid spacing in the streamwise and spanwise directions can be increased considerably, since only the outer region of the turbulent boundary layer, ![]() $y/\delta >0.1$, is treated with LES, while the inner region is handled with a RANS model. To appreciate the magnitude of this saving, Piomelli (Reference Piomelli2008) estimated that for
$y/\delta >0.1$, is treated with LES, while the inner region is handled with a RANS model. To appreciate the magnitude of this saving, Piomelli (Reference Piomelli2008) estimated that for ![]() $Re\approx 10^6$, the number of mesh cells required to resolve the inner region of the boundary layer, as required in WRLES, is around two orders of magnitude higher than the number of cells needed in the outer region. In this study, the Spalart–Allmaras one-equation RANS model is used to model turbulence quantities in the inner boundary layer, before switching rapidly to full LES away from the wall. The WMLES branch is designed to be activated in the presence of unsteady inflow conditions provided that the grid is sufficiently fine for resolving the dominant eddies found within a turbulent boundary layer. More details of the WMLES model can be found in Appendix A and in the paper of Shur et al. (Reference Shur, Spalart, Strelets and Travin2008).
$Re\approx 10^6$, the number of mesh cells required to resolve the inner region of the boundary layer, as required in WRLES, is around two orders of magnitude higher than the number of cells needed in the outer region. In this study, the Spalart–Allmaras one-equation RANS model is used to model turbulence quantities in the inner boundary layer, before switching rapidly to full LES away from the wall. The WMLES branch is designed to be activated in the presence of unsteady inflow conditions provided that the grid is sufficiently fine for resolving the dominant eddies found within a turbulent boundary layer. More details of the WMLES model can be found in Appendix A and in the paper of Shur et al. (Reference Shur, Spalart, Strelets and Travin2008).
The inlet boundary conditions to the LES domain are obtained from the RANS domain, for which the Spalart–Allmaras turbulence model is used, details of which can be found in the paper of Spalart & Allmaras (Reference Spalart and Allmaras1992). The current work uses a formulation without the trip term or ft2 term implemented, and with a limiter on the modified vorticity term to prevent negative values. The Spalart–Allmaras turbulence model was chosen for the background RANS calculation as it is particularly well calibrated for use on boundary layer flows and follows the methodology applied in earlier studies using similar techniques on turbulent boundary layers (Mockett, Haase & Schwamborn Reference Mockett, Haase and Schwamborn2017). In order to transition effectively from the RANS-modelled description of the flow in the precursor calculation to the region of LES, turbulence fluctuations in the velocity field must be introduced as these are not present in the averaged flow field of the RANS calculation. The synthetic eddy method (SEM), first proposed by Jarrin et al. (Reference Jarrin, Benhamadouche, Laurence and Prosser2006), is an efficient method used to introduce fluctuations to the velocity field at the LES inlet that can be applied to inhomogeneous fields. The method superimposes a prescribed number of randomly positioned eddies onto the mean velocity field, which are then scaled to match the spatial estimate of turbulence provided from the RANS model. The resulting fluctuating velocity field contains turbulent structures that are coherent in both time and space, and exist over a range of scales. Further details of the method used in this investigation, including improvements to the original SEM, are presented in the work by Skillen, Revell & Craft (Reference Skillen, Revell and Craft2016).
In this study, the finite volume code OpenFOAM-v1812 is used (Weller et al. Reference Weller, Tabor, Jasak and Fureby1999). For the LES, the coupled momentum and pressure equations are solved using the PISO algorithm with the time integration performed using a second-order backwards differencing, and spatial discretisation done using second-order schemes. For the precursor RANS calculation, the SIMPLE algorithm is used for the coupling of the momentum and pressure equations, with spatial discretisation performed using second-order schemes.
2.2. Boundary conditions
For the precursor two-dimensional RANS calculation, the domain is set up following the validation case of Rumsey, Smith & Huang (Reference Rumsey, Smith and Huang2009). The velocity inlet boundary condition is defined by a uniform Dirichlet condition ![]() $U_x = U_0 = 70\,{\rm m}\,{\rm s}^{-1}$. The outlet and top velocity boundary conditions are zero-gradient Neumann conditions, while the lower boundary has an initial section of a symmetrical boundary condition followed by a no-slip wall, as shown in figure 2. The pressure inlet condition is zero-gradient Neumann, with the other pressure boundaries zero-value Dirichlet conditions. The turbulence quantity for the Spalart–Allmaras model at the inflow is set to be three times the kinematic viscosity,
$U_x = U_0 = 70\,{\rm m}\,{\rm s}^{-1}$. The outlet and top velocity boundary conditions are zero-gradient Neumann conditions, while the lower boundary has an initial section of a symmetrical boundary condition followed by a no-slip wall, as shown in figure 2. The pressure inlet condition is zero-gradient Neumann, with the other pressure boundaries zero-value Dirichlet conditions. The turbulence quantity for the Spalart–Allmaras model at the inflow is set to be three times the kinematic viscosity, ![]() $\tilde {\nu } = 3\nu$, based on the recommendation by Spalart & Rumsey (Reference Spalart and Rumsey2007).
$\tilde {\nu } = 3\nu$, based on the recommendation by Spalart & Rumsey (Reference Spalart and Rumsey2007).
For the LES domain, the SEM is used to define the inlet velocity, based on the information from the precursor RANS calculation. The turbulence quantities at the inflow are taken from the value of ![]() $\tilde {\nu }$ from the precursor RANS model multiplied by the blending functions
$\tilde {\nu }$ from the precursor RANS model multiplied by the blending functions ![]() $f_B$ and
$f_B$ and ![]() $f_{e1}$ given in Appendix A as (A2a,b) and (A4a,b). A no-slip condition is applied along the lower wall, whilst the outlet and top velocity boundary conditions are zero-gradient Neumann conditions, and the front and back boundaries are periodic in the lateral direction as vortex generators are often found in arrays and match the set-up used by Liu et al. (Reference Liu, Piomelli and Spalart1996). The pressure inlet condition is zero-gradient Neumann with the top, wall and outlet pressure boundaries defined with zero-value Dirichlet conditions.
$f_{e1}$ given in Appendix A as (A2a,b) and (A4a,b). A no-slip condition is applied along the lower wall, whilst the outlet and top velocity boundary conditions are zero-gradient Neumann conditions, and the front and back boundaries are periodic in the lateral direction as vortex generators are often found in arrays and match the set-up used by Liu et al. (Reference Liu, Piomelli and Spalart1996). The pressure inlet condition is zero-gradient Neumann with the top, wall and outlet pressure boundaries defined with zero-value Dirichlet conditions.
2.3. Vortices
The vortex generators themselves are not resolved in this study. Instead, a simple vortex model is used to represent their downstream impact on the mean velocity field. The model is then combined with both the RANS turbulent boundary layer profile and the synthetic turbulence fluctuations to provide the inlet condition for the LES domain. In this way, the LES domain can be considered to start immediately downstream of the vortex generator.
A velocity field is generated to model the inclusion of the vortex by using the Batchelor vortex model (Batchelor Reference Batchelor1964). In order to model a vortex pair, two Batchelor vortices are introduced, and in order to enforce the non-permeable condition imposed by the solid wall, two additional mirror vortices are also included beneath the wall, as illustrated in figure 3, corresponding to each of the real vortices. The velocity fields of the individual vortices are created using a form of the Batchelor vortex equations that Velte, Hansen & Okulov (Reference Velte, Hansen and Okulov2009) found matched experimental results. The azimuthal velocity is defined by
where ![]() $q$ is the strength of the vortex,
$q$ is the strength of the vortex, ![]() $r$ is the distance away from the centre of the vortex, and
$r$ is the distance away from the centre of the vortex, and ![]() $R$ is a length scale corresponding to the radius of the vortex core. To model the streamwise velocity deficit introduced in real vortex generators by the delta-wing-shaped devices, a velocity component in the streamwise component is included, defined by
$R$ is a length scale corresponding to the radius of the vortex core. To model the streamwise velocity deficit introduced in real vortex generators by the delta-wing-shaped devices, a velocity component in the streamwise component is included, defined by
where ![]() $q_w$ is the strength of the wake, and the constant
$q_w$ is the strength of the wake, and the constant ![]() $\ln (2)$ is used to set the magnitude of
$\ln (2)$ is used to set the magnitude of ![]() $V_x$ at the edge of the core to be half the maximum magnitude. Two vortices and their corresponding mirror vortices can then be defined with centres in the wall-normal direction
$V_x$ at the edge of the core to be half the maximum magnitude. Two vortices and their corresponding mirror vortices can then be defined with centres in the wall-normal direction ![]() $y = \pm H_v$, and in the spanwise direction at
$y = \pm H_v$, and in the spanwise direction at ![]() $z = \pm S_v/2$. In order to enforce the no-slip condition at the wall, the azimuthal velocity is reduced linearly from distance
$z = \pm S_v/2$. In order to enforce the no-slip condition at the wall, the azimuthal velocity is reduced linearly from distance ![]() $y/\delta _0 = 0.1$, where
$y/\delta _0 = 0.1$, where ![]() $\delta _0$ is the boundary layer height at the LES inlet location. The Batchelor vortex model presented provides an approximation of the vortices found in the wake of a vortex generator and makes the assumption that the vortices are rotationally symmetrical and do not contain a radial component. The effects of these assumptions are considered relatively minor compared to the contribution of the azimuthal velocity component. Only the effect of the vortices on the velocity field is considered here, and no additional turbulence is introduced beyond that from the boundary layer. This limitation of the approach is difficult to avoid as a model of the additional turbulence would depend strongly on the specific geometry of the vortex generators. In § 4.1, the resulting flow of this model is compared to that found experimentally in the wake of a pair of vortex generators by Pauley & Eaton (Reference Pauley and Eaton1988). The comparison suggests that the flow would not be particularly sensitive to additional turbulence contributions, with the interaction between the vortices and the boundary layer turbulence dominating the behaviour.
$\delta _0$ is the boundary layer height at the LES inlet location. The Batchelor vortex model presented provides an approximation of the vortices found in the wake of a vortex generator and makes the assumption that the vortices are rotationally symmetrical and do not contain a radial component. The effects of these assumptions are considered relatively minor compared to the contribution of the azimuthal velocity component. Only the effect of the vortices on the velocity field is considered here, and no additional turbulence is introduced beyond that from the boundary layer. This limitation of the approach is difficult to avoid as a model of the additional turbulence would depend strongly on the specific geometry of the vortex generators. In § 4.1, the resulting flow of this model is compared to that found experimentally in the wake of a pair of vortex generators by Pauley & Eaton (Reference Pauley and Eaton1988). The comparison suggests that the flow would not be particularly sensitive to additional turbulence contributions, with the interaction between the vortices and the boundary layer turbulence dominating the behaviour.

Figure 3. Diagram showing the set-up of the vortex pair at the inlet to the LES region and the definition of the parameters used in their creation.
The strength (![]() $q$) and radius (
$q$) and radius (![]() $R$) of the vortices can be defined independently in order to achieve a configuration that represents the vortices generated by a skewed vortex generator. As shown in figure 3, when the flow direction is skewed by angle
$R$) of the vortices can be defined independently in order to achieve a configuration that represents the vortices generated by a skewed vortex generator. As shown in figure 3, when the flow direction is skewed by angle ![]() $\alpha$, the relative angles of the vortex generators are
$\alpha$, the relative angles of the vortex generators are ![]() $\beta \pm \alpha$, where
$\beta \pm \alpha$, where ![]() $\beta$ is the designed angle of the vortex generator. It is then this relative angle that correlates to the strength of each vortex. In this study, the effects of varying vortex configurations are investigated by varying the relative signs of the vortices, with
$\beta$ is the designed angle of the vortex generator. It is then this relative angle that correlates to the strength of each vortex. In this study, the effects of varying vortex configurations are investigated by varying the relative signs of the vortices, with ![]() $q_1/q_2 = -1$ describing counter-rotating vortices, and
$q_1/q_2 = -1$ describing counter-rotating vortices, and ![]() $q_1/q_2 = 1$ co-rotating vortices. The separation distance (
$q_1/q_2 = 1$ co-rotating vortices. The separation distance (![]() $S_v$) between the vortices for both counter-rotating and co-rotating vortex pairs, and the effect of varying the skew angle (
$S_v$) between the vortices for both counter-rotating and co-rotating vortex pairs, and the effect of varying the skew angle (![]() $\alpha$), are explored in § 4.3.
$\alpha$), are explored in § 4.3.
2.4. Mesh
The meshes used for the WMLES calculations are constructed according to best practice guidelines from a study of the same baseline case in the EU project ‘Go4Hybrid’ (Mockett et al. Reference Mockett, Haase and Schwamborn2017), and focus on capturing accurately the outer part of the boundary layer at an efficient resolution. The main mesh characteristics for the WMLES cases with and without vortices included are presented alongside those of the RANS mesh in table 1.
Table 1. Properties of the meshes used for both cases.

For the LES calculations, the total number of grid points is ![]() $N_{xyz} \approx 7.6 \times 10^6$ for the mesh used for the turbulent boundary layer only. When the vortices are introduced, the domain size is increased in the spanwise direction from
$N_{xyz} \approx 7.6 \times 10^6$ for the mesh used for the turbulent boundary layer only. When the vortices are introduced, the domain size is increased in the spanwise direction from ![]() $5\delta _0$ to
$5\delta _0$ to ![]() $12.5\delta _0$ in order to capture the vortices as they develop downstream; this specific width is chosen to match the width of the domain used in the reference study by Liu et al. (Reference Liu, Piomelli and Spalart1996). Additional refinement is also included in the
$12.5\delta _0$ in order to capture the vortices as they develop downstream; this specific width is chosen to match the width of the domain used in the reference study by Liu et al. (Reference Liu, Piomelli and Spalart1996). Additional refinement is also included in the ![]() $y$-direction to account for the slight increase in boundary layer height, which leads to a larger mesh of size
$y$-direction to account for the slight increase in boundary layer height, which leads to a larger mesh of size ![]() $N_{xyz} \approx 20 \times 10^6$. The wall-normal grid size for the turbulent boundary layer flow and the corresponding blending behaviour is shown to be performing as designed in § 3. The sensitivity to the grid spacing with the inclusion of vortices is shown through the comparison of the vortex development on different grids in § 4.1.
$N_{xyz} \approx 20 \times 10^6$. The wall-normal grid size for the turbulent boundary layer flow and the corresponding blending behaviour is shown to be performing as designed in § 3. The sensitivity to the grid spacing with the inclusion of vortices is shown through the comparison of the vortex development on different grids in § 4.1.
3. Zero pressure gradient turbulent boundary layer
In order to verify the proposed methodology, an initial investigation was conducted on a ZPG turbulent boundary layer free from the influence of vortices. The free stream velocity in this case is ![]() $U_0 = 70\,{\rm m}\,{\rm s}^{-1}$, with viscosity
$U_0 = 70\,{\rm m}\,{\rm s}^{-1}$, with viscosity ![]() $\nu = 1.48305\times 10^{-5}\,{\rm m}^{2}\,{\rm s}^{-1}$, resulting in a Reynolds number per metre
$\nu = 1.48305\times 10^{-5}\,{\rm m}^{2}\,{\rm s}^{-1}$, resulting in a Reynolds number per metre ![]() $Re/x = 4.72\times 10^6 \,{\rm m}^{-1}$. From the precursor RANS calculation, the mean flow and turbulence statistics were taken in order to produce the inlet condition for the LES region.
$Re/x = 4.72\times 10^6 \,{\rm m}^{-1}$. From the precursor RANS calculation, the mean flow and turbulence statistics were taken in order to produce the inlet condition for the LES region.
The LES domain is selected to begin at the point in the domain where the Reynolds number based on the momentum thickness (![]() $\theta$) of the boundary layer is
$\theta$) of the boundary layer is ![]() ${Re_{\theta _0} = {U_0 \theta _0}/{\nu } = 3040}$, and the initial boundary layer thickness is
${Re_{\theta _0} = {U_0 \theta _0}/{\nu } = 3040}$, and the initial boundary layer thickness is ![]() $\delta _0 = 5.8\times 10^{-3}\,{\rm m}$.
$\delta _0 = 5.8\times 10^{-3}\,{\rm m}$.
The profile of mean streamwise velocity (![]() $U$) is compared to experimental data from DeGraaff & Eaton (Reference DeGraaff and Eaton2000) at a downstream location where
$U$) is compared to experimental data from DeGraaff & Eaton (Reference DeGraaff and Eaton2000) at a downstream location where ![]() $Re_{\theta } = 5200$, as shown in figure 4, along with profiles of the turbulence shear and normal stresses. The quantities denoted with a
$Re_{\theta } = 5200$, as shown in figure 4, along with profiles of the turbulence shear and normal stresses. The quantities denoted with a ![]() $+$ are normalised by the wall friction velocity
$+$ are normalised by the wall friction velocity ![]() $u_{\tau } = \sqrt {\tau _w/\rho }$, where the wall shear stress is
$u_{\tau } = \sqrt {\tau _w/\rho }$, where the wall shear stress is ![]() $\tau _w = {\partial u}/{\partial y}\vert _w$, and are plotted over the distance from the wall in wall units
$\tau _w = {\partial u}/{\partial y}\vert _w$, and are plotted over the distance from the wall in wall units ![]() $y+ = {y u_{\tau }}/{\nu }$ to display the values close to the wall, and with outer units
$y+ = {y u_{\tau }}/{\nu }$ to display the values close to the wall, and with outer units ![]() $y/\delta$ to show the performance away from the wall. The turbulence model is active in the near-wall region, up to
$y/\delta$ to show the performance away from the wall. The turbulence model is active in the near-wall region, up to ![]() $y+ \approx 100$, after which there is a switch to LES, and the modelled shear stress drops to zero. A small velocity mismatch in the log layer corresponds to this switch from RANS to LES, which is characteristic of this model and due to the low resolution in the near-wall region (see e.g. Gritskevich, Garbaruk & Menter Reference Gritskevich, Garbaruk and Menter2017). The LES framework is otherwise shown to calculate accurately the first and second moment statistics of the turbulent flow, particularly in the outer region
$y+ \approx 100$, after which there is a switch to LES, and the modelled shear stress drops to zero. A small velocity mismatch in the log layer corresponds to this switch from RANS to LES, which is characteristic of this model and due to the low resolution in the near-wall region (see e.g. Gritskevich, Garbaruk & Menter Reference Gritskevich, Garbaruk and Menter2017). The LES framework is otherwise shown to calculate accurately the first and second moment statistics of the turbulent flow, particularly in the outer region ![]() $y/\delta >0.1$, corresponding approximately to
$y/\delta >0.1$, corresponding approximately to ![]() $y+>200$, which is the region where the vortex will be introduced.
$y+>200$, which is the region where the vortex will be introduced.

Figure 4. Velocity and Reynolds stress profiles at ![]() $Re_{\theta } = 5200$, with crosses showing experimental data from DeGraaff & Eaton (Reference DeGraaff and Eaton2000). Profiles are given in (a–c) wall units and (d–f) outer units.
$Re_{\theta } = 5200$, with crosses showing experimental data from DeGraaff & Eaton (Reference DeGraaff and Eaton2000). Profiles are given in (a–c) wall units and (d–f) outer units.
Downstream of the inlet, the imposed synthetic fluctuations rapidly bring about the resolution of realistic turbulent structures in the outer region, where the LES is active, as shown in figure 5. This can be seen by the fast convergence of the power spectral density (PSD) plot with streamwise location. This adjustment period occurs at a slower rate in the inner layer since the SEM is not active in the RANS region near the wall. To measure the ‘recovery length’ at the wall, the coefficient of friction ![]() $C_f = \tau _w / (0.5 \rho U_0^2)$ is plotted along the length of the plate in figure 5. There is an initial drop in
$C_f = \tau _w / (0.5 \rho U_0^2)$ is plotted along the length of the plate in figure 5. There is an initial drop in ![]() $C_f$ at the very start, due to a lack of prescribed turbulence in this region, before the flow recovers and
$C_f$ at the very start, due to a lack of prescribed turbulence in this region, before the flow recovers and ![]() $C_f$ returns to match the DNS (Schlatter & Örlü Reference Schlatter and Örlü2010) and experimental (DeGraaff & Eaton Reference DeGraaff and Eaton2000; Osterlund, Lindgren & Johansson Reference Osterlund, Lindgren and Johansson2003) values. In order to reduce the recovery length required for the development of the turbulence statistics, an investigation into the effect of the prescribed length scales in each direction,
$C_f$ returns to match the DNS (Schlatter & Örlü Reference Schlatter and Örlü2010) and experimental (DeGraaff & Eaton Reference DeGraaff and Eaton2000; Osterlund, Lindgren & Johansson Reference Osterlund, Lindgren and Johansson2003) values. In order to reduce the recovery length required for the development of the turbulence statistics, an investigation into the effect of the prescribed length scales in each direction, ![]() $\boldsymbol{\sigma} _{i}$, used in the generation of the turbulent structures by the SEM, was conducted. In this study, this quantity is taken to be one of the forms
$\boldsymbol{\sigma} _{i}$, used in the generation of the turbulent structures by the SEM, was conducted. In this study, this quantity is taken to be one of the forms
where ![]() $k$ is the turbulence kinetic energy,
$k$ is the turbulence kinetic energy, ![]() $\varepsilon$ is the turbulence time scale, and
$\varepsilon$ is the turbulence time scale, and ![]() $\boldsymbol{\mathsf{R}}_{ii}$ are the normal turbulence stresses, with the subscript
$\boldsymbol{\mathsf{R}}_{ii}$ are the normal turbulence stresses, with the subscript ![]() $i$ denoting the direction
$i$ denoting the direction ![]() $(x, y, z)$. These give either an isotropic or an anisotropic eddy shape, respectively. As a linear Boussinesq representation is used in the RANS domain, the Reynolds stresses are calculated for the flat plate using the Wilcox hypothesis as follows, as suggested in Laraufie & Deck (Reference Laraufie and Deck2013):
$(x, y, z)$. These give either an isotropic or an anisotropic eddy shape, respectively. As a linear Boussinesq representation is used in the RANS domain, the Reynolds stresses are calculated for the flat plate using the Wilcox hypothesis as follows, as suggested in Laraufie & Deck (Reference Laraufie and Deck2013):

Figure 5. (a) Power spectral density (PSD) of the streamwise velocity, sampled at a height ![]() $y=0.5\delta _0$, for various downstream locations. (b) Coefficient of friction along the length of the domain showing the development length for the different length scale definitions compared to DNS data, experimental data and the Coles–Femholz correlation.
$y=0.5\delta _0$, for various downstream locations. (b) Coefficient of friction along the length of the domain showing the development length for the different length scale definitions compared to DNS data, experimental data and the Coles–Femholz correlation.
Figure 6 presents the different length scales employed with the SEM at the inlet to the LES domain at ![]() $Re_{\theta } = 3040$. Also shown is the length scale calculated using (3.1) but with the
$Re_{\theta } = 3040$. Also shown is the length scale calculated using (3.1) but with the ![]() $\boldsymbol{\mathsf{R}}_{ii}$ values taken from the DNS data of Schlatter & Örlü (Reference Schlatter and Örlü2010) to give a more accurate definition for comparison. Figure 5 indicates that the development length is significantly shortened by the introduction of an anisotropic length scale when compared to an isotropic length scale. Furthermore, the results using the Wilcox length scale are very similar to those when using DNS data, which indicates that the former is sufficient for this flow. Further cases presented here therefore use the Wilcox anisotropic length scale definition. The approximate development length determined from figure 5 is highlighted in relevant future plots by the shaded region at the start of the domain.
$\boldsymbol{\mathsf{R}}_{ii}$ values taken from the DNS data of Schlatter & Örlü (Reference Schlatter and Örlü2010) to give a more accurate definition for comparison. Figure 5 indicates that the development length is significantly shortened by the introduction of an anisotropic length scale when compared to an isotropic length scale. Furthermore, the results using the Wilcox length scale are very similar to those when using DNS data, which indicates that the former is sufficient for this flow. Further cases presented here therefore use the Wilcox anisotropic length scale definition. The approximate development length determined from figure 5 is highlighted in relevant future plots by the shaded region at the start of the domain.

Figure 6. Length scale definitions used in the SEM inlet condition varying in the wall-normal direction reconstructed using (a) an isotropic length scale, (b) an anisotropic length scale (from Laraufie & Deck Reference Laraufie and Deck2013), and (c) a DNS length scale (from Schlatter & Örlü Reference Schlatter and Örlü2010).
4. The incorporation of vortex pairs
4.1. Validation of method
The central focus in this paper is the vortex generator study reported by Pauley & Eaton (Reference Pauley and Eaton1988), later replicated numerically by Liu et al. (Reference Liu, Piomelli and Spalart1996) using LES with a rescaling method proposed by Spalart & Watmuff (Reference Spalart and Watmuff1993) to rescale the spatially developing boundary layer in a periodic domain. They introduced the vortex pairs using a body force of a similar field as that used in the present work, described in § 2.3. In the current study, the Batchelor vortices are applied at the location corresponding to the first measurement point in the experiment, immediately downstream of the vortex generator. These vortices, henceforth referred to as the primary vortices, were generated with a separation distance ![]() $S_v = 11\delta _0/4$, at height above the wall
$S_v = 11\delta _0/4$, at height above the wall ![]() $h_v = 5\delta _0/8$, with radii
$h_v = 5\delta _0/8$, with radii ![]() $R_1 = R_2 = 2.1\delta _0/8$ and the vortex strength in (2.2),
$R_1 = R_2 = 2.1\delta _0/8$ and the vortex strength in (2.2), ![]() $q_1 = -q_2 = 0.37 U_0$. These setting were selected to match the velocity profiles used by Liu et al. (Reference Liu, Piomelli and Spalart1996), as shown in figure 7. These profiles match closely between the current method of applying the vortices to the velocity field of the inlet and the method of applying a body force used by Liu et al. (Reference Liu, Piomelli and Spalart1996). In (2.3),
$q_1 = -q_2 = 0.37 U_0$. These setting were selected to match the velocity profiles used by Liu et al. (Reference Liu, Piomelli and Spalart1996), as shown in figure 7. These profiles match closely between the current method of applying the vortices to the velocity field of the inlet and the method of applying a body force used by Liu et al. (Reference Liu, Piomelli and Spalart1996). In (2.3), ![]() $q_w$ is set as
$q_w$ is set as ![]() $1.25 |q|$ so that the local minimum streamwise velocity, at the vortex core, is
$1.25 |q|$ so that the local minimum streamwise velocity, at the vortex core, is ![]() $u = 0.45 U_0$, matching the value in the experiment (Liu et al. Reference Liu, Piomelli and Spalart1996).
$u = 0.45 U_0$, matching the value in the experiment (Liu et al. Reference Liu, Piomelli and Spalart1996).

Figure 7. The mean velocity components in the ![]() $x$-,
$x$-, ![]() $y$- and
$y$- and ![]() $z$-directions applied at the inlet to the LES domain compared to a Batchelor vortex and the inlet used by Liu et al. (Reference Liu, Piomelli and Spalart1996). The profiles of
$z$-directions applied at the inlet to the LES domain compared to a Batchelor vortex and the inlet used by Liu et al. (Reference Liu, Piomelli and Spalart1996). The profiles of ![]() $U$ and
$U$ and ![]() $W$ are located at the vortex core location in the
$W$ are located at the vortex core location in the ![]() $z$-direction, and the
$z$-direction, and the ![]() $V$ profiles are shown to each side of the vortex core.
$V$ profiles are shown to each side of the vortex core.
Downstream of the inlet, the development of the peak streamwise vorticity ![]() $\omega _x^{max}$, where the vorticity is defined as the curl of the velocity field
$\omega _x^{max}$, where the vorticity is defined as the curl of the velocity field ![]() $\boldsymbol{\omega} _i = \boldsymbol {\nabla } \times \boldsymbol{u}_i$, is shown along the length of the plate in figure 8. This is compared to corresponding values reported in both previous LES and experimental studies. The peak vorticity decay closely matches that reported by Liu et al. (Reference Liu, Piomelli and Spalart1996). In both the present work and the results of Liu et al., the vortex diffuses at a slightly greater rate than the experiment, particularly in the region
$\boldsymbol{\omega} _i = \boldsymbol {\nabla } \times \boldsymbol{u}_i$, is shown along the length of the plate in figure 8. This is compared to corresponding values reported in both previous LES and experimental studies. The peak vorticity decay closely matches that reported by Liu et al. (Reference Liu, Piomelli and Spalart1996). In both the present work and the results of Liu et al., the vortex diffuses at a slightly greater rate than the experiment, particularly in the region ![]() $x/\delta _0>20$. This discrepancy may be due to different levels of turbulence present in the experiment. In contrast, the reference RANS results from Kim & Patel (Reference Kim and Patel1994), reproduced in figure 8, can be seen to drastically under-predict this quantity. It is well established that standard RANS models, based on the linear Boussinesq hypothesis, fail to capture the turbulence at the vortex core, which arises due to the direct link between mean strain rate and turbulence Reynolds stresses. Excessive turbulence levels diffuse the momentum, thus the vorticity is reduced. More recent RANS results from Spalart et al. (Reference Spalart, Shur, Strelets and Travin2015) demonstrated some improvement by incorporating curvature correction, but still found an over-prediction in the downstream diffusion of the vortex, and subsequently lower levels of vorticity. The results of the coarser grid in figure 8 give confidence in the results obtained with the mesh at higher resolution.
$x/\delta _0>20$. This discrepancy may be due to different levels of turbulence present in the experiment. In contrast, the reference RANS results from Kim & Patel (Reference Kim and Patel1994), reproduced in figure 8, can be seen to drastically under-predict this quantity. It is well established that standard RANS models, based on the linear Boussinesq hypothesis, fail to capture the turbulence at the vortex core, which arises due to the direct link between mean strain rate and turbulence Reynolds stresses. Excessive turbulence levels diffuse the momentum, thus the vorticity is reduced. More recent RANS results from Spalart et al. (Reference Spalart, Shur, Strelets and Travin2015) demonstrated some improvement by incorporating curvature correction, but still found an over-prediction in the downstream diffusion of the vortex, and subsequently lower levels of vorticity. The results of the coarser grid in figure 8 give confidence in the results obtained with the mesh at higher resolution.

Figure 8. The evolution of the peak streamwise vorticity along the streamwise direction compared to Liu et al. (Reference Liu, Piomelli and Spalart1996), Kim & Patel (Reference Kim and Patel1994) and Pauley & Eaton (Reference Pauley and Eaton1988).
Further detailed comparison is presented in figure 9, showing a slice through the primary vortices at location ![]() $15\delta _0$ downstream of the inlet. At this location, the contours of a number of second-order statistics were plotted: the turbulence shear stress
$15\delta _0$ downstream of the inlet. At this location, the contours of a number of second-order statistics were plotted: the turbulence shear stress ![]() $-\overline {{u}'{v}'}$, the turbulence kinetic energy
$-\overline {{u}'{v}'}$, the turbulence kinetic energy ![]() $k = 0.5(\overline {{u}'{u}'} + \overline {{v}'{v}'} + \overline {{w}'{w}'})$, and the turbulence anisotropy
$k = 0.5(\overline {{u}'{u}'} + \overline {{v}'{v}'} + \overline {{w}'{w}'})$, and the turbulence anisotropy ![]() $-(\overline {{v}'{v}'}-\overline {{w}'{w}'})$. These are compared to the same plots from both the LES and experimental studies (Pauley & Eaton Reference Pauley and Eaton1988; Liu et al. Reference Liu, Piomelli and Spalart1996). The position, size and levels of the contours are observed to be in strong agreement with experimental results, slightly more so than those reported in the LES study of Liu et al., particularly if one examines the spanwise position of the primary vortex. The contours of the turbulence shear stress highlight a region of positive shear stress at the core, i.e. where
$-(\overline {{v}'{v}'}-\overline {{w}'{w}'})$. These are compared to the same plots from both the LES and experimental studies (Pauley & Eaton Reference Pauley and Eaton1988; Liu et al. Reference Liu, Piomelli and Spalart1996). The position, size and levels of the contours are observed to be in strong agreement with experimental results, slightly more so than those reported in the LES study of Liu et al., particularly if one examines the spanwise position of the primary vortex. The contours of the turbulence shear stress highlight a region of positive shear stress at the core, i.e. where ![]() $-\overline {{u}'{v}'} < 0$.
$-\overline {{u}'{v}'} < 0$.

Figure 9. Contour plots at location ![]() $x = 16\delta _0$ showing the computed (a,d,g) turbulence shear stress, (b,e,h) turbulence kinetic energy, and (c, f,i) turbulence anisotropy for (a–c) the current study, compared to (d–f) the previous LES study (Liu et al. Reference Liu, Piomelli and Spalart1996) and (g–i) the experimental study (Pauley & Eaton Reference Pauley and Eaton1988). (Solid lines show positive contours, and dashed lines show negative contours.)
$x = 16\delta _0$ showing the computed (a,d,g) turbulence shear stress, (b,e,h) turbulence kinetic energy, and (c, f,i) turbulence anisotropy for (a–c) the current study, compared to (d–f) the previous LES study (Liu et al. Reference Liu, Piomelli and Spalart1996) and (g–i) the experimental study (Pauley & Eaton Reference Pauley and Eaton1988). (Solid lines show positive contours, and dashed lines show negative contours.)
Line plots at this station (![]() $x = 16\delta _0$) for the mean velocity components and the turbulence shear stress are shown in Figure 10, comparing the results to those of a coarser mesh defined in table 1. These show that the first-order statistics of the flow are independent of the mesh. From this point onwards, the standard mesh with cells
$x = 16\delta _0$) for the mean velocity components and the turbulence shear stress are shown in Figure 10, comparing the results to those of a coarser mesh defined in table 1. These show that the first-order statistics of the flow are independent of the mesh. From this point onwards, the standard mesh with cells ![]() $N_{xyz} \approx 20 \times 10^6$ is used for all results.
$N_{xyz} \approx 20 \times 10^6$ is used for all results.

Figure 10. Line plots at location ![]() $x = 16\delta _0$ showing the mean velocity components computed using the standard and coarse meshes. The profiles of
$x = 16\delta _0$ showing the mean velocity components computed using the standard and coarse meshes. The profiles of ![]() $U$ and
$U$ and ![]() $W$ are located at the vortex core location in the
$W$ are located at the vortex core location in the ![]() $z$-direction, and the
$z$-direction, and the ![]() $V$ profiles are shown to each side of the vortex.
$V$ profiles are shown to each side of the vortex.
4.2. Counter-rotating, co-rotating and single-vortex flows
Once validated, the Batchelor vortex used to model the effects of the vortex generator can be adjusted easily, as described in § 2.3. This allows for a range of other vortex generator configurations to be investigated with relative ease by varying the parameters shown in figure 3. In the present subsection, results for a series of cases representing both counter-rotating and co-rotating vortex pairs and a single vortex are presented and discussed. The vortex properties used in these cases are given in table 2.
Table 2. Properties of baseline counter-rotating, co-rotating and single-vortex flows.
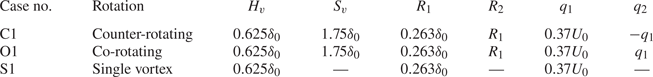
To start with, we compare three baseline cases, here referred to as case C1, the counter-rotating pair considered in § 4.1, case O1, which has the same set-up but with co-rotating vortices, and case S1, with a single vortex having the same strength and starting location.
4.2.1. Flow structure
Figures 11–13 display a visualisation of the flow in cases C1, O1 and S1, respectively. The plots include both ![]() $Q$-isocontours calculated from the instantaneous and time-averaged velocity:
$Q$-isocontours calculated from the instantaneous and time-averaged velocity:

Figure 11. Isocontours of the second invariant of the velocity gradient tensor (![]() $Q$) for the C1 case. Mean flow contours are shown in red, and instantaneous contours are coloured blue and yellow for negative and positive spanwise vorticity (
$Q$) for the C1 case. Mean flow contours are shown in red, and instantaneous contours are coloured blue and yellow for negative and positive spanwise vorticity (![]() $\omega _z$), respectively.
$\omega _z$), respectively.

Figure 12. Isocontours of the second invariant of the velocity gradient tensor (![]() $Q$) for the O1 case. Mean flow contours are shown in red, and instantaneous contours are coloured blue and yellow for negative and positive spanwise vorticity (
$Q$) for the O1 case. Mean flow contours are shown in red, and instantaneous contours are coloured blue and yellow for negative and positive spanwise vorticity (![]() $\omega _z$), respectively.
$\omega _z$), respectively.

Figure 13. Isocontours of the second invariant of the velocity gradient tensor (![]() $Q$) for the S1 case. Mean flow contours are shown in red, and instantaneous contours are coloured blue and yellow for negative and positive spanwise vorticity (
$Q$) for the S1 case. Mean flow contours are shown in red, and instantaneous contours are coloured blue and yellow for negative and positive spanwise vorticity (![]() $\omega _z$), respectively.
$\omega _z$), respectively.
Contours of ![]() $Q_{mean} = 2 \times 10^6$ are shown in red. These highlight the development of the mean vortices introduced by using the Batchelor vortex model as described in (2.2). The formation of a secondary, smaller vortex can be seen as the primary vortex interacts with the wall. Contours of
$Q_{mean} = 2 \times 10^6$ are shown in red. These highlight the development of the mean vortices introduced by using the Batchelor vortex model as described in (2.2). The formation of a secondary, smaller vortex can be seen as the primary vortex interacts with the wall. Contours of ![]() $Q_{inst} = 1 \times 10^5$ are clipped to show only those where the mean spanwise velocity is
$Q_{inst} = 1 \times 10^5$ are clipped to show only those where the mean spanwise velocity is ![]() $U_{z} > 5$ in the direction of the vortex, to highlight the instantaneous turbulent structures present over the top of the main vortex. The introduction of the turbulent structures at the inlet, and their interaction with the vortices, can be seen clearly. We also observe the formation of pairs of counter-rotating ring vortices, encircling the primary vortex highlighted in figures 11–13. These structures are coloured yellow and blue with positive and negative values of
$U_{z} > 5$ in the direction of the vortex, to highlight the instantaneous turbulent structures present over the top of the main vortex. The introduction of the turbulent structures at the inlet, and their interaction with the vortices, can be seen clearly. We also observe the formation of pairs of counter-rotating ring vortices, encircling the primary vortex highlighted in figures 11–13. These structures are coloured yellow and blue with positive and negative values of ![]() $\omega _z$, respectively. Initially, these ring vortices remain relatively coherent and grow in strength, before subsequently breaking down, due to both vortex–vortex and vortex–turbulence interactions. In the O1 case shown in figure 12, the two primary co-rotating vortices merge at location
$\omega _z$, respectively. Initially, these ring vortices remain relatively coherent and grow in strength, before subsequently breaking down, due to both vortex–vortex and vortex–turbulence interactions. In the O1 case shown in figure 12, the two primary co-rotating vortices merge at location ![]() $\approx 15\delta _0$.
$\approx 15\delta _0$.
Figures 14(a,b) display the trajectories of the vortex cores from plan and side views, respectively. All vortices remain within the boundary layer for the full extent of the domain. As well as spreading apart, the counter-rotating vortices rise up within the boundary, although they do not rise as high as a single vortex, suggesting that the proximity to the counter-rotating vortex is holding them closer to the wall. The co-rotating vortices combine and migrate to one side, while they also rise significantly higher than the counter-rotating pair, before settling just below the edge of the boundary layer.

Figure 14. Trajectory of the vortex cores along the length of the developing boundary layer for cases C1, O1 and S1, for (a) plan view and (b) side view. The grey region at the start of the domain represents the SEM development region. In the side view plot, the boundary layer thickness (![]() $\delta$) of an undisturbed boundary layer is shown in light grey for reference. (c) Integral of the positive shear stress over a plane. (d) Average shape factor along the length of the boundary layer. (e, f) Displacement and momentum thicknesses separately normalised by the case with no vortices present.
$\delta$) of an undisturbed boundary layer is shown in light grey for reference. (c) Integral of the positive shear stress over a plane. (d) Average shape factor along the length of the boundary layer. (e, f) Displacement and momentum thicknesses separately normalised by the case with no vortices present.
The shape factor ![]() $H$ is also plotted in figure 14(d) for these cases. This quantity, the ratio of the displacement thickness
$H$ is also plotted in figure 14(d) for these cases. This quantity, the ratio of the displacement thickness ![]() $\delta ^*$ to momentum thickness
$\delta ^*$ to momentum thickness ![]() $\theta$, provides a measure of how close to the wall the momentum is contained. A lower value of
$\theta$, provides a measure of how close to the wall the momentum is contained. A lower value of ![]() $H$ therefore represents a more effective vortex generator configuration. Note that the quantity is averaged over a spatial region equal to the full
$H$ therefore represents a more effective vortex generator configuration. Note that the quantity is averaged over a spatial region equal to the full ![]() $xz$ plane. It can be seen that the co-rotating pair, case O1, initially exhibits the lowest
$xz$ plane. It can be seen that the co-rotating pair, case O1, initially exhibits the lowest ![]() $H$, due perhaps to the movement of the smaller vortex towards the wall. At the point where the vortices merge, the co-rotating pair becomes less effective at transferring momentum to the vicinity of the wall, since the combined vortex settles in a location higher in the boundary layer than for the counter-rotating case C1. In all three cases, it can be seen that the shape factor is significantly lower than that of an undisturbed turbulent boundary layer. In the separate plots of displacement and momentum thickness shown in figures 14(e, f), respectively, it is shown that both thicknesses initially rise for the co-rotating and single vortices, whereas they initially drop for the counter-rotating case. This drop for the counter-rotating case can be attributed to the growing area of thinned boundary layer between the two vortices that is not present in the other cases. Case S1 is less effective at transferring momentum towards the wall, likely as with a single vortex the total circulation introduced is also lower. Figure 14(c) also displays a plot of the total positive shear stress over a plane,
$H$, due perhaps to the movement of the smaller vortex towards the wall. At the point where the vortices merge, the co-rotating pair becomes less effective at transferring momentum to the vicinity of the wall, since the combined vortex settles in a location higher in the boundary layer than for the counter-rotating case C1. In all three cases, it can be seen that the shape factor is significantly lower than that of an undisturbed turbulent boundary layer. In the separate plots of displacement and momentum thickness shown in figures 14(e, f), respectively, it is shown that both thicknesses initially rise for the co-rotating and single vortices, whereas they initially drop for the counter-rotating case. This drop for the counter-rotating case can be attributed to the growing area of thinned boundary layer between the two vortices that is not present in the other cases. Case S1 is less effective at transferring momentum towards the wall, likely as with a single vortex the total circulation introduced is also lower. Figure 14(c) also displays a plot of the total positive shear stress over a plane, ![]() $\iint ( \overline {u'v'} )_{pos}$, along
$\iint ( \overline {u'v'} )_{pos}$, along ![]() $x$, which is referred to later on.
$x$, which is referred to later on.
4.2.2. Vorticity and shear stress
Figures 15–17 describe the downstream development of axial vorticity and both streamwise and spanwise shear stresses, for cases C1, O1 and S1, respectively. For case C1, shown in figure 15, the vorticity contours show how the primary vortices interact with the wall and generate secondary vortices near the wall. These secondary vortices are then pulled outwards and away from the wall by the primary vortices. The primary vortices reduce in strength and gradually move apart along the length of the boundary layer.

Figure 15. Contour plots for case C1, showing (a,d,g,j,m,p,s,v) the streamwise vorticity, and the turbulence shear stresses (b,e,h,k,n,q,t,w) ![]() $\overline {u'v'}$ and (c, f,i,l,o,r,u,x)
$\overline {u'v'}$ and (c, f,i,l,o,r,u,x) ![]() $\overline {u'w'}$, with slices in the
$\overline {u'w'}$, with slices in the ![]() $yz$ plane taken at locations
$yz$ plane taken at locations ![]() $x/\delta _0 =0, 2, 5, 10, 15, 20, 30, 60$.
$x/\delta _0 =0, 2, 5, 10, 15, 20, 30, 60$.

Figure 16. Contour plots for case O1 showing (a,d,g,j,m,p,s,v) the streamwise vorticity, and and the turbulence shear stresses (b,e,h,k,n,q,t,w) ![]() $\overline {u'v'}$ and (c, f,i,l,o,r,u,x)
$\overline {u'v'}$ and (c, f,i,l,o,r,u,x) ![]() $\overline {u'w'}$, with slices in the
$\overline {u'w'}$, with slices in the ![]() $yz$ plane taken at locations
$yz$ plane taken at locations ![]() $x/\delta _0 =0, 2, 5, 10, 15, 20, 30, 60$.
$x/\delta _0 =0, 2, 5, 10, 15, 20, 30, 60$.

Figure 17. Contour plots for case S1 showing (a,d,g,j,m,p,s,v) the streamwise vorticity, and and the turbulence shear stresses (b,e,h,k,n,q,t,w) ![]() $\overline {u'v'}$ and (c, f,i,l,o,r,u,x)
$\overline {u'v'}$ and (c, f,i,l,o,r,u,x) ![]() $\overline {u'w'}$, with slices in the
$\overline {u'w'}$, with slices in the ![]() $yz$ plane taken at locations
$yz$ plane taken at locations ![]() $x/\delta _0 =0, 2, 5, 10, 15, 20, 30, 60$.
$x/\delta _0 =0, 2, 5, 10, 15, 20, 30, 60$.
The turbulence shear stress contour plots show that there is an area of considerable boundary layer thinning between the vortices. This is a good indication for the performance of the vortex generator in its ability to transfer momentum from the free stream closer to the wall and therefore delay the onset of potential separation. Also highlighted is the presence of an area of positive shear stress, shown in red. As discussed previously, this is an important factor in the preservation of the vortex, with the corresponding destruction of turbulence in the region slowing the diffusion of the vortex.
The contours of vorticity plots shown in figure 16 show a co-rotating vortex pair. In this case, both vortices initially move in the same direction before merging to form a single vortex from around ![]() $x=20\delta _0$. The merging of the vortices can also be seen in figure 14. It can be seen that the vortex starting at location
$x=20\delta _0$. The merging of the vortices can also be seen in figure 14. It can be seen that the vortex starting at location ![]() $z = -7\delta _0/8$ is pulled closer to the other vortex whilst also descending lower within the boundary layer. Conversely, the vortex that starts at location
$z = -7\delta _0/8$ is pulled closer to the other vortex whilst also descending lower within the boundary layer. Conversely, the vortex that starts at location ![]() $z=7\delta _0/8$ moves upwards. The lower vortex then passes underneath the other one before they combine at around
$z=7\delta _0/8$ moves upwards. The lower vortex then passes underneath the other one before they combine at around ![]() $x=20\delta _0$. Once the vortices have merged to form a single vortex, it continues to slowly move away from the wall at a height larger than that of the counter-rotating pair but still within the height of an undisturbed boundary layer.
$x=20\delta _0$. Once the vortices have merged to form a single vortex, it continues to slowly move away from the wall at a height larger than that of the counter-rotating pair but still within the height of an undisturbed boundary layer.
It can be seen from the contour plots of turbulence shear stress in figure 16 that at the point where the vortices merge, at ![]() $x=20\delta _0$, there is a significant drop in the positive shear stress. This is likely due to the increased shear flow that occurs as the two vortices approach each other. It can be seen in the contour plots in figure 16 that there is an area of strong, negative shear stress between the two vortex cores, supporting this hypothesis. In order to better assess this property, the shear stress is integrated in the area in the
$x=20\delta _0$, there is a significant drop in the positive shear stress. This is likely due to the increased shear flow that occurs as the two vortices approach each other. It can be seen in the contour plots in figure 16 that there is an area of strong, negative shear stress between the two vortex cores, supporting this hypothesis. In order to better assess this property, the shear stress is integrated in the area in the ![]() $yz$ plane where it is positive. This metric,
$yz$ plane where it is positive. This metric, ![]() $\iint ( \overline {u'v'} )_{pos}$, is then plotted against the streamwise direction and is shown for cases C1, O1 and S1 in figure 14. For the co-rotating vortex pairs, this shows a drop in positive shear stress as the vortices merge, followed by a significant rise.
$\iint ( \overline {u'v'} )_{pos}$, is then plotted against the streamwise direction and is shown for cases C1, O1 and S1 in figure 14. For the co-rotating vortex pairs, this shows a drop in positive shear stress as the vortices merge, followed by a significant rise.
4.2.3. Turbulence anisotropy and production
It is instructive to consider in more detail the nature of the observed levels of turbulence, both to aid the interpretation of the flow physics and to help us to understand RANS modelling of this flow. As discussed in § 1, previous attempts to use RANS models for these flows have demonstrated an inability to predict physics in the vortex core region. In this subsubsection, we consider the anisotropy of the turbulence, defined by
where ![]() ${\boldsymbol{\mathsf{\delta}}} _{ij}$ is the Kronecker delta function
${\boldsymbol{\mathsf{\delta}}} _{ij}$ is the Kronecker delta function
 \begin{equation} {\boldsymbol{\mathsf{\delta}}}_{ij} = \begin{cases} 1, & \text{if } i=j,\\ 0, & \text{otherwise}. \end{cases} \end{equation}
\begin{equation} {\boldsymbol{\mathsf{\delta}}}_{ij} = \begin{cases} 1, & \text{if } i=j,\\ 0, & \text{otherwise}. \end{cases} \end{equation}Also presented is the production of the turbulence kinetic energy which is calculated as
In figures 18–20, we display these quantities for cases C1, O1 and S1, respectively. The anisotropy is plotted using the colour map method proposed by Emory & Iaccarino (Reference Emory and Iaccarino2014). In this method, the componentality of the turbulence anisotropy at each point of the domain is allocated an RGB colour by mapping the eigenvalues ![]() $\lambda _i$ of the anisotropy tensor (
$\lambda _i$ of the anisotropy tensor (![]() $a_{ij}$) onto a barycentric map and assigning an RGB colour value to each position on this map:
$a_{ij}$) onto a barycentric map and assigning an RGB colour value to each position on this map:
 \begin{equation}
\left[ \begin{array}{@{}c@{}} {\rm
R}\\ {\rm G}\\ {\rm
B} \end{array} \right] = C_{1c}^*\left[ \begin{array}{@{}c@{}}
1\\ 0\\ 0 \end{array} \right] + C_{2c}^*\left[
\begin{array}{@{}c@{}} 0\\ 1\\ 0 \end{array} \right] +
C_{3c}^*\left[ \begin{array}{@{}c@{}} 0\\ 0\\ 1 \end{array}
\right],
\end{equation}
\begin{equation}
\left[ \begin{array}{@{}c@{}} {\rm
R}\\ {\rm G}\\ {\rm
B} \end{array} \right] = C_{1c}^*\left[ \begin{array}{@{}c@{}}
1\\ 0\\ 0 \end{array} \right] + C_{2c}^*\left[
\begin{array}{@{}c@{}} 0\\ 1\\ 0 \end{array} \right] +
C_{3c}^*\left[ \begin{array}{@{}c@{}} 0\\ 0\\ 1 \end{array}
\right],
\end{equation}where

Figure 18. Contour plots for case C1 of (a,d,g) turbulence kinetic energy ![]() $k$, (b,e,h) production of
$k$, (b,e,h) production of ![]() $k$,
$k$, ![]() $P_k$, and (c, f,i) anisotropy componentality. Slices are in the
$P_k$, and (c, f,i) anisotropy componentality. Slices are in the ![]() $yz$ plane at locations
$yz$ plane at locations ![]() $x/\delta _0 = 5, 15, 30$.
$x/\delta _0 = 5, 15, 30$.

Figure 19. Contour plots for case O1 of (a,d,g) turbulence kinetic energy ![]() $k$, (b,e,h) production of
$k$, (b,e,h) production of ![]() $k$,
$k$, ![]() $P_k$, and (c, f,i) anisotropy componentality. Slices are in the
$P_k$, and (c, f,i) anisotropy componentality. Slices are in the ![]() $yz$ plane at locations
$yz$ plane at locations ![]() $x/\delta _0 = 5, 12, 30$.
$x/\delta _0 = 5, 12, 30$.

Figure 20. Contour plots for case O1 of (a,d,g) turbulence kinetic energy ![]() $k$, (b,e,h) production of
$k$, (b,e,h) production of ![]() $k$,
$k$, ![]() $P_k$, and (c, f,i) anisotropy componentality. Slices are in the
$P_k$, and (c, f,i) anisotropy componentality. Slices are in the ![]() $yz$ plane at locations
$yz$ plane at locations ![]() $x/\delta _0 = 5, 15, 30$.
$x/\delta _0 = 5, 15, 30$.
The constants used to define the colour map are ![]() $C_{off} = 0.55$ and
$C_{off} = 0.55$ and ![]() $C_{exp} = 5$, such that distinct colours represent the three corners of the colour map (red, green and blue representing one component, axisymmetric two-component and isotropic turbulent structures, respectively) and the transition areas (yellow, cyan and magenta representing two-component, axisymmetric contraction and axisymmetric expansion, respectively). For clarity, a threshold is applied so that only areas of the flow where
$C_{exp} = 5$, such that distinct colours represent the three corners of the colour map (red, green and blue representing one component, axisymmetric two-component and isotropic turbulent structures, respectively) and the transition areas (yellow, cyan and magenta representing two-component, axisymmetric contraction and axisymmetric expansion, respectively). For clarity, a threshold is applied so that only areas of the flow where ![]() $k/U_0 > 0.005$ are shown.
$k/U_0 > 0.005$ are shown.
The contours of production in figure 18 show that in the initial development of the vortices, a ring of high turbulence kinetic energy production is formed around the centres of the two vortices. Further downstream, at ![]() $x=15\delta _0$, while the turbulence kinetic energy peaks at the centre of the vortices, a rapid drop in production is observed. Indeed, at the vortex core, the production takes small negative values, coloured red in the figure. This is due to the spatial lag between the Reynolds stresses and the mean strain field, and is a characteristic result of rotating turbulent flows. This leads to a reduction of turbulence in the core, which in turn helps to reduce diffusion and increase the coherence of the vortex structures downstream. This feature cannot be captured with standard, linear, RANS models without an appropriate correction term. In contrast to isolated vortices, the present configuration is more complex on account of the interaction of the vortex with the boundary layer, which provides a continual source of turbulence kinetic energy to the vortex core. The balance of these two effects is likely to be sensitive to the distance of the vortex from the wall, amongst other factors. This effect is also observed in the S1 case in figure 20, and in the O1 case in figure 19, where it peaks as the two co-rotating vortices approach each other before merging.
$x=15\delta _0$, while the turbulence kinetic energy peaks at the centre of the vortices, a rapid drop in production is observed. Indeed, at the vortex core, the production takes small negative values, coloured red in the figure. This is due to the spatial lag between the Reynolds stresses and the mean strain field, and is a characteristic result of rotating turbulent flows. This leads to a reduction of turbulence in the core, which in turn helps to reduce diffusion and increase the coherence of the vortex structures downstream. This feature cannot be captured with standard, linear, RANS models without an appropriate correction term. In contrast to isolated vortices, the present configuration is more complex on account of the interaction of the vortex with the boundary layer, which provides a continual source of turbulence kinetic energy to the vortex core. The balance of these two effects is likely to be sensitive to the distance of the vortex from the wall, amongst other factors. This effect is also observed in the S1 case in figure 20, and in the O1 case in figure 19, where it peaks as the two co-rotating vortices approach each other before merging.
Switching focus to the anisotropy plots, it is notable, in the context of the previous paragraph, that standard linear RANS models will not be able to account for the spatial lag between Reynolds stresses and the mean strain field. Furthermore, in shear flows dominated as in the present case, they will be limited in their ability to discern Reynolds stress anisotropy, in effect limiting their applicability to the blue regions of the graph for most of this flow, in some cases possibly also part of the cyan and magenta regions. In contrast, red and green regions, respectively referring to one- and two-component states of turbulence anisotropy, are beyond standard linear RANS models. The green regions above the vortices in the anisotropy plots in figures 18–20 show how as the mean flow outside the boundary layer is pulled in by the vortices, significant areas of axisymmetric two-component turbulence are found. Much of the areas of high production, near the surface of the wall and around the centre of the vortices, corresponds to red regions of the anisotropy plot. These are areas where turbulence tends towards a one-component state that represent characteristic near-wall streaks. Similar observations are made for the three cases C1, O1 and S1, highlighting the modelling challenge presented to RANS models for flows of this nature.
4.3. Parametric variation
To demonstrate the flexibility of the methodology proposed in § 4.1, we proceed to examine a series of different configurations of vortex pairs. In the following we report general trends observed by varying separation distance and effective skew angle for counter-rotating vortices.
4.3.1. Separation distance
For both counter-rotating and co-rotating vortex pairs, the effect of the separation distance ![]() $S_v$ on the dynamics of the vortices was investigated. The vortex paths in the
$S_v$ on the dynamics of the vortices was investigated. The vortex paths in the ![]() $xz$ plane are shown in figure 21. For the counter-rotating vortex pairs, the change in the separation distance at the inlet
$xz$ plane are shown in figure 21. For the counter-rotating vortex pairs, the change in the separation distance at the inlet ![]() $S_v$ correlates to a similar change in the vortex separation as they spread apart along the length of the domain. For the co-rotating pair, the inlet separation distance greatly affects the merging of the vortices; the closer together the vortices begin, the sooner they merge.
$S_v$ correlates to a similar change in the vortex separation as they spread apart along the length of the domain. For the co-rotating pair, the inlet separation distance greatly affects the merging of the vortices; the closer together the vortices begin, the sooner they merge.

Figure 21. Plots showing how the positions of the vortex cores in the ![]() $z$-direction vary along the length of the developing boundary layer. The vortex paths for a range of separation distances (
$z$-direction vary along the length of the developing boundary layer. The vortex paths for a range of separation distances (![]() $S_v$) are shown for (a) co-rotating and (b) counter-rotating vortex pairs.
$S_v$) are shown for (a) co-rotating and (b) counter-rotating vortex pairs.
The location in the streamwise direction at which the vortices combine affects the total circulation of the vortex. This can be explained by the corresponding drop in the positive shear stress. Figure 22 shows that at the point where the vortices merge, there is a drop in the total positive shear stress at the vortex cores. This then leads to a steeper drop in the total circulation, shown in figure 22 as the turbulence from the boundary layer acts to weaken the vortices. This in turn corresponds to a drop in the spanwise coefficient of friction (![]() $C_{f_z}$) on the wall, as shown in figure 23.
$C_{f_z}$) on the wall, as shown in figure 23.

Figure 22. Plots of (a) the integral of the positive shear stress in a plane, (b) total circulation over the length of the turbulent boundary layer, for co-rotating vortices with separation distances in the range ![]() $1.5 \leq S_v/\delta _0 \leq 2.5$.
$1.5 \leq S_v/\delta _0 \leq 2.5$.

Figure 23. Plots of coefficient of friction in (a,b) the ![]() $x$-direction, and (c,d) the
$x$-direction, and (c,d) the ![]() $z$-direction, for co-rotating vortices with various separation distances
$z$-direction, for co-rotating vortices with various separation distances ![]() $S_v$. Counter-rotating vortices are shown in (a,c), and co-rotating vortices in (b,d).
$S_v$. Counter-rotating vortices are shown in (a,c), and co-rotating vortices in (b,d).
For separation distances ![]() $S_v = 1.5 \delta _0$,
$S_v = 1.5 \delta _0$, ![]() $1.75 \delta _0$ and
$1.75 \delta _0$ and ![]() $2.0 \delta _0$, there is a clear dip at the positive turbulence shear stress around the location where the vortices merge, followed by a substantial peak. However, for separation distances
$2.0 \delta _0$, there is a clear dip at the positive turbulence shear stress around the location where the vortices merge, followed by a substantial peak. However, for separation distances ![]() $S_v > 2 \delta _0$, the drop in
$S_v > 2 \delta _0$, the drop in ![]() $\iint ( \overline {u'v'} )_{pos}$ is far more gradual. At separation distance
$\iint ( \overline {u'v'} )_{pos}$ is far more gradual. At separation distance ![]() $S_v = 2.25 \delta _0$, the area of positive shear stress recovers after merging; however, for
$S_v = 2.25 \delta _0$, the area of positive shear stress recovers after merging; however, for ![]() $S_v = 2.5\delta _0$, the integral drops to zero and no recovery is observed.
$S_v = 2.5\delta _0$, the integral drops to zero and no recovery is observed.
The effect of variable separation distance on the coefficient of friction at the wall is shown in figure 23, with both the streamwise (![]() $C_{f_x}$) and spanwise (
$C_{f_x}$) and spanwise (![]() $C_{f_z}$) values plotted for counter-rotating and co-rotating vortices. For counter-rotating vortex pairs, a higher separation distance corresponds to a faster rise in
$C_{f_z}$) values plotted for counter-rotating and co-rotating vortices. For counter-rotating vortex pairs, a higher separation distance corresponds to a faster rise in ![]() $C_{f_x}$. Although a higher
$C_{f_x}$. Although a higher ![]() $C_{f_x}$ corresponds to a higher drag force acting on the surface, it also suggests a higher resilience to separation, and shows the vortex generators working more effectively over a longer length. Vortices starting closer together are initially less effective, although in these cases,
$C_{f_x}$ corresponds to a higher drag force acting on the surface, it also suggests a higher resilience to separation, and shows the vortex generators working more effectively over a longer length. Vortices starting closer together are initially less effective, although in these cases, ![]() $C_{f_x}$ increases to levels observed in other cases further downstream as the vortices spread apart.
$C_{f_x}$ increases to levels observed in other cases further downstream as the vortices spread apart.
4.3.2. Skewed flow
In many practical applications, vortex generators are subject to yaw of the incoming flow. This could be due to either the misalignment of the vortex generators during installation or variations in the flow during operation, such as a vehicle under cornering conditions. This yaw angle leads to an imbalance in the vortex strength in a counter-rotating vortex pair. When investigating the effect of yaw angle, Lögdberg et al. (Reference Lögdberg, Fransson and Alfredsson2009) found that increasing the yaw angle in ![]() $0 \leq \beta \leq \alpha$ led to a linear increase in the strength of one vortex and a linear decrease in the other, with the total circulation remaining broadly constant. Following this, the relative strengths of the vortices
$0 \leq \beta \leq \alpha$ led to a linear increase in the strength of one vortex and a linear decrease in the other, with the total circulation remaining broadly constant. Following this, the relative strengths of the vortices ![]() $q_1$ and
$q_1$ and ![]() $q_2$ were varied whilst maintaining the total strength
$q_2$ were varied whilst maintaining the total strength ![]() $q_1 + q_2$, and it was taken that
$q_1 + q_2$, and it was taken that
Figure 24(a) shows how, by modelling the skew angle in this way, the average circulation over the full domain for the individual vortices follows a linear increase and decrease respectively with the total circulation remaining constant. This matches qualitatively the results of Lögdberg et al. (Reference Lögdberg, Fransson and Alfredsson2009).

Figure 24. Plots showing (a) the total circulation and the circulation of the contributing vortices, and (b) the difference in the average shape factor introduced by the change in angle over the whole domain as the skew angle ![]() $\alpha$ relative to the vortex generator angle
$\alpha$ relative to the vortex generator angle ![]() $\beta$ is varied. Plots of the coefficient of friction in (c) the
$\beta$ is varied. Plots of the coefficient of friction in (c) the ![]() $x$-direction and (d) the
$x$-direction and (d) the ![]() $z$-direction, for counter-rotating vortices with skew angles in the range
$z$-direction, for counter-rotating vortices with skew angles in the range ![]() $\alpha / \beta = 0\unicode{x2013}1$.
$\alpha / \beta = 0\unicode{x2013}1$.
Figure 24(b) displays how the angle of skew affects the total shape factor over the length of the boundary layer (![]() $H_{av}$). To highlight the change corresponding to the angle, this is shown relative to the shape factor of the case at
$H_{av}$). To highlight the change corresponding to the angle, this is shown relative to the shape factor of the case at ![]() $\alpha /\beta = 0$ by plotting
$\alpha /\beta = 0$ by plotting ![]() $H_{av} - H_0^{\circ }$. As the relative skew angle
$H_{av} - H_0^{\circ }$. As the relative skew angle ![]() $\alpha / \beta$ is increased in the range
$\alpha / \beta$ is increased in the range ![]() $0 \leq \alpha / \beta \leq 0.6$, the shape factor stays relatively consistent, with a slight decrease from the level found with
$0 \leq \alpha / \beta \leq 0.6$, the shape factor stays relatively consistent, with a slight decrease from the level found with ![]() $0^{\circ }$ of skew. This shows that over this range of skew angles, the effectiveness of the vortex generator to transfer momentum towards the wall and therefore delay the onset of separation is resistant to skew angle. At skew angles where
$0^{\circ }$ of skew. This shows that over this range of skew angles, the effectiveness of the vortex generator to transfer momentum towards the wall and therefore delay the onset of separation is resistant to skew angle. At skew angles where ![]() $0.8 \leq \alpha / \beta \leq 1$, there is an increase in the total shape factor of the downstream boundary layer that would correspond to a reduction in the vortex generator's effectiveness to delay the onset of separation. This step change in the performance of the vortex generator in
$0.8 \leq \alpha / \beta \leq 1$, there is an increase in the total shape factor of the downstream boundary layer that would correspond to a reduction in the vortex generator's effectiveness to delay the onset of separation. This step change in the performance of the vortex generator in ![]() $0.6<\alpha /\beta <0.8$ can also be seen in the coefficients of friction in figures 24(c,d). Here, two distinct groups can be seen in the behaviour of
$0.6<\alpha /\beta <0.8$ can also be seen in the coefficients of friction in figures 24(c,d). Here, two distinct groups can be seen in the behaviour of ![]() $C_{f_x}$ and
$C_{f_x}$ and ![]() $C_{f_z}$. For
$C_{f_z}$. For ![]() $0 \leq \alpha /\beta \leq 0.6$, higher values of
$0 \leq \alpha /\beta \leq 0.6$, higher values of ![]() $C_{f_x}$ and
$C_{f_x}$ and ![]() $C_{f_z}$ are displayed along the length of the domain, with a drop in both as
$C_{f_z}$ are displayed along the length of the domain, with a drop in both as ![]() $\alpha /\beta \geq 0.8$.
$\alpha /\beta \geq 0.8$.
5. Conclusions
In this study, we examined a range of cases investigating the effect of the properties of a vortex generator on the development of the streamwise vortices and their subsequent effect on the turbulent boundary layer. Vortex pairs in co-rotating and counter-rotating configurations have been investigated. The efficiency of the numerical method used has allowed for investigations into the effect of both the separation distance of the vortices and the skew angle of the incoming flow, whilst still capturing important turbulence properties accurately.
Initial work looking at an unaffected turbulent boundary layer allowed for the inlet turbulence generation method SEM to be optimised to reduce the development length. It was found that by providing an anisotropic definition of the turbulence length scale at the inlet, the development length was reduced from approximately 15 times the initial boundary layer height to approximately 6 times. By modelling the flow a short distance downstream of a vortex generator by using a pair of Batchelor vortices, the method was validated against previous LES and experimental studies for vortex generators. Both first-order statistics such as the peak streamwise vorticity and the total circulation, and second-order statistics of the turbulence, showed a strong correlation to these previous studies. Having made a direct comparison between the resulting flow developing from the theoretical vortex model and a previous experimental vortex generator flow, the method is applied to further configurations possible as a result of vortex generator design.
By varying the set-up of the Batchelor vortex model at the inlet to the LES domain, comparisons were made between co-rotating and counter-rotating vortex pairs and a single vortex. It was found that over the length of the domain, the counter-rotating pair produced a lower shape factor, thus more momentum is transferred close to the wall, delaying the potential onset of separation. However, it was also noted that as the vortices merge in a co-rotating vortex set-up, the proximity to the wall of one of the vortices, as it is pulled under the other, leads to better momentum transfer in this region, indicated by a lower shape factor. It was also found that by varying the separation distance for co-rotating vortices, the location of the vortices merging could be controlled. This could have the potential to improve the efficiency of the vortex generator if this merging location can be controlled adequately to match the location of the potential separation.
Also investigated was the effect of a skewed inlet flow condition to a vortex generator. This was modelled by an imbalance in the strength of the vortices generated, with the overall strength staying constant. This matched experimental results looking at vortex formation and allowed for the effectiveness of vortex generators in varying skew angle conditions to be assessed. It was found that over a broad range of inlet angles, the effectiveness of the vortices to exchange momentum close to the wall was unaffected, and only at particularly large angles was the effectiveness reduced. Although these variations are not related directly to the specific geometry changes of a vortex generator, they can aid in practical design decisions through the placement of the generators and through defining an effective operating range.
Funding
This research was funded by a MACE Beacon award. The authors would like to acknowledge the assistance given by Research IT and the use of the Computational Shared Facility at the University of Manchester. The authors would like to thank EPSRC for the computational time made available on the UK supercomputing facility ARCHER and ARCHER2 via the UK Turbulence Consortium (EP/R029326/1).
Declaration of interests
The authors report no conflict of interest.
Appendix A. IDDES
The WMLES branch of the IDDES model is implemented by providing a rapid switch between a RANS model near the wall and LES away from the wall. This switch is enabled by using a blended length scale definition, ![]() $L_{WMLES}$, common to DES implementations, and given by
$L_{WMLES}$, common to DES implementations, and given by
where ![]() $L_{RANS}$ and
$L_{RANS}$ and ![]() $L_{LES}$ are the RANS and LES length scales, respectively. The function
$L_{LES}$ are the RANS and LES length scales, respectively. The function ![]() $f_B$ switches smoothly from 1 near the wall to 0 away from the wall, based on the wall distance
$f_B$ switches smoothly from 1 near the wall to 0 away from the wall, based on the wall distance ![]() $d_w$ normalised by the largest cell size
$d_w$ normalised by the largest cell size ![]() $h_{max}$. It is defined empirically as
$h_{max}$. It is defined empirically as
The second empirical function, ![]() $f_e$, is included to alleviate the log-layer mismatch by artificially elevating the RANS Reynolds stresses near the wall. This function combines predefined effects of the wall distance with quantities defined by the flow:
$f_e$, is included to alleviate the log-layer mismatch by artificially elevating the RANS Reynolds stresses near the wall. This function combines predefined effects of the wall distance with quantities defined by the flow:
 \begin{gather} f_{e1} = \begin{cases} 2 \exp ({-}11.09 \alpha^2), & \text{if}\ \alpha \geq 0, \\ 2 \exp ({-}9.0 \alpha^2), & \text{if}\ \alpha < 0, \end{cases} \quad f_{e2} = 1.0 - \max[f_t, \, f_l] , \end{gather}
\begin{gather} f_{e1} = \begin{cases} 2 \exp ({-}11.09 \alpha^2), & \text{if}\ \alpha \geq 0, \\ 2 \exp ({-}9.0 \alpha^2), & \text{if}\ \alpha < 0, \end{cases} \quad f_{e2} = 1.0 - \max[f_t, \, f_l] , \end{gather}
where ![]() $r_{dl}$ and
$r_{dl}$ and ![]() $r_{dt}$ mark the laminar sublayer and logarithmic parts of the boundary layer, respectively. They are dependent on the solution and are given by
$r_{dt}$ mark the laminar sublayer and logarithmic parts of the boundary layer, respectively. They are dependent on the solution and are given by
 \begin{equation} r_{dt} = \frac{\nu_t}{\kappa^2 d_w^2 \max \left[ \left( \sum_{ij} (\partial \boldsymbol{u}_i / \partial \boldsymbol{x}_j)^2 \right)^{1/2} , \, 10^{{-}10}\right]} , \end{equation}
\begin{equation} r_{dt} = \frac{\nu_t}{\kappa^2 d_w^2 \max \left[ \left( \sum_{ij} (\partial \boldsymbol{u}_i / \partial \boldsymbol{x}_j)^2 \right)^{1/2} , \, 10^{{-}10}\right]} , \end{equation} \begin{equation} r_{dl} = \frac{\nu}{\kappa^2 d_w^2 \max \left[ \left( \sum_{ij} (\partial \boldsymbol{u}_i / \partial \boldsymbol{x}_j)^2 \right)^{1/2} , \, 10^{{-}10}\right]} . \end{equation}
\begin{equation} r_{dl} = \frac{\nu}{\kappa^2 d_w^2 \max \left[ \left( \sum_{ij} (\partial \boldsymbol{u}_i / \partial \boldsymbol{x}_j)^2 \right)^{1/2} , \, 10^{{-}10}\right]} . \end{equation}
The constants ![]() $c_t$ and
$c_t$ and ![]() $c_l$ are modified for the specific underlying turbulence model used. In the case of the Spalart–Allmaras model used, these are set as
$c_l$ are modified for the specific underlying turbulence model used. In the case of the Spalart–Allmaras model used, these are set as ![]() $c_t = 1.63$ and
$c_t = 1.63$ and ![]() $c_l = 3.55$.
$c_l = 3.55$.