Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-17T16:52:20.929Z Has data issue: false hasContentIssue false
  • English
  • Français

Experiments on Marangoni spreading – evidence of a new type of interfacial instability

Published online by Cambridge University Press:  07 March 2023

Xue Ma Open the ORCID record for Xue Ma [Opens in a new window] ,
Yao Huang ,
Yanru Huang ,
Zhanwei Liu Open the ORCID record for Zhanwei Liu [Opens in a new window] ,
Zhenzhen Li Open the ORCID record for Zhenzhen Li [Opens in a new window]  and
Jerzy M. Floryan Open the ORCID record for Jerzy M. Floryan [Opens in a new window]
Xue Ma
Affiliation:
School of Aerospace Engineering, Beijing Institute of Technology, 5th ZhongGuanCunNan Street, Haidian District, Beijing 100081, PR China
Yao Huang
Affiliation:
School of Aerospace Engineering, Beijing Institute of Technology, 5th ZhongGuanCunNan Street, Haidian District, Beijing 100081, PR China
Yanru Huang
Affiliation:
School of Aerospace Engineering, Beijing Institute of Technology, 5th ZhongGuanCunNan Street, Haidian District, Beijing 100081, PR China
Zhanwei Liu*
Affiliation:
School of Aerospace Engineering, Beijing Institute of Technology, 5th ZhongGuanCunNan Street, Haidian District, Beijing 100081, PR China
Zhenzhen Li*
Affiliation:
School of Aerospace Engineering, Beijing Institute of Technology, 5th ZhongGuanCunNan Street, Haidian District, Beijing 100081, PR China
Jerzy M. Floryan
Affiliation:
Department of Mechanical and Materials Engineering, Western University, London, Ontario N6A 5B9, Canada
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

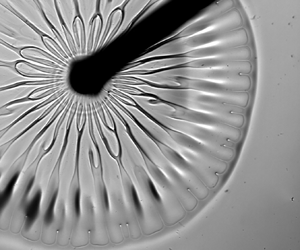
Marangoni spreading on thin films is widely observed in nature and applied in industry. It has serious implications for airway drug delivery, especially in surfactant displacement therapy. This paper reports the results of experimental investigations of a surfactant-laden droplet spreading on films made of more viscous Newtonian fluids as well as on films made of viscoelastic fluids. The experiments used particle seeding, the transmission-speckle method and particle tracking velocimetry (PTV) to determine the deformation of the film–droplet interface and to measure velocity fields. Radially aligned patterns were observed on Newtonian films. Similar patterns, but with much smaller wavenumber, were observed on viscoelastic films in combination with rapid azimuthal variations of the film thickness. The Saffman–Taylor instability at the film–droplet interface explains the formation of patterns on a more viscous Newtonian film, and their onset requires exceeding the critical capillary number. The pattern formation on viscoelastic films is correlated with an instability at the film–droplet–air contact line when the liquid is expelled radially by the spreading droplet. PTV revealed azimuthal variations of the velocity field in the vicinity of the contact line. The observed contact line instability is different from previously reported fingering instabilities of Newtonian thin films. A simple scaling law accounting for the Marangoni-stress-induced elastic shear deformation is proposed to describe the flow field in the patterns formed in the viscoelastic films.

JFM classification

Interfacial Flows (free surface): Contact lines Interfacial Flows (free surface): Thin films Non-Newtonian Flows: Viscoelasticity
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 958 , 10 March 2023 , A33
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afsar-Siddiqui, A.B., Luckham, P.F. & Matar, O.K. 2003 a The spreading of surfactant solutions on thin liquid films. Adv. Colloid Interface Sci. 106, 183–236.CrossRefGoogle ScholarPubMed
Afsar-Siddiqui, A.B., Luckham, P.F. & Matar, O.K. 2003 b Unstable spreading of aqueous anionic surfactant solutions on liquid films. Part 1. Sparingly soluble surfactant. Langmuir 19, 696–702.CrossRefGoogle Scholar
Atefi, E., Mann, J.A. Jr. & Tavana, H. 2014 Ultralow interfacial tensions of aqueous two-phase systems measured using drop shape. Langmuir 30, 9691–9699.CrossRefGoogle ScholarPubMed
Bacri, L., Debrégeas, G. & Brochard-Wyart, F. 1996 Experimental study of the spreading of a viscous droplet on a nonviscous liquid. Langmuir 12, 6708–6711.CrossRefGoogle Scholar
Bauman, T., Sullivan, T.M. & Middleman, S. 1982 Ribbing instability in coating flows: effect of polymer additives. Chem. Engng Commun. 14, 35–46.CrossRefGoogle Scholar
Borgas, M.S. & Grotberg, J.B. 1988 Monolayer flow on a thin film. J. Fluid Mech. 193, 151–170.CrossRefGoogle Scholar
Burton, L.J., Cheng, N., Vega, C., Andrés, J. & Bush, J.W.M. 2013 Biomimicry and the culinary arts. Bioinspir. Biomim. 8, 044003.CrossRefGoogle ScholarPubMed
Cachile, M. & Cazabat, A.M. 1999 Spontaneous spreading of surfactant solutions on hydrophilic surfaces: CnEm in ethylene and diethylene glycol. Langmuir 15, 1515–1521.CrossRefGoogle Scholar
Cachile, M., Schneemilch, M., Hamraoui, A. & Cazabat, A.M. 2002 Films driven by surface tension gradients. Adv. Colloid Interface Sci. 96, 59–74.CrossRefGoogle ScholarPubMed
Czechowski, L. & Floryan, J.M. 2001 Marangoni instability in a finite container—transition between short and long wavelengths modes. Trans. ASME J. Heat Transfer 123, 96–104.CrossRefGoogle Scholar
Deblais, A., Harich, R., Colin, A. & Kellay, H. 2015 Taming contact line instability for pattern formation. Nat. Commun. 7, 12458.CrossRefGoogle Scholar
Dontula, P., Macosko, C.W. & Scriven, L.E. 1998 Model elastic liquids with water-soluble polymers. AIChE J. 44, 1247–1255.CrossRefGoogle Scholar
Dunér, G., Garoff, S., Przybycien, T.M. & Tilton, R.D. 2016 Transient Marangoni transport of colloidal particles at the liquid/liquid interface caused by surfactant convective-diffusion under radial flow. J. Colloid Interface Sci. 462, 75–87.CrossRefGoogle ScholarPubMed
Dussaud, A.D. & Troian, S.M. 1998 Dynamics of spontaneous spreading with evaporation on a deep fluid layer. Phys. Fluids 10, 23–38.CrossRefGoogle Scholar
Floryan, J.M. & Chen, C. 1994 Thermocapillary convection and existence of continuous liquid layers in the absence of gravity. J. Fluid Mech. 277, 303–329.CrossRefGoogle Scholar
Gaillard, A., Roché, M., Lerouge, S., Gay, C., Lebon, L. & Limat, L. 2019 Viscoelastic liquid curtains: experimental results on the flow of a falling sheet of polymer solution. J. Fluid Mech. 873, 358–409.CrossRefGoogle Scholar
Gaver, D.P. & Grotberg, J.B. 1990 The dynamics of a localized surfactant on a thin film. J. Fluid Mech. 213, 127–148.CrossRefGoogle Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2002 Capillarity and Wetting Phenomena-Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
Graham, M.D. 2003 Interfacial hoop stress and instability of viscoelastic free surface flows. Phys. Fluids 15, 1702–1710.CrossRefGoogle Scholar
Grillet, A.M., Lee, A.G. & Shaqfeh, E.S.G. 1999 Observations of ribbing instabilities in elastic fluid flows with gravity stabilization. J. Fluid Mech. 399, 49–83.CrossRefGoogle Scholar
Grotberg, J.B. 2001 Respiratory fluid mechanics and transport processes. Annu. Rev. Biomed. Engng 3, 421–457.CrossRefGoogle ScholarPubMed
Helm, J.D. 2008 Digital image correlation for specimens with multiple growing cracks. Exp. Mech. 48, 753–762.CrossRefGoogle Scholar
Homsy, G.M. 1987 Viscous fingering in porous media. Annu. Rev. Fluid Mech. 19, 271–311.CrossRefGoogle Scholar
Hoult, D.P. 1972 Oil spreading on the sea. Annu. Rev. Fluid Mech. 4, 341–368.CrossRefGoogle Scholar
Iasella, S.V., Stetten, A.Z., Corcoran, T.E., Garoff, S., Przybycien, T.M. & Tilton, R.D. 2018 Aerosolizing lipid dispersions enables antibiotic transport across mimics of the lung airway surface even in the presence of pre-existing lipid monolayers. J. Aerosol. Med. Pulm. Drug. Deliv. 4, 212–220.CrossRefGoogle Scholar
Iasella, S.V., Sun, N., Zhang, X., Corcoran, T.E., Garoff, S., Przybycien, T.M. & Tilton, R.D. 2019 Flow regime transitions and effects on solute transport in surfactant-driven Marangoni flows. J. Colloid Interface Sci. 553, 136–147.CrossRefGoogle ScholarPubMed
Jensen, O.E. & Grotberg, J.B. 1992 Insoluble surfactant spreading on a thin viscous film: shock evolution and film rupture. J. Fluid Mech. 240, 259–288.CrossRefGoogle Scholar
Keiser, L., Bense, H., Colinet, P., Bico, J. & Reyssat, E. 2017 Marangoni bursting: evaporation-induced emulsification of binary mixtures on a liquid layer. Phys. Rev. Lett. 118, 074504.CrossRefGoogle ScholarPubMed
Kim, H., Boulogne, F., Um, E., Jacobi, I., Button, E. & Stone, H.A. 2016 Controlled uniform coating from the interplay of Marangoni flows and surface-adsorbed macromolecules. Phys. Rev. Lett. 116, 124501.CrossRefGoogle ScholarPubMed
Kim, H., Muller, K., Shardt, O., Afkhami, S. & Stone, H.A. 2017 Solutal marangoni flows of miscible liquids drive transport without surface contamination. Nat. Phys. 13, 1105–1111.CrossRefGoogle Scholar
Kim, J.-H. & Rothstein, J.P. 2015 Dynamic contact angle measurements of viscoelastic fluids. J. Non-Newtonian Fluid Mech. 225, 54–61.CrossRefGoogle Scholar
Koch, K., Dew, B., Corcoran, T.E., Przybycien, T.M., Tilton, R.D. & Garoff, S. 2011 Surface tension gradient driven spreading on aqueous mucin solutions: a possible route to enhanced pulmonary drug delivery. Mol. Pharmaceut. 8, 387–394.CrossRefGoogle ScholarPubMed
Koldeweij, R.B.J., van Capelleveen, B.F., Lohse, D. & Visser, C.W. 2019 Marangoni-driven spreading of miscible liquids in the binary pendant drop geometry. Soft Matt. 15, 8525–8531.CrossRefGoogle ScholarPubMed
Li, Z.Z., D'eramo, L., Lee, C., Monti, F., Yonger, M., Tabeling, P., Chollet, B., Bresson, B. & Tran, Y. 2015 Near-wall nano velocimetry based on total internal reflection fluorescence with continuous tracking. J. Fluid Mech. 766, 147–171.CrossRefGoogle Scholar
Limat, L. & Stone, H.A. 2004 Three-dimensional lubrication model of a contact line corner singularity. Europhys. Lett. 65, 365–371.CrossRefGoogle Scholar
Lindner, A., Bonn, D., Poiré, E.C., Amar, M.B. & Meunier, J. 2002 Viscous fingering in non-Newtonian fluids. J. Fluid Mech. 469, 237–256.CrossRefGoogle Scholar
Ma, X., Zhong, M.L., He, Y.F., Liu, Z.W. & Li, Z.Z. 2020 Fingering instability in Marangoni spreading on a deep layer of polymer solution. Phys. Fluids 32, 112112.CrossRefGoogle Scholar
Matar, O.K. & Craster, R.V. 2001 Models for Marangoni drying. Phys. Fluids 13, 1869–1883.CrossRefGoogle Scholar
Matar, O.K. & Craster, R.V. 2009 Dynamics of surfactant-assisted spreading. Soft Matt. 5, 3801–3809.CrossRefGoogle Scholar
Matar, O.K., Craster, R.V. & Warner, M.R.E. 2002 Surfactant transport on highly viscous surface films. J. Fluid Mech. 466, 85–111.CrossRefGoogle Scholar
Matar, O.K. & Troian, S.M. 1997 Linear stability analysis of an insoluble surfactant monolayer spreading on a thin liquid film. Phys. Fluids 9, 3645.CrossRefGoogle Scholar
Matar, O.K. & Troian, S.M. 1999 Spreading of a surfactant monolayer on a thin liquid film: onset and evolution of digitated structures. Chaos 9, 141.CrossRefGoogle ScholarPubMed
Motaghian, M., van Esbroeck, T., van der Linden, E. & Habibi, M. 2022 Interfacial instabilities in Marangoni-driven spreading of polymer solutions on soap films. J. Colloid Interface Sci. 612, 261–266.CrossRefGoogle ScholarPubMed
Mouat, A.P., Wood, C.E., Pye, J.E. & Burton, J.C. 2020 Tuning contact line dynamics and deposition patterns in volatile liquid mixtures. Phys. Rev. Lett. 124, 064502.CrossRefGoogle ScholarPubMed
Nikolov, A.D., Waan, D.T., Chengara, A., Koczo, K., Policello, G.A. & Kolossvary, I. 2002 Superspreading driven by Marangoni flow. Adv. Colloid Interface Sci. 96, 325–338.CrossRefGoogle ScholarPubMed
Oswald, P. 2009 Rheophysics-The Deformation and Flow of Matter. Cambridge University Press.Google Scholar
Pearson, J.R.A. 1958 On convection cells induced by surface tension. J. Fluid Mech. 4, 489–500.CrossRefGoogle Scholar
Pitts, E. & Greiller, J. 1961 The flow of thin liquid films between rollers. J. Fluid Mech. 11, 33–50.CrossRefGoogle Scholar
Podgorski, T., Flesselles, J.-M. & Limat, L. 2001 Corners, cusps, and pearls in running drops. Phys. Rev. Lett. 87, 036102.CrossRefGoogle ScholarPubMed
Roché, M., Li, Z., Griffiths, I.M., Le Roux, S., Cantat, I., Saint-Jalmes, A. & Stone, H.A. 2014 Marangoni flow of soluble amphiphiles. Phys. Rev. Lett. 112, 208302.CrossRefGoogle Scholar
Saffman, P.G. & Taylor, G. 1958 The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245, 311–329.Google Scholar
Shaqfeh, E.S.G. 1996 Purely elastic instabilities in viscometric flows. Annu. Rev. Fluid Mech. 28, 129–185.CrossRefGoogle Scholar
Shi, W.X., Huang, X.F. & Liu, Z.W. 2014 Transmission-lattice based geometric phase analysis for evaluating the dynamic deformation of a liquid surface. Opt. Express 36, 58–69.Google Scholar
Smitter, L.M., Guédez, J.F., Muller, A.J. & Saez, A.E. 2001 Interactions between poly(ethylene Oxide) and soldium dodecyl sulfate in elongational flows. J. Colloid Interface Sci. 236, 343–353.CrossRefGoogle Scholar
Spaid, M.A. & Homsy, G.M. 1997 Stability of viscoelastic dynamic contact lines: an experimental study. Phys. Fluids 9, 823–832.CrossRefGoogle Scholar
Spandagos, C., Goudoulas, T.B., Luckham, P.F. & Matar, O.K. 2012 a Surface tension-induced gel fracture. Part 1. Fracture of agar gels. Langmuir 28, 7197–7211.CrossRefGoogle ScholarPubMed
Spandagos, C., Goudoulas, T.B., Luckham, P.F. & Matar, O.K. 2012 b Surface tension-induced gel fracture. Part 2. Fracture of gelatin gels. Langmuir 28, 8017–8025.CrossRefGoogle ScholarPubMed
Stetten, A.Z., Iasella, S.V., Corcoran, T.E., Garoff, S., Przybycien, T.M. & Tilton, R.D. 2018 a Surfactant-induced Marangoni transport of lipids and therapeutics within the lung. Curr. Opin. Colloid Interface Sci. 36, 58–69.CrossRefGoogle ScholarPubMed
Stetten, A.Z., Moraca, G., Corcoran, T.E., Tristram-Nagle, S., Garoff, S., Przybycien, T.M. & Tilton, R.D. 2016 Enabling Marangoni flow at air-liquid interfaces through deposition of aerosolized lipid dispersions. J. Colloid Interface Sci. 484, 270–278.CrossRefGoogle ScholarPubMed
Stetten, A.Z., Treece, B.W., Corcoran, T.E., Garoff, S., Przybycien, T.M. & Tilton, R.D. 2018 b Evolution and disappearance of solvent drops on miscible polymer subphases. Colloid Surface A 546, 266–275.CrossRefGoogle ScholarPubMed
Sullivan, T.M. & Middleman, S. 1979 Roll coating in the presence of a fixed constraining boundary. Chem. Engng Commun. 3, 469–482.CrossRefGoogle Scholar
Tang, H.Y., Dong, H.M. & Liu, Z.W. 2017 Study on dynamic deformation synchronized measurement technology of double-layer liquid surfaces. Opt. Lasers Engng 98, 205–216.CrossRefGoogle Scholar
Troian, S.T., Herbolzheimer, E. & Safran, S.A. 1990 Model for the fingering instability of spreading surfactant drops. Phys. Rev. Lett. 65, 333–336.CrossRefGoogle ScholarPubMed
Troian, S.M., Wu, X.L. & Safran, S.A. 1989 Fingering instability in thin wetting films. Phys. Rev. Lett. 62, 1496–1500.CrossRefGoogle ScholarPubMed
Wang, X., Bonaccurso, E., Venzmer, J. & Garoff, S. 2015 Deposition of drops containing surfactants on liquid pools: movement of the contact line. Marangoni ridge, capillary waves and interfacial particles. Colloids Surf. A: Physicochem. Engng Aspects 486, 53–59.CrossRefGoogle Scholar
Wang, Z., Wu, H., Kang, K., Wang, S.B., Li, Y.H., Hou, W.J., Riaz, H., Li, L.A. & Li, C.W. 2019 DIC/Moire hybrid method based on regular patterns for deformation measurement. Opt. Express 27, 18435–18444.CrossRefGoogle ScholarPubMed
Warner, M.R.E., Craster, R.V. & Matar, O.K. 2004 a Fingering phenomena associated with insoluble surfactant spreading on thin liquid films. J. Fluid Mech. 510, 169–200.CrossRefGoogle Scholar
Warner, M.R.E., Craster, R.V. & Matar, O.K. 2004 b Fingering phenomena created by a soluble surfactant deposition on a thin liquid film. Phys. Fluids 16, 2933.CrossRefGoogle Scholar
Wodlei, F., Sebilleau, J., Magnaudet, J. & Pimienta, V. 2018 Marangoni-driven flower-like patterning of an evaporating drop spreading on a liquid substrate. Nat. Commun. 9, 820.CrossRefGoogle ScholarPubMed
Yamamoto, D., Nakajima, C., Shioi, A., Krafft, M.P. & Yoshikawa, K. 2015 The evolution of spatial ordering of oil drops fast spreading on a water surface. Nat. Commun. 6, 7189.CrossRefGoogle ScholarPubMed
Zhang, Y.L., Matar, O.K. & Craster, R.V. 2002 Surfactant spreading on a thin weakly viscoelastic film. J. Non-Newtonian Fluid Mech. 105, 53–78.CrossRefGoogle Scholar
Zhao, W.J., Ma, H.Z., Ji, W.J., Li, W.B., Wang, J., Yuan, Q.Z., Wang, Y.R. & Lan, D. 2021 Marangoni driven instability patterns of an N-hexadecane drop triggered by assistant solvent. Phys. Fluids 33, 024104.CrossRefGoogle Scholar

Ma et al. Supplementary Movie 1

Spreading of a surfactant-laden aqueous droplet on a more viscous viscoelastic (left) and Newtonian (right) thin liquid film. Both films have similar viscosities (22.7 mPa.s for the viscoelastic Boger 2 fluid, 21.5 mPa.s for the Newtonian PEG solution, fluid properties are given in Table 1). Rib-like structures characterized by low wavenumbers are formed at the Boger film - droplet interface (left), whereas radially aligned structures characterized by large wavenumbers are formed at the Newtonian film-droplet interface (right). Many very small fingers form at the end of spreading on Boger film (left) after deposition of a second surfactant-laden droplet.

Download Ma et al. Supplementary Movie 1(Video)
Video 13.6 MB

Ma et al. Supplementary Movie 2

See "Ma et al. Supplementary Movie Captions"

Download Ma et al. Supplementary Movie 2(Video)
Video 10.2 MB

Ma et al. Supplementary Movie 3

See "Ma et al. Supplementary Movie Captions"

Download Ma et al. Supplementary Movie 3(Video)
Video 6.2 MB

Ma et al. Supplementary Movie 4

See "Ma et al. Supplementary Movie Captions"

Download Ma et al. Supplementary Movie 4(Video)
Video 3.2 MB

Ma et al. Supplementary Movie 5

See "Ma et al. Supplementary Movie Captions"

Download Ma et al. Supplementary Movie 5(Video)
Video 13.9 MB
Supplementary material: File

Ma et al. Supplementary Movie Captions

Ma et al. Supplementary Movie Captions

Download Ma et al. Supplementary Movie Captions(File)
File 13.7 KB