No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
In the first part of this paper we state and prove a theorem concerning the partition (j; l, i) of an integer j into at most l integers 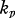 , none of which exceed i; l and i being themselves integers, (j; l, i) is thus the number of distinct solutions of the equations
, none of which exceed i; l and i being themselves integers, (j; l, i) is thus the number of distinct solutions of the equations
1.1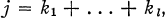
where the 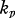 satisfy the inequalities
satisfy the inequalities
1.2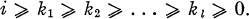
Please note a has been issued for this article.