Research Papers
Multitype branching processes based on exact progeny lengths of particles in a Galton-Watson branching process
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-8
-
- Article
- Export citation
A stochastic explosive reaction system with sampling
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 9-22
-
- Article
- Export citation
Representation of denumerable Markov chains with multiple states by weighted circuits
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 23-35
-
- Article
- Export citation
Slepian models for X2-processes with dependent components with application to envelope upcrossings
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 36-49
-
- Article
- Export citation
Commande optimale du processus de wiener
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 50-57
-
- Article
- Export citation
On the non-closure under convolution of the subexponential family
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 58-66
-
- Article
- Export citation
The limit distribution of the largest nearest-neighbour link in the unit d-cube
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 67-80
-
- Article
- Export citation
Modelling dependence in simple and indirect majority systems
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 81-88
-
- Article
- Export citation
Some results for repairable systems with general repair
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 89-102
-
- Article
- Export citation
Ballots, queues and random graphs
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 103-112
-
- Article
- Export citation
A proof of simple insensitive bounds for a pure overflow system
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 113-120
-
- Article
- Export citation
A generalization of little's law to moments of queue lengths and waiting times in closed, product-form queueing networks
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 121-133
-
- Article
- Export citation
Monotonicity of throughput in non-Markovian networks
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 134-141
-
- Article
- Export citation
On a non-Markovian time-dependent queueing system
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 142-151
-
- Article
- Export citation
M/G/1 queueing systems with returning customers
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 152-163
-
- Article
- Export citation
Short Communications
How large is the support of an ESS?
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 164-170
-
- Article
- Export citation
Asymptotic normality of some Graph-Related statistics
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 171-175
-
- Article
- Export citation
On some characterizations of the poisson process
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 176-181
-
- Article
- Export citation
On the maximum of gaussian fourier series emerging in the analysis of random vibrations
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 182-188
-
- Article
- Export citation
Time series formed from the superposition of discrete renewal processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 189-195
-
- Article
- Export citation

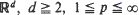 . For
. For  ; (2)
; (2) 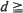 4,
4, 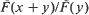 where
where 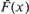 is the survival function of the failure-time of a new system. A general repair is represented as a sequence of random variables
is the survival function of the failure-time of a new system. A general repair is represented as a sequence of random variables