Relative dispersion in free-surface turbulence

Abstract

We report on an experimental study in which Lagrangian tracking is applied to millions of microscopic particles floating on the free surface of turbulent water. We leverage a large jet-stirred zero-mean-flow apparatus, where the Reynolds number is sufficiently high for an inertial range to emerge while the surface deformation remains minimal. Two-point statistics reveal specific features of the flow, deviating from the classic description derived for incompressible turbulence. The magnitude of the relative velocity is strongly intermittent, especially at small separations, leading to anomalous scaling of the second-order structure functions in the dissipative range. This is driven by the divergent component of the flow, leading to fast approaching/separation rates of nearby particles. The Lagrangian relative velocity shows strong persistence of the initial state, such that the ballistic pair separation extends to the inertial range of time delays. Based on these observations, we propose a classification of particle pairs based on their initial separation rate. When this is much smaller than the relative velocity prescribed by inertial scaling (which is the case for the majority of the observed particle pairs), the relative velocity transitions to a diffusive growth and the Richardson–Obukhov super-diffusive dispersion is recovered.

1. Introduction

The transport along the free surface bounding a turbulent liquid has long attracted the attention of scientists and engineers. A particularly evident and relevant instance is the dispersion of objects floating in natural bodies of water. Even when waves are negligibly small and the motion is essentially two-dimensional, upwellings from and downwellings into the bulk produce sources and sinks in the surface flow, respectively (Csanady 1963; Schumacher & Eckhardt 2002; Boffetta et al. 2004; Lovecchio, Marchioli & Soldati 2013). The velocity field is then rotational and compressible, exhibiting rich topology and complex dynamics in both the Eulerian and Lagrangian frames (Okubo 1970; Haller, Karrasch & Kogelbauer 2020). One of the crucial questions, for example in the context of plastic pollution (van Sebille et al. 2020), is the dispersion rate of small floating objects that follow the turbulent surface flow.

Turbulent dispersion is typically quantified by the statistical magnitude of the separation $\boldsymbol {r}$ between a pair of tracer particles over time $\tau$. Denoting with $\boldsymbol {r}_0$ the initial separation at time $\tau _0$ and with $\delta \boldsymbol {u}$ their relative velocity, $\boldsymbol {r}(\tau ) = \boldsymbol {r}_0+\int ^\tau _{\tau _0} \delta \boldsymbol {u}(\tau ')\, {\rm d} \tau '$. In homogeneous turbulence with zero mean flow, the transport is described by the mean square separation $\langle (r(\tau )-r_0)^2\rangle$ which is classically expected to evolve over three distinct regimes (Richardson 1926; Batchelor 1950; Salazar & Collins 2009). For times shorter than the eddy turnover time $t_0$ at scale $r_0$, i.e. $\tau \ll t_0 = \epsilon ^{-1/3}r_0^{2/3}$ (where $\epsilon$ is the turbulent dissipation rate), the relative velocity is highly self-correlated in time and the relative dispersion is ballistic, $\langle (r(\tau )-r_0)^2\rangle \sim \tau ^2$. For times longer than the integral time scale, $\tau \gg T_L$, the relative velocity is completely decorrelated from its initial state and the dispersion becomes diffusive, $\langle (r(\tau )-r_0)^2\rangle \sim \tau$. At intermediate times, $t_0 \ll \tau \ll T_L$, the relative velocity is presumed independent of the initial separation $r_0$ and influenced only by $\epsilon$, leading to a super-diffusive regime, $\langle (r(\tau )-r_0)^2\rangle \sim \tau ^3$. The latter was originally derived by Richardson (1926) assuming a scale-dependent effective diffusivity $\mathcal {K} \sim r^{4/3}$, consistent with the inertial-range scaling of the relative velocity (Obukhov 1941). The different regimes are associated with specific scaling relations of the velocity differences with separation, which in turn are at the basis of our understanding of the phenomenology of turbulence (Kolmogorov 1941). Specifically, the dichotomy between the ballistic and super-diffusive regimes is directly related to fundamental issues such as the intermittent nature of turbulence and its memory of initial conditions (Bourgoin et al. 2006; Elsinga, Ishihara & Hunt 2022). In practice, the existence and extent of the different dispersion regimes is crucial for predicting transport and mixing, especially in systems where a significant scale separation exists.

The topic, particularly the super-diffusive Richardson–Obukhov regime, has been widely debated, e.g. concerning its realizability and the role of the initial separation, separation rate and intermittency (e.g. Bourgoin et al. 2006; Scatamacchia, Biferale & Toschi 2012; Bitane, Homann & Bec 2012; Shnapp & Liberzon 2018; Tan & Ni 2022; Elsinga et al. 2022). One of the physical mechanisms proposed to rationalize this regime depicts it as a cascade of scale-dependent ballistic steps (Bourgoin 2015). Other interpretations propose that tracer particles, after losing memory of their initial state, sample the velocity space in random fashion, leading to a diffusive behaviour of the relative velocity, $\langle \delta \boldsymbol {u} (\tau )^2 \rangle \sim \tau$, and in turn to super-diffusive dispersion (Bitane et al. 2012).

How do small floating particles disperse along the free surface of turbulent flows? The influence of the non-solenoidal surface velocity was already emphasized by Csanady (1963) who analysed data from a field campaign in which floaters were released in Lake Huron. He found that regions of confluence could delay and even revert the pair separation process. Well-controlled laboratory studies on relative dispersion in free-surface turbulence are scarce. Cressman et al. (2004) imaged buoyant particles on the surface of a jet-stirred water tank, observing a dispersion rate significantly slower compared with the super-diffusive regime. This contrasted with the numerical simulations of Schumacher & Eckhardt (2002) who found mean square separations that agreed with the Richardson–Obukhov prediction. These and other computational studies also highlighted the stronger intermittency of the surface flow compared with three-dimensional incompressible turbulence, which was attributed to the compressibility of the velocity field (Lovecchio et al. 2013).

Here we leverage a large zero-mean-flow apparatus to study the relative motion along the quasi-flat free surface above homogeneous turbulence. Using high-speed, high-resolution imaging, we analyse Eulerian and Lagrangian two-point statistics and reveal the profound influence of the large relative velocities at small separations.

2. Methods

We track millions of floating microparticles (hollow glass spheres, 0.40 g cm$^{-3}$ in density, 75–90 $\mathrm {\mu }$m in diameter, Cospheric LLC) on the free surface of homogeneous turbulent water. The experimental apparatus, described in detail by Ruth & Coletti (2024), is illustrated in figure 1(a). It consists of a 2 m$^{3}$ tank, with two planar facing arrays of submersed pumps, firing jets in random sequence. The two random jet arrays are separated by a distance of 1.65 m, each lodging 64 pumps spaced 0.1 m from each other. The firing sequence, which follows the algorithm proposed by Variano & Cowen (2008), and the power supplied to each pump are dictated by programmable logic controllers. On average, one in eight pumps is on at a given time and fires for 3 s. Steady homogeneous turbulence is generated over a central region several times larger than the integral scale $L = O(0.1\ {\rm m})$. The free surface is located 0.07 m above the top row of jets, causing deformations of at most ${\sim }1$ mm even for the strongest turbulence level we consider, as characterized by laser-induced fluorescence (Ruth & Coletti 2024). The water surface is periodically skimmed and vacuumed to limit accumulation of surfactants. Though some contamination is unavoidable (Variano & Cowen 2013), the surface tension, measured via a Du Noüy ring at various points in time, remains at the standard value of 0.07 N m$^{-1}$ during the experiments. The small particle size and low mean areal concentration of $O(10)\ {\rm particles}\ {\rm cm}^{-2}$ minimize the risk of particle aggregation due to capillarity. Particles are only tracked if their centroid is more than 1 mm away from any other. Possible aggregates appear as larger objects and are discarded in post-processing. The individual particles are faithful tracers of the surface flow, as indicated by their small Stokes number. The latter can be estimated as $St \equiv \tau _p u_{rms}/L$ (Ouellette, O'Malley & Gollub 2008; Shin & Coletti 2024), where $u_{rms}$ is the root-mean-square particle velocity and $\tau _p = \rho _p d_p^2/(18\mu )$ is their response time. While this formulation is strictly valid for fully submerged particles, the order of magnitude $St = O(10^{-6})$ shows that particle inertia is negligible.

Figure 1. (a) Schematic of the experimental set-up. (b) A typical snapshot of trajectories coloured by the instantaneous velocity magnitude.

The floating particles are illuminated by light-emitting diode (LED) lamps and imaged by a CMOS camera (4 megapixel, VEO 640, Phantom) mounting a 25 mm lens (f/1.4 ZF.2, Milvus, Zeiss). The field of view is $0.1\ {\rm m}\times 0.1\ {\rm m}$, the resolution is $66\ \mathrm {\mu }{\rm m}\ {\rm pixel}^{-1}$ and the acquisition frequency is 200 Hz. The spatio-temporal resolution warrants subpixel accuracy in locating the particle centroids while keeping their inter-frame displacement to less than 5 pixels. Positions and velocities are obtained by convolving the trajectories with a Gaussian kernel of width 0.125 s (Voth et al. 2002; Berk & Coletti 2021). This is comparable to the Kolmogorov time scale, and it is verified that the precise duration of the kernel does not influence the quantitative results. The level of turbulence is varied by modulating the power supplied to the pumps, resulting in a range of Taylor-scale Reynolds numbers $Re_\lambda = 355$–$549$. This is much higher compared with previous studies ($Re_\lambda = 145$ in Schumacher & Eckhardt (2002) and $Re_\lambda = 140$ in Cressman et al. (2004)) and allows for the development of an inertial subrange. For each condition, we perform 20 independent measurement runs, for a total duration of 1800 s, and gather $O(10^6)$ trajectories longer than 50 frames.

The distance between the surface and the forcing region is less than one integral scale, which is significantly smaller compared with most previous experiments in which the turbulence was forced at depth (Brumley & Jirka 1987; McKenna & McGillis 2004; Herlina & Jirka 2008; Variano & Cowen 2008, 2013). Therefore, as discussed in Ruth & Coletti (2024), the spatial decay of turbulence away from the forcing region is limited; thus, the differences between the flow properties along the surface versus the bulk are mostly due to the free-surface boundary condition.

The main statistics of the free-surface turbulence are listed in table 1. The surface flow approximates zero-mean-flow homogeneous turbulence, which can be quantified by various metrics following Carter et al. (2016) and Esteban, Shrimpton & Ganapathisubramani (2019). The measured instantaneous velocity $\tilde {U}_i$ is decomposed into the local mean velocity $U_i$ and the local velocity fluctuations $u_i$, i.e. $\tilde {U}_i = U_i + u_i$. The root mean square of the velocity fluctuations (r.m.s. velocity) is defined as $u_i' = \sqrt {\overline {\langle u_i^2\rangle }}$, in which overline and angle brackets denote ensemble average and spatial average, respectively. The homogeneity deviation ${\rm HD} = 2\sigma _{u}/u'$, where $\sigma _{u}$ is the spatial deviation of the local ensemble average of the velocity fluctuations $\sqrt {\overline {u^2}}$ on the free surface, which quantifies the spatial variance of the turbulent fluctuations; the mean flow factor ${\rm MFF} = |\bar {U}|/u'$, which shows the strength of the mean flow relative to the velocity fluctuations; and the mean strain-rate factor ${\rm MSRF} = \langle \sqrt {(\partial U_1/\partial r_1)^2+(\partial U_2/\partial r_2)^2}\rangle /\overline {\sqrt {\langle (\partial u_1/\partial r_1)^2\rangle +\langle (\partial u_2/\partial r_2)^2\rangle }}$, which evaluates the strain rate of the mean flow relative to the turbulent strain rates. All the quantities are calculated over the field of view on the free surface. It is found that ${\rm HD} < 0.055$ for all the cases we tested, indicating good spatial homogeneity. With the exception of the lowest $Re_\lambda = 355$ case, ${\rm MFF}<0.065$, showing the mean flow is negligible relative to the turbulent fluctuations. The mean strain-rate factor is also low, i.e. ${\rm MSRF}<0.044$ for all the cases, confirming a low level of mean flow strain compared with its fluctuating counterpart. These quantities attain similar levels in the homogeneous bulk flow (Ruth & Coletti 2024).

Table 1. Main turbulence statistics of the experiments. Here $Re_\lambda$ is the Taylor-scale Reynolds number; $u_1'$ and $u_2'$ are the r.m.s. velocity parallel and perpendicular to the jetting direction, respectively; $\epsilon$ is the dissipation rate; $\eta$ and $\tau _\eta$ are the Kolmogorov length and time scale, respectively; $T_L$ is the integral time scale; and $u_{bulk}'$ and $\epsilon _{bulk}$ are the r.m.s. velocity and the dissipation rate in the bulk, respectively.

The level of large-scale anisotropy is comparable to that of similar set-ups and does not alter fundamental scaling laws (Carter et al. 2016; Carter & Coletti 2017; Esteban et al. 2019). The dissipation rate $\epsilon$ is estimated at the surface by assuming Kolmogorov (1941) scaling of the second-order velocity structure function over the inertial range, which has been found to approximately hold in free-surface turbulence (Cressman et al. 2004). Using values of $\epsilon _{bulk}$ measured in the bulk (Ruth & Coletti 2024) leads to quantitative differences in the Kolmogorov length $\eta$ and time $\tau _\eta$, but does not affect the trends and conclusions presented below. The integral time scale is evaluated from the e-fold decay of the Lagrangian autocorrelation of the particle velocity.

3. Results

3.1. Eulerian velocity differences and structure functions

In figure 2(a), we display probability distribution functions of the longitudinal relative velocity $\delta _r u = \delta \boldsymbol {u}\boldsymbol {\cdot } \boldsymbol {r}/r$, for a wide range of separations $r_0 = 11\eta$–$401\eta$. The distributions, shown for $Re_\lambda = 424$ and analogous in the other considered cases, display very strong intermittency, signalled by the broad exponential tails especially at small separations. This is quantified by the kurtosis plotted in figure 2(b), which only slowly approaches the Gaussian limit for integral-scale separations. Small-scale intermittency in three-dimensional incompressible turbulence at similar $Re_\lambda$ is far less pronounced, with kurtosis of the velocity gradients around 10 (Gylfason, Ayyalasomayajula & Warhaft 2004; Carter & Coletti 2017). The likelihood of extremely large velocity differences at small separations is interpreted as a consequence of the compressibility of the velocity field: in the presence of upwelling motions from beneath the surface, nearby floating particles separate explosively; vice versa, downwellings cause local confluence and large approaching rates between particle pairs.

Figure 2. (a) Probability distribution function (PDF) of velocity increments $\delta _{r_0} u$ with a series of separation distances $r_0$ at $Re_\lambda = 424$. (b) The kurtosis of PDF changes with increasing separation distance.

Such anomalously large relative velocities at small separations directly impact the Eulerian structure functions. In figure 3(a) we display the second-order structure functions $D_{ii}(r)=\langle |\boldsymbol {u}(\boldsymbol {x} +\boldsymbol {r})-\boldsymbol {u}(\boldsymbol {x} )|^2 \rangle$, where $\boldsymbol {u}(\boldsymbol {x})$ is the velocity fluctuation evaluated at the generic position $\boldsymbol {x}$, for the four considered levels of $Re_\lambda$. The longitudinal components $D_{ll}(r)$ are close to the transverse ones $3/4D_{tt}(r)$ and both approximately follow the scaling $D_{ii}(r) \sim r^{2/3}$ for separations $r \gg \eta$, as predicted by Kolmogorov (1941). However, at small separations, we observe a marked departure from the scaling $D_{ii}(r) \sim r^2$ expected for smooth flows in the dissipation range. The slope of the structure function at millimetric separations is in fact shallower than in the inertial subrange. This behaviour shares similarities with the formation of caustics displayed by inertial particles in turbulence (Bewley, Saw & Bodenschatz 2013; Bec, Gustavsson & Mehlig 2024). As those particles describe a compressible velocity field, intermittently large relative velocities result in anomalous scaling exponents of the structure functions at small scales, as shown in numerical simulations (Bec et al. 2010; Salazar & Collins 2012; Ireland, Bragg & Collins 2016) and laboratory experiments (Berk & Coletti 2021; Hassaini, Petersen & Coletti 2023). To investigate this analogy and explore the role of the non-solenoidal nature of the present velocity fields, we use the Helmholtz decomposition to compute the rotational and divergent components of the structure functions, respectively as (Lindborg 2015)

(3.1)$$\begin{gather} D_{rr} = D_{tt}+\int^r_0\frac{1}{r}(D_{tt}-D_{ll})\, {\rm d} r, \end{gather}$$

(3.2)$$\begin{gather}D_{dd} = D_{ll}-\int^r_0\frac{1}{r}(D_{tt}-D_{ll})\, {\rm d} r. \end{gather}$$

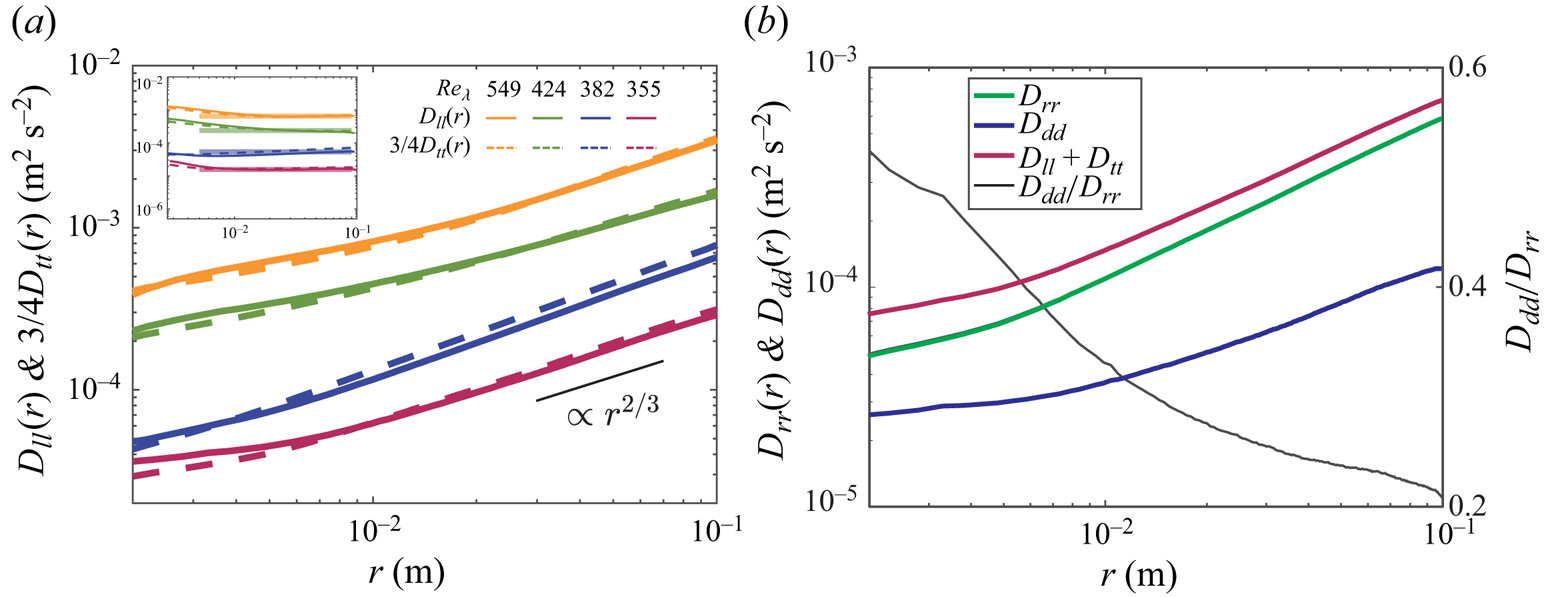
Figure 3. (a) Second-order structure functions at the indicated Reynolds numbers. Solid and dashed lines show the longitudinal and the transverse components, respectively. The inset shows the structure functions compensated by $(D_{ll}/C)^{3/2}/r$ and $(3/4D_{tt}/C)^{3/2}/r$ for the longitudinal and the transverse components, respectively. (b) The Helmholtz decomposition of $D_{ll}+D_{tt}$ into the rotational and divergent components $D_{rr}$ and $D_{dd}$ of the second-order structure function at $Re_\lambda = 355$. Also displayed is the ratio between divergent and rotational components $D_{dd}/D_{rr}$.

These are presented in figure 3(b) for the representative case $Re_\lambda = 355$. It appears that, while both components deviate from the $r^2$ scaling, the divergent one is majorly responsible for the effect at small separations, as also indicated by the growth of the ratio $D_{dd}/D_{rr}$ for decreasing $r$.

3.2. Mean squared separation of particle pairs

The same particle pairs used to evaluate two-point Eulerian statistics are used to investigate dispersion in the Lagrangian frame. Figure 4(a) reports the mean square separations as a function of time, shifted down by one decade with increasingly higher $Re_\lambda$ for illustration purposes. For all cases and over multiple decades in time, we observe a behaviour consistent with ballistic dispersion, with no sign of a transition to a super-diffusive regime. This suggests a persistence of the initial separation rate, as confirmed by the temporal evolution of the mean square relative velocity $\langle \delta _r u(\tau )^2 \rangle$ between particles initially separated by $\boldsymbol {r}_0$, shown in figure 4(b). Normalization by the mean initial relative velocity $\langle \delta _{r_0} u^2 \rangle =D_{ll}(r_0)$ produces a tight collapse of the data at unity, as the structure functions account for the ballistic separation at short times. Within experimental scatter, the relative velocity remains approximately constant even for $\tau > t_0$, which is equivalent to the scaling $\langle (r-r_0)^2\rangle \sim \tau ^2$ (Batchelor 1950; Tan & Ni 2022). In the following, we show how the lasting memory of the initial state is related to the fast separation/approaching rates.

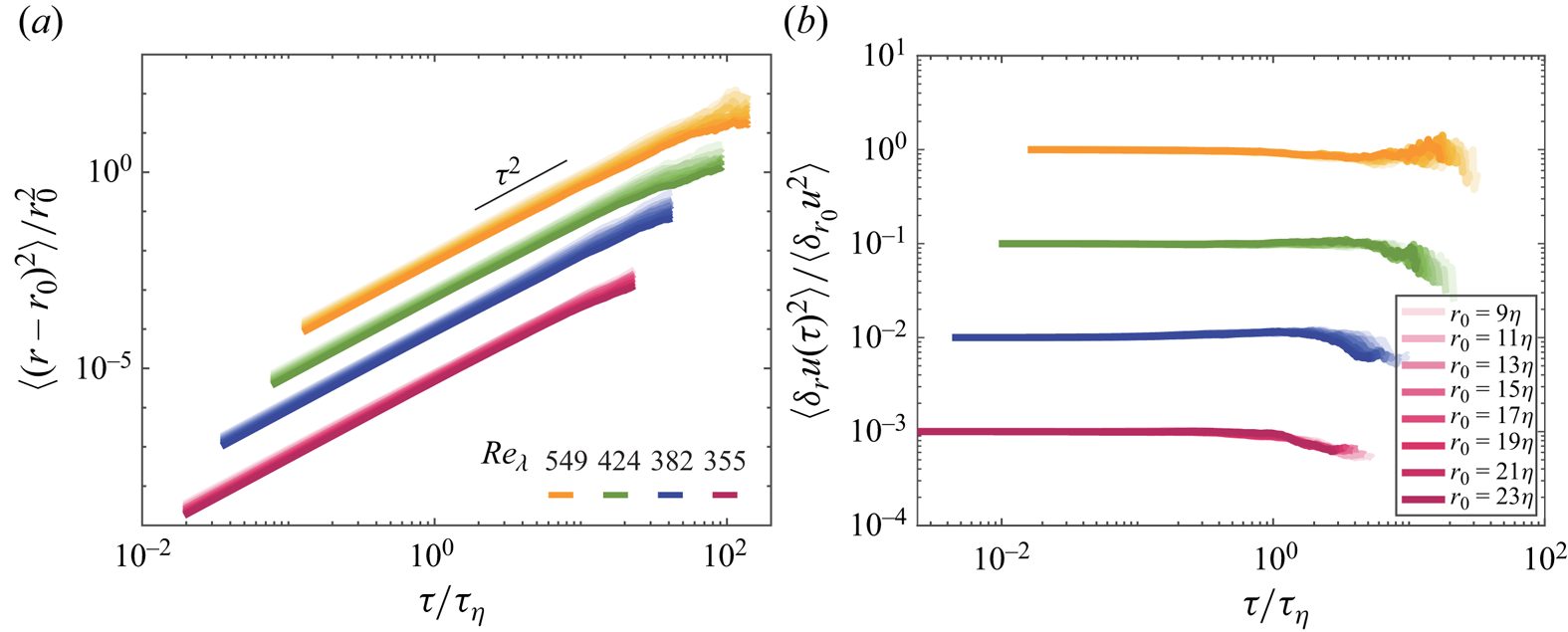
Figure 4. (a) Relative pair separation $\langle (r-r_0)^2\rangle$ for a series of initial separations $r_0$, with the colour of increasing $r_0$ gradually changing from light to dark. (b) The Lagrangian relative velocity $\langle \delta _{r}u(\tau )^2 \rangle$ compensated by the measured second-order structure function $\langle \delta _{r_0}u^2 \rangle$ with initial separation $r_0$. For the purpose of visibility, the curves corresponding to the three flow conditions $Re_\lambda = 355, 382$ and $424$ have been shifted down by three, two and one decade, respectively.

To gain insight into the evolution of the relative velocity, we perform a short-time Taylor expansion around its initial value:

(3.3) \begin{equation} \langle \delta_{r}u(\tau)^2 \rangle = \langle \delta_{r_0}u^2 \rangle + 2\left\langle \delta_{r_0}u(\tau)\frac{\partial \delta_{r}u(\tau)}{\partial \tau} \right\rangle_{\tau=0} \tau + O(\tau^2).\end{equation}

Assuming inertial scaling (Kolmogorov 1941), the second term in the right-hand side is of order $(r_0\epsilon )^{2/3}\tau /\tau _\eta$. Combining the well-known relationships $u'^2 \sim (\epsilon L)^{2/3}$, $u_\eta /u'\sim Re_\lambda ^{-1/4}$ and $\eta /L \sim Re_\lambda ^{-3/2}$, we write

(3.4)\begin{equation} \langle \delta_{r}u(\tau)^2 \rangle \approx \langle \delta_{r_0}u^2 \rangle + \mathcal{\xi}\left(\frac{r_0}{\eta}\right)^{2/3} Re_\lambda^{1/4}\epsilon \tau,\end{equation}

where $\mathcal {\xi }$ is a non-dimensional constant. Compared with the similar expression in Bitane et al. (2012), (3.4) explicitly incorporates the dependence of the diffusive term on the Reynolds number and initial separation. By balancing the first and second terms on the right-hand side of (3.4), we introduce the transition time scale $t_D = \langle \delta _{r_0}u^2 \rangle /[\mathcal {\xi }(r_0/\eta )^{2/3}Re_\lambda ^{1/4}\epsilon ]$. For $\tau \ll t_D$, the relative velocity is determined by the initial state, $\langle \delta _{r}u(\tau )^2 \rangle \approx \langle \delta _{r_0}u^2 \rangle$. For $\tau \gg t_D$, the diffusive behaviour dominates, $\langle \delta _{r}u(\tau )^2 \rangle \sim \tau$, which is equivalent to the Richardson–Obukhov regime $\langle (r-r_0)^2\rangle \sim \tau ^3$. Note that (3.4) implicitly requires $t_D \ll T_L$; i.e. sufficient time is needed for the super-diffusive regime to develop before the pair separations exceed the inertial range. In the present experiments, the mean initial relative velocity $\langle \delta _{r_0}u^2 \rangle$ is too large and the scale separation too small for the condition $t_D \ll T_L$ to be realized.

To quantify the influence of the initial relative velocity, we introduce a dimensionless parameter $s_0=|\delta _{r_0}u|/(r_0\epsilon )^{1/3}$: for each particle pair, it compares the initial relative velocity with that prescribed by inertial scaling. This is similar to the parameter $\gamma$ defined by Shnapp & Liberzon (2018), comparing the time over which the initial separation rate is retained against the eddy turnover time at the relevant scale. We then focus on pairs with $s_0$ smaller than a given threshold, applied to the initial velocity differences in both longitudinal and transverse directions (see Elsinga et al. 2022). Figure 5(a) illustrates the effect of reducing such threshold from $s_0 = 1$ (for which virtually all tracked pairs are considered) to $s_0 = 0.1$ (approximately 60 % of the pairs are considered), for the case $Re_\lambda =424$: the mean square separation is slowed down at the early stages, and the super-diffusive regime is approached at intermediate times. Figure 5(b) shows how, for all $Re_\lambda$, the mean relative velocity $\langle \delta _r u^2 \rangle$ of pairs with at most $s_0=0.1$ evolves according to (3.4). By fitting the data, we obtain $\mathcal {\xi } = 0.017 \pm 0.005$ for all Reynolds numbers, while the transition time scale is $t_D \approx 0.15$, 0.04, 0.02 and 0.01 s for $Re_\lambda =355, 382, 424$ and 549, respectively. The corresponding mean square separations in figure 5(c) confirm that, even enforcing such limitation on the initial separation rates, the Richardson–Obukhov regime emerges only at the larger $Re_\lambda$, for which the condition $t_D \ll T_L$ is strictly met. This is clearly highlighted by the compensated plots in figure 5(d), where only for $Re_\lambda = 424$ and 549 is the scaling $\langle (r-r_0)^2\rangle \sim \tau ^3$ achieved, and over a limited temporal range.

Figure 5. (a) Mean-squared separation for $s_0=1, 0.5, 0.25, 0.1$ with $Re_\lambda = 424$. (b) The Lagrangian relative velocity $\langle \delta _{r}u^2(\tau ) \rangle$ compensated by the measured second-order structure function $\langle \delta _{r_0}u^2 \rangle$ with initial separation distance $r_0$. For the purpose of visibility, the curves corresponding to the three flow conditions $Re_\lambda = 355, 382$ and $424$ have been shifted down by three, two and one decade, respectively. (c) Conditioned relative pair separation $\langle |\boldsymbol {r}-\boldsymbol {r}_0|^2 \rangle$ by $s_0=0.1$ for a series of initial separations $r_0$, with the colour of increasing $r_0$ gradually changing from light to dark. (d) The mean-squared separations compensated by the super-diffusive scaling $(\tau /t_D)^3$. The dashed lines highlight the plateau of the curves representing the compensated scaling $(\tau /t_D)^3$.

The role of the initial relative velocity between particle pairs is illustrated in figure 6 which displays sample trajectory pairs for $s_0=0.1$ and 1, both having an initial separation $r_0 = 10\eta$. The trajectory pairs are depicted in the space–time domain and coloured by the relative velocity. In the example at $s_0=0.1$ (figure 6a), the separation grows significantly in time, in particular for $\tau >t_D$, which is the hallmark of the super-diffusive regime. At later times, the motions of both particles in the pair decorrelate from each other, signalling that the diffusive long-time regime has been reached. In the example for $s_0 = 1$ (figure 6b), the relative velocity is initially higher but changes only marginally in time, as typical of the ballistic regime.

Figure 6. Trajectory pairs initially separated by $r_0 = 10\eta$ represented on the space–time domain and coloured by the relative velocity, for (a) $s_0=0.1$ and (b) $s_0=1$.

4. Conclusions

We have investigated the motion of microscopic particles floating above zero-mean-flow homogeneous turbulence, focusing on the case of minor surface deformations. The particles are bound to the surface by buoyancy and faithfully follow the local fluid fluctuations, describing therefore a rotational and compressible velocity field. The relatively high Reynolds number realized in the present experiments, along with the large number of long trajectories reconstructed over a wide range of initial separations, have allowed us to address fundamental questions on relative dispersion in this configuration. Specific features of the flow are revealed by two-point statistics, deviating from the classic description of incompressible turbulence. The relative velocity of the floating particles is strongly intermittent, especially for small separation distances. As indicated by Helmholtz decomposition, this is associated with the non-solenoidal nature of the velocity field: i.e. sources and sinks caused by upwelling and downwelling motions from and into the bulk, respectively. In analogy to caustics exhibited by inertial particles in turbulence, the compressibility of the surface flow leads to velocity structure functions that sharply deviate from the dissipative scaling of smooth incompressible flows.

The high probability of large separation/approaching rates of nearby particles profoundly impacts the relative dispersion. In particular, the Lagrangian relative velocity between particle pairs, rather than growing diffusively as expected in incompressible turbulence at high Reynolds numbers, persists beyond the local eddy turnover time. This results in a ballistic separation of the pairs that extends to time delays in the inertial range.

Based on these observations, we present a generalization of pair dispersion in free-surface turbulence, by classifying particle pairs based on the dimensionless parameter $s_0$. This compares the separation rate at the initial separation $r_0$ and the relative velocity following inertial scaling. Pairs with $s_0 < 0.1$, which account for more than half of the observations, separate sufficiently slowly to transition to the diffusive growth of relative velocity, and thus to super-diffusive dispersion. The framework may also help in interpreting observations in incompressible three-dimensional turbulent flows, where the Richardson–Obukhov regime has remained elusive. Such a direction, however, is outside the scope of our work.

Specifically for free-surface transport, the picture that emerges is strikingly consistent with that painted by Csanady (1963) in his appraising of the field data in Lake Huron: ‘The dispersal of floating objects was complicated by surface confluences, slicks and windrows, which under certain circumstances could completely reverse the diffusion process. In the absence of such disturbing effects, however, the dispersal of floating objects exhibited an increase in rate of growth with the size of the diffusing cloud, characteristic of relative turbulent diffusion.’ Indeed, once the pairs seemingly most influenced by the surface compressibility are resected from the data, the Richardson–Obukhov prediction is recovered. Our analysis further suggests that super-diffusive dispersion becomes more prevalent at very large $Re_\lambda$: this warrants an integral time scale much larger than $t_D$, which marks the transition to the scaling $\langle |r(\tau )-r_0 |^2 \rangle \sim \tau ^3$. This is consistent with the evidence that drifters in the ocean do exhibit this behaviour over intermediate times (Salazar & Collins 2009).

The non-zero divergence provides a mechanism that can directly alter relative dispersion. However, one cannot exclude that other specific aspects of free-surface turbulence may be at least partly responsible for the observed trends. In particular, the zero-stress boundary condition, which causes the vortices to connect perpendicular to the surface, results in long-lived attached structures (Shen et al. 1999). These may significantly contribute to the relative dispersion, though this cannot be directly ascertained by the present measurement.

The present findings also trigger other related and highly relevant questions. For example, based on fundamental understanding of particle-laden turbulence as well as recent field studies, one expects different transport properties for larger particles which filter some of the turbulent flow scales (Toschi & Bodenschatz 2009; Brandt & Coletti 2022; Sanness Salmon et al. 2023). Moreover, intense subsurface turbulence and/or wind shear may significantly deform the surface, with gravity–capillary waves impacting the dispersion in non-trivial ways. Finally, at significant number density, floating particles clustered by the surface flow are kept together by capillarity and grow increasingly large aggregates (Protière 2023; Shin & Coletti 2024) which may even back-react on the underlying flow. Dedicated investigations of those aspects are underway.