A regression model for pooled data in a two-stage survey under informative sampling with application for detecting and estimating the presence of transgenic corn

Abstract

Group-testing regression methods are effective for estimating and classifying binary responses and can substantially reduce the number of required diagnostic tests. However, there is no appropriate methodology when the sampling process is complex and informative. In these cases, researchers often ignore stratification and weights that can severely bias the estimates of the population parameters. In this paper, we develop group-testing regression models for analysing two-stage surveys with unequal selection probabilities and informative sampling. Weights are incorporated into the likelihood function using the pseudo-likelihood approach. A simulation study demonstrates that the proposed model reduces the bias in estimation considerably compared to other methods that ignore the weights. Finally, we apply the model for estimating the presence of transgenic corn in Mexico and we give the SAS code used for the analysis.

Introduction

Group testing is a technique used to screen samples for an attribute when samples are grouped into pools (or batches), and each pool is tested for the presence of the attribute; if a pool tests negative, then all samples in the pool are cleared of having the attribute. When the proportion of samples with the attribute is less than 10%, group testing is very attractive because it produces significant savings in the number of diagnostic tests required and time expended, and helps to preserve the anonymity of the tested subjects. First used by Dorfman (1943) for detecting soldiers with syphilis during the Second World War, group testing has been used to estimate the prevalence of a wide variety of diseases in humans, animals and plants (Cardoso et al., 1998; Kacena et al., 1998; Verstraeten et al., 1998; Muñoz-Zanzi et al., 2000; Tebbs and Bilder, 2004; Chen et al., 2009). It has also been used for analysing biomarker data (Delaigle and Hall, 2012), detecting drugs (Xie, 2001), solving problems in information theory (Wolf, 1985) and even in science fiction (Bilder, 2009).

Group-testing regression methods are available for fixed and mixed (fixed + random) effects (Farrington, 1992; Vansteelandt et al., 2000; Chen et al., 2009). Chen et al. (2009) presented group-testing regression models for imperfect diagnostic tests (with sensitivity and specificity of less than 1) with fixed and random effects, which produce the most accurate estimates when the sampling process is in clusters. More recently, McMahan et al. (2013) also provided group-testing regression models for mixed effects in the presence of dilution effects. Delaigle and Meister (2011) and Delaigle and Hall (2012) presented non-parametric group-testing regression models.

All the group-testing regression methods developed so far are based on the assumption that selection probabilities are the same for all clusters and individuals, and sampling weights are not required. Thus these methods are only valid when clusters are of the same size, and simple random samples of clusters and individuals are taken. Also, they do not take into account stratification at the cluster or individual levels. In the non-group-testing context for two-level linear (or linear mixed) and generalized linear mixed models, Graubard and Korn (1996), Pfeffermann et al. (1998), Korn and Graubard (2003), Grilli and Pratesi (2004), and Rabe-Hesketh and Skrondal (2006) discussed the proper use of sampling weights. However, no work has been done on incorporating sampling weights in group-testing regression models. Appropriate group-testing methodologies for a complex survey can result in substantial savings without significant loss of precision and can be used for estimating the prevalence of a rare attribute, such as transgenic corn or human diseases. For this reason, the aim of the present paper is to bring together the ideas of Chen et al. (2009) and Grilli and Pratesi (2004), which means generalizing the group-testing methodology to take into account the weights when a two-stage survey is performed, and we perform an application for detecting and estimating the presence of transgenic corn in Mexico. Researchers use complex sampling schemes (e.g. two or three stages with clusters and stratification and unequal selection probabilities) for collecting corn plants in a field and, to save resources, they use group testing on samples containing s plants to determine whether a transgene is present (Piñeyro-Nelson et al., 2009). However, due to the lack of an appropriate methodology for analysing data, they ignore the complex sampling design, which violates the basic assumptions underlying multilevel models.

A sampling process is informative when the sampling probabilities are related to the values of the outcome variable after conditioning on the model covariates (Pfeffermann et al., 2006). For example, assume that a two-stage sampling design is used for estimating the prevalence of transgenic corn in Mexico with fields as the primary sampling units and plants as the secondary sampling units. If fields are sampled with a probability that is proportional to field size (PPS), the sample of fields will tend to contain mostly large fields, and if field size is related to prevalence but not included among the model covariates, the sample of fields will not accurately represent the fields in the population and the sampling is informative (Pfeffermann et al., 2006). In the context of estimating transgenic corn in Mexico, this makes sense because most commercial corn fields are larger and more likely to contain transgenic corn than non-commercial corn fields. More examples of an informative sampling scheme being ignored in the inference process can be found in Kasprzyk et al. (1989), Skinner et al. (1989) and Pfeffermann (1993). In general terms, informative sampling results when the probability density of the sample data is different from the density of the population before sampling. Ignoring the sampling process in such cases may yield severely biased estimates of population model parameters, possibly leading to false inferences.

In theory, the effect of sample selection can be controlled by including all of the design covariates. However, this is often not practical because the design variables may not be available or known, or because there may be too many of them, making fitting and validation of such models a formidable task (Pfeffermann and Sverchkov, 2007). One approach for dealing with informative sampling that commonly produces good results is to include design (sampling) weights to account for unequal selection probabilities. Because the weights are incorporated in the likelihood function, this approach is called pseudo-maximum likelihood (PML). Another approach for dealing with this problem is the sample model; it consists of extracting the model for the sample data given the selected sample (Pfeffermann et al., 2006). However, with this approach it is sometimes not possible to extract the probability density function (pdf) for the sample data. For this reason, the PML approach is still the most popular approach and produces good results.

Before the PML approach, Grizzle et al. (1969) proposed using weighted least squares (WLS) for estimating logistic regression model parameters and standard errors for complex sample survey data (Landis et al., 1976). However, Binder (1981, 1983) presented the PML framework for fitting logistic regression and other generalized linear models to complex sample survey data as a technique for estimating model parameters. The PML approach to parameter estimation was combined with a linearized estimator of the variance–covariance matrix for the parameter estimates that accounted for complex sample design features. Further development and evaluation of the PML approach were presented in Roberts et al. (1987), Morel (1989) and Skinner et al. (1989). The PML approach is now the standard method for logistic regression modelling in all of the major software systems that support the analysis of complex sample survey data (Heeringa et al., 2010).

The prominent feature of this approach is that it utilizes the sampling weights to estimate the likelihood equations that would have been obtained in the case of a census. However, for mixed models, the PML approach needs the sampling weights for the sampled elements (level 1) and clusters (level 2). Because level 1 and level 2 weights appear in separate places within the PML estimator function, it is not sufficient to know the product of the level 1 and level 2 weights, as happens in conventional analyses. Also, level 1 weights have to be scaled to produce precise estimates of the variance components. For this reason, some rescaling methods have been proposed. Pfeffermann et al. (1998) and Korn and Graubard (2003), in the context of linear mixed models, point out that scaling the weights at level 1 produces estimates of the variance components (particularly the random-intercept variance) with little bias even in small samples.

The goal of this paper is to generalize the group-testing methodology to surveys conducted in two stages with stratification and different cluster sizes when sampling is informative. We solve this problem by using the PML approach and incorporating sampling weights at both levels to estimate the population likelihood equations that would have been obtained in the case of a census.

Why is it important to make inferences about the proportion of transgenic corn?

Mexico is the centre of origin and diversification of corn and many other plant species. The presence of transgenes in some corn landraces in Mexico has been confirmed by some studies (Quist and Chapela, 2001, 2002; Ortiz-García et al., 2005; Dyer et al., 2009; Piñeyro-Nelson et al., 2009). For this reason, there is great concern regarding possible gene flow as a result of outcrossing between transgenic crops and their landraces and wild relatives. However, the effects of transgenic maize outcrossing with traditional maize landraces and wild relatives such as Tripsacum and teocinte are virtually unknown (Hernández-Suárez et al., 2008). Although some studies have detected the presence of transgenes in maize landraces in Mexico, an estimate of the proportion of transgenic corn that is present in native corn landraces is needed to have a clear idea of the magnitude of the gene flow through outcrossing between transgenic crops and native maize. However, obtaining such an estimate is challenging for three reasons: (1) a diagnostic test is required to classify each plant as positive or negative; (2) it is impractical to use simple random sampling since we do not have a sampling frame for plants; and (3) diagnostic tests are expensive. Group testing is an excellent alternative for avoiding these problems, since instead of performing individual tests, a diagnostic test is performed on each pool (group of plants), which reduces the required number of diagnostic tests by 80%. However, as noted above, existing group-testing methods are not designed for complex surveys. For this reason, in the present paper we extend the group-testing methodology to an informative two-stage survey that takes into account the weights at the cluster and individual levels to obtain appropriate estimates of the parameter of interest.

Materials and methods

Sampling design and generalized linear model

Suppose that we have a population of M _h clusters in strata h (level 2 units, primary sampling units or fields) with h = 1, 2. By strata we mean the separation of the total target population into different groups based on certain categorical variables (i.e. moisture levels, spatial heterogeneity, fertility levels, regions, type of irrigation used, type of producer, etc.). These groups should be as homogeneous as possible, while the population between strata should be as heterogeneous as possible. We also define h* as substrata (homogeneous groups) inside each cluster. N _ih elementary units in the ith cluster at the hth strata (level 1 units, subjects or plants) are sampled following a two-stage sampling scheme. In the first stage, m _h  < M _h fields are selected with π _ih inclusion probabilities (i = 1, 2, …, M _h ) that are correlated with the cluster random effect (b _i ). In the second stage, n _ihh* plants are selected within the ith field, hth strata and substratum h* with probabilities π _j|ihh* (j = 1,2, …, N _ih ) that may be correlated with the outcomes after conditioning on the regressors x _ihh*j . Since the cluster random effect and the response variable are viewed as random under the model, so are the selection probabilities under informative sampling. The unconditional sample inclusion probabilities are then π _ihh*j  = π _j|ihh* π _ih .

Given that group testing will be used, plants must be assigned to pools in some way, and each pool is tested for a transgene. Suppose that n _ihh* plants from the ith field, hth strata and substratum h* are randomly assigned to one of the g _ihh* pools, such that there are s _ihh*j plants in pool j from field i, hth strata and substratum h*. Further, let y _ihh*jk  = 1 if the kth plant in the jth pool from field i, hth strata and substratum h* is transgenic, and y _ihh*jk  = 0 otherwise, for i = 1, 2, …, m _h , j = 1, 2, …, g _ihh* and k = 1, 2, …, s _ihh*j . Since we are using group testing and will only observe the response of each pool, we define the random variable Z _ihh*j  = 1, if the jth pool in the ith field, hth strata and substratum h* tests positive for transgenes, and Z _ihh*j  = 0 otherwise. Therefore, the two-level generalized linear mixed model for the response Z _ihh*j can be specified with the linear predictor of a generalized linear mixed model (Breslow and Clayton, 1993; Rabe-Hesketh and Skrondal, 2006):

(1) $${\eta _{ihh{^\ast}jk}} = {\beta _0} + {\beta_1}{x_{ihh^{\ast}jk}} + {b_i}.$$

Here β ₀ is the intercept, x _ihh*jk is a px1 covariate vector associated with fixed effects at the individual level, β ₁ is the slope, and b _i is the random effect of the ith field or cluster, which is Gaussian iid with mean zero and variance $\sigma _b^2 $ . The conditional distribution of y _ihh*jk is Bernoulli (p _ihh*jk ) which, assuming the logit link function $\; log ({{{p_{ihh*jk}}} {/} {1 - {p_{ihh*jk}}}})$ , gives:

(2) $${\,p_{ihh{^\ast}jk}} = {\,p_{ihh{^\ast}jk}}\left( {{\beta _0},{\beta _1},{\sigma _b}} \right)\; = {\rm exp}\big( {{\eta _{ihh{^\ast}jk}}} \big)/\big[ {1 + \exp \big( {{\eta _{ihh{^\ast}jk}}} \big)} \big].$$

Chen et al. (2009) assumed that, conditional on the random effect [b _i ], the probability of a positive pool taking into account the sensitivity (S _e ) and specificity (S _p ) of the diagnostic test is given as:

(3) $$P\left( {{Z_{ihh{^\ast}j}} = 1\left \vert {{b_i}} \right.} \right) = {S_e} + \left( {1 - {S_e} - {S_p}} \right)\mathop \prod \limits_{k = 1}^{{s_{ihh{^\ast}j}}} (1 - {\,p_{ihh{^\ast}jk}}).$$

S _e is the probability of a positive test given that a plant is transgenic (i.e. the ability of a test to correctly identify transgenic plants). S _p is the probability of a negative test given that the plant is not transgenic (i.e. the ability of the test to correctly identify non-transgenic plants). S _e and S _p are assumed to be constant and close to 1.

Incorporating weights in the PML

The PML approach is required when the sampling mechanism is informative. However, incorporating weights in the likelihood is complicated by the fact that the population log-likelihood is not a simple sum of elementary unit contributions, but rather a function of sums across level 2 and level 1 units. In addition, the implementation of the PML approach requires knowing the inclusion probabilities at both levels. Using only second-level weights or only first-level weights may yield poor results (Grilli and Pratesi, 2004).

Now let θ  = (β ₀, β ₁, σ _b ) denote the vector of all estimable parameters. The multilevel likelihood is calculated for each level of nesting and takes into account the weights. First, the conditional likelihood for pool j in field i is given by:

$${L_{ij}}({\bi \theta} \left \vert {{b_i}) = {{\left[ {P\left( {{Z_{ihh{^\ast}j}} = 1\left \vert {{b_i}} \right.} \right)} \right]}^{{Z_{ihh{^\ast}j}}}}} \right.{\left[ {1 - P\left( {{Z_{ijhh{^\ast}}} = 1\left \vert {{b_i}} \right.} \right)} \right]^{\left( {1 - {Z_{ihh{^\ast}j}}} \right)}}$$

where P(Z _ihh*j  = 1|b _i ) is defined in equation (3). We also assume two substrata. Next, to obtain the independent contribution of a field to the likelihood, field-level random effects are integrated out, as follows:

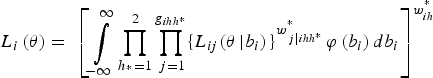$${L_i}\left( {\bi \theta} \right) = \; {\left[ {\mathop \int \limits_{ - \infty} ^\infty \mathop \prod \limits_{{h_{^\ast}} = 1}^2 \mathop \prod \limits_{\,j = 1}^{{g_{ihh{^\ast}}}} \{ {L_{ij}}{{({\bi \theta} \left \vert {{b_i})} \right.\}} ^{w_{\,j\left \vert {ihh{^\ast}} \right.}^{^\ast}}} \varphi \left( {{b_i}} \right)d{b_i}} \right]^{w_{ih}^{^\ast}}} $$

where g _ihh* is the number of pools in cluster i, strata h and substrata h*, where $w_{j\left\vert {ihh*} \right.}^* $ is the scaled weight for pool j in stratum h, field i and substratum h*, $w_{ih}^* $ is the field weight in stratum h, φ(b _i ) is the $N\left( {0,\; \sigma _b^2} \right)$ , with the final likelihood being the product of field likelihoods:

$$L = \mathop \prod \limits_{h = 1}^2 \mathop \prod \limits_{i = 1}^{{m_h}} {L_i}\left( {\bi \theta} \right).$$

Finally, combining the expression for all the fields (clusters), the overall marginal likelihood is

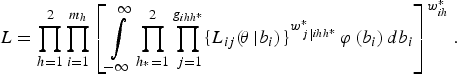(4) $$L = \prod\limits_{h = 1}^2 \prod\limits_{i = 1}^{{m_h}} \left[\int\limits_{ - \infty}^{\infty} \prod\limits_{{h_{^\ast}} = 1}^2 \prod\limits_{\,j = 1}^{g_{ihh^{\ast}}} \{L_{ij} (\!{\bi \theta} \left \vert {b_i}) \right.\}^{w_{\,j\left \vert {ihh^{\ast}} \right.}^{\ast}} \varphi \left( b_i \right) db_i \right]^{w_{ih}^{\ast}}. $$

Here the weights enter the log-pseudo-likelihood as if they were frequency weights, representing the number of times that each unit was replicated to estimate the likelihood that would have been obtained in a census. However, when survey data have been collected under a complex sample design, straightforward application of maximum likelihood estimator (MLE) procedures is no longer possible, for several reasons. First, the probabilities of selection of each cluster or individual are generally no longer equal. Sampling weights are thus required to estimate the finite population values of logistic regression model parameters. Second, the stratification and clustering of complex sample observations violates the assumption of independence of observations that is crucial to the standard MLE approach for estimating the sampling variances of the model parameters and choosing a reference distribution for the likelihood ratio test statistic (Heeringa et al., 2010). Also, when the sampling weights are related to the values of the model's outcome variable after conditioning on the model covariates, sampling is informative and the observed outcomes are no longer representative of the population outcomes. Thus the appropriate model for the sample data is different from the model for the finite population (Pfeffermann and Sverchkov, 2009).

Also, it is clear from the form of the likelihood (equation 4) that we cannot simply use one set of weights based on the overall inclusion probabilities; instead, we must use separate weights at each level, which implies that the self-weighting property of multistage designs is lost. The log-pseudo-likelihood is given as:

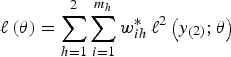(5) $$\ell \left( {\bi \theta} \right) = \sum\limits_{h = 1}^2 \sum\limits_{i = 1}^{m_h} w_{ih}^{\ast}\,\ell^2 \left(y_{\left( 2 \right)};{\bi \theta} \right)$$

where $\ell^2 (y_{( 2 )}; {\bi \theta}) = \log \left\{\mathop{\int}\nolimits_{-\infty}^{\infty} \exp \left[\mathop{\sum}\nolimits_{h_{\ast} = 1}^2 \sum\nolimits_{j = 1}^{g_{ihh \ast}} w_{j \vert {ihh \ast}}^{\ast} \log \left(L_{ij} ({\bi \theta} \vert {b_i}) \right) \right] \varphi \left({b_i} \right) d{b_i} \right\}$ . Maximization of the weighted log-likelihood (equation 5) involves computing several integrals that do not have a closed-form solution, so a numerical approximation technique is required. A standard solution to this problem is provided by using Gaussian quadrature (Pinheiro and Bates 2000; Rabe-Hesketh and Skrondal, 2006). However, since this method is based on a summation over an appropriate set of points, it is only efficient when the dimensionality of the integrals is low. The NLMIXED procedure of SAS (SAS, 2014) is a general procedure for fitting non-linear random effects models using adaptive Gaussian quadrature. For this reason, it will be implemented for maximizing the expression (equation 5). Another very important point is that inserting the weights in the log-likelihood implies using a consistent design estimator of the population score function.

The NLMIXED procedure of SAS (2014) has various optimization techniques to carry out maximization. The default, used in the simulations below, is a dual quasi-Newton algorithm, using the Cholesky factor of an approximate Hessian (SAS, 2014). Although the NLMIXED procedure does not include an option for PML estimation, Grilli and Pratesi (2004) show how to insert level 1 and 2 weights in the likelihood, as explained in the Illustrative example (Table 7). The sandwich estimator of the standard errors is provided in Appendix A.

Probability of selection

As mentioned earlier, when the sampling design is informative, maximizing the likelihood function given in equation (4), without weights, to obtain the MLEs of the parameters of interest may be seriously biased. For this reason, it is of paramount importance to incorporate design weights in the likelihood function. Considering two strata [i.e. M = (M ₁ + M ₂)] at the cluster level and that m _h clusters from each stratum are sampled with probabilities that are proportional to their sizes N _ih (number of units in the ith cluster at the hth strata), then the probability of selection of a cluster is

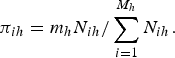(6) $${\pi _{ih}} = {m_h}{N_{ih}}/\mathop \sum \limits_{i = 1}^{{M_h}} {N_{ih}}.$$

Also, assume that in each cluster, the individuals are classified into two strata [i.e. n _ihh* = (n _i1h* + n _i2h*)], h* = 1, 2; and that a number of units n _ihh* is subsequently sampled from each cluster at each stratum, which implies that the probabilities of selection are:

(7) $$\; \; \; \; \; {\pi _{\,j\left \vert {ihh{^\ast}} \right.}} = {n_{ihh{^\ast}}}/{N_{ihh{^\ast}}}.$$

Such designs are self-weighting in the sense that all units have the same unconditional probability of selection. As an example of stratification of genetically modified corn plants, sampling fields at stage 1 could be stratified by irrigation (yes/no) or producer type (small or commercial), and while sampling plants at stage 2, strata could be based on plant or soil characteristics (e.g. moisture levels, spatial heterogeneity, fertility levels, etc.), which would correlate with the plant-level residuals. In this case, the unconditional probabilities are:

$${\pi _{ihh{^\ast}j}} = {\pi _{\,j\left \vert {ihh{^\ast}} \right.}}{\pi _{ih}} = {n_{ihh{^\ast}}}{m_h}{N_{ih}}/{N_{ihh{^\ast}}}\mathop \sum \limits_{i = 1}^{{M_h}} {N_{ih}}.$$

‘Raw’ design weights are obtained as the inverse of the probabilities of selection (w _ih  = 1/π _ih , w _j|ihh* = 1/π _j|ihh* and w _ihh*j  = 1/π _ihh*j ). However, these ‘raw’ weights need to be scaled to be used under a mixed model approach to avoid significant bias in the parameter estimates (Pfeffermann et al., 1998). For this reason, some scaling methods have been proposed. In general, most scaling methods produce better estimates than unweighted analyses. However, for the purpose of this research, we only consider three methods of scaling, which are reported as providing the least biased estimates in general. Due to the two-stage sampling process, we will have scaled weights for the two levels.

Level 1 scaling methods

Pfeffermann et al. (1998) and Korn and Graubard (2003) showed that scaling the weights is very important to obtain estimates with little bias even in small samples. However, they also state that it is not relevant for cluster weights, since multiplying the log-likelihood by a constant does not change the PML estimates (it simply inflates the information matrix by that constant). However, scaling level 1 weights on the small sample behaviour of the PML estimator is vital (Grilli and Pratesi, 2004). The most popular types of scaling are method A (or type 2), method B (or type 1) (Pfeffermann et al., 1998; Grilli and Pratesi, 2004; Rabe-Hesketh and Skrondal, 2006) and method D (Rabe-Hesketh and Skrondal, 2006). These three types of scaling methods are used in the simulation study (see below). At level 1 (elementary units) under method A (type 2), the scaled weight is obtained as:

(8) $$w_{\,j\vert ihh^{\ast}}^{\ast} = {w_{\,j \vert {ihh^{\ast}}}}/{\bar{w}_{\,j\vert ihh^{\ast}}}$$

where ${\bar w_{j\left\vert {ihh*} \right.}} = {{\mathop \sum \nolimits_j {w_{j\left\vert {ihh*} \right.}}} \over {{n_i}}}$ and n _i is the number of sample units in cluster i. With this scaling method, the new within-cluster weights add up to the cluster sample size $\sum\nolimits_j w_{j\left\vert {ihh \ast} \right.}^{\ast} = {n_i}$ . The scaled weight for method B (type 1) for level 1 is given by:

(9) $$w_{\,j\vert ihh^{\ast}}^{\ast} = w_{\,j \vert {ihh{^\ast}}}/n_i^{\ast} $$

where $n_i^* $ is the effective cluster sample size for cluster i, $n_i^* = {{\mathop \sum \nolimits_j w_{j\left\vert {ihh*} \right.}^2} \over {\mathop \sum \nolimits_j {w_{j\left\vert {ihh*} \right.}}}}$ . With this scaling method, the new within-cluster weights add up to the effective cluster sample size $n_i^* $ . Simulations in Pfeffermann et al. (1998) suggest that method B works better than method A for informative weights. Such a scaling factor was also used by Clogg and Eliason (1987) in a different context. Instead of scaling the level 1 weights, Graubard and Korn (1996) suggest a ‘method D’ which does not use any weights at level 1. This method D scales cluster weights as:

$$w_{ih}^{\ast} = \sum\limits_{\,j = 1}^{n_{ih}} w_{j\vert ihh^{\ast}}\, w_{ih},$$

and level 1 weights are $w_{j\left\vert {ihh*} \right.}^* = 1$ . This method seems appealing for pooled samples because we are mixing the information of s individuals. This implies that the weight of the pool is not required. Korn and Graubard (2003) pointed out that moment estimators of the variance components using these weights are approximately unbiased under non-informative sampling at level 1. The three methods proposed have an intuitive meaning, but do not always produce good results (Pfeffermann et al., 1998). Also, it is important to recall that we have conditional weights (w _j|ihh*) at the individual level; however, since we are pooling the material of s plants per pool, the weights for each pool can be incorporated in three ways: using the average weight of the individuals forming a particular pool, using the individual weights or using the sum of the s individual weights to form the pool weight.

Examples

Simulation example

A Monte Carlo experiment was carried out to assess the performance of PML estimation and the sandwich estimator under group testing. This experiment reflected the two-stage scheme explained above. First, finite population values with dichotomous responses were generated from the two-level superpopulation model with linear predictor η _ij  = β ₀ + b _i , with i = 1,2,…,M; ${b_i} \sim N\left( {0,\sigma _b^2} \right),$ response variable $Y_{ij}\vert {b_i} \sim {\rm binary} \left(p_i \right)$ , j = 1,2, …, N _i ; and logit link ${\rm log}\left( {{{{p_i}} \over {1 - {p_i}}}} \right)$ ; we used β ₀ = −4.4631, $\sigma _b^2 = 0.9888$ as our true model parameter values. Therefore, we simulated the individual responses, Y _ij , according to a Bernoulli distribution with mean p _i  = 1/(1 + exp(− β ₀ − b _i ). There were M = 300 clusters (level 2 units) that composed the finite population. These clusters were stratified into two strata by generating a normal random variable, $a_i \sim N (0,1)$ , independent of Y _ij , from which, if |a _i | >1, cluster i was assigned to stratum 1, and to stratum 2 otherwise. This stratification of clusters resulted in 83 clusters belonging to stratum 1 and 217 to stratum 2. The size of each cluster (N _ih ) was determined by ${N_{ih}} = 350 \exp \left(\tilde{b}_i \right)$ , with $\tilde{b_i}$ generated from $N\left( {0,\sigma _b^2} \right)$ , truncated below by − 0.1σ _b and above by 0.3σ _b . Therefore, the values of N _i in our finite population have a mean of 389.89 and a range between 317 and 472 individuals. We adopted an informative sampling process at both levels. For this reason, m _h clusters were selected with a probability proportional to a ‘measure of size’ X _ih , i.e. ${\pi _{ih}} = {m_h}{X_{ih}}/\mathop \sum \nolimits_{i = 1}^{{M_h}} {X_{ih}}$ , where the measured X _ih was determined in the same way as N _ih but with $\tilde{b_i}$ replaced by b _i , the random effect at level 2. Also, the individuals in each cluster were partitioned into two individual level strata such that if exp (1.6 + 0.1 * Y _ij  +  ${\epsilon}$ _ij) > 5.73, the individual was assigned to stratum 1; otherwise it was assigned to stratum 2, where ${\epsilon _{ij}}\approx {\rm Gamma}\left( {1,0.16} \right).\; \; $ Simple random samples were selected of 0.5n _ih1 and 0.5n _ih2 from the respective strata. The variable X _ih was used instead of the variable N _ih (in equation 6) and stratification at the individual level was performed to simulate a sampling process that is informative at both levels. It is important to point out that if we want an experiment that is informative only at level 2 (cluster level), stratification at level 1 (individual level) is not required. However, if we desire a process that is not informative, we need to use ${N_{ih}} = 350\,{\rm exp}\left( {{\hskip2pt\tilde{\hskip-3ptd}_i}} \right)$ instead of X _ih (equation 6), where $\tilde{d_i}$ is generated from N(0,1), truncated below by −0.1 and above by 0.3, and stratification at the individual level is not required.

To gain a clear understanding of the role of weighting methods in the accuracy of the results, six estimation methods were used for each simulated data set: (1) unweighted maximum likelihood; (2) PML using raw weights at the cluster level; (3) PML using raw weights at both levels; (4) PML using raw weights at the cluster level and scaling method A at the individual level; (5) PML using raw weights at the cluster level and scaling method B; and (6) PML using method D that only uses weights at the cluster level.

A two-stage sampling design for the finite population was implemented. In Table 1 (without covariates) and Table 2 (with a covariate), 100 individuals were selected from each cluster using stratified random sampling (50 from stratum 1 and 50 from stratum 2), and we used 24 clusters (8 from stratum 1 and 16 from stratum 2). In Table 3, we compared three sample sizes at individual levels (40, 80 and 120) per cluster with 24 clusters (8 from stratum 1 and 16 from stratum 2). The pools were formed with the individuals inside each cluster. For each combination of level 1 (plants) and level 2 (fields or cluster) samples, we simulated 600 data sets and estimated parameters using the weighting methods proposed. We observed that the sampling fraction at cluster level was 0.25 for stratum 1 and 0.75 for stratum 2. Computations were mostly performed in NLMIXED of SAS 9.4.

Table 1. Comparison of informative sampling at both levels, at the cluster level and at the individual level, and non-informative sampling. Simulation means and standard deviations (Std) of point estimators of the intercept (β ₀ = −4.4631 true value) and the second-level standard deviation (σ_b  = 0.9944 true value). Cluster sample m = 36 (12 from stratum 1 and 24 from stratum 2) under PPS. Elementary unit size n_j  = 100 (50 from stratum 1 and 50 from stratum 2) under SRS. Pool size (s). 600 simulations were performed for each scenario. Method 1: unweighted maximum likelihood; method 2: PML using raw weights at the cluster level; method 3: PML using raw weights at both levels; method 4: PML using raw weights at the cluster level and scaling Method A at the individual level; method 5: PML using raw weights at the cluster level and scaling method B; and method 6: PML using method D with weights at the cluster level

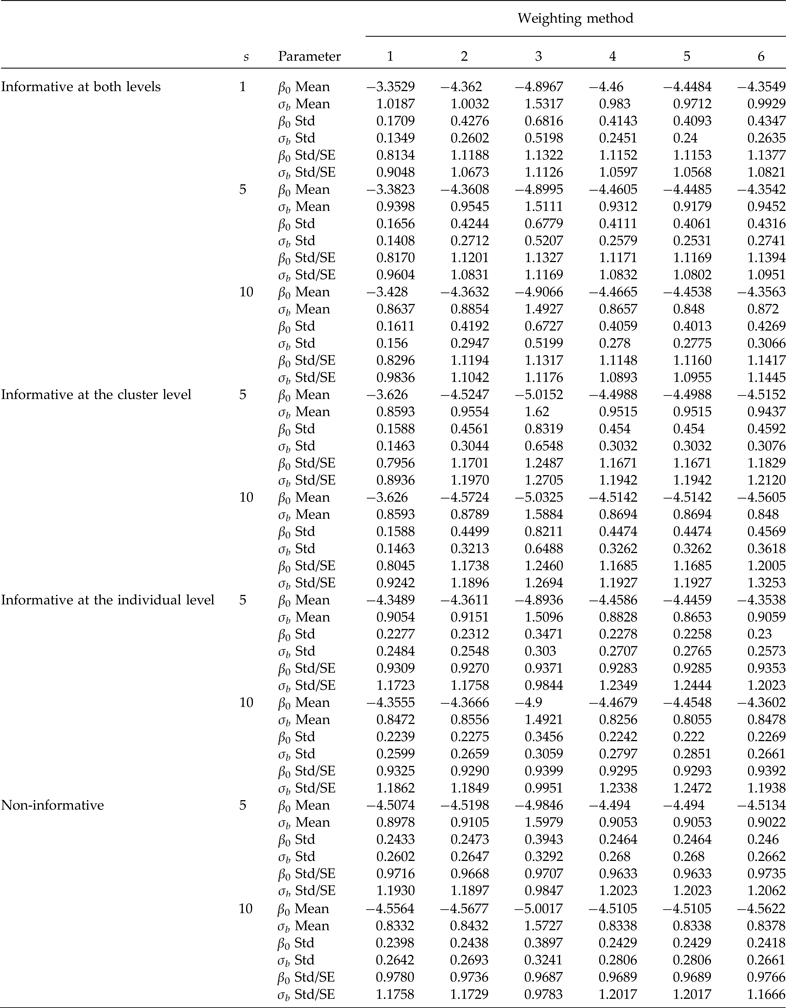
Table 2. Simulation means and standard deviations (Std) of the model with a covariate at the individual level (β ₀ = −4.7598, β ₁ = 0.8290 and σ _b  = 0.9820 true values). Cluster sample m = 24 (8 from stratum 1 and 16 from stratum 2) under PPS. Elementary unit size n_j  = 100 (50 from stratum 1 and 50 from stratum 2) under SRS. Pool size (s). 600 simulations were performed for each scenario. Method 1: unweighted maximum likelihood; method 2: PML using raw weights at the cluster level, method 3: PML using raw weights at both levels; method 4: PML using raw weights at the cluster level and scaling method A at the individual level; method 5: PML using raw weights at the cluster level and scaling method B; and method 6 PML using method D with weights at the cluster level

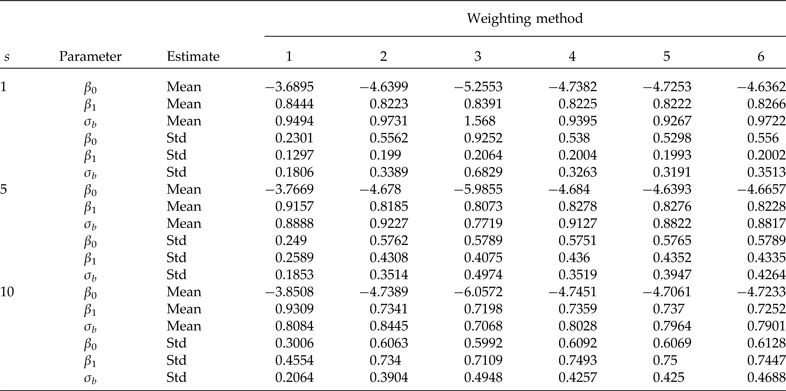
Table 3. Comparison using three different elementary unit sizes (n_j ) selected under SRS. Simulation means and standard deviations (Std) of point estimators of the intercept (β ₀ = −4.4631 true value) and the second-level standard deviation (σ_b  = 0.9944 true value). Cluster sample m = 24 (8 from stratum 1 and 16 from stratum 2) under PPS. Pool size (s). 600 simulations were performed for each scenario. Method 4: PML using raw weights at the cluster level and scaling method A at the individual level; method 5: PML using raw weights at the cluster level and scaling method B; and method 6: PML using method D with weights at the cluster level

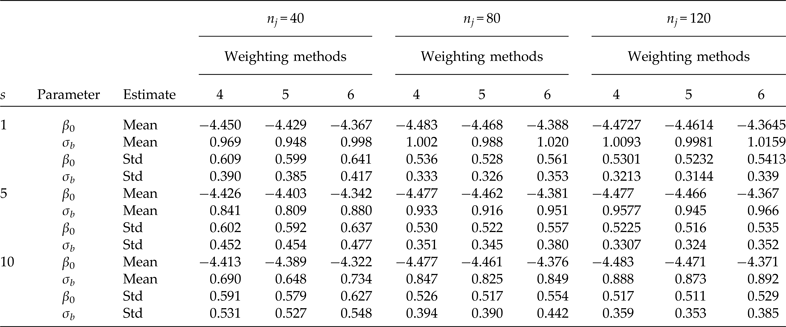
Estimating the proportion of transgenic corn in maize landrace accessions

A data set provided by one of the authors of the present paper was used for the application. The objective of this study was to estimate the adventitious presence of GMOs (transgenic corn) at the Mexico's National Genetic Resources Center in the region of Guanajuato, Mexico. This study is very important for reducing the risk of unknowingly storing maize landrace accessions with the adventitious presence of GMOs. Since it was not possible to do a census, a sample of 193 accessions of subtropical landraces was studied. However, weights at the cluster level (accession) were not obtained since these data were originally obtained under simple random sampling (SRS), but for purpose of the application we constructed the weight of each accession proportional to the accession's native area. Each accession was grown under field conditions at Celaya Experiment Station (Guanajuato, Mexico) of Mexico's National Forestry, Agricultural, and Livestock Research Institute (INIFAP) during the summer of 2012. Each accession consisted of 7 rows with 40 plants each. Then 3 of the 7 rows were selected at random; leaf tissue from each plant in these rows was harvested before anthesis. Forty leaf discs were collected from each plant and pooled (bulked) by row. In group testing notation this means that the pool size was 40 plants and that 3 pools were analysed for each accession. This pool size was chosen based on tests performed in the laboratory. The resulting pool of tissue samples was ground with liquid nitrogen and pulverized prior to deoxyribonucleic acid (DNA) extraction, which was performed according to the protocol of Saghai-Maroof et al. (1984), with the addition of 1% polyvinyl pyrrolidone (PVP) to the cetyltrimethylammonium bromide (CTAB) buffer. DNA quality was checked and concentrations were adjusted to 10 ng μl⁻¹. Detection of the 35S promoter was carried out with the TaqMan^® GMO Maize 35S Detection Kit from Life Technologies (Thermo Fisher Scientific, Waltham, Massachussetts, USA) following the manufacturer's recommendations. We considered a pool to be positive (presence of the 35S promoter in the tested pool) when both the endogenous gene and the 35S gene were amplified in the sample, the amplification curve had a Ct value between 20 and 30, and the amplification curve presented the three typical phases: exponential, linear and plateau. Also, each pool was tested with polymerase chain reaction (PCR) in real time for the amplification of the α-zein gene, but here we only report the analysis for the presence of the 35S promoter. It is important to point out that we are interested in estimating the proportion of the adventitious presence of GMOs (transgenic corn) in the native maize landrace accessions currently stored in Mexico's National Genetic Resources Center in Guanajuato, Mexico.

Results

Simulation study

Results of the simulation with and without covariates are given in Tables 1–3. Without covariates, the true values of the parameters are β ₀ = −4.4631 and $\sigma _b^2 = 0.9888$ . We reported the mean and standard deviations for the estimated parameters resulting from the 600 simulations.

For a sample of 36 clusters, Table 1 (informative at both levels) shows that ignoring the weights at both levels (method 1) produced a considerable overestimation of the β ₀ parameter, and an underestimation of the second-level standard deviation (σ _b ). Method 3, using raw weights at both levels, underestimated the fixed parameter, β ₀, and significantly overestimated the second-level standard deviation (σ _b ). However, using only raw weights at the cluster level and no weighting at the individual level (method 2) overestimated β ₀ and underestimated σ _b , but to a lesser degree than ignoring the two weights (method 1). Scaling the weights produces better results than method 1 (ignoring the weights) and method 3 (raw weights at both levels). Method 2 and the three scaled methods 4, 5 and 6 generally produce the least biased results of all methods. Estimates of β ₀ were reasonable and very close to the true values, but σ _b was still underestimated. Using a sample of 48 clusters, there is no clear improvement in the parameter estimates compared to using a sample of 36 clusters (data are not shown). Table 1 also shows that the ratio of the standard deviation of the parameter estimates in the simulation of the average standard errors converges to 1, which is expected when the sample size is large; this implies that the sandwich estimator is correct. Based on these results, scaled weights decreased the bias in the estimation of both parameters compared to no scaling; however, even when the weights were scaled, the results were biased, but to a much lesser degree. Also, using group testing produced results as precise as those of individual testing, but with the advantage that it considerably reduce the number of required diagnostic tests.

When the design is informative only at the cluster level (Table 1), method 1 produced highly biased results (serious overestimation of β ₀ and underestimation of σ _b ). Using the raw weights at both levels is not recommended because the estimates are still highly biased (Table 1). When only the raw cluster weights (method 2) are included, there is still considerable bias, and using scaled weights at the individual level and raw weights at the cluster level (methods 4 and 5) produced almost identical results and with small bias. This implies that using scaled weights is preferable.

When the design is informative only at the individual level (Table 1), using the raw weights (method 3) is not a good choice because the results still are highly biased. However, methods 1, 2, 4, 5 and 6 produced results with small bias (Table 1). This can be attributed to the way the informative sampling process was induced at each level. On the subject of regression of binary responses in a two-stage sampling, Grilli and Pratesi (2004) reported that when the sampling process is informative at the individual level, it is important to incorporate scaled weights. However, in their simulation they used β ₀ = 0 and a second-level standard deviation of 0.632 with the probit link.

When the sampling process is not informative, Table 1 shows that method 3 (raw weights at both levels) again underestimates β ₀ and overestimates σ _b . However, methods 1, 2, 4, 5 and 6 produced estimates of both parameters that are very close to the true values of β ₀ and σ _b , which corroborates that when the sampling process is not informative, weights are not required. In general, method 4 produced the best results.

For a fixed sample of clusters (Table 3, m = 24), we studied the behaviour of the parameter estimates (β ₀ and σ _b ) for three different sample sizes at the individual level (n _i ). Both parameters are considerably biased even with individual testing when the number of individuals per cluster is equal to n _i  = 40. A considerable improvement occurs when the number of individuals per cluster is equal to n _i  = 80. In this scenario, the estimate of β ₀ is close to the true value, but the estimate of the second-level standard deviation is still biased with group testing, and the problem is even worse when pool size s = 10. Finally, using 120 individuals per cluster produces less biased results than using 40 or 80, but the second-level standard deviation is still underestimated when using group testing.

Results from simulations used to study the performance of the model with a covariate at the individual level are given in Table 2. The model is the same as the model given in equation (1) described above, except that to include a covariate at the individual level, we generated data from a normal distribution with mean zero and variance 0.64, and used values of β ₀ = −4.7598, β ₁ = 0.8290 and σ _b  = 0.9820 (the code for the analysis is given in Appendix B). Table 2 indicates that the use of scaled weights (methods 4, 5 and 6) is effective for removing bias due to informative sampling. However, it is important to point out that the results are somewhat more biased than in the no covariate case. In general, the overall performance of the scaled weights is satisfactory.

Illustrative example

To illustrate the implementation of the analysis using NLMIXED of SAS 9.4, we present simulated data for a finite population of eight clusters within two regions (strata) and two substrata [which could be the fertility levels (FL) in each field]. On a smaller scale, these population data represent a typical population in which we can use PPS and stratified sampling for selecting the study units (Table 4). This population has a total of 163 plants distributed in 16 subgroups derived by combining region, field and FL levels. The total number of plants per region, field and subgroups are also given in Table 4.

Table 4. Population data including two regions, eight fields (clusters) and two strata per field (fertility levels, FL). The binary response of each plant is y, n _ihh* denotes total plants per combination of region, field and FL, N _ih denotes total plants per field in each stratum and N _h denotes total plants per region

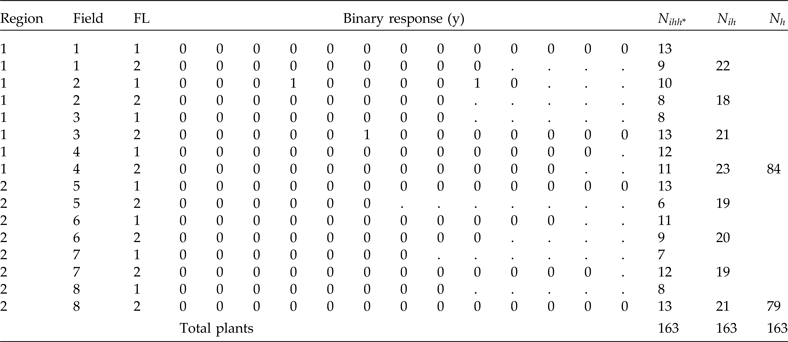
Suppose that a stratified sampling of two fields within each region and stratified sampling within each field at a fixed sample size of six plants per stratum are selected (π _ih  = 2N _ih /N _h , π _j|ihh* = 6/N _ihh*), where ${N_h} = \mathop \sum \nolimits_{i = 1}^{{M_h}} {N_{ih}}$ . Table 5 shows the sample that resulted from using this sampling procedure. Note that the total sample size is equal to 48 plants, which is obtained by multiplying 2 regions × 2 fields × 2 FL × 6 plants. First we will explain how the field raw weights are calculated. In Table 4 we see that the total number of plants in region 1 is N ₁ = 84, while the total numbers of plants in clusters 2 and 3 are N ₂₁ = 18 and N ₃₁ = 21, respectively. Therefore, the selection probabilities are ${\pi _{21}} = {{2\left( {18} \right)} \over {84}} = 0.4286$ , ${\pi _{31}} = {{2\left( {21} \right)} \over {84}} = 0.5$ and the corresponding sampling weights are ${w_{21}} = {1 \over {0.4286}} = 2.33$ and ${w_{31}} = {1 \over {0.5}} = 2.0$ . The remaining weights for the other fields are calculated in a similar manner.

Table 5. Sample obtained by taking two fields within each region under PPS and doing stratified sampling within each field using a fixed sample size of six plants per stratum under SRS

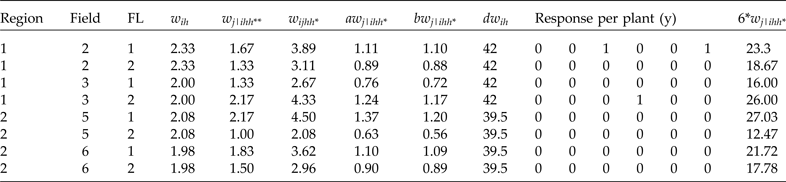
The conditional raw weights for each plant in the first row in Table 5, corresponding to region 1, field 2 and FL = 1, are calculated as follows. Here N ₂₁₁ is the total number of plants per combination of field 2, region 1, and FL 1, which is equal to 10 (see Table 4). Therefore, $\; \; {\pi _{j\left\vert {211} \right.}} = {6 \over {10}} = 0.6$ , and ${w_{j\left\vert {211} \right.}} = {1 \over {0.6}} = 1.67$ . For the conditional weight of the second row in Table 5, N ₂₁₂ = 8 (corresponding to field 2, region 1 and FL 2). Therefore, $ {\pi _{j\left\vert {212} \right.}} = {6 \over 8} = 0.75$ , and ${w_{j\left\vert {212} \right.}} = {1 \over {0.75}} = 1.33.$ To verify that the calculations of the raw weights are correct, it is important to calculate the raw unconditional weight of each individual, which is the product of the raw cluster weight multiplied by the conditional raw weights ( ${w_{ijhh*}} = {w_{ih}}*{w_{i\left\vert {ihh*} \right.}}$ ), and the sum of the individual total weights should be exactly (or very close to) the total number of individuals in the population. In this example, each calculated weight given in Table 5 is for six individuals in the sample, since the six plants that appear in each row of Table 5 have the same weight. This means that the sum of the unconditional raw weights (w _ijhh*) should be 163 (the total number of individuals in the population given in Table 4), and the unconditional raw weights for each row in Table 5 should be multiplied by 6 (last column of Table 5), since our total sample size is 48 individuals. Therefore, by obtaining the sum for the last column in Table 5, we verified that the sum is exactly 163. For more details on how to calculate raw weights, the reader should consult Lohr (2010) since the calculation of these weights is done using conventional methods.

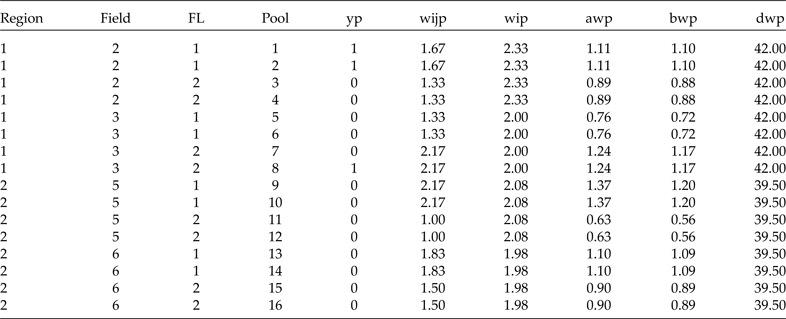
Table 6. Sample prepared in terms of pools for analysis

Since raw conditional weights are not the best option, as was observed previously, we will now show how to scale the weights. For scaling method A (aw _j|ihh*), first we obtain the average of the raw conditional weights (w _j|ihh*) in each cluster; then we divide each conditional weight by this average. For example, for field 2, the average conditional raw weight is equal to ${{6*1.67 + 6*1.33} \over {12}} = 1.5$ (this was calculated as a weighted average since 6 elements of each stratum in each cluster have the same weights). Therefore, the scaled weight using this method for the first conditional weight (row 1 in Table 5) is equal to $a{w_{j\left\vert {211} \right.}} = {{1.67} \over {1.5}} = 1.11$ . The corresponding conditional scaled A weight for the second row is equal to $a{w_{j\left\vert {212} \right.}} = {{1.33} \over {1.5}} = 0.89$ . The conditional scaled A weights for the other observations in the sample are obtained in exactly the same way. One way to check that these scaled conditional A weights are correct is that the sum of scaled conditional A weights in each cluster must be the same as the obtained sample size in each cluster (in this case, 12; for field 2 this is equal to [6(1.11) + 6(0.89)] = 12), and the sum of all the scaled weights must be the same as the total sample size (in this case, 48).

To obtain the conditional scaled B weights, we must first calculate the sum of all the conditional raw weights $(\mathop \sum \nolimits_j {w_{j/ihh*}})$ , then obtain $n_i^* = {{\mathop \sum \nolimits_j w_{j\left\vert {ihh*} \right.}^2} \over {\mathop \sum \nolimits_j {w_{j\left\vert {ihh*} \right.}}}}$ and, finally, the scaled B weights as $w_{j\left\vert {ihh*} \right.}^* = {w_{j\left\vert {ihh*} \right.}}/n_i^* $ . For cluster two, $\mathop \sum \nolimits_j {w_{j\left\vert {211} \right.}} = 6*1.67 + 6*1.33 = 18$ and $\mathop \sum \nolimits_j w_{j\left\vert {211} \right.}^2 = 6*{1.67^2} + 6*{1.33^2} = 27.35;$ then $n_2^* = {{27.35} \over {18}} = 1.52$ . Therefore, $b{w_{j\left\vert {211} \right.}} = {{1.67} \over {1.52}} = 1.10$ , while $b{w_{j\left\vert {212} \right.}} = {{1.33} \over {1.52}} = 0.88$ . Finally, the scaled D weights are obtained as $w_{ih}^* = \mathop \sum \nolimits_{j = 1}^{{n_i}} {w_{j\left\vert {ihh*} \right.}}{w_{ih}}$ . For field 2, this is equal to dw ₂₁ = 6*1.67*2.33 + 6*1.33*2.33 = 42. Scaled method D is calculated in the same way for the other clusters.

Now we have the complete sample (48 plants) and its corresponding weights. Since we will use group testing to classify the plants (positive or negative), we will form pools of size 3 at random in each cluster. For simplicity, let's assume that from each row (containing 6 plants) in Table 5 we form two pools; the first three plants go to pool 1, the second three to pool 2, and so on. Since we are forming the pools with the elements of the subgroup that resulted from the combination of region, field and FL, we will get exactly the same estimates if we use the average (of the three weights that form each pool) or individual weights. However, since we can form pools of size s at random with the elements of each cluster, this means that the weights in each pool are not always the same. Therefore, in Table 6 we present the data including the results in terms of pools and the average weights for each method. Here, of course, we are assuming that the diagnostic test used to classify each pool is perfect (S _e  = S _p  = 1). In Table 6, we show how to arrange the data resulting from any two-stage stratified cluster survey for analysis using group testing.

For analysis, the data should be prepared as in Table 6. That is, we need a column for region, a column for field (cluster), a column for FL, a column for the pool number (from 1 to 16 in this case), a column for the binary response of each pool (yp), a column for the level 1 raw conditional weight by pool (wijp), a column for the level 2 raw weight (wip) and three more columns for the scaled weights in terms of pools (awp, bwp and dwp). All different weights given in Table 6 are in terms of pools because the average of the three weights is used. Note that the finite population contains 8 clusters (fields 1 to 8), but in this sample only 4 of the 8 were selected: 2, 3, 5 and 6. We are interested in estimating the marginal probability of a particular transgene being present in the whole finite population and in the probability of this transgene being present in each cluster.

Table 7 gives the SAS NLMIXED code needed to perform the analysis with the information in Table 6. Note we form a data set in SAS using the names of the input variables as in the columns in Table 6 (Region, field, FL, pool, yp, wijp, wip, awp, bwp and dwp). The relevant output of this code is shown in two tables. The first table is called Parameter Estimates ( $\widehat{{{\beta _0}}}\; $  = −2.5057, denoted as b_0 estimate, and σ _b  = 0.6230 denoted as sd estimate). Therefore, the expected proportion of transgenic corn for the average field, p _i (b _i  = 0) is: $p = {1 \over {\left( {1 + exp\left( { - \widehat{{{\beta _0}}}} \right)} \right)}} = {1 \over {\left( {1 + exp\left( {2.5057} \right)} \right)}} = 0.0755$ . This means that the estimated probability of finding transgenic plants in the whole population is 7.55%. According to Breslow and Clayton (1993), we can approximate the marginal estimate of the proportion of transgenic plants in the entire population as: p = ${1 \over {\big( {1 + exp\big( { - {{\big( {1 + 0.346\sigma _b^2} \big)}^{ - 0.5}}\widehat{{{\beta _0}}}} \big)} \big)}}$  =  ${1 \over {\left( {1 + exp\left( {{{\left( {1 + 0.346 x {{0.6230}^2}} \right)}^{ - 0.5}}2.5057} \right)} \right)}}$  = 0.0869. This means that the estimated proportion of transgenic plants in the whole population is 8.69%. The second table, called Blups per field, contains the predicted proportions for each field. The predicted values are 0.112327 for cluster 2, 0.08450 for cluster 3, 0.05999 for cluster 5 and 0.05863 for cluster 6. Since these are Blups, they should be interpreted as the predicted probability that a particular transgene is present in each field. Field 2 has the highest probability of transgenes being present (0.112327) and field 6, the lowest (0.05863). Results of the program in Table 7 show that these results were run using weighting method 5, since we put the scaled B weights (bwp) in the augmented log-likelihood, and the raw cluster weights (wip) in the replicate statement. However, if you wish to run the analysis with a different weighting method, just replace bwp with the appropriate weight. For example, for method 3 (raw weights at both levels) you need to keep wip and replace bwp with wijp. One limitation of the code in Table 7 is that it does not take into account any covariates (see Appendix B for the SAS code if you have covariates).

Table 7. NLMIXED and GLIMMIX statements for two-stage group-testing regression under PPS

Application for estimating the proportion of transgenic corn

Since the data set contains a sample of 193 accessions, it is not practical to show all the details for the weight construction, but the construction process was the same as explained in detail in the illustrative example above. However, it is important to point out that the number of clusters (accessions) under study was 193, that the pool size was 40 plants, the total number of pools analysed was 664 and that for each pool we obtained a zero (35S promoter absent) and one (35S promoter present). We also assumed that sensitivity and specificity are equal to 1. Unfortunately, all 664 pools were negative and for purposes of illustrating the methodology, we added three positive pools to this real data set; these were pools 1, 10 and 19. The resulting parameter estimates using scaled A weights are $\widehat{{{\beta _0}}}$  = −20.173, denoted as b_0 estimate, and σ _b  = 7.4248 denoted as sd estimate. Therefore, the expected proportion of transgenic corn in an average accession, p _i (b _i  = 0) is: $p = {1 \over {\left( {1 + exp\left( { - \widehat{{{\beta _0}}}} \right)} \right)}} = {1 \over {\left( {1 + exp\left( {20.173} \right)} \right)}}$  = 1.73371E-09. This means that the estimated probability of finding transgenic plants in the whole area under study is very low. Given that we add three positive pools to this real data set, in any moment this result can be used as a valid expected proportion of transgenic corn in this area of Mexico.

Conclusions

In this paper, we present a generalization of the mixed regression group testing methodology for a complex survey in two stages with stratification and clusters of different sizes, when the sampling process is informative. The estimation process was performed using the average weights per pool for simplicity, which implied that the pools should be randomly formed inside each cluster. Our results are in line with those reported by Pfeffermann et al. (1998, 2006) (for a normal response), by Grilli and Pratesi (2004) and Rabe-Hesketh and Skrondal (2006) (for binary outcomes in the non-group-testing context). We found that when the sampling process is informative, weights at both levels should be included. However, we need to use scaled weights because using raw weights produces more bias than ignoring the weights altogether. Also, it is important to point out that if the sampling process is not informative, the weights at both levels should be ignored and the analysis can be performed using any of the previously developed packages for mixed group-testing regression models. However, the NLMIXED and GLIMMIX code given in this paper allows running the analysis with the six weighting methods proposed. From a practical point of view, if you get very similar results by ignoring the weights and using the three scaled weights (methods 4, 5 and 6), you should choose method 1 (ignoring the weights) because this means that your sampling process is not informative.

Also, it is important to stress that when covariates are not included in the linear predictor, the results when using group testing (with pool sizes 5 and 10) are almost the same as when using individual testing. This means that in this application, group-testing regression is as precise as individual regression. This result implies that group testing can be a useful approach for conducting complex surveys with small pool sizes (≤10) and forming the pools in each cluster. Also, including covariates at the individual level produced results that are very similar to those obtained without pooling (Table 2). However, more simulations need to be performed to see how well this methodology works with a larger pool size and more covariates. Although the data set used for the application was not really meaningful, it is important to point out that this methodology can be very useful for estimating the proportion of transgenic corn using a group-testing approach.

Although we can include individual weights or the sum of weights at the pool level, this requires further research. Using individual weights is expected to produce the same results as the average weights used in this investigation, when pools are formed with members of each stratum in each cluster. Since the log-likelihood function requires the information per cluster, we always recommend forming pools with members from the same cluster. For this reason, to perform a correct analysis with group testing in a two-stage sampling informative process requires using the pools, their corresponding outcomes (positive or negative) and raw weights at both levels (one cluster weight and the conditional weights of the individuals forming a pool). These raw weights at the individual level then need to be scaled to produce weighting methods 4, 5 and 6; finally, the NLMIXED and GLIMMIX code given in Table 7 and Appendix B can be used to perform the analysis. The resulting output using this code produces an estimate of β ₀ that can be used to estimate the marginal proportion of the characteristic of interest (as shown in the application). The code also produces Blups (predicted proportions), allowing researchers to obtain estimates not only for the whole population but for each cluster as well. Finally, the methodology developed here can be used to estimate any binary response using a complex informative sampling process. The overall utility of using our estimation approach is that it can save considerable resources when group testing is used in conjunction with complex sampling designs.