Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-17T13:26:30.589Z Has data issue: false hasContentIssue false
  • English
  • Français

ZERO-CYCLES ON NORMAL PROJECTIVE VARIETIES

Part of: Cycles and subschemes (Co)homology theory $K$-theory in geometry

Published online by Cambridge University Press:  11 February 2022

Mainak Ghosh  and
Amalendu Krishna Open the ORCID record for Amalendu Krishna [Opens in a new window]
Mainak Ghosh
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, 1 Homi Bhabha Road, Colaba, Mumbai 400005, India ([email protected])
Amalendu Krishna*
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore 560012, India
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove an extension of the Kato–Saito unramified class field theory for smooth projective schemes over a finite field to a class of normal projective schemes. As an application, we obtain Bloch’s formula for the Chow groups of 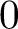$0$-cycles on such schemes. We identify the Chow group of 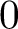$0$-cycles on a normal projective scheme over an algebraically closed field to the Suslin homology of its regular locus. Our final result is a Roitman torsion theorem for smooth quasiprojective schemes over algebraically closed fields. This completes the missing p-part in the torsion theorem of Spieß and Szamuely.

Keywords

singular varietiesalgebraic cyclesclass field theorySuslin homologyLefschetz theorems

MSC classification

Primary: 14C25: Algebraic cycles
Secondary: 14F42: Motivic cohomology; motivic homotopy theory 19E15: Algebraic cycles and motivic cohomology
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 5 , September 2023 , pp. 2241 - 2295
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altman, A. and Kleiman, S., Bertini theorems for hypersurface sections containing a subscheme, Comm. Algebra 7(8) (1979), 775–790.Google Scholar
Artin, E. and Tate, J., Class Field Theory, AMS Chelsea Publishing (American Mathematical Society, Providence, RI, 2000).Google Scholar
Binda, F. and Krishna, A., Zero cycles with modulus and zero cycles on singular varieties, Compos. Math. 154(1) (2018), 120–187.10.1112/S0010437X17007503CrossRefGoogle Scholar
Binda, F. and Krishna, A., Zero cycle groups on algebraic varieties, J. Éc. polytech. Math. (to appear), Preprint, 2021, https://arxiv.org/abs/2104.07968v2.Google Scholar
Binda, F., Krishna, A. and Saito, S., Bloch’s formula for 0-cycles with modulus and the higher dimensional class field theory, J. Alebraic Geom. (to appear), Preprint, 2020, https://arxiv.org/abs/2002.01856.Google Scholar
Binda, F. and Saito, S., Relative cycles with moduli and regulator maps, J. Math. Inst. Jussieu 18(6) (2019), 1233–1293.10.1017/S1474748017000391CrossRefGoogle Scholar
Biswas, J. and Srinivas, V., Roitman’s theorem for singular projective varieties, Compos. Math. 119(2) (1999), 213–237.10.1023/A:1001793226084CrossRefGoogle Scholar
Bloch, S., ${K}_2$ and algebraic cycles, Ann. of Math. (2) 99(2) (1974), 349–379.CrossRefGoogle Scholar
Bloch, S., Lectures on Algebraic Cycles, Duke University Mathematics Series, 4 (Duke University Press, Durham, North Carolina, 1976).Google Scholar
Cornell, G. and Silverman, J., Arithmetic Geometry (Springer, New York, 1986).CrossRefGoogle Scholar
de Jong, A. J. et al., The Stacks Project, 2020, http://stacks.math.columbia.edu.Google Scholar
Deglise, F., Bivariant theories in motivic stable homotopy, Doc. Math. 23 (2018), 997–1076.CrossRefGoogle Scholar
Deligne, P., Théorie de Hodge III, Publ. Math. Inst. Hautes Études Sci. 44(1) (1974), 5–77.Google Scholar
Deligne, P., La classe de cohomologie associée à un cycle, in Séminaire de Géométrie Algébriquedu Bois-Marie SGA 4 $\frac{1}{2}$ , LNM Series, 569, pp. 129–153 (Springer-Verlag, Berlin, 1977).10.1007/BFb0091521CrossRefGoogle Scholar
Friedlander, E., Suslin, A. and Voevodsky, V., Cycles, Transfers and Motivic Homology Theories, Annals of Mathematics Studies, 143 (Princeton University Press, Princeton, NJ, 2000).Google Scholar
Fujiwara, K., A proof of the absolute purity conjecture, Adv. Stud. Pure Math. 36 (2002), 144–173.Google Scholar
Fulton, W., Intersection Theory, 2nd ed., Ergebnisse der Mathematik und ihrer Grenzgebiete, 3 Folge, A Series of Modern Surveys in Mathematics, 2 (Springer-Verlag, Berlin, 1998).10.1007/978-1-4612-1700-8CrossRefGoogle Scholar
Geisser, T., Roitman’s theorem for normal schemes, Math. Res. Lett. 22(4) (2015), 1120–1144.10.4310/MRL.2015.v22.n4.a8CrossRefGoogle Scholar
Geisser, T. and Schmidt, A., Tame class field theory for singular varieties over finite fields, J. Eur. Math. Soc. 19(11) (2017), 3467–3488.10.4171/JEMS/744CrossRefGoogle Scholar
Ghosh, M. and Krishna, A., ‘Bertini theorems revisited’, Preprint, 2020, https://arxiv.org/abs/1912.09076v2.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique: I. Le langage des schémas, Publ. Math. Inst. Hautes Études Sci. 4(1) (1960), 5–228.10.1007/BF02684778CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Seconde partie, Publ. Math. Inst. Hautes Études Sci. 24(1) (1965), 5–231.Google Scholar
Grothendieck, A., Cohomologie locale des fasisceaux cohéerents et théorème de Lefschetz locaux et glabaux (SGA-2), in Séminaire de Géométrie Algébrique 2, pp. 1–287 (North-Holland, Amsterdam, 1968).Google Scholar
Grothendieck, A., Revétements étales et groupe fondamental (SGA 1), In Séminaire de Géométrie Algébrique du Bois-Marie 1960–1961, LNM Series, 224, pp. 1–447 (Springer-Verlag, Berlin, 1971).Google Scholar
Grothendieck, A. and Dieudonné, J., Eléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Seconde partie, Publ. Math. Inst. Hautes Études Sci. 20(1) (1964), 5–259.CrossRefGoogle Scholar
Gupta, R. and Krishna, A., $K$ -theory and 0-cycles on schemes, J. Algebraic Geom. 29(3) (2020), 547–601.10.1090/jag/744CrossRefGoogle Scholar
Gupta, R. and Krishna, A., Reciprocity for Kato-Saito idele class group with modulus, Preprint, 2021, https://arxiv.org/abs/2008.05719v3.Google Scholar
Hartshorne, R., Local Cohomology , LNM Series, 41 (Springer-Verlag, Berlin, 1967).Google Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, 52 (Springer-Verlag, New York, 1997).Google Scholar
Illusie, L., Complexe de de Rham-Witt et cohomologie cristalline, Ann. Sci. Éc. Norm. Supér. (4) 12(4) (1979), 501–661.10.24033/asens.1374CrossRefGoogle Scholar
Jannsen, U., Continuous Étale cohomology, Math. Ann. 280(2) (1988), 207–245.CrossRefGoogle Scholar
Jannsen, U., Saito, S. and Zhao, Y., Duality for relative logarithmic de Rham-Witt sheaves and wildly ramified class field theory over finite fields, Compos. Math. 154(6) (2018), 1306–1331.CrossRefGoogle Scholar
Kato, K., Milnor $K$ -theory and Chow group of zero cycles, in Applications of Algebraic K-Theory to Algebraic Geometry and Number Theory, Contemporary Mathematics, 55, pp. 241–255 (American Mathematical Society, Providence, RI, (1986).CrossRefGoogle Scholar
Kato, K. and Saito, S., Unramified class field theory of arithmetic surfaces, Ann. of Math. (2) 118(2) (1983), 241–275.CrossRefGoogle Scholar
Kato, K. and Saito, S., Global class field theory of arithmetic schemes, in Applications of Algebraic K-Theory to Algebraic Geometry and Number Theory, Contemporary Mathematics, 55, pp. 255–331 (American Mathematical Society, Providence, RI, 1986).Google Scholar
Kelly, S. and Saito, S., Weight homology of motives, Int. Math. Res. Not. IMRN 13 (2017), 3938–3984.Google Scholar
Kerz, M., Milnor K-theory of local rings with finite residue fields, J. Algebraic Geom. 19(1) (2010), 173–191.10.1090/S1056-3911-09-00514-1CrossRefGoogle Scholar
Kerz, M. and Saito, S., Chow group of 0-cycles with modulus and higher-dimensional class field theory, Duke Math. J. 165(15) (2016), 2811–2897.10.1215/00127094-3644902CrossRefGoogle Scholar
Krishna, A., Zero-cycles on a threefold with isolated singularities, J. Reine Angew. Math. 594 (2006), 93–115.Google Scholar
Krishna, A., An Artin-Rees theorem in $K$ -theory and applications to zero cycles, J. Algebraic Geom. 19(3) (2010), 555–598.10.1090/S1056-3911-09-00521-9CrossRefGoogle Scholar
Krishna, A., On 0-cycles with modulus, Algebra Number Theory 9(10) (2015), 2397–2415.CrossRefGoogle Scholar
Krishna, A., Murthy’s conjecture on 0-cycles, Invent. Math. 217(2) (2019), 549–602.CrossRefGoogle Scholar
Krishna, A. and Park, J., A module structure and a vanishing theorem for cycles with modulus, Math. Res. Lett. 24(4) (2017), 1147–1176.10.4310/MRL.2017.v24.n4.a10CrossRefGoogle Scholar
Krishna, A. and Srinivas, V., Zero cycles and $K$ -theory on normal surfaces, Ann. of Math. (2) 156(2) (2002), 155–195.10.2307/3597187CrossRefGoogle Scholar
Lang, S., Unramified class field theory over function fields in several variables, Ann. of Math. (2) 64(2) (1956), 285–325.CrossRefGoogle Scholar
Lang, S., Abelian Varieties , Interscience Tracts in Pure and Applied Mathematics, 7 (Interscience Publishers, New York, 1959).Google Scholar
Lee, Y. and Nakayama, N., Grothendieck duality and $\mathbb{Q}$ -Gorenstein morphisms, Publ. Res. Inst. Math. Sci. 54(3) (2018), 517–648.CrossRefGoogle Scholar
Levine, M., Bloch’s formula for singular surfaces, Topology 24(2) (1985), 165–174.CrossRefGoogle Scholar
Levine, M., Zero-cycles and $K$ -theory on singular varieties, Proc. Symp. Pure Math. 46(2) (1987), 451–462.10.1090/pspum/046.2/927992CrossRefGoogle Scholar
Levine, M. and Weibel, C., Zero cycles and complete intersections on singular varieties, J. Reine Angew. Math. 359 (1985), 106–120.Google Scholar
Lipman, J., Desingularization of two-dimensional schemes, Ann. of Math. (2) 107(2) (1978), 151–207.10.2307/1971141CrossRefGoogle Scholar
Matsumura, H., Commutative Ring Theory, Cambridge Studies in Advanced Mathematics, 8 (Cambridge University Press, Cambridge, 1997).Google Scholar
Mazza, C., Voevodsky, V. and Weibel, C., Lecture Notes on Motivic Cohomology, Clay Mathematics Monographs, 2 (American Mathematical Society, Providence, 2006).Google Scholar
Milne, J., Étale Cohomology , Princeton Mathematical Series, 33 (Princeton University Press, New Jersey, 1980).Google Scholar
Miyazaki, H., Cube invariance of higher Chow groups with modulus, J. Algebraic Geom. 28(2) (2019), 339–390.CrossRefGoogle Scholar
Navarro, A., Riemann-Roch for homotopy invariant $K$ -theory and Gysin morphisms, Adv. Math. 328 (2018), 501–554.10.1016/j.aim.2018.01.001CrossRefGoogle Scholar
Néron, A., Problèmes arithmétiques et géométriques rattachés à la notion de rang d’une courbe algébrique dans un corps, Bull. Soc. Math. France 80 (1952), 101–166.10.24033/bsmf.1427CrossRefGoogle Scholar
Pedrini, C. and Weibel, C., $K$ -theory and Chow groups on singular varieties, in Applications of algebraic K-theory to algebraic geometry and number theory, Contemporary Mathematics, 55, pp. 339–370 (American Mathematical Society, Providence, RI, 1986).Google Scholar
Poonen, B., Bertini theorems over finite fields, Ann. of Math. (2) 160(3) (2004), 1099–1127.CrossRefGoogle Scholar
Quillen, D., Higher algebraic $K$ -theory I, in Higher K-theories, LNM Series, 341, pp. 85–147 (Springer-Verlag, Berlin, 1973).Google Scholar
Ramachandran, N., Duality of Albanese and Picard 1-motives, $K$ -Theory 22(3) (2001), 271–301.10.1023/A:1011100812900CrossRefGoogle Scholar
Raskind, W., Abelian class field theory of arithmetic schemes, in K-theory and algebraic geometry: connections with quadratic forms and division algebras, Proc. Sympos. Pure Math., 58, Part-1, 85–187, Amer. Math. Soc., Providence, RI, 1995.Google Scholar
Roitman, A., The torsion of the group of 0-cycles modulo rational equivalence, Ann. of Math. (2) 111(3) (1980), 553–569.10.2307/1971109CrossRefGoogle Scholar
Rosenlicht, M., Generalized Jacobian varieties, Ann. of Math. (2) 59(3) (1954), 505–530.CrossRefGoogle Scholar
Saito, S. and Sato, K., A finiteness theorem for zero-cycles over $p$ -adic fields, Ann. of Math. (2) 172(3) (2010), 1593–1639.10.4007/annals.2010.172.1593CrossRefGoogle Scholar
Schmidt, A., Singular homology of arithmetic schemes, Algebra Number Theory 1(2) (2007), 183–222.CrossRefGoogle Scholar
Schmidt, A. and Spieß, M., Singular homology and class field theory of varieties over finite fields, J. Reine Angew. Math. 527 (2000), 13–36.Google Scholar
Serre, J.-P., Morphisme universels et variété d’Albanese, Séminaire Claude Chevalley, Tome 4, (1958–1959), no. 10, 1–22.Google Scholar
Serre, J.-P., Morphisme universels et différentielles de troisième espèce, Séminaire Claude Chevalley, Tome 4, (1958–1959), no. 11, 1–8.Google Scholar
Serre, J.-P., Algebraic Groups and Class Fields , Graduate Texts in Mathematics, 117 (Springer, New York, 1997).Google Scholar
Skorobogatov, A., Exponential sums, the geometry of hyperplane sections, and some diophantine problems, Israel J. Math. 80(3) (1992), 359–379.10.1007/BF02808077CrossRefGoogle Scholar
Spieß, M. and Szamuely, T., On the Albanese map for smooth quasi-projective varieties, Math. Ann. 325(1) (2003), 1–17.CrossRefGoogle Scholar
Suslin, A. and Voevodsky, V., Singular homology of abstract algebraic varieties, Invent. Math. 123(1) (1996), 61–94.10.1007/BF01232367CrossRefGoogle Scholar
Szamuely, T., Galois Groups and Fundamental Groups , Cambridge Studies in Advanced Mathematics, 117 (Cambridge University Press, Cambridge, 2009).Google Scholar
Thomason, R. and Trobaugh, T., Higher algebraic $K$ -theory of schemes and of derived categories, in The Grothendieck Festschrift, Vol. III, Progress in Mathematics, 88, pp. 247–435 (Birkhäuser Boston, Boston, MA, 1990).10.1007/978-0-8176-4576-2_10CrossRefGoogle Scholar
Weil, A., Sur les critéres d’équivalence en géométrique algébrique, Math. Ann. 128(1) (1954), 209–215.CrossRefGoogle Scholar
Wutz, F., Bertini Theorems for Smooth Hypersurface Sections Containing a Subscheme over Finite Fields, PhD thesis, Universität Regensburg, 2014.Google Scholar