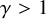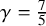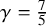1 Introduction
In this paper, we construct self-similar imploding solutions to the 3D isentropic compressible Euler equations
 $$ \begin{align} \begin{aligned} \partial_t (\rho u) + \div (\rho u \otimes u) + \nabla p(\rho) &= 0 , \\ \partial_t \rho + \div (\rho u)&=0 , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \partial_t (\rho u) + \div (\rho u \otimes u) + \nabla p(\rho) &= 0 , \\ \partial_t \rho + \div (\rho u)&=0 , \end{aligned} \end{align} $$
where here u is the velocity and
![]() $\rho $
the density, and we will assume the ideal gas law
$\rho $
the density, and we will assume the ideal gas law
![]() $p(\rho ) = \tfrac {1}{\gamma } \rho ^\gamma $
for
$p(\rho ) = \tfrac {1}{\gamma } \rho ^\gamma $
for
![]() $\gamma>1$
. Additionally, these self-similar solutions to Euler will be used as a basis to construct asymptotically self-similar solutions to the 3D isentropic compressible Navier-Stokes equations with density independent viscosity
$\gamma>1$
. Additionally, these self-similar solutions to Euler will be used as a basis to construct asymptotically self-similar solutions to the 3D isentropic compressible Navier-Stokes equations with density independent viscosity
 $$ \begin{align} \begin{aligned} \partial_t (\rho u) + \div (\rho u \otimes u) + \nabla p(\rho)-\mu_1\Delta u-(\mu_1+\mu_2)\nabla \div u &= 0 , \\ \partial_t \rho + \div (\rho u)&=0 , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \partial_t (\rho u) + \div (\rho u \otimes u) + \nabla p(\rho)-\mu_1\Delta u-(\mu_1+\mu_2)\nabla \div u &= 0 , \\ \partial_t \rho + \div (\rho u)&=0 , \end{aligned} \end{align} $$
for Lamé viscosity coefficients
![]() $(\mu _1,\mu _2)$
satisfying
$(\mu _1,\mu _2)$
satisfying
![]() $\mu _1>0$
and
$\mu _1>0$
and
![]() $2\mu _1+\mu _2> 0$
. In the case of the Navier-Stokes equations, we will assume the initial density to be constant at infinity in order to rule out the possibility that the singularities are an artifact of vacuum. Local well-posedness for the compressible Euler and Navier-Stokes equations (1.2) is classical (cf. [Reference Chemin20, Reference Danchin29, Reference Itaya49, Reference Kato55, Reference Lax60, Reference Majda65, Reference Nash74]).
$2\mu _1+\mu _2> 0$
. In the case of the Navier-Stokes equations, we will assume the initial density to be constant at infinity in order to rule out the possibility that the singularities are an artifact of vacuum. Local well-posedness for the compressible Euler and Navier-Stokes equations (1.2) is classical (cf. [Reference Chemin20, Reference Danchin29, Reference Itaya49, Reference Kato55, Reference Lax60, Reference Majda65, Reference Nash74]).
1.1 Background
1.1.1 Shock wave singularities
The prototypical singularity for the Euler equations is a shock wave, occurring when the speed of a disturbance exceeds the local speed of sound. Mathematically, one would like to provide a detailed description of both the formation of a shock and its development past the first singularity.
The first rigorous result in this direction is due to Lax [Reference Lax59]. Lax showed that in 1D, when writing the equation in terms of its Riemann invariants, one can use the method of characteristics to prove finite time singularity formation. The existence of finite time singularities in 2D and 3D was demonstrated by Sideris in [Reference Sideris81] via a virial type argument. Lebaud, in her seminal thesis work [Reference Lebaud61], provided the first detailed description of shock formation, in the context of one-dimensional p-systems, as well as proving development (see [Reference Chen and Dong22, Reference Kong58] for generalizations of Lebaud’s result).
In higher dimensions, Alinhac [Reference Alinhac3, Reference Alinhac2] was the first to provide a detailed description of shock formation for a class of quasilinear wave equations. Yin in [Reference Yin91] was able to adapt the work of Lebaud in order to prove shock formation and development in 3D under spherical symmetry (cf. [Reference Christodoulou and Lisibach25]). Within the sub-class of irrotational solutions, Christodoulou and Miao [Reference Christodoulou and Miao26] gave the first proof of shock formation in higher dimensions in the absence of symmetry (cf. [Reference Christodoulou24]). The work was extended by Luk and Speck to the 2D setting with nontrivial vorticity in [Reference Luk and Speck62].
In the work [Reference Buckmaster, Shkoller and Vicol14], the first author, Shkoller and Vicol developed a new self-similar framework in order to prove the existence and stability of shock wave formation for the Euler equations under azimuthal symmetry. This new framework provided the foundation for the works [Reference Buckmaster, Shkoller and Vicol13, Reference Buckmaster, Shkoller and Vicol15] by the same authors, which provided the first full detailed description of 3D shock formation in the presence of nontrivial vorticity and nonconstant entropy (see [Reference Luk and Speck63] for a recent related work of Luk and Speck in the framework of Christodoulou). As described above, the shock formation problem has been studied up to the time of the first singularity. The problem of maximal development has been very recently studied by Abbrescia and Speck [Reference Abbrescia and Speck1] and by Shkoller and Vicol [Reference Shkoller and Vicol80] using two very different approaches, in which solutions of the Euler equations are constructed for times that are much larger than the first blow-up time. In particular, the hypersurface of pre-shocks (or first singularities) is classified, and this is precisely the data required for the development problem.
In 2D, under azimuthal symmetry, the first author together with Drivas, Shkoller and Vicol were able to develop the singularity considered in the earlier work [Reference Buckmaster, Shkoller and Vicol14] in order to give the first full description of shock development, including the first description of weak discontinuities conjectured by Landau and Lifschitz.
1.1.2 Imploding solutions
While shock waves are the prototypical and possibly the sole stable form of singularity for the Euler equations, they are not the only form of singularity that can form from smooth initial data. It is a fundamentally interesting problem, both from a mathematical perspective and a physical perspective, to classify other forms of singularities resulting from smooth initial data.
Motivated by the classical work of Guderley [Reference Guderley41] (cf. [Reference Chisnell23, Reference Meyer ter Vehn and Schalk84]) on imploding solutions, Merle, Raphaël, Rodnianski and Szeftel, in the breakthrough work [Reference Merle, Raphaël, Rodnianski and Szeftel68], rigorously proved the existence of smooth radially symmetric imploding solutions to the isentropic compressible Euler equations for which the velocity and density become infinite at the time of singularity (cf. [Reference Jenssen and Johnson51, Reference Jenssen and Tsikkou52]). The work [Reference Merle, Raphaël, Rodnianski and Szeftel68] differs from the prior work of Guderley [Reference Guderley41] in a significant way: the solutions [Reference Merle, Raphaël, Rodnianski and Szeftel68] are smooth up until blow up, whereas the solutions [Reference Guderley41] represent solutions for which a shock has already formed. It should be noted that the solutions described in [Reference Merle, Raphaël, Rodnianski and Szeftel68] are highly unstable, which would make observing such solutions in numerical simulations or physical experiments extremely difficult. However, given that the structure of the solutions is now known, these solutions can be numerically computed as was done by Biasi in [Reference Biasi10], which provides a detailed numerical survey of the Merle et al. solutions.
In the companion works [Reference Merle, Raphaël, Rodnianski and Szeftel67, Reference Merle, Raphaël, Rodnianski and Szeftel69], the solutions constructed in [Reference Merle, Raphaël, Rodnianski and Szeftel68] have been used to construct asymptotically self-similar solutions to both the compressible Navier-Stokes equation (1.2) and the defocusing nonlinear Schrödinger equation – the later result resolving a major open problem in the field.
To describe the solutions of [Reference Merle, Raphaël, Rodnianski and Szeftel68], one must rewrite (1.1) in isentropic, radial form:
where for matters of simplicity, we restricted the problem to 3 dimensions. Letting
![]() $\sigma =\frac {1}{\alpha }\rho ^{\alpha }$
, for
$\sigma =\frac {1}{\alpha }\rho ^{\alpha }$
, for
![]() $\alpha =\frac {\gamma -1}{2}$
, denote the rescaled sound speed, one makes the following self-similar anzatz:
$\alpha =\frac {\gamma -1}{2}$
, denote the rescaled sound speed, one makes the following self-similar anzatz:
 $$ \begin{align} u(R,t)=r^{-1}\tfrac{R}{T-t} U\left(\log(\tfrac{R}{(T-t)^{\frac1r}})\right)\quad\mbox{and}\quad \sigma(R,t)=\alpha^{-\tfrac12}r^{-1} \tfrac{R}{T-t} S\left(\log(\tfrac{R}{(T-t)^{\frac1r}})\right), \end{align} $$
$$ \begin{align} u(R,t)=r^{-1}\tfrac{R}{T-t} U\left(\log(\tfrac{R}{(T-t)^{\frac1r}})\right)\quad\mbox{and}\quad \sigma(R,t)=\alpha^{-\tfrac12}r^{-1} \tfrac{R}{T-t} S\left(\log(\tfrac{R}{(T-t)^{\frac1r}})\right), \end{align} $$
where here r is a self-similar scaling parameter to be determined. Defining a new self-similar variable
![]() $\xi =\log (\tfrac {R}{(T-t)^{\frac 1r}})$
, then (1.3) reduces to an autonomous system of the form
$\xi =\log (\tfrac {R}{(T-t)^{\frac 1r}})$
, then (1.3) reduces to an autonomous system of the form

Figure 1 Imploding solutions in
![]() $(U,S)$
variables. Note that a singular coordinate change has been made in order to compactify the
$(U,S)$
variables. Note that a singular coordinate change has been made in order to compactify the
![]() $(U,S)$
coordinates.
$(U,S)$
coordinates.
The phase portrait for the case
![]() $\gamma =\frac 75$
,
$\gamma =\frac 75$
,
![]() $r=1.079404$
is represented in Figure 1. The red, green and black curves represent the vanishing of D,
$r=1.079404$
is represented in Figure 1. The red, green and black curves represent the vanishing of D,
![]() $N_U$
and
$N_U$
and
![]() $N_S$
respectively.
$N_S$
respectively.
![]() $P_0$
is a point in the compactified phase portrait, with finite value of U but
$P_0$
is a point in the compactified phase portrait, with finite value of U but
![]() $S = + \infty $
, and it will correspond to the values of
$S = + \infty $
, and it will correspond to the values of
![]() $(\bar U / R, \bar S / R)$
at the origin for our profiles.
$(\bar U / R, \bar S / R)$
at the origin for our profiles.
![]() $P_\infty $
is the point
$P_\infty $
is the point
![]() $(0, 0)$
, and it will correspond to values of the profiles at
$(0, 0)$
, and it will correspond to values of the profiles at
![]() $R = \infty $
(both profiles decay).
$R = \infty $
(both profiles decay).
![]() $P_s$
is a regular singular point of the dynamical system (1.5), and hence, one can construct integral curves which cross
$P_s$
is a regular singular point of the dynamical system (1.5), and hence, one can construct integral curves which cross
![]() $P_s$
. There exist two smooth integral curves that cross
$P_s$
. There exist two smooth integral curves that cross
![]() $P_s$
: one tangent to the direction
$P_s$
: one tangent to the direction
![]() $\nu _-$
and the other one tangent to
$\nu _-$
and the other one tangent to
![]() $\nu _+$
. The curve tangent to
$\nu _+$
. The curve tangent to
![]() $\nu _+$
corresponds to the Guderley solution, whereas the curve tangent to
$\nu _+$
corresponds to the Guderley solution, whereas the curve tangent to
![]() $\nu _-$
corresponds to solution found in [Reference Merle, Raphaël, Rodnianski and Szeftel68]. In order to create a globally defined self-similar solution, one must find an integral curve connecting
$\nu _-$
corresponds to solution found in [Reference Merle, Raphaël, Rodnianski and Szeftel68]. In order to create a globally defined self-similar solution, one must find an integral curve connecting
![]() $P_0$
to
$P_0$
to
![]() $P_{\infty }$
via
$P_{\infty }$
via
![]() $P_s$
. It is impossible to achieve this with the Guderley solution with a continuous integral curve; however, by adding a shock discontinuity, one may jump from one point in the phase portrait to another and hence describe a globally defined self-similar solution. The major difficulty faced in [Reference Merle, Raphaël, Rodnianski and Szeftel68] is that the alternate smooth integral curve in general also does not connect
$P_s$
. It is impossible to achieve this with the Guderley solution with a continuous integral curve; however, by adding a shock discontinuity, one may jump from one point in the phase portrait to another and hence describe a globally defined self-similar solution. The major difficulty faced in [Reference Merle, Raphaël, Rodnianski and Szeftel68] is that the alternate smooth integral curve in general also does not connect
![]() $P_0$
to
$P_0$
to
![]() $P_\infty $
; rather, it intersects the sonic line
$P_\infty $
; rather, it intersects the sonic line
![]() $D=0$
at a point other than
$D=0$
at a point other than
![]() $P_s$
leading to a solution that is not globally defined.Footnote
1
The authors, however, showed that for almost every
$P_s$
leading to a solution that is not globally defined.Footnote
1
The authors, however, showed that for almost every
![]() $\gamma>1$
, there exists an infinite sequence
$\gamma>1$
, there exists an infinite sequence
![]() $\{r_j\}$
, depending on
$\{r_j\}$
, depending on
![]() $\gamma $
, converging to some
$\gamma $
, converging to some
![]() $r^{\ast }$
, such that there exists a smooth curve connecting
$r^{\ast }$
, such that there exists a smooth curve connecting
![]() $P_0$
to
$P_0$
to
![]() $P_\infty $
. The condition on
$P_\infty $
. The condition on
![]() $\gamma $
for which the result holds is described in terms of the nonvanishing of an analytic function. This condition is not proven for any specific
$\gamma $
for which the result holds is described in terms of the nonvanishing of an analytic function. This condition is not proven for any specific
![]() $\gamma $
; however, it may be checked numerically. The analysis in [Reference Merle, Raphaël, Rodnianski and Szeftel68] becomes singular at
$\gamma $
; however, it may be checked numerically. The analysis in [Reference Merle, Raphaël, Rodnianski and Szeftel68] becomes singular at
![]() $\gamma =\frac 53$
, and so this specific, physically important case, corresponding to monatomic gas (helium), is not included in their theorem.
$\gamma =\frac 53$
, and so this specific, physically important case, corresponding to monatomic gas (helium), is not included in their theorem.
In the work [Reference Merle, Raphaël, Rodnianski and Szeftel69], the authors used the solutions of [Reference Merle, Raphaël, Rodnianski and Szeftel68] in order to show that for almost every
![]() $1<\gamma < \tfrac {2 + \sqrt 3}{\sqrt 3}$
, there exists an asymptotically self-similar solution to the compressible Navier-Stokes equation (1.2) that blows up in finite time. Existence of finite-time blow up for compressible Navier-Stokes was known previously for the case of compactly supported density [Reference Xin90] and rapidly decaying density [Reference Rozanova78]. Neither works, however, give a precise description of the singularity formation. Within this range of
$1<\gamma < \tfrac {2 + \sqrt 3}{\sqrt 3}$
, there exists an asymptotically self-similar solution to the compressible Navier-Stokes equation (1.2) that blows up in finite time. Existence of finite-time blow up for compressible Navier-Stokes was known previously for the case of compactly supported density [Reference Xin90] and rapidly decaying density [Reference Rozanova78]. Neither works, however, give a precise description of the singularity formation. Within this range of
![]() $\gamma $
, there exist self-similar solutions to the Euler equations for which the dissipation terms for the corresponding self-similar Navier-Stokes problem can be treated as exponentially decaying forcing due to the specific self-similar scaling. Applying stability analysis borrowed from [Reference Merle, Raphaël, Rodnianski and Szeftel67], the authors then use the solutions of [Reference Merle, Raphaël, Rodnianski and Szeftel69] to construct asymptotically self-similar solutions to (1.2) via a Brouwer fixed point argument. One caveat of the work [Reference Merle, Raphaël, Rodnianski and Szeftel69] is that the initial density of solutions is required to decay at infinity. Ideally, one would like to remove this condition in order to rule out the importance of the solution at infinity in the singularity formation process.
$\gamma $
, there exist self-similar solutions to the Euler equations for which the dissipation terms for the corresponding self-similar Navier-Stokes problem can be treated as exponentially decaying forcing due to the specific self-similar scaling. Applying stability analysis borrowed from [Reference Merle, Raphaël, Rodnianski and Szeftel67], the authors then use the solutions of [Reference Merle, Raphaël, Rodnianski and Szeftel69] to construct asymptotically self-similar solutions to (1.2) via a Brouwer fixed point argument. One caveat of the work [Reference Merle, Raphaël, Rodnianski and Szeftel69] is that the initial density of solutions is required to decay at infinity. Ideally, one would like to remove this condition in order to rule out the importance of the solution at infinity in the singularity formation process.
The works [Reference Merle, Raphaël, Rodnianski and Szeftel68] and [Reference Merle, Raphaël, Rodnianski and Szeftel69] leave open two important questions:
-
1. Do imploding solutions for Euler exist for all
 $\gamma>1$
?
$\gamma>1$
? -
2. Can one construct imploding solutions to the Navier-Stokes equation with initial density constant at infinity?
1.2 Main results
Theorem 1.1. Let
![]() $\gamma \in (1, +\infty )$
. There exists
$\gamma \in (1, +\infty )$
. There exists
![]() $r^{(3)}(\gamma ) \in (r_3(\gamma ), r_{4}(\gamma ))$
, such that there exists a smooth solution to (1.5) starting at
$r^{(3)}(\gamma ) \in (r_3(\gamma ), r_{4}(\gamma ))$
, such that there exists a smooth solution to (1.5) starting at
![]() $P_0$
and ending at
$P_0$
and ending at
![]() $P_\infty = (0, 0)$
, where
$P_\infty = (0, 0)$
, where
![]() $ (r_3(\gamma ), r_{4}(\gamma ))$
are defined in Section 1.4. This gives a smooth and radially symmetric self-similar solution to (1.3) of the form (1.4).
$ (r_3(\gamma ), r_{4}(\gamma ))$
are defined in Section 1.4. This gives a smooth and radially symmetric self-similar solution to (1.3) of the form (1.4).
Theorem 1.2. Let
![]() $\gamma = 7/5$
and
$\gamma = 7/5$
and
![]() $n \in \mathbb {N}$
be an odd number large enough. There exists
$n \in \mathbb {N}$
be an odd number large enough. There exists
![]() $r^{(n)}(\gamma ) \in (r_n(\gamma ), r_{n+1}(\gamma ))$
such that there exists a smooth solution to (1.5) starting at
$r^{(n)}(\gamma ) \in (r_n(\gamma ), r_{n+1}(\gamma ))$
such that there exists a smooth solution to (1.5) starting at
![]() $P_0$
and ending at
$P_0$
and ending at
![]() $P_\infty $
, where
$P_\infty $
, where
![]() $ r_j(\gamma )$
is defined in Section 1.4. This gives a smooth and radially symmetric self-similar solution to (1.3) of the form (1.4).
$ r_j(\gamma )$
is defined in Section 1.4. This gives a smooth and radially symmetric self-similar solution to (1.3) of the form (1.4).
Theorem 1.3. Let
![]() $\gamma = 7/5$
and
$\gamma = 7/5$
and
![]() $n \in \mathbb {N}$
be an odd number large enough. Let
$n \in \mathbb {N}$
be an odd number large enough. Let
![]() $(U^E, S^E)$
be the profiles of Theorem 1.2, solving (1.5). Then, for sufficiently small
$(U^E, S^E)$
be the profiles of Theorem 1.2, solving (1.5). Then, for sufficiently small
![]() $T>0$
, there exists a radially symmetric initial data
$T>0$
, there exists a radially symmetric initial data
![]() $(u_0,\rho _0)$
such that we have the following:
$(u_0,\rho _0)$
such that we have the following:
-
1. The initial density
 $\rho _0$
is constant at infinity:
$\rho _0$
is constant at infinity:  $$\begin{align*}\lim_{\left|x\right|\rightarrow\infty } \rho_0(x)=\rho_c. \end{align*}$$
$$\begin{align*}\lim_{\left|x\right|\rightarrow\infty } \rho_0(x)=\rho_c. \end{align*}$$
-
2. The initial data
 $(u_0,\rho _0)$
is smooth and has finite energy:
$(u_0,\rho _0)$
is smooth and has finite energy:  $$\begin{align*}\frac12 \int \rho_0 \left|u_0\right|{}^2+\frac{1}{\gamma(\gamma-1)}\int(\rho_0-\rho_c)^\gamma<\infty.\end{align*}$$
$$\begin{align*}\frac12 \int \rho_0 \left|u_0\right|{}^2+\frac{1}{\gamma(\gamma-1)}\int(\rho_0-\rho_c)^\gamma<\infty.\end{align*}$$
-
3. At time T, the solution
 $(u,\rho )$
becomes singular at the origin: for any
$(u,\rho )$
becomes singular at the origin: for any
 $\varepsilon>0$
$\varepsilon>0$
 $$\begin{align*}\lim_{t\rightarrow T}\sup_{R\in[0,\varepsilon)}\left|u(R,t)\right|=\infty\quad\mbox{and}\quad \lim_{t\rightarrow T}\rho(0,t)=\infty.\end{align*}$$
$$\begin{align*}\lim_{t\rightarrow T}\sup_{R\in[0,\varepsilon)}\left|u(R,t)\right|=\infty\quad\mbox{and}\quad \lim_{t\rightarrow T}\rho(0,t)=\infty.\end{align*}$$
-
4. The solution
 $(u,\rho )$
blows up in an asymptotically self-similar manner: for any fixed
$(u,\rho )$
blows up in an asymptotically self-similar manner: for any fixed
 $\xi \geq 0$
,
$\xi \geq 0$
,  $$\begin{align*}\lim_{t\rightarrow T}r\tfrac{T-t}{R}u\left((T-t)^{\frac1r}\exp(\xi),t\right)= U^E(\xi)\quad\mbox{and}\quad \lim_{t\rightarrow T} \alpha^{\tfrac12}r \tfrac{T-t}{R}\sigma\left((T-t)^{\frac1r}\exp(\xi),t\right)= S^E(\xi). \end{align*}$$
$$\begin{align*}\lim_{t\rightarrow T}r\tfrac{T-t}{R}u\left((T-t)^{\frac1r}\exp(\xi),t\right)= U^E(\xi)\quad\mbox{and}\quad \lim_{t\rightarrow T} \alpha^{\tfrac12}r \tfrac{T-t}{R}\sigma\left((T-t)^{\frac1r}\exp(\xi),t\right)= S^E(\xi). \end{align*}$$
Moreover, there exists a finite codimensional manifold of radially symmetric initial data satisfying the above conclusions (see Remark 8.4 for more details).
Remark 1.4. For simplicity, we will only prove Theorem 1.3 for the case
![]() $\mu _1=1$
and
$\mu _1=1$
and
![]() $\mu _2=-1$
. The general case follows analogously with minor changes to the energy estimates in Section 8.
$\mu _2=-1$
. The general case follows analogously with minor changes to the energy estimates in Section 8.
Remark 1.5. We note that as a corollary of the proof of Theorem 1.3, the statement of Theorem 1.3 holds with the Navier-Stokes equations (1.2) replaced by the Euler equations (1.1) for
![]() $\gamma =7/5$
. With some minor work, Theorem 1.3 can be extended to all
$\gamma =7/5$
. With some minor work, Theorem 1.3 can be extended to all
![]() $\gamma>1$
in the case of Euler by making use of the self-similar profiles of Theorem 1.1.
$\gamma>1$
in the case of Euler by making use of the self-similar profiles of Theorem 1.1.
1.3 Self-similar implosion in terms of Riemann invariants
Motivated by the works [Reference Buckmaster, Shkoller and Vicol13, Reference Buckmaster, Shkoller and Vicol14, Reference Buckmaster, Shkoller and Vicol15], we introduce the Riemann invariants
so that
One can now diagonalize (1.3) in terms of w and z, in order to rewrite (1.3) as a nonlinear transport equation
 $$ \begin{align}\begin{aligned} \partial_t w + \frac12(w+z+\alpha(w-z)) \partial_R w + \frac{\alpha}{2R}(w^2-z^2)&=0,\\ \partial_t z + \frac12(w+z-\alpha(w-z)) \partial_R z - \frac{\alpha}{2R}(w^2-z^2)&=0. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \partial_t w + \frac12(w+z+\alpha(w-z)) \partial_R w + \frac{\alpha}{2R}(w^2-z^2)&=0,\\ \partial_t z + \frac12(w+z-\alpha(w-z)) \partial_R z - \frac{\alpha}{2R}(w^2-z^2)&=0. \end{aligned} \end{align} $$
Employing the self-similar ansatz
where we recall
![]() $\xi =\log (\tfrac {R}{(T-t)^{\frac 1r}})$
, then we obtain
$\xi =\log (\tfrac {R}{(T-t)^{\frac 1r}})$
, then we obtain
 $$ \begin{align} \begin{aligned} (r+\frac12((1+2\alpha)W+(1-\alpha)Z))W+(1+\frac12(W+Z+\alpha(W-Z)))\partial_{\xi} W - \frac{\alpha}{2}Z^2&=0,\\ (r+\frac12((1-\alpha)W+(1+2\alpha)Z))Z+(1+\frac12(W+Z-\alpha(W-Z)))\partial_{\xi} Z - \frac{\alpha}{2}W^2&=0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (r+\frac12((1+2\alpha)W+(1-\alpha)Z))W+(1+\frac12(W+Z+\alpha(W-Z)))\partial_{\xi} W - \frac{\alpha}{2}Z^2&=0,\\ (r+\frac12((1-\alpha)W+(1+2\alpha)Z))Z+(1+\frac12(W+Z-\alpha(W-Z)))\partial_{\xi} Z - \frac{\alpha}{2}W^2&=0. \end{aligned} \end{align} $$
Rearranging, we obtain the autonomous system
 $$ \begin{align} \begin{aligned} \partial_{ \xi } W&= \frac{-(r+\frac12((1+2\alpha)W+(1-\alpha)Z))W+ \frac{\alpha}{2}Z^2}{1+\frac12(W+Z+\alpha(W-Z))}=\frac{N_W}{D_W},\\ \partial_{ \xi } Z&=\frac{-(r+\frac12((1-\alpha)W+(1+2\alpha)Z))Z+\frac{\alpha}{2}W^2}{1+\frac12(W+Z-\alpha(W-Z))}=\frac{N_Z}{D_Z}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \partial_{ \xi } W&= \frac{-(r+\frac12((1+2\alpha)W+(1-\alpha)Z))W+ \frac{\alpha}{2}Z^2}{1+\frac12(W+Z+\alpha(W-Z))}=\frac{N_W}{D_W},\\ \partial_{ \xi } Z&=\frac{-(r+\frac12((1-\alpha)W+(1+2\alpha)Z))Z+\frac{\alpha}{2}W^2}{1+\frac12(W+Z-\alpha(W-Z))}=\frac{N_Z}{D_Z}. \end{aligned} \end{align} $$
Figure 2 represents the phase portrait for the region
![]() $W-Z>0$
for which the density is positive. The red, purple and green lines correspond to
$W-Z>0$
for which the density is positive. The red, purple and green lines correspond to
![]() $D_Z=0$
,
$D_Z=0$
,
![]() $D_W=0$
and
$D_W=0$
and
![]() $N_Z=0$
, respectively. A key difference to the system (1.5) is that the denominator
$N_Z=0$
, respectively. A key difference to the system (1.5) is that the denominator
![]() $D_W$
does not vanish at
$D_W$
does not vanish at
![]() $P_s$
, which simplifies the analysis in a neighborhood of
$P_s$
, which simplifies the analysis in a neighborhood of
![]() $P_s$
. Unlike the self-similar variables
$P_s$
. Unlike the self-similar variables
![]() $(U,S)$
, the variables
$(U,S)$
, the variables
![]() $(W,Z)$
satisfy transport equations, which leads to the possibility of employing transport arguments in order to simplify the stability analysis. In particular, the
$(W,Z)$
satisfy transport equations, which leads to the possibility of employing transport arguments in order to simplify the stability analysis. In particular, the
![]() $(W,Z)$
variables give rise to a very geometric understanding of the imploding solution in terms of the trajectories of the W and Z waves:
$(W,Z)$
variables give rise to a very geometric understanding of the imploding solution in terms of the trajectories of the W and Z waves:
![]() $P_s$
is an unstable fixed point for the trajectories of Z-waves. Let
$P_s$
is an unstable fixed point for the trajectories of Z-waves. Let
![]() $P_s$
divide space into an interior (backward acoustic cone emanating from the singular point) and exterior region. Z-waves in the exterior region cannot cross into the interior region, whereas Z-waves in the interior region cross the origin to become W-waves, whereupon they cross
$P_s$
divide space into an interior (backward acoustic cone emanating from the singular point) and exterior region. Z-waves in the exterior region cannot cross into the interior region, whereas Z-waves in the interior region cross the origin to become W-waves, whereupon they cross
![]() $P_s$
and travel to the exterior region. Since the system (1.10) is autonomous, we are free to fix the location
$P_s$
and travel to the exterior region. Since the system (1.10) is autonomous, we are free to fix the location
![]() $\xi $
for which the solutions crosses
$\xi $
for which the solutions crosses
![]() $P_s$
. As such, we make the choice that
$P_s$
. As such, we make the choice that
![]() $P_s$
is located at
$P_s$
is located at
![]() $\xi =0$
.
$\xi =0$
.

Figure 2 Imploding solutions in
![]() $(W,Z)$
variables. Note that a singular coordinate change has been made in order to compactify the
$(W,Z)$
variables. Note that a singular coordinate change has been made in order to compactify the
![]() $(W,Z)$
coordinates. We have indicated in orange the type of smooth solutions we will find, crossing through
$(W,Z)$
coordinates. We have indicated in orange the type of smooth solutions we will find, crossing through
![]() $P_s$
with direction
$P_s$
with direction
![]() $v_-$
. On the left of
$v_-$
. On the left of
![]() $P_s$
the solution converges to
$P_s$
the solution converges to
![]() $P_\infty $
, while on the right, we show three possibilities for its behavior (it can start at
$P_\infty $
, while on the right, we show three possibilities for its behavior (it can start at
![]() $D_W = 0$
, at
$D_W = 0$
, at
![]() $P_0$
or at
$P_0$
or at
![]() $D_Z = 0$
).
$D_Z = 0$
).
Due to the singular nature of the coordinate transformation
![]() $R\mapsto \xi $
for R near
$R\mapsto \xi $
for R near
![]() $0$
, it is also helpful to introduce alternate self-similar coordinates. If we write
$0$
, it is also helpful to introduce alternate self-similar coordinates. If we write
 $$\begin{align*}\zeta=\frac{R}{(T-t)^{\frac{1}{r}}}=\exp(\xi),\end{align*}$$
$$\begin{align*}\zeta=\frac{R}{(T-t)^{\frac{1}{r}}}=\exp(\xi),\end{align*}$$
and write
 $$ \begin{align} \begin{aligned} w(R,t)&=r^{-1}(T-t)^{r^{-1}-1} \mathcal{W}(\zeta)=r^{-1} \frac{R}{T-t} W( \xi),\\ z(R,t)&=r^{-1} (T-t)^{r^{-1}-1} \mathcal{Z}(\zeta)=r^{-1}\frac{R}{T-t} Z( \xi), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} w(R,t)&=r^{-1}(T-t)^{r^{-1}-1} \mathcal{W}(\zeta)=r^{-1} \frac{R}{T-t} W( \xi),\\ z(R,t)&=r^{-1} (T-t)^{r^{-1}-1} \mathcal{Z}(\zeta)=r^{-1}\frac{R}{T-t} Z( \xi), \end{aligned} \end{align} $$
then (1.7) becomes
 $$ \begin{align} \begin{aligned} (r-1)\mathcal{W}+(\zeta+\frac12(\mathcal{W}+\mathcal{Z}+\alpha(\mathcal{W}-\mathcal{Z})))\partial_{\zeta} \mathcal{W} +\frac{\alpha}{2\zeta}(\mathcal{W}^2-\mathcal{Z}^2)&=0,\\ (r-1)\mathcal{Z}+(\zeta+\frac12(\mathcal{W}+\mathcal{Z}-\alpha(\mathcal{W}-\mathcal{Z})))\partial_{\zeta} \mathcal{Z} - \frac{\alpha}{2\zeta}(\mathcal{W}^2-\mathcal{Z}^2)&=0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (r-1)\mathcal{W}+(\zeta+\frac12(\mathcal{W}+\mathcal{Z}+\alpha(\mathcal{W}-\mathcal{Z})))\partial_{\zeta} \mathcal{W} +\frac{\alpha}{2\zeta}(\mathcal{W}^2-\mathcal{Z}^2)&=0,\\ (r-1)\mathcal{Z}+(\zeta+\frac12(\mathcal{W}+\mathcal{Z}-\alpha(\mathcal{W}-\mathcal{Z})))\partial_{\zeta} \mathcal{Z} - \frac{\alpha}{2\zeta}(\mathcal{W}^2-\mathcal{Z}^2)&=0. \end{aligned} \end{align} $$
This form of the equation will be useful in studying the solution at the origin
![]() $\zeta =0$
. A time-dependent version of these equations will also be used to study stability. Since we will be looking for solutions that are smooth at the origin, we can extend the solution to all of
$\zeta =0$
. A time-dependent version of these equations will also be used to study stability. Since we will be looking for solutions that are smooth at the origin, we can extend the solution to all of
![]() $\zeta \in \mathbb R$
by requiring that
$\zeta \in \mathbb R$
by requiring that
![]() $\mathcal {Z}(\zeta )=-\mathcal {W}(-\zeta )$
, The equations reduce to a single equation in
$\mathcal {Z}(\zeta )=-\mathcal {W}(-\zeta )$
, The equations reduce to a single equation in
![]() $\mathcal {W}$
:
$\mathcal {W}$
:
We first begin with a result for the maximal time of existence of solutions to the ODE (1.9). We also show that the system does not have periodic orbits.
Proposition 1.6. Let
![]() $(W_\star , Z_\star )\in \mathbb {R}^2$
such that
$(W_\star , Z_\star )\in \mathbb {R}^2$
such that
![]() $D_W(W_\star , Z_\star ) \neq 0$
and
$D_W(W_\star , Z_\star ) \neq 0$
and
![]() $D_Z(W_\star , Z_\star ) \neq 0$
and let
$D_Z(W_\star , Z_\star ) \neq 0$
and let
![]() $\xi _\star \in \mathbb {R}$
. There exists a smooth solution
$\xi _\star \in \mathbb {R}$
. There exists a smooth solution
![]() $W(\xi ), Z(\xi ):(\xi _1, \xi _2 ) \rightarrow \mathbb {R}$
to (1.9) such that
$W(\xi ), Z(\xi ):(\xi _1, \xi _2 ) \rightarrow \mathbb {R}$
to (1.9) such that
![]() $W(\xi _\star ) = W_\star $
,
$W(\xi _\star ) = W_\star $
,
![]() $Z (\xi _\star ) = Z_\star $
and
$Z (\xi _\star ) = Z_\star $
and
-
• Either
 $(W(\xi ), Z(\xi ))$
tends to a point of
$(W(\xi ), Z(\xi ))$
tends to a point of
 $\{ D_W = 0 \} \cup \{ D_Z = 0 \}$
as
$\{ D_W = 0 \} \cup \{ D_Z = 0 \}$
as
 $\xi \rightarrow \xi _1^+$
, or to infinity or to an equilibrium point. Moreover,
$\xi \rightarrow \xi _1^+$
, or to infinity or to an equilibrium point. Moreover,
 $\xi _1 = -\infty $
in the latter case.
$\xi _1 = -\infty $
in the latter case. -
• Either
 $(W(\xi ), Z(\xi ))$
tends to a point of
$(W(\xi ), Z(\xi ))$
tends to a point of
 $\{ D_W = 0 \} \cup \{ D_Z = 0 \}$
as
$\{ D_W = 0 \} \cup \{ D_Z = 0 \}$
as
 $\xi \rightarrow \xi _2^-$
, or to infinity or to an equilibrium point. Moreover,
$\xi \rightarrow \xi _2^-$
, or to infinity or to an equilibrium point. Moreover,
 $\xi _2 = +\infty $
in the latter case.
$\xi _2 = +\infty $
in the latter case.
The proof of Proposition 1.6 is given in Appendix A.1.
Remark 1.7. By local existence and uniqueness, we can divide the phase portrait in disjoint orbits ending either at the nullsets of
![]() $D_W$
,
$D_W$
,
![]() $D_Z$
or infinity. Let
$D_Z$
or infinity. Let
![]() $\Omega $
be the region where
$\Omega $
be the region where
![]() $D_W> 0, D_Z < 0$
. Let
$D_W> 0, D_Z < 0$
. Let
![]() $\Omega _1^{(r)}$
be the subset of points whose trajectories emanate from the halfline of
$\Omega _1^{(r)}$
be the subset of points whose trajectories emanate from the halfline of
![]() $D_Z = 0$
located to the right of
$D_Z = 0$
located to the right of
![]() $P_s$
and
$P_s$
and
![]() $\Omega _2^{(r)}$
be the points for whose trajectory emanates from
$\Omega _2^{(r)}$
be the points for whose trajectory emanates from
![]() $D_W=0$
.
$D_W=0$
.
1.4 Smooth self-similar imploding solution
In order to further analyze
![]() $P_s$
, it is helpful to consider the dynamical system under the change of variables
$P_s$
, it is helpful to consider the dynamical system under the change of variables
![]() $\xi \mapsto \psi $
where
$\xi \mapsto \psi $
where
![]() $\partial _\psi =-D_WD_Z\partial _\xi $
. The equation (1.10) becomes
$\partial _\psi =-D_WD_Z\partial _\xi $
. The equation (1.10) becomes
and
![]() $P_s$
becomes a stable stationary point of (1.14). The smooth integral curves of (1.10) correspond to slope-matching smooth curves with limit
$P_s$
becomes a stable stationary point of (1.14). The smooth integral curves of (1.10) correspond to slope-matching smooth curves with limit
![]() $P_s$
.
$P_s$
.
It is illustrative to consider the following simple system:
for some
![]() $\lambda _-<\lambda _+<0$
, which correspond to the eigenvalues of the system’s Jacobian. So long as
$\lambda _-<\lambda _+<0$
, which correspond to the eigenvalues of the system’s Jacobian. So long as
![]() $k=\frac {\lambda _-}{\lambda _+}\notin \mathbb {N}$
, the only smooth integral curves are along
$k=\frac {\lambda _-}{\lambda _+}\notin \mathbb {N}$
, the only smooth integral curves are along
![]() $x=0$
and
$x=0$
and
![]() $y=0$
. There do, however, exist non-smooth solutions of the form
$y=0$
. There do, however, exist non-smooth solutions of the form
![]() $y=Cx^k$
which are
$y=Cx^k$
which are
![]() $C^k$
regular and whose Taylor series agrees with the solution
$C^k$
regular and whose Taylor series agrees with the solution
![]() $y=0$
up to order
$y=0$
up to order
![]() $\lfloor k \rfloor $
(i.e., the largest integer smaller or equal to k).
$\lfloor k \rfloor $
(i.e., the largest integer smaller or equal to k).
Returning to our ODE (1.14), define
![]() $\lambda _-<\lambda _+<0$
to be the eigenvalues of the Jacobian of (1.14) at
$\lambda _-<\lambda _+<0$
to be the eigenvalues of the Jacobian of (1.14) at
![]() $P_s$
, and define
$P_s$
, and define
If
![]() $\nu _-$
,
$\nu _-$
,
![]() $\nu _+$
are the eigenvectors of the Jacobian of (1.14) associated with the eigenvalues
$\nu _+$
are the eigenvectors of the Jacobian of (1.14) associated with the eigenvalues
![]() $\lambda _-,\lambda _+$
, then we will be considering the smooth solutions of (1.10) with tangent parallel to
$\lambda _-,\lambda _+$
, then we will be considering the smooth solutions of (1.10) with tangent parallel to
![]() $\nu _-$
– the Guderley solutions correspond to the direction
$\nu _-$
– the Guderley solutions correspond to the direction
![]() $\nu _+$
. These two directions are illustrated in Figure 2.
$\nu _+$
. These two directions are illustrated in Figure 2.
We restrict the self-similar parameter r to
![]() $1<r<r^\ast $
, where
$1<r<r^\ast $
, where
 $$ \begin{align} r^\ast (\gamma ) = \begin{cases} \tfrac{2}{\left(\sqrt{2} \sqrt{\frac{1}{\gamma-1}}+1\right)^2}+1 & 1 < \gamma < \tfrac{5}{3} ,\\ \tfrac{3\gamma - 1 }{2 + \sqrt{3}(\gamma - 1)} & \gamma \geq \tfrac{5}{3}. \end{cases} \end{align} $$
$$ \begin{align} r^\ast (\gamma ) = \begin{cases} \tfrac{2}{\left(\sqrt{2} \sqrt{\frac{1}{\gamma-1}}+1\right)^2}+1 & 1 < \gamma < \tfrac{5}{3} ,\\ \tfrac{3\gamma - 1 }{2 + \sqrt{3}(\gamma - 1)} & \gamma \geq \tfrac{5}{3}. \end{cases} \end{align} $$
In this regime, k will be a monotonically increasing function of r, converging to
![]() $\infty $
as
$\infty $
as
![]() $r\rightarrow r^\ast $
(see Lemma 2.1).
$r\rightarrow r^\ast $
(see Lemma 2.1).
To study the behavior of the smooth solution corresponding to the direction
![]() $\nu _-$
around
$\nu _-$
around
![]() $P_s$
, which we denote
$P_s$
, which we denote
![]() $(W^{(r)},Z^{(r)})$
, we apply a Frobenius-like series expansion of the solution. As will be shown in Section 2.2, letting
$(W^{(r)},Z^{(r)})$
, we apply a Frobenius-like series expansion of the solution. As will be shown in Section 2.2, letting
![]() $(W_n,Z_n)$
denote the n-th Taylor coefficient of
$(W_n,Z_n)$
denote the n-th Taylor coefficient of
![]() $(W^{(r)},Z^{(r)})$
expanded at
$(W^{(r)},Z^{(r)})$
expanded at
![]() $P_s$
, then for
$P_s$
, then for
![]() $n\geq 2$
,
$n\geq 2$
,
where
![]() $(F_W, F_Z)$
are given in Section 2.2. For
$(F_W, F_Z)$
are given in Section 2.2. For
![]() $j\in \mathbb N$
, we define
$j\in \mathbb N$
, we define
![]() $r_j$
such that
$r_j$
such that
![]() $j=k(r_j)$
. Note that the denominator in (1.17) becomes singular as
$j=k(r_j)$
. Note that the denominator in (1.17) becomes singular as
![]() $k(r)$
approaches n and switches sign at
$k(r)$
approaches n and switches sign at
![]() $k(r)=n$
. This has a wiggling effect on the integral curve of the smooth solution, which in turn allows us to show that for a subset of
$k(r)=n$
. This has a wiggling effect on the integral curve of the smooth solution, which in turn allows us to show that for a subset of
![]() $\gamma>1$
and odd
$\gamma>1$
and odd
![]() $n\geq 3$
,
$n\geq 3$
,
-
1. For
 $r\in (r_n,r_{n+1})$
, the solution to the left of
$r\in (r_n,r_{n+1})$
, the solution to the left of
 $P_s$
converges to
$P_s$
converges to
 $P_{\infty }$
as
$P_{\infty }$
as
 $\xi \rightarrow \infty $
.
$\xi \rightarrow \infty $
. -
2. For
 $r=r_n+\varepsilon $
, the solution to the right of
$r=r_n+\varepsilon $
, the solution to the right of
 $P_s$
intersects the line
$P_s$
intersects the line
 $D_W = 0$
.
$D_W = 0$
. -
3. For
 $r=r_{n+1}-\varepsilon $
, the solution to the right of
$r=r_{n+1}-\varepsilon $
, the solution to the right of
 $P_s$
intersects the line
$P_s$
intersects the line
 $D_Z = 0$
.
$D_Z = 0$
.
More specifically, we show the above holds for
![]() $n=3$
and
$n=3$
and
![]() $\gamma \in (1, +\infty )$
, as well as the case
$\gamma \in (1, +\infty )$
, as well as the case
![]() $\gamma =\frac 75$
and n sufficiently large.Footnote
2
If we can prove 2 and 3, by a simple shooting argument, we obtain that there exists an
$\gamma =\frac 75$
and n sufficiently large.Footnote
2
If we can prove 2 and 3, by a simple shooting argument, we obtain that there exists an
![]() $r\in (r_n,r_{n+1})$
such that the solution curve connects
$r\in (r_n,r_{n+1})$
such that the solution curve connects
![]() $P_s$
to
$P_s$
to
![]() $P_0$
. Moreover, 1 implies that the solution connects
$P_0$
. Moreover, 1 implies that the solution connects
![]() $P_s$
to
$P_s$
to
![]() $P_\infty $
. We note that for the Einstein-Euler and Euler-Poisson systems, Guo, Hadžić and Jang in [Reference Guo, Hadzic and Jang43] and [Reference Guo, Hadžić and Jang42] apply similar arguments in the context of non-autonomous ODEs.
$P_\infty $
. We note that for the Einstein-Euler and Euler-Poisson systems, Guo, Hadžić and Jang in [Reference Guo, Hadzic and Jang43] and [Reference Guo, Hadžić and Jang42] apply similar arguments in the context of non-autonomous ODEs.
For the special case
![]() $\gamma =\frac 75$
, we aim at constructing a sequence of self-similar scalings
$\gamma =\frac 75$
, we aim at constructing a sequence of self-similar scalings
![]() $r^{(j)}$
satisfying
$r^{(j)}$
satisfying
![]() $r_j<r^{(j)}<r_{j+1}$
, for j odd and sufficiently large, as well as the corresponding smooth global solutions. A key ingredient to proving this is to determine a sign and lower bound on the Taylor coefficients of order j. Contrarily to the
$r_j<r^{(j)}<r_{j+1}$
, for j odd and sufficiently large, as well as the corresponding smooth global solutions. A key ingredient to proving this is to determine a sign and lower bound on the Taylor coefficients of order j. Contrarily to the
![]() $\gamma \geq \frac 53$
case, for
$\gamma \geq \frac 53$
case, for
![]() $\gamma <\frac 53$
, and
$\gamma <\frac 53$
, and
![]() $r=r^\ast $
, one may obtain a nontrivial Taylor expansion of the corresponding curve passing through
$r=r^\ast $
, one may obtain a nontrivial Taylor expansion of the corresponding curve passing through
![]() $P_s$
. By continuity, for
$P_s$
. By continuity, for
![]() $r<r^\ast $
, the corresponding Taylor series converges to that of
$r<r^\ast $
, the corresponding Taylor series converges to that of
![]() $r=r^\ast $
. Then, fixing
$r=r^\ast $
. Then, fixing
![]() $r<r^\ast $
, r sufficiently close to
$r<r^\ast $
, r sufficiently close to
![]() $r^\ast $
, one can deduce the sign and magnitudes of lower-order Taylor coefficients from those of
$r^\ast $
, one can deduce the sign and magnitudes of lower-order Taylor coefficients from those of
![]() $r^\ast $
. With this information, one can use an inductive argument to deduce information about the higher-order coefficients. Furthermore, we employ a computer-assisted proof to compute the first 10000 coefficient pairs
$r^\ast $
. With this information, one can use an inductive argument to deduce information about the higher-order coefficients. Furthermore, we employ a computer-assisted proof to compute the first 10000 coefficient pairs
![]() $(W_j,Z_j)$
at
$(W_j,Z_j)$
at
![]() $r=r^\ast $
with rigorous error bounds. While there is certainly room for improvement in terms of the amount of coefficients that we had to calculate using a computer-assisted approach, we decided to keep the asymptotic part of the analysis that treats the higher-order coefficients as simple as possible, at the expense of a slightly larger computation time. This part of the calculation takes about 14 hours on a single CPU.
$r=r^\ast $
with rigorous error bounds. While there is certainly room for improvement in terms of the amount of coefficients that we had to calculate using a computer-assisted approach, we decided to keep the asymptotic part of the analysis that treats the higher-order coefficients as simple as possible, at the expense of a slightly larger computation time. This part of the calculation takes about 14 hours on a single CPU.
In order to perform rigorous, error-free calculations, interval arithmetic will be used as part of the proof whenever needed. The main idea underlying this technique is to work with intervals which have representable numbers by the computer as endpoints in order to guarantee that the true result at any point belongs to the interval by which is represented. By doing so, we control all the errors (rounding, floating point arithmetic, etc.) incurred by the computer program while calculating the necessary quantities. Over the intervals, we define an arithmetic in such a way that we are guaranteed that for every
![]() $x \in X, y \in Y$
,
$x \in X, y \in Y$
,
for any operation
![]() $\star $
. For example,
$\star $
. For example,
 $$ \begin{align*} [\underline{x},\overline{x}] + [\underline{y},\overline{y}] & = [\underline{x} + \underline{y}, \overline{x} + \overline{y}] ,\\ [\underline{x},\overline{x}] \times [\underline{y},\overline{y}] & = [\min\{\underline{x}\underline{y},\underline{x}\overline{y},\overline{x}\underline{y},\overline{x}\overline{y}\},\max\{\underline{x}\underline{y},\underline{x}\overline{y},\overline{x}\underline{y},\overline{x}\overline{y}\}] . \end{align*} $$
$$ \begin{align*} [\underline{x},\overline{x}] + [\underline{y},\overline{y}] & = [\underline{x} + \underline{y}, \overline{x} + \overline{y}] ,\\ [\underline{x},\overline{x}] \times [\underline{y},\overline{y}] & = [\min\{\underline{x}\underline{y},\underline{x}\overline{y},\overline{x}\underline{y},\overline{x}\overline{y}\},\max\{\underline{x}\underline{y},\underline{x}\overline{y},\overline{x}\underline{y},\overline{x}\overline{y}\}] . \end{align*} $$
We can also define the interval version of a function
![]() $f(X)$
as an interval I that satisfies that for every
$f(X)$
as an interval I that satisfies that for every
![]() $x \in X$
,
$x \in X$
,
![]() $f(x) \in I$
. Even though in this paper we will only make use of basic functions, more complicated ones (such as special functions) over intervals can be defined as well.
$f(x) \in I$
. Even though in this paper we will only make use of basic functions, more complicated ones (such as special functions) over intervals can be defined as well.
Very early computer-assisted proofs were mostly constrained to finite dimensional problems [Reference Fefferman and de la Llave34, Reference Tucker85]. Slowly, more and more computational power has enabled harder problems to be tackled, including partial differential equations. We mention the pioneering papers of Plum [Reference Plum76, Reference Plum77] and Nakao [Reference Nakao71, Reference Nakao72] in this context, and more recent advances done by Fazekas–Pacella–Plum [Reference Fazekas, Pacella and Plum33] for the Lane Emden equation, van den Berg–Hénot–Lessard [Reference van den Berg, Hénot and Lessard88] for semilinear elliptic equations, Dahne–Gómez-Serrano–Hou and Gómez-Serrano–Orriols [Reference Dahne, Gómez-Serrano and Hou28, Reference Gómez-Serrano and Orriols40] for inverse spectral problems, Jaquette–Lessard–Takayasu [Reference Jaquette, Lessard and Takayasu50] for the non-conservative NLS equations, Dahne–Gómez-Serrano [Reference Dahne and Gómez-Serrano27] for the Burgers-Hilbert equation, Takayasu–Lessard–Jaquette–Okamoto [Reference Takayasu, Lessard, Jaquette and Okamoto82] for the complex in time nonlinear heat equation and Breden–Engel [Reference Breden and Engel11] for chaos in stochastically perturbed Hopf systems. We make no claim that this list is exhaustive, but we would like to emphasize the broad directions of the problems that the field (computer-assisted proofs in PDE) has been able to undertake over the last few years.
In the context of fluid mechanics, we highlight the following authors and equations: Kobayashi [Reference Kobayashi57] and Stokes’ extreme waves; Chen–Hou–Huang [Reference Chen, Hou and Huang21] and De Gregorio; Castro–Córdoba–Gómez-Serrano [Reference Castro, Córdoba and Gómez-Serrano19] and SQG; Enciso–Gómez-Serrano–Vergara [Reference Enciso, Gómez-Serrano and Vergara31] and Whitham; Arioli–Koch, Figueras–De la Llave, Gameiro–Lessard, Figueras–Gameiro–Lessard–De la Llave, Zgliczynski, Zgliczynski–Mischaikow [Reference Arioli and Koch5, Reference Figueras and de la Llave35, Reference Figueras, Gameiro, Lessard and de la Llave36, Reference Gameiro and Lessard37, Reference Zgliczyński92, Reference Zgliczyński and Mischaikow93] and Kuramoto–Shivasinsky; van den Berg–Breden–Lessard–van Veen, Arioli–Gazzola–Koch, Bedrossian–Punshon-Smith [Reference Arioli, Gazzola and Koch4, Reference Bedrossian and Punshon-Smith8, Reference van den Berg, Breden, Lessard and van Veen87] and Navier-Stokes.
We also refer the reader to the books [Reference Moore and Bierbaum70, Reference Tucker86] and to the survey [Reference Gómez-Serrano38] and the book [Reference Nakao, Plum and Watanabe73] for a more specific treatment of computer-assisted proofs in PDE.
In our concrete case, we will use the computer in two different parts of our strategy:
-
1. Computing (with rigorous bounds) a high amount of Taylor coefficients of a solution of an ODE at a singular point (Lemma A.27, Lemma A.28).
-
2. Validating the sign of polynomials of degree 7–11 with coefficients depending on 2 parameters using a branch and bound method (Proposition 3.2, Proposition 3.5, Proposition 4.5).
There is a rich history of papers that have used any of these two strategies in other contexts.
Regarding the first one, in the context of the parameterization method of stable and unstable manifolds for ODE, Cabré–Fontich–de la Llave [Reference Cabré, Fontich and de la Llave16, Reference Cabré, Fontich and de la Llave17, Reference Cabré, Fontich and de la Llave18]; for parabolic PDE, van den Berg–Jaquette–Mireles-James [Reference van den Berg, Jaquette and Mireles James89] and Barker–Mireles-James–Morgan [Reference Barker, Mireles James and Morgan7]; and for DDEs, Hénot–Lessard–Mireles-James [Reference Hénot, Lessard and Mireles James48] are examples. See also the book by Haro–Canadell–Figueras–Luque–Mondelo [Reference Haro, Canadell, Figueras, Luque and Mondelo47] for a more comprehensive list of references. A similar strategy has been employed to solve ODE by means of a Taylor expansion and automatic differentiation by Berz–Makino [Reference Berz and Makino9] and is also implemented in the CAPD library by Kapela–Mrozek–Wilczak–Zgliczynski [Reference Kapela, Mrozek, Wilczak and Zgliczyński54] and the COSY INFINITY library by Makino–Berz [Reference Makino and Berz66].
Regarding the second one, we highlight examples of computer-assisted proofs involving branch and bound methods – for example, the work of Day–Kalies–Wanner [Reference Day, Kalies and Wanner30] in homology, Tanaka [Reference Tanaka83] in elliptic PDE, Gómez-Serrano–Granero-Belinchón [Reference Gómez-Serrano and Granero-Belinchón39] in the Muskat problem, Bánhelyi–Csendes–Krisztin–Neumaier [Reference Bánhelyi, Csendes, Krisztin and Neumaier6] in Wright’s conjecture, Hales [Reference Hales45] in the Kepler conjecture, or Kearfott [Reference Kearfott56] in constrained optimization problems. See also the book by Hansen–Walster [Reference Hansen and Walster46] for more references.
We remark that in the recent paper [Reference Guo, Hadzic, Jang and Schrecker44], the authors Guo, Hadžić, Jang and Schrecker apply arguments of a very similar flavor (Taylor expansions, dynamical systems arguments and computer-assisted proofs) to construct smooth self-similar solutions the gravitational Euler-Poisson system.
1.5 Stability of the Euler solutions and the existence of asymptotically self-similar Navier-Stokes solutions
Let us begin by rewriting (1.2) under spherical symmetry, and in terms of the rescaled sound speed
![]() $\sigma $
:
$\sigma $
:
 $$ \begin{align} \begin{aligned} \partial_t u + u \partial_R u + \alpha\sigma \partial_R \sigma-\frac{1}{R^2\rho}\partial_R(R^2 \partial_Ru)+ \frac{2u}{R^2\rho}&=0, \\ \partial_t \sigma + u \partial_R \sigma+\frac{\alpha}{R^2}\sigma\partial_R(R^2u)&=0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \partial_t u + u \partial_R u + \alpha\sigma \partial_R \sigma-\frac{1}{R^2\rho}\partial_R(R^2 \partial_Ru)+ \frac{2u}{R^2\rho}&=0, \\ \partial_t \sigma + u \partial_R \sigma+\frac{\alpha}{R^2}\sigma\partial_R(R^2u)&=0. \end{aligned} \end{align} $$
We recall that for simplicity, we fixed
![]() $\mu _1=1$
and
$\mu _1=1$
and
![]() $\mu _2=-1$
. We again define our Riemann invariants as in (1.6). However, in place of the ansatz (1.11), we instead consider the following time-dependent ansatz:
$\mu _2=-1$
. We again define our Riemann invariants as in (1.6). However, in place of the ansatz (1.11), we instead consider the following time-dependent ansatz:
 $$ \begin{align*} w(R,t)&=r^{-1}(T-t)^{r^{-1}-1} \mathcal{W}(\tfrac{R}{(T-t)^{\frac1r}},-\tfrac{\log(T-t)}{r}),\\ z(R,t)&=r^{-1} (T-t)^{r^{-1}-1} \mathcal{Z}(\tfrac{R}{(T-t)^{\frac1r}}, -\tfrac{\log(T-t)}{r}). \end{align*} $$
$$ \begin{align*} w(R,t)&=r^{-1}(T-t)^{r^{-1}-1} \mathcal{W}(\tfrac{R}{(T-t)^{\frac1r}},-\tfrac{\log(T-t)}{r}),\\ z(R,t)&=r^{-1} (T-t)^{r^{-1}-1} \mathcal{Z}(\tfrac{R}{(T-t)^{\frac1r}}, -\tfrac{\log(T-t)}{r}). \end{align*} $$
We then define the self-similar variables
 $$\begin{align*}s=-\frac{\log(T-t)}{r},\quad \zeta=\frac{R}{(T-t)^{\frac{1}{r}}}=e^s R=\exp(\xi).\end{align*}$$
$$\begin{align*}s=-\frac{\log(T-t)}{r},\quad \zeta=\frac{R}{(T-t)^{\frac{1}{r}}}=e^s R=\exp(\xi).\end{align*}$$
The equation (1.18) then becomes
 $$ \begin{align} \begin{aligned} & (\partial_s +r-1)\mathcal{W}+(\zeta+\frac12(\mathcal{W}+\mathcal{Z}+\alpha(\mathcal{W}-\mathcal{Z})))\partial_{\zeta} \mathcal{W} +\frac{\alpha}{2\zeta}(\mathcal{W}^2-\mathcal{Z}^2)\\ &\qquad\qquad=\frac{r^{1+\frac{1}{\alpha}} 2^{1/\alpha}}{\alpha^{1/\alpha} \zeta^2((\mathcal{W}-\mathcal{Z}))^{\frac1\alpha}}e^{(2-r+\frac{1}{\alpha}(1-r))s}\left( \partial_{\zeta}(\zeta^2\partial_{\zeta}(\mathcal{W}+\mathcal{Z}))-2(\mathcal{W}+\mathcal{Z})\right),\\ & (\partial_s +r-1)\mathcal{Z}+(\zeta+\frac12(\mathcal{W}+\mathcal{Z}-\alpha(\mathcal{W}-\mathcal{Z})))\partial_{\zeta} \mathcal{Z} - \frac{\alpha}{2\zeta}(\mathcal{W}^2-\mathcal{Z}^2) \\ &\qquad\qquad=\frac{r^{1+\frac{1}{\alpha}} 2^{1/\alpha-1}}{\alpha^{1/\alpha} \zeta^2((\mathcal{W}-\mathcal{Z}))^{\frac1\alpha}}e^{(2-r+\frac{1}{\alpha}(1-r))s}\left( \partial_{\zeta}(\zeta^2\partial_{\zeta}(\mathcal{W}+\mathcal{Z}))- 2(\mathcal{W}+\mathcal{Z})\right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & (\partial_s +r-1)\mathcal{W}+(\zeta+\frac12(\mathcal{W}+\mathcal{Z}+\alpha(\mathcal{W}-\mathcal{Z})))\partial_{\zeta} \mathcal{W} +\frac{\alpha}{2\zeta}(\mathcal{W}^2-\mathcal{Z}^2)\\ &\qquad\qquad=\frac{r^{1+\frac{1}{\alpha}} 2^{1/\alpha}}{\alpha^{1/\alpha} \zeta^2((\mathcal{W}-\mathcal{Z}))^{\frac1\alpha}}e^{(2-r+\frac{1}{\alpha}(1-r))s}\left( \partial_{\zeta}(\zeta^2\partial_{\zeta}(\mathcal{W}+\mathcal{Z}))-2(\mathcal{W}+\mathcal{Z})\right),\\ & (\partial_s +r-1)\mathcal{Z}+(\zeta+\frac12(\mathcal{W}+\mathcal{Z}-\alpha(\mathcal{W}-\mathcal{Z})))\partial_{\zeta} \mathcal{Z} - \frac{\alpha}{2\zeta}(\mathcal{W}^2-\mathcal{Z}^2) \\ &\qquad\qquad=\frac{r^{1+\frac{1}{\alpha}} 2^{1/\alpha-1}}{\alpha^{1/\alpha} \zeta^2((\mathcal{W}-\mathcal{Z}))^{\frac1\alpha}}e^{(2-r+\frac{1}{\alpha}(1-r))s}\left( \partial_{\zeta}(\zeta^2\partial_{\zeta}(\mathcal{W}+\mathcal{Z}))- 2(\mathcal{W}+\mathcal{Z})\right). \end{aligned} \end{align} $$
The last term can be treated as an error so long as
or equivalently,
Given that we intend to restrict
![]() $r<r^\ast $
, by the definition of
$r<r^\ast $
, by the definition of
![]() $r^\ast $
given in (1.16), we conclude that we require
$r^\ast $
given in (1.16), we conclude that we require
which is clearly satisfied for
![]() $\gamma =\frac 75$
.
$\gamma =\frac 75$
.
Given a smooth globally defined self-similar solution to the Euler equation corresponding to a self-similar variable r satisfying (1.21), to prove the existence of an asymptotically self-similar solution to the Navier-Stokes equations, it will be sufficient to show the nonlinear stability of such a solution modulo finite modes of instability. The main ingredient is to first show linear stability of the self-similar Euler solutions. This was achieved in [Reference Merle, Raphaël, Rodnianski and Szeftel67] by writing the equation as a nonlinear wave equation and proving stability in terms of carefully weighted spaces. In the present work, a simpler approach is taken exploiting locality and the transport structure of the equation written in Riemann variables. In place of weighted spaces, we modify the equation outside a neighborhood of the backwards acoustic cone of the singularity in order to restrict the region of interest. Differing from the work [Reference Merle, Raphaël, Rodnianski and Szeftel67], we exploit the transport structure of the Riemann invariants in order to simplify the stability analysis. The nonlinear stability will rely on a topological argument in a similar vain to [Reference Merle, Raphaël, Rodnianski and Szeftel67, Reference Oh and Pasqualotto75] (see [Reference Buckmaster and Iyer12] for an alternate approach based on a Newton scheme).
1.6 Organization of paper
Section 2 describes Frobenius-like series expansions of the solution at
![]() $P_s$
and
$P_s$
and
![]() $P_0$
. In Section 3 and Section 4, we apply barrier arguments to describe the solution in the region outside (respectively inside) the backwards acoustic cone of the singularity. In Section 5, we complete the analysis of Section 3 for the case of
$P_0$
. In Section 3 and Section 4, we apply barrier arguments to describe the solution in the region outside (respectively inside) the backwards acoustic cone of the singularity. In Section 5, we complete the analysis of Section 3 for the case of
![]() $\gamma =7/5$
and
$\gamma =7/5$
and
![]() $r\rightarrow r^\ast $
. The section collects analysis related to the
$r\rightarrow r^\ast $
. The section collects analysis related to the
![]() $r\rightarrow r^\ast $
asymptotic limit. In Section 6, Theorem 1.1 and Theorem 1.2 are proved by combining the result of Proposition 4.1 with a shooting argument in order to connect
$r\rightarrow r^\ast $
asymptotic limit. In Section 6, Theorem 1.1 and Theorem 1.2 are proved by combining the result of Proposition 4.1 with a shooting argument in order to connect
![]() $P_s$
to
$P_s$
to
![]() $P_0$
by a smooth solution. Section 7 is dedicated to showing that the linearized operator of the Euler equations around the self-similar profile generates a contraction semigroup modulo finitely many instabilities. Finally in Section 8, we use the linear stability analysis of Section 7 in combination with a bootstrap and a topological argument in order to prove nonlinear stability for the Navier-Stokes equations for a manifold of initial data of finite codimension. In particular, Section 8 contains the proof of Theorem 1.3. Appendix A contains technical lemmas used throughout the proofs and properties of the phase portrait in the case
$P_0$
by a smooth solution. Section 7 is dedicated to showing that the linearized operator of the Euler equations around the self-similar profile generates a contraction semigroup modulo finitely many instabilities. Finally in Section 8, we use the linear stability analysis of Section 7 in combination with a bootstrap and a topological argument in order to prove nonlinear stability for the Navier-Stokes equations for a manifold of initial data of finite codimension. In particular, Section 8 contains the proof of Theorem 1.3. Appendix A contains technical lemmas used throughout the proofs and properties of the phase portrait in the case
![]() $\gamma = \frac 75$
. Appendix B summarizes the details of the computer-assisted proofs.
$\gamma = \frac 75$
. Appendix B summarizes the details of the computer-assisted proofs.
2 Expansion around
 $P_s$
and
$P_s$
and
 $P_0$
$P_0$
In this section, we describe the Frobenius-like series expansions of the smooth solutions passing through
![]() $P_s$
and starting at
$P_s$
and starting at
![]() $P_0$
. The general approach will be to obtain a recurrence for the coefficients of the expansion from imposing the ODE on the expansion. In the case of
$P_0$
. The general approach will be to obtain a recurrence for the coefficients of the expansion from imposing the ODE on the expansion. In the case of
![]() $P_s$
, we will obtain that the recurrence can be solved for
$P_s$
, we will obtain that the recurrence can be solved for
![]() $k \notin \mathbb N$
(due to a factor of the type
$k \notin \mathbb N$
(due to a factor of the type
![]() $m-k$
on the equation for the m-th coefficient). In the case of
$m-k$
on the equation for the m-th coefficient). In the case of
![]() $P_0$
, we will need to ensure that the appropriate conditions are met so that the profiles, in Cartesian variables, are smooth at
$P_0$
, we will need to ensure that the appropriate conditions are met so that the profiles, in Cartesian variables, are smooth at
![]() $R=0$
. The most elegant way of doing so will be reexpressing our recurrence in terms of a new function
$R=0$
. The most elegant way of doing so will be reexpressing our recurrence in terms of a new function
![]() $\mathcal {W}$
, that encodes W for positive arguments and a reflected version of Z for negative arguments. The smoothness of
$\mathcal {W}$
, that encodes W for positive arguments and a reflected version of Z for negative arguments. The smoothness of
![]() $\mathcal {W}$
at the origin will yield smoothness of both our profiles at the origin.
$\mathcal {W}$
at the origin will yield smoothness of both our profiles at the origin.
2.1 First-order expansion
We label the two solutions to
![]() $D_Z = N_Z = 0$
:
$D_Z = N_Z = 0$
:
 $$ \begin{align} \begin{aligned} P_s = (W_0, Z_0) &= \Big( \frac{\gamma^2 r+(\gamma+1) \mathcal{R}_1 -3 \gamma^2-2 \gamma r+10 \gamma-3 r-3}{4 (\gamma-1)^2} \\ & \qquad \frac{\gamma^2 r+(\gamma -3) \mathcal{R}_1 -3 \gamma^2-6 \gamma r+6 \gamma+9 r-7}{4 (\gamma-1)^2} \Big),\\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} P_s = (W_0, Z_0) &= \Big( \frac{\gamma^2 r+(\gamma+1) \mathcal{R}_1 -3 \gamma^2-2 \gamma r+10 \gamma-3 r-3}{4 (\gamma-1)^2} \\ & \qquad \frac{\gamma^2 r+(\gamma -3) \mathcal{R}_1 -3 \gamma^2-6 \gamma r+6 \gamma+9 r-7}{4 (\gamma-1)^2} \Big),\\ \end{aligned} \end{align} $$
 $$ \begin{align} \begin{aligned} \bar P_s = (\bar W_0, \bar Z_0) &= \Big( \frac{\gamma^2 r-(\gamma+1) \mathcal{R}_1-3 \gamma^2-2 \gamma r+10 \gamma-3 r-3}{4 (\gamma-1)^2}\ \\ & \qquad \frac{\gamma^2 r+(3-\gamma) \mathcal{R}_1 -3 \gamma^2-6 \gamma r+6 \gamma+9 r-7}{4 (\gamma-1)^2} \Big), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \bar P_s = (\bar W_0, \bar Z_0) &= \Big( \frac{\gamma^2 r-(\gamma+1) \mathcal{R}_1-3 \gamma^2-2 \gamma r+10 \gamma-3 r-3}{4 (\gamma-1)^2}\ \\ & \qquad \frac{\gamma^2 r+(3-\gamma) \mathcal{R}_1 -3 \gamma^2-6 \gamma r+6 \gamma+9 r-7}{4 (\gamma-1)^2} \Big), \end{aligned} \end{align} $$
where
The points
![]() $P_s$
and
$P_s$
and
![]() $\bar P_s$
are the only intersections of
$\bar P_s$
are the only intersections of
![]() $D_Z = N_Z = 0$
, so any possible smooth profile going from
$D_Z = N_Z = 0$
, so any possible smooth profile going from
![]() $P_0$
to
$P_0$
to
![]() $P_\infty $
will need to pass through one of them in order to cross
$P_\infty $
will need to pass through one of them in order to cross
![]() $D_Z = 0$
.
$D_Z = 0$
.
Let us consider the derivative of the smooth solutions to the ODE (1.10) with respect to
![]() $\xi $
at
$\xi $
at
![]() $P_s$
. The derivative of W at
$P_s$
. The derivative of W at
![]() $P_s$
to both solutions is given by
$P_s$
to both solutions is given by
Applying L’Hôpital, the derivative of Z at
![]() $P_s$
satisfies the second-degree equation
$P_s$
satisfies the second-degree equation
which leads to two possible values of
![]() $Z_1$
corresponding to the two smooth solutions passing through
$Z_1$
corresponding to the two smooth solutions passing through
![]() $P_s$
. The solution that we will work with corresponds to the vector
$P_s$
. The solution that we will work with corresponds to the vector
![]() $\nu _-=(W_1,Z_1)$
, where
$\nu _-=(W_1,Z_1)$
, where
 $$ \begin{align} \begin{aligned} W_1 &= \frac{\gamma \left(-3 \left(\mathcal{R}_1+6\right)-3 \gamma (r-3)+2 r\right)+\mathcal{R}_1+5 r+5}{4 (\gamma-1)^2} ,\\ Z_1 &= \frac{-\left(3 \gamma ^3-7 \gamma ^2+\gamma +11\right) r+\gamma (\gamma (9 \gamma -3 \mathcal{R}_1-25)+10 \mathcal{R}_1-4(\gamma-1) \mathcal{R}_2+27)-3 \mathcal{R}_1+4 (\gamma-1) \mathcal{R}_2-3}{4 (\gamma -1)^2 (\gamma +1)}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} W_1 &= \frac{\gamma \left(-3 \left(\mathcal{R}_1+6\right)-3 \gamma (r-3)+2 r\right)+\mathcal{R}_1+5 r+5}{4 (\gamma-1)^2} ,\\ Z_1 &= \frac{-\left(3 \gamma ^3-7 \gamma ^2+\gamma +11\right) r+\gamma (\gamma (9 \gamma -3 \mathcal{R}_1-25)+10 \mathcal{R}_1-4(\gamma-1) \mathcal{R}_2+27)-3 \mathcal{R}_1+4 (\gamma-1) \mathcal{R}_2-3}{4 (\gamma -1)^2 (\gamma +1)}, \end{aligned} \end{align} $$
and
 $$ \begin{align} \kern-12pt\begin{aligned} \mathcal{R}_2 &=\frac{1}{\gamma-1}\bigg(\gamma ((76-27 \gamma ) \gamma -71)-\left((3 \gamma -5) ((\gamma -5) \gamma +2) r^2\right)+(\gamma (\gamma (18 \gamma -52)+50)-8) r\\ &\qquad+\mathcal{R}_1 (9 (\gamma -2) \gamma +((2-3 \gamma ) \gamma +5) r+5)+18\bigg)^{\frac12}. \end{aligned} \end{align} $$
$$ \begin{align} \kern-12pt\begin{aligned} \mathcal{R}_2 &=\frac{1}{\gamma-1}\bigg(\gamma ((76-27 \gamma ) \gamma -71)-\left((3 \gamma -5) ((\gamma -5) \gamma +2) r^2\right)+(\gamma (\gamma (18 \gamma -52)+50)-8) r\\ &\qquad+\mathcal{R}_1 (9 (\gamma -2) \gamma +((2-3 \gamma ) \gamma +5) r+5)+18\bigg)^{\frac12}. \end{aligned} \end{align} $$
This value of
![]() $Z_1$
corresponds to the smooth solution that agrees up to order
$Z_1$
corresponds to the smooth solution that agrees up to order
![]() $\lfloor k \rfloor $
with all the non-smooth solutions around
$\lfloor k \rfloor $
with all the non-smooth solutions around
![]() $P_s$
(the simple example given in Section 1.4 is illustrative of this behavior).
$P_s$
(the simple example given in Section 1.4 is illustrative of this behavior).
Define the vector
![]() $\nu _+$
by
$\nu _+$
by
![]() $\nu _+=(W_1,\check Z_1)$
, where
$\nu _+=(W_1,\check Z_1)$
, where
 $$\begin{align*}\check Z_1 = -\frac{\left(3 \gamma ^3-7 \gamma ^2+\gamma +11\right) r-\gamma (\gamma (9 \gamma -3 \mathcal{R}_1-25)+10 \mathcal{R}_1+4 (\gamma-1)\mathcal{R}_2+27)+3 \mathcal{R}_1+4(\gamma-1) \mathcal{R}_2+3}{4 (\gamma -1)^2 (\gamma +1)} .\end{align*}$$
$$\begin{align*}\check Z_1 = -\frac{\left(3 \gamma ^3-7 \gamma ^2+\gamma +11\right) r-\gamma (\gamma (9 \gamma -3 \mathcal{R}_1-25)+10 \mathcal{R}_1+4 (\gamma-1)\mathcal{R}_2+27)+3 \mathcal{R}_1+4(\gamma-1) \mathcal{R}_2+3}{4 (\gamma -1)^2 (\gamma +1)} .\end{align*}$$
Then the two smooth solutions at
![]() $P_s$
have
$P_s$
have
![]() $\xi $
derivatives
$\xi $
derivatives
![]() $\nu _+=(W_1, Z_1)$
and
$\nu _+=(W_1, Z_1)$
and
![]() $\nu _-=(W_1, \check Z_1)$
.
$\nu _-=(W_1, \check Z_1)$
.
The vectors
![]() $\nu _-$
,
$\nu _-$
,
![]() $\nu _+$
are eigenvectors of the Jacobian J at
$\nu _+$
are eigenvectors of the Jacobian J at
![]() $P_s$
of the reparameterized system (1.14). In particular, the Jacobian J at
$P_s$
of the reparameterized system (1.14). In particular, the Jacobian J at
![]() $P_s$
is given by
$P_s$
is given by
 $$ \begin{align} J = \left( \begin{matrix} N_W (P_s) \partial_W D_Z (P_s) & N_W (P_s) \partial_Z D_Z (P_s) \\ D_W (P_s) \partial_W N_Z (P_s) & D_W (P_s) \partial_Z N_Z (P_s) \\ \end{matrix} \right). \end{align} $$
$$ \begin{align} J = \left( \begin{matrix} N_W (P_s) \partial_W D_Z (P_s) & N_W (P_s) \partial_Z D_Z (P_s) \\ D_W (P_s) \partial_W N_Z (P_s) & D_W (P_s) \partial_Z N_Z (P_s) \\ \end{matrix} \right). \end{align} $$
Note if
![]() $\nu = (\nu _W, \nu _Z)$
is an eigenvector of J, then it must satisfy the equation
$\nu = (\nu _W, \nu _Z)$
is an eigenvector of J, then it must satisfy the equation
Then, applying (2.4) and (2.5), we see that (2.9) is satisfied for
![]() $\nu =\nu _-,\nu _+$
and hence
$\nu =\nu _-,\nu _+$
and hence
![]() $\nu _-,\nu _+$
are eigenvectors of J. We let
$\nu _-,\nu _+$
are eigenvectors of J. We let
![]() $\lambda _+$
and
$\lambda _+$
and
![]() $\lambda _-$
be the eigenvalues corresponding to
$\lambda _-$
be the eigenvalues corresponding to
![]() $\nu _-$
and
$\nu _-$
and
![]() $\nu _+$
, respectively. We obtain the equations
$\nu _+$
, respectively. We obtain the equations
Lemma 2.1. Let
![]() $D_{Z, 1} = \nabla D_Z (P_s) (W_1, Z_1)$
. Then,
$D_{Z, 1} = \nabla D_Z (P_s) (W_1, Z_1)$
. Then,
where we recall in (1.15) we defined
![]() $k(r) = \frac {\lambda _+ }{\lambda _-}$
. Moreover, we have that
$k(r) = \frac {\lambda _+ }{\lambda _-}$
. Moreover, we have that
![]() $k(r)$
is a smooth monotonically increasing function for
$k(r)$
is a smooth monotonically increasing function for
![]() $r\in [1, r^\ast (\gamma ))$
such that
$r\in [1, r^\ast (\gamma ))$
such that
![]() $r(1) = 1$
,
$r(1) = 1$
,
![]() $\lim _{r\to r^\ast } k(r) = +\infty $
and
$\lim _{r\to r^\ast } k(r) = +\infty $
and
![]() $k'(r)> 0$
for all
$k'(r)> 0$
for all
![]() $r \in (1, r^\ast (\gamma ))$
. Thus,
$r \in (1, r^\ast (\gamma ))$
. Thus,
![]() $k(r)$
is a bijection between
$k(r)$
is a bijection between
![]() $[1, r^\ast (\gamma ))$
and
$[1, r^\ast (\gamma ))$
and
![]() $[1, +\infty )$
.
$[1, +\infty )$
.
Proof. Note that the parenthesis in (2.10) is
![]() $D_{Z, 1}$
. Then from (2.10) and (2.11), we obtain
$D_{Z, 1}$
. Then from (2.10) and (2.11), we obtain
 $$ \begin{align*} k(r)& = \frac{(\lambda_+ + \lambda_-) - \lambda_-}{\lambda_-}\\ &= \frac{ W_1 \partial_W D_Z (P_s) + \frac{W_1 D_W (P_s) }{N_W(P_s)} \partial_Z N_Z(P_s) - \left( \partial_W D_Z (P_s) W_1 + \partial_Z D_Z (P_s) Z_1 \right)}{D_{Z, 1}} \\ &= \frac{ \frac{W_1 D_W (P_s) }{N_W(P_s)} \partial_Z N_Z (P_s) - \partial_Z D_Z (P_s) Z_1 }{D_{Z, 1}} . \end{align*} $$
$$ \begin{align*} k(r)& = \frac{(\lambda_+ + \lambda_-) - \lambda_-}{\lambda_-}\\ &= \frac{ W_1 \partial_W D_Z (P_s) + \frac{W_1 D_W (P_s) }{N_W(P_s)} \partial_Z N_Z(P_s) - \left( \partial_W D_Z (P_s) W_1 + \partial_Z D_Z (P_s) Z_1 \right)}{D_{Z, 1}} \\ &= \frac{ \frac{W_1 D_W (P_s) }{N_W(P_s)} \partial_Z N_Z (P_s) - \partial_Z D_Z (P_s) Z_1 }{D_{Z, 1}} . \end{align*} $$
Noting also that
![]() $W_1 = \frac {N_W (P_s)}{D_W (P_s)}$
, we get the expression (2.12).
$W_1 = \frac {N_W (P_s)}{D_W (P_s)}$
, we get the expression (2.12).
In terms of
![]() $\check Z_1$
, we have that the fact that
$\check Z_1$
, we have that the fact that
![]() $(W_1, \check Z_1)$
is an eigenvector of J means
$(W_1, \check Z_1)$
is an eigenvector of J means
Dividing this by (2.10), we get that
 $$ \begin{align} k(r) = \frac{\check D_{Z, 1}}{D_{Z, 1}} = \frac{-4+(1+\gamma)\frac{r-1}{\gamma-1} - \mathcal{R}_2}{-4+(1+\gamma)\frac{r-1}{\gamma-1} + \mathcal{R}_2}, \end{align} $$
$$ \begin{align} k(r) = \frac{\check D_{Z, 1}}{D_{Z, 1}} = \frac{-4+(1+\gamma)\frac{r-1}{\gamma-1} - \mathcal{R}_2}{-4+(1+\gamma)\frac{r-1}{\gamma-1} + \mathcal{R}_2}, \end{align} $$
where
![]() $\check D_{Z, 1} = \nabla D_Z \cdot (W_1, \check Z_1)$
, and we have substituted
$\check D_{Z, 1} = \nabla D_Z \cdot (W_1, \check Z_1)$
, and we have substituted
![]() $D_{Z, 1}$
,
$D_{Z, 1}$
,
![]() $ \check D_{Z, 1}$
by their expressions in terms of
$ \check D_{Z, 1}$
by their expressions in terms of
![]() $\gamma , r, \mathcal {R}_i$
.
$\gamma , r, \mathcal {R}_i$
.
Now, we claim that
![]() $k(1) = 1$
. From (2.14), it suffices to show that
$k(1) = 1$
. From (2.14), it suffices to show that
![]() $\mathcal {R}_2 = 0$
at
$\mathcal {R}_2 = 0$
at
![]() $r=1$
. From (2.3), we have
$r=1$
. From (2.3), we have
![]() $\mathcal {R}_1 = 2(\gamma - 1)$
for
$\mathcal {R}_1 = 2(\gamma - 1)$
for
![]() $r=1$
. Plugging that into (2.7), we deduce that
$r=1$
. Plugging that into (2.7), we deduce that
![]() $\mathcal {R}_2 = 0$
for
$\mathcal {R}_2 = 0$
for
![]() $r=1$
.
$r=1$
.
We also claim that
![]() $k(r) \rightarrow +\infty $
as
$k(r) \rightarrow +\infty $
as
![]() $r \rightarrow r^\ast $
. From Lemma A.11, we have that
$r \rightarrow r^\ast $
. From Lemma A.11, we have that
![]() $D_{Z, 1}> 0$
for
$D_{Z, 1}> 0$
for
![]() $r \in [1, r^\ast )$
, and from Lemma A.12, we have
$r \in [1, r^\ast )$
, and from Lemma A.12, we have
![]() $\check D_{Z, 1}> 0$
for
$\check D_{Z, 1}> 0$
for
![]() $r \in [1, r^\ast ]$
. Using that
$r \in [1, r^\ast ]$
. Using that
![]() $D_{Z, 1} = 0$
for
$D_{Z, 1} = 0$
for
![]() $r = r^\ast $
(Lemma A.9), we conclude the desired limit.
$r = r^\ast $
(Lemma A.9), we conclude the desired limit.
Lastly, we show that
![]() $k'(r)> 0$
from equation (2.14) via a computer-assisted proof. The code can be found in the supplementary material, and details about the implementation can be found in Appendix B.
$k'(r)> 0$
from equation (2.14) via a computer-assisted proof. The code can be found in the supplementary material, and details about the implementation can be found in Appendix B.
2.2 Taylor expansion around
 $P_s$
(
$P_s$
(
 $\xi =0$
)
$\xi =0$
)
Let
![]() $(W^{(r)}(\xi ) ,Z^{(r)}(\xi ) )$
denote the smooth solution corresponding to the direction
$(W^{(r)}(\xi ) ,Z^{(r)}(\xi ) )$
denote the smooth solution corresponding to the direction
![]() $\nu _-$
defined in the previous section. Now consider its Taylor expansion around
$\nu _-$
defined in the previous section. Now consider its Taylor expansion around
![]() $P_s$
(i.e.,
$P_s$
(i.e.,
![]() $\xi =0$
):
$\xi =0$
):
 $$ \begin{align} \begin{aligned} W^{(r)} (\xi ) = \sum_{n=0}^\infty \frac{1}{n!} W_n \xi ^n, \quad\mbox{and}\quad Z^{(r)} (\xi ) = \sum_{n=0}^\infty \frac{1}{n!} Z_n \xi ^n. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} W^{(r)} (\xi ) = \sum_{n=0}^\infty \frac{1}{n!} W_n \xi ^n, \quad\mbox{and}\quad Z^{(r)} (\xi ) = \sum_{n=0}^\infty \frac{1}{n!} Z_n \xi ^n. \end{aligned} \end{align} $$
Let us also define the Taylor coefficients of
![]() $D_W, D_Z, N_W, N_Z$
as follows:
$D_W, D_Z, N_W, N_Z$
as follows:
 $$ \begin{align*} \begin{aligned} D_W(W^{(r)} (\xi ) , Z^{(r)} (\xi )) &= \sum_{n=0}^\infty \frac{1}{n!} D_{W, n} \xi^n, \qquad D_Z(W^{(r)} (\xi ) , Z^{(r)} (\xi )) = \sum_{n=0}^\infty \frac{1}{n!} D_{Z, n} \xi^n, \\ N_W(W^{(r)} (\xi ) , Z^{(r)} (\xi )) &= \sum_{n=0}^\infty \frac{1}{n!} N_{W, n} \xi^n, \qquad N_Z(W^{(r)} (\xi ) , Z^{(r)} (\xi )) = \sum_{n=0}^\infty \frac{1}{n!} N_{Z, n} \xi^n. \end{aligned}\nonumber \end{align*} $$
$$ \begin{align*} \begin{aligned} D_W(W^{(r)} (\xi ) , Z^{(r)} (\xi )) &= \sum_{n=0}^\infty \frac{1}{n!} D_{W, n} \xi^n, \qquad D_Z(W^{(r)} (\xi ) , Z^{(r)} (\xi )) = \sum_{n=0}^\infty \frac{1}{n!} D_{Z, n} \xi^n, \\ N_W(W^{(r)} (\xi ) , Z^{(r)} (\xi )) &= \sum_{n=0}^\infty \frac{1}{n!} N_{W, n} \xi^n, \qquad N_Z(W^{(r)} (\xi ) , Z^{(r)} (\xi )) = \sum_{n=0}^\infty \frac{1}{n!} N_{Z, n} \xi^n. \end{aligned}\nonumber \end{align*} $$
For
![]() $ \circ \in \{ W, Z \}$
,
$ \circ \in \{ W, Z \}$
,
![]() $D_\circ (W, Z)$
are first-degree polynomials in W and Z; hence,
$D_\circ (W, Z)$
are first-degree polynomials in W and Z; hence,
with the special case
![]() $D_{\circ , 0} = D_\circ (P_s)$
. In the case of
$D_{\circ , 0} = D_\circ (P_s)$
. In the case of
![]() $N_\circ $
, we have second-degree polynomials, so the gradient is not constant in
$N_\circ $
, we have second-degree polynomials, so the gradient is not constant in
![]() $(W, Z)$
. However, the Hessian matrix is, and we get the expression
$(W, Z)$
. However, the Hessian matrix is, and we get the expression
 $$ \begin{align} N_{\circ , n} = \nabla N_\circ \Big|_{P_s} \cdot (W_n, Z_n) + \sum_{j=1}^{n-1} \binom{n-1}{j-1} (W_{n-j}, Z_{n-j}) (HN_\circ )(W_j, Z_j)^\top, \qquad \circ \in \{ W, Z \},\;\; n\geq 1, \end{align} $$
$$ \begin{align} N_{\circ , n} = \nabla N_\circ \Big|_{P_s} \cdot (W_n, Z_n) + \sum_{j=1}^{n-1} \binom{n-1}{j-1} (W_{n-j}, Z_{n-j}) (HN_\circ )(W_j, Z_j)^\top, \qquad \circ \in \{ W, Z \},\;\; n\geq 1, \end{align} $$
with the special case
![]() $N_{\circ , 0} = N_\circ (P_s)$
.
$N_{\circ , 0} = N_\circ (P_s)$
.
Proposition 2.2. For
![]() $n\in \mathbb N$
, let
$n\in \mathbb N$
, let
![]() $r\in (r_n,r_{n+1})$
. If there is a solution to ODE (1.10) passing through
$r\in (r_n,r_{n+1})$
. If there is a solution to ODE (1.10) passing through
![]() $P_s$
at
$P_s$
at
![]() $\xi = 0$
with gradient
$\xi = 0$
with gradient
![]() $(W_1, Z_1)$
, their Taylor coefficients
$(W_1, Z_1)$
, their Taylor coefficients
![]() $W_m$
,
$W_m$
,
![]() $Z_m$
for
$Z_m$
for
![]() $m\geq 2$
satisfy the recursion relation
$m\geq 2$
satisfy the recursion relation
 $$ \begin{align} D_{W, 0} W_m &= N_{W, m-1} - \sum_{j=0}^{m-2} \binom{m-1}{j} D_{W, m-1-j} W_{j+1},\end{align} $$
$$ \begin{align} D_{W, 0} W_m &= N_{W, m-1} - \sum_{j=0}^{m-2} \binom{m-1}{j} D_{W, m-1-j} W_{j+1},\end{align} $$
 $$ \begin{align} Z_m D_{Z, 1} (m-k) &= - \sum_{j=1}^{m-2} \binom{m}{j} D_{Z, m-j} Z_{j+1} \nonumber \\&\qquad+\left( N_{Z, m} - (\partial_Z N_Z (P_s) ) Z_m\right) - Z_1 W_m \partial_W D_Z (P_s) . \end{align} $$
$$ \begin{align} Z_m D_{Z, 1} (m-k) &= - \sum_{j=1}^{m-2} \binom{m}{j} D_{Z, m-j} Z_{j+1} \nonumber \\&\qquad+\left( N_{Z, m} - (\partial_Z N_Z (P_s) ) Z_m\right) - Z_1 W_m \partial_W D_Z (P_s) . \end{align} $$
Moreover, the coefficients are iteratively solvable as both the coefficients
![]() $D_{W, 0}$
and
$D_{W, 0}$
and
![]() $D_{Z, 1} (m-k)$
are nonzero, and the expansion of the second line in (2.19) contains no terms involving
$D_{Z, 1} (m-k)$
are nonzero, and the expansion of the second line in (2.19) contains no terms involving
![]() $Z_m$
.
$Z_m$
.
Proof. Taking
![]() $m-1$
derivatives in equation (1.10), we obtain
$m-1$
derivatives in equation (1.10), we obtain
Expanding the derivatives, we immediately obtain (2.18). Moreover,
![]() $D_{W, 0} \neq 0$
as a consequence of Lemma A.10. Taking m derivatives in the equation (1.10), we analogously obtain
$D_{W, 0} \neq 0$
as a consequence of Lemma A.10. Taking m derivatives in the equation (1.10), we analogously obtain
 $$ \begin{align*} mD_{Z, 1} Z_m &= N_{Z, m} - \sum_{j=0}^{m-2} \binom{m}{j} D_{Z, m-j} Z_{j+1}. \end{align*} $$
$$ \begin{align*} mD_{Z, 1} Z_m &= N_{Z, m} - \sum_{j=0}^{m-2} \binom{m}{j} D_{Z, m-j} Z_{j+1}. \end{align*} $$
Now, we subtract the terms with
![]() $Z_m$
in the quantities
$Z_m$
in the quantities
![]() $N_{W, m}$
and
$N_{W, m}$
and
![]() $D_{Z, m}$
, obtaining
$D_{Z, m}$
, obtaining
 $$ \begin{align*} Z_m \left( m D_{Z, 1} - \partial_Z N_Z (P_s) + Z_1 \partial_Z D_Z \right) &= -\sum_{j=1}^{m-2} \binom{m}{j} D_{Z, m-j} Z_{j+1} \\&\quad+ \left( N_{Z, m} - \partial_Z N_Z (P_s) Z_m \right) + Z_1 \left( - D_{Z, m} + Z_m \partial_Z D_Z \right). \end{align*} $$
$$ \begin{align*} Z_m \left( m D_{Z, 1} - \partial_Z N_Z (P_s) + Z_1 \partial_Z D_Z \right) &= -\sum_{j=1}^{m-2} \binom{m}{j} D_{Z, m-j} Z_{j+1} \\&\quad+ \left( N_{Z, m} - \partial_Z N_Z (P_s) Z_m \right) + Z_1 \left( - D_{Z, m} + Z_m \partial_Z D_Z \right). \end{align*} $$
Note that the terms in the second line do not depend on
![]() $Z_m$
, as we have subtracted the dependence of
$Z_m$
, as we have subtracted the dependence of
![]() $D_{Z, m}$
and
$D_{Z, m}$
and
![]() $N_{Z, m}$
on
$N_{Z, m}$
on
![]() $Z_m$
(see equations (2.16) and (2.17)). Then, applying (2.12), we obtain (2.19). We have
$Z_m$
(see equations (2.16) and (2.17)). Then, applying (2.12), we obtain (2.19). We have
![]() $D_{Z, 1} \neq 0$
as a result of Lemma A.11.
$D_{Z, 1} \neq 0$
as a result of Lemma A.11.
Proposition 2.3. Let
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $I \subset (r_n, r_{n+1})$
a closed interval. There exists an absolute constant C (depending on I and
$I \subset (r_n, r_{n+1})$
a closed interval. There exists an absolute constant C (depending on I and
![]() $\gamma $
) such that we have the bounds
$\gamma $
) such that we have the bounds
For
![]() $\xi < 1/C$
, the series
$\xi < 1/C$
, the series
![]() $W^{(r)} (\xi ) = \sum W_i \xi ^i /i!$
and
$W^{(r)} (\xi ) = \sum W_i \xi ^i /i!$
and
![]() $Z^{(r)}(\xi ) = \sum Z_i \xi ^i / i!$
solve the ODE (1.10). Moreover, the functions
$Z^{(r)}(\xi ) = \sum Z_i \xi ^i / i!$
solve the ODE (1.10). Moreover, the functions
![]() $W^{(r)} (\xi ) , Z^{(r)} (\xi )$
are continuous with respect to
$W^{(r)} (\xi ) , Z^{(r)} (\xi )$
are continuous with respect to
![]() $r \in I$
.
$r \in I$
.
Proof. In this proof, we will use the following notation:
Then, from equations (2.16)–(2.19), we have
 $$ \begin{align} D_{W, 0} w_m m &= n_{W, m-1} - \sum_{j=0}^{m-2} d_{W, m-1-j} w_{j+1}(j+1),\end{align} $$
$$ \begin{align} D_{W, 0} w_m m &= n_{W, m-1} - \sum_{j=0}^{m-2} d_{W, m-1-j} w_{j+1}(j+1),\end{align} $$
 $$ \begin{align} z_m D_{Z, 1} (m-k) &= - \sum_{j=1}^{m-2} d_{Z, m-j} (j+1)z_{j+1} \nonumber \\ &\qquad+\underbrace{\left( n_{Z, m} - (\partial_Z N_Z (P_s) ) z_m\right)}_{g_m} - Z_1 w_m \partial_W D_Z (P_s) , \end{align} $$
$$ \begin{align} z_m D_{Z, 1} (m-k) &= - \sum_{j=1}^{m-2} d_{Z, m-j} (j+1)z_{j+1} \nonumber \\ &\qquad+\underbrace{\left( n_{Z, m} - (\partial_Z N_Z (P_s) ) z_m\right)}_{g_m} - Z_1 w_m \partial_W D_Z (P_s) , \end{align} $$
 $$ \begin{align} n_{\circ , m} &= \nabla N_\circ \Big|_{P_s} \cdot (w_m, z_m) + \frac{1}{m}\sum_{j=1}^{m-1} j (w_{m-j}, z_{m-j}) (HN_\circ )(w_j, z_j)^\top. \end{align} $$
$$ \begin{align} n_{\circ , m} &= \nabla N_\circ \Big|_{P_s} \cdot (w_m, z_m) + \frac{1}{m}\sum_{j=1}^{m-1} j (w_{m-j}, z_{m-j}) (HN_\circ )(w_j, z_j)^\top. \end{align} $$
We recall
![]() $D_{W, 0}, D_{Z, 1} \neq 0$
from Lemmas A.10 and A.11, so they are lower bounded in I. Let
$D_{W, 0}, D_{Z, 1} \neq 0$
from Lemmas A.10 and A.11, so they are lower bounded in I. Let
![]() $\mathfrak C_i$
denote the Catalan numbers. Then for some constant M, we inductively assume the bounds
$\mathfrak C_i$
denote the Catalan numbers. Then for some constant M, we inductively assume the bounds
for
![]() $3\leq i\leq m$
. Since the constant C in (2.20) is allowed to depend on n, choosing C sufficiently large, (2.20) trivially holds for all
$3\leq i\leq m$
. Since the constant C in (2.20) is allowed to depend on n, choosing C sufficiently large, (2.20) trivially holds for all
![]() $i\leq 2n+2$
. Let us now assume
$i\leq 2n+2$
. Let us now assume
![]() $m\geq 2n+2$
. By (2.21), we have
$m\geq 2n+2$
. By (2.21), we have
 $$ \begin{align} \left|w_{m+1}\right| &\lesssim\frac{1}{m} \left(\left| n_{W, m}\right| + \sum_{j=2}^{m-3} (j+1)\left|d_{W, m-j} \right|\left|w_{j+1}\right| + \sum_{ \substack{ j \in \{0, 1, \\ m-2, m-1 \} }}^{m-1} (j+1)\left|d_{W, m-j} \right|\left|w_{j+1}\right| \right)\nonumber\\ &\lesssim \mathfrak C_m M^{m-2}+M^{m-3}\sum_{j=0}^{m-2} \mathfrak C_{m-j} \mathfrak C_{j+1} + \mathfrak C_m M^{m-2}\nonumber\\ &\lesssim M^{m-2}\mathfrak C_{m+2}. \end{align} $$
$$ \begin{align} \left|w_{m+1}\right| &\lesssim\frac{1}{m} \left(\left| n_{W, m}\right| + \sum_{j=2}^{m-3} (j+1)\left|d_{W, m-j} \right|\left|w_{j+1}\right| + \sum_{ \substack{ j \in \{0, 1, \\ m-2, m-1 \} }}^{m-1} (j+1)\left|d_{W, m-j} \right|\left|w_{j+1}\right| \right)\nonumber\\ &\lesssim \mathfrak C_m M^{m-2}+M^{m-3}\sum_{j=0}^{m-2} \mathfrak C_{m-j} \mathfrak C_{j+1} + \mathfrak C_m M^{m-2}\nonumber\\ &\lesssim M^{m-2}\mathfrak C_{m+2}. \end{align} $$
Now we bound
![]() $g_{m+1}$
using (2.25) and (2.26):
$g_{m+1}$
using (2.25) and (2.26):
 $$ \begin{align} \left|g_{m+1}\right|&\lesssim \left|w_{m+1}\right| + \frac{1}{m+1}\sum_{j=1}^{m} j (\left|w_{m-j}\right|+\left| z_{m-j}\right|) (\left|w_j\right|+ \left|z_j\right|)\nonumber\\ &\lesssim M^{m-2}\mathfrak C_{m+2}. \end{align} $$
$$ \begin{align} \left|g_{m+1}\right|&\lesssim \left|w_{m+1}\right| + \frac{1}{m+1}\sum_{j=1}^{m} j (\left|w_{m-j}\right|+\left| z_{m-j}\right|) (\left|w_j\right|+ \left|z_j\right|)\nonumber\\ &\lesssim M^{m-2}\mathfrak C_{m+2}. \end{align} $$
We bound
![]() $z_{m+1}$
using (2.25), (2.26), (2.27) and
$z_{m+1}$
using (2.25), (2.26), (2.27) and
![]() $k \leq n+1 \leq \frac {m}{2}$
:
$k \leq n+1 \leq \frac {m}{2}$
:
 $$ \begin{align} \left|z_{m+1}\right| & \lesssim\frac{1}{m} \left(\sum_{j=1}^{m-1} \left|d_{Z, m+1-j} (j+1)z_{j+1} \right| +\left|g_{m+1}\right| + \left| w_{m+1}\right| \right)\nonumber\\ &\lesssim M^{m-2}\sum_{j=1}^{m-1} \mathfrak C_{m+1-j}\mathfrak C_{j+1}+M^{m-2}\mathfrak C_{m+2}\nonumber\\ &\lesssim M^{m-2}\mathfrak C_{m+3}. \end{align} $$
$$ \begin{align} \left|z_{m+1}\right| & \lesssim\frac{1}{m} \left(\sum_{j=1}^{m-1} \left|d_{Z, m+1-j} (j+1)z_{j+1} \right| +\left|g_{m+1}\right| + \left| w_{m+1}\right| \right)\nonumber\\ &\lesssim M^{m-2}\sum_{j=1}^{m-1} \mathfrak C_{m+1-j}\mathfrak C_{j+1}+M^{m-2}\mathfrak C_{m+2}\nonumber\\ &\lesssim M^{m-2}\mathfrak C_{m+3}. \end{align} $$
Finally, from (2.23)–(2.26) and (2.28), we obtain
Then, (2.25) follows for
![]() $i=m+1$
by (2.26), (2.28), (2.29), the assumption that M is chosen to be sufficiently large and
$i=m+1$
by (2.26), (2.28), (2.29), the assumption that M is chosen to be sufficiently large and
![]() $\mathfrak C_{m+3} \leq 4\mathfrak C_{m+2} \leq 16 \mathfrak C_{m+1}$
.
$\mathfrak C_{m+3} \leq 4\mathfrak C_{m+2} \leq 16 \mathfrak C_{m+1}$
.
Choosing C sufficiently large, from (2.25), we obtain (2.20). In particular, the series has a radius of convergence of at least
![]() $1/C$
, independently of
$1/C$
, independently of
![]() $r\in I$
(although depending on I).
$r\in I$
(although depending on I).
Lastly, we need to prove the continuity of the series with respect to the parameter r. We introduce the dependence of
![]() $W_j, Z_j$
with r, denoting the coefficients by
$W_j, Z_j$
with r, denoting the coefficients by
![]() $W_j(r), Z_j(r)$
. Let
$W_j(r), Z_j(r)$
. Let
![]() $W^{(r)} (\xi ) = \sum _j \frac {W_j(r)}{j!} \xi ^j$
, and denote similarly by
$W^{(r)} (\xi ) = \sum _j \frac {W_j(r)}{j!} \xi ^j$
, and denote similarly by
![]() $Z^{(r)}$
the series formed by
$Z^{(r)}$
the series formed by
![]() $Z_j(r)$
. We show continuity with respect to r for
$Z_j(r)$
. We show continuity with respect to r for
![]() $W^{(r)}$
; an analogous proof applies for
$W^{(r)}$
; an analogous proof applies for
![]() $Z^{(r)}$
. Let
$Z^{(r)}$
. Let
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
![]() $\delta> 0$
. For
$\delta> 0$
. For
![]() $r, \bar r \in I$
with
$r, \bar r \in I$
with
![]() $|r-\bar r| < \delta $
, we can bound
$|r-\bar r| < \delta $
, we can bound
 $$ \begin{align*} |W^{(r)} (\xi ) - W^{(\bar r)}(\xi )| &\leq \sum_{j=0}^{N-1} |W_j(r) - W_j(\bar r ) | \frac{|\xi |^j }{j!} + \sum_{j=N}^\infty |W_j(r)| \frac{|\xi |^j}{j!} + \sum_{j=N}^\infty |W_j(\bar r)| \frac{|\xi |^j}{j!} \\ &\leq \sum_{j=0}^{N-1} |W_j(r) - W_j(\bar r ) | \frac{|\xi |^j }{j!} + 2C\sum_{j=N}^\infty C^j |\xi|^j . \end{align*} $$
$$ \begin{align*} |W^{(r)} (\xi ) - W^{(\bar r)}(\xi )| &\leq \sum_{j=0}^{N-1} |W_j(r) - W_j(\bar r ) | \frac{|\xi |^j }{j!} + \sum_{j=N}^\infty |W_j(r)| \frac{|\xi |^j}{j!} + \sum_{j=N}^\infty |W_j(\bar r)| \frac{|\xi |^j}{j!} \\ &\leq \sum_{j=0}^{N-1} |W_j(r) - W_j(\bar r ) | \frac{|\xi |^j }{j!} + 2C\sum_{j=N}^\infty C^j |\xi|^j . \end{align*} $$
As
![]() $\xi < 1/C$
, we can take N large enough so that the last sum is smaller than
$\xi < 1/C$
, we can take N large enough so that the last sum is smaller than
![]() $\varepsilon /2$
. As the coefficients
$\varepsilon /2$
. As the coefficients
![]() $W_j(r)$
are continuous, there also exist
$W_j(r)$
are continuous, there also exist
![]() $\delta _j $
such that
$\delta _j $
such that
![]() $|W_j(r) - W_j (\bar r)| < \varepsilon /(2N)$
as long as
$|W_j(r) - W_j (\bar r)| < \varepsilon /(2N)$
as long as
![]() $|r-\overline {r}| < \delta _j$
. Therefore, taking
$|r-\overline {r}| < \delta _j$
. Therefore, taking
![]() $|\delta |< \min _{j=0,\ldots N-1} \delta _i$
, we have that
$|\delta |< \min _{j=0,\ldots N-1} \delta _i$
, we have that
![]() $|W^{(r)} - W^{(r+\delta )}| < \varepsilon $
, and this shows continuity with respect to r.
$|W^{(r)} - W^{(r+\delta )}| < \varepsilon $
, and this shows continuity with respect to r.
As one can see from (2.19), the n-th coefficient of the Taylor series is of order
![]() $O(|k-n|^{-1})$
, as
$O(|k-n|^{-1})$
, as
![]() $k \to n$
(equivalently,
$k \to n$
(equivalently,
![]() $r \to r_n$
). All the previous coefficients of the Taylor series are not singular as
$r \to r_n$
). All the previous coefficients of the Taylor series are not singular as
![]() $k\to n$
. However, the higher-order coefficients will not be
$k\to n$
. However, the higher-order coefficients will not be
![]() $O(1)$
, since they depend on
$O(1)$
, since they depend on
![]() $Z_n$
via the Taylor series recursion. The following Corollary studies the order in
$Z_n$
via the Taylor series recursion. The following Corollary studies the order in
![]() $\frac {1}{|k-n|}$
of the higher-order Taylor coefficients
$\frac {1}{|k-n|}$
of the higher-order Taylor coefficients
Corollary 2.4. We have the following asymptotics for r in a neighborhood of
![]() $r_n$
, with
$r_n$
, with
![]() $n \in \mathbb {N}$
:
$n \in \mathbb {N}$
:
In particular, for
![]() $m\leq n$
, we have
$m\leq n$
, we have
![]() $ \left |W_m\right |=O(1)$
, and for
$ \left |W_m\right |=O(1)$
, and for
![]() $m<n$
, we have
$m<n$
, we have
![]() $ \left |Z_m\right |=O(1)$
. We also have that
$ \left |Z_m\right |=O(1)$
. We also have that
![]() $\left |Z_n\right | = O(1 + |k-n|^{-1})$
.
$\left |Z_n\right | = O(1 + |k-n|^{-1})$
.
Proof. From Proposition 2.2, we can iteratively calculate
![]() $W_m$
and
$W_m$
and
![]() $Z_m$
with equations (2.16), (2.17), (2.18) and (2.19). Each coefficient is a rational function of the previous coefficients. From Lemma A.10 and Lemma A.11, we have
$Z_m$
with equations (2.16), (2.17), (2.18) and (2.19). Each coefficient is a rational function of the previous coefficients. From Lemma A.10 and Lemma A.11, we have
![]() $D_{W, 0}$
and
$D_{W, 0}$
and
![]() $D_{Z, 1}$
remain bounded away from
$D_{Z, 1}$
remain bounded away from
![]() $0$
for r in a neighborhood of
$0$
for r in a neighborhood of
![]() $r_n$
. We trivially have that for
$r_n$
. We trivially have that for
![]() $m<n$
, the factor
$m<n$
, the factor
![]() $m-k$
in (2.19) also remains bounded away from
$m-k$
in (2.19) also remains bounded away from
![]() $0$
. Then the result holds trivially for
$0$
. Then the result holds trivially for
![]() $W_m$
in the case
$W_m$
in the case
![]() $m\leq n$
and for
$m\leq n$
and for
![]() $Z_m$
in the case
$Z_m$
in the case
![]() $m<n$
. The case
$m<n$
. The case
![]() $m=n$
for
$m=n$
for
![]() $Z_m$
similarly holds using in addition that
$Z_m$
similarly holds using in addition that
![]() $k(r)$
has nonzero derivative at
$k(r)$
has nonzero derivative at
![]() $r=r_m$
(Lemma 2.1).
$r=r_m$
(Lemma 2.1).
For
![]() $m> n$
, each coefficient is a rational function of the previous one, with denominators only involving
$m> n$
, each coefficient is a rational function of the previous one, with denominators only involving
![]() $D_{Z, 1}$
,
$D_{Z, 1}$
,
![]() $D_{W, 0}$
and
$D_{W, 0}$
and
![]() $m-k$
, all of them bounded away from zero and infinity in a neighborhood of
$m-k$
, all of them bounded away from zero and infinity in a neighborhood of
![]() $r_m$
(as
$r_m$
(as
![]() $m> n$
). We will prove (2.30) via induction in m, supposing it holds for all coefficients of order
$m> n$
). We will prove (2.30) via induction in m, supposing it holds for all coefficients of order
![]() $<m$
.
$<m$
.
We start proving the induction step for
![]() $W_m$
. As a consequence of the induction hypothesis, we know that
$W_m$
. As a consequence of the induction hypothesis, we know that
![]() $D_{\circ , i}$
and
$D_{\circ , i}$
and
![]() $N_{\circ , i}$
are of the order
$N_{\circ , i}$
are of the order
![]() $O \left ( 1 + |k-n|^{-\left \lfloor \frac {i-1}{n-1} \right \rfloor } \right )$
for every
$O \left ( 1 + |k-n|^{-\left \lfloor \frac {i-1}{n-1} \right \rfloor } \right )$
for every
![]() $i < m$
. From expression (2.18) and the induction hypothesis, we have
$i < m$
. From expression (2.18) and the induction hypothesis, we have
 $$ \begin{align} \left|W_m\right|\lesssim 1+|k-n|^{-\left\lfloor \frac{m-2}{n-1} \right\rfloor} + \sum_{j=0}^{m-2} (1+ |k-n|^{-\left\lfloor \frac{m-j-2}{n-1} \right\rfloor})(1+ |k-n|^{-\left\lfloor \frac{j-1}{n-1} \right\rfloor})\lesssim 1+ |k-n|^{-\left\lfloor \frac{m-2}{n-1} \right\rfloor}, \end{align} $$
$$ \begin{align} \left|W_m\right|\lesssim 1+|k-n|^{-\left\lfloor \frac{m-2}{n-1} \right\rfloor} + \sum_{j=0}^{m-2} (1+ |k-n|^{-\left\lfloor \frac{m-j-2}{n-1} \right\rfloor})(1+ |k-n|^{-\left\lfloor \frac{j-1}{n-1} \right\rfloor})\lesssim 1+ |k-n|^{-\left\lfloor \frac{m-2}{n-1} \right\rfloor}, \end{align} $$
where we have used the floor concavity property
![]() $\left \lfloor x \right \rfloor + \left \lfloor y \right \rfloor \geq \left \lfloor x+y \right \rfloor $
for all
$\left \lfloor x \right \rfloor + \left \lfloor y \right \rfloor \geq \left \lfloor x+y \right \rfloor $
for all
![]() $ x, y \in \mathbb {R}^+$
. Thus, we obtain the desired estimate on
$ x, y \in \mathbb {R}^+$
. Thus, we obtain the desired estimate on
![]() $\left |W_m\right |$
.
$\left |W_m\right |$
.
Now consider
![]() $Z_m$
. For the first line of (2.19), we have
$Z_m$
. For the first line of (2.19), we have
 $$ \begin{align} \left|\sum_{j=1}^{m-2} \binom{m}{j} D_{Z, m-j} Z_{j+1}\right| &\lesssim \sum_{j=1}^{m-2} (1+ |k-n|^{-\left\lfloor \frac{m-j-1}{n-1} \right\rfloor} )(1+ |k-n|^{-\left\lfloor \frac{j}{n-1} \right\rfloor} )\lesssim 1+ |k-n|^{-\left\lfloor \frac{m-1}{n-1} \right\rfloor}. \end{align} $$
$$ \begin{align} \left|\sum_{j=1}^{m-2} \binom{m}{j} D_{Z, m-j} Z_{j+1}\right| &\lesssim \sum_{j=1}^{m-2} (1+ |k-n|^{-\left\lfloor \frac{m-j-1}{n-1} \right\rfloor} )(1+ |k-n|^{-\left\lfloor \frac{j}{n-1} \right\rfloor} )\lesssim 1+ |k-n|^{-\left\lfloor \frac{m-1}{n-1} \right\rfloor}. \end{align} $$
Now consider the second line of (2.19). Since the expansion of
![]() $N_{Z, m} - \partial _Z N_Z (P_s) Z_m$
does not involve
$N_{Z, m} - \partial _Z N_Z (P_s) Z_m$
does not involve
![]() $Z_m$
, we have from the induction hypothesis and (2.31) that
$Z_m$
, we have from the induction hypothesis and (2.31) that
 $$ \begin{align}& \left|\left( N_{Z, m} - (\partial_Z N_Z (P_s) ) Z_m\right) - Z_1 W_m \partial_W D_Z (P_s) \right|\nonumber\\&\quad \lesssim \sum_{i=0}^{m-1} (\left|W_i\right|+\left|Z_i\right|)\left|W_{m-i}\right|+\sum_{i=1}^{m-1}\left|Z_i\right|\left|Z_{m-i}\right|+\left|Z_1\right|\left|W_m\right| \nonumber\\&\quad \lesssim \sum_{i=0}^{i-1} (1+ |k-n|^{-\left\lfloor \frac{i-1}{n-1} \right\rfloor} )(1+ |k-n|^{-\left\lfloor \frac{m-i-2}{n-1} \right\rfloor} )+\sum_{i=1}^{m-1}(1+|k-n|^{-\left\lfloor \frac{i-1}{n-1} \right\rfloor})(1+ |k-n|^{-\left\lfloor \frac{m-i-1}{n-1} \right\rfloor})\nonumber\\& \qquad+1 +|k-n|^{-\left\lfloor \frac{m-2}{n-1} \right\rfloor} \nonumber\\&\quad\lesssim 1+|k-n|^{-\left\lfloor \frac{m-2}{n-1} \right\rfloor} . \end{align} $$
$$ \begin{align}& \left|\left( N_{Z, m} - (\partial_Z N_Z (P_s) ) Z_m\right) - Z_1 W_m \partial_W D_Z (P_s) \right|\nonumber\\&\quad \lesssim \sum_{i=0}^{m-1} (\left|W_i\right|+\left|Z_i\right|)\left|W_{m-i}\right|+\sum_{i=1}^{m-1}\left|Z_i\right|\left|Z_{m-i}\right|+\left|Z_1\right|\left|W_m\right| \nonumber\\&\quad \lesssim \sum_{i=0}^{i-1} (1+ |k-n|^{-\left\lfloor \frac{i-1}{n-1} \right\rfloor} )(1+ |k-n|^{-\left\lfloor \frac{m-i-2}{n-1} \right\rfloor} )+\sum_{i=1}^{m-1}(1+|k-n|^{-\left\lfloor \frac{i-1}{n-1} \right\rfloor})(1+ |k-n|^{-\left\lfloor \frac{m-i-1}{n-1} \right\rfloor})\nonumber\\& \qquad+1 +|k-n|^{-\left\lfloor \frac{m-2}{n-1} \right\rfloor} \nonumber\\&\quad\lesssim 1+|k-n|^{-\left\lfloor \frac{m-2}{n-1} \right\rfloor} . \end{align} $$
Combining (2.32) and (2.33), we obtain the desired estimate on
![]() $\left |Z_m\right |$
and hence conclude the proof by induction.
$\left |Z_m\right |$
and hence conclude the proof by induction.
2.3 Taylor expansion around
 $P_0$
$P_0$
We now aim to construct smooth solutions emanating from
![]() $P_0$
and reaching
$P_0$
and reaching
![]() $P_s$
at
$P_s$
at
![]() $\xi =0$
. Let us recall that
$\xi =0$
. Let us recall that
![]() $P_0$
is a point in the compactification of the phase portrait that corresponds to
$P_0$
is a point in the compactification of the phase portrait that corresponds to
![]() $\xi = 0$
, and where
$\xi = 0$
, and where
![]() $S = +\infty $
and U has finite value (in
$S = +\infty $
and U has finite value (in
![]() $W, Z$
coordinates,
$W, Z$
coordinates,
![]() $P_0$
is at infinity along a line parallel to
$P_0$
is at infinity along a line parallel to
![]() $W-Z = 0$
). Due to the singular nature of the coordinate change
$W-Z = 0$
). Due to the singular nature of the coordinate change
![]() $R\mapsto \xi $
near
$R\mapsto \xi $
near
![]() $R=0$
, and the singular nature of
$R=0$
, and the singular nature of
![]() $P_0$
, it is useful to instead work in terms of the self-similar coordinate
$P_0$
, it is useful to instead work in terms of the self-similar coordinate
![]() $\zeta =\exp (\xi )$
. Moreover, we will extend the values of
$\zeta =\exp (\xi )$
. Moreover, we will extend the values of
![]() $\zeta $
to negative
$\zeta $
to negative
![]() $\zeta $
as well considering a function
$\zeta $
as well considering a function
![]() $\mathcal {W} (\zeta )$
on the whole real line that is associated with W for
$\mathcal {W} (\zeta )$
on the whole real line that is associated with W for
![]() $\zeta> 0$
and with Z for negative
$\zeta> 0$
and with Z for negative
![]() $\zeta $
(see a precise definition below). In particular, we will search for a solution
$\zeta $
(see a precise definition below). In particular, we will search for a solution
![]() $\mathcal {W}$
to (1.13) for
$\mathcal {W}$
to (1.13) for
![]() $\zeta \in [-1,1]$
satisfying
$\zeta \in [-1,1]$
satisfying
![]() $(\mathcal {W}(1),-\mathcal {W}(-1))=(W_0,Z_0)$
. Such a solution would correspond to a profile
$(\mathcal {W}(1),-\mathcal {W}(-1))=(W_0,Z_0)$
. Such a solution would correspond to a profile
solving equation (1.10). Thus, one can understand Z as the natural continuation along
![]() $P_0$
(
$P_0$
(
![]() $\zeta = 0$
) of the W solution. Moreover, we will see that the singular nature of the point
$\zeta = 0$
) of the W solution. Moreover, we will see that the singular nature of the point
![]() $P_0$
is captured in the factors
$P_0$
is captured in the factors
![]() $\exp (-\xi )$
of (2.34), so that the function
$\exp (-\xi )$
of (2.34), so that the function
![]() $\mathcal {W} (\zeta )$
is smooth at
$\mathcal {W} (\zeta )$
is smooth at
![]() $\zeta = 0$
.
$\zeta = 0$
.
Proposition 2.5. For any
![]() $A> 0$
, there exists a solution
$A> 0$
, there exists a solution
![]() $\mathcal {W}$
to (1.13) in a neighborhood of
$\mathcal {W}$
to (1.13) in a neighborhood of
![]() $\zeta =0$
which can be written in terms of a convergent power series
$\zeta =0$
which can be written in terms of a convergent power series
 $$ \begin{align} \mathcal{W}(\zeta)=\sum_{i=0}^{\infty} w_i \zeta^i , \end{align} $$
$$ \begin{align} \mathcal{W}(\zeta)=\sum_{i=0}^{\infty} w_i \zeta^i , \end{align} $$
such that
![]() $w_0=A$
. Moreover, letting
$w_0=A$
. Moreover, letting
![]() $\gamma = 7/5$
and r sufficiently close to
$\gamma = 7/5$
and r sufficiently close to
![]() $r^\ast (\gamma )$
, or
$r^\ast (\gamma )$
, or
![]() $\gamma> 1$
with
$\gamma> 1$
with
![]() $r \in (r_3, r_4)$
, there exists a value of A such that the solution can be continued to
$r \in (r_3, r_4)$
, there exists a value of A such that the solution can be continued to
![]() $\zeta \in [-1,1]$
and
$\zeta \in [-1,1]$
and
![]() $(\mathcal {W}(1),-\mathcal {W}(-1))=(W_0,Z_0)$
. The solution corresponding to that value of A is continuous with respect to r.
$(\mathcal {W}(1),-\mathcal {W}(-1))=(W_0,Z_0)$
. The solution corresponding to that value of A is continuous with respect to r.
Proof. Let us start by writing
 $$ \begin{align*} \mathcal{V}=\zeta+\frac12(\mathcal{W}(\zeta)-\mathcal{W}(-\zeta)+\alpha(\mathcal{W}(\zeta)+\mathcal{W}(-\zeta))) \\ \mathcal{G}=-\left((r-1)\mathcal{W}+\frac{\alpha}{2\zeta}(\mathcal{W}^2(\zeta)-\mathcal{W}^2(-\zeta))\right), \end{align*} $$
$$ \begin{align*} \mathcal{V}=\zeta+\frac12(\mathcal{W}(\zeta)-\mathcal{W}(-\zeta)+\alpha(\mathcal{W}(\zeta)+\mathcal{W}(-\zeta))) \\ \mathcal{G}=-\left((r-1)\mathcal{W}+\frac{\alpha}{2\zeta}(\mathcal{W}^2(\zeta)-\mathcal{W}^2(-\zeta))\right), \end{align*} $$
so that (1.13) can be rewritten as
The coefficients
![]() $w_i$
will be determined by substituting the series (2.35) into the equation (2.36) in order to obtain a recursion formula. Writing
$w_i$
will be determined by substituting the series (2.35) into the equation (2.36) in order to obtain a recursion formula. Writing
![]() $\mathcal {V}(\zeta )=\sum _{i=0}^{\infty } v_i \zeta ^i$
and
$\mathcal {V}(\zeta )=\sum _{i=0}^{\infty } v_i \zeta ^i$
and
![]() $\mathcal {G}(\zeta )=\sum _{i=0}^{\infty } g_i \zeta ^i$
yields the expression
$\mathcal {G}(\zeta )=\sum _{i=0}^{\infty } g_i \zeta ^i$
yields the expression
 $$ \begin{align} (n+1)v_0 w_{n+1}=g_n-\sum_{i=0}^{n-1}(i+1)v_{n-i}w_{i+1}, \end{align} $$
$$ \begin{align} (n+1)v_0 w_{n+1}=g_n-\sum_{i=0}^{n-1}(i+1)v_{n-i}w_{i+1}, \end{align} $$
where

Rewriting (2.37) and using
![]() $v_0 = \alpha w_0$
, we obtain
$v_0 = \alpha w_0$
, we obtain

which gives an inductive definition of
![]() $w_i$
given
$w_i$
given
![]() $w_0=A$
. We now prove that the corresponding series is analytic in a small neighborhood of the origin. We inductively assume that
$w_0=A$
. We now prove that the corresponding series is analytic in a small neighborhood of the origin. We inductively assume that
where we recall
![]() $\mathfrak C_i$
denotes the Catalan numbers. We trivially get for
$\mathfrak C_i$
denotes the Catalan numbers. We trivially get for
![]() $i=0,1$
that
$i=0,1$
that
![]() $\left |w_i\right |+\left |\bar g_i\right |+\left |v_i\right |\lesssim 1$
. Then from (2.39), we have
$\left |w_i\right |+\left |\bar g_i\right |+\left |v_i\right |\lesssim 1$
. Then from (2.39), we have

Here, we used that
![]() $\mathfrak C_{n+1}=\sum _{i=0}^n\mathfrak C_i\mathfrak C_{n-i}$
and
$\mathfrak C_{n+1}=\sum _{i=0}^n\mathfrak C_i\mathfrak C_{n-i}$
and
![]() $ \mathfrak C_{i+1}\lesssim \mathfrak C_i\lesssim \mathfrak C_{i+1}$
. We can then use this bound together with the inductive hypothesis to bound
$ \mathfrak C_{i+1}\lesssim \mathfrak C_i\lesssim \mathfrak C_{i+1}$
. We can then use this bound together with the inductive hypothesis to bound
![]() $\bar g_{n+1}$
and
$\bar g_{n+1}$
and
![]() $v_{n+1}$
. For
$v_{n+1}$
. For
![]() $\bar g_{n+1}$
, we have
$\bar g_{n+1}$
, we have
 $$ \begin{align*} \left|\bar g_{n+1}\right|&\lesssim \left|w_{n+1}\right|+\left(\sum_{i=2}^{n}\left|w_iw_{n-i+2}\right|+ |w_1||w_{n+1}|\right)\lesssim M^{n-1}\mathfrak C_{n+1}.\nonumber \end{align*} $$
$$ \begin{align*} \left|\bar g_{n+1}\right|&\lesssim \left|w_{n+1}\right|+\left(\sum_{i=2}^{n}\left|w_iw_{n-i+2}\right|+ |w_1||w_{n+1}|\right)\lesssim M^{n-1}\mathfrak C_{n+1}.\nonumber \end{align*} $$
Finally, (2.40) implies
![]() $\left |v_{n+1}\right |\lesssim M^{n-1} \mathfrak C_{n+1}$
, closing the induction. Since
$\left |v_{n+1}\right |\lesssim M^{n-1} \mathfrak C_{n+1}$
, closing the induction. Since
![]() $\mathfrak C_i\leq 4^i$
, then we obtain that the power series that the series
$\mathfrak C_i\leq 4^i$
, then we obtain that the power series that the series
![]() $\mathcal {W}(\zeta )=\sum _{i=0}^{\infty } w_i \zeta ^i$
is analytic in a small neighborhood
$\mathcal {W}(\zeta )=\sum _{i=0}^{\infty } w_i \zeta ^i$
is analytic in a small neighborhood
![]() $(-\delta ,\delta )$
of the origin.
$(-\delta ,\delta )$
of the origin.
Under the change of variables
![]() $W(\log \zeta ) = \frac {1}{\zeta } \mathcal {W}(\zeta )$
(and analogously with Z), we have that (2.36) reads like ODE (1.10). Thus, we set
$W(\log \zeta ) = \frac {1}{\zeta } \mathcal {W}(\zeta )$
(and analogously with Z), we have that (2.36) reads like ODE (1.10). Thus, we set
![]() $(W(\log \frac \delta 2),Z(\log \frac \delta 2))= \frac 2 \delta (\mathcal {W}(\frac \delta 2),-\mathcal {W}(-\frac \delta 2))$
and solve (1.10). As each coefficient
$(W(\log \frac \delta 2),Z(\log \frac \delta 2))= \frac 2 \delta (\mathcal {W}(\frac \delta 2),-\mathcal {W}(-\frac \delta 2))$
and solve (1.10). As each coefficient
![]() $w_i$
is continuous with r, we have that
$w_i$
is continuous with r, we have that
![]() $\mathcal {W} $
, for a fixed
$\mathcal {W} $
, for a fixed
![]() $\zeta \in (-\delta /2, \delta _2)$
, is continuous with respect to r. This is done in exactly the same way as we did for
$\zeta \in (-\delta /2, \delta _2)$
, is continuous with respect to r. This is done in exactly the same way as we did for
![]() $(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
in Proposition 2.3. Thus, the continuations W and Z are also continuous with respect to r because of the stability of the ODE with respect to r.
$(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
in Proposition 2.3. Thus, the continuations W and Z are also continuous with respect to r because of the stability of the ODE with respect to r.
Finally, we need to prove that the solution
![]() $(W, Z)$
reaches
$(W, Z)$
reaches
![]() $P_s$
. If we consider the field
$P_s$
. If we consider the field
![]() $(N_W D_Z, N_Z D_W)$
(which reverses time because
$(N_W D_Z, N_Z D_W)$
(which reverses time because
![]() $D_Z < 0$
), our solution corresponds to a trajectory arriving at
$D_Z < 0$
), our solution corresponds to a trajectory arriving at
![]() $P_0$
. Let H be sufficiently large,
$P_0$
. Let H be sufficiently large,
![]() $P^{(H)}$
be the point
$P^{(H)}$
be the point
![]() $P_s + (H, -H)$
and
$P_s + (H, -H)$
and
![]() $\check P^{(H)}$
be the point in the same vertical as
$\check P^{(H)}$
be the point in the same vertical as
![]() $P^{(H)}$
and lying in
$P^{(H)}$
and lying in
![]() $D_Z = 0$
. We call
$D_Z = 0$
. We call
![]() $\mathcal {T}^{(H)}$
the triangle formed by
$\mathcal {T}^{(H)}$
the triangle formed by
![]() $P_s$
,
$P_s$
,
![]() $P^{(H)}$
and
$P^{(H)}$
and
![]() $\check P^{(H)}$
, which is drawn in Figure 3. We have that
$\check P^{(H)}$
, which is drawn in Figure 3. We have that
Let us argue that for
![]() $\zeta>0$
sufficiently small and H sufficiently large (depending on
$\zeta>0$
sufficiently small and H sufficiently large (depending on
![]() $\zeta $
), we will have that
$\zeta $
), we will have that
![]() $(W (\log \zeta ), Z (\log \zeta ))$
lies in
$(W (\log \zeta ), Z (\log \zeta ))$
lies in
![]() $\mathcal {T}^{(H)}$
. We just need to show that
$\mathcal {T}^{(H)}$
. We just need to show that
![]() $\frac {-4(r-1)}{3(\gamma - 1)}$
is bigger than
$\frac {-4(r-1)}{3(\gamma - 1)}$
is bigger than
![]() $W_0 + Z_0$
(which is the value of
$W_0 + Z_0$
(which is the value of
![]() $W+Z$
along the line
$W+Z$
along the line
![]() $\overline {P_s P^{(H)}}$
). We have that
$\overline {P_s P^{(H)}}$
). We have that
so we just need to show the right parenthesis is positive. Now,
where in the last inequality, we used
![]() $r < 2 - \frac {1}{\gamma }$
from Lemma A.6. Therefore, it suffices to show
$r < 2 - \frac {1}{\gamma }$
from Lemma A.6. Therefore, it suffices to show
![]() $-7 + 9 \gamma + r - 3 \gamma r> 0$
. Using again that
$-7 + 9 \gamma + r - 3 \gamma r> 0$
. Using again that
![]() $r < 2 - \frac {1}{\gamma }$
, we have that
$r < 2 - \frac {1}{\gamma }$
, we have that
We conclude that
![]() $(W (\log \zeta ), Z (\log \zeta ))$
lies in
$(W (\log \zeta ), Z (\log \zeta ))$
lies in
![]() $\mathcal {T}^{(H)}$
.
$\mathcal {T}^{(H)}$
.

Figure 3 Field
![]() $(N_W D_Z, N_Z D_W)$
in
$(N_W D_Z, N_Z D_W)$
in
![]() $(W, Z)$
coordinates for
$(W, Z)$
coordinates for
![]() $\gamma = \frac 53$
and
$\gamma = \frac 53$
and
![]() $r = \frac {11}{10}$
. The shaded area corresponds to the triangle
$r = \frac {11}{10}$
. The shaded area corresponds to the triangle
![]() $\mathcal {T}^{(1)}$
.
$\mathcal {T}^{(1)}$
.
We now show that the solution cannot come from the boundary of
![]() $\mathcal {T}^{(H)}$
except from point
$\mathcal {T}^{(H)}$
except from point
![]() $P_s$
. It suffices checking that the normal component of the field
$P_s$
. It suffices checking that the normal component of the field
![]() $(N_Z D_W, N_W D_Z)$
at each side of
$(N_Z D_W, N_W D_Z)$
at each side of
![]() $\mathcal {T}^{(H)}$
points outwards (except at the extremum
$\mathcal {T}^{(H)}$
points outwards (except at the extremum
![]() $P_s$
). For the vertical segment
$P_s$
). For the vertical segment
![]() $\overline {P_s P^{(H)} }$
, this is guaranteed by Lemma A.21, and for the side
$\overline {P_s P^{(H)} }$
, this is guaranteed by Lemma A.21, and for the side
![]() $\overline {P_s \check P^{(H)}}$
, this is guaranteed by Lemma A.22. For the side
$\overline {P_s \check P^{(H)}}$
, this is guaranteed by Lemma A.22. For the side
![]() $\overline {P^{(H)} \check P^{(H)} }$
, this follows from the fact that
$\overline {P^{(H)} \check P^{(H)} }$
, this follows from the fact that
![]() $N_W D_Z> 0$
(Lemma A.16). Using Proposition 1.6, the fact that
$N_W D_Z> 0$
(Lemma A.16). Using Proposition 1.6, the fact that
![]() $\mathcal {T}^{(H)}$
is bounded and that there are no equilibrium points in
$\mathcal {T}^{(H)}$
is bounded and that there are no equilibrium points in
![]() $\mathcal {T}^{(H)}$
the trajectory has to come from
$\mathcal {T}^{(H)}$
the trajectory has to come from
![]() $P_s$
. The fact that there are no equilibrium points on
$P_s$
. The fact that there are no equilibrium points on
![]() $\mathcal {T}^{(H)}$
follows from
$\mathcal {T}^{(H)}$
follows from
![]() $\mathcal {T}^{(H)} \subset \Omega $
and Lemma A.17 except for
$\mathcal {T}^{(H)} \subset \Omega $
and Lemma A.17 except for ![]() in the case
in the case
![]() $\gamma = 7/5$
, r sufficiently close to
$\gamma = 7/5$
, r sufficiently close to
![]() $r^\ast $
and the equilibrium point
$r^\ast $
and the equilibrium point ![]() . In that case, note that as
. In that case, note that as
![]() $\gamma = 7/5$
,
$\gamma = 7/5$
,
![]() $P_s$
is the point with highest Z of
$P_s$
is the point with highest Z of
![]() $\mathcal {T}^{(H)}$
, and by Lemma A.17,
$\mathcal {T}^{(H)}$
, and by Lemma A.17, ![]() has larger Z, so we deduce
has larger Z, so we deduce ![]() .
.
From now on, we will always choose A such that the solution reaches
![]() $P_s$
at
$P_s$
at
![]() $\xi = 0$
(that is,
$\xi = 0$
(that is,
![]() $\zeta = 1$
). We will let
$\zeta = 1$
). We will let
![]() $(W_r^o, Z_r^o)$
to be that solution in
$(W_r^o, Z_r^o)$
to be that solution in
![]() $(W, Z)$
variables. Therefore, in
$(W, Z)$
variables. Therefore, in
![]() $(W, Z)$
variables, we get the Taylor expansion
$(W, Z)$
variables, we get the Taylor expansion
 $$ \begin{align} W_r^o (\xi ) = Ae^{-\xi} + \sum_{j=0}^{\infty} W^o_{ r,j} \frac{e^{j \xi }}{j!}, \qquad Z_r^o (\xi) = - Ae^{-\xi} + \sum_{j=0}^{\infty} Z^o_{r,j} \frac{e^{j \xi} }{j!}\, \end{align} $$
$$ \begin{align} W_r^o (\xi ) = Ae^{-\xi} + \sum_{j=0}^{\infty} W^o_{ r,j} \frac{e^{j \xi }}{j!}, \qquad Z_r^o (\xi) = - Ae^{-\xi} + \sum_{j=0}^{\infty} Z^o_{r,j} \frac{e^{j \xi} }{j!}\, \end{align} $$
for some
![]() $W^o_{r,j} = (-1)^{j} Z^o_{r,j}$
. Moreover, the series (without the
$W^o_{r,j} = (-1)^{j} Z^o_{r,j}$
. Moreover, the series (without the
![]() $e^{-\xi }$
term) converges uniformly for
$e^{-\xi }$
term) converges uniformly for
![]() $\xi < M < 0$
for some M sufficiently negative.
$\xi < M < 0$
for some M sufficiently negative.
Remark 2.6. Note from the proof that the solution
![]() $(W_r^o, Z_r^o)$
will stay in the region
$(W_r^o, Z_r^o)$
will stay in the region
![]() $\Omega $
for
$\Omega $
for
![]() $\xi < 0$
. That is because the curve
$\xi < 0$
. That is because the curve
![]() $(W_r^o(\xi ), Z_r^o (\xi ))$
for
$(W_r^o(\xi ), Z_r^o (\xi ))$
for
![]() $\xi \in [-M', 0]$
will stay in some
$\xi \in [-M', 0]$
will stay in some
![]() $\mathcal {T}^{(M)}$
for sufficiently large M (as seen in the proof), and therefore, as
$\mathcal {T}^{(M)}$
for sufficiently large M (as seen in the proof), and therefore, as
![]() $\mathcal {T}^{(M)} \subset \Omega $
, we get that
$\mathcal {T}^{(M)} \subset \Omega $
, we get that
![]() $(W_r^o, Z_r^o)$
stays in
$(W_r^o, Z_r^o)$
stays in
![]() $\Omega $
for all
$\Omega $
for all
![]() $\xi < 0$
.
$\xi < 0$
.
Note also that
![]() $W_r^o (\xi )$
is decreasing for all
$W_r^o (\xi )$
is decreasing for all
![]() $\xi \in (-\infty , 0]$
. This follows from the fact that
$\xi \in (-\infty , 0]$
. This follows from the fact that
![]() $D_W> 0$
in
$D_W> 0$
in
![]() $\Omega $
and
$\Omega $
and
![]() $N_W < 0$
in
$N_W < 0$
in
![]() $\mathcal {T}^{(M)}$
for every M from Lemma A.16.
$\mathcal {T}^{(M)}$
for every M from Lemma A.16.
3 Left of
 $P_s$
$P_s$
This section is dedicated to showing properties of the solution left of
![]() $P_s$
in the phase portrait, which in the self-similar radial variable
$P_s$
in the phase portrait, which in the self-similar radial variable
![]() $\xi $
corresponds to the region
$\xi $
corresponds to the region
![]() $\xi>0$
, or equivalently, the region outside the backwards acoustic cone of the singularity. In particular, the main goal of this section is to prove the following proposition.
$\xi>0$
, or equivalently, the region outside the backwards acoustic cone of the singularity. In particular, the main goal of this section is to prove the following proposition.
Proposition 3.1. Suppose either
![]() $n=3$
with
$n=3$
with
![]() $\gamma \in (1, +\infty )$
or that
$\gamma \in (1, +\infty )$
or that
![]() $n\in \mathbb {N}$
is odd and sufficiently large with
$n\in \mathbb {N}$
is odd and sufficiently large with
![]() $\gamma = 7/5$
. Let
$\gamma = 7/5$
. Let
![]() $r\in (r_n, r_{n+1})$
. The smooth solution
$r\in (r_n, r_{n+1})$
. The smooth solution
![]() $W^{(r)} (\xi ), Z^{(r)} (\xi )$
defined in Proposition 2.3 can be continued up to
$W^{(r)} (\xi ), Z^{(r)} (\xi )$
defined in Proposition 2.3 can be continued up to
![]() $\xi = +\infty $
, and it satisfies
$\xi = +\infty $
, and it satisfies
![]() $\lim _{\xi \to +\infty } (W^{(r)} (\xi ), Z^{(r)} (\xi )) = (0,0) = P_\infty $
. Moreover, the solution stays in the region where
$\lim _{\xi \to +\infty } (W^{(r)} (\xi ), Z^{(r)} (\xi )) = (0,0) = P_\infty $
. Moreover, the solution stays in the region where
![]() $D_W> 0, D_Z > 0$
for all
$D_W> 0, D_Z > 0$
for all
![]() $\xi> 0$
.
$\xi> 0$
.
We will prove Proposition 3.1 using a double barrier argument. We will consider a barrier for the near-left region (
![]() $b^{\mathrm {nl}}(s)$
) and another one for the far-left region (
$b^{\mathrm {nl}}(s)$
) and another one for the far-left region (
![]() $b^{\mathrm {fl}}(t)$
). The field will point upwards along the barrier
$b^{\mathrm {fl}}(t)$
). The field will point upwards along the barrier
![]() $b^{\mathrm {fl}}(t)$
. The smooth solution starts below it, and so the barrier will be insufficient to bound the behavior of the smooth solution. The barrier
$b^{\mathrm {fl}}(t)$
. The smooth solution starts below it, and so the barrier will be insufficient to bound the behavior of the smooth solution. The barrier
![]() $b^{\mathrm {nl}}(s)$
will have the field pointing upwards, start above the smooth solution and will be valid over an interval sufficiently long to intersect
$b^{\mathrm {nl}}(s)$
will have the field pointing upwards, start above the smooth solution and will be valid over an interval sufficiently long to intersect
![]() $b^{\mathrm {fl}}(t)$
. Then, concatenating
$b^{\mathrm {fl}}(t)$
. Then, concatenating
![]() $b^{\mathrm {nl}}(s)$
(up to its intersection) with
$b^{\mathrm {nl}}(s)$
(up to its intersection) with
![]() $b^{\mathrm { fl}}(t)$
, one obtains a barrier bounding the trajectory of the smooth solution.
$b^{\mathrm { fl}}(t)$
, one obtains a barrier bounding the trajectory of the smooth solution.
Let us define the far-left barrier as
![]() $b^{\mathrm {fl}}(t) = (b^{\mathrm {fl}}_W (t), b^{\mathrm {fl}}_Z (t))$
, where
$b^{\mathrm {fl}}(t) = (b^{\mathrm {fl}}_W (t), b^{\mathrm {fl}}_Z (t))$
, where
where
![]() $B_1$
,
$B_1$
,
![]() $B_2$
and
$B_2$
and
![]() $B_3$
will be chosen to enforce that
$B_3$
will be chosen to enforce that ![]() and a first-order cancellation at this point. The point
and a first-order cancellation at this point. The point ![]() is defined as the only solution to
is defined as the only solution to
![]() $N_W(W, Z) = N_Z(W, Z) = 0$
in the region
$N_W(W, Z) = N_Z(W, Z) = 0$
in the region
![]() $\{ W> Z \}$
(there are two solutions in the symmetry axis
$\{ W> Z \}$
(there are two solutions in the symmetry axis
![]() $W=Z$
and another two solutions outside the axis, one in each halfplane).
$W=Z$
and another two solutions outside the axis, one in each halfplane). ![]() is given explicitly by
is given explicitly by

Moreover, if we do a first-order expansion around ![]() , we observe that one eigenvector of the matrix
, we observe that one eigenvector of the matrix
![]() $((\nabla N_W)/D_W, (\nabla N_Z )/D_Z)$
is given by
$((\nabla N_W)/D_W, (\nabla N_Z )/D_Z)$
is given by
![]() $(X_1, Y_1)$
with
$(X_1, Y_1)$
with
 $$ \begin{align*} \begin{aligned} \Theta &= -\sqrt{2 \left(53-3 \gamma \left(45 \gamma^3-110 \gamma+88\right)\right) r+\left(27 \gamma^2-30 \gamma+7\right)^2+(3 \gamma (\gamma (3 \gamma (\gamma+20)-94)+28)+25) r^2 } \\ &\qquad+3 \sqrt{3} \gamma^2 (r-5)+2 \sqrt{3} \gamma (r+7)-\sqrt{3} (r+3), \\ X_1 &= -2 \left(3 \gamma+4 \sqrt{3}-9\right) \left(3 \gamma^2 \left(r^2-3\right)-6 \gamma (r-2) r+6 \gamma-r (r+4)-1\right),\\ Y_1 &= \Theta \left( 3 \left(\sqrt{3}-1\right) \gamma r-\left(\sqrt{3}-3\right) (3 \gamma-1)-\left(3+\sqrt{3}\right) r \right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \Theta &= -\sqrt{2 \left(53-3 \gamma \left(45 \gamma^3-110 \gamma+88\right)\right) r+\left(27 \gamma^2-30 \gamma+7\right)^2+(3 \gamma (\gamma (3 \gamma (\gamma+20)-94)+28)+25) r^2 } \\ &\qquad+3 \sqrt{3} \gamma^2 (r-5)+2 \sqrt{3} \gamma (r+7)-\sqrt{3} (r+3), \\ X_1 &= -2 \left(3 \gamma+4 \sqrt{3}-9\right) \left(3 \gamma^2 \left(r^2-3\right)-6 \gamma (r-2) r+6 \gamma-r (r+4)-1\right),\\ Y_1 &= \Theta \left( 3 \left(\sqrt{3}-1\right) \gamma r-\left(\sqrt{3}-3\right) (3 \gamma-1)-\left(3+\sqrt{3}\right) r \right). \end{aligned} \end{align*} $$
In order to achieve the desired cancellations, we then choose
 $$ \begin{align} \begin{aligned} B_1 &= 2\frac{ (Y_0 - Z_0) X_1 - (X_0 - W_0 )Y_1 }{ X_1 Z_1 - W_1 Y_1 }, \\ B_2 &= 2\left( X_0 - W_0 - B_1 W_1 \right) , \\ B_3 &= 2 \left( Y_0 - Z_0 - B_1 Z_1 \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} B_1 &= 2\frac{ (Y_0 - Z_0) X_1 - (X_0 - W_0 )Y_1 }{ X_1 Z_1 - W_1 Y_1 }, \\ B_2 &= 2\left( X_0 - W_0 - B_1 W_1 \right) , \\ B_3 &= 2 \left( Y_0 - Z_0 - B_1 Z_1 \right). \end{aligned} \end{align} $$
It is clear that the definitions of
![]() $B_2$
and
$B_2$
and
![]() $B_3$
ensure that
$B_3$
ensure that
![]() $b^{\mathrm {fl}}_W (1) = X_0$
and
$b^{\mathrm {fl}}_W (1) = X_0$
and
![]() $b^{\mathrm {fl}}_Z (1) = Y_0$
, respectively.
$b^{\mathrm {fl}}_Z (1) = Y_0$
, respectively.
![]() $B_1$
is defined so that
$B_1$
is defined so that
![]() $(X_1, Y_1)$
is proportional to
$(X_1, Y_1)$
is proportional to
![]() $b^{\mathrm {fl}\, \prime }(0)$
. In particular, we will require
$b^{\mathrm {fl}\, \prime }(0)$
. In particular, we will require
 $$ \begin{align*} 0&=(X_1, Y_1)\wedge \frac{d}{dt}b^{\mathrm{fl}}\vert_{t=1} \\ &=(X_1, Y_1)\wedge (B_1 W_1 + B_2 , B_1 Z_1 + B_3)\\ &=(X_1, Y_1)\wedge \left( B_1 (-W_1 , -Z_1 ) + 2( X_0- W_0,Y_0- Z_0 ) \right). \end{align*} $$
$$ \begin{align*} 0&=(X_1, Y_1)\wedge \frac{d}{dt}b^{\mathrm{fl}}\vert_{t=1} \\ &=(X_1, Y_1)\wedge (B_1 W_1 + B_2 , B_1 Z_1 + B_3)\\ &=(X_1, Y_1)\wedge \left( B_1 (-W_1 , -Z_1 ) + 2( X_0- W_0,Y_0- Z_0 ) \right). \end{align*} $$
Solving for
![]() $B_1$
, one obtains the first equation of (3.3).
$B_1$
, one obtains the first equation of (3.3).
In order to check the validity of the barrier, we need to show the positivity of the seventh-degree polynomial
Note that the vector
![]() $(b_Z^{\mathrm {fl} \, \prime }(t), -b_W^{\mathrm {fl} \, \prime }(t))$
is normal to the curve
$(b_Z^{\mathrm {fl} \, \prime }(t), -b_W^{\mathrm {fl} \, \prime }(t))$
is normal to the curve
![]() $b^{\mathrm {fl}}(t)$
and points in the upwards direction.
$b^{\mathrm {fl}}(t)$
and points in the upwards direction.
Proposition 3.2. Let
![]() $\gamma \in (1, +\infty )$
and
$\gamma \in (1, +\infty )$
and
![]() $r\in (r_3, r_{4})$
. We have that
$r\in (r_3, r_{4})$
. We have that
![]() $P^{\mathrm {fl}} (t)> 0$
for every
$P^{\mathrm {fl}} (t)> 0$
for every
![]() $t\in (0, 1)$
. Moreover, we have that
$t\in (0, 1)$
. Moreover, we have that
![]() $D_W (b^{\mathrm {fl}}(t))> 0$
and
$D_W (b^{\mathrm {fl}}(t))> 0$
and
![]() $D_Z (b^{\mathrm {fl}}(t))> 0$
for any
$D_Z (b^{\mathrm {fl}}(t))> 0$
for any
![]() $t \in (0, 1]$
.
$t \in (0, 1]$
.
Proof. The statement
![]() $P^{\mathrm {fl}}(t)> 0$
for every
$P^{\mathrm {fl}}(t)> 0$
for every
![]() $t \in (0, 1)$
is proven via a computer-assisted proof. The code can be found in the supplementary material, and we refer to Appendix B for details about the implementation.
$t \in (0, 1)$
is proven via a computer-assisted proof. The code can be found in the supplementary material, and we refer to Appendix B for details about the implementation.
With respect to
![]() $D_Z (b^{\mathrm {fl}}(t))> 0$
, note that this is a second-degree polynomial vanishing at
$D_Z (b^{\mathrm {fl}}(t))> 0$
, note that this is a second-degree polynomial vanishing at
![]() $t=0$
. For
$t=0$
. For
![]() $t> 0$
small enough,
$t> 0$
small enough,
![]() $D_Z (b^{\mathrm {fl}}(t))> 0$
since the slope of
$D_Z (b^{\mathrm {fl}}(t))> 0$
since the slope of
![]() $b^{\mathrm {fl}}(t)$
coincides with the slope of the smooth solution (and
$b^{\mathrm {fl}}(t)$
coincides with the slope of the smooth solution (and
![]() $D_{Z, 1}> 0$
by Lemma A.11). Now, as
$D_{Z, 1}> 0$
by Lemma A.11). Now, as ![]() (Lemma A.26), the second-degree polynomial
(Lemma A.26), the second-degree polynomial
![]() $D_Z(b^{\mathrm {fl}}(t))$
cannot be non-positive at any
$D_Z(b^{\mathrm {fl}}(t))$
cannot be non-positive at any
![]() $0 < t_0 < 1$
because otherwise
$0 < t_0 < 1$
because otherwise
![]() $D_Z(b^{\mathrm {fl}}(t))$
would have three roots by continuity (one at
$D_Z(b^{\mathrm {fl}}(t))$
would have three roots by continuity (one at
![]() $t=0$
, and two in
$t=0$
, and two in
![]() $(0, 1)$
).
$(0, 1)$
).
Lastly,
![]() $D_W(b^{\mathrm {fl}}(t))$
is also a second-degree polynomial which is positive at
$D_W(b^{\mathrm {fl}}(t))$
is also a second-degree polynomial which is positive at
![]() $t=0$
and
$t=0$
and
![]() $t=1$
. It would need to have two roots in
$t=1$
. It would need to have two roots in
![]() $[0, 1]$
in order to be negative for some
$[0, 1]$
in order to be negative for some
![]() $t \in [0, 1]$
. That is impossible since its derivative at
$t \in [0, 1]$
. That is impossible since its derivative at
![]() $0$
is positive:
$0$
is positive:
![]() $b^{\mathrm {fl}}(t)$
agrees up to first order with the smooth solution and
$b^{\mathrm {fl}}(t)$
agrees up to first order with the smooth solution and
![]() $D_{W, 1}> 0$
by Lemma A.26.
$D_{W, 1}> 0$
by Lemma A.26.
For the case
![]() $\gamma = 7/5$
and
$\gamma = 7/5$
and
![]() $r\in (r_n, r_{n+1})$
for n odd large enough, we instead consider the barrier
$r\in (r_n, r_{n+1})$
for n odd large enough, we instead consider the barrier
 $$ \begin{align} b^{\mathrm{fl}}_{7/5}(t) = \left( W_0 + W_1t + \frac{W_2}{2} t^2 - \left( W_0 + W_1 + \frac{W_2}{2} \right) t^3, Z_0 + Z_1t + \frac{Z_2}{2}t^2 - \left( Z_0 + Z_1 + \frac{Z_2}{2} \right) t^3 \right). \end{align} $$
$$ \begin{align} b^{\mathrm{fl}}_{7/5}(t) = \left( W_0 + W_1t + \frac{W_2}{2} t^2 - \left( W_0 + W_1 + \frac{W_2}{2} \right) t^3, Z_0 + Z_1t + \frac{Z_2}{2}t^2 - \left( Z_0 + Z_1 + \frac{Z_2}{2} \right) t^3 \right). \end{align} $$
It is clear that the barrier matches up to second order at zero and that
![]() $b^{\mathrm {fl}}_{7/5}(1) = P_\infty = (0, 0)$
. In the very same way as before, we define the polynomial
$b^{\mathrm {fl}}_{7/5}(1) = P_\infty = (0, 0)$
. In the very same way as before, we define the polynomial
We have the same type of result.
Proposition 3.3. Let
![]() $\gamma = 7/5$
,
$\gamma = 7/5$
,
![]() $n \in \mathbb {N}$
large enough and
$n \in \mathbb {N}$
large enough and
![]() $r\in (r_n, r_{n+1})$
. We have that
$r\in (r_n, r_{n+1})$
. We have that
![]() $P^{\mathrm {fl}}_{7/5} (t)> 0$
for every
$P^{\mathrm {fl}}_{7/5} (t)> 0$
for every
![]() $t\in (0,1)$
. Moreover, we also have that
$t\in (0,1)$
. Moreover, we also have that
![]() $D_W (b^{\mathrm { fl}}_{7/5} (t))> 0$
for
$D_W (b^{\mathrm { fl}}_{7/5} (t))> 0$
for
![]() $t \in (0, 1)$
and
$t \in (0, 1)$
and
![]() $D_Z (b^{\mathrm {fl}}_{7/5} (t))> 0$
for
$D_Z (b^{\mathrm {fl}}_{7/5} (t))> 0$
for
![]() $t \in (0, 1) \setminus [t^{\mathrm {in}}_{7/5}, t^{\mathrm {out}}_{7/5}]$
, for some
$t \in (0, 1) \setminus [t^{\mathrm {in}}_{7/5}, t^{\mathrm {out}}_{7/5}]$
, for some
![]() $t^{\mathrm {in}}_{7/5}, t^{\mathrm {out}}_{7/5}$
such that
$t^{\mathrm {in}}_{7/5}, t^{\mathrm {out}}_{7/5}$
such that
![]() $D_Z(b^{\mathrm {fl}}_{7/5}(t^{\mathrm {in}}_{7/5})) = D_Z(b^{\mathrm {fl}}_{7/5}(t^{\mathrm {out}}_{7/5})) = 0$
.
$D_Z(b^{\mathrm {fl}}_{7/5}(t^{\mathrm {in}}_{7/5})) = D_Z(b^{\mathrm {fl}}_{7/5}(t^{\mathrm {out}}_{7/5})) = 0$
.
Moreover, the points
![]() $P^{\mathrm {in}}_{7/5} = b^{\mathrm {fl}}_{7/5}(t^{\mathrm {in}}_{7/5})$
and
$P^{\mathrm {in}}_{7/5} = b^{\mathrm {fl}}_{7/5}(t^{\mathrm {in}}_{7/5})$
and
![]() $P^{\mathrm {out}}_{7/5} = b^{\mathrm {fl}}_{7/5}(t^{\mathrm {out}}_{7/5})$
are located to the left of
$P^{\mathrm {out}}_{7/5} = b^{\mathrm {fl}}_{7/5}(t^{\mathrm {out}}_{7/5})$
are located to the left of
![]() $\bar P_s$
.
$\bar P_s$
.
Proof. We have that
![]() $D_W (b^{\mathrm {fl}}_{7/5}(t))$
is a third-degree polynomial. Calculating this polynomial at
$D_W (b^{\mathrm {fl}}_{7/5}(t))$
is a third-degree polynomial. Calculating this polynomial at
![]() $r = r^\ast (7/5)$
, we obtain
$r = r^\ast (7/5)$
, we obtain
As all the coefficients are positive, and we obtain that the coefficients of
![]() $D_W (b^{\mathrm {fl}}_{7/5}(t))$
are still positive for r sufficiently close to
$D_W (b^{\mathrm {fl}}_{7/5}(t))$
are still positive for r sufficiently close to
![]() $r^\ast (7/5)$
, so that
$r^\ast (7/5)$
, so that
![]() $D_W (b^{\mathrm {fl}}_{7/5}(t))> 0$
for
$D_W (b^{\mathrm {fl}}_{7/5}(t))> 0$
for
![]() $t \in (0, 1)$
.
$t \in (0, 1)$
.
With respect to
![]() $P^{\mathrm {fl}}_{7/5}(t)$
, we observe that this polynomial is a multiple of
$P^{\mathrm {fl}}_{7/5}(t)$
, we observe that this polynomial is a multiple of
![]() $t^3$
since the first three coefficients of
$t^3$
since the first three coefficients of
![]() $b^{\mathrm {fl}}_{7/5} (t)$
agree with those of the smooth solution passing through
$b^{\mathrm {fl}}_{7/5} (t)$
agree with those of the smooth solution passing through
![]() $P_s$
. We also have that
$P_s$
. We also have that
![]() $P_{7/5}^{\mathrm {fl}}(1) = 0$
because
$P_{7/5}^{\mathrm {fl}}(1) = 0$
because
![]() $N_W(P_\infty ) = N_Z (P_\infty ) = 0$
and
$N_W(P_\infty ) = N_Z (P_\infty ) = 0$
and
![]() $D_W(P_\infty ) = D_Z(P_\infty ) = 1$
. Moreover, we have that
$D_W(P_\infty ) = D_Z(P_\infty ) = 1$
. Moreover, we have that
 $$ \begin{align*} P_{7/5}^{\mathrm{fl} \; \prime}(1) &= b^{\mathrm{fl} \; \prime}_{7/5, Z}(1) D_Z (P_\infty ) \nabla N_W (P_\infty) \cdot b^{\mathrm{fl} \; \prime}_{7/5} (1) - b^{\mathrm{fl} \; \prime}_{7/5, W} (1) D_W (P_\infty ) \nabla N_Z (P_\infty ) \cdot b^{\mathrm{fl} \; \prime}_{7/5} (1) \\ &= b^{\mathrm{fl} \; \prime}_{7/5, Z}(1) (-r, 0) \cdot b^{\mathrm{fl} \; \prime}_{7/5} (1) - b^{\mathrm{fl} \; \prime}_{7/5, W} (1) (0, -r) \cdot b^{\mathrm{fl} \; \prime}_{7/5} (1) = 0. \end{align*} $$
$$ \begin{align*} P_{7/5}^{\mathrm{fl} \; \prime}(1) &= b^{\mathrm{fl} \; \prime}_{7/5, Z}(1) D_Z (P_\infty ) \nabla N_W (P_\infty) \cdot b^{\mathrm{fl} \; \prime}_{7/5} (1) - b^{\mathrm{fl} \; \prime}_{7/5, W} (1) D_W (P_\infty ) \nabla N_Z (P_\infty ) \cdot b^{\mathrm{fl} \; \prime}_{7/5} (1) \\ &= b^{\mathrm{fl} \; \prime}_{7/5, Z}(1) (-r, 0) \cdot b^{\mathrm{fl} \; \prime}_{7/5} (1) - b^{\mathrm{fl} \; \prime}_{7/5, W} (1) (0, -r) \cdot b^{\mathrm{fl} \; \prime}_{7/5} (1) = 0. \end{align*} $$
Therefore, we see that
![]() $P_{7/5}^{\mathrm {fl}}(t) = (1-t)^2 t^3 Q_{7/5}^{\mathrm {fl}}(t)$
for some sixth-degree polynomial
$P_{7/5}^{\mathrm {fl}}(t) = (1-t)^2 t^3 Q_{7/5}^{\mathrm {fl}}(t)$
for some sixth-degree polynomial
![]() $Q_{7/5}^{\mathrm {fl}}(t)$
. We just need to show that
$Q_{7/5}^{\mathrm {fl}}(t)$
. We just need to show that
![]() $Q_{7/5}^{\mathrm {fl}}(t)> 0$
for
$Q_{7/5}^{\mathrm {fl}}(t)> 0$
for
![]() $t \in (0, 1)$
. Calculating
$t \in (0, 1)$
. Calculating
![]() $Q_{7/5}^{\mathrm {fl}}(t)$
at
$Q_{7/5}^{\mathrm {fl}}(t)$
at
![]() $r=r^\ast $
, we obtain
$r=r^\ast $
, we obtain
 $$ \begin{align*} Q_{7/5}^{\mathrm{fl}}(t)\Big|_{r=r^\ast} &= 375 \left(17845372 \sqrt{5}-22507109\right) t^6+25 \left(242253290 \sqrt{5}-88777981\right) t^5 \\&\quad+10 \left(1945028708 \sqrt{5}-2421950855\right) t^4+660 \left(12759056 \sqrt{5}-8257439\right) t^3 \\&\quad +7260 \left(1604200 \sqrt{5}-2790277\right) t^2-21780 \left(137 \sqrt{5}-38799\right) t+313632 \left(6133 \sqrt{5}-7995\right). \end{align*} $$
$$ \begin{align*} Q_{7/5}^{\mathrm{fl}}(t)\Big|_{r=r^\ast} &= 375 \left(17845372 \sqrt{5}-22507109\right) t^6+25 \left(242253290 \sqrt{5}-88777981\right) t^5 \\&\quad+10 \left(1945028708 \sqrt{5}-2421950855\right) t^4+660 \left(12759056 \sqrt{5}-8257439\right) t^3 \\&\quad +7260 \left(1604200 \sqrt{5}-2790277\right) t^2-21780 \left(137 \sqrt{5}-38799\right) t+313632 \left(6133 \sqrt{5}-7995\right). \end{align*} $$
As all the coefficients are positive, they will be positive for r sufficiently close to
![]() $r^\ast $
, and therefore, for r sufficiently close to
$r^\ast $
, and therefore, for r sufficiently close to
![]() $r^\ast $
, we have that
$r^\ast $
, we have that
![]() $Q_{7/5}^{\mathrm {fl}}(t)> 0$
for
$Q_{7/5}^{\mathrm {fl}}(t)> 0$
for
![]() $t \in (0, 1)$
.
$t \in (0, 1)$
.
With respect to
![]() $D_Z$
, we have that
$D_Z$
, we have that
![]() $D_Z (b^{\mathrm {fl}}_{7/5}(t))$
is a multiple of t (as it vanishes at zero), and moreover,
$D_Z (b^{\mathrm {fl}}_{7/5}(t))$
is a multiple of t (as it vanishes at zero), and moreover,
for some
![]() $D_{Z, 3}^{\mathrm {fl}}$
. We have that
$D_{Z, 3}^{\mathrm {fl}}$
. We have that
![]() $D_{Z, 1}> 0$
from Lemma A.11, so the polynomial is initially positive. However, at
$D_{Z, 1}> 0$
from Lemma A.11, so the polynomial is initially positive. However, at
![]() $r = r^\ast $
, we have that
$r = r^\ast $
, we have that
![]() $D_{Z, 1} = 0$
,
$D_{Z, 1} = 0$
,
![]() $\frac {D_{Z, 2}}{2} = \frac {19-9\sqrt {5}}{264} < 0$
and
$\frac {D_{Z, 2}}{2} = \frac {19-9\sqrt {5}}{264} < 0$
and
![]() $\frac {D_{Z, 3}^{\mathrm {fl}}}{6} = \frac {245 + 9\sqrt {5}}{264}> 0$
. Therefore, it is clear that for r sufficiently close to
$\frac {D_{Z, 3}^{\mathrm {fl}}}{6} = \frac {245 + 9\sqrt {5}}{264}> 0$
. Therefore, it is clear that for r sufficiently close to
![]() $r^\ast $
, we have two real roots of the second-degree polynomial (3.7), which we define to be
$r^\ast $
, we have two real roots of the second-degree polynomial (3.7), which we define to be
![]() $t^{\mathrm {in}}_{7/5}$
and
$t^{\mathrm {in}}_{7/5}$
and
![]() $t^{\mathrm {out}}_{7/5}$
. Moreover, as
$t^{\mathrm {out}}_{7/5}$
. Moreover, as
![]() $D_{Z, 3}^{\mathrm {fl}}> 0$
, the sign of (3.7) is positive except for
$D_{Z, 3}^{\mathrm {fl}}> 0$
, the sign of (3.7) is positive except for
![]() $t \in [t^{\mathrm {in}}_{7/5}, t^{\mathrm {out}}_{7/5}]$
.
$t \in [t^{\mathrm {in}}_{7/5}, t^{\mathrm {out}}_{7/5}]$
.
Lastly, we just need to show that
![]() $b^{\mathrm {fl}}_{7/5}(t^{\mathrm {in}}_{7/5})$
is located to the left of
$b^{\mathrm {fl}}_{7/5}(t^{\mathrm {in}}_{7/5})$
is located to the left of
![]() $\bar P_s$
; that is, we need to check
$\bar P_s$
; that is, we need to check

This is checked in Lemma A.15.
We define the near-left barrier to be
 $$ \begin{align} \begin{aligned} b^{\mathrm{nl}}_{n, W} (s) &= \sum_{i=0}^n \frac{1}{i!} W_i s^i, \\b^{\mathrm{nl}}_{n, Z} (s) &= \sum_{i=0}^n \frac{1}{i!} Z_i s^i \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} b^{\mathrm{nl}}_{n, W} (s) &= \sum_{i=0}^n \frac{1}{i!} W_i s^i, \\b^{\mathrm{nl}}_{n, Z} (s) &= \sum_{i=0}^n \frac{1}{i!} Z_i s^i \end{aligned} \end{align} $$
and define
![]() $b^{\mathrm {nl}}_n (s) = (b^{\mathrm {nl}}_{n, W}(s), b^{\mathrm {nl}}_{n, Z}(s))$
. We have the following:
$b^{\mathrm {nl}}_n (s) = (b^{\mathrm {nl}}_{n, W}(s), b^{\mathrm {nl}}_{n, Z}(s))$
. We have the following:
Lemma 3.4. Let
![]() $n=3$
with any
$n=3$
with any
![]() $\gamma \in (1, +\infty )$
or either
$\gamma \in (1, +\infty )$
or either
![]() $n\in \mathbb {N}$
odd and sufficiently large with
$n\in \mathbb {N}$
odd and sufficiently large with
![]() $\gamma = 7/5$
. Let
$\gamma = 7/5$
. Let
![]() $r\in (r_n, r_{n+1})$
. We have that
$r\in (r_n, r_{n+1})$
. We have that
![]() $(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
is initially above
$(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
is initially above
![]() $b^{\mathrm {nl}}_n (s)$
for s and
$b^{\mathrm {nl}}_n (s)$
for s and
![]() $\xi $
sufficiently small. That is, for the same value of W, Z is higher for the smooth solution.
$\xi $
sufficiently small. That is, for the same value of W, Z is higher for the smooth solution.
Proof. Both curves
![]() $(W^{(r)}, Z^{(r)})(\xi )$
and
$(W^{(r)}, Z^{(r)})(\xi )$
and
![]() $b^{\mathrm {nl}}_n(s)$
agree in their Taylor expansions around
$b^{\mathrm {nl}}_n(s)$
agree in their Taylor expansions around
![]() $P_s$
up to order n. If the
$P_s$
up to order n. If the
![]() $(n+1)$
-th coefficient is given by a term
$(n+1)$
-th coefficient is given by a term
![]() $(W_{n+1}, Z_{n+1}) \frac {t^{n+1}}{(n+1)!}$
, this will have a normal component over the tangent line of size
$(W_{n+1}, Z_{n+1}) \frac {t^{n+1}}{(n+1)!}$
, this will have a normal component over the tangent line of size
![]() $- (W_1, Z_1) \wedge (W_{n+1}, Z_{n+1}) \frac {t^{n+1}}{(n+1)!}$
(where the sign is positive for a deviation above the tangent line at
$- (W_1, Z_1) \wedge (W_{n+1}, Z_{n+1}) \frac {t^{n+1}}{(n+1)!}$
(where the sign is positive for a deviation above the tangent line at
![]() $P_s$
and negative for a deviation below the tangent line at
$P_s$
and negative for a deviation below the tangent line at
![]() $P_s$
).
$P_s$
).
Therefore, we just need to check
This is done in Lemma A.26 for the case of
![]() $n = 3$
. For the case of
$n = 3$
. For the case of
![]() $\gamma = 7/5$
and n odd sufficiently large, this will follow from Section 5, concretely from Corollary 5.9.
$\gamma = 7/5$
and n odd sufficiently large, this will follow from Section 5, concretely from Corollary 5.9.
We now consider the
![]() $(4n-1)$
-th degree polynomial
$(4n-1)$
-th degree polynomial
whose sign determines the direction of the normal component of the barrier along
![]() $b^{\mathrm {nl}}_n(s)$
. In particular, we want
$b^{\mathrm {nl}}_n(s)$
. In particular, we want
![]() $P^{\mathrm {nl}}_n(t)$
to be positive, as this corresponds to the field pointing upwards.
$P^{\mathrm {nl}}_n(t)$
to be positive, as this corresponds to the field pointing upwards.
Proposition 3.5. Let
![]() $\gamma> 1$
,
$\gamma> 1$
,
![]() $n=3$
and
$n=3$
and
![]() $r\in (r_{3}, r_{4})$
. There exist
$r\in (r_{3}, r_{4})$
. There exist
![]() $s_\star $
and
$s_\star $
and
![]() $t_\star $
depending on r such that
$t_\star $
depending on r such that
![]() $b^{\mathrm {fl}}_n (t_\star ) = b^{\mathrm {nl}}_{n}(s_\star )$
. Moreover,
$b^{\mathrm {fl}}_n (t_\star ) = b^{\mathrm {nl}}_{n}(s_\star )$
. Moreover,
![]() $P^{\mathrm {nl}}_{n}(s)> 0$
,
$P^{\mathrm {nl}}_{n}(s)> 0$
,
![]() $D_Z( b^{\mathrm {nl}}_{n}(s) )> 0$
and
$D_Z( b^{\mathrm {nl}}_{n}(s) )> 0$
and
![]() $D_W (b^{\mathrm {nl}}_{n}(s))> 0$
for every
$D_W (b^{\mathrm {nl}}_{n}(s))> 0$
for every
![]() $s\in (0, s_\star ]$
.
$s\in (0, s_\star ]$
.
Proof. We first formulate the barrier
![]() $b^{\mathrm {fl}}(t)$
in implicit form using the resultant
$b^{\mathrm {fl}}(t)$
in implicit form using the resultant
 $$ \begin{align} B^{\mathrm{fl}} (W, Z) = \left| \begin{matrix} \frac{B_2}{2} & B_1 W_1 & W_0 - W & 0 \\ 0 & \frac{B_2}{2} & B_1 W_1 & W_0 - W \\ \frac{B_3}{2} & B_1 Z_1 & Z_0 - Z & 0 \\ 0 & \frac{B_3}{2} & B_1 Z_1 & Z_0 - Z \\ \end{matrix} \right|, \end{align} $$
$$ \begin{align} B^{\mathrm{fl}} (W, Z) = \left| \begin{matrix} \frac{B_2}{2} & B_1 W_1 & W_0 - W & 0 \\ 0 & \frac{B_2}{2} & B_1 W_1 & W_0 - W \\ \frac{B_3}{2} & B_1 Z_1 & Z_0 - Z & 0 \\ 0 & \frac{B_3}{2} & B_1 Z_1 & Z_0 - Z \\ \end{matrix} \right|, \end{align} $$
so that the equation
![]() $b^{\mathrm {fl}}(t_\star ) = b^{\mathrm {nl}}(s_\star )$
can be reformulated as
$b^{\mathrm {fl}}(t_\star ) = b^{\mathrm {nl}}(s_\star )$
can be reformulated as
![]() $B^{\mathrm {fl}}(b^{\mathrm {nl}}_n (t_\star ) ) = 0$
. Let us fix
$B^{\mathrm {fl}}(b^{\mathrm {nl}}_n (t_\star ) ) = 0$
. Let us fix
![]() $s_- = 35/100$
. We will divide the proof in five steps:
$s_- = 35/100$
. We will divide the proof in five steps:
-
1. For every
 $\gamma> 1$
, the polynomial
$\gamma> 1$
, the polynomial
 $B^{\mathrm {fl}}(b^{\mathrm {nl}}_3 (s))$
is negative for
$B^{\mathrm {fl}}(b^{\mathrm {nl}}_3 (s))$
is negative for
 $s>0$
sufficiently small for all
$s>0$
sufficiently small for all
 $r\in (r_3, r_4)$
.
$r\in (r_3, r_4)$
. -
2. For every
 $\gamma> 1$
, the polynomial
$\gamma> 1$
, the polynomial
 $B^{\mathrm {fl}}(b^{\mathrm {nl}}_3 (s_-(k-3 ))$
is positive for all
$B^{\mathrm {fl}}(b^{\mathrm {nl}}_3 (s_-(k-3 ))$
is positive for all
 $r\in (r_3, r_4)$
.
$r\in (r_3, r_4)$
. -
3. For every
 $\gamma> 1$
, we have
$\gamma> 1$
, we have
 $P^{\mathrm {nl}}_3(s)> 0$
for all
$P^{\mathrm {nl}}_3(s)> 0$
for all
 $s\in (0, s_-(k-3))$
and
$s\in (0, s_-(k-3))$
and
 $r\in (r_3, r_4)$
.
$r\in (r_3, r_4)$
. -
4. For every
 $\gamma> 1$
, we have
$\gamma> 1$
, we have
 $D_W (b^{\mathrm {nl}}_3(s))> 0$
for all
$D_W (b^{\mathrm {nl}}_3(s))> 0$
for all
 $s\in (0, s_-(k-3))$
and
$s\in (0, s_-(k-3))$
and
 $r\in (r_3, r_4)$
.
$r\in (r_3, r_4)$
. -
5. For every
 $\gamma> 1$
, we have
$\gamma> 1$
, we have
 $D_Z (b^{\mathrm {nl}}_3(s))> 0$
for all
$D_Z (b^{\mathrm {nl}}_3(s))> 0$
for all
 $s\in (0, s_- (k-3))$
and
$s\in (0, s_- (k-3))$
and
 $r\in (r_3, r_4)$
.
$r\in (r_3, r_4)$
.
From items 1 and 2, by continuity, there exists a value
![]() $s_\star \in (0, s_-(r-r_3)]$
such that
$s_\star \in (0, s_-(r-r_3)]$
such that
![]() $B^{\mathrm {fl}}(b^{\mathrm {nl}}_3(s_\star )) = 0$
, and therefore, there exists
$B^{\mathrm {fl}}(b^{\mathrm {nl}}_3(s_\star )) = 0$
, and therefore, there exists
![]() $t_\star $
such that
$t_\star $
such that
![]() $b^{\mathrm {fl}}(t_\star ) = b^{\mathrm {nl}}_3(s_\star )$
. Then, items 3, 4 and 5 give us the desired result.
$b^{\mathrm {fl}}(t_\star ) = b^{\mathrm {nl}}_3(s_\star )$
. Then, items 3, 4 and 5 give us the desired result.
Finally, we prove each of those steps with a computer-assisted proof. The code can be found in the supplementary material. We refer to Appendix B for details about the implementation.
Lastly, we require an analogous Proposition for the case where
![]() $\gamma = 7/5$
and k sufficiently large.
$\gamma = 7/5$
and k sufficiently large.
Proposition 3.6. Let
![]() $\gamma = 7/5$
, and n odd sufficiently large. There exist
$\gamma = 7/5$
, and n odd sufficiently large. There exist
![]() $s_{7/5,\mathrm {int}} $
and
$s_{7/5,\mathrm {int}} $
and
![]() $t_{7/5, \mathrm {int}} $
such that
$t_{7/5, \mathrm {int}} $
such that
![]() $b^{\mathrm {fl}}_{7/5, n} (t_{7/5, \mathrm {int}} ) = b^{\mathrm {nl}}_{n}(s_{7/5, \mathrm {int}})$
. Moreover,
$b^{\mathrm {fl}}_{7/5, n} (t_{7/5, \mathrm {int}} ) = b^{\mathrm {nl}}_{n}(s_{7/5, \mathrm {int}})$
. Moreover,
![]() $P^{\mathrm {nl}}_{n}(s)> 0$
and
$P^{\mathrm {nl}}_{n}(s)> 0$
and
![]() $D_W (b^{\mathrm {nl}}_{n}(s))> 0$
for every
$D_W (b^{\mathrm {nl}}_{n}(s))> 0$
for every
![]() $s \in (0, s_{7/5,\mathrm {int}} ]$
. Lastly, either
$s \in (0, s_{7/5,\mathrm {int}} ]$
. Lastly, either
![]() $D_Z( b^{\mathrm {nl}}_{n}(s) )> 0$
for
$D_Z( b^{\mathrm {nl}}_{n}(s) )> 0$
for
![]() $s \in (0, s_{7/5, \mathrm {int}} ]$
, or there exists some
$s \in (0, s_{7/5, \mathrm {int}} ]$
, or there exists some
![]() $s_{7/5, \mathrm {int}}' < s_{7/5, \mathrm {int}}$
such that
$s_{7/5, \mathrm {int}}' < s_{7/5, \mathrm {int}}$
such that
![]() $D_Z (b^{\mathrm {nl}}_{n}(s_{7/5, \mathrm {int}}')) = 0$
and the point
$D_Z (b^{\mathrm {nl}}_{n}(s_{7/5, \mathrm {int}}')) = 0$
and the point
![]() $b^{\mathrm {nl}}_{n}(s_{7/5, \mathrm {int}}')$
is located to the left of
$b^{\mathrm {nl}}_{n}(s_{7/5, \mathrm {int}}')$
is located to the left of
![]() $\bar P_s$
.
$\bar P_s$
.
The proof will require an asymptotic analysis of the Taylor series done in Section 5, and it can be found at the end of that section.
Proof of Proposition 3.1.
For
![]() $\gamma = 7/5$
and n sufficiently large, we can consider the closed region
$\gamma = 7/5$
and n sufficiently large, we can consider the closed region
![]() $\mathcal {T}$
of the plane which has a corner at
$\mathcal {T}$
of the plane which has a corner at
![]() $P_s$
and is enclosed by
$P_s$
and is enclosed by
![]() $b^{\mathrm {nl}}_{7/5,n}(t)$
,
$b^{\mathrm {nl}}_{7/5,n}(t)$
,
![]() $b^{\mathrm {fl}}_{7/5}(t)$
,
$b^{\mathrm {fl}}_{7/5}(t)$
,
![]() $D_Z = 0$
, the diagonal
$D_Z = 0$
, the diagonal
![]() $W = Z$
and the vertical line
$W = Z$
and the vertical line
![]() $W = W_0$
(starting at
$W = W_0$
(starting at
![]() $(W_0, W_0)$
, ending at
$(W_0, W_0)$
, ending at
![]() $P_s$
). The intersection between
$P_s$
). The intersection between
![]() $b^{\mathrm {nl}}_{7/5,n}(t)$
and
$b^{\mathrm {nl}}_{7/5,n}(t)$
and
![]() $b^{\mathrm {fl}}_{7/5}(t)$
is proven in Proposition 3.6. There are two intersection points between
$b^{\mathrm {fl}}_{7/5}(t)$
is proven in Proposition 3.6. There are two intersection points between
![]() $b^{\mathrm {fl}}_{7/5}(t)$
and
$b^{\mathrm {fl}}_{7/5}(t)$
and
![]() $D_Z = 0$
as indicated in Proposition 3.3. Note that Proposition 3.3 gives us two cases. In the first case, we go from
$D_Z = 0$
as indicated in Proposition 3.3. Note that Proposition 3.3 gives us two cases. In the first case, we go from
![]() $P_s$
to
$P_s$
to
![]() $P_\infty $
by following
$P_\infty $
by following
![]() $b^{\mathrm {nl}}_{7/5,n}(s)$
for
$b^{\mathrm {nl}}_{7/5,n}(s)$
for
![]() $0\leq s \leq s_{7/5, \mathrm {int}}$
, then
$0\leq s \leq s_{7/5, \mathrm {int}}$
, then
![]() $b^{fl}_{7/5}$
up to
$b^{fl}_{7/5}$
up to
![]() $P^{\mathrm {in}}_{7/5}$
, then
$P^{\mathrm {in}}_{7/5}$
, then
![]() $D_Z = 0$
up to
$D_Z = 0$
up to
![]() $P^{\mathrm { out}}_{7/5}$
and finally
$P^{\mathrm { out}}_{7/5}$
and finally
![]() $b^{\mathrm {fl}}_{7/5}(t)$
up to
$b^{\mathrm {fl}}_{7/5}(t)$
up to
![]() $P_\infty $
. In the second case, the path is the same except that we connect directly
$P_\infty $
. In the second case, the path is the same except that we connect directly
![]() $b^{\mathrm {nl}}_{3}$
with
$b^{\mathrm {nl}}_{3}$
with
![]() $D_Z = 0$
at
$D_Z = 0$
at
![]() $b^{\mathrm {nl}}_3(s_{7/5, \mathrm {int}}')$
. We should notice that in any case, the region of
$b^{\mathrm {nl}}_3(s_{7/5, \mathrm {int}}')$
. We should notice that in any case, the region of
![]() $D_Z = 0$
which forms part of
$D_Z = 0$
which forms part of
![]() $\mathcal {T}$
is always located to the left of
$\mathcal {T}$
is always located to the left of
![]() $\bar P_s$
(by Proposition 3.6 or Proposition 3.3). For general
$\bar P_s$
(by Proposition 3.6 or Proposition 3.3). For general
![]() $\gamma $
and
$\gamma $
and
![]() $r \in (r_3, r_4)$
, the endpoint of
$r \in (r_3, r_4)$
, the endpoint of
![]() $b^{\mathrm {fl}}(t)$
at
$b^{\mathrm {fl}}(t)$
at
![]() $t=1$
is
$t=1$
is ![]() , so we consider the same region with the addition of the barrier
, so we consider the same region with the addition of the barrier
![]() $b^{\mathrm {extra}} (t)= (X_0 - t, Y_0 + t)$
for
$b^{\mathrm {extra}} (t)= (X_0 - t, Y_0 + t)$
for
![]() $t \in [0, \frac 12 (X_0 - Y_0)]$
. That is, we take
$t \in [0, \frac 12 (X_0 - Y_0)]$
. That is, we take
![]() $\mathcal {T}$
to be enclosed by
$\mathcal {T}$
to be enclosed by
![]() $b^{\mathrm {nl}}_3(t)$
,
$b^{\mathrm {nl}}_3(t)$
,
![]() $b^{\mathrm {fl}}(t)$
,
$b^{\mathrm {fl}}(t)$
,
![]() $b^{\mathrm {extra}}(t)$
,
$b^{\mathrm {extra}}(t)$
,
![]() $W+Z = 0$
and
$W+Z = 0$
and
![]() $W=W_0$
. The intersection between
$W=W_0$
. The intersection between
![]() $b^{\mathrm {nl}}_3(t)$
and
$b^{\mathrm {nl}}_3(t)$
and
![]() $b^{\mathrm {fl}}(t)$
is guaranteed by Proposition 3.5. We show a sketch of region
$b^{\mathrm {fl}}(t)$
is guaranteed by Proposition 3.5. We show a sketch of region
![]() $\mathcal {T}$
in Figure 4 and Figure 5.
$\mathcal {T}$
in Figure 4 and Figure 5.

Figure 4 Region
![]() $\mathcal {T}$
for the case
$\mathcal {T}$
for the case
![]() $\gamma = 7/5$
and r sufficiently close to
$\gamma = 7/5$
and r sufficiently close to
![]() $r^\ast $
.
$r^\ast $
.

Figure 5 Region
![]() $\mathcal {T}$
for the case
$\mathcal {T}$
for the case
![]() $\gamma> 1$
and
$\gamma> 1$
and
![]() $r \in (r_3, r_4)$
.
$r \in (r_3, r_4)$
.
We will now show that the region
![]() $\mathcal {T}$
does not intersect the line
$\mathcal {T}$
does not intersect the line
![]() $D_W = 0$
. We first show that the line
$D_W = 0$
. We first show that the line
![]() $D_W = 0$
does not intersect
$D_W = 0$
does not intersect
![]() $b^{\mathrm {nl}}(t)$
and
$b^{\mathrm {nl}}(t)$
and
![]() $b^{\mathrm {fl}}(t)$
. For the case
$b^{\mathrm {fl}}(t)$
. For the case
![]() $r \in (r_3, r_4)$
, this follows as a consequence of Proposition 3.5 and Proposition 3.2, and for the case
$r \in (r_3, r_4)$
, this follows as a consequence of Proposition 3.5 and Proposition 3.2, and for the case
![]() $\gamma = 7/5$
, n odd sufficiently large, this is follows from Proposition 3.3 and Proposition 3.6. In the case
$\gamma = 7/5$
, n odd sufficiently large, this is follows from Proposition 3.3 and Proposition 3.6. In the case
![]() $r \in (r_3, r_4)$
, the fact that the line
$r \in (r_3, r_4)$
, the fact that the line
![]() $D_W = 0$
does not intersect
$D_W = 0$
does not intersect
![]() $b^{\mathrm {extra}}(t)$
follows from Lemma A.19. Moreover, as
$b^{\mathrm {extra}}(t)$
follows from Lemma A.19. Moreover, as
![]() $D_W$
is increasing with Z along
$D_W$
is increasing with Z along
![]() $W = W_0$
and is also increasing with t along
$W = W_0$
and is also increasing with t along
![]() $(t, t)$
, we conclude that
$(t, t)$
, we conclude that
![]() $D_W> 0$
in all
$D_W> 0$
in all
![]() $\partial \mathcal {T}$
. As
$\partial \mathcal {T}$
. As
![]() $D_W = 0$
is a straight line and
$D_W = 0$
is a straight line and
![]() $\mathcal {T}$
is connected, we obtain that
$\mathcal {T}$
is connected, we obtain that
![]() $D_W> 0$
in all
$D_W> 0$
in all
![]() $\mathcal {T}$
. The same reasoning allows us to say that
$\mathcal {T}$
. The same reasoning allows us to say that
![]() $\partial \mathcal {T}$
only intersects
$\partial \mathcal {T}$
only intersects
![]() $D_Z = 0$
at
$D_Z = 0$
at
![]() $P_s$
and (in the case where
$P_s$
and (in the case where
![]() $\gamma = \frac 75$
and r sufficiently close to
$\gamma = \frac 75$
and r sufficiently close to
![]() $r^\ast $
) the points in the segment between
$r^\ast $
) the points in the segment between
![]() $P^{\mathrm {in}}$
and
$P^{\mathrm {in}}$
and
![]() $P^{\mathrm {out}}$
defined in Proposition 3.3.
$P^{\mathrm {out}}$
defined in Proposition 3.3.
The smooth solution
![]() $W^{(r)}(\xi ), Z^{(r)} (\xi )$
is in
$W^{(r)}(\xi ), Z^{(r)} (\xi )$
is in
![]() $\mathcal {T}$
for small enough
$\mathcal {T}$
for small enough
![]() $\xi $
due to Lemma 3.4 and the fact that
$\xi $
due to Lemma 3.4 and the fact that
![]() $W_1 < 0$
(Lemmas A.26 and A.7). It cannot exit
$W_1 < 0$
(Lemmas A.26 and A.7). It cannot exit
![]() $\mathcal {T}$
through
$\mathcal {T}$
through
![]() $b^{\mathrm {nl}}(t)$
,
$b^{\mathrm {nl}}(t)$
,
![]() $b^{\mathrm {fl}}(t)$
or
$b^{\mathrm {fl}}(t)$
or
![]() $b^{\mathrm {extra}}(t)$
due to Proposition 3.5 and Proposition 3.6 (for
$b^{\mathrm {extra}}(t)$
due to Proposition 3.5 and Proposition 3.6 (for
![]() $b^{\mathrm {nl}}(t)$
), Proposition 3.2 and Proposition 3.3 (for
$b^{\mathrm {nl}}(t)$
), Proposition 3.2 and Proposition 3.3 (for
![]() $b^{\mathrm {fl}}(t)$
) and Lemma A.19 (for
$b^{\mathrm {fl}}(t)$
) and Lemma A.19 (for
![]() $b^{\mathrm {extra}}(t)$
,
$b^{\mathrm {extra}}(t)$
,
![]() $r \in (r_3, r_4)$
). In the case of
$r \in (r_3, r_4)$
). In the case of
![]() $\gamma = \frac 75$
and r close enough to
$\gamma = \frac 75$
and r close enough to
![]() $r^\ast $
, it cannot exit through
$r^\ast $
, it cannot exit through
![]() $D_Z = 0$
because that region is always located to the left of
$D_Z = 0$
because that region is always located to the left of
![]() $\bar P_s$
, and the field points inwards there (Lemma A.22). It cannot exit through the line
$\bar P_s$
, and the field points inwards there (Lemma A.22). It cannot exit through the line
![]() $W = Z$
because that line is an invariant of the field (
$W = Z$
because that line is an invariant of the field (
![]() $N_W / D_W, N_Z / D_Z$
is proportional to
$N_W / D_W, N_Z / D_Z$
is proportional to
![]() $(1, 1)$
in that diagonal). Also, it cannot exit through
$(1, 1)$
in that diagonal). Also, it cannot exit through
![]() $W = W_0$
since
$W = W_0$
since
![]() $N_W / D_W < 0$
(
$N_W / D_W < 0$
(
![]() $D_W> 0$
from last paragraph and
$D_W> 0$
from last paragraph and
![]() $N_W < 0$
from Lemma A.20).
$N_W < 0$
from Lemma A.20).
Therefore, as
![]() $\mathcal {T}$
is bounded, Proposition 1.6 yields that either
$\mathcal {T}$
is bounded, Proposition 1.6 yields that either
![]() $(W^{(r)}, Z^{(r)})$
converges to some point of
$(W^{(r)}, Z^{(r)})$
converges to some point of
![]() $\mathcal {T}$
with
$\mathcal {T}$
with
![]() $D_W = 0$
or
$D_W = 0$
or
![]() $D_Z=0$
or it converges to some equilibrium point inside
$D_Z=0$
or it converges to some equilibrium point inside
![]() $\mathcal {T}$
as
$\mathcal {T}$
as
![]() $\xi \rightarrow + \infty $
. There are no points with
$\xi \rightarrow + \infty $
. There are no points with
![]() $D_W = 0$
due to the second paragraph. The solution cannot converge to the points of
$D_W = 0$
due to the second paragraph. The solution cannot converge to the points of
![]() $D_Z = 0$
in the segment
$D_Z = 0$
in the segment
![]() $[P^{\mathrm {in}}_{7/5}, P^{\mathrm {out}}_{7/5}]$
because the field points inwards to
$[P^{\mathrm {in}}_{7/5}, P^{\mathrm {out}}_{7/5}]$
because the field points inwards to
![]() $\mathcal {T}$
in that segment (due to Proposition 3.3 and Lemma A.22). Now, we show that the situation where the solution converges to
$\mathcal {T}$
in that segment (due to Proposition 3.3 and Lemma A.22). Now, we show that the situation where the solution converges to
![]() $P_s$
is also not possible. As
$P_s$
is also not possible. As
![]() $P_s$
is the point with minimum Z in
$P_s$
is the point with minimum Z in
![]() $B_\varepsilon (P_s) \cap \mathcal {T}$
for
$B_\varepsilon (P_s) \cap \mathcal {T}$
for
![]() $\varepsilon $
small enough,Footnote
3
we would need to have points in
$\varepsilon $
small enough,Footnote
3
we would need to have points in
![]() $\mathcal {T}$
arbitrarily close to
$\mathcal {T}$
arbitrarily close to
![]() $P_s$
with
$P_s$
with
![]() $\frac {N_Z}{D_Z}> 0$
. In order to show that this does not happen, we just need to check that
$\frac {N_Z}{D_Z}> 0$
. In order to show that this does not happen, we just need to check that
![]() $D_Z> 0$
and
$D_Z> 0$
and
![]() $N_Z> 0$
in
$N_Z> 0$
in
![]() $(\mathcal {T} \setminus \{ P_s \}) \cap B_\varepsilon (P_s)$
for
$(\mathcal {T} \setminus \{ P_s \}) \cap B_\varepsilon (P_s)$
for
![]() $\varepsilon $
small enough. As the corner of
$\varepsilon $
small enough. As the corner of
![]() $\partial \mathcal {T}$
at
$\partial \mathcal {T}$
at
![]() $P_s$
has less than
$P_s$
has less than
![]() $\pi $
radians (because
$\pi $
radians (because
![]() $W_1 < 0$
), we just need to check
$W_1 < 0$
), we just need to check
![]() $\nabla D_Z (P_s) \cdot (W_1, Z_1)> 0$
,
$\nabla D_Z (P_s) \cdot (W_1, Z_1)> 0$
,
![]() $\nabla D_Z (P_s) \cdot (0, 1)$
,
$\nabla D_Z (P_s) \cdot (0, 1)$
,
![]() $\nabla N_Z (P_s) \cdot (W_1, Z_1)> 0$
and
$\nabla N_Z (P_s) \cdot (W_1, Z_1)> 0$
and
![]() $\nabla N_Z (P_s)\cdot (0,1)> 0$
. Clearly,
$\nabla N_Z (P_s)\cdot (0,1)> 0$
. Clearly,
![]() $\partial _Z D_Z = (\gamma + 1)/4> 0$
and
$\partial _Z D_Z = (\gamma + 1)/4> 0$
and
![]() $D_{Z, 1}, N_{Z, 1}, \partial _Z N_Z (P_s)> 0$
due to Lemmas A.11, A.26 and A.7.
$D_{Z, 1}, N_{Z, 1}, \partial _Z N_Z (P_s)> 0$
due to Lemmas A.11, A.26 and A.7.
Thus, we conclude that
![]() $W^{(r)}, Z^{(r)}$
converge to some equilibrium point of
$W^{(r)}, Z^{(r)}$
converge to some equilibrium point of
![]() $\mathcal {T}$
– that is, some point with
$\mathcal {T}$
– that is, some point with
![]() $N_W = N_Z = 0$
. There are four solutions to that system, which are
$N_W = N_Z = 0$
. There are four solutions to that system, which are ![]() . The point
. The point ![]() clearly lies in the half-plane
clearly lies in the half-plane
![]() $Z> W$
, so it is not in
$Z> W$
, so it is not in
![]() $\mathcal {T}$
. The point
$\mathcal {T}$
. The point
![]() $(-r, -r)$
is also never in
$(-r, -r)$
is also never in
![]() $\mathcal {T}$
. For the case
$\mathcal {T}$
. For the case
![]() $\gamma = 7/5$
, n sufficiently large, this is trivial and for the
$\gamma = 7/5$
, n sufficiently large, this is trivial and for the
![]() $r \in (r_3, r_4)$
case, this is because
$r \in (r_3, r_4)$
case, this is because
![]() $b^{\mathrm {extra}}(t)$
intersects
$b^{\mathrm {extra}}(t)$
intersects
![]() $W=Z$
at some point above
$W=Z$
at some point above
![]() $(-r, -r)$
(Lemma A.26).
$(-r, -r)$
(Lemma A.26).
Finally, we show that the solution does not converge to ![]() . For the case
. For the case
![]() $\gamma = 7/5$
with n sufficiently large, this point is discarded arguing that
$\gamma = 7/5$
with n sufficiently large, this point is discarded arguing that ![]() is not in
is not in
![]() $\mathcal {T}$
. We can parametrize
$\mathcal {T}$
. We can parametrize
![]() $b^{\mathrm {fl}}_{7/5}(t)$
by W because
$b^{\mathrm {fl}}_{7/5}(t)$
by W because
![]() $b^{\mathrm {fl}}_{7/5}(t)$
is decreasing by Lemma A.24, so all the points
$b^{\mathrm {fl}}_{7/5}(t)$
is decreasing by Lemma A.24, so all the points
![]() $(b^{\mathrm {fl}}_{7/5, W}(t), Z)$
with
$(b^{\mathrm {fl}}_{7/5, W}(t), Z)$
with
![]() $Z < b^{\mathrm {fl}}_{7/5, Z}(t)$
are outside
$Z < b^{\mathrm {fl}}_{7/5, Z}(t)$
are outside
![]() $\mathcal {T}$
. That is the case of
$\mathcal {T}$
. That is the case of ![]() due to Lemma A.24. Now we show that the solution does not converge to
due to Lemma A.24. Now we show that the solution does not converge to ![]() for the general
for the general
![]() $\gamma $
case with
$\gamma $
case with
![]() $r \in (r_3, r_4)$
. Note that
$r \in (r_3, r_4)$
. Note that ![]() is a saddle point of the field
is a saddle point of the field
![]() $(N_W D_Z, N_Z D_W)$
due to Lemma A.17. Therefore, there is only one direction along for trajectories converging to
$(N_W D_Z, N_Z D_W)$
due to Lemma A.17. Therefore, there is only one direction along for trajectories converging to ![]() , and will be given by the eigenvector of negative eigenvalue,
, and will be given by the eigenvector of negative eigenvalue,
![]() $v_-$
. We will see that there are not points in
$v_-$
. We will see that there are not points in
![]() $\mathcal {T}$
approaching
$\mathcal {T}$
approaching ![]() in direction
in direction
![]() $v_-$
(or
$v_-$
(or
![]() $-v_-$
), and that will conclude the proof.
$-v_-$
), and that will conclude the proof.
Let us fix the angles
![]() $-\pi \leq \theta _- < \theta _+ < \theta _- +\pi < \pi $
, so that
$-\pi \leq \theta _- < \theta _+ < \theta _- +\pi < \pi $
, so that
![]() $\theta _-, \theta _- +\pi $
indicate the angles of
$\theta _-, \theta _- +\pi $
indicate the angles of
![]() $v_-, -v_-$
and
$v_-, -v_-$
and
![]() $\theta _+, \theta _+ + \pi $
indicate the angles of
$\theta _+, \theta _+ + \pi $
indicate the angles of
![]() $v_+, -v_+$
. Locally around
$v_+, -v_+$
. Locally around ![]() , the angular component of the field around a saddle point points counterclockwise in the region
, the angular component of the field around a saddle point points counterclockwise in the region
![]() $\Theta _\circlearrowleft = (\theta _-, \theta _+)\cup (\theta _- + \pi , \theta _+ + \pi )$
, while it points clockwise in the region
$\Theta _\circlearrowleft = (\theta _-, \theta _+)\cup (\theta _- + \pi , \theta _+ + \pi )$
, while it points clockwise in the region
![]() $\Theta _\circlearrowright = (\theta _+, \theta _- +\pi )\cup (\theta _- + \pi , \theta _+ + 2\pi )$
. Let
$\Theta _\circlearrowright = (\theta _+, \theta _- +\pi )\cup (\theta _- + \pi , \theta _+ + 2\pi )$
. Let
![]() $\theta _{\mathrm {fl}}, \theta _{\mathrm {extra}} \in [-\pi , \pi )$
be the angles at which those barriers arrive to
$\theta _{\mathrm {fl}}, \theta _{\mathrm {extra}} \in [-\pi , \pi )$
be the angles at which those barriers arrive to ![]() . Note
. Note
![]() $\theta _{\mathrm {extra}} = 3\pi /4$
and note also
$\theta _{\mathrm {extra}} = 3\pi /4$
and note also
![]() $\theta _{\mathrm {fl}} < 3\pi /4$
by Lemma A.25. As the field points inwards to
$\theta _{\mathrm {fl}} < 3\pi /4$
by Lemma A.25. As the field points inwards to
![]() $\mathcal {T}$
on the barriers
$\mathcal {T}$
on the barriers
![]() $b^{\mathrm {fl}}$
and
$b^{\mathrm {fl}}$
and
![]() $b^{\mathrm {extra}}$
, we get that
$b^{\mathrm {extra}}$
, we get that
![]() $\theta _{\mathrm {fl}} \in \Theta _\circlearrowleft $
and
$\theta _{\mathrm {fl}} \in \Theta _\circlearrowleft $
and
![]() $\theta _{\mathrm {extra}} \in \Theta _\circlearrowright $
. Therefore, the set
$\theta _{\mathrm {extra}} \in \Theta _\circlearrowright $
. Therefore, the set
![]() $(\theta _{\mathrm {fl}}, \theta _{\mathrm {extra}}) \cap \{ \theta _+ - \pi , \theta _-, \theta _+, \theta _-+\pi , \theta _++\pi \}$
has an odd number of elements. If there are three elements, we get
$(\theta _{\mathrm {fl}}, \theta _{\mathrm {extra}}) \cap \{ \theta _+ - \pi , \theta _-, \theta _+, \theta _-+\pi , \theta _++\pi \}$
has an odd number of elements. If there are three elements, we get
![]() $\theta _{\mathrm {extra}} - \theta _{\mathrm {fl}}> \pi $
, which contradicts Lemma A.25, so there is only one element. If that element is
$\theta _{\mathrm {extra}} - \theta _{\mathrm {fl}}> \pi $
, which contradicts Lemma A.25, so there is only one element. If that element is
![]() $\theta _-$
or
$\theta _-$
or
![]() $\theta _- + \pi $
, we would get that
$\theta _- + \pi $
, we would get that
![]() $\theta _{\mathrm {fl}} \in \Theta _\circlearrowright $
and
$\theta _{\mathrm {fl}} \in \Theta _\circlearrowright $
and
![]() $\theta _{\mathrm {extra}} \in \Theta _\circlearrowleft $
, which is also a contradiction. Thus,
$\theta _{\mathrm {extra}} \in \Theta _\circlearrowleft $
, which is also a contradiction. Thus,
![]() $\theta _-, \theta _- + \pi \notin (\theta _{\mathrm {fl}}, \theta _{\mathrm {extra}})$
.
$\theta _-, \theta _- + \pi \notin (\theta _{\mathrm {fl}}, \theta _{\mathrm {extra}})$
.
4 Right of
 $P_s$
$P_s$
This section is dedicated to showing properties of the solution right of
![]() $P_s$
in the phase portrait, which in the self-similar radial variable
$P_s$
in the phase portrait, which in the self-similar radial variable
![]() $\xi $
corresponds to the region
$\xi $
corresponds to the region
![]() $\xi <0$
, or equivalently, the region within acoustic cone of the singularity. In particular, the main goal of this section is to prove the following proposition.
$\xi <0$
, or equivalently, the region within acoustic cone of the singularity. In particular, the main goal of this section is to prove the following proposition.
Proposition 4.1. Let us consider the smooth solution of Proposition 2.3 for
![]() $\xi < 0$
. Let either
$\xi < 0$
. Let either
![]() $n =3$
for
$n =3$
for
![]() $\gamma>1$
or
$\gamma>1$
or
![]() $n \in \mathbb {N}$
odd, and sufficiently large for
$n \in \mathbb {N}$
odd, and sufficiently large for
![]() $\gamma = 7/5$
. Then, there exist
$\gamma = 7/5$
. Then, there exist
![]() $r_u \in (r_{n}, r_{n+1})$
such that the smooth solution
$r_u \in (r_{n}, r_{n+1})$
such that the smooth solution
![]() $(W^{(r_u)}(\xi ), Z^{(r_u) }(\xi ))$
lies in
$(W^{(r_u)}(\xi ), Z^{(r_u) }(\xi ))$
lies in
![]() $\Omega _1^{(r_u)}$
and
$\Omega _1^{(r_u)}$
and
![]() $r_d \in (r_{n}, r_{n+1})$
such that the smooth solution lies in
$r_d \in (r_{n}, r_{n+1})$
such that the smooth solution lies in
![]() $\Omega _2^{(r_d)}$
(where here,
$\Omega _2^{(r_d)}$
(where here,
![]() $\Omega _1^{(r)}$
and
$\Omega _1^{(r)}$
and
![]() $\Omega _2^{(r)}$
are defined in Remark 1.7).
$\Omega _2^{(r)}$
are defined in Remark 1.7).
The strategy for the proof of this proposition will be similar to the proof of Proposition 3.1. We will consider a near-right barrier that matches up to the n-th (or
![]() $(n+1)$
-th) coefficients with the smooth solution, and we will also consider a far-right barrier that intersects the near-right barrier within the interval of its validity. This approach is similar to the one employed on the left, since in both cases, we need to use a local barrier that matches up to n-th order with the smooth solution in order to capture the singular behavior of
$(n+1)$
-th) coefficients with the smooth solution, and we will also consider a far-right barrier that intersects the near-right barrier within the interval of its validity. This approach is similar to the one employed on the left, since in both cases, we need to use a local barrier that matches up to n-th order with the smooth solution in order to capture the singular behavior of
![]() $Z_n$
. As in Section 3, we also concatenate this barrier with a global barrier (the far-right barrier) that matches better the behavior of the solution far from
$Z_n$
. As in Section 3, we also concatenate this barrier with a global barrier (the far-right barrier) that matches better the behavior of the solution far from
![]() $P_s$
. The main difference with respect to Section 3 is that here, we will work asymptotically as
$P_s$
. The main difference with respect to Section 3 is that here, we will work asymptotically as
![]() $r \rightarrow r_n^+$
or
$r \rightarrow r_n^+$
or
![]() $r \rightarrow r_{n+1}^-$
.
$r \rightarrow r_{n+1}^-$
.
We consider the near-right barrier
 $$ \begin{align*} \begin{aligned} b^{\mathrm{nr}}_{n, W} (t) &= \sum_{i=0}^n \frac{1}{i!} W_i (-t)^i, \\ b^{\mathrm{nr}}_{n, Z} (t) &= \sum_{i=0}^n \frac{1}{i!} Z_i (-t)^i + \frac{\beta_n}{(n+1)!}Z_{n} (-t)^{n+1}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} b^{\mathrm{nr}}_{n, W} (t) &= \sum_{i=0}^n \frac{1}{i!} W_i (-t)^i, \\ b^{\mathrm{nr}}_{n, Z} (t) &= \sum_{i=0}^n \frac{1}{i!} Z_i (-t)^i + \frac{\beta_n}{(n+1)!}Z_{n} (-t)^{n+1}, \end{aligned} \end{align*} $$
where
![]() $\beta _n$
is sufficiently large. We will always assume that
$\beta _n$
is sufficiently large. We will always assume that
![]() $r-r_n$
(or
$r-r_n$
(or
![]() $r_{n+1}-r$
) is sufficiently small depending on
$r_{n+1}-r$
) is sufficiently small depending on
![]() $\beta _n$
(or
$\beta _n$
(or
![]() $\beta _{n+1}$
). We will use the standard big-O notation whenever the implicit constant does not depend on
$\beta _{n+1}$
). We will use the standard big-O notation whenever the implicit constant does not depend on
![]() $\beta _n$
and whenever we use
$\beta _n$
and whenever we use
![]() $O_{\beta _n}$
, the implicit constant is allowed to depend on
$O_{\beta _n}$
, the implicit constant is allowed to depend on
![]() $\beta _n$
.
$\beta _n$
.
We also define the curve
![]() $b^{\mathrm {nr}}_n (t) = (b^{\mathrm {nr}}_{n, W}(t), b^{\mathrm {nr}}_{n, Z}(t))$
and consider the
$b^{\mathrm {nr}}_n (t) = (b^{\mathrm {nr}}_{n, W}(t), b^{\mathrm {nr}}_{n, Z}(t))$
and consider the
![]() $(4n+3)$
-th degree polynomial
$(4n+3)$
-th degree polynomial
As usual, the sign of
![]() $P^{\mathrm {nr}}_n(t)$
indicates the direction of the normal component of the field in this barrier. We have the following result for this sign.
$P^{\mathrm {nr}}_n(t)$
indicates the direction of the normal component of the field in this barrier. We have the following result for this sign.
Proposition 4.2. Let either
![]() $n \in \{ 3, 4 \}$
for
$n \in \{ 3, 4 \}$
for
![]() $\gamma>1$
or
$\gamma>1$
or
![]() $n \in \mathbb {N}$
sufficiently large for
$n \in \mathbb {N}$
sufficiently large for
![]() $\gamma = 7/5$
. There exist constants
$\gamma = 7/5$
. There exist constants
![]() $\varepsilon $
, c such that
$\varepsilon $
, c such that
-
• For n even and
 $r\in (r_{n} - \varepsilon , r_{n})$
, we have
$r\in (r_{n} - \varepsilon , r_{n})$
, we have
 $P^{\mathrm {nr}}_{n} (t) < 0$
for all
$P^{\mathrm {nr}}_{n} (t) < 0$
for all
 $t\in (0, c(n-k)^{1/n} )$
.
$t\in (0, c(n-k)^{1/n} )$
. -
• For n odd,
 $\beta _{n}$
sufficiently large and
$\beta _{n}$
sufficiently large and
 $r\in (r_{n}, r_{n}+\varepsilon )$
, we have
$r\in (r_{n}, r_{n}+\varepsilon )$
, we have
 $P^{\mathrm {nr}}_{n} (t)> 0$
for all
$P^{\mathrm {nr}}_{n} (t)> 0$
for all
 $t\in (0, c(k-n)^{1/(n-2)} \beta _{n})$
.
$t\in (0, c(k-n)^{1/(n-2)} \beta _{n})$
.
Proof. First, note that
![]() $P^{\mathrm {nr}}_n (t)$
is a multiple of
$P^{\mathrm {nr}}_n (t)$
is a multiple of
![]() $t^{n+1}$
since
$t^{n+1}$
since
![]() $b^{\mathrm {nr}}_n(t)$
matches the smooth solution up to n-th order. By Corollary 2.4, the only terms in
$b^{\mathrm {nr}}_n(t)$
matches the smooth solution up to n-th order. By Corollary 2.4, the only terms in
![]() $b^{\mathrm {nr}}_n (t)$
which are not
$b^{\mathrm {nr}}_n (t)$
which are not
![]() $O(1)$
in a neighborhood of
$O(1)$
in a neighborhood of
![]() $r_n$
are
$r_n$
are
![]() $\frac {1}{n!} Z_n (-t)^n$
and
$\frac {1}{n!} Z_n (-t)^n$
and
![]() $\frac {1}{(n+1)!} Z_n \beta _n (-t)^{n+1}$
, which are
$\frac {1}{(n+1)!} Z_n \beta _n (-t)^{n+1}$
, which are
![]() $O_{\beta _n}\left ( \frac {1}{k-n} \right )$
. Summing the terms, the asymptotics for
$O_{\beta _n}\left ( \frac {1}{k-n} \right )$
. Summing the terms, the asymptotics for
![]() $P^{\mathrm {nr}}_n (t)$
are given by
$P^{\mathrm {nr}}_n (t)$
are given by
 $$ \begin{align} \begin{aligned} P^{\mathrm{nr}}_n (t) &= C_1 Z_n t^{n+1} + C_2 Z_n^2 t^{2n-1} \\ &\qquad + O_{\beta_n}(t^{n+1} ) + O_{\beta_n}\left( \frac{t^{n+2}}{k-n} \right) + O_{\beta_n}\left( \frac{t^{2n}}{(k-n)^2 } \right) + O_{\beta_n}\left( \frac{t^{3n-1}}{(k-n)^3 } \right) + O_{\beta_n}\left( \frac{t^{4n-1}}{(k-n)^4 } \right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} P^{\mathrm{nr}}_n (t) &= C_1 Z_n t^{n+1} + C_2 Z_n^2 t^{2n-1} \\ &\qquad + O_{\beta_n}(t^{n+1} ) + O_{\beta_n}\left( \frac{t^{n+2}}{k-n} \right) + O_{\beta_n}\left( \frac{t^{2n}}{(k-n)^2 } \right) + O_{\beta_n}\left( \frac{t^{3n-1}}{(k-n)^3 } \right) + O_{\beta_n}\left( \frac{t^{4n-1}}{(k-n)^4 } \right), \end{aligned} \end{align} $$
for small t and
![]() $|k-n|$
. In order to calculate
$|k-n|$
. In order to calculate
![]() $C_1$
, we take
$C_1$
, we take
![]() $n+1$
derivatives in
$n+1$
derivatives in
![]() $P^{\mathrm {nr}}_n (t)$
and look for the terms with a factor
$P^{\mathrm {nr}}_n (t)$
and look for the terms with a factor
![]() $Z_n$
(as the rest of terms will be
$Z_n$
(as the rest of terms will be
![]() $O(1)$
, thus contributing to
$O(1)$
, thus contributing to
![]() $O(t^{n+1})$
in (4.2)). Note that
$O(t^{n+1})$
in (4.2)). Note that
![]() $P^{\mathrm {nl}}_n(t)$
already involves one derivative, so we will have terms with
$P^{\mathrm {nl}}_n(t)$
already involves one derivative, so we will have terms with
![]() $n+2$
derivatives in total. At
$n+2$
derivatives in total. At
![]() $t=0$
, we have
$t=0$
, we have
 $$ \begin{align*} (-1)^{n+2} \partial_t^{n+1} P^{\mathrm{nr}}_n &= (n+1)\beta_n Z_n (-\partial_t) D_Z (b^{\mathrm{nr}}_{n}) N_W (b^{\mathrm{nr}}_n) + Z_1 (-\partial_t)^{n+1} D_Z (b^{\mathrm{nr}}_n ) N_W (b^{\mathrm{nr}}_n )\\& \quad - W_1 (-\partial_t)^{n+1} N_Z (b^{\mathrm{nr}}_n ) D_W (b^{\mathrm{nr}}_n ) + O(|Z_n|) .\end{align*} $$
$$ \begin{align*} (-1)^{n+2} \partial_t^{n+1} P^{\mathrm{nr}}_n &= (n+1)\beta_n Z_n (-\partial_t) D_Z (b^{\mathrm{nr}}_{n}) N_W (b^{\mathrm{nr}}_n) + Z_1 (-\partial_t)^{n+1} D_Z (b^{\mathrm{nr}}_n ) N_W (b^{\mathrm{nr}}_n )\\& \quad - W_1 (-\partial_t)^{n+1} N_Z (b^{\mathrm{nr}}_n ) D_W (b^{\mathrm{nr}}_n ) + O(|Z_n|) .\end{align*} $$
Collecting the terms involving
![]() $Z_n\beta _n$
, we define
$Z_n\beta _n$
, we define
 $$ \begin{align} \begin{aligned} C_3 &= -(n+1)D_{Z, 1} N_W (P_s) - Z_1 \partial_Z D_Z (P_s) N_W (P_s) + W_1 \partial_Z N_Z (P_s) D_W (P_s) \\ &= N_W(P_s) \left( -(n+1)D_{Z, 1} - Z_1 \partial_Z D_Z (P_s) + \partial_Z N_Z (P_s)\right), \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} C_3 &= -(n+1)D_{Z, 1} N_W (P_s) - Z_1 \partial_Z D_Z (P_s) N_W (P_s) + W_1 \partial_Z N_Z (P_s) D_W (P_s) \\ &= N_W(P_s) \left( -(n+1)D_{Z, 1} - Z_1 \partial_Z D_Z (P_s) + \partial_Z N_Z (P_s)\right), \end{aligned}\end{align} $$
so that we obtain
As
![]() $\left |r_n-r\right |\leq \varepsilon $
and we are taking
$\left |r_n-r\right |\leq \varepsilon $
and we are taking
![]() $\varepsilon $
small, we may evaluate the sign of
$\varepsilon $
small, we may evaluate the sign of
![]() $C_3$
by looking at its sign at
$C_3$
by looking at its sign at
![]() $r=r_n$
, which by continuity will remain the same sign in a neighborhood of
$r=r_n$
, which by continuity will remain the same sign in a neighborhood of
![]() $k=n$
. Let us recall from Lemma 2.1 that
$k=n$
. Let us recall from Lemma 2.1 that
![]() $k = \frac {\check D_{Z, 1}}{D_{Z, 1}}$
, where
$k = \frac {\check D_{Z, 1}}{D_{Z, 1}}$
, where
![]() $\check D_{Z, 1} = \nabla D_Z (P_s) \cdot (W_1, \check Z_1)$
and
$\check D_{Z, 1} = \nabla D_Z (P_s) \cdot (W_1, \check Z_1)$
and
![]() $\check Z_1$
was defined in (2.1). Thus, using (4.3) at
$\check Z_1$
was defined in (2.1). Thus, using (4.3) at
![]() $k = n = \frac {\check D_{Z, 1}}{D_{Z, 1}}$
yields
$k = n = \frac {\check D_{Z, 1}}{D_{Z, 1}}$
yields
 $$ \begin{align} \frac{C_3}{N_{W, 0}} &= - \check D_{Z, 1} - D_{Z, 1} - Z_1 \partial_Z D_Z(P_s) + \partial_Z N_Z (P_s)\nonumber \\ &= -D_{Z, 1} - \partial_W D_Z (P_s) W_1 - \partial_Z D_Z (P_s) \left( \check Z_1 + Z_1 \right) + \partial_Z N_Z(P_s). \end{align} $$
$$ \begin{align} \frac{C_3}{N_{W, 0}} &= - \check D_{Z, 1} - D_{Z, 1} - Z_1 \partial_Z D_Z(P_s) + \partial_Z N_Z (P_s)\nonumber \\ &= -D_{Z, 1} - \partial_W D_Z (P_s) W_1 - \partial_Z D_Z (P_s) \left( \check Z_1 + Z_1 \right) + \partial_Z N_Z(P_s). \end{align} $$
Note
![]() $Z_1, \check Z_1$
are the two solutions of the second-degree equation
$Z_1, \check Z_1$
are the two solutions of the second-degree equation
and hence,
Substituting this expression into (4.4) and canceling terms, we deduce
Using Lemmas A.26 and A.11, we conclude that
![]() $C_3> 0$
for
$C_3> 0$
for
![]() $k=n$
, and thus, it is positive for r in a sufficiently small neighborhood of
$k=n$
, and thus, it is positive for r in a sufficiently small neighborhood of
![]() $r_n$
.
$r_n$
.
We have that
 $$ \begin{align*} C_1 = \frac{1}{(n+1)!Z_n}(-\partial_t)^{n+1} P^{\mathrm{nr}}_n (0) \geq \frac{(-1)^{n+1}}{(n+1)!} \left( \beta_n C_3 + O(1)\right). \end{align*} $$
$$ \begin{align*} C_1 = \frac{1}{(n+1)!Z_n}(-\partial_t)^{n+1} P^{\mathrm{nr}}_n (0) \geq \frac{(-1)^{n+1}}{(n+1)!} \left( \beta_n C_3 + O(1)\right). \end{align*} $$
Therefore, choosing
![]() $\beta _n$
sufficiently large, r close enough to
$\beta _n$
sufficiently large, r close enough to
![]() $r_n$
and using that
$r_n$
and using that
![]() $C_3> 0$
,
$C_3> 0$
,
We calculate the term
![]() $C_2$
in (4.2). Taking
$C_2$
in (4.2). Taking
![]() $2n-1$
derivatives in
$2n-1$
derivatives in
![]() $P^{\mathrm {nr}}_n (t)$
and looking for terms with
$P^{\mathrm {nr}}_n (t)$
and looking for terms with
![]() $Z_n^2$
, we obtain
$Z_n^2$
, we obtain
 $$ \begin{align*} (-1)^{2n} \partial_t ^{2n-1} P^{\mathrm{nr}}_n (t) = \binom{2n-1}{n} Z_n \partial_t^n D_Z (b^{\mathrm{nr}}_n ) N_W (P_s) + O_{\beta_n}\left( Z_n \right) . \end{align*} $$
$$ \begin{align*} (-1)^{2n} \partial_t ^{2n-1} P^{\mathrm{nr}}_n (t) = \binom{2n-1}{n} Z_n \partial_t^n D_Z (b^{\mathrm{nr}}_n ) N_W (P_s) + O_{\beta_n}\left( Z_n \right) . \end{align*} $$
Therefore,
 $$ \begin{align} C_2 = \frac{1}{(2n-1)!} \binom{2n-1}{n} \partial_Z D_Z (P_s) N_W (P_s) = \frac{1+\alpha}{2} \frac{1}{n!(n-1)!} N_W(P_s) < 0, \end{align} $$
$$ \begin{align} C_2 = \frac{1}{(2n-1)!} \binom{2n-1}{n} \partial_Z D_Z (P_s) N_W (P_s) = \frac{1+\alpha}{2} \frac{1}{n!(n-1)!} N_W(P_s) < 0, \end{align} $$
where the sign is due to Lemma A.26.
Now that we have analyzed
![]() $C_1$
and
$C_1$
and
![]() $C_2$
in (4.5) and (4.6); let us go back to (4.2) and consider the cases of n odd and even separately.
$C_2$
in (4.5) and (4.6); let us go back to (4.2) and consider the cases of n odd and even separately.
Odd n case. We have that
by (4.5) and (4.6). Moreover, we have that for odd n and r sufficiently close to
![]() $r_n$
from above,
$r_n$
from above,
![]() $Z_n> 0$
(Corollary 5.8 and Lemma A.31); moreover, assuming in addition that
$Z_n> 0$
(Corollary 5.8 and Lemma A.31); moreover, assuming in addition that
![]() $\beta _n$
is sufficiently large, and
$\beta _n$
is sufficiently large, and
![]() $t^{n-2} \leq c^{n-2} (k-n) \beta _n$
, the equation (4.2) yields
$t^{n-2} \leq c^{n-2} (k-n) \beta _n$
, the equation (4.2) yields
 $$ \begin{align*} P^{\mathrm{nr}}_n(t)> \frac{1}{2} C_1 Z_n t^{n+1} + C_2 Z_n^2 t^{2n-1} > t^{n+1} Z_n \beta_n \left( \frac{C_3}{4(n+1)!} - c^{n-2} |C_2| Z_n (k-n) \right). \end{align*} $$
$$ \begin{align*} P^{\mathrm{nr}}_n(t)> \frac{1}{2} C_1 Z_n t^{n+1} + C_2 Z_n^2 t^{2n-1} > t^{n+1} Z_n \beta_n \left( \frac{C_3}{4(n+1)!} - c^{n-2} |C_2| Z_n (k-n) \right). \end{align*} $$
Hence, since
![]() $Z_n (k-n) = O(1)$
, and we may choose c sufficiently small, we obtain that
$Z_n (k-n) = O(1)$
, and we may choose c sufficiently small, we obtain that
![]() $ P^{\mathrm {nr}}_n(t)>0$
.
$ P^{\mathrm {nr}}_n(t)>0$
.
Even n case. For this case, we obtain that for
![]() $\beta _n$
sufficiently large,
$\beta _n$
sufficiently large,
by (4.5) and (4.6). Moreover, for n even and r close to
![]() $r_n$
from below, we have that
$r_n$
from below, we have that
![]() $Z_n> 0$
(Lemma A.31 and Corollary 5.8). Therefore, taking
$Z_n> 0$
(Lemma A.31 and Corollary 5.8). Therefore, taking
![]() $\beta _n$
sufficiently large, r close enough from below to
$\beta _n$
sufficiently large, r close enough from below to
![]() $r_n$
and
$r_n$
and
![]() $t \leq c(n-k)^{1/n}$
, (4.2) yields
$t \leq c(n-k)^{1/n}$
, (4.2) yields
 $$ \begin{align*} P^{\mathrm{nr}}_n(t) &< \frac{1}{2}C_2 Z_n^2 t^{2n-1} + O_{\beta_n}\left( \frac{t^{2n}}{(n-k)^2} + \frac{t^{3n-1}}{(n-k)^3} + \frac{t^{4n-1}}{(n-k)^4} \right) \\ &= Z_n^2 t^{2n-1} \left( \frac{C_2}{2} + O_{\beta_n} \left( c(n-k)^{1/n} +c^n+c^{2n}\right) \right), \end{align*} $$
$$ \begin{align*} P^{\mathrm{nr}}_n(t) &< \frac{1}{2}C_2 Z_n^2 t^{2n-1} + O_{\beta_n}\left( \frac{t^{2n}}{(n-k)^2} + \frac{t^{3n-1}}{(n-k)^3} + \frac{t^{4n-1}}{(n-k)^4} \right) \\ &= Z_n^2 t^{2n-1} \left( \frac{C_2}{2} + O_{\beta_n} \left( c(n-k)^{1/n} +c^n+c^{2n}\right) \right), \end{align*} $$
which is negative as long as c is chosen small enough since
![]() $C_2 < 0$
.
$C_2 < 0$
.
Lemma 4.3. Let
![]() $n=3$
with
$n=3$
with
![]() $\gamma> 1$
or
$\gamma> 1$
or
![]() $n \in \mathbb {N}$
odd and sufficiently large for
$n \in \mathbb {N}$
odd and sufficiently large for
![]() $\gamma = 7/5$
. There exists
$\gamma = 7/5$
. There exists
![]() $\varepsilon> 0$
sufficiently small such that the following holds. For every
$\varepsilon> 0$
sufficiently small such that the following holds. For every
![]() $r\in (r_{n+1}-\varepsilon , r_{n})$
, we have a value
$r\in (r_{n+1}-\varepsilon , r_{n})$
, we have a value
![]() $ t_D>0$
with
$ t_D>0$
with
![]() $D_Z (b^{\mathrm {nr}}_{n+1} (t )) < 0$
for
$D_Z (b^{\mathrm {nr}}_{n+1} (t )) < 0$
for
![]() $t \in (0, t_D)$
and
$t \in (0, t_D)$
and
![]() $D_Z (b^{\mathrm {nr}}_{n+1} (t_D )) = 0$
. Moreover, we have
$D_Z (b^{\mathrm {nr}}_{n+1} (t_D )) = 0$
. Moreover, we have
![]() $t_D \lesssim (n+1-k)^{1/n}$
as
$t_D \lesssim (n+1-k)^{1/n}$
as
![]() $r \rightarrow r_{n+1}^-$
.
$r \rightarrow r_{n+1}^-$
.
Proof. We have that
![]() $D_Z (b^{\mathrm {nr}}_{n+1} (t))$
is a
$D_Z (b^{\mathrm {nr}}_{n+1} (t))$
is a
![]() $(n+2)$
-th degree polynomial, which is multiple of t since
$(n+2)$
-th degree polynomial, which is multiple of t since
Moreover, we have that at
![]() $t=0$
,
$t=0$
,
 $$ \begin{align} \begin{cases} \partial_t^i D_Z (b^{\mathrm{nr}}_{n+1} (t)) = (-1)^i \nabla D_Z (P_s) (W_{n+1}, Z_{n+1}), \qquad \text{ for } 1\leq i \leq n+1, \\ \partial_t^{n+2}D_Z (b^{\mathrm{nr}}_{n+1} (t)) = (-1) \nabla D_Z (P_s) (0, Z_{n+1} \beta_{n+1} ). \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \partial_t^i D_Z (b^{\mathrm{nr}}_{n+1} (t)) = (-1)^i \nabla D_Z (P_s) (W_{n+1}, Z_{n+1}), \qquad \text{ for } 1\leq i \leq n+1, \\ \partial_t^{n+2}D_Z (b^{\mathrm{nr}}_{n+1} (t)) = (-1) \nabla D_Z (P_s) (0, Z_{n+1} \beta_{n+1} ). \end{cases} \end{align} $$
Corollary 2.4 tells us that all the coefficients of
![]() $D_Z(b^{\mathrm {nr}}_{n+1}(t))$
are
$D_Z(b^{\mathrm {nr}}_{n+1}(t))$
are
![]() $O(1)$
for r in a small neighborhood of
$O(1)$
for r in a small neighborhood of
![]() $r_{n+1}$
, except for the
$r_{n+1}$
, except for the
![]() $(n+1)$
-th and
$(n+1)$
-th and
![]() $(n+2)$
-th coefficients, which are
$(n+2)$
-th coefficients, which are
![]() $O_{\beta _{n+1}} \left ( \frac {1}{n+1-k} \right )$
. We can thus write
$O_{\beta _{n+1}} \left ( \frac {1}{n+1-k} \right )$
. We can thus write
 $$ \begin{align} D_Z (b^{\mathrm{nr}}_{n+1} (t)) = -D_{Z, 1}t + \frac{\partial_Z D_Z (P_s) Z_{n+1} t^{n+1}}{(n+1)!} + O(t^2) + O \left( \frac{t^{n+2} \beta_{n+1}}{n+1-k} \right). \end{align} $$
$$ \begin{align} D_Z (b^{\mathrm{nr}}_{n+1} (t)) = -D_{Z, 1}t + \frac{\partial_Z D_Z (P_s) Z_{n+1} t^{n+1}}{(n+1)!} + O(t^2) + O \left( \frac{t^{n+2} \beta_{n+1}}{n+1-k} \right). \end{align} $$
We have that
![]() $-D_{Z, 1} < 0$
as a consequence of Lemma A.11 and Lemma A.7 and
$-D_{Z, 1} < 0$
as a consequence of Lemma A.11 and Lemma A.7 and
by Corollary 5.8 and Lemma A.31. Therefore, the polynomial
![]() $D_Z (b^{\mathrm {nr}}_{n+1} (t))$
is initially negative.
$D_Z (b^{\mathrm {nr}}_{n+1} (t))$
is initially negative.
Taking
![]() $t=C (n+1-k)^{1/n}$
and using Corollary 2.4, we can choose C sufficiently large so that
$t=C (n+1-k)^{1/n}$
and using Corollary 2.4, we can choose C sufficiently large so that
![]() $|D_{Z, 1} t| \leq \frac {1}{3} \left | \frac {\partial _Z D_Z (P_s) Z_{n+1} t^{n+1} }{(n+1)!} \right |$
for
$|D_{Z, 1} t| \leq \frac {1}{3} \left | \frac {\partial _Z D_Z (P_s) Z_{n+1} t^{n+1} }{(n+1)!} \right |$
for
![]() $r \in (r_{n+1}-\varepsilon , r_{n+1})$
. This constant C is allowed to depend on n. We can also choose
$r \in (r_{n+1}-\varepsilon , r_{n+1})$
. This constant C is allowed to depend on n. We can also choose
![]() $\varepsilon $
sufficiently small so that the error
$\varepsilon $
sufficiently small so that the error
![]() $O(t^2) + O(t^{n+2}\beta _{n+1} /(n+1-k))$
in (4.8) is smaller than
$O(t^2) + O(t^{n+2}\beta _{n+1} /(n+1-k))$
in (4.8) is smaller than
![]() $\frac {1}{3} \left | \frac {\partial _Z D_Z (P_s) Z_{n+1} t^{n+1} }{(n+1)!} \right |$
. With those choices, using (4.8) yields
$\frac {1}{3} \left | \frac {\partial _Z D_Z (P_s) Z_{n+1} t^{n+1} }{(n+1)!} \right |$
. With those choices, using (4.8) yields
 $$ \begin{align*} D_Z (b^{\mathrm{nr}}_{n+1} (t)) \geq \frac{\partial_Z D_Z (P_s) Z_{n+1} t^{n+1}}{(n+1)!} - \frac{2}{3} \left| \frac{\partial_Z D_Z (P_s) Z_{n+1} t^{n+1}}{(n+1)!} \right|> 0 \end{align*} $$
$$ \begin{align*} D_Z (b^{\mathrm{nr}}_{n+1} (t)) \geq \frac{\partial_Z D_Z (P_s) Z_{n+1} t^{n+1}}{(n+1)!} - \frac{2}{3} \left| \frac{\partial_Z D_Z (P_s) Z_{n+1} t^{n+1}}{(n+1)!} \right|> 0 \end{align*} $$
because
![]() $Z_{n+1}> 0$
. The proof of
$Z_{n+1}> 0$
. The proof of
![]() $Z_{n+1}> 0$
is in Lemma A.31 for
$Z_{n+1}> 0$
is in Lemma A.31 for
![]() $n = 3$
and will be done in Corollary 5.8 for the case
$n = 3$
and will be done in Corollary 5.8 for the case
![]() $\gamma = 7/5$
.
$\gamma = 7/5$
.
As
![]() $D_Z(b^{\mathrm {nr}}_{n+1}(t))$
is initially negative and is positive at
$D_Z(b^{\mathrm {nr}}_{n+1}(t))$
is initially negative and is positive at
![]() $t=C (n+1-k)^{1/n}$
, by continuity there exists a first time
$t=C (n+1-k)^{1/n}$
, by continuity there exists a first time
![]() $t_D \in (0, C(n+1-k)^{1/n} )$
at which
$t_D \in (0, C(n+1-k)^{1/n} )$
at which
![]() $D_Z (b^{\mathrm {nr}}_{n+1} (t_D)) = 0$
and
$D_Z (b^{\mathrm {nr}}_{n+1} (t_D)) = 0$
and
![]() $D_Z(b^{\mathrm {nr}}_{n+1} (t))$
is negative up to
$D_Z(b^{\mathrm {nr}}_{n+1} (t))$
is negative up to
![]() $t_D$
.
$t_D$
.
Lemma 4.4. Let either
![]() $\gamma \in (1, +\infty )$
with
$\gamma \in (1, +\infty )$
with
![]() $n=3$
or
$n=3$
or
![]() $\gamma = 7/5$
with n a sufficiently large odd number. There exist
$\gamma = 7/5$
with n a sufficiently large odd number. There exist
![]() $\beta _{n+1}, \varepsilon> 0$
such that for every
$\beta _{n+1}, \varepsilon> 0$
such that for every
![]() $r \in (r_{n+1} - \varepsilon , r_{n+1} )$
, the smooth solution
$r \in (r_{n+1} - \varepsilon , r_{n+1} )$
, the smooth solution
![]() $(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
is above the near-right barrier
$(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
is above the near-right barrier
![]() $b^{\mathrm {nr}}_{n+1} (t)$
for
$b^{\mathrm {nr}}_{n+1} (t)$
for
![]() $\xi < 0$
small enough in absolute value.
$\xi < 0$
small enough in absolute value.
Proof. First note that by definition, the Taylor expansion of
![]() $b^{\mathrm {nr}}_{n+1} (-t)$
agrees with the smooth solution up to order
$b^{\mathrm {nr}}_{n+1} (-t)$
agrees with the smooth solution up to order
![]() $n+1$
at
$n+1$
at
![]() $P_s$
. In particular, we have
$P_s$
. In particular, we have
Both
![]() $b^{\mathrm {nr}}_{n+1}(t)$
and
$b^{\mathrm {nr}}_{n+1}(t)$
and
![]() $(W^{(r)}(-t), Z^{(r)}(-t))$
start with slope
$(W^{(r)}(-t), Z^{(r)}(-t))$
start with slope
![]() $(-W_1, -Z_1)$
. Then, in order for
$(-W_1, -Z_1)$
. Then, in order for
![]() $b^{\mathrm {nr}}_{n+1} (t)$
to begin below the smooth solution, it suffices to check the geometric condition
$b^{\mathrm {nr}}_{n+1} (t)$
to begin below the smooth solution, it suffices to check the geometric condition
or equivalently,
Note that both sides are of order
![]() $\frac {1}{|k-n-1|}$
by Corollary 2.4 and
$\frac {1}{|k-n-1|}$
by Corollary 2.4 and
![]() $n \geq 3$
. The case
$n \geq 3$
. The case
![]() $n = 3$
follows from the fact that
$n = 3$
follows from the fact that
![]() $Z_{4}> 0$
(Lemma A.31) and
$Z_{4}> 0$
(Lemma A.31) and
![]() $W_1 < 0$
(Lemma A.26), taking
$W_1 < 0$
(Lemma A.26), taking
![]() $\beta _4$
sufficiently large. The case
$\beta _4$
sufficiently large. The case
![]() $\gamma = 7/5$
with n odd and sufficiently large would follow as long as we have
$\gamma = 7/5$
with n odd and sufficiently large would follow as long as we have
![]() $Z_{n+1}> 0$
, since
$Z_{n+1}> 0$
, since
![]() $W_1<0$
is guaranteed by Lemma A.7. The proof that
$W_1<0$
is guaranteed by Lemma A.7. The proof that
![]() $Z_{n+1}> 0$
will be delayed to Section 5 – specifically, this will be a consequence of Corollary 5.8).
$Z_{n+1}> 0$
will be delayed to Section 5 – specifically, this will be a consequence of Corollary 5.8).
We define a far-right barrier by
We define the coefficient
![]() $F_0 = \frac {-4(r-1)}{3(\gamma - 1)} = 2w_1$
, where
$F_0 = \frac {-4(r-1)}{3(\gamma - 1)} = 2w_1$
, where
![]() $w_1$
is given in Proposition 2.5, and we set
$w_1$
is given in Proposition 2.5, and we set
![]() $F_2 = 1/2$
. The coefficient
$F_2 = 1/2$
. The coefficient
![]() $F_1$
will be fixed later (given by (4.10)).
$F_1$
will be fixed later (given by (4.10)).
It is clear that
![]() $B^{\mathrm {fr}}(W_0, Z_0) = 0$
, and thus, the curve passes through
$B^{\mathrm {fr}}(W_0, Z_0) = 0$
, and thus, the curve passes through
![]() $P_s$
. As the second-degree summand has a factor
$P_s$
. As the second-degree summand has a factor
![]() $W+Z-F_0$
, it is clear that
$W+Z-F_0$
, it is clear that
![]() $B^{\mathrm {fr}}(W, Z) = 0$
has an asymptotic line parallel to the direction of
$B^{\mathrm {fr}}(W, Z) = 0$
has an asymptotic line parallel to the direction of
![]() $P_0$
. The value of
$P_0$
. The value of
![]() $F_0$
is the asymptotic value of
$F_0$
is the asymptotic value of
![]() $W+Z$
for the trajectory matching at
$W+Z$
for the trajectory matching at
![]() $P_0$
(this corresponds to matching another order at
$P_0$
(this corresponds to matching another order at
![]() $P_0$
). The value of
$P_0$
). The value of
![]() $F_1$
is chosen so that the slope of
$F_1$
is chosen so that the slope of
![]() $B^{\mathrm { fr}}(W,Z) = 0$
at
$B^{\mathrm { fr}}(W,Z) = 0$
at
![]() $P_s$
matches that of the smooth solution; that is,
$P_s$
matches that of the smooth solution; that is,
![]() $\nabla B^{\mathrm {fr}} (P_s) (W_1, Z_1) = 0$
. Therefore,
$\nabla B^{\mathrm {fr}} (P_s) (W_1, Z_1) = 0$
. Therefore,
which yields
In order to parametrize the curve
![]() $B^{\mathrm {fr}} = 0$
, we solve the system
$B^{\mathrm {fr}} = 0$
, we solve the system
 $$ \begin{align*} &\left( b^{\mathrm{fr}}_W(s) - W_0 \right) + \left( b^{\mathrm{fr}}_Z(s) - Z_0 \right) = s,\\ &B^{\mathrm{fr}} (b^{\mathrm{fr}}_W (s), b^{\mathrm{fr}}_Z(s) ) = \left( (b^{\mathrm{fr}}_W(s) - W_0) - F_2 (b^{\mathrm{fr}}_Z(s) - Z_0) \right) (s+W_0+Z_0-F_0) - F_1 s = 0\, \end{align*} $$
$$ \begin{align*} &\left( b^{\mathrm{fr}}_W(s) - W_0 \right) + \left( b^{\mathrm{fr}}_Z(s) - Z_0 \right) = s,\\ &B^{\mathrm{fr}} (b^{\mathrm{fr}}_W (s), b^{\mathrm{fr}}_Z(s) ) = \left( (b^{\mathrm{fr}}_W(s) - W_0) - F_2 (b^{\mathrm{fr}}_Z(s) - Z_0) \right) (s+W_0+Z_0-F_0) - F_1 s = 0\, \end{align*} $$
for s ranging from
![]() $0$
to
$0$
to
![]() $s^{\mathrm {fr}}_\infty = F_0 - W_0 - Z_0$
. Solving the system, we obtain
$s^{\mathrm {fr}}_\infty = F_0 - W_0 - Z_0$
. Solving the system, we obtain
 $$ \begin{align} \begin{cases} b^{\mathrm{fr}}_W (s) &\!\!\!\!= W_0 + \frac{1}{F_2 + 1} \left(F_2 s + \frac{F_1 s}{s+W_0+Z_0 - F_0} \right) = W_0 + \frac{1}{F_2+1} \left( F_2 s + \frac{F_1 s}{s-s^{\mathrm{fr}}_\infty} \right) , \\ b^{\mathrm{fr}}_Z (s) &\!\!\!\!= Z_0 + \frac{1}{F_2 + 1} \left( s - \frac{F_1 s}{s+W_0+Z_0 - F_0} \right) = Z_0 + \frac{1}{F_2+1} \left( s - \frac{F_1 s}{s-s_\infty^{\mathrm{fr}}} \right), \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} b^{\mathrm{fr}}_W (s) &\!\!\!\!= W_0 + \frac{1}{F_2 + 1} \left(F_2 s + \frac{F_1 s}{s+W_0+Z_0 - F_0} \right) = W_0 + \frac{1}{F_2+1} \left( F_2 s + \frac{F_1 s}{s-s^{\mathrm{fr}}_\infty} \right) , \\ b^{\mathrm{fr}}_Z (s) &\!\!\!\!= Z_0 + \frac{1}{F_2 + 1} \left( s - \frac{F_1 s}{s+W_0+Z_0 - F_0} \right) = Z_0 + \frac{1}{F_2+1} \left( s - \frac{F_1 s}{s-s_\infty^{\mathrm{fr}}} \right), \end{cases} \end{align} $$
and we define
![]() $b^{\mathrm {fr}}(s) = (b^{\mathrm {fr}}_W(s), b^{\mathrm {fr}}_Z (s))$
which goes from
$b^{\mathrm {fr}}(s) = (b^{\mathrm {fr}}_W(s), b^{\mathrm {fr}}_Z (s))$
which goes from
![]() $P_s$
at time
$P_s$
at time
![]() $s=0$
to
$s=0$
to
![]() $P_0$
at
$P_0$
at
![]() $s = s^{\mathrm {fr}}_\infty $
. We also define the barrier condition as
$s = s^{\mathrm {fr}}_\infty $
. We also define the barrier condition as
which is a rational function with powers of
![]() $(s-s_\infty ^{\mathrm {fr}})$
in the denominator.
$(s-s_\infty ^{\mathrm {fr}})$
in the denominator.
Let us remark that the value of
![]() $F_2 = 1/2$
is chosen ad-hoc so that
$F_2 = 1/2$
is chosen ad-hoc so that
![]() $P^{\mathrm {fr}}(s)$
is positive. In contrast,
$P^{\mathrm {fr}}(s)$
is positive. In contrast,
![]() $F_0$
and
$F_0$
and
![]() $F_1$
are carefully chosen to get cancellations of
$F_1$
are carefully chosen to get cancellations of
![]() $B^{\mathrm {fr}}$
at
$B^{\mathrm {fr}}$
at
![]() $P_s$
or
$P_s$
or
![]() $P_0$
. In particular,
$P_0$
. In particular,
![]() $F_2$
does not enforce any cancellation, and any slight modification of it would still yield a valid barrier.
$F_2$
does not enforce any cancellation, and any slight modification of it would still yield a valid barrier.
Proposition 4.5. Let either
![]() $n=3$
with
$n=3$
with
![]() $\gamma> 1$
or
$\gamma> 1$
or
![]() $n \in \mathbb {N}$
odd and sufficiently large with
$n \in \mathbb {N}$
odd and sufficiently large with
![]() $\gamma = 7/5$
. For r close enough from above to
$\gamma = 7/5$
. For r close enough from above to
![]() $r_n$
, we have that
$r_n$
, we have that
![]() $P^{\mathrm {fr}} (s)> 0$
for all
$P^{\mathrm {fr}} (s)> 0$
for all
![]() $s\in (0, s^{\mathrm {fr}}_\infty )$
.
$s\in (0, s^{\mathrm {fr}}_\infty )$
.
Proof. By continuity of
![]() $P^{\mathrm {fr}}$
with respect to r, we just need to prove this for
$P^{\mathrm {fr}}$
with respect to r, we just need to prove this for
![]() $r = r_3$
in the case of
$r = r_3$
in the case of
![]() $n = 3$
and for r close enough to
$n = 3$
and for r close enough to
![]() $r^\ast (7/5)$
for
$r^\ast (7/5)$
for
![]() $\gamma = 7/5$
. We prove the statement via a computer-assisted proof. The code can be found in the supplementary material, and we refer to Appendix B for details about the implementation.
$\gamma = 7/5$
. We prove the statement via a computer-assisted proof. The code can be found in the supplementary material, and we refer to Appendix B for details about the implementation.
Lemma 4.6. Let
![]() $n = 3$
with
$n = 3$
with
![]() $\gamma> 1$
or
$\gamma> 1$
or
![]() $n \in \mathbb {N}$
odd sufficiently large with
$n \in \mathbb {N}$
odd sufficiently large with
![]() $\gamma = 7/5$
. There exists
$\gamma = 7/5$
. There exists
![]() $\varepsilon> 0$
such that for every
$\varepsilon> 0$
such that for every
![]() $r\in (r_{n}, r_{n}+\varepsilon )$
, there exists a value
$r\in (r_{n}, r_{n}+\varepsilon )$
, there exists a value
![]() $t_F$
with
$t_F$
with
![]() $B^{\mathrm {fr}} (b^{\mathrm {nr}}_{n} (t_F )) = 0$
and
$B^{\mathrm {fr}} (b^{\mathrm {nr}}_{n} (t_F )) = 0$
and
![]() $B^{\mathrm {fr}} (b^{\mathrm {nr}}_{n} (t )) < 0$
for
$B^{\mathrm {fr}} (b^{\mathrm {nr}}_{n} (t )) < 0$
for
![]() $t \in (0, t_F)$
. Moreover, we have that
$t \in (0, t_F)$
. Moreover, we have that
![]() $t_F \lesssim _{n} (k-n )^{1/(n-2)}$
.
$t_F \lesssim _{n} (k-n )^{1/(n-2)}$
.
Proof. We consider the
![]() $(2n+2)$
-th degree polynomial
$(2n+2)$
-th degree polynomial
![]() $B^{\mathrm {fr}} (b^{\mathrm {nr}}_n (t))$
. We have that
$B^{\mathrm {fr}} (b^{\mathrm {nr}}_n (t))$
. We have that
![]() ${B^{\mathrm {fr}} (b^{\mathrm {nr}}_n (0)) = B^{\mathrm {fr}} (P_s) = 0}$
and
${B^{\mathrm {fr}} (b^{\mathrm {nr}}_n (0)) = B^{\mathrm {fr}} (P_s) = 0}$
and
![]() $\nabla B^{\mathrm {fr}} (P_s) (W_1, Z_1) = 0$
due to our choice of
$\nabla B^{\mathrm {fr}} (P_s) (W_1, Z_1) = 0$
due to our choice of
![]() $F_1$
. Therefore, the terms in the polynomial have
$F_1$
. Therefore, the terms in the polynomial have
![]() $t^2$
as a common factor. Taking into account Corollary 2.4, all the coefficients in
$t^2$
as a common factor. Taking into account Corollary 2.4, all the coefficients in
![]() $b^{\mathrm {nr}}_n (t)$
are
$b^{\mathrm {nr}}_n (t)$
are
![]() $O(1)$
around
$O(1)$
around
![]() $r\approx r_n$
except the n-th and
$r\approx r_n$
except the n-th and
![]() $(n+1)$
-th coefficients of
$(n+1)$
-th coefficients of
![]() $b_Z^{\mathrm {nr}}(t)$
. We get
$b_Z^{\mathrm {nr}}(t)$
. We get
 $$ \begin{align} \begin{aligned} B^{\mathrm{fr}} (b^{\mathrm{nr}}_n (t)) &= \frac{a^{\mathrm{nr}}_2}{2} t^2 + \frac{a^{\mathrm{nr}}_n}{n!(k-n)} t^n + O(t^3) + O_{\beta_n}\left( \frac{t^{n+1}}{k-n} \right) + O\left( \frac{ t^{2n}}{(k-n)^2} \right) + O_{\beta_n} \left( \frac{ t^{2n+1} }{(k-n)^2} \right) \\ &= \frac{a^{\mathrm{nr}}_2}{2} t^2 (1+o(1)) + \frac{a^{\mathrm{nr}}_n}{n!(k - n)} t^n (1+o(1))\, , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} B^{\mathrm{fr}} (b^{\mathrm{nr}}_n (t)) &= \frac{a^{\mathrm{nr}}_2}{2} t^2 + \frac{a^{\mathrm{nr}}_n}{n!(k-n)} t^n + O(t^3) + O_{\beta_n}\left( \frac{t^{n+1}}{k-n} \right) + O\left( \frac{ t^{2n}}{(k-n)^2} \right) + O_{\beta_n} \left( \frac{ t^{2n+1} }{(k-n)^2} \right) \\ &= \frac{a^{\mathrm{nr}}_2}{2} t^2 (1+o(1)) + \frac{a^{\mathrm{nr}}_n}{n!(k - n)} t^n (1+o(1))\, , \end{aligned} \end{align} $$
where in the last equality we are assuming
![]() $t \leq C (k-n)^{1/(n-2)}$
for some sufficiently large C and using that
$t \leq C (k-n)^{1/(n-2)}$
for some sufficiently large C and using that
![]() $k-n$
is sufficiently small depending on
$k-n$
is sufficiently small depending on
![]() $\beta _n$
.
$\beta _n$
.
We proceed to calculate
![]() $a^{\mathrm {nr}}_2$
and
$a^{\mathrm {nr}}_2$
and
![]() $a^{\mathrm {nr}}_n$
. We have that
$a^{\mathrm {nr}}_n$
. We have that
 $$ \begin{align*} B^{\mathrm{fr}}(W, Z) &= \nabla B^{\mathrm{fr}}(P_s) (W-W_0, Z-Z_0)^\top + (W-W_0, Z-Z_0) \frac{HB^{\mathrm{fr}}}{2} (W-W_0, Z-Z_0)^\top \\&= (-s_\infty^{\mathrm{fr}} - F_1, F_2s_\infty^{\mathrm{fr}} - F_1) (W-W_0, Z-Z_0)^\top \\&\quad + (W-W_0, Z-Z_0) \begin{pmatrix} 1 & (1-F_2)/2 \\ (1-F_2)/2 & -F_2 \end{pmatrix} (W-W_0, Z-Z_0)^\top. \end{align*} $$
$$ \begin{align*} B^{\mathrm{fr}}(W, Z) &= \nabla B^{\mathrm{fr}}(P_s) (W-W_0, Z-Z_0)^\top + (W-W_0, Z-Z_0) \frac{HB^{\mathrm{fr}}}{2} (W-W_0, Z-Z_0)^\top \\&= (-s_\infty^{\mathrm{fr}} - F_1, F_2s_\infty^{\mathrm{fr}} - F_1) (W-W_0, Z-Z_0)^\top \\&\quad + (W-W_0, Z-Z_0) \begin{pmatrix} 1 & (1-F_2)/2 \\ (1-F_2)/2 & -F_2 \end{pmatrix} (W-W_0, Z-Z_0)^\top. \end{align*} $$
Therefore, using
![]() $F_2 = 1/2$
, we obtain that
$F_2 = 1/2$
, we obtain that
 $$ \begin{align*} \frac{a_2^{\mathrm{nr}} }{2}&= \frac{1}{2} \left( -s_\infty^{\mathrm{fr}} W_2 - F_1W_2 + s_\infty^{\mathrm{fr}} Z_2/2 - F_1Z_2 \right) + W_1^2 + W_1Z_1/2 - Z_1^2/2 \\ &= \frac{s_\infty^{\mathrm{fr}}}{2} \left( -W_2 + Z_2/2 - (W_2+Z_2)\frac{Z_1/2-W_1}{W_1+Z_1}\right) + W_1^2 + W_1Z_1/2 - Z_1^2/2, \end{align*} $$
$$ \begin{align*} \frac{a_2^{\mathrm{nr}} }{2}&= \frac{1}{2} \left( -s_\infty^{\mathrm{fr}} W_2 - F_1W_2 + s_\infty^{\mathrm{fr}} Z_2/2 - F_1Z_2 \right) + W_1^2 + W_1Z_1/2 - Z_1^2/2 \\ &= \frac{s_\infty^{\mathrm{fr}}}{2} \left( -W_2 + Z_2/2 - (W_2+Z_2)\frac{Z_1/2-W_1}{W_1+Z_1}\right) + W_1^2 + W_1Z_1/2 - Z_1^2/2, \end{align*} $$
and
 $$ \begin{align*} \frac{a_n^{\mathrm{nr}}}{k-n} = \left( s_\infty^{\mathrm{fr}}/2 - F_1 \right) Z_n(-1)^n = -s^{\mathrm{fr}}_\infty \left( \frac{1}{2} - \frac{Z_1/2 - W_1}{W_1+Z_1} \right) Z_n, \end{align*} $$
$$ \begin{align*} \frac{a_n^{\mathrm{nr}}}{k-n} = \left( s_\infty^{\mathrm{fr}}/2 - F_1 \right) Z_n(-1)^n = -s^{\mathrm{fr}}_\infty \left( \frac{1}{2} - \frac{Z_1/2 - W_1}{W_1+Z_1} \right) Z_n, \end{align*} $$
where we have used
![]() $F_1 = s_\infty ^{\mathrm {fr}} \frac {Z_1/2 - W_1}{W_1+Z_1}$
. First, note that
$F_1 = s_\infty ^{\mathrm {fr}} \frac {Z_1/2 - W_1}{W_1+Z_1}$
. First, note that
![]() $s_\infty ^{\mathrm {fr}}> 0$
due to Lemma A.13. Second, we have that
$s_\infty ^{\mathrm {fr}}> 0$
due to Lemma A.13. Second, we have that
![]() $\frac {Z_1/2 - W_1}{W_1 + Z_1} \leq -1 $
for
$\frac {Z_1/2 - W_1}{W_1 + Z_1} \leq -1 $
for
![]() $r = r_3$
with
$r = r_3$
with
![]() $\gamma> 1$
and
$\gamma> 1$
and
![]() $r=r^\ast (7/5)$
for
$r=r^\ast (7/5)$
for
![]() $\gamma = 7/5$
due to Lemma A.29. These two facts allow us to conclude
$\gamma = 7/5$
due to Lemma A.29. These two facts allow us to conclude
where
![]() $Z_n> 0$
(Corollary 5.8 for
$Z_n> 0$
(Corollary 5.8 for
![]() $\gamma = 7/5$
, n sufficiently large and Lemma A.31 for
$\gamma = 7/5$
, n sufficiently large and Lemma A.31 for
![]() $r \in (r_3, r_4)$
).
$r \in (r_3, r_4)$
).
However, we have that Lemma A.30 guarantees
![]() $a_2^{\mathrm {nr}}> 0$
.
$a_2^{\mathrm {nr}}> 0$
.
Going back to (4.13), we have that
![]() $B^{\mathrm {fr}}(b^{\mathrm {nr}}_n(t))$
is initially positive for sufficiently small
$B^{\mathrm {fr}}(b^{\mathrm {nr}}_n(t))$
is initially positive for sufficiently small
![]() $t> 0$
. Define
$t> 0$
. Define
 $$ \begin{align} t_G = \left| \frac{n! a_2^{\mathrm{nr}}}{ 2 s_\infty^{\mathrm{fr}} Z_n} \right|{}^{1/(n-2)}. \end{align} $$
$$ \begin{align} t_G = \left| \frac{n! a_2^{\mathrm{nr}}}{ 2 s_\infty^{\mathrm{fr}} Z_n} \right|{}^{1/(n-2)}. \end{align} $$
Using (4.13) and (4.14), we have that
 $$ \begin{align*} B^{\mathrm{fr}} (b^{\mathrm{nr}}_n (t_G)) &= \frac{a^{\mathrm{nr}}_2}{2} t^2 (1+o(1)) + \frac{a^{\mathrm{nr}}_n}{n!(k - n)} t^2 \cdot \left| \frac{n! a_2^{\mathrm{nr}}}{ 2 s_\infty^{\mathrm{fr}} Z_n} \right| (1+o(1)) \\ &= \frac{a^{\mathrm{nr}}_2}{2} t^2 \left(1- \left| \frac{a^{\mathrm{nr}}_n}{(k-n)s_\infty^{\mathrm{fr}} Z_n } \right|(1+o(1)) +o(1)\right) \\ &\leq -\frac{a^{\mathrm{nr}}_2}{4} t^2 (1+o(1)). \end{align*} $$
$$ \begin{align*} B^{\mathrm{fr}} (b^{\mathrm{nr}}_n (t_G)) &= \frac{a^{\mathrm{nr}}_2}{2} t^2 (1+o(1)) + \frac{a^{\mathrm{nr}}_n}{n!(k - n)} t^2 \cdot \left| \frac{n! a_2^{\mathrm{nr}}}{ 2 s_\infty^{\mathrm{fr}} Z_n} \right| (1+o(1)) \\ &= \frac{a^{\mathrm{nr}}_2}{2} t^2 \left(1- \left| \frac{a^{\mathrm{nr}}_n}{(k-n)s_\infty^{\mathrm{fr}} Z_n } \right|(1+o(1)) +o(1)\right) \\ &\leq -\frac{a^{\mathrm{nr}}_2}{4} t^2 (1+o(1)). \end{align*} $$
By continuity, there exists some
![]() $t_F \in (0, t_G)$
such that
$t_F \in (0, t_G)$
such that
![]() $B^{\mathrm {fr}}(b^{\mathrm {nr}}_n(t_F)) = 0$
. Moreover, as
$B^{\mathrm {fr}}(b^{\mathrm {nr}}_n(t_F)) = 0$
. Moreover, as
![]() $B^{\mathrm {fr}}(b^{\mathrm {nr}}(t))$
is a polynomial, we can take
$B^{\mathrm {fr}}(b^{\mathrm {nr}}(t))$
is a polynomial, we can take
![]() $t_F$
to be the first such zero, so that
$t_F$
to be the first such zero, so that
![]() $B^{\mathrm {fr}}(b^{\mathrm {nr}}_n(t))> 0$
for
$B^{\mathrm {fr}}(b^{\mathrm {nr}}_n(t))> 0$
for
![]() $0 < t < t_F$
. Lastly, by (4.15), we conclude that
$0 < t < t_F$
. Lastly, by (4.15), we conclude that
![]() $t_F \leq t_G \lesssim _n (k-n)^{1/(n-2)}$
.
$t_F \leq t_G \lesssim _n (k-n)^{1/(n-2)}$
.
Lemma 4.7. Let either
![]() $\gamma> 1$
with
$\gamma> 1$
with
![]() $n=3$
or
$n=3$
or
![]() $\gamma = 7/5$
with
$\gamma = 7/5$
with
![]() $n\in \mathbb {N}$
odd, large enough. There exists
$n\in \mathbb {N}$
odd, large enough. There exists
![]() $\varepsilon , \delta , \beta _{n, 0 }> 0$
such that for every
$\varepsilon , \delta , \beta _{n, 0 }> 0$
such that for every
![]() $r\in (r_{n}, r_{n} + \varepsilon )$
,
$r\in (r_{n}, r_{n} + \varepsilon )$
,
![]() $\beta _{n}> \beta _{n, 0 }$
and
$\beta _{n}> \beta _{n, 0 }$
and
![]() $\xi \in (0,\delta )$
, the smooth solution
$\xi \in (0,\delta )$
, the smooth solution
![]() $(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
is below the near-right barrier
$(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
is below the near-right barrier
![]() $b^{\mathrm {nr}}_{n} (t)$
.
$b^{\mathrm {nr}}_{n} (t)$
.
Proof. We have to compare the first Taylor coefficients on the barrier which differ from those of the smooth solution (with
![]() $\xi $
replaced with
$\xi $
replaced with
![]() $-\xi $
) – that is, the
$-\xi $
) – that is, the
![]() $n+1$
-th. As
$n+1$
-th. As
![]() $n+1$
is even, they are given by
$n+1$
is even, they are given by
![]() $(W_{n+1}, Z_{n+1})$
for the smooth solution and
$(W_{n+1}, Z_{n+1})$
for the smooth solution and
![]() $(0, \beta _n Z_n )$
for
$(0, \beta _n Z_n )$
for
![]() $b^{\mathrm {nr}} (t)$
. Therefore,
$b^{\mathrm {nr}} (t)$
. Therefore,
![]() $b^{\mathrm {nr}}_n (t)$
is above the smooth one close to
$b^{\mathrm {nr}}_n (t)$
is above the smooth one close to
![]() $P_s$
if
$P_s$
if
or equivalently,
The case
![]() $n = 3$
follows from the fact that
$n = 3$
follows from the fact that
![]() $W_1 < 0$
(Lemma A.26) and
$W_1 < 0$
(Lemma A.26) and
![]() $Z_3> 0$
(Lemma A.31) provided that we take
$Z_3> 0$
(Lemma A.31) provided that we take
![]() $\beta _n$
sufficiently large. For the case
$\beta _n$
sufficiently large. For the case
![]() $\gamma = 7/5$
, n large enough, Lemma A.7 guarantees
$\gamma = 7/5$
, n large enough, Lemma A.7 guarantees
![]() $W_1 < 0$
, so we just need
$W_1 < 0$
, so we just need
![]() $Z_n> 0$
in order to conclude the statement. The proof that
$Z_n> 0$
in order to conclude the statement. The proof that
![]() $Z_n> 0$
will be delayed to Section 5: specifically, this will follow from Corollary 5.8.
$Z_n> 0$
will be delayed to Section 5: specifically, this will follow from Corollary 5.8.
Proof of Proposition 4.1.
Let us start with the existence of
![]() $r_u$
. From Proposition 4.2 and Lemmas 4.3 and 4.4, we have an
$r_u$
. From Proposition 4.2 and Lemmas 4.3 and 4.4, we have an
![]() $\varepsilon> 0$
small enough and a
$\varepsilon> 0$
small enough and a
![]() $\beta _{n+1}$
sufficiently large such that for every
$\beta _{n+1}$
sufficiently large such that for every
![]() $r\in (r_{n+1}-\varepsilon , r_{n+1})$
, the following holds:
$r\in (r_{n+1}-\varepsilon , r_{n+1})$
, the following holds:
-
1. The smooth solution
 $(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
is above the barrier
$(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
is above the barrier
 $b^{\mathrm {nr}}_{n+1}(t)$
for
$b^{\mathrm {nr}}_{n+1}(t)$
for
 $0> \xi > -\epsilon $
, for some
$0> \xi > -\epsilon $
, for some
 $\epsilon> 0$
sufficiently small.
$\epsilon> 0$
sufficiently small. -
2. There is a constant
 $C_1$
such that
$C_1$
such that
 $P^{\mathrm {nr}}_{n+1} (t) < 0$
for every
$P^{\mathrm {nr}}_{n+1} (t) < 0$
for every
 $t\in (0, C_1 (n+1-k)^{1/n})$
.
$t\in (0, C_1 (n+1-k)^{1/n})$
. -
3. There exists
 $t_D>0$
such that
$t_D>0$
such that
 $D_Z ( b^{\mathrm {nr}}_{n+1} (t_D)) = 0$
,
$D_Z ( b^{\mathrm {nr}}_{n+1} (t_D)) = 0$
,
 $D_Z(b^{\mathrm {nr}}_{n+1}(t)) < 0$
for
$D_Z(b^{\mathrm {nr}}_{n+1}(t)) < 0$
for
 $t \leq t_D$
; with
$t \leq t_D$
; with
 $t_D \leq C_2 (n+1-k)^{1/(n-1)}$
.
$t_D \leq C_2 (n+1-k)^{1/(n-1)}$
.
Therefore, taking r close enough to
![]() $r_{n+1}$
from below, we can ensure that
$r_{n+1}$
from below, we can ensure that
![]() $P^{\mathrm {nr}}_{n+1} (t) < 0$
up to the intersection of
$P^{\mathrm {nr}}_{n+1} (t) < 0$
up to the intersection of
![]() $b^{\mathrm {nr}}_{n+1}(t)$
with
$b^{\mathrm {nr}}_{n+1}(t)$
with
![]() $D_Z = 0$
. Consider the region delimited by
$D_Z = 0$
. Consider the region delimited by
![]() $b^{\mathrm {nr}}_{n+1}(t)$
and
$b^{\mathrm {nr}}_{n+1}(t)$
and
![]() $D_Z = 0$
inside
$D_Z = 0$
inside
![]() $\Omega $
. The region is bounded, and the solution cannot exit that region. Moreover, the solution cannot converge to an equilibrium point by Lemma A.17 (and Lemma A.18 for the case of
$\Omega $
. The region is bounded, and the solution cannot exit that region. Moreover, the solution cannot converge to an equilibrium point by Lemma A.17 (and Lemma A.18 for the case of ![]() ,
,
![]() $\gamma = 7/5$
, r sufficiently close to
$\gamma = 7/5$
, r sufficiently close to
![]() $r^\ast $
). Therefore, by Proposition 1.6, the solution must end in the right halfline of
$r^\ast $
). Therefore, by Proposition 1.6, the solution must end in the right halfline of
![]() $D_Z = 0$
starting at
$D_Z = 0$
starting at
![]() $P_s$
, thus lying in
$P_s$
, thus lying in
![]() $\Omega _1^{(r_u)}$
. This concludes the first part of Proposition 4.1.
$\Omega _1^{(r_u)}$
. This concludes the first part of Proposition 4.1.
From Proposition 4.2, Lemma 4.6 and Lemma 4.7, we choose
![]() $\beta _{n}$
sufficiently large and
$\beta _{n}$
sufficiently large and
![]() $\varepsilon> 0$
sufficiently small, depending on
$\varepsilon> 0$
sufficiently small, depending on
![]() $\beta _{n}$
(in particular, we assume
$\beta _{n}$
(in particular, we assume
![]() $\beta _n\ll (k-n)^{-1/(2n)}$
). Then the following holds:
$\beta _n\ll (k-n)^{-1/(2n)}$
). Then the following holds:
-
1. The smooth solution
 $(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
stays initially below the barrier
$(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
stays initially below the barrier
 $b^{\mathrm {nr}}_{n}(t)$
for
$b^{\mathrm {nr}}_{n}(t)$
for
 $-\epsilon < \xi < 0$
for some
$-\epsilon < \xi < 0$
for some
 $\epsilon> 0$
sufficiently small.
$\epsilon> 0$
sufficiently small. -
2. There is a constant
 $C_1$
such that
$C_1$
such that
 $P^{\mathrm {nr}}_{n} (t)> 0$
for every
$P^{\mathrm {nr}}_{n} (t)> 0$
for every
 $t\in (0, \beta _{n} C_1 (k-n)^{1/(n-2)}$
.
$t\in (0, \beta _{n} C_1 (k-n)^{1/(n-2)}$
. -
3. There exists a
 $0<t_F \leq C_2 (k-n)^{1/(n-2)}$
such that
$0<t_F \leq C_2 (k-n)^{1/(n-2)}$
such that
 $B^{\mathrm {fr}} ( b^{\mathrm {nr}}_{n}(t_F)) = 0$
and
$B^{\mathrm {fr}} ( b^{\mathrm {nr}}_{n}(t_F)) = 0$
and
 $B^{\mathrm {fr}} ( b^{\mathrm {nr}}_{n}(t)) < 0$
for
$B^{\mathrm {fr}} ( b^{\mathrm {nr}}_{n}(t)) < 0$
for
 $0 < t < t_F$
.
$0 < t < t_F$
.
We conclude that
![]() $P^{\mathrm {nr}}_n(t)> 0$
up to
$P^{\mathrm {nr}}_n(t)> 0$
up to
![]() $t_F$
, for r close enough to
$t_F$
, for r close enough to
![]() $r_n$
from above.
$r_n$
from above.
We define the barrier
![]() $b^{\mathrm {nr}}_{n} \ast B^{\mathrm {fr}}$
to be
$b^{\mathrm {nr}}_{n} \ast B^{\mathrm {fr}}$
to be
![]() $b^{\mathrm {nr}}_{n} (t)$
up to
$b^{\mathrm {nr}}_{n} (t)$
up to
![]() $t_F$
and then
$t_F$
and then
![]() $B^{\mathrm {fr}} = 0$
(with some parametrization starting at
$B^{\mathrm {fr}} = 0$
(with some parametrization starting at
![]() $t_F$
) up to
$t_F$
) up to
![]() $P_0$
. Using Proposition 4.5 and the fact that
$P_0$
. Using Proposition 4.5 and the fact that
![]() $P^{\mathrm {nr}}_n(t)> 0$
up to
$P^{\mathrm {nr}}_n(t)> 0$
up to
![]() $t_F$
, we know that the component of the field
$t_F$
, we know that the component of the field
![]() $\left ( N_W D_Z , N_Z D_W \right )$
points downwards. Let us consider
$\left ( N_W D_Z , N_Z D_W \right )$
points downwards. Let us consider
![]() $\Omega _d$
, the part of
$\Omega _d$
, the part of
![]() $\Omega $
below
$\Omega $
below
![]() $b^{\mathrm {nr}}_{n} \ast B^{\mathrm {fr}} $
.
$b^{\mathrm {nr}}_{n} \ast B^{\mathrm {fr}} $
.
The smooth solution
![]() $(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
is in
$(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
is in
![]() $\Omega _d$
for
$\Omega _d$
for
![]() $-\xi>0$
sufficiently small by point 1 above and cannot exit through
$-\xi>0$
sufficiently small by point 1 above and cannot exit through
![]() $b^{\mathrm {nr}}_{n} \ast B^{\mathrm {fr}}$
since the normal component points downwards. In particular, it cannot hit the halfline of
$b^{\mathrm {nr}}_{n} \ast B^{\mathrm {fr}}$
since the normal component points downwards. In particular, it cannot hit the halfline of
![]() $D_Z = 0$
to the right of
$D_Z = 0$
to the right of
![]() $P_s$
, so by Remark 1.7, it cannot lie in
$P_s$
, so by Remark 1.7, it cannot lie in
![]() $\Omega _1^{(r_d)}$
. In other words
$\Omega _1^{(r_d)}$
. In other words
![]() $\Omega _d \subset \bar \Omega _2^{(r_d)}$
. As
$\Omega _d \subset \bar \Omega _2^{(r_d)}$
. As
![]() $\Omega _d$
is open, it cannot have points of
$\Omega _d$
is open, it cannot have points of
![]() $\partial \Omega _2^{(r_d)}$
. Therefore,
$\partial \Omega _2^{(r_d)}$
. Therefore,
![]() $\Omega _d \subset \Omega _2^{(r_d )}$
, and we are done.
$\Omega _d \subset \Omega _2^{(r_d )}$
, and we are done.
5 Complete Section 3 for the case
 $r\rightarrow r^\ast $
$r\rightarrow r^\ast $
In this section, we fix
![]() $\gamma = 7/5$
. Our objective here is to complete the analysis we did in Section 3 for the case of
$\gamma = 7/5$
. Our objective here is to complete the analysis we did in Section 3 for the case of
![]() $\gamma = 7/5$
and
$\gamma = 7/5$
and
![]() $n $
sufficiently large. We will prove Proposition 3.6, and in Corollary 5.9, we will also conclude the proof of Lemma 3.4 for this case of
$n $
sufficiently large. We will prove Proposition 3.6, and in Corollary 5.9, we will also conclude the proof of Lemma 3.4 for this case of
![]() $\gamma = 7/5$
and k sufficiently large.
$\gamma = 7/5$
and k sufficiently large.
In order to do so, first we need to control the growth of the Taylor coefficients of the solution. In particular, we need to obtain the sign of
![]() $Z_n$
(with a lower bound of its magnitude) in order to guarantee that the behavior of the smooth solution when
$Z_n$
(with a lower bound of its magnitude) in order to guarantee that the behavior of the smooth solution when
![]() $r \approx r_n^+$
or
$r \approx r_n^+$
or
![]() $r\approx r_{n+1}^-$
is the expected one.
$r\approx r_{n+1}^-$
is the expected one.
Let us define
![]() $C_\ast = \lim _{r\to r^\ast } \frac {D_{Z, 2}}{2 k D_{Z, 1}}$
. With this definition, we will have that for
$C_\ast = \lim _{r\to r^\ast } \frac {D_{Z, 2}}{2 k D_{Z, 1}}$
. With this definition, we will have that for
![]() $1 \ll i \leq n$
, the coefficient
$1 \ll i \leq n$
, the coefficient
![]() $Z_i$
is approximately equal to
$Z_i$
is approximately equal to
![]() $C_\ast \frac {i^2 k}{i-k} Z_{i-1}$
. This idea is formalized in the following lemma. Let us define also the quantity
$C_\ast \frac {i^2 k}{i-k} Z_{i-1}$
. This idea is formalized in the following lemma. Let us define also the quantity
![]() $\bar C_\ast =0.95 C_\ast $
.
$\bar C_\ast =0.95 C_\ast $
.
Lemma 5.1. For k sufficiently large and
![]() $i \leq k$
we have that
$i \leq k$
we have that
 $$ \begin{align} \left| \frac{W_{i+1}}{Z_i}\right| &\leq 4, \end{align} $$
$$ \begin{align} \left| \frac{W_{i+1}}{Z_i}\right| &\leq 4, \end{align} $$
 $$ \begin{align} \left| \bar C_\ast \frac{(i+1)^2k}{i+1-k} \right| \leq\left| \frac{Z_{i+1}}{Z_i} \right| &\leq \left| 500\bar C_\ast \frac{(i+1) k}{i+1-k} \right|&\mbox{for }i< 160, \end{align} $$
$$ \begin{align} \left| \bar C_\ast \frac{(i+1)^2k}{i+1-k} \right| \leq\left| \frac{Z_{i+1}}{Z_i} \right| &\leq \left| 500\bar C_\ast \frac{(i+1) k}{i+1-k} \right|&\mbox{for }i< 160, \end{align} $$
 $$ \begin{align} \left| \bar C_\ast \frac{(i+1)^2 k}{i+1-k} \right| \leq\left| \frac{Z_{i+1}}{Z_i} \right|&\leq \left| 3\bar C_\ast \frac{(i+1)^2k}{i+1-k} \right|&\mbox{for }i\geq 160, \end{align} $$
$$ \begin{align} \left| \bar C_\ast \frac{(i+1)^2 k}{i+1-k} \right| \leq\left| \frac{Z_{i+1}}{Z_i} \right|&\leq \left| 3\bar C_\ast \frac{(i+1)^2k}{i+1-k} \right|&\mbox{for }i\geq 160, \end{align} $$
 $$ \begin{align} \left|Z_{i+1} - \bar C_\ast \frac{(i+1)^2 k}{i+1-k} Z_i\right|&\leq0.05|Z_{i+1}| &\mbox{for }i>10000. \end{align} $$
$$ \begin{align} \left|Z_{i+1} - \bar C_\ast \frac{(i+1)^2 k}{i+1-k} Z_i\right|&\leq0.05|Z_{i+1}| &\mbox{for }i>10000. \end{align} $$
Note that the inequality (5.4) is strictly stronger than (5.3).
Inequality (5.2) and inequality (5.3) for
![]() $i \leq 10000$
are proven via a computer-assisted argument (see Lemma A.28). Moreover, (5.1) for
$i \leq 10000$
are proven via a computer-assisted argument (see Lemma A.28). Moreover, (5.1) for
![]() $i\leq 10000$
is also proven via a computer-assisted proof (see Lemma A.27). In both cases, strict inequalities at
$i\leq 10000$
is also proven via a computer-assisted proof (see Lemma A.27). In both cases, strict inequalities at
![]() $r = r^\ast (7/5)$
are shown, and then one obtains the result by invoking continuity.
$r = r^\ast (7/5)$
are shown, and then one obtains the result by invoking continuity.
The proof of Lemma 5.1 will follow by induction. In Lemma 5.6, we show that given that the estimates in Lemma 5.1 hold for all
![]() $i< m$
for
$i< m$
for
![]() $10000\leq m\leq k$
, then (5.1) holds for
$10000\leq m\leq k$
, then (5.1) holds for
![]() $i=m$
. In Lemma 5.7 we show that given that the estimates in Lemma 5.1 hold for all
$i=m$
. In Lemma 5.7 we show that given that the estimates in Lemma 5.1 hold for all
![]() $i< m$
and (5.1) holds for
$i< m$
and (5.1) holds for
![]() $i\leq m$
, where
$i\leq m$
, where
![]() $10000\leq m\leq k$
, then (5.4) holds for
$10000\leq m\leq k$
, then (5.4) holds for
![]() $i=m$
.
$i=m$
.
The proof of (5.4) will be strongly based on the log-convexity of the Taylor terms. We will have that
![]() $|Z_a| \cdot |Z_{i-a}| \gg |Z_b| \cdot |Z_{i-b}|$
when
$|Z_a| \cdot |Z_{i-a}| \gg |Z_b| \cdot |Z_{i-b}|$
when
![]() $a \leq b \leq i-b \leq i-a$
. This will allow us to justify that all the terms in the Taylor recursion are dominated by the most extreme ones (those terms
$a \leq b \leq i-b \leq i-a$
. This will allow us to justify that all the terms in the Taylor recursion are dominated by the most extreme ones (those terms
![]() $Z_a Z_{i-a}$
on which either
$Z_a Z_{i-a}$
on which either
![]() $a \in \{0, 1 \}$
or
$a \in \{0, 1 \}$
or
![]() $a \in \{ i-1, i \}$
). Note that this
$a \in \{ i-1, i \}$
). Note that this
![]() $\mathrm{log}$
-convexity does not hold when
$\mathrm{log}$
-convexity does not hold when
![]() $i> k$
since, for example, taking k approximately equal to n, and n even, we have that
$i> k$
since, for example, taking k approximately equal to n, and n even, we have that
![]() $|Z_{3n/2}| \cdot | Z_{n/2} | = O(|k-n|^{-1})$
as
$|Z_{3n/2}| \cdot | Z_{n/2} | = O(|k-n|^{-1})$
as
![]() $k\to n$
, while
$k\to n$
, while
![]() $|Z_n|^2 = O(|k-n|^{-2})$
as
$|Z_n|^2 = O(|k-n|^{-2})$
as
![]() $k \to n$
. Therefore, for k sufficiently close to n, we have
$k \to n$
. Therefore, for k sufficiently close to n, we have
![]() $|Z_n|^2 \gg |Z_{3n/2}| \cdot | Z_{n/2} |$
. However, since
$|Z_n|^2 \gg |Z_{3n/2}| \cdot | Z_{n/2} |$
. However, since
![]() $Z_n$
is the first coefficient that blows up as
$Z_n$
is the first coefficient that blows up as
![]() $k \to n$
, it will be enough to have a lower bound on that coefficient to control the Taylor series, since the next ones will go with higher powers of
$k \to n$
, it will be enough to have a lower bound on that coefficient to control the Taylor series, since the next ones will go with higher powers of
![]() $\xi $
.
$\xi $
.
Remark 5.2. From Lemma A.7, we have that that
so that
![]() $\bar C_\ast = 0.95 \bar C_\ast $
is negative and
$\bar C_\ast = 0.95 \bar C_\ast $
is negative and
![]() $0.00283 < |\bar C_\ast | < 0.00284$
.
$0.00283 < |\bar C_\ast | < 0.00284$
.
Corollary 5.3. Assume (5.2)–(5.4) hold for all
![]() $i\leq m$
. If k is sufficiently large, then for all
$i\leq m$
. If k is sufficiently large, then for all
![]() $i\leq m$
, we have
$i\leq m$
, we have
 $$ \begin{align} \left|\frac{W_i}{Z_i}\right|\leq 2. \end{align} $$
$$ \begin{align} \left|\frac{W_i}{Z_i}\right|\leq 2. \end{align} $$
Proof. The inequality is shown for
![]() $i\leq 160$
in Lemma A.27.
$i\leq 160$
in Lemma A.27.
Recall that the inequality (5.4) is stronger than (5.3). Then, (5.1), (5.3) and (5.4) imply
 $$\begin{align*}\left|\frac{W_i}{Z_i}\right|\leq 4 \left|\frac{Z_{i-1}}{Z_i}\right|\leq 4 |\bar C_\ast| \left|\frac{i-k}{i^2k}\right|\leq 8 |\bar C_\ast|. \end{align*}$$
$$\begin{align*}\left|\frac{W_i}{Z_i}\right|\leq 4 \left|\frac{Z_{i-1}}{Z_i}\right|\leq 4 |\bar C_\ast| \left|\frac{i-k}{i^2k}\right|\leq 8 |\bar C_\ast|. \end{align*}$$
Then, we conclude by using Remark 5.2.
Whenever we use the sign
![]() $\lesssim $
in this section, the implicit constant will not depend on n. We also use the descending Pochhammer notation
$\lesssim $
in this section, the implicit constant will not depend on n. We also use the descending Pochhammer notation
![]() $a_{(b)} = a(a-1)(a-2)\ldots (a-b+1)$
for any real a and positive integer b. For simplicity, assume that
$a_{(b)} = a(a-1)(a-2)\ldots (a-b+1)$
for any real a and positive integer b. For simplicity, assume that
![]() $\sum _{j=a}^b$
is the sum starting at
$\sum _{j=a}^b$
is the sum starting at
![]() $\lceil a \rceil $
and ending at
$\lceil a \rceil $
and ending at
![]() $\lfloor b \rfloor $
whenever
$\lfloor b \rfloor $
whenever
![]() $a, b$
are not integers.
$a, b$
are not integers.
5.1 Convexity lemmas from our assumptions
Lemma 5.4. Assume (5.2)–(5.4) hold for all
![]() $i\leq m$
. Let
$i\leq m$
. Let
![]() $j \geq 2$
and
$j \geq 2$
and
![]() $m < k$
. Assume also
$m < k$
. Assume also
![]() $j \leq (m+1)/2$
, and
$j \leq (m+1)/2$
, and
![]() $m> 10000$
. Then we have the following:
$m> 10000$
. Then we have the following:
-
• For
 $j < 160$
, we have (5.6)
$j < 160$
, we have (5.6) $$ \begin{align} \begin{aligned} \binom{m+1}{j} |Z_jZ_{m+1-j}| &\leq \binom{m+1}{1} |Z_1Z_m| \left( \frac{600}{m}\right)^{j-1} ,\\ \binom{m+2}{j} |Z_j Z_{m+2-j}| &\leq \binom{m+2}{2} |Z_2 Z_m| \left( \frac{600}{m} \right)^{j-2}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \binom{m+1}{j} |Z_jZ_{m+1-j}| &\leq \binom{m+1}{1} |Z_1Z_m| \left( \frac{600}{m}\right)^{j-1} ,\\ \binom{m+2}{j} |Z_j Z_{m+2-j}| &\leq \binom{m+2}{2} |Z_2 Z_m| \left( \frac{600}{m} \right)^{j-2}. \end{aligned} \end{align} $$
-
• For
 $160 \leq j \leq m/10$
, we have that (5.7)
$160 \leq j \leq m/10$
, we have that (5.7) $$ \begin{align} \begin{aligned} \binom{m+1}{j} |Z_jZ_{m+1-j}| &\leq \binom{m+1}{1} |Z_1Z_m| \frac{1}{m^9} (1/3)^j ,\\ \binom{m+2}{j} |Z_j Z_{m+2-j}| &\leq \binom{m+2}{2} |Z_2 Z_m| \frac{1}{m^9} (1/3)^j. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \binom{m+1}{j} |Z_jZ_{m+1-j}| &\leq \binom{m+1}{1} |Z_1Z_m| \frac{1}{m^9} (1/3)^j ,\\ \binom{m+2}{j} |Z_j Z_{m+2-j}| &\leq \binom{m+2}{2} |Z_2 Z_m| \frac{1}{m^9} (1/3)^j. \end{aligned} \end{align} $$
-
• For
 $j \geq m/10$
, we have that (5.8)We note that the first inequality of (5.6) is also trivially true for
$j \geq m/10$
, we have that (5.8)We note that the first inequality of (5.6) is also trivially true for $$ \begin{align} \begin{aligned} \binom{m+1}{j} |Z_jZ_{m+1-j}| &\leq \binom{m+1}{1} |Z_1Z_m|(3/4)^{j/11}, \\ \binom{m+2}{j} |Z_j Z_{m+2-j}| &\leq \binom{m+2}{2} |Z_2 Z_m| (3/4)^{j/11}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \binom{m+1}{j} |Z_jZ_{m+1-j}| &\leq \binom{m+1}{1} |Z_1Z_m|(3/4)^{j/11}, \\ \binom{m+2}{j} |Z_j Z_{m+2-j}| &\leq \binom{m+2}{2} |Z_2 Z_m| (3/4)^{j/11}. \end{aligned} \end{align} $$
 $j=1$
.
$j=1$
.
Before we prove this lemma, let us prove an elementary bound on binomial coefficients. We first recall the classical bound
From this bound, we obtain the following bound on binomial coefficients.
Lemma 5.5. The following holds for any
![]() $n \geq 1$
.
$n \geq 1$
.
-
• If
 $1 \leq j \leq n/2$
, it holds that
$1 \leq j \leq n/2$
, it holds that
 $\binom {n}{j}^{-1} \leq 3 \frac {\sqrt {j} }{4^j}$
.
$\binom {n}{j}^{-1} \leq 3 \frac {\sqrt {j} }{4^j}$
. -
• If
 $j \leq n/10$
, it holds that
$j \leq n/10$
, it holds that
 $\binom {n}{j}^{-1} \leq \frac {j!}{(9n/10)^j}$
.
$\binom {n}{j}^{-1} \leq \frac {j!}{(9n/10)^j}$
.
Proof. For the first one, use Stirling’s bound and note that
![]() $\frac {j^j (n-j)^{n-j} }{n^n} = f(\alpha )^n$
where
$\frac {j^j (n-j)^{n-j} }{n^n} = f(\alpha )^n$
where
![]() $\alpha = j/n$
and
$\alpha = j/n$
and
![]() $f(\alpha ) = \alpha ^\alpha (1-\alpha )^{1-\alpha }$
. Checking the bound
$f(\alpha ) = \alpha ^\alpha (1-\alpha )^{1-\alpha }$
. Checking the bound
![]() $f(\alpha ) \leq 4^{-\alpha }$
for any
$f(\alpha ) \leq 4^{-\alpha }$
for any
![]() $\alpha \in [0, 1/2]$
concludes the proof. The second claim is clear from the definition of binomial number.
$\alpha \in [0, 1/2]$
concludes the proof. The second claim is clear from the definition of binomial number.
Proof of Lemma 5.4.
For the sake of brevity, let us just prove the first bound on each item (the proof for the second is exactly the same changing the indices accordingly). Let us start with (5.8). We bound
 $$ \begin{align} \left|Z_j\right|&\leq \left|Z_1\right| \prod_{i=1}^{159}\left| 500\bar C_\ast \frac{(i+1) k}{i+1-k} \right| \prod_{i=160}^{j-1} \left| 3\bar C_\ast \frac{(i+1)^2k}{i+1-k} \right| \leq \left|Z_1\right| \frac{\left(500 / 3\right)^{159}} {160!} \frac{(j!)^2\left|3\bar C_\ast k\right| ^{j-1}}{(k-2)_{(j-1)}}, \end{align} $$
$$ \begin{align} \left|Z_j\right|&\leq \left|Z_1\right| \prod_{i=1}^{159}\left| 500\bar C_\ast \frac{(i+1) k}{i+1-k} \right| \prod_{i=160}^{j-1} \left| 3\bar C_\ast \frac{(i+1)^2k}{i+1-k} \right| \leq \left|Z_1\right| \frac{\left(500 / 3\right)^{159}} {160!} \frac{(j!)^2\left|3\bar C_\ast k\right| ^{j-1}}{(k-2)_{(j-1)}}, \end{align} $$
and similarly,
 $$ \begin{align} \left|Z_{m+1-j}\right| & \leq |Z_m|\frac{\left|(m-k)_{(j-1)}\right|((m+1-j)!)^2}{\left|\bar C_\ast k\right|{}^{j-1} (m!)^2 } . \end{align} $$
$$ \begin{align} \left|Z_{m+1-j}\right| & \leq |Z_m|\frac{\left|(m-k)_{(j-1)}\right|((m+1-j)!)^2}{\left|\bar C_\ast k\right|{}^{j-1} (m!)^2 } . \end{align} $$
Substituting in these bounds and using the bound
![]() $\frac {\left |(m-k)_{(j-1)}\right |}{(k-2)_{(j-1)}} \leq 1$
, along with Lemma 5.5, we obtain
$\frac {\left |(m-k)_{(j-1)}\right |}{(k-2)_{(j-1)}} \leq 1$
, along with Lemma 5.5, we obtain
 $$ \begin{align*} \binom{m+1}{j} |Z_j Z_{m+1-j}| &\leq \binom{m+1}{j}\left|Z_1\right|\left|Z_m\right| \frac{3 ^{j-160} \cdot500 ^{159} (m+1)^2 } {160!} {\binom{m+1}{j}}^{-2}\ \\&\leq \binom{m+1}{1} |Z_1||Z_m| (m+1) \frac{3 ^{j-159} \cdot500 ^{159} } {160!} \frac{\sqrt j}{4^j}\\&\leq \binom{m+1}{1} |Z_1||Z_m| (3/4)^{j/11}\left((3/4)^{m/11}\sqrt{m}(m+1) \frac{(500/3)^{159}}{160!}\right) \\&\leq \binom{m+1}{1} |Z_1||Z_m| (3/4)^{j/11}, \end{align*} $$
$$ \begin{align*} \binom{m+1}{j} |Z_j Z_{m+1-j}| &\leq \binom{m+1}{j}\left|Z_1\right|\left|Z_m\right| \frac{3 ^{j-160} \cdot500 ^{159} (m+1)^2 } {160!} {\binom{m+1}{j}}^{-2}\ \\&\leq \binom{m+1}{1} |Z_1||Z_m| (m+1) \frac{3 ^{j-159} \cdot500 ^{159} } {160!} \frac{\sqrt j}{4^j}\\&\leq \binom{m+1}{1} |Z_1||Z_m| (3/4)^{j/11}\left((3/4)^{m/11}\sqrt{m}(m+1) \frac{(500/3)^{159}}{160!}\right) \\&\leq \binom{m+1}{1} |Z_1||Z_m| (3/4)^{j/11}, \end{align*} $$
where we used
![]() $j\leq m/10$
in the third inequality, and in the last inequality, we used that the last factor is bounded by 1 for
$j\leq m/10$
in the third inequality, and in the last inequality, we used that the last factor is bounded by 1 for
![]() $m\geq 10000$
. To obtain this last observation, we note
$m\geq 10000$
. To obtain this last observation, we note
 $$\begin{align*}\frac{d}{dm} \left( (3/4)^{m/11}\sqrt{m}(m+1) \right) \leq 0\quad \mbox{for }m\geq\frac{33+\sqrt{1089+4 \left(\log \left(\frac{4}{3}\right)-11\right) \log \left(\frac{4}{3}\right)}-4 \log (2)+\log (9)}{\log \left(\frac{256}{81}\right)}.\end{align*}$$
$$\begin{align*}\frac{d}{dm} \left( (3/4)^{m/11}\sqrt{m}(m+1) \right) \leq 0\quad \mbox{for }m\geq\frac{33+\sqrt{1089+4 \left(\log \left(\frac{4}{3}\right)-11\right) \log \left(\frac{4}{3}\right)}-4 \log (2)+\log (9)}{\log \left(\frac{256}{81}\right)}.\end{align*}$$
In particular, the inequality holds for
![]() $m\geq 100$
. Thus, the desired inequality holds as a consequence of
$m\geq 100$
. Thus, the desired inequality holds as a consequence of
Let us now show (5.7). We apply (5.10), (5.11), Lemma 5.5 using
![]() $160\leq j \leq m/10$
,
$160\leq j \leq m/10$
,
 $$ \begin{align*} \begin{aligned} \binom{m+1}{j} |Z_j Z_{m+1-j}| &\leq \binom{m+1}{1} |Z_1||Z_m| (m+1) \frac{3 ^{j-160} \cdot500 ^{159} } {160!} \frac{j!}{(9(m+1)/10)^j} \\ &\leq \binom{m+1}{1} |Z_1||Z_m| \frac1{3^j m^9}\frac{10^j\cdot j!}{m^{j-9}} \frac{500^{159} }{ 3^{160}\cdot 160!} \\ &\leq \binom{m+1}{1} |Z_1||Z_m| \frac1{3^j m^9} \sqrt{2\pi j}m^9 \left(\frac{10 j}{e m}\right)^j \frac{500^{159} e^{\frac1{12j}}}{ 3^{160}\cdot 160!} \\ &\leq \binom{m+1}{1} |Z_1||Z_m| \frac1{3^j m^9} m^{10} \left(\frac{10j}{ e m}\right)^j \frac{2\cdot 500^{159} }{ 3^{160}\cdot 160!}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \binom{m+1}{j} |Z_j Z_{m+1-j}| &\leq \binom{m+1}{1} |Z_1||Z_m| (m+1) \frac{3 ^{j-160} \cdot500 ^{159} } {160!} \frac{j!}{(9(m+1)/10)^j} \\ &\leq \binom{m+1}{1} |Z_1||Z_m| \frac1{3^j m^9}\frac{10^j\cdot j!}{m^{j-9}} \frac{500^{159} }{ 3^{160}\cdot 160!} \\ &\leq \binom{m+1}{1} |Z_1||Z_m| \frac1{3^j m^9} \sqrt{2\pi j}m^9 \left(\frac{10 j}{e m}\right)^j \frac{500^{159} e^{\frac1{12j}}}{ 3^{160}\cdot 160!} \\ &\leq \binom{m+1}{1} |Z_1||Z_m| \frac1{3^j m^9} m^{10} \left(\frac{10j}{ e m}\right)^j \frac{2\cdot 500^{159} }{ 3^{160}\cdot 160!}, \end{aligned} \end{align*} $$
where we used (5.9). Observe that
![]() $\frac {d}{dj}\left (\frac {10j}{ e m}\right )^j \leq 0$
for
$\frac {d}{dj}\left (\frac {10j}{ e m}\right )^j \leq 0$
for
![]() $j\leq \frac {m}{10}$
. Then (5.7) follows once we note that for
$j\leq \frac {m}{10}$
. Then (5.7) follows once we note that for
![]() $160\leq j\leq \frac m{10}$
and
$160\leq j\leq \frac m{10}$
and
![]() $m\geq 10000$
, we have
$m\geq 10000$
, we have
 $$\begin{align*}m^{10} \left(\frac{10j}{ e m}\right)^j \frac{2\cdot 500^{159} }{ 3^{160}\cdot 160!}\leq m^{-150} \frac{2\cdot 500^{159}\cdot 1600^{160} }{ (3e)^{160}\cdot 160!}\leq 1.\end{align*}$$
$$\begin{align*}m^{10} \left(\frac{10j}{ e m}\right)^j \frac{2\cdot 500^{159} }{ 3^{160}\cdot 160!}\leq m^{-150} \frac{2\cdot 500^{159}\cdot 1600^{160} }{ (3e)^{160}\cdot 160!}\leq 1.\end{align*}$$
Finally, let us show (5.6) for
![]() $j < 160$
. Then by (5.2), we have
$j < 160$
. Then by (5.2), we have
 $$ \begin{align} \left|Z_j\right|&\leq \left|Z_1\right| \prod_{i=1}^{j-1} \left| 500\bar C_\ast \frac{(i+1) k}{i+1-k} \right| \leq \left|Z_1\right| \frac{j!\left|500 \bar C_\ast k\right| ^{j-1}}{(k-2)_{(j-1)}}, \end{align} $$
$$ \begin{align} \left|Z_j\right|&\leq \left|Z_1\right| \prod_{i=1}^{j-1} \left| 500\bar C_\ast \frac{(i+1) k}{i+1-k} \right| \leq \left|Z_1\right| \frac{j!\left|500 \bar C_\ast k\right| ^{j-1}}{(k-2)_{(j-1)}}, \end{align} $$
and (5.11) holds. Thus,
 $$ \begin{align*} \begin{aligned} \binom{m+1}{1} |Z_j Z_{m+1-j}| &\leq \binom{m+1}{j} |Z_1||Z_m| \frac{(m-j+1)!500^{j-1}}{m!} \\ &\leq \binom{m+1}{j} |Z_1||Z_m| \frac{101}{100}\frac{(m-j+1)^{m-j+\frac32}(500e)^{j-1}}{m^{m+\frac12}}\\ &\leq \binom{m+1}{1} |Z_1||Z_m| \left( \frac{600}{m} \right)^{j-1} \frac{101}{100}\left(\frac{m-j+1}{m}\right )^{m-j+1}\left(\frac{5 e}{6}\right)^{j-1}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \binom{m+1}{1} |Z_j Z_{m+1-j}| &\leq \binom{m+1}{j} |Z_1||Z_m| \frac{(m-j+1)!500^{j-1}}{m!} \\ &\leq \binom{m+1}{j} |Z_1||Z_m| \frac{101}{100}\frac{(m-j+1)^{m-j+\frac32}(500e)^{j-1}}{m^{m+\frac12}}\\ &\leq \binom{m+1}{1} |Z_1||Z_m| \left( \frac{600}{m} \right)^{j-1} \frac{101}{100}\left(\frac{m-j+1}{m}\right )^{m-j+1}\left(\frac{5 e}{6}\right)^{j-1}. \end{aligned} \end{align*} $$
Then to conclude, we observe that
 $$\begin{align*}\frac{d}{dj} \left( \left(\frac{m-j+1}{m}\right )^{m-j+1}\left(\frac{5 e}{6}\right)^{j-1} \right)\leq 0,\end{align*}$$
$$\begin{align*}\frac{d}{dj} \left( \left(\frac{m-j+1}{m}\right )^{m-j+1}\left(\frac{5 e}{6}\right)^{j-1} \right)\leq 0,\end{align*}$$
which is negative so long as
![]() $j\leq \frac {6+m}{6}$
, which is clearly satisfied. Then, substituting
$j\leq \frac {6+m}{6}$
, which is clearly satisfied. Then, substituting
![]() $j=2$
, we obtain (5.6) as a consequence of
$j=2$
, we obtain (5.6) as a consequence of
 $$\begin{align*}\frac{101}{100}\left(\frac{m-j+1}{m}\right )^{m-j+1}\left(\frac{5 e}{6}\right)^{j-1}\leq \frac{101}{100} \left(\frac{m-1}{m}\right )^{m-1}\left(\frac{5 e}{6}\right)\leq 1\,\end{align*}$$
$$\begin{align*}\frac{101}{100}\left(\frac{m-j+1}{m}\right )^{m-j+1}\left(\frac{5 e}{6}\right)^{j-1}\leq \frac{101}{100} \left(\frac{m-1}{m}\right )^{m-1}\left(\frac{5 e}{6}\right)\leq 1\,\end{align*}$$
for
![]() $m\geq 10000 $
.
$m\geq 10000 $
.
5.2 Closing the induction for
 $W_i$
$W_i$
Let us recall the following bounds from Lemma A.8. If
![]() $r \in (r_n, r_{n+1})$
, for n sufficiently large, then for any
$r \in (r_n, r_{n+1})$
, for n sufficiently large, then for any
![]() $i, j \in \left \{ W, Z \right \}$
,
$i, j \in \left \{ W, Z \right \}$
,
 $$ \begin{align} \begin{aligned} D_{W, 0} \leq 2|Z_0|,\quad |Z_1| \leq 3/10, \quad |W_1| \leq 1/2, \\ |\partial_i N_\circ (P_s)| \leq 2,\quad |\partial_i D_\circ | \leq 3/5, \quad |\partial_i \partial_j N_\circ (P_s) | \leq 7/5. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} D_{W, 0} \leq 2|Z_0|,\quad |Z_1| \leq 3/10, \quad |W_1| \leq 1/2, \\ |\partial_i N_\circ (P_s)| \leq 2,\quad |\partial_i D_\circ | \leq 3/5, \quad |\partial_i \partial_j N_\circ (P_s) | \leq 7/5. \end{aligned} \end{align} $$
Lemma 5.6. Assuming the estimates in Lemma 5.1 hold for all
![]() $i< m$
where we take
$i< m$
where we take
![]() $10000\leq m\leq k$
, then (5.1) holds for
$10000\leq m\leq k$
, then (5.1) holds for
![]() $i=m$
.
$i=m$
.
Proof. Let us rewrite equation (2.18) as
 $$ \begin{align} \begin{aligned} D_{W, 0} W_{m+1} &= (\partial_Z N_W (P_s) - W_1 \partial_Z D_W ) Z_m+ (N_{W, m} - \partial_ZN_W(P_s)Z_m) \\&\quad - W_1\partial_W D_Z(P_s) W_m - \sum_{j=1}^{m-1} \binom{m}{j}D_{W, m-j} W_{j+1} =\mathrm{I}+\mathrm{II}+\mathrm{III}+\mathrm{IV}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} D_{W, 0} W_{m+1} &= (\partial_Z N_W (P_s) - W_1 \partial_Z D_W ) Z_m+ (N_{W, m} - \partial_ZN_W(P_s)Z_m) \\&\quad - W_1\partial_W D_Z(P_s) W_m - \sum_{j=1}^{m-1} \binom{m}{j}D_{W, m-j} W_{j+1} =\mathrm{I}+\mathrm{II}+\mathrm{III}+\mathrm{IV}. \end{aligned} \end{align} $$
Taking the limit
![]() $r\rightarrow r^\ast $
yields
$r\rightarrow r^\ast $
yields
(see Lemma A.7). Thus, if we take k sufficiently large, we obtain
 $$ \begin{align} \left|\mathrm{I}\right|\leq \left( \frac{2}{5+3 \sqrt{5}}+o(1) \right) \left|Z_m\right|\leq \frac{2}{5}\left|Z_m\right|. \end{align} $$
$$ \begin{align} \left|\mathrm{I}\right|\leq \left( \frac{2}{5+3 \sqrt{5}}+o(1) \right) \left|Z_m\right|\leq \frac{2}{5}\left|Z_m\right|. \end{align} $$
Now consider
![]() $\mathrm {II}$
. Applying (5.1)–(5.4), (5.5), Lemma 5.4 and (5.13),
$\mathrm {II}$
. Applying (5.1)–(5.4), (5.5), Lemma 5.4 and (5.13),
 $$ \begin{align} \left|\mathrm{II}\right| &= \left| \partial_W N_W (P_s) W_{m} + \frac{1}{2}\sum_{j=1}^{m-1} \binom{m}{j} (W_j, Z_j)^\top HN_W \cdot (W_{m-j}, Z_{m-j}) \right|\nonumber \\&\leq 2|W_{m}| + 5 \sum_{j=1}^{m/2} \binom{m}{j} |Z_{j}| \left|HN_W\right||Z_{m-j}| \nonumber\\&\leq 8|Z_{m-1}| + 14\sum_{j=1}^{m/2} \binom{m}{j} |Z_{j}| |Z_{m-j}|\nonumber \\&\leq 8|Z_m| + 14\binom{m}{1} |Z_1 Z_{m-1}| \left( \sum_{j=1}^{160} \left( \frac{600}{m} \right)^{j-1} + \frac{1}{m^9}\sum_{j=161}^{m/10} (1/3)^{j} + \sum_{j=m/10}^{m/2} (3/4)^{j/11} \right)\nonumber \\&\leq 8|Z_m| + \frac{21}{5}m |Z_{m-1}| \left( \frac{10}{9} + \frac{1}{1000} + \frac{1}{1000} \right) \nonumber\\& \leq 5m|Z_{m-1}|\leq \frac{5\left|k-m\right|}{|\bar C_\ast|m k} |Z_{m}|\leq \frac{1700}{m } |Z_{m}|, \end{align} $$
$$ \begin{align} \left|\mathrm{II}\right| &= \left| \partial_W N_W (P_s) W_{m} + \frac{1}{2}\sum_{j=1}^{m-1} \binom{m}{j} (W_j, Z_j)^\top HN_W \cdot (W_{m-j}, Z_{m-j}) \right|\nonumber \\&\leq 2|W_{m}| + 5 \sum_{j=1}^{m/2} \binom{m}{j} |Z_{j}| \left|HN_W\right||Z_{m-j}| \nonumber\\&\leq 8|Z_{m-1}| + 14\sum_{j=1}^{m/2} \binom{m}{j} |Z_{j}| |Z_{m-j}|\nonumber \\&\leq 8|Z_m| + 14\binom{m}{1} |Z_1 Z_{m-1}| \left( \sum_{j=1}^{160} \left( \frac{600}{m} \right)^{j-1} + \frac{1}{m^9}\sum_{j=161}^{m/10} (1/3)^{j} + \sum_{j=m/10}^{m/2} (3/4)^{j/11} \right)\nonumber \\&\leq 8|Z_m| + \frac{21}{5}m |Z_{m-1}| \left( \frac{10}{9} + \frac{1}{1000} + \frac{1}{1000} \right) \nonumber\\& \leq 5m|Z_{m-1}|\leq \frac{5\left|k-m\right|}{|\bar C_\ast|m k} |Z_{m}|\leq \frac{1700}{m } |Z_{m}|, \end{align} $$
where in the last inequality we used Remark 5.2. Here, we used the estimate
 $$\begin{align*}\left|HN_W\right|{}_{\infty}\leq \max_{i=1,2}\sum_{j=1,2}\left|(HN_W)_{ij}\right|\leq \frac{14}{5}.\end{align*}$$
$$\begin{align*}\left|HN_W\right|{}_{\infty}\leq \max_{i=1,2}\sum_{j=1,2}\left|(HN_W)_{ij}\right|\leq \frac{14}{5}.\end{align*}$$
To estimate
![]() $\mathrm {III}$
, we first note that by (5.1)–(5.4),
$\mathrm {III}$
, we first note that by (5.1)–(5.4),
using again Remark 5.2. Therefore, using (5.13), we obtain
Lastly, let us consider
![]() $\mathrm {IV}$
. We remark that
$\mathrm {IV}$
. We remark that
![]() $D_{W, i}= \frac {3W_i+2Z_i}5$
for
$D_{W, i}= \frac {3W_i+2Z_i}5$
for
![]() $i\geq 1$
. Then applying (5.1)–(5.4), (5.5), Lemma 5.4 and (5.13),
$i\geq 1$
. Then applying (5.1)–(5.4), (5.5), Lemma 5.4 and (5.13),
 $$ \begin{align} \left|\mathrm{IV}\right| &\leq \frac{1}{5}\sum_{j=1}^{m-1} \binom{m}{j} |3W_{m-j}+2Z_{m-j}| |W_{j+1}| \nonumber\\ &\leq \frac{32}{5}\sum_{j=1}^{m-1} \binom{m}{j} |Z_{m-j}| |Z_{j}| \nonumber \\&\leq 13 \sum_{j=1}^{m/2} \binom{m}{j} |Z_j||Z_{m-j}|\nonumber \\ &\leq 13 m |Z_1||Z_{m-1}| \left( \sum_{j=1}^{160} \left( \frac{600}{m} \right)^{j-1} + \frac{1}{m^9}\sum_{j=160}^{m/10} (1/3)^j + \sum_{j=m/10}^{m/2} (3/4)^{j/11} \right)\nonumber \\ &\leq 14 m |Z_1||Z_{m-1}| \leq \frac{5}{m|\bar C_\ast|} |Z_m| \leq \frac{2000}{m} |Z_m|, \end{align} $$
$$ \begin{align} \left|\mathrm{IV}\right| &\leq \frac{1}{5}\sum_{j=1}^{m-1} \binom{m}{j} |3W_{m-j}+2Z_{m-j}| |W_{j+1}| \nonumber\\ &\leq \frac{32}{5}\sum_{j=1}^{m-1} \binom{m}{j} |Z_{m-j}| |Z_{j}| \nonumber \\&\leq 13 \sum_{j=1}^{m/2} \binom{m}{j} |Z_j||Z_{m-j}|\nonumber \\ &\leq 13 m |Z_1||Z_{m-1}| \left( \sum_{j=1}^{160} \left( \frac{600}{m} \right)^{j-1} + \frac{1}{m^9}\sum_{j=160}^{m/10} (1/3)^j + \sum_{j=m/10}^{m/2} (3/4)^{j/11} \right)\nonumber \\ &\leq 14 m |Z_1||Z_{m-1}| \leq \frac{5}{m|\bar C_\ast|} |Z_m| \leq \frac{2000}{m} |Z_m|, \end{align} $$
where we used Remark 5.2 in the last inequality.
Then combining (5.15)–(5.18), we obtain
 $$\begin{align*}\left|D_{W, 0} W_{m+1}\right| \leq \left(\frac{2}{5}+\frac{1700}{m }+\frac{450}{m^2}+\frac{2000}{m}\right)\left|Z_m\right| \leq \left|Z_m\right|. \end{align*}$$
$$\begin{align*}\left|D_{W, 0} W_{m+1}\right| \leq \left(\frac{2}{5}+\frac{1700}{m }+\frac{450}{m^2}+\frac{2000}{m}\right)\left|Z_m\right| \leq \left|Z_m\right|. \end{align*}$$
Noting
from Lemma A.7, then for k sufficiently large, we obtain our claim.
5.3 Closing the induction for
 $Z_i$
$Z_i$
Lemma 5.7. Assuming the estimates in Lemma 5.1 hold for all
![]() $i< m$
where we take
$i< m$
where we take
![]() $10000\leq m\leq k$
, and (5.1) holds for
$10000\leq m\leq k$
, and (5.1) holds for
![]() $i=m$
, then (5.4) holds for
$i=m$
, then (5.4) holds for
![]() $i=m$
.
$i=m$
.
Proof. Let us recall (2.19)
 $$ \begin{align*} Z_{m+1} D_{Z, 1} (m+1-k) &= -\binom{m+1}{m-1} D_{Z, 2} Z_{m} - \sum_{j=1}^{m-2} \binom{m+1}{j} D_{Z, m+1-j} Z_{j+1} \nonumber \\ &\quad+\left( N_{Z, m+1} - (\partial_Z N_Z (P_s) ) Z_{m+1}\right) - Z_1 W_{m+1} \partial_W D_Z (P_s) \\ &= -\frac m 2 (1 + m)D_{Z, 2} Z_{m} +\mathrm{I}+\mathrm{II}+\mathrm{III}. \end{align*} $$
$$ \begin{align*} Z_{m+1} D_{Z, 1} (m+1-k) &= -\binom{m+1}{m-1} D_{Z, 2} Z_{m} - \sum_{j=1}^{m-2} \binom{m+1}{j} D_{Z, m+1-j} Z_{j+1} \nonumber \\ &\quad+\left( N_{Z, m+1} - (\partial_Z N_Z (P_s) ) Z_{m+1}\right) - Z_1 W_{m+1} \partial_W D_Z (P_s) \\ &= -\frac m 2 (1 + m)D_{Z, 2} Z_{m} +\mathrm{I}+\mathrm{II}+\mathrm{III}. \end{align*} $$
Applying (5.5), Lemma 5.4 and (5.13),
 $$ \begin{align} \left|\mathrm{I}\right|&\leq \frac{1}{5}\sum_{j=1}^{m-2} \binom{m+1}{j} (3\left|W_{ m+1-j }\right|+2\left|Z_{ m+1-j }\right|) \left|Z_{j+1}\right| \nonumber \\ &\leq \frac{8}{5}\sum_{j=1}^{m-2} \binom{m+1}{j} \left|Z_{m+1-j}\right| \left|Z_{j+1}\right| \nonumber \\ &\leq \frac{16}{5}\sum_{j=1}^{(m+1)/2} \binom{m+1}{j} \left|Z_{m+1-j}\right| \left|Z_{j+1}\right| \nonumber \\ &= \frac{16}{5}\sum_{j=2}^{(m+2)/2} \frac{j}{m+2} \binom{m+2}{j} \left|Z_{m+2-j}\right| \left|Z_{j}\right| \nonumber \\ &\leq \frac{16}{5}(m+1) |Z_1 Z_m| \left( \sum_{j=2}^{160} j\left( \frac{600}{m} \right)^{j-1} + \frac{1}{m^9}\sum_{j=161}^{m/10} j(1/3)^{j} + \sum_{j=m/10}^{(m-2)/2} j(3/4)^{j/11} \right) \nonumber \\ & \leq \frac {m}{10}|Z_m|. \end{align} $$
$$ \begin{align} \left|\mathrm{I}\right|&\leq \frac{1}{5}\sum_{j=1}^{m-2} \binom{m+1}{j} (3\left|W_{ m+1-j }\right|+2\left|Z_{ m+1-j }\right|) \left|Z_{j+1}\right| \nonumber \\ &\leq \frac{8}{5}\sum_{j=1}^{m-2} \binom{m+1}{j} \left|Z_{m+1-j}\right| \left|Z_{j+1}\right| \nonumber \\ &\leq \frac{16}{5}\sum_{j=1}^{(m+1)/2} \binom{m+1}{j} \left|Z_{m+1-j}\right| \left|Z_{j+1}\right| \nonumber \\ &= \frac{16}{5}\sum_{j=2}^{(m+2)/2} \frac{j}{m+2} \binom{m+2}{j} \left|Z_{m+2-j}\right| \left|Z_{j}\right| \nonumber \\ &\leq \frac{16}{5}(m+1) |Z_1 Z_m| \left( \sum_{j=2}^{160} j\left( \frac{600}{m} \right)^{j-1} + \frac{1}{m^9}\sum_{j=161}^{m/10} j(1/3)^{j} + \sum_{j=m/10}^{(m-2)/2} j(3/4)^{j/11} \right) \nonumber \\ & \leq \frac {m}{10}|Z_m|. \end{align} $$
Applying (5.1), (5.5), Lemma 5.4 and (5.13),
 $$ \begin{align} \left|\mathrm{II}\right| &= \left|\partial_W N_Z (P_s) W_{m+1} \right|+ \sum_{j=1}^{m/2} \binom{m+1}{j} \left|(W_j, Z_j)^\top HN_Z \cdot (W_{m+1-j}, Z_{m+1-j}) \right|\nonumber\\&\leq 2|W_{m+1}| +(m+1) \left|(W_1, Z_1)^\top HN_Z \cdot (W_{m}, Z_{m}) \right|+ \sum_{j=2}^{m/2} \binom{m+1}{j} \left|(W_j, Z_j)^\top HN_Z \cdot (W_{m+1-j}, Z_{m+1-j}) \right|\nonumber\\&\leq 8|Z_{m}| +(m+1) \left|(W_1, Z_1)^\top HN_Z \cdot (W_{m}, Z_{m}) \right|+ 5\sum_{j=2}^{m/2} \binom{m+1}{j} |Z_{j}| |Z_{m+1-j}|\nonumber\\&\leq 8|Z_{m}| +(m+1) \left|(W_1, Z_1)^\top HN_Z \cdot (W_{m}, Z_{m}) \right|\nonumber\\&\quad+ 5(m+1) |Z_1 Z_m| \left( \sum_{j=2}^{160} \left( \frac{600}{m} \right)^{j-1} + \frac{1}{m^9}\sum_{j=161}^{m/10} (1/3)^{j} + \sum_{j=m/10}^{(m+1)/2} (3/4)^{j/11} \right) \nonumber\\&\leq (m+1) \left|(W_1, Z_1)^\top HN_Z \cdot (W_{m}, Z_{m}) \right|+ \frac{m}{10} | Z_m|. \end{align} $$
$$ \begin{align} \left|\mathrm{II}\right| &= \left|\partial_W N_Z (P_s) W_{m+1} \right|+ \sum_{j=1}^{m/2} \binom{m+1}{j} \left|(W_j, Z_j)^\top HN_Z \cdot (W_{m+1-j}, Z_{m+1-j}) \right|\nonumber\\&\leq 2|W_{m+1}| +(m+1) \left|(W_1, Z_1)^\top HN_Z \cdot (W_{m}, Z_{m}) \right|+ \sum_{j=2}^{m/2} \binom{m+1}{j} \left|(W_j, Z_j)^\top HN_Z \cdot (W_{m+1-j}, Z_{m+1-j}) \right|\nonumber\\&\leq 8|Z_{m}| +(m+1) \left|(W_1, Z_1)^\top HN_Z \cdot (W_{m}, Z_{m}) \right|+ 5\sum_{j=2}^{m/2} \binom{m+1}{j} |Z_{j}| |Z_{m+1-j}|\nonumber\\&\leq 8|Z_{m}| +(m+1) \left|(W_1, Z_1)^\top HN_Z \cdot (W_{m}, Z_{m}) \right|\nonumber\\&\quad+ 5(m+1) |Z_1 Z_m| \left( \sum_{j=2}^{160} \left( \frac{600}{m} \right)^{j-1} + \frac{1}{m^9}\sum_{j=161}^{m/10} (1/3)^{j} + \sum_{j=m/10}^{(m+1)/2} (3/4)^{j/11} \right) \nonumber\\&\leq (m+1) \left|(W_1, Z_1)^\top HN_Z \cdot (W_{m}, Z_{m}) \right|+ \frac{m}{10} | Z_m|. \end{align} $$
Note
 $$\begin{align*}HN_Z (P_s) = \begin{pmatrix} \frac{\gamma-1}{2} & \frac{\gamma-3}{4} \\ \frac{\gamma-3}{4} & -\gamma \\ \end{pmatrix} = \frac{1}{5} \begin{pmatrix} 1 & -2 \\ -2 & -7 \end{pmatrix},\end{align*}$$
$$\begin{align*}HN_Z (P_s) = \begin{pmatrix} \frac{\gamma-1}{2} & \frac{\gamma-3}{4} \\ \frac{\gamma-3}{4} & -\gamma \\ \end{pmatrix} = \frac{1}{5} \begin{pmatrix} 1 & -2 \\ -2 & -7 \end{pmatrix},\end{align*}$$
and
![]() $\lim _{r\rightarrow r^\ast }(W_1,Z_1)=(5-3 \sqrt {5}) \left (\frac 14,-\frac 16\right )$
from Lemma A.7. Hence,
$\lim _{r\rightarrow r^\ast }(W_1,Z_1)=(5-3 \sqrt {5}) \left (\frac 14,-\frac 16\right )$
from Lemma A.7. Hence,
Thus, for k sufficiently large, we have
Combining this estimate with (5.20), we obtain
Finally, applying (5.1), (5.13) to
![]() $\mathrm {III}$
yields
$\mathrm {III}$
yields
Hence, combining (5.19)–(5.21), we obtain
 $$ \begin{align*} \left| Z_{m+1} D_{Z, 1} (m+1-k) +\frac m 2 (1 + m)D_{Z, 2} Z_{m}\right| \leq \left|\mathrm{I}\right|+ \left|\mathrm{II}\right|+ \left|\mathrm{III}\right| \leq \left( \frac{1}{10} + 1 + \frac 1 m\right) m|Z_m|\leq \frac32 m|Z_m|. \end{align*} $$
$$ \begin{align*} \left| Z_{m+1} D_{Z, 1} (m+1-k) +\frac m 2 (1 + m)D_{Z, 2} Z_{m}\right| \leq \left|\mathrm{I}\right|+ \left|\mathrm{II}\right|+ \left|\mathrm{III}\right| \leq \left( \frac{1}{10} + 1 + \frac 1 m\right) m|Z_m|\leq \frac32 m|Z_m|. \end{align*} $$
Thus,
 $$ \begin{align*} \left| Z_{m+1} (m+1-k) \frac{2 D_{Z, 1}}{(m+1)m D_{Z, 2}} + Z_m \right| \leq \frac{3}{(m+1)|D_{Z, 2}|} |Z_m| . \end{align*} $$
$$ \begin{align*} \left| Z_{m+1} (m+1-k) \frac{2 D_{Z, 1}}{(m+1)m D_{Z, 2}} + Z_m \right| \leq \frac{3}{(m+1)|D_{Z, 2}|} |Z_m| . \end{align*} $$
Using
from Lemma A.7, we obtain
 $$\begin{align*}\left| Z_{m+1} (m+1-k) \frac{2 D_{Z, 1}}{(m+1)m D_{Z, 2}} + Z_m \right| \leq \frac{2}{50} |Z_m|,\end{align*}$$
$$\begin{align*}\left| Z_{m+1} (m+1-k) \frac{2 D_{Z, 1}}{(m+1)m D_{Z, 2}} + Z_m \right| \leq \frac{2}{50} |Z_m|,\end{align*}$$
from which we obtain (5.4).
5.4 Further corollaries of Lemma 5.1
Corollary 5.8. Let
![]() $\gamma = 7/5$
, n odd sufficiently large and
$\gamma = 7/5$
, n odd sufficiently large and
![]() $r \in (r_n, r_{n+1})$
. We have that
$r \in (r_n, r_{n+1})$
. We have that
![]() $Z_n> 0$
and
$Z_n> 0$
and
![]() $Z_{n+1} < 0$
. Moreover, we have
$Z_{n+1} < 0$
. Moreover, we have
 $$ \begin{align} \frac{ k^n}{k-n} |\bar C_\ast|^n \lesssim\frac{Z_n}{n!} \lesssim \frac{n k^n}{k-n } |\bar C_\ast|^n \left( \frac{1.05}{0.95} \right)^{n} . \end{align} $$
$$ \begin{align} \frac{ k^n}{k-n} |\bar C_\ast|^n \lesssim\frac{Z_n}{n!} \lesssim \frac{n k^n}{k-n } |\bar C_\ast|^n \left( \frac{1.05}{0.95} \right)^{n} . \end{align} $$
In particular,
![]() $\left ( \frac {|Z_n|}{n!} (k-n) \right )^{1/n} \approx n$
.
$\left ( \frac {|Z_n|}{n!} (k-n) \right )^{1/n} \approx n$
.
Proof. By Lemma A.28, we have
which by a liberal choice of implicit constant may be rewritten as
 $$\begin{align*}|\bar C_\ast|^{10000} \frac{{10000}! k^{10000}}{|({10000}-k)_{(10000)}|} \lesssim \frac{-Z_{10000}}{10000!} \lesssim |\bar C_\ast|^{10000} \frac{n! k^{10000}}{|({10000}-k)_{(10000)}|}\left( \frac{1.05}{0.95} \right)^{10000}.\end{align*}$$
$$\begin{align*}|\bar C_\ast|^{10000} \frac{{10000}! k^{10000}}{|({10000}-k)_{(10000)}|} \lesssim \frac{-Z_{10000}}{10000!} \lesssim |\bar C_\ast|^{10000} \frac{n! k^{10000}}{|({10000}-k)_{(10000)}|}\left( \frac{1.05}{0.95} \right)^{10000}.\end{align*}$$
Then, applying (5.4) successively yields
 $$\begin{align*}|\bar C_\ast|^n \frac{n! k^n}{|(n-k)_{(n)}|} \lesssim \frac{Z_n}{n!} \lesssim |\bar C_\ast|^n \frac{n! k^n}{|(n-k)_{(n)}|}\left( \frac{1.05}{0.95} \right)^{n}. \end{align*}$$
$$\begin{align*}|\bar C_\ast|^n \frac{n! k^n}{|(n-k)_{(n)}|} \lesssim \frac{Z_n}{n!} \lesssim |\bar C_\ast|^n \frac{n! k^n}{|(n-k)_{(n)}|}\left( \frac{1.05}{0.95} \right)^{n}. \end{align*}$$
We notice that
![]() $(k-n)(n-1)! \leq |(n-k)_{(n)}| \leq (k-n) n!$
, which follows by canceling the factor
$(k-n)(n-1)! \leq |(n-k)_{(n)}| \leq (k-n) n!$
, which follows by canceling the factor
![]() $(k-n)$
and bounding
$(k-n)$
and bounding
![]() $1 \leq (k-n+1) \leq 2$
,
$1 \leq (k-n+1) \leq 2$
,
![]() $2 \leq (k-n+2) \leq 3$
,
$2 \leq (k-n+2) \leq 3$
,
![]() $\dots $
. Thus, we obtain (5.22).
$\dots $
. Thus, we obtain (5.22).
Finally, we note the statement
![]() $Z_{n+1}<0$
follows as a consequence of (5.4) and (5.22).
$Z_{n+1}<0$
follows as a consequence of (5.4) and (5.22).
Note that this Corollary concludes the proof of Lemmas 4.4 and 4.7.
Corollary 5.9. We have that for
![]() $\gamma = 7/5$
and n odd and sufficiently large (
$\gamma = 7/5$
and n odd and sufficiently large (
![]() $r \in (r_n, r_{n+1})$
),
$r \in (r_n, r_{n+1})$
),
Proof. From Lemma 5.1, we have that
![]() $|W_{n+1}| \lesssim |Z_n| \lesssim \frac {n+1-k}{(n+1)^2k }|Z_{n+1}| \lesssim \frac {|Z_{n+1}|}{n^2}$
. Using Corollary 5.8, we have
$|W_{n+1}| \lesssim |Z_n| \lesssim \frac {n+1-k}{(n+1)^2k }|Z_{n+1}| \lesssim \frac {|Z_{n+1}|}{n^2}$
. Using Corollary 5.8, we have
![]() $Z_{n+1} < 0$
.
$Z_{n+1} < 0$
.
Let us note that this Corollary ends the proof of Lemma 3.4 for the case of
![]() $\gamma = 7/5$
and sufficiently large odd n. We will now show how Lemma 5.1 implies
$\gamma = 7/5$
and sufficiently large odd n. We will now show how Lemma 5.1 implies
![]() $\log $
-convexity of
$\log $
-convexity of
![]() $\frac {Z_i}{i!}$
.
$\frac {Z_i}{i!}$
.
From Lemma 5.1, we can compare the size of
![]() $|Z_i|$
with
$|Z_i|$
with
![]() $|Z_{i+1}|$
. The following Lemma just applies Lemma 5.1 for all
$|Z_{i+1}|$
. The following Lemma just applies Lemma 5.1 for all
![]() $i = a, a+1, \ldots n-1$
and concatenates those bounds in order to obtain a direct comparison between
$i = a, a+1, \ldots n-1$
and concatenates those bounds in order to obtain a direct comparison between
![]() $|Z_a|$
and
$|Z_a|$
and
![]() $|Z_n|$
.
$|Z_n|$
.
Lemma 5.10. For k sufficiently large, we have that for any
![]() $a \leq n = \lfloor k \rfloor $
,
$a \leq n = \lfloor k \rfloor $
,
 $$ \begin{align*} \frac{|Z_{a}| }{a!} \lesssim \left( \frac{Z_n}{n!} \right)^{a/n} \binom{n}{a}^{-1} \left( \frac{1.05}{0.95} \right)^{\frac{a(n-a)}{n}} (k-n)^{a/n-\lfloor a/n \rfloor} . \end{align*} $$
$$ \begin{align*} \frac{|Z_{a}| }{a!} \lesssim \left( \frac{Z_n}{n!} \right)^{a/n} \binom{n}{a}^{-1} \left( \frac{1.05}{0.95} \right)^{\frac{a(n-a)}{n}} (k-n)^{a/n-\lfloor a/n \rfloor} . \end{align*} $$
Proof. Let us start supposing
![]() $a < n$
, so that
$a < n$
, so that
![]() $a/n - \lfloor a/n \rfloor = a/n$
. Writing
$a/n - \lfloor a/n \rfloor = a/n$
. Writing
![]() $\frac {Z_a}{a!} = \prod _{j=1}^a \frac {1}{j} \frac {Z_j}{Z_{j-1}}$
and
$\frac {Z_a}{a!} = \prod _{j=1}^a \frac {1}{j} \frac {Z_j}{Z_{j-1}}$
and
![]() $\frac {Z_n}{n!} = \prod _{j=1}^n \frac {1}{j} \frac {Z_j}{Z_{j-1}}$
, the statement is equivalent to
$\frac {Z_n}{n!} = \prod _{j=1}^n \frac {1}{j} \frac {Z_j}{Z_{j-1}}$
, the statement is equivalent to
 $$ \begin{align*} \left( \prod_{j=1}^{a} \frac{|Z_j|}{|Z_{j-1}| jk} \right)^{1-a/n} \lesssim \left( \prod_{j=a+1}^{n} \frac{|Z_j|}{|Z_{j-1}| jk} \right)^{a/n} \binom{n}{a}^{-1} \left( \frac{1.05}{0.95} \right)^{ \frac{a(n-a)}{n}} (k-n)^{a/n}. \end{align*} $$
$$ \begin{align*} \left( \prod_{j=1}^{a} \frac{|Z_j|}{|Z_{j-1}| jk} \right)^{1-a/n} \lesssim \left( \prod_{j=a+1}^{n} \frac{|Z_j|}{|Z_{j-1}| jk} \right)^{a/n} \binom{n}{a}^{-1} \left( \frac{1.05}{0.95} \right)^{ \frac{a(n-a)}{n}} (k-n)^{a/n}. \end{align*} $$
Using Lemma 5.1, the left-hand-side is
![]() $\lesssim \prod _{j=1}^a \frac {j}{k-j}\bar C_\ast \left ( \frac {1.05}{0.95} \right )^a$
and the parenthesis in the right-hand-side is
$\lesssim \prod _{j=1}^a \frac {j}{k-j}\bar C_\ast \left ( \frac {1.05}{0.95} \right )^a$
and the parenthesis in the right-hand-side is
![]() $\gtrsim \prod _{j=a+1}^n \frac {j}{k-j}\bar C_\ast $
. Thus, it just suffices to show
$\gtrsim \prod _{j=a+1}^n \frac {j}{k-j}\bar C_\ast $
. Thus, it just suffices to show
 $$ \begin{align*} &\left( \prod_{j=1}^{a} \frac{j}{k-j} \bar C_\ast \right)^{1-a/n} \left( \frac{1.05}{0.95} \right)^{a(1-a/n)} \lesssim \left( \prod_{j=a+1}^{n} \frac{j\bar C_\ast}{k-j} \right)^{a/n} \binom{n}{a}^{-1} \left( \frac{1.05}{0.95} \right)^{ \frac{a(n-a)}{n}} (k-n)^{a/n} \\ \Leftrightarrow &\left( \prod_{j=1}^{a} \frac{j}{k-j} \right)^{1-a/n} \lesssim \left( \prod_{j=a+1}^{n} \frac{j}{k-j} \right)^{\frac{a}{n}} \binom{n}{a}^{-1} (k-n)^{a/n} \\ \Leftarrow &\left( \frac{a!}{n! /(n-a)! }\right)^{1-a/n} \lesssim \left( \frac{n!/a!}{(n-a)! (k-n)} \right)^{\frac{a}{n}} \binom{n}{a}^{-1} (k-n)^{a/n}. \end{align*} $$
$$ \begin{align*} &\left( \prod_{j=1}^{a} \frac{j}{k-j} \bar C_\ast \right)^{1-a/n} \left( \frac{1.05}{0.95} \right)^{a(1-a/n)} \lesssim \left( \prod_{j=a+1}^{n} \frac{j\bar C_\ast}{k-j} \right)^{a/n} \binom{n}{a}^{-1} \left( \frac{1.05}{0.95} \right)^{ \frac{a(n-a)}{n}} (k-n)^{a/n} \\ \Leftrightarrow &\left( \prod_{j=1}^{a} \frac{j}{k-j} \right)^{1-a/n} \lesssim \left( \prod_{j=a+1}^{n} \frac{j}{k-j} \right)^{\frac{a}{n}} \binom{n}{a}^{-1} (k-n)^{a/n} \\ \Leftarrow &\left( \frac{a!}{n! /(n-a)! }\right)^{1-a/n} \lesssim \left( \frac{n!/a!}{(n-a)! (k-n)} \right)^{\frac{a}{n}} \binom{n}{a}^{-1} (k-n)^{a/n}. \end{align*} $$
As the last inequality is in fact an equality, we are done with the case
![]() $a < n$
. For the case
$a < n$
. For the case
![]() $a=n$
, all the implications work the same except the last one, as we should erase the factor
$a=n$
, all the implications work the same except the last one, as we should erase the factor
![]() $(k-n)$
(this is because
$(k-n)$
(this is because
![]() $\prod _{j=a+1}^n (k-j)$
has no factors for
$\prod _{j=a+1}^n (k-j)$
has no factors for
![]() $a=n$
, so we cannot extract a factor
$a=n$
, so we cannot extract a factor
![]() $(k-n)$
). Thus, erasing the factors
$(k-n)$
). Thus, erasing the factors
![]() $(k-n)$
(and their powers) in all the equations, the proof works the same for
$(k-n)$
(and their powers) in all the equations, the proof works the same for
![]() $a=n$
. As
$a=n$
. As
![]() $a/n - \lfloor a/n \rfloor = 0$
for
$a/n - \lfloor a/n \rfloor = 0$
for
![]() $a=n$
, the statement is also correct in that case.
$a=n$
, the statement is also correct in that case.
5.5 Estimates on P - Validity of the near-left barrier
Let us recall
![]() $b^{\mathrm {nl}}_{n, W}(s) = \sum _{i=0}^n \frac {W_i}{i!} s^i$
,
$b^{\mathrm {nl}}_{n, W}(s) = \sum _{i=0}^n \frac {W_i}{i!} s^i$
,
![]() $b^{\mathrm {nl}}_{n, Z}(s) = \sum _{i=0}^n \frac {Z_i}{i!} s^i$
and
$b^{\mathrm {nl}}_{n, Z}(s) = \sum _{i=0}^n \frac {Z_i}{i!} s^i$
and
In order to obtain the sign of
![]() $P^{\mathrm {nl}}_n(s)$
, we prove the following lemma:
$P^{\mathrm {nl}}_n(s)$
, we prove the following lemma:
Proposition 5.11. For any s with
![]() $0 \leq s^{n-2} \leq 3 \frac {|D_{Z, 2}^\ast | }{2 \partial _Z D_Z}\frac {n!}{Z_n} $
, we have
$0 \leq s^{n-2} \leq 3 \frac {|D_{Z, 2}^\ast | }{2 \partial _Z D_Z}\frac {n!}{Z_n} $
, we have
 $$ \begin{align} P^{\mathrm{nl}}_n(s) = n \frac{Z_n}{n!} \frac{N_{W, 0} D_{Z, 2}}{2} s^{n+1} \left( 1 +O \left( \frac1n \right) \right) + n\left(\frac{Z_n}{n!} \right)^2 \partial_Z D_ZN_{W, 0} s^{2n-1} \left( 1 +O \left( \frac1n \right) \right). \end{align} $$
$$ \begin{align} P^{\mathrm{nl}}_n(s) = n \frac{Z_n}{n!} \frac{N_{W, 0} D_{Z, 2}}{2} s^{n+1} \left( 1 +O \left( \frac1n \right) \right) + n\left(\frac{Z_n}{n!} \right)^2 \partial_Z D_ZN_{W, 0} s^{2n-1} \left( 1 +O \left( \frac1n \right) \right). \end{align} $$
Moreover, letting
 $$ \begin{align} s_{7/5, \mathrm{val}} = \left( \frac{99}{100}\frac{|D_{Z, 2}|}{2 \partial_Z D_Z} \frac{n!}{Z_n} \right)^{\frac{1}{n-2}}, \end{align} $$
$$ \begin{align} s_{7/5, \mathrm{val}} = \left( \frac{99}{100}\frac{|D_{Z, 2}|}{2 \partial_Z D_Z} \frac{n!}{Z_n} \right)^{\frac{1}{n-2}}, \end{align} $$
we have that
![]() $P^{\mathrm {nl}}_n(s)> 0$
for
$P^{\mathrm {nl}}_n(s)> 0$
for
![]() $s \in (0, s_{7/5, \mathrm {val}} )$
.
$s \in (0, s_{7/5, \mathrm {val}} )$
.
Before we prove Proposition 5.11, we need a few auxiliary lemmas.
In what follows, it will be useful to introduce the following notation: Let us define the discrepancy
![]() $\ell $
of a number a as
$\ell $
of a number a as
We also define
 $$\begin{align*}\genfrac{[}{]}{0pt}{}{n}{a} = \binom{n}{a} \left( \frac{0.95}{1.05} \right)^{(a(n-a))/n}.\end{align*}$$
$$\begin{align*}\genfrac{[}{]}{0pt}{}{n}{a} = \binom{n}{a} \left( \frac{0.95}{1.05} \right)^{(a(n-a))/n}.\end{align*}$$
The brackets behave asymptotically like the binomial coefficients in the sense that they are symmetric. We have
![]() $\genfrac {[}{]}{0pt}{}{n}{a}^{-1} \lesssim \frac {1}{n^a}$
if a is fixed, and we also have
$\genfrac {[}{]}{0pt}{}{n}{a}^{-1} \lesssim \frac {1}{n^a}$
if a is fixed, and we also have
![]() $\genfrac {[}{]}{0pt}{}{n}{a}^{-1} \lesssim \frac {1}{n^{10}} 3^{-\ell (a)}$
for any
$\genfrac {[}{]}{0pt}{}{n}{a}^{-1} \lesssim \frac {1}{n^{10}} 3^{-\ell (a)}$
for any
![]() $1\leq a\leq n$
with
$1\leq a\leq n$
with
![]() $\ell (a) \geq 10$
.
$\ell (a) \geq 10$
.
The strategy toward Proposition 5.11 is to develop a Taylor series for
![]() $P^{\mathrm {{nl}}}_n(s)$
and bound all the terms except the dominant ones. In Lemma 5.12, we will bound the i-th coefficient for
$P^{\mathrm {{nl}}}_n(s)$
and bound all the terms except the dominant ones. In Lemma 5.12, we will bound the i-th coefficient for
![]() $i \leq n$
, and in Lemma 5.13, we will extract the main contributions of the
$i \leq n$
, and in Lemma 5.13, we will extract the main contributions of the
![]() $(n+1)$
-th and
$(n+1)$
-th and
![]() $(2n-1)$
-th terms. Those correspond to the main terms in (5.23). Lastly, in the proof of Proposition 5.11, we will deal with all the i-th Taylor coefficients, for
$(2n-1)$
-th terms. Those correspond to the main terms in (5.23). Lastly, in the proof of Proposition 5.11, we will deal with all the i-th Taylor coefficients, for
![]() $i \geq n+2$
,
$i \geq n+2$
,
![]() $i \neq 2n-1$
. In all those proofs, we will develop the expressions in terms of
$i \neq 2n-1$
. In all those proofs, we will develop the expressions in terms of
![]() $|Z_i|$
(or
$|Z_i|$
(or
![]() $|W_i| \lesssim |Z_{i-1}|$
), and we will observe that the term arising from
$|W_i| \lesssim |Z_{i-1}|$
), and we will observe that the term arising from
![]() $|Z_a| |Z_b| |Z_c| | Z_d |$
is proportional to
$|Z_a| |Z_b| |Z_c| | Z_d |$
is proportional to
![]() $\genfrac {[}{]}{0pt}{}{n}{a}^{-1} \genfrac {[}{]}{0pt}{}{n}{b}^{-1} \genfrac {[}{]}{0pt}{}{n}{c}^{-1} \genfrac {[}{]}{0pt}{}{n}{d}^{-1}$
. Since that is smaller than
$\genfrac {[}{]}{0pt}{}{n}{a}^{-1} \genfrac {[}{]}{0pt}{}{n}{b}^{-1} \genfrac {[}{]}{0pt}{}{n}{c}^{-1} \genfrac {[}{]}{0pt}{}{n}{d}^{-1}$
. Since that is smaller than
![]() $n^{-\ell (a, b, c, d) }$
, we will be able to show that the terms with small discrepancy dominate, and they will correspond exactly to the main contributions from the
$n^{-\ell (a, b, c, d) }$
, we will be able to show that the terms with small discrepancy dominate, and they will correspond exactly to the main contributions from the
![]() $(n+1)$
-th and
$(n+1)$
-th and
![]() $(2n-1)$
-th terms of the Taylor series.
$(2n-1)$
-th terms of the Taylor series.
Lemma 5.12. Let n be an odd number sufficiently large and
![]() $ i \leq n$
. We have that
$ i \leq n$
. We have that
 $$ \begin{align*} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_{n} (0)}{(i-1)!} \lesssim i \left( \frac{|Z_n|}{n!}\right)^{i/n} \frac{(k-n)^{i/n - \lfloor i/n \rfloor}}{n^{\min \{7, \ell (i) \} }}. \end{align*} $$
$$ \begin{align*} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_{n} (0)}{(i-1)!} \lesssim i \left( \frac{|Z_n|}{n!}\right)^{i/n} \frac{(k-n)^{i/n - \lfloor i/n \rfloor}}{n^{\min \{7, \ell (i) \} }}. \end{align*} $$
Proof. Let us recall (3.10):
We have that
![]() $|D_{\circ , i}| \lesssim |\partial ^i_s b_{n, Z}^{\mathrm {nl}}(s)|$
and
$|D_{\circ , i}| \lesssim |\partial ^i_s b_{n, Z}^{\mathrm {nl}}(s)|$
and
![]() $|\partial ^i_s (N_Z(b_n^{\mathrm {nl}}(s)))| \lesssim |\partial ^i_s (b_{n,Z}^{\mathrm {nl}}(s)^2)| + |\partial _s^i b_Z^{\mathrm {nl}}(s)| \lesssim |\partial ^i_s (b_Z^{\mathrm {nl}}(s)^2)|$
. Using Lemma 5.10,
$|\partial ^i_s (N_Z(b_n^{\mathrm {nl}}(s)))| \lesssim |\partial ^i_s (b_{n,Z}^{\mathrm {nl}}(s)^2)| + |\partial _s^i b_Z^{\mathrm {nl}}(s)| \lesssim |\partial ^i_s (b_Z^{\mathrm {nl}}(s)^2)|$
. Using Lemma 5.10,
 $$ \begin{align} \partial^{i-1}_s P^{\mathrm{nl}}_{n} (0) &\lesssim |\partial^{i-1}_s (b_{n, Z}^{\mathrm{nl\, \prime}}(s) b_{n, Z}^{\mathrm{nl}}(s)^3)(0)| = \sum_{\mathcal{J}_i} \frac{(i-1)!}{(a-1)!b!c!d!} |Z_a||Z_b||Z_c||Z_d| \nonumber \\ & \lesssim \sum_{\mathcal{J}_i} \frac{i!}{a!b!c!d!} |Z_a||Z_b||Z_c||Z_d| \nonumber \\ &\lesssim i! \left( \frac{|Z_n|}{n!} \right)^{i/n} (k-n)^{i/n - \lfloor i/n \rfloor} \sum_{\mathcal{J}_i} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \genfrac{[}{]}{0pt}{}{n}{d}^{-1} , \end{align} $$
$$ \begin{align} \partial^{i-1}_s P^{\mathrm{nl}}_{n} (0) &\lesssim |\partial^{i-1}_s (b_{n, Z}^{\mathrm{nl\, \prime}}(s) b_{n, Z}^{\mathrm{nl}}(s)^3)(0)| = \sum_{\mathcal{J}_i} \frac{(i-1)!}{(a-1)!b!c!d!} |Z_a||Z_b||Z_c||Z_d| \nonumber \\ & \lesssim \sum_{\mathcal{J}_i} \frac{i!}{a!b!c!d!} |Z_a||Z_b||Z_c||Z_d| \nonumber \\ &\lesssim i! \left( \frac{|Z_n|}{n!} \right)^{i/n} (k-n)^{i/n - \lfloor i/n \rfloor} \sum_{\mathcal{J}_i} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \genfrac{[}{]}{0pt}{}{n}{d}^{-1} , \end{align} $$
where
In the last inequality, we also used that the function
![]() $x-\lfloor x \rfloor $
is subadditive. Let us decompose
$x-\lfloor x \rfloor $
is subadditive. Let us decompose
![]() $\mathcal {J}_i = \mathcal {J}_i' \sqcup \mathcal {J}_i"$
with
$\mathcal {J}_i = \mathcal {J}_i' \sqcup \mathcal {J}_i"$
with
![]() $\mathcal {J}_i', \mathcal {J}_i"$
given by
$\mathcal {J}_i', \mathcal {J}_i"$
given by
 $$ \begin{align*} \mathcal{J}_i' = \mathcal{J}_i \cap \left\{ (a, b, c, d) \in \mathbb{Z}^4: \ell (a, b, c, d) \geq 10 \right\}, \\ \mathcal{J}_i" = \mathcal{J}_i \cap \left\{ (a, b, c, d) \in \mathbb{Z}^4: \ell (a, b, c, d) < 10 \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{J}_i' = \mathcal{J}_i \cap \left\{ (a, b, c, d) \in \mathbb{Z}^4: \ell (a, b, c, d) \geq 10 \right\}, \\ \mathcal{J}_i" = \mathcal{J}_i \cap \left\{ (a, b, c, d) \in \mathbb{Z}^4: \ell (a, b, c, d) < 10 \right\}. \end{align*} $$
As
![]() $|\mathcal {J}_i'| \lesssim n^3$
, we have that
$|\mathcal {J}_i'| \lesssim n^3$
, we have that
 $$ \begin{align} \sum_{\mathcal{J}_i'} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \genfrac{[}{]}{0pt}{}{n}{d}^{-1} \lesssim |\mathcal{J}_i'| \frac{1}{n^{10}} \lesssim \frac{1}{n^7}. \end{align} $$
$$ \begin{align} \sum_{\mathcal{J}_i'} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \genfrac{[}{]}{0pt}{}{n}{d}^{-1} \lesssim |\mathcal{J}_i'| \frac{1}{n^{10}} \lesssim \frac{1}{n^7}. \end{align} $$
However,
![]() $| \mathcal {J}_i" | \lesssim 1$
, so we deduce
$| \mathcal {J}_i" | \lesssim 1$
, so we deduce
 $$ \begin{align} \sum_{\mathcal{J}_i"} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \genfrac{[}{]}{0pt}{}{n}{d}^{-1} \lesssim | \mathcal{J}_i"| \max_{\mathcal{J}_i"} \frac{1}{n^{\ell (a, b, c, d)}} \lesssim \frac{1}{n^{\ell (i)}}, \end{align} $$
$$ \begin{align} \sum_{\mathcal{J}_i"} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \genfrac{[}{]}{0pt}{}{n}{d}^{-1} \lesssim | \mathcal{J}_i"| \max_{\mathcal{J}_i"} \frac{1}{n^{\ell (a, b, c, d)}} \lesssim \frac{1}{n^{\ell (i)}}, \end{align} $$
where we are using superadditivity of the discrepancy:
![]() $\ell (a)+\ell (b)+\ell (c)+\ell (d) \geq \ell (i)$
.
$\ell (a)+\ell (b)+\ell (c)+\ell (d) \geq \ell (i)$
.
Plugging in (5.26) and (5.27) into (5.25), we conclude the proof.
Now, recall that
![]() $\partial ^{i-1}_s P^{\mathrm {nl}}_n (0) = 0$
for any
$\partial ^{i-1}_s P^{\mathrm {nl}}_n (0) = 0$
for any
![]() $i \leq n+1$
. The previous lemma will guarantee that
$i \leq n+1$
. The previous lemma will guarantee that
![]() $\partial ^{i-1}_s P^{\mathrm {nl}}_n (0)$
are not dominant for
$\partial ^{i-1}_s P^{\mathrm {nl}}_n (0)$
are not dominant for
![]() $i \neq n+2, 2n$
. Let us thus analyze the precise order of the
$i \neq n+2, 2n$
. Let us thus analyze the precise order of the
![]() $(n+2)$
-th and
$(n+2)$
-th and
![]() $(2n)$
-th derivatives of P.
$(2n)$
-th derivatives of P.
Lemma 5.13. We have that for odd n, sufficiently large,
 $$ \begin{align} \frac{\partial^{n+1}_s P^{\mathrm{nl}}_n (0)}{(n+1)!} &= n \frac{Z_n}{n!} \frac{N_{W, 0} D_{Z, 2}}{2}\left(1+O\left( \frac1n \right) \right) , \end{align} $$
$$ \begin{align} \frac{\partial^{n+1}_s P^{\mathrm{nl}}_n (0)}{(n+1)!} &= n \frac{Z_n}{n!} \frac{N_{W, 0} D_{Z, 2}}{2}\left(1+O\left( \frac1n \right) \right) , \end{align} $$
 $$ \begin{align} \frac{\partial^{2n-1}_s P^{\mathrm{nl}}_n (0)}{(2n-1)!} &= n\left(\frac{Z_n}{n!} \right)^2 N_{W, 0} \partial_Z D_Z\left(1+O\left( \frac1n \right) \right). \end{align} $$
$$ \begin{align} \frac{\partial^{2n-1}_s P^{\mathrm{nl}}_n (0)}{(2n-1)!} &= n\left(\frac{Z_n}{n!} \right)^2 N_{W, 0} \partial_Z D_Z\left(1+O\left( \frac1n \right) \right). \end{align} $$
Proof. The strategy is similar to the one in Lemma 5.12. The main difference is that in Lemma 5.12, we bounded every term, while here, we will identify the dominant terms (which will be the ones with the least discrepancy) and bound the rest.
Let us start showing (5.28). Let us define
 $$ \begin{align} \mathcal{B} &= \binom{n+1}{2} Z_n N_{W, 0} D_{Z, 2} + (n+1)n Z_n N_{W, 1} D_{Z, 1} + (n+1) Z_1 N_{W, n} D_{Z, 1} \nonumber\\&\quad + (n+1) Z_2 N_{W, 0} D_{Z, n} + (n+1) Z_1 N_{W, 1} Z_n - \binom{n+1}{2} W_n N_{Z, 2} D_{W, 0} - (n+1)n W_n N_{Z, 1} D_{W, 1}\nonumber\\&\quad - (n+1) W_1 N_{Z, n} D_{W, 1} - (n+1) W_2 N_{Z, n} D_{W, 0} - (n+1) W_1 N_{Z, 1} D_{W, n} \nonumber\\&\quad -W_1N_{Z,n+1}D_{W,0}, \end{align} $$
$$ \begin{align} \mathcal{B} &= \binom{n+1}{2} Z_n N_{W, 0} D_{Z, 2} + (n+1)n Z_n N_{W, 1} D_{Z, 1} + (n+1) Z_1 N_{W, n} D_{Z, 1} \nonumber\\&\quad + (n+1) Z_2 N_{W, 0} D_{Z, n} + (n+1) Z_1 N_{W, 1} Z_n - \binom{n+1}{2} W_n N_{Z, 2} D_{W, 0} - (n+1)n W_n N_{Z, 1} D_{W, 1}\nonumber\\&\quad - (n+1) W_1 N_{Z, n} D_{W, 1} - (n+1) W_2 N_{Z, n} D_{W, 0} - (n+1) W_1 N_{Z, 1} D_{W, n} \nonumber\\&\quad -W_1N_{Z,n+1}D_{W,0}, \end{align} $$
which corresponds to all the monomials of
![]() $\partial _s^{n+1} P^{\mathrm {nl}}_n (0)$
where there are factors with n derivatives. In particular, following the same reasoning as in (5.25), we have that
$\partial _s^{n+1} P^{\mathrm {nl}}_n (0)$
where there are factors with n derivatives. In particular, following the same reasoning as in (5.25), we have that
 $$ \begin{align} \left| \partial_s^{n+1} P^{\mathrm{nl}}_n (0) - \mathcal{B} \right| \lesssim (n+2)! \left( \frac{|Z_n|}{n!} \right)^{1+2/n} (k-n)^{2/n} \sum_{\widetilde{\mathcal{J}}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \genfrac{[}{]}{0pt}{}{n}{d}^{-1}, \end{align} $$
$$ \begin{align} \left| \partial_s^{n+1} P^{\mathrm{nl}}_n (0) - \mathcal{B} \right| \lesssim (n+2)! \left( \frac{|Z_n|}{n!} \right)^{1+2/n} (k-n)^{2/n} \sum_{\widetilde{\mathcal{J}}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \genfrac{[}{]}{0pt}{}{n}{d}^{-1}, \end{align} $$
where
Note that for any tuple
![]() $(a, b, c, d)$
with
$(a, b, c, d)$
with
![]() $a+b+c+d = n+2$
, we have that
$a+b+c+d = n+2$
, we have that
![]() $\ell (a,b,c,d) \geq \ell (n+2) = 2$
and that the discrepancy is even. As
$\ell (a,b,c,d) \geq \ell (n+2) = 2$
and that the discrepancy is even. As
![]() $\mathcal {B}$
from equation (5.30) contains precisely the monomials of discrepancy
$\mathcal {B}$
from equation (5.30) contains precisely the monomials of discrepancy
![]() $2$
of
$2$
of
![]() $\partial _s^{n+1} P^{\mathrm {nl}}_n(0)$
, every addend in the right-hand side of (5.31) has discrepancy greater or equal than
$\partial _s^{n+1} P^{\mathrm {nl}}_n(0)$
, every addend in the right-hand side of (5.31) has discrepancy greater or equal than
![]() $4$
.
$4$
.
Now, using the same reasoning as in the proof of Lemma 5.12 (decomposing
![]() $\widetilde {\mathcal {J}}$
according to the discrepancy being smaller or greater than
$\widetilde {\mathcal {J}}$
according to the discrepancy being smaller or greater than
![]() $10$
), we have that
$10$
), we have that
 $$ \begin{align} \sum_{\widetilde{\mathcal{J}}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \genfrac{[}{]}{0pt}{}{n}{d}^{-1} \lesssim \frac{1}{n^4}. \end{align} $$
$$ \begin{align} \sum_{\widetilde{\mathcal{J}}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \genfrac{[}{]}{0pt}{}{n}{d}^{-1} \lesssim \frac{1}{n^4}. \end{align} $$
However, from (5.30), we see that
 $$ \begin{align} \mathcal{B} &= \binom{n+1}{2} Z_n N_{W, 0} D_{Z, 2} + O\left( n^2 |Z_n| D_{Z, 1} \right) + O \left( n|Z_n| \right) + O \left( n^2 |W_n| \right)\nonumber \\ &= \binom{n+1}{2} Z_n N_{W, 0} D_{Z, 2} + O(n|Z_n|), \end{align} $$
$$ \begin{align} \mathcal{B} &= \binom{n+1}{2} Z_n N_{W, 0} D_{Z, 2} + O\left( n^2 |Z_n| D_{Z, 1} \right) + O \left( n|Z_n| \right) + O \left( n^2 |W_n| \right)\nonumber \\ &= \binom{n+1}{2} Z_n N_{W, 0} D_{Z, 2} + O(n|Z_n|), \end{align} $$
since
![]() $|D_{Z, 1}| \lesssim \frac {1}{k} \lesssim \frac {1}{n}$
(Lemma A.7) and
$|D_{Z, 1}| \lesssim \frac {1}{k} \lesssim \frac {1}{n}$
(Lemma A.7) and
![]() $|W_n| \lesssim |Z_{n-1}| \lesssim n|Z_n|$
(Lemma 5.1).
$|W_n| \lesssim |Z_{n-1}| \lesssim n|Z_n|$
(Lemma 5.1).
From equations (5.31)–(5.33), we conclude that
 $$ \begin{align*} \frac{\partial_s^{n+1} P_n^{\mathrm{nl}}(0)}{(n+1)!} &= \frac{1}{(n+1)!} \binom{n+1}{2} Z_n N_{W, 0} D_{Z, 2} + O \left( \frac{n|Z_n|}{(n+1)!} \right) + O \left( \frac{1}{n^3} \left( \frac{|Z_n|}{n!} \right)^{1+2/n} (k-n)^{2/n} \right) \\ &= n \frac{N_{W, 0} D_{Z, 2}}{2} \frac{Z_n}{n!} + O\left( \frac{|Z_n|}{n!} \right) + O \left( \frac{|Z_n|}{n!} \cdot \frac{1}{n^3} \left( \frac{|Z_n|(n-k) }{n!}\right)^{2/n} \right) \\ &= n \frac{Z_n}{n!} \frac{N_{W, 0} D_{Z, 2}}{2}\left(1+O\left( \frac1n \right) \right), \end{align*} $$
$$ \begin{align*} \frac{\partial_s^{n+1} P_n^{\mathrm{nl}}(0)}{(n+1)!} &= \frac{1}{(n+1)!} \binom{n+1}{2} Z_n N_{W, 0} D_{Z, 2} + O \left( \frac{n|Z_n|}{(n+1)!} \right) + O \left( \frac{1}{n^3} \left( \frac{|Z_n|}{n!} \right)^{1+2/n} (k-n)^{2/n} \right) \\ &= n \frac{N_{W, 0} D_{Z, 2}}{2} \frac{Z_n}{n!} + O\left( \frac{|Z_n|}{n!} \right) + O \left( \frac{|Z_n|}{n!} \cdot \frac{1}{n^3} \left( \frac{|Z_n|(n-k) }{n!}\right)^{2/n} \right) \\ &= n \frac{Z_n}{n!} \frac{N_{W, 0} D_{Z, 2}}{2}\left(1+O\left( \frac1n \right) \right), \end{align*} $$
where we have used Corollary 5.8 in the last equality and the fact that
![]() $|N_{W, 0} D_{Z, 2}| \gtrsim 1$
(Lemma A.7).
$|N_{W, 0} D_{Z, 2}| \gtrsim 1$
(Lemma A.7).
Now, let us show (5.29). Let us define

which corresponds to all the monomials of
![]() $\partial _s^{n+1} P^{\mathrm {nl}}_n (0)$
where there are two factors with n derivatives. In particular, following the same reasoning as in (5.25), we have that
$\partial _s^{n+1} P^{\mathrm {nl}}_n (0)$
where there are two factors with n derivatives. In particular, following the same reasoning as in (5.25), we have that

where
Note that for any tuple
![]() $(a, b, c, d)$
with
$(a, b, c, d)$
with
![]() $a+b+c+d = 2n$
, we have that the discrepancy is even. As
$a+b+c+d = 2n$
, we have that the discrepancy is even. As ![]() from equation (5.34) contains precisely the monomials of discrepancy
from equation (5.34) contains precisely the monomials of discrepancy
![]() $0$
of
$0$
of
![]() $\partial _s^{n+1} P^{\mathrm {nl}}_n(0)$
, every addend in the right-hand side of (5.35) has discrepancy greater or equal than
$\partial _s^{n+1} P^{\mathrm {nl}}_n(0)$
, every addend in the right-hand side of (5.35) has discrepancy greater or equal than
![]() $2$
.
$2$
.
Now, using the same reasoning as in the proof of Lemma 5.12, we have that

However, from (5.34) and using
![]() $|W_n| \lesssim |Z_{n-1}| \lesssim \frac {1}{n^3} |Z_n|$
(Lemma 5.1), we have that
$|W_n| \lesssim |Z_{n-1}| \lesssim \frac {1}{n^3} |Z_n|$
(Lemma 5.1), we have that

Finally, using (5.35)–(5.37), we conclude that
 $$ \begin{align*} \frac{\partial_s^{n+1} P_n^{\mathrm{nl}}(0)}{(n+1)!} &= n N_{W, 0} \partial_Z D_Z \left( \frac{Z_n}{n!} \right)^2 + O \left( \left( \frac{Z_n}{n!} \right)^2 \frac{1}{n^2} \right) + O \left( \left( \frac{|Z_n|}{n!} \right)^{2} \frac{1}{n} \right) \\&= n\left(\frac{Z_n}{n!} \right)^2 N_{W, 0} \partial_Z D_Z\left(1+O\left( \frac1n \right) \right). \end{align*} $$
$$ \begin{align*} \frac{\partial_s^{n+1} P_n^{\mathrm{nl}}(0)}{(n+1)!} &= n N_{W, 0} \partial_Z D_Z \left( \frac{Z_n}{n!} \right)^2 + O \left( \left( \frac{Z_n}{n!} \right)^2 \frac{1}{n^2} \right) + O \left( \left( \frac{|Z_n|}{n!} \right)^{2} \frac{1}{n} \right) \\&= n\left(\frac{Z_n}{n!} \right)^2 N_{W, 0} \partial_Z D_Z\left(1+O\left( \frac1n \right) \right). \end{align*} $$
In the second equality, we used
![]() $|N_{W, 0} \partial _Z D_Z| = \frac {1+\gamma }{4} |N_{W, 0}| \gtrsim 1$
from Lemma A.7.
$|N_{W, 0} \partial _Z D_Z| = \frac {1+\gamma }{4} |N_{W, 0}| \gtrsim 1$
from Lemma A.7.
Proof of Proposition 5.11.
Let us start showing equation (5.23). First of all, let us notice that the assumption
![]() $s^{n-2} \leq 3 |\frac {D_{Z, 2}^\ast n!}{2\partial _Z D_Z Z_n}|$
yields
$s^{n-2} \leq 3 |\frac {D_{Z, 2}^\ast n!}{2\partial _Z D_Z Z_n}|$
yields
 $$\begin{align*}s \lesssim \left( \frac{n!}{|Z_n|} \right)^{1/(n-2)} \lesssim \frac{1}{n}\,\end{align*}$$
$$\begin{align*}s \lesssim \left( \frac{n!}{|Z_n|} \right)^{1/(n-2)} \lesssim \frac{1}{n}\,\end{align*}$$
as a consequence of Corollary 5.8. Applying Lemma 5.12, we obtain
 $$ \begin{align*} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_n(0)}{(i-1)!}s^{i-1} &\lesssim \frac{n}{s} \frac{1}{n^{\min \{7, \ell (i) \}}} \left( \frac{|Z_n| s}{n!}\right)^{i/n} \lesssim n s \frac{|Z_n| s^n}{n!} \frac{1}{s^2 n^{\min \{ 7, \ell (i) \}}} \left( s^2 \right)^{i/n - 1}\\ & = n s \frac{|Z_n| s^n}{n!} \frac{ s^{2i/n - 4}}{ n^{\min \{ 7, \ell (i) \}}}, \end{align*} $$
$$ \begin{align*} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_n(0)}{(i-1)!}s^{i-1} &\lesssim \frac{n}{s} \frac{1}{n^{\min \{7, \ell (i) \}}} \left( \frac{|Z_n| s}{n!}\right)^{i/n} \lesssim n s \frac{|Z_n| s^n}{n!} \frac{1}{s^2 n^{\min \{ 7, \ell (i) \}}} \left( s^2 \right)^{i/n - 1}\\ & = n s \frac{|Z_n| s^n}{n!} \frac{ s^{2i/n - 4}}{ n^{\min \{ 7, \ell (i) \}}}, \end{align*} $$
where we have used
![]() $\frac {|Z_n| s^n}{n!} \lesssim s^2$
from our hypothesis on s. Let us consider the case
$\frac {|Z_n| s^n}{n!} \lesssim s^2$
from our hypothesis on s. Let us consider the case
![]() $ i \geq 2n+1$
. Then, since
$ i \geq 2n+1$
. Then, since
![]() $s \lesssim 1/n$
and as
$s \lesssim 1/n$
and as
![]() $2i/n-4> 0$
, we have
$2i/n-4> 0$
, we have
This can be further bounded, up to a constant multiple by
![]() $ \frac {1}{n^2}$
for all
$ \frac {1}{n^2}$
for all
![]() $i> 2n+1$
and
$i> 2n+1$
and
![]() $i\neq 3n$
. For the cases
$i\neq 3n$
. For the cases
![]() $i=2n+1,3n$
, this quantity can be bounded by a constant multiple of
$i=2n+1,3n$
, this quantity can be bounded by a constant multiple of
![]() $\frac {1}{n}$
. Thus,
$\frac {1}{n}$
. Thus,
 $$ \begin{align*} \sum_{i=2n+1}^{4n} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_n(0)}{(i-1)!}s^{i-1} = O \left( n s \frac{|Z_n| s^n}{n!} \cdot \frac{1}{n} \right). \end{align*} $$
$$ \begin{align*} \sum_{i=2n+1}^{4n} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_n(0)}{(i-1)!}s^{i-1} = O \left( n s \frac{|Z_n| s^n}{n!} \cdot \frac{1}{n} \right). \end{align*} $$
Now, for the case
![]() $n+3 \leq i \leq 2n-1$
, we have
$n+3 \leq i \leq 2n-1$
, we have
![]() $i/n-\lfloor i/n\rfloor = i/n-1$
, and we argue with Lemma 5.12 as follows:
$i/n-\lfloor i/n\rfloor = i/n-1$
, and we argue with Lemma 5.12 as follows:
 $$ \begin{align} \begin{aligned} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_n(0)}{(i-1)!}s^{i-1} &\lesssim \frac{1}{n^{\min \{7, \ell (i) \}}} \frac{n}{s} \left( \frac{|Z_n| s^n}{n!}\right)^{i/n} (k-n)^{i/n-1} \\ &\leq n s \left( \frac{|Z_n| s^n}{n!} \right) s^{i-n-2} \left( \frac{|Z_n| (k-n)}{n!}\right)^{(i-n)/n} \frac{1}{n^{\min \{7, \ell (i) \}}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_n(0)}{(i-1)!}s^{i-1} &\lesssim \frac{1}{n^{\min \{7, \ell (i) \}}} \frac{n}{s} \left( \frac{|Z_n| s^n}{n!}\right)^{i/n} (k-n)^{i/n-1} \\ &\leq n s \left( \frac{|Z_n| s^n}{n!} \right) s^{i-n-2} \left( \frac{|Z_n| (k-n)}{n!}\right)^{(i-n)/n} \frac{1}{n^{\min \{7, \ell (i) \}}}. \end{aligned} \end{align} $$
Labeling
![]() $\mathcal {I} = s^{i-n-2} \left ( \frac {|Z_n|(k-n)}{n!} \right )^{(i-n)/n}$
, we have by Corollary 5.8
$\mathcal {I} = s^{i-n-2} \left ( \frac {|Z_n|(k-n)}{n!} \right )^{(i-n)/n}$
, we have by Corollary 5.8
 $$ \begin{align*} \mathcal{I}^{(n-2)/(i-n-2)} &= \frac{|Z_n| s^{n-2}}{n!} \left( \frac{|Z_n|(k-n)}{n!} \right)^{\frac{-2i+4n}{in-n^2-2n}}(k-n) \\&\lesssim \left( nk^n |\bar C_\ast|^n \left( \frac{1.05}{0.95} \right)^n \right)^{\frac{-2i+4n}{in-n^2-2n}} \\ &\lesssim \left( n^{1/n} (n+1) \frac{1.05 |\bar C_\ast|}{0.95} \right)^{\frac{n(-2i+4n)}{in-n^2-2n}}, \end{align*} $$
$$ \begin{align*} \mathcal{I}^{(n-2)/(i-n-2)} &= \frac{|Z_n| s^{n-2}}{n!} \left( \frac{|Z_n|(k-n)}{n!} \right)^{\frac{-2i+4n}{in-n^2-2n}}(k-n) \\&\lesssim \left( nk^n |\bar C_\ast|^n \left( \frac{1.05}{0.95} \right)^n \right)^{\frac{-2i+4n}{in-n^2-2n}} \\ &\lesssim \left( n^{1/n} (n+1) \frac{1.05 |\bar C_\ast|}{0.95} \right)^{\frac{n(-2i+4n)}{in-n^2-2n}}, \end{align*} $$
where we used the hypothesis
![]() $s^{n-2} \lesssim \frac {n!}{|Z_n|}$
in the second line. Now, raising the inequality to the
$s^{n-2} \lesssim \frac {n!}{|Z_n|}$
in the second line. Now, raising the inequality to the
![]() $\frac {i-n-2}{n-2}$
-th power, we obtain
$\frac {i-n-2}{n-2}$
-th power, we obtain
![]() $\mathcal {I} \lesssim n^{(4n-2i)/(n-2)}$
. Going back to (5.38), we have that
$\mathcal {I} \lesssim n^{(4n-2i)/(n-2)}$
. Going back to (5.38), we have that
 $$ \begin{align*} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_n(0)}{(i-1)!}s^{i-1} \lesssim n s \left( \frac{|Z_n| s^n}{n!} \right) \frac{ n^{(4n-2i)/(n-2)}}{n^{\min \{7, \ell (i) \}}}. \end{align*} $$
$$ \begin{align*} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_n(0)}{(i-1)!}s^{i-1} \lesssim n s \left( \frac{|Z_n| s^n}{n!} \right) \frac{ n^{(4n-2i)/(n-2)}}{n^{\min \{7, \ell (i) \}}}. \end{align*} $$
Note
 $$\begin{align*}\frac{ n^{(4n-2i)/(n-2)}}{n^{\min \{7, \ell (i) \}}}\lesssim \begin{cases} \frac1n & \mbox{for }i=n+3,2n-1\\ \frac1{n^2} & \mbox{for }n+4\leq i \leq 2n-2 \end{cases}. \end{align*}$$
$$\begin{align*}\frac{ n^{(4n-2i)/(n-2)}}{n^{\min \{7, \ell (i) \}}}\lesssim \begin{cases} \frac1n & \mbox{for }i=n+3,2n-1\\ \frac1{n^2} & \mbox{for }n+4\leq i \leq 2n-2 \end{cases}. \end{align*}$$
Therefore, we obtain
 $$ \begin{align*} \sum_{i=n+3}^{2n-1} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_n(0)}{(i-1)!}s^{i-1} = O \left( n s \frac{|Z_n| s^n}{n!} \cdot \frac{1}{n} \right), \end{align*} $$
$$ \begin{align*} \sum_{i=n+3}^{2n-1} \frac{\partial_s^{i-1} P^{\mathrm{nl}}_n(0)}{(i-1)!}s^{i-1} = O \left( n s \frac{|Z_n| s^n}{n!} \cdot \frac{1}{n} \right), \end{align*} $$
which concludes the proof of equation (5.23).
Now, from equation (5.23), we have that
 $$ \begin{align} P^{\mathrm{nl}}_n(s) = \frac{Z_n}{n!}ns^{n+1}N_{W, 0} \left( \frac{D_{Z, 2}}{2}\left( 1+O \left( \frac1n \right) \right) + \frac{Z_n}{n!} \partial_Z D_Z s^{n-2}\left( 1+O \left( \frac1n \right) \right) \right) , \end{align} $$
$$ \begin{align} P^{\mathrm{nl}}_n(s) = \frac{Z_n}{n!}ns^{n+1}N_{W, 0} \left( \frac{D_{Z, 2}}{2}\left( 1+O \left( \frac1n \right) \right) + \frac{Z_n}{n!} \partial_Z D_Z s^{n-2}\left( 1+O \left( \frac1n \right) \right) \right) , \end{align} $$
up to
![]() $s^{n-2} = \frac {3|D_{Z, 2}|}{2 \partial _Z D_Z} \frac {n!}{Z_n}$
. In particular, taking
$s^{n-2} = \frac {3|D_{Z, 2}|}{2 \partial _Z D_Z} \frac {n!}{Z_n}$
. In particular, taking
![]() $s_{7/5, \mathrm {val}}$
such that
$s_{7/5, \mathrm {val}}$
such that
![]() $s_{7/5, \mathrm {val}}^{n-2} = \frac {99}{100}\frac {|D_{Z, 2}|}{2 \partial _Z D_Z} \frac {n!}{Z_n}$
, the approximation (5.39) is valid, and moreover,
$s_{7/5, \mathrm {val}}^{n-2} = \frac {99}{100}\frac {|D_{Z, 2}|}{2 \partial _Z D_Z} \frac {n!}{Z_n}$
, the approximation (5.39) is valid, and moreover,
 $$\begin{align*}\left| \frac{D_{Z, 2}}{2}\right|\geq \frac{100}{99}\left|\frac{Z_n}{n!} \partial_Z D_Z s^{n-2}\right|\,\end{align*}$$
$$\begin{align*}\left| \frac{D_{Z, 2}}{2}\right|\geq \frac{100}{99}\left|\frac{Z_n}{n!} \partial_Z D_Z s^{n-2}\right|\,\end{align*}$$
for
![]() $s \leq s_{7/5, \mathrm {val}}$
. Therefore, for n sufficiently large, the sign of
$s \leq s_{7/5, \mathrm {val}}$
. Therefore, for n sufficiently large, the sign of
![]() $P^{\mathrm {nl}}_n(s )$
for every
$P^{\mathrm {nl}}_n(s )$
for every
![]() $0 \leq s \leq s_{7/5, \mathrm {val}}$
is given by the sign of
$0 \leq s \leq s_{7/5, \mathrm {val}}$
is given by the sign of
![]() $Z_n N_{W, 0} D_{Z, 2}$
. Using Lemma A.7, and the fact that
$Z_n N_{W, 0} D_{Z, 2}$
. Using Lemma A.7, and the fact that
![]() $Z_n> 0$
from Corollary 5.8, we have that
$Z_n> 0$
from Corollary 5.8, we have that
![]() $P^{\mathrm {nl}}_n(s)> 0$
up to
$P^{\mathrm {nl}}_n(s)> 0$
up to
![]() $s_{7/5, \mathrm {val}}$
.
$s_{7/5, \mathrm {val}}$
.
5.6 Intersection with the far-left barrier and proof of Proposition 3.6
Let us recall that for
![]() $\gamma = 7/5$
and n sufficiently large, we take the far-left barrier to be
$\gamma = 7/5$
and n sufficiently large, we take the far-left barrier to be
 $$ \begin{align*} b_{7/5}^{\mathrm{fl}} (t) = \left( W_0 + W_1 t + \frac12 W_2 t^2 - \left(W_0 + W_1 + \frac{W_2}{2}\right) t^3, Z_0 + Z_1 t + \frac12 Z_2 t^2 - \left(Z_0 + Z_1 + \frac{Z_2}{2}\right)t^3 \right). \end{align*} $$
$$ \begin{align*} b_{7/5}^{\mathrm{fl}} (t) = \left( W_0 + W_1 t + \frac12 W_2 t^2 - \left(W_0 + W_1 + \frac{W_2}{2}\right) t^3, Z_0 + Z_1 t + \frac12 Z_2 t^2 - \left(Z_0 + Z_1 + \frac{Z_2}{2}\right)t^3 \right). \end{align*} $$
We formulate the barrier in implicit form looking at
 $$ \begin{align*} B^{\mathrm{fl}}_{7/5} (W, Z) &= \mathrm{Res}_t \Big( -\left( W_0 + W_1 + \frac12 W_2 \right) t^3 + \frac12 W_2t^2 + W_1 t + W_0 - W, \\& \qquad\qquad -\left( Z_0 + Z_1 + \frac12 Z_2 \right) t^3 + \frac12 Z_2t^2 + Z_1 t + Z_0 - Z \Big) \\&= \begin{vmatrix} - \left( W_0 + W_1 + \frac{W_2}{2} \right) & \frac{W_2}{2} & W_1 & W_0 - W &0 & 0 \\ 0 & - \left( W_0 + W_1 + \frac{W_2}{2} \right) & \frac{W_2}{2} & W_1 & W_0 - W & 0 \\ 0 & 0 &- \left( W_0 + W_1 + \frac{W_2}{2} \right) & \frac{W_2}{2} & W_1 & W_0 - W\\ - \left( Z_0 + Z_1 + \frac{Z_2}{2} \right) & \frac{Z_2}{2} & Z_1 & Z_0 - Z &0 & 0 \\ 0 & - \left( Z_0 + Z_1 + \frac{Z_2}{2} \right) & \frac{Z_2}{2} & Z_1 & Z_0 - Z & 0 \\ 0 & 0 &- \left( Z_0 + Z_1 +\frac{Z_2}{2}\right) & \frac{Z_2}{2} & Z_1 & Z_0 - Z\\ \end{vmatrix}, \end{align*} $$
$$ \begin{align*} B^{\mathrm{fl}}_{7/5} (W, Z) &= \mathrm{Res}_t \Big( -\left( W_0 + W_1 + \frac12 W_2 \right) t^3 + \frac12 W_2t^2 + W_1 t + W_0 - W, \\& \qquad\qquad -\left( Z_0 + Z_1 + \frac12 Z_2 \right) t^3 + \frac12 Z_2t^2 + Z_1 t + Z_0 - Z \Big) \\&= \begin{vmatrix} - \left( W_0 + W_1 + \frac{W_2}{2} \right) & \frac{W_2}{2} & W_1 & W_0 - W &0 & 0 \\ 0 & - \left( W_0 + W_1 + \frac{W_2}{2} \right) & \frac{W_2}{2} & W_1 & W_0 - W & 0 \\ 0 & 0 &- \left( W_0 + W_1 + \frac{W_2}{2} \right) & \frac{W_2}{2} & W_1 & W_0 - W\\ - \left( Z_0 + Z_1 + \frac{Z_2}{2} \right) & \frac{Z_2}{2} & Z_1 & Z_0 - Z &0 & 0 \\ 0 & - \left( Z_0 + Z_1 + \frac{Z_2}{2} \right) & \frac{Z_2}{2} & Z_1 & Z_0 - Z & 0 \\ 0 & 0 &- \left( Z_0 + Z_1 +\frac{Z_2}{2}\right) & \frac{Z_2}{2} & Z_1 & Z_0 - Z\\ \end{vmatrix}, \end{align*} $$
which is positive if
![]() $(W, Z)$
is above the the barrier and negative if it is below. Thus, we study the function
$(W, Z)$
is above the the barrier and negative if it is below. Thus, we study the function
![]() $f(s)= B^{\mathrm {fl}}(b^{\mathrm {nl}}_n (s))$
. Let us define
$f(s)= B^{\mathrm {fl}}(b^{\mathrm {nl}}_n (s))$
. Let us define
Lemma 5.14. Let n be an odd number sufficiently large,
![]() $\gamma = \frac 75$
and
$\gamma = \frac 75$
and
![]() $r \in (r_n, r_{n+1})$
. We have that
$r \in (r_n, r_{n+1})$
. We have that
![]() $a_3 < 0$
and
$a_3 < 0$
and
![]() $a_n> 0$
.
$a_n> 0$
.
Proof. The statement
![]() $a_n> 0$
follows from
$a_n> 0$
follows from
![]() $\partial _Z B^{\mathrm {fl}}_{7/5} (W_0, Z_0)>0$
(Lemma A.7) and
$\partial _Z B^{\mathrm {fl}}_{7/5} (W_0, Z_0)>0$
(Lemma A.7) and
![]() $Z_n> 0$
(Corollary 5.8). The proof of
$Z_n> 0$
(Corollary 5.8). The proof of
![]() $a_3 < 0$
is computer-assisted and can be found in the supplementary material, and we refer to Appendix B for the implementation.
$a_3 < 0$
is computer-assisted and can be found in the supplementary material, and we refer to Appendix B for the implementation.
Lemma 5.15. For any given constant
![]() $C>0$
, and
$C>0$
, and
![]() $0\leq s^{n-3} \leq C\frac {n!}{Z_n}$
,
$0\leq s^{n-3} \leq C\frac {n!}{Z_n}$
,
 $$ \begin{align} f(s) = a_3 s^3+ a_n s^n + O\left( \frac{|a_3| s^3 +| a_n | s^n }{n}\right), \end{align} $$
$$ \begin{align} f(s) = a_3 s^3+ a_n s^n + O\left( \frac{|a_3| s^3 +| a_n | s^n }{n}\right), \end{align} $$
where the implicit constant in the big-O notation is permitted to depend on C.
Proof. This will follow in a very similar way as Lemma 5.13, using Lemma 5.10 to bound intermediate terms, so we omit most of the details. First of all, let us note that
![]() $s \lesssim 1/n$
from Corollary 5.8.
$s \lesssim 1/n$
from Corollary 5.8.
Now, we note that
![]() $f(s)$
is a
$f(s)$
is a
![]() $3n$
-th degree polynomial multiple of
$3n$
-th degree polynomial multiple of
![]() $s^3$
because both
$s^3$
because both
![]() $B^{\mathrm {fl}}$
and
$B^{\mathrm {fl}}$
and
![]() $b^{\mathrm {nl}}$
agree up to second order. Therefore,
$b^{\mathrm {nl}}$
agree up to second order. Therefore,
 $$ \begin{align} f(s) = a_3 s^3 + a_n s^n + \sum_{i=4, i\neq n}^{3n} \frac{1}{i!} (\partial_s^i f)(0) + \left( \frac{1}{n!} |(\partial_s^n f)(0)| - a_n \right) s^n. \end{align} $$
$$ \begin{align} f(s) = a_3 s^3 + a_n s^n + \sum_{i=4, i\neq n}^{3n} \frac{1}{i!} (\partial_s^i f)(0) + \left( \frac{1}{n!} |(\partial_s^n f)(0)| - a_n \right) s^n. \end{align} $$
As
![]() $B^{\mathrm {fl}}_{7/5}(W, Z)$
is a third-degree polynomial, similarly to Lemma 5.13, we have that the i-th coefficient is bounded as
$B^{\mathrm {fl}}_{7/5}(W, Z)$
is a third-degree polynomial, similarly to Lemma 5.13, we have that the i-th coefficient is bounded as

and
 $$ \begin{align}\nonumber \left( \frac{1}{n!} |(\partial_s^n f)(0)| - a_n \right) s^n &\lesssim s^n \left( \sum_{\substack{ a+b+c = n, \\ 0\leq a, b, c < n}} \frac{|Z_a||Z_b||Z_c|}{a!b!c!} + \frac{|W_n|}{n!} \right) \lesssim s^n \left( \sum_{\substack{ a+b+c = n, \\ 0\leq a, b, c < n}} \frac{|Z_a||Z_b||Z_c|}{a!b!c!} + \frac{|Z_{n-1}|}{n!} \right) \\ &\lesssim \left(\frac{Z_n s^n}{n!} \right) \left( \sum_{\substack{ a+b+c = n, \\ 0\leq a, b, c < n}} \left( \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} (k-n) \right) + \frac{k-n}{n^3} \right). \end{align} $$
$$ \begin{align}\nonumber \left( \frac{1}{n!} |(\partial_s^n f)(0)| - a_n \right) s^n &\lesssim s^n \left( \sum_{\substack{ a+b+c = n, \\ 0\leq a, b, c < n}} \frac{|Z_a||Z_b||Z_c|}{a!b!c!} + \frac{|W_n|}{n!} \right) \lesssim s^n \left( \sum_{\substack{ a+b+c = n, \\ 0\leq a, b, c < n}} \frac{|Z_a||Z_b||Z_c|}{a!b!c!} + \frac{|Z_{n-1}|}{n!} \right) \\ &\lesssim \left(\frac{Z_n s^n}{n!} \right) \left( \sum_{\substack{ a+b+c = n, \\ 0\leq a, b, c < n}} \left( \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} (k-n) \right) + \frac{k-n}{n^3} \right). \end{align} $$
From (5.44), we directly see that the last term of (5.42) satisfies the stated bound in (5.41). Thus, we just need to bound the sum in (5.42).
From (5.43), we see that the term with
![]() $i = n + 1$
also satisfies the bound in (5.41), since
$i = n + 1$
also satisfies the bound in (5.41), since
![]() $\left |\frac {Z_n s^n}{n!}\right |=O( 1/n )$
and
$\left |\frac {Z_n s^n}{n!}\right |=O( 1/n )$
and
![]() $Z_n s^n/n! \leq 1$
. The terms with
$Z_n s^n/n! \leq 1$
. The terms with
![]() $n+2 \leq i \leq 2n-2$
added all together also satisfy the bound, as the parenthesis is
$n+2 \leq i \leq 2n-2$
added all together also satisfy the bound, as the parenthesis is
![]() $O( 1/n^2 )$
(so that the sum of all those terms is
$O( 1/n^2 )$
(so that the sum of all those terms is
![]() $O(\frac 1n |a_n| s^n)$
). For the terms with
$O(\frac 1n |a_n| s^n)$
). For the terms with
![]() $2n-1 \leq i \leq 3n$
, note that
$2n-1 \leq i \leq 3n$
, note that
 $$ \begin{align*} \left( \frac{Z_n s^n}{n!} \right)^{i/n} \lesssim \left( |a_n| s^n \right)\left( \frac{Z_n s^n}{n!} \right)^{i/n-1} \lesssim \left( |a_n| s^n \right) s^{3 (n-2)/n}, \end{align*} $$
$$ \begin{align*} \left( \frac{Z_n s^n}{n!} \right)^{i/n} \lesssim \left( |a_n| s^n \right)\left( \frac{Z_n s^n}{n!} \right)^{i/n-1} \lesssim \left( |a_n| s^n \right) s^{3 (n-2)/n}, \end{align*} $$
so they are all
![]() $O(1/n^2)|a_n| s^n$
and their sum also satisfies the stated bound in (5.41).
$O(1/n^2)|a_n| s^n$
and their sum also satisfies the stated bound in (5.41).
Lastly, we need to show that the contribution of terms with
![]() $4 \leq i \leq n-1$
in (5.42) is
$4 \leq i \leq n-1$
in (5.42) is
![]() $O \left ( \frac {|a_3|s^3 + |a_n|s^n}{n}\right )$
. We have
$O \left ( \frac {|a_3|s^3 + |a_n|s^n}{n}\right )$
. We have
 $$ \begin{align} \sum_{i=4}^{n-1} \frac{|a_i| s^i}{i!} &\lesssim s^3 \sum_{i=4}^{n-1} s^{i-3} \left( \frac{Z_n (k-n) }{n!} \right)^{i/n} \sum_{\substack{ a+b+c = i, \\ 0\leq a, b, c \leq n}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \nonumber \\ & \lesssim s^3 \sum_{i=4}^{n-1} \left( \frac{s^{n-3} |Z_n| }{n!} (k-n)\right)^{(i-3)/(n-3)} \left( \frac{Z_n (n-k)}{n!}\right)^{(3n-3i)/(n(n-3))} \sum_{\substack{ a+b+c = i, \\ 0\leq a, b, c \leq n}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \nonumber \\ & \lesssim s^3 \sum_{i=4}^{n-1} n^{\frac{3n}{n^2/2}} \sum_{\substack{ a+b+c = i, \\ 0\leq a, b, c \leq n}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \nonumber \\ &\lesssim s^3 \sum_{i=4}^{n-1} \sum_{\substack{ a+b+c = i, \\ 0\leq a, b, c \leq n}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1}, \end{align} $$
$$ \begin{align} \sum_{i=4}^{n-1} \frac{|a_i| s^i}{i!} &\lesssim s^3 \sum_{i=4}^{n-1} s^{i-3} \left( \frac{Z_n (k-n) }{n!} \right)^{i/n} \sum_{\substack{ a+b+c = i, \\ 0\leq a, b, c \leq n}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \nonumber \\ & \lesssim s^3 \sum_{i=4}^{n-1} \left( \frac{s^{n-3} |Z_n| }{n!} (k-n)\right)^{(i-3)/(n-3)} \left( \frac{Z_n (n-k)}{n!}\right)^{(3n-3i)/(n(n-3))} \sum_{\substack{ a+b+c = i, \\ 0\leq a, b, c \leq n}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \nonumber \\ & \lesssim s^3 \sum_{i=4}^{n-1} n^{\frac{3n}{n^2/2}} \sum_{\substack{ a+b+c = i, \\ 0\leq a, b, c \leq n}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1} \nonumber \\ &\lesssim s^3 \sum_{i=4}^{n-1} \sum_{\substack{ a+b+c = i, \\ 0\leq a, b, c \leq n}} \genfrac{[}{]}{0pt}{}{n}{a}^{-1} \genfrac{[}{]}{0pt}{}{n}{b}^{-1} \genfrac{[}{]}{0pt}{}{n}{c}^{-1}, \end{align} $$
where we have used Corollary 5.8 for bounding
![]() $\frac {Z_n (n-k)}{n!}$
and our hypothesis for bounding
$\frac {Z_n (n-k)}{n!}$
and our hypothesis for bounding
![]() $\frac {Z_ns^{n-3}}{n!} \lesssim 1$
. Lastly, one can check that the sum in (5.45) is
$\frac {Z_ns^{n-3}}{n!} \lesssim 1$
. Lastly, one can check that the sum in (5.45) is
![]() $O(1/n)$
, and this concludes our statement because
$O(1/n)$
, and this concludes our statement because
![]() $|a_3| \gtrsim 1$
.
$|a_3| \gtrsim 1$
.
Proof of Proposition 3.6.
Combining Lemma 5.14 and Lemma 5.15, we have that
![]() $f(s) < 0$
for s small enough and
$f(s) < 0$
for s small enough and
![]() $f(s)> 0$
for
$f(s)> 0$
for
 $$ \begin{align*} s = \left( \frac{2|a_3|}{|Z_n \partial_Z B^{\mathrm{fl}}_{7/5} (W_0, Z_0)| / n!} \right)^{1/(n-3)}. \end{align*} $$
$$ \begin{align*} s = \left( \frac{2|a_3|}{|Z_n \partial_Z B^{\mathrm{fl}}_{7/5} (W_0, Z_0)| / n!} \right)^{1/(n-3)}. \end{align*} $$
In particular, there exists a value of
![]() $s_{7/5, int}$
with
$s_{7/5, int}$
with
![]() $s_{7/5, int}^{n-3} \lesssim \frac {n!}{Z_n}$
such that
$s_{7/5, int}^{n-3} \lesssim \frac {n!}{Z_n}$
such that
![]() $B_{7/5}^{\mathrm {fl}} (b^{\mathrm {nl}}_{7/5}(s_{7/5, int})) = 0$
; that is, the far-left and near-left barriers intersect.
$B_{7/5}^{\mathrm {fl}} (b^{\mathrm {nl}}_{7/5}(s_{7/5, int})) = 0$
; that is, the far-left and near-left barriers intersect.
As we know that the near-left barrier is valid up to
 $$ \begin{align*} s_{7/5,\mathrm{val}} = \left( \frac{99}{100}\frac{|D_{Z, 2}|}{2 \partial_Z D_Z} \frac{n!}{Z_n} \right)^{1/(n-2)}, \end{align*} $$
$$ \begin{align*} s_{7/5,\mathrm{val}} = \left( \frac{99}{100}\frac{|D_{Z, 2}|}{2 \partial_Z D_Z} \frac{n!}{Z_n} \right)^{1/(n-2)}, \end{align*} $$
for n sufficiently large, it is clear that
![]() $s_{7/5, \mathrm {val}}> s_{7/5, \mathrm {int}}$
.
$s_{7/5, \mathrm {val}}> s_{7/5, \mathrm {int}}$
.
From Proposition 5.11, we have that
![]() $P^{\mathrm {nl}}_{n}(s)> 0$
up to
$P^{\mathrm {nl}}_{n}(s)> 0$
up to
![]() $s_{7/5, \mathrm {val}}> s_{7/5, \mathrm {int}}$
, and that
$s_{7/5, \mathrm {val}}> s_{7/5, \mathrm {int}}$
, and that
![]() $b^{\mathrm {nl}}_n(s)$
intersects
$b^{\mathrm {nl}}_n(s)$
intersects
![]() $b^{\mathrm {fl}}_{7/5}(t)$
at
$b^{\mathrm {fl}}_{7/5}(t)$
at
![]() $s_{7/5, \mathrm {int}}$
. Let us check that
$s_{7/5, \mathrm {int}}$
. Let us check that
![]() $D_Z (b^{\mathrm {nl}}_n (s))> 0$
and
$D_Z (b^{\mathrm {nl}}_n (s))> 0$
and
![]() $D_W (b^{\mathrm {nl}}_n(s))> 0$
for
$D_W (b^{\mathrm {nl}}_n(s))> 0$
for
![]() $s \in (0, s_{7/5}^{\mathrm {int}})$
. Now, notice that
$s \in (0, s_{7/5}^{\mathrm {int}})$
. Now, notice that
 $$ \begin{align*} D_W (b^{\mathrm{nl}}_n(s)) &= D_{W, 0} + \sum_{i=1}^{n} \frac{s^i}{i!} \nabla D_W (P_s) \cdot (W_i, Z_i) = D_{W, 0} + \frac{\partial_Z D_W Z_n}{n!}s^n + O \left( \frac{1 + |Z_n|s^n/n!}{n}\right) \end{align*} $$
$$ \begin{align*} D_W (b^{\mathrm{nl}}_n(s)) &= D_{W, 0} + \sum_{i=1}^{n} \frac{s^i}{i!} \nabla D_W (P_s) \cdot (W_i, Z_i) = D_{W, 0} + \frac{\partial_Z D_W Z_n}{n!}s^n + O \left( \frac{1 + |Z_n|s^n/n!}{n}\right) \end{align*} $$
for
![]() $s^{n-1} \lesssim \frac {n!}{Z_n}$
, using the same reasoning as the one used in Proposition 5.11 or Lemma 5.15. Noting that
$s^{n-1} \lesssim \frac {n!}{Z_n}$
, using the same reasoning as the one used in Proposition 5.11 or Lemma 5.15. Noting that
![]() $\partial _Z D_W = \frac 25$
(as
$\partial _Z D_W = \frac 25$
(as
![]() $\gamma = \frac 75$
) and
$\gamma = \frac 75$
) and
![]() $D_{W, 0}> 0$
(Lemma A.10), we get the result for
$D_{W, 0}> 0$
(Lemma A.10), we get the result for
![]() $D_W (b^{\mathrm {nl}}_n(s))$
.
$D_W (b^{\mathrm {nl}}_n(s))$
.
In order to treat the case of
![]() $D_Z (b^{\mathrm {nl}}_n(s))$
, note that
$D_Z (b^{\mathrm {nl}}_n(s))$
, note that
![]() $D_{Z, 1}> 0$
, so
$D_{Z, 1}> 0$
, so
![]() $D_Z (b^{\mathrm {nl}}_n(s))$
is initially positive. However, if
$D_Z (b^{\mathrm {nl}}_n(s))$
is initially positive. However, if
![]() $b^{\mathrm {nl}}_n(s)$
crosses
$b^{\mathrm {nl}}_n(s)$
crosses
![]() $D_Z = 0$
between
$D_Z = 0$
between
![]() $P_s$
and
$P_s$
and
![]() $\bar P_s$
before
$\bar P_s$
before
![]() $s_{7/5}^{\mathrm {int}}$
, by Lemma A.22, we would have that the field
$s_{7/5}^{\mathrm {int}}$
, by Lemma A.22, we would have that the field
![]() $(N_W D_Z, N_Z D_W)$
points upwards at that point contradicting
$(N_W D_Z, N_Z D_W)$
points upwards at that point contradicting
![]() $P^{\mathrm {nl}}_n(s)> 0$
, from Proposition 3.6. If
$P^{\mathrm {nl}}_n(s)> 0$
, from Proposition 3.6. If
![]() $b^{\mathrm {nl}}_n(s)$
crosses
$b^{\mathrm {nl}}_n(s)$
crosses
![]() $D_Z = 0$
to the left of
$D_Z = 0$
to the left of
![]() $\bar P_s$
, at some other time
$\bar P_s$
, at some other time
![]() $s < s_{7/5}^{\mathrm {int}}$
, we fall under the second case considered in Proposition 3.6.
$s < s_{7/5}^{\mathrm {int}}$
, we fall under the second case considered in Proposition 3.6.
6 Proof of Theorems 1.1 and 1.2
We finally give the proof of Theorem 1.1 and Theorem 1.2. By Proposition 3.1, we have that in either the case
![]() $\gamma \in (1, +\infty )$
and
$\gamma \in (1, +\infty )$
and
![]() $r \in (r_3, r_{4})$
or the case
$r \in (r_3, r_{4})$
or the case
![]() $\gamma =\frac 75$
and
$\gamma =\frac 75$
and
![]() $r\in (r_{n}, r_{n+1})$
for n odd and sufficiently large, the smooth solution
$r\in (r_{n}, r_{n+1})$
for n odd and sufficiently large, the smooth solution
![]() $(W^{(r)}, Z^{(r)})$
, given in Proposition 2.3, connects
$(W^{(r)}, Z^{(r)})$
, given in Proposition 2.3, connects
![]() $P_s$
to
$P_s$
to
![]() $P_\infty $
. It remains to apply a shooting argument, in conjunction with Proposition 4.1, to show that the smooth solution connects
$P_\infty $
. It remains to apply a shooting argument, in conjunction with Proposition 4.1, to show that the smooth solution connects
![]() $P_0$
to
$P_0$
to
![]() $P_s$
.
$P_s$
.
Let us fix
![]() $n \in \mathbb {N}$
odd and
$n \in \mathbb {N}$
odd and
![]() $r\in (r_{n}, r_{n+1})$
. Due to Proposition 4.1, we know that there exist
$r\in (r_{n}, r_{n+1})$
. Due to Proposition 4.1, we know that there exist
![]() $r_d, r_u \in (r_{n}, r_{n+1})$
such that
$r_d, r_u \in (r_{n}, r_{n+1})$
such that
![]() $(W^{(r)}, Z^{(r)})$
lies in
$(W^{(r)}, Z^{(r)})$
lies in
![]() $\Omega _2^{(r)}$
and
$\Omega _2^{(r)}$
and
![]() $\Omega _1^{(r)}$
, respectively. Set
$\Omega _1^{(r)}$
, respectively. Set
![]() $\delta>0$
sufficiently small such that for all
$\delta>0$
sufficiently small such that for all
![]() $r\in [r_d,r_u]$
, the Taylor series (2.15) for
$r\in [r_d,r_u]$
, the Taylor series (2.15) for
![]() $(W^{(r)},Z^{(r)})$
converges for all
$(W^{(r)},Z^{(r)})$
converges for all
![]() $\xi \in [-\delta ,0]$
. By Lemma A.26 and Lemma A.7,
$\xi \in [-\delta ,0]$
. By Lemma A.26 and Lemma A.7,
![]() $W_1<0$
. Thus, by continuity and compactness, we may take
$W_1<0$
. Thus, by continuity and compactness, we may take
![]() $\delta $
smaller if need be to guarantee that
$\delta $
smaller if need be to guarantee that
for all
![]() $\xi \in [-\delta ,0]$
. In particular, the curve
$\xi \in [-\delta ,0]$
. In particular, the curve
![]() $(W^{(r)},Z^{(r)})$
for
$(W^{(r)},Z^{(r)})$
for
![]() $\xi \in [-\delta ,0]$
is a graph with respect to its W coordinate.
$\xi \in [-\delta ,0]$
is a graph with respect to its W coordinate.
Let
![]() $(W_r^o (\xi ), Z_r^o (\xi ))$
be the curve defined in (2.41). By Remark 2.6,
$(W_r^o (\xi ), Z_r^o (\xi ))$
be the curve defined in (2.41). By Remark 2.6,
![]() $W_r^o(\xi )$
is increasing with
$W_r^o(\xi )$
is increasing with
![]() $| \xi |$
for
$| \xi |$
for
![]() $\xi \in (-\infty ,0]$
. Thus, the curve
$\xi \in (-\infty ,0]$
. Thus, the curve
![]() $(W_r^o (\xi ), Z_r^o (\xi ))$
is also a graph with respect to its W coordinate.
$(W_r^o (\xi ), Z_r^o (\xi ))$
is also a graph with respect to its W coordinate.
Fix
![]() $(W_\ast ,Z_\ast )=(W^{(r)}(-\delta ),Z^{(r)}(-\delta ))$
, and define
$(W_\ast ,Z_\ast )=(W^{(r)}(-\delta ),Z^{(r)}(-\delta ))$
, and define
![]() $Z^o_\ast $
to be such that
$Z^o_\ast $
to be such that
![]() $(W_\ast ,Z^o_\ast )$
is a point on the curve
$(W_\ast ,Z^o_\ast )$
is a point on the curve
![]() $(W_r^o (\xi ), Z_r^o (\xi ))$
. We then define
$(W_r^o (\xi ), Z_r^o (\xi ))$
. We then define
![]() $e:[r_d,r_u]\mapsto \mathbb R$
by
$e:[r_d,r_u]\mapsto \mathbb R$
by
By definition, e is a continuous function in r. Moreover, as a consequence of Proposition 4.1 we have
![]() $e(r_d)<0$
and
$e(r_d)<0$
and
![]() $e(r_u)>0$
. Hence, by continuity, there exists a
$e(r_u)>0$
. Hence, by continuity, there exists a
![]() $r^{(n)}\in (r_d,r_u)$
such that
$r^{(n)}\in (r_d,r_u)$
such that
![]() $e(r)=0$
. Therefore, by the uniqueness in Proposition 1.6, for
$e(r)=0$
. Therefore, by the uniqueness in Proposition 1.6, for
![]() $r= r^{(n)}$
, we have
$r= r^{(n)}$
, we have
![]() $(W^{(r)},Z^{(r)})=(W_r^o (\xi ), Z_r^o (\xi ))$
. Thus, we conclude that the smooth curve corresponding to
$(W^{(r)},Z^{(r)})=(W_r^o (\xi ), Z_r^o (\xi ))$
. Thus, we conclude that the smooth curve corresponding to
![]() $r = r^{(n)}$
connects
$r = r^{(n)}$
connects
![]() $P_0$
to
$P_0$
to
![]() $P_\infty $
through the point
$P_\infty $
through the point
![]() $P_s$
, concluding the proofs of Theorem 1.1 and Theorem 1.2.
$P_s$
, concluding the proofs of Theorem 1.1 and Theorem 1.2.
7 Linear Stability of the Profile
In this section, we will study the linearized operator of the Euler equations around the self-similar profiles we have found. The stability for the Euler equation will follow in general, while in the Navier-Stokes case, we need to restrict the parameter r to a regime where the self-similar profile dominates the dissipation. The strategy will be to cut off the equation and study the linearized operator in a compact region
![]() $| \zeta | < 2$
. Following the strategy of [Reference Merle, Raphaël, Rodnianski and Szeftel67], we show that the linearized operator is maximal and accretive in the appropriate spaces. Maximality corresponds to the existence of solutions of the ODE determined by this operator, while accretivity corresponds to the fact that the operator has damping. Both properties give us, via a functional analysis argument, that the compactified linearized operator generates a contraction semigroup modulo finitely many instabilities. That is the main result of this section. The nonlinear stability and the treatment of the equation outside our compact region
$| \zeta | < 2$
. Following the strategy of [Reference Merle, Raphaël, Rodnianski and Szeftel67], we show that the linearized operator is maximal and accretive in the appropriate spaces. Maximality corresponds to the existence of solutions of the ODE determined by this operator, while accretivity corresponds to the fact that the operator has damping. Both properties give us, via a functional analysis argument, that the compactified linearized operator generates a contraction semigroup modulo finitely many instabilities. That is the main result of this section. The nonlinear stability and the treatment of the equation outside our compact region
![]() $| \zeta | < 2$
will be delayed to Section 8.
$| \zeta | < 2$
will be delayed to Section 8.
Remark 7.1. Let us note that from the proof that for
![]() $r = r^{(n)}$
,
$r = r^{(n)}$
,
![]() $W^{(r)}(\zeta )$
is increasing in
$W^{(r)}(\zeta )$
is increasing in
![]() $\xi \in (-\infty , 0]$
, so in particular,
$\xi \in (-\infty , 0]$
, so in particular,
![]() $W^{(r)}(\xi )> 0$
for all
$W^{(r)}(\xi )> 0$
for all
![]() $\xi \in (-\infty , 0]$
. Moreover, we have that
$\xi \in (-\infty , 0]$
. Moreover, we have that
![]() $D_Z ( W^{(r)}, Z^{(r)}) < 0$
for
$D_Z ( W^{(r)}, Z^{(r)}) < 0$
for
![]() $\xi < 0$
, and for the
$\xi < 0$
, and for the
![]() $\gamma = \frac 75$
case, this implies that
$\gamma = \frac 75$
case, this implies that
![]() $Z^{(r)}(\xi ) < 0$
for
$Z^{(r)}(\xi ) < 0$
for
![]() $\xi < 0$
. Thus, in the
$\xi < 0$
. Thus, in the
![]() $\gamma = \frac 75$
, we have that
$\gamma = \frac 75$
, we have that
![]() $(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
lies in the region
$(W^{(r)} (\xi ), Z^{(r)} (\xi ))$
lies in the region
![]() $W>0, Z<0$
for
$W>0, Z<0$
for
![]() $\xi \in (-\infty , 0]$
.
$\xi \in (-\infty , 0]$
.
7.1 Linearization and localization
Let ![]() represent an exact self-similar solution to the Euler equations solving (1.12). We now consider a solution
represent an exact self-similar solution to the Euler equations solving (1.12). We now consider a solution
![]() $(\mathcal {W},\mathcal {Z})$
to the time-dependent Navier-Stokes equation (1.19) and the difference
$(\mathcal {W},\mathcal {Z})$
to the time-dependent Navier-Stokes equation (1.19) and the difference
Then,
![]() $(\widetilde {W}, \widetilde {Z})$
satisfy the equations
$(\widetilde {W}, \widetilde {Z})$
satisfy the equations

Defining

then (7.1) becomes

where
![]() $\mathcal {F}_{\mathrm {dis}}$
,
$\mathcal {F}_{\mathrm {dis}}$
,
![]() $\mathcal {F}_{\mathrm {nl}, \widetilde {W}}$
,
$\mathcal {F}_{\mathrm {nl}, \widetilde {W}}$
,
![]() $\mathcal {F}_{\mathrm {nl}, \widetilde {Z}}$
are, respectively, the dissipative forcing, the nonlinear forcing term in the equation for
$\mathcal {F}_{\mathrm {nl}, \widetilde {Z}}$
are, respectively, the dissipative forcing, the nonlinear forcing term in the equation for
![]() $\widetilde {W}$
and the the nonlinear forcing term in the equation for
$\widetilde {W}$
and the the nonlinear forcing term in the equation for
![]() $\widetilde {Z}$
. Since we look for solutions
$\widetilde {Z}$
. Since we look for solutions
![]() $(\mathcal {W},\mathcal {Z})$
which are smooth when transformed into Cartesian coordinates, we may extend the solutions to
$(\mathcal {W},\mathcal {Z})$
which are smooth when transformed into Cartesian coordinates, we may extend the solutions to
![]() $\zeta \in \mathbb R$
by imposing the restriction
$\zeta \in \mathbb R$
by imposing the restriction
Then, (7.1) becomes
We also let
![]() $\mathcal {U}=\frac {\mathcal {W}+\mathcal {Z}}{2}$
and
$\mathcal {U}=\frac {\mathcal {W}+\mathcal {Z}}{2}$
and
![]() $\mathcal {S}=\frac {\mathcal {W}-\mathcal {Z}}{2}$
be the self-similar velocity and sound speed, respectively, which satisfy the equations
$\mathcal {S}=\frac {\mathcal {W}-\mathcal {Z}}{2}$
be the self-similar velocity and sound speed, respectively, which satisfy the equations
 $$ \begin{align} \begin{aligned} (\partial_s +r-1)\mathcal{U}+(\zeta+\mathcal{U})\partial_{\zeta} \mathcal{U} +\alpha \mathcal{S}\partial_{\zeta}S&=\mathcal{F}_{\mathrm{dis}},\\ (\partial_s +r-1)\mathcal{S}+(\zeta+\mathcal{U})\partial_{\zeta} \mathcal{S} +\frac{\alpha \mathcal{S}}{\zeta^2}\partial_{\zeta}(\zeta^2 \mathcal{U})&=0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\partial_s +r-1)\mathcal{U}+(\zeta+\mathcal{U})\partial_{\zeta} \mathcal{U} +\alpha \mathcal{S}\partial_{\zeta}S&=\mathcal{F}_{\mathrm{dis}},\\ (\partial_s +r-1)\mathcal{S}+(\zeta+\mathcal{U})\partial_{\zeta} \mathcal{S} +\frac{\alpha \mathcal{S}}{\zeta^2}\partial_{\zeta}(\zeta^2 \mathcal{U})&=0. \end{aligned} \end{align} $$
We let ![]() and
and ![]() denote the self-similar velocity and sound speed of the exact self-similar Euler profile. Taking the difference
denote the self-similar velocity and sound speed of the exact self-similar Euler profile. Taking the difference
leads to the equation

In order to simply our analysis, we will now introduce cut-offs and additional damping to (7.3) and (7.6) which will have the effect of localizing our analysis around a neighborhood of the acoustic light-cone of the singularity. Let
![]() $\chi _1$
be a cut-off function which is
$\chi _1$
be a cut-off function which is
![]() $1$
for
$1$
for
![]() $| \zeta | \leq \frac {6}{5}$
and it is supported on
$| \zeta | \leq \frac {6}{5}$
and it is supported on
![]() $ |\zeta | \leq \frac {7}{5}$
. Define also
$ |\zeta | \leq \frac {7}{5}$
. Define also
![]() $\chi _2$
to be a cut-off function such that
$\chi _2$
to be a cut-off function such that
![]() $\chi _2(\zeta )=1$
for
$\chi _2(\zeta )=1$
for
![]() $| \zeta | \leq \frac {8}{5}$
and it is supported on
$| \zeta | \leq \frac {8}{5}$
and it is supported on
![]() $| \zeta | \leq \frac {9}{5}$
. For a large constant
$| \zeta | \leq \frac {9}{5}$
. For a large constant
![]() $J>0$
, define
$J>0$
, define

We then consider the truncated equations

Note that the truncated equations are not themselves closed since
![]() $(\widetilde {W},\widetilde {Z})$
appear in the forcing terms. Adding the equations (7.3) closes (7.7). The truncated analogue of
$(\widetilde {W},\widetilde {Z})$
appear in the forcing terms. Adding the equations (7.3) closes (7.7). The truncated analogue of
![]() $(\widetilde {U},\widetilde {S})$
, given by
$(\widetilde {U},\widetilde {S})$
, given by
![]() $(\widetilde {U}_t,\widetilde {S}_t)=\frac 12(\widetilde {W}_t+\widetilde {Z}_t,\widetilde {W}_t-\widetilde {Z}_t)$
, satisfy the equations
$(\widetilde {U}_t,\widetilde {S}_t)=\frac 12(\widetilde {W}_t+\widetilde {Z}_t,\widetilde {W}_t-\widetilde {Z}_t)$
, satisfy the equations

To further distinguish the original equation, we will adopt the notation

where here, the subscript ‘e’ stands for extended. Then by an abuse of notation, we free up the notation
![]() $\widetilde {U}$
,
$\widetilde {U}$
,
![]() $\widetilde {S}$
,
$\widetilde {S}$
,
![]() $\widetilde {W}$
,
$\widetilde {W}$
,
![]() $\widetilde {Z}$
,
$\widetilde {Z}$
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() $ \mathcal {F}_{\tilde W}$
,
$ \mathcal {F}_{\tilde W}$
,
![]() $ \mathcal {F}_{\tilde Z}$
to refer to either the corresponding notation with the ‘t’ or ‘e’ subscript. For the remainder of the section, we will restrict our attention to the truncated equation, and so we will drop the ‘t’ subscript. In particular, we will consider the linear operator
$ \mathcal {F}_{\tilde Z}$
to refer to either the corresponding notation with the ‘t’ or ‘e’ subscript. For the remainder of the section, we will restrict our attention to the truncated equation, and so we will drop the ‘t’ subscript. In particular, we will consider the linear operator
![]() $\mathcal {L}=(\mathcal {L}_W,\mathcal {L}_Z)$
associated with (7.7) where
$\mathcal {L}=(\mathcal {L}_W,\mathcal {L}_Z)$
associated with (7.7) where
or in
![]() $(U,S)$
variables,
$(U,S)$
variables,
![]() $\mathcal {L}=(\mathcal {L}_U,\mathcal {L}_S)$
where
$\mathcal {L}=(\mathcal {L}_U,\mathcal {L}_S)$
where

The parameter J will be chosen sufficiently large in order that the operator
![]() $\mathcal {L}$
is well behaved in the region
$\mathcal {L}$
is well behaved in the region
![]() $[\frac {6}{5},2]$
.
$[\frac {6}{5},2]$
.
Using the definition of
![]() $\mathcal {L} = (\mathcal {L}_U, \mathcal {L}_S)$
in (7.9), we may rewrite (7.7) as
$\mathcal {L} = (\mathcal {L}_U, \mathcal {L}_S)$
in (7.9), we may rewrite (7.7) as
where
 $$ \begin{align*} \mathcal{F}_{t, \mathrm{nl}} = (\mathcal{F}_{t, \widetilde{U}}, \mathcal{F}_{t, \widetilde{S}}) = \left( \chi_2 \frac{\mathcal{F}_{\mathrm{nl}, \widetilde{W}} + \mathcal{F}_{\mathrm{nl}, \widetilde{Z}} }{2}, \chi_2 \frac{\mathcal{F}_{\mathrm{nl}, \widetilde{W}} - \mathcal{F}_{\mathrm{nl}, \widetilde{Z}} }{2}\right) \qquad \mbox{ and } \qquad \mathcal{F}_{t, \mathrm{dis}} = (\chi_2 \mathcal{F}_{\mathrm{dis}}, 0 ). \end{align*} $$
$$ \begin{align*} \mathcal{F}_{t, \mathrm{nl}} = (\mathcal{F}_{t, \widetilde{U}}, \mathcal{F}_{t, \widetilde{S}}) = \left( \chi_2 \frac{\mathcal{F}_{\mathrm{nl}, \widetilde{W}} + \mathcal{F}_{\mathrm{nl}, \widetilde{Z}} }{2}, \chi_2 \frac{\mathcal{F}_{\mathrm{nl}, \widetilde{W}} - \mathcal{F}_{\mathrm{nl}, \widetilde{Z}} }{2}\right) \qquad \mbox{ and } \qquad \mathcal{F}_{t, \mathrm{dis}} = (\chi_2 \mathcal{F}_{\mathrm{dis}}, 0 ). \end{align*} $$
Dissipativity of the operator
Remark 7.2. For some m (which will be chosen to be sufficiently large), we consider the space X to be the subspace of tuples
![]() $(U, S)$
, where U is a radially symmetric vector field and S a radially symmetric smooth function, and where
$(U, S)$
, where U is a radially symmetric vector field and S a radially symmetric smooth function, and where
![]() $U, S \in H_0^{2m} (B(0, 2))$
. We equip X with the usual
$U, S \in H_0^{2m} (B(0, 2))$
. We equip X with the usual
![]() $H^{2m}$
norm
$H^{2m}$
norm
Similarly, we let
![]() $\dot H^{2m}$
denote the corresponding homogeneous norm.
$\dot H^{2m}$
denote the corresponding homogeneous norm.
Moreover, we will sometimes consider the function
![]() $W (\zeta ) = S (| \zeta |) + \text {sign}(\zeta ) U(| \zeta |)$
defined for
$W (\zeta ) = S (| \zeta |) + \text {sign}(\zeta ) U(| \zeta |)$
defined for
![]() $\zeta \in [-2, 2]$
. We will say that
$\zeta \in [-2, 2]$
. We will say that
![]() $W \in X$
if the corresponding pair
$W \in X$
if the corresponding pair
![]() $(U, S)$
(which can be uniquely determined from W) is in X. By abuse of notation, we define the
$(U, S)$
(which can be uniquely determined from W) is in X. By abuse of notation, we define the
![]() $H^{2m}$
norm on W as
$H^{2m}$
norm on W as
![]() $\| W \|_{H^{2m}} = \|(U, S) \|_{H^{2m}}$
in that case.
$\| W \|_{H^{2m}} = \|(U, S) \|_{H^{2m}}$
in that case.
We then define the domain of our linear operator
![]() $\mathcal {L}=(\mathcal {L}_U,\mathcal {L}_S)$
to be the space
$\mathcal {L}=(\mathcal {L}_U,\mathcal {L}_S)$
to be the space
Lemma 7.3. For any N, there exists a finite codimension subspace of X where for any
![]() $0 \leq i \leq 2m$
, the following holds:
$0 \leq i \leq 2m$
, the following holds:
We let
![]() $Y_N$
denote that subspace.
$Y_N$
denote that subspace.
Proof. First of all, note that by interpolation, it suffices to show the claim for
![]() $i=0$
. Now, for a pair
$i=0$
. Now, for a pair
![]() $(U, S)$
, we consider the torus
$(U, S)$
, we consider the torus
![]() $\mathbb {T}^3 = [-\pi , \pi ]^3$
and extend
$\mathbb {T}^3 = [-\pi , \pi ]^3$
and extend
![]() $U_i(y), S(y)$
to be zero for
$U_i(y), S(y)$
to be zero for
![]() $y \in \mathbb {T}^3 \setminus B(0, 2)$
. Consider the Fourier series of
$y \in \mathbb {T}^3 \setminus B(0, 2)$
. Consider the Fourier series of
![]() $U_i, S$
as functions over
$U_i, S$
as functions over
![]() $\mathbb {T}^3$
.
$\mathbb {T}^3$
.
Now, we let the space
![]() $Y_N$
to be the finite codimension subspace of X defined by the finite set of linear equations
$Y_N$
to be the finite codimension subspace of X defined by the finite set of linear equations
for
![]() $i=1,2,3$
. Then, for such
$i=1,2,3$
. Then, for such
![]() $U_i$
, we have that
$U_i$
, we have that
The same reasoning applies to S, and we conclude our result.
Lemma 7.4. There exists sufficiently large N depending on J, which is chosen sufficiently large depending on m such that if
![]() $P_N$
is the orthogonal projection
$P_N$
is the orthogonal projection
![]() $P_N: X \rightarrow Y_N$
, then
$P_N: X \rightarrow Y_N$
, then
![]() $P_N \circ \mathcal {L} $
is dissipative on
$P_N \circ \mathcal {L} $
is dissipative on
![]() $Y_N$
, satisfying the bound
$Y_N$
, satisfying the bound
for all
![]() $(U,S)\in Y_N$
.
$(U,S)\in Y_N$
.
Proof. We will use the notation
![]() $O_m$
to indicate cases where the constant may depend on m, while we use O as usual our usual big-O notation (the constant is universal).
$O_m$
to indicate cases where the constant may depend on m, while we use O as usual our usual big-O notation (the constant is universal).
First note that since
![]() $P_N \circ \mathcal {L} $
is a real operator, mapping real valued function to real valued functions, it suffices to prove the bound
$P_N \circ \mathcal {L} $
is a real operator, mapping real valued function to real valued functions, it suffices to prove the bound
for
![]() $(U,S)$
real valued.
$(U,S)$
real valued.
Let us study the inner product
![]() $\langle \mathcal {L} (U, S), (U, S) \rangle _{\dot H^{2m}}$
, and we will treat the projection at the end. Let us recall that
$\langle \mathcal {L} (U, S), (U, S) \rangle _{\dot H^{2m}}$
, and we will treat the projection at the end. Let us recall that

Now, we proceed to study the terms in
 $$ \begin{align} \begin{aligned} -\langle \mathcal{L}(U, S), (U, S) \rangle_{\dot H^{2m}} &= \int_{B(0, 2)}\Delta^m \left( J(1-\chi_1) U + \chi_2 \mathcal{K}_U + \mathcal{V}_U \right)\cdot \Delta^m U \\ & \qquad + \int_{B(0, 2)}\Delta^m \left( J(1-\chi_1) S + \chi_2 \mathcal{K}_S + \mathcal{V}_S \right) \Delta^m S. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} -\langle \mathcal{L}(U, S), (U, S) \rangle_{\dot H^{2m}} &= \int_{B(0, 2)}\Delta^m \left( J(1-\chi_1) U + \chi_2 \mathcal{K}_U + \mathcal{V}_U \right)\cdot \Delta^m U \\ & \qquad + \int_{B(0, 2)}\Delta^m \left( J(1-\chi_1) S + \chi_2 \mathcal{K}_S + \mathcal{V}_S \right) \Delta^m S. \end{aligned} \end{align} $$
First of all, let us note that
 $$ \begin{align*} J \int_{B(0, 2)} \Delta^m \left( (1-\chi_1) U \right) \cdot \Delta^m U &= J \int_{B(0, 2)} (1-\chi_1) | \Delta^m U|^2 + O_m \left( J \| U \|_{H^{2m}} \left( \| U \|_{H^{2m-1}} + \| S \|_{H^{2m-1}} \right) \right),\nonumber \\ J \int_{B(0, 2)} \Delta^m \left( (1-\chi_1) S \right) \cdot \Delta^m S &= J \int_{B(0, 2)} (1-\chi_1) | \Delta^m S|^2 + O_m \left( J \| S \|_{H^{2m}} \left( \| U \|_{H^{2m-1}} + \| S \|_{H^{2m-1}} \right) \right). \end{align*} $$
$$ \begin{align*} J \int_{B(0, 2)} \Delta^m \left( (1-\chi_1) U \right) \cdot \Delta^m U &= J \int_{B(0, 2)} (1-\chi_1) | \Delta^m U|^2 + O_m \left( J \| U \|_{H^{2m}} \left( \| U \|_{H^{2m-1}} + \| S \|_{H^{2m-1}} \right) \right),\nonumber \\ J \int_{B(0, 2)} \Delta^m \left( (1-\chi_1) S \right) \cdot \Delta^m S &= J \int_{B(0, 2)} (1-\chi_1) | \Delta^m S|^2 + O_m \left( J \| S \|_{H^{2m}} \left( \| U \|_{H^{2m-1}} + \| S \|_{H^{2m-1}} \right) \right). \end{align*} $$
Choosing N sufficiently large, dependent on J, which in turn is chosen sufficiently large, dependent on m, we can ensure as a consequence of Lemma 7.3 that the error is
![]() $O( \| (U, S) \|_{ H^{2m}}^2 )$
. Therefore, we get that
$O( \| (U, S) \|_{ H^{2m}}^2 )$
. Therefore, we get that
 $$ \begin{align} \begin{aligned} J \int_{B(0, 2)} \Delta^m \left( (1-\chi_1) U \right) \cdot \Delta^m U &= J \int_{B(0, 2)} (1-\chi_1) | \Delta^m U|^2 + O \left( \| (U, S) \|_{\dot H^{2m}}^2 \right) ,\\ J \int_{B(0, 2)} \Delta^m \left( (1-\chi_1) S \right) \cdot \Delta^m S &= J \int_{B(0, 2)} (1-\chi_1) | \Delta^m S|^2 + O \left( \| (U, S) \|_{\dot H^{2m}}^2 \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} J \int_{B(0, 2)} \Delta^m \left( (1-\chi_1) U \right) \cdot \Delta^m U &= J \int_{B(0, 2)} (1-\chi_1) | \Delta^m U|^2 + O \left( \| (U, S) \|_{\dot H^{2m}}^2 \right) ,\\ J \int_{B(0, 2)} \Delta^m \left( (1-\chi_1) S \right) \cdot \Delta^m S &= J \int_{B(0, 2)} (1-\chi_1) | \Delta^m S|^2 + O \left( \| (U, S) \|_{\dot H^{2m}}^2 \right). \end{aligned} \end{align} $$
For the terms
![]() $\Delta ^m (\chi _2 \mathcal {K})$
in (7.11), we note the following: The terms where all the derivatives fall on U or S are bounded in
$\Delta ^m (\chi _2 \mathcal {K})$
in (7.11), we note the following: The terms where all the derivatives fall on U or S are bounded in
![]() $L^2$
as
$L^2$
as
![]() $O( \|(U, S) \|_{\dot H^{2m}})$
, where the implicit constant is independent of m. The rest of the terms have at most
$O( \|(U, S) \|_{\dot H^{2m}})$
, where the implicit constant is independent of m. The rest of the terms have at most
![]() $2m-1$
derivatives on U or S, so are simply bounded in
$2m-1$
derivatives on U or S, so are simply bounded in
![]() $L^2$
as
$L^2$
as
![]() $O_m (\| U \|_{H^{2m-1}} + \| S \|_{H^{2m-1}} )$
. Putting this altogether yields
$O_m (\| U \|_{H^{2m-1}} + \| S \|_{H^{2m-1}} )$
. Putting this altogether yields
 $$ \begin{align} \int_{B(0, 2)} \left( \Delta^m (\chi_2 \mathcal{K}_U) \cdot \Delta^m U + \Delta^m (\chi_2 \mathcal{K}_S) \Delta^m S \right) &= O_m \left( \left( \| U \|_{H^{2m-1}} + \| S \|_{H^{2m-1}} \right) \| (U, S) \|_{\dot H^{2m}} \right) \nonumber\\&\quad+O \left( \| (U, S) \|_{\dot H^{2m}}^2 \right) \nonumber \\ & = O \left( \| (U, S) \|_{\dot H^{2m}}^2 \right). \end{align} $$
$$ \begin{align} \int_{B(0, 2)} \left( \Delta^m (\chi_2 \mathcal{K}_U) \cdot \Delta^m U + \Delta^m (\chi_2 \mathcal{K}_S) \Delta^m S \right) &= O_m \left( \left( \| U \|_{H^{2m-1}} + \| S \|_{H^{2m-1}} \right) \| (U, S) \|_{\dot H^{2m}} \right) \nonumber\\&\quad+O \left( \| (U, S) \|_{\dot H^{2m}}^2 \right) \nonumber \\ & = O \left( \| (U, S) \|_{\dot H^{2m}}^2 \right). \end{align} $$
The last equality is due to the fact that we take N large enough in terms of m and apply Lemma 7.3.
Lastly, let us treat the terms coming from
![]() $\mathcal {V}_U$
and
$\mathcal {V}_U$
and
![]() $\mathcal {V}_S$
in (7.11). From Lemma A.4,
$\mathcal {V}_S$
in (7.11). From Lemma A.4,

If we take N sufficiently large in terms of m and use Lemma 7.3, these errors are
![]() $O( \| (U, S) \|_{\dot H^{2m}}^2 )$
. Therefore, we see from (7.14) that
$O( \| (U, S) \|_{\dot H^{2m}}^2 )$
. Therefore, we see from (7.14) that

where we have defined

Integrating by parts, we see that
Integration by parts also shows that
Finally, we also have
Plugging (7.17)–(7.19) into (7.15), we obtain

Plugging (7.12), (7.13) and (7.20) in (7.11), we obtain that

for some absolute constant C. Now, we claim that we can choose
![]() $J \gg m$
such that
$J \gg m$
such that
In order to show (7.22), let us divide
![]() $B(0, 2)$
in two regions. We define
$B(0, 2)$
in two regions. We define
![]() $R_1$
as the region where
$R_1$
as the region where
![]() $\chi _2 = 1$
and define
$\chi _2 = 1$
and define
![]() $R_2$
as the region of
$R_2$
as the region of
![]() $B(0, 2)$
where
$B(0, 2)$
where
![]() $\chi _2 < 1$
. In particular, we have that
$\chi _2 < 1$
. In particular, we have that
![]() $\chi _1 = 0$
on
$\chi _1 = 0$
on
![]() $R_2$
.
$R_2$
.
Region
![]() $R_1$
. In this region, as
$R_1$
. In this region, as
![]() $\chi _2 = 1$
and
$\chi _2 = 1$
and
![]() $\chi _1 \leq 1$
, it suffices to show
$\chi _1 \leq 1$
, it suffices to show
As we can choose m sufficiently large, we just need to show that
for some
![]() $\varepsilon> 0$
and every
$\varepsilon> 0$
and every
![]() $\zeta \in [0, 7/5]$
. This is implied by Lemma A.36 taking
$\zeta \in [0, 7/5]$
. This is implied by Lemma A.36 taking
![]() $\varepsilon = \eta _{\mathrm {damp}}$
.
$\varepsilon = \eta _{\mathrm {damp}}$
.
Region
![]() $R_2$
. In this region, as
$R_2$
. In this region, as
![]() $\chi _1 = 0$
, it suffices to satisfy
$\chi _1 = 0$
, it suffices to satisfy
It is trivial that we can satisfy this inequality because the right-hand side is a bounded function for
![]() $\zeta \in [0, 2]$
, and we can take J sufficiently large, depending on m.
$\zeta \in [0, 2]$
, and we can take J sufficiently large, depending on m.
Therefore, we conclude that (7.22) holds, and inserting this in (7.21), we conclude
Assuming N is sufficiently large, applying Lemma 7.3, the bound (7.23) yields
Note that
![]() $(1-P_N) \circ \mathcal {L} (U, S)$
has image in a finite dimension space which is the orthogonal complement to the space
$(1-P_N) \circ \mathcal {L} (U, S)$
has image in a finite dimension space which is the orthogonal complement to the space
![]() $Y_N$
where
$Y_N$
where
![]() $(U, S)$
lie. Therefore,
$(U, S)$
lie. Therefore,
![]() $\langle (1-P_N)\circ \mathcal {L} (U, S), (U, S) \rangle _{ H^{2m}} = 0$
, and we conclude
$\langle (1-P_N)\circ \mathcal {L} (U, S), (U, S) \rangle _{ H^{2m}} = 0$
, and we conclude
that is, that our operator
![]() $P_N \circ \mathcal {L}$
is dissipative on
$P_N \circ \mathcal {L}$
is dissipative on
![]() $Y_N$
.
$Y_N$
.
Maximality
Before we prove our main maximality result, let us prove the following auxiliary lemma that will help us deal with the point
![]() $\zeta =\frac 95$
where both
$\zeta =\frac 95$
where both ![]() and
and ![]() vanish.
vanish.
Lemma 7.5. For
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $a<2$
, consider the following ODE:
$a<2$
, consider the following ODE:
on the region
![]() $[a,2]$
, for smooth
$[a,2]$
, for smooth
![]() $\mathcal {D}$
,
$\mathcal {D}$
,
![]() $\mathcal {V}$
and f. For some
$\mathcal {V}$
and f. For some
![]() $a<b<2$
, let us further assume that
$a<b<2$
, let us further assume that
![]() $\mathcal {V}(x)=0$
for
$\mathcal {V}(x)=0$
for
![]() $x\in [b,2]$
and
$x\in [b,2]$
and
![]() $\mathcal {V}(x)>0$
for
$\mathcal {V}(x)>0$
for
![]() $x\in [a,b)$
. Then, assuming
$x\in [a,b)$
. Then, assuming
![]() $\lambda>0$
is sufficiently large, (7.24) has a unique smooth solution. Moreover,
$\lambda>0$
is sufficiently large, (7.24) has a unique smooth solution. Moreover,
![]() $(u,f)$
may be taken to be vector valued, in which case
$(u,f)$
may be taken to be vector valued, in which case
![]() $u_0$
is a vector, and
$u_0$
is a vector, and
![]() $\mathcal {D}$
is taken to be matrix valued and
$\mathcal {D}$
is taken to be matrix valued and
![]() $\mathcal {V}$
remains scalar valued.
$\mathcal {V}$
remains scalar valued.
Proof. For concreteness, let us assume
![]() $a=0$
and
$a=0$
and
![]() $b=1$
. We also assume u to be scalar valued since the vector valued case will follow from an identical proof.
$b=1$
. We also assume u to be scalar valued since the vector valued case will follow from an identical proof.
By standard ODE theory, there exists a unique smooth u to (7.24) on the region
![]() $[0,1)$
. Moreover, assuming
$[0,1)$
. Moreover, assuming
![]() $ \lambda>0$
is sufficiently large, on the region
$ \lambda>0$
is sufficiently large, on the region
![]() $[1,2]$
, (7.24) has the unique smooth solution
$[1,2]$
, (7.24) has the unique smooth solution
![]() $u=\frac {f}{\lambda +\mathcal {D}}$
. Thus, it suffices to verify that the resulting solution u is smooth at
$u=\frac {f}{\lambda +\mathcal {D}}$
. Thus, it suffices to verify that the resulting solution u is smooth at
![]() $x=1$
. In particular, we need to show
$x=1$
. In particular, we need to show
By the Leibniz rule,
 $$\begin{align*}\mathcal{V} u^{(n+1)}=-(\lambda+\mathcal{D}+n{\mathcal{V}}') u^{(n)}\underbrace{-\sum_{k=2}^{n} \binom{n}{k} u^{(n-k+1)}{\mathcal{V}}^{(k)}-\sum_{k=1}^{n} \binom{n}{k} u^{(n-k)}{\mathcal{D}}^{(k)}+f^{(n)}}_{\mathcal{F}_n}. \end{align*}$$
$$\begin{align*}\mathcal{V} u^{(n+1)}=-(\lambda+\mathcal{D}+n{\mathcal{V}}') u^{(n)}\underbrace{-\sum_{k=2}^{n} \binom{n}{k} u^{(n-k+1)}{\mathcal{V}}^{(k)}-\sum_{k=1}^{n} \binom{n}{k} u^{(n-k)}{\mathcal{D}}^{(k)}+f^{(n)}}_{\mathcal{F}_n}. \end{align*}$$
By Grönwall’s inequality, for
![]() $0<x_0<x<1$
,
$0<x_0<x<1$
,
![]() $x_0$
sufficiently close to
$x_0$
sufficiently close to
![]() $1$
, we have
$1$
, we have
 $$ \begin{align*} \left|u^{(n)}(x)\right|&\leq e^{-\int_{x_0}^x \frac{\lambda}{\mathcal{V}}}\left(\left|u^{(n)}({x_0})\right|+\int_{x_0}^x \frac{e^{\int_{x_0}^{x'} \frac{\lambda}{\mathcal{V}}}}{\mathcal{V}(x')} \left(\left|\mathcal{F}_n(x')\right|+\left|u^{(n)}({x'})\right|\left(\left|\mathcal{D}(x')\right|+n\left|\mathcal{V}'(x')\right|\right)\right)\,dx'\ \right)\\ &\leq e^{-\int_{x_0}^x \frac{\lambda}{\mathcal{V}}}\left(\left|u^{(n)}({x_0})\right|+\int_{x_0}^x \frac{1}{\lambda}\left(\frac{d}{dx'}e^{\int_{x_0}^{x'} \frac{\lambda}{\mathcal{V}}} \right)\left(\left|\mathcal{F}_n(x')\right|+C\left|u^{(n)}({x'})\right|\right)\,dx' \right)\\ &\leq e^{-\int_{x_0}^x \frac{\lambda}{\mathcal{V}}}\left|u^{(n)}({x_0})\right|+\frac{1}{\lambda}\left(\left\|\mathcal{F}_n\right\|_{L^{\infty}[x_0,x]}+C\left\|u^{(n)}\right\|_{L^{\infty}[x_0,x]}\right)\, \end{align*} $$
$$ \begin{align*} \left|u^{(n)}(x)\right|&\leq e^{-\int_{x_0}^x \frac{\lambda}{\mathcal{V}}}\left(\left|u^{(n)}({x_0})\right|+\int_{x_0}^x \frac{e^{\int_{x_0}^{x'} \frac{\lambda}{\mathcal{V}}}}{\mathcal{V}(x')} \left(\left|\mathcal{F}_n(x')\right|+\left|u^{(n)}({x'})\right|\left(\left|\mathcal{D}(x')\right|+n\left|\mathcal{V}'(x')\right|\right)\right)\,dx'\ \right)\\ &\leq e^{-\int_{x_0}^x \frac{\lambda}{\mathcal{V}}}\left(\left|u^{(n)}({x_0})\right|+\int_{x_0}^x \frac{1}{\lambda}\left(\frac{d}{dx'}e^{\int_{x_0}^{x'} \frac{\lambda}{\mathcal{V}}} \right)\left(\left|\mathcal{F}_n(x')\right|+C\left|u^{(n)}({x'})\right|\right)\,dx' \right)\\ &\leq e^{-\int_{x_0}^x \frac{\lambda}{\mathcal{V}}}\left|u^{(n)}({x_0})\right|+\frac{1}{\lambda}\left(\left\|\mathcal{F}_n\right\|_{L^{\infty}[x_0,x]}+C\left\|u^{(n)}\right\|_{L^{\infty}[x_0,x]}\right)\, \end{align*} $$
for some constant C independent of n, where we used that
![]() $n\left \|\mathcal {V}'\right \|_{L^\infty [x_0,1]}$
can be made arbitrarily small by assuming
$n\left \|\mathcal {V}'\right \|_{L^\infty [x_0,1]}$
can be made arbitrarily small by assuming
![]() $x_0$
to be sufficiently close to
$x_0$
to be sufficiently close to
![]() $1$
. Assuming
$1$
. Assuming
![]() $\frac {C}{ \lambda }\le \frac 12$
, we obtain
$\frac {C}{ \lambda }\le \frac 12$
, we obtain
By induction on n (and an appropriate choice of
![]() $x_0$
for each n), we conclude that u is smooth at
$x_0$
for each n), we conclude that u is smooth at
![]() $x=1$
.
$x=1$
.
Lemma 7.6. Consider
![]() $J, m, N$
chosen as in Lemma 7.4. For sufficiently large
$J, m, N$
chosen as in Lemma 7.4. For sufficiently large
![]() $\lambda>0$
, we have that for every
$\lambda>0$
, we have that for every
![]() $F=(F_U,F_S)\in X$
, then there exists
$F=(F_U,F_S)\in X$
, then there exists
![]() $(U,S)\in \mathcal {D}(\mathcal {L})$
such that
$(U,S)\in \mathcal {D}(\mathcal {L})$
such that
Proof. Let us rewrite the equation (7.25) in terms of
 $$\begin{align*}W(\zeta)=\begin{cases}U(\zeta)+S(\zeta)&\mbox{for }\zeta\geq 0\\ -U(-\zeta)+S(-\zeta)&\mbox{for }\zeta\leq 0\end{cases},\end{align*}$$
$$\begin{align*}W(\zeta)=\begin{cases}U(\zeta)+S(\zeta)&\mbox{for }\zeta\geq 0\\ -U(-\zeta)+S(-\zeta)&\mbox{for }\zeta\leq 0\end{cases},\end{align*}$$
which leads to the equation
where
 $$\begin{align*}Z ( \zeta) = -W (-\zeta)\quad\mbox{and}\quad F_W(\zeta)=\begin{cases}F_U(\zeta)+F_S(\zeta)&\mbox{for }\zeta\geq 0\\ -F_U(-\zeta)+F_S(-\zeta)&\mbox{for }\zeta\leq 0\end{cases} .\end{align*}$$
$$\begin{align*}Z ( \zeta) = -W (-\zeta)\quad\mbox{and}\quad F_W(\zeta)=\begin{cases}F_U(\zeta)+F_S(\zeta)&\mbox{for }\zeta\geq 0\\ -F_U(-\zeta)+F_S(-\zeta)&\mbox{for }\zeta\leq 0\end{cases} .\end{align*}$$
We consider first the problem (7.26) for the case
![]() $F_W=\chi \mathcal {F}$
, where
$F_W=\chi \mathcal {F}$
, where
![]() $\mathcal {F}$
is analytic and
$\mathcal {F}$
is analytic and
![]() $\chi $
is a cut-off function that is
$\chi $
is a cut-off function that is
![]() $1$
on
$1$
on
![]() $[-\frac 32,\frac 32]$
and has compact support in
$[-\frac 32,\frac 32]$
and has compact support in
![]() $[-2,2]$
. Clearly, such
$[-2,2]$
. Clearly, such
![]() $F_W$
are dense in X. Let us rewrite (7.26) as
$F_W$
are dense in X. Let us rewrite (7.26) as

For the analysis around
![]() $P_s$
, it will also be useful to write a separate equation for
$P_s$
, it will also be useful to write a separate equation for
![]() $ Z$
:
$ Z$
:
and

Consider the formal power series expansions of
![]() $(W, Z)$
at
$(W, Z)$
at
![]() $\zeta =1$
(i.e.,
$\zeta =1$
(i.e.,
![]() $ W=\sum _{i \geq 0} w_i (\zeta -1)^i$
and
$ W=\sum _{i \geq 0} w_i (\zeta -1)^i$
and
![]() $ Z = \sum _{i \geq 0} z_i(\zeta -1)^i$
). Writing in addition
$ Z = \sum _{i \geq 0} z_i(\zeta -1)^i$
). Writing in addition ![]() and
and
![]() $\mathcal {G}_{ Z}(W,Z)=\sum _{i \geq 0} g_{ Z,i} (\zeta -1)^i$
, then substituting these expansions into (7.27) and (7.28) yields
$\mathcal {G}_{ Z}(W,Z)=\sum _{i \geq 0} g_{ Z,i} (\zeta -1)^i$
, then substituting these expansions into (7.27) and (7.28) yields


Let us rewrite
![]() $g_{ Z,n+1}$
as
$g_{ Z,n+1}$
as
Then, (7.30) can be rewritten as

Thus, assuming
![]() $\lambda $
is sufficiently large and using
$\lambda $
is sufficiently large and using ![]() (Lemma (A.11)), one may solve the recurrence relations (7.29) and (7.30) uniquely by setting
(Lemma (A.11)), one may solve the recurrence relations (7.29) and (7.30) uniquely by setting
![]() $w_0 = A$
, and
$w_0 = A$
, and
![]() $z_0$
is determined from (7.28). Furthermore, from the analyticity of
$z_0$
is determined from (7.28). Furthermore, from the analyticity of ![]() at
at
![]() $\zeta =1$
(which is a consequence of Proposition Proposition 2.3) and F, we obtain that the series converges absolutely to obtain a solution
$\zeta =1$
(which is a consequence of Proposition Proposition 2.3) and F, we obtain that the series converges absolutely to obtain a solution
![]() $(W,Z)$
in a neighborhood of
$(W,Z)$
in a neighborhood of
![]() $\zeta =1$
. The solution can be extended to a
$\zeta =1$
. The solution can be extended to a
![]() $C^\infty $
solution on
$C^\infty $
solution on
![]() $\zeta \in (0,\frac 95)$
by standard ODE arguments, using that the only zero of
$\zeta \in (0,\frac 95)$
by standard ODE arguments, using that the only zero of
![]() $\mathcal {V}_{\bar Z} (\zeta )$
or
$\mathcal {V}_{\bar Z} (\zeta )$
or
![]() $\mathcal {V}_{\bar W} (\zeta )$
with
$\mathcal {V}_{\bar W} (\zeta )$
with
![]() $\zeta \in (0, \frac 95 )$
is
$\zeta \in (0, \frac 95 )$
is
![]() $\mathcal {V}_{\bar Z} (1) = 0$
. This just follows from the observation that
$\mathcal {V}_{\bar Z} (1) = 0$
. This just follows from the observation that
![]() $\mathcal {V}_{\bar Z} = \zeta D_Z^E$
and
$\mathcal {V}_{\bar Z} = \zeta D_Z^E$
and
![]() $\mathcal {V}_{\bar W} = \zeta D_W^E$
(where we use the superindex E to indicate we refer to the Euler scaling and self-similar profiles from Sections 2–6). Applying Lemma 7.5, we can further extend the solution to a
$\mathcal {V}_{\bar W} = \zeta D_W^E$
(where we use the superindex E to indicate we refer to the Euler scaling and self-similar profiles from Sections 2–6). Applying Lemma 7.5, we can further extend the solution to a
![]() $C^\infty $
solution on
$C^\infty $
solution on
![]() $\zeta \in (0,2]$
. Note in order to apply Lemma 7.5, we let
$\zeta \in (0,2]$
. Note in order to apply Lemma 7.5, we let
![]() $(a,b)=(\frac 65,\frac 95)$
and
$(a,b)=(\frac 65,\frac 95)$
and ![]() .
.
We will apply a shooting argument in order to choose A such that W is smooth at
![]() $\zeta =0$
. First we show that there exists
$\zeta =0$
. First we show that there exists
![]() $A^\ast $
such that if
$A^\ast $
such that if
![]() $(W_{A^\ast },Z_{A^\ast })$
and
$(W_{A^\ast },Z_{A^\ast })$
and
![]() $(W_{-A^\ast },Z_{-A^\ast })$
correspond to the smooth solutions to (7.27) and (7.28) for
$(W_{-A^\ast },Z_{-A^\ast })$
correspond to the smooth solutions to (7.27) and (7.28) for
![]() $\zeta \in (0,1]$
satisfying
$\zeta \in (0,1]$
satisfying
![]() $W(1)=A^\ast $
and
$W(1)=A^\ast $
and
![]() $W(1)=-A^\ast $
, respectively, then we have
$W(1)=-A^\ast $
, respectively, then we have
for all
![]() $\zeta \in (0,1]$
.
$\zeta \in (0,1]$
.
Note that by (7.28), we have that
Note for
![]() $\gamma =\frac 75$
, we have
$\gamma =\frac 75$
, we have
Hence, for k sufficiently large, by continuity, ![]() . Thus, choosing
. Thus, choosing ![]() and
and ![]() , from (7.33), we obtain
, from (7.33), we obtain
![]() $ Z_{A^\ast }(1)\geq \frac {A^\ast }{C\lambda }$
for C some depending on
$ Z_{A^\ast }(1)\geq \frac {A^\ast }{C\lambda }$
for C some depending on ![]() .
.
We claim that
![]() $W_{A^\ast }\geq \frac {A^\ast }{2}$
and
$W_{A^\ast }\geq \frac {A^\ast }{2}$
and
![]() $Z_{A^\ast }\geq \frac {A^\ast }{C'\lambda }$
for all
$Z_{A^\ast }\geq \frac {A^\ast }{C'\lambda }$
for all
![]() $\zeta \in (0,1]$
and some large constant
$\zeta \in (0,1]$
and some large constant
![]() $C'> C$
. Suppose the statement is false. Then there must exist a largest
$C'> C$
. Suppose the statement is false. Then there must exist a largest
![]() $\zeta '\in (0,1)$
such that either
$\zeta '\in (0,1)$
such that either
-
1.
 $W_{A^\ast }(\zeta ')=\frac {A^\ast }{2}$
and
$W_{A^\ast }(\zeta ')=\frac {A^\ast }{2}$
and
 $W_{A^\ast }'(\zeta ')\geq 0$
.
$W_{A^\ast }'(\zeta ')\geq 0$
. -
2.
 $Z_{A^\ast }(\zeta ')=\frac {A^\ast }{\lambda C'}$
and
$Z_{A^\ast }(\zeta ')=\frac {A^\ast }{\lambda C'}$
and
 $Z_{A^\ast }'(\zeta ')\geq 0$
.
$Z_{A^\ast }'(\zeta ')\geq 0$
.
Consider the first the case. If
![]() $W_{A^\ast }(\zeta ')=\frac {A^\ast }{2}$
, then
$W_{A^\ast }(\zeta ')=\frac {A^\ast }{2}$
, then

In the second line, we absorbed many terms by
![]() $-\frac { \lambda W_{A^\ast }}{2} $
. In the third line, we used that
$-\frac { \lambda W_{A^\ast }}{2} $
. In the third line, we used that
![]() $W_{A^\ast }(\zeta ')=\frac {A^\ast }{2}$
,
$W_{A^\ast }(\zeta ')=\frac {A^\ast }{2}$
, ![]() is positive and
is positive and ![]() is positive by Remark 7.1. Thus, we arrive at a contradiction, using that
is positive by Remark 7.1. Thus, we arrive at a contradiction, using that

from Lemma A.37 and
![]() $Z_{A^\ast } \geq \frac {A^\ast }{C' \lambda }> 0$
.
$Z_{A^\ast } \geq \frac {A^\ast }{C' \lambda }> 0$
.
Now consider the second case,
![]() $Z_{A^\ast (\zeta ')}= \frac {A^\ast }{C'\lambda }$
. Thus, we get
$Z_{A^\ast (\zeta ')}= \frac {A^\ast }{C'\lambda }$
. Thus, we get

In the first inequality, we have used that ![]() . In the second one, we have bounded most of the terms from
. In the second one, we have bounded most of the terms from ![]() simply by
simply by
![]() $C"Z_{A^\ast }$
, being
$C"Z_{A^\ast }$
, being
![]() $C"$
a constant sufficiently large. In the third one, we used our value for
$C"$
a constant sufficiently large. In the third one, we used our value for
![]() $Z_{A^\ast } = \frac {A^\ast }{C'\lambda }$
and the fact that
$Z_{A^\ast } = \frac {A^\ast }{C'\lambda }$
and the fact that ![]() is negative for
is negative for
![]() $\zeta \in (0, 1]$
(Remark 7.1), and we also used
$\zeta \in (0, 1]$
(Remark 7.1), and we also used

from Lemma A.38. Choosing
![]() $C' = 400$
and
$C' = 400$
and
![]() $A^\ast , \lambda $
to be sufficiently large, we get a contradiction from (7.36).
$A^\ast , \lambda $
to be sufficiently large, we get a contradiction from (7.36).
The second inequality of (7.32) follows analogously, enlarging
![]() $A^\ast $
if needed.
$A^\ast $
if needed.
As a consequence of (7.32), for any
![]() $0<\delta <1$
, there exists a map
$0<\delta <1$
, there exists a map
![]() $\mathcal {F}_\delta :[-1,1]\rightarrow [-A^\ast ,A^\ast ]$
such that if
$\mathcal {F}_\delta :[-1,1]\rightarrow [-A^\ast ,A^\ast ]$
such that if
![]() $(W,Z)$
is the smooth solution on
$(W,Z)$
is the smooth solution on
![]() $(0,2]$
corresponding to
$(0,2]$
corresponding to
![]() $W(1)=\mathcal {F}_\delta (z)$
, then
$W(1)=\mathcal {F}_\delta (z)$
, then
We now want to show such solutions
![]() $(W,Z)$
can be bounded on the region
$(W,Z)$
can be bounded on the region
![]() $[\delta ,2]$
, independent of the choice of
$[\delta ,2]$
, independent of the choice of
![]() $\delta $
and
$\delta $
and
![]() $z\in [-1,1]$
. We introduce a parameter M (that will be taken sufficiently large), and we note that on the region
$z\in [-1,1]$
. We introduce a parameter M (that will be taken sufficiently large), and we note that on the region
![]() $\left [ \frac {1}{M \lambda }, 2 \right ]$
, we have the bound
$\left [ \frac {1}{M \lambda }, 2 \right ]$
, we have the bound
for some constant
![]() $C_1$
, depending on
$C_1$
, depending on
![]() $\lambda $
and M, independent of z and
$\lambda $
and M, independent of z and
![]() $\delta $
.
$\delta $
.
Since
![]() $\lambda $
may be chosen sufficiently large, dependent on
$\lambda $
may be chosen sufficiently large, dependent on
![]() $F_W, F_Z$
, we can rewrite (7.27) and (7.28) as
$F_W, F_Z$
, we can rewrite (7.27) and (7.28) as

Setting
![]() $U = \frac {W+Z}{2}, S = \frac {W-Z}{2}$
, and using
$U = \frac {W+Z}{2}, S = \frac {W-Z}{2}$
, and using
we obtain

We used that ![]() and that
and that ![]() is uniformly bounded close to
is uniformly bounded close to
![]() $\zeta = 0$
.
$\zeta = 0$
.
Defining ![]() , From (7.39), we obtain
, From (7.39), we obtain
 $$ \begin{align} \begin{aligned} \left| \partial_\zeta U + \frac{C_2 U}{\zeta} \right| \leq C_3 \lambda \sqrt{U^2 + S^2} \qquad \mbox{ and } \qquad \left| \partial_\zeta S \right| \leq C_3 \lambda \sqrt{U^2 + S^2}\, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left| \partial_\zeta U + \frac{C_2 U}{\zeta} \right| \leq C_3 \lambda \sqrt{U^2 + S^2} \qquad \mbox{ and } \qquad \left| \partial_\zeta S \right| \leq C_3 \lambda \sqrt{U^2 + S^2}\, \end{aligned} \end{align} $$
for some new constant
![]() $C_3>0$
. Let us define
$C_3>0$
. Let us define
 $$ \begin{align} A = \left| \frac{C_2 U(\zeta)}{\zeta} \right| ,\qquad B = C_3 \lambda \sqrt{U^2+S^2}\qquad \mbox{ and } \qquad G = U^2 + S^2. \end{align} $$
$$ \begin{align} A = \left| \frac{C_2 U(\zeta)}{\zeta} \right| ,\qquad B = C_3 \lambda \sqrt{U^2+S^2}\qquad \mbox{ and } \qquad G = U^2 + S^2. \end{align} $$
Let us work under the hypothesis that
![]() $A> 10B$
for some
$A> 10B$
for some
![]() $\zeta $
. Without loss of generality, let us also assume that
$\zeta $
. Without loss of generality, let us also assume that
![]() $U(\zeta )> 0$
. Then,
$U(\zeta )> 0$
. Then,
 $$ \begin{align*} -\partial_{\zeta} A &= -\partial_{\zeta} \frac{C_2 U(\zeta)}{\zeta} \geq \frac{C_2 U}{\zeta^2} - \frac{C_2 \left(-C_2U/\zeta \right)}{\zeta} - \left| \frac{C_2 \left( C_3 \lambda \sqrt{U^2 + S^2} \right)}{\zeta} \right| = \frac{1+C_2}{\zeta} A - \frac{C_2}{\zeta} B \geq M\lambda A , \\-\partial_{\zeta} B &= -\frac{BG'}{2G } \leq B\frac{\zeta A^2 /C_2}{B^2 /(C_3^2 \lambda^2) } + 2C_3 \lambda B \leq \zeta\frac{\lambda^2 C_3^2}{10 C_2} A + 2 C_3 \lambda B = \frac{\lambda C_3^2}{10 M C_2} A + 2 C_3 \lambda B \leq C_4 \lambda A, \end{align*} $$
$$ \begin{align*} -\partial_{\zeta} A &= -\partial_{\zeta} \frac{C_2 U(\zeta)}{\zeta} \geq \frac{C_2 U}{\zeta^2} - \frac{C_2 \left(-C_2U/\zeta \right)}{\zeta} - \left| \frac{C_2 \left( C_3 \lambda \sqrt{U^2 + S^2} \right)}{\zeta} \right| = \frac{1+C_2}{\zeta} A - \frac{C_2}{\zeta} B \geq M\lambda A , \\-\partial_{\zeta} B &= -\frac{BG'}{2G } \leq B\frac{\zeta A^2 /C_2}{B^2 /(C_3^2 \lambda^2) } + 2C_3 \lambda B \leq \zeta\frac{\lambda^2 C_3^2}{10 C_2} A + 2 C_3 \lambda B = \frac{\lambda C_3^2}{10 M C_2} A + 2 C_3 \lambda B \leq C_4 \lambda A, \end{align*} $$
where
![]() $C_4$
is independent of
$C_4$
is independent of
![]() $M, \lambda $
. Then, taking M to be sufficiently large so that
$M, \lambda $
. Then, taking M to be sufficiently large so that
![]() $M> 10 C_4$
, we see that the hypothesis
$M> 10 C_4$
, we see that the hypothesis
![]() $A> 10B$
for some
$A> 10B$
for some
![]() $\zeta '$
, implies that the same hypothesis holds for all smaller
$\zeta '$
, implies that the same hypothesis holds for all smaller
![]() $\zeta \in [\delta , \zeta ']$
. Taking
$\zeta \in [\delta , \zeta ']$
. Taking
![]() $\zeta '$
to be the largest
$\zeta '$
to be the largest
![]() $\zeta \in [\delta , \frac {1}{M \lambda }]$
such that
$\zeta \in [\delta , \frac {1}{M \lambda }]$
such that
![]() $A \geq 10B$
(or
$A \geq 10B$
(or
![]() $\zeta ' = \delta $
if there is no such
$\zeta ' = \delta $
if there is no such
![]() $\zeta $
exists), we obtain the following:
$\zeta $
exists), we obtain the following:
-
• In the region
 $(\delta , \zeta ')$
, we have
$(\delta , \zeta ')$
, we have
 $A \geq 10B$
, and moreover,
$A \geq 10B$
, and moreover,
 $U(\zeta )$
has constant sign in this interval.
$U(\zeta )$
has constant sign in this interval. -
• In the region
 $\left ( \zeta ', \frac {1}{M \lambda } \right )$
, we have
$\left ( \zeta ', \frac {1}{M \lambda } \right )$
, we have
 $A < 10B$
.
$A < 10B$
.
Let us first treat the region
![]() $\zeta ' < \zeta < \frac {1}{M \lambda }$
. As
$\zeta ' < \zeta < \frac {1}{M \lambda }$
. As
![]() $A < 10B$
, we obtain that
$A < 10B$
, we obtain that
![]() $|U'| \leq 11 C_3 \lambda \sqrt {U^2 + S^2}$
. Thus,
$|U'| \leq 11 C_3 \lambda \sqrt {U^2 + S^2}$
. Thus,
Integrating, we get that for all
![]() $\zeta \in \left ( \zeta ', \frac {1}{\lambda M} \right )$
,
$\zeta \in \left ( \zeta ', \frac {1}{\lambda M} \right )$
,
 $$ \begin{align} G(\zeta) \leq G \left( \frac{1}{\lambda M} \right) e^{\frac{24 C_3}{M}} \leq C_{M, \lambda} , \end{align} $$
$$ \begin{align} G(\zeta) \leq G \left( \frac{1}{\lambda M} \right) e^{\frac{24 C_3}{M}} \leq C_{M, \lambda} , \end{align} $$
where
![]() $C_{M, \lambda }$
is sufficiently large depending on M and
$C_{M, \lambda }$
is sufficiently large depending on M and
![]() $\lambda $
(independent of
$\lambda $
(independent of
![]() $z, \delta $
).
$z, \delta $
).
In the region
![]() $\delta < \zeta < \zeta '$
, using
$\delta < \zeta < \zeta '$
, using
![]() $A> 10B$
in equation (7.40), we see that
$A> 10B$
in equation (7.40), we see that
![]() $U'$
has the same sign as
$U'$
has the same sign as
![]() $\frac {-C_2 U}{\zeta }$
, so
$\frac {-C_2 U}{\zeta }$
, so
![]() $U^2$
is decreasing in
$U^2$
is decreasing in
![]() $\delta < \zeta < \zeta '$
. Therefore, for
$\delta < \zeta < \zeta '$
. Therefore, for
![]() $\zeta \in [\delta , \zeta ']$
, we have
$\zeta \in [\delta , \zeta ']$
, we have
Using (7.43) in (7.40), we obtain that
Using the initial condition
![]() $|S(\zeta ')| \leq C_{\lambda , M}$
implied by (7.42), we deduce that for
$|S(\zeta ')| \leq C_{\lambda , M}$
implied by (7.42), we deduce that for
![]() $\zeta \in [\delta , \zeta ']$
,
$\zeta \in [\delta , \zeta ']$
,
for some
![]() $\bar C_{M, \lambda }$
sufficiently large, independent of z and
$\bar C_{M, \lambda }$
sufficiently large, independent of z and
![]() $\delta $
. Finally, recalling
$\delta $
. Finally, recalling
![]() $W = U+S$
,
$W = U+S$
,
![]() $Z = U-S$
, (7.42)–(7.44) give us a bound on
$Z = U-S$
, (7.42)–(7.44) give us a bound on
![]() $|W|$
and
$|W|$
and
![]() $|Z|$
independent of
$|Z|$
independent of
![]() $\delta , z$
for all
$\delta , z$
for all
![]() $\zeta \in \left ( \delta , \frac {1}{M \lambda } \right )$
.
$\zeta \in \left ( \delta , \frac {1}{M \lambda } \right )$
.
To summarize, there exists a map
![]() $\mathcal {F}_\delta :[-1,1]\rightarrow [-A^\ast ,A^\ast ]$
such that if
$\mathcal {F}_\delta :[-1,1]\rightarrow [-A^\ast ,A^\ast ]$
such that if
![]() $(W,Z)$
is the smooth solution on
$(W,Z)$
is the smooth solution on
![]() $(0,2]$
corresponding to
$(0,2]$
corresponding to
![]() $W(1)=\mathcal {F}_\delta (z)$
, then
$W(1)=\mathcal {F}_\delta (z)$
, then
![]() $W(\delta )+Z(\delta )=z$
and we have a bound on
$W(\delta )+Z(\delta )=z$
and we have a bound on
![]() $|W|$
and
$|W|$
and
![]() $|Z|$
independent of
$|Z|$
independent of
![]() $\delta , z$
for all
$\delta , z$
for all
![]() $\zeta \in \left ( \delta , \frac {1}{M \lambda } \right )$
. Now we wish to show that there exists a continuous solution map
$\zeta \in \left ( \delta , \frac {1}{M \lambda } \right )$
. Now we wish to show that there exists a continuous solution map
![]() $\mathcal {G}$
, mapping any
$\mathcal {G}$
, mapping any
![]() $w_0$
to an analytic solution
$w_0$
to an analytic solution
![]() $(W,Z)$
to equation (7.26) on the region
$(W,Z)$
to equation (7.26) on the region
![]() $\zeta \in (-\frac 12,\frac 12)$
such that
$\zeta \in (-\frac 12,\frac 12)$
such that
![]() $W(0)=w_0$
. With these two maps,
$W(0)=w_0$
. With these two maps,
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
, we will be able use a fixed point argument to construct a smooth solution to (7.26) on
$\mathcal {G}$
, we will be able use a fixed point argument to construct a smooth solution to (7.26) on
![]() $\zeta \in [-2,2]$
.
$\zeta \in [-2,2]$
.
We will now repeat an expansion argument in line with the expansion in the proof of Proposition 2.5. Writing
![]() $ W=\sum _{i \geq 0} w_i \zeta ^i$
,
$ W=\sum _{i \geq 0} w_i \zeta ^i$
, ![]() ,
,
![]() $\mathcal {G}_{ W}=\sum _{i \geq 0} g_i \zeta ^i$
and
$\mathcal {G}_{ W}=\sum _{i \geq 0} g_i \zeta ^i$
and ![]() , then substituting these formal expansions into (7.27), we obtain
, then substituting these formal expansions into (7.27), we obtain

Let us rewrite
![]() $g_{ n}$
as
$g_{ n}$
as
then, using ![]() we have
we have

Since ![]() , then (7.45) can be used to define
, then (7.45) can be used to define
![]() $w_i$
given
$w_i$
given
![]() $w_0$
. Since
$w_0$
. Since
![]() $(\bar W,\bar Z,F_W)$
are analytic, it is easy to see that the formal series converges producing an analytic solution in a small neighborhood of
$(\bar W,\bar Z,F_W)$
are analytic, it is easy to see that the formal series converges producing an analytic solution in a small neighborhood of
![]() $\zeta =0$
.
$\zeta =0$
.
Let us denote the solution map
![]() $w_0\mapsto W$
restricted to
$w_0\mapsto W$
restricted to
![]() $w_0\in [-2C, 2C]$
by
$w_0\in [-2C, 2C]$
by
![]() $\mathcal {G}$
. Then by continuity, there exists some
$\mathcal {G}$
. Then by continuity, there exists some
![]() $\delta '>0$
such that the solutions in the range of
$\delta '>0$
such that the solutions in the range of
![]() $\mathcal {G}$
are all analytic on the region
$\mathcal {G}$
are all analytic on the region
![]() $\zeta \in [-\delta ',\delta ']$
.
$\zeta \in [-\delta ',\delta ']$
.
Now, we consider the map
![]() $w_0 \mapsto \mathcal {G} (w_0)(\delta )$
for some
$w_0 \mapsto \mathcal {G} (w_0)(\delta )$
for some
![]() $0 < \delta < \delta '$
sufficiently small. We can take
$0 < \delta < \delta '$
sufficiently small. We can take
![]() $\delta $
sufficiently small so that:
$\delta $
sufficiently small so that:
-
• In the range of
 $\mathcal {G}$
, we have
$\mathcal {G}$
, we have
 $\left |W+Z\right | = \left |W(\zeta ) - W(-\zeta )\right | \leq 1$
for all
$\left |W+Z\right | = \left |W(\zeta ) - W(-\zeta )\right | \leq 1$
for all
 $\zeta \in (-\delta ,\delta )$
.
$\zeta \in (-\delta ,\delta )$
. -
• The map
 $w_0 \mapsto \mathcal {G} (w_0)(\delta )$
has a range that covers
$w_0 \mapsto \mathcal {G} (w_0)(\delta )$
has a range that covers
 $[-C, C]$
(recall
$[-C, C]$
(recall
 $w_0 \in [-2C, 2C]$
).
$w_0 \in [-2C, 2C]$
). -
• The map
 $w_0 \mapsto \mathcal {G} (w_0)(\delta )$
is injective.
$w_0 \mapsto \mathcal {G} (w_0)(\delta )$
is injective.
The first two items follow from
![]() $W(\zeta ) = w_0 + O(\delta )$
when
$W(\zeta ) = w_0 + O(\delta )$
when
![]() $\zeta \in (-\delta , \delta )$
, so let us argue the third one. Considering
$\zeta \in (-\delta , \delta )$
, so let us argue the third one. Considering
![]() $w_0, w_0' \in [-2C, 2C]$
, we use (7.45) to define
$w_0, w_0' \in [-2C, 2C]$
, we use (7.45) to define
![]() $w_i, w_i'$
via the Taylor recurrence. We have
$w_i, w_i'$
via the Taylor recurrence. We have
Now, from (7.45), and using the formula for
![]() $\bar g_n$
from (2.38), we have
$\bar g_n$
from (2.38), we have

Letting
![]() $d_i = w_{i} - w_i'$
, we see that
$d_i = w_{i} - w_i'$
, we see that
 $$ \begin{align*} n |d_{n+1}| \lesssim n \sum_{i=0}^n |d_i| + \sum_{j=1}^n |d_j| \cdot |w_{n+1-j}|. \end{align*} $$
$$ \begin{align*} n |d_{n+1}| \lesssim n \sum_{i=0}^n |d_i| + \sum_{j=1}^n |d_j| \cdot |w_{n+1-j}|. \end{align*} $$
Choosing
![]() $\delta $
sufficiently small, we can assume
$\delta $
sufficiently small, we can assume
![]() $|w_i| \lesssim 1/(3\delta )^i$
, and in that case, the equation above allows to close an induction argument for the bound
$|w_i| \lesssim 1/(3\delta )^i$
, and in that case, the equation above allows to close an induction argument for the bound
![]() $|d_i| \leq C |d_0| / (2\delta )^i$
, for some constant C independent of
$|d_i| \leq C |d_0| / (2\delta )^i$
, for some constant C independent of
![]() $\delta , w_0, w_0'$
and
$\delta , w_0, w_0'$
and
![]() $\delta $
sufficiently small. Therefore,
$\delta $
sufficiently small. Therefore,
![]() $|w_i - w_i'| \lesssim |w_0-w_0'|/(2\delta )^i$
, and from (7.46), we conclude the injectivity.
$|w_i - w_i'| \lesssim |w_0-w_0'|/(2\delta )^i$
, and from (7.46), we conclude the injectivity.
Now, since
![]() $w_0 \mapsto \mathcal {G} (w_0)(\delta )$
is injective and covers
$w_0 \mapsto \mathcal {G} (w_0)(\delta )$
is injective and covers
![]() $[-C, C]$
, we define
$[-C, C]$
, we define
![]() $\mathcal {H}:[-C,C]\rightarrow [-2C,2C]$
to be its inverse map restricted to
$\mathcal {H}:[-C,C]\rightarrow [-2C,2C]$
to be its inverse map restricted to
![]() $[-C, C]$
. Therefore,
$[-C, C]$
. Therefore,
![]() $\mathcal {H}$
takes the value of a smooth solution W at
$\mathcal {H}$
takes the value of a smooth solution W at
![]() $\zeta = \delta $
and outputs the value that W has at
$\zeta = \delta $
and outputs the value that W has at
![]() $\zeta = 0$
. Now, we consider the following map
$\zeta = 0$
. Now, we consider the following map
![]() $z \mapsto z'$
, where
$z \mapsto z'$
, where
![]() $z'$
is defined as follows. First, we construct
$z'$
is defined as follows. First, we construct
![]() $(W, Z) = \mathcal {F}_\delta (z)$
, which we recall that is the smooth solution on
$(W, Z) = \mathcal {F}_\delta (z)$
, which we recall that is the smooth solution on
![]() $(0, 2]$
with
$(0, 2]$
with
![]() $W(\delta ) + Z(\delta ) = z$
. Then, we apply
$W(\delta ) + Z(\delta ) = z$
. Then, we apply
![]() $\mathcal {H} (W(\delta ))$
to obtain the value of
$\mathcal {H} (W(\delta ))$
to obtain the value of
![]() $w_0$
that generates a smooth solution around
$w_0$
that generates a smooth solution around
![]() $\zeta = 0$
with that corresponding value of
$\zeta = 0$
with that corresponding value of
![]() $W(\delta )$
. Finally, we let
$W(\delta )$
. Finally, we let
![]() $\check W = \mathcal {G} (\mathcal {H} (W(\delta ))$
be the smooth solution generated by that
$\check W = \mathcal {G} (\mathcal {H} (W(\delta ))$
be the smooth solution generated by that
![]() $w_0$
, and define
$w_0$
, and define
![]() $z' = \check W(\delta ) - \check W(-\delta )$
to be its corresponding value of
$z' = \check W(\delta ) - \check W(-\delta )$
to be its corresponding value of
![]() $\check W+\check Z$
at
$\check W+\check Z$
at
![]() $\zeta = \delta $
. Since
$\zeta = \delta $
. Since
![]() $z \mapsto z'$
maps the interval
$z \mapsto z'$
maps the interval
![]() $[-1, 1]$
to
$[-1, 1]$
to
![]() $[-1, 1]$
and it is continuous, Brouwer’s fixed point theorem ensures the existence of a fixed point z. For such z, we have that
$[-1, 1]$
and it is continuous, Brouwer’s fixed point theorem ensures the existence of a fixed point z. For such z, we have that
![]() $W(\delta ) + Z(\delta ) = z = z' = \check W(\delta ) -\check W(-\delta )$
. Note that by construction of the map
$W(\delta ) + Z(\delta ) = z = z' = \check W(\delta ) -\check W(-\delta )$
. Note that by construction of the map
![]() $z \mapsto z'$
, we always have
$z \mapsto z'$
, we always have
![]() $W(\delta ) = \check W(\delta )$
, since the definition of
$W(\delta ) = \check W(\delta )$
, since the definition of
![]() $\check W(\delta ) = \mathcal {G} (\mathcal {H} ( W(\delta ))$
is the solution constructed via a Taylor series at zero that passes through
$\check W(\delta ) = \mathcal {G} (\mathcal {H} ( W(\delta ))$
is the solution constructed via a Taylor series at zero that passes through
![]() $(\delta , W(\delta ))$
. Therefore, we have that
$(\delta , W(\delta ))$
. Therefore, we have that
![]() $(W(\delta ), Z(\delta ) ) = (\check W (\delta ) , -\check W(-\delta ))$
, and by standard uniqueness of ODE solutions, we conclude they are the same solution. Since
$(W(\delta ), Z(\delta ) ) = (\check W (\delta ) , -\check W(-\delta ))$
, and by standard uniqueness of ODE solutions, we conclude they are the same solution. Since
![]() $\check W (\zeta )$
is smooth for
$\check W (\zeta )$
is smooth for
![]() $\zeta \in (-\delta , \delta )$
and
$\zeta \in (-\delta , \delta )$
and
![]() $(W(\zeta ), Z(\zeta ))$
for
$(W(\zeta ), Z(\zeta ))$
for
![]() $\zeta \in (0, 2]$
, we see that
$\zeta \in (0, 2]$
, we see that
![]() $\check W(\zeta )$
is smooth for
$\check W(\zeta )$
is smooth for
![]() $\zeta \in [-2, 2]$
.
$\zeta \in [-2, 2]$
.
Let
![]() $\aleph $
be the space of functions that can be written as
$\aleph $
be the space of functions that can be written as
![]() $F=\chi (\mathcal {F}_U,\mathcal {F}_S)$
, for
$F=\chi (\mathcal {F}_U,\mathcal {F}_S)$
, for
![]() $(\mathcal {F}_U,\mathcal {F}_S)$
analytic and
$(\mathcal {F}_U,\mathcal {F}_S)$
analytic and
![]() $\chi $
a smooth cut-off function,
$\chi $
a smooth cut-off function,
![]() $1$
on
$1$
on
![]() $[0,\frac 32]$
and compactly supported on
$[0,\frac 32]$
and compactly supported on
![]() $[0,2)$
.Footnote
4
Then for every
$[0,2)$
.Footnote
4
Then for every
![]() $F\in \aleph $
, we have shown there exists
$F\in \aleph $
, we have shown there exists
![]() $(U,S)\in \mathcal {D}(\mathcal {L})$
satisfying (7.25). Now given a
$(U,S)\in \mathcal {D}(\mathcal {L})$
satisfying (7.25). Now given a
![]() $F\in X$
and a sequence
$F\in X$
and a sequence
![]() $F_{j}\in \aleph $
converging to F in X, it remains to show that the corresponding sequence
$F_{j}\in \aleph $
converging to F in X, it remains to show that the corresponding sequence
![]() $(U_j,S_j)\in \mathcal {D}(\mathcal {L})$
solving (7.25) converges in
$(U_j,S_j)\in \mathcal {D}(\mathcal {L})$
solving (7.25) converges in
![]() $\mathcal {D}(\mathcal {L})$
.
$\mathcal {D}(\mathcal {L})$
.
Observe that
 $$ \begin{align*} \langle F_i -F_j,~(U_i-U_j,~S_i-S_j) \rangle_{H^{2m}}&= \langle -\mathcal{L}(U_i-U_j,~S_i-S_j) ,~(U_i-U_j,~S_i-S_j) \rangle_{H^{2m}}\\&\qquad+\lambda \left\|(U_i-U_j,~S_i-S_j)\right\|_{H^{2m}}^2 \\ &\gtrsim \left\|P_N\mathcal{L}(U_i-U_j,~S_i-S_j) \right\|_{H^{2m}}^2+ \left\|(I-P_N)\mathcal{L}(U_i-U_j,~S_i-S_j) \right\|_{H^{2m}}^2\\&\qquad +\lambda \left\|(U_i-U_j,~S_i-S_j)\right\|_{H^{2m}}^2\\ &\gtrsim \lambda \left\|(U_i-U_j,~S_i-S_j)\right\|_{H^{2m}}^2, \end{align*} $$
$$ \begin{align*} \langle F_i -F_j,~(U_i-U_j,~S_i-S_j) \rangle_{H^{2m}}&= \langle -\mathcal{L}(U_i-U_j,~S_i-S_j) ,~(U_i-U_j,~S_i-S_j) \rangle_{H^{2m}}\\&\qquad+\lambda \left\|(U_i-U_j,~S_i-S_j)\right\|_{H^{2m}}^2 \\ &\gtrsim \left\|P_N\mathcal{L}(U_i-U_j,~S_i-S_j) \right\|_{H^{2m}}^2+ \left\|(I-P_N)\mathcal{L}(U_i-U_j,~S_i-S_j) \right\|_{H^{2m}}^2\\&\qquad +\lambda \left\|(U_i-U_j,~S_i-S_j)\right\|_{H^{2m}}^2\\ &\gtrsim \lambda \left\|(U_i-U_j,~S_i-S_j)\right\|_{H^{2m}}^2, \end{align*} $$
where we used Lemma 7.4, that
![]() $\mathcal {L}$
is bounded on the finite dimensional orthogonal complement of
$\mathcal {L}$
is bounded on the finite dimensional orthogonal complement of
![]() $Y_N$
and that we are free to take
$Y_N$
and that we are free to take
![]() $\lambda $
arbitrarily large. By Cauchy–Schwarz, we conclude
$\lambda $
arbitrarily large. By Cauchy–Schwarz, we conclude
Thus, since
![]() $F_j$
forms a Cauchy sequence, so is
$F_j$
forms a Cauchy sequence, so is
![]() $(U_j,S_j)$
, which concludes the proof.
$(U_j,S_j)$
, which concludes the proof.
Corollary 7.7. For all
![]() $\delta _g> 0$
sufficiently small, we can write our linearized operator
$\delta _g> 0$
sufficiently small, we can write our linearized operator
![]() $\mathcal {L}$
as
$\mathcal {L}$
as
for some
![]() $A_0$
maximally dissipative on X, and K is some compact operator on X.
$A_0$
maximally dissipative on X, and K is some compact operator on X.
Proof. First of all, recall that
![]() $P_N : X \rightarrow Y_N$
is the projection onto the finite dimensional subspace
$P_N : X \rightarrow Y_N$
is the projection onto the finite dimensional subspace
![]() $Y_N$
. From Lemma 7.4 we have that
$Y_N$
. From Lemma 7.4 we have that
for every
![]() $(U, S) \in Y_N$
, so in particular,
$(U, S) \in Y_N$
, so in particular,
![]() $P_N \mathcal {L} + \delta _g$
is dissipative on
$P_N \mathcal {L} + \delta _g$
is dissipative on
![]() $Y_N$
.
$Y_N$
.
Lemma 7.6 implies that
![]() $P_N \mathcal {L} + \delta _g - \lambda :X \rightarrow X$
is surjective for sufficiently large
$P_N \mathcal {L} + \delta _g - \lambda :X \rightarrow X$
is surjective for sufficiently large
![]() $\lambda $
. Since
$\lambda $
. Since
![]() $ Y_N$
has finite codimension
$ Y_N$
has finite codimension
![]() $\text {cod}_X(Y_N)$
, the surjectivity of
$\text {cod}_X(Y_N)$
, the surjectivity of
![]() $\mathcal {L}+\delta _g - \lambda $
on X implies that there exists some finite codimension space
$\mathcal {L}+\delta _g - \lambda $
on X implies that there exists some finite codimension space
![]() $\widetilde {Y}_N \subset Y_N$
(of finite codimension
$\widetilde {Y}_N \subset Y_N$
(of finite codimension
![]() $\text {cod}_X(\widetilde {Y}_N) \leq 2 \text {cod}_X(Y_N)$
) such that
$\text {cod}_X(\widetilde {Y}_N) \leq 2 \text {cod}_X(Y_N)$
) such that
![]() $\widetilde {P}_N \mathcal {L}+\delta _g - \lambda : \widetilde {Y}_N \rightarrow \widetilde {Y}_N$
is surjective on
$\widetilde {P}_N \mathcal {L}+\delta _g - \lambda : \widetilde {Y}_N \rightarrow \widetilde {Y}_N$
is surjective on
![]() $\widetilde {Y}_N$
. Here,
$\widetilde {Y}_N$
. Here,
![]() $\widetilde {P}_N$
denotes the orthogonal projection to
$\widetilde {P}_N$
denotes the orthogonal projection to
![]() $\widetilde {Y}_N$
.
$\widetilde {Y}_N$
.
Thus, we get that
![]() $\widetilde {P}_N \mathcal {L} + \delta _g$
is a maximally dissipative operator on the finite codimension space
$\widetilde {P}_N \mathcal {L} + \delta _g$
is a maximally dissipative operator on the finite codimension space
![]() $\widetilde {Y}_N$
. Let
$\widetilde {Y}_N$
. Let
![]() $A_0$
be a maximally dissipative operator on X that agrees with
$A_0$
be a maximally dissipative operator on X that agrees with
![]() $\mathcal {L}+\delta _g$
on
$\mathcal {L}+\delta _g$
on
![]() $\widetilde {Y}_N$
. For instance, one may define
$\widetilde {Y}_N$
. For instance, one may define
![]() $A_0$
to be
$A_0$
to be
![]() $-\text {Id}$
on
$-\text {Id}$
on
![]() $\widetilde {Y}_N^\perp $
, and this clearly makes
$\widetilde {Y}_N^\perp $
, and this clearly makes
![]() $A_0: X \rightarrow X$
maximally dissipative. In particular, we have the equality
$A_0: X \rightarrow X$
maximally dissipative. In particular, we have the equality
![]() $\widetilde {P}_N \mathcal {L} = A_0 - \delta _g$
over the finite codimension space
$\widetilde {P}_N \mathcal {L} = A_0 - \delta _g$
over the finite codimension space
![]() $\widetilde {Y}_N$
. Letting
$\widetilde {Y}_N$
. Letting
![]() $K_1 = (1-\widetilde {P}_N)\mathcal {L}$
, which is compact because it has finite dimensional rank, we get
$K_1 = (1-\widetilde {P}_N)\mathcal {L}$
, which is compact because it has finite dimensional rank, we get
![]() $\mathcal {L} = A_0 - \delta _g + K_1$
over
$\mathcal {L} = A_0 - \delta _g + K_1$
over
![]() $\widetilde {Y}_N$
.
$\widetilde {Y}_N$
.
Then, let
![]() $K_2$
be an operator which is zero over
$K_2$
be an operator which is zero over
![]() $\widetilde {Y}_N$
, and it is defined as
$\widetilde {Y}_N$
, and it is defined as
![]() $\mathcal {L} - A_0 + \delta _g - K_1$
on
$\mathcal {L} - A_0 + \delta _g - K_1$
on
![]() $\widetilde {Y}_N^\perp $
. Again,
$\widetilde {Y}_N^\perp $
. Again,
![]() $K_2$
is compact, as it has finite dimensional rank. Moreover, we get that the equality
$K_2$
is compact, as it has finite dimensional rank. Moreover, we get that the equality
holds both over
![]() $\widetilde {Y}_N$
and over
$\widetilde {Y}_N$
and over
![]() $\widetilde {Y}_N^\perp $
. Therefore, it holds over all X, and letting
$\widetilde {Y}_N^\perp $
. Therefore, it holds over all X, and letting
![]() $K = K_1 + K_2$
, we conclude that
$K = K_1 + K_2$
, we conclude that
![]() $\mathcal {L} = A_0 - \delta _g + K$
for some
$\mathcal {L} = A_0 - \delta _g + K$
for some
![]() $A_0$
maximally dissipative,
$A_0$
maximally dissipative,
![]() $\delta _g> 0$
and K compact.
$\delta _g> 0$
and K compact.
7.2 Abstract results on maximally dissipative operators
We first recall some basic properties of maximally dissipative operators (see [Reference Lumer and Phillips64, Reference Schmüdgen79]).
Lemma 7.8 (Properties of maximally dissipative operators).
Let
![]() $A_0$
be a maximally dissipative operator on a Hilbert space H. Then, we have that
$A_0$
be a maximally dissipative operator on a Hilbert space H. Then, we have that
-
•
 $A_0$
is closed.
$A_0$
is closed. -
•
 $\sigma (A_0) \subset \{ \lambda \in \mathbb {C} : \Re (\lambda ) \leq 0 \}$
.
$\sigma (A_0) \subset \{ \lambda \in \mathbb {C} : \Re (\lambda ) \leq 0 \}$
. -
• For every
 $\lambda \in \mathbb {C}$
with
$\lambda \in \mathbb {C}$
with
 $\Re \lambda> 0$
, we have that
$\Re \lambda> 0$
, we have that
 $(-A_0 + \lambda ) : D(A_0) \rightarrow H$
is a bijection and moreover
$(-A_0 + \lambda ) : D(A_0) \rightarrow H$
is a bijection and moreover
 $\| (-A_0 + \lambda )^{-1} \|_{L(H \rightarrow D(A_0))} \leq \Re (\lambda )^{-1}$
.
$\| (-A_0 + \lambda )^{-1} \|_{L(H \rightarrow D(A_0))} \leq \Re (\lambda )^{-1}$
. -
•
 $A_0^\ast $
is also maximally dissipative.
$A_0^\ast $
is also maximally dissipative. -
• (Lumer-Phillips theorem):
 $A_0$
generates a strongly continuous semigroup on H.
$A_0$
generates a strongly continuous semigroup on H.
Definition 7.9. We define the growth bound of a semigroup T on H as
We also define
where the essential seminorm is defined as
Lemma 7.10 (Growth bound [Reference Engel and Nagel32]).
Let us suppose that A generates the continuous semigroup T. Let
![]() $\sigma (A)$
be the spectrum of A and let us consider
$\sigma (A)$
be the spectrum of A and let us consider
![]() $s(A) = \sup _{\lambda \in \sigma (A)} \Re (\lambda )$
. Then
$s(A) = \sup _{\lambda \in \sigma (A)} \Re (\lambda )$
. Then
Moreover, for any,
![]() $w> w_{\mathrm {ess}}(T)$
have that
$w> w_{\mathrm {ess}}(T)$
have that
![]() $\sigma (A) \cap \{ \lambda \in \mathbb {C} : \Re (\lambda )> w \}$
is a finite set of eigenvalues with finite algebraic multiplicity.
$\sigma (A) \cap \{ \lambda \in \mathbb {C} : \Re (\lambda )> w \}$
is a finite set of eigenvalues with finite algebraic multiplicity.
Lemma 7.11. Let
![]() $A_0$
be a maximally dissipative operator and consider
$A_0$
be a maximally dissipative operator and consider
![]() $A = A_0 - \delta _g + K$
where
$A = A_0 - \delta _g + K$
where
![]() $\delta _g> 0$
and K compact. Then we have
$\delta _g> 0$
and K compact. Then we have
-
1. The set
 $\Lambda = \sigma (A) \cap \{ \lambda \in \mathbb {C} : \Re (\lambda )> -\delta _g/2\}$
is finite and formed only by eigenvalues of A. Moreover, each
$\Lambda = \sigma (A) \cap \{ \lambda \in \mathbb {C} : \Re (\lambda )> -\delta _g/2\}$
is finite and formed only by eigenvalues of A. Moreover, each
 $\lambda \in \Lambda $
has finite algebraic multiplicity. That is, if we let
$\lambda \in \Lambda $
has finite algebraic multiplicity. That is, if we let
 $\mu _{\lambda }$
to be the first natural such that
$\mu _{\lambda }$
to be the first natural such that
 $\mathrm {ker} (A-\lambda \text {Id} )^{\mu _{\lambda }} = \mathrm {ker} (A- \lambda \text {Id} )^{\mu _\lambda + 1}$
, we have that the vector space (7.47)is finite dimensional.
$\mathrm {ker} (A-\lambda \text {Id} )^{\mu _{\lambda }} = \mathrm {ker} (A- \lambda \text {Id} )^{\mu _\lambda + 1}$
, we have that the vector space (7.47)is finite dimensional. $$ \begin{align} V = \bigoplus_{\lambda \in \Lambda} \mathrm{ker} (A - \lambda \text{Id})^{\mu_{\lambda}}\, \end{align} $$
$$ \begin{align} V = \bigoplus_{\lambda \in \Lambda} \mathrm{ker} (A - \lambda \text{Id})^{\mu_{\lambda}}\, \end{align} $$
-
2. Consider
 $A^\ast = A_0^\ast - \delta _g + K^\ast $
and let
$A^\ast = A_0^\ast - \delta _g + K^\ast $
and let
 $\Lambda ^\ast = \sigma (A^\ast ) \cap \{ \lambda \in \mathbb {C} : \Re (\lambda )>- \delta _g/2\}$
. As before, we define (7.48)We have that both V and
$\Lambda ^\ast = \sigma (A^\ast ) \cap \{ \lambda \in \mathbb {C} : \Re (\lambda )>- \delta _g/2\}$
. As before, we define (7.48)We have that both V and $$ \begin{align} V^\ast = \bigoplus_{\lambda \in \Lambda^\ast} \mathrm{ker} (A^\ast - \lambda \text{Id})^{\mu_{\lambda}^\ast}. \end{align} $$
$$ \begin{align} V^\ast = \bigoplus_{\lambda \in \Lambda^\ast} \mathrm{ker} (A^\ast - \lambda \text{Id})^{\mu_{\lambda}^\ast}. \end{align} $$
 $V^{\ast \, \perp }$
are invariant under A. We also have that
$V^{\ast \, \perp }$
are invariant under A. We also have that
 $\Lambda ^\ast = \overline {\Lambda }$
and
$\Lambda ^\ast = \overline {\Lambda }$
and
 $\mu _\lambda = \mu _{\overline {\lambda }}^\ast $
. Moreover, we have the decomposition
$\mu _\lambda = \mu _{\overline {\lambda }}^\ast $
. Moreover, we have the decomposition
 $H = V \oplus V^{\ast \, \perp }$
.
$H = V \oplus V^{\ast \, \perp }$
.
-
3. The linear transformation
 $A|_V: V\rightarrow V$
obtained by restricting A to the finite dimensional space V has all its eigenvalues with real part larger than
$A|_V: V\rightarrow V$
obtained by restricting A to the finite dimensional space V has all its eigenvalues with real part larger than
 $-\delta _g / 2$
. In particular, there is some basis such that we can express where
$-\delta _g / 2$
. In particular, there is some basis such that we can express where $$ \begin{align*} A|_V = \begin{bmatrix} J_1 & & & \\ & J_2 & & \\ & & \ddots & \\ & & & J_\ell \end{bmatrix}, \qquad \mbox{ where } \qquad J_i = \begin{bmatrix} \lambda_i & \delta_g/10 & & \\ & \lambda_i & \ddots & \\ & & \ddots & \delta_g/10\\ & & & \lambda_i \end{bmatrix}, \end{align*} $$
$$ \begin{align*} A|_V = \begin{bmatrix} J_1 & & & \\ & J_2 & & \\ & & \ddots & \\ & & & J_\ell \end{bmatrix}, \qquad \mbox{ where } \qquad J_i = \begin{bmatrix} \lambda_i & \delta_g/10 & & \\ & \lambda_i & \ddots & \\ & & \ddots & \delta_g/10\\ & & & \lambda_i \end{bmatrix}, \end{align*} $$
 $\lambda _i$
are the eigenvalues of
$\lambda _i$
are the eigenvalues of
 $A|_V$
. In that basis, we have that (7.49)Moreover, letting
$A|_V$
. In that basis, we have that (7.49)Moreover, letting $$ \begin{align} w^T \cdot A|_V \cdot w \geq \frac{-6\delta_g}{10} \| w \|^2, \qquad \forall w \in \mathbb{R}^N. \end{align} $$
$$ \begin{align} w^T \cdot A|_V \cdot w \geq \frac{-6\delta_g}{10} \| w \|^2, \qquad \forall w \in \mathbb{R}^N. \end{align} $$
 $T(t)$
be the semigroup generated by A, for any
$T(t)$
be the semigroup generated by A, for any
 $v \in V^{\ast \, \perp }$
, we have (7.50)
$v \in V^{\ast \, \perp }$
, we have (7.50) $$ \begin{align} \| T(t) v \|_H \lesssim e^{-\delta_g t/2} \| v \|_H. \end{align} $$
$$ \begin{align} \| T(t) v \|_H \lesssim e^{-\delta_g t/2} \| v \|_H. \end{align} $$
Lemma 7.11 is very similar to Lemma 3.3 in [Reference Merle, Raphaël, Rodnianski and Szeftel67]. We, however, provide a proof for completeness.
Proof.
Item 1. Lemma 7.8 tells us that
![]() $A_0$
generates a contraction semigroup
$A_0$
generates a contraction semigroup
![]() $T_0(t)$
. Therefore, we have that
$T_0(t)$
. Therefore, we have that
![]() $A_0-\delta _g$
generates a contraction semigroup
$A_0-\delta _g$
generates a contraction semigroup
![]() $T_1(t) = e^{-\delta _g t}T_0(t)$
, such that
$T_1(t) = e^{-\delta _g t}T_0(t)$
, such that
![]() $w_0(T_1), w_{\mathrm {ess}}(T_1) \leq -\delta _g$
.
$w_0(T_1), w_{\mathrm {ess}}(T_1) \leq -\delta _g$
.
Thus, as K is compact,
![]() $A_0 -\delta _g-K$
generates a continuous semigroup
$A_0 -\delta _g-K$
generates a continuous semigroup
![]() $T(t)$
as well, and as
$T(t)$
as well, and as
![]() $w_{\mathrm {ess}}$
is invariant under compact perturbations, we have that
$w_{\mathrm {ess}}$
is invariant under compact perturbations, we have that
![]() $w_{\mathrm {ess}}(T) \leq -\delta _g$
. In particular, applying Lemma 7.10 for
$w_{\mathrm {ess}}(T) \leq -\delta _g$
. In particular, applying Lemma 7.10 for
![]() $w = \frac {-1}{2} \delta _g$
, we see that
$w = \frac {-1}{2} \delta _g$
, we see that
![]() $\Lambda $
consists of finitely many eigenvalues with finite algebraic multiplicity.
$\Lambda $
consists of finitely many eigenvalues with finite algebraic multiplicity.
The fact that the spaces
![]() $\mathrm {ker}(A-\lambda _i \text {Id})^{\mu _{\lambda }}$
are linearly independent for a finite set of different
$\mathrm {ker}(A-\lambda _i \text {Id})^{\mu _{\lambda }}$
are linearly independent for a finite set of different
![]() $\lambda _i$
is well-known in linear algebra.
$\lambda _i$
is well-known in linear algebra.
Item 2. It is clear that
![]() $\mathrm {ker}(A-\lambda \text {Id})^{\mu _\lambda }$
is invariant under A: if
$\mathrm {ker}(A-\lambda \text {Id})^{\mu _\lambda }$
is invariant under A: if
![]() $v \in \mathrm {ker}(A-\lambda \text {Id})^{\mu _\lambda }$
, we just have
$v \in \mathrm {ker}(A-\lambda \text {Id})^{\mu _\lambda }$
, we just have
As a consequence, V remains invariant under A.
Applying the argument from Item 1 to
![]() $A^\ast $
, we find that
$A^\ast $
, we find that
![]() $\Lambda ^\ast $
is finite, and consequently,
$\Lambda ^\ast $
is finite, and consequently,
![]() $V^\ast $
is finite dimensional. In addition, as above, we find that
$V^\ast $
is finite dimensional. In addition, as above, we find that
![]() $V^\ast $
is invariant under
$V^\ast $
is invariant under
![]() $A^\ast $
. Therefore, for any
$A^\ast $
. Therefore, for any
![]() $v \in V^{\ast \, \perp }, w \in V^\ast $
$v \in V^{\ast \, \perp }, w \in V^\ast $
since
![]() $A^\ast w \in V^\ast $
. Thus,
$A^\ast w \in V^\ast $
. Thus,
![]() $Av \in V^{ \ast \, \perp }$
, and we have shown that
$Av \in V^{ \ast \, \perp }$
, and we have shown that
![]() $V^{\ast \, \perp }$
is invariant under A.
$V^{\ast \, \perp }$
is invariant under A.
Now suppose
![]() $\lambda \in \Lambda ^\ast \setminus \Lambda $
. As
$\lambda \in \Lambda ^\ast \setminus \Lambda $
. As
![]() $\Re (\lambda )> -\delta _g/2$
and
$\Re (\lambda )> -\delta _g/2$
and
![]() $\lambda \notin \Lambda $
; hence, the resolvent
$\lambda \notin \Lambda $
; hence, the resolvent
![]() $(A-\lambda \text {Id} )^{-1}$
is a bounded operator. Therefore,
$(A-\lambda \text {Id} )^{-1}$
is a bounded operator. Therefore,
![]() $(A^\ast - \overline {\lambda } \text {Id} ) u = v$
is equivalent to
$(A^\ast - \overline {\lambda } \text {Id} ) u = v$
is equivalent to
By the Riesz representation theorem, we have a unique such
![]() $u\in H$
, and moreover, the map
$u\in H$
, and moreover, the map
![]() $v\mapsto u$
is bounded. This shows that
$v\mapsto u$
is bounded. This shows that
![]() $\overline {\Lambda ^\ast } \subset \Lambda $
; however, since
$\overline {\Lambda ^\ast } \subset \Lambda $
; however, since
![]() $A^{\ast \, \ast } = A$
, an analogous argument for
$A^{\ast \, \ast } = A$
, an analogous argument for
![]() $A^\ast $
shows that
$A^\ast $
shows that
![]() $\Lambda \subset \overline {\Lambda ^\ast } $
, and hence,
$\Lambda \subset \overline {\Lambda ^\ast } $
, and hence,
![]() $\overline {\Lambda ^\ast } =\Lambda $
.
$\overline {\Lambda ^\ast } =\Lambda $
.
Before showing that the multiplicities are equal, let us show that
![]() $H = V \oplus V^{\ast \, \perp }$
. Let us note that V is the image of H under the projector
$H = V \oplus V^{\ast \, \perp }$
. Let us note that V is the image of H under the projector
for some curve
![]() $\Gamma $
enclosing
$\Gamma $
enclosing
![]() $\Lambda $
. However, as
$\Lambda $
. However, as
![]() $\overline {\Lambda } = \Lambda ^\ast $
, we get that
$\overline {\Lambda } = \Lambda ^\ast $
, we get that
![]() $P(A^\ast ) = P(A)^\ast $
. Therefore, using
$P(A^\ast ) = P(A)^\ast $
. Therefore, using
![]() $\text {Im}(P(A^\ast ))^\perp = \mathrm {ker}(P(A))$
and the decomposition
$\text {Im}(P(A^\ast ))^\perp = \mathrm {ker}(P(A))$
and the decomposition
![]() $H = \mathrm {ker}(P(A)) \oplus \text {Im}(P(A))$
(since
$H = \mathrm {ker}(P(A)) \oplus \text {Im}(P(A))$
(since
![]() $P(A)$
is a projector) yields the desired decomposition
$P(A)$
is a projector) yields the desired decomposition
![]() $H = V^{\ast \, \perp } \oplus V$
.
$H = V^{\ast \, \perp } \oplus V$
.
Lastly, let us show that
![]() $\mu _\lambda = \mu _{\overline {\lambda }}^\ast $
. Without loss of generality, assume
$\mu _\lambda = \mu _{\overline {\lambda }}^\ast $
. Without loss of generality, assume
![]() $\mu _{\lambda }> \mu _{\overline {\lambda }}^\ast $
. Then we have that
$\mu _{\lambda }> \mu _{\overline {\lambda }}^\ast $
. Then we have that
However, as
![]() $\mu _{\lambda }> \mu _{\overline {\lambda }}^\ast $
, there exists some
$\mu _{\lambda }> \mu _{\overline {\lambda }}^\ast $
, there exists some
![]() $v \in V$
such that the term
$v \in V$
such that the term
![]() $v' = \left ( A - \lambda \text {Id} \right )^{\mu _{\overline {\lambda }}^\ast }v \neq 0$
. It is clear that
$v' = \left ( A - \lambda \text {Id} \right )^{\mu _{\overline {\lambda }}^\ast }v \neq 0$
. It is clear that
![]() $v' \in V$
, since V is an invariant subspace of A. Therefore, we have that
$v' \in V$
, since V is an invariant subspace of A. Therefore, we have that
![]() $v' \in V$
,
$v' \in V$
,
![]() $v' \in V^{\ast \, \perp }$
and
$v' \in V^{\ast \, \perp }$
and
![]() $v \neq 0$
. However, this is impossible due to the decomposition
$v \neq 0$
. However, this is impossible due to the decomposition
![]() $H = V\oplus V^{\ast \, \perp }$
.
$H = V\oplus V^{\ast \, \perp }$
.
Item 3. If
![]() $\lambda $
is an eigenvalue of
$\lambda $
is an eigenvalue of
![]() $A|_V$
, we have that there exists
$A|_V$
, we have that there exists
![]() $v \in V$
with
$v \in V$
with
![]() $A v = \lambda v$
. As
$A v = \lambda v$
. As
![]() $v \in V$
, we have that
$v \in V$
, we have that
![]() $\lambda \in \Lambda $
, and therefore,
$\lambda \in \Lambda $
, and therefore,
![]() $\Re (\lambda )> -\delta _g/2$
.
$\Re (\lambda )> -\delta _g/2$
.
Now, we express
![]() $A|_V$
in its Jordan normal form and obtain some blocks
$A|_V$
in its Jordan normal form and obtain some blocks
![]() $\widetilde {J}_i$
with
$\widetilde {J}_i$
with
![]() $\lambda _i$
on the diagonal and
$\lambda _i$
on the diagonal and
![]() $1$
on the superdiagonal of each block. Consider
$1$
on the superdiagonal of each block. Consider
![]() $D_i$
to be the diagonal matrix with elements
$D_i$
to be the diagonal matrix with elements
![]() $1, \delta _g/10, (\delta _g/10)^2, \ldots $
on its diagonal. Then, we have that
$1, \delta _g/10, (\delta _g/10)^2, \ldots $
on its diagonal. Then, we have that
![]() $D_i^{-1} \widetilde {J}_i D_i = J_i$
, so we can obtain the desired form by applying the change of basis dictated by
$D_i^{-1} \widetilde {J}_i D_i = J_i$
, so we can obtain the desired form by applying the change of basis dictated by
![]() $D_i$
to the Jordan normal form.
$D_i$
to the Jordan normal form.
In order to show (7.49), we show that
![]() $A|_V + \frac {6\delta _g}{10} I$
is semipositive definite. It suffices to show that each of its blocks
$A|_V + \frac {6\delta _g}{10} I$
is semipositive definite. It suffices to show that each of its blocks
![]() $J_i + \frac {6 \delta _g}{10} I$
is semipositive definite. Suppose that the block is of size k. Then, as
$J_i + \frac {6 \delta _g}{10} I$
is semipositive definite. Suppose that the block is of size k. Then, as
![]() $\Re \lambda \geq - \frac {\delta _g}{2}$
, we have
$\Re \lambda \geq - \frac {\delta _g}{2}$
, we have
 $$ \begin{align*} w^T \cdot (J_i + \frac{6 \delta_g}{10} I) \cdot w \geq \sum_{j=1}^k \frac{\delta_g}{10} w_i^2 - \frac{\delta_g}{10} \sum_{j=1}^{k-1} |w_j | |w_{j+1}| \geq \frac{\delta_g}{20} \sum_{j=1}^{k-1} (w_j^2 + w_{j+1}^2 - 2|w_j | |w_{j+1}|) \geq 0. \end{align*} $$
$$ \begin{align*} w^T \cdot (J_i + \frac{6 \delta_g}{10} I) \cdot w \geq \sum_{j=1}^k \frac{\delta_g}{10} w_i^2 - \frac{\delta_g}{10} \sum_{j=1}^{k-1} |w_j | |w_{j+1}| \geq \frac{\delta_g}{20} \sum_{j=1}^{k-1} (w_j^2 + w_{j+1}^2 - 2|w_j | |w_{j+1}|) \geq 0. \end{align*} $$
As
![]() $V^{\ast \, \perp }$
is invariant under A, we can consider
$V^{\ast \, \perp }$
is invariant under A, we can consider
![]() $T_{\mathrm {sta}}(t) = T|_{V^{\ast \, \perp }}(t)$
, the restriction to the semigroup to that space, which is clearly generated by
$T_{\mathrm {sta}}(t) = T|_{V^{\ast \, \perp }}(t)$
, the restriction to the semigroup to that space, which is clearly generated by
![]() $A_s = A|_{V^{\ast \, \perp }}$
.
$A_s = A|_{V^{\ast \, \perp }}$
.
On the one hand, we have that
since those contraction semigroups differ by a compact operator.
On the other hand, if
![]() $\sigma (A_s)$
had any element
$\sigma (A_s)$
had any element
![]() $\lambda $
with
$\lambda $
with
![]() $\Re (\lambda )> -\delta _g/2$
, we can apply the same reasoning as in 1 to say that
$\Re (\lambda )> -\delta _g/2$
, we can apply the same reasoning as in 1 to say that
![]() $\lambda $
has to be an eigenvalue. Thus, we would have an eigenvector
$\lambda $
has to be an eigenvalue. Thus, we would have an eigenvector
![]() $v \in V^{\ast \, \perp }$
with
$v \in V^{\ast \, \perp }$
with
![]() $Av = \lambda v$
and
$Av = \lambda v$
and
![]() $\Re (\lambda )> -\delta _g/2$
. This is a contradiction since
$\Re (\lambda )> -\delta _g/2$
. This is a contradiction since
![]() $\mathrm {ker}(A - \lambda \text {Id}) \subset V$
for those
$\mathrm {ker}(A - \lambda \text {Id}) \subset V$
for those
![]() $\lambda $
. Thus, we get that
$\lambda $
. Thus, we get that
Combining (7.51) and (7.52) via Lemma 7.10, we get that
![]() $w_0(T_{\mathrm {sta}}) \leq -\delta _g/2$
, and we conclude the proof.
$w_0(T_{\mathrm {sta}}) \leq -\delta _g/2$
, and we conclude the proof.
7.3 Smoothness of eigenfunctions
Let us remark that due to Corollary 7.7, we have that our operator
![]() $\mathcal {L}$
can be written as
$\mathcal {L}$
can be written as
![]() $A_0 - \delta _g + K$
for some K compact,
$A_0 - \delta _g + K$
for some K compact,
![]() $\delta _g> 0$
and
$\delta _g> 0$
and
![]() $A_0$
maximally dissipative. Therefore, we are under the hypothesis of Lemma 7.11 on the space X. From now on, let us denote
$A_0$
maximally dissipative. Therefore, we are under the hypothesis of Lemma 7.11 on the space X. From now on, let us denote
Lemma 7.12. Let
![]() $(\widetilde {U}_t, \widetilde {S}_t)$
be radially symmetric. Let
$(\widetilde {U}_t, \widetilde {S}_t)$
be radially symmetric. Let
![]() $\chi _0$
be a cut-off function supported on
$\chi _0$
be a cut-off function supported on
![]() $[0, \frac 65]$
which takes value
$[0, \frac 65]$
which takes value
![]() $1$
in
$1$
in
![]() $[0, 1]$
. Then, there exists an absolute constant C independent of
$[0, 1]$
. Then, there exists an absolute constant C independent of
![]() $m, J, N$
such that
$m, J, N$
such that
Proof. Let us denote
Let us note that on the support of
![]() $\chi _0$
, we have that
$\chi _0$
, we have that
![]() $\chi _1 = \chi _2 = 1$
. Therefore, in this region, we have the equalities
$\chi _1 = \chi _2 = 1$
. Therefore, in this region, we have the equalities

Taking C big enough such that ![]() , we have
, we have

Therefore, we get

Corollary 7.13. If
![]() $\lambda $
is an eigenvalue of our operator
$\lambda $
is an eigenvalue of our operator
![]() $\mathcal {L}$
, we necessarily have that
$\mathcal {L}$
, we necessarily have that
![]() $\Re (\lambda ) \leq C$
.
$\Re (\lambda ) \leq C$
.
Proof. Let
![]() $\nu = (\nu _U, \nu _S)$
be an eigenfunction of
$\nu = (\nu _U, \nu _S)$
be an eigenfunction of
![]() $\mathcal {L}$
. As these may be complex, let us write
$\mathcal {L}$
. As these may be complex, let us write
![]() $\nu _U = \nu _U^r + i\nu _U^i$
and
$\nu _U = \nu _U^r + i\nu _U^i$
and
![]() $\nu _S = \nu _S^r + i\nu _S^i$
for their decompositions into real and imaginary parts. Let us also denote
$\nu _S = \nu _S^r + i\nu _S^i$
for their decompositions into real and imaginary parts. Let us also denote
![]() $\nu ^r = (\nu _U^r, \nu _S^r)$
and
$\nu ^r = (\nu _U^r, \nu _S^r)$
and
![]() $\nu ^i = (\nu _U^i, \nu _S^i)$
. As the operator
$\nu ^i = (\nu _U^i, \nu _S^i)$
. As the operator
![]() $\mathcal {L}$
sends real functions into real functions, we have that
$\mathcal {L}$
sends real functions into real functions, we have that
 $$ \begin{align*} \int \chi_0 \Re \left( \nu_U \cdot \overline{\mathcal{L}_U \nu} + \nu_S \overline{\mathcal{L}_S \nu_S} \right) &= \int \chi_0\left( \nu_U^r \cdot \mathcal{L}_U \nu_U^r + \nu_S^r \mathcal{L}_S \nu_S^r \right) + \int \chi_0\left( \nu_U^i \cdot \mathcal{L}_U \nu_U^i + \nu_S^i \mathcal{L}_S \nu_S^i \right) \\ &\leq C \int \chi_0 \left(| \nu_U^r |^2 + (\nu_S^r)^2 +| \nu_U^i |^2 + (\nu_S^i)^2 \right), \end{align*} $$
$$ \begin{align*} \int \chi_0 \Re \left( \nu_U \cdot \overline{\mathcal{L}_U \nu} + \nu_S \overline{\mathcal{L}_S \nu_S} \right) &= \int \chi_0\left( \nu_U^r \cdot \mathcal{L}_U \nu_U^r + \nu_S^r \mathcal{L}_S \nu_S^r \right) + \int \chi_0\left( \nu_U^i \cdot \mathcal{L}_U \nu_U^i + \nu_S^i \mathcal{L}_S \nu_S^i \right) \\ &\leq C \int \chi_0 \left(| \nu_U^r |^2 + (\nu_S^r)^2 +| \nu_U^i |^2 + (\nu_S^i)^2 \right), \end{align*} $$
where in the last inequality, we used Lemma 7.12 for the pairs
![]() $(\nu _U^r, \nu _S^r)$
and
$(\nu _U^r, \nu _S^r)$
and
![]() $(\nu _U^i, \nu _S^i)$
. Using that
$(\nu _U^i, \nu _S^i)$
. Using that
![]() $\nu $
is an eigenfunction of eigenvalue
$\nu $
is an eigenfunction of eigenvalue
![]() $\lambda $
in the left-hand side of the previous equation, we obtain that
$\lambda $
in the left-hand side of the previous equation, we obtain that
This concludes our claim.
Lemma 7.14. If
![]() $\delta _g>0$
is chosen sufficiently small and
$\delta _g>0$
is chosen sufficiently small and
![]() $\{\nu _{i,U},\nu _{i,S}\}_{i=1,\dots ,N}$
are the eigenfunctions corresponding to the eigenvalues
$\{\nu _{i,U},\nu _{i,S}\}_{i=1,\dots ,N}$
are the eigenfunctions corresponding to the eigenvalues
![]() $\Lambda $
defined in Lemma 7.11 applied to the operator
$\Lambda $
defined in Lemma 7.11 applied to the operator
![]() $A_0$
defined in Corollary 7.7, then
$A_0$
defined in Corollary 7.7, then
![]() $\{\nu _{i,U},\nu _{i,S}\}_{i=1,\dots ,N}$
are smooth.
$\{\nu _{i,U},\nu _{i,S}\}_{i=1,\dots ,N}$
are smooth.
Proof. Fixing
![]() $\delta _g>0$
sufficiently small, let
$\delta _g>0$
sufficiently small, let
![]() $\{\nu _{i,U},\nu _{i,S}\}_{i=1,\dots ,N}$
be the eigenfunctions corresponding to the eigenvalues
$\{\nu _{i,U},\nu _{i,S}\}_{i=1,\dots ,N}$
be the eigenfunctions corresponding to the eigenvalues
![]() $\Lambda $
defined in Lemma 7.11 applied to the operator
$\Lambda $
defined in Lemma 7.11 applied to the operator
![]() $A_0$
defined in Corollary 7.7. By Sobolev embedding, the eigenfunctions are
$A_0$
defined in Corollary 7.7. By Sobolev embedding, the eigenfunctions are
![]() $C^{2m-1}$
.
$C^{2m-1}$
.
Fix i, let
![]() $\lambda +\delta _g$
be the eigenvalue associated with
$\lambda +\delta _g$
be the eigenvalue associated with
![]() $(\nu _{i,U},\nu _{i,S})$
and define
$(\nu _{i,U},\nu _{i,S})$
and define
![]() $(W,Z)=(\nu _{i,U}+\nu _{i,S}, \nu _{i,U}-\nu _{i,S})$
. Then
$(W,Z)=(\nu _{i,U}+\nu _{i,S}, \nu _{i,U}-\nu _{i,S})$
. Then

We extend
![]() $(W,Z)$
in the usual way by requiring
$(W,Z)$
in the usual way by requiring
![]() $Z(\zeta )=-W(-\zeta )$
. By simple ODE analysis, we obtain that
$Z(\zeta )=-W(-\zeta )$
. By simple ODE analysis, we obtain that
![]() $(W,Z)$
are smooth away from
$(W,Z)$
are smooth away from
![]() $\zeta =0,1$
. At
$\zeta =0,1$
. At
![]() $\zeta =0,1$
, and we compare
$\zeta =0,1$
, and we compare
![]() $(W,Z)$
to the power series. At
$(W,Z)$
to the power series. At
![]() $\zeta =1$
, we may use (7.31) in order to construct a power series expansion around
$\zeta =1$
, we may use (7.31) in order to construct a power series expansion around
![]() $\zeta =1$
. In order to construct the series, we are using that
$\zeta =1$
. In order to construct the series, we are using that
![]() $\Re \lambda>-\frac {\delta _g}2$
, and hence. the prefactor
$\Re \lambda>-\frac {\delta _g}2$
, and hence. the prefactor
in (7.31) is positive assuming that
![]() $n\geq 2m-1$
and m is chosen sufficiently large, dependent on
$n\geq 2m-1$
and m is chosen sufficiently large, dependent on
![]() $\delta _g$
– here, we are also using the lower bound Lemma A.11 on
$\delta _g$
– here, we are also using the lower bound Lemma A.11 on ![]() . Let
. Let
![]() $(\check W, \check Z)$
denote the solution obtained via power series expansion in a small neighborhood
$(\check W, \check Z)$
denote the solution obtained via power series expansion in a small neighborhood
![]() $[1-\delta ,1+\delta ]$
of
$[1-\delta ,1+\delta ]$
of
![]() $\zeta =1$
such that
$\zeta =1$
such that
![]() $W(1)=\check W(1)$
. We necessarily have that all derivatives of
$W(1)=\check W(1)$
. We necessarily have that all derivatives of
![]() $(W,Z)$
and
$(W,Z)$
and
![]() $(\check W,\check Z)$
agree up to order
$(\check W,\check Z)$
agree up to order
![]() $2m-1$
at
$2m-1$
at
![]() $\zeta =1$
. Let
$\zeta =1$
. Let
![]() $(\widetilde {W},\widetilde {Z})=( W-\check W, Z-\check W)$
. Then for
$(\widetilde {W},\widetilde {Z})=( W-\check W, Z-\check W)$
. Then for
![]() $\zeta \in [1-\delta ,1+\delta ]$
, we have
$\zeta \in [1-\delta ,1+\delta ]$
, we have
![]() $(\widetilde {W},\widetilde {Z})=O((\zeta -1)^{2m-1})$
.
$(\widetilde {W},\widetilde {Z})=O((\zeta -1)^{2m-1})$
.
Suppose for
![]() $\zeta \in [1-\delta ,1+\delta ]$
, C is chosen larger enough such that
$\zeta \in [1-\delta ,1+\delta ]$
, C is chosen larger enough such that

Then, by Grönwall, we have for
![]() $1+\bar \delta <\zeta <1+\delta $
,
$1+\bar \delta <\zeta <1+\delta $
,
By an energy estimate, we can bound
![]() $\lambda $
independent of m. Then since m can be chosen sufficiently large, we can take
$\lambda $
independent of m. Then since m can be chosen sufficiently large, we can take
![]() $\bar \delta $
to zero to conclude that
$\bar \delta $
to zero to conclude that
![]() $(\check W,\check Z)\equiv 0$
in the region
$(\check W,\check Z)\equiv 0$
in the region
![]() $\zeta \in [1,1+\delta ]$
. An analogous argument holds in the region
$\zeta \in [1,1+\delta ]$
. An analogous argument holds in the region
![]() $\zeta \in [1-\delta ,1]$
. In particular, we have shown that
$\zeta \in [1-\delta ,1]$
. In particular, we have shown that
![]() $(W,Z)$
is smooth in a neighborhood of
$(W,Z)$
is smooth in a neighborhood of
![]() $\zeta =1$
. A similar Grönwall argument using (7.45) to construct the local analytic solution can be used to prove
$\zeta =1$
. A similar Grönwall argument using (7.45) to construct the local analytic solution can be used to prove
![]() $(W,Z)$
are smooth in a neighborhood of
$(W,Z)$
are smooth in a neighborhood of
![]() $\zeta =0$
.
$\zeta =0$
.
Corollary 7.15. There exists a finite dimensional orthonormal basis of smooth functions
![]() $\{\psi _{i,U},\psi _{i,S}\}_{i=1,\dots ,N}$
for the space V defined in Lemma 7.11 for the operator
$\{\psi _{i,U},\psi _{i,S}\}_{i=1,\dots ,N}$
for the space V defined in Lemma 7.11 for the operator
![]() $A_0$
defined in Corollary 7.7.
$A_0$
defined in Corollary 7.7.
Proof. Let
![]() $\{\nu _{i,U},\nu _{i,S}\}_{i=1,\dots ,M}$
be the sequence of smooth eigenvectors defined in Lemma 7.14. For each
$\{\nu _{i,U},\nu _{i,S}\}_{i=1,\dots ,M}$
be the sequence of smooth eigenvectors defined in Lemma 7.14. For each
![]() $i= 1,\dots ,M $
, define
$i= 1,\dots ,M $
, define
Each
![]() $(\tilde \psi _{i,U},\tilde \psi _{i,S}) $
is smooth by definition and span V. The sequence of functions
$(\tilde \psi _{i,U},\tilde \psi _{i,S}) $
is smooth by definition and span V. The sequence of functions
![]() $\{\psi _{i,U},\psi _{i,S}\}_{i=1,\dots ,N}$
can then be constructed via a standard Gram-Schmidt argument.
$\{\psi _{i,U},\psi _{i,S}\}_{i=1,\dots ,N}$
can then be constructed via a standard Gram-Schmidt argument.
Remark 7.16. Let us note that, moreover, with our definition of
![]() $\mathcal {L}$
, the functions
$\mathcal {L}$
, the functions
![]() $\psi _{i, U}, \psi _{i, S}$
are compactly supported in
$\psi _{i, U}, \psi _{i, S}$
are compactly supported in
![]() $\zeta \leq \frac 95$
, which is the support of
$\zeta \leq \frac 95$
, which is the support of
![]() $\chi _2$
. As the functions
$\chi _2$
. As the functions
![]() $\psi _{i, U}$
and
$\psi _{i, U}$
and
![]() $\psi _{i, S}$
are linear combinations of
$\psi _{i, S}$
are linear combinations of
![]() $\tilde \psi _{i, U}$
and
$\tilde \psi _{i, U}$
and
![]() $\tilde \psi _{i, S}$
, respectively, it suffices to check that
$\tilde \psi _{i, S}$
, respectively, it suffices to check that
![]() $\tilde \psi _{i, U}$
and
$\tilde \psi _{i, U}$
and
![]() $\tilde \psi _{i, S}$
are supported on
$\tilde \psi _{i, S}$
are supported on
![]() $\zeta \leq \frac 95$
.
$\zeta \leq \frac 95$
.
Indeed, note on the one hand that
![]() $\mathcal {L}(\tilde \psi _i) = \lambda _i (\tilde \psi _{i, U}, \tilde \psi _{i, S})$
with
$\mathcal {L}(\tilde \psi _i) = \lambda _i (\tilde \psi _{i, U}, \tilde \psi _{i, S})$
with
![]() $\Re (\lambda _i)> -\delta _g/2$
. On the other hand, from (7.9), we get that
$\Re (\lambda _i)> -\delta _g/2$
. On the other hand, from (7.9), we get that
outside the support of
![]() $\chi _2$
.
$\chi _2$
.
As J is taken to be sufficiently large,
![]() $-J \ll 1\ll \frac {-\delta _g}{2} < \lambda _i$
. Equation (7.53) contradicts that
$-J \ll 1\ll \frac {-\delta _g}{2} < \lambda _i$
. Equation (7.53) contradicts that
![]() $\lambda _i$
is the eigenvalue of
$\lambda _i$
is the eigenvalue of
![]() $\tilde \psi _i$
unless both
$\tilde \psi _i$
unless both
![]() $\tilde \psi _{i, U}$
and
$\tilde \psi _{i, U}$
and
![]() $\tilde \psi _{i, S}$
vanish identically outside the support of
$\tilde \psi _{i, S}$
vanish identically outside the support of
![]() $\chi _2$
. Thus,
$\chi _2$
. Thus,
![]() $\psi _{i, U}, \psi _{i, S}$
are compactly supported on
$\psi _{i, U}, \psi _{i, S}$
are compactly supported on
![]() $\zeta \leq \frac 95$
.
$\zeta \leq \frac 95$
.
8 Nonlinear stability
For brevity, we will use the notation
![]() $\left \|\cdot \right \|_{X}$
in place of
$\left \|\cdot \right \|_{X}$
in place of
![]() $\left \|\cdot \right \|_{H^{2m}(B(0,2))}$
(this is consistent with the definition of the space X given in Remark 7.2).
$\left \|\cdot \right \|_{H^{2m}(B(0,2))}$
(this is consistent with the definition of the space X given in Remark 7.2).
Our aim is to show that there exists a finite codimensional manifold of initial data that lead to asymptotically self-similar implosion. To make this more precise, suppose we are given initial data
![]() $(\mathcal {U}_0',\mathcal {S}_0')$
such that the difference
$(\mathcal {U}_0',\mathcal {S}_0')$
such that the difference
![]() $ (\widetilde {U}_0',\widetilde {S}_0')=(\mathcal {U}_0',\mathcal {S}_0')-(\ddot {U},\ddot {S})$
satisfies the following assumptions:
$ (\widetilde {U}_0',\widetilde {S}_0')=(\mathcal {U}_0',\mathcal {S}_0')-(\ddot {U},\ddot {S})$
satisfies the following assumptions:
where here,
![]() $\delta _0$
and
$\delta _0$
and
![]() $\delta _1$
are constants satisfying the relation
$\delta _1$
are constants satisfying the relation
and
![]() $\chi _2$
is the cut-off function defined in Section 7.
$\chi _2$
is the cut-off function defined in Section 7.
We will moreover assume a high-order weighted energy estimate on
![]() $ (\widetilde {U}_0',\widetilde {S}_0')$
. For some
$ (\widetilde {U}_0',\widetilde {S}_0')$
. For some
![]() $\zeta _0$
and
$\zeta _0$
and
![]() $\eta _{w}$
yet to be determined, we let
$\eta _{w}$
yet to be determined, we let
![]() $\phi $
be a smooth function that is
$\phi $
be a smooth function that is
![]() $1$
on the region
$1$
on the region
![]() $[-\zeta _0, \zeta _0]$
and behaves like
$[-\zeta _0, \zeta _0]$
and behaves like
![]() $\zeta ^{2(1-\eta _{w})}$
for
$\zeta ^{2(1-\eta _{w})}$
for
![]() $\zeta \geq \zeta _0$
. We then assume
$\zeta \geq \zeta _0$
. We then assume
![]() $ (\widetilde {U}_0',\widetilde {S}_0')$
satisfies the bound
$ (\widetilde {U}_0',\widetilde {S}_0')$
satisfies the bound
for K satisfying
![]() $ \delta _0 \ll 1/K \ll \eta _{w}$
.
$ \delta _0 \ll 1/K \ll \eta _{w}$
.
For the convenience of the reader, we collect the following chain of inequalities:
where we recall
![]() $\delta _g$
is defined at the beginning of Section 7.3 and
$\delta _g$
is defined at the beginning of Section 7.3 and
![]() $\delta _{\mathrm {dis}}$
is defined in (1.20).
$\delta _{\mathrm {dis}}$
is defined in (1.20).
With the assumptions (8.1) and (8.2), we will show there exists
![]() $\{ a_i \}_{i=1}^N$
satisfying
$\{ a_i \}_{i=1}^N$
satisfying
![]() $|a| \leq \delta _1$
, such that the initial data
$|a| \leq \delta _1$
, such that the initial data
 $$ \begin{align} ( \mathcal{U}_0', \mathcal{S}_0' ) = \left( \ddot{U} + \widetilde{U}_0' + \sum_{i=1}^N a_i \psi_{i, U} ,~ \ddot{S} + \widetilde{S}_0' + \sum_{i=1}^N a_i \psi_{i, S} \right)\, \end{align} $$
$$ \begin{align} ( \mathcal{U}_0', \mathcal{S}_0' ) = \left( \ddot{U} + \widetilde{U}_0' + \sum_{i=1}^N a_i \psi_{i, U} ,~ \ddot{S} + \widetilde{S}_0' + \sum_{i=1}^N a_i \psi_{i, S} \right)\, \end{align} $$
leads to a global solution
![]() $(\mathcal {U},\mathcal {S})$
to (7.5), and moreover, if one sets
$(\mathcal {U},\mathcal {S})$
to (7.5), and moreover, if one sets
![]() $ (\widetilde {U},\widetilde {S})=(\mathcal {U},\mathcal {S})-(\ddot {U},\ddot {S})$
, then
$ (\widetilde {U},\widetilde {S})=(\mathcal {U},\mathcal {S})-(\ddot {U},\ddot {S})$
, then
for any
![]() $\zeta $
. The key ingredient to proving this statement is the linear stability of truncated problem considered in Section 7. To make this link precise, given
$\zeta $
. The key ingredient to proving this statement is the linear stability of truncated problem considered in Section 7. To make this link precise, given
![]() $( \mathcal {U}_0, \mathcal {S}_0 ) $
, define its truncation
$( \mathcal {U}_0, \mathcal {S}_0 ) $
, define its truncation
![]() $( \mathcal {U}_{0,t}, \mathcal {S}_{0,t})$
as
$( \mathcal {U}_{0,t}, \mathcal {S}_{0,t})$
as
We then let
![]() $( \mathcal {U}_{t}, \mathcal {S}_{t})$
be the solution to truncated equation (7.7) corresponding to such initial data. Let us recall that all the cut-offs introduced in the truncated equation are constantly equal to
$( \mathcal {U}_{t}, \mathcal {S}_{t})$
be the solution to truncated equation (7.7) corresponding to such initial data. Let us recall that all the cut-offs introduced in the truncated equation are constantly equal to
![]() $1$
for
$1$
for
![]() $|\zeta | \leq \frac {6}{5}$
. We thus have the following.
$|\zeta | \leq \frac {6}{5}$
. We thus have the following.
Lemma 8.1. The solution to the truncated equation and the solution to the original equation agree on
![]() $[0, \frac 65 ]$
.
$[0, \frac 65 ]$
.
Proof. Subtracting the two solutions written in terms of their
![]() $(U, S)$
variables, we obtain that their difference
$(U, S)$
variables, we obtain that their difference
![]() $(U, S)$
satisfies
$(U, S)$
satisfies
 $$ \begin{align*} (\partial_s + r - 1) U + (\zeta + \ddot{U}) \partial_\zeta U + \alpha \ddot{S} \partial_\zeta S + \widetilde{U} \partial_\zeta \ddot{U} + \alpha S \partial_\zeta \ddot{S} &= 0, \\ (\partial_s + r - 1) S + (\zeta + \ddot{U}) \partial_\zeta S + \alpha \ddot{S} \div ( U) + \widetilde{U} \partial_\zeta \ddot{S} + \alpha S \div (\ddot{U}) &= 0\, \end{align*} $$
$$ \begin{align*} (\partial_s + r - 1) U + (\zeta + \ddot{U}) \partial_\zeta U + \alpha \ddot{S} \partial_\zeta S + \widetilde{U} \partial_\zeta \ddot{U} + \alpha S \partial_\zeta \ddot{S} &= 0, \\ (\partial_s + r - 1) S + (\zeta + \ddot{U}) \partial_\zeta S + \alpha \ddot{S} \div ( U) + \widetilde{U} \partial_\zeta \ddot{S} + \alpha S \div (\ddot{U}) &= 0\, \end{align*} $$
on a ball
![]() $B(0, 6/5)$
and with zero initial conditions on that ball. Applying energy estimates, we see that
$B(0, 6/5)$
and with zero initial conditions on that ball. Applying energy estimates, we see that
 $$ \begin{align*} \frac{\partial_s}{2} \int_{B(0, 6/5)} \left( | U |^2 + S^2 \right) &\leq -\int_{B(0, 6/5)} (\zeta + \ddot{U}) \frac{\partial_\zeta}{2} \left( | U |^2 + S^2 \right) - \int_{B(0, 6/5)} \alpha \ddot{S} \div(S U) + C_1 \int_{B(0, 6/5)} \left( U^2 + S^2 \right) \\&\leq -\int_{\partial B(0, 6/5)} \left( \frac{\zeta + \ddot{U}}{2} (| U |^2 + S^2) + \alpha \ddot{S} S U \right) + C_2 \int_{B(0, 6/5)} \left( U^2 + S^2 \right) \\&\leq \int_{\partial B(0, 6/5)} \frac{-\zeta - \ddot{U} + \alpha \ddot{S}}{2} (| U |^2 + S^2) + C_3 \int_{B(0, 6/5)} \left( U^2 + S^2 \right) \\&\leq C_3 \int_{B(0, 6/5)} \left( |U|^2 + S^2 \right), \end{align*} $$
$$ \begin{align*} \frac{\partial_s}{2} \int_{B(0, 6/5)} \left( | U |^2 + S^2 \right) &\leq -\int_{B(0, 6/5)} (\zeta + \ddot{U}) \frac{\partial_\zeta}{2} \left( | U |^2 + S^2 \right) - \int_{B(0, 6/5)} \alpha \ddot{S} \div(S U) + C_1 \int_{B(0, 6/5)} \left( U^2 + S^2 \right) \\&\leq -\int_{\partial B(0, 6/5)} \left( \frac{\zeta + \ddot{U}}{2} (| U |^2 + S^2) + \alpha \ddot{S} S U \right) + C_2 \int_{B(0, 6/5)} \left( U^2 + S^2 \right) \\&\leq \int_{\partial B(0, 6/5)} \frac{-\zeta - \ddot{U} + \alpha \ddot{S}}{2} (| U |^2 + S^2) + C_3 \int_{B(0, 6/5)} \left( U^2 + S^2 \right) \\&\leq C_3 \int_{B(0, 6/5)} \left( |U|^2 + S^2 \right), \end{align*} $$
where
![]() $C_1, C_2, C_3$
are some absolute constants, and we have used Lemma A.33 in the last inequality. In particular, as U and S are zero at time
$C_1, C_2, C_3$
are some absolute constants, and we have used Lemma A.33 in the last inequality. In particular, as U and S are zero at time
![]() $s_0$
in
$s_0$
in
![]() $B\left ( 0, \frac 65 \right )$
, we conclude that they are zero for all times, and both solutions agree for all times and
$B\left ( 0, \frac 65 \right )$
, we conclude that they are zero for all times, and both solutions agree for all times and
![]() $\zeta \in \left [ 0, \frac 65 \right ]$
.
$\zeta \in \left [ 0, \frac 65 \right ]$
.
Given a solution
![]() $( \mathcal {U}_{t}, \mathcal {S}_{t})$
to (7.7), we will consider
$( \mathcal {U}_{t}, \mathcal {S}_{t})$
to (7.7), we will consider
![]() $\| P_{\mathrm {uns}} (\mathcal {U}_t, \mathcal {S}_t ) \|_X$
. Our first result is to show that as long as the unstable modes are controlled, we can control the extended solution
$\| P_{\mathrm {uns}} (\mathcal {U}_t, \mathcal {S}_t ) \|_X$
. Our first result is to show that as long as the unstable modes are controlled, we can control the extended solution
![]() $(\mathcal {U},\mathcal {S})$
in a high-order weighted Sobolev norm. In particular, we will bound
$(\mathcal {U},\mathcal {S})$
in a high-order weighted Sobolev norm. In particular, we will bound
Specifically, in Section 8.1, we will prove the following:
Proposition 8.2. Let us take
![]() $\delta _0^{3/2} \ll \delta _1 \ll \delta _0$
. Let us assume that our initial data satisfies
$\delta _0^{3/2} \ll \delta _1 \ll \delta _0$
. Let us assume that our initial data satisfies
and that letting
![]() $\mathcal {U}_0 = \ddot {U} + \widetilde {U}_0$
,
$\mathcal {U}_0 = \ddot {U} + \widetilde {U}_0$
,
![]() $\mathcal {S} = \ddot {S} + \widetilde {S}_0$
, its derivatives satisfy the decay estimates
$\mathcal {S} = \ddot {S} + \widetilde {S}_0$
, its derivatives satisfy the decay estimates
Moreover, let us assume that our solution is defined for
![]() $s \in [s_0, s_1]$
and for every
$s \in [s_0, s_1]$
and for every
![]() $s \in [s_0, s_1]$
, we have
$s \in [s_0, s_1]$
, we have
Then, we have the bounds
for all
![]() $s \in [s_0, s_1]$
.
$s \in [s_0, s_1]$
.
By local existence and a standard continuation argument, Proposition 8.2 implies that the solution
![]() $( \mathcal {U}, \mathcal {S})$
is well defined and satisfies the bound (8.9) so long as the unstable modes satisfy the bound
$( \mathcal {U}, \mathcal {S})$
is well defined and satisfies the bound (8.9) so long as the unstable modes satisfy the bound
![]() $\| P_{\mathrm {uns}} (\widetilde {U}_t, \widetilde {S}_t) \|_X \leq \delta _1$
.
$\| P_{\mathrm {uns}} (\widetilde {U}_t, \widetilde {S}_t) \|_X \leq \delta _1$
.
In Section 8.2, we will prove, via a standard topological argument, the existence of a choice of
![]() $\{a_i\}$
leading to a global bounded converging asymptotically to
$\{a_i\}$
leading to a global bounded converging asymptotically to
![]() $(\ddot {U}, \ddot {S})$
.
$(\ddot {U}, \ddot {S})$
.
Proposition 8.3. Let us consider
![]() $(\widetilde {U}_0', \widetilde {S}_0')$
smooth and satisfying the initial conditions
$(\widetilde {U}_0', \widetilde {S}_0')$
smooth and satisfying the initial conditions
 $$ \begin{align} \begin{aligned} \| (\widetilde{U}_{0, t}', \widetilde{S}_{0, t})' \|_X \leq \frac{\delta_0}{4}, \qquad E_{2K} (\mathcal{U}_0', \mathcal{S}_0'; s_0) \leq \frac{\bar E}{4}, \qquad \| \widetilde{U}_0' \|_{L^\infty}, \| \widetilde{S}_0' \|_{L^\infty} \leq \frac{9\delta_1}{10} ,\\ \ddot{S} + \widetilde{S}_0' \geq \frac{\delta_1}{2}, \qquad | \nabla \mathcal{S}_0' | + | \nabla \mathcal{U}_0' | \lesssim \frac{1}{\langle \zeta \rangle} \qquad | \nabla^2 \mathcal{U}_0' | + | \nabla^2 \mathcal{S}_0' | \lesssim \frac{1}{ \langle \zeta \rangle^2}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \| (\widetilde{U}_{0, t}', \widetilde{S}_{0, t})' \|_X \leq \frac{\delta_0}{4}, \qquad E_{2K} (\mathcal{U}_0', \mathcal{S}_0'; s_0) \leq \frac{\bar E}{4}, \qquad \| \widetilde{U}_0' \|_{L^\infty}, \| \widetilde{S}_0' \|_{L^\infty} \leq \frac{9\delta_1}{10} ,\\ \ddot{S} + \widetilde{S}_0' \geq \frac{\delta_1}{2}, \qquad | \nabla \mathcal{S}_0' | + | \nabla \mathcal{U}_0' | \lesssim \frac{1}{\langle \zeta \rangle} \qquad | \nabla^2 \mathcal{U}_0' | + | \nabla^2 \mathcal{S}_0' | \lesssim \frac{1}{ \langle \zeta \rangle^2}, \end{aligned} \end{align} $$
and moreover such that
![]() $P_{\mathrm {uns}} (\widetilde {U}_{0, t}', \widetilde {S}_{0, t}' ) = 0$
, for
$P_{\mathrm {uns}} (\widetilde {U}_{0, t}', \widetilde {S}_{0, t}' ) = 0$
, for
![]() $\widetilde {U}_{0,t}' = \chi _2 \widetilde {U}_0'$
and
$\widetilde {U}_{0,t}' = \chi _2 \widetilde {U}_0'$
and
![]() $\widetilde {S}_{0, t}' = \chi _2 \widetilde {S}_0'$
Then, we have that there exist specific values of
$\widetilde {S}_{0, t}' = \chi _2 \widetilde {S}_0'$
Then, we have that there exist specific values of
![]() $a_i$
such that we have the following: Let
$a_i$
such that we have the following: Let
![]() $(\mathcal {U}_0, \mathcal {S}_0)$
be defined by (8.3) and
$(\mathcal {U}_0, \mathcal {S}_0)$
be defined by (8.3) and
![]() $(\mathcal {U}_{0, t}, \mathcal {S}_{0, t})$
defined by (8.4). Let also
$(\mathcal {U}_{0, t}, \mathcal {S}_{0, t})$
defined by (8.4). Let also
![]() $\widetilde {U}_0 = \mathcal {U}_0 - \ddot {U}$
,
$\widetilde {U}_0 = \mathcal {U}_0 - \ddot {U}$
,
![]() $\widetilde {S}_0 = \mathcal {S}_0 - \ddot {S}$
,
$\widetilde {S}_0 = \mathcal {S}_0 - \ddot {S}$
,
![]() $\widetilde {U}_{0, t} = \mathcal {U}_{0, t} - \chi _2 \ddot {U}$
,
$\widetilde {U}_{0, t} = \mathcal {U}_{0, t} - \chi _2 \ddot {U}$
,
![]() $\widetilde {S}_{0, t} = \mathcal {S}_{0, t} - \chi _2 \ddot {S}$
.
$\widetilde {S}_{0, t} = \mathcal {S}_{0, t} - \chi _2 \ddot {S}$
.
Then, the equations (7.6) and (7.8) can be solved globally for all
![]() $s \geq s_0$
, and moreover, we obtain smooth solutions that satisfy the estimates
$s \geq s_0$
, and moreover, we obtain smooth solutions that satisfy the estimates
and
where we recall
![]() $\widetilde {U}_e$
and
$\widetilde {U}_e$
and
![]() $\widetilde {S}_e$
refer to the whole perturbation (without any cut-off) solving the extended equation (7.6).
$\widetilde {S}_e$
refer to the whole perturbation (without any cut-off) solving the extended equation (7.6).
Given the inequalities in (8.10), we may safely assume that the equations 8.6–8.7 will be satisfied for
![]() $\mathcal {U}_0, \mathcal {S}_0$
.
$\mathcal {U}_0, \mathcal {S}_0$
.
Now, let us see how to conclude Theorem 1.3 from Proposition 8.3. The proofs of Proposition 8.2 and Proposition 8.3 will be delayed for now and will constitute the bulk of this section.
Let us specify the initial data
![]() $(\widetilde {U}_0', \widetilde {S}_0')$
. We consider
$(\widetilde {U}_0', \widetilde {S}_0')$
. We consider
![]() $\zeta _u> 3$
such that
$\zeta _u> 3$
such that
![]() $\ddot {U} \leq \frac 34 \delta _1$
for
$\ddot {U} \leq \frac 34 \delta _1$
for
![]() $\zeta> \zeta _u$
and let
$\zeta> \zeta _u$
and let
 $$ \begin{align*} \mathfrak B_U = \left\{\zeta \, : \zeta> \zeta_u \right\} \qquad \mbox{ and } \qquad \mathfrak B_S = \left\{ \zeta \, : \, \ddot{S}(\zeta) \leq \frac34 \delta_1 \right \}. \end{align*} $$
$$ \begin{align*} \mathfrak B_U = \left\{\zeta \, : \zeta> \zeta_u \right\} \qquad \mbox{ and } \qquad \mathfrak B_S = \left\{ \zeta \, : \, \ddot{S}(\zeta) \leq \frac34 \delta_1 \right \}. \end{align*} $$
We let
![]() $\chi _3 : \mathbb {R}_{\geq 0} \rightarrow \mathbb {R}$
be a smooth cut-off function supported on
$\chi _3 : \mathbb {R}_{\geq 0} \rightarrow \mathbb {R}$
be a smooth cut-off function supported on
![]() $[0, 1]$
and equal to
$[0, 1]$
and equal to
![]() $1$
on
$1$
on
![]() $[0, 1/2]$
, and we let
$[0, 1/2]$
, and we let
![]() $\lambda> 1$
be a parameter to be fixed. We define the initial data
$\lambda> 1$
be a parameter to be fixed. We define the initial data
![]() $\widetilde {U}_0', \widetilde {S}_0'$
as follows:
$\widetilde {U}_0', \widetilde {S}_0'$
as follows:
 $$ \begin{align*} \widetilde{U}_0'(\zeta) = -\ddot{U} (\zeta) \chi_3 \left( \lambda \cdot \mathrm{d}(\zeta, \mathfrak B_U )\right), \qquad \mbox{ and } \qquad \widetilde{S}_0' (\zeta) = \left( \frac34 \delta_1 - \ddot{S} (\zeta) \right)\chi_3 \left( \lambda \cdot \mathrm{d}( \zeta, \mathfrak B_S ) \right), \end{align*} $$
$$ \begin{align*} \widetilde{U}_0'(\zeta) = -\ddot{U} (\zeta) \chi_3 \left( \lambda \cdot \mathrm{d}(\zeta, \mathfrak B_U )\right), \qquad \mbox{ and } \qquad \widetilde{S}_0' (\zeta) = \left( \frac34 \delta_1 - \ddot{S} (\zeta) \right)\chi_3 \left( \lambda \cdot \mathrm{d}( \zeta, \mathfrak B_S ) \right), \end{align*} $$
where
![]() $\mathrm {d}$
is the distance function. That is, we fix
$\mathrm {d}$
is the distance function. That is, we fix
![]() $\widetilde {U}_0'$
and
$\widetilde {U}_0'$
and
![]() $\widetilde {S}_0'$
to be
$\widetilde {S}_0'$
to be
![]() $-\ddot {U}$
and
$-\ddot {U}$
and
![]() $\frac 34 \delta _1 - \ddot {S}$
in the regions
$\frac 34 \delta _1 - \ddot {S}$
in the regions
![]() $\mathfrak B_U$
and
$\mathfrak B_U$
and
![]() $\mathfrak B_S$
respectively. Outside that region, our definition gives a smooth extension of
$\mathfrak B_S$
respectively. Outside that region, our definition gives a smooth extension of
![]() $\widetilde {U}_0', \widetilde {S}_0'$
that guarantees that they are supported in a
$\widetilde {U}_0', \widetilde {S}_0'$
that guarantees that they are supported in a
![]() $\frac {1}{\lambda }$
-neighborhood of
$\frac {1}{\lambda }$
-neighborhood of
![]() $\mathfrak B_U$
and
$\mathfrak B_U$
and
![]() $\mathfrak B_S$
, respectively.
$\mathfrak B_S$
, respectively.
Let us note that
![]() $\mathcal {U}_0'$
is zero for
$\mathcal {U}_0'$
is zero for
![]() $\zeta $
large enough and
$\zeta $
large enough and
![]() $\mathcal {S}_0'$
is
$\mathcal {S}_0'$
is
![]() $\frac 34 \delta _1$
for
$\frac 34 \delta _1$
for
![]() $\zeta $
large enough. This clearly follows from the fact that
$\zeta $
large enough. This clearly follows from the fact that
![]() $\ddot {U}$
and
$\ddot {U}$
and
![]() $\ddot {S}$
decay (Lemma A.39), so for
$\ddot {S}$
decay (Lemma A.39), so for
![]() $\zeta $
sufficiently large, we will have
$\zeta $
sufficiently large, we will have
![]() $\zeta \in \mathfrak B_U$
and
$\zeta \in \mathfrak B_U$
and
![]() $\zeta \in \mathfrak B_S$
. Let us also note that
$\zeta \in \mathfrak B_S$
. Let us also note that
![]() $\mathfrak B_U, \mathfrak B_S \subset (3, \infty )$
because
$\mathfrak B_U, \mathfrak B_S \subset (3, \infty )$
because
![]() $\zeta _u> 3$
and Lemma A.32. Therefore, as
$\zeta _u> 3$
and Lemma A.32. Therefore, as
![]() $\widetilde {U}_0', \widetilde {S}_0'$
are supported in
$\widetilde {U}_0', \widetilde {S}_0'$
are supported in
![]() $\frac {1}{\lambda }$
-neighborhoods of
$\frac {1}{\lambda }$
-neighborhoods of
![]() $\mathfrak B_U$
and
$\mathfrak B_U$
and
![]() $\mathfrak B_S$
(and
$\mathfrak B_S$
(and
![]() $\lambda> 1$
), we have that
$\lambda> 1$
), we have that
![]() $\widetilde {U}_0', \widetilde {S}_0'$
are zero for
$\widetilde {U}_0', \widetilde {S}_0'$
are zero for
![]() $\zeta \leq 2$
.
$\zeta \leq 2$
.
Now, all the estimates from (8.10) are trivial. We have
![]() $\widetilde {U}_{0, t}' = \widetilde {S}_{0, t}' = 0$
because
$\widetilde {U}_{0, t}' = \widetilde {S}_{0, t}' = 0$
because
![]() $\widetilde {U}_0', \widetilde {S}_0'$
are zero for
$\widetilde {U}_0', \widetilde {S}_0'$
are zero for
![]() $\zeta \leq 2$
. As
$\zeta \leq 2$
. As
![]() $\mathcal {U}_0', \mathcal {S}_0'$
are constant for
$\mathcal {U}_0', \mathcal {S}_0'$
are constant for
![]() $\zeta $
large enough, we have that the integral defining
$\zeta $
large enough, we have that the integral defining
![]() $E_{2K}(\mathcal {U}_0', \mathcal {S}_0')^2$
converges, so it is less than
$E_{2K}(\mathcal {U}_0', \mathcal {S}_0')^2$
converges, so it is less than
![]() $\frac {\bar E^2}{16}$
provided we take
$\frac {\bar E^2}{16}$
provided we take
![]() $\bar E$
sufficiently large. We clearly have
$\bar E$
sufficiently large. We clearly have
for
![]() $\zeta \in \mathfrak B_U$
and
$\zeta \in \mathfrak B_U$
and
![]() $\mathfrak B_S$
, respectively. Therefore, taking
$\mathfrak B_S$
, respectively. Therefore, taking
![]() $\lambda $
to be large enough, the third and fourth inequalities from (8.10) are satisfied because
$\lambda $
to be large enough, the third and fourth inequalities from (8.10) are satisfied because
![]() $\widetilde {U}_0'$
and
$\widetilde {U}_0'$
and
![]() $\widetilde {S}'$
are supported on
$\widetilde {S}'$
are supported on
![]() $\frac {1}{\lambda }$
neighborhoods of
$\frac {1}{\lambda }$
neighborhoods of
![]() $\mathfrak B_U$
,
$\mathfrak B_U$
,
![]() $\mathfrak B_S$
. The two last inequalities of (8.10) follow directly from the fact that
$\mathfrak B_S$
. The two last inequalities of (8.10) follow directly from the fact that
![]() $\mathcal {U}_0', \mathcal {S}_0'$
are constant for sufficiently large
$\mathcal {U}_0', \mathcal {S}_0'$
are constant for sufficiently large
![]() $\zeta $
.
$\zeta $
.
Now, we apply Proposition 8.3 to
![]() $(\widetilde {U}_0', \widetilde {S}_0')$
. Note that as
$(\widetilde {U}_0', \widetilde {S}_0')$
. Note that as
![]() $\psi _{i, U}, \psi _{i, S}$
are supported in
$\psi _{i, U}, \psi _{i, S}$
are supported in
![]() $\zeta < 2$
(Remark 7.16), we have that
$\zeta < 2$
(Remark 7.16), we have that
Moreover, Proposition 8.3 gives us a global solution
![]() $(\widetilde {U}, \widetilde {S})$
to (7.6), which taking
$(\widetilde {U}, \widetilde {S})$
to (7.6), which taking
![]() $\mathcal {U} = \widetilde {U} + \ddot {U}$
and
$\mathcal {U} = \widetilde {U} + \ddot {U}$
and
![]() $\mathcal {S} = \widetilde {U} + \ddot {U}$
yields a solution
$\mathcal {S} = \widetilde {U} + \ddot {U}$
yields a solution
![]() $(\mathcal {U}, \mathcal {S})$
to (7.5). Undoing the self-similar change of variables by taking
$(\mathcal {U}, \mathcal {S})$
to (7.5). Undoing the self-similar change of variables by taking
where
we obtain that
![]() $u(R, t), \sigma (R, t)$
for
$u(R, t), \sigma (R, t)$
for
![]() $t \in [0, T)$
satisfy equation (1.18). We may recover
$t \in [0, T)$
satisfy equation (1.18). We may recover
![]() $\rho $
from taking
$\rho $
from taking
![]() $\rho = (\alpha \sigma )^{\frac {1}{\alpha }}$
, and then
$\rho = (\alpha \sigma )^{\frac {1}{\alpha }}$
, and then
![]() $(u, \rho )$
satisfies (1.3). It is clear from (8.13) and the changes performed that
$(u, \rho )$
satisfies (1.3). It is clear from (8.13) and the changes performed that
![]() $u(R, 0)$
will be zero for R large enough and
$u(R, 0)$
will be zero for R large enough and
![]() $\rho (R, 0)$
will be constant for R large enough (let us denote that constant by
$\rho (R, 0)$
will be constant for R large enough (let us denote that constant by
![]() $\rho _c$
). Then, the items 1 and 2 of Theorem 1.3 are satisfied.
$\rho _c$
). Then, the items 1 and 2 of Theorem 1.3 are satisfied.
Moreover, we see from Proposition 8.3 and (8.14) that
so we see that
![]() $\sigma (0, t)$
tends to
$\sigma (0, t)$
tends to
![]() $+\infty $
since
$+\infty $
since
![]() $\ddot {S}(0)> 0$
as a consequence of Lemma A.32. This implies the
$\ddot {S}(0)> 0$
as a consequence of Lemma A.32. This implies the
![]() $\rho $
limit stated in item 3 of Theorem 1.3.
$\rho $
limit stated in item 3 of Theorem 1.3.
In addition, we know from Proposition 8.3 that
![]() $\mathcal {U} (1, s) \rightarrow \ddot {U} (1)$
and
$\mathcal {U} (1, s) \rightarrow \ddot {U} (1)$
and
![]() $\mathcal {S} (\zeta , s) \rightarrow \ddot {S} (\zeta )$
as
$\mathcal {S} (\zeta , s) \rightarrow \ddot {S} (\zeta )$
as
![]() $s \rightarrow \infty $
, which implies item 4 of Theorem 1.3.
$s \rightarrow \infty $
, which implies item 4 of Theorem 1.3.
Finally, we show the u limit stated in item 3 of Theorem 1.3. First note that
Then, assuming r is sufficiently close to
![]() $r^\ast $
, we obtain from Lemma A.7 that
$r^\ast $
, we obtain from Lemma A.7 that
![]() $\bar U(1)\neq 0$
. Since
$\bar U(1)\neq 0$
. Since
![]() $\mathcal {U} (\zeta , s) \rightarrow \ddot {U} (\zeta )$
, we obtain the u limit stated in item 3 of Theorem 1.3.
$\mathcal {U} (\zeta , s) \rightarrow \ddot {U} (\zeta )$
, we obtain the u limit stated in item 3 of Theorem 1.3.
Remark 8.4. Observe that our construction of
![]() $(\widetilde {U}_0', \widetilde {S}_0')$
allows for small perturbations in all the norms considered (the norms appearing in (8.10)). The functions
$(\widetilde {U}_0', \widetilde {S}_0')$
allows for small perturbations in all the norms considered (the norms appearing in (8.10)). The functions
![]() $(\mathcal {U}_0, \mathcal {S}_0)$
can be defined as before in (8.3) up to small perturbations in the coefficients
$(\mathcal {U}_0, \mathcal {S}_0)$
can be defined as before in (8.3) up to small perturbations in the coefficients
![]() $a_i$
. In particular, the conclusion of Proposition 8.3 holds for a finite codimension manifold of radial initial data.
$a_i$
. In particular, the conclusion of Proposition 8.3 holds for a finite codimension manifold of radial initial data.
8.1 Proof of Proposition 8.2
We will prove Proposition 8.2 via a bootstrap argument. Thus, we will assume equations 8.6–8.9 hold for
![]() $s \in [s_0, s_1]$
and show an improvement on (8.9) – specifically,
$s \in [s_0, s_1]$
and show an improvement on (8.9) – specifically,
for all
![]() $s \in [s_0, s_1]$
. Showing the improved bounds (8.15) and (8.16) would clearly conclude the proof of Proposition 8.2 because
$s \in [s_0, s_1]$
. Showing the improved bounds (8.15) and (8.16) would clearly conclude the proof of Proposition 8.2 because
![]() $E_{2K}(s)$
,
$E_{2K}(s)$
,
![]() $\| \widetilde {U}(\cdot , s) \|_{L^\infty }$
and
$\| \widetilde {U}(\cdot , s) \|_{L^\infty }$
and
![]() $\| \widetilde {S} (\cdot , s) \|_{L^\infty }$
are continuous with respect to s.
$\| \widetilde {S} (\cdot , s) \|_{L^\infty }$
are continuous with respect to s.
From now on, and for the rest of this subsection, we will always assume that (8.6)–(8.9) hold and that
![]() $s \in [s_0, s_1]$
. In order to show equations (8.15) and (8.16), we divide the proof in three steps. First, we will derive a series of consequences of the assumptions (8.6)–(8.9). Secondly, we will show (8.15), and thirdly, we will show (8.16). This subsection is organized in three different parts according to those three steps.
$s \in [s_0, s_1]$
. In order to show equations (8.15) and (8.16), we divide the proof in three steps. First, we will derive a series of consequences of the assumptions (8.6)–(8.9). Secondly, we will show (8.15), and thirdly, we will show (8.16). This subsection is organized in three different parts according to those three steps.
Before doing any of those steps, let us introduce some definitions. Due to Lemma A.39, and recalling that
![]() $\delta _0^{3/2} \ll \delta _1 \ll \delta _0 \ll 1$
, we know that there exists a value of
$\delta _0^{3/2} \ll \delta _1 \ll \delta _0 \ll 1$
, we know that there exists a value of
![]() $\zeta _0$
such that
$\zeta _0$
such that
In particular, from
![]() $\| \widetilde {S} \|_{L^\infty } \leq \delta _0$
in (8.9), we have that
$\| \widetilde {S} \|_{L^\infty } \leq \delta _0$
in (8.9), we have that
Let us also define the weight
![]() $\phi (\zeta )$
that we will use for the energy. We fix
$\phi (\zeta )$
that we will use for the energy. We fix
 $$ \begin{align*} \phi(\zeta ) = \begin{cases} 1 & \mbox{ for } \zeta \leq \zeta_0, \\ \frac{ \zeta^{2(1-\eta_w)} }{ 2 \zeta_0^{2(1-\eta_w)} }&\mbox{ for }\zeta \geq 4 \zeta_0\, \end{cases} \end{align*} $$
$$ \begin{align*} \phi(\zeta ) = \begin{cases} 1 & \mbox{ for } \zeta \leq \zeta_0, \\ \frac{ \zeta^{2(1-\eta_w)} }{ 2 \zeta_0^{2(1-\eta_w)} }&\mbox{ for }\zeta \geq 4 \zeta_0\, \end{cases} \end{align*} $$
and choose
![]() $\phi (\zeta )$
in the region
$\phi (\zeta )$
in the region
![]() $\zeta _0 \leq \zeta \leq 4 \zeta _0$
so that it is smooth and
$\zeta _0 \leq \zeta \leq 4 \zeta _0$
so that it is smooth and
hold globally.
8.1.1 Consequences of the bootstrap
Let us stress once again that for all the results in this subsection, we are implicitly assuming that (8.6)–(8.9) hold and that
![]() $s \in [s_0, s_1]$
.
$s \in [s_0, s_1]$
.
Lemma 8.5. We have the following inequalities for the
![]() $2K-1$
derivatives:
$2K-1$
derivatives:
 $$ \begin{align} \phi^{(2K-1)/2} |\nabla^{2K-1} \mathcal{U}| + \phi^{(2K-1)/2} |\nabla^{2K-1} \mathcal{S} | \lesssim \frac{\bar{E} }{\zeta^{1/2} \phi^{1/2}}. \end{align} $$
$$ \begin{align} \phi^{(2K-1)/2} |\nabla^{2K-1} \mathcal{U}| + \phi^{(2K-1)/2} |\nabla^{2K-1} \mathcal{S} | \lesssim \frac{\bar{E} }{\zeta^{1/2} \phi^{1/2}}. \end{align} $$
Moreover, for
![]() $0 \leq j \leq 2K-2$
and
$0 \leq j \leq 2K-2$
and
![]() $\zeta> \zeta _0$
, we have
$\zeta> \zeta _0$
, we have
 $$ \begin{align} \begin{aligned} \phi^{j/2} |\nabla ^{j} \mathcal{U}|+\phi^{j/2} |\nabla^{j} \mathcal{S} | &\lesssim \delta_0^{(2K-1-j)/(2K-1)} \left( \frac{\bar{E} }{\zeta^{1/2} \phi^{1/2}} \right)^{j/(2K-1)} . \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \phi^{j/2} |\nabla ^{j} \mathcal{U}|+\phi^{j/2} |\nabla^{j} \mathcal{S} | &\lesssim \delta_0^{(2K-1-j)/(2K-1)} \left( \frac{\bar{E} }{\zeta^{1/2} \phi^{1/2}} \right)^{j/(2K-1)} . \end{aligned} \end{align} $$
Finally, for
![]() $0 \leq j \leq 2K-2$
, we also have the global inequality
$0 \leq j \leq 2K-2$
, we also have the global inequality
Proof. We have the following bound on any
![]() $2K-1$
-th derivative of
$2K-1$
-th derivative of
![]() $\mathcal {S}$
:
$\mathcal {S}$
:
 $$ \begin{align} | \partial^{2K-1} \mathcal{S} (\zeta) | &\leq \int_{\zeta_1}^\infty \left|\partial^{2K}\mathcal{S}\right| dz \nonumber\\ &\leq \left( \int_{\zeta}^\infty \left|\partial^{2K}\mathcal{S}\right| ^2 z^2 \phi(z)^{2K} dz \right)^{1/2} \left( \int_{\zeta}^\infty \frac{1}{ z^2 \phi (z)^{2K} } dz \right)^{1/2} \nonumber\\ &\lesssim \bar{E} \left( \int_{\zeta}^\infty \frac{1}{z^2 \phi (z)^{2K} } dz \right)^{1/2} \lesssim \bar{E} \left( \frac{1}{\zeta \phi (\zeta)^{2K}} \right)^{1/2} \lesssim \bar{E} \phi^{-K}\zeta^{-\frac12}. \end{align} $$
$$ \begin{align} | \partial^{2K-1} \mathcal{S} (\zeta) | &\leq \int_{\zeta_1}^\infty \left|\partial^{2K}\mathcal{S}\right| dz \nonumber\\ &\leq \left( \int_{\zeta}^\infty \left|\partial^{2K}\mathcal{S}\right| ^2 z^2 \phi(z)^{2K} dz \right)^{1/2} \left( \int_{\zeta}^\infty \frac{1}{ z^2 \phi (z)^{2K} } dz \right)^{1/2} \nonumber\\ &\lesssim \bar{E} \left( \int_{\zeta}^\infty \frac{1}{z^2 \phi (z)^{2K} } dz \right)^{1/2} \lesssim \bar{E} \left( \frac{1}{\zeta \phi (\zeta)^{2K}} \right)^{1/2} \lesssim \bar{E} \phi^{-K}\zeta^{-\frac12}. \end{align} $$
This yields the estimate on
![]() $\nabla ^{2K-1} \mathcal {S}$
implied by (8.20).
$\nabla ^{2K-1} \mathcal {S}$
implied by (8.20).
Now, for the region
![]() $\zeta> \zeta _0$
, we have that
$\zeta> \zeta _0$
, we have that
![]() $|\ddot {S} (\zeta )| \lesssim \delta _0$
, and by (8.9), we also have that
$|\ddot {S} (\zeta )| \lesssim \delta _0$
, and by (8.9), we also have that
![]() $| \widetilde {S} (\zeta )| \leq \delta _0$
. Therefore,
$| \widetilde {S} (\zeta )| \leq \delta _0$
. Therefore,
![]() $| \mathcal {S} (\zeta )| \lesssim \delta _0$
. Using interpolation (Lemma A.1) between
$| \mathcal {S} (\zeta )| \lesssim \delta _0$
. Using interpolation (Lemma A.1) between
![]() $| \mathcal {S} (\zeta )| \lesssim \delta _0$
and
$| \mathcal {S} (\zeta )| \lesssim \delta _0$
and
![]() $\phi ^K | \nabla ^{2K-1} \mathcal {S} | \frac {\zeta ^{1/2}}{\bar E} \lesssim 1$
in the region
$\phi ^K | \nabla ^{2K-1} \mathcal {S} | \frac {\zeta ^{1/2}}{\bar E} \lesssim 1$
in the region
![]() $[\zeta _0, +\infty )$
, we conclude the estimate on
$[\zeta _0, +\infty )$
, we conclude the estimate on
![]() $\nabla ^{j}\mathcal {S}$
implied by (8.21).
$\nabla ^{j}\mathcal {S}$
implied by (8.21).
Integrating (8.23), we obtain
 $$ \begin{align} \left|\partial^{2K-2} \mathcal{S} (\zeta)\right|\lesssim \bar{E}\frac{\zeta_0^{1/2}}{\phi (\zeta_0)^K } = \bar E \zeta_0^{1/2} \, , \end{align} $$
$$ \begin{align} \left|\partial^{2K-2} \mathcal{S} (\zeta)\right|\lesssim \bar{E}\frac{\zeta_0^{1/2}}{\phi (\zeta_0)^K } = \bar E \zeta_0^{1/2} \, , \end{align} $$
which shows (8.22) for
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $j = 2K-2$
. Standard
$j = 2K-2$
. Standard
![]() $L^\infty $
interpolation (Gagliardo-Nirenberg) yields
$L^\infty $
interpolation (Gagliardo-Nirenberg) yields
using that in
![]() $B(0, \zeta _0)$
, we have that
$B(0, \zeta _0)$
, we have that
![]() $\phi = 1$
. For the region
$\phi = 1$
. For the region
![]() $\zeta> \zeta _0$
, note that weighted interpolation (Lemma A.1) between
$\zeta> \zeta _0$
, note that weighted interpolation (Lemma A.1) between
![]() $\| \mathcal {S} \|_{L^\infty } \lesssim 1$
and (8.24) yields
$\| \mathcal {S} \|_{L^\infty } \lesssim 1$
and (8.24) yields
which together with (8.25) shows (8.22) for
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
In order to obtain the bound for
![]() $\widetilde {S}$
, recall that
$\widetilde {S}$
, recall that
![]() $\mathcal {S} = \widetilde {S} + \ddot {S}$
, and then note that
$\mathcal {S} = \widetilde {S} + \ddot {S}$
, and then note that
![]() $\| \phi ^{j/2} \nabla ^j \ddot {S} \|_{L^\infty } \lesssim 1$
due to Lemma A.39. Therefore, we conclude the desired bound also for
$\| \phi ^{j/2} \nabla ^j \ddot {S} \|_{L^\infty } \lesssim 1$
due to Lemma A.39. Therefore, we conclude the desired bound also for
![]() $\widetilde {S}$
. The bounds for
$\widetilde {S}$
. The bounds for
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $\widetilde {U}$
are proven in the same way as we did with
$\widetilde {U}$
are proven in the same way as we did with
![]() $\mathcal {S}, \widetilde {S}$
.
$\mathcal {S}, \widetilde {S}$
.
Lemma 8.6. We have that
 $$ \begin{align*} \mathcal{S} \geq \frac{\delta_1}{4} \left\langle \frac{\zeta}{\zeta_0} \right\rangle^{-(r-1)}. \end{align*} $$
$$ \begin{align*} \mathcal{S} \geq \frac{\delta_1}{4} \left\langle \frac{\zeta}{\zeta_0} \right\rangle^{-(r-1)}. \end{align*} $$
Proof. The statement clearly holds for
![]() $\zeta < \zeta _0$
from (8.18). Thus, let us work on the region
$\zeta < \zeta _0$
from (8.18). Thus, let us work on the region
![]() $\mathcal {O} = [\zeta _0, \infty )$
. Let us recall that
$\mathcal {O} = [\zeta _0, \infty )$
. Let us recall that
![]() $\mathcal {S}$
solves
$\mathcal {S}$
solves
By (8.21), we have that
 $$ \begin{align} \begin{aligned} \| \mathcal{U}\|_{L^\infty (\mathcal{O} )} +\| \mathcal{S}\|_{L^\infty (\mathcal{O} )}&\lesssim \delta_0 , \\ \| \phi^{1/2} \nabla \mathcal{U} \|_{L^\infty (\mathcal{O} )} + \| \phi^{1/2} \nabla \mathcal{S} \|_{L^\infty (\mathcal{O} )}& \lesssim \delta_0^{(2K-2)/(2K-1)} \bar E^{1/(2K-1)} \lesssim \delta_0^{9/10} \bar{E}^{1/10} \ll \delta_0^{4/5}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \| \mathcal{U}\|_{L^\infty (\mathcal{O} )} +\| \mathcal{S}\|_{L^\infty (\mathcal{O} )}&\lesssim \delta_0 , \\ \| \phi^{1/2} \nabla \mathcal{U} \|_{L^\infty (\mathcal{O} )} + \| \phi^{1/2} \nabla \mathcal{S} \|_{L^\infty (\mathcal{O} )}& \lesssim \delta_0^{(2K-2)/(2K-1)} \bar E^{1/(2K-1)} \lesssim \delta_0^{9/10} \bar{E}^{1/10} \ll \delta_0^{4/5}. \end{aligned} \end{align} $$
Let us also define
![]() $\omega _{\ddot {\zeta }, \ddot {s}} (s) = \left ( \ddot {\zeta } e^{(s-\ddot {s})} \right )^{r-1} \mathcal {S} (\ddot {\zeta } e^{s-\ddot {s}}, s )$
. Then, using (8.27) in (8.26), we obtain that
$\omega _{\ddot {\zeta }, \ddot {s}} (s) = \left ( \ddot {\zeta } e^{(s-\ddot {s})} \right )^{r-1} \mathcal {S} (\ddot {\zeta } e^{s-\ddot {s}}, s )$
. Then, using (8.27) in (8.26), we obtain that
Now, note that
![]() $\frac {-1}{2} + \frac {r-1}{2} <- \frac 1{10}$
because
$\frac {-1}{2} + \frac {r-1}{2} <- \frac 1{10}$
because
![]() $r < r^\ast (\gamma ) < 3-\sqrt {3} $
; hence,
$r < r^\ast (\gamma ) < 3-\sqrt {3} $
; hence,
 $$\begin{align*}{\phi \left( \ddot{\zeta} e^{s-\ddot{s}} \right)^{\frac{-1}{2} + \frac{r-1}{2-2\eta_w}} \lesssim \left( \frac{\ddot{\zeta} e^{s-\ddot{s}} }{ \zeta_0 } \right)^{-\frac{2}{10}(1-\eta_w) } \leq e^{ \frac{-1}{10} (s-\bar s)}},\end{align*}$$
$$\begin{align*}{\phi \left( \ddot{\zeta} e^{s-\ddot{s}} \right)^{\frac{-1}{2} + \frac{r-1}{2-2\eta_w}} \lesssim \left( \frac{\ddot{\zeta} e^{s-\ddot{s}} }{ \zeta_0 } \right)^{-\frac{2}{10}(1-\eta_w) } \leq e^{ \frac{-1}{10} (s-\bar s)}},\end{align*}$$
where we used that
![]() $\eta _w$
is sufficiently small and assumed
$\eta _w$
is sufficiently small and assumed
![]() $\ddot {\zeta } \geq \zeta _0$
. Thus, we obtain
$\ddot {\zeta } \geq \zeta _0$
. Thus, we obtain
 $$ \begin{align} \frac{1}{\zeta_0^{r-1}} \left| \partial_s \omega_{\ddot{\zeta}, \ddot{s}} (s) \right| \lesssim \delta_0^{9/5}e^{ \frac{-1}{10}(s-\bar s)}\, \end{align} $$
$$ \begin{align} \frac{1}{\zeta_0^{r-1}} \left| \partial_s \omega_{\ddot{\zeta}, \ddot{s}} (s) \right| \lesssim \delta_0^{9/5}e^{ \frac{-1}{10}(s-\bar s)}\, \end{align} $$
for any
![]() $s \geq \ddot {s}$
with
$s \geq \ddot {s}$
with
![]() $\ddot {s}, s \in [s_0, s_1]$
and any
$\ddot {s}, s \in [s_0, s_1]$
and any
![]() $\ddot {\zeta } \geq \zeta _0$
.
$\ddot {\zeta } \geq \zeta _0$
.
Integrating (8.29), we obtain
 $$ \begin{align} \frac{1}{\zeta_0^{r-1}} \left| \omega_{\ddot{\zeta}, \ddot{s}} (s) - \ddot{\zeta}^{r-1} \mathcal{S} (\ddot{\zeta}, \ddot{s}) \right| \lesssim \delta_0^{9/5} \ll \delta_1 \delta_0^{1/5}. \end{align} $$
$$ \begin{align} \frac{1}{\zeta_0^{r-1}} \left| \omega_{\ddot{\zeta}, \ddot{s}} (s) - \ddot{\zeta}^{r-1} \mathcal{S} (\ddot{\zeta}, \ddot{s}) \right| \lesssim \delta_0^{9/5} \ll \delta_1 \delta_0^{1/5}. \end{align} $$
Now, for any
![]() $\zeta \in \mathcal {O}$
and
$\zeta \in \mathcal {O}$
and
![]() $s \in [s_0, s_1]$
, there exists
$s \in [s_0, s_1]$
, there exists
![]() $\ddot {\zeta } \geq \zeta _0, \ddot {s} \in [s_0, s_1]$
such that
$\ddot {\zeta } \geq \zeta _0, \ddot {s} \in [s_0, s_1]$
such that
![]() $(\ddot {\zeta }, \ddot {s}) \in \{ \zeta _0 \} \times [s_0, s_1] \cup [\zeta _0, \infty ) \times \{ s_0 \}$
and
$(\ddot {\zeta }, \ddot {s}) \in \{ \zeta _0 \} \times [s_0, s_1] \cup [\zeta _0, \infty ) \times \{ s_0 \}$
and
![]() $\ddot {\zeta } e^{s-\ddot {s}} = \zeta $
. Fixing such conditions for
$\ddot {\zeta } e^{s-\ddot {s}} = \zeta $
. Fixing such conditions for
![]() $\ddot {\zeta }, \ddot {s}$
, we have
$\ddot {\zeta }, \ddot {s}$
, we have
This is due to (8.18) for
![]() $\ddot {\zeta } = \zeta _0$
and due to (8.6) for
$\ddot {\zeta } = \zeta _0$
and due to (8.6) for
![]() $\ddot {s} = s_0$
. From (8.30)–(8.31), we conclude
$\ddot {s} = s_0$
. From (8.30)–(8.31), we conclude
 $$ \begin{align*} \frac{\omega_{\ddot{\zeta}, \ddot{s}} (s)}{\zeta_0^{r-1}} \geq \frac12 \frac{ \ddot{\zeta}^{r-1} }{\zeta_0^{r-1}} \delta_1 - \delta_0^{1/5} \delta_1 \geq \frac14 \frac{ \ddot{\zeta}^{r-1} }{\zeta_0^{r-1} } \delta_1 \geq \frac14 \delta_1. \end{align*} $$
$$ \begin{align*} \frac{\omega_{\ddot{\zeta}, \ddot{s}} (s)}{\zeta_0^{r-1}} \geq \frac12 \frac{ \ddot{\zeta}^{r-1} }{\zeta_0^{r-1}} \delta_1 - \delta_0^{1/5} \delta_1 \geq \frac14 \frac{ \ddot{\zeta}^{r-1} }{\zeta_0^{r-1} } \delta_1 \geq \frac14 \delta_1. \end{align*} $$
Recalling that
![]() $\zeta = \ddot {\zeta } e^{s-\ddot {s}}$
, we get that
$\zeta = \ddot {\zeta } e^{s-\ddot {s}}$
, we get that
 $$ \begin{align*} \frac{\zeta^{r-1}}{\zeta_0^{r-1}} \mathcal{S} (\zeta, s) \geq \frac14 \delta_1\, \end{align*} $$
$$ \begin{align*} \frac{\zeta^{r-1}}{\zeta_0^{r-1}} \mathcal{S} (\zeta, s) \geq \frac14 \delta_1\, \end{align*} $$
for
![]() $\zeta \geq \zeta _0$
, and this completes the proof.
$\zeta \geq \zeta _0$
, and this completes the proof.
Lemma 8.7. Assume
![]() $\zeta> \zeta _0$
. Then, we have that
$\zeta> \zeta _0$
. Then, we have that
where here, we use the notation
![]() $\lesssim _{\delta _1}$
to imply that the implicit constant in the inequality may depend on
$\lesssim _{\delta _1}$
to imply that the implicit constant in the inequality may depend on
![]() $\delta _1$
.
$\delta _1$
.
Proof. From (7.5), we have that
Now, let us define
![]() $\omega _{\ddot {\zeta }, \ddot {s}} (s) = \ddot {\zeta }^r e^{(s-\ddot {s})r} \nabla \mathcal {S} ( \ddot {\zeta } e^{s-\ddot {s}}, s)$
. With this definition and using (8.22), we have that
$\omega _{\ddot {\zeta }, \ddot {s}} (s) = \ddot {\zeta }^r e^{(s-\ddot {s})r} \nabla \mathcal {S} ( \ddot {\zeta } e^{s-\ddot {s}}, s)$
. With this definition and using (8.22), we have that
 $$ \begin{align} \left|\partial_s \omega_{\ddot{\zeta}, \ddot{s}} (s)\right|\lesssim_{\delta_1} \left( \frac{ 1 }{ \phi \left( \ddot{\zeta} e^{s-\ddot{s}} \right) } \left( \ddot{\zeta} e^{s-\ddot{s}} \right)^r \right) \lesssim_{\delta_1} \left( \ddot{\zeta} e^{s-\ddot{s}} \right)^{-2+2\eta_w+r}. \end{align} $$
$$ \begin{align} \left|\partial_s \omega_{\ddot{\zeta}, \ddot{s}} (s)\right|\lesssim_{\delta_1} \left( \frac{ 1 }{ \phi \left( \ddot{\zeta} e^{s-\ddot{s}} \right) } \left( \ddot{\zeta} e^{s-\ddot{s}} \right)^r \right) \lesssim_{\delta_1} \left( \ddot{\zeta} e^{s-\ddot{s}} \right)^{-2+2\eta_w+r}. \end{align} $$
Now, we assume that either
![]() $\ddot {\zeta } = \zeta _0$
or
$\ddot {\zeta } = \zeta _0$
or
![]() $\ddot {s} = s_0$
. Therefore,
$\ddot {s} = s_0$
. Therefore,
Using both (8.33) and (8.34), we obtain that
and this shows our estimate for any
![]() $(\zeta , s) = (\ddot {\zeta } e^{s-\ddot {s}}, s)$
such that
$(\zeta , s) = (\ddot {\zeta } e^{s-\ddot {s}}, s)$
such that
![]() $s \geq \ddot {s}$
and either
$s \geq \ddot {s}$
and either
![]() $\ddot {\zeta } = \zeta _0$
or
$\ddot {\zeta } = \zeta _0$
or
![]() $\ddot {s} = s_0$
. As any
$\ddot {s} = s_0$
. As any
![]() $(\zeta , s)$
with
$(\zeta , s)$
with
![]() $\zeta \geq \zeta _0$
,
$\zeta \geq \zeta _0$
,
![]() $s \geq s_0$
can be written in that way, this finishes our proof.
$s \geq s_0$
can be written in that way, this finishes our proof.
Lemma 8.8. We have that
 $$ \begin{align} \begin{aligned} \phi^{j/2} \left| \nabla^j \left( \frac{1}{\mathcal{S}^{1/\alpha}} \right) \right| &\lesssim_{\delta_1} \langle \zeta \rangle^{(r-1)/\alpha} \left( \langle \zeta \rangle^{r-1/2} \phi^{-1} \right)^{j/(2K-2)} \, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \phi^{j/2} \left| \nabla^j \left( \frac{1}{\mathcal{S}^{1/\alpha}} \right) \right| &\lesssim_{\delta_1} \langle \zeta \rangle^{(r-1)/\alpha} \left( \langle \zeta \rangle^{r-1/2} \phi^{-1} \right)^{j/(2K-2)} \, \end{aligned} \end{align} $$
for any
![]() $0 \leq j \leq 2K-1$
.
$0 \leq j \leq 2K-1$
.
Proof. First, let us note that
 $$ \begin{align} \left|\nabla^j \left( \frac{1}{\mathcal{S}^{1/\alpha}} \right) \right| \lesssim_j \frac{1}{\mathcal{S}^{1/\alpha }}\sum_{j_1 + \ldots + j_\ell = j} \frac{| \nabla^{j_1} \mathcal{S} |}{\mathcal{S} } \cdot \ldots \cdot \frac{| \nabla^{j_1} \mathcal{S} |}{\mathcal{S} }. \end{align} $$
$$ \begin{align} \left|\nabla^j \left( \frac{1}{\mathcal{S}^{1/\alpha}} \right) \right| \lesssim_j \frac{1}{\mathcal{S}^{1/\alpha }}\sum_{j_1 + \ldots + j_\ell = j} \frac{| \nabla^{j_1} \mathcal{S} |}{\mathcal{S} } \cdot \ldots \cdot \frac{| \nabla^{j_1} \mathcal{S} |}{\mathcal{S} }. \end{align} $$
Equation (8.35) follows clearly for the case
![]() $\zeta \leq \zeta _0$
by uniform bounds on
$\zeta \leq \zeta _0$
by uniform bounds on
![]() $\phi $
in this region and the inequality
$\phi $
in this region and the inequality
![]() $\frac {1}{\mathcal {S}^{1/\alpha + j}} \leq \delta _1^{-j-1/\alpha } \lesssim _{\delta _1} 1$
implied by equation (8.18). Therefore, let us assume from now that
$\frac {1}{\mathcal {S}^{1/\alpha + j}} \leq \delta _1^{-j-1/\alpha } \lesssim _{\delta _1} 1$
implied by equation (8.18). Therefore, let us assume from now that
![]() $\zeta \geq \zeta _0$
.
$\zeta \geq \zeta _0$
.
Now, we want to analyze each factor in (8.36) for
![]() $\zeta \geq \zeta _0$
. We first claim that for any
$\zeta \geq \zeta _0$
. We first claim that for any
![]() $1 \leq j \leq 2K-1$
, we have
$1 \leq j \leq 2K-1$
, we have
In order to see this, we apply interpolation (as in Lemma A.1) between (8.20) and (8.32), obtaining
 $$ \begin{align*} 1 &\gtrsim_{\delta_1} \left| \nabla^j \mathcal{S} \zeta^{\left( 1-\frac{j-1}{2K-2}\right) r} \left( \phi(\zeta)^{K} \zeta^{1/2} \right)^{\frac{j-1}{2K-2}}\right| = \left| \nabla^j \mathcal{S} \zeta^r \phi(\zeta)^{j/2} \phi(\zeta)^{\frac{j-K}{2K-2}} \left( \zeta^{1/2-r} \right)^{\frac{j-1}{2K-2}}\right|. \end{align*} $$
$$ \begin{align*} 1 &\gtrsim_{\delta_1} \left| \nabla^j \mathcal{S} \zeta^{\left( 1-\frac{j-1}{2K-2}\right) r} \left( \phi(\zeta)^{K} \zeta^{1/2} \right)^{\frac{j-1}{2K-2}}\right| = \left| \nabla^j \mathcal{S} \zeta^r \phi(\zeta)^{j/2} \phi(\zeta)^{\frac{j-K}{2K-2}} \left( \zeta^{1/2-r} \right)^{\frac{j-1}{2K-2}}\right|. \end{align*} $$
Now, as
![]() $\frac {1}{K} \ll \eta _w \ll 1$
, observe that
$\frac {1}{K} \ll \eta _w \ll 1$
, observe that
![]() $\zeta \phi (\zeta )^{-\frac {K}{2K-2}} \gtrsim _{\delta _1} \zeta ^{1-(1-\eta _w) \left ( 1+\frac {1}{K-1} \right ) } \gtrsim 1$
. This concludes (8.37).
$\zeta \phi (\zeta )^{-\frac {K}{2K-2}} \gtrsim _{\delta _1} \zeta ^{1-(1-\eta _w) \left ( 1+\frac {1}{K-1} \right ) } \gtrsim 1$
. This concludes (8.37).
Now using (8.37) and the lower bound from Lemma 8.6, we get that
 $$ \begin{align*} \left| \frac{ \nabla^j \mathcal{S} }{\mathcal{S}} \right| &\lesssim_{\delta_1} \frac{1}{\mathcal{S}}\phi (\zeta)^{-j/2} \zeta^{-(r-1)} \left( \zeta^{r-1/2} \right)^{-\frac{j-1}{2K-2}} \phi (\zeta)^{- \frac{j}{2K-2} } \\ & \leq \phi(\zeta)^{-j/2} \left( \zeta^{r-1/2} \right)^{-\frac{j-1}{2K-2}} \phi(\zeta)^{- \frac{j}{2K-2} } . \end{align*} $$
$$ \begin{align*} \left| \frac{ \nabla^j \mathcal{S} }{\mathcal{S}} \right| &\lesssim_{\delta_1} \frac{1}{\mathcal{S}}\phi (\zeta)^{-j/2} \zeta^{-(r-1)} \left( \zeta^{r-1/2} \right)^{-\frac{j-1}{2K-2}} \phi (\zeta)^{- \frac{j}{2K-2} } \\ & \leq \phi(\zeta)^{-j/2} \left( \zeta^{r-1/2} \right)^{-\frac{j-1}{2K-2}} \phi(\zeta)^{- \frac{j}{2K-2} } . \end{align*} $$
Plugging this into (8.36), we have that
 $$ \begin{align*} \left| \nabla^j \left( \frac{1}{\mathcal{S}^{1/\alpha}} \right) \right| \lesssim_{\delta_1} \frac{1}{\mathcal{S}^{1/\alpha}}\phi(\zeta)^{-j/2} \left( \zeta^{r-1/2} \phi(\zeta)^{-1} \right)^{j/(2K-2)}. \end{align*} $$
$$ \begin{align*} \left| \nabla^j \left( \frac{1}{\mathcal{S}^{1/\alpha}} \right) \right| \lesssim_{\delta_1} \frac{1}{\mathcal{S}^{1/\alpha}}\phi(\zeta)^{-j/2} \left( \zeta^{r-1/2} \phi(\zeta)^{-1} \right)^{j/(2K-2)}. \end{align*} $$
Using again Lemma 8.6 to bound
![]() $\frac {1}{\mathcal {S}^{1/\alpha }}$
, we obtain the desired result.
$\frac {1}{\mathcal {S}^{1/\alpha }}$
, we obtain the desired result.
Lemma 8.9. There exist values
![]() $C_1, C$
independent of all the other parameters such that
$C_1, C$
independent of all the other parameters such that
and
for every
![]() $\zeta> C_1$
.
$\zeta> C_1$
.
Proof. From (7.5), letting
![]() $W = \mathcal {U} + \mathcal {S}$
and
$W = \mathcal {U} + \mathcal {S}$
and
![]() $Z = \mathcal {U} - \mathcal {S}$
, we have
$Z = \mathcal {U} - \mathcal {S}$
, we have
 $$ \begin{align} \begin{aligned} (\partial_s +r-1) W + (\zeta + \mathcal{U} + \alpha \mathcal{S} ) \partial_\zeta W &= \mathcal{F}_{\mathrm{dis}} - \frac{2\alpha \mathcal{S}}{\zeta } \mathcal{U} , \\ (\partial_s +r-1) Z + (\zeta + \mathcal{U} - \alpha \mathcal{S}) \partial_\zeta Z &= \mathcal{F}_{\mathrm{dis}} + \frac{2\alpha \mathcal{S}}{\zeta } \mathcal{U}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\partial_s +r-1) W + (\zeta + \mathcal{U} + \alpha \mathcal{S} ) \partial_\zeta W &= \mathcal{F}_{\mathrm{dis}} - \frac{2\alpha \mathcal{S}}{\zeta } \mathcal{U} , \\ (\partial_s +r-1) Z + (\zeta + \mathcal{U} - \alpha \mathcal{S}) \partial_\zeta Z &= \mathcal{F}_{\mathrm{dis}} + \frac{2\alpha \mathcal{S}}{\zeta } \mathcal{U}. \end{aligned} \end{align} $$
Denote
![]() $E_W = (\mathcal {U} + \alpha \mathcal {S})$
and
$E_W = (\mathcal {U} + \alpha \mathcal {S})$
and
![]() $E_Z = (\mathcal {U} - \alpha \mathcal {S})$
. Taking one derivative in (8.40), we obtain
$E_Z = (\mathcal {U} - \alpha \mathcal {S})$
. Taking one derivative in (8.40), we obtain
 $$ \begin{align} \begin{aligned} (\partial_s +r) \partial_\zeta W + (\zeta + E_W) \partial_\zeta^2 W &= \partial_\zeta \mathcal{F}_{\mathrm{dis}} - 2\alpha \partial_\zeta\left( \frac{ \mathcal{S} \mathcal{U}}{\zeta } \right) - \partial_\zeta E_W \partial_\zeta W , \\ (\partial_s +r) \partial_\zeta Z + (\zeta + E_Z) \partial_\zeta^2 Z &= \partial_\zeta \mathcal{F}_{\mathrm{dis}} + 2 \alpha \partial_\zeta \left( \frac{ \mathcal{S} \mathcal{U}}{\zeta } \right) - \partial_\zeta E_Z \partial_\zeta Z, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\partial_s +r) \partial_\zeta W + (\zeta + E_W) \partial_\zeta^2 W &= \partial_\zeta \mathcal{F}_{\mathrm{dis}} - 2\alpha \partial_\zeta\left( \frac{ \mathcal{S} \mathcal{U}}{\zeta } \right) - \partial_\zeta E_W \partial_\zeta W , \\ (\partial_s +r) \partial_\zeta Z + (\zeta + E_Z) \partial_\zeta^2 Z &= \partial_\zeta \mathcal{F}_{\mathrm{dis}} + 2 \alpha \partial_\zeta \left( \frac{ \mathcal{S} \mathcal{U}}{\zeta } \right) - \partial_\zeta E_Z \partial_\zeta Z, \end{aligned} \end{align} $$
and taking two derivatives in (8.40)
 $$ \begin{align} \begin{aligned} (\partial_s +r+1) \partial_\zeta^2 W + (\zeta+ E_W) \partial_\zeta^3 W &= \partial_\zeta^2 \mathcal{F}_{\mathrm{dis}} - 2\alpha \partial_\zeta^2 \left( \frac{ \mathcal{S} \mathcal{U}}{\zeta } \right) - 2\partial_\zeta E_W \partial_\zeta^2 W - \partial_\zeta^2 E_W \partial_\zeta W, \\ (\partial_s +r+1)\partial_\zeta^2 Z + (\zeta + E_Z) \partial_\zeta^3 Z &= \partial_\zeta^2 \mathcal{F}_{\mathrm{dis}} + 2 \alpha \partial_\zeta^2 \left( \frac{ \mathcal{S} \mathcal{U}}{\zeta } \right) - 2 \partial_\zeta E_Z \partial_\zeta^2 Z - \partial_\zeta^2 E_Z \partial_\zeta Z. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\partial_s +r+1) \partial_\zeta^2 W + (\zeta+ E_W) \partial_\zeta^3 W &= \partial_\zeta^2 \mathcal{F}_{\mathrm{dis}} - 2\alpha \partial_\zeta^2 \left( \frac{ \mathcal{S} \mathcal{U}}{\zeta } \right) - 2\partial_\zeta E_W \partial_\zeta^2 W - \partial_\zeta^2 E_W \partial_\zeta W, \\ (\partial_s +r+1)\partial_\zeta^2 Z + (\zeta + E_Z) \partial_\zeta^3 Z &= \partial_\zeta^2 \mathcal{F}_{\mathrm{dis}} + 2 \alpha \partial_\zeta^2 \left( \frac{ \mathcal{S} \mathcal{U}}{\zeta } \right) - 2 \partial_\zeta E_Z \partial_\zeta^2 Z - \partial_\zeta^2 E_Z \partial_\zeta Z. \end{aligned} \end{align} $$
Now, we claim
We have
 $$ \begin{align} \begin{aligned} \left| \partial_\zeta \mathcal{F}_{\mathrm{dis}}\right| &\lesssim e^{-\delta_{\mathrm{dis}}s_0} \left( \frac{| \nabla^3 \mathcal{U} | }{\mathcal{S}^{1/\alpha}} + \frac{| \nabla^2 \mathcal{U} | | \nabla \mathcal{S} |}{\mathcal{S}^{1+1/\alpha}} \right) \\ \left| \partial_\zeta^2 \mathcal{F}_{\mathrm{dis}}\right| &\lesssim e^{-\delta_{\mathrm{dis}}s_0} \left( \frac{| \nabla^4 \mathcal{U} |}{\mathcal{S}^{1/\alpha}} + \frac{ | \nabla^3 \mathcal{U} | | \nabla \mathcal{S} | }{\mathcal{S}^{1+1/\alpha}} + \frac{| \nabla^2 \mathcal{U} | | \nabla^2 \mathcal{S} |}{\mathcal{S}^{1+1/\alpha}} + \frac{| \nabla^2 \mathcal{U} | | \nabla \mathcal{S} |^2}{\mathcal{S}^{2+1/\alpha}} \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left| \partial_\zeta \mathcal{F}_{\mathrm{dis}}\right| &\lesssim e^{-\delta_{\mathrm{dis}}s_0} \left( \frac{| \nabla^3 \mathcal{U} | }{\mathcal{S}^{1/\alpha}} + \frac{| \nabla^2 \mathcal{U} | | \nabla \mathcal{S} |}{\mathcal{S}^{1+1/\alpha}} \right) \\ \left| \partial_\zeta^2 \mathcal{F}_{\mathrm{dis}}\right| &\lesssim e^{-\delta_{\mathrm{dis}}s_0} \left( \frac{| \nabla^4 \mathcal{U} |}{\mathcal{S}^{1/\alpha}} + \frac{ | \nabla^3 \mathcal{U} | | \nabla \mathcal{S} | }{\mathcal{S}^{1+1/\alpha}} + \frac{| \nabla^2 \mathcal{U} | | \nabla^2 \mathcal{S} |}{\mathcal{S}^{1+1/\alpha}} + \frac{| \nabla^2 \mathcal{U} | | \nabla \mathcal{S} |^2}{\mathcal{S}^{2+1/\alpha}} \right). \end{aligned} \end{align} $$
Using (8.18) and (8.22) in (8.44), we see that for
![]() $\zeta < \zeta _0$
,
$\zeta < \zeta _0$
,
 $$ \begin{align*} \left| \partial_\zeta \mathcal{F}_{\mathrm{dis}}\right| &\lesssim e^{-\delta_{\mathrm{dis}}s_0} \frac{(\zeta_0^{1/2} \bar E)^{\frac{3}{2K-2}}}{\delta_0^{1+1/\alpha}} \ll e^{-\delta_{\mathrm{dis}} s_0/2} \ll \frac{1}{\zeta_0}, \\ \left| \partial_\zeta^2 \mathcal{F}_{\mathrm{dis}}\right| &\lesssim e^{-\delta_{\mathrm{dis}}s_0} \frac{(\zeta_0^{1/2} \bar E)^{\frac{4}{2K-2}}}{\delta_0^{2+1/\alpha}} \ll e^{-\delta_{\mathrm{dis}} s_0/2} \ll \frac{1}{\zeta_0^2}, \end{align*} $$
$$ \begin{align*} \left| \partial_\zeta \mathcal{F}_{\mathrm{dis}}\right| &\lesssim e^{-\delta_{\mathrm{dis}}s_0} \frac{(\zeta_0^{1/2} \bar E)^{\frac{3}{2K-2}}}{\delta_0^{1+1/\alpha}} \ll e^{-\delta_{\mathrm{dis}} s_0/2} \ll \frac{1}{\zeta_0}, \\ \left| \partial_\zeta^2 \mathcal{F}_{\mathrm{dis}}\right| &\lesssim e^{-\delta_{\mathrm{dis}}s_0} \frac{(\zeta_0^{1/2} \bar E)^{\frac{4}{2K-2}}}{\delta_0^{2+1/\alpha}} \ll e^{-\delta_{\mathrm{dis}} s_0/2} \ll \frac{1}{\zeta_0^2}, \end{align*} $$
so (8.43) holds for the region
![]() $\zeta < \zeta _0$
. For the region
$\zeta < \zeta _0$
. For the region
![]() $\zeta> \zeta _0$
, from (8.21), we have
$\zeta> \zeta _0$
, from (8.21), we have
where we have used that
![]() $\zeta _0$
is sufficiently large, dependent on
$\zeta _0$
is sufficiently large, dependent on
![]() $\bar E$
. Thus, from Lemma 8.6 and (8.44), we see that
$\bar E$
. Thus, from Lemma 8.6 and (8.44), we see that
 $$ \begin{align*} \left| \partial_\zeta \mathcal{F}_{\mathrm{dis}}\right| &\lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}}s_0} \frac{ \phi^{-3/2} }{\zeta^{-(r-1)\left( 1 + 1/\alpha \right)}} \lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}}s_0} \zeta^{-3+4\eta_w+ (r-1) \left( 1 + \frac{1}{\alpha} \right)}, \\ \left| \partial_\zeta^2 \mathcal{F}_{\mathrm{dis}}\right| &\lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}}s_0} \frac{ \phi^{-2} }{\zeta^{-(r-1)\left( 2 + 1/\alpha \right)}} \lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}}s_0} \zeta^{-4+4\eta_w+(r-1) \left( 2 + \frac{1}{\alpha} \right)}. \end{align*} $$
$$ \begin{align*} \left| \partial_\zeta \mathcal{F}_{\mathrm{dis}}\right| &\lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}}s_0} \frac{ \phi^{-3/2} }{\zeta^{-(r-1)\left( 1 + 1/\alpha \right)}} \lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}}s_0} \zeta^{-3+4\eta_w+ (r-1) \left( 1 + \frac{1}{\alpha} \right)}, \\ \left| \partial_\zeta^2 \mathcal{F}_{\mathrm{dis}}\right| &\lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}}s_0} \frac{ \phi^{-2} }{\zeta^{-(r-1)\left( 2 + 1/\alpha \right)}} \lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}}s_0} \zeta^{-4+4\eta_w+(r-1) \left( 2 + \frac{1}{\alpha} \right)}. \end{align*} $$
Thus, using that
![]() $(r-1) \left ( 2 + \frac 1\alpha \right ) < 2$
(due to Lemma A.6),
$(r-1) \left ( 2 + \frac 1\alpha \right ) < 2$
(due to Lemma A.6),
![]() $\eta _w$
is sufficiently small and that
$\eta _w$
is sufficiently small and that
![]() $e^{-\delta _{\mathrm {dis}} s_0}$
is sufficiently small depending on
$e^{-\delta _{\mathrm {dis}} s_0}$
is sufficiently small depending on
![]() $\delta _i$
, we conclude (8.43) for
$\delta _i$
, we conclude (8.43) for
![]() $\zeta> \zeta _0$
.
$\zeta> \zeta _0$
.
Using
![]() $L^\infty $
-interpolation between
$L^\infty $
-interpolation between
![]() $| \widetilde {U} |, | \widetilde {S} | \leq \delta _0$
and (8.22), we have that for
$| \widetilde {U} |, | \widetilde {S} | \leq \delta _0$
and (8.22), we have that for
![]() $i \in \{0, 1, 2\}$
,
$i \in \{0, 1, 2\}$
,
In particular, using Lemma A.39, this shows our statement for
![]() $C_1 < \zeta < \delta _0^{-1/2}$
, so from now on, we will take
$C_1 < \zeta < \delta _0^{-1/2}$
, so from now on, we will take
![]() $C_1' = \delta _0^{-1/2}$
, and we can assume
$C_1' = \delta _0^{-1/2}$
, and we can assume
![]() $\zeta> C_1'$
. In particular, we have
$\zeta> C_1'$
. In particular, we have
Using the estimates
 $$ \begin{align*} 2 \alpha \left| \partial_\zeta \left( \frac{\mathcal{U} \mathcal{S}}{\zeta} \right) \right| \leq 2\alpha | \mathcal{U} \mathcal{S} | + 2\alpha | \partial_\zeta \mathcal{U} \mathcal{S} | + 2 \alpha | \mathcal{U} \partial_\zeta \mathcal{S} | \leq \frac{1}{\zeta}, \end{align*} $$
$$ \begin{align*} 2 \alpha \left| \partial_\zeta \left( \frac{\mathcal{U} \mathcal{S}}{\zeta} \right) \right| \leq 2\alpha | \mathcal{U} \mathcal{S} | + 2\alpha | \partial_\zeta \mathcal{U} \mathcal{S} | + 2 \alpha | \mathcal{U} \partial_\zeta \mathcal{S} | \leq \frac{1}{\zeta}, \end{align*} $$
(8.43) and (8.45), then from (8.41), we obtain
 $$ \begin{align} \begin{aligned} \left| \left( \partial_s +r - 1 - \frac{E_W}{\zeta} \right) \zeta \partial_\zeta W + (\zeta + E_W) \partial_\zeta (\zeta \partial_\zeta W ) \right| &\leq 2 + \frac{r-1}{10} \zeta \partial_\zeta W, \\ \left| \left( \partial_s +r - 1 - \frac{E_Z}{\zeta} \right) \zeta \partial_\zeta Z + (\zeta + E_Z) \partial_\zeta (\zeta \partial_\zeta Z ) \right| &\leq 2 + \frac{r-1}{10} \zeta \partial_\zeta Z . \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left| \left( \partial_s +r - 1 - \frac{E_W}{\zeta} \right) \zeta \partial_\zeta W + (\zeta + E_W) \partial_\zeta (\zeta \partial_\zeta W ) \right| &\leq 2 + \frac{r-1}{10} \zeta \partial_\zeta W, \\ \left| \left( \partial_s +r - 1 - \frac{E_Z}{\zeta} \right) \zeta \partial_\zeta Z + (\zeta + E_Z) \partial_\zeta (\zeta \partial_\zeta Z ) \right| &\leq 2 + \frac{r-1}{10} \zeta \partial_\zeta Z . \end{aligned} \end{align} $$
Now, let us define the trajectories
starting at
![]() $(\bar \zeta , \bar s)$
such that either
$(\bar \zeta , \bar s)$
such that either
![]() $\ddot {\zeta } = C_1'$
or
$\ddot {\zeta } = C_1'$
or
![]() $\ddot {s} = s_0$
. Using (8.45) and noting that
$\ddot {s} = s_0$
. Using (8.45) and noting that
![]() $\delta _0$
is sufficiently small depending on
$\delta _0$
is sufficiently small depending on
![]() $\eta _w$
, we can assume that
$\eta _w$
, we can assume that
![]() $\Upsilon _W, \Upsilon _Z$
are increasing and have derivatives between
$\Upsilon _W, \Upsilon _Z$
are increasing and have derivatives between
![]() $\frac {9}{10}\zeta $
and
$\frac {9}{10}\zeta $
and
![]() $\frac {11}{10}\zeta $
. Thus,
$\frac {11}{10}\zeta $
. Thus,
Let us also define
Using definitions (8.47) and (8.49) in (8.46), together with (8.45), we get
for
![]() $\circ \in \{ W, Z\}$
.
$\circ \in \{ W, Z\}$
.
Now, we claim that there exists some
![]() $C_2$
, sufficiently large and independent of all the other parameters, such that
$C_2$
, sufficiently large and independent of all the other parameters, such that
This is a consequence of
which is trivial for
![]() $\ddot {\zeta } = C_1$
and follows from (8.7) for
$\ddot {\zeta } = C_1$
and follows from (8.7) for
![]() $\ddot {s} = s_0$
.
$\ddot {s} = s_0$
.
Taking
![]() $C_3 = C_2 + \frac {3}{r-1}$
, we have that
$C_3 = C_2 + \frac {3}{r-1}$
, we have that
![]() $\left | \Theta ^{(W)} \right |, \left | \Theta ^{(S)} \right | \leq C_3$
. This is clearly true at
$\left | \Theta ^{(W)} \right |, \left | \Theta ^{(S)} \right | \leq C_3$
. This is clearly true at
![]() $s = \ddot {s}$
due to (8.51), and the inequality cannot break due to (8.50). Therefore, we get that
$s = \ddot {s}$
due to (8.51), and the inequality cannot break due to (8.50). Therefore, we get that
which yields
and completes the proof of (8.38).
Now, we study (8.42). First of all, let us note that
 $$ \begin{align} \begin{aligned} |\partial_\zeta W| \left| \partial_\zeta^2 E_W \right| &= |\partial_\zeta W| \left| \frac{1+\alpha}{2} \partial_\zeta^2 W + \frac{1-\alpha}{2} \partial_\zeta^2 Z \right| \leq \frac{C_3}{\zeta} \left( | \partial_\zeta^2 W | + | \partial_\zeta^2 Z | \right),\\ |\partial_\zeta Z| \left| \partial_\zeta^2 E_Z \right| &= |\partial_\zeta Z| \left| \frac{1-\alpha}{2} \partial_\zeta^2 W + \frac{1+\alpha}{2} \partial_\zeta^2 Z \right| \leq \frac{C_3}{\zeta} \left( | \partial_\zeta^2 W | + | \partial_\zeta^2 Z | \right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} |\partial_\zeta W| \left| \partial_\zeta^2 E_W \right| &= |\partial_\zeta W| \left| \frac{1+\alpha}{2} \partial_\zeta^2 W + \frac{1-\alpha}{2} \partial_\zeta^2 Z \right| \leq \frac{C_3}{\zeta} \left( | \partial_\zeta^2 W | + | \partial_\zeta^2 Z | \right),\\ |\partial_\zeta Z| \left| \partial_\zeta^2 E_Z \right| &= |\partial_\zeta Z| \left| \frac{1-\alpha}{2} \partial_\zeta^2 W + \frac{1+\alpha}{2} \partial_\zeta^2 Z \right| \leq \frac{C_3}{\zeta} \left( | \partial_\zeta^2 W | + | \partial_\zeta^2 Z | \right), \end{aligned} \end{align} $$
and
 $$ \begin{align} \left| 2 \alpha \partial_\zeta^2 \left( \frac{\mathcal{S} \mathcal{U}}{\zeta} \right) \right| \leq \frac{1}{\zeta^2} + 4 \alpha \frac{\partial_\zeta \mathcal{S} \partial_\zeta \mathcal{U}}{\zeta} + \frac{2 \alpha}{\zeta} \left( |\mathcal{S} \partial_\zeta^2 \mathcal{U}| + | \mathcal{U} \partial_\zeta^2 \mathcal{S} | \right) \leq \frac{1+C_3^2}{\zeta^2} + \frac{1}{10\zeta} \left( | \partial_\zeta^2 W | + | \partial_\zeta^2 Z | \right), \end{align} $$
$$ \begin{align} \left| 2 \alpha \partial_\zeta^2 \left( \frac{\mathcal{S} \mathcal{U}}{\zeta} \right) \right| \leq \frac{1}{\zeta^2} + 4 \alpha \frac{\partial_\zeta \mathcal{S} \partial_\zeta \mathcal{U}}{\zeta} + \frac{2 \alpha}{\zeta} \left( |\mathcal{S} \partial_\zeta^2 \mathcal{U}| + | \mathcal{U} \partial_\zeta^2 \mathcal{S} | \right) \leq \frac{1+C_3^2}{\zeta^2} + \frac{1}{10\zeta} \left( | \partial_\zeta^2 W | + | \partial_\zeta^2 Z | \right), \end{align} $$
where we used (8.45) and (8.52). Let us also note from (8.52) that
Taking
![]() $C_3$
larger if needed, and using (8.43), (8.45) and (8.53)–(8.55) in (8.42), we get that
$C_3$
larger if needed, and using (8.43), (8.45) and (8.53)–(8.55) in (8.42), we get that
 $$ \begin{align*} \left| \left( \partial_s +r-1 - \frac{2E_W}{\zeta} \right) \zeta^2 \partial_\zeta^2 W + (\zeta+ E_W) \partial_\zeta \left( \zeta^2\partial_\zeta^2 W \right) \right| &\leq 2+C_3^2 + \frac{4C_3}{\zeta} \left( | \zeta^2\partial_\zeta^2 W | + | \zeta^2\partial_\zeta^2 Z | \right), \\ \left| \left( \partial_s +r-1 - \frac{2E_Z}{\zeta} \right) \zeta^2 \partial_\zeta^2 Z + (\zeta + E_Z) \partial_\zeta \left( \zeta^2 \partial_\zeta^2 Z \right) \right| &\leq 2+C_3^2 + \frac{4 C_3}{\zeta} \left( | \zeta^2\partial_\zeta^2 W | + | \zeta^2\partial_\zeta^2 Z | \right). \end{align*} $$
$$ \begin{align*} \left| \left( \partial_s +r-1 - \frac{2E_W}{\zeta} \right) \zeta^2 \partial_\zeta^2 W + (\zeta+ E_W) \partial_\zeta \left( \zeta^2\partial_\zeta^2 W \right) \right| &\leq 2+C_3^2 + \frac{4C_3}{\zeta} \left( | \zeta^2\partial_\zeta^2 W | + | \zeta^2\partial_\zeta^2 Z | \right), \\ \left| \left( \partial_s +r-1 - \frac{2E_Z}{\zeta} \right) \zeta^2 \partial_\zeta^2 Z + (\zeta + E_Z) \partial_\zeta \left( \zeta^2 \partial_\zeta^2 Z \right) \right| &\leq 2+C_3^2 + \frac{4 C_3}{\zeta} \left( | \zeta^2\partial_\zeta^2 W | + | \zeta^2\partial_\zeta^2 Z | \right). \end{align*} $$
Defining
using (8.45) and recalling that
![]() $\zeta , \Upsilon _W, \Upsilon _Z> C_1' = \delta _0^{-1/2}$
is sufficiently large, we have
$\zeta , \Upsilon _W, \Upsilon _Z> C_1' = \delta _0^{-1/2}$
is sufficiently large, we have
 $$ \begin{align} \begin{aligned} \left| \partial_s \Xi^{(W)} + \left( r-1 \right) \Xi^{(W)} \right| &\leq 2 + C_3^2 + \frac{r-1}{10 \Upsilon_W^{1/2}}\left( \left| \Xi^{(W)} \right| + \frac{\Upsilon_W^{2}}{\Upsilon_Z^2}\left| \Xi^{(Z)} \circ (\Upsilon_Z^{-1} \circ \Upsilon_W ) \right| \right) \\ &\leq 2 + C_3^2 + \frac{r-1}{10}\left( \left| \Xi^{(W)} \right| + \left| \Xi^{(Z)} \circ (\Upsilon_Z^{-1} \circ \Upsilon_W ) \right| \right) ,\\ \left| \partial_s \Xi^{(Z)} + \left( r-1 \right) \Xi^{(Z)} \right| &\leq 2 + C_3^2 + \frac{r-1}{10 \Upsilon_Z^{1/2}}\left( \left| \Xi^{(Z)} \right| + \frac{\Upsilon_Z^{2}}{\Upsilon_W^2} \left| \Xi^{(W)} \circ (\Upsilon_W^{-1} \circ \Upsilon_Z )\right| \right) \\ &\leq 2 + C_3^2 + \frac{r-1}{10}\left( \left| \Xi^{(Z)} \right| + \left| \Xi^{(W)} \circ (\Upsilon_W^{-1} \circ \Upsilon_Z )\right| \right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left| \partial_s \Xi^{(W)} + \left( r-1 \right) \Xi^{(W)} \right| &\leq 2 + C_3^2 + \frac{r-1}{10 \Upsilon_W^{1/2}}\left( \left| \Xi^{(W)} \right| + \frac{\Upsilon_W^{2}}{\Upsilon_Z^2}\left| \Xi^{(Z)} \circ (\Upsilon_Z^{-1} \circ \Upsilon_W ) \right| \right) \\ &\leq 2 + C_3^2 + \frac{r-1}{10}\left( \left| \Xi^{(W)} \right| + \left| \Xi^{(Z)} \circ (\Upsilon_Z^{-1} \circ \Upsilon_W ) \right| \right) ,\\ \left| \partial_s \Xi^{(Z)} + \left( r-1 \right) \Xi^{(Z)} \right| &\leq 2 + C_3^2 + \frac{r-1}{10 \Upsilon_Z^{1/2}}\left( \left| \Xi^{(Z)} \right| + \frac{\Upsilon_Z^{2}}{\Upsilon_W^2} \left| \Xi^{(W)} \circ (\Upsilon_W^{-1} \circ \Upsilon_Z )\right| \right) \\ &\leq 2 + C_3^2 + \frac{r-1}{10}\left( \left| \Xi^{(Z)} \right| + \left| \Xi^{(W)} \circ (\Upsilon_W^{-1} \circ \Upsilon_Z )\right| \right), \end{aligned} \end{align} $$
where in the second and fourth lines, we used (8.48). We can pick a constant
![]() $C_4$
sufficiently large so that
$C_4$
sufficiently large so that
 $$ \begin{align} \begin{aligned} \left| \Xi^{(W)} (\ddot{s}) \right| &= \left| \ddot{\zeta}^{2} \partial_\zeta^2 \left( \ddot{U} ( \ddot{\zeta}, \ddot{s}) + \widetilde{U} ( \ddot{\zeta}, \ddot{s}) + \ddot{S} (\ddot{\zeta}, \ddot{s}) + \widetilde{S} (\ddot{\zeta}, \ddot{s}) \right) \right| \leq C_4, \\ \left| \Xi^{(Z)} (\ddot{s}) \right| &= \left| \ddot{\zeta}^{2} \partial_\zeta^2 \left( \ddot{U} ( \ddot{\zeta}, \ddot{s}) + \widetilde{U} ( \ddot{\zeta}, \ddot{s})- \ddot{S} (\ddot{\zeta}, \ddot{s}) - \widetilde{S} (\ddot{\zeta}, \ddot{s}) \right) \right| \leq C_4. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left| \Xi^{(W)} (\ddot{s}) \right| &= \left| \ddot{\zeta}^{2} \partial_\zeta^2 \left( \ddot{U} ( \ddot{\zeta}, \ddot{s}) + \widetilde{U} ( \ddot{\zeta}, \ddot{s}) + \ddot{S} (\ddot{\zeta}, \ddot{s}) + \widetilde{S} (\ddot{\zeta}, \ddot{s}) \right) \right| \leq C_4, \\ \left| \Xi^{(Z)} (\ddot{s}) \right| &= \left| \ddot{\zeta}^{2} \partial_\zeta^2 \left( \ddot{U} ( \ddot{\zeta}, \ddot{s}) + \widetilde{U} ( \ddot{\zeta}, \ddot{s})- \ddot{S} (\ddot{\zeta}, \ddot{s}) - \widetilde{S} (\ddot{\zeta}, \ddot{s}) \right) \right| \leq C_4. \end{aligned} \end{align} $$
This is clear if
![]() $\ddot {\zeta } = C_1'$
(as
$\ddot {\zeta } = C_1'$
(as
![]() $C_4$
can depend on
$C_4$
can depend on
![]() $C_1$
) and follows from equation (8.7) for
$C_1$
) and follows from equation (8.7) for
![]() $\ddot {s} = s$
.
$\ddot {s} = s$
.
Finally, taking
![]() $C_5 = C_4 + \frac {2}{r-1} (2+C_3^2)$
, we conclude that
$C_5 = C_4 + \frac {2}{r-1} (2+C_3^2)$
, we conclude that
![]() $\Xi ^{(W)}, \Xi ^{(Z)} \leq C_5$
. This follows from (8.58) for
$\Xi ^{(W)}, \Xi ^{(Z)} \leq C_5$
. This follows from (8.58) for
![]() $s = \bar s$
, and the inequality cannot break for
$s = \bar s$
, and the inequality cannot break for
![]() $s> \bar s$
due to equation (8.57). Therefore,
$s> \bar s$
due to equation (8.57). Therefore,
 $$ \begin{align*} | \partial_{\zeta}^2 W \circ \Upsilon_W | \leq \frac{C_5}{ \Upsilon_W^2 } \qquad \mbox{ and } \qquad | \partial_{\zeta}^2 Z \circ \Upsilon_Z | \leq \frac{C_5}{ \Upsilon_Z^2 }, \end{align*} $$
$$ \begin{align*} | \partial_{\zeta}^2 W \circ \Upsilon_W | \leq \frac{C_5}{ \Upsilon_W^2 } \qquad \mbox{ and } \qquad | \partial_{\zeta}^2 Z \circ \Upsilon_Z | \leq \frac{C_5}{ \Upsilon_Z^2 }, \end{align*} $$
which yields
Finally, as any Cartesian second derivative of a radial function is a linear combination of
![]() $\partial _\zeta ^2$
,
$\partial _\zeta ^2$
,
![]() $\frac {\partial _\zeta }{\zeta }$
and
$\frac {\partial _\zeta }{\zeta }$
and
![]() $\frac {1}{\zeta ^2}$
, we conclude (8.39) from (8.45), (8.52) and (8.59).
$\frac {1}{\zeta ^2}$
, we conclude (8.39) from (8.45), (8.52) and (8.59).
Corollary 8.10. There exists some absolute constant
![]() $\bar C$
such that
$\bar C$
such that
Moreover,
Proof. Let
![]() $C, C_1$
be the constants from the statement of Lemma 8.9. Let
$C, C_1$
be the constants from the statement of Lemma 8.9. Let
![]() $C_2 = \max \{ C_1, 1 \}$
. Using Lemma 8.9, we have
$C_2 = \max \{ C_1, 1 \}$
. Using Lemma 8.9, we have
 $$ \begin{align} \| \nabla^2 \mathcal{U} \|_{L^2(B(0, C_2)^c)}^2 \leq C^2 \int_{B(0, C_2)^c} \frac{d\zeta}{\zeta^{4}} = 4 \pi C^2 \int_{C_2}^\infty \zeta^{-2} d\zeta = 4 \pi C^2 \frac{1}{C_2} \leq 4 \pi C^2. \end{align} $$
$$ \begin{align} \| \nabla^2 \mathcal{U} \|_{L^2(B(0, C_2)^c)}^2 \leq C^2 \int_{B(0, C_2)^c} \frac{d\zeta}{\zeta^{4}} = 4 \pi C^2 \int_{C_2}^\infty \zeta^{-2} d\zeta = 4 \pi C^2 \frac{1}{C_2} \leq 4 \pi C^2. \end{align} $$
On the ball
![]() $B(0, C_2)$
, we have
$B(0, C_2)$
, we have
 $$ \begin{align} \| \nabla^2 \mathcal{U} \|_{L^2 (B(0, C_2))}^2 &\leq C_2^3 \| \nabla^2 \mathcal{U} \|_{L^\infty}^2 \leq C_2^3 \left( \| \ddot{U} \|_{W^{2, \infty}} + \| \nabla^2 \widetilde{U} \|_{L^\infty} \right) \nonumber \\ &\leq C_2^3 \left( \| \ddot{U} \|_{W^{2, \infty}} + \| \widetilde{U} \|_{L^\infty}^{\frac{2K-4}{2K-2}} \| \nabla^{2K-2} \widetilde{U} \|_{L^\infty}^{\frac{2}{2K-2}} \right) \nonumber \\ &\lesssim 1 + \delta_0^{\frac{2K-4}{2K-2}} \left( \bar E \zeta_0^{1/2} \right)^{\frac{2}{2K-2}} \lesssim 1, \end{align} $$
$$ \begin{align} \| \nabla^2 \mathcal{U} \|_{L^2 (B(0, C_2))}^2 &\leq C_2^3 \| \nabla^2 \mathcal{U} \|_{L^\infty}^2 \leq C_2^3 \left( \| \ddot{U} \|_{W^{2, \infty}} + \| \nabla^2 \widetilde{U} \|_{L^\infty} \right) \nonumber \\ &\leq C_2^3 \left( \| \ddot{U} \|_{W^{2, \infty}} + \| \widetilde{U} \|_{L^\infty}^{\frac{2K-4}{2K-2}} \| \nabla^{2K-2} \widetilde{U} \|_{L^\infty}^{\frac{2}{2K-2}} \right) \nonumber \\ &\lesssim 1 + \delta_0^{\frac{2K-4}{2K-2}} \left( \bar E \zeta_0^{1/2} \right)^{\frac{2}{2K-2}} \lesssim 1, \end{align} $$
where in the third inequality, we used (8.9), (8.22) and Lemma A.39. Combining (8.62) and (8.63) and taking
![]() $\bar C$
sufficiently large, we obtain equation (8.60) for
$\bar C$
sufficiently large, we obtain equation (8.60) for
![]() $ \nabla ^2 \mathcal {U} $
. The result for
$ \nabla ^2 \mathcal {U} $
. The result for
![]() $\nabla ^2 \mathcal {S} $
is obtained in an analogous way.
$\nabla ^2 \mathcal {S} $
is obtained in an analogous way.
Then, estimate (8.61) just follows from
![]() $L^2$
-interpolation. For
$L^2$
-interpolation. For
![]() $\mathcal {U}$
, we have
$\mathcal {U}$
, we have
Then the required estimate on
![]() $\mathcal {U}$
follows by (8.60) and noting that
$\mathcal {U}$
follows by (8.60) and noting that
An analogous estimate holds for
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Lemma 8.11. We have that
Proof. Writing the expression for
![]() $\mathcal {F}_{\mathrm {dis}}$
from (7.2) in
$\mathcal {F}_{\mathrm {dis}}$
from (7.2) in
![]() $(U, S)$
coordinates, we have that
$(U, S)$
coordinates, we have that
 $$ \begin{align} |\mathcal{F}_{e, \mathrm{dis}}| \lesssim \left| e^{-\delta_{\mathrm{dis}} s} \frac{\Delta \mathcal{U}}{\mathcal{S}^{1/\alpha}}\right| \lesssim e^{-\delta_{\mathrm{dis}} s/2} e^{-\delta_{\mathrm{dis}}s_0/2} \frac{|\Delta \mathcal{U}|}{\mathcal{S}^{1/\alpha}}. \end{align} $$
$$ \begin{align} |\mathcal{F}_{e, \mathrm{dis}}| \lesssim \left| e^{-\delta_{\mathrm{dis}} s} \frac{\Delta \mathcal{U}}{\mathcal{S}^{1/\alpha}}\right| \lesssim e^{-\delta_{\mathrm{dis}} s/2} e^{-\delta_{\mathrm{dis}}s_0/2} \frac{|\Delta \mathcal{U}|}{\mathcal{S}^{1/\alpha}}. \end{align} $$
Lemma 8.5 and Lemma 8.6 give us
 $$ \begin{align} \frac{| \Delta \mathcal{U} |}{\mathcal{S}^{1/\alpha}} \lesssim_{\delta_1} \frac{\zeta^{(r-1)/\alpha }}{\phi} \lesssim_{\delta_1} 1, \end{align} $$
$$ \begin{align} \frac{| \Delta \mathcal{U} |}{\mathcal{S}^{1/\alpha}} \lesssim_{\delta_1} \frac{\zeta^{(r-1)/\alpha }}{\phi} \lesssim_{\delta_1} 1, \end{align} $$
using the definition of
![]() $\phi $
and the inequality
$\phi $
and the inequality
![]() $\frac {r^\ast -1}{\alpha } < 2$
from Lemma A.6. Combining (8.65) and (8.66), and using that
$\frac {r^\ast -1}{\alpha } < 2$
from Lemma A.6. Combining (8.65) and (8.66), and using that
![]() $s_0$
is large enough (depending on
$s_0$
is large enough (depending on
![]() $\delta _0, \delta _1$
), we obtain the bound for
$\delta _0, \delta _1$
), we obtain the bound for
![]() $\mathcal {F}_{e,\mathrm {dis}}$
.
$\mathcal {F}_{e,\mathrm {dis}}$
.
Using the embedding
![]() $L^\infty (B(0, 2)) \rightarrow L^2 (B(0, 2))$
, we get
$L^\infty (B(0, 2)) \rightarrow L^2 (B(0, 2))$
, we get
Note for
![]() $\zeta < \frac 65$
, we have that
$\zeta < \frac 65$
, we have that
![]() $\mathcal {S} (\zeta )> \ddot {S} (\zeta ) - \delta _1 \gtrsim 1$
, so
$\mathcal {S} (\zeta )> \ddot {S} (\zeta ) - \delta _1 \gtrsim 1$
, so
![]() $\frac {1}{\mathcal {S}} \lesssim 1$
. Therefore,
$\frac {1}{\mathcal {S}} \lesssim 1$
. Therefore,
 $$ \begin{align} e^{-\delta_{\mathrm{dis}} s} \left| \Delta^m \left( \frac{\Delta \mathcal{U}}{\mathcal{S}^{1/\alpha}} \right) \right| &\lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}} s} \left| \sum_{i+j=2m} | \nabla^{i+2} \mathcal{U} | \left| \nabla^{j} \left( \frac{1}{\mathcal{S}^{1/\alpha}} \right) \right| \right| \nonumber \\ &\lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}} s} \left| \sum_{i+j=2m} | \nabla^{i+2} \mathcal{U} | \sum_{j_1 + \ldots + j_\ell = j} | \nabla^{j_1} \mathcal{S} | \ldots | \nabla^{j_\ell} \mathcal{S} | \right| \nonumber\\ &\lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}} s_0/2} e^{-\delta_{\mathrm{dis}} s/2} . \end{align} $$
$$ \begin{align} e^{-\delta_{\mathrm{dis}} s} \left| \Delta^m \left( \frac{\Delta \mathcal{U}}{\mathcal{S}^{1/\alpha}} \right) \right| &\lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}} s} \left| \sum_{i+j=2m} | \nabla^{i+2} \mathcal{U} | \left| \nabla^{j} \left( \frac{1}{\mathcal{S}^{1/\alpha}} \right) \right| \right| \nonumber \\ &\lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}} s} \left| \sum_{i+j=2m} | \nabla^{i+2} \mathcal{U} | \sum_{j_1 + \ldots + j_\ell = j} | \nabla^{j_1} \mathcal{S} | \ldots | \nabla^{j_\ell} \mathcal{S} | \right| \nonumber\\ &\lesssim_{\delta_1} e^{-\delta_{\mathrm{dis}} s_0/2} e^{-\delta_{\mathrm{dis}} s/2} . \end{align} $$
From (8.68), noting that
![]() $s_0$
is chosen sufficiently large in terms of
$s_0$
is chosen sufficiently large in terms of
![]() $\delta _1$
, we get that
$\delta _1$
, we get that
Plugging (8.69) and the first bound of the statement into (8.67), we obtain the second bound of the statement.
Now, let us show the estimate for
![]() $\| \mathcal {F}_{e, \mathrm {nl}} \|_{L^\infty }$
. Writing
$\| \mathcal {F}_{e, \mathrm {nl}} \|_{L^\infty }$
. Writing
![]() $\mathcal {F}_{\mathrm {nl}}$
from (7.2) in
$\mathcal {F}_{\mathrm {nl}}$
from (7.2) in
![]() $(U, S)$
coordinates, we have that
$(U, S)$
coordinates, we have that
We know from (8.9) that
![]() $\| \widetilde {U} \|_{L^\infty }, \| \widetilde {S} \|_{L^\infty } \leq \delta _0$
and from Lemma 8.5 that
$\| \widetilde {U} \|_{L^\infty }, \| \widetilde {S} \|_{L^\infty } \leq \delta _0$
and from Lemma 8.5 that
![]() $\| \nabla ^{2K-2} \widetilde {U} \|_{L^\infty }, \| \nabla ^{2K-2} \widetilde {S} \|_{L^\infty } \lesssim \bar {E}$
. Using
$\| \nabla ^{2K-2} \widetilde {U} \|_{L^\infty }, \| \nabla ^{2K-2} \widetilde {S} \|_{L^\infty } \lesssim \bar {E}$
. Using
![]() $L^\infty $
-interpolation between both bounds, we obtain
$L^\infty $
-interpolation between both bounds, we obtain
for
![]() $0\leq \ell \leq 2K-2$
. Applying (8.71) to (8.70), we obtain
$0\leq \ell \leq 2K-2$
. Applying (8.71) to (8.70), we obtain
 $$ \begin{align} \| \mathcal{F}_{\mathrm{nl}, \widetilde{U}} \|_{L^\infty} + \| \mathcal{F}_{\mathrm{nl}, \widetilde{S}} \|_{L^\infty} \lesssim \delta_0^{2} \left( \frac{\bar{E}}{\delta_0} \right)^{1/(2K-2)} \ll \delta_1, \end{align} $$
$$ \begin{align} \| \mathcal{F}_{\mathrm{nl}, \widetilde{U}} \|_{L^\infty} + \| \mathcal{F}_{\mathrm{nl}, \widetilde{S}} \|_{L^\infty} \lesssim \delta_0^{2} \left( \frac{\bar{E}}{\delta_0} \right)^{1/(2K-2)} \ll \delta_1, \end{align} $$
where the last inequality is due to the fact that
![]() $\delta _0^{3/2} \ll \delta _1$
.
$\delta _0^{3/2} \ll \delta _1$
.
For the last inequality of (8.64), using that
![]() $H^{2m}$
is an algebra, from (8.71). we get that
$H^{2m}$
is an algebra, from (8.71). we get that
 $$ \begin{align} \| \Delta^m (\chi_2 \mathcal{F}_{\mathrm{nl}, \widetilde{U}} ) \|_{L^2} + \| \Delta^m (\chi_2 \mathcal{F}_{\mathrm{nl}, \widetilde{S}} ) \|_{L^2} &\lesssim \| \mathcal{F}_{\mathrm{nl}, \widetilde{U}} \|_{X} + \| \mathcal{F}_{\mathrm{nl}, \widetilde{S}} \|_{X} \nonumber \\ &\lesssim_m \left( \| \widetilde{U} \|_{W^{2m, \infty}} + \| \widetilde{S} \|_{W^{2m, \infty}} \right) \left( \| \widetilde{U} \|_{W^{2m+1, \infty}} + \| \widetilde{S} \|_{W^{2m+1, \infty}} \right) \nonumber \\ &\lesssim \delta_0^{(2K-2-2m)/(2K-2)} \bar{E}^{2m/(2K-2)} \delta_0^{(2K-3-2m)/(2K-2)} \bar{E}^{(2m+1)/(2K-2)} \nonumber \\ &= \delta_0^2 \left( \frac{\bar{E}}{\delta_0} \right)^{(4m+1)/(2K-2)} \ll \delta_1 , \end{align} $$
$$ \begin{align} \| \Delta^m (\chi_2 \mathcal{F}_{\mathrm{nl}, \widetilde{U}} ) \|_{L^2} + \| \Delta^m (\chi_2 \mathcal{F}_{\mathrm{nl}, \widetilde{S}} ) \|_{L^2} &\lesssim \| \mathcal{F}_{\mathrm{nl}, \widetilde{U}} \|_{X} + \| \mathcal{F}_{\mathrm{nl}, \widetilde{S}} \|_{X} \nonumber \\ &\lesssim_m \left( \| \widetilde{U} \|_{W^{2m, \infty}} + \| \widetilde{S} \|_{W^{2m, \infty}} \right) \left( \| \widetilde{U} \|_{W^{2m+1, \infty}} + \| \widetilde{S} \|_{W^{2m+1, \infty}} \right) \nonumber \\ &\lesssim \delta_0^{(2K-2-2m)/(2K-2)} \bar{E}^{2m/(2K-2)} \delta_0^{(2K-3-2m)/(2K-2)} \bar{E}^{(2m+1)/(2K-2)} \nonumber \\ &= \delta_0^2 \left( \frac{\bar{E}}{\delta_0} \right)^{(4m+1)/(2K-2)} \ll \delta_1 , \end{align} $$
where in the last inequality, we used
![]() $m \ll K$
,
$m \ll K$
,
![]() $\delta _0^{3/2} \ll \delta _1$
and
$\delta _0^{3/2} \ll \delta _1$
and
![]() $\bar E\ll \frac {1}{\delta _0}$
.
$\bar E\ll \frac {1}{\delta _0}$
.
Equation (8.72) and the embedding
![]() $L^\infty (B(0, 2)) \rightarrow L^2(B(0, 2))$
yield
$L^\infty (B(0, 2)) \rightarrow L^2(B(0, 2))$
yield
where we used
![]() $\delta _0^{3/2} \ll \delta _1$
and
$\delta _0^{3/2} \ll \delta _1$
and
![]() $\delta _0\ll \frac {1}{\bar E}$
. Combining (8.73) with (8.74), we conclude our bound for
$\delta _0\ll \frac {1}{\bar E}$
. Combining (8.73) with (8.74), we conclude our bound for
![]() $\mathcal {F}_{t, \mathrm {nl}}$
.
$\mathcal {F}_{t, \mathrm {nl}}$
.
8.1.2 Proof of the bootstrap estimate (8.15)
Our strategy will be the following. First, we will show that we have
![]() $L^\infty $
estimates in a compact region
$L^\infty $
estimates in a compact region
![]() $\zeta < \frac 65$
. As the extended and truncated solutions agree on that region (Lemma 8.1), we can do that for the truncated equation, for which we have very precise information about its linearized operator (due to Section 7). Then, we will propagate those
$\zeta < \frac 65$
. As the extended and truncated solutions agree on that region (Lemma 8.1), we can do that for the truncated equation, for which we have very precise information about its linearized operator (due to Section 7). Then, we will propagate those
![]() $L^\infty $
estimates for the extended equation to the region
$L^\infty $
estimates for the extended equation to the region
![]() $\zeta> \frac 65$
using trajectory estimates.
$\zeta> \frac 65$
using trajectory estimates.
Lemma 8.12. Under the bootstrap assumptions (8.9), we get the stronger bound
Proof. By Lemma 8.1, the truncated solution and the extended solution agree on
![]() $B \left (0, \frac 65 \right )$
. Then,
$B \left (0, \frac 65 \right )$
. Then,
 $$ \begin{align} \| \widetilde{U}_e \|_{L^\infty (B(0, 6/5))} = \| \widetilde{U}_t \|_{L^\infty(B(0, 6/5))} \lesssim \| \widetilde{U}_t \|_{H^{2m} (B(0, 6/5))} \lesssim \| \widetilde{U}_t \|_{\dot{H}^{2m}(B(0, 6/5))} \leq \int_{B(0, 2)} \left( \Delta^m \widetilde{U}_t \right)^2, \end{align} $$
$$ \begin{align} \| \widetilde{U}_e \|_{L^\infty (B(0, 6/5))} = \| \widetilde{U}_t \|_{L^\infty(B(0, 6/5))} \lesssim \| \widetilde{U}_t \|_{H^{2m} (B(0, 6/5))} \lesssim \| \widetilde{U}_t \|_{\dot{H}^{2m}(B(0, 6/5))} \leq \int_{B(0, 2)} \left( \Delta^m \widetilde{U}_t \right)^2, \end{align} $$
where we used that the
![]() $H^{2m}(B(0, 2))$
norm is equivalent to the
$H^{2m}(B(0, 2))$
norm is equivalent to the
![]() $\dot {H}^{2m}(B(0, 2))$
norm since
$\dot {H}^{2m}(B(0, 2))$
norm since
![]() $\widetilde {U}_t$
vanishes at the boundary. An analogous calculation shows the same bound for
$\widetilde {U}_t$
vanishes at the boundary. An analogous calculation shows the same bound for
![]() $\widetilde {S}_e$
. Now, we claim
$\widetilde {S}_e$
. Now, we claim
 $$ \begin{align} \| (\widetilde{U}_t, \widetilde{S}_t ) \|_X \leq \left( 2 + \frac{4}{\delta_g} \right) \delta_1. \end{align} $$
$$ \begin{align} \| (\widetilde{U}_t, \widetilde{S}_t ) \|_X \leq \left( 2 + \frac{4}{\delta_g} \right) \delta_1. \end{align} $$
It is clear that (8.75) follows directly from (8.76) and (8.77), so it remains to show (8.77).
Clearly, (8.77) is true at
![]() $s = s_0$
by our assumptions on the initial conditions (8.6). Let us recall that by (8.8), the unstable part
$s = s_0$
by our assumptions on the initial conditions (8.6). Let us recall that by (8.8), the unstable part
![]() $P_{\mathrm {uns}}(\widetilde {U}, \widetilde {S}) = (1-P_{\mathrm {sta}})(\widetilde {U}, \widetilde {S})$
will have X norm at most
$P_{\mathrm {uns}}(\widetilde {U}, \widetilde {S}) = (1-P_{\mathrm {sta}})(\widetilde {U}, \widetilde {S})$
will have X norm at most
![]() $\delta _1$
, so in order to show (8.77), we just need to ensure that
$\delta _1$
, so in order to show (8.77), we just need to ensure that
![]() $\| P_{\mathrm {sta}} (\widetilde {u} ,\widetilde {\sigma }) \|_X \leq \delta _1 (1+4/\delta _g)$
.
$\| P_{\mathrm {sta}} (\widetilde {u} ,\widetilde {\sigma }) \|_X \leq \delta _1 (1+4/\delta _g)$
.
Let us recall that the truncated problem (7.7) reads
where the forcings
![]() $\mathcal {F}_{t, \mathrm {dis}}, \mathcal {F}_{t, \mathrm {nl}}$
are calculated via solving the extended equation.
$\mathcal {F}_{t, \mathrm {dis}}, \mathcal {F}_{t, \mathrm {nl}}$
are calculated via solving the extended equation.
Projecting the previous equation and using that
![]() $\mathcal {L}$
is invariant on
$\mathcal {L}$
is invariant on
![]() $V^{\ast \, \perp }$
, we get
$V^{\ast \, \perp }$
, we get
By Duhamel, the solution to the linear equation (8.78) is given by
 $$ \begin{align*} P_{\mathrm{sta}} (\widetilde{U}_t(s), \widetilde{S}_t(S)) = T(s) P_{\mathrm{sta}} (\widetilde{U}_{t, 0}, \widetilde{S}_{t, 0} ) + \int_{s_0}^s T(s-\tilde s) (P_{\mathrm{sta}}\mathcal{F}_{t, \mathrm{dis}}(\tilde{s}) + P_{\mathrm{sta}} \mathcal{F}_{t, \mathrm{nl}} (\tilde{s}) ) d\tilde{s}, \end{align*} $$
$$ \begin{align*} P_{\mathrm{sta}} (\widetilde{U}_t(s), \widetilde{S}_t(S)) = T(s) P_{\mathrm{sta}} (\widetilde{U}_{t, 0}, \widetilde{S}_{t, 0} ) + \int_{s_0}^s T(s-\tilde s) (P_{\mathrm{sta}}\mathcal{F}_{t, \mathrm{dis}}(\tilde{s}) + P_{\mathrm{sta}} \mathcal{F}_{t, \mathrm{nl}} (\tilde{s}) ) d\tilde{s}, \end{align*} $$
where we recall that
![]() $T(s)$
is the contraction semigroup generated by
$T(s)$
is the contraction semigroup generated by
![]() $\mathcal {L}$
. Recall also that
$\mathcal {L}$
. Recall also that
![]() $\| (\widetilde {U}_{t, 0}, \widetilde {S}_{t, 0}) \|_X \leq \delta _1$
due to the hypothesis of Proposition 8.2 and that the semigroup has an exponential decay in the stable space from (7.50). Using those two observations together with Lemma 8.11, we estimate
$\| (\widetilde {U}_{t, 0}, \widetilde {S}_{t, 0}) \|_X \leq \delta _1$
due to the hypothesis of Proposition 8.2 and that the semigroup has an exponential decay in the stable space from (7.50). Using those two observations together with Lemma 8.11, we estimate
 $$ \begin{align*} \left\| P_{\mathrm{sta}} (\widetilde{U}_t(s), \widetilde{S}_t(s)) \right\|_X \leq \delta_1 + \int_{s_0}^s 2 \delta_1 e^{-(\widetilde{s}-s_0)\delta_g/2}d \widetilde{s} \leq \left( 1 + \frac{4}{\delta_g} \right) \delta_1, \end{align*} $$
$$ \begin{align*} \left\| P_{\mathrm{sta}} (\widetilde{U}_t(s), \widetilde{S}_t(s)) \right\|_X \leq \delta_1 + \int_{s_0}^s 2 \delta_1 e^{-(\widetilde{s}-s_0)\delta_g/2}d \widetilde{s} \leq \left( 1 + \frac{4}{\delta_g} \right) \delta_1, \end{align*} $$
and we are done.
Now as
![]() $\delta _1/\delta _g \ll \delta _0$
, it is clear that we get (8.15) in the region
$\delta _1/\delta _g \ll \delta _0$
, it is clear that we get (8.15) in the region
![]() $\zeta < \frac 65$
. The objective is to extend the estimate from Lemma 8.12 to the whole space. We will chose some parameter
$\zeta < \frac 65$
. The objective is to extend the estimate from Lemma 8.12 to the whole space. We will chose some parameter
![]() $\zeta _1$
and divide the argument in two different regions, the region
$\zeta _1$
and divide the argument in two different regions, the region
![]() $6/5\leq \zeta \leq \zeta _1$
and the region
$6/5\leq \zeta \leq \zeta _1$
and the region
![]() $\zeta> \zeta _1$
. The strategy is similar for both regions, since it will be based on trajectory estimates. The fundamental difference is that in the region
$\zeta> \zeta _1$
. The strategy is similar for both regions, since it will be based on trajectory estimates. The fundamental difference is that in the region
![]() $6/5 \leq \zeta \leq \zeta _1$
, the profiles are not small, and we will not be able to extract decay for the perturbation along the trajectories. However, one can bound the amount of time the trajectory stays in this region by a constant, and therefore, the profiles will only grow by a constant factor between
$6/5 \leq \zeta \leq \zeta _1$
, the profiles are not small, and we will not be able to extract decay for the perturbation along the trajectories. However, one can bound the amount of time the trajectory stays in this region by a constant, and therefore, the profiles will only grow by a constant factor between
![]() $\zeta = 6/5$
and
$\zeta = 6/5$
and
![]() $\zeta = \zeta _1$
. In contrast, the profiles will be small for
$\zeta = \zeta _1$
. In contrast, the profiles will be small for
![]() $\zeta> \zeta _1$
, and one can show that the damping part of the linearized operator dominates in this regime. This will give exponential decay for the perturbations in the region
$\zeta> \zeta _1$
, and one can show that the damping part of the linearized operator dominates in this regime. This will give exponential decay for the perturbations in the region
![]() $\zeta \geq \zeta _1$
.
$\zeta \geq \zeta _1$
.
Let us recall the equation for
![]() $\widetilde {W}$
, which reads
$\widetilde {W}$
, which reads
 $$ \begin{align} \begin{aligned} & (\partial_s +r-1+\frac{\alpha}{\zeta}\ddot{W}+\frac{1+\alpha}2\partial_{\zeta}\ddot{W})\widetilde{W} + \left( \zeta+ \frac{1+\alpha}{2} \ddot{W} + \frac{1-\alpha}{2} \ddot{Z} \right) \partial_\zeta \widetilde{W} + \left( \frac{1-\alpha}{2} \partial_{\zeta} \ddot{W} -\frac{\alpha \ddot{Z}}{\zeta} \right)\widetilde{Z} \\ &\qquad\qquad = \mathcal{F}_{\mathrm{dis}} + \mathcal{F}_{\mathrm{nl}, W}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & (\partial_s +r-1+\frac{\alpha}{\zeta}\ddot{W}+\frac{1+\alpha}2\partial_{\zeta}\ddot{W})\widetilde{W} + \left( \zeta+ \frac{1+\alpha}{2} \ddot{W} + \frac{1-\alpha}{2} \ddot{Z} \right) \partial_\zeta \widetilde{W} + \left( \frac{1-\alpha}{2} \partial_{\zeta} \ddot{W} -\frac{\alpha \ddot{Z}}{\zeta} \right)\widetilde{Z} \\ &\qquad\qquad = \mathcal{F}_{\mathrm{dis}} + \mathcal{F}_{\mathrm{nl}, W}. \end{aligned} \end{align} $$
Let us define
Let us define the trajectories
![]() $\ddot {\Upsilon }_W^{(\zeta _\star , s_\star )}$
and
$\ddot {\Upsilon }_W^{(\zeta _\star , s_\star )}$
and
![]() $\ddot {\Upsilon }_Z^{(\zeta _\star , s_\star )}$
solving the following ODEs:
$\ddot {\Upsilon }_Z^{(\zeta _\star , s_\star )}$
solving the following ODEs:
 $$ \begin{align} \partial_s \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}(s) &= \left( \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}(s) + \frac{1+\alpha}{2} \ddot{W}( \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}(s)) + \frac{1-\alpha}{2} \ddot{Z}(\ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}(s) ) \right), \end{align} $$
$$ \begin{align} \partial_s \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}(s) &= \left( \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}(s) + \frac{1+\alpha}{2} \ddot{W}( \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}(s)) + \frac{1-\alpha}{2} \ddot{Z}(\ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}(s) ) \right), \end{align} $$
 $$ \begin{align} \partial_s \ddot{\Upsilon}_Z^{(\zeta_\star, s_\star)}(s) &= \left( \ddot{\Upsilon}_Z^{(\zeta_\star, s_\star)}(s) + \frac{1-\alpha}{2} \ddot{W}(\ddot{\Upsilon}_Z^{(\zeta_\star, s_\star)}(s)) + \frac{1+\alpha}{2} \ddot{Z}(\ddot{\Upsilon}_Z^{(\zeta_\star, s_\star)}(s) ) \right), \end{align} $$
$$ \begin{align} \partial_s \ddot{\Upsilon}_Z^{(\zeta_\star, s_\star)}(s) &= \left( \ddot{\Upsilon}_Z^{(\zeta_\star, s_\star)}(s) + \frac{1-\alpha}{2} \ddot{W}(\ddot{\Upsilon}_Z^{(\zeta_\star, s_\star)}(s)) + \frac{1+\alpha}{2} \ddot{Z}(\ddot{\Upsilon}_Z^{(\zeta_\star, s_\star)}(s) ) \right), \end{align} $$
and starting at the point
![]() $\ddot {\Upsilon }_W^{(\zeta _\star , s_\star )} (s_\star ) = \ddot {\Upsilon }_Z^{(\zeta _\star , s_\star )}(s_\star ) = \zeta _\star $
. To ease the notation, we usually omit superindex
$\ddot {\Upsilon }_W^{(\zeta _\star , s_\star )} (s_\star ) = \ddot {\Upsilon }_Z^{(\zeta _\star , s_\star )}(s_\star ) = \zeta _\star $
. To ease the notation, we usually omit superindex
![]() $(\zeta _\star , s_\star )$
.
$(\zeta _\star , s_\star )$
.
Using (8.80)–(8.82), from (8.79), we obtain
where we have also used Lemma 8.11 to bound the forcings. In an analogous way, we obtain
Let us also note that there exists some large enough constant
![]() $C_1$
such that for any
$C_1$
such that for any
![]() $(\zeta _\star , s_\star )$
such that either
$(\zeta _\star , s_\star )$
such that either
![]() $ \zeta _\star = \frac 65$
or
$ \zeta _\star = \frac 65$
or
![]() $s_\star = s_0$
, we have
$s_\star = s_0$
, we have
 $$ \begin{align} |\widetilde{W} (\zeta_\star, s_\star) |, |\widetilde{Z} (\zeta_\star, s_\star) | \leq C_1 \frac{\delta_1}{\delta_g}. \end{align} $$
$$ \begin{align} |\widetilde{W} (\zeta_\star, s_\star) |, |\widetilde{Z} (\zeta_\star, s_\star) | \leq C_1 \frac{\delta_1}{\delta_g}. \end{align} $$
This follows from (8.6) for
![]() $s_\star = s_0$
and from Lemma 8.12 for
$s_\star = s_0$
and from Lemma 8.12 for
![]() $ \zeta _\star = \frac 65$
. We will always assume that our trajectories start at a point
$ \zeta _\star = \frac 65$
. We will always assume that our trajectories start at a point
![]() $(\zeta _\star , s_\star )$
that is either in
$(\zeta _\star , s_\star )$
that is either in
![]() $\left [ \frac 65, \infty \right ) \times \{ s_0 \}$
or in
$\left [ \frac 65, \infty \right ) \times \{ s_0 \}$
or in
![]() $\left \{ \frac 65 \right \} \times [s_0, s_1]$
, so the above condition will always be satisfied.
$\left \{ \frac 65 \right \} \times [s_0, s_1]$
, so the above condition will always be satisfied.
Observe also that for
![]() $\zeta> \frac 65$
, the right-hand sides of (8.81) and (8.82) are larger than
$\zeta> \frac 65$
, the right-hand sides of (8.81) and (8.82) are larger than
![]() $\frac {\ddot {\Upsilon }_W}{C_0}$
and
$\frac {\ddot {\Upsilon }_W}{C_0}$
and
![]() $\frac {\ddot {\Upsilon }_Z}{C_0}$
, respectively, for some absolute constant
$\frac {\ddot {\Upsilon }_Z}{C_0}$
, respectively, for some absolute constant
![]() $C_0$
, due to Lemma A.33. Therefore, as
$C_0$
, due to Lemma A.33. Therefore, as
![]() $\zeta _\star \geq \frac 65$
, we obtain that
$\zeta _\star \geq \frac 65$
, we obtain that
 $$ \begin{align} \partial_s \ddot{\Upsilon}_\circ (s) \geq \frac{\ddot{\Upsilon}_\circ ( s)}{C_0}, \qquad \ddot{\Upsilon}_\circ^{(\zeta_\star, s_\star)} (s) \geq \ddot{\zeta}_\star e^{(s-s_\star)/C_0}, \end{align} $$
$$ \begin{align} \partial_s \ddot{\Upsilon}_\circ (s) \geq \frac{\ddot{\Upsilon}_\circ ( s)}{C_0}, \qquad \ddot{\Upsilon}_\circ^{(\zeta_\star, s_\star)} (s) \geq \ddot{\zeta}_\star e^{(s-s_\star)/C_0}, \end{align} $$
where
![]() $\circ \in \{ W, Z\}$
, and in the second inequality, we are integrating the first inequality one from
$\circ \in \{ W, Z\}$
, and in the second inequality, we are integrating the first inequality one from
![]() $s_\star $
to s.
$s_\star $
to s.
Now, we estimate
![]() $\widetilde {W}, \widetilde {Z}$
in the region
$\widetilde {W}, \widetilde {Z}$
in the region
![]() $(\zeta , s) \in \left [ \frac 65, \infty \right ) \times [s_0, s_1]$
. As the profiles decay (Lemma A.39), there exists some
$(\zeta , s) \in \left [ \frac 65, \infty \right ) \times [s_0, s_1]$
. As the profiles decay (Lemma A.39), there exists some
![]() $\zeta _1$
such that
$\zeta _1$
such that
![]() $J(\zeta ) < \frac {r-1}{4}$
for
$J(\zeta ) < \frac {r-1}{4}$
for
![]() $\zeta> \zeta _1$
. We treat different the cases where
$\zeta> \zeta _1$
. We treat different the cases where
![]() $\frac 65 < \zeta < \zeta _1$
and
$\frac 65 < \zeta < \zeta _1$
and
![]() $\zeta> \zeta _1$
.
$\zeta> \zeta _1$
.
Case
![]() $\frac 65 < \zeta < \zeta _1$
. Let us fix a large enough constant
$\frac 65 < \zeta < \zeta _1$
. Let us fix a large enough constant
![]() $C_2$
so that
$C_2$
so that
![]() $J(\zeta ) + (r-1) < C_2$
for
$J(\zeta ) + (r-1) < C_2$
for
![]() $\zeta \in \left [\frac 65, \zeta _1 \right ]$
. Then, from (8.83)–(8.84), we have
$\zeta \in \left [\frac 65, \zeta _1 \right ]$
. Then, from (8.83)–(8.84), we have
 $$ \begin{align} \begin{aligned} \left| \partial_s \widetilde{W} ( \ddot{\Upsilon}_W (s), s) \right| \leq 2\delta_1 + C_2 \left( \left| \widetilde{W} ( \ddot{\Upsilon}_W (s), s) \right| + \left| \widetilde{Z} ( \ddot{\Upsilon}_W (s), s) \right| \right) ,\\ \left| \partial_s \widetilde{Z} ( \ddot{\Upsilon}_Z (s), s) \right| \leq 2\delta_1 + C_2 \left( \left| \widetilde{W} ( \ddot{\Upsilon}_Z (s), s) \right| + \left| \widetilde{Z} ( \ddot{\Upsilon}_Z (s), s) \right| \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left| \partial_s \widetilde{W} ( \ddot{\Upsilon}_W (s), s) \right| \leq 2\delta_1 + C_2 \left( \left| \widetilde{W} ( \ddot{\Upsilon}_W (s), s) \right| + \left| \widetilde{Z} ( \ddot{\Upsilon}_W (s), s) \right| \right) ,\\ \left| \partial_s \widetilde{Z} ( \ddot{\Upsilon}_Z (s), s) \right| \leq 2\delta_1 + C_2 \left( \left| \widetilde{W} ( \ddot{\Upsilon}_Z (s), s) \right| + \left| \widetilde{Z} ( \ddot{\Upsilon}_Z (s), s) \right| \right). \end{aligned} \end{align} $$
Now, we claim that
for some constant
![]() $C_3$
sufficiently large. It is clear that this holds whenever
$C_3$
sufficiently large. It is clear that this holds whenever
![]() $\zeta = \frac 65$
or
$\zeta = \frac 65$
or
![]() $\ddot {s} = s_0$
due to (8.85). Let us show (8.88) by contradiction. Let
$\ddot {s} = s_0$
due to (8.85). Let us show (8.88) by contradiction. Let
![]() $s_b$
the first time at which (8.88) fails. Assume that it fails at
$s_b$
the first time at which (8.88) fails. Assume that it fails at
![]() $\zeta = \zeta _b$
and, without loss of generality, assume that
$\zeta = \zeta _b$
and, without loss of generality, assume that
because the case where
![]() $\widetilde {W}(\zeta _b, s_b)$
is negative or the case where the bound fails for
$\widetilde {W}(\zeta _b, s_b)$
is negative or the case where the bound fails for
![]() $\widetilde {Z}$
are analogous.
$\widetilde {Z}$
are analogous.
As
![]() $(\zeta _b, s_b) \in \left [ \frac 65, \zeta _1 \right ] \times [s_0, s_1]$
, and the field of the ODE of
$(\zeta _b, s_b) \in \left [ \frac 65, \zeta _1 \right ] \times [s_0, s_1]$
, and the field of the ODE of
![]() $\ddot {\Upsilon }_W$
is positive (see (8.86)), there is a unique starting point
$\ddot {\Upsilon }_W$
is positive (see (8.86)), there is a unique starting point
![]() $(\zeta _\star , s_\star ) \in \left [ \frac 65, \zeta _1 \right ] \times \{ s_0 \} \cup \left \{ \frac 65 \right \} \times [s_0, s_1]$
such that the trajectory
$(\zeta _\star , s_\star ) \in \left [ \frac 65, \zeta _1 \right ] \times \{ s_0 \} \cup \left \{ \frac 65 \right \} \times [s_0, s_1]$
such that the trajectory
![]() $\left ( \ddot {\Upsilon }_W^{(\zeta _\star , s_\star )}(s), s \right )$
passes through
$\left ( \ddot {\Upsilon }_W^{(\zeta _\star , s_\star )}(s), s \right )$
passes through
![]() $(\zeta _b, s_b)$
. That is,
$(\zeta _b, s_b)$
. That is,
![]() $\Upsilon ^{(\zeta _\star , s_\star )}(s_b) = \zeta _b$
. Let us fix that pair
$\Upsilon ^{(\zeta _\star , s_\star )}(s_b) = \zeta _b$
. Let us fix that pair
![]() $(\zeta _\star , s_\star )$
.
$(\zeta _\star , s_\star )$
.
As equation (8.88) ceases to hold along
![]() $(\Upsilon _W(s), s)$
at time
$(\Upsilon _W(s), s)$
at time
![]() $s_b$
, the derivative of the left-hand side is greater than the derivative of the right-hand side, yielding
$s_b$
, the derivative of the left-hand side is greater than the derivative of the right-hand side, yielding
 $$ \begin{align} \partial_s \widetilde{W} ( \ddot{\Upsilon}_W (s_b), s_b) &\geq \frac{C_1 \delta_1}{\delta_g} e^{C_3 \ddot{\Upsilon}_W(s_b)}C_3 \partial_s \ddot{\Upsilon}_W(s_b)\nonumber\\& \geq \frac{C_1C_3 \delta_1}{\delta_g} e^{C_3 \ddot{\Upsilon}_W(s_b)} \frac{ \ddot{\Upsilon}_W (s_b)}{C_0}= \frac{C_1 C_3 \delta_1}{\delta_g} e^{C_3 \zeta_b} \frac{\zeta_b}{C_0}, \end{align} $$
$$ \begin{align} \partial_s \widetilde{W} ( \ddot{\Upsilon}_W (s_b), s_b) &\geq \frac{C_1 \delta_1}{\delta_g} e^{C_3 \ddot{\Upsilon}_W(s_b)}C_3 \partial_s \ddot{\Upsilon}_W(s_b)\nonumber\\& \geq \frac{C_1C_3 \delta_1}{\delta_g} e^{C_3 \ddot{\Upsilon}_W(s_b)} \frac{ \ddot{\Upsilon}_W (s_b)}{C_0}= \frac{C_1 C_3 \delta_1}{\delta_g} e^{C_3 \zeta_b} \frac{\zeta_b}{C_0}, \end{align} $$
where in the second inequality, we used (8.85).
However, plugging (8.89) into (8.87) at time
![]() $s_b$
, we get
$s_b$
, we get
where in the last inequality, we used
![]() $\delta _g \leq 1$
and
$\delta _g \leq 1$
and
![]() $C_1, C_2> 1$
(they are constants large enough; we can enlarge them if needed).
$C_1, C_2> 1$
(they are constants large enough; we can enlarge them if needed).
Comparing (8.90) with (8.91), we get a contradiction as long as
![]() $C_3 \frac { \zeta _b}{C_0}> 4C_2$
, which can be easily enforced by taking
$C_3 \frac { \zeta _b}{C_0}> 4C_2$
, which can be easily enforced by taking
![]() $C_3 = \frac {4C_0C_2}{6/5}$
because
$C_3 = \frac {4C_0C_2}{6/5}$
because
![]() $\zeta _b> \frac 65$
. Therefore, we conclude that (8.88) holds, which gives a uniform bound
$\zeta _b> \frac 65$
. Therefore, we conclude that (8.88) holds, which gives a uniform bound
for the region
![]() $\frac 65 \leq \zeta \leq \zeta _1$
and some large constant
$\frac 65 \leq \zeta \leq \zeta _1$
and some large constant
![]() $C_4$
. As
$C_4$
. As
![]() $\frac {C_4}{\delta _g}\delta _1 \ll \delta _0$
, note that we now have (8.15) in the region
$\frac {C_4}{\delta _g}\delta _1 \ll \delta _0$
, note that we now have (8.15) in the region
![]() $\zeta \leq \zeta _1$
. Finally, let us treat the region
$\zeta \leq \zeta _1$
. Finally, let us treat the region
![]() $\zeta> \zeta _1$
.
$\zeta> \zeta _1$
.
Case
![]() $ \zeta> \zeta _1$
. First of all, note that the previous case yields that
$ \zeta> \zeta _1$
. First of all, note that the previous case yields that
 $$ \begin{align} |\widetilde{W}(\zeta_1, s)|, |\widetilde{Z} (\zeta_1, s)| \leq C_4 \frac{\delta_1}{\delta_g}\, \end{align} $$
$$ \begin{align} |\widetilde{W}(\zeta_1, s)|, |\widetilde{Z} (\zeta_1, s)| \leq C_4 \frac{\delta_1}{\delta_g}\, \end{align} $$
for all
![]() $s \in [s_0, s_1]$
. Let us recall that
$s \in [s_0, s_1]$
. Let us recall that
![]() $\zeta _1$
was defined so that
$\zeta _1$
was defined so that
![]() $|J(\zeta )| \leq \frac {r-1}{4}$
in this region
$|J(\zeta )| \leq \frac {r-1}{4}$
in this region
![]() $\zeta> \zeta _1$
. Therefore, from (8.83) and (8.84), we have
$\zeta> \zeta _1$
. Therefore, from (8.83) and (8.84), we have
 $$ \begin{align} \begin{aligned} \left| (\partial_s + r - 1) \widetilde{W} ( \ddot{\Upsilon}_W (s), s) \right| &\leq 2\delta_1 + \frac{r-1}{4} \left( \| \widetilde{W}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } + \| \widetilde{Z}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } \right), \\ \left| (\partial_s + r - 1) \widetilde{Z} ( \ddot{\Upsilon}_Z (s), s) \right| &\leq 2\delta_1 + \frac{r-1}{4} \left( \| \widetilde{W}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } + \| \widetilde{Z}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left| (\partial_s + r - 1) \widetilde{W} ( \ddot{\Upsilon}_W (s), s) \right| &\leq 2\delta_1 + \frac{r-1}{4} \left( \| \widetilde{W}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } + \| \widetilde{Z}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } \right), \\ \left| (\partial_s + r - 1) \widetilde{Z} ( \ddot{\Upsilon}_Z (s), s) \right| &\leq 2\delta_1 + \frac{r-1}{4} \left( \| \widetilde{W}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } + \| \widetilde{Z}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } \right). \end{aligned} \end{align} $$
We claim that
 $$ \begin{align} | \widetilde{W} (\zeta, s) |, | \widetilde{Z} (\zeta, s | < 2C_4 \frac{\delta_1}{\delta_g}\, \end{align} $$
$$ \begin{align} | \widetilde{W} (\zeta, s) |, | \widetilde{Z} (\zeta, s | < 2C_4 \frac{\delta_1}{\delta_g}\, \end{align} $$
for all
![]() $\zeta \geq \zeta _1$
and
$\zeta \geq \zeta _1$
and
![]() $s \in [s_0, s_1]$
. This clearly holds at
$s \in [s_0, s_1]$
. This clearly holds at
![]() $\zeta = \zeta _1$
or
$\zeta = \zeta _1$
or
![]() $s = s_0$
due to (8.6) and (8.93). Let
$s = s_0$
due to (8.6) and (8.93). Let
![]() $s_b$
be the first time at which equation (8.95) breaks down, and suppose that happens at
$s_b$
be the first time at which equation (8.95) breaks down, and suppose that happens at
![]() $\zeta _b$
. Without loss of generality, assume that
$\zeta _b$
. Without loss of generality, assume that
![]() $\widetilde {W}(\zeta _b, s_b) = 2C_4 \frac {\delta _1}{\delta _g}$
. Let us consider the trajectory passing through
$\widetilde {W}(\zeta _b, s_b) = 2C_4 \frac {\delta _1}{\delta _g}$
. Let us consider the trajectory passing through
![]() $(\zeta _b, s_b)$
. Then, from (8.94), we have
$(\zeta _b, s_b)$
. Then, from (8.94), we have
 $$ \begin{align*} 0 &\leq \partial_s \widetilde{W}( \ddot{\Upsilon}_W(s), s) \Big|_{s=s_b} \\ &\leq -(r-1)\left( 2C_4 \frac{\delta_1}{\delta_g} \right) + 2\delta_1 + \frac{(r-1)}{4} \left( \| \widetilde{W}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } + \| \widetilde{Z}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } \right) \\ &\leq -(r-1)\left( 2C_4 \frac{\delta_1}{\delta_g} \right) + 2\delta_1 + (r-1)\left( C_4 \frac{\delta_1}{\delta_g} \right) \\ &\leq - \frac{r-1}{2} C_4 \frac{\delta_1}{\delta_g}. \end{align*} $$
$$ \begin{align*} 0 &\leq \partial_s \widetilde{W}( \ddot{\Upsilon}_W(s), s) \Big|_{s=s_b} \\ &\leq -(r-1)\left( 2C_4 \frac{\delta_1}{\delta_g} \right) + 2\delta_1 + \frac{(r-1)}{4} \left( \| \widetilde{W}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } + \| \widetilde{Z}(\cdot, s) \|_{L^\infty[\zeta_1, \infty) } \right) \\ &\leq -(r-1)\left( 2C_4 \frac{\delta_1}{\delta_g} \right) + 2\delta_1 + (r-1)\left( C_4 \frac{\delta_1}{\delta_g} \right) \\ &\leq - \frac{r-1}{2} C_4 \frac{\delta_1}{\delta_g}. \end{align*} $$
In the third inequality, we used that (8.95) is still true at
![]() $s=s_b$
with a non-strict inequality by continuity. Thus, we get a contradiction, and this shows that such
$s=s_b$
with a non-strict inequality by continuity. Thus, we get a contradiction, and this shows that such
![]() $(\zeta _b, s_b)$
cannot exist, so (8.95) holds for any
$(\zeta _b, s_b)$
cannot exist, so (8.95) holds for any
![]() $ \zeta \geq \zeta _1$
and
$ \zeta \geq \zeta _1$
and
![]() $s \geq s_0$
.
$s \geq s_0$
.
Combining equation (8.95) with Lemma 8.12 and equation (8.92), and using that
![]() $\frac {\delta _1}{\delta _g} \ll \delta _0$
, we conclude equation (8.15).
$\frac {\delta _1}{\delta _g} \ll \delta _0$
, we conclude equation (8.15).
8.1.3 Proof of bootstrap estimate (8.16)
As in the previous subsections, we work under the assumptions (8.6)–(8.9). In this subsection, we will show the improved bound (8.16), concluding the proof of Proposition 8.2. We will do so via high-order weighted energy estimates, which we will do directly on our extended equation.
We divide the proof in three steps. First, we will show that the dominant terms on a high derivative of a quadratic term are those where all (or all except one) derivatives fall on the same factor. The second step will be to treat the dominant terms in the energy calculation, using integration by parts in a similar way as one would do for the classical energy estimates. In our third and final step, we treat the term coming from the dissipation, which one cannot expect to bound (since it has more derivatives than our energy). Thus, the strategy is to extract the correct sign for this term.
We take K Laplacians in (7.5). Note that
![]() $\Delta ^K (y F) = y\Delta ^K F + 2K \div \Delta ^{K-1}F$
for any vector field F. Thus,
$\Delta ^K (y F) = y\Delta ^K F + 2K \div \Delta ^{K-1}F$
for any vector field F. Thus,
 $$ \begin{align} \begin{aligned} \Delta^K (y \nabla \mathcal{S}) &= y \cdot \Delta^K \nabla \mathcal{S} + 2K \div \Delta^{K-1} \nabla \mathcal{S} = y \cdot \nabla \Delta^K \mathcal{S} + 2K \Delta^K \mathcal{S} ,\\ \Delta^K (y \nabla \mathcal{U}_i) &= y \cdot \Delta^K \nabla \mathcal{U}_i + 2K \div \Delta^{K-1} \nabla \mathcal{U}_i = y \cdot \nabla \Delta^K \mathcal{U}_i + 2K \Delta^K \mathcal{U}_i. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \Delta^K (y \nabla \mathcal{S}) &= y \cdot \Delta^K \nabla \mathcal{S} + 2K \div \Delta^{K-1} \nabla \mathcal{S} = y \cdot \nabla \Delta^K \mathcal{S} + 2K \Delta^K \mathcal{S} ,\\ \Delta^K (y \nabla \mathcal{U}_i) &= y \cdot \Delta^K \nabla \mathcal{U}_i + 2K \div \Delta^{K-1} \nabla \mathcal{U}_i = y \cdot \nabla \Delta^K \mathcal{U}_i + 2K \Delta^K \mathcal{U}_i. \end{aligned} \end{align} $$
We have also used that
![]() $\Delta \nabla f = \nabla \Delta f$
and that
$\Delta \nabla f = \nabla \Delta f$
and that
![]() $\Delta f = \div \nabla f$
. Taking K Laplacians in (7.5) and using (8.96), we obtain
$\Delta f = \div \nabla f$
. Taking K Laplacians in (7.5) and using (8.96), we obtain
 $$ \begin{align} \begin{aligned} (\partial_s + r -1 + 2K )\Delta^K \mathcal{U}_i + y\cdot \nabla \Delta^K \mathcal{U}_i + \Delta^K (\mathcal{U} \cdot \nabla \mathcal{U}_i) + \alpha \Delta^K (\mathcal{S} \partial_i \mathcal{S}) &= \frac{r^{1+\frac{1}{\alpha}}}{\alpha^{1/\alpha} } e^{-\delta_{\mathrm{dis}} s} \Delta^K \frac{\Delta \mathcal{U}_i}{ \mathcal{S}^{1/\alpha }}, \\ (\partial_s + r - 1 + 2K)\Delta^K \mathcal{S} + y \cdot \nabla \Delta^K \mathcal{S} + \alpha \Delta^K (\mathcal{S} \div \mathcal{U}) + \Delta^K (\mathcal{U} \cdot \nabla \mathcal{S}) &= 0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\partial_s + r -1 + 2K )\Delta^K \mathcal{U}_i + y\cdot \nabla \Delta^K \mathcal{U}_i + \Delta^K (\mathcal{U} \cdot \nabla \mathcal{U}_i) + \alpha \Delta^K (\mathcal{S} \partial_i \mathcal{S}) &= \frac{r^{1+\frac{1}{\alpha}}}{\alpha^{1/\alpha} } e^{-\delta_{\mathrm{dis}} s} \Delta^K \frac{\Delta \mathcal{U}_i}{ \mathcal{S}^{1/\alpha }}, \\ (\partial_s + r - 1 + 2K)\Delta^K \mathcal{S} + y \cdot \nabla \Delta^K \mathcal{S} + \alpha \Delta^K (\mathcal{S} \div \mathcal{U}) + \Delta^K (\mathcal{U} \cdot \nabla \mathcal{S}) &= 0. \end{aligned} \end{align} $$
Now, we multiply each equation by
![]() $\phi ^{2K} \Delta ^K \mathcal {U}_i$
or
$\phi ^{2K} \Delta ^K \mathcal {U}_i$
or
![]() $\phi ^{2K} \Delta ^K \mathcal {S}$
, respectively, in order to do energy estimates. First of all, we claim that as a consequence of Lemma A.5,
$\phi ^{2K} \Delta ^K \mathcal {S}$
, respectively, in order to do energy estimates. First of all, we claim that as a consequence of Lemma A.5,
 $$ \begin{align} \begin{aligned} \left\| \left( \Delta^K (\mathcal{U} \cdot \nabla \mathcal{U}_i ) - \mathcal{U} \nabla \Delta^K \mathcal{U}_i - 2K \partial_\zeta \mathcal{U} \Delta^K \mathcal{U}_i \right) \phi^{K} \right\|_{L^2} &= O \left( \bar{E} \right), \\ \left\| \left( \Delta^K (\mathcal{S} \nabla \mathcal{S}) - \mathcal{S} \nabla \Delta^K \mathcal{S} - 2K \nabla \mathcal{S} \Delta^K \mathcal{S} \right) \phi^{K} \right\|_{L^2} &= O \left( \bar{E} \right), \\ \left\| \left( \Delta^K (\mathcal{U} \cdot \nabla \mathcal{S}) - \mathcal{U} \cdot \nabla \Delta^K \mathcal{S} - 2K \partial_\zeta \mathcal{U} \cdot \Delta^K \mathcal{S} \right) \phi^{K} \right\|_{L^2} &= O \left( \bar{E} \right), \\ \left\| \left( \Delta^K (\mathcal{S} \div (\mathcal{U})) - \mathcal{S} \div ( \Delta^K \mathcal{U} ) - 2K \nabla \mathcal{S} \cdot \Delta^K \mathcal{U} \right) \phi^{K} \right\|_{L^2} &= O \left( \bar{E} \right). \\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\| \left( \Delta^K (\mathcal{U} \cdot \nabla \mathcal{U}_i ) - \mathcal{U} \nabla \Delta^K \mathcal{U}_i - 2K \partial_\zeta \mathcal{U} \Delta^K \mathcal{U}_i \right) \phi^{K} \right\|_{L^2} &= O \left( \bar{E} \right), \\ \left\| \left( \Delta^K (\mathcal{S} \nabla \mathcal{S}) - \mathcal{S} \nabla \Delta^K \mathcal{S} - 2K \nabla \mathcal{S} \Delta^K \mathcal{S} \right) \phi^{K} \right\|_{L^2} &= O \left( \bar{E} \right), \\ \left\| \left( \Delta^K (\mathcal{U} \cdot \nabla \mathcal{S}) - \mathcal{U} \cdot \nabla \Delta^K \mathcal{S} - 2K \partial_\zeta \mathcal{U} \cdot \Delta^K \mathcal{S} \right) \phi^{K} \right\|_{L^2} &= O \left( \bar{E} \right), \\ \left\| \left( \Delta^K (\mathcal{S} \div (\mathcal{U})) - \mathcal{S} \div ( \Delta^K \mathcal{U} ) - 2K \nabla \mathcal{S} \cdot \Delta^K \mathcal{U} \right) \phi^{K} \right\|_{L^2} &= O \left( \bar{E} \right). \\ \end{aligned} \end{align} $$
However, to apply Lemma A.5, we need to verify its hypotheses.
Verifying the Hypotheses of Lemma A.5. We start checking Hypothesis (A.25). Let
![]() $2 \leq j \leq 2K-1$
,
$2 \leq j \leq 2K-1$
,
![]() $\beta = \frac {j-2}{2K-3}$
,
$\beta = \frac {j-2}{2K-3}$
,
![]() $p = \frac {2}{\beta }$
. We have that
$p = \frac {2}{\beta }$
. We have that
 $$ \begin{align} &\int_{\mathbb{R}^3} \left( | \nabla^j \mathcal{U} | + | \nabla^j \mathcal{S} | \right)^2 \left( | \nabla^{2K+1-j} \mathcal{U} | + | \nabla^{2K+1-j} \mathcal{S} | \right)^2 \nonumber \\ & \qquad \leq \left( \int_{\mathbb{R}^3} \left( | \nabla^j \mathcal{U} | + | \nabla^{j} \mathcal{S} | \right)^{2p} \right)^{1/p} \left( \int_{\mathbb{R}^3} \left( | \nabla^{2K+1-j} \mathcal{U} | + | \nabla^{2K+1-j} \mathcal{S} | \right)^{2p/(p-1)} \right)^{1-1/p} \nonumber \\ & \qquad \leq \left( \| \nabla^2 \mathcal{U} \|_{L^\infty} + \| \nabla^2 \mathcal{S} \|_{L^\infty} \right)^{2\beta} \left( \| \nabla^{2K-1} \mathcal{U} \|_{L^2} + \| \nabla^{2K-1} \mathcal{S} \|_{L^2} \right)^{2(1-\beta)} \nonumber \\ &\qquad \qquad \cdot \left( \| \nabla^2 \mathcal{U} \|_{L^\infty} + \| \nabla^2 \mathcal{S} \|_{L^\infty} \right)^{2(1-\beta)} \left( \| \nabla^{2K-1} \mathcal{U} \|_{L^2} + \| \nabla^{2K-1} \mathcal{S} \|_{L^2} \right)^{2\beta} \nonumber \\ &\qquad \leq \left( \| \nabla^{2K-1} \mathcal{U} \|_{L^2} + \| \nabla^{2K-1} \mathcal{S} \|_{L^2} \right)^2 \left( \| \nabla^2 \mathcal{U} \|_{L^\infty} + \| \nabla^2 \mathcal{S} \|_{L^\infty} \right)^2 \nonumber ,\\ &\qquad\lesssim \bar{E}^{\frac{2K-3}{2K-2}} \end{align} $$
$$ \begin{align} &\int_{\mathbb{R}^3} \left( | \nabla^j \mathcal{U} | + | \nabla^j \mathcal{S} | \right)^2 \left( | \nabla^{2K+1-j} \mathcal{U} | + | \nabla^{2K+1-j} \mathcal{S} | \right)^2 \nonumber \\ & \qquad \leq \left( \int_{\mathbb{R}^3} \left( | \nabla^j \mathcal{U} | + | \nabla^{j} \mathcal{S} | \right)^{2p} \right)^{1/p} \left( \int_{\mathbb{R}^3} \left( | \nabla^{2K+1-j} \mathcal{U} | + | \nabla^{2K+1-j} \mathcal{S} | \right)^{2p/(p-1)} \right)^{1-1/p} \nonumber \\ & \qquad \leq \left( \| \nabla^2 \mathcal{U} \|_{L^\infty} + \| \nabla^2 \mathcal{S} \|_{L^\infty} \right)^{2\beta} \left( \| \nabla^{2K-1} \mathcal{U} \|_{L^2} + \| \nabla^{2K-1} \mathcal{S} \|_{L^2} \right)^{2(1-\beta)} \nonumber \\ &\qquad \qquad \cdot \left( \| \nabla^2 \mathcal{U} \|_{L^\infty} + \| \nabla^2 \mathcal{S} \|_{L^\infty} \right)^{2(1-\beta)} \left( \| \nabla^{2K-1} \mathcal{U} \|_{L^2} + \| \nabla^{2K-1} \mathcal{S} \|_{L^2} \right)^{2\beta} \nonumber \\ &\qquad \leq \left( \| \nabla^{2K-1} \mathcal{U} \|_{L^2} + \| \nabla^{2K-1} \mathcal{S} \|_{L^2} \right)^2 \left( \| \nabla^2 \mathcal{U} \|_{L^\infty} + \| \nabla^2 \mathcal{S} \|_{L^\infty} \right)^2 \nonumber ,\\ &\qquad\lesssim \bar{E}^{\frac{2K-3}{2K-2}} \end{align} $$
where in the first inequality, we use Hölder and in the second one, we use endpoint Gagliardo-Nirenberg for each integral. In the last inequality, we are also using (8.61) and
![]() $ | \nabla ^2 \mathcal {U} |+ | \nabla ^2 \mathcal {S} | \lesssim 1$
, which follows from
$ | \nabla ^2 \mathcal {U} |+ | \nabla ^2 \mathcal {S} | \lesssim 1$
, which follows from
![]() $| \nabla ^2 \widetilde {U} |+ | \nabla ^2 \widetilde {S} | \lesssim 1$
which itself follows from interpolating
$| \nabla ^2 \widetilde {U} |+ | \nabla ^2 \widetilde {S} | \lesssim 1$
which itself follows from interpolating
![]() $|\widetilde {U}|, |\widetilde {S}| \leq \delta _0$
(equation (8.9)) with (8.22).
$|\widetilde {U}|, |\widetilde {S}| \leq \delta _0$
(equation (8.9)) with (8.22).
Now let
![]() $\mathcal {B}_2 = \mathbb {R}^3 \setminus B(0, \zeta _0)$
. Now, we let
$\mathcal {B}_2 = \mathbb {R}^3 \setminus B(0, \zeta _0)$
. Now, we let
![]() $\beta ' = \frac {j-1}{2K-1}$
and
$\beta ' = \frac {j-1}{2K-1}$
and
![]() $q = \frac {2}{\beta '}$
. We have that
$q = \frac {2}{\beta '}$
. We have that
 $$ \begin{align} & \int_{\mathcal{B}_2} \left( | \nabla^j \mathcal{U} | + | \nabla^j \mathcal{S} | \right)^2 \left( | \nabla^{2K+1-j} \mathcal{U} | + | \nabla^{2K+1-j} \mathcal{S} | \right)^2 \phi^{2K} \nonumber \\& \quad \leq \left( \int_{\mathcal{B}_2} \left( | \nabla^j \mathcal{U} | + | \nabla^j \mathcal{S} | \right)^{2q} \phi^{2K \beta' q} \right)^{1/q} \left( \int_{\mathcal{B}_2} \left( | \nabla^{2K+1-j} \mathcal{U} | + | \nabla^{2K+1-j} \mathcal{S}| \right)^{2q/(q-1)} \phi^{2qK (1-\beta')/(q-1)} \right)^{1-1/q} \nonumber \\& \quad \lesssim \left[ \left( \| \nabla \mathcal{U} \|_{L^\infty (\mathcal{B}_2)}| + \| \nabla \mathcal{S} \|_{L^\infty (\mathcal{B}_2)} \right)^{2\beta'} \left( \| \phi^{2K} \nabla^{2K} \mathcal{U} \|_{L^2} + \| \nabla^{2K} \mathcal{S} \|_{L^2} \right)^{2(1-\beta')}\right.\nonumber\\& \qquad\ \left. + \left( \| \nabla \mathcal{U} \|_{L^\infty (\mathcal{B}_2)}+ \| \nabla \mathcal{S} \|_{L^\infty (\mathcal{B}_2)} \right)^2 \right] \nonumber \\&\qquad \cdot \left[ \left( \| \nabla \mathcal{U} \|_{L^\infty (\mathcal{B}_2)} + \| \nabla \mathcal{S} \|_{L^\infty (\mathcal{B}_2)} \right)^{2(1-\beta')} \left( \| \nabla^{2K} \mathcal{U} \phi^{2K} \|_{L^2} + \| \nabla^{2K} \mathcal{S} \phi^{2K} \|_{L^2} \right)^{2 \beta'}\right. \nonumber\\& \qquad\quad \left. + \left( \| \nabla \mathcal{U} \|_{L^\infty (\mathcal{B}_2)} + \| \nabla \mathcal{S} \|_{L^\infty (\mathcal{B}_2)} \right)^2 \right] \nonumber \\& \quad \lesssim \left[ \delta_0^{2\beta'} \bar E^{1-\beta'}+ \delta_0 \right] \cdot \left[ \delta_0^{2(1-\beta')} \bar E^{\beta'} + \delta_0 \right] \lesssim \delta_0 \bar E. \end{align} $$
$$ \begin{align} & \int_{\mathcal{B}_2} \left( | \nabla^j \mathcal{U} | + | \nabla^j \mathcal{S} | \right)^2 \left( | \nabla^{2K+1-j} \mathcal{U} | + | \nabla^{2K+1-j} \mathcal{S} | \right)^2 \phi^{2K} \nonumber \\& \quad \leq \left( \int_{\mathcal{B}_2} \left( | \nabla^j \mathcal{U} | + | \nabla^j \mathcal{S} | \right)^{2q} \phi^{2K \beta' q} \right)^{1/q} \left( \int_{\mathcal{B}_2} \left( | \nabla^{2K+1-j} \mathcal{U} | + | \nabla^{2K+1-j} \mathcal{S}| \right)^{2q/(q-1)} \phi^{2qK (1-\beta')/(q-1)} \right)^{1-1/q} \nonumber \\& \quad \lesssim \left[ \left( \| \nabla \mathcal{U} \|_{L^\infty (\mathcal{B}_2)}| + \| \nabla \mathcal{S} \|_{L^\infty (\mathcal{B}_2)} \right)^{2\beta'} \left( \| \phi^{2K} \nabla^{2K} \mathcal{U} \|_{L^2} + \| \nabla^{2K} \mathcal{S} \|_{L^2} \right)^{2(1-\beta')}\right.\nonumber\\& \qquad\ \left. + \left( \| \nabla \mathcal{U} \|_{L^\infty (\mathcal{B}_2)}+ \| \nabla \mathcal{S} \|_{L^\infty (\mathcal{B}_2)} \right)^2 \right] \nonumber \\&\qquad \cdot \left[ \left( \| \nabla \mathcal{U} \|_{L^\infty (\mathcal{B}_2)} + \| \nabla \mathcal{S} \|_{L^\infty (\mathcal{B}_2)} \right)^{2(1-\beta')} \left( \| \nabla^{2K} \mathcal{U} \phi^{2K} \|_{L^2} + \| \nabla^{2K} \mathcal{S} \phi^{2K} \|_{L^2} \right)^{2 \beta'}\right. \nonumber\\& \qquad\quad \left. + \left( \| \nabla \mathcal{U} \|_{L^\infty (\mathcal{B}_2)} + \| \nabla \mathcal{S} \|_{L^\infty (\mathcal{B}_2)} \right)^2 \right] \nonumber \\& \quad \lesssim \left[ \delta_0^{2\beta'} \bar E^{1-\beta'}+ \delta_0 \right] \cdot \left[ \delta_0^{2(1-\beta')} \bar E^{\beta'} + \delta_0 \right] \lesssim \delta_0 \bar E. \end{align} $$
In the first inequality, we used Hölder. In the second inequality, we used Gagliardo-Nirenberg (Lemma A.2). In the third inequality, we used that
![]() $\| \nabla ^{2K} \mathcal {U} \|_{L^2} \lesssim \| \Delta ^K \mathcal {U} \|_{L^2}$
(and the same for
$\| \nabla ^{2K} \mathcal {U} \|_{L^2} \lesssim \| \Delta ^K \mathcal {U} \|_{L^2}$
(and the same for
![]() $\mathcal {S}$
), and
$\mathcal {S}$
), and
Combining (8.99) with (8.100), we see that Hypothesis (A.25) is satisfied.
Now, let us check Hypothesis (A.26). The first part trivially holds due to our bootstrap hypothesis (8.9). For the second part, note that Corollary 8.10 yields
so we just need to treat the region
![]() $\zeta> \zeta _0$
. Let
$\zeta> \zeta _0$
. Let
![]() $\mathcal {B}_2 = \mathbb {R}^3 \setminus B(0, \zeta _0)$
. Using Lemma A.3, we have that
$\mathcal {B}_2 = \mathbb {R}^3 \setminus B(0, \zeta _0)$
. Using Lemma A.3, we have that
where we have used that
![]() $\| \mathcal {U} \|_{L^\infty }, \| \zeta ^{-2} \|_{L^2(\mathcal {B}_1)} \lesssim 1$
. Now, note that
$\| \mathcal {U} \|_{L^\infty }, \| \zeta ^{-2} \|_{L^2(\mathcal {B}_1)} \lesssim 1$
. Now, note that
![]() $\frac {\phi ^{1/4} \zeta ^{1/K}}{\langle \zeta \rangle ^{1/2} } \leq 1$
because
$\frac {\phi ^{1/4} \zeta ^{1/K}}{\langle \zeta \rangle ^{1/2} } \leq 1$
because
![]() $\phi ^{1/2} \leq \zeta ^{1-\eta _w}$
and
$\phi ^{1/2} \leq \zeta ^{1-\eta _w}$
and
![]() $\frac {1}{K} \ll \eta _w$
. Therefore, multiplying the weight in (8.102) by
$\frac {1}{K} \ll \eta _w$
. Therefore, multiplying the weight in (8.102) by
![]() $ \frac {\phi ^{1/4} \zeta ^{1/K}}{\langle \zeta \rangle ^{1/2} }$
, we obtain
$ \frac {\phi ^{1/4} \zeta ^{1/K}}{\langle \zeta \rangle ^{1/2} }$
, we obtain
 $$ \begin{align} \left\| \phi^K \nabla^{2K-1} \mathcal{U} \frac{1}{\phi^{1/4} \langle \zeta \rangle^{1/2}} \right\|_{L^2(\mathcal{B}_1)} \lesssim \bar E^{1-1/(2K)}. \end{align} $$
$$ \begin{align} \left\| \phi^K \nabla^{2K-1} \mathcal{U} \frac{1}{\phi^{1/4} \langle \zeta \rangle^{1/2}} \right\|_{L^2(\mathcal{B}_1)} \lesssim \bar E^{1-1/(2K)}. \end{align} $$
Combining (8.101) with (8.103), we conclude Hypothesis (A.26) holds for
![]() $\mathcal {U}$
. The case of
$\mathcal {U}$
. The case of
![]() $\mathcal {S}$
is completely analogous.
$\mathcal {S}$
is completely analogous.
Finally, let us check Hypothesis (A.27). The second part follows directly from (8.38) in Lemma 8.9. For the first part, note that
 $$ \begin{align*} \| \mathcal{U} \|_{W^{3, \infty}} &\leq \| \ddot{U} \|_{W^{3, \infty}} + \| \widetilde{U} \|_{W^{3, \infty}} \\ & \lesssim 1 + O_K(1) \| \widetilde{U} \|_{L^\infty}^{(2K-5)/(2K-2)} \left( \| \widetilde{U} \|_{L^\infty}^{3/(2K-2)} + \| \nabla^{2K-2} \widetilde{U} \|_{L^\infty}^{3/(2K-2)} \right) \\ & \lesssim 1 + \delta_0^{1/2} \left( \bar E \zeta_0^{1/2} \right)^{3/(2K-2)} \lesssim 1, \end{align*} $$
$$ \begin{align*} \| \mathcal{U} \|_{W^{3, \infty}} &\leq \| \ddot{U} \|_{W^{3, \infty}} + \| \widetilde{U} \|_{W^{3, \infty}} \\ & \lesssim 1 + O_K(1) \| \widetilde{U} \|_{L^\infty}^{(2K-5)/(2K-2)} \left( \| \widetilde{U} \|_{L^\infty}^{3/(2K-2)} + \| \nabla^{2K-2} \widetilde{U} \|_{L^\infty}^{3/(2K-2)} \right) \\ & \lesssim 1 + \delta_0^{1/2} \left( \bar E \zeta_0^{1/2} \right)^{3/(2K-2)} \lesssim 1, \end{align*} $$
where we have used Lemma A.39,
![]() $L^\infty $
-interpolation,
$L^\infty $
-interpolation,
![]() $\| \widetilde {U} \|_{L^\infty } \leq \delta _0$
(from (8.9)) and equation (8.22).
$\| \widetilde {U} \|_{L^\infty } \leq \delta _0$
(from (8.9)) and equation (8.22).
The proof is analogous for
![]() $\mathcal {S}$
, and this concludes checking all the hypotheses of Lemma A.5.
$\mathcal {S}$
, and this concludes checking all the hypotheses of Lemma A.5.
Main energy calculation. Let us go back to (8.97). Let
![]() $\mathcal {J}$
denote the dissipative term
$\mathcal {J}$
denote the dissipative term
 $$ \begin{align*} \mathcal{J} = \int \frac{r^{1+\frac{1}{\alpha}} }{\alpha^{\frac1\alpha} }e^{-\delta_{\mathrm{dis}} s} \Delta^K \frac{\Delta \mathcal{U}}{ \mathcal{S}^{1/\alpha }} \Delta^K \mathcal{U} \phi^{2K}. \end{align*} $$
$$ \begin{align*} \mathcal{J} = \int \frac{r^{1+\frac{1}{\alpha}} }{\alpha^{\frac1\alpha} }e^{-\delta_{\mathrm{dis}} s} \Delta^K \frac{\Delta \mathcal{U}}{ \mathcal{S}^{1/\alpha }} \Delta^K \mathcal{U} \phi^{2K}. \end{align*} $$
Then, using (8.98), we obtain that
 $$ \begin{align} \frac{\partial_s}{2} \left( E_{2K}^2 \right) &= -(2K+r-1) E_{2K}^2 + \frac{1}{2} \int \div(y \phi^{2K} ) \left( (\Delta^K \mathcal{U}_i)^2 + (\Delta^K \mathcal{S} )^2 \right) \nonumber \\& \quad - \sum_{i=1}^3 \int \mathcal{U} \cdot \nabla \Delta^K \mathcal{U}_i \Delta^K \mathcal{U}_i \phi^{2K} - 2K \int \partial_\zeta \mathcal{U} (\Delta^K \mathcal{U})^2 \phi^{2K} \nonumber \\& \quad - \alpha \int \mathcal{S} \nabla \Delta^K \mathcal{S} \cdot \Delta^K \mathcal{U} \phi^{2K} - 2K \alpha \int \Delta^K \mathcal{S} \nabla \mathcal{S} \cdot \Delta^K \mathcal{U} \phi^{2K} \nonumber \\& \quad - \int \mathcal{U} \cdot \nabla \Delta^K \mathcal{S} \Delta^K \mathcal{S} \phi^{2K} - 2K \int \partial_\zeta \mathcal{U} (\Delta^K \mathcal{S})^2 \phi^{2K} \nonumber \\& \quad - \alpha \int \mathcal{S} \div (\Delta^K \mathcal{U}) \Delta^K \mathcal{S} \phi^{2K} - 2K \alpha \int \nabla \mathcal{S} \cdot \Delta^K \mathcal{U} \Delta^K \mathcal{S} \phi^{2K} + \mathcal{J} + O (\bar{E}^2 ) \nonumber \\&= -2K E_{2K}^2 + \frac12 \int \div \left( y\phi^{2K} + \mathcal{U} \phi^{2K} \right) \left( (\Delta^K \mathcal{U})^2 + (\Delta^K \mathcal{S})^2 \right) \nonumber \\& \quad - 2K \int \partial_\zeta \mathcal{U} \left( (\Delta^K \mathcal{U})^2 + (\Delta^K \mathcal{S})^2 \right) \phi^{2K} \nonumber \\& \quad - \alpha \int \mathcal{S} \div( \Delta^K \mathcal{S} \cdot \Delta^K \mathcal{U} )\phi^{2K} - 4K \alpha \int \Delta^K \mathcal{S} \nabla \mathcal{S} \cdot \Delta^K \mathcal{U} \phi^{2K} + \mathcal{J} + O (\bar{E}^2 )\nonumber \\&\leq -2K \int (1+\partial_\zeta \mathcal{U} - \alpha | \nabla \mathcal{S} |) \left( (\Delta^K \mathcal{U} )^2 + (\Delta^K \mathcal{S})^2 \right) \phi^{2K} \nonumber \\& \quad + \frac12 \int (\zeta + | \mathcal{U} | + \alpha \mathcal{S}) | \nabla (\phi^{2K}) | \left( (\Delta^K \mathcal{U})^2 + (\Delta^K \mathcal{S})^2 \right) + \mathcal{J} + O (\bar{E}^2 )\nonumber \\& = -2K \int \left( 1 + \partial_\zeta \mathcal{U} - \alpha | \nabla \mathcal{S} | - \frac{| \nabla \phi|}{2\phi} \left( \zeta + | \mathcal{U} | + \alpha S \right) \right) \left( (\Delta^K \mathcal{U})^2 + (\Delta^K \mathcal{S})^2 \right) \phi^{2K} + \mathcal{J} + O (\bar{E}^2 ) , \end{align} $$
$$ \begin{align} \frac{\partial_s}{2} \left( E_{2K}^2 \right) &= -(2K+r-1) E_{2K}^2 + \frac{1}{2} \int \div(y \phi^{2K} ) \left( (\Delta^K \mathcal{U}_i)^2 + (\Delta^K \mathcal{S} )^2 \right) \nonumber \\& \quad - \sum_{i=1}^3 \int \mathcal{U} \cdot \nabla \Delta^K \mathcal{U}_i \Delta^K \mathcal{U}_i \phi^{2K} - 2K \int \partial_\zeta \mathcal{U} (\Delta^K \mathcal{U})^2 \phi^{2K} \nonumber \\& \quad - \alpha \int \mathcal{S} \nabla \Delta^K \mathcal{S} \cdot \Delta^K \mathcal{U} \phi^{2K} - 2K \alpha \int \Delta^K \mathcal{S} \nabla \mathcal{S} \cdot \Delta^K \mathcal{U} \phi^{2K} \nonumber \\& \quad - \int \mathcal{U} \cdot \nabla \Delta^K \mathcal{S} \Delta^K \mathcal{S} \phi^{2K} - 2K \int \partial_\zeta \mathcal{U} (\Delta^K \mathcal{S})^2 \phi^{2K} \nonumber \\& \quad - \alpha \int \mathcal{S} \div (\Delta^K \mathcal{U}) \Delta^K \mathcal{S} \phi^{2K} - 2K \alpha \int \nabla \mathcal{S} \cdot \Delta^K \mathcal{U} \Delta^K \mathcal{S} \phi^{2K} + \mathcal{J} + O (\bar{E}^2 ) \nonumber \\&= -2K E_{2K}^2 + \frac12 \int \div \left( y\phi^{2K} + \mathcal{U} \phi^{2K} \right) \left( (\Delta^K \mathcal{U})^2 + (\Delta^K \mathcal{S})^2 \right) \nonumber \\& \quad - 2K \int \partial_\zeta \mathcal{U} \left( (\Delta^K \mathcal{U})^2 + (\Delta^K \mathcal{S})^2 \right) \phi^{2K} \nonumber \\& \quad - \alpha \int \mathcal{S} \div( \Delta^K \mathcal{S} \cdot \Delta^K \mathcal{U} )\phi^{2K} - 4K \alpha \int \Delta^K \mathcal{S} \nabla \mathcal{S} \cdot \Delta^K \mathcal{U} \phi^{2K} + \mathcal{J} + O (\bar{E}^2 )\nonumber \\&\leq -2K \int (1+\partial_\zeta \mathcal{U} - \alpha | \nabla \mathcal{S} |) \left( (\Delta^K \mathcal{U} )^2 + (\Delta^K \mathcal{S})^2 \right) \phi^{2K} \nonumber \\& \quad + \frac12 \int (\zeta + | \mathcal{U} | + \alpha \mathcal{S}) | \nabla (\phi^{2K}) | \left( (\Delta^K \mathcal{U})^2 + (\Delta^K \mathcal{S})^2 \right) + \mathcal{J} + O (\bar{E}^2 )\nonumber \\& = -2K \int \left( 1 + \partial_\zeta \mathcal{U} - \alpha | \nabla \mathcal{S} | - \frac{| \nabla \phi|}{2\phi} \left( \zeta + | \mathcal{U} | + \alpha S \right) \right) \left( (\Delta^K \mathcal{U})^2 + (\Delta^K \mathcal{S})^2 \right) \phi^{2K} + \mathcal{J} + O (\bar{E}^2 ) , \end{align} $$
where we have used (8.9). Now, we claim that
 $$ \begin{align} \left( 1 + \partial_\zeta \mathcal{U} - \alpha | \nabla \mathcal{S} | - \frac{| \nabla \phi|}{2\phi} \left( \zeta + | \mathcal{U} | + \alpha S \right) \right) \geq \eta\, \end{align} $$
$$ \begin{align} \left( 1 + \partial_\zeta \mathcal{U} - \alpha | \nabla \mathcal{S} | - \frac{| \nabla \phi|}{2\phi} \left( \zeta + | \mathcal{U} | + \alpha S \right) \right) \geq \eta\, \end{align} $$
for some positive constant
![]() $\eta $
. In the region
$\eta $
. In the region
![]() $\zeta < \zeta _0$
, we have that
$\zeta < \zeta _0$
, we have that
![]() $\nabla \phi = 0$
and
$\nabla \phi = 0$
and
![]() $1 + \partial _\zeta \ddot {U} - \alpha | \nabla \ddot {S} | \geq \eta _{\mathrm {damp}}> 0$
due to Lemma A.36. Therefore, taking
$1 + \partial _\zeta \ddot {U} - \alpha | \nabla \ddot {S} | \geq \eta _{\mathrm {damp}}> 0$
due to Lemma A.36. Therefore, taking
![]() $\delta _0$
small enough and using that
$\delta _0$
small enough and using that
![]() $| \partial _\zeta \widetilde {U} |, | \nabla \widetilde {S} | \lesssim \delta _0^{(2K-1)/(2K-2)} \bar {E}^{1/(2K-2)}$
(equation (8.71)), we conclude that (8.105) holds for
$| \partial _\zeta \widetilde {U} |, | \nabla \widetilde {S} | \lesssim \delta _0^{(2K-1)/(2K-2)} \bar {E}^{1/(2K-2)}$
(equation (8.71)), we conclude that (8.105) holds for
![]() $\eta \leq \frac 12 \eta _{\mathrm {damp}}$
and
$\eta \leq \frac 12 \eta _{\mathrm {damp}}$
and
![]() $\zeta < \zeta _0$
.
$\zeta < \zeta _0$
.
In the region
![]() $\zeta> \zeta _0$
, equation (8.105) reduces to show
$\zeta> \zeta _0$
, equation (8.105) reduces to show
since the remaining terms are
![]() $ O (\delta _0^{(2K-1)/(2K-2)} \bar {E}^{1/(2K-2)})$
by (8.71).
$ O (\delta _0^{(2K-1)/(2K-2)} \bar {E}^{1/(2K-2)})$
by (8.71).
Using that
![]() $|\nabla \phi | \zeta \leq 2(1-\eta _w ) \phi $
, we conclude that taking
$|\nabla \phi | \zeta \leq 2(1-\eta _w ) \phi $
, we conclude that taking
![]() $\delta _0$
small enough (8.105) holds for
$\delta _0$
small enough (8.105) holds for
![]() $\eta < \frac 12 \eta _w$
.
$\eta < \frac 12 \eta _w$
.
Putting everything together, we have that (8.105) holds globally for
![]() $\eta = \frac 12 \min \{ \eta _{\mathrm {damp}}, \eta _w \}$
, and plugging this in (8.104), we conclude
$\eta = \frac 12 \min \{ \eta _{\mathrm {damp}}, \eta _w \}$
, and plugging this in (8.104), we conclude
Sign on the dissipative term. We proceed by estimating
![]() $\mathcal {J}$
by subtracting off the highest-order term. Letting
$\mathcal {J}$
by subtracting off the highest-order term. Letting
 $$ \begin{align*} \mathcal{G}^2 = \sum_{i=1}^3 \int \frac{( \nabla \Delta^K \mathcal{U}_i )^2}{\mathcal{S}^{1/\alpha}} \phi^{2K}, \end{align*} $$
$$ \begin{align*} \mathcal{G}^2 = \sum_{i=1}^3 \int \frac{( \nabla \Delta^K \mathcal{U}_i )^2}{\mathcal{S}^{1/\alpha}} \phi^{2K}, \end{align*} $$
integrating by parts, and using Cauchy-Schwarz, we have that
 $$ \begin{align} \left| \frac{\alpha^{1/\alpha} }{r^{1+1/\alpha }} e^{\delta_{\mathrm{dis}} s}\mathcal{J} + \mathcal{G}^2 \right| &\leq \mathcal{G} \sum_{i=2}^{2K} \binom{2K-1}{i-2} \left( \int \frac{\mathcal{S}^{1/\alpha}}{\phi} |\partial^i \mathcal{U}|^2 \phi^i \left( \partial^{2K+1-i} \left( \frac{1}{\mathcal{S}^{1 / \alpha}} \right) \right)^2 \phi^{2K+1-i} \right)^{1/2} \nonumber \\&\leq \mathcal{G} \Bigg( (2K-1) \left( \int | \partial^{2K} \mathcal{U} |^2 \phi^{2K} \right)^{1/2} \left\| \mathcal{S}^{1/\alpha} \left| \nabla \left( \frac{1}{\mathcal{S}^{1/\alpha}} \right) \right| \right\|^{1/2}_{L^\infty} \nonumber \\&\quad+\sum_{i=2}^{2K-1} \binom{2K-1}{i-2} \left( \int_{\mathcal{B}_1} \frac{\mathcal{S}^{1/\alpha}}{\phi} |\partial^i \mathcal{U}|^2 \phi^i \left( \partial^{2K+1-i} \left( \frac{1}{\mathcal{S}^{1 / \alpha}} \right) \right)^2 \phi^{2K+1-i} \right)^{1/2} \nonumber \\&\quad+\sum_{i=2}^{2K-1} \binom{2K-1}{i-2} \left( \int_{\mathcal{B}_2} \frac{\mathcal{S}^{1/\alpha}}{\phi} |\partial^i \mathcal{U}|^2 \phi^i \left( \partial^{2K+1-i} \left( \frac{1}{\mathcal{S}^{1 / \alpha}} \right) \right)^2 \phi^{2K+1-i} \right)^{1/2} \Bigg) \nonumber \\&= \mathcal{G} (\mathcal{Q}_1 + \mathcal{Q}_2 + \mathcal{Q}_3 ), \end{align} $$
$$ \begin{align} \left| \frac{\alpha^{1/\alpha} }{r^{1+1/\alpha }} e^{\delta_{\mathrm{dis}} s}\mathcal{J} + \mathcal{G}^2 \right| &\leq \mathcal{G} \sum_{i=2}^{2K} \binom{2K-1}{i-2} \left( \int \frac{\mathcal{S}^{1/\alpha}}{\phi} |\partial^i \mathcal{U}|^2 \phi^i \left( \partial^{2K+1-i} \left( \frac{1}{\mathcal{S}^{1 / \alpha}} \right) \right)^2 \phi^{2K+1-i} \right)^{1/2} \nonumber \\&\leq \mathcal{G} \Bigg( (2K-1) \left( \int | \partial^{2K} \mathcal{U} |^2 \phi^{2K} \right)^{1/2} \left\| \mathcal{S}^{1/\alpha} \left| \nabla \left( \frac{1}{\mathcal{S}^{1/\alpha}} \right) \right| \right\|^{1/2}_{L^\infty} \nonumber \\&\quad+\sum_{i=2}^{2K-1} \binom{2K-1}{i-2} \left( \int_{\mathcal{B}_1} \frac{\mathcal{S}^{1/\alpha}}{\phi} |\partial^i \mathcal{U}|^2 \phi^i \left( \partial^{2K+1-i} \left( \frac{1}{\mathcal{S}^{1 / \alpha}} \right) \right)^2 \phi^{2K+1-i} \right)^{1/2} \nonumber \\&\quad+\sum_{i=2}^{2K-1} \binom{2K-1}{i-2} \left( \int_{\mathcal{B}_2} \frac{\mathcal{S}^{1/\alpha}}{\phi} |\partial^i \mathcal{U}|^2 \phi^i \left( \partial^{2K+1-i} \left( \frac{1}{\mathcal{S}^{1 / \alpha}} \right) \right)^2 \phi^{2K+1-i} \right)^{1/2} \Bigg) \nonumber \\&= \mathcal{G} (\mathcal{Q}_1 + \mathcal{Q}_2 + \mathcal{Q}_3 ), \end{align} $$
where we have divided the integrals in the regions
![]() $\mathcal {B}_1 = B(0, \zeta _0)$
and
$\mathcal {B}_1 = B(0, \zeta _0)$
and
![]() $\mathcal {B}_2 = \mathbb {R}^3 \setminus \mathcal {B}_1$
. Using Lemma 8.8, we have that
$\mathcal {B}_2 = \mathbb {R}^3 \setminus \mathcal {B}_1$
. Using Lemma 8.8, we have that
where in the last equality, we have used Lemma A.6 and
![]() $\mathcal {S} \langle \zeta \rangle ^{(r-1)} \lesssim 1$
by Lemma 8.6.
$\mathcal {S} \langle \zeta \rangle ^{(r-1)} \lesssim 1$
by Lemma 8.6.
In order to bound
![]() $\mathcal {Q}_2$
, we use again Lemma 8.8 and note that
$\mathcal {Q}_2$
, we use again Lemma 8.8 and note that
![]() $\phi (\zeta ) \lesssim _{\zeta _0, K} 1$
in
$\phi (\zeta ) \lesssim _{\zeta _0, K} 1$
in
![]() $\mathcal {B}_1$
. We obtain
$\mathcal {B}_1$
. We obtain
 $$ \begin{align} \mathcal{Q}_2 &\lesssim_{K, \bar E, \delta_0, \zeta_0} \sum_{i=2}^{2K-1} \left( \int_{\mathcal{B}_1} \mathcal{S}^{1/\alpha} |\partial^i \mathcal{U}|^2 \langle \zeta \rangle^{2\frac{r-1}{\alpha}} \right)^{1/2} \nonumber \\ &\lesssim_{K, \bar E, \delta_0, \zeta_0} \left( \int_{\mathcal{B}_1} \frac{1}{\zeta^{1/2}} \right)^{1/2} \lesssim_{K, \bar E, \delta_0, \zeta_0} 1, \end{align} $$
$$ \begin{align} \mathcal{Q}_2 &\lesssim_{K, \bar E, \delta_0, \zeta_0} \sum_{i=2}^{2K-1} \left( \int_{\mathcal{B}_1} \mathcal{S}^{1/\alpha} |\partial^i \mathcal{U}|^2 \langle \zeta \rangle^{2\frac{r-1}{\alpha}} \right)^{1/2} \nonumber \\ &\lesssim_{K, \bar E, \delta_0, \zeta_0} \left( \int_{\mathcal{B}_1} \frac{1}{\zeta^{1/2}} \right)^{1/2} \lesssim_{K, \bar E, \delta_0, \zeta_0} 1, \end{align} $$
where in the second inequality, we also used (8.20) (for
![]() $i=2K-1$
) and (8.21) (for
$i=2K-1$
) and (8.21) (for
![]() $i \leq 2K-2$
).
$i \leq 2K-2$
).
Lastly, let us bound
![]() $\mathcal {Q}_3$
. Note that in
$\mathcal {Q}_3$
. Note that in
![]() $\mathcal {B}_2$
, we have (8.20), which yields
$\mathcal {B}_2$
, we have (8.20), which yields
 $$ \begin{align*} |\nabla^i \mathcal{U}| \phi^{i/2} &\lesssim \bar{E} \left( \frac{1}{\zeta^{1/2} \phi^{1/2}} \right)^{\frac{i}{2K-1}}. \end{align*} $$
$$ \begin{align*} |\nabla^i \mathcal{U}| \phi^{i/2} &\lesssim \bar{E} \left( \frac{1}{\zeta^{1/2} \phi^{1/2}} \right)^{\frac{i}{2K-1}}. \end{align*} $$
Plugging this into
![]() $\mathcal {Q}_3$
and using Lemma 8.8, we obtain
$\mathcal {Q}_3$
and using Lemma 8.8, we obtain
 $$ \begin{align*} \mathcal{Q}_3 \lesssim_{K, \bar E, \delta_0} \sum_{i=2}^{2K} \left( \int \frac{\mathcal{S}^{1/\alpha}}{\phi} \left( \frac{1}{\zeta \phi (\zeta) } \right)^{\frac{i}{2K-1}} \langle \zeta \rangle^{\frac{2(r-1)}{\alpha}} \left( \langle \zeta \rangle^{2r-1} \phi^{-2} \right)^{\frac{2K+1-i}{2K-2}} \right)^{1/2} . \end{align*} $$
$$ \begin{align*} \mathcal{Q}_3 \lesssim_{K, \bar E, \delta_0} \sum_{i=2}^{2K} \left( \int \frac{\mathcal{S}^{1/\alpha}}{\phi} \left( \frac{1}{\zeta \phi (\zeta) } \right)^{\frac{i}{2K-1}} \langle \zeta \rangle^{\frac{2(r-1)}{\alpha}} \left( \langle \zeta \rangle^{2r-1} \phi^{-2} \right)^{\frac{2K+1-i}{2K-2}} \right)^{1/2} . \end{align*} $$
Noting that
![]() $1 \lesssim _{\delta _0, \zeta _0} \langle \zeta \rangle ^{2r} \phi (\zeta )^{-1}$
, and using Lemma 8.6, we get
$1 \lesssim _{\delta _0, \zeta _0} \langle \zeta \rangle ^{2r} \phi (\zeta )^{-1}$
, and using Lemma 8.6, we get
 $$ \begin{align} \mathcal{Q}_3 &\lesssim_{K, \bar E, \delta_0, \zeta_0} \sum_{i=2}^{2K} \left( \int \frac{\langle \zeta \rangle^{-(r-1)/\alpha}}{\phi} \langle \zeta \rangle^{\frac{2(r-1)}{\alpha}}\langle \zeta \rangle^{2r-1} \phi^{-2} \right)^{1/2} \nonumber \\ &= \sum_{i=2}^{2K} \left( \int \frac{1}{\phi^3} \langle \zeta \rangle^{(r-1) (2+1/\alpha)}\langle \zeta \rangle \right)^{1/2} \nonumber \\ &\lesssim_{K, \bar E, \delta_0, \zeta_0} \left( \int \frac{\langle \zeta \rangle^3}{\phi^3 (\zeta )}\right)^{1/2} \nonumber \\ & \lesssim_{K, \bar E, \delta_0, \zeta_0} 1, \end{align} $$
$$ \begin{align} \mathcal{Q}_3 &\lesssim_{K, \bar E, \delta_0, \zeta_0} \sum_{i=2}^{2K} \left( \int \frac{\langle \zeta \rangle^{-(r-1)/\alpha}}{\phi} \langle \zeta \rangle^{\frac{2(r-1)}{\alpha}}\langle \zeta \rangle^{2r-1} \phi^{-2} \right)^{1/2} \nonumber \\ &= \sum_{i=2}^{2K} \left( \int \frac{1}{\phi^3} \langle \zeta \rangle^{(r-1) (2+1/\alpha)}\langle \zeta \rangle \right)^{1/2} \nonumber \\ &\lesssim_{K, \bar E, \delta_0, \zeta_0} \left( \int \frac{\langle \zeta \rangle^3}{\phi^3 (\zeta )}\right)^{1/2} \nonumber \\ & \lesssim_{K, \bar E, \delta_0, \zeta_0} 1, \end{align} $$
where in the third line, we used Lemma A.6.
Using (8.108)–(8.110) in (8.107), we conclude that
 $$ \begin{align*} \left| \frac{\alpha^{1/\alpha} }{r^{1+1/\alpha }} e^{\delta_{\mathrm{dis}} s}\mathcal{J} + \mathcal{G}^2 \right| \lesssim_{\delta_0, K, \bar E, \zeta_0} \mathcal{G} . \end{align*} $$
$$ \begin{align*} \left| \frac{\alpha^{1/\alpha} }{r^{1+1/\alpha }} e^{\delta_{\mathrm{dis}} s}\mathcal{J} + \mathcal{G}^2 \right| \lesssim_{\delta_0, K, \bar E, \zeta_0} \mathcal{G} . \end{align*} $$
Thus, as
![]() $s_0$
is sufficiently large in terms of
$s_0$
is sufficiently large in terms of
![]() $K, \bar E, \delta _0, \zeta _0$
, we get
$K, \bar E, \delta _0, \zeta _0$
, we get
and in particular,
Plugging (8.111) into (8.106), we deduce
for some universal constant
![]() $\widetilde {C}$
. In the second inequality, we are using that K can be taken large enough in terms of
$\widetilde {C}$
. In the second inequality, we are using that K can be taken large enough in terms of
![]() $\widetilde {C}, \eta $
– in particular, such that
$\widetilde {C}, \eta $
– in particular, such that
![]() $K> \frac {5 \widetilde {C}}{\eta }$
.
$K> \frac {5 \widetilde {C}}{\eta }$
.
Finally, as
![]() $E_{2K}(s_0) \leq \bar E/2$
, it is clear that
$E_{2K}(s_0) \leq \bar E/2$
, it is clear that
![]() $E_{2K}(s)$
can never go above
$E_{2K}(s)$
can never go above
![]() $\bar E/2$
, as it would contradict (8.112). Therefore,
$\bar E/2$
, as it would contradict (8.112). Therefore,
![]() $E_{2K}(s) \leq \bar E/2$
, and we conclude (8.16). This finishes the proof of Proposition 8.2.
$E_{2K}(s) \leq \bar E/2$
, and we conclude (8.16). This finishes the proof of Proposition 8.2.
8.2 Topological argument for the initial unstable coefficients
In this subsection, we prove Proposition 8.3. In particular, we will always assume (8.6) and (8.7). Whenever we have (8.8), we may apply Proposition 8.2 and thus deduce (8.9). In such cases, we are in the hypotheses of the previous subsection, so we may use any result of that subsection.
For this subsection, we will assume that all the variables make reference to the truncated equation, and we will use the subscript ’e’ whenever we want to make reference to the extended equation.
Let us define
 $$ \begin{align*} \kappa_i (s) = \left\langle (\widetilde{U}_t (\cdot, s), \widetilde{S}_t (\cdot, s) ), (\psi_{i, U}, \psi_{i, S} ) \right\rangle, \qquad \kappa (s) = \sum_{i=1}^N (\psi_{i, U}, \psi_{i, S} ) \kappa_i(s). \end{align*} $$
$$ \begin{align*} \kappa_i (s) = \left\langle (\widetilde{U}_t (\cdot, s), \widetilde{S}_t (\cdot, s) ), (\psi_{i, U}, \psi_{i, S} ) \right\rangle, \qquad \kappa (s) = \sum_{i=1}^N (\psi_{i, U}, \psi_{i, S} ) \kappa_i(s). \end{align*} $$
Note that as
![]() $(\psi _{i, U}, \psi _{i, S})$
form an orthonormal base of V (by Corollary 7.15), the norm
$(\psi _{i, U}, \psi _{i, S})$
form an orthonormal base of V (by Corollary 7.15), the norm
![]() $\sqrt {\sum _i \kappa _i^2}$
is just the norm inherited from X, which we denote by
$\sqrt {\sum _i \kappa _i^2}$
is just the norm inherited from X, which we denote by
![]() $| \kappa |_X$
. We will also work with another norm on
$| \kappa |_X$
. We will also work with another norm on
![]() $\kappa $
. We define the metric B to be the canonical metric associated to the basis of item 3 in Lemma 7.11 (where we take
$\kappa $
. We define the metric B to be the canonical metric associated to the basis of item 3 in Lemma 7.11 (where we take
![]() $A = \mathcal {L}$
due to Corollary 7.7). In particular, equation (7.49) yields
$A = \mathcal {L}$
due to Corollary 7.7). In particular, equation (7.49) yields
As any two norms are equivalent on a finite dimensional vector space, we have that
![]() $| \cdot |_X$
and
$| \cdot |_X$
and
![]() $| \cdot |_B$
are equivalent norms. Moreover, both depend only on the space X and
$| \cdot |_B$
are equivalent norms. Moreover, both depend only on the space X and
![]() $\delta _g$
, so we have that
$\delta _g$
, so we have that
![]() $| w |_X \lesssim _m | w |_B \lesssim _m | w (s)|_X$
.
$| w |_X \lesssim _m | w |_B \lesssim _m | w (s)|_X$
.
It will be useful to consider the following exponentially contracting regions for the unstable modes:
 $$ \begin{align} \begin{aligned} \mathcal{R}(s) &= \{ w \in \mathbb{R}^N \mid | w |_X \leq \delta_1 e^{-\frac{7}{10} \delta_g (s-s_0)}\} \, ,\\ \widetilde{ \mathcal{R} }(s) &= \{ w \in \mathbb{R}^N \mid | w |_B \leq \delta_1^{ \frac{11}{10} } e^{- \frac{7}{10}\delta_g (s-s_0)}\}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathcal{R}(s) &= \{ w \in \mathbb{R}^N \mid | w |_X \leq \delta_1 e^{-\frac{7}{10} \delta_g (s-s_0)}\} \, ,\\ \widetilde{ \mathcal{R} }(s) &= \{ w \in \mathbb{R}^N \mid | w |_B \leq \delta_1^{ \frac{11}{10} } e^{- \frac{7}{10}\delta_g (s-s_0)}\}, \end{aligned} \end{align} $$
where we clearly have
![]() $\widetilde {\mathcal {R}} (s) \Subset \mathcal {R}(s)$
as
$\widetilde {\mathcal {R}} (s) \Subset \mathcal {R}(s)$
as
![]() $|w|_X \lesssim _m |w|_B$
.
$|w|_X \lesssim _m |w|_B$
.
Lemma 8.13. Provided that
![]() $\kappa (s) \in \mathcal {R} (s)$
for
$\kappa (s) \in \mathcal {R} (s)$
for
![]() $s \in [s_0, s_1]$
and assuming our initial data hypothesis
$s \in [s_0, s_1]$
and assuming our initial data hypothesis
we have that
Proof. First of all, note that
![]() $\kappa (s) \in \mathcal {R}(s)$
implies (8.8), so we have (8.9), and we are in the hypothesis of the previous subsection.
$\kappa (s) \in \mathcal {R}(s)$
implies (8.8), so we have (8.9), and we are in the hypothesis of the previous subsection.
We claim that
It is clear that (8.118) implies (8.116), since
![]() $\| P_{\mathrm {uns}}(\widetilde {u}, \widetilde {\sigma }) \|_X = |\kappa (s) |$
, which is smaller than
$\| P_{\mathrm {uns}}(\widetilde {u}, \widetilde {\sigma }) \|_X = |\kappa (s) |$
, which is smaller than
![]() $\delta _1 e^{- \frac {7}{10} \delta _g (s-s_0)}$
by hypothesis. Therefore, it suffices to show (8.117) or (8.118). Assume by contradiction that either (8.117) or (8.118) are violated at some first time
$\delta _1 e^{- \frac {7}{10} \delta _g (s-s_0)}$
by hypothesis. Therefore, it suffices to show (8.117) or (8.118). Assume by contradiction that either (8.117) or (8.118) are violated at some first time
![]() $s' \leq s_1$
.
$s' \leq s_1$
.
Case 1: (8.118) breaks at
![]() $s=s'$
. Let
$s=s'$
. Let
![]() $s \in [s_0, s']$
. By (8.64),
$s \in [s_0, s']$
. By (8.64),
![]() $ \delta _1 \ll \delta _g \ll \delta _{\mathrm {dis}}$
, continuity on (8.117) and that
$ \delta _1 \ll \delta _g \ll \delta _{\mathrm {dis}}$
, continuity on (8.117) and that
![]() $s_0$
is chosen sufficiently large dependent on
$s_0$
is chosen sufficiently large dependent on
![]() $\delta _1$
, we have
$\delta _1$
, we have
 $$ \begin{align} \begin{aligned} \left\| \mathcal{F}_{\mathrm{dis}} (\cdot, s) \right\|_{X} &\leq \delta_1 e^{-\delta_{\mathrm{dis}} s/2} \leq \delta_1^{3/2} e^{- \frac{9}{10}\delta_g (s-s_0)}, \\ \left\| \mathcal{F}_{\mathrm{nl}} (\cdot, s) \right\|_{X} &\leq \delta_1^{3/2} e^{- \frac{9}{10} \delta_g (s-s_0)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left\| \mathcal{F}_{\mathrm{dis}} (\cdot, s) \right\|_{X} &\leq \delta_1 e^{-\delta_{\mathrm{dis}} s/2} \leq \delta_1^{3/2} e^{- \frac{9}{10}\delta_g (s-s_0)}, \\ \left\| \mathcal{F}_{\mathrm{nl}} (\cdot, s) \right\|_{X} &\leq \delta_1^{3/2} e^{- \frac{9}{10} \delta_g (s-s_0)}. \end{aligned} \end{align} $$
However, as the stable space
![]() $V^{\ast \, \perp }$
is invariant under
$V^{\ast \, \perp }$
is invariant under
![]() $\mathcal {L}$
(by Lemma 7.11), we get the commutation relation
$\mathcal {L}$
(by Lemma 7.11), we get the commutation relation
![]() $P_{\mathrm {sta}} \mathcal {L} = \mathcal {L} P_{\mathrm {sta}}$
. Therefore, taking the projection
$P_{\mathrm {sta}} \mathcal {L} = \mathcal {L} P_{\mathrm {sta}}$
. Therefore, taking the projection
![]() $P_{\mathrm {sta}}$
on (7.10), we get
$P_{\mathrm {sta}}$
on (7.10), we get
By Duhamel, we get
 $$ \begin{align*} P_{\mathrm{sta}}(\widetilde{u} (\cdot, s), \widetilde{\sigma} (\cdot, s)) = T(s-s_0)P_{\mathrm{sta}} (\widetilde{u}_0, \widetilde{\sigma}_0) + \int_{s_0}^s T(s-\ddot{s}) P_{\mathrm{sta}}\mathcal{F}_{\mathrm{nl}} (\cdot, \ddot{s}) d\ddot{s} + \int_{s_0}^s T (s-\ddot{s}) P_{\mathrm{sta}}\mathcal{F}_{\mathrm{dis}} (\cdot, \ddot{s}) d\ddot{s}. \end{align*} $$
$$ \begin{align*} P_{\mathrm{sta}}(\widetilde{u} (\cdot, s), \widetilde{\sigma} (\cdot, s)) = T(s-s_0)P_{\mathrm{sta}} (\widetilde{u}_0, \widetilde{\sigma}_0) + \int_{s_0}^s T(s-\ddot{s}) P_{\mathrm{sta}}\mathcal{F}_{\mathrm{nl}} (\cdot, \ddot{s}) d\ddot{s} + \int_{s_0}^s T (s-\ddot{s}) P_{\mathrm{sta}}\mathcal{F}_{\mathrm{dis}} (\cdot, \ddot{s}) d\ddot{s}. \end{align*} $$
Now, using the bound on
![]() $T(s)$
over
$T(s)$
over
![]() $V_{\mathrm {sta}}$
(equation (7.50)), we get
$V_{\mathrm {sta}}$
(equation (7.50)), we get
 $$ \begin{align*} \| P_{\mathrm{sta}}(\widetilde{u} (\cdot, s), \widetilde{\sigma} (\cdot, s)) \|_X &\leq e^{- \frac12 \delta_g (s-s_0)} \|(\widetilde{u}_0, \widetilde{\sigma}_0)\|_X + \int_{s_0}^s e^{- \frac12 \delta_g (s-\ddot{s})} \left( \| \mathcal{F}_{\mathrm{nl}} (\cdot, \ddot{s})\|_X + \| \mathcal{F}_{\mathrm{dis}} (\cdot, \ddot{s}) \|_X \right) d\ddot{s} \\ &\leq e^{- \frac12 \delta_g (s-s_0)}\delta_1 + 2 \delta_1^{3/2} \int_{s_0}^s e^{-\delta_g \left( \frac12 (s-\ddot{s})+ \frac{9}{10}(\ddot{s}-s_0) \right) } d\ddot{s} \\ &\leq e^{- \frac12 \delta_g (s-s_0)}\delta_1 + 2 \delta_1^{3/2} e^{- \frac12 \delta_g(s-s_0)} \int_{s_0}^\infty e^{- \frac{4}{10} \delta_g (\ddot{s}-s_0)/2} d\ddot{s} \\ &\leq \left( 1 + \frac{5\delta_1^{1/2}}{\delta_g} \right)\delta_1 e^{- \frac12 \delta_g (s-s_0)} \leq \frac32 \delta_1 e^{- \frac12 \delta_g (s-s_0)}. \end{align*} $$
$$ \begin{align*} \| P_{\mathrm{sta}}(\widetilde{u} (\cdot, s), \widetilde{\sigma} (\cdot, s)) \|_X &\leq e^{- \frac12 \delta_g (s-s_0)} \|(\widetilde{u}_0, \widetilde{\sigma}_0)\|_X + \int_{s_0}^s e^{- \frac12 \delta_g (s-\ddot{s})} \left( \| \mathcal{F}_{\mathrm{nl}} (\cdot, \ddot{s})\|_X + \| \mathcal{F}_{\mathrm{dis}} (\cdot, \ddot{s}) \|_X \right) d\ddot{s} \\ &\leq e^{- \frac12 \delta_g (s-s_0)}\delta_1 + 2 \delta_1^{3/2} \int_{s_0}^s e^{-\delta_g \left( \frac12 (s-\ddot{s})+ \frac{9}{10}(\ddot{s}-s_0) \right) } d\ddot{s} \\ &\leq e^{- \frac12 \delta_g (s-s_0)}\delta_1 + 2 \delta_1^{3/2} e^{- \frac12 \delta_g(s-s_0)} \int_{s_0}^\infty e^{- \frac{4}{10} \delta_g (\ddot{s}-s_0)/2} d\ddot{s} \\ &\leq \left( 1 + \frac{5\delta_1^{1/2}}{\delta_g} \right)\delta_1 e^{- \frac12 \delta_g (s-s_0)} \leq \frac32 \delta_1 e^{- \frac12 \delta_g (s-s_0)}. \end{align*} $$
In the second inequality, we used (8.119) and (8.115). Clearly, this last inequality at
![]() $s=s'$
implies (8.118), so that we arrive to contradiction, because we supposed (8.118) broke at time
$s=s'$
implies (8.118), so that we arrive to contradiction, because we supposed (8.118) broke at time
![]() $s=s'$
.
$s=s'$
.
Case 2: (8.117) breaks at
![]() $s=s'$
. By assumption, we have
$s=s'$
. By assumption, we have
By continuity on (8.118), we also have
so using that
![]() $| \kappa (s') | \leq \delta _1 e^{-\frac {7}{10}\delta _g (s'-s_0)}$
by hypothesis, we get
$| \kappa (s') | \leq \delta _1 e^{-\frac {7}{10}\delta _g (s'-s_0)}$
by hypothesis, we get
Interpolating between (8.22) and (8.121), we get that
where we used
![]() $m \ll K$
and
$m \ll K$
and
![]() $\delta _1\ll \frac {1}{\bar E} $
in the last inequality.
$\delta _1\ll \frac {1}{\bar E} $
in the last inequality.
From (8.70), we obtain that
This clearly contradicts (8.120).
As the unstable space V is invariant under
![]() $\mathcal {L}$
(by Lemma 7.11, with
$\mathcal {L}$
(by Lemma 7.11, with
![]() $A = \mathcal {L}$
from Corollary 7.7), we get the commutation relation
$A = \mathcal {L}$
from Corollary 7.7), we get the commutation relation
![]() $P_{\mathrm {uns}} \mathcal {L} = \mathcal {L} P_{\mathrm {uns}}$
. Therefore, taking the projection
$P_{\mathrm {uns}} \mathcal {L} = \mathcal {L} P_{\mathrm {uns}}$
. Therefore, taking the projection
![]() $P_{\mathrm {uns}}$
on (7.10), we get that
$P_{\mathrm {uns}}$
on (7.10), we get that
![]() $\kappa $
satisfies the ODE
$\kappa $
satisfies the ODE
 $$ \begin{align} \begin{cases} \kappa'(s) &\!\!\!\!= \mathcal{L} |_{V} \kappa (s) + P_{\mathrm{uns}} \mathcal{F}_{\mathrm{dis}} + P_{\mathrm{uns}} \mathcal{F}_{\mathrm{nl}}, \\ \kappa_i (s_0) &\!\!\!\!= a_i\, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \kappa'(s) &\!\!\!\!= \mathcal{L} |_{V} \kappa (s) + P_{\mathrm{uns}} \mathcal{F}_{\mathrm{dis}} + P_{\mathrm{uns}} \mathcal{F}_{\mathrm{nl}}, \\ \kappa_i (s_0) &\!\!\!\!= a_i\, \end{cases} \end{align} $$
for some initial values
![]() $a_i$
.
$a_i$
.
For the solution corresponding to the initial data given in (8.3), for
![]() $|a| \leq \delta _1$
, we define the stopping time
$|a| \leq \delta _1$
, we define the stopping time
Lemma 8.14 (Outgoing property).
Let us suppose
![]() $|a_i| \leq \delta _0$
and that
$|a_i| \leq \delta _0$
and that
![]() $\kappa \in \widetilde {\mathcal {R}}$
at times
$\kappa \in \widetilde {\mathcal {R}}$
at times
![]() $s\in [s_0, s_1]$
and that at time
$s\in [s_0, s_1]$
and that at time
![]() $s_1 \geq s_0$
, we have
$s_1 \geq s_0$
, we have
That is,
![]() $\kappa (s_1) \in \partial ( \widetilde {\mathcal {R}} (s_1) )$
. Then, we have that
$\kappa (s_1) \in \partial ( \widetilde {\mathcal {R}} (s_1) )$
. Then, we have that
![]() $\kappa (s) \notin \widetilde {\mathcal {R}} (s)$
for s close enough to
$\kappa (s) \notin \widetilde {\mathcal {R}} (s)$
for s close enough to
![]() $s_1$
from above. That is,
$s_1$
from above. That is,
![]() $\kappa (s)$
exits
$\kappa (s)$
exits
![]() $\widetilde {\mathcal {R}}(s)$
at
$\widetilde {\mathcal {R}}(s)$
at
![]() $s = s_1$
.
$s = s_1$
.
Proof. Given that
![]() $\kappa (s_1) \in \partial (\widetilde {\mathcal {R}}(s_1))$
, we have that
$\kappa (s_1) \in \partial (\widetilde {\mathcal {R}}(s_1))$
, we have that
![]() $\kappa (s)$
will be exiting
$\kappa (s)$
will be exiting
![]() $\widetilde {\mathcal {R}} (s)$
at time
$\widetilde {\mathcal {R}} (s)$
at time
![]() $s = s_1$
if and only if
$s = s_1$
if and only if
which using (8.124) can be written as
On the one hand, we have from equation (8.113) that
On the other hand, we have that
 $$ \begin{align} \langle P_{\mathrm{uns}} \mathcal{F}_{\mathrm{dis}}, \kappa (s_1) \rangle + \langle P_{\mathrm{uns}} \mathcal{F}_{\mathrm{nl}} (\cdot, s_1), \kappa (s_1) \rangle & \leq \left\| P_{\mathrm{uns}} \mathcal{F}_{\mathrm{dis}} (\cdot, s_1) \right\|_B |\kappa (s_1)|_B + \| P_{\mathrm{uns}} \mathcal{F}_{\mathrm{nl}} \|_B |\kappa (s_1)|_B \nonumber \\ & \lesssim_m \left( \left\| P_{\mathrm{uns}} \mathcal{F}_{\mathrm{dis}} (\cdot, s_1) \right\|_X + \| P_{\mathrm{uns}} \mathcal{F}_{\mathrm{nl}} (\cdot, s_1) \|_X \right) \frac{| \kappa (s_1) |_B^2}{\delta_1^{\frac{11}{10}} e^{- \frac{7}{10}\delta_g (s_1-s_0)}} \nonumber \\ & \leq \left( \left\| \mathcal{F}_{\mathrm{dis}} (\cdot, s_1) \right\|_X + \| \mathcal{F}_{\mathrm{nl}} (\cdot, s_1) \|_X \right) \frac{| \kappa (s_1) |_B^2}{\delta_1^{\frac{11}{10}} e^{-\frac{7}{10}\delta_g (s_1-s_0)}} \nonumber \\ & \leq \delta_1^{\frac32} e^{- \frac{9}{10} \delta_g (s_1-s_0)} \frac{| \kappa (s_1) |_B^2}{ \delta_1^{\frac{11}{10}} e^{- \frac{7}{10} \delta_g (s_1-s_0)} } \nonumber \\ &= \delta_1^{\frac{4}{10}} e^{- \frac{2}{10}\delta_g (s_1-s_0)} | \kappa (s_1) |_B^2, \end{align} $$
$$ \begin{align} \langle P_{\mathrm{uns}} \mathcal{F}_{\mathrm{dis}}, \kappa (s_1) \rangle + \langle P_{\mathrm{uns}} \mathcal{F}_{\mathrm{nl}} (\cdot, s_1), \kappa (s_1) \rangle & \leq \left\| P_{\mathrm{uns}} \mathcal{F}_{\mathrm{dis}} (\cdot, s_1) \right\|_B |\kappa (s_1)|_B + \| P_{\mathrm{uns}} \mathcal{F}_{\mathrm{nl}} \|_B |\kappa (s_1)|_B \nonumber \\ & \lesssim_m \left( \left\| P_{\mathrm{uns}} \mathcal{F}_{\mathrm{dis}} (\cdot, s_1) \right\|_X + \| P_{\mathrm{uns}} \mathcal{F}_{\mathrm{nl}} (\cdot, s_1) \|_X \right) \frac{| \kappa (s_1) |_B^2}{\delta_1^{\frac{11}{10}} e^{- \frac{7}{10}\delta_g (s_1-s_0)}} \nonumber \\ & \leq \left( \left\| \mathcal{F}_{\mathrm{dis}} (\cdot, s_1) \right\|_X + \| \mathcal{F}_{\mathrm{nl}} (\cdot, s_1) \|_X \right) \frac{| \kappa (s_1) |_B^2}{\delta_1^{\frac{11}{10}} e^{-\frac{7}{10}\delta_g (s_1-s_0)}} \nonumber \\ & \leq \delta_1^{\frac32} e^{- \frac{9}{10} \delta_g (s_1-s_0)} \frac{| \kappa (s_1) |_B^2}{ \delta_1^{\frac{11}{10}} e^{- \frac{7}{10} \delta_g (s_1-s_0)} } \nonumber \\ &= \delta_1^{\frac{4}{10}} e^{- \frac{2}{10}\delta_g (s_1-s_0)} | \kappa (s_1) |_B^2, \end{align} $$
where we used equation (8.125) in the second line and Lemma 8.11 in the fourth one.
Combining equations (8.128) and (8.129), and choosing
![]() $\delta _1$
sufficiently small dependent on
$\delta _1$
sufficiently small dependent on
![]() $\delta _g$
, we conclude equation (8.127).
$\delta _g$
, we conclude equation (8.127).
Proposition 8.15. There exists specific initial conditions
![]() $a_i$
such that
$a_i$
such that
![]() $| a |_X \leq \delta _1$
and the
$| a |_X \leq \delta _1$
and the
![]() $\kappa (s)$
defined by the ODE (8.124) satisfies that
$\kappa (s)$
defined by the ODE (8.124) satisfies that
![]() $\kappa (s) \in \mathcal {R}$
for all
$\kappa (s) \in \mathcal {R}$
for all
![]() $s \geq s_0$
.
$s \geq s_0$
.
Moreover, for such initial conditions
![]() $a_i = \kappa _i(s_0)$
, we have that
$a_i = \kappa _i(s_0)$
, we have that
Proof. We argue by contradiction, so let us suppose that for any such initial conditions
![]() $a_i$
, there exists a time of exit
$a_i$
, there exists a time of exit
![]() $s_a$
such that
$s_a$
such that
![]() $\kappa _i$
exits
$\kappa _i$
exits
![]() $\widetilde {\mathcal {R}}$
after
$\widetilde {\mathcal {R}}$
after
![]() $s = s_a$
and let us define
$s = s_a$
and let us define
![]() $b_i(a) = \kappa _i (s_a)$
. Due to Lemma 8.14, we can equivalently define
$b_i(a) = \kappa _i (s_a)$
. Due to Lemma 8.14, we can equivalently define
![]() $(b_i, s_a)$
letting
$(b_i, s_a)$
letting
First, let us argue that the mapping
![]() $a\rightarrow s_a$
is continuous (in the domain where
$a\rightarrow s_a$
is continuous (in the domain where
![]() $s_a \neq +\infty $
). Let
$s_a \neq +\infty $
). Let
![]() $a, \bar a \in \widetilde {\mathcal {R}} (s_0)$
so that
$a, \bar a \in \widetilde {\mathcal {R}} (s_0)$
so that
![]() $s_a, s_{\bar a}$
are finite, and let
$s_a, s_{\bar a}$
are finite, and let
![]() $\kappa (s)$
and
$\kappa (s)$
and
![]() $\bar \kappa (s)$
be the unstable modes corresponding to the solutions with initial conditions dictated by a and
$\bar \kappa (s)$
be the unstable modes corresponding to the solutions with initial conditions dictated by a and
![]() $\bar a$
. By local existence of solutions [Reference Danchin29], we can extend
$\bar a$
. By local existence of solutions [Reference Danchin29], we can extend
![]() $\kappa (s)$
up to some time
$\kappa (s)$
up to some time
![]() $s_a + \varepsilon $
for some
$s_a + \varepsilon $
for some
![]() $\varepsilon $
sufficiently small. Also, by Lemma 8.14 (and again taking
$\varepsilon $
sufficiently small. Also, by Lemma 8.14 (and again taking
![]() $\varepsilon $
sufficiently small), we can ensure that
$\varepsilon $
sufficiently small), we can ensure that
![]() $\kappa (s_a + \varepsilon ) \notin \widetilde {\mathcal {R}} (s_a + \varepsilon )$
. Let
$\kappa (s_a + \varepsilon ) \notin \widetilde {\mathcal {R}} (s_a + \varepsilon )$
. Let
![]() $\varepsilon ' = \frac 12 \mathrm {d}_B (\kappa (s_a + \varepsilon ), \widetilde {\mathcal {R}}(s_a + \varepsilon ))$
. By stability [Reference Danchin29], there exists
$\varepsilon ' = \frac 12 \mathrm {d}_B (\kappa (s_a + \varepsilon ), \widetilde {\mathcal {R}}(s_a + \varepsilon ))$
. By stability [Reference Danchin29], there exists
![]() $\delta $
sufficiently small such that
$\delta $
sufficiently small such that
![]() $|a-\bar a |_B \leq \delta $
guarantees
$|a-\bar a |_B \leq \delta $
guarantees
![]() $|\kappa (s_a + \varepsilon ) - \bar \kappa (s_a + \varepsilon )|_B \leq \frac 12 \varepsilon '$
. In that case,
$|\kappa (s_a + \varepsilon ) - \bar \kappa (s_a + \varepsilon )|_B \leq \frac 12 \varepsilon '$
. In that case,
![]() $\bar \kappa (s_a + \varepsilon ) \notin \widetilde {\mathcal {R}}(s_a + \varepsilon )$
, and we deduce
$\bar \kappa (s_a + \varepsilon ) \notin \widetilde {\mathcal {R}}(s_a + \varepsilon )$
, and we deduce
![]() $s_{\bar a} < s_a + \varepsilon $
. In a symmetric way, we can find
$s_{\bar a} < s_a + \varepsilon $
. In a symmetric way, we can find
![]() $\bar \delta $
such that if
$\bar \delta $
such that if
![]() $|a - \bar a |_B \leq \bar \delta $
, then
$|a - \bar a |_B \leq \bar \delta $
, then
![]() $s_a < s_{\bar a} + \varepsilon $
. Thus, we conclude that
$s_a < s_{\bar a} + \varepsilon $
. Thus, we conclude that
![]() $a \rightarrow s_a$
is continuous. As a consequence,
$a \rightarrow s_a$
is continuous. As a consequence,
![]() $b_i = \kappa _i (s_a)$
is also continuous with respect to a, as it is the composition of continuous functions.
$b_i = \kappa _i (s_a)$
is also continuous with respect to a, as it is the composition of continuous functions.
Now, we define the mapping
![]() $H : B_B (1) \rightarrow \partial B_B (1)$
as follows. For each
$H : B_B (1) \rightarrow \partial B_B (1)$
as follows. For each
![]() $\vartheta \in V$
with
$\vartheta \in V$
with
![]() $| \vartheta |_B \leq 1$
, consider
$| \vartheta |_B \leq 1$
, consider
![]() $a = \delta _1^{\frac {11}{10}} \vartheta $
and evolve (8.124) with
$a = \delta _1^{\frac {11}{10}} \vartheta $
and evolve (8.124) with
![]() $\kappa (s_0) = a$
. As we are supposing every initial data exits
$\kappa (s_0) = a$
. As we are supposing every initial data exits
![]() $\widetilde {\mathcal {R}}(s)$
at some s, we have a time
$\widetilde {\mathcal {R}}(s)$
at some s, we have a time
![]() $s_a$
and the corresponding values
$s_a$
and the corresponding values
![]() $b_i (a)$
such that
$b_i (a)$
such that
![]() $|b(a)|_B = \delta _1^{\frac {11}{10}} e^{-\delta _g (s_a-s_0)} $
. We now consider
$|b(a)|_B = \delta _1^{\frac {11}{10}} e^{-\delta _g (s_a-s_0)} $
. We now consider
![]() $H(\vartheta )$
to be
$H(\vartheta )$
to be
![]() $\frac {b(a)}{|b(a)|_B}$
, which is trivially on the boundary of
$\frac {b(a)}{|b(a)|_B}$
, which is trivially on the boundary of
![]() $B_{B} (1)$
. As
$B_{B} (1)$
. As
![]() $b(a)$
is continuous, we also get that H is continuous. Moreover, note that H is just the identity on the boundary of the ball, as
$b(a)$
is continuous, we also get that H is continuous. Moreover, note that H is just the identity on the boundary of the ball, as
![]() $|a|_B = \delta _1^{\frac {11}{10}}$
implies
$|a|_B = \delta _1^{\frac {11}{10}}$
implies
![]() $s_a = s_0$
and
$s_a = s_0$
and
![]() $b(a) = a$
due to Lemma 8.14.
$b(a) = a$
due to Lemma 8.14.
Therefore, we have constructed a mapping H from the the unit ball on V to its boundary which is continuous and is the identity restricted to its boundary. The map
![]() $-H$
would therefore have no fixed point, contradicting Brouwer’s fixed point theorem. Therefore, there must exist at least a N-tuple of values for
$-H$
would therefore have no fixed point, contradicting Brouwer’s fixed point theorem. Therefore, there must exist at least a N-tuple of values for
![]() $a_i$
such that
$a_i$
such that
![]() $\kappa (s) \in \widetilde {\mathcal {R}}(s)$
for all
$\kappa (s) \in \widetilde {\mathcal {R}}(s)$
for all
![]() $s \geq s_0$
.
$s \geq s_0$
.
Now, with that value for
![]() $a_i$
, we conclude the unstable projections of
$a_i$
, we conclude the unstable projections of
![]() $\widetilde {u}, \widetilde {\sigma }$
in X are always bounded by
$\widetilde {u}, \widetilde {\sigma }$
in X are always bounded by
![]() $\delta _1 e^{- \frac {7}{10}\delta _g (s-s_0)}$
. Therefore, for such
$\delta _1 e^{- \frac {7}{10}\delta _g (s-s_0)}$
. Therefore, for such
![]() $a_i$
, we have (8.8), so we can apply Proposition 8.2 and obtain (8.9), which gives us the desired bounds.
$a_i$
, we have (8.8), so we can apply Proposition 8.2 and obtain (8.9), which gives us the desired bounds.
From Proposition 8.15, we conclude the bound 8.11 on Proposition 8.3. Moreover, by Proposition 8.2, we see that
![]() $E_{2K}$
,
$E_{2K}$
,
![]() $\| \widetilde {U} \|_{L^\infty }$
and
$\| \widetilde {U} \|_{L^\infty }$
and
![]() $\| \widetilde {S} \|_{L^\infty }$
remain bounded uniformly in time. Thus, the local-wellposedness results [Reference Danchin29] imply that the solution to (7.6) can be continued for all times. As (7.8) is a linear equation, and the forcing remains bounded due to Lemma 8.11, it can also be continued for all times.
$\| \widetilde {S} \|_{L^\infty }$
remain bounded uniformly in time. Thus, the local-wellposedness results [Reference Danchin29] imply that the solution to (7.6) can be continued for all times. As (7.8) is a linear equation, and the forcing remains bounded due to Lemma 8.11, it can also be continued for all times.
Thus, the only thing that remains to show from Proposition 8.3 is equation (8.12). Let us show it. In the region
![]() $\zeta \leq \frac 65$
, Lemma 8.1 gives us that
$\zeta \leq \frac 65$
, Lemma 8.1 gives us that
![]() $\widetilde {U}_t = \widetilde {U}_e$
and
$\widetilde {U}_t = \widetilde {U}_e$
and
![]() $\widetilde {S}_t = \widetilde {S}_e$
, so
$\widetilde {S}_t = \widetilde {S}_e$
, so
Therefore, for
![]() $\zeta \leq \frac 65$
, we obtain equation (8.12) from (8.11).
$\zeta \leq \frac 65$
, we obtain equation (8.12) from (8.11).
Now let us show equation (8.12) for
![]() $\zeta> \frac 65$
. From now on, we will only refer to the extended equation, so we drop the subindex ‘e’. The approach will be similar to the one we followed for closing the
$\zeta> \frac 65$
. From now on, we will only refer to the extended equation, so we drop the subindex ‘e’. The approach will be similar to the one we followed for closing the
![]() $L^\infty $
estimates. Let us change to
$L^\infty $
estimates. Let us change to
![]() $W, Z$
variables and recall the definitions of
$W, Z$
variables and recall the definitions of
![]() $J(\zeta ), \ddot {\Upsilon }_W, \ddot {\Upsilon }_Z$
from (8.80)–(8.82). Whenever we want to indicate the initial condition of
$J(\zeta ), \ddot {\Upsilon }_W, \ddot {\Upsilon }_Z$
from (8.80)–(8.82). Whenever we want to indicate the initial condition of
![]() $\Upsilon _\circ (s)$
, we will use the notation
$\Upsilon _\circ (s)$
, we will use the notation
![]() $\Upsilon _\circ ^{(\zeta _\star , s_\star )}(s)$
, which is the only trajectory such that
$\Upsilon _\circ ^{(\zeta _\star , s_\star )}(s)$
, which is the only trajectory such that
![]() $\Upsilon _\circ (s_\star ) = \zeta _\star $
. Let us also recall that there exists some
$\Upsilon _\circ (s_\star ) = \zeta _\star $
. Let us also recall that there exists some
![]() $\zeta _1$
such that
$\zeta _1$
such that
![]() $| J(\zeta ) | \leq \frac {r-1}{4}$
for
$| J(\zeta ) | \leq \frac {r-1}{4}$
for
![]() $\zeta> \zeta _1$
.
$\zeta> \zeta _1$
.
For the region
![]() $\frac 65 \leq \zeta \leq \zeta _1$
, we argue by contradiction. Let us note that in this region, equation (8.87) holds for a sufficiently large
$\frac 65 \leq \zeta \leq \zeta _1$
, we argue by contradiction. Let us note that in this region, equation (8.87) holds for a sufficiently large
![]() $C_2$
. Let
$C_2$
. Let
![]() $C_1, C_3$
be sufficiently large constants. We claim
$C_1, C_3$
be sufficiently large constants. We claim
in the region
![]() $\frac 65 \leq \zeta \leq \zeta _1$
. Note that if
$\frac 65 \leq \zeta \leq \zeta _1$
. Note that if
![]() $C_1$
is taken sufficiently large, this is satisfied at
$C_1$
is taken sufficiently large, this is satisfied at
![]() $s=s_0$
because of our initial conditions hypothesis and at
$s=s_0$
because of our initial conditions hypothesis and at
![]() $\zeta = \frac 65$
, because we already have (8.12) in the region
$\zeta = \frac 65$
, because we already have (8.12) in the region
![]() $\zeta \leq \frac 65$
. In order to show it for other
$\zeta \leq \frac 65$
. In order to show it for other
![]() $\zeta $
and s, we argue by contradiction and suppose that (8.130) holds until time
$\zeta $
and s, we argue by contradiction and suppose that (8.130) holds until time
![]() $s_b> s_0$
, and is broken at some point
$s_b> s_0$
, and is broken at some point
![]() $\zeta _b \in \left ( \frac 65 , \zeta _1 \right ]$
. Without loss of generality, we have that
$\zeta _b \in \left ( \frac 65 , \zeta _1 \right ]$
. Without loss of generality, we have that
because the cases where (8.130) breaks with
![]() $\widetilde {W}$
being negative or where it breaks for
$\widetilde {W}$
being negative or where it breaks for
![]() $\widetilde {Z}$
are analogous. Let
$\widetilde {Z}$
are analogous. Let
![]() $(\zeta _\star , s_\star )$
such that either
$(\zeta _\star , s_\star )$
such that either
![]() $\zeta _\star = \frac 65 $
or
$\zeta _\star = \frac 65 $
or
![]() $s_\star = s_0$
and
$s_\star = s_0$
and
![]() $\ddot {\Upsilon }_W^{(\zeta _\star , s_\star )} (s_b) = \zeta _b$
. As
$\ddot {\Upsilon }_W^{(\zeta _\star , s_\star )} (s_b) = \zeta _b$
. As
![]() $s_b$
is the first time at which equation (8.130) breaks, we have that
$s_b$
is the first time at which equation (8.130) breaks, we have that
 $$ \begin{align} \partial_s \left( \widetilde{W} (\ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}, s) \right) \Big|_{s = s_b} &\geq \partial_s \left( C_1 \delta_1 e^{-\frac{7}{10} \delta_g (s-s_0)} e^{C_3 \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)} }\right) \Big|_{s=s_b} \nonumber \\ &\geq C_1 \delta_1 e^{- \frac{7}{10} \delta_g (s_b-s_0)} e^{C_3 \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)} (s_b)} \left( \frac{7}{10} \delta_g + C_3 \frac{\ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}(s_b) }{C_0} \right), \nonumber\\ &\geq C_1 \delta_1 e^{-\frac{7}{10} \delta_g (s_b-s_0)} e^{C_3 \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)} (s_b)} \cdot \frac{C_3 }{C_0} \cdot \frac65 , \end{align} $$
$$ \begin{align} \partial_s \left( \widetilde{W} (\ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}, s) \right) \Big|_{s = s_b} &\geq \partial_s \left( C_1 \delta_1 e^{-\frac{7}{10} \delta_g (s-s_0)} e^{C_3 \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)} }\right) \Big|_{s=s_b} \nonumber \\ &\geq C_1 \delta_1 e^{- \frac{7}{10} \delta_g (s_b-s_0)} e^{C_3 \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)} (s_b)} \left( \frac{7}{10} \delta_g + C_3 \frac{\ddot{\Upsilon}_W^{(\zeta_\star, s_\star)}(s_b) }{C_0} \right), \nonumber\\ &\geq C_1 \delta_1 e^{-\frac{7}{10} \delta_g (s_b-s_0)} e^{C_3 \ddot{\Upsilon}_W^{(\zeta_\star, s_\star)} (s_b)} \cdot \frac{C_3 }{C_0} \cdot \frac65 , \end{align} $$
where in the second inequality, we used equation (8.86) and in the third one
![]() $\ddot {\Upsilon }_W^{(\zeta _\star , s_\star )} \geq \frac 65$
(by (8.86)).
$\ddot {\Upsilon }_W^{(\zeta _\star , s_\star )} \geq \frac 65$
(by (8.86)).
However, combining (8.87) with (8.131), we see that
Now, comparing (8.132) and (8.133), and taking
![]() $C_3$
sufficiently large with respect to
$C_3$
sufficiently large with respect to
![]() $C_1$
, we arrive to contradiction. Therefore, we conclude (8.130) for some constants
$C_1$
, we arrive to contradiction. Therefore, we conclude (8.130) for some constants
![]() $C_1, C_3$
. As
$C_1, C_3$
. As
![]() $C_3, \zeta _1$
are constants,
$C_3, \zeta _1$
are constants,
![]() $e^{C_3 \zeta _1} \lesssim 1$
, so this shows (8.12) in the region
$e^{C_3 \zeta _1} \lesssim 1$
, so this shows (8.12) in the region
![]() $\frac 65 \leq \zeta \leq \zeta _1$
.
$\frac 65 \leq \zeta \leq \zeta _1$
.
Finally, we need to show (8.12) in the region
![]() $\zeta> \zeta _1$
. We will do it by bootstrap. Let
$\zeta> \zeta _1$
. We will do it by bootstrap. Let
![]() $C_4$
be a sufficiently large constant and let us assume that
$C_4$
be a sufficiently large constant and let us assume that
We will show the reinforced estimate
which implies that (8.134) cannot be broken. From equations (8.79)–(8.80), we get that
 $$ \begin{align} \left| (\partial_s +r-1)\widetilde{W} + \left( \zeta+ \frac{1+\alpha}{2} \ddot{W} + \frac{1-\alpha}{2} \ddot{Z} \right) \partial_\zeta \widetilde{W} \right| \leq J(\zeta) \left( | \widetilde{W} | + | \widetilde{Z} | \right) + \mathcal{F}_{\mathrm{dis}} + \mathcal{F}_{\mathrm{nl}, W}. \end{align} $$
$$ \begin{align} \left| (\partial_s +r-1)\widetilde{W} + \left( \zeta+ \frac{1+\alpha}{2} \ddot{W} + \frac{1-\alpha}{2} \ddot{Z} \right) \partial_\zeta \widetilde{W} \right| \leq J(\zeta) \left( | \widetilde{W} | + | \widetilde{Z} | \right) + \mathcal{F}_{\mathrm{dis}} + \mathcal{F}_{\mathrm{nl}, W}. \end{align} $$
Using equation (8.134) in (8.136), and recalling that
![]() $J(\zeta ) \leq \frac {r-1}{4}$
in the region
$J(\zeta ) \leq \frac {r-1}{4}$
in the region
![]() $\zeta> \zeta _1$
, we obtain that
$\zeta> \zeta _1$
, we obtain that
 $$ \begin{align} \left| (\partial_s +r-1)\widetilde{W} + \left( \zeta+ \frac{1+\alpha}{2} \ddot{W} + \frac{1-\alpha}{2} \ddot{Z} \right) \partial_\zeta \widetilde{W} \right| \leq \frac{r-1}{2} \delta_1 C_4 e^{- \frac{7}{10} \delta_g (s-s_0)} + \mathcal{F}_{\mathrm{dis}} + \mathcal{F}_{\mathrm{nl}, W}. \end{align} $$
$$ \begin{align} \left| (\partial_s +r-1)\widetilde{W} + \left( \zeta+ \frac{1+\alpha}{2} \ddot{W} + \frac{1-\alpha}{2} \ddot{Z} \right) \partial_\zeta \widetilde{W} \right| \leq \frac{r-1}{2} \delta_1 C_4 e^{- \frac{7}{10} \delta_g (s-s_0)} + \mathcal{F}_{\mathrm{dis}} + \mathcal{F}_{\mathrm{nl}, W}. \end{align} $$
We recall from (8.64) that
In addition, as
![]() $\zeta \geq \zeta _1$
, we have from (7.2) that
$\zeta \geq \zeta _1$
, we have from (7.2) that
 $$ \begin{align} | \mathcal{F}_{\mathrm{nl}, W} | & \lesssim \left( | \widetilde{W} | + | \widetilde{Z} | \right) \left( | \widetilde{W} | + | \partial_\zeta \widetilde{W} | \right) \nonumber \\ & \leq \delta_1 e^{- \frac{7}{10} \delta_g (s-s_0)} \cdot \left( | \widetilde{W} | + | \partial_\zeta \widetilde{W} | \right), \end{align} $$
$$ \begin{align} | \mathcal{F}_{\mathrm{nl}, W} | & \lesssim \left( | \widetilde{W} | + | \widetilde{Z} | \right) \left( | \widetilde{W} | + | \partial_\zeta \widetilde{W} | \right) \nonumber \\ & \leq \delta_1 e^{- \frac{7}{10} \delta_g (s-s_0)} \cdot \left( | \widetilde{W} | + | \partial_\zeta \widetilde{W} | \right), \end{align} $$
where we bounded the first factor by (8.134). Now from (8.20), we get that
![]() $|\partial _\zeta ^{2K-1} \widetilde {W}| \lesssim \bar E$
, and from (8.134), we get that
$|\partial _\zeta ^{2K-1} \widetilde {W}| \lesssim \bar E$
, and from (8.134), we get that
![]() $| \widetilde {W} | \leq \delta _1$
. Applying
$| \widetilde {W} | \leq \delta _1$
. Applying
![]() $L^\infty $
interpolation between those two bounds, we get
$L^\infty $
interpolation between those two bounds, we get
Plugging this into (8.139), we obtain that
Using equations (8.138) and (8.140) in (8.137), we obtain that
 $$ \begin{align*} \left| (\partial_s +r-1)\widetilde{W} + \left( \zeta+ \frac{1+\alpha}{2} \ddot{W} + \frac{1-\alpha}{2} \ddot{Z} \right) \partial_\zeta \widetilde{W} \right| \leq \frac{r-1}{2} \delta_1 C_4 e^{- \frac{7}{10} \delta_g (s-s_0)} + \delta_1^{3/2} e^{- \frac{7}{10} \delta_g (s-s_0)}. \end{align*} $$
$$ \begin{align*} \left| (\partial_s +r-1)\widetilde{W} + \left( \zeta+ \frac{1+\alpha}{2} \ddot{W} + \frac{1-\alpha}{2} \ddot{Z} \right) \partial_\zeta \widetilde{W} \right| \leq \frac{r-1}{2} \delta_1 C_4 e^{- \frac{7}{10} \delta_g (s-s_0)} + \delta_1^{3/2} e^{- \frac{7}{10} \delta_g (s-s_0)}. \end{align*} $$
Recalling the definition of
![]() $\ddot {\Upsilon }_W$
from (8.81), we can rewrite this equation as
$\ddot {\Upsilon }_W$
from (8.81), we can rewrite this equation as
 $$ \begin{align} \left| (\partial_s +r-1)\widetilde{W} (\ddot{\Upsilon}_W (s), s) \right| \leq \left( \frac{r-1}{2} + \frac{\delta_1^{1/2}}{C_4} \right) C_4 \delta_1 e^{- \frac{7}{10} \delta_g (s-s_0)} \leq \frac{3(r-1)}{5} C_4 \delta_1 e^{- \frac{7}{10} \delta_g (s-s_0)}. \end{align} $$
$$ \begin{align} \left| (\partial_s +r-1)\widetilde{W} (\ddot{\Upsilon}_W (s), s) \right| \leq \left( \frac{r-1}{2} + \frac{\delta_1^{1/2}}{C_4} \right) C_4 \delta_1 e^{- \frac{7}{10} \delta_g (s-s_0)} \leq \frac{3(r-1)}{5} C_4 \delta_1 e^{- \frac{7}{10} \delta_g (s-s_0)}. \end{align} $$
Now, we conclude (8.135) by contradiction. Equation (8.135) clearly holds for
![]() $s = s_0$
, and also holds for
$s = s_0$
, and also holds for
![]() $\zeta = \zeta _1$
because we know (8.12) in the region
$\zeta = \zeta _1$
because we know (8.12) in the region
![]() $\frac 65 \leq \zeta \leq \zeta _1$
. Moreover, if (8.135) breaks for some trajectory at
$\frac 65 \leq \zeta \leq \zeta _1$
. Moreover, if (8.135) breaks for some trajectory at
![]() $s_b$
, without loss of generality, we would have
$s_b$
, without loss of generality, we would have
However, (8.141) implies
so we obtain the desired contradiction. The cases where (8.135) breaks with
![]() $\widetilde {W}$
being negative, or where it breaks for
$\widetilde {W}$
being negative, or where it breaks for
![]() $\widetilde {Z}$
, are handled completely analogously.
$\widetilde {Z}$
, are handled completely analogously.
Therefore, we have shown (8.135) under the assumption of (8.134), which allows us to conclude (8.135) by bootstrap. This proves (8.12) for
![]() $\zeta \geq \zeta _1$
, so it finalizes the proof of Proposition 8.3.
$\zeta \geq \zeta _1$
, so it finalizes the proof of Proposition 8.3.
A Auxiliary Lemmas
A.1 Proof of Proposition 1.6.
Proof of Proposition 1.6.
Let us start by proving that there are no non-degenerate closed curves C (not crossing the nullsets of the denominators) such that the field
![]() $\left ( \frac {N_W}{D_W} , \frac {N_Z}{D_Z} \right )$
is tangent with constant direction to the curve at each point of C. If there was such a curve, it would also be tangent to the polynomial field
$\left ( \frac {N_W}{D_W} , \frac {N_Z}{D_Z} \right )$
is tangent with constant direction to the curve at each point of C. If there was such a curve, it would also be tangent to the polynomial field
![]() $\tilde F = (N_W D_Z , N_Z D_W )$
.
$\tilde F = (N_W D_Z , N_Z D_W )$
.
By Poincaré-Hopf theorem, there has to be some equilibrium point P in the interior of C. Moreover, as C does not cross
![]() $D_W = 0$
or
$D_W = 0$
or
![]() $D_Z = 0$
, any equilibrium point inside C has to be a solution of
$D_Z = 0$
, any equilibrium point inside C has to be a solution of
![]() $N_W = N_Z = 0$
. Thus, C has to be in the region
$N_W = N_Z = 0$
. Thus, C has to be in the region
![]() $W> Z$
, by Lemma A.17, the only such point is
$W> Z$
, by Lemma A.17, the only such point is ![]() and it is a saddle point for all
and it is a saddle point for all
![]() $\gamma> 1$
,
$\gamma> 1$
,
![]() $r < \frac {3\gamma -1}{2+\sqrt {3}(\gamma -1)}$
. By Poincaré-Hopf theorem, a closed orbit cannot contain just a saddle equilibrium point, so we conclude there is no such curve C for all
$r < \frac {3\gamma -1}{2+\sqrt {3}(\gamma -1)}$
. By Poincaré-Hopf theorem, a closed orbit cannot contain just a saddle equilibrium point, so we conclude there is no such curve C for all
![]() $\gamma> 1$
,
$\gamma> 1$
,
![]() $r < \frac {3\gamma -1}{2+\sqrt {3}(\gamma -1)}$
. Note that by Lemma A.23, this covers the case
$r < \frac {3\gamma -1}{2+\sqrt {3}(\gamma -1)}$
. Note that by Lemma A.23, this covers the case
![]() $\gamma> 1$
,
$\gamma> 1$
,
![]() $r \in (r_3, r_4)$
.
$r \in (r_3, r_4)$
.
Now, let us show that such curve C does not exist also in the case
![]() $\gamma = 7/5$
and r close enough to
$\gamma = 7/5$
and r close enough to
![]() $r^\ast $
. By the same reasoning as above, C has to encircle the point
$r^\ast $
. By the same reasoning as above, C has to encircle the point ![]() (which is no longer a saddle point). By Lemma A.17, we have that
(which is no longer a saddle point). By Lemma A.17, we have that ![]() lies in the region
lies in the region
![]() $D_W> 0, D_Z < 0$
, and as C does not intersect
$D_W> 0, D_Z < 0$
, and as C does not intersect
![]() $D_W = 0$
or
$D_W = 0$
or
![]() $D_Z = 0$
, we have that C is also contained in the region
$D_Z = 0$
, we have that C is also contained in the region
![]() $\Omega $
(that is, the region where
$\Omega $
(that is, the region where
![]() $D_W> 0, D_Z < 0$
). Now, we let
$D_W> 0, D_Z < 0$
). Now, we let ![]() be the intersection of the branch of
be the intersection of the branch of
![]() $N_W = 0$
passing through
$N_W = 0$
passing through ![]() with the nullset
with the nullset
![]() $D_Z = 0$
. We also let
$D_Z = 0$
. We also let ![]() be the point in the same horizontal of
be the point in the same horizontal of ![]() which lies over
which lies over
![]() $D_Z = 0$
. We define the region
$D_Z = 0$
. We define the region
![]() $\mathcal {T}$
to be the triangular region enclosed by
$\mathcal {T}$
to be the triangular region enclosed by
![]() $N_W = 0$
, the horizontal segment from
$N_W = 0$
, the horizontal segment from ![]() to
to ![]() and
and
![]() $D_Z = 0$
. We call those parts of
$D_Z = 0$
. We call those parts of
![]() $\partial \mathcal {T}$
by
$\partial \mathcal {T}$
by
![]() $S_1, S_2, S_3$
, respectively. As
$S_1, S_2, S_3$
, respectively. As
![]() $\mathcal {T}$
is a region from
$\mathcal {T}$
is a region from ![]() to
to
![]() $D_Z = 0$
, and our curve C encloses
$D_Z = 0$
, and our curve C encloses ![]() and stays in
and stays in
![]() $D_Z < 0$
, it necessarily has to pass through
$D_Z < 0$
, it necessarily has to pass through
![]() $\mathcal {T}$
and has to cross either
$\mathcal {T}$
and has to cross either
![]() $S_1$
or
$S_1$
or
![]() $S_2$
in the outwards direction. We get our final contradiction by Lemma A.14, which asserts that the field
$S_2$
in the outwards direction. We get our final contradiction by Lemma A.14, which asserts that the field
![]() $(N_W D_Z, N_Z D_W)$
points inwards to
$(N_W D_Z, N_Z D_W)$
points inwards to
![]() $\mathcal {T}$
both in
$\mathcal {T}$
both in
![]() $S_1$
and
$S_1$
and
![]() $S_2$
for
$S_2$
for
![]() $\gamma = 7/5$
and r sufficiently close to
$\gamma = 7/5$
and r sufficiently close to
![]() $r^\ast $
.
$r^\ast $
.
By our previous reasoning, the orbits of our system are the orbits of the modified field
![]() $(N_W D_Z, N_Z D_W )$
, as long as the orbit does not intersect the nullset of
$(N_W D_Z, N_Z D_W )$
, as long as the orbit does not intersect the nullset of
![]() $D_W$
or
$D_W$
or
![]() $D_Z$
. By Picard-Lindelöf’s theorem, those trajectories exist locally. Moreover, by Poincaré-Bedixson (and the previous fact that there are no periodic orbits), every bounded semitrajectory converges to an equilibrium point.
$D_Z$
. By Picard-Lindelöf’s theorem, those trajectories exist locally. Moreover, by Poincaré-Bedixson (and the previous fact that there are no periodic orbits), every bounded semitrajectory converges to an equilibrium point.
However, those trajectories may intersect
![]() $D_W = 0$
or
$D_W = 0$
or
![]() $D_Z = 0$
, which give singularities for the change of variables between the fields
$D_Z = 0$
, which give singularities for the change of variables between the fields
![]() $(N_W/D_W, N_Z/D_Z)$
and
$(N_W/D_W, N_Z/D_Z)$
and
![]() $(N_W D_Z, N_Z D_W)$
. Therefore, we add the possibility that the trajectory of the original system intersects those nullsets. We have thus seen that the trajectories (from left or right) either are unbounded, or converge to an equilibrium point, or converge to a point of the nullsets
$(N_W D_Z, N_Z D_W)$
. Therefore, we add the possibility that the trajectory of the original system intersects those nullsets. We have thus seen that the trajectories (from left or right) either are unbounded, or converge to an equilibrium point, or converge to a point of the nullsets
![]() $D_W = 0, D_Z = 0$
.
$D_W = 0, D_Z = 0$
.
In the case of reaching an equilibrium, as all equilibria are hyperbolic, Hartman-Grobman ensures that the rate of convergence is exponentially fast, reaching the equilibrium in infinite time.
A.2 Interpolation Lemmas
Lemma A.1. Let
![]() $a \geq 1$
and consider
$a \geq 1$
and consider
![]() $\mathcal {O} = [a, \infty )$
. Let
$\mathcal {O} = [a, \infty )$
. Let
![]() $\beta _1 \in (0, 1)$
. Then, for any
$\beta _1 \in (0, 1)$
. Then, for any
![]() $0\leq i\leq n$
,
$0\leq i\leq n$
,
![]() $\beta _2\in \mathbb R$
, we have the interpolation inequality
$\beta _2\in \mathbb R$
, we have the interpolation inequality
Proof. First, let us define
and
![]() $g(x) = x^{\alpha _2} f(\Phi (x))$
for some
$g(x) = x^{\alpha _2} f(\Phi (x))$
for some
![]() $\alpha _1> 0, \alpha _2$
to be fixed later. Using Faa di Bruno for the m-th derivative of the composition and identifying the only term where m derivatives fall on f, we have
$\alpha _1> 0, \alpha _2$
to be fixed later. Using Faa di Bruno for the m-th derivative of the composition and identifying the only term where m derivatives fall on f, we have
 $$ \begin{align} \left| \partial^m_x g(x) - x^{\alpha_{1} m + \alpha_2} f^{(m)}(\Phi (x)) \right| \lesssim_m \sum_{i=0}^{m-1} f^{(i)} (\Phi(x)) x^{\alpha_{1} i + \alpha_2 - (m-i)}, \end{align} $$
$$ \begin{align} \left| \partial^m_x g(x) - x^{\alpha_{1} m + \alpha_2} f^{(m)}(\Phi (x)) \right| \lesssim_m \sum_{i=0}^{m-1} f^{(i)} (\Phi(x)) x^{\alpha_{1} i + \alpha_2 - (m-i)}, \end{align} $$
where i corresponds to the quantity of derivatives falling on f.
Let
![]() $\widetilde {O} = [\Phi ^{-1} (a), +\infty ) \subset [1, +\infty )$
. By the Kolmogorov-Landau inequality on the halfline, we have
$\widetilde {O} = [\Phi ^{-1} (a), +\infty ) \subset [1, +\infty )$
. By the Kolmogorov-Landau inequality on the halfline, we have
Using (A.2) and (A.3), we obtain
 $$ \begin{align} \left\| x^{\alpha_{1} m + \alpha_2} f^{(m)}(\Phi (x)) \right\|_{L^\infty (\widetilde{O}) } \lesssim_n \sum_{j=0}^{m-1} \left\| f^{(j)} (\Phi(x)) x^{\alpha_{1} j + \alpha_2 - (m-j)} \right\|_{L^\infty (\widetilde{O})} + \| g(x) \|_{L^\infty (\widetilde{O})}^{1-m/n} \| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )}^{m/n}. \end{align} $$
$$ \begin{align} \left\| x^{\alpha_{1} m + \alpha_2} f^{(m)}(\Phi (x)) \right\|_{L^\infty (\widetilde{O}) } \lesssim_n \sum_{j=0}^{m-1} \left\| f^{(j)} (\Phi(x)) x^{\alpha_{1} j + \alpha_2 - (m-j)} \right\|_{L^\infty (\widetilde{O})} + \| g(x) \|_{L^\infty (\widetilde{O})}^{1-m/n} \| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )}^{m/n}. \end{align} $$
Applying (A.4) i times, we conclude that for any
![]() $0 \leq i \leq n$
,
$0 \leq i \leq n$
,
However, taking
![]() $m=n$
in (A.2) and using (A.5), we see that
$m=n$
in (A.2) and using (A.5), we see that
 $$ \begin{align*} \left\| \partial_x^n g(x) - x^{\alpha_{1} n + \alpha_2} f^{(n)}(\Phi (x)) \right\|_{L^\infty (\mathcal{O})} &\lesssim_n \| g(x) \|_{L^\infty (\widetilde{O})} + \sum_{j=0}^{n-1} \| g(x) \|_{L^\infty (\widetilde{O})}^{1-j/n} \| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )}^{j/n} \\ &\lesssim_n \| g(x) \|_{L^\infty (\widetilde{O} )} + \| g(x) \|_{L^\infty (\widetilde{O})}^{1/n} \| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )}^{(n-1)/n}, \end{align*} $$
$$ \begin{align*} \left\| \partial_x^n g(x) - x^{\alpha_{1} n + \alpha_2} f^{(n)}(\Phi (x)) \right\|_{L^\infty (\mathcal{O})} &\lesssim_n \| g(x) \|_{L^\infty (\widetilde{O})} + \sum_{j=0}^{n-1} \| g(x) \|_{L^\infty (\widetilde{O})}^{1-j/n} \| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )}^{j/n} \\ &\lesssim_n \| g(x) \|_{L^\infty (\widetilde{O} )} + \| g(x) \|_{L^\infty (\widetilde{O})}^{1/n} \| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )}^{(n-1)/n}, \end{align*} $$
so there exists some constant
![]() $C_n$
such that
$C_n$
such that
 $$ \begin{align*} \| \partial_x^n g(x) \|_{L^\infty (\widetilde{O}) } &\leq \| x^{\alpha_{1} n + \alpha_2} f^{(n)} (\Phi (x)) \|_{L^\infty (\widetilde{O})} + C_n \| g(x) \|_{L^\infty (\widetilde{O} )} + C_n \| g(x) \|_{L^\infty (\widetilde{O})}^{1/n} \| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )}^{(n-1)/n} \\& \leq \| x^{\alpha_{1} n + \alpha_2} f^{(n)} (\Phi (x)) \|_{L^\infty (\widetilde{O})} + C_n \| g(x) \|_{L^\infty (\widetilde{O} )} \\& \quad + C_n \frac{\| g(x) \|_{L^\infty (\widetilde{O})} \widetilde{C}^n }{n} + \frac{C_n}{\widetilde{C}^{n/(n-1)}} \frac{\| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )}}{n/(n-1)} \\& \leq \| x^{\alpha_{1} n + \alpha_2} f^{(n)} (\Phi (x)) \|_{L^\infty (\widetilde{O})} + \frac{1}{2} \| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )} + O_n \left( \| g(x) \|_{L^\infty (\widetilde{O} )} \right), \end{align*} $$
$$ \begin{align*} \| \partial_x^n g(x) \|_{L^\infty (\widetilde{O}) } &\leq \| x^{\alpha_{1} n + \alpha_2} f^{(n)} (\Phi (x)) \|_{L^\infty (\widetilde{O})} + C_n \| g(x) \|_{L^\infty (\widetilde{O} )} + C_n \| g(x) \|_{L^\infty (\widetilde{O})}^{1/n} \| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )}^{(n-1)/n} \\& \leq \| x^{\alpha_{1} n + \alpha_2} f^{(n)} (\Phi (x)) \|_{L^\infty (\widetilde{O})} + C_n \| g(x) \|_{L^\infty (\widetilde{O} )} \\& \quad + C_n \frac{\| g(x) \|_{L^\infty (\widetilde{O})} \widetilde{C}^n }{n} + \frac{C_n}{\widetilde{C}^{n/(n-1)}} \frac{\| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )}}{n/(n-1)} \\& \leq \| x^{\alpha_{1} n + \alpha_2} f^{(n)} (\Phi (x)) \|_{L^\infty (\widetilde{O})} + \frac{1}{2} \| \partial^n_x g(x) \|_{L^\infty (\widetilde{O} )} + O_n \left( \| g(x) \|_{L^\infty (\widetilde{O} )} \right), \end{align*} $$
where the second inequality holds for any
![]() $\widetilde {C}> 0$
due to Young’s inequality, and for the third inequality, we chose
$\widetilde {C}> 0$
due to Young’s inequality, and for the third inequality, we chose
![]() $\widetilde {C} = 2 C_n$
. Therefore, we get
$\widetilde {C} = 2 C_n$
. Therefore, we get
Now, plugging in (A.6) into (A.5), we obtain
 $$ \begin{align} \left\| x^{\alpha_{1} i + \alpha_2} f^{(i)} (\Phi (x)) \right\|_{L^\infty (\widetilde{O}) } &\lesssim_n \left\| g(x) \right\|_{L^\infty (\widetilde{O})} + \| g(x) \|_{L^\infty (\widetilde{O})}^{1-i/n} \| x^{\alpha_{1} n + \alpha_2} f^{(n)} (\Phi (x)) \|_{L^\infty (\widetilde{O} )}^{i/n} \nonumber \\ &= \left\| x^{\alpha_2} f(\Phi (x) ) \right\|_{L^\infty (\widetilde{O})} + \| x^{\alpha_2} f(\Phi (x)) \|_{L^\infty (\widetilde{O})}^{1-i/n} \| x^{\alpha_{1} n + \alpha_2} f^{(n)} (\Phi (x)) \|_{L^\infty (\widetilde{O} )}^{i/n} . \end{align} $$
$$ \begin{align} \left\| x^{\alpha_{1} i + \alpha_2} f^{(i)} (\Phi (x)) \right\|_{L^\infty (\widetilde{O}) } &\lesssim_n \left\| g(x) \right\|_{L^\infty (\widetilde{O})} + \| g(x) \|_{L^\infty (\widetilde{O})}^{1-i/n} \| x^{\alpha_{1} n + \alpha_2} f^{(n)} (\Phi (x)) \|_{L^\infty (\widetilde{O} )}^{i/n} \nonumber \\ &= \left\| x^{\alpha_2} f(\Phi (x) ) \right\|_{L^\infty (\widetilde{O})} + \| x^{\alpha_2} f(\Phi (x)) \|_{L^\infty (\widetilde{O})}^{1-i/n} \| x^{\alpha_{1} n + \alpha_2} f^{(n)} (\Phi (x)) \|_{L^\infty (\widetilde{O} )}^{i/n} . \end{align} $$
Letting
![]() $z = \Phi (x) = \frac {1}{\alpha _{1}+1} x^{\alpha _{1}+1} $
and writing (A.7) in terms of z, we obtain
$z = \Phi (x) = \frac {1}{\alpha _{1}+1} x^{\alpha _{1}+1} $
and writing (A.7) in terms of z, we obtain
 $$ \begin{align*} \left\| z^{\frac{\alpha_{1}i + \alpha_2}{\alpha_{1}+1}} f^{(i)} (z) \right\|_{L^\infty (\mathcal{O}) } \lesssim_{n} \frac{\left\| z^{\frac{\alpha_2}{\alpha_1+1}}f(z ) \right\|_{L^\infty (\mathcal{O})}}{(\alpha_{1}+1)^{\frac{\alpha_{1}}{\alpha_{1}+1}i}} + \left\| z^{\frac{\alpha_2}{\alpha_1+1}} f(z) \right\|_{L^\infty (\mathcal{O})}^{1-i/n} \left\| z^{\frac{\alpha_{1}n+\alpha_2}{\alpha_{1}+1} } f^{(n)} (z) \right\|_{L^\infty (\mathcal{O} )}^{i/n} . \end{align*} $$
$$ \begin{align*} \left\| z^{\frac{\alpha_{1}i + \alpha_2}{\alpha_{1}+1}} f^{(i)} (z) \right\|_{L^\infty (\mathcal{O}) } \lesssim_{n} \frac{\left\| z^{\frac{\alpha_2}{\alpha_1+1}}f(z ) \right\|_{L^\infty (\mathcal{O})}}{(\alpha_{1}+1)^{\frac{\alpha_{1}}{\alpha_{1}+1}i}} + \left\| z^{\frac{\alpha_2}{\alpha_1+1}} f(z) \right\|_{L^\infty (\mathcal{O})}^{1-i/n} \left\| z^{\frac{\alpha_{1}n+\alpha_2}{\alpha_{1}+1} } f^{(n)} (z) \right\|_{L^\infty (\mathcal{O} )}^{i/n} . \end{align*} $$
Taking
![]() $\alpha _{1}> 0$
such that
$\alpha _{1}> 0$
such that
![]() $\beta _1 = \frac {\alpha _{1}}{\alpha _{1}+1}$
and taking
$\beta _1 = \frac {\alpha _{1}}{\alpha _{1}+1}$
and taking
![]() $\alpha _2 = (1+\alpha _1) \beta _2$
, we obtain the desired inequality. It is clear that this imposes
$\alpha _2 = (1+\alpha _1) \beta _2$
, we obtain the desired inequality. It is clear that this imposes
![]() $\beta _1 \in (0, 1)$
.
$\beta _1 \in (0, 1)$
.
Lemma A.2. Let
![]() $a \geq 1$
and consider
$a \geq 1$
and consider
![]() $\mathcal {O} = \mathbb {R}^3 \setminus B(0, a)$
. Let
$\mathcal {O} = \mathbb {R}^3 \setminus B(0, a)$
. Let
![]() $\kappa \in (0, 1-2/n)$
. We have that for any
$\kappa \in (0, 1-2/n)$
. We have that for any
![]() $0 \leq i \leq n$
,
$0 \leq i \leq n$
,
 $$ \begin{align} \left( \int_{\mathcal{O}} |x|^{2 \kappa n} \left( | \nabla^i f | (x) \right)^p \right)^{1/p} \lesssim_{n} \left( \int_{\mathcal{O}} | x |^{2 \kappa n} \left( | \nabla^n f |(x) \right)^2 \right)^{\beta/2} \left\| f (x) \right\|_{L^\infty (\mathcal{O} )}^{1-\beta} + \| f (x)\|_{L^\infty (\mathcal{O})}, \end{align} $$
$$ \begin{align} \left( \int_{\mathcal{O}} |x|^{2 \kappa n} \left( | \nabla^i f | (x) \right)^p \right)^{1/p} \lesssim_{n} \left( \int_{\mathcal{O}} | x |^{2 \kappa n} \left( | \nabla^n f |(x) \right)^2 \right)^{\beta/2} \left\| f (x) \right\|_{L^\infty (\mathcal{O} )}^{1-\beta} + \| f (x)\|_{L^\infty (\mathcal{O})}, \end{align} $$
where
![]() $\beta = i/n$
and
$\beta = i/n$
and
![]() $\frac {1}{p} = \frac {\beta }{2}$
.
$\frac {1}{p} = \frac {\beta }{2}$
.
Proof. First, due to Gagliardo-Nirenberg inequality for bounded domains, we have that there exist absolute constants
![]() $C_1, C_2$
such that we have
$C_1, C_2$
such that we have
where A is the annulus where
![]() $1 \leq | x | \leq 4$
. Now, for any
$1 \leq | x | \leq 4$
. Now, for any
![]() $\lambda $
, let
$\lambda $
, let
![]() $\lambda A$
be the annulus
$\lambda A$
be the annulus
![]() $\lambda \leq | x | \leq 2\lambda $
. We can write (A.9) in terms of
$\lambda \leq | x | \leq 2\lambda $
. We can write (A.9) in terms of
![]() $f_\lambda (x) = f(\lambda x)$
which is a function defined on
$f_\lambda (x) = f(\lambda x)$
which is a function defined on
![]() $\lambda A$
. We obtain
$\lambda A$
. We obtain
Noting that
![]() $ip = n \beta p = 2n$
, we have that
$ip = n \beta p = 2n$
, we have that
 $$ \begin{align} \lambda^{2\kappa n} \left\| \nabla^i f_{\lambda} \right\|_{L^p (\lambda A)}^p &\leq C_1 \lambda^{2\kappa n} \left\| \nabla^n f_\lambda \right\|_{L^2(\lambda A)}^2 \| f \|_{L^\infty(\lambda A)}^{p-2} + C_2 \lambda^{3-2n(1-\kappa)} \| f_\lambda \|_{L^\infty (\lambda A)}^p \nonumber \\ &\leq C_1 \lambda^{2\kappa n} \left\| \nabla^n f_\lambda \right\|_{L^2(\lambda A)}^2 \| f \|_{L^\infty(\lambda A)}^{p-2} + C_2 \lambda^{-1} \| f_\lambda \|_{L^\infty (\lambda A)}^p, \end{align} $$
$$ \begin{align} \lambda^{2\kappa n} \left\| \nabla^i f_{\lambda} \right\|_{L^p (\lambda A)}^p &\leq C_1 \lambda^{2\kappa n} \left\| \nabla^n f_\lambda \right\|_{L^2(\lambda A)}^2 \| f \|_{L^\infty(\lambda A)}^{p-2} + C_2 \lambda^{3-2n(1-\kappa)} \| f_\lambda \|_{L^\infty (\lambda A)}^p \nonumber \\ &\leq C_1 \lambda^{2\kappa n} \left\| \nabla^n f_\lambda \right\|_{L^2(\lambda A)}^2 \| f \|_{L^\infty(\lambda A)}^{p-2} + C_2 \lambda^{-1} \| f_\lambda \|_{L^\infty (\lambda A)}^p, \end{align} $$
where in the second inequality, we used
![]() $1-\kappa \geq 2/n$
. Now, note that any function g defined over
$1-\kappa \geq 2/n$
. Now, note that any function g defined over
![]() $\lambda A$
has a corresponding f defined over A such that
$\lambda A$
has a corresponding f defined over A such that
![]() $g = f_\lambda $
. Therefore, (A.11) holds for all g over
$g = f_\lambda $
. Therefore, (A.11) holds for all g over
![]() $\lambda A$
.
$\lambda A$
.
Finally, we combine all those estimates at different scales. Set
![]() $\lambda _j=a2^{j-\frac 12}$
. Let us consider functions
$\lambda _j=a2^{j-\frac 12}$
. Let us consider functions
![]() $g_j$
such that
$g_j$
such that
![]() $g_j = g$
for
$g_j = g$
for
![]() $a2^j \leq | x | \leq a 2^{j+1}$
and
$a2^j \leq | x | \leq a 2^{j+1}$
and
![]() $g_j$
is supported on some
$g_j$
is supported on some
![]() $\lambda _j A$
, and moreover, we have that
$\lambda _j A$
, and moreover, we have that
for
![]() $B_j = \{ x: a 2^j \leq | x | \leq a 2^{j+1} \}\subset \lambda _j A$
and some constant
$B_j = \{ x: a 2^j \leq | x | \leq a 2^{j+1} \}\subset \lambda _j A$
and some constant
![]() $C_3>0$
. Using (A.11) for
$C_3>0$
. Using (A.11) for
![]() $g_j$
, we have that
$g_j$
, we have that
 $$ \begin{align*} \int_{\mathcal{O}} | x |^{2 \kappa n} \left( | \nabla^i g|(x) \right)^p &\leq \sum_{j=0}^\infty (4\lambda_j)^{2\kappa n} \left\| \nabla^i g_j \right\|_{L^p(\lambda_j A)}^p \\ &\leq C_1 \sum_{j \geq 0} \lambda_j^{2\kappa n} \left\| \nabla^n g_j \right\|_{L^2(\lambda_j A)}^2 \| g_j \|_{L^\infty(\lambda_j A)}^{p-2} + C_2 \sum_{j \geq 0} \lambda^{-1} \| g_j \|_{L^\infty (\lambda_j A)} \\ &\leq 16^n C_1 C_3^p \| g \|_{L^\infty (\mathcal{O} )}^{p-2} \sum_{j \geq 0} \lambda_j^{2\kappa n} \left\| \nabla^n g_j \right\|_{L^2(B_j)}^2 + 16^n C_2 C_3^p \| g \|_{L^\infty (\mathcal{O})}^p \sum_{j \geq 0} \lambda_j^{-1} \\ &= 16^n C_1 C_3^p \| g \|_{L^\infty (\mathcal{O} )}^{p-2} \sum_{j \geq 0} \lambda_j^{2\kappa n} \left\| \nabla^n g_j \right\|_{L^2(B_j)}^2 + 16^n C_2 C_3^p \| g \|_{L^\infty (\mathcal{O})}^p \frac{2}{a}. \end{align*} $$
$$ \begin{align*} \int_{\mathcal{O}} | x |^{2 \kappa n} \left( | \nabla^i g|(x) \right)^p &\leq \sum_{j=0}^\infty (4\lambda_j)^{2\kappa n} \left\| \nabla^i g_j \right\|_{L^p(\lambda_j A)}^p \\ &\leq C_1 \sum_{j \geq 0} \lambda_j^{2\kappa n} \left\| \nabla^n g_j \right\|_{L^2(\lambda_j A)}^2 \| g_j \|_{L^\infty(\lambda_j A)}^{p-2} + C_2 \sum_{j \geq 0} \lambda^{-1} \| g_j \|_{L^\infty (\lambda_j A)} \\ &\leq 16^n C_1 C_3^p \| g \|_{L^\infty (\mathcal{O} )}^{p-2} \sum_{j \geq 0} \lambda_j^{2\kappa n} \left\| \nabla^n g_j \right\|_{L^2(B_j)}^2 + 16^n C_2 C_3^p \| g \|_{L^\infty (\mathcal{O})}^p \sum_{j \geq 0} \lambda_j^{-1} \\ &= 16^n C_1 C_3^p \| g \|_{L^\infty (\mathcal{O} )}^{p-2} \sum_{j \geq 0} \lambda_j^{2\kappa n} \left\| \nabla^n g_j \right\|_{L^2(B_j)}^2 + 16^n C_2 C_3^p \| g \|_{L^\infty (\mathcal{O})}^p \frac{2}{a}. \end{align*} $$
As
![]() $a \geq 1$
, we have that
$a \geq 1$
, we have that
![]() $\frac {2}{a} \leq 2$
, and this concludes our proof. Note that
$\frac {2}{a} \leq 2$
, and this concludes our proof. Note that
![]() $C_1, C_2, C_3, p$
are independent of
$C_1, C_2, C_3, p$
are independent of
![]() $ \kappa , n, a$
.
$ \kappa , n, a$
.
Lemma A.3. Let
![]() $a \geq 1$
and consider
$a \geq 1$
and consider
![]() $\mathcal {O} = \mathbb {R}^3 \setminus B(0, a)$
. Let
$\mathcal {O} = \mathbb {R}^3 \setminus B(0, a)$
. Let
![]() $\kappa \in (0, 1-2/n )$
and
$\kappa \in (0, 1-2/n )$
and
![]() $\kappa '\in \mathbb R$
. We have that for any
$\kappa '\in \mathbb R$
. We have that for any
![]() $0 \leq i \leq n$
,
$0 \leq i \leq n$
,
where
![]() $\beta = i/n$
.
$\beta = i/n$
.
Proof. We will follow an analogous strategy to the proof of Lemma A.3. The principal difference is that in place of (A.9), we use the following Gagliardo-Nirenberg inequality:
where A is the annulus where
![]() $1 \leq | x | \leq 4$
and
$1 \leq | x | \leq 4$
and
![]() $C_1, C_2$
are some absolute constants. Given (A.13), one argues in a completely analogous manner as for Lemma A.3.
$C_1, C_2$
are some absolute constants. Given (A.13), one argues in a completely analogous manner as for Lemma A.3.
Lemma A.4. Let
![]() $f, g$
be radially symmetric scalar funcitons over
$f, g$
be radially symmetric scalar funcitons over
![]() $\mathbb {R}^3$
and
$\mathbb {R}^3$
and
![]() $F, G$
to be radially symmetric vector fields over
$F, G$
to be radially symmetric vector fields over
![]() $\mathbb {R}^3$
. Let us assume that
$\mathbb {R}^3$
. Let us assume that
![]() $f, F_i \in W^{2m, \infty }$
and
$f, F_i \in W^{2m, \infty }$
and
![]() $g, G_i \in H^{2m}$
. We have the following inequalities:
$g, G_i \in H^{2m}$
. We have the following inequalities:
Proof. Equation (A.15) and equation (A.17) are clear by examination because we are subtracting exactly the terms where m or
![]() $m+1$
derivatives fall on g or G. For equation (A.17), note also that
$m+1$
derivatives fall on g or G. For equation (A.17), note also that
![]() $\div (\Delta ^m G) = \Delta ^m \div (G)$
because
$\div (\Delta ^m G) = \Delta ^m \div (G)$
because
![]() $\Delta G = \nabla \div (G) $
for radial G.
$\Delta G = \nabla \div (G) $
for radial G.
Let us consider the equation (A.16) by expanding
![]() $\Delta ^m(F \nabla g)$
. We clearly have
$\Delta ^m(F \nabla g)$
. We clearly have
 $$ \begin{align} \Delta^m (F \nabla g ) &= \left( \sum_i \partial_i^2 \right)^m \sum_j F_j \partial_j g = \sum_j \left( F_j \partial_j \left( \sum_i \partial_i^2 \right)^mg \right) \nonumber \\&\quad + \sum_j \left( 2m \sum_{k} \partial_k F_j \partial_k \partial_j \left( \sum_i \partial_i^2 \right)^{m-1} g \right) + O \left( \| F \|_{W^{2m , \infty}} \| g \|_{H^{2m-1}} \right) \nonumber \\ &= F \nabla \Delta^m g + 2m \sum_{k, j} \partial_k F_j \partial_{k} \partial_j \Delta^{m-1} g + O_m \left( \| F \|_{W^{2m , \infty}} \| g \|_{H^{2m-1}} \right). \end{align} $$
$$ \begin{align} \Delta^m (F \nabla g ) &= \left( \sum_i \partial_i^2 \right)^m \sum_j F_j \partial_j g = \sum_j \left( F_j \partial_j \left( \sum_i \partial_i^2 \right)^mg \right) \nonumber \\&\quad + \sum_j \left( 2m \sum_{k} \partial_k F_j \partial_k \partial_j \left( \sum_i \partial_i^2 \right)^{m-1} g \right) + O \left( \| F \|_{W^{2m , \infty}} \| g \|_{H^{2m-1}} \right) \nonumber \\ &= F \nabla \Delta^m g + 2m \sum_{k, j} \partial_k F_j \partial_{k} \partial_j \Delta^{m-1} g + O_m \left( \| F \|_{W^{2m , \infty}} \| g \|_{H^{2m-1}} \right). \end{align} $$
Now, we claim that for a radially symmetric field F,
 $$ \begin{align} \partial_a F_b = \frac{y_a y_b}{\zeta^2} \left( \partial_\zeta F - \frac{F}{\zeta} \right) + \frac{\delta_{a, b} F}{\zeta}, \end{align} $$
$$ \begin{align} \partial_a F_b = \frac{y_a y_b}{\zeta^2} \left( \partial_\zeta F - \frac{F}{\zeta} \right) + \frac{\delta_{a, b} F}{\zeta}, \end{align} $$
which follows just from writing
![]() $F_b = F \frac {x_b}{\zeta }$
, where F is the radial component of F, and expanding
$F_b = F \frac {x_b}{\zeta }$
, where F is the radial component of F, and expanding
![]() $\partial _a \left ( F \frac {x_b}{\zeta } \right )$
. Using (A.19), we see that
$\partial _a \left ( F \frac {x_b}{\zeta } \right )$
. Using (A.19), we see that
 $$ \begin{align} \sum_{k, j} \partial_k F_j \partial_k \partial_j \Delta^{m-1} g &= \left( \partial_\zeta F - \frac{F}{\zeta} \right) \sum_{k, j} \frac{y_k y_j}{\zeta^2} \partial_k \partial_j \Delta^{m-1} g + \frac{F}{\zeta} \Delta^m g \nonumber \\ &= \left( \partial_\zeta F - \frac{F}{\zeta} \right) \partial_{\zeta}^2 \Delta^{m-1} g + \frac{F}{\zeta} \Delta^m g \nonumber \\ &= \left( \partial_\zeta F - \frac{F}{\zeta} \right) \left( \Delta^m g - \frac{2}{\zeta} \partial_\zeta \Delta^{m-1}g \right) + \frac{F}{\zeta} \Delta^m \nonumber \\ &= \partial_\zeta F \Delta^m g + \frac{\partial_\zeta F - F/\zeta}{\zeta} \partial_\zeta \Delta^{m-1} g. \end{align} $$
$$ \begin{align} \sum_{k, j} \partial_k F_j \partial_k \partial_j \Delta^{m-1} g &= \left( \partial_\zeta F - \frac{F}{\zeta} \right) \sum_{k, j} \frac{y_k y_j}{\zeta^2} \partial_k \partial_j \Delta^{m-1} g + \frac{F}{\zeta} \Delta^m g \nonumber \\ &= \left( \partial_\zeta F - \frac{F}{\zeta} \right) \partial_{\zeta}^2 \Delta^{m-1} g + \frac{F}{\zeta} \Delta^m g \nonumber \\ &= \left( \partial_\zeta F - \frac{F}{\zeta} \right) \left( \Delta^m g - \frac{2}{\zeta} \partial_\zeta \Delta^{m-1}g \right) + \frac{F}{\zeta} \Delta^m \nonumber \\ &= \partial_\zeta F \Delta^m g + \frac{\partial_\zeta F - F/\zeta}{\zeta} \partial_\zeta \Delta^{m-1} g. \end{align} $$
In the second equality, we have used that
![]() $\sum _{k, j} \frac {y_k y_j}{\zeta ^2} \partial _k \partial _j = \partial _{\zeta }^2$
, which follows from the fact that
$\sum _{k, j} \frac {y_k y_j}{\zeta ^2} \partial _k \partial _j = \partial _{\zeta }^2$
, which follows from the fact that
![]() $\left [ \partial _\zeta , \frac {y_k}{\zeta } \right ]$
and
$\left [ \partial _\zeta , \frac {y_k}{\zeta } \right ]$
and
 $$ \begin{align} \partial_\zeta^2 = \partial_\zeta \sum_{j} \frac{y_j}{\zeta} \partial_j = \sum_j \frac{y_j}{\zeta} \partial_\zeta \partial_j = \sum_{j, k} \frac{y_j y_k}{\zeta^2} \partial_{j, k}. \end{align} $$
$$ \begin{align} \partial_\zeta^2 = \partial_\zeta \sum_{j} \frac{y_j}{\zeta} \partial_j = \sum_j \frac{y_j}{\zeta} \partial_\zeta \partial_j = \sum_{j, k} \frac{y_j y_k}{\zeta^2} \partial_{j, k}. \end{align} $$
Substituting (A.20) in (A.18), we have
 $$ \begin{align} \Delta^m (F \nabla g) = F \nabla \Delta^m g + 2m \left( \partial_\zeta F \Delta^m g + \frac{\partial_\zeta F - F/\zeta}{\zeta} \partial_\zeta \Delta^{m-1} g \right) + O_m \left( \| F \|_{W^{2m , \infty}} \| g \|_{H^{2m-1}} \right). \end{align} $$
$$ \begin{align} \Delta^m (F \nabla g) = F \nabla \Delta^m g + 2m \left( \partial_\zeta F \Delta^m g + \frac{\partial_\zeta F - F/\zeta}{\zeta} \partial_\zeta \Delta^{m-1} g \right) + O_m \left( \| F \|_{W^{2m , \infty}} \| g \|_{H^{2m-1}} \right). \end{align} $$
Finally, note that
![]() $\left \| \frac {\partial _\zeta F - F/\zeta }{\zeta } \right \|_{\infty } \lesssim \left \| F \right \|_{W^{2m, \infty }}$
because of the radial symmetry of F. This completes the proof of (A.16).
$\left \| \frac {\partial _\zeta F - F/\zeta }{\zeta } \right \|_{\infty } \lesssim \left \| F \right \|_{W^{2m, \infty }}$
because of the radial symmetry of F. This completes the proof of (A.16).
Finally, let us show (A.14). Analyzing
![]() $\Delta ^m (F\nabla G_i)$
, we have that
$\Delta ^m (F\nabla G_i)$
, we have that
 $$ \begin{align} \Delta^m (F \nabla G_i ) &= F \cdot \nabla \Delta^m G_i + 2m \sum_{j, k} \partial_j F_k \partial_{j} \partial_k \Delta^{m-1} G_i + O \left( \| F \|_{W^{2m, \infty}} \| G \|_{H^{2m-1}} \right) \nonumber \\&= F \cdot \nabla \Delta^m G_i + 2m \left( \partial_\zeta F - \frac{F}{\zeta} \right) \partial_\zeta^2 \left( \frac{y_i}{\zeta} \Delta^{m-1} G \right) \nonumber \\&\quad + 2m \frac{F}{\zeta} \Delta^m G_i + O \left( \| F \|_{W^{2m, \infty}} \| G \|_{H^{2m-1}} \right) \nonumber \\&= F \cdot \nabla \Delta^m G_i + 2m \left( \partial_\zeta F - \frac{F}{\zeta} \right) \frac{y_i}{\zeta} \left( \Delta^{m} G - \frac{2 \zeta \partial_\zeta - 2}{\zeta^2} \Delta^{m-1} G \right) \nonumber \\&\quad + 2m \frac{F}{\zeta} \Delta^m G_i + O \left( \| F \|_{W^{2m, \infty}} \| G \|_{H^{2m-1}} \right) \nonumber \\&= F \cdot \nabla \Delta^m G_i + 2m \partial_\zeta F \Delta^m G_i - 2m \frac{ \partial_\zeta F - \frac{F}{\zeta} }{\zeta} \frac{y_i}{\zeta} \frac{2 \zeta \partial_\zeta - 2 }{\zeta} \Delta^{m-1} G \nonumber \\& \quad + O \left( \| F \|_{W^{2m, \infty}} \| G \|_{H^{2m-1}} \right) . \end{align} $$
$$ \begin{align} \Delta^m (F \nabla G_i ) &= F \cdot \nabla \Delta^m G_i + 2m \sum_{j, k} \partial_j F_k \partial_{j} \partial_k \Delta^{m-1} G_i + O \left( \| F \|_{W^{2m, \infty}} \| G \|_{H^{2m-1}} \right) \nonumber \\&= F \cdot \nabla \Delta^m G_i + 2m \left( \partial_\zeta F - \frac{F}{\zeta} \right) \partial_\zeta^2 \left( \frac{y_i}{\zeta} \Delta^{m-1} G \right) \nonumber \\&\quad + 2m \frac{F}{\zeta} \Delta^m G_i + O \left( \| F \|_{W^{2m, \infty}} \| G \|_{H^{2m-1}} \right) \nonumber \\&= F \cdot \nabla \Delta^m G_i + 2m \left( \partial_\zeta F - \frac{F}{\zeta} \right) \frac{y_i}{\zeta} \left( \Delta^{m} G - \frac{2 \zeta \partial_\zeta - 2}{\zeta^2} \Delta^{m-1} G \right) \nonumber \\&\quad + 2m \frac{F}{\zeta} \Delta^m G_i + O \left( \| F \|_{W^{2m, \infty}} \| G \|_{H^{2m-1}} \right) \nonumber \\&= F \cdot \nabla \Delta^m G_i + 2m \partial_\zeta F \Delta^m G_i - 2m \frac{ \partial_\zeta F - \frac{F}{\zeta} }{\zeta} \frac{y_i}{\zeta} \frac{2 \zeta \partial_\zeta - 2 }{\zeta} \Delta^{m-1} G \nonumber \\& \quad + O \left( \| F \|_{W^{2m, \infty}} \| G \|_{H^{2m-1}} \right) . \end{align} $$
Noting as before that
![]() $\frac {\partial _\zeta F - F/\zeta }{\zeta }$
is bounded in
$\frac {\partial _\zeta F - F/\zeta }{\zeta }$
is bounded in
![]() $L^\infty $
because of the symmetry and noting that
$L^\infty $
because of the symmetry and noting that
 $$ \begin{align} \frac{2 \zeta \partial_\zeta - 2}{\zeta} \Delta^{m-1} G = \left( 3 \partial_\zeta - \div \right) \Delta^{m-1} G, \end{align} $$
$$ \begin{align} \frac{2 \zeta \partial_\zeta - 2}{\zeta} \Delta^{m-1} G = \left( 3 \partial_\zeta - \div \right) \Delta^{m-1} G, \end{align} $$
we conclude (A.14).
Lemma A.5. Let us assume that
![]() $\mathcal {U}$
is a radially symmetric vector field and
$\mathcal {U}$
is a radially symmetric vector field and
![]() $\mathcal {S}$
is a radially symmetric scalar field. Let us denote the radial variable by
$\mathcal {S}$
is a radially symmetric scalar field. Let us denote the radial variable by
![]() $\zeta $
. Let
$\zeta $
. Let
![]() $\phi $
be some radially symmetric weight with
$\phi $
be some radially symmetric weight with
![]() $\phi \geq 1$
,
$\phi \geq 1$
,
![]() $\phi = 1$
on
$\phi = 1$
on
![]() $B(0, 1)$
and
$B(0, 1)$
and
![]() $\phi (\zeta )^{1/2} \leq \zeta $
for
$\phi (\zeta )^{1/2} \leq \zeta $
for
![]() $\zeta> 1$
.
$\zeta> 1$
.
Moreover, we assume that for any
![]() $0 \leq i \leq 2K$
, we have
$0 \leq i \leq 2K$
, we have
for some
![]() $\bar \varepsilon \ll 2^{-4K}$
. Let us also assume
$\bar \varepsilon \ll 2^{-4K}$
. Let us also assume
and
Then, we have
Proof. Equations (A.29) and (A.31) just follow from distributing the derivatives in
![]() $\Delta ^K (\mathcal {S} \nabla \mathcal {S})$
or
$\Delta ^K (\mathcal {S} \nabla \mathcal {S})$
or
![]() $\Delta ^K (\mathcal {S} \div (U))$
, respectively. For example, equation (A.29) follows from
$\Delta ^K (\mathcal {S} \div (U))$
, respectively. For example, equation (A.29) follows from
 $$ \begin{align*} \phi^K \left| \Delta^K (\mathcal{S} \nabla \mathcal{S}) - \mathcal{S} \nabla \Delta^K \mathcal{S} - 2K \nabla \mathcal{S} \Delta^K \mathcal{S} \right| \leq \sum_{i=0}^{2K-2} \binom{2K}{i} | \nabla^{2K-i} \mathcal{S} | | \nabla^{i+1} \mathcal{S} | \phi^K, \end{align*} $$
$$ \begin{align*} \phi^K \left| \Delta^K (\mathcal{S} \nabla \mathcal{S}) - \mathcal{S} \nabla \Delta^K \mathcal{S} - 2K \nabla \mathcal{S} \Delta^K \mathcal{S} \right| \leq \sum_{i=0}^{2K-2} \binom{2K}{i} | \nabla^{2K-i} \mathcal{S} | | \nabla^{i+1} \mathcal{S} | \phi^K, \end{align*} $$
so that
Equation (A.31) is shown in a completely analogous way.
Let us now show (A.30). Reasoning in the exact same way as we did to obtain (A.22), we have that
 $$ \begin{align*} &\left| \Delta^K ( \mathcal{U} \nabla \mathcal{S}) - \mathcal{U} \nabla \Delta^K \mathcal{S} - 2K \left( \partial_\zeta \mathcal{U} \Delta^K \mathcal{S} + \frac{\partial_\zeta \mathcal{U} - \mathcal{U}/\zeta}{\zeta} \partial_\zeta \Delta^{K-1} \mathcal{S} \right) \right| \\ & \qquad \leq | \nabla^{2K} \mathcal{U} | | \nabla \mathcal{S} | + 2^{2K}\sum_{i=1}^{2K-2} | \nabla^{2K-i} \mathcal{U} | | \nabla^{i+1} \mathcal{S} |. \end{align*} $$
$$ \begin{align*} &\left| \Delta^K ( \mathcal{U} \nabla \mathcal{S}) - \mathcal{U} \nabla \Delta^K \mathcal{S} - 2K \left( \partial_\zeta \mathcal{U} \Delta^K \mathcal{S} + \frac{\partial_\zeta \mathcal{U} - \mathcal{U}/\zeta}{\zeta} \partial_\zeta \Delta^{K-1} \mathcal{S} \right) \right| \\ & \qquad \leq | \nabla^{2K} \mathcal{U} | | \nabla \mathcal{S} | + 2^{2K}\sum_{i=1}^{2K-2} | \nabla^{2K-i} \mathcal{U} | | \nabla^{i+1} \mathcal{S} |. \end{align*} $$
Using (A.25) and (A.26), we obtain that
 $$ \begin{align} &\left\| \left( \Delta^K (\mathcal{U} \cdot \nabla \mathcal{S}) - \mathcal{U} \cdot \nabla \Delta^K \mathcal{S} - 2K \partial_\zeta \mathcal{U} \cdot \Delta^K \mathcal{S} \right) \phi^{K} \right\|_{L^2} \nonumber\\ &\quad\leq 2K \left\| \frac{\partial_\zeta \mathcal{U} - \mathcal{U}/\zeta}{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} \left\| \frac{\phi^{K}}{\zeta^{1/2} \phi^{1/4}} \nabla^{2K-1} \mathcal{S} \right\|_{L^2} + 2^{2K} \bar \varepsilon^{1/2} \bar E \nonumber \\&\quad\lesssim \bar E + 2K \bar \varepsilon^{1/2} \bar E \left\| \frac{ \partial_\zeta \mathcal{U} - \mathcal{U} / \zeta }{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} \nonumber \\&\quad\lesssim \bar E \left( 1 + \left\| \frac{ \partial_\zeta \mathcal{U} - \frac{\mathcal{U}}{\zeta} }{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} \right). \end{align} $$
$$ \begin{align} &\left\| \left( \Delta^K (\mathcal{U} \cdot \nabla \mathcal{S}) - \mathcal{U} \cdot \nabla \Delta^K \mathcal{S} - 2K \partial_\zeta \mathcal{U} \cdot \Delta^K \mathcal{S} \right) \phi^{K} \right\|_{L^2} \nonumber\\ &\quad\leq 2K \left\| \frac{\partial_\zeta \mathcal{U} - \mathcal{U}/\zeta}{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} \left\| \frac{\phi^{K}}{\zeta^{1/2} \phi^{1/4}} \nabla^{2K-1} \mathcal{S} \right\|_{L^2} + 2^{2K} \bar \varepsilon^{1/2} \bar E \nonumber \\&\quad\lesssim \bar E + 2K \bar \varepsilon^{1/2} \bar E \left\| \frac{ \partial_\zeta \mathcal{U} - \mathcal{U} / \zeta }{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} \nonumber \\&\quad\lesssim \bar E \left( 1 + \left\| \frac{ \partial_\zeta \mathcal{U} - \frac{\mathcal{U}}{\zeta} }{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} \right). \end{align} $$
Consider the regions
![]() $\mathcal {B}_1 = B(0, 1)$
and
$\mathcal {B}_1 = B(0, 1)$
and
![]() $\mathcal {B}_2 = \mathbb {R}^3 \setminus \mathcal {B}_1$
. We have that
$\mathcal {B}_2 = \mathbb {R}^3 \setminus \mathcal {B}_1$
. We have that
 $$ \begin{align} \left\| \frac{ \partial_\zeta \mathcal{U} - \mathcal{U}/\zeta }{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} &\leq \left\| \frac{ \partial_\zeta \mathcal{U} - \mathcal{U} / \zeta}{\zeta} \right\|_{L^\infty(\mathcal{B}_2)} + \left\| \partial_\zeta \mathcal{U} \right\|_{L^\infty(\mathcal{B}_2)}+ \left\| \mathcal{U} \right\|_{L^\infty(\mathcal{B}_1)} \nonumber \\ &\leq \left\| \mathcal{U} \right\|_{W^{3, \infty}} + \left\| \partial_\zeta \mathcal{U} \right\|_{L^\infty(\mathcal{B}_2)}+ \left\| \mathcal{U} \right\|_{L^\infty(\mathcal{B}_2)} \nonumber \\ &\lesssim 1, \end{align} $$
$$ \begin{align} \left\| \frac{ \partial_\zeta \mathcal{U} - \mathcal{U}/\zeta }{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} &\leq \left\| \frac{ \partial_\zeta \mathcal{U} - \mathcal{U} / \zeta}{\zeta} \right\|_{L^\infty(\mathcal{B}_2)} + \left\| \partial_\zeta \mathcal{U} \right\|_{L^\infty(\mathcal{B}_2)}+ \left\| \mathcal{U} \right\|_{L^\infty(\mathcal{B}_1)} \nonumber \\ &\leq \left\| \mathcal{U} \right\|_{W^{3, \infty}} + \left\| \partial_\zeta \mathcal{U} \right\|_{L^\infty(\mathcal{B}_2)}+ \left\| \mathcal{U} \right\|_{L^\infty(\mathcal{B}_2)} \nonumber \\ &\lesssim 1, \end{align} $$
where in the first inequality, we used
![]() $\phi (\zeta )^{1/4} \leq \zeta ^{1/2}$
, and in the last inequality, we used (A.27). Plugging (A.33) into (A.32), we conclude (A.30).
$\phi (\zeta )^{1/4} \leq \zeta ^{1/2}$
, and in the last inequality, we used (A.27). Plugging (A.33) into (A.32), we conclude (A.30).
Lastly, let us show (A.28). In the same way as we obtained (A.23), we have that
 $$ \begin{align*} &\left| \Delta^K (\mathcal{U} \cdot \nabla \mathcal{U}_i) - \mathcal{U} \cdot \nabla \Delta^K \mathcal{U}_i - 2K \partial_\zeta \mathcal{U} \Delta^K \mathcal{U}_i + 2K \frac{ \partial_\zeta \mathcal{U} - \frac{\mathcal{U}}{\zeta} }{\zeta} \frac{y_i}{\zeta} \frac{2 \zeta \partial_\zeta - 2 }{\zeta} \Delta^{m-1} \mathcal{U} \right| \nonumber \\& \quad \leq | \nabla^{2K} \mathcal{U} | | \nabla \mathcal{U} | + 2^{2K} \sum_{i=1}^{2K-2} | \nabla^{2K-i} \mathcal{U} | | \nabla^{i+1} \mathcal{U}_i |. \end{align*} $$
$$ \begin{align*} &\left| \Delta^K (\mathcal{U} \cdot \nabla \mathcal{U}_i) - \mathcal{U} \cdot \nabla \Delta^K \mathcal{U}_i - 2K \partial_\zeta \mathcal{U} \Delta^K \mathcal{U}_i + 2K \frac{ \partial_\zeta \mathcal{U} - \frac{\mathcal{U}}{\zeta} }{\zeta} \frac{y_i}{\zeta} \frac{2 \zeta \partial_\zeta - 2 }{\zeta} \Delta^{m-1} \mathcal{U} \right| \nonumber \\& \quad \leq | \nabla^{2K} \mathcal{U} | | \nabla \mathcal{U} | + 2^{2K} \sum_{i=1}^{2K-2} | \nabla^{2K-i} \mathcal{U} | | \nabla^{i+1} \mathcal{U}_i |. \end{align*} $$
Using (A.24), (A.25) and (A.26), we get that
 $$ \begin{align*} &\left\|\left( \Delta^K (\mathcal{U} \cdot \nabla \mathcal{U}_i) - \mathcal{U} \cdot \nabla \Delta^K \mathcal{U}_i - 2K \partial_\zeta \mathcal{U} \Delta^K \mathcal{U}_i \right) \phi^K \right\|_{L^2} \\&\quad \leq 2K \left\| \frac{ \partial_\zeta \mathcal{U} - \frac{\mathcal{U}}{\zeta} }{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} \left\| \frac{\phi^{K}}{\langle \zeta \rangle^{1/2} \phi^{1/4}} (3 \partial_\zeta - \div ) \Delta^{K-1} \mathcal{U} \right\|_{L^2} + \bar E + 2^{2K} \bar \varepsilon^{1/2} \bar E \\&\quad \leq 2K \bar \varepsilon^{1/2} \bar E \left\| \frac{ \partial_\zeta \mathcal{U} - \frac{\mathcal{U}}{\zeta} }{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} + 2 \bar E. \end{align*} $$
$$ \begin{align*} &\left\|\left( \Delta^K (\mathcal{U} \cdot \nabla \mathcal{U}_i) - \mathcal{U} \cdot \nabla \Delta^K \mathcal{U}_i - 2K \partial_\zeta \mathcal{U} \Delta^K \mathcal{U}_i \right) \phi^K \right\|_{L^2} \\&\quad \leq 2K \left\| \frac{ \partial_\zeta \mathcal{U} - \frac{\mathcal{U}}{\zeta} }{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} \left\| \frac{\phi^{K}}{\langle \zeta \rangle^{1/2} \phi^{1/4}} (3 \partial_\zeta - \div ) \Delta^{K-1} \mathcal{U} \right\|_{L^2} + \bar E + 2^{2K} \bar \varepsilon^{1/2} \bar E \\&\quad \leq 2K \bar \varepsilon^{1/2} \bar E \left\| \frac{ \partial_\zeta \mathcal{U} - \frac{\mathcal{U}}{\zeta} }{\zeta} \langle \zeta \rangle^{1/2} \phi^{1/4} \right\|_{L^\infty} + 2 \bar E. \end{align*} $$
Explicit computations
Lemma A.6. For every
![]() $\gamma>1 $
, we have that
$\gamma>1 $
, we have that
![]() $r^\ast (\gamma ) < 2-\frac {1}{\gamma }$
. Equivalently,
$r^\ast (\gamma ) < 2-\frac {1}{\gamma }$
. Equivalently,
 $$ \begin{align*} 2> (r^\ast (\gamma) - 1)\left( 2+ \frac{1}{\alpha} \right).\nonumber \end{align*} $$
$$ \begin{align*} 2> (r^\ast (\gamma) - 1)\left( 2+ \frac{1}{\alpha} \right).\nonumber \end{align*} $$
We also have
![]() $r^\ast (\gamma ) < \gamma $
.
$r^\ast (\gamma ) < \gamma $
.
Proof. For
![]() $\gamma \leq \frac {5}{3}$
, we have that
$\gamma \leq \frac {5}{3}$
, we have that
 $$ \begin{align*} 2 - \frac{1}{\gamma} - r^\ast (\gamma) = \frac{ \left(2 \sqrt{2}-\sqrt{\gamma -1}\right) \sqrt{\gamma -1} }{ \left(\sqrt{2} \sqrt{\frac{1}{\gamma -1}}+1\right)^2 \gamma }, \end{align*} $$
$$ \begin{align*} 2 - \frac{1}{\gamma} - r^\ast (\gamma) = \frac{ \left(2 \sqrt{2}-\sqrt{\gamma -1}\right) \sqrt{\gamma -1} }{ \left(\sqrt{2} \sqrt{\frac{1}{\gamma -1}}+1\right)^2 \gamma }, \end{align*} $$
which is positive, as
![]() $\gamma - 1 < 2\sqrt {2}$
. However, for
$\gamma - 1 < 2\sqrt {2}$
. However, for
![]() $\gamma> \frac {5}{3}$
,
$\gamma> \frac {5}{3}$
,
 $$ \begin{align*} 2 - \frac{1}{\gamma} - r^\ast (\gamma) = \frac{ (\gamma -1) \left(\left(2 \sqrt{3}-3\right) \gamma -\sqrt{3}+2\right) }{\left(\sqrt{3} (\gamma -1)+2\right) \gamma}> 0. \end{align*} $$
$$ \begin{align*} 2 - \frac{1}{\gamma} - r^\ast (\gamma) = \frac{ (\gamma -1) \left(\left(2 \sqrt{3}-3\right) \gamma -\sqrt{3}+2\right) }{\left(\sqrt{3} (\gamma -1)+2\right) \gamma}> 0. \end{align*} $$
This concludes the proof of
![]() $r^\ast (\gamma ) < 2-\frac {1}{\gamma }$
. As a consequence, we get
$r^\ast (\gamma ) < 2-\frac {1}{\gamma }$
. As a consequence, we get
 $$ \begin{align*} r^\ast (\gamma) - \gamma < -\gamma + 2 - \frac{1}{\gamma} = \frac{-(\gamma - 1)^2}{\gamma} < 0, \end{align*} $$
$$ \begin{align*} r^\ast (\gamma) - \gamma < -\gamma + 2 - \frac{1}{\gamma} = \frac{-(\gamma - 1)^2}{\gamma} < 0, \end{align*} $$
so we also get
![]() $\gamma> r^\ast (\gamma )$
. Finally, note that
$\gamma> r^\ast (\gamma )$
. Finally, note that
 $$ \begin{align*} 2> (r^\ast (\gamma) - 1)\left( 2+ \frac{1}{\alpha} \right) \Leftrightarrow 1 > (r^\ast (\gamma) - 1) \frac{\gamma}{\gamma - 1} \Leftrightarrow \frac{\gamma}{\gamma - 1} > r^\ast (\gamma ) - 1 \Leftrightarrow 2 - \frac{1}{\gamma} < r^\ast (\gamma ).\\[-41pt] \end{align*} $$
$$ \begin{align*} 2> (r^\ast (\gamma) - 1)\left( 2+ \frac{1}{\alpha} \right) \Leftrightarrow 1 > (r^\ast (\gamma) - 1) \frac{\gamma}{\gamma - 1} \Leftrightarrow \frac{\gamma}{\gamma - 1} > r^\ast (\gamma ) - 1 \Leftrightarrow 2 - \frac{1}{\gamma} < r^\ast (\gamma ).\\[-41pt] \end{align*} $$
Lemma A.7. For
![]() $\gamma = 7/5$
, we have that
$\gamma = 7/5$
, we have that
 $$ \begin{align*} \lim_{r\rightarrow r^\ast }D_{Z, 2} &= \frac{19 - 9 \sqrt 5}{132} < 0, & \lim_{r\rightarrow r^\ast}W_1 &= \frac{5-3 \sqrt{5}}{4} < 0, \\\lim_{r\rightarrow r^\ast} D_{W,0} &= \frac{\sqrt{5} - 1}{2}> 0, & \lim_{r\rightarrow r^\ast}Z_1 &= \frac{3 \sqrt{5} - 5}{6} > 0, \\\lim_{r\rightarrow r^\ast} N_{W,0} &= -\frac52 + \sqrt{5} < 0 & \lim_{r \rightarrow r^\ast } \partial_Z N_Z (P_s) &= \frac{3(-5+7\sqrt{5})}{20}> 0, \\\lim_{r \rightarrow r^\ast} D_{Z, 1} k &= \frac{3 \sqrt{5} - 1}{4} > 0, & \lim_{r\rightarrow r^\ast} k N_{Z, 1} &= \frac{25-9\sqrt{5}}{12} > 0 , \\\lim_{r \rightarrow r^\ast}(\partial_Z N_W (P_s) - W_1 \partial_Z D_W ) &= \frac{1-\sqrt{5}}{2} < 0, & \lim_{r\rightarrow r^\ast} \frac{D_{Z, 2}}{2 k D_{Z, 1}} &= \frac{-29 + 12 \sqrt 5 }{726} < 0, \\\lim_{r \rightarrow r^\ast} \partial_Z B^{\mathrm{fl}}_{7/5}(W_0, Z_0) &= 625 \frac{-58951 + 26559 \sqrt{5} }{1254528}>0, & \lim_{r\rightarrow r^\ast} Z_0 &= -\sqrt{5} < 0. \end{align*} $$
$$ \begin{align*} \lim_{r\rightarrow r^\ast }D_{Z, 2} &= \frac{19 - 9 \sqrt 5}{132} < 0, & \lim_{r\rightarrow r^\ast}W_1 &= \frac{5-3 \sqrt{5}}{4} < 0, \\\lim_{r\rightarrow r^\ast} D_{W,0} &= \frac{\sqrt{5} - 1}{2}> 0, & \lim_{r\rightarrow r^\ast}Z_1 &= \frac{3 \sqrt{5} - 5}{6} > 0, \\\lim_{r\rightarrow r^\ast} N_{W,0} &= -\frac52 + \sqrt{5} < 0 & \lim_{r \rightarrow r^\ast } \partial_Z N_Z (P_s) &= \frac{3(-5+7\sqrt{5})}{20}> 0, \\\lim_{r \rightarrow r^\ast} D_{Z, 1} k &= \frac{3 \sqrt{5} - 1}{4} > 0, & \lim_{r\rightarrow r^\ast} k N_{Z, 1} &= \frac{25-9\sqrt{5}}{12} > 0 , \\\lim_{r \rightarrow r^\ast}(\partial_Z N_W (P_s) - W_1 \partial_Z D_W ) &= \frac{1-\sqrt{5}}{2} < 0, & \lim_{r\rightarrow r^\ast} \frac{D_{Z, 2}}{2 k D_{Z, 1}} &= \frac{-29 + 12 \sqrt 5 }{726} < 0, \\\lim_{r \rightarrow r^\ast} \partial_Z B^{\mathrm{fl}}_{7/5}(W_0, Z_0) &= 625 \frac{-58951 + 26559 \sqrt{5} }{1254528}>0, & \lim_{r\rightarrow r^\ast} Z_0 &= -\sqrt{5} < 0. \end{align*} $$
Proof. We compute the limits using their formulas and obtain the results above.
Lemma A.8. For
![]() $\gamma = 7/5$
and n sufficiently large with
$\gamma = 7/5$
and n sufficiently large with
![]() $r \in (r_n, r_{n+1})$
, we have
$r \in (r_n, r_{n+1})$
, we have
 $$ \begin{align*} D_{W, 0} &\leq 2|Z_0|, &\qquad |Z_1| &\leq 3/10, &\qquad |W_1| &\leq 1/2, \\ |\partial_i N_\circ (P_s)| &\leq 2, &\qquad |\partial_i D_\circ | &\leq 3/5, &\qquad |\partial_i \partial_j N_\circ (P_s) | &\leq 7/5, \end{align*} $$
$$ \begin{align*} D_{W, 0} &\leq 2|Z_0|, &\qquad |Z_1| &\leq 3/10, &\qquad |W_1| &\leq 1/2, \\ |\partial_i N_\circ (P_s)| &\leq 2, &\qquad |\partial_i D_\circ | &\leq 3/5, &\qquad |\partial_i \partial_j N_\circ (P_s) | &\leq 7/5, \end{align*} $$
for any
![]() $i, j \in \left \{ W, Z \right \}$
.
$i, j \in \left \{ W, Z \right \}$
.
Proof. The first three items follow from the limits of
![]() $D_{W, 0}$
,
$D_{W, 0}$
,
![]() $Z_0$
,
$Z_0$
,
![]() $Z_1$
and
$Z_1$
and
![]() $W_1$
as
$W_1$
as
![]() $r \rightarrow r^\ast $
in Lemma A.7. For
$r \rightarrow r^\ast $
in Lemma A.7. For
![]() $|\partial _i N_\circ (P_s)| \leq 2$
, note that
$|\partial _i N_\circ (P_s)| \leq 2$
, note that
 $$ \begin{align*} \lim_{r \to r^\ast} \nabla N_W (P_s) = \left( \frac{7}{4}-\frac{29}{4 \sqrt{5}},1-\frac{4}{\sqrt{5}}\right), \qquad \lim_{r \to r^\ast} \nabla N_Z (P_s) = \left( \frac{1}{10} \left(7 \sqrt{5}-5\right),\frac{3}{20} \left(7 \sqrt{5}-5\right)\right), \end{align*} $$
$$ \begin{align*} \lim_{r \to r^\ast} \nabla N_W (P_s) = \left( \frac{7}{4}-\frac{29}{4 \sqrt{5}},1-\frac{4}{\sqrt{5}}\right), \qquad \lim_{r \to r^\ast} \nabla N_Z (P_s) = \left( \frac{1}{10} \left(7 \sqrt{5}-5\right),\frac{3}{20} \left(7 \sqrt{5}-5\right)\right), \end{align*} $$
and all the components on those limits are smaller than
![]() $2$
in absolute value. Lastly, for the last two items, let us write the expressions of
$2$
in absolute value. Lastly, for the last two items, let us write the expressions of
![]() $D_\circ , N_\circ $
for
$D_\circ , N_\circ $
for
![]() $\gamma = 7/5$
, which are
$\gamma = 7/5$
, which are
 $$ \begin{align*} \begin{aligned} D_W(W, Z) &= 1 + \frac{3}{5}W + \frac{2}{5} Z, \quad \quad N_W (W, Z) = -r W-\frac{7 W^2}{10}-\frac{2 WZ}{5}+\frac{Z^2}{10}, \\ D_Z(W, Z) &= 1 + \frac{2}{5}W + \frac{3}{5} Z, \quad \quad N_Z (W, Z) = -r Z-\frac{7 Z^2}{10}-\frac{2 WZ}{5}+\frac{W^2}{10}. \\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} D_W(W, Z) &= 1 + \frac{3}{5}W + \frac{2}{5} Z, \quad \quad N_W (W, Z) = -r W-\frac{7 W^2}{10}-\frac{2 WZ}{5}+\frac{Z^2}{10}, \\ D_Z(W, Z) &= 1 + \frac{2}{5}W + \frac{3}{5} Z, \quad \quad N_Z (W, Z) = -r Z-\frac{7 Z^2}{10}-\frac{2 WZ}{5}+\frac{W^2}{10}. \\ \end{aligned} \end{align*} $$
It is clear that any first derivative of
![]() $D_\circ $
is at most
$D_\circ $
is at most
![]() $3/5$
in absolute value and any second derivative of
$3/5$
in absolute value and any second derivative of
![]() $N_\circ $
is at most
$N_\circ $
is at most
![]() $7/5$
in absolute value.
$7/5$
in absolute value.
Lemma A.9. Let
![]() $\gamma \in (1, +\infty )$
. We have that
$\gamma \in (1, +\infty )$
. We have that
![]() $D_{Z, 1} = 0$
for
$D_{Z, 1} = 0$
for
![]() $r = r^\ast (\gamma )$
.
$r = r^\ast (\gamma )$
.
Proof. We separate in two cases:
![]() $1 < \gamma \leq \frac {5}{3}$
and
$1 < \gamma \leq \frac {5}{3}$
and
![]() $\gamma> \frac 53$
. For each case, we compute the limit
$\gamma> \frac 53$
. For each case, we compute the limit
 $$ \begin{align*} \lim_{r \to r^\ast } D_{Z, 1} = \lim_{r \to r^\ast } \left( 1 + \frac{3-\gamma}{4} W_1 + \frac{1 + \gamma}{4} Z_1 \right) = 0 \end{align*} $$
$$ \begin{align*} \lim_{r \to r^\ast } D_{Z, 1} = \lim_{r \to r^\ast } \left( 1 + \frac{3-\gamma}{4} W_1 + \frac{1 + \gamma}{4} Z_1 \right) = 0 \end{align*} $$
using equation (2.6).
Lemma A.10. Let us recall
![]() $D_{W, 0} = D_W (W_0, Z_0)$
. For every
$D_{W, 0} = D_W (W_0, Z_0)$
. For every
![]() $\gamma \in (1, +\infty )$
and
$\gamma \in (1, +\infty )$
and
![]() $r\in (1, r^\ast (\gamma ))$
, we have
$r\in (1, r^\ast (\gamma ))$
, we have
![]() $D_{W, 0}> 0$
.
$D_{W, 0}> 0$
.
Proof. We have that
Now, if
![]() $\gamma \geq 3$
, this is clearly positive. If
$\gamma \geq 3$
, this is clearly positive. If
![]() $\gamma < 3$
, we see that
$\gamma < 3$
, we see that
![]() $1+\gamma - (3 - \gamma )r$
decreases with r. Therefore, it suffices to check that
$1+\gamma - (3 - \gamma )r$
decreases with r. Therefore, it suffices to check that
![]() $1+\gamma - (3-\gamma )r^\ast (\gamma )>0$
to conclude that
$1+\gamma - (3-\gamma )r^\ast (\gamma )>0$
to conclude that
![]() $D_{W, 0}> 0$
. For
$D_{W, 0}> 0$
. For
![]() $1 < \gamma < \frac 53$
, we obtain
$1 < \gamma < \frac 53$
, we obtain
 $$ \begin{align*} 1+\gamma - (3-\gamma)r^\ast (\gamma) = \frac{4 (\gamma -1)}{\frac{\sqrt{2}}{\sqrt{\gamma -1}}+1}> 0. \end{align*} $$
$$ \begin{align*} 1+\gamma - (3-\gamma)r^\ast (\gamma) = \frac{4 (\gamma -1)}{\frac{\sqrt{2}}{\sqrt{\gamma -1}}+1}> 0. \end{align*} $$
For
![]() $\gamma \geq \frac 53$
, we obtain
$\gamma \geq \frac 53$
, we obtain
 $$ \begin{align*} 1+\gamma - (3-\gamma)r^\ast (\gamma) = \frac{\gamma -1 }{(\sqrt{3} (\gamma -1)+2)} \left(\left(3+\sqrt{3}\right) \gamma +\sqrt{3}-5\right), \end{align*} $$
$$ \begin{align*} 1+\gamma - (3-\gamma)r^\ast (\gamma) = \frac{\gamma -1 }{(\sqrt{3} (\gamma -1)+2)} \left(\left(3+\sqrt{3}\right) \gamma +\sqrt{3}-5\right), \end{align*} $$
where both the numerator and denominator on the fraction are clearly positive since
![]() $\gamma \geq \frac 53$
. The last factor is also positive since
$\gamma \geq \frac 53$
. The last factor is also positive since
![]() $\frac {5-\sqrt {3}}{3+\sqrt {3}} < \frac 53$
.
$\frac {5-\sqrt {3}}{3+\sqrt {3}} < \frac 53$
.
Lemma A.11. Let us recall
![]() $D_{Z, 1} = \nabla D_Z (P_s) (W_1, Z_1)$
. For every
$D_{Z, 1} = \nabla D_Z (P_s) (W_1, Z_1)$
. For every
![]() $\gamma \in (1, +\infty )$
and
$\gamma \in (1, +\infty )$
and
![]() $r\in [1, r^\ast (\gamma ))$
, we have
$r\in [1, r^\ast (\gamma ))$
, we have
![]() $D_{Z, 1}> 0$
.
$D_{Z, 1}> 0$
.
Proof. First of all,
![]() $D_{Z, 1} = -\frac {3-5\gamma +(1+\gamma )r + \mathcal {R}_2 (\gamma - 1)}{4(\gamma - 1)}$
, so it suffices to show that the numerator is negative. Using Lemma A.6, we have that
$D_{Z, 1} = -\frac {3-5\gamma +(1+\gamma )r + \mathcal {R}_2 (\gamma - 1)}{4(\gamma - 1)}$
, so it suffices to show that the numerator is negative. Using Lemma A.6, we have that
 $$ \begin{align} 3-5\gamma+(1+\gamma)r \leq 3-5\gamma+(1+\gamma) \left( 2 - \frac{1}{\gamma }\right) = \frac{-(\gamma - 1) (3\gamma - 1)}{\gamma} < 0. \end{align} $$
$$ \begin{align} 3-5\gamma+(1+\gamma)r \leq 3-5\gamma+(1+\gamma) \left( 2 - \frac{1}{\gamma }\right) = \frac{-(\gamma - 1) (3\gamma - 1)}{\gamma} < 0. \end{align} $$
Therefore, the proof would follow if we show that
Now, using Lemma A.6 again, we have
 $$ \begin{align*} 1-3\gamma+(\gamma+1)r < 1-3\gamma+(\gamma+1)\left( 2 - \frac{1}{\gamma} \right) = \frac{-(\gamma - 1)^2}{\gamma} < 0. \end{align*} $$
$$ \begin{align*} 1-3\gamma+(\gamma+1)r < 1-3\gamma+(\gamma+1)\left( 2 - \frac{1}{\gamma} \right) = \frac{-(\gamma - 1)^2}{\gamma} < 0. \end{align*} $$
Therefore, if
![]() $\gamma \leq \frac 53$
, both summands in (A.35) are positive, and we are done. Thus, we just need to show that (A.35) is positive for
$\gamma \leq \frac 53$
, both summands in (A.35) are positive, and we are done. Thus, we just need to show that (A.35) is positive for
![]() $\gamma> \frac 53$
. It suffices to show that
$\gamma> \frac 53$
. It suffices to show that
For
![]() $\gamma \geq \frac 53$
, we have that
$\gamma \geq \frac 53$
, we have that
so we conclude that the inequality in (A.36) for all
![]() $r \in (1, r^\ast (\gamma ))$
.
$r \in (1, r^\ast (\gamma ))$
.
Lemma A.12. Let us recall
![]() $\check D_{Z, 1} = \nabla D_Z (P_s) (W_1, \check Z_1)$
. For every
$\check D_{Z, 1} = \nabla D_Z (P_s) (W_1, \check Z_1)$
. For every
![]() $\gamma \in (1, +\infty )$
and
$\gamma \in (1, +\infty )$
and
![]() $r \in [1, r^\ast (\gamma )]$
, we have
$r \in [1, r^\ast (\gamma )]$
, we have
![]() $\check D_{Z, 1}> 0$
.
$\check D_{Z, 1}> 0$
.
Proof. We have that
![]() $\check D_{Z, 1} = -\frac {3+r-5\gamma + r\gamma - (\gamma - 1)\mathcal {R}_2}{4(\gamma - 1)}$
, so we just need to show that the numerator is negative. This follows from
$\check D_{Z, 1} = -\frac {3+r-5\gamma + r\gamma - (\gamma - 1)\mathcal {R}_2}{4(\gamma - 1)}$
, so we just need to show that the numerator is negative. This follows from
![]() $-5\gamma +3+r+r\gamma < 0$
, which was justified in (A.34).
$-5\gamma +3+r+r\gamma < 0$
, which was justified in (A.34).
Lemma A.13. Let us recall
![]() $s_\infty ^{\mathrm {fr}} = F_0 - W_0 - Z_0 = \frac {-4(r-1)}{3(\gamma - 1)} - W_0 - Z_0$
. Let either
$s_\infty ^{\mathrm {fr}} = F_0 - W_0 - Z_0 = \frac {-4(r-1)}{3(\gamma - 1)} - W_0 - Z_0$
. Let either
![]() $\gamma> 1$
and
$\gamma> 1$
and
![]() $r = r_3$
or
$r = r_3$
or
![]() $\gamma = 7/5$
and
$\gamma = 7/5$
and
![]() $r = r^\ast (7/5)$
. We have that
$r = r^\ast (7/5)$
. We have that
![]() $s_\infty ^{\mathrm {fr}}> 0$
.
$s_\infty ^{\mathrm {fr}}> 0$
.
Proof. We have that
Lemma A.23 yields
 $$ \begin{align*} 9 \gamma - 7 +(1-3\gamma)r> 9 \gamma - 7 +(1-3\gamma) \left( 2 - \frac{1}{\gamma} \right) = 3\gamma - 2 - \frac{1}{\gamma} > 0, \end{align*} $$
$$ \begin{align*} 9 \gamma - 7 +(1-3\gamma)r> 9 \gamma - 7 +(1-3\gamma) \left( 2 - \frac{1}{\gamma} \right) = 3\gamma - 2 - \frac{1}{\gamma} > 0, \end{align*} $$
so (A.37) is positive because
where in the last inequality, we used (A.42).
Properties of the phase portrait
Lemma A.14. Let
![]() $\gamma = 7/5$
and r sufficiently close to
$\gamma = 7/5$
and r sufficiently close to
![]() $r^\ast $
. Let us recall that the region
$r^\ast $
. Let us recall that the region
![]() $\mathcal {T}$
is the triangular region enclosed by
$\mathcal {T}$
is the triangular region enclosed by
![]() $N_W = 0$
, the horizontal segment from
$N_W = 0$
, the horizontal segment from ![]() to
to ![]() and
and
![]() $D_Z = 0$
. We call those parts of
$D_Z = 0$
. We call those parts of
![]() $\partial \mathcal {T}$
by
$\partial \mathcal {T}$
by
![]() $S_1, S_2, S_3$
, respectively. Then, the field
$S_1, S_2, S_3$
, respectively. Then, the field
![]() $(N_W D_Z, N_Z D_W)$
points inwards to
$(N_W D_Z, N_Z D_W)$
points inwards to
![]() $\mathcal {T}$
both in
$\mathcal {T}$
both in
![]() $S_1$
and
$S_1$
and
![]() $S_2$
.
$S_2$
.
Proof. The field over
![]() $N_W=0$
can be simply written as
$N_W=0$
can be simply written as
![]() $(0, N_Z D_W)$
. The branch of
$(0, N_Z D_W)$
. The branch of
![]() $N_W = 0$
passing through
$N_W = 0$
passing through ![]() can be parametrized as
can be parametrized as
in the region
![]() $W \geq Z$
. Its derivative satisfies
$W \geq Z$
. Its derivative satisfies
 $$ \begin{align*} Z ' &= \frac{2 \sqrt{W (10 r+11 W)}-5 r-11 W}{\sqrt{W (10 r+11 W)}}\\& \leq \frac{7W + 7\sqrt{rW}-5 r-11 W}{\sqrt{W (10 r+11 W)}} \leq \frac{ 8\sqrt{rW}-4 r-4 W}{\sqrt{W (10 r+11 W)}} = \frac{-4(\sqrt{W} - \sqrt{r})^2}{\sqrt{W (10 r+11 W)}} < 0, \end{align*} $$
$$ \begin{align*} Z ' &= \frac{2 \sqrt{W (10 r+11 W)}-5 r-11 W}{\sqrt{W (10 r+11 W)}}\\& \leq \frac{7W + 7\sqrt{rW}-5 r-11 W}{\sqrt{W (10 r+11 W)}} \leq \frac{ 8\sqrt{rW}-4 r-4 W}{\sqrt{W (10 r+11 W)}} = \frac{-4(\sqrt{W} - \sqrt{r})^2}{\sqrt{W (10 r+11 W)}} < 0, \end{align*} $$
where we used that
![]() $\sqrt {11}<7/2$
in the first inequality. Therefore, as Z decreases with W, the field
$\sqrt {11}<7/2$
in the first inequality. Therefore, as Z decreases with W, the field
![]() $(0, N_ZD_W)$
will point inwards to
$(0, N_ZD_W)$
will point inwards to
![]() $\mathcal {T}$
on
$\mathcal {T}$
on
![]() $S_1$
if
$S_1$
if
![]() $N_ZD_W> 0$
. We have that
$N_ZD_W> 0$
. We have that
![]() $D_W> 0$
as
$D_W> 0$
as
![]() $\mathcal {T}$
is in
$\mathcal {T}$
is in
![]() $\Omega $
. With respect to
$\Omega $
. With respect to
![]() $N_Z$
, note that it intersects our branch of
$N_Z$
, note that it intersects our branch of
![]() $N_W$
at two points:
$N_W$
at two points:
![]() $(0, 0)$
and
$(0, 0)$
and ![]() (the other two intersections of
(the other two intersections of
![]() $N_W=0$
and
$N_W=0$
and
![]() $N_Z = 0$
from Lemma A.17 correspond to the other branch). Therefore, the sign of
$N_Z = 0$
from Lemma A.17 correspond to the other branch). Therefore, the sign of
![]() $N_Z$
at
$N_Z$
at
![]() $S_1$
is the opposite one to the one after
$S_1$
is the opposite one to the one after ![]() . Taking asymptotics of
. Taking asymptotics of
![]() $N_Z$
over the branch (A.38), we see
$N_Z$
over the branch (A.38), we see
 $$ \begin{align*} N_Z(W, 2W - \sqrt{10rW + 11W^2} ) &= \frac{8}{5} \left(2 W^{3/2} \sqrt{10 r+11 W}-7 W^2\right)+r \left(\sqrt{W} \sqrt{10 r+11 W}-9 W\right) \\ &= \frac85 (-7 + 2 \sqrt{11}) W^2 + O\left( W^{3/2} \right), \end{align*} $$
$$ \begin{align*} N_Z(W, 2W - \sqrt{10rW + 11W^2} ) &= \frac{8}{5} \left(2 W^{3/2} \sqrt{10 r+11 W}-7 W^2\right)+r \left(\sqrt{W} \sqrt{10 r+11 W}-9 W\right) \\ &= \frac85 (-7 + 2 \sqrt{11}) W^2 + O\left( W^{3/2} \right), \end{align*} $$
and as
![]() $2\sqrt {11} < 7$
, we get that
$2\sqrt {11} < 7$
, we get that
![]() $N_Z$
is negative between
$N_Z$
is negative between ![]() and infinity over the branch (A.38), so it is positive over
and infinity over the branch (A.38), so it is positive over
![]() $S_1$
.
$S_1$
.
Now let us evaluate the field over
![]() $S_2$
. As
$S_2$
. As
![]() $S_2$
is horizontal, the field
$S_2$
is horizontal, the field
![]() $(N_W D_Z, N_Z D_W)$
will point inwards if
$(N_W D_Z, N_Z D_W)$
will point inwards if
![]() $N_Z D_W> 0$
. Similarly as before,
$N_Z D_W> 0$
. Similarly as before,
![]() $D_W> 0$
because
$D_W> 0$
because
![]() $\mathcal {T}$
lies on
$\mathcal {T}$
lies on
![]() $\Omega $
. With respect to
$\Omega $
. With respect to
![]() $N_Z$
, we have that
$N_Z$
, we have that
which is positive for
![]() $t> 0$
, so we also get
$t> 0$
, so we also get
![]() $N_Z> 0$
.
$N_Z> 0$
.
Lemma A.15. For
![]() $\gamma = \frac 75$
, and r close enough to
$\gamma = \frac 75$
, and r close enough to
![]() $r^\ast (7/5)$
, we have that
$r^\ast (7/5)$
, we have that

Proof. As
![]() $\gamma = \frac 75$
is fixed, Proposition 2.2 together with equations (2.1), (2.2), (2.6) give formulas for all the coefficients, depending on r and its radicals
$\gamma = \frac 75$
is fixed, Proposition 2.2 together with equations (2.1), (2.2), (2.6) give formulas for all the coefficients, depending on r and its radicals
![]() $\mathcal {R}_1, \mathcal {R}_2$
(given in equations (2.3), (2.7)). As
$\mathcal {R}_1, \mathcal {R}_2$
(given in equations (2.3), (2.7)). As
![]() $b^{\mathrm {fl}}$
only depends on those coefficients, we get expressions for
$b^{\mathrm {fl}}$
only depends on those coefficients, we get expressions for
![]() $D_{Z, 1}, D_{Z, 2}, D_{Z, 3}^{\mathrm {fl}}$
, depending on them.
$D_{Z, 1}, D_{Z, 2}, D_{Z, 3}^{\mathrm {fl}}$
, depending on them.
Using that for
![]() $\gamma = 7/5$
, we have
$\gamma = 7/5$
, we have
 $$ \begin{align} r &= \frac{7}{4}-\frac{1}{8} \sqrt{5} \sqrt{5 \mathcal{R}_1^2+4}, \\ \mathcal{R}_2 &= \frac{1}{4} \sqrt{\mathcal{R}_1 \left(-24 \sqrt{5} \sqrt{5 \mathcal{R}_1^2+4}-95 \mathcal{R}_1+80\right)-12 \sqrt{5} \sqrt{5 \mathcal{R}_1^2+4}+184} \nonumber, \end{align} $$
$$ \begin{align} r &= \frac{7}{4}-\frac{1}{8} \sqrt{5} \sqrt{5 \mathcal{R}_1^2+4}, \\ \mathcal{R}_2 &= \frac{1}{4} \sqrt{\mathcal{R}_1 \left(-24 \sqrt{5} \sqrt{5 \mathcal{R}_1^2+4}-95 \mathcal{R}_1+80\right)-12 \sqrt{5} \sqrt{5 \mathcal{R}_1^2+4}+184} \nonumber, \end{align} $$
we can express both sides of equation (A.39) just in terms of
![]() $\mathcal {R}_1$
. Taylor expanding
$\mathcal {R}_1$
. Taylor expanding
![]() $\mathcal {R}_1$
, we obtain
$\mathcal {R}_1$
, we obtain

so we conclude that (A.39) holds if
![]() $\mathcal {R}_1$
is sufficiently small. However, for
$\mathcal {R}_1$
is sufficiently small. However, for
![]() $\gamma = \frac 75$
, we have that
$\gamma = \frac 75$
, we have that
![]() $r^\ast = \frac 14 (7 - \sqrt {5})$
. From (A.40), we see that
$r^\ast = \frac 14 (7 - \sqrt {5})$
. From (A.40), we see that
![]() $\mathcal {R}_1 \rightarrow 0$
as
$\mathcal {R}_1 \rightarrow 0$
as
![]() $r \rightarrow r^\ast $
, so we are done.
$r \rightarrow r^\ast $
, so we are done.
Lemma A.16. Let us recall that
![]() $\mathcal {T}^{(M)}$
is the triangle with vertices
$\mathcal {T}^{(M)}$
is the triangle with vertices
![]() $P_s$
,
$P_s$
,
![]() $P_s + (M, -M)$
and
$P_s + (M, -M)$
and
![]() $P_s + (M, h)$
, where h is such that this third point falls on the line
$P_s + (M, h)$
, where h is such that this third point falls on the line
![]() $D_Z = 0$
. We have that
$D_Z = 0$
. We have that
![]() $N_W < 0$
on
$N_W < 0$
on
![]() $\mathcal {T}^{(M)}$
for any
$\mathcal {T}^{(M)}$
for any
![]() $M> 0$
.
$M> 0$
.
Proof. A generic point of
![]() $\mathcal {T}^{(M)}$
can be written as
$\mathcal {T}^{(M)}$
can be written as
![]() $P = P_s + t(1, s)$
, where s is between
$P = P_s + t(1, s)$
, where s is between
![]() $-1$
and
$-1$
and
![]() $-\frac {1-\alpha }{1+\alpha }$
. Thus,
$-\frac {1-\alpha }{1+\alpha }$
. Thus,
 $$ \begin{align*} N_W (P) &= N_W(P_s) + t\nabla N_W(P_s) \cdot (1, s) + t^2(1, s) \frac{HN_W}{2} (1, s) \\ &= N_{W, 0} + \frac{1}{4} t \Big( (-4 r-4 \gamma W_0+\gamma Z_0-3 Z_0)+ s(\gamma W_0-3 W_0+2 \gamma Z_0-2 Z_0) \Big) \\ &\quad +\frac{1}{4}t^2 \Big( (\gamma -1) s^2+ (\gamma -3) s - 2\gamma \Big) \\ &= N_{W, 0} + \frac{t}{4} A + \frac{t^2}{4} B. \end{align*} $$
$$ \begin{align*} N_W (P) &= N_W(P_s) + t\nabla N_W(P_s) \cdot (1, s) + t^2(1, s) \frac{HN_W}{2} (1, s) \\ &= N_{W, 0} + \frac{1}{4} t \Big( (-4 r-4 \gamma W_0+\gamma Z_0-3 Z_0)+ s(\gamma W_0-3 W_0+2 \gamma Z_0-2 Z_0) \Big) \\ &\quad +\frac{1}{4}t^2 \Big( (\gamma -1) s^2+ (\gamma -3) s - 2\gamma \Big) \\ &= N_{W, 0} + \frac{t}{4} A + \frac{t^2}{4} B. \end{align*} $$
We have that
![]() $N_{W, 0} < 0$
due to Lemmas A.26 and A.7. We will conclude the proof by showing that
$N_{W, 0} < 0$
due to Lemmas A.26 and A.7. We will conclude the proof by showing that
![]() $A < 0$
and
$A < 0$
and
![]() $B < 0$
for
$B < 0$
for
![]() $s \in \left [ -1, -\frac {1-\alpha }{1+\alpha } \right ]$
.
$s \in \left [ -1, -\frac {1-\alpha }{1+\alpha } \right ]$
.
Let us start showing
![]() $B < 0$
. As B is a second-degree polynomial in s with positive second derivative, it will be negative for
$B < 0$
. As B is a second-degree polynomial in s with positive second derivative, it will be negative for
![]() $s \in \left [ -1, -\frac {1-\alpha }{1+\alpha } \right ]$
as long as it is negative in both extrema. We have that
$s \in \left [ -1, -\frac {1-\alpha }{1+\alpha } \right ]$
as long as it is negative in both extrema. We have that
and this concludes
![]() $B < 0$
.
$B < 0$
.
Now, we show
![]() $A < 0$
. As A is an affine function of s, in order to show that it is negative for
$A < 0$
. As A is an affine function of s, in order to show that it is negative for
![]() $s \in \left [ -1, -\frac {1-\alpha }{1+\alpha } \right ]$
, it suffices to show it at both extrema. We have that
$s \in \left [ -1, -\frac {1-\alpha }{1+\alpha } \right ]$
, it suffices to show it at both extrema. We have that
 $$ \begin{align*} (\gamma^2-1)A\Big|_{s = -\frac{1-\alpha}{1+\alpha} } = -8\mathcal{R}_1 \gamma + 4 \underbrace{\left( 3 \gamma ^2-10 \gamma +3+\left(-3 \gamma ^2+6 \gamma +1\right) r \right)}_C, \end{align*} $$
$$ \begin{align*} (\gamma^2-1)A\Big|_{s = -\frac{1-\alpha}{1+\alpha} } = -8\mathcal{R}_1 \gamma + 4 \underbrace{\left( 3 \gamma ^2-10 \gamma +3+\left(-3 \gamma ^2+6 \gamma +1\right) r \right)}_C, \end{align*} $$
so it suffices to show
![]() $C < 0$
. As C is an affine function of r, it suffices to check its sign at
$C < 0$
. As C is an affine function of r, it suffices to check its sign at
![]() $r=1$
and
$r=1$
and
![]() $r=r^\ast $
:
$r=r^\ast $
:
 $$ \begin{align*} C\Big|_{r=1} &= 4-4\gamma < 0, \\ C \Big|_{r=r^\ast} &= -\left(\sqrt{3}-1\right) (\gamma -1) (3 \gamma -1) < 0, \quad \mbox{ for } \gamma>\frac53, \\ C \Big|_{r=r^\ast} &= \frac{-2 (\gamma -1) \left(3 \gamma-1 +4 \sqrt{2} \sqrt{\frac{1}{\gamma -1}}\right)}{ \left( 1 + \sqrt{\frac{2}{\gamma - 1}} \right)^2 } < 0 \quad \mbox{ for } 1 < \gamma \leq \frac53. \end{align*} $$
$$ \begin{align*} C\Big|_{r=1} &= 4-4\gamma < 0, \\ C \Big|_{r=r^\ast} &= -\left(\sqrt{3}-1\right) (\gamma -1) (3 \gamma -1) < 0, \quad \mbox{ for } \gamma>\frac53, \\ C \Big|_{r=r^\ast} &= \frac{-2 (\gamma -1) \left(3 \gamma-1 +4 \sqrt{2} \sqrt{\frac{1}{\gamma -1}}\right)}{ \left( 1 + \sqrt{\frac{2}{\gamma - 1}} \right)^2 } < 0 \quad \mbox{ for } 1 < \gamma \leq \frac53. \end{align*} $$
Finally, we need to show that
![]() $A |_{s=-1}$
is also negative. We have that
$A |_{s=-1}$
is also negative. We have that
 $$ \begin{align} A \Big|_{s=-1} = -3(\gamma +1) \mathcal{R}_1 + \underbrace{9 \gamma ^2-22 \gamma +1 +\left(-3 \gamma ^2-2 \gamma +17\right) r}_D. \end{align} $$
$$ \begin{align} A \Big|_{s=-1} = -3(\gamma +1) \mathcal{R}_1 + \underbrace{9 \gamma ^2-22 \gamma +1 +\left(-3 \gamma ^2-2 \gamma +17\right) r}_D. \end{align} $$
We again split into two cases,
![]() $1 < \gamma < 3$
and
$1 < \gamma < 3$
and
![]() $\gamma \geq 3$
.
$\gamma \geq 3$
.
For the case
![]() $1 < \gamma < 3$
, we will show
$1 < \gamma < 3$
, we will show
![]() $D < 0$
, which trivially gives
$D < 0$
, which trivially gives
![]() $A|_{s=-1} < 0$
from (A.41). As D is an affine function of r, it suffices to show that it is negative at
$A|_{s=-1} < 0$
from (A.41). As D is an affine function of r, it suffices to show that it is negative at
![]() $r=1$
and at
$r=1$
and at
![]() $r = 1+\frac {2}{\left (1+\sqrt {\frac {2}{\gamma -1}}\right )^2} \geq r^\ast $
. We have that
$r = 1+\frac {2}{\left (1+\sqrt {\frac {2}{\gamma -1}}\right )^2} \geq r^\ast $
. We have that
 $$ \begin{align*} D\Big|_{r=1} = 6 (\gamma-3)(\gamma-1) < 0, \quad \mbox{ and } \quad D\Big|_{r = 1+\frac{2}{\left(1+\sqrt{\frac{2}{\gamma -1}}\right)^2}} = 3(\gamma-3)\gamma \sqrt{\frac{2}{\gamma -1}} -4 < 0. \end{align*} $$
$$ \begin{align*} D\Big|_{r=1} = 6 (\gamma-3)(\gamma-1) < 0, \quad \mbox{ and } \quad D\Big|_{r = 1+\frac{2}{\left(1+\sqrt{\frac{2}{\gamma -1}}\right)^2}} = 3(\gamma-3)\gamma \sqrt{\frac{2}{\gamma -1}} -4 < 0. \end{align*} $$
For the case
![]() $\gamma \geq 3$
, we will show that
$\gamma \geq 3$
, we will show that
![]() $9(\gamma +1)^2 \mathcal {R}_1^2> D^2$
. This clearly implies that
$9(\gamma +1)^2 \mathcal {R}_1^2> D^2$
. This clearly implies that
![]() $A|_{s=-1} < 0$
from (A.41). We have that
$A|_{s=-1} < 0$
from (A.41). We have that
 $$ \begin{align*} \frac{9(\gamma+1)^2 \mathcal{R}_1^2 - D^2}{16(\gamma - 1)} = 27 \gamma^2 - 10 \gamma -5 + \left(-6 \gamma^2 - 28 \gamma +10\right) r + \left( -3 \gamma^2 + 2\gamma + 13 \right) r^2. \end{align*} $$
$$ \begin{align*} \frac{9(\gamma+1)^2 \mathcal{R}_1^2 - D^2}{16(\gamma - 1)} = 27 \gamma^2 - 10 \gamma -5 + \left(-6 \gamma^2 - 28 \gamma +10\right) r + \left( -3 \gamma^2 + 2\gamma + 13 \right) r^2. \end{align*} $$
For
![]() $\gamma> 3$
, both the terms in r and
$\gamma> 3$
, both the terms in r and
![]() $r^2$
in the previous equation are negative; thus, the expression is decreasing. In particular, we can lower bound it by its value at
$r^2$
in the previous equation are negative; thus, the expression is decreasing. In particular, we can lower bound it by its value at
![]() $r=r^\ast $
; that is,
$r=r^\ast $
; that is,
 $$ \begin{align*} \frac{9(\gamma+1)^2 \mathcal{R}_1^2 - D^2}{16(\gamma - 1)} &\geq 27 \gamma^2 - 10 \gamma -5 + \left(-6 \gamma^2 - 28 \gamma +10\right) r^\ast + \left( -3 \gamma^2 + 2\gamma + 13 \right) \left( r^\ast \right)^2 \\ &= \frac{6 (\gamma -1)^2 \left(3 \left(3-\sqrt{3}\right) \gamma ^2-2 \left(7-\sqrt{3}\right) \gamma +5 \sqrt{3}-7\right)}{\left(\sqrt{3} (\gamma - 1) + 2\right)^2}. \end{align*} $$
$$ \begin{align*} \frac{9(\gamma+1)^2 \mathcal{R}_1^2 - D^2}{16(\gamma - 1)} &\geq 27 \gamma^2 - 10 \gamma -5 + \left(-6 \gamma^2 - 28 \gamma +10\right) r^\ast + \left( -3 \gamma^2 + 2\gamma + 13 \right) \left( r^\ast \right)^2 \\ &= \frac{6 (\gamma -1)^2 \left(3 \left(3-\sqrt{3}\right) \gamma ^2-2 \left(7-\sqrt{3}\right) \gamma +5 \sqrt{3}-7\right)}{\left(\sqrt{3} (\gamma - 1) + 2\right)^2}. \end{align*} $$
Noting that the second-degree polynomial
![]() $\left (3 \left (3-\sqrt {3}\right ) \gamma ^2-2 \left (7-\sqrt {3}\right ) \gamma +5 \sqrt {3}-7\right )$
is positive for
$\left (3 \left (3-\sqrt {3}\right ) \gamma ^2-2 \left (7-\sqrt {3}\right ) \gamma +5 \sqrt {3}-7\right )$
is positive for
![]() $\gamma> 3$
, we are done.
$\gamma> 3$
, we are done.
Lemma A.17. There are three points in our phase portrait
![]() $W - Z \geq 0$
at which
$W - Z \geq 0$
at which
![]() $N_W = N_Z = 0$
, which are
$N_W = N_Z = 0$
, which are
![]() $(0, 0)$
,
$(0, 0)$
,
![]() $(-r, -r)$
,
$(-r, -r)$
, ![]() .
.
-
• For
 $\gamma> 1$
and
$\gamma> 1$
and
 $r \in (r_3, r_4)$
, no equilibrium point is in the region
$r \in (r_3, r_4)$
, no equilibrium point is in the region
 $\Omega $
. Moreover, the point
$\Omega $
. Moreover, the point  is a saddle point of the field
is a saddle point of the field
 $(N_W D_Z, N_Z D_W)$
.
$(N_W D_Z, N_Z D_W)$
. -
• For
 $\gamma = 7/5$
and r sufficiently close to
$\gamma = 7/5$
and r sufficiently close to
 $r^\ast $
, only the point
$r^\ast $
, only the point  is in
is in
 $\Omega $
, and it lies in the region
$\Omega $
, and it lies in the region
 $Z> Z_0$
.
$Z> Z_0$
.
Proof. From Bézout’s theorem, there are at most four solutions to
![]() $N_W = N_Z = 0$
. By direct substitution in the expressions of
$N_W = N_Z = 0$
. By direct substitution in the expressions of
![]() $N_W, N_Z$
, it is clear that
$N_W, N_Z$
, it is clear that
![]() $(0, 0)$
,
$(0, 0)$
,
![]() $(-r, -r)$
,
$(-r, -r)$
,

are those four solutions. It is also clear that the last one lies in
![]() $W-Z<0$
. Now, recall
$W-Z<0$
. Now, recall
![]() $\Omega $
is the region of
$\Omega $
is the region of
![]() $W-Z\geq 0$
, where
$W-Z\geq 0$
, where
![]() $D_W> 0$
and
$D_W> 0$
and
![]() $D_Z < 0$
. Note that
$D_Z < 0$
. Note that
![]() $D_Z(0, 0) = 1$
,
$D_Z(0, 0) = 1$
,
![]() $D_W(-r,-r) = 1-r<0$
, so the only equilibrium point that can possibly lie on
$D_W(-r,-r) = 1-r<0$
, so the only equilibrium point that can possibly lie on
![]() $\Omega $
is
$\Omega $
is ![]() .
.
For the case
![]() $r \in (r_3, r_4)$
, a direct calculation gives us
$r \in (r_3, r_4)$
, a direct calculation gives us
From Lemma A.23, we have
![]() $r_4 < \frac {3\gamma - 1}{2+\sqrt {3}(\gamma -1)}$
. Therefore, in the case
$r_4 < \frac {3\gamma - 1}{2+\sqrt {3}(\gamma -1)}$
. Therefore, in the case
![]() $r \in (r_3, r_4)$
, we get that
$r \in (r_3, r_4)$
, we get that

For
![]() $\gamma = 7/5$
and
$\gamma = 7/5$
and
![]() $r = r^\ast (\gamma )$
, we get
$r = r^\ast (\gamma )$
, we get
Recall that
![]() $Y_0$
is the Z coordinate of
$Y_0$
is the Z coordinate of ![]() . At
. At
![]() $\gamma = 7/5$
and
$\gamma = 7/5$
and
![]() $r = r^\ast $
, we have
$r = r^\ast $
, we have
 $$ \begin{align*} Y_0 = -\frac{5 \left(1+\sqrt{3}\right) \left(4+\sqrt{5}\right)}{4 \left(1+\sqrt{5}\right)^2}> -\sqrt{5} = Z_0.\nonumber \end{align*} $$
$$ \begin{align*} Y_0 = -\frac{5 \left(1+\sqrt{3}\right) \left(4+\sqrt{5}\right)}{4 \left(1+\sqrt{5}\right)^2}> -\sqrt{5} = Z_0.\nonumber \end{align*} $$
Lastly, we need to show that for the case
![]() $\gamma>1$
,
$\gamma>1$
,
![]() $r\in (r_3, r_4)$
, we have that
$r\in (r_3, r_4)$
, we have that ![]() is a saddle point of
is a saddle point of
![]() $(N_W D_Z, N_Z D_W)$
. We calculate the Jacobian at
$(N_W D_Z, N_Z D_W)$
. We calculate the Jacobian at ![]() , and its eigenvalues are given by
, and its eigenvalues are given by
 $$ \begin{align*} \lambda_\pm &= \frac{r}{2 (1-3 \gamma )^2} \left( (-9 \gamma^2 +18 \gamma - 5) +(15 \gamma^2 -18\gamma -1) r \pm \sqrt{B} \right) = \frac{r}{2 (1-3 \gamma )^2} \left(A \pm \sqrt{B} \right), \\ B &= \left(27 \gamma ^2-30 \gamma +7\right)^2+(3 \gamma (\gamma (3 \gamma (\gamma +20)-94)+28)+25) r^2+\left(106-6 \gamma \left(45 \gamma ^3-110 \gamma +88\right)\right) r. \end{align*} $$
$$ \begin{align*} \lambda_\pm &= \frac{r}{2 (1-3 \gamma )^2} \left( (-9 \gamma^2 +18 \gamma - 5) +(15 \gamma^2 -18\gamma -1) r \pm \sqrt{B} \right) = \frac{r}{2 (1-3 \gamma )^2} \left(A \pm \sqrt{B} \right), \\ B &= \left(27 \gamma ^2-30 \gamma +7\right)^2+(3 \gamma (\gamma (3 \gamma (\gamma +20)-94)+28)+25) r^2+\left(106-6 \gamma \left(45 \gamma ^3-110 \gamma +88\right)\right) r. \end{align*} $$
Let
![]() $r' = \frac {3 \gamma -1}{\sqrt {3} (\gamma -1)+2}$
. We will show that
$r' = \frac {3 \gamma -1}{\sqrt {3} (\gamma -1)+2}$
. We will show that
![]() $B>0, A>0$
and
$B>0, A>0$
and
![]() $A^2-B> 0$
for all
$A^2-B> 0$
for all
![]() $r \in (1, r')$
. This directly gives that
$r \in (1, r')$
. This directly gives that
![]() $\lambda _+> 0, \lambda _-<0$
for
$\lambda _+> 0, \lambda _-<0$
for
![]() $r \in (1, r')$
. Assume
$r \in (1, r')$
. Assume
![]() $r'> r_4$
by Lemma A.23, and we would be done.
$r'> r_4$
by Lemma A.23, and we would be done.
We start with
![]() $A> 0$
. As A is affine with respect to r, it suffices to check that A is positive for
$A> 0$
. As A is affine with respect to r, it suffices to check that A is positive for
![]() $r=1$
and for
$r=1$
and for
![]() $r=r'$
. This follows from
$r=r'$
. This follows from
 $$ \begin{align*} A \Big|_{r=1} = 6(\gamma^2-1)>0, \qquad A \Big|_{r=r'} = \frac{((6+2\sqrt{3})\gamma + (9 - 5\sqrt{3})(\gamma - 1) ) (3\gamma - 1)(\gamma - 1)}{2 + (\gamma - 1)\sqrt{3} } > 0. \end{align*} $$
$$ \begin{align*} A \Big|_{r=1} = 6(\gamma^2-1)>0, \qquad A \Big|_{r=r'} = \frac{((6+2\sqrt{3})\gamma + (9 - 5\sqrt{3})(\gamma - 1) ) (3\gamma - 1)(\gamma - 1)}{2 + (\gamma - 1)\sqrt{3} } > 0. \end{align*} $$
Now, we show
![]() $B> 0$
. As an auxiliary step, we will show that
$B> 0$
. As an auxiliary step, we will show that
![]() $\frac {d}{dr} B < 0$
. As
$\frac {d}{dr} B < 0$
. As
![]() $\frac {d}{dr} B$
is an affine function of r, it suffices to show that for
$\frac {d}{dr} B$
is an affine function of r, it suffices to show that for
![]() $r=1$
and
$r=1$
and
![]() $r=r'$
, we have
$r=r'$
, we have
 $$ \begin{align*} \frac{d}{dr}\Big|_{r=1} B &= -12 (\gamma -1) (\gamma +1) (21 \gamma^2- 30\gamma +13) < 0, \\ \frac{d}{dr}\Big|_{r=r'} B &= -\frac{2 (\gamma -1) (3 \gamma -1) \left( 9 \left(5 \sqrt{3}-1\right) \gamma ^3+\left(15 \sqrt{3}-99\right) \gamma ^2+\left(213-105 \sqrt{3}\right) \gamma +53 \sqrt{3}-81\right)}{\sqrt{3} (\gamma - 1)+2} < 0. \end{align*} $$
$$ \begin{align*} \frac{d}{dr}\Big|_{r=1} B &= -12 (\gamma -1) (\gamma +1) (21 \gamma^2- 30\gamma +13) < 0, \\ \frac{d}{dr}\Big|_{r=r'} B &= -\frac{2 (\gamma -1) (3 \gamma -1) \left( 9 \left(5 \sqrt{3}-1\right) \gamma ^3+\left(15 \sqrt{3}-99\right) \gamma ^2+\left(213-105 \sqrt{3}\right) \gamma +53 \sqrt{3}-81\right)}{\sqrt{3} (\gamma - 1)+2} < 0. \end{align*} $$
Therefore,
![]() $B \geq B|_{r=r'}$
, so it suffices to show that
$B \geq B|_{r=r'}$
, so it suffices to show that
![]() $B|_{r=r'}> 0$
. We have that
$B|_{r=r'}> 0$
. We have that
 $$ \begin{align*} B\Big|_{r=r'} = \frac{6 (3\gamma-1)^2(\gamma-1)^2 \left( (19\sqrt{3}-18) \gamma^2 + (60-34\sqrt{3}) \gamma (\gamma-1) + 26-15 \sqrt{3}\right) }{\left(\sqrt{3} \gamma -\sqrt{3}+2\right)^2}> 0. \end{align*} $$
$$ \begin{align*} B\Big|_{r=r'} = \frac{6 (3\gamma-1)^2(\gamma-1)^2 \left( (19\sqrt{3}-18) \gamma^2 + (60-34\sqrt{3}) \gamma (\gamma-1) + 26-15 \sqrt{3}\right) }{\left(\sqrt{3} \gamma -\sqrt{3}+2\right)^2}> 0. \end{align*} $$
Finally, let us show that
![]() $A^2 - B> 0$
. We have that
$A^2 - B> 0$
. We have that
 $$ \begin{align*} \frac{A^2 - B}{24(\gamma-1)(3\gamma-1)} &= \underbrace{9 \gamma ^2-6 \gamma +1 +(4-12 \gamma ) r +\left(-3 \gamma ^2+6 \gamma +1\right) r^2}_{C}. \end{align*} $$
$$ \begin{align*} \frac{A^2 - B}{24(\gamma-1)(3\gamma-1)} &= \underbrace{9 \gamma ^2-6 \gamma +1 +(4-12 \gamma ) r +\left(-3 \gamma ^2+6 \gamma +1\right) r^2}_{C}. \end{align*} $$
Now note that C is a second order polynomial of r and
In particular, for any
![]() $\varepsilon $
sufficiently small, C is positive at
$\varepsilon $
sufficiently small, C is positive at
![]() $r = r'-\varepsilon $
. As C is a polynomial of r, positive at
$r = r'-\varepsilon $
. As C is a polynomial of r, positive at
![]() $r=1$
and
$r=1$
and
![]() $r = r'-\varepsilon $
, it has an even quantity of roots (counted with multiplicity) in the interval
$r = r'-\varepsilon $
, it has an even quantity of roots (counted with multiplicity) in the interval
![]() $(1, r'-\varepsilon )$
. Therefore, as C is a second-degree polynomial of r and it has a root at
$(1, r'-\varepsilon )$
. Therefore, as C is a second-degree polynomial of r and it has a root at
![]() $r=r'$
, there are no roots in the interval
$r=r'$
, there are no roots in the interval
![]() $[1, r'-\varepsilon )$
. As we can take
$[1, r'-\varepsilon )$
. As we can take
![]() $\varepsilon $
sufficiently small, we conclude that C is positive for all
$\varepsilon $
sufficiently small, we conclude that C is positive for all
![]() $r \in [1, r')$
.
$r \in [1, r')$
.
Lemma A.18. Let
![]() $\gamma = 7/5$
and r sufficiently close to
$\gamma = 7/5$
and r sufficiently close to
![]() $r^\ast (7/5)$
. Let
$r^\ast (7/5)$
. Let
![]() $P' = \left ( W_0 - T_{\mathrm {DW}}, Z_0 \right )$
for
$P' = \left ( W_0 - T_{\mathrm {DW}}, Z_0 \right )$
for
![]() $T_{\mathrm {DW}} = \frac {5}{3} \left (\sqrt {4 r^2-14 r+11}-2 r+3\right )$
. We have that
$T_{\mathrm {DW}} = \frac {5}{3} \left (\sqrt {4 r^2-14 r+11}-2 r+3\right )$
. We have that
![]() $D_W(P') = 0$
and that along the horizontal segment
$D_W(P') = 0$
and that along the horizontal segment
![]() $[P', P_s]$
, the field
$[P', P_s]$
, the field
![]() $(N_W D_W, N_Z D_W)$
points downwards.
$(N_W D_W, N_Z D_W)$
points downwards.
Proof. Using the formulas for
![]() $W_0, Z_0$
in (2.1), we get that
$W_0, Z_0$
in (2.1), we get that
![]() $D_W(P') = 0$
. Then, we need to show that the sign of the third-degree polynomial
$D_W(P') = 0$
. Then, we need to show that the sign of the third-degree polynomial
![]() $N_Z (W_0 - t, Z_0) D_W(W_0 - t, Z_0)$
is negative for
$N_Z (W_0 - t, Z_0) D_W(W_0 - t, Z_0)$
is negative for
![]() $t \in (0, T_{\mathrm {DW}})$
. We clearly have that
$t \in (0, T_{\mathrm {DW}})$
. We clearly have that
![]() $N_Z (W_0 - t, Z_0) D_W(W_0 - t, Z_0)$
vanishes at
$N_Z (W_0 - t, Z_0) D_W(W_0 - t, Z_0)$
vanishes at
![]() $0$
(because
$0$
(because
![]() $N_Z(P_s) = 0$
) and
$N_Z(P_s) = 0$
) and
![]() $T_{\mathrm {DW}}$
(because
$T_{\mathrm {DW}}$
(because
![]() $D_W(P') = 0$
). At
$D_W(P') = 0$
). At
![]() $r = r^\ast $
, we have
$r = r^\ast $
, we have
so the first-degree polynomial above is negative also for r sufficiently close to
![]() $r^\ast $
.
$r^\ast $
.
Lemma A.19. Let us recall that for
![]() $\gamma \in (1, +\infty )$
and
$\gamma \in (1, +\infty )$
and
![]() $r \in (r_3, r_4)$
, we define
$r \in (r_3, r_4)$
, we define
where
![]() $X_0, Y_0$
are defined in (3.2). Let us also define
$X_0, Y_0$
are defined in (3.2). Let us also define
![]() $t_f^{\mathrm {extra}} = \frac 12 (X_0 - Y_0)$
. We have that
$t_f^{\mathrm {extra}} = \frac 12 (X_0 - Y_0)$
. We have that
![]() $D_W(b^{\mathrm {extra}}(t))> 0$
and
$D_W(b^{\mathrm {extra}}(t))> 0$
and
![]() $D_Z (b^{\mathrm {extra}}(t))> 0$
for all
$D_Z (b^{\mathrm {extra}}(t))> 0$
for all
![]() $t \in (0, t_f^{\mathrm { extra}}]$
. Moreover, if we let
$t \in (0, t_f^{\mathrm { extra}}]$
. Moreover, if we let
we have that
![]() $P^{\mathrm {extra}}(t)> 0$
for all
$P^{\mathrm {extra}}(t)> 0$
for all
![]() $t \in (0, t_f^{\mathrm {extra}})$
.
$t \in (0, t_f^{\mathrm {extra}})$
.
Proof. By direct calculation, we get that
 $$ \begin{align*} t_f^{\mathrm{extra}} &= \frac{2 \sqrt{3} r}{3 \gamma -1}, \\ (6\gamma - 2) D_W(b^{\mathrm{extra}}(t)) &= 2 (3 \gamma -1)+2 \left(\sqrt{3} \gamma -\sqrt{3}-2\right) r-(\gamma -1 ) (3 \gamma -1) t ,\\ (6\gamma - 2) D_Z(b^{\mathrm{extra}}(t)) &= 2 (3 \gamma -1)-2 \left(\sqrt{3} \gamma -\sqrt{3}+2\right) r+(\gamma -1) (3 \gamma -1) t ,\\ \frac{(3\gamma - 1)^2}{t (\gamma - 1) }P^{\mathrm{extra}}(t) &= -4 \sqrt{3} r (-3 \gamma +2 r+1)+(3 \gamma -1 ) (2 r+1-3 \gamma ) t. \end{align*} $$
$$ \begin{align*} t_f^{\mathrm{extra}} &= \frac{2 \sqrt{3} r}{3 \gamma -1}, \\ (6\gamma - 2) D_W(b^{\mathrm{extra}}(t)) &= 2 (3 \gamma -1)+2 \left(\sqrt{3} \gamma -\sqrt{3}-2\right) r-(\gamma -1 ) (3 \gamma -1) t ,\\ (6\gamma - 2) D_Z(b^{\mathrm{extra}}(t)) &= 2 (3 \gamma -1)-2 \left(\sqrt{3} \gamma -\sqrt{3}+2\right) r+(\gamma -1) (3 \gamma -1) t ,\\ \frac{(3\gamma - 1)^2}{t (\gamma - 1) }P^{\mathrm{extra}}(t) &= -4 \sqrt{3} r (-3 \gamma +2 r+1)+(3 \gamma -1 ) (2 r+1-3 \gamma ) t. \end{align*} $$
The second expression is clearly decreasing, and the third one increasing. With respect to the fourth one, note that
![]() $-3\gamma + 2r + 1 \leq -\gamma +1 < 0$
due to Lemma A.6, so it is also decreasing. Thus, we just need to show the following quantities are positive:
$-3\gamma + 2r + 1 \leq -\gamma +1 < 0$
due to Lemma A.6, so it is also decreasing. Thus, we just need to show the following quantities are positive:
 $$ \begin{align*} (6\gamma - 2) D_W(b^{\mathrm{extra}}(t_f^{\mathrm{extra}})) &= -2-4r+6\gamma> 0 ,\\ (6\gamma - 2) D_Z(b^{\mathrm{extra}}(0)) &= -2 + 6\gamma + 2r(-2+\sqrt{3}-\sqrt{3}\gamma), \\ \frac{(3\gamma - 1)^2}{t (\gamma - 1) }P^{\mathrm{extra}}(t_f^{\mathrm{extra}}) &= -2 \sqrt{3} r (1+2r-3\gamma) > 0. \end{align*} $$
$$ \begin{align*} (6\gamma - 2) D_W(b^{\mathrm{extra}}(t_f^{\mathrm{extra}})) &= -2-4r+6\gamma> 0 ,\\ (6\gamma - 2) D_Z(b^{\mathrm{extra}}(0)) &= -2 + 6\gamma + 2r(-2+\sqrt{3}-\sqrt{3}\gamma), \\ \frac{(3\gamma - 1)^2}{t (\gamma - 1) }P^{\mathrm{extra}}(t_f^{\mathrm{extra}}) &= -2 \sqrt{3} r (1+2r-3\gamma) > 0. \end{align*} $$
The first and the third expressions are trivially positive (recall
![]() $r^\ast < \gamma $
from Lemma A.6). The second expression is clearly decreasing with r, and it vanishes at
$r^\ast < \gamma $
from Lemma A.6). The second expression is clearly decreasing with r, and it vanishes at
![]() $r = \frac {3\gamma - 1}{2+\sqrt {3}(\gamma - 1)}$
. Therefore, we just need to show that
$r = \frac {3\gamma - 1}{2+\sqrt {3}(\gamma - 1)}$
. Therefore, we just need to show that
![]() $r_4 < \frac {3\gamma - 1}{2+\sqrt {3}(\gamma - 1)}$
. This is shown in Lemma A.23.
$r_4 < \frac {3\gamma - 1}{2+\sqrt {3}(\gamma - 1)}$
. This is shown in Lemma A.23.
Lemma A.20. Let S be the vertical segment between
![]() $(W_0, Z_0)$
and
$(W_0, Z_0)$
and
![]() $(W_0, W_0)$
. Let either
$(W_0, W_0)$
. Let either
![]() $(\gamma , r) = (7/5, r^\ast )$
or
$(\gamma , r) = (7/5, r^\ast )$
or
![]() $(\gamma , r) \in (1, +\infty ) \times (r_3, r_4)$
. We have that
$(\gamma , r) \in (1, +\infty ) \times (r_3, r_4)$
. We have that
![]() $N_W(P) < 0$
for any
$N_W(P) < 0$
for any
![]() $P \in S$
.
$P \in S$
.
Proof. The second-degree polynomial
![]() $N_W(W_0, y)$
(in y) has second derivative
$N_W(W_0, y)$
(in y) has second derivative
![]() $\frac {\gamma - 1}{2}> 0$
. As we want to show that the polynomial is negative for
$\frac {\gamma - 1}{2}> 0$
. As we want to show that the polynomial is negative for
![]() $y \in [Z_0, W_0]$
, it suffices to show it at the endpoints. Clearly,
$y \in [Z_0, W_0]$
, it suffices to show it at the endpoints. Clearly,
![]() $N_W(W_0, Z_0) = N_{W, 0} < 0$
in our range of
$N_W(W_0, Z_0) = N_{W, 0} < 0$
in our range of
![]() $(\gamma , r)$
because of Lemmas A.26 and A.7. Observe that
$(\gamma , r)$
because of Lemmas A.26 and A.7. Observe that
 $$ \begin{align*} 16(\gamma - 1)^4 N_W(W_0, W_0) &= A\cdot B \\ &=\left( 3(\gamma-3)\left(\gamma-\frac13 \right) + ( -5\gamma^2 +10\gamma - 1 )r -(1+\gamma) \mathcal{R}_1 \right) \\ &\qquad \cdot \left( -3(\gamma-3)\left( \gamma - \frac13 \right) + (\gamma -3)(\gamma +1) r + (\gamma +1) \mathcal{R}_1 \right). \end{align*} $$
$$ \begin{align*} 16(\gamma - 1)^4 N_W(W_0, W_0) &= A\cdot B \\ &=\left( 3(\gamma-3)\left(\gamma-\frac13 \right) + ( -5\gamma^2 +10\gamma - 1 )r -(1+\gamma) \mathcal{R}_1 \right) \\ &\qquad \cdot \left( -3(\gamma-3)\left( \gamma - \frac13 \right) + (\gamma -3)(\gamma +1) r + (\gamma +1) \mathcal{R}_1 \right). \end{align*} $$
In the case
![]() $\gamma = 7/5$
,
$\gamma = 7/5$
,
![]() $r = r^\ast (7/5)$
, we obtain
$r = r^\ast (7/5)$
, we obtain
![]() $A \cdot B = \frac {64}{625} (-45+17\sqrt {5}) < 0$
. From now on, let us assume
$A \cdot B = \frac {64}{625} (-45+17\sqrt {5}) < 0$
. From now on, let us assume
![]() $r \in (r_3, r_4)$
.
$r \in (r_3, r_4)$
.
We first show
![]() $B> 0$
. If
$B> 0$
. If
![]() $\gamma \in (1, 3)$
, as
$\gamma \in (1, 3)$
, as
![]() $(\gamma -3)(\gamma +1)r$
decreases with r, and
$(\gamma -3)(\gamma +1)r$
decreases with r, and
![]() $r < r_4 < \frac {3\gamma - 1}{2+\sqrt {3}(\gamma - 1)}$
, we get
$r < r_4 < \frac {3\gamma - 1}{2+\sqrt {3}(\gamma - 1)}$
, we get
 $$ \begin{align*} B &> \left( 3(\gamma-3)\left(\gamma-\frac13 \right) + ( -5\gamma^2 +10\gamma - 1 ) \frac{3\gamma - 1}{2+\sqrt{3}(\gamma - 1)} \right) \\ &= \frac{-\left(\sqrt{3}-1\right) (\gamma -3) (\gamma -1) (3 \gamma -1)}{(2+\sqrt{3} (\gamma-1))} > 0. \end{align*} $$
$$ \begin{align*} B &> \left( 3(\gamma-3)\left(\gamma-\frac13 \right) + ( -5\gamma^2 +10\gamma - 1 ) \frac{3\gamma - 1}{2+\sqrt{3}(\gamma - 1)} \right) \\ &= \frac{-\left(\sqrt{3}-1\right) (\gamma -3) (\gamma -1) (3 \gamma -1)}{(2+\sqrt{3} (\gamma-1))} > 0. \end{align*} $$
Now, let us assume that
![]() $\gamma \geq 3$
. We get that
$\gamma \geq 3$
. We get that
We claim
![]() $\frac {dB}{dr} < 0$
. As
$\frac {dB}{dr} < 0$
. As
![]() $|-3 (\gamma -2) \gamma |>(\gamma -3)^2 r$
(because
$|-3 (\gamma -2) \gamma |>(\gamma -3)^2 r$
(because
![]() $\gamma , \gamma -2> \gamma -3$
and
$\gamma , \gamma -2> \gamma -3$
and
![]() $3>r$
), the claim
$3>r$
), the claim
![]() $\frac {dB}{dr} < 0$
follows from
$\frac {dB}{dr} < 0$
follows from
Therefore, to prove
![]() $B> 0$
, we just need to show
$B> 0$
, we just need to show
![]() $B> 0$
at
$B> 0$
at
![]() $r = r^\ast $
. We have that
$r = r^\ast $
. We have that
 $$ \begin{align*} B|_{r = r^\ast} = \frac{8 \left(\sqrt{3}-1\right) (\gamma -1)^2}{\sqrt{3} \gamma -\sqrt{3}+2}> 0. \end{align*} $$
$$ \begin{align*} B|_{r = r^\ast} = \frac{8 \left(\sqrt{3}-1\right) (\gamma -1)^2}{\sqrt{3} \gamma -\sqrt{3}+2}> 0. \end{align*} $$
Now, let us prove
![]() $A < 0$
. If we have
$A < 0$
. If we have
![]() $-5\gamma ^2 + 10\gamma - 1 \leq 0$
,
$-5\gamma ^2 + 10\gamma - 1 \leq 0$
,
 $$ \begin{align*} A &= \left( 3(\gamma-3)\left(\gamma-\frac13 \right) + ( -5\gamma^2 +10\gamma - 1 )r -(1+\gamma) \mathcal{R}_1 \right) \\ &\leq \left( 3(\gamma-3)\left(\gamma-\frac13 \right) + ( -5\gamma^2 +10\gamma - 1 ) \right) = 2-2\gamma^2 < 0. \end{align*} $$
$$ \begin{align*} A &= \left( 3(\gamma-3)\left(\gamma-\frac13 \right) + ( -5\gamma^2 +10\gamma - 1 )r -(1+\gamma) \mathcal{R}_1 \right) \\ &\leq \left( 3(\gamma-3)\left(\gamma-\frac13 \right) + ( -5\gamma^2 +10\gamma - 1 ) \right) = 2-2\gamma^2 < 0. \end{align*} $$
Thus, we just need to consider the case where
![]() $-5\gamma ^2 + 10\gamma - 1> 0$
, which is
$-5\gamma ^2 + 10\gamma - 1> 0$
, which is
![]() $\gamma < 1 + \frac {2}{\sqrt {5}}$
. From now on, let us assume
$\gamma < 1 + \frac {2}{\sqrt {5}}$
. From now on, let us assume
![]() $\gamma < 1 + \frac {2}{\sqrt {5}}$
. In that case, we have that
$\gamma < 1 + \frac {2}{\sqrt {5}}$
. In that case, we have that
![]() $r < \frac {2}{\left (\sqrt {2} \sqrt {\frac {1}{\gamma -1}}+1\right )^2}+1$
. Therefore, we have that
$r < \frac {2}{\left (\sqrt {2} \sqrt {\frac {1}{\gamma -1}}+1\right )^2}+1$
. Therefore, we have that
 $$ \begin{align*} A &\leq 3(\gamma-3)\left(\gamma-\frac13 \right) + ( -5\gamma^2 +10\gamma - 1 ) \left( \frac{2}{\left(\sqrt{2} \sqrt{\frac{1}{\gamma -1}}+1\right)^2}+1 \right) \\ &\leq -\frac{4 \sqrt{\gamma -1} \left(\left(3 \sqrt{\gamma -1}+\sqrt{2}\right) \gamma -\sqrt{\gamma -1}+\sqrt{2}\right) }{\left(\sqrt{2} \sqrt{\frac{1}{\gamma -1}}+1\right)^2}. \end{align*} $$
$$ \begin{align*} A &\leq 3(\gamma-3)\left(\gamma-\frac13 \right) + ( -5\gamma^2 +10\gamma - 1 ) \left( \frac{2}{\left(\sqrt{2} \sqrt{\frac{1}{\gamma -1}}+1\right)^2}+1 \right) \\ &\leq -\frac{4 \sqrt{\gamma -1} \left(\left(3 \sqrt{\gamma -1}+\sqrt{2}\right) \gamma -\sqrt{\gamma -1}+\sqrt{2}\right) }{\left(\sqrt{2} \sqrt{\frac{1}{\gamma -1}}+1\right)^2}. \end{align*} $$
Noting
![]() $\sqrt {2}> \sqrt {\gamma - 1}$
, we see that all the terms in parenthesis in the last expression are positive, so we conclude
$\sqrt {2}> \sqrt {\gamma - 1}$
, we see that all the terms in parenthesis in the last expression are positive, so we conclude
![]() $A < 0$
, and we are done.
$A < 0$
, and we are done.
Lemma A.21. Let
![]() $\gamma> 1$
. Consider the
$\gamma> 1$
. Consider the
![]() $S_1$
the diagonal halfline of slope
$S_1$
the diagonal halfline of slope
![]() $-1$
from
$-1$
from
![]() $P_s$
– that is, the halfline given by
$P_s$
– that is, the halfline given by
![]() $(W_0 + t, Z_0 - t)$
for
$(W_0 + t, Z_0 - t)$
for
![]() $t> 0$
. We have that
$t> 0$
. We have that
Proof. We have that
 $$ \begin{align*} \frac{2}{t} \left( N_W D_Z + N_Z D_W \right) \Big|_{(W_0+t, Z_0-t)} &= t \left(2 (\gamma -1) r + 4 (\gamma +2)+6 W_0+3 \left(\gamma ^2+1\right) Z_0\right) \\ &\quad +4 r (W_0+4 Z_0+2) +4 \left(W_0 (3 Z_0+2)+3 \gamma Z_0^2+(3 \gamma +2)Z_0+4\right) \\ &= At + B. \end{align*} $$
$$ \begin{align*} \frac{2}{t} \left( N_W D_Z + N_Z D_W \right) \Big|_{(W_0+t, Z_0-t)} &= t \left(2 (\gamma -1) r + 4 (\gamma +2)+6 W_0+3 \left(\gamma ^2+1\right) Z_0\right) \\ &\quad +4 r (W_0+4 Z_0+2) +4 \left(W_0 (3 Z_0+2)+3 \gamma Z_0^2+(3 \gamma +2)Z_0+4\right) \\ &= At + B. \end{align*} $$
We will just prove that A and B are both negative, which yields the desired statement.
For B, we have that
As
![]() $-9 \gamma ^2+22 \gamma -17$
is negative for all real
$-9 \gamma ^2+22 \gamma -17$
is negative for all real
![]() $\gamma $
,
$\gamma $
,
![]() $B < 0$
just follows if we show the following quantity is positive:
$B < 0$
just follows if we show the following quantity is positive:
Thus, we just need to show
![]() $(3\gamma - 5)r+2> 0$
. This is trivial for
$(3\gamma - 5)r+2> 0$
. This is trivial for
![]() $\gamma \geq \frac 53$
, and for
$\gamma \geq \frac 53$
, and for
![]() $\gamma < \frac 53$
, Lemma A.6 yields
$\gamma < \frac 53$
, Lemma A.6 yields
 $$ \begin{align} (3\gamma - 5)r+2> \left( 3\gamma - 5 \right) \left( 2 - \frac{1}{\gamma} \right) + 2 = \frac{(6\gamma - 5)(\gamma - 1)}{\gamma} > 0. \end{align} $$
$$ \begin{align} (3\gamma - 5)r+2> \left( 3\gamma - 5 \right) \left( 2 - \frac{1}{\gamma} \right) + 2 = \frac{(6\gamma - 5)(\gamma - 1)}{\gamma} > 0. \end{align} $$
Now, let us show that
![]() $A < 0$
. We have that
$A < 0$
. We have that
By Lemma A.6, we have
 $$ \begin{align*} -9 \gamma +(3 \gamma -1) r + 7 \leq -9 \gamma +(3 \gamma -1) \left( 2 - \frac{1}{\gamma} \right) + 7 = 2 + \frac{1}{\gamma} - 3\gamma < 0. \end{align*} $$
$$ \begin{align*} -9 \gamma +(3 \gamma -1) r + 7 \leq -9 \gamma +(3 \gamma -1) \left( 2 - \frac{1}{\gamma} \right) + 7 = 2 + \frac{1}{\gamma} - 3\gamma < 0. \end{align*} $$
Therefore, in order to show (A.43), it suffices to note
where
![]() $(3\gamma -5)r+2> 0$
was already shown in (A.42).
$(3\gamma -5)r+2> 0$
was already shown in (A.42).
Lemma A.22. Let H be the halfline of
![]() $D_Z = 0$
which is to the right of
$D_Z = 0$
which is to the right of
![]() $P_s$
. We have that
$P_s$
. We have that
![]() $\nabla D_Z \cdot (N_W D_Z, N_Z D_W) \geq 0$
on H. Moreover,
$\nabla D_Z \cdot (N_W D_Z, N_Z D_W) \geq 0$
on H. Moreover,
![]() $\nabla D_Z \cdot (N_W D_Z, N_Z D_W)$
is negative between
$\nabla D_Z \cdot (N_W D_Z, N_Z D_W)$
is negative between
![]() $\bar P_s$
and
$\bar P_s$
and
![]() $P_s$
, and positive again to the left of
$P_s$
, and positive again to the left of
![]() $\bar P_s$
.
$\bar P_s$
.
Proof. The intersection of
![]() $D_W= 0$
and
$D_W= 0$
and
![]() $D_Z = 0$
is
$D_Z = 0$
is
![]() $(-1, -1)$
, which on the diagonal
$(-1, -1)$
, which on the diagonal
![]() $W = Z$
; thus, it is the leftmost point of
$W = Z$
; thus, it is the leftmost point of
![]() $D_Z$
in our region of interest
$D_Z$
in our region of interest
![]() $W> Z$
. On H, we have
$W> Z$
. On H, we have
Therefore, we just need to analyze the sign
![]() $N_Z> 0$
. The system
$N_Z> 0$
. The system
![]() $N_Z = D_Z = 0$
has two solutions (by Bézout), which are
$N_Z = D_Z = 0$
has two solutions (by Bézout), which are
![]() $P_s$
and
$P_s$
and
![]() $\bar P_s$
. From their formulas (2.1) and (2.2), we see that
$\bar P_s$
. From their formulas (2.1) and (2.2), we see that
![]() $P_s$
is the rightmost. Thus,
$P_s$
is the rightmost. Thus,
![]() $N_Z$
will have constant sign on H, so we just need to check the sign on
$N_Z$
will have constant sign on H, so we just need to check the sign on
![]() $N_Z$
at infinity along the direction of H, given by
$N_Z$
at infinity along the direction of H, given by
![]() $\nabla D_Z^\perp = \left ( \frac {1+\alpha }{2}, -\frac {1-\alpha }{2} \right )$
. We get
$\nabla D_Z^\perp = \left ( \frac {1+\alpha }{2}, -\frac {1-\alpha }{2} \right )$
. We get
 $$ \begin{align*} \lim_{t \to \infty} \frac{1}{t^2} N_Z \left( \frac{1+\gamma}{4}t, -\frac{3-\gamma}{4} t \right) = \frac{1}{8} \left(\gamma^2 - 2\gamma + 1 \right) = \frac{1}{8} (\gamma - 1)^2> 0.\\[-41pt] \end{align*} $$
$$ \begin{align*} \lim_{t \to \infty} \frac{1}{t^2} N_Z \left( \frac{1+\gamma}{4}t, -\frac{3-\gamma}{4} t \right) = \frac{1}{8} \left(\gamma^2 - 2\gamma + 1 \right) = \frac{1}{8} (\gamma - 1)^2> 0.\\[-41pt] \end{align*} $$
Computer-assisted Lemmas
Lemma A.23. We have that
![]() $r_4 < \frac {3\gamma - 1}{2+\sqrt {3}(\gamma - 1)}$
for all
$r_4 < \frac {3\gamma - 1}{2+\sqrt {3}(\gamma - 1)}$
for all
![]() $\gamma>1$
.
$\gamma>1$
.
Proof. If
![]() $\gamma \geq \frac 53$
, the proof follows trivially because
$\gamma \geq \frac 53$
, the proof follows trivially because
![]() $r^\ast (\gamma ) = \frac {3\gamma - 1}{2+\sqrt {3}(\gamma - 1)}$
. If
$r^\ast (\gamma ) = \frac {3\gamma - 1}{2+\sqrt {3}(\gamma - 1)}$
. If
![]() $1<\gamma <\frac 53$
, the proof is computer-assisted, and we refer to Appendix B for details about the implementation.
$1<\gamma <\frac 53$
, the proof is computer-assisted, and we refer to Appendix B for details about the implementation.
Lemma A.24. Let
![]() $r = r^\ast $
and
$r = r^\ast $
and
![]() $\gamma = 7/5$
. Let us recall (3.5)
$\gamma = 7/5$
. Let us recall (3.5)
 $$ \begin{align*} b^{\mathrm{fl}}_{7/5}(t) = \left( W_0 + W_1 t + \frac{W_2}{2} t^2 - \left( W_0 + W_1 + \frac{W_2}{2} \right)t^3 , Z_0 + Z_1 t + \frac{Z_2}{2} t^2 - \left( Z_0 + Z_1 + \frac{Z_2}{2} \right)t^3 \right), \end{align*} $$
$$ \begin{align*} b^{\mathrm{fl}}_{7/5}(t) = \left( W_0 + W_1 t + \frac{W_2}{2} t^2 - \left( W_0 + W_1 + \frac{W_2}{2} \right)t^3 , Z_0 + Z_1 t + \frac{Z_2}{2} t^2 - \left( Z_0 + Z_1 + \frac{Z_2}{2} \right)t^3 \right), \end{align*} $$
and (3.2)

There exists some
![]() $t_W \in (0, 1)$
such that
$t_W \in (0, 1)$
such that
![]() $b^{\mathrm {fl}}_{7/5, W} (t_W) = X_0$
and
$b^{\mathrm {fl}}_{7/5, W} (t_W) = X_0$
and
![]() $b^{\mathrm {fl}}_{7/5, Z}(t_W)> Y_0$
. That is,
$b^{\mathrm {fl}}_{7/5, Z}(t_W)> Y_0$
. That is, ![]() is below
is below
![]() $b^{\mathrm {fl}}_{7/5}(t)$
. Moreover, we have that
$b^{\mathrm {fl}}_{7/5}(t)$
. Moreover, we have that
![]() $b^{\mathrm {fl}}_{7/5, W}(t)$
is decreasing for
$b^{\mathrm {fl}}_{7/5, W}(t)$
is decreasing for
![]() $t\in (0, t_W)$
.
$t\in (0, t_W)$
.
Proof. The first part of the proof is computer-assisted, and we refer to Appendix B for details about the implementation. In order to show that
![]() $b^{\mathrm {fl}}_{7/5, W}(t)$
is decreasing, we calculate the polynomial at
$b^{\mathrm {fl}}_{7/5, W}(t)$
is decreasing, we calculate the polynomial at
![]() $\gamma = 7/5$
,
$\gamma = 7/5$
,
![]() $r = r^\ast $
. We obtain
$r = r^\ast $
. We obtain
which is globally negative.
Lemma A.25. Let
![]() $\gamma> 1$
and
$\gamma> 1$
and
![]() $r \in (r_3, r_4)$
. Let
$r \in (r_3, r_4)$
. Let
![]() $\theta _{\mathrm {extra}} = \frac 34 \pi $
and
$\theta _{\mathrm {extra}} = \frac 34 \pi $
and
![]() $\theta _{\mathrm {fl}} \in [-\pi , \pi )$
be the angle
$\theta _{\mathrm {fl}} \in [-\pi , \pi )$
be the angle
 $$ \begin{align*} \theta_{\mathrm{fl}} = - \arctan \left( \frac{ b_Z^{\mathrm{fl \; \prime}}(1) }{ b_W^{\mathrm{fl \; \prime}}(1) } \right), \end{align*} $$
$$ \begin{align*} \theta_{\mathrm{fl}} = - \arctan \left( \frac{ b_Z^{\mathrm{fl \; \prime}}(1) }{ b_W^{\mathrm{fl \; \prime}}(1) } \right), \end{align*} $$
that is, the angle formed by
![]() $b^{\mathrm {fl}}(t)$
for
$b^{\mathrm {fl}}(t)$
for
![]() $t\in [0, 1]$
when arriving at
$t\in [0, 1]$
when arriving at ![]() at
at
![]() $t=1$
.
$t=1$
.
Then, we have that
![]() $\theta _{\mathrm {fl}} < \theta _{\mathrm {extra}}$
and
$\theta _{\mathrm {fl}} < \theta _{\mathrm {extra}}$
and
![]() $\theta _{\mathrm {fl}}> \theta _{\mathrm {extra}} - \pi $
.
$\theta _{\mathrm {fl}}> \theta _{\mathrm {extra}} - \pi $
.
Proof. We need to show that
![]() $-\frac {\pi }{4} \leq \theta _{\mathrm {fl}} \leq \frac {3\pi }{4}$
, or equivalently, that the vector
$-\frac {\pi }{4} \leq \theta _{\mathrm {fl}} \leq \frac {3\pi }{4}$
, or equivalently, that the vector
![]() $-b^{\mathrm {fl\; \prime }}(1)$
has angle between
$-b^{\mathrm {fl\; \prime }}(1)$
has angle between
![]() $-\frac {\pi }{4}$
and
$-\frac {\pi }{4}$
and
![]() $\frac {3\pi }{4}$
. That is equivalent to
$\frac {3\pi }{4}$
. That is equivalent to
![]() $-b^{\mathrm {fl\; \prime }}(1) \cdot (1, 1)> 0$
. We show that
$-b^{\mathrm {fl\; \prime }}(1) \cdot (1, 1)> 0$
. We show that
![]() $b^{\mathrm {fl\; \prime }}_W(1) + b^{\mathrm {fl\; \prime }}_Z(1) < 0$
with a computer-assisted proof. Details about the implementation can be found in Appendix B.
$b^{\mathrm {fl\; \prime }}_W(1) + b^{\mathrm {fl\; \prime }}_Z(1) < 0$
with a computer-assisted proof. Details about the implementation can be found in Appendix B.
Lemma A.26. Let
![]() $\gamma \in (1, + \infty )$
and
$\gamma \in (1, + \infty )$
and
![]() $r \in (r_3, r_4)$
. We have that
$r \in (r_3, r_4)$
. We have that

Proof. The first five inequalities are done with a computer-assisted proof. We refer to Appendix B for details about the implementation. Let us start with
![]() $\partial _Z N_Z (P_s)$
. We have that
$\partial _Z N_Z (P_s)$
. We have that
We have that
because the polynomial
![]() $3\gamma ^2 - 7\gamma + 6$
does not have real roots. For
$3\gamma ^2 - 7\gamma + 6$
does not have real roots. For
![]() $1 < \gamma \leq \frac 53$
, we get that
$1 < \gamma \leq \frac 53$
, we get that
 $$ \begin{align*} A \geq A \Big|_{r=r^\ast} = \frac{ 4 (\gamma +1) \left(2 \sqrt{2} \gamma \sqrt{\gamma -1} + \left( \sqrt{2} \sqrt{\gamma -1}+4\right) (\gamma - 1)\right) }{ \left(\frac{\sqrt{2}}{\sqrt{\gamma -1}}+1\right)^2}> 0, \end{align*} $$
$$ \begin{align*} A \geq A \Big|_{r=r^\ast} = \frac{ 4 (\gamma +1) \left(2 \sqrt{2} \gamma \sqrt{\gamma -1} + \left( \sqrt{2} \sqrt{\gamma -1}+4\right) (\gamma - 1)\right) }{ \left(\frac{\sqrt{2}}{\sqrt{\gamma -1}}+1\right)^2}> 0, \end{align*} $$
and for
![]() $\gamma \geq \frac 53$
,
$\gamma \geq \frac 53$
,
 $$ \begin{align*} A &\geq A \Big|_{r=r^\ast} = \frac{ 9 \left(\sqrt{3}-1\right) \gamma ^2+\left(30-14 \sqrt{3}\right) \gamma +9 \sqrt{3}-25 }{ \sqrt{3} (\gamma -1)+2 } \\ & \geq \frac{ 9 \left(\sqrt{3}-1\right)+\left(30-14 \sqrt{3}\right)+9 \sqrt{3}-25 }{ \sqrt{3} (\gamma -1)+2 } = \frac{ 4 (\sqrt{3}-1) }{ \sqrt{3} (\gamma -1)+2 }> 0. \end{align*} $$
$$ \begin{align*} A &\geq A \Big|_{r=r^\ast} = \frac{ 9 \left(\sqrt{3}-1\right) \gamma ^2+\left(30-14 \sqrt{3}\right) \gamma +9 \sqrt{3}-25 }{ \sqrt{3} (\gamma -1)+2 } \\ & \geq \frac{ 9 \left(\sqrt{3}-1\right)+\left(30-14 \sqrt{3}\right)+9 \sqrt{3}-25 }{ \sqrt{3} (\gamma -1)+2 } = \frac{ 4 (\sqrt{3}-1) }{ \sqrt{3} (\gamma -1)+2 }> 0. \end{align*} $$
Therefore, we get that
![]() $A> 0$
globally. If
$A> 0$
globally. If
![]() $\gamma \leq 3$
, we get that
$\gamma \leq 3$
, we get that
![]() $B = (-3\gamma + 1)(\gamma - 3) \geq 0$
, so we are done. From now on, let us assume
$B = (-3\gamma + 1)(\gamma - 3) \geq 0$
, so we are done. From now on, let us assume
![]() $\gamma> 3$
. We will show that
$\gamma> 3$
. We will show that
![]() $A^2 - B^2 \mathcal {R}_1^2> 0$
, which will conclude the proof of the sign of
$A^2 - B^2 \mathcal {R}_1^2> 0$
, which will conclude the proof of the sign of
![]() $\partial _Z N_Z (P_s)$
. We have
$\partial _Z N_Z (P_s)$
. We have
 $$ \begin{align*} A^2 - B^2\mathcal{R}_1^2 & = 32 (\gamma -1)^2 \left(2 \gamma (\gamma (9 \gamma -14)+9)+(\gamma (\gamma (3 \gamma -11)+17)-1) r^2-4 \gamma (3 (\gamma -2) \gamma +7) r\right) \\ & = 32 (\gamma -1)^2 C, \end{align*} $$
$$ \begin{align*} A^2 - B^2\mathcal{R}_1^2 & = 32 (\gamma -1)^2 \left(2 \gamma (\gamma (9 \gamma -14)+9)+(\gamma (\gamma (3 \gamma -11)+17)-1) r^2-4 \gamma (3 (\gamma -2) \gamma +7) r\right) \\ & = 32 (\gamma -1)^2 C, \end{align*} $$
so we need to show
![]() $C> 0$
. We have
$C> 0$
. We have
so
 $$ \begin{align*} \frac{d}{dr} C &\leq \frac{d}{dr} \Big|_{r=r^\ast} C = \frac{-2(\gamma - 1)}{2 + \sqrt{3} (\gamma - 1)} \left( 3 \left(2 \sqrt{3}-3\right) \gamma ^3+\left(39-12 \sqrt{3}\right) \gamma ^2+\left(14 \sqrt{3}-47\right) \gamma +1 \right) \\ &\leq \frac{-2(\gamma - 1)}{2 + \sqrt{3} (\gamma - 1)} \left( 3 \left(2 \sqrt{3}-3\right) \gamma \cdot 9+\left(39-12 \sqrt{3}\right) \gamma \cdot 3 +\left(14 \sqrt{3}-47\right) \gamma +1 \right) \\ & \leq \frac{-2(\gamma - 1)}{2 + \sqrt{3} (\gamma - 1)} \left( 1 + (32\sqrt{3} - 11) \gamma \right) < 0. \end{align*} $$
$$ \begin{align*} \frac{d}{dr} C &\leq \frac{d}{dr} \Big|_{r=r^\ast} C = \frac{-2(\gamma - 1)}{2 + \sqrt{3} (\gamma - 1)} \left( 3 \left(2 \sqrt{3}-3\right) \gamma ^3+\left(39-12 \sqrt{3}\right) \gamma ^2+\left(14 \sqrt{3}-47\right) \gamma +1 \right) \\ &\leq \frac{-2(\gamma - 1)}{2 + \sqrt{3} (\gamma - 1)} \left( 3 \left(2 \sqrt{3}-3\right) \gamma \cdot 9+\left(39-12 \sqrt{3}\right) \gamma \cdot 3 +\left(14 \sqrt{3}-47\right) \gamma +1 \right) \\ & \leq \frac{-2(\gamma - 1)}{2 + \sqrt{3} (\gamma - 1)} \left( 1 + (32\sqrt{3} - 11) \gamma \right) < 0. \end{align*} $$
Finally, we have
 $$ \begin{align*} \frac{(2 + \sqrt{3} (\gamma - 1))^2}{ -(\gamma -1)} C &\leq \frac{(2 + \sqrt{3} (\gamma - 1))^2}{ -(\gamma -1)} C \Big|_{r=r^\ast} \\ &= \left(9 \left(4 \sqrt{3}-9\right) \gamma ^4+\left(300-156 \sqrt{3}\right) \gamma ^3+\left(220 \sqrt{3}-438\right) \gamma ^2+\left(204-100 \sqrt{3}\right) \gamma -1\right) \\ &\leq \left(9 \left(4 \sqrt{3}-9\right) \gamma ^3 \cdot 3+\left(300-156 \sqrt{3}\right) \gamma ^3+\left(220 \sqrt{3}-438\right) \gamma \cdot 3+\left(204-100 \sqrt{3}\right) \gamma -1\right) \\ &= \left(57-48 \sqrt{3}\right) \gamma ^3+10 \left(56 \sqrt{3}-111\right) \gamma -1 < 0. \end{align*} $$
$$ \begin{align*} \frac{(2 + \sqrt{3} (\gamma - 1))^2}{ -(\gamma -1)} C &\leq \frac{(2 + \sqrt{3} (\gamma - 1))^2}{ -(\gamma -1)} C \Big|_{r=r^\ast} \\ &= \left(9 \left(4 \sqrt{3}-9\right) \gamma ^4+\left(300-156 \sqrt{3}\right) \gamma ^3+\left(220 \sqrt{3}-438\right) \gamma ^2+\left(204-100 \sqrt{3}\right) \gamma -1\right) \\ &\leq \left(9 \left(4 \sqrt{3}-9\right) \gamma ^3 \cdot 3+\left(300-156 \sqrt{3}\right) \gamma ^3+\left(220 \sqrt{3}-438\right) \gamma \cdot 3+\left(204-100 \sqrt{3}\right) \gamma -1\right) \\ &= \left(57-48 \sqrt{3}\right) \gamma ^3+10 \left(56 \sqrt{3}-111\right) \gamma -1 < 0. \end{align*} $$
Now, we show ![]() . We get that
. We get that
Now, this quantity vanishes at
![]() $r = \frac {3\gamma - 1}{2+\sqrt {3}(\gamma -1)}$
, and by Lemma A.23,
$r = \frac {3\gamma - 1}{2+\sqrt {3}(\gamma -1)}$
, and by Lemma A.23,
![]() $r_4 < \frac {3\gamma - 1}{2+\sqrt {3}(\gamma -1)}$
.
$r_4 < \frac {3\gamma - 1}{2+\sqrt {3}(\gamma -1)}$
.
Lastly, from (3.2),
Lemma A.27. For
![]() $\gamma = 7/5$
and
$\gamma = 7/5$
and
![]() $r = r^\ast (7/5)$
, we have that
$r = r^\ast (7/5)$
, we have that
![]() $|W_i/Z_i|< 2$
for all
$|W_i/Z_i|< 2$
for all
![]() $0 \leq i \leq 160$
.
$0 \leq i \leq 160$
.
Proof. We prove the statement via a computer-assisted proof. The code can be found in the supplementary material, and we refer to Appendix B for details about the implementation.
Lemma A.28. Let
![]() $\gamma = 7/5$
and
$\gamma = 7/5$
and
![]() $r = r^\ast (7/5)$
. For any
$r = r^\ast (7/5)$
. For any
![]() $i \leq 160$
, we have
$i \leq 160$
, we have
 $$ \begin{align*} \left| \bar C_\ast (i+1)^2 \right| < \left| \frac{Z_{i+1}}{Z_i} \right| < \left| \bar C_\ast (i+1)^2 \frac{500}{i+1} \right|. \end{align*} $$
$$ \begin{align*} \left| \bar C_\ast (i+1)^2 \right| < \left| \frac{Z_{i+1}}{Z_i} \right| < \left| \bar C_\ast (i+1)^2 \frac{500}{i+1} \right|. \end{align*} $$
For
![]() $160 \leq i \leq 10000$
, we have the further refinement
$160 \leq i \leq 10000$
, we have the further refinement
 $$ \begin{align*} \left| \bar C_\ast (i+1)^2 \right| < \left| \frac{Z_{i+1}}{Z_i} \right| < \left| 3\bar C_\ast (i+1)^2 \right|. \end{align*} $$
$$ \begin{align*} \left| \bar C_\ast (i+1)^2 \right| < \left| \frac{Z_{i+1}}{Z_i} \right| < \left| 3\bar C_\ast (i+1)^2 \right|. \end{align*} $$
Moreover,
Proof. We prove the statement via a computer-assisted proof. The code can be found in the supplementary material, and we refer to Appendix B for details about the implementation.
Lemma A.29. Let either
![]() $\gamma> 1 $
and
$\gamma> 1 $
and
![]() $r = r_3$
or
$r = r_3$
or
![]() $\gamma = 7/5$
and
$\gamma = 7/5$
and
![]() $r = r^\ast (7/5)$
. We have that
$r = r^\ast (7/5)$
. We have that
![]() $\frac {Z_1/2 - W_1}{W_1 + Z_1} \leq -1$
.
$\frac {Z_1/2 - W_1}{W_1 + Z_1} \leq -1$
.
Proof. The proof for
![]() $r = r_3$
is computer-assisted. The code can be found in the supplementary material, and details about the implementation can be found in Appendix B. For the case
$r = r_3$
is computer-assisted. The code can be found in the supplementary material, and details about the implementation can be found in Appendix B. For the case
![]() $\gamma = 7/5$
,
$\gamma = 7/5$
,
![]() $r = r^\ast ( 7/5 )$
, we have that
$r = r^\ast ( 7/5 )$
, we have that
Lemma A.30. Let us recall
 $$ \begin{align*} a_2^{\mathrm{nr}} = \frac{s_\infty^{\mathrm{fr}}}{2} \left( -W_2 + Z_2/2 - (W_2+Z_2)\frac{Z_1/2-W_1}{W_1+Z_1}\right) + W_1^2 + W_1Z_1/2 - Z_1^2/2. \end{align*} $$
$$ \begin{align*} a_2^{\mathrm{nr}} = \frac{s_\infty^{\mathrm{fr}}}{2} \left( -W_2 + Z_2/2 - (W_2+Z_2)\frac{Z_1/2-W_1}{W_1+Z_1}\right) + W_1^2 + W_1Z_1/2 - Z_1^2/2. \end{align*} $$
Let either
![]() $\gamma> 1$
and
$\gamma> 1$
and
![]() $r = r_3$
or
$r = r_3$
or
![]() $\gamma = 7/5$
and
$\gamma = 7/5$
and
![]() $r = r^\ast (7/5)$
. We have that
$r = r^\ast (7/5)$
. We have that
![]() $a_2^{\mathrm {nr}}> 0$
.
$a_2^{\mathrm {nr}}> 0$
.
Proof. The proof is computer-assisted. The code can be found in the supplementary material, and details about the implementation can be found in Appendix B.
Lemma A.31. Let
![]() $\gamma> 1$
. We have that
$\gamma> 1$
. We have that
![]() $Z_3> 0$
for r close enough to
$Z_3> 0$
for r close enough to
![]() $r_3$
from above and
$r_3$
from above and
![]() $Z_4> 0$
for r close enough to
$Z_4> 0$
for r close enough to
![]() $r_4$
from below. In other words, we have that
$r_4$
from below. In other words, we have that
 $$ \begin{align*} Z_3(3-k) < 0 \quad \quad \text{for} \; \; r = r_3,\\ Z_4(4-k)> 0 \quad \quad \text{for} \; \; r = r_4. \end{align*} $$
$$ \begin{align*} Z_3(3-k) < 0 \quad \quad \text{for} \; \; r = r_3,\\ Z_4(4-k)> 0 \quad \quad \text{for} \; \; r = r_4. \end{align*} $$
Proof. The proof is computer-assisted, and we refer to Appendix B for details about the implementation.
Additional properties of the profiles
Let us recall that ![]() and
and ![]() , where
, where
![]() $\xi =\log \zeta $
and
$\xi =\log \zeta $
and
![]() $(W^E, Z^E)$
is a solution to the ODE (1.10). We use the notation
$(W^E, Z^E)$
is a solution to the ODE (1.10). We use the notation
![]() $D_W^E$
to denote the function
$D_W^E$
to denote the function
We define
![]() $D_Z^E$
,
$D_Z^E$
,
![]() $N_W^E$
and
$N_W^E$
and
![]() $N_Z^E$
in an analogous fashion.
$N_Z^E$
in an analogous fashion.
Lemma A.32. We have that ![]() .
.
Our profile for Euler is in the region
![]() $W^E-Z^E> 0$
and cannot cross
$W^E-Z^E> 0$
and cannot cross
![]() $W^E = Z^E$
because it is an invariant manifold of the ODE (1.10). Therefore,
$W^E = Z^E$
because it is an invariant manifold of the ODE (1.10). Therefore, ![]() .
.
Lemma A.33. We have that ![]() is uniformly bounded and strictly positive for
is uniformly bounded and strictly positive for
![]() $\zeta> 1$
. Moreover,
$\zeta> 1$
. Moreover, ![]() for all
for all
![]() $\zeta> \frac 65$
and some
$\zeta> \frac 65$
and some
![]() $\varepsilon> 0$
sufficiently small. We also have that
$\varepsilon> 0$
sufficiently small. We also have that ![]() for all
for all
![]() $\zeta> \frac 65$
and some
$\zeta> \frac 65$
and some
![]() $\varepsilon '> 0$
.
$\varepsilon '> 0$
.
Proof. Passing to
![]() $W^E, Z^E, \xi $
coordinates, the stated inequality reads
$W^E, Z^E, \xi $
coordinates, the stated inequality reads
 $$ \begin{align*} e^{\xi} \left(1 + W^E(\xi) \frac{1 - \alpha}{2} + Z^E (\xi) \frac{1 + \alpha}{2} \right) = e^{\xi} D_Z^E (\xi)< 0\,\nonumber \end{align*} $$
$$ \begin{align*} e^{\xi} \left(1 + W^E(\xi) \frac{1 - \alpha}{2} + Z^E (\xi) \frac{1 + \alpha}{2} \right) = e^{\xi} D_Z^E (\xi)< 0\,\nonumber \end{align*} $$
for
![]() $\xi> 0$
. Now, let us recall that our profile
$\xi> 0$
. Now, let us recall that our profile
![]() $(W(\xi ), Z(\xi ))$
is given by Proposition 3.1 for
$(W(\xi ), Z(\xi ))$
is given by Proposition 3.1 for
![]() $\xi> 0$
. In particular,
$\xi> 0$
. In particular,
![]() $D_Z^E> 0$
.
$D_Z^E> 0$
.
With respect to the second claim, just note that the solution converges to
![]() $P_\infty = (0, 0)$
(with
$P_\infty = (0, 0)$
(with
![]() $D_Z (P_\infty ) = 1$
), so in particular, we will have that
$D_Z (P_\infty ) = 1$
), so in particular, we will have that
![]() $D_Z^E(\xi )> \varepsilon $
for
$D_Z^E(\xi )> \varepsilon $
for
![]() $\xi> C$
, where C is a sufficiently large constant. Then, as
$\xi> C$
, where C is a sufficiently large constant. Then, as
![]() $[\log (6/5), C]$
is a compact interval where
$[\log (6/5), C]$
is a compact interval where
![]() $D_Z^E> 0$
, we can find an
$D_Z^E> 0$
, we can find an
![]() $\varepsilon> 0$
sufficiently small that bounds
$\varepsilon> 0$
sufficiently small that bounds
![]() $D_Z$
from below. Therefore, as
$D_Z$
from below. Therefore, as
![]() $e^{\xi } = \zeta $
, we conclude that
$e^{\xi } = \zeta $
, we conclude that
![]() $e^{\xi } D_Z^E(\xi )> \varepsilon \zeta $
.
$e^{\xi } D_Z^E(\xi )> \varepsilon \zeta $
.
With respect to the third claim, just note that ![]() corresponds to
corresponds to
![]() $\xi D_W^E(\log \zeta )$
. By Proposition 3.1, we have that
$\xi D_W^E(\log \zeta )$
. By Proposition 3.1, we have that
![]() $D_W^E> 0$
for
$D_W^E> 0$
for
![]() $\xi> \log (6/5)$
, and using the same argument as in the paragraph above for
$\xi> \log (6/5)$
, and using the same argument as in the paragraph above for
![]() $D_Z^E$
, we conclude that
$D_Z^E$
, we conclude that
![]() $e^{\xi } D_W^E(\xi )> \zeta \varepsilon '$
for every
$e^{\xi } D_W^E(\xi )> \zeta \varepsilon '$
for every
![]() $\xi> \log (6/5)$
and some
$\xi> \log (6/5)$
and some
![]() $\varepsilon '> 0$
sufficiently small.
$\varepsilon '> 0$
sufficiently small.
Lemma A.34. For
![]() $\gamma = 7/5$
, r sufficiently close to
$\gamma = 7/5$
, r sufficiently close to
![]() $r^\ast $
and
$r^\ast $
and
![]() $\zeta <1$
, we have that
$\zeta <1$
, we have that ![]() .
.
Proof. Writing this in
![]() $(W, Z)$
variables, we need to show that
$(W, Z)$
variables, we need to show that
![]() $W^E - Z^E +\frac {N_W^E}{D_W^E} - \frac {N_Z^E}{D_Z^E}> 0$
. As for
$W^E - Z^E +\frac {N_W^E}{D_W^E} - \frac {N_Z^E}{D_Z^E}> 0$
. As for
![]() $\zeta < 1$
(that is,
$\zeta < 1$
(that is,
![]() $\xi < 0$
), we have
$\xi < 0$
), we have
![]() $D_W> 0, D_Z < 0$
, and we can reduce to show negativity of
$D_W> 0, D_Z < 0$
, and we can reduce to show negativity of
 $$ \begin{align*} & D_W^E D_Z^E (W^E - Z^E) + N_W^E D_Z^E - N_Z^E D_W^E \\ & \qquad = \frac{-1}{10}(W-Z) \left(-\sqrt{4 r^2-14 r+11}+2 r+W+Z-1\right) \left(\sqrt{4 r^2-14 r+11}+2 r+W+Z-1\right). \end{align*} $$
$$ \begin{align*} & D_W^E D_Z^E (W^E - Z^E) + N_W^E D_Z^E - N_Z^E D_W^E \\ & \qquad = \frac{-1}{10}(W-Z) \left(-\sqrt{4 r^2-14 r+11}+2 r+W+Z-1\right) \left(\sqrt{4 r^2-14 r+11}+2 r+W+Z-1\right). \end{align*} $$
As
![]() $W> Z$
, it suffices to show that for
$W> Z$
, it suffices to show that for
![]() $\xi> 0$
, the
$\xi> 0$
, the
![]() $Z^E$
stays above
$Z^E$
stays above
![]() $Z_\Delta (W) = \sqrt {4 r^2-14 r+11}-2 r-W+1$
.
$Z_\Delta (W) = \sqrt {4 r^2-14 r+11}-2 r-W+1$
.
![]() $Z_\Delta (W)$
is a diagonal line of slope
$Z_\Delta (W)$
is a diagonal line of slope
![]() $-1$
passing through
$-1$
passing through
![]() $P_s$
, and from the proof of Proposition 2.5 (see also Lemma A.21), we have that our solution stays above.
$P_s$
, and from the proof of Proposition 2.5 (see also Lemma A.21), we have that our solution stays above.
Lemma A.35. For
![]() $\gamma = 7/5$
, r sufficiently close to
$\gamma = 7/5$
, r sufficiently close to
![]() $r^\ast $
and
$r^\ast $
and
![]() $\zeta> 1$
, we have that
$\zeta> 1$
, we have that
 $$ \begin{align} M:=- \frac{1-\alpha}{1+\alpha} D_Z^E + D_W^E + \left( \frac{1+\alpha}{2} - \frac{(1-\alpha)^2}{2(1+\alpha)} \right) \frac{N_W^E}{D_W^E}> 0. \end{align} $$
$$ \begin{align} M:=- \frac{1-\alpha}{1+\alpha} D_Z^E + D_W^E + \left( \frac{1+\alpha}{2} - \frac{(1-\alpha)^2}{2(1+\alpha)} \right) \frac{N_W^E}{D_W^E}> 0. \end{align} $$
Proof. Given that the solution is in the region
![]() $D_W> 0$
, it suffices to show positivity for
$D_W> 0$
, it suffices to show positivity for
Let us recall from the proof of Proposition 3.6 that
![]() $(W^E, Z^E)$
is contained in the triangle T delimited by the lines
$(W^E, Z^E)$
is contained in the triangle T delimited by the lines
![]() $W = W_0$
,
$W = W_0$
,
![]() $W=Z$
and
$W=Z$
and
![]() $D_Z = 0$
. As both T and (A.46) depend continuously on r, we reduce to show that every point of T satisfies (A.46) for
$D_Z = 0$
. As both T and (A.46) depend continuously on r, we reduce to show that every point of T satisfies (A.46) for
![]() $r=r^\ast (7/5)$
. Thus, let us fix
$r=r^\ast (7/5)$
. Thus, let us fix
![]() $r=r^\ast $
from now on.
$r=r^\ast $
from now on.
Solving (A.46) in W, we see that the previous quantity is positive if
![]() $W_{(-)}(Z) \leq W \leq W_{(+)}(Z)$
, where
$W_{(-)}(Z) \leq W \leq W_{(+)}(Z)$
, where
![]() $W_{(i)}(Z)$
are given by
$W_{(i)}(Z)$
are given by
 $$ \begin{align*} W_{(\pm)}(Z) = \frac{1}{4} \left(+5 \sqrt{5}-3 \pm \sqrt{16 Z^2+64 Z-30 \sqrt{5}+294}\right),\nonumber \end{align*} $$
$$ \begin{align*} W_{(\pm)}(Z) = \frac{1}{4} \left(+5 \sqrt{5}-3 \pm \sqrt{16 Z^2+64 Z-30 \sqrt{5}+294}\right),\nonumber \end{align*} $$
and the radical is positive for all Z. Now, the triangle T is contained in
![]() $-1 \leq W \leq W_0$
because the rightmost side of T is
$-1 \leq W \leq W_0$
because the rightmost side of T is
![]() $W = W_0$
and the leftmost point is
$W = W_0$
and the leftmost point is
![]() $(-1, -1)$
(the intersection of
$(-1, -1)$
(the intersection of
![]() $D_Z = 0$
and
$D_Z = 0$
and
![]() $W=Z$
). Thus, it suffices to show that
$W=Z$
). Thus, it suffices to show that
![]() $W_{(-)}(Z) < -1$
and
$W_{(-)}(Z) < -1$
and
![]() $W_0 < W_{(+)}(Z)$
.
$W_0 < W_{(+)}(Z)$
.
We have that
 $$ \begin{align*} 4 (-1-W_{(-)}(Z)) &= -5 \sqrt{5}-1 + \sqrt{16 Z (Z+4)-30 \sqrt{5}+294}, \\ 4 ( W_{(+)}(Z) - W_0 ) &= 7-\sqrt{5} + \sqrt{16 Z (Z+4)-30 \sqrt{5}+294}, \end{align*} $$
$$ \begin{align*} 4 (-1-W_{(-)}(Z)) &= -5 \sqrt{5}-1 + \sqrt{16 Z (Z+4)-30 \sqrt{5}+294}, \\ 4 ( W_{(+)}(Z) - W_0 ) &= 7-\sqrt{5} + \sqrt{16 Z (Z+4)-30 \sqrt{5}+294}, \end{align*} $$
where we recall that the radical is positive for all Z. The second expression is clearly positive, and the first one is also positive because
Lemma A.36. For
![]() $\gamma = 7/5$
and r sufficiently close to
$\gamma = 7/5$
and r sufficiently close to
![]() $r^\ast $
, there exists a value
$r^\ast $
, there exists a value
![]() $\eta _{\mathrm {damp}}> 0$
such that
$\eta _{\mathrm {damp}}> 0$
such that ![]() globally.
globally.
Proof. First, observe

and similarly,

Let us first reduce to show that (A.47) is greater than
![]() $\eta _{\mathrm {damp}}$
. In the region
$\eta _{\mathrm {damp}}$
. In the region
![]() $\zeta \leq 1$
, Lemma A.34 yields that
$\zeta \leq 1$
, Lemma A.34 yields that ![]() , so it is clear that
, so it is clear that ![]() is given by (A.47). With respect to the region
is given by (A.47). With respect to the region
![]() $\zeta> 1$
, note that (A.48)
$\zeta> 1$
, note that (A.48)
![]() $ {=}\ \frac {1-\alpha }{1+\alpha }$
(A.47) + (A.45). Therefore, as (A.45) is positive by Lemma A.35, is also suffices to show that (A.47) is lower bounded by some
$ {=}\ \frac {1-\alpha }{1+\alpha }$
(A.47) + (A.45). Therefore, as (A.45) is positive by Lemma A.35, is also suffices to show that (A.47) is lower bounded by some
![]() $\eta _{\mathrm {damp}}> 0$
. In order to show this, we divide in two cases:
$\eta _{\mathrm {damp}}> 0$
. In order to show this, we divide in two cases:
![]() $\xi \leq 0$
and
$\xi \leq 0$
and
![]() $\xi> 0$
.
$\xi> 0$
.
Case
![]() $\xi < 0$
. We start showing (A.47) is greater than
$\xi < 0$
. We start showing (A.47) is greater than
![]() $\eta _{\mathrm {damp}}> 0$
for
$\eta _{\mathrm {damp}}> 0$
for
![]() $\zeta \leq 1$
(that is,
$\zeta \leq 1$
(that is,
![]() $\xi \leq 0$
). As we will show that this is strictly positive at
$\xi \leq 0$
). As we will show that this is strictly positive at
![]() $\xi = 0$
and as
$\xi = 0$
and as
![]() $\xi \rightarrow -\infty $
, by compactness (say, reparametrizing the domain), we can reduce to showing that (A.47) is positive.
$\xi \rightarrow -\infty $
, by compactness (say, reparametrizing the domain), we can reduce to showing that (A.47) is positive.
Let us start noting that the statement is true at
![]() $\xi = 0$
because
$\xi = 0$
because
![]() $D_{Z, 1}> 0$
due to Lemma A.7. Now, we show it for
$D_{Z, 1}> 0$
due to Lemma A.7. Now, we show it for
![]() $\xi < 0$
. As
$\xi < 0$
. As
![]() $D_W> 0, D_Z < 0$
in this region, we need to show negativity for
$D_W> 0, D_Z < 0$
in this region, we need to show negativity for
 $$ \begin{align} A = 50 D_W D_Z (A.47) &= Z^2 (-(12 r+W-23))-30 r (W+1) Z \nonumber \\ &\qquad +W (-4 r (2 W+5) +W (W+21)+70) +56 W Z+80 Z+50. \end{align} $$
$$ \begin{align} A = 50 D_W D_Z (A.47) &= Z^2 (-(12 r+W-23))-30 r (W+1) Z \nonumber \\ &\qquad +W (-4 r (2 W+5) +W (W+21)+70) +56 W Z+80 Z+50. \end{align} $$
Solving in Z, we get that we need to show Z is below
 $$ \begin{align*} f(W) &=\frac{\sqrt{g(W)}+30 r W+30 r-56 W-80}{2 (-12 r-W+23)}, \qquad \mbox{ where }\\ g(W) &= (-30 r W-30 r+56 W+80)^2-4 (-12 r-W+23) \left(-8 r W^2-20 r W+W^3+21 W^2+70 W+50\right). \end{align*} $$
$$ \begin{align*} f(W) &=\frac{\sqrt{g(W)}+30 r W+30 r-56 W-80}{2 (-12 r-W+23)}, \qquad \mbox{ where }\\ g(W) &= (-30 r W-30 r+56 W+80)^2-4 (-12 r-W+23) \left(-8 r W^2-20 r W+W^3+21 W^2+70 W+50\right). \end{align*} $$
For
![]() $W> W_0$
and r close to
$W> W_0$
and r close to
![]() $r^\ast $
, we have
$r^\ast $
, we have
![]() $g(W)> 0$
. Note that our solution can also be parametrized as some
$g(W)> 0$
. Note that our solution can also be parametrized as some
![]() $Z_\ast (W)$
because it is decreasing in W (by Remark 2.6). We know that
$Z_\ast (W)$
because it is decreasing in W (by Remark 2.6). We know that
![]() $Z_\ast (W) < f(W)$
for W close enough (from above) to
$Z_\ast (W) < f(W)$
for W close enough (from above) to
![]() $W_0$
because we already checked the sign for
$W_0$
because we already checked the sign for
![]() $\xi = 0$
. Moreover, we have
$\xi = 0$
. Moreover, we have
![]() $f(W) = -W + (6-5r) + O(1/W)$
, while
$f(W) = -W + (6-5r) + O(1/W)$
, while
![]() $Z_\ast (W) = -W - \frac {4(r-1)}{3(\gamma - 1)} + O(1/W)$
from the proof of Proposition 2.5. Thus, as
$Z_\ast (W) = -W - \frac {4(r-1)}{3(\gamma - 1)} + O(1/W)$
from the proof of Proposition 2.5. Thus, as
![]() $6-5r^\ast> \frac {-4(r^\ast -1)}{6/5}$
, we also have that
$6-5r^\ast> \frac {-4(r^\ast -1)}{6/5}$
, we also have that
![]() $Z_\ast (W) < f(W)$
for W sufficiently large. Thus, by continuity, if
$Z_\ast (W) < f(W)$
for W sufficiently large. Thus, by continuity, if
![]() $Z_\ast (W)$
crosses
$Z_\ast (W)$
crosses
![]() $f(W)$
at some
$f(W)$
at some
![]() $W \in (W_0, +\infty )$
, it has to do so in both directions. We show that this is impossible by checking that the field
$W \in (W_0, +\infty )$
, it has to do so in both directions. We show that this is impossible by checking that the field
![]() $(N_W D_Z, N_Z D_W)$
points always to the same side of the curve
$(N_W D_Z, N_Z D_W)$
points always to the same side of the curve
![]() $(W, f(W))$
. Indeed, defining
$(W, f(W))$
. Indeed, defining
we have that
![]() $P_f(W) < 0$
for r sufficiently close to
$P_f(W) < 0$
for r sufficiently close to
![]() $r^\ast $
. Clearly, we have that
$r^\ast $
. Clearly, we have that
![]() $P_f(W_0) = 0$
because
$P_f(W_0) = 0$
because
![]() $N_Z(P_s) = D_Z (P_s) = 0$
. Moreover, we have that
$N_Z(P_s) = D_Z (P_s) = 0$
. Moreover, we have that
so we get that
![]() $P_f'(W_0)$
is negative for r close enough (from below) to
$P_f'(W_0)$
is negative for r close enough (from below) to
![]() $r^\ast $
. Therefore, it suffices to check
$r^\ast $
. Therefore, it suffices to check
![]() $\frac {P_f(W)}{(W-W_0)^3} \Big |_{r=r^\ast }> 0$
. Let us fix
$\frac {P_f(W)}{(W-W_0)^3} \Big |_{r=r^\ast }> 0$
. Let us fix
![]() $r = r^\ast $
for the rest of this case. We have that
$r = r^\ast $
for the rest of this case. We have that
 $$ \begin{align*} P_f(W) &= \frac{ P_{f, 1}(W) + P_{f, 2}(W) \sqrt{ g(W) } }{ 100 (2 + 3\sqrt{5} - W)^5 \sqrt{ g(W)} } \\ P_{f, 1}(W) &= 880 \sqrt{5} W^9+872 W^9+467 \sqrt{5} W^8-5115 W^8-15117 \sqrt{5} W^7-74695 W^7 -447170 \sqrt{5} W^6 \\ &\quad -864890 W^6-3634655 \sqrt{5} W^5-4535775 W^5-14090850 \sqrt{5} W^4-19856150 W^4\\ &\quad -47811625 \sqrt{5} W^3 -23786875 W^3 -72742000 \sqrt{5} W^2-32280000 W^2-104707875 \sqrt{5} W\\ &\quad +80830625 W-59254375 \sqrt{5}+84001875 \\ P_{f, 2}(W) &= -435 \sqrt{5} W^7-439 W^7+664 \sqrt{5} W^6+2140 W^6+21074 \sqrt{5} W^5+41470 W^5+167470 \sqrt{5} W^4\\ &\quad +329040 W^4 +887560 \sqrt{5} W^3 +853650 W^3+1794425 \sqrt{5} W^2+2377375 W^2+3598525 \sqrt{5} W\\ &\quad -570125 W +2233125 \sqrt{5}-1711375. \end{align*} $$
$$ \begin{align*} P_f(W) &= \frac{ P_{f, 1}(W) + P_{f, 2}(W) \sqrt{ g(W) } }{ 100 (2 + 3\sqrt{5} - W)^5 \sqrt{ g(W)} } \\ P_{f, 1}(W) &= 880 \sqrt{5} W^9+872 W^9+467 \sqrt{5} W^8-5115 W^8-15117 \sqrt{5} W^7-74695 W^7 -447170 \sqrt{5} W^6 \\ &\quad -864890 W^6-3634655 \sqrt{5} W^5-4535775 W^5-14090850 \sqrt{5} W^4-19856150 W^4\\ &\quad -47811625 \sqrt{5} W^3 -23786875 W^3 -72742000 \sqrt{5} W^2-32280000 W^2-104707875 \sqrt{5} W\\ &\quad +80830625 W-59254375 \sqrt{5}+84001875 \\ P_{f, 2}(W) &= -435 \sqrt{5} W^7-439 W^7+664 \sqrt{5} W^6+2140 W^6+21074 \sqrt{5} W^5+41470 W^5+167470 \sqrt{5} W^4\\ &\quad +329040 W^4 +887560 \sqrt{5} W^3 +853650 W^3+1794425 \sqrt{5} W^2+2377375 W^2+3598525 \sqrt{5} W\\ &\quad -570125 W +2233125 \sqrt{5}-1711375. \end{align*} $$
We obtain that
 $$ \begin{align*} Q_f(W) &= P_f(W) \left( P_{f, 1}(W) - P_{f, 2}(W)\sqrt{g(W)} \right) \sqrt{P_{f, 0}(W)} = \frac{P_{f, 1}(W)^2 - P_{f, 2}(W)^2 P_{f, 0}(W) }{ 100 (2 + 3\sqrt{5} - W)^5} \\ &= P_{f, 4}(W) (W + \sqrt{5})^2 (W+1) (W-W_0)^3, \end{align*} $$
$$ \begin{align*} Q_f(W) &= P_f(W) \left( P_{f, 1}(W) - P_{f, 2}(W)\sqrt{g(W)} \right) \sqrt{P_{f, 0}(W)} = \frac{P_{f, 1}(W)^2 - P_{f, 2}(W)^2 P_{f, 0}(W) }{ 100 (2 + 3\sqrt{5} - W)^5} \\ &= P_{f, 4}(W) (W + \sqrt{5})^2 (W+1) (W-W_0)^3, \end{align*} $$
where
 $$ \begin{align*} P_{f, 4}(W) &= 70 \left(11+\sqrt{5}\right) W^7+\left(-1520-1340 \sqrt{5}\right) W^6+\left(-45150-5730 \sqrt{5}\right) W^5 \\ &\quad +\left(-176050-45630 \sqrt{5}\right) W^4+\left(-259900-123200 \sqrt{5}\right) W^3 \\ &\quad+\left(216300 \sqrt{5}-795000\right) W^2+\left(991250 \sqrt{5}-2159250\right) W+624750 \sqrt{5}-1336250. \end{align*} $$
$$ \begin{align*} P_{f, 4}(W) &= 70 \left(11+\sqrt{5}\right) W^7+\left(-1520-1340 \sqrt{5}\right) W^6+\left(-45150-5730 \sqrt{5}\right) W^5 \\ &\quad +\left(-176050-45630 \sqrt{5}\right) W^4+\left(-259900-123200 \sqrt{5}\right) W^3 \\ &\quad+\left(216300 \sqrt{5}-795000\right) W^2+\left(991250 \sqrt{5}-2159250\right) W+624750 \sqrt{5}-1336250. \end{align*} $$
![]() $P_{f, 4}(W)$
only has a single root for
$P_{f, 4}(W)$
only has a single root for
![]() $W> W_0$
. Let us call x to that root. We have that
$W> W_0$
. Let us call x to that root. We have that
![]() $P_{f, 4}(W) < 0$
for
$P_{f, 4}(W) < 0$
for
![]() $W \in [W_0, x)$
and
$W \in [W_0, x)$
and
![]() $P_{f, 4}(W)> 0$
for
$P_{f, 4}(W)> 0$
for
![]() $W \in (x, \infty )$
. Therefore,
$W \in (x, \infty )$
. Therefore,
![]() $Q_f(W)$
is also negative for
$Q_f(W)$
is also negative for
![]() $W \in (W_0, x)$
and positive for
$W \in (W_0, x)$
and positive for
![]() $W \in (x, \infty )$
. Letting
$W \in (x, \infty )$
. Letting
![]() $P_{f, 5}(W) = P_{f, 1}(W) - P_{f, 2}(W)\sqrt {g(W)}$
, we have that
$P_{f, 5}(W) = P_{f, 1}(W) - P_{f, 2}(W)\sqrt {g(W)}$
, we have that
![]() $P_f(W) P_{f, 5}(W) = Q_f(W)$
. Moreover, we have that
$P_f(W) P_{f, 5}(W) = Q_f(W)$
. Moreover, we have that
 $$ \begin{align*} P_{f, 5}(10) &= -625 \left(3087362507+371529853 \sqrt{5}+\sqrt{9412199900256492638+2656241362034147990 \sqrt{5}}\right) < 0, \\ P_{f, 5}(15) &= 20000 \left(-336818691+1184891137 \sqrt{5}+\sqrt{6 \left(557-33 \sqrt{5}\right)} \left(19411872 \sqrt{5}-461659\right)\right)> 0, \end{align*} $$
$$ \begin{align*} P_{f, 5}(10) &= -625 \left(3087362507+371529853 \sqrt{5}+\sqrt{9412199900256492638+2656241362034147990 \sqrt{5}}\right) < 0, \\ P_{f, 5}(15) &= 20000 \left(-336818691+1184891137 \sqrt{5}+\sqrt{6 \left(557-33 \sqrt{5}\right)} \left(19411872 \sqrt{5}-461659\right)\right)> 0, \end{align*} $$
so the only root of
![]() $Q_f(W)$
for
$Q_f(W)$
for
![]() $W> W_0$
(which is simple) is a zero of
$W> W_0$
(which is simple) is a zero of
![]() $P_{f, 5}(W)$
. In particular,
$P_{f, 5}(W)$
. In particular,
![]() $P_f (W)$
does not vanish for
$P_f (W)$
does not vanish for
![]() $W> W_0$
.
$W> W_0$
.
Case
![]() $\xi> 0$
. First of all, as
$\xi> 0$
. First of all, as
![]() $(W^E, Z^E)$
goes from
$(W^E, Z^E)$
goes from
![]() $P_s$
to
$P_s$
to
![]() $P_\infty = (0, 0)$
, it can be parametrized by some compact domain; therefore, we just need to show (A.47) is positive for
$P_\infty = (0, 0)$
, it can be parametrized by some compact domain; therefore, we just need to show (A.47) is positive for
![]() $\xi> 0$
, and we will automatically get a positive lower bound by compactness. As in this region we have
$\xi> 0$
, and we will automatically get a positive lower bound by compactness. As in this region we have
![]() $D_W^E, D_Z^E> 0$
, this corresponds to showing that (A.49) is positive. Solving (A.49) as in the previous case, this is true as long as
$D_W^E, D_Z^E> 0$
, this corresponds to showing that (A.49) is positive. Solving (A.49) as in the previous case, this is true as long as
![]() $W> f(W)$
.
$W> f(W)$
.
Let us recall that for
![]() $\xi> 0$
, the solution
$\xi> 0$
, the solution
![]() $(W^E, Z^E)$
is inside a triangle T formed by the lines
$(W^E, Z^E)$
is inside a triangle T formed by the lines
![]() $D_Z = 0$
,
$D_Z = 0$
,
![]() $W = Z$
and
$W = Z$
and
![]() $W = W_0$
; in particular,
$W = W_0$
; in particular,
![]() $W^E$
is between
$W^E$
is between
![]() $-1$
and
$-1$
and
![]() $W_0$
(left and right extrema of the triangle) for
$W_0$
(left and right extrema of the triangle) for
![]() $\xi> 0$
. There are three simple roots of
$\xi> 0$
. There are three simple roots of
![]() $D_Z (W, f(W))$
, given by
$D_Z (W, f(W))$
, given by
![]() $-1$
,
$-1$
,
![]() $\bar W_0$
and
$\bar W_0$
and
![]() $W_0$
. Using that
$W_0$
. Using that
![]() $D_Z(W, f(W)) < 0$
for
$D_Z(W, f(W)) < 0$
for
![]() $W> W_0$
from the previous case, we conclude that
$W> W_0$
from the previous case, we conclude that
![]() $D_Z(W, f(W))$
is positive for
$D_Z(W, f(W))$
is positive for
![]() $W \in (\bar W_0, W_0)$
and negative for
$W \in (\bar W_0, W_0)$
and negative for
![]() $W \in (-1, \bar W_0)$
. As
$W \in (-1, \bar W_0)$
. As
![]() $D_Z^E> 0$
, this automatically yields that
$D_Z^E> 0$
, this automatically yields that
![]() $(W^E, Z^E)$
lies in the region
$(W^E, Z^E)$
lies in the region
![]() $W> f(W)$
for
$W> f(W)$
for
![]() $W \in (-1, \bar W_0)$
(for a given fixed W, the points with
$W \in (-1, \bar W_0)$
(for a given fixed W, the points with
![]() $D_Z> 0$
lie above those with
$D_Z> 0$
lie above those with
![]() $D_Z < 0$
). Thus, we just need to deal with the region
$D_Z < 0$
). Thus, we just need to deal with the region
![]() $W \in (\bar W_0, W_0)$
.
$W \in (\bar W_0, W_0)$
.
From our proof of Proposition 3.6, we have that
![]() $(W^E, Z^E)$
lies in the region
$(W^E, Z^E)$
lies in the region
![]() $\mathcal {T} \subset T$
, which has lower boundary
$\mathcal {T} \subset T$
, which has lower boundary
![]() $b^{\mathrm {nl}}_{7/5}(t)$
or
$b^{\mathrm {nl}}_{7/5}(t)$
or
![]() $b^{\mathrm {fl}}_{7/5}(t)$
for
$b^{\mathrm {fl}}_{7/5}(t)$
for
![]() $W \in (\bar W_0, W_0)$
. Thus, it suffices to show that the sign of (A.49) is positive at
$W \in (\bar W_0, W_0)$
. Thus, it suffices to show that the sign of (A.49) is positive at
![]() $b^{\mathrm {nl}}_{7/5}(t)$
and
$b^{\mathrm {nl}}_{7/5}(t)$
and
![]() $b^{\mathrm {fl}}_{7/5}(t)$
.
$b^{\mathrm {fl}}_{7/5}(t)$
.
Let us start with
![]() $b^{\mathrm {fl}}_{7/5}(t)$
. We define the quantity
$b^{\mathrm {fl}}_{7/5}(t)$
. We define the quantity
It is clear that this is a polynomial in t, multiple of t because
![]() $b^{\mathrm {fl}}_{7/5}(0) = P_s$
and
$b^{\mathrm {fl}}_{7/5}(0) = P_s$
and
![]() $D_Z(P_s) = N_Z(P_s) = 0$
. We have that
$D_Z(P_s) = N_Z(P_s) = 0$
. We have that
 $$ \begin{align*} \lim_{r\rightarrow \left( r^\ast \right)^- } \frac{S_{7/5}^{\mathrm{fl}}(0)}{r^\ast - r} = \frac{1}{605} \left(205-89 \sqrt{5}\right)> 0, \end{align*} $$
$$ \begin{align*} \lim_{r\rightarrow \left( r^\ast \right)^- } \frac{S_{7/5}^{\mathrm{fl}}(0)}{r^\ast - r} = \frac{1}{605} \left(205-89 \sqrt{5}\right)> 0, \end{align*} $$
so we can reduce to show
![]() $ \frac {S_{7/5}^{\mathrm {fl}}(t)}{t^3} \Big |_{r=r^\ast }> 0$
. For the rest of the treatment of
$ \frac {S_{7/5}^{\mathrm {fl}}(t)}{t^3} \Big |_{r=r^\ast }> 0$
. For the rest of the treatment of
![]() $b^{\mathrm {fl}}(t)$
, let us assume
$b^{\mathrm {fl}}(t)$
, let us assume
![]() $r= r^\ast $
. We have that
$r= r^\ast $
. We have that
 $$ \begin{align*} \frac{S_{7/5}^{\mathrm{fl}}(t)}{t^3} \Big|_{r=r^\ast} &= \frac{1}{ 15552 \left(14661 \sqrt{5}-32783\right) } \Big( 454726725 \sqrt{5} t^6-1016799875 t^6-479229660 \sqrt{5} t^5 \\ & +1071590100 t^5+899397288 \sqrt{5} t^4-2011113480 t^4-1391938278 \sqrt{5} t^3+3112468598 t^3 \\ &+833713587 \sqrt{5}t^2-1864240269 t^2-834718230 \sqrt{5} t\\ &+1866486726 t+746056440 \sqrt{5}-1668233016 \Big), \end{align*} $$
$$ \begin{align*} \frac{S_{7/5}^{\mathrm{fl}}(t)}{t^3} \Big|_{r=r^\ast} &= \frac{1}{ 15552 \left(14661 \sqrt{5}-32783\right) } \Big( 454726725 \sqrt{5} t^6-1016799875 t^6-479229660 \sqrt{5} t^5 \\ & +1071590100 t^5+899397288 \sqrt{5} t^4-2011113480 t^4-1391938278 \sqrt{5} t^3+3112468598 t^3 \\ &+833713587 \sqrt{5}t^2-1864240269 t^2-834718230 \sqrt{5} t\\ &+1866486726 t+746056440 \sqrt{5}-1668233016 \Big), \end{align*} $$
and this polynomial is positive for all
![]() $t \in \mathbb {R}$
.
$t \in \mathbb {R}$
.
Lastly, we need to show that (A.49) is positive at
![]() $b^{\mathrm {nl}}_{7/5}(s)$
for
$b^{\mathrm {nl}}_{7/5}(s)$
for
![]() $s \leq s_{7/5, \mathrm {int}}$
defined in the proof of Proposition 3.6. Let us recall
$s \leq s_{7/5, \mathrm {int}}$
defined in the proof of Proposition 3.6. Let us recall
![]() $ s_{7/5, \mathrm {int}}^{n-3} \lesssim \frac {n!}{Z_n}$
also from the proof of Proposition 3.6. We define
$ s_{7/5, \mathrm {int}}^{n-3} \lesssim \frac {n!}{Z_n}$
also from the proof of Proposition 3.6. We define
which is a
![]() $3n$
-th degree polynomial. Following the same proof as in Lemma 5.12, we get that for
$3n$
-th degree polynomial. Following the same proof as in Lemma 5.12, we get that for
![]() $2 \leq i \leq 3n$
,
$2 \leq i \leq 3n$
,
 $$ \begin{align*} \frac{\partial^i S_{7/5}^{\mathrm{nl}} (s)}{i!} \lesssim \left( \frac{|Z_n|}{n!} \right)^{i/n} \frac{(k-n)^{i/n - \lfloor i/n \rfloor}}{n^{\min \{ 7, \ell (i) \} }}. \end{align*} $$
$$ \begin{align*} \frac{\partial^i S_{7/5}^{\mathrm{nl}} (s)}{i!} \lesssim \left( \frac{|Z_n|}{n!} \right)^{i/n} \frac{(k-n)^{i/n - \lfloor i/n \rfloor}}{n^{\min \{ 7, \ell (i) \} }}. \end{align*} $$
Thus, we get
 $$ \begin{align*} S_{7/5}^{\mathrm{nl}} (s) - S_{7/5}^{\mathrm{nl\; \prime }} (0)s &\lesssim \sum_{i=2}^{n-1} \left( \frac{|Z_n| (k-n)}{n!}s^n \right)^{i/n} \frac{1}{n^{\min \{ 7, \ell (i) \} }} + \sum_{i=n}^{3n} \left( \frac{|Z_n|}{n!}s^n \right)^{i/n} \frac{1}{n^{\min \{ 7, \ell (i) \} }}. \end{align*} $$
$$ \begin{align*} S_{7/5}^{\mathrm{nl}} (s) - S_{7/5}^{\mathrm{nl\; \prime }} (0)s &\lesssim \sum_{i=2}^{n-1} \left( \frac{|Z_n| (k-n)}{n!}s^n \right)^{i/n} \frac{1}{n^{\min \{ 7, \ell (i) \} }} + \sum_{i=n}^{3n} \left( \frac{|Z_n|}{n!}s^n \right)^{i/n} \frac{1}{n^{\min \{ 7, \ell (i) \} }}. \end{align*} $$
Now let
![]() $s_0 = \left ( \frac {n!}{|Z_n|} \right )^{1/(n-2)}$
. By Corollary 5.8, we have that
$s_0 = \left ( \frac {n!}{|Z_n|} \right )^{1/(n-2)}$
. By Corollary 5.8, we have that
![]() $s_0 \lesssim \frac {1}{n}$
. Assuming
$s_0 \lesssim \frac {1}{n}$
. Assuming
![]() $s \leq s_0$
, we have
$s \leq s_0$
, we have
 $$ \begin{align} S_{7/5}^{\mathrm{nl}} (s) - S_{7/5}^{\mathrm{nl\; \prime }} (0)s &\lesssim s^2 \sum_{i=2}^{3n} \frac{1}{n^{\min \{ 7, \ell (i) \} }} \lesssim s^2. \end{align} $$
$$ \begin{align} S_{7/5}^{\mathrm{nl}} (s) - S_{7/5}^{\mathrm{nl\; \prime }} (0)s &\lesssim s^2 \sum_{i=2}^{3n} \frac{1}{n^{\min \{ 7, \ell (i) \} }} \lesssim s^2. \end{align} $$
Moreover,
 $$ \begin{align} S_{7/5}^{\mathrm{nl\; \prime }} (0) = \frac{1-\alpha}{2} N_{W, 0} D_{Z, 1} + \frac{1+\alpha}{2} D_{W, 0} N_{Z, 1} = \frac{ \frac{1-\alpha}{2} W_1 + \frac{1+\alpha}{2} Z_1 }{D_{W, 0} D_{Z, 1}} = \frac{1}{D_{W, 0}}> 0, \end{align} $$
$$ \begin{align} S_{7/5}^{\mathrm{nl\; \prime }} (0) = \frac{1-\alpha}{2} N_{W, 0} D_{Z, 1} + \frac{1+\alpha}{2} D_{W, 0} N_{Z, 1} = \frac{ \frac{1-\alpha}{2} W_1 + \frac{1+\alpha}{2} Z_1 }{D_{W, 0} D_{Z, 1}} = \frac{1}{D_{W, 0}}> 0, \end{align} $$
where the last inequality is due to Lemma A.7. We conclude from (A.50)–(A.51) and from the fact that
![]() $s_0 \lesssim \frac {1}{n}$
that for
$s_0 \lesssim \frac {1}{n}$
that for
![]() $0 \leq s \leq s_0$
,
$0 \leq s \leq s_0$
,
 $$ \begin{align*} S_{7/5}^{\mathrm{nl}} (s) = \frac{s}{D_{W, 0}} \left( 1 + O \left( \frac{1}{n} \right) \right), \end{align*} $$
$$ \begin{align*} S_{7/5}^{\mathrm{nl}} (s) = \frac{s}{D_{W, 0}} \left( 1 + O \left( \frac{1}{n} \right) \right), \end{align*} $$
and in particular, it is positive. As we have that
![]() $s_{7/5, \mathrm {int}}^{n-3} \lesssim \frac {n!}{Z_n} = s_0^{n-2}$
, we get that
$s_{7/5, \mathrm {int}}^{n-3} \lesssim \frac {n!}{Z_n} = s_0^{n-2}$
, we get that
![]() $s_{7/5, \mathrm {int}} < s_0$
for n sufficiently large (r sufficiently close to
$s_{7/5, \mathrm {int}} < s_0$
for n sufficiently large (r sufficiently close to
![]() $r^\ast $
), so we are done.
$r^\ast $
), so we are done.
Lemma A.37. We have that for all
![]() $\zeta \in (0, 1)$
,
$\zeta \in (0, 1)$
,

Proof. Note that on the variables used for the Euler profile, this is just saying that our profile is in the region
 $$ \begin{align*} A = \alpha Z^E - \frac{1-\alpha}{2} \left( W^E + \frac{N_W^E }{D_W^E}\right) + \frac{1}{100} < 0 \end{align*} $$
$$ \begin{align*} A = \alpha Z^E - \frac{1-\alpha}{2} \left( W^E + \frac{N_W^E }{D_W^E}\right) + \frac{1}{100} < 0 \end{align*} $$
for
![]() $\xi < 0$
. From our proof of Theorem 1.2, we know that
$\xi < 0$
. From our proof of Theorem 1.2, we know that
![]() $(W^E(\xi ), Z^E(\xi )) \in \Omega $
for
$(W^E(\xi ), Z^E(\xi )) \in \Omega $
for
![]() $\xi < 0$
, and we recall that
$\xi < 0$
, and we recall that
![]() $\Omega $
is defined to be the region where
$\Omega $
is defined to be the region where
![]() $D_W> 0, D_Z < 0$
. In particular, it suffices to show that
$D_W> 0, D_Z < 0$
. In particular, it suffices to show that
is negative in
![]() $\Omega $
. As
$\Omega $
. As
![]() $500AD_W$
is continuous with respect to r and
$500AD_W$
is continuous with respect to r and
![]() $\Omega $
is independent of r, we may just show this at
$\Omega $
is independent of r, we may just show this at
![]() $r=r^+$
, and the result will hold true in a neighborhood of
$r=r^+$
, and the result will hold true in a neighborhood of
![]() $r^+$
by continuity.
$r^+$
by continuity.
We get that
![]() $500AD_W$
is negative for
$500AD_W$
is negative for
![]() $Z \in (Z_{(1)}(W), Z_{(2)}(W))$
, where
$Z \in (Z_{(1)}(W), Z_{(2)}(W))$
, where
![]() $Z_{(i)}(W)$
are the two branches of the hyperbola implicitly defined by (A.52) and they are given at
$Z_{(i)}(W)$
are the two branches of the hyperbola implicitly defined by (A.52) and they are given at
![]() $r=r^+$
by
$r=r^+$
by
 $$ \begin{align*} Z_{(1)}(W) &= \frac{1}{20} \left(-30 W-51-\sqrt{500 W^2 + 1000\sqrt{5} W+2501}\right), \\ Z_{(2)}(W) &= \frac{1}{20} \left(-30 W-51+\sqrt{500 W^2 + 1000\sqrt{5} W+2501}\right), \end{align*} $$
$$ \begin{align*} Z_{(1)}(W) &= \frac{1}{20} \left(-30 W-51-\sqrt{500 W^2 + 1000\sqrt{5} W+2501}\right), \\ Z_{(2)}(W) &= \frac{1}{20} \left(-30 W-51+\sqrt{500 W^2 + 1000\sqrt{5} W+2501}\right), \end{align*} $$
where the second-degree polynomials inside the square root are positive for all
![]() $W \in \mathbb R$
. However,
$W \in \mathbb R$
. However,
![]() $\Omega $
is given by
$\Omega $
is given by
![]() $\frac {-5-3W}{2} < Z < \frac {-5-2W}{3}$
for
$\frac {-5-3W}{2} < Z < \frac {-5-2W}{3}$
for
![]() $W> -1$
, so we just need to show
$W> -1$
, so we just need to show
![]() $Z_{(1)}(W) < \frac {-5-3W}{2}$
and
$Z_{(1)}(W) < \frac {-5-3W}{2}$
and
![]() $\frac {-5-2W}{3} < Z_{(2)}(W)$
for all
$\frac {-5-2W}{3} < Z_{(2)}(W)$
for all
![]() $W> -1$
.
$W> -1$
.
Let us start with
![]() $Z_{(1)}(W) < \frac {-5-3W}{2}$
. We have that
$Z_{(1)}(W) < \frac {-5-3W}{2}$
. We have that
 $$ \begin{align} 20 \left( \frac{-5-3W}{2} - Z_{(1)}(W) \right) = 1+\sqrt{500 W^2 + 1000\sqrt{5} W+2501}> 0. \end{align} $$
$$ \begin{align} 20 \left( \frac{-5-3W}{2} - Z_{(1)}(W) \right) = 1+\sqrt{500 W^2 + 1000\sqrt{5} W+2501}> 0. \end{align} $$
With respect to
![]() $\frac {-5-2W}{3} < Z_{(2)}(W)$
, we have
$\frac {-5-2W}{3} < Z_{(2)}(W)$
, we have
 $$ \begin{align} 60\left( Z_{(2)}(W) + \frac{5+2W}{3} \right) = -53-50 W+3 \sqrt{500 (W + \sqrt{5})^2 + 1}. \end{align} $$
$$ \begin{align} 60\left( Z_{(2)}(W) + \frac{5+2W}{3} \right) = -53-50 W+3 \sqrt{500 (W + \sqrt{5})^2 + 1}. \end{align} $$
To show that (A.54) is positive, it suffices to show that the term with the square root dominates. That is the case as
where we used
![]() $W \geq -1$
to conclude the last inequality.
$W \geq -1$
to conclude the last inequality.
Lemma A.38. We have that for every
![]() $\zeta \in (0, 1)$
,
$\zeta \in (0, 1)$
,

Proof. This is equivalent to show positivity for
 $$ \begin{align*} \nonumber B = \alpha W^E - \frac{1-\alpha}{2} \left( Z^E + \frac{N_Z^E}{D_Z^E} \right) - \frac{1}{100}, \end{align*} $$
$$ \begin{align*} \nonumber B = \alpha W^E - \frac{1-\alpha}{2} \left( Z^E + \frac{N_Z^E}{D_Z^E} \right) - \frac{1}{100}, \end{align*} $$
when
![]() $\xi < 0$
. From our proof of Theorem 1.2, we know that
$\xi < 0$
. From our proof of Theorem 1.2, we know that
![]() $(W^E (\xi ), Z^E(\xi )) \in \Omega $
for
$(W^E (\xi ), Z^E(\xi )) \in \Omega $
for
![]() $\xi < 0$
. In particular,
$\xi < 0$
. In particular,
![]() $D_Z < 0$
, so it suffices to show negativity for
$D_Z < 0$
, so it suffices to show negativity for
Solving the polynomial in (A.55) in Z, one finds that (A.55) is negative for
![]() $Z \in (Z_{(-)}, Z_{(+)})$
, where
$Z \in (Z_{(-)}, Z_{(+)})$
, where
Let us recall from Remark 2.6 that our solution is decreasing in W, so we can parametrize it as
![]() $Z_\ast (W)$
. Thus, we have to show
$Z_\ast (W)$
. Thus, we have to show
![]() $Z_{(-)}(W) < Z_\ast (W) < Z_{(+)}(W)$
for
$Z_{(-)}(W) < Z_\ast (W) < Z_{(+)}(W)$
for
![]() $W> W_0$
.
$W> W_0$
.
Let us start with
![]() $Z_\ast (W) < Z_{(+)}(W)$
. As we know that the solution is in
$Z_\ast (W) < Z_{(+)}(W)$
. As we know that the solution is in
![]() $\Omega $
(where
$\Omega $
(where
![]() $D_Z < 0$
) for
$D_Z < 0$
) for
![]() $\xi < 0$
, it suffices to show that
$\xi < 0$
, it suffices to show that
![]() $Z_{(+)}(W)> \frac {-5-2W}{3}$
, as
$Z_{(+)}(W)> \frac {-5-2W}{3}$
, as
![]() $Z = \frac {-5-2W}{3}$
is the line at which
$Z = \frac {-5-2W}{3}$
is the line at which
![]() $D_Z = 0$
. By continuity, we may take
$D_Z = 0$
. By continuity, we may take
![]() $r = r^\ast $
, and note
$r = r^\ast $
, and note
 $$ \begin{align} 120 \left( Z_{(+)}(W) + \frac{5+2W}{3} \right) = -100 W+150 \sqrt{5}-241 +3 \sqrt{200 W \left(10 W-30 \sqrt{5}+49\right)-14700 \sqrt{5}+34509}. \end{align} $$
$$ \begin{align} 120 \left( Z_{(+)}(W) + \frac{5+2W}{3} \right) = -100 W+150 \sqrt{5}-241 +3 \sqrt{200 W \left(10 W-30 \sqrt{5}+49\right)-14700 \sqrt{5}+34509}. \end{align} $$
The second-degree polynomial inside the square root is always positive, and moreover, it dominates the expression, since
 $$ \begin{align*} &9 \left(200 W \left(10 W-30 \sqrt{5}+49\right)-14700 \sqrt{5}+34509\right)-\left(-100 W+150 \sqrt{5}-241\right)^2 \\ &\qquad = 8000 \left(W+\frac{1}{2} \left(5-3 \sqrt{5}\right)\right)^2> 0, \end{align*} $$
$$ \begin{align*} &9 \left(200 W \left(10 W-30 \sqrt{5}+49\right)-14700 \sqrt{5}+34509\right)-\left(-100 W+150 \sqrt{5}-241\right)^2 \\ &\qquad = 8000 \left(W+\frac{1}{2} \left(5-3 \sqrt{5}\right)\right)^2> 0, \end{align*} $$
so (A.57) is positive.
Now, let us show
![]() $Z_\ast (W)> Z_{(-)}(W)$
. First of all, note from Proposition 2.5 that
$Z_\ast (W)> Z_{(-)}(W)$
. First of all, note from Proposition 2.5 that
![]() $Z_\ast (W) = -W + O(1)$
. While doing series in (A.56), we get that
$Z_\ast (W) = -W + O(1)$
. While doing series in (A.56), we get that
![]() $Z_{(-)}(W) = \frac {-3-\sqrt {5}}{2} W + O(1)$
, so the inequality is clearly true for W sufficiently large. For W sufficiently close (from above) to
$Z_{(-)}(W) = \frac {-3-\sqrt {5}}{2} W + O(1)$
, so the inequality is clearly true for W sufficiently large. For W sufficiently close (from above) to
![]() $W_0$
, we also have that (A.55) is negative because it is zero for
$W_0$
, we also have that (A.55) is negative because it is zero for
![]() $W = W_0$
(as
$W = W_0$
(as
![]() $D_Z = 0$
) and
$D_Z = 0$
) and
 $$ \begin{align*} & (-203 + 200r) (-Z_1) + 40 Z_0 (-Z_1) + 40 W_0 (-W_1) + 60 W_0 (-Z_1) + 60 Z_0 (-W_1) + 98 (-W_1) \\ & \qquad = \sqrt{r^\ast - r} \left( \frac{-1}{33} \sqrt{42979610 \sqrt{5}-92240400} + o(1) \right), \end{align*} $$
$$ \begin{align*} & (-203 + 200r) (-Z_1) + 40 Z_0 (-Z_1) + 40 W_0 (-W_1) + 60 W_0 (-Z_1) + 60 Z_0 (-W_1) + 98 (-W_1) \\ & \qquad = \sqrt{r^\ast - r} \left( \frac{-1}{33} \sqrt{42979610 \sqrt{5}-92240400} + o(1) \right), \end{align*} $$
as
![]() $r \rightarrow r^\ast $
and
$r \rightarrow r^\ast $
and
![]() $\sqrt {42979610 \sqrt {5}-92240400}> 0$
.
$\sqrt {42979610 \sqrt {5}-92240400}> 0$
.
Therefore, as
![]() $Z_\ast (W)$
is above
$Z_\ast (W)$
is above
![]() $Z_{(-)}(W)$
for W sufficiently large and for W sufficiently close to
$Z_{(-)}(W)$
for W sufficiently large and for W sufficiently close to
![]() $W_0$
, we just need to discard the case that
$W_0$
, we just need to discard the case that
![]() $Z_\ast (W)$
crosses
$Z_\ast (W)$
crosses
![]() $Z_{(-)}(W)$
in both directions at some intermediate points. This is impossible because the field
$Z_{(-)}(W)$
in both directions at some intermediate points. This is impossible because the field
![]() $(N_W D_Z, N_Z D_W)$
points always to the left of
$(N_W D_Z, N_Z D_W)$
points always to the left of
![]() $(W, Z_{(-)}(W))$
for
$(W, Z_{(-)}(W))$
for
![]() $W \in (W_0, +\infty )$
. Concretely, if we define
$W \in (W_0, +\infty )$
. Concretely, if we define
we will show that
![]() $P_{(-)}(W)> 0$
for all
$P_{(-)}(W)> 0$
for all
![]() $W> W_0$
. As we have
$W> W_0$
. As we have
![]() $P_{(-)}(W_0) = 0$
(because
$P_{(-)}(W_0) = 0$
(because
![]() $N_Z(P_s) = D_Z(P_s) = 0$
) and
$N_Z(P_s) = D_Z(P_s) = 0$
) and
 $$ \begin{align*} \lim_{r \to (r^\ast)^-} \frac{P_{(-)}'(W_0)}{ \sqrt{ r^\ast - r } } = \frac{1}{9} \sqrt{425427 \sqrt{5}-815045}> 0, \end{align*} $$
$$ \begin{align*} \lim_{r \to (r^\ast)^-} \frac{P_{(-)}'(W_0)}{ \sqrt{ r^\ast - r } } = \frac{1}{9} \sqrt{425427 \sqrt{5}-815045}> 0, \end{align*} $$
we can reduce to show that
![]() $\frac {P_{(-)}(W)}{(W-W_0)^2} \Big |_{r=r^\ast }> 0$
. Defining
$\frac {P_{(-)}(W)}{(W-W_0)^2} \Big |_{r=r^\ast }> 0$
. Defining
 $$ \begin{align*} P_{(-)}^{(0)}(W) &= 200 W \left(10 W-30 \sqrt{5}+49\right)-14700 \sqrt{5}+34509, \\ P_{(-)}^{(1)}(W) &= 28000000 W^4-114000000 \sqrt{5} W^3+205000000 W^3-509000000 \sqrt{5} W^2 +1158252000 W^2 \\ &\quad-464135000 \sqrt{5} W+1041517700 W+1596837600 \sqrt{5}-3572154667 \\ P_{(-)}^{(2)}(W) &= 600000 W^3-1600000 \sqrt{5} W^2+2920000 W^2-2862000 \sqrt{5} W+6371200 W\\ &\quad+6167650 \sqrt{5}-13689861, \end{align*} $$
$$ \begin{align*} P_{(-)}^{(0)}(W) &= 200 W \left(10 W-30 \sqrt{5}+49\right)-14700 \sqrt{5}+34509, \\ P_{(-)}^{(1)}(W) &= 28000000 W^4-114000000 \sqrt{5} W^3+205000000 W^3-509000000 \sqrt{5} W^2 +1158252000 W^2 \\ &\quad-464135000 \sqrt{5} W+1041517700 W+1596837600 \sqrt{5}-3572154667 \\ P_{(-)}^{(2)}(W) &= 600000 W^3-1600000 \sqrt{5} W^2+2920000 W^2-2862000 \sqrt{5} W+6371200 W\\ &\quad+6167650 \sqrt{5}-13689861, \end{align*} $$
we have that
![]() $P_{(-)}^{(0)}(W)> 0$
for all
$P_{(-)}^{(0)}(W)> 0$
for all
![]() $W \in \mathbb {R}$
. We also have that
$W \in \mathbb {R}$
. We also have that
 $$ \begin{align*} Q_{(-)}(W) &= P_{(-)}(W) \frac{ \sqrt{P_{(-)}^{(0)}(W)} \left( P_{(-)}^{(1)}(W) - \sqrt{ P_{(-)}^{(0)}(W)} P_{(-)}^{(2)}(W) \right)}{ (W-W_0)^2 } \Big|_{r=r^\ast} \\ &= 80000000 W^6+\left(780000000-240000000 \sqrt{5}\right) W^5+\left(3051240000-1554000000 \sqrt{5}\right) W^4 \\ &\quad +\left(2544792000-1196400000 \sqrt{5}\right) W^3+\left(5195893000 \sqrt{5}-11358448560\right) W^2 \\ &\quad +\left(193380463-85410820 \sqrt{5}\right) W -1096899300 \sqrt{5}+2427799463, \end{align*} $$
$$ \begin{align*} Q_{(-)}(W) &= P_{(-)}(W) \frac{ \sqrt{P_{(-)}^{(0)}(W)} \left( P_{(-)}^{(1)}(W) - \sqrt{ P_{(-)}^{(0)}(W)} P_{(-)}^{(2)}(W) \right)}{ (W-W_0)^2 } \Big|_{r=r^\ast} \\ &= 80000000 W^6+\left(780000000-240000000 \sqrt{5}\right) W^5+\left(3051240000-1554000000 \sqrt{5}\right) W^4 \\ &\quad +\left(2544792000-1196400000 \sqrt{5}\right) W^3+\left(5195893000 \sqrt{5}-11358448560\right) W^2 \\ &\quad +\left(193380463-85410820 \sqrt{5}\right) W -1096899300 \sqrt{5}+2427799463, \end{align*} $$
and the polynomial
![]() $Q_{(-)}(W)$
is positive for
$Q_{(-)}(W)$
is positive for
![]() $W \geq W_0$
at
$W \geq W_0$
at
![]() $r=r^\ast $
. Therefore, we have that
$r=r^\ast $
. Therefore, we have that
![]() $\frac {P_{(-)}(W)}{(W-W_0)^2} \Big |_{r=r^\ast }$
does not change signs for
$\frac {P_{(-)}(W)}{(W-W_0)^2} \Big |_{r=r^\ast }$
does not change signs for
![]() $W \geq W_0$
. Its sign is positive because
$W \geq W_0$
. Its sign is positive because
 $$ \begin{align*} P_{(-)}(2) = \frac{15532539-5956350 \sqrt{5}+\frac{1743962911-759810800 \sqrt{5}}{\sqrt{6901-\frac{8900 \sqrt{5}}{3}}}}{800000}> 0. \end{align*} $$
$$ \begin{align*} P_{(-)}(2) = \frac{15532539-5956350 \sqrt{5}+\frac{1743962911-759810800 \sqrt{5}}{\sqrt{6901-\frac{8900 \sqrt{5}}{3}}}}{800000}> 0. \end{align*} $$
Lemma A.39. We have that our smooth self-similar profiles have the following asymptotics as
![]() $\zeta \rightarrow \infty $
:
$\zeta \rightarrow \infty $
:
Moreover, we have that for
![]() $\delta $
sufficiently small, there exists
$\delta $
sufficiently small, there exists
![]() $\zeta _0> 0$
such that
$\zeta _0> 0$
such that
for every
![]() $\zeta ' \leq \zeta _0 \leq \zeta $
.
$\zeta ' \leq \zeta _0 \leq \zeta $
.
Proof. To show ![]() and
and ![]() . Near
. Near
![]() $(W_E,Z_E)=0$
, we have
$(W_E,Z_E)=0$
, we have
which implies
![]() $W_E,Z_E=O(e^{-r\xi })=O(\zeta ^{-r})$
, which translates to
$W_E,Z_E=O(e^{-r\xi })=O(\zeta ^{-r})$
, which translates to ![]() .
.
and we obtain an analogous bound for ![]() .
.
Assuming (A.58) holds inductively for
![]() $i=0,\ldots m$
, then by the Leibniz rule,
$i=0,\ldots m$
, then by the Leibniz rule,

Thus, by Grönwall, we obtain (A.58) for
![]() $i=m+1$
.
$i=m+1$
.
B Implementation details of the computer-assisted part
In this appendix, we discuss the technical details about the implementation of the different rigorous numerical computations that appear in the proofs throughout the paper. We performed the rigorous computations using the Arb library [Reference Johansson53] and specifically its C implementation. We attach the code as supplementary material. See Table 2 for the specific programs/commands to run each Lemma/Proposition, with more details in the Supplementary Material. Since the code is long, as an extra step in guaranteeing correctness, we further verified the C implementation of functions against a numerical implementation in Mathematica. We only attach here the C version since it is the only mathematically rigorous implementation. We have also sacrificed efficiency by readability, and some parts of the code could be optimized (e.g., the splitting between the regimes
![]() $\gamma \sim 1$
and
$\gamma \sim 1$
and
![]() $\gamma \sim \infty $
could be optimized function by function, or the calculation of the more complicated barriers could also be optimized, as well as the aspect ratio – see below for a precise definition). Instead, we decided to write a much more modular design with many small functions performing simple tasks, at the price of sometimes duplicating code.
$\gamma \sim \infty $
could be optimized function by function, or the calculation of the more complicated barriers could also be optimized, as well as the aspect ratio – see below for a precise definition). Instead, we decided to write a much more modular design with many small functions performing simple tasks, at the price of sometimes duplicating code.
Table 1 Performance of the code in the different Lemmas/Propositions and regions.

Table 2 Executables and compilation commands for the different Lemmas.

Other times, we found empirically that the gain in precision from a higher-order method vs a lower-order method (for example, using
![]() $f\left (\frac {a+b}{2}\right ) + \frac {b-a}{2}f'([a,b])$
instead of
$f\left (\frac {a+b}{2}\right ) + \frac {b-a}{2}f'([a,b])$
instead of
![]() $f([a,b])$
as an enclosure of f) was beaten by the computational cost of the former, and the net execution time was comparable for both methods. In such a case, we decided to keep the lower-order method to gain in readability.
$f([a,b])$
as an enclosure of f) was beaten by the computational cost of the former, and the net execution time was comparable for both methods. In such a case, we decided to keep the lower-order method to gain in readability.
The implementation is split into several files dealing with the basic functions (such as
![]() $W_0$
,
$W_0$
,
![]() $Z_0$
for example), more complicated functions needed for the barriers (e.g.,
$Z_0$
for example), more complicated functions needed for the barriers (e.g.,
![]() $P^{nl}$
) and an additional general utility file.
$P^{nl}$
) and an additional general utility file.
There are two versions of the basic and barriers’ files depending on whether
![]() $\gamma \in [1,3]$
or
$\gamma \in [1,3]$
or
![]() $\gamma \in [3,\infty )$
, and an extra file with additional functions for the case
$\gamma \in [3,\infty )$
, and an extra file with additional functions for the case
![]() $\gamma = \frac 75$
. The rationale behind the splitting is that different desingularizations of the functions are required for the respective cases. In the former case, we will work with the variables
$\gamma = \frac 75$
. The rationale behind the splitting is that different desingularizations of the functions are required for the respective cases. In the former case, we will work with the variables
![]() $\tilde {\gamma } = \gamma -1, \tilde {r} = \frac {r-1}{\gamma -1}$
due to the singular behavior of the functions as
$\tilde {\gamma } = \gamma -1, \tilde {r} = \frac {r-1}{\gamma -1}$
due to the singular behavior of the functions as
![]() $\gamma \to 1$
. In the latter, we will work with the variables
$\gamma \to 1$
. In the latter, we will work with the variables
![]() $\gamma _{\mathrm {inv}} = \frac {1}{\gamma } \in [0,\frac 13] $
, and
$\gamma _{\mathrm {inv}} = \frac {1}{\gamma } \in [0,\frac 13] $
, and
![]() $\beta $
, where
$\beta $
, where
![]() $r = \frac {13}{10} - \gamma _{\mathrm {inv}}\left (\frac {5}{12}\right ) + \frac {3}{20}\beta $
. This change of variables is used to map the region
$r = \frac {13}{10} - \gamma _{\mathrm {inv}}\left (\frac {5}{12}\right ) + \frac {3}{20}\beta $
. This change of variables is used to map the region
![]() $\Omega = \{\gamma _{\mathrm {inv}} \in [0,\frac 13] , r \in (r_3(\gamma ), r_4(\gamma )\}$
into a rectangular-like region to avoid recalculating or bounding
$\Omega = \{\gamma _{\mathrm {inv}} \in [0,\frac 13] , r \in (r_3(\gamma ), r_4(\gamma )\}$
into a rectangular-like region to avoid recalculating or bounding
![]() $r_3(\gamma )$
and
$r_3(\gamma )$
and
![]() $r_4(\gamma )$
every time, leading to smaller errors. For performance reasons and because of Lemma A.31 or Proposition 4.5, we computed an enclosure of
$r_4(\gamma )$
every time, leading to smaller errors. For performance reasons and because of Lemma A.31 or Proposition 4.5, we computed an enclosure of
![]() $r_3(\gamma _{\mathrm {inv}}),r_4(\gamma _{\mathrm {inv}})$
and
$r_3(\gamma _{\mathrm {inv}}),r_4(\gamma _{\mathrm {inv}})$
and
![]() $\tilde {r}_3(\tilde {\gamma }), \tilde {r}_4(\tilde {\gamma })$
via the following Lemmas:
$\tilde {r}_3(\tilde {\gamma }), \tilde {r}_4(\tilde {\gamma })$
via the following Lemmas:
Lemma B.1. Let
![]() $\gamma \geq 3 $
. Then
$\gamma \geq 3 $
. Then
![]() $\beta _3 \in \bar {\beta _3}$
, where
$\beta _3 \in \bar {\beta _3}$
, where
 $$ \begin{align*} \bar{\beta}_3(\gamma_{\mathrm{inv}}) & = (-0.12274496668801302 \gamma_{\mathrm{inv}}^8 + 0.42078810964241387 \gamma_{\mathrm{inv}}^7 - 0.623996430280739 \gamma_{\mathrm{inv}}^6 \\ & + 0.4105016227331515 \gamma_{\mathrm{inv}}^5 + 0.20672452719140819 \gamma_{\mathrm{inv}}^4 - 1.0572166089549326 \gamma_{\mathrm{inv}}^3 \\ & + 1.804198700610401 \gamma_{\mathrm{inv}}^2 - 0.35416295479734694 \gamma_{\mathrm{inv}} + 0.09216512413383933) + 10^{-7}[-1,1], \end{align*} $$
$$ \begin{align*} \bar{\beta}_3(\gamma_{\mathrm{inv}}) & = (-0.12274496668801302 \gamma_{\mathrm{inv}}^8 + 0.42078810964241387 \gamma_{\mathrm{inv}}^7 - 0.623996430280739 \gamma_{\mathrm{inv}}^6 \\ & + 0.4105016227331515 \gamma_{\mathrm{inv}}^5 + 0.20672452719140819 \gamma_{\mathrm{inv}}^4 - 1.0572166089549326 \gamma_{\mathrm{inv}}^3 \\ & + 1.804198700610401 \gamma_{\mathrm{inv}}^2 - 0.35416295479734694 \gamma_{\mathrm{inv}} + 0.09216512413383933) + 10^{-7}[-1,1], \end{align*} $$
and
Lemma B.2. Let
![]() $\gamma \geq 3 $
. Then
$\gamma \geq 3 $
. Then
![]() $\beta _4 \in \bar {\beta _4}$
, where
$\beta _4 \in \bar {\beta _4}$
, where
 $$ \begin{align*} \bar{\beta}_4(\gamma_{\mathrm{inv}}) & = (-0.04469537027555534\gamma_{\mathrm{inv}}^8 + 0.27333057184133175\gamma_{\mathrm{inv}}^7 - 0.7172811883027264\gamma_{\mathrm{inv}}^6 \\ & + 0.9255018926764634*\gamma_{\mathrm{inv}}^5 - 0.4952968302717332\gamma_{\mathrm{inv}}^4 - 0.6817068021865448\gamma_{\mathrm{inv}}^3 \\ & + 1.8794062687026156\gamma_{\mathrm{inv}}^2 - 1.0362653478653305\gamma_{\mathrm{inv}} + 0.6762522531779247) + 10^{-7}[-1,1], \end{align*} $$
$$ \begin{align*} \bar{\beta}_4(\gamma_{\mathrm{inv}}) & = (-0.04469537027555534\gamma_{\mathrm{inv}}^8 + 0.27333057184133175\gamma_{\mathrm{inv}}^7 - 0.7172811883027264\gamma_{\mathrm{inv}}^6 \\ & + 0.9255018926764634*\gamma_{\mathrm{inv}}^5 - 0.4952968302717332\gamma_{\mathrm{inv}}^4 - 0.6817068021865448\gamma_{\mathrm{inv}}^3 \\ & + 1.8794062687026156\gamma_{\mathrm{inv}}^2 - 1.0362653478653305\gamma_{\mathrm{inv}} + 0.6762522531779247) + 10^{-7}[-1,1], \end{align*} $$
and
Lemma B.3. Let
![]() $1 < \gamma \leq 3$
. Then
$1 < \gamma \leq 3$
. Then
![]() $\tilde {r}_3 \in \bar {\tilde {r}}_3$
, where
$\tilde {r}_3 \in \bar {\tilde {r}}_3$
, where
 $$ \begin{align*} \bar{\tilde{r}}_3(\tilde{\gamma}) & = 0.12958483718253389 - 0.055797750679595685(\tilde{\gamma} - 1) + 0.025268384121421402(\tilde{\gamma} - 1)^2 \\ &\quad - 0.012079846976628505(\tilde{\gamma} - 1)^3 + 0.006116771307938418(\tilde{\gamma} - 1)^4 \\ &\quad - 0.0032535214532335432(\tilde{\gamma} - 1)^5 + 0.0016116474810902726(\tilde{\gamma} - 1)^6 \\ &\quad - 0.0008337203606963439(\tilde{\gamma} - 1)^7 + 0.001012190680858338(\tilde{\gamma} - 1)^8 \\ &\quad - 0.0007409251358921898(\tilde{\gamma} - 1)^9 - 0.00036102326965520293(\tilde{\gamma} - 1)^{10} \\ &\quad + 0.0003377160636686555(\tilde{\gamma} - 1)^{11} + 0.0004026573999596568(\tilde{\gamma} - 1)^{12} \\ &\quad - 0.00028839031633197794(\tilde{\gamma} - 1)^{13} + 10^{-6}[-1,1]. \end{align*} $$
$$ \begin{align*} \bar{\tilde{r}}_3(\tilde{\gamma}) & = 0.12958483718253389 - 0.055797750679595685(\tilde{\gamma} - 1) + 0.025268384121421402(\tilde{\gamma} - 1)^2 \\ &\quad - 0.012079846976628505(\tilde{\gamma} - 1)^3 + 0.006116771307938418(\tilde{\gamma} - 1)^4 \\ &\quad - 0.0032535214532335432(\tilde{\gamma} - 1)^5 + 0.0016116474810902726(\tilde{\gamma} - 1)^6 \\ &\quad - 0.0008337203606963439(\tilde{\gamma} - 1)^7 + 0.001012190680858338(\tilde{\gamma} - 1)^8 \\ &\quad - 0.0007409251358921898(\tilde{\gamma} - 1)^9 - 0.00036102326965520293(\tilde{\gamma} - 1)^{10} \\ &\quad + 0.0003377160636686555(\tilde{\gamma} - 1)^{11} + 0.0004026573999596568(\tilde{\gamma} - 1)^{12} \\ &\quad - 0.00028839031633197794(\tilde{\gamma} - 1)^{13} + 10^{-6}[-1,1]. \end{align*} $$
Lemma B.4. Let
![]() $1 < \gamma \leq 3$
. Then
$1 < \gamma \leq 3$
. Then
![]() $\tilde {r}_4 \in \bar {\tilde {r}}_4$
, where
$\tilde {r}_4 \in \bar {\tilde {r}}_4$
, where
 $$ \begin{align*} \bar{\tilde{r}}_4(\tilde{\gamma}) & = 0.17138836639778826 - 0.07719915367902941(\tilde{\gamma} - 1) + 0.037195168499089215(\tilde{\gamma} - 1)^2 \\ &\quad - 0.01925242261821647(\tilde{\gamma} - 1)^3 + 0.010950870775304766(\tilde{\gamma} - 1)^4 \\ &\quad - 0.0066817396642915305(\tilde{\gamma} - 1)^5 + 0.0023871873304486257(\tilde{\gamma} - 1)^6 \\ &\quad - 0.0005906689017045608(\tilde{\gamma} - 1)^7 + 0.005507190023795072(\tilde{\gamma} - 1)^8 \\ &\quad - 0.00526607727745243(\tilde{\gamma} - 1)^9 - 0.004296434160444562(\tilde{\gamma} - 1)^{10} \\ &\quad + 0.0042797575355271456(\tilde{\gamma} - 1)^{11} + 0.002982168551811326(\tilde{\gamma} - 1)^{12} \\ &\quad - 0.0025067232778351023(\tilde{\gamma} - 1)^{13} +10^{-6}[-2,2]. \end{align*} $$
$$ \begin{align*} \bar{\tilde{r}}_4(\tilde{\gamma}) & = 0.17138836639778826 - 0.07719915367902941(\tilde{\gamma} - 1) + 0.037195168499089215(\tilde{\gamma} - 1)^2 \\ &\quad - 0.01925242261821647(\tilde{\gamma} - 1)^3 + 0.010950870775304766(\tilde{\gamma} - 1)^4 \\ &\quad - 0.0066817396642915305(\tilde{\gamma} - 1)^5 + 0.0023871873304486257(\tilde{\gamma} - 1)^6 \\ &\quad - 0.0005906689017045608(\tilde{\gamma} - 1)^7 + 0.005507190023795072(\tilde{\gamma} - 1)^8 \\ &\quad - 0.00526607727745243(\tilde{\gamma} - 1)^9 - 0.004296434160444562(\tilde{\gamma} - 1)^{10} \\ &\quad + 0.0042797575355271456(\tilde{\gamma} - 1)^{11} + 0.002982168551811326(\tilde{\gamma} - 1)^{12} \\ &\quad - 0.0025067232778351023(\tilde{\gamma} - 1)^{13} +10^{-6}[-2,2]. \end{align*} $$
Any statement that has to be proved in
![]() $\Omega $
for
$\Omega $
for
![]() $\gamma \geq 3$
will be proved in the region
$\gamma \geq 3$
will be proved in the region
![]() $\Omega ' = \{\gamma _{\mathrm {inv}} \in [0, \frac 13], \beta \in [\bar \beta _{3}(\gamma _{\mathrm {inv}}),\bar \beta _{4}(\gamma _{\mathrm { inv}})]\}$
, or conversely, in
$\Omega ' = \{\gamma _{\mathrm {inv}} \in [0, \frac 13], \beta \in [\bar \beta _{3}(\gamma _{\mathrm {inv}}),\bar \beta _{4}(\gamma _{\mathrm { inv}})]\}$
, or conversely, in
![]() $\Omega ' = \{\tilde {\gamma } \in [0, 2], \tilde {r} \in [\bar { \tilde {r}}_{3}(\tilde {\gamma }),\bar { \tilde {r}}_{4}(\tilde {\gamma })]\}$
in the case
$\Omega ' = \{\tilde {\gamma } \in [0, 2], \tilde {r} \in [\bar { \tilde {r}}_{3}(\tilde {\gamma }),\bar { \tilde {r}}_{4}(\tilde {\gamma })]\}$
in the case
![]() $\gamma \leq 3$
, which will imply the correctness of the statement in
$\gamma \leq 3$
, which will imply the correctness of the statement in
![]() $\Omega $
thanks to the monotonicity of
$\Omega $
thanks to the monotonicity of
![]() $r(\beta )$
with
$r(\beta )$
with
![]() $\beta $
,
$\beta $
,
![]() $r(\tilde {r})$
with
$r(\tilde {r})$
with
![]() $\tilde {r}$
as well as the monotonicity of
$\tilde {r}$
as well as the monotonicity of
![]() $k(r)$
(cf. Lemma 2.1):
$k(r)$
(cf. Lemma 2.1):
Throughout the code, we will also desingularize the different variables in such a way that there is a finite limit whenever
![]() $\gamma $
tends to the singular point (either 1 or
$\gamma $
tends to the singular point (either 1 or
![]() $\infty $
). For example, instead of calculating
$\infty $
). For example, instead of calculating
![]() $W_0$
or
$W_0$
or
![]() $Z_0$
, we will calculate
$Z_0$
, we will calculate
![]() $\frac {W_0}{\gamma _{\mathrm {inv}}}$
and
$\frac {W_0}{\gamma _{\mathrm {inv}}}$
and
![]() $\frac {Z_0}{\gamma _{\mathrm {inv}}}$
, respectively, to be able to reach the corresponding limits as
$\frac {Z_0}{\gamma _{\mathrm {inv}}}$
, respectively, to be able to reach the corresponding limits as
![]() $\gamma _{\mathrm {inv}} \rightarrow 0$
.
$\gamma _{\mathrm {inv}} \rightarrow 0$
.
An important desingularization in the case
![]() $1 < \gamma \leq 3$
is the following. If one expands
$1 < \gamma \leq 3$
is the following. If one expands
![]() $W_k$
or
$W_k$
or
![]() $Z_k$
in powers of
$Z_k$
in powers of
![]() $\tilde {\gamma } = \gamma -1$
, it is easy to obtain that
$\tilde {\gamma } = \gamma -1$
, it is easy to obtain that
![]() $W_k = \frac {W_k^{\mathrm {s}}}{\tilde {\gamma }} + W_k^{\mathrm {ns}}$
, where
$W_k = \frac {W_k^{\mathrm {s}}}{\tilde {\gamma }} + W_k^{\mathrm {ns}}$
, where
![]() $W_k^{\mathrm {s}}, W_k^{\mathrm {ns}}$
are
$W_k^{\mathrm {s}}, W_k^{\mathrm {ns}}$
are
![]() $O(1)$
. However,
$O(1)$
. However,
![]() $W_k + Z_k = O(1)$
introduces an extra cancellation, and this appears at many levels. In contrast with the case
$W_k + Z_k = O(1)$
introduces an extra cancellation, and this appears at many levels. In contrast with the case
![]() $\gamma \geq 3$
, a homogeneous desingularization is not possible anymore. To remedy this situation, we will perform two steps. The first one is to split the recurrence for
$\gamma \geq 3$
, a homogeneous desingularization is not possible anymore. To remedy this situation, we will perform two steps. The first one is to split the recurrence for
![]() $W_k$
and
$W_k$
and
![]() $Z_k$
into
$Z_k$
into
![]() $W_k^{\mathrm {s}}, Z_k^{\mathrm {s}}, W_k^{\mathrm {ns}}, Z_k^{\mathrm { ns}}$
. In particular, this yields
$W_k^{\mathrm {s}}, Z_k^{\mathrm {s}}, W_k^{\mathrm {ns}}, Z_k^{\mathrm { ns}}$
. In particular, this yields
 $$ \begin{align*} D_{W,i} & = \frac12 W_i^{\mathrm{s}} + \frac{1+\alpha}{2}W_i^{\mathrm{ns}} + \frac{1-\alpha}{2}Z_i^{\mathrm{ns}} ,\\ D_{Z,i} & = \frac12 Z_i^{\mathrm{s}} + \frac{1+\alpha}{2}Z_i^{\mathrm{ns}} + \frac{1-\alpha}{2}W_i^{\mathrm{ns}}, \end{align*} $$
$$ \begin{align*} D_{W,i} & = \frac12 W_i^{\mathrm{s}} + \frac{1+\alpha}{2}W_i^{\mathrm{ns}} + \frac{1-\alpha}{2}Z_i^{\mathrm{ns}} ,\\ D_{Z,i} & = \frac12 Z_i^{\mathrm{s}} + \frac{1+\alpha}{2}Z_i^{\mathrm{ns}} + \frac{1-\alpha}{2}W_i^{\mathrm{ns}}, \end{align*} $$
and (for
![]() $W_n^{\mathrm {ns}}$
)
$W_n^{\mathrm {ns}}$
)
 $$ \begin{align*} D_{W,0} W_n^{\mathrm{ns}} & = -\sum_{j=0}^{n-2}\binom{n-1}{j}DW_{n+1-j}W_{j+1}^{\mathrm{ns}} + \frac14 \sum_{j=0}^{n-1}\binom{n-1}{j}(W_{j}^{\mathrm{ns}}-Z_{j}^{\mathrm{ns}})W_{n-1-j}^{\mathrm{s}} + \tilde{N}_{W,n-1}^{\mathrm{ns}} + R_{W,n-1} + W_n^{\mathrm{s}} \frac{r-1}{\gamma-1}, \\ \tilde{N}_{W,n-1}^{\mathrm{ns}} & = \nabla N_W^{\mathrm{ns}} \cdot (W_{n-1}^{\mathrm{ns}},Z_{n-1}^{\mathrm{ns}}) + \frac12 \sum_{j=1}^{n-1} \binom{n}{j}(W_j^{\mathrm{ns}},Z_j^{\mathrm{ns}}) HN_W (W_{n-1-j}^{\mathrm{ns}},Z_{n-1-j}^{\mathrm{ ns}})^{\top}, \\ \nabla N_W^{\mathrm{ns}} & = \left(-r-W_0^{\mathrm{ns}}-\frac12 Z_0^{\mathrm{ns}} - \frac54 W_0^s - (\gamma-1)W_0^{\mathrm{ns}} + \frac{\gamma-1}{4}Z_0^{\mathrm{ns}},-\frac12 W_0^{\mathrm{ns}} - \frac14 W_0^{\mathrm{s}} + \frac{\gamma-1}{4}W_0^{\mathrm{ns}} + \frac{\gamma-1}{2} Z_0^{\mathrm{ns}}\right) ,\\ R_{W,i} & = \sum_{j=1}^{i} \binom{i}{j}W_j^s\left(-\frac54 W_{i-j}^{\mathrm{ns}} - \frac14 Z_{i-j}^{\mathrm{ns}}\right), \end{align*} $$
$$ \begin{align*} D_{W,0} W_n^{\mathrm{ns}} & = -\sum_{j=0}^{n-2}\binom{n-1}{j}DW_{n+1-j}W_{j+1}^{\mathrm{ns}} + \frac14 \sum_{j=0}^{n-1}\binom{n-1}{j}(W_{j}^{\mathrm{ns}}-Z_{j}^{\mathrm{ns}})W_{n-1-j}^{\mathrm{s}} + \tilde{N}_{W,n-1}^{\mathrm{ns}} + R_{W,n-1} + W_n^{\mathrm{s}} \frac{r-1}{\gamma-1}, \\ \tilde{N}_{W,n-1}^{\mathrm{ns}} & = \nabla N_W^{\mathrm{ns}} \cdot (W_{n-1}^{\mathrm{ns}},Z_{n-1}^{\mathrm{ns}}) + \frac12 \sum_{j=1}^{n-1} \binom{n}{j}(W_j^{\mathrm{ns}},Z_j^{\mathrm{ns}}) HN_W (W_{n-1-j}^{\mathrm{ns}},Z_{n-1-j}^{\mathrm{ ns}})^{\top}, \\ \nabla N_W^{\mathrm{ns}} & = \left(-r-W_0^{\mathrm{ns}}-\frac12 Z_0^{\mathrm{ns}} - \frac54 W_0^s - (\gamma-1)W_0^{\mathrm{ns}} + \frac{\gamma-1}{4}Z_0^{\mathrm{ns}},-\frac12 W_0^{\mathrm{ns}} - \frac14 W_0^{\mathrm{s}} + \frac{\gamma-1}{4}W_0^{\mathrm{ns}} + \frac{\gamma-1}{2} Z_0^{\mathrm{ns}}\right) ,\\ R_{W,i} & = \sum_{j=1}^{i} \binom{i}{j}W_j^s\left(-\frac54 W_{i-j}^{\mathrm{ns}} - \frac14 Z_{i-j}^{\mathrm{ns}}\right), \end{align*} $$
and (for
![]() $Z_n^{\mathrm {ns}}$
)
$Z_n^{\mathrm {ns}}$
)
 $$ \begin{align*} (n-k)D_{Z,1} Z_n^{\mathrm{ns}} & = -\sum_{j=1}^{n-2}\binom{n}{j}DZ_{n-j}Z_{j+1}^{\mathrm{ns}} - \frac14 \sum_{j=1}^{n-1}\binom{n}{j}(Z_{n-j}^{\mathrm{ns}}-W_{n-j}^{\mathrm{ns}})W_{j}^{\mathrm{s}} + W_n^{\mathrm{s}} \left(\frac{r-1}{\gamma-1} + \frac14(W_0^{\mathrm{ns}} - Z_0^{\mathrm{ns}})\right) ,\\ & + \frac12 W_n^{\mathrm{s}} Z_1^{\mathrm{ns}} - \frac{1-\alpha}{2} Z_1^{\mathrm{ns}} W_n^{\mathrm{ns}} + \frac14 W_0^{\mathrm{s}} W_n^{\mathrm{ns}} + \left(-\frac12 Z_0^{\mathrm{ns}} + \frac14 W_0^s + \frac{\gamma-1}{2}W_0^{\mathrm{ns}} + \frac{\gamma-1}{4}Z_0^{\mathrm{ns}}\right)W_n^{\mathrm{ns}}, \\ & + \tilde{Q}_{Z,n}^{\mathrm{ns}} + R_{Z,n} \\ \tilde{Q}_{Z,n}^{\mathrm{ns}} & = \frac12 \sum_{j=1}^{n-1} \binom{n}{j}(W_j^{\mathrm{ns}},Z_j^{\mathrm{ns}}) HN_Z (W_{n-1-j}^{\mathrm{ns}},Z_{n-1-j}^{\mathrm{ns}})^{\top} ,\\ R_{Z,i} & = \sum_{j=1}^{i} \binom{i}{j}Z_j^s\left(-\frac54 Z_{i-j}^{\mathrm{ns}} - \frac14 W_{i-j}^{\mathrm{ns}}\right), \end{align*} $$
$$ \begin{align*} (n-k)D_{Z,1} Z_n^{\mathrm{ns}} & = -\sum_{j=1}^{n-2}\binom{n}{j}DZ_{n-j}Z_{j+1}^{\mathrm{ns}} - \frac14 \sum_{j=1}^{n-1}\binom{n}{j}(Z_{n-j}^{\mathrm{ns}}-W_{n-j}^{\mathrm{ns}})W_{j}^{\mathrm{s}} + W_n^{\mathrm{s}} \left(\frac{r-1}{\gamma-1} + \frac14(W_0^{\mathrm{ns}} - Z_0^{\mathrm{ns}})\right) ,\\ & + \frac12 W_n^{\mathrm{s}} Z_1^{\mathrm{ns}} - \frac{1-\alpha}{2} Z_1^{\mathrm{ns}} W_n^{\mathrm{ns}} + \frac14 W_0^{\mathrm{s}} W_n^{\mathrm{ns}} + \left(-\frac12 Z_0^{\mathrm{ns}} + \frac14 W_0^s + \frac{\gamma-1}{2}W_0^{\mathrm{ns}} + \frac{\gamma-1}{4}Z_0^{\mathrm{ns}}\right)W_n^{\mathrm{ns}}, \\ & + \tilde{Q}_{Z,n}^{\mathrm{ns}} + R_{Z,n} \\ \tilde{Q}_{Z,n}^{\mathrm{ns}} & = \frac12 \sum_{j=1}^{n-1} \binom{n}{j}(W_j^{\mathrm{ns}},Z_j^{\mathrm{ns}}) HN_Z (W_{n-1-j}^{\mathrm{ns}},Z_{n-1-j}^{\mathrm{ns}})^{\top} ,\\ R_{Z,i} & = \sum_{j=1}^{i} \binom{i}{j}Z_j^s\left(-\frac54 Z_{i-j}^{\mathrm{ns}} - \frac14 W_{i-j}^{\mathrm{ns}}\right), \end{align*} $$
as well as
![]() $Z_k^{\mathrm {s}} = -W_k^{\mathrm {s}} = -Z_{k-1}^{\mathrm {s}}$
for all
$Z_k^{\mathrm {s}} = -W_k^{\mathrm {s}} = -Z_{k-1}^{\mathrm {s}}$
for all
![]() $k \geq 1$
. Moreover, we will propagate estimates of the form ‘singular’ and ‘non-singular’ into some of the building blocks of the barriers. The second step is related to this phenomenon and concerns the observation of the following cancellation (we write it for a generic barrier though it applies everywhere):
$k \geq 1$
. Moreover, we will propagate estimates of the form ‘singular’ and ‘non-singular’ into some of the building blocks of the barriers. The second step is related to this phenomenon and concerns the observation of the following cancellation (we write it for a generic barrier though it applies everywhere):
where the barrier
![]() $b = (b_W,b_Z)$
is split into the singular and non-singular parts
$b = (b_W,b_Z)$
is split into the singular and non-singular parts
![]() $b^{\mathrm {s}} = (b_W^{\mathrm {s}}, b_Z^{\mathrm {s}}), b^{\mathrm {ns}} = (b_W^{\mathrm {ns}},b_Z^{\mathrm {ns}})$
, respectively, and we have used the fact that
$b^{\mathrm {s}} = (b_W^{\mathrm {s}}, b_Z^{\mathrm {s}}), b^{\mathrm {ns}} = (b_W^{\mathrm {ns}},b_Z^{\mathrm {ns}})$
, respectively, and we have used the fact that
![]() $(b_Z')^{\mathrm {s}} = -(b_W')^{\mathrm {s}}$
and we exploit an extra cancellation in
$(b_Z')^{\mathrm {s}} = -(b_W')^{\mathrm {s}}$
and we exploit an extra cancellation in
![]() $N_W D_Z + N_Z D_W$
writing it in terms of
$N_W D_Z + N_Z D_W$
writing it in terms of
![]() $W + Z$
and
$W + Z$
and
![]() $W - Z$
.
$W - Z$
.
The general philosophy is to run a branch and bound algorithm for all the open conditions that have to be checked throughout the paper. We will first enclose the condition at a given box in parameter space (which is at most 2 dimensional). For instance, in the
![]() $\gamma \geq 3$
case, starting from a subset of
$\gamma \geq 3$
case, starting from a subset of
![]() $\Omega '$
, where we picked either
$\Omega '$
, where we picked either
![]() $\{\gamma _{\mathrm {inv}} \in \gamma _{\mathrm {inv}}^{K,N} = [\frac {K-1}{N} \frac 13,\frac {K}{N} \frac 13], \quad \beta \in [\bar {\beta }_3(\gamma _{\mathrm {inv}}^{K,N}),\bar {\beta }_4(\gamma _{\mathrm {inv}}^{K,N})], K, N \in \mathbb {Z}\}$
(for the most demanding calculations) or the full set
$\{\gamma _{\mathrm {inv}} \in \gamma _{\mathrm {inv}}^{K,N} = [\frac {K-1}{N} \frac 13,\frac {K}{N} \frac 13], \quad \beta \in [\bar {\beta }_3(\gamma _{\mathrm {inv}}^{K,N}),\bar {\beta }_4(\gamma _{\mathrm {inv}}^{K,N})], K, N \in \mathbb {Z}\}$
(for the most demanding calculations) or the full set
![]() $\{\gamma _{\mathrm {inv}} \in [0, \frac 13],\beta \in [0,0.7]\}$
for the least demanding ones. In the case
$\{\gamma _{\mathrm {inv}} \in [0, \frac 13],\beta \in [0,0.7]\}$
for the least demanding ones. In the case
![]() $\gamma \leq 3$
, the least demanding intervals are taken to be
$\gamma \leq 3$
, the least demanding intervals are taken to be
![]() $\{(\tilde {\gamma },\tilde {r}) \in [0,1] \times [0.125,0.335] \} \cup \{(\tilde {\gamma },\tilde {r}) \in [1,2] \times [0.085,0.195] \}$
. For the specific values of K and N used, please see Table 1. If the enclosure gives a definite sign, we accept (or reject) it, depending on whether the sign is the desired one or not. If the enclosure does not give a sign, we split the box in 2 across one of the dimensions and call this procedure recursively. The program keeps dividing unless a certain tolerance (
$\{(\tilde {\gamma },\tilde {r}) \in [0,1] \times [0.125,0.335] \} \cup \{(\tilde {\gamma },\tilde {r}) \in [1,2] \times [0.085,0.195] \}$
. For the specific values of K and N used, please see Table 1. If the enclosure gives a definite sign, we accept (or reject) it, depending on whether the sign is the desired one or not. If the enclosure does not give a sign, we split the box in 2 across one of the dimensions and call this procedure recursively. The program keeps dividing unless a certain tolerance (
![]() $10^{-10}$
) in the maximum length in any dimension of the box is reached, in which case the program fails. In our case, this tolerance was never met. In order to select which direction to split by, a reasonable criterion should be to keep an aspect ratio proportional to the gradient of the function to be evaluated. Instead, due to the costly evaluation or estimation of that gradient, we determined empirically that keeping an aspect ratio of around 10 optimized the running time for
$10^{-10}$
) in the maximum length in any dimension of the box is reached, in which case the program fails. In our case, this tolerance was never met. In order to select which direction to split by, a reasonable criterion should be to keep an aspect ratio proportional to the gradient of the function to be evaluated. Instead, due to the costly evaluation or estimation of that gradient, we determined empirically that keeping an aspect ratio of around 10 optimized the running time for
![]() $\gamma \geq 3$
(in
$\gamma \geq 3$
(in
![]() $\beta ,\gamma _{\mathrm {inv}}$
variables) and an aspect ratio of
$\beta ,\gamma _{\mathrm {inv}}$
variables) and an aspect ratio of
![]() $\frac 15$
(in
$\frac 15$
(in
![]() $\tilde {r},\tilde {\gamma }$
variables) in the case
$\tilde {r},\tilde {\gamma }$
variables) in the case
![]() $\gamma \leq 3$
. For example, this meant that we split along the
$\gamma \leq 3$
. For example, this meant that we split along the
![]() $\beta $
direction if the width in the
$\beta $
direction if the width in the
![]() $\beta $
direction was bigger than 10 times the width in the
$\beta $
direction was bigger than 10 times the width in the
![]() $\gamma _{\mathrm {inv}}$
direction, otherwise along the
$\gamma _{\mathrm {inv}}$
direction, otherwise along the
![]() $\gamma _{\mathrm {inv}}$
one. For the cases where the problem is 1-dimensional, we treat is as a 2-dimensional one with width 0 in one of the dimensions.
$\gamma _{\mathrm {inv}}$
one. For the cases where the problem is 1-dimensional, we treat is as a 2-dimensional one with width 0 in one of the dimensions.
In Table 1, we presented the maximum times (per run) of the different parts of the code. In total, our computations ran for at most about 5000 CPU hours, although a more realistic estimate is between 3000 and 4000 CPU hours. We have also included the logs from the cluster runs as supplementary material to provide a more detailed estimate of the runtime.
We now move on to the specific details of the corresponding lemmas and propositions, in the order in which they appear on the paper:
Details of Lemma 2.1: We start by using the formulation (2.14) writing
It is enough to check that
We can write condition (B.1) as
![]() $T_1(r,\gamma ) + T_2(r,\gamma ) \mathcal {R}_1 < 0$
, where
$T_1(r,\gamma ) + T_2(r,\gamma ) \mathcal {R}_1 < 0$
, where
 $$ \begin{align*} T_1(r,\gamma) & = 4 (\gamma -1) (3 \gamma - 1) \left(\gamma^2 r-3 \gamma^2-14 \gamma r+14 \gamma+17 r-15\right), \\ T_2(r,\gamma) & = (\gamma +1)^2 (3 \gamma -5) (r-1). \end{align*} $$
$$ \begin{align*} T_1(r,\gamma) & = 4 (\gamma -1) (3 \gamma - 1) \left(\gamma^2 r-3 \gamma^2-14 \gamma r+14 \gamma+17 r-15\right), \\ T_2(r,\gamma) & = (\gamma +1)^2 (3 \gamma -5) (r-1). \end{align*} $$
We first show that
![]() $T_1(r, \gamma ) < 0$
. Clearly, we just need to show negativity for
$T_1(r, \gamma ) < 0$
. Clearly, we just need to show negativity for
![]() $\left (\gamma ^2 r-3 \gamma ^2-14 \gamma r+14 \gamma +17 r-15\right )$
. As this expression is affine in r and
$\left (\gamma ^2 r-3 \gamma ^2-14 \gamma r+14 \gamma +17 r-15\right )$
. As this expression is affine in r and
![]() $r^\ast (\gamma ) < 2 - \frac {1}{\gamma }$
(by Lemma A.6), it suffices to show negativity for the endpoints
$r^\ast (\gamma ) < 2 - \frac {1}{\gamma }$
(by Lemma A.6), it suffices to show negativity for the endpoints
![]() $r = 1$
and
$r = 1$
and
![]() $r=2 - \frac {1}{\gamma }$
. We have that
$r=2 - \frac {1}{\gamma }$
. We have that
 $$ \begin{align*} \left(\gamma^2 r-3 \gamma^2-14 \gamma r+14 \gamma+17 r-15\right) \Big|_{r=1} &= 2 - 2\gamma^2 < 0, \\ \left(\gamma^2 r-3 \gamma^2-14 \gamma r+14 \gamma+17 r-15\right) \Big|_{r=2-1/\gamma} &= - \frac{(17 + \gamma)(\gamma - 1)^2}{\gamma} < 0. \end{align*} $$
$$ \begin{align*} \left(\gamma^2 r-3 \gamma^2-14 \gamma r+14 \gamma+17 r-15\right) \Big|_{r=1} &= 2 - 2\gamma^2 < 0, \\ \left(\gamma^2 r-3 \gamma^2-14 \gamma r+14 \gamma+17 r-15\right) \Big|_{r=2-1/\gamma} &= - \frac{(17 + \gamma)(\gamma - 1)^2}{\gamma} < 0. \end{align*} $$
Therefore,
![]() $T_1(r, \gamma ) < 0$
. As we trivially have
$T_1(r, \gamma ) < 0$
. As we trivially have
![]() $T_2(r, \gamma ) < 0$
for
$T_2(r, \gamma ) < 0$
for
![]() $\gamma \leq \frac 53$
, this concludes the case
$\gamma \leq \frac 53$
, this concludes the case
![]() $\gamma \leq \frac 53$
. For the case
$\gamma \leq \frac 53$
. For the case
![]() $\gamma> \frac 53$
, it suffices to show that
$\gamma> \frac 53$
, it suffices to show that
![]() $\frac {1}{\gamma ^8}(T_1^2 - T_2^2 \mathcal {R}_1^2)> 0$
. We check with a computer-assisted proof that this is positive for
$\frac {1}{\gamma ^8}(T_1^2 - T_2^2 \mathcal {R}_1^2)> 0$
. We check with a computer-assisted proof that this is positive for
![]() $\gamma \geq 5/3$
and
$\gamma \geq 5/3$
and
![]() $1 \leq r \leq 2$
. As
$1 \leq r \leq 2$
. As
![]() $r^\ast < 2-\frac {1}{\gamma } < 2$
, this ends our proof.
$r^\ast < 2-\frac {1}{\gamma } < 2$
, this ends our proof.
Details of Proposition 3.2: Our choice of
![]() $b^{\mathrm {fl}}(t)$
ensures that
$b^{\mathrm {fl}}(t)$
ensures that
![]() $P^{\mathrm {fl}}(t)$
is a
$P^{\mathrm {fl}}(t)$
is a
![]() $7^{\mathrm {th}}$
-degree polynomial multiple of
$7^{\mathrm {th}}$
-degree polynomial multiple of
![]() $t^2(1-t)^2$
. Thus, it suffices to check the positivity of
$t^2(1-t)^2$
. Thus, it suffices to check the positivity of
![]() $Q^{\mathrm {fl}}(t) = P^{\mathrm {fl}}(t)/(t^2(1-t)^2)$
, which is a
$Q^{\mathrm {fl}}(t) = P^{\mathrm {fl}}(t)/(t^2(1-t)^2)$
, which is a
![]() $3^{rd}$
-degree polynomial. We validate the condition that
$3^{rd}$
-degree polynomial. We validate the condition that
![]() $Q^{\mathrm {fl} \,\prime }(t)$
is increasing, either by validating
$Q^{\mathrm {fl} \,\prime }(t)$
is increasing, either by validating
![]() $Q^{\mathrm {fl} \,\prime \prime \prime }(1) = Q^{\mathrm {fl} \,\prime \prime \prime }(t) < 0$
and
$Q^{\mathrm {fl} \,\prime \prime \prime }(1) = Q^{\mathrm {fl} \,\prime \prime \prime }(t) < 0$
and
![]() $Q^{\mathrm {fl} \,\prime \prime }(1)> 0$
(in the case
$Q^{\mathrm {fl} \,\prime \prime }(1)> 0$
(in the case
![]() $\gamma \geq 3$
) or by validating
$\gamma \geq 3$
) or by validating
![]() $Q^{\mathrm {fl} \,\prime \prime }(0)> 0$
and
$Q^{\mathrm {fl} \,\prime \prime }(0)> 0$
and
![]() $Q^{\mathrm {fl} \,\prime \prime }(1)> 0$
, which is enough since
$Q^{\mathrm {fl} \,\prime \prime }(1)> 0$
, which is enough since
![]() $Q^{\mathrm {fl} \,\prime \prime }(t)$
is linear (in the case
$Q^{\mathrm {fl} \,\prime \prime }(t)$
is linear (in the case
![]() $\gamma \leq 3$
). Therefore, in both cases,
$\gamma \leq 3$
). Therefore, in both cases,
![]() $Q^{\mathrm {fl} \,\prime }(t) < Q^{\mathrm {fl} \,\prime }(1)$
and
$Q^{\mathrm {fl} \,\prime }(t) < Q^{\mathrm {fl} \,\prime }(1)$
and
![]() $Q^{\mathrm {fl}}(t)> Q^{\mathrm {fl}}(1) - \max \{Q^{\mathrm {fl}\,\prime }(1),0\}$
. We validate
$Q^{\mathrm {fl}}(t)> Q^{\mathrm {fl}}(1) - \max \{Q^{\mathrm {fl}\,\prime }(1),0\}$
. We validate
![]() $Q^{\mathrm {fl}}(1) - \max \{Q^{\mathrm {fl}\,\prime }(1),0\}>0$
. In order to optimize the code, we do not perform divisions by
$Q^{\mathrm {fl}}(1) - \max \{Q^{\mathrm {fl}\,\prime }(1),0\}>0$
. In order to optimize the code, we do not perform divisions by
![]() $1-t$
or t and read the coefficients of
$1-t$
or t and read the coefficients of
![]() $Q^{\mathrm {fl}}$
off the coefficients of
$Q^{\mathrm {fl}}$
off the coefficients of
![]() $P^{\mathrm {fl}}$
.
$P^{\mathrm {fl}}$
.
The case
![]() $\gamma \leq 3$
presents an extra complication since
$\gamma \leq 3$
presents an extra complication since
![]() $\tilde {\gamma }Q^{\mathrm {fl}}(\tilde {\gamma },t) \sim \tilde {\gamma }F_1(\tilde {\gamma },t) + (t-1)F_2(t)$
for some smooth functions
$\tilde {\gamma }Q^{\mathrm {fl}}(\tilde {\gamma },t) \sim \tilde {\gamma }F_1(\tilde {\gamma },t) + (t-1)F_2(t)$
for some smooth functions
![]() $F_1$
and
$F_1$
and
![]() $F_2$
, and thus, it is impossible to determine the sign out of a uniform bound on the evaluation of
$F_2$
, and thus, it is impossible to determine the sign out of a uniform bound on the evaluation of
![]() $Q^{\mathrm {fl}} \tilde {\gamma }$
(which is what one can compute with the previously described desingularization) due to its vanishing at
$Q^{\mathrm {fl}} \tilde {\gamma }$
(which is what one can compute with the previously described desingularization) due to its vanishing at
![]() $\tilde {\gamma } = 0, t = 1$
. Instead, we have to work harder and further extract the leading, subleading and the rest of the terms out of expanding
$\tilde {\gamma } = 0, t = 1$
. Instead, we have to work harder and further extract the leading, subleading and the rest of the terms out of expanding
![]() $Z_k = \frac {Z_k^{\mathrm {s}}}{\tilde {\gamma }} + Z_k^c + \tilde {\gamma }Z_k^{\mathrm {desing},2}$
, where
$Z_k = \frac {Z_k^{\mathrm {s}}}{\tilde {\gamma }} + Z_k^c + \tilde {\gamma }Z_k^{\mathrm {desing},2}$
, where
![]() $Z_k^{\mathrm {s}}, Z_k^c, Z_k^{\mathrm {desing},2}$
are
$Z_k^{\mathrm {s}}, Z_k^c, Z_k^{\mathrm {desing},2}$
are
![]() $O(1)$
, and analogously,
$O(1)$
, and analogously,
![]() $W_k$
and all the barriers. In order to extract a sign out of
$W_k$
and all the barriers. In order to extract a sign out of
![]() $Q^{\mathrm {fl}}(\tilde {\gamma },1)$
, we will extract a sign out of
$Q^{\mathrm {fl}}(\tilde {\gamma },1)$
, we will extract a sign out of
![]() $F_1(\tilde {\gamma },1)$
.
$F_1(\tilde {\gamma },1)$
.
Details of Proposition 3.5: Throughout this proposition, we renormalize in
![]() $\gamma $
as explained above in order to have meaningful limits of the relevant quantities as
$\gamma $
as explained above in order to have meaningful limits of the relevant quantities as
![]() $\gamma _{\mathrm {inv}} \to 0$
. We discuss in detail the case
$\gamma _{\mathrm {inv}} \to 0$
. We discuss in detail the case
![]() $\gamma \geq 3$
: the case
$\gamma \geq 3$
: the case
![]() $\gamma \leq 3$
is done in an analogous way, considering the desingularization and splitting into the singular and non-singular parts of the relevant quantities outlined above. For steps 1, 2, 4, 5, we additionally consider the polynomials under the following change of variables:
$\gamma \leq 3$
is done in an analogous way, considering the desingularization and splitting into the singular and non-singular parts of the relevant quantities outlined above. For steps 1, 2, 4, 5, we additionally consider the polynomials under the following change of variables:
![]() $\tilde {s} = s(k-3)$
to make the validation region constant. In steps 1 and 2, we use the following formula:
$\tilde {s} = s(k-3)$
to make the validation region constant. In steps 1 and 2, we use the following formula:
 $$ \begin{align*} \frac{B^{\mathrm{fl}}}{\gamma_{\mathrm{inv}}^4[s^2(k-3)^2]} & = \frac14\left(\frac{B_2}{\gamma_{\mathrm{inv}}}\right)^2\left(\frac{(Z_0-Z)}{\gamma_{\mathrm{inv}}[s(k-3)]}\right)^2 + \frac14\left(\frac{B_3}{\gamma_{\mathrm{inv}}}\right)^2\left(\frac{(W_0-W)}{\gamma_{\mathrm{inv}}[s(k-3)]}\right)^2 \\ &\quad - \frac12\left(\frac{B_2}{\gamma_{\mathrm{inv}}}\right)\left(\frac{B_3}{\gamma_{\mathrm{inv}}}\right)\left(\frac{(Z_0-Z)}{\gamma_{\mathrm{inv}}[s(k-3)]}\right)\left(\frac{(W_0-W)}{\gamma_{\mathrm{inv}}[s(k-3)]}\right) \\ &\quad + \frac12 B_1^2 \frac{(B_2 Z_1 - B_3 W_1)}{\gamma_{\mathrm{inv}}^2}\frac{(Z_1(W_0-W) - W_1(Z_0-Z))}{\gamma_{\mathrm{inv}}^2[s^2(k-3)^2]}. \end{align*} $$
$$ \begin{align*} \frac{B^{\mathrm{fl}}}{\gamma_{\mathrm{inv}}^4[s^2(k-3)^2]} & = \frac14\left(\frac{B_2}{\gamma_{\mathrm{inv}}}\right)^2\left(\frac{(Z_0-Z)}{\gamma_{\mathrm{inv}}[s(k-3)]}\right)^2 + \frac14\left(\frac{B_3}{\gamma_{\mathrm{inv}}}\right)^2\left(\frac{(W_0-W)}{\gamma_{\mathrm{inv}}[s(k-3)]}\right)^2 \\ &\quad - \frac12\left(\frac{B_2}{\gamma_{\mathrm{inv}}}\right)\left(\frac{B_3}{\gamma_{\mathrm{inv}}}\right)\left(\frac{(Z_0-Z)}{\gamma_{\mathrm{inv}}[s(k-3)]}\right)\left(\frac{(W_0-W)}{\gamma_{\mathrm{inv}}[s(k-3)]}\right) \\ &\quad + \frac12 B_1^2 \frac{(B_2 Z_1 - B_3 W_1)}{\gamma_{\mathrm{inv}}^2}\frac{(Z_1(W_0-W) - W_1(Z_0-Z))}{\gamma_{\mathrm{inv}}^2[s^2(k-3)^2]}. \end{align*} $$
Note that there is an extra cancellation in the last parenthesis of the last term, yielding
 $$ \begin{align*} \frac{Z_1(W_0-W) - W_1(Z_0-Z)}{\gamma_{\mathrm{inv}}^2s^2(k-3)^2} &= \frac12\frac{(Z_2 W_1-W_2 Z_1)}{\gamma_{\mathrm{inv}}^2} + \frac16 s \left(Z_{3}^{\mathrm{norm,1}} \frac{W_1}{\gamma_{\mathrm{inv}}} - \frac{W_3 Z_1}{\gamma_{\mathrm{ inv}}^2} (k-3)\right),\\Z_{3}^{\mathrm{norm,1}} &= Z_3(k-3). \end{align*} $$
$$ \begin{align*} \frac{Z_1(W_0-W) - W_1(Z_0-Z)}{\gamma_{\mathrm{inv}}^2s^2(k-3)^2} &= \frac12\frac{(Z_2 W_1-W_2 Z_1)}{\gamma_{\mathrm{inv}}^2} + \frac16 s \left(Z_{3}^{\mathrm{norm,1}} \frac{W_1}{\gamma_{\mathrm{inv}}} - \frac{W_3 Z_1}{\gamma_{\mathrm{ inv}}^2} (k-3)\right),\\Z_{3}^{\mathrm{norm,1}} &= Z_3(k-3). \end{align*} $$
Steps 4 and 5: Here,
![]() $\tilde {s}$
is split into the two cases
$\tilde {s}$
is split into the two cases
![]() $[0,0.175]$
and
$[0,0.175]$
and
![]() $[0.175,0.35]$
, and we simply evaluate at the whole interval in
$[0.175,0.35]$
, and we simply evaluate at the whole interval in
![]() $\tilde {s}$
. We further desingularize
$\tilde {s}$
. We further desingularize
![]() $D_Z$
and prove the sign condition for
$D_Z$
and prove the sign condition for
![]() $\frac {D_Z}{s(k-3)}$
instead to ensure strict inequality for
$\frac {D_Z}{s(k-3)}$
instead to ensure strict inequality for
![]() $\tilde {s} \sim 0$
.
$\tilde {s} \sim 0$
.
Step 3: Throughout this part, we will compute
![]() $P^{\mathrm {nl}}(t(k-3))$
. A natural desingularization (in t) would be to consider
$P^{\mathrm {nl}}(t(k-3))$
. A natural desingularization (in t) would be to consider
![]() $\tilde {s} = t(k-3)$
and desingularize as in the previous steps. This is problematic, however, since, for example,
$\tilde {s} = t(k-3)$
and desingularize as in the previous steps. This is problematic, however, since, for example,
![]() $W_3t^3(k-3)^3$
and
$W_3t^3(k-3)^3$
and
![]() $Z_3 t^3 (k-3)^3$
do not desingularize in the same way (in the latter case, to desingularize,
$Z_3 t^3 (k-3)^3$
do not desingularize in the same way (in the latter case, to desingularize,
![]() $Z_3$
should be paired with a factor of
$Z_3$
should be paired with a factor of
![]() $k-3$
). In fact, the natural desingularization (in t and
$k-3$
). In fact, the natural desingularization (in t and
![]() $k-3$
) should be
$k-3$
) should be
![]() $\frac {P^{\mathrm {nl}}(t(k-3))}{t^4(k-3)^3}$
. In order to overcome this complication, we will divide every summand in t by the highest possible power of
$\frac {P^{\mathrm {nl}}(t(k-3))}{t^4(k-3)^3}$
. In order to overcome this complication, we will divide every summand in t by the highest possible power of
![]() $k-3$
in W or Z, keeping track of it, multiply out to compose the power series of the products and finally multiply by powers of
$k-3$
in W or Z, keeping track of it, multiply out to compose the power series of the products and finally multiply by powers of
![]() $k-3$
if needed. The reason for doing it this way (as opposed to dividing by
$k-3$
if needed. The reason for doing it this way (as opposed to dividing by
![]() $k-3$
whenever it is needed) is that
$k-3$
whenever it is needed) is that
![]() $k-3$
may potentially be 0, so division by
$k-3$
may potentially be 0, so division by
![]() $k-3$
will not yield any meaningful results. In particular, our methods will return the following vectors, from which we will construct the functions
$k-3$
will not yield any meaningful results. In particular, our methods will return the following vectors, from which we will construct the functions
![]() $N, D$
and b: (in parenthesis the terms corresponding to the power series for the different degrees of t)
$N, D$
and b: (in parenthesis the terms corresponding to the power series for the different degrees of t)
 $$ \begin{align*} W & = (W_0, W_1, \frac12 W_2, \frac16 W_3 (k-3)), \quad Z = (Z_0, Z_1, \frac12 Z_2, \frac16 Z_3^{\mathrm{norm,1}}), \\ b_W^{\prime} & = (W_1,W_2, \frac12 W_3(k-3), \quad b_Z^{\prime} = (Z_1, Z_2, \frac12 Z_3^{\mathrm{norm,1}}) ,\\ WZ & = (W_0Z_0, W_1Z_0 + W_0Z_1, W_1Z_1 + \frac12 W_2 Z_0 + \frac12 W_0 Z_2, \\ & \frac16 W_0 Z_3^{\mathrm{norm,1}} + \frac16 W_3 Z_0 (k-3) + \frac12 W_2 Z_1 (k-3) + \frac12 W_1 Z_2 (k-3), \\ & \frac16 W_1 Z_3^{\mathrm{norm,1}} + \frac16 W_3 Z_1 (k-3) + \frac14 W_2 Z_2 (k-3), \frac{1}{12} W_2 Z_3^{\mathrm{norm,1}} + \frac{1}{12} W_3 Z_2(k-3), \frac{1}{36} Z_3^{\mathrm{norm,1}} W_3 (k-3)) \\ W^2 & = (W_0^2, 2 W_0 W_1, W_1^2+W_0 W_2, W_1 W_2 (k-3) + \frac13 W_0 W_3 (k-3), \frac14 W_2^2 (k-3) + \frac13 W_1 W_3 (k-3), \\ & \frac16 W_2 W_3 (k-3), \frac{1}{36} W_3^2 (k-3)^2) ,\\ Z^2 & = (Z_0^2, 2 Z_0 Z_1, Z_1^2+Z_0 Z_2, Z_1 Z_2(k-3) + \frac{1}{3} Z_0 Z_3^{\mathrm{norm,1}}, \frac14 Z_2^2 (k-3) + \frac13 Z_1 Z_3^{\mathrm{norm,1}}, \frac16 Z_2 Z_3^{\mathrm{norm,1}}, \frac{1}{36} (Z_3^{\mathrm{norm,1}})^2), \end{align*} $$
$$ \begin{align*} W & = (W_0, W_1, \frac12 W_2, \frac16 W_3 (k-3)), \quad Z = (Z_0, Z_1, \frac12 Z_2, \frac16 Z_3^{\mathrm{norm,1}}), \\ b_W^{\prime} & = (W_1,W_2, \frac12 W_3(k-3), \quad b_Z^{\prime} = (Z_1, Z_2, \frac12 Z_3^{\mathrm{norm,1}}) ,\\ WZ & = (W_0Z_0, W_1Z_0 + W_0Z_1, W_1Z_1 + \frac12 W_2 Z_0 + \frac12 W_0 Z_2, \\ & \frac16 W_0 Z_3^{\mathrm{norm,1}} + \frac16 W_3 Z_0 (k-3) + \frac12 W_2 Z_1 (k-3) + \frac12 W_1 Z_2 (k-3), \\ & \frac16 W_1 Z_3^{\mathrm{norm,1}} + \frac16 W_3 Z_1 (k-3) + \frac14 W_2 Z_2 (k-3), \frac{1}{12} W_2 Z_3^{\mathrm{norm,1}} + \frac{1}{12} W_3 Z_2(k-3), \frac{1}{36} Z_3^{\mathrm{norm,1}} W_3 (k-3)) \\ W^2 & = (W_0^2, 2 W_0 W_1, W_1^2+W_0 W_2, W_1 W_2 (k-3) + \frac13 W_0 W_3 (k-3), \frac14 W_2^2 (k-3) + \frac13 W_1 W_3 (k-3), \\ & \frac16 W_2 W_3 (k-3), \frac{1}{36} W_3^2 (k-3)^2) ,\\ Z^2 & = (Z_0^2, 2 Z_0 Z_1, Z_1^2+Z_0 Z_2, Z_1 Z_2(k-3) + \frac{1}{3} Z_0 Z_3^{\mathrm{norm,1}}, \frac14 Z_2^2 (k-3) + \frac13 Z_1 Z_3^{\mathrm{norm,1}}, \frac16 Z_2 Z_3^{\mathrm{norm,1}}, \frac{1}{36} (Z_3^{\mathrm{norm,1}})^2), \end{align*} $$
and the powers of
![]() $k-3$
we have divided by (as functions of the powers of t) are given by:
$k-3$
we have divided by (as functions of the powers of t) are given by:
In the end, we validate
![]() $P^{\mathrm {nl}}(\tilde {s}_{-})> 0$
and
$P^{\mathrm {nl}}(\tilde {s}_{-})> 0$
and
![]() $P^{\mathrm {nl,\prime }}([0,\tilde {s}_{-}]) < 0$
.
$P^{\mathrm {nl,\prime }}([0,\tilde {s}_{-}]) < 0$
.
Details of Proposition 4.5: In principle, it is clear that
![]() $P^{\mathrm {fr}} (s)(s-s_\infty ^{\mathrm {fr}})^5 $
is a polynomial in s, as we have up to five times the denominator
$P^{\mathrm {fr}} (s)(s-s_\infty ^{\mathrm {fr}})^5 $
is a polynomial in s, as we have up to five times the denominator
![]() $(s-s_\infty ^{\mathrm {fr}})$
in (4.12). However, the two cancellations at
$(s-s_\infty ^{\mathrm {fr}})$
in (4.12). However, the two cancellations at
![]() $P_0$
(because
$P_0$
(because
![]() $b^{\mathrm {fr}}(0) = P_s$
and the choice of
$b^{\mathrm {fr}}(0) = P_s$
and the choice of
![]() $F_1$
) give us that
$F_1$
) give us that
![]() $P^{\mathrm {fr}}(s)(s-s_\infty ^{\mathrm {fr}})^5$
is multiple of
$P^{\mathrm {fr}}(s)(s-s_\infty ^{\mathrm {fr}})^5$
is multiple of
![]() $s^2$
.
$s^2$
.
However, we have that
![]() $B^{\mathrm {fr}}(W, Z)$
is bounded if
$B^{\mathrm {fr}}(W, Z)$
is bounded if
![]() $(W, Z)$
is the solution starting at
$(W, Z)$
is the solution starting at
![]() $P_0$
(instead of growing quadratically with
$P_0$
(instead of growing quadratically with
![]() $|W|+|Z|$
). This is because
$|W|+|Z|$
). This is because
![]() $W+Z-W_0-Z_0$
is bounded over this solution and
$W+Z-W_0-Z_0$
is bounded over this solution and
![]() $W+Z-F_0 \lesssim \frac {1}{|W|+|Z|}$
over this solution (due to the choice of
$W+Z-F_0 \lesssim \frac {1}{|W|+|Z|}$
over this solution (due to the choice of
![]() $F_0$
). Those two cancellations imply that
$F_0$
). Those two cancellations imply that
![]() $P^{\mathrm {fr}}(s)(s-s_\infty ^{\mathrm {fr}})^5$
is in fact a multiple of
$P^{\mathrm {fr}}(s)(s-s_\infty ^{\mathrm {fr}})^5$
is in fact a multiple of
![]() $(s-s_\infty ^{\mathrm {fr}})^2$
. Therefore, it suffices to check that the sign of the polynomial
$(s-s_\infty ^{\mathrm {fr}})^2$
. Therefore, it suffices to check that the sign of the polynomial
![]() $Q^{\mathrm {fr}}(s) = P^{\mathrm {fr}}(s)(s-s_\infty )^3/s^2$
is positive.
$Q^{\mathrm {fr}}(s) = P^{\mathrm {fr}}(s)(s-s_\infty )^3/s^2$
is positive.
In order to reduce the dimension of the problem, we use Lemma B.1 (so that we will evaluate at
![]() $\beta = \bar {\beta }_3$
for
$\beta = \bar {\beta }_3$
for
![]() $\gamma \geq 3$
and
$\gamma \geq 3$
and
![]() $\tilde {r} = \bar {\tilde {r}}_3$
for
$\tilde {r} = \bar {\tilde {r}}_3$
for
![]() $\gamma \leq 3$
) and hence deal with a 1-dimensional problem. In the former case, we also renormalize s via
$\gamma \leq 3$
) and hence deal with a 1-dimensional problem. In the former case, we also renormalize s via
![]() $\tilde {s} = \frac {s}{\gamma _{\mathrm {inv}}}$
to ensure convergence to a finite value as
$\tilde {s} = \frac {s}{\gamma _{\mathrm {inv}}}$
to ensure convergence to a finite value as
![]() $\gamma _{\mathrm {inv}} \to 0$
(this includes the right scaling with respect to
$\gamma _{\mathrm {inv}} \to 0$
(this includes the right scaling with respect to
![]() $\gamma _{\mathrm {inv}}$
in
$\gamma _{\mathrm {inv}}$
in
![]() $s_{\infty }^{\mathrm {fr}}$
as well). In the latter, we apply the desingularization scheme described above without desingularizing s.
$s_{\infty }^{\mathrm {fr}}$
as well). In the latter, we apply the desingularization scheme described above without desingularizing s.
In order to bound
![]() $Q^{\mathrm {fr}}(\tilde {s}) = a_0 + a_1 \tilde {s} + a_2 \tilde {s}^2 + a_3 \tilde {s}^3 + a_4 \tilde {s}^4$
or
$Q^{\mathrm {fr}}(\tilde {s}) = a_0 + a_1 \tilde {s} + a_2 \tilde {s}^2 + a_3 \tilde {s}^3 + a_4 \tilde {s}^4$
or
![]() $Q^{\mathrm {fr}}(s) = a_0 + a_1 s + a_2 s^2 + a_3 s^3 + a_4 s^4$
, we validate the conditions
$Q^{\mathrm {fr}}(s) = a_0 + a_1 s + a_2 s^2 + a_3 s^3 + a_4 s^4$
, we validate the conditions
![]() $a_2 < 0$
and
$a_2 < 0$
and
 $$ \begin{align*} \left\{ \begin{array}{cc} a_0 - \frac{a_1^2}{4 a_2} + |a_3|\left(\frac{s^{\mathrm{fr}}_{\infty}}{\gamma_{\mathrm{inv}}}\right)^3 + |a_4|\left(\frac{s^{\mathrm{fr}}_{\infty}}{\gamma_{\mathrm{inv}}}\right)^4 < 0 & \text{ for } \gamma \geq \frac53 ,\\ a_0 - \frac{a_1^2}{4 a_2} + |a_3|\left(s^{\mathrm{fr}}_{\infty}\right)^3 + |a_4|\left(s^{\mathrm{fr}}_{\infty}\right)^4 < 0 & \text{ for } \gamma \leq \frac53, \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{cc} a_0 - \frac{a_1^2}{4 a_2} + |a_3|\left(\frac{s^{\mathrm{fr}}_{\infty}}{\gamma_{\mathrm{inv}}}\right)^3 + |a_4|\left(\frac{s^{\mathrm{fr}}_{\infty}}{\gamma_{\mathrm{inv}}}\right)^4 < 0 & \text{ for } \gamma \geq \frac53 ,\\ a_0 - \frac{a_1^2}{4 a_2} + |a_3|\left(s^{\mathrm{fr}}_{\infty}\right)^3 + |a_4|\left(s^{\mathrm{fr}}_{\infty}\right)^4 < 0 & \text{ for } \gamma \leq \frac53, \end{array} \right. \end{align*} $$
where we are bounding the first 3 terms of the polynomial by its maximum, given that they correspond to a negative parabola.
The case
![]() $\gamma = \frac 75, r = r^{\ast }$
is done directly using the framework of
$\gamma = \frac 75, r = r^{\ast }$
is done directly using the framework of
![]() $\gamma \geq 3$
since the desingularization is simpler.
$\gamma \geq 3$
since the desingularization is simpler.
Details of Lemma 5.14: Instead of computing the
![]() $6 \times 6$
determinant directly, we write it in block form, apply the formula
$6 \times 6$
determinant directly, we write it in block form, apply the formula
 $\text {det}\left (\begin {array}{cc} A & B \\ C & D \end {array}\right ) = \text {det}(A)\text {det}(D - CA^{-1}B)$
and compute the determinants on the right-hand side. The above formula holds so long as A is invertible (which we ensure along the calculation). The computations of the determinants on the right-hand side of the equation are comparatively more efficient since A is triangular and the expression for
$\text {det}\left (\begin {array}{cc} A & B \\ C & D \end {array}\right ) = \text {det}(A)\text {det}(D - CA^{-1}B)$
and compute the determinants on the right-hand side. The above formula holds so long as A is invertible (which we ensure along the calculation). The computations of the determinants on the right-hand side of the equation are comparatively more efficient since A is triangular and the expression for
![]() $A^{-1}$
is simple.
$A^{-1}$
is simple.
Details of Lemma A.23: The condition is equivalent to
![]() $\frac {3 - \sqrt {3}}{2 + \sqrt {3}\tilde {\gamma }} - \tilde {r}_4> 0$
, which is what we actually validate.
$\frac {3 - \sqrt {3}}{2 + \sqrt {3}\tilde {\gamma }} - \tilde {r}_4> 0$
, which is what we actually validate.
Details of Lemma A.24: In order to prove the first part, we will take the full interval
![]() $T_W = (0.6019, 0.6021)$
and prove that on the one hand,
$T_W = (0.6019, 0.6021)$
and prove that on the one hand,
![]() $b^{\mathrm {fl}}_{7/5, Z} (T_W)> Y_0$
, and on the other,
$b^{\mathrm {fl}}_{7/5, Z} (T_W)> Y_0$
, and on the other,
![]() $b^{\mathrm {fl}}_{7/5, W} (0.6019) < X_0, b^{\mathrm {fl}}_{7/5, W} (0.6021)> X_0$
.
$b^{\mathrm {fl}}_{7/5, W} (0.6019) < X_0, b^{\mathrm {fl}}_{7/5, W} (0.6021)> X_0$
.
Details of Lemma A.25: We apply the same renormalization/desingularization as in Proposition 3.2.
Details of Lemma A.26 (fifth inequality): The inequality is problematic due to
![]() $W_4,Z_4$
blowing up at
$W_4,Z_4$
blowing up at
![]() $r_3$
and
$r_3$
and
![]() $Z_4$
blowing up at
$Z_4$
blowing up at
![]() $r_4$
as well. Instead, in the case
$r_4$
as well. Instead, in the case
![]() $\gamma \geq 3$
, we implemented a method that returned
$\gamma \geq 3$
, we implemented a method that returned
![]() $W_4^{\mathrm {norm,2}} = \frac {1}{\gamma _{\mathrm {inv}}}W_4(k-3)$
and
$W_4^{\mathrm {norm,2}} = \frac {1}{\gamma _{\mathrm {inv}}}W_4(k-3)$
and
![]() $Z_4^{norm,2} = \frac {1}{\gamma _{\mathrm {inv}}}Z_4(k-3)(k-4)$
adapting equations 2.18–2.19 accordingly and proved instead
$Z_4^{norm,2} = \frac {1}{\gamma _{\mathrm {inv}}}Z_4(k-3)(k-4)$
adapting equations 2.18–2.19 accordingly and proved instead
In the case
![]() $\gamma \leq 3$
, we split
$\gamma \leq 3$
, we split
![]() $W_k = \frac {W_k^{\mathrm {s}}}{\tilde {\gamma }} + W_k^{\mathrm {ns}}, Z_k = \frac {Z_k^{\mathrm {s}}}{\tilde {\gamma }} + Z_k^{\mathrm {ns}}$
and, respectively,
$W_k = \frac {W_k^{\mathrm {s}}}{\tilde {\gamma }} + W_k^{\mathrm {ns}}, Z_k = \frac {Z_k^{\mathrm {s}}}{\tilde {\gamma }} + Z_k^{\mathrm {ns}}$
and, respectively,
![]() $W_4^{\mathrm {norm,2,*}} = W_4^{*}(k-3), Z_4^{\mathrm {norm,2,*}} = Z_4^{*}(k-3)(k-4)$
for
$W_4^{\mathrm {norm,2,*}} = W_4^{*}(k-3), Z_4^{\mathrm {norm,2,*}} = Z_4^{*}(k-3)(k-4)$
for
![]() $* = \{s,ns\}$
. Using that
$* = \{s,ns\}$
. Using that
![]() $Z_k^{\mathrm {s}} = -W_k^{\mathrm {s}}$
for all k, it is enough to validate the conditions
$Z_k^{\mathrm {s}} = -W_k^{\mathrm {s}}$
for all k, it is enough to validate the conditions
 $$ \begin{align*} (Z_4^{\mathrm{norm,2,ns}} W_1^{\mathrm{ns}} - W_4^{\mathrm{norm,2,ns}} Z_1^{\mathrm{ns}} (k-4)) < 0, \\ -(Z_4^{\mathrm{norm,2,ns}} + (k-4) W_4^{\mathrm{norm,2,ns}} + (k-3)(k-4)(W_1^{\mathrm{ns}} + Z_1^{\mathrm{ns}})> 0. \end{align*} $$
$$ \begin{align*} (Z_4^{\mathrm{norm,2,ns}} W_1^{\mathrm{ns}} - W_4^{\mathrm{norm,2,ns}} Z_1^{\mathrm{ns}} (k-4)) < 0, \\ -(Z_4^{\mathrm{norm,2,ns}} + (k-4) W_4^{\mathrm{norm,2,ns}} + (k-3)(k-4)(W_1^{\mathrm{ns}} + Z_1^{\mathrm{ns}})> 0. \end{align*} $$
Details of Lemmas A.26 (top row inequalities): In the case
![]() $\gamma \geq 3$
, we desingularize by computing
$\gamma \geq 3$
, we desingularize by computing
![]() $\frac {N_{W,0}}{\gamma _{\mathrm {inv}}}$
and
$\frac {N_{W,0}}{\gamma _{\mathrm {inv}}}$
and
![]() $\frac {N_{Z,1}}{\gamma _{\mathrm {inv}}}$
in order for them to have finite limits as
$\frac {N_{Z,1}}{\gamma _{\mathrm {inv}}}$
in order for them to have finite limits as
![]() $\gamma _{\mathrm {inv}} \to 0$
. Similarly, in the case
$\gamma _{\mathrm {inv}} \to 0$
. Similarly, in the case
![]() $\gamma \leq 3$
, we desingularize by computing
$\gamma \leq 3$
, we desingularize by computing
![]() $N_{W,0}\tilde {\gamma }$
and
$N_{W,0}\tilde {\gamma }$
and
![]() $N_{Z,1}\tilde {\gamma }$
in order for them to have finite limits as
$N_{Z,1}\tilde {\gamma }$
in order for them to have finite limits as
![]() $\tilde {\gamma } \to 0$
.
$\tilde {\gamma } \to 0$
.
Details of Lemmas A.27, A.28: The implementation is straightforward; however, due to the large numbers that appear throughout the process (
![]() $Z_{10000} \sim 10^{46770}$
), ultra-high precision is required to avoid overestimation and to be able to extract the signs out of the relevant quantities. We used 2000 bits to accomplish this.
$Z_{10000} \sim 10^{46770}$
), ultra-high precision is required to avoid overestimation and to be able to extract the signs out of the relevant quantities. We used 2000 bits to accomplish this.
Details of Lemmas A.29, A.30: In the case
![]() $\gamma \geq 3$
, we renormalize
$\gamma \geq 3$
, we renormalize
![]() $s_{\infty }^{\mathrm {fr}}$
by considering
$s_{\infty }^{\mathrm {fr}}$
by considering
![]() $\frac {s_{\infty }^{\mathrm {fr}}}{\gamma _{\mathrm {inv}}}$
and proceed as in previous Lemmas. In the case
$\frac {s_{\infty }^{\mathrm {fr}}}{\gamma _{\mathrm {inv}}}$
and proceed as in previous Lemmas. In the case
![]() $\gamma \leq 3$
, we do not renormalize with respect to
$\gamma \leq 3$
, we do not renormalize with respect to
![]() $\gamma $
. We also remark that in the case
$\gamma $
. We also remark that in the case
![]() $\gamma = \frac 75$
, it is enough to validate the condition
$\gamma = \frac 75$
, it is enough to validate the condition
![]() $W_1 + Z_1 < 0$
thanks to Lemma A.27.
$W_1 + Z_1 < 0$
thanks to Lemma A.27.
Details of Lemma A.31: The inequality is also problematic due to
![]() $Z_3$
blowing up at
$Z_3$
blowing up at
![]() $r_3$
and
$r_3$
and
![]() $Z_4$
blowing up at
$Z_4$
blowing up at
![]() $r_4$
. We generalized the implementation of
$r_4$
. We generalized the implementation of
![]() $Z_n^{norm,1}$
in 3.5 to return
$Z_n^{norm,1}$
in 3.5 to return
![]() $Z_n^{norm,1} = \frac {1}{\gamma _{\mathrm {inv}}}Z_n(k-n)$
for any given n in the case
$Z_n^{norm,1} = \frac {1}{\gamma _{\mathrm {inv}}}Z_n(k-n)$
for any given n in the case
![]() $\gamma \geq 3$
and to return
$\gamma \geq 3$
and to return
![]() $Z_n^{norm,1,*} = Z_n^{*}(k-n), * = \{s,ns\}$
in the case
$Z_n^{norm,1,*} = Z_n^{*}(k-n), * = \{s,ns\}$
in the case
![]() $\gamma \leq 3$
. In the latter case, since
$\gamma \leq 3$
. In the latter case, since
![]() $Z_n^s$
is uniformly bounded (in
$Z_n^s$
is uniformly bounded (in
![]() $\tilde {\gamma }$
) at
$\tilde {\gamma }$
) at
![]() $r=r_n$
, it is enough to check the conditions
$r=r_n$
, it is enough to check the conditions
![]() $Z_3^{norm,1,ns} < 0$
and
$Z_3^{norm,1,ns} < 0$
and
![]() $Z_4^{norm,1,ns}> 0$
at
$Z_4^{norm,1,ns}> 0$
at
![]() $\tilde {r}_3$
and
$\tilde {r}_3$
and
![]() $\tilde {r}_4$
, respectively.
$\tilde {r}_4$
, respectively.
Details of Lemmas B.1, B.2, B.3, B.4: Straightforward since the quantities are not singular.
Competing interests
The authors have no competing interest to declare.
Data availability statement
The code can be accessed via the supplementary material.
The codes from the computer-assisted proof, a README with instructions to run them, as well as logs with the results (including timings) are provided as supplementary material.
Ethical standards
No ethical standards were required in the pursuit of this research.
Author contributions
All authors contributed equally.
Funding statement
T.B. was supported by the NSF grant DMS-1900149, a Simons Foundation Mathematical and Physical Sciences Collaborative Grant and a grant from the Institute for Advanced Study. G.C.-L. was supported by a grant from the Centre de Formació Interdisciplinària Superior, a MOBINT-MIF grant from the Generalitat de Catalunya, a Praecis Presidential Fellowship from the Massachusetts Institute of Technology and NSF grants DMS-2052651 and DMS-1764403. G.C.-L. would also like to thank the Department of Mathematics at Princeton University for partially supporting him during his stay at Princeton and for their warm hospitality. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program through the grant agreement 852741 (G.C.-L. and J.G.-S.). G.C-L. and J.G.-S. have been partially supported by the MICINN (Spain) research grant number PID2021–125021NA–I00. J.G.-S. was partially supported by NSF through Grants DMS-1763356, DMS-2245017 and DMS-2247537. J.G.-S has been partially supported by the AGAUR project 2021-SGR-0087 (Catalunya). This material is based upon work supported by the National Science Foundation under Grant No. DMS-1929284 while J.G.-S. was in residence at the Institute for Computational and Experimental Research in Mathematics in Providence, RI, during the program ‘Hamiltonian Methods in Dispersive and Wave Evolution Equations’. This work is supported by the Spanish State Research Agency, through the Severo Ochoa and María de Maeztu Program for Centers and Units of Excellence in R&D (CEX2020-001084-M). We thank Princeton University and the Institute for Advanced Study for computing facilities via the Princeton Research Computing resources and the School of Natural Sciences Computing resources, respectively. Part of this research was conducted using computational resources and services at the Center for Computation and Visualization, Brown University. The programs ran on the batch queue: for more specific details about the hardware please check https://docs.ccv.brown.edu/oscar/system-overview.