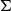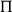1. Introduction
Dependent type theory is based on the notion of family of types indexed by a type, and the basic operations are the reindexing and the sums and products of such families: the
![]() $\Sigma$
-types and
$\Sigma$
-types and
![]() $\Pi$
-types constructors. On the other hand, the geometer’s toolbox contains methods to study spaces by means of “bundles,” that is, using families of spaces indexed by the space of interest (vector bundles, sheaves…). There also, bundles can be pulled back along a morphism and sometimes pushed forward in two different ways (additively or multiplicatively). This has suggested an analogy where
$\Pi$
-types constructors. On the other hand, the geometer’s toolbox contains methods to study spaces by means of “bundles,” that is, using families of spaces indexed by the space of interest (vector bundles, sheaves…). There also, bundles can be pulled back along a morphism and sometimes pushed forward in two different ways (additively or multiplicatively). This has suggested an analogy where
![]() $\Sigma$
-types can be understood as total spaces of families, while
$\Sigma$
-types can be understood as total spaces of families, while
![]() $\Pi$
-types can be regarded as spaces of sections of families.
$\Pi$
-types can be regarded as spaces of sections of families.
The fact that the pushforwards are not always defined is the source of an interesting feature: it distinguishes the classes of maps along which these pushforwards exist: locally contractible and proper morphisms.
In Section 2, we introduce an abstract notion of smooth and proper maps associated with any category
![]() $\mathbb{C}$
. This is done in the setting of fibered/indexed categories over a base category
$\mathbb{C}$
. This is done in the setting of fibered/indexed categories over a base category
![]() $\mathcal{B}$
. The smooth (proper) maps are the maps
$\mathcal{B}$
. The smooth (proper) maps are the maps
![]() $u:X\to Y$
in
$u:X\to Y$
in
![]() $\mathcal{B}$
along which the base change functor
$\mathcal{B}$
along which the base change functor
![]() $u^*:\mathbb{C}(Y)\to \mathbb{C}(X)$
admits a left adjoint
$u^*:\mathbb{C}(Y)\to \mathbb{C}(X)$
admits a left adjoint
![]() $u_!$
(a right adjoint
$u_!$
(a right adjoint
![]() $u_*$
) compatible with reindexing/base change (aka the Beck–Chevalley conditions). Then Section 3 details many examples in logic, category theory, topology, and geometry, where we show how our abstract definitions connect to existing notions of smoothness and properness.
$u_*$
) compatible with reindexing/base change (aka the Beck–Chevalley conditions). Then Section 3 details many examples in logic, category theory, topology, and geometry, where we show how our abstract definitions connect to existing notions of smoothness and properness.
Conventions
The paper is written in the context of
![]() $\infty$
-categories (Lurie, Reference Lurie2009; Cisinski, Reference Cisinski2019), but we are simplifying the terminology and simply saying “category” for
$\infty$
-categories (Lurie, Reference Lurie2009; Cisinski, Reference Cisinski2019), but we are simplifying the terminology and simply saying “category” for
![]() $\infty$
-category and “1-categories” for the truncated notion. We denote by
$\infty$
-category and “1-categories” for the truncated notion. We denote by
![]() $\mathsf{Set}$
(
$\mathsf{Set}$
(
![]() $\mathsf{SET}$
) the 1-category of small (large) sets and by
$\mathsf{SET}$
) the 1-category of small (large) sets and by
![]() $\mathsf{Cat}$
(
$\mathsf{Cat}$
(
![]() $\mathsf{CAT}$
) the (
$\mathsf{CAT}$
) the (
![]() $\infty$
-)category of small (large) (
$\infty$
-)category of small (large) (
![]() $\infty$
-)categories. Consequently, we refer to
$\infty$
-)categories. Consequently, we refer to
![]() $\infty$
-functors simply as “functors,” so that under the (
$\infty$
-functors simply as “functors,” so that under the (
![]() $\infty$
-categorical) Grothendieck construction, small fibered categories correspond to functors into
$\infty$
-categorical) Grothendieck construction, small fibered categories correspond to functors into
![]() $\mathsf{Cat}$
. The categories of functors from
$\mathsf{Cat}$
. The categories of functors from
![]() $C$
to
$C$
to
![]() $D$
are denoted
$D$
are denoted
![]() $\left [C,D\right ]$
. The arrow category of a category
$\left [C,D\right ]$
. The arrow category of a category
![]() $C$
is denoted
$C$
is denoted
![]() ${C}^{\to }$
.
${C}^{\to }$
.
2. Abstract Setting
Let
![]() $\kappa$
be a cardinal and
$\kappa$
be a cardinal and
![]() $\mathsf{Set}^{\lt \kappa }$
be the category of sets of cardinality strictly smaller than
$\mathsf{Set}^{\lt \kappa }$
be the category of sets of cardinality strictly smaller than
![]() $\kappa$
. The elementary operations on sets are the sum and product of a family of sets. For
$\kappa$
. The elementary operations on sets are the sum and product of a family of sets. For
![]() $I$
an arbitrary set, an
$I$
an arbitrary set, an
![]() $I$
-indexed family (
$I$
-indexed family (
![]() $I$
-family for short) in
$I$
-family for short) in
![]() $\mathsf{Set}^{\lt \kappa }$
is a functor
$\mathsf{Set}^{\lt \kappa }$
is a functor
![]() $I\to \mathsf{Set}^{\lt \kappa }$
, and the sum and product of
$I\to \mathsf{Set}^{\lt \kappa }$
, and the sum and product of
![]() $I$
-families are the left and right adjoint to the constant family functor
$I$
-families are the left and right adjoint to the constant family functor
![]() $\mathsf{Set}^{\lt \kappa } \to \left [I,{\mathsf{Set}^{\lt \kappa }}\right ]$
. Given
$\mathsf{Set}^{\lt \kappa } \to \left [I,{\mathsf{Set}^{\lt \kappa }}\right ]$
. Given
![]() $\kappa$
, one can ask for what sets
$\kappa$
, one can ask for what sets
![]() $I$
the sum and product of
$I$
the sum and product of
![]() $I$
-families of
$I$
-families of
![]() $\kappa$
-small sets are
$\kappa$
-small sets are
![]() $\kappa$
-small. Let
$\kappa$
-small. Let
![]() $\sigma$
be a cardinal, such that for any cardinal
$\sigma$
be a cardinal, such that for any cardinal
![]() $\rho \lt \kappa$
, we have
$\rho \lt \kappa$
, we have
![]() $\sigma \rho \lt \kappa$
. Then
$\sigma \rho \lt \kappa$
. Then
![]() $\mathsf{Set}^{\lt \kappa }$
admits sums indexed by objects in
$\mathsf{Set}^{\lt \kappa }$
admits sums indexed by objects in
![]() $\mathsf{Set}^{\lt \sigma }$
. Let
$\mathsf{Set}^{\lt \sigma }$
. Let
![]() $\Sigma (\kappa )$
be the supremum of all such cardinals
$\Sigma (\kappa )$
be the supremum of all such cardinals
![]() $\sigma$
. We shall call
$\sigma$
. We shall call
![]() $\Sigma (\kappa )$
the smooth bound of
$\Sigma (\kappa )$
the smooth bound of
![]() $\kappa$
. The cardinal
$\kappa$
. The cardinal
![]() $\kappa$
is regular if and only if
$\kappa$
is regular if and only if
![]() $\kappa =\Sigma (\kappa )$
. Similarly, let
$\kappa =\Sigma (\kappa )$
. Similarly, let
![]() $\pi$
be a cardinal, such that for any cardinal
$\pi$
be a cardinal, such that for any cardinal
![]() $\rho \lt \kappa$
, we have
$\rho \lt \kappa$
, we have
![]() $\rho ^\pi \lt \kappa$
. Then
$\rho ^\pi \lt \kappa$
. Then
![]() $\mathsf{Set}^{\lt \kappa }$
admits products indexed by objects in
$\mathsf{Set}^{\lt \kappa }$
admits products indexed by objects in
![]() $\mathsf{Set}^{\lt \pi }$
. Let
$\mathsf{Set}^{\lt \pi }$
. Let
![]() $\Pi (\kappa )$
be the supremum of all such cardinals
$\Pi (\kappa )$
be the supremum of all such cardinals
![]() $\pi$
. We shall call
$\pi$
. We shall call
![]() $\Pi (\kappa )$
the proper bound of
$\Pi (\kappa )$
the proper bound of
![]() $\kappa$
. The cardinal
$\kappa$
. The cardinal
![]() $\kappa$
is inaccessible if and only if
$\kappa$
is inaccessible if and only if
![]() $\kappa =\Pi (\kappa )=\Sigma (\kappa )$
.
$\kappa =\Pi (\kappa )=\Sigma (\kappa )$
.
More generally, we can replace the category
![]() $\mathsf{Set}^{\lt \kappa }$
by any category
$\mathsf{Set}^{\lt \kappa }$
by any category
![]() $C$
and extract the classes of sets
$C$
and extract the classes of sets
![]() $\Sigma (C)$
and
$\Sigma (C)$
and
![]() $\Pi (C)$
indexing the sums and products that exist in
$\Pi (C)$
indexing the sums and products that exist in
![]() $C$
. We shall call
$C$
. We shall call
![]() $\Sigma (C)$
the smooth calibration of
$\Sigma (C)$
the smooth calibration of
![]() $C$
and
$C$
and
![]() $\Pi (C)$
the proper calibration of
$\Pi (C)$
the proper calibration of
![]() $C$
.Footnote
1
$C$
.Footnote
1
We are going to propose an abstract setting for the definition of smooth and proper calibrations and illustrate it with many examples. The category
![]() $C$
will be a fibration over some base category
$C$
will be a fibration over some base category
![]() $B$
with finite limits, and the calibrations
$B$
with finite limits, and the calibrations
![]() $\Sigma (C)$
and
$\Sigma (C)$
and
![]() $\Pi (C)$
will be defined as subfibrations of the codomain fibration of
$\Pi (C)$
will be defined as subfibrations of the codomain fibration of
![]() $B$
.
$B$
.
2.1 Calibrations and families
We fix a category
![]() $\mathcal{B}$
with finite limits.
$\mathcal{B}$
with finite limits.
Definition 1. (
![]() $\mathcal{B}$
-category). A functor
$\mathcal{B}$
-category). A functor
![]() $\mathbb{C}:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
is called a
$\mathbb{C}:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
is called a
![]() $\mathcal{B}$
-category (or simply a category when
$\mathcal{B}$
-category (or simply a category when
![]() $\mathcal{B}$
is clear from the context). A (
$\mathcal{B}$
is clear from the context). A (
![]() $\mathcal{B}$
-)functor between
$\mathcal{B}$
-)functor between
![]() $\mathcal{B}$
-categories is simply a natural transformation. There is an equivalence between the category of
$\mathcal{B}$
-categories is simply a natural transformation. There is an equivalence between the category of
![]() $\mathcal{B}$
-categories and the category of fibrations in categories (aka Grothendieck fibrations, or cartesian fibrations)
$\mathcal{B}$
-categories and the category of fibrations in categories (aka Grothendieck fibrations, or cartesian fibrations)
![]() $\mathcal{C}\to \mathcal{B}$
(Lurie, Reference Lurie2009, Theorem 3.2.0.1 and Section 3.3.2). We shall treat the two objects
$\mathcal{C}\to \mathcal{B}$
(Lurie, Reference Lurie2009, Theorem 3.2.0.1 and Section 3.3.2). We shall treat the two objects
![]() $\mathbb{C}$
and
$\mathbb{C}$
and
![]() $\mathcal{C}$
as equivalent and go back and forth between them. We systematically use the same letter in different fonts
$\mathcal{C}$
as equivalent and go back and forth between them. We systematically use the same letter in different fonts
![]() $\mathbb{C}$
/
$\mathbb{C}$
/
![]() $\mathcal{C}$
to denote whether we are considering the functorial (aka indexed) or the fibrational point of view on
$\mathcal{C}$
to denote whether we are considering the functorial (aka indexed) or the fibrational point of view on
![]() $\mathcal{B}$
-categories.
$\mathcal{B}$
-categories.
Definition 2. (Universe). Since
![]() $\mathcal{B}$
is assumed with finite limits, the codomain functor
$\mathcal{B}$
is assumed with finite limits, the codomain functor
![]() ${\mathcal{B}}^{\to }\to \mathcal{B}$
is a cartesian fibration, and we denote by
${\mathcal{B}}^{\to }\to \mathcal{B}$
is a cartesian fibration, and we denote by
![]() $\mathbb{B}:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
the corresponding functor (sending an object
$\mathbb{B}:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
the corresponding functor (sending an object
![]() $X$
to the slice category
$X$
to the slice category
![]() $\mathcal{B}{_{/X}}$
). We shall refer to
$\mathcal{B}{_{/X}}$
). We shall refer to
![]() $\mathbb{B}$
as the universe of
$\mathbb{B}$
as the universe of
![]() $\mathcal{B}$
.
$\mathcal{B}$
.
Since
![]() $\mathcal{B}$
has a terminal object, the terminal functor
$\mathcal{B}$
has a terminal object, the terminal functor
![]() $1:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
is a subfunctor of the universe
$1:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
is a subfunctor of the universe
![]() $\mathbb{B}$
. The corresponding fibration is the identity of
$\mathbb{B}$
. The corresponding fibration is the identity of
![]() $\mathcal{B}$
. Equivalently, it corresponds to the subcodomain fibration
$\mathcal{B}$
. Equivalently, it corresponds to the subcodomain fibration
![]() $\mathcal{B}=\mathcal{B}^\simeq \subset{\mathcal{B}}^{\to }$
spanned by the isomorphisms.Footnote
2
$\mathcal{B}=\mathcal{B}^\simeq \subset{\mathcal{B}}^{\to }$
spanned by the isomorphisms.Footnote
2
Definition 3. (Calibration). A calibration is a subuniverse
![]() $\mathbb{U}\subset \mathbb{B}$
(i.e., a subfibration
$\mathbb{U}\subset \mathbb{B}$
(i.e., a subfibration
![]() $\mathcal{U}\subset{\mathcal{B}}^{\to }$
). The constant calibration is the calibration
$\mathcal{U}\subset{\mathcal{B}}^{\to }$
). The constant calibration is the calibration
![]() $1\to \mathbb{B}$
. A calibration is pointed if it contains the constant calibration (equivalently, if
$1\to \mathbb{B}$
. A calibration is pointed if it contains the constant calibration (equivalently, if
![]() $\mathcal{U}\subset{\mathcal{B}}^{\to }$
contains all isomorphisms). A calibration
$\mathcal{U}\subset{\mathcal{B}}^{\to }$
contains all isomorphisms). A calibration
![]() $\mathbb{U}\subset \mathbb{B}$
is regular if it is pointed, and the corresponding class of maps in
$\mathbb{U}\subset \mathbb{B}$
is regular if it is pointed, and the corresponding class of maps in
![]() $\mathcal{B}$
is closed under composition.
$\mathcal{B}$
is closed under composition.
A regular calibration defines a wide subcategory of
![]() $\mathcal{B}$
(since it contains all isomorphisms). In fact, regular calibrations are in bijection with wide subcategories of
$\mathcal{B}$
(since it contains all isomorphisms). In fact, regular calibrations are in bijection with wide subcategories of
![]() $\mathcal{B}$
whose maps are closed under base change in
$\mathcal{B}$
whose maps are closed under base change in
![]() $\mathcal{B}$
.
$\mathcal{B}$
.
Definition 4. (Family construction). We fix a
![]() $\mathcal{B}$
-category
$\mathcal{B}$
-category
![]() $\mathbb{C}$
, with associated fibration
$\mathbb{C}$
, with associated fibration
![]() $\mathcal{C}\to \mathcal{B}$
. Let
$\mathcal{C}\to \mathcal{B}$
. Let
![]() $\mathcal{U}\subset{\mathcal{B}}^{\to } \xrightarrow{cod} \mathcal{B}$
be a subfibration of the codomain fibration. The fibration
$\mathcal{U}\subset{\mathcal{B}}^{\to } \xrightarrow{cod} \mathcal{B}$
be a subfibration of the codomain fibration. The fibration
![]() $\mathsf{Fam}_{\mathcal{U}}(\mathcal{C})$
of
$\mathsf{Fam}_{\mathcal{U}}(\mathcal{C})$
of
![]() $\mathcal{U}$
-indexed families of objects in
$\mathcal{U}$
-indexed families of objects in
![]() $\mathcal{C}$
is defined as the functor
$\mathcal{C}$
is defined as the functor
![]() $\phi$
in the diagram
$\phi$
in the diagram

(where the square is a fiber product). Following our typographic convention, we denote by
![]() $\mathsf{Fam}_{\mathbb{U}}(\mathbb{C})$
the associated functor
$\mathsf{Fam}_{\mathbb{U}}(\mathbb{C})$
the associated functor
![]() $\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
(and call it the
$\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
(and call it the
![]() $\mathcal{B}$
-category of
$\mathcal{B}$
-category of
![]() $\mathbb{U}$
-indexed families of objects in
$\mathbb{U}$
-indexed families of objects in
![]() $\mathbb{C}$
). Its value at an object
$\mathbb{C}$
). Its value at an object
![]() $I$
in
$I$
in
![]() $\mathcal{B}$
is the category of pairs
$\mathcal{B}$
is the category of pairs
![]() $(u:U\to I \in \mathcal{U},C\in \mathbb{C}(U))$
(with the obvious notion of morphism).
$(u:U\to I \in \mathcal{U},C\in \mathbb{C}(U))$
(with the obvious notion of morphism).
2.2 Sums and products
The family construction associated with the constant calibration is the identity:
![]() $\mathbb{C} = \mathsf{Fam}_1(\mathbb{C})$
. If
$\mathbb{C} = \mathsf{Fam}_1(\mathbb{C})$
. If
![]() $\mathbb{U}$
is a pointed calibration we get a canonical functor
$\mathbb{U}$
is a pointed calibration we get a canonical functor
![]() $\Delta _{\mathbb{U}}:\mathbb{C}=\mathsf{Fam}_1(\mathbb{C})\to \mathsf{Fam}_{\mathbb{U}}(\mathbb{C})$
.
$\Delta _{\mathbb{U}}:\mathbb{C}=\mathsf{Fam}_1(\mathbb{C})\to \mathsf{Fam}_{\mathbb{U}}(\mathbb{C})$
.
Definition 5. Let
![]() $\mathbb{U}$
be a pointed calibration on
$\mathbb{U}$
be a pointed calibration on
![]() $\mathcal{B}$
. A (
$\mathcal{B}$
. A (
![]() $\mathcal{B}$
-)category
$\mathcal{B}$
-)category
![]() $\mathbb{C}$
has
$\mathbb{C}$
has
![]() $\mathbb{U}$
-indexed sums (products) if the canonical functor
$\mathbb{U}$
-indexed sums (products) if the canonical functor
![]() $\Delta _{\mathbb{U}}:\mathbb{C}\to \mathsf{Fam}_{\mathbb{U}}(\mathbb{C})$
has a left (right) adjoint.
$\Delta _{\mathbb{U}}:\mathbb{C}\to \mathsf{Fam}_{\mathbb{U}}(\mathbb{C})$
has a left (right) adjoint.
The following result is proved for 1-categories in Streicher (2020). The statement extends to
![]() $\infty$
-categories as well. So do a range of expected results from Streicher (2020) and Moens (Reference Moens1982) about fibrations with internal sums. This has been developed by Buchholtz and Weinberger (Reference Buchholtz and Weinberger2023) and Weinberger (Reference Weinberger2024) in the type theory of synthetic
$\infty$
-categories as well. So do a range of expected results from Streicher (2020) and Moens (Reference Moens1982) about fibrations with internal sums. This has been developed by Buchholtz and Weinberger (Reference Buchholtz and Weinberger2023) and Weinberger (Reference Weinberger2024) in the type theory of synthetic
![]() $\infty$
-categories (Riehl and Shulman, Reference Riehl and Shulman2017; Riehl, Reference Riehl2023a) (internally to any
$\infty$
-categories (Riehl and Shulman, Reference Riehl and Shulman2017; Riehl, Reference Riehl2023a) (internally to any
![]() $\infty$
-topos, see Shulman (2020); Riehl (Reference Riehl2023b); Weinberger (Reference Weinberger2022)). See also the work on internal
$\infty$
-topos, see Shulman (2020); Riehl (Reference Riehl2023b); Weinberger (Reference Weinberger2022)). See also the work on internal
![]() $\infty$
-categories in an arbitrary
$\infty$
-categories in an arbitrary
![]() $\infty$
-topos by Martini (Reference Martini2022), Martini and Wolf (Reference Martini and Wolf2023a, Reference Martini and Wolf2023b).
$\infty$
-topos by Martini (Reference Martini2022), Martini and Wolf (Reference Martini and Wolf2023a, Reference Martini and Wolf2023b).
Proposition 6. (Bénabou–Streicher). If
![]() $\mathbb{U}$
is a regular calibration, then
$\mathbb{U}$
is a regular calibration, then
![]() $\mathsf{Fam}_{\mathbb{U}}(\mathbb{C})$
is the free cocompletion of
$\mathsf{Fam}_{\mathbb{U}}(\mathbb{C})$
is the free cocompletion of
![]() $\mathbb{C}$
for sums indexed by objects in
$\mathbb{C}$
for sums indexed by objects in
![]() $\mathbb{U}$
. A pointed calibration
$\mathbb{U}$
. A pointed calibration
![]() $\mathbb{U}$
is regular if and only if
$\mathbb{U}$
is regular if and only if
![]() $\mathbb{U}$
has
$\mathbb{U}$
has
![]() $\mathbb{U}$
-indexed sums.
$\mathbb{U}$
-indexed sums.
Remark 7. The notion of regular calibration corresponds in dependent type theory to the notion of a subuniverse closed under
![]() $\Sigma$
-types and containing the terminal type.
$\Sigma$
-types and containing the terminal type.
Proposition 8.
For every category with finite limits
![]() $\mathcal{B}$
, the universe
$\mathcal{B}$
, the universe
![]() $\mathbb{B}$
always has
$\mathbb{B}$
always has
![]() $\mathbb{B}$
-indexed sums. A map is proper if and only if all its pullbacks are exponentiable maps in
$\mathbb{B}$
-indexed sums. A map is proper if and only if all its pullbacks are exponentiable maps in
![]() $\mathcal{B}$
. In particular, the universe
$\mathcal{B}$
. In particular, the universe
![]() $\mathbb{B}$
has
$\mathbb{B}$
has
![]() $\mathbb{B}$
-indexed products if and only if
$\mathbb{B}$
-indexed products if and only if
![]() $\mathcal{B}$
is a locally cartesian closed category.
$\mathcal{B}$
is a locally cartesian closed category.
Sketch of the proof. The left adjoints
![]() $f_!$
always exist and are given by composition with
$f_!$
always exist and are given by composition with
![]() $f$
. The Beck–Chevalley conditions are fulfilled since they amount to the cancellation property for pullback squares. The right adjoint
$f$
. The Beck–Chevalley conditions are fulfilled since they amount to the cancellation property for pullback squares. The right adjoint
![]() $f_*$
exists for every map
$f_*$
exists for every map
![]() $f$
if and only if
$f$
if and only if
![]() $\mathcal{B}$
is a locally cartesian closed category. Then the Beck–Chevalley conditions are deduced by adjunction from those for
$\mathcal{B}$
is a locally cartesian closed category. Then the Beck–Chevalley conditions are deduced by adjunction from those for
![]() $f_!$
.
$f_!$
.
2.3 Smooth and proper maps
We fix a category
![]() $\mathcal{B}$
with finite limits and a
$\mathcal{B}$
with finite limits and a
![]() $\mathcal{B}$
-category
$\mathcal{B}$
-category
![]() $\mathbb{C}:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
.
$\mathbb{C}:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
.
Definition 9. (Smooth & proper maps). A map
![]() $u:X\to Y$
in
$u:X\to Y$
in
![]() $\mathcal{B}$
is called left (right) Beck–Chevalley for
$\mathcal{B}$
is called left (right) Beck–Chevalley for
![]() $\mathbb{C}$
if for any cartesian square
$\mathbb{C}$
if for any cartesian square

the maps
![]() $u^*$
and
$u^*$
and
![]() $\bar u ^*$
have left (right) adjoints
$\bar u ^*$
have left (right) adjoints

and the corresponding mate natural transformation is invertible
A map
![]() $u:X\to Y$
in
$u:X\to Y$
in
![]() $\mathcal{B}$
is called smooth, or stably left Beck–Chevalley (proper, or stably right Beck–Chevalley) if every base change of
$\mathcal{B}$
is called smooth, or stably left Beck–Chevalley (proper, or stably right Beck–Chevalley) if every base change of
![]() $u$
is left (right) Beck–Chevalley. The relation of these operations with quantification in logic is recalled in Table 2.
$u$
is left (right) Beck–Chevalley. The relation of these operations with quantification in logic is recalled in Table 2.
The classes of
![]() $\mathbb{C}$
-smooth and
$\mathbb{C}$
-smooth and
![]() $\mathbb{C}$
-proper maps are closed under base change and define subfibrations of the codomain fibration of
$\mathbb{C}$
-proper maps are closed under base change and define subfibrations of the codomain fibration of
![]() $\mathcal{B}$
. Equivalently, they define regular calibrations
$\mathcal{B}$
. Equivalently, they define regular calibrations
![]() $\Sigma (\mathbb{C}) \subset \mathbb{B}\supset \Pi (\mathbb{C})$
of the universe of
$\Sigma (\mathbb{C}) \subset \mathbb{B}\supset \Pi (\mathbb{C})$
of the universe of
![]() $\mathbb{B}$
, called the smooth calibration and the proper calibration of
$\mathbb{B}$
, called the smooth calibration and the proper calibration of
![]() $\mathbb{C}$
. The interest of the notions is in the following result.
$\mathbb{C}$
. The interest of the notions is in the following result.
Proposition 10.
The smooth (proper) calibration of
![]() $\mathbb{C}$
is the largest calibration for which
$\mathbb{C}$
is the largest calibration for which
![]() $\mathbb{C}$
admits sums (products).
$\mathbb{C}$
admits sums (products).
Proof.
Unfolding the condition that
![]() $\Delta _{\mathbb{U}}:\mathbb{C}\to \mathsf{Fam}_{\mathbb{U}}(\mathbb{C})$
has a left (right) adjoint, we find that the left adjoint exists if and only if all maps in
$\Delta _{\mathbb{U}}:\mathbb{C}\to \mathsf{Fam}_{\mathbb{U}}(\mathbb{C})$
has a left (right) adjoint, we find that the left adjoint exists if and only if all maps in
![]() $\mathcal{U}$
are smooth (proper); see Streicher (2020).
$\mathcal{U}$
are smooth (proper); see Streicher (2020).
Remark 11. When
![]() $\mathcal{B}$
is the 1-category of sets or the
$\mathcal{B}$
is the 1-category of sets or the
![]() $\infty$
-category of spaces, the Beck–Chevalley conditions simplify for the functors
$\infty$
-category of spaces, the Beck–Chevalley conditions simplify for the functors
![]() $\mathbb{C}:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
, which send colimits to limits. In that case, we have
$\mathbb{C}:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
, which send colimits to limits. In that case, we have
![]() $\mathbb{C}(X) = \mathbb{C}(1)^X$
, and the compatibility with base change holds for free as soon as the adjoint functors exist.
$\mathbb{C}(X) = \mathbb{C}(1)^X$
, and the compatibility with base change holds for free as soon as the adjoint functors exist.
The characterization of the smooth and proper maps can be quite difficult in practice. In the setting where the category
![]() $\mathbb{C}$
has a forgetful functor into the universe
$\mathbb{C}$
has a forgetful functor into the universe
![]() $\mathbb{B}$
(typically, when
$\mathbb{B}$
(typically, when
![]() $\mathbb{C}$
classifies objects in
$\mathbb{C}$
classifies objects in
![]() $\mathbb{B}$
with an extra structure, notably when
$\mathbb{B}$
with an extra structure, notably when
![]() $\mathbb{C}$
is a calibration), stricter notions of smooth and proper maps can be defined, which are easier to characterize in practice.
$\mathbb{C}$
is a calibration), stricter notions of smooth and proper maps can be defined, which are easier to characterize in practice.
Definition 12. (Strict smoothness/properness). Let
![]() $\mathbb{C}:\mathcal{B}^{\mathrm{op}} \to \mathsf{CAT}$
be equipped with a natural transformation
$\mathbb{C}:\mathcal{B}^{\mathrm{op}} \to \mathsf{CAT}$
be equipped with a natural transformation
![]() $U:\mathbb{C}\to \mathbb{B}$
to the universe of
$U:\mathbb{C}\to \mathbb{B}$
to the universe of
![]() $\mathbb{B}$
(typically the inclusion of a subuniverse). For
$\mathbb{B}$
(typically the inclusion of a subuniverse). For
![]() $f:X\to Y$
a map in
$f:X\to Y$
a map in
![]() $\mathcal{B}$
, we have a commutative square
$\mathcal{B}$
, we have a commutative square

Recall from Proposition 8 that the functor
![]() $f^*:\mathcal{B}{_{/Y}}\to \mathcal{B}{_{/X}}$
has always a left adjoint
$f^*:\mathcal{B}{_{/Y}}\to \mathcal{B}{_{/X}}$
has always a left adjoint
![]() $f_!$
given by composition with
$f_!$
given by composition with
![]() $f$
and that the right adjoint
$f$
and that the right adjoint
![]() $f_*$
exists if and only if
$f_*$
exists if and only if
![]() $f$
is an exponentiable map in
$f$
is an exponentiable map in
![]() $\mathcal{B}$
. We shall say that a
$\mathcal{B}$
. We shall say that a
![]() $\mathbb{C}$
-smooth map is strictly smooth if the mate
$\mathbb{C}$
-smooth map is strictly smooth if the mate
![]() $f_!U_X \to U_Y\;f_!$
is invertible. We shall say that a
$f_!U_X \to U_Y\;f_!$
is invertible. We shall say that a
![]() $\mathbb{C}$
-proper map is strictly proper if it is exponentiable in
$\mathbb{C}$
-proper map is strictly proper if it is exponentiable in
![]() $\mathcal{B}$
(i.e., if
$\mathcal{B}$
(i.e., if
![]() $f_*$
exists) and if the mate
$f_*$
exists) and if the mate
![]() $U_Yf_* \to f_*U_X$
is invertible. Essentially, this says that a map
$U_Yf_* \to f_*U_X$
is invertible. Essentially, this says that a map
![]() $f$
is strictly smooth if
$f$
is strictly smooth if
![]() $f_!$
can be computed by composition with
$f_!$
can be computed by composition with
![]() $f$
in
$f$
in
![]() $\mathcal{B}$
, and that it is strictly proper if
$\mathcal{B}$
, and that it is strictly proper if
![]() $f_*$
can be computed by exponentiation along
$f_*$
can be computed by exponentiation along
![]() $f$
in
$f$
in
![]() $\mathcal{B}$
.
$\mathcal{B}$
.
Remark 13. We shall see that such maps are sometimes easier to characterize in practice. In particular, when
![]() $\mathbb{C}$
is a calibration, a map is strictly smooth if the corresponding class
$\mathbb{C}$
is a calibration, a map is strictly smooth if the corresponding class
![]() $\mathcal{C}$
of maps in
$\mathcal{C}$
of maps in
![]() $\mathcal{B}$
is closed under composition with every pullback of
$\mathcal{B}$
is closed under composition with every pullback of
![]() $f$
. And a map
$f$
. And a map
![]() $f$
is strictly proper if it is exponentiable and the functor
$f$
is strictly proper if it is exponentiable and the functor
![]() $f_*$
sends maps in
$f_*$
sends maps in
![]() $\mathcal{C}$
to maps in
$\mathcal{C}$
to maps in
![]() $\mathcal{C}$
.
$\mathcal{C}$
.
Lemma 14.
If
![]() $\mathbb{C}\subset \mathbb{B}$
is a regular calibration, then a
$\mathbb{C}\subset \mathbb{B}$
is a regular calibration, then a
![]() $\mathbb{C}$
-smooth map is strict if and only if it is in
$\mathbb{C}$
-smooth map is strict if and only if it is in
![]() $\mathcal{C}\subset{\mathcal{B}}^{\to }$
.
$\mathcal{C}\subset{\mathcal{B}}^{\to }$
.
Proof.
A map
![]() $u:X\to Y$
is strict if composition with
$u:X\to Y$
is strict if composition with
![]() $u$
sends maps
$u$
sends maps
![]() $r:\bar X\to X$
in
$r:\bar X\to X$
in
![]() $\mathcal{C}$
to maps
$\mathcal{C}$
to maps
![]() $\bar X\to Y$
in
$\bar X\to Y$
in
![]() $\mathcal{C}$
. Applied to
$\mathcal{C}$
. Applied to
![]() $r=\mathrm{id}_X$
, this implies that
$r=\mathrm{id}_X$
, this implies that
![]() $u$
is in
$u$
is in
![]() $\mathcal{C}$
and that every strict smooth map is in
$\mathcal{C}$
and that every strict smooth map is in
![]() $\mathcal{C}$
. The converse is true by regularity of
$\mathcal{C}$
. The converse is true by regularity of
![]() $\mathbb{C}$
.
$\mathbb{C}$
.
A modality on the category
![]() $\mathcal{B}$
is a (unique) factorization system
$\mathcal{B}$
is a (unique) factorization system
![]() $(\mathcal{L},\mathcal{R})$
such that the factorization (or equivalently the left class
$(\mathcal{L},\mathcal{R})$
such that the factorization (or equivalently the left class
![]() $\mathcal{L}$
) is stable under base change. In this situation, both classes
$\mathcal{L}$
) is stable under base change. In this situation, both classes
![]() $\mathcal{L}$
and
$\mathcal{L}$
and
![]() $\mathcal{R}$
define calibrations
$\mathcal{R}$
define calibrations
![]() $\mathbb{L}\subset \mathbb{B}\supset \mathbb{R}$
and
$\mathbb{L}\subset \mathbb{B}\supset \mathbb{R}$
and
![]() $\mathbb{R}$
is even a reflective calibration (with the reflection given by the factorization) (Anel et al., Reference Anel, Biedermann, Finster and Joyal2020; Rijke et al., Reference Rijke, Shulman and Spitters2019).
$\mathbb{R}$
is even a reflective calibration (with the reflection given by the factorization) (Anel et al., Reference Anel, Biedermann, Finster and Joyal2020; Rijke et al., Reference Rijke, Shulman and Spitters2019).
Lemma 15.
If
![]() $\mathbb{C}=\mathbb{R}\subset \mathbb{B}$
is the subuniverse of the right class of a modality on
$\mathbb{C}=\mathbb{R}\subset \mathbb{B}$
is the subuniverse of the right class of a modality on
![]() $\mathcal{B}$
, then every map in
$\mathcal{B}$
, then every map in
![]() $\mathcal{B}$
is
$\mathcal{B}$
is
![]() $\mathbb{C}$
-smooth.
$\mathbb{C}$
-smooth.
Proof.
For a map
![]() $u:X\to Y$
in
$u:X\to Y$
in
![]() $\mathcal{B}$
, and
$\mathcal{B}$
, and
![]() $r:\bar X\to X$
in
$r:\bar X\to X$
in
![]() $\mathcal{R}$
, the left adjoint
$\mathcal{R}$
, the left adjoint
![]() $u_!(r)$
is given by the right map of the
$u_!(r)$
is given by the right map of the
![]() $(\mathcal{L},\mathcal{R})$
-factorization of the map composite map
$(\mathcal{L},\mathcal{R})$
-factorization of the map composite map
![]() $\bar X\to X\to Y$
. It satisfies the Beck–Chevalley condition because the factorization is stable under base change.
$\bar X\to X\to Y$
. It satisfies the Beck–Chevalley condition because the factorization is stable under base change.
Notice that Lemmas 14 and 15 together provide examples where smooth and strictly smooth maps do not coincide.
We consider now the case of a weak factorization system
![]() $(\mathcal{L},\mathcal{R})$
on
$(\mathcal{L},\mathcal{R})$
on
![]() $\mathcal{B}$
. The class
$\mathcal{B}$
. The class
![]() $\mathcal{R}$
is still closed under base change and defines a regular calibration
$\mathcal{R}$
is still closed under base change and defines a regular calibration
![]() $\mathbb{R}\subset \mathbb{B}$
(but not the class
$\mathbb{R}\subset \mathbb{B}$
(but not the class
![]() $\mathcal{L}$
in general). The following lemma is a classical trick to recognize proper maps.
$\mathcal{L}$
in general). The following lemma is a classical trick to recognize proper maps.
Lemma 16.
If
![]() $\mathbb{C}=\mathbb{R}\subset \mathbb{B}$
if the regular calibration is associated with the right class of a weak factorization system
$\mathbb{C}=\mathbb{R}\subset \mathbb{B}$
if the regular calibration is associated with the right class of a weak factorization system
![]() $(\mathcal{L},\mathcal{R})$
on
$(\mathcal{L},\mathcal{R})$
on
![]() $\mathcal{B}$
, then a map
$\mathcal{B}$
, then a map
![]() $u$
is strictly
$u$
is strictly
![]() $\mathbb{C}$
-proper if and only if for any base change
$\mathbb{C}$
-proper if and only if for any base change
![]() $\bar u\to u$
, the functor
$\bar u\to u$
, the functor
![]() $\bar u^*$
preserves the class
$\bar u^*$
preserves the class
![]() $\mathcal{L}$
. In particular, if the factorization system
$\mathcal{L}$
. In particular, if the factorization system
![]() $(\mathcal{L},\mathcal{R})$
is a modality, then every map is strictly proper.
$(\mathcal{L},\mathcal{R})$
is a modality, then every map is strictly proper.
Proof.
A map
![]() $u$
is strictly proper if, for any base change
$u$
is strictly proper if, for any base change
![]() $\bar u\to u$
, the functor
$\bar u\to u$
, the functor
![]() $\bar u_*$
preserves the maps in
$\bar u_*$
preserves the maps in
![]() $\mathcal{R}$
, but this is equivalent to
$\mathcal{R}$
, but this is equivalent to
![]() $\bar u^*$
preserving the class
$\bar u^*$
preserving the class
![]() $\mathcal{L}$
. And when
$\mathcal{L}$
. And when
![]() $(\mathcal{L},\mathcal{R})$
is a modality, every
$(\mathcal{L},\mathcal{R})$
is a modality, every
![]() $\bar u^*$
preserves the class
$\bar u^*$
preserves the class
![]() $\mathcal{L}$
.
$\mathcal{L}$
.
Definition 17. (Acyclic and localic maps). A map
![]() $u:X\to Y$
in
$u:X\to Y$
in
![]() $\mathcal{B}$
is called
$\mathcal{B}$
is called
![]() $\mathbb{C}$
-pre-acyclic if
$\mathbb{C}$
-pre-acyclic if
![]() $u^*:\mathbb{C}(Y)\to \mathbb{C}(X)$
is an equivalence. A map
$u^*:\mathbb{C}(Y)\to \mathbb{C}(X)$
is an equivalence. A map
![]() $u:X\to Y$
in
$u:X\to Y$
in
![]() $\mathcal{B}$
is called
$\mathcal{B}$
is called
![]() $\mathbb{C}$
-acyclic if every base change of
$\mathbb{C}$
-acyclic if every base change of
![]() $u$
is
$u$
is
![]() $\mathbb{C}$
-pre-acyclic. We denote by
$\mathbb{C}$
-pre-acyclic. We denote by
![]() $\mathrm{A}(\mathbb{C})$
(Alpha) the codomain subfibration of
$\mathrm{A}(\mathbb{C})$
(Alpha) the codomain subfibration of
![]() $\mathbb{C}$
-acyclic maps. Acyclic maps are always both smooth and proper. A map is called
$\mathbb{C}$
-acyclic maps. Acyclic maps are always both smooth and proper. A map is called
![]() $\mathbb{C}$
-localic if it is right orthogonal to
$\mathbb{C}$
-localic if it is right orthogonal to
![]() $\mathbb{C}$
-acyclic maps. We denote by
$\mathbb{C}$
-acyclic maps. We denote by
![]() $\Lambda (\mathbb{C})$
the codomain subfibration of
$\Lambda (\mathbb{C})$
the codomain subfibration of
![]() $\mathbb{C}$
-localic maps.
$\mathbb{C}$
-localic maps.
The name “acyclic” is motivated by the following result. The name “localic” is motivated by an application to topos theory (see third example of Section 3.3). In an
![]() $\infty$
-topos
$\infty$
-topos
![]() $\mathcal{E}$
, an acyclic class is a class of maps containing all isomorphisms, closed under composition and base change, and under colimits in the arrow category of
$\mathcal{E}$
, an acyclic class is a class of maps containing all isomorphisms, closed under composition and base change, and under colimits in the arrow category of
![]() $\mathcal{E}$
(Anel et al., Reference Anel, Biedermann, Finster and Joyal2022, Definition 3.2.8). If
$\mathcal{E}$
(Anel et al., Reference Anel, Biedermann, Finster and Joyal2022, Definition 3.2.8). If
![]() $(\mathcal{L},\mathcal{R})$
is a (unique) factorization system on
$(\mathcal{L},\mathcal{R})$
is a (unique) factorization system on
![]() $\mathcal{E}$
, the class
$\mathcal{E}$
, the class
![]() $\mathcal{L}$
is acyclic if and only if
$\mathcal{L}$
is acyclic if and only if
![]() $(\mathcal{L},\mathcal{R})$
is a modality.
$(\mathcal{L},\mathcal{R})$
is a modality.
Lemma 18.
If
![]() $\mathcal{B}$
is an
$\mathcal{B}$
is an
![]() $\infty$
-topos and if
$\infty$
-topos and if
![]() $\mathbb{C}:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
sends colimits to limits, then the class of
$\mathbb{C}:\mathcal{B}^{\mathrm{op}}\to \mathsf{CAT}$
sends colimits to limits, then the class of
![]() $\mathbb{C}$
-acyclic maps is an acyclic class.
$\mathbb{C}$
-acyclic maps is an acyclic class.
Proof.
It is easy to see from the definition that
![]() $\mathrm{A}(\mathbb{C})$
contains all isomorphisms and is closed under composition and base change. It is also closed under small colimits in
$\mathrm{A}(\mathbb{C})$
contains all isomorphisms and is closed under composition and base change. It is also closed under small colimits in
![]() ${\mathcal{B}}^{\to }$
since the functor
${\mathcal{B}}^{\to }$
since the functor
![]() $\mathbb{C}$
send colimits to limits and
$\mathbb{C}$
send colimits to limits and
![]() $\mathrm{A}(\mathbb{C})$
is the inverse image of the class
$\mathrm{A}(\mathbb{C})$
is the inverse image of the class
![]() $\mathsf{CAT}^\simeq \subset{\mathsf{CAT}}^{\to }$
, which is closed under limits.
$\mathsf{CAT}^\simeq \subset{\mathsf{CAT}}^{\to }$
, which is closed under limits.
The
![]() $\mathbb{C}$
-acyclic and
$\mathbb{C}$
-acyclic and
![]() $\mathbb{C}$
-localic maps sometimes form a factorization system on
$\mathbb{C}$
-localic maps sometimes form a factorization system on
![]() $\mathcal{B}$
. When this the case, it is always a modality since both classes are stable by base change by definition.
$\mathcal{B}$
. When this the case, it is always a modality since both classes are stable by base change by definition.
3. Examples
3.1 Set theory and type theory
The examples are summarized in Table 1.
Table 1. Examples from set theory and type theory

Any 1-category
![]() $C$
represents a functor
$C$
represents a functor
![]() $\mathcal{B}^{\mathrm{op}}=\mathsf{Set}^{\mathrm{op}}\to \mathsf{CAT}$
, sending
$\mathcal{B}^{\mathrm{op}}=\mathsf{Set}^{\mathrm{op}}\to \mathsf{CAT}$
, sending
![]() $I$
to
$I$
to
![]() $C^I$
. In this setting, all conditions on maps can be computed fiberwise. A set
$C^I$
. In this setting, all conditions on maps can be computed fiberwise. A set
![]() $I$
is smooth (proper) if the coproduct
$I$
is smooth (proper) if the coproduct
![]() $\coprod _I:C^I\to C$
(product functor
$\coprod _I:C^I\to C$
(product functor
![]() $\prod _I:C^I\to C$
) exists. Notice that in this case, the Beck–Chevalley condition is always fulfilled since everything is determined fiberwise (Remark 11). A map is smooth (proper) if its fibers are smooth (proper) sets. If
$\prod _I:C^I\to C$
) exists. Notice that in this case, the Beck–Chevalley condition is always fulfilled since everything is determined fiberwise (Remark 11). A map is smooth (proper) if its fibers are smooth (proper) sets. If
![]() $C$
is the terminal category, every set is smooth and proper. If
$C$
is the terminal category, every set is smooth and proper. If
![]() $C$
is the initial category, the smooth (proper) maps are the surjections. A set
$C$
is the initial category, the smooth (proper) maps are the surjections. A set
![]() $I$
is acyclic if
$I$
is acyclic if
![]() $C\to C^I$
is an equivalence. If
$C\to C^I$
is an equivalence. If
![]() $C$
is the terminal category, every set is acyclic (and every map is acyclic). If
$C$
is the terminal category, every set is acyclic (and every map is acyclic). If
![]() $C$
is the empty category, the acyclic sets are the nonempty sets (the acyclic maps are surjections, and the localic maps are the injections). If
$C$
is the empty category, the acyclic sets are the nonempty sets (the acyclic maps are surjections, and the localic maps are the injections). If
![]() $C$
is otherwise, the only acyclic sets are the singletons; thus, the acyclic maps are the bijections, and every map is localic.
$C$
is otherwise, the only acyclic sets are the singletons; thus, the acyclic maps are the bijections, and every map is localic.
Similar considerations hold when
![]() $\mathcal{B}=\mathcal{S}$
is the
$\mathcal{B}=\mathcal{S}$
is the
![]() $\infty$
-category of spaces and
$\infty$
-category of spaces and
![]() $C$
some
$C$
some
![]() $\infty$
-category. In particular, Remark 11 applies, and the Beck–Chevalley conditions are always fulfilled.
$\infty$
-category. In particular, Remark 11 applies, and the Beck–Chevalley conditions are always fulfilled.
The second example is the one detailed in the introduction of Section 2. It is an instance of the previous example if and only if
![]() $\kappa$
is a regular cardinal (use
$\kappa$
is a regular cardinal (use
![]() $C=\mathsf{Set}^{\lt \kappa }$
). The example of the fibration of subsets (or of injections) is the case
$C=\mathsf{Set}^{\lt \kappa }$
). The example of the fibration of subsets (or of injections) is the case
![]() $\kappa =2$
. Every map
$\kappa =2$
. Every map
![]() $u:I\to J$
is smooth and proper. The functors
$u:I\to J$
is smooth and proper. The functors
![]() $u_!$
and
$u_!$
and
![]() $u_*$
are the two direct images of subsets, classically related to existential and universal quantifiers (
$u_*$
are the two direct images of subsets, classically related to existential and universal quantifiers (
![]() $u_!A = \{j\ |\ \exists a\in A, a\in u^{-1}(j)\}$
,
$u_!A = \{j\ |\ \exists a\in A, a\in u^{-1}(j)\}$
,
![]() $u_*A = \{j\ |\ \forall a\in A, a\in u^{-1}(j)\}$
). More generally, the setting of sets and subsets could be replaced by a hyperdoctrine in the sense of Lawvere (Reference Lawvere1970, Reference Lawvere2006) and Seely (Reference Seely1983). We recall the correspondence between logical quantifiers and the adjoints to base change in Table 2.
$u_*A = \{j\ |\ \forall a\in A, a\in u^{-1}(j)\}$
). More generally, the setting of sets and subsets could be replaced by a hyperdoctrine in the sense of Lawvere (Reference Lawvere1970, Reference Lawvere2006) and Seely (Reference Seely1983). We recall the correspondence between logical quantifiers and the adjoints to base change in Table 2.
Table 2. Quantifiers and direct images

In the case of the codomain fibration, we have seen in Proposition 8 that all maps are smooth and that proper maps are the exponentiable maps whose pullbacks are also exponentiable. All the projections
![]() $X\times Y\to X$
are proper if and only if the category
$X\times Y\to X$
are proper if and only if the category
![]() $\mathcal{B}$
is cartesian closed, and all the maps are proper if and only if the category
$\mathcal{B}$
is cartesian closed, and all the maps are proper if and only if the category
![]() $\mathcal{B}$
is locally cartesian closed. In this setting, only the isomorphisms are acylic and every map is localic.
$\mathcal{B}$
is locally cartesian closed. In this setting, only the isomorphisms are acylic and every map is localic.
Another example related to type theory is that of a category
![]() $\mathcal{B}$
with a
$\mathcal{B}$
with a
![]() $\pi$
-clan structure in the sense of Joyal (Reference Joyal2020). The clan structure distinguishes a class of maps in
$\pi$
-clan structure in the sense of Joyal (Reference Joyal2020). The clan structure distinguishes a class of maps in
![]() $\mathcal{D}\subset \mathcal{B}$
closed under base change and containing all isomorphisms, or equivalently a regular calibration
$\mathcal{D}\subset \mathcal{B}$
closed under base change and containing all isomorphisms, or equivalently a regular calibration
![]() $\mathbb{D}\subset \mathbb{B}$
. This implies that strict smooth maps are exactly the maps in
$\mathbb{D}\subset \mathbb{B}$
. This implies that strict smooth maps are exactly the maps in
![]() $\mathcal{D}$
. And the definition of the
$\mathcal{D}$
. And the definition of the
![]() $\pi$
-clan structure says that every map in
$\pi$
-clan structure says that every map in
![]() $\mathcal{D}$
is strictly proper (Joyal, Reference Joyal2020, Definition 2.4.1).
$\mathcal{D}$
is strictly proper (Joyal, Reference Joyal2020, Definition 2.4.1).
If
![]() $\mathcal{B}$
is a cartesian closed 1-category with a subobject classifier (e.g., 1-topos), we consider the example of a dominance, which is a regular calibration of monomorphisms classified by a subobject
$\mathcal{B}$
is a cartesian closed 1-category with a subobject classifier (e.g., 1-topos), we consider the example of a dominance, which is a regular calibration of monomorphisms classified by a subobject
![]() $\mathcal{O}\subset \Omega$
of the subobject classifier (Escardó, Reference Escardó2004; Hyland, Reference Hyland, Carboni, Pedicchio and Rosolini1991; Rosolini, 2020). Intuitively, the object
$\mathcal{O}\subset \Omega$
of the subobject classifier (Escardó, Reference Escardó2004; Hyland, Reference Hyland, Carboni, Pedicchio and Rosolini1991; Rosolini, 2020). Intuitively, the object
![]() $\mathcal{O}$
classifies the subobjects meant to be “open” in the sense of topology, and the exponential
$\mathcal{O}$
classifies the subobjects meant to be “open” in the sense of topology, and the exponential
![]() $\mathcal{O}^A\subset \Omega ^A$
is the lattice of open subobjects sitting within that of all subobjects. The smooth (proper) maps define a notion of open (compact) maps in the sense of topology. The strictly smooth maps are those classified by
$\mathcal{O}^A\subset \Omega ^A$
is the lattice of open subobjects sitting within that of all subobjects. The smooth (proper) maps define a notion of open (compact) maps in the sense of topology. The strictly smooth maps are those classified by
![]() $\mathcal{O}$
(Lemma 14). The strictly proper maps are those maps for which the direct image can be computed within the posets of all subobjects. Acyclic and localic maps are considered in the literature, but (seemingly) only with the base change property along cartesian projections and not along arbitrary maps. They are called
$\mathcal{O}$
(Lemma 14). The strictly proper maps are those maps for which the direct image can be computed within the posets of all subobjects. Acyclic and localic maps are considered in the literature, but (seemingly) only with the base change property along cartesian projections and not along arbitrary maps. They are called
![]() $\mathcal{O}$
-equable maps and
$\mathcal{O}$
-equable maps and
![]() $\mathcal{O}$
-replete maps in Hyland (Reference Hyland, Carboni, Pedicchio and Rosolini1991).
$\mathcal{O}$
-replete maps in Hyland (Reference Hyland, Carboni, Pedicchio and Rosolini1991).
When
![]() $\mathcal{B}$
is a 1-topos, any Grothendieck topology defines a dominance
$\mathcal{B}$
is a 1-topos, any Grothendieck topology defines a dominance
![]() $\Omega _j\subset \Omega$
where
$\Omega _j\subset \Omega$
where
![]() $\Omega _j$
is the classifier of closed monos. In this case, all maps are smooth, the closed monos are the strictly smooth maps. The acyclic maps are the maps inverted in the localization by the topology, and the localic maps are the relative sheaves. A map
$\Omega _j$
is the classifier of closed monos. In this case, all maps are smooth, the closed monos are the strictly smooth maps. The acyclic maps are the maps inverted in the localization by the topology, and the localic maps are the relative sheaves. A map
![]() $A\to 1$
is proper if and only if
$A\to 1$
is proper if and only if
![]() $A$
it is quasi-compact (every covering family has a covering finite subfamily). General proper maps can be described by a relative version of the same condition.
$A$
it is quasi-compact (every covering family has a covering finite subfamily). General proper maps can be described by a relative version of the same condition.
The
![]() $\infty$
-category
$\infty$
-category
![]() $\mathcal{S}$
of
$\mathcal{S}$
of
![]() $\infty$
-groupoids is a higher categorical model for dependent type theory with univalence: precisely, the small subuniverses correspond to univalent maps in
$\infty$
-groupoids is a higher categorical model for dependent type theory with univalence: precisely, the small subuniverses correspond to univalent maps in
![]() $\mathcal{S}$
. It seems difficult to describe the smooth, proper, acyclic, and localic maps for an arbitrary subuniverse, but it is easier with strict smooth and proper maps. We shall only consider the subuniverse of
$\mathcal{S}$
. It seems difficult to describe the smooth, proper, acyclic, and localic maps for an arbitrary subuniverse, but it is easier with strict smooth and proper maps. We shall only consider the subuniverse of
![]() $\kappa$
-small spaces. When
$\kappa$
-small spaces. When
![]() $\kappa$
is regular, the strict smooth maps are the maps with
$\kappa$
is regular, the strict smooth maps are the maps with
![]() $\kappa$
-small fibers by Lemma 14. When
$\kappa$
-small fibers by Lemma 14. When
![]() $\kappa$
is inaccessible, the strict proper maps are the maps with
$\kappa$
is inaccessible, the strict proper maps are the maps with
![]() $\kappa$
-small fibers by Lemma 16. In particular, if
$\kappa$
-small fibers by Lemma 16. In particular, if
![]() $\kappa$
is the inaccessible cardinal bounding the size of small objects, all maps are smooth and proper. In this case, the acyclic maps are reduced to equivalences and all maps are localic.
$\kappa$
is the inaccessible cardinal bounding the size of small objects, all maps are smooth and proper. In this case, the acyclic maps are reduced to equivalences and all maps are localic.
In the example of an
![]() $\infty$
-topos
$\infty$
-topos
![]() $\mathcal{E}$
, we denote the universe by
$\mathcal{E}$
, we denote the universe by
![]() $\mathbb{E}$
.Footnote
3
By definition of an
$\mathbb{E}$
.Footnote
3
By definition of an
![]() $\infty$
-topos, the functor
$\infty$
-topos, the functor
![]() $\mathbb{E}:\mathcal{E}^{\mathrm{op}}\to \mathsf{CAT}$
sends colimits of
$\mathbb{E}:\mathcal{E}^{\mathrm{op}}\to \mathsf{CAT}$
sends colimits of
![]() $\mathcal{E}$
to limits in
$\mathcal{E}$
to limits in
![]() $\mathsf{CAT}$
, and the interesting subuniverses are those satisfying a similar condition (corresponding to local classes of maps (Lurie, Reference Lurie2009, Proposition 6.1.3.7)). For
$\mathsf{CAT}$
, and the interesting subuniverses are those satisfying a similar condition (corresponding to local classes of maps (Lurie, Reference Lurie2009, Proposition 6.1.3.7)). For
![]() $n\geq -2$
, we denote by
$n\geq -2$
, we denote by
![]() $\mathcal{C}_n$
and
$\mathcal{C}_n$
and
![]() $\mathcal{T}_n$
the classes of
$\mathcal{T}_n$
the classes of
![]() $n$
-connected and
$n$
-connected and
![]() $n$
-truncated maps. For example, the class
$n$
-truncated maps. For example, the class
![]() $\mathcal{C}_{-1}$
and
$\mathcal{C}_{-1}$
and
![]() $\mathcal{T}_{-1}$
are the classes of surjections and monomorphisms. Every map can be factored uniquely into an
$\mathcal{T}_{-1}$
are the classes of surjections and monomorphisms. Every map can be factored uniquely into an
![]() $n$
-connected map followed by an
$n$
-connected map followed by an
![]() $n$
-truncated maps, and this factorization is stable under base change (it is a modality). The class
$n$
-truncated maps, and this factorization is stable under base change (it is a modality). The class
![]() $\mathcal{T}_n$
contains all isomorphisms, is closed under composition, and is local. It defines a regular calibration
$\mathcal{T}_n$
contains all isomorphisms, is closed under composition, and is local. It defines a regular calibration
![]() $\mathbb{T}_n\subset \mathbb{E}$
, which is also a reflective subuniverse (where the reflection is given by the factorization). Every map is smooth for
$\mathbb{T}_n\subset \mathbb{E}$
, which is also a reflective subuniverse (where the reflection is given by the factorization). Every map is smooth for
![]() $\mathbb{T}$
, and the strict smooth maps are those in
$\mathbb{T}$
, and the strict smooth maps are those in
![]() $\mathbb{T}$
. Every map is strictly proper (hence proper) for
$\mathbb{T}$
. Every map is strictly proper (hence proper) for
![]() $\mathbb{T}$
because dependent products preserve the truncation level of objects. The
$\mathbb{T}$
because dependent products preserve the truncation level of objects. The
![]() $\mathbb{T}_n$
-acyclic maps and
$\mathbb{T}_n$
-acyclic maps and
![]() $\mathbb{T}_n$
-localic maps can be characterized as the
$\mathbb{T}_n$
-localic maps can be characterized as the
![]() $(n+1)$
-connected maps and
$(n+1)$
-connected maps and
![]() $(n+1)$
-truncated maps (see below).
$(n+1)$
-truncated maps (see below).
More generally, a modality on
![]() $\mathcal{E}$
is a (unique) factorization system
$\mathcal{E}$
is a (unique) factorization system
![]() $(\mathcal{L},\mathcal{R})$
on
$(\mathcal{L},\mathcal{R})$
on
![]() $\mathcal{E}$
such that both classes are stable under base change. Then both classes
$\mathcal{E}$
such that both classes are stable under base change. Then both classes
![]() $\mathcal{L}$
and
$\mathcal{L}$
and
![]() $\mathcal{R}$
are local by Anel et al. (Reference Anel, Biedermann, Finster and Joyal2020, Proposition 3.6.5) and define subuniverses
$\mathcal{R}$
are local by Anel et al. (Reference Anel, Biedermann, Finster and Joyal2020, Proposition 3.6.5) and define subuniverses
![]() $\mathbb{L},\mathbb{R}\subset \mathbb{E}:\mathcal{E}^{\mathrm{op}}\to \mathsf{CAT}$
. We shall consider the case
$\mathbb{L},\mathbb{R}\subset \mathbb{E}:\mathcal{E}^{\mathrm{op}}\to \mathsf{CAT}$
. We shall consider the case
![]() $\mathbb{C}=\mathbb{R}$
. Since the class
$\mathbb{C}=\mathbb{R}$
. Since the class
![]() $\mathcal{R}$
is closed under composition and base change, Lemma 14 shows that the strict smooth maps are all maps in
$\mathcal{R}$
is closed under composition and base change, Lemma 14 shows that the strict smooth maps are all maps in
![]() $\mathcal{R}$
. But the subuniverse actually admits sums indexed by all maps in
$\mathcal{R}$
. But the subuniverse actually admits sums indexed by all maps in
![]() $\mathcal{E}$
. Given a map
$\mathcal{E}$
. Given a map
![]() $u:X\to Y$
in
$u:X\to Y$
in
![]() $\mathcal{E}$
and a map
$\mathcal{E}$
and a map
![]() $r:\bar X\to X$
in
$r:\bar X\to X$
in
![]() $\mathcal{R}$
, the
$\mathcal{R}$
, the
![]() $(\mathcal{L},\mathcal{R})$
-factorization of the composite map
$(\mathcal{L},\mathcal{R})$
-factorization of the composite map
![]() $\bar X\to X\to Y$
gives maps
$\bar X\to X\to Y$
gives maps
![]() $\bar X\to \bar Y$
in
$\bar X\to \bar Y$
in
![]() $\mathcal{L}$
and
$\mathcal{L}$
and
![]() $r':\bar Y\to Y$
in
$r':\bar Y\to Y$
in
![]() $\mathcal{R}$
. The image of
$\mathcal{R}$
. The image of
![]() $r$
by
$r$
by
![]() $u_!$
is the map
$u_!$
is the map
![]() $\bar Y\to Y$
. The Beck–Chevalley condition holds because the factorization is stable under base change. A more conceptual way to see this is to say that
$\bar Y\to Y$
. The Beck–Chevalley condition holds because the factorization is stable under base change. A more conceptual way to see this is to say that
![]() $\mathbb{R}$
is in fact a reflective subuniverse (where the reflection is given by the factorization) and therefore complete under all sums existing in
$\mathbb{R}$
is in fact a reflective subuniverse (where the reflection is given by the factorization) and therefore complete under all sums existing in
![]() $\mathbb{E}$
.
$\mathbb{E}$
.
In this example, it seems difficult to describe the proper maps without further assumptions on
![]() $\mathbb{R}$
. However, the acyclic maps are exactly the maps in the décalage of the class
$\mathbb{R}$
. However, the acyclic maps are exactly the maps in the décalage of the class
![]() $\mathcal{L}$
(Anel et al., Reference Anel, Biedermann, Finster and Joyal2024, 2.2.7) (they are also the “fiberwise
$\mathcal{L}$
(Anel et al., Reference Anel, Biedermann, Finster and Joyal2024, 2.2.7) (they are also the “fiberwise
![]() $\mathbb{R}$
-equivalences” of Anel et al. (Reference Anel, Biedermann, Finster and Joyal2022, Def. 3.3.1)). In particular, they form an acyclic class in
$\mathbb{R}$
-equivalences” of Anel et al. (Reference Anel, Biedermann, Finster and Joyal2022, Def. 3.3.1)). In particular, they form an acyclic class in
![]() $\mathcal{E}$
(Anel et al., Reference Anel, Biedermann, Finster and Joyal2022, Theorem 3.3.9). In this context, acyclic and localic maps define a modality on
$\mathcal{E}$
(Anel et al., Reference Anel, Biedermann, Finster and Joyal2022, Theorem 3.3.9). In this context, acyclic and localic maps define a modality on
![]() $\mathcal{E}$
, which is detailled in Anel et al. (Reference Anel, Biedermann, Finster and Joyal2023, Theorem 2.3.32).
$\mathcal{E}$
, which is detailled in Anel et al. (Reference Anel, Biedermann, Finster and Joyal2023, Theorem 2.3.32).
Finally, any left-exact localization of
![]() $\infty$
-topoi
$\infty$
-topoi
![]() $q^*:\mathcal{E}\to \mathcal{E}[\mathcal{W}^{-1}]$
provides a modality
$q^*:\mathcal{E}\to \mathcal{E}[\mathcal{W}^{-1}]$
provides a modality
![]() $(\mathcal{W},\mathcal{F})$
on
$(\mathcal{W},\mathcal{F})$
on
![]() $\mathcal{E}$
, where
$\mathcal{E}$
, where
![]() $\mathcal{W}$
is the class if maps inverted by
$\mathcal{W}$
is the class if maps inverted by
![]() $q^*$
and
$q^*$
and
![]() $\mathcal{F}$
are the class of “relative sheaves” (Rijke et al., Reference Rijke, Shulman and Spitters2019; Anel et al., Reference Anel, Biedermann, Finster and Joyal2022). Such a modality is left-exact in the sense that the factorization of a map preserves finite limits (in the arrow category). In fact, there is a bijection between left-exact localizations and left-exact modalities (Anel et al., Reference Anel, Biedermann, Finster and Joyal2022). Let
$\mathcal{F}$
are the class of “relative sheaves” (Rijke et al., Reference Rijke, Shulman and Spitters2019; Anel et al., Reference Anel, Biedermann, Finster and Joyal2022). Such a modality is left-exact in the sense that the factorization of a map preserves finite limits (in the arrow category). In fact, there is a bijection between left-exact localizations and left-exact modalities (Anel et al., Reference Anel, Biedermann, Finster and Joyal2022). Let
![]() $\mathbb{W}\subset \mathbb{E}\supset \mathbb{F}$
be the corresponding subuniverses. If
$\mathbb{W}\subset \mathbb{E}\supset \mathbb{F}$
be the corresponding subuniverses. If
![]() $\mathbb{E}':\mathcal{E}[\mathcal{W}^{-1}]^{\mathrm{op}}\to \mathsf{CAT}$
is the universe of the
$\mathbb{E}':\mathcal{E}[\mathcal{W}^{-1}]^{\mathrm{op}}\to \mathsf{CAT}$
is the universe of the
![]() $\infty$
-topos
$\infty$
-topos
![]() $\mathcal{E}[\mathcal{W}^{-1}]$
, one can show that
$\mathcal{E}[\mathcal{W}^{-1}]$
, one can show that
![]() $\mathbb{F}=\mathbb{E}'\circ q^*:\mathcal{E}^{\mathrm{op}}\to \mathsf{CAT}$
. Since left-exact modalities are fixed by décalage (Anel et al., Reference Anel, Biedermann, Finster and Joyal2024, Lemma 2.4.6 (1)), the acyclic (localic) maps coincides with the class
$\mathbb{F}=\mathbb{E}'\circ q^*:\mathcal{E}^{\mathrm{op}}\to \mathsf{CAT}$
. Since left-exact modalities are fixed by décalage (Anel et al., Reference Anel, Biedermann, Finster and Joyal2024, Lemma 2.4.6 (1)), the acyclic (localic) maps coincides with the class
![]() $\mathcal{W}$
(
$\mathcal{W}$
(
![]() $\mathcal{F}$
).
$\mathcal{F}$
).
3.2 Category theory
We now consider examples from category theory. The study of fibrations of categories was the motivation of Grothendieck for introducing his notion of smooth and proper functors. The examples are summarized in Table 3.
Table 3. Examples from category theory

The first example is that of the universe of
![]() $\mathcal{B}=\mathsf{Cat}$
. It will be the base of all the other examples. We denote by
$\mathcal{B}=\mathsf{Cat}$
. It will be the base of all the other examples. We denote by
![]() $\mathsf{\mathbb{C} at}$
the universe of
$\mathsf{\mathbb{C} at}$
the universe of
![]() $\mathsf{Cat}$
(which can be thought of either as the codomain fibration, or as the slice functor
$\mathsf{Cat}$
(which can be thought of either as the codomain fibration, or as the slice functor
![]() $C\mapsto \mathsf{Cat}{_{/C}}$
). The category
$C\mapsto \mathsf{Cat}{_{/C}}$
). The category
![]() $\mathsf{Cat}$
is cartesian closed but not locally cartesian closed. The exponentiable functors are the Conduché fibrations (see Ayala and Francis (Reference Ayala and Francis2020, Lemma 1.11) for a higher categorical account). The acyclic maps are the equivalences of categories and every functor is localic.
$\mathsf{Cat}$
is cartesian closed but not locally cartesian closed. The exponentiable functors are the Conduché fibrations (see Ayala and Francis (Reference Ayala and Francis2020, Lemma 1.11) for a higher categorical account). The acyclic maps are the equivalences of categories and every functor is localic.
The following examples will study various kinds of “fibrations” conditions on functors. This will lead to consider functors
![]() $\mathbb{C}:\mathsf{Cat}^{\mathrm{op}} \to \mathsf{CAT}$
with a natural forgetful morphism
$\mathbb{C}:\mathsf{Cat}^{\mathrm{op}} \to \mathsf{CAT}$
with a natural forgetful morphism
![]() $\mathbb{C}\to \mathsf{\mathbb{C} at}$
into the universe of
$\mathbb{C}\to \mathsf{\mathbb{C} at}$
into the universe of
![]() $\mathsf{Cat}$
(or equivalently a morphism between the corresponding fibrations over
$\mathsf{Cat}$
(or equivalently a morphism between the corresponding fibrations over
![]() $\mathsf{Cat}$
).
$\mathsf{Cat}$
).
Let us start with the the functor
![]() $\mathsf{LFib}:\mathsf{Cat}^{\mathrm{op}}\to \mathsf{CAT}$
sending a category
$\mathsf{LFib}:\mathsf{Cat}^{\mathrm{op}}\to \mathsf{CAT}$
sending a category
![]() $C$
to its category
$C$
to its category
![]() $\mathsf{LFib}(C) = \left [C,\mathcal{S}\right ]$
of (small) left fibrations. This functor is (up to size issues) representable by the category
$\mathsf{LFib}(C) = \left [C,\mathcal{S}\right ]$
of (small) left fibrations. This functor is (up to size issues) representable by the category
![]() $\mathcal{S}$
. The Grothendieck construction provides a natural transformation
$\mathcal{S}$
. The Grothendieck construction provides a natural transformation
![]() $\mathsf{LFib}(C) \to \mathsf{Cat}{_{/C}}$
, and we can talk about strict notions. Recall that the left fibrations are the right class of a (unique) factorization system on
$\mathsf{LFib}(C) \to \mathsf{Cat}{_{/C}}$
, and we can talk about strict notions. Recall that the left fibrations are the right class of a (unique) factorization system on
![]() $\mathsf{Cat}$
, whereas the left class is that of initial functors. The characterization of smooth and proper maps is open. The previous factorization system is not stable under base change, and we cannot apply Lemma 15. But the strict smooth maps are exactly the left fibrations themselves. The class of proper functors contains right fibrations And we can use Lemma 16 to characterize the strict proper maps as the exponentiable functors
$\mathsf{Cat}$
, whereas the left class is that of initial functors. The characterization of smooth and proper maps is open. The previous factorization system is not stable under base change, and we cannot apply Lemma 15. But the strict smooth maps are exactly the left fibrations themselves. The class of proper functors contains right fibrations And we can use Lemma 16 to characterize the strict proper maps as the exponentiable functors
![]() $u:C\to D$
such that for any base change
$u:C\to D$
such that for any base change
![]() $\bar u\to u$
, the pullback along
$\bar u\to u$
, the pullback along
![]() $\bar u$
preserves the class of initial functors. This is exactly the notion of proper functor of Lurie (Reference Lurie2009, dual of Definition 4.1.2.9) and the notion of smooth functor of Grothendieck in Pursuing Stacks and also in Joyal (Reference Joyal2008, 21.1) and Cisinski (Reference Cisinski2019, dual of Definition 4.4.1).Footnote
4
In particular, right fibrations are strict proper functors for
$\bar u$
preserves the class of initial functors. This is exactly the notion of proper functor of Lurie (Reference Lurie2009, dual of Definition 4.1.2.9) and the notion of smooth functor of Grothendieck in Pursuing Stacks and also in Joyal (Reference Joyal2008, 21.1) and Cisinski (Reference Cisinski2019, dual of Definition 4.4.1).Footnote
4
In particular, right fibrations are strict proper functors for
![]() $\mathsf{LFib}$
. The previous characterization of strict proper functors shows that they are also left-final functors in the sense of Ayala–Francis since they satisfy the condition of Ayala and Francis (Reference Ayala and Francis2020, Lemma 4.1.1 (a)). However, the condition to be left-final seems strictly weaker. In the dual situation of right fibrations, the notion of smooth and proper are reversed.
$\mathsf{LFib}$
. The previous characterization of strict proper functors shows that they are also left-final functors in the sense of Ayala–Francis since they satisfy the condition of Ayala and Francis (Reference Ayala and Francis2020, Lemma 4.1.1 (a)). However, the condition to be left-final seems strictly weaker. In the dual situation of right fibrations, the notion of smooth and proper are reversed.
Finally, we can look at the example of (small) cocartesian (and cartesian) fibrations. The functor of interest is
![]() $C\mapsto \mathsf{CcFib}(C) = \left [C, \mathsf{Cat}\right ]$
. Up to size issues, it is represented by
$C\mapsto \mathsf{CcFib}(C) = \left [C, \mathsf{Cat}\right ]$
. Up to size issues, it is represented by
![]() $\mathsf{Cat}$
itself. The class of cocartesian fibrations is almost the right class of a weak factorization system on
$\mathsf{Cat}$
itself. The class of cocartesian fibrations is almost the right class of a weak factorization system on
![]() $\mathsf{Cat}$
(in 1-categories, it is the right class of an algebraic factorization system, Bourke and Garner (Reference Bourke and Garner2014)). The corresponding left class is the class of fully faithful left adjoint functor. Any functor
$\mathsf{Cat}$
(in 1-categories, it is the right class of an algebraic factorization system, Bourke and Garner (Reference Bourke and Garner2014)). The corresponding left class is the class of fully faithful left adjoint functor. Any functor
![]() $f:C\to D$
admits a factorization
$f:C\to D$
admits a factorization
![]() $C\to f\downarrow D\to D$
into a fully faithful left adjoint functor followed by a cocartesian fibration (where
$C\to f\downarrow D\to D$
into a fully faithful left adjoint functor followed by a cocartesian fibration (where
![]() $f\downarrow D$
if the fiber product of
$f\downarrow D$
if the fiber product of
![]() $C\to D \xleftarrow{dom}{D}^{\to }$
). Again, the smooth and proper maps are difficult to find. The strict smooth maps are the cocartesian fibrations themselves. The previous factorization is enough to apply Lemma 16 to characterize the strictly proper maps as the exponentiable functors
$C\to D \xleftarrow{dom}{D}^{\to }$
). Again, the smooth and proper maps are difficult to find. The strict smooth maps are the cocartesian fibrations themselves. The previous factorization is enough to apply Lemma 16 to characterize the strictly proper maps as the exponentiable functors
![]() $u:C\to D$
such that
$u:C\to D$
such that
![]() $u^*$
preserves fully faithful left adjoint functors. This class includes that of cartesian fibrations. In the dual situation of cartesian fibrations, the notion of smooth and proper are reversed.
$u^*$
preserves fully faithful left adjoint functors. This class includes that of cartesian fibrations. In the dual situation of cartesian fibrations, the notion of smooth and proper are reversed.
In all the “fibration” examples, the acyclic maps are the equivalences and every functor is localic. To see this, recall that a functor
![]() $u:C\to D$
induces an equivalence
$u:C\to D$
induces an equivalence
![]() $u_!:\mathcal{S}^C\rightleftarrows \mathcal{S}^D:u^*$
if and only if it is a Morita equivalence. The acyclic maps are Morita equivalences, which are stable under base change. This implies that they must be (essentially) surjective functors. Since
$u_!:\mathcal{S}^C\rightleftarrows \mathcal{S}^D:u^*$
if and only if it is a Morita equivalence. The acyclic maps are Morita equivalences, which are stable under base change. This implies that they must be (essentially) surjective functors. Since
![]() $u_!$
is an equivalence,
$u_!$
is an equivalence,
![]() $u$
is fully faithful and is therefore an actual equivalence.
$u$
is fully faithful and is therefore an actual equivalence.
3.3 Topology and geometry
We now consider examples where the base category
![]() $\mathcal{B}$
is a category of topological or geometrical objects. We are going to see a tight connection between direct images functors and classical topological conditions. The examples are summarized in Table 4.
$\mathcal{B}$
is a category of topological or geometrical objects. We are going to see a tight connection between direct images functors and classical topological conditions. The examples are summarized in Table 4.
Table 4. Examples from topology and geometry

In the first example,
![]() $\mathcal{B}=\mathsf{Locale}$
is the category of localesFootnote
5
with the codomain fibration. Every map is smooth, and the proper maps are the exponentiable ones. The exponentiable locales are the locally compact ones (i.e., the locales such that
$\mathcal{B}=\mathsf{Locale}$
is the category of localesFootnote
5
with the codomain fibration. Every map is smooth, and the proper maps are the exponentiable ones. The exponentiable locales are the locally compact ones (i.e., the locales such that
![]() ${\mathrm{Op}\left (X\right )}$
is a continuous lattice) (Johnstone, Reference Johnstone1982, Theorem 4.11). Acyclic maps are the isomorphisms, and every map is localic.
${\mathrm{Op}\left (X\right )}$
is a continuous lattice) (Johnstone, Reference Johnstone1982, Theorem 4.11). Acyclic maps are the isomorphisms, and every map is localic.
The next example is that of the functor
![]() $\mathsf{Locale}^{\mathrm{op}}\to \mathsf{CAT}$
sending a locale
$\mathsf{Locale}^{\mathrm{op}}\to \mathsf{CAT}$
sending a locale
![]() $X$
to its frame
$X$
to its frame
![]() $\mathrm{Op}\left (X\right )$
of open domains. This functor is represented by the Sierpiński space. Let us say that a map is an open immersion if it is isomorphism to the inclusion of an open. The fibration corresponding to
$\mathrm{Op}\left (X\right )$
of open domains. This functor is represented by the Sierpiński space. Let us say that a map is an open immersion if it is isomorphism to the inclusion of an open. The fibration corresponding to
![]() $\mathrm{Op}\left (-\right )$
is the subfibration of the codomain fibration of
$\mathrm{Op}\left (-\right )$
is the subfibration of the codomain fibration of
![]() $\mathsf{Locale}$
spanned by open immersions. This shows that the notion of strict smooth and proper maps makes sense.
$\mathsf{Locale}$
spanned by open immersions. This shows that the notion of strict smooth and proper maps makes sense.
The smooth morphisms are almost by definition the open morphisms of topology (this can be shown directly, or deduced from the similar result for topoi (Johnstone, Reference Johnstone2002, Lemma C.3.1.10), see also Escardó (Reference Escardó2004)). By Lemma 14, the strict smooth maps are the open immersions that are also open morphisms, but that is the case of every open immersion. The proper morphisms are the proper morphisms of topology (i.e., the universally closed morphisms, this can be seen directly by considering left adjoints on the posets
![]() ${\mathrm{Op}\left (X\right )}^{\mathrm{op}}$
, or deduced from topos theory (Johnstone, Reference Johnstone2002, Lemma C.3.2.81), see also Escardó (Reference Escardó2004, Reference Escardó2020)). The characterization of strict proper maps is open. An open immersion is proper if and only if it is isomorphic to the inclusion of a clopen. The computation of acyclic and localic maps is straighforward.
${\mathrm{Op}\left (X\right )}^{\mathrm{op}}$
, or deduced from topos theory (Johnstone, Reference Johnstone2002, Lemma C.3.2.81), see also Escardó (Reference Escardó2004, Reference Escardó2020)). The characterization of strict proper maps is open. An open immersion is proper if and only if it is isomorphic to the inclusion of a clopen. The computation of acyclic and localic maps is straighforward.
In the third example,
![]() $\mathcal{B}$
is the category of 1-topoi and geometric morphisms (Johnstone, Reference Johnstone2002); Anel and Joyal, Reference Anel, Joyal, Anel and Catren2021)). If we look at the codomain fibration, the only nontrivial class of maps is that of exponentiable maps (Johnstone and Joyal, Reference Johnstone and Joyal1982).
$\mathcal{B}$
is the category of 1-topoi and geometric morphisms (Johnstone, Reference Johnstone2002); Anel and Joyal, Reference Anel, Joyal, Anel and Catren2021)). If we look at the codomain fibration, the only nontrivial class of maps is that of exponentiable maps (Johnstone and Joyal, Reference Johnstone and Joyal1982).
Another important fibration is the one of open sub-1-topoi (or open immersions), sending a 1-topos
![]() $\mathsf X$
to the poset of subterminal objects in its category of sheaves
$\mathsf X$
to the poset of subterminal objects in its category of sheaves
![]() $\mathrm{Sh}({\mathsf X})$
(its dual 1-logos in the sense of Anel and Joyal (Reference Anel, Joyal, Anel and Catren2021)). This fibration is represented by the Sierpiński topos (dual to the 1-logos
$\mathrm{Sh}({\mathsf X})$
(its dual 1-logos in the sense of Anel and Joyal (Reference Anel, Joyal, Anel and Catren2021)). This fibration is represented by the Sierpiński topos (dual to the 1-logos
![]() ${\mathsf{Set}}^{\to }$
). The identification of smooth maps as open morphisms of 1-topoi is done in Johnstone (Reference Johnstone2002, Theorem C.3.1.28), and that of proper maps as proper morphisms of 1-topoi is done in Moerdijk and Vermeulen (Reference Moerdijk and Vermeulen2000, Corollary I.5.9) and in Johnstone (Reference Johnstone2002, Theorem C.3.1.28). Both references use a “weak” version of Beck–Chevalley conditions (where the mate transformation is only monic) for arbitrary sheaves. But restricted to subterminal objects, this condition recovers the one from Definition 9, and this can be shown to be equivalent to the weak condition (see Johnstone, Reference Johnstone2002, Proposition A.4.1.17, and Moerdijk and Vermeulen, Reference Moerdijk and Vermeulen2000, Proposition 3.2).
${\mathsf{Set}}^{\to }$
). The identification of smooth maps as open morphisms of 1-topoi is done in Johnstone (Reference Johnstone2002, Theorem C.3.1.28), and that of proper maps as proper morphisms of 1-topoi is done in Moerdijk and Vermeulen (Reference Moerdijk and Vermeulen2000, Corollary I.5.9) and in Johnstone (Reference Johnstone2002, Theorem C.3.1.28). Both references use a “weak” version of Beck–Chevalley conditions (where the mate transformation is only monic) for arbitrary sheaves. But restricted to subterminal objects, this condition recovers the one from Definition 9, and this can be shown to be equivalent to the weak condition (see Johnstone, Reference Johnstone2002, Proposition A.4.1.17, and Moerdijk and Vermeulen, Reference Moerdijk and Vermeulen2000, Proposition 3.2).
Open immersions can be composed and define a regular calibration on
![]() $\mathsf{Topos}$
. Then, Lemma 14 shows that the strict smooth maps are exactly the open immersion of 1-topoi. The characterization of strict proper maps is open. An open immersion of 1-topoi is proper if it is also the inclusion of a closed sub-1-topoi (corresponding to a decidable subterminal object). Interestingly, in this example, the notion of acyclic and localic maps recover the hyperconnected and localic morphisms of topoi (this is in fact the motivation for the name localic). The proof is straightforward for hyperconnected maps, and the fact that the right orthogonal to hyperconnected morphisms are the localic morphisms is Johnstone (Reference Johnstone2002, Lemma A.4.6.4).
$\mathsf{Topos}$
. Then, Lemma 14 shows that the strict smooth maps are exactly the open immersion of 1-topoi. The characterization of strict proper maps is open. An open immersion of 1-topoi is proper if it is also the inclusion of a closed sub-1-topoi (corresponding to a decidable subterminal object). Interestingly, in this example, the notion of acyclic and localic maps recover the hyperconnected and localic morphisms of topoi (this is in fact the motivation for the name localic). The proof is straightforward for hyperconnected maps, and the fact that the right orthogonal to hyperconnected morphisms are the localic morphisms is Johnstone (Reference Johnstone2002, Lemma A.4.6.4).
The next example is the case of the fibration of étale maps over the category of 1-topoi, sending a 1-topos
![]() $\mathsf X$
to its category of sheaves of sets (its dual 1-logos)
$\mathsf X$
to its category of sheaves of sets (its dual 1-logos)
![]() $\mathrm{Sh}({\mathsf X})$
. This fibration is representable by the “object classifier” or the “topos line” (which we shall denote
$\mathrm{Sh}({\mathsf X})$
. This fibration is representable by the “object classifier” or the “topos line” (which we shall denote
![]() $\mathsf A$
, its 1-logos of sheaves is
$\mathsf A$
, its 1-logos of sheaves is
![]() $\left [{\mathsf{finset}},\mathsf{Set}\right ]$
) and the existence of sums and products for the étale fibration can be interpreted as sums and products structures on the 1-topos
$\left [{\mathsf{finset}},\mathsf{Set}\right ]$
) and the existence of sums and products for the étale fibration can be interpreted as sums and products structures on the 1-topos
![]() $\mathsf A$
. In this case, the smooth maps are the locally connected morphisms of 1-topoi (Johnstone, Reference Johnstone2002, Corollary C.3.3.16), and the proper maps are the tidy morphisms of 1-topoi (see Moerdijk and Vermeulen, Reference Moerdijk and Vermeulen2000, Corollary III.4.9, or Johnstone, Reference Johnstone2002, Corollary C.3.4.11). The strict smooth maps are all the étale morphisms. The characterization of strict proper maps is open. In this setting, the acyclic maps are the equivalences, and every map is localic.
$\mathsf A$
. In this case, the smooth maps are the locally connected morphisms of 1-topoi (Johnstone, Reference Johnstone2002, Corollary C.3.3.16), and the proper maps are the tidy morphisms of 1-topoi (see Moerdijk and Vermeulen, Reference Moerdijk and Vermeulen2000, Corollary III.4.9, or Johnstone, Reference Johnstone2002, Corollary C.3.4.11). The strict smooth maps are all the étale morphisms. The characterization of strict proper maps is open. In this setting, the acyclic maps are the equivalences, and every map is localic.
Interestingly, not every étale map is proper: the intersection of the two classes is the class of finite maps. This means that the “topos line”
![]() $\mathsf A$
does not have arbitrary products indexed by itself, but only finite products. This might be surprising since categories of sheaves are always locally cartesian closed, but the dependent products are not preserved by geometric morphisms, only finite products are.
$\mathsf A$
does not have arbitrary products indexed by itself, but only finite products. This might be surprising since categories of sheaves are always locally cartesian closed, but the dependent products are not preserved by geometric morphisms, only finite products are.
The generalization of the previous results to
![]() $\infty$
-topoi is quite rich! For the case of the codomain fibration, exponentiable
$\infty$
-topoi is quite rich! For the case of the codomain fibration, exponentiable
![]() $\infty$
-topoi have been characterized in Lurie (Reference Lurie2017, Theorem 21.1.6.12) and Anel and Lejay (Reference Anel and Lejay2019). The case of the fibration of étale morphisms has been studied recently by Martini and Wolf. If
$\infty$
-topoi have been characterized in Lurie (Reference Lurie2017, Theorem 21.1.6.12) and Anel and Lejay (Reference Anel and Lejay2019). The case of the fibration of étale morphisms has been studied recently by Martini and Wolf. If
![]() $\mathcal{B}=\mathsf{Topos}_\infty$
is the category of
$\mathcal{B}=\mathsf{Topos}_\infty$
is the category of
![]() $\infty$
-topoi and
$\infty$
-topoi and
![]() $\mathbb{C}({\mathsf X}) ={\mathrm{Sh}_\infty \!\left ({\mathsf X} \right )}$
is the category of higher sheaves (the
$\mathbb{C}({\mathsf X}) ={\mathrm{Sh}_\infty \!\left ({\mathsf X} \right )}$
is the category of higher sheaves (the
![]() $\infty$
-logos dual to
$\infty$
-logos dual to
![]() $\mathsf X$
), then the smooth maps are the locally contractible morphisms of
$\mathsf X$
), then the smooth maps are the locally contractible morphisms of
![]() $\infty$
-topoi Martini (Reference Martini and Wolf2023), and the proper maps are the proper morphisms of
$\infty$
-topoi Martini (Reference Martini and Wolf2023), and the proper maps are the proper morphisms of
![]() $\infty$
-topoi (Lurie, Reference Lurie2009; Martini and Wolf Reference Martini and Wolf2023a, Reference Martini and Wolf2023b) The acyclic maps are equivalences, and every map is localic.
$\infty$
-topoi (Lurie, Reference Lurie2009; Martini and Wolf Reference Martini and Wolf2023a, Reference Martini and Wolf2023b) The acyclic maps are equivalences, and every map is localic.
It is interesting to restrict the fibration of higher sheaves (aka higher etale morphisms) to
![]() $n$
-truncated sheaves only (the case
$n$
-truncated sheaves only (the case
![]() $n=-1$
recovers the fibration of open immersions). In this case, it is easy to adapt the results of Martini and Wolf to characterize the smooth maps as some locally
$n=-1$
recovers the fibration of open immersions). In this case, it is easy to adapt the results of Martini and Wolf to characterize the smooth maps as some locally
![]() $n$
-connected morphisms of
$n$
-connected morphisms of
![]() $\infty$
-topoi,Footnote
6
and the proper maps are the
$\infty$
-topoi,Footnote
6
and the proper maps are the
![]() $n$
-proper morphisms of
$n$
-proper morphisms of
![]() $\infty$
-topoi.Footnote
7
The strict smooth maps are the
$\infty$
-topoi.Footnote
7
The strict smooth maps are the
![]() $n$
-truncated étale morphisms of topoi. The corresponding acyclic and localic maps define notions of hyper-
$n$
-truncated étale morphisms of topoi. The corresponding acyclic and localic maps define notions of hyper-
![]() $(n+1)$
-connected morphisms and
$(n+1)$
-connected morphisms and
![]() $(n+1)$
-localic morphisms, and every geometric morphism should factor into a hyper-
$(n+1)$
-localic morphisms, and every geometric morphism should factor into a hyper-
![]() $(n+1)$
-connected morphism followed by a
$(n+1)$
-connected morphism followed by a
![]() $(n+1)$
-localic morphism. Moreover, an
$(n+1)$
-localic morphism. Moreover, an
![]() $\infty$
-topos
$\infty$
-topos
![]() $\mathsf X$
should be
$\mathsf X$
should be
![]() $n$
-localic in the sense of Lurie (Reference Lurie2009, Definition 6.4.5.8) if and only if the morphism
$n$
-localic in the sense of Lurie (Reference Lurie2009, Definition 6.4.5.8) if and only if the morphism
![]() ${\mathsf X}\to 1$
is
${\mathsf X}\to 1$
is
![]() $n$
-localic in the previous sense.
$n$
-localic in the previous sense.
Étale maps define a regular calibration of the universe of
![]() $\mathsf{Topos}_\infty$
, and the notions of strictly smooth and strictly proper maps can be defined. By Lemma 14, the strict smooth maps are exactly the etale maps. The strict proper maps are exponentiable maps
$\mathsf{Topos}_\infty$
, and the notions of strictly smooth and strictly proper maps can be defined. By Lemma 14, the strict smooth maps are exactly the etale maps. The strict proper maps are exponentiable maps
![]() $u$
whose direct image
$u$
whose direct image
![]() $u_*$
preserves etale maps. Their characterization is open.
$u_*$
preserves etale maps. Their characterization is open.
The last example of Table 4 is in algebraic geometry, where the base category is the category
![]() $\mathsf{Sch}$
of (noetherian) schemes, and the functor
$\mathsf{Sch}$
of (noetherian) schemes, and the functor
![]() $\mathsf{Sch}^{\mathrm{op}} \to \mathsf{CAT}$
is the one sending a scheme
$\mathsf{Sch}^{\mathrm{op}} \to \mathsf{CAT}$
is the one sending a scheme
![]() $X$
to its category of torsion étale sheaves (Freitag and Kiehl, Reference Freitag and Kiehl1988). The characterization of smooth and proper maps in general is open but Freitag and Kiehl (Reference Freitag and Kiehl1988, Theorems 6.1 and 7.3) show that smooth morphisms of schemes are smooth maps (if the torsion is prime to the characteristic) and that proper morphisms of schemes are proper maps. This setting is the one that inspired Grothendieck to name his notions of smooth and proper functors (Maltsiniotis, Reference Maltsiniotis2005). The characterization of acyclic and localic maps is an open question.
$X$
to its category of torsion étale sheaves (Freitag and Kiehl, Reference Freitag and Kiehl1988). The characterization of smooth and proper maps in general is open but Freitag and Kiehl (Reference Freitag and Kiehl1988, Theorems 6.1 and 7.3) show that smooth morphisms of schemes are smooth maps (if the torsion is prime to the characteristic) and that proper morphisms of schemes are proper maps. This setting is the one that inspired Grothendieck to name his notions of smooth and proper functors (Maltsiniotis, Reference Maltsiniotis2005). The characterization of acyclic and localic maps is an open question.
Acknowledgments
The authors are happy to dedicate this paper to André Joyal on the occasion of his 80th birthday. The focus on examples is a homage to André, who has drilled their importance into the head of the first author.
The authors would like to thank the anonymous referee for valuable feedback, as well as Carlo Angiuli, Steve Awodey, Reid Barton, Denis-Charles Cisinski, Jonas Frey, Louis Martini, Anders Mörtberg, Emily Riehl, Jon Sterling, Thomas Streicher, Andrew Swan, and Sebastian Wolf for numerous discussions around this material. Special thanks to Denis-Charles Cisinski for his comments on an earlier version and to Jon Sterling for pointing out to us the example of dominances.
This material is based upon work supported by the Air Force Office of Scientific Research under award number FA9550-23-1-0434 and by the US Army Research Office under MURI Grant W911NF-20-1-0082. The second author wishes to thank the Department of Mathematics at the Johns Hopkins University for hosting him as part of the latter project. He also thanks the Max Planck Institute for Mathematics in Bonn for its hospitality and financial support during some stages of this work.