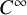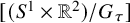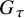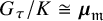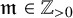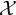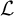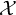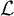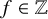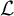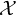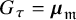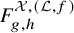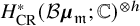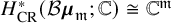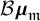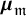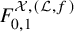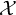1 Introduction
Open Gromov-Witten (GW) invariants of toric Calabi-Yau 3-folds have been studied extensively by both mathematicians and physicists. They correspond to ‘A-model topological open string amplitudes’ in the physics literature and can be interpreted as intersection numbers of certain moduli spaces of holomorphic maps from bordered Riemann surfaces to the 3-fold with boundaries in a Lagrangian submanifold. The physics prediction of these open GW invariants comes from string dualities: mirror symmetry relates the A-model topological string theory of a Calabi-Yau 3-fold X to the B-model topological string theory of the mirror Calabi-Yau 3-fold
![]() $\check {X}$
; the large- N duality relates the A-model topological string theory on Calabi-Yau 3-folds (of complex dimension three) to the Chern-Simons theory on 3-manifolds (of real dimension three).
$\check {X}$
; the large- N duality relates the A-model topological string theory on Calabi-Yau 3-folds (of complex dimension three) to the Chern-Simons theory on 3-manifolds (of real dimension three).
1.1 Open GW invariants of smooth toric Calabi-Yau 3-folds
Aganagic-Vafa [Reference Aganagic and Vafa6] introduce a class of Lagrangian submanifolds in smooth semi-projective toric Calabi-Yau 3-folds, which are diffeomorphic to
![]() $S^1\times \mathbb {R} ^2$
. By mirror symmetry, Aganagic-Vafa and Aganagic-Klemm-Vafa [Reference Aganagic and Vafa6, Reference Aganagic, Klemm and Vafa5] relate genus-zero open GW invariants (disk invariants) of a smooth toric Calabi-Yau 3-fold X relative to such a Lagrangian submanifold L to the classical Abel-Jacobi map of the mirror Calabi-Yau 3-fold
$S^1\times \mathbb {R} ^2$
. By mirror symmetry, Aganagic-Vafa and Aganagic-Klemm-Vafa [Reference Aganagic and Vafa6, Reference Aganagic, Klemm and Vafa5] relate genus-zero open GW invariants (disk invariants) of a smooth toric Calabi-Yau 3-fold X relative to such a Lagrangian submanifold L to the classical Abel-Jacobi map of the mirror Calabi-Yau 3-fold
![]() $\check {X}$
, which can be further related to the Abel-Jacobi map to the mirror curve of X. This conjecture is proved in full generality in [Reference Fang and Liu33].
$\check {X}$
, which can be further related to the Abel-Jacobi map to the mirror curve of X. This conjecture is proved in full generality in [Reference Fang and Liu33].
By the large-N duality, Aganagic-Klemm-Mariño-Vafa propose the topological vertex [Reference Aganagic, Klemm, Mariño and Vafa4], an algorithm of computing all genera generating functions
![]() $F_{\beta ',\mu _1, \ldots , \mu _h}$
of open GW invariants of
$F_{\beta ',\mu _1, \ldots , \mu _h}$
of open GW invariants of
![]() $(X,L)$
obtained by fixing a topological type of the map (determined by the degree
$(X,L)$
obtained by fixing a topological type of the map (determined by the degree
![]() $\beta '\in H_2(X,L; \mathbb {Z} )$
and winding numbers
$\beta '\in H_2(X,L; \mathbb {Z} )$
and winding numbers
![]() $\mu _1,\ldots , \mu _h\in H_1(L; \mathbb {Z} )= \mathbb {Z} $
) and summing over the genus of the domain. The algorithm of the topological vertex is proved in full generality in [Reference Maulik, Oblomkov and Okounkov60].
$\mu _1,\ldots , \mu _h\in H_1(L; \mathbb {Z} )= \mathbb {Z} $
) and summing over the genus of the domain. The algorithm of the topological vertex is proved in full generality in [Reference Maulik, Oblomkov and Okounkov60].
Bouchard-Klemm-Mariño-Pasquetti propose the Remodeling Conjecture [Reference Bouchard, Klemm, Mariño and Pasquetti8], an algorithm for constructing the B-model topological open string amplitudes in all genera of
![]() $\check {X}$
following [Reference Mariño58], using Eynard-Orantin’s topological recursion from the theory of matrix models [Reference Eynard and Orantin30]. Combined with the mirror symmetry prediction, this gives an algorithm for computing generating functions
$\check {X}$
following [Reference Mariño58], using Eynard-Orantin’s topological recursion from the theory of matrix models [Reference Eynard and Orantin30]. Combined with the mirror symmetry prediction, this gives an algorithm for computing generating functions
![]() $F_{g,h}$
of open GW invariants of
$F_{g,h}$
of open GW invariants of
![]() $(X,L)$
obtained by fixing a topological type of the domain (determined by the genus g and number h of boundary circles) and summing over the topological types of the map. Eynard-Orantin studied the Remodeling Conjecture for any smooth symplectic toric Calabi-Yau threefolds [Reference Eynard and Orantin31].
$(X,L)$
obtained by fixing a topological type of the domain (determined by the genus g and number h of boundary circles) and summing over the topological types of the map. Eynard-Orantin studied the Remodeling Conjecture for any smooth symplectic toric Calabi-Yau threefolds [Reference Eynard and Orantin31].
1.2 Open GW invariants for 3-dimensional Calabi-Yau smooth toric DM stacks
There have been attempts to generalise some of the above results to 3-dimensional Calabi-Yau smooth toric Deligne-Mumford (DM) stacks. The closed GW theory of orbifolds has been studied for a long time. The physics literature dates back to the early 1990s, such as [Reference Cecotti and Vafa17, Reference Zaslow74], which studies the quantum cohomology ring of orbifolds. The mathematical definition is given by Chen-Ruan [Reference Chen and Ruan22] for symplectic orbifolds and by Abramovich-Graber-Vistoli [Reference Abramovich, Graber and Vistoli2, Reference Abramovich, Graber and Vistoli3] for smooth DM stacks. Toric varieties are defined by a fan, while smooth toric DM stacks are defined by a stacky fan [Reference Borisov, Chen and Smith7]. The coarse moduli of a smooth toric DM stack
![]() $\mathcal {X}$
is a toric variety
$\mathcal {X}$
is a toric variety
![]() $X_\Sigma $
defined by a simplicial fan
$X_\Sigma $
defined by a simplicial fan
![]() $\Sigma $
. A toric orbifold is a smooth toric DM stack with a trivial generic stabiliser. Any smooth toric DM stack
$\Sigma $
. A toric orbifold is a smooth toric DM stack with a trivial generic stabiliser. Any smooth toric DM stack
![]() $\mathcal {X}$
is a K-gerbe over its rigidification
$\mathcal {X}$
is a K-gerbe over its rigidification
![]() $\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
, where K is the generic stabiliser (which is a finite abelian group) and
$\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
, where K is the generic stabiliser (which is a finite abelian group) and
![]() $\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
is a toric orbifold.
$\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
is a toric orbifold.
The definition of Aganagic-Vafa branes can be extended to the setting of 3-dimensional Calabi-Yau smooth toric DM stacks with semi-projective coarse moduli spaces. These branes are diffeomorphic to
![]() $[(S^1\times \mathbb {R} ^2)/G_\tau ]$
, where
$[(S^1\times \mathbb {R} ^2)/G_\tau ]$
, where
![]() $G_\tau $
is a finite abelian group containing the generic stabiliser K. The open GW invariants of 3-dimensional Calabi-Yau smooth toric DM stacks are defined via localisation [Reference Ross66], generalising the methods in [Reference Katz and Liu49]. By localisation, open and closed GW invariants of a smooth toric Calabi-Yau 3-fold can be obtained by glueing the GW vertex, a generating function of open GW invariants of
$G_\tau $
is a finite abelian group containing the generic stabiliser K. The open GW invariants of 3-dimensional Calabi-Yau smooth toric DM stacks are defined via localisation [Reference Ross66], generalising the methods in [Reference Katz and Liu49]. By localisation, open and closed GW invariants of a smooth toric Calabi-Yau 3-fold can be obtained by glueing the GW vertex, a generating function of open GW invariants of
![]() $ \mathbb {C} ^3$
, which can be reduced to a generating function of certain cubic Hodge integrals [Reference Diaconescu and Florea29]. Similarly, open and closed orbifold GW invariants of a 3-dimensional Calabi-Yau smooth toric DM stack can be obtained by glueing the orbifold GW vertex, a generating function of open GW invariants of
$ \mathbb {C} ^3$
, which can be reduced to a generating function of certain cubic Hodge integrals [Reference Diaconescu and Florea29]. Similarly, open and closed orbifold GW invariants of a 3-dimensional Calabi-Yau smooth toric DM stack can be obtained by glueing the orbifold GW vertex, a generating function of open GW invariants of
![]() $[ \mathbb {C} ^3/G]$
(where G is a finite abelian subgroup of
$[ \mathbb {C} ^3/G]$
(where G is a finite abelian subgroup of
![]() $SL(3, \mathbb {C} )$
), which can be reduced to a generating function of certain cubic abelian Hurwitz-Hodge integrals [Reference Ross66]. The GW vertex has been evaluated in the general case [Reference Li, Liu, Liu and Zhou57, Reference Maulik, Oblomkov and Okounkov60]. The orbifold GW vertex has been evaluated for
$SL(3, \mathbb {C} )$
), which can be reduced to a generating function of certain cubic abelian Hurwitz-Hodge integrals [Reference Ross66]. The GW vertex has been evaluated in the general case [Reference Li, Liu, Liu and Zhou57, Reference Maulik, Oblomkov and Okounkov60]. The orbifold GW vertex has been evaluated for
![]() $[ \mathbb {C} ^2/ \mathbb {Z} _n]\times \mathbb {C} $
, where
$[ \mathbb {C} ^2/ \mathbb {Z} _n]\times \mathbb {C} $
, where
![]() $ \mathbb {C} ^2/\mathbb {Z}_n$
is the
$ \mathbb {C} ^2/\mathbb {Z}_n$
is the
![]() $A_{n-1}$
surface singularity [Reference Zong77, Reference Ross and Zong68, Reference Ross and Zong69, Reference Ross67], but not in the general case.
$A_{n-1}$
surface singularity [Reference Zong77, Reference Ross and Zong68, Reference Ross and Zong69, Reference Ross67], but not in the general case.
As for mirror symmetry, a mirror theorem for disk invariants of
![]() $[\mathbb {C}^3/\mathbb {Z}_4]$
is proved in [Reference Brini and Cavalieri11]. The Remodeling Conjecture is also expected to predict higher genus open GW invariants of toric Calabi-Yau 3-orbifolds via mirror symmetry [Reference Bouchard, Klemm, Mariño and Pasquetti8, Reference Bouchard, Klemm, Mariño and Pasquetti9].
$[\mathbb {C}^3/\mathbb {Z}_4]$
is proved in [Reference Brini and Cavalieri11]. The Remodeling Conjecture is also expected to predict higher genus open GW invariants of toric Calabi-Yau 3-orbifolds via mirror symmetry [Reference Bouchard, Klemm, Mariño and Pasquetti8, Reference Bouchard, Klemm, Mariño and Pasquetti9].
1.3 Summary of results
In this paper, we study open-closed orbifold GW invariants of a 3-dimensional Calabi-Yau smooth toric DM stack
![]() $\mathcal {X}$
relative to an Aganagic-Vafa A-brane
$\mathcal {X}$
relative to an Aganagic-Vafa A-brane
![]() $\mathcal {L}$
at all genera.
$\mathcal {L}$
at all genera.
Open GW invariants of the pair
![]() $(\mathcal {X}, \mathcal {L})$
count holomorphic maps from orbicurves to
$(\mathcal {X}, \mathcal {L})$
count holomorphic maps from orbicurves to
![]() $\mathcal {X}$
with boundaries mapped to
$\mathcal {X}$
with boundaries mapped to
![]() $\mathcal {L}$
. Open-closed orbifold GW invariants of the pair
$\mathcal {L}$
. Open-closed orbifold GW invariants of the pair
![]() $(\mathcal {X},\mathcal {L})$
depend on the following discrete data:
$(\mathcal {X},\mathcal {L})$
depend on the following discrete data:
-
(i) topological type
 $(g,h)$
of the domain orbicurve
$(g,h)$
of the domain orbicurve
 $(\Sigma ,\partial \Sigma )$
, where g is the genus and h is the number of boundary holes;
$(\Sigma ,\partial \Sigma )$
, where g is the genus and h is the number of boundary holes; -
(ii) number of interior marked points n;
-
(iii) topological type of the map
 $u:(\Sigma ,\partial \Sigma =\coprod _{i=1}^h R_i )\to (\mathcal {X},\mathcal {L})$
given by the degree
$u:(\Sigma ,\partial \Sigma =\coprod _{i=1}^h R_i )\to (\mathcal {X},\mathcal {L})$
given by the degree
 $\beta ' =u_*[\Sigma ]\in H_2(\mathcal {X},\mathcal {L}; \mathbb {Z} )$
and each
$\beta ' =u_*[\Sigma ]\in H_2(\mathcal {X},\mathcal {L}; \mathbb {Z} )$
and each
 $[u_*(R_i)]\in H_1(\mathcal {L}; \mathbb {Z} )\cong \mathbb {Z} \times G_\tau $
, collectively denoted by
$[u_*(R_i)]\in H_1(\mathcal {L}; \mathbb {Z} )\cong \mathbb {Z} \times G_\tau $
, collectively denoted by
 $ {\vec {\mu }} =([u_*(R_1)],\dots , [u_*(R_h)])$
;
$ {\vec {\mu }} =([u_*(R_1)],\dots , [u_*(R_h)])$
; -
(iv) framing
 $f\in \mathbb {Z} $
of the Aganagic-Vafa A-brane
$f\in \mathbb {Z} $
of the Aganagic-Vafa A-brane
 $\mathcal {L}$
.
$\mathcal {L}$
.
Let
![]() $\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
be the moduli space parametrising holomorphic maps with discrete data (i)-(iii). We use the evaluation maps
$\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
be the moduli space parametrising holomorphic maps with discrete data (i)-(iii). We use the evaluation maps
![]() $\mathrm {ev}_i$
,
$\mathrm {ev}_i$
,
![]() $i=1,\ldots , n$
at interior points to pull back classes in the orbifold Chen-Ruan cohomology
$i=1,\ldots , n$
at interior points to pull back classes in the orbifold Chen-Ruan cohomology
![]() $H^*_ {\mathrm {CR}} (\mathcal {X})$
of
$H^*_ {\mathrm {CR}} (\mathcal {X})$
of
![]() $\mathcal {X}$
to obtain open-closed GW invariants. More precisely,
$\mathcal {X}$
to obtain open-closed GW invariants. More precisely,
![]() $\mathcal {L}$
intersects a unique
$\mathcal {L}$
intersects a unique
![]() $1$
-dimensional orbit
$1$
-dimensional orbit
![]() $\mathfrak {o}_\tau \cong \mathbb {C} ^*\times \mathcal {B} G_\tau $
. Given
$\mathfrak {o}_\tau \cong \mathbb {C} ^*\times \mathcal {B} G_\tau $
. Given
![]() $\gamma _1,\ldots , \gamma _n\in H_ {\mathrm {CR}} ^*(\mathcal {X}; \mathbb {Q} )$
, we define open-closed orbifold GW invariant
$\gamma _1,\ldots , \gamma _n\in H_ {\mathrm {CR}} ^*(\mathcal {X}; \mathbb {Q} )$
, we define open-closed orbifold GW invariant
![]() $\langle \gamma _1,\ldots ,\gamma _n\rangle ^{\mathcal {X},(\mathcal {L},f)}_{g,\beta ', {\vec {\mu }} }$
via localisation using a circle action determined by the framing
$\langle \gamma _1,\ldots ,\gamma _n\rangle ^{\mathcal {X},(\mathcal {L},f)}_{g,\beta ', {\vec {\mu }} }$
via localisation using a circle action determined by the framing
![]() $f\in \mathbb {Z} $
; this is a rational number depending on f and can be viewed as an equivariant invariant. We also provide another definition based on algebraic relative Gromov-Witten theory, which agrees with the above definition up to a sign depending on the choice of orientation on
$f\in \mathbb {Z} $
; this is a rational number depending on f and can be viewed as an equivariant invariant. We also provide another definition based on algebraic relative Gromov-Witten theory, which agrees with the above definition up to a sign depending on the choice of orientation on
![]() $\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
. This generalises the definition in [Reference Li, Liu, Liu and Zhou57] for smooth toric Calabi-Yau 3-folds and specifies an orientation on
$\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
. This generalises the definition in [Reference Li, Liu, Liu and Zhou57] for smooth toric Calabi-Yau 3-folds and specifies an orientation on
![]() $\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
compatible with the canonical orientation on moduli of relative stable maps determined by the complex structure.
$\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
compatible with the canonical orientation on moduli of relative stable maps determined by the complex structure.
When
![]() $\mathcal {X}$
is a symplectic toric Calabi-Yau 3-orbifolds (i.e., when the generic stabiliser K is trivial),
$\mathcal {X}$
is a symplectic toric Calabi-Yau 3-orbifolds (i.e., when the generic stabiliser K is trivial),
![]() $G_\tau \cong \boldsymbol {\mu }_{\mathfrak {m}}$
is cyclic. In this case, for each topological type
$G_\tau \cong \boldsymbol {\mu }_{\mathfrak {m}}$
is cyclic. In this case, for each topological type
![]() $(g,h)$
of the domain bordered Riemann surface, we define a generating function
$(g,h)$
of the domain bordered Riemann surface, we define a generating function
![]() $F_{g,h}^{\mathcal {X},(\mathcal {L},f)}$
of open-closed GW invariants that takes value in
$F_{g,h}^{\mathcal {X},(\mathcal {L},f)}$
of open-closed GW invariants that takes value in
![]() $H^*_ {\mathrm {CR}} (\mathcal {B} G; \mathbb {C} )^{\otimes h}$
, where
$H^*_ {\mathrm {CR}} (\mathcal {B} G; \mathbb {C} )^{\otimes h}$
, where
![]() $H^*_ {\mathrm {CR}} (\mathcal {B} G; \mathbb {C} )=\oplus _{\lambda \in G} \mathbb {C} \mathbf {1}_\lambda $
.
$H^*_ {\mathrm {CR}} (\mathcal {B} G; \mathbb {C} )=\oplus _{\lambda \in G} \mathbb {C} \mathbf {1}_\lambda $
.
In particular, the disk potential
![]() $F_{0,1}^{\mathcal {X},(\mathcal {L},f)}$
takes values in
$F_{0,1}^{\mathcal {X},(\mathcal {L},f)}$
takes values in
![]() $H^*_ {\mathrm {CR}} (\mathcal {B} G; \mathbb {C} )$
. When
$H^*_ {\mathrm {CR}} (\mathcal {B} G; \mathbb {C} )$
. When
![]() $\mathcal {L}$
is an outer brane,Footnote
1
the A-model disk potential is
$\mathcal {L}$
is an outer brane,Footnote
1
the A-model disk potential is
 $$\begin{align*}F_{0,1}^{\mathcal{X},(\mathcal{L},f)}(\boldsymbol{\tau}_2, X)=\sum_{\beta',n\geq 0} \sum_{(\mu, \lambda)\in H_1(\mathcal{L}; \mathbb{Z} )\cong \mathbb{Z} \times G_\tau} \frac{\langle (\boldsymbol{\tau}_2)^n\rangle^{\mathcal{X},(\mathcal{L},f)}_{0,\beta',(\mu,\lambda)}}{n!} \cdot X^\mu (\xi_0)^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}} \end{align*}$$
$$\begin{align*}F_{0,1}^{\mathcal{X},(\mathcal{L},f)}(\boldsymbol{\tau}_2, X)=\sum_{\beta',n\geq 0} \sum_{(\mu, \lambda)\in H_1(\mathcal{L}; \mathbb{Z} )\cong \mathbb{Z} \times G_\tau} \frac{\langle (\boldsymbol{\tau}_2)^n\rangle^{\mathcal{X},(\mathcal{L},f)}_{0,\beta',(\mu,\lambda)}}{n!} \cdot X^\mu (\xi_0)^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}} \end{align*}$$
where
![]() $\boldsymbol {\tau }_2$
is certain equivariant second Chen-Ruan cohomology class of
$\boldsymbol {\tau }_2$
is certain equivariant second Chen-Ruan cohomology class of
![]() $\mathcal {X}$
,
$\mathcal {X}$
,
![]() $\xi _0$
is an
$\xi _0$
is an
![]() $\mathfrak {m}$
th root of
$\mathfrak {m}$
th root of
![]() $-1$
, and
$-1$
, and
![]() $\bar {\lambda }\in \{0,1,\ldots ,\mathfrak {m}-1\}$
corresponds to
$\bar {\lambda }\in \{0,1,\ldots ,\mathfrak {m}-1\}$
corresponds to
![]() $\lambda \in G$
under a group isomorphism
$\lambda \in G$
under a group isomorphism
![]() $G_\tau \cong \mathbb {Z} /\mathfrak {m} \mathbb {Z} $
. The precise definition of
$G_\tau \cong \mathbb {Z} /\mathfrak {m} \mathbb {Z} $
. The precise definition of
![]() $\boldsymbol {\tau }_2$
and
$\boldsymbol {\tau }_2$
and
![]() $F_{(0,1)}^{\mathcal {X},(\mathcal {L},f)}$
will be given in Section 3.13. (Throughout the paper,
$F_{(0,1)}^{\mathcal {X},(\mathcal {L},f)}$
will be given in Section 3.13. (Throughout the paper,
![]() $\beta '$
denotes a relative homology class in
$\beta '$
denotes a relative homology class in
![]() $H_2(\mathcal {X},\mathcal {L}; \mathbb {Z} )$
, whereas
$H_2(\mathcal {X},\mathcal {L}; \mathbb {Z} )$
, whereas
![]() $\beta $
denotes an absolute homology class in
$\beta $
denotes an absolute homology class in
![]() $H_2(\mathcal {X}; \mathbb {Z} )$
.) In this paper, we prove a mirror theorem regarding the disk potential
$H_2(\mathcal {X}; \mathbb {Z} )$
.) In this paper, we prove a mirror theorem regarding the disk potential
![]() $F_{0,1}^{\mathcal {X},(\mathcal {L},f)}$
when
$F_{0,1}^{\mathcal {X},(\mathcal {L},f)}$
when
![]() $\mathcal {X}$
is a semi-projective toric Calabi-Yau 3-orbifold. Mirror symmetry relates the A-model topological string theory on a Calabi-Yau 3-fold to the B-model topological string theory on the mirror Calabi-Yau 3-fold. The mirror of a semi-projective toric Calabi-Yau 3-fold is a Calabi-Yau hypersurface in
$\mathcal {X}$
is a semi-projective toric Calabi-Yau 3-orbifold. Mirror symmetry relates the A-model topological string theory on a Calabi-Yau 3-fold to the B-model topological string theory on the mirror Calabi-Yau 3-fold. The mirror of a semi-projective toric Calabi-Yau 3-fold is a Calabi-Yau hypersurface in
![]() $ \mathbb {C} ^2\times ( \mathbb {C} ^*)^2$
defined by an equation
$ \mathbb {C} ^2\times ( \mathbb {C} ^*)^2$
defined by an equation
![]() $uv=H(x,y,q)$
, where
$uv=H(x,y,q)$
, where
![]() $(u,v)\in \mathbb {C} ^2$
,
$(u,v)\in \mathbb {C} ^2$
,
![]() $(x,y)\in ( \mathbb {C} ^*)^2$
and q is the complex moduli parametrising the B-model. The function
$(x,y)\in ( \mathbb {C} ^*)^2$
and q is the complex moduli parametrising the B-model. The function
![]() $H(x,y,q)$
is determined by both the combinatorial toric data of
$H(x,y,q)$
is determined by both the combinatorial toric data of
![]() $\mathcal {X}$
and the framed brane
$\mathcal {X}$
and the framed brane
![]() $(\mathcal {L},f)$
. The affine curve
$(\mathcal {L},f)$
. The affine curve
![]() $C_q=\{H(x,y,q)=0\}$
in
$C_q=\{H(x,y,q)=0\}$
in
![]() $( \mathbb {C} ^*)^2$
is called the mirror curve. We can fix a labelling of the
$( \mathbb {C} ^*)^2$
is called the mirror curve. We can fix a labelling of the
![]() $\mathfrak {m}$
points with
$\mathfrak {m}$
points with
![]() $x=0$
on the mirror curve by the elements in
$x=0$
on the mirror curve by the elements in
![]() $G_\tau ^*=\mathrm {Hom}(G, \mathbb {C} ^*)\cong \mathbb {Z} /\mathfrak {m} \mathbb {Z} $
. For each
$G_\tau ^*=\mathrm {Hom}(G, \mathbb {C} ^*)\cong \mathbb {Z} /\mathfrak {m} \mathbb {Z} $
. For each
![]() $\eta \in G_\tau ^*$
, there is a small open neighbourhood
$\eta \in G_\tau ^*$
, there is a small open neighbourhood
![]() $U^\epsilon _\eta $
in the (compactified) mirror curve of the
$U^\epsilon _\eta $
in the (compactified) mirror curve of the
![]() $x=0$
point labelled by
$x=0$
point labelled by
![]() $\eta $
and a branch
$\eta $
and a branch
![]() $(\log y)_{U_\eta ^\epsilon }$
of
$(\log y)_{U_\eta ^\epsilon }$
of
![]() $\log y$
defined on
$\log y$
defined on
![]() $U_\eta ^\epsilon $
, where
$U_\eta ^\epsilon $
, where
![]() $y=y(x,q)$
is defined implicitly by the equation
$y=y(x,q)$
is defined implicitly by the equation
![]() $H(x,y,q)=0$
. When
$H(x,y,q)=0$
. When
![]() $\mathcal {L}$
is an outer brane, the closure of the 1-dimensional orbit intersecting
$\mathcal {L}$
is an outer brane, the closure of the 1-dimensional orbit intersecting
![]() $\mathcal {L}$
contains a unique torus fixed (stacky) point
$\mathcal {L}$
contains a unique torus fixed (stacky) point
![]() $\mathfrak {p}_ {\sigma } = \mathcal {B} G_ {\sigma } $
, where
$\mathfrak {p}_ {\sigma } = \mathcal {B} G_ {\sigma } $
, where
![]() $G_ {\sigma } $
is the inertia group of
$G_ {\sigma } $
is the inertia group of
![]() $\mathfrak {p}_ {\sigma } $
. With the above convention, we state our open mirror theorem as follows.
$\mathfrak {p}_ {\sigma } $
. With the above convention, we state our open mirror theorem as follows.
Theorem 1.1. Under the closed mirror map
![]() $\boldsymbol {\tau }_2=\boldsymbol {\tau }_2(q)$
and the open mirror map
$\boldsymbol {\tau }_2=\boldsymbol {\tau }_2(q)$
and the open mirror map
![]() $X=xe^{A(q)}$
(the explicit formula of
$X=xe^{A(q)}$
(the explicit formula of
![]() $\boldsymbol {\tau }_2(q)$
and
$\boldsymbol {\tau }_2(q)$
and
![]() $A(q)$
will be given in Section 4),
$A(q)$
will be given in Section 4),
 $$\begin{align*}x\frac{\partial}{\partial x}\left(\sum_{\eta \in \boldsymbol{\mu}^*_{\mathfrak{m}}}(\log y)_{U_\eta^\epsilon} (q,x) \phi_\eta \right) = \frac{\partial^2}{\partial x^2} F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2,X), \end{align*}$$
$$\begin{align*}x\frac{\partial}{\partial x}\left(\sum_{\eta \in \boldsymbol{\mu}^*_{\mathfrak{m}}}(\log y)_{U_\eta^\epsilon} (q,x) \phi_\eta \right) = \frac{\partial^2}{\partial x^2} F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2,X), \end{align*}$$
where
![]() $\{\phi _\eta \}_{\eta \in G}$
is the canonical basis of
$\{\phi _\eta \}_{\eta \in G}$
is the canonical basis of
![]() $H^*_ {\mathrm {CR}} (\mathcal {B} G_\tau; \mathbb {C} )$
.
$H^*_ {\mathrm {CR}} (\mathcal {B} G_\tau; \mathbb {C} )$
.
Remark 1.2. The definition of the disk function
![]() $F_{0,1}^{\mathcal {X},(\mathcal {L},f)}$
and the formulation of the above Theorem 1.1 are slightly different from those in the first version of this paper in 2012 [Reference Fang, Liu and Tseng34], but the above Theorem 1.1 implies [Reference Fang, Liu and Tseng34, Theorem 1.1], which is used to prove an open version of Ruan’s Crepant Resolution Conjecture for disk invariants of toric Calabi-Yau 3-orbifold relative to an effective outer Aganagic-Vafa brane [Reference Ke and Zhou50].
$F_{0,1}^{\mathcal {X},(\mathcal {L},f)}$
and the formulation of the above Theorem 1.1 are slightly different from those in the first version of this paper in 2012 [Reference Fang, Liu and Tseng34], but the above Theorem 1.1 implies [Reference Fang, Liu and Tseng34, Theorem 1.1], which is used to prove an open version of Ruan’s Crepant Resolution Conjecture for disk invariants of toric Calabi-Yau 3-orbifold relative to an effective outer Aganagic-Vafa brane [Reference Ke and Zhou50].
1.4 Similar results for compact Lagrangian tori
There are other open GW invariants relative to different types of Lagrangian submanifolds. C.-H. Cho [Reference Cho15] and J. Solomon [Reference Solomon70] define disk invariants of a compact symplectic manifold in real dimensions four and six relative to a Lagrangian submanifold that is the fixed locus of an anti-symplectic involution. The mirror theorem for disk invariants for the quintic 3-fold relative to the real quintic is conjectured in [Reference Walcher72] and proved in [Reference Pandharipande, Solomon and Walcher63]. It has been generalised to compact Calabi-Yau 3-folds that are projective complete intersections [Reference Popa and Zinger64], where a mirror theorem for genus one open GW invariants (annulus invariants) is also proved.
Open orbifold GW invariants of compact toric orbifolds with respect to Lagrangian torus fibres of the moment map are defined in [Reference Cho and Poddar24], which generalises the work of [Reference Fukaya, Oh, Ohta and Ono38] on compact toric manifolds. The third author and collaborators prove mirror theorems on disk invariants in this context [Reference Chan, Lau, Leung and Tseng20, Reference Chan, Cho, Lau and Tseng18]. The third author and collaborators also prove mirror theorems on disk invariants of toric Calabi-Yau manifolds/orbifolds (which must be noncompact) with respect to Lagrangian torus fibres of the Gross fibration [Reference Chan, Lau and Tseng21, Reference Chan, Cho, Lau and Tseng19].
1.5 Applications
The main theorem (Theorem 1.1) of this paper has several applications. Here we mention two important applications:
-
○ As mentioned in Remark 1.2 above, Theorem 1.1 has been applied to prove an open version of Ruan’s Crepant Resolution Conjecture for disk invariants of a toric Calabi-Yau 3-orbifold relative to an effective outer Aganagic-Vafa brane [Reference Ke and Zhou50]. Using Theorem 1.1, S. Yu [Reference Yu73] proves an open version of Crepant Transformation Conjecture (and in particular the Crepant Resolution Conjecture) for disk invariants of a semi-projective toric Calabi-Yau 3-orbifold relative to a general (effective or ineffective, inner or outer) Aganagic-Vafa brane defined in Section 3.3 of this paper. This generalises the Open Crepant Resolution Conjecture (OCRC) for disk invariants of
 $[ \mathbb {C} ^2/ \mathbb {Z} _n]\times \mathbb {C} $
relative to possibly ineffective Aganagic-Vafa branes proved in [Reference Brini, Cavalieri and Ross12].
$[ \mathbb {C} ^2/ \mathbb {Z} _n]\times \mathbb {C} $
relative to possibly ineffective Aganagic-Vafa branes proved in [Reference Brini, Cavalieri and Ross12]. -
○ Recently, the first two authors and Zong prove the BKMP Remodeling Conjecture for all semi-projective toric Calabi-Yau 3-orbifolds [Reference Fang, Liu and Zong36]. Theorem 1.1 is one of the key ingredients of this proof.
1.6 Overview of the paper
The rest of the paper is organised as follows. In Section 2, we review the necessary materials concerning smooth toric DM stacks. In Section 3, we apply localisation to relate open-closed GW invariants and descendant GW invariants of 3-dimensional smooth Calabi-Yau toric DM stacks. In Section 4, we prove a mirror theorem for orbifold disk invariants.
2 Smooth toric DM stacks
In this section, we follow the definitions in [Reference Iritani47, Section 3.1], with slightly different notation. We work over
![]() $ \mathbb {C} $
.
$ \mathbb {C} $
.
2.1 Definition
Let N be a finitely generated abelian group, and let
![]() $N_{\mathbb {R}} =N\otimes _{\mathbb {Z}} \mathbb {R} $
. We have a short exact sequence of (additive) abelian groups:
$N_{\mathbb {R}} =N\otimes _{\mathbb {Z}} \mathbb {R} $
. We have a short exact sequence of (additive) abelian groups:
where
![]() $N_ {\mathrm {tor}} $
is the subgroup of torsion elements in N. Then
$N_ {\mathrm {tor}} $
is the subgroup of torsion elements in N. Then
![]() $N_ {\mathrm {tor}} $
is a finite abelian group and
$N_ {\mathrm {tor}} $
is a finite abelian group and
![]() $\bar {N}= \mathbb {Z} ^n$
, where
$\bar {N}= \mathbb {Z} ^n$
, where
![]() $n=\dim _{\mathbb {R}} N_{\mathbb {R}} $
. The natural projection
$n=\dim _{\mathbb {R}} N_{\mathbb {R}} $
. The natural projection
![]() $N\to \bar {N}$
is denoted
$N\to \bar {N}$
is denoted
![]() $b\mapsto \bar {b}$
. A smooth toric DM stack is an extension of toric varieties [Reference Fulton39, Reference Borisov, Chen and Smith7]. A smooth toric DM stack is given by the following data:
$b\mapsto \bar {b}$
. A smooth toric DM stack is an extension of toric varieties [Reference Fulton39, Reference Borisov, Chen and Smith7]. A smooth toric DM stack is given by the following data:
-
○
 $b_1,\dots , b_{r'} \in N$
that generate a subgroup of N of finite index, and
$b_1,\dots , b_{r'} \in N$
that generate a subgroup of N of finite index, and -
○ a simplicial fan
 $\Sigma $
in
$\Sigma $
in
 $N_{\mathbb {R}} $
such that the set of
$N_{\mathbb {R}} $
such that the set of
 $1$
-cones is where
$1$
-cones is where $$ \begin{align*}\{\rho_1,\dots,\rho_{r'}\}, \end{align*} $$
$$ \begin{align*}\{\rho_1,\dots,\rho_{r'}\}, \end{align*} $$
 $\rho _i= \mathbb {R} _{\ge 0} \bar b_i$
,
$\rho _i= \mathbb {R} _{\ge 0} \bar b_i$
,
 $i=1,\dots , r'$
.
$i=1,\dots , r'$
.
The datum
![]() $\mathbf \Sigma =(\Sigma , (b_1,\dots , b_{r'}))$
is a stacky fan in the sense of [Reference Borisov, Chen and Smith7]. The vectors
$\mathbf \Sigma =(\Sigma , (b_1,\dots , b_{r'}))$
is a stacky fan in the sense of [Reference Borisov, Chen and Smith7]. The vectors
![]() $b_1,\dots , b_{r'}$
may or may not generate N; if they do not, we choose additional vectors
$b_1,\dots , b_{r'}$
may or may not generate N; if they do not, we choose additional vectors
![]() $b_{r'+1},\dots , b_r$
such that
$b_{r'+1},\dots , b_r$
such that
![]() $b_1,\dots , b_r$
generate N. There is a surjective group homomorphism
$b_1,\dots , b_r$
generate N. There is a surjective group homomorphism
 $$ \begin{align*} \phi : {\widetilde{N}} :=\oplus_{i=1}^r \mathbb{Z} & {\tilde{b}} _i \longrightarrow N,\\ & {\tilde{b}} _i \mapsto b_i. \end{align*} $$
$$ \begin{align*} \phi : {\widetilde{N}} :=\oplus_{i=1}^r \mathbb{Z} & {\tilde{b}} _i \longrightarrow N,\\ & {\tilde{b}} _i \mapsto b_i. \end{align*} $$
Define
![]() $\mathbb {L} :=\mathrm {Ker}(\phi ) \cong \mathbb {Z} ^k$
, where
$\mathbb {L} :=\mathrm {Ker}(\phi ) \cong \mathbb {Z} ^k$
, where
![]() $k:=r-n$
. Then we have the following short exact sequence of finitely generated abelian groups:
$k:=r-n$
. Then we have the following short exact sequence of finitely generated abelian groups:
Applying
![]() $ - \otimes _{\mathbb {Z}} \mathbb {C} ^*$
to equation (1), we obtain an exact sequence of abelian groups
$ - \otimes _{\mathbb {Z}} \mathbb {C} ^*$
to equation (1), we obtain an exact sequence of abelian groups
where
 $$ \begin{align*} \mathbb{T} &:= N\otimes_{\mathbb{Z}} \mathbb{C} ^* =\bar{N}\otimes_{\mathbb{Z}} \mathbb{C} ^* \cong ( \mathbb{C} ^*)^n,\\ {\widetilde{ \mathbb{T} }} &:= {\widetilde{N}} \otimes_{\mathbb{Z}} \mathbb{C} ^* \cong ( \mathbb{C} ^*)^r,\\ G &:= \mathbb{L}\otimes_{\mathbb{Z}} \mathbb{C} ^* \cong ( \mathbb{C} ^*)^k,\\ K &:= {\mathrm{Tor}} _1^{ \mathbb{Z} }(N, \mathbb{C} ^*)\cong N_ {\mathrm{tor}}. \end{align*} $$
$$ \begin{align*} \mathbb{T} &:= N\otimes_{\mathbb{Z}} \mathbb{C} ^* =\bar{N}\otimes_{\mathbb{Z}} \mathbb{C} ^* \cong ( \mathbb{C} ^*)^n,\\ {\widetilde{ \mathbb{T} }} &:= {\widetilde{N}} \otimes_{\mathbb{Z}} \mathbb{C} ^* \cong ( \mathbb{C} ^*)^r,\\ G &:= \mathbb{L}\otimes_{\mathbb{Z}} \mathbb{C} ^* \cong ( \mathbb{C} ^*)^k,\\ K &:= {\mathrm{Tor}} _1^{ \mathbb{Z} }(N, \mathbb{C} ^*)\cong N_ {\mathrm{tor}}. \end{align*} $$
The action of
![]() $ {\widetilde { \mathbb {T} }} $
on itself extends to a
$ {\widetilde { \mathbb {T} }} $
on itself extends to a
![]() $ {\widetilde { \mathbb {T} }} $
-action on
$ {\widetilde { \mathbb {T} }} $
-action on
![]() $ \mathbb {C} ^r = \mathrm {Spec} \mathbb {C} [Z_1,\dots , Z_r]$
. The torus G acts on
$ \mathbb {C} ^r = \mathrm {Spec} \mathbb {C} [Z_1,\dots , Z_r]$
. The torus G acts on
![]() $ \mathbb {C} ^r$
via the group homomorphism
$ \mathbb {C} ^r$
via the group homomorphism
![]() $G\to {\widetilde { \mathbb {T} }} $
in equation (2), so
$G\to {\widetilde { \mathbb {T} }} $
in equation (2), so
![]() $K\subset G$
acts on
$K\subset G$
acts on
![]() $ \mathbb {C} ^r$
trivially. The isomorphism
$ \mathbb {C} ^r$
trivially. The isomorphism
![]() $K\cong N_ {\mathrm {tor}} $
is not canonical.
$K\cong N_ {\mathrm {tor}} $
is not canonical.
With the above preparation, we are now ready to define a smooth toric DM stack
![]() $\mathcal {X}$
. Let
$\mathcal {X}$
. Let
be the set of anti-cones; note that
![]() $\{r'+1,\ldots , r\} \subset I$
for any anti-cone
$\{r'+1,\ldots , r\} \subset I$
for any anti-cone
![]() $I\subset \mathcal {A}$
. Given
$I\subset \mathcal {A}$
. Given
![]() $I\subset \{1,\ldots , r\}$
, let
$I\subset \{1,\ldots , r\}$
, let
![]() $ \mathbb {C} ^I$
be the subvariety of
$ \mathbb {C} ^I$
be the subvariety of
![]() $ \mathbb {C} ^r$
defined by the ideal in
$ \mathbb {C} ^r$
defined by the ideal in
![]() $ \mathbb {C} [Z_1,\ldots , Z_r]$
generated by
$ \mathbb {C} [Z_1,\ldots , Z_r]$
generated by
![]() $\{ Z_i \mid i\notin I\}$
. Define the smooth toric DM stack
$\{ Z_i \mid i\notin I\}$
. Define the smooth toric DM stack
![]() $\mathcal {X}$
as the quotient stack
$\mathcal {X}$
as the quotient stack
where
 $$ \begin{align*}U_{\mathcal{A}}:= \mathbb{C} ^r \backslash \bigcup_{I\notin \mathcal A} \mathbb{C} ^I = \bigcap_{I\notin \mathcal{A}} \left( \mathbb{C} ^r \backslash \mathbb{C} ^I\right). \end{align*} $$
$$ \begin{align*}U_{\mathcal{A}}:= \mathbb{C} ^r \backslash \bigcup_{I\notin \mathcal A} \mathbb{C} ^I = \bigcap_{I\notin \mathcal{A}} \left( \mathbb{C} ^r \backslash \mathbb{C} ^I\right). \end{align*} $$
Note that for
![]() $i=r'+1,\ldots ,r$
,
$i=r'+1,\ldots ,r$
,
![]() $ \mathbb {R} _{\geq 0} b_i$
is not a cone in
$ \mathbb {R} _{\geq 0} b_i$
is not a cone in
![]() $\Sigma $
, so
$\Sigma $
, so
![]() $\{ i\}' := \{1,\ldots , r\} \backslash \{i\} \notin \mathcal {A}$
. Therefore,
$\{ i\}' := \{1,\ldots , r\} \backslash \{i\} \notin \mathcal {A}$
. Therefore,
 $$ \begin{align*}U_{\mathcal{A}} \subset \bigcap_{i=r'+1}^r \left( \mathbb{C} ^r\backslash \mathbb{C} ^{\{i\}'}\right) = \mathbb{C} ^{r'}\times ( \mathbb{C} ^*)^{r-r'}. \end{align*} $$
$$ \begin{align*}U_{\mathcal{A}} \subset \bigcap_{i=r'+1}^r \left( \mathbb{C} ^r\backslash \mathbb{C} ^{\{i\}'}\right) = \mathbb{C} ^{r'}\times ( \mathbb{C} ^*)^{r-r'}. \end{align*} $$
The stack
![]() $\mathcal {X}$
contains the DM torus
$\mathcal {X}$
contains the DM torus
![]() $\mathcal {T} := [ {\widetilde { \mathbb {T} }} /G]$
as a dense open subset, and the
$\mathcal {T} := [ {\widetilde { \mathbb {T} }} /G]$
as a dense open subset, and the
![]() $ {\widetilde { \mathbb {T} }} $
-action on
$ {\widetilde { \mathbb {T} }} $
-action on
![]() $U_{\mathcal {A}}$
descends to a
$U_{\mathcal {A}}$
descends to a
![]() $\mathcal {T}$
-action on
$\mathcal {T}$
-action on
![]() $\mathcal {X}$
. The smooth toric DM stack
$\mathcal {X}$
. The smooth toric DM stack
![]() $\mathcal {X}$
is a toric orbifold if the G-action on
$\mathcal {X}$
is a toric orbifold if the G-action on
![]() $ {\widetilde { \mathbb {T} }} $
is free.
$ {\widetilde { \mathbb {T} }} $
is free.
Let
![]() $G^ {\mathrm {rig}} = G/K$
. Then
$G^ {\mathrm {rig}} = G/K$
. Then
![]() $G^ {\mathrm {rig}} $
acts freely on
$G^ {\mathrm {rig}} $
acts freely on
![]() $ {\widetilde { \mathbb {T} }} $
and
$ {\widetilde { \mathbb {T} }} $
and
![]() $ {\widetilde { \mathbb {T} }} /G^ {\mathrm {rig}} = \mathbb {T} $
. The rigidification of the smooth toric DM stack
$ {\widetilde { \mathbb {T} }} /G^ {\mathrm {rig}} = \mathbb {T} $
. The rigidification of the smooth toric DM stack
![]() $\mathcal {X}$
is the toric orbifold
$\mathcal {X}$
is the toric orbifold
The coarse moduli space of the stack
![]() $\mathcal {X}$
is the simplical toric variety
$\mathcal {X}$
is the simplical toric variety
![]() $X_\Sigma $
defined by the simplicial fan
$X_\Sigma $
defined by the simplicial fan
![]() $\Sigma $
in
$\Sigma $
in
![]() $N_{\mathbb {R}} \cong \mathbb {R} ^n$
. By [Reference Fantechi, Mann and Nironi37, Theorem I], the morphism
$N_{\mathbb {R}} \cong \mathbb {R} ^n$
. By [Reference Fantechi, Mann and Nironi37, Theorem I], the morphism
![]() $\mathcal {X}\to X_\Sigma $
factors canonically via toric morphisms
$\mathcal {X}\to X_\Sigma $
factors canonically via toric morphisms
where
-
○
 $\mathcal {X}\longrightarrow \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
is a K-gerbe over
$\mathcal {X}\longrightarrow \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
is a K-gerbe over
 $\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
;
$\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
; -
○
 $\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} \longrightarrow \mathcal {X}^ {\mathrm {can}} $
is a fibred product of roots of toric divisors;
$\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} \longrightarrow \mathcal {X}^ {\mathrm {can}} $
is a fibred product of roots of toric divisors; -
○
 $\mathcal {X}^ {\mathrm {can}} \longrightarrow X_\Sigma $
is the minimal orbifold having
$\mathcal {X}^ {\mathrm {can}} \longrightarrow X_\Sigma $
is the minimal orbifold having
 $X_\Sigma $
as coarse moduli space.
$X_\Sigma $
as coarse moduli space.
Restricting equation (3) to the open substack
![]() $\mathcal {T} \subset \mathcal {X}$
, one obtains
$\mathcal {T} \subset \mathcal {X}$
, one obtains
![]() $\mathcal {T} \cong \mathbb {T} \times \mathcal {B} K \longrightarrow \mathbb {T} \longrightarrow \mathbb {T} \longrightarrow \mathbb {T} $
, where
$\mathcal {T} \cong \mathbb {T} \times \mathcal {B} K \longrightarrow \mathbb {T} \longrightarrow \mathbb {T} \longrightarrow \mathbb {T} $
, where
![]() $ \mathbb {T} \times \mathcal {B} K \longrightarrow \mathbb {T} $
is the projection to the first factor and
$ \mathbb {T} \times \mathcal {B} K \longrightarrow \mathbb {T} $
is the projection to the first factor and
![]() $ \mathbb {T} \longrightarrow \mathbb {T} $
is the identity map.
$ \mathbb {T} \longrightarrow \mathbb {T} $
is the identity map.
Remark 2.1. The purpose of introducing additional vectors
![]() $b_{r'+1},\dots , b_{r}$
is to ensure that G is connected. The stacky fan
$b_{r'+1},\dots , b_{r}$
is to ensure that G is connected. The stacky fan
![]() $\mathbf \Sigma $
together with the extra vectors
$\mathbf \Sigma $
together with the extra vectors
![]() $b_{r'+1},\dots , b_r$
is an extended stacky fan in the sense of Jiang [Reference Jiang48]. It follows from the definition that
$b_{r'+1},\dots , b_r$
is an extended stacky fan in the sense of Jiang [Reference Jiang48]. It follows from the definition that
![]() $\{r'+1,\dots , r\}\subset I$
for any
$\{r'+1,\dots , r\}\subset I$
for any
![]() $I\in \mathcal A$
.
$I\in \mathcal A$
.
Let M,
![]() $ {\widetilde {M}} $
, and
$ {\widetilde {M}} $
, and
![]() $\mathbb {L}^\vee $
be the character lattices of the tori
$\mathbb {L}^\vee $
be the character lattices of the tori
![]() $ \mathbb {T} $
,
$ \mathbb {T} $
,
![]() $ {\widetilde { \mathbb {T} }} $
and G, respectively:
$ {\widetilde { \mathbb {T} }} $
and G, respectively:
 $$ \begin{align*} M &= \mathrm{Hom}(N, \mathbb{Z} ) = \mathrm{Hom}( \mathbb{T} , \mathbb{C} ^*), \\ {\widetilde{M}} &= \mathrm{Hom}( {\widetilde{N}} , \mathbb{Z} )= \mathrm{Hom}( {\widetilde{ \mathbb{T} }} , \mathbb{C} ^*),\\ \mathbb{L}^\vee &= \mathrm{Hom}(\mathbb{L}, \mathbb{Z} ) =\mathrm{Hom}(G, \mathbb{C} ^*). \end{align*} $$
$$ \begin{align*} M &= \mathrm{Hom}(N, \mathbb{Z} ) = \mathrm{Hom}( \mathbb{T} , \mathbb{C} ^*), \\ {\widetilde{M}} &= \mathrm{Hom}( {\widetilde{N}} , \mathbb{Z} )= \mathrm{Hom}( {\widetilde{ \mathbb{T} }} , \mathbb{C} ^*),\\ \mathbb{L}^\vee &= \mathrm{Hom}(\mathbb{L}, \mathbb{Z} ) =\mathrm{Hom}(G, \mathbb{C} ^*). \end{align*} $$
Applying
![]() $\mathrm {Hom}(-, \mathbb {Z} )$
to equation (1), we obtain the following exact sequence of (additive) abelian groups:
$\mathrm {Hom}(-, \mathbb {Z} )$
to equation (1), we obtain the following exact sequence of (additive) abelian groups:
Therefore, the group homomorphism
![]() $\psi ^\vee : {\widetilde {M}} \longrightarrow \mathbb {L}^\vee $
is surjective if and only if
$\psi ^\vee : {\widetilde {M}} \longrightarrow \mathbb {L}^\vee $
is surjective if and only if
![]() $N_ {\mathrm {tor}} =0$
.
$N_ {\mathrm {tor}} =0$
.
We now consider a class of examples of 3-dimensional Calabi-Yau smooth toric DM stacks of the form
![]() $[ \mathbb {C} ^3/ \mathbb {Z} _3]$
. Let
$[ \mathbb {C} ^3/ \mathbb {Z} _3]$
. Let
![]() $\omega =e^{\frac {2\pi \sqrt {-1}}{3}}$
be the generator of
$\omega =e^{\frac {2\pi \sqrt {-1}}{3}}$
be the generator of
![]() $ \mathbb {Z} _3$
. Given
$ \mathbb {Z} _3$
. Given
![]() $i,j,k\in \{0,1,2\}$
such that
$i,j,k\in \{0,1,2\}$
such that
![]() $i+j+k\in 3 \mathbb {Z} $
, we define
$i+j+k\in 3 \mathbb {Z} $
, we define
![]() $\mathcal {X}_{i,j,k}$
to be the quotient stack of the following
$\mathcal {X}_{i,j,k}$
to be the quotient stack of the following
![]() $ \mathbb {Z} _3$
-action on
$ \mathbb {Z} _3$
-action on
![]() $ \mathbb {C} ^3$
:
$ \mathbb {C} ^3$
:
In the following example, we consider
Example 2.2.
-
1.
 $\mathcal {X}=\mathcal {X}_{1,1,1}$
(see Figure 1). The toric data are given as follows:
$\mathcal {X}=\mathcal {X}_{1,1,1}$
(see Figure 1). The toric data are given as follows:  $$ \begin{gather*} N= \mathbb{Z} ^3,\quad N_ {\mathrm{tor}} =0;\\ b_1=(1,0,1),b_2=(0,1,1),b_3=(-1,-1,1),b_4=(0,0,1);\\ r=4,r'=3,k=1;\\ \Sigma=\{\text{the}\ 3\text{-cone spanned by}\ \{b_1,b_2,b_3\},\ \text{and its faces, and faces of faces, etc.}\};\\ \mathcal{A}=\{I\subset\{1,2,3,4\}: 4\in I\};\\ \mathbb{L}\cong \mathbb{Z} ,\quad \mathbb{L}^\vee\cong \mathbb{Z} ;\\ \end{gather*} $$
$$ \begin{gather*} N= \mathbb{Z} ^3,\quad N_ {\mathrm{tor}} =0;\\ b_1=(1,0,1),b_2=(0,1,1),b_3=(-1,-1,1),b_4=(0,0,1);\\ r=4,r'=3,k=1;\\ \Sigma=\{\text{the}\ 3\text{-cone spanned by}\ \{b_1,b_2,b_3\},\ \text{and its faces, and faces of faces, etc.}\};\\ \mathcal{A}=\{I\subset\{1,2,3,4\}: 4\in I\};\\ \mathbb{L}\cong \mathbb{Z} ,\quad \mathbb{L}^\vee\cong \mathbb{Z} ;\\ \end{gather*} $$

Figure 1
 $\mathcal {X}_{1,1,1}$
and its crepant resolution
$\mathcal {X}_{1,1,1}$
and its crepant resolution
 $\mathcal {O}_{ \mathbb {P} ^2}(-3)$
.
$\mathcal {O}_{ \mathbb {P} ^2}(-3)$
. -
2.
 $\mathcal {X}=\mathcal {X}_{1,2,0}$
, transversal
$\mathcal {X}=\mathcal {X}_{1,2,0}$
, transversal
 $A_2$
-singularity (see Figure 2). The toric data are given as follows:
$A_2$
-singularity (see Figure 2). The toric data are given as follows:  $$ \begin{gather*} N= \mathbb{Z} ^3,\quad N_ {\mathrm{tor}} =0;\\ b_1=(1,0,1),b_2=(0,3,1),b_3=(0,0,1),b_4=(0,1,1), b_5=(0,2,1);\\ r=5,r'=3,k=2;\\ \Sigma=\{\text{the}\ 3\text{-cone spanned by}\ \{b_1,b_2,b_3\},\ \text{and its faces, and faces of faces, etc.}\};\\ \mathcal{A}=\{I\subset\{1,2,3,4,5\}: \{ 4, 5\} \subset I \};\\ \mathbb{L}\cong \mathbb{Z} ^2,\quad \mathbb{L}^\vee\cong \mathbb{Z} ^2. \end{gather*} $$
$$ \begin{gather*} N= \mathbb{Z} ^3,\quad N_ {\mathrm{tor}} =0;\\ b_1=(1,0,1),b_2=(0,3,1),b_3=(0,0,1),b_4=(0,1,1), b_5=(0,2,1);\\ r=5,r'=3,k=2;\\ \Sigma=\{\text{the}\ 3\text{-cone spanned by}\ \{b_1,b_2,b_3\},\ \text{and its faces, and faces of faces, etc.}\};\\ \mathcal{A}=\{I\subset\{1,2,3,4,5\}: \{ 4, 5\} \subset I \};\\ \mathbb{L}\cong \mathbb{Z} ^2,\quad \mathbb{L}^\vee\cong \mathbb{Z} ^2. \end{gather*} $$

Figure 2
 $\mathcal {X}_{1,2,0}$
and its (partial) crepant resolutions.
$\mathcal {X}_{1,2,0}$
and its (partial) crepant resolutions. -
3.
 $\mathcal {X}=\mathcal {X}_{0,0,0}$
. The toric data is given as follows:
$\mathcal {X}=\mathcal {X}_{0,0,0}$
. The toric data is given as follows:  $$ \begin{gather*} N= \mathbb{Z} ^3\oplus \mathbb{Z} _3 \quad N_ {\mathrm{tor}} = \mathbb{Z} _3;\\ b_1=(1,0,0,0),b_2=(0,1,0,0),b_3=(0,0,1,0),b_4=(1,0,0,1);\\ r=4,r'=3,k=1;\\ \Sigma=\{\text{the}\ 3\text{-cone spanned by}\ \{b_1,b_2,b_3\},\ \text{and its faces, and faces of faces, etc.}\};\\ \mathcal{A}=\{I\subset\{1,2,3,4\}: 4\in I \};\\ \mathbb{L}\cong \mathbb{Z} ,\quad \mathbb{L}^\vee\cong \mathbb{Z}. \end{gather*} $$
$$ \begin{gather*} N= \mathbb{Z} ^3\oplus \mathbb{Z} _3 \quad N_ {\mathrm{tor}} = \mathbb{Z} _3;\\ b_1=(1,0,0,0),b_2=(0,1,0,0),b_3=(0,0,1,0),b_4=(1,0,0,1);\\ r=4,r'=3,k=1;\\ \Sigma=\{\text{the}\ 3\text{-cone spanned by}\ \{b_1,b_2,b_3\},\ \text{and its faces, and faces of faces, etc.}\};\\ \mathcal{A}=\{I\subset\{1,2,3,4\}: 4\in I \};\\ \mathbb{L}\cong \mathbb{Z} ,\quad \mathbb{L}^\vee\cong \mathbb{Z}. \end{gather*} $$
2.2 Equivariant line bundles and torus-invariant Cartier divisors
A character
![]() $\chi \in {\widetilde {M}} $
gives a
$\chi \in {\widetilde {M}} $
gives a
![]() $ {\widetilde { \mathbb {T} }} $
-action on
$ {\widetilde { \mathbb {T} }} $
-action on
![]() $ \mathbb {C} ^r \times \mathbb {C} $
by
$ \mathbb {C} ^r \times \mathbb {C} $
by
where
Therefore
![]() $ \mathbb {C} ^r\times \mathbb {C} $
can be viewed as the total space of a
$ \mathbb {C} ^r\times \mathbb {C} $
can be viewed as the total space of a
![]() $ {\widetilde { \mathbb {T} }} $
-equivariant line bundle
$ {\widetilde { \mathbb {T} }} $
-equivariant line bundle
![]() $ {\widetilde {L}} _\chi $
over
$ {\widetilde {L}} _\chi $
over
![]() $ \mathbb {C} ^r$
. If
$ \mathbb {C} ^r$
. If
 $$ \begin{align*}\chi(\tilde{t}_1,\ldots, \tilde{t}_r) =\prod_{i=1}^r \tilde{t}_i^{c_i}, \end{align*} $$
$$ \begin{align*}\chi(\tilde{t}_1,\ldots, \tilde{t}_r) =\prod_{i=1}^r \tilde{t}_i^{c_i}, \end{align*} $$
where
![]() $c_1,\ldots , c_r\in \mathbb {Z} $
, then
$c_1,\ldots , c_r\in \mathbb {Z} $
, then
 $$ \begin{align*}{\widetilde{L}} _{\chi}= \mathcal{O}_{ \mathbb{C} ^r}(\sum_{i=1}^r c_i {\widetilde{\mathcal{D}}}_i), \end{align*} $$
$$ \begin{align*}{\widetilde{L}} _{\chi}= \mathcal{O}_{ \mathbb{C} ^r}(\sum_{i=1}^r c_i {\widetilde{\mathcal{D}}}_i), \end{align*} $$
where
![]() $ {\widetilde {\mathcal {D}}}_i$
is the
$ {\widetilde {\mathcal {D}}}_i$
is the
![]() $ {\widetilde { \mathbb {T} }} $
-divisor in
$ {\widetilde { \mathbb {T} }} $
-divisor in
![]() $ \mathbb {C} ^r$
defined by
$ \mathbb {C} ^r$
defined by
![]() $Z_i=0$
. We have
$Z_i=0$
. We have
where the first isomorphism is given by
![]() $\chi \mapsto {\widetilde {L}} _\chi $
and the second isomorphism is given by the
$\chi \mapsto {\widetilde {L}} _\chi $
and the second isomorphism is given by the
![]() $ {\widetilde { \mathbb {T} }} $
-equivariant first Chern class
$ {\widetilde { \mathbb {T} }} $
-equivariant first Chern class
![]() $(c_1)_{ {\widetilde { \mathbb {T} }} }$
. Define
$(c_1)_{ {\widetilde { \mathbb {T} }} }$
. Define
Then
![]() $\{ D_1^{\mathcal {T}},\ldots , D_r^{\mathcal {T}} \}$
is a
$\{ D_1^{\mathcal {T}},\ldots , D_r^{\mathcal {T}} \}$
is a
![]() $ \mathbb {Z} $
-basis of
$ \mathbb {Z} $
-basis of
![]() $H^2_{ {\widetilde { \mathbb {T} }} }( \mathbb {C} ^r; \mathbb {Z} )\cong {\widetilde {M}} $
dual to the
$H^2_{ {\widetilde { \mathbb {T} }} }( \mathbb {C} ^r; \mathbb {Z} )\cong {\widetilde {M}} $
dual to the
![]() $ \mathbb {Z} $
-basis
$ \mathbb {Z} $
-basis
![]() $\{ {\tilde {b}} _1,\ldots , {\tilde {b}} _r\}$
of
$\{ {\tilde {b}} _1,\ldots , {\tilde {b}} _r\}$
of
![]() $ {\widetilde {N}} $
. We have a commutative diagram
$ {\widetilde {N}} $
. We have a commutative diagram

where
![]() $\iota _{\mathcal {T}}^*$
is a surjective group homomorphism induced by the inclusion
$\iota _{\mathcal {T}}^*$
is a surjective group homomorphism induced by the inclusion
![]() $\iota : U_{\mathcal {A}}\hookrightarrow \mathbb {C} ^r$
, and
$\iota : U_{\mathcal {A}}\hookrightarrow \mathbb {C} ^r$
, and
 $$ \begin{align*}\mathrm{Ker}(\iota_{\mathcal{T}}^*)= \bigoplus_{i=r'+1}^r \mathbb{Z} D_i^{\mathcal{T}}. \end{align*} $$
$$ \begin{align*}\mathrm{Ker}(\iota_{\mathcal{T}}^*)= \bigoplus_{i=r'+1}^r \mathbb{Z} D_i^{\mathcal{T}}. \end{align*} $$
Therefore,
Let
![]() $\bar {D}_i^{\mathcal {T}} := \iota _{\mathcal {T}}^* D_i^{\mathcal {T}}$
. Then
$\bar {D}_i^{\mathcal {T}} := \iota _{\mathcal {T}}^* D_i^{\mathcal {T}}$
. Then
and
 $$ \begin{align*}H^2_{\mathcal{T}}(\mathcal{X}; \mathbb{Z} ) = \bigoplus_{i=1}^{r'} \mathbb{Z} \bar{D}^{\mathcal{T}}_i \cong \mathbb{Z} ^{r'}. \end{align*} $$
$$ \begin{align*}H^2_{\mathcal{T}}(\mathcal{X}; \mathbb{Z} ) = \bigoplus_{i=1}^{r'} \mathbb{Z} \bar{D}^{\mathcal{T}}_i \cong \mathbb{Z} ^{r'}. \end{align*} $$
For
![]() $i=1,\ldots ,r'$
,
$i=1,\ldots ,r'$
,
![]() $ {\widetilde {\mathcal {D}}}_i\cap U_{\mathcal {A}}$
is a
$ {\widetilde {\mathcal {D}}}_i\cap U_{\mathcal {A}}$
is a
![]() $ {\widetilde { \mathbb {T} }} $
-divisor in
$ {\widetilde { \mathbb {T} }} $
-divisor in
![]() $U_{\mathcal {A}}$
, and it descends to a
$U_{\mathcal {A}}$
, and it descends to a
![]() $ \mathbb {T} $
-divisor
$ \mathbb {T} $
-divisor
![]() $\mathcal {D}_i$
in
$\mathcal {D}_i$
in
![]() $\mathcal {X}$
. We have
$\mathcal {X}$
. We have
For
![]() $i=r'+1,\ldots , r$
,
$i=r'+1,\ldots , r$
,
![]() $ {\widetilde {\mathcal {D}}}_i\cap U_{\mathcal {A}}$
is empty, so it is the zero
$ {\widetilde {\mathcal {D}}}_i\cap U_{\mathcal {A}}$
is empty, so it is the zero
![]() $ {\widetilde { \mathbb {T} }} $
-divisor.
$ {\widetilde { \mathbb {T} }} $
-divisor.
2.3 Line bundles and Cartier divisors
We have group isomorphisms
where the first isomorphism is given by
![]() $\chi \in \mathbb {L}^\vee =\mathrm {Hom}(G, \mathbb {C} ^*)\mapsto {\widetilde {L}} _\chi $
and the second isomorphism is given by the G-equivariant first Chern class
$\chi \in \mathbb {L}^\vee =\mathrm {Hom}(G, \mathbb {C} ^*)\mapsto {\widetilde {L}} _\chi $
and the second isomorphism is given by the G-equivariant first Chern class
![]() $(c_1)_G$
. We have a commutative diagram
$(c_1)_G$
. We have a commutative diagram

where
![]() $\iota ^*$
is a surjective group homomorphism induced by the inclusion
$\iota ^*$
is a surjective group homomorphism induced by the inclusion
![]() $\iota : U_{\mathcal {A}}\hookrightarrow \mathbb {C} ^r$
. The surjective map
$\iota : U_{\mathcal {A}}\hookrightarrow \mathbb {C} ^r$
. The surjective map
![]() $H^2_G( \mathbb {C} ^r; \mathbb {Z} )\to H^2(\mathcal {X}; \mathbb {Z} )$
is the restriction of the Kirwan map
$H^2_G( \mathbb {C} ^r; \mathbb {Z} )\to H^2(\mathcal {X}; \mathbb {Z} )$
is the restriction of the Kirwan map
Define
Then
 $$ \begin{align*}\mathrm{Ker}(\iota^*)= \bigoplus_{i=r'+1}^r \mathbb{Z} D_i. \end{align*} $$
$$ \begin{align*}\mathrm{Ker}(\iota^*)= \bigoplus_{i=r'+1}^r \mathbb{Z} D_i. \end{align*} $$
Therefore,
Recall that
![]() $\psi ^\vee : {\widetilde {M}} \longrightarrow \mathbb {L}^\vee $
is surjective if and only if
$\psi ^\vee : {\widetilde {M}} \longrightarrow \mathbb {L}^\vee $
is surjective if and only if
![]() $N_ {\mathrm {tor}} =0$
. Let
$N_ {\mathrm {tor}} =0$
. Let
The map
given by
is surjective if and only if
![]() $N_ {\mathrm {tor}} =0$
. In general,
$N_ {\mathrm {tor}} =0$
. In general,
![]() $\mathrm {Coker}(\psi ^\vee )\cong \mathrm {Coker}(\bar {\psi }^\vee )$
is a finite abelian group.
$\mathrm {Coker}(\psi ^\vee )\cong \mathrm {Coker}(\bar {\psi }^\vee )$
is a finite abelian group.
Pick a
![]() $ \mathbb {Z} $
-basis
$ \mathbb {Z} $
-basis
![]() $\{e_1,\ldots , e_k\}$
of
$\{e_1,\ldots , e_k\}$
of
![]() $\mathbb {L}\cong \mathbb {Z} ^k$
, and let
$\mathbb {L}\cong \mathbb {Z} ^k$
, and let
![]() $\{e_1^\vee ,\ldots , e_k^\vee \}$
be the dual
$\{e_1^\vee ,\ldots , e_k^\vee \}$
be the dual
![]() $ \mathbb {Z} $
-basis of
$ \mathbb {Z} $
-basis of
![]() $\mathbb {L}^\vee $
. For each
$\mathbb {L}^\vee $
. For each
![]() $a\in \{1,\ldots ,k\}$
, we define a charge vector
$a\in \{1,\ldots ,k\}$
, we define a charge vector
by
 $$ \begin{align*}\psi(e_a)=\sum_{i=1}^r l^{(a)}_i {\tilde{b}} _i, \end{align*} $$
$$ \begin{align*}\psi(e_a)=\sum_{i=1}^r l^{(a)}_i {\tilde{b}} _i, \end{align*} $$
where
![]() $\psi : \mathbb {L} \longrightarrow {\widetilde {N}} $
is the inclusion map. Then
$\psi : \mathbb {L} \longrightarrow {\widetilde {N}} $
is the inclusion map. Then
 $$ \begin{align*}D_i=\psi^\vee(D_i^{\mathcal{T}})=\sum_{a=1}^k l^{(a)}_i e_a^\vee,\quad i=1,\ldots,r, \end{align*} $$
$$ \begin{align*}D_i=\psi^\vee(D_i^{\mathcal{T}})=\sum_{a=1}^k l^{(a)}_i e_a^\vee,\quad i=1,\ldots,r, \end{align*} $$
and
 $$ \begin{align*}\sum_{i=1}^r l^{(a)}_{i} b_{i} = \phi\circ \psi(e_a)=0,\quad a=1,\ldots, k. \end{align*} $$
$$ \begin{align*}\sum_{i=1}^r l^{(a)}_{i} b_{i} = \phi\circ \psi(e_a)=0,\quad a=1,\ldots, k. \end{align*} $$
Example 2.3. We use the notation in Example 2.2.
-
1.
 $\mathcal {X}=\mathcal {X}_{1,1,1}$
.
$\mathcal {X}=\mathcal {X}_{1,1,1}$
.  $$ \begin{gather*} D_1=D_2=D_3=1,\ D_4=-3;\\ l^{(1)}=(1,1,1,-3);\\ {\mathrm{Pic}} _{\mathcal{T}}(\mathcal{X})\cong \mathbb{Z} ^3,\quad {\mathrm{Pic}} (\mathcal{X})\cong \mathbb{Z} /3 \mathbb{Z}; \end{gather*} $$
$$ \begin{gather*} D_1=D_2=D_3=1,\ D_4=-3;\\ l^{(1)}=(1,1,1,-3);\\ {\mathrm{Pic}} _{\mathcal{T}}(\mathcal{X})\cong \mathbb{Z} ^3,\quad {\mathrm{Pic}} (\mathcal{X})\cong \mathbb{Z} /3 \mathbb{Z}; \end{gather*} $$
-
2.
 $\mathcal {X}=\mathcal {X}_{1,2,0}$
.
$\mathcal {X}=\mathcal {X}_{1,2,0}$
.  $$ \begin{gather*} D_1=(0,0),\ D_2= (0,1),\ D_3=(1,0),\ D_4=(-2,1),\ D_5=(1,-2);\\ l^{(1)}=(0,0,1,-2,1),\ l^{(2)}= (0,1,0,1,-2);\\ {\mathrm{Pic}} _{\mathcal{T}}(\mathcal{X})= \mathbb{Z} ^3,\quad {\mathrm{Pic}} (\mathcal{X}) = \mathbb{Z} ^2 \big/ \big( \mathbb{Z} (-2,1)\oplus \mathbb{Z} (1,-2)\big) \cong \mathbb{Z} /3 \mathbb{Z}. \end{gather*} $$
$$ \begin{gather*} D_1=(0,0),\ D_2= (0,1),\ D_3=(1,0),\ D_4=(-2,1),\ D_5=(1,-2);\\ l^{(1)}=(0,0,1,-2,1),\ l^{(2)}= (0,1,0,1,-2);\\ {\mathrm{Pic}} _{\mathcal{T}}(\mathcal{X})= \mathbb{Z} ^3,\quad {\mathrm{Pic}} (\mathcal{X}) = \mathbb{Z} ^2 \big/ \big( \mathbb{Z} (-2,1)\oplus \mathbb{Z} (1,-2)\big) \cong \mathbb{Z} /3 \mathbb{Z}. \end{gather*} $$
-
3.
 $\mathcal {X}=\mathcal {X}_{0,0,0}$
.
$\mathcal {X}=\mathcal {X}_{0,0,0}$
.  $$ \begin{gather*} D_1=3,\ D_2= 0 ,\ D_3= 0,\ D_4=-3;\\ l^{(1)}=(3,0,0,-3);\\ {\mathrm{Pic}} _{\mathcal{T}}(\mathcal{X})= \mathbb{Z} ^3,\quad {\mathrm{Pic}} (\mathcal{X}) = \mathbb{Z} /3 \mathbb{Z}. \end{gather*} $$
$$ \begin{gather*} D_1=3,\ D_2= 0 ,\ D_3= 0,\ D_4=-3;\\ l^{(1)}=(3,0,0,-3);\\ {\mathrm{Pic}} _{\mathcal{T}}(\mathcal{X})= \mathbb{Z} ^3,\quad {\mathrm{Pic}} (\mathcal{X}) = \mathbb{Z} /3 \mathbb{Z}. \end{gather*} $$
2.4 Torus invariant subvarieties and their generic stabilisers
Let
![]() $\Sigma (d)$
be the set of d-dimensional cones. For each
$\Sigma (d)$
be the set of d-dimensional cones. For each
![]() $ {\sigma } \in \Sigma (d)$
, we define
$ {\sigma } \in \Sigma (d)$
, we define
Then
![]() $|I_ {\sigma } '|=d$
and
$|I_ {\sigma } '|=d$
and
![]() $|I_ {\sigma } |=r-d$
. Let
$|I_ {\sigma } |=r-d$
. Let
![]() $\tilde {V}( {\sigma } )\subset U_{\mathcal {A}}$
be the closed subvariety defined by the ideal of
$\tilde {V}( {\sigma } )\subset U_{\mathcal {A}}$
be the closed subvariety defined by the ideal of
![]() $ \mathbb {C} [Z_1,\ldots , Z_r]$
generated by
$ \mathbb {C} [Z_1,\ldots , Z_r]$
generated by
Then
![]() $\mathcal {V}( {\sigma } ) := [ {\widetilde {V}} ( {\sigma } )/G]$
is an
$\mathcal {V}( {\sigma } ) := [ {\widetilde {V}} ( {\sigma } )/G]$
is an
![]() $(n-d)$
-dimensional
$(n-d)$
-dimensional
![]() $\mathcal {T}$
-invariant closed substack of
$\mathcal {T}$
-invariant closed substack of
![]() $\mathcal {X}= [U_{\mathcal {A}}/G]$
.
$\mathcal {X}= [U_{\mathcal {A}}/G]$
.
The group homomorphism
![]() $G\cong ( \mathbb {C} ^*)^k \longrightarrow {\widetilde { \mathbb {T} }} \cong ( \mathbb {C} ^*)^r$
is given by
$G\cong ( \mathbb {C} ^*)^k \longrightarrow {\widetilde { \mathbb {T} }} \cong ( \mathbb {C} ^*)^r$
is given by
where
![]() $\chi _i\in \mathrm {Hom}(G, \mathbb {C} ^*)=\mathbb {L}^\vee $
is given by
$\chi _i\in \mathrm {Hom}(G, \mathbb {C} ^*)=\mathbb {L}^\vee $
is given by
 $$ \begin{align*}\chi_i(u_1,\ldots, u_k)= \prod_{a=1}^k u_a^{ l_i^{(a)} }. \end{align*} $$
$$ \begin{align*}\chi_i(u_1,\ldots, u_k)= \prod_{a=1}^k u_a^{ l_i^{(a)} }. \end{align*} $$
Let
Then
![]() $G_ {\sigma } $
is the generic stabiliser of
$G_ {\sigma } $
is the generic stabiliser of
![]() $\mathcal {V}( {\sigma } )$
. It is a finite subgroup of G. If
$\mathcal {V}( {\sigma } )$
. It is a finite subgroup of G. If
![]() $\tau \subset {\sigma } $
, then
$\tau \subset {\sigma } $
, then
![]() $I_ {\sigma } \subset I_\tau $
, so
$I_ {\sigma } \subset I_\tau $
, so
![]() $G_\tau \subset G_ {\sigma } $
. There are two special cases:
$G_\tau \subset G_ {\sigma } $
. There are two special cases:
-
○ Let
 $\{0\}$
be the unique 0-dimensional cone. Then
$\{0\}$
be the unique 0-dimensional cone. Then
 $G_{\{0\}}=K$
is the generic stabiliser of
$G_{\{0\}}=K$
is the generic stabiliser of
 $\mathcal {V}(\{0\})=\mathcal {X}$
.
$\mathcal {V}(\{0\})=\mathcal {X}$
. -
○ If
 $ {\sigma } \in \Sigma (n)$
, where
$ {\sigma } \in \Sigma (n)$
, where
 $n=\dim _{\mathbb {C}} \mathcal {X}$
, then
$n=\dim _{\mathbb {C}} \mathcal {X}$
, then
 $\mathfrak {p}_ {\sigma } := \mathcal {V}( {\sigma } )$
is a
$\mathfrak {p}_ {\sigma } := \mathcal {V}( {\sigma } )$
is a
 $\mathcal {T}$
-fixed point in
$\mathcal {T}$
-fixed point in
 $\mathcal {X}$
, and
$\mathcal {X}$
, and
 $\mathfrak {p}_ {\sigma } =\mathcal {B} G_ {\sigma } $
.
$\mathfrak {p}_ {\sigma } =\mathcal {B} G_ {\sigma } $
.
Example 2.4. We use the notation in Example 2.2. Let
![]() $ {\sigma } \subset N_{\mathbb {R}} \cong \mathbb {R} ^3$
denote the 3-dimensional cone spanned by
$ {\sigma } \subset N_{\mathbb {R}} \cong \mathbb {R} ^3$
denote the 3-dimensional cone spanned by
![]() $\bar {b}_1,\bar {b}_2,\bar {b}_3$
. For
$\bar {b}_1,\bar {b}_2,\bar {b}_3$
. For
![]() $j=1,2,3$
, let
$j=1,2,3$
, let
![]() $\tau _j$
denote the 2-dimensional cone in
$\tau _j$
denote the 2-dimensional cone in
![]() $N_{\mathbb {R}} $
spanned by
$N_{\mathbb {R}} $
spanned by
![]() $\{\bar {b}_i: i\in \{1,2,3\}-\{j\}\}$
.
$\{\bar {b}_i: i\in \{1,2,3\}-\{j\}\}$
.
-
1.
 $\mathcal {X}=\mathcal {X}_{1,1,1}$
:
$\mathcal {X}=\mathcal {X}_{1,1,1}$
:
 $G_ {\sigma } = \mathbb {Z} _3,\quad G_{\tau _1}=G_{\tau _2}=G_{\tau _3}=\{1\}$
.
$G_ {\sigma } = \mathbb {Z} _3,\quad G_{\tau _1}=G_{\tau _2}=G_{\tau _3}=\{1\}$
. -
2.
 $\mathcal {X}=\mathcal {X}_{1,2,0}$
:
$\mathcal {X}=\mathcal {X}_{1,2,0}$
:
 $G_ {\sigma } = \mathbb {Z} _3 = G_{\tau _3}, \quad G_{\tau _1}=G_{\tau _2}=\{1\}$
.
$G_ {\sigma } = \mathbb {Z} _3 = G_{\tau _3}, \quad G_{\tau _1}=G_{\tau _2}=\{1\}$
. -
3.
 $\mathcal {X}=\mathcal {X}_{0,0,0}$
:
$\mathcal {X}=\mathcal {X}_{0,0,0}$
:
 $G_ {\sigma } = \mathbb {Z} _3 = G_{\tau _1}=G_{\tau _2}=G_{\tau _3}$
.
$G_ {\sigma } = \mathbb {Z} _3 = G_{\tau _1}=G_{\tau _2}=G_{\tau _3}$
.
Define the set of flags in
![]() $\Sigma $
to be
$\Sigma $
to be
Given
![]() $(\tau , {\sigma } )\in F(\Sigma )$
, let
$(\tau , {\sigma } )\in F(\Sigma )$
, let
![]() $\mathfrak {l}_\tau :=\mathcal {V}(\tau )$
be the 1-dimensional
$\mathfrak {l}_\tau :=\mathcal {V}(\tau )$
be the 1-dimensional
![]() $\mathcal {T}$
-invariant subvariety of
$\mathcal {T}$
-invariant subvariety of
![]() $\mathcal {X}$
. Then
$\mathcal {X}$
. Then
![]() $\mathfrak {p}_ {\sigma } $
is contained in
$\mathfrak {p}_ {\sigma } $
is contained in
![]() $\mathfrak {l}_\tau $
. There is a unique
$\mathfrak {l}_\tau $
. There is a unique
![]() $i\in \{1,\ldots , r'\}$
such that
$i\in \{1,\ldots , r'\}$
such that
![]() $i\in I^{\prime }_ {\sigma } \setminus I^{\prime }_\tau $
. The representation of
$i\in I^{\prime }_ {\sigma } \setminus I^{\prime }_\tau $
. The representation of
![]() $G_ {\sigma } $
on the tangent line
$G_ {\sigma } $
on the tangent line
![]() $T_{\mathfrak {p}_ {\sigma } }\mathfrak {l}_\tau $
to
$T_{\mathfrak {p}_ {\sigma } }\mathfrak {l}_\tau $
to
![]() $\mathfrak {l}_\tau $
at the stacky point
$\mathfrak {l}_\tau $
at the stacky point
![]() $\mathfrak {p}_ {\sigma } $
is given by
$\mathfrak {p}_ {\sigma } $
is given by
![]() $\chi _{(\tau , {\sigma } )}:= \chi _i|_{G_ {\sigma } }: G_ {\sigma } \to \mathbb {C} ^*$
. The image
$\chi _{(\tau , {\sigma } )}:= \chi _i|_{G_ {\sigma } }: G_ {\sigma } \to \mathbb {C} ^*$
. The image
![]() $\chi _i(G_ {\sigma } ) \subset \mathbb {C} ^*$
is a cyclic subgroup of
$\chi _i(G_ {\sigma } ) \subset \mathbb {C} ^*$
is a cyclic subgroup of
![]() $ \mathbb {C} ^*$
; we define the order of this group to be
$ \mathbb {C} ^*$
; we define the order of this group to be
![]() $r(\tau , {\sigma } )$
. Then there is a short exact sequence of finite abelian groups:
$r(\tau , {\sigma } )$
. Then there is a short exact sequence of finite abelian groups:
where
![]() $\boldsymbol {\mu }_a=\{ z\in \mathbb {C} ^*\mid z^a=1\}$
is the group of ath roots of unity.
$\boldsymbol {\mu }_a=\{ z\in \mathbb {C} ^*\mid z^a=1\}$
is the group of ath roots of unity.
2.5 The extended nef cone and the extended Mori cone
In this paragraph,
![]() $ \mathbb {F} = \mathbb {Q} $
,
$ \mathbb {F} = \mathbb {Q} $
,
![]() $ \mathbb {R} $
or
$ \mathbb {R} $
or
![]() $ \mathbb {C} $
. Given a finitely generated abelian group
$ \mathbb {C} $
. Given a finitely generated abelian group
![]() $\Lambda $
with
$\Lambda $
with
![]() $\Lambda /\Lambda _ {\mathrm {tor}} \cong \mathbb {Z} ^m$
, define
$\Lambda /\Lambda _ {\mathrm {tor}} \cong \mathbb {Z} ^m$
, define
![]() $\Lambda _{\mathbb {F}} = \Lambda \otimes _{\mathbb {Z}} \mathbb {F} \cong \mathbb {F} ^m$
. We have the following short exact sequences of vector spaces:
$\Lambda _{\mathbb {F}} = \Lambda \otimes _{\mathbb {Z}} \mathbb {F} \cong \mathbb {F} ^m$
. We have the following short exact sequences of vector spaces:
 $$ \begin{align*} & 0\to \mathbb{L}_{\mathbb{F}} \to {\widetilde{N}} _{\mathbb{F}} \to N_{\mathbb{F}} \to 0,\\ & 0\to M_{\mathbb{F}} \to {\widetilde{M}} _{\mathbb{F}} \to \mathbb{L}^\vee_{\mathbb{F}} \to 0. \end{align*} $$
$$ \begin{align*} & 0\to \mathbb{L}_{\mathbb{F}} \to {\widetilde{N}} _{\mathbb{F}} \to N_{\mathbb{F}} \to 0,\\ & 0\to M_{\mathbb{F}} \to {\widetilde{M}} _{\mathbb{F}} \to \mathbb{L}^\vee_{\mathbb{F}} \to 0. \end{align*} $$
We also have the following isomorphisms of vector spaces over
![]() $ \mathbb {F} $
:
$ \mathbb {F} $
:
 $$ \begin{align*} & H^2(\mathcal{X}; \mathbb{F} )\cong H^2(X; \mathbb{F} ) \cong \mathbb{L}^\vee_{\mathbb{F}} /\oplus_{i=r'+1}^r \mathbb{F} D_i,\\ & H^2_{\mathcal{T}}(\mathcal{X}; \mathbb{F} ) \cong H^2_{\mathbb{T}} (X; \mathbb{F} ) \cong {\widetilde{M}} _{\mathbb{F}} /\oplus_{i=r'+1}^r \mathbb{F} D_i^{\mathcal{T}}, \end{align*} $$
$$ \begin{align*} & H^2(\mathcal{X}; \mathbb{F} )\cong H^2(X; \mathbb{F} ) \cong \mathbb{L}^\vee_{\mathbb{F}} /\oplus_{i=r'+1}^r \mathbb{F} D_i,\\ & H^2_{\mathcal{T}}(\mathcal{X}; \mathbb{F} ) \cong H^2_{\mathbb{T}} (X; \mathbb{F} ) \cong {\widetilde{M}} _{\mathbb{F}} /\oplus_{i=r'+1}^r \mathbb{F} D_i^{\mathcal{T}}, \end{align*} $$
where X is the coarse moduli space of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
From now on, we assume all the maximal cones in
![]() $\Sigma $
are n-dimensional, where
$\Sigma $
are n-dimensional, where
![]() $n=\dim _{\mathbb {C}} \mathcal {X}$
. Given a maximal cone
$n=\dim _{\mathbb {C}} \mathcal {X}$
. Given a maximal cone
![]() $ {\sigma } \in \Sigma (n)$
, we define
$ {\sigma } \in \Sigma (n)$
, we define
Then
![]() $\mathbb {K}_ {\sigma } ^\vee $
is a sublattice of
$\mathbb {K}_ {\sigma } ^\vee $
is a sublattice of
![]() $\mathbb {L}^\vee $
of finite index. We define the extended
$\mathbb {L}^\vee $
of finite index. We define the extended
![]() $ {\sigma } $
-nef cone to be
$ {\sigma } $
-nef cone to be
which is a k-dimensional cone in
![]() $\mathbb {L}^\vee _{\mathbb {R}} \cong \mathbb {R} ^k$
. The extended nef cone of the extended stacky fan
$\mathbb {L}^\vee _{\mathbb {R}} \cong \mathbb {R} ^k$
. The extended nef cone of the extended stacky fan
![]() $(\Sigma ,b_1,\ldots , b_r)$
is
$(\Sigma ,b_1,\ldots , b_r)$
is
The extended
![]() $ {\sigma } $
-Kähler cone
$ {\sigma } $
-Kähler cone
![]() $ {\widetilde {C}} _ {\sigma } $
is defined to be the interior of
$ {\widetilde {C}} _ {\sigma } $
is defined to be the interior of
![]() $\widetilde { {\mathrm {Nef}} }_ {\sigma } $
; the extended Kähler cone of
$\widetilde { {\mathrm {Nef}} }_ {\sigma } $
; the extended Kähler cone of
![]() $\mathcal {X}$
,
$\mathcal {X}$
,
![]() $ {\widetilde {C}} _{\mathcal {X}}$
, is defined to be the interior of the extended nef cone
$ {\widetilde {C}} _{\mathcal {X}}$
, is defined to be the interior of the extended nef cone
![]() $\widetilde { {\mathrm {Nef}} }_{\mathcal {X}}$
.
$\widetilde { {\mathrm {Nef}} }_{\mathcal {X}}$
.
Let
![]() $\mathbb {K}_ {\sigma } $
be the dual lattice of
$\mathbb {K}_ {\sigma } $
be the dual lattice of
![]() $\mathbb {K}_ {\sigma } ^\vee $
; it can be viewed as an additive subgroup of
$\mathbb {K}_ {\sigma } ^\vee $
; it can be viewed as an additive subgroup of
![]() $\mathbb {L}_{\mathbb {Q}} $
:
$\mathbb {L}_{\mathbb {Q}} $
:
where
![]() $\langle -, -\rangle $
is the natural pairing between
$\langle -, -\rangle $
is the natural pairing between
![]() $\mathbb {L}^\vee _{\mathbb {Q}} $
and
$\mathbb {L}^\vee _{\mathbb {Q}} $
and
![]() $\mathbb {L}_{\mathbb {Q}} $
. Define
$\mathbb {L}_{\mathbb {Q}} $
. Define
Then
![]() $\mathbb {K}$
is a subset (which is not necessarily a subgroup) of
$\mathbb {K}$
is a subset (which is not necessarily a subgroup) of
![]() $\mathbb {L}_{\mathbb {Q}} $
, and
$\mathbb {L}_{\mathbb {Q}} $
, and
![]() $\mathbb {L}\subset \mathbb {K}$
.
$\mathbb {L}\subset \mathbb {K}$
.
We define the extended
![]() $ {\sigma } $
-Mori cone
$ {\sigma } $
-Mori cone
![]() $\widetilde { {\mathrm {NE}} }_ {\sigma } \subset \mathbb {L}_{\mathbb {R}} $
to be the dual cone of
$\widetilde { {\mathrm {NE}} }_ {\sigma } \subset \mathbb {L}_{\mathbb {R}} $
to be the dual cone of
![]() $\widetilde { {\mathrm {Nef}} }_ {\sigma } \subset \mathbb {L}_{\mathbb {R}} ^\vee $
:
$\widetilde { {\mathrm {Nef}} }_ {\sigma } \subset \mathbb {L}_{\mathbb {R}} ^\vee $
:
It is a k-dimensional cone in
![]() $\mathbb {L}_{\mathbb {R}} $
. The extended Mori cone of the extended stacky fan
$\mathbb {L}_{\mathbb {R}} $
. The extended Mori cone of the extended stacky fan
![]() $(\Sigma ,b_1,\ldots , b_r)$
is
$(\Sigma ,b_1,\ldots , b_r)$
is
Finally, we define
Example 2.5.
-
1.
 $\mathcal {X}=\mathcal {X}_{1,1,1}$
(see Figure 3).
$\mathcal {X}=\mathcal {X}_{1,1,1}$
(see Figure 3).  $$ \begin{gather*} \mathbb{K}^\vee \cong 3 \mathbb{Z} , \quad \widetilde{ {\mathrm{Nef}} }_{\mathcal{X}}= \mathbb{R} _{\leq 0};\\ \mathbb{K} \cong \frac{1}{3} \mathbb{Z} , \quad \widetilde{ {\mathrm{NE}} }_{\mathcal{X}}= \mathbb{R} _{\leq 0},\quad \mathbb{K}_{\mathrm{eff}}=\frac{1}{3} \mathbb{Z} _{\leq 0}. \end{gather*} $$
$$ \begin{gather*} \mathbb{K}^\vee \cong 3 \mathbb{Z} , \quad \widetilde{ {\mathrm{Nef}} }_{\mathcal{X}}= \mathbb{R} _{\leq 0};\\ \mathbb{K} \cong \frac{1}{3} \mathbb{Z} , \quad \widetilde{ {\mathrm{NE}} }_{\mathcal{X}}= \mathbb{R} _{\leq 0},\quad \mathbb{K}_{\mathrm{eff}}=\frac{1}{3} \mathbb{Z} _{\leq 0}. \end{gather*} $$

Figure 3
 $\mathbb {K}_{\mathrm {eff}}$
of
$\mathbb {K}_{\mathrm {eff}}$
of
 $\mathcal {X}_{1,1,1}$
and its crepant resolution
$\mathcal {X}_{1,1,1}$
and its crepant resolution
 $\mathcal {O}_{ \mathbb {P} ^2}(-3)$
.
$\mathcal {O}_{ \mathbb {P} ^2}(-3)$
. -
2.
 $\mathcal {X}=\mathcal {X}_{1,2,0}$
(see Figures 4 and 5).
$\mathcal {X}=\mathcal {X}_{1,2,0}$
(see Figures 4 and 5).  $$ \begin{gather*} \mathbb{K}^\vee\cong \mathbb{Z} (-2,1)\oplus \mathbb{Z} (1,-2),\quad \widetilde{ {\mathrm{Nef}} }_{\mathcal{X}}= \mathbb{R} _{\geq 0}(-2,1) + \mathbb{R} _{\geq 0}(1,-2);\\ \mathbb{K}\cong \mathbb{Z} \Big(-\frac{2}{3}, -\frac{1}{3}\Big)\oplus \mathbb{Z} \Big(-\frac{1}{3}, -\frac{2}{3}\Big), \quad \widetilde{ {\mathrm{NE}} }_{\mathcal{X}} = \mathbb{R} _{\geq 0} \Big(-\frac{2}{3}, -\frac{1}{3}\Big) + \mathbb{R} _{\geq 0}\Big(-\frac{1}{3}, -\frac{2}{3}\Big),\\ \mathbb{K}_{\mathrm{eff}} = \mathbb{Z} _{\geq 0}\Big(-\frac{2}{3},-\frac{1}{3}\Big) + \mathbb{Z} _{\geq 0}\Big(-\frac{1}{3},-\frac{2}{3}\Big). \end{gather*} $$
$$ \begin{gather*} \mathbb{K}^\vee\cong \mathbb{Z} (-2,1)\oplus \mathbb{Z} (1,-2),\quad \widetilde{ {\mathrm{Nef}} }_{\mathcal{X}}= \mathbb{R} _{\geq 0}(-2,1) + \mathbb{R} _{\geq 0}(1,-2);\\ \mathbb{K}\cong \mathbb{Z} \Big(-\frac{2}{3}, -\frac{1}{3}\Big)\oplus \mathbb{Z} \Big(-\frac{1}{3}, -\frac{2}{3}\Big), \quad \widetilde{ {\mathrm{NE}} }_{\mathcal{X}} = \mathbb{R} _{\geq 0} \Big(-\frac{2}{3}, -\frac{1}{3}\Big) + \mathbb{R} _{\geq 0}\Big(-\frac{1}{3}, -\frac{2}{3}\Big),\\ \mathbb{K}_{\mathrm{eff}} = \mathbb{Z} _{\geq 0}\Big(-\frac{2}{3},-\frac{1}{3}\Big) + \mathbb{Z} _{\geq 0}\Big(-\frac{1}{3},-\frac{2}{3}\Big). \end{gather*} $$

Figure 4 The secondary fan of the crepant resolution of
 $\mathcal {X}_{1,2,0}$
.
$\mathcal {X}_{1,2,0}$
.
Figure 5
 $\mathbb {K}_{\mathrm {eff}}$
of
$\mathbb {K}_{\mathrm {eff}}$
of
 $\mathcal {X}_{1,2,0}$
and its (partial) crepant resolutions.
$\mathcal {X}_{1,2,0}$
and its (partial) crepant resolutions. -
3.
 $\mathcal {X}=\mathcal {X}_{0,0,0}$
.
$\mathcal {X}=\mathcal {X}_{0,0,0}$
.  $$ \begin{gather*} \mathbb{K}^\vee\cong 3 \mathbb{Z} ,\quad \widetilde{ {\mathrm{Nef}} }_{\mathcal{X}}= \mathbb{R} _{\leq 0};\\ \mathbb{K}\cong \frac{1}{3} \mathbb{Z} , \quad \widetilde{ {\mathrm{NE}} }_{\mathcal{X}} = \mathbb{R} _{\leq 0},\quad \mathbb{K}_{\mathrm{eff}} =\frac{1}{3} \mathbb{Z} _{\leq 0}. \end{gather*} $$
$$ \begin{gather*} \mathbb{K}^\vee\cong 3 \mathbb{Z} ,\quad \widetilde{ {\mathrm{Nef}} }_{\mathcal{X}}= \mathbb{R} _{\leq 0};\\ \mathbb{K}\cong \frac{1}{3} \mathbb{Z} , \quad \widetilde{ {\mathrm{NE}} }_{\mathcal{X}} = \mathbb{R} _{\leq 0},\quad \mathbb{K}_{\mathrm{eff}} =\frac{1}{3} \mathbb{Z} _{\leq 0}. \end{gather*} $$
Assumption 2.6. From now on, we make the following assumptions on
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
-
(a) The coarse moduli space
 $X_\Sigma $
of
$X_\Sigma $
of
 $\mathcal {X}$
is semi-projective.
$\mathcal {X}$
is semi-projective. -
(b) We may choose
 $b_{r'+1},\ldots , b_r$
such that
$b_{r'+1},\ldots , b_r$
such that
 $\hat \rho :=D_1+\dots + D_r$
is contained in the closure of the extended Kähler cone
$\hat \rho :=D_1+\dots + D_r$
is contained in the closure of the extended Kähler cone
 $ {\widetilde {C}} _{\mathcal {X}}$
.
$ {\widetilde {C}} _{\mathcal {X}}$
.
Remark 2.7.
-
1. We make the above assumptions (a) and (b) so that the equivariant mirror theorem [Reference Coates, Corti, Iritani and Tseng27, Theorem 31] takes a particularly simple form. See Section 4.1 in this paper for the precise statement.
-
2. By [Reference Cox, Little and Schenck28, Proposition 14.4.1],
 $X_\Sigma $
is semi-projective if and only if
$X_\Sigma $
is semi-projective if and only if
 $|\Sigma |$
is equal to the cone spanned by
$|\Sigma |$
is equal to the cone spanned by
 $b_1,\ldots , b_r$
. For example, the total space of
$b_1,\ldots , b_r$
. For example, the total space of
 $\mathcal {O}_{ \mathbb {P} ^1}(-3)\oplus \mathcal {O}_{ \mathbb {P} ^1}(1)$
is a smooth toric Calabi-Yau 3-fold that is not semi-projective (see Figure 6).
$\mathcal {O}_{ \mathbb {P} ^1}(-3)\oplus \mathcal {O}_{ \mathbb {P} ^1}(1)$
is a smooth toric Calabi-Yau 3-fold that is not semi-projective (see Figure 6).
Figure 6
 $\mathcal {O}_{ \mathbb {P} ^1}(-3)\oplus \mathcal {O}_{ \mathbb {P} ^1}(1)$
.
$\mathcal {O}_{ \mathbb {P} ^1}(-3)\oplus \mathcal {O}_{ \mathbb {P} ^1}(1)$
. -
3. When
 $\mathcal {X}$
is a Calabi-Yau smooth toric DM stack, Assumption (b) holds if its coarse moduli space
$\mathcal {X}$
is a Calabi-Yau smooth toric DM stack, Assumption (b) holds if its coarse moduli space
 $X_\Sigma $
has a toric crepant resolution of singularities; see [Reference Iritani47, Remark 3.4]. By [Reference Cox, Little and Schenck28, Proposition 11.4.19], any 3-dimensional Gorenstein toric variety
$X_\Sigma $
has a toric crepant resolution of singularities; see [Reference Iritani47, Remark 3.4]. By [Reference Cox, Little and Schenck28, Proposition 11.4.19], any 3-dimensional Gorenstein toric variety
 $X_\Sigma $
has a resolution of singularities
$X_\Sigma $
has a resolution of singularities
 $\phi :X_{\Sigma '}\to X_{\Sigma }$
such that
$\phi :X_{\Sigma '}\to X_{\Sigma }$
such that
 $\phi $
is projective and crepant. So Assumption 2.6 (b) holds for any 3-dimensional Calabi-Yau smooth toric DM stacks.
$\phi $
is projective and crepant. So Assumption 2.6 (b) holds for any 3-dimensional Calabi-Yau smooth toric DM stacks.
2.6 Smooth toric DM stacks as symplectic quotients
Let
![]() $G_{\mathbb {R}} \cong U(1)^k$
be the maximal compact subgroup of
$G_{\mathbb {R}} \cong U(1)^k$
be the maximal compact subgroup of
![]() $G\cong ( \mathbb {C} ^*)^k$
. Then the Lie algebra of
$G\cong ( \mathbb {C} ^*)^k$
. Then the Lie algebra of
![]() $G_{\mathbb {R}} $
is
$G_{\mathbb {R}} $
is
![]() $\mathbb {L}_{\mathbb {R}} $
. Let
$\mathbb {L}_{\mathbb {R}} $
. Let
 $$ \begin{align*}{\widetilde{\mu}} : \mathbb{C} ^r\to \mathbb{L}^\vee_{\mathbb{R}} =\bigoplus_{a=1}^k \mathbb{R} e_a ^\vee \end{align*} $$
$$ \begin{align*}{\widetilde{\mu}} : \mathbb{C} ^r\to \mathbb{L}^\vee_{\mathbb{R}} =\bigoplus_{a=1}^k \mathbb{R} e_a ^\vee \end{align*} $$
be the moment map of the Hamiltonian
![]() $G_{\mathbb {R}} $
-action on
$G_{\mathbb {R}} $
-action on
![]() $ \mathbb {C} ^r$
, equipped with the Kähler form
$ \mathbb {C} ^r$
, equipped with the Kähler form
 $$ \begin{align*}\sqrt{-1} \sum_{i=1}^r dZ_i\wedge d\bar{Z}_i. \end{align*} $$
$$ \begin{align*}\sqrt{-1} \sum_{i=1}^r dZ_i\wedge d\bar{Z}_i. \end{align*} $$
Then
 $$ \begin{align*}{\widetilde{\mu}} (Z_1,\ldots, Z_r) = \sum_{i=1}^r \sum_{a=1}^k l_i^{(a)}|Z_i|^2 e^\vee_a. \end{align*} $$
$$ \begin{align*}{\widetilde{\mu}} (Z_1,\ldots, Z_r) = \sum_{i=1}^r \sum_{a=1}^k l_i^{(a)}|Z_i|^2 e^\vee_a. \end{align*} $$
If
![]() $\mathbf {r}=\sum _{a=1}^k r_a e_a^\vee $
is in the extended Kähler cone of
$\mathbf {r}=\sum _{a=1}^k r_a e_a^\vee $
is in the extended Kähler cone of
![]() $\mathcal {X}$
, then
$\mathcal {X}$
, then
The generic stabiliser K (which is a finite subgroup of
![]() $G\cong ( \mathbb {C} ^*)^k$
) is contained in the maximal compact subgroup
$G\cong ( \mathbb {C} ^*)^k$
) is contained in the maximal compact subgroup
![]() $G_{\mathbb {R}} $
of G. The quotient
$G_{\mathbb {R}} $
of G. The quotient
![]() $G_{\mathbb {R}} ^ {\mathrm {rig}} := G_{\mathbb {R}} /K\cong U(1)^k$
is the maximal compact subgroup of
$G_{\mathbb {R}} ^ {\mathrm {rig}} := G_{\mathbb {R}} /K\cong U(1)^k$
is the maximal compact subgroup of
![]() $G^ {\mathrm {rig}} =G/K\cong ( \mathbb {C} ^*)^k$
, and
$G^ {\mathrm {rig}} =G/K\cong ( \mathbb {C} ^*)^k$
, and
as a symplectic quotient.
The real numbers
![]() $r_1,\ldots , r_k$
are extended Kähler parameters. The symplectic structure
$r_1,\ldots , r_k$
are extended Kähler parameters. The symplectic structure
![]() $\omega (\mathbf {r})$
depends on
$\omega (\mathbf {r})$
depends on
![]() $\mathbf {r}$
. The map
$\mathbf {r}$
. The map
![]() $\mathbf {r}\mapsto [\omega (\mathbf {r})]$
is given by
$\mathbf {r}\mapsto [\omega (\mathbf {r})]$
is given by
![]() $\mathbb {L}^\vee _{\mathbb {R}} \to H^2(\mathcal {X}; \mathbb {R} )$
. Let
$\mathbb {L}^\vee _{\mathbb {R}} \to H^2(\mathcal {X}; \mathbb {R} )$
. Let
![]() $T_a=-r_a+\sqrt {-1}\theta _a$
be complexified extended Kähler parameters of
$T_a=-r_a+\sqrt {-1}\theta _a$
be complexified extended Kähler parameters of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
2.7 The inertia stack and the Chen-Ruan orbifold cohomology
Given
![]() $ {\sigma } \in \Sigma $
, define
$ {\sigma } \in \Sigma $
, define
 $$ \begin{align*}\mathrm{Box}( {\sigma} ):=\Big\{ v\in N: \bar{v}=\sum_{i\in I^{\prime}_ {\sigma} } c_i \bar{b}_i, \quad 0\leq c_i <1\Big\}. \end{align*} $$
$$ \begin{align*}\mathrm{Box}( {\sigma} ):=\Big\{ v\in N: \bar{v}=\sum_{i\in I^{\prime}_ {\sigma} } c_i \bar{b}_i, \quad 0\leq c_i <1\Big\}. \end{align*} $$
Then
![]() $N_ {\mathrm {tor}} \subset \mathrm {Box}( {\sigma } )\subset N$
. If
$N_ {\mathrm {tor}} \subset \mathrm {Box}( {\sigma } )\subset N$
. If
![]() $ {\sigma } $
is a d-dimensional cone, then the set
$ {\sigma } $
is a d-dimensional cone, then the set
![]() $\{ \sum _{i\in I^{\prime }_ {\sigma } } c_i \bar {b}_i: c_i\in \mathbb {R} , 0\leq c_i<1 \}$
is a fundamental domain of the action of
$\{ \sum _{i\in I^{\prime }_ {\sigma } } c_i \bar {b}_i: c_i\in \mathbb {R} , 0\leq c_i<1 \}$
is a fundamental domain of the action of
![]() $\displaystyle { \bar {N}_ {\sigma } =\oplus _{i\in I^{\prime }_ {\sigma } } \mathbb {Z} \bar {b}_i \cong \mathbb {Z} ^d }$
on
$\displaystyle { \bar {N}_ {\sigma } =\oplus _{i\in I^{\prime }_ {\sigma } } \mathbb {Z} \bar {b}_i \cong \mathbb {Z} ^d }$
on
![]() $\displaystyle { N_ {\sigma } \otimes _{ \mathbb {Z} } \mathbb {R} = \oplus _{i\in I^{\prime }_{ {\sigma } }} \mathbb {R} \bar {b}_i\cong \mathbb {R} ^d}$
. If
$\displaystyle { N_ {\sigma } \otimes _{ \mathbb {Z} } \mathbb {R} = \oplus _{i\in I^{\prime }_{ {\sigma } }} \mathbb {R} \bar {b}_i\cong \mathbb {R} ^d}$
. If
![]() $\tau \subset \sigma $
, then
$\tau \subset \sigma $
, then
![]() $I^{\prime }_\tau \subset I^{\prime }_ {\sigma } $
, so
$I^{\prime }_\tau \subset I^{\prime }_ {\sigma } $
, so
![]() $\mathrm {Box}(\tau )\subset \mathrm {Box}( {\sigma } )$
.
$\mathrm {Box}(\tau )\subset \mathrm {Box}( {\sigma } )$
.
Let
![]() $ {\sigma } \in \Sigma (n)$
be a maximal cone in
$ {\sigma } \in \Sigma (n)$
be a maximal cone in
![]() $\Sigma $
. We have a short exact sequence of abelian groups
$\Sigma $
. We have a short exact sequence of abelian groups
which can be identified with the following short exact sequence of multiplicative abelian groups
where
![]() $G_{\mathbb {R}} \cong U(1)^k$
is the maximal compact subgroup of
$G_{\mathbb {R}} \cong U(1)^k$
is the maximal compact subgroup of
![]() $G\cong ( \mathbb {C} ^*)^k$
, and
$G\cong ( \mathbb {C} ^*)^k$
, and
![]() $(G/G_ {\sigma } )_{\mathbb {R}} \cong U(1)^k$
is the maximal compact subgroup of
$(G/G_ {\sigma } )_{\mathbb {R}} \cong U(1)^k$
is the maximal compact subgroup of
![]() $(G/G_ {\sigma } )\cong ( \mathbb {C} ^*)^k$
.
$(G/G_ {\sigma } )\cong ( \mathbb {C} ^*)^k$
.
Given a real number x, we recall some standard notation:
![]() $\lfloor x \rfloor $
is the greatest integer less than or equal to x,
$\lfloor x \rfloor $
is the greatest integer less than or equal to x,
![]() $\lceil x \rceil $
is the least integer greater or equal to x and
$\lceil x \rceil $
is the least integer greater or equal to x and
![]() $\{ x\} = x-\lfloor x \rfloor $
is the fractional part of x. Define
$\{ x\} = x-\lfloor x \rfloor $
is the fractional part of x. Define
![]() $v: \mathbb {K}_ {\sigma } \to N$
by
$v: \mathbb {K}_ {\sigma } \to N$
by
 $$ \begin{align*}v(\beta)= \sum_{i=1}^r \lceil \langle D_i,\beta\rangle\rceil b_i. \end{align*} $$
$$ \begin{align*}v(\beta)= \sum_{i=1}^r \lceil \langle D_i,\beta\rangle\rceil b_i. \end{align*} $$
Then
so
![]() $v(\beta )\in \mathrm {Box}( {\sigma } )$
. Indeed, v induces a bijection
$v(\beta )\in \mathrm {Box}( {\sigma } )$
. Indeed, v induces a bijection
![]() $K_ {\sigma } /\mathbb {L}\cong \mathrm {Box}( {\sigma } )$
.
$K_ {\sigma } /\mathbb {L}\cong \mathrm {Box}( {\sigma } )$
.
For any
![]() $\tau \in \Sigma $
, there exists
$\tau \in \Sigma $
, there exists
![]() $ {\sigma } \in \Sigma (n)$
such that
$ {\sigma } \in \Sigma (n)$
such that
![]() $\tau \subset {\sigma } $
. The bijection
$\tau \subset {\sigma } $
. The bijection
![]() $G_ {\sigma } \to \mathrm {Box}( {\sigma } )$
restricts to a bijection
$G_ {\sigma } \to \mathrm {Box}( {\sigma } )$
restricts to a bijection
![]() $G_\tau \to \mathrm {Box}(\tau )$
.
$G_\tau \to \mathrm {Box}(\tau )$
.
Define
Then
![]() $N_ {\mathrm {tor}} \subset \mathrm {Box}(\mathbf \Sigma ) \subset N$
. There is a bijection
$N_ {\mathrm {tor}} \subset \mathrm {Box}(\mathbf \Sigma ) \subset N$
. There is a bijection
![]() $\mathbb {K}/\mathbb {L}\to \mathrm {Box}(\mathbf \Sigma )$
.
$\mathbb {K}/\mathbb {L}\to \mathrm {Box}(\mathbf \Sigma )$
.
Given
![]() $v\in \mathrm {Box}( {\sigma } )$
, where
$v\in \mathrm {Box}( {\sigma } )$
, where
![]() $ {\sigma } \in \Sigma (d)$
, define
$ {\sigma } \in \Sigma (d)$
, define
![]() $c_i(v)\in [0,1)\cap \mathbb {Q} $
by
$c_i(v)\in [0,1)\cap \mathbb {Q} $
by
Suppose that
![]() $k \in G_ {\sigma } $
corresponds to
$k \in G_ {\sigma } $
corresponds to
![]() $v\in \mathrm {Box}( {\sigma } )$
under the bijection
$v\in \mathrm {Box}( {\sigma } )$
under the bijection
![]() $G_ {\sigma } \cong \mathrm {Box}( {\sigma } )$
. Then
$G_ {\sigma } \cong \mathrm {Box}( {\sigma } )$
. Then
 $$ \begin{align*}\chi_i(k) = \begin{cases} 1, & i\in I_ {\sigma} ,\\ e^{2\pi\sqrt{-1} c_i(v)},& i \in I^{\prime}_ {\sigma}. \end{cases} \end{align*} $$
$$ \begin{align*}\chi_i(k) = \begin{cases} 1, & i\in I_ {\sigma} ,\\ e^{2\pi\sqrt{-1} c_i(v)},& i \in I^{\prime}_ {\sigma}. \end{cases} \end{align*} $$
Define
Let
![]() $IU=\{(z,k)\in U_{\mathcal {A}}\times G\mid k\cdot z = z\}$
, and let G act on
$IU=\{(z,k)\in U_{\mathcal {A}}\times G\mid k\cdot z = z\}$
, and let G act on
![]() $IU$
by
$IU$
by
![]() $h\cdot (z,k)= (h\cdot z,k)$
. The inertia stack
$h\cdot (z,k)= (h\cdot z,k)$
. The inertia stack
![]() $\mathcal {I}\mathcal {X}$
of
$\mathcal {I}\mathcal {X}$
of
![]() $\mathcal {X}$
is defined to be the quotient stack
$\mathcal {X}$
is defined to be the quotient stack
Note that
![]() $(z=(Z_1,\ldots ,Z_r), k)\in IU$
if and only if
$(z=(Z_1,\ldots ,Z_r), k)\in IU$
if and only if
So
where
The connected components of
![]() $\mathcal {I}\mathcal {X}$
are
$\mathcal {I}\mathcal {X}$
are
The involution
![]() $IU\to IU$
,
$IU\to IU$
,
![]() $(z,k)\mapsto (z,k^{-1})$
induces involutions
$(z,k)\mapsto (z,k^{-1})$
induces involutions
![]() $\mathrm {inv}:\mathcal {I}\mathcal {X}\to \mathcal {I}\mathcal {X}$
and
$\mathrm {inv}:\mathcal {I}\mathcal {X}\to \mathcal {I}\mathcal {X}$
and
![]() $\mathrm {inv}:\mathrm {Box}(\mathbf \Sigma )\to \mathrm {Box}(\mathbf \Sigma )$
such that
$\mathrm {inv}:\mathrm {Box}(\mathbf \Sigma )\to \mathrm {Box}(\mathbf \Sigma )$
such that
![]() $\mathrm {inv}(\mathcal {X}_v)=\mathcal {X}_{\mathrm {inv}(v)}$
.
$\mathrm {inv}(\mathcal {X}_v)=\mathcal {X}_{\mathrm {inv}(v)}$
.
In the remainder of this subsection, we consider rational cohomology and write
![]() $H^*(-)$
instead of
$H^*(-)$
instead of
![]() $H^*(-; \mathbb {Q} )$
.
$H^*(-; \mathbb {Q} )$
.
As a graded vector space over
![]() $ \mathbb {Q} $
(and as the state-space of the relevant quantum theory in physics [Reference Zaslow74]), the Chen-Ruan orbifold cohomology [Reference Chen and Ruan23] is defined to be
$ \mathbb {Q} $
(and as the state-space of the relevant quantum theory in physics [Reference Zaslow74]), the Chen-Ruan orbifold cohomology [Reference Chen and Ruan23] is defined to be
Let
![]() $\mathbf 1_v$
be the unit in
$\mathbf 1_v$
be the unit in
![]() $H^*(\mathcal {X}_v)$
. Then
$H^*(\mathcal {X}_v)$
. Then
![]() $\mathbf 1_v\in H^{2\mathrm {age}(v)}_ {\mathrm {CR}} (\mathcal {X})$
. In particular,
$\mathbf 1_v\in H^{2\mathrm {age}(v)}_ {\mathrm {CR}} (\mathcal {X})$
. In particular,
Suppose that
![]() $\mathcal {X}$
is a proper toric DM stack. Then the orbifold Poincaré pairing on
$\mathcal {X}$
is a proper toric DM stack. Then the orbifold Poincaré pairing on
![]() $H^*_ {\mathrm {CR}} (\mathcal {X})$
is defined as
$H^*_ {\mathrm {CR}} (\mathcal {X})$
is defined as
We also have an equivariant pairing on
![]() $H^*_{ {\mathrm {CR}} , \mathbb {T} }(\mathcal {X})$
:
$H^*_{ {\mathrm {CR}} , \mathbb {T} }(\mathcal {X})$
:
where
is the equivariant pushforward to a point. When
![]() $\mathcal {X}$
is not proper, equation (5) is not defined, but we can still define via equation (6) an equivariant pairing
$\mathcal {X}$
is not proper, equation (5) is not defined, but we can still define via equation (6) an equivariant pairing
![]() $H^*_{ {\mathrm {CR}} , \mathbb {T} }(\mathcal {X})\otimes H^*_{ {\mathrm {CR}} , \mathbb {T} }(\mathcal {X}) \to \mathcal {Q}_{\mathbb {T}} $
, where
$H^*_{ {\mathrm {CR}} , \mathbb {T} }(\mathcal {X})\otimes H^*_{ {\mathrm {CR}} , \mathbb {T} }(\mathcal {X}) \to \mathcal {Q}_{\mathbb {T}} $
, where
![]() $\mathcal {Q}_{\mathbb {T}} $
is the fractional field of the ring
$\mathcal {Q}_{\mathbb {T}} $
is the fractional field of the ring
![]() $H^*(B \mathbb {T} )$
.
$H^*(B \mathbb {T} )$
.
Example 2.8.
-
1.
 $\mathcal {X}=\mathcal {X}_{1,1,1}$
.
$\mathcal {X}=\mathcal {X}_{1,1,1}$
.  $$ \begin{gather*} N= \mathbb{Z} ^3,\quad \mathrm{Box}(\mathbf \Sigma)=\{(0,0,0),(0,0,1),(0,0,2)\};\\ H^0_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_{(0,0,0)},\ H^2_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_{(0,0,1)},\ H^4_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_{(0,0,2)}. \end{gather*} $$
$$ \begin{gather*} N= \mathbb{Z} ^3,\quad \mathrm{Box}(\mathbf \Sigma)=\{(0,0,0),(0,0,1),(0,0,2)\};\\ H^0_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_{(0,0,0)},\ H^2_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_{(0,0,1)},\ H^4_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_{(0,0,2)}. \end{gather*} $$
-
2.
 $\mathcal {X}=\mathcal {X}_{1,2,0}$
.
$\mathcal {X}=\mathcal {X}_{1,2,0}$
.  $$ \begin{gather*} N= \mathbb{Z} ^3,\quad \mathrm{Box}(\mathbf \Sigma)=\{ (0,0,0), (0,2,1), (0,1,1)\};\\ H^0_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_{(0,0,0)},\quad H^2_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_{(0,2,1)} \oplus \mathbb{Q} \mathbf 1_{(0,1,1)}. \end{gather*} $$
$$ \begin{gather*} N= \mathbb{Z} ^3,\quad \mathrm{Box}(\mathbf \Sigma)=\{ (0,0,0), (0,2,1), (0,1,1)\};\\ H^0_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_{(0,0,0)},\quad H^2_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_{(0,2,1)} \oplus \mathbb{Q} \mathbf 1_{(0,1,1)}. \end{gather*} $$
-
3.
 $\mathcal {X}=\mathcal {X}_{0,0,0}$
.
$\mathcal {X}=\mathcal {X}_{0,0,0}$
.  $$ \begin{gather*} N= \mathbb{Z} ^3\oplus \mathbb{Z} _3,\quad \mathrm{Box}(\mathbf \Sigma)=N_ {\mathrm{tor}} = \mathbb{Z} _3=\{0,1,2\};\\ H^0_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_0\oplus \mathbb{Q} \mathbf{1}_1 \oplus \mathbb{Q} \mathbf{1}_2. \end{gather*} $$
$$ \begin{gather*} N= \mathbb{Z} ^3\oplus \mathbb{Z} _3,\quad \mathrm{Box}(\mathbf \Sigma)=N_ {\mathrm{tor}} = \mathbb{Z} _3=\{0,1,2\};\\ H^0_ {\mathrm{CR}} (\mathcal{X})= \mathbb{Q} \mathbf{1}_0\oplus \mathbb{Q} \mathbf{1}_1 \oplus \mathbb{Q} \mathbf{1}_2. \end{gather*} $$
3 All genus open-closed Gromov-Witten invariants
In this section,
![]() $\mathcal {X}$
is a 3-dimensional Calabi-Yau smooth Deligne-Mumford stack.
$\mathcal {X}$
is a 3-dimensional Calabi-Yau smooth Deligne-Mumford stack.
3.1 Rigidification
The rigidification
![]() $\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
of
$\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
of
![]() $\mathcal {X}$
is a toric Calabi-Yau 3-orbifold. The Calabi-Yau condition implies
$\mathcal {X}$
is a toric Calabi-Yau 3-orbifold. The Calabi-Yau condition implies
![]() $\mathcal {X}^{ {\mathrm {rig}} }=\mathcal {X}^{ {\mathrm {can}} }$
, where
$\mathcal {X}^{ {\mathrm {rig}} }=\mathcal {X}^{ {\mathrm {can}} }$
, where
![]() $\mathcal {X}^{ {\mathrm {can}} }$
is determined by the simplicial fan
$\mathcal {X}^{ {\mathrm {can}} }$
is determined by the simplicial fan
![]() $\Sigma $
and then by choosing each
$\Sigma $
and then by choosing each
![]() $b_i$
to be the primitive generator of each
$b_i$
to be the primitive generator of each
![]() $1$
-cone (compare to equation (3) in Section 2.1). Let
$1$
-cone (compare to equation (3) in Section 2.1). Let
![]() $\mathcal {T}'$
(respectively,
$\mathcal {T}'$
(respectively,
![]() $ \mathbb {T} '$
) be the subtorus of
$ \mathbb {T} '$
) be the subtorus of
![]() $\mathcal {T}\cong ( \mathbb {C} ^*)^3 \times \mathcal {B} K$
(respectively,
$\mathcal {T}\cong ( \mathbb {C} ^*)^3 \times \mathcal {B} K$
(respectively,
![]() $ \mathbb {T} \cong ( \mathbb {C} ^*)^3$
) preserving the Calabi-Yau 3-form on
$ \mathbb {T} \cong ( \mathbb {C} ^*)^3$
) preserving the Calabi-Yau 3-form on
![]() $\mathcal {X}$
(respectively,
$\mathcal {X}$
(respectively,
![]() $\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
). Then
$\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
). Then
![]() $ \mathbb {T} '\cong ( \mathbb {C} ^*)^2$
and
$ \mathbb {T} '\cong ( \mathbb {C} ^*)^2$
and
![]() $\mathcal {T}'\cong ( \mathbb {C} ^*)^2 \times \mathcal {B} K$
. There is a primitive
$\mathcal {T}'\cong ( \mathbb {C} ^*)^2 \times \mathcal {B} K$
. There is a primitive
![]() $\mathsf {u}_3 \in M=\mathrm {Hom}( \mathbb {T} , \mathbb {C} ^*)\cong \mathbb {Z} ^3$
such that
$\mathsf {u}_3 \in M=\mathrm {Hom}( \mathbb {T} , \mathbb {C} ^*)\cong \mathbb {Z} ^3$
such that
![]() $\mathrm {Ker}(\mathsf {u}_3)= \mathbb {T} '$
. Define
$\mathrm {Ker}(\mathsf {u}_3)= \mathbb {T} '$
. Define
![]() $M':=M/\langle \mathsf {u}_3 \rangle \cong \mathbb {Z} ^2$
. Then
$M':=M/\langle \mathsf {u}_3 \rangle \cong \mathbb {Z} ^2$
. Then
![]() $\bar {N}':=\mathsf {u}_3^\perp =\{ \mathsf {v} \in \bar {N}: \langle \mathsf {u}_3, \mathsf {v} \rangle =0\}$
is the dual lattice of
$\bar {N}':=\mathsf {u}_3^\perp =\{ \mathsf {v} \in \bar {N}: \langle \mathsf {u}_3, \mathsf {v} \rangle =0\}$
is the dual lattice of
![]() $M'=\mathrm {Hom}( \mathbb {T} ', \mathbb {C} ^*)$
.
$M'=\mathrm {Hom}( \mathbb {T} ', \mathbb {C} ^*)$
.
The simplicial fan
![]() $\Sigma $
is determined by a convex polytope
$\Sigma $
is determined by a convex polytope
![]() $\Delta \subset N^{\prime }_{\mathbb {R}} =\bar {N}'\otimes _{\mathbb {Z}} \mathbb {R} $
together with a triangulation of
$\Delta \subset N^{\prime }_{\mathbb {R}} =\bar {N}'\otimes _{\mathbb {Z}} \mathbb {R} $
together with a triangulation of
![]() $\Delta $
, where all the vertices are in the lattice
$\Delta $
, where all the vertices are in the lattice
![]() $\bar {N}$
. The fan
$\bar {N}$
. The fan
![]() $\Sigma $
is a cone over this triangulation in
$\Sigma $
is a cone over this triangulation in
![]() $N^{\prime }_{1, \mathbb {R} }\subset N_{\mathbb {R}} $
, where
$N^{\prime }_{1, \mathbb {R} }\subset N_{\mathbb {R}} $
, where
![]() $N^{\prime }_{1, \mathbb {R} }=\{ \mathsf {v}\in N_{\mathbb {R}} : \langle \mathsf {u}_3, \mathsf {v}\rangle =1\}$
.
$N^{\prime }_{1, \mathbb {R} }=\{ \mathsf {v}\in N_{\mathbb {R}} : \langle \mathsf {u}_3, \mathsf {v}\rangle =1\}$
.
3.2 Toric graph
Let
![]() $ \mathbb {T} _{\mathbb {R}} \cong U(1)^3$
(respectively,
$ \mathbb {T} _{\mathbb {R}} \cong U(1)^3$
(respectively,
![]() $ \mathbb {T} ^{\prime }_{\mathbb {R}} \cong U(1)^2$
) be the maximal compact subgroup of
$ \mathbb {T} ^{\prime }_{\mathbb {R}} \cong U(1)^2$
) be the maximal compact subgroup of
![]() $ \mathbb {T} \cong ( \mathbb {C} ^*)^3$
(respectively,
$ \mathbb {T} \cong ( \mathbb {C} ^*)^3$
(respectively,
![]() $ \mathbb {T} '\cong ( \mathbb {C} ^*)^2$
), and we choose an
$ \mathbb {T} '\cong ( \mathbb {C} ^*)^2$
), and we choose an
![]() $\mathbf {r}$
in the extended Kähler cone. The
$\mathbf {r}$
in the extended Kähler cone. The
![]() $ \mathbb {T} $
-action on
$ \mathbb {T} $
-action on
![]() $\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
restricts to a Hamiltonian
$\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
restricts to a Hamiltonian
![]() $ \mathbb {T} _{\mathbb {R}} $
-action on the Kähler orbifold
$ \mathbb {T} _{\mathbb {R}} $
-action on the Kähler orbifold
![]() $(\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} ,\omega (\mathbf {r}))$
. Since
$(\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} ,\omega (\mathbf {r}))$
. Since
![]() $M_{\mathbb {R}} $
(respectively,
$M_{\mathbb {R}} $
(respectively,
![]() $M_{\mathbb {R}} '$
) is canonically identified with the dual of the Lie algebra of
$M_{\mathbb {R}} '$
) is canonically identified with the dual of the Lie algebra of
![]() $ \mathbb {T} _{\mathbb {R}} $
(respectively,
$ \mathbb {T} _{\mathbb {R}} $
(respectively,
![]() $ \mathbb {T} ^{\prime }_{\mathbb {R}} $
), the Kähler form
$ \mathbb {T} ^{\prime }_{\mathbb {R}} $
), the Kähler form
![]() $\omega (\mathbf {r})$
determines a moment map
$\omega (\mathbf {r})$
determines a moment map
![]() $\mu _{ \mathbb {T} _{\mathbb {R}} }: \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} \longrightarrow M_{\mathbb {R}} $
up to translation by a vector in
$\mu _{ \mathbb {T} _{\mathbb {R}} }: \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} \longrightarrow M_{\mathbb {R}} $
up to translation by a vector in
![]() $M_{\mathbb {R}} $
. The image
$M_{\mathbb {R}} $
. The image
![]() $\mu _{ \mathbb {T} _{\mathbb {R}} }(\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} )$
is a convex polyhedron. The moment map
$\mu _{ \mathbb {T} _{\mathbb {R}} }(\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} )$
is a convex polyhedron. The moment map
![]() $\mu _{ \mathbb {T} ^{\prime }_{\mathbb {R}} }:\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} \longrightarrow M^{\prime }_{\mathbb {R}} $
is the composition
$\mu _{ \mathbb {T} ^{\prime }_{\mathbb {R}} }:\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} \longrightarrow M^{\prime }_{\mathbb {R}} $
is the composition
![]() $\pi \circ \mu _{T_{\mathbb {R}} }$
, where
$\pi \circ \mu _{T_{\mathbb {R}} }$
, where
![]() $\pi :M_{\mathbb {R}} \cong \mathbb {R} ^3 \to M^{\prime }_{ \mathbb {R} }\cong \mathbb {R} ^2$
is the projection. The map
$\pi :M_{\mathbb {R}} \cong \mathbb {R} ^3 \to M^{\prime }_{ \mathbb {R} }\cong \mathbb {R} ^2$
is the projection. The map
![]() $\mu _{ \mathbb {T} ^{\prime }_{\mathbb {R}} }$
is surjective. Let
$\mu _{ \mathbb {T} ^{\prime }_{\mathbb {R}} }$
is surjective. Let
![]() $\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} _1 \subset \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
be the union of 0-dimensional and 1-dimensional
$\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} _1 \subset \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
be the union of 0-dimensional and 1-dimensional
![]() $ \mathbb {T} $
-orbits in
$ \mathbb {T} $
-orbits in
![]() $\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
. The toric graph is defined by
$\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
. The toric graph is defined by
![]() $\Gamma := \mu _{T_{\mathbb {R}} '}(\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} _1)\subset M^{\prime }_{\mathbb {R}} \cong \mathbb {R} ^2$
. It is determined by the Kähler class
$\Gamma := \mu _{T_{\mathbb {R}} '}(\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} _1)\subset M^{\prime }_{\mathbb {R}} \cong \mathbb {R} ^2$
. It is determined by the Kähler class
![]() $[\omega (\mathbf {r})]\in H^2(\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}}; \mathbb {R} )=H^2(X_\Sigma; \mathbb {R} )$
up to translation by a vector in
$[\omega (\mathbf {r})]\in H^2(\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}}; \mathbb {R} )=H^2(X_\Sigma; \mathbb {R} )$
up to translation by a vector in
![]() $M^{\prime }_{\mathbb {R}} $
. The vertices (respectively, edges) of
$M^{\prime }_{\mathbb {R}} $
. The vertices (respectively, edges) of
![]() $\Gamma $
are in one-to-one correspondence to
$\Gamma $
are in one-to-one correspondence to
![]() $3$
-dimensional (respectively,
$3$
-dimensional (respectively,
![]() $2$
-dimensional) cones in
$2$
-dimensional) cones in
![]() $\Sigma $
. Conversely, the Kähler class
$\Sigma $
. Conversely, the Kähler class
![]() $[\omega (\mathbf {r})]\in H^2(\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}}; \mathbb {R} )$
is determined by the toric graph.
$[\omega (\mathbf {r})]\in H^2(\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}}; \mathbb {R} )$
is determined by the toric graph.
Pulling back under the map
![]() $\mathcal {X}\longrightarrow \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
defines a one-to-one correspondence between Kähler forms/classes on
$\mathcal {X}\longrightarrow \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
defines a one-to-one correspondence between Kähler forms/classes on
![]() $\mathcal {X}$
and on its rigidification
$\mathcal {X}$
and on its rigidification
![]() $\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
.
$\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
.
3.3 Aganagic-Vafa A-branes
In [Reference Aganagic and Vafa6], Aganagic-Vafa introduced a class of Lagrangian submanifolds of semi-projective smooth toric Calabi-Yau 3-folds. In this section, we generalise this construction and define Aganagic-Vafa A-branes in a general 3-dimensional Calabi-Yau smooth toric DM stack with semi-projective coarse moduli space.
Let
![]() $\mathcal {X}=[ {\widetilde {\mu }} ^{-1}(\mathbf {r})/G_{\mathbb {R}} ]$
be a 3-dimensional Calabi-Yau smooth toric DM stack, where
$\mathcal {X}=[ {\widetilde {\mu }} ^{-1}(\mathbf {r})/G_{\mathbb {R}} ]$
be a 3-dimensional Calabi-Yau smooth toric DM stack, where
 $$ \begin{align*}\mathbf{r} =\sum_{a=1}^k r_a e_a^\vee \in {\widetilde{C}} (\mathcal{X})\subset \mathbb{L}^\vee_{\mathbb{R}} , \end{align*} $$
$$ \begin{align*}\mathbf{r} =\sum_{a=1}^k r_a e_a^\vee \in {\widetilde{C}} (\mathcal{X})\subset \mathbb{L}^\vee_{\mathbb{R}} , \end{align*} $$
and
![]() $ {\widetilde {\mu }} ^{-1}(\mathbf {r})\subset \mathbb {C} ^{k+3}$
is defined by the following equations:
$ {\widetilde {\mu }} ^{-1}(\mathbf {r})\subset \mathbb {C} ^{k+3}$
is defined by the following equations:
 $$ \begin{align*}\sum_{i=1}^{k+3} l_i^{(a)} |X_i|^2 =r_a,\quad a=1,\ldots, k. \end{align*} $$
$$ \begin{align*}\sum_{i=1}^{k+3} l_i^{(a)} |X_i|^2 =r_a,\quad a=1,\ldots, k. \end{align*} $$
Write
![]() $X_i=\rho _i e^{\sqrt {-1}\phi _i}$
, where
$X_i=\rho _i e^{\sqrt {-1}\phi _i}$
, where
![]() $\rho _i=|X_i|$
. An Aganagic-Vafa brane is a Lagrangian suborbifold of
$\rho _i=|X_i|$
. An Aganagic-Vafa brane is a Lagrangian suborbifold of
![]() $\mathcal {X}$
of the form
$\mathcal {X}$
of the form
where
 $$ \begin{align*}{\widetilde{L}} =\left\{ (X_1,\ldots, X_{k+3})\in {\widetilde{\mu}} ^{-1}(\mathbf{r}): \sum_{i=1}^{k+3}\hat{l}^1_i |X_i|^2=c_1, \sum_{i=1}^{k+3} \hat{l}_i^2 |X_i|^2 = c_2, \sum_{i=1}^{k+3}\phi_i =\mathrm{const} \right\} \end{align*} $$
$$ \begin{align*}{\widetilde{L}} =\left\{ (X_1,\ldots, X_{k+3})\in {\widetilde{\mu}} ^{-1}(\mathbf{r}): \sum_{i=1}^{k+3}\hat{l}^1_i |X_i|^2=c_1, \sum_{i=1}^{k+3} \hat{l}_i^2 |X_i|^2 = c_2, \sum_{i=1}^{k+3}\phi_i =\mathrm{const} \right\} \end{align*} $$
for some
![]() $\hat {l}^\alpha _i \in \mathbb {Z} , \sum _{i=1}^{k+3}\hat {l}^\alpha _i =0$
,
$\hat {l}^\alpha _i \in \mathbb {Z} , \sum _{i=1}^{k+3}\hat {l}^\alpha _i =0$
,
![]() $\alpha =1,2$
. Note that the action of
$\alpha =1,2$
. Note that the action of
![]() $G_{\mathbb {R}} $
on
$G_{\mathbb {R}} $
on
![]() $ \mathbb {C} ^{k+3}$
preserves the subsets
$ \mathbb {C} ^{k+3}$
preserves the subsets
![]() $ {\widetilde {\mu }} ^{-1}(\mathbf {r})$
and
$ {\widetilde {\mu }} ^{-1}(\mathbf {r})$
and
![]() $ {\widetilde {L}} $
. If we view
$ {\widetilde {L}} $
. If we view
![]() $\mathcal {X} = [ {\widetilde {\mu }} ^{-1}(\mathbf {r})/G_{\mathbb {R}} ]$
as a Lie groupoid (and in particular a category), then
$\mathcal {X} = [ {\widetilde {\mu }} ^{-1}(\mathbf {r})/G_{\mathbb {R}} ]$
as a Lie groupoid (and in particular a category), then
![]() $\mathcal {L}=[ {\widetilde {L}} /G_{\mathbb {R}} ]$
is a full subcategory.
$\mathcal {L}=[ {\widetilde {L}} /G_{\mathbb {R}} ]$
is a full subcategory.
An Aganagic-Vafa brane
![]() $\mathcal {L}$
intersects a unique 1-dimensional orbit
$\mathcal {L}$
intersects a unique 1-dimensional orbit
![]() $\mathfrak {o}_\tau \cong \mathbb {C} ^*\times \mathcal {B} G_\tau $
along
$\mathfrak {o}_\tau \cong \mathbb {C} ^*\times \mathcal {B} G_\tau $
along
![]() $\mathcal {S}_\tau := \mathcal {L}\cap \mathfrak {o}_\tau \cong S^1\times \mathcal {B} G_\tau $
. The inclusion
$\mathcal {S}_\tau := \mathcal {L}\cap \mathfrak {o}_\tau \cong S^1\times \mathcal {B} G_\tau $
. The inclusion
![]() $\mathcal {S}_\tau \subset \mathcal {L}$
is a homotopic equivalence, so the fundamental group of
$\mathcal {S}_\tau \subset \mathcal {L}$
is a homotopic equivalence, so the fundamental group of
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
In particular, it is abelian, so it is isomorphic to its abelianisation
![]() $H_1(\mathcal {L}; \mathbb {Z} )$
.
$H_1(\mathcal {L}; \mathbb {Z} )$
.
If
![]() $(\tau , {\sigma } )\in F(\Sigma )$
, then there is an inclusion
$(\tau , {\sigma } )\in F(\Sigma )$
, then there is an inclusion
![]() $\iota ^{(\tau , {\sigma } )}: \mathcal {S}_\tau \hookrightarrow \mathcal {X}_ {\sigma } =[ \mathbb {C} ^3/G_ {\sigma } ]$
that induces
$\iota ^{(\tau , {\sigma } )}: \mathcal {S}_\tau \hookrightarrow \mathcal {X}_ {\sigma } =[ \mathbb {C} ^3/G_ {\sigma } ]$
that induces
3.4 Moduli spaces of stable maps to
 $(\mathcal {X},\mathcal {L})$
$(\mathcal {X},\mathcal {L})$
In [Reference Katz and Liu49], Katz-Liu introduced stable maps to a symplectic manifold with Lagrangian boundary conditions at all genera; the domain of such a map is a prestable bordered Riemann surface: that is, a smooth or nodal bordered Riemann surface. (See also [Reference Liu55], [Reference Fukaya, Oh, Ohta and Ono38].) In [Reference Cho and Poddar24, Section 2], Cho-Poddar define stable maps to a symplectic orbifold
![]() $\mathcal {X}$
with Lagrangian boundary conditions, under the assumption that the Lagrangian suborbifold
$\mathcal {X}$
with Lagrangian boundary conditions, under the assumption that the Lagrangian suborbifold
![]() $\mathcal {L}$
does not contain any stacky points (so that
$\mathcal {L}$
does not contain any stacky points (so that
![]() $\mathcal {L}$
is indeed a smooth manifold); the domain of such a map is a prestable bordered orbifold Riemann surface in the sense of [Reference Cho and Poddar24, Section 2]: that is, a smooth or nodal bordered orbifold Riemann surface, where a stacky point is either an interior marked point or an interior node.
$\mathcal {L}$
is indeed a smooth manifold); the domain of such a map is a prestable bordered orbifold Riemann surface in the sense of [Reference Cho and Poddar24, Section 2]: that is, a smooth or nodal bordered orbifold Riemann surface, where a stacky point is either an interior marked point or an interior node.
In general,
![]() $\mathcal {L}$
is a suborbifold that contains stacky points. To obtain compactness of the moduli spaces when
$\mathcal {L}$
is a suborbifold that contains stacky points. To obtain compactness of the moduli spaces when
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {L}$
are compact, one needs to allow orbifold structures at boundary marked points and boundary nodes. In the present paper,
$\mathcal {L}$
are compact, one needs to allow orbifold structures at boundary marked points and boundary nodes. In the present paper,
![]() $\mathcal {L}$
may contain stacky points, but we do not need to allow orbifold structures on the boundary of the domain for the following two reasons:
$\mathcal {L}$
may contain stacky points, but we do not need to allow orbifold structures on the boundary of the domain for the following two reasons:
-
(i) Our enumerative problem only requires interior insertions, so we do not need to introduce any boundary marked points.
-
(ii) In our case,
 $\mathcal {X}$
and
$\mathcal {X}$
and
 $\mathcal {L}$
are noncompact, and we will define and compute open GW invariants by torus localisation on moduli space of stable maps
$\mathcal {L}$
are noncompact, and we will define and compute open GW invariants by torus localisation on moduli space of stable maps
 $\mathcal {X}$
with boundaries in
$\mathcal {X}$
with boundaries in
 $\mathcal {L}$
. If a stable map represents a torus fixed point in the moduli space, then any node in the domain must be mapped to a torus fixed (scheme or stacky) point in
$\mathcal {L}$
. If a stable map represents a torus fixed point in the moduli space, then any node in the domain must be mapped to a torus fixed (scheme or stacky) point in
 $\mathcal {X}$
, but
$\mathcal {X}$
, but
 $\mathcal {L}$
does not contain any torus fixed point, so the domain does not contain any boundary nodes.
$\mathcal {L}$
does not contain any torus fixed point, so the domain does not contain any boundary nodes.
Let
![]() $(\Sigma ,x_1,\ldots , x_n)$
be a prestable bordered orbifold Riemann surface with n interior marked point. Then the coarse moduli space
$(\Sigma ,x_1,\ldots , x_n)$
be a prestable bordered orbifold Riemann surface with n interior marked point. Then the coarse moduli space
![]() $(\bar {\Sigma },\bar {x}_1,\ldots , \bar {x}_n)$
is a prestable bordered Riemann surface with n interior marked points, defined in [Reference Katz and Liu49, Section 3.6] and [Reference Liu55, Section 3.2]. We define the topological type
$(\bar {\Sigma },\bar {x}_1,\ldots , \bar {x}_n)$
is a prestable bordered Riemann surface with n interior marked points, defined in [Reference Katz and Liu49, Section 3.6] and [Reference Liu55, Section 3.2]. We define the topological type
![]() $(g,h)$
of
$(g,h)$
of
![]() $\Sigma $
to be the topological type of
$\Sigma $
to be the topological type of
![]() $\bar {\Sigma }$
(see [Reference Liu55, Section 3.2]).
$\bar {\Sigma }$
(see [Reference Liu55, Section 3.2]).
Let
![]() $(\Sigma ,\partial \Sigma )$
be a prestable bordered orbifold Riemann surface of type
$(\Sigma ,\partial \Sigma )$
be a prestable bordered orbifold Riemann surface of type
![]() $(g,h)$
, and let
$(g,h)$
, and let
![]() $\partial \Sigma = R_1\cup \cdots \cup R_h$
be union of connected components. Each connected component is a circle that contains no orbifold points. A (bordered) prestable map to the pair
$\partial \Sigma = R_1\cup \cdots \cup R_h$
be union of connected components. Each connected component is a circle that contains no orbifold points. A (bordered) prestable map to the pair
![]() $(\mathcal {X},\mathcal {L})$
is a map
$(\mathcal {X},\mathcal {L})$
is a map
![]() $u:(\Sigma ,\partial \Sigma )\to (\mathcal {X},\mathcal {L})$
, where
$u:(\Sigma ,\partial \Sigma )\to (\mathcal {X},\mathcal {L})$
, where
![]() $\Sigma $
is a prestable bordered orbifold Riemann surface such that
$\Sigma $
is a prestable bordered orbifold Riemann surface such that
![]() $u\circ \nu :\hat {\Sigma }\to \mathcal {X}$
is holomorphic, where
$u\circ \nu :\hat {\Sigma }\to \mathcal {X}$
is holomorphic, where
![]() $\nu : \hat {\Sigma }\to \Sigma $
is the normalisation (so
$\nu : \hat {\Sigma }\to \Sigma $
is the normalisation (so
![]() $\hat {\Sigma }$
is a possibly disconnected smooth bordered orbifold Riemann surface); a prestable map to
$\hat {\Sigma }$
is a possibly disconnected smooth bordered orbifold Riemann surface); a prestable map to
![]() $(\mathcal {X},\mathcal {L})$
is stable if its automorphism group is finite. The topological type of a stable map u is given by the degree
$(\mathcal {X},\mathcal {L})$
is stable if its automorphism group is finite. The topological type of a stable map u is given by the degree
![]() $\beta '= \bar {u}_*[\bar {\Sigma }]\in H_2(X,L; \mathbb {Z} )$
(where X and L are the coarse moduli spaces of
$\beta '= \bar {u}_*[\bar {\Sigma }]\in H_2(X,L; \mathbb {Z} )$
(where X and L are the coarse moduli spaces of
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {L}$
respectively, and
$\mathcal {L}$
respectively, and
![]() $\bar {u}:\bar {\Sigma }\to X$
is the map between coarse moduli spaces) and
$\bar {u}:\bar {\Sigma }\to X$
is the map between coarse moduli spaces) and
![]() $\bar \mu _i=u_*[R_i] = (\mu _i, \lambda _i)\in H_1(\mathcal {L}; \mathbb {Z} )\cong \mathbb {Z} \times G_\tau $
(where
$\bar \mu _i=u_*[R_i] = (\mu _i, \lambda _i)\in H_1(\mathcal {L}; \mathbb {Z} )\cong \mathbb {Z} \times G_\tau $
(where
![]() $\mu _i\in \mathbb {Z} $
is the winding number and
$\mu _i\in \mathbb {Z} $
is the winding number and
![]() $\lambda _i\in G_\tau $
is the monodromy). Given
$\lambda _i\in G_\tau $
is the monodromy). Given
![]() $\beta '\in H_2(X,L; \mathbb {Z} )$
and
$\beta '\in H_2(X,L; \mathbb {Z} )$
and
Let
![]() $\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
be the moduli space of stable maps of type
$\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
be the moduli space of stable maps of type
![]() $(g,h)$
, degree
$(g,h)$
, degree
![]() $\beta '$
, winding numbers
$\beta '$
, winding numbers
![]() $\mu _i\in \mathbb {Z} $
and monodromies
$\mu _i\in \mathbb {Z} $
and monodromies
![]() $\lambda _i\in G_\tau $
, with n interior marked points.
$\lambda _i\in G_\tau $
, with n interior marked points.
3.5 The tangent-obstruction complex and the virtual dimension
Similar to [Reference Katz and Liu49, Section 4.2], the tangent space
![]() $\mathcal {T}_\xi ^1$
and the obstruction space
$\mathcal {T}_\xi ^1$
and the obstruction space
![]() $\mathcal {T}_\xi ^2$
at a moduli point
$\mathcal {T}_\xi ^2$
at a moduli point
fit into the following exact sequence of real vector spaces:
 $$ \begin{align} \begin{aligned} 0 \to & \mathrm{Aut}((\Sigma,x_1,\ldots,x_n),\partial\Sigma)\to H^0(\Sigma,\partial\Sigma,u^*T_{\mathcal{X}}, (u|_{\partial\Sigma})^*T_{\mathcal{L}})\to \mathcal{T}^1_\xi \\ \to & \mathrm{Def}((\Sigma,x_1,\ldots, x_n),\partial\Sigma)\to H^1(\Sigma,\partial\Sigma, u^*T_{\mathcal{X}}, (u|_{\partial\Sigma})^* T_{\mathcal{L}})\to \mathcal{T}^2_\xi, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 0 \to & \mathrm{Aut}((\Sigma,x_1,\ldots,x_n),\partial\Sigma)\to H^0(\Sigma,\partial\Sigma,u^*T_{\mathcal{X}}, (u|_{\partial\Sigma})^*T_{\mathcal{L}})\to \mathcal{T}^1_\xi \\ \to & \mathrm{Def}((\Sigma,x_1,\ldots, x_n),\partial\Sigma)\to H^1(\Sigma,\partial\Sigma, u^*T_{\mathcal{X}}, (u|_{\partial\Sigma})^* T_{\mathcal{L}})\to \mathcal{T}^2_\xi, \end{aligned} \end{align} $$
where
-
○
 $\mathrm {Aut}((\Sigma ,x_1,\ldots , x_n),\partial \Sigma )$
is the space of infinitesimal automorphism of the domain
$\mathrm {Aut}((\Sigma ,x_1,\ldots , x_n),\partial \Sigma )$
is the space of infinitesimal automorphism of the domain
 $((\Sigma ,x_1,\ldots , x_n),\partial \Sigma )$
and is equal to
$((\Sigma ,x_1,\ldots , x_n),\partial \Sigma )$
and is equal to
 $H^0(\Sigma ,\partial \Sigma , T_{\Sigma }(-\sum _{j=1}^nx_j), T_{\partial \Sigma })$
when
$H^0(\Sigma ,\partial \Sigma , T_{\Sigma }(-\sum _{j=1}^nx_j), T_{\partial \Sigma })$
when
 $\Sigma $
is a smooth bordered orbifold Riemann surface;
$\Sigma $
is a smooth bordered orbifold Riemann surface; -
○
 $\mathrm {Def}((\Sigma ,x_1,\ldots , x_n),\partial \Sigma )$
is the space of infinitesimal deformations of the domain, and is equal to
$\mathrm {Def}((\Sigma ,x_1,\ldots , x_n),\partial \Sigma )$
is the space of infinitesimal deformations of the domain, and is equal to
 $H^1(\Sigma ,\partial \Sigma ,T_{\Sigma }(-\sum _{j=1}^n x_i), T_{\partial \Sigma })$
when
$H^1(\Sigma ,\partial \Sigma ,T_{\Sigma }(-\sum _{j=1}^n x_i), T_{\partial \Sigma })$
when
 $\Sigma $
is a smooth bordered orbifold Riemann surface;
$\Sigma $
is a smooth bordered orbifold Riemann surface; -
○
 $H^0(\Sigma ,\partial \Sigma ,u^*T_{\mathcal {X}}, (u|_{\partial \Sigma })^*T_{\mathcal {L}})$
is the space of infinitesimal deformation of the map for a fixed domain;
$H^0(\Sigma ,\partial \Sigma ,u^*T_{\mathcal {X}}, (u|_{\partial \Sigma })^*T_{\mathcal {L}})$
is the space of infinitesimal deformation of the map for a fixed domain; -
○
 $H^1(\Sigma ,\partial \Sigma ,u^*T_{\mathcal {X}},(u|_{\partial \Sigma })^*T_{\mathcal {L}})$
is the space of obstructions to deforming the map for a fixed domain.
$H^1(\Sigma ,\partial \Sigma ,u^*T_{\mathcal {X}},(u|_{\partial \Sigma })^*T_{\mathcal {L}})$
is the space of obstructions to deforming the map for a fixed domain.
Globally on the moduli space
![]() $\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L},\beta ', {\vec {\mu }} )$
, there is an exact sequence of sheaves
$\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L},\beta ', {\vec {\mu }} )$
, there is an exact sequence of sheaves
whose fibre at the moduli point
![]() $\xi $
is equation (7).
$\xi $
is equation (7).
Let
![]() $\mathfrak {M}_{(g,h),n}$
be the moduli of prestable bordered orbifold Riemann surfaces of type
$\mathfrak {M}_{(g,h),n}$
be the moduli of prestable bordered orbifold Riemann surfaces of type
![]() $(g,h)$
with n interior marked point. Then
$(g,h)$
with n interior marked point. Then
![]() $\mathfrak {M}_{(g,h),n}$
is a differentiable stack (with corners) of real dimension
$\mathfrak {M}_{(g,h),n}$
is a differentiable stack (with corners) of real dimension
There are evaluation maps (at interior marked points)
Given
![]() $\vec {v}=(v_1,\ldots , v_n)$
, where
$\vec {v}=(v_1,\ldots , v_n)$
, where
![]() $v_1,\ldots , v_n\in \mathrm {Box}(\mathbf \Sigma )$
, define
$v_1,\ldots , v_n\in \mathrm {Box}(\mathbf \Sigma )$
, define
 $$ \begin{align*}\overline{\mathcal{M}}_{(g,h),\vec{v}}(\mathcal{X},\mathcal{L}\mid\beta', {\vec{\mu}} ) := \bigcap_{j=1}^n \mathrm{ev}_j^{-1}(\mathcal{X}_{v_j}). \end{align*} $$
$$ \begin{align*}\overline{\mathcal{M}}_{(g,h),\vec{v}}(\mathcal{X},\mathcal{L}\mid\beta', {\vec{\mu}} ) := \bigcap_{j=1}^n \mathrm{ev}_j^{-1}(\mathcal{X}_{v_j}). \end{align*} $$
Suppose that
![]() $\xi \in \overline {\mathcal {M}}_{(g,h),\vec {v}}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
. By the Riemann-Roch theorem for prestable bordered orbifold Riemann surface (which can be derived by combining the proof of the Riemann-Roch theorem for prestable bordered Riemann surfaces and prestable orbifold closed Riemann surfaces),
$\xi \in \overline {\mathcal {M}}_{(g,h),\vec {v}}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
. By the Riemann-Roch theorem for prestable bordered orbifold Riemann surface (which can be derived by combining the proof of the Riemann-Roch theorem for prestable bordered Riemann surfaces and prestable orbifold closed Riemann surfaces),
 $$ \begin{align} &\dim_{\mathbb{R}} H^0(\Sigma,\partial\Sigma,u^*T_{\mathcal{X}}, (u|_{\partial\Sigma})^*T_{\mathcal{L}}) -\dim_{\mathbb{R}} H^1(\Sigma,\partial\Sigma, u^*T_{\mathcal{X}}, (u|_{\partial\Sigma})^*T_{\mathcal{L}}) \nonumber \\ &\quad = 3(2-2g-h) - 2\sum_{j=1}^n \mathrm{age}(v_j). \end{align} $$
$$ \begin{align} &\dim_{\mathbb{R}} H^0(\Sigma,\partial\Sigma,u^*T_{\mathcal{X}}, (u|_{\partial\Sigma})^*T_{\mathcal{L}}) -\dim_{\mathbb{R}} H^1(\Sigma,\partial\Sigma, u^*T_{\mathcal{X}}, (u|_{\partial\Sigma})^*T_{\mathcal{L}}) \nonumber \\ &\quad = 3(2-2g-h) - 2\sum_{j=1}^n \mathrm{age}(v_j). \end{align} $$
The above equation (10) is the relative virtual dimension of
![]() $\overline {\mathcal {M}}_{(g,h),\vec {v}}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )\rightarrow \mathfrak {M}_{(g,h),n}$
that sends a stable map to its domain. The virtual (real) dimension of
$\overline {\mathcal {M}}_{(g,h),\vec {v}}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )\rightarrow \mathfrak {M}_{(g,h),n}$
that sends a stable map to its domain. The virtual (real) dimension of
![]() $\overline {\mathcal {M}}_{{ (g,h)},\vec {v}}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
is equal to
$\overline {\mathcal {M}}_{{ (g,h)},\vec {v}}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
is equal to
 $$ \begin{align*}\dim_{\mathbb{R}} \mathcal{T}^1_\xi - \dim_{\mathbb{R}} \mathcal{T}^2_\xi = 2 \sum_{j=1}^n(1-\mathrm{age}(v_j)), \end{align*} $$
$$ \begin{align*}\dim_{\mathbb{R}} \mathcal{T}^1_\xi - \dim_{\mathbb{R}} \mathcal{T}^2_\xi = 2 \sum_{j=1}^n(1-\mathrm{age}(v_j)), \end{align*} $$
where
![]() $\mathrm {age}(v_j)\in \{0,1,2\}$
.
$\mathrm {age}(v_j)\in \{0,1,2\}$
.
3.6 Torus action and equivariant invariants
Let
![]() $ \mathbb {T} ^{\prime }_{\mathbb {R}} \cong U(1)^2$
be the maximal compact subgroup of
$ \mathbb {T} ^{\prime }_{\mathbb {R}} \cong U(1)^2$
be the maximal compact subgroup of
![]() $ \mathbb {T} '\cong ( \mathbb {C} ^*)^2$
. For any
$ \mathbb {T} '\cong ( \mathbb {C} ^*)^2$
. For any
![]() $t \in \mathbb {T} ^{\prime }_{\mathbb {R}} $
, the map
$t \in \mathbb {T} ^{\prime }_{\mathbb {R}} $
, the map
![]() $\phi _t: \mathcal {X} \to \mathcal {X}$
given by
$\phi _t: \mathcal {X} \to \mathcal {X}$
given by
![]() $x\mapsto t\cdot x$
is an automorphism of the smooth toric DM stack
$x\mapsto t\cdot x$
is an automorphism of the smooth toric DM stack
![]() $\mathcal {X}$
, and
$\mathcal {X}$
, and
![]() $\phi _t(\mathcal {L}) =\mathcal {L}$
, so
$\phi _t(\mathcal {L}) =\mathcal {L}$
, so
![]() $ \mathbb {T} ^{\prime }_{\mathbb {R}} $
acts on the moduli spaces
$ \mathbb {T} ^{\prime }_{\mathbb {R}} $
acts on the moduli spaces
![]() $\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L} \mid \beta ', {\vec {\mu }} )$
; here we use the notion of group actions on stacks in [Reference Romagny65]. Let
$\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L} \mid \beta ', {\vec {\mu }} )$
; here we use the notion of group actions on stacks in [Reference Romagny65]. Let
![]() $F \subset \overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
be the substack of
$F \subset \overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
be the substack of
![]() $ \mathbb {T} ^{\prime }_{\mathbb {R}} $
fixed points. The restriction of the exact sequence equation (8) to the substack F is the direct sum of two exact sequences
$ \mathbb {T} ^{\prime }_{\mathbb {R}} $
fixed points. The restriction of the exact sequence equation (8) to the substack F is the direct sum of two exact sequences
where equation (11) is the subcomplex fixed by the torus action. The virtual tangent bundle
![]() $\mathcal {T}^ {\mathrm {vir}} _F$
of F is
$\mathcal {T}^ {\mathrm {vir}} _F$
of F is
whose ranks can be different on different connected components of F. We will see that each connected component of F is a compact orbifold and that
![]() $\mathcal {T}^ {\mathrm {vir}} _F$
is equal to the tangent bundle
$\mathcal {T}^ {\mathrm {vir}} _F$
is equal to the tangent bundle
![]() $\mathcal {T}_F$
of F. So
$\mathcal {T}_F$
of F. So
The virtual normal bundle
![]() $N^ {\mathrm {vir}} $
of F in
$N^ {\mathrm {vir}} $
of F in
![]() $\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
is
$\overline {\mathcal {M}}_{(g,h),n}(\mathcal {X},\mathcal {L}\mid \beta ', {\vec {\mu }} )$
is
Given
![]() $\gamma _1,\ldots , \gamma _n \in H^*_{ \mathbb {T} ', {\mathrm {CR}} }(\mathcal {X}; \mathbb {Q} )=H^*_{ \mathbb {T} ^{\prime }_{\mathbb {R}} , {\mathrm {CR}} }(\mathcal {X}, \mathbb {Q} )$
, we define
$\gamma _1,\ldots , \gamma _n \in H^*_{ \mathbb {T} ', {\mathrm {CR}} }(\mathcal {X}; \mathbb {Q} )=H^*_{ \mathbb {T} ^{\prime }_{\mathbb {R}} , {\mathrm {CR}} }(\mathcal {X}, \mathbb {Q} )$
, we define
 $$ \begin{align} \langle \gamma_1,\ldots, \gamma_n\rangle^{\mathcal{X},\mathcal{L}, \mathbb{T} _{\mathbb{R}} '}_{g,\beta', {\vec{\mu}} }:= \int_{[F]^{ {\mathrm{vir}} }} \frac{\prod_{j=1}^n (\mathrm{ev}_j^*\gamma_i)|_F}{e_{ \mathbb{T} _{\mathbb{R}} '}(N^ {\mathrm{vir}} )} \in \mathcal{Q}_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }, \end{align} $$
$$ \begin{align} \langle \gamma_1,\ldots, \gamma_n\rangle^{\mathcal{X},\mathcal{L}, \mathbb{T} _{\mathbb{R}} '}_{g,\beta', {\vec{\mu}} }:= \int_{[F]^{ {\mathrm{vir}} }} \frac{\prod_{j=1}^n (\mathrm{ev}_j^*\gamma_i)|_F}{e_{ \mathbb{T} _{\mathbb{R}} '}(N^ {\mathrm{vir}} )} \in \mathcal{Q}_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }, \end{align} $$
where
![]() $\mathcal {Q}_{ \mathbb {T} _{\mathbb {R}} '}$
is the fractional field of
$\mathcal {Q}_{ \mathbb {T} _{\mathbb {R}} '}$
is the fractional field of
![]() $H^*_{ \mathbb {T} _{\mathbb {R}} '}(\mathrm {point}; \mathbb {Q} )$
, and
$H^*_{ \mathbb {T} _{\mathbb {R}} '}(\mathrm {point}; \mathbb {Q} )$
, and
 $$ \begin{align*}\frac{1}{e_{ \mathbb{T} _{\mathbb{R}} '}(N^ {\mathrm{vir}} _F)} =\frac{e_{ \mathbb{T} _{\mathbb{R}} '}(\mathcal{T}^{2,m})}{e_{ \mathbb{T} _{\mathbb{R}} '}(\mathcal{T}^{1,m}) }=\frac{ e_{ \mathbb{T} _{\mathbb{R}} '}(B_1^m) e_{ \mathbb{T} _{\mathbb{R}} '}(B_5^m)}{e_{ \mathbb{T} _{\mathbb{R}} '}(B_2^m)e_{ \mathbb{T} _{\mathbb{R}} '}(B_4^m)}. \end{align*} $$
$$ \begin{align*}\frac{1}{e_{ \mathbb{T} _{\mathbb{R}} '}(N^ {\mathrm{vir}} _F)} =\frac{e_{ \mathbb{T} _{\mathbb{R}} '}(\mathcal{T}^{2,m})}{e_{ \mathbb{T} _{\mathbb{R}} '}(\mathcal{T}^{1,m}) }=\frac{ e_{ \mathbb{T} _{\mathbb{R}} '}(B_1^m) e_{ \mathbb{T} _{\mathbb{R}} '}(B_5^m)}{e_{ \mathbb{T} _{\mathbb{R}} '}(B_2^m)e_{ \mathbb{T} _{\mathbb{R}} '}(B_4^m)}. \end{align*} $$
More precisely, the definition in equation (13) also requires an orientation on the virtual tangent bundle
![]() $\mathcal {T}^1 -\mathcal {T}^2$
, which we will specify later.
$\mathcal {T}^1 -\mathcal {T}^2$
, which we will specify later.
3.7 Tangent weights: the 3-torus, the Calabi-Yau 2-torus, and the framing 1-torus
Let
![]() $\mathfrak {o}_\tau \cong \mathbb {C} ^*\times \mathcal {B} G_\tau $
be the unique 1-dimensional
$\mathfrak {o}_\tau \cong \mathbb {C} ^*\times \mathcal {B} G_\tau $
be the unique 1-dimensional
![]() $ \mathbb {T} $
-orbit that intersects the Aganagic-Vafa A-brane
$ \mathbb {T} $
-orbit that intersects the Aganagic-Vafa A-brane
![]() $\mathcal {L}$
, where
$\mathcal {L}$
, where
![]() $\tau \in \Sigma (2)$
, as before. Let
$\tau \in \Sigma (2)$
, as before. Let
![]() $\mathfrak {l}_\tau $
be the closure of
$\mathfrak {l}_\tau $
be the closure of
![]() $\mathfrak {o}_\tau $
, and let
$\mathfrak {o}_\tau $
, and let
![]() $\ell _\tau $
be the coarse moduli of
$\ell _\tau $
be the coarse moduli of
![]() $\mathfrak {l}_\tau $
. Then
$\mathfrak {l}_\tau $
. Then
![]() $\ell _\tau $
is either
$\ell _\tau $
is either
![]() $ \mathbb {P} ^1$
or
$ \mathbb {P} ^1$
or
![]() $ \mathbb {C} $
.
$ \mathbb {C} $
.
Definition 3.1. We say
![]() $\mathcal {L}$
is an inner brane if
$\mathcal {L}$
is an inner brane if
![]() $\ell _\tau \cong \mathbb {P} ^1$
; we say
$\ell _\tau \cong \mathbb {P} ^1$
; we say
![]() $\mathcal {L}$
is an outer brane if
$\mathcal {L}$
is an outer brane if
![]() $\ell _\tau \cong \mathbb {C} $
.
$\ell _\tau \cong \mathbb {C} $
.
If
![]() $\mathcal {L}$
is an outer brane, let
$\mathcal {L}$
is an outer brane, let
![]() $ {\sigma } \in \Sigma (3)$
be the unique 3-cone such that
$ {\sigma } \in \Sigma (3)$
be the unique 3-cone such that
![]() $(\tau , {\sigma } )\in F(\Sigma )$
; if
$(\tau , {\sigma } )\in F(\Sigma )$
; if
![]() $\mathcal {L}$
is an inner brane, we choose
$\mathcal {L}$
is an inner brane, we choose
![]() $ {\sigma } \in \Sigma (3)$
such that
$ {\sigma } \in \Sigma (3)$
such that
![]() $(\tau , {\sigma } )\in F(\Sigma )$
, and let
$(\tau , {\sigma } )\in F(\Sigma )$
, and let
![]() $ {\sigma } _- \in \Sigma (3)$
denote the other choice, so that
$ {\sigma } _- \in \Sigma (3)$
denote the other choice, so that
![]() $\mathfrak {p}_ {\sigma } $
and
$\mathfrak {p}_ {\sigma } $
and
![]() $\mathfrak {p}_{ \sigma_{-}}$
are the two torus fixed points in
$\mathfrak {p}_{ \sigma_{-}}$
are the two torus fixed points in
![]() $\mathfrak {l}_\tau $
. For inner branes, we also denote
$\mathfrak {l}_\tau $
. For inner branes, we also denote
![]() $ {\sigma } _+= {\sigma } $
.
$ {\sigma } _+= {\sigma } $
.
By permuting
![]() $b_1,\ldots , b_r$
if necessary, we may assume that
$b_1,\ldots , b_r$
if necessary, we may assume that
![]() $I^{\prime }_{ {\sigma } }=\{1,2,3\}$
, and
$I^{\prime }_{ {\sigma } }=\{1,2,3\}$
, and
![]() $(\tau _1,\sigma )= (\tau ,\sigma )$
,
$(\tau _1,\sigma )= (\tau ,\sigma )$
,
![]() $(\tau _2,\sigma )$
and
$(\tau _2,\sigma )$
and
![]() $(\tau _3,\sigma )$
are three flags in the toric graph in the counterclockwise direction such that
$(\tau _3,\sigma )$
are three flags in the toric graph in the counterclockwise direction such that
Here we fixed an orientation of
![]() $ \mathbb {R} ^2$
. If
$ \mathbb {R} ^2$
. If
![]() $\mathcal {L}$
is an inner brane, we assume in addition
$\mathcal {L}$
is an inner brane, we assume in addition
![]() $I^{\prime }_{ {\sigma } _-}=\{ 2,3, 4\}$
.
$I^{\prime }_{ {\sigma } _-}=\{ 2,3, 4\}$
.
Recall from Section 2.4 that for any flag
![]() $(\tau , {\sigma } )\in F(\Sigma )$
,
$(\tau , {\sigma } )\in F(\Sigma )$
,
![]() $\chi _{(\tau , {\sigma } )}\in \mathrm {Hom}(G_ {\sigma } , \mathbb {C} ^*)$
is the character of the 1-dimensional
$\chi _{(\tau , {\sigma } )}\in \mathrm {Hom}(G_ {\sigma } , \mathbb {C} ^*)$
is the character of the 1-dimensional
![]() $G_ {\sigma } $
representation
$G_ {\sigma } $
representation
![]() $T_{\mathfrak {p}_ {\sigma } }\mathfrak {l}_\tau $
. Let
$T_{\mathfrak {p}_ {\sigma } }\mathfrak {l}_\tau $
. Let
Then we have the following two short exact sequences of finite abelian groups:
Note that for any
![]() $\lambda \in G_\tau $
,
$\lambda \in G_\tau $
,
![]() $\chi _{(\tau , {\sigma } )}(\lambda )=1$
and
$\chi _{(\tau , {\sigma } )}(\lambda )=1$
and
![]() $\chi _{(\tau _2, {\sigma } )}(\lambda )\chi _{(\tau _3, {\sigma } )}(\lambda )=1$
. Let
$\chi _{(\tau _2, {\sigma } )}(\lambda )\chi _{(\tau _3, {\sigma } )}(\lambda )=1$
. Let
![]() $\bar {\lambda }$
denote the unique element in
$\bar {\lambda }$
denote the unique element in
![]() $\{0,1,\ldots ,\mathfrak {m}-1\}$
such that
$\{0,1,\ldots ,\mathfrak {m}-1\}$
such that
Let
![]() $\mathsf {u}_3\in M$
be defined as in Section 3.1, so that
$\mathsf {u}_3\in M$
be defined as in Section 3.1, so that
![]() $\langle \mathsf {u}_3, \bar {b}_i\rangle =1$
. We may choose a
$\langle \mathsf {u}_3, \bar {b}_i\rangle =1$
. We may choose a
![]() $ \mathbb {Z} $
-basis
$ \mathbb {Z} $
-basis
![]() $\{ \mathsf {v}_1,\mathsf {v}_2, \mathsf {v}_3\}$
of
$\{ \mathsf {v}_1,\mathsf {v}_2, \mathsf {v}_3\}$
of
![]() $\bar {N}$
such that
$\bar {N}$
such that
![]() $ \langle \mathsf {u}_3,\mathsf {v}_i\rangle =\delta _{i,3}$
, and
$ \langle \mathsf {u}_3,\mathsf {v}_i\rangle =\delta _{i,3}$
, and
Moreover, the choice
![]() $(\mathsf {v}_1,\mathsf {v}_2,\mathsf {v}_3)$
is unique if we require
$(\mathsf {v}_1,\mathsf {v}_2,\mathsf {v}_3)$
is unique if we require
![]() $\mathfrak {s} \in \{0,1,\ldots ,\mathfrak {r}-1\}$
. Let
$\mathfrak {s} \in \{0,1,\ldots ,\mathfrak {r}-1\}$
. Let
![]() $\{ \mathsf {u}_1,\mathsf {u}_2,\mathsf {u}_3\}$
be the
$\{ \mathsf {u}_1,\mathsf {u}_2,\mathsf {u}_3\}$
be the
![]() $ \mathbb {Z} $
-basis of M that is dual to the
$ \mathbb {Z} $
-basis of M that is dual to the
![]() $ \mathbb {Z} $
-basis
$ \mathbb {Z} $
-basis
![]() $\{\mathsf {v}_1,\mathsf {v}_2,\mathsf {v}_2\}$
of
$\{\mathsf {v}_1,\mathsf {v}_2,\mathsf {v}_2\}$
of
![]() $\bar {N}$
. Let
$\bar {N}$
. Let
![]() $\{\mathsf {w}_1,\mathsf {w}_2,\mathsf {w}_3\}$
be the
$\{\mathsf {w}_1,\mathsf {w}_2,\mathsf {w}_3\}$
be the
![]() $ \mathbb {Q} $
-basis of
$ \mathbb {Q} $
-basis of
![]() $M_{\mathbb {Q}} $
that is dual to the
$M_{\mathbb {Q}} $
that is dual to the
![]() $ \mathbb {Q} $
-basis
$ \mathbb {Q} $
-basis
![]() $\{ \bar {b}_1,\bar {b}_2, \bar {b}_3\}$
of
$\{ \bar {b}_1,\bar {b}_2, \bar {b}_3\}$
of
![]() $N_{\mathbb {Q}} = N\otimes _{ \mathbb {Z} } \mathbb {Q} $
. Then
$N_{\mathbb {Q}} = N\otimes _{ \mathbb {Z} } \mathbb {Q} $
. Then
Moreover, for
![]() $i\in \{1,2,3\}$
,
$i\in \{1,2,3\}$
,
The inclusion
![]() $ \mathbb {T} '\subset \mathbb {T} $
induces the following surjective ring homomorphism
$ \mathbb {T} '\subset \mathbb {T} $
induces the following surjective ring homomorphism
where
![]() $R= \mathbb {Z} $
or
$R= \mathbb {Z} $
or
![]() $ \mathbb {Q} $
.
$ \mathbb {Q} $
.
Given a framing that is an integer
![]() $f\in \mathbb {Z} $
, let
$f\in \mathbb {Z} $
, let
![]() $ \mathbb {T} _f \subset \mathbb {T} '$
be the kernel of the character
$ \mathbb {T} _f \subset \mathbb {T} '$
be the kernel of the character
![]() $\mathsf {u}_2'-f\mathsf {u}^{\prime }_1\in \mathrm {Hom}( \mathbb {T} '; \mathbb {C} ^*)$
. Then
$\mathsf {u}_2'-f\mathsf {u}^{\prime }_1\in \mathrm {Hom}( \mathbb {T} '; \mathbb {C} ^*)$
. Then
![]() $ \mathbb {T} _f\cong \mathbb {C} ^*$
is a 1-dimensional subtorus of the Calabi-Yau torus
$ \mathbb {T} _f\cong \mathbb {C} ^*$
is a 1-dimensional subtorus of the Calabi-Yau torus
![]() $ \mathbb {T} '$
. The inclusion
$ \mathbb {T} '$
. The inclusion
![]() $ \mathbb {T} _f\subset \mathbb {T} '$
induces a surjective ring homomorphism
$ \mathbb {T} _f\subset \mathbb {T} '$
induces a surjective ring homomorphism
where
![]() $R= \mathbb {Z} $
or
$R= \mathbb {Z} $
or
![]() $ \mathbb {Q} $
. For
$ \mathbb {Q} $
. For
![]() $i=1,2,3$
, let
$i=1,2,3$
, let
![]() $\mathsf {w}^{\prime }_i$
denote the image of
$\mathsf {w}^{\prime }_i$
denote the image of
![]() $\mathsf {w}_i$
under the ring homomorphism equation (14), and let
$\mathsf {w}_i$
under the ring homomorphism equation (14), and let
![]() $\mathsf {w}^f_i$
denote the image of
$\mathsf {w}^f_i$
denote the image of
![]() $\mathsf {w}^{\prime }_i$
under the ring homomorphism in (15). Then
$\mathsf {w}^{\prime }_i$
under the ring homomorphism in (15). Then
and
![]() $\mathsf {w}^f_i = w_i \mathsf {u}$
, where
$\mathsf {w}^f_i = w_i \mathsf {u}$
, where
![]() $w_i\in \mathbb {Q} $
are given by
$w_i\in \mathbb {Q} $
are given by
3.8 Disk factors as equivariant open GW invariants
A framed Aganagic-Vafa Lagrangian brane is a pair
![]() $(\mathcal {L},f)$
, where
$(\mathcal {L},f)$
, where
![]() $\mathcal {L}$
is an Aganagic-Vafa brane together with a choice of a flag
$\mathcal {L}$
is an Aganagic-Vafa brane together with a choice of a flag
![]() $(\tau , {\sigma } )\in F(\Sigma )$
such that
$(\tau , {\sigma } )\in F(\Sigma )$
such that
![]() $\mathfrak {o}_\tau $
is the unique 1-dimensional orbit intersecting
$\mathfrak {o}_\tau $
is the unique 1-dimensional orbit intersecting
![]() $\mathcal {L}$
and a choice of framing
$\mathcal {L}$
and a choice of framing
![]() $f\in \mathbb {Z} $
. Given a framed Aganagic-Vafa Lagrangian brane
$f\in \mathbb {Z} $
. Given a framed Aganagic-Vafa Lagrangian brane
![]() $(\mathcal {L},f)$
, we choose an isomorphism
$(\mathcal {L},f)$
, we choose an isomorphism
![]() $\pi _1(\mathcal {L}) \cong \mathbb {Z} \times G_\tau $
such that if
$\pi _1(\mathcal {L}) \cong \mathbb {Z} \times G_\tau $
such that if
![]() $h=\iota _*^{(\tau , {\sigma } )}(d_0,\lambda )$
(where
$h=\iota _*^{(\tau , {\sigma } )}(d_0,\lambda )$
(where
![]() $\iota _*^{(\tau , {\sigma } )}$
is defined in Section 3.3); then
$\iota _*^{(\tau , {\sigma } )}$
is defined in Section 3.3); then
Let
![]() $\ell _\tau $
be the coarse moduli of
$\ell _\tau $
be the coarse moduli of
![]() $\mathfrak {l}_\tau $
, as before. Let
$\mathfrak {l}_\tau $
, as before. Let
![]() $p_ {\sigma } \in \ell _\tau $
be the coarse moduli of
$p_ {\sigma } \in \ell _\tau $
be the coarse moduli of
![]() $\mathfrak {p}_ {\sigma } \cong \mathcal {B} G_ {\sigma } $
, and let
$\mathfrak {p}_ {\sigma } \cong \mathcal {B} G_ {\sigma } $
, and let
![]() $S_\tau := L\cap \ell _\tau \cong S^1$
be the coarse moduli of
$S_\tau := L\cap \ell _\tau \cong S^1$
be the coarse moduli of
![]() $\mathcal {S}_\tau =\mathcal {L}\cap \mathfrak {l}_\tau \cong S^1\times \mathcal {B} G_\tau $
.
$\mathcal {S}_\tau =\mathcal {L}\cap \mathfrak {l}_\tau \cong S^1\times \mathcal {B} G_\tau $
.
3.8.1
 $(\mathcal {L},f)$
is a framed outer brane
$(\mathcal {L},f)$
is a framed outer brane
In this case
![]() $\ell _\tau = \mathbb {C} $
. Let
$\ell _\tau = \mathbb {C} $
. Let
![]() $D\subset \ell _\tau $
be the disk that contains
$D\subset \ell _\tau $
be the disk that contains
![]() $p_ {\sigma } $
with boundary
$p_ {\sigma } $
with boundary
![]() $S_\tau $
, oriented by the complex structure on
$S_\tau $
, oriented by the complex structure on
![]() $\ell _\tau $
, and let
$\ell _\tau $
, and let
![]() $b=[D]\in H_2(X,L; \mathbb {Z} )$
. Given
$b=[D]\in H_2(X,L; \mathbb {Z} )$
. Given
![]() $(d_0,\lambda )\in H_1(\mathcal {L}; \mathbb {Z} )\cong \mathbb {Z} \times G_\tau $
, where
$(d_0,\lambda )\in H_1(\mathcal {L}; \mathbb {Z} )\cong \mathbb {Z} \times G_\tau $
, where
![]() $d_0>0$
, define
$d_0>0$
, define
The virtual real dimension of
![]() $\overline {\mathcal {M}}(d_0,\lambda )$
is
$\overline {\mathcal {M}}(d_0,\lambda )$
is
![]() $2(1-\mathrm {age}(h(d_0,\lambda )))$
, where
$2(1-\mathrm {age}(h(d_0,\lambda )))$
, where
![]() $h(d_0,\lambda ):= \iota _*^{(\tau , {\sigma } )}(d_0,\lambda )\in G_\sigma $
. Define the disk factor
$h(d_0,\lambda ):= \iota _*^{(\tau , {\sigma } )}(d_0,\lambda )\in G_\sigma $
. Define the disk factor
which is a rational function in
![]() $\mathsf {w}_1',\mathsf {w}_2'$
, homogeneous of degree
$\mathsf {w}_1',\mathsf {w}_2'$
, homogeneous of degree
![]() $\mathrm {age}(h(d_0,\lambda ))-1$
. The disk factor is computed in [Reference Brini and Cavalieri11] when
$\mathrm {age}(h(d_0,\lambda ))-1$
. The disk factor is computed in [Reference Brini and Cavalieri11] when
![]() $G_ {\sigma } $
is cyclic and in [Reference Ross66, Section 3.3] for general
$G_ {\sigma } $
is cyclic and in [Reference Ross66, Section 3.3] for general
![]() $G_ {\sigma } $
. In our notation, the formula in [Reference Ross66, Section 3.3] saysFootnote
2
$G_ {\sigma } $
. In our notation, the formula in [Reference Ross66, Section 3.3] saysFootnote
2
 $$ \begin{align} \begin{aligned} D_{d_0,\lambda}= \left(\frac{\mathfrak{r}\mathsf{w}^{\prime}_1}{d_0}\right)^{\mathrm{age}(h(d_0,\lambda))-1} \frac{1}{d_0 |G_\tau|} \cdot \frac{ \prod_{a=1}^{ \lfloor \frac{d_0}{\mathfrak{r}}\rfloor+ \mathrm{age}(h(d_0,\lambda)) -1}\left( \frac{d_0 \mathsf{w}^{\prime}_2}{\mathfrak{r}\mathsf{w}^{\prime}_1} + a-c_2\left(h(d_0,\lambda)\right) \right) }{\lfloor \frac{d_0}{\mathfrak{r}}\rfloor!} \end{aligned}, \end{align} $$
$$ \begin{align} \begin{aligned} D_{d_0,\lambda}= \left(\frac{\mathfrak{r}\mathsf{w}^{\prime}_1}{d_0}\right)^{\mathrm{age}(h(d_0,\lambda))-1} \frac{1}{d_0 |G_\tau|} \cdot \frac{ \prod_{a=1}^{ \lfloor \frac{d_0}{\mathfrak{r}}\rfloor+ \mathrm{age}(h(d_0,\lambda)) -1}\left( \frac{d_0 \mathsf{w}^{\prime}_2}{\mathfrak{r}\mathsf{w}^{\prime}_1} + a-c_2\left(h(d_0,\lambda)\right) \right) }{\lfloor \frac{d_0}{\mathfrak{r}}\rfloor!} \end{aligned}, \end{align} $$
where
![]() $c_i(\cdot )\in \mathbb {Q} \cap [0,1)$
is defined in Section 2.7. More explicitly,
$c_i(\cdot )\in \mathbb {Q} \cap [0,1)$
is defined in Section 2.7. More explicitly,
 $$ \begin{align*}c_2(h(d_0,\lambda)) = \left\langle d_0 w_2 -\frac{\bar{\lambda}}{\mathfrak{m}}\right\rangle. \end{align*} $$
$$ \begin{align*}c_2(h(d_0,\lambda)) = \left\langle d_0 w_2 -\frac{\bar{\lambda}}{\mathfrak{m}}\right\rangle. \end{align*} $$
3.8.2
 $(\mathcal {L},f)$
is a framed inner brane
$(\mathcal {L},f)$
is a framed inner brane
In this case
![]() $\ell _\tau \cong \mathbb {P} ^1$
. It contains two torus fixed points
$\ell _\tau \cong \mathbb {P} ^1$
. It contains two torus fixed points
![]() $p_+ = p_ {\sigma } $
and
$p_+ = p_ {\sigma } $
and
![]() $p_-=p_{ {\sigma } _-}$
, where
$p_-=p_{ {\sigma } _-}$
, where
![]() $ {\sigma } _- \in \Sigma (3)$
. The circle
$ {\sigma } _- \in \Sigma (3)$
. The circle
![]() $S_\tau $
is the intersection of two disks
$S_\tau $
is the intersection of two disks
![]() $D_+$
and
$D_+$
and
![]() $D_-$
that contain
$D_-$
that contain
![]() $p_+$
and
$p_+$
and
![]() $p_-$
, respectively. Let
$p_-$
, respectively. Let
Then
![]() $[D_-]=\alpha -b\in H_2(X,L; \mathbb {Z} )$
. Given
$[D_-]=\alpha -b\in H_2(X,L; \mathbb {Z} )$
. Given
![]() $(d_0,\lambda )\in H_1(\mathcal {L}; \mathbb {Z} )\cong \mathbb {Z} \times G_\tau $
, where
$(d_0,\lambda )\in H_1(\mathcal {L}; \mathbb {Z} )\cong \mathbb {Z} \times G_\tau $
, where
![]() $d_0\neq 0$
, we define
$d_0\neq 0$
, we define
 $$ \begin{align*}\overline{\mathcal{M}}(d_0,\lambda) := \begin{cases} \overline{\mathcal{M}}_{(0,1),1}(\mathcal{X},\mathcal{L}\mid d_0 b, (d_0,\lambda)), & d_0>0,\\ \overline{\mathcal{M}}_{(0,1),1}(\mathcal{X},\mathcal{L}\mid -d_0(\alpha-b), (d_0, \lambda)), & d_0<0. \end{cases} \end{align*} $$
$$ \begin{align*}\overline{\mathcal{M}}(d_0,\lambda) := \begin{cases} \overline{\mathcal{M}}_{(0,1),1}(\mathcal{X},\mathcal{L}\mid d_0 b, (d_0,\lambda)), & d_0>0,\\ \overline{\mathcal{M}}_{(0,1),1}(\mathcal{X},\mathcal{L}\mid -d_0(\alpha-b), (d_0, \lambda)), & d_0<0. \end{cases} \end{align*} $$
Then
 $$ \begin{align*}\mathrm{virtual\ dimension\ of\ }\overline{\mathcal{M}}(d_0,\lambda)= \begin{cases} 1 -\mathrm{age}(h^+(d_0,\lambda)), & d_0>0,\\ 1-\mathrm{age}(h^-(d_0,\lambda)), & d_0<0, \end{cases} \end{align*} $$
$$ \begin{align*}\mathrm{virtual\ dimension\ of\ }\overline{\mathcal{M}}(d_0,\lambda)= \begin{cases} 1 -\mathrm{age}(h^+(d_0,\lambda)), & d_0>0,\\ 1-\mathrm{age}(h^-(d_0,\lambda)), & d_0<0, \end{cases} \end{align*} $$
where
![]() $h^{\pm }(d_0,\lambda ) = \iota _*^{(\tau , {\sigma } _\pm )}(d_0,\lambda )\in G_{ {\sigma } _\pm }$
. Define
$h^{\pm }(d_0,\lambda ) = \iota _*^{(\tau , {\sigma } _\pm )}(d_0,\lambda )\in G_{ {\sigma } _\pm }$
. Define
 $$ \begin{align*}D_{d_0,\lambda}:= \begin{cases} \langle 1_{h^+(d_0,\lambda)}\rangle_{0,d_0 b, (d_0,\lambda)}^{\mathcal{X},\mathcal{L}, \mathbb{T} ^{\prime}_{\mathbb{R}} }, & d_0>0,\\ & \\ \langle 1_{h^-(d_0,\lambda)}\rangle_{0,-d_0 (\alpha-b), (d_0,\lambda)}^{\mathcal{X}, \mathcal{L}, \mathbb{T} ^{\prime}_{\mathbb{R}} }, & d_0 <0. \end{cases}. \end{align*} $$
$$ \begin{align*}D_{d_0,\lambda}:= \begin{cases} \langle 1_{h^+(d_0,\lambda)}\rangle_{0,d_0 b, (d_0,\lambda)}^{\mathcal{X},\mathcal{L}, \mathbb{T} ^{\prime}_{\mathbb{R}} }, & d_0>0,\\ & \\ \langle 1_{h^-(d_0,\lambda)}\rangle_{0,-d_0 (\alpha-b), (d_0,\lambda)}^{\mathcal{X}, \mathcal{L}, \mathbb{T} ^{\prime}_{\mathbb{R}} }, & d_0 <0. \end{cases}. \end{align*} $$
Then
![]() $D_{d_0,\lambda }$
is a rational function in
$D_{d_0,\lambda }$
is a rational function in
![]() $\mathsf {u}^{\prime }_1,\mathsf {u}^{\prime }_2$
, homogeneous of degree
$\mathsf {u}^{\prime }_1,\mathsf {u}^{\prime }_2$
, homogeneous of degree
![]() $\mathrm {age}(h^\pm (d_0,\lambda ))-1$
if
$\mathrm {age}(h^\pm (d_0,\lambda ))-1$
if
![]() $\pm d_0>0$
.
$\pm d_0>0$
.
More precisely, the disk factor
![]() $D_{d_0,\lambda }$
is defined up to a sign depending on choice of orientation of
$D_{d_0,\lambda }$
is defined up to a sign depending on choice of orientation of
![]() $\overline {\mathcal {M}}(d_0,\lambda )$
, which will be clarified in Section 3.11 by relative GW invariants.
$\overline {\mathcal {M}}(d_0,\lambda )$
, which will be clarified in Section 3.11 by relative GW invariants.
3.9 Normal bundle to
 $\mathfrak {l}_\tau $
$\mathfrak {l}_\tau $
Let
![]() $\mathcal {L}$
be an inner brane so that
$\mathcal {L}$
be an inner brane so that
![]() $\mathfrak {l}_\tau $
is a proper smooth toric DM curve. Let
$\mathfrak {l}_\tau $
is a proper smooth toric DM curve. Let
![]() $\hat {\mathfrak {l}}_\tau $
be the image of
$\hat {\mathfrak {l}}_\tau $
be the image of
![]() $\mathfrak {l}_\tau $
under the morphism
$\mathfrak {l}_\tau $
under the morphism
![]() $\mathcal {X}\to \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
. We have
$\mathcal {X}\to \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
. We have
where
![]() $\mathfrak {l}_\tau \to \hat {\mathfrak {l}}_\tau $
is a K-banded gerbe,
$\mathfrak {l}_\tau \to \hat {\mathfrak {l}}_\tau $
is a K-banded gerbe,
![]() $\hat {\mathfrak {l}}_\tau \to \mathfrak {l}_\tau ^ {\mathrm {rig}} $
is a
$\hat {\mathfrak {l}}_\tau \to \mathfrak {l}_\tau ^ {\mathrm {rig}} $
is a
![]() $\boldsymbol {\mu }_\mathfrak{m}$
-banded gerbe and
$\boldsymbol {\mu }_\mathfrak{m}$
-banded gerbe and
![]() $\mathfrak {l}_\tau \to \mathfrak {l}_\tau ^ {\mathrm {rig}} $
is a
$\mathfrak {l}_\tau \to \mathfrak {l}_\tau ^ {\mathrm {rig}} $
is a
![]() $G_\tau $
-banded gerbe. The normal bundle
$G_\tau $
-banded gerbe. The normal bundle
![]() $\mathfrak {l}_\tau $
in
$\mathfrak {l}_\tau $
in
![]() $\mathcal {X}$
is a direct sum of two
$\mathcal {X}$
is a direct sum of two
![]() $ \mathbb {T} $
-equivariant line bundles over
$ \mathbb {T} $
-equivariant line bundles over
![]() $\mathfrak {l}_\tau $
:
$\mathfrak {l}_\tau $
:
where
![]() $L_2=\mathcal {O}_{\mathcal {X}}(\mathcal {D}_2)\big |_{\mathfrak {l}_\tau }$
and
$L_2=\mathcal {O}_{\mathcal {X}}(\mathcal {D}_2)\big |_{\mathfrak {l}_\tau }$
and
![]() $L_3 =\mathcal {O}_{\mathcal {X}}(\mathcal {D}_3)\big |_{\mathfrak {l}_\tau }$
. The total space of
$L_3 =\mathcal {O}_{\mathcal {X}}(\mathcal {D}_3)\big |_{\mathfrak {l}_\tau }$
. The total space of
![]() $N_{\mathfrak {l}_\tau /\mathcal {X}}$
is a smooth toric DM stack that is isomorphic to the open substack
$N_{\mathfrak {l}_\tau /\mathcal {X}}$
is a smooth toric DM stack that is isomorphic to the open substack
![]() $\mathcal {Y}:= \mathcal {X}_{ {\sigma } }\cup \mathcal {X}_{ {\sigma } _-}$
of
$\mathcal {Y}:= \mathcal {X}_{ {\sigma } }\cup \mathcal {X}_{ {\sigma } _-}$
of
![]() $\mathcal {X}$
. Let
$\mathcal {X}$
. Let
![]() $\hat {\mathcal {D}}_i$
be the image of
$\hat {\mathcal {D}}_i$
be the image of
![]() $\mathcal {D}_i$
under
$\mathcal {D}_i$
under
![]() $\mathcal {X}\to \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
. Then
$\mathcal {X}\to \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
. Then
where
![]() $\hat {L}_2 =\mathcal {O}_{\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} }(\hat {\mathcal {D}}_2)\big |_{\hat {\mathfrak {l}}_\tau }$
and
$\hat {L}_2 =\mathcal {O}_{\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} }(\hat {\mathcal {D}}_2)\big |_{\hat {\mathfrak {l}}_\tau }$
and
![]() $\hat {L}_3 =\mathcal {O}_{\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} }(\hat {\mathcal {D}}_3)\big |_{\hat {\mathfrak {l}}_\tau }$
. The total space of
$\hat {L}_3 =\mathcal {O}_{\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} }(\hat {\mathcal {D}}_3)\big |_{\hat {\mathfrak {l}}_\tau }$
. The total space of
![]() $N_{\hat {\mathfrak {l}}_\tau /{\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} }}$
is a toric orbifold that is isomorphic to the open substack
$N_{\hat {\mathfrak {l}}_\tau /{\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} }}$
is a toric orbifold that is isomorphic to the open substack
![]() $\mathcal {Y}^ {\mathrm {rig}} =\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} _ {\sigma } \cup \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} _{ {\sigma } _-}$
of the toric orbifold
$\mathcal {Y}^ {\mathrm {rig}} =\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} _ {\sigma } \cup \mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} _{ {\sigma } _-}$
of the toric orbifold
![]() $\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
.
$\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
.
Let
![]() $\Sigma _0$
be the simplicial fan in
$\Sigma _0$
be the simplicial fan in
![]() $N_{\mathbb {R}} $
consisting of
$N_{\mathbb {R}} $
consisting of
![]() $ {\sigma } $
,
$ {\sigma } $
,
![]() $ {\sigma } _-$
and their subcones. The stacky fan of
$ {\sigma } _-$
and their subcones. The stacky fan of
![]() $\mathcal {Y}^ {\mathrm {rig}} $
is given by
$\mathcal {Y}^ {\mathrm {rig}} $
is given by
![]() $(\Sigma _0, (\bar {b}_1, \bar {b}_2, \bar {b}_3, \bar {b}_4))$
, where
$(\Sigma _0, (\bar {b}_1, \bar {b}_2, \bar {b}_3, \bar {b}_4))$
, where
where c is some integer. For inner branes, we also denote
![]() $\mathfrak {r}_+=\mathfrak {r}$
. We have
$\mathfrak {r}_+=\mathfrak {r}$
. We have
![]() $\mathcal {Y} =[U/G_0]$
, where
$\mathcal {Y} =[U/G_0]$
, where
 $$ \begin{align*} U&=\{(Z_1,Z_2,Z_3,Z_4)\in \mathbb{C} ^4: (Z_1,Z_4)\neq (0,0)\},\\ G_0&=\{ (\tilde{t}_1,\tilde{t}_2,\tilde{t}_3,\tilde{t}_4)\in ( \mathbb{C} ^*)^4: \tilde{t}_1^{\mathfrak{r}} (\tilde{t}_4)^{-\mathfrak{r}_-} = (\tilde{t}_1)^{-\mathfrak{s}}\tilde{t}_2^{\mathfrak{m}} \tilde{t}_4^c =\tilde{t}_1\tilde{t}_2\tilde{t}_3\tilde{t}_4=1\}. \end{align*} $$
$$ \begin{align*} U&=\{(Z_1,Z_2,Z_3,Z_4)\in \mathbb{C} ^4: (Z_1,Z_4)\neq (0,0)\},\\ G_0&=\{ (\tilde{t}_1,\tilde{t}_2,\tilde{t}_3,\tilde{t}_4)\in ( \mathbb{C} ^*)^4: \tilde{t}_1^{\mathfrak{r}} (\tilde{t}_4)^{-\mathfrak{r}_-} = (\tilde{t}_1)^{-\mathfrak{s}}\tilde{t}_2^{\mathfrak{m}} \tilde{t}_4^c =\tilde{t}_1\tilde{t}_2\tilde{t}_3\tilde{t}_4=1\}. \end{align*} $$
We have a short exact sequence of abelian groups:
where
![]() $G_{\mathfrak {r},\mathfrak {r}_-}=\{ (\tilde {t}_1,\tilde {t}_4)\in ( \mathbb {C} ^*)^2: \tilde {t}_1^{\mathfrak {r}} (\tilde {t}_4)^{-\mathfrak {r}_-}=1\}$
and
$G_{\mathfrak {r},\mathfrak {r}_-}=\{ (\tilde {t}_1,\tilde {t}_4)\in ( \mathbb {C} ^*)^2: \tilde {t}_1^{\mathfrak {r}} (\tilde {t}_4)^{-\mathfrak {r}_-}=1\}$
and
![]() $\chi _i(\tilde {t}_1,\tilde {t}_2, \tilde {t}_3, \tilde {t}_4)=\tilde {t}_i$
. The subgroup
$\chi _i(\tilde {t}_1,\tilde {t}_2, \tilde {t}_3, \tilde {t}_4)=\tilde {t}_i$
. The subgroup
![]() $\boldsymbol {\mu }_{\mathfrak {m}}$
of
$\boldsymbol {\mu }_{\mathfrak {m}}$
of
![]() $G_0$
acts trivially on
$G_0$
acts trivially on
![]() $V =\{ (Z_1,Z_2,Z_3,Z_4)\in U_{\mathcal {A}}: Z_2=Z_3=0\}$
, so the
$V =\{ (Z_1,Z_2,Z_3,Z_4)\in U_{\mathcal {A}}: Z_2=Z_3=0\}$
, so the
![]() $G_0$
-action on V factors through a
$G_0$
-action on V factors through a
![]() $G_{\mathfrak {r},\mathfrak {r}_-}$
-action on V, and
$G_{\mathfrak {r},\mathfrak {r}_-}$
-action on V, and
where
![]() $\mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}$
denotes the football obtained by glueing
$\mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}$
denotes the football obtained by glueing
![]() $[ \mathbb {C} /\boldsymbol {\mu }_{\mathfrak {r}}]$
and
$[ \mathbb {C} /\boldsymbol {\mu }_{\mathfrak {r}}]$
and
![]() $[ \mathbb {C} /\boldsymbol {\mu }_{\mathfrak {r}-}]$
along
$[ \mathbb {C} /\boldsymbol {\mu }_{\mathfrak {r}-}]$
along
![]() $[ \mathbb {C} ^*/\boldsymbol {\mu }_{\mathfrak {r}}] \cong [ \mathbb {C} ^*/\boldsymbol {\mu }_{\mathfrak {r}_-}]\cong \mathbb {C} ^*$
. The two torus fixed points in
$[ \mathbb {C} ^*/\boldsymbol {\mu }_{\mathfrak {r}}] \cong [ \mathbb {C} ^*/\boldsymbol {\mu }_{\mathfrak {r}_-}]\cong \mathbb {C} ^*$
. The two torus fixed points in
![]() $\mathfrak {l}_{\tau }^ {\mathrm {rig}} $
are
$\mathfrak {l}_{\tau }^ {\mathrm {rig}} $
are
and
![]() $\mathfrak {l}_\tau ^ {\mathrm {rig}} - \{ \mathfrak {p}_x, \mathfrak {p}_y\} \cong \mathbb {C} ^*$
. We have a surjective group homomorphism
$\mathfrak {l}_\tau ^ {\mathrm {rig}} - \{ \mathfrak {p}_x, \mathfrak {p}_y\} \cong \mathbb {C} ^*$
. We have a surjective group homomorphism
![]() $ \mathbb {Z} \oplus \mathbb {Z} \to {\mathrm {Pic}} (\mathfrak {l}_\tau ^ {\mathrm {rig}} )$
sending
$ \mathbb {Z} \oplus \mathbb {Z} \to {\mathrm {Pic}} (\mathfrak {l}_\tau ^ {\mathrm {rig}} )$
sending
![]() $(n_x,n_y)$
to
$(n_x,n_y)$
to
![]() $\mathcal {O}_{\mathfrak {l}_\tau ^ {\mathrm {rig}} }(n_x \mathfrak {p}_x + n_y \mathfrak {p}_y)$
; the kernel is
$\mathcal {O}_{\mathfrak {l}_\tau ^ {\mathrm {rig}} }(n_x \mathfrak {p}_x + n_y \mathfrak {p}_y)$
; the kernel is
![]() $ \mathbb {Z} (\mathfrak {r},-\mathfrak {r}_-)$
.
$ \mathbb {Z} (\mathfrak {r},-\mathfrak {r}_-)$
.
Let
![]() $\mathcal {O}(-1)$
denote the tautological line bundle over
$\mathcal {O}(-1)$
denote the tautological line bundle over
![]() $\mathcal {B} \mathbb {C} ^*$
associated with the fundamental representation
$\mathcal {B} \mathbb {C} ^*$
associated with the fundamental representation
![]() $ \mathbb {C} ^* \to GL(1, \mathbb {C} )$
,
$ \mathbb {C} ^* \to GL(1, \mathbb {C} )$
,
![]() $t\mapsto t$
. Given a line bundle L over a DM stack
$t\mapsto t$
. Given a line bundle L over a DM stack
![]() $\mathcal {Z}$
and a positive integer
$\mathcal {Z}$
and a positive integer
![]() $\mathfrak {m}$
, let
$\mathfrak {m}$
, let
![]() $\sqrt [\mathfrak {m}]{L/\mathcal {Z}}$
denote the following fibre product (compare to [Reference Cadman14, Definition 2.2.6]):
$\sqrt [\mathfrak {m}]{L/\mathcal {Z}}$
denote the following fibre product (compare to [Reference Cadman14, Definition 2.2.6]):

where the morphism
![]() $\phi _L: \mathcal {Z} \longrightarrow \mathcal {B} \mathbb {C} ^*$
is defined by L (so that
$\phi _L: \mathcal {Z} \longrightarrow \mathcal {B} \mathbb {C} ^*$
is defined by L (so that
![]() $\phi _L^*\mathcal {O}(-1)= L$
), and
$\phi _L^*\mathcal {O}(-1)= L$
), and
![]() $\mathcal {B} \mathbb {C} ^*\to \mathcal {B} \mathbb {C} ^*$
is induced by the
$\mathcal {B} \mathbb {C} ^*\to \mathcal {B} \mathbb {C} ^*$
is induced by the
![]() $\mathfrak {m}$
th power map from
$\mathfrak {m}$
th power map from
![]() $ \mathbb {C} ^*$
to itself. Then
$ \mathbb {C} ^*$
to itself. Then
![]() $p_1:\sqrt [\mathfrak {m}]{L/\mathcal {Z}} \to \mathcal {Z}$
is a
$p_1:\sqrt [\mathfrak {m}]{L/\mathcal {Z}} \to \mathcal {Z}$
is a
![]() $\boldsymbol {\mu }_{\mathfrak {m}}$
-banded gerbe. Let
$\boldsymbol {\mu }_{\mathfrak {m}}$
-banded gerbe. Let
![]() $\sqrt [\mathfrak {m}]{L}:=p_2^*\mathcal {O}(-1)\in {\mathrm {Pic}} (\sqrt [\mathfrak {m}]{L/\mathcal {Z}})$
. Then
$\sqrt [\mathfrak {m}]{L}:=p_2^*\mathcal {O}(-1)\in {\mathrm {Pic}} (\sqrt [\mathfrak {m}]{L/\mathcal {Z}})$
. Then
![]() $(\sqrt [\mathfrak {m}]{L})^{\otimes \mathfrak {m}}= p_1^*L$
: that is,
$(\sqrt [\mathfrak {m}]{L})^{\otimes \mathfrak {m}}= p_1^*L$
: that is,
![]() $\sqrt [\mathfrak {m}]{L}$
is an
$\sqrt [\mathfrak {m}]{L}$
is an
![]() $\mathfrak{m}$
th root of
$\mathfrak{m}$
th root of
![]() $p_1^*L$
.
$p_1^*L$
.
It is straightforward to check that
-
○
 $\hat {\mathfrak {l}}_\tau $
is isomorphic to
$\hat {\mathfrak {l}}_\tau $
is isomorphic to
 $\sqrt [\mathfrak {m}]{\mathcal {O}_{\mathfrak {l}_\tau ^ {\mathrm {rig}} }(\mathfrak {s}\mathfrak {p}_x - c\mathfrak {p}_y)/\mathfrak {l}^ {\mathrm {rig}} _\tau }$
as a
$\sqrt [\mathfrak {m}]{\mathcal {O}_{\mathfrak {l}_\tau ^ {\mathrm {rig}} }(\mathfrak {s}\mathfrak {p}_x - c\mathfrak {p}_y)/\mathfrak {l}^ {\mathrm {rig}} _\tau }$
as a
 $\boldsymbol {\mu }_{\mathfrak {m}}$
-banded gerbe over
$\boldsymbol {\mu }_{\mathfrak {m}}$
-banded gerbe over
 $\mathfrak {l}_\tau ^ {\mathrm {rig}} \cong \mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}$
, and
$\mathfrak {l}_\tau ^ {\mathrm {rig}} \cong \mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}$
, and -
○
 $\hat {L}_2 \cong \sqrt [\mathfrak {m}]{\mathcal {O}_{\mathfrak {l}_\tau ^ {\mathrm {rig}} }(\mathfrak {s}\mathfrak {p}_x-c\mathfrak {p}_y)}$
,
$\hat {L}_2 \cong \sqrt [\mathfrak {m}]{\mathcal {O}_{\mathfrak {l}_\tau ^ {\mathrm {rig}} }(\mathfrak {s}\mathfrak {p}_x-c\mathfrak {p}_y)}$
,
 $\hat {L}_3 = \hat {L}_2^{-1} \otimes p_1^*\mathcal {O}_{\mathfrak {l}_\tau ^ {\mathrm {rig}} }(-\mathfrak {p}_x-\mathfrak {p}_y)$
, where
$\hat {L}_3 = \hat {L}_2^{-1} \otimes p_1^*\mathcal {O}_{\mathfrak {l}_\tau ^ {\mathrm {rig}} }(-\mathfrak {p}_x-\mathfrak {p}_y)$
, where
 $p_1: \hat {\mathfrak {l}}_\tau \to \mathfrak {l}_\tau ^ {\mathrm {rig}} $
and
$p_1: \hat {\mathfrak {l}}_\tau \to \mathfrak {l}_\tau ^ {\mathrm {rig}} $
and
 $\mathcal {O}_{\mathfrak {l}_\tau ^ {\mathrm {rig}} }(-\mathfrak {p}_x-\mathfrak {p}_y)$
is the cotangent bundle of
$\mathcal {O}_{\mathfrak {l}_\tau ^ {\mathrm {rig}} }(-\mathfrak {p}_x-\mathfrak {p}_y)$
is the cotangent bundle of
 $\mathfrak {l}_\tau ^ {\mathrm {rig}} $
.
$\mathfrak {l}_\tau ^ {\mathrm {rig}} $
.
3.10 Degeneration
Let
![]() $\Sigma _1 =\{ \{0\}, \mathbb {R} _{\geq 0} \mathsf {v}_1, \mathbb {R} _{\geq 0}(-\mathsf {v}_1)\}$
be the complete 1-dimensional fan in
$\Sigma _1 =\{ \{0\}, \mathbb {R} _{\geq 0} \mathsf {v}_1, \mathbb {R} _{\geq 0}(-\mathsf {v}_1)\}$
be the complete 1-dimensional fan in
![]() $ \mathbb {R} \mathsf {v}_1\cong \mathbb {R} $
, and let
$ \mathbb {R} \mathsf {v}_1\cong \mathbb {R} $
, and let
![]() $\Sigma _2=\{ \{0\}, \mathbb {R} _{\geq 0} \mathsf {v}_4 , \mathbb {R} _{\geq 0}(-\mathsf {v}_4)\}$
be the complete 1-dimensional fan in
$\Sigma _2=\{ \{0\}, \mathbb {R} _{\geq 0} \mathsf {v}_4 , \mathbb {R} _{\geq 0}(-\mathsf {v}_4)\}$
be the complete 1-dimensional fan in
![]() $ \mathbb {R} \mathsf {v}_4\cong \mathbb {R} $
. Then
$ \mathbb {R} \mathsf {v}_4\cong \mathbb {R} $
. Then
![]() $X_{\Sigma _1}=X_{\Sigma _2}= \mathbb {P} ^1$
. The stacky fan
$X_{\Sigma _1}=X_{\Sigma _2}= \mathbb {P} ^1$
. The stacky fan
![]() $(\Sigma _1, (\mathfrak {r}\mathsf {v}_1,-\mathfrak {r}_-\mathsf {v}_1))$
defines the 1-dimensional toric orbifold
$(\Sigma _1, (\mathfrak {r}\mathsf {v}_1,-\mathfrak {r}_-\mathsf {v}_1))$
defines the 1-dimensional toric orbifold
![]() $\mathcal {F}_{\mathfrak {r},-\mathfrak {r}_-}$
, and the stacky fan
$\mathcal {F}_{\mathfrak {r},-\mathfrak {r}_-}$
, and the stacky fan
defines the 2-dimensional toric orbifold
![]() $\mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}\times \mathbb {P} ^1$
. The 1-dimensional cones in the fan
$\mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}\times \mathbb {P} ^1$
. The 1-dimensional cones in the fan
![]() $\Sigma _1\times \Sigma _2$
are
$\Sigma _1\times \Sigma _2$
are
![]() $\{ \rho _i = \mathbb {R} _{\geq 0}b_i': 1\leq i\leq 4\}$
. Let
$\{ \rho _i = \mathbb {R} _{\geq 0}b_i': 1\leq i\leq 4\}$
. Let
![]() $\Sigma '$
be the fan obtained by adding a 1-dimensional cone
$\Sigma '$
be the fan obtained by adding a 1-dimensional cone
![]() $\rho _5 = \mathbb {R} _{\geq 0} b_5'$
, where
$\rho _5 = \mathbb {R} _{\geq 0} b_5'$
, where
![]() $b_5'=-\mathsf {v}_1-\mathsf {v}_4$
. Let
$b_5'=-\mathsf {v}_1-\mathsf {v}_4$
. Let
![]() $\mathcal {S}'$
be the 2-dimensional toric orbifold defined by the stacky fan
$\mathcal {S}'$
be the 2-dimensional toric orbifold defined by the stacky fan
![]() $\mathbf {\Sigma }'=(\Sigma ',(b_1',b_2',b_3',b_4',b_5'))$
, and let
$\mathbf {\Sigma }'=(\Sigma ',(b_1',b_2',b_3',b_4',b_5'))$
, and let
![]() $\mathfrak {l}_i'=\mathcal {V}(\rho _i) \subset \mathcal {S}'$
be 1-dimensional closed toric substack associated with the ray
$\mathfrak {l}_i'=\mathcal {V}(\rho _i) \subset \mathcal {S}'$
be 1-dimensional closed toric substack associated with the ray
![]() $\rho _i$
. The morphism
$\rho _i$
. The morphism
![]() $\mathbf {\Sigma '}\to \mathbf {\Sigma }_{\Box }$
of stacky fans induces a morphism
$\mathbf {\Sigma '}\to \mathbf {\Sigma }_{\Box }$
of stacky fans induces a morphism
![]() $\nu : \mathcal {S}' \to \mathcal {F}_{\mathfrak {r},\mathfrak {r}_-} \times \mathbb {P} ^1$
of toric orbifolds;
$\nu : \mathcal {S}' \to \mathcal {F}_{\mathfrak {r},\mathfrak {r}_-} \times \mathbb {P} ^1$
of toric orbifolds;
![]() $\nu $
contracts the divisor
$\nu $
contracts the divisor
![]() $\mathfrak {l}^{\prime }_5$
to the torus fixed point
$\mathfrak {l}^{\prime }_5$
to the torus fixed point
![]() $[0,1]\times [0,1] \cong \mathcal {B} \boldsymbol {\mu }_{\mathfrak {r}_-}$
in
$[0,1]\times [0,1] \cong \mathcal {B} \boldsymbol {\mu }_{\mathfrak {r}_-}$
in
![]() $\mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}\times \mathbb {P} ^1$
. Let
$\mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}\times \mathbb {P} ^1$
. Let
![]() $p: \mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}\times \mathbb {P} ^1\to \mathbb {P} ^1$
be the projection to the second factor. The composition
$p: \mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}\times \mathbb {P} ^1\to \mathbb {P} ^1$
be the projection to the second factor. The composition
![]() $\pi ':= p\circ \nu $
is a flat morphism, and
$\pi ':= p\circ \nu $
is a flat morphism, and
where
![]() $\mathfrak {l}^{\prime }_3\cong \mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}$
,
$\mathfrak {l}^{\prime }_3\cong \mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}$
,
![]() $\mathfrak {l}^{\prime }_4 \cong \mathcal {F}_{\mathfrak {r},1}$
, and
$\mathfrak {l}^{\prime }_4 \cong \mathcal {F}_{\mathfrak {r},1}$
, and
![]() $\mathfrak {l}^{\prime }_5\cong \mathcal {F}_{1,\mathfrak {r}_-}$
. The torus fixed points in
$\mathfrak {l}^{\prime }_5\cong \mathcal {F}_{1,\mathfrak {r}_-}$
. The torus fixed points in
![]() $\mathcal {S}'$
are
$\mathcal {S}'$
are
where
![]() $p_z$
is a scheme point.
$p_z$
is a scheme point.
Given any
![]() $f\in \mathbb {Z} $
, define
$f\in \mathbb {Z} $
, define
which is a
![]() $\boldsymbol {\mu }_{\mathfrak {m}}$
-banded gerbe over
$\boldsymbol {\mu }_{\mathfrak {m}}$
-banded gerbe over
![]() $\mathcal {S}'$
, and let
$\mathcal {S}'$
, and let
![]() $\hat {q}: \hat {\mathcal {S}} \to \mathcal {S}'=\mathcal {S}^ {\mathrm {rig}} $
be the morphism to the rigidification. Define
$\hat {q}: \hat {\mathcal {S}} \to \mathcal {S}'=\mathcal {S}^ {\mathrm {rig}} $
be the morphism to the rigidification. Define
![]() $\pi := \hat {q}\circ \pi ': \mathcal {S}\to \mathbb {P} ^1$
, and let
$\pi := \hat {q}\circ \pi ': \mathcal {S}\to \mathbb {P} ^1$
, and let
![]() $\hat {\mathfrak {l}}_i\subset \mathcal {S}$
be the divisor that corresponds to
$\hat {\mathfrak {l}}_i\subset \mathcal {S}$
be the divisor that corresponds to
![]() $\mathfrak {l}_i'\subset \mathcal {S}'$
under
$\mathfrak {l}_i'\subset \mathcal {S}'$
under
![]() $\hat {q}:\hat {\mathcal {S}}\to \mathcal {S}'$
. Then
$\hat {q}:\hat {\mathcal {S}}\to \mathcal {S}'$
. Then
![]() $\hat {q}_i:= \hat {q}|_{\mathfrak {l}_i}: \hat {\mathfrak {l}}_i\to \mathfrak {l}^{\prime }_i =\hat {\mathfrak {l}}_i^ {\mathrm {rig}} $
is a
$\hat {q}_i:= \hat {q}|_{\mathfrak {l}_i}: \hat {\mathfrak {l}}_i\to \mathfrak {l}^{\prime }_i =\hat {\mathfrak {l}}_i^ {\mathrm {rig}} $
is a
![]() $\boldsymbol {\mu }_{\mathfrak {m}}$
-banded gerbe. We have
$\boldsymbol {\mu }_{\mathfrak {m}}$
-banded gerbe. We have
Define
![]() $\tilde {L}_2, \tilde {L}_3 \in {\mathrm {Pic}} (\hat {\mathcal {S}})$
by
$\tilde {L}_2, \tilde {L}_3 \in {\mathrm {Pic}} (\hat {\mathcal {S}})$
by
Then
For
![]() $i\in \{2,3\}$
, define
$i\in \{2,3\}$
, define
![]() $\hat {L}_i^+ = \tilde {L}_i\big |_{\hat {\mathfrak {l}}_4}$
and
$\hat {L}_i^+ = \tilde {L}_i\big |_{\hat {\mathfrak {l}}_4}$
and
![]() $\hat {L}_i^- =\tilde {L}_i\big |_{\hat {\mathfrak {l}}_5}$
. Then
$\hat {L}_i^- =\tilde {L}_i\big |_{\hat {\mathfrak {l}}_5}$
. Then
 $$ \begin{align*}\begin{array}{ll} \hat{L}_2^+= \sqrt[\mathfrak{m}]{\mathcal{O}_{\mathfrak{l}_4'}(\mathfrak{s}\mathfrak{p}_x^\infty+fp_z )}, & \hat{L}_3^+ = \sqrt[\mathfrak{m}]{\mathcal{O}_{\mathfrak{l}^{\prime}_4}(-\mathfrak{s}\mathfrak{p}^\infty_x-fp_z)}\otimes \hat{q}_4^*\mathcal{O}_{\mathfrak{l}^{\prime}_4}(-\mathfrak{p}_x^\infty),\\[6pt] \hat{L}_2^-= \sqrt[\mathfrak{m}]{\mathcal{O}_{\mathfrak{l}^{\prime}_5}(-c \mathfrak{p}_y^\infty-fp_z)}, & \hat{L}_3^- = \sqrt[\mathfrak{m}]{\mathcal{O}_{\mathfrak{l}^{\prime}_5}(c \mathfrak{p}^\infty_y + fp_z)}\otimes \hat{q}_5^*\mathcal{O}_{\mathfrak{l}^{\prime}_5}(-\mathfrak{p}_y^\infty). \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ll} \hat{L}_2^+= \sqrt[\mathfrak{m}]{\mathcal{O}_{\mathfrak{l}_4'}(\mathfrak{s}\mathfrak{p}_x^\infty+fp_z )}, & \hat{L}_3^+ = \sqrt[\mathfrak{m}]{\mathcal{O}_{\mathfrak{l}^{\prime}_4}(-\mathfrak{s}\mathfrak{p}^\infty_x-fp_z)}\otimes \hat{q}_4^*\mathcal{O}_{\mathfrak{l}^{\prime}_4}(-\mathfrak{p}_x^\infty),\\[6pt] \hat{L}_2^-= \sqrt[\mathfrak{m}]{\mathcal{O}_{\mathfrak{l}^{\prime}_5}(-c \mathfrak{p}_y^\infty-fp_z)}, & \hat{L}_3^- = \sqrt[\mathfrak{m}]{\mathcal{O}_{\mathfrak{l}^{\prime}_5}(c \mathfrak{p}^\infty_y + fp_z)}\otimes \hat{q}_5^*\mathcal{O}_{\mathfrak{l}^{\prime}_5}(-\mathfrak{p}_y^\infty). \end{array} \end{align*} $$
To summarise:
-
○
 $\hat {\mathcal {S}}$
is a degeneration from
$\hat {\mathcal {S}}$
is a degeneration from
 $\hat {\mathfrak {l}}_\tau $
to a nodal DM curve
$\hat {\mathfrak {l}}_\tau $
to a nodal DM curve
 $\hat {\mathfrak {l}}_4 \cup \hat {\mathfrak {l}}_5$
, and
$\hat {\mathfrak {l}}_4 \cup \hat {\mathfrak {l}}_5$
, and
 $\mathcal {S}'=\hat {\mathcal {S}}^ {\mathrm {rig}} $
is a degeneration from the football
$\mathcal {S}'=\hat {\mathcal {S}}^ {\mathrm {rig}} $
is a degeneration from the football
 $\mathfrak {l}_\tau ^ {\mathrm {rig}} \cong \mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}$
to the nodal DM curve
$\mathfrak {l}_\tau ^ {\mathrm {rig}} \cong \mathcal {F}_{\mathfrak {r},\mathfrak {r}_-}$
to the nodal DM curve
 $\mathfrak {l}_4'\cup \mathfrak {l}_5'$
.
$\mathfrak {l}_4'\cup \mathfrak {l}_5'$
. -
○ For
 $i=2,3$
, the line bundle
$i=2,3$
, the line bundle
 $\tilde {L}_i$
on
$\tilde {L}_i$
on
 $\hat {\mathcal {S}}$
defines a degeneration of the line bundle
$\hat {\mathcal {S}}$
defines a degeneration of the line bundle
 $\hat {L}_i\to \hat {\mathfrak {l}}_\tau $
to a line bundle on
$\hat {L}_i\to \hat {\mathfrak {l}}_\tau $
to a line bundle on
 $\hat {\mathfrak {l}}_4\cup \hat {\mathfrak {l}}_5$
that restricts to
$\hat {\mathfrak {l}}_4\cup \hat {\mathfrak {l}}_5$
that restricts to
 $\hat {L}_i^+$
on
$\hat {L}_i^+$
on
 $\hat {\mathfrak {l}}_4$
and
$\hat {\mathfrak {l}}_4$
and
 $\hat {L}_i^-$
on
$\hat {L}_i^-$
on
 $\hat {\mathfrak {l}}_5$
.
$\hat {\mathfrak {l}}_5$
. -
○
 $\hat {\mathcal {S}}$
,
$\hat {\mathcal {S}}$
,
 $\tilde {L}_i$
,
$\tilde {L}_i$
,
 $\hat {\mathfrak {l}}_4$
,
$\hat {\mathfrak {l}}_4$
,
 $\hat {\mathfrak {l}}_5$
, and
$\hat {\mathfrak {l}}_5$
, and
 $\hat {L}^\pm _i$
depend on f, while
$\hat {L}^\pm _i$
depend on f, while
 $\mathcal {S}'$
,
$\mathcal {S}'$
,
 $\mathfrak {l}_4'$
and
$\mathfrak {l}_4'$
and
 $\mathfrak {l}_5'$
do not.
$\mathfrak {l}_5'$
do not.
Moreover, the total space of
![]() $\tilde {L}_2\oplus \tilde {L}_3 \to {\hat {\mathcal {S}}} $
is a 4-dimensional toric orbifold
$\tilde {L}_2\oplus \tilde {L}_3 \to {\hat {\mathcal {S}}} $
is a 4-dimensional toric orbifold
![]() $\hat {\mathcal {W}}$
defined by a stacky fan
$\hat {\mathcal {W}}$
defined by a stacky fan
where
![]() $\Sigma _f$
is a simplicial fan in
$\Sigma _f$
is a simplicial fan in
![]() $\bigoplus _{i=1}^4 \mathbb {R} \mathsf {v}_i$
, and
$\bigoplus _{i=1}^4 \mathbb {R} \mathsf {v}_i$
, and
![]() $(\bar {b}_1,\ldots ,-\mathsf {v}_1-f\mathsf {v}_2 -\mathsf {v}_4)$
is a 7-tuple of vectors in
$(\bar {b}_1,\ldots ,-\mathsf {v}_1-f\mathsf {v}_2 -\mathsf {v}_4)$
is a 7-tuple of vectors in
![]() $\bar {N}\oplus \mathbb {Z} \mathsf {v}_4 \cong \mathbb {Z} ^4$
. Let
$\bar {N}\oplus \mathbb {Z} \mathsf {v}_4 \cong \mathbb {Z} ^4$
. Let
![]() $\mathcal {W}$
be the 4-dimensional smooth toric DM stack defined by the the stacky fan
$\mathcal {W}$
be the 4-dimensional smooth toric DM stack defined by the the stacky fan
where
![]() $\tilde {\mathsf {v}}_1,\tilde {\mathsf {v}}_2 \in N$
are lifts of
$\tilde {\mathsf {v}}_1,\tilde {\mathsf {v}}_2 \in N$
are lifts of
![]() $\mathsf {v}_1,\mathsf {v}_2 \in \bar {N}$
, so that
$\mathsf {v}_1,\mathsf {v}_2 \in \bar {N}$
, so that
![]() $(b_1,\ldots , -\tilde {\mathsf {v}}_1- f\tilde {\mathsf {v}}_2- \mathsf {v}_4)$
is a 7-tuple of elements in
$(b_1,\ldots , -\tilde {\mathsf {v}}_1- f\tilde {\mathsf {v}}_2- \mathsf {v}_4)$
is a 7-tuple of elements in
![]() $N\oplus \mathbb {Z} \mathsf {v}_4$
. Then
$N\oplus \mathbb {Z} \mathsf {v}_4$
. Then
![]() $\mathcal {W}$
is a K-banded gerbe over
$\mathcal {W}$
is a K-banded gerbe over
![]() $\hat {\mathcal {W}} =\mathcal {W}^ {\mathrm {rig}} $
and is a degeneration from the total space
$\hat {\mathcal {W}} =\mathcal {W}^ {\mathrm {rig}} $
and is a degeneration from the total space
![]() $\mathcal {Y}$
of
$\mathcal {Y}$
of
![]() $N_{\mathfrak {l}_\tau /\mathcal {X}}$
to the total space
$N_{\mathfrak {l}_\tau /\mathcal {X}}$
to the total space
![]() $\mathcal {Y}_\infty $
of a direct sum
$\mathcal {Y}_\infty $
of a direct sum
![]() $L_2^\infty \oplus L_3^\infty $
of line bundles over a nodal DM curve
$L_2^\infty \oplus L_3^\infty $
of line bundles over a nodal DM curve
![]() $\mathfrak {l}_+\cup \mathfrak {l}_-$
;
$\mathfrak {l}_+\cup \mathfrak {l}_-$
;
![]() $\mathfrak {l}_+\cup \mathfrak {l}_-$
is a K-banded gerbe over
$\mathfrak {l}_+\cup \mathfrak {l}_-$
is a K-banded gerbe over
![]() $\hat {\mathfrak {l}}_4\cup \hat {\mathfrak {l}}_5$
and a
$\hat {\mathfrak {l}}_4\cup \hat {\mathfrak {l}}_5$
and a
![]() $G_\tau $
-banded gerbe over
$G_\tau $
-banded gerbe over
![]() $\mathfrak {l}_4'\cup \mathfrak {l}_5'$
. For
$\mathfrak {l}_4'\cup \mathfrak {l}_5'$
. For
![]() $i=2,3$
, let
$i=2,3$
, let
![]() $L_i^\pm = L_i^\infty |_{\mathfrak {l}_\pm }$
. Then
$L_i^\pm = L_i^\infty |_{\mathfrak {l}_\pm }$
. Then
![]() $L_i^\pm $
is the pullback of
$L_i^\pm $
is the pullback of
![]() $\hat {L}_i^\pm $
. Let
$\hat {L}_i^\pm $
. Let
![]() $\mathfrak {p}_0\cong \mathcal {B} G_\tau $
be the node that is the intersection of
$\mathfrak {p}_0\cong \mathcal {B} G_\tau $
be the node that is the intersection of
![]() $\mathfrak {l}_+$
and
$\mathfrak {l}_+$
and
![]() $\mathfrak {l}_-$
, and let
$\mathfrak {l}_-$
, and let
![]() $\mathfrak {p}_\pm $
be the unique torus fixed point in
$\mathfrak {p}_\pm $
be the unique torus fixed point in
![]() $\mathfrak {l}_\pm -\{ \mathfrak {p}_0\}$
. Then
$\mathfrak {l}_\pm -\{ \mathfrak {p}_0\}$
. Then
![]() $\mathfrak {p}_+ \cong \mathcal {B} G_ {\sigma } $
and
$\mathfrak {p}_+ \cong \mathcal {B} G_ {\sigma } $
and
![]() $\mathfrak {p}_-\cong \mathcal {B} G_{ {\sigma } _-}$
. Define
$\mathfrak {p}_-\cong \mathcal {B} G_{ {\sigma } _-}$
. Define
![]() $ \mathbb {T} '$
weights
$ \mathbb {T} '$
weights
Then
![]() $\mathsf {w}^+_i=\mathsf {w}^{\prime }_i$
is given by equation (16),
$\mathsf {w}^+_i=\mathsf {w}^{\prime }_i$
is given by equation (16),
![]() $\mathsf {w}_1^\pm +\mathsf {w}_2^\pm +\mathsf {w}_3^\pm =0$
, and
$\mathsf {w}_1^\pm +\mathsf {w}_2^\pm +\mathsf {w}_3^\pm =0$
, and
We also have
The above weights are summarised in Figure 7 below.

Figure 7 Degenerated
![]() $N_{\mathfrak {l}_\tau /\mathcal {X}}$
and the
$N_{\mathfrak {l}_\tau /\mathcal {X}}$
and the
![]() $ \mathbb {T} '$
-weights.
$ \mathbb {T} '$
-weights.
3.11 Disk factors as equivariant relative GW invariants
When
![]() $d_0>0$
, let
$d_0>0$
, let
![]() $\overline {\mathcal {M}}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0,(d_0,\lambda ))$
be the moduli space of relative maps to
$\overline {\mathcal {M}}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0,(d_0,\lambda ))$
be the moduli space of relative maps to
![]() $(\mathfrak {l}_+,\mathfrak {p}_0)$
with the relative condition
$(\mathfrak {l}_+,\mathfrak {p}_0)$
with the relative condition
![]() $(d_0,\lambda )$
, where
$(d_0,\lambda )$
, where
![]() $\lambda \in G_\tau $
[Reference Abramovich and Fantechi1]. A relative stable map to
$\lambda \in G_\tau $
[Reference Abramovich and Fantechi1]. A relative stable map to
![]() $(\mathfrak {l}_+,\mathfrak {p}_0)$
is a morphism to
$(\mathfrak {l}_+,\mathfrak {p}_0)$
is a morphism to
![]() $\mathfrak {l}_+[m]$
that is the union of
$\mathfrak {l}_+[m]$
that is the union of
![]() $\mathfrak {l}_+$
and a chain of m copies of
$\mathfrak {l}_+$
and a chain of m copies of
![]() $ \mathbb {P} ^1\times \mathcal {B} G_\lambda $
. Let
$ \mathbb {P} ^1\times \mathcal {B} G_\lambda $
. Let
![]() $\mathcal {M}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0,(d_0,\lambda ))\subset \overline {\mathcal {M}}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0,(d_0,\lambda ))$
be the open substack where the target is
$\mathcal {M}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0,(d_0,\lambda ))\subset \overline {\mathcal {M}}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0,(d_0,\lambda ))$
be the open substack where the target is
![]() $\mathfrak {l}_+[0]=\mathfrak {l}_+$
. The tangent space
$\mathfrak {l}_+[0]=\mathfrak {l}_+$
. The tangent space
![]() $\mathcal {T}^1_\xi $
and the obstruction space
$\mathcal {T}^1_\xi $
and the obstruction space
![]() $\mathcal {T}^2_\xi $
at a moduli point
$\mathcal {T}^2_\xi $
at a moduli point
![]() $\xi =[u:(\mathcal {C},x,y)\to (\mathfrak {l}_+,\mathfrak {p}_0)]$
in
$\xi =[u:(\mathcal {C},x,y)\to (\mathfrak {l}_+,\mathfrak {p}_0)]$
in
![]() $\mathcal {M}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0,(d_0,\lambda ))$
(where
$\mathcal {M}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0,(d_0,\lambda ))$
(where
![]() $u^{-1}(\mathfrak {p}_0)= d_0 y$
as Cartier divisors) fit into the following exact sequence of complex vector spaces:
$u^{-1}(\mathfrak {p}_0)= d_0 y$
as Cartier divisors) fit into the following exact sequence of complex vector spaces:
 $$ \begin{align} \begin{aligned} 0 \to & \mathrm{Ext}^0(\Omega_{\mathcal{C}}(x+y), \mathcal{O}_{\mathcal{C}})\to H^0(\mathcal{C}, u^*(T_{\mathfrak{l}_+}(-\mathfrak{p}_0)) \to \mathcal{T}^1_\xi \\ \to & \mathrm{Ext}^1(\Omega_{\mathcal{C}}(x+y),\mathcal{O}_{\mathcal{C}}) \to H^1(\mathcal{C}, u^*(T_{\mathfrak{l}_+}(-\mathfrak{p}_0)) \to \mathcal{T}^2_\xi. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 0 \to & \mathrm{Ext}^0(\Omega_{\mathcal{C}}(x+y), \mathcal{O}_{\mathcal{C}})\to H^0(\mathcal{C}, u^*(T_{\mathfrak{l}_+}(-\mathfrak{p}_0)) \to \mathcal{T}^1_\xi \\ \to & \mathrm{Ext}^1(\Omega_{\mathcal{C}}(x+y),\mathcal{O}_{\mathcal{C}}) \to H^1(\mathcal{C}, u^*(T_{\mathfrak{l}_+}(-\mathfrak{p}_0)) \to \mathcal{T}^2_\xi. \end{aligned} \end{align} $$
Globally on
![]() $\mathcal {M}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0,(d_0,\lambda ))$
, there is an exact sequence of sheaves
$\mathcal {M}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0,(d_0,\lambda ))$
, there is an exact sequence of sheaves
whose fibre at the moduli point
![]() $\xi $
is equation (21).
$\xi $
is equation (21).
Let
![]() $\pi :\mathcal {U}_+\to \mathcal {M}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0 ,(d_0,\lambda ))$
be the universal domain curve, and let
$\pi :\mathcal {U}_+\to \mathcal {M}_{0,1}(\mathfrak {l}_+/\mathfrak {p}_0 ,(d_0,\lambda ))$
be the universal domain curve, and let
![]() $F_+:\mathcal {U}_+\to \mathfrak {l}_+$
be the evaluation map. We define
$F_+:\mathcal {U}_+\to \mathfrak {l}_+$
be the evaluation map. We define
where
![]() $R^\bullet \pi _*$
is the K-theoretic push-forward.
$R^\bullet \pi _*$
is the K-theoretic push-forward.
For
![]() $d_0>0$
, we define
$d_0>0$
, we define
 $$ \begin{align*} D_{d_0,\lambda}&=\langle 1_{h^+(d_0,\lambda)} \rangle^{\mathcal{X},\mathcal{L},T_{\mathbb{R}} '}_{0,d_0 b,(d_0,\lambda )} \\ &=\int_{[\mathcal{M}_{0,1}(\mathfrak{l}_+,\mathfrak{p}_0,(d_0,\lambda))]^ {\mathrm{vir}} } \mathrm{ev}^*(1_{h^+(d_0,\lambda)})e_{ \mathbb{T} '}(V^+_{0,1}). \end{align*} $$
$$ \begin{align*} D_{d_0,\lambda}&=\langle 1_{h^+(d_0,\lambda)} \rangle^{\mathcal{X},\mathcal{L},T_{\mathbb{R}} '}_{0,d_0 b,(d_0,\lambda )} \\ &=\int_{[\mathcal{M}_{0,1}(\mathfrak{l}_+,\mathfrak{p}_0,(d_0,\lambda))]^ {\mathrm{vir}} } \mathrm{ev}^*(1_{h^+(d_0,\lambda)})e_{ \mathbb{T} '}(V^+_{0,1}). \end{align*} $$
When
![]() $d_0<0$
, let
$d_0<0$
, let
![]() $\overline {\mathcal {M}}_{0,1}(\mathfrak {l}_-/\mathfrak {p}_0, (-d_0,\lambda ^{-1}))$
be the moduli space of relative stable maps to
$\overline {\mathcal {M}}_{0,1}(\mathfrak {l}_-/\mathfrak {p}_0, (-d_0,\lambda ^{-1}))$
be the moduli space of relative stable maps to
![]() $(\mathfrak {l}_-,\mathfrak {p}_0)$
with relative condition
$(\mathfrak {l}_-,\mathfrak {p}_0)$
with relative condition
![]() $(-d_0,\lambda ^{-1})$
, and let
$(-d_0,\lambda ^{-1})$
, and let
![]() $\mathcal {M}_{0,1}(\mathfrak {l}_-/\mathfrak {p}_0,(-d_0,\lambda ^{-1}))$
be the open substack where the target is
$\mathcal {M}_{0,1}(\mathfrak {l}_-/\mathfrak {p}_0,(-d_0,\lambda ^{-1}))$
be the open substack where the target is
![]() $\mathfrak {l}_-$
. Let
$\mathfrak {l}_-$
. Let
![]() $\pi :\mathcal {U}_-\to \mathcal {M}_{0,1}(\mathfrak {l}_-/\mathfrak {p}_0 ,(-d_0,\lambda ^{-1}))$
be the universal domain curve, and let
$\pi :\mathcal {U}_-\to \mathcal {M}_{0,1}(\mathfrak {l}_-/\mathfrak {p}_0 ,(-d_0,\lambda ^{-1}))$
be the universal domain curve, and let
![]() $F_-:\mathcal {U}_-\to \mathfrak {l}_-$
be the evaluation map. We define
$F_-:\mathcal {U}_-\to \mathfrak {l}_-$
be the evaluation map. We define
and define
 $$ \begin{align*} D_{d_0,\lambda}&=\langle 1_{h^-(d_0,\lambda)} \rangle^{\mathcal{X},\mathcal{L},T^{\prime}_{\mathbb{R}} }_{0,-d_0 (\alpha-b), (d_0,\lambda))} \\ &=\int_{[\mathcal{M}_{0,1}(\mathfrak{l}_-,\mathfrak{p}_0,(-d_0,\lambda^{-1}))]^ {\mathrm{vir}} } \mathrm{ev}^*(1_{h^-(d_0,\lambda)})e_{ \mathbb{T} '}(V^-_{0,1}). \end{align*} $$
$$ \begin{align*} D_{d_0,\lambda}&=\langle 1_{h^-(d_0,\lambda)} \rangle^{\mathcal{X},\mathcal{L},T^{\prime}_{\mathbb{R}} }_{0,-d_0 (\alpha-b), (d_0,\lambda))} \\ &=\int_{[\mathcal{M}_{0,1}(\mathfrak{l}_-,\mathfrak{p}_0,(-d_0,\lambda^{-1}))]^ {\mathrm{vir}} } \mathrm{ev}^*(1_{h^-(d_0,\lambda)})e_{ \mathbb{T} '}(V^-_{0,1}). \end{align*} $$
Let
![]() $u:(\mathcal {C},x,y)\to \mathfrak {l}_+ $
be a relative stable map that represents a point in
$u:(\mathcal {C},x,y)\to \mathfrak {l}_+ $
be a relative stable map that represents a point in
![]() $\mathcal {M}$
. Suppose that u is fixed by the torus action. Recall that
$\mathcal {M}$
. Suppose that u is fixed by the torus action. Recall that
![]() $c_i:G_ {\sigma } \to [0,1)\cap \mathbb {Q} $
is defined by
$c_i:G_ {\sigma } \to [0,1)\cap \mathbb {Q} $
is defined by
![]() $\chi _i(k)=\exp (2\pi \sqrt {-1}c_i(k))$
. In the computation below, let
$\chi _i(k)=\exp (2\pi \sqrt {-1}c_i(k))$
. In the computation below, let
![]() $k^\pm =h^\pm (d_0,\lambda )$
. For
$k^\pm =h^\pm (d_0,\lambda )$
. For
![]() $j=1, 2,3$
, let
$j=1, 2,3$
, let
![]() $\epsilon _j= c_j(k^+)$
. Then
$\epsilon _j= c_j(k^+)$
. Then
![]() $\epsilon _1=\langle \frac {d_0}{\mathfrak {r}_+}\rangle $
. We have the following weights
$\epsilon _1=\langle \frac {d_0}{\mathfrak {r}_+}\rangle $
. We have the following weights
 $$ \begin{align*} {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^0(\mathcal{C},u^*L_1^+) \bigr) = \sum_{a=0}^{\lfloor d_0w_1\rfloor} e^{a \frac{\mathsf{u}_1'}{d_0}},&\quad {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^1(\mathcal{C},u^*L_1^+) \bigr) = 0, \\[6pt] {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^0(\mathcal{C},u^*L_2^+\otimes \mathcal{O}_y) \bigr) = \delta_{\langle d_0w_2- \epsilon_2\rangle, 0} e^{\frac{\mathsf{u}_2'-f\mathsf{u}_1'}{\mathfrak{m}}},&\quad {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^1(\mathcal{C},u^*L_2^+\otimes \mathcal{O}_y) \bigr) = 0, \end{align*} $$
$$ \begin{align*} {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^0(\mathcal{C},u^*L_1^+) \bigr) = \sum_{a=0}^{\lfloor d_0w_1\rfloor} e^{a \frac{\mathsf{u}_1'}{d_0}},&\quad {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^1(\mathcal{C},u^*L_1^+) \bigr) = 0, \\[6pt] {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^0(\mathcal{C},u^*L_2^+\otimes \mathcal{O}_y) \bigr) = \delta_{\langle d_0w_2- \epsilon_2\rangle, 0} e^{\frac{\mathsf{u}_2'-f\mathsf{u}_1'}{\mathfrak{m}}},&\quad {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^1(\mathcal{C},u^*L_2^+\otimes \mathcal{O}_y) \bigr) = 0, \end{align*} $$
 $$ \begin{align*} {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^0(\mathcal{C}, u^*L^+_2) \bigr) &= \begin{cases} \displaystyle{ \sum_{a= -\lfloor d_0w_2-\epsilon_2\rfloor}^0 e^{\mathsf{w}^{\prime}_2+(a-\epsilon_2) \frac{\mathsf{u}^{\prime}_1}{d_0 } } }, & f \geq 0,\\ 0, & f<0,\\ \end{cases} \\[6pt] {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^1(\mathcal{C}, u^*L^+_2) \bigr) &= \begin{cases} 0, & f \geq 0,\\ \displaystyle{ \sum_{a=1}^{-\lfloor d_0w_2-\epsilon_2\rfloor-1} e^{\mathsf{w}^{\prime}_2+(a-\epsilon_2)\frac{\mathsf{u}^{\prime}_1}{d_0 } } }, & f<0 \end{cases}\\[6pt] {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^0(\mathcal{C}, u^*L^+_3) \bigr) &= \begin{cases} \displaystyle{ \sum_{a=-\lfloor d_0w_3-\epsilon_3\rfloor}^0 e^{\mathsf{w}^{\prime}_3+(a-\epsilon_3) \frac{\mathsf{u}^{\prime}_1}{d_0 } } }, & f<0,\\ 0, & f\geq 0,\\ \end{cases}\\[6pt] {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^1(\mathcal{C}, u^*L^+_3) \bigr) &= \begin{cases} 0, & f<0 ,\\ \displaystyle{ \sum_{a=1}^{-\lfloor d_0w_3 - \epsilon_3\rfloor-1} e^{\mathsf{w}^{\prime}_3+(a-\epsilon_3)\frac{\mathsf{u}^{\prime}_1}{d_0 } } }, & f\geq 0. \end{cases} \end{align*} $$
$$ \begin{align*} {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^0(\mathcal{C}, u^*L^+_2) \bigr) &= \begin{cases} \displaystyle{ \sum_{a= -\lfloor d_0w_2-\epsilon_2\rfloor}^0 e^{\mathsf{w}^{\prime}_2+(a-\epsilon_2) \frac{\mathsf{u}^{\prime}_1}{d_0 } } }, & f \geq 0,\\ 0, & f<0,\\ \end{cases} \\[6pt] {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^1(\mathcal{C}, u^*L^+_2) \bigr) &= \begin{cases} 0, & f \geq 0,\\ \displaystyle{ \sum_{a=1}^{-\lfloor d_0w_2-\epsilon_2\rfloor-1} e^{\mathsf{w}^{\prime}_2+(a-\epsilon_2)\frac{\mathsf{u}^{\prime}_1}{d_0 } } }, & f<0 \end{cases}\\[6pt] {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^0(\mathcal{C}, u^*L^+_3) \bigr) &= \begin{cases} \displaystyle{ \sum_{a=-\lfloor d_0w_3-\epsilon_3\rfloor}^0 e^{\mathsf{w}^{\prime}_3+(a-\epsilon_3) \frac{\mathsf{u}^{\prime}_1}{d_0 } } }, & f<0,\\ 0, & f\geq 0,\\ \end{cases}\\[6pt] {\mathrm{ch}} _{ \mathbb{T} '}\bigl( H^1(\mathcal{C}, u^*L^+_3) \bigr) &= \begin{cases} 0, & f<0 ,\\ \displaystyle{ \sum_{a=1}^{-\lfloor d_0w_3 - \epsilon_3\rfloor-1} e^{\mathsf{w}^{\prime}_3+(a-\epsilon_3)\frac{\mathsf{u}^{\prime}_1}{d_0 } } }, & f\geq 0. \end{cases} \end{align*} $$
and the following identities
 $$ \begin{align*} \sum_{a=-\lfloor w_3d_0-\epsilon_3 \rfloor}^0 e^{\mathsf{w}^{\prime}_3+(a-\epsilon_3) \frac{\mathsf{u}^{\prime}_1}{d_0 } } &= \sum_{a=d_0w_1+\epsilon_2+\epsilon_3}^{-\lfloor d_0 w_2-\epsilon_2\rfloor -1 + \delta_{\langle d_0 w_2-\epsilon_2 \rangle , 0}} e^{-\mathsf{w}^{\prime}_2 +(\epsilon_2-a)\frac{\mathsf{u}^{\prime}_1}{d_0 }} \\[6pt] \sum_{a=1}^{-\lfloor w_3 d_0 +1 - \epsilon_3 \rfloor} e^{\mathsf{w}^{\prime}_3+(a-\epsilon_3)\frac{\mathsf{u}^{\prime}_1}{d_0 } } &= \sum_{a=-\lfloor d_0w_2-\epsilon_2\rfloor +\delta_{\langle d_0w_2-\epsilon_2 \rangle}}^{\frac{d_0 }{s^+_1} +\epsilon_2+\epsilon_3-1} e^{-\mathsf{w}^{\prime}_2 +(\epsilon_2-a)\frac{\mathsf{u}_1'}{d_0 }}\\[6pt] d_0w_1 + \epsilon_2 +\epsilon_3 &= \left\lfloor \frac{d_0 }{s^+_1} \right\rfloor + \mathrm{age}(k^+). \end{align*} $$
$$ \begin{align*} \sum_{a=-\lfloor w_3d_0-\epsilon_3 \rfloor}^0 e^{\mathsf{w}^{\prime}_3+(a-\epsilon_3) \frac{\mathsf{u}^{\prime}_1}{d_0 } } &= \sum_{a=d_0w_1+\epsilon_2+\epsilon_3}^{-\lfloor d_0 w_2-\epsilon_2\rfloor -1 + \delta_{\langle d_0 w_2-\epsilon_2 \rangle , 0}} e^{-\mathsf{w}^{\prime}_2 +(\epsilon_2-a)\frac{\mathsf{u}^{\prime}_1}{d_0 }} \\[6pt] \sum_{a=1}^{-\lfloor w_3 d_0 +1 - \epsilon_3 \rfloor} e^{\mathsf{w}^{\prime}_3+(a-\epsilon_3)\frac{\mathsf{u}^{\prime}_1}{d_0 } } &= \sum_{a=-\lfloor d_0w_2-\epsilon_2\rfloor +\delta_{\langle d_0w_2-\epsilon_2 \rangle}}^{\frac{d_0 }{s^+_1} +\epsilon_2+\epsilon_3-1} e^{-\mathsf{w}^{\prime}_2 +(\epsilon_2-a)\frac{\mathsf{u}_1'}{d_0 }}\\[6pt] d_0w_1 + \epsilon_2 +\epsilon_3 &= \left\lfloor \frac{d_0 }{s^+_1} \right\rfloor + \mathrm{age}(k^+). \end{align*} $$
The
![]() $ \mathbb {T} '$
-equivariant Euler classes are
$ \mathbb {T} '$
-equivariant Euler classes are
 $$ \begin{align*} e_{ \mathbb{T} '}(B_1^m) &= 1,\\[6pt] e_{ \mathbb{T} '}(B_2^m) &= \lfloor d_0 w_1 \rfloor! \left(\frac{\mathsf{u}^{\prime}_1}{d_0} \right)^{\lfloor d_0w_1 \rfloor}, \\[6pt] \frac{e_{ \mathbb{T} '}(B_5^m)}{e_{ \mathbb{T} '}(B_4^m)} &= (-1)^{\lceil d_0 w_2-\epsilon_2 \rceil +\lfloor d_0w_1 \rfloor +\mathrm{age}(k^+)-1} \prod_{a =1}^{\lfloor d_0w_1 \rfloor + \mathrm{age}(k^+) -1} \left(\mathsf{w}^{\prime}_2 + (a-\epsilon_2)\frac{\mathsf{u}^{\prime}_1}{d_0}\right). \end{align*} $$
$$ \begin{align*} e_{ \mathbb{T} '}(B_1^m) &= 1,\\[6pt] e_{ \mathbb{T} '}(B_2^m) &= \lfloor d_0 w_1 \rfloor! \left(\frac{\mathsf{u}^{\prime}_1}{d_0} \right)^{\lfloor d_0w_1 \rfloor}, \\[6pt] \frac{e_{ \mathbb{T} '}(B_5^m)}{e_{ \mathbb{T} '}(B_4^m)} &= (-1)^{\lceil d_0 w_2-\epsilon_2 \rceil +\lfloor d_0w_1 \rfloor +\mathrm{age}(k^+)-1} \prod_{a =1}^{\lfloor d_0w_1 \rfloor + \mathrm{age}(k^+) -1} \left(\mathsf{w}^{\prime}_2 + (a-\epsilon_2)\frac{\mathsf{u}^{\prime}_1}{d_0}\right). \end{align*} $$
Since
![]() $|\mathrm {Aut}(f)| = d_0|G_\tau |$
, by localisation,
$|\mathrm {Aut}(f)| = d_0|G_\tau |$
, by localisation,
 $$ \begin{align*} D_{d_0,\lambda} &=D(d_0,k^+,k^-) = \frac{1}{|\mathrm{Aut}(f)|} \frac{e_{ \mathbb{T} '}(B_1^m) e_{ \mathbb{T} '}(B_5^m)}{e_{ \mathbb{T} '}(B_2^m) e_{ \mathbb{T} '}(B_4^m)} \\ = &\frac{1}{d_0|G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0 w_1\rfloor + \mathrm{age}(k^+) -1}(\mathsf{w}^{\prime}_2 + (a-\epsilon_2)\frac{\mathsf{u}^{\prime}_1}{d_0})} {\lfloor d_0 w_1\rfloor! (\frac{\mathsf{u}^{\prime}_1}{d_0})^{\lfloor d_0w_1\rfloor}} \cdot (-1)^{\lceil d_0w_2-\epsilon_2\rceil +\lfloor d_0w_1\rfloor +\mathrm{age}(k^+)-1 } \\ =&(-1)^{\lceil d_0w_2-\epsilon_2\rceil +\lfloor d_0w_1\rfloor +\mathrm{age}(k^+)-1 } \Big(\frac{\mathsf{u}_1'}{d_0}\Big)^{\mathrm{age}(k^+)-1} \cdot \frac{1}{d_0|G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0w_1\rfloor +\mathrm{age}(k^+)-1} (\frac{d_0 \mathsf{w}^{\prime}_2}{s^+_1\mathsf{w}^{\prime}_1} +a-\epsilon_2)} {\lfloor d_0w_1\rfloor !} \\ = &- (-1)^{\lfloor d_0w_3+\frac{\bar\lambda}{\mathfrak{m}} \rfloor } \Big(\frac{\mathsf{u}_1'}{d_0}\Big)^{\mathrm{age}(k^+)-1} \cdot \frac{1}{d_0|G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0w_1\rfloor +\mathrm{age}(k^+)-1} (\frac{d_0 \mathsf{w}^{\prime}_2}{s^+_1\mathsf{w}^{\prime}_1} +a-\epsilon_2)} {\lfloor d_0w_1\rfloor !} \end{align*} $$
$$ \begin{align*} D_{d_0,\lambda} &=D(d_0,k^+,k^-) = \frac{1}{|\mathrm{Aut}(f)|} \frac{e_{ \mathbb{T} '}(B_1^m) e_{ \mathbb{T} '}(B_5^m)}{e_{ \mathbb{T} '}(B_2^m) e_{ \mathbb{T} '}(B_4^m)} \\ = &\frac{1}{d_0|G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0 w_1\rfloor + \mathrm{age}(k^+) -1}(\mathsf{w}^{\prime}_2 + (a-\epsilon_2)\frac{\mathsf{u}^{\prime}_1}{d_0})} {\lfloor d_0 w_1\rfloor! (\frac{\mathsf{u}^{\prime}_1}{d_0})^{\lfloor d_0w_1\rfloor}} \cdot (-1)^{\lceil d_0w_2-\epsilon_2\rceil +\lfloor d_0w_1\rfloor +\mathrm{age}(k^+)-1 } \\ =&(-1)^{\lceil d_0w_2-\epsilon_2\rceil +\lfloor d_0w_1\rfloor +\mathrm{age}(k^+)-1 } \Big(\frac{\mathsf{u}_1'}{d_0}\Big)^{\mathrm{age}(k^+)-1} \cdot \frac{1}{d_0|G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0w_1\rfloor +\mathrm{age}(k^+)-1} (\frac{d_0 \mathsf{w}^{\prime}_2}{s^+_1\mathsf{w}^{\prime}_1} +a-\epsilon_2)} {\lfloor d_0w_1\rfloor !} \\ = &- (-1)^{\lfloor d_0w_3+\frac{\bar\lambda}{\mathfrak{m}} \rfloor } \Big(\frac{\mathsf{u}_1'}{d_0}\Big)^{\mathrm{age}(k^+)-1} \cdot \frac{1}{d_0|G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0w_1\rfloor +\mathrm{age}(k^+)-1} (\frac{d_0 \mathsf{w}^{\prime}_2}{s^+_1\mathsf{w}^{\prime}_1} +a-\epsilon_2)} {\lfloor d_0w_1\rfloor !} \end{align*} $$
Let
![]() $\mathsf {u}:= \iota _f^* \mathsf {u}^{\prime }_1 \in H^2( \mathbb {T} _f; \mathbb {Z} )$
. Then
$\mathsf {u}:= \iota _f^* \mathsf {u}^{\prime }_1 \in H^2( \mathbb {T} _f; \mathbb {Z} )$
. Then
![]() $H^*( \mathbb {T} _f; \mathbb {Q} )= \mathbb {Q} [\mathsf {u}]$
and
$H^*( \mathbb {T} _f; \mathbb {Q} )= \mathbb {Q} [\mathsf {u}]$
and
![]() $\iota _f^*\mathsf {u}_2'=f\mathsf {u}$
. Define
$\iota _f^*\mathsf {u}_2'=f\mathsf {u}$
. Define
![]() $D_{d_0,\lambda ,f}=\iota _{f}^* D_{d_0,\lambda }$
. Hence when
$D_{d_0,\lambda ,f}=\iota _{f}^* D_{d_0,\lambda }$
. Hence when
![]() $d_0>0$
,
$d_0>0$
,
 $$ \begin{align*} & D_{d_0,\lambda,f} \\ &\quad = -(-1)^{\lfloor d_0w_3+\frac{\bar \lambda}{\mathfrak{m}}\rfloor}\left(\frac{\mathsf{u}}{d_0}\right)^{\mathrm{age}(h^+(d_0,\lambda))-1} \cdot \frac{1}{d_0|G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0w_1\rfloor +\mathrm{age}(h^+(d_0,\lambda))-1} (d_0 w_2 +a-c_2(h^+(d_0,\lambda))} {\lfloor d_0w_1\rfloor !}. \end{align*} $$
$$ \begin{align*} & D_{d_0,\lambda,f} \\ &\quad = -(-1)^{\lfloor d_0w_3+\frac{\bar \lambda}{\mathfrak{m}}\rfloor}\left(\frac{\mathsf{u}}{d_0}\right)^{\mathrm{age}(h^+(d_0,\lambda))-1} \cdot \frac{1}{d_0|G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0w_1\rfloor +\mathrm{age}(h^+(d_0,\lambda))-1} (d_0 w_2 +a-c_2(h^+(d_0,\lambda))} {\lfloor d_0w_1\rfloor !}. \end{align*} $$
If
![]() $d_0 <0$
, similar computation shows (notice
$d_0 <0$
, similar computation shows (notice
![]() $\overline { \lambda ^{-1}}=(1-\delta _{\bar \lambda ,0})(\mathfrak{m}-\bar \lambda )\in \{0,\dots ,\mathfrak{m}-1\}$
)
$\overline { \lambda ^{-1}}=(1-\delta _{\bar \lambda ,0})(\mathfrak{m}-\bar \lambda )\in \{0,\dots ,\mathfrak{m}-1\}$
)
 $$ \begin{align*} D_{d_0 ,\lambda,f} &= -(-1)^{\lfloor d_0w_2^- + \left(1-\frac{\bar\lambda}{m}-\delta_{\bar \lambda,0}\right)\rfloor} \left(\frac{\mathsf{u}}{d_0 }\right)^{\mathrm{age}(h^-(d_0,\lambda))-1} \\ &\quad \cdot \frac{1}{-d_0 |G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0 w_1^- \rfloor+\mathrm{age}(h^-(d_0,\lambda))-1}(d_0w_3^--c_3(h^-(d_0,\lambda))+a)}{\lfloor d_0w_1^-\rfloor!}. \end{align*} $$
$$ \begin{align*} D_{d_0 ,\lambda,f} &= -(-1)^{\lfloor d_0w_2^- + \left(1-\frac{\bar\lambda}{m}-\delta_{\bar \lambda,0}\right)\rfloor} \left(\frac{\mathsf{u}}{d_0 }\right)^{\mathrm{age}(h^-(d_0,\lambda))-1} \\ &\quad \cdot \frac{1}{-d_0 |G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0 w_1^- \rfloor+\mathrm{age}(h^-(d_0,\lambda))-1}(d_0w_3^--c_3(h^-(d_0,\lambda))+a)}{\lfloor d_0w_1^-\rfloor!}. \end{align*} $$
If
![]() $\mathcal {L}$
is an outer brane, it is the same as
$\mathcal {L}$
is an outer brane, it is the same as
![]() $d_0>0$
. Define
$d_0>0$
. Define
 $$ \begin{align*} D_{d_0,\lambda,f} &= -(-1)^{\lfloor d_0w_3+ \frac{\bar \lambda}{\mathfrak{m}}\rfloor}\big(\frac{\mathsf{u}}{d_0} \big)^{\mathrm{age}(h(d_0,\lambda))-1} \cdot \frac{1}{d_0|G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0w_1\rfloor +\mathrm{age}(h(d_0,\lambda))-1} (d_0 w_2 +a-c_2(h(d_0,\lambda))} {\lfloor d_0w_1\rfloor !}. \end{align*} $$
$$ \begin{align*} D_{d_0,\lambda,f} &= -(-1)^{\lfloor d_0w_3+ \frac{\bar \lambda}{\mathfrak{m}}\rfloor}\big(\frac{\mathsf{u}}{d_0} \big)^{\mathrm{age}(h(d_0,\lambda))-1} \cdot \frac{1}{d_0|G_\tau|}\frac{\prod_{a=1}^{\lfloor d_0w_1\rfloor +\mathrm{age}(h(d_0,\lambda))-1} (d_0 w_2 +a-c_2(h(d_0,\lambda))} {\lfloor d_0w_1\rfloor !}. \end{align*} $$
3.12 Open-closed GW invariants and descendant GW invariants
For any torus fixed point
![]() $\mathfrak {p}_ {\sigma } $
of
$\mathfrak {p}_ {\sigma } $
of
![]() $\mathcal {X}$
, where
$\mathcal {X}$
, where
![]() $ {\sigma } \in \Sigma (3)$
, we have
$ {\sigma } \in \Sigma (3)$
, we have
The inclusion
![]() $\iota _ {\sigma } : \mathfrak {p}_ {\sigma } \hookrightarrow \mathcal {X}$
induces
$\iota _ {\sigma } : \mathfrak {p}_ {\sigma } \hookrightarrow \mathcal {X}$
induces
Define
Proposition 3.2 (framed inner brane)
Suppose that
![]() $(\mathcal {L},f)$
is a framed inner brane and
$(\mathcal {L},f)$
is a framed inner brane and
where
![]() $(\mu _j,\lambda _j)\in H_1(\mathcal {L}; \mathbb {Z} )\cong \mathbb {Z} \times \mathcal {B} G_\tau $
. Let
$(\mu _j,\lambda _j)\in H_1(\mathcal {L}; \mathbb {Z} )\cong \mathbb {Z} \times \mathcal {B} G_\tau $
. Let
![]() $J_\pm =\{ j\in \{1,\ldots ,h\}: \pm \mu _j>0\}$
, and let
$J_\pm =\{ j\in \{1,\ldots ,h\}: \pm \mu _j>0\}$
, and let
![]() $k_j^\pm = h^\pm (\mu _j,\lambda _j)$
. Then
$k_j^\pm = h^\pm (\mu _j,\lambda _j)$
. Then
 $$ \begin{align*} & \langle \gamma_1,\ldots, \gamma_n\rangle_{g,\beta', {\vec{\mu}} }^{\mathcal{X}, (\mathcal{L},f)}=\prod_{j=1}^h D^{\prime}_{\mu_j,\lambda_j,f} \\ &\quad \cdot \int_{[\overline{\mathcal{M}}_{g,n+h}(\mathcal{X},\beta)]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i \prod_{j\in J_+}\mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} _+, (h^+(d_0,\lambda_j))^{-1}} \prod_{j\in J_-} \mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} _-, (h^-(d_0,\lambda_j))^{-1}} \big)} {\prod_{j=1}^h\frac{\mathsf{u}}{\mu_j}(\frac{\mathsf{u}}{\mu_j} -\bar{\psi}_{n+j})}, \end{align*} $$
$$ \begin{align*} & \langle \gamma_1,\ldots, \gamma_n\rangle_{g,\beta', {\vec{\mu}} }^{\mathcal{X}, (\mathcal{L},f)}=\prod_{j=1}^h D^{\prime}_{\mu_j,\lambda_j,f} \\ &\quad \cdot \int_{[\overline{\mathcal{M}}_{g,n+h}(\mathcal{X},\beta)]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i \prod_{j\in J_+}\mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} _+, (h^+(d_0,\lambda_j))^{-1}} \prod_{j\in J_-} \mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} _-, (h^-(d_0,\lambda_j))^{-1}} \big)} {\prod_{j=1}^h\frac{\mathsf{u}}{\mu_j}(\frac{\mathsf{u}}{\mu_j} -\bar{\psi}_{n+j})}, \end{align*} $$
where
 $$ \begin{align*}\beta\in H_2(\mathcal{X}),\quad \beta'= \beta + \Big(\sum_{j\in J_+} \mu_j\Big)b -\Big(\sum_{j\in J_-} \mu_j\Big)(\alpha-b) \in H_2(\mathcal{X},\mathcal{L}). \end{align*} $$
$$ \begin{align*}\beta\in H_2(\mathcal{X}),\quad \beta'= \beta + \Big(\sum_{j\in J_+} \mu_j\Big)b -\Big(\sum_{j\in J_-} \mu_j\Big)(\alpha-b) \in H_2(\mathcal{X},\mathcal{L}). \end{align*} $$
Proof. There exists
![]() $\beta \in H_2(\mathcal {X})$
such that
$\beta \in H_2(\mathcal {X})$
such that
 $$ \begin{align*}\beta'=\beta +\Big(\sum_{j\in J_+} \mu_j \Big)b + \sum_{j\in J_-}(-\mu_j)(\alpha-b). \end{align*} $$
$$ \begin{align*}\beta'=\beta +\Big(\sum_{j\in J_+} \mu_j \Big)b + \sum_{j\in J_-}(-\mu_j)(\alpha-b). \end{align*} $$
Let
![]() $\langle k_j^+\rangle $
be the cyclic subgroup generated by
$\langle k_j^+\rangle $
be the cyclic subgroup generated by
![]() $k_j^+$
, and let
$k_j^+$
, and let
![]() $r_j$
be the cardinality of
$r_j$
be the cardinality of
![]() $\langle k_j^+\rangle $
for
$\langle k_j^+\rangle $
for
![]() $j\in J_+$
and
$j\in J_+$
and
![]() $r_j$
be the cardinality of
$r_j$
be the cardinality of
![]() $\langle k_j^-\rangle $
for
$\langle k_j^-\rangle $
for
![]() $j\in J_-$
.
$j\in J_-$
.
We have
 $$ \begin{align*} \overline{\mathcal{M}}_{(g,h),n}(\mathcal{X},\mathcal{L}\mid \beta', {\vec{\mu}} )^{ \mathbb{T} ^{\prime}_{\mathbb{R}} } &= \bigcup_{ {\Gamma} \in G_{g,n}(\mathcal{X},\mathcal{L}\mid \beta', {\vec{\mu}} )} F_\Gamma \\ \overline{\mathcal{M}}_{g,n+h}(\mathcal{X}, \beta)^{ \mathbb{T} ^{\prime}_{\mathbb{R}} } = \overline{\mathcal{M}}_{g,n+h}(\mathcal{X}, \beta)^{ \mathbb{T} '} &= \bigcup_{ {\hat{ {\Gamma} }} \in G_{g,n+h}(\mathcal{X},\beta) } F_{ {\hat{ {\Gamma} }} }. \end{align*} $$
$$ \begin{align*} \overline{\mathcal{M}}_{(g,h),n}(\mathcal{X},\mathcal{L}\mid \beta', {\vec{\mu}} )^{ \mathbb{T} ^{\prime}_{\mathbb{R}} } &= \bigcup_{ {\Gamma} \in G_{g,n}(\mathcal{X},\mathcal{L}\mid \beta', {\vec{\mu}} )} F_\Gamma \\ \overline{\mathcal{M}}_{g,n+h}(\mathcal{X}, \beta)^{ \mathbb{T} ^{\prime}_{\mathbb{R}} } = \overline{\mathcal{M}}_{g,n+h}(\mathcal{X}, \beta)^{ \mathbb{T} '} &= \bigcup_{ {\hat{ {\Gamma} }} \in G_{g,n+h}(\mathcal{X},\beta) } F_{ {\hat{ {\Gamma} }} }. \end{align*} $$
In the remaining part of this subsection, we use the following abbreviations:
 $$ \begin{align*} & \mathcal{M} = \overline{\mathcal{M}}_{g,n}(\mathcal{X},\mathcal{L}\mid \beta', {\vec{\mu}} ),\quad \hat{\mathcal{M}} = \overline{\mathcal{M}}_{g,n+h}(\mathcal{X}, \beta), \\ & \mathcal{M}_j = \begin{cases} \overline{\mathcal{M}}_{(0,1),1}(\mathcal{X},\mathcal{L}\mid \mu_j b, (\mu_j,\lambda)), & j\in J_+\\ \overline{\mathcal{M}}_{(0,1),1}(\mathcal{X}, \mathcal{L}\mid -\mu_j(\alpha-b), (\mu_j, \lambda)), & j\in J_- \end{cases} \\ & \mathcal{G} = G_{g,n}(\mathcal{X},\mathcal{L}\mid \beta', {\vec{\mu}} ),\quad \hat{\mathcal{G}} = G_{g,n+h}(\mathcal{X},\beta)\\ & \mathbf{x}=(x_1,\ldots, x_n),\quad \mathbf{y}=(y_1,\ldots, y_h). \end{align*} $$
$$ \begin{align*} & \mathcal{M} = \overline{\mathcal{M}}_{g,n}(\mathcal{X},\mathcal{L}\mid \beta', {\vec{\mu}} ),\quad \hat{\mathcal{M}} = \overline{\mathcal{M}}_{g,n+h}(\mathcal{X}, \beta), \\ & \mathcal{M}_j = \begin{cases} \overline{\mathcal{M}}_{(0,1),1}(\mathcal{X},\mathcal{L}\mid \mu_j b, (\mu_j,\lambda)), & j\in J_+\\ \overline{\mathcal{M}}_{(0,1),1}(\mathcal{X}, \mathcal{L}\mid -\mu_j(\alpha-b), (\mu_j, \lambda)), & j\in J_- \end{cases} \\ & \mathcal{G} = G_{g,n}(\mathcal{X},\mathcal{L}\mid \beta', {\vec{\mu}} ),\quad \hat{\mathcal{G}} = G_{g,n+h}(\mathcal{X},\beta)\\ & \mathbf{x}=(x_1,\ldots, x_n),\quad \mathbf{y}=(y_1,\ldots, y_h). \end{align*} $$
Given
![]() $u:(\Sigma ,\mathbf {x},\partial \Sigma )\to (\mathcal {X}, \mathcal {L})$
that represents a point
$u:(\Sigma ,\mathbf {x},\partial \Sigma )\to (\mathcal {X}, \mathcal {L})$
that represents a point
![]() $\xi \in \mathcal {M}^{ \mathbb {T} ^{\prime }_{\mathbb {R}} }$
, we have
$\xi \in \mathcal {M}^{ \mathbb {T} ^{\prime }_{\mathbb {R}} }$
, we have
 $$ \begin{align*}\Sigma = \mathcal{C} \cup \bigcup_{j=1}^h D_j, \end{align*} $$
$$ \begin{align*}\Sigma = \mathcal{C} \cup \bigcup_{j=1}^h D_j, \end{align*} $$
where
![]() $\mathcal {C}$
is an orbicurve of genus g,
$\mathcal {C}$
is an orbicurve of genus g,
![]() $x_1,\ldots , x_n \in \mathcal {C}$
,
$x_1,\ldots , x_n \in \mathcal {C}$
,
![]() $D_j = [\{ z\in \mathbb {C} \mid |z|\leq 1\}/ \mathbb {Z} _{r_j}]$
,
$D_j = [\{ z\in \mathbb {C} \mid |z|\leq 1\}/ \mathbb {Z} _{r_j}]$
,
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $D_j$
intersect at
$D_j$
intersect at
![]() $y_j = B \mathbb {Z} _{r_j}$
. Let
$y_j = B \mathbb {Z} _{r_j}$
. Let
![]() $u_j=u|_{D_j}$
and
$u_j=u|_{D_j}$
and
![]() $\hat {u}= u|_{\mathcal {C}}$
. Then
$\hat {u}= u|_{\mathcal {C}}$
. Then
-
1. For
 $j=1,\ldots , h$
,
$j=1,\ldots , h$
,
 $u_j: (D_j,\partial D_j)\to (\mathcal {X}, \mathcal {L})$
represents a point in
$u_j: (D_j,\partial D_j)\to (\mathcal {X}, \mathcal {L})$
represents a point in
 $\mathcal {M}_j^{ \mathbb {T} ^{\prime }_{\mathbb {R}} }$
.
$\mathcal {M}_j^{ \mathbb {T} ^{\prime }_{\mathbb {R}} }$
. -
2.
 $\hat {u}:(\mathcal {C},\mathbf {x},\mathbf {y})\to \mathcal {X}$
represents a point
$\hat {u}:(\mathcal {C},\mathbf {x},\mathbf {y})\to \mathcal {X}$
represents a point
 $\hat {\xi }\in \hat {\mathcal {M}}^{ \mathbb {T} '}$
, and
$\hat {\xi }\in \hat {\mathcal {M}}^{ \mathbb {T} '}$
, and
 $\hat {u}(\mathbf {y}_j) =[\mathfrak {p}_\pm , (k_j^\pm )^{-1}] \in \mathcal {I} \mathfrak {p}_\pm \subset \mathcal {I}\mathcal {X}$
if
$\hat {u}(\mathbf {y}_j) =[\mathfrak {p}_\pm , (k_j^\pm )^{-1}] \in \mathcal {I} \mathfrak {p}_\pm \subset \mathcal {I}\mathcal {X}$
if
 $j\in J_\pm $
.
$j\in J_\pm $
.
Let
![]() $x_{n+j}=y_j$
. Let
$x_{n+j}=y_j$
. Let
![]() $F_ {\Gamma } $
be the connected component of
$F_ {\Gamma } $
be the connected component of
![]() $\mathcal {M}^{ \mathbb {T} '}$
associated to the decorated graph
$\mathcal {M}^{ \mathbb {T} '}$
associated to the decorated graph
![]() $ {\Gamma } \in \mathcal {G}$
, and let
$ {\Gamma } \in \mathcal {G}$
, and let
![]() $F_{ {\hat { {\Gamma } }} }$
be the connected component of
$F_{ {\hat { {\Gamma } }} }$
be the connected component of
![]() $\hat {\mathcal {M}}^{ \mathbb {T} ^{\prime }_{\mathbb {R}} }$
associated to the decorated graph
$\hat {\mathcal {M}}^{ \mathbb {T} ^{\prime }_{\mathbb {R}} }$
associated to the decorated graph
![]() $\hat {\Gamma } \in \mathcal {G}$
. Then for any
$\hat {\Gamma } \in \mathcal {G}$
. Then for any
![]() $ {\Gamma } \in \mathcal {G}$
there exists
$ {\Gamma } \in \mathcal {G}$
there exists
![]() $ {\hat { {\Gamma } }} \in \hat {\mathcal {G}}$
such that
$ {\hat { {\Gamma } }} \in \hat {\mathcal {G}}$
such that
if
![]() $j\in J_\pm $
, and
$j\in J_\pm $
, and
![]() $F_{ {\Gamma } }$
can be identified with
$F_{ {\Gamma } }$
can be identified with
![]() $F_{ {\hat { {\Gamma } }} }$
up to a finite morphism. More precisely,
$F_{ {\hat { {\Gamma } }} }$
up to a finite morphism. More precisely,
 $$ \begin{align*} [F_ {\Gamma} ]^ {\mathrm{vir}} &= \prod_{j\in J_+} \frac{|G_{ {\sigma} _+}|}{r_j|\mathrm{Aut}(u_j)|} \prod_{j\in J_-} \frac{|G_{ {\sigma} _-}|}{r_j|\mathrm{Aut}(u_j)|} [F_{ {\hat{ {\Gamma} }} }]^ {\mathrm{vir}} \\ &=\prod_{j\in J_+} \frac{s^+_1}{r_j\mu_j} \prod_{j\in J_-} \frac{s^-_1}{-r_j\mu_j} [F_{ {\hat{ {\Gamma} }} }]^ {\mathrm{vir}}. \end{align*} $$
$$ \begin{align*} [F_ {\Gamma} ]^ {\mathrm{vir}} &= \prod_{j\in J_+} \frac{|G_{ {\sigma} _+}|}{r_j|\mathrm{Aut}(u_j)|} \prod_{j\in J_-} \frac{|G_{ {\sigma} _-}|}{r_j|\mathrm{Aut}(u_j)|} [F_{ {\hat{ {\Gamma} }} }]^ {\mathrm{vir}} \\ &=\prod_{j\in J_+} \frac{s^+_1}{r_j\mu_j} \prod_{j\in J_-} \frac{s^-_1}{-r_j\mu_j} [F_{ {\hat{ {\Gamma} }} }]^ {\mathrm{vir}}. \end{align*} $$
We have
 $$ \begin{align*}\frac{1}{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N_ {\Gamma} ^ {\mathrm{vir}} )} =\frac{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_1^m) e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_5^m)}{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_2^m) e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_4^m)},\quad \frac{1}{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N_ {\hat{ {\Gamma} }} ^ {\mathrm{vir}} )} =\frac{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_1^m) e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_5^m) }{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_2^m) e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_4^m)}, \end{align*} $$
$$ \begin{align*}\frac{1}{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N_ {\Gamma} ^ {\mathrm{vir}} )} =\frac{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_1^m) e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_5^m)}{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_2^m) e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_4^m)},\quad \frac{1}{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N_ {\hat{ {\Gamma} }} ^ {\mathrm{vir}} )} =\frac{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_1^m) e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_5^m) }{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_2^m) e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_4^m)}, \end{align*} $$
where
 $$ \begin{align*} e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_1^m)&= e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_1^m), \\ e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_4^m) &= e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_4^m) \prod_{j\in J_+}\left(\frac{\mathsf{u}_1'}{r_j \mu_j} -\frac{\bar{\psi}_j}{r_j}\right) \prod_{j\in J_-}\left(\frac{\mathsf{u}_1'}{r_j \mu_j}-\frac{\bar{\psi}_j}{r_j}\right) \end{align*} $$
$$ \begin{align*} e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_1^m)&= e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_1^m), \\ e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(B_4^m) &= e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(\hat{B}_4^m) \prod_{j\in J_+}\left(\frac{\mathsf{u}_1'}{r_j \mu_j} -\frac{\bar{\psi}_j}{r_j}\right) \prod_{j\in J_-}\left(\frac{\mathsf{u}_1'}{r_j \mu_j}-\frac{\bar{\psi}_j}{r_j}\right) \end{align*} $$
For
![]() $k=0,1$
and
$k=0,1$
and
![]() $j=1,\ldots , h$
, let
$j=1,\ldots , h$
, let
Then there is a long exact sequence
 $$ \begin{align*} & 0 \to B_2 \to \hat{B}_2 \oplus \bigoplus_{j=1}^h H^0(D_j) \to \bigoplus_{j\in J_+} (T_{\mathfrak{p}_+}\mathcal{X})^{k_j^+}\oplus \bigoplus_{j\in J_-} (T_{\mathfrak{p}_-}\mathcal{X})^{k_j^-} \\ & \to B_5 \to \hat{B}_5 \oplus \bigoplus_{j=1}^h H^1(D_j)\to 0, \end{align*} $$
$$ \begin{align*} & 0 \to B_2 \to \hat{B}_2 \oplus \bigoplus_{j=1}^h H^0(D_j) \to \bigoplus_{j\in J_+} (T_{\mathfrak{p}_+}\mathcal{X})^{k_j^+}\oplus \bigoplus_{j\in J_-} (T_{\mathfrak{p}_-}\mathcal{X})^{k_j^-} \\ & \to B_5 \to \hat{B}_5 \oplus \bigoplus_{j=1}^h H^1(D_j)\to 0, \end{align*} $$
where
![]() $(T_{\mathfrak {p}_\pm }\mathcal {X})^{k_j^\pm }$
denote the
$(T_{\mathfrak {p}_\pm }\mathcal {X})^{k_j^\pm }$
denote the
![]() $k_j^\pm $
-invariant part of
$k_j^\pm $
-invariant part of
![]() $T_{\mathfrak {p}_\pm }\mathcal {X}$
. Note that
$T_{\mathfrak {p}_\pm }\mathcal {X}$
. Note that
 $$ \begin{align*} \frac{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(H^1(D_j)^m)}{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(H^0(D_j)^m)} = |\mu_j ||G_\tau| D_{\mu_j,\lambda_j}. \end{align*} $$
$$ \begin{align*} \frac{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(H^1(D_j)^m)}{e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(H^0(D_j)^m)} = |\mu_j ||G_\tau| D_{\mu_j,\lambda_j}. \end{align*} $$
Let
 $$ \begin{align*} e_{ \mathbb{T} _f}(N^ {\mathrm{vir}} _\Gamma) &:= \iota_f^* e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N^ {\mathrm{vir}} _\Gamma) = e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N^ {\mathrm{vir}} _\Gamma)\Big|_{\mathsf{u}_1'=\mathsf{u}, \mathsf{u}_2'=f\mathsf{u}},\\ e_{ \mathbb{T} _f}(N^ {\mathrm{vir}} _ {\hat{ {\Gamma} }} ) &:= \iota_f^* e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N^ {\mathrm{vir}} _ {\hat{ {\Gamma} }} ) = e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N^ {\mathrm{vir}} _ {\hat{ {\Gamma} }} )\Big|_{\mathsf{u}_1'=\mathsf{u}, \mathsf{u}_2'=f\mathsf{u}}. \end{align*} $$
$$ \begin{align*} e_{ \mathbb{T} _f}(N^ {\mathrm{vir}} _\Gamma) &:= \iota_f^* e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N^ {\mathrm{vir}} _\Gamma) = e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N^ {\mathrm{vir}} _\Gamma)\Big|_{\mathsf{u}_1'=\mathsf{u}, \mathsf{u}_2'=f\mathsf{u}},\\ e_{ \mathbb{T} _f}(N^ {\mathrm{vir}} _ {\hat{ {\Gamma} }} ) &:= \iota_f^* e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N^ {\mathrm{vir}} _ {\hat{ {\Gamma} }} ) = e_{ \mathbb{T} ^{\prime}_{\mathbb{R}} }(N^ {\mathrm{vir}} _ {\hat{ {\Gamma} }} )\Big|_{\mathsf{u}_1'=\mathsf{u}, \mathsf{u}_2'=f\mathsf{u}}. \end{align*} $$
Given
![]() $\gamma _1,\ldots ,\gamma _n \in H^*_{ {\mathrm {CR}} , \mathbb {T} _f}(\mathcal {X})$
, we define
$\gamma _1,\ldots ,\gamma _n \in H^*_{ {\mathrm {CR}} , \mathbb {T} _f}(\mathcal {X})$
, we define
 $$ \begin{align*} &\langle \gamma_1,\dots,\gamma_h\rangle^{\mathcal{X},(\mathcal{L},f)}_{\beta',((\mu_1,\lambda_1),\dots,(\mu_h,\lambda_h))}:=\int_{[F_ {\Gamma} ]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i\big)|_{F_\Gamma}}{e_{ \mathbb{T} _f}(N_ {\Gamma} ^ {\mathrm{vir}} )} \\ =& \prod_{j\in J_+ }\frac{\mathfrak{r}_+}{r_j\mu_j} \prod_{j\in J_-}\frac{\mathfrak{r}_-}{- r_j\mu_j} \prod_{j=1}^h (|\mu_j||G_\tau|D_{\mu_j, \lambda_j,f}) \\ &\cdot \int_{[F_{ {\hat{ {\Gamma} }} }]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i \prod_{j\in J_+}\mathrm{ev}_{n+j}^*\phi_{ {\sigma} _+, (k_j^+)^{-1}} \prod_{j\in J_-} \mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} _-, (k_j^-)^{-1}}\big)|_{F_\Gamma}} {\prod_{j\in J_+}(\frac{\mathsf{u}_1'}{r_j \mu_j} -\frac{\bar{\psi}_{n+j}}{r_j}) \prod_{j\in J_-}(\frac{\mathsf{u}_1'}{r_j \mu_j} -\frac{\bar{\psi}_{n+j}}{r_j})e_{ \mathbb{T} _f}(N_ {\hat{ {\Gamma} }} ^ {\mathrm{vir}} )} \\ =& \prod_{j=1}^hD^{\prime}_{\mu_j,\lambda_j,f} \cdot \int_{[F_{ {\hat{ {\Gamma} }} }]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i \prod_{j\in J_+}\mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} _+, (k_j^+)^{-1}} \prod_{j\in J_-}\mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} _-, (k_j^-)^{-1}}\big)|_{F_\Gamma}}{ \prod_{j=1}^h\frac{\mathsf{u}}{\mu_j}(\frac{\mathsf{u}}{\mu_j} -\bar{\psi}_{n+j})e_{ \mathbb{T} _f}(N_ {\hat{ {\Gamma} }} ^ {\mathrm{vir}} )} \end{align*} $$
$$ \begin{align*} &\langle \gamma_1,\dots,\gamma_h\rangle^{\mathcal{X},(\mathcal{L},f)}_{\beta',((\mu_1,\lambda_1),\dots,(\mu_h,\lambda_h))}:=\int_{[F_ {\Gamma} ]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i\big)|_{F_\Gamma}}{e_{ \mathbb{T} _f}(N_ {\Gamma} ^ {\mathrm{vir}} )} \\ =& \prod_{j\in J_+ }\frac{\mathfrak{r}_+}{r_j\mu_j} \prod_{j\in J_-}\frac{\mathfrak{r}_-}{- r_j\mu_j} \prod_{j=1}^h (|\mu_j||G_\tau|D_{\mu_j, \lambda_j,f}) \\ &\cdot \int_{[F_{ {\hat{ {\Gamma} }} }]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i \prod_{j\in J_+}\mathrm{ev}_{n+j}^*\phi_{ {\sigma} _+, (k_j^+)^{-1}} \prod_{j\in J_-} \mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} _-, (k_j^-)^{-1}}\big)|_{F_\Gamma}} {\prod_{j\in J_+}(\frac{\mathsf{u}_1'}{r_j \mu_j} -\frac{\bar{\psi}_{n+j}}{r_j}) \prod_{j\in J_-}(\frac{\mathsf{u}_1'}{r_j \mu_j} -\frac{\bar{\psi}_{n+j}}{r_j})e_{ \mathbb{T} _f}(N_ {\hat{ {\Gamma} }} ^ {\mathrm{vir}} )} \\ =& \prod_{j=1}^hD^{\prime}_{\mu_j,\lambda_j,f} \cdot \int_{[F_{ {\hat{ {\Gamma} }} }]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i \prod_{j\in J_+}\mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} _+, (k_j^+)^{-1}} \prod_{j\in J_-}\mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} _-, (k_j^-)^{-1}}\big)|_{F_\Gamma}}{ \prod_{j=1}^h\frac{\mathsf{u}}{\mu_j}(\frac{\mathsf{u}}{\mu_j} -\bar{\psi}_{n+j})e_{ \mathbb{T} _f}(N_ {\hat{ {\Gamma} }} ^ {\mathrm{vir}} )} \end{align*} $$
where
 $$ \begin{align*}& D^{\prime}_{d_0,\lambda,f} \\ &= \begin{cases} \displaystyle{ -(-1)^{\lfloor d_0w^+_3 + \frac{\bar \lambda}{\mathfrak{m}}\rfloor}\Big(\frac{\mathsf{u}}{d_0}\Big)^{\mathrm{age}(k^+)} \cdot \frac{\mathfrak{r}_+}{d_0}\cdot \frac{\prod_{a=1}^{\lfloor d_0w^+_1\rfloor +\mathrm{age}(k^+)-1} (d_0 w^+_2 +a-c_2(k^+))} {\lfloor d_0w^+_1\rfloor !}}, \quad d_0>0, & \\ & \\ \displaystyle{ -(-1)^{\lfloor d_0w_2^- + (1-\frac{\bar\lambda}{\mathfrak{m}}-\delta_{\bar \lambda,0})\rfloor} \Big(\frac{\mathsf{u}}{d_0 }\Big)^{\mathrm{age}(k^-)} \cdot \frac{\mathfrak{r}_-}{-d_0}\cdot \frac{\prod_{a=1}^{\lfloor d_0 w_1^- \rfloor+\mathrm{age}(k^-)-1}(d_0w_3^--c_3(k^-)+a)}{\lfloor d_0w_1^-\rfloor!} } , \quad d_0<0. & \\ \end{cases} \end{align*} $$
$$ \begin{align*}& D^{\prime}_{d_0,\lambda,f} \\ &= \begin{cases} \displaystyle{ -(-1)^{\lfloor d_0w^+_3 + \frac{\bar \lambda}{\mathfrak{m}}\rfloor}\Big(\frac{\mathsf{u}}{d_0}\Big)^{\mathrm{age}(k^+)} \cdot \frac{\mathfrak{r}_+}{d_0}\cdot \frac{\prod_{a=1}^{\lfloor d_0w^+_1\rfloor +\mathrm{age}(k^+)-1} (d_0 w^+_2 +a-c_2(k^+))} {\lfloor d_0w^+_1\rfloor !}}, \quad d_0>0, & \\ & \\ \displaystyle{ -(-1)^{\lfloor d_0w_2^- + (1-\frac{\bar\lambda}{\mathfrak{m}}-\delta_{\bar \lambda,0})\rfloor} \Big(\frac{\mathsf{u}}{d_0 }\Big)^{\mathrm{age}(k^-)} \cdot \frac{\mathfrak{r}_-}{-d_0}\cdot \frac{\prod_{a=1}^{\lfloor d_0 w_1^- \rfloor+\mathrm{age}(k^-)-1}(d_0w_3^--c_3(k^-)+a)}{\lfloor d_0w_1^-\rfloor!} } , \quad d_0<0. & \\ \end{cases} \end{align*} $$
Suppose that
![]() $(\mathcal {L},f)$
is a framed outer brane. Define
$(\mathcal {L},f)$
is a framed outer brane. Define
 $$ \begin{align*}D^{\prime}_{d_0,\lambda,f}= -(-1)^{\lfloor d_0w_3+ \frac{\bar \lambda}{\mathfrak{m}}\rfloor}\Big(\frac{\mathsf{u}}{d_0}\Big)^{\mathrm{age}(k)} \cdot \frac{\mathfrak{r}}{d_0}\cdot \frac{\prod_{a=1}^{\lfloor d_0w_1\rfloor +\mathrm{age}(k)-1} (d_0 w_2 +a-c_2(k))} {\lfloor d_0w_1\rfloor !}, \end{align*} $$
$$ \begin{align*}D^{\prime}_{d_0,\lambda,f}= -(-1)^{\lfloor d_0w_3+ \frac{\bar \lambda}{\mathfrak{m}}\rfloor}\Big(\frac{\mathsf{u}}{d_0}\Big)^{\mathrm{age}(k)} \cdot \frac{\mathfrak{r}}{d_0}\cdot \frac{\prod_{a=1}^{\lfloor d_0w_1\rfloor +\mathrm{age}(k)-1} (d_0 w_2 +a-c_2(k))} {\lfloor d_0w_1\rfloor !}, \end{align*} $$
where
![]() $k=h(d_0,\lambda )$
. By the
$k=h(d_0,\lambda )$
. By the
![]() $d_0>0$
part of the proof of Proposition 3.2, we obtain:
$d_0>0$
part of the proof of Proposition 3.2, we obtain:
Proposition 3.3 (framed outer brane)
Suppose that
![]() $(\mathcal {L},f)$
is a framed inner brane and
$(\mathcal {L},f)$
is a framed inner brane and
![]() $ {\vec {\mu }} =((\mu _1,\lambda _1),\ldots , (\mu _h,\lambda _h))$
, where
$ {\vec {\mu }} =((\mu _1,\lambda _1),\ldots , (\mu _h,\lambda _h))$
, where
![]() $(\mu _j,\lambda _j)\in H_1(\mathcal {L}; \mathbb {Z} )$
. Then
$(\mu _j,\lambda _j)\in H_1(\mathcal {L}; \mathbb {Z} )$
. Then
 $$ \begin{align*}\langle \gamma_1,\ldots, \gamma_n\rangle_{g,\beta', {\vec{\mu}} }^{\mathcal{X}, (\mathcal{L},f)} =\prod_{j=1}^h D^{\prime}_{\mu_j,\lambda,f} \cdot \int_{[\overline{\mathcal{M}}_{g,n+h}(\mathcal{X},\beta)]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i \prod_{j=1}^h\mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} , (h(d_0,\lambda))^{-1}}\big)} {\prod_{j=1}^h\frac{\mathsf{u}}{\mu_j}(\frac{\mathsf{u}}{\mu_j} -\bar{\psi}_{n+j})}, \end{align*} $$
$$ \begin{align*}\langle \gamma_1,\ldots, \gamma_n\rangle_{g,\beta', {\vec{\mu}} }^{\mathcal{X}, (\mathcal{L},f)} =\prod_{j=1}^h D^{\prime}_{\mu_j,\lambda,f} \cdot \int_{[\overline{\mathcal{M}}_{g,n+h}(\mathcal{X},\beta)]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i \prod_{j=1}^h\mathrm{ev}_{n+j}^*\phi^f_{ {\sigma} , (h(d_0,\lambda))^{-1}}\big)} {\prod_{j=1}^h\frac{\mathsf{u}}{\mu_j}(\frac{\mathsf{u}}{\mu_j} -\bar{\psi}_{n+j})}, \end{align*} $$
where
 $$ \begin{align*}\beta\in H_2(\mathcal{X}),\quad \beta'= \beta + \Big(\sum_{j=1}^h \mu_j\Big)b. \end{align*} $$
$$ \begin{align*}\beta\in H_2(\mathcal{X}),\quad \beta'= \beta + \Big(\sum_{j=1}^h \mu_j\Big)b. \end{align*} $$
3.13 Generating functions of open-closed GW invariants
From now on, we assume the generic stabiliser K is trivial so that
![]() $\mathcal {X}=\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
is a toric Calabi-Yau 3-orbifold. Then
$\mathcal {X}=\mathcal {X}^ {\mathrm {{\kern1.5pt}rig}} $
is a toric Calabi-Yau 3-orbifold. Then
is a group isomorphism. We have
![]() $\bar {N}=N$
and
$\bar {N}=N$
and
![]() $\bar {b}_i=\bar {b}_i$
. In particular,
$\bar {b}_i=\bar {b}_i$
. In particular,
There exists
![]() $m_a,n_a\in \mathbb {Z} $
, such that
$m_a,n_a\in \mathbb {Z} $
, such that
Introduce variables
![]() $\{ X_j \mid j=1,\ldots ,h\}$
, and let
$\{ X_j \mid j=1,\ldots ,h\}$
, and let
 $$ \begin{align*}\boldsymbol{\tau}_2 = \sum_{i=1}^m \tau_i u_i, \end{align*} $$
$$ \begin{align*}\boldsymbol{\tau}_2 = \sum_{i=1}^m \tau_i u_i, \end{align*} $$
where
![]() $u_1,\ldots , u_m$
form a basis of
$u_1,\ldots , u_m$
form a basis of
![]() $H^2_ {\mathrm {CR}} (\mathcal {X}; \mathbb {Q} )$
. We choose
$H^2_ {\mathrm {CR}} (\mathcal {X}; \mathbb {Q} )$
. We choose
![]() $ \mathbb {T} '$
-equivariant lifting of
$ \mathbb {T} '$
-equivariant lifting of
![]() $\boldsymbol {\tau }_2$
as follows: for each
$\boldsymbol {\tau }_2$
as follows: for each
![]() $u_i\in H^2_ {\mathrm {CR}} (\mathcal {X}; \mathbb {Q} )$
, we choose the unique
$u_i\in H^2_ {\mathrm {CR}} (\mathcal {X}; \mathbb {Q} )$
, we choose the unique
![]() $ \mathbb {T} '$
-equivariant lifting
$ \mathbb {T} '$
-equivariant lifting
![]() $u_i^{ \mathbb {T} '} \in H^2_{ {\mathrm {CR}} , \mathbb {T} '}(\mathcal {X}; \mathbb {Q} )$
such that
$u_i^{ \mathbb {T} '} \in H^2_{ {\mathrm {CR}} , \mathbb {T} '}(\mathcal {X}; \mathbb {Q} )$
such that
![]() $\iota _ {\sigma } ^* u_i^{ \mathbb {T} '} = 0\in H^2_{ {\mathrm {CR}} , \mathbb {T} '}(\mathfrak {p}_ {\sigma }; \mathbb {Q} )$
, where
$\iota _ {\sigma } ^* u_i^{ \mathbb {T} '} = 0\in H^2_{ {\mathrm {CR}} , \mathbb {T} '}(\mathfrak {p}_ {\sigma }; \mathbb {Q} )$
, where
![]() $\iota _ {\sigma } ^*: H^2_{ {\mathrm {CR}} , \mathbb {T} '}(\mathcal {X}; \mathbb {Q} )\to H^2_{ {\mathrm {CR}} , \mathbb {T} '}(\mathfrak {p}_ {\sigma }; \mathbb {Q} )$
is induced by the inclusion map
$\iota _ {\sigma } ^*: H^2_{ {\mathrm {CR}} , \mathbb {T} '}(\mathcal {X}; \mathbb {Q} )\to H^2_{ {\mathrm {CR}} , \mathbb {T} '}(\mathfrak {p}_ {\sigma }; \mathbb {Q} )$
is induced by the inclusion map
![]() $\iota _ {\sigma } :\mathfrak {p}_ {\sigma } \to \mathcal {X}$
.
$\iota _ {\sigma } :\mathfrak {p}_ {\sigma } \to \mathcal {X}$
.
We define
![]() $\xi _0:= e^{-\pi \sqrt {-1}/\mathfrak {m}}$
. If
$\xi _0:= e^{-\pi \sqrt {-1}/\mathfrak {m}}$
. If
![]() $(\mathcal {L},f)$
is a framed outer brane, define
$(\mathcal {L},f)$
is a framed outer brane, define
 $$ \begin{align} \begin{aligned} & F_{g,h}^{\mathcal{X},(\mathcal{L},f)}(\boldsymbol{\tau}_2, Q^b, X_1,\ldots,X_h)\\ &\quad = \sum_{\beta', n\geq 0}\sum_{(\mu_j, \lambda_j)\in H_1(\mathcal{L}; \mathbb{Z} )} \frac{\langle (\iota_f^*\boldsymbol{\tau}_2) ^n\rangle_{g,\beta,(\mu_1,\lambda_1),\ldots, (\mu_h,\lambda_h)}^{\mathcal{X},(\mathcal{L},f)}}{n!} \prod_{j=1}^h (Q^bX_j)^{\mu_j} \cdot \xi_0^{\bar{\lambda}_1} \mathbf{1}_{\lambda_1^{-1}} \otimes \cdots \otimes \xi_0^{\bar{\lambda}_h} \mathbf{1} _{\lambda_h^{-1}}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & F_{g,h}^{\mathcal{X},(\mathcal{L},f)}(\boldsymbol{\tau}_2, Q^b, X_1,\ldots,X_h)\\ &\quad = \sum_{\beta', n\geq 0}\sum_{(\mu_j, \lambda_j)\in H_1(\mathcal{L}; \mathbb{Z} )} \frac{\langle (\iota_f^*\boldsymbol{\tau}_2) ^n\rangle_{g,\beta,(\mu_1,\lambda_1),\ldots, (\mu_h,\lambda_h)}^{\mathcal{X},(\mathcal{L},f)}}{n!} \prod_{j=1}^h (Q^bX_j)^{\mu_j} \cdot \xi_0^{\bar{\lambda}_1} \mathbf{1}_{\lambda_1^{-1}} \otimes \cdots \otimes \xi_0^{\bar{\lambda}_h} \mathbf{1} _{\lambda_h^{-1}}, \end{aligned} \end{align} $$
which is a function that takes values in
![]() $H^*_ {\mathrm {CR}} (\mathcal {B} G_\tau; \mathbb {C} )^{\otimes h}$
, where
$H^*_ {\mathrm {CR}} (\mathcal {B} G_\tau; \mathbb {C} )^{\otimes h}$
, where
When
![]() $\lambda =1$
is the identity element of
$\lambda =1$
is the identity element of
![]() $G_\tau $
,
$G_\tau $
,
![]() $\mathbf {1}_1=1$
is the unit of
$\mathbf {1}_1=1$
is the unit of
![]() $H^*_ {\mathrm {CR}} (\mathcal {B} G_\tau; \mathbb {C} )$
.
$H^*_ {\mathrm {CR}} (\mathcal {B} G_\tau; \mathbb {C} )$
.
If
![]() $(\mathcal {L},f)$
is a framed inner brane, define
$(\mathcal {L},f)$
is a framed inner brane, define
 $$ \begin{align} \begin{aligned} & F_{g,h}^{\mathcal{X},(\mathcal{L},f)}(\boldsymbol{\tau}_2, Q^b, X_1,\ldots, X_h) = \sum_{\beta', n\geq 0}\sum_{(\mu_j,\lambda_j)\in H_1(\mathcal{L}; \mathbb{Z} )} \frac{\langle (\iota_f^*\boldsymbol{\tau}_2)^n\rangle_{g,\beta,(\mu_1,\lambda_1),\ldots, (\mu_h,\lambda_h)}^{\mathcal{X},(\mathcal{L},f)}}{n!} \\ & \quad \quad \cdot \prod_{\substack{ j\in \{1,\ldots, h\}\\ \mu_j>0} } (Q^b X_j)^{\mu_j} \prod_{\substack{ j\in \{1,\ldots, h\}\\ \mu_j<0} } (Q^{b-\alpha}X_j)^{\mu_j} \cdot \xi_0^{\bar{\lambda}_1} \mathbf{1}_{\lambda_1^{-1}} \otimes \cdots \otimes \xi_0^{\bar{\lambda}_h} \mathbf{1}_{\lambda_h^{-1}}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & F_{g,h}^{\mathcal{X},(\mathcal{L},f)}(\boldsymbol{\tau}_2, Q^b, X_1,\ldots, X_h) = \sum_{\beta', n\geq 0}\sum_{(\mu_j,\lambda_j)\in H_1(\mathcal{L}; \mathbb{Z} )} \frac{\langle (\iota_f^*\boldsymbol{\tau}_2)^n\rangle_{g,\beta,(\mu_1,\lambda_1),\ldots, (\mu_h,\lambda_h)}^{\mathcal{X},(\mathcal{L},f)}}{n!} \\ & \quad \quad \cdot \prod_{\substack{ j\in \{1,\ldots, h\}\\ \mu_j>0} } (Q^b X_j)^{\mu_j} \prod_{\substack{ j\in \{1,\ldots, h\}\\ \mu_j<0} } (Q^{b-\alpha}X_j)^{\mu_j} \cdot \xi_0^{\bar{\lambda}_1} \mathbf{1}_{\lambda_1^{-1}} \otimes \cdots \otimes \xi_0^{\bar{\lambda}_h} \mathbf{1}_{\lambda_h^{-1}}, \end{aligned} \end{align} $$
which is a function that takes values in
![]() $H^*_ {\mathrm {CR}} (\mathcal {B} G_\tau; \mathbb {C} )^{\otimes h}$
.
$H^*_ {\mathrm {CR}} (\mathcal {B} G_\tau; \mathbb {C} )^{\otimes h}$
.
3.14 The equivariant J-function and the disk potential
Let
![]() $\{u_i\}_{i=1}^N$
be a homogeneous basis of
$\{u_i\}_{i=1}^N$
be a homogeneous basis of
![]() $H^*_{ \mathbb {T} , {\mathrm {CR}} }(\mathcal {X}; \mathbb {Q} )$
and
$H^*_{ \mathbb {T} , {\mathrm {CR}} }(\mathcal {X}; \mathbb {Q} )$
and
![]() $\{u^i\}_{i=1}^N$
be its dual basis. Define
$\{u^i\}_{i=1}^N$
be its dual basis. Define
 $$ \begin{align*}\boldsymbol{\tau} =\sum_{i=1}^N \tau_i u_i =\boldsymbol{\tau}_0+ \boldsymbol{\tau}_2 + \boldsymbol{\tau}_{>2}, \end{align*} $$
$$ \begin{align*}\boldsymbol{\tau} =\sum_{i=1}^N \tau_i u_i =\boldsymbol{\tau}_0+ \boldsymbol{\tau}_2 + \boldsymbol{\tau}_{>2}, \end{align*} $$
where
The J-function [Reference Tseng71, Reference Coates and Givental26, Reference Givental40] is a
![]() $H^*_{ \mathbb {T} , {\mathrm {CR}} }(\mathcal {X})$
-valued function:
$H^*_{ \mathbb {T} , {\mathrm {CR}} }(\mathcal {X})$
-valued function:
 $$ \begin{align*}J(\boldsymbol{\tau},z):= 1+\sum_{\beta\ge 0, n\ge 0} \frac{1}{n!}\sum_{i=1}^N \left\langle 1,\boldsymbol{\tau}^n, \frac{u_i}{z-\bar \psi}\right\rangle^{\mathcal{X}, \mathbb{T} }_{0,\beta} u^i. \end{align*} $$
$$ \begin{align*}J(\boldsymbol{\tau},z):= 1+\sum_{\beta\ge 0, n\ge 0} \frac{1}{n!}\sum_{i=1}^N \left\langle 1,\boldsymbol{\tau}^n, \frac{u_i}{z-\bar \psi}\right\rangle^{\mathcal{X}, \mathbb{T} }_{0,\beta} u^i. \end{align*} $$
Then
 $$ \begin{align*}\iota_ {\sigma} ^* J(\boldsymbol{\tau},z)\Big|_{\mathsf{u}_1=\mathsf{u},\, \mathsf{u}_2=f\mathsf{u},\, \mathsf{u}_3=0} =\sum_{k\in G_ {\sigma} } J^f_{ {\sigma} ,k}(\boldsymbol{\tau},z) \mathbf{1}_k, \end{align*} $$
$$ \begin{align*}\iota_ {\sigma} ^* J(\boldsymbol{\tau},z)\Big|_{\mathsf{u}_1=\mathsf{u},\, \mathsf{u}_2=f\mathsf{u},\, \mathsf{u}_3=0} =\sum_{k\in G_ {\sigma} } J^f_{ {\sigma} ,k}(\boldsymbol{\tau},z) \mathbf{1}_k, \end{align*} $$
where
 $$ \begin{align*}J_{ {\sigma} ,k}^f(\boldsymbol{\tau},z)= \delta_{k,1} +\sum_{\beta\ge 0, n\ge 0} \frac{1}{n!} \sum_{i=1}^N \left\langle 1, (\iota_f^*\boldsymbol{\tau})^n, \frac{|G_ {\sigma} |\phi^f_{ {\sigma} ,k^{-1}}}{z-\bar \psi}\right\rangle^{\mathcal{X}, \mathbb{T} _f}_{0,\beta}. \end{align*} $$
$$ \begin{align*}J_{ {\sigma} ,k}^f(\boldsymbol{\tau},z)= \delta_{k,1} +\sum_{\beta\ge 0, n\ge 0} \frac{1}{n!} \sum_{i=1}^N \left\langle 1, (\iota_f^*\boldsymbol{\tau})^n, \frac{|G_ {\sigma} |\phi^f_{ {\sigma} ,k^{-1}}}{z-\bar \psi}\right\rangle^{\mathcal{X}, \mathbb{T} _f}_{0,\beta}. \end{align*} $$
As a special case of Proposition 3.3,
 $$ \begin{align*} \langle \gamma_1,\ldots, \gamma_n\rangle_{0,\beta+d_0 b,(d_0 ,k)}^{\mathcal{X},(\mathcal{L},f)} &= D^{\prime}_{d_0 ,\lambda,f} \int_{[\overline{\mathcal{M}}_{0,n+1}(\mathcal{X},\beta)]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i\cup \mathrm{ev}_{n+1}^*\phi^f_{(h^+(d_0,\lambda))^{-1}}\big)}{\frac{\mathsf{u}}{d_0}(\frac{\mathsf{u}}{d_0} -\bar{\psi}_{n+1})}\\ &= D^{\prime}_{d_0 ,\lambda,f} \left\langle 1,\gamma_1,\dots,\gamma_n,\frac{\phi^f_{(h^+(d_0,\lambda))^{-1}}}{\frac{\mathsf{u}}{d_0} -\bar{\psi}} \right\rangle^{\mathcal{X}}_{0,\beta}; \end{align*} $$
$$ \begin{align*} \langle \gamma_1,\ldots, \gamma_n\rangle_{0,\beta+d_0 b,(d_0 ,k)}^{\mathcal{X},(\mathcal{L},f)} &= D^{\prime}_{d_0 ,\lambda,f} \int_{[\overline{\mathcal{M}}_{0,n+1}(\mathcal{X},\beta)]^ {\mathrm{vir}} } \frac{ \big(\prod_{i=1}^n\mathrm{ev}_i^*\gamma_i\cup \mathrm{ev}_{n+1}^*\phi^f_{(h^+(d_0,\lambda))^{-1}}\big)}{\frac{\mathsf{u}}{d_0}(\frac{\mathsf{u}}{d_0} -\bar{\psi}_{n+1})}\\ &= D^{\prime}_{d_0 ,\lambda,f} \left\langle 1,\gamma_1,\dots,\gamma_n,\frac{\phi^f_{(h^+(d_0,\lambda))^{-1}}}{\frac{\mathsf{u}}{d_0} -\bar{\psi}} \right\rangle^{\mathcal{X}}_{0,\beta}; \end{align*} $$
 $$ \begin{align*} F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2,Q^b, X_1) &= \sum_{\beta,n\geq 0} \sum_{(d_0 ,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} \frac{1}{n!}\langle (\iota_f^*\boldsymbol{\tau}_2)^n\rangle^{\mathcal{X},(\mathcal{L},f)}_{0,\beta+d_0 b,(d_0 ,\lambda)} (Q^bX)^{d_0} \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}\\ &= \frac{1}{|G_ {\sigma} |}\sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} (Q^b X_1)^{d_0} D^{\prime}_{d_0 ,\lambda,f} J^f_{ {\sigma} ,h^+(d_0,\lambda)}\Big(\boldsymbol{\tau}_2 ,\frac{\mathsf{u}}{d_0}\Big)\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*} F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2,Q^b, X_1) &= \sum_{\beta,n\geq 0} \sum_{(d_0 ,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} \frac{1}{n!}\langle (\iota_f^*\boldsymbol{\tau}_2)^n\rangle^{\mathcal{X},(\mathcal{L},f)}_{0,\beta+d_0 b,(d_0 ,\lambda)} (Q^bX)^{d_0} \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}\\ &= \frac{1}{|G_ {\sigma} |}\sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} (Q^b X_1)^{d_0} D^{\prime}_{d_0 ,\lambda,f} J^f_{ {\sigma} ,h^+(d_0,\lambda)}\Big(\boldsymbol{\tau}_2 ,\frac{\mathsf{u}}{d_0}\Big)\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
Proposition 3.4. Let
![]() $X=Q^b X_1$
. If
$X=Q^b X_1$
. If
![]() $(\mathcal {L},f)$
is a framed outer brane, then
$(\mathcal {L},f)$
is a framed outer brane, then
 $$ \begin{align*}F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2,X) = \frac{1}{|G_ {\sigma} |} \sum_{(d_0 ,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} X^{d_0} D^{\prime}_{d_0 ,\lambda,f}J^f_{ {\sigma} ,h^+(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0} \Big) \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*}F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2,X) = \frac{1}{|G_ {\sigma} |} \sum_{(d_0 ,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} X^{d_0} D^{\prime}_{d_0 ,\lambda,f}J^f_{ {\sigma} ,h^+(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0} \Big) \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
If
![]() $(\mathcal {L},f)$
is a framed inner brane, then
$(\mathcal {L},f)$
is a framed inner brane, then
 $$ \begin{align*} F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2, Q, X) &= \frac{1}{|G_ {\sigma} |}\sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} ), d_0>0} X^{d_0} D^{\prime}_{d_0 ,\lambda,f} J^f_{ {\sigma} _+,h^+(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0}\Big) \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}} \\ &\quad + \frac{1}{|G_ {\sigma} |} \sum_{(d_0 ,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} ), d_0 <0} X^{d_0} Q^{-d_0 \alpha} D^{\prime}_{d_0,\lambda,f}J^f_{ {\sigma} _-,h^-(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0}\Big) \cdot \frac{\mathfrak{r}_+}{\mathfrak{r}_-} \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*} F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2, Q, X) &= \frac{1}{|G_ {\sigma} |}\sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} ), d_0>0} X^{d_0} D^{\prime}_{d_0 ,\lambda,f} J^f_{ {\sigma} _+,h^+(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0}\Big) \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}} \\ &\quad + \frac{1}{|G_ {\sigma} |} \sum_{(d_0 ,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} ), d_0 <0} X^{d_0} Q^{-d_0 \alpha} D^{\prime}_{d_0,\lambda,f}J^f_{ {\sigma} _-,h^-(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0}\Big) \cdot \frac{\mathfrak{r}_+}{\mathfrak{r}_-} \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
4 Mirror symmetry for the disk amplitudes
4.1 The equivariant I-function and the equivariant mirror theorem
We choose
![]() $p_1,\ldots , p_k \in \mathbb {L}^\vee \cap \widetilde { {\mathrm {Nef}} }_{\mathcal {X}}$
such that
$p_1,\ldots , p_k \in \mathbb {L}^\vee \cap \widetilde { {\mathrm {Nef}} }_{\mathcal {X}}$
such that
-
○
 $\{p_1,\ldots ,p_k\}$
is a
$\{p_1,\ldots ,p_k\}$
is a
 $ \mathbb {Q} $
-basis of
$ \mathbb {Q} $
-basis of
 $\mathbb {L}^\vee _{\mathbb {Q}} $
.
$\mathbb {L}^\vee _{\mathbb {Q}} $
. -
○
 $\{\bar {p}_1,\ldots , \bar {p}_{k'}\}$
is a
$\{\bar {p}_1,\ldots , \bar {p}_{k'}\}$
is a
 $ \mathbb {Q} $
-basis of
$ \mathbb {Q} $
-basis of
 $H^2(\mathcal {X}; \mathbb {Q} )$
.
$H^2(\mathcal {X}; \mathbb {Q} )$
. -
○
 $p_a=D_{3+a}$
for
$p_a=D_{3+a}$
for
 $a= k'+1,\dots ,k$
.
$a= k'+1,\dots ,k$
.
We define charges
![]() $m^{(a)}_i\in \mathbb {Q} $
by
$m^{(a)}_i\in \mathbb {Q} $
by
![]() $D_i=\sum _{a=1}^k m^{(a)}_i p_a$
.
$D_i=\sum _{a=1}^k m^{(a)}_i p_a$
.
Let
![]() $q^{\prime }_0,q_1,\ldots , q_k$
be
$q^{\prime }_0,q_1,\ldots , q_k$
be
![]() $k+1$
formal variables, and define
$k+1$
formal variables, and define
![]() $q^\beta = q_1^{\langle p_1,\beta \rangle } \cdots q_k^{\langle p_k,\beta \rangle }$
for
$q^\beta = q_1^{\langle p_1,\beta \rangle } \cdots q_k^{\langle p_k,\beta \rangle }$
for
![]() $\beta \in \mathbb {K}$
. We take the equivariant lifting
$\beta \in \mathbb {K}$
. We take the equivariant lifting
![]() $\bar p^{\mathcal {T}}_a\in H^2_{\mathbb {T}} (\mathcal {X}; \mathbb {Q} )$
of
$\bar p^{\mathcal {T}}_a\in H^2_{\mathbb {T}} (\mathcal {X}; \mathbb {Q} )$
of
![]() $\bar p_a\in H^2(\mathcal {X}; \mathbb {Q} )$
. The equivariant I-function is an
$\bar p_a\in H^2(\mathcal {X}; \mathbb {Q} )$
. The equivariant I-function is an
![]() $H^*_{ {\mathrm {CR}} , \mathbb {T} } (\mathcal {X})$
-valued power series defined as follows [Reference Iritani47]:
$H^*_{ {\mathrm {CR}} , \mathbb {T} } (\mathcal {X})$
-valued power series defined as follows [Reference Iritani47]:
 $$ \begin{align*} I(q_0',q,z) &= e^{\frac{\log q^{\prime}_0+\sum_{a=1}^{k'} \bar p_a^{\mathcal{T}} \log q_a}{z}} \sum_{\beta\in \mathbb{K}_{\mathrm{eff}}} q^\beta \prod_{i=1}^{r'} \frac{\prod_{m=\lceil \langle D_i, \beta \rangle \rceil}^\infty (\bar D^{\mathcal{T}}_i +(\langle D_i,\beta\rangle -m)z)}{\prod_{m=0}^\infty(\bar D^{\mathcal{T}}_i+(\langle D_i,\beta\rangle -m)z)} \\ & \quad \cdot \prod_{i=r'+1}^r \frac{\prod_{m=\lceil \langle D_i, \beta \rangle \rceil}^\infty (\langle D_i,\beta\rangle -m)z} {\prod_{m=0}^\infty(\langle D_i,\beta\rangle -m)z} \mathbf{1}_{v(\beta)}, \end{align*} $$
$$ \begin{align*} I(q_0',q,z) &= e^{\frac{\log q^{\prime}_0+\sum_{a=1}^{k'} \bar p_a^{\mathcal{T}} \log q_a}{z}} \sum_{\beta\in \mathbb{K}_{\mathrm{eff}}} q^\beta \prod_{i=1}^{r'} \frac{\prod_{m=\lceil \langle D_i, \beta \rangle \rceil}^\infty (\bar D^{\mathcal{T}}_i +(\langle D_i,\beta\rangle -m)z)}{\prod_{m=0}^\infty(\bar D^{\mathcal{T}}_i+(\langle D_i,\beta\rangle -m)z)} \\ & \quad \cdot \prod_{i=r'+1}^r \frac{\prod_{m=\lceil \langle D_i, \beta \rangle \rceil}^\infty (\langle D_i,\beta\rangle -m)z} {\prod_{m=0}^\infty(\langle D_i,\beta\rangle -m)z} \mathbf{1}_{v(\beta)}, \end{align*} $$
where
![]() $q^\beta =\prod _{a=1}^k q_a^{\langle p_a,\beta \rangle }$
. Note that
$q^\beta =\prod _{a=1}^k q_a^{\langle p_a,\beta \rangle }$
. Note that
![]() $\langle p_a,\beta \rangle \geq 0$
for
$\langle p_a,\beta \rangle \geq 0$
for
![]() $\beta \in \mathbb {K}_{\mathrm {eff}}$
. The equivariant I-function can be rewritten as
$\beta \in \mathbb {K}_{\mathrm {eff}}$
. The equivariant I-function can be rewritten as
 $$ \begin{align*} I(q_0',q,z) &= e^{\frac{\log q^{\prime}_0+\sum_{a=1}^{k'} \bar p_a^{\mathcal{T}} \log q_a}{z}} \sum_{\beta\in \mathbb{K}_{\mathrm{eff}}} \frac{q^\beta}{z^{\langle \hat \rho ,\beta\rangle + \mathrm{age}(v(\beta))} } \prod_{i=1}^{r'} \frac{\prod_{m=\lceil \langle D_i, \beta \rangle \rceil}^\infty ( \frac{\bar D^{\mathcal{T}}_i}{z} +\langle D_i,\beta\rangle -m)} {\prod_{m=0}^\infty(\frac{\bar D^{\mathcal{T}}_i}{z}+ \langle D_i,\beta\rangle -m)} \\ & \quad \cdot \prod_{i=r'+1}^r \frac{\prod_{m=\lceil \langle D_i, \beta \rangle \rceil}^\infty (\langle D_i,\beta\rangle -m)}{\prod_{m=0}^\infty(\langle D_i,\beta\rangle -m)} \mathbf{1}_{v(\beta)}, \end{align*} $$
$$ \begin{align*} I(q_0',q,z) &= e^{\frac{\log q^{\prime}_0+\sum_{a=1}^{k'} \bar p_a^{\mathcal{T}} \log q_a}{z}} \sum_{\beta\in \mathbb{K}_{\mathrm{eff}}} \frac{q^\beta}{z^{\langle \hat \rho ,\beta\rangle + \mathrm{age}(v(\beta))} } \prod_{i=1}^{r'} \frac{\prod_{m=\lceil \langle D_i, \beta \rangle \rceil}^\infty ( \frac{\bar D^{\mathcal{T}}_i}{z} +\langle D_i,\beta\rangle -m)} {\prod_{m=0}^\infty(\frac{\bar D^{\mathcal{T}}_i}{z}+ \langle D_i,\beta\rangle -m)} \\ & \quad \cdot \prod_{i=r'+1}^r \frac{\prod_{m=\lceil \langle D_i, \beta \rangle \rceil}^\infty (\langle D_i,\beta\rangle -m)}{\prod_{m=0}^\infty(\langle D_i,\beta\rangle -m)} \mathbf{1}_{v(\beta)}, \end{align*} $$
where
![]() $\hat \rho = D_1+\cdots +D_r \in {\widetilde {C}} _{\mathcal {X}}$
.
$\hat \rho = D_1+\cdots +D_r \in {\widetilde {C}} _{\mathcal {X}}$
.
Since
![]() $\mathcal {X}$
is a Calabi-Yau orbifold,
$\mathcal {X}$
is a Calabi-Yau orbifold,
![]() $\mathrm {age}(v)$
is an integer for any
$\mathrm {age}(v)$
is an integer for any
![]() $v\in \mathrm {Box}(\mathbf \Sigma )$
. Then
$v\in \mathrm {Box}(\mathbf \Sigma )$
. Then
Let
![]() $\mathcal {Q}= \mathbb {Q} (\mathsf {u}_1,\mathsf {u}_2,\mathsf {u}_3)$
be the fractional field of
$\mathcal {Q}= \mathbb {Q} (\mathsf {u}_1,\mathsf {u}_2,\mathsf {u}_3)$
be the fractional field of
![]() $H^*_{ \mathbb {T} }(\mathrm {point}; \mathbb {Q} )$
:
$H^*_{ \mathbb {T} }(\mathrm {point}; \mathbb {Q} )$
:
 $$ \begin{align*} H^0_{ {\mathrm{CR}} , \mathbb{T} }(\mathcal{X};\mathcal{Q}) &= \mathcal{Q} \mathbf{1} , \\ H^2_{ {\mathrm{CR}} , \mathbb{T} }(\mathcal{X};\mathcal{Q}) &= \bigoplus_{a=1}^{k'}\mathcal{Q} {\bar{p}_a^{\mathcal{T}}}\oplus \bigoplus_{\substack{v\in {\mathrm{Box}(\mathbf \Sigma)}\\ \mathrm{age}(v)=1}} \mathcal{Q} \mathbf{1}_v. \end{align*} $$
$$ \begin{align*} H^0_{ {\mathrm{CR}} , \mathbb{T} }(\mathcal{X};\mathcal{Q}) &= \mathcal{Q} \mathbf{1} , \\ H^2_{ {\mathrm{CR}} , \mathbb{T} }(\mathcal{X};\mathcal{Q}) &= \bigoplus_{a=1}^{k'}\mathcal{Q} {\bar{p}_a^{\mathcal{T}}}\oplus \bigoplus_{\substack{v\in {\mathrm{Box}(\mathbf \Sigma)}\\ \mathrm{age}(v)=1}} \mathcal{Q} \mathbf{1}_v. \end{align*} $$
Recall that the embedding of the stacky fixed point
![]() $\mathfrak {p}_\sigma $
is
$\mathfrak {p}_\sigma $
is
![]() $\iota _\sigma :\mathfrak {p}_\sigma \to \mathcal {X}$
. We choose the lifting
$\iota _\sigma :\mathfrak {p}_\sigma \to \mathcal {X}$
. We choose the lifting
![]() $\bar {p}^{\mathcal {T}}_a$
such that
$\bar {p}^{\mathcal {T}}_a$
such that
![]() $\iota _\sigma ^*\bar {p}^{\mathcal {T}}_a=0$
.
$\iota _\sigma ^*\bar {p}^{\mathcal {T}}_a=0$
.
For
![]() $i=1,\ldots , r$
, we will define
$i=1,\ldots , r$
, we will define
![]() $\Omega _i \subset \mathbb {K}_{\mathrm {eff}}-\{0\}$
and
$\Omega _i \subset \mathbb {K}_{\mathrm {eff}}-\{0\}$
and
![]() $A_i(q)$
supported on
$A_i(q)$
supported on
![]() $\Omega _i$
. We observe that if
$\Omega _i$
. We observe that if
![]() $\beta \in \mathbb {K}_{\mathrm {eff}}$
and
$\beta \in \mathbb {K}_{\mathrm {eff}}$
and
![]() $v(\beta )=0$
, then
$v(\beta )=0$
, then
![]() $\langle D_i,\beta \rangle \in \mathbb {Z} $
for
$\langle D_i,\beta \rangle \in \mathbb {Z} $
for
![]() $i=1,\ldots , r$
.
$i=1,\ldots , r$
.
-
○ For
 $i=1,\ldots ,r'$
, let Then
$i=1,\ldots ,r'$
, let Then $$ \begin{align*}\Omega_i =\left \{ \beta\in \mathbb{K}_{\mathrm{eff}}: v(\beta)=0, \langle D_i,\beta\rangle <0 \mathrm{\ and\ } \langle D_j, \beta \rangle \geq 0 \mathrm{\ for\ } j\in \{1,\ldots, r\}-\{i\} \right \}. \end{align*} $$
$$ \begin{align*}\Omega_i =\left \{ \beta\in \mathbb{K}_{\mathrm{eff}}: v(\beta)=0, \langle D_i,\beta\rangle <0 \mathrm{\ and\ } \langle D_j, \beta \rangle \geq 0 \mathrm{\ for\ } j\in \{1,\ldots, r\}-\{i\} \right \}. \end{align*} $$
 $\Omega _i\subset \{ \beta \in \mathbb {K}_{\mathrm {eff}}: v(\beta )=0, \beta \neq 0\}$
. We define
$\Omega _i\subset \{ \beta \in \mathbb {K}_{\mathrm {eff}}: v(\beta )=0, \beta \neq 0\}$
. We define  $$ \begin{align*}A_i(q):=\sum_{\beta \in \Omega_i} q^\beta \frac{(-1)^{-\langle D_i,\beta\rangle-1}(-\langle D_i, \beta\rangle -1)! }{ \prod_{j\in\{1,\ldots, r\}-\{i\}}\langle D_j,\beta\rangle!}. \end{align*} $$
$$ \begin{align*}A_i(q):=\sum_{\beta \in \Omega_i} q^\beta \frac{(-1)^{-\langle D_i,\beta\rangle-1}(-\langle D_i, \beta\rangle -1)! }{ \prod_{j\in\{1,\ldots, r\}-\{i\}}\langle D_j,\beta\rangle!}. \end{align*} $$
-
○ For
 $i=r'+1,\ldots , r$
, let and define
$i=r'+1,\ldots , r$
, let and define $$ \begin{align*}\Omega_i := \{ \beta\in \mathbb{K}_{\mathrm{eff}}: v(\beta)= b_i, \langle D_j, \beta\rangle \notin \mathbb{Z} _{<0} \mathrm{\ for\ }j=1,\ldots, r\}, \end{align*} $$
$$ \begin{align*}\Omega_i := \{ \beta\in \mathbb{K}_{\mathrm{eff}}: v(\beta)= b_i, \langle D_j, \beta\rangle \notin \mathbb{Z} _{<0} \mathrm{\ for\ }j=1,\ldots, r\}, \end{align*} $$
 $$ \begin{align*}A_i(q) = \sum_{\beta\in \Omega_i} q^\beta \prod_{j=1}^r \frac{\prod_{m=\lceil \langle D_j, \beta \rangle \rceil}^\infty (\langle D_j,\beta\rangle -m)}{\prod_{m=0}^\infty(\langle D_j,\beta\rangle -m)}. \end{align*} $$
$$ \begin{align*}A_i(q) = \sum_{\beta\in \Omega_i} q^\beta \prod_{j=1}^r \frac{\prod_{m=\lceil \langle D_j, \beta \rangle \rceil}^\infty (\langle D_j,\beta\rangle -m)}{\prod_{m=0}^\infty(\langle D_j,\beta\rangle -m)}. \end{align*} $$
Let
![]() $ {\sigma } $
be the smallest cone containing
$ {\sigma } $
be the smallest cone containing
![]() $b_i$
. Then
$b_i$
. Then
 $$ \begin{align*}b_i=\sum_{j\in I_ {\sigma} '}c_j(b_i)b_j, \end{align*} $$
$$ \begin{align*}b_i=\sum_{j\in I_ {\sigma} '}c_j(b_i)b_j, \end{align*} $$
where
![]() $c_j(b_i)\in (0,1)$
and
$c_j(b_i)\in (0,1)$
and
![]() $\sum _{j\in I_ {\sigma } '}c_j(b_i)=1$
. There exists a unique
$\sum _{j\in I_ {\sigma } '}c_j(b_i)=1$
. There exists a unique
![]() $D_i^\vee \in \mathbb {L}_{\mathbb {Q}} $
such that
$D_i^\vee \in \mathbb {L}_{\mathbb {Q}} $
such that
 $$ \begin{align*}\langle D_j, D_i^\vee\rangle =\begin{cases} 1, & j=i,\\ -c_j(b_i), & j\in I^{\prime}_ {\sigma} ,\\ 0, & j\in I_ {\sigma} -\{i\}. \end{cases} \end{align*} $$
$$ \begin{align*}\langle D_j, D_i^\vee\rangle =\begin{cases} 1, & j=i,\\ -c_j(b_i), & j\in I^{\prime}_ {\sigma} ,\\ 0, & j\in I_ {\sigma} -\{i\}. \end{cases} \end{align*} $$
Then
 $$ \begin{align*}I(q_0',q,z)= 1 +\frac{1}{z}(\log q_0' \mathbf{1}+\sum_{a=1}^{k'} \log(q_a)\bar{p}^{\mathcal{T}}_a + \sum_{i=1}^{r'} A_i(q) \bar{D}_i^{\mathcal{T}}+ \sum_{i=r'+1}^r A_i(q) \mathbf{1}_{b_i}) + o(z^{-1}). \end{align*} $$
$$ \begin{align*}I(q_0',q,z)= 1 +\frac{1}{z}(\log q_0' \mathbf{1}+\sum_{a=1}^{k'} \log(q_a)\bar{p}^{\mathcal{T}}_a + \sum_{i=1}^{r'} A_i(q) \bar{D}_i^{\mathcal{T}}+ \sum_{i=r'+1}^r A_i(q) \mathbf{1}_{b_i}) + o(z^{-1}). \end{align*} $$
For
![]() $i=1,\ldots , r'$
,
$i=1,\ldots , r'$
,
 $$ \begin{align*}\bar{\mathcal{D}}^{\mathcal{T}}_i =\sum_{a=1}^{k'}m_i^{(a)} \bar{p}_a^{\mathcal{T}} +\lambda_i, \end{align*} $$
$$ \begin{align*}\bar{\mathcal{D}}^{\mathcal{T}}_i =\sum_{a=1}^{k'}m_i^{(a)} \bar{p}_a^{\mathcal{T}} +\lambda_i, \end{align*} $$
where
![]() $\lambda _i\in H^2(B \mathbb {T}; \mathbb {Q} )$
. Let
$\lambda _i\in H^2(B \mathbb {T}; \mathbb {Q} )$
. Let
![]() $S_a(q):=\sum _{i=1}^{r'} m_i^{(a)} A_i(q)$
. Then
$S_a(q):=\sum _{i=1}^{r'} m_i^{(a)} A_i(q)$
. Then
 $$ \begin{align*}I(q_0',q,z)= 1 +\frac{1}{z}( (\log q_0' +\sum_{i=1}^{r'}\lambda_i A_i(q)) \mathbf{1} +\sum_{a=1}^{k'} (\log(q_a) + S_a(q)) \bar{p}^{\mathcal{T}}_a + \sum_{i=r'+1}^r A_i(q) \mathbf{1}_{b_i}) + o(z^{-1}). \end{align*} $$
$$ \begin{align*}I(q_0',q,z)= 1 +\frac{1}{z}( (\log q_0' +\sum_{i=1}^{r'}\lambda_i A_i(q)) \mathbf{1} +\sum_{a=1}^{k'} (\log(q_a) + S_a(q)) \bar{p}^{\mathcal{T}}_a + \sum_{i=r'+1}^r A_i(q) \mathbf{1}_{b_i}) + o(z^{-1}). \end{align*} $$
Recall that the
![]() $ \mathbb {T} $
-equivariant J-function for
$ \mathbb {T} $
-equivariant J-function for
![]() $\mathcal {X}$
is
$\mathcal {X}$
is
 $$ \begin{align*}J(\boldsymbol{\tau},z)=1+\sum_{\beta\ge 0, n\ge 0} \sum_{i=1}^N \frac{1}{n!} \langle 1,\boldsymbol{\tau}^n, \frac{u_i}{z-\bar \psi}\rangle^{\mathcal{X}, \mathbb{T} }_{0,\beta} u^i, \end{align*} $$
$$ \begin{align*}J(\boldsymbol{\tau},z)=1+\sum_{\beta\ge 0, n\ge 0} \sum_{i=1}^N \frac{1}{n!} \langle 1,\boldsymbol{\tau}^n, \frac{u_i}{z-\bar \psi}\rangle^{\mathcal{X}, \mathbb{T} }_{0,\beta} u^i, \end{align*} $$
where
![]() $\{u_i\}_{i=1}^N$
is an
$\{u_i\}_{i=1}^N$
is an
![]() $H^*(B \mathbb {T} )$
-basis of
$H^*(B \mathbb {T} )$
-basis of
![]() $H^*_{\mathbb {T}} (\mathcal {X}; \mathbb {Q} )$
and
$H^*_{\mathbb {T}} (\mathcal {X}; \mathbb {Q} )$
and
![]() $\{u^i\}_{i=1}^N$
is the dual basis. Assume
$\{u^i\}_{i=1}^N$
is the dual basis. Assume
![]() $u_0=\mathbf {1}$
,
$u_0=\mathbf {1}$
,
![]() $u_a=\bar p^{\mathcal {T}}_a$
for
$u_a=\bar p^{\mathcal {T}}_a$
for
![]() $a=1,\dots , k'$
and
$a=1,\dots , k'$
and
![]() $u_a=\mathbf {1}_{b_{a+3}}$
for
$u_a=\mathbf {1}_{b_{a+3}}$
for
![]() $a=k'+1,\dots , k$
. The mirror theorem for toric orbifolds [Reference Coates, Corti, Iritani and Tseng27] implies the following theorem.
$a=k'+1,\dots , k$
. The mirror theorem for toric orbifolds [Reference Coates, Corti, Iritani and Tseng27] implies the following theorem.
Theorem 4.1 (Coates-Corti-Iritani-Tseng [Reference Coates, Corti, Iritani and Tseng27])
If the toric orbifold
![]() $\mathcal {X}$
satisfies Assumption 2.6, then
$\mathcal {X}$
satisfies Assumption 2.6, then
where the equivariant closed mirror map
![]() $(q_0',q)\mapsto \tau _0(q_0',q)1 + \boldsymbol {\tau }_2(q)$
is determined by the first-order term in the asymptotic expansion of the I-function
$(q_0',q)\mapsto \tau _0(q_0',q)1 + \boldsymbol {\tau }_2(q)$
is determined by the first-order term in the asymptotic expansion of the I-function
More explicitly, the equivariant closed mirror map is given by
 $$ \begin{align} \tau_0 &= \log(q_0') +\sum_{i=1}^{r'} \lambda_i A_i(q), \nonumber\\ \tau_a &= \begin{cases} \log(q_a)+ S_a(q), & 1\leq a\leq k',\\ A_{a-3}(q), & k'+1\leq a\leq k. \end{cases}. \end{align} $$
$$ \begin{align} \tau_0 &= \log(q_0') +\sum_{i=1}^{r'} \lambda_i A_i(q), \nonumber\\ \tau_a &= \begin{cases} \log(q_a)+ S_a(q), & 1\leq a\leq k',\\ A_{a-3}(q), & k'+1\leq a\leq k. \end{cases}. \end{align} $$
4.2 The pullback of the disk potential under the mirror map
By Proposition 3.4, if
![]() $(\mathcal {L},f)$
is a framed outer brane, then
$(\mathcal {L},f)$
is a framed outer brane, then
 $$ \begin{align*}F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2,Q,X) = \frac{1}{|G_ {\sigma} |} \sum_{(d_0 ,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} X^{d_0} D^{\prime}_{d_0,\lambda,f}J^f_{ {\sigma} ,h(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0}\Big) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*}F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2,Q,X) = \frac{1}{|G_ {\sigma} |} \sum_{(d_0 ,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} X^{d_0} D^{\prime}_{d_0,\lambda,f}J^f_{ {\sigma} ,h(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0}\Big) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}}. \end{align*} $$
Let
![]() $F^{\mathcal {X},(\mathcal {L},f)}(q,X)$
be the pullback of
$F^{\mathcal {X},(\mathcal {L},f)}(q,X)$
be the pullback of
![]() $F^{\mathcal {X},(\mathcal {L},f)}_{0,1}(\boldsymbol {\tau }_2,Q, X)$
under the closed mirror map.
$F^{\mathcal {X},(\mathcal {L},f)}_{0,1}(\boldsymbol {\tau }_2,Q, X)$
under the closed mirror map.
By Proposition 3.4, if
![]() $(\mathcal {L},f)$
is a framed inner brane, then
$(\mathcal {L},f)$
is a framed inner brane, then
 $$ \begin{align*} & F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2 ,Q, X) \\ &\quad =\frac{1}{|G_ {\sigma} |} \sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} ), d_0>0} X^{d_0} D^{\prime}_{d_0,\lambda,f}J^{f}_{ {\sigma} _+,h^+(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0}\Big) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}} \\ &\qquad + \frac{1}{|G_ {\sigma} |} \sum_{(d_0,k^+, k^-)\in H_{\tau, {\sigma} _+, {\sigma} _-}, d_0 <0} X^{d_0} Q^{-d_0 \alpha} D^{\prime}_{d_0,\lambda,f}J^{f}_{ {\sigma} _-,h^-(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0 }\Big)\cdot \frac{\mathfrak{r}_+}{\mathfrak{r}_-} \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*} & F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(\boldsymbol{\tau}_2 ,Q, X) \\ &\quad =\frac{1}{|G_ {\sigma} |} \sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} ), d_0>0} X^{d_0} D^{\prime}_{d_0,\lambda,f}J^{f}_{ {\sigma} _+,h^+(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0}\Big) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}} \\ &\qquad + \frac{1}{|G_ {\sigma} |} \sum_{(d_0,k^+, k^-)\in H_{\tau, {\sigma} _+, {\sigma} _-}, d_0 <0} X^{d_0} Q^{-d_0 \alpha} D^{\prime}_{d_0,\lambda,f}J^{f}_{ {\sigma} _-,h^-(d_0,\lambda)}\Big(\boldsymbol{\tau}_2,\frac{\mathsf{u}}{d_0 }\Big)\cdot \frac{\mathfrak{r}_+}{\mathfrak{r}_-} \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
Given
![]() $ {\sigma } \in \Sigma (3)$
,
$ {\sigma } \in \Sigma (3)$
,
![]() $k\in G_ {\sigma } $
, and
$k\in G_ {\sigma } $
, and
![]() $f\in \mathbb {Z} $
, define
$f\in \mathbb {Z} $
, define
![]() $I_{ {\sigma } ,k}^f(q,z)$
by
$I_{ {\sigma } ,k}^f(q,z)$
by
 $$ \begin{align*}\iota_ {\sigma} ^* I(q,z)\Big|_{\mathsf{u}_1=\mathsf{u},\, \mathsf{u}_2=f\mathsf{u},\, \mathsf{u}_3=0} =\sum_{k\in G_ {\sigma} }I_{ {\sigma} ,k}^f(q,z)\mathbf{1}_k. \end{align*} $$
$$ \begin{align*}\iota_ {\sigma} ^* I(q,z)\Big|_{\mathsf{u}_1=\mathsf{u},\, \mathsf{u}_2=f\mathsf{u},\, \mathsf{u}_3=0} =\sum_{k\in G_ {\sigma} }I_{ {\sigma} ,k}^f(q,z)\mathbf{1}_k. \end{align*} $$
Since a toric Calabi-Yau orbifold satisfies the weak Fano condition, by the equivariant mirror theorem (Theorem 4.1), we may write
![]() $F^{\mathcal {X},(\mathcal {L},f)}(q,X)$
in terms of
$F^{\mathcal {X},(\mathcal {L},f)}(q,X)$
in terms of
![]() $I_{ {\sigma } ,k}^f(q,z)$
in case of an outer brane and in terms of
$I_{ {\sigma } ,k}^f(q,z)$
in case of an outer brane and in terms of
![]() $I_{ {\sigma } _+,k^+}^f(q,z)$
and
$I_{ {\sigma } _+,k^+}^f(q,z)$
and
![]() $I_{ {\sigma } _-,k^-}^{f}(q,z)$
in case of an inner brane.
$I_{ {\sigma } _-,k^-}^{f}(q,z)$
in case of an inner brane.
Lemma 4.2. If
![]() $(\mathcal {L},f)$
is a framed outer brane, then
$(\mathcal {L},f)$
is a framed outer brane, then
 $$ \begin{align} F_{0,1}^{\mathcal{X},(\mathcal{L},f)}(q,X) = \frac{1}{|G_ {\sigma} |} \sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} X^{d_0} D^{\prime}_{d_0,\lambda,f} e^{\frac{-d_0 \tau_0(q) }{\mathsf{u}}} I^f_{ {\sigma} ,h(d_0,\lambda)}\Big(q,\frac{\mathsf{u}}{d_0}\Big) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}}. \end{align} $$
$$ \begin{align} F_{0,1}^{\mathcal{X},(\mathcal{L},f)}(q,X) = \frac{1}{|G_ {\sigma} |} \sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} X^{d_0} D^{\prime}_{d_0,\lambda,f} e^{\frac{-d_0 \tau_0(q) }{\mathsf{u}}} I^f_{ {\sigma} ,h(d_0,\lambda)}\Big(q,\frac{\mathsf{u}}{d_0}\Big) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}}. \end{align} $$
If
![]() $(\mathcal {L},f)$
is a framed inner brane, then
$(\mathcal {L},f)$
is a framed inner brane, then
 $$ \begin{align*} & F_{0,1}^{\mathcal{X},(\mathcal{L},f^+,f^-)}(q,X) \\ &\quad = \frac{1}{|G_ {\sigma} |} \sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} ), d_0>0} X^{d_0} D^{\prime}_{d_0,\lambda,f} e^{\frac{-d_0 \tau_0(q) }{\mathsf{u}}}I^{f}_{ {\sigma} _+,h^+(d_0,\lambda)}\Big(q,\frac{\mathsf{u}}{d_0}\Big) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}} \\ &\qquad + \frac{1}{|G_ {\sigma} |}\sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} ), d_0 <0} X^{d_0} Q^{-d_0 \alpha} D^{\prime}_{d_0,\lambda,f} e^{\frac{-d_0 \tau_0(q)}{\mathsf{u}}} I^{f}_{ {\sigma} _-,h^-(d_0,\lambda)}\Big(q,\frac{\mathsf{u}}{d_0} \Big) \cdot \frac{\mathfrak{r}_+}{\mathfrak{r}_-} \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*} & F_{0,1}^{\mathcal{X},(\mathcal{L},f^+,f^-)}(q,X) \\ &\quad = \frac{1}{|G_ {\sigma} |} \sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} ), d_0>0} X^{d_0} D^{\prime}_{d_0,\lambda,f} e^{\frac{-d_0 \tau_0(q) }{\mathsf{u}}}I^{f}_{ {\sigma} _+,h^+(d_0,\lambda)}\Big(q,\frac{\mathsf{u}}{d_0}\Big) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}} \\ &\qquad + \frac{1}{|G_ {\sigma} |}\sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} ), d_0 <0} X^{d_0} Q^{-d_0 \alpha} D^{\prime}_{d_0,\lambda,f} e^{\frac{-d_0 \tau_0(q)}{\mathsf{u}}} I^{f}_{ {\sigma} _-,h^-(d_0,\lambda)}\Big(q,\frac{\mathsf{u}}{d_0} \Big) \cdot \frac{\mathfrak{r}_+}{\mathfrak{r}_-} \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}}. \end{align*} $$
Let
![]() $(\mathcal {L},f)$
be a framed brane, and let
$(\mathcal {L},f)$
be a framed brane, and let
![]() $\tau $
,
$\tau $
,
![]() $ {\sigma } = {\sigma } _+, {\sigma } _-$
be defined as in Section 3.3. Recall that
$ {\sigma } = {\sigma } _+, {\sigma } _-$
be defined as in Section 3.3. Recall that
 $$ \begin{align*} & I^{\prime}_ {\sigma} = \{ i\in \{1,\ldots,r'\}: \rho_i\subset {\sigma} \} =\{1,2, 3 \},\quad I_ {\sigma} = \{1,\ldots, r\} \setminus I^{\prime}_ {\sigma} ,\\ & I^{\prime}_\tau = \{i\in \{1,\ldots, r'\}:\rho_i\subset \tau\}= \{2, 3\},\quad I_\tau =\{1,\ldots, r\} \setminus I^{\prime}_\tau,\\ & \mathbb{K}_{\mathrm{eff}, {\sigma} } = \{ \beta\in \mathbb{L}_{\mathbb{Q}} : \langle D_i, \beta\rangle \in \mathbb{Z} _{\geq 0} \mathrm{\ for\ } i\in I_ {\sigma} \}. \end{align*} $$
$$ \begin{align*} & I^{\prime}_ {\sigma} = \{ i\in \{1,\ldots,r'\}: \rho_i\subset {\sigma} \} =\{1,2, 3 \},\quad I_ {\sigma} = \{1,\ldots, r\} \setminus I^{\prime}_ {\sigma} ,\\ & I^{\prime}_\tau = \{i\in \{1,\ldots, r'\}:\rho_i\subset \tau\}= \{2, 3\},\quad I_\tau =\{1,\ldots, r\} \setminus I^{\prime}_\tau,\\ & \mathbb{K}_{\mathrm{eff}, {\sigma} } = \{ \beta\in \mathbb{L}_{\mathbb{Q}} : \langle D_i, \beta\rangle \in \mathbb{Z} _{\geq 0} \mathrm{\ for\ } i\in I_ {\sigma} \}. \end{align*} $$
In case that
![]() $\mathcal {L}$
is inner,
$\mathcal {L}$
is inner,
 $$ \begin{align*} &I^{\prime}_{ {\sigma} _-}=\{2,3,4\},\ I_{ {\sigma} _-}=\{1,\dots,r\}\backslash I^{\prime}_{ {\sigma} _-}\\ &\mathbb{K}_{\mathrm{eff}, {\sigma} -} = \{ \beta\in \mathbb{L}_{\mathbb{Q}} : \langle D_i, \beta\rangle \in \mathbb{Z} _{\geq 0} \mathrm{\ for\ } i\in I_{{ {\sigma} _-}}\}. \end{align*} $$
$$ \begin{align*} &I^{\prime}_{ {\sigma} _-}=\{2,3,4\},\ I_{ {\sigma} _-}=\{1,\dots,r\}\backslash I^{\prime}_{ {\sigma} _-}\\ &\mathbb{K}_{\mathrm{eff}, {\sigma} -} = \{ \beta\in \mathbb{L}_{\mathbb{Q}} : \langle D_i, \beta\rangle \in \mathbb{Z} _{\geq 0} \mathrm{\ for\ } i\in I_{{ {\sigma} _-}}\}. \end{align*} $$
Let
![]() $\mathsf {b}_{ {\sigma } ,i}=\iota _ {\sigma } ^* \bar {D}^{\mathcal {T}}_i \in H^2_{ \mathbb {T} }(\mathfrak {p}_ {\sigma }; \mathbb {Q} )=H^2(B \mathbb {T}; \mathbb {Q} )$
for
$\mathsf {b}_{ {\sigma } ,i}=\iota _ {\sigma } ^* \bar {D}^{\mathcal {T}}_i \in H^2_{ \mathbb {T} }(\mathfrak {p}_ {\sigma }; \mathbb {Q} )=H^2(B \mathbb {T}; \mathbb {Q} )$
for
![]() $1\leq i\leq r$
, and then
$1\leq i\leq r$
, and then
![]() $\mathsf {b}_i=0$
for
$\mathsf {b}_i=0$
for
![]() $r'+1\leq i\leq r$
. For
$r'+1\leq i\leq r$
. For
![]() $\beta \in \mathbb {K}_{\mathrm {eff}, {\sigma } }$
, define an
$\beta \in \mathbb {K}_{\mathrm {eff}, {\sigma } }$
, define an
![]() $H^*({ B \mathbb {T} }; \mathbb {Q} )$
-valued
$H^*({ B \mathbb {T} }; \mathbb {Q} )$
-valued
 $$ \begin{align} I( {\sigma} ,\beta): = \prod_{i=1}^r \frac{\prod_{m=\lceil \langle D_i, \beta \rangle \rceil}^\infty (\mathsf{b}_{ {\sigma} ,i} +(\langle D_i,\beta\rangle -m)\frac{\mathsf{u}_1}{d_0})} {\prod_{m=0}^\infty(\mathsf{b}_{ {\sigma} ,i} +(\langle D_i,\beta\rangle -m)\frac{\mathsf{u}_1}{d_0})}. \end{align} $$
$$ \begin{align} I( {\sigma} ,\beta): = \prod_{i=1}^r \frac{\prod_{m=\lceil \langle D_i, \beta \rangle \rceil}^\infty (\mathsf{b}_{ {\sigma} ,i} +(\langle D_i,\beta\rangle -m)\frac{\mathsf{u}_1}{d_0})} {\prod_{m=0}^\infty(\mathsf{b}_{ {\sigma} ,i} +(\langle D_i,\beta\rangle -m)\frac{\mathsf{u}_1}{d_0})}. \end{align} $$
Recall that
![]() $\iota _ {\sigma } ^*\bar {p}_a^{\mathcal {T}}=0$
, so
$\iota _ {\sigma } ^*\bar {p}_a^{\mathcal {T}}=0$
, so
 $$ \begin{align*}\iota_ {\sigma} ^* I(q,z)|_{z=\frac{\mathsf{u}_1}{d_0}} = \sum_{\beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} } } e^{\frac{d_0}{\mathsf{u}_1}\log q_0'} q^\beta I( {\sigma} ,\beta) \mathbf{1}_{v(\beta)}. \end{align*} $$
$$ \begin{align*}\iota_ {\sigma} ^* I(q,z)|_{z=\frac{\mathsf{u}_1}{d_0}} = \sum_{\beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} } } e^{\frac{d_0}{\mathsf{u}_1}\log q_0'} q^\beta I( {\sigma} ,\beta) \mathbf{1}_{v(\beta)}. \end{align*} $$
With the above notation, if
![]() $\mathcal {L}$
is an outer brane, we can rewrite
$\mathcal {L}$
is an outer brane, we can rewrite
![]() $F_{0,1}^{\mathcal {X},(\mathcal {L},f)}(q,X)$
as
$F_{0,1}^{\mathcal {X},(\mathcal {L},f)}(q,X)$
as
 $$ \begin{align*}F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(q,X)=\frac{1}{|G_ {\sigma} |} \sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} \sum_{\beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} }, v(\beta)=h(d_0,\lambda)} x^{d_0} q^\beta D^{\prime}_{d_0,\lambda,f}I^f( {\sigma} ,\beta) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}}, \end{align*} $$
$$ \begin{align*}F^{\mathcal{X},(\mathcal{L},f)}_{0,1}(q,X)=\frac{1}{|G_ {\sigma} |} \sum_{(d_0,\lambda)\in H_1(\mathcal{L}; \mathbb{Z} )} \sum_{\beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} }, v(\beta)=h(d_0,\lambda)} x^{d_0} q^\beta D^{\prime}_{d_0,\lambda,f}I^f( {\sigma} ,\beta) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}}, \end{align*} $$
where
![]() $I^f( {\sigma } ,\beta )=I( {\sigma } ,\beta )|_{\mathsf {u}_1=\mathsf {u},\, \mathsf {u}_2=f\mathsf {u},\, \mathsf {u}_3=0}$
, and
$I^f( {\sigma } ,\beta )=I( {\sigma } ,\beta )|_{\mathsf {u}_1=\mathsf {u},\, \mathsf {u}_2=f\mathsf {u},\, \mathsf {u}_3=0}$
, and
 $$ \begin{align*}x=X \exp\left(\frac{\log q_0'-\tau_0(q)}{\mathsf{u}_1}\right) \end{align*} $$
$$ \begin{align*}x=X \exp\left(\frac{\log q_0'-\tau_0(q)}{\mathsf{u}_1}\right) \end{align*} $$
is the B-brane moduli parameter.
Following [Reference Lerche and Mayr51, Reference Mayr59], we define extended charge vectors
 $$ \begin{align*}\{m^{(a)}_i\}_{i=1,\dots,r}^{a=0,\dots,k}=\begin{pmatrix} w_1 & w_2 & w_3 & 0 & \dots\\ & & \{ m^{(a)}_i\}_{i=1,\dots,r}^{a=1,\dots,k} & \end{pmatrix}, \end{align*} $$
$$ \begin{align*}\{m^{(a)}_i\}_{i=1,\dots,r}^{a=0,\dots,k}=\begin{pmatrix} w_1 & w_2 & w_3 & 0 & \dots\\ & & \{ m^{(a)}_i\}_{i=1,\dots,r}^{a=1,\dots,k} & \end{pmatrix}, \end{align*} $$
such that
![]() $m^{(0)}_i=w_i$
for
$m^{(0)}_i=w_i$
for
![]() $i=1,2,3$
and
$i=1,2,3$
and
![]() $m^{(0)}_i=0$
for
$m^{(0)}_i=0$
for
![]() $i=4,\dots , r$
. Recall that
$i=4,\dots , r$
. Recall that
 $$ \begin{align*}\tau_0 + \sum_{a=1}^{k'} \tau_a \bar{p}_a^{\mathcal{T}} + \sum_{a=k'+1}^k \tau_a \mathbf{1}_{b_{a+3}} = \log q_0' + \sum_{a=1}^{k'} \log q_a \bar{p}_a^{\mathcal{T}} +\sum_{i=1}^{r'} A_i(q)\bar{\mathcal{D}}^{\mathcal{T}}_i +\sum_{i=r'+1}^r A_i(q)\mathbf{1}_{b_i}. \end{align*} $$
$$ \begin{align*}\tau_0 + \sum_{a=1}^{k'} \tau_a \bar{p}_a^{\mathcal{T}} + \sum_{a=k'+1}^k \tau_a \mathbf{1}_{b_{a+3}} = \log q_0' + \sum_{a=1}^{k'} \log q_a \bar{p}_a^{\mathcal{T}} +\sum_{i=1}^{r'} A_i(q)\bar{\mathcal{D}}^{\mathcal{T}}_i +\sum_{i=r'+1}^r A_i(q)\mathbf{1}_{b_i}. \end{align*} $$
We pull back the above identity under
![]() $\iota _ {\sigma } ^*$
. Since
$\iota _ {\sigma } ^*$
. Since
we get
 $$ \begin{align*}\tau_0(q_0',q)=\log q^{\prime}_0+ \sum_{i=1}^{r'} m^{(0)}_i A_i(q) \mathsf{v}. \end{align*} $$
$$ \begin{align*}\tau_0(q_0',q)=\log q^{\prime}_0+ \sum_{i=1}^{r'} m^{(0)}_i A_i(q) \mathsf{v}. \end{align*} $$
So the open mirror map is given by
 $$ \begin{align} \log X = \log x + \sum_{i=1}^{r'} m^{(0)}_i A_i(q). \end{align} $$
$$ \begin{align} \log X = \log x + \sum_{i=1}^{r'} m^{(0)}_i A_i(q). \end{align} $$
If
![]() $\mathcal {L}$
is inner, we further set
$\mathcal {L}$
is inner, we further set
![]() $Q=q$
. Denote the pullback of the disk potential
$Q=q$
. Denote the pullback of the disk potential
![]() $W^{\mathcal {X},(\mathcal {L},f)}(q,x)$
to be the pullback of
$W^{\mathcal {X},(\mathcal {L},f)}(q,x)$
to be the pullback of
![]() $F_{0,1}^{\mathcal {X},(\mathcal {L},f)}(q,X)$
under this open mirror map. Then by Lemma 4.2,
$F_{0,1}^{\mathcal {X},(\mathcal {L},f)}(q,X)$
under this open mirror map. Then by Lemma 4.2,
 $$ \begin{align} |G_ {\sigma} | W^{\mathcal{X},(\mathcal{L},f)}(q,x)=\begin{cases}\displaystyle{\sum_{\substack{d_0>0,\beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} } \\ v(\beta)=h(d_0,\lambda)}} x^{d_0}q^\beta D^{\prime}_{d_0,\lambda,f} I^f(\sigma,\beta) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}} },& \mathcal{L}\ \text{is outer,}\\ \\ \displaystyle{\sum_{\substack{d_0>0,\beta \in \mathbb{K}_{\mathrm{eff}, {\sigma} _+} \\ v(\beta)=h^+(d_0,\lambda)}} x^{d_0}q^\beta D^{\prime}_{d_0,\lambda,f} I^f(\sigma^+,\beta) \xi_0^{\bar{\lambda}}}\mathbf{1}_{\lambda^{-1}} \\\qquad\qquad\displaystyle{+\frac{\mathfrak{r}_+}{\mathfrak{r}_-}\sum_{\substack{d_0<0, \beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} _-} \\ v(\beta)=h^-(d_0,\lambda)}} x^{d_0}q^{\beta-d_0\alpha} D^{\prime}_{d_0,\lambda,f} I^f(\sigma^-,\beta) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}} },& \mathcal{L}\ \text{is inner}. \end{cases} \end{align} $$
$$ \begin{align} |G_ {\sigma} | W^{\mathcal{X},(\mathcal{L},f)}(q,x)=\begin{cases}\displaystyle{\sum_{\substack{d_0>0,\beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} } \\ v(\beta)=h(d_0,\lambda)}} x^{d_0}q^\beta D^{\prime}_{d_0,\lambda,f} I^f(\sigma,\beta) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}} },& \mathcal{L}\ \text{is outer,}\\ \\ \displaystyle{\sum_{\substack{d_0>0,\beta \in \mathbb{K}_{\mathrm{eff}, {\sigma} _+} \\ v(\beta)=h^+(d_0,\lambda)}} x^{d_0}q^\beta D^{\prime}_{d_0,\lambda,f} I^f(\sigma^+,\beta) \xi_0^{\bar{\lambda}}}\mathbf{1}_{\lambda^{-1}} \\\qquad\qquad\displaystyle{+\frac{\mathfrak{r}_+}{\mathfrak{r}_-}\sum_{\substack{d_0<0, \beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} _-} \\ v(\beta)=h^-(d_0,\lambda)}} x^{d_0}q^{\beta-d_0\alpha} D^{\prime}_{d_0,\lambda,f} I^f(\sigma^-,\beta) \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}} },& \mathcal{L}\ \text{is inner}. \end{cases} \end{align} $$
Given
![]() ${\widetilde {\beta }}=(d_0,\beta )\in \mathbb {Z} \times \mathbb {K}_ {\sigma } $
, define the extended or open sector pairing to be
${\widetilde {\beta }}=(d_0,\beta )\in \mathbb {Z} \times \mathbb {K}_ {\sigma } $
, define the extended or open sector pairing to be
Recall that
![]() $\{D_i: i\in I_ {\sigma } \}$
is a
$\{D_i: i\in I_ {\sigma } \}$
is a
![]() $ \mathbb {Q} $
-basis of
$ \mathbb {Q} $
-basis of
![]() $\mathbb {L}^\vee _{\mathbb {Q}} \cong \mathbb {Q} ^k$
and a
$\mathbb {L}^\vee _{\mathbb {Q}} \cong \mathbb {Q} ^k$
and a
![]() $ \mathbb {Z} $
-basis of
$ \mathbb {Z} $
-basis of
![]() $\mathbb {K}_ {\sigma } ^{{ \vee }}\cong \mathbb {Z} ^k$
. Let
$\mathbb {K}_ {\sigma } ^{{ \vee }}\cong \mathbb {Z} ^k$
. Let
![]() $v_a= D_{a+3}$
for
$v_a= D_{a+3}$
for
![]() $a=1,\dots , k$
., and let
$a=1,\dots , k$
., and let
![]() $\{ h_a\}_{a=1,\ldots ,k}$
be the dual
$\{ h_a\}_{a=1,\ldots ,k}$
be the dual
![]() $ \mathbb {Q} $
-basis of
$ \mathbb {Q} $
-basis of
![]() $\mathbb {L}_{\mathbb {Q}} $
. Then
$\mathbb {L}_{\mathbb {Q}} $
. Then
![]() $\{h_a\}_{a=1,\ldots ,k}$
is a
$\{h_a\}_{a=1,\ldots ,k}$
is a
![]() $ \mathbb {Z} $
-basis of
$ \mathbb {Z} $
-basis of
![]() $\mathbb {K}_ {\sigma } \cong \mathbb {Z} ^k$
, and
$\mathbb {K}_ {\sigma } \cong \mathbb {Z} ^k$
, and
 $$ \begin{align*}\mathbb{K}_{\mathrm{eff}, {\sigma} } =\sum_{a=1}^k \mathbb{Z} _{\geq 0} h_a. \end{align*} $$
$$ \begin{align*}\mathbb{K}_{\mathrm{eff}, {\sigma} } =\sum_{a=1}^k \mathbb{Z} _{\geq 0} h_a. \end{align*} $$
Given any
![]() $(d_0,\beta )\in \mathbb {Z} \times \mathbb {K}_ {\sigma } $
, define
$(d_0,\beta )\in \mathbb {Z} \times \mathbb {K}_ {\sigma } $
, define
 $$ \begin{align*}q^{{\widetilde{\beta}}} = x^{d_0} q^\beta = x^{d_0} \prod_{a=1}^k q_a^{\langle p_a,\beta\rangle}. \end{align*} $$
$$ \begin{align*}q^{{\widetilde{\beta}}} = x^{d_0} q^\beta = x^{d_0} \prod_{a=1}^k q_a^{\langle p_a,\beta\rangle}. \end{align*} $$
Define
Theorem 4.3. Assuming the Aganagic-Vafa brane
![]() $(\mathcal {L},f)$
is either inner or outer,
$(\mathcal {L},f)$
is either inner or outer,
 $$ \begin{align} W^{\mathcal{X},(\mathcal{L},f)}(q,x)=\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L}) \\ v(\beta)=h(d_0,\lambda)}} q^{\widetilde{\beta}} A^{\mathcal{X},(\mathcal{L},f)}_{{\widetilde{\beta}}}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}, \end{align} $$
$$ \begin{align} W^{\mathcal{X},(\mathcal{L},f)}(q,x)=\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L}) \\ v(\beta)=h(d_0,\lambda)}} q^{\widetilde{\beta}} A^{\mathcal{X},(\mathcal{L},f)}_{{\widetilde{\beta}}}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}, \end{align} $$
where
 $$ \begin{align*} A^{\mathcal{X},(\mathcal{L},f)}_{{\widetilde{\beta}}=(d_0,\beta)}= \frac{- (-1)^{\lfloor \langle D_3,{\widetilde{\beta}} \rangle \rfloor} }{\mathfrak{m} d_0 \prod_{i\in I_\tau} \langle D_i,{\widetilde{\beta}}\rangle!} \cdot \frac{\Gamma(-\langle D_{3},{\widetilde{\beta}} \rangle) }{\Gamma(\langle D_{2},{\widetilde{\beta}} \rangle+1)}. \end{align*} $$
$$ \begin{align*} A^{\mathcal{X},(\mathcal{L},f)}_{{\widetilde{\beta}}=(d_0,\beta)}= \frac{- (-1)^{\lfloor \langle D_3,{\widetilde{\beta}} \rangle \rfloor} }{\mathfrak{m} d_0 \prod_{i\in I_\tau} \langle D_i,{\widetilde{\beta}}\rangle!} \cdot \frac{\Gamma(-\langle D_{3},{\widetilde{\beta}} \rangle) }{\Gamma(\langle D_{2},{\widetilde{\beta}} \rangle+1)}. \end{align*} $$
Proof. Assume
![]() $\mathcal {L}$
is an outer brane. Let
$\mathcal {L}$
is an outer brane. Let
![]() ${\widetilde {\beta }}=(d_0,\beta )$
, and let
${\widetilde {\beta }}=(d_0,\beta )$
, and let
![]() $\epsilon _j =c_{j}(v)$
for
$\epsilon _j =c_{j}(v)$
for
![]() $j=1,2,3$
. By equation (29) (and recall that
$j=1,2,3$
. By equation (29) (and recall that
![]() $|G_ {\sigma } |=\mathfrak {r}\mathfrak {m}$
),
$|G_ {\sigma } |=\mathfrak {r}\mathfrak {m}$
),
 $$ \begin{align*}W^{\mathcal{X},(\mathcal{L},f)}(q,x)= \frac{1}{\mathfrak{r} \mathfrak{m}} \sum_{\substack{d_0>0\\ \beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} } \\ v(\beta)=h(d_0,\lambda)}} x^{d_0}q^\beta D^{\prime}_{d_0,\lambda,f} I^f(\sigma,\beta)\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*}W^{\mathcal{X},(\mathcal{L},f)}(q,x)= \frac{1}{\mathfrak{r} \mathfrak{m}} \sum_{\substack{d_0>0\\ \beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} } \\ v(\beta)=h(d_0,\lambda)}} x^{d_0}q^\beta D^{\prime}_{d_0,\lambda,f} I^f(\sigma,\beta)\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
Given any
![]() $\beta \in \mathbb {K}_{\mathrm {eff}, {\sigma } }$
, we have
$\beta \in \mathbb {K}_{\mathrm {eff}, {\sigma } }$
, we have
![]() $\lceil \langle D_{j},\beta \rangle \rceil -\epsilon _j =\langle D_{j},\beta \rangle $
for
$\lceil \langle D_{j},\beta \rangle \rceil -\epsilon _j =\langle D_{j},\beta \rangle $
for
![]() $j=1, 2,3$
, and
$j=1, 2,3$
, and
![]() $\lceil \langle D_i, \beta \rangle \rceil =\langle D_i,\beta \rangle $
for
$\lceil \langle D_i, \beta \rangle \rceil =\langle D_i,\beta \rangle $
for
![]() $i\in I_ {\sigma } $
. The disk factors
$i\in I_ {\sigma } $
. The disk factors
 $$ \begin{align*} D^{\prime}_{d_0,\lambda,f}&= -(-1)^{\lfloor d_0 w_3 +\frac{\bar \lambda}{m}\rfloor} \frac{\mathfrak{r}}{d_0} \left ( \frac{\mathsf{u}}{d_0} \right)^{\mathrm{age}(h(d_0,\lambda))} \frac{\prod_{a=1}^{\lfloor d_0 w_1 \rfloor + \mathrm{age}(h(d_0,\lambda)) -1} (d_0w_2 + a-\epsilon_2)}{\lfloor d_0w_1 \rfloor!} \\ &= -(-1)^{\lfloor d_0 w_3+\frac{\bar \lambda}{m}\rfloor } \frac{\mathfrak{r}}{d_0} \left ( \frac{\mathsf{u}}{d_0} \right)^{\mathrm{age}(h(d_0,\lambda))}\frac{1}{\Gamma(w_1d_0-\epsilon_1+1)}\cdot \frac{\Gamma(-w_3d_0+\epsilon_3)}{\Gamma(w_2d_0-\epsilon_2+1)}. \end{align*} $$
$$ \begin{align*} D^{\prime}_{d_0,\lambda,f}&= -(-1)^{\lfloor d_0 w_3 +\frac{\bar \lambda}{m}\rfloor} \frac{\mathfrak{r}}{d_0} \left ( \frac{\mathsf{u}}{d_0} \right)^{\mathrm{age}(h(d_0,\lambda))} \frac{\prod_{a=1}^{\lfloor d_0 w_1 \rfloor + \mathrm{age}(h(d_0,\lambda)) -1} (d_0w_2 + a-\epsilon_2)}{\lfloor d_0w_1 \rfloor!} \\ &= -(-1)^{\lfloor d_0 w_3+\frac{\bar \lambda}{m}\rfloor } \frac{\mathfrak{r}}{d_0} \left ( \frac{\mathsf{u}}{d_0} \right)^{\mathrm{age}(h(d_0,\lambda))}\frac{1}{\Gamma(w_1d_0-\epsilon_1+1)}\cdot \frac{\Gamma(-w_3d_0+\epsilon_3)}{\Gamma(w_2d_0-\epsilon_2+1)}. \end{align*} $$
The pullback of the coefficients of the I-function is
 $$ \begin{align*} I^f( {\sigma} ,\beta) &= \Big(\frac{\mathsf{u}}{d_0} \Big)^{-\mathrm{age}(h(d_0,\lambda))}\frac{1}{\prod_{i\in I_\sigma}\Gamma(\langle D_i,\beta \rangle+1)} \\ &\quad \cdot \frac{\Gamma(w_1d_0-\epsilon_1+1)}{\Gamma(\langle D_1,{\widetilde{\beta}} \rangle +1)}\cdot \frac{\Gamma(w_2d_0-\epsilon_2+1)}{\Gamma(\langle D_2,{\widetilde{\beta}} \rangle +1)}\cdot \frac{\Gamma(w_3d_0-\epsilon_3+1)}{\Gamma(\langle D_3,{\widetilde{\beta}} \rangle +1)}. \end{align*} $$
$$ \begin{align*} I^f( {\sigma} ,\beta) &= \Big(\frac{\mathsf{u}}{d_0} \Big)^{-\mathrm{age}(h(d_0,\lambda))}\frac{1}{\prod_{i\in I_\sigma}\Gamma(\langle D_i,\beta \rangle+1)} \\ &\quad \cdot \frac{\Gamma(w_1d_0-\epsilon_1+1)}{\Gamma(\langle D_1,{\widetilde{\beta}} \rangle +1)}\cdot \frac{\Gamma(w_2d_0-\epsilon_2+1)}{\Gamma(\langle D_2,{\widetilde{\beta}} \rangle +1)}\cdot \frac{\Gamma(w_3d_0-\epsilon_3+1)}{\Gamma(\langle D_3,{\widetilde{\beta}} \rangle +1)}. \end{align*} $$
Hence
 $$ \begin{align*}W^{\mathcal{X},(\mathcal{L},f)}(q,x)=\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\v(\beta)=h(d_0,\lambda)}} x^{d_0} q^\beta A^{\mathcal{X},(\mathcal{L},f)}_{(d_0,\beta)} \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}}, \end{align*} $$
$$ \begin{align*}W^{\mathcal{X},(\mathcal{L},f)}(q,x)=\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\v(\beta)=h(d_0,\lambda)}} x^{d_0} q^\beta A^{\mathcal{X},(\mathcal{L},f)}_{(d_0,\beta)} \xi_0^{\bar{\lambda}} \mathbf{1}_{\lambda^{-1}}, \end{align*} $$
where
 $$ \begin{align*}A^{\mathcal{X}, (\mathcal{L},f)}_{{\widetilde{\beta}}} = (-1)^{\lfloor \langle D_3,{\widetilde{\beta}} \rangle \rfloor} \frac{-1}{\mathfrak{m} d_0} \frac{1}{\prod_{i\in I_\tau}\Gamma(\langle D_i,{\widetilde{\beta}} \rangle +1)}\cdot \frac{\Gamma (-\langle D_3,{\widetilde{\beta}} \rangle )}{\Gamma (\langle D_2,{\widetilde{\beta}} \rangle+1)}. \end{align*} $$
$$ \begin{align*}A^{\mathcal{X}, (\mathcal{L},f)}_{{\widetilde{\beta}}} = (-1)^{\lfloor \langle D_3,{\widetilde{\beta}} \rangle \rfloor} \frac{-1}{\mathfrak{m} d_0} \frac{1}{\prod_{i\in I_\tau}\Gamma(\langle D_i,{\widetilde{\beta}} \rangle +1)}\cdot \frac{\Gamma (-\langle D_3,{\widetilde{\beta}} \rangle )}{\Gamma (\langle D_2,{\widetilde{\beta}} \rangle+1)}. \end{align*} $$
Note that
![]() $\mathbb {K}_{\mathrm {eff}}(\mathcal {X},\mathcal {L})\subset \mathbb {Z} _{>0} \times \mathbb {K}_{\mathrm {eff}, {\sigma } }$
, and for any
$\mathbb {K}_{\mathrm {eff}}(\mathcal {X},\mathcal {L})\subset \mathbb {Z} _{>0} \times \mathbb {K}_{\mathrm {eff}, {\sigma } }$
, and for any
![]() $(d_0,\beta )\in ( \mathbb {Z} _{>0}\times \mathbb {K}_{\mathrm {eff}, {\sigma } }) \backslash \mathbb {K}_{\mathrm {eff}}(\mathcal {X},\mathcal {L})$
,
$(d_0,\beta )\in ( \mathbb {Z} _{>0}\times \mathbb {K}_{\mathrm {eff}, {\sigma } }) \backslash \mathbb {K}_{\mathrm {eff}}(\mathcal {X},\mathcal {L})$
,
![]() $A^{\mathcal {X},(\mathcal {L},f)}_{(d_0,\beta )}=0$
.
$A^{\mathcal {X},(\mathcal {L},f)}_{(d_0,\beta )}=0$
.
In case
![]() $\mathcal {L}$
is inner, by equation (29),
$\mathcal {L}$
is inner, by equation (29),
where
 $$ \begin{align*} I_+&=\sum_{\substack{d_0>0, \beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} _+}\\v(\beta)=h^+(d_0,\lambda)}} x^{d_0} q^\beta \frac{-1}{\mathfrak{m} d_0} \frac{(-1)^{\lfloor w^+_3 d_0 +\langle D_3,\beta \rangle \rfloor}}{\prod_{i\in I_{\sigma^+}}\Gamma(\langle D_i,\beta \rangle +1)} \\ &\quad \cdot \frac{\Gamma (-w^+_3d_0 -\langle D_3, \beta \rangle )}{\Gamma (w^+_2d_0+\langle D_2,\beta \rangle+1)\Gamma(w^+_1d_0+\langle D_1,\beta \rangle +1)}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}},\\ I_-&=\sum_{\substack{d_0<0, \beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} _-}\\v(\beta)=h^-(d_0,\lambda)}} x^{d_0}q^{\beta-d_0\alpha} \frac{-1}{\mathfrak{m} d_0} \frac{(-1)^{\lfloor w^-_2 d_0 +\langle D_2,\beta \rangle \rfloor}}{\prod_{i\in I_{\sigma^-}}\Gamma(\langle D_i,\beta \rangle +1)} \\ &\quad \cdot \frac{\Gamma (-w^-_2d_0 -\langle D_2, \beta \rangle )}{\Gamma (w^-_3d_0+\langle D_3,\beta \rangle+1)\Gamma(w^-_1d_0+\langle D_4,\beta \rangle +1)}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}\\ &=\sum_{\substack{\beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} _-}\\\langle \beta,D_4\rangle+w_1^-d_0\in \mathbb{Z} _{\geq 0}\\d_0<0, v(\beta)=h^-(d_0,\lambda)}} x^{d_0}q^{\beta-d_0\alpha} \frac{-1}{\mathfrak{m} d_0} \frac{(-1)^{\lfloor w^-_2 d_0 +\langle D_2,\beta \rangle \rfloor}}{\prod_{i\in I_{\sigma^-}}\Gamma(\langle D_i,\beta \rangle +1)} \\ &\quad \cdot \frac{\Gamma (-w^-_2d_0 -\langle D_2, \beta \rangle )}{\Gamma (w^-_3d_0+\langle D_3,\beta \rangle+1)\Gamma(w^-_1d_0+\langle D_4,\beta \rangle +1)}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*} I_+&=\sum_{\substack{d_0>0, \beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} _+}\\v(\beta)=h^+(d_0,\lambda)}} x^{d_0} q^\beta \frac{-1}{\mathfrak{m} d_0} \frac{(-1)^{\lfloor w^+_3 d_0 +\langle D_3,\beta \rangle \rfloor}}{\prod_{i\in I_{\sigma^+}}\Gamma(\langle D_i,\beta \rangle +1)} \\ &\quad \cdot \frac{\Gamma (-w^+_3d_0 -\langle D_3, \beta \rangle )}{\Gamma (w^+_2d_0+\langle D_2,\beta \rangle+1)\Gamma(w^+_1d_0+\langle D_1,\beta \rangle +1)}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}},\\ I_-&=\sum_{\substack{d_0<0, \beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} _-}\\v(\beta)=h^-(d_0,\lambda)}} x^{d_0}q^{\beta-d_0\alpha} \frac{-1}{\mathfrak{m} d_0} \frac{(-1)^{\lfloor w^-_2 d_0 +\langle D_2,\beta \rangle \rfloor}}{\prod_{i\in I_{\sigma^-}}\Gamma(\langle D_i,\beta \rangle +1)} \\ &\quad \cdot \frac{\Gamma (-w^-_2d_0 -\langle D_2, \beta \rangle )}{\Gamma (w^-_3d_0+\langle D_3,\beta \rangle+1)\Gamma(w^-_1d_0+\langle D_4,\beta \rangle +1)}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}\\ &=\sum_{\substack{\beta\in \mathbb{K}_{\mathrm{eff}, {\sigma} _-}\\\langle \beta,D_4\rangle+w_1^-d_0\in \mathbb{Z} _{\geq 0}\\d_0<0, v(\beta)=h^-(d_0,\lambda)}} x^{d_0}q^{\beta-d_0\alpha} \frac{-1}{\mathfrak{m} d_0} \frac{(-1)^{\lfloor w^-_2 d_0 +\langle D_2,\beta \rangle \rfloor}}{\prod_{i\in I_{\sigma^-}}\Gamma(\langle D_i,\beta \rangle +1)} \\ &\quad \cdot \frac{\Gamma (-w^-_2d_0 -\langle D_2, \beta \rangle )}{\Gamma (w^-_3d_0+\langle D_3,\beta \rangle+1)\Gamma(w^-_1d_0+\langle D_4,\beta \rangle +1)}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
We have
and
![]() $\langle D_i,\alpha \rangle =0$
for
$\langle D_i,\alpha \rangle =0$
for
![]() $i\in I\backslash \{1, 2, 3, 4\}$
. So for
$i\in I\backslash \{1, 2, 3, 4\}$
. So for
![]() $\beta \in \mathbb {K}_{\mathrm {eff}, {\sigma } _-}$
,
$\beta \in \mathbb {K}_{\mathrm {eff}, {\sigma } _-}$
,
 $$ \begin{align*} \langle D_{1},\beta\rangle &= \langle D_{1}, \beta-d_0\alpha\rangle + d_0w_1^+,\\ w_2^-d_0 +\langle D_{2}, \beta \rangle &= w^+_2d_0 +\langle D_{2}, \beta-d_0\alpha\rangle, \\ w_3^-d_0 +\langle D_{3}, \beta \rangle &= w_3^+d_0 +\langle D_{3}, \beta-d_0\alpha\rangle, \\ d_0w_1^- +\langle D_{4},\beta\rangle &= \langle D_{4}, \beta-d_0\alpha\rangle. \end{align*} $$
$$ \begin{align*} \langle D_{1},\beta\rangle &= \langle D_{1}, \beta-d_0\alpha\rangle + d_0w_1^+,\\ w_2^-d_0 +\langle D_{2}, \beta \rangle &= w^+_2d_0 +\langle D_{2}, \beta-d_0\alpha\rangle, \\ w_3^-d_0 +\langle D_{3}, \beta \rangle &= w_3^+d_0 +\langle D_{3}, \beta-d_0\alpha\rangle, \\ d_0w_1^- +\langle D_{4},\beta\rangle &= \langle D_{4}, \beta-d_0\alpha\rangle. \end{align*} $$
Since the conditions
![]() $\langle \beta ,D_4\rangle +w_1^-d_0\in \mathbb {Z} _{\geq _0}$
and
$\langle \beta ,D_4\rangle +w_1^-d_0\in \mathbb {Z} _{\geq _0}$
and
![]() $\beta \in \mathbb {K}_{\mathrm {eff}, {\sigma } _-}$
imply
$\beta \in \mathbb {K}_{\mathrm {eff}, {\sigma } _-}$
imply
![]() $(d_0,\beta -d_0\alpha ) \in \mathbb {K}_{\mathrm {eff}}(\mathcal {X},\mathcal {L})$
,
$(d_0,\beta -d_0\alpha ) \in \mathbb {K}_{\mathrm {eff}}(\mathcal {X},\mathcal {L})$
,
 $$ \begin{align*} I_- &= \sum_{\substack{(d_0,\beta-d_0\alpha)\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\d_0<0}} x^{d_0}q^{\beta-d_0\alpha} \frac{-1}{\mathfrak{m} d_0} \frac{(-1)^{\lfloor w^+_2 d_0 +\langle D_2,\beta-d_0\alpha \rangle \rfloor}}{\prod_{i\in I_{\sigma^+}}\Gamma(\langle D_i,\beta-d_0\alpha \rangle +1)} \\ &\quad \cdot \frac{\Gamma (-w^+_2d_0 -\langle D_2, \beta-d_0\alpha \rangle )}{\Gamma (w^+_3d_0+\langle D_3,\beta-d_0\alpha \rangle+1)\Gamma(w^+_1d_0+\langle D_1,\beta-d_0\alpha \rangle +1)}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*} I_- &= \sum_{\substack{(d_0,\beta-d_0\alpha)\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\d_0<0}} x^{d_0}q^{\beta-d_0\alpha} \frac{-1}{\mathfrak{m} d_0} \frac{(-1)^{\lfloor w^+_2 d_0 +\langle D_2,\beta-d_0\alpha \rangle \rfloor}}{\prod_{i\in I_{\sigma^+}}\Gamma(\langle D_i,\beta-d_0\alpha \rangle +1)} \\ &\quad \cdot \frac{\Gamma (-w^+_2d_0 -\langle D_2, \beta-d_0\alpha \rangle )}{\Gamma (w^+_3d_0+\langle D_3,\beta-d_0\alpha \rangle+1)\Gamma(w^+_1d_0+\langle D_1,\beta-d_0\alpha \rangle +1)}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
So
 $$ \begin{align*}I_++I_-=\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\v(\beta)=h^+(d_0,\lambda)}} x^{d_0} q^\beta \frac{-1}{\mathfrak{m} d_0} \frac{(-1)^{\lfloor \langle D_3,{\widetilde{\beta}} \rangle \rfloor}}{\prod_{i\in I_{\sigma^+}}\Gamma(\langle D_i,{\widetilde{\beta}} \rangle +1)}\cdot \frac{\Gamma ( -\langle D_3, {\widetilde{\beta}} \rangle )}{\Gamma (\langle D_2,{\widetilde{\beta}} \rangle+1)\Gamma(\langle D_1,{\widetilde{\beta}} \rangle +1)}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*}I_++I_-=\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\v(\beta)=h^+(d_0,\lambda)}} x^{d_0} q^\beta \frac{-1}{\mathfrak{m} d_0} \frac{(-1)^{\lfloor \langle D_3,{\widetilde{\beta}} \rangle \rfloor}}{\prod_{i\in I_{\sigma^+}}\Gamma(\langle D_i,{\widetilde{\beta}} \rangle +1)}\cdot \frac{\Gamma ( -\langle D_3, {\widetilde{\beta}} \rangle )}{\Gamma (\langle D_2,{\widetilde{\beta}} \rangle+1)\Gamma(\langle D_1,{\widetilde{\beta}} \rangle +1)}\xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
Remark 4.4. When
![]() $\mathcal {L}$
is an outer brane, the condition
$\mathcal {L}$
is an outer brane, the condition
![]() ${\widetilde {\beta }}=(d_0,\beta )\in \mathbb{K}_{\mathrm{eff}}(\mathcal {X},\mathcal {L})$
implies
${\widetilde {\beta }}=(d_0,\beta )\in \mathbb{K}_{\mathrm{eff}}(\mathcal {X},\mathcal {L})$
implies
![]() $d_0>0$
. One has
$d_0>0$
. One has
 $$ \begin{align*}\sum_{a=1}^k \langle D_{a+3},\beta \rangle b_{a+3}=-\sum_{i=1}^3 \langle D_i,\beta \rangle b_i. \end{align*} $$
$$ \begin{align*}\sum_{a=1}^k \langle D_{a+3},\beta \rangle b_{a+3}=-\sum_{i=1}^3 \langle D_i,\beta \rangle b_i. \end{align*} $$
Since
![]() $\langle D_{a+3},\beta \rangle \geq 0$
, the fan
$\langle D_{a+3},\beta \rangle \geq 0$
, the fan
![]() $\Sigma $
is convex, and this is an outer brane, every
$\Sigma $
is convex, and this is an outer brane, every
![]() $1$
-cone
$1$
-cone
![]() $b_i$
is on the same side of the plane spanned by
$b_i$
is on the same side of the plane spanned by
![]() $b_2,b_3$
. Therefore,
$b_2,b_3$
. Therefore,
![]() $\langle \beta , D_1 \rangle \leq 0$
. From
$\langle \beta , D_1 \rangle \leq 0$
. From
![]() $w_1 d_0 +\langle D_1,\beta \rangle \in \mathbb {Z} _{\geq 0}$
, we see that
$w_1 d_0 +\langle D_1,\beta \rangle \in \mathbb {Z} _{\geq 0}$
, we see that
![]() $d_0>0$
.
$d_0>0$
.
4.3 The B-model and the framed mirror curve
The mirror B-model to the toric Calabi-Yau threefold
![]() $\mathcal {X}$
is another noncompact Calabi-Yau hypersurface
$\mathcal {X}$
is another noncompact Calabi-Yau hypersurface
![]() $Y\subset \mathbb {C} ^2\times ( \mathbb {C} ^*)^2$
, constructed as the Hori-Vafa mirror [Reference Hori and Vafa45]. It is equivalent to an affine mirror curve
$Y\subset \mathbb {C} ^2\times ( \mathbb {C} ^*)^2$
, constructed as the Hori-Vafa mirror [Reference Hori and Vafa45]. It is equivalent to an affine mirror curve
![]() $C_q \subset ( \mathbb {C} ^*)^2$
. We state the relevant mirror prediction for disk amplitudes from [Reference Aganagic and Vafa6, Reference Aganagic, Klemm and Vafa5].
$C_q \subset ( \mathbb {C} ^*)^2$
. We state the relevant mirror prediction for disk amplitudes from [Reference Aganagic and Vafa6, Reference Aganagic, Klemm and Vafa5].
4.3.1 Toric degeneration
The main reference of this subsection is [Reference Nishinou and Siebert61, Section 3].
The set
is a top-dimensional convex cone in
![]() $\mathbb {L}^\vee _{\mathbb {Q}} \cong \mathbb {Q} ^{k}$
. The cone
$\mathbb {L}^\vee _{\mathbb {Q}} \cong \mathbb {Q} ^{k}$
. The cone
![]() $\Theta _0$
together with its faces is a fan in
$\Theta _0$
together with its faces is a fan in
![]() $\mathbb {L}^\vee _{\mathbb {R}} $
denoted by
$\mathbb {L}^\vee _{\mathbb {R}} $
denoted by
![]() $\Theta $
. This fan determines a k-dimensional affine toric variety
$\Theta $
. This fan determines a k-dimensional affine toric variety
![]() $X_{\Theta }$
.
$X_{\Theta }$
.
Consider the exact sequence induced from equation (4) (notice
![]() $N_ {\mathrm {tor}} =0$
)
$N_ {\mathrm {tor}} =0$
)
where
![]() $M'=M/\langle \mathsf {v}_3 \rangle $
and
$M'=M/\langle \mathsf {v}_3 \rangle $
and
![]() $ {\widetilde {M}} '= {\widetilde {M}} / \langle \phi ^\vee (\mathsf {v}_3) \rangle .$
Let
$ {\widetilde {M}} '= {\widetilde {M}} / \langle \phi ^\vee (\mathsf {v}_3) \rangle .$
Let
![]() $D^{\prime \mathcal {T}}_i$
be the image of
$D^{\prime \mathcal {T}}_i$
be the image of
![]() $D^{\mathcal {T}}_i$
when passing to
$D^{\mathcal {T}}_i$
when passing to
![]() $ {\widetilde {M}} '$
. For any proper subset
$ {\widetilde {M}} '$
. For any proper subset
![]() $I\subset \{1,\dots ,r\}$
and a cone
$I\subset \{1,\dots ,r\}$
and a cone
![]() $\upsilon \in \Theta $
, define
$\upsilon \in \Theta $
, define
Define a fan
This fan determines a toric variety
![]() $X_{\widetilde {\Theta }}$
. There is a fan morphism
$X_{\widetilde {\Theta }}$
. There is a fan morphism
![]() $\rho ': \widetilde \Theta \to \Theta $
, which induces a flat family of toric surfaces
$\rho ': \widetilde \Theta \to \Theta $
, which induces a flat family of toric surfaces
![]() $\rho : X_{\widetilde {\Theta }}\to X_{\Theta }$
.
$\rho : X_{\widetilde {\Theta }}\to X_{\Theta }$
.
Let
![]() $\Theta _0'\subset \mathbb {L}^\vee _{ \mathbb {Q} }$
be the cone spanned by
$\Theta _0'\subset \mathbb {L}^\vee _{ \mathbb {Q} }$
be the cone spanned by
![]() $p_1,\ldots , p_{k}$
. Let
$p_1,\ldots , p_{k}$
. Let
![]() $\mathbb {L}^{\prime \vee } := \bigoplus _{a=1}^{k} \mathbb {Z} p_a$
and let
$\mathbb {L}^{\prime \vee } := \bigoplus _{a=1}^{k} \mathbb {Z} p_a$
and let
![]() $\mathbb {L}'$
be the dual lattice. Then
$\mathbb {L}'$
be the dual lattice. Then
![]() $\mathbb {L}^{\prime \vee }$
is a sublattice of
$\mathbb {L}^{\prime \vee }$
is a sublattice of
![]() $\mathbb {L}^\vee $
of finite index, and
$\mathbb {L}^\vee $
of finite index, and
![]() $\mathbb {L}$
is a sublattice of
$\mathbb {L}$
is a sublattice of
![]() $\mathbb {L}'$
of finite index. Let
$\mathbb {L}'$
of finite index. Let
![]() $\Theta _0^\vee $
and
$\Theta _0^\vee $
and
![]() $\Theta _0^{\prime \vee }$
be the dual cones of
$\Theta _0^{\prime \vee }$
be the dual cones of
![]() $\Theta _0$
and
$\Theta _0$
and
![]() $\Theta _0'$
, respectively. We have inclusions
$\Theta _0'$
, respectively. We have inclusions
Since
![]() $\Theta _0^\vee \cap \mathbb {L}$
is a subset of
$\Theta _0^\vee \cap \mathbb {L}$
is a subset of
![]() $\Theta _0^{\prime \vee } \cap \mathbb {L}'$
, we have an injective ring homomorphism
$\Theta _0^{\prime \vee } \cap \mathbb {L}'$
, we have an injective ring homomorphism
where
![]() $q_1,\ldots , q_{k}$
are the variables in Section 4.1. Taking the spectrum, we obtain a morphism
$q_1,\ldots , q_{k}$
are the variables in Section 4.1. Taking the spectrum, we obtain a morphism
and a cartesian diagram

where
![]() $\widetilde {\rho }:{\mathfrak {X}}\to \mathbb {A} ^{k}$
is a flat family of toric surfaces.
$\widetilde {\rho }:{\mathfrak {X}}\to \mathbb {A} ^{k}$
is a flat family of toric surfaces.
We choose a Kähler class
![]() $[\omega (\eta )]\in H^2(X_\Sigma; \mathbb {Z} )$
associated to a lattice point
$[\omega (\eta )]\in H^2(X_\Sigma; \mathbb {Z} )$
associated to a lattice point
![]() $\eta \in \mathbb {L}^\vee $
;
$\eta \in \mathbb {L}^\vee $
;
![]() $[\omega (\eta )]$
is the first Chern class of some ample line bundle over
$[\omega (\eta )]$
is the first Chern class of some ample line bundle over
![]() $X_\Sigma $
. Then it determines a toric graph
$X_\Sigma $
. Then it determines a toric graph
![]() $\Gamma \in M^{\prime }_{\mathbb {R}} \cong \mathbb {R} ^2$
up to translation by an element in
$\Gamma \in M^{\prime }_{\mathbb {R}} \cong \mathbb {R} ^2$
up to translation by an element in
![]() $M'\cong \mathbb {Z} ^2$
(see Section 3.2). The toric graph gives a polyhedral decomposition of
$M'\cong \mathbb {Z} ^2$
(see Section 3.2). The toric graph gives a polyhedral decomposition of
![]() $M_{\mathbb {Q}} $
in the sense of [Reference Nishinou and Siebert61, Section 3]. It is a covering
$M_{\mathbb {Q}} $
in the sense of [Reference Nishinou and Siebert61, Section 3]. It is a covering
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $M_{\mathbb {Q}} $
by strongly convex lattice polyhedra. The asymptotic fan of
$M_{\mathbb {Q}} $
by strongly convex lattice polyhedra. The asymptotic fan of
![]() $\mathcal {P}$
is defined to be
$\mathcal {P}$
is defined to be
The fan
![]() $\Sigma _{\mathcal {P}}=\widetilde \Theta \cap \rho ^{\prime -1}(0)$
defines a toric surface
$\Sigma _{\mathcal {P}}=\widetilde \Theta \cap \rho ^{\prime -1}(0)$
defines a toric surface
![]() $\mathbb {S}$
, which is the same as the toric surface given by the defining polytope
$\mathbb {S}$
, which is the same as the toric surface given by the defining polytope
![]() $\Delta $
. For each
$\Delta $
. For each
![]() $\Pi \in \mathcal {P}$
, let
$\Pi \in \mathcal {P}$
, let
![]() $C(\Pi )\subset M^{\prime }_{\mathbb {Q}} \times \mathbb {Q} _{\geq 0}$
be the closure of the cone over
$C(\Pi )\subset M^{\prime }_{\mathbb {Q}} \times \mathbb {Q} _{\geq 0}$
be the closure of the cone over
![]() $\Xi \times \{1\}$
in
$\Xi \times \{1\}$
in
![]() $M^{\prime }_{\mathbb {Q}} \times \mathbb {Q} $
. Then
$M^{\prime }_{\mathbb {Q}} \times \mathbb {Q} $
. Then
is a fan in
![]() $M^{\prime }_{\mathbb {Q}} \times \mathbb {Q} $
with support
$M^{\prime }_{\mathbb {Q}} \times \mathbb {Q} $
with support
![]() $|\widetilde {\Sigma }_{\mathcal {P}}|= M_{\mathbb {Q}} '\times \mathbb {Q} _{\geq 0}$
. The projection
$|\widetilde {\Sigma }_{\mathcal {P}}|= M_{\mathbb {Q}} '\times \mathbb {Q} _{\geq 0}$
. The projection
![]() $\pi ':M^{\prime }_{\mathbb {Q}} \times \mathbb {Q} \to \mathbb {Q} $
to the second factor defines a map from the fan
$\pi ':M^{\prime }_{\mathbb {Q}} \times \mathbb {Q} \to \mathbb {Q} $
to the second factor defines a map from the fan
![]() $\widetilde {\Sigma }_{\mathcal {P}}$
to the fan
$\widetilde {\Sigma }_{\mathcal {P}}$
to the fan
![]() $\{0, \mathbb {Q} _{\geq 0} \}$
. This map of fans determines a flat toric morphism
$\{0, \mathbb {Q} _{\geq 0} \}$
. This map of fans determines a flat toric morphism
![]() $\pi : X_{\widetilde {\Sigma }_{\mathcal {P}}}\to \mathbb {A} ^1$
, where
$\pi : X_{\widetilde {\Sigma }_{\mathcal {P}}}\to \mathbb {A} ^1$
, where
![]() $X_{\widetilde {\Sigma }_{\mathcal {P}}}$
is the toric 3-fold defined by the fan
$X_{\widetilde {\Sigma }_{\mathcal {P}}}$
is the toric 3-fold defined by the fan
![]() $\widetilde {\Sigma }_{\mathcal {P}}$
. Let t be a closed point in
$\widetilde {\Sigma }_{\mathcal {P}}$
. Let t be a closed point in
![]() $ \mathbb {A} ^1$
, and let
$ \mathbb {A} ^1$
, and let
![]() $X_t$
denote the fibre of
$X_t$
denote the fibre of
![]() $\pi $
over t. Then
$\pi $
over t. Then
![]() $X_t\cong \mathbb {S}$
for
$X_t\cong \mathbb {S}$
for
![]() $t\neq 0$
. As shown in [Reference Nishinou and Siebert61], when
$t\neq 0$
. As shown in [Reference Nishinou and Siebert61], when
![]() $t=0$
, we have a union of irreducible components, where each
$t=0$
, we have a union of irreducible components, where each
![]() $\mathbb {S}_\upsilon $
is the toric surface defined by the polytope
$\mathbb {S}_\upsilon $
is the toric surface defined by the polytope
![]() $\Delta _\upsilon $
(recall that each
$\Delta _\upsilon $
(recall that each
![]() $3$
-cone is a cone over a triangle
$3$
-cone is a cone over a triangle
![]() $\Delta _\upsilon \subset \Delta $
in
$\Delta _\upsilon \subset \Delta $
in
![]() $N_{\mathbb {R}} $
)
$N_{\mathbb {R}} $
)
If
![]() $\upsilon ' \in \Sigma (2)$
,
$\upsilon ' \in \Sigma (2)$
,
![]() $\upsilon \in \Sigma (3)$
and
$\upsilon \in \Sigma (3)$
and
![]() $\upsilon ' \subset \upsilon $
,
$\upsilon ' \subset \upsilon $
,
![]() $\upsilon '$
corresponds to a torus invariant divisor
$\upsilon '$
corresponds to a torus invariant divisor
![]() $ \mathbb {D} _{\upsilon '} \subset \mathbb {S}_{\upsilon }$
. We have the following commutative diagram:
$ \mathbb {D} _{\upsilon '} \subset \mathbb {S}_{\upsilon }$
. We have the following commutative diagram:

The polytope
![]() $\mathrm {Hull}( {\tilde {b}} _1,\dots , {\tilde {b}} _r)\subset {\widetilde {N}} $
lies on the hyperplane
$\mathrm {Hull}( {\tilde {b}} _1,\dots , {\tilde {b}} _r)\subset {\widetilde {N}} $
lies on the hyperplane
![]() $\langle \phi ^\vee (\mathsf {u}_3),\bullet \rangle =1$
. It determines a polytope on
$\langle \phi ^\vee (\mathsf {u}_3),\bullet \rangle =1$
. It determines a polytope on
![]() $ {\widetilde {N}} '=\{\langle \phi ^\vee (\mathsf {u}_3),\bullet \rangle =0\}$
up to a translation. The associated line bundle
$ {\widetilde {N}} '=\{\langle \phi ^\vee (\mathsf {u}_3),\bullet \rangle =0\}$
up to a translation. The associated line bundle
![]() $\mathfrak L$
on
$\mathfrak L$
on
![]() $X_{\widetilde \Theta }$
has sections
$X_{\widetilde \Theta }$
has sections
![]() $u_i,\ i=1,\dots , r$
associated to each integer point in this polytope. Define
$u_i,\ i=1,\dots , r$
associated to each integer point in this polytope. Define
 $$\begin{align*}u=\sum_{i=1}^{r} u_i,\quad \widetilde{\mathfrak{C}}=u^{-1}(0). \end{align*}$$
$$\begin{align*}u=\sum_{i=1}^{r} u_i,\quad \widetilde{\mathfrak{C}}=u^{-1}(0). \end{align*}$$
The divisor
![]() $\widetilde {\mathfrak {C}}\subset X_{\widetilde {\Theta }}$
. Let
$\widetilde {\mathfrak {C}}\subset X_{\widetilde {\Theta }}$
. Let
![]() $\mathfrak {C}:=\widetilde {\nu }^{-1}(\widetilde {\mathfrak {C}})\subset {\mathfrak {X}}$
be the pullback divisor under the morphism
$\mathfrak {C}:=\widetilde {\nu }^{-1}(\widetilde {\mathfrak {C}})\subset {\mathfrak {X}}$
be the pullback divisor under the morphism
![]() $\widetilde {\nu }:{\mathfrak {X}}\to X_{\widetilde {\Theta }}$
. Then
$\widetilde {\nu }:{\mathfrak {X}}\to X_{\widetilde {\Theta }}$
. Then
![]() $\mathfrak {C}\to \mathbb {A} ^{k}$
is a flat family of curves over
$\mathfrak {C}\to \mathbb {A} ^{k}$
is a flat family of curves over
![]() $ \mathbb {A} ^{k}$
.
$ \mathbb {A} ^{k}$
.
For
![]() $q\neq 0$
,
$q\neq 0$
,
![]() $\mathfrak {C}_q= \widetilde {\rho }^{-1}(q)\cap \mathfrak {C}$
can be identified with the zero locus of
$\mathfrak {C}_q= \widetilde {\rho }^{-1}(q)\cap \mathfrak {C}$
can be identified with the zero locus of
 $$ \begin{align} H_q(x,y)= x^{\mathfrak{r}}y^{-\mathfrak{s}-\mathfrak{r} f} + y^{\mathfrak{m}} +1 + \sum_{a=1}^k s_a (q) x^{m_a} y^{n_a-f m_a}, \end{align} $$
$$ \begin{align} H_q(x,y)= x^{\mathfrak{r}}y^{-\mathfrak{s}-\mathfrak{r} f} + y^{\mathfrak{m}} +1 + \sum_{a=1}^k s_a (q) x^{m_a} y^{n_a-f m_a}, \end{align} $$
where
![]() $x^{\mathfrak {r}} y^{-\mathfrak {s}-\mathfrak {r} f}= u_1 u_3^{-1}$
,
$x^{\mathfrak {r}} y^{-\mathfrak {s}-\mathfrak {r} f}= u_1 u_3^{-1}$
,
![]() $y^{\mathfrak {m}}=u_2 u_3^{-1}$
while
$y^{\mathfrak {m}}=u_2 u_3^{-1}$
while
![]() $s_a(q)x^{m_a} y^{n_a-f m_a}=u_{3+a} u_3^{-1}$
for
$s_a(q)x^{m_a} y^{n_a-f m_a}=u_{3+a} u_3^{-1}$
for
![]() $a=1,\ldots ,k$
. Here
$a=1,\ldots ,k$
. Here
![]() $x,y$
are affine coordinates of the toric surface
$x,y$
are affine coordinates of the toric surface
![]() $\mathbb {S}$
.
$\mathbb {S}$
.
For any
![]() $\beta \in \mathbb {K}_{\mathrm {eff}}$
, let
$\beta \in \mathbb {K}_{\mathrm {eff}}$
, let
![]() $s^\beta =\prod _{a=1}^k s_a^{\langle D_{a+3},\beta \rangle }$
. If we write
$s^\beta =\prod _{a=1}^k s_a^{\langle D_{a+3},\beta \rangle }$
. If we write
![]() $p_a=\sum _{b=1}^k p^b_a D_{b+3}$
, we have
$p_a=\sum _{b=1}^k p^b_a D_{b+3}$
, we have
 $$ \begin{align} s_a=\prod_{b=1}^k q_b^{p^a_b},\quad s^\beta=q^\beta. \end{align} $$
$$ \begin{align} s_a=\prod_{b=1}^k q_b^{p^a_b},\quad s^\beta=q^\beta. \end{align} $$
Denote
![]() $s^{\widetilde {\beta }}=x^{d_0} s^\beta $
for
$s^{\widetilde {\beta }}=x^{d_0} s^\beta $
for
![]() ${\widetilde {\beta }}= (d_0,\beta) $
.
${\widetilde {\beta }}= (d_0,\beta) $
.
When
![]() $q=0$
, we have a union of irreducible components
$q=0$
, we have a union of irreducible components
Each irreducible component
![]() $\mathbb {S}_{{\upsilon }}$
of the central fibre
$\mathbb {S}_{{\upsilon }}$
of the central fibre
![]() $X_0$
is given by the equation
$X_0$
is given by the equation
![]() $\{u_i=0,\ b_i\notin \upsilon \}$
. On
$\{u_i=0,\ b_i\notin \upsilon \}$
. On
![]() $\mathbb {S}_{{ {\sigma } _+}}$
, the coordinates in the affine chart
$\mathbb {S}_{{ {\sigma } _+}}$
, the coordinates in the affine chart
![]() $u_3\neq 0$
are
$u_3\neq 0$
are
while on
![]() $\mathbb {S}_{{ {\sigma } _-}}$
, the coordinates are
$\mathbb {S}_{{ {\sigma } _-}}$
, the coordinates are
Here
![]() $b_4=m_1\mathsf {v}_1 + n_1 \mathsf {v}_2+\mathsf {v}_3$
,
$b_4=m_1\mathsf {v}_1 + n_1 \mathsf {v}_2+\mathsf {v}_3$
,
![]() $m_1=-\mathfrak {s}^-$
and
$m_1=-\mathfrak {s}^-$
and
![]() $\alpha =[\mathfrak {l}_{\tau }]$
. Define
$\alpha =[\mathfrak {l}_{\tau }]$
. Define
 $$ \begin{align*} U=&\{ (q_1,\ldots,q_k)\in ( \mathbb{C} ^*)^{k}\times \mathbb{C} ^{k-k'}: \mathfrak{C}_{q} \mathrm{\ is\ smooth\ }\\ &\text{and intersects}\ \partial \mathbb{S}\ \text{transversally at distinct points} \}. \end{align*} $$
$$ \begin{align*} U=&\{ (q_1,\ldots,q_k)\in ( \mathbb{C} ^*)^{k}\times \mathbb{C} ^{k-k'}: \mathfrak{C}_{q} \mathrm{\ is\ smooth\ }\\ &\text{and intersects}\ \partial \mathbb{S}\ \text{transversally at distinct points} \}. \end{align*} $$
Then U is a dense open subset of
![]() $ \mathbb {A} ^{k}$
.
$ \mathbb {A} ^{k}$
.
4.3.2 Mirror curve and the mirror conjecture for disk amplitudes
When
![]() $q\neq 0$
, we denote
$q\neq 0$
, we denote
![]() $C_q=\mathfrak {C}_q\setminus (\partial \mathbb {S})$
. Thus the mirror curve
$C_q=\mathfrak {C}_q\setminus (\partial \mathbb {S})$
. Thus the mirror curve
![]() $C_q\subset ( \mathbb {C} ^*)^2$
is given by equation (33). On
$C_q\subset ( \mathbb {C} ^*)^2$
is given by equation (33). On
![]() $\bar C_{0,\upsilon }$
, when
$\bar C_{0,\upsilon }$
, when
![]() $x=0$
, there are m points, called large radius limit (LRL) points. They are given by
$x=0$
, there are m points, called large radius limit (LRL) points. They are given by
If
![]() $\mathcal {L}$
is outer, these points are smooth points in
$\mathcal {L}$
is outer, these points are smooth points in
![]() $\bar C_{0, {\sigma } }\subset \mathfrak {C}_0$
; if
$\bar C_{0, {\sigma } }\subset \mathfrak {C}_0$
; if
![]() $\mathcal {L}$
is inner, they are the nodal points
$\mathcal {L}$
is inner, they are the nodal points
![]() $\bar C_{0, {\sigma } _+}\cap \bar C_{0, {\sigma } _-}$
.
$\bar C_{0, {\sigma } _+}\cap \bar C_{0, {\sigma } _-}$
.
The group
![]() $G^*_ {\sigma } =\{(t_1,t_2)\in ( \mathbb {C} ^*)^2|t_1^{\mathfrak {r}} =t_2^{\mathfrak {s}},t_2^{\mathfrak {m}}=1\}$
fits into the short exact sequence
$G^*_ {\sigma } =\{(t_1,t_2)\in ( \mathbb {C} ^*)^2|t_1^{\mathfrak {r}} =t_2^{\mathfrak {s}},t_2^{\mathfrak {m}}=1\}$
fits into the short exact sequence
where
![]() $G_\sigma ^{{ *}}\to \boldsymbol {\mu }^*_{\mathfrak {m}}$
is given by
$G_\sigma ^{{ *}}\to \boldsymbol {\mu }^*_{\mathfrak {m}}$
is given by
![]() $(t_1,t_2)\mapsto t_2$
. Let
$(t_1,t_2)\mapsto t_2$
. Let
Then
![]() $G^*_\sigma =\{\chi _1^j \chi _2^l|j\in \{0,\dots ,\mathfrak {r} -1\},l\in \{0,\dots ,\mathfrak {m}-1\}\}$
. It pairs with
$G^*_\sigma =\{\chi _1^j \chi _2^l|j\in \{0,\dots ,\mathfrak {r} -1\},l\in \{0,\dots ,\mathfrak {m}-1\}\}$
. It pairs with
![]() $G_ {\sigma } $
by
$G_ {\sigma } $
by
and acts on the family of compactified mirror curves
![]() $\bar {\mathcal C}$
by
$\bar {\mathcal C}$
by
 $$ \begin{align*} \chi_1\cdot (x,y,s_a)&=(e^{2\pi\sqrt{-1}\frac{1}{\mathfrak{r}}}x,y,e^{-2\pi\sqrt{-1}c^\sigma_1(b_{a+3})}s_a),\\ \chi_2\cdot (x,y,s_a)&=(e^{2\pi\sqrt{-1}\frac{s+\mathfrak{r} f}{\mathfrak{r} \mathfrak{m}}}x,e^{2\pi\sqrt{-1}\frac{1}{\mathfrak{m}}}y,e^{-2\pi\sqrt{-1}c^\sigma_2(b_{a+3})}s_a). \end{align*} $$
$$ \begin{align*} \chi_1\cdot (x,y,s_a)&=(e^{2\pi\sqrt{-1}\frac{1}{\mathfrak{r}}}x,y,e^{-2\pi\sqrt{-1}c^\sigma_1(b_{a+3})}s_a),\\ \chi_2\cdot (x,y,s_a)&=(e^{2\pi\sqrt{-1}\frac{s+\mathfrak{r} f}{\mathfrak{r} \mathfrak{m}}}x,e^{2\pi\sqrt{-1}\frac{1}{\mathfrak{m}}}y,e^{-2\pi\sqrt{-1}c^\sigma_2(b_{a+3})}s_a). \end{align*} $$
Here
![]() $c_i^\sigma (b_{a+3})$
is defined as
$c_i^\sigma (b_{a+3})$
is defined as
![]() $h_{a+3}=\sum _{i=1}^3c_i^\sigma (b_{a+3}) b_i$
. The group
$h_{a+3}=\sum _{i=1}^3c_i^\sigma (b_{a+3}) b_i$
. The group
![]() $\boldsymbol {\mu }_{\mathfrak {m}}^*$
acts freely and transitively on the set of LRL points (
$\boldsymbol {\mu }_{\mathfrak {m}}^*$
acts freely and transitively on the set of LRL points (
![]() $x=0$
on
$x=0$
on
![]() $\bar C_{0, {\sigma } _+}$
).
$\bar C_{0, {\sigma } _+}$
).
Given
![]() $\bar {\eta }\in \{0,1,\ldots , \mathfrak {m} -1\}$
, let
$\bar {\eta }\in \{0,1,\ldots , \mathfrak {m} -1\}$
, let
![]() $\eta \in G_\tau ^*$
be the element associated to the character
$\eta \in G_\tau ^*$
be the element associated to the character
 $$ \begin{align*}\chi_\eta: G_\tau \to \mathbb{C} ^*,\quad \chi_\eta(\lambda)= \exp \left(\frac{2\pi\sqrt{-1}}{\mathfrak{m}} \bar{\eta}\bar{\lambda} \right). \end{align*} $$
$$ \begin{align*}\chi_\eta: G_\tau \to \mathbb{C} ^*,\quad \chi_\eta(\lambda)= \exp \left(\frac{2\pi\sqrt{-1}}{\mathfrak{m}} \bar{\eta}\bar{\lambda} \right). \end{align*} $$
Then
![]() $\bar {\eta }\mapsto \eta $
is a bijection from
$\bar {\eta }\mapsto \eta $
is a bijection from
![]() $\{0,1,\ldots ,\mathfrak {m}-1\}$
to
$\{0,1,\ldots ,\mathfrak {m}-1\}$
to
![]() $G_\tau ^*$
. Given
$G_\tau ^*$
. Given
![]() $\eta \in G_\tau ^*$
, define
$\eta \in G_\tau ^*$
, define
![]() $\mathfrak {u}_\eta \in \mathfrak {C}_0$
by
$\mathfrak {u}_\eta \in \mathfrak {C}_0$
by
For a small
![]() $\epsilon $
, one can always find small
$\epsilon $
, one can always find small
![]() $\epsilon '(\epsilon )<\epsilon $
such that when
$\epsilon '(\epsilon )<\epsilon $
such that when
![]() $\|q\|< \epsilon '(\epsilon )$
the following set
$\|q\|< \epsilon '(\epsilon )$
the following set
 $$ \begin{align*}U^{\epsilon,\epsilon'}=\begin{cases} \{(x,q),|x|<\epsilon,U\}, \quad \mathcal{L}\ \text{is outer;}\\ \{(x,q),|x|<\epsilon, |q^\alpha x^{-1}|<\epsilon\ \text{whenever}\ \|q\|<\epsilon'\} , \quad \mathcal{L}\ \text{is inner;} \end{cases} \end{align*} $$
$$ \begin{align*}U^{\epsilon,\epsilon'}=\begin{cases} \{(x,q),|x|<\epsilon,U\}, \quad \mathcal{L}\ \text{is outer;}\\ \{(x,q),|x|<\epsilon, |q^\alpha x^{-1}|<\epsilon\ \text{whenever}\ \|q\|<\epsilon'\} , \quad \mathcal{L}\ \text{is inner;} \end{cases} \end{align*} $$
is not empty. Let
![]() $U^\epsilon =U^{\epsilon ,\epsilon '(\epsilon )}\times \{\|q\|< \epsilon '(\epsilon ),q\in U\}\subset \mathfrak {C}$
. When
$U^\epsilon =U^{\epsilon ,\epsilon '(\epsilon )}\times \{\|q\|< \epsilon '(\epsilon ),q\in U\}\subset \mathfrak {C}$
. When
![]() $\epsilon $
is sufficiently small,
$\epsilon $
is sufficiently small,
![]() $U^{\epsilon ,\epsilon '(\epsilon )}$
is a disjoint union of
$U^{\epsilon ,\epsilon '(\epsilon )}$
is a disjoint union of
![]() $\mathfrak {m}$
small contractible regions when
$\mathfrak {m}$
small contractible regions when
![]() $\mathcal {L}$
is outer, or is a disjoint union of m annuli when
$\mathcal {L}$
is outer, or is a disjoint union of m annuli when
![]() $\mathcal {L}$
is inner. Let
$\mathcal {L}$
is inner. Let
![]() $U^\epsilon _\eta $
be the unique connected component of
$U^\epsilon _\eta $
be the unique connected component of
![]() $U^\epsilon $
containing
$U^\epsilon $
containing
![]() $\mathfrak u_\eta $
. So
$\mathfrak u_\eta $
. So
![]() $\log y$
is well defined on
$\log y$
is well defined on
![]() $U^\epsilon _\eta $
up to an integral multiple of
$U^\epsilon _\eta $
up to an integral multiple of
![]() $2\pi \sqrt {-1}$
, and it could be written as a power series in x when
$2\pi \sqrt {-1}$
, and it could be written as a power series in x when
![]() $\mathcal {L}$
is outer, and a Laurent series in x when
$\mathcal {L}$
is outer, and a Laurent series in x when
![]() $\mathcal {L}$
is inner.
$\mathcal {L}$
is inner.
Define
 $$ \begin{align*}\phi_\eta:=\frac{1}{\mathfrak{m}}\sum_{\lambda\in G_\tau} \chi_\eta(\lambda^{-1})\mathbf{1}_\lambda. \end{align*} $$
$$ \begin{align*}\phi_\eta:=\frac{1}{\mathfrak{m}}\sum_{\lambda\in G_\tau} \chi_\eta(\lambda^{-1})\mathbf{1}_\lambda. \end{align*} $$
Then
![]() $\{ \phi _\eta : \eta \in G_1^*\}$
is the canonical basis of
$\{ \phi _\eta : \eta \in G_1^*\}$
is the canonical basis of
![]() $H^*_ {\mathrm {CR}} (\mathcal {B}\mu _{\mathfrak {m}})$
, and
$H^*_ {\mathrm {CR}} (\mathcal {B}\mu _{\mathfrak {m}})$
, and
 $$ \begin{align*}\mathbf{1}_\lambda=\sum_{\eta \in \boldsymbol{\mu}_{\mathfrak{m}}^*} \chi_\eta (\lambda) \phi_\eta. \end{align*} $$
$$ \begin{align*}\mathbf{1}_\lambda=\sum_{\eta \in \boldsymbol{\mu}_{\mathfrak{m}}^*} \chi_\eta (\lambda) \phi_\eta. \end{align*} $$
We prove the following mirror theorem for disk amplitudes. Note that the ambiguity in
![]() $\log y$
does not play any role in the statement.
$\log y$
does not play any role in the statement.
Theorem 4.5.
 $$\begin{align*}x\frac{\partial}{\partial x}\sum_{\eta \in \boldsymbol{\mu}_m^*}(\log y|_{U^\epsilon_\eta})\phi_\eta =\left (x\frac{\partial}{\partial x}\right)^2 W^{\mathcal{X},(\mathcal{L},f)}(q,x)=\left (x\frac{\partial}{\partial x}\right)^2 F_{0,1}^{\mathcal{X},(\mathcal{L},f)}(\boldsymbol{\tau}_2,X).\end{align*}$$
$$\begin{align*}x\frac{\partial}{\partial x}\sum_{\eta \in \boldsymbol{\mu}_m^*}(\log y|_{U^\epsilon_\eta})\phi_\eta =\left (x\frac{\partial}{\partial x}\right)^2 W^{\mathcal{X},(\mathcal{L},f)}(q,x)=\left (x\frac{\partial}{\partial x}\right)^2 F_{0,1}^{\mathcal{X},(\mathcal{L},f)}(\boldsymbol{\tau}_2,X).\end{align*}$$
Here s and q are related by equation (34). The A-model flat coordinates
![]() $\boldsymbol {\tau }_2,X$
and the B-model coordinates
$\boldsymbol {\tau }_2,X$
and the B-model coordinates
![]() $q,x$
are related by the mirror maps in equation (25) and equation (28).
$q,x$
are related by the mirror maps in equation (25) and equation (28).
Remark 4.6.
-
(i) Theorem 4.5 for smooth toric Calabi-Yau 3-folds was conjectured in [Reference Aganagic and Vafa6, Reference Aganagic, Klemm and Vafa5] and proved in [Reference Fang and Liu33].
-
(ii) Theorem 4.5 can also be written as
where the integral is indefinite and $$\begin{align*}\int \sum_{\eta\in \boldsymbol{\mu}_m^*} \left(\log y\frac{dx}{x}|_{U^\epsilon_\eta}\right)\phi_\eta" =" W^{\mathcal{X},(\mathcal{L},f)}(q,x),\end{align*}$$
$$\begin{align*}\int \sum_{\eta\in \boldsymbol{\mu}_m^*} \left(\log y\frac{dx}{x}|_{U^\epsilon_\eta}\right)\phi_\eta" =" W^{\mathcal{X},(\mathcal{L},f)}(q,x),\end{align*}$$
 $"="$
means their instanton parts are equal in the following sense. The left side is the sum of a power series with no constant term in x and an extra term in the form of
$"="$
means their instanton parts are equal in the following sense. The left side is the sum of a power series with no constant term in x and an extra term in the form of
 $f(q)\log x+c$
. The power series part is equal to the right side. Note that the constant ambiguity in the indefinite integral is irrelevant here. If
$f(q)\log x+c$
. The power series part is equal to the right side. Note that the constant ambiguity in the indefinite integral is irrelevant here. If
 $\mathcal {X}$
is a smooth variety, then
$\mathcal {X}$
is a smooth variety, then
 $\boldsymbol {\mu }_m^*$
is trivial, and we revert to the original form of the conjecture in [Reference Aganagic and Vafa6, Reference Aganagic, Klemm and Vafa5]. We will prove this conjecture in the next subsection.
$\boldsymbol {\mu }_m^*$
is trivial, and we revert to the original form of the conjecture in [Reference Aganagic and Vafa6, Reference Aganagic, Klemm and Vafa5]. We will prove this conjecture in the next subsection.
4.4 Open mirror theorem for disk amplitudes
Lemma 4.7. The solution v to the exponential polynomial equation
 $$ \begin{align} \sum_{a=0}^k t_a e^{r_a v}- e^v +1=0 \end{align} $$
$$ \begin{align} \sum_{a=0}^k t_a e^{r_a v}- e^v +1=0 \end{align} $$
around
![]() $t_0=\dots ={t}_k=0, v=0$
is in the following power series form:
$t_0=\dots ={t}_k=0, v=0$
is in the following power series form:
 $$ \begin{align} v=\sum_{\substack{l_0,\dots,l_k=0\\ (l_0,\dots,l_k)\neq 0}}^{\infty} \frac{(r_0l_0 + \dots r_k l_k -1)_{(l_0+\dots+l_k-1)}}{l_0!\dots l_k!} t_0^{l_0}\dots t_k^{l_k}. \end{align} $$
$$ \begin{align} v=\sum_{\substack{l_0,\dots,l_k=0\\ (l_0,\dots,l_k)\neq 0}}^{\infty} \frac{(r_0l_0 + \dots r_k l_k -1)_{(l_0+\dots+l_k-1)}}{l_0!\dots l_k!} t_0^{l_0}\dots t_k^{l_k}. \end{align} $$
Here we adopt the Pochhammer symbol
 $$ \begin{align*}(a)_n=\frac{\Gamma(a+1)}{\Gamma(a-n+1)}=\begin{cases} a(a-1)\cdots(a-n+1),\quad n>0;\\ 1,\quad n=0;\\\frac{1}{(a+1)\dots(a-n)},\quad n<0;\end{cases}\end{align*} $$
$$ \begin{align*}(a)_n=\frac{\Gamma(a+1)}{\Gamma(a-n+1)}=\begin{cases} a(a-1)\cdots(a-n+1),\quad n>0;\\ 1,\quad n=0;\\\frac{1}{(a+1)\dots(a-n)},\quad n<0;\end{cases}\end{align*} $$
where
![]() $a\in \mathbb {C} $
and
$a\in \mathbb {C} $
and
![]() $n\in \mathbb {Z} $
.
$n\in \mathbb {Z} $
.
Proof. See Appendix A.
Starting from the above observation, we prove Theorem 4.5 in this section. To find the expansion of
![]() $\log y$
on
$\log y$
on
![]() $U^\epsilon _\eta $
, we assume
$U^\epsilon _\eta $
, we assume
where v is a power series in q and x. Setting
 $$ \begin{align*} &\xi_{\bar\eta}=e^{\frac{2\pi\sqrt{-1}}{\mathfrak{m}}\bar{\eta}},\ t_0=x^{\mathfrak{r}} (\xi_0\xi_{\bar \eta})^{-s-\mathfrak{r} f},\ r_0=-w_2\mathfrak{r},\\ &t_a=s_ax^{m_a} (\xi_0\xi_{\bar\eta})^{n_a-fm_a},\ r_a=\frac{n_a-fm_a}{\mathfrak{m}}, \end{align*} $$
$$ \begin{align*} &\xi_{\bar\eta}=e^{\frac{2\pi\sqrt{-1}}{\mathfrak{m}}\bar{\eta}},\ t_0=x^{\mathfrak{r}} (\xi_0\xi_{\bar \eta})^{-s-\mathfrak{r} f},\ r_0=-w_2\mathfrak{r},\\ &t_a=s_ax^{m_a} (\xi_0\xi_{\bar\eta})^{n_a-fm_a},\ r_a=\frac{n_a-fm_a}{\mathfrak{m}}, \end{align*} $$
the mirror curve is
 $$ \begin{align*}H(x,y)=\sum_{a=0}^k t_a e^{r_a v}-e^v+1=0. \end{align*} $$
$$ \begin{align*}H(x,y)=\sum_{a=0}^k t_a e^{r_a v}-e^v+1=0. \end{align*} $$
Let
![]() $ \mathbb {D} _{\mathrm {eff}}(\mathcal {X},\mathcal {L})=\{{\widetilde {\beta }}=(d_0,\beta ) \in \mathbb {Z} \times \mathbb {L}|\langle {\widetilde {\beta }},D_i \rangle \in \mathbb {Z} _{\geq 0},i\neq 2,3\}$
. So
$ \mathbb {D} _{\mathrm {eff}}(\mathcal {X},\mathcal {L})=\{{\widetilde {\beta }}=(d_0,\beta ) \in \mathbb {Z} \times \mathbb {L}|\langle {\widetilde {\beta }},D_i \rangle \in \mathbb {Z} _{\geq 0},i\neq 2,3\}$
. So
![]() $\mathbb {K}_{\mathrm {eff}}(\mathcal {X},\mathcal {L})\subset \mathbb {D} _{\mathrm {eff}}(\mathcal {X},\mathcal {L})$
. By Lemma 4.7,
$\mathbb {K}_{\mathrm {eff}}(\mathcal {X},\mathcal {L})\subset \mathbb {D} _{\mathrm {eff}}(\mathcal {X},\mathcal {L})$
. By Lemma 4.7,
 $$ \begin{align*} v&=\sum_{\substack{l_0,\dots,l_k=0\\ (l_0,\dots, l_k)\neq 0}}^\infty\frac{(r_0l_0+\dots r_k l_k -1)_{(l_0+\dots + l_k -1)}}{l_0!\dots l_k!}\prod_{a=0}^k t_a^{l_a}.\\ &=-\sum_{{\widetilde{\beta}}\in \mathbb{D} _{\mathrm{eff}}(\mathcal{X},\mathcal{L})} (\xi_0\xi_{\bar{\eta}})^{-m\langle D_2,{\widetilde{\beta}}\rangle}\frac{(-\langle D_2,{\widetilde{\beta}} \rangle-1)_{(-\langle D_2,{\widetilde{\beta}} \rangle - \langle D_3,{\widetilde{\beta}} \rangle -1)}}{\prod_{i\in I_\tau} \langle D_i,{\widetilde{\beta}} \rangle!} x^{d_0} \prod_{a=1}^ks_a^{\langle D_{a+3}, {\widetilde{\beta}}\rangle }\\ &=-\sum_{{\widetilde{\beta}}\in \mathbb{D} _{\mathrm{eff}}(\mathcal{X},\mathcal{L})} (\xi_0)^{-m\langle D_3,{\widetilde{\beta}}\rangle}(\xi_{\bar \eta})^{-m\langle D_2,{\widetilde{\beta}} \rangle} \frac{(-\langle D_3,{\widetilde{\beta}} \rangle-1)_{(-\langle D_2,{\widetilde{\beta}} \rangle - \langle D_3,{\widetilde{\beta}} \rangle -1)}}{\prod_{i\in I_\tau} \langle D_i,{\widetilde{\beta}} \rangle!} x^{d_0}q^\beta. \end{align*} $$
$$ \begin{align*} v&=\sum_{\substack{l_0,\dots,l_k=0\\ (l_0,\dots, l_k)\neq 0}}^\infty\frac{(r_0l_0+\dots r_k l_k -1)_{(l_0+\dots + l_k -1)}}{l_0!\dots l_k!}\prod_{a=0}^k t_a^{l_a}.\\ &=-\sum_{{\widetilde{\beta}}\in \mathbb{D} _{\mathrm{eff}}(\mathcal{X},\mathcal{L})} (\xi_0\xi_{\bar{\eta}})^{-m\langle D_2,{\widetilde{\beta}}\rangle}\frac{(-\langle D_2,{\widetilde{\beta}} \rangle-1)_{(-\langle D_2,{\widetilde{\beta}} \rangle - \langle D_3,{\widetilde{\beta}} \rangle -1)}}{\prod_{i\in I_\tau} \langle D_i,{\widetilde{\beta}} \rangle!} x^{d_0} \prod_{a=1}^ks_a^{\langle D_{a+3}, {\widetilde{\beta}}\rangle }\\ &=-\sum_{{\widetilde{\beta}}\in \mathbb{D} _{\mathrm{eff}}(\mathcal{X},\mathcal{L})} (\xi_0)^{-m\langle D_3,{\widetilde{\beta}}\rangle}(\xi_{\bar \eta})^{-m\langle D_2,{\widetilde{\beta}} \rangle} \frac{(-\langle D_3,{\widetilde{\beta}} \rangle-1)_{(-\langle D_2,{\widetilde{\beta}} \rangle - \langle D_3,{\widetilde{\beta}} \rangle -1)}}{\prod_{i\in I_\tau} \langle D_i,{\widetilde{\beta}} \rangle!} x^{d_0}q^\beta. \end{align*} $$
Suppose that
![]() $\mathcal {L}$
is an outer brane. For any
$\mathcal {L}$
is an outer brane. For any
![]() ${\widetilde {\beta }}=(d_0,\beta ) \in \mathbb {D} _{\mathrm {eff}}(\mathcal {X},\mathcal {L})$
, we have
${\widetilde {\beta }}=(d_0,\beta ) \in \mathbb {D} _{\mathrm {eff}}(\mathcal {X},\mathcal {L})$
, we have
Let
![]() $\lambda = d_0(\mathsf {v}_1+f\mathsf {v}_2)-v(\beta )+N_ {\sigma } \in G_\tau $
. Then
$\lambda = d_0(\mathsf {v}_1+f\mathsf {v}_2)-v(\beta )+N_ {\sigma } \in G_\tau $
. Then
![]() $h(d_0,\lambda )=v(\beta ) \in G_ {\sigma } $
. If
$h(d_0,\lambda )=v(\beta ) \in G_ {\sigma } $
. If
![]() $\mathcal {L}$
is an inner brane, we replace
$\mathcal {L}$
is an inner brane, we replace
![]() $ {\sigma } $
by
$ {\sigma } $
by
![]() $ {\sigma } _+$
in the above discussion and define
$ {\sigma } _+$
in the above discussion and define
![]() $\lambda \in G_1$
similarly. Then
$\lambda \in G_1$
similarly. Then
So
 $$ \begin{align*}\xi_{\bar\eta}^{-\langle D_2,{\widetilde{\beta}}\rangle} = \exp \left(-\frac{2\pi\sqrt{-1}}{\mathfrak{m}}\bar{\eta}\bar{\lambda}\right) = \chi_\eta(\lambda^{-1}). \end{align*} $$
$$ \begin{align*}\xi_{\bar\eta}^{-\langle D_2,{\widetilde{\beta}}\rangle} = \exp \left(-\frac{2\pi\sqrt{-1}}{\mathfrak{m}}\bar{\eta}\bar{\lambda}\right) = \chi_\eta(\lambda^{-1}). \end{align*} $$
It follows that
 $$ \begin{align*} &x\frac{\partial}{\partial x}\sum_{\eta \in \boldsymbol{\mu}_m^*}(\log y)_{U_\eta^\epsilon}\phi_\eta \\ &\quad =-\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\h(d_0,\lambda)=v(\beta)}} (\xi_0)^{-\mathfrak{m}\langle D_3,{\widetilde{\beta}}\rangle} \frac{d_0(-\langle D_3,{\widetilde{\beta}} \rangle-1)_{(-\langle D_2,{\widetilde{\beta}} \rangle - \langle D_3,{\widetilde{\beta}} \rangle -1)}}{\mathfrak{m}\prod_{i\in I_\tau} \langle D_i,{\widetilde{\beta}} \rangle!} \sum_{\eta \in \boldsymbol{\mu}^*_m}\chi_\eta (\lambda^{-1})\phi_\eta x^{d_0}q^\beta\\ &\quad =-\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\h(d_0,\lambda)=v(\beta)}} (\xi_0)^{-\mathfrak{m}\lfloor \langle D_3,{\widetilde{\beta}}\rangle \rfloor} \frac{d_0(-\langle D_3,{\widetilde{\beta}} \rangle-1)_{(-\langle D_2,{\widetilde{\beta}} \rangle - \langle D_3,{\widetilde{\beta}} \rangle -1)}}{\mathfrak{m}\prod_{i\in I_\tau} \langle D_i,{\widetilde{\beta}} \rangle!} \sum_{\eta \in \boldsymbol{\mu}^*_{\mathfrak{m}}}(\xi_0)^{\bar \lambda} \chi_\eta(\lambda^{-1})\phi_\eta x^{d_0}q^\beta\\ &\quad =\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\h(d_0,\lambda)=v(\beta)}} -(-1)^{\lfloor \langle D_3,{\widetilde{\beta}}\rangle \rfloor} \frac{d_0\Gamma(-\langle D_3,{\widetilde{\beta}} \rangle)}{\mathfrak{m}\Gamma(\langle D_2,{\widetilde{\beta}} \rangle+1) \prod_{i\in I_\tau} \Gamma(\langle D_i,{\widetilde{\beta}} \rangle+1)} x^{d_0}q^\beta \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*} &x\frac{\partial}{\partial x}\sum_{\eta \in \boldsymbol{\mu}_m^*}(\log y)_{U_\eta^\epsilon}\phi_\eta \\ &\quad =-\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\h(d_0,\lambda)=v(\beta)}} (\xi_0)^{-\mathfrak{m}\langle D_3,{\widetilde{\beta}}\rangle} \frac{d_0(-\langle D_3,{\widetilde{\beta}} \rangle-1)_{(-\langle D_2,{\widetilde{\beta}} \rangle - \langle D_3,{\widetilde{\beta}} \rangle -1)}}{\mathfrak{m}\prod_{i\in I_\tau} \langle D_i,{\widetilde{\beta}} \rangle!} \sum_{\eta \in \boldsymbol{\mu}^*_m}\chi_\eta (\lambda^{-1})\phi_\eta x^{d_0}q^\beta\\ &\quad =-\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\h(d_0,\lambda)=v(\beta)}} (\xi_0)^{-\mathfrak{m}\lfloor \langle D_3,{\widetilde{\beta}}\rangle \rfloor} \frac{d_0(-\langle D_3,{\widetilde{\beta}} \rangle-1)_{(-\langle D_2,{\widetilde{\beta}} \rangle - \langle D_3,{\widetilde{\beta}} \rangle -1)}}{\mathfrak{m}\prod_{i\in I_\tau} \langle D_i,{\widetilde{\beta}} \rangle!} \sum_{\eta \in \boldsymbol{\mu}^*_{\mathfrak{m}}}(\xi_0)^{\bar \lambda} \chi_\eta(\lambda^{-1})\phi_\eta x^{d_0}q^\beta\\ &\quad =\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\h(d_0,\lambda)=v(\beta)}} -(-1)^{\lfloor \langle D_3,{\widetilde{\beta}}\rangle \rfloor} \frac{d_0\Gamma(-\langle D_3,{\widetilde{\beta}} \rangle)}{\mathfrak{m}\Gamma(\langle D_2,{\widetilde{\beta}} \rangle+1) \prod_{i\in I_\tau} \Gamma(\langle D_i,{\widetilde{\beta}} \rangle+1)} x^{d_0}q^\beta \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
On the other hand,
 $$ \begin{align*} &\Big (x\frac{\partial}{\partial x}\Big)^2 W^{\mathcal{X},(\mathcal{L},f)}(x,q)\\ &\quad =\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\h(d_0,\lambda)=v(\beta)}}- (-1)^{\lfloor \langle D_3,{\widetilde{\beta}}\rangle \rfloor} \frac{d_0\Gamma(-\langle D_3,{\widetilde{\beta}} \rangle)}{\mathfrak{m}\Gamma(\langle D_2,{\widetilde{\beta}} \rangle+1)\prod_{i\in I_\tau} \Gamma(\langle D_i,{\widetilde{\beta}} \rangle+1)} x^{d_0}q^\beta \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
$$ \begin{align*} &\Big (x\frac{\partial}{\partial x}\Big)^2 W^{\mathcal{X},(\mathcal{L},f)}(x,q)\\ &\quad =\sum_{\substack{{\widetilde{\beta}}\in \mathbb{K}_{\mathrm{eff}}(\mathcal{X},\mathcal{L})\\h(d_0,\lambda)=v(\beta)}}- (-1)^{\lfloor \langle D_3,{\widetilde{\beta}}\rangle \rfloor} \frac{d_0\Gamma(-\langle D_3,{\widetilde{\beta}} \rangle)}{\mathfrak{m}\Gamma(\langle D_2,{\widetilde{\beta}} \rangle+1)\prod_{i\in I_\tau} \Gamma(\langle D_i,{\widetilde{\beta}} \rangle+1)} x^{d_0}q^\beta \xi_0^{\bar{\lambda}}\mathbf{1}_{\lambda^{-1}}. \end{align*} $$
Thus Theorem 4.5 follows.
A Proof of Lemma 4.7
In this appendix, we obtain a power series solution to the following exponential polynomial where
![]() $r_a\in \mathbb {R} $
$r_a\in \mathbb {R} $
 $$ \begin{align} 1-e^v+ \sum_{a=1}^k t_a e^{r_a v}=0 \end{align} $$
$$ \begin{align} 1-e^v+ \sum_{a=1}^k t_a e^{r_a v}=0 \end{align} $$
around
![]() $t_1=\dots =t_k=0$
by oscillatory integral and inverse Laplace transform. Note that the notation here is slightly different from that in Lemma 4.7: the sum in the above equation (37) starts from
$t_1=\dots =t_k=0$
by oscillatory integral and inverse Laplace transform. Note that the notation here is slightly different from that in Lemma 4.7: the sum in the above equation (37) starts from
![]() $a=1$
, whereas the sum in equation (35) in Lemma 4.7 starts from
$a=1$
, whereas the sum in equation (35) in Lemma 4.7 starts from
![]() $a=0$
.
$a=0$
.
We also consider the following equation where
![]() $f,r_a\in \mathbb {Z} _{>0}$
:
$f,r_a\in \mathbb {Z} _{>0}$
:
 $$ \begin{align} L(X,Y)=1+XY^{-f}+Y+\sum_{a=1}^k s_a Y^{r_a}=0. \end{align} $$
$$ \begin{align} L(X,Y)=1+XY^{-f}+Y+\sum_{a=1}^k s_a Y^{r_a}=0. \end{align} $$
Let
![]() $X=e^{-x}$
and
$X=e^{-x}$
and
![]() $Y=e^{-y}$
. This equation identifies with equation (37) after setting
$Y=e^{-y}$
. This equation identifies with equation (37) after setting
![]() $X=0$
and a change of variables
$X=0$
and a change of variables
![]() $v=\sqrt {-1}\pi -y, t_a=(-1)^{r_a}s_a$
.
$v=\sqrt {-1}\pi -y, t_a=(-1)^{r_a}s_a$
.
Lemma A.1. For equation (37), one can expand v as a power series in
![]() $t_a$
, where each coefficient is a rational function of
$t_a$
, where each coefficient is a rational function of
![]() $r_a$
. For equation (38), the variable Y can be expanded as a power series of
$r_a$
. For equation (38), the variable Y can be expanded as a power series of
![]() $(-1)^{r_a}s_a$
and
$(-1)^{r_a}s_a$
and
![]() $(-1)^fX$
around
$(-1)^fX$
around
![]() $Y=-1$
with each coefficient rational in
$Y=-1$
with each coefficient rational in
![]() $r_a$
and f. One can also expand Y as a power series of
$r_a$
and f. One can also expand Y as a power series of
![]() $s_a$
and
$s_a$
and
![]() $(-X)^{\frac {1}{f}}$
around
$(-X)^{\frac {1}{f}}$
around
![]() $Y=0$
with each coefficient rational in
$Y=0$
with each coefficient rational in
![]() $r_a$
and f.
$r_a$
and f.
Proof. This is done by elementary recursive calculation. We illustrate the expansion at
![]() $Y=0$
for equation (38). The equation can be written as
$Y=0$
for equation (38). The equation can be written as
 $$\begin{align*}Y^f+Y^{f+1}+\sum_{a=1}^k s_a Y^{r_a+f}=((-X)^{\frac{1}{f}})^f. \end{align*}$$
$$\begin{align*}Y^f+Y^{f+1}+\sum_{a=1}^k s_a Y^{r_a+f}=((-X)^{\frac{1}{f}})^f. \end{align*}$$
Implicit function theorem (applying to
![]() $Y(Y+1+\sum _{a=1}^k s_aY^{r_a})^{\frac {1}{f}}=(-X)^{\frac {1}{f}}$
) says Y is analytic in
$Y(Y+1+\sum _{a=1}^k s_aY^{r_a})^{\frac {1}{f}}=(-X)^{\frac {1}{f}}$
) says Y is analytic in
![]() $(-X)^{\frac {1}{f}}$
and
$(-X)^{\frac {1}{f}}$
and
![]() $s_a$
around
$s_a$
around
![]() $(X,Y,s)=(0,0,0)$
, and recursive calculation shows each coefficient is a rational function of lower degree coefficients.
$(X,Y,s)=(0,0,0)$
, and recursive calculation shows each coefficient is a rational function of lower degree coefficients.
We consider an affine curve
and its partial compactification
![]() $\bar C \subset \mathbb {C} ^2$
with two points
$\bar C \subset \mathbb {C} ^2$
with two points
![]() $(X,Y)=(0,0)$
and
$(X,Y)=(0,0)$
and
![]() $(X,Y)=(0,-1+O(s))$
added. Let
$(X,Y)=(0,-1+O(s))$
added. Let
![]() $e^{-x_0}$
be the branch point of the map
$e^{-x_0}$
be the branch point of the map
![]() $(X,Y)\mapsto X$
such that
$(X,Y)\mapsto X$
such that
![]() $e^{-x_0}=-\frac {1}{4}+O(s)$
. Let
$e^{-x_0}=-\frac {1}{4}+O(s)$
. Let
![]() $\gamma _{s}$
be the oriented Lefschetz thimble that passes through the ramification point
$\gamma _{s}$
be the oriented Lefschetz thimble that passes through the ramification point
![]() $(e^{-x_0}, e^{-y_0})=(-\frac {1}{4}+O(s), -\frac {1}{2}+O(s))$
and goes from
$(e^{-x_0}, e^{-y_0})=(-\frac {1}{4}+O(s), -\frac {1}{2}+O(s))$
and goes from
![]() $(X,Y)=(0,-1+O(s))$
to
$(X,Y)=(0,-1+O(s))$
to
![]() $(X,Y)=(0,0)$
. So the coordinate on
$(X,Y)=(0,0)$
. So the coordinate on
![]() $\gamma _s$
is z such that
$\gamma _s$
is z such that
![]() $x-x_0=z^2$
. We choose the sign of z such that
$x-x_0=z^2$
. We choose the sign of z such that
![]() $(X,Y)=(0,0)$
is at
$(X,Y)=(0,0)$
is at
![]() $z=+\infty $
.
$z=+\infty $
.
Lemma A.2.
 $$ \begin{align*}\int_{\gamma_{s}} e^{-ux} ydx=\sum_{l_1,\dots,l_k \geq 0} e^{ \sqrt{-1}\pi(-(f+1)u+\sum_{a=1}^k r_al_a)} \frac{\Gamma(u)\Gamma(fu+\sum_{a=1}^k r_a l_a)}{\Gamma((f+1)u+\sum_{a=1}^k ( r_a-1)l_a+1)} \frac{\prod_{a=1}^k s_a^{l_a}}{l_1!\dots l_k!}. \end{align*} $$
$$ \begin{align*}\int_{\gamma_{s}} e^{-ux} ydx=\sum_{l_1,\dots,l_k \geq 0} e^{ \sqrt{-1}\pi(-(f+1)u+\sum_{a=1}^k r_al_a)} \frac{\Gamma(u)\Gamma(fu+\sum_{a=1}^k r_a l_a)}{\Gamma((f+1)u+\sum_{a=1}^k ( r_a-1)l_a+1)} \frac{\prod_{a=1}^k s_a^{l_a}}{l_1!\dots l_k!}. \end{align*} $$
Proof. Consider a Landau-Ginzburg model
![]() $W_{s}:( \mathbb {C} ^*)^3\to \mathbb {C} $
, where
$W_{s}:( \mathbb {C} ^*)^3\to \mathbb {C} $
, where
 $$ \begin{align*} W_{s}=X_1 X_2^{-f}X_3+X_2 X_3 +X_3+\sum_{a=1}^k s_a X_2^{r_a} X_3 -u \log X_1. \end{align*} $$
$$ \begin{align*} W_{s}=X_1 X_2^{-f}X_3+X_2 X_3 +X_3+\sum_{a=1}^k s_a X_2^{r_a} X_3 -u \log X_1. \end{align*} $$
Define
![]() $\check {t}_1 =X_1 X_2^{-f} X_3, \check {t}_2 = X_2 X_3, \hat t_1 =X_1 X_2^{-f}, \hat t_2= X_2.$
$\check {t}_1 =X_1 X_2^{-f} X_3, \check {t}_2 = X_2 X_3, \hat t_1 =X_1 X_2^{-f}, \hat t_2= X_2.$
Let
![]() $X_3\in \Gamma _3$
be a cycle that counterclockwise encircles the positive real axis, starting and ending on the positive real infinity. We require that the argument of each
$X_3\in \Gamma _3$
be a cycle that counterclockwise encircles the positive real axis, starting and ending on the positive real infinity. We require that the argument of each
![]() $X_3\in \Gamma _3$
takes every value in
$X_3\in \Gamma _3$
takes every value in
![]() $(0,2\pi )$
once. Define the relative connected cycle
$(0,2\pi )$
once. Define the relative connected cycle
![]() $\Gamma _{s}$
to be
$\Gamma _{s}$
to be
When
![]() $|s|<\epsilon $
for small
$|s|<\epsilon $
for small
![]() $\epsilon $
, the superpotential
$\epsilon $
, the superpotential
![]() $\mathrm {Re}(W)\to \infty $
in the noncompact direction of
$\mathrm {Re}(W)\to \infty $
in the noncompact direction of
![]() $\Gamma _{s}$
. On
$\Gamma _{s}$
. On
![]() $\Gamma _{s}$
the logarithm is taken in the following way: when
$\Gamma _{s}$
the logarithm is taken in the following way: when
![]() $X_3<0$
and
$X_3<0$
and
![]() $s=0$
,
$s=0$
,
Since the cycle
![]() $\Gamma _{s}$
is simply connected and deforms continuously with respect to s, this choice is fixed. Evaluate the following oscillatory integral of
$\Gamma _{s}$
is simply connected and deforms continuously with respect to s, this choice is fixed. Evaluate the following oscillatory integral of
![]() $W_{s}$
:
$W_{s}$
:
 $$ \begin{align*} I(u)=&\int_{\Gamma_s} e^{-W_{s}} \frac{dX_1}{X_1} \frac{dX_2}{X_2} \frac{dX_3}{X_3}\\ =&\int_{\Gamma_s} \exp(-\sum_{a=1}^k s_a \check{t}_2^{r_a} X_3^{1-r_a}-\check{t}_1-\check{t}_2-X_3 +u \log \check{t}_1 + f u\log\check{t}_2 - (f+1)u \log X_3) \frac{d\check{t}_1}{\check{t}_1}\frac{d\check{t}_2}{\check{t}_2}\frac{dX_3}{X_3}\\ =&\int_{\Gamma_{s} } e^{-\sum_{a=1}^k s_a \check{t}_2^{r_a} X_3^{1-r_a}-\check{t}_1-\check{t}_2-X_3} \check{t}_1^u \check{t}_2^{fu} e^{-(f+1)u (\log X_3-\sqrt{-1}\pi)} e^{-(f+1)\sqrt{-1}\pi u} \frac{d\check{t}_1}{\check{t}_1}\frac{d\check{t}_2}{\check{t}_2}\frac{dX_3}{X_3}\\ =&-e^{-(f+1)\sqrt{-1}\pi u} \sum_{l_1,\dots, l_k\geq 0} (-1)^{\sum_{a=1}^k (r_a-1)l_a} \prod_{a=1}^k\frac{(-s_a)^{l_a}}{l_a!} \Big ( \int_{\check{t}_1>0} e^{-\check{t}_1} \check{t}_1^{u-1} d\check{t}_1 \Big) \\ &\cdot \Big( \int_{\check{t}_2>0} e^{-\check{t}_2} \check{t}_2^{\sum_{a=0}^k r_a l_a+fu-1} d\check{t}_2 \Big ) \cdot \Big (\int_{X_3 \in \Gamma_3} e^{-X_3} e^{(\log X_3-\sqrt{-1}\pi)( \sum_{a=1}^k (1-r_a)l_a-(f+1)u-1)} dX_3 \Big )\\ =&2\pi\sqrt{-1}e^{-(f+1)\sqrt{-1}\pi u} \sum_{l_1,\dots,l_k\geq 0} (-1)^ {\sum_{a=1}^k r_a l_a } \prod_{a=1}^k\frac{s_a^{l_a}}{l_a!} \frac{\Gamma(u) \Gamma(fu+\sum_{a=1}^k r_a l_a )}{\Gamma((f+1)u+\sum_{a=1}^k (r_a -1) l_a +1)}. \end{align*} $$
$$ \begin{align*} I(u)=&\int_{\Gamma_s} e^{-W_{s}} \frac{dX_1}{X_1} \frac{dX_2}{X_2} \frac{dX_3}{X_3}\\ =&\int_{\Gamma_s} \exp(-\sum_{a=1}^k s_a \check{t}_2^{r_a} X_3^{1-r_a}-\check{t}_1-\check{t}_2-X_3 +u \log \check{t}_1 + f u\log\check{t}_2 - (f+1)u \log X_3) \frac{d\check{t}_1}{\check{t}_1}\frac{d\check{t}_2}{\check{t}_2}\frac{dX_3}{X_3}\\ =&\int_{\Gamma_{s} } e^{-\sum_{a=1}^k s_a \check{t}_2^{r_a} X_3^{1-r_a}-\check{t}_1-\check{t}_2-X_3} \check{t}_1^u \check{t}_2^{fu} e^{-(f+1)u (\log X_3-\sqrt{-1}\pi)} e^{-(f+1)\sqrt{-1}\pi u} \frac{d\check{t}_1}{\check{t}_1}\frac{d\check{t}_2}{\check{t}_2}\frac{dX_3}{X_3}\\ =&-e^{-(f+1)\sqrt{-1}\pi u} \sum_{l_1,\dots, l_k\geq 0} (-1)^{\sum_{a=1}^k (r_a-1)l_a} \prod_{a=1}^k\frac{(-s_a)^{l_a}}{l_a!} \Big ( \int_{\check{t}_1>0} e^{-\check{t}_1} \check{t}_1^{u-1} d\check{t}_1 \Big) \\ &\cdot \Big( \int_{\check{t}_2>0} e^{-\check{t}_2} \check{t}_2^{\sum_{a=0}^k r_a l_a+fu-1} d\check{t}_2 \Big ) \cdot \Big (\int_{X_3 \in \Gamma_3} e^{-X_3} e^{(\log X_3-\sqrt{-1}\pi)( \sum_{a=1}^k (1-r_a)l_a-(f+1)u-1)} dX_3 \Big )\\ =&2\pi\sqrt{-1}e^{-(f+1)\sqrt{-1}\pi u} \sum_{l_1,\dots,l_k\geq 0} (-1)^ {\sum_{a=1}^k r_a l_a } \prod_{a=1}^k\frac{s_a^{l_a}}{l_a!} \frac{\Gamma(u) \Gamma(fu+\sum_{a=1}^k r_a l_a )}{\Gamma((f+1)u+\sum_{a=1}^k (r_a -1) l_a +1)}. \end{align*} $$
Here we use the Hankel’s formula:
 $$ \begin{align*}\frac{\sqrt{-1}}{2\pi}\int_{\Gamma_3} e^{-z(\log(t)-\sqrt{-1}\pi)}e^{-t} dt=\frac{1}{\Gamma(z)}. \end{align*} $$
$$ \begin{align*}\frac{\sqrt{-1}}{2\pi}\int_{\Gamma_3} e^{-z(\log(t)-\sqrt{-1}\pi)}e^{-t} dt=\frac{1}{\Gamma(z)}. \end{align*} $$
By Hori-Iqbal-Vafa [Reference Hori, Iqbal and Vafa44], this oscillatory integral could be reduced to a Laplace transform on the curve C. Introduce two variables
![]() $v^+,v^-\in \mathbb {C} $
, and the extended cycle
$v^+,v^-\in \mathbb {C} $
, and the extended cycle
Define
![]() $H=\frac {W_s}{X_3}$
. Define the holomorphic volume form
$H=\frac {W_s}{X_3}$
. Define the holomorphic volume form
We reduce the oscillatory integral to the curve C as follows. Let
![]() $ {\tilde {\Gamma }}_{\mathrm {red}} =\{(\hat t_1,\hat t_2)|\arg \hat t_1=\arg \hat t_2\}\times \{v^+=-\overline {v^-}\}.$
$ {\tilde {\Gamma }}_{\mathrm {red}} =\{(\hat t_1,\hat t_2)|\arg \hat t_1=\arg \hat t_2\}\times \{v^+=-\overline {v^-}\}.$
 $$ \begin{align*} I(u)=&\frac{1}{2\sqrt{-1}\pi} \int_{ {\tilde{\Gamma}} _s} e^{-X_3 (H-v^+ v^-)}e^{-ux} \frac{d X_1}{ X_1}\frac{d X_2}{X_2} dX_3 dv^+ dv^-\\ =& \frac{1}{2\sqrt{-1}\pi} \int_{ {\tilde{\Gamma}}_{\mathrm{red}} } \delta(H-v^+ v^-) e^{-ux} \frac{d X_1}{ X_1}\frac{d X_2}{X_2} dv^+ dv^-\\ =&- \int_{ {\tilde{\Gamma}}_{\mathrm{red}} \cap \{H-v^+ v^-=0\}} e^{-ux} \frac{d X_1}{ X_1}\frac{d X_2}{X_2}\frac{dv^-}{v^-}. \end{align*} $$
$$ \begin{align*} I(u)=&\frac{1}{2\sqrt{-1}\pi} \int_{ {\tilde{\Gamma}} _s} e^{-X_3 (H-v^+ v^-)}e^{-ux} \frac{d X_1}{ X_1}\frac{d X_2}{X_2} dX_3 dv^+ dv^-\\ =& \frac{1}{2\sqrt{-1}\pi} \int_{ {\tilde{\Gamma}}_{\mathrm{red}} } \delta(H-v^+ v^-) e^{-ux} \frac{d X_1}{ X_1}\frac{d X_2}{X_2} dv^+ dv^-\\ =&- \int_{ {\tilde{\Gamma}}_{\mathrm{red}} \cap \{H-v^+ v^-=0\}} e^{-ux} \frac{d X_1}{ X_1}\frac{d X_2}{X_2}\frac{dv^-}{v^-}. \end{align*} $$
This integration is further reduced to the curve
![]() $C=\{H(e^{-x},e^{-y})=0\}$
as follows:
$C=\{H(e^{-x},e^{-y})=0\}$
as follows:
 $$ \begin{align*}I(u) & =- \int_{ {\tilde{\Gamma}}_{\mathrm{red}} \cap \{H-v^+ v^-=0\}} e^{-ux}dx dy \frac{dv^-}{v^-}= 2\sqrt{-1}\pi\int_{\gamma_s} e^{-ux} y dx. \end{align*} $$
$$ \begin{align*}I(u) & =- \int_{ {\tilde{\Gamma}}_{\mathrm{red}} \cap \{H-v^+ v^-=0\}} e^{-ux}dx dy \frac{dv^-}{v^-}= 2\sqrt{-1}\pi\int_{\gamma_s} e^{-ux} y dx. \end{align*} $$
Notice that we use the fact that
![]() $d(e^{-ux} ydx\frac {dv^-}{v^-})=-e^{-ux} \Omega $
near
$d(e^{-ux} ydx\frac {dv^-}{v^-})=-e^{-ux} \Omega $
near
![]() $ {\tilde {\Gamma }}_{\mathrm {red}} \cap \{H-v^+ v^-=0\}$
.
$ {\tilde {\Gamma }}_{\mathrm {red}} \cap \{H-v^+ v^-=0\}$
.
The function
![]() $\frac {dy}{dx}$
is a meromorphic function on the partially compactified curve
$\frac {dy}{dx}$
is a meromorphic function on the partially compactified curve
![]() $\bar C$
with the only pole at
$\bar C$
with the only pole at
![]() $x_0$
. Its expansion at
$x_0$
. Its expansion at
![]() $(X,Y)=(0,-1+O(s))$
is a power series in X, while its expansion at
$(X,Y)=(0,-1+O(s))$
is a power series in X, while its expansion at
![]() $(X,Y)=(0,0)$
is a series in
$(X,Y)=(0,0)$
is a series in
![]() $X^{\frac {1}{f}}$
. Denote
$X^{\frac {1}{f}}$
. Denote
![]() $g^\pm (x)=\frac {dy}{dx}\vert _{z=\pm \sqrt {x-x_0}}$
. Then
$g^\pm (x)=\frac {dy}{dx}\vert _{z=\pm \sqrt {x-x_0}}$
. Then
![]() $g^-$
is a power series in X and
$g^-$
is a power series in X and
![]() $s_a$
, while
$s_a$
, while
![]() $g^+$
is a power series in
$g^+$
is a power series in
![]() $X^{\frac {1}{f}}$
and
$X^{\frac {1}{f}}$
and
![]() $s_a$
. Since they are expansions of
$s_a$
. Since they are expansions of
![]() $\frac {dy}{dx}=\frac {XdY}{YdX}$
regarding the curve equation (38), as series of
$\frac {dy}{dx}=\frac {XdY}{YdX}$
regarding the curve equation (38), as series of
![]() $(-1)^f X$
,
$(-1)^f X$
,
![]() $(-1)^{r_a}s_a$
and
$(-1)^{r_a}s_a$
and
![]() $(-X)^{\frac {1}{f}}$
,
$(-X)^{\frac {1}{f}}$
,
![]() $s_a$
respectively, their coefficients are rational in
$s_a$
respectively, their coefficients are rational in
![]() $r_a$
and f by Lemma A.1.
$r_a$
and f by Lemma A.1.
By Lemma A.2, the ‘classical Laplace transform’ is
 $$ \begin{align*} \mathfrak G(u)=&\int_{x-x_0\in \mathbb{R} ^+} e^{-u(x-x_0)}(g^+(x)-g^-(x))d(x-x_0)\\ =&\int_{x-x_0\in \mathbb{R} ^+}e^{-u(x-x_0)} \left(\frac{dy}{dx}\right) d(x-x_0)=u e^{ux_0}\int_{\gamma_s} e^{-ux} ydx\\ =&\sum_{l_1,\dots,l_k\geq 0} u e^{ux_0}e^{\sqrt{-1}\pi(-(f+1)u+\sum_{a=1}^k r_al_a)} \frac{\Gamma(u)\Gamma(fu+\sum_{a=1}^kr_a l_a)}{\Gamma((f+1)u + \sum_{a=1}^k(r_a-1)l_a+1)}\frac{\prod_{a=1}^k s_a^{l_a}}{l_1!\dots l_k!}. \end{align*} $$
$$ \begin{align*} \mathfrak G(u)=&\int_{x-x_0\in \mathbb{R} ^+} e^{-u(x-x_0)}(g^+(x)-g^-(x))d(x-x_0)\\ =&\int_{x-x_0\in \mathbb{R} ^+}e^{-u(x-x_0)} \left(\frac{dy}{dx}\right) d(x-x_0)=u e^{ux_0}\int_{\gamma_s} e^{-ux} ydx\\ =&\sum_{l_1,\dots,l_k\geq 0} u e^{ux_0}e^{\sqrt{-1}\pi(-(f+1)u+\sum_{a=1}^k r_al_a)} \frac{\Gamma(u)\Gamma(fu+\sum_{a=1}^kr_a l_a)}{\Gamma((f+1)u + \sum_{a=1}^k(r_a-1)l_a+1)}\frac{\prod_{a=1}^k s_a^{l_a}}{l_1!\dots l_k!}. \end{align*} $$
By the inverse Laplace transform formula,
 $$ \begin{align*} (g^+-g^-)=\int_{u=-\infty \sqrt{-1}+ T}^{u=+\infty\sqrt{-1}+T}\mathfrak G(u)e^{u(x-x_0)}du, \end{align*} $$
$$ \begin{align*} (g^+-g^-)=\int_{u=-\infty \sqrt{-1}+ T}^{u=+\infty\sqrt{-1}+T}\mathfrak G(u)e^{u(x-x_0)}du, \end{align*} $$
where T is large enough that all poles of
![]() $\mathfrak G(u)$
are on the left of the integration contour. Here the inverse Laplace transform takes residues around poles of
$\mathfrak G(u)$
are on the left of the integration contour. Here the inverse Laplace transform takes residues around poles of
![]() $\Gamma (u)$
and
$\Gamma (u)$
and
![]() $\Gamma (fu+\sum _{a=1}^kr_al_a)$
. Taking the residues around all poles (other than the possible pole at
$\Gamma (fu+\sum _{a=1}^kr_al_a)$
. Taking the residues around all poles (other than the possible pole at
![]() $u=0$
) of
$u=0$
) of
![]() $\Gamma (fu+\sum _{a=1}^k r_a l_a)$
gives a series of
$\Gamma (fu+\sum _{a=1}^k r_a l_a)$
gives a series of
![]() $(-X)^{\frac {1}{f}}$
with coefficients rational in
$(-X)^{\frac {1}{f}}$
with coefficients rational in
![]() $r_a$
and f, denoted by
$r_a$
and f, denoted by
![]() $h^+$
$h^+$
 $$ \begin{align*} h^+&=\sum_{l>0,l_1,\dots, l_k\geq 0}h^+_{l,l_1,\dots,l_k} \prod_{a=1}^k s_a^{l_a}((-X)^{\frac{1}{f}})^l \\&=\sum_{l>0,l_1,\dots, l_k\geq 0}(-l/f)e^{\sqrt{-1}\pi(-\frac{f+1}{f}l+\sum_{a=1}^k r_a l_a)}(X^{\frac{1}{f}})^l \frac{\Gamma(-\frac{l}{f})\mathrm{Res}_{u=-\frac{l}{f}}\Gamma(fu+\sum_{a=1}^k r_a l_a)}{\Gamma(-\frac{l(f+1)}{f}+\sum_{a=1}^k(r_a-1)l_a+1)}\frac{\prod_{a=1}^k s_a^{l_a}}{l_1!\dots l_k!}\\ &=\sum_{l>0,l_1,\dots, l_k\geq 0}(-l/f)(-X)^{\frac{l}{f}}\frac{\Gamma(-\frac{l}{f})}{\Gamma(-\frac{l(f+1)}{f}+\sum_{a=1}^k(r_a-1)l_a+1)f}\frac{\prod_{a=1}^k s_a^{l_a}}{l!l_1!\dots l_k!}; \end{align*} $$
$$ \begin{align*} h^+&=\sum_{l>0,l_1,\dots, l_k\geq 0}h^+_{l,l_1,\dots,l_k} \prod_{a=1}^k s_a^{l_a}((-X)^{\frac{1}{f}})^l \\&=\sum_{l>0,l_1,\dots, l_k\geq 0}(-l/f)e^{\sqrt{-1}\pi(-\frac{f+1}{f}l+\sum_{a=1}^k r_a l_a)}(X^{\frac{1}{f}})^l \frac{\Gamma(-\frac{l}{f})\mathrm{Res}_{u=-\frac{l}{f}}\Gamma(fu+\sum_{a=1}^k r_a l_a)}{\Gamma(-\frac{l(f+1)}{f}+\sum_{a=1}^k(r_a-1)l_a+1)}\frac{\prod_{a=1}^k s_a^{l_a}}{l_1!\dots l_k!}\\ &=\sum_{l>0,l_1,\dots, l_k\geq 0}(-l/f)(-X)^{\frac{l}{f}}\frac{\Gamma(-\frac{l}{f})}{\Gamma(-\frac{l(f+1)}{f}+\sum_{a=1}^k(r_a-1)l_a+1)f}\frac{\prod_{a=1}^k s_a^{l_a}}{l!l_1!\dots l_k!}; \end{align*} $$
while taking residues around the poles of
![]() $\Gamma (u)$
(other than the possible pole at
$\Gamma (u)$
(other than the possible pole at
![]() $u=0$
), we get a power series in X
$u=0$
), we get a power series in X
 $$ \begin{align*} h^-=&\sum_{l>0, l_1,\dots,l_k\geq 0} (-l) X^l e^{\sqrt{-1}\pi(-(f+1)l+\sum_{a=1}^k r_al_a)} \frac{\mathrm{Res}_{u=-l}(\Gamma(u))\Gamma(-fl+\sum_{a=1}^kr_a l_a)}{\Gamma(-(f+1)l +\sum_{a=1}^k(r_a-1)l_a+1)}\frac{\prod_{a=1}^k s_a^{l_a}}{l_1!\dots l_k!}\\ =&\sum_{l>0, l_1,\dots,l_k\geq 0} (-l) ((-1)^fX)^l \frac{\Gamma(-fl+\sum_{a=1}^kr_a l_a)}{\Gamma(-(f+1)l +\sum_{a=1}^k(r_a-1)l_a+1)l!}\frac{\prod_{a=1}^k ((-1)^{r_a}s_a)^{l_a}}{l_1!\dots l_k!}. \end{align*} $$
$$ \begin{align*} h^-=&\sum_{l>0, l_1,\dots,l_k\geq 0} (-l) X^l e^{\sqrt{-1}\pi(-(f+1)l+\sum_{a=1}^k r_al_a)} \frac{\mathrm{Res}_{u=-l}(\Gamma(u))\Gamma(-fl+\sum_{a=1}^kr_a l_a)}{\Gamma(-(f+1)l +\sum_{a=1}^k(r_a-1)l_a+1)}\frac{\prod_{a=1}^k s_a^{l_a}}{l_1!\dots l_k!}\\ =&\sum_{l>0, l_1,\dots,l_k\geq 0} (-l) ((-1)^fX)^l \frac{\Gamma(-fl+\sum_{a=1}^kr_a l_a)}{\Gamma(-(f+1)l +\sum_{a=1}^k(r_a-1)l_a+1)l!}\frac{\prod_{a=1}^k ((-1)^{r_a}s_a)^{l_a}}{l_1!\dots l_k!}. \end{align*} $$
So
![]() $g^+-g^-=h^++h^-+\text {const.}$
, where the constant difference (in X) arises since we don’t consider the residue around
$g^+-g^-=h^++h^-+\text {const.}$
, where the constant difference (in X) arises since we don’t consider the residue around
![]() $u=0$
. For any degree
$u=0$
. For any degree
![]() $l\geq 1$
, choose
$l\geq 1$
, choose
![]() $f>l$
such that the term
$f>l$
such that the term
![]() $((-X)^{\frac {1}{f}})^l\prod _{a=1}^k s_a^{l_a}$
in
$((-X)^{\frac {1}{f}})^l\prod _{a=1}^k s_a^{l_a}$
in
![]() $g^+$
is not a monomial in X and thus can only come from
$g^+$
is not a monomial in X and thus can only come from
![]() $h^+$
. Since the coefficient of the term is rational in f, it has to be equal to the corresponding term
$h^+$
. Since the coefficient of the term is rational in f, it has to be equal to the corresponding term
![]() $h^+_{l,l_1,\dots ,l_k}$
for all
$h^+_{l,l_1,\dots ,l_k}$
for all
![]() $f>0$
. Therefore
$f>0$
. Therefore
![]() $g^+=h^++\mathrm {const.}$
and
$g^+=h^++\mathrm {const.}$
and
![]() $-g^-=h^-$
. Note here that
$-g^-=h^-$
. Note here that
![]() $g^-$
is the expansion of
$g^-$
is the expansion of
![]() $\frac {dy}{dx}$
, and since y is analytic in X at
$\frac {dy}{dx}$
, and since y is analytic in X at
![]() $(X,Y)=(0,-1+O(s))$
,
$(X,Y)=(0,-1+O(s))$
,
![]() $-g^-$
has no degree
$-g^-$
has no degree
![]() $0$
term and does not differ from
$0$
term and does not differ from
![]() $h^-$
by a degree
$h^-$
by a degree
![]() $0$
term in X.
$0$
term in X.
Suppose the expansion of y at
![]() $(X,Y)=(0,-1+O(s))$
is
$(X,Y)=(0,-1+O(s))$
is
![]() $y=A_0 +\sum _{l>0} A_l X^l$
, then the expansion of
$y=A_0 +\sum _{l>0} A_l X^l$
, then the expansion of
![]() $\frac {dy}{dx}$
at this point is
$\frac {dy}{dx}$
at this point is
 $$ \begin{align*}g^-=\frac{dy}{dx}=-\sum_{l>0} l A_l X^l. \end{align*} $$
$$ \begin{align*}g^-=\frac{dy}{dx}=-\sum_{l>0} l A_l X^l. \end{align*} $$
Therefore, for
![]() $l\geq 1$
,
$l\geq 1$
,
 $$ \begin{align} A_l=-\sum_{l_1,\dots,l_k\geq 0} e^{\sqrt{-1}\pi(- fl+\sum_{a=1}^k r_al_a)} \frac{\Gamma(-fl+\sum_{a=1}^kr_a l_a)}{\Gamma(-(f+1)l + \sum_{a=1}^k(r_a-1)l_a+1)}\frac{\prod_{a=1}^k s_a^{l_a}}{l_1!\dots l_k!}. \end{align} $$
$$ \begin{align} A_l=-\sum_{l_1,\dots,l_k\geq 0} e^{\sqrt{-1}\pi(- fl+\sum_{a=1}^k r_al_a)} \frac{\Gamma(-fl+\sum_{a=1}^kr_a l_a)}{\Gamma(-(f+1)l + \sum_{a=1}^k(r_a-1)l_a+1)}\frac{\prod_{a=1}^k s_a^{l_a}}{l_1!\dots l_k!}. \end{align} $$
We prove Lemma 4.7 by induction. The statement is true for
![]() $k=0$
trivially. Assume it is true for
$k=0$
trivially. Assume it is true for
![]() $k=\mathfrak {m}-1\ (\mathfrak {m}\geq 1)$
. For
$k=\mathfrak {m}-1\ (\mathfrak {m}\geq 1)$
. For
![]() $k=\mathfrak {m}$
, we first assume
$k=\mathfrak {m}$
, we first assume
![]() $r_{\mathfrak {m}}\in \mathbb {Z} _{<0}$
and all other
$r_{\mathfrak {m}}\in \mathbb {Z} _{<0}$
and all other
![]() $r_a$
(
$r_a$
(
![]() $a=1,\dots ,\mathfrak {m}-1$
) are positive integers. By the induction assumption, we know the expansion is given as in Lemma 4.7 for terms of degree
$a=1,\dots ,\mathfrak {m}-1$
) are positive integers. By the induction assumption, we know the expansion is given as in Lemma 4.7 for terms of degree
![]() $0$
in
$0$
in
![]() $t_{\mathfrak {m}}$
. Let
$t_{\mathfrak {m}}$
. Let
![]() $f=-r_{\mathfrak {m}}$
. After a change of variables
$f=-r_{\mathfrak {m}}$
. After a change of variables
![]() $v=\sqrt {-1}\pi -y$
,
$v=\sqrt {-1}\pi -y$
,
![]() $(-1)^{r_a}s_a=t_a$
for
$(-1)^{r_a}s_a=t_a$
for
![]() $a=1,\dots ,{\mathfrak {m}-1}$
and
$a=1,\dots ,{\mathfrak {m}-1}$
and
![]() $X=(-1)^ft_{\mathfrak {m}}$
, we obtain Equation (38). Then from Equation (39), we know the expansion of y for positive degree terms in X and thus conclude that for positive degree terms in
$X=(-1)^ft_{\mathfrak {m}}$
, we obtain Equation (38). Then from Equation (39), we know the expansion of y for positive degree terms in X and thus conclude that for positive degree terms in
![]() $t_{\mathfrak {m}}$
, the lemma also holds. Then for all degrees, the lemma holds
$t_{\mathfrak {m}}$
, the lemma also holds. Then for all degrees, the lemma holds
 $$\begin{align*}v=\sum_{\substack{l_1,\dots,l_k=1\\ (l_1,\dots,l_k)\neq 0}}^\infty \frac{(r_1l_1 + \dots r_k l_k -1)_{(l_1+\dots+l_k-1)}}{l_1!\dots l_k!} t_1^{l_1}\dots t_k^{l_k}. \end{align*}$$
$$\begin{align*}v=\sum_{\substack{l_1,\dots,l_k=1\\ (l_1,\dots,l_k)\neq 0}}^\infty \frac{(r_1l_1 + \dots r_k l_k -1)_{(l_1+\dots+l_k-1)}}{l_1!\dots l_k!} t_1^{l_1}\dots t_k^{l_k}. \end{align*}$$
Each coefficient is a rational function of
![]() $r_1,\dots ,r_{\mathfrak {m}}$
. The above equation holds for
$r_1,\dots ,r_{\mathfrak {m}}$
. The above equation holds for
![]() $r_1,\dots , r_{\mathfrak {m}-1}\in \mathbb {Z} _{>0}$
and
$r_1,\dots , r_{\mathfrak {m}-1}\in \mathbb {Z} _{>0}$
and
![]() $r_{\mathfrak {m}}\in \mathbb {Z} _{<0}$
, so it is true for all
$r_{\mathfrak {m}}\in \mathbb {Z} _{<0}$
, so it is true for all
![]() $r_a\in \mathbb {R} $
.
$r_a\in \mathbb {R} $
.
Acknowledgements
The first author would like to thank Kwokwai Chan, Naichung Conan Leung and Yongbin Ruan for valuable discussions. We wish to thank Song Yu for corrections to the previous version of this paper. We wish to thank the anonymous referees for their comments and suggestions.
Conflicts of Interest
None.
Funding statement
The research of the first author was partially supported by NSF DMS-1206667, a start-up grant at Peking University, NSFC 11831017, NSFC 11890661 and NSFC 12125101. The research of the second author was partially supported by NSF DMS-1159416 and NSF DMS-1206667. The research of the third author was partially supported by a Simons Foundation Collaboration Grant and NSF DMS-1506551.