Let {ξ; t = 1, 2, …} be a stationary normal sequence with zero means, unit variances, and covariances 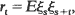 let
let 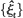 be independent and standard normal, and write
be independent and standard normal, and write 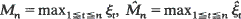 . In this paper we find bounds on
. In this paper we find bounds on 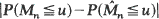 which are roughly of the order
which are roughly of the order
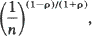 where ρ is the maximal correlation, ρ =sup {0, r1, r2, …}. It is further shown that, at least for m-dependent sequences, the bounds are of the right order and, in a simple example, the errors are evaluated numerically. Bounds of the same order on the rate of convergence of the point processes of exceedances of one or several levels are obtained using a ‘representation' approach (which seems to be of rather wide applicability). As corollaries we obtain rates of convergence of several functionals of the point processes, including the joint distribution function of the k largest values amongst ξ1, …, ξn.
where ρ is the maximal correlation, ρ =sup {0, r1, r2, …}. It is further shown that, at least for m-dependent sequences, the bounds are of the right order and, in a simple example, the errors are evaluated numerically. Bounds of the same order on the rate of convergence of the point processes of exceedances of one or several levels are obtained using a ‘representation' approach (which seems to be of rather wide applicability). As corollaries we obtain rates of convergence of several functionals of the point processes, including the joint distribution function of the k largest values amongst ξ1, …, ξn.