Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T08:13:35.114Z Has data issue: false hasContentIssue false
  • English
  • Français

The rate of convergence of extremes of stationary normal sequences

Published online by Cambridge University Press:  01 July 2016

Holger Rootzén
Holger Rootzén*
Affiliation:
University of Copenhagen
*
∗Postal address; Institute of Mathematical Statistics, 5 Universitetsparken, University of Copenhagen, DK-2100 Copenhagen 0, Denmark.
Get access Rights & Permissions [Opens in a new window]

Abstract

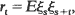Let {ξ; t = 1, 2, …} be a stationary normal sequence with zero means, unit variances, and covariances let 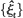be independent and standard normal, and write 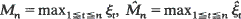. In this paper we find bounds on 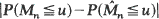which are roughly of the order 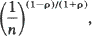where ρ is the maximal correlation, ρ =sup {0, r1, r2, …}. It is further shown that, at least for m-dependent sequences, the bounds are of the right order and, in a simple example, the errors are evaluated numerically. Bounds of the same order on the rate of convergence of the point processes of exceedances of one or several levels are obtained using a ‘representation' approach (which seems to be of rather wide applicability). As corollaries we obtain rates of convergence of several functionals of the point processes, including the joint distribution function of the k largest values amongst ξ1, …, ξn.

Keywords

MAXIMA OF NORMAL SEQUENCESEXTREME VALUES
Type
Research Article
Information
Advances in Applied Probability , Volume 15 , Issue 1 , March 1983 , pp. 54 - 80
Copyright
Copyright © Applied Probability Trust 1983 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported in part by the Office of Naval Research under contract N 0014-75-C-0809.

References

Berman, S. M. (1964) Limit theorems for the maximum term in stationary sequences. Ann. Math. Statist. 35, 502–516.CrossRefGoogle Scholar
Fisher, R. A. and Tippett, L. H. C. (1928) Limiting forms of the frequency distribution of the largest or smallest member of a sample. Proc. Camb. Phil. Soc. 24, 180–190.CrossRefGoogle Scholar
Gumbel, E. J. (1958) Statistics of Extremes. Columbia University Press, New York.CrossRefGoogle Scholar
Hall, P. (1979) The rate of convergence of normal extremes. J. Appl. Prob. 16, 433–439.CrossRefGoogle Scholar
Kallenberg, O. (1976) Random Measures. Academic Press, New York.Google Scholar
Leadbetter, M. R., Lindgren, G. and Rootzen, H. (1978) Conditions for the convergence in distribution of maxima of stationary normal processes. Stoch. Proc. Appl. 8, 131–139.CrossRefGoogle Scholar
Leadbetter, M. R., Lindgren, G. and Rootzen, H. (1982) Extremes and Related Properties of Stationary Sequences and Processes. Springer-Verlag, Berlin.Google Scholar
Nair, A. K. (1981) Asymptotic distribution and moments of sample extremes. Ann. Prob. 9, 150–153.CrossRefGoogle Scholar
Piterbarg, V. I. (1978) Asymptotic expansions for the probability of large excursions of Gaussian processes. Soviet Math. Dokl. 19, 1279–1283.Google Scholar
Serfling, R. J. (1975) A general Poisson approximation theorem. Ann. Prob. 3, 726–731.CrossRefGoogle Scholar
Slepian, D. (1962) The one-sided barrier problem for Gaussian noise. Bell System Tech. J. 41, 463–501.CrossRefGoogle Scholar
Watts, V., Rootzen, H. and Leadbetter, M. R. (1982) On limiting distributions of intermediate order statistics from stationary sequences. Ann. Prob. 10, 653–662.CrossRefGoogle Scholar