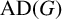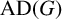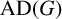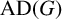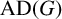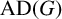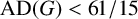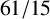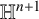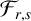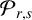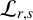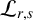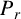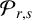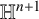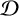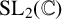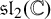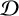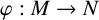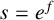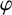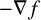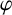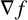In this article, we study rational matrix representations of VZ p-groups (p is any prime). Using our findings on VZ p-groups, we explicitly obtain all inequivalent irreducible rational matrix representations of all p-groups of order $\leq p^4$. Furthermore, we establish combinatorial formulae to determine the Wedderburn decompositions of rational group algebras for VZ p-groups and all p-groups of order $\leq p^4$, ensuring simplicity in the process.

Using the special value at $u=1$ of Artin–Ihara L-functions, we associate to every $\mathbb {Z}$-cover of a finite connected graph a polynomial, which we call the Ihara polynomial. We show that the number of spanning trees for the finite intermediate graphs of such a cover can be expressed in terms of the Pierce–Lehmer sequence associated to a factor of the Ihara polynomial. This allows us to express the asymptotic growth of the number of spanning trees in terms of the Mahler measure of this polynomial. Specialising to the situation where the base graph is a bouquet or the dumbbell graph gives us back previous results in the literature for circulant and I-graphs (including the generalised Petersen graphs). We also express the p-adic valuation of the number of spanning trees of the finite intermediate graphs in terms of the p-adic Mahler measure of the Ihara polynomial. When applied to a particular $\mathbb {Z}$-cover, our result gives us back Lengyel’s calculation of the p-adic valuations of Fibonacci numbers.

We study the asymptotic behaviour of the least energy solutions to the following class of nonlocal Neumann problems:

$$ \begin{align*} \begin{cases} { d(-\Delta)^{s}u+ u= \vert u\vert^{p-1}u } & \text{in } \Omega, \\ {u>0} & \text{in } \Omega, \\ { \mathcal{N}_{s}u=0 } & \text{in } \mathbb{R}^{n}\setminus \overline{\Omega}, \end{cases} \end{align*} $$

where $\Omega \subset \mathbb {R}^{n}$ is a bounded domain of class $C^{1,1}$, $1<p<({n+s})/({n-s}),\,n>\max \{1, 2s \}, 0<s<1, d>0$ and $\mathcal {N}_{s}u$ is the nonlocal Neumann derivative. We show that for small $d,$ the least energy solutions $u_d$ of the above problem achieve an $L^{\infty }$-bound independent of $d.$ Using this together with suitable $L^{r}$-estimates on $u_d,$ we show that the least energy solution $u_d$ achieves a maximum on the boundary of $\Omega $ for d sufficiently small.

This paper is the first of a two part series devoted to describing relations between congruence and crystallographic braid groups. We recall and introduce some elements belonging to congruence braid groups and we establish some (iso)-morphisms between crystallographic braid groups and corresponding quotients of congruence braid groups.

This article introduces the Clairaut conformal Riemannian map. This notion includes the previously studied notions of Clairaut conformal submersion, Clairaut Riemannian submersion, and the Clairaut Riemannian map as particular cases, and is well known in the classical theory of surfaces. Toward this, we find the necessary and sufficient condition for a conformal Riemannian map 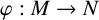$\varphi : M \to N$ between Riemannian manifolds to be a Clairaut conformal Riemannian map with girth 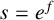$s = e^f$. We show that the fibers of 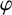$\varphi $ are totally umbilical with mean curvature vector field the negative gradient of the logarithm of the girth function, that is, 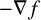$-\nabla f$. Using this, we obtain a local splitting of M as a warped product and a usual product, if the horizontal space is integrable (under some appropriate hypothesis). We also provide some examples of the Clairaut conformal Riemannian maps to confirm our main theorem. We observe that the Laplacian of the logarithmic girth, that is, of f, on the total manifold takes the special form. It reduces to the Laplacian on the horizontal distribution, and if it is nonnegative, the universal covering space of M becomes a product manifold, under some hypothesis on f. Analysis of the Laplacian of f also yields the splitting of the universal covering space of M as a warped product under some appropriate conditions. We calculate the sectional curvature and mixed sectional curvature of M when f is a distance function. We also find the relationships between the total manifold and the fibers being symmetrical and, in particular, having constant sectional curvature, and from there, we compare their universal covering spaces, if fibers are also complete, provided f is a distance function. We also find a condition on the curvature tensor of the fibers to be semi-symmetric, provided that the total manifold is semi-symmetric and f is a distance function. In turn, this gives the warped product of symmetric, semi-symmetric spaces into two symmetric, semi-symmetric subspaces (under some hypothesis). Also if the Hessian or the Laplacian of the Riemannian curvature tensor fields is zero, or has a harmonic curvature tensor, then the fibers of 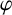$\varphi $ also satisfy the same property, if f is also a distance function. By obtaining Bochner-type formulas for Clairaut conformal Riemannian maps, we establish the relations between the divergences of the Ricci curvature tensor on fibers and horizontal space and the corresponding scalar curvature. We also study the horizontal Killing vector field of constant length and show that they are parallel under appropriate hypotheses. This in turn gives the splitting of the total manifold, if it admits a horizontal parallel Killing vector field and if the horizontal space is integrable. Finally, assuming that 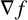$\nabla f$ is a nontrivial gradient Ricci soliton on M, we prove that any vertical vector field is incompressible and hence the volume form of the fiber is invariant under the flow of the vector field.

We study analogues of Kronecker coefficients for symmetric inverse semigroups, for dual symmetric inverse semigroups and for the inverse semigroups of bijections between subquotients of finite sets. In all cases, we reduce the problem of determination of such coefficients to some group-theoretic and combinatorial problems. For symmetric inverse semigroups, we provide an explicit formula in terms of the classical Kronecker and Littlewood–Richardson coefficients for symmetric groups.

Let $B(\Omega )$ be a Banach space of holomorphic functions on a bounded connected domain $\Omega $ in ${{\mathbb C}^n}$. In this paper, we establish a criterion for $B(\Omega )$ to be reflexive via evaluation functions on $B(\Omega )$, that is, $B(\Omega )$ is reflexive if and only if the evaluation functions span the dual space $(B(\Omega ))^{*} $.

In this paper, we study the singular boundary value problem

$$ \begin{align*} \begin{cases} \Delta_\infty^h u=\lambda f(x,u,Du) \quad &\mathrm{in}\; \Omega, \\ u>0\quad &\mathrm{in}\; \Omega,\\ u=0 \quad &\mathrm{on} \;\partial\Omega, \end{cases} \end{align*} $$

where $\lambda>0$ is a parameter, $h>1$ and $\Delta _\infty ^h u=|Du|^{h-3} \langle D^2uDu,Du \rangle $ is the highly degenerate and h-homogeneous operator related to the infinity Laplacian. The nonlinear term $f(x,t,p):\Omega \times (0,\infty )\times \mathbb {R}^{n}\rightarrow \mathbb {R}$ is a continuous function and may exhibit singularity at $t\rightarrow 0^{+}$. We establish the comparison principle by the double variables method for the general equation $\Delta _\infty ^h u=F(x,u,Du)$ under some conditions on the term $F(x,t,p)$. Then, we establish the existence of viscosity solutions to the singular boundary value problem in a bounded domain based on Perron’s method and the comparison principle. Finally, we obtain the existence result in the entire Euclidean space by the approximation procedure. In this procedure, we also establish the local Lipschitz continuity of the viscosity solution.

We prove a nonarchimedean analogue of Jørgensen’s inequality, and use it to deduce several algebraic convergence results. As an application, we show that every dense subgroup of ${\mathrm {SL}_2}(K)$, where K is a p-adic field, contains two elements that generate a dense subgroup of ${\mathrm {SL}_2}(K)$, which is a special case of a result by Breuillard and Gelander [‘On dense free subgroups of Lie groups’, J. Algebra 261(2) (2003), 448–467]. We also list several other related results, which are well known to experts, but not easy to locate in the literature; for example, we show that a nonelementary subgroup of ${\mathrm {SL}_2}(K)$ over a nonarchimedean local field K is discrete if and only if each of its two-generator subgroups is discrete.

The Dehn quandle of a closed orientable surface is the set of isotopy classes of nonseparating simple closed curves with a natural quandle structure arising from Dehn twists. In this paper, we consider the finiteness of some canonical quotients of these quandles. For a surface of positive genus, we give a precise description of the 2-quandle of its Dehn quandle. Further, with some exceptions for genus more than 2, we determine all values of n for which the n-quandle of its Dehn quandle is finite. The result can be thought of as the Dehn quandle analogue of a similar result of Hoste and Shanahan for link quandles [‘Links with finite n-quandles’, Algebr. Geom. Topol. 17(5) (2017), 2807–2823]. We also compute the size of the smallest nontrivial quandle quotient of the Dehn quandle of a surface. Along the way, we prove that the involutory quotient of an Artin quandle is precisely the corresponding Coxeter quandle, and also determine the smallest nontrivial quotient of a braid quandle.

We establish a generalized Rieffel correspondence for ideals in equivalent Fell bundles.

In this article, we prove a generalized Rodrigues formula for a wide class of holonomic Laurent series, which yields a new linear independence criterion concerning their values at algebraic points. This generalization yields a new construction of Padé approximations including those for Gauss hypergeometric functions. In particular, we obtain a linear independence criterion over a number field concerning values of Gauss hypergeometric functions, allowing the parameters of Gauss hypergeometric functions to vary.

Let $G=(V, E)$ be a locally finite graph with the vertex set V and the edge set E, where both V and E are infinite sets. By dividing the graph G into a sequence of finite subgraphs, the existence of a sequence of local solutions to several equations involving the p-Laplacian and the poly-Laplacian systems is confirmed on each subgraph, and the global existence for each equation on graph G is derived by the convergence of these local solutions. Such results extend the recent work of Grigor’yan, Lin and Yang [J. Differential Equations, 261 (2016), 4924–4943; Rev. Mat. Complut., 35 (2022), 791–813]. The method in this paper also provides an idea for investigating similar problems on infinite graphs.

Given any rectangular polyhedron $3$ -manifold $\mathcal {P}$ tiled with unit cubes, we find infinitely many explicit directions related to cubic algebraic numbers such that all half-infinite geodesics in these directions are uniformly distributed in $\mathcal {P}$ .