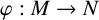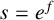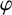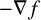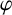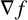GEOMETRY OF CLAIRAUT CONFORMAL RIEMANNIAN MAPS

Abstract

This article introduces the Clairaut conformal Riemannian map. This notion includes the previously studied notions of Clairaut conformal submersion, Clairaut Riemannian submersion, and the Clairaut Riemannian map as particular cases, and is well known in the classical theory of surfaces. Toward this, we find the necessary and sufficient condition for a conformal Riemannian map $\varphi : M \to N$ between Riemannian manifolds to be a Clairaut conformal Riemannian map with girth $s = e^f$. We show that the fibers of $\varphi $ are totally umbilical with mean curvature vector field the negative gradient of the logarithm of the girth function, that is, $-\nabla f$. Using this, we obtain a local splitting of M as a warped product and a usual product, if the horizontal space is integrable (under some appropriate hypothesis). We also provide some examples of the Clairaut conformal Riemannian maps to confirm our main theorem. We observe that the Laplacian of the logarithmic girth, that is, of f, on the total manifold takes the special form. It reduces to the Laplacian on the horizontal distribution, and if it is nonnegative, the universal covering space of M becomes a product manifold, under some hypothesis on f. Analysis of the Laplacian of f also yields the splitting of the universal covering space of M as a warped product under some appropriate conditions. We calculate the sectional curvature and mixed sectional curvature of M when f is a distance function. We also find the relationships between the total manifold and the fibers being symmetrical and, in particular, having constant sectional curvature, and from there, we compare their universal covering spaces, if fibers are also complete, provided f is a distance function. We also find a condition on the curvature tensor of the fibers to be semi-symmetric, provided that the total manifold is semi-symmetric and f is a distance function. In turn, this gives the warped product of symmetric, semi-symmetric spaces into two symmetric, semi-symmetric subspaces (under some hypothesis). Also if the Hessian or the Laplacian of the Riemannian curvature tensor fields is zero, or has a harmonic curvature tensor, then the fibers of $\varphi $ also satisfy the same property, if f is also a distance function. By obtaining Bochner-type formulas for Clairaut conformal Riemannian maps, we establish the relations between the divergences of the Ricci curvature tensor on fibers and horizontal space and the corresponding scalar curvature. We also study the horizontal Killing vector field of constant length and show that they are parallel under appropriate hypotheses. This in turn gives the splitting of the total manifold, if it admits a horizontal parallel Killing vector field and if the horizontal space is integrable. Finally, assuming that $\nabla f$ is a nontrivial gradient Ricci soliton on M, we prove that any vertical vector field is incompressible and hence the volume form of the fiber is invariant under the flow of the vector field.

1. Introduction

The geometry of Riemannian submersions has been effectively studied by several geometers since its formulation (see for example, [6, 11, 23, 33]). The theory of the Riemannian submersion was further generalized to that of the conformal submersion [8, 15] and the Riemannian map [7] independently. In 2010, Şahin generalized the idea of the conformal submersion and the Riemannian map to the conformal Riemannian map [31].

The well-known Clairaut relation states that for every geodesic $\gamma $ on a surface of revolution M, $(e^f \circ \gamma ) \sin \vartheta $ is constant, where $e^f$ is the distance of a point of M from the axis of rotation, and $\vartheta $ is the angle between the tangent vector of the geodesic and the meridian. Bishop [4] introduced the concept of the Clairaut Riemannian submersion using Clairaut’s relation for geodesics on surfaces of revolution [2, 29]. In 2017, the Clairaut condition for Riemannian maps was introduced by Şahin in [32]. Using a similar approach, Meena and Zawadzki extended the Clairaut condition for the conformal submersion in [19]. The current paper generalizes the concept of the Clairaut Riemannian submersion [4], the Clairaut conformal submersion [19], and the Clairaut Riemannian map [32] to the Clairaut conformal Riemannian map.

Note that these maps have possible applications in many different areas. For example, Riemannian submersions have applications in Yang–Mills theory, Klauza–Klein theory, gravity, relativity, supergravity theory, superstring theory, Morse theory, and so forth [6, 24, 33].

The conformal maps are the maps that preserve angles. Understanding the conformal Riemannian maps is fundamental for various branches of mathematics, including complex analysis, differential geometry, and theoretical physics. They provide a powerful tool for studying geometric structures, and have far-reaching applications in both pure and applied mathematics. The conformal factors of conformal maps provide an appropriate deformation that furnishes realistic models in applications. The conformal maps have applications in many areas, including the study of minimal surfaces, harmonic functions, and finding the solutions of partial differential equations. They are also essential in the theory of Riemann surfaces. In hyperbolic geometry, which is a non-Euclidean geometry, conformal maps play a crucial role in understanding the relationships between different models of hyperbolic space [30]. The conformal mappings also have applications in gravity [21], medical science (brain imaging), and computer graphics [12, 36–38, 43]. In addition, conformal maps are the most suitable candidates for harmonic morphisms; see [3, page 106].

The Riemannian maps satisfy the generalized eikonal equation, which is useful to build some quantum models [7]. We note that under certain regularity conditions, Riemannian maps (so called semi-Riemannian maps) were also considered in semi-Riemannian geometry with applications (see the book by Garcia-Rio and Kupeli [10]). The Clairaut theorem is a foundational mathematical tool with widespread applications across various scientific and engineering areas. Consequently, there are many possible applications of the Clairaut conformal maps in mathematics, physics, medical science, computer graphics, and so forth.

The paper is organized as follows. Section 2 is devoted to the preliminaries, which are used throughout the paper. In Section 3, we first define Clairaut conformal Riemannian maps and characterize them using the Clairaut relation. One relation is that the fibers are totally umbilical, which yields the splitting of total manifolds under appropriate conditions.

Section 4 deals with the Laplacian of the logarithm girth function. Employing suitable hypotheses on M, f, and so forth, we again get some splitting-type results.

Section 5 deals with the geometry of the Clairaut conformal Riemannian maps using distance functions, that is, $C^2$ functions f satisfying $\|{\nabla }f\|^2 = 1$ [26]. The important geometric properties, like symmetry, semi-symmetry, and so forth, of fibers are studied if the total manifold of the Clairaut conformal Riemannian map also satisfies the same property, provided that the logarithm of the girth of the map is a distance function. We also obtain splitting-type results in this section for these spaces.

In Section 6, we obtain generalized Bochner formulas for Clairaut conformal Riemannian maps. As an application, we study vertical and horizontal Killing vector fields of constant length, and consequently obtain the splitting of the fibers and the horizontal space, when it is integrable, under some appropriate geometric conditions.

Section 7 is the last section of the paper, which contains two subsections. In Section 7.1, we prove contracted-type Bianchi identities for the Clairaut conformal Riemannian maps. In Section 7.2, we study the geometry of the Clairaut conformal Riemannian maps whose total manifolds admit a Ricci soliton.

2. Preliminaries

In this section, we describe some preliminaries on the conformal Riemannian maps, which are used throughout our paper.

Let $\varphi : (M^m, g) \to (M^{\prime m'}, g')$ be a smooth map between Riemannian manifolds and $\varphi _{\ast p}: T_p M \to T_{\varphi (p)}M'$ be its differential map. We decompose the tangent space $T_{p}M$ into the kernel space of $\varphi _{\ast p}$ and its orthogonal complementary space. Also, we decompose the tangent space $T_{\varphi (p)}M'$ into the range space of $\varphi _{\ast p}$ and its orthogonal complementary space at a point $\varphi (p)\in M'$ . Then we can write

$$ \begin{align*} T_p M= (\ker \varphi_{\ast p}) \oplus(\ker \varphi_{\ast p})^\bot = \nu_p \oplus \mathfrak{h}_p \end{align*} $$

and

$$ \begin{align*} T_{\varphi(p)}M' = (\mathrm{range}~ \varphi_{\ast p}) \oplus(\mathrm{range}~ \varphi_{\ast p})^\bot. \end{align*} $$

The conformal Riemannian map ([31, Definition 1]): A map $\varphi :(M^m, g)$ $\to $ $(M^{\prime m'}, g')$ is said to be a conformal Riemannian map at $p \in M$ if $0 < \mathrm {rank}~ \varphi _{\ast p} \leq \min \{m, m'\}$ and there is dilation $\rho : M \to \mathbb {R}^{+}$ such that

(2-1) $$ \begin{align} g'(\varphi_{\ast p} X, \varphi_{\ast p} Y) = \rho^2(p) g(X, Y) \end{align} $$

for all $X, Y \in \Gamma (\ker \varphi _{\ast p})^\perp $ . The map $\varphi $ is called a conformal Riemannian map if $\varphi $ is a conformal Riemannian map at each point of M.

In what follows, the conformal Riemannian map means the conformal Riemannian map with dilation $\rho $ .

The O’Neill tensors ([23, Section 2]): These tensors, commonly denoted by A and T, are defined as

(2-2) $$ \begin{align} A_{\xi_1} \xi_2= \mathfrak{h} \,\nabla_{\mathfrak{h}\xi_1} \nu \xi_2 + \nu \,\nabla_{\mathfrak{h}\xi_1} \mathfrak{h}\xi_2, \end{align} $$

(2-3) $$ \begin{align} T_{\xi_1} \xi_2= \mathfrak{h} \,\nabla_{\nu \xi_1} \nu \xi_2 + \nu \,\nabla_{\nu \xi_1} \mathfrak{h}\xi_2, \end{align} $$

for all $\xi _1, \xi _2 \in \Gamma (TM)$ , where $\,\nabla $ is the Levi-Civita connection of g. For any $\xi _1 \in \Gamma (TM) $ , the tensors $T_{\xi _1}$ and $A_{\xi _1}$ are skew-symmetric operators on $(\Gamma (TM),g)$ reversing the horizontal and vertical distributions.

It is also easy to see that T is vertical, that is, $T_{\xi _1} = T_{\nu \xi _1} $ and A is horizontal, that is, $A_{\xi _1} = A_{\mathfrak {h}\xi _1} $ . We note that the tensor field T satisfies $T_U W = T_W U\ \text{for all} U,W \in \Gamma (\ker \varphi _\ast )$ . See [23] for more details on these tensors.

Now from (2-2) and (2-3), we have for all $X, Y \in \Gamma (\ker \varphi _\ast )^\bot $ and $U, V \in \Gamma (\ker \varphi _\ast )$ :

(2-4) $$ \begin{align} \nabla_U V &= T_U V + \nu \,\nabla_U V = T_U V + {\hat{\nabla}}_U V, \end{align} $$

(2-5) $$ \begin{align} \hspace{-11pt}\nabla_X U &= A_X U + \nu \,\nabla_X U,\qquad\qquad\quad\end{align} $$

(2-6) $$ \begin{align} \hspace{-11pt}\nabla_X Y &= A_X Y + \mathfrak{h} \,\nabla_X Y.\qquad\qquad\quad\end{align} $$

Totally umbilical fibers ([33, (5.40)]): A Riemannian map has totally umbilical fibers if

$$ \begin{align*} T_U V = g(U, V) H\quad\mathrm{or}\quad T_U X = -g(H, X)U \end{align*} $$

for all $U, V \in \Gamma (\ker \varphi _\ast )$ and $X \in \Gamma (\ker \varphi _\ast )^\perp $ , where the mean curvature vector field of the fiber is defined as

$$ \begin{align*} H = \frac{1}{r}\sum_{i=1}^{r} T_{U_i} U_{i} \end{align*} $$

for $\{U_i\}_{i=1}^{r}$ , an orthonormal basis of the fiber of $\varphi $ .

The second fundamental form of a Riemannian map ([33, Definition 23]): The second fundamental form of a Riemannian map $\varphi $ is defined as

(2-7) $$ \begin{align} ({\,\nabla} \varphi_\ast) (\xi_1, \xi_2) = {\,\nabla}_{\xi_1}^\varphi \varphi_\ast ({\xi_2}) - \varphi_\ast({\,\nabla}_{\xi_1} \xi_2) \end{align} $$

for all $\xi _1, \xi _2 \in \Gamma (TM)$ . Here ${\,\nabla }_{\xi _1}^\varphi \varphi _\ast ({\xi _2}) = {\,\nabla }_{\varphi _\ast \xi _1}^{\prime } {\varphi _\ast \xi _2}$ , where $\,\nabla '$ is the Levi-Civita connection on $M'$ and $\,\nabla ^\varphi $ is the pull back of the connection of $\,\nabla '$ under $\varphi $ .

The adjoint of the covariant derivative ([26, page 59]): The adjoint of the covariant derivative of $(0,~ k)$ -tensor $\mathcal {T}$ is defined as

(2-8) $$ \begin{align} (\,\nabla^{\ast}~ \mathcal{T})(X_2, X_3,\ldots,X_k) = \sum_{i=1}^{m} (\nabla_{E_i} \mathcal{T})(E_i, X_2,\ldots,X_k), \end{align} $$

where $\{X_{i}\}_{1 \leq i \leq m}$ are smooth vector fields and $\{E_i\}_{1 \leq i \leq m}$ is an orthonormal frame in some neighborhood of $p \in M$ .

Further, it follows that

(2-9) $$ \begin{align} \nabla^{*} \,\nabla \mathcal{T} = \mathrm{trace } \,\nabla^2 \mathcal{T} = \Delta \mathcal{T}, \end{align} $$

where $\,\nabla \mathcal {T}$ and $\Delta \mathcal {T}$ denote the covariant derivative and Laplacian of $\mathcal {T}$ , respectively.

Now we recall some results that are used later in our investigation.

Lemma 2.1 [31 Lemma 4.1].

Let $\varphi : (M^m, g) \to (M^{\prime m'}, g')$ be a conformal Riemannian map between Riemannian manifolds. Then

$$ \begin{align*} \sum\limits_{a = r+1}^{m} g'((\nabla \varphi_\ast)(X, Y), \bar{Z}_a)\bar{Z}_a = X (\ln \rho) \bar{Y} + Y (\ln \rho) \bar{X} -g(X, Y)~ \varphi_\ast (\nabla \ln \rho), \end{align*} $$

where $\{\bar {Z}_a\}_{a = r+1}^{m}$ is an orthonormal frame of $\mathrm {range}~\varphi _\ast $ in some neighborhood of $\varphi (p)$ , and $X, Y \in \Gamma (\ker \varphi _\ast )^\bot $ are the horizontal lifts of $\bar {X}, \bar {Y}$ , respectively.

Thus, we have the following decomposition.

Lemma 2.2 [34, Theorem 2.1].

Let $\varphi : (M, g) \to (M', g')$ be a conformal Riemannian map between Riemannian manifolds. Then

$$ \begin{align*} (\nabla \varphi_\ast) (X, Y)= (\nabla \varphi_\ast)^{(\mathrm{range}~ \varphi_\ast)} (X, Y) + (\nabla \varphi_\ast)^{(\mathrm{range}~ \varphi_\ast)^\perp} (X, Y), \end{align*} $$

where

(2-10) $$ \begin{align} (\nabla \varphi_\ast)^{(\mathrm{range}~ \varphi_\ast)} (X, Y) = X (\ln \rho) \varphi_\ast Y + Y (\ln \rho) \varphi_\ast X -g(X, Y) \varphi_\ast (\nabla \ln \rho) \end{align} $$

for all basic vector fields $X, Y$ .

In what follows, we require the fundamental tensor A for the conformal Riemannian map, which has the following expression.

Proposition 2.3 [13, Lemma 2.1].

Let $\varphi : (M, g) \to (M', g')$ be a conformal Riemannian map between Riemannian manifolds. Then

$$ \begin{align*} 2 A_X Y = \nu [X, Y] - \rho^2 g(X, Y) \bigg(\nabla_\nu \frac{1}{\rho^2}\bigg) \end{align*} $$

for all $X, Y \in \Gamma (\ker \varphi _\ast )^\bot $ .

It is interesting to know under what conditions a given Riemannian manifold splits. We use the following splitting theorem in this context.

Theorem 2.4 (Splitting theorem (see [16, Theorem 6.1, page 187])).

Suppose $(M^m, g)$ is a connected and complete Riemannian manifold admitting a nonzero parallel vector field. Then the universal cover of $(M, g)$ splits isometrically as a product $N^{(m-1)} \times \mathbb {R}$ , where N is a Riemannian submanifold of N.

3. The Clairaut conformal Riemannian maps

In this section, we explore the geometry of Clairaut conformal Riemannian maps. First, we characterize the geodesics of conformal Riemannian maps (Proposition 3.1). Then using this characterization, we obtain a necessary and sufficient condition for a conformal Riemannian map to be a Clairaut conformal Riemannian map. It turns out that, in this case, the fibers of $\varphi $ are totally umbilical with mean curvature vector field $-\nabla f$ (Theorem 3.2). From this main result (under some hypothesis), we obtain the splitting of the total manifold as the warped product or usual product of horizontal integral submanifolds of M and fibers (Corollary 3.4). We also give an example and a family of Clairaut conformal Riemannian maps and show that they indeed satisfy the necessary and sufficient conditions of Theorem 3.2.

We recall that the Clairaut condition for Riemannian and conformal submersions was first studied by [4, 19], respectively. Also, the Clairaut condition for Riemannian maps was explored in [32]. In this article, we further generalize this notion to introduce the Clairaut conformal Riemannian map and investigate its geometry in detail.

Clairaut conformal Riemannian map: A conformal Riemannian map $\varphi : (M, g)\to (M', g')$ between Riemannian manifolds is said to be the Clairaut conformal Riemannian map if there is a function $s: M \to \mathbb {R}^{+}$ such that for every geodesic $\gamma $ on M, the function $(s \circ \gamma ) \sin \vartheta (t)$ is constant along $\gamma $ , where for all t, $\vartheta (t)$ is the angle between $\dot {\gamma }(t)$ and the horizontal space at $\gamma (t)$ . Following the terminology already used in [1], we call s the girth of the Clairaut conformal Riemannian map.

We know that with the help of Clairaut’s theorem, we can find all the geodesics on a surface of revolution. It should also be observed that the notion of the Clairaut conformal Riemannian map is based on the geodesic curve. We find necessary and sufficient conditions for a curve on the total space $(M, g)$ to be a geodesic, by using techniques similar to [19, 32].

Proposition 3.1. Let $\varphi : (M, g)\to (M', g')$ be a conformal Riemannian map between Riemannian manifolds. Let $\gamma : I \to M$ be a regular curve on M such that $U(t) = \nu \dot {\gamma }(t)$ and $X(t)= \mathfrak {h} \dot {\gamma }(t)$ . Then $\gamma $ is a geodesic on M if and only if

(3-1) $$ \begin{align} A_X X + \nu \,\nabla_X U + T_U X + {\nu \,\nabla_U U}=0 \end{align} $$

and

(3-2) $$ \begin{align} {\,\nabla}_X^\varphi \varphi_\ast X & = 2X (\ln \rho) \varphi_\ast X - \|X\|^2 \varphi_\ast (\nabla \ln \rho) \nonumber \\ &\quad + (\nabla \varphi_\ast)^{(\mathrm{range}~ \varphi_\ast)^\perp} (X, X) - \varphi_\ast(2 A_X U + T_U U). \end{align} $$

Now we prove the main result of this section, that is, we find a necessary and sufficient condition for a conformal Riemannian map to be the Clairaut conformal Riemannian map.

Theorem 3.2. Let $\varphi : (M, g)\to (M', g')$ be a conformal Riemannian map between Riemannian manifolds such that the fibers of $\varphi $ are connected. Then $\varphi $ is the Clairaut conformal Riemannian map with girth $s = e^f$ , where f is a smooth function on M, if and only if the fibers of $\varphi $ are totally umbilical with the mean curvature vector field $-\nabla f$ , and also the dilation $\rho $ along each fiber of $\varphi $ is constant.

Proof. First we prove that $\varphi $ is a Clairaut conformal Riemannian map with $s = e^f$ if and only if for any geodesic $\gamma : I \rightarrow M$ with $U(t)= \nu \dot {\gamma }(t)$ and $X(t)= \mathfrak {h} \dot {\gamma }(t)$ , $t \in I \subset \mathbb {R}$ , the equation

(3-3) $$ \begin{align} &g(U(t), U(t)) g(\dot{\gamma}(t), (\nabla f)_{\gamma(t)} ) \nonumber\\ &\quad+\frac{\rho^2}{2}g\bigg(\nabla_\nu \frac{1}{\rho^2}, U(t) \bigg) g(X(t), X(t)) + g((T_U U)(t), X(t)) = 0 \end{align} $$

is satisfied. To prove this, let $\vartheta (t) \in [0, {\pi }/{2}]$ denote the angle between $\dot {\gamma }(t)$ and $X(t)$ . Let the speed of $\gamma $ be constant, $a = \|\dot {\gamma }\|^2$ (say). Now

(3-4) $$ \begin{align} g(X, X) = a \cos^2 \vartheta(t) \end{align} $$

and

(3-5) $$ \begin{align} g(U, U) = a \sin^2 \vartheta(t). \end{align} $$

Differentiating (3-4) and substituting (3-2) yields that

(3-6) $$ \begin{align} g(A_X X, U) - g (T_U U, X) = - a \sin \vartheta(t) \cos \vartheta (t) \frac{d \vartheta } {dt}. \end{align} $$

Moreover, $\varphi $ is a Clairaut conformal Riemannian map with $s=e^f$ if and only if ${d}/{dt} (e^{f\circ \gamma } \sin \vartheta ) = 0$ , that is,

(3-7) $$ \begin{align} \cos\vartheta \frac{d\vartheta}{dt} + \sin\vartheta \frac{df}{dt}= 0. \end{align} $$

By (3-5), (3-6), and (3-7), and using Proposition 2.3, we confirm (3-3).

If at any $t_0$ , $\dot {\gamma } \in \Gamma (\ker \varphi _\ast )$ , that is, $X(t_0) = 0$ , then by (3-3),

$$ \begin{align*}g(U, U) g(U, \nabla f) = 0;\end{align*} $$

this implies that $U(f) = 0$ . Thus, f is constant on any fiber as the fibers are connected. Consequently, $\,\nabla f$ is horizontal.

Hence, by similar arguments to those in [19], we obtain a pair of equations:

(3-8) $$ \begin{align} g(T_U U, X) + g(U, U) g(X, \nabla f) =0 \end{align} $$

and

(3-9) $$ \begin{align} \frac{\rho^2}{2} g(X, X) g\bigg(U, \nabla_\nu \frac{1}{\rho^2}\bigg) =0 \end{align} $$

for all vertical U and horizontal X.

From (3-8), it follows that the fibers are totally umbilical with mean curvature vector field $-\mathfrak {h} \,\nabla f = - \,\nabla f$ (as shown above, $\nabla f$ is the horizontal vector field). Also, from (3-9), we conclude that $\rho $ is constant along fibers. This completes the proof.

Remark 3.3.

1. (i) Henceforth, (3-8) and (3-9) are referred to as the Clairaut conditions. We call the function f in the above theorem the logarithmic girth function [1]. In the next section, we explore the geometry of this function in detail.

2. (ii) The proof of Theorem 3.2 shows that f and the dilation $\rho $ are constant on any fiber. Hence, f and $\rho $ can be regarded as functions on the horizontal space (when the horizontal space is integrable).

3. (iii) In view of the above remark, we see that indeed the geometry of the Clairaut conformal Riemannian map $\varphi $ is concentrated on horizontal space. Hence, we can regard it as a horizontal Clairaut conformal Riemannian map.

It should be noted that Garcia-Rio and Kupeli obtained splitting theorems for Riemannian manifolds by assuming the existence of Riemannian maps between them under certain conditions on Ricci curvature, scalar curvature, and the tension field [9]. Now using the above theorem, we obtain the splitting of the total manifold under some hypotheses.

Note: In what follows, we denote the universal covering space of a manifold N by  $\tilde {N}$ .

Corollary 3.4. Let $\varphi $ satisfy the hypotheses of Theorem 3.2, and also suppose that $\varphi $ is the Clairaut conformal Riemannian map with girth $s = e^f$ , where f is a smooth function on M. Let the horizontal space be integrable and $L_{\mathfrak {h}}$ denote a leaf of the horizontal space, and let $F_{\nu }$ denote a fiber of $\varphi $ . Then, we have the following.

1. (i) M splits as $M = {L_{\mathfrak {h}}}\times _f F_{\nu }$ , that is, M is a locally twisted product of the leaf of the horizontal space and the fiber. In particular, if the horizontal space is one-dimensional, then $ M$ is locally the warped product ${L_{\mathfrak {h}}}\times _f F_{\nu }$ , where $ {L_{\mathfrak {h}}}$ is of dimension $1$ . Consequently, $\tilde M$ splits as $\tilde M = {\tilde L_{\mathfrak {h}}} \times _f \tilde {F_{\nu }}$ , that is, the universal covering space of M is isometric to the warped product of the universal covering space of the leaf of the horizontal space and the universal covering space of the fiber.

2. (ii) If $\mathrm {Hess } f = 0$ , then we have local splitting of M as ${L_{\mathfrak {h}}}\times F_{\nu }$ , and isometric splitting of $\tilde M$ as $\tilde M = {\tilde L_{\mathfrak {h}}} \times \tilde {F_{\nu }}$ .

Proof. (i) From Theorem 3.2, if $\varphi $ is a Clairaut conformal Riemannian map, then the fibers of $\varphi $ are totally umbilical and $\rho $ is constant along the fibers of $\varphi $ . Also by hypothesis, as the horizontal space is integrable, A is zero (see [6, pages 10 and 11]). Therefore, $L_{\mathfrak {h}}$ is totally geodesic. Thus, by [28, Proposition 3(b)], M is the locally twisted product of the leaf of the horizontal space and the fiber. Clearly, by Remark 3.3(ii), we can regard f to be a function on the space ${L_{\mathfrak {h}}}$ . Hence, the twisted product reduces to the warped product. The second conclusion follows from the de Rham decomposition-type theorem [28, Theorem 1].

(ii) If $\mathrm {Hess } f = 0$ on M, then the fibers of $\varphi $ give rise to a spherical foliation on M (see [22]), as in this case, the mean curvature vector field of the fibers of $\varphi $ is parallel. Hence, by the Clairaut condition (3-8), T is parallel and consequently, $T \equiv 0$ . This implies that $F_{\nu }$ is totally geodesic. Thus we affirm [28, Corollary 1(ii)].

Corollary 3.5. Let $\varphi $ satisfy the hypotheses of Theorem 3.2, and also suppose that $\varphi $ is the Clairaut conformal Riemannian map with girth $s = e^f$ , where f is a smooth function on M. If the map $\varphi $ is totally geodesic, then $\varphi $ becomes a simply Clairaut Riemannian map and we have local splitting of M as ${L_{\mathfrak {h}}} \times F_{\nu }$ , and isometric splitting of $\tilde M$ as $\tilde M = {\tilde L_{\mathfrak {h}}} \times {\tilde F_{\nu }}$ .

Proof. If the map $\varphi $ is totally geodesic, then from (2-10), it follows that $\rho $ is constant along the leaves of the horizontal space. From Remark 3.3(ii), $\rho $ is constant along the fibers of $\varphi $ . Hence, $\rho $ is constant on M and therefore, $\varphi $ is a simply Clairaut Riemannian map. From Proposition 3.1 and Theorem 3.2, we conclude that in this case, $A = 0$ and $T = 0$ . Consequently, the conclusion follows from [28, Proposition 3(d)].

Example 3.6. Consider two Riemannian manifolds

$$ \begin{align*}\!(M = \mathbb {R}^{4}, g = e^{2x_1} dx_1^2 + e^{2x_1} dx_2^2+ e^{2x_2} dx_3^2 + e^{2x_3} dx_4^2)\end{align*} $$

and

$$ \begin{align*}(M' = \mathbb {R}^{3}, g' = dy_1^2 + dy_2^2 + dy_3^2 + dy_4^2).\qquad\qquad\quad\end{align*} $$

Let $\varphi : (M, g) \to (M', g')$ be given by

$$ \begin{align*} \varphi(x_1, x_2, x_3, x_4) = (\cos x_1, \sin x_1, \cos x_2, \sin x_2). \end{align*} $$

Then

$$ \begin{align*} \ker \varphi_\ast = \mathrm{span } \{ E_3, E_4\}\quad\text{and}\quad (\ker \varphi_\ast)^\perp = \mathrm{span} \{ E_1, E_2\}, \end{align*} $$

where $\{E_1 = e^{-x_1} {\partial }/{\partial x_1}, E_2 = e^{-x_1} {\partial }/{\partial x_2}, E_3 = e^{-x_2} {\partial }/{\partial x_3}, E_4 = e^{-x_3} {\partial }/{\partial x_4}\}$ is an ortho- normal basis of $T_p M$ for all $p\in M$ . Let $\{E_i^{\prime } = {\partial }/{\partial y_i}$ for $i = 1, 2, 3, 4\}$ be a basis of $T_{\varphi (p)} M'$ . An easy computation shows that $\varphi $ is the conformal Riemannian map with dilation $\rho = e^{-x_1}$ . Clearly, the dilation is constant on $\ker \varphi _\ast $ . The covariant derivatives using Christoffel symbols for the metric g are

$$ \begin{align*} \,\nabla_{E_3} E_3 = - e^{-x_1} E_2,\quad \,\nabla_{E_4} E_3 = e^{-x_2} E_4,\quad \,\nabla_{E_3} E_4 = 0\quad \mathrm{and}\quad \,\nabla_{E_4} E_4 = - e^{-x_2} E_3. \end{align*} $$

Then for $U \in \Gamma (\ker \varphi _\ast )$ and $a_1, a_2 \in \mathbb {R}$ ,

$$ \begin{align*} \,\nabla_U U &= \,\nabla_{a_1 E_3 + a_2 E_4} (a_1 E_3 + a_2 E_4) \nonumber \\ &= - a_1^2 e^{-x_1} E_2 - a_2^2 e^{-x_2} E_3 + a_1 a_2 e^{-x_2} E_4. \end{align*} $$

Consequently,

$$ \begin{align*} T_U U= \mathfrak{h} (\nabla_U U) = e^{-x_1} E_2. \end{align*} $$

In conclusion, $\varphi $ is the Clairaut conformal Riemannian map with dilation $\rho = e^{-x_1}$ and logarithmic girth function $f = {-x_2}/({a_1^2 + a_2^2})$ .

Example 3.7. Let $M = M_1 ~{}_\rho \times _{s} M_2$ be a doubly warped product [24] of two Riemannian manifolds $(M_1, g_{\mathfrak {h}})$ and $(M_2, g_\nu )$ with the Riemannian metric

$$ \begin{align*} g = (\rho \circ \varphi_2)^2 \varphi_1^\ast(g_{\mathfrak{h}}) + (s \circ \varphi_1)^2 \varphi_2^\ast(g_\nu), \end{align*} $$

where s and $\rho $ are positive smooth functions on $M_1$ and $M_2$ . We can see the first projection $\varphi _1 : M_1 ~{}_\rho \times _{s} M_2 \to M_1$ is a conformal submersion onto $M_1$ whose vertical and horizontal spaces at $(p_1,~ p_2)$ are identified with $T_{p_2} M_2$ and $T_{p_1} M_1$ , respectively. Since the horizontal distribution is integrable, the O’Neill tensor A vanishes. Now, to compute another O’Neill tensor T, we use Koszul’s formula to get

$$ \begin{align*} T_U V = - g(U, V) ~ \nabla_{\mathfrak{h}} \log (s), \end{align*} $$

where $U, V \in \Gamma (\ker {\varphi _1}_{\ast })$ . Thus, any fiber of $\varphi _1$ turns out to be totally umbilical. Also, we can prove easily that $\rho $ is constant along the fibers of $\varphi _1$ . We now consider the conformal immersion $\varphi _2 : M_1 \to M_1 ~{}_\rho \times _{s} M_2$ ; then the composite map $\varphi _2 \circ \varphi _1$ is a conformal Riemannian map. Moreover, projection $\varphi _1$ and map $\varphi _2 \circ \varphi _1$ have the same vertical distribution. Hence, $\varphi _2 \circ \varphi _1$ is a Clairaut conformal Riemannian map with dilation $\rho $ and girth s.

Note: It should be noted that in the following, $\varphi $ denotes the Clairaut conformal Riemannian map between Riemannian manifolds $(M^m,g)$ and $(M^{\prime m'}, g')$ with girth $s = e^f$ and dilation $\rho $ .

4. The Laplacian of the logarithmic girth function

In this section, we study the Laplacian of the logarithmic girth function on the fibers, total manifold, and on the vertical and horizontal spaces. From the analysis of the Laplacian, we split the total manifold in various contexts.

Remark 4.1. Note that because $\,\nabla f$ is horizontal,

$$ \begin{align*} \mathrm{\hat{H}ess } f(U, V) = \hat{\nabla}^2f(U, V) = g(\nabla_{U} \nu \,\nabla f , V) = 0. \end{align*} $$

Thus, the Laplacian on the fibers $\hat {\Delta } f$ vanishes.

Theorem 4.2. If $\Delta f$ denotes the Laplacian on M, then

(4-1) $$ \begin{align} \Delta f = \frac{1}{\rho^2} \mathrm{div}_{(\mathrm{range}~\varphi_\ast)}(\varphi_\ast \,\nabla f) - (m-r) g(\nabla f, \nabla \ln \rho), \end{align} $$

where $r = \dim (\ker \varphi _\ast )$ and $(m - r) = \dim (\ker \varphi _\ast )^\perp $ .

Proof. The Laplacian of a function f on the fibers is zero (see Remark 4.1).

However, the Laplacian of a function f on M is defined as

$$ \begin{align*} \Delta f = \mathrm{trace \ Hess}~ f(\xi_1, \xi_2), \end{align*} $$

where $\xi _1, \xi _2 \in \Gamma (TM)$ . Then

$$ \begin{align*} \Delta f & =\sum\limits_{i = 1}^{r} g(\nabla_{U_i} \,\nabla f, U_i) + \sum\limits_{j=r+1}^{m} g(\nabla_{X_j} \,\nabla f, X_j) \nonumber\\ & =-\sum\limits_{i = 1}^{r} g(\nabla_{U_i} U_i, \nabla f) + \frac{1}{\rho^2}\sum\limits_{j=r+1}^{m} g'(\varphi_\ast(\nabla_{X_j} \,\nabla f), \varphi_\ast(X_j))\\ & = \frac{1}{\rho^2}\sum\limits_{j=r+1}^{m} g'(\varphi_\ast(\nabla_{X_j} \,\nabla f), \varphi_\ast(X_j)), \end{align*} $$

where $\{U_i\}_{i=1}^{r}$ and $\{X_j\}_{j= r+1}^{m}$ are orthonormal frames of $\ker \varphi _\ast $ and $(\ker \varphi _\ast )^\perp $ , respectively, in a neighborhood of some fixed $p \in M$ , which are parallel at $p \in M$ . Now, using (2-7) and the fact that fibers are totally umbilical with mean curvature vector field $-\nabla f$ (Theorem 3.2), in the above equation, we get at p,

$$ \begin{align*} \Delta f &= \frac{1}{\rho^2} \sum_{j =r+1}^{m}g'(\nabla_{X_j}^\varphi \varphi_\ast (\nabla f)-(\nabla \varphi_\ast)(X_j, \nabla f), \varphi_\ast X_j)\\&= \frac{1}{\rho^2} \sum_{j =r+1}^{m} \{ g'(\nabla_{\varphi_\ast X_j}^{\prime} (\varphi_\ast (\nabla f)), \varphi_\ast X_j) - g'((\nabla \varphi_\ast)(X_j, \nabla f), \varphi_\ast X_j)\}. \end{align*} $$

Finally, applying Lemmas 2.2 and 2.1 in the above equation, after some simplifications, we get at p,

$$ \begin{align*} \Delta f = \frac{1}{\rho^2} \mathrm{div}_{(\mathrm{range}~\varphi_\ast)}(\varphi_\ast \,\nabla f) - (m-r) g(\nabla f, \nabla \ln \rho).\\[-42pt] \end{align*} $$

Remark 4.3. By the above theorem, we observe that the Laplacian on the total manifold $\Delta f$ is the same as the Laplacian on the horizontal space $\Delta ^{\mathfrak {h}} f$ , because the Laplacian on the vertical space $\Delta ^\nu f$ vanishes.

Corollary 4.4. If M is compact and if $f = C \rho $ , where $C> 0$ is some constant, then both f and $\rho $ are constants. Consequently, the fibers of $\varphi $ are totally geodesic, $\varphi $ becomes simply a Riemannian map, and $\tilde M$ is the product manifold, provided that the horizontal space is integrable. In particular, the same conclusion follows if the horizontal space is of dimension one.

Proof. From (4-1),

$$ \begin{align*} \Delta f = \frac{1}{\rho^2} \mathrm{div}_{(\mathrm{range}~ \varphi_\ast)}(\varphi_\ast \,\nabla f) - (m-r) g(\nabla f, \nabla \ln \rho). \end{align*} $$

By hypothesis, it follows that

$$ \begin{align*} \int\nolimits_{M} f g(\nabla f, \nabla f)\,d\Omega_M = 0. \end{align*} $$

This shows that f is constant and hence the conclusion follows.

Note that both $\,\nabla f$ and $\nabla \rho $ are horizontal vectors, as $\rho $ is constant on each fiber of $\varphi $ (Theorem 3.2). In particular, if the horizontal space is of dimension $1$ , then clearly $f = C \rho $ and the same conclusion holds and the splitting occurs with horizontal leaves (connected) being of one dimension.

Proposition 4.5. Suppose that M is complete. If $\Delta ^{\mathfrak {h}}f$ is nonnegative and $\|df\| \in L^1(M)$ , then f is a constant function on M.

Proof. By Remark 4.1,

$$ \begin{align*} \Delta f = \Delta^{\mathfrak{h}}f. \end{align*} $$

Since $\Delta ^{\mathfrak {h}}f \geq 0$ , $\Delta f \geq 0$ . Then by the corollary in [42, Section 1], if $\int _{M} \|df\| < \infty $ , then $\Delta f = 0$ . However, then $\Delta {f}^2 = 2 f \Delta f + 2 \|df\|^2 = 2 \|df\|^2$ . But again, by the same argument as above, as $\|df\| \in L^1(M)$ , $\Delta {f}^2 = 0$ . Consequently, f is a constant function on M.

Corollary 4.6. Under the hypotheses of the above proposition, the following hold.

1. (i) Any regular curve on M is a geodesic.

2. (ii) If the horizontal space is integrable, then we have local splitting of M as ${L_{\mathfrak {h}}} \times F_{\nu }$ , and isometric splitting of $\tilde M$ as $\tilde M = {\tilde L_{\mathfrak {h}}} \times {\tilde F_{\nu }}$ .

Proof. As in this case f is constant (the conformal factor $\rho $ is non-constant), we obtain the following.

1. (i) By (3-7), $\cos \vartheta ~ ({d \vartheta }/{dt}) = 0$ , which implies either $\vartheta $ is constant or $\vartheta $ is an integral multiple of $\pi /2$ . In any case, the Clairaut condition implies that any regular curve is a geodesic. Hence item (i) follows.

2. (ii) Because f is constant, the fibers of $\varphi $ are totally geodesic submanifolds of M and hence $T_U U \equiv 0$ . Therefore, item (ii) follows, if the horizontal space is integrable ([28, Proposition 3(d)]).

5. Geometry of fibers if the logarithmic girth function is a distance function

In this section, we mainly show that the fibers of a Clairaut conformal Riemannian map satisfy some central geometric properties like symmetry, semi-symmetry (under some hypothesis on the curvature tensor), provided that the total manifold satisfies the same condition and if the logarithmic girth function f is a distance function, that is, $\|\,\nabla f\| \equiv 1$ . In particular, we obtain that if $\tilde {M}$ is isometric to a Euclidean space or sphere or hyperbolic space, then the universal covering space of the fibers is isometric to a sphere or sphere of radius ${1}/\!{\sqrt 2}$ or Euclidean space, respectively. We also confirm the splitting of the universal coverings of symmetric spaces and semi-symmetric spaces (under some conditions).

We use the techniques of [26, Theorem 9.4.2] for the general computations involved in this section. In what follows, we use the Riemannian curvature tensor R of M defined by

$$ \begin{align*} R(\xi_1, \xi_2)\xi_3 = \,\nabla_{\xi_1} \,\nabla_{\xi_2} \xi_3 - \,\nabla_{\xi_2} \,\nabla_{\xi_1} \xi_3 - \,\nabla_{[\xi_1, \xi_2]} \xi_3, \end{align*} $$

where $\xi _1, \xi _2, \xi _3 \in \Gamma (TM)$ .

In this section, we use the concepts of symmetric space, semi-symmetric space, and harmonic curvature tensor.

Symmetric space [26]: A Riemannian manifold is locally symmetric if and only if $\,\nabla R \equiv 0$ . A locally symmetric Riemannian manifold is called globally symmetric if it is complete and also simply connected.

Space form [26]: A complete Riemannian manifold of constant sectional curvature is called a Riemannian space form.

In particular, the space of constant sectional curvature is a locally symmetric space.

Semi-symmetric space [35]: A Riemannian manifold is said to be semi-symmetric if $R(\xi _1, \xi _2)\cdot R = 0$ for $\xi _1, \xi _2 \in \Gamma (TM)$ . The equation $R(\xi _1, \xi _2) \cdot R = 0$ is equivalent to

$$ \begin{align*} (R(\xi_1, \xi_2) \cdot R)(\xi_3, \xi_4)\xi_5 &= R(\xi_1, \xi_2) R(\xi_3, \xi_4)\xi_5 - R(R(\xi_1, \xi_2)\xi_3, \xi_4)\xi_5 \\ &\quad - R(\xi_3, R(\xi_1, \xi_2)\xi_4)\xi_5 - R(\xi_3, \xi_4)R(\xi_1, \xi_2)\xi_5 \end{align*} $$

for all ${\xi _1, \xi _2, \xi _3, \xi _4, \xi _5} \in \Gamma (TM)$ .

For the detailed study of semi-symmetric spaces, we refer to [35] and the references therein.

Harmonic curvature tensor [26]: A Riemannian manifold is said to have harmonic curvature tensor if $\Delta R = 0$ (see (2-9)).

For some applications of the harmonic curvature tensor, see [27].

Proposition 5.1. Let $\varphi : (M, g)\to (M', g')$ be a Clairaut conformal Riemannian map between Riemannian manifolds with $s = e^f$ . If f is a distance function, then for $U, V, W, E \in \Gamma (\ker \varphi _\ast )$ and $X, Y \in \Gamma (\ker \varphi _\ast )^\perp $ ,

(5-1) $$ \begin{align} g(R(U, V)W, E) &= g(\hat{R}(U, V)W, E) - g(V, W) g(U, E) + g(U, W) g(V, E), \end{align} $$

(5-2) $$ \begin{align} g(R(U, V)W, X) &= -g(V, W) g(\nabla_U \,\nabla f, X) + g(U, W) g(\nabla_V \,\nabla f, X),\qquad\quad \end{align} $$

(5-3) $$ \begin{align} g(R(U, X)Y, V) &= g((\nabla_U A)_X Y, V) + g(A_X U, A_Y V) \nonumber\\ &\quad -g(\nabla_X \,\nabla f, Y) g(U, V) - X(f)Y(f) g(U, V),\qquad\qquad \end{align} $$

where R and $\hat {R}$ denote the Riemannian curvature tensors of M and fibers of $\varphi $ , respectively.

Proof. Using Theorem 3.2 and the fact that $\|\,\nabla f\|^2 = 1$ in the first three statements of [13, Lemma 2.2], we get the required result.

Corollary 5.2. Under the hypothesis of the above proposition, if $U, V, X$ are mutually linearly independent vectors, then the following statements hold.

1. (i) $\mathrm {sec}(U, V) = \mathrm {\hat {s}ec} (U, V) - ({\{\|U\|^2 \|V\|^2 - g(U, V)^2\}})/{\|U \wedge V\|^2}$ , where $\mathrm {\hat {s}ec}(U, V)$ denotes the sectional curvature of the plane P spanned by $U, V$ on the fibers of $\varphi $ . Consequently, if M has nonnegative sectional curvatures, then the fibers of $\varphi $ too have nonnegative sectional curvatures.

2. (ii) $\mathrm {sec}(U, X) = ({\|A_X U\|^2 - \{g(\nabla _X \,\nabla f, X) + X(f)^2\} \|U\|^2 })/{\|X\|^2 \|U\|^2}$ , where $\mathrm {sec}(U, X)$ denotes the mix sectional curvature of the plane P spanned by $U, X$ on M. Consequently, we have the inequality:

   $$ \begin{align*} \mathrm{sec}(U, X) \geq \frac{-\{g(\nabla_X \,\nabla f, X) + X(f)^2\}}{\|X\|^2}. \end{align*} $$

The equality holds in the above inequality if and only if the horizontal space is integrable.

Proof. Let $U, V$ be two linearly independent vectors. Now, substituting $W = U$ and $E = V$ in (5-1),

$$ \begin{align*} g(R(U, V, V, U)) = g(\hat{R}(U, V, V, U)) - g(U, U) g(V, V) + (g(U, V))^2, \end{align*} $$

which shows that

$$ \begin{align*} \mathrm{sec}(U, V) = \mathrm{\hat{s}ec } (U, V) - \frac{\|U\|^2 \|V\|^2}{\|U \wedge V\|^2} + \frac{g(U, V)^2}{\|U \wedge V\|^2}. \end{align*} $$

Now, by the Cauchy–Schwarz inequality, we obtain the strict inequality:

$$ \begin{align*} \mathrm{sec}(U, V) < \mathrm{\hat{s}ec}(U, V). \end{align*} $$

Therefore, it follows that if $\mathrm {sec}(U, V) \geq 0$ , then $\mathrm {\hat {s}ec}(U, V) \geq 0$ .

Similarly, let $X, U$ be two linearly independent vectors. Now, substituting $V = U$ and $Y = X$ in (5-3),

$$ \begin{align*} g(R(U, X, X, U)) = \|A_X U\|^2 - \{g(\nabla_X \,\nabla f, X) + X(f)^2\} \|U\|^2, \end{align*} $$

which proves that

$$ \begin{align*} \mathrm{sec}(U, X) = \frac{\|A_X U\|^2 - \{g(\nabla_X \,\nabla f, X) + X(f)^2\} \|U\|^2 }{\|X\|^2 \|U\|^2}. \end{align*} $$

Clearly, the last inequality and the equality statement follow in an obvious way.

Remark 5.3. By (5-1) and (5-2),

$$ \begin{align*} \nu R(U, V)W = \hat{R}(U, V)W - g(V, W) U + g(U, W) V \end{align*} $$

and

$$ \begin{align*} \mathfrak{h} R(U, V)W = - g(V, W) \,\nabla_U \,\nabla f + g(U, W) \,\nabla_V \,\nabla f. \end{align*} $$

Theorem 5.4. If M is locally symmetric, then the fibers of $\varphi $ are also locally symmetric provided that $\|\,\nabla f \| =1$ .

Proof. Since M is symmetric, we have $(\nabla _E R)(U, V, W) = 0$ for all $E, U, V, W$ $\in $ $\Gamma (\ker \varphi _\ast )$ , which means $\nu (\nabla _E R)(U, V, W) = 0$ and $\mathfrak {h}(\nabla _E R)(U, V, W) = 0$ . Thus,

$$ \begin{align*} 0 &= \nu (\nabla_E R)(U, V, W) = \nu \,\nabla_E (R(U, V, W)) - \nu R(\nabla_E U, V, W) \nonumber \\ &\quad - \nu R(U, \nabla_E V, W) - \nu R(U, V, \nabla_E W). \end{align*} $$

Using (2-4) and then a Clairaut condition (Remark 3.3) in the above equation yields

$$ \begin{align*} 0 &= \nu \,\nabla_E (R(U, V, W)) - \nu R({\hat{\nabla}_E} U, V, W) + R(\nabla f, V, W) g(E, U) \nonumber \\ &\quad - \nu R(U, {\hat{\nabla}_E} V, W) + R(U, \nabla f, W) g(E, V) \\ &\quad - \nu R(U, V, {\hat{\nabla}_E} W) + R(U, V, \nabla f) g(E, W). \end{align*} $$

Substituting Remark 5.3 in the above equation,

$$ \begin{align*} &\nu \,\nabla_E (\nu R(U, V, W) + \mathfrak{h} R(U, V, W)) - \nu R({\hat{\nabla}_E} U, V, W) \nonumber \\ &\quad - \nu R(U, {\hat{\nabla}_E} V, W)- \nu R(U, V, {\hat{\nabla}_E} W) = 0. \end{align*} $$

Again applying Remark 5.3 in the above equation,

$$ \begin{align*} &\hat{\nabla}_E (\hat{R}(U, V)W) -\nu \,\nabla_E (g(V, W) U) + \nu \,\nabla_E (g(U, W) V) + T_E \mathfrak{h} R(U, V, W)\\ &\quad- \hat{R}({\hat{\nabla}_E} U, V)W + g(V, W) {\hat{\nabla}_E} U - g({\hat{\nabla}_E} U, W) V \\ &\quad- \hat{R}(U, {\hat{\nabla}_E} V) W + g({\hat{\nabla}_E} V, W) U - g(U, W) {\hat{\nabla}_E} V \\ &\quad - \hat{R}(U, V){\hat{\nabla}_E} W + g(V, {\hat{\nabla}_E} W) U - g(U, {\hat{\nabla}_E} W) V = 0. \end{align*} $$

Since we have $T_E \mathfrak {h} R(U, V, W) = \mathfrak {h} R(U, V, W)(f) E = 0$ , employing (5-2) and the fact that f is a distance function in the aforementioned equation, we conclude that

$$ \begin{align*} (\hat{\nabla}_E \hat{R})(U, V, W) = 0.\\[-38pt] \end{align*} $$

Corollary 5.5. Let M satisfy the hypothesis of the above theorem. Suppose that the horizontal space is integrable and complete, then it must be a locally symmetric subspace of M and consequently, locally $M = {L_{\mathfrak {h}}} \times _f {F_{\nu }}$ and $\tilde M = {\tilde L_{\mathfrak {h}}} \times _f {\tilde F_{\nu }} $ is a warped product of two symmetric subspaces of M, where f is a distance function.

Proof. The first part of the proof follows from [25, Propositions 2.2 and 2.3] and the second part follows from [28, Proposition 3(b)].

Proposition 5.6. Suppose that the fibers of $\varphi $ are complete. If M is a space form having sectional curvatures k, then the fibers are also space forms having sectional curvatures $(k+1)$ and in particular are symmetric as well.

Proof. From Remark 5.3,

(5-4) $$ \begin{align} R(U, V, W) = \hat{R}(U, V, W) - g(V, W) U + g(U, W) V. \end{align} $$

Since M has constant sectional curvature k, using the well-known form of the curvature tensor [26] and (5-4),

$$ \begin{align*} \hat{R}(U, V, W) = (k+1)\{g(V, W)U - g(U, W)V\} \end{align*} $$

for all $U, V, W \in \Gamma (\ker \varphi _\ast )$ . Thus, the fibers have constant sectional curvature $(k+1)$ . This completes the proof.

Corollary 5.7. Under the hypothesis of the above proposition, the following hold.

1. (i) If $k = 0$ , that is, $\tilde M$ is isometric to Euclidean space $\mathbb {R}^{m}$ , then $\tilde {F_\nu }$ is isometric to the unit sphere $\mathbb {S}^{r}$ .

2. (ii) If $k = 1$ , that is, $\tilde M$ is isometric to $\mathbb {S}^m$ , then $\tilde {F_\nu }$ is isometric to a sphere $\mathbb {S}^{r}$ of radius ${1}/\!{\sqrt 2}$ .

3. (iii) If $k = -1$ , that is, $\tilde M$ is isometric to $\mathbb {H}^m$ of curvature $-$ 1, then $\tilde {F_\nu }$ is isometric to a Euclidean space $\mathbb {R}^{r}$ .

Following the proof of Corollary 5.5, we obtain the following corollary.

Corollary 5.8. Let $\tilde M$ be as in the above corollary. Suppose that the horizontal space is complete and integrable, then the following warped products occur.

1. (i) If $k =0$ , then $\tilde L_{\mathfrak {h}}$ must be a totally geodesic submanifold of $\mathbb {R}^m$ , that is, it must be $\mathbb {R}^{m-r}$ . Hence, $\mathbb {R}^m = \mathbb {R}^{m-r}\times _f \mathbb {S}^r(1)$ .

2. (ii) If $k =1$ , then by similar arguments to those given for item (i), $\mathbb {S}^m(1) = \mathbb {S}^{m-r}(1)\times _f \mathbb {S}^r ({1}/\!\sqrt{2})$ .

3. (iii) If $k= -1$ , then $\mathbb {H}^m = \mathbb {H}^{m-r}\times _f \mathbb {R}^{r}$ .

Theorem 5.9. Suppose the horizontal space is integrable and M is semi-symmetric, then the fibers of $\varphi $ are semi-symmetric. If $E, U, V, W, F \in \Gamma (\ker \varphi _\ast )$ , the following condition holds:

$$ \begin{align*} & \hat{R}(E, F, W, V) U - \hat{R}(E, F, W, U)V - g(V, E) \hat{R}(U, F, W) \\ &\quad + g(U, E) \hat{R}(V, F, W) - g(V, F) \hat{R}(E, U, W) + g(U, F) \hat{R}(E, V, W) \\ &\quad- g(V, W) \hat{R}(E, F, U) + g(U, W) \hat{R}(E, F, V) = 0. \end{align*} $$

Proof. Since M is semi-symmetric [35], we have $({R}(U, V) \cdot {R})(E, F) W = 0$ for all $E, U, V, W, F\in \Gamma (\ker \varphi _\ast )$ , which means that $\nu (({R}(U, V) \cdot {R})(E, F) W) = 0$ and $\mathfrak {h}(({R}(U, V) \cdot {R})(E, F) W) = 0$ . Then $\nu (({R}(U, V) \cdot {R})(E, F) W) = 0$ implies

$$ \begin{align*} &\nu R(U,V) R(E, F)W - \nu R(R(U,V)E,F)W \\ &\quad- \nu R(E, R(U,V)F)W - \nu R(E,F)R(U,V)W = 0. \end{align*} $$

This can be written as

$$ \begin{align*} &\nu R( U,V, \nu R (E,F,W)) - \nu R(U,V, \mathfrak{h} R(E,F,W)) - \nu R(\nu R (U,V)E,F,W) \\ &\quad- \nu R(\mathfrak{h} R(U,V)E, F,W) -\nu R( E, \nu R (U,V,F),W) - \nu R( E,\mathfrak{h} R (U,V,F),W) \\ &\quad - \nu R( E,F, \nu R (U,V,W)) - \nu R( E,F, \mathfrak{h} R (U,V,W)) = 0. \end{align*} $$

Applying the equations of Remark 5.3 in the above equation,

$$ \begin{align*} &\hat{R}(U,V,\nu R(E,F,W)) - g(V, R(E,F,W))U + g(U, R(E,F,W))V \\ &\quad - \hat{R}(R(U,V,E),F,W) + g(F, W)\nu R(U,V,E) - g(\nu R(U,V,E),W)F\\ &\quad - \hat{R}(E, \nu R(U,V,F),W) + g(\nu R(U,V,F),W)E - g(E,W)\nu R(U,V,F) \\ &\quad - \hat{R}(E,F,R(U,V,W)) + g(F,\nu R(U,V,W))E -g(E,\nu R(U,V,W))F\\ &\quad- g(\mathfrak{h} \,\nabla_V \,\nabla f, R(E,F,W))U - g(U,V) A_{\,\nabla f} \mathfrak{h} R(E,F,W)\\ &\quad- g(\mathfrak{h} \,\nabla_W \,\nabla f, R(U,V,E))F - g(F,W) A_{\,\nabla f} \mathfrak{h} R(U,V,E)\\ &\quad + g(\mathfrak{h} \,\nabla_W \,\nabla f, R(U,V,F))E + g(E,W) A_{\,\nabla f} \mathfrak{h} R(U,V,F)\\ &\quad -g(\mathfrak{h} \,\nabla_F \,\nabla f, R(U,V,W))E - g(E,F) A_{\,\nabla f} \mathfrak{h} R(U,V,W) = 0. \end{align*} $$

Again applying the equations of Remark 5.3 in the above equation yields

$$ \begin{align*} &(\hat{R}(U, V) \cdot \hat{R})(E, F) W - \hat{R}(E,F,W,V)U + \hat{R}(E,F,W,U)V \\ &\quad + g(V,E)\hat{R}(U,F,W) - \hat{R}(V,F,W) g(U,E) + g(V,F)\hat{R}(E,U,W) \\ &\quad - g(U,F)\hat{R}(E,V,W) + g(V,W) \hat{R}(E,F,U) - g(U,W)\hat{R}(E,F,V) \\ &\quad- g(\mathfrak{h} \,\nabla_V \,\nabla f, R(E,F,W))U - g(U,V) A_{\,\nabla f} \mathfrak{h} R(E,F,W)\\ &\quad - g(\mathfrak{h} \,\nabla_W \,\nabla f, R(U,V,E))F -g(F,W) A_{\,\nabla f} \mathfrak{h} R(U,V,E)\\ &\quad +g(\mathfrak{h} \,\nabla_W \,\nabla f, R(U,V,F))E - g(E,W) A_{\,\nabla f} \mathfrak{h} R(U,V,F)\\ &\quad -g(\mathfrak{h} \,\nabla_F \,\nabla f, R(U,V,W))E - g(F,E) A_{\,\nabla f} \mathfrak{h} R(U,V,W) = 0. \end{align*} $$

This completes the proof.

Again along similar lines to the proof of Corollary 5.5, we can obtain the following corollary.

Corollary 5.10. Let M satisfy the hypothesis of the above theorem. Suppose that the horizontal space is integrable and complete, then $\tilde M = \tilde {L_{\mathfrak {h}}} \times _f \tilde {F_{\nu }}$ , that is, $\tilde M$ is a warped product of two semi-symmetric subspaces of $\tilde M$ .

Theorem 5.11. The following statements hold.

1. (i) If the Hessian of the curvature tensor of M vanishes, then the fibers of $\varphi $ have harmonic curvature tensors.

2. (ii) If M has harmonic curvature tensor, then the fibers of $\varphi $ have harmonic Riemannian curvature tensors.

Proof. Fix a point $p \in M$ and let $\{U_i\}_{i= 1}^{r}$ be an orthonormal frame of $\ker \varphi _{\ast }$ in the neighborhood of p. Let $U, V, W, E$ be vertical vector fields in the neighborhood of p and that are parallel at $p \in M$ . Suppose that the Hessian of the curvature tensor of M is zero, that is,

$$ \begin{align*} (\text{Hess }R)(U, V, W, E) = 0\quad \text{for all } U, V, W, E \in \Gamma(\ker \varphi_{\ast }).\end{align*} $$

Then, we have $(\nabla ^{\ast }~ \nabla R)(U, V, W, E) = 0$ (see (2-9)). This implies

$$ \begin{align*} \nu (\nabla^{\ast}~ \nabla R)(U, V, W, E) = 0. \end{align*} $$

Substituting (2-8) in the above equation,

$$ \begin{align*} \nu \sum\limits_{i=1}^{r}(\nabla_{U_i} \,\nabla_{U_i} R)(U, V, W, E) = 0. \end{align*} $$

Equivalently,

$$ \begin{align*} &\nu \sum\limits_{i=1}^{r} \{\nabla_{U_i} ((\nabla_{U_i} R)(U, V, W, E)) - (\nabla_{U_i} R) (\nabla_{U_i} U, V, W, E) - (\nabla_{U_i} R) (U, \nabla_{U_i} V, W, E) \\ &\quad - (\nabla_{U_i} R) (U, V, \nabla_{U_i} W, E)- (\nabla_{U_i} R) (U, V, W, \nabla_{U_i} E)\} = 0. \end{align*} $$

Since $\,\nabla _{U_i} U = \,\nabla _{U_i} V = \,\nabla _{U_i} W = \,\nabla _{U_i} E = 0$ at p, the aforementioned equation gives at p,

$$ \begin{align*} \nu \sum \limits_{i=1}^{r} \,\nabla_{U_i} ((\nabla_{U_i} R)(U, V, W, E))= 0. \end{align*} $$

Hence, at p,

$$ \begin{align*} & \nu \sum \limits_{i=1}^{r} \,\nabla_{U_i} \{\nabla_{U_i} (R(U, V, W, E)) - R (\nabla_{U_i} U, V, W, E) - R (U, \nabla_{U_i} V, W, E) \\ &\quad - R (U, V, \nabla_{U_i} W, E)- R (U, V, W, \nabla_{U_i} E)\} = 0. \end{align*} $$

Substituting $\,\nabla _{U_i} U = \,\nabla _{U_i} V = \,\nabla _{U_i} W = \,\nabla _{U_i} E = 0$ at p in the above equation, we have at p,

$$ \begin{align*} \nu \sum \limits_{i=1}^{r} \,\nabla_{U_i} (\nabla_{U_i} (R(U, V, W, E))) = 0. \end{align*} $$

Employing (5-1) in the above equation, we get at $p \in M$ ,

$$ \begin{align*} \nu \sum \limits_{i=1}^{r} \{\nabla_{U_i} (\nabla_{U_i} (\hat{R}(U, V, W, E)- g(V, W) g(U, E) + g(U, W) g(V, E)))\} = 0. \end{align*} $$

Thus, at $p \in M$ ,

$$ \begin{align*} &\nu \sum \limits_{i=1}^{r} \,\nabla_{U_i} \{\nabla_{U_i} (\hat{R}(U, V, W, E))- \,\nabla_{U_i} g(V, W) g(U, E) - g(V, W) \,\nabla_{U_i} g(U, E) \\ &\quad + \,\nabla_{U_i} g(U, W) g(V, E) + g(U, W) \,\nabla_{U_i} g(V, E)\} = 0. \end{align*} $$

Again as $\,\nabla _{U_i} U = \,\nabla _{U_i} V = \,\nabla _{U_i} W = \,\nabla _{U_i} E = 0$ at $p \in M$ , the aforementioned equation at p reduces to

$$ \begin{align*} \nu \sum \limits_{i=1}^{r} \,\nabla_{U_i} (\nabla_{U_i} (\hat{R}(U, V, W, E))) = 0. \end{align*} $$

Finally, applying (2-8) in the above equation, at p,

$$ \begin{align*} (\hat{\nabla}^\ast~ \hat{\nabla} \hat{R})(U, V, W, E) = 0. \end{align*} $$

Thus, by (2-9), we obtain $\hat {\Delta } \hat {R} = 0$ at p. This completes the proof of statement (i).

Now to prove statement (ii), we proceed as follows. Suppose that M has harmonic curvature tensor, that is, $\Delta R = 0$ . Then we have [26],

$$ \begin{align*} \text{trace Hess } R(U, V, W, E) = 0\quad \text{for all } U, V, W, E \in \Gamma(\ker \varphi_{\ast}).\end{align*} $$

Equivalently,

(5-5) $$ \begin{align} \sum\limits_{\overset{i,j=1}{i\neq j}}^{r} \text{Hess }R(U_i, U_j, U_j, U_i) = 0, \end{align} $$

where $\{U_i\}_{i= 1}^{r}$ is an orthonormal frame in a neighborhood of $p \in M$ , which is parallel at $p \in M$ . Using (2-9) in (5-5), we have at $p \in M$ ,

$$ \begin{align*} \nu \sum\limits_{\overset{i,j=1}{i\neq j}}^{r} (\nabla^{\ast}~ \nabla R)(U_i, U_j, U_j, U_i) = 0. \end{align*} $$

Employing (2-8) in the aforementioned equation, we get at $p \in M$ ,

$$ \begin{align*} \nu \sum\limits_{\overset{i,j=1}{i\neq j}}^{r} (\nabla_{U_i} \,\nabla_{U_i} R)(U_i, U_j, U_j, U_i) = 0. \end{align*} $$

Since we have $\,\nabla _{U_i} U_i = 0 = \,\nabla _{U_i} U_j$ at $p \in M$ , the aforementioned equation at p reduces to

$$ \begin{align*} \nu \sum\limits_{\overset{i,j=1}{i\neq j}}^{r} \,\nabla_{U_i} ((\nabla_{U_i} R)(U_i, U_j, U_j, U_i)) = 0. \end{align*} $$

Now substituting $\,\nabla _{U_i} U_i = 0 = \,\nabla _{U_i} U_j$ at $p \in M$ in the above equation, we obtain at p,

(5-6) $$ \begin{align} \nu \sum\limits_{\overset{i,j=1}{i\neq j}}^{r} \,\nabla_{U_i} (\nabla_{U_i} (R(U_i, U_j, U_j, U_i))) = 0. \end{align} $$

Substituting (5-1) in (5-6) at p,

$$ \begin{align*} \nu \sum\limits_{\overset{i,j=1}{i\neq j}}^{r} \,\nabla_{U_i} (\nabla_{U_i} (\hat{R}(U_i, U_j, U_j, U_i) - r(r-1))) = 0. \end{align*} $$

This implies at p,

$$ \begin{align*} \nu \sum\limits_{\overset{i,j=1}{i\neq j}}^{r} \,\nabla_{U_i} (\nabla_{U_i} \hat{R}(U_i, U_j, U_j, U_i)) = 0. \end{align*} $$

Again applying $\,\nabla _{U_i} U_i = 0 = \,\nabla _{U_i} U_j$ at p, the aforementioned equation reduces to

$$ \begin{align*} \nu \sum\limits_{\overset{i,j=1}{i\neq j}}^{r} (\nabla_{U_i} \,\nabla_{U_i} \hat{R})(U_i, U_j, U_j, U_i) = 0. \end{align*} $$

Thus, equivalently at p,

$$ \begin{align*} \sum\limits_{\overset{i,j=1}{i\neq j}}^{r} (\hat{\nabla}_{U_i} \hat{\nabla}_{U_i} \hat{R})(U_i, U_j, U_j, U_i) = 0. \end{align*} $$

By Definition (2-8), at p, the above equation reduces to

$$ \begin{align*} \sum\limits_{\overset{i,j=1}{i\neq j}}^{r} (\hat{\nabla}^\ast~ \hat{\nabla} \hat{R})(U_i, U_j, U_j, U_i) = 0. \end{align*} $$

Finally, (2-9) shows that at p, $\hat {\Delta } \hat {R} = 0$ . This completes the required proof.

6. The Bochner-type formulas

In this section, we derive some Bochner-type formulas and use them to study vertical and horizontal Killing fields on M. Our approach here should be compared with [27, Lemma 2.1]. As an application of the Bochner-type formulas obtained in this section, we find Bochner formulas for horizontal and vertical Killing vector fields. In particular, we show that if M admits a horizontal Killing vector field, then under some assumptions, it is parallel. This yields the splitting of $\tilde M$ as a warped product if the horizontal space is integrable: $\tilde M = (N \times {\mathbb R}) \times _f \tilde F_{\nu }$ .

Killing vector field [26]: A smooth vector field $\xi $ on M is a Killing vector field on M if $L_{\xi } g = 0$ .

We begin by proving a result about the Lie derivative of a vector field.

Lemma 6.1. Let $\Delta ^\nu $ , $\Delta ^{\mathfrak {h}}$ denote the Laplacian operators on the vertical and the horizontal spaces, respectively. In addition, $\mathrm {\hat {R}ic}$ and $\mathrm {Ric}^{(\ker \varphi _\ast )^\perp }$ denote the Ricci tensors of the fibers of $\varphi $ and horizontal space, respectively. Then for a vertical vector field U and horizontal vector field X, the following statements hold.

1. (i) $\mathrm {trace}^\nu (\nabla _{(\cdot )} L_X g)((\cdot ), X) = -r(X(f))^2$ .

2. (ii) $\mathrm {trace}^{\mathfrak {h}}(\nabla _{(\cdot )} L_X g)((\cdot ), X) = \tfrac 12 \Delta ^{\mathfrak {h}} \|X\|^2 - \|\,\nabla _{\mathfrak {h}} X\|^2 + \mathrm {Ric}^{(\ker \varphi _\ast )^\perp } (X, X) + \,\nabla _X \mathrm {div}{}_{\mathfrak {h}} (X)$ .

3. (iii) $\mathrm {trace}^\nu (\nabla _{(\cdot )} L_U g)((\cdot ), U) = \tfrac 12 \Delta ^\nu \|U\|^2 - \|\,\nabla _{\nu } U\|^2 + \,\nabla _U \mathrm {div}{}_\nu (U)+ \mathrm {\hat {R}ic}(U, U) + (1-r) \|U\|^2 \|\,\nabla f\|^2$ .

4. (iv) $\mathrm {trace}^{\mathfrak {h}} (\nabla _{(\cdot )} L_U g)((\cdot ), U) = \tfrac 12 \Delta ^{\mathfrak {h}} \|U\|^2 - \|\nu \,\nabla _{\mathfrak {h}} U\|^2 - g(U, U) \mathrm {div}_{\mathfrak {h}} (\nabla f)$

   $- \mathrm {trace}^{\mathfrak {h}} (g(\nu \,\nabla _{(\cdot )} U, U) df (\cdot ))$ .

5. (v) $\mathrm {trace}^\nu (\nabla _{(\cdot )} L_U g)((\cdot ), X) = \mathrm {trace}^\nu (g(\nabla _{(\cdot )} \,\nabla _X U, (\cdot ))) - 2 X(f) ~\mathrm {div}_\nu (U)$ .

6. (vi) $\mathrm {trace}^{\mathfrak {h}} (\nabla _{(\cdot )} L_U g)((\cdot ), X) = 0$ .

7. (vii) $\mathrm {trace}^\nu (\nabla _{(\cdot )} L_X g)((\cdot ), U) = 0$ .

8. (viii) $\mathrm {trace}^{\mathfrak {h}} (\nabla _{(\cdot )} L_X g)((\cdot ), U) =0$ .

Proof. Let $\{U_i\}_{1 \leq i \leq r}$ and $\{X_j\}_{r+1 \leq j \leq m}$ be orthonormal frames in a neighborhood of $p \in M$ that are parallel at p. Now again at p,

$$ \begin{align*} &(\nabla_{U_i} L_X g)(U_i, X) = \nabla_{U_i} (L_X g (U_i, X)) - L_X g(\nabla_{U_i} U_i, X) - L_X g(U_i, \nabla_{U_i} X)\\[5pt] &\quad = \nabla_{U_i} \{g(\mathfrak{h} \,\nabla_{U_i} X, X) + g(\nabla_X X, U_i)\} - g(\nabla_{U_i} X, \nabla_{U_i} X) - g(\nabla_{\,\nabla_{{U_i}} X} X, U_i)\\[5pt] &\quad = \nabla_{U_i} (g(A_X X, U_i)) - g(\mathfrak{h}\,\nabla_{U_i} X, \mathfrak{h}\,\nabla_{U_i} X) - g(\nu \,\nabla_{U_i} X, \nu \,\nabla_{U_i} X) \\[5pt] &\qquad - g(\nabla_{\mathfrak{h}\,\nabla_{{U_i}} X} X, U_i) - g(\nabla_{\nu \,\nabla_{{U_i}} X} X, U_i) = -g(T_{U_i}X, T_{U_i}X). \end{align*} $$

Now, by the skew-symmetry of tensor T and a Clairaut condition (Remark 3.3), we have $g(T_U V, X) = -g(T_U X, V) = -g(U, V) g(\nabla f, X)$ . Consequently, $T_U X = X(f) U$ . Substituting this in the above equation, we get the proof of statement (i).

Also at p,

$$ \begin{align*} &\sum\limits_{j = r+1}^{m}(\nabla_{X_j} L_X g)(X_j, X) \nonumber \\[5pt] &\quad = \sum\limits_{j = r+1}^{m} \{\nabla_{X_j} (L_X g (X_j, X)) - L_X g(\nabla_{X_j} X_j, X) - L_X g(X_j, \nabla_{X_j} X)\} \nonumber \\[5pt] &\quad= \sum\limits_{j = r+1}^{m} \,\nabla_{X_j} g(\nabla_{X_j} X, X) + \sum\limits_{j = r+1}^{m}\,\nabla_{X_j} g(\nabla_X X, X_j) \nonumber \\[5pt] &\qquad-\sum\limits_{j = r+1}^{m}g(\nabla_{X_j} X, \nabla_{X_j} X) -\sum\limits_{j = r+1}^{m} g(\nabla_{\,\nabla_{{X_j}} X} X, X_j). \end{align*} $$

This implies at p,

$$ \begin{align*} &\sum\limits_{j = r+1}^{m}(\nabla_{X_j} L_X g)(X_j, X) \\ &\quad=\sum\limits_{j = r+1}^{m} \{\nabla_{X_j} (g(\nabla_{X_j} X, X)) + g(\nabla_{X_j} \,\nabla_X X, X_j) - g(\nabla_{\,\nabla_{{X_j}} X} X, X_j)\} - \|\,\nabla_{\mathfrak{h}} X\|^2\\ &\quad = \frac{1}{2} \Delta^{\mathfrak{h}} \|X\|^2 - \|\,\nabla_{\mathfrak{h}} X\|^2 + \sum\limits_{j = r+1}^{m} \{g(\nabla_{X_j} \,\nabla_X X, X_j) - g(\nabla_{\,\nabla_{{X_j}} X} X, X_j)\} \\ &\quad = \frac{1}{2} \Delta^{\mathfrak{h}} \|X\|^2 - \|\,\nabla_{\mathfrak{h}} X\|^2 + \sum\limits_{j = r+1}^{m}\{g(R(X_j, X)X, X_j) + g(\nabla_X \,\nabla_{{X_j}} X, X_j)\} \\ &\quad = \frac{1}{2} \Delta^{\mathfrak{h}} \|X\|^2 - \|\,\nabla_{\mathfrak{h}} X\|^2 +\mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, X) + \nabla_X \mathrm{div}_{\mathfrak{h}} (X), \end{align*} $$

which completes the proof of statement (ii).

Next again at p,

$$ \begin{align*} &(\nabla_{U_i} L_U g)(U_i, U) = \,\nabla_{U_i} (L_U g (U_i, U)) - L_U g(U_i, \nabla_{U_i} U)\\ &\quad= \,\nabla_{U_i} \{g(\nabla_{U_i} U, U) + g(\nabla_U U, U_i)\} - g(\nabla_{U_i} U, \nabla_{U_i} U) - g(\nabla_{\,\nabla_{{U_i}} U} U, U_i)\\ &\quad=\,\nabla_{U_i} (g(\nabla_{U_i} U, U)) + g(\nabla_{U_i} \,\nabla_U U, U_i) - |\,\nabla_{\nu} U|^2 - g(\nabla_{\,\nabla_{{U_i}} U} U, U_i) \\ &\quad = \tfrac{1}{2} \Delta^\nu \|U\|^2 - \|\,\nabla_{\nu} U\|^2 + g(R(U_i, U)U, U_i) + \,\nabla_U \mathrm{div}_\nu (U). \end{align*} $$

Employing [13] and then Theorem 3.2 in the aforementioned equation, we get the proof of statement (iii).

In addition, at p,

$$ \begin{align*} &\sum\limits_{j = r+1}^{m}(\nabla_{X_j} L_U g)(X_j, U) = \sum\limits_{j = r+1}^{m} \{\nabla_{X_j} (L_U g (X_j, U)) - L_U g(X_j, \nabla_{X_j} U)\}\nonumber \\ &\quad = \sum\limits_{j = r+1}^{m} \,\nabla_{X_j} g(\nu \,\nabla_{X_j} U, U) + \sum\limits_{j = r+1}^{m}\,\nabla_{X_j} g(\mathfrak{h}\,\nabla_U U, X_j) \nonumber \\ &\qquad-\sum\limits_{j = r+1}^{m}g(\nabla_{X_j} U, \nabla_{X_j} U) -\sum\limits_{j = r+1}^{m} g(\nabla_{\,\nabla_{{X_j}} U} U, X_j)\nonumber \\ &\quad =\sum\limits_{j = r+1}^{m} \,\nabla_{X_j} (g(\nabla_{X_j} U, U)) - \sum\limits_{j = r+1}^{m}\,\nabla_{X_j} (g(U, U)\,\nabla f, X_j) -\sum\limits_{j = r+1}^{m}g(\mathfrak{h}\nabla_{X_j} U, \mathfrak{h}\nabla_{X_j} U) \nonumber \\ &\qquad - \sum\limits_{j = r+1}^{m}g(\nu\,\nabla_{X_j} U, \nu\,\nabla_{X_j} U) -\sum\limits_{j = r+1}^{m} g(\nabla_{\mathfrak{h}\,\nabla_{{X_j}} U} U, X_j) -\sum\limits_{j = r+1}^{m} g(\nabla_{\nu \nabla_{{X_j}} U} U, X_j) \nonumber\\ &\quad = \frac{1}{2} \Delta^{\mathfrak{h}} \|U\|^2 - \|\nu \,\nabla_{\mathfrak{h}} U\|^2 -\sum\limits_{j = r+1}^{m}g(\nu \,\nabla_{X_j} U, U) X_j(f) -\sum\limits_{j = r+1}^{m}g(U, U) g(\nabla_{X_j} \nabla f, X_j) \nonumber \\ &\quad = \frac{1}{2} \Delta^{\mathfrak{h}} \|U\|^2 - \|\nu \,\nabla_{\mathfrak{h}} U\|^2 -g(U, U)~\mathrm{div}_{\mathfrak{h}} (\nabla f) -\sum\limits_{j = r+1}^{m}g(\nu \,\nabla_{X_j} U, U) X_j(f), \end{align*} $$

which is the same as statement (iv).

By similar computations, one can prove the remaining statements.

Theorem 6.2. Let $\Delta ^\nu $ and $\Delta ^{\mathfrak {h}}$ denote the Laplace operator on the vertical and the horizontal space, respectively. In addition, $\mathrm {Ric}$ , $\mathrm {\hat {R}ic}$ , and $\mathrm {Ric}^{(\ker \varphi _\ast )^\perp }$ denote the Ricci tensor of M, fibers of $\varphi $ , and horizontal space, respectively. Let $\xi \in \Gamma (TM)$ and write $\xi = X + U$ . Then the generalized Bochner formulas are

(6-1) $$ \begin{align} \mathrm{div}(L_{{\xi}} g) ({\xi}) &= \tfrac{1}{2} \Delta^{\mathfrak{h}} \|X\|^2 - \|\,\nabla_{\mathfrak{h}} X\|^2 +\mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, X) + \,\nabla_X \mathrm{div}_{\mathfrak{h}} (X) -r(X(f))^2 \nonumber \\ &\quad + \tfrac{1}{2} \Delta^\nu \|U\|^2 - \|\,\nabla_{\nu} U\|^2 + \,\nabla_U \mathrm{div}_\nu (U)+ \mathrm{\hat{R}ic}(U, U) + (1-r) \|U\|^2 \|\,\nabla f\|^2 \nonumber \\ &\quad + \tfrac{1}{2} \Delta^{\mathfrak{h}} \|U\|^2 - \|\nu \,\nabla_{\mathfrak{h}} U\|^2 -g(U, U)\mathrm{div}_{\mathfrak{h}} (\nabla f) - \mathrm{ trace}^{\mathfrak{h}} (g(\nu \,\nabla_{(\cdot)} U, U) df (\cdot)) \nonumber \\ &\quad + \mathrm{ trace}^\nu(g(\nabla_{(\cdot)} \,\nabla_X U, (\cdot))) - 2 X(f) \mathrm{div}_\nu (U). \end{align} $$

(6-2) $$ \begin{align} \tfrac{1}{2}\mathrm{div}(L_{\,\nabla f} g) ({\xi}) &= \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, \nabla f) + \nabla_X \mathrm{div}_{\mathfrak{h}} (\nabla f) -r X(f) \|\,\nabla f\|^2. \end{align} $$

Further,

(6-3) $$ \begin{align} \mathrm{div}(\mathrm{Hess } f) &= \mathrm{Ric}|_{(\ker \varphi_\ast)} (\nabla f) + \mathrm{Ric}|_{(\ker \varphi_\ast)^\perp} (\nabla f) + \nabla (\Delta f). \end{align} $$

Proof. Let $\{U_i\}_{1 \leq i \leq r}$ and $\{X_j\}_{r+1 \leq j \leq m}$ be orthonormal frames in a neighborhood of $p \in M$ that are parallel at p. Then at p,

(6-4) $$ \begin{align} \mathrm{div}(L_{{\xi}} g) ({\xi}) = \mathrm{div}(L_{X} g) (X) + \mathrm{div}(L_{X} g) (U) + \mathrm{div}(L_{U} g) (X) + \mathrm{div}(L_{U} g) (U). \end{align} $$

Clearly at p,

$$ \begin{align*} \mathrm{div}(L_{X} g) (X) = \sum\limits_{i=1}^{r} (\nabla_{U_i} L_X g)(U_i, X) + \sum\limits_{j = r+1}^{m} (\nabla_{X_j} L_X g)(X_j, X). \end{align*} $$

Applying Lemma 6.1 at p in the above equation,

(6-5) $$ \begin{align} \mathrm{div}(L_{X} g) (X) &= \tfrac{1}{2} \Delta^{\mathfrak{h}} \|X\|^2 - \|\,\nabla_{\mathfrak{h}} X\|^2 +\mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, X) \nonumber \\ &\quad + \nabla_X \mathrm{div}_{\mathfrak{h}} (X) - r (X(f))^2. \end{align} $$

Also at p,

$$ \begin{align*} \mathrm{div}(L_{U} g) (U) = \sum\limits_{i=1}^{r} (\nabla_{U_i} L_U g)(U_i, U) + \sum\limits_{j = r+1}^{m} (\nabla_{X_j} L_U g)(X_j, U). \end{align*} $$

Again employing Lemma 6.1 at p in the above equation yields

(6-6) $$ \begin{align} \mathrm{div}(L_{U} g) (U) &= \frac{1}{2} \Delta^\nu \|U\|^2 - \|\,\nabla_{\nu} U\|^2 + \,\nabla_U \mathrm{div}_\nu (U)+ \mathrm{\hat{R}ic}(U, U) \nonumber \\ &\quad + (1-r) \|U\|^2 \|\,\nabla f\|^2 + \frac{1}{2} \Delta^{\mathfrak{h}} \|U\|^2 - \|\nu \,\nabla_{\mathfrak{h}} U\|^2 \nonumber \\ &\quad - g(U, U)~\mathrm{div}_{\mathfrak{h}} (\nabla f) -\sum\limits_{j = r+1}^{m}g(\nu \,\nabla_{X_j}U, U) X_j(f). \end{align} $$

We have at p,

$$ \begin{align*} \mathrm{div}(L_{U} g) (X) = \sum\limits_{i=1}^{r} (\nabla_{U_i} L_U g)(U_i, X) + \sum\limits_{j = r+1}^{m} (\nabla_{X_j} L_U g)(X_j, X). \end{align*} $$

Again applying Lemma 6.1 in the aforementioned equation yields at p,

(6-7) $$ \begin{align} \mathrm{div}(L_{U} g) (X) = \sum\limits_{i=1}^{r} g(\nabla_{U_i} \,\nabla_X U, U_i) - 2 X(f) \mathrm{div}_\nu (U). \end{align} $$

Finally, at p,

$$ \begin{align*} \mathrm{div}(L_{X} g) (U) = \sum\limits_{i=1}^{r} (\nabla_{U_i} L_X g)(U_i, U) + \sum\limits_{j = r+1}^{m} (\nabla_{X_j} L_X g)(X_j, U). \end{align*} $$

Repeatedly using Lemma 6.1 in the above equation at p yields

(6-8) $$ \begin{align} \mathrm{div}(L_{X} g) (U) = 0. \end{align} $$

Then using consecutively (6-5), (6-6), (6-7) and (6-8) in (6-4), we conclude the proof of (6-1).

To prove (6-2), we proceed as follows. Clearly, at p,

(6-9) $$ \begin{align} \mathrm{div}(L_{\,\nabla f} g) ({\xi})& = \mathrm{div}(L_{\,\nabla f} g) (X) + \mathrm{div}(L_{\,\nabla f} g) (U)\nonumber \\ & = \sum\limits_{i=1}^{r} (\nabla_{U_i} L_{\,\nabla f} g)(U_i, X) + \sum\limits_{j = r+1}^{m} (\nabla_{X_j} L_{\,\nabla f} g)(X_j, X) \nonumber \\ &\quad + \sum\limits_{i=1}^{r} (\nabla_{U_i} L_{\,\nabla f} g)(U_i, U) + \sum\limits_{j = r+1}^{m} (\nabla_{X_j} L_{\,\nabla f} g)(X_j, U) \nonumber \\ & = \sum\limits_{i=1}^{r} (\nabla_{U_i} L_{\,\nabla f} g)(U_i, X) + \sum\limits_{j = r+1}^{m} (\nabla_{X_j} L_{\,\nabla f} g)(X_j, X). \end{align} $$

Also at p,

$$ \begin{align*} &(\nabla_{U_i} L_{\,\nabla f} g)(U_i, X) = \,\nabla_{U_i} (L_{\,\nabla f} g (U_i, X)) - L_{\,\nabla f} g(\nabla_{U_i} U_i, {\,\nabla f}) - L_{\,\nabla f} (g(U_i, \nabla_{U_i} X)) \\ &\quad = \,\nabla_{U_i} \{g(\mathfrak{h} \,\nabla_{U_i} {\,\nabla f}, X) + g(\nabla_X {\,\nabla f}, U_i)\} -g(\nabla_{U_i} {\,\nabla f}, \nabla_{U_i} X) - g(\nabla_{\,\nabla_{{U_i}} X} {\,\nabla f}, U_i)\\ &\quad = - 2g(\nu \,\nabla_{U_i} {\,\nabla f}, \nu \,\nabla_{U_i} X) -2 g({\mathfrak{h} \,\nabla_{{U_i}} {\,\nabla f}}, \mathfrak{h} \,\nabla_{U_i} X) = -2g(T_{U_i} {\,\nabla f}, T_{U_i}X). \end{align*} $$

Recall that the tensor T is skew-symmetric (see Section 2) and also we have the Clairaut condition (Remark 3.3). Therefore, we have $T_U X = X(f) U$ . Substituting in the above equation, we get at p,

(6-10) $$ \begin{align} \sum\limits_{i=1}^{r} (\nabla_{U_i} L_{\,\nabla f} g)(U_i, X) = - 2 r \|\,\nabla f\|^2 X(f). \end{align} $$

In addition, at p,

(6-11) $$ \begin{align} &\sum\limits_{j = r+1}^{m}(\nabla_{X_j} L_{\,\nabla f} g)(X_j, X) \nonumber \\ &\quad= \sum\limits_{j = r+1}^{m} \{\nabla_{X_j} (L_{\,\nabla f} g (X_j, X)) - L_{\,\nabla f} g(\nabla_{X_j} X_j, X) - L_{\,\nabla f} g(X_j, \nabla_{X_j} X)\}\nonumber \\ &\quad = \sum\limits_{j = r+1}^{m} \,\nabla_{X_j} g(\nabla_{X_j} {\,\nabla f}, X) + \sum\limits_{j = r+1}^{m}\,\nabla_{X_j} g(\nabla_X {\,\nabla f}, X_j) \nonumber \\ &\qquad -\sum\limits_{j = r+1}^{m}g(\nabla_{X_j} {\,\nabla f}, \nabla_{X_j} X) -\sum\limits_{j = r+1}^{m} g(\nabla_{\,\nabla_{{X_j}} X} {\,\nabla f}, X_j)\nonumber \\ &\quad =2\sum\limits_{j = r+1}^{m} \{g(\nabla_{X_j} \,\nabla_X {\,\nabla f}, X_j) - g(\mathfrak{h} \,\nabla_{\mathfrak{h}\,\nabla_{{X_j}} X} {\,\nabla f}, X_j)\} \nonumber \\ &\quad = 2 \sum\limits_{j = r+1}^{m}\{g(R(X_j, X){\,\nabla f}, X_j) + g(\nabla_X \,\nabla_{{X_j}} {\,\nabla f}, X_j)\} \nonumber \\ &\quad = 2~ \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, {\,\nabla f}) + 2~ \nabla_X \mathrm{div}_{\mathfrak{h}} ({\,\nabla f}). \end{align} $$

Using (6-10) and (6-11) in (6-9), we obtain (6-2).

Toward proving (6-3) we proceed as follows.

We have the following at p:

(6-12) $$ \begin{align} &\mathrm{div}(L_{\,\nabla f} g) ({\xi}) = \sum\limits_{i=1}^{r} (\nabla_{U_i} L_{\,\nabla f} g)(U_i, {\xi}) + \sum\limits_{j = r+1}^{m} (\nabla_{X_j} L_{\,\nabla f} g)(X_j, {\xi}) \nonumber \\ &\quad =\sum\limits_{i=1}^{r}\,\nabla_{U_i} (L_{\,\nabla f}g(U_i, {\xi})) - \sum\limits_{i=1}^{r} L_{\,\nabla f} g(U_i, \nabla_{U_i} {\xi}) \nonumber \\&\qquad+ \sum\limits_{j = r+1}^{m} \,\nabla_{X_j} (L_{\nabla f}g(X_j, {\xi})) -\sum\limits_{j = r+1}^{m} L_{\nabla f}g(X_j, \nabla_{X_j} {\xi})\nonumber \\ &\quad =2\sum\limits_{i=1}^{r} \,\nabla_{U_i} (g(\nabla_{U_i} \,\nabla f, {\xi})) - 2\sum\limits_{i=1}^{r} g(\nabla_{U_i} \,\nabla f, \nabla_{U_i} {\xi}) \nonumber \\&\qquad + 2\sum\limits_{j = r+1}^{m} \nabla_{X_j} (g(\nabla_{X_j} \,\nabla f, {\xi})) - 2 \sum\limits_{j = r+1}^{m}g(\nabla_{X_j} \,\nabla f, \nabla_{X_j} {\xi})\nonumber \\&\quad =2\sum\limits_{i=1}^{r} \nabla_{U_i} (g(\nabla_{{\xi}} \,\nabla f, U_i)) - 2\sum\limits_{i=1}^{r} g(\nabla_{U_i} \,\nabla f, \nabla_{U_i} {\xi}) \nonumber \\ &\qquad + 2\sum\limits_{j = r+1}^{m} \nabla_{X_j} (g(\nabla_{{\xi}} \,\nabla f, X_j)) - 2 \sum\limits_{j = r+1}^{m}g(\nabla_{X_j} \,\nabla f, \nabla_{X_j} {\xi}) \nonumber \\ &\quad = 2\sum\limits_{i=1}^{r} g(\nabla_{U_i} \,\nabla_{{\xi}} \,\nabla f, U_i) - 2\sum\limits_{i=1}^{r} g(\nabla_{U_i} \,\nabla f, \nabla_{U_i} {\xi}) \nonumber \\ &\qquad + 2\sum\limits_{j = r+1}^{m} g(\nabla_{X_j} \,\nabla_{{\xi}} \,\nabla f, X_j) - 2 \sum\limits_{j = r+1}^{m}g(\nabla_{X_j} \,\nabla f, \nabla_{X_j} {\xi}). \end{align} $$

We know that at p,

$$ \begin{align*} g(R(U_i, {\xi}) \,\nabla f, U_i) = g(\nabla_{U_i} \,\nabla_{{\xi}} \,\nabla f - \,\nabla_{{\xi}} \,\nabla_{U_i} \,\nabla f - \,\nabla_{\,\nabla_{U_i} {\xi}} \,\nabla f, U_i), \end{align*} $$

which implies at p,

$$ \begin{align*} g(\nabla_{U_i} \,\nabla_{{\xi}} \,\nabla f, U_i) = g(R(U_i, {\xi}) \,\nabla f, U_i) + g(\nabla_{{\xi}} \,\nabla_{U_i} \,\nabla f, U_i) + g(\nabla_{\,\nabla_{U_i} {\xi}} \,\nabla f, U_i). \end{align*} $$

Similarly, we have at p,

$$ \begin{align*} g(\nabla_{X_j} \,\nabla_{{\xi}} \,\nabla f, X_j) = g(R(X_j, {\xi}) \,\nabla f, X_j) + g(\nabla_{{\xi}} \,\nabla_{X_j} \,\nabla f, X_j) + g(\nabla_{\,\nabla_{X_j} {\xi}} \,\nabla f, X_j). \end{align*} $$

Substituting these equations in (6-12), we get at p,

$$ \begin{align*} &\mathrm{div}(L_{\,\nabla f} g) ({\xi}) = 2\sum\limits_{i=1}^{r} g(R(U_i, {\xi}) \,\nabla f, U_i) + 2\sum\limits_{i=1}^{r} g(\nabla_{{\xi}} \,\nabla_{U_i} \,\nabla f, U_i) \nonumber \\ &\qquad + 2\sum\limits_{j = r+1}^{m} g(R(X_j, {\xi}) \,\nabla f, X_j) + 2\sum\limits_{j = r+1}^{m} g(\nabla_{{\xi}} \,\nabla_{X_j} \,\nabla f, X_j) \nonumber \\ &\quad =2\sum\limits_{i=1}^{r} g(R(\nabla f, U_i)U_i, {\xi}) + 2 \nabla_{{\xi}} \mathrm{div}_\nu (\nabla f) \nonumber\\ &\qquad+ 2\sum\limits_{j = r+1}^{m} g(R(\nabla f, X_j)X_j, {\xi}) + 2 \nabla_{{\xi}} \mathrm{div}_{\mathfrak{h}} (\nabla f) \nonumber \\ &\quad = 2~ \mathrm{Ric}|_{(\ker \varphi_\ast)} (\nabla f, {\xi}) + 2~ \mathrm{Ric}|_{(\ker \varphi_\ast)^\perp} (\nabla f, {\xi}) + 2~ \nabla_{{\xi}} (\mathrm{div}_\nu (\nabla f) + \mathrm{div}_{\mathfrak{h}} (\nabla f)), \end{align*} $$

which implies the required proof.

Remark 6.3. If X and U are Killing vector fields on M, then ${\xi } = X + U$ is also a Killing vector field. As $L_{X} g = 0$ and $L_{U} g = 0$ implies that $\mathrm {div}(X) = 0$ and $\mathrm {div}(U) = 0$ , from the Bochner formula in Theorem 6.2,

$$ \begin{align*} &\tfrac{1}{2} \{\Delta^{\mathfrak{h}} \|X\|^2 + \Delta \|U\|^2 \} \nonumber \\ &\quad = \|\,\nabla_{\nu} U\|^2 + \|\nu \,\nabla_{\mathfrak{h}} U\|^2 + \|\,\nabla_{\mathfrak{h}} X\|^2 + (r -1) \|U\|^2 \|\,\nabla f\|^2 - \mathrm{\hat{R}ic}(U, U) \nonumber \\ &\qquad - \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, X) + r(X(f))^2 + g(U, U)~\mathrm{div}{}_{\mathfrak{h}} (\nabla f) \nonumber \\ &\qquad +\mathrm{ trace}^{\mathfrak{h}}(df(\cdot) \,\nabla_{(\cdot)} U) - \mathrm{ trace}^\nu(g(\nabla_{(\cdot)} \,\nabla_X U, (\cdot))). \end{align*} $$

As an application of the generalized Bochner formula, the following results can be proved easily.

Corollary 6.4. If ${\xi } = X$ is the Killing vector field, then

(6-13) $$ \begin{align} \tfrac{1}{2} \Delta^{\mathfrak{h}} \|X\|^2 = \|\,\nabla_{\mathfrak{h}} X\|^2 - \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, X) + r(X(f))^2. \end{align} $$

In particular, if $X = \,\nabla f$ is the Killing vector field, then

(6-14) $$ \begin{align} \tfrac{1}{2} \Delta^{\mathfrak{h}} \|\,\nabla f\|^2 = \|\,\nabla_{\mathfrak{h}} \,\nabla f\|^2 - \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (\nabla f, \nabla f) + r \|\,\nabla(f)\|^2. \end{align} $$

Corollary 6.5. If ${\xi } = U$ is the Killing vector field, then

(6-15) $$ \begin{align} \tfrac{1}{2} \Delta \|U\|^2 &= \|\,\nabla_{\nu} U\|^2 + \|\nu \,\nabla_{\mathfrak{h}} U\|^2 + (r -1) \|U\|^2 \|\,\nabla f\|^2 \nonumber \\ &\quad + g(U, U)~\mathrm{div}_{\mathfrak{h}} (\nabla f)+\mathrm{ trace}^{\mathfrak{h}}(df(\cdot) \,\nabla_{(\cdot)} U) - \mathrm{trace}^\nu(g(\nabla_{(\cdot)} \,\nabla_X U, (\cdot))). \end{align} $$

Remark 6.6. We can compare the generalized Bochner formula (6-1) with the Bochner formula of [27, Lemma 2.1]. We observe that $\mathrm {div}(\mathrm {Hess } f)$ obtained in [27] and (6-3) obtained here are similar. Also our formulas for the Killing vector field (6-13) and (6-14) are similar. However, the generalized formulas obtained in Remark 6.3 and in (6-15) differ drastically. This shows how the geometry of a Clairaut conformal Riemannian map is rich, in comparison.

Corollary 6.7. Suppose a Clairaut conformal Riemannian map has nonconstant girth and an integrable horizontal space with $\mathrm {Ric}^{(\ker \varphi _\ast )^\perp } (X, X) \leq 0$ . Let X be a horizontal Killing vector field, which attains its maximum on $L_{\mathfrak {h}}$ (in particular, this condition is satisfied if $L_{\mathfrak {h}}$ is compact), then X is a parallel Killing vector field. Thus, the universal covering space of the leaves of the horizontal space splits as $(N \times {\mathbb R})$ , (where N is a submanifold of M) and hence, $\tilde M = (N \times {\mathbb R}) \times _f \tilde F_{\nu }$ is a warped product if the horizontal space is integrable.

Proof. Suppose X is Killing, $\mathfrak {h}$ is integrable, then as $\mathrm {Ric}^{(\ker \varphi _\ast )^\perp } (X, X) \leq 0$ , by (6-13), $\|X\|^2$ is subharmonic function on each leaf $L_{\mathfrak {h}}$ . If $\|X\|$ attains a maximum value, then $\|X\|$ is constant. This yields that X is a parallel vector field. This shows that $\tilde {L_{\mathfrak {h}}}$ splits as $N \times {\mathbb R}$ (Theorem 2.4). Thus, in turn, we obtain the product $\tilde M = (N \times {\mathbb R}) \times \tilde F_{\nu }$ by [28, Proposition 3(b)] if the horizontal space is integrable.

In particular, if $L_{\mathfrak {h}}$ is compact, then $\|X\|$ attains a maximum value and the above argument follows.

From, Corollary 6.4, we obtain the following corollary.

Corollary 6.8. If there exists a constant-length horizontal Killing vector field X such that $\mathrm {Ric}^{(\ker \varphi _\ast )^\perp } (X, X) \leq 0$ , then X must be parallel. In particular, if f is a distance function and $\,\nabla f$ is a Killing field, then it is parallel, that is, $\mathrm {Hess} f = 0$ . Then $\tilde M = (N \times {\mathbb R}) \times \tilde F_{\nu }$ , that is, $\tilde M$ is the product of $(N \times {\mathbb R})$ and a fiber if the horizontal space is integrable (Corollary 3.4).

Remark 6.9. If the girth of the Clairaut conformal Riemannian is nonconstant, then if U is a constant-length Killing vertical vector field such that $\mathrm {div}_{\mathfrak {h}} (\nabla f) \geq 0$ , then using Corollary 6.5 and Lemma 6.1, we easily see that $\mathrm {\hat {R}ic} (U, U) \leq 0$ .

Theorem 6.10. For $U \in \Gamma (\ker \varphi _\ast )$ and $X \in \Gamma (\ker \varphi _\ast )^\perp $ :

1. (i) $\mathrm {div}(\mathrm {Hess } f) (X) = \mathrm {div}_{\mathfrak h}(\nabla ^2 f) (X) = \mathrm {Ric}^{(\ker \varphi _\ast )^\perp } (X, \nabla f) +\! \nabla _X \mathrm {div}_{\mathfrak {h}} (\nabla f) - r X(f) \|\nabla f\|^2$ ;

2. (ii) $\mathrm {div}(\mathrm {Hess } f) (U) = - \|\,\nabla f\|^2 \mathrm {div}_\nu (U) = \mathrm {\hat {d}iv} (L_{\,\nabla f} g)(U)$ ,

where $\mathrm {\hat {d}iv}$ and $\mathrm {div}$ denote divergence on the fibers of $\varphi $ and M, respectively. In addition, $r = \dim (\ker \varphi _\ast )$ .

Proof. Let $\{U_i\}_{1 \leq i \leq r}$ and $\{X_j\}_{r+1 \leq j \leq m}$ be orthonormal parallel frames in a neighborhood of $p \in M$ that are parallel at p. We know that at p,

(6-16) $$ \begin{align} &\mathrm{div}(L_{\,\nabla f} g) (X) = \sum\limits_{i=1}^{r} (\nabla_{U_i} L_{\,\nabla f} g)(U_i, X) + \sum\limits_{j = r+1}^{m} (\nabla_{X_j} L_{\,\nabla f} g)(X_j, X) \nonumber \\ &\quad =\sum\limits_{i=1}^{r}\,\nabla_{U_i} (L_{\,\nabla f}g(U_i, X)) - \sum\limits_{i=1}^{r} L_{\,\nabla f}g(U_i, \nabla_{U_i} X) \nonumber \\ &\qquad+ \sum\limits_{j = r+1}^{m} \,\nabla_{X_j} (L_{\,\nabla f}g(X_j, X)) -\sum\limits_{j = r+1}^{m} L_{\,\nabla f}g(X_j, \nabla_{X_j} X)\nonumber \\ &\quad = 2\sum\limits_{j = r+1}^{m} \{ \nabla_{X_j} (g(\nabla_{X} \,\nabla f, X_j)) - g(\nabla_{X_j} \,\nabla f, \nabla_{X_j} X) \} - 2\sum\limits_{i=1}^{r} g(\nabla_{U_i} \,\nabla f, \nabla_{U_i} X) \nonumber \\ &\quad= 2\sum\limits_{j = r+1}^{m}\{g(\nabla_{X_j} \nabla_{X} \nabla f, X_j) -g(\mathfrak{h}\nabla_{X_j} \nabla f, \mathfrak{h} \nabla_{X_j} X) \} - 2\sum\limits_{i=1}^{r} g(\nu \nabla_{U_i} \nabla f, \nu \nabla_{U_i} X) \nonumber \\ &\quad= 2\sum\limits_{j = r+1}^{m} \{g(\nabla_{X_j} \,\nabla_{X} \,\nabla f, X_j) -g(\mathfrak{h}\,\nabla_{X_j} \,\nabla f, \mathfrak{h} \,\nabla_{X_j} X) \} - 2\sum\limits_{i=1}^{r} g(\|\,\nabla f\|^2 U_i, X(f)U_i). \end{align} $$

At p, using

$$ \begin{align*} R(X_j, X) \,\nabla f = \,\nabla_{X_j} \,\nabla_{X} \,\nabla f - \nabla_{X} \,\nabla_{X_j} \,\nabla f - \nabla_{\,\nabla_{X_j} X} \,\nabla f \end{align*} $$

in (6-16), we get at p,

$$ \begin{align*} \mathrm{div}(L_{\,\nabla f} g) (X) & =2\sum\limits_{j = r+1}^{m}\{g(R(X_j, X)\,\nabla f, X_j) + g(\nabla_X \,\nabla_{X_j} \,\nabla f, X_j)\} - 2r X(f) \|\,\nabla f\|^2 \nonumber \\ & = 2 \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, \nabla f) + 2 \,\nabla_X \mathrm{div}_{\mathfrak{h}} (\nabla f) - 2r X(f) \|\,\nabla f\|^2, \end{align*} $$

which implies the proof of item (i).

However, we have at p,

$$ \begin{align*} &\mathrm{div}(L_{\,\nabla f} g) (U) = \sum\limits_{i=1}^{r} (\nabla_{U_i} L_{\,\nabla f} g)(U_i, U) + \sum\limits_{j = r+1}^{m} (\nabla_{X_j} L_{\,\nabla f} g)(X_j, U) \nonumber \\ &\quad =\sum\limits_{i=1}^{r}\,\nabla_{U_i} (L_{\,\nabla f} g(U_i, U)) - \sum\limits_{i=1}^{r} L_{\,\nabla f}g(U_i, \nabla_{U_i} U) \nonumber \\ &\qquad + \sum\limits_{j = r+1}^{m} \,\nabla_{X_j} (L_{\,\nabla f}g(X_j, U)) -\sum\limits_{j = r+1}^{m} L_{\,\nabla f}g(X_j, \nabla_{X_j} U)\nonumber \\ &\quad =- 2\sum\limits_{i=1}^{r} g(\nabla_{U_i} \,\nabla f, \nabla_{U_i} U) + \sum\limits_{j = r+1}^{m} \,\nabla_{X_j} (g(\nabla_{X_j} \,\nabla f, U)) \nonumber \\ &\qquad + \sum\limits_{j = r+1}^{m} \,\nabla_{X_j} (g(\nabla_{U} \,\nabla f, X_j)) - 2 \sum\limits_{j = r+1}^{m}g(\nabla_{X_j} \,\nabla f, \nabla_{X_j} U)\nonumber \\ &\quad =-2\sum\limits_{i=1}^{r} g(\|\,\nabla f\|^2 U_i, \nu \,\nabla_{U_i} U) = -2 \|\,\nabla f\|^2 \mathrm{div}{}_\nu (U) = \mathrm{\hat{d}iv} (L_{\,\nabla f} g)(U), \end{align*} $$

which completes the proof.

7. Contracted-type Bianchi identities and their applications to Ricci solitons

In this section, we derive the contracted-type Bianchi identities in the context when the total manifold admits a Clairaut conformal Riemannian map. The well-known contracted Bianchi identity ([26, Proposition 3.15]) states that on any Riemannian manifold,

$$ \begin{align*} d\mathrm{{S}} = 2 \mbox{div} (\mathrm{Ric}), \end{align*} $$

where S denotes the scalar curvature of the manifold.

This identity has wider applications and in particular, is used in the study of Ricci solitons (see for example, [27]). In addition, we see its applications to Ricci solitons on total manifolds admitting Clairaut conformal Riemannian maps.

7.1. Contracted-type Bianchi identities

In this subsection, we derive the contracted-type vertical and horizontal Bianchi identities in our context, which are used in our study in Section 7.2.

Proposition 7.1. For $U \in \Gamma (\ker \varphi _\ast )$ and $X \in \Gamma (\ker \varphi _\ast )^\perp $ ,

$$ \begin{align*} d \hat{S} (U) (p) = \hat{\nabla} \hat{S} (U) (p) = 2~ \mathrm{\hat{d}iv } \mathrm{\hat{R}ic }(U) (p) \end{align*} $$

and

$$ \begin{align*} d S^{(\ker\varphi_{\ast})^\perp} (X) (p) = \,\nabla_X S^{(\ker \varphi_{\ast})^\perp} (p) = 2 ~\mathrm{div}_{\mathfrak h} ~\mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X) (p), \end{align*} $$

where $\mathrm {\hat {R}ic}$ and $\mathrm {Ric}^{(\ker \varphi _\ast )^\perp }$ , respectively, denote the Ricci tensor of a fiber of $\varphi $ and the horizontal space. Also, $\hat {S}$ and $S^{(\ker \varphi _{\ast })^\perp }$ denote the scalar curvature of the fiber of $\varphi $ and the scalar curvature of M restricted to the horizontal space, respectively. In addition, $\mathrm {\hat {d}iv}$ and $\mathrm {div}_{\mathfrak h}$ denote the divergence on the fiber of $\varphi $ and the horizontal space, respectively.

Proof. Let $\{U_i\}_{1 \leq i \leq r}$ be an orthonormal frame of $\ker \varphi _{\ast }$ in a neighborhood of $p \in M$ , parallel at p. Therefore, the scalar curvature of a fiber is at p:

$$ \begin{align*} \hat{S} = \text{trace } \mathrm{\hat{R}ic} = \sum\limits_{i=1}^{r} g(\mathrm{\hat{R}ic}(U_i), U_i). \end{align*} $$

Thus, at p,

$$ \begin{align*} \hat{\nabla}_U \hat{S} (p)& = \hat{\nabla}_U \bigg\{\sum\limits_{i,j=1; i \neq j}^{r} g(\hat{R}(U_i, U_j) U_j, U_i)\bigg\} \nonumber \\ & = \sum\limits_{i,j=1; i \neq j}^{r} \hat{\nabla}_U (g(\hat{R}(U_i, U_j) U_j, U_i)) \nonumber \\ & = \sum\limits_{i,j=1; i \neq j}^{r} g((\hat{\nabla}_U \hat{R})(U_i, U_j) U_j, U_i) - \sum\limits_{i,j=1; i \neq j}^{r} g( \hat{R}(\hat{\nabla}_U U_i, U_j) U_j, U_i) \nonumber \\ &\quad - \sum\limits_{i,j=1; i \neq j}^{r} g( \hat{R}(U_i, \hat{\nabla}_U U_j) U_j, U_i) +\sum\limits_{i,j=1; i \neq j}^{r} g( \hat{R}(U_i, U_j) \hat{\nabla}_U U_j, U_i) \nonumber \\ &\quad + \sum\limits_{i,j=1; i \neq j}^{r} g( \hat{R}(U_i, U_j) U_j, \hat{\nabla}_U U_i). \end{align*} $$

As $\{U_i\}_{1 \leq i \leq r}$ is an orthonormal frame parallel at p,

$$ \begin{align*} \hat{\nabla}_U \hat{S} (p) = \sum\limits_{i,j=1; i \neq j}^{r} g((\hat{\nabla}_U \hat{R})(U_i, U_j) U_j, U_i). \end{align*} $$

Applying the second Bianchi identity to the aforementioned equation,

$$ \begin{align*} \hat{\nabla}_U \hat{S} (p) &= -\sum\limits_{i,j=1; i \neq j}^{r}\{g((\hat{\nabla}_{U_i} \hat{R})(U_j, U) U_j, U_i) + g((\hat{\nabla}_{U_j} \hat{R})(U, U_i) U_j, U_i)\}\nonumber \\ & = -\sum\limits_{i,j=1; i \neq j}^{r} \{(\hat{\nabla}_{U_i} \hat{R})(U_j, U, U_j, U_i) + (\hat{\nabla}_{U_j} \hat{R})(U, U_i, U_j, U_i)\} \nonumber \\ & = 2\sum\limits_{i,j=1; i \neq j}^{r} (\hat{\nabla}_{U_i} \hat{R})(U_i, U_j, U_j, U) = 2\sum\limits_{i,j=1; i \neq j}^{r} g((\hat{\nabla}_{U_i} \hat{R})(U_i, U_j) U_j, U) \nonumber \\ & = 2\sum\limits_{i,j=1; i \neq j}^{r} \hat{\nabla}_{U_i} (g(\hat{R}(U_i, U_j) U_j, U)) = 2\sum\limits_{i,j=1; i \neq j}^{r} \hat{\nabla}_{U_i}g(\mathrm{\hat{R}ic}(U), U_i). \end{align*} $$

Finally,

$$ \begin{align*} \hat{\nabla}_U \hat{S} (p) = 2\sum\limits_{i,j=1; i \neq j}^{r} g(\hat{\nabla}_{U_i}\mathrm{\hat{R}ic}(U), U_i) = 2 \mathrm{\hat{d}iv}~ \mathrm{\hat{R}ic}(U) (p). \end{align*} $$

By similar arguments, we can prove the other statements.

7.2. Applications to Ricci solitons

In recent years, geometers (including the first author) studied the geometry of smooth maps using Ricci soliton [13, 17, 18, 20, 39–41]. In this subsection, we study geometry of a Clairaut conformal Riemannian map, when the total manifold admits a nontrivial Ricci soliton.

Ricci solitons are the self-similar solutions of the Ricci flow. The concept of Ricci flow was first introduced by Hamilton [14] in 1982, motivated by the work of Eells and Sampson [5] on the harmonic map and the flow was given by the equation

$$ \begin{align*} \frac{\partial g}{\partial t}=-2 \mathrm{Ric}. \end{align*} $$

Thus, Ricci solitons turn out to be the generalizations of the Einstein metrics and are the solutions of the equation

(7-1) $$ \begin{align} \mathrm{Ric}(g) + \tfrac{1}{2}{L}_{X} g = \lambda g, \end{align} $$

where $\lambda $ is a real constant. The soliton is said to be shrinking if $\lambda < 0$ , steady if $\lambda = 0$ , and expanding if $\lambda> 0$ .

In what follows, we need the following results for the analysis of Ricci solitons.

If we do the computation using bases in a neighborhood of p that are parallel at p, then [13, Lemma 2.3] gives the following proposition.

Proposition 7.2. For $U,V \in \Gamma (\ker \varphi _\ast ) $ and $X \in \Gamma (\ker \varphi _\ast )^\perp $ ,

$$ \begin{align*} \mathrm{Ric}(U,V) &= \mathrm{\hat{R}ic}(U,V) + r \|\,\nabla f\|^2g(U,V),\\ \mathrm{Ric}(U,X) &= -(r+1) g(\nabla_X \,\nabla f, U), \end{align*} $$

where $r= \dim (\ker \varphi _\ast )$ and $(m - r) = \dim (\ker \varphi _\ast )^\perp $ .

Remark 7.3. If f is a distance function, then by Proposition 7.2,

(7-2) $$ \begin{align} \mathrm{Ric}(U, U) = \mathrm{\hat{R}ic}(U, U) + r \|U\|^2. \end{align} $$

If the fibers of $\varphi $ are Einstein with Einstein constant $\hat {\mu }$ , then (7-2) gives

$$ \begin{align*} \mathrm{Ric}(U, U) = (\hat{\mu} + r ) \|U\|^2. \end{align*} $$

If M is an Einstein manifold with Einstein constant $\mu $ , then (7-2) implies

$$ \begin{align*} \mathrm{\hat{R}ic}(U, U) = ( \mu - r) \|U\|^2. \end{align*} $$

Therefore, the fibers are also Einstein with Einstein constant $( \mu - r)$ . In particular, if $(\mu - r) = 0$ , then the fibers are Ricci flat.

Remark 7.4. If the total manifold of a Clairaut conformal Riemannian map admits the gradient Ricci soliton $\,\nabla f$ , which is the gradient of the logarithmic girth function, then its scalar curvature satisfies

$$ \begin{align*} S = \lambda m - \Delta^{\mathfrak{h}} f. \end{align*} $$

The last equation follows by tracing (7-1) and the fact that $\,\nabla f$ is a horizontal vector field.

Theorem 7.5. Let $\varphi : (M, g)\to (M', g')$ be a Clairaut conformal Riemannian map between Riemannian manifolds. Suppose that $(M, g)$ admits a Ricci soliton with the potential vector field $X \in \Gamma {(\ker \varphi _\ast )^\perp }$ . Then the scalar curvature of the fibers is constant and hence $(r \|\,\nabla f\|^2 - X(f))$ is a constant function on the fiber. Therefore, for $U \in \Gamma (\ker \varphi _\ast )$ ,

(7-3) $$ \begin{align} \mathrm{\hat{d}iv}~ \mathrm{\hat{R}ic}(U) (p)= 0, \end{align} $$

where $\mathrm {\hat {R}ic}$ denotes the Ricci tensor of the fibers of $\varphi $ and $\mathrm {\hat {d}iv}$ denotes the divergence on the fibers of $\varphi $ .

Proof. As $(M, g)$ admits a Ricci soliton with the potential vector field $X \in \Gamma {(\ker \varphi _\ast )^\perp }$ , by hypothesis, for $U, V \in \Gamma (\ker \varphi _\ast )$ ,

$$ \begin{align*} \tfrac{1}{2} (L_X g)(U, V) + \mathrm{Ric}(U, V) = \lambda g(U, V), \end{align*} $$

which can be written as

$$ \begin{align*} \tfrac{1}{2} \{g(\nabla_U X, V) + g(\nabla_V X, U)\} + \mathrm{Ric}(U, V) = \lambda g(U, V) \end{align*} $$

or

$$ \begin{align*} -\tfrac{1}{2} \{g(\mathfrak{h} \,\nabla_U V, X) + g(\mathfrak{h} \,\nabla_V U, X)\} + \mathrm{Ric}(U, V) = \lambda g(U, V). \end{align*} $$

Using (2-4),

$$ \begin{align*} - g(T_U V, X) + \mathrm{Ric}(U, V) = \lambda g(U, V). \end{align*} $$

Using the Clairaut condition in the above equation,

$$ \begin{align*} g(U, V) X(f) + \mathrm{Ric}(U, V) = \lambda g(U, V). \end{align*} $$

Choose $\{U_i\}_{1 \leq i \leq r}$ and $\{X_j\}_{r+1 \leq j \leq m}$ to be orthonormal frames of $\ker \varphi _{\ast }$ and $(\ker \varphi _{\ast })^\perp $ in a neighborhood of p that are parallel at p. Then applying Proposition 7.2 in the above equation, we affirm at p,

$$ \begin{align*} \mathrm{\hat{R}ic} (U, V) = (r \|\,\nabla f\|^2 - X(f) + \lambda) g(U, V). \end{align*} $$

Tracing the above equation,

(7-4) $$ \begin{align} \hat{S} (p)= (r \|\,\nabla f\|^2 - X(f) + \lambda)~ r. \end{align} $$

Hence,

$$ \begin{align*} \hat{\nabla}_U \hat{S} (p) = 0. \end{align*} $$

Therefore, the scalar curvature of the fibers of $\varphi $ is constant. Thus, (7-3) follows from Proposition 7.1. Also, we see from (7-4) that on the fibers of $\varphi $ , $(r \|\,\nabla f\|^2 - X(f))$ is a constant function (as we assume that fibers are connected). Let $(r \|\,\nabla f\|^2 - X(f)) = C$ , constant on the fibers of $\varphi $ . This implies that the scalar curvature of the fibers is $(C + \lambda ) r$ .

Corollary 7.6. Under the hypotheses of the above theorem, if $X = \,\nabla f$ , then any $U\in \Gamma {(\ker \varphi _\ast )}$ is an incompressible vector field, and hence $L_U \Omega = 0$ , where $\Omega $ is a volume form of the fiber. Therefore, the volume form of the fiber is invariant under the flow of U.

Proof. By the Ricci soliton equation, for $U, V \in \Gamma (\ker \varphi _\ast )$ ,

$$ \begin{align*} \tfrac{1}{2} (L_{\,\nabla f} g)(U, V) + \mathrm{Ric}(U, V) = \lambda g(U, V). \end{align*} $$

Using Proposition 7.2 in the above equation yields

$$ \begin{align*} \tfrac{1}{2} (L_{\,\nabla f} g)(U, V) + \mathrm{\hat{R}ic} (U, V) = (r \|\,\nabla f\|^2 + \lambda) g(U, V). \end{align*} $$

Thus,

$$ \begin{align*} \tfrac{1}{2} \mathrm{\hat{d}iv} (L_{\,\nabla f} g)(U) + \mathrm{\hat{d}iv} \mathrm{\hat{R}ic} (U) = 0. \end{align*} $$

Applying Theorem 6.10 in the aforementioned equation, we affirm

$$ \begin{align*} \tfrac{1}{2} \mathrm{div} (\nabla^2 f) (U) = - \mathrm{\hat{d}iv} ~\mathrm{\hat{R}ic}(U). \end{align*} $$

This implies

$$ \begin{align*} \|\,\nabla f\|^2 \mathrm{div}_\nu (U) = 2 ~\mathrm{\hat{d}iv}~ \mathrm{\hat{R}ic}(U) = 0 \end{align*} $$

by (7-3). Thus, $L_{U}\Omega =\mathrm {div}_\nu (U) ~\Omega = 0$ , where $\Omega $ is the volume form of the fiber of $\varphi $ . Hence, the corollary follows.

Theorem 7.7. Let $\varphi : (M, g)\to (M', g')$ be a conformal Riemannian map between Riemannian manifolds. Suppose that $(M, g)$ admits a Ricci soliton with the potential vector field $\,\nabla f \in \Gamma {(\ker \varphi _\ast )^\perp }$ . Then for $X, Y \in \Gamma (\ker \varphi _\ast )^\perp $ ,

(7-5) $$ \begin{align} \tfrac{1}{2} \,\nabla_X S^{(\ker \varphi_{\ast})^\perp} (p) &= r ~ (1-r) X(f) \|\,\nabla f\|^2 - (1-r) ~\mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, \nabla f) \nonumber \\ &\quad- (1-r) ~ \nabla_X \Delta f + r\ \mathrm{trace}^{\mathfrak{h}}(L_{(\cdot)} (df\otimes df))(X, (\cdot)). \end{align} $$

Also, $S^{(\ker \varphi _\ast )^\perp } = \lambda (m-r) + r \|\,\nabla f\|^2 + (r-1) \Delta f$ . Therefore, if $(\ker \varphi _\ast )^\perp $ is integrable, then $S^{(\ker \varphi _\ast )^\perp }$ denotes the scalar curvature of the leaves of $(\ker \varphi _\ast )^\perp $ .

Proof. We have, by the Ricci soliton equation, for $X, Y \in \Gamma (\ker \varphi _\ast )^\perp $ ,

$$ \begin{align*} \tfrac{1}{2} (L_{\,\nabla f} g)(X, Y) + \mathrm{Ric}(X, Y) = \lambda g(X, Y). \end{align*} $$

This implies

$$ \begin{align*} \nabla^2 f(X, Y) + \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, Y) + \sum\limits_{i=1}^{r} g(R(U_i, X)Y, U_i) = \lambda g(X, Y). \end{align*} $$

Using [13, Lemma 2.2],

(7-6) $$ \begin{align} &\,\nabla^2 f(X, Y) + \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, Y) + \sum\limits_{i=1}^{r} g((\nabla_{U_i} A)_X Y, U_i) \nonumber \\ &\quad - \sum\limits_{i=1}^{r} g((\nabla_X T)_{U_i} Y, U_i) - \sum\limits_{i=1}^{r} g(T_{U_i} X, T_{U_i} Y) = \lambda g(X, Y). \end{align} $$

As

(7-7) $$ \begin{align} \sum\limits_{i=1}^{r}g((\nabla_{U_i} A)_X Y, U_i) &= \sum\limits_{i=1}^{r} g(\nabla_{U_i} A_X Y - A(\nabla_{U_i} X, Y) - A(X, \nabla_{U_i} Y), U_i) \nonumber \\ & = \sum\limits_{i=1}^{r} g(\nabla_{U_i} A_X Y, U_i) = \mathrm{div}_\nu (A_X Y), \end{align} $$

clearly,

$$ \begin{align*} \sum\limits_{i=1}^{r} g((\nabla_X T)_{U_i} Y, U_i) = \sum\limits_{i=1}^{r} g(\nabla_{X} T_{U_i} Y - T(\nabla_X U_i, Y) - T(U_i, \nabla_X Y), U_i). \end{align*} $$

As $T_U X = X(f) U$ , the above expressions reduce to

(7-8) $$ \begin{align} \sum\limits_{i=1}^{r} g((\nabla_X T)_{U_i} Y, U_i) &= \sum\limits_{i=1}^{r} g(\nabla_{X} (Y(f) U_i) - Y(f) \nu \,\nabla_X U_i - \mathfrak{h} (\nabla_X Y)(f) U_i, U_i) \nonumber \\ &= g(Y, \nabla_X \,\nabla f) ~r, \end{align} $$

and

(7-9) $$ \begin{align} \sum\limits_{i=1}^{r} g(T_{U_i} X, T_{U_i} Y) = \sum\limits_{i=1}^{r} g(-X(f) U_i, - Y(f) U_i) = r X(f) Y(f). \end{align} $$

Employing (7-7), (7-8), and (7-9) in (7-6) yields

(7-10) $$ \begin{align} &\,\nabla^2 f(X, Y) + \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, Y) + \mathrm{div}_\nu (A_X Y) \nonumber \\ &\quad - g(Y, \nabla_X \,\nabla f) ~r - r X(f) Y(f) = \lambda g(X, Y). \end{align} $$

Equivalently,

$$ \begin{align*} & (1 - r) (\nabla^2 f)(X, Y) + \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, Y) \\ &\quad + \mathrm{div}_\nu (A_X Y) - r X(f) Y(f) = \lambda g(X, Y). \end{align*} $$

This can be rewritten as

$$ \begin{align*} (1 - r) (\nabla^2 f) + \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} + \mathrm{div}_\nu (A) - r~ (d f \otimes d f) = \lambda g. \end{align*} $$

Consequently,

(7-11) $$ \begin{align} &(1 - r) \mathrm{div}_{\mathfrak h}(\nabla^2 f)(X) + \mathrm{div}_{\mathfrak h} (\mathrm{Ric}^{(\ker \varphi_\ast)^\perp})(X) \nonumber \\ &\quad + \mathrm{div}_{\mathfrak h} (\mathrm{div}_\nu (A))(X) - r~ \mathrm{div}_{\mathfrak h} (d f \otimes d f)(X) = \lambda ~\mathrm{div}_{\mathfrak h} (g)(X). \end{align} $$

We know that

$$ \begin{align*} \mathrm{div}_{\mathfrak h} (g)(X) &= 0,\\ \mathrm{div}_{\mathfrak h} (\mathrm{div}_\nu (A)) (X) &= \mathrm{div}_{\mathfrak h} \bigg(\sum \limits_{i=1}^{r} g(\nabla_{U_{i}} A, U_{i})\bigg)(X) = 0, \end{align*} $$

and

$$ \begin{align*} \mathrm{div}_{\mathfrak h} (d f \otimes d f)(X)& = \sum\limits_{j= r+1}^{m} (\nabla_{X_j} (df\otimes df))(X, X_j)\\ & = \sum\limits_{j= r+1}^{m} (\nabla_{X_j} (df \otimes df (X, X_j)) - (df \otimes df)(\nabla_{X_j} X, X_j))\\ & = \sum\limits_{j= r+1}^{m}(\nabla_{X_j} (df(X) df(X_j)) - df(\nabla_{X_j} X) df(X_j)) \\ & =\sum\limits_{j= r+1}^{m} ((L_{X_j} (df\otimes df))(X, X_j) - df(X_j) df(\nabla_X X_j))\\ & = \sum\limits_{j= r+1}^{m}(L_{X_j} (df\otimes df))(X, X_j), \end{align*} $$

where $\{X_j\}_{j= r+1}^{m}$ is an orthonormal frame of $(\ker \varphi _\ast )^\perp $ parallel at p. Then applying Theorem 6.10 and Proposition 7.1 with the above expressions in (7-11), we obtain the required proof of (7-5).

Further, (7-10) can be written as

$$ \begin{align*} & \tfrac{1}{2} (L_{\,\nabla f} g)(X, Y) + \mathrm{Ric}^{(\ker \varphi_\ast)^\perp} (X, Y) + \mathrm{div}_\nu (A_X Y) \\ &\quad - r g(Y, \nabla_X \,\nabla f) - r X(f) Y(f) = \lambda g(X, Y). \end{align*} $$

Tracing the above equation yields

$$ \begin{align*} \mathrm{div}_{\mathfrak{h}} (\nabla f) + S^{(\ker \varphi_\ast)^\perp} - r \sum\limits_{j=r+1}^{m}g(X_j, \nabla_{X_j} \,\nabla f) - r \sum\limits_{j=r+1}^{m} X_j(f) X_j(f) = \lambda (m-r), \end{align*} $$

where $\{X_j\}_{j=r+1}^{m}$ is an orthonormal frame of $(\ker \varphi _\ast )^\perp $ parallel at p. Thus,

$$ \begin{align*} S^{(\ker \varphi_\ast)^\perp} = \lambda (m-r) + r \|\,\nabla f\|^2 + (r-1) \Delta^{\mathfrak{h}} f. \end{align*} $$

Hence, the assertion of the theorem follows.

Theorem 7.8. Suppose that $(M, g)$ admits a Ricci soliton with the potential vector field $U \in \Gamma {(\ker \varphi _\ast )}$ . Then the following statements hold.

1. (i) The fibers of $\varphi $ , in fact, admit the almost Ricci soliton with the potential vector vector field U.

2. (ii) Let $\mathrm {\hat {R}ic}$ denote the Ricci curvature of the fibers of $\varphi $ . Then,

   $$ \begin{align*} \mathrm{\hat{R}ic}(U, U) = \|\,\nabla_{\nu} U\|^2 - \tfrac{1}{2} \Delta^\nu \|U\|^2 + (r-1) \|U\|^2 \|\,\nabla f\|^2. \end{align*} $$

Proof. Let $\{U_i\}_{1 \leq i \leq r}$ be an orthonormal frame of $\ker \varphi _{\ast }$ around p that is parallel at p. Since M admits the Ricci soliton $U \in \Gamma {(\ker \varphi _\ast )}$ with constant $\lambda $ , for $U, V, W \in \Gamma (\ker \varphi _\ast )$ ,

(7-12) $$ \begin{align} \tfrac{1}{2} (L_U g)(V, W) + \mathrm{Ric}(V, W) = \lambda g(V, W). \end{align} $$

Using Proposition 7.2 in the above equation,

$$ \begin{align*} \tfrac{1}{2}(L_U g)(V, W) +\mathrm{\hat{R}ic} (V, W) = (r \|\,\nabla f\|^2 + \lambda) g(V, W). \end{align*} $$

This implies that the fibers of $\varphi $ admit the almost Ricci soliton U.

Further, by tracing the above equation,

$$ \begin{align*} \mathrm{\hat{d}iv}_\nu(U) + \hat{S} = (r \|\,\nabla f\|^2 + \lambda) ~r. \end{align*} $$

This implies

(7-13) $$ \begin{align} \hat{\nabla}_U \mathrm{\hat{d}iv}_\nu(U) + \hat{\nabla}_U \hat{S} = 0. \end{align} $$

By (7-12),

(7-14) $$ \begin{align} \mathrm{\hat{d}iv} (L_U g) (U) + 2 ~\mathrm{\hat{d}iv}~ \mathrm{\hat{R}ic}(U) = 0. \end{align} $$

Comparing (7-13) and (7-14) and applying Proposition 7.1,

$$ \begin{align*} \hat{\nabla}_U \mathrm{\hat{d}iv}_\nu (U) = \mathrm{\hat{d}iv} (L_U g) (U). \end{align*} $$

As $\mathrm {\hat {d}iv} (L_U g) (U) = \sum _{i=1}^{r} (\nabla _{U_i} L_U g)(U_i, U)$ , applying Lemma 6.1(iii) in the aforementioned equation proves item (ii).