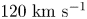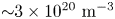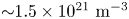Quadruple Langmuir probe characterization of different fuel gases in a plasma deflagration accelerator

Abstract

Astrophysical flows may be studied by reproducing similar conditions using a coaxial plasma accelerator operating in the deflagration regime (or plasma deflagration accelerator). This allows for the recreation and investigation of dynamics present in complex highly coupled plasma systems at the laboratory scale. We report on measurements of the plasma density, temperature, plasma potential and velocity found using a quadruple Langmuir probe (QLP) on such a deflagration accelerator in the form of the Stanford Coaxial High ENerGy (CHENG) device operating with multiple gases – specifically argon, nitrogen and hydrogen. Experiments show a general decrease in bulk plasma velocity with gas atomic mass from upwards of $120\ {\rm km}\ {\rm s}^{-1}$ with hydrogen to less than $30\ {\rm km}\ {\rm s}^{-1}$ with argon. There was an accompanying increase in peak plasma density with increasing atomic mass from ${\sim }3\times 10^{20}\ {\rm m}^{-3}$ with hydrogen to ${\sim }1.5 \times 10^{21}\ {\rm m}^{-3}$ with argon. It was found that the momentum flux and internal energy density also generally increase with atomic mass while the particle flux is constant between shots. Further investigation is needed to understand these correlations and the underlying physics. Lastly, comparisons with scaling laws show that while the CHENG device may be operated in such a way as to simulate the effects of bulk solar wind movement, it may not properly capture the thermal effects.

1. Introduction

Astrophysical jets and flows are common in the universe. Found in nebula, young star objects and galactic nuclei, many of these jets have velocities well in the $100\unicode{x2013}300\ {\rm km}\ {\rm s}^{-1}$ range. Furthermore, they manage to stay collimated and narrow over incredibly long distances and time scales (Borkowski & Harrington 1997; Reipurth & Ball 2001; Balick & Frank 2002). Yet despite their commonplace in nature and recent interest in such plasma jets, they remain poorly understood – specifically their formation dynamics, the role of instabilities in their dynamics and their interactions with their surroundings. As such, it is imperative that a method for replicating similar occurrences at the laboratory scale be developed to isolate and understand some of the phenomena and dynamics behind such jets.

The Stanford Plasma Physics Laboratory has constructed a Co-axial High ENerGy (CHENG) source that serves as a plasma deflagration accelerator, which, with inexpensive upkeep and high repeatability, has been shown to generate jets with the appropriate temporo-spatial properties for scaling to astrophysical phenomena of interest. A host of diagnostics also allows for greater accessibility compared to conventional laser-generated systems (Underwood, Loebner & Cappelli 2017). Prior measurements and characterization on this device were largely carried out on hydrogen but astrophysical jets are often made of other atomic constituents. Furthermore, there has been recent interest in investigating the device's suitability for studying the solar winds’ interactions with a proposed electric sail (e-sail) design (Schneider et al. 2017). Rahman et al. (1991) provides necessary scaling laws for a laboratory scale solar wind replicator, while Fu et al. (2020) provides updated values and comparisons to a device built specifically to replicate the solar wind. As such, it is of interest to further characterize the CHENG device and its jet properties, particularly when operating on a range of gases or gas mixtures.

In this work, we report on measurements of the flow properties when operating on nitrogen (${\rm N}_2$), hydrogen (${\rm H}_2$) and argon (Ar) using a quadruple electrostatic (Langmuir) probe (QLP). Section 2 lays out the physics of the accelerator and the theoretical basis for the electrostatic probe with special attention paid to theories governing this probe – specifically Bohm and Laframboise's approximations for determining collected current. Section 3 presents the experimental set-up, procedures used for acquiring the data and the results with key points of discussion. Section 4 provides a summary of our experiments, with conclusions pertaining to the source's viability for potential e-sail studies.

2. Background

2.1. Deflagration accelerator

The CHENG deflagration plasma accelerator is a pulsed device developed by D.Y. Cheng, as a variant of an original design by Marshall (Marshall 1960; Cheng & Wang 1973). As shown in figure 1, it features 15 outer stainless steel 5-mm diameter rods and one central copper 7.5 mm diameter rod in a coaxial rod configuration. The rods are all 26 cm long and the outer array is approximately 5 cm in diameter. The outer rods have a clear polycarbonate sleeve around the assembly for gas containment. This set-up is mounted on a vacuum chamber that is kept in the $10^{-5}$ to $10^{-6}$ torr ($10^{-6}$ to $10^{-7}$ kPa) range when running experiments. This is sufficiently low for inducing the deflagration mode as opposed to the detonation mode, as discussed in prior studies from our laboratory (Loebner, Underwood & Cappelli 2015b).

Figure 1. (a) Cross-sectional view of the deflagration accelerator illustrating the current lines (blue) in the plasma post-ionization and the induced magnetic field lines (black). The induced $\boldsymbol {J} \times \boldsymbol {B}$ Lorentz force (red arrows) accelerates the plasma down the length of the accelerator resulting in a pinch and a shear stabilized plasma jet about the pinch. (b) Long exposure image of the deflagration accelerator.

The electrodes are connected to a high voltage $56\ \mathrm {\mu }{\rm F}$ capacitor bank with charging capacities of up to 20 kV. The outer array of electrodes serve as the anodes and the inner rod serves as the cathode. At the base of the accelerator is a fast opening custom gas valve that is opened for $\sim$1 ms injecting a set amount of neutral gas when pressurized to a set value. The injected gas resulting from the sudden opening of the value in the presence of the high voltage, breaks down naturally along the Paschen curve's low pressure branch resulting in a current carrying plasma with current flowing in the cathode-pointing radial direction. This current generates an azimuthal magnetic field and the current and induced magnetic field yield a $\boldsymbol {J}\times \boldsymbol {B}$ force which accelerates the plasma particles along the axial direction to high velocities.

At the end of the electrodes, the current lines cant and bow in such a way as to radially compress the plasma particles on axis driving a pinch about which a high energy plasma forms and a high density plasma jet expands due to the formation of a magnetic nozzle. This expansion of this finite pressure plasma into a vacuum is referred to as a deflagration in the literature. This deflagration mode characterized here typically lasts of the order of $10\unicode{x2013}20\ \mathrm {\mu }{\rm s}$, depending primarily on the transmission inductance and the bank capacitance. That said, as the bulk of the current carrying plasma exits the accelerator, the current passes through zero and a voltage is induced to keep the current stable – much as in an inductor. This leads to inductive charging and ringdown resulting in subsequent restrikes, producing a weak detonation mode due to the presence of neutral gas still in the barrel of the accelerator. The differences and transitions between the two modes are explored further in our prior studies (Loebner et al. 2015b).

2.2. Quadruple Langmuir probe

The quadruple Langmuir probe (QLP) is a diagnostic system based on three Langmuir probes oriented in the direction of the bulk plasma flow and one oriented perpendicular to the direction of bulk flow. A schematic of the probe used in our studies is illustrated in figure 2.

Figure 2. Diagram of the quadruple Langmuir probe as used in this experiment. Probes 2–4 are biased relative to probe 1. The resulting currents driven by a passing plasma can be used to infer the time-resolved density, temperature, potential and velocity of the plasma.

As seen in the figure, three of the probes (the perpendicular and two of the parallel probes) are differentially biased relative to the fourth probe. When placed in the plasma flow, the current through each probe can be measured using four wideband current monitors. The current through each probe has a nonlinear dependence on plasma density, temperature, Mach number and potential. The theory used to describe these relationships are discussed in § 2.2.1. The theory allows for determining all four plasma properties at the probe location by solving a system of governing nonlinear equations. This system of equations can be solved at each measurement time step thereby providing acquisition of temporally resolved values for each of these properties at the probe location.

Note that using these systems of equations to solve for these properties is possible because this QLP operates in the ‘current-mode’. This is as compared with the typical ‘voltage-mode’ probe configurations which require voltage sweeps to develop a current versus voltage curve from which plasma characteristics might be developed (Gatsonis et al. 2004). This current-mode operation allows for measurements to be taken on transient plasma phenomena such as that present in the CHENG accelerator.

2.2.1. Laframboise and Bohm methods

The relation between the measured currents and the voltages can be found by considering the current flow through the probe. As with general electrostatic probes, the current collected has contributions due to both ions and electrons:

(2.1)\begin{equation} I_{{\rm probe}} = I_i - I_e, \end{equation}

where $I_i$ and $I_e$ denote the ion and electron current, respectively. For probes exposed to a plasma flow with a probe potential less than the plasma potential $(\phi _{{\rm probe}} \leqslant \phi _{{\rm plasma}})$, the probes retard electron collection. Note that all equations used in the theory presented below assume Maxwell–Boltzmann electron energy distributions, collisionless sheaths and probe separation distances greater than their respective sheath thicknesses to minimize interaction effects between probes. A more detailed discussion of these assumptions and requirements is discussed by Gatsonis et al. (2004). With these assumptions, the electron current can be described by the following equation, where $k_b$ is the Boltzmann constant and $T_e$ is the electron temperature:

(2.2)\begin{equation} I_{e} = A_{{\rm probe}}J_{e0}\exp\left[ -\frac{e}{k_bT_e}(\phi_{{\rm plasma}}-\phi_{{\rm probe}}) \right]. \end{equation}

The collected electron current is a function of $A_{{\rm probe}}$, the probe collection area – parallel or perpendicular to the plasma flow – and an augmentation to the random current density which is defined as the current when both the sheath thickness and the plasma bulk velocity are zero. The random current density for any charged species (electrons or ions), denoted by the subscript $s = e, i$, is given as

(2.3)\begin{equation} J_{s0} = n_{s}e \left(\frac{k_bT_s}{2{\rm \pi} m_s}\right)^{1/2}. \end{equation}

In contrast to the electron current collected as described by (2.2), the ion current collected is more complicated as it depends on the direction of flow, the ratio of the local probe radius to the Debye length of the plasma, $r_p/\lambda _D$, and the ratio, $T_i/Z_iT_e$. Here $Z_i$ is the ion charge number. If $5 \leqslant r_p/\lambda _D \leqslant 100$ and $T_i/Z_iT_e \leqslant 1$, the ion current to a probe parallel to the direction of flow is given via empirical fitting to Laframboise's data (Laframboise 1966; Peterson & Talbot 1970) as

(2.4)\begin{equation} I_{{\parallel},i} = A_{{\parallel}}J_{i0}\left[\beta +\frac{e}{k_bT_{i}}(\phi_{{\rm plasma}}-\phi_{{\rm probe}}) \right]^\alpha, \end{equation}

where

(2.5)\begin{equation} \alpha = \frac{2.9}{\ln(r_p/\lambda_D)+2.3}+0.07\left(\frac{T_i}{Z_iT_e}\right)^{0.75}-0.34 \end{equation}

and

(2.6)\begin{equation} \beta = 1.5+\frac{T_i}{Z_iT_e} \left[0.85+0.135\left(\ln\left[\frac{r_p}{\lambda_D}\right]\right)^3\right]. \end{equation}

In contrast, when $r_p/\lambda _D \geqslant 100$, (2.4) is invalid and a thin sheath must be assumed which leads to the below Bohm expression for the ion current for the parallel probes (Chen & Sekiguchi 1965):

(2.7)\begin{equation} I_{{\parallel},i} = A_{{\parallel}}n_ie\sqrt{\frac{k_bT_i}{m_i}}\exp\left(-\frac{1}{2}\right). \end{equation}

In either case, the perpendicular ion current is given by Kanal (1964) as

(2.8)\begin{equation} I_{{\perp} i} = A_{{\perp},i}n_ie\left(\frac{k_bT}{2{\rm \pi} m_i}\right)^{1/2}\frac{2}{\sqrt{\rm \pi}}\exp\left[{-}S_i^2\right]\sum_{j=0}^{\infty} \left(\frac{S_i^j}{j!}\right)^2\varGamma\left(j+\frac{3}{2}\right) \end{equation}

for $a \sim r_p$, where

(2.9)\begin{equation} S_i = \frac{u_i}{c_i} \end{equation}

and $a$ is the sheath diameter. Here, $S_i$ is the ion Mach number defined as the ratio of the ion drift velocity, $u_i$, to the most probable thermal speed, $c_i$:

(2.10)\begin{equation} c_i = \sqrt{\frac{2k_bT_i}{m_i}}. \end{equation}

Assuming quasineutrality ($n_e=n_i=n$) and local thermal equilibrium ($T_i=T_e=T$), a suite of nonlinear equations may be developed relating the probe currents and the plasma temperature, density and potential via the Laframboise approximation for $5 \leqslant r_p/\lambda _D \leqslant 100$:

(2.11)\begin{equation} \left.\begin{gathered} I_{1} = A_{{\parallel}}J_{e0}\exp\left(-\frac{e\phi_{p1}}{k_bT}\right)-A_{{\parallel}}J_{i0}\left[\beta +\frac{e\phi_{p1}}{k_bT}\right]^\alpha \\ I_{2} = A_{{\parallel}}J_{e0}\exp\left(-\frac{e(\phi_{p1}+\phi_{12})}{k_bT}\right)-A_{{\parallel}}J_{i0}\left[\beta +\frac{e(\phi_{p1}+\phi_{12})}{k_bT}\right]^\alpha \\ I_{3} = A_{{\parallel}}J_{e0}\exp\left(-\frac{e(\phi_{p1}+\phi_{13})}{k_bT}\right)-A_{{\parallel}}J_{i0}\left[\beta +\frac{e(\phi_{p1}+\phi_{13})}{k_bT}\right]^\alpha \\ I_{4} = A_{{\perp},e}J_{e0}\exp\left(-\frac{e(\phi_{p1}+\phi_{14})}{k_bT}\right)-A_{{\perp},i}J_{i0}\frac{2}{\sqrt{\rm \pi}}\exp\left[{-}S_i^2\right]\sum_{j=0}^{\infty} \left(\frac{S_i^j}{j!}\right)^2\varGamma\left(j+\frac{3}{2}\right) \end{gathered}\right\}, \end{equation}

where the notation $\varGamma$ is the gamma function, $\phi _{p1}$ represents the plasma potential relative to probe 1, and $\phi _{12}$, $\phi _{13}$ and $\phi _{14}$ are the potentials of probe 1 relative to probe 2, 3 and 4, respectively. The corresponding Bohm expressions for $r_p/\lambda _D \geqslant 100$ are

(2.12)\begin{gather} \left.\begin{gathered} I_{1} = A_{{\parallel}}J_{e0}\exp\left(-\frac{e\phi_{p1}}{k_bT}\right)-A_{{\parallel}}n_ee\sqrt{\frac{k_bT}{m_i}}\exp\left(-\frac{1}{2}\right) \\ I_{2} = A_{{\parallel}}J_{e0}\exp\left(-\frac{e(\phi_{p1}+\phi_{12})}{k_bT}\right)-A_{{\parallel}}n_ee\sqrt{\frac{k_bT}{m_i}}\exp\left(-\frac{1}{2}\right) \\ I_{3} = A_{{\parallel}}J_{e0}\exp\left(-\frac{e(\phi_{p1}+\phi_{13})}{k_bT}\right)-A_{{\parallel}}n_ee\sqrt{\frac{k_bT}{m_i}}\exp\left(-\frac{1}{2}\right) \\ I_{4} = A_{{\perp},e}J_{e0}\exp\left(-\frac{e(\phi_{p1}+\phi_{14})}{k_bT}\right)-A_{{\perp},i}J_{i0}\frac{2}{\sqrt{\rm \pi}}\exp\left[{-}S_i^2\right]\sum_{j=0}^{\infty} \left(\frac{S_i^j}{j!}\right)^2\varGamma\left(j+\frac{3}{2}\right) \end{gathered}\right\}. \end{gather}

Note $A_{\perp,e}$ and $A_{\perp,i}$ refer to the probe collection area for electrons and ions, respectively, in the perpendicular probe. These differ from the parallel probe collection area, $A_{\parallel }$, because of the wake effect present in high-Mach-number flows ($S_i \geqslant 3$) causing a low ion density region behind the perpendicular probe and a corresponding low electron density because of quasi-neutrality as discussed by Burton, DelMedico & Andrews (1993) and Segall & Koopman (1973), and supported by work from Tan (1973). The high thermal velocity of the electrons allows for collection on the front half of the cylindrical probe while the ion collection area is limited to the projected rectangular area of the cylinder leading to

(2.13)\begin{gather} A_{{\parallel}} = 2{\rm \pi} rl, \end{gather}

(2.14)\begin{gather}A_{{\perp},e} = {\rm \pi}rl = A_{{\parallel}}/2, \end{gather}

(2.15)\begin{gather}A_{{\perp},i} = 2rl = A_{{\parallel}}/{\rm \pi}. \end{gather}

It should be noted that this method of incorporating the ion Mach number in (2.11) and (2.12) differs from that used by Johnson & Murphree (1969) which considers only the ratio of $I_3$ and $I_4$ for deriving the Mach number. Their method requires $\phi _{13} \approx \phi _{14}$ and assumes that the electron current contribution is minimal which may be true under the relatively high bias voltage and low plasma temperature present in their experiment. Furthermore, they extrapolate the ion current to zero bias voltage to minimize the effect of artificially large ion currents due to increased sheath diameter. The method shown above in (2.11) and (2.12) relaxes these requirements and includes the electron current flow. It is similar to that presented by Gatsonis et al. (2004). In contrast to Gatsonis et al., however, the ion current density and masses are used for the ion current in (2.8), (2.11) and (2.12), and the correction factors for the electron and ion currents in the perpendicular probe are included.

The above systems of equations may be solved using a nonlinear system of equation solvers at each time step assuming the current in each probe can be measured as a function of time. The initial guess of each state variable provided can be obtained by solving the algebraically reduced system as treated by Burton et al. (1993) and Gatsonis et al. (2004). These values may also be used to determine which system of equations to use for processing at each time step. The initial guess for the Mach number was taken to be three which is the lower limit of the Mach number expected based on velocities found using a simple PMT set-up on the CHENG facility.

3. Experimental characterization

3.1. Set-up

For these experiments, the QLP was placed 30 cm away from the expected pinch location of the CHENG deflagration source. The QLP was constructed with $250\ \mathrm {\mu } \textrm {m}$ diameter tungsten wires placed in a four-bore 150 mm long alumina ceramic rod. Each probe had an exposed length of 6 mm. The ceramic rod was supported by an acrylic extension arm to hold the set-up at the location of interest. The tungsten probes were soldered to high voltage wires through a feed-through vacuum bulkhead to the necessary circuitry and a Tektronics oscilloscope. The Pearson current monitors (Pearson Electronics models 2877) on each of the wires for probes 2–4 were connected to three of the channels on the oscilloscope with the last one attached to a Rogowski coil monitoring the discharge current at the capacitors for the accelerator. This discharge current was used to trigger the recording of the probe signals on the oscilloscope. The fourth current for probe 1 was calculated knowing the summation of currents should be zero (i.e. $I_1 = -I_2-I_3-I_4$). The biasing of the probes was accomplished with batteries such that $\phi _{12} = 3.10$ V and $\phi _{13} = \phi _{14} = 19.37$ V. The 3.10 V was attained by two 1.5 V batteries connected in series while the 19.37 V was attained by two 9 V batteries connected in series. There was no variation found in the voltage of the batteries while the discharges were taken – likely due to the minimal current/charge loading on the battery.

Discharges were undertaken at voltages from 3 to 7 kV on hydrogen, nitrogen and argon gas corresponding to energies of approximately 250 J to 1.4 kJ. Discharges at higher voltages with the QLP were avoided as its placement so close to the exit plane of the CHENG source made it subject to arcing. The valve was set such that the plenum pressure was 40 psi gauge (276 kPa) and the charging voltage was 900 V. This resulted in approximately 500 mg of gas injection into the system for each shot (Loebner, Underwood & Cappelli 2015a). Figure 3 illustrates the experimental set-up of the QLP in the CHENG device's vacuum chamber.

Figure 3. Experimental set-up illustrating QLP position relative to the exit plane of the plasma accelerator.

3.2. Analysis

Current traces from the oscilloscope were analysed. The oscilloscope was set to the maximum temporal resolution without interpolating, corresponding to a time interval of 100 ps. The recorded data were then post-processed and averaged every 50 points (every 5 ns) – the results of which were then used to set up the nonlinear systems of equations for solving with MATLAB's built-in nonlinear least square solver, lsqnonlin. Error propagation was performed following the scheme as discussed by Gatsonis et al. (2004). It was assumed that ions were singly ionized. It was also assumed that the energy of the plasma is such that the bulk of the ions for the nitrogen and hydrogen gases were fully dissociated. As such, the masses of atomic hydrogen and nitrogen were used for the calculations. Finally, the summation term for the ion collection current was taken only to $j = 150$ to aid in computational time.

3.3. Characterization results

The result of analysis for a 3 kV nitrogen shot is shown in figure 4. Note the two regions of increased density, temperature and plasma potential around $12\ \mathrm {\mu } \textrm {s}$ and again at $24\ \mathrm {\mu } \textrm {s}$. The first and larger increase corresponds to the deflagration mode plasma, and the smaller to a subsequent detonation mode due to the ringdown and inductive charging of the capacitors. This time difference matches the results for what would be expected with a ringdown half-period time of ${\sim }10\ \mathrm {\mu } \textrm {s}$. The Mach number and velocity are more complex in their shapes. Considering the region around $12\ \mathrm {\mu } \textrm {s}$, there is an increase in calculated Mach number and velocity around $10\ \mathrm {\mu } \textrm {s}$, which follows as the fastest particles arrive at the QLP position first. The Mach number and velocity decrease as the slower bulk plasma arrives around $12\ \mathrm {\mu } \textrm {s}$ and increase again around $15\ \mathrm {\mu } \textrm {s}$. This second increase in the Mach number is likely due to the plasma temperature falling off as reflected in the much more modest increase in velocity and may also be due to a reduction in density. There is a third increase in the plasma velocity around $24\ \mathrm {\mu } \textrm {s}$ corresponding to the arrival of the detonation. The detonation, unlike the deflagration, is characterized by a shock front effect so the distribution of particles is not as wide as in the deflagration case and shows up only as a jump in conditions around $24\ \mathrm {\mu } \textrm {s}$ in density, potential, temperature and velocity. The detonation features grow in relative size at higher voltages – owing to larger voltage amplitudes which can drive stronger detonations in the leftover gas.

Figure 4. QLP currents and calculated plasma parameters from a 3 kV $\textrm {N}_2$ discharge. Note the error bars are plotted every other time step for clarity.

Inspection of the Mach number graph suggests there is a ceiling of approximately 11 in value, as reflected by the flat region in the Mach number around $10\ \mathrm {\mu } \textrm {s}$ in figure 4. This flattening of Mach numbers at 11 is due to the aforementioned $j=150$ limit used in the ion current summation per (2.8). Plotting the coefficient of the ion current, $\exp [-S_i^2]\sum _{j=0}^{\infty } ({S_i^j}/{j!})^2\varGamma (j+\frac {3}{2})$, for various final values of $j$, as done in figure 5, shows the maximum Mach number calculable increases with more summation terms. It may not be worthwhile to calculate with a large number of terms from a computational standpoint, but any limit on $j$ induces an artificial limit on the Mach number calculable using the current QLP theory. Also shown is a comparison of these lines to a simple $\textrm {coefficient} = \textrm {Mach}$ number line which matches up well at higher Mach numbers ($S_i > 7$ results in less than 0.5 % difference) and may, instead, be used for high-Mach-number regimes of calculation. This flattening effect applies to both the method described by Gatsonis et al. (2004), and the method described by Johnson & Murphree (1969) and Burton et al. (1993), as shown in figure 6(a). The same graphs are shown in figure 6(b) with the incorporated correction for high Mach numbers.

Figure 5. Ion current collection coefficients as a function of Mach number for various numbers of summation terms depicting implicit maximum Mach numbers. A $\textrm {Coefficient} = S_i$ line is shown for comparison and agrees well with the coefficient calculation at higher Mach numbers.

Figure 6. (a) A comparison of the Mach numbers found using the ratio method per Johnson and Murphree, and the full ion current methods for both the Bohm and Laframboise systems of equations with 150 summation terms. (b) A comparison of the same but with a correction applied which uses the Mach number itself instead of the summations as the coefficient for the ion current for high Mach numbers.

It is beneficial to consider the electron and ion currents to verify the need for the incorporation of ion Mach number per Gatsonis instead of the ratio method used by Johnson and Murphree, and Burton. As shown in figure 6, there is a non-trivial difference between the two methods. As discussed in § 2.2.1, the ratio method requires the electron currents for both $I_3$ and $I_4$ to be zero or to evolve in a specific manner as to maintain the ratio of ion currents. A plot of the calculated ion and electron currents for both $I_3$ and $I_4$ is shown in figure 7. The equations for the ion and electron $I_3$ agree across theories so, at the minimum, the electron current for $I_3$ must be negligible. As shown, this is not necessarily true thereby substantiating the need for the full equation for incorporating the ion Mach number per Gatsonis’ method.

Figure 7. Calculated ion and electron currents from probe 3 and 4. The calculated electron currents are non-zero during the bulk of the deflagration which implies the ratio method for calculating the Mach number is not applicable.

All discharges on the CHENG device were analysed in a similar fashion and the results are tabulated below in table 1 reflecting the peak properties (density, plasma potential and temperature) for each values. The Mach number and velocity are reported at the time of peak density. It should be noted that the argon discharges at 3 kV produced multiple local maxima in the currents measured during each deflagration, suggesting the presence of restrikes – perhaps due to Argon's relatively high ionization energy – or instabilities in the pinch. These produce periods of anomalously high values and asymptotic behaviour for the derived plasma parameters. The peak results tabulated for argon ignore those periods of asymptotic behaviour.

Table 1. Peak plasma properties as measured by the QLP during the deflagration portion of the shot cycle for $\textrm {H}_2$, $\textrm {N}_2$ and Ar. Note that the above velocity is reflected at the time of maximum density.

A review of the data suggests a general increase in peak density and potential with increasing atomic mass and increasing voltage. Peak temperature seems to stay the same regardless of atomic mass and charge voltage. Bulk plasma velocity and Mach number, however, decrease with increases in both atomic mass and charging voltage. This is unexpected as intuition suggests there should be an increase in energy with increasing charging voltage which should result in an increase in velocity. The data were further analysed by looking at the peak ion momentum density, $p$, and the corresponding ion energy density, $\varepsilon$, for all shots per (3.1) and (3.2) below where $c_v$ is the specific heat and is assumed to be $3k_b/2$ for fully dissociated diatomic or monatomic gases.

(3.1)\begin{gather} p = m_in_iu_i, \end{gather}

(3.2)\begin{gather}\varepsilon = c_vk_bT_in_i+\tfrac{1}{2}m_iu_i^2n_i. \end{gather}

The peak momentum and corresponding energy densities are shown in table 2. As shown, the peak momentum density for each gas increases with increasing atomic mass. In fact, the increase is nearly proportional to atomic mass, suggesting the peak flux of ionized particles may be constant regardless of gas. This flux is also tabulated in table 2 and, as shown, is the same for all shots aside from argon at 3 kV and nitrogen at 7 kV. Furthermore, the internal energy density, as calculated, is constant for each gas regardless of charging voltage suggesting the energy coupling mechanisms at play may be partially invariant to charging voltage.

Table 2. Plasma properties at peak momentum density as measured by the QLP during the deflagration portion of the shot cycle for $\textrm {H}_2$, $\textrm {N}_2$ and Ar. Minimal change is noted in particle flux while momentum density and energy density exhibit dependence on atomic mass.

The assumption of thermal equilibrium and single ionization may now be revisited and tested for consistency. The calculated temperatures are of the same order of magnitude as the $\sim$25 eV ion temperatures found in the device using Doppler broadened impurity lines measured using emission spectroscopy (Loebner 2017), suggesting at least partial thermal equilibrium. Such ion and electron temperatures, if the flow is taken to be in Saha equilibrium, would correspond to nitrogen charge states of the order of 5–7 and argon charge states of the order of 8–13 for the densities found. However, the residence time of the plasma is not sufficiently long to allow for ‘ionization’ equilibrium to be established. For ‘ionization’ equilibrium, we would expect a residence time of the flow within the high temperature ensuing jet, $\tau _{r}$, to be much longer than the characteristic time scale for ionization, $\tau _{i}$, which would be the inverse of the ionization rate. The ionization rate may expressed as

(3.3)\begin{equation} \nu_{{\rm ionization}} = \sigma_in_ic_e = \sigma_in_i\sqrt{\frac{2k_bT_e}{m_e}}. \end{equation}

The absolute ionization collision cross-section of singly ionized nitrogen atoms by $\sim$25.8 eV electrons (higher than the temperatures measured in our nitrogen experiments) is $7 \times 10^{-23} \ \textrm {m}^{2}$ (Lecointre et al. 2013). Assuming a density of ${\approx }10^{21}$ – although the pinch has a higher density, the resident time within the pinch region is minimal – the characteristic time for ionization is approximately $\tau _{i} = (2.1\times 10^{5})^{-1} = 4.6\times 10^{-6}$ s. Considering a residence time, $\tau _{r}$, associated with a measured velocity of ${\approx }4 \times 10^{4}\ \textrm {m}\ \textrm {s}^{-1}$, over an approximate span of 0.1 m, we find $\tau _{r} = 6.3\times 10^{-6}$ s. As a consequence, since $\tau _{i} \approx \tau _{r}$,we do not expect a significant fraction of doubly ionized nitrogen in the flow. Similar conclusions can be drawn for argon using the cross-sections determined for singly ionized argon (Belic, Lecointre & Defrance 2010).

3.4. Applicability to solar winds

The plasma properties shown in table 1 allow for comparisons with the laboratory scaling as provided by Rahman et al. (1991) and Fu et al. (2020). Table 3 reflects the numbers for the solar wind along with some of the values from the CHENG device for hydrogen – as that would best replicate the solar winds – at 3 and 5 kV using the peak values from the QLP analysis. Note that the calculations and results provided are in cgs units to match the original paper. All four parameters depend on the magnetic flux density at the location of interest. No measurements have been taken of the magnetic flux density but an equilibrium model, developed by Loebner (2017), provides an approximation at the pinch location. By assuming a simple radial decay and a linear scaling with voltage, the magnetic flux density may be approximated at the QLP location. The magnetic Reynolds number, $R_m$, and the Hall parameter, $R_H$, depend on the size of the object being placed in the chamber. For e-sail work, a $250\ \mathrm {\mu } \textrm {m}$ wire is the most likely target so a characteristic radius of $125\ \mathrm {\mu } \textrm {m}$ has been used for the calculations.

Table 3. Values of solar wind properties and scaling parameters along with their corresponding values for the hydrogen plasma generated by the CHENG device. Here, $\rho _o$ is the mass density of the plasma, $\varOmega _e$ is the electron cyclotron frequency, $r_{iL}$ is the Larmor radius and $x_o$ is the characteristic length of the object being studied.

As shown, although the CHENG device can be operated such that the dynamic beta, $\beta _d$, closely matches that of the solar wind, the thermal beta, $\beta _p$, is approximately an order of magnitude larger than the solar winds’, suggesting that studies pertaining to the thermal effects of the solar winds would not be properly captured by the CHENG device. Furthermore, the magnetic Reynolds number and the Hall parameter are off by orders of magnitude, but the requirement for these is that they be much larger than 1. These last two parameters are more relevant for simulating magnetosphere conditions (Rahman et al. 1991; Fu et al. 2020) and are strongly dependent on the characteristic radius of the object placed downstream of the CHENG device. By choosing large enough objects, these parameters may be worked so as to meet the scaling requirements.

4. Conclusions

We have presented a review and consolidation of theories behind the use of quadruple Langmuir probes in highly ionized high speed plasma flows, pointing out some limitations and the implicit assumptions behind them. We use these theories to interpret measurements carried out in the far-field of a pulsed plasma deflagration (CHENG) accelerator operating on argon, hydrogen and nitrogen. Preliminary indications suggest that the energy coupling is not as dependent on charging voltage as previously thought, and is, instead, dependent on atomic mass for the tested parameters. It was also found that the peak particle flux is consistent between shots and gases suggesting that neutral gas flux may be a limiting parameter. The results are examined within the framework of the possible use of this deflagration source as a means of replicating certain properties of the solar wind. Future work will consider different neutral gas inflow rates to further investigate the operating parameters that can influence the particle flux. Simulations and/or experiments will also be done to better understand the magnetic fields produced on the accelerator.