Published online by Cambridge University Press: 20 November 2018
For Dewitt super groups  $G$ modeled via an underlying finitely generated Grassmann algebra it is well known that when there exists a body group
$G$ modeled via an underlying finitely generated Grassmann algebra it is well known that when there exists a body group 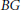 $BG$ compatible with the group operation on
$BG$ compatible with the group operation on  $G$, then, generically, the kernel
$G$, then, generically, the kernel 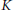 $K$ of the body homomorphism is nilpotent. This is not true when the underlying Grassmann algebra is infinitely generated. We show that it is quasi-nilpotent in the sense that as a Banach Lie group its Lie algebra
$K$ of the body homomorphism is nilpotent. This is not true when the underlying Grassmann algebra is infinitely generated. We show that it is quasi-nilpotent in the sense that as a Banach Lie group its Lie algebra  $\kappa$ has the property that for each
$\kappa$ has the property that for each 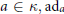 $a\,\in \,\kappa ,\,\text{a}{{\text{d}}_{a}}$ has a zero spectrum. We also show that the exponential mapping from
$a\,\in \,\kappa ,\,\text{a}{{\text{d}}_{a}}$ has a zero spectrum. We also show that the exponential mapping from  $\kappa$ to
$\kappa$ to 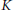 $K$ is surjective and that
$K$ is surjective and that 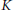 $K$ is a quotient manifold of the Banach space
$K$ is a quotient manifold of the Banach space  $\kappa$ via a lattice in
$\kappa$ via a lattice in  $\kappa$.
$\kappa$.