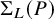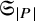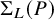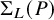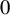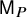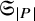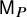1 Introduction
Schur labeled skew shape posets naturally appear in the context of the celebrated Stanley’s P-partitions conjecture. Let
![]() $\mathsf {P}_n$
be the set of posets with underlying set
$\mathsf {P}_n$
be the set of posets with underlying set
![]() $[n] := \{1,2,\ldots , n\}$
. Each poset
$[n] := \{1,2,\ldots , n\}$
. Each poset
![]() $P \in \mathsf {P}_n$
can be identified with the labeled poset
$P \in \mathsf {P}_n$
can be identified with the labeled poset
![]() $(P, \omega )$
with the labeling
$(P, \omega )$
with the labeling
![]() $\omega : P \rightarrow [n]$
given by
$\omega : P \rightarrow [n]$
given by
![]() $\omega (i) = i$
. Consequently, to each poset
$\omega (i) = i$
. Consequently, to each poset
![]() $P\in \mathsf {P}_n$
, one can associate the following generating function for its P-partitions:
$P\in \mathsf {P}_n$
, one can associate the following generating function for its P-partitions:
 $$\begin{align*}K_{P} := \sum_{f: P\text{-partition}} x_1^{|f^{-1}(1)|} x_2^{|f^{-1}(2)|} \cdots. \end{align*}$$
$$\begin{align*}K_{P} := \sum_{f: P\text{-partition}} x_1^{|f^{-1}(1)|} x_2^{|f^{-1}(2)|} \cdots. \end{align*}$$
In 1972, Stanley [Reference Stanley34, p. 81] proposed a conjecture stating that
![]() $K_P$
is a symmetric function if and only if P is a Schur labeled skew shape poset. For the precise definition of Schur labeled skew shape posets, refer to Section 2.3. While this conjecture has been verified to be true for all posets P with
$K_P$
is a symmetric function if and only if P is a Schur labeled skew shape poset. For the precise definition of Schur labeled skew shape posets, refer to Section 2.3. While this conjecture has been verified to be true for all posets P with
![]() $|P| \le 8$
, it remains an open question in the general case (see [Reference McNamara28]). We denote by
$|P| \le 8$
, it remains an open question in the general case (see [Reference McNamara28]). We denote by
![]() $\mathsf {SP}_n$
the set of all Schur labeled skew shape posets in
$\mathsf {SP}_n$
the set of all Schur labeled skew shape posets in
![]() $\mathsf {P}_n$
.
$\mathsf {P}_n$
.
Regular posets were introduced by Björner–Wachs [Reference Björner and Wachs8] during their investigation of the convex subsets of the symmetric group
![]() $\mathfrak {S}_n$
on
$\mathfrak {S}_n$
on
![]() $\{1,2, \ldots n\}$
under the right weak Bruhat order. For
$\{1,2, \ldots n\}$
under the right weak Bruhat order. For
![]() $P \in \mathsf {P}_n$
with the partial order
$P \in \mathsf {P}_n$
with the partial order
![]() $\preceq $
, let
$\preceq $
, let
![]() $\Sigma _R(P)$
be the set of permutations
$\Sigma _R(P)$
be the set of permutations
![]() $\pi \in \mathfrak {S}_n$
satisfying that if
$\pi \in \mathfrak {S}_n$
satisfying that if
![]() $x \preceq y$
, then
$x \preceq y$
, then
![]() $\pi ^{-1}(x) \le \pi ^{-1}(y)$
. They observed that every convex subset of
$\pi ^{-1}(x) \le \pi ^{-1}(y)$
. They observed that every convex subset of
![]() $\mathfrak {S}_n$
under the right weak Bruhat order appears as
$\mathfrak {S}_n$
under the right weak Bruhat order appears as
![]() $\Sigma _R(P)$
for some
$\Sigma _R(P)$
for some
![]() $P \in \mathsf {P}_n$
, and every right weak Bruhat interval in
$P \in \mathsf {P}_n$
, and every right weak Bruhat interval in
![]() $\mathfrak {S}_n$
is convex. This observation led them to characterize the posets
$\mathfrak {S}_n$
is convex. This observation led them to characterize the posets
![]() $P \in \mathsf {P}_n$
satisfying that
$P \in \mathsf {P}_n$
satisfying that
![]() $\Sigma _R(P)$
is a right weak Bruhat interval. They introduced the notion of regular posets and proved that
$\Sigma _R(P)$
is a right weak Bruhat interval. They introduced the notion of regular posets and proved that
![]() $P \in \mathsf {P}_n$
is a regular poset if and only if
$P \in \mathsf {P}_n$
is a regular poset if and only if
![]() $\Sigma _R(P)$
is a right weak Bruhat interval in
$\Sigma _R(P)$
is a right weak Bruhat interval in
![]() $\mathfrak {S}_n$
. For the definition of regular posets, refer to Definition 2.3. We denote by
$\mathfrak {S}_n$
. For the definition of regular posets, refer to Definition 2.3. We denote by
![]() $\mathsf {RP}_n$
the set of all regular posets in
$\mathsf {RP}_n$
the set of all regular posets in
![]() $\mathsf {P}_n$
.
$\mathsf {P}_n$
.
Let
![]() $\mathsf {RSP}_n := \mathsf {RP}_n \cap \mathsf {SP}_n$
. In the following, we explain the reason why we consider regular Schur labeled skew shape posets from the perspective of the representation theory of the
$\mathsf {RSP}_n := \mathsf {RP}_n \cap \mathsf {SP}_n$
. In the following, we explain the reason why we consider regular Schur labeled skew shape posets from the perspective of the representation theory of the
![]() $0$
-Hecke algebra.
$0$
-Hecke algebra.
In 1996, Duchamp, Krob, Leclerc and Thibon [Reference Duchamp, Krob, Leclerc and Thibon12] showed that the Grothendieck ring of the tower of
![]() $0$
-Hecke algebras
$0$
-Hecke algebras
![]() $\bigoplus _{n\ge 0}H_n(0)$
, when equipped with addition and multiplication from direct sum and induction product, is isomorphic to the ring
$\bigoplus _{n\ge 0}H_n(0)$
, when equipped with addition and multiplication from direct sum and induction product, is isomorphic to the ring
![]() $\mathrm {QSym}$
of quasisymmetric functions. To be precise, they showed that the map
$\mathrm {QSym}$
of quasisymmetric functions. To be precise, they showed that the map
called the quasisymmetric characteristic, is a ring isomorphism. Here,
![]() $\mathcal {G}_0(H_n(0)\text{-}\mathbf {mod})$
is the Grothendieck group of the category
$\mathcal {G}_0(H_n(0)\text{-}\mathbf {mod})$
is the Grothendieck group of the category
![]() $H_n(0)\text{-}\mathbf {mod}$
of finitely generated left
$H_n(0)\text{-}\mathbf {mod}$
of finitely generated left
![]() $H_n(0)$
-modules,
$H_n(0)$
-modules,
![]() $\alpha $
is a composition,
$\alpha $
is a composition,
![]() $\mathbf {F}_\alpha $
is the irreducible
$\mathbf {F}_\alpha $
is the irreducible
![]() $H_n(0)$
-module attached to
$H_n(0)$
-module attached to
![]() $\alpha $
, and
$\alpha $
, and
![]() $F_\alpha $
is the fundamental quasisymmetric function attached to
$F_\alpha $
is the fundamental quasisymmetric function attached to
![]() $\alpha $
(for more details, see Section 2.4). Afterwards, Bergeron–Li [Reference Bergeron and Li5] showed that the map
$\alpha $
(for more details, see Section 2.4). Afterwards, Bergeron–Li [Reference Bergeron and Li5] showed that the map
![]() $\mathrm {ch}$
is not just a ring isomorphism but also a Hopf algebra isomorphism. In 2002, Duchamp–Hivert–Thibon [Reference Duchamp, Hivert and Thibon11] associated a right
$\mathrm {ch}$
is not just a ring isomorphism but also a Hopf algebra isomorphism. In 2002, Duchamp–Hivert–Thibon [Reference Duchamp, Hivert and Thibon11] associated a right
![]() $H_n(0)$
-module
$H_n(0)$
-module
![]() $M_P$
with each poset
$M_P$
with each poset
![]() $P \in \mathsf {P}_n$
, such that the image of
$P \in \mathsf {P}_n$
, such that the image of
![]() $M_P$
under the quasisymmetric characteristic is
$M_P$
under the quasisymmetric characteristic is
![]() $K_P$
. This was achieved by defining a suitable right
$K_P$
. This was achieved by defining a suitable right
![]() $H_n(0)$
-action on
$H_n(0)$
-action on
![]() $\Sigma _R(P)$
.
$\Sigma _R(P)$
.
Since the middle of 2010, various left
![]() $0$
-Hecke modules, each equipped with a tableau basis and yielding an important quasisymmetric characteristic image, have been constructed ([Reference Bardwell and Searles2, Reference Berg, Bergeron, Saliola, Serrano and Zabrocki4, Reference Searles32, Reference Tewari and van Willigenburg37, Reference Tewari and van Willigenburg38]). In order to handle these modules in a uniform manner, Jung–Kim–Lee–Oh [Reference Jung, Kim, Lee and Oh19] introduced a left
$0$
-Hecke modules, each equipped with a tableau basis and yielding an important quasisymmetric characteristic image, have been constructed ([Reference Bardwell and Searles2, Reference Berg, Bergeron, Saliola, Serrano and Zabrocki4, Reference Searles32, Reference Tewari and van Willigenburg37, Reference Tewari and van Willigenburg38]). In order to handle these modules in a uniform manner, Jung–Kim–Lee–Oh [Reference Jung, Kim, Lee and Oh19] introduced a left
![]() $H_n(0)$
-module
$H_n(0)$
-module
![]() $\mathsf {B}(I)$
, referred to as the weak Bruhat interval module associated with I, for each left weak Bruhat interval I in
$\mathsf {B}(I)$
, referred to as the weak Bruhat interval module associated with I, for each left weak Bruhat interval I in
![]() $\mathfrak {S}_n$
. Furthermore, they showed that
$\mathfrak {S}_n$
. Furthermore, they showed that
![]() $\bigoplus _{n \ge 0} \mathcal {G}_0(\mathscr {B}_n)$
is isomorphic to
$\bigoplus _{n \ge 0} \mathcal {G}_0(\mathscr {B}_n)$
is isomorphic to
![]() $\mathrm {QSym}$
as Hopf algebras, where
$\mathrm {QSym}$
as Hopf algebras, where
![]() $\mathscr {B}_n$
is the full subcategory of
$\mathscr {B}_n$
is the full subcategory of
![]() $H_n(0)$
-
$H_n(0)$
-
![]() $\mathbf {mod}$
consisting of objects that are direct sums of finitely many isomorphic copies of weak Bruhat interval modules of
$\mathbf {mod}$
consisting of objects that are direct sums of finitely many isomorphic copies of weak Bruhat interval modules of
![]() $H_n(0)$
. Recently, Choi–Kim–Oh [Reference Choi, Kim and Oh9] clarified the exact relationship between the weak Bruhat interval modules and the
$H_n(0)$
. Recently, Choi–Kim–Oh [Reference Choi, Kim and Oh9] clarified the exact relationship between the weak Bruhat interval modules and the
![]() $0$
-Hecke modules
$0$
-Hecke modules
![]() $M_P$
, using Björner–Wachs’ characterization. More precisely, they constructed a contravariant functor
$M_P$
, using Björner–Wachs’ characterization. More precisely, they constructed a contravariant functor
![]() $\mathcal {F}:{H_n(0)\text{-}\mathbf {mod}} \rightarrow \mathbf {mod}\text{-}H_n(0)$
that preserves the quasisymmetric characteristic and showed that
$\mathcal {F}:{H_n(0)\text{-}\mathbf {mod}} \rightarrow \mathbf {mod}\text{-}H_n(0)$
that preserves the quasisymmetric characteristic and showed that
![]() $M_P = \mathcal {F}(\mathsf {B}(\Sigma _L(P)))$
, where
$M_P = \mathcal {F}(\mathsf {B}(\Sigma _L(P)))$
, where
![]() $\mathbf {mod}\text{-}H_n(0)$
is the category of finitely generated right
$\mathbf {mod}\text{-}H_n(0)$
is the category of finitely generated right
![]() $H_n(0)$
-modules and
$H_n(0)$
-modules and
![]() $\Sigma _L(P) := \{\gamma ^{-1} \mid \gamma \in \Sigma _R(P)\}$
for
$\Sigma _L(P) := \{\gamma ^{-1} \mid \gamma \in \Sigma _R(P)\}$
for
![]() $P \in \mathsf {RP}_n$
. For technical reasons, we use a slightly different
$P \in \mathsf {RP}_n$
. For technical reasons, we use a slightly different
![]() $0$
-Hecke module, denoted as
$0$
-Hecke module, denoted as
![]() $\mathsf {M}_P$
, instead of Duchamp, Hivert and Thibon’s module
$\mathsf {M}_P$
, instead of Duchamp, Hivert and Thibon’s module
![]() $M_P$
. This module is a left
$M_P$
. This module is a left
![]() $H_n(0)$
-module with the basis
$H_n(0)$
-module with the basis
![]() $\Sigma _L(P)$
. For the detailed definition of
$\Sigma _L(P)$
. For the detailed definition of
![]() $\mathsf {M}_P$
, refer to Definition 2.8.
$\mathsf {M}_P$
, refer to Definition 2.8.
The aim of this paper is to give a comprehensive investigation of regular Schur labeled skew shape posets and their associated
![]() $0$
-Hecke modules.
$0$
-Hecke modules.
In Section 3, we provide an explicit description of
![]() $\Sigma _L(P)$
for
$\Sigma _L(P)$
for
![]() $P \in \mathsf {RSP}_n$
. We first introduce a Schur labeling
$P \in \mathsf {RSP}_n$
. We first introduce a Schur labeling
![]() $\tau _P$
, which is a bijective tableau uniquely determined by suitable conditions. For details, see Equation (3.2). Let
$\tau _P$
, which is a bijective tableau uniquely determined by suitable conditions. For details, see Equation (3.2). Let
![]() $\lambda /\mu $
be the shape of
$\lambda /\mu $
be the shape of
![]() $\tau _P$
. Then
$\tau _P$
. Then
![]() $\tau _P$
gives rise to a reading, denoted
$\tau _P$
gives rise to a reading, denoted
![]() $\mathsf {read}_{\tau _P}$
, on the set
$\mathsf {read}_{\tau _P}$
, on the set
![]() $\mathrm {SYT}(\lambda /\mu )$
of standard Young tableaux of shape
$\mathrm {SYT}(\lambda /\mu )$
of standard Young tableaux of shape
![]() $\lambda /\mu $
. We show that all permutations in
$\lambda /\mu $
. We show that all permutations in
![]() $\Sigma _L(P)$
appear as reading words of standard Young tableaux of shape
$\Sigma _L(P)$
appear as reading words of standard Young tableaux of shape
![]() $\lambda /\mu $
, i.e.,
$\lambda /\mu $
, i.e.,
![]() $ \Sigma _L(P) = \mathsf {read}_{\tau _P}(\mathrm {SYT}(\lambda /\mu )) $
(Lemma 3.2). Then, we derive that
$ \Sigma _L(P) = \mathsf {read}_{\tau _P}(\mathrm {SYT}(\lambda /\mu )) $
(Lemma 3.2). Then, we derive that
where
![]() $T_{\lambda /\mu }$
(resp.
$T_{\lambda /\mu }$
(resp.
![]() $T^{\prime}_{\lambda /\mu }$
) is the standard Young tableau obtained by filling the Young diagram of shape
$T^{\prime}_{\lambda /\mu }$
) is the standard Young tableau obtained by filling the Young diagram of shape
![]() $\lambda /\mu $
by
$\lambda /\mu $
by
![]() $1, 2, \ldots , n$
from left to right starting with the top row (resp. from top to bottom starting with leftmost column) (Theorem 3.9).
$1, 2, \ldots , n$
from left to right starting with the top row (resp. from top to bottom starting with leftmost column) (Theorem 3.9).
In Section 4, we introduce an equivalence relation
![]() $\overset {D}{\simeq }$
on the set
$\overset {D}{\simeq }$
on the set
![]() $\mathrm {Int}(n)$
of left weak Bruhat intervals in
$\mathrm {Int}(n)$
of left weak Bruhat intervals in
![]() $\mathfrak {S}_n$
. This relation is defined by
$\mathfrak {S}_n$
. This relation is defined by
![]() $I_1 \overset {D}{\simeq } I_2$
if there is a descent-preserving poset isomorphism between
$I_1 \overset {D}{\simeq } I_2$
if there is a descent-preserving poset isomorphism between
![]() $I_1$
and
$I_1$
and
![]() $I_2$
. We show that every equivalence class C is of the form
$I_2$
. We show that every equivalence class C is of the form
where
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $\sigma _1$
are the minimal and maximal elements in
$\sigma _1$
are the minimal and maximal elements in
![]() $\{\sigma \mid [\sigma , \rho ]_L \in C\}$
, respectively, and
$\{\sigma \mid [\sigma , \rho ]_L \in C\}$
, respectively, and
![]() $\xi _C = \rho \sigma ^{-1}$
for any
$\xi _C = \rho \sigma ^{-1}$
for any
![]() $[\sigma , \rho ]_L \in C$
(Theorem 4.6). In the case where
$[\sigma , \rho ]_L \in C$
(Theorem 4.6). In the case where
![]() $P \in \mathsf {RSP}_n$
, we show in Theorem 4.7 that the equivalence class of
$P \in \mathsf {RSP}_n$
, we show in Theorem 4.7 that the equivalence class of
![]() $\Sigma _L(P)$
is given by
$\Sigma _L(P)$
is given by
In Section 5, we classify the
![]() $H_n(0)$
-modules
$H_n(0)$
-modules
![]() $\mathsf {M}_P$
up to isomorphism as P ranges over
$\mathsf {M}_P$
up to isomorphism as P ranges over
![]() $\mathsf {RSP}_n$
. We show in Theorem 5.5 that for
$\mathsf {RSP}_n$
. We show in Theorem 5.5 that for
![]() $P, Q \in \mathsf {RSP}_n$
,
$P, Q \in \mathsf {RSP}_n$
,
The ‘if’ part is straightforward and can be derived from Equation (1.1). As for the ‘only if’ part, it can be verified by showing that when
![]() $\tau _P$
and
$\tau _P$
and
![]() $\tau _Q$
have different shapes, it results in either nonisomorphic projective covers or nonisomorphic injective hulls of
$\tau _Q$
have different shapes, it results in either nonisomorphic projective covers or nonisomorphic injective hulls of
![]() $\mathsf {M}_P$
and
$\mathsf {M}_P$
and
![]() $\mathsf {M}_Q$
. To accomplish this, we compute both a projective cover and an injective hull of
$\mathsf {M}_Q$
. To accomplish this, we compute both a projective cover and an injective hull of
![]() $\mathsf {M}_P$
for
$\mathsf {M}_P$
for
![]() $P \in \mathsf {RSP}_n$
(Lemma 5.4).
$P \in \mathsf {RSP}_n$
(Lemma 5.4).
In Section 6, we first prove that a poset
![]() $P \in \mathsf {P}_n$
is a regular Schur labeled skew shape poset if and only if
$P \in \mathsf {P}_n$
is a regular Schur labeled skew shape poset if and only if
![]() $\Sigma _L(P)$
is dual plactic-closed (Theorem 6.4). This improves Malvenuto’s result [Reference Malvenuto27, Theorem 1], which states that if
$\Sigma _L(P)$
is dual plactic-closed (Theorem 6.4). This improves Malvenuto’s result [Reference Malvenuto27, Theorem 1], which states that if
![]() $\Sigma _L(P)$
is dual plactic-closed, then
$\Sigma _L(P)$
is dual plactic-closed, then
![]() $P \in \mathsf {SP}_n$
. Then, we introduce the notion of a distinguished filtration of an
$P \in \mathsf {SP}_n$
. Then, we introduce the notion of a distinguished filtration of an
![]() $H_n(0)$
-module M with respect to a linearly independent subset
$H_n(0)$
-module M with respect to a linearly independent subset
![]() $\mathcal {B}$
of
$\mathcal {B}$
of
![]() $\mathrm {QSym}_n$
(Definition 6.5). If such a filtration is available, we have a representation theoretic interpretation of the expansion of
$\mathrm {QSym}_n$
(Definition 6.5). If such a filtration is available, we have a representation theoretic interpretation of the expansion of
![]() $\mathrm {ch}([M])$
in
$\mathrm {ch}([M])$
in
![]() $\mathcal {B}$
. The existence of a distinguished filtration is quite nontrivial as seen in Example 6.6. However, using the characterization given in Theorem 6.4, we show that
$\mathcal {B}$
. The existence of a distinguished filtration is quite nontrivial as seen in Example 6.6. However, using the characterization given in Theorem 6.4, we show that
![]() $\mathsf {M}_P$
admits a distinguished filtration with respect to the Schur basis when
$\mathsf {M}_P$
admits a distinguished filtration with respect to the Schur basis when
![]() $P \in \mathsf {RSP}_n$
(Theorem 6.7).
$P \in \mathsf {RSP}_n$
(Theorem 6.7).
The final section is mainly devoted to further issues concerned with the classification and decomposition of the
![]() $0$
-Hecke modules
$0$
-Hecke modules
![]() $\mathsf {M}_P$
. We discuss the classification problem for
$\mathsf {M}_P$
. We discuss the classification problem for
![]() $\{\mathsf {M}_P \mid P \in \mathsf {SP}_n\}$
and
$\{\mathsf {M}_P \mid P \in \mathsf {SP}_n\}$
and
![]() $\{\mathsf {M}_P \mid P \in \mathsf {RP}_n\}$
. In particular, we expect that for
$\{\mathsf {M}_P \mid P \in \mathsf {RP}_n\}$
. In particular, we expect that for
![]() $P, Q \in \mathsf {RP}_n$
,
$P, Q \in \mathsf {RP}_n$
,
![]() $\mathsf {M}_P \cong \mathsf {M}_Q$
if and only if
$\mathsf {M}_P \cong \mathsf {M}_Q$
if and only if
![]() $\Sigma _L(P) \overset {D}{\simeq } \Sigma _L(Q)$
(Conjecture 7.2). The decomposition problem is also discussed for the
$\Sigma _L(P) \overset {D}{\simeq } \Sigma _L(Q)$
(Conjecture 7.2). The decomposition problem is also discussed for the
![]() $0$
-Hecke modules
$0$
-Hecke modules
![]() $\mathsf {M}_P$
when
$\mathsf {M}_P$
when
![]() $P \in \mathsf {RSP}_n$
. Based on experimental data, we expect that for
$P \in \mathsf {RSP}_n$
. Based on experimental data, we expect that for
![]() $P \in \mathsf {RSP}_n$
,
$P \in \mathsf {RSP}_n$
,
![]() $\mathsf {M}_P$
is indecomposable if and only if
$\mathsf {M}_P$
is indecomposable if and only if
![]() $\mathrm {sh}(\tau _P)$
is disconnected and does not contain any disconnected ribbon (Conjecture 7.5). At the end of this section, we provide a remark on how to recover
$\mathrm {sh}(\tau _P)$
is disconnected and does not contain any disconnected ribbon (Conjecture 7.5). At the end of this section, we provide a remark on how to recover
![]() $\mathsf {M}_P$
for
$\mathsf {M}_P$
for
![]() $P \in \mathsf {RSP}_n$
from a module of the generic Hecke algebra
$P \in \mathsf {RSP}_n$
from a module of the generic Hecke algebra
![]() $H_n(q)$
by specializing q to
$H_n(q)$
by specializing q to
![]() $0$
.
$0$
.
In the appendix, we give a tableau description of
![]() $\mathsf {M}_P$
for
$\mathsf {M}_P$
for
![]() $P \in \mathsf {RSP}_n$
. For a skew partition
$P \in \mathsf {RSP}_n$
. For a skew partition
![]() $\lambda /\mu $
of size n, we construct an
$\lambda /\mu $
of size n, we construct an
![]() $H_n(0)$
-module
$H_n(0)$
-module
![]() $X_{\lambda /\mu }$
with standard Young tableaux of shape
$X_{\lambda /\mu }$
with standard Young tableaux of shape
![]() $\lambda /\mu $
as basis elements. This module can be viewed as a representative of the isomorphism class of
$\lambda /\mu $
as basis elements. This module can be viewed as a representative of the isomorphism class of
![]() $\mathsf {M}_P$
in the category
$\mathsf {M}_P$
in the category
![]() $H_n(0)\text{-}\mathbf {mod}$
for every
$H_n(0)\text{-}\mathbf {mod}$
for every
![]() $P \in \mathsf {RSP}_n$
with
$P \in \mathsf {RSP}_n$
with
![]() $\mathrm {sh}(\tau _P) = \lambda /\mu $
.
$\mathrm {sh}(\tau _P) = \lambda /\mu $
.
2 Preliminaries
For integers m and n, we define
![]() $[m,n]$
and
$[m,n]$
and
![]() $[n]$
to be the intervals
$[n]$
to be the intervals
![]() $\{t\in \mathbb Z \mid m\le t \le n\}$
and
$\{t\in \mathbb Z \mid m\le t \le n\}$
and
![]() $\{t\in \mathbb Z \mid 1\le t \le n\}$
, respectively. Throughout this paper, n will denote a nonnegative integer unless otherwise stated.
$\{t\in \mathbb Z \mid 1\le t \le n\}$
, respectively. Throughout this paper, n will denote a nonnegative integer unless otherwise stated.
2.1 Compositions, Young diagrams and bijective tableaux
A composition
![]() $\alpha $
of n, denoted by
$\alpha $
of n, denoted by
![]() $\alpha \models n$
, is a finite ordered list of positive integers
$\alpha \models n$
, is a finite ordered list of positive integers
![]() $(\alpha _1,\alpha _2,\ldots , \alpha _k)$
satisfying
$(\alpha _1,\alpha _2,\ldots , \alpha _k)$
satisfying
![]() $\sum _{i=1}^k \alpha _i = n$
. We call
$\sum _{i=1}^k \alpha _i = n$
. We call
![]() $\alpha _i$
(
$\alpha _i$
(
![]() $1 \le i \le k$
) a part of
$1 \le i \le k$
) a part of
![]() $\alpha $
,
$\alpha $
,
![]() $k =: \ell (\alpha )$
the length of
$k =: \ell (\alpha )$
the length of
![]() $\alpha $
, and
$\alpha $
, and
![]() $n =:|\alpha |$
the size of
$n =:|\alpha |$
the size of
![]() $\alpha $
. And we define the empty composition
$\alpha $
. And we define the empty composition
![]() $\varnothing $
to be the unique composition of size and length
$\varnothing $
to be the unique composition of size and length
![]() $0$
. Whenever necessary, we set
$0$
. Whenever necessary, we set
![]() $\alpha _i = 0$
for all
$\alpha _i = 0$
for all
![]() $i> \ell (\alpha )$
.
$i> \ell (\alpha )$
.
Given
![]() $\alpha = (\alpha _1,\alpha _2,\ldots ,\alpha _k) \models n$
and
$\alpha = (\alpha _1,\alpha _2,\ldots ,\alpha _k) \models n$
and
![]() $I = \{i_1 < i_2 < \cdots < i_{l}\} \subseteq [n-1]$
, let
$I = \{i_1 < i_2 < \cdots < i_{l}\} \subseteq [n-1]$
, let
 $$ \begin{align*} \mathrm{set}(\alpha) &:= \{\alpha_1,\alpha_1+\alpha_2,\ldots, \alpha_1 + \alpha_2 + \cdots + \alpha_{k-1}\}, \text{ and} \\\mathrm{comp}(I) &:= (i_1,i_2 - i_1, i_3 - i_2, \ldots,n-i_{l}). \end{align*} $$
$$ \begin{align*} \mathrm{set}(\alpha) &:= \{\alpha_1,\alpha_1+\alpha_2,\ldots, \alpha_1 + \alpha_2 + \cdots + \alpha_{k-1}\}, \text{ and} \\\mathrm{comp}(I) &:= (i_1,i_2 - i_1, i_3 - i_2, \ldots,n-i_{l}). \end{align*} $$
The set of compositions of n is in bijection with the set of subsets of
![]() $[n-1]$
under the correspondence
$[n-1]$
under the correspondence
![]() $\alpha \mapsto \mathrm {set}(\alpha )$
(or
$\alpha \mapsto \mathrm {set}(\alpha )$
(or
![]() $I \mapsto \mathrm {comp}(I)$
). The reverse composition
$I \mapsto \mathrm {comp}(I)$
). The reverse composition
![]() $\alpha ^{\mathrm {r}}$
of
$\alpha ^{\mathrm {r}}$
of
![]() $\alpha $
is defined to be the composition
$\alpha $
is defined to be the composition
![]() $(\alpha _k, \alpha _{k-1}, \ldots , \alpha _1)$
, and the complement
$(\alpha _k, \alpha _{k-1}, \ldots , \alpha _1)$
, and the complement
![]() $\alpha ^{\mathrm {c}}$
of
$\alpha ^{\mathrm {c}}$
of
![]() $\alpha $
is defined to be the unique composition satisfying
$\alpha $
is defined to be the unique composition satisfying
![]() $\mathrm {set}(\alpha ^c) = [n-1] \setminus \mathrm {set}(\alpha )$
.
$\mathrm {set}(\alpha ^c) = [n-1] \setminus \mathrm {set}(\alpha )$
.
If a composition
![]() $\lambda = (\lambda _1, \lambda _2, \ldots , \lambda _k) \models n$
satisfies
$\lambda = (\lambda _1, \lambda _2, \ldots , \lambda _k) \models n$
satisfies
![]() $\lambda _1 \ge \lambda _2 \ge \cdots \ge \lambda _k$
, then it is called a partition of n and denoted as
$\lambda _1 \ge \lambda _2 \ge \cdots \ge \lambda _k$
, then it is called a partition of n and denoted as
![]() $\lambda \vdash n$
. Given two partitions
$\lambda \vdash n$
. Given two partitions
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
with
$\mu $
with
![]() $\ell (\lambda ) \ge \ell (\mu )$
, we write
$\ell (\lambda ) \ge \ell (\mu )$
, we write
![]() $\lambda \supseteq \mu $
if
$\lambda \supseteq \mu $
if
![]() $\lambda _i \geq \mu _i$
for all
$\lambda _i \geq \mu _i$
for all
![]() $1 \le i \le \ell (\mu )$
. A skew partition
$1 \le i \le \ell (\mu )$
. A skew partition
![]() $\lambda /\mu $
is a pair
$\lambda /\mu $
is a pair
![]() $(\lambda , \mu )$
of partitions with
$(\lambda , \mu )$
of partitions with
![]() $\lambda \supseteq \mu $
. We call
$\lambda \supseteq \mu $
. We call
![]() $|\lambda /\mu | := |\lambda | - |\mu |$
the size of
$|\lambda /\mu | := |\lambda | - |\mu |$
the size of
![]() $\lambda /\mu $
. In the case where
$\lambda /\mu $
. In the case where
![]() $\lambda \supset \mu \supset \nu $
, we say that
$\lambda \supset \mu \supset \nu $
, we say that
![]() $\lambda /\mu $
extends
$\lambda /\mu $
extends
![]() $\mu /\nu $
.
$\mu /\nu $
.
Given a partition
![]() $\lambda $
, we define the Young diagram
$\lambda $
, we define the Young diagram
![]() $\mathtt {yd}(\lambda )$
of
$\mathtt {yd}(\lambda )$
of
![]() $\lambda $
to be the left-justified array of n boxes, where the ith row from the top has
$\lambda $
to be the left-justified array of n boxes, where the ith row from the top has
![]() $\lambda _i$
boxes for
$\lambda _i$
boxes for
![]() $1 \le i \le k$
. Similarly, given a skew partition
$1 \le i \le k$
. Similarly, given a skew partition
![]() $\lambda / \mu $
, we define the Young diagram
$\lambda / \mu $
, we define the Young diagram
![]() $\mathtt {yd}(\lambda / \mu )$
of
$\mathtt {yd}(\lambda / \mu )$
of
![]() $\lambda / \mu $
to be the Young diagram
$\lambda / \mu $
to be the Young diagram
![]() $\mathtt {yd}(\lambda )$
with all boxes belonging to
$\mathtt {yd}(\lambda )$
with all boxes belonging to
![]() $\mathtt {yd}(\mu )$
removed. A Young diagram is called connected if for each pair of consecutive rows, there are at least two boxes (one in each row) which have a common edge. A skew partition is called connected if the corresponding Young diagram is connected, and it is called basic if the corresponding Young diagram contains neither empty rows nor empty columns. In this paper, every skew partition is assumed to be basic unless otherwise stated.
$\mathtt {yd}(\mu )$
removed. A Young diagram is called connected if for each pair of consecutive rows, there are at least two boxes (one in each row) which have a common edge. A skew partition is called connected if the corresponding Young diagram is connected, and it is called basic if the corresponding Young diagram contains neither empty rows nor empty columns. In this paper, every skew partition is assumed to be basic unless otherwise stated.
For two skew partitions
![]() $\lambda /\mu $
and
$\lambda /\mu $
and
![]() $\nu /\kappa $
, we define
$\nu /\kappa $
, we define
![]() $\lambda /\mu \star \nu /\kappa $
to be the skew partition whose Young diagram is obtained by taking a rectangle of empty squares with the same number of rows as
$\lambda /\mu \star \nu /\kappa $
to be the skew partition whose Young diagram is obtained by taking a rectangle of empty squares with the same number of rows as
![]() $\mathtt {yd}(\lambda /\mu )$
and the same number of columns as
$\mathtt {yd}(\lambda /\mu )$
and the same number of columns as
![]() $\mathtt {yd}(\nu /\kappa )$
, and putting
$\mathtt {yd}(\nu /\kappa )$
, and putting
![]() $\mathtt {yd}(\nu /\kappa )$
below and
$\mathtt {yd}(\nu /\kappa )$
below and
![]() $\mathtt {yd}(\lambda /\mu )$
to the right of this rectangle. For instance, if
$\mathtt {yd}(\lambda /\mu )$
to the right of this rectangle. For instance, if
![]() $\lambda /\mu = (2,2)$
and
$\lambda /\mu = (2,2)$
and
![]() $\nu /\kappa = (3,2)/(1)$
, then
$\nu /\kappa = (3,2)/(1)$
, then
![]() $\lambda /\mu \star \nu /\kappa = (5,5,3,2)/(3,3,1)$
and
$\lambda /\mu \star \nu /\kappa = (5,5,3,2)/(3,3,1)$
and

Given a skew partition
![]() $\lambda /\mu $
of size n, a bijective tableau of shape
$\lambda /\mu $
of size n, a bijective tableau of shape
![]() $\lambda / \mu $
is a filling of
$\lambda / \mu $
is a filling of
![]() $\mathtt {yd}(\lambda / \mu )$
with distinct entries in
$\mathtt {yd}(\lambda / \mu )$
with distinct entries in
![]() $[n]$
. For later use, we denote by
$[n]$
. For later use, we denote by
![]() $\tau _0^{\lambda /\mu }$
(resp.
$\tau _0^{\lambda /\mu }$
(resp.
![]() $\tau _1^{\lambda /\mu }$
) the bijective tableau of shape
$\tau _1^{\lambda /\mu }$
) the bijective tableau of shape
![]() $\lambda / \mu $
obtained by filling
$\lambda / \mu $
obtained by filling
![]() $1, 2, \ldots , n$
from right to left starting with the top row (resp. from top to bottom starting with the rightmost column). If
$1, 2, \ldots , n$
from right to left starting with the top row (resp. from top to bottom starting with the rightmost column). If
![]() $\lambda /\mu $
is clear in the context, we will drop the superscript
$\lambda /\mu $
is clear in the context, we will drop the superscript
![]() $\lambda /\mu $
from
$\lambda /\mu $
from
![]() $\tau _0^{\lambda /\mu }$
and
$\tau _0^{\lambda /\mu }$
and
![]() $\tau _1^{\lambda /\mu }$
. Again, letting
$\tau _1^{\lambda /\mu }$
. Again, letting
![]() $\lambda / \mu = (2,2) \star (3,2) / (1)$
, we have
$\lambda / \mu = (2,2) \star (3,2) / (1)$
, we have

A bijective tableau is referred to as a standard Young tableau if the elements in each row are arranged in increasing order from left to right, and the elements in each column are arranged in increasing order from top to bottom. We denote by
![]() $\mathrm {SYT}(\lambda / \mu )$
the set of all standard Young tableaux of shape
$\mathrm {SYT}(\lambda / \mu )$
the set of all standard Young tableaux of shape
![]() $\lambda / \mu $
. And we let
$\lambda / \mu $
. And we let
![]() $\mathrm {SYT}_n := \bigcup _{\lambda \vdash n} \mathrm {SYT}(\lambda )$
.
$\mathrm {SYT}_n := \bigcup _{\lambda \vdash n} \mathrm {SYT}(\lambda )$
.
2.2 Weak Bruhat orders on the symmetric group
Let
![]() $\mathfrak {S}_n$
denote the symmetric group on
$\mathfrak {S}_n$
denote the symmetric group on
![]() $[n]$
. Every permutation
$[n]$
. Every permutation
![]() $\sigma \in \mathfrak {S}_n$
can be expressed as a product of simple transpositions
$\sigma \in \mathfrak {S}_n$
can be expressed as a product of simple transpositions
![]() $s_i := (i,i+1)$
for
$s_i := (i,i+1)$
for
![]() $1 \leq i \leq n-1$
. A reduced expression for
$1 \leq i \leq n-1$
. A reduced expression for
![]() $\sigma $
is an expression that represents
$\sigma $
is an expression that represents
![]() $\sigma $
in the shortest possible length, and the length
$\sigma $
in the shortest possible length, and the length
![]() $\ell (\sigma )$
of
$\ell (\sigma )$
of
![]() $\sigma $
is the number of simple transpositions in any reduced expression for
$\sigma $
is the number of simple transpositions in any reduced expression for
![]() $\sigma $
. Let
$\sigma $
. Let
It is well known that if
![]() $\sigma = w_1 w_2 \cdots w_n$
in one-line notation, then
$\sigma = w_1 w_2 \cdots w_n$
in one-line notation, then
 $$ \begin{align*} \begin{aligned} \mathrm{Des}_L(\sigma) & = \{ i \in [n-1] \mid i\text{ is right of }i+1\text{ in }w_1 w_2 \cdots w_n \} \quad \text{and} \\ \mathrm{Des}_R(\sigma) & = \{ i \in [n-1] \mid w_i> w_{i+1} \}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathrm{Des}_L(\sigma) & = \{ i \in [n-1] \mid i\text{ is right of }i+1\text{ in }w_1 w_2 \cdots w_n \} \quad \text{and} \\ \mathrm{Des}_R(\sigma) & = \{ i \in [n-1] \mid w_i> w_{i+1} \}. \end{aligned} \end{align*} $$
The left weak Bruhat order
![]() $\preceq _L$
(resp. right weak Bruhat order
$\preceq _L$
(resp. right weak Bruhat order
![]() $\preceq _R$
) on
$\preceq _R$
) on
![]() $\mathfrak {S}_n$
is the partial order on
$\mathfrak {S}_n$
is the partial order on
![]() $\mathfrak {S}_n$
whose covering relation
$\mathfrak {S}_n$
whose covering relation
![]() $\preceq _L^{\mathrm {c}}$
(resp.
$\preceq _L^{\mathrm {c}}$
(resp.
![]() $\preceq _R^{\mathrm {c}}$
) is given as follows:
$\preceq _R^{\mathrm {c}}$
) is given as follows:
Although these two weak Bruhat orders are not identical, there exists a poset isomorphism
For each
![]() $\gamma \in \mathfrak {S}_n$
, let
$\gamma \in \mathfrak {S}_n$
, let
 $$ \begin{align*} \mathrm{Inv}_L(\gamma) & := \{(i,j) \mid 1 \le i < j \le n \text{ and } \gamma(i)> \gamma(j) \} \quad \text{and} \\ \mathrm{Inv}_R(\gamma) & := \{(\gamma(i), \gamma(j)) \mid 1 \le i < j \le n \text{ and } \gamma(i)> \gamma(j)\}. \end{align*} $$
$$ \begin{align*} \mathrm{Inv}_L(\gamma) & := \{(i,j) \mid 1 \le i < j \le n \text{ and } \gamma(i)> \gamma(j) \} \quad \text{and} \\ \mathrm{Inv}_R(\gamma) & := \{(\gamma(i), \gamma(j)) \mid 1 \le i < j \le n \text{ and } \gamma(i)> \gamma(j)\}. \end{align*} $$
Then, for
![]() $\sigma , \rho \in \mathfrak {S}_n$
,
$\sigma , \rho \in \mathfrak {S}_n$
,
 $$ \begin{align*} & \sigma \preceq_L \rho \quad \text{if and only if} \quad \mathrm{Inv}_L(\sigma) \subseteq \mathrm{Inv}_L(\rho) \quad \text{and}\\ & \sigma \preceq_R \rho \quad \text{if and only if} \quad \mathrm{Inv}_R(\sigma) \subseteq \mathrm{Inv}_R(\rho). \end{align*} $$
$$ \begin{align*} & \sigma \preceq_L \rho \quad \text{if and only if} \quad \mathrm{Inv}_L(\sigma) \subseteq \mathrm{Inv}_L(\rho) \quad \text{and}\\ & \sigma \preceq_R \rho \quad \text{if and only if} \quad \mathrm{Inv}_R(\sigma) \subseteq \mathrm{Inv}_R(\rho). \end{align*} $$
Given
![]() $\sigma , \rho \in \mathfrak {S}_n$
, the left weak Bruhat interval
$\sigma , \rho \in \mathfrak {S}_n$
, the left weak Bruhat interval
![]() $[\sigma , \rho ]_L$
(resp. the right weak Bruhat interval
$[\sigma , \rho ]_L$
(resp. the right weak Bruhat interval
![]() $[\sigma , \rho ]_R$
) denotes the closed interval
$[\sigma , \rho ]_R$
) denotes the closed interval
![]() $\{\gamma \in \mathfrak {S}_n \mid \sigma \preceq _L \gamma \preceq _L \rho \}$
(resp.
$\{\gamma \in \mathfrak {S}_n \mid \sigma \preceq _L \gamma \preceq _L \rho \}$
(resp.
![]() $\{\gamma \in \mathfrak {S}_n \mid \sigma \preceq _R \gamma \preceq _R \rho \}$
) with respect to the left weak Bruhat order (resp. the right weak Bruhat order).
$\{\gamma \in \mathfrak {S}_n \mid \sigma \preceq _R \gamma \preceq _R \rho \}$
) with respect to the left weak Bruhat order (resp. the right weak Bruhat order).
For later use, we introduce the following lemma.
Lemma 2.1 [Reference Björner and Brenti6, Proposition 3.1.6]
For
![]() $\sigma ,\rho \in \mathfrak {S}_n$
with
$\sigma ,\rho \in \mathfrak {S}_n$
with
![]() $\sigma \preceq _R \rho $
, the map
$\sigma \preceq _R \rho $
, the map
![]() $[\sigma , \rho ]_R \rightarrow [\mathrm {id}, \sigma ^{-1}\rho ]_R, \gamma \mapsto \sigma ^{-1} \gamma $
is a poset isomorphism. Equivalently, for
$[\sigma , \rho ]_R \rightarrow [\mathrm {id}, \sigma ^{-1}\rho ]_R, \gamma \mapsto \sigma ^{-1} \gamma $
is a poset isomorphism. Equivalently, for
![]() $\sigma ,\rho \in \mathfrak {S}_n$
with
$\sigma ,\rho \in \mathfrak {S}_n$
with
![]() $\sigma \preceq _L \rho $
, the map
$\sigma \preceq _L \rho $
, the map
![]() $[\sigma ,\rho ]_L \rightarrow [\mathrm {id}, \rho \sigma ^{-1}]_L,\gamma \mapsto \gamma \sigma ^{-1}$
is a poset isomorphism.
$[\sigma ,\rho ]_L \rightarrow [\mathrm {id}, \rho \sigma ^{-1}]_L,\gamma \mapsto \gamma \sigma ^{-1}$
is a poset isomorphism.
Let us collect notations which will be used later. For
![]() $S \subseteq \mathfrak {S}_n$
and
$S \subseteq \mathfrak {S}_n$
and
![]() $\xi \in \mathfrak {S}_n$
, let
$\xi \in \mathfrak {S}_n$
, let
We use
![]() $w_0$
to denote the longest element in
$w_0$
to denote the longest element in
![]() $\mathfrak {S}_n$
. For
$\mathfrak {S}_n$
. For
![]() $I \subseteq [n-1]$
, let
$I \subseteq [n-1]$
, let
![]() $\mathfrak {S}_{I}$
be the parabolic subgroup of
$\mathfrak {S}_{I}$
be the parabolic subgroup of
![]() $\mathfrak {S}_n$
generated by
$\mathfrak {S}_n$
generated by
![]() $\{s_i \mid i\in I\}$
and
$\{s_i \mid i\in I\}$
and
![]() $w_0(I)$
the longest element in
$w_0(I)$
the longest element in
![]() $\mathfrak {S}_{I}$
. For
$\mathfrak {S}_{I}$
. For
![]() $\alpha \models n$
, let
$\alpha \models n$
, let
![]() $w_0(\alpha ) := w_0(\mathrm {set}(\alpha ))$
. Finally, for
$w_0(\alpha ) := w_0(\mathrm {set}(\alpha ))$
. Finally, for
![]() $\sigma \in \mathfrak {S}_n$
, we let
$\sigma \in \mathfrak {S}_n$
, we let
![]() $\sigma ^{w_0} := w_0 \sigma w_0$
.
$\sigma ^{w_0} := w_0 \sigma w_0$
.
Lemma 2.2 [Reference Björner and Wachs7, Theorem 6.2]
For
![]() $I \subseteq J \subseteq [n-1]$
, we have
$I \subseteq J \subseteq [n-1]$
, we have
2.3 Regular posets and Schur labeled skew shape posets
Let
![]() $\mathsf {P}_n$
be the set of posets whose underlying set is
$\mathsf {P}_n$
be the set of posets whose underlying set is
![]() $[n]$
. Given
$[n]$
. Given
![]() $P \in \mathsf {P}_n$
, we write the partial order of P as
$P \in \mathsf {P}_n$
, we write the partial order of P as
![]() $\preceq _P$
.
$\preceq _P$
.
Definition 2.3 [Reference Björner and Wachs8, p. 110]
A poset
![]() $P \in \mathsf {P}_n$
is said to be regular if the following holds: for all
$P \in \mathsf {P}_n$
is said to be regular if the following holds: for all
![]() $x,y,z \in [n]$
with
$x,y,z \in [n]$
with
![]() $x \preceq _P z$
, if
$x \preceq _P z$
, if
![]() $x < y < z$
or
$x < y < z$
or
![]() $z<y<x$
, then
$z<y<x$
, then
![]() $x \preceq _P y$
or
$x \preceq _P y$
or
![]() $y \preceq _P z$
.
$y \preceq _P z$
.
We denote by
![]() $\mathsf {RP}_n$
the set of all regular posets in
$\mathsf {RP}_n$
the set of all regular posets in
![]() $\mathsf {P}_n$
. In the following, we will explain how regular posets can be characterized in terms of left weak Bruhat intervals.
$\mathsf {P}_n$
. In the following, we will explain how regular posets can be characterized in terms of left weak Bruhat intervals.
Given
![]() $P \in \mathsf {P}_n$
, let
$P \in \mathsf {P}_n$
, let
Throughout this paper,
![]() $\Sigma _L(P)$
is considered as the set of all linear extensions of P under the correspondence
$\Sigma _L(P)$
is considered as the set of all linear extensions of P under the correspondence
![]() $\sigma \mapsto ([n], \preceq _E)$
, where
$\sigma \mapsto ([n], \preceq _E)$
, where
![]() $\preceq _E$
is the total order on
$\preceq _E$
is the total order on
![]() $[n]$
given by
$[n]$
given by
![]() $\sigma ^{-1}(1) \preceq _E \sigma ^{-1}(2) \preceq _E \cdots \preceq _E \sigma ^{-1}(n)$
.
$\sigma ^{-1}(1) \preceq _E \sigma ^{-1}(2) \preceq _E \cdots \preceq _E \sigma ^{-1}(n)$
.
Theorem 2.4 [Reference Björner and Wachs8, Theorem 6.8]
Let
![]() $U \subseteq \mathfrak {S}_n$
with
$U \subseteq \mathfrak {S}_n$
with
![]() $|U|> 1$
. The following conditions are equivalent:
$|U|> 1$
. The following conditions are equivalent:
-
(1) U is a left weak Bruhat interval.
-
(2)
 $U = \Sigma _L(P)$
for some
$U = \Sigma _L(P)$
for some
 $P \in \mathsf {RP}_n$
.
$P \in \mathsf {RP}_n$
.
Consider the map
where
![]() $\mathscr {P}(\mathfrak {S}_n)$
is the power set of
$\mathscr {P}(\mathfrak {S}_n)$
is the power set of
![]() $\mathfrak {S}_n$
. One can see that
$\mathfrak {S}_n$
. One can see that
![]() $\unicode{x3b7} $
is injective. Combining this with Theorem 2.4, we obtain a one-to-one correspondence
$\unicode{x3b7} $
is injective. Combining this with Theorem 2.4, we obtain a one-to-one correspondence
where
![]() $\mathrm {Int}(n)$
is the set of nonempty left weak Bruhat intervals in
$\mathrm {Int}(n)$
is the set of nonempty left weak Bruhat intervals in
![]() $\mathfrak {S}_n$
.
$\mathfrak {S}_n$
.
Next, let us introduce Schur labeled skew shape posets. Let
![]() $\lambda / \mu $
be a skew partition of size n. Given a bijective tableau
$\lambda / \mu $
be a skew partition of size n. Given a bijective tableau
![]() $\tau $
of shape
$\tau $
of shape
![]() $\lambda /\mu $
, we define
$\lambda /\mu $
, we define
![]() $\mathsf {poset}(\tau )$
to be the poset
$\mathsf {poset}(\tau )$
to be the poset
![]() $([n], \preceq _\tau )$
, where
$([n], \preceq _\tau )$
, where
The Hasse diagram of
![]() $\mathsf {poset}(\tau )$
can be obtained by rotating
$\mathsf {poset}(\tau )$
can be obtained by rotating
![]() $\tau 135^\circ $
counterclockwise.Footnote 1
$\tau 135^\circ $
counterclockwise.Footnote 1
Example 2.5. Let
![]() $\lambda / \mu = (2,2) \star (3,2) / (1)$
. For the bijective tableaux
$\lambda / \mu = (2,2) \star (3,2) / (1)$
. For the bijective tableaux
![]() $\tau _0$
and
$\tau _0$
and
![]() $\tau _1$
of shape
$\tau _1$
of shape
![]() $\lambda /\mu $
introduced in Section 2.1, we have
$\lambda /\mu $
introduced in Section 2.1, we have

A Schur labeling of shape
![]() $\lambda / \mu $
is a bijective tableau of shape
$\lambda / \mu $
is a bijective tableau of shape
![]() $\lambda / \mu $
such that the entries in each row decrease from left to right and the entries in each column increase from top to bottom. Let
$\lambda / \mu $
such that the entries in each row decrease from left to right and the entries in each column increase from top to bottom. Let
![]() $\mathsf {S}(\lambda /\mu )$
be the set of all Schur labelings of shape
$\mathsf {S}(\lambda /\mu )$
be the set of all Schur labelings of shape
![]() $\lambda / \mu $
. Since
$\lambda / \mu $
. Since
![]() $\tau _0$
and
$\tau _0$
and
![]() $\tau _1$
are Schur labelings of shape
$\tau _1$
are Schur labelings of shape
![]() $\lambda /\mu $
,
$\lambda /\mu $
,
![]() $\mathsf {S}(\lambda /\mu )$
is nonempty. Set
$\mathsf {S}(\lambda /\mu )$
is nonempty. Set
 $$\begin{align*}\mathsf{SP}(\lambda/\mu) := \{\mathsf{poset}(\tau) \mid \tau \in \mathsf{S}(\lambda/\mu) \} \quad \text{and} \quad \mathsf{SP}_n := \bigcup_{ |\lambda/\mu| = n } \mathsf{SP}(\lambda/\mu). \end{align*}$$
$$\begin{align*}\mathsf{SP}(\lambda/\mu) := \{\mathsf{poset}(\tau) \mid \tau \in \mathsf{S}(\lambda/\mu) \} \quad \text{and} \quad \mathsf{SP}_n := \bigcup_{ |\lambda/\mu| = n } \mathsf{SP}(\lambda/\mu). \end{align*}$$
Definition 2.6. A poset
![]() $P \in \mathsf {P}_n$
is said to be a Schur labeled skew shape poset if it is contained in
$P \in \mathsf {P}_n$
is said to be a Schur labeled skew shape poset if it is contained in
![]() $\mathsf {SP}_n$
.
$\mathsf {SP}_n$
.
Remark 2.7. In some papers, for instance [Reference Malvenuto27, Reference McNamara28], authors used a different convention than ours for Schur labeling. We adopt the definition of Schur labeling used in Stanley’s paper [Reference Stanley34].
For simplicity, we set
![]() $\mathsf {RSP}_n := \mathsf {RP}_n \cap \mathsf {SP}_n$
.
$\mathsf {RSP}_n := \mathsf {RP}_n \cap \mathsf {SP}_n$
.
2.4 The
 $0$
-Hecke algebra and the quasisymmetric characteristic
$0$
-Hecke algebra and the quasisymmetric characteristic
The
![]() $0$
-Hecke algebra
$0$
-Hecke algebra
![]() $H_n(0)$
is the associative
$H_n(0)$
is the associative
![]() $\mathbb C$
-algebra with
$\mathbb C$
-algebra with
![]() $1$
generated by
$1$
generated by
![]() $\pi _1,\pi _2,\ldots ,\pi _{n-1}$
subject to the following relations:
$\pi _1,\pi _2,\ldots ,\pi _{n-1}$
subject to the following relations:
 $$ \begin{align*} \pi_i^2 &= \pi_i \quad \text{for }1\le i \le n-1,\\ \pi_i \pi_{i+1} \pi_i &= \pi_{i+1} \pi_i \pi_{i+1} \quad \text{for }1\le i \le n-2,\\ \pi_i \pi_j &=\pi_j \pi_i \quad \text{if }|i-j| \ge 2. \end{align*} $$
$$ \begin{align*} \pi_i^2 &= \pi_i \quad \text{for }1\le i \le n-1,\\ \pi_i \pi_{i+1} \pi_i &= \pi_{i+1} \pi_i \pi_{i+1} \quad \text{for }1\le i \le n-2,\\ \pi_i \pi_j &=\pi_j \pi_i \quad \text{if }|i-j| \ge 2. \end{align*} $$
For each
![]() $1 \leq i \leq n-1$
, let
$1 \leq i \leq n-1$
, let
![]() $\overline {\pi }_i := \pi _i - 1$
. Then,
$\overline {\pi }_i := \pi _i - 1$
. Then,
![]() $\{\overline {\pi }_i \mid i = 1, 2, \ldots , n-1\}$
is also a generating set of
$\{\overline {\pi }_i \mid i = 1, 2, \ldots , n-1\}$
is also a generating set of
![]() $H_n(0)$
.
$H_n(0)$
.
For any reduced expression
![]() $s_{i_1} s_{i_2} \cdots s_{i_p}$
for
$s_{i_1} s_{i_2} \cdots s_{i_p}$
for
![]() $\sigma \in \mathfrak {S}_n$
, let
$\sigma \in \mathfrak {S}_n$
, let
It is well known that these elements are independent of the choices of reduced expressions, and both
![]() $\{\pi _\sigma \mid \sigma \in \mathfrak {S}_n\}$
and
$\{\pi _\sigma \mid \sigma \in \mathfrak {S}_n\}$
and
![]() $\{\overline {\pi }_\sigma \mid \sigma \in \mathfrak {S}_n\}$
are
$\{\overline {\pi }_\sigma \mid \sigma \in \mathfrak {S}_n\}$
are
![]() $\mathbb C$
-bases for
$\mathbb C$
-bases for
![]() $H_n(0)$
.
$H_n(0)$
.
According to [Reference Norton30], there are
![]() $2^{n-1}$
pairwise nonisomorphic irreducible
$2^{n-1}$
pairwise nonisomorphic irreducible
![]() $H_n(0)$
-modules which are naturally indexed by compositions of n. To be precise, for each composition
$H_n(0)$
-modules which are naturally indexed by compositions of n. To be precise, for each composition
![]() $\alpha $
of n, there exists an irreducible
$\alpha $
of n, there exists an irreducible
![]() $H_n(0)$
-module
$H_n(0)$
-module
![]() $\mathbf {F}_{\alpha }:=\mathbb C v_{\alpha }$
endowed with the
$\mathbf {F}_{\alpha }:=\mathbb C v_{\alpha }$
endowed with the
![]() $H_n(0)$
-action defined as follows: for each
$H_n(0)$
-action defined as follows: for each
![]() $1 \le i \le n-1$
,
$1 \le i \le n-1$
,
 $$\begin{align*}\pi_i \cdot v_\alpha = \begin{cases} 0 & i \in \mathrm{set}(\alpha),\\ v_\alpha & i \notin \mathrm{set}(\alpha). \end{cases} \end{align*}$$
$$\begin{align*}\pi_i \cdot v_\alpha = \begin{cases} 0 & i \in \mathrm{set}(\alpha),\\ v_\alpha & i \notin \mathrm{set}(\alpha). \end{cases} \end{align*}$$
Let
![]() $H_n(0)\text{-}\mathbf {mod}$
be the category of finite dimensional left
$H_n(0)\text{-}\mathbf {mod}$
be the category of finite dimensional left
![]() $H_n(0)$
-modules and
$H_n(0)$
-modules and
![]() $\mathcal {R}(H_n(0))$
the
$\mathcal {R}(H_n(0))$
the
![]() $\mathbb Z$
-span of the set of (representatives of) isomorphism classes of modules in
$\mathbb Z$
-span of the set of (representatives of) isomorphism classes of modules in
![]() $H_n(0)\text{-}\mathbf {mod}$
. We denote by
$H_n(0)\text{-}\mathbf {mod}$
. We denote by
![]() $[M]$
the isomorphism class corresponding to an
$[M]$
the isomorphism class corresponding to an
![]() $H_n(0)$
-module M. The Grothendieck group
$H_n(0)$
-module M. The Grothendieck group
![]() $\mathcal {G}_0(H_n(0))$
of
$\mathcal {G}_0(H_n(0))$
of
![]() $H_n(0)$
-
$H_n(0)$
-
![]() $\mathbf {mod}$
is the quotient of
$\mathbf {mod}$
is the quotient of
![]() $\mathcal {R}(H_n(0))$
modulo the relations
$\mathcal {R}(H_n(0))$
modulo the relations
![]() $[M] = [M'] + [M"]$
whenever there exists a short exact sequence
$[M] = [M'] + [M"]$
whenever there exists a short exact sequence
![]() $0 \rightarrow M' \rightarrow M \rightarrow M" \rightarrow 0$
. The equivalence classes of the irreducible
$0 \rightarrow M' \rightarrow M \rightarrow M" \rightarrow 0$
. The equivalence classes of the irreducible
![]() $H_n(0)$
-modules form a
$H_n(0)$
-modules form a
![]() $\mathbb Z$
-basis for
$\mathbb Z$
-basis for
![]() $\mathcal {G}_0(H_n(0))$
. Let
$\mathcal {G}_0(H_n(0))$
. Let
Let us review the connection between
![]() $\mathcal {G}$
and the ring
$\mathcal {G}$
and the ring
![]() $\mathrm {QSym}$
of quasisymmetric functions. For the definition of quasisymmetric functions, see [Reference Stanley35, Section 7.19]. For a composition
$\mathrm {QSym}$
of quasisymmetric functions. For the definition of quasisymmetric functions, see [Reference Stanley35, Section 7.19]. For a composition
![]() $\alpha $
, the fundamental quasisymmetric function
$\alpha $
, the fundamental quasisymmetric function
![]() $F_\alpha $
, which was firstly introduced in [Reference Gessel16], is defined by
$F_\alpha $
, which was firstly introduced in [Reference Gessel16], is defined by
 $$\begin{align*}F_\varnothing = 1 \quad \text{and} \quad F_\alpha = \sum_{\substack{1 \le i_1 \le i_2 \le \cdots \le i_n \\ i_j < i_{j+1} \text{ if } j \in \mathrm{set}(\alpha)}} x_{i_1}x_{i_2} \cdots x_{i_n} \quad \text{if }\alpha \neq \varnothing. \end{align*}$$
$$\begin{align*}F_\varnothing = 1 \quad \text{and} \quad F_\alpha = \sum_{\substack{1 \le i_1 \le i_2 \le \cdots \le i_n \\ i_j < i_{j+1} \text{ if } j \in \mathrm{set}(\alpha)}} x_{i_1}x_{i_2} \cdots x_{i_n} \quad \text{if }\alpha \neq \varnothing. \end{align*}$$
It is known that
![]() $\{F_\alpha \mid \alpha \text { is a composition}\}$
is a
$\{F_\alpha \mid \alpha \text { is a composition}\}$
is a
![]() $\mathbb Z$
-basis for
$\mathbb Z$
-basis for
![]() $\mathrm {QSym}$
. When M is an
$\mathrm {QSym}$
. When M is an
![]() $H_m(0)$
-module and N is an
$H_m(0)$
-module and N is an
![]() $H_n(0)$
-module, we write
$H_n(0)$
-module, we write
![]() $M \boxtimes N$
for the induction product of M and N; that is,
$M \boxtimes N$
for the induction product of M and N; that is,
Here,
![]() $H_m(0) \otimes H_n(0)$
is viewed as the subalgebra of
$H_m(0) \otimes H_n(0)$
is viewed as the subalgebra of
![]() $H_{m+n}(0)$
generated by
$H_{m+n}(0)$
generated by
![]() $\{\pi _i \mid i \in [m+n-1] \setminus \{m\} \}$
. The induction product induces a multiplication on
$\{\pi _i \mid i \in [m+n-1] \setminus \{m\} \}$
. The induction product induces a multiplication on
![]() $\mathcal {G}$
. It was shown in [Reference Duchamp, Krob, Leclerc and Thibon12] that the linear map
$\mathcal {G}$
. It was shown in [Reference Duchamp, Krob, Leclerc and Thibon12] that the linear map
called quasisymmetric characteristic, is a ring isomorphism. Indeed, it turns out to be a Hopf algebra isomorphism when
![]() $\mathcal {G}$
has the comultiplication induced from restriction.
$\mathcal {G}$
has the comultiplication induced from restriction.
It is well known that
![]() $H_n(0)$
has the automorphisms
$H_n(0)$
has the automorphisms
![]() $\unicode{x3b8} $
and
$\unicode{x3b8} $
and
![]() $\unicode{x3c6} $
, as well as the anti-automorphism
$\unicode{x3c6} $
, as well as the anti-automorphism
![]() $\unicode{x3c7} $
, defined in the following manner:
$\unicode{x3c7} $
, defined in the following manner:
 $$ \begin{align*} &\unicode{x3c6}: H_n(0) \rightarrow H_n(0), \quad \pi_i \mapsto \pi_{n-i} \quad \text{for }1 \le i \le n-1,\\ &\unicode{x3b8}: H_n(0) \rightarrow H_n(0), \quad \pi_i \mapsto - \overline{\pi}_i \quad \text{for }1 \le i \le n-1, \\ &\unicode{x3c7}: H_n(0) \rightarrow H_n(0), \quad \pi_i \mapsto \pi_i \quad \text{for }1 \le i \le n-1 \end{align*} $$
$$ \begin{align*} &\unicode{x3c6}: H_n(0) \rightarrow H_n(0), \quad \pi_i \mapsto \pi_{n-i} \quad \text{for }1 \le i \le n-1,\\ &\unicode{x3b8}: H_n(0) \rightarrow H_n(0), \quad \pi_i \mapsto - \overline{\pi}_i \quad \text{for }1 \le i \le n-1, \\ &\unicode{x3c7}: H_n(0) \rightarrow H_n(0), \quad \pi_i \mapsto \pi_i \quad \text{for }1 \le i \le n-1 \end{align*} $$
(for instance, see [Reference Fayers13, Reference Krob and Thibon22, Reference Lascoux, Leclerc and Thibon24, Reference Lascoux and Schützenberger25]). These maps commute with each other.
Note that an automorphism
![]() $\mu $
of
$\mu $
of
![]() $H_n(0)$
induces a covariant functor
$H_n(0)$
induces a covariant functor
called the
![]() $\mu $
-twist. Similarly, an anti-automorphism
$\mu $
-twist. Similarly, an anti-automorphism
![]() $\nu $
of
$\nu $
of
![]() $H_n(0)$
induces a contravariant functor
$H_n(0)$
induces a contravariant functor
called the
![]() $\nu $
-twist. For the precise definitions of
$\nu $
-twist. For the precise definitions of
![]() $\mathbf {T}^{+}_\mu $
and
$\mathbf {T}^{+}_\mu $
and
![]() $\mathbf {T}^{-}_\nu $
, see [Reference Jung, Kim, Lee and Oh19, Subsection 3.4]. In [Reference Fayers13, Proposition 3.3.], it was shown that
$\mathbf {T}^{-}_\nu $
, see [Reference Jung, Kim, Lee and Oh19, Subsection 3.4]. In [Reference Fayers13, Proposition 3.3.], it was shown that
for
![]() $\alpha \models n$
. Let
$\alpha \models n$
. Let
![]() $\unicode{x3c1} $
and
$\unicode{x3c1} $
and
![]() $\unicode{x3c8} $
be the automorphisms of
$\unicode{x3c8} $
be the automorphisms of
![]() $\mathrm {QSym}$
defined by
$\mathrm {QSym}$
defined by
for every composition
![]() $\alpha $
. For a finite dimensional
$\alpha $
. For a finite dimensional
![]() $H_n(0)$
-module M, it holds that
$H_n(0)$
-module M, it holds that
 $$ \begin{align} \begin{array}{c} \mathrm{ch}( [\mathbf{T}^{+}_\unicode{x3c6}(M)] ) = \unicode{x3c1} \circ \mathrm{ch}([M]), \quad \mathrm{ch} ( [\mathbf{T}^{+}_\unicode{x3b8}(M)] ) = \unicode{x3c8} \circ \mathrm{ch}([M]),\\[1ex] \text{and} \quad \mathrm{ch} ( [\mathbf{T}^{-}_\unicode{x3c7}(M)] ) = \mathrm{ch}([M]). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{c} \mathrm{ch}( [\mathbf{T}^{+}_\unicode{x3c6}(M)] ) = \unicode{x3c1} \circ \mathrm{ch}([M]), \quad \mathrm{ch} ( [\mathbf{T}^{+}_\unicode{x3b8}(M)] ) = \unicode{x3c8} \circ \mathrm{ch}([M]),\\[1ex] \text{and} \quad \mathrm{ch} ( [\mathbf{T}^{-}_\unicode{x3c7}(M)] ) = \mathrm{ch}([M]). \end{array} \end{align} $$
2.5 Modules arising from posets and weak Bruhat interval modules
Let
![]() $P\in \mathsf {P}_n$
. In [Reference Duchamp, Hivert and Thibon11, Definition 3.18], Duchamp, Hivert and Thibon defined a right
$P\in \mathsf {P}_n$
. In [Reference Duchamp, Hivert and Thibon11, Definition 3.18], Duchamp, Hivert and Thibon defined a right
![]() $H_n(0)$
-module
$H_n(0)$
-module
![]() $M_P$
associated with P. In this paper, we are primarily concerned with left modules, so we introduce a left
$M_P$
associated with P. In this paper, we are primarily concerned with left modules, so we introduce a left
![]() $H_n(0)$
-module, denoted as
$H_n(0)$
-module, denoted as
![]() $\mathsf {M}_P$
, associated with P.
$\mathsf {M}_P$
, associated with P.
Definition 2.8. Let
![]() $P \in \mathsf {P}_n$
. Define
$P \in \mathsf {P}_n$
. Define
![]() $\mathsf {M}_P$
to be the left
$\mathsf {M}_P$
to be the left
![]() $H_n(0)$
-module with
$H_n(0)$
-module with
![]() $\mathbb C \Sigma _{L}(P)$
as the underlying space and with the
$\mathbb C \Sigma _{L}(P)$
as the underlying space and with the
![]() $H_n(0)$
-action defined by
$H_n(0)$
-action defined by
 $$ \begin{align} \pi_{i} \cdot \gamma := \begin{cases} \gamma & \text{if }i \in \mathrm{Des}_L(\gamma), \\ 0 & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \notin \Sigma_{L}(P), \\ s_i \gamma & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \in \Sigma_{L}(P). \end{cases} \end{align} $$
$$ \begin{align} \pi_{i} \cdot \gamma := \begin{cases} \gamma & \text{if }i \in \mathrm{Des}_L(\gamma), \\ 0 & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \notin \Sigma_{L}(P), \\ s_i \gamma & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \in \Sigma_{L}(P). \end{cases} \end{align} $$
One can see that the
![]() $H_n(0)$
-action provided in Equation (2.3) is well-defined through a slight modification of the proof in [Reference Duchamp, Hivert and Thibon11, Subsection 3.9] that
$H_n(0)$
-action provided in Equation (2.3) is well-defined through a slight modification of the proof in [Reference Duchamp, Hivert and Thibon11, Subsection 3.9] that
![]() $M_P$
is a well-defined right
$M_P$
is a well-defined right
![]() $H_n(0)$
-module. Indeed, there is a close connection between
$H_n(0)$
-module. Indeed, there is a close connection between
![]() $\mathsf {M}_P$
and
$\mathsf {M}_P$
and
![]() $M_P$
. Let
$M_P$
. Let
![]() $\mathbf {mod}\text{-}H_n(0)$
be the category of finite dimensional right
$\mathbf {mod}\text{-}H_n(0)$
be the category of finite dimensional right
![]() $H_n(0)$
-modules. In [Reference Choi, Kim and Oh9, Subsection 4.3], the authors introduced a contravariant functor
$H_n(0)$
-modules. In [Reference Choi, Kim and Oh9, Subsection 4.3], the authors introduced a contravariant functor
that preserves quasisymmetric characteristics.Footnote 2 Using this functor, it is not difficult to see that
Since the underlying set of P is
![]() $[n]$
, we can regard P as the labeled poset
$[n]$
, we can regard P as the labeled poset
![]() $(P, \omega )$
with the labeling
$(P, \omega )$
with the labeling
![]() $\omega : P \rightarrow [n]$
given by
$\omega : P \rightarrow [n]$
given by
![]() $\omega (i) = i$
. Under this consideration, a map
$\omega (i) = i$
. Under this consideration, a map
![]() $f: [n] \rightarrow \mathbb Z_{\ge 0}$
is called a P-partition if it satisfies the following conditions:
$f: [n] \rightarrow \mathbb Z_{\ge 0}$
is called a P-partition if it satisfies the following conditions:
-
(1) If
 $i \preceq _P j$
, then
$i \preceq _P j$
, then
 $f(i) \le f(j)$
.
$f(i) \le f(j)$
. -
(2) If
 $i \preceq _P j$
and
$i \preceq _P j$
and
 $i> j$
, then
$i> j$
, then
 $f(i) < f(j)$
.
$f(i) < f(j)$
.
We define the P-partition generating function
![]() $K_P$
of P by
$K_P$
of P by
 $$\begin{align*}K_{P} := \sum_{f: P\text{-partition}} x_1^{|f^{-1}(1)|} x_2^{|f^{-1}(2)|} \cdots. \end{align*}$$
$$\begin{align*}K_{P} := \sum_{f: P\text{-partition}} x_1^{|f^{-1}(1)|} x_2^{|f^{-1}(2)|} \cdots. \end{align*}$$
Theorem 2.9. For
![]() $P \in \mathsf {P}_n$
, the following hold.
$P \in \mathsf {P}_n$
, the following hold.
-
(1)
 $\mathrm {ch}([\mathsf {M}_P]) = \unicode{x3c8} (K_{P})$
.
$\mathrm {ch}([\mathsf {M}_P]) = \unicode{x3c8} (K_{P})$
. -
(2) If
 $P \in \mathsf {SP}(\lambda /\mu )$
for a skew partition
$P \in \mathsf {SP}(\lambda /\mu )$
for a skew partition
 $\lambda /\mu $
, then
$\lambda /\mu $
, then
 $\mathrm {ch}([\mathsf {M}_P]) = s_{\lambda /\mu }$
.
$\mathrm {ch}([\mathsf {M}_P]) = s_{\lambda /\mu }$
.
Proof. (1) It was shown in [Reference Duchamp, Hivert and Thibon11, Theorem 3.21(i)] that the (right) quasisymmetric characteristic of
![]() $M_P$
is given by
$M_P$
is given by
![]() $K_P$
. Since
$K_P$
. Since
![]() $\mathsf {M}_P \cong \mathbf {T}^{+}_\unicode{x3b8} \circ \mathbf {T}^{-}_\unicode{x3c7} \circ \mathcal {F}_n^{-1}(M_P)$
, the assertion follows from Equation (2.2).
$\mathsf {M}_P \cong \mathbf {T}^{+}_\unicode{x3b8} \circ \mathbf {T}^{-}_\unicode{x3c7} \circ \mathcal {F}_n^{-1}(M_P)$
, the assertion follows from Equation (2.2).
(2) In the same manner as in [Reference Stanley35, Subsection 7.19], one can see that
![]() $K_P = s_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}}$
. Here,
$K_P = s_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}}$
. Here,
![]() $\lambda ^{\mathrm {t}}$
and
$\lambda ^{\mathrm {t}}$
and
![]() $\mu ^{\mathrm {t}}$
are the transposes of
$\mu ^{\mathrm {t}}$
are the transposes of
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
, respectively. Now the assertion can be derived from the well-known identity
$\mu $
, respectively. Now the assertion can be derived from the well-known identity
![]() $\unicode{x3c8} (s_{\lambda /\mu }) = s_{\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}}}$
(for instance, see [Reference Luoto, Mykytiuk and van Willigenburg26, Subsection 3.6]).
$\unicode{x3c8} (s_{\lambda /\mu }) = s_{\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}}}$
(for instance, see [Reference Luoto, Mykytiuk and van Willigenburg26, Subsection 3.6]).
Next, let us introduce weak Bruhat interval modules, which were introduced by Jung, Kim, Lee and Oh [Reference Jung, Kim, Lee and Oh19] to provide a unified method for dealing with
![]() $H_n(0)$
-modules constructed using tableaux.
$H_n(0)$
-modules constructed using tableaux.
Definition 2.10 [Reference Jung, Kim, Lee and Oh19, Definition 1]
For each left weak Bruhat interval
![]() $[\sigma , \rho ]_L$
in
$[\sigma , \rho ]_L$
in
![]() $\mathfrak {S}_n$
, define
$\mathfrak {S}_n$
, define
![]() $\mathsf {B}([\sigma , \rho ]_L)$
(simply,
$\mathsf {B}([\sigma , \rho ]_L)$
(simply,
![]() $\mathsf {B}(\sigma , \rho )$
) to be the
$\mathsf {B}(\sigma , \rho )$
) to be the
![]() $H_n(0)$
-module with
$H_n(0)$
-module with
![]() $\mathbb C[\sigma ,\rho ]_L$
as the underlying space and with the
$\mathbb C[\sigma ,\rho ]_L$
as the underlying space and with the
![]() $H_n(0)$
-action defined by
$H_n(0)$
-action defined by
 $$ \begin{align*} \pi_i \cdot \gamma := \begin{cases} \gamma & \text{if }i \in \mathrm{Des}_L(\gamma), \\ 0 & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \notin [\sigma,\rho]_L, \\ s_i \gamma & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \in [\sigma,\rho]_L. \end{cases} \end{align*} $$
$$ \begin{align*} \pi_i \cdot \gamma := \begin{cases} \gamma & \text{if }i \in \mathrm{Des}_L(\gamma), \\ 0 & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \notin [\sigma,\rho]_L, \\ s_i \gamma & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \in [\sigma,\rho]_L. \end{cases} \end{align*} $$
This module is called the weak Bruhat interval module associated to
![]() $[\sigma ,\rho ]_L$
.
$[\sigma ,\rho ]_L$
.
We can deduce from Theorem 2.4 that for every
![]() $[\sigma , \rho ]_L \in \mathrm {Int}(n)$
, there exists a unique poset
$[\sigma , \rho ]_L \in \mathrm {Int}(n)$
, there exists a unique poset
![]() $P\in \mathsf {P}_n$
such that
$P\in \mathsf {P}_n$
such that
![]() $\Sigma _L(P)=[\sigma , \rho ]_L$
. Since both
$\Sigma _L(P)=[\sigma , \rho ]_L$
. Since both
![]() $\mathsf {B}(\sigma , \rho )$
and
$\mathsf {B}(\sigma , \rho )$
and
![]() $\mathsf {M}_P$
share
$\mathsf {M}_P$
share
![]() $[\sigma , \rho ]_L$
as their basis and exhibit identical
$[\sigma , \rho ]_L$
as their basis and exhibit identical
![]() $H_n(0)$
-actions on this set, we can conclude that
$H_n(0)$
-actions on this set, we can conclude that
![]() $\mathsf {B}(\sigma , \rho )$
is indeed equal to
$\mathsf {B}(\sigma , \rho )$
is indeed equal to
![]() $\mathsf {M}_P$
.
$\mathsf {M}_P$
.
Remark 2.11. The weak Bruhat interval modules are equipped with the structure of semi-combinatorial
![]() $H_n(0)$
-modules due to Hivert, Novelli and Thibon [Reference Hivert, Novelli and Thibon17] and also that of diagram modules due to Searles [Reference Searles33]. More precisely,
$H_n(0)$
-modules due to Hivert, Novelli and Thibon [Reference Hivert, Novelli and Thibon17] and also that of diagram modules due to Searles [Reference Searles33]. More precisely,
-
(1)
 $\mathsf {B}(\sigma ,\rho )$
is the semi-combinatorial
$\mathsf {B}(\sigma ,\rho )$
is the semi-combinatorial
 $H_n(0)$
-module associated to the Yang-Baxter interval
$H_n(0)$
-module associated to the Yang-Baxter interval
 $[Y_{\sigma }(\mathrm {id}), Y_{\rho }(\mathrm {id})]$
, and
$[Y_{\sigma }(\mathrm {id}), Y_{\rho }(\mathrm {id})]$
, and -
(2) it was shown in [Reference Searles33, Subsection 7.3] that
 $\mathsf {B}(\sigma ,\rho )$
is isomorphic to a diagram module
$\mathsf {B}(\sigma ,\rho )$
is isomorphic to a diagram module
 $\widehat {\mathbf {N}}_{\mathsf {StdTab}(D)}$
.
$\widehat {\mathbf {N}}_{\mathsf {StdTab}(D)}$
.
3 The weak Bruhat interval structure of
 $\Sigma _L(P)$
for
$\Sigma _L(P)$
for
 $P \in \mathsf {RSP}_n$
$P \in \mathsf {RSP}_n$
Let
![]() $P \in \mathsf {RSP}_n$
. In this section, we explicitly describe the left weak Bruhat interval
$P \in \mathsf {RSP}_n$
. In this section, we explicitly describe the left weak Bruhat interval
![]() $\Sigma _L(P)$
in terms of reading words of standard Young tableaux. To begin with, we introduce readings for bijective tableaux.
$\Sigma _L(P)$
in terms of reading words of standard Young tableaux. To begin with, we introduce readings for bijective tableaux.
Definition 3.1. Let
![]() $\tau $
be a bijective tableau of shape
$\tau $
be a bijective tableau of shape
![]() $\lambda / \mu $
. The
$\lambda / \mu $
. The
![]() $\tau $
-reading is the map
$\tau $
-reading is the map
where
![]() $\mathsf {read}_\tau (T)$
is the permutation in
$\mathsf {read}_\tau (T)$
is the permutation in
![]() $\mathfrak {S}_n$
given by
$\mathfrak {S}_n$
given by
![]() $\mathsf {read}_\tau (T)(k) = T_{\tau ^{-1}(k)}$
for
$\mathsf {read}_\tau (T)(k) = T_{\tau ^{-1}(k)}$
for
![]() $1 \le k \le n$
. We call
$1 \le k \le n$
. We call
![]() $\mathsf {read}_\tau (T)$
the
$\mathsf {read}_\tau (T)$
the
![]() $\tau $
-reading word of T.
$\tau $
-reading word of T.
Given a bijective tableaux T of shape
![]() $\lambda / \mu $
, the permutation
$\lambda / \mu $
, the permutation
![]() $\mathsf {read}_{\tau }(T)$
in one-line notation can be obtained by reading the entries of T in the order given by
$\mathsf {read}_{\tau }(T)$
in one-line notation can be obtained by reading the entries of T in the order given by
![]() $\tau ^{-1}(1), \tau ^{-1}(2), \ldots , \tau ^{-1}(n)$
. For instance, if
$\tau ^{-1}(1), \tau ^{-1}(2), \ldots , \tau ^{-1}(n)$
. For instance, if  and
and  , then
, then
![]() $\mathsf {read}_{\tau }(T) = 53412$
. With this definition, we have the following lemma.
$\mathsf {read}_{\tau }(T) = 53412$
. With this definition, we have the following lemma.
Lemma 3.2. For any bijective tableau
![]() $\tau $
of shape
$\tau $
of shape
![]() $\lambda / \mu $
,
$\lambda / \mu $
,
![]() $\Sigma _L(\mathsf {poset}(\tau )) = \mathsf {read}_\tau (\mathrm {SYT}(\lambda /\mu ))$
.
$\Sigma _L(\mathsf {poset}(\tau )) = \mathsf {read}_\tau (\mathrm {SYT}(\lambda /\mu ))$
.
Proof. We first show that
![]() $\mathsf {read}_\tau (\mathrm {SYT}(\lambda /\mu )) \subseteq \Sigma _L(\mathsf {poset}(\tau ))$
. To do this, take any
$\mathsf {read}_\tau (\mathrm {SYT}(\lambda /\mu )) \subseteq \Sigma _L(\mathsf {poset}(\tau ))$
. To do this, take any
![]() $T \in \mathrm {SYT}(\lambda /\mu )$
and
$T \in \mathrm {SYT}(\lambda /\mu )$
and
![]() $i,j \in [n]$
with
$i,j \in [n]$
with
![]() $i \preceq _\tau j$
(for the definition of
$i \preceq _\tau j$
(for the definition of
![]() $\preceq _\tau $
, see Equation (2.1). Let
$\preceq _\tau $
, see Equation (2.1). Let
![]() $B_1$
and
$B_1$
and
![]() $B_2$
be the boxes in
$B_2$
be the boxes in
![]() $\mathtt {yd}(\lambda /\mu )$
such that
$\mathtt {yd}(\lambda /\mu )$
such that
![]() $\tau _{B_1} = i$
and
$\tau _{B_1} = i$
and
![]() $\tau _{B_2} = j$
. Since
$\tau _{B_2} = j$
. Since
![]() $i \preceq _\tau j$
,
$i \preceq _\tau j$
,
![]() $B_1$
is weakly upper-left of
$B_1$
is weakly upper-left of
![]() $B_2$
in
$B_2$
in
![]() $\mathtt {yd}(\lambda /\mu )$
. This implies that
$\mathtt {yd}(\lambda /\mu )$
. This implies that
Therefore,
![]() $\mathsf {read}_\tau (T) \in \Sigma _L(\mathsf {poset}(\tau ))$
.
$\mathsf {read}_\tau (T) \in \Sigma _L(\mathsf {poset}(\tau ))$
.
To complete the proof, let us show that
![]() $|\Sigma _L(\mathsf {poset}(\tau ))| = |\mathsf {read}_\tau (\mathrm {SYT}(\lambda /\mu ))|$
. Note that
$|\Sigma _L(\mathsf {poset}(\tau ))| = |\mathsf {read}_\tau (\mathrm {SYT}(\lambda /\mu ))|$
. Note that
 $$ \begin{align*} \mathrm{ch}([\mathsf{M}_{\mathsf{poset}(\tau^{\lambda/\mu}_0)}]) = \sum_{\gamma \in \Sigma_L(\mathsf{poset}(\tau^{\lambda/\mu}_0))} F_{\mathrm{comp}(\mathrm{Des}_L(\gamma))^{\mathrm{c}}} \quad \text{and} \quad \mathrm{ch}([\mathsf{M}_{\mathsf{poset}(\tau^{\lambda/\mu}_0)}]) = s_{\lambda/\mu}, \end{align*} $$
$$ \begin{align*} \mathrm{ch}([\mathsf{M}_{\mathsf{poset}(\tau^{\lambda/\mu}_0)}]) = \sum_{\gamma \in \Sigma_L(\mathsf{poset}(\tau^{\lambda/\mu}_0))} F_{\mathrm{comp}(\mathrm{Des}_L(\gamma))^{\mathrm{c}}} \quad \text{and} \quad \mathrm{ch}([\mathsf{M}_{\mathsf{poset}(\tau^{\lambda/\mu}_0)}]) = s_{\lambda/\mu}, \end{align*} $$
where the second equality follows from Theorem 2.9(2). Putting these together with the well-known equality
![]() $s_{\lambda / \mu } = \sum _{T \in \mathrm {SYT}(\lambda / \mu )} F_{\mathrm {comp}(T)}$
, we have
$s_{\lambda / \mu } = \sum _{T \in \mathrm {SYT}(\lambda / \mu )} F_{\mathrm {comp}(T)}$
, we have
 $$ \begin{align} \sum_{\gamma \in \Sigma_L(\mathsf{poset}(\tau^{\lambda/\mu}_0))} F_{\mathrm{comp}(\mathrm{Des}_L(\gamma))^{\mathrm{c}}} = \sum_{T \in \mathrm{SYT}(\lambda/\mu)} F_{\mathrm{comp}(T)}. \end{align} $$
$$ \begin{align} \sum_{\gamma \in \Sigma_L(\mathsf{poset}(\tau^{\lambda/\mu}_0))} F_{\mathrm{comp}(\mathrm{Des}_L(\gamma))^{\mathrm{c}}} = \sum_{T \in \mathrm{SYT}(\lambda/\mu)} F_{\mathrm{comp}(T)}. \end{align} $$
Here,
![]() $\mathrm {comp}(T) = \mathrm {comp}(\{i \in [n-1] \mid i\text { is weakly right of }i+1\text { in }T\})$
. As a consequence of Equation (3.1), we have
$\mathrm {comp}(T) = \mathrm {comp}(\{i \in [n-1] \mid i\text { is weakly right of }i+1\text { in }T\})$
. As a consequence of Equation (3.1), we have
The purpose of the remainder of this section is to describe the minimum and maximum of
![]() $\Sigma _L(P)$
with respect to
$\Sigma _L(P)$
with respect to
![]() $\preceq _L$
.
$\preceq _L$
.
As a first step, we deal with a characterization of regular Schur labeled skew shape posets. For this purpose, the following definition is necessary.
Definition 3.3. Let
![]() $\lambda /\mu $
be a skew partition of size n. A Schur labeling
$\lambda /\mu $
be a skew partition of size n. A Schur labeling
![]() $\tau $
of shape
$\tau $
of shape
![]() $\lambda / \mu $
is said to be distinguished if
$\lambda / \mu $
is said to be distinguished if
![]() $\tau _B \geq \tau _{B'}$
whenever B is weakly below and weakly left of
$\tau _B \geq \tau _{B'}$
whenever B is weakly below and weakly left of
![]() $B'$
for boxes
$B'$
for boxes
![]() $B, B' \in \mathtt {yd}(\lambda /\mu )$
.
$B, B' \in \mathtt {yd}(\lambda /\mu )$
.
Example 3.4. Consider the Schur labelings of shape
![]() $(3,2,2)/(1)$
$(3,2,2)/(1)$

One sees that
![]() $\tau _0^{(3,2,2)/(1)}$
and
$\tau _0^{(3,2,2)/(1)}$
and
![]() $\tau _1^{(3,2,2)/(1)}$
are distinguished, whereas
$\tau _1^{(3,2,2)/(1)}$
are distinguished, whereas
![]() $\tau $
is non-distinguished since
$\tau $
is non-distinguished since
![]() $1$
appears weakly below and weakly left of
$1$
appears weakly below and weakly left of
![]() $2$
in
$2$
in
![]() $\tau $
.
$\tau $
.
Let
![]() $\mathsf {DS}(\lambda / \mu )$
be the set of all distinguished Schur labelings of shape
$\mathsf {DS}(\lambda / \mu )$
be the set of all distinguished Schur labelings of shape
![]() $\lambda / \mu $
. For any Schur labeling
$\lambda / \mu $
. For any Schur labeling
![]() $\tau $
, let
$\tau $
, let
![]() $\mathsf {cnt}_i(\tau )$
be the set of entries in the ith connected component of
$\mathsf {cnt}_i(\tau )$
be the set of entries in the ith connected component of
![]() $\tau $
from the top. For each
$\tau $
from the top. For each
![]() $P \in \mathsf {SP}_n$
, there exists a unique Schur labeling
$P \in \mathsf {SP}_n$
, there exists a unique Schur labeling
![]() $\tau $
such that
$\tau $
such that
 $$ \begin{align} &(\text{i})\ \mathrm{sh}(\tau)\text{ is basic},\nonumber\\ &(\text{ii})\ \mathsf{poset}(\tau) = P,\text{ and}\\ &(\text{iii})\ \mathrm{min}(\mathsf{cnt}_i(\tau)) < \mathrm{min}(\mathsf{cnt}_j(\tau))\text{ for }1 \leq i < j \leq k,\text{ where }k\text{ is the number of connected components}\nonumber\\ &\quad\text{of }P.\nonumber \end{align} $$
$$ \begin{align} &(\text{i})\ \mathrm{sh}(\tau)\text{ is basic},\nonumber\\ &(\text{ii})\ \mathsf{poset}(\tau) = P,\text{ and}\\ &(\text{iii})\ \mathrm{min}(\mathsf{cnt}_i(\tau)) < \mathrm{min}(\mathsf{cnt}_j(\tau))\text{ for }1 \leq i < j \leq k,\text{ where }k\text{ is the number of connected components}\nonumber\\ &\quad\text{of }P.\nonumber \end{align} $$
We denote this Schur labeling as
![]() $\tau _P$
. One can easily see that for
$\tau _P$
. One can easily see that for
![]() $P \in \mathsf {SP}_n$
,
$P \in \mathsf {SP}_n$
,
![]() $\tau _P$
is distinguished if and only if every connected component of
$\tau _P$
is distinguished if and only if every connected component of
![]() $\tau _P$
is filled with consecutive integers.
$\tau _P$
is filled with consecutive integers.
Example 3.5. Given two Schur labeled skew shape posets

we have that

Lemma 3.6. For
![]() $P \in \mathsf {SP}_n$
, P is regular if and only if
$P \in \mathsf {SP}_n$
, P is regular if and only if
![]() $\tau _P$
is distinguished.
$\tau _P$
is distinguished.
Proof. To prove the ‘only if’ part, assume that P is a regular Schur labeled skew shape poset and
![]() $\lambda / \mu $
is the shape of
$\lambda / \mu $
is the shape of
![]() $\tau _P$
. We claim that every connected component of
$\tau _P$
. We claim that every connected component of
![]() $\tau _P$
is filled with consecutive integers. Take an arbitrary connected component
$\tau _P$
is filled with consecutive integers. Take an arbitrary connected component
![]() $\mathsf {C}$
of
$\mathsf {C}$
of
![]() $\tau _P$
. Let
$\tau _P$
. Let
![]() $B_1$
be the box at the top of the rightmost column of
$B_1$
be the box at the top of the rightmost column of
![]() $\mathsf {C}$
and
$\mathsf {C}$
and
![]() $B_2$
the box at the bottom of the leftmost column of
$B_2$
the box at the bottom of the leftmost column of
![]() $\mathsf {C}$
. Then, we may choose boxes
$\mathsf {C}$
. Then, we may choose boxes
![]() $A_0:= B_1, A_2, A_3, \ldots , A_k := B_2$
satisfying that for all
$A_0:= B_1, A_2, A_3, \ldots , A_k := B_2$
satisfying that for all
![]() $1 \le i \le k-1$
,
$1 \le i \le k-1$
,
![]() $A_{i+1}$
is weakly below and weakly left of
$A_{i+1}$
is weakly below and weakly left of
![]() $A_i$
and
$A_i$
and
![]() $A_{i}, A_{i+1}$
are in the same row or in the same column. Let
$A_{i}, A_{i+1}$
are in the same row or in the same column. Let
![]() $m \in [(\tau _P)_{B_1}, (\tau _P)_{B_2}]$
. Then, there exists a unique index
$m \in [(\tau _P)_{B_1}, (\tau _P)_{B_2}]$
. Then, there exists a unique index
![]() $1 \leq i \leq k-1$
such that
$1 \leq i \leq k-1$
such that
![]() $(\tau _P)_{A_i} \leq m \leq (\tau _P)_{A_{i+1}}$
. Since P is regular, one of the following holds:
$(\tau _P)_{A_i} \leq m \leq (\tau _P)_{A_{i+1}}$
. Since P is regular, one of the following holds:
-
(i) If
 $(\tau _P)_{A_i} \preceq _P (\tau _P)_{A_{i+1}}$
, then
$(\tau _P)_{A_i} \preceq _P (\tau _P)_{A_{i+1}}$
, then
 $(\tau _P)_{A_i} \preceq _P m$
or
$(\tau _P)_{A_i} \preceq _P m$
or
 $m \preceq _P (\tau _P)_{A_{i+1}}$
.
$m \preceq _P (\tau _P)_{A_{i+1}}$
. -
(ii) If
 $(\tau _P)_{A_{i+1}} \preceq _P (\tau _P)_{A_{i}}$
, then
$(\tau _P)_{A_{i+1}} \preceq _P (\tau _P)_{A_{i}}$
, then
 $(\tau _P)_{A_{i+1}} \preceq _P m$
or
$(\tau _P)_{A_{i+1}} \preceq _P m$
or
 $m \preceq _P (\tau _P)_{A_{i}}$
.
$m \preceq _P (\tau _P)_{A_{i}}$
.
It follows that
![]() $(\tau _P)_{A_i}$
, m and
$(\tau _P)_{A_i}$
, m and
![]() $(\tau _P)_{A_{i+1}}$
appear in the same connected component; that is, m appears in
$(\tau _P)_{A_{i+1}}$
appear in the same connected component; that is, m appears in
![]() $\mathsf {C}$
. Thus,
$\mathsf {C}$
. Thus,
![]() $\tau _P$
is distinguished.
$\tau _P$
is distinguished.
Next, to prove the ‘if’ part, assume that
![]() $\tau _P$
is a distinguished Schur labeling and
$\tau _P$
is a distinguished Schur labeling and
![]() $\lambda / \mu $
is the shape of
$\lambda / \mu $
is the shape of
![]() $\tau _P$
. Let
$\tau _P$
. Let
![]() $B_1, B_2 \in \mathtt {yd}(\lambda /\mu )$
with
$B_1, B_2 \in \mathtt {yd}(\lambda /\mu )$
with
![]() $(\tau _P)_{B_1} \prec _{\tau _P} (\tau _P)_{B_2}$
. By the definition of
$(\tau _P)_{B_1} \prec _{\tau _P} (\tau _P)_{B_2}$
. By the definition of
![]() $\prec _{\tau _P}$
,
$\prec _{\tau _P}$
,
![]() $B_1$
and
$B_1$
and
![]() $B_2$
are in the same connected component. In order to establish the regularity of P, we need to prove that either
$B_2$
are in the same connected component. In order to establish the regularity of P, we need to prove that either
![]() $(\tau _P)_{B_1} \preceq _{\tau _P} (\tau _P)_C$
or
$(\tau _P)_{B_1} \preceq _{\tau _P} (\tau _P)_C$
or
![]() $(\tau _P)_{C} \preceq _{\tau _P} (\tau _P)_{B_2}$
for all
$(\tau _P)_{C} \preceq _{\tau _P} (\tau _P)_{B_2}$
for all
![]() $C \in \mathtt {yd}(\lambda /\mu )$
satisfying
$C \in \mathtt {yd}(\lambda /\mu )$
satisfying
![]() $(\tau _P)_{B_1} < (\tau _P)_C < (\tau _P)_{B_2}$
or
$(\tau _P)_{B_1} < (\tau _P)_C < (\tau _P)_{B_2}$
or
![]() $(\tau _P)_{B_1}> (\tau _P)_C > (\tau _P)_{B_2}$
.
$(\tau _P)_{B_1}> (\tau _P)_C > (\tau _P)_{B_2}$
.
Assume that there exists
![]() $C \in \mathtt {yd}(\lambda /\mu )$
such that
$C \in \mathtt {yd}(\lambda /\mu )$
such that
![]() $(\tau _P)_{B_1} < (\tau _P)_C < (\tau _P)_{B_2}$
. Since
$(\tau _P)_{B_1} < (\tau _P)_C < (\tau _P)_{B_2}$
. Since
![]() $\tau _P$
is a Schur labeling and
$\tau _P$
is a Schur labeling and
![]() $(\tau _P)_{B_1} \prec _{\tau _P} (\tau _P)_{B_2}$
, the inequality
$(\tau _P)_{B_1} \prec _{\tau _P} (\tau _P)_{B_2}$
, the inequality
![]() $(\tau _P)_{B_1} < (\tau _P)_{B_2}$
implies that
$(\tau _P)_{B_1} < (\tau _P)_{B_2}$
implies that
![]() $B_2$
is strictly below
$B_2$
is strictly below
![]() $B_1$
. In addition, since
$B_1$
. In addition, since
![]() $\tau _P$
is distinguished and
$\tau _P$
is distinguished and
![]() $(\tau _P)_{B_1},(\tau _P)_{B_2}$
appear in the same connected component in
$(\tau _P)_{B_1},(\tau _P)_{B_2}$
appear in the same connected component in
![]() $\tau _P$
,
$\tau _P$
,
![]() $(\tau _P)_{C}$
appears in the same connected component with them in
$(\tau _P)_{C}$
appears in the same connected component with them in
![]() $\tau _P$
. Suppose for the sake of contradiction that
$\tau _P$
. Suppose for the sake of contradiction that
![]() $(\tau _P)_{B_1} \not \preceq _{\tau _P} (\tau _P)_C$
and
$(\tau _P)_{B_1} \not \preceq _{\tau _P} (\tau _P)_C$
and
![]() $(\tau _P)_{C} \not \preceq _{\tau _P} (\tau _P)_{B_2}$
. Then C satisfies one of the following conditions:
$(\tau _P)_{C} \not \preceq _{\tau _P} (\tau _P)_{B_2}$
. Then C satisfies one of the following conditions:
-
(i) C is strictly above
 $B_1$
and strictly right of
$B_1$
and strictly right of
 $B_2$
.
$B_2$
. -
(ii) C is strictly left of
 $B_1$
and strictly below
$B_1$
and strictly below
 $B_2$
.
$B_2$
.
However, since
![]() $\tau _P$
is a Schur labeling and
$\tau _P$
is a Schur labeling and
![]() $(\tau _P)_{B_1} < (\tau _P)_C$
, C cannot satisfy (i). Similarly, since
$(\tau _P)_{B_1} < (\tau _P)_C$
, C cannot satisfy (i). Similarly, since
![]() $\tau _P$
is a Schur labeling and
$\tau _P$
is a Schur labeling and
![]() $(\tau _P)_{C} < (\tau _P)_{B_2}$
, C cannot satisfy (ii). Therefore,
$(\tau _P)_{C} < (\tau _P)_{B_2}$
, C cannot satisfy (ii). Therefore,
![]() $(\tau _P)_{B_1} \preceq _{\tau _P} (\tau _P)_C$
or
$(\tau _P)_{B_1} \preceq _{\tau _P} (\tau _P)_C$
or
![]() $(\tau _P)_{C} \preceq _{\tau _P} (\tau _P)_{B_2}$
. In a similar way, one can show that if there exists
$(\tau _P)_{C} \preceq _{\tau _P} (\tau _P)_{B_2}$
. In a similar way, one can show that if there exists
![]() $C \in \mathtt {yd}(\lambda /\mu )$
such that
$C \in \mathtt {yd}(\lambda /\mu )$
such that
![]() $(\tau _P)_{B_1}> (\tau _P)_C > (\tau _P)_{B_2}$
, then
$(\tau _P)_{B_1}> (\tau _P)_C > (\tau _P)_{B_2}$
, then
![]() $(\tau _P)_{B_1} \preceq _{\tau _P} (\tau _P)_C$
or
$(\tau _P)_{B_1} \preceq _{\tau _P} (\tau _P)_C$
or
![]() $(\tau _P)_{C} \preceq _{\tau _P} (\tau _P)_{B_2}$
. Thus, P is regular.
$(\tau _P)_{C} \preceq _{\tau _P} (\tau _P)_{B_2}$
. Thus, P is regular.
Note that
![]() $\tau _{\mathsf {poset}(\tau )} = \tau $
for any
$\tau _{\mathsf {poset}(\tau )} = \tau $
for any
![]() $\tau \in \mathsf {DS}(\lambda / \mu )$
. Considering this property together with Lemma 3.6, one can see that the map
$\tau \in \mathsf {DS}(\lambda / \mu )$
. Considering this property together with Lemma 3.6, one can see that the map
 $$ \begin{align} \Phi: \mathsf{RSP}_n \rightarrow \bigcup_{|\lambda/\mu| = n} \mathsf{DS}(\lambda/\mu), \quad P \mapsto \tau_P \end{align} $$
$$ \begin{align} \Phi: \mathsf{RSP}_n \rightarrow \bigcup_{|\lambda/\mu| = n} \mathsf{DS}(\lambda/\mu), \quad P \mapsto \tau_P \end{align} $$
is a bijection and its inverse is given by
![]() $\tau \mapsto \mathsf {poset}(\tau )$
.
$\tau \mapsto \mathsf {poset}(\tau )$
.
As a second step, we provide a lemma that will be used throughout this paper.
Lemma 3.7. For
![]() $T \in \mathrm {SYT}(\lambda /\mu )$
,
$T \in \mathrm {SYT}(\lambda /\mu )$
,
![]() $\{\mathsf {read}_\tau (T) \mid \tau \in \mathsf {DS}(\lambda /\mu )\} = [\mathsf {read}_{\tau _0}(T), \mathsf {read}_{\tau _1}(T)]_R$
.
$\{\mathsf {read}_\tau (T) \mid \tau \in \mathsf {DS}(\lambda /\mu )\} = [\mathsf {read}_{\tau _0}(T), \mathsf {read}_{\tau _1}(T)]_R$
.
Proof. Let us show the inclusion
![]() $\{\mathsf {read}_\tau (T) \mid \tau \in \mathsf {DS}(\lambda /\mu )\} \subseteq [\mathsf {read}_{\tau _0}(T), \mathsf {read}_{\tau _1}(T)]_R$
. This can be done by proving
$\{\mathsf {read}_\tau (T) \mid \tau \in \mathsf {DS}(\lambda /\mu )\} \subseteq [\mathsf {read}_{\tau _0}(T), \mathsf {read}_{\tau _1}(T)]_R$
. This can be done by proving
![]() $\mathsf {read}_{\tau _0}(T) \preceq _R \mathsf {read}_{\tau }(T)$
and
$\mathsf {read}_{\tau _0}(T) \preceq _R \mathsf {read}_{\tau }(T)$
and
![]() $\mathsf {read}_{\tau }(T) \preceq _R \mathsf {read}_{\tau _1}(T)$
for all
$\mathsf {read}_{\tau }(T) \preceq _R \mathsf {read}_{\tau _1}(T)$
for all
![]() $\tau \in \mathsf {DS}(\lambda /\mu )$
. Since the method of proof for the latter inequality is essentially the same as that for the former one, we omit the proof for the latter inequality. Let
$\tau \in \mathsf {DS}(\lambda /\mu )$
. Since the method of proof for the latter inequality is essentially the same as that for the former one, we omit the proof for the latter inequality. Let
![]() $\tau \in \mathsf {DS}(\lambda /\mu )$
and
$\tau \in \mathsf {DS}(\lambda /\mu )$
and
![]() $(i,j) \in \mathrm {Inv}_R(\mathsf {read}_{\tau _0}(T))$
. Since
$(i,j) \in \mathrm {Inv}_R(\mathsf {read}_{\tau _0}(T))$
. Since
![]() ${i> j}$
and
${i> j}$
and
![]() $\mathsf {read}_{\tau _0}(T)^{-1}(i) < \mathsf {read}_{\tau _0}(T)^{-1}(j)$
, the box
$\mathsf {read}_{\tau _0}(T)^{-1}(i) < \mathsf {read}_{\tau _0}(T)^{-1}(j)$
, the box
![]() $T^{-1}(j)$
is placed strictly left and weakly below
$T^{-1}(j)$
is placed strictly left and weakly below
![]() $T^{-1}(i)$
. This, together with the definition of distinguished Schur labeling, implies that
$T^{-1}(i)$
. This, together with the definition of distinguished Schur labeling, implies that
![]() $\tau _{T^{-1}(i)} < \tau _{T^{-1}(j)}$
; equivalently,
$\tau _{T^{-1}(i)} < \tau _{T^{-1}(j)}$
; equivalently,
![]() $\mathsf {read}_{\tau }(T)^{-1}(i) < \mathsf {read}_{\tau }(T)^{-1}(j)$
. It follows that
$\mathsf {read}_{\tau }(T)^{-1}(i) < \mathsf {read}_{\tau }(T)^{-1}(j)$
. It follows that
![]() $(i,j) \in \mathrm {Inv}_R(\mathsf {read}_{\tau }(T))$
. Since we chose an arbitrary
$(i,j) \in \mathrm {Inv}_R(\mathsf {read}_{\tau }(T))$
. Since we chose an arbitrary
![]() $(i,j) \in \mathrm {Inv}_R(\mathsf {read}_{\tau _0}(T))$
, we have the inclusion
$(i,j) \in \mathrm {Inv}_R(\mathsf {read}_{\tau _0}(T))$
, we have the inclusion
![]() $\mathrm {Inv}_R(\mathsf {read}_{\tau _0}(T)) \subseteq \mathrm {Inv}_R(\mathsf {read}_{\tau }(T))$
. Therefore,
$\mathrm {Inv}_R(\mathsf {read}_{\tau _0}(T)) \subseteq \mathrm {Inv}_R(\mathsf {read}_{\tau }(T))$
. Therefore,
![]() $\mathsf {read}_{\tau _0}(T) \preceq _R \mathsf {read}_{\tau }(T)$
.
$\mathsf {read}_{\tau _0}(T) \preceq _R \mathsf {read}_{\tau }(T)$
.
Let us show the opposite inclusion
![]() $\{\mathsf {read}_\tau (T) \mid \tau \in \mathsf {DS}(\lambda /\mu )\} \supseteq [\mathsf {read}_{\tau _0}(T), \mathsf {read}_{\tau _1}(T)]_R$
. Since
$\{\mathsf {read}_\tau (T) \mid \tau \in \mathsf {DS}(\lambda /\mu )\} \supseteq [\mathsf {read}_{\tau _0}(T), \mathsf {read}_{\tau _1}(T)]_R$
. Since
![]() $\{\mathsf {read}_\tau (T) \mid \tau \text {is a bijective tableau of shape} \lambda / \mu \}$
is equal to
$\{\mathsf {read}_\tau (T) \mid \tau \text {is a bijective tableau of shape} \lambda / \mu \}$
is equal to
![]() $\mathfrak {S}_n$
as a set, the inclusion can be obtained by proving that
$\mathfrak {S}_n$
as a set, the inclusion can be obtained by proving that
![]() $\mathsf {read}_\tau (T) \notin [\mathsf {read}_{\tau _0}(T), \mathsf {read}_{\tau _1}(T)]_R$
for all bijective tableaux
$\mathsf {read}_\tau (T) \notin [\mathsf {read}_{\tau _0}(T), \mathsf {read}_{\tau _1}(T)]_R$
for all bijective tableaux
![]() $\tau $
of shape
$\tau $
of shape
![]() $\lambda /\mu $
with
$\lambda /\mu $
with
![]() $\tau \notin \mathsf {DS}(\lambda /\mu )$
. To prove it, choose an arbitrary bijective tableau
$\tau \notin \mathsf {DS}(\lambda /\mu )$
. To prove it, choose an arbitrary bijective tableau
![]() $\tau $
of shape
$\tau $
of shape
![]() $\lambda /\mu $
with
$\lambda /\mu $
with
![]() $\tau \notin \mathsf {DS}(\lambda /\mu )$
. Since
$\tau \notin \mathsf {DS}(\lambda /\mu )$
. Since
![]() $\tau \notin \mathsf {DS}(\lambda /\mu )$
, there exists
$\tau \notin \mathsf {DS}(\lambda /\mu )$
, there exists
![]() $ 1 \leq i < j \leq n$
such that i is weakly below and weakly left of j in
$ 1 \leq i < j \leq n$
such that i is weakly below and weakly left of j in
![]() $\tau $
. Set
$\tau $
. Set
![]() $x := T_{\tau ^{-1}(i)}$
and
$x := T_{\tau ^{-1}(i)}$
and
![]() $y := T_{\tau ^{-1}(j)}$
. Then, x appears left of y in
$y := T_{\tau ^{-1}(j)}$
. Then, x appears left of y in
![]() $\mathsf {read}_\tau (T)$
. However, since
$\mathsf {read}_\tau (T)$
. However, since
![]() $\tau _0, \tau _1 \in \mathsf {DS}(\lambda /\mu )$
, we have
$\tau _0, \tau _1 \in \mathsf {DS}(\lambda /\mu )$
, we have
![]() $(\tau _0)_{\tau ^{-1}(i)}> (\tau _0)_{\tau ^{-1}(j)}$
and
$(\tau _0)_{\tau ^{-1}(i)}> (\tau _0)_{\tau ^{-1}(j)}$
and
![]() $(\tau _1)_{\tau ^{-1}(i)}> (\tau _1)_{\tau ^{-1}(j)}$
, which implies that x appears right of y in both
$(\tau _1)_{\tau ^{-1}(i)}> (\tau _1)_{\tau ^{-1}(j)}$
, which implies that x appears right of y in both
![]() $\mathsf {read}_{\tau _0}(T)$
and
$\mathsf {read}_{\tau _0}(T)$
and
![]() $\mathsf {read}_{\tau _1}(T)$
. If
$\mathsf {read}_{\tau _1}(T)$
. If
![]() $x < y$
, then
$x < y$
, then
![]() $(y, x) \in \mathrm {Inv}_R(\mathsf {read}_{\tau _0}(T))$
and
$(y, x) \in \mathrm {Inv}_R(\mathsf {read}_{\tau _0}(T))$
and
![]() $(y, x) \notin \mathrm {Inv}_R(\mathsf {read}_\tau (T))$
, thus
$(y, x) \notin \mathrm {Inv}_R(\mathsf {read}_\tau (T))$
, thus
![]() $\mathrm {Inv}_R(\mathsf {read}_{\tau _0}(T)) \not \subseteq \mathrm {Inv}_R(\mathsf {read}_{\tau }(T))$
. Similarly, if
$\mathrm {Inv}_R(\mathsf {read}_{\tau _0}(T)) \not \subseteq \mathrm {Inv}_R(\mathsf {read}_{\tau }(T))$
. Similarly, if
![]() $x> y$
, then
$x> y$
, then
![]() $\mathrm {Inv}_R(\mathsf {read}_\tau (T)) \not \subseteq \mathrm {Inv}_R(\mathsf {read}_{\tau _1}(T))$
. Hence,
$\mathrm {Inv}_R(\mathsf {read}_\tau (T)) \not \subseteq \mathrm {Inv}_R(\mathsf {read}_{\tau _1}(T))$
. Hence,
![]() $\mathsf {read}_\tau (T) \notin [\mathsf {read}_{\tau _0}(T), \mathsf {read}_{\tau _1}(T)]_R$
.
$\mathsf {read}_\tau (T) \notin [\mathsf {read}_{\tau _0}(T), \mathsf {read}_{\tau _1}(T)]_R$
.
As a last step, we define two specific standard Young tableaux. For a skew partition
![]() $\lambda /\mu $
of size n, let
$\lambda /\mu $
of size n, let
![]() $T_{\lambda /\mu }$
(resp.
$T_{\lambda /\mu }$
(resp.
![]() $T^{\prime}_{\lambda /\mu }$
) be the standard Young tableau obtained by filling
$T^{\prime}_{\lambda /\mu }$
) be the standard Young tableau obtained by filling
![]() $\mathtt {yd}(\lambda /\mu )$
by
$\mathtt {yd}(\lambda /\mu )$
by
![]() $1, 2, \ldots , n$
from left to right starting with the top row (resp. from top to bottom starting with leftmost column).
$1, 2, \ldots , n$
from left to right starting with the top row (resp. from top to bottom starting with leftmost column).
Example 3.8. Let
![]() $\lambda / \mu = (2,2) \star (3,2) / (1)$
. Then
$\lambda / \mu = (2,2) \star (3,2) / (1)$
. Then

Now, we are ready prove the main theorem of this section.
Theorem 3.9. Let
![]() $P \in \mathsf {RSP}_n$
and
$P \in \mathsf {RSP}_n$
and
![]() $\lambda /\mu = \mathrm {sh}(\tau _P)$
. Then
$\lambda /\mu = \mathrm {sh}(\tau _P)$
. Then
Proof. Due to Theorem 2.4 and Lemma 3.2, it suffices to show that
![]() $\mathsf {read}_{\tau _P}(T_{\lambda /\mu })$
is minimal and
$\mathsf {read}_{\tau _P}(T_{\lambda /\mu })$
is minimal and
![]() $\mathsf {read}_{\tau _P}(T^{\prime}_{\lambda /\mu })$
is maximal in
$\mathsf {read}_{\tau _P}(T^{\prime}_{\lambda /\mu })$
is maximal in
![]() $\mathsf {read}_{\tau _P}(\mathrm {SYT}(\lambda /\mu ))$
with respect to
$\mathsf {read}_{\tau _P}(\mathrm {SYT}(\lambda /\mu ))$
with respect to
![]() $\preceq _L$
. Let
$\preceq _L$
. Let
![]() $T \in \mathrm {SYT}(\lambda / \mu )$
. In the case where
$T \in \mathrm {SYT}(\lambda / \mu )$
. In the case where
![]() $\tau _P = \tau _0$
, one can easily see that
$\tau _P = \tau _0$
, one can easily see that
In the case where
![]() $\tau _P \neq \tau _0$
, we consider the equality
$\tau _P \neq \tau _0$
, we consider the equality
which follows from Definition 3.1. By Lemma 3.6, we have
![]() $\tau _P \in \mathsf {DS}(\lambda /\mu )$
; therefore, combining Lemma 3.7 with Equation (3.5) yields that
$\tau _P \in \mathsf {DS}(\lambda /\mu )$
; therefore, combining Lemma 3.7 with Equation (3.5) yields that
Now, we have that
 $$ \begin{align*} \ell(\mathsf{read}_{\tau_P}(T)) - \ell(\mathsf{read}_{\tau_P}(T_{\lambda/\mu})) & = \ell(\mathsf{read}_{\tau_0}(T)) - \ell(\mathsf{read}_{\tau_0}(T_{\lambda/\mu})) \\ & = \ell(\mathsf{read}_{\tau_0}(T) \mathsf{read}_{\tau_0}(T_{\lambda/\mu})^{-1}) & \text{by Equation }({3.4}) \\ & = \ell(\mathsf{read}_{\tau_P}(T) \mathsf{read}_{\tau_P}(T_{\lambda/\mu})^{-1}) & \text{by Definition }{3.1}. \end{align*} $$
$$ \begin{align*} \ell(\mathsf{read}_{\tau_P}(T)) - \ell(\mathsf{read}_{\tau_P}(T_{\lambda/\mu})) & = \ell(\mathsf{read}_{\tau_0}(T)) - \ell(\mathsf{read}_{\tau_0}(T_{\lambda/\mu})) \\ & = \ell(\mathsf{read}_{\tau_0}(T) \mathsf{read}_{\tau_0}(T_{\lambda/\mu})^{-1}) & \text{by Equation }({3.4}) \\ & = \ell(\mathsf{read}_{\tau_P}(T) \mathsf{read}_{\tau_P}(T_{\lambda/\mu})^{-1}) & \text{by Definition }{3.1}. \end{align*} $$
Therefore,
![]() $\mathsf {read}_{\tau _P}(T_{\lambda /\mu }) \preceq _L \mathsf {read}_{\tau _P}(T)$
. In the same manner, we can prove that
$\mathsf {read}_{\tau _P}(T_{\lambda /\mu }) \preceq _L \mathsf {read}_{\tau _P}(T)$
. In the same manner, we can prove that
![]() $\mathsf {read}_{\tau _P}(T) \preceq _L \mathsf {read}_{\tau _P}(T^{\prime}_{\lambda /\mu })$
.
$\mathsf {read}_{\tau _P}(T) \preceq _L \mathsf {read}_{\tau _P}(T^{\prime}_{\lambda /\mu })$
.
4 An equivalence relation on
 $\mathrm {Int}(n)$
$\mathrm {Int}(n)$
Recall that
![]() $\mathrm {Int}(n)$
denotes the set of nonempty left weak Bruhat intervals in
$\mathrm {Int}(n)$
denotes the set of nonempty left weak Bruhat intervals in
![]() $\mathfrak {S}_n$
; that is,
$\mathfrak {S}_n$
; that is,
For
![]() $I_1, I_2 \in \mathrm {Int}(n)$
, a poset isomorphism
$I_1, I_2 \in \mathrm {Int}(n)$
, a poset isomorphism
![]() $f: (I_1, \preceq _L) \rightarrow (I_2, \preceq _L)$
is called descent-preserving if
$f: (I_1, \preceq _L) \rightarrow (I_2, \preceq _L)$
is called descent-preserving if
![]() $\mathrm {Des}_L(\gamma ) = \mathrm {Des}_L(f(\gamma ))$
for all
$\mathrm {Des}_L(\gamma ) = \mathrm {Des}_L(f(\gamma ))$
for all
![]() $\gamma \in I_1$
. In this section, we study the classification of left weak Bruhat intervals in
$\gamma \in I_1$
. In this section, we study the classification of left weak Bruhat intervals in
![]() $\mathrm {Int}(n)$
up to descent-preserving poset isomorphism. In particular, in the case where
$\mathrm {Int}(n)$
up to descent-preserving poset isomorphism. In particular, in the case where
![]() ${P \in \mathsf {RSP}_n}$
, we explicitly describe the isomorphism class of
${P \in \mathsf {RSP}_n}$
, we explicitly describe the isomorphism class of
![]() $\Sigma _L(P)$
.
$\Sigma _L(P)$
.
We begin by explaining the reason why we consider descent-preserving poset isomorphisms. Note that every interval
![]() $I \in \mathrm {Int}(n)$
can be represented by the colored digraph whose vertices are given by the permutations in I and
$I \in \mathrm {Int}(n)$
can be represented by the colored digraph whose vertices are given by the permutations in I and
![]() $\{1,2,\ldots , n-1\}$
-colored arrows are given by
$\{1,2,\ldots , n-1\}$
-colored arrows are given by
For intervals
![]() $I_1, I_2 \in \mathrm {Int}(n)$
, a map
$I_1, I_2 \in \mathrm {Int}(n)$
, a map
![]() $f: I_1 \rightarrow I_2$
is called a colored digraph isomorphism if f is bijective and satisfies that for all
$f: I_1 \rightarrow I_2$
is called a colored digraph isomorphism if f is bijective and satisfies that for all
![]() $\gamma , \gamma ' \in I_1$
and
$\gamma , \gamma ' \in I_1$
and
![]() $1 \leq i \leq n-1$
,
$1 \leq i \leq n-1$
,
If there exists a descent-preserving colored digraph isomorphism between two intervals
![]() $I_1$
and
$I_1$
and
![]() $I_2$
, then
$I_2$
, then
![]() $\mathsf {B}(I_1)$
is isomorphic to
$\mathsf {B}(I_1)$
is isomorphic to
![]() $\mathsf {B}(I_2)$
. Motivated by this fact, in [Reference Jung, Kim, Lee and Oh19, Subsection 3.1], the authors posed the classification problem of weak Bruhat intervals up to descent-preserving colored digraph isomorphism.
$\mathsf {B}(I_2)$
. Motivated by this fact, in [Reference Jung, Kim, Lee and Oh19, Subsection 3.1], the authors posed the classification problem of weak Bruhat intervals up to descent-preserving colored digraph isomorphism.
A colored digraph isomorphism between
![]() $I_1$
and
$I_1$
and
![]() $I_2$
is a poset isomorphism with respect to
$I_2$
is a poset isomorphism with respect to
![]() $\preceq _L$
, but a poset isomorphism
$\preceq _L$
, but a poset isomorphism
![]() $f: I_1 \rightarrow I_2$
may not be a colored digraph isomorphism. For instance, the poset isomorphism
$f: I_1 \rightarrow I_2$
may not be a colored digraph isomorphism. For instance, the poset isomorphism
![]() $f: [1234, 2134]_L \rightarrow [1234, 1324]_L$
defined by
$f: [1234, 2134]_L \rightarrow [1234, 1324]_L$
defined by
![]() $f(1234) = 1234$
and
$f(1234) = 1234$
and
![]() $f(2134) = 1324$
is not a colored digraph isomorphism since
$f(2134) = 1324$
is not a colored digraph isomorphism since

However, if a poset isomorphism between left weak Bruhat intervals is descent-preserving, it indeed proves to be a colored digraph isomorphism.
Proposition 4.1. Let
![]() $I_1, I_2 \in \mathrm {Int}(n)$
. Every descent-preserving poset isomorphism
$I_1, I_2 \in \mathrm {Int}(n)$
. Every descent-preserving poset isomorphism
![]() $f: I_1 \rightarrow I_2$
is a colored digraph isomorphism.
$f: I_1 \rightarrow I_2$
is a colored digraph isomorphism.
Proof. Let
![]() $\gamma , \gamma ' \in I_1$
with
$\gamma , \gamma ' \in I_1$
with
![]() $\gamma \preceq _L^c \gamma '$
. Since f is a poset isomorphism, we have
$\gamma \preceq _L^c \gamma '$
. Since f is a poset isomorphism, we have
![]() $f(\gamma ) \preceq _L^c f(\gamma ')$
. Let
$f(\gamma ) \preceq _L^c f(\gamma ')$
. Let
![]() $i,j \in [n-1]$
, satisfying
$i,j \in [n-1]$
, satisfying
![]() $\gamma ' = s_i \gamma $
and
$\gamma ' = s_i \gamma $
and
![]() $f(\gamma ') = s_j f(\gamma )$
. For the assertion, it suffices to show that
$f(\gamma ') = s_j f(\gamma )$
. For the assertion, it suffices to show that
![]() $i = j$
. Let
$i = j$
. Let
![]() $D_1 := \mathrm {Des}_L(\gamma )$
and
$D_1 := \mathrm {Des}_L(\gamma )$
and
![]() $D_2 := \mathrm {Des}_L(\gamma ')$
. Since
$D_2 := \mathrm {Des}_L(\gamma ')$
. Since
![]() $\gamma ' = s_i \gamma $
, we have
$\gamma ' = s_i \gamma $
, we have
In addition, since
![]() $D_1 = \mathrm {Des}_L(f(\gamma ))$
,
$D_1 = \mathrm {Des}_L(f(\gamma ))$
,
![]() $D_2 = \mathrm {Des}_L(f(\gamma '))$
and
$D_2 = \mathrm {Des}_L(f(\gamma '))$
and
![]() $f(\gamma ') = s_j f(\gamma )$
, we have
$f(\gamma ') = s_j f(\gamma )$
, we have
![]() $j \in D_2 \setminus D_1$
, and it follows that j is one of
$j \in D_2 \setminus D_1$
, and it follows that j is one of
![]() $i-1$
, i, and
$i-1$
, i, and
![]() $i+1$
.
$i+1$
.
If
![]() $j = i-1$
, then
$j = i-1$
, then
![]() $i-1, i \in D_2$
. It follows that
$i-1, i \in D_2$
. It follows that
equivalently,
This implies that
![]() $j=i-1 \in D_1$
, which is a contradiction to
$j=i-1 \in D_1$
, which is a contradiction to
![]() $j \notin \mathrm {Des}_L(f(\gamma ))$
. Therefore,
$j \notin \mathrm {Des}_L(f(\gamma ))$
. Therefore,
![]() $j\neq i-1$
.
$j\neq i-1$
.
In a similar manner, one can show that
![]() $j \neq i+1$
. Hence,
$j \neq i+1$
. Hence,
![]() $j = i$
, as required.
$j = i$
, as required.
Proposition 4.1 says that classifying weak Bruhat intervals up to descent-preserving colored digraph isomorphism is equivalent to classifying weak Bruhat intervals up to descent-preserving poset isomorphism. With this equivalence in mind, we introduce an equivalence relation, whose reflexivity, symmetricity and transitivity are obvious.
Definition 4.2. We define an equivalence relation
![]() $\overset {D}{\simeq }$
on
$\overset {D}{\simeq }$
on
![]() $\mathrm {Int}(n)$
by
$\mathrm {Int}(n)$
by
![]() $I_1 \overset {D}{\simeq } I_2$
if there is a descent-preserving (poset) isomorphism between
$I_1 \overset {D}{\simeq } I_2$
if there is a descent-preserving (poset) isomorphism between
![]() $(I_1, \preceq _L)$
and
$(I_1, \preceq _L)$
and
![]() $(I_2, \preceq _L)$
.
$(I_2, \preceq _L)$
.
For each equivalence class C, we define
By Proposition 4.1,
![]() $\xi _C$
does not depend on the choice of
$\xi _C$
does not depend on the choice of
![]() $[\sigma , \rho ]_L \in C$
. We also define
$[\sigma , \rho ]_L \in C$
. We also define
From now on, we always regard
![]() $\overline {\mathrm {min}}(C)$
and
$\overline {\mathrm {min}}(C)$
and
![]() $\overline {\mathrm {max}}(C)$
as subposets of
$\overline {\mathrm {max}}(C)$
as subposets of
![]() $(\mathfrak {S}_n, \preceq _R)$
.
$(\mathfrak {S}_n, \preceq _R)$
.
The following lemma is the initial step in the proof of the main result of this section (Theorem 4.6).
Lemma 4.3. Let C be an equivalence class under
![]() $\overset {D}{\simeq }$
with
$\overset {D}{\simeq }$
with
![]() $\ell (\xi _C) = 1$
. Then,
$\ell (\xi _C) = 1$
. Then,
![]() $\overline {\mathrm {min}}(C)$
is a right weak Bruhat interval in
$\overline {\mathrm {min}}(C)$
is a right weak Bruhat interval in
![]() $(\mathfrak {S}_n, \preceq _R)$
.
$(\mathfrak {S}_n, \preceq _R)$
.
Before proving the lemma, we provide an outline of the proof for the reader’s understanding. We first classify the equivalence classes under consideration according to the set X in Equation (4.2). Then, case by case, we show that
![]() $\overline {\mathrm {min}}(C)$
has a unique minimal element
$\overline {\mathrm {min}}(C)$
has a unique minimal element
![]() $\sigma _0$
. In particular, in Case 3, we introduce a specific permutation
$\sigma _0$
. In particular, in Case 3, we introduce a specific permutation
![]() $\mathbf {w}_0$
and show that it is the unique minimal element of
$\mathbf {w}_0$
and show that it is the unique minimal element of
![]() $\overline {\mathrm {min}}(C)$
. Using these results, we next show that
$\overline {\mathrm {min}}(C)$
. Using these results, we next show that
![]() $\overline {\mathrm {min}}(C)$
has the unique maximal element
$\overline {\mathrm {min}}(C)$
has the unique maximal element
![]() $\sigma _1$
. Finally, we show that
$\sigma _1$
. Finally, we show that
![]() $[\sigma _0, \sigma _1]_R \subseteq \overline {\mathrm {min}}(C)$
.
$[\sigma _0, \sigma _1]_R \subseteq \overline {\mathrm {min}}(C)$
.
Proof. From the condition
![]() $\ell (\xi _C) = 1$
, it follows that
$\ell (\xi _C) = 1$
, it follows that
![]() $\xi _C = s_{i_0}$
for some
$\xi _C = s_{i_0}$
for some
![]() $i_0 \in [n-1]$
.
$i_0 \in [n-1]$
.
First, let us prove that there exists a unique minimal element in
![]() $\overline {\mathrm {min}}(C)$
. Let
$\overline {\mathrm {min}}(C)$
. Let
and
One sees that
![]() $\{i_0\} \subseteq X \subseteq \{i_0 - 1, i_0, i_0 + 1\}$
, and therefore, X can be one of the following:
$\{i_0\} \subseteq X \subseteq \{i_0 - 1, i_0, i_0 + 1\}$
, and therefore, X can be one of the following:
Case 1:
![]() $X = \{i_0 - 1, i_0, i_0 + 1\}$
. Since
$X = \{i_0 - 1, i_0, i_0 + 1\}$
. Since
![]() $i_0 - 1, i_0+1 \in D_1$
and
$i_0 - 1, i_0+1 \in D_1$
and
![]() $i_0 \notin D_1$
,
$i_0 \notin D_1$
,
in one-line notation. Considering this equality, one can see that
![]() $[w_0(D_1), s_{i_0} w_0(D_1)]_L \in C$
. By Lemma 2.2,
$[w_0(D_1), s_{i_0} w_0(D_1)]_L \in C$
. By Lemma 2.2,
![]() $w_0(D_1) \preceq _R \sigma $
for all
$w_0(D_1) \preceq _R \sigma $
for all
![]() $\sigma \in \mathfrak {S}_n$
with
$\sigma \in \mathfrak {S}_n$
with
![]() $\mathrm {Des}_L(\sigma ) = D_1$
. Thus,
$\mathrm {Des}_L(\sigma ) = D_1$
. Thus,
![]() $w_0(D_1)$
is a unique minimal element in
$w_0(D_1)$
is a unique minimal element in
![]() $\overline {\mathrm {min}}(C)$
.
$\overline {\mathrm {min}}(C)$
.
Case 2:
![]() $X = \{i_0\}$
. In this case, we have
$X = \{i_0\}$
. In this case, we have
in one-line notation. Considering this equality, one can see that
![]() $[s_{i_0} w_0(D_2), w_0(D_2)]_L \in C$
. Again, by Lemma 2.2,
$[s_{i_0} w_0(D_2), w_0(D_2)]_L \in C$
. Again, by Lemma 2.2,
![]() $w_0(D_2) \preceq _R \sigma $
for all
$w_0(D_2) \preceq _R \sigma $
for all
![]() $\sigma \in \mathfrak {S}_n$
with
$\sigma \in \mathfrak {S}_n$
with
![]() $\mathrm {Des}_L(\sigma ) = D_2$
. Thus,
$\mathrm {Des}_L(\sigma ) = D_2$
. Thus,
![]() $s_{i_0} w_0(D_2)$
is a unique minimal element in
$s_{i_0} w_0(D_2)$
is a unique minimal element in
![]() $\overline {\mathrm {min}}(C)$
.
$\overline {\mathrm {min}}(C)$
.
Case 3:
![]() $X = \{i_0-1, i_0\}$
. When
$X = \{i_0-1, i_0\}$
. When
![]() $i_0 + 1 \notin D_1$
, following the way as in Case 1, one can see that
$i_0 + 1 \notin D_1$
, following the way as in Case 1, one can see that
![]() $w_0(D_1)$
is a unique minimal element in
$w_0(D_1)$
is a unique minimal element in
![]() $\overline {\mathrm {min}}(C)$
.
$\overline {\mathrm {min}}(C)$
.
From now on, assume that
![]() $i_0 + 1 \in D_1$
. We begin by introducing necessary notation. Let
$i_0 + 1 \in D_1$
. We begin by introducing necessary notation. Let
And set
Let
-
•
 $\mathbf {w}^{(1)}$
be the longest element of the subgroup
$\mathbf {w}^{(1)}$
be the longest element of the subgroup
 $\mathfrak {S}_{D_1 \cap [p_1 - 1]}$
of
$\mathfrak {S}_{D_1 \cap [p_1 - 1]}$
of
 $\mathfrak {S}_{p_1}$
,
$\mathfrak {S}_{p_1}$
, -
•
 $\mathbf {w}^{(2)}$
be the longest element of
$\mathbf {w}^{(2)}$
be the longest element of
 $\mathfrak {S}_{p_2}$
,
$\mathfrak {S}_{p_2}$
, -
•
 $\mathbf {w}^{(3)}$
be the longest element of
$\mathbf {w}^{(3)}$
be the longest element of
 $\mathfrak {S}_{p_3}$
, and
$\mathfrak {S}_{p_3}$
, and -
•
 $\mathbf {w}^{(4)}$
be the longest element of the subgroup
$\mathbf {w}^{(4)}$
be the longest element of the subgroup
 $\mathfrak {S}_{D_1 \cap [p_4 -1]}$
of
$\mathfrak {S}_{D_1 \cap [p_4 -1]}$
of
 $\mathfrak {S}_{p_4}$
.
$\mathfrak {S}_{p_4}$
.
With this notation, we define
![]() $\mathbf {w}_0$
to be the permutation given by
$\mathbf {w}_0$
to be the permutation given by
 $$\begin{align*}\mathbf{w}_0(k) := \begin{cases} \mathbf{w}^{(1)}(k) & \text{if }k \in [p_1], \\ \mathbf{w}^{(2)}(k - p_1) + (i_0 + 1) & \text{if }k \in [p_1 +1, p_1 + p_2], \\ i_0 & \text{if }k = p_1 + p_2 + 1, \\ \mathbf{w}^{(3)}(k - (p_1 + p_2 + 1)) + (\mathsf{m}_1 - 1) & \text{if }k \in [p_1 + p_2 + 2, p_1 + p_2 + p_3 + 1], \\ i_0 + 1 & \text{if }k = p_1 + p_2 + p_3 + 2, \\ \mathbf{w}^{(4)}(k - (p_1 + p_2 + p_3 + 2)) + (\mathsf{m}_2 + 1) & \text{if }k \in [p_1 + p_2 + p_3 + 3, n]. \end{cases} \end{align*}$$
$$\begin{align*}\mathbf{w}_0(k) := \begin{cases} \mathbf{w}^{(1)}(k) & \text{if }k \in [p_1], \\ \mathbf{w}^{(2)}(k - p_1) + (i_0 + 1) & \text{if }k \in [p_1 +1, p_1 + p_2], \\ i_0 & \text{if }k = p_1 + p_2 + 1, \\ \mathbf{w}^{(3)}(k - (p_1 + p_2 + 1)) + (\mathsf{m}_1 - 1) & \text{if }k \in [p_1 + p_2 + 2, p_1 + p_2 + p_3 + 1], \\ i_0 + 1 & \text{if }k = p_1 + p_2 + p_3 + 2, \\ \mathbf{w}^{(4)}(k - (p_1 + p_2 + p_3 + 2)) + (\mathsf{m}_2 + 1) & \text{if }k \in [p_1 + p_2 + p_3 + 3, n]. \end{cases} \end{align*}$$
It should be remarked that
 $$ \begin{align*} \mathbf{w}_0([1,p_1]) &= [1,\mathsf{m}_1-1], \\ \mathbf{w}_0([p_1+1,p_1+p_2]) & = [i_0+2,\mathsf{m}_2+1], \\ \mathbf{w}_0(p_1+p_2+1) &= i_0, \\ \mathbf{w}_0([p_1+p_2+2,p_1+p_2+p_3+1]) &= [\mathsf{m}_1, i_0-1], \\ \mathbf{w}_0(p_1+p_2+p_3+2) &= i_0+1, \quad \text{and} \\ \mathbf{w}_0([p_1+p_2+p_3+3,n]) &= [\mathsf{m}_2+2, n]. \end{align*} $$
$$ \begin{align*} \mathbf{w}_0([1,p_1]) &= [1,\mathsf{m}_1-1], \\ \mathbf{w}_0([p_1+1,p_1+p_2]) & = [i_0+2,\mathsf{m}_2+1], \\ \mathbf{w}_0(p_1+p_2+1) &= i_0, \\ \mathbf{w}_0([p_1+p_2+2,p_1+p_2+p_3+1]) &= [\mathsf{m}_1, i_0-1], \\ \mathbf{w}_0(p_1+p_2+p_3+2) &= i_0+1, \quad \text{and} \\ \mathbf{w}_0([p_1+p_2+p_3+3,n]) &= [\mathsf{m}_2+2, n]. \end{align*} $$
From the definition of
![]() $\mathbf {w}_0$
, it follows that
$\mathbf {w}_0$
, it follows that
![]() $[\mathbf {w}_0, s_{i_0} \mathbf {w}_0]_L \in C$
; equivalently,
$[\mathbf {w}_0, s_{i_0} \mathbf {w}_0]_L \in C$
; equivalently,
![]() $\mathbf {w}_0 \in \overline {\mathrm {min}}(C)$
. We claim that
$\mathbf {w}_0 \in \overline {\mathrm {min}}(C)$
. We claim that
![]() $\mathbf {w}_0$
is a unique minimal element in
$\mathbf {w}_0$
is a unique minimal element in
![]() $\overline {\mathrm {min}}(C)$
. This can be verified by showing that every minimal element in
$\overline {\mathrm {min}}(C)$
. This can be verified by showing that every minimal element in
![]() $\overline {\mathrm {min}}(C)$
is equal to
$\overline {\mathrm {min}}(C)$
is equal to
![]() $\mathbf {w}_0$
. Let
$\mathbf {w}_0$
. Let
![]() $\sigma _0$
be a minimal element in
$\sigma _0$
be a minimal element in
![]() $\overline {\mathrm {min}}(C)$
. Set
$\overline {\mathrm {min}}(C)$
. Set
 $$ \begin{align*} \begin{array}{l} \mathcal{I}_{\mathrm{L}} := \{\sigma_0(k) \mid 1 \le k < \sigma_0^{-1}(i_0)\}, \\[.5ex] \mathcal{I}_{\mathrm{C}} := \{\sigma_0(k) \mid \sigma_0^{-1}(i_0) < k < \sigma_0^{-1}(i_0+1) \}, \\[.5ex] \mathcal{I}_{\mathrm{R}} := \{\sigma_0(k) \mid \sigma_0^{-1}(i_0 + 1) < k \le n\}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} \mathcal{I}_{\mathrm{L}} := \{\sigma_0(k) \mid 1 \le k < \sigma_0^{-1}(i_0)\}, \\[.5ex] \mathcal{I}_{\mathrm{C}} := \{\sigma_0(k) \mid \sigma_0^{-1}(i_0) < k < \sigma_0^{-1}(i_0+1) \}, \\[.5ex] \mathcal{I}_{\mathrm{R}} := \{\sigma_0(k) \mid \sigma_0^{-1}(i_0 + 1) < k \le n\}. \end{array} \end{align*} $$
To begin with, we establish the equalities
These equalities are derived by verifying the following claims.
Claim 1.
![]() $\mathcal {I}_{\mathrm {C}} = [\mathsf {m}_1, i_0 - 1]$
. Let us show
$\mathcal {I}_{\mathrm {C}} = [\mathsf {m}_1, i_0 - 1]$
. Let us show
![]() $\mathcal {I}_{\mathrm {C}} \subseteq [\mathsf {m}_1, i_0 - 1]$
. First, to prove
$\mathcal {I}_{\mathrm {C}} \subseteq [\mathsf {m}_1, i_0 - 1]$
. First, to prove
![]() $\mathcal {I}_{\mathrm {C}} \subseteq [i_0 - 1]$
, we assume that there exists
$\mathcal {I}_{\mathrm {C}} \subseteq [i_0 - 1]$
, we assume that there exists
![]() $i \in \mathcal {I}_{\mathrm {C}}$
such that
$i \in \mathcal {I}_{\mathrm {C}}$
such that
![]() $i \geq i_0$
. Let
$i \geq i_0$
. Let
By the definition of
![]() $\mathcal {I}_{\mathrm {C}}$
,
$\mathcal {I}_{\mathrm {C}}$
,
![]() $i_0,i_0+1 \notin \mathcal {I}_{\mathrm {C}}$
. If
$i_0,i_0+1 \notin \mathcal {I}_{\mathrm {C}}$
. If
![]() $i_0 + 2 \in \mathcal {I}_{\mathrm {C}}$
, then
$i_0 + 2 \in \mathcal {I}_{\mathrm {C}}$
, then
![]() $i_0 + 1 \in D_1 \setminus D_2$
, which contradicts the assumption that
$i_0 + 1 \in D_1 \setminus D_2$
, which contradicts the assumption that
![]() $i_0 +1 \notin X$
. Since
$i_0 +1 \notin X$
. Since
![]() $\sigma _0(k_1) \in \mathcal {I}_{\mathrm {C}}$
, it follows that
$\sigma _0(k_1) \in \mathcal {I}_{\mathrm {C}}$
, it follows that
![]() $\sigma _0(k_1) \geq i_0 + 3$
. And, by the choice of
$\sigma _0(k_1) \geq i_0 + 3$
. And, by the choice of
![]() $k_1$
, we have
$k_1$
, we have
![]() $\sigma _0(k_1 + 1) \leq i_0+1$
. Putting these together yields that
$\sigma _0(k_1 + 1) \leq i_0+1$
. Putting these together yields that
![]() $[\sigma _0 s_{k_1}, s_{i_0} \sigma _0s_{k_1}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
$[\sigma _0 s_{k_1}, s_{i_0} \sigma _0s_{k_1}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
![]() $\sigma _0 s_{k_1} \prec _R \sigma _0$
. This contradicts the minimality of
$\sigma _0 s_{k_1} \prec _R \sigma _0$
. This contradicts the minimality of
![]() $\sigma _0$
in
$\sigma _0$
in
![]() $\overline {\mathrm {min}}(C)$
; therefore,
$\overline {\mathrm {min}}(C)$
; therefore,
![]() $\mathcal {I}_{\mathrm {C}} \subseteq [i_0 - 1]$
. Next, to prove
$\mathcal {I}_{\mathrm {C}} \subseteq [i_0 - 1]$
. Next, to prove
![]() $\mathcal {I}_{\mathrm {C}} \subseteq [\mathsf {m}_1, n]$
, we assume that there exists
$\mathcal {I}_{\mathrm {C}} \subseteq [\mathsf {m}_1, n]$
, we assume that there exists
![]() $i \in \mathcal {I}_{\mathrm {C}}$
such that
$i \in \mathcal {I}_{\mathrm {C}}$
such that
![]() $i < \mathsf {m}_1$
. Let
$i < \mathsf {m}_1$
. Let
By the choice of
![]() $k_2$
, we have
$k_2$
, we have
![]() $\sigma _0(k_2) + 1 \le \mathsf {m}_1 \le \sigma _0(k_2 - 1)$
. In addition, if
$\sigma _0(k_2) + 1 \le \mathsf {m}_1 \le \sigma _0(k_2 - 1)$
. In addition, if
![]() $\sigma _0(k_2) + 1 = \mathsf {m}_1 = \sigma _0(k_2 - 1)$
, then
$\sigma _0(k_2) + 1 = \mathsf {m}_1 = \sigma _0(k_2 - 1)$
, then
![]() $\mathsf {m}_1 - 1 \in \mathrm {Des}_L(\sigma _0)$
, which cannot happen by the definition of
$\mathsf {m}_1 - 1 \in \mathrm {Des}_L(\sigma _0)$
, which cannot happen by the definition of
![]() $\mathsf {m}_1$
. Therefore,
$\mathsf {m}_1$
. Therefore,
![]() $\sigma _0(k_2) + 1 < \sigma _0(k_2 - 1)$
, which implies that
$\sigma _0(k_2) + 1 < \sigma _0(k_2 - 1)$
, which implies that
![]() $[\sigma _0 s_{k_2 - 1}, s_{i_0} \sigma _0 s_{k_2 - 1}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
$[\sigma _0 s_{k_2 - 1}, s_{i_0} \sigma _0 s_{k_2 - 1}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
![]() $\sigma _0 s_{k_2 - 1} \prec _R \sigma _0$
. This contradicts the minimality of
$\sigma _0 s_{k_2 - 1} \prec _R \sigma _0$
. This contradicts the minimality of
![]() $\sigma _0$
in
$\sigma _0$
in
![]() $\overline {\mathrm {min}}(C)$
. Thus,
$\overline {\mathrm {min}}(C)$
. Thus,
![]() $\mathcal {I}_{\mathrm {C}} \subseteq [\mathsf {m}_1, i_0 - 1]$
.
$\mathcal {I}_{\mathrm {C}} \subseteq [\mathsf {m}_1, i_0 - 1]$
.
Let us show
![]() $\mathcal {I}_{\mathrm {C}} \supseteq [\mathsf {m}_1, i_0 - 1]$
. Assume for the sake of contradiction that there exists
$\mathcal {I}_{\mathrm {C}} \supseteq [\mathsf {m}_1, i_0 - 1]$
. Assume for the sake of contradiction that there exists
![]() $i \in [\mathsf {m}_1, i_0 - 1]$
such that
$i \in [\mathsf {m}_1, i_0 - 1]$
such that
![]() $i \notin \mathcal {I}_{\mathrm {C}}$
. Let j be the maximal element in
$i \notin \mathcal {I}_{\mathrm {C}}$
. Let j be the maximal element in
![]() $[\mathsf {m}_1, i_0 - 1]$
such that
$[\mathsf {m}_1, i_0 - 1]$
such that
![]() $j \notin \mathcal {I}_{\mathrm {C}}$
. Since
$j \notin \mathcal {I}_{\mathrm {C}}$
. Since
![]() $i_0 - 1 \in X$
, we have
$i_0 - 1 \in X$
, we have
![]() $i_0 - 1 \in \mathcal {I}_{\mathrm {C}}$
. It follows that
$i_0 - 1 \in \mathcal {I}_{\mathrm {C}}$
. It follows that
![]() $j < i_0 - 1$
, so
$j < i_0 - 1$
, so
![]() $j+1 \in [\mathsf {m}_1,i_0-1]$
. Combining this with the maximality of j, we have
$j+1 \in [\mathsf {m}_1,i_0-1]$
. Combining this with the maximality of j, we have
![]() $j+1 \in \mathcal {I}_{\mathrm {C}}$
. And, by the definition of
$j+1 \in \mathcal {I}_{\mathrm {C}}$
. And, by the definition of
![]() $\mathsf {m}_1$
, we have
$\mathsf {m}_1$
, we have
![]() $j \in D_1$
. Putting these together yields that
$j \in D_1$
. Putting these together yields that
![]() $j \in \mathcal {I}_{\mathrm {R}}$
. Let
$j \in \mathcal {I}_{\mathrm {R}}$
. Let
If
![]() $\sigma _0(k_3 -1) \le \sigma _0(k_3) + 1$
, then
$\sigma _0(k_3 -1) \le \sigma _0(k_3) + 1$
, then
![]() $\sigma _0(k_3 -1) \le j + 1 < i_0$
. So,
$\sigma _0(k_3 -1) \le j + 1 < i_0$
. So,
![]() $\sigma _0(k_3 - 1) \neq i_0 + 1$
, which implies
$\sigma _0(k_3 - 1) \neq i_0 + 1$
, which implies
![]() $\sigma _0(k_3 -1) \in \mathcal {I}_{\mathrm {R}}$
. This, together with the minimality of
$\sigma _0(k_3 -1) \in \mathcal {I}_{\mathrm {R}}$
. This, together with the minimality of
![]() $k_3$
, yields that
$k_3$
, yields that
![]() $j+1 \le \sigma _0(k_3 -1)$
. It follows that
$j+1 \le \sigma _0(k_3 -1)$
. It follows that
![]() $\sigma _0(k_3 - 1) = j + 1$
, which is a contradiction because
$\sigma _0(k_3 - 1) = j + 1$
, which is a contradiction because
![]() $\sigma _0(k_3 -1) \in \mathcal {I}_{\mathrm {R}}$
, but
$\sigma _0(k_3 -1) \in \mathcal {I}_{\mathrm {R}}$
, but
![]() $j+1 \in \mathcal {I}_{\mathrm {C}}$
. Therefore, we have
$j+1 \in \mathcal {I}_{\mathrm {C}}$
. Therefore, we have
![]() $\sigma _0(k_3) + 1 < \sigma _0(k_3-1)$
. In addition, since
$\sigma _0(k_3) + 1 < \sigma _0(k_3-1)$
. In addition, since
![]() $j < i_0 - 1$
, we have
$j < i_0 - 1$
, we have
![]() $\sigma _0(k_3) < i_0 - 1$
. Putting these together yields that
$\sigma _0(k_3) < i_0 - 1$
. Putting these together yields that
![]() $[\sigma _0 s_{k_3 - 1}, s_{i_0} \sigma _0 s_{k_3 - 1}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
$[\sigma _0 s_{k_3 - 1}, s_{i_0} \sigma _0 s_{k_3 - 1}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
![]() $\sigma _0 s_{k_3 - 1} \prec _R \sigma _0$
, which contradicts the minimality of
$\sigma _0 s_{k_3 - 1} \prec _R \sigma _0$
, which contradicts the minimality of
![]() $\sigma _0$
in
$\sigma _0$
in
![]() $\overline {\mathrm {min}}(C)$
. Thus,
$\overline {\mathrm {min}}(C)$
. Thus,
![]() $\mathcal {I}_{\mathrm {C}} \supseteq [\mathsf {m}_1, i_0 - 1]$
.
$\mathcal {I}_{\mathrm {C}} \supseteq [\mathsf {m}_1, i_0 - 1]$
.
Claim 2.
![]() $[\mathsf {m}_1 -1] \cup [i_0+2, \mathsf {m}_2+1] \subseteq \mathcal {I}_{\mathrm {L}}$
. By the definition of
$[\mathsf {m}_1 -1] \cup [i_0+2, \mathsf {m}_2+1] \subseteq \mathcal {I}_{\mathrm {L}}$
. By the definition of
![]() $\mathsf {m}_2$
, we have
$\mathsf {m}_2$
, we have
![]() $[i_0 + 1, \mathsf {m}_2] \subseteq \mathrm {Des}_L(\sigma _0)$
. Since
$[i_0 + 1, \mathsf {m}_2] \subseteq \mathrm {Des}_L(\sigma _0)$
. Since
![]() $i_0+2 \notin \mathcal {I}_{\mathrm {C}}$
, we have
$i_0+2 \notin \mathcal {I}_{\mathrm {C}}$
, we have
![]() $[i_0+2, \mathsf {m}_2+1] \subseteq \mathcal {I}_{\mathrm {L}}$
. To prove
$[i_0+2, \mathsf {m}_2+1] \subseteq \mathcal {I}_{\mathrm {L}}$
. To prove
![]() $[\mathsf {m}_1 - 1] \subseteq \mathcal {I}_{\mathrm {L}}$
, suppose that there exists
$[\mathsf {m}_1 - 1] \subseteq \mathcal {I}_{\mathrm {L}}$
, suppose that there exists
![]() $i \in [\mathsf {m}_1 - 1]$
such that
$i \in [\mathsf {m}_1 - 1]$
such that
![]() $i \notin \mathcal {I}_{\mathrm {L}}$
. Let
$i \notin \mathcal {I}_{\mathrm {L}}$
. Let
Since
![]() $\sigma _0(k_4) \notin \mathcal {I}_{\mathrm {L}}$
and
$\sigma _0(k_4) \notin \mathcal {I}_{\mathrm {L}}$
and
![]() $\sigma _0(k_4) < \mathsf {m}_1$
, we have
$\sigma _0(k_4) < \mathsf {m}_1$
, we have
![]() $\sigma _0(k_4) \in \mathcal {I}_{\mathrm {R}}$
. This implies that
$\sigma _0(k_4) \in \mathcal {I}_{\mathrm {R}}$
. This implies that
![]() $\sigma _0(k_4-1) \notin \mathcal {I}_{\mathrm {L}} \cup \{i_0\} \cup \mathcal {I}_{\mathrm {C}}$
. In addition, the minimality of
$\sigma _0(k_4-1) \notin \mathcal {I}_{\mathrm {L}} \cup \{i_0\} \cup \mathcal {I}_{\mathrm {C}}$
. In addition, the minimality of
![]() $k_4$
gives
$k_4$
gives
![]() $\sigma _0(k_4 - 1) \geq \mathsf {m}_1$
. Since
$\sigma _0(k_4 - 1) \geq \mathsf {m}_1$
. Since
![]() $[\mathsf {m}_1, i_0-1] = \mathcal {I}_{\mathrm {C}}$
, we have
$[\mathsf {m}_1, i_0-1] = \mathcal {I}_{\mathrm {C}}$
, we have
![]() $\sigma _0(k_4 - 1) \geq i_0+1$
. Putting the above inequalities together, we have
$\sigma _0(k_4 - 1) \geq i_0+1$
. Putting the above inequalities together, we have
and so
![]() $\sigma _0(k_4) + 2 < \sigma _0(k_4 - 1)$
. It follows that
$\sigma _0(k_4) + 2 < \sigma _0(k_4 - 1)$
. It follows that
![]() $[\sigma _0 s_{k_4 - 1}, s_{i_0} \sigma _0 s_{k_4 - 1}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
$[\sigma _0 s_{k_4 - 1}, s_{i_0} \sigma _0 s_{k_4 - 1}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
![]() $\sigma _0 s_{k_4 - 1} \prec _R \sigma _0$
. This contradicts the minimality of
$\sigma _0 s_{k_4 - 1} \prec _R \sigma _0$
. This contradicts the minimality of
![]() $\sigma _0$
in
$\sigma _0$
in
![]() $\overline {\mathrm {min}}(C)$
; thus,
$\overline {\mathrm {min}}(C)$
; thus,
![]() $[\mathsf {m}_1 - 1] \subseteq \mathcal {I}_{\mathrm {L}}$
.
$[\mathsf {m}_1 - 1] \subseteq \mathcal {I}_{\mathrm {L}}$
.
Claim 3.
![]() $[\mathsf {m}_2 + 2,n] \subseteq \mathcal {I}_{\mathrm {R}}$
. Suppose that there exists
$[\mathsf {m}_2 + 2,n] \subseteq \mathcal {I}_{\mathrm {R}}$
. Suppose that there exists
![]() $i \in [\mathsf {m}_2 + 2,n]$
such that
$i \in [\mathsf {m}_2 + 2,n]$
such that
![]() $i \notin \mathcal {I}_{\mathrm {R}}$
. Let
$i \notin \mathcal {I}_{\mathrm {R}}$
. Let
Since
![]() $k_5 \notin \mathcal {I}_{\mathrm {R}}$
and
$k_5 \notin \mathcal {I}_{\mathrm {R}}$
and
![]() $\sigma _0(k_5)> i_0 + 1$
, we have
$\sigma _0(k_5)> i_0 + 1$
, we have
![]() $\sigma _0(k_5) \in \mathcal {I}_{\mathrm {L}}$
, which implies that
$\sigma _0(k_5) \in \mathcal {I}_{\mathrm {L}}$
, which implies that
![]() $\sigma _0(k_5 + 1) \notin \mathcal {I}_{\mathrm {R}}$
. By the maximality of
$\sigma _0(k_5 + 1) \notin \mathcal {I}_{\mathrm {R}}$
. By the maximality of
![]() $k_5$
, we have
$k_5$
, we have
![]() $\sigma _0(k_5+1) \le \mathsf {m}_2 + 1$
. If
$\sigma _0(k_5+1) \le \mathsf {m}_2 + 1$
. If
![]() $\sigma _0(k_5+1) < \mathsf {m}_2 + 1$
, then
$\sigma _0(k_5+1) < \mathsf {m}_2 + 1$
, then
If
![]() $\sigma _0(k_5+1) = \mathsf {m}_2 + 1$
, then
$\sigma _0(k_5+1) = \mathsf {m}_2 + 1$
, then
![]() $\sigma _0^{-1}(\mathsf {m}_2 + 2)> k_5+1$
due to the maximality of
$\sigma _0^{-1}(\mathsf {m}_2 + 2)> k_5+1$
due to the maximality of
![]() $\mathsf {m}_2$
, so
$\mathsf {m}_2$
, so
![]() $\sigma _0(k_5) \neq \mathsf {m}_2 + 2$
, which implies
$\sigma _0(k_5) \neq \mathsf {m}_2 + 2$
, which implies
Putting these together with the inequalities
![]() $\sigma _0(k_5) \ge \mathsf {m}_2 + 2>i_0 + 2$
yields that
$\sigma _0(k_5) \ge \mathsf {m}_2 + 2>i_0 + 2$
yields that
![]() $[\sigma _0 s_{k_5}, s_{i_0} \sigma _0 s_{k_5}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
$[\sigma _0 s_{k_5}, s_{i_0} \sigma _0 s_{k_5}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
![]() $\sigma _0 s_{k_5} \prec _R \sigma _0$
. This contradicts the minimality of
$\sigma _0 s_{k_5} \prec _R \sigma _0$
. This contradicts the minimality of
![]() $\sigma _0$
in
$\sigma _0$
in
![]() $\overline {\mathrm {min}}(C)$
; thus,
$\overline {\mathrm {min}}(C)$
; thus,
![]() $[\mathsf {m}_2 + 2, n] \subseteq \mathcal {I}_{\mathrm {R}}$
.
$[\mathsf {m}_2 + 2, n] \subseteq \mathcal {I}_{\mathrm {R}}$
.
Now, we are ready to show that
![]() $\sigma _0 = \mathbf {w}_0$
. Let
$\sigma _0 = \mathbf {w}_0$
. Let
We claim that
![]() $\mathcal {I}^{(1)}_{\mathrm {L}} = [\mathsf {m}_1-1]$
and
$\mathcal {I}^{(1)}_{\mathrm {L}} = [\mathsf {m}_1-1]$
and
![]() $\mathcal {I}^{(2)}_{\mathrm {L}} = [i_0+2, \mathsf {m}_2+1]$
. We may assume that
$\mathcal {I}^{(2)}_{\mathrm {L}} = [i_0+2, \mathsf {m}_2+1]$
. We may assume that
![]() $\mathsf {m}_1> 1$
; otherwise, the claim is obvious. To prove our claim, suppose that there exists
$\mathsf {m}_1> 1$
; otherwise, the claim is obvious. To prove our claim, suppose that there exists
![]() $i \in \mathcal {I}^{(1)}_{\mathrm {L}}$
such that
$i \in \mathcal {I}^{(1)}_{\mathrm {L}}$
such that
![]() $i \in [i_0+2,\mathsf {m}_2+1]$
. Then, there exists
$i \in [i_0+2,\mathsf {m}_2+1]$
. Then, there exists
![]() $1 \le k < \sigma _0^{-1}(i_0) - 1$
such that
$1 \le k < \sigma _0^{-1}(i_0) - 1$
such that
![]() $\sigma _0(k) \in [i_0+2, \mathsf {m}_2 + 1]$
and
$\sigma _0(k) \in [i_0+2, \mathsf {m}_2 + 1]$
and
![]() $\sigma _0(k + 1) \in [\mathsf {m}_1 - 1]$
. It follows that
$\sigma _0(k + 1) \in [\mathsf {m}_1 - 1]$
. It follows that
![]() $[\sigma _0 s_{k}, s_{i_0} \sigma _0 s_{k}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
$[\sigma _0 s_{k}, s_{i_0} \sigma _0 s_{k}]_L \overset {D}{\simeq } [\sigma _0, s_{i_0}\sigma _0]_L$
and
![]() $\sigma _0 s_{k} \prec _R \sigma _0$
. Again, this contradicts the minimality of
$\sigma _0 s_{k} \prec _R \sigma _0$
. Again, this contradicts the minimality of
![]() $\sigma _0$
in
$\sigma _0$
in
![]() $\overline {\mathrm {min}}(C)$
, so
$\overline {\mathrm {min}}(C)$
, so
Putting Lemma 2.2, Equation (4.3), Equation (4.4) and the minimality of
![]() $\sigma _0$
together, we conclude that
$\sigma _0$
together, we conclude that
![]() $\sigma _0 = \mathbf {w}_0$
.
$\sigma _0 = \mathbf {w}_0$
.
Case 4:
![]() $X = \{i_0, i_0 + 1\}$
. Take
$X = \{i_0, i_0 + 1\}$
. Take
![]() $[\sigma , s_{i_0} \sigma ]_L \in C$
and let
$[\sigma , s_{i_0} \sigma ]_L \in C$
and let
![]() $C'$
be the equivalence class of
$C'$
be the equivalence class of
![]() $[\sigma ^{w_0}, (s_{i_0} \sigma )^{w_0}]_L$
. By mimicking Equation (4.1) and Equation (4.2), we define
$[\sigma ^{w_0}, (s_{i_0} \sigma )^{w_0}]_L$
. By mimicking Equation (4.1) and Equation (4.2), we define
Since
![]() $D^{\prime}_1 = \{ n-i \mid i \in D_1\}$
and
$D^{\prime}_1 = \{ n-i \mid i \in D_1\}$
and
![]() $D^{\prime}_2 = \{ n-i \mid i \in D_2\}$
, we have
$D^{\prime}_2 = \{ n-i \mid i \in D_2\}$
, we have
Following the proof of Case 3, we see that
![]() $\overline {\mathrm {min}}(C')$
has a unique minimal element
$\overline {\mathrm {min}}(C')$
has a unique minimal element
![]() $\mathbf {w}^{\prime}_0$
. And one can easily see that the map
$\mathbf {w}^{\prime}_0$
. And one can easily see that the map
![]() $f: \overline {\mathrm {min}}(C) \rightarrow \overline {\mathrm {min}}(C')$
,
$f: \overline {\mathrm {min}}(C) \rightarrow \overline {\mathrm {min}}(C')$
,
![]() $\gamma \mapsto \gamma ^{w_0}$
is a well-defined bijection and that for
$\gamma \mapsto \gamma ^{w_0}$
is a well-defined bijection and that for
![]() $\gamma _1, \gamma _2 \in \overline {\mathrm {min}}(C)$
,
$\gamma _1, \gamma _2 \in \overline {\mathrm {min}}(C)$
,
![]() $\gamma _1 \preceq _R \gamma _2$
if and only if
$\gamma _1 \preceq _R \gamma _2$
if and only if
![]() $f(\gamma _1) \preceq _R f(\gamma _2)$
. Thus,
$f(\gamma _1) \preceq _R f(\gamma _2)$
. Thus,
![]() $(\mathbf {w}^{\prime}_0)^{w_0}$
is a unique minimal element in
$(\mathbf {w}^{\prime}_0)^{w_0}$
is a unique minimal element in
![]() $\overline {\mathrm {min}}(C')$
.
$\overline {\mathrm {min}}(C')$
.
Second, we will show that
![]() $\overline {\mathrm {min}}(C)$
has a unique maximal element. Recall that we take
$\overline {\mathrm {min}}(C)$
has a unique maximal element. Recall that we take
![]() $[\sigma , s_{i_0} \sigma ]_L \in C$
. Let
$[\sigma , s_{i_0} \sigma ]_L \in C$
. Let
![]() $C"$
be the equivalence class of
$C"$
be the equivalence class of
![]() $[s_{i_0} \sigma w_0, \sigma w_0]_L$
. Due to the previous arguments, we know that there is a unique minimal element
$[s_{i_0} \sigma w_0, \sigma w_0]_L$
. Due to the previous arguments, we know that there is a unique minimal element
![]() $\gamma _0$
in
$\gamma _0$
in
![]() $\overline {\mathrm {min}}(C")$
. One can easily see that the map
$\overline {\mathrm {min}}(C")$
. One can easily see that the map
![]() $g: \overline {\mathrm {min}}(C) \rightarrow \overline {\mathrm {min}}(C")$
,
$g: \overline {\mathrm {min}}(C) \rightarrow \overline {\mathrm {min}}(C")$
,
![]() $\gamma \mapsto \gamma w_0$
is a well-defined bijection and that for
$\gamma \mapsto \gamma w_0$
is a well-defined bijection and that for
![]() $\gamma _1, \gamma _2 \in \overline {\mathrm {min}}(C)$
,
$\gamma _1, \gamma _2 \in \overline {\mathrm {min}}(C)$
,
![]() $\gamma _1 \preceq _R \gamma _2$
if and only if
$\gamma _1 \preceq _R \gamma _2$
if and only if
![]() $g(\gamma _1) \succeq _R g(\gamma _2)$
. Therefore,
$g(\gamma _1) \succeq _R g(\gamma _2)$
. Therefore,
![]() $\gamma _0 w_0$
is the unique maximal element in
$\gamma _0 w_0$
is the unique maximal element in
![]() $\overline {\mathrm {min}}(C)$
.
$\overline {\mathrm {min}}(C)$
.
Finally, we will show that
![]() $\overline {\mathrm {min}}(C)$
is a right weak Bruhat interval in
$\overline {\mathrm {min}}(C)$
is a right weak Bruhat interval in
![]() $(\mathfrak {S}_n, \preceq _R)$
. Let
$(\mathfrak {S}_n, \preceq _R)$
. Let
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $\sigma _1$
be the minimal and maximal elements in
$\sigma _1$
be the minimal and maximal elements in
![]() $\overline {\mathrm {min}}(C)$
, respectively. Let
$\overline {\mathrm {min}}(C)$
, respectively. Let
![]() $\gamma \in [\sigma _0, \sigma _1]_R$
. Since
$\gamma \in [\sigma _0, \sigma _1]_R$
. Since
![]() $\mathrm {Des}_L(\sigma _0) = \mathrm {Des}_L(\sigma _1)$
, we have
$\mathrm {Des}_L(\sigma _0) = \mathrm {Des}_L(\sigma _1)$
, we have
![]() $\mathrm {Des}_L(\gamma ) = \mathrm {Des}_L(\sigma _0)$
by Lemma 2.2. Next, let us examine
$\mathrm {Des}_L(\gamma ) = \mathrm {Des}_L(\sigma _0)$
by Lemma 2.2. Next, let us examine
![]() $\mathrm {Des}_L(s_{i_0}\gamma )$
. Since
$\mathrm {Des}_L(s_{i_0}\gamma )$
. Since
![]() $\mathrm {Des}_L(\sigma _0) = \mathrm {Des}_L(\gamma )$
, it follows that
$\mathrm {Des}_L(\sigma _0) = \mathrm {Des}_L(\gamma )$
, it follows that
![]() $\gamma \preceq _L s_{i_0} \gamma $
. By Lemma 2.1, we have that
$\gamma \preceq _L s_{i_0} \gamma $
. By Lemma 2.1, we have that
![]() $s_{i_0} \gamma \in [s_{i_0}\sigma _0, s_{i_0}\sigma _1]_{R}$
. Since
$s_{i_0} \gamma \in [s_{i_0}\sigma _0, s_{i_0}\sigma _1]_{R}$
. Since
![]() $\mathrm {Des}_L(s_{i_0} \sigma _0) =\mathrm {Des}_L(s_{i_0} \sigma _1)$
, we have
$\mathrm {Des}_L(s_{i_0} \sigma _0) =\mathrm {Des}_L(s_{i_0} \sigma _1)$
, we have
![]() $\mathrm {Des}_L(s_{i_0}\gamma ) = \mathrm {Des}_L(s_{i_0}\sigma _0)$
by Lemma 2.2. Thus,
$\mathrm {Des}_L(s_{i_0}\gamma ) = \mathrm {Des}_L(s_{i_0}\sigma _0)$
by Lemma 2.2. Thus,
![]() ${\gamma \in \overline {\mathrm {min}}(C)}$
.
${\gamma \in \overline {\mathrm {min}}(C)}$
.
Example 4.4. Let
![]() $C \subseteq \mathrm {Int}(4)$
be the equivalence class of
$C \subseteq \mathrm {Int}(4)$
be the equivalence class of
![]() $[2134, 2143]_L$
. One sees that
$[2134, 2143]_L$
. One sees that
So,
![]() $\overline {\mathrm {min}}(C) = \{2134,2314,2341\}$
and
$\overline {\mathrm {min}}(C) = \{2134,2314,2341\}$
and
![]() $\overline {\mathrm {max}}(C) = \{2143,2413,2431\}$
which are equal to
$\overline {\mathrm {max}}(C) = \{2143,2413,2431\}$
which are equal to
![]() $[2134, 2341]_R$
and
$[2134, 2341]_R$
and
![]() $[2143,2431]_R$
, respectively. For the readers’ convenience, we draw the left weak Bruhat intervals in C within the left weak Bruhat graph of
$[2143,2431]_R$
, respectively. For the readers’ convenience, we draw the left weak Bruhat intervals in C within the left weak Bruhat graph of
![]() $\mathfrak {S}_4$
on the left-hand side of Figure 1. We also draw the right weak Bruhat intervals
$\mathfrak {S}_4$
on the left-hand side of Figure 1. We also draw the right weak Bruhat intervals
![]() $\overline {\mathrm {min}}(C)$
and
$\overline {\mathrm {min}}(C)$
and
![]() $\overline {\mathrm {max}}(C)$
within the right weak Bruhat graph of
$\overline {\mathrm {max}}(C)$
within the right weak Bruhat graph of
![]() $\mathfrak {S}_4$
on the right-hand side of Figure 1.
$\mathfrak {S}_4$
on the right-hand side of Figure 1.

Figure 1 The left weak Bruhat intervals in C on
![]() $(\mathfrak {S}_4, \preceq _L)$
and the right weak Bruhat intervals
$(\mathfrak {S}_4, \preceq _L)$
and the right weak Bruhat intervals
![]() $\overline {\mathrm {min}}(C)$
and
$\overline {\mathrm {min}}(C)$
and
![]() $\overline {\mathrm {max}}(C)$
on
$\overline {\mathrm {max}}(C)$
on
![]() $(\mathfrak {S}_4, \preceq _R)$
in Example 4.4.
$(\mathfrak {S}_4, \preceq _R)$
in Example 4.4.
Lemma 4.5. The intersection of two right weak Bruhat intervals in
![]() $\mathfrak {S}_n$
is again a right weak Bruhat interval.
$\mathfrak {S}_n$
is again a right weak Bruhat interval.
Proof. It is well known that
![]() $(\mathfrak {S}_n, \preceq _R)$
is a lattice; that is, every two-element subset
$(\mathfrak {S}_n, \preceq _R)$
is a lattice; that is, every two-element subset
![]() $\{\gamma _1,\gamma _2\} \subseteq \mathfrak {S}_n$
has the least upper bound and greatest lower bound (for example, see [Reference Björner and Brenti6, Section 3.2]). Combining this with the fact
$\{\gamma _1,\gamma _2\} \subseteq \mathfrak {S}_n$
has the least upper bound and greatest lower bound (for example, see [Reference Björner and Brenti6, Section 3.2]). Combining this with the fact
![]() $|\mathfrak {S}_n| < \infty $
, we derive the desired result.
$|\mathfrak {S}_n| < \infty $
, we derive the desired result.
The following theorem provides significant information regarding equivalence classes under
![]() $\overset {D}{\simeq }$
.
$\overset {D}{\simeq }$
.
Theorem 4.6. Let C be an equivalence class under
![]() $\overset {D}{\simeq }$
. Then
$\overset {D}{\simeq }$
. Then
![]() $\overline {\mathrm {min}}(C)$
and
$\overline {\mathrm {min}}(C)$
and
![]() $\overline {\mathrm {max}}(C)$
are right weak Bruhat intervals in
$\overline {\mathrm {max}}(C)$
are right weak Bruhat intervals in
![]() $(\mathfrak {S}_n, \preceq _R)$
.
$(\mathfrak {S}_n, \preceq _R)$
.
Proof. Note that
![]() $\sigma \preceq _L \xi _C \sigma $
for any
$\sigma \preceq _L \xi _C \sigma $
for any
![]() $\sigma \in \overline {\mathrm {min}}(C)$
and that
$\sigma \in \overline {\mathrm {min}}(C)$
and that
![]() $\overline {\mathrm {max}}(C) = \xi _C \cdot \overline {\mathrm {min}}(C)$
. If we prove that
$\overline {\mathrm {max}}(C) = \xi _C \cdot \overline {\mathrm {min}}(C)$
. If we prove that
![]() $\overline {\mathrm {min}}(C)$
is a right weak Bruhat interval, then Lemma 2.1 implies that
$\overline {\mathrm {min}}(C)$
is a right weak Bruhat interval, then Lemma 2.1 implies that
![]() $\overline {\mathrm {max}}(C)$
is also a right weak Bruhat interval. So we will only prove that
$\overline {\mathrm {max}}(C)$
is also a right weak Bruhat interval. So we will only prove that
![]() $\overline {\mathrm {min}}(C)$
is a right weak Bruhat interval.
$\overline {\mathrm {min}}(C)$
is a right weak Bruhat interval.
When
![]() $\ell (\xi _C) = 0$
, the assertion follows from Lemma 2.2. From now on, assume that
$\ell (\xi _C) = 0$
, the assertion follows from Lemma 2.2. From now on, assume that
![]() $\ell (\xi _C) \geq 1$
. We will prove the assertion by using mathematical induction on
$\ell (\xi _C) \geq 1$
. We will prove the assertion by using mathematical induction on
![]() $\ell (\xi _C)$
. When
$\ell (\xi _C)$
. When
![]() $\ell (\xi _C) = 1$
, the assertion is true by Lemma 4.3. Let k be an arbitrary positive integer and suppose that the assertion holds for every equivalence class
$\ell (\xi _C) = 1$
, the assertion is true by Lemma 4.3. Let k be an arbitrary positive integer and suppose that the assertion holds for every equivalence class
![]() $C \in \mathscr {C}(n)$
with
$C \in \mathscr {C}(n)$
with
![]() $\ell (\xi _C) \leq k$
. Let
$\ell (\xi _C) \leq k$
. Let
![]() $C \in \mathscr {C}(n)$
with
$C \in \mathscr {C}(n)$
with
![]() $\ell (\xi _C) = k+1$
. Set
$\ell (\xi _C) = k+1$
. Set
Given
![]() $i \in \mathcal {A}$
and
$i \in \mathcal {A}$
and
![]() $\sigma \in \overline {\mathrm {min}}(C)$
, note that
$\sigma \in \overline {\mathrm {min}}(C)$
, note that
for all
![]() $\sigma ' \in \overline {\mathrm {min}}(C)$
. This says that the equivalence classes of
$\sigma ' \in \overline {\mathrm {min}}(C)$
. This says that the equivalence classes of
![]() $[\sigma , s_i \sigma ]_L$
and
$[\sigma , s_i \sigma ]_L$
and
![]() $[s_i\sigma , \xi _C \sigma ]_L$
do not depend on
$[s_i\sigma , \xi _C \sigma ]_L$
do not depend on
![]() $\sigma \in \overline {\mathrm {min}}(C)$
. For each
$\sigma \in \overline {\mathrm {min}}(C)$
. For each
![]() $i \in \mathcal {A}$
, we set
$i \in \mathcal {A}$
, we set
 $$ \begin{align*} E_i & := \text{the equivalence class of }[\sigma, s_i \sigma]_L, \\ E^{\prime}_i & := \text{the equivalence class of }[s_i \sigma, \xi_C \sigma]_L \end{align*} $$
$$ \begin{align*} E_i & := \text{the equivalence class of }[\sigma, s_i \sigma]_L, \\ E^{\prime}_i & := \text{the equivalence class of }[s_i \sigma, \xi_C \sigma]_L \end{align*} $$
for any
![]() $\sigma \in \overline {\mathrm {min}}(C)$
. Then, we set
$\sigma \in \overline {\mathrm {min}}(C)$
. Then, we set
Now, the desired assertion can be achieved by proving the following claims:
-
(i)
 $\overline {\mathrm {min}}(C) = J$
.
$\overline {\mathrm {min}}(C) = J$
. -
(ii) J is a right weak Bruhat interval.
First, let us prove
![]() $\overline {\mathrm {min}}(C) = J$
. By the definition of
$\overline {\mathrm {min}}(C) = J$
. By the definition of
![]() $J_i$
, we have
$J_i$
, we have
![]() $s_i \sigma \in J_i$
for all
$s_i \sigma \in J_i$
for all
![]() $i \in \mathcal {A}$
and
$i \in \mathcal {A}$
and
![]() $\sigma \in \overline {\mathrm {min}}(C)$
. It follows that
$\sigma \in \overline {\mathrm {min}}(C)$
. It follows that
![]() $\overline {\mathrm {min}}(C) \subseteq J$
. To prove the opposite inclusion
$\overline {\mathrm {min}}(C) \subseteq J$
. To prove the opposite inclusion
![]() $\overline {\mathrm {min}}(C) \supseteq J$
, take
$\overline {\mathrm {min}}(C) \supseteq J$
, take
![]() $\sigma \in J$
. By the definition of J, we have
$\sigma \in J$
. By the definition of J, we have
And Lemma 2.1 implies that
Putting these together yields that
![]() $[\sigma , \xi _C \sigma ]_L \in C$
; therefore,
$[\sigma , \xi _C \sigma ]_L \in C$
; therefore,
![]() $\sigma \in \overline {\mathrm {min}}(C)$
.
$\sigma \in \overline {\mathrm {min}}(C)$
.
Next, let us prove that J is a right weak Bruhat interval. Due to Lemma 4.5, it suffices to show that
![]() $s_i \cdot J_i$
is a right weak Bruhat interval for
$s_i \cdot J_i$
is a right weak Bruhat interval for
![]() $i \in \mathcal {A}$
. Let us fix
$i \in \mathcal {A}$
. Let us fix
![]() $i \in \mathcal {A}$
. Since
$i \in \mathcal {A}$
. Since
![]() $\ell (\xi _{E_i}) = 1$
and
$\ell (\xi _{E_i}) = 1$
and
![]() $\ell (\xi _{E^{\prime}_i}) = k$
,
$\ell (\xi _{E^{\prime}_i}) = k$
,
![]() $\overline {\mathrm {max}}(E_i)$
and
$\overline {\mathrm {max}}(E_i)$
and
![]() $\overline {\mathrm {min}}(E^{\prime}_i)$
are right weak Bruhat intervals by the induction hypothesis. Combining this with Lemma 4.5 yields that
$\overline {\mathrm {min}}(E^{\prime}_i)$
are right weak Bruhat intervals by the induction hypothesis. Combining this with Lemma 4.5 yields that
![]() $J_i$
is a right weak Bruhat interval. In addition, we have
$J_i$
is a right weak Bruhat interval. In addition, we have
![]() $s_i \gamma \preceq _L \gamma $
for all
$s_i \gamma \preceq _L \gamma $
for all
![]() $\gamma \in J_i$
. Therefore, by Lemma 2.1,
$\gamma \in J_i$
. Therefore, by Lemma 2.1,
![]() $s_i \cdot J_i$
is a right weak Bruhat interval.
$s_i \cdot J_i$
is a right weak Bruhat interval.
According to Theorem 4.6, every equivalence class C can be expressed as follows:
where
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $\sigma _1$
represent the minimal and maximal elements in
$\sigma _1$
represent the minimal and maximal elements in
![]() $\overline {\mathrm {min}}(C)$
, respectively. In particular, when C is the equivalence class of
$\overline {\mathrm {min}}(C)$
, respectively. In particular, when C is the equivalence class of
![]() $\Sigma _L(P)$
for
$\Sigma _L(P)$
for
![]() $P \in \mathsf {RSP}_n$
, we can provide an explicit description of it.
$P \in \mathsf {RSP}_n$
, we can provide an explicit description of it.
Theorem 4.7. Let
![]() $P \in \mathsf {RSP}_n$
and C the equivalence class of
$P \in \mathsf {RSP}_n$
and C the equivalence class of
![]() $\Sigma _L(P)$
under
$\Sigma _L(P)$
under
![]() $\overset {D}{\simeq }$
. Then
$\overset {D}{\simeq }$
. Then
Proof. Let
![]() $\lambda /\mu = \mathrm {sh}(\tau _P)$
. Combining Equation (3.3) with Theorem 3.9 yields that
$\lambda /\mu = \mathrm {sh}(\tau _P)$
. Combining Equation (3.3) with Theorem 3.9 yields that
Therefore, for the assertion, we have only to show the equality
First, let us show that
![]() $\{[\mathsf {read}_{\tau }(T_{\lambda /\mu }), \mathsf {read}_{\tau }(T^{\prime}_{\lambda /\mu })]_L \mid \tau \in \mathsf {DS}(\lambda /\mu ) \} \subseteq C$
. This can be done by proving that for
$\{[\mathsf {read}_{\tau }(T_{\lambda /\mu }), \mathsf {read}_{\tau }(T^{\prime}_{\lambda /\mu })]_L \mid \tau \in \mathsf {DS}(\lambda /\mu ) \} \subseteq C$
. This can be done by proving that for
![]() $\tau \in \mathsf {DS}(\lambda /\mu )$
, the map
$\tau \in \mathsf {DS}(\lambda /\mu )$
, the map
 $$ \begin{align*} f_{P;\tau}: [\mathsf{read}_{\tau_P}(T_{\lambda/\mu}), \mathsf{read}_{\tau_P}(T^{\prime}_{\lambda/\mu})]_L & \rightarrow [\mathsf{read}_{\tau}(T_{\lambda/\mu}), \mathsf{read}_{\tau}(T^{\prime}_{\lambda/\mu})]_L \\ \mathsf{read}_{\tau_P}(T) &\mapsto \mathsf{read}_{\tau}(T) \quad (T\in \mathrm{SYT}(\lambda / \mu)) \end{align*} $$
$$ \begin{align*} f_{P;\tau}: [\mathsf{read}_{\tau_P}(T_{\lambda/\mu}), \mathsf{read}_{\tau_P}(T^{\prime}_{\lambda/\mu})]_L & \rightarrow [\mathsf{read}_{\tau}(T_{\lambda/\mu}), \mathsf{read}_{\tau}(T^{\prime}_{\lambda/\mu})]_L \\ \mathsf{read}_{\tau_P}(T) &\mapsto \mathsf{read}_{\tau}(T) \quad (T\in \mathrm{SYT}(\lambda / \mu)) \end{align*} $$
is a descent-preserving isomorphism. Let us fix
![]() $\tau \in \mathsf {DS}(\lambda /\mu )$
. The definition of
$\tau \in \mathsf {DS}(\lambda /\mu )$
. The definition of
![]() $\tau $
-reading implies that for any
$\tau $
-reading implies that for any
![]() $T_1,T_2 \in \mathrm {SYT}(\lambda /\mu )$
,
$T_1,T_2 \in \mathrm {SYT}(\lambda /\mu )$
,
and therefore,
![]() $f_{P;\tau }$
is a poset isomorphism. To show that
$f_{P;\tau }$
is a poset isomorphism. To show that
![]() $f_{P;\tau }$
is descent-preserving, choose arbitrary
$f_{P;\tau }$
is descent-preserving, choose arbitrary
![]() $T \in \mathrm {SYT}(\lambda /\mu )$
and
$T \in \mathrm {SYT}(\lambda /\mu )$
and
![]() $i \in \mathrm {Des}_L(\mathsf {read}_{\tau _P}(T))$
. Combining the conditions
$i \in \mathrm {Des}_L(\mathsf {read}_{\tau _P}(T))$
. Combining the conditions
![]() $T \in \mathrm {SYT}(\lambda /\mu )$
and
$T \in \mathrm {SYT}(\lambda /\mu )$
and
![]() $\tau _P \in \mathsf {DS}(\lambda /\mu )$
with
$\tau _P \in \mathsf {DS}(\lambda /\mu )$
with
![]() $i \in \mathrm {Des}_L(\mathsf {read}_{\tau _P}(T))$
yields that
$i \in \mathrm {Des}_L(\mathsf {read}_{\tau _P}(T))$
yields that
![]() $i+1$
appears weakly above and strictly right of i in T. It follows that
$i+1$
appears weakly above and strictly right of i in T. It follows that
![]() $i \in \mathrm {Des}_L(\mathsf {read}_{\tau }(T))$
, so
$i \in \mathrm {Des}_L(\mathsf {read}_{\tau }(T))$
, so
![]() $\mathrm {Des}_L(\mathsf {read}_{\tau _P}(T)) \subseteq \mathrm {Des}_L(\mathsf {read}_{\tau }(T))$
. In the same manner, one can show that
$\mathrm {Des}_L(\mathsf {read}_{\tau _P}(T)) \subseteq \mathrm {Des}_L(\mathsf {read}_{\tau }(T))$
. In the same manner, one can show that
![]() $\mathrm {Des}_L(\mathsf {read}_{\tau }(T)) \subseteq \mathrm {Des}_L(\mathsf {read}_{\tau _P}(T))$
. Therefore,
$\mathrm {Des}_L(\mathsf {read}_{\tau }(T)) \subseteq \mathrm {Des}_L(\mathsf {read}_{\tau _P}(T))$
. Therefore,
![]() $f_{P;\tau }$
is a descent-preserving isomorphism.
$f_{P;\tau }$
is a descent-preserving isomorphism.
Next, let us show
![]() $C \subseteq \{[\mathsf {read}_{\tau }(T_{\lambda /\mu }), \mathsf {read}_{\tau }(T^{\prime}_{\lambda /\mu })]_L \mid \tau \in \mathsf {DS}(\lambda /\mu ) \}$
. In the previous paragraph, we prove that
$C \subseteq \{[\mathsf {read}_{\tau }(T_{\lambda /\mu }), \mathsf {read}_{\tau }(T^{\prime}_{\lambda /\mu })]_L \mid \tau \in \mathsf {DS}(\lambda /\mu ) \}$
. In the previous paragraph, we prove that
![]() $[\mathsf {read}_{\tau }(T_{\lambda /\mu }), \mathsf {read}_{\tau }(T^{\prime}_{\lambda /\mu })]_L \in C$
for any
$[\mathsf {read}_{\tau }(T_{\lambda /\mu }), \mathsf {read}_{\tau }(T^{\prime}_{\lambda /\mu })]_L \in C$
for any
![]() $\tau \in \mathsf {DS}(\lambda /\mu )$
. This implies that
$\tau \in \mathsf {DS}(\lambda /\mu )$
. This implies that
![]() $\mathsf {read}_{\tau }(T^{\prime}_{\lambda /\mu }) = \xi _C \mathsf {read}_{\tau }(T_{\lambda /\mu })$
, and so it suffices to show that
$\mathsf {read}_{\tau }(T^{\prime}_{\lambda /\mu }) = \xi _C \mathsf {read}_{\tau }(T_{\lambda /\mu })$
, and so it suffices to show that
Due to Lemma 3.7, this inclusion can be obtained by proving
Let
![]() $\gamma \in \overline {\mathrm {min}}(C)$
. Since
$\gamma \in \overline {\mathrm {min}}(C)$
. Since
![]() $\mathsf {read}_{\tau _0}(T_{\lambda /\mu }) \in \overline {\mathrm {min}}(C)$
, we have
$\mathsf {read}_{\tau _0}(T_{\lambda /\mu }) \in \overline {\mathrm {min}}(C)$
, we have
![]() $\mathrm {Des}_L(\mathsf {read}_{\tau _0}(T_{\lambda /\mu })) = \mathrm {Des}_L(\gamma )$
. In addition, by the definitions of
$\mathrm {Des}_L(\mathsf {read}_{\tau _0}(T_{\lambda /\mu })) = \mathrm {Des}_L(\gamma )$
. In addition, by the definitions of
![]() $\tau _0$
and
$\tau _0$
and
![]() $T_{\lambda /\mu }$
, we have
$T_{\lambda /\mu }$
, we have
![]() $\mathsf {read}_{\tau _0}(T_{\lambda /\mu }) = w_0(\alpha ^{\mathrm {c}})$
, where
$\mathsf {read}_{\tau _0}(T_{\lambda /\mu }) = w_0(\alpha ^{\mathrm {c}})$
, where
![]() $\alpha = (\lambda _1 - \mu _1, \lambda _2 - \mu _2, \ldots , \lambda _{\ell (\lambda )} - \mu _{\ell (\lambda )})$
. Putting these equalities together with Lemma 2.2 yields that
$\alpha = (\lambda _1 - \mu _1, \lambda _2 - \mu _2, \ldots , \lambda _{\ell (\lambda )} - \mu _{\ell (\lambda )})$
. Putting these equalities together with Lemma 2.2 yields that
![]() $\mathsf {read}_{\tau _0}(T_{\lambda /\mu }) \preceq _{R} \gamma $
. Similarly, we have
$\mathsf {read}_{\tau _0}(T_{\lambda /\mu }) \preceq _{R} \gamma $
. Similarly, we have
where
![]() $\beta = (\lambda ^{\mathrm {t}}_1 - \mu ^{\mathrm {t}}_1, \lambda ^{\mathrm {t}}_2 - \mu ^{\mathrm {t}}_2, \ldots , \lambda ^{\mathrm {t}}_{\ell (\lambda ^{\mathrm {t}})} - \mu ^{\mathrm {t}}_{\ell (\lambda ^{\mathrm {t}})})$
. This, together with Lemma 2.2, yields that
$\beta = (\lambda ^{\mathrm {t}}_1 - \mu ^{\mathrm {t}}_1, \lambda ^{\mathrm {t}}_2 - \mu ^{\mathrm {t}}_2, \ldots , \lambda ^{\mathrm {t}}_{\ell (\lambda ^{\mathrm {t}})} - \mu ^{\mathrm {t}}_{\ell (\lambda ^{\mathrm {t}})})$
. This, together with Lemma 2.2, yields that
![]() $\xi _C\gamma \preceq _{R} \mathsf {read}_{\tau _1}(T^{\prime}_{\lambda /\mu })$
. Since
$\xi _C\gamma \preceq _{R} \mathsf {read}_{\tau _1}(T^{\prime}_{\lambda /\mu })$
. Since
![]() $\mathsf {read}_{\tau _1}(T_{\lambda /\mu }) \preceq _L \mathsf {read}_{\tau _1}(T^{\prime}_{\lambda /\mu }) = \xi _C \mathsf {read}_{\tau _1}(T_{\lambda /\mu })$
, we have
$\mathsf {read}_{\tau _1}(T_{\lambda /\mu }) \preceq _L \mathsf {read}_{\tau _1}(T^{\prime}_{\lambda /\mu }) = \xi _C \mathsf {read}_{\tau _1}(T_{\lambda /\mu })$
, we have
![]() $\gamma \preceq _{R} \mathsf {read}_{\tau _1}(T_{\lambda /\mu })$
. Therefore,
$\gamma \preceq _{R} \mathsf {read}_{\tau _1}(T_{\lambda /\mu })$
. Therefore,
![]() $\gamma \in [\mathsf {read}_{\tau _0}(T_{\lambda /\mu }), \mathsf {read}_{\tau _1}(T_{\lambda /\mu })]_R$
, as desired.
$\gamma \in [\mathsf {read}_{\tau _0}(T_{\lambda /\mu }), \mathsf {read}_{\tau _1}(T_{\lambda /\mu })]_R$
, as desired.
Theorem 4.7 tells us that
![]() $\{\Sigma _L(P) \mid P \in \mathsf {RSP}_n \}$
is closed under
$\{\Sigma _L(P) \mid P \in \mathsf {RSP}_n \}$
is closed under
![]() $\overset {D}{\simeq }$
and the equivalence classes inside it are parametrized by the skew partitions of size n. Given a skew partition
$\overset {D}{\simeq }$
and the equivalence classes inside it are parametrized by the skew partitions of size n. Given a skew partition
![]() $\lambda /\mu $
of size n, let
$\lambda /\mu $
of size n, let
![]() $C_{\lambda /\mu }$
be the equivalence class parametrized by
$C_{\lambda /\mu }$
be the equivalence class parametrized by
![]() $\lambda /\mu $
; that is,
$\lambda /\mu $
; that is,
Corollary 4.8. With the above notation, we have
 $$\begin{align*}\{\Sigma_L(P) \mid P \in \mathsf{RSP}_n \} = \bigsqcup_{|\lambda/\mu| = n} C_{\lambda / \mu} \quad (\text{disjoint union}). \end{align*}$$
$$\begin{align*}\{\Sigma_L(P) \mid P \in \mathsf{RSP}_n \} = \bigsqcup_{|\lambda/\mu| = n} C_{\lambda / \mu} \quad (\text{disjoint union}). \end{align*}$$
5 The classification of
 $\mathsf {M}_P$
’s for
$\mathsf {M}_P$
’s for
 $P \in \mathsf {RSP}_n$
$P \in \mathsf {RSP}_n$
Let
![]() $P, Q \in \mathsf {RSP}_n$
. By combining Proposition 4.1 with Theorem 4.7, we can see that if
$P, Q \in \mathsf {RSP}_n$
. By combining Proposition 4.1 with Theorem 4.7, we can see that if
![]() $\tau _P$
and
$\tau _P$
and
![]() $\tau _Q$
have the same shape, then the
$\tau _Q$
have the same shape, then the
![]() $H_n(0)$
-modules
$H_n(0)$
-modules
![]() $\mathsf {M}_P$
and
$\mathsf {M}_P$
and
![]() $\mathsf {M}_Q$
are isomorphic. The purpose of this section is to demonstrate that the converse of this implication also holds. Let us briefly explain our strategy. First, we provide both a projective cover and an injective hull of
$\mathsf {M}_Q$
are isomorphic. The purpose of this section is to demonstrate that the converse of this implication also holds. Let us briefly explain our strategy. First, we provide both a projective cover and an injective hull of
![]() $\mathsf {M}_P$
for every
$\mathsf {M}_P$
for every
![]() $P \in \mathsf {RSP}_n$
. We discover that these modules are completely determined by the shape of
$P \in \mathsf {RSP}_n$
. We discover that these modules are completely determined by the shape of
![]() $\tau _P$
, as demonstrated in Lemma 5.4. Then, we establish that if
$\tau _P$
, as demonstrated in Lemma 5.4. Then, we establish that if
![]() $\tau _P$
and
$\tau _P$
and
![]() $\tau _Q$
have different shapes,
$\tau _Q$
have different shapes,
![]() $\mathsf {M}_P$
and
$\mathsf {M}_P$
and
![]() $\mathsf {M}_Q$
have either nonisomorphic projective covers or nonisomorphic injective hulls, as proven in Theorem 5.5.
$\mathsf {M}_Q$
have either nonisomorphic projective covers or nonisomorphic injective hulls, as proven in Theorem 5.5.
To begin with, we present a brief overview of the background knowledge concerning projective modules and injective modules of the
![]() $0$
-Hecke algebras. In [Reference Duchamp, Hivert and Thibon11, Proposition 4.1], it was shown that
$0$
-Hecke algebras. In [Reference Duchamp, Hivert and Thibon11, Proposition 4.1], it was shown that
![]() $H_n(0)$
is a Frobenius algebra. It is well known that every Frobenius algebra is self injective, and for a finitely generated module M of a self injective algebra, M is projective if and only if it is injective (for instance, see [Reference Benson3, Proposition 1.6.2]). In [Reference Norton30], a complete list of non-isomorphic projective indecomposable
$H_n(0)$
is a Frobenius algebra. It is well known that every Frobenius algebra is self injective, and for a finitely generated module M of a self injective algebra, M is projective if and only if it is injective (for instance, see [Reference Benson3, Proposition 1.6.2]). In [Reference Norton30], a complete list of non-isomorphic projective indecomposable
![]() $H_n(0)$
-modules was provided.
$H_n(0)$
-modules was provided.
In the work [Reference Jung, Kim, Lee and Oh19], it was shown that this list can also be expressed in terms of weak Bruhat interval modules, specifically as
![]() $\{\mathbf {P}_\alpha \mid \alpha \models n\}$
, where
$\{\mathbf {P}_\alpha \mid \alpha \models n\}$
, where
We note that
![]() $\mathbf {P}_\alpha / \mathrm {rad} \; \mathbf {P}_\alpha $
is isomorphic to
$\mathbf {P}_\alpha / \mathrm {rad} \; \mathbf {P}_\alpha $
is isomorphic to
![]() $\mathbf {F}_\alpha $
, where
$\mathbf {F}_\alpha $
, where
![]() $\mathrm {rad} \; \mathbf {P}_\alpha $
is the radical of
$\mathrm {rad} \; \mathbf {P}_\alpha $
is the radical of
![]() $\mathbf {P}_\alpha $
, the intersection of maximal submodules of
$\mathbf {P}_\alpha $
, the intersection of maximal submodules of
![]() $\mathbf {P}_\alpha $
.
$\mathbf {P}_\alpha $
.
In the following, we recall the definition of a projective cover and an injective hull. Let M be a finitely generated
![]() $H_n(0)$
-module. A projective cover of M is a pair
$H_n(0)$
-module. A projective cover of M is a pair
![]() $(\boldsymbol {P}, f)$
consisting of a projective
$(\boldsymbol {P}, f)$
consisting of a projective
![]() $H_n(0)$
-module
$H_n(0)$
-module
![]() $\boldsymbol {P}$
and an
$\boldsymbol {P}$
and an
![]() $H_n(0)$
-module epimorphism
$H_n(0)$
-module epimorphism
![]() $f: \boldsymbol {P} \rightarrow M$
such that
$f: \boldsymbol {P} \rightarrow M$
such that
![]() $\ker (f) \subseteq \mathrm {rad}(\boldsymbol {P})$
. An injective hull of M is a pair
$\ker (f) \subseteq \mathrm {rad}(\boldsymbol {P})$
. An injective hull of M is a pair
![]() $(\boldsymbol {I}, \iota )$
, where
$(\boldsymbol {I}, \iota )$
, where
![]() $\boldsymbol {I}$
is an injective
$\boldsymbol {I}$
is an injective
![]() $H_n(0)$
-module and
$H_n(0)$
-module and
![]() $\iota : M \rightarrow \boldsymbol {I}$
is an
$\iota : M \rightarrow \boldsymbol {I}$
is an
![]() $H_n(0)$
-module monomorphism satisfying
$H_n(0)$
-module monomorphism satisfying
![]() $\iota (M) \supseteq \mathrm {soc}(\boldsymbol {I})$
. Here,
$\iota (M) \supseteq \mathrm {soc}(\boldsymbol {I})$
. Here,
![]() $\mathrm {soc}(\boldsymbol {I})$
is the socle of
$\mathrm {soc}(\boldsymbol {I})$
is the socle of
![]() $\boldsymbol {I}$
, the sum of all irreducible submodules of
$\boldsymbol {I}$
, the sum of all irreducible submodules of
![]() $\boldsymbol {I}$
. A projective cover and an injective hull of M always exist, and they are unique up to isomorphism. For more information, refer to [Reference Auslander, Reiten and Smalø1, Reference Lam23].
$\boldsymbol {I}$
. A projective cover and an injective hull of M always exist, and they are unique up to isomorphism. For more information, refer to [Reference Auslander, Reiten and Smalø1, Reference Lam23].
The projective modules introduced by Huang [Reference Huang18] play an important role in describing the projective cover and injective hull of
![]() $\mathsf {M}_P$
for
$\mathsf {M}_P$
for
![]() $P \in \mathsf {RSP}_n$
. We briefly review these projective modules from the viewpoint of weak Bruhat interval modules. A generalized composition
$P \in \mathsf {RSP}_n$
. We briefly review these projective modules from the viewpoint of weak Bruhat interval modules. A generalized composition
![]() ${\boldsymbol {\unicode{x3b1} }}$
of n is a formal expression
${\boldsymbol {\unicode{x3b1} }}$
of n is a formal expression
![]() $\alpha ^{(1)} \star \alpha ^{(2)} \star \cdots \star \alpha ^{(k)}$
, where
$\alpha ^{(1)} \star \alpha ^{(2)} \star \cdots \star \alpha ^{(k)}$
, where
![]() $\alpha ^{(i)} \models n_i$
for positive integers
$\alpha ^{(i)} \models n_i$
for positive integers
![]() $n_i$
’s with
$n_i$
’s with
![]() $n_1 + n_2 + \cdots + n_k = n$
. For compositions
$n_1 + n_2 + \cdots + n_k = n$
. For compositions
![]() $\alpha = (\alpha _1, \alpha _2, \ldots , \alpha _{\ell (\alpha )})$
and
$\alpha = (\alpha _1, \alpha _2, \ldots , \alpha _{\ell (\alpha )})$
and
![]() $\beta = (\beta _1, \beta _2, \ldots , \beta _{\ell (\beta )})$
, let
$\beta = (\beta _1, \beta _2, \ldots , \beta _{\ell (\beta )})$
, let
For a generalized composition
![]() ${\boldsymbol {\unicode{x3b1} }} = \alpha ^{(1)} \star \alpha ^{(2)} \star \cdots \star \alpha ^{(k)}$
, let
${\boldsymbol {\unicode{x3b1} }} = \alpha ^{(1)} \star \alpha ^{(2)} \star \cdots \star \alpha ^{(k)}$
, let
and let
and
![]() ${\boldsymbol {\unicode{x3b1} }}^{\mathrm {c} \cdot \mathrm {r}} := ({\boldsymbol {\unicode{x3b1} }}^{\mathrm {c}})^{\mathrm {r}}$
. Normally,
${\boldsymbol {\unicode{x3b1} }}^{\mathrm {c} \cdot \mathrm {r}} := ({\boldsymbol {\unicode{x3b1} }}^{\mathrm {c}})^{\mathrm {r}}$
. Normally,
![]() $({\boldsymbol {\unicode{x3b1} }}_{\bullet })^{\mathrm {c}} \neq ({\boldsymbol {\unicode{x3b1} }}^{\mathrm {c}})_{\bullet }$
and
$({\boldsymbol {\unicode{x3b1} }}_{\bullet })^{\mathrm {c}} \neq ({\boldsymbol {\unicode{x3b1} }}^{\mathrm {c}})_{\bullet }$
and
![]() $({\boldsymbol {\unicode{x3b1} }}_{\odot })^{\mathrm {c}} \neq ({\boldsymbol {\unicode{x3b1} }}^{\mathrm {c}})_{\odot }$
for a generalized composition
$({\boldsymbol {\unicode{x3b1} }}_{\odot })^{\mathrm {c}} \neq ({\boldsymbol {\unicode{x3b1} }}^{\mathrm {c}})_{\odot }$
for a generalized composition
![]() ${\boldsymbol {\unicode{x3b1} }}$
. Despite the potential for confusion, for the sake of brevity, we denote
${\boldsymbol {\unicode{x3b1} }}$
. Despite the potential for confusion, for the sake of brevity, we denote
![]() $({\boldsymbol {\unicode{x3b1} }}_{\bullet })^{\mathrm {c}}$
and
$({\boldsymbol {\unicode{x3b1} }}_{\bullet })^{\mathrm {c}}$
and
![]() $({\boldsymbol {\unicode{x3b1} }}_{\odot })^{\mathrm {c}}$
as
$({\boldsymbol {\unicode{x3b1} }}_{\odot })^{\mathrm {c}}$
as
![]() ${\boldsymbol {\unicode{x3b1} }}_{\bullet }^{\mathrm {c}}$
and
${\boldsymbol {\unicode{x3b1} }}_{\bullet }^{\mathrm {c}}$
and
![]() ${\boldsymbol {\unicode{x3b1} }}_{\odot }^{\mathrm {c}}$
, respectively. Then, we define
${\boldsymbol {\unicode{x3b1} }}_{\odot }^{\mathrm {c}}$
, respectively. Then, we define
Huang decomposed
![]() $\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}}$
into projective indecomposable modules, and thus showed that it is projective. To be precise, the following lemma was shown.
$\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}}$
into projective indecomposable modules, and thus showed that it is projective. To be precise, the following lemma was shown.
Lemma 5.1 [Reference Huang18, Theorem 3.3]
For a generalized composition
![]() ${\boldsymbol {\unicode{x3b1} }} = \alpha ^{(1)} \star \alpha ^{(2)} \star \cdots \star \alpha ^{(k)}$
of n,
${\boldsymbol {\unicode{x3b1} }} = \alpha ^{(1)} \star \alpha ^{(2)} \star \cdots \star \alpha ^{(k)}$
of n,
 $$\begin{align*}\mathbf{P}_{\boldsymbol{\unicode{x3b1}}} \cong \mathbf{P}_{\alpha^{(1)}} \boxtimes \mathbf{P}_{\alpha^{(2)}} \boxtimes \cdots \boxtimes \mathbf{P}_{\alpha^{(k)}} \cong \bigoplus_{\beta \in [{\boldsymbol{\unicode{x3b1}}}]} \mathbf{P}_\beta, \end{align*}$$
$$\begin{align*}\mathbf{P}_{\boldsymbol{\unicode{x3b1}}} \cong \mathbf{P}_{\alpha^{(1)}} \boxtimes \mathbf{P}_{\alpha^{(2)}} \boxtimes \cdots \boxtimes \mathbf{P}_{\alpha^{(k)}} \cong \bigoplus_{\beta \in [{\boldsymbol{\unicode{x3b1}}}]} \mathbf{P}_\beta, \end{align*}$$
where
![]() $[{\boldsymbol {\unicode{x3b1} }}] := \{\alpha ^{(1)} \; \square \; \alpha ^{(2)} \; \square \; \cdots \; \square \; \alpha ^{(k)} \mid \square = \cdot \; \text {or} \; \odot \}$
.
$[{\boldsymbol {\unicode{x3b1} }}] := \{\alpha ^{(1)} \; \square \; \alpha ^{(2)} \; \square \; \cdots \; \square \; \alpha ^{(k)} \mid \square = \cdot \; \text {or} \; \odot \}$
.
It is clear from Lemma 5.1 that if
![]() ${\boldsymbol {\unicode{x3b1} }}$
and
${\boldsymbol {\unicode{x3b1} }}$
and
![]() ${\boldsymbol {\unicode{x3b2} }}$
are distinct generalized compositions of n, then
${\boldsymbol {\unicode{x3b2} }}$
are distinct generalized compositions of n, then
![]() $\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
and
$\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
and
![]() $\mathbf {P}_{\boldsymbol {\unicode{x3b2} }}$
are nonisomorphic. Let
$\mathbf {P}_{\boldsymbol {\unicode{x3b2} }}$
are nonisomorphic. Let
![]() ${\boldsymbol {\unicode{x3b1} }}$
be a generalized composition of n. For
${\boldsymbol {\unicode{x3b1} }}$
be a generalized composition of n. For
![]() $\rho \in [w_0({\boldsymbol {\unicode{x3b1} }}_\odot ^{\mathrm {c}}), w_0 w_0({\boldsymbol {\unicode{x3b1} }}_\odot )]_L$
, let
$\rho \in [w_0({\boldsymbol {\unicode{x3b1} }}_\odot ^{\mathrm {c}}), w_0 w_0({\boldsymbol {\unicode{x3b1} }}_\odot )]_L$
, let
![]() $\Upsilon _{{\boldsymbol {\unicode{x3b1} }};\rho }: \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}} \rightarrow \mathsf {B}(w_0({\boldsymbol {\unicode{x3b1} }}_\bullet ^{\mathrm {c}}), \rho )$
be a
$\Upsilon _{{\boldsymbol {\unicode{x3b1} }};\rho }: \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}} \rightarrow \mathsf {B}(w_0({\boldsymbol {\unicode{x3b1} }}_\bullet ^{\mathrm {c}}), \rho )$
be a
![]() $\mathbb C$
-linear map given by
$\mathbb C$
-linear map given by
 $$\begin{align*}\gamma \mapsto\begin{cases}\gamma & \text{if }\gamma \in [w_0({\boldsymbol{\unicode{x3b1}}}_\bullet^{\mathrm{c}}), \rho]_L,\\0 & \text{if }\gamma \in [w_0({\boldsymbol{\unicode{x3b1}}}_\bullet^{\mathrm{c}}), w_0 w_0({\boldsymbol{\unicode{x3b1}}}_\odot)]_L \setminus [w_0({\boldsymbol{\unicode{x3b1}}}_\bullet^{\mathrm{c}}), \rho]_L.\end{cases} \end{align*}$$
$$\begin{align*}\gamma \mapsto\begin{cases}\gamma & \text{if }\gamma \in [w_0({\boldsymbol{\unicode{x3b1}}}_\bullet^{\mathrm{c}}), \rho]_L,\\0 & \text{if }\gamma \in [w_0({\boldsymbol{\unicode{x3b1}}}_\bullet^{\mathrm{c}}), w_0 w_0({\boldsymbol{\unicode{x3b1}}}_\odot)]_L \setminus [w_0({\boldsymbol{\unicode{x3b1}}}_\bullet^{\mathrm{c}}), \rho]_L.\end{cases} \end{align*}$$
Clearly,
![]() $\Upsilon _{{\boldsymbol {\unicode{x3b1} }};\rho }$
is an
$\Upsilon _{{\boldsymbol {\unicode{x3b1} }};\rho }$
is an
![]() $H_n(0)$
-module epimorphism. In addition, it follows from [Reference Kim and Yoo20, Lemma 6.2] that
$H_n(0)$
-module epimorphism. In addition, it follows from [Reference Kim and Yoo20, Lemma 6.2] that
![]() $\ker (\Upsilon _{{\boldsymbol {\unicode{x3b1} }};\rho }) \subseteq \mathrm {rad} (\mathbf {P}_{\boldsymbol {\unicode{x3b1} }})$
. Consequently, we have the following lemma.
$\ker (\Upsilon _{{\boldsymbol {\unicode{x3b1} }};\rho }) \subseteq \mathrm {rad} (\mathbf {P}_{\boldsymbol {\unicode{x3b1} }})$
. Consequently, we have the following lemma.
Lemma 5.2. [(cf. [Reference Kim and Yoo20, Lemma 6.2])] For a generalized composition
![]() ${\boldsymbol {\unicode{x3b1} }}$
of n and
${\boldsymbol {\unicode{x3b1} }}$
of n and
![]() $\rho \in [w_0({\boldsymbol {\unicode{x3b1} }}_\odot ^{\mathrm {c}}), w_0 w_0({\boldsymbol {\unicode{x3b1} }}_\odot )]_L$
, the pair
$\rho \in [w_0({\boldsymbol {\unicode{x3b1} }}_\odot ^{\mathrm {c}}), w_0 w_0({\boldsymbol {\unicode{x3b1} }}_\odot )]_L$
, the pair
![]() $(\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}, \Upsilon _{{\boldsymbol {\unicode{x3b1} }};\rho })$
is a projective cover of
$(\mathbf {P}_{\boldsymbol {\unicode{x3b1} }}, \Upsilon _{{\boldsymbol {\unicode{x3b1} }};\rho })$
is a projective cover of
![]() $\mathsf {B}(w_0({\boldsymbol {\unicode{x3b1} }}_\bullet ^{\mathrm {c}}), \rho )$
.
$\mathsf {B}(w_0({\boldsymbol {\unicode{x3b1} }}_\bullet ^{\mathrm {c}}), \rho )$
.
Let us provide notation and a lemma needed to describe a projective cover and an injective hull of
![]() $\mathsf {M}_P$
for
$\mathsf {M}_P$
for
![]() $P \in \mathsf {RSP}_n$
. For a connected skew partition
$P \in \mathsf {RSP}_n$
. For a connected skew partition
![]() $\lambda / \mu $
of size n, define
$\lambda / \mu $
of size n, define
And, for a disconnected skew partition
![]() $\lambda / \mu $
of size n, define
$\lambda / \mu $
of size n, define
where
![]() $\lambda /\mu = \lambda ^{(1)} / \mu ^{(1)} \star \lambda ^{(2)} / \mu ^{(2)} \star \cdots \star \lambda ^{(k)} / \mu ^{(k)}$
with connected skew partitions
$\lambda /\mu = \lambda ^{(1)} / \mu ^{(1)} \star \lambda ^{(2)} / \mu ^{(2)} \star \cdots \star \lambda ^{(k)} / \mu ^{(k)}$
with connected skew partitions
![]() $\lambda ^{(i)} / \mu ^{(i)}$
’s
$\lambda ^{(i)} / \mu ^{(i)}$
’s
![]() $(1\le i \le k)$
.
$(1\le i \le k)$
.
Lemma 5.3. Let
![]() $\lambda /\mu $
be a skew partition of size n.
$\lambda /\mu $
be a skew partition of size n.
-
(1)
 $\mathsf {read}_{\tau _0}(T_{\lambda /\mu }) = w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )_{\bullet }^{\mathrm {c}})$
.
$\mathsf {read}_{\tau _0}(T_{\lambda /\mu }) = w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )_{\bullet }^{\mathrm {c}})$
. -
(2)
 $\mathsf {read}_{\tau _0}(T^{\prime}_{\lambda /\mu }) \in [w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )_{\odot }^{\mathrm {c}}), w_0w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )_{\odot })]_L$
.
$\mathsf {read}_{\tau _0}(T^{\prime}_{\lambda /\mu }) \in [w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )_{\odot }^{\mathrm {c}}), w_0w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )_{\odot })]_L$
.
Proof. By the definition of
![]() ${\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )$
, the assertion (1) is clear. In addition, one can easily see that
${\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )$
, the assertion (1) is clear. In addition, one can easily see that
![]() $\mathrm {Des}_R(\mathsf {read}_{\tau _0}(T^{\prime}_{\lambda /\mu })) = \mathrm {set}({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )_{\odot }^{\mathrm {c}})$
. So, by Lemma 2.2, the assertion (2) follows.
$\mathrm {Des}_R(\mathsf {read}_{\tau _0}(T^{\prime}_{\lambda /\mu })) = \mathrm {set}({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )_{\odot }^{\mathrm {c}})$
. So, by Lemma 2.2, the assertion (2) follows.
Let
![]() $P \in \mathsf {RSP}_n$
and
$P \in \mathsf {RSP}_n$
and
![]() $\lambda /\mu = \mathrm {sh}(\tau _P)$
. By Theorem 3.9,
$\lambda /\mu = \mathrm {sh}(\tau _P)$
. By Theorem 3.9,
![]() $\mathsf {M}_P = \mathsf {B}(\mathsf {read}_{\tau _P}(T_{\lambda /\mu }), \mathsf {read}_{\tau _P}(T^{\prime}_{\lambda /\mu }))$
. Furthermore, by Theorem 4.7, we have an
$\mathsf {M}_P = \mathsf {B}(\mathsf {read}_{\tau _P}(T_{\lambda /\mu }), \mathsf {read}_{\tau _P}(T^{\prime}_{\lambda /\mu }))$
. Furthermore, by Theorem 4.7, we have an
![]() $H_n(0)$
-module isomorphism
$H_n(0)$
-module isomorphism
Set
Combining Lemma 5.2 and Lemma 5.3 implies that the pair
![]() $\left (\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )}, \eta _P\right )$
is a projective cover of
$\left (\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )}, \eta _P\right )$
is a projective cover of
![]() $\mathsf {M}_P$
.
$\mathsf {M}_P$
.
To find an injective hull of
![]() $\mathsf {M}_P$
, we note that
$\mathsf {M}_P$
, we note that
Combining these equalities with [Reference Jung, Kim, Lee and Oh19, Theorem 4] yields the following
![]() $H_n(0)$
-module isomorphism:
$H_n(0)$
-module isomorphism:
 $$ \begin{align*} g_1: \mathbf{T}^{-}_{\widehat{\unicode{x3b8}}} \left( \mathsf{M}_{\mathsf{poset}(\tau_1^{\lambda^{\mathrm{t}}/\mu^{\mathrm{t}}})}\right) &\rightarrow \mathsf{M}_{\mathsf{poset}(\tau_0^{\lambda/\mu})}, \\ \gamma^* &\mapsto (-1)^{\ell(\gamma \; \mathsf{read}_{\tau_1}(T^{\prime}_{\lambda^{\mathrm{t}}/\mu^{\mathrm{t}}})^{-1})} \gamma w_0, \end{align*} $$
$$ \begin{align*} g_1: \mathbf{T}^{-}_{\widehat{\unicode{x3b8}}} \left( \mathsf{M}_{\mathsf{poset}(\tau_1^{\lambda^{\mathrm{t}}/\mu^{\mathrm{t}}})}\right) &\rightarrow \mathsf{M}_{\mathsf{poset}(\tau_0^{\lambda/\mu})}, \\ \gamma^* &\mapsto (-1)^{\ell(\gamma \; \mathsf{read}_{\tau_1}(T^{\prime}_{\lambda^{\mathrm{t}}/\mu^{\mathrm{t}}})^{-1})} \gamma w_0, \end{align*} $$
where
![]() $\gamma \in [\mathsf {read}_{\tau _1}(T_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}}), \mathsf {read}_{\tau _1}(T^{\prime}_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})]_L$
and
$\gamma \in [\mathsf {read}_{\tau _1}(T_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}}), \mathsf {read}_{\tau _1}(T^{\prime}_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})]_L$
and
![]() $\gamma ^\ast $
denotes the dual of
$\gamma ^\ast $
denotes the dual of
![]() $\gamma $
with respect to the basis
$\gamma $
with respect to the basis
![]() $[\mathsf {read}_{\tau _1}(T_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}}), \mathsf {read}_{\tau _1}(T^{\prime}_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})]_L$
for
$[\mathsf {read}_{\tau _1}(T_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}}), \mathsf {read}_{\tau _1}(T^{\prime}_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})]_L$
for
![]() $\mathsf {M}_{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})}$
. Set
$\mathsf {M}_{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})}$
. Set
Again, by [Reference Jung, Kim, Lee and Oh19, Theorem 4], we have the
![]() $H_n(0)$
-module isomorphism
$H_n(0)$
-module isomorphism
 $$ \begin{align*} g_2: \mathbf{T}^{-}_{\widehat{\unicode{x3b8}}} \left( \mathbf{P}_{{\boldsymbol{\unicode{x3b1}}}_{\mathrm{proj}}(\lambda^{\mathrm{t}} / \mu^{\mathrm{t}})}\right) &\rightarrow \mathbf{P}_{{\boldsymbol{\unicode{x3b1}}}_{\mathrm{inj}}(\lambda/\mu)}, \\ \gamma^* &\mapsto (-1)^{\ell(\gamma (w_0w_0({\boldsymbol{\unicode{x3b1}}}_{\mathrm{inj}}(\lambda/\mu)_{\odot}))^{-1})} \gamma w_0, \end{align*} $$
$$ \begin{align*} g_2: \mathbf{T}^{-}_{\widehat{\unicode{x3b8}}} \left( \mathbf{P}_{{\boldsymbol{\unicode{x3b1}}}_{\mathrm{proj}}(\lambda^{\mathrm{t}} / \mu^{\mathrm{t}})}\right) &\rightarrow \mathbf{P}_{{\boldsymbol{\unicode{x3b1}}}_{\mathrm{inj}}(\lambda/\mu)}, \\ \gamma^* &\mapsto (-1)^{\ell(\gamma (w_0w_0({\boldsymbol{\unicode{x3b1}}}_{\mathrm{inj}}(\lambda/\mu)_{\odot}))^{-1})} \gamma w_0, \end{align*} $$
where
![]() $\gamma \in [ w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}})_{\bullet }^{\mathrm {c}}), w_0w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}})_{\odot }) ]_L$
and
$\gamma \in [ w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}})_{\bullet }^{\mathrm {c}}), w_0w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}})_{\odot }) ]_L$
and
![]() $\gamma ^\ast $
denotes the dual of
$\gamma ^\ast $
denotes the dual of
![]() $\gamma $
with respect to the basis
$\gamma $
with respect to the basis
![]() $[ w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}})_{\bullet }^{\mathrm {c}}), w_0w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}})_{\odot }) ]_L$
for
$[ w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}})_{\bullet }^{\mathrm {c}}), w_0w_0({\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}})_{\odot }) ]_L$
for
![]() $\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}})}$
. Set
$\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} / \mu ^{\mathrm {t}})}$
. Set
![]() $\eta _{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})} := f_{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})} \circ \Upsilon _{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}); \mathsf {read}_{\tau _0}(T^{\prime}_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})}$
. As above, the pair
$\eta _{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})} := f_{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})} \circ \Upsilon _{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}); \mathsf {read}_{\tau _0}(T^{\prime}_{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})}$
. As above, the pair
 $\left (\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} /\mu ^{\mathrm {t}})}, \eta _{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})}\right )$
is a projective cover of
$\left (\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} /\mu ^{\mathrm {t}})}, \eta _{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})}\right )$
is a projective cover of
![]() $\mathsf {M}_{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})}$
. And since
$\mathsf {M}_{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})}$
. And since
![]() $\mathbf {T}^{-}_{\widehat {\unicode{x3b8} }}$
is contravariant,
$\mathbf {T}^{-}_{\widehat {\unicode{x3b8} }}$
is contravariant,
 $\left ( \mathbf {T}^{-}_{\widehat {\unicode{x3b8} }} \left ( \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} /\mu ^{\mathrm {t}})} \right ), \mathbf {T}^{-}_{\widehat {\unicode{x3b8} }} \left ( \eta _{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})} \right ) \right )$
is an injective hull of
$\left ( \mathbf {T}^{-}_{\widehat {\unicode{x3b8} }} \left ( \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{\mathrm {t}} /\mu ^{\mathrm {t}})} \right ), \mathbf {T}^{-}_{\widehat {\unicode{x3b8} }} \left ( \eta _{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})} \right ) \right )$
is an injective hull of
![]() $\mathbf {T}^{-}_{\widehat {\unicode{x3b8} }}(\mathsf {M}_{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})})$
(for the definition of
$\mathbf {T}^{-}_{\widehat {\unicode{x3b8} }}(\mathsf {M}_{\mathsf {poset}(\tau _1^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}})})$
(for the definition of
![]() $\mathbf {T}^{-}_{\widehat {\unicode{x3b8} }} $
, see Section 2.4). Consequently, the pair
$\mathbf {T}^{-}_{\widehat {\unicode{x3b8} }} $
, see Section 2.4). Consequently, the pair
![]() $\left (\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\lambda /\mu )}, \iota _P\right )$
is an injective hull of
$\left (\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\lambda /\mu )}, \iota _P\right )$
is an injective hull of
![]() $\mathsf {M}_P$
, where
$\mathsf {M}_P$
, where
 $$\begin{align*}\iota_P = g_2 \circ \mathbf{T}^{-}_{\widehat{\unicode{x3b8}}} \left( \eta_{\mathsf{poset}(\tau_1^{\lambda^{\mathrm{t}}/\mu^{\mathrm{t}}})} \right) \circ g_1^{-1} \circ f_P^{-1}. \end{align*}$$
$$\begin{align*}\iota_P = g_2 \circ \mathbf{T}^{-}_{\widehat{\unicode{x3b8}}} \left( \eta_{\mathsf{poset}(\tau_1^{\lambda^{\mathrm{t}}/\mu^{\mathrm{t}}})} \right) \circ g_1^{-1} \circ f_P^{-1}. \end{align*}$$
To summarize, we can state the following lemma.
Lemma 5.4. Let
![]() $P \in \mathsf {RSP}_n$
and
$P \in \mathsf {RSP}_n$
and
![]() $\lambda /\mu = \mathrm {sh}(\tau _P)$
.
$\lambda /\mu = \mathrm {sh}(\tau _P)$
.
-
(1)
 $\left ( \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )}, \eta _P \right )$
is a projective cover of
$\left ( \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )}, \eta _P \right )$
is a projective cover of
 $\mathsf {M}_P$
.
$\mathsf {M}_P$
. -
(2)
 $\left (\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\lambda /\mu )}, \iota _P \right )$
is an injective hull of
$\left (\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\lambda /\mu )}, \iota _P \right )$
is an injective hull of
 $\mathsf {M}_P$
.
$\mathsf {M}_P$
.
Now, we are ready to state the classification of
![]() $\mathsf {M}_P$
’s for
$\mathsf {M}_P$
’s for
![]() $P \in \mathsf {RSP}_n$
up to
$P \in \mathsf {RSP}_n$
up to
![]() $H_n(0)$
-module isomorphism.
$H_n(0)$
-module isomorphism.
Theorem 5.5. Let
![]() $P, Q \in \mathsf {RSP}_n$
. Then
$P, Q \in \mathsf {RSP}_n$
. Then
Proof. The ‘if’ part follows from Proposition 4.1 and Theorem 4.7. To prove the ‘only if’ part, suppose that
![]() $\mathsf {M}_{P} \cong \mathsf {M}_{Q}$
. For simplicity, let
$\mathsf {M}_{P} \cong \mathsf {M}_{Q}$
. For simplicity, let
![]() $\lambda /\mu = \mathrm {sh}(\tau _{P})$
and
$\lambda /\mu = \mathrm {sh}(\tau _{P})$
and
![]() $\nu /\kappa = \mathrm {sh}(\tau _{Q})$
. By Lemma 5.4,
$\nu /\kappa = \mathrm {sh}(\tau _{Q})$
. By Lemma 5.4,
![]() $\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )} \cong \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\nu /\kappa )}$
and
$\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu )} \cong \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\nu /\kappa )}$
and
![]() $\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\lambda /\mu )} \cong \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\nu /\kappa )}$
, and therefore,
$\mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\lambda /\mu )} \cong \mathbf {P}_{{\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\nu /\kappa )}$
, and therefore,
![]() ${\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu ) = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\nu /\kappa )$
and
${\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu ) = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\nu /\kappa )$
and
![]() ${\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\lambda /\mu ) = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\nu /\kappa )$
. Since
${\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\lambda /\mu ) = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\nu /\kappa )$
. Since
![]() ${\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu ) = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\nu /\kappa )$
, the number of boxes in the same row of
${\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu ) = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\nu /\kappa )$
, the number of boxes in the same row of
![]() $\mathtt {yd}(\lambda /\mu )$
and
$\mathtt {yd}(\lambda /\mu )$
and
![]() $\mathtt {yd}(\nu /\kappa )$
are the same. Similarly, since
$\mathtt {yd}(\nu /\kappa )$
are the same. Similarly, since
![]() ${\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\lambda /\mu ) = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\nu /\kappa )$
, the number of boxes in the same column of
${\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\lambda /\mu ) = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {inj}}(\nu /\kappa )$
, the number of boxes in the same column of
![]() $\mathtt {yd}(\lambda /\mu )$
and
$\mathtt {yd}(\lambda /\mu )$
and
![]() $\mathtt {yd}(\nu /\kappa )$
are same. Thus, we have
$\mathtt {yd}(\nu /\kappa )$
are same. Thus, we have
![]() $\lambda /\mu = \nu /\kappa $
.
$\lambda /\mu = \nu /\kappa $
.
Note that Theorem 5.5 is the classification theorem concerning the class of
![]() $H_n(0)$
-modules
$H_n(0)$
-modules
![]() $\{\mathsf {M}_P \mid P \in \mathsf {RSP}_n\}$
. Consequently, a natural question arises: can this theorem be extended to the classes
$\{\mathsf {M}_P \mid P \in \mathsf {RSP}_n\}$
. Consequently, a natural question arises: can this theorem be extended to the classes
![]() $\{\mathsf {M}_P \mid P \in \mathsf {RP}_n\}$
or
$\{\mathsf {M}_P \mid P \in \mathsf {RP}_n\}$
or
![]() $\{\mathsf {M}_P \mid P \in \mathsf {SP}_n\}$
? This question appears to be highly nontrivial, as it involves the investigation of a broader set of modules. As a specific instance, let us examine the characterization of posets
$\{\mathsf {M}_P \mid P \in \mathsf {SP}_n\}$
? This question appears to be highly nontrivial, as it involves the investigation of a broader set of modules. As a specific instance, let us examine the characterization of posets
![]() $Q \in \mathsf {RP}_n$
such that
$Q \in \mathsf {RP}_n$
such that
![]() $\mathsf {M}_Q \cong \mathsf {M}_P$
when
$\mathsf {M}_Q \cong \mathsf {M}_P$
when
![]() $P \in \mathsf {RSP}_n$
. This problem can be readily addressed by assuming the validity of the following conjecture due to Stanley.
$P \in \mathsf {RSP}_n$
. This problem can be readily addressed by assuming the validity of the following conjecture due to Stanley.
Conjecture 5.6 [Reference Stanley34, p. 81]
For
![]() $P \in \mathsf {P}_n$
, if
$P \in \mathsf {P}_n$
, if
![]() $K_P$
is symmetric, then
$K_P$
is symmetric, then
![]() $P \in \mathsf {SP}_n$
.
$P \in \mathsf {SP}_n$
.
In more detail, by combining Stanley’s conjecture with Theorem 2.9(1), we can deduce that
![]() $\mathrm {ch}([\mathsf {M}_Q])$
is not symmetric, and as a consequence,
$\mathrm {ch}([\mathsf {M}_Q])$
is not symmetric, and as a consequence,
![]() $\mathsf {M}_Q \not \cong \mathsf {M}_P$
unless
$\mathsf {M}_Q \not \cong \mathsf {M}_P$
unless
![]() $Q \in \mathsf {SP}_n$
. This observation leads to the following conclusion from Theorem 5.5:
$Q \in \mathsf {SP}_n$
. This observation leads to the following conclusion from Theorem 5.5:
If the shape of
![]() $\tau _P$
is non-skew, it is indeed possible to derive this conjectural identity without depending on the validity of Stanley’s conjecture (see Proposition 7.1). However, tackling the general case remains beyond our current comprehension. For further discussions on classifications, refer to Section 7.1.
$\tau _P$
is non-skew, it is indeed possible to derive this conjectural identity without depending on the validity of Stanley’s conjecture (see Proposition 7.1). However, tackling the general case remains beyond our current comprehension. For further discussions on classifications, refer to Section 7.1.
6 A characterization of regular Schur labeled skew shape posets P and distinguished filtrations of
 $\mathsf {M}_P$
$\mathsf {M}_P$
In this section, we prove that a poset
![]() $P \in \mathsf {P}_n$
is a regular Schur labeled skew shape poset if and only if
$P \in \mathsf {P}_n$
is a regular Schur labeled skew shape poset if and only if
![]() $\Sigma _L(P)$
is dual plactic closed (Theorem 6.4). Then, by considering the dual plactic closedness of
$\Sigma _L(P)$
is dual plactic closed (Theorem 6.4). Then, by considering the dual plactic closedness of
![]() $\Sigma _L(P)$
, we construct filtrations
$\Sigma _L(P)$
, we construct filtrations
such that
![]() $\mathrm {ch}([M_{k}/M_{k-1}])$
is a Schur function for all
$\mathrm {ch}([M_{k}/M_{k-1}])$
is a Schur function for all
![]() $1 \leq k \leq l$
(Theorem 6.7).
$1 \leq k \leq l$
(Theorem 6.7).
6.1 A characterization of regular Schur labeled skew shape posets
Let
![]() $P \in \mathsf {P}_n$
and let
$P \in \mathsf {P}_n$
and let
![]() $\Sigma _R(P) :=\{\gamma ^{-1} \mid \gamma \in \Sigma _L(P)\}$
. In [Reference Malvenuto27, Fact 1], it was stated that if
$\Sigma _R(P) :=\{\gamma ^{-1} \mid \gamma \in \Sigma _L(P)\}$
. In [Reference Malvenuto27, Fact 1], it was stated that if
![]() $P \in \mathsf {SP}_n$
, then
$P \in \mathsf {SP}_n$
, then
![]() $\Sigma _R(P)$
is plactic-closed. This, however, is not true. For instance, considering the case where
$\Sigma _R(P)$
is plactic-closed. This, however, is not true. For instance, considering the case where
![]() $\lambda /\mu = (3,2)/(2)$
and
$\lambda /\mu = (3,2)/(2)$
and  , we have
, we have
which is not plactic-closed.
The purpose of this subsection is to prove that
![]() $P \in \mathsf {RSP}_n$
if and only if
$P \in \mathsf {RSP}_n$
if and only if
![]() $\Sigma _R(P)$
is plactic-closed. We begin by providing background knowledge relevant to the plactic congruence. For instance, see [Reference Björner and Brenti6, Reference Fulton14, Reference Sagan31, Reference Stanley35].
$\Sigma _R(P)$
is plactic-closed. We begin by providing background knowledge relevant to the plactic congruence. For instance, see [Reference Björner and Brenti6, Reference Fulton14, Reference Sagan31, Reference Stanley35].
For
![]() $\sigma \in \mathfrak {S}_n$
and
$\sigma \in \mathfrak {S}_n$
and
![]() $1 < i < n$
, we write
$1 < i < n$
, we write
![]() $\sigma \overset {1}{\cong } \sigma s_i$
if
$\sigma \overset {1}{\cong } \sigma s_i$
if
And we write
![]() $\sigma \overset {2}{\cong } \sigma s_{i-1}$
if
$\sigma \overset {2}{\cong } \sigma s_{i-1}$
if
The Knuth equivalence (or plactic congruence) is an equivalence relation
![]() $\overset {K}{\cong }$
on
$\overset {K}{\cong }$
on
![]() $\mathfrak {S}_n$
defined by
$\mathfrak {S}_n$
defined by
![]() $\sigma \overset {K}{\cong } \rho $
if and only if there are
$\sigma \overset {K}{\cong } \rho $
if and only if there are
![]() $\gamma _1,\gamma _2, \ldots , \gamma _k \in \mathfrak {S}_n$
such that
$\gamma _1,\gamma _2, \ldots , \gamma _k \in \mathfrak {S}_n$
such that
where
![]() $a_1,a_2,\ldots a_{k-1} \in \{1,2\}$
. A subset S of
$a_1,a_2,\ldots a_{k-1} \in \{1,2\}$
. A subset S of
![]() $\mathfrak {S}_n$
is called plactic-closed if for any
$\mathfrak {S}_n$
is called plactic-closed if for any
![]() $\sigma \in S$
, every
$\sigma \in S$
, every
![]() $\rho \in \mathfrak {S}_n$
with
$\rho \in \mathfrak {S}_n$
with
![]() $\rho \overset {K}{\cong } \sigma $
is also an element of S; in other words, S is a union of equivalence classes under
$\rho \overset {K}{\cong } \sigma $
is also an element of S; in other words, S is a union of equivalence classes under
![]() $\overset {K}{\cong }$
.
$\overset {K}{\cong }$
.
The dual Knuth equivalence (or dual plactic congruence) is an equivalence relation
![]() $\overset {K^*}{\cong }$
on
$\overset {K^*}{\cong }$
on
![]() $\mathfrak {S}_n$
defined by
$\mathfrak {S}_n$
defined by
A subset S of
![]() $\mathfrak {S}_n$
is called dual plactic-closed if for any
$\mathfrak {S}_n$
is called dual plactic-closed if for any
![]() $\sigma \in S$
, every
$\sigma \in S$
, every
![]() $\rho \in \mathfrak {S}_n$
with
$\rho \in \mathfrak {S}_n$
with
![]() $\rho \overset {K^*}{\cong } \sigma $
is also an element of S; in other words, S is a union of equivalence classes under
$\rho \overset {K^*}{\cong } \sigma $
is also an element of S; in other words, S is a union of equivalence classes under
![]() $\overset {K^*}{\cong }$
.
$\overset {K^*}{\cong }$
.
The Knuth and dual Knuth equivalences are closely related to the Robinson–Schensted correspondence, which is a one-to-one correspondence between
![]() $\mathfrak {S}_n$
and
$\mathfrak {S}_n$
and
![]() $\bigcup _{\lambda \vdash n} \mathrm {SYT}(\lambda ) \times \mathrm {SYT}(\lambda )$
. For
$\bigcup _{\lambda \vdash n} \mathrm {SYT}(\lambda ) \times \mathrm {SYT}(\lambda )$
. For
![]() $\sigma \in \mathfrak {S}_n$
, we use the notation
$\sigma \in \mathfrak {S}_n$
, we use the notation
![]() $(\mathtt {ins}(\sigma ), \mathtt {rec}(\sigma ))$
to represent the image of
$(\mathtt {ins}(\sigma ), \mathtt {rec}(\sigma ))$
to represent the image of
![]() $\sigma $
under this bijection. We call
$\sigma $
under this bijection. We call
![]() $\mathtt {ins}(\sigma )$
and
$\mathtt {ins}(\sigma )$
and
![]() $\mathtt {rec}(\sigma )$
as the insertion tableau and recording tableau of
$\mathtt {rec}(\sigma )$
as the insertion tableau and recording tableau of
![]() $\sigma $
, respectively. It is well known that
$\sigma $
, respectively. It is well known that
![]() $\mathtt {ins}(\sigma ) = \mathtt {rec}(\sigma ^{-1})$
and
$\mathtt {ins}(\sigma ) = \mathtt {rec}(\sigma ^{-1})$
and
Putting these together, one can easily derive that
For a subset S of
![]() $\mathfrak {S}_n$
, S is plactic-closed if and only if
$\mathfrak {S}_n$
, S is plactic-closed if and only if
![]() $\{\gamma ^{-1} \mid \gamma \in S\}$
is dual plactic-closed. Based on this fact, we will consider the claim that
$\{\gamma ^{-1} \mid \gamma \in S\}$
is dual plactic-closed. Based on this fact, we will consider the claim that
![]() $\Sigma _R(P)$
is plactic-closed and the claim that
$\Sigma _R(P)$
is plactic-closed and the claim that
![]() $\Sigma _L(P)$
is dual plactic-closed to be identical.
$\Sigma _L(P)$
is dual plactic-closed to be identical.
Let us collect the terminologies and lemmas necessary for the proof of the main result of this subsection. Let T be a standard Young tableau of skew shape. Denote by
![]() $\mathrm {Rect}(T)$
the rectification of T – that is, the unique standard Young tableau of partition shape obtained by applying jeu de taquin slides to T (see [Reference Fulton14, Section 1.2]). Then
$\mathrm {Rect}(T)$
the rectification of T – that is, the unique standard Young tableau of partition shape obtained by applying jeu de taquin slides to T (see [Reference Fulton14, Section 1.2]). Then
Define
![]() $T^{\mathrm {t}}$
to be the tableau obtained from T by flipping it along its main diagonal.
$T^{\mathrm {t}}$
to be the tableau obtained from T by flipping it along its main diagonal.
Lemma 6.1. Let
![]() $\lambda / \mu $
be a skew partition and
$\lambda / \mu $
be a skew partition and
![]() $T \in \mathrm {SYT}(\lambda /\mu )$
. Then
$T \in \mathrm {SYT}(\lambda /\mu )$
. Then
Proof. It is well known that
(for instance, see [Reference Sagan31, Theorems 3.2.3]). Therefore, due to Equation (6.1), the assertion can be verified by showing that
Applying Taşkin’s result [Reference Taskin36, Proposition 3.2.5] to the weak orderFootnote 3 on
![]() $\mathrm {SYT}_n$
given in [Reference Taskin36, Definition 3.1.3], we derive that for
$\mathrm {SYT}_n$
given in [Reference Taskin36, Definition 3.1.3], we derive that for
![]() $\sigma , \rho \in \mathfrak {S}_n$
with
$\sigma , \rho \in \mathfrak {S}_n$
with
![]() $\sigma \preceq _R \rho $
,
$\sigma \preceq _R \rho $
,
Here,
![]() $\trianglelefteq $
denotes the dominance order on the set of partitions of n. And, Lemma 3.7 says that
$\trianglelefteq $
denotes the dominance order on the set of partitions of n. And, Lemma 3.7 says that
Note that
Since
![]() $\mathsf {read}_{\tau ^{\lambda /\mu }_1}(T) = \mathsf {read}_{\tau ^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}}_0}(T^{\mathrm {t}}) w_0$
, it follows from Equation (6.2) that
$\mathsf {read}_{\tau ^{\lambda /\mu }_1}(T) = \mathsf {read}_{\tau ^{\lambda ^{\mathrm {t}}/\mu ^{\mathrm {t}}}_0}(T^{\mathrm {t}}) w_0$
, it follows from Equation (6.2) that
Now, the equality in Equation (6.3) is obtained by combining Equation (6.4), Equation (6.5) and Equation (6.6).
We introduce two important results due to Malvenuto [Reference Malvenuto27].
Lemma 6.2 [Reference Malvenuto27, Theorem 1]
For
![]() $P \in \mathsf {P}_n$
, if
$P \in \mathsf {P}_n$
, if
![]() $\Sigma _R(P)$
is plactic-closed, then P is a Schur labeled skew shape poset.
$\Sigma _R(P)$
is plactic-closed, then P is a Schur labeled skew shape poset.
For
![]() $P \in \mathsf {P}_n$
, we say a subposet Q of P is convex if Q satisfies the property that for any
$P \in \mathsf {P}_n$
, we say a subposet Q of P is convex if Q satisfies the property that for any
![]() $x \in P$
if there exist
$x \in P$
if there exist
![]() $y_1, y_2 \in Q$
such that
$y_1, y_2 \in Q$
such that
![]() $y_1 \preceq _P x \preceq _P y_2$
, then
$y_1 \preceq _P x \preceq _P y_2$
, then
![]() $x \in Q$
. For a subposet
$x \in Q$
. For a subposet
![]() $Q = \{i_1 < i_2 < \cdots <i_{|Q|} \}$
of
$Q = \{i_1 < i_2 < \cdots <i_{|Q|} \}$
of
![]() $P \in \mathsf {P}_n$
, the standardization of Q, denoted by
$P \in \mathsf {P}_n$
, the standardization of Q, denoted by
![]() $\mathsf {st}(Q)$
, is the poset obtained from Q by replacing
$\mathsf {st}(Q)$
, is the poset obtained from Q by replacing
![]() $i_j$
with j for
$i_j$
with j for
![]() $1 \leq j \leq |Q|$
.
$1 \leq j \leq |Q|$
.
Lemma 6.3 [Reference Malvenuto27, Corollary 1]
Let
![]() $P \in \mathsf {P}_n$
such that
$P \in \mathsf {P}_n$
such that
![]() $\Sigma _R(P)$
is plactic-closed. For any convex subposet Q of P,
$\Sigma _R(P)$
is plactic-closed. For any convex subposet Q of P,
![]() $\Sigma _R(\mathsf {st}(Q))$
is plactic-closed.
$\Sigma _R(\mathsf {st}(Q))$
is plactic-closed.
Now, we are ready to prove the main result of this subsection.
Theorem 6.4. For
![]() $P \in \mathsf {P}_n$
, P is a regular Schur labeled skew shape poset if and only if
$P \in \mathsf {P}_n$
, P is a regular Schur labeled skew shape poset if and only if
![]() $\Sigma _L(P)$
is dual plactic-closed.
$\Sigma _L(P)$
is dual plactic-closed.
Proof. To establish the ‘only if’ part, let
![]() $P \in \mathsf {RSP}_n$
and
$P \in \mathsf {RSP}_n$
and
![]() $\lambda /\mu = \mathrm {sh}(\tau _P)$
. Due to Lemma 3.2, we have that
$\lambda /\mu = \mathrm {sh}(\tau _P)$
. Due to Lemma 3.2, we have that
We claim that
![]() $\mathsf {read}_{\tau _P}(\mathrm {SYT}(\lambda /\mu ))$
is dual plactic-closed.
$\mathsf {read}_{\tau _P}(\mathrm {SYT}(\lambda /\mu ))$
is dual plactic-closed.
As mentioned in [Reference Garsia and Remmel15, Property A], one can easily see that
![]() $\mathsf {read}_{\tau _0}(\mathrm {SYT}(\lambda /\mu ))$
is dual plactic-closed.Footnote 4 In addition, by Lemma 6.1, we have
$\mathsf {read}_{\tau _0}(\mathrm {SYT}(\lambda /\mu ))$
is dual plactic-closed.Footnote 4 In addition, by Lemma 6.1, we have
Therefore, given
![]() $T \in \mathrm {SYT}(\lambda /\mu )$
, if we show that
$T \in \mathrm {SYT}(\lambda /\mu )$
, if we show that
then we have
Let
![]() $T, U \in \mathrm {SYT}(\lambda /\mu )$
with
$T, U \in \mathrm {SYT}(\lambda /\mu )$
with
![]() $\mathsf {read}_{\tau _0}(T) \overset {K^*}{\cong } \mathsf {read}_{\tau _0}(U)$
. Since
$\mathsf {read}_{\tau _0}(T) \overset {K^*}{\cong } \mathsf {read}_{\tau _0}(U)$
. Since
![]() $\mathsf {read}_{\tau _0}(\mathrm {SYT}(\lambda /\mu ))$
is dual plactic-closed, there exist standard Young tableaux
$\mathsf {read}_{\tau _0}(\mathrm {SYT}(\lambda /\mu ))$
is dual plactic-closed, there exist standard Young tableaux
![]() $T_0 := T, T_1, \ldots , T_l := U$
of shape
$T_0 := T, T_1, \ldots , T_l := U$
of shape
![]() $\lambda /\mu $
such that for any
$\lambda /\mu $
such that for any
![]() $1 \leq k \leq l$
,
$1 \leq k \leq l$
,
Combining Equation (6.7) with the equality
![]() $\mathrm {sh}(\mathtt {ins}(\mathsf {read}_{\tau _0}(T_k))) = \mathrm {sh}(\mathtt {ins}(\mathsf {read}_{\tau _0}(T)))$
, we have
$\mathrm {sh}(\mathtt {ins}(\mathsf {read}_{\tau _0}(T_k))) = \mathrm {sh}(\mathtt {ins}(\mathsf {read}_{\tau _0}(T)))$
, we have
Note that Equation (6.4) is equivalent to the statement that for
![]() $\sigma , \rho \in \mathfrak {S}_n$
with
$\sigma , \rho \in \mathfrak {S}_n$
with
![]() $\sigma \preceq _L \rho $
,
$\sigma \preceq _L \rho $
,
Putting Equation (6.8) together with Equation (6.9), we have
![]() $\mathsf {read}_{\tau _P}(T) \overset {K^*}{\cong } \mathsf {read}_{\tau _P}(U)$
. Since we chose arbitrary
$\mathsf {read}_{\tau _P}(T) \overset {K^*}{\cong } \mathsf {read}_{\tau _P}(U)$
. Since we chose arbitrary
![]() $T,U \in \mathrm {SYT}(\lambda /\mu )$
, we conclude that
$T,U \in \mathrm {SYT}(\lambda /\mu )$
, we conclude that
![]() $\mathsf {read}_{\tau _P}(\mathrm {SYT}(\lambda /\mu ))$
is dual plactic-closed.
$\mathsf {read}_{\tau _P}(\mathrm {SYT}(\lambda /\mu ))$
is dual plactic-closed.
To establish the ‘if’ part of the assertion, we prove the contraposition; that is, if P is not a regular Schur labeled skew shape poset, then
![]() $\Sigma _L(P)$
is not dual plactic-closed. If P is not a Schur labeled skew shape poset, then Lemma 6.2 says that
$\Sigma _L(P)$
is not dual plactic-closed. If P is not a Schur labeled skew shape poset, then Lemma 6.2 says that
![]() $\Sigma _L(P)$
is not dual plactic-closed. So, we assume that
$\Sigma _L(P)$
is not dual plactic-closed. So, we assume that
![]() $P \in \mathsf {P}_n$
is a non-regular Schur labeled skew shape poset.
$P \in \mathsf {P}_n$
is a non-regular Schur labeled skew shape poset.
One can easily check that if
![]() $n = 1,2,3$
, then
$n = 1,2,3$
, then
![]() $\Sigma _L(P)$
is not dual plactic-closed. Suppose
$\Sigma _L(P)$
is not dual plactic-closed. Suppose
![]() $n> 3$
. Then, by Lemma 3.6,
$n> 3$
. Then, by Lemma 3.6,
![]() $\tau _P$
is a non-distinguished Schur labeling. This implies that there exists
$\tau _P$
is a non-distinguished Schur labeling. This implies that there exists
![]() $k \in \mathbb Z_{>0}$
such that
$k \in \mathbb Z_{>0}$
such that
![]() $\mathsf {cnt}_{k}(\tau _P)$
is not filled with consecutive integers. Let
$\mathsf {cnt}_{k}(\tau _P)$
is not filled with consecutive integers. Let
![]() $k_0$
be the minimum among these integers and let
$k_0$
be the minimum among these integers and let
![]() $m_0$
be the minimum element among
$m_0$
be the minimum element among
![]() $m \in \mathsf {cnt}_{k_0}(\tau _P)$
such that
$m \in \mathsf {cnt}_{k_0}(\tau _P)$
such that
![]() $m + 1 \notin \mathsf {cnt}_{k_0}(\tau _P)$
. Since
$m + 1 \notin \mathsf {cnt}_{k_0}(\tau _P)$
. Since
![]() $\mathsf {cnt}_{k_0}(\tau _P)$
is not filled with consecutive integers, we can choose
$\mathsf {cnt}_{k_0}(\tau _P)$
is not filled with consecutive integers, we can choose
Since
![]() $m_0$
and
$m_0$
and
![]() $m_1$
are in the same connected component of the Schur labeling
$m_1$
are in the same connected component of the Schur labeling
![]() $\tau _P$
and
$\tau _P$
and
![]() $m_0 < m_1$
, we can take
$m_0 < m_1$
, we can take
![]() $m_{-1} \in \mathsf {cnt}_{k_0}(\tau _P)$
such that
$m_{-1} \in \mathsf {cnt}_{k_0}(\tau _P)$
such that
![]() $m_{-1} < m_1$
and
$m_{-1} < m_1$
and
![]() $m_{-1}$
is adjacent to
$m_{-1}$
is adjacent to
![]() $m_1$
. Here, the sentence ‘
$m_1$
. Here, the sentence ‘
![]() $m_{-1}$
is adjacent to
$m_{-1}$
is adjacent to
![]() $m_1$
’ means that the box containing
$m_1$
’ means that the box containing
![]() $m_{-1}$
and that containing
$m_{-1}$
and that containing
![]() $m_{1}$
share an edge. We note that
$m_{1}$
share an edge. We note that
![]() $m_{-1}$
can be
$m_{-1}$
can be
![]() $m_0$
. Because of the choice of
$m_0$
. Because of the choice of
![]() $m_1$
, we have
$m_1$
, we have
![]() $m_{-1} < m_0+1 < m_1$
. Let Q be the subposet of P whose underlying set is
$m_{-1} < m_0+1 < m_1$
. Let Q be the subposet of P whose underlying set is
![]() $\{m_{-1}, m_0 + 1, m_1\}$
. In P,
$\{m_{-1}, m_0 + 1, m_1\}$
. In P,
![]() $m_1$
covers
$m_1$
covers
![]() $m_{-1}$
and
$m_{-1}$
and
![]() $m_0 + 1$
is incomparable with both
$m_0 + 1$
is incomparable with both
![]() $m_1$
and
$m_1$
and
![]() $m_{-1}$
. This implies that Q is a convex subposet of P. In addition, since
$m_{-1}$
. This implies that Q is a convex subposet of P. In addition, since
![]() $m_{-1} < m_0 + 1 < m_1$
, we have
$m_{-1} < m_0 + 1 < m_1$
, we have
![]() $\Sigma _L(\mathsf {st}(Q)) = \{123,132,213\}$
or
$\Sigma _L(\mathsf {st}(Q)) = \{123,132,213\}$
or
![]() $\Sigma _L(\mathsf {st}(Q)) = \{312,231,321\}$
. Thus,
$\Sigma _L(\mathsf {st}(Q)) = \{312,231,321\}$
. Thus,
![]() $\Sigma _L(\mathsf {st}(Q))$
is not dual plactic closed. Combining this with Lemma 6.3 yields that
$\Sigma _L(\mathsf {st}(Q))$
is not dual plactic closed. Combining this with Lemma 6.3 yields that
![]() $\Sigma _L(P)$
is not dual plactic closed, as desired.
$\Sigma _L(P)$
is not dual plactic closed, as desired.
6.2 Distinguished filtrations of
 $\mathsf {M}_P$
for
$\mathsf {M}_P$
for
 $P \in \mathsf {RSP}_n$
$P \in \mathsf {RSP}_n$
We begin by introducing the definition of distinguished filtrations.
Definition 6.5. Let
![]() $\mathcal {B} = \{\mathcal {B}_\alpha \mid \alpha \in I\}$
be a linearly independent subset of
$\mathcal {B} = \{\mathcal {B}_\alpha \mid \alpha \in I\}$
be a linearly independent subset of
![]() $\mathrm {QSym}_n$
with the property that
$\mathrm {QSym}_n$
with the property that
![]() $\mathcal {B}_\alpha $
is F-positive for all
$\mathcal {B}_\alpha $
is F-positive for all
![]() $\alpha \in I$
, where I is an index set. Given a finite dimensional
$\alpha \in I$
, where I is an index set. Given a finite dimensional
![]() $H_n(0)$
-module M, a distinguished filtration of M with respect to
$H_n(0)$
-module M, a distinguished filtration of M with respect to
![]() $\mathcal {B}$
is an
$\mathcal {B}$
is an
![]() $H_n(0)$
-submodule series of M
$H_n(0)$
-submodule series of M
such that for all
![]() $1 \leq k \leq l$
,
$1 \leq k \leq l$
,
![]() $\mathrm {ch}([M_k / M_{k-1}]) = \mathcal {B}_\alpha $
for some
$\mathrm {ch}([M_k / M_{k-1}]) = \mathcal {B}_\alpha $
for some
![]() $\alpha \in I$
.
$\alpha \in I$
.
As seen in Example 6.6, a distinguished filtration of M with respect to
![]() $\mathcal {B}$
may not exist even if
$\mathcal {B}$
may not exist even if
![]() $\mathrm {ch}([M])$
expands positively in
$\mathrm {ch}([M])$
expands positively in
![]() $\mathcal {B}$
. This is because the category
$\mathcal {B}$
. This is because the category
![]() $H_n(0)\text{-}\mathbf {mod}$
is neither semisimple nor representation-finite when
$H_n(0)\text{-}\mathbf {mod}$
is neither semisimple nor representation-finite when
![]() $n> 3$
([Reference Deng and Yang10, Reference Duchamp, Hivert and Thibon11]).
$n> 3$
([Reference Deng and Yang10, Reference Duchamp, Hivert and Thibon11]).
Example 6.6. Let
![]() $\mathcal {B} = \{s_\lambda \mid \lambda \vdash 4 \}$
. For
$\mathcal {B} = \{s_\lambda \mid \lambda \vdash 4 \}$
. For
![]() $B = \{2314, 1423, 3214,2413, 1432, 3412\}$
, let M be the
$B = \{2314, 1423, 3214,2413, 1432, 3412\}$
, let M be the
![]() $H_4(0)$
-module with underlying space
$H_4(0)$
-module with underlying space
![]() $\mathbb C B$
and with the
$\mathbb C B$
and with the
![]() $H_4(0)$
-action defined by
$H_4(0)$
-action defined by
 $$ \begin{align*} \pi_{i} \cdot \gamma := \begin{cases} \gamma & \text{if }i \in \mathrm{Des}_L(\gamma), \\ 0 & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \notin B, \\ s_i \gamma & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \in B. \end{cases} \end{align*} $$
$$ \begin{align*} \pi_{i} \cdot \gamma := \begin{cases} \gamma & \text{if }i \in \mathrm{Des}_L(\gamma), \\ 0 & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \notin B, \\ s_i \gamma & \text{if }i \notin \mathrm{Des}_L(\gamma)\text{ and }s_i\gamma \in B. \end{cases} \end{align*} $$
The
![]() $H_4(0)$
-action on
$H_4(0)$
-action on
![]() $B \cup \{ 0 \}$
is illustrated in the following figure:
$B \cup \{ 0 \}$
is illustrated in the following figure:

One sees that
So, if there exists a distinguished filtration of M with respect to
![]() $\mathcal {B}$
, then there exists a three-dimensional
$\mathcal {B}$
, then there exists a three-dimensional
![]() $H_4(0)$
-submodule N of M such that
$H_4(0)$
-submodule N of M such that
![]() $\mathrm {ch}([N])$
is equal to either
$\mathrm {ch}([N])$
is equal to either
![]() $s_{(3,1)}$
or
$s_{(3,1)}$
or
![]() $s_{(2,1,1)}$
. We claim that such a submodule N does not exist.
$s_{(2,1,1)}$
. We claim that such a submodule N does not exist.
Note that
Here,
![]() $\mathbb C \{3214\}$
and
$\mathbb C \{3214\}$
and
![]() $\mathbb C \{1432\}$
are irreducible. And
$\mathbb C \{1432\}$
are irreducible. And
![]() $\mathbb C \{2314 - 3214, 1423-1432, 2413, 3412 \}$
is indecomposable since it is isomorphic to a submodule of the injective indecomposable module
$\mathbb C \{2314 - 3214, 1423-1432, 2413, 3412 \}$
is indecomposable since it is isomorphic to a submodule of the injective indecomposable module
![]() $\mathbf {P}_{(1,2,1)}$
. Therefore, Equation (6.10) is a decomposition of M into indecomposables. The
$\mathbf {P}_{(1,2,1)}$
. Therefore, Equation (6.10) is a decomposition of M into indecomposables. The
![]() $H_4(0)$
-action on
$H_4(0)$
-action on
![]() $\{2314 - 3214, 1423-1432, 2413, 3412, 3214, 1432\} \cup \{ 0 \}$
is illustrated in the following figure:
$\{2314 - 3214, 1423-1432, 2413, 3412, 3214, 1432\} \cup \{ 0 \}$
is illustrated in the following figure:

The injective hulls of
![]() $\mathbb C \{2314 - 3214, 1423-1432, 2413, 3412 \}$
,
$\mathbb C \{2314 - 3214, 1423-1432, 2413, 3412 \}$
,
![]() $\mathbb C \{3214\}$
and
$\mathbb C \{3214\}$
and
![]() $\mathbb C \{1432\}$
are
$\mathbb C \{1432\}$
are
![]() $\mathbf {P}_{(1,2,1)}$
,
$\mathbf {P}_{(1,2,1)}$
,
![]() $\mathbf {P}_{(1,3)}$
and
$\mathbf {P}_{(1,3)}$
and
![]() $\mathbf {P}_{(3,1)}$
, respectively. This implies that the socle of M is
$\mathbf {P}_{(3,1)}$
, respectively. This implies that the socle of M is
![]() $\mathbb C\{3412\} \oplus \mathbb C \{3214\} \oplus \mathbb C \{1432\}$
. It follows that for every three-dimensional submodule N of M,
$\mathbb C\{3412\} \oplus \mathbb C \{3214\} \oplus \mathbb C \{1432\}$
. It follows that for every three-dimensional submodule N of M,
![]() $1 \le \dim \mathrm {soc}(N) \le 3$
. We list all three-dimensional submodules N of M in Table 1. Based on this, we conclude that there are no
$1 \le \dim \mathrm {soc}(N) \le 3$
. We list all three-dimensional submodules N of M in Table 1. Based on this, we conclude that there are no
![]() $H_4(0)$
-submodules N of M such that
$H_4(0)$
-submodules N of M such that
![]() $\mathrm {ch}([N]) = s_{(3,1)}$
or
$\mathrm {ch}([N]) = s_{(3,1)}$
or
![]() $s_{(2,1,1)}$
.
$s_{(2,1,1)}$
.
Table 1 The complete list of three-dimensional submodules of M in Example 6.6.

Let
![]() $f \in \mathrm {QSym}_n$
and
$f \in \mathrm {QSym}_n$
and
![]() $\mathcal {B} = \{\mathcal {B}_\alpha \mid \alpha \in I \}$
be the linearly independent set given in Definition 6.5. When f expands positively in
$\mathcal {B} = \{\mathcal {B}_\alpha \mid \alpha \in I \}$
be the linearly independent set given in Definition 6.5. When f expands positively in
![]() $\mathcal {B}$
, that is,
$\mathcal {B}$
, that is,
finding an
![]() $H_n(0)$
-module M such that
$H_n(0)$
-module M such that
-
(C1)
 $\mathrm {ch}([M]) = f$
,
$\mathrm {ch}([M]) = f$
, -
(C2) it is not a direct sum of irreducible modules, yet it possesses a combinatorial model that can be effectively handled, and
-
(C3) it has a distinguished filtration with respect to
 $\mathcal {B}$
$\mathcal {B}$
is a very important problem in the sense that this filtration can be considered as a nice representation theoretic interpretation of Equation (6.11).
In this subsection, we focus on the above problem in the case where
![]() $\mathcal {B}$
is
$\mathcal {B}$
is
![]() $\mathcal {S} := \{s_{\lambda } \mid \lambda \vdash n \}$
and
$\mathcal {S} := \{s_{\lambda } \mid \lambda \vdash n \}$
and
![]() $f = s_{\lambda /\mu }$
for a skew partition
$f = s_{\lambda /\mu }$
for a skew partition
![]() $\lambda /\mu $
of size n. Note that for all
$\lambda /\mu $
of size n. Note that for all
![]() $P \in \mathsf {RSP}_n$
with
$P \in \mathsf {RSP}_n$
with
![]() $\mathrm {sh}(\tau _P) = \lambda /\mu $
,
$\mathrm {sh}(\tau _P) = \lambda /\mu $
,
![]() $\mathsf {M}_P$
satisfies (C1) and (C2) because
$\mathsf {M}_P$
satisfies (C1) and (C2) because
![]() $\mathrm {ch}([\mathsf {M}_P]) = s_{\lambda /\mu }$
by Theorem 2.9(2) and it has a combinatorial model
$\mathrm {ch}([\mathsf {M}_P]) = s_{\lambda /\mu }$
by Theorem 2.9(2) and it has a combinatorial model
![]() $\Sigma _L(P)$
. In the following, we show that
$\Sigma _L(P)$
. In the following, we show that
![]() $\mathsf {M}_P$
satisfies (C3).
$\mathsf {M}_P$
satisfies (C3).
Theorem 6.7. For every
![]() $P \in \mathsf {RSP}_n$
,
$P \in \mathsf {RSP}_n$
,
![]() $\mathsf {M}_P$
has a distinguished filtration with respect to
$\mathsf {M}_P$
has a distinguished filtration with respect to
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Proof. To begin with, we choose any total order
![]() $\ll $
on
$\ll $
on
![]() $\mathrm {SYT}_n$
subject to the condition that
$\mathrm {SYT}_n$
subject to the condition that
Write
![]() $\{\mathtt {rec}(\gamma ) \mid \gamma \in \Sigma _L(P) \}$
as
$\{\mathtt {rec}(\gamma ) \mid \gamma \in \Sigma _L(P) \}$
as
For
![]() $0 \leq k \leq l$
, set
$0 \leq k \leq l$
, set
It is clear that
![]() $\emptyset = B_0 \subset B_1 \subset B_2 \subset \cdots \subset B_l$
. And, by Theorem 6.4, we have
$\emptyset = B_0 \subset B_1 \subset B_2 \subset \cdots \subset B_l$
. And, by Theorem 6.4, we have
![]() $B_l = \Sigma _L(P)$
. We claim that
$B_l = \Sigma _L(P)$
. We claim that
is a distinguished filtration of
![]() $\mathsf {M}_P$
with respect to
$\mathsf {M}_P$
with respect to
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
First, we show that for
![]() $1 \leq k \leq l$
,
$1 \leq k \leq l$
,
Take any
![]() $i \in [n-1]$
and
$i \in [n-1]$
and
![]() $\gamma \in B_k$
. If
$\gamma \in B_k$
. If
![]() $\pi _i \cdot \gamma = 0$
or
$\pi _i \cdot \gamma = 0$
or
![]() $\gamma $
, then there is nothing to prove. Assume that
$\gamma $
, then there is nothing to prove. Assume that
![]() $\pi _i \cdot \gamma = s_i \gamma $
. Then, by the definition of
$\pi _i \cdot \gamma = s_i \gamma $
. Then, by the definition of
![]() $H_n(0)$
-action on
$H_n(0)$
-action on
![]() $\mathsf {M}_P$
, we have
$\mathsf {M}_P$
, we have
![]() $\gamma \preceq _L s_i \gamma $
. Combining this inequality with Equation (6.9) yields that
$\gamma \preceq _L s_i \gamma $
. Combining this inequality with Equation (6.9) yields that
This implies that
![]() $s_i \gamma \in B_k$
, as desired.
$s_i \gamma \in B_k$
, as desired.
Next, we show that the filtration given in Equation (6.13) is distinguished with respect to
![]() $\mathcal {S}$
. For
$\mathcal {S}$
. For
![]() $1 \le k \le l$
,
$1 \le k \le l$
,
![]() $\{\gamma + M_{k-1} \mid \gamma \in B_k \setminus B_{k-1}\}$
is a basis for
$\{\gamma + M_{k-1} \mid \gamma \in B_k \setminus B_{k-1}\}$
is a basis for
![]() $M_k / M_{k-1}$
and
$M_k / M_{k-1}$
and
![]() $B_k \setminus B_{k-1}$
is an equivalence class under
$B_k \setminus B_{k-1}$
is an equivalence class under
![]() $\overset {K^*}{\cong }$
. It follows that
$\overset {K^*}{\cong }$
. It follows that
![]() $\mathrm {ch}([M_k / M_{k-1}])$
is a Schur function; more precisely,
$\mathrm {ch}([M_k / M_{k-1}])$
is a Schur function; more precisely,
![]() $\mathrm {ch}([M_k / M_{k-1}]) = s_{\mathrm {sh}(T_k)^{\mathrm {t}}}$
.
$\mathrm {ch}([M_k / M_{k-1}]) = s_{\mathrm {sh}(T_k)^{\mathrm {t}}}$
.
Example 6.8. Let
![]() $P = \mathsf {poset}(\tau _0^{(4,2,1)/(2,1)})$
. Following the method presented in the proof of Theorem 6.7, we will construct two distinguished filtrations of
$P = \mathsf {poset}(\tau _0^{(4,2,1)/(2,1)})$
. Following the method presented in the proof of Theorem 6.7, we will construct two distinguished filtrations of
![]() $\mathsf {M}_P$
with respect to
$\mathsf {M}_P$
with respect to
![]() $\{s_{\lambda } \mid \lambda \vdash 4 \}$
by choosing two distinct total orders on
$\{s_{\lambda } \mid \lambda \vdash 4 \}$
by choosing two distinct total orders on
![]() $\mathrm {SYT}_4$
.
$\mathrm {SYT}_4$
.
Note that
![]() $\{\mathtt {rec}(\gamma ) \mid \gamma \in \Sigma _L(P)\}$
is given by
$\{\mathtt {rec}(\gamma ) \mid \gamma \in \Sigma _L(P)\}$
is given by


Figure 2 The
![]() $H_4(0)$
-action on the basis
$H_4(0)$
-action on the basis
![]() $\Sigma _L(P) = [2134, 4321]_L$
for
$\Sigma _L(P) = [2134, 4321]_L$
for
![]() $\mathsf {M}_P$
and the sets
$\mathsf {M}_P$
and the sets
![]() $B^{\prime}_k (1 \leq k \leq 5)$
in Example 6.8.
$B^{\prime}_k (1 \leq k \leq 5)$
in Example 6.8.
and
![]() $\mathrm {sh}(Q_1) \triangleleft \mathrm {sh}(Q_2) = \mathrm {sh}(Q_3) \triangleleft \mathrm {sh}(Q_4) \triangleleft \mathrm {sh}(Q_5)$
. Choose a total order
$\mathrm {sh}(Q_1) \triangleleft \mathrm {sh}(Q_2) = \mathrm {sh}(Q_3) \triangleleft \mathrm {sh}(Q_4) \triangleleft \mathrm {sh}(Q_5)$
. Choose a total order
![]() $\ll _1$
(resp.
$\ll _1$
(resp.
![]() $\ll _2$
) on
$\ll _2$
) on
![]() $\mathrm {SYT}_4$
satisfying both Equation (6.12) and
$\mathrm {SYT}_4$
satisfying both Equation (6.12) and
![]() $Q_2 \ll _1 Q_3$
(resp.
$Q_2 \ll _1 Q_3$
(resp.
![]() $Q_3 \ll _2 Q_2$
). For
$Q_3 \ll _2 Q_2$
). For
![]() $1 \leq k \leq 5$
, let
$1 \leq k \leq 5$
, let
When we use
![]() $\ll _1$
, we let
$\ll _1$
, we let
and when we use
![]() $\ll _2$
, we let
$\ll _2$
, we let
Then
is the desired distinguished filtration of
![]() $\mathsf {M}_P$
with respect to
$\mathsf {M}_P$
with respect to
![]() $\{s_\lambda \mid \lambda \vdash 4 \}$
.
$\{s_\lambda \mid \lambda \vdash 4 \}$
.
For the readers’ convenience, we draw the
![]() $H_4(0)$
-action on the basis
$H_4(0)$
-action on the basis
![]() $\Sigma _L(P) = [2134, 4321]_L$
for
$\Sigma _L(P) = [2134, 4321]_L$
for
![]() $\mathsf {M}_P$
and the sets
$\mathsf {M}_P$
and the sets
![]() $B^{\prime}_k (1 \leq k \leq 5)$
in Figure 2.
$B^{\prime}_k (1 \leq k \leq 5)$
in Figure 2.
7 Further avenues
In this section, we discuss future directions regarding the classification problem, the decomposition problem, and how to recover
![]() $\mathsf {M}_P$
for
$\mathsf {M}_P$
for
![]() $P \in \mathsf {RSP}_n$
from a module of the generic Hecke algebra
$P \in \mathsf {RSP}_n$
from a module of the generic Hecke algebra
![]() $H_n(q)$
by specializing q to
$H_n(q)$
by specializing q to
![]() $0$
.
$0$
.
7.1 The classification problem
In Theorem 5.5, we successfully classify
![]() $\mathsf {M}_P$
for
$\mathsf {M}_P$
for
![]() $P \in \mathsf {RSP}_n$
. To be precise, we show that for
$P \in \mathsf {RSP}_n$
. To be precise, we show that for
![]() $P, Q \in \mathsf {RSP}_n$
,
$P, Q \in \mathsf {RSP}_n$
,
Recall that
![]() $\mathsf {RSP}_n = \mathsf {RP}_n \cap \mathsf {SP}_n$
. Hence, it would be natural to consider the classification problem for
$\mathsf {RSP}_n = \mathsf {RP}_n \cap \mathsf {SP}_n$
. Hence, it would be natural to consider the classification problem for
![]() $\{\mathsf {M}_P \mid P \in \mathsf {SP}_n\}$
and
$\{\mathsf {M}_P \mid P \in \mathsf {SP}_n\}$
and
![]() $\{\mathsf {M}_P \mid P \in \mathsf {RP}_n\}$
.
$\{\mathsf {M}_P \mid P \in \mathsf {RP}_n\}$
.
7.1.1 A remark on the classification problem for
 $\{\mathsf {M}_P \mid P \in \mathsf {SP}_n \}$
$\{\mathsf {M}_P \mid P \in \mathsf {SP}_n \}$
Since the notion ‘the shape of
![]() $\tau _P$
’ is available for
$\tau _P$
’ is available for
![]() $P \in \mathsf {SP}_n$
, one may expect that the classification given in Equation (7.1) can be extended to
$P \in \mathsf {SP}_n$
, one may expect that the classification given in Equation (7.1) can be extended to
![]() $\{\mathsf {M}_P \mid P \in \mathsf {SP}_n\}$
. Unfortunately, this expectation turns out to be false.
$\{\mathsf {M}_P \mid P \in \mathsf {SP}_n\}$
. Unfortunately, this expectation turns out to be false.
Let

Then
![]() $\mathsf {M}_{\mathsf {poset}(\tau _i)} (i = 1,2,3)$
is decomposed into indecomposables as follows:
$\mathsf {M}_{\mathsf {poset}(\tau _i)} (i = 1,2,3)$
is decomposed into indecomposables as follows:
 $$ \begin{align*} \mathsf{M}_{\mathsf{poset}(\tau_1)} & \cong \mathbf{P}_{(4)} \oplus \mathbf{P}_{(2,2)}, \\ \mathsf{M}_{\mathsf{poset}(\tau_2)} & \cong \mathbf{F}_{(1,2,1)} \oplus \mathsf{B}(4213, 4312) \oplus \mathbf{F}_{(3,1)} \oplus \mathbf{F}_{(2,2)} \oplus \mathbf{F}_{(4)}, \\ \mathsf{M}_{\mathsf{poset}(\tau_3)} & \cong \mathbf{F}_{(1,2,1)} \oplus \mathsf{B}(4213, 4312) \oplus \mathsf{B}(2431, 3421) \oplus \mathbf{F}_{(4)}, \end{align*} $$
$$ \begin{align*} \mathsf{M}_{\mathsf{poset}(\tau_1)} & \cong \mathbf{P}_{(4)} \oplus \mathbf{P}_{(2,2)}, \\ \mathsf{M}_{\mathsf{poset}(\tau_2)} & \cong \mathbf{F}_{(1,2,1)} \oplus \mathsf{B}(4213, 4312) \oplus \mathbf{F}_{(3,1)} \oplus \mathbf{F}_{(2,2)} \oplus \mathbf{F}_{(4)}, \\ \mathsf{M}_{\mathsf{poset}(\tau_3)} & \cong \mathbf{F}_{(1,2,1)} \oplus \mathsf{B}(4213, 4312) \oplus \mathsf{B}(2431, 3421) \oplus \mathbf{F}_{(4)}, \end{align*} $$
where
![]() $\mathsf {B}(4213, 4312)$
and
$\mathsf {B}(4213, 4312)$
and
![]() $\mathsf {B}(2431, 3421)$
are
$\mathsf {B}(2431, 3421)$
are
![]() $2$
-dimensional indecomposable modules. These decompositions show that
$2$
-dimensional indecomposable modules. These decompositions show that
![]() $\mathsf {M}_{\mathsf {poset}(\tau _1)}$
,
$\mathsf {M}_{\mathsf {poset}(\tau _1)}$
,
![]() $\mathsf {M}_{\mathsf {poset}(\tau _2)}$
and
$\mathsf {M}_{\mathsf {poset}(\tau _2)}$
and
![]() $\mathsf {M}_{\mathsf {poset}(\tau _3)}$
are pairwise non-isomorphic although all
$\mathsf {M}_{\mathsf {poset}(\tau _3)}$
are pairwise non-isomorphic although all
![]() $\tau _{\mathsf {poset}(\tau _i)}$
’s have the same shape.
$\tau _{\mathsf {poset}(\tau _i)}$
’s have the same shape.
Table 2 Seven pairs
![]() $(I_1^{(k)}, I_2^{(k)})$
in
$(I_1^{(k)}, I_2^{(k)})$
in
![]() $\mathfrak {A}_6$
.
$\mathfrak {A}_6$
.

7.1.2 A conjecture on the classification problem for
 $\{\mathsf {M}_P \mid P \in \mathsf {RP}_n \}$
$\{\mathsf {M}_P \mid P \in \mathsf {RP}_n \}$
Note that for
![]() $P \in \mathsf {RP}_n$
, the notion ‘the shape of
$P \in \mathsf {RP}_n$
, the notion ‘the shape of
![]() $\tau _P$
’ has not been defined. This leads us to introduce a classification of
$\tau _P$
’ has not been defined. This leads us to introduce a classification of
![]() $\{\mathsf {M}_P \mid P \in \mathsf {RSP}_n\}$
without using this notion. To be precise, by combining Theorem 4.7 and Theorem 5.5, we derive that for
$\{\mathsf {M}_P \mid P \in \mathsf {RSP}_n\}$
without using this notion. To be precise, by combining Theorem 4.7 and Theorem 5.5, we derive that for
![]() $P, Q \in \mathsf {RSP}_n$
,
$P, Q \in \mathsf {RSP}_n$
,
We expect that this classification can be extended to
![]() $\mathsf {RP}_n$
in its current form. The validity of this expectation has been checked for values of n up to 6 with the aid of the computer program SageMath. Let us provide an overview of our verification process. We first classify all left weak Bruhat intervals in
$\mathsf {RP}_n$
in its current form. The validity of this expectation has been checked for values of n up to 6 with the aid of the computer program SageMath. Let us provide an overview of our verification process. We first classify all left weak Bruhat intervals in
![]() $\mathfrak {S}_n$
(
$\mathfrak {S}_n$
(
![]() $n \leq 6$
) up to descent-preserving isomorphism and choose a complete list
$n \leq 6$
) up to descent-preserving isomorphism and choose a complete list
![]() $\mathfrak {I}_n$
of inequivalent representatives. Next, we let
$\mathfrak {I}_n$
of inequivalent representatives. Next, we let
![]() $\mathfrak {A}_n$
be the set of all unordered pairs
$\mathfrak {A}_n$
be the set of all unordered pairs
![]() $([\sigma _1, \rho _1]_L, [\sigma _2, \rho _2]_L)$
of intervals in
$([\sigma _1, \rho _1]_L, [\sigma _2, \rho _2]_L)$
of intervals in
![]() $\mathfrak {I}_n$
satisfying that
$\mathfrak {I}_n$
satisfying that
![]() $[\sigma _1, \rho _1]_L \neq [\sigma _2, \rho _2]_L$
and
$[\sigma _1, \rho _1]_L \neq [\sigma _2, \rho _2]_L$
and
Note that Equation (7.3) is a necessary condition for
![]() $\mathsf {B}(\sigma _1, \rho _1) \cong \mathsf {B}(\sigma _2, \rho _2)$
. Finally, we show that for all
$\mathsf {B}(\sigma _1, \rho _1) \cong \mathsf {B}(\sigma _2, \rho _2)$
. Finally, we show that for all
![]() $(I_1, I_2) \in \mathfrak {A}_n$
,
$(I_1, I_2) \in \mathfrak {A}_n$
,
![]() $\mathsf {B}(I_1) \not \cong \mathsf {B}(I_2)$
. When
$\mathsf {B}(I_1) \not \cong \mathsf {B}(I_2)$
. When
![]() $n \leq 5$
, there is nothing to prove because
$n \leq 5$
, there is nothing to prove because
![]() $\mathfrak {A}_n = \emptyset $
. When
$\mathfrak {A}_n = \emptyset $
. When
![]() $n = 6$
,
$n = 6$
,
![]() $\mathfrak {A}_6$
has fourteen pairs. Note that if
$\mathfrak {A}_6$
has fourteen pairs. Note that if
![]() $(I_1, I_2) \in \mathfrak {A}_6$
, then
$(I_1, I_2) \in \mathfrak {A}_6$
, then
![]() $(w_0 \cdot I_1 \cdot {w_0}, w_0 \cdot I_2 \cdot {w_0}) \in \mathfrak {A}_6$
and
$(w_0 \cdot I_1 \cdot {w_0}, w_0 \cdot I_2 \cdot {w_0}) \in \mathfrak {A}_6$
and
Therefore, it suffices to examine seven pairs
![]() $(I_1^{(k)}, I_2^{(k)})$
listed in Table 2. For
$(I_1^{(k)}, I_2^{(k)})$
listed in Table 2. For
![]() $3 \leq k \leq 7$
, using Lemma 5.2, one can see that the projective covers of
$3 \leq k \leq 7$
, using Lemma 5.2, one can see that the projective covers of
![]() $\mathsf {B}(I_1^{(k)})$
and
$\mathsf {B}(I_1^{(k)})$
and
![]() $\mathsf {B}(I_2^{(k)})$
are not isomorphic. Therefore,
$\mathsf {B}(I_2^{(k)})$
are not isomorphic. Therefore,
![]() $\mathsf {B}(I_1^{(k)})$
and
$\mathsf {B}(I_1^{(k)})$
and
![]() $\mathsf {B}(I_2^{(k)})$
are not isomorphic. For
$\mathsf {B}(I_2^{(k)})$
are not isomorphic. For
![]() $k = 1, 2$
, one can see that
$k = 1, 2$
, one can see that
![]() $\mathsf {B}(I_1^{(k)})$
and
$\mathsf {B}(I_1^{(k)})$
and
![]() $\mathsf {B}(I_2^{(k)})$
are not isomorphic in a brute force manner.
$\mathsf {B}(I_2^{(k)})$
are not isomorphic in a brute force manner.
Let us give another evidence for our expectation. Specifically, we show that Equation (7.2) holds when
![]() $P \in \mathsf {RSP}_n$
,
$P \in \mathsf {RSP}_n$
,
![]() $Q \in \mathsf {RP}_n$
, and
$Q \in \mathsf {RP}_n$
, and
![]() $\mathrm {ch}([\mathsf {M}_P])$
is a Schur function. This can be derived from the proposition presented below.
$\mathrm {ch}([\mathsf {M}_P])$
is a Schur function. This can be derived from the proposition presented below.
Proposition 7.1. Let P be a poset in
![]() $\mathsf {RSP}_n$
such that
$\mathsf {RSP}_n$
such that
![]() $\mathrm {ch}([\mathsf {M}_P])$
is a Schur function.
$\mathrm {ch}([\mathsf {M}_P])$
is a Schur function.
-
(1) If
 $Q \in \mathsf {P}_n$
satisfies that
$Q \in \mathsf {P}_n$
satisfies that
 $\mathsf {M}_Q \cong \mathsf {M}_P$
, then
$\mathsf {M}_Q \cong \mathsf {M}_P$
, then
 $Q \in \mathsf {RSP}_n$
.
$Q \in \mathsf {RSP}_n$
. -
(2) The isomorphism class of
 $\mathsf {M}_P$
within
$\mathsf {M}_P$
within
 $\{\mathsf {M}_Q \mid Q \in \mathsf {P}_n \}$
is equal to the isomorphism class of
$\{\mathsf {M}_Q \mid Q \in \mathsf {P}_n \}$
is equal to the isomorphism class of
 $\mathsf {M}_P$
within
$\mathsf {M}_P$
within
 $\{\mathsf {M}_Q \mid Q \in \mathsf {RSP}_n \}$
as sets.
$\{\mathsf {M}_Q \mid Q \in \mathsf {RSP}_n \}$
as sets.
Proof. (1) Suppose that
![]() $\mathrm {ch}([\mathsf {M}_P]) = s_{\lambda }$
for some
$\mathrm {ch}([\mathsf {M}_P]) = s_{\lambda }$
for some
![]() $\lambda \vdash n$
. By [Reference van Willigenburg39, Theorem 2.2],
$\lambda \vdash n$
. By [Reference van Willigenburg39, Theorem 2.2],
![]() $\mathrm {sh}(\tau _P)$
is either
$\mathrm {sh}(\tau _P)$
is either
![]() $\lambda $
or
$\lambda $
or
![]() $\lambda ^\circ $
, where
$\lambda ^\circ $
, where
![]() $\lambda ^\circ $
denotes the skew partition whose Young diagram is obtained by rotating
$\lambda ^\circ $
denotes the skew partition whose Young diagram is obtained by rotating
![]() $\mathtt {yd}(\lambda )$
by
$\mathtt {yd}(\lambda )$
by
![]() $180^\circ $
.
$180^\circ $
.
First, we consider the case where
![]() $\mathrm {sh}(\tau _P) = \lambda $
. Let
$\mathrm {sh}(\tau _P) = \lambda $
. Let
![]() $f: \mathsf {M}_P \rightarrow \mathsf {M}_Q$
be an
$f: \mathsf {M}_P \rightarrow \mathsf {M}_Q$
be an
![]() $H_n(0)$
-module isomorphism. By Theorem 3.9, we see that
$H_n(0)$
-module isomorphism. By Theorem 3.9, we see that
![]() $\Sigma _L(P) = [\mathsf {read}_{\tau _P} (T_{\lambda }), \mathsf {read}_{\tau _P}(T^{\prime}_{\lambda })]_L$
, and therefore,
$\Sigma _L(P) = [\mathsf {read}_{\tau _P} (T_{\lambda }), \mathsf {read}_{\tau _P}(T^{\prime}_{\lambda })]_L$
, and therefore,
![]() $\mathsf {read}_{\tau _P} (T_{\lambda })$
is a cyclic generator of
$\mathsf {read}_{\tau _P} (T_{\lambda })$
is a cyclic generator of
![]() $\mathsf {M}_P$
. In addition, in view of [Reference Searles32, Lemma 3.12], we have that
$\mathsf {M}_P$
. In addition, in view of [Reference Searles32, Lemma 3.12], we have that
Combining (7.4) with the equality
![]() $\mathrm {ch}([\mathsf {M}_P]) = \mathrm {ch}([\mathsf {M}_Q])$
, we can deduce that there exists a unique
$\mathrm {ch}([\mathsf {M}_P]) = \mathrm {ch}([\mathsf {M}_Q])$
, we can deduce that there exists a unique
![]() $\sigma \in \Sigma _L(Q)$
such that
$\sigma \in \Sigma _L(Q)$
such that
![]() $\mathrm {Des}_L(\sigma ) \supseteq \mathrm {Des}_L(\mathsf {read}_{\tau _P}(T_{\lambda }))$
. This fact implies that
$\mathrm {Des}_L(\sigma ) \supseteq \mathrm {Des}_L(\mathsf {read}_{\tau _P}(T_{\lambda }))$
. This fact implies that
![]() $f(\mathsf {read}_{\tau _P}(T_{\lambda })) = c \sigma $
for some nonzero
$f(\mathsf {read}_{\tau _P}(T_{\lambda })) = c \sigma $
for some nonzero
![]() $c \in \mathbb C$
. We may assume that
$c \in \mathbb C$
. We may assume that
![]() $c = 1$
by considering the isomorphism
$c = 1$
by considering the isomorphism
![]() $\frac {1}{c}f$
instead of f. Since f is an
$\frac {1}{c}f$
instead of f. Since f is an
![]() $H_n(0)$
-module isomorphism,
$H_n(0)$
-module isomorphism,
![]() $\Sigma _L(Q)$
is equal to
$\Sigma _L(Q)$
is equal to
![]() $f(\Sigma _L(P))$
and therefore is a left weak Bruhat interval. Furthermore, it holds that
$f(\Sigma _L(P))$
and therefore is a left weak Bruhat interval. Furthermore, it holds that
As a consequence, we obtain a descent-preserving isomorphism
![]() $f|_{\Sigma _L(P)}: \Sigma _L(P) \rightarrow \Sigma _L(Q)$
. Now the assertion follows from Theorem 4.7.
$f|_{\Sigma _L(P)}: \Sigma _L(P) \rightarrow \Sigma _L(Q)$
. Now the assertion follows from Theorem 4.7.
Next, consider the case where
![]() $\mathrm {sh}(\tau _P) = \lambda ^\circ $
. Let
$\mathrm {sh}(\tau _P) = \lambda ^\circ $
. Let
![]() $\overline {P}^*$
and
$\overline {P}^*$
and
![]() $\overline {Q}^*$
be the posets in
$\overline {Q}^*$
be the posets in
![]() $\mathsf {P}_n$
whose orders are defined by
$\mathsf {P}_n$
whose orders are defined by
respectively. Since P is a poset in
![]() $\mathsf {RSP}_n$
with
$\mathsf {RSP}_n$
with
![]() $\mathrm {sh}(\tau _P) = \lambda ^\circ $
,
$\mathrm {sh}(\tau _P) = \lambda ^\circ $
,
![]() $\overline {P}^*$
is a poset in
$\overline {P}^*$
is a poset in
![]() $\mathsf {RSP}_n$
with
$\mathsf {RSP}_n$
with
![]() $\mathrm {sh}(\tau _{\overline {P}^*}) = \lambda $
. By [Reference Choi, Kim and Oh9, Theorem 3.6(a)], we have
$\mathrm {sh}(\tau _{\overline {P}^*}) = \lambda $
. By [Reference Choi, Kim and Oh9, Theorem 3.6(a)], we have
![]() $\mathsf {M}_{\overline {P}^*} \cong \mathbf {T}^+_{\unicode{x3c6} } (\mathsf {M}_{P})$
and
$\mathsf {M}_{\overline {P}^*} \cong \mathbf {T}^+_{\unicode{x3c6} } (\mathsf {M}_{P})$
and
![]() $\mathsf {M}_{\overline {Q}^*} \cong \mathbf {T}^+_{\unicode{x3c6} } (\mathsf {M}_{Q})$
, which implies that
$\mathsf {M}_{\overline {Q}^*} \cong \mathbf {T}^+_{\unicode{x3c6} } (\mathsf {M}_{Q})$
, which implies that
![]() $\mathsf {M}_{\overline {Q}^*} \cong \mathsf {M}_{\overline {P}^*}$
. It follows from the first case that
$\mathsf {M}_{\overline {Q}^*} \cong \mathsf {M}_{\overline {P}^*}$
. It follows from the first case that
![]() $\overline {Q}^* \in \mathsf {RSP}_n$
, thus
$\overline {Q}^* \in \mathsf {RSP}_n$
, thus
![]() $Q \in \mathsf {RSP}_n$
.
$Q \in \mathsf {RSP}_n$
.
(2) It follows from (1).
Based on these evidences, we propose the following conjecture.
Conjecture 7.2. Let
![]() $P, Q \in \mathsf {RP}_n$
. If
$P, Q \in \mathsf {RP}_n$
. If
![]() $\mathsf {M}_P \cong \mathsf {M}_Q$
, then
$\mathsf {M}_P \cong \mathsf {M}_Q$
, then
![]() $\Sigma _L(P) \overset {D}{\simeq } \Sigma _L(Q)$
.
$\Sigma _L(P) \overset {D}{\simeq } \Sigma _L(Q)$
.
We remark that the converse of Conjecture 7.2 holds due to Proposition 4.1.
7.2 The decomposition problem of
 $\mathsf {M}_P$
for
$\mathsf {M}_P$
for
 $P \in \mathsf {RSP}_n$
$P \in \mathsf {RSP}_n$
A Young diagram of skew shape is called a ribbon if it does not contain any
![]() $2\times 2$
square. For simplicity, we call a skew partition a ribbon if the corresponding Young diagram is a ribbon. Note that our ribbons are not necessarily connected. Consider a skew partition
$2\times 2$
square. For simplicity, we call a skew partition a ribbon if the corresponding Young diagram is a ribbon. Note that our ribbons are not necessarily connected. Consider a skew partition
such that
![]() $\lambda ^{(i)} / \mu ^{(i)}$
is connected for all
$\lambda ^{(i)} / \mu ^{(i)}$
is connected for all
![]() $1 \le i \le k$
. We say that
$1 \le i \le k$
. We say that
![]() $\lambda / \mu $
contains a disconnected ribbon if there exists an index
$\lambda / \mu $
contains a disconnected ribbon if there exists an index
![]() $1 \le j \le k-1$
such that both
$1 \le j \le k-1$
such that both
![]() $\lambda ^{(j)} / \mu ^{(j)}$
and
$\lambda ^{(j)} / \mu ^{(j)}$
and
![]() $\lambda ^{(j+1)} / \mu ^{(j+1)}$
are ribbons. With this notation, we state the following proposition.
$\lambda ^{(j+1)} / \mu ^{(j+1)}$
are ribbons. With this notation, we state the following proposition.
Proposition 7.3. Let
![]() $P \in \mathsf {RSP}_n$
.
$P \in \mathsf {RSP}_n$
.
-
(1) If
 $\mathrm {sh}(\tau _P)$
is connected, then
$\mathrm {sh}(\tau _P)$
is connected, then
 $\mathsf {M}_P$
is indecomposable.
$\mathsf {M}_P$
is indecomposable. -
(2) If
 $\mathrm {sh}(\tau _P)$
contains a disconnected ribbon, then
$\mathrm {sh}(\tau _P)$
contains a disconnected ribbon, then
 $\mathsf {M}_P$
is not indecomposable.
$\mathsf {M}_P$
is not indecomposable.
Proof. (1) It follows from Lemma 5.4.
(2) Suppose that
![]() $\mathrm {sh}(\tau _P)$
contains a disconnected ribbon. Let
$\mathrm {sh}(\tau _P)$
contains a disconnected ribbon. Let
![]() $\lambda /\mu = \mathrm {sh}(\tau _P)$
. Write
$\lambda /\mu = \mathrm {sh}(\tau _P)$
. Write
![]() $\lambda /\mu $
as
$\lambda /\mu $
as
![]() $\lambda ^{(1)} / \mu ^{(1)} \star \lambda ^{(2)} / \mu ^{(2)} \star \cdots \star \lambda ^{(k)} / \mu ^{(k)}$
, where
$\lambda ^{(1)} / \mu ^{(1)} \star \lambda ^{(2)} / \mu ^{(2)} \star \cdots \star \lambda ^{(k)} / \mu ^{(k)}$
, where
![]() $\lambda ^{(i)} / \mu ^{(i)}$
is connected for all
$\lambda ^{(i)} / \mu ^{(i)}$
is connected for all
![]() $1 \le i \le k$
and both
$1 \le i \le k$
and both
![]() $\lambda ^{(j)} / \mu ^{(j)}$
and
$\lambda ^{(j)} / \mu ^{(j)}$
and
![]() $\lambda ^{(j+1)} / \mu ^{(j+1)}$
are ribbons for some
$\lambda ^{(j+1)} / \mu ^{(j+1)}$
are ribbons for some
![]() $1 \leq j \leq k-1$
.
$1 \leq j \leq k-1$
.
In Appendix A, we constructed an
![]() $H_n(0)$
-module
$H_n(0)$
-module
![]() $X_{\lambda /\mu }$
satisfying that
$X_{\lambda /\mu }$
satisfying that
![]() $X_{\lambda /\mu } \cong \mathsf {M}_P$
. From now on, we will prove the assertion for
$X_{\lambda /\mu } \cong \mathsf {M}_P$
. From now on, we will prove the assertion for
![]() $X_{\lambda /\mu }$
instead of
$X_{\lambda /\mu }$
instead of
![]() $\mathsf {M}_P$
. By Proposition A.2(1), we have the
$\mathsf {M}_P$
. By Proposition A.2(1), we have the
![]() $H_n(0)$
-module isomorphism
$H_n(0)$
-module isomorphism
Set
![]() $X^{(1)} := X_{\lambda ^{(1)} / \mu ^{(1)}} \boxtimes \cdots \boxtimes X_{\lambda ^{(j-1)} / \mu ^{(j-1)}}$
and
$X^{(1)} := X_{\lambda ^{(1)} / \mu ^{(1)}} \boxtimes \cdots \boxtimes X_{\lambda ^{(j-1)} / \mu ^{(j-1)}}$
and
![]() $X^{(2)} := X_{\lambda ^{(j+2)} / \mu ^{(j+2)}} \boxtimes \cdots \boxtimes X_{\lambda ^{(k)} / \mu ^{(k)}}$
. Since
$X^{(2)} := X_{\lambda ^{(j+2)} / \mu ^{(j+2)}} \boxtimes \cdots \boxtimes X_{\lambda ^{(k)} / \mu ^{(k)}}$
. Since
![]() $\lambda ^{(j)}/\mu ^{(j)}$
and
$\lambda ^{(j)}/\mu ^{(j)}$
and
![]() $\lambda ^{(j+1)}/\mu ^{(j+1)}$
are ribbons,
$\lambda ^{(j+1)}/\mu ^{(j+1)}$
are ribbons,
![]() $X_{\lambda ^{(j)}/\mu ^{(j)}} \cong \mathbf {P}_\alpha $
and
$X_{\lambda ^{(j)}/\mu ^{(j)}} \cong \mathbf {P}_\alpha $
and
![]() $X_{\lambda ^{(j+1)}/\mu ^{(j+1)}} \cong \mathbf {P}_\beta $
, where
$X_{\lambda ^{(j+1)}/\mu ^{(j+1)}} \cong \mathbf {P}_\beta $
, where
![]() $\alpha = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{(j)} / \mu ^{(j)})$
and
$\alpha = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{(j)} / \mu ^{(j)})$
and
![]() $\beta = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{(j+1)} / \mu ^{(j+1)})$
. Therefore,
$\beta = {\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda ^{(j+1)} / \mu ^{(j+1)})$
. Therefore,
Combining Lemma 5.1 with the fact that
![]() $\boxtimes $
is distributive over
$\boxtimes $
is distributive over
![]() $\oplus $
, we derive the
$\oplus $
, we derive the
![]() $H_n(0)$
-module isomorphism
$H_n(0)$
-module isomorphism
This shows
![]() $X_{\lambda /\mu }$
is not indecomposable.
$X_{\lambda /\mu }$
is not indecomposable.
The contraposition of Proposition 7.3(2) says that if
![]() $\mathsf {M}_P$
is indecomposable, then
$\mathsf {M}_P$
is indecomposable, then
![]() $\mathrm {sh}(\tau _P)$
does not contain any disconnected ribbon. We ask if the converse is true. In the case where
$\mathrm {sh}(\tau _P)$
does not contain any disconnected ribbon. We ask if the converse is true. In the case where
![]() $\mathrm {sh}(\tau _P)$
is connected, it is true by Proposition 7.3(1). In the case where
$\mathrm {sh}(\tau _P)$
is connected, it is true by Proposition 7.3(1). In the case where
![]() $\mathrm {sh}(\tau _P)$
is disconnected, we verified its validity when
$\mathrm {sh}(\tau _P)$
is disconnected, we verified its validity when
![]() $|P| \leq 6$
. Indeed, this was done by showing that
$|P| \leq 6$
. Indeed, this was done by showing that
![]() $\mathrm {End}(\mathsf {M}_P)$
has no idempotent except for
$\mathrm {End}(\mathsf {M}_P)$
has no idempotent except for
![]() $0$
and
$0$
and
![]() $\mathrm {id}$
. Refer to the following example.
$\mathrm {id}$
. Refer to the following example.
Example 7.4. Let
![]() $\lambda /\mu = (3,3,1)/(1,1)$
and
$\lambda /\mu = (3,3,1)/(1,1)$
and
![]() $P = \mathsf {poset}(\tau _0^{\lambda /\mu })$
. Then,
$P = \mathsf {poset}(\tau _0^{\lambda /\mu })$
. Then,
![]() $\Sigma _L(P) = [21435, 42531]_L$
is a basis for
$\Sigma _L(P) = [21435, 42531]_L$
is a basis for
![]() $\mathsf {M}_P$
. Let
$\mathsf {M}_P$
. Let
![]() $f \in \mathrm {End}(\mathsf {M}_P)$
be an idempotent and let
$f \in \mathrm {End}(\mathsf {M}_P)$
be an idempotent and let
 $$ \begin{align*}f(21435) = \sum_{\gamma \in [21435, 42531]_L} c_\gamma \gamma \quad (c_\gamma \in \mathbb C). \end{align*} $$
$$ \begin{align*}f(21435) = \sum_{\gamma \in [21435, 42531]_L} c_\gamma \gamma \quad (c_\gamma \in \mathbb C). \end{align*} $$
Note that
Since f is an
![]() $H_5(0)$
-module homomorphism, this equality implies that
$H_5(0)$
-module homomorphism, this equality implies that
![]() $c_\gamma = 0$
for all
$c_\gamma = 0$
for all
![]() $\gamma \in [21435, 42531]_L \setminus \{21435,21543,42531\}$
. In addition,
$\gamma \in [21435, 42531]_L \setminus \{21435,21543,42531\}$
. In addition,
![]() $c_{21543} = 0$
since
$c_{21543} = 0$
since
Hence,
![]() $f - c_{21435} \, \mathrm {id}$
is an
$f - c_{21435} \, \mathrm {id}$
is an
![]() $H_5(0)$
-module homomorphism such that
$H_5(0)$
-module homomorphism such that
 $$\begin{align*}(f - c_{21435} \mathrm{id}) (\gamma) = \begin{cases} c_{42531} 42531 & \text{if }\gamma = 21435,\\ 0 & \text{if }\gamma \in [21435, 42531]_L \setminus \{21435\}, \end{cases} \end{align*}$$
$$\begin{align*}(f - c_{21435} \mathrm{id}) (\gamma) = \begin{cases} c_{42531} 42531 & \text{if }\gamma = 21435,\\ 0 & \text{if }\gamma \in [21435, 42531]_L \setminus \{21435\}, \end{cases} \end{align*}$$
and therefore,
![]() $(f - c_{21435} \mathrm {id})^2 = 0$
. Since f is an idempotent, the possible values for
$(f - c_{21435} \mathrm {id})^2 = 0$
. Since f is an idempotent, the possible values for
![]() $c_{21435}$
are
$c_{21435}$
are
![]() $0$
or
$0$
or
![]() $1$
. Using the fact that f is an idempotent again, we have that
$1$
. Using the fact that f is an idempotent again, we have that
![]() $c_{42531} = 0$
. As a consequence, f is
$c_{42531} = 0$
. As a consequence, f is
![]() $0$
or
$0$
or
![]() $\mathrm {id}$
.
$\mathrm {id}$
.
Based on the above discussion, we propose the following conjecture.
Conjecture 7.5. Let
![]() $P \in \mathsf {RSP}_n$
. Suppose that
$P \in \mathsf {RSP}_n$
. Suppose that
![]() $\mathrm {sh}(\tau _P)$
is disconnected and does not contain any disconnected ribbon. Then,
$\mathrm {sh}(\tau _P)$
is disconnected and does not contain any disconnected ribbon. Then,
![]() $\mathsf {M}_P$
is indecomposable.
$\mathsf {M}_P$
is indecomposable.
7.3 Recovering
 $\mathsf {M}_P$
for
$\mathsf {M}_P$
for
 $P \in \mathsf {RSP}_n$
from an
$P \in \mathsf {RSP}_n$
from an
 $H_n(q)$
-module by specializing q to
$H_n(q)$
-module by specializing q to
 $0$
$0$
Let
![]() $q \in \mathbb C$
. The Hecke algebra
$q \in \mathbb C$
. The Hecke algebra
![]() $H_n(q)$
is the associative
$H_n(q)$
is the associative
![]() $\mathbb C$
-algebra with
$\mathbb C$
-algebra with
![]() $1$
generated by
$1$
generated by
![]() $T_1, T_2, \ldots , T_{n-1}$
subject to the following relations:
$T_1, T_2, \ldots , T_{n-1}$
subject to the following relations:
 $$ \begin{align*} T_i^2 &= (q-1) T_i + q \quad \text{for }1\le i \le n-1,\\ T_i T_{i+1} T_i &= T_{i+1} T_i T_{i+1} \quad \text{for }1\le i \le n-2,\\ T_i T_j &=T_j T_i \quad \text{if }|i-j| \ge 2. \end{align*} $$
$$ \begin{align*} T_i^2 &= (q-1) T_i + q \quad \text{for }1\le i \le n-1,\\ T_i T_{i+1} T_i &= T_{i+1} T_i T_{i+1} \quad \text{for }1\le i \le n-2,\\ T_i T_j &=T_j T_i \quad \text{if }|i-j| \ge 2. \end{align*} $$
Let
![]() $q \in \mathbb C$
be generic; that is, q is neither zero nor a root of unity. It is well known that
$q \in \mathbb C$
be generic; that is, q is neither zero nor a root of unity. It is well known that
![]() $H_n(q)$
is isomorphic to the group algebra
$H_n(q)$
is isomorphic to the group algebra
![]() $\mathbb C[\mathfrak {S}_n]$
, and thus, the category of left finite dimensional
$\mathbb C[\mathfrak {S}_n]$
, and thus, the category of left finite dimensional
![]() $H_n(q)$
-modules is semisimple and there exists a ring isomorphism ([Reference Krob and Thibon22, Section 3.2])
$H_n(q)$
-modules is semisimple and there exists a ring isomorphism ([Reference Krob and Thibon22, Section 3.2])
Here,
![]() $\bigoplus _{n\ge 0} \mathcal {G}_0(H_n(q))$
is the Grothendieck ring of the tower of generic Hecke algebras equipped with addition and multiplication from direct sum and induction product,
$\bigoplus _{n\ge 0} \mathcal {G}_0(H_n(q))$
is the Grothendieck ring of the tower of generic Hecke algebras equipped with addition and multiplication from direct sum and induction product,
![]() $\mathrm {Sym}$
is the ring of symmetric functions, and
$\mathrm {Sym}$
is the ring of symmetric functions, and
![]() $V^\lambda (q)$
is the irreducible
$V^\lambda (q)$
is the irreducible
![]() $H_n(q)$
-module attached to a partition
$H_n(q)$
-module attached to a partition
![]() $\lambda $
of size n. The explicit description of
$\lambda $
of size n. The explicit description of
![]() $V^{\lambda }(q)$
can be found in [Reference King and Wybourne21, p.7].
$V^{\lambda }(q)$
can be found in [Reference King and Wybourne21, p.7].
Let
![]() $P \in \mathsf {RSP}_n$
. Viewing q as an indeterminate, one may ask if
$P \in \mathsf {RSP}_n$
. Viewing q as an indeterminate, one may ask if
![]() $\mathsf {M}_P$
can be obtained from an
$\mathsf {M}_P$
can be obtained from an
![]() $H_n(q)$
-module by specializing q to
$H_n(q)$
-module by specializing q to
![]() $0$
. However, it should be noted that the process of ‘specializing q to
$0$
. However, it should be noted that the process of ‘specializing q to
![]() $0$
’ depends on the choice of bases for the
$0$
’ depends on the choice of bases for the
![]() $H_n(q)$
-module under consideration, as illustrated in the example below.
$H_n(q)$
-module under consideration, as illustrated in the example below.
Example 7.6. The irreducible
![]() $H_3(q)$
-module
$H_3(q)$
-module
![]() $V^{(2,1)}(q)$
has the underlying space
$V^{(2,1)}(q)$
has the underlying space
![]() $\mathbb C\{v_1, v_2\}$
, and the
$\mathbb C\{v_1, v_2\}$
, and the
![]() $H_3(q)$
-action defined by
$H_3(q)$
-action defined by
 $$ \begin{align*} \begin{cases} T_1 \cdot v_1 = -v_1, \\ T_2 \cdot v_1 = v_2, \end{cases} \quad \text{and} \quad\quad \begin{cases} T_1 \cdot v_2 = -q^2 v_1 + q v_2, \\ T_2 \cdot v_2 = qv_1 + (q - 1)v_2. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} T_1 \cdot v_1 = -v_1, \\ T_2 \cdot v_1 = v_2, \end{cases} \quad \text{and} \quad\quad \begin{cases} T_1 \cdot v_2 = -q^2 v_1 + q v_2, \\ T_2 \cdot v_2 = qv_1 + (q - 1)v_2. \end{cases} \end{align*} $$
By the specialization
![]() $q = 0$
, we have the
$q = 0$
, we have the
![]() $H_3(0)$
-action on
$H_3(0)$
-action on
![]() $\mathbb C\{v_1, v_2\}$
defined by
$\mathbb C\{v_1, v_2\}$
defined by
 $$ \begin{align*} \begin{cases} \overline{\pi}_1 \cdot v_1 = -v_1, \\ \overline{\pi}_2 \cdot v_1 = v_2, \end{cases} \quad \text{and} \quad\quad \begin{cases} \overline{\pi}_1 \cdot v_2 = 0, \\ \overline{\pi}_2 \cdot v_2 = - v_2. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \overline{\pi}_1 \cdot v_1 = -v_1, \\ \overline{\pi}_2 \cdot v_1 = v_2, \end{cases} \quad \text{and} \quad\quad \begin{cases} \overline{\pi}_1 \cdot v_2 = 0, \\ \overline{\pi}_2 \cdot v_2 = - v_2. \end{cases} \end{align*} $$
The resulting module is isomorphic to
![]() $\mathbf {T}^{+}_\unicode{x3b8} (\mathsf {M}_{P_1})$
, where
$\mathbf {T}^{+}_\unicode{x3b8} (\mathsf {M}_{P_1})$
, where
![]() $P_1 = \mathsf {poset}(\tau _0^{(2,1)}) \in \mathsf {RSP}_3$
.
$P_1 = \mathsf {poset}(\tau _0^{(2,1)}) \in \mathsf {RSP}_3$
.
However, if we choose the basis
![]() $\{w_1 := qv_1 - v_2, w_2 := (q^2 - q) v_1 - q v_2\}$
for
$\{w_1 := qv_1 - v_2, w_2 := (q^2 - q) v_1 - q v_2\}$
for
![]() $V^{(2,1)}(q)$
, then we have
$V^{(2,1)}(q)$
, then we have
 $$ \begin{align*} \begin{cases} T_1 \cdot w_1 = w_2, \\ T_2 \cdot w_1 = -w_1, \end{cases} \quad \text{and} \quad\quad \begin{cases} T_1 \cdot w_2 = qw_1 + (q-1)w_2, \\ T_2 \cdot w_2 = -q^2 w_1 + q w_2. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} T_1 \cdot w_1 = w_2, \\ T_2 \cdot w_1 = -w_1, \end{cases} \quad \text{and} \quad\quad \begin{cases} T_1 \cdot w_2 = qw_1 + (q-1)w_2, \\ T_2 \cdot w_2 = -q^2 w_1 + q w_2. \end{cases} \end{align*} $$
By the specialization
![]() $q = 0$
, we have the
$q = 0$
, we have the
![]() $H_3(0)$
-action on
$H_3(0)$
-action on
![]() $\mathbb C\{w_1, w_2\}$
defined by
$\mathbb C\{w_1, w_2\}$
defined by
 $$ \begin{align*} \begin{cases} \overline{\pi}_1 \cdot w_1 = w_2, \\ \overline{\pi}_2 \cdot w_1 = -w_1, \end{cases} \quad \text{and} \quad\quad \begin{cases} \overline{\pi}_1 \cdot w_2 = -w_2, \\ \overline{\pi}_2 \cdot w_2 = 0. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \overline{\pi}_1 \cdot w_1 = w_2, \\ \overline{\pi}_2 \cdot w_1 = -w_1, \end{cases} \quad \text{and} \quad\quad \begin{cases} \overline{\pi}_1 \cdot w_2 = -w_2, \\ \overline{\pi}_2 \cdot w_2 = 0. \end{cases} \end{align*} $$
The resulting module is isomorphic to
![]() $\mathbf {T}^{+}_\unicode{x3b8} (\mathsf {M}_{P_2})$
, where
$\mathbf {T}^{+}_\unicode{x3b8} (\mathsf {M}_{P_2})$
, where
![]() $P_2 = \mathsf {poset}(\tau _0^{(2,2)/(1)}) \in \mathsf {RSP}_3$
. It is worthwhile to remark that while
$P_2 = \mathsf {poset}(\tau _0^{(2,2)/(1)}) \in \mathsf {RSP}_3$
. It is worthwhile to remark that while
![]() $\mathbf {T}^{+}_\unicode{x3b8} (\mathsf {M}_{P_1})$
and
$\mathbf {T}^{+}_\unicode{x3b8} (\mathsf {M}_{P_1})$
and
![]() $\mathbf {T}^{+}_\unicode{x3b8} (\mathsf {M}_{P_2})$
have the same quasisymmetric characteristic
$\mathbf {T}^{+}_\unicode{x3b8} (\mathsf {M}_{P_2})$
have the same quasisymmetric characteristic
![]() $\textbf {ch}_q([V^{(2,1)}(q)])$
, they are not isomorphic.
$\textbf {ch}_q([V^{(2,1)}(q)])$
, they are not isomorphic.
We expect that for
![]() $P \in \mathsf {RSP}_n$
,
$P \in \mathsf {RSP}_n$
,
![]() $\mathbf {T}^{+}_\unicode{x3b8} (\mathsf {M}_P)$
can be obtained from an
$\mathbf {T}^{+}_\unicode{x3b8} (\mathsf {M}_P)$
can be obtained from an
![]() $H_n(q)$
-module, whose image under
$H_n(q)$
-module, whose image under
![]() $\textbf {ch}_q$
equals
$\textbf {ch}_q$
equals
![]() $K_P$
, by applying the specialization
$K_P$
, by applying the specialization
![]() $q = 0$
to a suitable basis.
$q = 0$
to a suitable basis.
A A tableau description of
 $\mathsf {M}_P$
for
$\mathsf {M}_P$
for
 $P \in \mathsf {RSP}_n$
$P \in \mathsf {RSP}_n$
Let
![]() $P \in \mathsf {RSP}_n$
. Note that
$P \in \mathsf {RSP}_n$
. Note that
![]() $\Sigma _L(P)$
is a basis of
$\Sigma _L(P)$
is a basis of
![]() $\mathsf {M}_P$
consisting of permutations. Here, we construct an
$\mathsf {M}_P$
consisting of permutations. Here, we construct an
![]() $H_n(0)$
-module that is isomorphic to
$H_n(0)$
-module that is isomorphic to
![]() $\mathsf {M}_P$
and has a tableau basis.
$\mathsf {M}_P$
and has a tableau basis.
For a skew partition
![]() $\lambda / \mu $
of size n, consider the bijection
$\lambda / \mu $
of size n, consider the bijection
Let
![]() $\widetilde {f}: \mathbb C\mathrm {SYT}(\lambda /\mu ) \rightarrow \mathsf {M}_{\mathsf {poset}(\tau _0^{\lambda /\mu })}$
be the
$\widetilde {f}: \mathbb C\mathrm {SYT}(\lambda /\mu ) \rightarrow \mathsf {M}_{\mathsf {poset}(\tau _0^{\lambda /\mu })}$
be the
![]() $\mathbb C$
-linear isomorphism obtained by extending f by linearity. We endow
$\mathbb C$
-linear isomorphism obtained by extending f by linearity. We endow
![]() $\mathbb C\mathrm {SYT}(\lambda /\mu )$
with an
$\mathbb C\mathrm {SYT}(\lambda /\mu )$
with an
![]() $H_n(0)$
-module structure by letting
$H_n(0)$
-module structure by letting
One can see that for
![]() $T \in \mathrm {SYT}(\lambda /\mu )$
and
$T \in \mathrm {SYT}(\lambda /\mu )$
and
![]() $1 \le i \le n-1$
,
$1 \le i \le n-1$
,
 $$\begin{align*}\pi_i \cdot T = \begin{cases} T & \text{if }i\text{ is strictly left of }i+1\text{ in }T,\\ 0 & \text{if }i\text{ and }i+1\text{ are in the same column of }T,\\ s_i \cdot T & \text{if }i\text{ is strictly right of }i + 1\text{ in }T. \end{cases} \end{align*}$$
$$\begin{align*}\pi_i \cdot T = \begin{cases} T & \text{if }i\text{ is strictly left of }i+1\text{ in }T,\\ 0 & \text{if }i\text{ and }i+1\text{ are in the same column of }T,\\ s_i \cdot T & \text{if }i\text{ is strictly right of }i + 1\text{ in }T. \end{cases} \end{align*}$$
Here,
![]() $s_i \cdot T$
is the tableau obtained from T by swapping i and
$s_i \cdot T$
is the tableau obtained from T by swapping i and
![]() $i+1$
. We denote the resulting module by
$i+1$
. We denote the resulting module by
![]() $X_{\lambda /\mu }$
. By Theorem 5.5, we have
$X_{\lambda /\mu }$
. By Theorem 5.5, we have
-
•
 $\mathsf {M}_P \cong X_{\mathrm {sh}(\tau _P)}$
for
$\mathsf {M}_P \cong X_{\mathrm {sh}(\tau _P)}$
for
 $P \in \mathsf {RSP}_n$
, and
$P \in \mathsf {RSP}_n$
, and -
•
 $X_{\lambda /\mu } \not \cong X_{\nu /\kappa }$
for distinct skew partitions
$X_{\lambda /\mu } \not \cong X_{\nu /\kappa }$
for distinct skew partitions
 $\lambda /\mu $
,
$\lambda /\mu $
,
 $\nu /\kappa $
of size n.
$\nu /\kappa $
of size n.
Therefore,
![]() $X_{\mathrm {sh}(\tau _P)}$
can be viewed as a representative of the isomorphism class of
$X_{\mathrm {sh}(\tau _P)}$
can be viewed as a representative of the isomorphism class of
![]() $\mathsf {M}_P$
in the category
$\mathsf {M}_P$
in the category
![]() $H_n(0)\text{-}\mathbf {mod}$
.
$H_n(0)\text{-}\mathbf {mod}$
.
Remark A.1. (1) For a composition
![]() $\alpha $
, Searles [Reference Searles32] constructed an indecomposable
$\alpha $
, Searles [Reference Searles32] constructed an indecomposable
![]() $0$
-Hecke module
$0$
-Hecke module
![]() $\mathsf {X}_\alpha $
whose image under the quasisymmetric characteristic is an extended Schur function. In particular, when
$\mathsf {X}_\alpha $
whose image under the quasisymmetric characteristic is an extended Schur function. In particular, when
![]() $\alpha $
is a partition, our
$\alpha $
is a partition, our
![]() $X_\alpha $
is identical to
$X_\alpha $
is identical to
![]() $\mathsf {X}_{\alpha }$
.
$\mathsf {X}_{\alpha }$
.
(2) For a generalized composition
![]() ${\boldsymbol {\unicode{x3b1} }}$
, let
${\boldsymbol {\unicode{x3b1} }}$
, let
![]() $\lambda /\mu $
be a unique skew partition satisfying the conditions that
$\lambda /\mu $
be a unique skew partition satisfying the conditions that
![]() ${\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu ) = {\boldsymbol {\unicode{x3b1} }}$
and
${\boldsymbol {\unicode{x3b1} }}_{\mathrm {proj}}(\lambda /\mu ) = {\boldsymbol {\unicode{x3b1} }}$
and
![]() $\lambda /\mu $
is a ribbon. Then,
$\lambda /\mu $
is a ribbon. Then,
![]() $X_{\lambda /\mu } \cong \mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
.
$X_{\lambda /\mu } \cong \mathbf {P}_{\boldsymbol {\unicode{x3b1} }}$
.
The following proposition shows how
![]() $X_{\lambda /\mu }$
’s behave with respect to induction product, restrictions and (anti-)automorphism twists of
$X_{\lambda /\mu }$
’s behave with respect to induction product, restrictions and (anti-)automorphism twists of
![]() $\unicode{x3c6} $
and
$\unicode{x3c6} $
and
![]() ${\widehat {\unicode{x3b8} }}$
.
${\widehat {\unicode{x3b8} }}$
.
Proposition A.2. We have the following isomorphisms.
-
(1) For skew partitions
 $\lambda /\mu $
of size n and
$\lambda /\mu $
of size n and
 $\nu /\kappa $
of size m,
$\nu /\kappa $
of size m,  $$\begin{align*}X_{\lambda/\mu} \boxtimes X_{\nu/\kappa} \cong X_{\lambda/\mu \star \nu/\kappa} \quad \text{as }H_{n+m}(0)\text{-modules.} \end{align*}$$
$$\begin{align*}X_{\lambda/\mu} \boxtimes X_{\nu/\kappa} \cong X_{\lambda/\mu \star \nu/\kappa} \quad \text{as }H_{n+m}(0)\text{-modules.} \end{align*}$$
-
(2) For a skew partition
 $\lambda /\mu $
of size n and
$\lambda /\mu $
of size n and
 $1 \leq k \leq n-1$
,
$1 \leq k \leq n-1$
,  $$\begin{align*}X_{\lambda/\mu} \downarrow_{H_k(0) \otimes H_{n-k}(0)} \cong \bigoplus_{\substack{|\nu/\mu| = k \\ \mu \subset \nu \subset \lambda}} X_{\overline{\nu/\mu}} \otimes X_{\overline{\lambda/\nu}} \quad \text{as }H_k(0) \otimes H_{n-k}(0)\text{-modules}. \end{align*}$$
$$\begin{align*}X_{\lambda/\mu} \downarrow_{H_k(0) \otimes H_{n-k}(0)} \cong \bigoplus_{\substack{|\nu/\mu| = k \\ \mu \subset \nu \subset \lambda}} X_{\overline{\nu/\mu}} \otimes X_{\overline{\lambda/\nu}} \quad \text{as }H_k(0) \otimes H_{n-k}(0)\text{-modules}. \end{align*}$$
Here,
 $\overline {\nu /\mu }$
and
$\overline {\nu /\mu }$
and
 $\overline {\lambda /\nu }$
denote the basic skew partitions whose Young diagrams are obtained from
$\overline {\lambda /\nu }$
denote the basic skew partitions whose Young diagrams are obtained from
 $\mathtt {yd}(\nu /\mu )$
and
$\mathtt {yd}(\nu /\mu )$
and
 $\mathtt {yd}(\lambda /\nu )$
, respectively, by removing empty rows and empty columns.
$\mathtt {yd}(\lambda /\nu )$
, respectively, by removing empty rows and empty columns. -
(3) For a skew partition
 $\lambda /\mu $
of size n,
$\lambda /\mu $
of size n,  $$\begin{align*}\mathbf{T}^{+}_\unicode{x3c6}(X_{\lambda/\mu}) \cong X_{(\lambda/\mu)^\circ} \quad \text{and} \quad \mathbf{T}^{-}_{\widehat{\unicode{x3b8}}}(X_{\lambda/\mu}) \cong X_{\lambda^{\mathrm{t}}/\mu^{\mathrm{t}}}. \end{align*}$$
$$\begin{align*}\mathbf{T}^{+}_\unicode{x3c6}(X_{\lambda/\mu}) \cong X_{(\lambda/\mu)^\circ} \quad \text{and} \quad \mathbf{T}^{-}_{\widehat{\unicode{x3b8}}}(X_{\lambda/\mu}) \cong X_{\lambda^{\mathrm{t}}/\mu^{\mathrm{t}}}. \end{align*}$$
Here,
 $(\lambda /\mu )^\circ $
is the skew partition whose Young diagram is obtained by rotating
$(\lambda /\mu )^\circ $
is the skew partition whose Young diagram is obtained by rotating
 $\mathtt {yd}(\lambda /\mu )$
by
$\mathtt {yd}(\lambda /\mu )$
by
 $180^\circ $
.
$180^\circ $
.
Proof. The first assertion follows from [Reference Jung, Kim, Lee and Oh19, Lemma 4], the second from [Reference Jung, Kim, Lee and Oh19, Theorem 2] and the third from [Reference Jung, Kim, Lee and Oh19, Theorem 4].
Acknowledgements
The authors are deeply grateful to the anonymous referees for their meticulous reading of the manuscript and their invaluable advice. We would especially like to express our sincere thanks to the referee for bringing references [Reference Lascoux, Leclerc and Thibon24, Reference Lascoux and Schützenberger25] and the contents of Section 7.3 to our attention.
Competing interest
The authors have no competing interest to declare.
Funding statement
The first author was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean Government (No. NRF-2020R1A5A1016126) and Basic Science Research Program through NRF funded by the Ministry of Education (No. RS-2023-00240377). The second author was supported by NRF grant funded by the Korean Government (No. NRF-2020R1F1A1A01071055), Basic Science Research Program through NRF funded by the Ministry of Education (No. RS-2023-00271282), NRF grant funded by the Korea government (MSIT) (No. RS-2024-00342349), the Sogang University Research Grant of 2024 (No. 202412001.01), and the BK21 FOUR program through the NRF under the Department of Mathematics at Sogang University ‘Nurturing team for creative and convergent mathematical science talents’. The third author was supported by NRF grant funded by the Korean Government (No. NRF-2020R1F1A1A01071055) and by NRF grant funded by the Korea government (MSIT) (No. RS-2024-00342349).