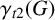GRAPHS WITH SEMITOTAL DOMINATION NUMBER HALF THEIR ORDER

Abstract

In an isolate-free graph G, a subset S of vertices is a semitotal dominating set of G if it is a dominating set of G and every vertex in S is within distance 2 of another vertex of S. The semitotal domination number of G, denoted by $\gamma _{t2}(G)$, is the minimum cardinality of a semitotal dominating set in G. Goddard, Henning and McPillan [‘Semitotal domination in graphs’, Utilitas Math. 94 (2014), 67–81] characterised the trees and graphs of minimum degree 2 with semitotal domination number half their order. In this paper, we characterise all graphs whose semitotal domination number is half their order.

1 Introduction

In this paper, we consider only finite simple undirected graphs. A subset D of vertices in a graph G is a dominating set of G if every vertex of $V(G)\setminus D$ is adjacent to a vertex in D. The minimum cardinality $\gamma (G)$ of a dominating set is called the dominating number. Similarly, D is a total dominating set of G if every vertex of $V(G)$ is adjacent to a vertex in D and the minimum cardinality $\gamma _{t}(G)$ of a total dominating set is called the total dominating number of G. The study of a total dominating set is meaningful only in an isolate-free graph. Since 1997, domination and its variations have been extensively studied (see, for example, [2, 5, 10]).

Semitotal domination, introduced by Goddard et al. [1] is a relaxed form of total domination. A subset D of vertices in an isolate-free graph G is a semitotal dominating set, abbreviated semi-TD-set, of G if it is a dominating set of G and every vertex in D is within distance 2 of another vertex of D. The semitotal domination number of G, denoted by $\gamma _{t2}(G)$ , is the minimum cardinality of a semi-TD-set in G. We refer to a minimum semi-TD-set of G as a $\gamma _{t2}(G)$ -set.

Two edges in a graph G are independent if they are not adjacent in G. A matching in G is a set of pairwise independent edges. The matching number of G is the maximum cardinality of a matching in G.

Since every total dominating set of an isolate-free graph G is a semi-TD-set of G and every semi-TD-set of an isolate-free graph G is a dominating set of G, we observe that $\gamma (G)\leq \gamma _{t2}(G)\leq \gamma _{t}(G)$ . However, the semitotal domination number is very different from the domination and total domination number. For example, the total domination number cannot be compared with the matching number, while the semitotal domination number is comparable with the matching number and cannot be greater than the matching number plus one (see [6, 7]). That makes the study of the semitotal domination number interesting.

There has been much work to determine bounds for the semitotal domination number of graphs (see, for example, [1, 3, 4, 7–9, 11, 12]). Goddard et al. [1] proved that if G is a connected graph of order $n\geqslant 4$ , then $\gamma _{t2}(G)\leqslant {n}/{2}$ , and characterised the trees and graphs of minimum degree 2 achieving this bound.

Theorem 1.1 [1].

If G is a connected graph of order $n\geqslant 4$ , then $\gamma _{t2}(G)\leq {n}/{2}$ .

We aim to characterise the infinite families of graphs that achieve equality in the bound in Theorem 1.1. In Section 2, we give some basic definitions and some useful results as preliminaries. In Section 3, we give our main theorem characterising the graphs whose semitotal domination number is half their order (Theorem 3.1).

2 Preliminaries

In this section, we introduce some basic definitions and some useful results.

Let G be a connected finite simple undirected graph with vertex set $V(G)$ , edge set $E(G)$ and order $n=|V(G)|$ . Let u, v be two vertices in $V(G)$ . If $uv\in E(G)$ , then we say u, v are adjacent, u is a neighbour of v and vice versa. We denote by $N_G(v)$ the neighbourhood of v and by $N_G[v]$ the closed neighbourhood of v. The degree of v is $d_G(v)=|N_G(v)|$ . Denote by $\delta (G)$ the minimum degree of G. A leaf of G is a vertex of degree 1, a support vertex of G is a vertex adjacent to at least one leaf and a strong support vertex of G is a support vertex adjacent to at least two leaves. Denote the sets of leaves, support vertices and strong support vertices of G by $L(G)$ , $S(G)$ and $S'(G)$ , respectively.

For a subset S of $V(G)$ and a vertex v of $V(G)$ , we denote $N_{S}(v)=N_{G}(v)\cap S$ , $G[S]$ as the subgraph of G induced by S, and $G-S$ as the graph obtained from G by deleting the vertices in S. Moreover, denote $N_{H}(v)=N_{V(H)}(v)$ , where H is a subgraph of G. We call a path connecting vertices u and v a $(u,v)$ -path. The distance $d_G(u,v)$ between u and v is the length of a shortest $(u,v)$ -path in G. As usual, a cycle and a path of order n are denoted by $C_n$ and $P_n$ , respectively. For a positive integer r, $[r]$ denotes $\{1,\ldots ,r\}$ . If there is no confusion, the subscript G is omitted.

Seven graphs $G_1$ – $G_7$ are shown in Figure 1. Let U be a connected graph and for each vertex v of U, add either a $P_2$ , or a $P_4$ or a $C_4$ , and identify v with one end of the path or one vertex of the cycle. Let G denote the resulting graph and let $\mathcal {G}$ be the family of all such graphs G that are not isomorphic to $P_2$ . We call the graph U used to construct the graph G an underlying graph of G. A graph of $\mathcal {G}$ is illustrated in Figure 2. Let $\mathcal {G}_1$ be the subfamily of $\mathcal {G}$ for which every vertex in every U has $C_4$ added.

Figure 1 Eleven special graphs.

Figure 2 A graph of $\mathcal {G}$ .

Goddard et al. [1] provided a characterisation of the graphs whose minimum degree is at least two and whose semi-total domination number is half their order.

Theorem 2.1 [1].

Let G be a connected graph of order $n\geq 4$ with minimum degree at least 2. Then $\gamma _{t2}(G)={n}/{2}$ if and only if G is either $C_6$ or $C_8$ or a spanning subgraph of $K_4$ or a graph of $\mathcal {G}_1$ .

We have the following observation.

Observation 2.2. Let G be a graph of $\{G_3,G_4,G_5,G_6,G_7\}\cup (\mathcal {G}\setminus \{P_4,P_6\})$ and v be a support vertex of G but not in U, where U is an underlying graph of G if $G\in \mathcal {G}$ . Then $\gamma _{t2}(G-N_G[v])\leq \gamma _{t2}(G)-2$ .

3 The main theorem

Theorem 3.1. Let G be a connected graph of order n. Then $\gamma _{t2}(G)={n}/{2}$ if and only if $G\in \{K_{1,3},G_1,G_2,K_4,C_6,C_8,G_3,G_4,G_5,G_6,G_7\}\cup \mathcal {G}$ .

Proof. Suppose that G is a connected graph of order n. If G is one of the graphs listed above, then it is easy to verify that $\gamma _{t2}(G)= {n}/{2}$ . Thus, it suffices to prove the necessity. Assume $\gamma _{t2}(G)={n}/{2}$ . We proceed by induction on the order n. Since $\gamma _{t2}(G)$ is an integer of size at least 2, n is an even number of size at least 4. If $n=4$ , then G is a spanning subgraph of $K_4$ , implying that $G\in \{P_4,C_4,K_{1,3},G_1,G_2,K_4\}$ . We note that $\{P_4,C_4\}\subseteq \mathcal {G}$ . The desired result follows for $n=4$ and we may now assume that $n\geq 6$ .

We prove two claims relating to the set of support vertices of G.

Claim 1. Let u be a vertex of $S(G)$ . Then there exists a $\gamma _{t2}(G)$ -set containing u.

Proof. Let u be a vertex of $S(G)$ and D be a $\gamma _{t2}(G)$ -set. If $u\in D$ , then the claim follows. Thus, we may assume that $u\notin D$ . Let $u_1$ be a leaf in G adjacent to u. To dominate $u_1$ , we must have $u_1\in D$ . Since D is a semi-TD-set of G, we note that $(N(u)\setminus \{u_1\})\cap D\neq \emptyset $ . Hence, $(D\setminus \{u_1\})\cup \{u\}$ is a $\gamma _{t2}(G)$ -set, as desired.

Claim 2. $S'(G)=\emptyset $ .

Proof. Suppose to the contrary that $S'(G)\neq \emptyset $ . Let u be a vertex of $S'(G)$ , and $u_1$ and $u_2$ be two leaves adjacent to u. Let $G'=G-\{u_1\}$ . Then $G'$ is a connected graph of order $n'=n-1$ . Since $n\geq 6$ , $n'\geq 5$ . By Theorem 1.1, $\gamma _{t2}(G')\leq {n'}/{2}$ . Note that $u\in S(G')$ . Arguments similar to Claim 1 show that there is a $\gamma _{t2}(G')$ -set containing u, say $D'$ . Observe that $D'$ is also a semi-TD-set of G. Thus, $\gamma _{t2}(G)\leq |D'|=\gamma _{t2}(G')\leq {n'}/{2}<{n}/{2}$ , which is a contradiction.

Recall that $n\geq 6$ . If $\delta (G)\geq 2$ , then G is either $C_6$ or $C_8$ or a graph of $\mathcal {G}_1$ by Theorem 2.1. It follows that $G\in \{C_6,C_8\}\cup \mathcal {G}$ , as desired. Thus, it remains to consider the case when $\delta (G)=1$ . Let $v_1$ be a vertex of degree 1 and $v_2$ be the support vertex adjacent to $v_1$ . Let H be a component of $G-\{v_1,v_2\}$ and $G'=G-V(H)$ . Then $G'$ is a connected graph of order $n'=n-|V(H)|$ . Note that $\{v_1,v_2\}\subseteq V(G')$ . If $n'=3$ or $|V(H)|=1$ , then $v_2\in S'(G)$ , which contradicts Claim 2. Thus, $n'=2$ or $n'\geq 4$ , and $|V(H)|\geq 2$ . When $n'=2$ , let $D_1=\{v_2\}$ . When $n'\geq 4$ , it follows from Theorem 1.1 that $\gamma _{t2}(G')\leq {n'}/{2}$ . Analogous arguments as in Claim 1 show that there exists a $\gamma _{t2}(G')$ -set containing $v_2$ , say $D_1$ . Hence, no matter what $n'$ is, we have $v_2\in D_1$ and $|D_1|\leq {n'}/{2}$ .

Claim 3. If $|V(H)|\leq 3$ , then $G\in \mathcal {G}$ .

Proof. Assume $|V(H)|\leq 3$ . Since $n\geq 6$ , $n'=n-|V(H)|\geq 3$ . Combined with the fact that $n'=2$ or $n'\geq 4$ and $|V(H)|\geq 2$ , we have $n'\geq 4$ and $|V(H)|=2$ or 3. It follows that $D_1$ is a $\gamma _{t2}(G')$ -set containing $v_2$ and there exists a vertex w in H such that $N_H[w]=V(H)$ . Thus, $D_1\cup \{w\}$ is a semi-TD-set of G. Further, $\gamma _{t2}(G)\ {\leq}\ |D_1|\ {+}\ 1\ {\leq}\ {n'}/{2}\ {+}\ 1\ {\leq}\ {(n-|V(H)|)}/{2}\ {+}\ 1\ {\leq}\ {(n-2)}/{2}\ {+}\ 1\ {\leq}\ {n}/{2}$ . Since $\gamma _{t2}(G)={n}/{2}$ , we note that $|D_1|={n'}/{2}$ and $|V(H)|=2$ . Let $H=w_1w_2$ . Without loss of generality, consider $v_2w_1\in~E(G)$ . If $v_2w_2\in E(G)$ , then $D_1$ is a semi-TD-set of G. Further, $\gamma _{t2}(G)\leq |D_1|\leq {n'}/{2}<{n}/{2}$ , which is a contradiction. Thus, $v_2w_2\notin E(G)$ .

By the inductive hypothesis, $G'\in \{K_{1,3},G_1,G_2,K_4,C_6,C_8,G_3,G_4,G_5,G_6,G_7\}\cup \mathcal {G}$ . Observe that $v_2\in S(G')$ . Combined with Claim 2, $G'\in \{G_1,G_3,G_4,G_5,G_6,G_7\}\cup \mathcal {G}$ . If $G'\cong G_1$ , then $n=6$ and $\{v_2,w_1\}$ is a semi-TD-set of G, which contradicts $\gamma _{t2}(G)=~{n}/{2}$ . Thus, $G'\in \{G_3,G_4,G_5,G_6,G_7\}\cup \mathcal {G}$ . Note that if $G'\in \{P_4,P_6\}$ , then $G\in \mathcal {G}$ , as desired. Thus, we may assume that $G'\notin \{P_4,P_6\}$ . If $v_2\notin V(U)$ , where U is an underlying graph of $G'$ when $G'\in \mathcal {G}$ , then there is a $\gamma _{t2}(G'-N_{G'}[v_2])$ -set, say $D'$ , with size at most $\gamma _{t2}(G')-2$ by Observation 2.2. Observe that $D'\cup \{v_2,w_1\}$ is a semi-TD-set of G. Thus, $\gamma _{t2}(G)\leq |D'|+2\leq \gamma _{t2}(G')={n'}/{2}<{n}/{2}$ , which is a contradiction. Hence, $G'\in \mathcal {G}$ and $v_2\in V(U)$ for any underlying graph U of $G'$ . Therefore, $G\in \mathcal {G}$ .

By Claim 3, we may assume that $|V(H)|\geq 4$ for any component H of $G-\{v_1,v_2\}$ , for otherwise, the desired result follows. Let $D_2$ be a $\gamma _{t2}(H)$ -set. By Theorem 1.1, $|D_2|\leq {|V(H)|}/{2}$ . Observe that $D_1\cup D_2$ is a semi-TD-set of G. Thus, $\gamma _{t2}(G)\leq |D_1|+|D_2|\leq {n'}/{2}+{|V(H)|}/{2}={n}/{2}$ . Since $\gamma _{t2}(G)={n}/{2}$ , we note that $|D_1|={n'}/{2}$ and $|D_2|=~{|V(H)|}/{2}$ . Applying the inductive hypothesis to H and $G'$ of order $n'\geq 4$ shows that they both belong to $ \{K_{1,3},G_1,G_2,K_4,C_6,C_8,G_3,G_4,G_5,G_6,G_7\}\cup \mathcal {G}$ . Let $w_1$ be a vertex in H adjacent to $v_2$ . We prove the following claim.

Claim 4. If $H\in \{K_{1,3},G_1,G_2,K_4,C_6,C_8,G_3,G_4,G_5,G_6,G_7\}$ , then $G\in \{G_3,G_6,G_7\}$ .

Proof. When $H\in \{K_{1,3},G_1,G_2,K_4\}$ , there exists a vertex w in H such that $N_{H}[w]=V(H)$ . Recall that $v_2\in D_1$ . Thus, $D_1\cup \{w\}$ is a semi-TD-set of G. Further, $\gamma _{t2}(G)\leq |D_1|+1\leq {n'}/{2}+1={(n-4)}/{2}+1<{n}/{2}$ , which is a contradiction.

When $H\cong C_6$ , let $w_2$ and $w_3$ be the two vertices with a distance of 2 from $w_1$ in H. Observe that if $D_1$ is a $\gamma _{t2}(G')$ -set or $|N_H(v_2)|\geq 2$ , then $D_1\cup \{w_2,w_3\}$ is a semi-TD-set of G. Further, $\gamma _{t2}(G)\leq |D_1|+2\leq {n'}/{2}+2={(n-6)}/{2}+2<{n}/{2}$ , which is a contradiction. Hence, $D_1$ is not a $\gamma _{t2}(G')$ -set and $|N_H(v_2)|=1$ . It follows that $n'=2$ and $G\cong G_3$ .

When $H\cong C_8$ , without loss of generality, we can assume $H=w_1w_2\cdots w_8w_1$ . Then $D_1\cup \{w_2,w_5,w_7\}$ is a semi-TD-set of G. Thus, $\gamma _{t2}(G)\leq |D_1|+3\leq {n'}/{2}+3={(n-8)}/{2}+3<{n}/{2}$ , which is a contradiction.

When $H\in \{G_3,G_4,G_5,G_6,G_7\}$ , we note that $S(H)\neq \emptyset $ . If there exists a vertex $u\in S(H)$ such that $d_{G}(v_2,u)\leq 2$ , then $D_1\cup D'\cup \{u\}$ is a semi-TD-set of G, where $D'$ is a $\gamma _{t2}(H-N_H[u])$ -set. By Observation 2.2, $|D'|\leq \gamma _{t2}(H)-2$ . It follows that $\gamma _{t2}(G)\leq |D_1|+|D'|+1\leq {n'}/{2}+\gamma _{t2}(H)-1={(n-|V(H)|)}/{2}+{|V(H)|}/{2}-1<{n}/{2}$ , which is a contradiction. Thus, $d_{G}(v_2,u)\geq 2$ for any vertex u of $S(H)$ .

If $H\cong G_3$ , then $|S(H)|=1$ . Let $S(H)=\{x\}$ , $x_1$ be the vertex of degree 3 in H, and $x_2,\ldots ,x_6$ be the five vertices in H that are not adjacent to x, where $x_ix_{i+1}\in E(H)$ for $i\in [5]$ . It follows that $N_{H}[x]\cap N(v_2)=\emptyset $ . So $\{x_2,\ldots ,x_6\}\cap N(v_2)\neq \emptyset $ . Without loss of generality, consider $\{x_2,x_3,x_4\}\cap N(v_2)\neq \emptyset $ . Then $D_1\cup \{x,x_3,x_6\}$ is a semi-TD-set of G. Further, $\gamma _{t2}(G)\leq |D_1|+3\leq {n'}/{2}+3={(n-8)}/{2}+3<{n}/{2}$ , which is a contradiction. Thus, $H\ncong G_3$ and $H\in \{G_4,G_5,G_6,G_7\}$ .

Since $d_{G}(v_2,u)\geq 2$ for any vertex u of $S(H)$ , it follows that

$$ \begin{align*}\bigg(\bigcup_{u\in S(H)}N_{H}[u]\bigg)\cap N(v_2)=\emptyset \quad\text{and}\quad N_{H}(v_2)\subseteq V(H)\setminus \bigg(\bigcup_{u\in S(H)}N_{H}[u]\bigg).\end{align*} $$

Next, observe that if $D_1$ is a $\gamma _{t2}(G')$ -set or $|N_{H}(v_2)|\geq 2$ , then there exists a vertex y in $V(H)\setminus (\bigcup _{u\in S(H)}N_{H}[u])$ such that $D_1\cup S(H)\cup \{y\}$ is a semi-TD-set of G and $\gamma _{t2}(G)\leq |D_1|+|S(H)|+1\leq {n'}/{2}+{(|V(H)|-4)}/{2}+1={(n-|V(H)|)}/{2}+{(|V(H)|-4)}/{2}+1<{n}/{2}$ , which is a contradiction. Thus, $D_1$ is not a $\gamma _{t2}(G')$ -set and $|N_{H}(v_2)|=1$ , implying that $n'=2$ . Hence, $H\in \{G_4,G_5,G_6\}$ and $G\in \{G_6,G_7\}$ .

By Claim 4, we may assume that $H\in \mathcal {G}$ for any component H of $G-\{v_1,v_2\}$ , for otherwise, the desired result follows. It follows that $G'\in \{P_2,G_4,G_5\}\cup \mathcal {G}$ . According to the structure of H, there exists a $\gamma _{t2}(H)$ -set containing $w_1$ . Without loss of generality, we can assume $w_1\in D_2$ . If $G'\in \{G_4,G_5\}$ , then there exists a vertex x in $V(G')\setminus (\bigcup _{u\in S(G')}N_{G'}[u])$ such that $D_2\cup S(G')\cup \{x\}$ is a semi-TD-set of G. It follows that $\gamma _{t2}(G)\leq |D_2|+|S(G')|+1={|V(H)|}/{2}+3={(n-8)}/{2}+3<{n}/{2}$ , which is a contradiction. Thus, $G'\notin \{G_4,G_5\}$ and $G'\in \{P_2\}\cup \mathcal {G}$ .

Claim 5. If $G'\in \mathcal {G}$ , then there exists an underlying graph $U_1$ of $G'$ such that $v_2\in~V(U_1)$ .

Proof. Assume $G'\in \mathcal {G}$ . Note that $v_2\in S(G')$ . If $G'\in \{P_4,P_6\}$ , then there exists an underlying graph of $G'$ such that $v_2$ is in it, as desired. Thus, we may assume that $G'\notin \{P_4,P_6\}$ . Let $U_1$ be an underlying graph of H. If $v_2\notin V(U_1)$ , then $\gamma _{t2}(G'-N_{G'}[v_2])\leq \gamma _{t2}(G')-2$ by Observation 2.2. Let $D'$ be a $\gamma _{t2}(G'-N_{G'}[v_2])$ -set. Then $D'\cup \{v_2\}\cup D_2$ is a semi-TD-set of G. Further, $\gamma _{t2}(G)\leq |D'|+1+|D_2|\leq \gamma _{t2}(G')-2+1+{|V(H)|}/{2} \leq {n'}/{2}-1+{|V(H)|}/{2}<{n}/{2}$ , which is a contradiction. Thus, $v_2\in V(U_1)$ .

We proceed with the following final claim.

Claim 6. If $|V(H)|=4$ , then $G\in \mathcal {G}$ .

Proof. Assume $|V(H)|=4$ . Since $H\in \mathcal {G}$ , we note that $H\in \{P_4,C_4\}$ . Let $V(H)=\{x_1, x_2,x_3,x_4\}$ , where $x_ix_{i+1}\in E(H)$ for $i\in [3]$ . Suppose $v_2x_1\in E(G)$ . Then ${N_{H}(v_2)=\{x_1\}}$ , otherwise $D_1\cup \{x_3\}$ is a semi-TD-set of G and $\gamma _{t2}(G)\leq |D_1|+1\leq {n'}/{2}+1={(n-4)}/{2}+1<{n}/{2}$ , which is a contradiction. When $G'\cong P_2$ , we have $G\in \mathcal {G}$ . When $G'\in \mathcal {G}$ , combined with Claim 5, we have $G\in \mathcal {G}$ . Similarly, if $v_2x_4\in E(G)$ , then $G\in \mathcal {G}$ . Thus, we may assume that $v_2x_1\notin E(G)$ and $v_2x_4\notin E(G)$ . It follows that $N_{H}(v_2)\subseteq \{x_2,x_3\}$ . When $H\cong P_4$ , combine $G'\in \{P_2\}\cup \mathcal {G}$ with Claim 5 to get $G\in \mathcal {G}$ . When $H\cong C_4$ , analogous arguments as the case of $v_2x_1\in E(G)$ show that $G\in \mathcal {G}$ .

By Claim 6, we may assume that $|V(H)|\geq 6$ , for otherwise, the desired result follows. Let $U_2$ be an underlying graph of H. If $N_{H}(v_2)\subseteq V(U_2)$ , then it follows from $G'\in \{P_2\}\cup \mathcal {G}$ and Claim 5 that $G\in \mathcal {G}$ . Thus, it remains to discuss the case of $N_{H}(v_2)\nsubseteq V(U_2)$ . Without loss of generality, consider $w_1\notin V(U_2)$ .

Suppose that $w_1$ is on a $P_4$ -addition. Let $x_2$ be the support vertex of H on this $P_4$ -addition. Then $w_1\in N_{H}[x_2]$ . If $H\notin \{P_4,P_6\}$ , then $\gamma _{t2}(H-N_H[x_2])\leq \gamma _{t2}(H)-2$ by Observation 2.2. Let $D'$ be a $\gamma _{t2}(H-N_H[x_2])$ -set. Then $D_1\cup D'\cup \{x_2\}$ is a semi-TD-set of G. Further, $\gamma _{t2}(G)\leq |D_1|+|D'|+1\leq {n'}/{2}+ \gamma _{t2}(H)-1={(n-|V(H)|)}/{2} +{|V(H)|}/{2}-1 <{n}/{2}$ , which is a contradiction. Thus, $H\in \{P_4,P_6\}$ . Recall that $|V(H)|\geq 6$ . So $H\cong P_6$ .

Without loss of generality, let $H=x_1x_2\cdots x_6$ . Then $w_1=x_1$ , or $x_2$ or $x_3$ . If $\{x_4,x_5,x_6\}\cap N_{H}(v_2)\neq \emptyset $ , then $D_1\cup \{x_2,x_5\}$ is a semi-TD-set of G. Further, $\gamma _{t2}(G)\leq |D_1|+2\leq {n'}/{2}+2={(n-6)}/{2} +2 <{n}/{2}$ , which is a contradiction. Thus, $\{x_4,x_5,x_6\}\cap N_{H}(v_2)=\emptyset $ . When $v_2x_1\notin E(G)$ , we note that $N_{H}(v_2)\subseteq \{x_2,x_3\}$ . Combining $G'\in \{P_2\}\cup \mathcal {G}$ and Claim 5 gives $G\in \mathcal {G}$ . When $v_2x_1\in E(G)$ , we have $G'\cong P_2$ and $N_{H}(v_2)=\{x_1\}$ , otherwise $D_1\cup \{x_3,x_5\}$ is a semi-TD-set of G and $\gamma _{t2}(G)\leq |D_1|+2\leq {n'}/{2}+2={(n-6)}/{2}+2 <{n}/{2}$ , which is a contradiction. Observe that $G\cong P_8\in \mathcal {G}$ .

Next, suppose that $w_1$ is on a $C_4$ -addition. Let y be the farthest vertex of H from $U_2$ on this $C_4$ -addition. Then $w_1\in N_{H}[y]$ . If $|V(H)|\geq 8$ , then $\gamma _{t2}(H-N_{H}[y])\leq \gamma _{t2}(H)-2$ by the structure of H. Let $D'$ be a $\gamma _{t2}(H-N_H[y])$ -set. Observe that $D_1\cup D'\cup \{y\}$ is a semi-TD-set of G. Further,

$$ \begin{align*}\gamma_{t2}(G)\leq |D_1|+|D'|+1\leq{n'}/{2}+\gamma_{t2}(H)-1={(n-|V(H)|)}/{2} +{|V(H)|}/{2}-1 <{n}/{2}, \end{align*} $$

which is a contradiction. Thus, $|V(H)|=6$ . It follows that H is constructed by the underlying graph $P_2$ with a $P_2$ -addition and a $C_4$ -addition. Note that $D_1$ is not a $\gamma _{t2}(G')$ -set and $|N_H(v_2)|=1$ , otherwise $\gamma _{t2}(G)\leq |D_1|+2\leq {(n-6)}/{2}+2<{n}/{2}$ , which is a contradiction. Hence, $G'\cong P_2$ and $G\in \{G_4,G_5\}$ .

Finally, suppose that any vertex of $N_{H}(v_2)$ is not on the $P_4$ -additions and $C_4$ -additions. Thus, $w_1$ is on a $P_2$ -addition. Recall that $|V(H)|\geq 6$ . Observe that if $D_1$ is a $\gamma _{t2}(G')$ -set or $|N_H(v_2)|\geq 2$ , then we have $\gamma _{t2}(G)\leq |D_1|+\gamma _{t2}(H)-1\leq {(n-|V(H)|)}/{2}+\gamma _{t2}(H)-1<{n}/{2}$ , which is a contradiction. Thus, $D_1$ is not a $\gamma _{t2}(G')$ -set and $|N_H(v_2)|=1$ . It follows that $G'\cong P_2$ . Therefore, $G\in \mathcal {G}$ .