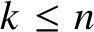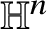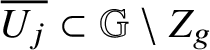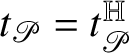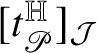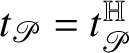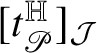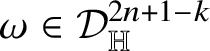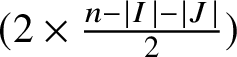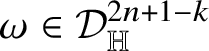1 Introduction
The celebrated Rademacher’s theorem [Reference Rademacher82] states that a Lipschitz continuous function
![]() $f:{\mathbb R}^{h}\to {\mathbb R}^{k}$
is differentiable almost everywhere in
$f:{\mathbb R}^{h}\to {\mathbb R}^{k}$
is differentiable almost everywhere in
![]() ${\mathbb R}^{h}$
; in particular, the graph of f in
${\mathbb R}^{h}$
; in particular, the graph of f in
![]() ${\mathbb R}^{h+k}$
has an h-dimensional tangent plane at almost all of its points. One of the consequences of Rademacher’s theorem is the following Lusin-type result, which stems from Whitney’s extension theorem [Reference Whitney96]: for every
${\mathbb R}^{h+k}$
has an h-dimensional tangent plane at almost all of its points. One of the consequences of Rademacher’s theorem is the following Lusin-type result, which stems from Whitney’s extension theorem [Reference Whitney96]: for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $g\in C^{1}({\mathbb R}^{h},{\mathbb R}^{k})$
that coincides with f out of a set of measure at most
$g\in C^{1}({\mathbb R}^{h},{\mathbb R}^{k})$
that coincides with f out of a set of measure at most
![]() $\varepsilon $
. From the viewpoint of geometric measure theory, this means that Lipschitz-regular objects (functions, submanifolds, etc.) are essentially as nice as
$\varepsilon $
. From the viewpoint of geometric measure theory, this means that Lipschitz-regular objects (functions, submanifolds, etc.) are essentially as nice as
![]() $C^{1}$
-smooth ones and has profound implications; for instance, in the theory of rectifiable sets and currents [Reference Federer42, Reference Mattila72, Reference Simon90].
$C^{1}$
-smooth ones and has profound implications; for instance, in the theory of rectifiable sets and currents [Reference Federer42, Reference Mattila72, Reference Simon90].
The present article aims to develop a similar theory for submanifolds with (intrinsic) Lipschitz regularity in sub-Riemannian Heisenberg groups. Before introducing our results, we feel the need to list them at least quickly. We believe that our main result is a Rademacher-type theorem for intrinsic Lipschitz graphs, which was the main open problem since the beginning of this theory. Some applications – namely, a Lusin-type result and an area formula for intrinsic Lipschitz graphs – are provided here as well; however, we believe that further consequences are yet to come concerning, for instance, rectifiability and minimal submanifolds in Heisenberg groups. Some of the tools we develop for proving our main result are worth mentioning; in fact, we prove an extension result for intrinsic Lipschitz graphs as well as the fact that they can be uniformly approximated by smooth graphs. Both results stem from what can be considered as another contribution of the present article; that is, a new definition of intrinsic Lipschitz graphs that is equivalent to the original one, introduced by B. Franchi, R. Serapioni and F. Serra Cassano and now widely accepted. Recall, in fact, that intrinsic Lipschitz graphs in Heisenberg groups played a fundamental role in the recent proof by A. Naor and R. Young [Reference Naor and Young79] of the ‘vertical versus horizontal’ isoperimetric inequality in
![]() ${\mathbb H}^{n}$
that settled the longstanding question of determining the approximation ratio of the Goemans–Linial algorithm for the sparsest cut problem. Let us also say that our proof of Rademacher’s theorem heavily uses the language of currents in Heisenberg groups; a key result is for us (a version of) the celebrated constancy theorem [Reference Federer42, Reference Simon90, Reference Krantz and Parks65]. From the technical point of view, the use of currents constitutes the hardest part of the article; in fact, currents in Heisenberg groups are defined in terms of the complex of differential forms introduced by M. Rumin in [Reference Rumin85, Reference Rumin86], which is not easy to handle. Among other things, we had to provide a convenient basis of Rumin’s covectors that could be fruitfully employed in the computation of Rumin’s exterior derivatives. We were surprised by the fact that the use of standard Young tableaux from combinatorics proved to be crucial in performing this task.
${\mathbb H}^{n}$
that settled the longstanding question of determining the approximation ratio of the Goemans–Linial algorithm for the sparsest cut problem. Let us also say that our proof of Rademacher’s theorem heavily uses the language of currents in Heisenberg groups; a key result is for us (a version of) the celebrated constancy theorem [Reference Federer42, Reference Simon90, Reference Krantz and Parks65]. From the technical point of view, the use of currents constitutes the hardest part of the article; in fact, currents in Heisenberg groups are defined in terms of the complex of differential forms introduced by M. Rumin in [Reference Rumin85, Reference Rumin86], which is not easy to handle. Among other things, we had to provide a convenient basis of Rumin’s covectors that could be fruitfully employed in the computation of Rumin’s exterior derivatives. We were surprised by the fact that the use of standard Young tableaux from combinatorics proved to be crucial in performing this task.
It is time to introduce and discuss our results more appropriately.
1.1 Heisenberg groups and intrinsic graphs
For
![]() $n\geq 1$
, the Heisenberg group
$n\geq 1$
, the Heisenberg group
![]() ${\mathbb H}^{n}$
is the connected, simply connected and nilpotent Lie group associated with the Lie algebra
${\mathbb H}^{n}$
is the connected, simply connected and nilpotent Lie group associated with the Lie algebra
![]() ${\mathfrak h}$
with
${\mathfrak h}$
with
![]() $2n+1$
generators
$2n+1$
generators
![]() $X_{1},\dots ,X_{n},Y_{1},\dots ,Y_{n},T$
; all Lie brackets between these generators are null except for
$X_{1},\dots ,X_{n},Y_{1},\dots ,Y_{n},T$
; all Lie brackets between these generators are null except for
The algebra
![]() ${\mathfrak h}$
is stratified, as it can be decomposed as
${\mathfrak h}$
is stratified, as it can be decomposed as
![]() ${\mathfrak h}={\mathfrak h}_{1}\oplus {\mathfrak h}_{2}$
with
${\mathfrak h}={\mathfrak h}_{1}\oplus {\mathfrak h}_{2}$
with
![]() ${\mathfrak h}_{1}:=\operatorname *{\mathrm {span}}\{X_{j},Y_{j}:j=1,\dots ,n\}$
and
${\mathfrak h}_{1}:=\operatorname *{\mathrm {span}}\{X_{j},Y_{j}:j=1,\dots ,n\}$
and
![]() ${\mathfrak h}_{2}:=\operatorname *{\mathrm {span}}\{T\}$
. The first layer
${\mathfrak h}_{2}:=\operatorname *{\mathrm {span}}\{T\}$
. The first layer
![]() ${\mathfrak h}_{1}$
in the stratification is called horizontal.
${\mathfrak h}_{1}$
in the stratification is called horizontal.
It will often be convenient to identify
![]() ${\mathbb H}^{n}$
with
${\mathbb H}^{n}$
with
![]() ${\mathbb R}^{2n+1}$
by exponential coordinates
${\mathbb R}^{2n+1}$
by exponential coordinates
where
![]() $\exp :{\mathfrak h}\to {\mathbb H}^{n}$
is the exponential map and 0 is the group identity. The Heisenberg group is a homogeneous group according to [Reference Folland and Stein43]; indeed, for
$\exp :{\mathfrak h}\to {\mathbb H}^{n}$
is the exponential map and 0 is the group identity. The Heisenberg group is a homogeneous group according to [Reference Folland and Stein43]; indeed, for
![]() $\lambda>0$
the maps
$\lambda>0$
the maps
![]() $\delta _{\lambda }(x,y,t):=(\lambda x,\lambda y,\lambda ^{2} t)$
determine a one-parameter family of group automorphisms of
$\delta _{\lambda }(x,y,t):=(\lambda x,\lambda y,\lambda ^{2} t)$
determine a one-parameter family of group automorphisms of
![]() ${\mathbb H}^{n}$
called dilations. We endow
${\mathbb H}^{n}$
called dilations. We endow
![]() ${\mathbb H}^{n}$
with a left-invariant and homogeneous distance d, so that
${\mathbb H}^{n}$
with a left-invariant and homogeneous distance d, so that
It will be convenient to assume that d is rotationally invariant; that is, that
where we set
![]() $\|p\|_{\mathbb H}:=d(0,p)$
for every
$\|p\|_{\mathbb H}:=d(0,p)$
for every
![]() $p\in {\mathbb H}^{n}$
. Relevant examples of rotationally invariant distances are the well-known Carnot–Carathéodory and Korányi (or Cygan–Korányi) distances.
$p\in {\mathbb H}^{n}$
. Relevant examples of rotationally invariant distances are the well-known Carnot–Carathéodory and Korányi (or Cygan–Korányi) distances.
An intensive search for a robust intrinsic notion of
![]() $C^{1}$
or Lipschitz regularity for submanifolds was conducted in the last two decades; in fact (see [Reference Ambrosio and Kirchheim3]), the Heisenberg group
$C^{1}$
or Lipschitz regularity for submanifolds was conducted in the last two decades; in fact (see [Reference Ambrosio and Kirchheim3]), the Heisenberg group
![]() ${\mathbb H}^{1}$
is purely k-unrectifiable, in the sense of [Reference Federer42], for
${\mathbb H}^{1}$
is purely k-unrectifiable, in the sense of [Reference Federer42], for
![]() $k=2,3,4$
. It can, however, be stated that the theory of
$k=2,3,4$
. It can, however, be stated that the theory of
![]() ${\mathbb H}$
-regular submanifolds (i.e., submanifolds with intrinsic
${\mathbb H}$
-regular submanifolds (i.e., submanifolds with intrinsic
![]() $C^{1}$
regularity) is well-established; see, for instance, the beautiful paper [Reference Franchi, Serapioni and Serra Cassano51]. It turns out that
$C^{1}$
regularity) is well-established; see, for instance, the beautiful paper [Reference Franchi, Serapioni and Serra Cassano51]. It turns out that
![]() ${\mathbb H}$
-regular submanifolds in
${\mathbb H}$
-regular submanifolds in
![]() ${\mathbb H}^{n}$
of low dimension
${\mathbb H}^{n}$
of low dimension
![]() $k\in \{1,\dots ,n\}$
are k-dimensional submanifolds of class
$k\in \{1,\dots ,n\}$
are k-dimensional submanifolds of class
![]() $C^{1}$
(in the Euclidean sense) that are tangent to the horizontal bundle
$C^{1}$
(in the Euclidean sense) that are tangent to the horizontal bundle
![]() ${\mathfrak h}_{1}$
. On the contrary,
${\mathfrak h}_{1}$
. On the contrary,
![]() ${\mathbb H}$
-regular submanifolds of low codimension
${\mathbb H}$
-regular submanifolds of low codimension
![]() $k\in \{1,\dots ,n\}$
are more complicated: they are (locally) noncritical level sets of
$k\in \{1,\dots ,n\}$
are more complicated: they are (locally) noncritical level sets of
![]() ${\mathbb R}^{k}$
-valued maps on
${\mathbb R}^{k}$
-valued maps on
![]() ${\mathbb H}^{n}$
with continuous horizontal derivatives (see Subsection 4.4 for precise definitions) and, as a matter of fact, they can have fractal Euclidean dimension [Reference Kirchheim and Serra Cassano63].
${\mathbb H}^{n}$
with continuous horizontal derivatives (see Subsection 4.4 for precise definitions) and, as a matter of fact, they can have fractal Euclidean dimension [Reference Kirchheim and Serra Cassano63].
A key tool for the study of
![]() ${\mathbb H}$
-regular submanifolds is provided by intrinsic graphs. Assume that
${\mathbb H}$
-regular submanifolds is provided by intrinsic graphs. Assume that
![]() ${\mathbb V},{\mathbb W}$
are homogeneous complementary subgroups of
${\mathbb V},{\mathbb W}$
are homogeneous complementary subgroups of
![]() ${\mathbb H}^{n}$
; that is, that they are invariant under dilations,
${\mathbb H}^{n}$
; that is, that they are invariant under dilations,
![]() ${\mathbb V}\cap {\mathbb W}=\{0\}$
and
${\mathbb V}\cap {\mathbb W}=\{0\}$
and
![]() ${\mathbb H}^{n}={\mathbb W}{\mathbb V}={\mathbb V}{\mathbb W}$
; given
${\mathbb H}^{n}={\mathbb W}{\mathbb V}={\mathbb V}{\mathbb W}$
; given
![]() $A\subset {\mathbb W}$
and a map
$A\subset {\mathbb W}$
and a map
![]() $\phi :A\to {\mathbb V}$
, the intrinsic graph of
$\phi :A\to {\mathbb V}$
, the intrinsic graph of
![]() $\phi $
is
$\phi $
is
![]() $\mathrm {gr}_{\phi }:=\{w\phi (w):w\in A\}\subset {\mathbb H}^{n}$
. It is worth recalling that, if
$\mathrm {gr}_{\phi }:=\{w\phi (w):w\in A\}\subset {\mathbb H}^{n}$
. It is worth recalling that, if
![]() ${\mathbb V},{\mathbb W}$
are homogeneous and complementary subgroups, then one of the two is necessarily horizontal (i.e., contained in
${\mathbb V},{\mathbb W}$
are homogeneous and complementary subgroups, then one of the two is necessarily horizontal (i.e., contained in
![]() $\exp ({\mathfrak h}_{1})$
), abelian and of dimension
$\exp ({\mathfrak h}_{1})$
), abelian and of dimension
![]() $k\leq n$
, while the other has dimension
$k\leq n$
, while the other has dimension
![]() $2n+1-k\geq n+1$
, is normal and contains the group center
$2n+1-k\geq n+1$
, is normal and contains the group center
![]() $\exp ({\mathfrak h}_{2})$
; see [Reference Franchi, Serapioni and Serra Cassano51, Remark 3.12]. The first appearance of intrinsic graphs is most likely to be attributed to the implicit function theorem of the fundamental paper [Reference Franchi, Serapioni and Serra Cassano48], where the authors prove an
$\exp ({\mathfrak h}_{2})$
; see [Reference Franchi, Serapioni and Serra Cassano51, Remark 3.12]. The first appearance of intrinsic graphs is most likely to be attributed to the implicit function theorem of the fundamental paper [Reference Franchi, Serapioni and Serra Cassano48], where the authors prove an
![]() ${\mathbb H}$
-rectifiability result for (boundaries of) sets with finite perimeter in
${\mathbb H}$
-rectifiability result for (boundaries of) sets with finite perimeter in
![]() ${\mathbb H}^{n}$
. As a matter of fact,
${\mathbb H}^{n}$
. As a matter of fact,
![]() ${\mathbb H}$
-regular submanifolds are locally intrinsic graphs whose properties have been studied in many papers (see, e.g., [Reference Ambrosio, Serra Cassano and Vittone4, Reference Antonelli, Di Donato and Don5, Reference Antonelli, Di Donato, Don and Le Donne6, Reference Arena and Serapioni9, Reference Bigolin and Serra Cassano17, Reference Bigolin and Serra Cassano18, Reference Citti and Manfredini29, Reference Corni32, Reference Corni and Magnani33, Reference Di Donato36, Reference Di Donato35, Reference Di Donato, Fässler and Orponen37, Reference Franchi, Serapioni and Serra Cassano51, Reference Julia, Nicolussi Golo and Vittone61, Reference Magnani70, Reference Monti and Vittone76]).
${\mathbb H}$
-regular submanifolds are locally intrinsic graphs whose properties have been studied in many papers (see, e.g., [Reference Ambrosio, Serra Cassano and Vittone4, Reference Antonelli, Di Donato and Don5, Reference Antonelli, Di Donato, Don and Le Donne6, Reference Arena and Serapioni9, Reference Bigolin and Serra Cassano17, Reference Bigolin and Serra Cassano18, Reference Citti and Manfredini29, Reference Corni32, Reference Corni and Magnani33, Reference Di Donato36, Reference Di Donato35, Reference Di Donato, Fässler and Orponen37, Reference Franchi, Serapioni and Serra Cassano51, Reference Julia, Nicolussi Golo and Vittone61, Reference Magnani70, Reference Monti and Vittone76]).
Intrinsic graphs also provide the language for introducing a theory of Lipschitz submanifolds in
![]() ${\mathbb H}^{n}$
. Observe that, while for the case of low-dimensional submanifolds one could simply consider Euclidean Lipschitz submanifolds that are almost everywhere (a.e.) tangent to the horizontal distribution, for submanifolds of low codimension there is no immediate way of modifying the ‘level set definition’ of
${\mathbb H}^{n}$
. Observe that, while for the case of low-dimensional submanifolds one could simply consider Euclidean Lipschitz submanifolds that are almost everywhere (a.e.) tangent to the horizontal distribution, for submanifolds of low codimension there is no immediate way of modifying the ‘level set definition’ of
![]() ${\mathbb H}$
-regularity into a Lipschitz one. Intrinsic Lipschitz graphs in
${\mathbb H}$
-regularity into a Lipschitz one. Intrinsic Lipschitz graphs in
![]() ${\mathbb H}^{n}$
first appeared in [Reference Franchi, Serapioni and Serra Cassano50]; their definition is stated in terms of a suitable cone property. Given
${\mathbb H}^{n}$
first appeared in [Reference Franchi, Serapioni and Serra Cassano50]; their definition is stated in terms of a suitable cone property. Given
![]() $\alpha>0$
, consider the homogeneous cone of axis
$\alpha>0$
, consider the homogeneous cone of axis
![]() ${\mathbb V}$
and aperture
${\mathbb V}$
and aperture
![]() $\alpha $
,
$\alpha $
,
We say that a map
![]() $\phi :A\subset {\mathbb W}\to {\mathbb V}$
is intrinsic Lipschitz if there exists
$\phi :A\subset {\mathbb W}\to {\mathbb V}$
is intrinsic Lipschitz if there exists
![]() $\alpha>0$
such that
$\alpha>0$
such that
Intrinsic Lipschitz graphs can be introduced in the more general framework of Carnot groups: apart from the elementary basics contained in Section 2, we refer to [Reference Franchi and Serapioni53] for a beautiful introduction to the topic and to [Reference Bigolin, Caravenna and Serra Cassano16, Reference Chousionis, Fässler and Orponen27, Reference Citti, Manfredini, Pinamonti and Serra Cassano30, Reference Di Donato, Fässler and Orponen37, Reference Don, Le Donne, Moisala and Vittone38, Reference Fässler, Orponen and Rigot41, Reference Franchi, Marchi and Serapioni44, Reference Franchi, Penso and Serapioni45, Reference Nicolussi Golo and Serra Cassano80, Reference Serapioni87, Reference Serra Cassano88] for several facets of the theory.
1.2 Rademacher’s theorem for intrinsic Lipschitz graphs and consequences
One of the main questions about intrinsic Lipschitz graphs concerns their almost everywhere ‘intrinsic’ differentiability. Consider an intrinsic Lipschitz map
![]() $\phi :A\to {\mathbb V}$
defined on some relatively open subset
$\phi :A\to {\mathbb V}$
defined on some relatively open subset
![]() $A\subset {\mathbb W}$
. If
$A\subset {\mathbb W}$
. If
![]() ${\mathbb W}$
has low dimension
${\mathbb W}$
has low dimension
![]() $k\leq n$
, then (see [Reference Antonelli and Merlo8] or also [Reference Franchi, Serapioni and Serra Cassano50, Remark 3.11], [Reference Franchi and Serapioni53, Proposition 3.7])
$k\leq n$
, then (see [Reference Antonelli and Merlo8] or also [Reference Franchi, Serapioni and Serra Cassano50, Remark 3.11], [Reference Franchi and Serapioni53, Proposition 3.7])
![]() $\mathrm {gr}_{\phi }$
is a k-dimensional submanifold with Euclidean Lipschitz regularity that is a.e. tangent to the horizontal bundle
$\mathrm {gr}_{\phi }$
is a k-dimensional submanifold with Euclidean Lipschitz regularity that is a.e. tangent to the horizontal bundle
![]() ${\mathfrak h}_{1}$
; therefore, the problem reduces to the case of
${\mathfrak h}_{1}$
; therefore, the problem reduces to the case of
![]() ${\mathbb H}$
-regular graphs with low codimension
${\mathbb H}$
-regular graphs with low codimension
![]() $k=\dim {\mathbb V}\leq n$
. A positive answer ([Reference Franchi, Serapioni and Serra Cassano52]) is known only for the case of codimension
$k=\dim {\mathbb V}\leq n$
. A positive answer ([Reference Franchi, Serapioni and Serra Cassano52]) is known only for the case of codimension
![]() $k=1$
; in fact, in this case
$k=1$
; in fact, in this case
![]() $\mathrm {gr}_{\phi }$
is (part of) the boundary of a set with finite
$\mathrm {gr}_{\phi }$
is (part of) the boundary of a set with finite
![]() ${\mathbb H}$
-perimeter ([Reference Capogna, Danielli and Garofalo25, Reference Franchi, Serapioni and Serra Cassano46]) in
${\mathbb H}$
-perimeter ([Reference Capogna, Danielli and Garofalo25, Reference Franchi, Serapioni and Serra Cassano46]) in
![]() ${\mathbb H}^{n}$
and one can use the rectifiability result [Reference Franchi, Serapioni and Serra Cassano48] available for such sets. A Rademacher-type theorem for intrinsic Lipschitz functions of codimension 1 was proved in Carnot groups of type
${\mathbb H}^{n}$
and one can use the rectifiability result [Reference Franchi, Serapioni and Serra Cassano48] available for such sets. A Rademacher-type theorem for intrinsic Lipschitz functions of codimension 1 was proved in Carnot groups of type
![]() $\star $
; see [Reference Franchi, Marchi and Serapioni44]. After a preliminary version of the present article was made public, it was found that the Rademacher theorem may dramatically fail for intrinsic Lipschitz graphs of codimension 2 (or higher) even in certain Carnot groups of step 2; see [Reference Julia, Nicolussi Golo and Vittone60]. In this article, we provide a full solution to the problem in
$\star $
; see [Reference Franchi, Marchi and Serapioni44]. After a preliminary version of the present article was made public, it was found that the Rademacher theorem may dramatically fail for intrinsic Lipschitz graphs of codimension 2 (or higher) even in certain Carnot groups of step 2; see [Reference Julia, Nicolussi Golo and Vittone60]. In this article, we provide a full solution to the problem in
![]() ${\mathbb H}^{n}$
, as stated in our main result.
${\mathbb H}^{n}$
, as stated in our main result.
Theorem 1.1. If
![]() $A\subset {\mathbb W}$
is open and
$A\subset {\mathbb W}$
is open and
![]() $\phi :A\to {\mathbb V}$
is intrinsic Lipschitz, then
$\phi :A\to {\mathbb V}$
is intrinsic Lipschitz, then
![]() $\phi $
is intrinsically differentiable at almost every point of A.
$\phi $
is intrinsically differentiable at almost every point of A.
In Theorem 1.1, ‘almost every’ must be understood with respect to a Haar measure on the subgroup
![]() ${\mathbb W}$
; for instance, the Hausdorff measure of dimension
${\mathbb W}$
; for instance, the Hausdorff measure of dimension
![]() $2n+2-k$
. Concerning the notion of intrinsic differentiability (see Subsection 4.2), recall that left-translations and dilations of intrinsic Lipschitz graphs are intrinsic Lipschitz graphs; in particular, for every
$2n+2-k$
. Concerning the notion of intrinsic differentiability (see Subsection 4.2), recall that left-translations and dilations of intrinsic Lipschitz graphs are intrinsic Lipschitz graphs; in particular, for every
![]() $w\in A$
and every
$w\in A$
and every
![]() $\lambda>0$
there exists an intrinsic Lipschitz
$\lambda>0$
there exists an intrinsic Lipschitz
![]() $\phi _{w}^{\lambda }:B\to {\mathbb V}$
, defined on some open subset
$\phi _{w}^{\lambda }:B\to {\mathbb V}$
, defined on some open subset
![]() $B\subset {\mathbb W}$
, such that
$B\subset {\mathbb W}$
, such that
 $$ \begin{align*} \delta_{\lambda}((w\phi(w))^{-1}\mathrm{gr}_{\phi})=\mathrm{gr}_{\phi_{w}^{\lambda}}. \end{align*} $$
$$ \begin{align*} \delta_{\lambda}((w\phi(w))^{-1}\mathrm{gr}_{\phi})=\mathrm{gr}_{\phi_{w}^{\lambda}}. \end{align*} $$
One then says ([Reference Arena and Serapioni9, §3.3]) that
![]() $\phi $
is intrinsically differentiable at w if, as
$\phi $
is intrinsically differentiable at w if, as
![]() $\lambda \to +\infty $
, the blow-ups
$\lambda \to +\infty $
, the blow-ups
![]() $\phi _{w}^{\lambda }$
converge locally uniformly on
$\phi _{w}^{\lambda }$
converge locally uniformly on
![]() ${\mathbb W}$
to an intrinsic linear map; that is, to a map
${\mathbb W}$
to an intrinsic linear map; that is, to a map
![]() $\psi :{\mathbb W}\to {\mathbb V}$
such that
$\psi :{\mathbb W}\to {\mathbb V}$
such that
![]() $\mathrm {gr}_{\psi }$
is a homogeneous subgroup of
$\mathrm {gr}_{\psi }$
is a homogeneous subgroup of
![]() ${\mathbb H}^{n}$
with codimension k. This subgroup, which is necessarily vertical (i.e., it contains the center of
${\mathbb H}^{n}$
with codimension k. This subgroup, which is necessarily vertical (i.e., it contains the center of
![]() ${\mathbb H}^{n}$
) and normal, is called tangent subgroup to
${\mathbb H}^{n}$
) and normal, is called tangent subgroup to
![]() $\mathrm {gr}_{\phi }$
at
$\mathrm {gr}_{\phi }$
at
![]() $w\phi (w)$
and is denoted by
$w\phi (w)$
and is denoted by
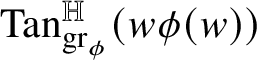 ${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}(w\phi (w))$
.
${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}(w\phi (w))$
.
For the reader’s convenience, the proof of Theorem 1.1 is sketched at the end of the Introduction. We are now going to introduce a few consequences of our main result: the first one is a Lusin-type theorem for intrinsic Lipschitz graphs.
Theorem 1.2. Let
![]() $A\subset {\mathbb W}$
be an open set and
$A\subset {\mathbb W}$
be an open set and
![]() $\phi :A\to {\mathbb V}$
an intrinsic Lipschitz function. Then for every
$\phi :A\to {\mathbb V}$
an intrinsic Lipschitz function. Then for every
![]() $\varepsilon>0$
there exists an intrinsic Lipschitz function
$\varepsilon>0$
there exists an intrinsic Lipschitz function
![]() $\psi :A\to {\mathbb V}$
such that
$\psi :A\to {\mathbb V}$
such that
![]() $\mathrm {gr}_{\psi }$
is a
$\mathrm {gr}_{\psi }$
is a
![]() ${\mathbb H}$
-regular submanifold and
${\mathbb H}$
-regular submanifold and
 $$ \begin{align*} {\mathscr S}^{Q-k}((\mathrm{gr}_{\phi}\,\Delta\, \mathrm{gr}_{\psi})\cup\{p\in\mathrm{gr}_{\phi}\cap \mathrm{gr}_{\psi}:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi}}(p)\})<\varepsilon. \end{align*} $$
$$ \begin{align*} {\mathscr S}^{Q-k}((\mathrm{gr}_{\phi}\,\Delta\, \mathrm{gr}_{\psi})\cup\{p\in\mathrm{gr}_{\phi}\cap \mathrm{gr}_{\psi}:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi}}(p)\})<\varepsilon. \end{align*} $$
As is customary, the integer
![]() $Q:=2n+2$
denotes the homogeneous dimension of
$Q:=2n+2$
denotes the homogeneous dimension of
![]() ${\mathbb H}^{n}$
and
${\mathbb H}^{n}$
and
![]() ${\mathscr S}^{Q-k}$
is the spherical Hausdorff measure of dimension
${\mathscr S}^{Q-k}$
is the spherical Hausdorff measure of dimension
![]() $Q-k$
; by
$Q-k$
; by
![]() $A\Delta B:=(A\setminus B)\cup (B\setminus A)$
we denote the symmetric difference of sets
$A\Delta B:=(A\setminus B)\cup (B\setminus A)$
we denote the symmetric difference of sets
![]() $A,B$
. Theorem 1.2 is part of Theorem 7.2; the latter stems from the equivalent definition of intrinsic Lipschitz graphs provided by Theorem 1.4 and is proved by an adaptation of the classical argument of Whitney’s extension theorem; see also [Reference Franchi, Serapioni and Serra Cassano48, Reference Franchi, Serapioni and Serra Cassano49, Reference Vittone92, Reference Vodop’yanov and Pupyshev94]. Theorem 1.2 implies that, as in the Euclidean case, the notion of
$A,B$
. Theorem 1.2 is part of Theorem 7.2; the latter stems from the equivalent definition of intrinsic Lipschitz graphs provided by Theorem 1.4 and is proved by an adaptation of the classical argument of Whitney’s extension theorem; see also [Reference Franchi, Serapioni and Serra Cassano48, Reference Franchi, Serapioni and Serra Cassano49, Reference Vittone92, Reference Vodop’yanov and Pupyshev94]. Theorem 1.2 implies that, as in the Euclidean case, the notion of
![]() ${\mathbb H}$
-rectifiability (Definition 4.22) can be equivalently defined in terms of either
${\mathbb H}$
-rectifiability (Definition 4.22) can be equivalently defined in terms of either
![]() ${\mathbb H}$
-regular submanifolds or intrinsic Lipschitz graphs; see Corollary 7.4. We refer to [Reference Antonelli and Le Donne7, Reference Bigolin and Vittone19, Reference Chousionis, Fässler and Orponen27, Reference Chousionis, Magnani and Tyson28, Reference Cole and Pauls31, Reference Di Donato, Fässler and Orponen37, Reference Fässler, Orponen and Rigot41, Reference Mattila, Serapioni and Serra Cassano73, Reference Merlo74, Reference Merlo75] for more about rectifiability in Heisenberg groups.
${\mathbb H}$
-regular submanifolds or intrinsic Lipschitz graphs; see Corollary 7.4. We refer to [Reference Antonelli and Le Donne7, Reference Bigolin and Vittone19, Reference Chousionis, Fässler and Orponen27, Reference Chousionis, Magnani and Tyson28, Reference Cole and Pauls31, Reference Di Donato, Fässler and Orponen37, Reference Fässler, Orponen and Rigot41, Reference Mattila, Serapioni and Serra Cassano73, Reference Merlo74, Reference Merlo75] for more about rectifiability in Heisenberg groups.
We stress the fact that Rademacher’s Theorem 1.1 also allows defining a canonical current
 carried by the graph of an intrinsic Lipschitz map
carried by the graph of an intrinsic Lipschitz map
![]() $\phi :{\mathbb W}\to {\mathbb V}$
. This current turns out to have zero boundary; see Proposition 7.5.
$\phi :{\mathbb W}\to {\mathbb V}$
. This current turns out to have zero boundary; see Proposition 7.5.
A further consequence of Theorem 1.2 is an area formula for intrinsic Lipschitz graphs of low codimension. For
![]() ${\mathbb H}$
-regular submanifolds, area formulae are proved in [Reference Franchi, Serapioni and Serra Cassano48, Reference Franchi, Serapioni and Serra Cassano51, Reference Ambrosio, Serra Cassano and Vittone4] for submanifolds of codimension 1 and in [Reference Corni and Magnani33] for higher codimension (see also [Reference Magnani71]). For intrinsic Lipschitz graphs of low dimension, an area formula is proved in [Reference Antonelli and Merlo8, Theorem 1.1]. Our area formula is stated in Theorem 1.3 and, once Lusin’s Theorem 1.2 is available, it is a quite simple consequence of [Reference Corni and Magnani33, Theorem 1.2], where a similar area formula is proved for intrinsic graphs that are also
${\mathbb H}$
-regular submanifolds, area formulae are proved in [Reference Franchi, Serapioni and Serra Cassano48, Reference Franchi, Serapioni and Serra Cassano51, Reference Ambrosio, Serra Cassano and Vittone4] for submanifolds of codimension 1 and in [Reference Corni and Magnani33] for higher codimension (see also [Reference Magnani71]). For intrinsic Lipschitz graphs of low dimension, an area formula is proved in [Reference Antonelli and Merlo8, Theorem 1.1]. Our area formula is stated in Theorem 1.3 and, once Lusin’s Theorem 1.2 is available, it is a quite simple consequence of [Reference Corni and Magnani33, Theorem 1.2], where a similar area formula is proved for intrinsic graphs that are also
![]() ${\mathbb H}$
-regular submanifolds. As in [Reference Corni and Magnani33], the symbol
${\mathbb H}$
-regular submanifolds. As in [Reference Corni and Magnani33], the symbol
![]() $J^{\phi }\phi (w)$
denotes the intrinsic Jacobian of
$J^{\phi }\phi (w)$
denotes the intrinsic Jacobian of
![]() $\phi $
at w (see Definition 4.9), while
$\phi $
at w (see Definition 4.9), while
![]() $C_{n,k}$
denotes a positive constant, depending only on
$C_{n,k}$
denotes a positive constant, depending only on
![]() $n,k$
and the distance d, which will be introduced later in Proposition 1.9.
$n,k$
and the distance d, which will be introduced later in Proposition 1.9.
Theorem 1.3. Assume that the subgroups
![]() ${\mathbb W},{\mathbb V}$
are orthogonalFootnote
1
and let
${\mathbb W},{\mathbb V}$
are orthogonalFootnote
1
and let
![]() $\phi :A\to {\mathbb V}$
be an intrinsic Lipschitz map defined on some Borel subset
$\phi :A\to {\mathbb V}$
be an intrinsic Lipschitz map defined on some Borel subset
![]() $A\subset {\mathbb W}$
; then for every Borel function
$A\subset {\mathbb W}$
; then for every Borel function
![]() $h:\mathrm {gr}_{\phi }\to [0,+\infty )$
, there holds
$h:\mathrm {gr}_{\phi }\to [0,+\infty )$
, there holds
 $$ \begin{align*} \int_{\mathrm{gr}_{\phi}} h \:d{\mathscr S}^{Q-k} =C_{n,k}\int_{A} (h\circ\Phi)J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}, \end{align*} $$
$$ \begin{align*} \int_{\mathrm{gr}_{\phi}} h \:d{\mathscr S}^{Q-k} =C_{n,k}\int_{A} (h\circ\Phi)J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}, \end{align*} $$
where
![]() $\Phi $
denotes the graph map
$\Phi $
denotes the graph map
![]() $\Phi (w):=w\phi (w).$
$\Phi (w):=w\phi (w).$
By abuse of notation,
![]() ${\mathscr L}^{2n+1-k}$
denotes the Haar measure on
${\mathscr L}^{2n+1-k}$
denotes the Haar measure on
![]() ${\mathbb W}$
associated with the canonical identification of
${\mathbb W}$
associated with the canonical identification of
![]() ${\mathbb W}$
with
${\mathbb W}$
with
![]() ${\mathbb R}^{2n+1-k}$
induced by exponential coordinates. It is worth observing that Theorem 1.3 and Proposition 1.9 are the only points where we use the rotational invariance of the distance d. In case of general distances, area formulae for intrinsic Lipschitz graphs can be easily deduced using Theorem 1.2 and [Reference Corni and Magnani33, Theorem 1.2], but they are slightly more complicated than ours, as they involve a certain area factor that depends on the tangent plane to the graph.
${\mathbb R}^{2n+1-k}$
induced by exponential coordinates. It is worth observing that Theorem 1.3 and Proposition 1.9 are the only points where we use the rotational invariance of the distance d. In case of general distances, area formulae for intrinsic Lipschitz graphs can be easily deduced using Theorem 1.2 and [Reference Corni and Magnani33, Theorem 1.2], but they are slightly more complicated than ours, as they involve a certain area factor that depends on the tangent plane to the graph.
1.3 Equivalent definition, extension and approximation of intrinsic Lipschitz graphs
We now introduce two of the ingredients needed in the proof of Theorem 1.1 that are of independent interest: namely, an extension theorem for intrinsic Lipschitz graphs in the spirit of the classical McShane–Whitney theorem and an approximation result by means of smooth graphs. They are stated in Theorems 1.5 and 1.6 and are both based on a new, equivalent definition of intrinsic Lipschitz graphs (Theorem 1.4), which can be regarded as another contribution of this article.
Our alternative definition of intrinsic Lipschitz graphs appeared in [Reference Vittone93] for graphs of codimension 1; it can be seen as a generalisation of the original level-set definition of
![]() ${\mathbb H}$
-regular submanifolds. Observe, however, that it is not immediate to give a level-set definition even for Lipschitz submanifolds of codimension 1 in
${\mathbb H}$
-regular submanifolds. Observe, however, that it is not immediate to give a level-set definition even for Lipschitz submanifolds of codimension 1 in
![]() ${\mathbb R}^{n}$
; in fact, every closed set
${\mathbb R}^{n}$
; in fact, every closed set
![]() $S\subset {\mathbb R}^{n}$
is the level set of some Lipschitz function; for instance, the distance from S. Anyway, we leave as an exercise to the reader the following observation, which was actually the starting point of [Reference Vittone93]: a set
$S\subset {\mathbb R}^{n}$
is the level set of some Lipschitz function; for instance, the distance from S. Anyway, we leave as an exercise to the reader the following observation, which was actually the starting point of [Reference Vittone93]: a set
![]() $S\subset {\mathbb R}^{n}={\mathbb R}^{n-1}\times {\mathbb R}$
is (contained in) the graph of a Lipschitz function
$S\subset {\mathbb R}^{n}={\mathbb R}^{n-1}\times {\mathbb R}$
is (contained in) the graph of a Lipschitz function
![]() $\phi :{\mathbb R}^{n-1}\to {\mathbb R}$
if and only if there exist
$\phi :{\mathbb R}^{n-1}\to {\mathbb R}$
if and only if there exist
![]() $\delta>0$
and a Lipschitz function
$\delta>0$
and a Lipschitz function
![]() $f:{\mathbb R}^{n}\to {\mathbb R}$
such that
$f:{\mathbb R}^{n}\to {\mathbb R}$
such that
![]() $S\subset \{x\in {\mathbb R}^{n}:f(x)=0\}$
and
$S\subset \{x\in {\mathbb R}^{n}:f(x)=0\}$
and
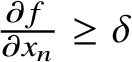 $\frac {\partial f}{\partial {x_{n}}}\geq \delta $
a.e. on
$\frac {\partial f}{\partial {x_{n}}}\geq \delta $
a.e. on
![]() ${\mathbb R}^{n}$
.
${\mathbb R}^{n}$
.
Since their proofs present no extra difficulty with respect to the Heisenberg case, Theorems 1.4, 1.5 and 1.6 are stated in the more general setting of a Carnot group
![]() ${\mathbb G}$
where two homogeneous complementary subgroups
${\mathbb G}$
where two homogeneous complementary subgroups
![]() ${\mathbb W},{\mathbb V}$
are fixed with
${\mathbb W},{\mathbb V}$
are fixed with
![]() ${\mathbb V}$
horizontal. This means that
${\mathbb V}$
horizontal. This means that
![]() ${\mathbb V}\subset \exp ({\mathfrak g}_{1})$
, where
${\mathbb V}\subset \exp ({\mathfrak g}_{1})$
, where
![]() ${\mathfrak g}_{1}$
is the first layer in the stratification of the Lie algebra of
${\mathfrak g}_{1}$
is the first layer in the stratification of the Lie algebra of
![]() ${\mathbb G}$
. When
${\mathbb G}$
. When
![]() ${\mathbb V}$
is horizontal, we say that an intrinsic Lipschitz graph
${\mathbb V}$
is horizontal, we say that an intrinsic Lipschitz graph
![]() $\phi :{\mathbb W}\to {\mathbb V}$
is co-horizontal; see [Reference Antonelli, Di Donato, Don and Le Donne6]. Observe that
$\phi :{\mathbb W}\to {\mathbb V}$
is co-horizontal; see [Reference Antonelli, Di Donato, Don and Le Donne6]. Observe that
![]() ${\mathbb V}$
is necessarily abelian and there exists a homogeneous isomorphism according to which we can identify
${\mathbb V}$
is necessarily abelian and there exists a homogeneous isomorphism according to which we can identify
![]() ${\mathbb V}$
with
${\mathbb V}$
with
![]() ${\mathbb R}^{k}$
; see (2.5). This identification is understood in the scalar product appearing in (1.2).
${\mathbb R}^{k}$
; see (2.5). This identification is understood in the scalar product appearing in (1.2).
Theorem 1.4. Assume that a splitting
![]() ${\mathbb G}={\mathbb W}{\mathbb V}$
is fixed in such a way that the subgroup
${\mathbb G}={\mathbb W}{\mathbb V}$
is fixed in such a way that the subgroup
![]() ${\mathbb V}$
is horizontal; set
${\mathbb V}$
is horizontal; set
![]() $k:=\dim {\mathbb V}$
. If
$k:=\dim {\mathbb V}$
. If
![]() $S\subset {\mathbb G}$
is not empty, then the following statements are equivalent:
$S\subset {\mathbb G}$
is not empty, then the following statements are equivalent:
-
(a) there exist
 $A\subset {\mathbb W}$
and an intrinsic Lipschitz map
$A\subset {\mathbb W}$
and an intrinsic Lipschitz map
 $\phi :A\to {\mathbb V}$
such that
$\phi :A\to {\mathbb V}$
such that
 $S=\mathrm {gr}_{\phi }$
;
$S=\mathrm {gr}_{\phi }$
; -
(b) there exist
 $\delta>0$
and a Lipschitz map
$\delta>0$
and a Lipschitz map
 $f:{\mathbb G}\to {\mathbb R}^{k}$
such that (1.1)
$f:{\mathbb G}\to {\mathbb R}^{k}$
such that (1.1) $$ \begin{align} & S\subset \{x\in{\mathbb G}:f(x)=0\} \end{align} $$
(1.2)
$$ \begin{align} & S\subset \{x\in{\mathbb G}:f(x)=0\} \end{align} $$
(1.2) $$ \begin{align} \text{and}\quad& \langle f(xv)-f(x),v\rangle \geq \delta|v|^{2}\qquad\text{for every }v\in{\mathbb V}\text{ and }x\in{\mathbb G}. \end{align} $$
$$ \begin{align} \text{and}\quad& \langle f(xv)-f(x),v\rangle \geq \delta|v|^{2}\qquad\text{for every }v\in{\mathbb V}\text{ and }x\in{\mathbb G}. \end{align} $$
It is worth remarking that, if
![]() $X_{1},\dots , X_{k}\in {\mathfrak g}_{1}$
are such that
$X_{1},\dots , X_{k}\in {\mathfrak g}_{1}$
are such that
![]() ${\mathbb V}=\exp (\operatorname *{\mathrm {span}}\{X_{1},\dots ,X_{k}\})$
, then statement (1.2) is equivalent to the a.e. uniform ellipticity (a.k.a. coercivity) of the matrix col
${\mathbb V}=\exp (\operatorname *{\mathrm {span}}\{X_{1},\dots ,X_{k}\})$
, then statement (1.2) is equivalent to the a.e. uniform ellipticity (a.k.a. coercivity) of the matrix col
![]() $[\,X_{1}f(x)\,|\,\dots \,|\,X_{k} f(x)\,]$
; see Remark 2.7. In case
$[\,X_{1}f(x)\,|\,\dots \,|\,X_{k} f(x)\,]$
; see Remark 2.7. In case
![]() $k=1$
, Theorem 1.4 was proved in [Reference Vittone93, Theorem 3.2].
$k=1$
, Theorem 1.4 was proved in [Reference Vittone93, Theorem 3.2].
Let us underline two of the most interesting features of this alternative definition. First, it allows for a definition of co-horizontal intrinsic Lipschitz submanifolds in the more general setting of Carnot–Carathéodory spaces, as in [Reference Vittone93]. Second, it gives gratis an extension result for intrinsic Lipschitz maps; in fact (Remark 2.8), the level set
![]() $\{x\in {\mathbb G}:f(x)=0\}$
appearing in (1.1) is the graph of an intrinsic Lipschitz map that is defined on the whole
$\{x\in {\mathbb G}:f(x)=0\}$
appearing in (1.1) is the graph of an intrinsic Lipschitz map that is defined on the whole
![]() ${\mathbb W}$
and extends
${\mathbb W}$
and extends
![]() $\phi $
. We can then state the following result.
$\phi $
. We can then state the following result.
Theorem 1.5. Let
![]() $A\subset {\mathbb W}$
and
$A\subset {\mathbb W}$
and
![]() $\phi :A\to {\mathbb V}$
be a co-horizontal intrinsic Lipschitz graph; then there exists an intrinsic Lipschitz extension
$\phi :A\to {\mathbb V}$
be a co-horizontal intrinsic Lipschitz graph; then there exists an intrinsic Lipschitz extension
![]() $\tilde {\phi }:{\mathbb W}\to {\mathbb V}$
of
$\tilde {\phi }:{\mathbb W}\to {\mathbb V}$
of
![]() $\phi $
. Moreover,
$\phi $
. Moreover,
![]() $\tilde {\phi }$
can be chosen in such a way that its intrinsic Lipschitz constant is controlled in terms of the intrinsic Lipschitz constant of
$\tilde {\phi }$
can be chosen in such a way that its intrinsic Lipschitz constant is controlled in terms of the intrinsic Lipschitz constant of
![]() $\phi $
.
$\phi $
.
Theorem 1.5 was proved in [Reference Vittone93, Proposition 3.4] for the case of codimension
![]() $k=1$
; see also [Reference Franchi, Serapioni and Serra Cassano52, Reference Franchi and Serapioni53, Reference Naor and Young79, Reference Rigot84].
$k=1$
; see also [Reference Franchi, Serapioni and Serra Cassano52, Reference Franchi and Serapioni53, Reference Naor and Young79, Reference Rigot84].
In Proposition 2.10 we use a standard approximation argument based on group convolutions (see, e.g., [Reference Folland and Stein43, §1.B]) to show that the function f appearing in Theorem 1.4 can be chosen with the additional property that
![]() $f\in C^{\infty }(\{x\in {\mathbb G}:f(x)\neq 0\})$
. This fact has the following consequence.
$f\in C^{\infty }(\{x\in {\mathbb G}:f(x)\neq 0\})$
. This fact has the following consequence.
Theorem 1.6. Let
![]() $A\subset {\mathbb W}$
and
$A\subset {\mathbb W}$
and
![]() $\phi :A\to {\mathbb V}$
be a co-horizontal intrinsic Lipschitz graph. Then there exists a sequence
$\phi :A\to {\mathbb V}$
be a co-horizontal intrinsic Lipschitz graph. Then there exists a sequence
![]() $(\phi _{i})_{i\in \mathbb N}$
of
$(\phi _{i})_{i\in \mathbb N}$
of
![]() $C^{\infty }$
-regular and intrinsic Lipschitz maps
$C^{\infty }$
-regular and intrinsic Lipschitz maps
![]() $\phi _{i}:{\mathbb W}\to {\mathbb V}$
such that
$\phi _{i}:{\mathbb W}\to {\mathbb V}$
such that
Moreover, the intrinsic Lipschitz constant of
![]() $\phi _{i}$
is bounded, uniformly in i, in terms of the intrinsic Lipschitz constant of
$\phi _{i}$
is bounded, uniformly in i, in terms of the intrinsic Lipschitz constant of
![]() $\phi $
.
$\phi $
.
A similar result has been proved in [Reference Citti, Manfredini, Pinamonti and Serra Cassano30] for intrinsic Lipschitz graphs of codimension 1 in Heisenberg groups; see also [Reference Ambrosio, Serra Cassano and Vittone4, Reference Antonelli, Di Donato, Don and Le Donne6, Reference Monti and Vittone76, Reference Vittone93].
1.4 Currents and the constancy theorem
As in the classical setting, currents in Heisenberg groups are defined in duality with spaces of smooth forms with compact support; here, however, the De Rham complex must be replaced by the complex introduced by M. Rumin [Reference Rumin85, Reference Rumin86] in the setting of contact manifolds. The construction of the spaces
![]() $\Omega _{\mathbb H}^{m}$
of Heisenberg differential m -forms is detailed in Subsection 3.2; here we only recall that, for
$\Omega _{\mathbb H}^{m}$
of Heisenberg differential m -forms is detailed in Subsection 3.2; here we only recall that, for
![]() $1\leq k\leq n$
, Heisenberg forms of codimension k are smooth functions on
$1\leq k\leq n$
, Heisenberg forms of codimension k are smooth functions on
![]() ${\mathbb H}^{n}$
with values in a certain subspace
${\mathbb H}^{n}$
with values in a certain subspace
![]() ${\mathcal J}^{2n+1-k}$
of
${\mathcal J}^{2n+1-k}$
of
![]() $(2n+1-k)$
-covectors. We denote by
$(2n+1-k)$
-covectors. We denote by
![]() ${\mathcal J}_{2n+1-k}$
the (formal) dual of
${\mathcal J}_{2n+1-k}$
the (formal) dual of
![]() ${\mathcal J}^{2n+1-k}$
; clearly, every
${\mathcal J}^{2n+1-k}$
; clearly, every
![]() $(2n+1-k)$
-vector t canonically induces an element
$(2n+1-k)$
-vector t canonically induces an element
![]() $[t]_{{\mathcal J}}\in {\mathcal J}_{2n+1-k}$
defined by
$[t]_{{\mathcal J}}\in {\mathcal J}_{2n+1-k}$
defined by
![]() $[t]_{{\mathcal J}}(\lambda ):=\langle \, t\mid \lambda \,\rangle $
, where
$[t]_{{\mathcal J}}(\lambda ):=\langle \, t\mid \lambda \,\rangle $
, where
![]() $\langle \,\cdot \mid \cdot \,\rangle $
is the standard pairing vectors-covectors. See Subsection 3.1 and Subsection 3.2 for more details.
$\langle \,\cdot \mid \cdot \,\rangle $
is the standard pairing vectors-covectors. See Subsection 3.1 and Subsection 3.2 for more details.
The starting point of the theory of Heisenberg currents is the existence of a linear second-order operator
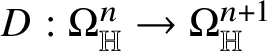 $D:\Omega _{\mathbb H}^{n}\to \Omega _{\mathbb H}^{n+1}$
such that the sequence
$D:\Omega _{\mathbb H}^{n}\to \Omega _{\mathbb H}^{n+1}$
such that the sequence
 $$ \begin{align*} 0\to{\mathbb R}\to\Omega_{\mathbb H}^{0}\stackrel{d}{\to}\Omega_{\mathbb H}^{1}\stackrel{d}{\to}\dots\stackrel{d}{\to}\Omega_{\mathbb H}^{n}\stackrel{D}{\to}\Omega_{\mathbb H}^{n+1}\stackrel{d}{\to} \dots \stackrel{d}{\to}\Omega_{\mathbb H}^{2n+1}\to 0 \end{align*} $$
$$ \begin{align*} 0\to{\mathbb R}\to\Omega_{\mathbb H}^{0}\stackrel{d}{\to}\Omega_{\mathbb H}^{1}\stackrel{d}{\to}\dots\stackrel{d}{\to}\Omega_{\mathbb H}^{n}\stackrel{D}{\to}\Omega_{\mathbb H}^{n+1}\stackrel{d}{\to} \dots \stackrel{d}{\to}\Omega_{\mathbb H}^{2n+1}\to 0 \end{align*} $$
is exact, where d is (the operator induced by) the standard exterior derivative. A Heisenberg m-current
![]() ${\mathsf T}$
is by definition a continuous linear functional on the space
${\mathsf T}$
is by definition a continuous linear functional on the space
![]() ${\mathcal D}_{\mathbb H}^{m}\subset \Omega _{\mathbb H}^{m}$
of Heisenberg m-forms with compact support. The boundary
${\mathcal D}_{\mathbb H}^{m}\subset \Omega _{\mathbb H}^{m}$
of Heisenberg m-forms with compact support. The boundary
![]() $\partial {\mathsf T}$
of
$\partial {\mathsf T}$
of
![]() ${\mathsf T}$
is the Heisenberg
${\mathsf T}$
is the Heisenberg
![]() $(m-1)$
-current defined, for every
$(m-1)$
-current defined, for every
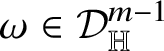 $\omega \in {\mathcal D}_{\mathbb H}^{m-1}$
, by
$\omega \in {\mathcal D}_{\mathbb H}^{m-1}$
, by
 $$ \begin{align*} \begin{array}{ll} \partial {\mathsf T}(\omega):={\mathsf T}(d\omega)&\quad\text{if }m\neq n+1\\ \partial {\mathsf T}(\omega):={\mathsf T}(D\omega)&\quad\text{if }m= n+1. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \partial {\mathsf T}(\omega):={\mathsf T}(d\omega)&\quad\text{if }m\neq n+1\\ \partial {\mathsf T}(\omega):={\mathsf T}(D\omega)&\quad\text{if }m= n+1. \end{array} \end{align*} $$
We say that
![]() ${\mathsf T}$
is locally normal if both
${\mathsf T}$
is locally normal if both
![]() ${\mathsf T}$
and
${\mathsf T}$
and
![]() $\partial {\mathsf T}$
have locally finite mass; that is, if they have order 0 in the sense of distributions. Recall that, if
$\partial {\mathsf T}$
have locally finite mass; that is, if they have order 0 in the sense of distributions. Recall that, if
![]() ${\mathsf T}$
has locally finite mass, then there exist a Radon measure
${\mathsf T}$
has locally finite mass, then there exist a Radon measure
![]() $\mu $
on
$\mu $
on
![]() ${\mathbb H}^{n}$
and a locally
${\mathbb H}^{n}$
and a locally
![]() $\mu $
-integrable function
$\mu $
-integrable function
![]() $\tau $
with values in a suitable space of multivectors (which, for
$\tau $
with values in a suitable space of multivectors (which, for
![]() $m\geq n+1$
, is precisely
$m\geq n+1$
, is precisely
![]() ${\mathcal J}_{m}$
) such that
${\mathcal J}_{m}$
) such that
![]() ${\mathsf T}=\tau \mu $
, where
${\mathsf T}=\tau \mu $
, where
 $$ \begin{align*} \tau\mu(\omega):=\int_{{\mathbb H}^{n}}\langle\,\tau(p)\mid\omega(p)\,\rangle\,d\mu(p)\qquad\text{for every }\omega\in{\mathcal D}_{\mathbb H}^{m}. \end{align*} $$
$$ \begin{align*} \tau\mu(\omega):=\int_{{\mathbb H}^{n}}\langle\,\tau(p)\mid\omega(p)\,\rangle\,d\mu(p)\qquad\text{for every }\omega\in{\mathcal D}_{\mathbb H}^{m}. \end{align*} $$
One can also assume that
![]() $|\tau |=1\ \mu $
-a.e., where
$|\tau |=1\ \mu $
-a.e., where
![]() $|\cdot |$
denotes some fixed norm on multivectorsFootnote
2
; in this case, we write
$|\cdot |$
denotes some fixed norm on multivectorsFootnote
2
; in this case, we write
![]() $\!\vec {\,{\mathsf T}}$
and
$\!\vec {\,{\mathsf T}}$
and
![]() $\|{\mathsf T}\|$
in place of
$\|{\mathsf T}\|$
in place of
![]() $\tau $
and
$\tau $
and
![]() $\mu $
, respectively.
$\mu $
, respectively.
Relevant examples of currents will be for us those concentrated on
![]() ${\mathbb H}$
-rectifiable sets of low codimension. Recall that a set
${\mathbb H}$
-rectifiable sets of low codimension. Recall that a set
![]() $R\subset {\mathbb H}^{n}$
is locally
$R\subset {\mathbb H}^{n}$
is locally
![]() ${\mathbb H}$
-rectifiable of codimension
${\mathbb H}$
-rectifiable of codimension
![]() $k\in \{1,\dots ,n\}$
if
$k\in \{1,\dots ,n\}$
if
![]() is locally finite and R can be covered by countably many
is locally finite and R can be covered by countably many
![]() ${\mathbb H}$
-regular submanifolds of codimension k plus a
${\mathbb H}$
-regular submanifolds of codimension k plus a
![]() ${\mathscr S}^{Q-k}$
-negligible set. In this case, a (unit) approximate tangent
${\mathscr S}^{Q-k}$
-negligible set. In this case, a (unit) approximate tangent
![]() $(2n+1-k)$
-vector
$(2n+1-k)$
-vector
 $t^{\mathbb H}_{R}(p)$
to R can be defined at
$t^{\mathbb H}_{R}(p)$
to R can be defined at
![]() ${\mathscr S}^{Q-k}$
-a.e.
${\mathscr S}^{Q-k}$
-a.e.
![]() $p\in {\mathbb R}$
; see Subsection 4.4. We denote by
$p\in {\mathbb R}$
; see Subsection 4.4. We denote by
![]() the Heisenberg current
the Heisenberg current
 naturally associated with R.
naturally associated with R.
A fundamental result in the classical theory of currents is the constancy theorem (see, e.g., [Reference Federer42, 4.1.7] and [Reference Simon90, Theorem 26.27]), which states that, if
![]() ${\mathsf T}$
is an n-dimensional current in
${\mathsf T}$
is an n-dimensional current in
![]() ${\mathbb R}^{n}$
such that
${\mathbb R}^{n}$
such that
![]() $\partial {\mathsf T}=0$
, then
$\partial {\mathsf T}=0$
, then
![]() ${\mathsf T}$
is constant; that is, there exists
${\mathsf T}$
is constant; that is, there exists
![]() $c\in {\mathbb R}$
such that
$c\in {\mathbb R}$
such that
 ${\mathsf T}(\omega )=c\int _{{\mathbb R}^{n}}\omega $
for every smooth n-form
${\mathsf T}(\omega )=c\int _{{\mathbb R}^{n}}\omega $
for every smooth n-form
![]() $\omega $
with compact support. A more general version of the constancy theorem can be proved for currents supported on an m-dimensional plane
$\omega $
with compact support. A more general version of the constancy theorem can be proved for currents supported on an m-dimensional plane
![]() ${\mathscr P}\subset {\mathbb R}^{n}$
: if
${\mathscr P}\subset {\mathbb R}^{n}$
: if
![]() ${\mathsf T}$
is an m-current with support in
${\mathsf T}$
is an m-current with support in
![]() ${\mathscr P}$
and such that
${\mathscr P}$
and such that
![]() $\partial {\mathsf T}=0$
, then there exists
$\partial {\mathsf T}=0$
, then there exists
![]() $c\in {\mathbb R}$
such that
$c\in {\mathbb R}$
such that
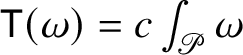 ${\mathsf T}(\omega )=c\int _{{\mathscr P}}\omega $
for every smooth m-form
${\mathsf T}(\omega )=c\int _{{\mathscr P}}\omega $
for every smooth m-form
![]() $\omega $
with compact support. For this statement, see, for example, [Reference Krantz and Parks65, Proposition 7.3.5]. The following Theorem 1.7 can be considered as the Heisenberg analogue of this more general constancy theorem; besides its importance for the present article, Theorem 1.7 is a fundamental tool for the outcomes of the recent [Reference Julia, Nicolussi Golo and Vittone62].
$\omega $
with compact support. For this statement, see, for example, [Reference Krantz and Parks65, Proposition 7.3.5]. The following Theorem 1.7 can be considered as the Heisenberg analogue of this more general constancy theorem; besides its importance for the present article, Theorem 1.7 is a fundamental tool for the outcomes of the recent [Reference Julia, Nicolussi Golo and Vittone62].
Theorem 1.7. Let
![]() $k\in \{1,\dots ,n\}$
be fixed and let
$k\in \{1,\dots ,n\}$
be fixed and let
![]() ${\mathsf T}$
be a Heisenberg
${\mathsf T}$
be a Heisenberg
![]() $(2n+1-k)$
-current supported on a vertical plane
$(2n+1-k)$
-current supported on a vertical plane
![]() ${\mathscr P}\subset {\mathbb H}^{n}$
of dimension
${\mathscr P}\subset {\mathbb H}^{n}$
of dimension
![]() $2n+1-k$
. Assume that
$2n+1-k$
. Assume that
![]() $\partial {\mathsf T}=0$
; then there exists a constant
$\partial {\mathsf T}=0$
; then there exists a constant
![]() $c\in {\mathbb R}$
such that
$c\in {\mathbb R}$
such that
![]() .
.
Using a procedure involving projection on planes (see [Reference Šilhavý89, Theorem 4.2]; let us mention also [Reference Alberti and Marchese1, §5] and [Reference Alberti, Massaccesi and Stepanov2] for some related results), the (version on planes of the) constancy theorem in
![]() ${\mathbb R}^{n}$
has the following consequence: if
${\mathbb R}^{n}$
has the following consequence: if
![]() $R\subset {\mathbb R}^{n}$
is an m-rectifiable set and
$R\subset {\mathbb R}^{n}$
is an m-rectifiable set and
![]() ${\mathsf T}=\tau \mu $
is a normal m-current, where
${\mathsf T}=\tau \mu $
is a normal m-current, where
![]() $\mu $
is a Radon measure and
$\mu $
is a Radon measure and
![]() $\tau $
is a locally
$\tau $
is a locally
![]() $\mu $
-integrable m-vectorfield with
$\mu $
-integrable m-vectorfield with
![]() $\tau \neq 0 \ \mu $
-a.e., then
$\tau \neq 0 \ \mu $
-a.e., then
-
(i)
 is absolutely continuous with respect to the Hausdorff measure
is absolutely continuous with respect to the Hausdorff measure
 and
and -
(ii)
 $\tau $
is tangent to R at
$\tau $
is tangent to R at
 $\mu $
-almost every point of R.
$\mu $
-almost every point of R.
A consequence of this fact, which might help explaining its geometric meaning, is the following one: if
![]() ${\mathsf T}=\tau \mu $
is a normal current concentratedFootnote
3
on a rectifiable set R, then
${\mathsf T}=\tau \mu $
is a normal current concentratedFootnote
3
on a rectifiable set R, then
![]() and
and
![]() $\tau $
is necessarily tangent to
$\tau $
is necessarily tangent to
![]() $R \ \mu $
-almost everywhere.Footnote
4
$R \ \mu $
-almost everywhere.Footnote
4
In our proof of Rademacher’s Theorem 1.1, we will utilise the following result, which is the Heisenberg counterpart of the ‘tangency’ property (ii) above; we were not able to deduce any ‘absolute continuity’ statement analogous to (i) because no good notion of projection on planes is available in
![]() ${\mathbb H}^{n}$
. Notice, however, that, in the special case when
${\mathbb H}^{n}$
. Notice, however, that, in the special case when
![]() ${\mathsf T}$
is concentrated on a vertical plane, Theorem 1.7 allows deducing a complete result including absolute continuity.
${\mathsf T}$
is concentrated on a vertical plane, Theorem 1.7 allows deducing a complete result including absolute continuity.
Theorem 1.8. Let
![]() $k\in \{1,\dots ,n\}$
and let a locally normal Heisenberg
$k\in \{1,\dots ,n\}$
and let a locally normal Heisenberg
![]() $(2n+1-k)$
-current
$(2n+1-k)$
-current
![]() ${\mathsf T}$
and a locally
${\mathsf T}$
and a locally
![]() ${\mathbb H}$
-rectifiable set
${\mathbb H}$
-rectifiable set
![]() $R\subset {\mathbb H}^{n}$
of codimension k be fixed. Then
$R\subset {\mathbb H}^{n}$
of codimension k be fixed. Then
 $$ \begin{align*} \!\vec{\,{\mathsf T}}(p)\text{ is a multiple of }[t^{\mathbb H}_{R}(p)]_{{\mathcal J}}\qquad \text{for }\|{\mathsf T}\|_{a}\text{-a.e. }p. \end{align*} $$
$$ \begin{align*} \!\vec{\,{\mathsf T}}(p)\text{ is a multiple of }[t^{\mathbb H}_{R}(p)]_{{\mathcal J}}\qquad \text{for }\|{\mathsf T}\|_{a}\text{-a.e. }p. \end{align*} $$
In Theorem 1.8 we decomposed
![]() $\|{\mathsf T}\|=\|{\mathsf T}\|_{a}+\|{\mathsf T}\|_{s}$
as the sum of the absolutely continuous and singular part of
$\|{\mathsf T}\|=\|{\mathsf T}\|_{a}+\|{\mathsf T}\|_{s}$
as the sum of the absolutely continuous and singular part of
![]() $\|{\mathsf T}\|$
with respect to
$\|{\mathsf T}\|$
with respect to
![]() . Observe that
. Observe that
![]() $t^{\mathbb H}_{R}$
is defined only
$t^{\mathbb H}_{R}$
is defined only
![]() ${\mathscr S}^{Q-k}$
-almost everywhere on R; hence, it could be undefined on a set with positive
${\mathscr S}^{Q-k}$
-almost everywhere on R; hence, it could be undefined on a set with positive
![]() $\|{\mathsf T}\|_{s}$
-measure. The geometric content of Theorem 1.8 is again clear: for a current
$\|{\mathsf T}\|_{s}$
-measure. The geometric content of Theorem 1.8 is again clear: for a current
![]() ${\mathsf T}$
concentrated on R to be normal, it is necessary that
${\mathsf T}$
concentrated on R to be normal, it is necessary that
![]() $\!\vec {\,{\mathsf T}}$
is almost everywhere tangent to R.
$\!\vec {\,{\mathsf T}}$
is almost everywhere tangent to R.
The proof of Theorem 1.8 follows a blow-up strategy according to which one can prove that, at
![]() ${\mathscr S}^{Q-k}$
-a.e.
${\mathscr S}^{Q-k}$
-a.e.
![]() $p\in R$
, the current
$p\in R$
, the current
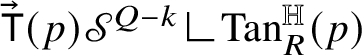 has zero boundary, where
has zero boundary, where
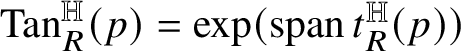 ${\mathrm {Tan}}^{\mathbb H}_{R}(p)=\exp (\operatorname *{\mathrm {span}} t^{\mathbb H}_{R}(p))$
is the approximate tangent plane to R at p. Proposition 5.3 shows that this is possible only if
${\mathrm {Tan}}^{\mathbb H}_{R}(p)=\exp (\operatorname *{\mathrm {span}} t^{\mathbb H}_{R}(p))$
is the approximate tangent plane to R at p. Proposition 5.3 shows that this is possible only if
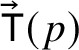 $\!\vec {\,{\mathsf T}}(p)$
is a multiple of
$\!\vec {\,{\mathsf T}}(p)$
is a multiple of
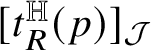 $[t^{\mathbb H}_{R}(p)]_{{\mathcal J}}$
. Proposition 5.3 is essentially a simpler version of Theorem 1.7; its classical counterpart can be found, for instance, in [Reference Giaquinta, Modica and Souček57, Lemma 1 in §3.3.2]. The proof of Proposition 5.3
Footnote
5
consists in feeding the given boundaryless current with (the differential of) enough test forms in order to eventually deduce the desired ‘tangency’ property. Apart from the computational difficulties pertaining to the second-order operator D (at least in case
$[t^{\mathbb H}_{R}(p)]_{{\mathcal J}}$
. Proposition 5.3 is essentially a simpler version of Theorem 1.7; its classical counterpart can be found, for instance, in [Reference Giaquinta, Modica and Souček57, Lemma 1 in §3.3.2]. The proof of Proposition 5.3
Footnote
5
consists in feeding the given boundaryless current with (the differential of) enough test forms in order to eventually deduce the desired ‘tangency’ property. Apart from the computational difficulties pertaining to the second-order operator D (at least in case
![]() $k=n$
), one demanding task we had to face was the search for a convenient basis of
$k=n$
), one demanding task we had to face was the search for a convenient basis of
![]() ${\mathcal J}^{2n+1-k}$
; see Subsection 1.5.
${\mathcal J}^{2n+1-k}$
; see Subsection 1.5.
We conclude this section with an important observation. Assume that S is an oriented submanifold of codimension k that is (Euclidean)
![]() $C^{1}$
-regular; in particular, the tangent vector
$C^{1}$
-regular; in particular, the tangent vector
![]() $t^{\mathbb H}_{S}$
is defined except at characteristic points of S, which, however, are
$t^{\mathbb H}_{S}$
is defined except at characteristic points of S, which, however, are
![]() ${\mathscr S}^{Q-k}$
-negligible [Reference Balogh15, Reference Magnani69]. Then, on the one side, S induces the natural Heisenberg current
${\mathscr S}^{Q-k}$
-negligible [Reference Balogh15, Reference Magnani69]. Then, on the one side, S induces the natural Heisenberg current
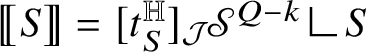 ; on the other side, associated to S is also the classical current
; on the other side, associated to S is also the classical current
![]() defined by
defined by
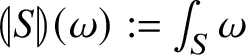 for every
for every
![]() $(2n+1-k)$
-form
$(2n+1-k)$
-form
![]() $\omega $
with compact support. The following fact holds true provided the homogeneous distance d is rotationally invariant.
$\omega $
with compact support. The following fact holds true provided the homogeneous distance d is rotationally invariant.
Proposition 1.9. Let
![]() $k\in \{1,\dots ,n\}$
; then there exists a positive constant
$k\in \{1,\dots ,n\}$
; then there exists a positive constant
![]() $C_{n,k}$
, depending on
$C_{n,k}$
, depending on
![]() $n,k$
and the rotationally invariant distance d, such that for every
$n,k$
and the rotationally invariant distance d, such that for every
![]() $C^{1}$
-regular submanifold
$C^{1}$
-regular submanifold
![]() $S\subset {\mathbb H}^{n}$
of codimension k,
$S\subset {\mathbb H}^{n}$
of codimension k,

In particular, if S is a submanifold without boundary, then
![]() is a Heisenberg
is a Heisenberg
![]() $(2n-k)$
-current.
$(2n-k)$
-current.
In other words,
![]() and
and
![]() coincide, as Heisenberg currents, up to a multiplicative constant. This is remarkable. The first part of the statement of Proposition 1.9 is proved in Lemma 3.31, while the second one is a consequence of the fact that the operator D is the composition of the differential d with another operator; see Corollary 3.34. For the exact value of
coincide, as Heisenberg currents, up to a multiplicative constant. This is remarkable. The first part of the statement of Proposition 1.9 is proved in Lemma 3.31, while the second one is a consequence of the fact that the operator D is the composition of the differential d with another operator; see Corollary 3.34. For the exact value of
![]() $C_{n,k}$
, see Remark 4.21. Proposition 1.9 is crucial in the proof of our main result Theorem 1.1.
$C_{n,k}$
, see Remark 4.21. Proposition 1.9 is crucial in the proof of our main result Theorem 1.1.
1.5 A basis for Rumin’s spaces
 ${\mathcal J}^{2n+1-k}$
${\mathcal J}^{2n+1-k}$
We believe it is worth introducing, at least quickly, the basis of
![]() ${\mathcal J}^{2n+1-k}$
that we use; we need some preliminary notation. Assume that the elements of a finite subset
${\mathcal J}^{2n+1-k}$
that we use; we need some preliminary notation. Assume that the elements of a finite subset
![]() $M\subset \mathbb N$
with cardinality
$M\subset \mathbb N$
with cardinality
![]() $|M|=m$
are arranged (each element of M appearing exactly once) in a tableau with two rows, the first row displaying
$|M|=m$
are arranged (each element of M appearing exactly once) in a tableau with two rows, the first row displaying
![]() $\ell \geq \frac m2$
elements
$\ell \geq \frac m2$
elements
 $R^{1}_{1},\dots ,R^{1}_{\ell }$
and the second one displaying
$R^{1}_{1},\dots ,R^{1}_{\ell }$
and the second one displaying
![]() $m-\ell \geq 0$
elements
$m-\ell \geq 0$
elements
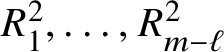 $R^{2}_{1},\dots ,R^{2}_{m-\ell }$
, as follows:
$R^{2}_{1},\dots ,R^{2}_{m-\ell }$
, as follows:

Such an R is called Young tableau (see, e.g., [Reference Fulton55]). Clearly, R has to be read as a
![]() $(2\times \ell )$
rectangular tableau when
$(2\times \ell )$
rectangular tableau when
![]() $\ell =m/2$
while, in case
$\ell =m/2$
while, in case
![]() $\ell =m$
, we agree that the second row is empty. Given such an R, define the
$\ell =m$
, we agree that the second row is empty. Given such an R, define the
![]() $2\ell $
-covector
$2\ell $
-covector
 $$ \begin{align*} \alpha_{R}:=(dxy_{R^{1}_{1}}- dxy_{R^{2}_{1}})\wedge(dxy_{R^{1}_{2}}- dxy_{R^{2}_{2}})\wedge\dots\wedge(dxy_{R^{1}_{m-\ell}}- dxy_{R^{2}_{m-\ell}})\wedge dxy_{R^{1}_{m-\ell+1}}\wedge\dots\wedge dxy_{R^{1}_{\ell}}, \end{align*} $$
$$ \begin{align*} \alpha_{R}:=(dxy_{R^{1}_{1}}- dxy_{R^{2}_{1}})\wedge(dxy_{R^{1}_{2}}- dxy_{R^{2}_{2}})\wedge\dots\wedge(dxy_{R^{1}_{m-\ell}}- dxy_{R^{2}_{m-\ell}})\wedge dxy_{R^{1}_{m-\ell+1}}\wedge\dots\wedge dxy_{R^{1}_{\ell}}, \end{align*} $$
where for shortness we set
![]() $dxy_{i}:=dx_{i}\wedge dy_{i}$
; when
$dxy_{i}:=dx_{i}\wedge dy_{i}$
; when
![]() $\ell =m$
(i.e., when the second row of R is empty), we agree that
$\ell =m$
(i.e., when the second row of R is empty), we agree that
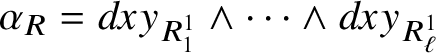 $\alpha _{R}=dxy_{R^{1}_{1}}\wedge \dots \wedge dxy_{R^{1}_{\ell }}$
. One key observation is the fact that
$\alpha _{R}=dxy_{R^{1}_{1}}\wedge \dots \wedge dxy_{R^{1}_{\ell }}$
. One key observation is the fact that
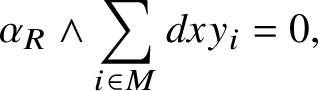 $$ \begin{align} \alpha_{R}\wedge\sum_{i\in M}dxy_{i}=0, \end{align} $$
$$ \begin{align} \alpha_{R}\wedge\sum_{i\in M}dxy_{i}=0, \end{align} $$
which is essentially a consequence of the equality
![]() $(dxy_{i}-dxy_{j})\wedge (dxy_{i}+dxy_{j})=0$
.
$(dxy_{i}-dxy_{j})\wedge (dxy_{i}+dxy_{j})=0$
.
Before stating Proposition 1.10, we need some further notation. First, we say that R is a standard Young tableau when the elements in each row and each column of R are in increasing order; that is, when
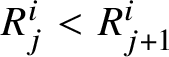 $R^{i}_{j}<R^{i}_{j+1}$
and
$R^{i}_{j}<R^{i}_{j+1}$
and
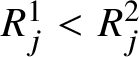 $R^{1}_{j}<R^{2}_{j}$
. Second, given
$R^{1}_{j}<R^{2}_{j}$
. Second, given
![]() $I=\{i_{1},\dots ,i_{|I|}\}\subset \{1,\dots ,n\}$
with
$I=\{i_{1},\dots ,i_{|I|}\}\subset \{1,\dots ,n\}$
with
![]() $i_{1}<i_{2}<\dots <i_{|I|}$
, we write
$i_{1}<i_{2}<\dots <i_{|I|}$
, we write
Eventually, we denote by
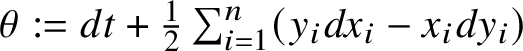 $\theta :=dt+\frac 12\sum _{i=1}^{n}(y_{i}dx_{i}-x_{i}dy_{i})$
the contact form on
$\theta :=dt+\frac 12\sum _{i=1}^{n}(y_{i}dx_{i}-x_{i}dy_{i})$
the contact form on
![]() ${\mathbb H}^{n}$
, which is left-invariant and then can be thought of as a covector in
${\mathbb H}^{n}$
, which is left-invariant and then can be thought of as a covector in
![]() $\Large \wedge ^{1}{\mathfrak h}$
. Observe that
$\Large \wedge ^{1}{\mathfrak h}$
. Observe that
![]() $\theta $
vanishes on horizontal vectors.
$\theta $
vanishes on horizontal vectors.
Proposition 1.10. For every
![]() $k\in \{1,\dots ,n\}$
, a basis of
$k\in \{1,\dots ,n\}$
, a basis of
![]() ${\mathcal J}^{2n+1-k}$
is provided by the elements of the form
${\mathcal J}^{2n+1-k}$
is provided by the elements of the form
![]() $dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
, where
$dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
, where
![]() $(I,J,R)$
ranges among those triples such that
$(I,J,R)$
ranges among those triples such that
-
•
 $I\subset \{1,\dots ,n\}$
,
$I\subset \{1,\dots ,n\}$
,
 $J\subset \{1,\dots ,n\}$
,
$J\subset \{1,\dots ,n\}$
,
 $|I|+|J|\leq k$
and
$|I|+|J|\leq k$
and
 $I\cap J=\emptyset $
;
$I\cap J=\emptyset $
; -
• R is a standard Young tableau containing the elements of
 $\{1,\dots ,n\}\setminus (I\cup J)$
arranged in two rows of length, respectively,
$\{1,\dots ,n\}\setminus (I\cup J)$
arranged in two rows of length, respectively,
 $(2n-k-|I|-|J|)/2$
and
$(2n-k-|I|-|J|)/2$
and
 $(k-|I|-|J|)/2$
.
$(k-|I|-|J|)/2$
.
Proposition 1.10 follows from Corollary 3.22. Observe that the tableaux R appearing in the statement are rectangular exactly in case
![]() $k=n$
. In this case, it might happen that
$k=n$
. In this case, it might happen that
![]() $I\cup J=\{1,\dots ,n\}$
; that is, that R is the empty table. If so, we agree that
$I\cup J=\{1,\dots ,n\}$
; that is, that R is the empty table. If so, we agree that
![]() $\alpha _{R}=1$
. It is also worth observing that the covectors
$\alpha _{R}=1$
. It is also worth observing that the covectors
![]() $\lambda _{I,J,R}=dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
appearing in Proposition 1.10 indeed belong to
$\lambda _{I,J,R}=dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
appearing in Proposition 1.10 indeed belong to
![]() ${\mathcal J}^{2n+1-k}$
because
${\mathcal J}^{2n+1-k}$
because
![]() $\lambda _{I,J,R}\wedge \theta =0$
(by definition) and
$\lambda _{I,J,R}\wedge \theta =0$
(by definition) and
![]() $\lambda _{I,J,R}\wedge d\theta =0$
, which comes as a consequence of (1.4) and the fact that
$\lambda _{I,J,R}\wedge d\theta =0$
, which comes as a consequence of (1.4) and the fact that
![]() $d\theta =-\sum _{i=1}^{n} dxy_{i}$
is, up to a sign, the standard symplectic form.
$d\theta =-\sum _{i=1}^{n} dxy_{i}$
is, up to a sign, the standard symplectic form.
During the preparation of this article, we became aware that a basis of
![]() ${\mathcal J}^{2n+1-k}$
is provided also in the paper [Reference Baldi, Barnabei and Franchi11]: however, the basis in [Reference Baldi, Barnabei and Franchi11] is presented by induction on n, while ours is given directly and is somewhat manageable in the computations we need.
${\mathcal J}^{2n+1-k}$
is provided also in the paper [Reference Baldi, Barnabei and Franchi11]: however, the basis in [Reference Baldi, Barnabei and Franchi11] is presented by induction on n, while ours is given directly and is somewhat manageable in the computations we need.
1.6 Sketch of the proof of Rademacher’s Theorem 1.1
For the reader’s convenience, we provide a sketch of the proof of our main result. Let
![]() $\phi :A\subset {\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz; by Theorem 1.5 we can assume that
$\phi :A\subset {\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz; by Theorem 1.5 we can assume that
![]() $A={\mathbb W}$
. We now use Theorem 1.6 to produce a sequence of smooth maps
$A={\mathbb W}$
. We now use Theorem 1.6 to produce a sequence of smooth maps
![]() $\phi _{i}:{\mathbb W}\to {\mathbb V}$
converging uniformly to
$\phi _{i}:{\mathbb W}\to {\mathbb V}$
converging uniformly to
![]() $\phi $
: it can be easily proved that the associated Heisenberg currents
$\phi $
: it can be easily proved that the associated Heisenberg currents
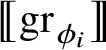 converge (possibly up to a subsequence) to a current
converge (possibly up to a subsequence) to a current
![]() ${\mathsf T}$
supported on
${\mathsf T}$
supported on
![]() $\mathrm {gr}_{\phi }$
and, actually, that
$\mathrm {gr}_{\phi }$
and, actually, that
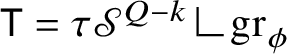 for some bounded function
for some bounded function
![]() $\tau :\mathrm {gr}_{\phi }\to {\mathcal J}_{2n+1-k}\setminus \{0\}$
. Moreover, we have
$\tau :\mathrm {gr}_{\phi }\to {\mathcal J}_{2n+1-k}\setminus \{0\}$
. Moreover, we have
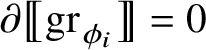 for every i because of Proposition 1.9; therefore, also
for every i because of Proposition 1.9; therefore, also
![]() $\partial {\mathsf T}=0$
. As we will see, this equality carries the relevant geometric information.
$\partial {\mathsf T}=0$
. As we will see, this equality carries the relevant geometric information.
Our aim is to prove that, at a.e.
![]() $w\in {\mathbb W}$
, the blow-up of
$w\in {\mathbb W}$
, the blow-up of
![]() $\phi $
at w (i.e., the limit as
$\phi $
at w (i.e., the limit as
![]() $r\to +\infty $
of
$r\to +\infty $
of
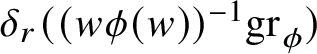 $\delta _{r}((w\phi (w))^{-1}\mathrm {gr}_{\phi })$
) is the graph of an intrinsic linear map; a priori, however, there could exist many possible blow-up limits
$\delta _{r}((w\phi (w))^{-1}\mathrm {gr}_{\phi })$
) is the graph of an intrinsic linear map; a priori, however, there could exist many possible blow-up limits
![]() $\psi $
associated with different diverging scaling sequences
$\psi $
associated with different diverging scaling sequences
![]() $(r_{j})_{j}$
. In Lemma 4.16 we prove the following: for a.e.
$(r_{j})_{j}$
. In Lemma 4.16 we prove the following: for a.e.
![]() $\bar {w}\in {\mathbb W}$
, all of the possible blow-ups
$\bar {w}\in {\mathbb W}$
, all of the possible blow-ups
![]() $\psi $
of
$\psi $
of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
are t-invariant; that is,
$\bar {w}$
are t-invariant; that is,
The proof of Lemma 4.16 makes use of Rademacher’s theorem proved for the case of codimension 1 in [Reference Franchi, Serapioni and Serra Cassano52].
Let then
![]() $\bar {w}$
be such a point and fix a t-invariant blow-up
$\bar {w}$
be such a point and fix a t-invariant blow-up
![]() $\psi $
of
$\psi $
of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
associated with a scaling sequence
$\bar {w}$
associated with a scaling sequence
![]() $(r_{j})_{j}$
. It is a good point to notice that, being both intrinsic Lipschitz (because it is the limit of uniformly intrinsic Lipschitz maps) and t-invariant,
$(r_{j})_{j}$
. It is a good point to notice that, being both intrinsic Lipschitz (because it is the limit of uniformly intrinsic Lipschitz maps) and t-invariant,
![]() $\psi $
is necessarily Euclidean Lipschitz; see Lemma 4.15. Consider now the current
$\psi $
is necessarily Euclidean Lipschitz; see Lemma 4.15. Consider now the current
![]() ${\mathsf T}_{\infty }$
defined (up to passing to a subsequence) as the blow-up limit along
${\mathsf T}_{\infty }$
defined (up to passing to a subsequence) as the blow-up limit along
![]() $(r_{j})_{j}$
of
$(r_{j})_{j}$
of
![]() ${\mathsf T}$
at
${\mathsf T}$
at
![]() $\bar p:=\bar {w}\phi (\bar {w})\in \mathrm {gr}_{\phi }$
, namely,
$\bar p:=\bar {w}\phi (\bar {w})\in \mathrm {gr}_{\phi }$
, namely,
 $$ \begin{align*} {\mathsf T}_{\infty}:=\lim_{j\to\infty}(\delta_{r_{j}}\circ L_{\bar p^{-1}})_\#{\mathsf T}, \end{align*} $$
$$ \begin{align*} {\mathsf T}_{\infty}:=\lim_{j\to\infty}(\delta_{r_{j}}\circ L_{\bar p^{-1}})_\#{\mathsf T}, \end{align*} $$
where
![]() $L_{\bar p^{-1}}$
denotes left-translation by
$L_{\bar p^{-1}}$
denotes left-translation by
![]() $\bar p^{-1}$
and the subscript
$\bar p^{-1}$
and the subscript
![]() $\#$
denotes push-forward. If one assumes that
$\#$
denotes push-forward. If one assumes that
![]() $\bar p$
is also a Lebesgue point (in a suitable sense) of the function
$\bar p$
is also a Lebesgue point (in a suitable sense) of the function
![]() $\tau $
, then the following properties hold for
$\tau $
, then the following properties hold for
![]() ${\mathsf T}_{\infty }$
:
${\mathsf T}_{\infty }$
:
-
•
 for some positive and bounded function f on
for some positive and bounded function f on
 $\mathrm {gr}_{\psi }$
;
$\mathrm {gr}_{\psi }$
; -
•
 $\mathrm {gr}_{\psi }$
is locally Euclidean rectifiable and, in particular, it is locally
$\mathrm {gr}_{\psi }$
is locally Euclidean rectifiable and, in particular, it is locally
 ${\mathbb H}$
-rectifiable;
${\mathbb H}$
-rectifiable; -
•
 $\partial {\mathsf T}_{\infty }=0$
, because
$\partial {\mathsf T}_{\infty }=0$
, because
 ${\mathsf T}_{\infty }$
is limit of boundaryless currents.
${\mathsf T}_{\infty }$
is limit of boundaryless currents.
We can then apply Theorem 1.8 to deduce that
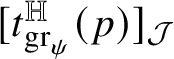 $[t^{\mathbb H}_{\mathrm {gr}_{\psi }}(p)]_{{\mathcal J}}$
is a multiple of
$[t^{\mathbb H}_{\mathrm {gr}_{\psi }}(p)]_{{\mathcal J}}$
is a multiple of
![]() $\tau (\bar p)$
for a.e.
$\tau (\bar p)$
for a.e.
![]() $p\in \mathrm {gr}_{\psi }$
. By t-invariance, the unit tangent vector
$p\in \mathrm {gr}_{\psi }$
. By t-invariance, the unit tangent vector
![]() $t_{\mathrm {gr}_{\psi }}(p)$
coincides with
$t_{\mathrm {gr}_{\psi }}(p)$
coincides with
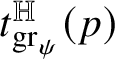 $t^{\mathbb H}_{\mathrm {gr}_{\psi }}(p)$
. Summarising, we have a t-invariant Euclidean Lipschitz submanifold
$t^{\mathbb H}_{\mathrm {gr}_{\psi }}(p)$
. Summarising, we have a t-invariant Euclidean Lipschitz submanifold
![]() $\mathrm {gr}_{\psi }$
whose unit tangent vector
$\mathrm {gr}_{\psi }$
whose unit tangent vector
![]() $t_{\mathrm {gr}_{\psi }}$
is always vertical (i.e., of the form
$t_{\mathrm {gr}_{\psi }}$
is always vertical (i.e., of the form
![]() $t_{\mathrm {gr}_{\psi }}=t^{\prime }\wedge T$
for a suitable multivector
$t_{\mathrm {gr}_{\psi }}=t^{\prime }\wedge T$
for a suitable multivector
![]() $t^{\prime }$
) and has the property that, for a.e. point p,
$t^{\prime }$
) and has the property that, for a.e. point p,
![]() $[t_{\mathrm {gr}_{\psi }}(p)]_{{\mathcal J}}$
is a multiple of
$[t_{\mathrm {gr}_{\psi }}(p)]_{{\mathcal J}}$
is a multiple of
![]() $\tau (\bar p)\in {\mathcal J}_{2n+1-k}\setminus \{0\}$
. If we could guarantee that there is a unique (up to a sign) unit simple vector
$\tau (\bar p)\in {\mathcal J}_{2n+1-k}\setminus \{0\}$
. If we could guarantee that there is a unique (up to a sign) unit simple vector
![]() $\bar t$
that is vertical and such that
$\bar t$
that is vertical and such that
![]() $[\,\bar t\,]_{{\mathcal J}}$
is a multiple of
$[\,\bar t\,]_{{\mathcal J}}$
is a multiple of
![]() $\tau (\bar p)$
, then we would conclude that
$\tau (\bar p)$
, then we would conclude that
![]() $\mathrm {gr}_{\psi }$
is always tangent to that particular
$\mathrm {gr}_{\psi }$
is always tangent to that particular
![]() $\bar t$
; that is, that
$\bar t$
; that is, that
![]() $\mathrm {gr}_{\psi }$
is a vertical plane
$\mathrm {gr}_{\psi }$
is a vertical plane
![]() ${\mathscr P}$
. Since
${\mathscr P}$
. Since
![]() $\bar t$
(and then
$\bar t$
(and then
![]() ${\mathscr P}$
) depends only on
${\mathscr P}$
) depends only on
![]() $\bar p$
and not on the particular sequence
$\bar p$
and not on the particular sequence
![]() $(r_{j})_{j}$
, the blow-up
$(r_{j})_{j}$
, the blow-up
![]() ${\mathscr P}$
is unique and is the graph of an intrinsic linear map
${\mathscr P}$
is unique and is the graph of an intrinsic linear map
![]() $\psi $
: this would conclude the proof.
$\psi $
: this would conclude the proof.
Unluckily, this is not always the case; in fact, in the second Heisenberg group
![]() ${\mathbb H}^{2}$
the unit simple vertical 3-vectors
${\mathbb H}^{2}$
the unit simple vertical 3-vectors
![]() $X_{1}\wedge Y_{1}\wedge T$
and
$X_{1}\wedge Y_{1}\wedge T$
and
![]() $-X_{2}\wedge Y_{2}\wedge T$
have the property that
$-X_{2}\wedge Y_{2}\wedge T$
have the property that
This, however, is basically the worst-case scenario. A key, technically demanding result is Proposition 3.38, where we prove that there exist at most two linearly independent unit simple vertical vectors
![]() $\bar t_{1},\bar t_{2}$
such that
$\bar t_{1},\bar t_{2}$
such that
![]() $[ \bar t_{1}]_{{\mathcal J}} = [\bar t_{2}]_{{\mathcal J}}$
are multiples of
$[ \bar t_{1}]_{{\mathcal J}} = [\bar t_{2}]_{{\mathcal J}}$
are multiples of
![]() $\tau (\bar p)$
; moreover, the planes
$\tau (\bar p)$
; moreover, the planes
![]() ${\mathscr P}_{1},{\mathscr P}_{2}$
associated (respectively) with
${\mathscr P}_{1},{\mathscr P}_{2}$
associated (respectively) with
![]() $\pm \bar t_{1},\pm \bar t_{2}$
are not rank 1 connected; that is,
$\pm \bar t_{1},\pm \bar t_{2}$
are not rank 1 connected; that is,
![]() $\dim {\mathscr P}_{1}\cap {\mathscr P}_{2}$
has codimension at least 2 in
$\dim {\mathscr P}_{1}\cap {\mathscr P}_{2}$
has codimension at least 2 in
![]() ${\mathscr P}_{1}$
(equivalently, in
${\mathscr P}_{1}$
(equivalently, in
![]() ${\mathscr P}_{2}$
). This means that the vertical Euclidean Lipschitz submanifold
${\mathscr P}_{2}$
). This means that the vertical Euclidean Lipschitz submanifold
![]() $\mathrm {gr}_{\psi }$
has at most two possible tangent planes
$\mathrm {gr}_{\psi }$
has at most two possible tangent planes
![]() ${\mathscr P}_{1},{\mathscr P}_{2}$
; however (see, e.g., [Reference Ball and James14, Proposition 1] or [Reference Müller78, Proposition 2.1]), the fact that these two planes are not rank 1 connected forces
${\mathscr P}_{1},{\mathscr P}_{2}$
; however (see, e.g., [Reference Ball and James14, Proposition 1] or [Reference Müller78, Proposition 2.1]), the fact that these two planes are not rank 1 connected forces
![]() $\mathrm {gr}_{\psi }$
to be a plane (either
$\mathrm {gr}_{\psi }$
to be a plane (either
![]() ${\mathscr P}_{1}$
or
${\mathscr P}_{1}$
or
![]() ${\mathscr P}_{2}$
) itself.
${\mathscr P}_{2}$
) itself.
This is not the conclusion yet: we have for the moment proved that, for a.e.
![]() $\bar {w}\in {\mathbb W}$
, all of the possible blow-ups of
$\bar {w}\in {\mathbb W}$
, all of the possible blow-ups of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
are either the map
$\bar {w}$
are either the map
![]() $\psi _{1}$
parametrising
$\psi _{1}$
parametrising
![]() ${\mathscr P}_{1}$
or the map
${\mathscr P}_{1}$
or the map
![]() $\psi _{2}$
parametrising
$\psi _{2}$
parametrising
![]() ${\mathscr P}_{2}$
; both are determined by
${\mathscr P}_{2}$
; both are determined by
![]() $\tau (\bar p)$
(i.e., by
$\tau (\bar p)$
(i.e., by
![]() $\bar {w}$
) only. However, it is not difficult to observe that the family of all possible blow-ups of
$\bar {w}$
) only. However, it is not difficult to observe that the family of all possible blow-ups of
![]() $\phi $
at a fixed point must enjoy a suitable connectedness property; hence, it cannot consist of the two points
$\phi $
at a fixed point must enjoy a suitable connectedness property; hence, it cannot consist of the two points
![]() $\psi _{1},\psi _{2}$
only. This proves the uniqueness of blow-ups and concludes the proof of our main result.
$\psi _{1},\psi _{2}$
only. This proves the uniqueness of blow-ups and concludes the proof of our main result.
1.7 Structure of the article
In Section 2 we introduce intrinsic Lipschitz graphs in Carnot groups and prove Theorems 1.4, 1.5 and 1.6. Heisenberg groups are introduced in Section 3, where we focus on the algebraic preliminary material, in particular, about multilinear algebra and Rumin’s complex. We also provide the basis of Rumin’s spaces of Proposition 1.10, introduce Heisenberg currents and prove Proposition 1.9. Eventually, we state Proposition 3.38, which we use in the proof of Rademacher’s Theorem 1.1 and whose long and tedious proof is postponed to Appendix A. In Section 4 we deal with intrinsic Lipschitz graphs of low codimension; in particular, we define intrinsic differentiability and we prove the crucial Lemma 4.16. We also introduce
![]() ${\mathbb H}$
-regular submanifolds and
${\mathbb H}$
-regular submanifolds and
![]() ${\mathbb H}$
-rectifiable sets and we study (Euclidean)
${\mathbb H}$
-rectifiable sets and we study (Euclidean)
![]() $C^{1}$
-regular intrinsic graphs. Section 5 is devoted to the proof of the constancy-type Theorems 1.7 and 1.8. The proof of Rademacher’s Theorem 1.1 is provided in Section 6. Section 7 contains the applications of our main result concerning Lusin’s Theorem 1.2, the equivalence between
$C^{1}$
-regular intrinsic graphs. Section 5 is devoted to the proof of the constancy-type Theorems 1.7 and 1.8. The proof of Rademacher’s Theorem 1.1 is provided in Section 6. Section 7 contains the applications of our main result concerning Lusin’s Theorem 1.2, the equivalence between
![]() ${\mathbb H}$
-rectifiability and ‘Lipschitz’
${\mathbb H}$
-rectifiability and ‘Lipschitz’
![]() ${\mathbb H}$
-rectifiability (Corollary 7.4) and the area formula of Theorem 1.3.
${\mathbb H}$
-rectifiability (Corollary 7.4) and the area formula of Theorem 1.3.
2 Intrinsic Lipschitz graphs in Carnot groups: extension and approximation results
In this section we introduce Carnot groups and intrinsic Lipschitz graphs; our goal is to prove the extension and approximation results stated in Theorems 1.5 and 1.6. These two results are used later in the article for intrinsic Lipschitz graphs in Heisenberg groups; however, they can be proved with no extra effort in the wider setting of Carnot groups, and we will therefore operate in this framework, which also allows for some simplifications in the notation. The presentation of Carnot groups will be only minimal, and we refer to [Reference Folland and Stein43, Reference Bonfiglioli, Lanconelli and Uguzzoni20, Reference Gromov58, Reference Le Donne66, Reference Serra Cassano88] for a more comprehensive treatment. The reader looking for a thorough account on intrinsic Lipschitz graphs might instead consult [Reference Franchi and Serapioni53].
2.1 Carnot groups: algebraic and metric preliminaries
A Carnot (or stratified) group is a connected, simply connected and nilpotent Lie group whose Lie algebra
![]() ${\mathfrak g}$
is stratified; that is, it possesses a decomposition
${\mathfrak g}$
is stratified; that is, it possesses a decomposition
![]() ${\mathfrak g}={\mathfrak g}_{1}\oplus \dots \oplus {\mathfrak g}_{s}$
such that
${\mathfrak g}={\mathfrak g}_{1}\oplus \dots \oplus {\mathfrak g}_{s}$
such that
We refer to the integer s as the step of
![]() ${\mathbb G}$
and to
${\mathbb G}$
and to
![]() $m:=\,$
dim
$m:=\,$
dim
![]() ${\mathfrak g}_{1}$
as its rank; we also denote by d the topological dimension of
${\mathfrak g}_{1}$
as its rank; we also denote by d the topological dimension of
![]() ${\mathbb G}$
. The group identity is denoted by
${\mathbb G}$
. The group identity is denoted by
![]() $0$
and, as is customary, we identify
$0$
and, as is customary, we identify
![]() ${\mathfrak g}$
,
${\mathfrak g}$
,
![]() $T_{0}{\mathbb G}$
and the algebra of left-invariant vector fields on
$T_{0}{\mathbb G}$
and the algebra of left-invariant vector fields on
![]() ${\mathbb G}$
. The elements of
${\mathbb G}$
. The elements of
![]() ${\mathfrak g}_{1}$
are referred to as horizontal.
${\mathfrak g}_{1}$
are referred to as horizontal.
The exponential map
![]() $\exp :{\mathfrak g}\to {\mathbb G}$
is a diffeomorphism and, given a basis
$\exp :{\mathfrak g}\to {\mathbb G}$
is a diffeomorphism and, given a basis
![]() $X_{1},\dots ,X_{d}$
of
$X_{1},\dots ,X_{d}$
of
![]() ${\mathfrak g}$
, we will often identify
${\mathfrak g}$
, we will often identify
![]() ${\mathbb G}$
with
${\mathbb G}$
with
![]() ${\mathbb R}^{d}$
by means of exponential coordinates:
${\mathbb R}^{d}$
by means of exponential coordinates:
We will also assume that the basis is adapted to the stratification; that is, that
 $$ \begin{align*} & X_{1},\dots,X_{m} \text{ is a basis of }{\mathfrak g}_{1}\text{ and}\\ & \forall\ j=2,\dots,s,\ X_{\dim ({\mathfrak g}_{1}\oplus\cdots\oplus{\mathfrak g}_{j-1})+1},\dots, X_{\dim ({\mathfrak g}_{1}\oplus\cdots\oplus{\mathfrak g}_{j})}\text{ is a basis of }{\mathfrak g}_{j}\text{.} \end{align*} $$
$$ \begin{align*} & X_{1},\dots,X_{m} \text{ is a basis of }{\mathfrak g}_{1}\text{ and}\\ & \forall\ j=2,\dots,s,\ X_{\dim ({\mathfrak g}_{1}\oplus\cdots\oplus{\mathfrak g}_{j-1})+1},\dots, X_{\dim ({\mathfrak g}_{1}\oplus\cdots\oplus{\mathfrak g}_{j})}\text{ is a basis of }{\mathfrak g}_{j}\text{.} \end{align*} $$
In these coordinates, one has
 $$ \begin{align} X_{i}(x)=\partial_{x_{i}}+\sum_{j=m+1}^{d} P_{i,j}(x)\partial_{x_{j}}\quad\text{for every }i=1,\dots,m \end{align} $$
$$ \begin{align} X_{i}(x)=\partial_{x_{i}}+\sum_{j=m+1}^{d} P_{i,j}(x)\partial_{x_{j}}\quad\text{for every }i=1,\dots,m \end{align} $$
for suitable polynomial functions
![]() $P_{i,j}$
. A one-parameter family
$P_{i,j}$
. A one-parameter family
![]() $\{\delta _{\lambda }\}_{\lambda>0}$
of dilations
$\{\delta _{\lambda }\}_{\lambda>0}$
of dilations
![]() $\delta _{\lambda }:{\mathfrak g}\to {\mathfrak g}$
is defined by (linearly extending)
$\delta _{\lambda }:{\mathfrak g}\to {\mathfrak g}$
is defined by (linearly extending)
 $$ \begin{align*} \delta_{\lambda}(X):=\lambda^{j} X\text{ for any }X\in{\mathfrak g}_{j}\text{;} \end{align*} $$
$$ \begin{align*} \delta_{\lambda}(X):=\lambda^{j} X\text{ for any }X\in{\mathfrak g}_{j}\text{;} \end{align*} $$
notice that dilations are Lie algebra homomorphisms and
![]() $\delta _{\lambda \mu }=\delta _{\lambda }\circ \delta _{\mu }$
. By composition with
$\delta _{\lambda \mu }=\delta _{\lambda }\circ \delta _{\mu }$
. By composition with
![]() $\exp $
, one can then define a one-parameter family, for which we use the same symbol, of group isomorphisms
$\exp $
, one can then define a one-parameter family, for which we use the same symbol, of group isomorphisms
![]() $\delta _{\lambda }:{\mathbb G}\to {\mathbb G}$
.
$\delta _{\lambda }:{\mathbb G}\to {\mathbb G}$
.
We fix a left-invariant homogeneous distance d on
![]() ${\mathbb G}$
, so that
${\mathbb G}$
, so that
We use d to denote both the distance on
![]() ${\mathbb G}$
and its topological dimension, but no confusion will ever arise. We denote by
${\mathbb G}$
and its topological dimension, but no confusion will ever arise. We denote by
![]() $B(x,r)$
the open ball of center
$B(x,r)$
the open ball of center
![]() $x\in {\mathbb G}$
and radius
$x\in {\mathbb G}$
and radius
![]() $r>0$
; it will also be convenient to denote by
$r>0$
; it will also be convenient to denote by
![]() $\|\cdot \|_{{\mathbb G}}$
the homogeneous norm defined for
$\|\cdot \|_{{\mathbb G}}$
the homogeneous norm defined for
![]() $x\in {\mathbb G}$
by
$x\in {\mathbb G}$
by
![]() $\|x\|_{{\mathbb G}}:=d(0,x)$
. Recall that
$\|x\|_{{\mathbb G}}:=d(0,x)$
. Recall that
![]() ${\mathscr L}^{d}$
is a Haar measure on
${\mathscr L}^{d}$
is a Haar measure on
![]() ${\mathbb G}\equiv {\mathbb R}^{d}$
and that the homogeneous dimension of
${\mathbb G}\equiv {\mathbb R}^{d}$
and that the homogeneous dimension of
![]() ${\mathbb G}$
is the integer
${\mathbb G}$
is the integer
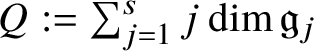 $Q:=\sum _{j=1}^{s} j\dim {\mathfrak g}_{j}$
. One has
$Q:=\sum _{j=1}^{s} j\dim {\mathfrak g}_{j}$
. One has
The number Q is always greater than d (apart from the Euclidean case
![]() $s=1$
) and it coincides with the Hausdorff dimension of
$s=1$
) and it coincides with the Hausdorff dimension of
![]() ${\mathbb G}$
. Since the Hausdorff Q-dimensional measure is also a Haar measure, it coincides with
${\mathbb G}$
. Since the Hausdorff Q-dimensional measure is also a Haar measure, it coincides with
![]() ${\mathscr L}^{d}$
up to a constant.
${\mathscr L}^{d}$
up to a constant.
Given a measurable function
![]() $f:{\mathbb G}\to {\mathbb R}$
, we denote by
$f:{\mathbb G}\to {\mathbb R}$
, we denote by
![]() $\nabla _{{\mathbb G}} f=(X_{1}f,\dots ,X_{m}f)$
its horizontal derivatives in the sense of distributions. It is well-known that, if f is Lipschitz continuous, then it is Pansu differentiable almost everywhere [Reference Pansu81] and, in particular, the pointwise horizontal gradient
$\nabla _{{\mathbb G}} f=(X_{1}f,\dots ,X_{m}f)$
its horizontal derivatives in the sense of distributions. It is well-known that, if f is Lipschitz continuous, then it is Pansu differentiable almost everywhere [Reference Pansu81] and, in particular, the pointwise horizontal gradient
![]() $\nabla _{{\mathbb G}} f$
exists almost everywhere on
$\nabla _{{\mathbb G}} f$
exists almost everywhere on
![]() ${\mathbb G}$
. Moreover (see, e.g., [Reference Franchi, Serapioni and Serra Cassano47, Reference Garofalo and Nhieu56]), we have
${\mathbb G}$
. Moreover (see, e.g., [Reference Franchi, Serapioni and Serra Cassano47, Reference Garofalo and Nhieu56]), we have
where Lipschitz continuity, of course, is meant with respect to the homogeneous distance d on
![]() ${\mathbb G}$
. It is worth mentioning that the Lipschitz constant of f is bounded by
${\mathbb G}$
. It is worth mentioning that the Lipschitz constant of f is bounded by
![]() $\|\nabla _{{\mathbb G}} f\|_{L^{\infty }({\mathbb G})}$
, apart from multiplicative constants that depend only on the distance d, both from below and from above.
$\|\nabla _{{\mathbb G}} f\|_{L^{\infty }({\mathbb G})}$
, apart from multiplicative constants that depend only on the distance d, both from below and from above.
We will need the following result later, proved in [Reference Vittone93, Lemma 2.2], where we denote by
![]() $\overrightarrow {\exp }(X)(x)$
the point reached in unit time by the integral curve of a vector field X starting at a point x.
$\overrightarrow {\exp }(X)(x)$
the point reached in unit time by the integral curve of a vector field X starting at a point x.
Lemma 2.1. Let
![]() $f:{\mathbb R}^{d}\to {\mathbb R}$
be a continuous function and let Y be a smooth vector field in
$f:{\mathbb R}^{d}\to {\mathbb R}$
be a continuous function and let Y be a smooth vector field in
![]() ${\mathbb R}^{d}$
. Assume that
${\mathbb R}^{d}$
. Assume that
![]() $Yf\geq \delta $
holds, in the sense of distributions, on an open set
$Yf\geq \delta $
holds, in the sense of distributions, on an open set
![]() $U\subset {\mathbb R}^{d}$
and for a suitable
$U\subset {\mathbb R}^{d}$
and for a suitable
![]() $\delta \in {\mathbb R}$
. If
$\delta \in {\mathbb R}$
. If
![]() $x\in U$
and
$x\in U$
and
![]() $T>0$
are such that
$T>0$
are such that
![]() $\overrightarrow {\exp }(hY)(x)\in U$
for every
$\overrightarrow {\exp }(hY)(x)\in U$
for every
![]() $h\in [0,T)$
, then
$h\in [0,T)$
, then
2.2 Intrinsic Lipschitz graphs
Following [Reference Franchi and Serapioni53], we fix a splitting
![]() ${\mathbb G}={\mathbb W}{\mathbb V}$
in terms of a couple
${\mathbb G}={\mathbb W}{\mathbb V}$
in terms of a couple
![]() ${\mathbb W},{\mathbb V}$
of homogeneous (i.e., invariant under dilations) and complementary (i.e.,
${\mathbb W},{\mathbb V}$
of homogeneous (i.e., invariant under dilations) and complementary (i.e.,
![]() ${\mathbb W}\cap {\mathbb V}=\{0\}$
and
${\mathbb W}\cap {\mathbb V}=\{0\}$
and
![]() ${\mathbb G}={\mathbb W}{\mathbb V}$
) Lie subgroups of
${\mathbb G}={\mathbb W}{\mathbb V}$
) Lie subgroups of
![]() ${\mathbb G}$
. In exponential coordinates,
${\mathbb G}$
. In exponential coordinates,
![]() ${\mathbb W},{\mathbb V}$
are linear subspaces of
${\mathbb W},{\mathbb V}$
are linear subspaces of
![]() ${\mathbb G}\equiv {\mathbb R}^{d}$
. Clearly, the splitting induces for every
${\mathbb G}\equiv {\mathbb R}^{d}$
. Clearly, the splitting induces for every
![]() $x\in {\mathbb G}$
a unique decomposition
$x\in {\mathbb G}$
a unique decomposition
![]() $x=x_{{\mathbb W}} x_{{\mathbb V}}$
such that
$x=x_{{\mathbb W}} x_{{\mathbb V}}$
such that
![]() $x_{{\mathbb W}}\in {\mathbb W}$
and
$x_{{\mathbb W}}\in {\mathbb W}$
and
![]() $x_{{\mathbb V}}\in {\mathbb V}$
; we will sometimes refer to the maps
$x_{{\mathbb V}}\in {\mathbb V}$
; we will sometimes refer to the maps
![]() $x\mapsto x_{{\mathbb W}}$
and
$x\mapsto x_{{\mathbb W}}$
and
![]() $x\mapsto x_{{\mathbb V}}$
as the projections of
$x\mapsto x_{{\mathbb V}}$
as the projections of
![]() ${\mathbb G}$
on
${\mathbb G}$
on
![]() ${\mathbb W}$
and on
${\mathbb W}$
and on
![]() ${\mathbb V}$
, respectively.
${\mathbb V}$
, respectively.
Given
![]() $A\subset {\mathbb W}$
and a map
$A\subset {\mathbb W}$
and a map
![]() $\phi :A\to {\mathbb V}$
, the intrinsic graph
$\phi :A\to {\mathbb V}$
, the intrinsic graph
![]() $\mathrm {gr}_{\phi }$
of
$\mathrm {gr}_{\phi }$
of
![]() $\phi $
is the set
$\phi $
is the set
The notion of intrinsic Lipschitz continuity for maps
![]() $\phi $
from
$\phi $
from
![]() ${\mathbb W}$
to
${\mathbb W}$
to
![]() ${\mathbb V}$
was introduced by B. Franchi, R. Serapioni and F. Serra Cassano [Reference Franchi, Serapioni and Serra Cassano50] in terms of a cone property for
${\mathbb V}$
was introduced by B. Franchi, R. Serapioni and F. Serra Cassano [Reference Franchi, Serapioni and Serra Cassano50] in terms of a cone property for
![]() $\mathrm {gr}_{\phi }$
. The intrinsic cone
$\mathrm {gr}_{\phi }$
. The intrinsic cone
![]() ${\mathscr C}_{\alpha }$
of aperture
${\mathscr C}_{\alpha }$
of aperture
![]() $\alpha> 0$
and axis
$\alpha> 0$
and axis
![]() ${\mathbb V}$
is
${\mathbb V}$
is
Observe that
![]() ${\mathscr C}_{\alpha }$
is homogeneous (invariant under dilations) and that
${\mathscr C}_{\alpha }$
is homogeneous (invariant under dilations) and that
![]() ${\mathbb V}\subset {\mathscr C}_{\alpha }$
. For
${\mathbb V}\subset {\mathscr C}_{\alpha }$
. For
![]() $x\in {\mathbb G}$
we also introduce the cone
$x\in {\mathbb G}$
we also introduce the cone
![]() ${\mathscr C}_{\alpha }(x):=x{\mathscr C}_{\alpha }$
with vertex x.
${\mathscr C}_{\alpha }(x):=x{\mathscr C}_{\alpha }$
with vertex x.
Definition 2.2. Let
![]() $A\subset {\mathbb W}$
; we say that
$A\subset {\mathbb W}$
; we say that
![]() $\phi :A\to {\mathbb V}$
is intrinsic Lipschitz if there exists
$\phi :A\to {\mathbb V}$
is intrinsic Lipschitz if there exists
![]() $\alpha>0$
such that
$\alpha>0$
such that
The intrinsic Lipschitz constant of
![]() $\phi $
is
$\phi $
is
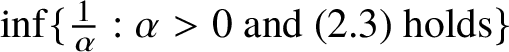 $\inf \{\frac 1\alpha :\alpha>0\text { and~(2.3) holds}\}$
.
$\inf \{\frac 1\alpha :\alpha>0\text { and~(2.3) holds}\}$
.
Since all homogeneous distances on
![]() ${\mathbb G}$
are equivalent, Definition 2.2 is clearly independent from the fixed distance d on the group. It was proved in [Reference Franchi and Serapioni53, Theorem 3.9] that, if
${\mathbb G}$
are equivalent, Definition 2.2 is clearly independent from the fixed distance d on the group. It was proved in [Reference Franchi and Serapioni53, Theorem 3.9] that, if
![]() $\phi :{\mathbb W}\to {\mathbb V}$
is an entire intrinsic Lipschitz map, then the Hausdorff dimension of
$\phi :{\mathbb W}\to {\mathbb V}$
is an entire intrinsic Lipschitz map, then the Hausdorff dimension of
![]() $\mathrm {gr}_{\phi }$
is the same as the Hausdorff dimension of the domain
$\mathrm {gr}_{\phi }$
is the same as the Hausdorff dimension of the domain
![]() ${\mathbb W}$
; actually, the corresponding Hausdorff measure on
${\mathbb W}$
; actually, the corresponding Hausdorff measure on
![]() $\mathrm {gr}_{\phi }$
is Ahlfors regular and then also locally finite on
$\mathrm {gr}_{\phi }$
is Ahlfors regular and then also locally finite on
![]() $\mathrm {gr}_{\phi }$
. This implies that for entire intrinsic Lipschitz graphs one has
$\mathrm {gr}_{\phi }$
. This implies that for entire intrinsic Lipschitz graphs one has
 $$ \begin{align} {\mathscr L}^{d}(\mathrm{gr}_{\phi})=0, \end{align} $$
$$ \begin{align} {\mathscr L}^{d}(\mathrm{gr}_{\phi})=0, \end{align} $$
provided, of course, we are not in the trivial case
![]() ${\mathbb W}={\mathbb G}$
,
${\mathbb W}={\mathbb G}$
,
![]() ${\mathbb V}=\{0\}$
. As one can imagine, the equality (2.4) holds, however, for every intrinsic Lipschitz
${\mathbb V}=\{0\}$
. As one can imagine, the equality (2.4) holds, however, for every intrinsic Lipschitz
![]() $\phi :A\subset {\mathbb W}\to {\mathbb V}$
provided
$\phi :A\subset {\mathbb W}\to {\mathbb V}$
provided
![]() ${\mathbb W}\neq {\mathbb G}$
: one way of proving this fact is by noticing that
${\mathbb W}\neq {\mathbb G}$
: one way of proving this fact is by noticing that
![]() ${\mathscr L}^{d}({\mathscr C}_{\alpha }(x)\cap B(x,r))$
is a fixed fraction of
${\mathscr L}^{d}({\mathscr C}_{\alpha }(x)\cap B(x,r))$
is a fixed fraction of
![]() ${\mathscr L}^{d}( B(x,r))$
; hence,
${\mathscr L}^{d}( B(x,r))$
; hence,
![]() $\mathrm {gr}_{\phi }$
cannot have points of density 1 and (2.4) follows by Lebesgue’s differentiation theorem in doubling metric spaces (see, e.g., [Reference Heinonen59, Theorem 1.8]).
$\mathrm {gr}_{\phi }$
cannot have points of density 1 and (2.4) follows by Lebesgue’s differentiation theorem in doubling metric spaces (see, e.g., [Reference Heinonen59, Theorem 1.8]).
Remark 2.3. For the purpose of future references, we observe the following easy fact. Let
![]() $S\subset {\mathbb G}$
and
$S\subset {\mathbb G}$
and
![]() $\alpha>0$
be fixed; if
$\alpha>0$
be fixed; if
then
![]() $S=\mathrm {gr}_{\phi }$
for suitable
$S=\mathrm {gr}_{\phi }$
for suitable
![]() $\phi :A\to {\mathbb V}$
(which is clearly intrinsic Lipschitz) and
$\phi :A\to {\mathbb V}$
(which is clearly intrinsic Lipschitz) and
![]() $A\subset {\mathbb W}$
. See, for example, [Reference Franchi and Serapioni53, §2.2.3].
$A\subset {\mathbb W}$
. See, for example, [Reference Franchi and Serapioni53, §2.2.3].
2.3 A level set definition of co-horizontal intrinsic Lipschitz graphs
From now on we assume that the splitting
![]() ${\mathbb W}{\mathbb V}$
of
${\mathbb W}{\mathbb V}$
of
![]() ${\mathbb G}$
is fixed in such a way that
${\mathbb G}$
is fixed in such a way that
![]() ${\mathbb V}$
is not trivial (
${\mathbb V}$
is not trivial (
![]() ${\mathbb V}\neq \{0\}$
) and it is horizontal; that is,
${\mathbb V}\neq \{0\}$
) and it is horizontal; that is,
![]() ${\mathbb V}\subset \exp ({\mathfrak g}_{1})$
. Of course, this poses some algebraic restrictions: for instance,
${\mathbb V}\subset \exp ({\mathfrak g}_{1})$
. Of course, this poses some algebraic restrictions: for instance,
![]() ${\mathbb V}$
is forced to be abelian. Moreover, it can be easily checked that free Carnot groups (of step at least
${\mathbb V}$
is forced to be abelian. Moreover, it can be easily checked that free Carnot groups (of step at least
![]() $2$
) have no splitting such that
$2$
) have no splitting such that
![]() ${\mathbb V}$
is horizontal and
${\mathbb V}$
is horizontal and
![]() $\dim {\mathbb V}\geq 2$
. Nonetheless, the theory we are going to develop here is rich enough to include intrinsic Lipschitz graphs of codimension 1 in any Carnot group (in fact, every 1-dimensional horizontal subgroup
$\dim {\mathbb V}\geq 2$
. Nonetheless, the theory we are going to develop here is rich enough to include intrinsic Lipschitz graphs of codimension 1 in any Carnot group (in fact, every 1-dimensional horizontal subgroup
![]() ${\mathbb V}$
of a Carnot group provides a splitting
${\mathbb V}$
of a Carnot group provides a splitting
![]() ${\mathbb W}{\mathbb V}$
for some
${\mathbb W}{\mathbb V}$
for some
![]() ${\mathbb W}$
) and intrinsic Lipschitz graphs of codimension at most n in the Heisenberg group
${\mathbb W}$
) and intrinsic Lipschitz graphs of codimension at most n in the Heisenberg group
![]() ${\mathbb H}^{n}$
, which are the main object of study of the present article.
${\mathbb H}^{n}$
, which are the main object of study of the present article.
With such assumptions on the splitting
![]() ${\mathbb W}{\mathbb V}$
, intrinsic Lipschitz graphs
${\mathbb W}{\mathbb V}$
, intrinsic Lipschitz graphs
![]() $\Phi :A\subset {\mathbb W}\to {\mathbb V}$
will be called co-horizontal (see [Reference Antonelli, Di Donato, Don and Le Donne6]). We denote by k the topological dimension of
$\Phi :A\subset {\mathbb W}\to {\mathbb V}$
will be called co-horizontal (see [Reference Antonelli, Di Donato, Don and Le Donne6]). We denote by k the topological dimension of
![]() ${\mathbb V}$
and we assume without loss of generality that the adapted basis
${\mathbb V}$
and we assume without loss of generality that the adapted basis
![]() $X_{1},\dots ,X_{d}$
of
$X_{1},\dots ,X_{d}$
of
![]() ${\mathfrak g}$
has been fixed in such a way that
${\mathfrak g}$
has been fixed in such a way that
We consequently identify
![]() ${\mathbb V}$
with
${\mathbb V}$
with
![]() ${\mathbb R}^{k}$
through the map
${\mathbb R}^{k}$
through the map
and we accordingly write
![]() $ v=(v_{1},\dots ,v_{k})\in {\mathbb V}$
. The map in (2.5) turns out to be a group isomorphism as well as a bi-Lipschitz map between
$ v=(v_{1},\dots ,v_{k})\in {\mathbb V}$
. The map in (2.5) turns out to be a group isomorphism as well as a bi-Lipschitz map between
![]() $({\mathbb R}^{k},|\cdot |)$
and
$({\mathbb R}^{k},|\cdot |)$
and
![]() $({\mathbb V},d)$
: this proves that the Hausdorff dimension of
$({\mathbb V},d)$
: this proves that the Hausdorff dimension of
![]() ${\mathbb V}$
equals the topological dimension k. We observe that, since the flow of a left-invariant vector field corresponds to right multiplication, we have
${\mathbb V}$
equals the topological dimension k. We observe that, since the flow of a left-invariant vector field corresponds to right multiplication, we have
In particular, the projections on the factors
![]() ${\mathbb W},{\mathbb V}$
can be written as
${\mathbb W},{\mathbb V}$
can be written as
 $$ \begin{align*} x_{{\mathbb V}}=\exp(x_{1}X_{1}+\dots+x_{k}X_{k}),\qquad x_{{\mathbb W}} =x\,x_{{\mathbb V}}^{-1}=\overrightarrow{\exp}(-(x_{1}X_{1}+\dots+x_{k}X_{k}))(x) \end{align*} $$
$$ \begin{align*} x_{{\mathbb V}}=\exp(x_{1}X_{1}+\dots+x_{k}X_{k}),\qquad x_{{\mathbb W}} =x\,x_{{\mathbb V}}^{-1}=\overrightarrow{\exp}(-(x_{1}X_{1}+\dots+x_{k}X_{k}))(x) \end{align*} $$
and are therefore smooth maps.
Our first goal is to provide the equivalent characterisation of co-horizontal intrinsic Lipschitz graphs stated in Theorem 1.4. However, we need some preparatory lemmata as well as some extra convention about notation. First, we introduce the homogeneous (pseudo)-norm
 $$ \begin{align*} \|x\|_{*}:=\left(\sum_{j=1}^{s} \sum_{i:X_{i}\in{\mathfrak g}_{j}}|x_{i}|^{\frac{2\;\!s!}{j}}\right)^{\frac1{2\;\!s!}},\qquad x\in{\mathbb G}, \end{align*} $$
$$ \begin{align*} \|x\|_{*}:=\left(\sum_{j=1}^{s} \sum_{i:X_{i}\in{\mathfrak g}_{j}}|x_{i}|^{\frac{2\;\!s!}{j}}\right)^{\frac1{2\;\!s!}},\qquad x\in{\mathbb G}, \end{align*} $$
which is equivalent to
![]() $\|\cdot \|_{{\mathbb G}}$
in the sense that there exists
$\|\cdot \|_{{\mathbb G}}$
in the sense that there exists
![]() $C_{*}\geq 1$
such that
$C_{*}\geq 1$
such that
Observe that
![]() $x\mapsto \|x\|_{*}$
is of class
$x\mapsto \|x\|_{*}$
is of class
![]() $C^{\infty }$
in
$C^{\infty }$
in
![]() ${\mathbb G}\setminus \{0\}$
. Second, given
${\mathbb G}\setminus \{0\}$
. Second, given
![]() $i\in \{1,\dots ,k\}$
,
$i\in \{1,\dots ,k\}$
,
![]() $\beta>0$
and
$\beta>0$
and
![]() $\varepsilon>0$
, we introduce the homogeneous cone
$\varepsilon>0$
, we introduce the homogeneous cone
 $$ \begin{align*} \begin{aligned} {\mathscr C}_{i,\beta,\varepsilon} :=& \left\{wv:w\in{\mathbb W},\ v\in{\mathbb V},\ |v_{i}|+\varepsilon\sum_{j\in\{1,\dots,k\}\setminus\{i\}}|v_{j}|\geq \beta\|w\|_{*}\right\}\\ = & \left\{x\in{\mathbb G}:|x_{i}|+\varepsilon\sum_{j\in\{1,\dots,k\}\setminus\{i\}}|x_{j}|\geq \beta\|x_{{\mathbb W}}\|_{*}\right\}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} {\mathscr C}_{i,\beta,\varepsilon} :=& \left\{wv:w\in{\mathbb W},\ v\in{\mathbb V},\ |v_{i}|+\varepsilon\sum_{j\in\{1,\dots,k\}\setminus\{i\}}|v_{j}|\geq \beta\|w\|_{*}\right\}\\ = & \left\{x\in{\mathbb G}:|x_{i}|+\varepsilon\sum_{j\in\{1,\dots,k\}\setminus\{i\}}|x_{j}|\geq \beta\|x_{{\mathbb W}}\|_{*}\right\}, \end{aligned} \end{align*} $$
where we used the fact that
![]() $x_{{\mathbb V}}=(x_{1},\dots ,x_{k})$
. Third, if
$x_{{\mathbb V}}=(x_{1},\dots ,x_{k})$
. Third, if
![]() $t\in {\mathbb R}$
and
$t\in {\mathbb R}$
and
![]() $f:D\to {\mathbb R}$
is a real-valued function defined on some set D, we denote by
$f:D\to {\mathbb R}$
is a real-valued function defined on some set D, we denote by
![]() $\{f\geq t\}$
the set
$\{f\geq t\}$
the set
![]() $\{x\in D:f(x)\geq t\}$
. Similar conventions are understood when writing
$\{x\in D:f(x)\geq t\}$
. Similar conventions are understood when writing
![]() $\{f>t\},\ \{f<t\},\ \{f=t\},\ \{t_{1}<f<t_{2}\}$
, etc.
$\{f>t\},\ \{f<t\},\ \{f=t\},\ \{t_{1}<f<t_{2}\}$
, etc.
Lemma 2.4. For every
![]() $i\in \{1,\dots ,k\}$
,
$i\in \{1,\dots ,k\}$
,
![]() $\beta>0$
and
$\beta>0$
and
![]() $\varepsilon \in (0,1)$
there exists a 1-homogeneous Lipschitz function
$\varepsilon \in (0,1)$
there exists a 1-homogeneous Lipschitz function
![]() $f_{i,\beta ,\varepsilon }:{\mathbb G}\to {\mathbb R}$
such that
$f_{i,\beta ,\varepsilon }:{\mathbb G}\to {\mathbb R}$
such that
 $$ \begin{align} 1\leq X_{i}f_{i,\beta,\varepsilon}\leq 3\quad{\mathscr L}^{d}\text{-a.e. on }{\mathbb G} \hphantom{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\end{align} $$
$$ \begin{align} 1\leq X_{i}f_{i,\beta,\varepsilon}\leq 3\quad{\mathscr L}^{d}\text{-a.e. on }{\mathbb G} \hphantom{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\end{align} $$
 $$ \begin{align} \varepsilon\leq X_{\ell} f_{i,\beta,\varepsilon}\leq 3\varepsilon\quad{\mathscr L}^{d}\text{-a.e. on }{\mathbb G}\quad \forall\ \ell\in\{1,\dots,k\}\setminus\{i\} \end{align} $$
$$ \begin{align} \varepsilon\leq X_{\ell} f_{i,\beta,\varepsilon}\leq 3\varepsilon\quad{\mathscr L}^{d}\text{-a.e. on }{\mathbb G}\quad \forall\ \ell\in\{1,\dots,k\}\setminus\{i\} \end{align} $$
Moreover, if
![]() $0<\beta \leq \bar \beta $
, then the Lipschitz constant of
$0<\beta \leq \bar \beta $
, then the Lipschitz constant of
![]() $f_{i,\beta ,\varepsilon }$
can be controlled in terms of
$f_{i,\beta ,\varepsilon }$
can be controlled in terms of
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\bar \beta $
only.
$\bar \beta $
only.
Proof. Without loss of generality, we can assume that
![]() $i=1$
. For
$i=1$
. For
![]() $x\in {\mathbb G}$
, define
$x\in {\mathbb G}$
, define
 $$ \begin{align*} f(x):=\left\{ \begin{array}{l@{\quad}l} 2[x_{1}+\varepsilon(x_{2}+\dots+x_{k})-\beta\| x_{{\mathbb W}}\|_{*}]\quad & \text{if }|x_{1}+\varepsilon(x_{2}+\dots+x_{k})|\leq 2\beta\| x_{{\mathbb W}}\|_{*} \\ (x_{1}+\varepsilon(x_{2}+\dots+x_{k})) & \text{if }x_{1}+\varepsilon(x_{2}+\dots+x_{k})> 2\beta\| x_{{\mathbb W}}\|_{*}\\ 3[x_{1}+\varepsilon(x_{2}+\dots+x_{k})] & \text{if }x_{1}+\varepsilon(x_{2}+\dots+x_{k})<- 2\beta\| x_{{\mathbb W}}\|_{*}. \end{array} \right. \end{align*} $$
$$ \begin{align*} f(x):=\left\{ \begin{array}{l@{\quad}l} 2[x_{1}+\varepsilon(x_{2}+\dots+x_{k})-\beta\| x_{{\mathbb W}}\|_{*}]\quad & \text{if }|x_{1}+\varepsilon(x_{2}+\dots+x_{k})|\leq 2\beta\| x_{{\mathbb W}}\|_{*} \\ (x_{1}+\varepsilon(x_{2}+\dots+x_{k})) & \text{if }x_{1}+\varepsilon(x_{2}+\dots+x_{k})> 2\beta\| x_{{\mathbb W}}\|_{*}\\ 3[x_{1}+\varepsilon(x_{2}+\dots+x_{k})] & \text{if }x_{1}+\varepsilon(x_{2}+\dots+x_{k})<- 2\beta\| x_{{\mathbb W}}\|_{*}. \end{array} \right. \end{align*} $$
We prove that
![]() $f_{1,\beta ,\varepsilon }:=f$
satisfies all of the claimed statements. Property (2.7) and the homogeneity of f are immediate. Property (2.10) is equivalent to the implication
$f_{1,\beta ,\varepsilon }:=f$
satisfies all of the claimed statements. Property (2.7) and the homogeneity of f are immediate. Property (2.10) is equivalent to the implication
which one can easily check. The function f is continuous on
![]() ${\mathbb G}$
and smooth on
${\mathbb G}$
and smooth on
![]() ${\mathbb G}\setminus D$
, where
${\mathbb G}\setminus D$
, where
Since D is
![]() ${\mathscr L}^{d}$
-negligible, statements (2.8) and (2.9) follow if we prove that for every
${\mathscr L}^{d}$
-negligible, statements (2.8) and (2.9) follow if we prove that for every
![]() $\ell =2,\dots ,k$
,
$\ell =2,\dots ,k$
,
Using (2.1) one gets
 $$ \begin{align} \begin{array}{l@{\quad }l} \nabla_{{\mathbb G}} f(x)=(1,\varepsilon,\dots,\varepsilon,0,\dots,0) & \text{if }x_{1}+\varepsilon(x_{2}+\dots+x_{k})> 2\beta\| x_{{\mathbb W}}\|_{*}\\ \nabla_{{\mathbb G}} f(x)=(3,3\varepsilon,\dots,3\varepsilon,0,\dots,0)\quad & \text{if }x_{1}+\varepsilon(x_{2}+\dots+x_{k})<- 2\beta\| x_{{\mathbb W}}\|_{*}\,. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{l@{\quad }l} \nabla_{{\mathbb G}} f(x)=(1,\varepsilon,\dots,\varepsilon,0,\dots,0) & \text{if }x_{1}+\varepsilon(x_{2}+\dots+x_{k})> 2\beta\| x_{{\mathbb W}}\|_{*}\\ \nabla_{{\mathbb G}} f(x)=(3,3\varepsilon,\dots,3\varepsilon,0,\dots,0)\quad & \text{if }x_{1}+\varepsilon(x_{2}+\dots+x_{k})<- 2\beta\| x_{{\mathbb W}}\|_{*}\,. \end{array} \end{align} $$
We now notice that, for any
![]() $x\in {\mathbb G}$
, the map
$x\in {\mathbb G}$
, the map
![]() $y\mapsto y_{{\mathbb W}}$
is constant on the coset
$y\mapsto y_{{\mathbb W}}$
is constant on the coset
![]() $x{\mathbb V}$
, which is a smooth submanifold tangent to
$x{\mathbb V}$
, which is a smooth submanifold tangent to
![]() $X_{1},\dots ,X_{k}$
. This implies that
$X_{1},\dots ,X_{k}$
. This implies that
which, together with (2.12), implies (2.11).
We have only to check that f is Lipschitz continuous on
![]() ${\mathbb G}$
and that a bound on the Lipschitz constant can be given in terms of
${\mathbb G}$
and that a bound on the Lipschitz constant can be given in terms of
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\bar \beta $
. Taking into account (2.12) and the continuity of f on
$\bar \beta $
. Taking into account (2.12) and the continuity of f on
![]() ${\mathbb G}$
, by (2.2) it is enough to prove the function
${\mathbb G}$
, by (2.2) it is enough to prove the function
![]() $g:{\mathbb G}\to {\mathbb R}$
defined by
$g:{\mathbb G}\to {\mathbb R}$
defined by
satisfies
for some positive C. Since
![]() $x\mapsto x_{{\mathbb W}}$
is smooth on
$x\mapsto x_{{\mathbb W}}$
is smooth on
![]() ${\mathbb G}$
and
${\mathbb G}$
and
![]() $\|\cdot \|_{*}$
is smooth on
$\|\cdot \|_{*}$
is smooth on
![]() ${\mathbb G}\setminus \{0\}$
, we get that g is smooth on
${\mathbb G}\setminus \{0\}$
, we get that g is smooth on
![]() ${\mathbb G}\setminus {\mathbb V}$
. Moreover, g is 1-homogeneous; thus,
${\mathbb G}\setminus {\mathbb V}$
. Moreover, g is 1-homogeneous; thus,
![]() $\nabla _{{\mathbb G}} g$
is 0-homogeneous (i.e., invariant under dilations) and continuous on
$\nabla _{{\mathbb G}} g$
is 0-homogeneous (i.e., invariant under dilations) and continuous on
![]() ${\mathbb G}\setminus {\mathbb V}$
. Inequality (2.13) will then follow if we prove that
${\mathbb G}\setminus {\mathbb V}$
. Inequality (2.13) will then follow if we prove that
in turn, this inequality and the bound (in terms of
![]() $\varepsilon ,\bar \beta $
) on the Lipschitz constant of f follow by proving that
$\varepsilon ,\bar \beta $
) on the Lipschitz constant of f follow by proving that
The set
![]() ${\mathbb V}$
is closed, while
${\mathbb V}$
is closed, while
![]() $\partial B(0,1)\cap \{x\in {\mathbb G}:|x_{1}+\varepsilon (x_{2}+\dots +x_{k})|\leq \bar \beta \| x_{{\mathbb W}}\|_{*}\}$
is compact; since they are disjoint, they have positive distance and the continuity of
$\partial B(0,1)\cap \{x\in {\mathbb G}:|x_{1}+\varepsilon (x_{2}+\dots +x_{k})|\leq \bar \beta \| x_{{\mathbb W}}\|_{*}\}$
is compact; since they are disjoint, they have positive distance and the continuity of
![]() $\nabla _{{\mathbb G}} g$
on
$\nabla _{{\mathbb G}} g$
on
![]() ${\mathbb G}\setminus {\mathbb V}$
ensures that
${\mathbb G}\setminus {\mathbb V}$
ensures that
 $$ \begin{align*} \sup \big\{|\nabla_{{\mathbb G}} g(x)|:x\in\partial B(0,1)\text{ and }|x_{1}+\varepsilon(x_{2}+\dots+x_{k})|\leq \bar\beta\| x_{{\mathbb W}}\|_{*}\big\} < +\infty, \end{align*} $$
$$ \begin{align*} \sup \big\{|\nabla_{{\mathbb G}} g(x)|:x\in\partial B(0,1)\text{ and }|x_{1}+\varepsilon(x_{2}+\dots+x_{k})|\leq \bar\beta\| x_{{\mathbb W}}\|_{*}\big\} < +\infty, \end{align*} $$
which is (2.14) and allows us to conclude.
Lemma 2.5. Let
![]() $A\subset {\mathbb W}$
be nonempty and let
$A\subset {\mathbb W}$
be nonempty and let
![]() $\phi :A\to {\mathbb V}$
be intrinsic Lipschitz. Then for every
$\phi :A\to {\mathbb V}$
be intrinsic Lipschitz. Then for every
![]() $\varepsilon \in (0,1)$
and
$\varepsilon \in (0,1)$
and
![]() $i\in \{1,\dots ,k\}$
there exists a Lipschitz function
$i\in \{1,\dots ,k\}$
there exists a Lipschitz function
![]() $f_{i,\varepsilon }:{\mathbb G}\to {\mathbb R}$
such that
$f_{i,\varepsilon }:{\mathbb G}\to {\mathbb R}$
such that
 $$ \begin{align} & 1\leq X_{i}f_{i,\varepsilon}\leq 3 \qquad{\mathscr L}^{d}\text{-a.e. on }{\mathbb G} \hphantom{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\end{align} $$
$$ \begin{align} & 1\leq X_{i}f_{i,\varepsilon}\leq 3 \qquad{\mathscr L}^{d}\text{-a.e. on }{\mathbb G} \hphantom{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\end{align} $$
 $$ \begin{align} & \varepsilon \leq X_{\ell} f_{i,\varepsilon}\leq 3\varepsilon\qquad{\mathscr L}^{d}\text{-a.e. on }{\mathbb G}\quad \forall\ell\in\{1,\dots,k\}\setminus\{i\}. \end{align} $$
$$ \begin{align} & \varepsilon \leq X_{\ell} f_{i,\varepsilon}\leq 3\varepsilon\qquad{\mathscr L}^{d}\text{-a.e. on }{\mathbb G}\quad \forall\ell\in\{1,\dots,k\}\setminus\{i\}. \end{align} $$
Moreover, if the intrinsic Lipschitz constant of
![]() $\phi $
is not greater than
$\phi $
is not greater than
![]() $\bar \alpha>0$
, then the Lipschitz constant of
$\bar \alpha>0$
, then the Lipschitz constant of
![]() $f_{i,\varepsilon }$
can be bounded in terms of
$f_{i,\varepsilon }$
can be bounded in terms of
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\bar \alpha $
only.
$\bar \alpha $
only.
Proof. Assume that the intrinsic Lipschitz constant of
![]() $\phi $
is not greater than some
$\phi $
is not greater than some
![]() $\bar \Lambda>0$
and define
$\bar \Lambda>0$
and define
![]() $\alpha :=(2\Lambda )^{-1}$
; then (2.3) holds for such
$\alpha :=(2\Lambda )^{-1}$
; then (2.3) holds for such
![]() $\alpha $
. Recalling that the constant
$\alpha $
. Recalling that the constant
![]() $C_{*}>0$
was introduced in (2.6), we set
$C_{*}>0$
was introduced in (2.6), we set
![]() $\beta :=k\:\!C_{*}^{2}/\alpha $
. Taking into account the inequalities
$\beta :=k\:\!C_{*}^{2}/\alpha $
. Taking into account the inequalities
 $$ \begin{align*} & |x_{i}|+\varepsilon\!\!\!\sum_{j\in\{1,\dots,k\}\setminus\{i\}}\!\!\!\!|x_{j}|\ \leq |x_{1}|+\dots+|x_{k}|\leq k\|x_{{\mathbb V}}\|_{*}\leq kC_{*}\|x_{{\mathbb V}}\|_{{\mathbb G}},\\ & \beta\|x_{{\mathbb W}}\|_{*} \geq \beta\|x_{{\mathbb W}}\|_{{\mathbb G}}/{C_{*}} \end{align*} $$
$$ \begin{align*} & |x_{i}|+\varepsilon\!\!\!\sum_{j\in\{1,\dots,k\}\setminus\{i\}}\!\!\!\!|x_{j}|\ \leq |x_{1}|+\dots+|x_{k}|\leq k\|x_{{\mathbb V}}\|_{*}\leq kC_{*}\|x_{{\mathbb V}}\|_{{\mathbb G}},\\ & \beta\|x_{{\mathbb W}}\|_{*} \geq \beta\|x_{{\mathbb W}}\|_{{\mathbb G}}/{C_{*}} \end{align*} $$
we obtain the inclusion
![]() ${\mathscr C}_{i,\beta ,\varepsilon }\subset {\mathscr C}_{\alpha }$
. For
${\mathscr C}_{i,\beta ,\varepsilon }\subset {\mathscr C}_{\alpha }$
. For
![]() $y\in {\mathbb G}$
, set
$y\in {\mathbb G}$
, set
![]() $f_{y}(x):=f_{i,\beta ,\varepsilon }(y^{-1}x)$
, where
$f_{y}(x):=f_{i,\beta ,\varepsilon }(y^{-1}x)$
, where
![]() $f_{i,\beta ,\varepsilon }$
is the function provided by Lemma 2.4, and define
$f_{i,\beta ,\varepsilon }$
is the function provided by Lemma 2.4, and define
 $$ \begin{align*} f(x):=\sup_{y\in \mathrm{gr}_{\phi}} f_{y}(x). \end{align*} $$
$$ \begin{align*} f(x):=\sup_{y\in \mathrm{gr}_{\phi}} f_{y}(x). \end{align*} $$
We prove that
![]() $f_{i,\varepsilon }:=f$
satisfies the claimed statement.
$f_{i,\varepsilon }:=f$
satisfies the claimed statement.
Let
![]() $x\in \mathrm {gr}_{\phi }$
; then
$x\in \mathrm {gr}_{\phi }$
; then
![]() $f(x)\geq f_{x}(x)=0$
, while for every
$f(x)\geq f_{x}(x)=0$
, while for every
![]() $y\in \mathrm {gr}_{\phi }\setminus \{x\}$
one has
$y\in \mathrm {gr}_{\phi }\setminus \{x\}$
one has
![]() $f_{y}(x)<0$
because of (2.10) and
$f_{y}(x)<0$
because of (2.10) and
This proves that
![]() $f(x)=0$
, which is (2.15).
$f(x)=0$
, which is (2.15).
The functions
![]() $f_{y}$
are uniformly Lipschitz continuous; hence, f shares the same Lipschitz continuity. Let
$f_{y}$
are uniformly Lipschitz continuous; hence, f shares the same Lipschitz continuity. Let
![]() $x\in {\mathbb G}$
be fixed; then for every
$x\in {\mathbb G}$
be fixed; then for every
![]() $\eta>0$
there exists
$\eta>0$
there exists
![]() $y\in \mathrm {gr}_{\phi }$
such that
$y\in \mathrm {gr}_{\phi }$
such that
Since
![]() $X_{i} f_{y}\geq 1$
, by Lemma 2.1 we have for every
$X_{i} f_{y}\geq 1$
, by Lemma 2.1 we have for every
![]() $t\geq 0$
$t\geq 0$
 $$ \begin{align*} f(\overrightarrow{\exp}(tX_{i})(x))\geq f_{y}(\overrightarrow{\exp}(tX_{i})(x))\geq f_{y}(x) +t\geq f(x)+t -\eta. \end{align*} $$
$$ \begin{align*} f(\overrightarrow{\exp}(tX_{i})(x))\geq f_{y}(\overrightarrow{\exp}(tX_{i})(x))\geq f_{y}(x) +t\geq f(x)+t -\eta. \end{align*} $$
By the arbitrariness of
![]() $\eta $
, one obtains
$\eta $
, one obtains
that is,
![]() $X_{i}f\geq 1$
a.e. on
$X_{i}f\geq 1$
a.e. on
![]() ${\mathbb G}$
. A similar argument, using
${\mathbb G}$
. A similar argument, using
![]() $g:=-f$
and the inequality
$g:=-f$
and the inequality
![]() $X_{i}g\geq -3$
, shows that
$X_{i}g\geq -3$
, shows that
![]() $f(\overrightarrow {\exp }(tX_{i})(x))\leq f(x)+3t$
for every
$f(\overrightarrow {\exp }(tX_{i})(x))\leq f(x)+3t$
for every
![]() $t\geq 0$
; that is, that
$t\geq 0$
; that is, that
![]() $X_{i}f\leq 3$
a.e. on
$X_{i}f\leq 3$
a.e. on
![]() ${\mathbb G}$
. This proves (2.16).
${\mathbb G}$
. This proves (2.16).
The proof of (2.17) is completely analogous and we omit it.
The following lemma is most likely well-known; however, we provide a proof for the sake of completeness.
Lemma 2.6. Let
![]() $f:{\mathbb R}^{k}\to {\mathbb R}^{k}$
be a Lipschitz map such that there exists
$f:{\mathbb R}^{k}\to {\mathbb R}^{k}$
be a Lipschitz map such that there exists
![]() $\delta>0$
for which
$\delta>0$
for which
Then there exists a unique
![]() $\bar {x}\in {\mathbb R}^{k}$
such that
$\bar {x}\in {\mathbb R}^{k}$
such that
![]() $f(\bar {x})=0$
.
$f(\bar {x})=0$
.
Proof. We reason by induction on k and leave the case
![]() $k=1$
as an exercise to the reader. We assume that the lemma holds for some
$k=1$
as an exercise to the reader. We assume that the lemma holds for some
![]() $k\geq 1$
and we prove it for
$k\geq 1$
and we prove it for
![]() $k+1$
.
$k+1$
.
By the 1-dimensional case of the lemma, for every
![]() $x\in {\mathbb R}^{k}$
there exists a unique
$x\in {\mathbb R}^{k}$
there exists a unique
![]() $g(x)\in {\mathbb R}$
such that
$g(x)\in {\mathbb R}$
such that
![]() $f_{k+1}(x,g(x))=0$
; we claim that g is Lipschitz continuous. Letting L denote the Lipschitz constant of f, we indeed have for every
$f_{k+1}(x,g(x))=0$
; we claim that g is Lipschitz continuous. Letting L denote the Lipschitz constant of f, we indeed have for every
![]() $x,y\in {\mathbb R}^{k}$
$x,y\in {\mathbb R}^{k}$
 $$ \begin{align*} f_{k+1}(y,g(x)+\tfrac L\delta|y-x|) \stackrel{(2.18)}{\geq} & f_{k+1}(y,g(x)) + L|y-x|\\ \stackrel{\phantom{(2.18)}}{\geq} & f_{k+1}(x,g(x)) - L|y-x| + L|y-x|\ =\ 0 \end{align*} $$
$$ \begin{align*} f_{k+1}(y,g(x)+\tfrac L\delta|y-x|) \stackrel{(2.18)}{\geq} & f_{k+1}(y,g(x)) + L|y-x|\\ \stackrel{\phantom{(2.18)}}{\geq} & f_{k+1}(x,g(x)) - L|y-x| + L|y-x|\ =\ 0 \end{align*} $$
and
 $$ \begin{align*} f_{k+1}(y,g(x)-\tfrac L\delta|y-x|) \stackrel{(2.18)}{\leq} & f_{k+1}(y,g(x)) - L|y-x|\\ \stackrel{\phantom{(2.18)}}{\leq} & f_{k+1}(x,g(x)) + L|y-x| - L|y-x|\ =\ 0. \end{align*} $$
$$ \begin{align*} f_{k+1}(y,g(x)-\tfrac L\delta|y-x|) \stackrel{(2.18)}{\leq} & f_{k+1}(y,g(x)) - L|y-x|\\ \stackrel{\phantom{(2.18)}}{\leq} & f_{k+1}(x,g(x)) + L|y-x| - L|y-x|\ =\ 0. \end{align*} $$
The last two displayed formulae imply that
 $$ \begin{align*} g(x)-\tfrac L\delta|y-x| \leq g(y) \leq g(x)+\tfrac L\delta|y-x|, \end{align*} $$
$$ \begin{align*} g(x)-\tfrac L\delta|y-x| \leq g(y) \leq g(x)+\tfrac L\delta|y-x|, \end{align*} $$
and the Lipschitz continuity of g follows. In particular, the function
![]() $h:{\mathbb R}^{k}\to {\mathbb R}^{k}$
defined by
$h:{\mathbb R}^{k}\to {\mathbb R}^{k}$
defined by
![]() $h(z):=(f_{1},\dots ,f_{k})(z,g(z))$
is Lipschitz continuous; since
$h(z):=(f_{1},\dots ,f_{k})(z,g(z))$
is Lipschitz continuous; since
by inductive assumption there is a unique
![]() $\bar z\in {\mathbb R}^{k}$
such that
$\bar z\in {\mathbb R}^{k}$
such that
![]() $h(\bar z)=0$
. It follows that
$h(\bar z)=0$
. It follows that
![]() $\bar {x}:=(\bar z,g(\bar z))$
is the unique zero of f, which concludes the proof.
$\bar {x}:=(\bar z,g(\bar z))$
is the unique zero of f, which concludes the proof.
Before passing to the the main proof of this section, we recall once more that
![]() ${\mathbb V}$
is identified with
${\mathbb V}$
is identified with
![]() ${\mathbb R}^{k}$
by
${\mathbb R}^{k}$
by
This identification is understood, in particular, when considering scalar products between elements of
![]() ${\mathbb R}^{k}$
and
${\mathbb R}^{k}$
and
![]() ${\mathbb V}$
as in (1.2).
${\mathbb V}$
as in (1.2).
Remark 2.7. It is easily seen that, for a given Lipschitz map
![]() $f:{\mathbb G}\to {\mathbb R}^{k}$
, statement (1.2) is equivalent to the uniform ellipticity (a.k.a. coercivity) of the matrix col
$f:{\mathbb G}\to {\mathbb R}^{k}$
, statement (1.2) is equivalent to the uniform ellipticity (a.k.a. coercivity) of the matrix col
![]() $[X_{1}f|\dots |X_{k} f]$
; that is, to the fact that
$[X_{1}f|\dots |X_{k} f]$
; that is, to the fact that
in the sense of bilinear forms, where I denotes the
![]() $k\times k$
identity matrix. Observe that such a matrix is defined a.e. on
$k\times k$
identity matrix. Observe that such a matrix is defined a.e. on
![]() ${\mathbb G}$
by Pansu’s theorem [Reference Pansu81, Théorème 2].
${\mathbb G}$
by Pansu’s theorem [Reference Pansu81, Théorème 2].
Proof of Theorem 1.4.
Step 1. We prove the implication (a)
![]() $\Rightarrow $
(b). Consider the map
$\Rightarrow $
(b). Consider the map
 $$ \begin{align*} f:=(f_{1,\varepsilon},\dots,f_{k,\varepsilon}):{\mathbb G}\to{\mathbb R}^{k}, \end{align*} $$
$$ \begin{align*} f:=(f_{1,\varepsilon},\dots,f_{k,\varepsilon}):{\mathbb G}\to{\mathbb R}^{k}, \end{align*} $$
where
![]() $\varepsilon \in (0,1)$
will be determined later and the functions
$\varepsilon \in (0,1)$
will be determined later and the functions
![]() $f_{i,\varepsilon }$
are provided by Lemma 2.5. The inclusion (1.1) follows from (2.15). In order to prove (1.2), we first observe that for
$f_{i,\varepsilon }$
are provided by Lemma 2.5. The inclusion (1.1) follows from (2.15). In order to prove (1.2), we first observe that for
![]() ${\mathscr L}^{d}$
-a.e.
${\mathscr L}^{d}$
-a.e.
![]() $x\in {\mathbb G}$
and
$x\in {\mathbb G}$
and
![]() ${\mathscr L}^{k}$
-a.e.
${\mathscr L}^{k}$
-a.e.
![]() $v\in {\mathbb R}^{k}\equiv {\mathbb V}$
one has
$v\in {\mathbb R}^{k}\equiv {\mathbb V}$
one has
 $$ \begin{align*} \langle f(xv)-f(x),v\rangle =& \int_{0}^{1} \left\langle \sum_{j=1}^{k}v_{j}X_{j}f(x\delta_{t}v),v\right\rangle\:dt, \end{align*} $$
$$ \begin{align*} \langle f(xv)-f(x),v\rangle =& \int_{0}^{1} \left\langle \sum_{j=1}^{k}v_{j}X_{j}f(x\delta_{t}v),v\right\rangle\:dt, \end{align*} $$
where we used the fact that
![]() $x\delta _{t}v=\overrightarrow {\exp }(t(v_{1}X_{1}+\dots +v_{k}X_{k}))(x)$
. Therefore,
$x\delta _{t}v=\overrightarrow {\exp }(t(v_{1}X_{1}+\dots +v_{k}X_{k}))(x)$
. Therefore,
 $$ \begin{align*} \langle f(xv)-f(x),v\rangle = & \int_{0}^{1} \sum_{i,j=1}^{k}v_{i}v_{j}X_{j}f_{i}(x\delta_{t}v) \:dt\\ = & \int_{0}^{1} \sum_{i=1}^{k}v_{i}^{2}X_{i}f_{i}(x\delta_{t}v) \:dt + \int_{0}^{1} \sum_{\substack{i,j=1,\dots, k\\i\neq j}}v_{i}v_{j}X_{j}f_{i}(x\delta_{t}v) \:dt\\ \geq & (1-3(k^{2}-k)\varepsilon) |v|^{2}, \end{align*} $$
$$ \begin{align*} \langle f(xv)-f(x),v\rangle = & \int_{0}^{1} \sum_{i,j=1}^{k}v_{i}v_{j}X_{j}f_{i}(x\delta_{t}v) \:dt\\ = & \int_{0}^{1} \sum_{i=1}^{k}v_{i}^{2}X_{i}f_{i}(x\delta_{t}v) \:dt + \int_{0}^{1} \sum_{\substack{i,j=1,\dots, k\\i\neq j}}v_{i}v_{j}X_{j}f_{i}(x\delta_{t}v) \:dt\\ \geq & (1-3(k^{2}-k)\varepsilon) |v|^{2}, \end{align*} $$
where in the last inequality we used (2.16) and (2.17). If
![]() $k=1$
, this inequality is (1.2) with
$k=1$
, this inequality is (1.2) with
![]() $\delta =1$
; if
$\delta =1$
; if
![]() $k\geq 2$
, (1.2) follows with
$k\geq 2$
, (1.2) follows with
![]() $\delta =1/2$
provided we choose
$\delta =1/2$
provided we choose
![]() $ \varepsilon =(6(k^{2}-k))^{-1}$
. This proves the implication (a)
$ \varepsilon =(6(k^{2}-k))^{-1}$
. This proves the implication (a)
![]() $\Rightarrow $
(b).
$\Rightarrow $
(b).
Step 2. We now prove the converse implication (b)
![]() $\Rightarrow $
(a); it is enough to prove that
$\Rightarrow $
(a); it is enough to prove that
![]() $Z_{f}:=\{f=0\}$
is the intrinsic graph of some intrinsic Lipschitz function
$Z_{f}:=\{f=0\}$
is the intrinsic graph of some intrinsic Lipschitz function
![]() $\phi :{\mathbb W}\to {\mathbb V}$
. For every
$\phi :{\mathbb W}\to {\mathbb V}$
. For every
![]() $w\in {\mathbb W}$
, define
$w\in {\mathbb W}$
, define
![]() $f_{w}:{\mathbb V}\equiv {\mathbb R}^{k}\to {\mathbb R}^{k}$
as
$f_{w}:{\mathbb V}\equiv {\mathbb R}^{k}\to {\mathbb R}^{k}$
as
![]() $f_{w}(v):=f(wv)$
. By Lemma 2.6 there is a unique
$f_{w}(v):=f(wv)$
. By Lemma 2.6 there is a unique
![]() $\bar v=\bar v(w)$
such that
$\bar v=\bar v(w)$
such that
![]() $f_{w}(\bar v)=0$
; we define
$f_{w}(\bar v)=0$
; we define
![]() $\phi :{\mathbb W}\to {\mathbb V}$
by
$\phi :{\mathbb W}\to {\mathbb V}$
by
![]() $\phi (w):=\bar v$
. For
$\phi (w):=\bar v$
. For
![]() $\lambda \in (0,1)$
, which will be fixed later, we introduce the homogeneous cone
$\lambda \in (0,1)$
, which will be fixed later, we introduce the homogeneous cone
 $$ \begin{align*} D_{\lambda}:=\bigcup_{v\in{\mathbb V}} \overline{B(v,\lambda \|v\|_{{\mathbb G}})}=\bigcup_{v\in{\mathbb V}} v\overline{B(0,\lambda \|v\|_{{\mathbb G}})}. \end{align*} $$
$$ \begin{align*} D_{\lambda}:=\bigcup_{v\in{\mathbb V}} \overline{B(v,\lambda \|v\|_{{\mathbb G}})}=\bigcup_{v\in{\mathbb V}} v\overline{B(0,\lambda \|v\|_{{\mathbb G}})}. \end{align*} $$
By a simple topological argument (see, e.g., [Reference Don, Massaccesi and Vittone39, Remark A.2]) there exists
![]() $\alpha =\alpha (\lambda )>0$
such that
$\alpha =\alpha (\lambda )>0$
such that
![]() ${\mathscr C}_{\alpha }\subset D_{\lambda }$
; in order to prove that
${\mathscr C}_{\alpha }\subset D_{\lambda }$
; in order to prove that
![]() $\phi $
is intrinsic Lipschitz, it is sufficient to show that
$\phi $
is intrinsic Lipschitz, it is sufficient to show that
To this aim, for every
![]() $x\in Z_{f}$
and every
$x\in Z_{f}$
and every
![]() $y\in xD_{\lambda }\setminus \{x\}$
, one has by definition
$y\in xD_{\lambda }\setminus \{x\}$
, one has by definition
Denoting by L the Lipschitz constant of f we obtain
 $$ \begin{align*} \langle f(y),v\rangle = & \langle f(xvz)-f(xv),v\rangle + \langle f(xv)-f(x),v\rangle\\ \geq & - L\,d(0,z)|v| + \delta|v|^{2} \\ \geq & -L\lambda\,d(0,v)|v|+ \delta|v|^{2}\\ \geq & -L\lambda\, C_{*}\|v\|_{*}|v|+ \delta|v|^{2}\\ \geq & (\delta-L\lambda C_{*}c_{k})|v|^{2} \end{align*} $$
$$ \begin{align*} \langle f(y),v\rangle = & \langle f(xvz)-f(xv),v\rangle + \langle f(xv)-f(x),v\rangle\\ \geq & - L\,d(0,z)|v| + \delta|v|^{2} \\ \geq & -L\lambda\,d(0,v)|v|+ \delta|v|^{2}\\ \geq & -L\lambda\, C_{*}\|v\|_{*}|v|+ \delta|v|^{2}\\ \geq & (\delta-L\lambda C_{*}c_{k})|v|^{2} \end{align*} $$
for some positive constant
![]() $c_{k}$
depending on k only. It follows that, provided
$c_{k}$
depending on k only. It follows that, provided
![]() $\lambda $
is chosen small enough, one has
$\lambda $
is chosen small enough, one has
![]() $\langle f(y),v\rangle>0$
; hence,
$\langle f(y),v\rangle>0$
; hence,
![]() $f(y)\neq 0$
and
$f(y)\neq 0$
and
![]() $y\notin Z_{f}$
. This proves (2.20) and concludes the proof of the theorem.
$y\notin Z_{f}$
. This proves (2.20) and concludes the proof of the theorem.
Remark 2.8. In Step 2 of the previous proof we showed that, if f is as in Theorem 1.4 (b), then the level set
![]() $\{f=0\}$
is an entire intrinsic Lipschitz graph; that is, it is the intrinsic graph of a
$\{f=0\}$
is an entire intrinsic Lipschitz graph; that is, it is the intrinsic graph of a
![]() ${\mathbb V}$
-valued map
${\mathbb V}$
-valued map
![]() $\phi $
defined on the whole
$\phi $
defined on the whole
![]() ${\mathbb W}$
.
${\mathbb W}$
.
Remark 2.9. It is worth pointing out that, in the implication (b)
![]() $\Rightarrow $
(a), the aperture
$\Rightarrow $
(a), the aperture
![]() $\alpha $
depends, apart from geometric quantities, only on the Lipschitz and coercivity constants
$\alpha $
depends, apart from geometric quantities, only on the Lipschitz and coercivity constants
![]() $L,\delta $
of f. More precisely, if f is as in Theorem 1.4 (b), the Lipschitz constant L of f is not greater than some
$L,\delta $
of f. More precisely, if f is as in Theorem 1.4 (b), the Lipschitz constant L of f is not greater than some
![]() $\bar L>0$
and the coercivity constant
$\bar L>0$
and the coercivity constant
![]() $\delta $
is not smaller than some
$\delta $
is not smaller than some
![]() $\bar \delta>0$
, then the aperture
$\bar \delta>0$
, then the aperture
![]() $\alpha $
(and hence the intrinsic Lipschitz constant of
$\alpha $
(and hence the intrinsic Lipschitz constant of
![]() $\phi $
) can be controlled in terms of
$\phi $
) can be controlled in terms of
![]() $\bar L$
and
$\bar L$
and
![]() $\bar \delta $
only.
$\bar \delta $
only.
A similar remark applies at the level of the implication (a)
![]() $\Rightarrow $
(b); in fact, if
$\Rightarrow $
(b); in fact, if
![]() $\phi $
is as in Theorem 1.4 (a) and the intrinsic Lipschitz constant of
$\phi $
is as in Theorem 1.4 (a) and the intrinsic Lipschitz constant of
![]() $\phi $
is not greater than some positive
$\phi $
is not greater than some positive
![]() $\Lambda $
, then statement (b) in Theorem 1.4 holds with
$\Lambda $
, then statement (b) in Theorem 1.4 holds with
![]() $\delta =1/2$
and (by the second part of Lemma 2.5) a function f with Lipschitz constant bounded in terms of
$\delta =1/2$
and (by the second part of Lemma 2.5) a function f with Lipschitz constant bounded in terms of
![]() $\Lambda $
only.
$\Lambda $
only.
2.4 Extension and smooth approximation of co-horizontal intrinsic Lipschitz maps
Given Remark 2.8, Theorem 1.5 is an immediate consequence of Theorem 1.4.
Proof of Theorem 1.5.
Let
![]() $S:=\mathrm {gr}_{\phi }$
and consider
$S:=\mathrm {gr}_{\phi }$
and consider
![]() $f:{\mathbb G}\to {\mathbb R}$
as given by Theorem 1.4 (b); by Remark 2.8, the level set
$f:{\mathbb G}\to {\mathbb R}$
as given by Theorem 1.4 (b); by Remark 2.8, the level set
![]() $Z_{f}:=\{f=0\}$
is the graph of an intrinsic Lipschitz function
$Z_{f}:=\{f=0\}$
is the graph of an intrinsic Lipschitz function
![]() $\tilde {\phi }:{\mathbb W}\to {\mathbb V}$
defined on the whole
$\tilde {\phi }:{\mathbb W}\to {\mathbb V}$
defined on the whole
![]() ${\mathbb W}$
. Since
${\mathbb W}$
. Since
![]() $\mathrm {gr}_{\phi }=S\subset Z_{f}=\mathrm {gr}_{\tilde {\phi }}$
,
$\mathrm {gr}_{\phi }=S\subset Z_{f}=\mathrm {gr}_{\tilde {\phi }}$
,
![]() $\tilde {\phi }$
is an extension of
$\tilde {\phi }$
is an extension of
![]() $\phi $
. The bound on the intrinsic Lipschitz constant of
$\phi $
. The bound on the intrinsic Lipschitz constant of
![]() $\tilde {\phi }$
follows from Remark 2.9.
$\tilde {\phi }$
follows from Remark 2.9.
We now state a technical improvement of Theorem 1.4 that will provide the key tool in the proof of the approximation result stated in Theorem 1.6. In case
![]() $k=1$
, Proposition 2.10 should be compared with [Reference Vittone93, Lemma 4.3].
$k=1$
, Proposition 2.10 should be compared with [Reference Vittone93, Lemma 4.3].
Proposition 2.10. Let
![]() $A\subset {\mathbb W}$
be nonempty and
$A\subset {\mathbb W}$
be nonempty and
![]() $\phi :A\to {\mathbb V}$
be intrinsic Lipschitz. Then there exist
$\phi :A\to {\mathbb V}$
be intrinsic Lipschitz. Then there exist
![]() $\delta>0$
and a Lipschitz map
$\delta>0$
and a Lipschitz map
![]() $f:{\mathbb G}\to {\mathbb R}^{k}$
such that (1.1) (with
$f:{\mathbb G}\to {\mathbb R}^{k}$
such that (1.1) (with
![]() $S:=\mathrm {gr}_{\phi }$
) and (1.2) hold together with
$S:=\mathrm {gr}_{\phi }$
) and (1.2) hold together with
Moreover, if the intrinsic Lipschitz constant of
![]() $\phi $
is not greater than some positive
$\phi $
is not greater than some positive
![]() $\Lambda $
, then the statement holds with
$\Lambda $
, then the statement holds with
![]() $\delta =1/4$
and a function
$\delta =1/4$
and a function
![]() $f:{\mathbb G}\to {\mathbb R}$
with Lipschitz constant bounded in terms of
$f:{\mathbb G}\to {\mathbb R}$
with Lipschitz constant bounded in terms of
![]() $\Lambda $
only.
$\Lambda $
only.
Proof. By Theorem 1.4 and Remark 2.7 there exist
![]() $\delta>0$
and a Lipschitz function
$\delta>0$
and a Lipschitz function
![]() $g:{\mathbb G}\to {\mathbb R}^{k}$
such that S is contained in the level set
$g:{\mathbb G}\to {\mathbb R}^{k}$
such that S is contained in the level set
![]() $Z_{g}:=\{g=0\}$
and
$Z_{g}:=\{g=0\}$
and
By Remark 2.9, one can also assume
![]() $\delta =1/4$
and that the Lipschitz constant of g is bounded in terms of
$\delta =1/4$
and that the Lipschitz constant of g is bounded in terms of
![]() $\Lambda $
only. For
$\Lambda $
only. For
![]() $j\in \mathbb N$
, choose
$j\in \mathbb N$
, choose
-
(i) bounded open sets
 $(U_{j})_{j\in \mathbb N}$
such that
$(U_{j})_{j\in \mathbb N}$
such that
 $\overline {U_{j}}\subset {\mathbb G}\setminus Z_{g}$
and
$\overline {U_{j}}\subset {\mathbb G}\setminus Z_{g}$
and
 ${\mathbb G}\setminus Z_{g}=\cup _{j} U_{j}$
;
${\mathbb G}\setminus Z_{g}=\cup _{j} U_{j}$
; -
(ii) positive numbers
 $\varepsilon _{j}$
such that
$\varepsilon _{j}$
such that
 $\varepsilon _{j}<d(U_{j},Z_{g})$
;
$\varepsilon _{j}<d(U_{j},Z_{g})$
; -
(iii) nonnegative functions
 $u_{j}\in C^{\infty }_{c}(U_{j})$
forming a partition of the unity on
$u_{j}\in C^{\infty }_{c}(U_{j})$
forming a partition of the unity on
 ${\mathbb G}\setminus Z_{g}$
; that is,
${\mathbb G}\setminus Z_{g}$
; that is,
 $\sum _{j} u_{j}=1\text { on }{\mathbb G}\setminus Z_{g}$
.
$\sum _{j} u_{j}=1\text { on }{\mathbb G}\setminus Z_{g}$
.
We can also assume that
![]() $\sum _{j} \chi _{U_{j}} \leq M$
for some
$\sum _{j} \chi _{U_{j}} \leq M$
for some
![]() $M>0$
, where
$M>0$
, where
![]() $\chi _{U_{j}} $
denotes the characteristic function of
$\chi _{U_{j}} $
denotes the characteristic function of
![]() $U_{j}$
. Notice, in particular, that the sum in (iii) is locally finite.
$U_{j}$
. Notice, in particular, that the sum in (iii) is locally finite.
We are going to use the group convolution
![]() $\star $
(see, e.g., [Reference Folland and Stein43, Chapter 1]). Here we only recall that, given
$\star $
(see, e.g., [Reference Folland and Stein43, Chapter 1]). Here we only recall that, given
![]() $G:{\mathbb G}\to {\mathbb R}^{k}$
and
$G:{\mathbb G}\to {\mathbb R}^{k}$
and
![]() $H\in C^{\infty }_{c}({\mathbb G})$
, the group convolution
$H\in C^{\infty }_{c}({\mathbb G})$
, the group convolution
 $$ \begin{align*} (G\star H)(x):=\int_{{\mathbb G}} G(y^{-1}x)H(y)d{\mathscr L}^{d}(y)= \int_{{\mathbb G}} G(y)H(xy^{-1})d{\mathscr L}^{d}(y) \end{align*} $$
$$ \begin{align*} (G\star H)(x):=\int_{{\mathbb G}} G(y^{-1}x)H(y)d{\mathscr L}^{d}(y)= \int_{{\mathbb G}} G(y)H(xy^{-1})d{\mathscr L}^{d}(y) \end{align*} $$
is a smooth function satisfying
We fix a positive kernel
![]() $K\in C^{\infty }_{c}(B(0,1))$
such that
$K\in C^{\infty }_{c}(B(0,1))$
such that
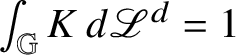 $\int _{{\mathbb G}} K\,d{\mathscr L}^{d}=1$
and, for
$\int _{{\mathbb G}} K\,d{\mathscr L}^{d}=1$
and, for
![]() $\varepsilon>0$
, we set
$\varepsilon>0$
, we set
![]() $K_{\varepsilon }:=\varepsilon ^{-Q}K\circ \delta _{1/\varepsilon }$
. Possibly reducing
$K_{\varepsilon }:=\varepsilon ^{-Q}K\circ \delta _{1/\varepsilon }$
. Possibly reducing
![]() $\varepsilon _{j}>0$
, as specified later in (2.23), (2.25) and (2.26), define
$\varepsilon _{j}>0$
, as specified later in (2.23), (2.25) and (2.26), define
 $$ \begin{align*} f:=\begin{cases} \sum_{j} u_{j} (g\star K_{\varepsilon_{j}})\qquad &\text{on }{\mathbb G}\setminus Z_{g}\\ 0 &\text{on } Z_{g}. \end{cases} \end{align*} $$
$$ \begin{align*} f:=\begin{cases} \sum_{j} u_{j} (g\star K_{\varepsilon_{j}})\qquad &\text{on }{\mathbb G}\setminus Z_{g}\\ 0 &\text{on } Z_{g}. \end{cases} \end{align*} $$
Notice that the sum above is locally finite. We also observe that (1.1) holds because
![]() $S\subset Z_{g}\subset \{f=0\}$
; actually, the equality
$S\subset Z_{g}\subset \{f=0\}$
; actually, the equality
![]() $Z_{g}=\{f=0\}$
will come as a byproduct of what follows.
$Z_{g}=\{f=0\}$
will come as a byproduct of what follows.
We first check that f is continuous on
![]() ${\mathbb G}$
; it is clearly smooth on
${\mathbb G}$
; it is clearly smooth on
![]() ${\mathbb G}\setminus Z_{g}$
and hence continuity has to be checked only at points of
${\mathbb G}\setminus Z_{g}$
and hence continuity has to be checked only at points of
![]() $Z_{g}$
. Up to reducing
$Z_{g}$
. Up to reducing
![]() $\varepsilon _{j}$
, we can assume that
$\varepsilon _{j}$
, we can assume that
so that
 $$ \begin{align*} |f(x)-g(x)|\leq\sum_{j} u_{j}(x)\:| (g\star K_{\varepsilon_{j}})(x)-g(x)|\leq d(x,Z_{g})\qquad\forall\ x\in{\mathbb G}\setminus Z_{g}. \end{align*} $$
$$ \begin{align*} |f(x)-g(x)|\leq\sum_{j} u_{j}(x)\:| (g\star K_{\varepsilon_{j}})(x)-g(x)|\leq d(x,Z_{g})\qquad\forall\ x\in{\mathbb G}\setminus Z_{g}. \end{align*} $$
This implies that f is continuous also on
![]() $Z_{g}=\{g=0\}$
because, for every
$Z_{g}=\{g=0\}$
because, for every
![]() $\bar {x}\in Z_{g}$
, one has
$\bar {x}\in Z_{g}$
, one has
 $$ \begin{align*} \lim_{x\to\bar{x}} |f(x)-f(\bar{x})| =\lim_{x\to\bar{x}} |f(x)| \leq\lim_{x\to\bar{x}} |g(x)|+d(x,\bar{x})=0. \end{align*} $$
$$ \begin{align*} \lim_{x\to\bar{x}} |f(x)-f(\bar{x})| =\lim_{x\to\bar{x}} |f(x)| \leq\lim_{x\to\bar{x}} |g(x)|+d(x,\bar{x})=0. \end{align*} $$
We prove that f is Lipschitz continuous on
![]() ${\mathbb G}$
. Since
${\mathbb G}$
. Since
![]() $Z_{g}$
is an intrinsic Lipschitz graph, by (2.4) we have
$Z_{g}$
is an intrinsic Lipschitz graph, by (2.4) we have
![]() ${\mathscr L}^{d}(Z_{g})=0$
; by (2.2), it is then enough to prove that
${\mathscr L}^{d}(Z_{g})=0$
; by (2.2), it is then enough to prove that
![]() $|\nabla _{{\mathbb G}} f|$
is bounded on
$|\nabla _{{\mathbb G}} f|$
is bounded on
![]() ${\mathbb G}\setminus Z_{g}$
. Using the properties of convolutions and the fact that
${\mathbb G}\setminus Z_{g}$
. Using the properties of convolutions and the fact that
![]() $\sum _{j} \nabla _{{\mathbb G}} u_{j}=0$
, one gets
$\sum _{j} \nabla _{{\mathbb G}} u_{j}=0$
, one gets
 $$ \begin{align} \nabla_{{\mathbb G}} f = & \sum_{j}(g\star K_{\varepsilon_{j}})\otimes(\nabla_{{\mathbb G}} u_{j}) + \sum_{j} u_{j}((\nabla_{{\mathbb G}} g)\star K_{\varepsilon_{j}})\nonumber\\ =& \sum_{j}(g\star K_{\varepsilon_{j}}-g)\otimes(\nabla_{{\mathbb G}} u_{j}) + \sum_{j} u_{j}((\nabla_{{\mathbb G}} g)\star K_{\varepsilon_{j}}). \end{align} $$
$$ \begin{align} \nabla_{{\mathbb G}} f = & \sum_{j}(g\star K_{\varepsilon_{j}})\otimes(\nabla_{{\mathbb G}} u_{j}) + \sum_{j} u_{j}((\nabla_{{\mathbb G}} g)\star K_{\varepsilon_{j}})\nonumber\\ =& \sum_{j}(g\star K_{\varepsilon_{j}}-g)\otimes(\nabla_{{\mathbb G}} u_{j}) + \sum_{j} u_{j}((\nabla_{{\mathbb G}} g)\star K_{\varepsilon_{j}}). \end{align} $$
The second sum in (2.24) is bounded by
![]() $\|\nabla _{{\mathbb G}} g\|_{L^{\infty }({\mathbb G})}$
and then by a multiple of the Lipschitz constant L of g; possibly reducing
$\|\nabla _{{\mathbb G}} g\|_{L^{\infty }({\mathbb G})}$
and then by a multiple of the Lipschitz constant L of g; possibly reducing
![]() $\varepsilon _{j}$
, we can assume that
$\varepsilon _{j}$
, we can assume that
 $$ \begin{align} |g\star K_{\varepsilon_{j}}-g|\leq (\sup |\nabla_{{\mathbb G}} u_{j}|)^{-1}\qquad \text{on }U_{j} \end{align} $$
$$ \begin{align} |g\star K_{\varepsilon_{j}}-g|\leq (\sup |\nabla_{{\mathbb G}} u_{j}|)^{-1}\qquad \text{on }U_{j} \end{align} $$
so that the first sum in (2.24) is bounded by M. This proves that f is Lipschitz continuous on
![]() ${\mathbb G}$
with Lipschitz constant bounded in terms of the Lipschitz constant of g (and then in terms of
${\mathbb G}$
with Lipschitz constant bounded in terms of the Lipschitz constant of g (and then in terms of
![]() $\Lambda $
only).
$\Lambda $
only).
Eventually, we have to check that f satisfies (1.2); we prove this by checking the equivalent inequality (2.19). Writing
![]() $\widehat \nabla _{{\mathbb G}} f:=\text {col}[X_{1}f|\dots |X_{k} f]$
and reasoning as in (2.24), we obtain
$\widehat \nabla _{{\mathbb G}} f:=\text {col}[X_{1}f|\dots |X_{k} f]$
and reasoning as in (2.24), we obtain
 $$ \begin{align*} \widehat\nabla_{{\mathbb G}} f = \sum_{j}(g\star K_{\varepsilon_{j}}-g)\otimes(\widehat\nabla_{{\mathbb G}} u_{j}) + \sum_{j} u_{j}((\widehat\nabla_{{\mathbb G}} g)\star K_{\varepsilon_{j}})=: A+B. \end{align*} $$
$$ \begin{align*} \widehat\nabla_{{\mathbb G}} f = \sum_{j}(g\star K_{\varepsilon_{j}}-g)\otimes(\widehat\nabla_{{\mathbb G}} u_{j}) + \sum_{j} u_{j}((\widehat\nabla_{{\mathbb G}} g)\star K_{\varepsilon_{j}})=: A+B. \end{align*} $$
By (2.22) we have
![]() $B\geq 2\delta I$
a.e. on
$B\geq 2\delta I$
a.e. on
![]() ${\mathbb G}$
. Given
${\mathbb G}$
. Given
![]() $\eta>0$
, possibly reducing
$\eta>0$
, possibly reducing
![]() $\varepsilon _{j}$
we can assume that
$\varepsilon _{j}$
we can assume that
 $$ \begin{align} |g\star K_{\varepsilon_{j}}-g|\leq \eta(\sup |\widehat\nabla_{{\mathbb G}} u_{j}|)^{-1}\qquad \text{on }U_{j} \end{align} $$
$$ \begin{align} |g\star K_{\varepsilon_{j}}-g|\leq \eta(\sup |\widehat\nabla_{{\mathbb G}} u_{j}|)^{-1}\qquad \text{on }U_{j} \end{align} $$
so that
![]() $\|A\|_{L^{\infty }({\mathbb G})}\leq M\eta $
. Inequality (2.19) immediately follows provided one chooses
$\|A\|_{L^{\infty }({\mathbb G})}\leq M\eta $
. Inequality (2.19) immediately follows provided one chooses
![]() $\eta =\eta (\delta )$
small enough. The proof is complete.
$\eta =\eta (\delta )$
small enough. The proof is complete.
We have all of the tools needed for the proof of the approximation result stated in Theorem 1.6.
Proof of Theorem 1.6.
By Theorem 1.5 we can assume without loss of generality that
![]() $A={\mathbb W}$
. Let
$A={\mathbb W}$
. Let
![]() $f:{\mathbb G}\to {\mathbb R}^{k}$
be as in Proposition 2.10; for
$f:{\mathbb G}\to {\mathbb R}^{k}$
be as in Proposition 2.10; for
![]() $i\in \mathbb N$
, we consider
$i\in \mathbb N$
, we consider
By Theorem 1.4 (applied to the function
![]() $f-(1/i,0,\dots ,0)$
) and Remark 2.8, for every
$f-(1/i,0,\dots ,0)$
) and Remark 2.8, for every
![]() $i\in \mathbb N$
the level set
$i\in \mathbb N$
the level set
![]() $Z_{i}$
is the graph of an intrinsic Lipschitz function
$Z_{i}$
is the graph of an intrinsic Lipschitz function
![]() $\phi _{i}:{\mathbb W}\to {\mathbb V}$
defined on the whole
$\phi _{i}:{\mathbb W}\to {\mathbb V}$
defined on the whole
![]() ${\mathbb W}$
. By Remark 2.9, the intrinsic Lipschitz constant of
${\mathbb W}$
. By Remark 2.9, the intrinsic Lipschitz constant of
![]() $\phi _{i}$
is bounded (uniformly in i) in terms of the intrinsic Lipschitz constant of
$\phi _{i}$
is bounded (uniformly in i) in terms of the intrinsic Lipschitz constant of
![]() $\phi $
. Recalling once more the identification
$\phi $
. Recalling once more the identification
![]() ${\mathbb V}\equiv {\mathbb R}^{k}$
, which gives the equality
${\mathbb V}\equiv {\mathbb R}^{k}$
, which gives the equality
![]() $\phi _{i}(w)=\phi (w)(\phi _{i}(w)-\phi (w))$
, we have for every
$\phi _{i}(w)=\phi (w)(\phi _{i}(w)-\phi (w))$
, we have for every
![]() $w\in {\mathbb W}$
$w\in {\mathbb W}$
 $$ \begin{align*} \delta |\phi_{i}(w)-\phi(w)|^{2} & \leq \left\langle f(w\phi_{i}(w))-f(w\phi(w)), \phi_{i}(w)-\phi(w)\right\rangle\\ &\leq |f(w\phi_{i}(w))-f(w\phi(w))|\:|\phi_{i}(w)-\phi(w)|\\ &= \frac{|\phi_{i}(w)-\phi(w)|}{i}\,, \end{align*} $$
$$ \begin{align*} \delta |\phi_{i}(w)-\phi(w)|^{2} & \leq \left\langle f(w\phi_{i}(w))-f(w\phi(w)), \phi_{i}(w)-\phi(w)\right\rangle\\ &\leq |f(w\phi_{i}(w))-f(w\phi(w))|\:|\phi_{i}(w)-\phi(w)|\\ &= \frac{|\phi_{i}(w)-\phi(w)|}{i}\,, \end{align*} $$
which proves that
![]() $\phi _{i}\to \phi $
uniformly as
$\phi _{i}\to \phi $
uniformly as
![]() $i\to \infty $
.
$i\to \infty $
.
We have only to show that each
![]() $\phi _{i}$
is
$\phi _{i}$
is
![]() $C^{\infty }$
smooth. The quickest way is probably to reason in exponential coordinates of the second type; that is, to identify
$C^{\infty }$
smooth. The quickest way is probably to reason in exponential coordinates of the second type; that is, to identify
![]() ${\mathbb G}\equiv {\mathbb R}^{d}$
by
${\mathbb G}\equiv {\mathbb R}^{d}$
by
Since
![]() ${\mathbb V}$
is abelian, we have for every
${\mathbb V}$
is abelian, we have for every
![]() $j=1,\dots ,k$
,
$j=1,\dots ,k$
,
 $$ \begin{align*} &\exp(x_{k+1}X_{k+1}+\dots+x_{d}X_{d})\exp(x_{1}X_{1}+\dots+x_{k}X_{k})\\ &\quad = \exp(x_{k+1}X_{k+1}+\dots+x_{d}X_{d})\exp(x_{1}X_{1}+\dots+\widehat{x_{j}X_{j}}+\dots+x_{k}X_{k})\exp(x_{j}X_{j})\\ &\quad =\overrightarrow{\exp}(x_{j}X_{j})\Big(\overrightarrow{\exp}(x_{1}X_{1}+\dots+\widehat{x_{j}X_{j}}+\dots+x_{k}X_{k})\big(\overrightarrow{\exp}(x_{k+1}X_{k+1}+\dots+x_{d}X_{d})(0)\big)\Big), \end{align*} $$
$$ \begin{align*} &\exp(x_{k+1}X_{k+1}+\dots+x_{d}X_{d})\exp(x_{1}X_{1}+\dots+x_{k}X_{k})\\ &\quad = \exp(x_{k+1}X_{k+1}+\dots+x_{d}X_{d})\exp(x_{1}X_{1}+\dots+\widehat{x_{j}X_{j}}+\dots+x_{k}X_{k})\exp(x_{j}X_{j})\\ &\quad =\overrightarrow{\exp}(x_{j}X_{j})\Big(\overrightarrow{\exp}(x_{1}X_{1}+\dots+\widehat{x_{j}X_{j}}+\dots+x_{k}X_{k})\big(\overrightarrow{\exp}(x_{k+1}X_{k+1}+\dots+x_{d}X_{d})(0)\big)\Big), \end{align*} $$
which proves that in these coordinates
![]() $X_{j}=\partial _{x_{j}}$
for all
$X_{j}=\partial _{x_{j}}$
for all
![]() $j=1,\dots ,k$
. Since
$j=1,\dots ,k$
. Since
![]() $f\in C^{\infty }({\mathbb R}^{d}\setminus \{f=0\})$
, the classical implicit function theorem ensures that the level set
$f\in C^{\infty }({\mathbb R}^{d}\setminus \{f=0\})$
, the classical implicit function theorem ensures that the level set
![]() $Z_{i}=\{f=(1/i,0,\dots ,0)\}$
is the graph of a
$Z_{i}=\{f=(1/i,0,\dots ,0)\}$
is the graph of a
![]() $C^{\infty }$
smooth function
$C^{\infty }$
smooth function
![]() $\psi _{i}=\psi _{i}(x_{k+1},\dots ,x_{d}):{\mathbb R}^{d-k}\to {\mathbb R}^{k}$
. Writing
$\psi _{i}=\psi _{i}(x_{k+1},\dots ,x_{d}):{\mathbb R}^{d-k}\to {\mathbb R}^{k}$
. Writing
![]() $x=(x^{\prime },x^{\prime \prime })\in {\mathbb R}^{k}\times {\mathbb R}^{d-k}$
, we observe that
$x=(x^{\prime },x^{\prime \prime })\in {\mathbb R}^{k}\times {\mathbb R}^{d-k}$
, we observe that
 $$ \begin{align*} \phantom{\Longleftrightarrow }& x=(x_{1},\dots,x_{d})\in Z_{i}\\ \Longleftrightarrow & x^{\prime}=(x_{1},\dots,x_{k})=\psi_{i}(x^{\prime\prime})\\ \Longleftrightarrow & x=\overrightarrow{\exp}\Big((\psi_{i}(x^{\prime\prime}))_{1}X_{1}+\dots+(\psi_{i}(x^{\prime\prime}))_{k}X_{k})(\overrightarrow{\exp}(x_{k+1}X_{k+1}+\dots+x_{d}X_{d})(0)\Big)\\ \Longleftrightarrow & x= \exp(x_{k+1}X_{k+1}+\dots+x_{d}X_{d})\exp((\psi_{i}(x^{\prime\prime}))_{1}X_{1}+\dots+(\psi_{i}(x^{\prime\prime}))_{k}X_{k}), \end{align*} $$
$$ \begin{align*} \phantom{\Longleftrightarrow }& x=(x_{1},\dots,x_{d})\in Z_{i}\\ \Longleftrightarrow & x^{\prime}=(x_{1},\dots,x_{k})=\psi_{i}(x^{\prime\prime})\\ \Longleftrightarrow & x=\overrightarrow{\exp}\Big((\psi_{i}(x^{\prime\prime}))_{1}X_{1}+\dots+(\psi_{i}(x^{\prime\prime}))_{k}X_{k})(\overrightarrow{\exp}(x_{k+1}X_{k+1}+\dots+x_{d}X_{d})(0)\Big)\\ \Longleftrightarrow & x= \exp(x_{k+1}X_{k+1}+\dots+x_{d}X_{d})\exp((\psi_{i}(x^{\prime\prime}))_{1}X_{1}+\dots+(\psi_{i}(x^{\prime\prime}))_{k}X_{k}), \end{align*} $$
which in turn proves that
![]() $\phi _{i}$
and
$\phi _{i}$
and
![]() $\psi _{i}$
coincide as maps from
$\psi _{i}$
coincide as maps from
![]() ${\mathbb W}$
to
${\mathbb W}$
to
![]() ${\mathbb V}$
. This proves that
${\mathbb V}$
. This proves that
![]() $\phi _{i}$
is smooth, as wished.
$\phi _{i}$
is smooth, as wished.
3 The Heisenberg group
From now on we will always work in Heisenberg groups, which provide the most notable examples of Carnot groups; we refer to [Reference Capogna, Danielli, Pauls and Tyson26] for a thorough introduction. For every
![]() $n\geq 1$
, the nth Heisenberg group
$n\geq 1$
, the nth Heisenberg group
![]() ${\mathbb H}^{n}$
is the connected, simply connected and nilpotent Lie group
${\mathbb H}^{n}$
is the connected, simply connected and nilpotent Lie group
![]() ${\mathbb H}^{n}$
associated with the
${\mathbb H}^{n}$
associated with the
![]() $(2n+1)$
-dimensional stratified Lie algebra
$(2n+1)$
-dimensional stratified Lie algebra
![]() ${\mathfrak h}$
generated by elements
${\mathfrak h}$
generated by elements
![]() $X_{1},\dots ,X_{n},Y_{1},\dots ,Y_{n},T$
whose Lie brackets vanish except for
$X_{1},\dots ,X_{n},Y_{1},\dots ,Y_{n},T$
whose Lie brackets vanish except for
The algebra stratification is given by
![]() ${\mathfrak h}={\mathfrak h}_{1}\oplus {\mathfrak h}_{2}$
, where
${\mathfrak h}={\mathfrak h}_{1}\oplus {\mathfrak h}_{2}$
, where
the second layer
![]() ${\mathfrak h}_{2}$
is the center of the algebra.
${\mathfrak h}_{2}$
is the center of the algebra.
We identify
![]() ${\mathbb H}^{n}$
with
${\mathbb H}^{n}$
with
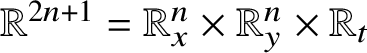 ${\mathbb R}^{2n+1}={\mathbb R}^{n}_{x}\times {\mathbb R}^{n}_{y}\times {\mathbb R}_{t}$
by means of exponential coordinates
${\mathbb R}^{2n+1}={\mathbb R}^{n}_{x}\times {\mathbb R}^{n}_{y}\times {\mathbb R}_{t}$
by means of exponential coordinates
In these coordinates, the group law reads as
 $$ \begin{align*} (x,y,t)(x^{\prime},y^{\prime},t^{\prime})=(x+x^{\prime},y+y^{\prime},t+t^{\prime}+ \tfrac12 \langle x,y^{\prime}\rangle-\tfrac12\langle x^{\prime},y\rangle), \end{align*} $$
$$ \begin{align*} (x,y,t)(x^{\prime},y^{\prime},t^{\prime})=(x+x^{\prime},y+y^{\prime},t+t^{\prime}+ \tfrac12 \langle x,y^{\prime}\rangle-\tfrac12\langle x^{\prime},y\rangle), \end{align*} $$
and left-invariant vector fields have the form
 $$ \begin{align*} X_{j}=\partial_{x_{j}}-\frac{y_{j}}2 \partial_{t},\qquad Y_{j}=\partial_{y_{j}}+\frac{x_{j}}2\partial_{t},\qquad T=\partial_{t}. \end{align*} $$
$$ \begin{align*} X_{j}=\partial_{x_{j}}-\frac{y_{j}}2 \partial_{t},\qquad Y_{j}=\partial_{y_{j}}+\frac{x_{j}}2\partial_{t},\qquad T=\partial_{t}. \end{align*} $$
We also observe that, in exponential coordinates, we have
![]() $p^{-1}=-p$
for every
$p^{-1}=-p$
for every
![]() $p\in {\mathbb H}^{n}$
. As in Section 2, a one-parameter family
$p\in {\mathbb H}^{n}$
. As in Section 2, a one-parameter family
![]() $(\delta _{\lambda })_{\lambda>0}$
of group automorphisms is provided by the dilations
$(\delta _{\lambda })_{\lambda>0}$
of group automorphisms is provided by the dilations
![]() $\delta _{\lambda }(x,y,t):=(\lambda x,\lambda y,\lambda ^{2} t)$
.
$\delta _{\lambda }(x,y,t):=(\lambda x,\lambda y,\lambda ^{2} t)$
.
We fix a homogeneous distance d on
![]() ${\mathbb H}^{n}$
and we denote by
${\mathbb H}^{n}$
and we denote by
![]() $B(p,r)$
,
$B(p,r)$
,
![]() $p\in {\mathbb H}^{n}$
,
$p\in {\mathbb H}^{n}$
,
![]() $r>0$
, the associated open balls; for
$r>0$
, the associated open balls; for
![]() $p\in {\mathbb H}^{n}$
we also write
$p\in {\mathbb H}^{n}$
we also write
![]() $\|p\|_{\mathbb H}:=d(0,p)$
. It will be convenient to assume that d is rotationally invariant; that is, that
$\|p\|_{\mathbb H}:=d(0,p)$
. It will be convenient to assume that d is rotationally invariant; that is, that
Relevant examples of rotationally invariant homogeneous distances are provided by the Carnot–Carathéodory distance
![]() $d_{cc}$
,
$d_{cc}$
,
 $$ \begin{align*} d_{cc}(p,q):=\inf\left\{\|h\|_{L^{1}([0,1],{\mathbb R}^{2n})} : \begin{array}{l} \text{the curve }\gamma_{h}:[0,1]\to{\mathbb H}^{n}\text{ defined by}\\ \gamma_{h}(0)=p,\ \dot\gamma_{h}=\sum_{j=1}^{n}(h_{j}X_{j}+h_{j+n}Y_{j})(\gamma_{h})\\ \text{has final point }\gamma_{h}(1)=q \end{array} \right\}, \end{align*} $$
$$ \begin{align*} d_{cc}(p,q):=\inf\left\{\|h\|_{L^{1}([0,1],{\mathbb R}^{2n})} : \begin{array}{l} \text{the curve }\gamma_{h}:[0,1]\to{\mathbb H}^{n}\text{ defined by}\\ \gamma_{h}(0)=p,\ \dot\gamma_{h}=\sum_{j=1}^{n}(h_{j}X_{j}+h_{j+n}Y_{j})(\gamma_{h})\\ \text{has final point }\gamma_{h}(1)=q \end{array} \right\}, \end{align*} $$
by the left-invariant distance
![]() $d_{\infty }$
(see [Reference Franchi, Serapioni and Serra Cassano48, Proposition 2.1]) such that
$d_{\infty }$
(see [Reference Franchi, Serapioni and Serra Cassano48, Proposition 2.1]) such that
and by the Korányi (or Cygan–Korányi; see [Reference Cygan34]) distance
![]() $d_{K}$
defined by
$d_{K}$
defined by
 $$ \begin{align} d_{K}(0,(x,y,t)):=\big((|x|^{2}+|y|^{2})^{2}+16t^{2}\big)^{1/4}. \end{align} $$
$$ \begin{align} d_{K}(0,(x,y,t)):=\big((|x|^{2}+|y|^{2})^{2}+16t^{2}\big)^{1/4}. \end{align} $$
The Lebesgue measure
![]() ${\mathscr L}^{2n+1}$
is a Haar measure on
${\mathscr L}^{2n+1}$
is a Haar measure on
![]() ${\mathbb H}^{n}\equiv {\mathbb R}^{2n+1}$
and
${\mathbb H}^{n}\equiv {\mathbb R}^{2n+1}$
and
![]() $Q:=2n+2$
is the homogeneous dimension of
$Q:=2n+2$
is the homogeneous dimension of
![]() ${\mathbb H}^{n}$
; in particular,
${\mathbb H}^{n}$
; in particular,
Actually, the Hausdorff and spherical Hausdorff measures
![]() ${\mathscr H}^{Q},{\mathscr S}^{Q}$
are also Haar measure in
${\mathscr H}^{Q},{\mathscr S}^{Q}$
are also Haar measure in
![]() ${\mathbb H}^{n}$
; hence,
${\mathbb H}^{n}$
; hence,
![]() ${\mathscr L}^{2n+1},{\mathscr H}^{Q}$
and
${\mathscr L}^{2n+1},{\mathscr H}^{Q}$
and
![]() ${\mathscr S}^{Q}$
coincide up to multiplicative constants. Recall in particular that the spherical Hausdorff measure
${\mathscr S}^{Q}$
coincide up to multiplicative constants. Recall in particular that the spherical Hausdorff measure
![]() ${\mathscr S}^{k}$
of dimension
${\mathscr S}^{k}$
of dimension
![]() $k\geq 0$
is defined by
$k\geq 0$
is defined by
 $$ \begin{align*} {\mathscr S}^{k}(E):=\lim_{\delta\to 0^{+}} \inf\left\{ \sum_{i=0}^{\infty} (2r_{i})^{k}:E\subset\bigcup_{i=0}^{\infty} B(p_{i},r_{i})\text{ for some }p_{i}\in{\mathbb H}^{n},r_{i}\in(0,\delta)\right\}. \end{align*} $$
$$ \begin{align*} {\mathscr S}^{k}(E):=\lim_{\delta\to 0^{+}} \inf\left\{ \sum_{i=0}^{\infty} (2r_{i})^{k}:E\subset\bigcup_{i=0}^{\infty} B(p_{i},r_{i})\text{ for some }p_{i}\in{\mathbb H}^{n},r_{i}\in(0,\delta)\right\}. \end{align*} $$
One of the aims of this section is to introduce Rumin’s complex of differential forms in
![]() ${\mathbb H}^{n}$
, for which we follow the presentations in [Reference Franchi, Serapioni and Serra Cassano51, Reference Rumin86].
${\mathbb H}^{n}$
, for which we follow the presentations in [Reference Franchi, Serapioni and Serra Cassano51, Reference Rumin86].
3.1 Multilinear algebra
The Heisenberg group
![]() ${\mathbb H}^{n}$
is a contact manifold. The contact form
${\mathbb H}^{n}$
is a contact manifold. The contact form
![]() $\theta $
defined by
$\theta $
defined by
![]() $\theta _{|{\mathfrak h}_{1}}=0$
and
$\theta _{|{\mathfrak h}_{1}}=0$
and
![]() $\theta (T)=1$
satisfies
$\theta (T)=1$
satisfies
![]() $\theta \wedge (d\theta )^{n}\neq 0$
and, actually, the
$\theta \wedge (d\theta )^{n}\neq 0$
and, actually, the
![]() $2n+1$
-form
$2n+1$
-form
![]() $\theta \wedge (d\theta )^{n}$
is a left-invariant volume form. In coordinates,
$\theta \wedge (d\theta )^{n}$
is a left-invariant volume form. In coordinates,
 $$ \begin{align*} \theta=dt+\frac12\sum_{j=1}^{n}(y_{j}dx_{j}-x_{j}dy_{j}), \end{align*} $$
$$ \begin{align*} \theta=dt+\frac12\sum_{j=1}^{n}(y_{j}dx_{j}-x_{j}dy_{j}), \end{align*} $$
while
 $$ \begin{align*} d\theta=-\sum_{j=1}^{n} dx_{j}\wedge dy_{j} \end{align*} $$
$$ \begin{align*} d\theta=-\sum_{j=1}^{n} dx_{j}\wedge dy_{j} \end{align*} $$
is the standard symplectic 2-form in
![]() ${\mathbb R}^{2n}$
, up to a sign. Notice that the basis
${\mathbb R}^{2n}$
, up to a sign. Notice that the basis
![]() $dx_{1},\dots ,dy_{n},\theta $
is the dual basis to
$dx_{1},\dots ,dy_{n},\theta $
is the dual basis to
![]() $X_{1},\dots ,Y_{n},T$
; observe also that here we are identifying the dual of
$X_{1},\dots ,Y_{n},T$
; observe also that here we are identifying the dual of
![]() ${\mathfrak h}$
with left-invariant 1-forms on
${\mathfrak h}$
with left-invariant 1-forms on
![]() ${\mathbb H}^{n}$
, in the same way as the algebra
${\mathbb H}^{n}$
, in the same way as the algebra
![]() ${\mathfrak h}$
can be identified with left-invariant vector fields.
${\mathfrak h}$
can be identified with left-invariant vector fields.
It will sometimes be convenient to denote the family
![]() $X_{1},\dots ,Y_{n},T$
by
$X_{1},\dots ,Y_{n},T$
by
![]() $W_{1},\dots ,W_{2n+1}$
, where
$W_{1},\dots ,W_{2n+1}$
, where
 $$ \begin{align} \begin{aligned} & W_{j}:=X_{j} &&\text{if }1\leq j\leq n\\ & W_{j}:=Y_{j-n}\qquad &&\text{if }n+1\leq j\leq 2n\\ & W_{2n+1}:=T. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & W_{j}:=X_{j} &&\text{if }1\leq j\leq n\\ & W_{j}:=Y_{j-n}\qquad &&\text{if }n+1\leq j\leq 2n\\ & W_{2n+1}:=T. \end{aligned} \end{align} $$
Analogously, we use
![]() $\theta _{1},\dots ,\theta _{2n+1}$
to denote, respectively,
$\theta _{1},\dots ,\theta _{2n+1}$
to denote, respectively,
![]() $dx_{1},\dots ,dy_{n},\theta $
. Given a subset
$dx_{1},\dots ,dy_{n},\theta $
. Given a subset
![]() $I\subset \{1,\dots ,2n+1\}$
, we write
$I\subset \{1,\dots ,2n+1\}$
, we write
![]() $I=\{i_{1},\dots ,i_{k}\}$
for
$I=\{i_{1},\dots ,i_{k}\}$
for
![]() $i_{1}<i_{2}<\dots <i_{k}$
and we denote by
$i_{1}<i_{2}<\dots <i_{k}$
and we denote by
![]() $W_{I},\theta _{I}$
the (formal) exterior products
$W_{I},\theta _{I}$
the (formal) exterior products
We also denote by
![]() $|I|$
the cardinality of I. We can now introduce the exterior algebras
$|I|$
the cardinality of I. We can now introduce the exterior algebras
![]() $\Large \wedge _{\ast }{\mathfrak h}$
and
$\Large \wedge _{\ast }{\mathfrak h}$
and
![]() $\Large \wedge ^{\ast }{\mathfrak h}$
of (multi)vectors and (multi-)covectors as
$\Large \wedge ^{\ast }{\mathfrak h}$
of (multi)vectors and (multi-)covectors as
 $$ \begin{align*} \Large\wedge_{\ast}{\mathfrak h}:=\bigoplus_{k=0}^{2n+1}\Large\wedge_{k}{\mathfrak h},\qquad \Large\wedge^{\ast}{\mathfrak h}:=\bigoplus_{k=0}^{2n+1}\Large\wedge^{k}{\mathfrak h} \end{align*} $$
$$ \begin{align*} \Large\wedge_{\ast}{\mathfrak h}:=\bigoplus_{k=0}^{2n+1}\Large\wedge_{k}{\mathfrak h},\qquad \Large\wedge^{\ast}{\mathfrak h}:=\bigoplus_{k=0}^{2n+1}\Large\wedge^{k}{\mathfrak h} \end{align*} $$
where
![]() $\Large \wedge _{0}{\mathfrak h}=\Large \wedge ^{0}{\mathfrak h}={\mathbb R}$
and
$\Large \wedge _{0}{\mathfrak h}=\Large \wedge ^{0}{\mathfrak h}={\mathbb R}$
and
 $$ \begin{align*} & \Large\wedge_{k}{\mathfrak h}:=\operatorname*{\mathrm{span}}\{W_{I}:I\subset\{1,\dots,2n+1\}\text{ with }|I|=k\}\\ & \Large\wedge^{k}{\mathfrak h}:=\operatorname*{\mathrm{span}}\{\theta_{I}:I\subset\{1,\dots,2n+1\}\text{ with }|I|=k\}. \end{align*} $$
$$ \begin{align*} & \Large\wedge_{k}{\mathfrak h}:=\operatorname*{\mathrm{span}}\{W_{I}:I\subset\{1,\dots,2n+1\}\text{ with }|I|=k\}\\ & \Large\wedge^{k}{\mathfrak h}:=\operatorname*{\mathrm{span}}\{\theta_{I}:I\subset\{1,\dots,2n+1\}\text{ with }|I|=k\}. \end{align*} $$
The elements of
![]() $\Large \wedge _{k}{\mathfrak h}$
and
$\Large \wedge _{k}{\mathfrak h}$
and
![]() $\Large \wedge ^{k}{\mathfrak h}$
are called, respectively, k-vectors and k-covectors. The inner product on
$\Large \wedge ^{k}{\mathfrak h}$
are called, respectively, k-vectors and k-covectors. The inner product on
![]() ${\mathfrak h}$
making
${\mathfrak h}$
making
![]() $W_{1},\dots ,W_{2n+1}$
an orthonormal frame can be naturally extended to
$W_{1},\dots ,W_{2n+1}$
an orthonormal frame can be naturally extended to
![]() $\Large \wedge _{k}{\mathfrak h}$
in such a way that the elements
$\Large \wedge _{k}{\mathfrak h}$
in such a way that the elements
![]() $W_{I}$
form an orthonormal frame. In this way, one can define an explicit isomorphism
$W_{I}$
form an orthonormal frame. In this way, one can define an explicit isomorphism
by requiring
![]() $\langle w\mid v^{\ast }\rangle := \langle w,v\rangle $
for every
$\langle w\mid v^{\ast }\rangle := \langle w,v\rangle $
for every
![]() $w\in \Large \wedge _{k}{\mathfrak h}$
, where
$w\in \Large \wedge _{k}{\mathfrak h}$
, where
![]() $\langle \,\cdot \mid \cdot \,\rangle $
denotes duality pairing between vectors and covectors.
$\langle \,\cdot \mid \cdot \,\rangle $
denotes duality pairing between vectors and covectors.
We analogously introduce the exterior algebras of horizontal vectors and covectors
 $$ \begin{align*} \Large\wedge_{\ast}{\mathfrak h}_{1}:=\bigoplus_{k=0}^{2n}\Large\wedge_{k}{\mathfrak h}_{1},\qquad \Large\wedge^{\ast}{\mathfrak h}_{1}:=\bigoplus_{k=0}^{2n}\Large\wedge^{k}{\mathfrak h}_{1} \end{align*} $$
$$ \begin{align*} \Large\wedge_{\ast}{\mathfrak h}_{1}:=\bigoplus_{k=0}^{2n}\Large\wedge_{k}{\mathfrak h}_{1},\qquad \Large\wedge^{\ast}{\mathfrak h}_{1}:=\bigoplus_{k=0}^{2n}\Large\wedge^{k}{\mathfrak h}_{1} \end{align*} $$
where
 $$ \begin{align*} & \Large\wedge_{k}{\mathfrak h}_{1}:=\operatorname*{\mathrm{span}}\{W_{I}:I\subset\{1,\dots,2n\}\text{ with }|I|=k\}\\ & \Large\wedge^{k}{\mathfrak h}_{1}:=\operatorname*{\mathrm{span}}\{\theta_{I}:I\subset\{1,\dots,2n\}\text{ with }|I|=k\}. \end{align*} $$
$$ \begin{align*} & \Large\wedge_{k}{\mathfrak h}_{1}:=\operatorname*{\mathrm{span}}\{W_{I}:I\subset\{1,\dots,2n\}\text{ with }|I|=k\}\\ & \Large\wedge^{k}{\mathfrak h}_{1}:=\operatorname*{\mathrm{span}}\{\theta_{I}:I\subset\{1,\dots,2n\}\text{ with }|I|=k\}. \end{align*} $$
Remark 3.1. Given
![]() $\tau \in \Large \wedge _{k}{\mathfrak h}$
and
$\tau \in \Large \wedge _{k}{\mathfrak h}$
and
![]() $\lambda \in \Large \wedge ^{k}{\mathfrak h}$
,
$\lambda \in \Large \wedge ^{k}{\mathfrak h}$
,
![]() $1\leq k\leq 2n$
, we denote by
$1\leq k\leq 2n$
, we denote by
![]() $\tau _{{\mathfrak h}_{1}}$
and
$\tau _{{\mathfrak h}_{1}}$
and
![]() $\lambda _{{\mathfrak h}_{1}}$
their horizontal component; that is, the unique
$\lambda _{{\mathfrak h}_{1}}$
their horizontal component; that is, the unique
![]() $\tau _{{\mathfrak h}_{1}}\in \Large \wedge _{k}{\mathfrak h}_{1}$
and
$\tau _{{\mathfrak h}_{1}}\in \Large \wedge _{k}{\mathfrak h}_{1}$
and
![]() $\lambda _{{\mathfrak h}_{1}}\in \Large \wedge ^{k}{\mathfrak h}_{1}$
such that
$\lambda _{{\mathfrak h}_{1}}\in \Large \wedge ^{k}{\mathfrak h}_{1}$
such that
![]() $\tau =\tau _{{\mathfrak h}_{1}}+\sigma \wedge T$
and
$\tau =\tau _{{\mathfrak h}_{1}}+\sigma \wedge T$
and
![]() $\lambda =\lambda _{{\mathfrak h}_{1}}+\mu \wedge \theta $
for some (unique)
$\lambda =\lambda _{{\mathfrak h}_{1}}+\mu \wedge \theta $
for some (unique)
![]() $\sigma \in \Large \wedge _{k-1}{\mathfrak h}_{1},\mu \in \Large \wedge ^{k-1}{\mathfrak h}_{1}$
.
$\sigma \in \Large \wedge _{k-1}{\mathfrak h}_{1},\mu \in \Large \wedge ^{k-1}{\mathfrak h}_{1}$
.
Of special importance for us are vertical planes, which we now introduce. As is customary, given a nonzero simple k-vector
![]() $\tau =\tau _{1}\wedge \dots \wedge \tau _{k}$
, we denote by
$\tau =\tau _{1}\wedge \dots \wedge \tau _{k}$
, we denote by
![]() $\operatorname *{\mathrm {span}}\tau $
the linear space generated by
$\operatorname *{\mathrm {span}}\tau $
the linear space generated by
![]() $\tau _{1},\dots , \tau _{k}$
; equivalently,
$\tau _{1},\dots , \tau _{k}$
; equivalently,
![]() $\operatorname *{\mathrm {span}}\tau =\{v:v\wedge \tau =0\}$
.
$\operatorname *{\mathrm {span}}\tau =\{v:v\wedge \tau =0\}$
.
Definition 3.2. A set
![]() ${\mathscr P}\subset {\mathbb H}^{n}$
is a vertical plane of dimension k if there exists a nonzero
${\mathscr P}\subset {\mathbb H}^{n}$
is a vertical plane of dimension k if there exists a nonzero
![]() $\tau \in \Large \wedge _{k-1}{\mathfrak h}_{1}$
such that
$\tau \in \Large \wedge _{k-1}{\mathfrak h}_{1}$
such that
In exponential coordinates, a vertical plane
![]() ${\mathscr P}$
is a k-dimensional linear subspace of
${\mathscr P}$
is a k-dimensional linear subspace of
![]() ${\mathbb H}^{n}\equiv {\mathbb R}^{2n+1}={\mathbb R}^{2n}\times {\mathbb R}$
of the form
${\mathbb H}^{n}\equiv {\mathbb R}^{2n+1}={\mathbb R}^{2n}\times {\mathbb R}$
of the form
![]() $V\times {\mathbb R}$
for some
$V\times {\mathbb R}$
for some
![]() $(k-1)$
-dimensional subspace
$(k-1)$
-dimensional subspace
![]() $V\subset {\mathbb R}^{2n}$
. A vertical plane is always a normal subgroup of
$V\subset {\mathbb R}^{2n}$
. A vertical plane is always a normal subgroup of
![]() ${\mathbb H}^{n}$
.
${\mathbb H}^{n}$
.
3.2 Differential forms and Rumin’s complex
The spaces
![]() ${\mathfrak h}$
,
${\mathfrak h}$
,
![]() ${\mathfrak h}_{1}$
,
${\mathfrak h}_{1}$
,
![]() $\Large \wedge _{k}{\mathfrak h}$
,
$\Large \wedge _{k}{\mathfrak h}$
,
![]() $\Large \wedge ^{k}{\mathfrak h}$
,
$\Large \wedge ^{k}{\mathfrak h}$
,
![]() $\Large \wedge _{k}{\mathfrak h}_{1}$
,
$\Large \wedge _{k}{\mathfrak h}_{1}$
,
![]() $\Large \wedge ^{k}{\mathfrak h}_{1}$
, as well as the spaces
$\Large \wedge ^{k}{\mathfrak h}_{1}$
, as well as the spaces
![]() ${\mathcal I}^{k}$
and
${\mathcal I}^{k}$
and
![]() ${\mathcal J}^{2n+1-k}$
introduced in (3.6), canonically induce several bundles on
${\mathcal J}^{2n+1-k}$
introduced in (3.6), canonically induce several bundles on
![]() ${\mathbb H}^{n}$
, which we will denote by using the same symbol. The same convention applies to dual and quotient spaces of such spaces. As is customary, we denote by
${\mathbb H}^{n}$
, which we will denote by using the same symbol. The same convention applies to dual and quotient spaces of such spaces. As is customary, we denote by
![]() $\Omega ^{k}$
the space of smooth differential k-forms on
$\Omega ^{k}$
the space of smooth differential k-forms on
![]() ${\mathbb H}^{n}$
; that is, the space of smooth sections of
${\mathbb H}^{n}$
; that is, the space of smooth sections of
![]() $\Large \wedge ^{k}{\mathfrak h}$
(seen as a bundle on
$\Large \wedge ^{k}{\mathfrak h}$
(seen as a bundle on
![]() ${\mathbb H}^{n}$
).
${\mathbb H}^{n}$
).
We now recall some of the spaces of differential forms introduced by M. Rumin in [Reference Rumin85, Reference Rumin86]. As before, we identify the left-invariant 2-form
![]() $d\theta $
in
$d\theta $
in
![]() ${\mathbb H}^{n}$
with a 2-covector in
${\mathbb H}^{n}$
with a 2-covector in
![]() $\Large \wedge ^{2}{\mathfrak h}$
and we define
$\Large \wedge ^{2}{\mathfrak h}$
and we define
 $$ \begin{align} \begin{aligned} \mathcal I^{k}:=&\{\lambda\wedge\theta+\mu\wedge d\theta:\textstyle\lambda\in\Large\wedge^{k-1}{\mathfrak h},\mu\in\Large\wedge^{k-2}{\mathfrak h}\}, \\ {\mathcal J}^{k}:=&\{\textstyle\lambda\in\Large\wedge^{k}{\mathfrak h}:\lambda\wedge\theta=\lambda\wedge d\theta=0\}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathcal I^{k}:=&\{\lambda\wedge\theta+\mu\wedge d\theta:\textstyle\lambda\in\Large\wedge^{k-1}{\mathfrak h},\mu\in\Large\wedge^{k-2}{\mathfrak h}\}, \\ {\mathcal J}^{k}:=&\{\textstyle\lambda\in\Large\wedge^{k}{\mathfrak h}:\lambda\wedge\theta=\lambda\wedge d\theta=0\}, \end{aligned} \end{align} $$
where we adopted the convention that
![]() $\Large \wedge ^{i}{\mathfrak h}=\{0\}$
if
$\Large \wedge ^{i}{\mathfrak h}=\{0\}$
if
![]() $i<0$
. Observe that
$i<0$
. Observe that
![]() $\mathcal I^{0}=\{0\}$
. The space
$\mathcal I^{0}=\{0\}$
. The space
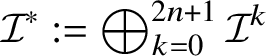 $\mathcal I^{*}:=\bigoplus _{k=0}^{2n+1}\mathcal I^{k}$
is the graded ideal generated by
$\mathcal I^{*}:=\bigoplus _{k=0}^{2n+1}\mathcal I^{k}$
is the graded ideal generated by
![]() $\theta $
, while
$\theta $
, while
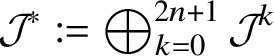 ${\mathcal J}^{*}:=\bigoplus _{k=0}^{2n+1}{\mathcal J}^{k}$
is the annihilator of
${\mathcal J}^{*}:=\bigoplus _{k=0}^{2n+1}{\mathcal J}^{k}$
is the annihilator of
![]() $\mathcal I^{*}$
. As observed in [Reference Rumin86] (see also [Reference Franchi, Serapioni and Serra Cassano51, page 166]), for
$\mathcal I^{*}$
. As observed in [Reference Rumin86] (see also [Reference Franchi, Serapioni and Serra Cassano51, page 166]), for
![]() $1\leq k\leq n$
we have
$1\leq k\leq n$
we have
![]() ${\mathcal J}^{k}=\{0\}$
and
${\mathcal J}^{k}=\{0\}$
and
![]() $\mathcal I^{2n+1-k}=\Large \wedge ^{2n+1-k}{\mathfrak h}$
; these equalities are, in essence, consequences of the fact that the Lefschetz operator
Footnote
6
$\mathcal I^{2n+1-k}=\Large \wedge ^{2n+1-k}{\mathfrak h}$
; these equalities are, in essence, consequences of the fact that the Lefschetz operator
Footnote
6
![]() $L:\Large \wedge ^{h}{\mathfrak h}_{1}\to \Large \wedge ^{h+2}{\mathfrak h}_{1}$
defined by
$L:\Large \wedge ^{h}{\mathfrak h}_{1}\to \Large \wedge ^{h+2}{\mathfrak h}_{1}$
defined by
![]() $L(\lambda ):=\lambda \wedge d\theta $
is injective for
$L(\lambda ):=\lambda \wedge d\theta $
is injective for
![]() $h\leq n-1$
and surjective for
$h\leq n-1$
and surjective for
![]() $h\geq n-1$
; see, for instance, the beautiful proof in [Reference Bryant, Griffiths and Grossman21, Proposition 1.1].
$h\geq n-1$
; see, for instance, the beautiful proof in [Reference Bryant, Griffiths and Grossman21, Proposition 1.1].
Remark 3.3. Recalling the notation introduced in Remark 3.1, it can be easily proved that
![]() $\lambda _{{\mathfrak h}_{1}}=0$
for every
$\lambda _{{\mathfrak h}_{1}}=0$
for every
![]() $\lambda \in {\mathcal J}^{k}$
. In particular, there exists a unique
$\lambda \in {\mathcal J}^{k}$
. In particular, there exists a unique
![]() $\lambda _{H}\in \Large \wedge ^{k-1}{\mathfrak h}_{1}$
such that
$\lambda _{H}\in \Large \wedge ^{k-1}{\mathfrak h}_{1}$
such that
![]() $\lambda =\lambda _{H}\wedge \theta $
; hence,
$\lambda =\lambda _{H}\wedge \theta $
; hence,
We also notice that
![]() $\lambda _{H}\wedge d\theta =0$
.
$\lambda _{H}\wedge d\theta =0$
.
Remark 3.4. For
![]() $k\geq n+1$
it is convenient to introduce the (formal) dual space
$k\geq n+1$
it is convenient to introduce the (formal) dual space
![]() ${\mathcal J}_{k}:=({\mathcal J}^{k})^{*}$
. Observe that every multivector
${\mathcal J}_{k}:=({\mathcal J}^{k})^{*}$
. Observe that every multivector
![]() $\tau \in \Large \wedge _{k}{\mathfrak h}$
canonically induces an element
$\tau \in \Large \wedge _{k}{\mathfrak h}$
canonically induces an element
![]() $[\tau ]_{{\mathcal J}}\in {\mathcal J}_{k}$
defined by
$[\tau ]_{{\mathcal J}}\in {\mathcal J}_{k}$
defined by
Equivalently,
![]() $[\tau ]_{{\mathcal J}}$
is the equivalence class of
$[\tau ]_{{\mathcal J}}$
is the equivalence class of
![]() $\tau $
in the quotient of
$\tau $
in the quotient of
![]() $\Large \wedge _{k}{\mathfrak h}$
by its subspace
$\Large \wedge _{k}{\mathfrak h}$
by its subspace
![]() $({\mathcal J}^{k})^{\perp }$
.
$({\mathcal J}^{k})^{\perp }$
.
Let us introduce the spaces
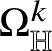 $\Omega _{\mathbb H}^{k}$
of Heisenberg differential k-forms
$\Omega _{\mathbb H}^{k}$
of Heisenberg differential k-forms
 $$ \begin{align*} & \Omega_{\mathbb H}^{k}:= C^{\infty}\big({\mathbb H}^{n},\tfrac{\large\wedge^{k}{\mathfrak h}}{\mathcal I^{k}}\big)=\left\{\text{smooth sections of }\tfrac{\large\wedge^{k}{\mathfrak h}}{\mathcal I^{k}}\right\},&&\text{if }0\leq k\leq n\\ & \Omega_{\mathbb H}^{k}:= C^{\infty}({\mathbb H}^{n},{\mathcal J}^{k})=\left\{\text{smooth sections of }{\mathcal J}^{k}\right\},&&\text{if }n+1\leq k\leq 2n+1. \end{align*} $$
$$ \begin{align*} & \Omega_{\mathbb H}^{k}:= C^{\infty}\big({\mathbb H}^{n},\tfrac{\large\wedge^{k}{\mathfrak h}}{\mathcal I^{k}}\big)=\left\{\text{smooth sections of }\tfrac{\large\wedge^{k}{\mathfrak h}}{\mathcal I^{k}}\right\},&&\text{if }0\leq k\leq n\\ & \Omega_{\mathbb H}^{k}:= C^{\infty}({\mathbb H}^{n},{\mathcal J}^{k})=\left\{\text{smooth sections of }{\mathcal J}^{k}\right\},&&\text{if }n+1\leq k\leq 2n+1. \end{align*} $$
Clearly,
 $\Omega _{\mathbb H}^{0}=C^{\infty }({\mathbb H}^{n})$
. Denoting exterior differentiation byFootnote
7
d, we observe that, if
$\Omega _{\mathbb H}^{0}=C^{\infty }({\mathbb H}^{n})$
. Denoting exterior differentiation byFootnote
7
d, we observe that, if
![]() $k\geq n+1$
, then
$k\geq n+1$
, then
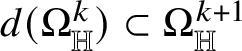 $d(\Omega _{\mathbb H}^{k})\subset \Omega _{\mathbb H}^{k+1}$
. If
$d(\Omega _{\mathbb H}^{k})\subset \Omega _{\mathbb H}^{k+1}$
. If
![]() $ k\leq n-1$
, we have
$ k\leq n-1$
, we have
![]() $d(\mathcal I^{k})\subset \mathcal I^{k+1}$
; hence, d passes to the quotient. All in all, for
$d(\mathcal I^{k})\subset \mathcal I^{k+1}$
; hence, d passes to the quotient. All in all, for
![]() $k\in \{0,\dots ,2n\}\setminus \{n\}$
a well-defined operator
$k\in \{0,\dots ,2n\}\setminus \{n\}$
a well-defined operator
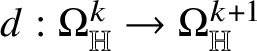 $d:\Omega _{\mathbb H}^{k}\to \Omega _{\mathbb H}^{k+1}$
is induced by exterior differentiation. The following fundamental result was proved by M. Rumin [Reference Rumin86]; see also [Reference Franchi, Serapioni and Serra Cassano51, Theorem 5.9].
$d:\Omega _{\mathbb H}^{k}\to \Omega _{\mathbb H}^{k+1}$
is induced by exterior differentiation. The following fundamental result was proved by M. Rumin [Reference Rumin86]; see also [Reference Franchi, Serapioni and Serra Cassano51, Theorem 5.9].
Theorem 3.5. There exists a second-order differential operator
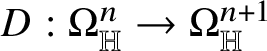 $D:\Omega _{\mathbb H}^{n}\to \Omega _{\mathbb H}^{n+1}$
such that the sequence
$D:\Omega _{\mathbb H}^{n}\to \Omega _{\mathbb H}^{n+1}$
such that the sequence
 $$ \begin{align*} 0\to{\mathbb R}\to\Omega_{\mathbb H}^{0}\stackrel{d}{\to}\Omega_{\mathbb H}^{1}\stackrel{d}{\to}\dots\stackrel{d}{\to}\Omega_{\mathbb H}^{n}\stackrel{D}{\to}\Omega_{\mathbb H}^{n+1}\stackrel{d}{\to} \dots \stackrel{d}{\to}\Omega_{\mathbb H}^{2n+1}\to 0 \end{align*} $$
$$ \begin{align*} 0\to{\mathbb R}\to\Omega_{\mathbb H}^{0}\stackrel{d}{\to}\Omega_{\mathbb H}^{1}\stackrel{d}{\to}\dots\stackrel{d}{\to}\Omega_{\mathbb H}^{n}\stackrel{D}{\to}\Omega_{\mathbb H}^{n+1}\stackrel{d}{\to} \dots \stackrel{d}{\to}\Omega_{\mathbb H}^{2n+1}\to 0 \end{align*} $$
is exact.
The construction of the operator D is crucial for our purposes, and we recall it here. First, as already mentioned, the Lefschetz operator
![]() $L:\Large \wedge ^{n-1}{\mathbb R}^{2n}\to \Large \wedge ^{n+1}{\mathbb R}^{2n}$
defined by
$L:\Large \wedge ^{n-1}{\mathbb R}^{2n}\to \Large \wedge ^{n+1}{\mathbb R}^{2n}$
defined by
![]() $L(\lambda )=\lambda \wedge d\theta $
is bijective. Second, observe that
$L(\lambda )=\lambda \wedge d\theta $
is bijective. Second, observe that
 $$ \begin{align} \frac{\Large\wedge^{n}{\mathfrak h}}{\mathcal I^{n}}=\frac{\Large\wedge^{n}{\mathfrak h}_{1}}{\{\mu\wedge d\theta:\mu\in\Large\wedge^{n-2}{\mathfrak h}_{1}\}}. \end{align} $$
$$ \begin{align} \frac{\Large\wedge^{n}{\mathfrak h}}{\mathcal I^{n}}=\frac{\Large\wedge^{n}{\mathfrak h}_{1}}{\{\mu\wedge d\theta:\mu\in\Large\wedge^{n-2}{\mathfrak h}_{1}\}}. \end{align} $$
We are going to define an operator D on smooth sections of
![]() $\Large \wedge ^{n}{\mathfrak h}_{1}$
and prove that it passes to the quotient modulo smooth sections of
$\Large \wedge ^{n}{\mathfrak h}_{1}$
and prove that it passes to the quotient modulo smooth sections of
![]() $\{\mu \wedge d\theta :\mu \in \Large \wedge ^{n-2}{\mathfrak h}_{1}\}$
. Given a smooth section
$\{\mu \wedge d\theta :\mu \in \Large \wedge ^{n-2}{\mathfrak h}_{1}\}$
. Given a smooth section
![]() $\alpha $
of
$\alpha $
of
![]() $\Large \wedge ^{n}{\mathfrak h}_{1}$
, we set
$\Large \wedge ^{n}{\mathfrak h}_{1}$
, we set
 $$ \begin{align*} D\alpha &:= d\big(\alpha-\theta\wedge L^{-1}((d\alpha)_{{\mathfrak h}_{1}})\big),\\ &{\kern3pt}= d\big(\alpha+(-1)^{n} L^{-1}((d\alpha)_{{\mathfrak h}_{1}})\wedge\theta\big), \end{align*} $$
$$ \begin{align*} D\alpha &:= d\big(\alpha-\theta\wedge L^{-1}((d\alpha)_{{\mathfrak h}_{1}})\big),\\ &{\kern3pt}= d\big(\alpha+(-1)^{n} L^{-1}((d\alpha)_{{\mathfrak h}_{1}})\wedge\theta\big), \end{align*} $$
where we used the notation in Remark 3.1. We have to prove that
![]() $D(\beta \wedge d\theta )=0$
for every smooth section
$D(\beta \wedge d\theta )=0$
for every smooth section
![]() $\beta $
of
$\beta $
of
![]() $\Large \wedge ^{n-2}{\mathfrak h}_{1}$
. Inasmuch as
$\Large \wedge ^{n-2}{\mathfrak h}_{1}$
. Inasmuch as
 $$ \begin{align*} & L^{-1}((d(\beta\wedge d\theta))_{{\mathfrak h}_{1}} )=L^{-1}((d\beta\wedge d\theta)_{{\mathfrak h}_{1}})=L^{-1}((d\beta)_{{\mathfrak h}_{1}}\wedge d\theta)=(d\beta)_{{\mathfrak h}_{1}}\\ & d(\beta\wedge d\theta)=(-1)^{n-1}d(d\beta\wedge\theta), \end{align*} $$
$$ \begin{align*} & L^{-1}((d(\beta\wedge d\theta))_{{\mathfrak h}_{1}} )=L^{-1}((d\beta\wedge d\theta)_{{\mathfrak h}_{1}})=L^{-1}((d\beta)_{{\mathfrak h}_{1}}\wedge d\theta)=(d\beta)_{{\mathfrak h}_{1}}\\ & d(\beta\wedge d\theta)=(-1)^{n-1}d(d\beta\wedge\theta), \end{align*} $$
we deduce that
 $$ \begin{align*} D(\beta\wedge d\theta) & = d(\beta\wedge d\theta + (-1)^{n}(d\beta)_{{\mathfrak h}_{1}}\wedge\theta)\\ &= (-1)^{n-1} d(d\beta\wedge\theta - (d\beta)_{{\mathfrak h}_{1}}\wedge\theta)\\ &= (-1)^{n-1} d((d\beta)_{{\mathfrak h}_{1}}\wedge\theta - (d\beta)_{{\mathfrak h}_{1}}\wedge\theta)=0, \end{align*} $$
$$ \begin{align*} D(\beta\wedge d\theta) & = d(\beta\wedge d\theta + (-1)^{n}(d\beta)_{{\mathfrak h}_{1}}\wedge\theta)\\ &= (-1)^{n-1} d(d\beta\wedge\theta - (d\beta)_{{\mathfrak h}_{1}}\wedge\theta)\\ &= (-1)^{n-1} d((d\beta)_{{\mathfrak h}_{1}}\wedge\theta - (d\beta)_{{\mathfrak h}_{1}}\wedge\theta)=0, \end{align*} $$
as wished.
This proves that D is well-defined as a linear operator
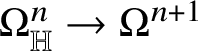 $\Omega _{\mathbb H}^{n}\to \Omega ^{n+1}$
. We have to check that
$\Omega _{\mathbb H}^{n}\to \Omega ^{n+1}$
. We have to check that
 $D(\Omega _{\mathbb H}^{n})\subset \Omega _{\mathbb H}^{n+1}$
; that is, that
$D(\Omega _{\mathbb H}^{n})\subset \Omega _{\mathbb H}^{n+1}$
; that is, that
![]() $D\alpha \wedge \theta =D\alpha \wedge d\theta =0$
for every
$D\alpha \wedge \theta =D\alpha \wedge d\theta =0$
for every
![]() $\alpha \in \Omega _{\mathbb H}^{n}$
. To this aim, let us write
$\alpha \in \Omega _{\mathbb H}^{n}$
. To this aim, let us write
![]() $(d\alpha )_{\mathfrak v}:=d\alpha -(d\alpha )_{{\mathfrak h}_{1}}$
to denote the ‘vertical’ part of
$(d\alpha )_{\mathfrak v}:=d\alpha -(d\alpha )_{{\mathfrak h}_{1}}$
to denote the ‘vertical’ part of
![]() $d\alpha $
, which can be written as
$d\alpha $
, which can be written as
![]() $(d\alpha )_{\mathfrak v}=\theta \wedge \beta _{\alpha }$
for a suitable smooth section
$(d\alpha )_{\mathfrak v}=\theta \wedge \beta _{\alpha }$
for a suitable smooth section
![]() $\beta _{\alpha }$
of
$\beta _{\alpha }$
of
![]() $\Large \wedge ^{n}{\mathfrak h}_{1}$
. Then
$\Large \wedge ^{n}{\mathfrak h}_{1}$
. Then

This implies that
![]() $D\alpha \wedge \theta =0$
and, as a consequence,
$D\alpha \wedge \theta =0$
and, as a consequence,
![]() $0=d(D\alpha \wedge \theta )=(-1)^{n+1}D\alpha \wedge d\theta $
, as wished.
$0=d(D\alpha \wedge \theta )=(-1)^{n+1}D\alpha \wedge d\theta $
, as wished.
Example 3.6. Let us compute the operator
 $D:\Omega _{\mathbb H}^{1}\to \Omega _{\mathbb H}^{2}$
in the first Heisenberg group
$D:\Omega _{\mathbb H}^{1}\to \Omega _{\mathbb H}^{2}$
in the first Heisenberg group
![]() ${\mathbb H}^{1}$
. Given
${\mathbb H}^{1}$
. Given
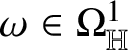 $\omega \in \Omega _{\mathbb H}^{1}$
, we choose a smooth section
$\omega \in \Omega _{\mathbb H}^{1}$
, we choose a smooth section
![]() $\alpha $
of
$\alpha $
of
![]() $\Large \wedge ^{1}{\mathfrak h}_{1}$
that is a representative of
$\Large \wedge ^{1}{\mathfrak h}_{1}$
that is a representative of
![]() $\omega $
in the quotient (3.7). Writing
$\omega $
in the quotient (3.7). Writing
![]() $\alpha =f dx+g dy$
, we have
$\alpha =f dx+g dy$
, we have
and, clearly,
![]() $L^{-1}((d\alpha )_{{\mathfrak h}_{1}})=Yf-Xg$
. Therefore,
$L^{-1}((d\alpha )_{{\mathfrak h}_{1}})=Yf-Xg$
. Therefore,

See also [Reference Baldi, Franchi, Tchou and Tesi13, Example B.2] and [Reference Baldi and Franchi12, Example 3.11].
We refer to [Reference Baldi and Franchi12, Example 3.12] for the computation of the operator D in
![]() ${\mathbb H}^{2}$
.
${\mathbb H}^{2}$
.
Remark 3.7. It is sometimes convenient to have a unique symbol to denote the differential operators in Rumin’s complex. Following [Reference Franchi and Tripaldi54], we then define
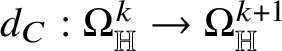 $d_{C}:\Omega ^{k}_{\mathbb H}\to \Omega ^{k+1}_{\mathbb H}$
by
$d_{C}:\Omega ^{k}_{\mathbb H}\to \Omega ^{k+1}_{\mathbb H}$
by
![]() $d_{C}=d$
, if
$d_{C}=d$
, if
![]() $k\neq n$
, and
$k\neq n$
, and
![]() $d_{C}=D$
, if
$d_{C}=D$
, if
![]() $k=n$
.
$k=n$
.
Remark 3.8. For
![]() $k\leq n$
, an interesting interpretation of
$k\leq n$
, an interesting interpretation of
 $\tfrac {\large\wedge ^{k}{\mathfrak h}}{\mathcal I^{k}}$
and
$\tfrac {\large\wedge ^{k}{\mathfrak h}}{\mathcal I^{k}}$
and
![]() ${\mathcal J}^{2n+1-k}$
as spaces of integrable covectors is provided in [Reference Franchi, Serapioni and Serra Cassano51, Theorem 2.9].
${\mathcal J}^{2n+1-k}$
as spaces of integrable covectors is provided in [Reference Franchi, Serapioni and Serra Cassano51, Theorem 2.9].
3.3
 ${\mathbb H}$
-linear maps
${\mathbb H}$
-linear maps
We now introduce the notion of
![]() ${\mathbb H}$
-linear maps in
${\mathbb H}$
-linear maps in
![]() ${\mathbb H}^{n}$
, which are among the most simple examples of contact maps (see, e.g., [Reference Korányi and Reimann64]), and study their behaviour on Heisenberg forms. For a finer study of the relations between Heisenberg forms and contact maps, see, for example, [Reference Canarecci24, Chapter 3]. The results in this section will be applied especially, but not exclusively, to left-translations and dilations in
${\mathbb H}^{n}$
, which are among the most simple examples of contact maps (see, e.g., [Reference Korányi and Reimann64]), and study their behaviour on Heisenberg forms. For a finer study of the relations between Heisenberg forms and contact maps, see, for example, [Reference Canarecci24, Chapter 3]. The results in this section will be applied especially, but not exclusively, to left-translations and dilations in
![]() ${\mathbb H}^{n}$
and their compositions.
${\mathbb H}^{n}$
and their compositions.
Definition 3.9. A map
![]() ${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
is
${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
is
![]() ${\mathbb H}$
-linear if it is a group homomorphism that is also homogeneous; that is,
${\mathbb H}$
-linear if it is a group homomorphism that is also homogeneous; that is,
![]() $\delta _{r}(\mathcal Lp)={\mathcal L}(\delta _{r} p)$
for any
$\delta _{r}(\mathcal Lp)={\mathcal L}(\delta _{r} p)$
for any
![]() $p\in {\mathbb H}^{n}$
and any
$p\in {\mathbb H}^{n}$
and any
![]() $r>0$
.
$r>0$
.
It is not difficult to prove that
![]() ${\mathcal L}$
is
${\mathcal L}$
is
![]() ${\mathbb H}$
-linear if and only if
${\mathbb H}$
-linear if and only if
![]() $\mathfrak l:=\exp ^{-1}\circ {\mathcal L}\circ \exp :{\mathfrak h}\to {\mathfrak h}$
is a Lie algebra homomorphism; see, for example, [Reference Magnani67, §3.1] and the references therein. In particular,
$\mathfrak l:=\exp ^{-1}\circ {\mathcal L}\circ \exp :{\mathfrak h}\to {\mathfrak h}$
is a Lie algebra homomorphism; see, for example, [Reference Magnani67, §3.1] and the references therein. In particular,
Moreover, if for every
![]() $p\in {\mathbb H}^{n}$
one canonically identifies
$p\in {\mathbb H}^{n}$
one canonically identifies
![]() $T_{p}{\mathbb H}^{n}\equiv T_{0}{\mathbb H}^{n}={\mathfrak h}$
by means of the differential of the left-translation by
$T_{p}{\mathbb H}^{n}\equiv T_{0}{\mathbb H}^{n}={\mathfrak h}$
by means of the differential of the left-translation by
![]() $p^{-1}$
, then the differential
$p^{-1}$
, then the differential
![]() $d{\mathcal L}$
of
$d{\mathcal L}$
of
![]() ${\mathcal L}$
is constant; that is,
${\mathcal L}$
is constant; that is,
This easily follows by computing the differential at p of
![]() ${\mathcal L}(q)={\mathcal L}(p){\mathcal L}(p^{-1}q)$
.
${\mathcal L}(q)={\mathcal L}(p){\mathcal L}(p^{-1}q)$
.
By abuse of notation, we use a unique symbol
![]() ${\mathcal L}_{*}$
to denote any of
${\mathcal L}_{*}$
to denote any of
![]() $d{\mathcal L}_{p}$
,
$d{\mathcal L}_{p}$
,
![]() $d{\mathcal L}_{0}$
and
$d{\mathcal L}_{0}$
and
![]() $\mathfrak l$
. Similarly, the symbol
$\mathfrak l$
. Similarly, the symbol
![]() ${\mathcal L}^{*}$
denotes any of the associated pullback actions
${\mathcal L}^{*}$
denotes any of the associated pullback actions
 $(d{\mathcal L}_{p})^{*}:T_{{\mathcal L}(p)}^{*}{\mathbb H}^{n}\to T_{p}^{*}{\mathbb H}^{n}$
,
$(d{\mathcal L}_{p})^{*}:T_{{\mathcal L}(p)}^{*}{\mathbb H}^{n}\to T_{p}^{*}{\mathbb H}^{n}$
,
![]() $(d{\mathcal L}_{0})^{*}:T_{0}^{*}{\mathbb H}^{n}\to T_{0}^{*}{\mathbb H}^{n}$
and
$(d{\mathcal L}_{0})^{*}:T_{0}^{*}{\mathbb H}^{n}\to T_{0}^{*}{\mathbb H}^{n}$
and
![]() $\mathfrak l^{*}:\Large \wedge ^{1}{\mathfrak h}\to \Large \wedge ^{1}{\mathfrak h}$
. We also use the symbols
$\mathfrak l^{*}:\Large \wedge ^{1}{\mathfrak h}\to \Large \wedge ^{1}{\mathfrak h}$
. We also use the symbols
![]() ${\mathcal L}_{*},{\mathcal L}^{*}$
to denote the induced maps
${\mathcal L}_{*},{\mathcal L}^{*}$
to denote the induced maps
![]() ${\mathcal L}_{*}:\Large \wedge _{*}{\mathfrak h}\to \Large \wedge _{*}{\mathfrak h}$
and
${\mathcal L}_{*}:\Large \wedge _{*}{\mathfrak h}\to \Large \wedge _{*}{\mathfrak h}$
and
![]() ${\mathcal L}^{*}:\Large \wedge ^{*}{\mathfrak h}\to \Large \wedge ^{*}{\mathfrak h}$
defined by
${\mathcal L}^{*}:\Large \wedge ^{*}{\mathfrak h}\to \Large \wedge ^{*}{\mathfrak h}$
defined by
and
Proposition 3.10. Let
![]() ${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
be a
${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
be a
![]() ${\mathbb H}$
-linear isomorphism; then the pullbacks of
${\mathbb H}$
-linear isomorphism; then the pullbacks of
![]() $\theta $
and
$\theta $
and
![]() $d\theta $
satisfy
$d\theta $
satisfy
where
![]() $c_{\mathcal L}\neq 0$
is definedFootnote
8
by
$c_{\mathcal L}\neq 0$
is definedFootnote
8
by
![]() ${\mathcal L}_{*}(T)=c_{\mathcal L} T$
.
${\mathcal L}_{*}(T)=c_{\mathcal L} T$
.
Proof. Since pullback and exterior derivative commute, it is sufficient to prove the first assertion in (3.10). It is proved in [Reference Warner95, §3.15] that, since
![]() $\theta $
is left-invariant,
$\theta $
is left-invariant,
![]() $d{\mathcal L}^{*}(\theta )$
is left-invariant as well. By (3.9), we have
$d{\mathcal L}^{*}(\theta )$
is left-invariant as well. By (3.9), we have
![]() ${\mathcal L}^{*}(\theta )=0$
on
${\mathcal L}^{*}(\theta )=0$
on
![]() ${\mathfrak h}_{1}$
; hence,
${\mathfrak h}_{1}$
; hence,
![]() ${\mathcal L}^{*}(\theta )$
is a scalar multiple of
${\mathcal L}^{*}(\theta )$
is a scalar multiple of
![]() $\theta $
. The statement follows because
$\theta $
. The statement follows because
![]() ${\mathcal L}^{*}(\theta )(T)=\theta ({\mathcal L}_{*}(T))=\theta (c_{\mathcal L} T)=c_{\mathcal L}$
.
${\mathcal L}^{*}(\theta )(T)=\theta ({\mathcal L}_{*}(T))=\theta (c_{\mathcal L} T)=c_{\mathcal L}$
.
Proposition 3.11. Let
![]() ${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
be a
${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
be a
![]() ${\mathbb H}$
-linear isomorphism; then
${\mathbb H}$
-linear isomorphism; then
-
(i) if
 $1\leq k\leq n$
,
$1\leq k\leq n$
,
 ${\mathcal L}^{*}:\Large \wedge ^{k}{\mathfrak h}\to \Large \wedge ^{k}{\mathfrak h}$
passes to the quotient and defines an isomorphism
${\mathcal L}^{*}:\Large \wedge ^{k}{\mathfrak h}\to \Large \wedge ^{k}{\mathfrak h}$
passes to the quotient and defines an isomorphism
 ${\mathcal L}^{*}:\Large \wedge ^{k}{\mathfrak h}/\mathcal I^{k}\to \Large \wedge ^{k}{\mathfrak h}/\mathcal I^{k}$
;
${\mathcal L}^{*}:\Large \wedge ^{k}{\mathfrak h}/\mathcal I^{k}\to \Large \wedge ^{k}{\mathfrak h}/\mathcal I^{k}$
; -
(ii) if
 $n+1\leq k\leq 2n$
,
$n+1\leq k\leq 2n$
,
 ${\mathcal L}^{*}({\mathcal J}^{k})={\mathcal J}^{k}$
.
${\mathcal L}^{*}({\mathcal J}^{k})={\mathcal J}^{k}$
.
Proof. (i) If
![]() $1\leq k\leq n$
, it is enough to show that
$1\leq k\leq n$
, it is enough to show that
![]() ${\mathcal L}^{*}(\mathcal I^{k})=\mathcal I^{k}$
. For every
${\mathcal L}^{*}(\mathcal I^{k})=\mathcal I^{k}$
. For every
![]() $\lambda \in \Large \wedge ^{k-1}{\mathfrak h}$
and
$\lambda \in \Large \wedge ^{k-1}{\mathfrak h}$
and
![]() $\mu \in \Large \wedge ^{k-2}{\mathfrak h}$
, we have by Proposition 3.10
$\mu \in \Large \wedge ^{k-2}{\mathfrak h}$
, we have by Proposition 3.10
hence,
![]() ${\mathcal L}^{*}(\mathcal I^{k})\subset \mathcal I^{k}$
. The equality
${\mathcal L}^{*}(\mathcal I^{k})\subset \mathcal I^{k}$
. The equality
![]() ${\mathcal L}^{*}(\mathcal I^{k})= \mathcal I^{k}$
follows because
${\mathcal L}^{*}(\mathcal I^{k})= \mathcal I^{k}$
follows because
![]() ${\mathcal L}^{*}$
is a isomorphism.
${\mathcal L}^{*}$
is a isomorphism.
(ii) Given
![]() $\lambda \in {\mathcal J}^{k}$
we have
$\lambda \in {\mathcal J}^{k}$
we have
 $$ \begin{align*} {\mathcal L}^{*}(\lambda)\wedge\theta= c_{\mathcal L}^{-1} {\mathcal L}^{*}(\lambda\wedge \theta)=0\quad\text{and}\quad {\mathcal L}^{*}(\lambda)\wedge d\theta= c_{\mathcal L}^{-1} {\mathcal L}^{*}(\lambda\wedge d\theta)=0, \end{align*} $$
$$ \begin{align*} {\mathcal L}^{*}(\lambda)\wedge\theta= c_{\mathcal L}^{-1} {\mathcal L}^{*}(\lambda\wedge \theta)=0\quad\text{and}\quad {\mathcal L}^{*}(\lambda)\wedge d\theta= c_{\mathcal L}^{-1} {\mathcal L}^{*}(\lambda\wedge d\theta)=0, \end{align*} $$
hence
![]() ${\mathcal L}^{*}(\lambda )\in {\mathcal J}^{k}$
. This proves the inclusion
${\mathcal L}^{*}(\lambda )\in {\mathcal J}^{k}$
. This proves the inclusion
![]() ${\mathcal L}^{*}({\mathcal J}^{k})\subset {\mathcal J}^{k}$
, and the equality follows again because
${\mathcal L}^{*}({\mathcal J}^{k})\subset {\mathcal J}^{k}$
, and the equality follows again because
![]() ${\mathcal L}^{*}$
is an isomorphism.
${\mathcal L}^{*}$
is an isomorphism.
Proposition 3.11 has the following consequence that we will later use when
![]() ${\mathcal L}$
is (a composition of) dilations and left-translations. Compare with [Reference Canarecci24, Theorem 3.2.1].
${\mathcal L}$
is (a composition of) dilations and left-translations. Compare with [Reference Canarecci24, Theorem 3.2.1].
Corollary 3.12. Let
![]() ${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
be a
${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
be a
![]() ${\mathbb H}$
-linear isomorphism; then the pullback
${\mathbb H}$
-linear isomorphism; then the pullback
![]() ${\mathcal L}^{*}$
commutes with the differential operators in Rumin’s complex; that is, for every
${\mathcal L}^{*}$
commutes with the differential operators in Rumin’s complex; that is, for every
![]() $k\in \{1,\dots ,2n\}$
,
$k\in \{1,\dots ,2n\}$
,
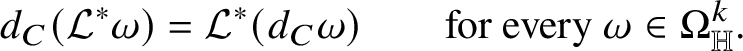 $$ \begin{align*} d_{C}({\mathcal L}^{*}\omega)={\mathcal L}^{*}(d_{C}\omega)\qquad\text{for every } \omega\in\Omega^{k}_{\mathbb H}. \end{align*} $$
$$ \begin{align*} d_{C}({\mathcal L}^{*}\omega)={\mathcal L}^{*}(d_{C}\omega)\qquad\text{for every } \omega\in\Omega^{k}_{\mathbb H}. \end{align*} $$
Proof. When
![]() $k\neq n$
, this is a simple consequence of Proposition 3.11 and the fact that
$k\neq n$
, this is a simple consequence of Proposition 3.11 and the fact that
![]() ${\mathcal L}^{*}$
commutes with exterior differentiation
${\mathcal L}^{*}$
commutes with exterior differentiation
![]() $d=d_{C}$
.
$d=d_{C}$
.
When
![]() $k=n$
, we have
$k=n$
, we have
![]() $d_{C}=D$
and some computations are needed. For every
$d_{C}=D$
and some computations are needed. For every
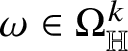 $\omega \in \Omega ^{k}_{\mathbb H}$
we fix a representative
$\omega \in \Omega ^{k}_{\mathbb H}$
we fix a representative
![]() $\alpha \in C^{\infty }({\mathbb H}^{n},\Large \wedge ^{n}{\mathfrak h}_{1})$
of the equivalence class
$\alpha \in C^{\infty }({\mathbb H}^{n},\Large \wedge ^{n}{\mathfrak h}_{1})$
of the equivalence class
![]() $\omega $
in the quotient in the right-hand side of (3.7). By Proposition 3.11,
$\omega $
in the quotient in the right-hand side of (3.7). By Proposition 3.11,
![]() ${\mathcal L}^{*}\alpha $
is a representative of
${\mathcal L}^{*}\alpha $
is a representative of
![]() ${\mathcal L}^{*}\omega $
and we can compute
${\mathcal L}^{*}\omega $
and we can compute
 $$ \begin{align*} D({\mathcal L}^{*}\omega) & = d\big({\mathcal L}^{*}\alpha-\theta\wedge L^{-1}((d{\mathcal L}^{*}\alpha)_{{\mathfrak h}_{1}})\big)\\ & = d\big({\mathcal L}^{*}\alpha-\theta\wedge L^{-1}(({\mathcal L}^{*}(d\alpha))_{{\mathfrak h}_{1}})\big)\\ & = d\big({\mathcal L}^{*}\alpha-{\mathcal L}^{*}(\theta/c_{\mathcal L})\wedge L^{-1}({\mathcal L}^{*}((d\alpha)_{{\mathfrak h}_{1}}))\big), \end{align*} $$
$$ \begin{align*} D({\mathcal L}^{*}\omega) & = d\big({\mathcal L}^{*}\alpha-\theta\wedge L^{-1}((d{\mathcal L}^{*}\alpha)_{{\mathfrak h}_{1}})\big)\\ & = d\big({\mathcal L}^{*}\alpha-\theta\wedge L^{-1}(({\mathcal L}^{*}(d\alpha))_{{\mathfrak h}_{1}})\big)\\ & = d\big({\mathcal L}^{*}\alpha-{\mathcal L}^{*}(\theta/c_{\mathcal L})\wedge L^{-1}({\mathcal L}^{*}((d\alpha)_{{\mathfrak h}_{1}}))\big), \end{align*} $$
where we used Proposition 3.10. The latter also gives
 $$ \begin{align*} {\mathcal L}^{*}((d\alpha)_{{\mathfrak h}_{1}}) &={\mathcal L}^{*}(L^{-1}(d\alpha)_{{\mathfrak h}_{1}}\wedge d\theta)\\ &={\mathcal L}^{*}(L^{-1}(d\alpha)_{{\mathfrak h}_{1}})\wedge{\mathcal L}^{*}( d\theta)\\ &=c_{\mathcal L} {\mathcal L}^{*}(L^{-1}(d\alpha)_{{\mathfrak h}_{1}})\wedge d\theta \end{align*} $$
$$ \begin{align*} {\mathcal L}^{*}((d\alpha)_{{\mathfrak h}_{1}}) &={\mathcal L}^{*}(L^{-1}(d\alpha)_{{\mathfrak h}_{1}}\wedge d\theta)\\ &={\mathcal L}^{*}(L^{-1}(d\alpha)_{{\mathfrak h}_{1}})\wedge{\mathcal L}^{*}( d\theta)\\ &=c_{\mathcal L} {\mathcal L}^{*}(L^{-1}(d\alpha)_{{\mathfrak h}_{1}})\wedge d\theta \end{align*} $$
so that
 $$ \begin{align*} L^{-1}( {\mathcal L}^{*}((d\alpha)_{{\mathfrak h}_{1}}) ) = c_{\mathcal L} {\mathcal L}^{*}(L^{-1}(d\alpha)_{{\mathfrak h}_{1}}). \end{align*} $$
$$ \begin{align*} L^{-1}( {\mathcal L}^{*}((d\alpha)_{{\mathfrak h}_{1}}) ) = c_{\mathcal L} {\mathcal L}^{*}(L^{-1}(d\alpha)_{{\mathfrak h}_{1}}). \end{align*} $$
Therefore,
 $$ \begin{align*} D({\mathcal L}^{*}\omega) & = d\big({\mathcal L}^{*}\alpha-{\mathcal L}^{*}(\theta/c_{\mathcal L})\wedge c_{\mathcal L} {\mathcal L}^{*}(L^{-1}(d\alpha)_{{\mathfrak h}_{1}})\big)\\ &= d\big({\mathcal L}^{*}(\alpha-\theta\wedge(L^{-1}(d\alpha)_{{\mathfrak h}_{1}}))\big)\\ &={\mathcal L}^{*}\big(d(\alpha-\theta\wedge(L^{-1}(d\alpha)_{{\mathfrak h}_{1}}))\big)\\ &= {\mathcal L}^{*}(D\omega) \end{align*} $$
$$ \begin{align*} D({\mathcal L}^{*}\omega) & = d\big({\mathcal L}^{*}\alpha-{\mathcal L}^{*}(\theta/c_{\mathcal L})\wedge c_{\mathcal L} {\mathcal L}^{*}(L^{-1}(d\alpha)_{{\mathfrak h}_{1}})\big)\\ &= d\big({\mathcal L}^{*}(\alpha-\theta\wedge(L^{-1}(d\alpha)_{{\mathfrak h}_{1}}))\big)\\ &={\mathcal L}^{*}\big(d(\alpha-\theta\wedge(L^{-1}(d\alpha)_{{\mathfrak h}_{1}}))\big)\\ &= {\mathcal L}^{*}(D\omega) \end{align*} $$
and the proof is concluded.
We recall that the notion of vertical plane was introduced in Definition 3.2. Given natural numbers
![]() $a,b$
such that
$a,b$
such that
![]() $1\leq a+b\leq n$
, we denote by
$1\leq a+b\leq n$
, we denote by
![]() ${{\mathscr P}_{a,b}}\subset {\mathbb H}^{n}$
the
${{\mathscr P}_{a,b}}\subset {\mathbb H}^{n}$
the
![]() $(2a+b+1)$
-dimensional vertical plane
$(2a+b+1)$
-dimensional vertical plane
 $$ \begin{align} \begin{aligned} \!\!\: {{\mathscr P}_{a,b}}:=\:& \{(x,y,t)\in{\mathbb H}^{n}:x_{i}=y_{j}=0\text{ for all }a+b+1\leq i\leq n \text{ and }a+1\leq j\leq n\}\\ =\:& \begin{cases} \{(x_{1},\dots,x_{a+b},0,\dots,0,y_{1},\dots,y_{a},0,\dots,0,t)\}\quad & \text{if }a\geq 1\text{ and } a+b<n\\ \{(x_{1},\dots,x_{n},y_{1},\dots,y_{a},0,\dots,0,t)\}\quad & \text{if }a\geq 1\text{ and } a+b=n\\ \{(x_{1},\dots,x_{b},0,\dots,0,t)\}\quad & \text{if }a=0. \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \!\!\: {{\mathscr P}_{a,b}}:=\:& \{(x,y,t)\in{\mathbb H}^{n}:x_{i}=y_{j}=0\text{ for all }a+b+1\leq i\leq n \text{ and }a+1\leq j\leq n\}\\ =\:& \begin{cases} \{(x_{1},\dots,x_{a+b},0,\dots,0,y_{1},\dots,y_{a},0,\dots,0,t)\}\quad & \text{if }a\geq 1\text{ and } a+b<n\\ \{(x_{1},\dots,x_{n},y_{1},\dots,y_{a},0,\dots,0,t)\}\quad & \text{if }a\geq 1\text{ and } a+b=n\\ \{(x_{1},\dots,x_{b},0,\dots,0,t)\}\quad & \text{if }a=0. \end{cases} \end{aligned} \end{align} $$
As shown by the following proposition, the planes
![]() ${{\mathscr P}_{a,b}}$
can be considered as canonical models for vertical planes in
${{\mathscr P}_{a,b}}$
can be considered as canonical models for vertical planes in
![]() ${\mathbb H}^{n}$
.
${\mathbb H}^{n}$
.
Proposition 3.13. Let
![]() ${\mathscr P}\subset {\mathbb R}^{2n+1}\equiv {\mathbb H}^{n}$
be a vertical plane; then there exist nonnegative integers
${\mathscr P}\subset {\mathbb R}^{2n+1}\equiv {\mathbb H}^{n}$
be a vertical plane; then there exist nonnegative integers
![]() $a,b$
and an
$a,b$
and an
![]() ${\mathbb H}$
-linear isomorphism
${\mathbb H}$
-linear isomorphism
![]() ${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
such that
${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
such that
 $$ \begin{align*} \begin{aligned} & a+b\leq n\quad\text{and}\quad \dim {\mathscr P}=2a+b+1\\ & {\mathcal L}^{*}(\theta)=\theta,\quad {\mathcal L}^{*}(d\theta)=d\theta\quad\text{and}\quad {\mathcal L}({\mathscr P})={{\mathscr P}_{a,b}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & a+b\leq n\quad\text{and}\quad \dim {\mathscr P}=2a+b+1\\ & {\mathcal L}^{*}(\theta)=\theta,\quad {\mathcal L}^{*}(d\theta)=d\theta\quad\text{and}\quad {\mathcal L}({\mathscr P})={{\mathscr P}_{a,b}}. \end{aligned} \end{align*} $$
Proof. The set
![]() $V:=\exp ^{-1}(\{(x,y,t)\in {\mathscr P}:t=0\})$
is a vector subspace of
$V:=\exp ^{-1}(\{(x,y,t)\in {\mathscr P}:t=0\})$
is a vector subspace of
![]() ${\mathfrak h}_{1}$
. If
${\mathfrak h}_{1}$
. If
![]() $\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
is the Lie algebra isomorphism provided by the following Lemma 3.14, then
$\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
is the Lie algebra isomorphism provided by the following Lemma 3.14, then
![]() ${\mathcal L}:=\exp \circ \mathfrak l\circ \exp ^{-1}$
is an
${\mathcal L}:=\exp \circ \mathfrak l\circ \exp ^{-1}$
is an
![]() ${\mathbb H}$
-linear isomorphism, which, by Proposition 3.10, satisfies the statement of the present proposition.
${\mathbb H}$
-linear isomorphism, which, by Proposition 3.10, satisfies the statement of the present proposition.
Lemma 3.14. Let
![]() $V\subset {\mathfrak h}_{1}$
be a linear subspace with
$V\subset {\mathfrak h}_{1}$
be a linear subspace with
![]() $\dim V\geq 1$
. Then there exist nonnegative integers
$\dim V\geq 1$
. Then there exist nonnegative integers
![]() $a,b$
and a Lie algebra isomorphism
$a,b$
and a Lie algebra isomorphism
![]() $\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
such that
$\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
such that
![]() $\dim V=2a+b$
,
$\dim V=2a+b$
,
![]() $\mathfrak l(T)=T$
and
$\mathfrak l(T)=T$
and
 $$ \begin{align*} \mathfrak l(V)= \begin{cases} \operatorname*{\mathrm{span}}\{X_{1},\dots,X_{a+b},Y_{1},\dots,Y_{a}\}\qquad& \text{if }a\geq 1\\ \operatorname*{\mathrm{span}}\{X_{1},\dots,X_{b}\}\qquad& \text{if }a=0. \end{cases} \end{align*} $$
$$ \begin{align*} \mathfrak l(V)= \begin{cases} \operatorname*{\mathrm{span}}\{X_{1},\dots,X_{a+b},Y_{1},\dots,Y_{a}\}\qquad& \text{if }a\geq 1\\ \operatorname*{\mathrm{span}}\{X_{1},\dots,X_{b}\}\qquad& \text{if }a=0. \end{cases} \end{align*} $$
Moreover,
![]() $a=0$
if and only if
$a=0$
if and only if
![]() $[V,V]=\{0\}$
; that is, if and only if V is an abelian subalgebra of
$[V,V]=\{0\}$
; that is, if and only if V is an abelian subalgebra of
![]() ${\mathfrak h}$
.
${\mathfrak h}$
.
Proof. We first recall the canonical symplectic structure on
![]() ${\mathfrak h}_{1}$
, which is provided by the bilinear skew-symmetric form
${\mathfrak h}_{1}$
, which is provided by the bilinear skew-symmetric form
Notice that
![]() $d\theta $
(seen as a 2-covector at
$d\theta $
(seen as a 2-covector at
![]() $0$
; that is, as an element of
$0$
; that is, as an element of
![]() $\Large \wedge ^{2}{\mathfrak h}$
) satisfies
$\Large \wedge ^{2}{\mathfrak h}$
) satisfies
which can be easily checked by testing
![]() $d\theta $
on a basis
$d\theta $
on a basis
![]() $X_{i}\wedge X_{j},X_{i}\wedge Y_{j},Y_{i}\wedge Y_{j}$
of
$X_{i}\wedge X_{j},X_{i}\wedge Y_{j},Y_{i}\wedge Y_{j}$
of
![]() $\Large \wedge ^{2}{\mathfrak h}_{1}$
.
$\Large \wedge ^{2}{\mathfrak h}_{1}$
.
We borrow some language and notation from [Reference Artin10, Chapter 3]. Let
be the radical of V and let
![]() $b:=\dim \text {rad}(V)$
. Choose a subspace U of V such that
$b:=\dim \text {rad}(V)$
. Choose a subspace U of V such that
![]() $V=$
rad
$V=$
rad
![]() $(V)\oplus U$
; U is clearly nonsingular; that is, for every
$(V)\oplus U$
; U is clearly nonsingular; that is, for every
![]() $X\in U$
there exists
$X\in U$
there exists
![]() $X^{\prime }\in U$
such that
$X^{\prime }\in U$
such that
![]() $[X,X^{\prime }]\neq 0$
. By [Reference Artin10, Theorem 3.7], the dimension of
$[X,X^{\prime }]\neq 0$
. By [Reference Artin10, Theorem 3.7], the dimension of
![]() $ U$
is even and we set
$ U$
is even and we set
![]() $\dim U=2a$
.
$\dim U=2a$
.
If
![]() $a\geq 1$
, by [Reference Artin10, Theorem 3.7] there exists a basis
$a\geq 1$
, by [Reference Artin10, Theorem 3.7] there exists a basis
![]() $\widetilde X_{1},\dots ,\widetilde X_{a},\widetilde Y_{1},\dots , \widetilde Y_{a}$
of U such that
$\widetilde X_{1},\dots ,\widetilde X_{a},\widetilde Y_{1},\dots , \widetilde Y_{a}$
of U such that
 $$ \begin{align*} B(\widetilde X_{i},\widetilde X_{j})=0,\quad B(\widetilde Y_{i},\widetilde Y_{j})=0\quad\text{and}\quad B(\widetilde X_{i},\widetilde Y_{j})=\delta_{ij},\qquad i,j\in\{1,\dots,a\}; \end{align*} $$
$$ \begin{align*} B(\widetilde X_{i},\widetilde X_{j})=0,\quad B(\widetilde Y_{i},\widetilde Y_{j})=0\quad\text{and}\quad B(\widetilde X_{i},\widetilde Y_{j})=\delta_{ij},\qquad i,j\in\{1,\dots,a\}; \end{align*} $$
that is,
 $$ \begin{align*} [\widetilde X_{i},\widetilde X_{j}]=0,\quad [\widetilde Y_{i},\widetilde Y_{j}]=0\quad\text{and}\quad [\widetilde X_{i},\widetilde Y_{j}]=\delta_{ij}T,\qquad i,j\in\{1,\dots,a\}. \end{align*} $$
$$ \begin{align*} [\widetilde X_{i},\widetilde X_{j}]=0,\quad [\widetilde Y_{i},\widetilde Y_{j}]=0\quad\text{and}\quad [\widetilde X_{i},\widetilde Y_{j}]=\delta_{ij}T,\qquad i,j\in\{1,\dots,a\}. \end{align*} $$
If
![]() $b\geq 1$
, fix a basis
$b\geq 1$
, fix a basis
![]() $\widetilde X_{a+1},\dots ,\widetilde X_{a+b}$
of rad
$\widetilde X_{a+1},\dots ,\widetilde X_{a+b}$
of rad
![]() $(V)$
.
$(V)$
.
We can now define
![]() $\mathfrak l^{\prime }:V\to {\mathfrak h}_{1}$
by
$\mathfrak l^{\prime }:V\to {\mathfrak h}_{1}$
by
 $$ \begin{align*} \mathfrak l^{\prime}(\widetilde X_{i})=X_{i}\quad\text{and}\quad \mathfrak l^{\prime}(\widetilde Y_{j})=Y_{j} \end{align*} $$
$$ \begin{align*} \mathfrak l^{\prime}(\widetilde X_{i})=X_{i}\quad\text{and}\quad \mathfrak l^{\prime}(\widetilde Y_{j})=Y_{j} \end{align*} $$
for all integers
![]() $1\leq i\leq a+b$
and
$1\leq i\leq a+b$
and
![]() $1\leq j\leq b$
. Notice that
$1\leq j\leq b$
. Notice that
![]() $\mathfrak l^{\prime }$
is an isometry of V into
$\mathfrak l^{\prime }$
is an isometry of V into
![]() ${\mathfrak h}_{1}$
; that is,
${\mathfrak h}_{1}$
; that is,
By Witt’s theorem (see [Reference Artin10, Theorem 3.9]),
![]() $\mathfrak l^{\prime }$
can be extended to an isometry
$\mathfrak l^{\prime }$
can be extended to an isometry
![]() $\mathfrak l^{\prime \prime }:{\mathfrak h}_{1}\to {\mathfrak h}_{1}$
; that is, a map satisfying
$\mathfrak l^{\prime \prime }:{\mathfrak h}_{1}\to {\mathfrak h}_{1}$
; that is, a map satisfying
![]() $[\mathfrak l^{\prime \prime }(X),\mathfrak l^{\prime \prime }(Y)]=[X,Y]$
for every
$[\mathfrak l^{\prime \prime }(X),\mathfrak l^{\prime \prime }(Y)]=[X,Y]$
for every
![]() $X,Y\in {\mathfrak h}_{1}$
. Finally, we extend
$X,Y\in {\mathfrak h}_{1}$
. Finally, we extend
![]() $\mathfrak l^{\prime \prime }$
to
$\mathfrak l^{\prime \prime }$
to
![]() $\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
by setting
$\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
by setting
![]() $\mathfrak l_{|{\mathfrak h}_{1}}:=\mathfrak l^{\prime \prime }$
and
$\mathfrak l_{|{\mathfrak h}_{1}}:=\mathfrak l^{\prime \prime }$
and
![]() $\mathfrak l(T):=T$
. The map
$\mathfrak l(T):=T$
. The map
![]() $\mathfrak l$
provides the desired Lie algebra isomorphism.
$\mathfrak l$
provides the desired Lie algebra isomorphism.
Remark 3.15. Under the same assumptions of Lemma 3.14, if
![]() $[V,V]=0$
, then the Lie algebra isomorphism
$[V,V]=0$
, then the Lie algebra isomorphism
![]() $\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
provided by Lemma 3.14 can be chosen in such a way that
$\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
provided by Lemma 3.14 can be chosen in such a way that
![]() $\mathfrak l$
is an isometry of
$\mathfrak l$
is an isometry of
![]() ${\mathfrak h}$
when endowed with the scalar product making
${\mathfrak h}$
when endowed with the scalar product making
![]() $X_{1},\dots ,X_{n},Y_{1},\dots ,Y_{n},T$
orthonormal. Observe in particular that here the term isometry has a different meaning than in the proof of Lemma 3.14.
$X_{1},\dots ,X_{n},Y_{1},\dots ,Y_{n},T$
orthonormal. Observe in particular that here the term isometry has a different meaning than in the proof of Lemma 3.14.
Let us prove our statement. As in the proof of Lemma 3.14, fix a basis
![]() $\widetilde X_{1},\dots ,\widetilde X_{b}$
of
$\widetilde X_{1},\dots ,\widetilde X_{b}$
of
![]() $V=\text {rad}(V)$
. Consider the linear isomorphism
$V=\text {rad}(V)$
. Consider the linear isomorphism
![]() $J:{\mathfrak h}_{1}\to {\mathfrak h}_{1}$
defined by
$J:{\mathfrak h}_{1}\to {\mathfrak h}_{1}$
defined by
We observe that
![]() $B(X,Y)=\langle X,JY\rangle $
for
$B(X,Y)=\langle X,JY\rangle $
for
![]() $X,Y\in {\mathfrak h}_{1}$
and that J is an isometry of
$X,Y\in {\mathfrak h}_{1}$
and that J is an isometry of
![]() ${\mathfrak h}_{1}$
. Set
${\mathfrak h}_{1}$
. Set
![]() $\widetilde Y_{i}:=J(\widetilde X_{i})$
and observe that, since
$\widetilde Y_{i}:=J(\widetilde X_{i})$
and observe that, since
![]() $V=\text {rad}(V)\subset (J(V))^{\perp }$
, the elements
$V=\text {rad}(V)\subset (J(V))^{\perp }$
, the elements
![]() $\{\widetilde X_{i},\widetilde Y_{i}:i=1,\dots ,b\}$
form an orthonormal basis of
$\{\widetilde X_{i},\widetilde Y_{i}:i=1,\dots ,b\}$
form an orthonormal basis of
![]() $V\oplus J(V)$
.
$V\oplus J(V)$
.
Consider
![]() $W:=(V\oplus J(V))^{\perp }$
; then
$W:=(V\oplus J(V))^{\perp }$
; then
![]() $W=W^{\prime }\oplus \operatorname *{\mathrm {span}}\{T\}$
where
$W=W^{\prime }\oplus \operatorname *{\mathrm {span}}\{T\}$
where
![]() $W^{\prime }:=(V\oplus J(V))^{\perp }\cap {\mathfrak h}_{1}$
. We claim that
$W^{\prime }:=(V\oplus J(V))^{\perp }\cap {\mathfrak h}_{1}$
. We claim that
![]() $J(W^{\prime })=W^{\prime }$
; by dimensional reasons, it suffices to prove that
$J(W^{\prime })=W^{\prime }$
; by dimensional reasons, it suffices to prove that
![]() $J(W^{\prime })\subset W^{\prime }$
, and this follows because, for every
$J(W^{\prime })\subset W^{\prime }$
, and this follows because, for every
![]() $X\in W^{\prime }$
and
$X\in W^{\prime }$
and
![]() $Y\in V$
, there holds
$Y\in V$
, there holds
 $$ \begin{align*} & \langle JX,Y\rangle = -\langle X,JY\rangle =0\\ & \langle JX,JY\rangle = \langle X,Y\rangle =0. \end{align*} $$
$$ \begin{align*} & \langle JX,Y\rangle = -\langle X,JY\rangle =0\\ & \langle JX,JY\rangle = \langle X,Y\rangle =0. \end{align*} $$
We can now exhibit a Lie algebra isomorphism
![]() $\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
that is also an isometry. First, we define
$\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
that is also an isometry. First, we define
![]() $\mathfrak l (T)=T$
and
$\mathfrak l (T)=T$
and
If
![]() $W^{\prime }=\{0\}$
, the proof is concluded. Otherwise, we fix a unit element
$W^{\prime }=\{0\}$
, the proof is concluded. Otherwise, we fix a unit element
![]() $\widetilde X_{b+1}\in W^{\prime }$
and, defining
$\widetilde X_{b+1}\in W^{\prime }$
and, defining
![]() $\widetilde Y_{b+1}:=J(\widetilde X_{b+1})\in W^{\prime }$
, we set
$\widetilde Y_{b+1}:=J(\widetilde X_{b+1})\in W^{\prime }$
, we set
If
![]() $W^{\prime }=\operatorname *{\mathrm {span}}\{\widetilde X_{b+1},\widetilde Y_{b+1}\}$
, the proof is concluded; otherwise, we fix a unit element
$W^{\prime }=\operatorname *{\mathrm {span}}\{\widetilde X_{b+1},\widetilde Y_{b+1}\}$
, the proof is concluded; otherwise, we fix a unit element
![]() $\widetilde X_{b+2}\in W^{\prime }\cap \operatorname *{\mathrm {span}}\{\widetilde X_{b+1},\widetilde Y_{b+1}\}^{\perp }$
and, defining
$\widetilde X_{b+2}\in W^{\prime }\cap \operatorname *{\mathrm {span}}\{\widetilde X_{b+1},\widetilde Y_{b+1}\}^{\perp }$
and, defining
![]() $\widetilde Y_{b+2}:=J(\widetilde X_{b+2})\in W^{\prime }\cap \operatorname *{\mathrm {span}}\{\widetilde X_{b+1},\widetilde Y_{b+1}\}^{\perp }$
, we set
$\widetilde Y_{b+2}:=J(\widetilde X_{b+2})\in W^{\prime }\cap \operatorname *{\mathrm {span}}\{\widetilde X_{b+1},\widetilde Y_{b+1}\}^{\perp }$
, we set
It is clear that this construction can be iterated and that it eventually stops providing as a final outcome the desired isometric Lie algebra isomorphism
![]() $\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
.
$\mathfrak l:{\mathfrak h}\to {\mathfrak h}$
.
Remark 3.16. Under the same assumptions of Proposition 3.13, if the vertical plane
![]() ${\mathscr P}$
is an abelian subgroup of
${\mathscr P}$
is an abelian subgroup of
![]() ${\mathbb H}^{n}$
(i.e., if
${\mathbb H}^{n}$
(i.e., if
![]() $a=0$
), then the
$a=0$
), then the
![]() ${\mathbb H}$
-linear isomorphism
${\mathbb H}$
-linear isomorphism
![]() ${\mathcal L}$
provided by Proposition 3.13 can be chosen to be an isometry of
${\mathcal L}$
provided by Proposition 3.13 can be chosen to be an isometry of
![]() ${\mathbb H}^{n}$
. This is an easy consequence of Remark 3.15 and the rotational invariance of the distance d.
${\mathbb H}^{n}$
. This is an easy consequence of Remark 3.15 and the rotational invariance of the distance d.
In particular, if
![]() ${\mathbb V}\subset \exp ({\mathfrak h}_{1})$
is a horizontal (and necessarily abelian) subgroup of
${\mathbb V}\subset \exp ({\mathfrak h}_{1})$
is a horizontal (and necessarily abelian) subgroup of
![]() ${\mathbb H}^{n}$
, we can consider the vertical subgroup
${\mathbb H}^{n}$
, we can consider the vertical subgroup
![]() ${\mathscr P}$
generated by
${\mathscr P}$
generated by
![]() ${\mathbb V}$
and
${\mathbb V}$
and
![]() $\exp (\operatorname *{\mathrm {span}}\{T\})$
and deduce that there exists an isometric
$\exp (\operatorname *{\mathrm {span}}\{T\})$
and deduce that there exists an isometric
![]() ${\mathbb H}$
-linear isomorphism
${\mathbb H}$
-linear isomorphism
![]() ${\mathcal L}$
of
${\mathcal L}$
of
![]() ${\mathbb H}^{n}$
such that
${\mathbb H}^{n}$
such that
where
![]() $k:=\dim {\mathbb V}$
.
$k:=\dim {\mathbb V}$
.
3.4 A basis for Rumin’s spaces
In this section we provide a basis for Rumin’s spaces
![]() ${\mathcal J}^{n+1},\dots ,{\mathcal J}^{2n}$
; since later in the article we will denote by k the codimension of the involved objects, we fix k such that
${\mathcal J}^{n+1},\dots ,{\mathcal J}^{2n}$
; since later in the article we will denote by k the codimension of the involved objects, we fix k such that
![]() $1\leq k\leq n$
and study
$1\leq k\leq n$
and study
![]() ${\mathcal J}^{2n+1-k}$
. By Remark 3.3, this space coincides with
${\mathcal J}^{2n+1-k}$
. By Remark 3.3, this space coincides with
![]() $\{\lambda \wedge \theta :\lambda \in \Large \wedge ^{2n-k}{\mathfrak h}_{1},\lambda \wedge d\theta =0\}$
; hence, one is led to the study of the kernel of the Lefschetz operator
$\{\lambda \wedge \theta :\lambda \in \Large \wedge ^{2n-k}{\mathfrak h}_{1},\lambda \wedge d\theta =0\}$
; hence, one is led to the study of the kernel of the Lefschetz operator
![]() $\lambda \mapsto \lambda \wedge d\theta $
.
$\lambda \mapsto \lambda \wedge d\theta $
.
We write
![]() $h:=2n-k$
and, identifying
$h:=2n-k$
and, identifying
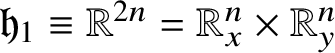 ${\mathfrak h}_{1}\equiv {\mathbb R}^{2n}={\mathbb R}^{n}_{x}\times {\mathbb R}^{n}_{y}$
, we denote by L the operator
${\mathfrak h}_{1}\equiv {\mathbb R}^{2n}={\mathbb R}^{n}_{x}\times {\mathbb R}^{n}_{y}$
, we denote by L the operator
Since
![]() $h\geq n$
, the operator
$h\geq n$
, the operator
![]() $L:\Large \wedge ^{h}{\mathbb R}^{2n}\to \Large \wedge ^{h+2}{\mathbb R}^{2n}$
is surjective ([Reference Bryant, Griffiths and Grossman21, Proposition 1.1]).
$L:\Large \wedge ^{h}{\mathbb R}^{2n}\to \Large \wedge ^{h+2}{\mathbb R}^{2n}$
is surjective ([Reference Bryant, Griffiths and Grossman21, Proposition 1.1]).
We need some preliminary notation. For every
![]() $i\in \{1,\dots ,n\}$
we use the compact notation
$i\in \{1,\dots ,n\}$
we use the compact notation
![]() $dxy_{i}:=dx_{i}\wedge dy_{i}$
, so that
$dxy_{i}:=dx_{i}\wedge dy_{i}$
, so that
![]() $d\theta =-(dxy_{1}+\dots +dxy_{n})$
. Moreover, for every
$d\theta =-(dxy_{1}+\dots +dxy_{n})$
. Moreover, for every
![]() $I\subset \{1,\dots ,n\}$
we denote by
$I\subset \{1,\dots ,n\}$
we denote by
![]() $|I|$
the cardinality of I and, if
$|I|$
the cardinality of I and, if
![]() $I=\{i_{1},i_{2},\dots ,i_{|I|}\}$
with
$I=\{i_{1},i_{2},\dots ,i_{|I|}\}$
with
![]() $i_{1}<\dots <i_{|I|}$
, we define
$i_{1}<\dots <i_{|I|}$
, we define
 $$ \begin{align*} & dx_{I}:=dx_{i_{1}}\wedge dx_{i_{2}}\wedge\dots\wedge dx_{i_{|I|}}\in\Large\wedge^{|I|}{\mathbb R}^{2n}\\ & dy_{I}:=dy_{i_{1}}\wedge dy_{i_{2}}\wedge\dots\wedge dy_{i_{|I|}}\in\Large\wedge^{|I|}{\mathbb R}^{2n}\\ & dxy_{I}:=dxy_{i_{1}}\wedge dxy_{i_{2}}\wedge\dots\wedge dxy_{i_{|I|}}\in\Large\wedge^{2|I|}{\mathbb R}^{2n}. \end{align*} $$
$$ \begin{align*} & dx_{I}:=dx_{i_{1}}\wedge dx_{i_{2}}\wedge\dots\wedge dx_{i_{|I|}}\in\Large\wedge^{|I|}{\mathbb R}^{2n}\\ & dy_{I}:=dy_{i_{1}}\wedge dy_{i_{2}}\wedge\dots\wedge dy_{i_{|I|}}\in\Large\wedge^{|I|}{\mathbb R}^{2n}\\ & dxy_{I}:=dxy_{i_{1}}\wedge dxy_{i_{2}}\wedge\dots\wedge dxy_{i_{|I|}}\in\Large\wedge^{2|I|}{\mathbb R}^{2n}. \end{align*} $$
For
![]() $I=\emptyset $
we agree that
$I=\emptyset $
we agree that
![]() $dx_{\emptyset }=dy_{\emptyset }=dxy_{\emptyset }=1$
. It will also be convenient to set for
$dx_{\emptyset }=dy_{\emptyset }=dxy_{\emptyset }=1$
. It will also be convenient to set for
![]() $i\in \{1,\dots ,2n\}$
$i\in \{1,\dots ,2n\}$
and, accordingly,
whenever
![]() $I=\{i_{1},i_{2},\dots ,i_{|I|}\}$
with
$I=\{i_{1},i_{2},\dots ,i_{|I|}\}$
with
![]() $1\leq i_{1}<\dots <i_{|I|}\leq 2n$
.
$1\leq i_{1}<\dots <i_{|I|}\leq 2n$
.
A basis of
![]() $\Large \wedge ^{h}{\mathbb R}^{2n}$
is given by the family
$\Large \wedge ^{h}{\mathbb R}^{2n}$
is given by the family
![]() $\{dx_{I}\wedge dy_{J}\wedge dxy_{K}\}_{(I,J,K)}$
, where
$\{dx_{I}\wedge dy_{J}\wedge dxy_{K}\}_{(I,J,K)}$
, where
![]() $(I,J,K)$
range among all (ordered) triples of pairwise disjoint subsets
$(I,J,K)$
range among all (ordered) triples of pairwise disjoint subsets
![]() $I,J,K$
of
$I,J,K$
of
![]() $\{1,\dots ,n\}$
such that
$\{1,\dots ,n\}$
such that
![]() $|I|+|J|+2|K|=h$
. In particular, one can write
$|I|+|J|+2|K|=h$
. In particular, one can write
 $$ \begin{align*} \Large\wedge^{h}{\mathbb R}^{2n}=\bigoplus_{(I,J)} dx_{I}\wedge dy_{J}\wedge\Large\wedge^{h, I,J}{\mathbb R}^{2n}, \end{align*} $$
$$ \begin{align*} \Large\wedge^{h}{\mathbb R}^{2n}=\bigoplus_{(I,J)} dx_{I}\wedge dy_{J}\wedge\Large\wedge^{h, I,J}{\mathbb R}^{2n}, \end{align*} $$
where the sum ranges among all ordered pairs
![]() $(I,J)$
of disjoint
$(I,J)$
of disjoint
![]() $I,J\subset \{1,\dots ,n\}$
such that
$I,J\subset \{1,\dots ,n\}$
such that
![]() $0\leq |I|+|J|\leq h$
and
$0\leq |I|+|J|\leq h$
and
![]() $\Large \wedge ^{h, I,J}{\mathbb R}^{2n}$
is defined by
$\Large \wedge ^{h, I,J}{\mathbb R}^{2n}$
is defined by
 $$ \begin{align*} \Large\wedge^{h, I,J}{\mathbb R}^{2n}:=\operatorname*{\mathrm{span}}\{dxy_{K}:K\subset\{1,\dots,n\}\setminus(I\cup J)\text{ and }|I|+|J|+2|K|=h\}. \end{align*} $$
$$ \begin{align*} \Large\wedge^{h, I,J}{\mathbb R}^{2n}:=\operatorname*{\mathrm{span}}\{dxy_{K}:K\subset\{1,\dots,n\}\setminus(I\cup J)\text{ and }|I|+|J|+2|K|=h\}. \end{align*} $$
The parity of
![]() $|I|+|J|$
is necessarily the same of h. Observe also that
$|I|+|J|$
is necessarily the same of h. Observe also that
more precisely, for every
![]() $\alpha \in \Large \wedge ^{h, I,J}{\mathbb R}^{2n}$
one has
$\alpha \in \Large \wedge ^{h, I,J}{\mathbb R}^{2n}$
one has
 $$ \begin{align*} L(dx_{I}\wedge dy_{J}\wedge\alpha)=-dx_{I}\wedge dy_{J}\wedge \alpha\wedge\sum_{i\in\{1,\dots,n\}\setminus( I\cup J)}dx_{i}\wedge dy_{i}. \end{align*} $$
$$ \begin{align*} L(dx_{I}\wedge dy_{J}\wedge\alpha)=-dx_{I}\wedge dy_{J}\wedge \alpha\wedge\sum_{i\in\{1,\dots,n\}\setminus( I\cup J)}dx_{i}\wedge dy_{i}. \end{align*} $$
In particular,
 $$ \begin{align} \ker L=\bigoplus_{(I,J)}dx_{I}\wedge dy_{J}\wedge \ker L_{h,I,J}, \end{align} $$
$$ \begin{align} \ker L=\bigoplus_{(I,J)}dx_{I}\wedge dy_{J}\wedge \ker L_{h,I,J}, \end{align} $$
where
![]() $L_{h,I,J}:\Large \wedge ^{h, I,J}{\mathbb R}^{2n}\to \Large \wedge ^{h+2, I,J}{\mathbb R}^{2n}$
is defined by
$L_{h,I,J}:\Large \wedge ^{h, I,J}{\mathbb R}^{2n}\to \Large \wedge ^{h+2, I,J}{\mathbb R}^{2n}$
is defined by
 $$ \begin{align*} L_{h,I,J}(\alpha):=-\alpha\wedge\sum_{i\in\{1,\dots,n\}\setminus( I\cup J)}dx_{i}\wedge dy_{i}. \end{align*} $$
$$ \begin{align*} L_{h,I,J}(\alpha):=-\alpha\wedge\sum_{i\in\{1,\dots,n\}\setminus( I\cup J)}dx_{i}\wedge dy_{i}. \end{align*} $$
There is a canonical isomorphism
 $\iota :\Large \wedge ^{h,I,J}{\mathbb R}^{2n}\to \Large \wedge _{D}^{2\ell }{\mathbb R}^{2m}$
, where
$\iota :\Large \wedge ^{h,I,J}{\mathbb R}^{2n}\to \Large \wedge _{D}^{2\ell }{\mathbb R}^{2m}$
, where
 $$ \begin{align} \begin{aligned} &\ell:=({h-|I|-|J|})/2,\qquad m:=n-|I|-|J|,\\ &\Large\wedge^{2\ell}_{D}{\mathbb R}^{2m}:=\operatorname*{\mathrm{span}}\{dxy_{K}:K\subset\{1,\dots,m\},|K|=\ell\}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\ell:=({h-|I|-|J|})/2,\qquad m:=n-|I|-|J|,\\ &\Large\wedge^{2\ell}_{D}{\mathbb R}^{2m}:=\operatorname*{\mathrm{span}}\{dxy_{K}:K\subset\{1,\dots,m\},|K|=\ell\}, \end{aligned} \end{align} $$
according to which
![]() $\iota \circ L_{h,I,J}= L\circ \iota $
. The study of
$\iota \circ L_{h,I,J}= L\circ \iota $
. The study of
![]() $\ker L_{h,I,J}$
(which, by (3.13), determines
$\ker L_{h,I,J}$
(which, by (3.13), determines
![]() $\ker L$
) is thus equivalent to the study of the kernel of the restriction
$\ker L$
) is thus equivalent to the study of the kernel of the restriction
 $$ \begin{align*} L_{D}:=L_{{\big|}\large\wedge^{2\ell}_{D}{\mathbb R}^{2m}}. \end{align*} $$
$$ \begin{align*} L_{D}:=L_{{\big|}\large\wedge^{2\ell}_{D}{\mathbb R}^{2m}}. \end{align*} $$
Remark 3.17. The objects introduced so far are well-defined unless
![]() $|I|+|J|=n$
; that is, if
$|I|+|J|=n$
; that is, if
![]() $m=0$
. This can happen only if
$m=0$
. This can happen only if
![]() $h=n$
and gives that also
$h=n$
and gives that also
![]() $\ell =0$
. In this case, we agree that
$\ell =0$
. In this case, we agree that
![]() $\Large \wedge ^{h,I,J}{\mathbb R}^{2n}=\Large \wedge ^{2\ell }{\mathbb R}^{2m}={\mathbb R}$
,
$\Large \wedge ^{h,I,J}{\mathbb R}^{2n}=\Large \wedge ^{2\ell }{\mathbb R}^{2m}={\mathbb R}$
,
![]() $\Large \wedge ^{h+2,I,J}{\mathbb R}^{2n}=\Large \wedge ^{2\ell +2}{\mathbb R}^{2m}=\{0\}$
and
$\Large \wedge ^{h+2,I,J}{\mathbb R}^{2n}=\Large \wedge ^{2\ell +2}{\mathbb R}^{2m}=\{0\}$
and
![]() $L_{D}=0$
. It is immediate to check that, for every such
$L_{D}=0$
. It is immediate to check that, for every such
![]() $I,J$
, one has
$I,J$
, one has
![]() $L(dx_{I}\wedge dy_{J})=0$
.
$L(dx_{I}\wedge dy_{J})=0$
.
Observe that
 $L(\Large \wedge ^{2\ell }_{D}{\mathbb R}^{2m})\subset \Large \wedge ^{2\ell +2}_{D}{\mathbb R}^{2m}$
; hence,
$L(\Large \wedge ^{2\ell }_{D}{\mathbb R}^{2m})\subset \Large \wedge ^{2\ell +2}_{D}{\mathbb R}^{2m}$
; hence,
![]() $L_{D}$
maps
$L_{D}$
maps
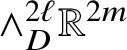 $\Large \wedge ^{2\ell }_{D}{\mathbb R}^{2m}$
on
$\Large \wedge ^{2\ell }_{D}{\mathbb R}^{2m}$
on
 $\Large \wedge ^{2\ell +2}_{D}{\mathbb R}^{2m}$
. It is understood that, when
$\Large \wedge ^{2\ell +2}_{D}{\mathbb R}^{2m}$
. It is understood that, when
![]() $\ell =m$
,
$\ell =m$
,
 $\Large \wedge ^{2\ell +2}_{D}{\mathbb R}^{2m}=\{0\}$
and
$\Large \wedge ^{2\ell +2}_{D}{\mathbb R}^{2m}=\{0\}$
and
![]() $L_{D}=0$
. Notice also that the inequality
$L_{D}=0$
. Notice also that the inequality
![]() $2\ell \geq m$
holds because
$2\ell \geq m$
holds because
![]() $h\geq n$
.
$h\geq n$
.
Lemma 3.18. The operator
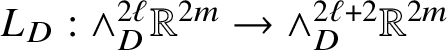 $L_{D}:\Large \wedge ^{2\ell }_{D}{\mathbb R}^{2m}\to \Large \wedge ^{2\ell +2}_{D}{\mathbb R}^{2m}$
is surjective for every integer
$L_{D}:\Large \wedge ^{2\ell }_{D}{\mathbb R}^{2m}\to \Large \wedge ^{2\ell +2}_{D}{\mathbb R}^{2m}$
is surjective for every integer
![]() $\ell $
such that
$\ell $
such that
![]() $m\leq 2\ell \leq 2m$
. In particular,
$m\leq 2\ell \leq 2m$
. In particular,
 $$ \begin{align*} \dim\ker L_{D}=\dim \Large\wedge^{2\ell}_{D}{\mathbb R}^{2m}-\dim\Large\wedge^{2\ell+2}_{D}{\mathbb R}^{2m}=\binom m\ell-\binom m{\ell+1}, \end{align*} $$
$$ \begin{align*} \dim\ker L_{D}=\dim \Large\wedge^{2\ell}_{D}{\mathbb R}^{2m}-\dim\Large\wedge^{2\ell+2}_{D}{\mathbb R}^{2m}=\binom m\ell-\binom m{\ell+1}, \end{align*} $$
where we agree that
 $\binom m{m+1} =0$
.
$\binom m{m+1} =0$
.
Proof. When
![]() $2\ell =2m$
, there is nothing to prove. For the remaining cases, it suffices to prove that, for every
$2\ell =2m$
, there is nothing to prove. For the remaining cases, it suffices to prove that, for every
![]() $i=1,\dots , m$
, the operator
$i=1,\dots , m$
, the operator
 $$ \begin{align*} L_{D}^{i}:=\underbrace{L_{D}\circ\dots\circ L_{D}}_{\textit{i}\text{ times}}:\Large\wedge_{D}^{m-i}{\mathbb R}^{2m}\to\Large\wedge_{D}^{m+i}{\mathbb R}^{2m} \end{align*} $$
$$ \begin{align*} L_{D}^{i}:=\underbrace{L_{D}\circ\dots\circ L_{D}}_{\textit{i}\text{ times}}:\Large\wedge_{D}^{m-i}{\mathbb R}^{2m}\to\Large\wedge_{D}^{m+i}{\mathbb R}^{2m} \end{align*} $$
is bijective. Since
 $\dim \Large \wedge _{D}^{m-i}{\mathbb R}^{2m} = \dim \Large \wedge _{D}^{m+i}{\mathbb R}^{2m}$
, this is an immediate consequence of the bijectivity of
$\dim \Large \wedge _{D}^{m-i}{\mathbb R}^{2m} = \dim \Large \wedge _{D}^{m+i}{\mathbb R}^{2m}$
, this is an immediate consequence of the bijectivity of
![]() $L^{i}:\Large \wedge ^{m-i}{\mathbb R}^{2m}\to \Large \wedge ^{m+i}{\mathbb R}^{2m}$
; see [Reference Bryant, Griffiths and Grossman21, Proposition 1.1].
$L^{i}:\Large \wedge ^{m-i}{\mathbb R}^{2m}\to \Large \wedge ^{m+i}{\mathbb R}^{2m}$
; see [Reference Bryant, Griffiths and Grossman21, Proposition 1.1].
We now provide a basis of
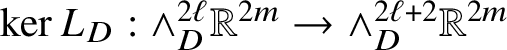 $\ker L_{D}:\Large \wedge _{D}^{2\ell }{\mathbb R}^{2m}\to \Large \wedge _{D}^{2\ell +2}{\mathbb R}^{2m}$
for
$\ker L_{D}:\Large \wedge _{D}^{2\ell }{\mathbb R}^{2m}\to \Large \wedge _{D}^{2\ell +2}{\mathbb R}^{2m}$
for
![]() $m\leq 2\ell \leq 2m$
. Assume that the numbers
$m\leq 2\ell \leq 2m$
. Assume that the numbers
![]() $1,\dots ,m$
have been arranged (each number appearing exactly once) in a tableau
$1,\dots ,m$
have been arranged (each number appearing exactly once) in a tableau
![]() $ R$
with two rows, the first row having
$ R$
with two rows, the first row having
![]() $\ell $
elements
$\ell $
elements
 $R^{1}_{1},\dots ,R^{1}_{\ell }$
and the second having
$R^{1}_{1},\dots ,R^{1}_{\ell }$
and the second having
![]() $m-\ell $
elements
$m-\ell $
elements
 $R^{2}_{1},\dots ,R^{2}_{m-\ell }$
, as follows:
$R^{2}_{1},\dots ,R^{2}_{m-\ell }$
, as follows:

where, clearly, R has to be read as a
![]() $(2\times \ell )$
rectangular matrix when
$(2\times \ell )$
rectangular matrix when
![]() $2\ell =m$
. As is customary, we call Young tableau such a tableau; see [Reference Fulton55]. When
$2\ell =m$
. As is customary, we call Young tableau such a tableau; see [Reference Fulton55]. When
![]() $m=\ell =0$
, we agree that the tableau is empty. When
$m=\ell =0$
, we agree that the tableau is empty. When
![]() $m=\ell \geq 1$
, we agree that R has one row only (the second row is empty).
$m=\ell \geq 1$
, we agree that R has one row only (the second row is empty).
Given such a Young tableau R, consider the covector
 $\alpha _{R}\in \Large \wedge ^{2\ell }_{D}{\mathbb R}^{2m}$
defined by
$\alpha _{R}\in \Large \wedge ^{2\ell }_{D}{\mathbb R}^{2m}$
defined by
 $$ \begin{align} \alpha_{R}:=(dxy_{R^{1}_{1}}- dxy_{R^{2}_{1}})\wedge(dxy_{R^{1}_{2}}- dxy_{R^{2}_{2}})\wedge\dots\wedge(dxy_{R^{1}_{m-\ell}}- dxy_{R^{2}_{m-\ell}})\wedge dxy_{R^{1}_{m-\ell+1}}\wedge\dots\wedge dxy_{R^{1}_{\ell}}. \end{align} $$
$$ \begin{align} \alpha_{R}:=(dxy_{R^{1}_{1}}- dxy_{R^{2}_{1}})\wedge(dxy_{R^{1}_{2}}- dxy_{R^{2}_{2}})\wedge\dots\wedge(dxy_{R^{1}_{m-\ell}}- dxy_{R^{2}_{m-\ell}})\wedge dxy_{R^{1}_{m-\ell+1}}\wedge\dots\wedge dxy_{R^{1}_{\ell}}. \end{align} $$
When
![]() $m=\ell =0$
, we agree that
$m=\ell =0$
, we agree that
![]() $\alpha _{R}:=1$
, while if
$\alpha _{R}:=1$
, while if
![]() $m=\ell \geq 1$
we set
$m=\ell \geq 1$
we set
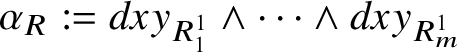 $ \alpha _{R}:=dxy_{R^{1}_{1}}\wedge \dots \wedge dxy_{R^{1}_{m}}$
. Using the equality
$ \alpha _{R}:=dxy_{R^{1}_{1}}\wedge \dots \wedge dxy_{R^{1}_{m}}$
. Using the equality
![]() $(dxy_{i}-dxy_{j})\wedge (dxy_{i}+dxy_{j})=0$
, valid for every
$(dxy_{i}-dxy_{j})\wedge (dxy_{i}+dxy_{j})=0$
, valid for every
![]() $i,j=1,\dots ,m$
, one can easily check that
$i,j=1,\dots ,m$
, one can easily check that
It follows that, for every Young tableau R,
![]() $\alpha _{R}$
belongs to
$\alpha _{R}$
belongs to
![]() $\ker L_{D}$
.
$\ker L_{D}$
.
Consider now the set
![]() $\mathscr R$
of standard Young tableaux; that is, of those Young tableaux R such that the entries in each row and in each column are in increasing order:
$\mathscr R$
of standard Young tableaux; that is, of those Young tableaux R such that the entries in each row and in each column are in increasing order:
 $$ \begin{align*} \begin{array}{ccccccccccccc} R^{1}_{1} & < & R^{1}_{2} & < & \ \cdots\ & < & R^{1}_{m-\ell} & < & R^{1}_{m-\ell+1} & < & \ \cdots\ & < & R^{1}_{\ell}\\ \wedge && \wedge && &&\wedge\\ R^{2}_{1} & < & R^{2}_{2} & < & \ \cdots\ & < & R^{2}_{m-\ell}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccccccccccccc} R^{1}_{1} & < & R^{1}_{2} & < & \ \cdots\ & < & R^{1}_{m-\ell} & < & R^{1}_{m-\ell+1} & < & \ \cdots\ & < & R^{1}_{\ell}\\ \wedge && \wedge && &&\wedge\\ R^{2}_{1} & < & R^{2}_{2} & < & \ \cdots\ & < & R^{2}_{m-\ell}. \end{array} \end{align*} $$
Notice that a standard Young tableau R always satisfies
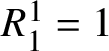 $R^{1}_{1}=1$
. The following lemma shows that the family
$R^{1}_{1}=1$
. The following lemma shows that the family
![]() $\{\alpha _{R}\}_{R\in \mathscr R}\subset \ker L_{D}$
is made by linearly independent covectors.
$\{\alpha _{R}\}_{R\in \mathscr R}\subset \ker L_{D}$
is made by linearly independent covectors.
Lemma 3.19. Let
![]() $m,\ell $
be integers such that
$m,\ell $
be integers such that
![]() $0\leq m\leq 2\ell \leq 2m$
and let
$0\leq m\leq 2\ell \leq 2m$
and let
![]() $\mathscr R$
be the set of standard Young tableaux with two rows of width
$\mathscr R$
be the set of standard Young tableaux with two rows of width
![]() $\ell $
and
$\ell $
and
![]() $m-\ell $
, as in (3.15). Then the elements
$m-\ell $
, as in (3.15). Then the elements
![]() $\{\alpha _{R}\}_{R\in \mathscr R}$
defined in (3.16) are linearly independent.
$\{\alpha _{R}\}_{R\in \mathscr R}$
defined in (3.16) are linearly independent.
Proof. When
![]() $m=0$
also
$m=0$
also
![]() $\ell =0$
and the family
$\ell =0$
and the family
![]() $\{\alpha _{R}\}_{R\in \mathscr R}$
is made by a unique element
$\{\alpha _{R}\}_{R\in \mathscr R}$
is made by a unique element
![]() $\alpha _{R}=1$
; there is nothing to prove. When
$\alpha _{R}=1$
; there is nothing to prove. When
![]() $\ell =m$
, the family
$\ell =m$
, the family
![]() $\mathscr R$
is made by the single standard Young tableau
$\mathscr R$
is made by the single standard Young tableau
 Therefore,
Therefore,
![]() $\{\alpha _{R}\}_{R\in \mathscr R}=\{dxy_{1}\wedge \dots \wedge dxy_{m}\}$
is made by linearly independent vectors, as wished.
$\{\alpha _{R}\}_{R\in \mathscr R}=\{dxy_{1}\wedge \dots \wedge dxy_{m}\}$
is made by linearly independent vectors, as wished.
We therefore assume that
![]() $1\leq m\leq 2\ell \leq 2m-2$
. Let us begin with some preliminary considerations. Given a Young tableau R, we denote by
$1\leq m\leq 2\ell \leq 2m-2$
. Let us begin with some preliminary considerations. Given a Young tableau R, we denote by
![]() $\sigma (R)$
the sum
$\sigma (R)$
the sum
 $R^{1}_{1}+R^{1}_{2}+\dots + R^{1}_{\ell }$
of the elements in the first row of R. Clearly, there exists an integer
$R^{1}_{1}+R^{1}_{2}+\dots + R^{1}_{\ell }$
of the elements in the first row of R. Clearly, there exists an integer
![]() $M=M(m,\ell )$
such that
$M=M(m,\ell )$
such that
moreover, there is a unique
![]() $R_{min}\in \mathscr R$
such that
$R_{min}\in \mathscr R$
such that
![]() $\sigma (R)=1+\dots +\ell $
, namely,
$\sigma (R)=1+\dots +\ell $
, namely,

Let
![]() $\overline R\in \mathscr R$
be fixed and let
$\overline R\in \mathscr R$
be fixed and let
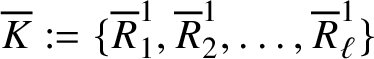 $\overline K:=\{\overline R^{1}_{1},\overline R^{1}_{2},\dots ,\overline R^{1}_{\ell }\}$
be the subset of
$\overline K:=\{\overline R^{1}_{1},\overline R^{1}_{2},\dots ,\overline R^{1}_{\ell }\}$
be the subset of
![]() $\{1,\dots ,m\}$
containing the
$\{1,\dots ,m\}$
containing the
![]() $\ell $
elements in the first row of
$\ell $
elements in the first row of
![]() $\overline R$
. We claim that, if
$\overline R$
. We claim that, if
(in particular, by the pigeonhole principle, each column of R contains exactly one element of
![]() $\overline K$
), then
$\overline K$
), then
Indeed, for every tableau R as in (3.18) there exist a permutation
![]() $\pi $
of
$\pi $
of
![]() $\{1,\dots ,\ell \}$
and a function
$\{1,\dots ,\ell \}$
and a function
![]() $u:\{1,\dots ,\ell \}\to \{1,2\}$
such that
$u:\{1,\dots ,\ell \}\to \{1,2\}$
such that
 $$ \begin{align*} R^{u(j)}_{j}=\overline R^{1}_{\pi(j)}\qquad\text{for all }j=1,\dots,\ell\text{.} \end{align*} $$
$$ \begin{align*} R^{u(j)}_{j}=\overline R^{1}_{\pi(j)}\qquad\text{for all }j=1,\dots,\ell\text{.} \end{align*} $$
Therefore,
 $$ \begin{align} \sigma(R)=\sum_{j=1}^{\ell} R^{1}_{j}\leq \sum_{j=1}^{\ell} R^{u(j)}_{j}=\sum_{j=1}^{\ell}\overline R^{1}_{\pi(j)}=\sigma(\overline R); \end{align} $$
$$ \begin{align} \sigma(R)=\sum_{j=1}^{\ell} R^{1}_{j}\leq \sum_{j=1}^{\ell} R^{u(j)}_{j}=\sum_{j=1}^{\ell}\overline R^{1}_{\pi(j)}=\sigma(\overline R); \end{align} $$
notice that equality holds if and only if
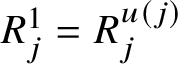 $R^{1}_{j}=R^{u(j)}_{j}$
for every
$R^{1}_{j}=R^{u(j)}_{j}$
for every
![]() $j=1,\dots ,\ell $
; that is, if and only if
$j=1,\dots ,\ell $
; that is, if and only if
 $$ \begin{align*} \{ R^{1}_{1}, R^{1}_{2},\dots, R^{1}_{\ell}\} = \{\overline R^{1}_{1},\overline R^{1}_{2},\dots,\overline R^{1}_{\ell}\}. \end{align*} $$
$$ \begin{align*} \{ R^{1}_{1}, R^{1}_{2},\dots, R^{1}_{\ell}\} = \{\overline R^{1}_{1},\overline R^{1}_{2},\dots,\overline R^{1}_{\ell}\}. \end{align*} $$
Since a standard Young tableau is uniquely determined once one fixes the set of elements of the first row, equality in (3.20) holds if and only if
![]() $R=\overline R$
.
$R=\overline R$
.
We now prove the lemma. Assume that there are real coefficients
![]() $(b_{R})_{R\in \mathscr R}$
, such that
$(b_{R})_{R\in \mathscr R}$
, such that
![]() $\sum _{R\in \mathscr R}b_{R}\alpha _{R}=0$
; we prove that all of the coefficients
$\sum _{R\in \mathscr R}b_{R}\alpha _{R}=0$
; we prove that all of the coefficients
![]() $b_{R}$
are null. We perform this task reasoning by induction on
$b_{R}$
are null. We perform this task reasoning by induction on
![]() $\bar s=1+\dots +\ell ,\dots ,M$
and showing that
$\bar s=1+\dots +\ell ,\dots ,M$
and showing that
Consider first the case
![]() $\bar s=1+\dots +\ell $
; we need to prove that
$\bar s=1+\dots +\ell $
; we need to prove that
![]() $b_{R_{min}}=0$
. For every
$b_{R_{min}}=0$
. For every
![]() $R\in \mathscr R$
let us write
$R\in \mathscr R$
let us write
![]() $\alpha _{R}=\sum _{K} c_{R,K} dxy_{K}$
, where the sum ranges among all
$\alpha _{R}=\sum _{K} c_{R,K} dxy_{K}$
, where the sum ranges among all
![]() $K\subset \{1,\dots ,m\}$
with
$K\subset \{1,\dots ,m\}$
with
![]() $|K|=\ell $
and
$|K|=\ell $
and
![]() $c_{R,K}$
are suitable real numbers. We claim that, defining
$c_{R,K}$
are suitable real numbers. We claim that, defining
![]() $\overline K:=\{1,2,\dots ,\ell \}$
, then
$\overline K:=\{1,2,\dots ,\ell \}$
, then
This would be enough to conclude; indeed, one would have
 $$ \begin{align*} 0= \sum_{R\in\mathscr R}b_{R}\alpha_{R} = \sum_{K} \sum_{R\in\mathscr R}b_{R}c_{R,K} dxy_{K}= b_{R_{min}} dxy_{\overline K} + \sum_{K\neq \overline K} \sum_{R\in\mathscr R}b_{R}c_{R,K} dxy_{K}, \end{align*} $$
$$ \begin{align*} 0= \sum_{R\in\mathscr R}b_{R}\alpha_{R} = \sum_{K} \sum_{R\in\mathscr R}b_{R}c_{R,K} dxy_{K}= b_{R_{min}} dxy_{\overline K} + \sum_{K\neq \overline K} \sum_{R\in\mathscr R}b_{R}c_{R,K} dxy_{K}, \end{align*} $$
which gives
![]() $b_{R_{min}}=0$
, as desired.
$b_{R_{min}}=0$
, as desired.
We prove (3.21): by the very definition (3.16) of
![]() $\alpha _{R}$
, we see that for every K one has
$\alpha _{R}$
, we see that for every K one has
![]() $c_{R,K}=0$
unless each column of R contains (exactly) one element of K (in which case,
$c_{R,K}=0$
unless each column of R contains (exactly) one element of K (in which case,
![]() $c_{R,K}\in \{1,-1\}$
). Using this observation with
$c_{R,K}\in \{1,-1\}$
). Using this observation with
![]() $K=\overline K$
, (3.21) follows because, by the implication (3.18)
$K=\overline K$
, (3.21) follows because, by the implication (3.18)
![]() $\Rightarrow $
(3.19), the only standard Young tableau such that each of its columns contains one element of
$\Rightarrow $
(3.19), the only standard Young tableau such that each of its columns contains one element of
![]() $\overline K$
is
$\overline K$
is
![]() $R_{min}$
itself, because any other standard Young tableau R with such a property would satisfy
$R_{min}$
itself, because any other standard Young tableau R with such a property would satisfy
![]() $\sigma (R)<1+\dots +\ell $
.
$\sigma (R)<1+\dots +\ell $
.
Assume now that
![]() $b_{R}=0$
for every
$b_{R}=0$
for every
![]() $R\in \mathscr R$
such that
$R\in \mathscr R$
such that
![]() $\sigma (R)\leq \overline s-1$
; we prove that
$\sigma (R)\leq \overline s-1$
; we prove that
![]() $b_{R}=0$
for every (fixed)
$b_{R}=0$
for every (fixed)
![]() $\overline R$
such that
$\overline R$
such that
![]() $\sigma (\overline R)=\overline s$
. Let
$\sigma (\overline R)=\overline s$
. Let
 $\overline K:=\{\overline R^{1}_{1},\dots ,\overline R^{1}_{\ell }\}$
be the set formed by the elements in the first row of
$\overline K:=\{\overline R^{1}_{1},\dots ,\overline R^{1}_{\ell }\}$
be the set formed by the elements in the first row of
![]() $\overline R$
; we claim that
$\overline R$
; we claim that
 $$ \begin{align} c_{R,\overline K}=0\qquad\text{for every }R\in\mathscr R\setminus \{\overline R\}\text{ such that }\sigma(R)\geq\overline s. \end{align} $$
$$ \begin{align} c_{R,\overline K}=0\qquad\text{for every }R\in\mathscr R\setminus \{\overline R\}\text{ such that }\sigma(R)\geq\overline s. \end{align} $$
This would be enough to conclude; indeed, one would have
 $$ \begin{align*} 0= \sum_{R\in\mathscr R}b_{R}\alpha_{R}= \sum_{\substack{R\in\mathscr R\\\sigma(R)\geq \overline s}}b_{R}\alpha_{R} = \sum_{K} \sum_{\substack{R\in\mathscr R\\\sigma(R)\geq \overline s}}b_{R}c_{R,K} dxy_{K}= b_{\overline R} dxy_{\overline K} + \sum_{K\neq \overline K} \sum_{\substack{R\in\mathscr R\\\sigma(R)\geq \overline s}}b_{R}c_{R,K} dxy_{K}, \end{align*} $$
$$ \begin{align*} 0= \sum_{R\in\mathscr R}b_{R}\alpha_{R}= \sum_{\substack{R\in\mathscr R\\\sigma(R)\geq \overline s}}b_{R}\alpha_{R} = \sum_{K} \sum_{\substack{R\in\mathscr R\\\sigma(R)\geq \overline s}}b_{R}c_{R,K} dxy_{K}= b_{\overline R} dxy_{\overline K} + \sum_{K\neq \overline K} \sum_{\substack{R\in\mathscr R\\\sigma(R)\geq \overline s}}b_{R}c_{R,K} dxy_{K}, \end{align*} $$
which would give
![]() $b_{\overline R}=0$
, as desired.
$b_{\overline R}=0$
, as desired.
Claim (3.22) can be proved similarly as before: by the definition of
![]() $\alpha _{R}$
, for a standard Young tableau R one has
$\alpha _{R}$
, for a standard Young tableau R one has
![]() $c_{R,\overline K}=0$
unless each column of R contains (exactly) one element of
$c_{R,\overline K}=0$
unless each column of R contains (exactly) one element of
![]() $\overline K$
; in particular, (3.22) follows from the implication (3.18)
$\overline K$
; in particular, (3.22) follows from the implication (3.18)
![]() $\Rightarrow $
(3.19).
$\Rightarrow $
(3.19).
The cardinality of
![]() $\mathscr R$
can be computed using the hook length formula, also known as Frame–Robinson–Thrall formula. We refer to [Reference Fulton55, page 53]: such a formula states that the cardinality of
$\mathscr R$
can be computed using the hook length formula, also known as Frame–Robinson–Thrall formula. We refer to [Reference Fulton55, page 53]: such a formula states that the cardinality of
![]() $\mathscr R$
equals
$\mathscr R$
equals
 $$ \begin{align*} &\frac{m!}{(\ell+1)\ell(\ell-1)\cdots(2\ell-m+2)\;1\cdot\;(2\ell-m)\cdots 2\cdot 1\;\cdot\; (m-\ell)(m-\ell-1)\cdots1}\\ &\quad = \frac{m!}{(\ell+1)!(m-\ell)!}(2\ell-m+1) \ =\ \frac{m!}{(\ell+1)!(m-\ell)!}(\ell+1-(m-\ell))\\ &\quad =\binom m\ell-\binom m{\ell+1} \end{align*} $$
$$ \begin{align*} &\frac{m!}{(\ell+1)\ell(\ell-1)\cdots(2\ell-m+2)\;1\cdot\;(2\ell-m)\cdots 2\cdot 1\;\cdot\; (m-\ell)(m-\ell-1)\cdots1}\\ &\quad = \frac{m!}{(\ell+1)!(m-\ell)!}(2\ell-m+1) \ =\ \frac{m!}{(\ell+1)!(m-\ell)!}(\ell+1-(m-\ell))\\ &\quad =\binom m\ell-\binom m{\ell+1} \end{align*} $$
provided
![]() $\ell <m$
. If
$\ell <m$
. If
![]() $\ell =m$
, then the cardinality of
$\ell =m$
, then the cardinality of
![]() $\mathscr R$
is 1. In both cases, Lemma 3.18 implies that the cardinality of
$\mathscr R$
is 1. In both cases, Lemma 3.18 implies that the cardinality of
![]() $\mathscr R$
is equal to
$\mathscr R$
is equal to
![]() $\dim \ker L_{D}$
. Together with Lemma 3.19, this proves that
$\dim \ker L_{D}$
. Together with Lemma 3.19, this proves that
![]() $\{\alpha _{R}\}_{R\in \mathscr R}$
is a basis of
$\{\alpha _{R}\}_{R\in \mathscr R}$
is a basis of
![]() $\ker L_{D}$
.
$\ker L_{D}$
.
We can summarise the discussion above as follows.
Proposition 3.20. Consider integer numbers
![]() $n,h$
such that
$n,h$
such that
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $n\leq h\leq 2n$
. Then a basis of the kernel of
$n\leq h\leq 2n$
. Then a basis of the kernel of
![]() $L:\Large \wedge ^{h}{\mathbb R}^{2n}\to \Large \wedge ^{h+2}{\mathbb R}^{2n}$
is given by the elements of the form
$L:\Large \wedge ^{h}{\mathbb R}^{2n}\to \Large \wedge ^{h+2}{\mathbb R}^{2n}$
is given by the elements of the form
![]() $dx_{I}\wedge dy_{J}\wedge \alpha _{R}$
where
$dx_{I}\wedge dy_{J}\wedge \alpha _{R}$
where
-
•
 $I,J$
are disjoint subsets of
$I,J$
are disjoint subsets of
 $\{1,\dots ,n\}$
;
$\{1,\dots ,n\}$
; -
•
 $\alpha _{R}$
is defined as in (3.16) and R is a standard Young tableau where the elements of
$\alpha _{R}$
is defined as in (3.16) and R is a standard Young tableau where the elements of
 $\{1,\dots ,n\}\setminus (I\cup J)$
are arranged in two rows, the first one having
$\{1,\dots ,n\}\setminus (I\cup J)$
are arranged in two rows, the first one having
 $(h-|I|-|J|)/2$
elements and the second one having
$(h-|I|-|J|)/2$
elements and the second one having
 $(2n-h-|I|-|J|)/2$
elements.
$(2n-h-|I|-|J|)/2$
elements.
Remark 3.21. It follows from (3.17) that, given
![]() $I,J\subset \{1,\dots ,n\}$
disjoint and a (nonnecessarily standard) Young tableau Q containing the elements of
$I,J\subset \{1,\dots ,n\}$
disjoint and a (nonnecessarily standard) Young tableau Q containing the elements of
![]() $\{1,\dots ,n\}\setminus (I\cup J)$
, the covector
$\{1,\dots ,n\}\setminus (I\cup J)$
, the covector
![]() $dx_{I}\wedge dy_{J}\wedge \alpha _{Q}$
is in the kernel of L. Moreover, by (3.13),
$dx_{I}\wedge dy_{J}\wedge \alpha _{Q}$
is in the kernel of L. Moreover, by (3.13),
![]() $dx_{I}\wedge dy_{J}\wedge \alpha _{Q}$
can be written as a linear combination of covectors of the form
$dx_{I}\wedge dy_{J}\wedge \alpha _{Q}$
can be written as a linear combination of covectors of the form
![]() $dx_{I}\wedge dy_{J}\wedge \alpha _{R}$
where R ranges among all standard Young tableaux with the same shape and containing the same elements as Q.
$dx_{I}\wedge dy_{J}\wedge \alpha _{R}$
where R ranges among all standard Young tableaux with the same shape and containing the same elements as Q.
Proposition 3.20 has the following immediate consequence.
Corollary 3.22. Let
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $1\leq k\leq n$
be integers. Then a basis of
$1\leq k\leq n$
be integers. Then a basis of
![]() ${\mathcal J}^{2n+1-k}$
is given by the elements of the form
${\mathcal J}^{2n+1-k}$
is given by the elements of the form
![]() $dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
where
$dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
where
![]() $I,J,R$
are given by Proposition 3.20 with
$I,J,R$
are given by Proposition 3.20 with
![]() $h:=2n-k$
.
$h:=2n-k$
.
Proof. We observed at the beginning of the section that
 $$ \begin{align*} {\mathcal J}^{2n+1-k}=\{\lambda\wedge\theta:\lambda\in\Large\wedge^{2n-k}{\mathfrak h}_{1}\text{ and }\lambda\wedge d\theta=0\}. \end{align*} $$
$$ \begin{align*} {\mathcal J}^{2n+1-k}=\{\lambda\wedge\theta:\lambda\in\Large\wedge^{2n-k}{\mathfrak h}_{1}\text{ and }\lambda\wedge d\theta=0\}. \end{align*} $$
The statement now easily follows from Proposition 3.20.
Proposition 1.10 is now an easy consequence of Corollary 3.22.
We feel it might be useful to provide some simple examples before continuing our analysis.
Example 3.23. When
![]() $n=2$
, the space
$n=2$
, the space
![]() ${\mathcal J}^{n+1}={\mathcal J}^{3}$
in
${\mathcal J}^{n+1}={\mathcal J}^{3}$
in
![]() ${\mathbb H}^{2}$
is 5-dimensional. The corresponding basis
${\mathbb H}^{2}$
is 5-dimensional. The corresponding basis
![]() $dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
provided by Proposition 1.10 is displayed on the left column of the following table, while on the right column the corresponding triple
$dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
provided by Proposition 1.10 is displayed on the left column of the following table, while on the right column the corresponding triple
![]() $(I,J,R)$
appears:
$(I,J,R)$
appears:

where
![]() $\emptyset $
denotes either the empty set or the empty tableau. See also [Reference Baldi and Franchi12, Example 3.12].
$\emptyset $
denotes either the empty set or the empty tableau. See also [Reference Baldi and Franchi12, Example 3.12].
Example 3.24. When
![]() $n=3$
, the space
$n=3$
, the space
![]() ${\mathcal J}^{5}$
in
${\mathcal J}^{5}$
in
![]() ${\mathbb H}^{3}$
is 14-dimensional; let us write the basis provided by Proposition 1.10. Observe that here
${\mathbb H}^{3}$
is 14-dimensional; let us write the basis provided by Proposition 1.10. Observe that here
![]() $n=3$
,
$n=3$
,
![]() $k=2$
and
$k=2$
and
![]() $h=4$
. We first determine the triples
$h=4$
. We first determine the triples
![]() $(I,J,R)$
: since
$(I,J,R)$
: since
![]() $|I|+|J|$
is not greater than
$|I|+|J|$
is not greater than
![]() $ k=2$
and has the same parity as
$ k=2$
and has the same parity as
![]() $h=4$
, either
$h=4$
, either
![]() $|I|+|J|=0$
or
$|I|+|J|=0$
or
![]() $|I|+|J|=2$
.
$|I|+|J|=2$
.
If
![]() $|I|+|J|=0$
, then
$|I|+|J|=0$
, then
![]() $m=3$
,
$m=3$
,
![]() $\ell =2$
and all of the indices 1, 2, 3 appear in the tableau R, whose rows have lengths
$\ell =2$
and all of the indices 1, 2, 3 appear in the tableau R, whose rows have lengths
![]() $2$
and
$2$
and
![]() $1$
, respectively. It is immediate to check that R can be only one of the following two tableaux:
$1$
, respectively. It is immediate to check that R can be only one of the following two tableaux:

which, respectively, provide the elements
of
![]() ${\mathcal J}^{5}$
. If
${\mathcal J}^{5}$
. If
![]() $|I|+|J|=2$
, then
$|I|+|J|=2$
, then
![]() $I\cup J=\{a,b\}$
for some
$I\cup J=\{a,b\}$
for some
![]() $a,b\in \{1,2,3\}$
and the tableau R contains the unique remaining index
$a,b\in \{1,2,3\}$
and the tableau R contains the unique remaining index
![]() $c\in \{1,2,3\}\setminus \{a,b\}$
; in particular, the second row of R is empty (in fact, here
$c\in \{1,2,3\}\setminus \{a,b\}$
; in particular, the second row of R is empty (in fact, here
![]() $\ell =m=1$
) and
$\ell =m=1$
) and

. This produces the following elements of
![]() ${\mathcal J}^{5}$
:
${\mathcal J}^{5}$
:
 $$ \begin{align} & dx_{a}\wedge dx_{b}\wedge dx_{c}\wedge dy_{c}\wedge\theta\qquad\text{provided }a<b\nonumber\\ & dx_{a}\wedge dy_{b}\wedge dx_{c}\wedge dy_{c}\wedge\theta\\ & dy_{a}\wedge dy_{b}\wedge dx_{c}\wedge dy_{c}\wedge\theta\qquad\text{provided }a<b\nonumber \end{align} $$
$$ \begin{align} & dx_{a}\wedge dx_{b}\wedge dx_{c}\wedge dy_{c}\wedge\theta\qquad\text{provided }a<b\nonumber\\ & dx_{a}\wedge dy_{b}\wedge dx_{c}\wedge dy_{c}\wedge\theta\\ & dy_{a}\wedge dy_{b}\wedge dx_{c}\wedge dy_{c}\wedge\theta\qquad\text{provided }a<b\nonumber \end{align} $$
and, as
![]() $a,b,c$
vary in
$a,b,c$
vary in
![]() $\{1,2,3\}$
, each of the covectors in (3.24) provides, respectively, three, six and three elements of
$\{1,2,3\}$
, each of the covectors in (3.24) provides, respectively, three, six and three elements of
![]() ${\mathcal J}^{5}$
. All in all, a basis of
${\mathcal J}^{5}$
. All in all, a basis of
![]() ${\mathcal J}^{5}$
is provided by the 2+12 elements displayed in (3.23) and (3.24).
${\mathcal J}^{5}$
is provided by the 2+12 elements displayed in (3.23) and (3.24).
Remark 3.25. The difference between the lengths of the first and second rows of every standard Young tableau R appearing in Proposition 1.10 (respectively, in Proposition 3.20) is determined by k (respectively by h) and it is equal to
![]() $n-k$
(respectively to
$n-k$
(respectively to
![]() $h-n$
). In particular, the standard Young tableaux R appearing in Proposition 1.10 (respectively in Proposition 3.20) are rectangular (the two rows have the same length) if and only if
$h-n$
). In particular, the standard Young tableaux R appearing in Proposition 1.10 (respectively in Proposition 3.20) are rectangular (the two rows have the same length) if and only if
![]() $k=n$
(respectively if
$k=n$
(respectively if
![]() $h=n$
).
$h=n$
).
Remark 3.26. It follows from Remark 3.21 that, given
![]() $I,J\subset \{1,\dots ,n\}$
disjoint and a (nonnecessarily standard) Young tableau Q containing the elements of
$I,J\subset \{1,\dots ,n\}$
disjoint and a (nonnecessarily standard) Young tableau Q containing the elements of
![]() $\{1,\dots ,n\}\setminus (I\cup J)$
, the covector
$\{1,\dots ,n\}\setminus (I\cup J)$
, the covector
![]() $dx_{I}\wedge dy_{J}\wedge \alpha _{Q}\wedge \theta $
belongs to
$dx_{I}\wedge dy_{J}\wedge \alpha _{Q}\wedge \theta $
belongs to
![]() ${\mathcal J}^{|I|+|J|+2\ell +1}$
, where
${\mathcal J}^{|I|+|J|+2\ell +1}$
, where
![]() $\ell $
denotes the length of the first row of Q, and it can be written as a linear combination of the elements
$\ell $
denotes the length of the first row of Q, and it can be written as a linear combination of the elements
![]() $dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \in {\mathcal J}^{|I|+|J|+2\ell +1}$
where R ranges among the standard Young tableaux with the same shape and containing the same elements as Q.
$dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \in {\mathcal J}^{|I|+|J|+2\ell +1}$
where R ranges among the standard Young tableaux with the same shape and containing the same elements as Q.
Remark 3.27. It is a good point to state, for future reference, the following property of the basis provided by Proposition 1.10.
Let
![]() $a,b$
be fixed nonnegative integers such that
$a,b$
be fixed nonnegative integers such that
![]() $a+b\leq n$
and
$a+b\leq n$
and
![]() $n\leq 2a+b\leq 2n$
. Let
$n\leq 2a+b\leq 2n$
. Let
![]() $(I,J,R)$
range among the triples such that
$(I,J,R)$
range among the triples such that
![]() $\{dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \}_{(I,J,R)}$
is the basis of
$\{dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \}_{(I,J,R)}$
is the basis of
![]() ${\mathcal J}^{2a+b+1}$
provided by Proposition 1.10; that is,
${\mathcal J}^{2a+b+1}$
provided by Proposition 1.10; that is,
-
•
 $I,J$
are disjoint subsets of
$I,J$
are disjoint subsets of
 $\{1,\dots ,n\}$
such that
$\{1,\dots ,n\}$
such that
 $|I|+|J|\leq 2n-2a-b$
;
$|I|+|J|\leq 2n-2a-b$
; -
• R is a standard Young tableau where the elements of
 $\{1,\dots ,n\}\setminus (I\cup J)$
are arranged in two rows, the first one having
$\{1,\dots ,n\}\setminus (I\cup J)$
are arranged in two rows, the first one having
 $(2a+b-|I|-|J|)/2$
elements and the second one having
$(2a+b-|I|-|J|)/2$
elements and the second one having
 $(2n-2a-b-|I|-|J|)/2$
elements.
$(2n-2a-b-|I|-|J|)/2$
elements.
Then either

or
where, in (3.25)
-
•
 $I=\emptyset $
if
$I=\emptyset $
if
 $b=0$
,
$b=0$
, -
• R is the empty tableau if
 $a=0$
,
$a=0$
, -
• R has to be interpreted as a rectangular
 $2\times a$
matrix if
$2\times a$
matrix if
 $n=2a+b$
and
$n=2a+b$
and
 $a\geq 1$
.
$a\geq 1$
.
Let us prove what is claimed. If either
![]() $ I\neq \{a+1,\dots ,a+b\}$
or
$ I\neq \{a+1,\dots ,a+b\}$
or
![]() $ J\neq \emptyset $
, then (3.26) holds. If instead
$ J\neq \emptyset $
, then (3.26) holds. If instead
![]() $I=\{a+1,\dots ,a+b\}$
and
$I=\{a+1,\dots ,a+b\}$
and
![]() $J=\emptyset $
, then the shape of R (i.e., the lengths of its rows) is necessarily the same as the tableau displayed in (3.25) and R contains precisely the elements
$J=\emptyset $
, then the shape of R (i.e., the lengths of its rows) is necessarily the same as the tableau displayed in (3.25) and R contains precisely the elements
![]() $\{1,\dots ,a,a+b+1,\dots ,n\}$
. We have
$\{1,\dots ,a,a+b+1,\dots ,n\}$
. We have
 $$ \begin{align} \begin{aligned} &\langle X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\wedge T\mid dx_{I}\wedge dy_{J}\wedge \alpha_{R}\wedge\theta\rangle\\ &\quad =\pm\langle X_{1}\wedge\dots\wedge X_{a}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \alpha_{R}\rangle, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\langle X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\wedge T\mid dx_{I}\wedge dy_{J}\wedge \alpha_{R}\wedge\theta\rangle\\ &\quad =\pm\langle X_{1}\wedge\dots\wedge X_{a}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \alpha_{R}\rangle, \end{aligned} \end{align} $$
where the sign is determined by a and b. By its definition (3.16),
![]() $\alpha _{R}$
can be written as a sum
$\alpha _{R}$
can be written as a sum
![]() $\sum _{S} \sigma (S) dxy_{S}$
, where
$\sum _{S} \sigma (S) dxy_{S}$
, where
![]() $\sigma (S)\in \{1,-1\}$
is a proper sign and the sum ranges among all subsets
$\sigma (S)\in \{1,-1\}$
is a proper sign and the sum ranges among all subsets
![]() $S\subset \{1,\dots ,a,a+b+1,\dots ,n\}$
(i.e., S is a subset of the set of the entries of R) of cardinality a that contain exactly one element from each column of R. It is clear that
$S\subset \{1,\dots ,a,a+b+1,\dots ,n\}$
(i.e., S is a subset of the set of the entries of R) of cardinality a that contain exactly one element from each column of R. It is clear that
If R is such that at least one of its columns contains no elements of
![]() $\{1,\dots ,a\}$
, then none of the S’s appearing in the sum
$\{1,\dots ,a\}$
, then none of the S’s appearing in the sum
![]() $\alpha _{R}=\sum _{S} \sigma (S) dxy_{S}$
is
$\alpha _{R}=\sum _{S} \sigma (S) dxy_{S}$
is
![]() $\{1,\dots ,a\}$
, and by (3.27)
$\{1,\dots ,a\}$
, and by (3.27)
If all of the a columns of R contain at least one element of
![]() $\{1,\dots ,a\}$
, then each of these columns contains exactly one such element. Since R is a standard Young tableau, the sum of the elements of the first row of R is at most
$\{1,\dots ,a\}$
, then each of these columns contains exactly one such element. Since R is a standard Young tableau, the sum of the elements of the first row of R is at most
![]() $1+\dots +a$
, but this sum is clearly also at least
$1+\dots +a$
, but this sum is clearly also at least
![]() $1+\dots +a$
. It follows that the first line of R is made by the elements
$1+\dots +a$
. It follows that the first line of R is made by the elements
![]() $1,\dots ,a$
(in increasing order) and that the remaining elements
$1,\dots ,a$
(in increasing order) and that the remaining elements
![]() $a+b+1,\dots ,n$
(not belonging to I, J or the first line of R) have to be placed, in increasing order, in the second line of R. This proves that R must be the one in (3.25) and concludes the proof.
$a+b+1,\dots ,n$
(not belonging to I, J or the first line of R) have to be placed, in increasing order, in the second line of R. This proves that R must be the one in (3.25) and concludes the proof.
3.5 Heisenberg currents
For every
![]() $k=0,\dots ,2n+1$
, we introduce the spaces
$k=0,\dots ,2n+1$
, we introduce the spaces
 ${\mathcal D}_{\mathbb H}^{k}\subset \Omega _{\mathbb H}^{k}$
of compactly supported smooth Heisenberg k-forms; that is,
${\mathcal D}_{\mathbb H}^{k}\subset \Omega _{\mathbb H}^{k}$
of compactly supported smooth Heisenberg k-forms; that is,
 $$ \begin{align*}
& {\mathcal D}_{\mathbb H}^{k}:= C_{c}^{\infty}\big({\mathbb H}^{n},\tfrac{\large\wedge^{k}{\mathfrak h}}{\mathcal I^{k}}\big)
&&\text{if }0\leq k\leq n\\
& {\mathcal D}_{\mathbb H}^{k}:= C_{c}^{\infty}({\mathbb H}^{n},{\mathcal J}^{k})
&&\text{if }n+1\leq k\leq 2n+1, \end{align*} $$
$$ \begin{align*}
& {\mathcal D}_{\mathbb H}^{k}:= C_{c}^{\infty}\big({\mathbb H}^{n},\tfrac{\large\wedge^{k}{\mathfrak h}}{\mathcal I^{k}}\big)
&&\text{if }0\leq k\leq n\\
& {\mathcal D}_{\mathbb H}^{k}:= C_{c}^{\infty}({\mathbb H}^{n},{\mathcal J}^{k})
&&\text{if }n+1\leq k\leq 2n+1, \end{align*} $$
and we observe that
![]() $d_{C}$
maps
$d_{C}$
maps
 ${\mathcal D}_{\mathbb H}^{k}$
to
${\mathcal D}_{\mathbb H}^{k}$
to
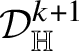 ${\mathcal D}_{\mathbb H}^{k+1}$
. We endow the space
${\mathcal D}_{\mathbb H}^{k+1}$
. We endow the space
 ${\mathcal D}_{\mathbb H}^{k}$
with the natural topology induced by the topology of the space
${\mathcal D}_{\mathbb H}^{k}$
with the natural topology induced by the topology of the space
![]() ${\mathcal D}^{k}$
of compactly supported k-forms on
${\mathcal D}^{k}$
of compactly supported k-forms on
![]() ${\mathbb H}^{n}$
.
${\mathbb H}^{n}$
.
Definition 3.28. Given
![]() $k\in \{0,\dots ,2n+1\}$
, we denote by
$k\in \{0,\dots ,2n+1\}$
, we denote by
![]() ${\mathcal D}_{{\mathbb H},k}$
the space of continuous linear functionals on
${\mathcal D}_{{\mathbb H},k}$
the space of continuous linear functionals on
 ${\mathcal D}_{\mathbb H}^{k}$
. An element of
${\mathcal D}_{\mathbb H}^{k}$
. An element of
![]() ${\mathcal D}_{{\mathbb H},k}$
is called Heisenberg k-dimensional current or, for shortness, Heisenberg k-current.
${\mathcal D}_{{\mathbb H},k}$
is called Heisenberg k-dimensional current or, for shortness, Heisenberg k-current.
For every
![]() $k\in \{1,\dots ,2n+1\}$
and every Heisenberg k-current
$k\in \{1,\dots ,2n+1\}$
and every Heisenberg k-current
![]() ${\mathsf T}\in {\mathcal D}_{{\mathbb H},k}$
, we denote by
${\mathsf T}\in {\mathcal D}_{{\mathbb H},k}$
, we denote by
![]() $\partial {\mathsf T}$
the Heisenberg
$\partial {\mathsf T}$
the Heisenberg
![]() $(k-1)$
-current defined, for every
$(k-1)$
-current defined, for every
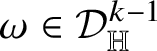 $\omega \in {\mathcal D}_{\mathbb H}^{k-1}$
, by
$\omega \in {\mathcal D}_{\mathbb H}^{k-1}$
, by
![]() $\partial {\mathsf T}(\omega ):={\mathsf T}(d_{C}\omega )$
(recall Remark 3.7). Namely,
$\partial {\mathsf T}(\omega ):={\mathsf T}(d_{C}\omega )$
(recall Remark 3.7). Namely,
 $$ \begin{align*} \begin{array}{ll} \partial{\mathsf T}(\omega):={\mathsf T}(d\omega)\quad& \text{if }k\neq n+1\\ \partial{\mathsf T}(\omega):={\mathsf T}(D\omega)&\text{if }k= n+1. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \partial{\mathsf T}(\omega):={\mathsf T}(d\omega)\quad& \text{if }k\neq n+1\\ \partial{\mathsf T}(\omega):={\mathsf T}(D\omega)&\text{if }k= n+1. \end{array} \end{align*} $$
It is not our aim to introduce here the mass of a current (see [Reference Franchi, Serapioni and Serra Cassano51, Definition 5.12] and [Reference Canarecci22, Definitions 2.5 and 2.6]), which would require introducing a notion of comass ([Reference Federer42, 4.1.7]) on Rumin’s spaces of covectors. For our purposes, it will be enough to introduce the notion of current with finite mass (see Definition 3.29), and to this end any choice of (co)mass on covectors is equivalent. We denote by
![]() $|\cdot |$
the standard norm on
$|\cdot |$
the standard norm on
![]() $\Large \wedge ^{*}{\mathfrak h}$
(in particular,
$\Large \wedge ^{*}{\mathfrak h}$
(in particular,
![]() $|\cdot |$
is defined on
$|\cdot |$
is defined on
![]() ${\mathcal J}^{k}$
for
${\mathcal J}^{k}$
for
![]() $k\geq n+1$
) and we agree that, for every
$k\geq n+1$
) and we agree that, for every
![]() $1\leq k\leq n$
and
$1\leq k\leq n$
and
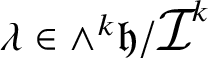 $\lambda \in \Large \wedge ^{k}{\mathfrak h}/\mathcal I^{k}$
,
$\lambda \in \Large \wedge ^{k}{\mathfrak h}/\mathcal I^{k}$
,
 $$ \begin{align} |\lambda|:=\min\left\{|\nu|:\nu\in\Large\wedge^{k}{\mathfrak h}_{1},\ [\nu]=\lambda\right\} \end{align} $$
$$ \begin{align} |\lambda|:=\min\left\{|\nu|:\nu\in\Large\wedge^{k}{\mathfrak h}_{1},\ [\nu]=\lambda\right\} \end{align} $$
where
![]() $[\nu ]$
is the equivalence class of
$[\nu ]$
is the equivalence class of
![]() $\nu $
in the quotient
$\nu $
in the quotient
![]() ${\Large \wedge ^{k}{\mathfrak h}_{1}}/{\{\mu \wedge d\theta :\mu \in \Large \wedge ^{k-2}{\mathfrak h}_{1}\}}$
(recall (3.7)). The quantity
${\Large \wedge ^{k}{\mathfrak h}_{1}}/{\{\mu \wedge d\theta :\mu \in \Large \wedge ^{k-2}{\mathfrak h}_{1}\}}$
(recall (3.7)). The quantity
![]() $|\cdot |$
is a norm on
$|\cdot |$
is a norm on
![]() ${\Large \wedge ^{k}}{\mathfrak h}/{\mathcal I^{k}}$
.
${\Large \wedge ^{k}}{\mathfrak h}/{\mathcal I^{k}}$
.
Definition 3.29. Let
![]() $k\in \{1,\dots ,2n\}$
be fixed. We say that a current
$k\in \{1,\dots ,2n\}$
be fixed. We say that a current
![]() ${\mathsf T}\in {\mathcal D}_{{\mathbb H},k}$
has finite mass if there exists
${\mathsf T}\in {\mathcal D}_{{\mathbb H},k}$
has finite mass if there exists
![]() $M_{{\mathsf T}}\in {\mathbb R}$
such that
$M_{{\mathsf T}}\in {\mathbb R}$
such that
 $$ \begin{align*} |{\mathsf T}(\omega)|\leq M_{\mathsf T} \sup_{p\in{\mathbb H}^{n}}|\omega(p)|\qquad\text{for every }\omega\in{{\mathcal D}}_{\mathbb H}^{k}. \end{align*} $$
$$ \begin{align*} |{\mathsf T}(\omega)|\leq M_{\mathsf T} \sup_{p\in{\mathbb H}^{n}}|\omega(p)|\qquad\text{for every }\omega\in{{\mathcal D}}_{\mathbb H}^{k}. \end{align*} $$
The current
![]() ${\mathsf T}$
has locally finite mass if, for each compact set
${\mathsf T}$
has locally finite mass if, for each compact set
![]() $K\subset {\mathbb H}^{n}$
, there exists
$K\subset {\mathbb H}^{n}$
, there exists
![]() $M_{{\mathsf T},K}\in {\mathbb R}$
such that
$M_{{\mathsf T},K}\in {\mathbb R}$
such that
 $$ \begin{align*} |{\mathsf T}(\omega)|\leq M_{{\mathsf T},K} \sup_{p\in{\mathbb H}^{n}}|\omega(p)|\qquad\text{for every }\omega\in{\mathcal D}_{\mathbb H}^{k}\text{ with support in }K. \end{align*} $$
$$ \begin{align*} |{\mathsf T}(\omega)|\leq M_{{\mathsf T},K} \sup_{p\in{\mathbb H}^{n}}|\omega(p)|\qquad\text{for every }\omega\in{\mathcal D}_{\mathbb H}^{k}\text{ with support in }K. \end{align*} $$
Finally,
![]() ${\mathsf T}$
is normal (respectively, locally normal) if both
${\mathsf T}$
is normal (respectively, locally normal) if both
![]() ${\mathsf T}$
and
${\mathsf T}$
and
![]() $\partial {\mathsf T}$
have finite mass (respectively locally finite mass).
$\partial {\mathsf T}$
have finite mass (respectively locally finite mass).
Remark 3.30. The reader familiar with the theory of distributions will realise that a Heisenberg k-current has locally finite mass if and only if it has order 0 in the sense of distributions; equivalently, if it is a measure taking values in a proper space of k-vectors. More precisely, if
![]() ${\mathsf T}$
is a k-current with locally finite mass, then there exist a locally finite (nonnegative) measure
${\mathsf T}$
is a k-current with locally finite mass, then there exist a locally finite (nonnegative) measure
![]() $\mu $
and a
$\mu $
and a
![]() $\mu $
-measurable function
$\mu $
-measurable function
![]() $\tau $
, taking values in
$\tau $
, taking values in
![]() ${\mathcal J}_{k}$
(if
${\mathcal J}_{k}$
(if
![]() $k\geq n+1$
; recall Remark 3.4) or in the dual space
$k\geq n+1$
; recall Remark 3.4) or in the dual space
![]() $({\Large \wedge ^{k}{\mathfrak h}}/{\mathcal I^{k}})^{*}$
(if
$({\Large \wedge ^{k}{\mathfrak h}}/{\mathcal I^{k}})^{*}$
(if
![]() $k\leq n$
), such that
$k\leq n$
), such that
![]() ${\mathsf T}=\tau \mu $
; that is,
${\mathsf T}=\tau \mu $
; that is,
 $$ \begin{align*} {\mathsf T}(\omega)=\int\langle\tau\mid \omega\rangle\,d\mu\qquad\text{for every }\omega\in{\mathcal D}_{\mathbb H}^{k}. \end{align*} $$
$$ \begin{align*} {\mathsf T}(\omega)=\int\langle\tau\mid \omega\rangle\,d\mu\qquad\text{for every }\omega\in{\mathcal D}_{\mathbb H}^{k}. \end{align*} $$
As done in the Introduction, one can also assume that
![]() $|\tau |=1 \ \mu $
-a.e. In this case, we denote
$|\tau |=1 \ \mu $
-a.e. In this case, we denote
![]() $\tau $
and
$\tau $
and
![]() $\mu $
by, respectively,
$\mu $
by, respectively,
![]() $\!\vec {\,{\mathsf T}}$
and
$\!\vec {\,{\mathsf T}}$
and
![]() $\|{\mathsf T}\|$
and write
$\|{\mathsf T}\|$
and write
![]() ${\mathsf T}=\!\vec {\,{\mathsf T}} \|{\mathsf T}\|$
.
${\mathsf T}=\!\vec {\,{\mathsf T}} \|{\mathsf T}\|$
.
As in Subsection 3.4, for the rest of the present section we denote by k the codimension, rather than the dimension, of a current or submanifold. We focus on the low-codimensional case and we fix
![]() $k\in \{1,\dots ,n\}$
.
$k\in \{1,\dots ,n\}$
.
Recall that every
![]() $C^{1}$
-regular oriented submanifold
$C^{1}$
-regular oriented submanifold
![]() $S\subset {\mathbb H}^{n}$
of codimension k naturally induces a
$S\subset {\mathbb H}^{n}$
of codimension k naturally induces a
![]() $(2n+1-k)$
-dimensional classical current
$(2n+1-k)$
-dimensional classical current
defined, for every smooth and compactly supported
![]() $(2n+1-k)$
-form
$(2n+1-k)$
-form
![]() $\omega $
in
$\omega $
in
![]() ${\mathbb H}^{n}$
, by
${\mathbb H}^{n}$
, by

where
![]() $t_{S}$
is a unit
$t_{S}$
is a unit
![]() $(2n+1-k)$
-vector tangent to S and with positive orientation and
$(2n+1-k)$
-vector tangent to S and with positive orientation and
![]() $d\text {vol}_{S}$
is the surface measure on S induced by the left-invariant Riemannian metric on
$d\text {vol}_{S}$
is the surface measure on S induced by the left-invariant Riemannian metric on
![]() ${\mathbb H}^{n}$
making
${\mathbb H}^{n}$
making
![]() $X_{1},\dots ,Y_{n},T$
orthonormal.
$X_{1},\dots ,Y_{n},T$
orthonormal.
Using the notation in Remark 3.1, for every
![]() $p\in S$
we can write
$p\in S$
we can write
for a unique
![]() $\eta _{S}(p)\in \Large \wedge _{2n-k}{\mathfrak h}_{1}$
. Notice that
$\eta _{S}(p)\in \Large \wedge _{2n-k}{\mathfrak h}_{1}$
. Notice that
![]() $\eta _{S}(p)= 0$
if and only if p is a characteristic point of S; that is,
$\eta _{S}(p)= 0$
if and only if p is a characteristic point of S; that is,
![]() $T_{p}S\subset {\mathfrak h}_{1}$
.
$T_{p}S\subset {\mathfrak h}_{1}$
.
Assume now that
![]() $p\in S$
is not a characteristic point; then, the intersection
$p\in S$
is not a characteristic point; then, the intersection
![]() $T_{p}S\cap {\mathfrak h}_{1}$
is a
$T_{p}S\cap {\mathfrak h}_{1}$
is a
![]() $(2n-k)$
-dimensional plane and it is immediate to check that
$(2n-k)$
-dimensional plane and it is immediate to check that
![]() $T_{p}S\cap {\mathfrak h}_{1}=\operatorname *{\mathrm {span}}\eta _{S}(p)$
. Therefore, the unit vector
$T_{p}S\cap {\mathfrak h}_{1}=\operatorname *{\mathrm {span}}\eta _{S}(p)$
. Therefore, the unit vector
 $$ \begin{align} \tau^{\mathbb H}_{S}(p):=\frac{\eta_{S}(p)}{|\eta_{S}(p)|} \end{align} $$
$$ \begin{align} \tau^{\mathbb H}_{S}(p):=\frac{\eta_{S}(p)}{|\eta_{S}(p)|} \end{align} $$
is canonically associated with the linear subspace
![]() $T_{p}S\cap {\mathfrak h}_{1}$
. We denote by
$T_{p}S\cap {\mathfrak h}_{1}$
. We denote by
 $t^{\mathbb H}_{S}:=\tau ^{\mathbb H}_{S}\wedge T$
the (horizontal) tangent vector to S. Geometrically,
$t^{\mathbb H}_{S}:=\tau ^{\mathbb H}_{S}\wedge T$
the (horizontal) tangent vector to S. Geometrically,
![]() $t^{\mathbb H}_{S}$
characterises the blow-up limit of S at p; in fact,
$t^{\mathbb H}_{S}$
characterises the blow-up limit of S at p; in fact,
 $$ \begin{align*} \lim_{r\to +\infty} \delta_{r} (p^{-1}S) = \exp(\operatorname*{\mathrm{span}} t^{\mathbb H}_{S}(p)), \end{align*} $$
$$ \begin{align*} \lim_{r\to +\infty} \delta_{r} (p^{-1}S) = \exp(\operatorname*{\mathrm{span}} t^{\mathbb H}_{S}(p)), \end{align*} $$
where the limit is taken with respect to local Hausdorff convergence of sets. See, for example, [Reference Magnani68].
With this notation, we define the Heisenberg current
by

The definition is well-posed because the Hausdorff measure
![]() ${\mathscr S}^{Q-k}$
is locally finite on S (see, e.g., [Reference Magnani68]) and the set of characteristic points of S, where in principle
${\mathscr S}^{Q-k}$
is locally finite on S (see, e.g., [Reference Magnani68]) and the set of characteristic points of S, where in principle
![]() $t^{\mathbb H}_{S}$
is not defined, is
$t^{\mathbb H}_{S}$
is not defined, is
![]() ${\mathscr S}^{Q-k}$
-negligible ([Reference Balogh15, 69]).
${\mathscr S}^{Q-k}$
-negligible ([Reference Balogh15, 69]).
The next result, though very simple, has to our knowledge never been noticed in the literature. Lemma 3.31 and the subsequent Corollary 3.34 prove Proposition 1.9, which will play a crucial role in the sequel.
Lemma 3.31. Let
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $k\in \{1,\dots ,n\}$
be fixed. Then there exists
$k\in \{1,\dots ,n\}$
be fixed. Then there exists
![]() $C_{n,k}>0$
such that, for every oriented and
$C_{n,k}>0$
such that, for every oriented and
![]() $C^{1}$
-smooth submanifold S of
$C^{1}$
-smooth submanifold S of
![]() ${\mathbb H}^{n}$
of dimension
${\mathbb H}^{n}$
of dimension
![]() $2n+1-k$
, one has
$2n+1-k$
, one has

Proof. By [Reference Magnani68, Theorem 1.2] (see also [Reference Magnani71, Theorem 8.1 and Proposition 8.7]), there exists a positive constant
![]() $C_{n,k}$
such that
$C_{n,k}$
such that

where
![]() $\eta _{S}(p)$
is as in (3.29). We remark that one is allowed to apply [Reference Magnani68, Theorem 1.2] because of the rotational invariance (3.1) of the distance d; see [Reference Magnani68, Proposition 4.5]. Therefore,
$\eta _{S}(p)$
is as in (3.29). We remark that one is allowed to apply [Reference Magnani68, Theorem 1.2] because of the rotational invariance (3.1) of the distance d; see [Reference Magnani68, Proposition 4.5]. Therefore,

and by Remark 3.3,

This concludes the proof.
Remark 3.32. The constant
![]() $C_{n,k}$
provided by Lemma 3.31 actually also depends on the distance d. However, we omit this dependence.
$C_{n,k}$
provided by Lemma 3.31 actually also depends on the distance d. However, we omit this dependence.
Remark 3.33. Let S be as in Lemma 3.31. The definition of the Heisenberg current
![]() depends on
depends on
![]() ${\mathscr S}^{Q-k}$
; that is, on the choice of the rotationally invariant distance d. On the contrary, the classical current
${\mathscr S}^{Q-k}$
; that is, on the choice of the rotationally invariant distance d. On the contrary, the classical current
![]() is a purely differential object – there is no metric involved. Therefore, Lemma 3.31 suggests that
is a purely differential object – there is no metric involved. Therefore, Lemma 3.31 suggests that
 ${\mathscr S}^{Q-k}_{*}:={\mathscr S}^{Q-k}/C_{n,k}$
, which does not depend on the choice of d, might be the correctly normalised spherical Hausdorff measure on
${\mathscr S}^{Q-k}_{*}:={\mathscr S}^{Q-k}/C_{n,k}$
, which does not depend on the choice of d, might be the correctly normalised spherical Hausdorff measure on
![]() ${\mathbb H}^{n}$
.
${\mathbb H}^{n}$
.
The following result is very simple.
Corollary 3.34. Let
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $k\in \{1,\dots ,n\}$
be fixed. If S is an oriented
$k\in \{1,\dots ,n\}$
be fixed. If S is an oriented
![]() $C^{1}$
-smooth submanifold of
$C^{1}$
-smooth submanifold of
![]() ${\mathbb H}^{n}$
of codimension k and without boundary, then
${\mathbb H}^{n}$
of codimension k and without boundary, then
![]() .
.
Proof. If
![]() $k<n$
, by Lemma 3.31 and Stokes’ theorem we have for every
$k<n$
, by Lemma 3.31 and Stokes’ theorem we have for every
 $\omega \in {\mathcal D}_{\mathbb H}^{2n-k}$
$\omega \in {\mathcal D}_{\mathbb H}^{2n-k}$
Similarly, when
![]() $k=n$
we have for every
$k=n$
we have for every
![]() $\omega \in {\mathcal D}_{\mathbb H}^{n}$
$\omega \in {\mathcal D}_{\mathbb H}^{n}$
because, by definition of D, the form
![]() $D\omega $
is exact.
$D\omega $
is exact.
3.6 Rank 1 connection and a property of tangent vectors to vertical planes
We conclude the present Section 3 by stating a technical result, Proposition 3.38, which will be of the utmost relevance in the proof of Rademacher’s Theorem 1.1. Since the proof of Proposition 3.38 is quite long and involved, for the moment we only state it and postpone its proof to Appendix A.
Let us start with a preliminary definition.
Definition 3.35. Let V be a real vector space of dimension
![]() $\ell $
and let m be an integer such that
$\ell $
and let m be an integer such that
![]() $1\leq m<\ell $
. We say that two m-dimensional vector subspaces
$1\leq m<\ell $
. We say that two m-dimensional vector subspaces
![]() ${\mathscr P}_{1},{\mathscr P}_{2}$
of V are rank 1 connected if
${\mathscr P}_{1},{\mathscr P}_{2}$
of V are rank 1 connected if
![]() $\dim {\mathscr P}_{1}\cap {\mathscr P}_{2}\geq m-1$
.
$\dim {\mathscr P}_{1}\cap {\mathscr P}_{2}\geq m-1$
.
The terminology chosen in Definition 3.35 is borrowed from some classical problems in the calculus of variations; see, for example, [Reference Ball and James14, Reference Müller78]. Some motivations are provided by the following Remark 3.36, which we state for future reference and where we identify linear applications and matrices.
Remark 3.36. Let
![]() $W,V$
be real vector spaces of dimensions
$W,V$
be real vector spaces of dimensions
![]() $m\geq 1$
and
$m\geq 1$
and
![]() $\ell \geq 1$
, respectively. Let also
$\ell \geq 1$
, respectively. Let also
![]() $L_{1},L_{2}:W\to V$
be linear maps and, for
$L_{1},L_{2}:W\to V$
be linear maps and, for
![]() $i=1,2$
, let
$i=1,2$
, let
![]() ${\mathscr P}_{i}:=\{(w,L_{i}(w))\in W\times V:w\in W\}$
be the graph of
${\mathscr P}_{i}:=\{(w,L_{i}(w))\in W\times V:w\in W\}$
be the graph of
![]() $L_{i}$
. Then the following statements are equivalent:
$L_{i}$
. Then the following statements are equivalent:
-
(a) the vector subspaces
 ${\mathscr P}_{1},{\mathscr P}_{2} $
of
${\mathscr P}_{1},{\mathscr P}_{2} $
of
 $W\times V$
are rank 1 connected;
$W\times V$
are rank 1 connected; -
(b) either
 $L_{1}=L_{2}$
or rank
$L_{1}=L_{2}$
or rank
 $(L_{1}-L_{2})=1$
.
$(L_{1}-L_{2})=1$
.
The subsequent Lemma 3.37 motivates the terminology in Definition 3.35: recall, in fact, that simple multivectors are sometimes called rank 1 multivectors. Before stating Lemma 3.37, let us fix some standard language. If
![]() ${\mathscr P}\subset V$
is a m-dimensional vector subspace and
${\mathscr P}\subset V$
is a m-dimensional vector subspace and
![]() $t\in \Large \wedge _{m} V$
is not null, we say that t is tangent to
$t\in \Large \wedge _{m} V$
is not null, we say that t is tangent to
![]() ${\mathscr P}$
if t is simple and it can be written as
${\mathscr P}$
if t is simple and it can be written as
![]() $t=v_{1}\wedge \dots \wedge v_{m}$
for some basis
$t=v_{1}\wedge \dots \wedge v_{m}$
for some basis
![]() $v_{1},\dots , v_{m}$
of
$v_{1},\dots , v_{m}$
of
![]() ${\mathscr P}$
. Equivalently, t is tangent to
${\mathscr P}$
. Equivalently, t is tangent to
![]() ${\mathscr P}$
if and only if
${\mathscr P}$
if and only if
![]() $\operatorname *{\mathrm {span}} t:=\{v\in V:v\wedge t=0\}$
coincides with
$\operatorname *{\mathrm {span}} t:=\{v\in V:v\wedge t=0\}$
coincides with
![]() ${\mathscr P}$
. Needless to say, if t and s are both tangent to
${\mathscr P}$
. Needless to say, if t and s are both tangent to
![]() ${\mathscr P}$
, then t and s are linearly dependent; that is, t is a multiple of s (and vice versa).
${\mathscr P}$
, then t and s are linearly dependent; that is, t is a multiple of s (and vice versa).
Lemma 3.37. Let V be a real vector space of dimension
![]() $\ell $
and let m be an integer such that
$\ell $
and let m be an integer such that
![]() $1\leq m \leq \ell $
; let also
$1\leq m \leq \ell $
; let also
![]() ${\mathscr P}_{1},{\mathscr P}_{2}$
be fixed m-dimensional vector subspaces of V. Then the following statements are equivalent:
${\mathscr P}_{1},{\mathscr P}_{2}$
be fixed m-dimensional vector subspaces of V. Then the following statements are equivalent:
-
(a)
 ${\mathscr P}_{1},{\mathscr P}_{2}$
are rank 1 connected;
${\mathscr P}_{1},{\mathscr P}_{2}$
are rank 1 connected; -
(b) for every couple of simple vectors
 $t_{1},t_{2}\in \Large \wedge _{m} V$
tangent to
$t_{1},t_{2}\in \Large \wedge _{m} V$
tangent to
 ${\mathscr P}_{1},{\mathscr P}_{2}$
(respectively), the difference
${\mathscr P}_{1},{\mathscr P}_{2}$
(respectively), the difference
 $t_{1}-t_{2}$
is a simple m-vector;
$t_{1}-t_{2}$
is a simple m-vector; -
(c) there exists a couple of simple vectors
 $t_{1},t_{2}\in \Large \wedge _{m} V$
tangent to
$t_{1},t_{2}\in \Large \wedge _{m} V$
tangent to
 ${\mathscr P}_{1},{\mathscr P}_{2}$
(respectively) such that the difference
${\mathscr P}_{1},{\mathscr P}_{2}$
(respectively) such that the difference
 $t_{1}-t_{2}$
is a simple m-vector.
$t_{1}-t_{2}$
is a simple m-vector.
The proof of Lemma 3.37 is quite simple; nonetheless, it is provided in Appendix A for the sake of completeness.
After recalling Definition 3.2 (vertical planes) and the notation
![]() $[\,\cdot \,]_{{\mathcal J}}$
introduced in Remark 3.4, we can eventually state the following result.
$[\,\cdot \,]_{{\mathcal J}}$
introduced in Remark 3.4, we can eventually state the following result.
Proposition 3.38. Let
![]() $k\in \{1,\dots ,n\}$
and
$k\in \{1,\dots ,n\}$
and
![]() $\zeta \in {\mathcal J}_{2n+1-k}$
be fixed with
$\zeta \in {\mathcal J}_{2n+1-k}$
be fixed with
![]() $\zeta \neq 0$
. Then
$\zeta \neq 0$
. Then
-
(i) if
 $k<n$
, there exists at most one
$k<n$
, there exists at most one
 $(2n+1-k)$
-dimensional vertical plane
$(2n+1-k)$
-dimensional vertical plane
 ${\mathscr P}$
whose unit tangent vector
${\mathscr P}$
whose unit tangent vector
 $t_{{\mathscr P}}=t_{{\mathscr P}}^{\mathbb H}$
is such that
$t_{{\mathscr P}}=t_{{\mathscr P}}^{\mathbb H}$
is such that
 $[t_{{\mathscr P}}^{\mathbb H}]_{{\mathcal J}}$
is a multiple of
$[t_{{\mathscr P}}^{\mathbb H}]_{{\mathcal J}}$
is a multiple of
 $\zeta $
;
$\zeta $
; -
(ii) if
 $k=n$
, there exist at most two vertical
$k=n$
, there exist at most two vertical
 $(n+1)$
-planes
$(n+1)$
-planes
 ${\mathscr P}$
whose unit tangent vectors
${\mathscr P}$
whose unit tangent vectors
 $t_{{\mathscr P}}=t_{{\mathscr P}}^{\mathbb H}$
are such that
$t_{{\mathscr P}}=t_{{\mathscr P}}^{\mathbb H}$
are such that
 $[t_{{\mathscr P}}^{\mathbb H}]_{{\mathcal J}}$
is a multiple of
$[t_{{\mathscr P}}^{\mathbb H}]_{{\mathcal J}}$
is a multiple of
 $\zeta $
. Moreover, if
$\zeta $
. Moreover, if
 ${\mathscr P}_{1},{\mathscr P}_{2}$
are two different such planes, then
${\mathscr P}_{1},{\mathscr P}_{2}$
are two different such planes, then
 ${{\mathscr P}_{1}}$
and
${{\mathscr P}_{1}}$
and
 ${{\mathscr P}_{2}}$
are not rank 1 connected.
${{\mathscr P}_{2}}$
are not rank 1 connected.
As we said, the long proof of Proposition 3.38 is postponed to Appendix A. It is, however, worth observing that the nonuniqueness phenomenon allowed for by statement (ii) above can indeed occur. In fact, consider the vertical 3-planes in
![]() ${\mathbb H}^{2}$
,
${\mathbb H}^{2}$
,
Unit tangent vectors are provided by
 $$ \begin{align*} t^{\mathbb H}_{{\mathscr P}_{1}}=X_{1}\wedge Y_{1}\wedge T\quad\text{and}\quad t^{\mathbb H}_{{\mathscr P}_{2}}=-X_{2}\wedge Y_{2}\wedge T \end{align*} $$
$$ \begin{align*} t^{\mathbb H}_{{\mathscr P}_{1}}=X_{1}\wedge Y_{1}\wedge T\quad\text{and}\quad t^{\mathbb H}_{{\mathscr P}_{2}}=-X_{2}\wedge Y_{2}\wedge T \end{align*} $$
and, using, for instance, Example 3.23, one can easily check that
 $[t^{\mathbb H}_{{\mathscr P}_{1}}]_{{\mathcal J}}=[t^{\mathbb H}_{{\mathscr P}_{2}}]_{{\mathcal J}}$
. Observe that
$[t^{\mathbb H}_{{\mathscr P}_{1}}]_{{\mathcal J}}=[t^{\mathbb H}_{{\mathscr P}_{2}}]_{{\mathcal J}}$
. Observe that
![]() ${\mathscr P}_{1}$
and
${\mathscr P}_{1}$
and
![]() ${\mathscr P}_{2}$
are not rank 1 connected, as stated by Proposition 3.38. The latter also guarantees that no vertical plane
${\mathscr P}_{2}$
are not rank 1 connected, as stated by Proposition 3.38. The latter also guarantees that no vertical plane
![]() ${\mathscr P}\neq {\mathscr P}_{1}$
such that
${\mathscr P}\neq {\mathscr P}_{1}$
such that
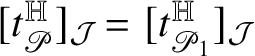 $[t^{\mathbb H}_{{\mathscr P}}]_{{\mathcal J}}=[t^{\mathbb H}_{{\mathscr P}_{1}}]_{{\mathcal J}}$
exists other than
$[t^{\mathbb H}_{{\mathscr P}}]_{{\mathcal J}}=[t^{\mathbb H}_{{\mathscr P}_{1}}]_{{\mathcal J}}$
exists other than
![]() ${\mathscr P}_{2}$
. See also Remarks A.2 and A.4.
${\mathscr P}_{2}$
. See also Remarks A.2 and A.4.
4 Intrinsic Lipschitz graphs in Heisenberg groups
Though already introduced in Section 2, for the reader’s convenience we now recall the notion of intrinsic Lipschitz graph. Assume that a splitting of
![]() ${\mathbb H}^{n}$
is fixed; namely, let
${\mathbb H}^{n}$
is fixed; namely, let
![]() ${\mathbb W},{\mathbb V}$
be homogeneous (i.e., invariant under dilations) and complementary (i.e.,
${\mathbb W},{\mathbb V}$
be homogeneous (i.e., invariant under dilations) and complementary (i.e.,
![]() ${\mathbb W}\cap {\mathbb V}=\{0\}$
and
${\mathbb W}\cap {\mathbb V}=\{0\}$
and
![]() ${\mathbb H}^{n}={\mathbb W}{\mathbb V}$
) subgroups of
${\mathbb H}^{n}={\mathbb W}{\mathbb V}$
) subgroups of
![]() ${\mathbb H}^{n}$
. Each
${\mathbb H}^{n}$
. Each
![]() $p\in {\mathbb H}^{n}$
possesses a unique decomposition
$p\in {\mathbb H}^{n}$
possesses a unique decomposition
![]() $p=p_{{\mathbb W}} p_{{\mathbb V}}$
as a product of elements
$p=p_{{\mathbb W}} p_{{\mathbb V}}$
as a product of elements
![]() $p_{{\mathbb W}}\in {\mathbb W}$
,
$p_{{\mathbb W}}\in {\mathbb W}$
,
![]() $p_{{\mathbb V}}\in {\mathbb V}$
. For
$p_{{\mathbb V}}\in {\mathbb V}$
. For
![]() $\alpha \geq 0$
, the homogeneous cone
$\alpha \geq 0$
, the homogeneous cone
![]() $C_{\alpha }$
along
$C_{\alpha }$
along
![]() ${\mathbb V}$
is
${\mathbb V}$
is
The set
![]() $C_{\alpha }$
is homogeneous (i.e., invariant under dilations) and
$C_{\alpha }$
is homogeneous (i.e., invariant under dilations) and
![]() $0\in C_{\alpha }$
; actually,
$0\in C_{\alpha }$
; actually,
![]() ${\mathbb V}\subset C_{\alpha }$
. For
${\mathbb V}\subset C_{\alpha }$
. For
![]() $p\in {\mathbb H}^{n}$
we set
$p\in {\mathbb H}^{n}$
we set
![]() $C_{\alpha }(p):=pC_{\alpha }$
. Observe that
$C_{\alpha }(p):=pC_{\alpha }$
. Observe that
![]() $C_{\alpha }$
coincides with the cone
$C_{\alpha }$
coincides with the cone
![]() ${\mathscr C}_{1/\alpha }$
defined in Subsection 2.2: the reason for this change in notation is that, from now on, we will more frequently deal with the intrinsic Lipschitz constants of maps rather than with the apertures of the associated cones.
${\mathscr C}_{1/\alpha }$
defined in Subsection 2.2: the reason for this change in notation is that, from now on, we will more frequently deal with the intrinsic Lipschitz constants of maps rather than with the apertures of the associated cones.
Given
![]() $A\subset {\mathbb W}$
and a map
$A\subset {\mathbb W}$
and a map
![]() $\phi :{\mathbb W}\to {\mathbb V}$
, the intrinsic graph of
$\phi :{\mathbb W}\to {\mathbb V}$
, the intrinsic graph of
![]() $\phi $
is the set
$\phi $
is the set
We hereafter adopt the convention that, whenever a map
![]() $\phi :A\to {\mathbb V}$
is introduced, we denote by
$\phi :A\to {\mathbb V}$
is introduced, we denote by
![]() $\Phi :A\to {\mathbb H}^{n}$
the associated graph map
$\Phi :A\to {\mathbb H}^{n}$
the associated graph map
![]() $\Phi (w):=w\phi (w)$
; in particular,
$\Phi (w):=w\phi (w)$
; in particular,
![]() $\mathrm {gr}_{\phi }=\Phi (A)$
.
$\mathrm {gr}_{\phi }=\Phi (A)$
.
Definition 4.1. Let
![]() $A\subset {\mathbb W}$
; we say that a map
$A\subset {\mathbb W}$
; we say that a map
![]() $\phi :A\to {\mathbb V}$
is intrinsic Lipschitz continuous if there exists
$\phi :A\to {\mathbb V}$
is intrinsic Lipschitz continuous if there exists
![]() $\alpha>0$
such that
$\alpha>0$
such that
We call intrinsic Lipschitz constant of
![]() $\phi $
the infimum of those positive
$\phi $
the infimum of those positive
![]() $\alpha $
for which (4.1) holds.
$\alpha $
for which (4.1) holds.
Intrinsic Lipschitz maps of low dimension (
![]() $\dim {\mathbb W}\leq n$
) are Euclidean Lipschitz continuous and the Hausdorff dimension of their graphs equals the topological one; that is,
$\dim {\mathbb W}\leq n$
) are Euclidean Lipschitz continuous and the Hausdorff dimension of their graphs equals the topological one; that is,
![]() $\dim {\mathbb W}$
. See [Reference Franchi, Serapioni and Serra Cassano50, Remark 3.11], [Reference Franchi and Serapioni53, Proposition 3.7] or [Reference Antonelli and Merlo8]. On the contrary, intrinsic Lipschitz maps of low codimension
$\dim {\mathbb W}$
. See [Reference Franchi, Serapioni and Serra Cassano50, Remark 3.11], [Reference Franchi and Serapioni53, Proposition 3.7] or [Reference Antonelli and Merlo8]. On the contrary, intrinsic Lipschitz maps of low codimension
![]() $k=\dim {\mathbb V}\leq n$
are not better than Euclidean
$k=\dim {\mathbb V}\leq n$
are not better than Euclidean
![]() $1/2$
-Hölder continuous; see Remark 4.5. Despite this fractal behaviour (see also [Reference Kirchheim and Serra Cassano63]), they enjoy good metric properties: for instance, the Hausdorff dimension of their graphs is the same,
$1/2$
-Hölder continuous; see Remark 4.5. Despite this fractal behaviour (see also [Reference Kirchheim and Serra Cassano63]), they enjoy good metric properties: for instance, the Hausdorff dimension of their graphs is the same,
![]() $Q-k$
, as
$Q-k$
, as
![]() ${\mathbb W}$
, and the
${\mathbb W}$
, and the
![]() $(Q-k)$
-dimensional Hausdorff measure on their graph is even
$(Q-k)$
-dimensional Hausdorff measure on their graph is even
![]() $(Q-k)$
-Ahlfors regular; see Remark 4.6 and the references therein.
$(Q-k)$
-Ahlfors regular; see Remark 4.6 and the references therein.
4.1 Intrinsic Lipschitz graphs of low codimension
We are interested in intrinsic Lipschitz graphs of codimension at most n; we then assume that
![]() $k:=\dim {\mathbb V}$
is a positive integer not greater than n. It can be easily checked (see, e.g., [Reference Franchi, Serapioni and Serra Cassano51, Remark 3.12]) that this forces
$k:=\dim {\mathbb V}$
is a positive integer not greater than n. It can be easily checked (see, e.g., [Reference Franchi, Serapioni and Serra Cassano51, Remark 3.12]) that this forces
![]() ${\mathbb V}$
to be abelian; by Remark 3.16, up to an isometric group isomorphism of
${\mathbb V}$
to be abelian; by Remark 3.16, up to an isometric group isomorphism of
![]() ${\mathbb H}^{n}$
, one can always assume that
${\mathbb H}^{n}$
, one can always assume that
Moreover, it follows from [Reference Franchi and Serapioni53, Proposition 3.1] (alternatively, from Theorem 1.4) that, if
![]() ${\mathbb W},{\mathbb W}^{\prime }$
are complementary to
${\mathbb W},{\mathbb W}^{\prime }$
are complementary to
![]() ${\mathbb V}$
and
${\mathbb V}$
and
![]() $S\subset {\mathbb H}^{n}$
is such that
$S\subset {\mathbb H}^{n}$
is such that
![]() $S=\mathrm {gr}_{\phi }$
for some intrinsic Lipschitz
$S=\mathrm {gr}_{\phi }$
for some intrinsic Lipschitz
![]() $\phi :A\to {\mathbb V}$
with
$\phi :A\to {\mathbb V}$
with
![]() $A\subset {\mathbb W}$
, then there exists
$A\subset {\mathbb W}$
, then there exists
![]() $ A^{\prime }\subset {\mathbb W}^{\prime }$
and an intrinsic Lipschitz map
$ A^{\prime }\subset {\mathbb W}^{\prime }$
and an intrinsic Lipschitz map
![]() $\phi ^{\prime }: A^{\prime }\to {\mathbb V}$
such that
$\phi ^{\prime }: A^{\prime }\to {\mathbb V}$
such that
![]() $S=\mathrm {gr}_{\phi ^{\prime }}$
. In particular, it will not be restrictive (see also Remark 6.1) to assume that
$S=\mathrm {gr}_{\phi ^{\prime }}$
. In particular, it will not be restrictive (see also Remark 6.1) to assume that
 $$ \begin{align} \begin{aligned} &{\mathbb W}=\exp(\operatorname*{\mathrm{span}}\{X_{k+1},\dots,X_{n},Y_{1},\dots,Y_{n},T\}) &&\text{if }1\leq k\leq n-1\\ &{\mathbb W}=\exp(\operatorname*{\mathrm{span}}\{Y_{1},\dots,Y_{n},T\}) &&\text{if }k=n. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &{\mathbb W}=\exp(\operatorname*{\mathrm{span}}\{X_{k+1},\dots,X_{n},Y_{1},\dots,Y_{n},T\}) &&\text{if }1\leq k\leq n-1\\ &{\mathbb W}=\exp(\operatorname*{\mathrm{span}}\{Y_{1},\dots,Y_{n},T\}) &&\text{if }k=n. \end{aligned} \end{align} $$
Hence, from now on we work with the subgroups
![]() ${\mathbb W},{\mathbb V}$
defined in (4.2) and (4.3). In coordinates
${\mathbb W},{\mathbb V}$
defined in (4.2) and (4.3). In coordinates
 $$ \begin{align} &{\mathbb V}=\{(x,y,t)\in{\mathbb R}^{n}\times{\mathbb R}^{n}\times{\mathbb R}:y=0,\ x_{k+1}=\ldots=x_{n}=t=0\} &&\text{if }1\leq k\leq n-1\nonumber\\ &{\mathbb V}=\{(x,y,t)\in{\mathbb R}^{n}\times{\mathbb R}^{n}\times{\mathbb R}:y=0,\ t=0\} &&\text{if }k=n\\ &{\mathbb W}=\{(x,y,t)\in{\mathbb R}^{n}\times{\mathbb R}^{n}\times{\mathbb R}:x_{1}=\ldots=x_{k}=0\}.\nonumber \end{align} $$
$$ \begin{align} &{\mathbb V}=\{(x,y,t)\in{\mathbb R}^{n}\times{\mathbb R}^{n}\times{\mathbb R}:y=0,\ x_{k+1}=\ldots=x_{n}=t=0\} &&\text{if }1\leq k\leq n-1\nonumber\\ &{\mathbb V}=\{(x,y,t)\in{\mathbb R}^{n}\times{\mathbb R}^{n}\times{\mathbb R}:y=0,\ t=0\} &&\text{if }k=n\\ &{\mathbb W}=\{(x,y,t)\in{\mathbb R}^{n}\times{\mathbb R}^{n}\times{\mathbb R}:x_{1}=\ldots=x_{k}=0\}.\nonumber \end{align} $$
For simplicity, we will write
![]() $v\in {\mathbb V}$
and
$v\in {\mathbb V}$
and
![]() $w\in {\mathbb W}$
as
$w\in {\mathbb W}$
as
 $$ \begin{align} & v=(x_{1},\dots,x_{k})\in{\mathbb R}^{k}\nonumber\\ & w=(x_{k+1},\dots,x_{n},y_{1},\dots,y_{n},t)\in{\mathbb R}^{2n+1-k} &&\text{if }1\leq k\leq n-1\\ & w=(y_{1},\dots,y_{n},t)\in{\mathbb R}^{n+1} &&\text{if }k=n.\nonumber \end{align} $$
$$ \begin{align} & v=(x_{1},\dots,x_{k})\in{\mathbb R}^{k}\nonumber\\ & w=(x_{k+1},\dots,x_{n},y_{1},\dots,y_{n},t)\in{\mathbb R}^{2n+1-k} &&\text{if }1\leq k\leq n-1\\ & w=(y_{1},\dots,y_{n},t)\in{\mathbb R}^{n+1} &&\text{if }k=n.\nonumber \end{align} $$
Notice that, if
![]() $p=(x,y,t)$
, then
$p=(x,y,t)$
, then
![]() $p_{{\mathbb V}}=(x_{1},\dots ,x_{k})$
. Observe also that the measure
$p_{{\mathbb V}}=(x_{1},\dots ,x_{k})$
. Observe also that the measure
![]() ${\mathscr L}^{2n+1-k}$
induced on
${\mathscr L}^{2n+1-k}$
induced on
![]() ${\mathbb W}$
by the identification
${\mathbb W}$
by the identification
![]() ${\mathbb W}\equiv {\mathbb R}^{2n+1-k}$
in (4.5) is a Haar measure on
${\mathbb W}\equiv {\mathbb R}^{2n+1-k}$
in (4.5) is a Haar measure on
![]() ${\mathbb W}$
that is also
${\mathbb W}$
that is also
![]() $(Q-k)$
-homogeneous; that is,
$(Q-k)$
-homogeneous; that is,
In particular,
![]() ${\mathscr L}^{2n+1-k}$
coincides, up to multiplicative factors, with the Hausdorff
${\mathscr L}^{2n+1-k}$
coincides, up to multiplicative factors, with the Hausdorff
![]() ${\mathscr H}^{Q-k}$
and spherical Hausdorff
${\mathscr H}^{Q-k}$
and spherical Hausdorff
![]() ${\mathscr S}^{Q-k}$
measures on
${\mathscr S}^{Q-k}$
measures on
![]() ${\mathbb W}$
.
${\mathbb W}$
.
We now write the intrinsic graph map
![]() $\Phi $
in coordinates: writing
$\Phi $
in coordinates: writing
![]() $w\in {\mathbb W}\equiv {\mathbb R}^{2n+1-k}$
and
$w\in {\mathbb W}\equiv {\mathbb R}^{2n+1-k}$
and
![]() $\phi (w)\in {\mathbb V}\equiv {\mathbb R}^{k}$
as in (4.5), one gets
$\phi (w)\in {\mathbb V}\equiv {\mathbb R}^{k}$
as in (4.5), one gets
 $$ \begin{align} \begin{array}{ll} \Phi(w)=(\phi(w),x_{k+1},\dots,x_{n},y_{1},\dots,y_{n},t-\tfrac 12\langle \phi(w),(y_{1},\dots,y_{k})\rangle)&\text{if }1\leq k\leq n-1\\ \Phi(w)=(\phi(w),y_{1},\dots,y_{n},t-\tfrac 12\langle \phi(w),y\rangle) &\text{if }k=n, \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} \Phi(w)=(\phi(w),x_{k+1},\dots,x_{n},y_{1},\dots,y_{n},t-\tfrac 12\langle \phi(w),(y_{1},\dots,y_{k})\rangle)&\text{if }1\leq k\leq n-1\\ \Phi(w)=(\phi(w),y_{1},\dots,y_{n},t-\tfrac 12\langle \phi(w),y\rangle) &\text{if }k=n, \end{array} \end{align} $$
where the scalar products appearing in (4.7) are those of
![]() ${\mathbb R}^{k}$
. Let us write an equivalent analytic formulation for (4.1). Clearly, the latter is equivalent to require that
${\mathbb R}^{k}$
. Let us write an equivalent analytic formulation for (4.1). Clearly, the latter is equivalent to require that
Since
![]() ${\mathbb W}$
is a normal subgroup and
${\mathbb W}$
is a normal subgroup and
![]() ${\mathbb V}$
is commutative, we have
${\mathbb V}$
is commutative, we have
 $$ \begin{align*} (-\phi(w^{\prime}))(-w^{\prime})w\phi(w) = \underbrace{(-\phi(w^{\prime}))(-w^{\prime})w\phi(w^{\prime})}_{\in{\mathbb W}}\underbrace{(\phi(w)-\phi(w^{\prime}))}_{\in{\mathbb V}\equiv{\mathbb R}^{k}} \end{align*} $$
$$ \begin{align*} (-\phi(w^{\prime}))(-w^{\prime})w\phi(w) = \underbrace{(-\phi(w^{\prime}))(-w^{\prime})w\phi(w^{\prime})}_{\in{\mathbb W}}\underbrace{(\phi(w)-\phi(w^{\prime}))}_{\in{\mathbb V}\equiv{\mathbb R}^{k}} \end{align*} $$
and (4.8) is equivalent to
After a boring computation (which we omit) and writing
![]() $w=(x_{k+1},\dots ,y_{n},t)$
and
$w=(x_{k+1},\dots ,y_{n},t)$
and
![]() $w^{\prime }=(x_{k+1}^{\prime },\dots ,y_{n}^{\prime },t^{\prime })$
, when
$w^{\prime }=(x_{k+1}^{\prime },\dots ,y_{n}^{\prime },t^{\prime })$
, when
![]() $k<n$
we obtain that (4.1) is equivalent to
$k<n$
we obtain that (4.1) is equivalent to
 $$ \begin{align} &|\phi(w)-\phi(w')| \notag \\ &\quad < \alpha \left\|\left(x_{k+1}-x_{k+1}',\dots,y_{n}-y_{n}',t-t'-\sum_{j=1}^{k}\phi_{j}(w')(y_{j}-y_{j}')+\frac 12\sum_{j=k+1}^{n}(x_{j}y_{j}'-x_{j}'y_{j})\right) \right\|_{\mathbb H} \end{align} $$
$$ \begin{align} &|\phi(w)-\phi(w')| \notag \\ &\quad < \alpha \left\|\left(x_{k+1}-x_{k+1}',\dots,y_{n}-y_{n}',t-t'-\sum_{j=1}^{k}\phi_{j}(w')(y_{j}-y_{j}')+\frac 12\sum_{j=k+1}^{n}(x_{j}y_{j}'-x_{j}'y_{j})\right) \right\|_{\mathbb H} \end{align} $$
for all points
![]() $w=(x_{k+1},\dots ,y_{n},t)$
,
$w=(x_{k+1},\dots ,y_{n},t)$
,
![]() $w^{\prime }=(x_{k+1}^{\prime },\dots ,y_{n}^{\prime },t^{\prime })\in A$
with
$w^{\prime }=(x_{k+1}^{\prime },\dots ,y_{n}^{\prime },t^{\prime })\in A$
with
![]() $w\neq w^{\prime }$
. If
$w\neq w^{\prime }$
. If
![]() $k=n$
, the formula above reads as
$k=n$
, the formula above reads as
 $$ \begin{align} |\phi(w)-\phi(w^{\prime})| < \alpha \left\|\left(y_{1}-y_{1}^{\prime},\dots,y_{n}-y_{n}^{\prime},t-t^{\prime}-\sum_{j=1}^{k}\phi_{j}(w^{\prime})(y_{j}-y_{j}^{\prime})\right) \right\|_{\mathbb H} \end{align} $$
$$ \begin{align} |\phi(w)-\phi(w^{\prime})| < \alpha \left\|\left(y_{1}-y_{1}^{\prime},\dots,y_{n}-y_{n}^{\prime},t-t^{\prime}-\sum_{j=1}^{k}\phi_{j}(w^{\prime})(y_{j}-y_{j}^{\prime})\right) \right\|_{\mathbb H} \end{align} $$
for all
![]() $w=(y_{1},\dots ,y_{n},t)$
,
$w=(y_{1},\dots ,y_{n},t)$
,
![]() $w^{\prime }=(y_{1}^{\prime },\dots ,y_{n}^{\prime },t^{\prime })\in A$
,
$w^{\prime }=(y_{1}^{\prime },\dots ,y_{n}^{\prime },t^{\prime })\in A$
,
![]() $w\neq w^{\prime }$
.
$w\neq w^{\prime }$
.
It is convenient to point out some basic facts about intrinsic Lipschitz functions.
Remark 4.2. Let
![]() $\phi :A\subset {\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz with intrinsic Lipschitz constant not greater than
$\phi :A\subset {\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz with intrinsic Lipschitz constant not greater than
![]() $\alpha $
and assume that
$\alpha $
and assume that
![]() $\phi (0)=0$
; then,
$\phi (0)=0$
; then,
![]() $|\phi (w)|\leq \alpha \|w\|_{\mathbb H}$
for every
$|\phi (w)|\leq \alpha \|w\|_{\mathbb H}$
for every
![]() $w\in {\mathbb W}$
. In order to prove this statement, it is enough to plug
$w\in {\mathbb W}$
. In order to prove this statement, it is enough to plug
![]() $w^{\prime }=0$
in (4.9) and (4.10).
$w^{\prime }=0$
in (4.9) and (4.10).
Remark 4.3. Assume that
![]() ${\mathbb H}^{n}$
is endowed with the distance
${\mathbb H}^{n}$
is endowed with the distance
![]() $d_{\infty }$
defined in (3.2) and let
$d_{\infty }$
defined in (3.2) and let
![]() $\alpha \leq 1/2$
be fixed. Then, for every intrinsic Lipschitz
$\alpha \leq 1/2$
be fixed. Then, for every intrinsic Lipschitz
![]() $\phi :{\mathbb W}\to {\mathbb V}$
with intrinsic Lipschitz constant not greater than
$\phi :{\mathbb W}\to {\mathbb V}$
with intrinsic Lipschitz constant not greater than
![]() $\alpha $
there holds
$\alpha $
there holds
We can assume without loss of generality that
![]() $q=0$
; using Remark 4.2,
$q=0$
; using Remark 4.2,
 $$ \begin{align*} |p_{{\mathbb V}}| &=|\phi(p_{{\mathbb W}})| \leq \alpha d_{\infty}(0,p_{{\mathbb W}})\\ &\leq\alpha(d_{\infty}(0,p)+ d_{\infty}(p,p_{{\mathbb W}}))\leq \alpha d_{\infty}(0,p) + \tfrac 12 d_{\infty}(p_{{\mathbb V}},0) =\alpha d_{\infty}(0,p) + \tfrac 12 |p_{{\mathbb V}}|, \end{align*} $$
$$ \begin{align*} |p_{{\mathbb V}}| &=|\phi(p_{{\mathbb W}})| \leq \alpha d_{\infty}(0,p_{{\mathbb W}})\\ &\leq\alpha(d_{\infty}(0,p)+ d_{\infty}(p,p_{{\mathbb W}}))\leq \alpha d_{\infty}(0,p) + \tfrac 12 d_{\infty}(p_{{\mathbb V}},0) =\alpha d_{\infty}(0,p) + \tfrac 12 |p_{{\mathbb V}}|, \end{align*} $$
which is (4.11).
Remark 4.4. Assume that
![]() ${\mathbb H}^{n}$
is endowed with the distance
${\mathbb H}^{n}$
is endowed with the distance
![]() $d_{\infty }$
defined in (3.2). Then, for every
$d_{\infty }$
defined in (3.2). Then, for every
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $\bar \alpha =\bar \alpha (\varepsilon ,n,k)>0$
such that the following holds: for every intrinsic Lipschitz map
$\bar \alpha =\bar \alpha (\varepsilon ,n,k)>0$
such that the following holds: for every intrinsic Lipschitz map
![]() $\phi :{\mathbb W}\to {\mathbb V}$
with intrinsic Lipschitz constant not greater than
$\phi :{\mathbb W}\to {\mathbb V}$
with intrinsic Lipschitz constant not greater than
![]() $\bar \alpha $
,
$\bar \alpha $
,
The second equality in (4.12) is trivial (and, actually, it holds for every
![]() $\phi :{\mathbb W}\to {\mathbb V}$
) because
$\phi :{\mathbb W}\to {\mathbb V}$
) because
 $$ \begin{align*} d_{\infty}(p,\mathrm{gr}_{\phi})\leq d_{\infty}(p,\Phi(p_{{\mathbb W}}))=d_{\infty}(p_{{\mathbb W}} p_{{\mathbb V}},p_{{\mathbb W}} \phi(p_{{\mathbb W}}))=d_{\infty}(0,(p_{{\mathbb V}})^{-1}\phi(p_{{\mathbb W}}))=|p_{{\mathbb V}}-\phi(p_{{\mathbb W}})|. \end{align*} $$
$$ \begin{align*} d_{\infty}(p,\mathrm{gr}_{\phi})\leq d_{\infty}(p,\Phi(p_{{\mathbb W}}))=d_{\infty}(p_{{\mathbb W}} p_{{\mathbb V}},p_{{\mathbb W}} \phi(p_{{\mathbb W}}))=d_{\infty}(0,(p_{{\mathbb V}})^{-1}\phi(p_{{\mathbb W}}))=|p_{{\mathbb V}}-\phi(p_{{\mathbb W}})|. \end{align*} $$
In order to prove the first inequality in (4.12), we argue by contradiction. Assume that there exists
![]() $\bar \varepsilon>0$
such that, for every
$\bar \varepsilon>0$
such that, for every
![]() $i\in \mathbb N$
, there exist
$i\in \mathbb N$
, there exist
![]() $p_{i}\in {\mathbb H}^{n}$
and
$p_{i}\in {\mathbb H}^{n}$
and
![]() $\phi _{i}:{\mathbb W}\to {\mathbb V}$
such that
$\phi _{i}:{\mathbb W}\to {\mathbb V}$
such that
![]() $\phi _{i}$
is intrinsic Lipschitz with intrinsic Lipschitz constant not greater than
$\phi _{i}$
is intrinsic Lipschitz with intrinsic Lipschitz constant not greater than
![]() $1/i$
and
$1/i$
and
Up to a left translation we can assume that
![]() $(p_{i})_{{\mathbb W}}=0$
and
$(p_{i})_{{\mathbb W}}=0$
and
![]() $\phi _{i}(0)=0$
for all i; in particular,
$\phi _{i}(0)=0$
for all i; in particular,
![]() $p_{i}\in {\mathbb V}$
for all i and, up to a dilation, we can also assume that
$p_{i}\in {\mathbb V}$
for all i and, up to a dilation, we can also assume that
![]() $d_{\infty }(p_{i},0)=1$
, so that (4.13) becomes
$d_{\infty }(p_{i},0)=1$
, so that (4.13) becomes
where the points
![]() $\bar p_{i}\in \mathrm {gr}_{\phi _{i}}$
are chosen so that
$\bar p_{i}\in \mathrm {gr}_{\phi _{i}}$
are chosen so that
![]() $d_{\infty }(p_{i},\bar p_{i})=d_{\infty }(p_{i},\mathrm {gr}_{\phi _{i}})$
. Observe that
$d_{\infty }(p_{i},\bar p_{i})=d_{\infty }(p_{i},\mathrm {gr}_{\phi _{i}})$
. Observe that
![]() $d_{\infty }(0,\bar p_{i})\leq d_{\infty }(0, p_{i}) +d_{\infty }(p_{i},\bar p_{i})<2$
; in particular, up to extracting a subsequence there exist
$d_{\infty }(0,\bar p_{i})\leq d_{\infty }(0, p_{i}) +d_{\infty }(p_{i},\bar p_{i})<2$
; in particular, up to extracting a subsequence there exist
![]() $p\in {\mathbb V}$
and
$p\in {\mathbb V}$
and
![]() $\bar p\in B(0,2) $
such that
$\bar p\in B(0,2) $
such that
![]() $p_{i}\to p\in {\mathbb V}$
and
$p_{i}\to p\in {\mathbb V}$
and
![]() $\bar p_{i}\to \bar p$
as
$\bar p_{i}\to \bar p$
as
![]() $i\to +\infty $
; clearly,
$i\to +\infty $
; clearly,
![]() $d_{\infty }(p,0)=1$
. By Remark 4.2 we have that
$d_{\infty }(p,0)=1$
. By Remark 4.2 we have that
![]() $\phi _{i}\to 0$
uniformly on compact sets of
$\phi _{i}\to 0$
uniformly on compact sets of
![]() ${\mathbb W}$
(equivalently,
${\mathbb W}$
(equivalently,
![]() $\mathrm {gr}_{\phi _{i}}\to {\mathbb W}$
with respect to the local Hausdorff convergence of closed sets in
$\mathrm {gr}_{\phi _{i}}\to {\mathbb W}$
with respect to the local Hausdorff convergence of closed sets in
![]() ${\mathbb H}^{n}$
), in particular,
${\mathbb H}^{n}$
), in particular,
![]() $\bar p\in {\mathbb W}$
. Letting
$\bar p\in {\mathbb W}$
. Letting
![]() $i\to +\infty $
in (4.14) provides
$i\to +\infty $
in (4.14) provides
However, writing
![]() $p=(p_{1},\dots ,p_{k},0,\dots ,0)$
and
$p=(p_{1},\dots ,p_{k},0,\dots ,0)$
and
![]() $\bar p=(0,\dots ,0,\bar p_{k+1},\dots ,\bar p_{2n+1})$
, we notice that
$\bar p=(0,\dots ,0,\bar p_{k+1},\dots ,\bar p_{2n+1})$
, we notice that
a contradiction.
Remark 4.5. It follows from (4.9)–(4.10) that, if
![]() $K\subset {\mathbb W}$
is compact and
$K\subset {\mathbb W}$
is compact and
![]() $\phi :{\mathbb W}\to {\mathbb V}$
is intrinsic Lipschitz with intrinsic Lipschitz constant
$\phi :{\mathbb W}\to {\mathbb V}$
is intrinsic Lipschitz with intrinsic Lipschitz constant
![]() $\alpha $
, then there exists
$\alpha $
, then there exists
![]() $M=M(\alpha ,\phi (0),K)$
such that
$M=M(\alpha ,\phi (0),K)$
such that
![]() $|\phi |\leq M$
on K.
$|\phi |\leq M$
on K.
In particular, one can apply [Reference Franchi, Serapioni and Serra Cassano52, Proposition 4.8] to get the following: for every
![]() $\alpha>0$
and every compact set
$\alpha>0$
and every compact set
![]() $K\subset {\mathbb W}$
there exists
$K\subset {\mathbb W}$
there exists
![]() $C=C(\alpha ,K)>0$
such that, for every
$C=C(\alpha ,K)>0$
such that, for every
![]() $w,w^{\prime }\in K$
and every intrinsic Lipschitz
$w,w^{\prime }\in K$
and every intrinsic Lipschitz
![]() $\phi :{\mathbb W}\to {\mathbb V}$
with
$\phi :{\mathbb W}\to {\mathbb V}$
with
![]() $\phi (0)=0$
and intrinsic Lipschitz constant not greater than
$\phi (0)=0$
and intrinsic Lipschitz constant not greater than
![]() $\alpha $
, the
$\alpha $
, the
![]() $1/2$
-Hölder estimate
$1/2$
-Hölder estimate
holds, where
![]() $|\cdot |$
denotes the Euclidean norm in
$|\cdot |$
denotes the Euclidean norm in
![]() ${\mathbb W}\equiv {\mathbb R}^{2n+1-k}$
.
${\mathbb W}\equiv {\mathbb R}^{2n+1-k}$
.
Remark 4.6. It was proved in [Reference Franchi and Serapioni53, Theorem 3.9] that the
![]() $(Q-k)$
-dimensional Hausdorff measure on intrinsic Lipschitz graphs graphs is
$(Q-k)$
-dimensional Hausdorff measure on intrinsic Lipschitz graphs graphs is
![]() $(Q-k)$
-Ahlfors regular; in particular, intrinsic Lipschitz graphs have the same Hausdorff dimension
$(Q-k)$
-Ahlfors regular; in particular, intrinsic Lipschitz graphs have the same Hausdorff dimension
![]() $Q-k$
of the domain
$Q-k$
of the domain
![]() ${\mathbb W}$
. Actually, the statement of [Reference Franchi and Serapioni53, Theorem 3.9] is more quantitative; in fact, it states that for every
${\mathbb W}$
. Actually, the statement of [Reference Franchi and Serapioni53, Theorem 3.9] is more quantitative; in fact, it states that for every
![]() $\alpha>0$
there exists
$\alpha>0$
there exists
![]() $C_{1}=C_{1}(\alpha )>0$
such that, for every intrinsic Lipschitz function
$C_{1}=C_{1}(\alpha )>0$
such that, for every intrinsic Lipschitz function
![]() $\phi :{\mathbb W}\to {\mathbb V}$
whose intrinsic Lipschitz constant is not greater than
$\phi :{\mathbb W}\to {\mathbb V}$
whose intrinsic Lipschitz constant is not greater than
![]() $\alpha $
, one has
$\alpha $
, one has
 $$ \begin{align} {C_{1}}^{-1} r^{Q-k} \leq {\mathscr S}^{Q-k}(\mathrm{gr}_{\phi}\cap B(p,r)) \leq C_{1} r^{Q-k}\qquad\forall\, p\in\mathrm{gr}_{\phi},\ r>0. \end{align} $$
$$ \begin{align} {C_{1}}^{-1} r^{Q-k} \leq {\mathscr S}^{Q-k}(\mathrm{gr}_{\phi}\cap B(p,r)) \leq C_{1} r^{Q-k}\qquad\forall\, p\in\mathrm{gr}_{\phi},\ r>0. \end{align} $$
Let us point out for future reference one further consequence that is implicitly proved in [Reference Franchi and Serapioni53, Theorem 3.9]. Denote by
![]() $\pi _{{\mathbb W}}:{\mathbb H}^{n}\to {\mathbb W}$
the projection
$\pi _{{\mathbb W}}:{\mathbb H}^{n}\to {\mathbb W}$
the projection
![]() $\pi _{{\mathbb W}}(p):=p_{{\mathbb W}}$
; by [Reference Franchi and Serapioni53, formula (44)] there exists a constant
$\pi _{{\mathbb W}}(p):=p_{{\mathbb W}}$
; by [Reference Franchi and Serapioni53, formula (44)] there exists a constant
![]() $C_{2}=C_{2}(\alpha )\in (0,1)$
such that, for every
$C_{2}=C_{2}(\alpha )\in (0,1)$
such that, for every
![]() $\phi $
as above,
$\phi $
as above,
By [Reference Franchi and Serapioni53, Lemma 2.20], which states that there exists
![]() $C_{3}>0$
such that
$C_{3}>0$
such that
we deduce that

for a suitable
![]() $C_{4}=C_{4}(\alpha )>0$
, where
$C_{4}=C_{4}(\alpha )>0$
, where
![]() $\Phi _\#$
denotes push-forward of measures. Since
$\Phi _\#$
denotes push-forward of measures. Since
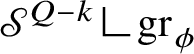
is a doubling measure, one can differentiate the measure
with respect to
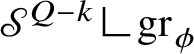
(see, e.g., [Reference Rigot83]) to get the existence of
 $g:\mathrm {gr}_{\phi }\to [{C_{4}}^{-1},C_{4}]$
such that
$g:\mathrm {gr}_{\phi }\to [{C_{4}}^{-1},C_{4}]$
such that
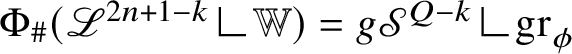
. Equivalently, there exists a measurable function
 $J_{\phi }:{\mathbb W}\to [{C_{4}}^{-1},C_{4}]$
such that
$J_{\phi }:{\mathbb W}\to [{C_{4}}^{-1},C_{4}]$
such that

Theorem 1.3 (proved later in Section 7) will show that
![]() $J_{\phi }$
coincides with the intrinsic Jacobian determinant
$J_{\phi }$
coincides with the intrinsic Jacobian determinant
![]() $J^{\phi }\phi $
of
$J^{\phi }\phi $
of
![]() $\phi $
(see Definition 4.9) up to a multiplicative constant. We will, of course, need to consider
$\phi $
(see Definition 4.9) up to a multiplicative constant. We will, of course, need to consider
![]() $J_{\phi }$
and
$J_{\phi }$
and
![]() $J^{\phi }\phi $
as separate notions until Theorem 1.3 is proved, and we therefore ask the reader to remember that the two objects are distinguished even though quite similar in notation.
$J^{\phi }\phi $
as separate notions until Theorem 1.3 is proved, and we therefore ask the reader to remember that the two objects are distinguished even though quite similar in notation.
4.2 Intrinsic differentiability and blow-ups of intrinsic Lipschitz maps
Left-translations of intrinsic Lipschitz graphs are also intrinsic Lipschitz graphs. When
![]() $A\subset {\mathbb W}$
,
$A\subset {\mathbb W}$
,
![]() $\bar {w}\in A$
and an intrinsic Lipschitz map
$\bar {w}\in A$
and an intrinsic Lipschitz map
![]() $\phi :A\to {\mathbb V}$
are fixed and one sets
$\phi :A\to {\mathbb V}$
are fixed and one sets
![]() $\bar p:=\bar {w}\phi (\bar {w})$
; then (see [Reference Arena and Serapioni9, Proposition 3.6] or [Reference Franchi and Serapioni53, Proposition 2.21])
$\bar p:=\bar {w}\phi (\bar {w})$
; then (see [Reference Arena and Serapioni9, Proposition 3.6] or [Reference Franchi and Serapioni53, Proposition 2.21])
 $\bar p^{-1}\mathrm {gr}_{\phi }$
is the intrinsic Lipschitz graph of the map
$\bar p^{-1}\mathrm {gr}_{\phi }$
is the intrinsic Lipschitz graph of the map
![]() $\phi _{\bar {w}}:\bar p^{-1}A\phi (\bar {w})\to {\mathbb V}$
defined by
$\phi _{\bar {w}}:\bar p^{-1}A\phi (\bar {w})\to {\mathbb V}$
defined by
We observe that the domain
![]() $\bar p^{-1}A\phi (\bar {w})=\phi (\bar {w})^{-1}\bar {w}^{-1} A\phi (\bar {w})$
of
$\bar p^{-1}A\phi (\bar {w})=\phi (\bar {w})^{-1}\bar {w}^{-1} A\phi (\bar {w})$
of
![]() $\phi _{\bar {w}}$
is a subset of
$\phi _{\bar {w}}$
is a subset of
![]() ${\mathbb W}$
because
${\mathbb W}$
because
![]() ${\mathbb W}$
is a normal subgroup; moreover,
${\mathbb W}$
is a normal subgroup; moreover,
![]() $\phi _{\bar {w}}(0)=0$
by construction. Clearly,
$\phi _{\bar {w}}(0)=0$
by construction. Clearly,
![]() $\phi _{\bar {w}}$
has the same intrinsic Lipschitz constant as
$\phi _{\bar {w}}$
has the same intrinsic Lipschitz constant as
![]() $\phi $
.
$\phi $
.
Dilations of intrinsic Lipschitz graphs are intrinsic Lipschitz graphs too: if A and
![]() $\phi $
are as above,
$\phi $
are as above,
![]() $r>0$
and
$r>0$
and
![]() $\phi (0)=0$
, then
$\phi (0)=0$
, then
![]() $\delta _{r}(\mathrm {gr}_{\phi })$
is the intrinsic Lipschitz graph of the function
$\delta _{r}(\mathrm {gr}_{\phi })$
is the intrinsic Lipschitz graph of the function
![]() $\phi ^{r}:\delta _{r} A\to {\mathbb V}$
defined by
$\phi ^{r}:\delta _{r} A\to {\mathbb V}$
defined by
The intrinsic Lipschitz constant of
![]() $\phi ^{r}$
equals the one of
$\phi ^{r}$
equals the one of
![]() $\phi $
.
$\phi $
.
Definition 4.7. Let
![]() $\phi :A\to {\mathbb V}$
be a map defined on a (relatively) open subset
$\phi :A\to {\mathbb V}$
be a map defined on a (relatively) open subset
![]() $A\subset {\mathbb W}$
. We say that
$A\subset {\mathbb W}$
. We say that
![]() $\bar {\phi }:{\mathbb W}\to {\mathbb V}$
is a blow-up of
$\bar {\phi }:{\mathbb W}\to {\mathbb V}$
is a blow-up of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}\in A$
if there exists a sequence
$\bar {w}\in A$
if there exists a sequence
![]() $(r_{j})_{j}$
such that
$(r_{j})_{j}$
such that
![]() $r_{j}\to +\infty $
as
$r_{j}\to +\infty $
as
![]() $j\to +\infty $
and
$j\to +\infty $
and
 $$ \begin{align*} \lim_{j\to\infty} (\phi_{\bar{w}})^{r_{j}}=\bar{\phi}\qquad\text{locally uniformly on }{\mathbb W}\text{.} \end{align*} $$
$$ \begin{align*} \lim_{j\to\infty} (\phi_{\bar{w}})^{r_{j}}=\bar{\phi}\qquad\text{locally uniformly on }{\mathbb W}\text{.} \end{align*} $$
Remark 4.8. Clearly, every blow-up
![]() $\bar {\phi }$
of
$\bar {\phi }$
of
![]() $\phi $
is such that
$\phi $
is such that
![]() $\bar {\phi }(0)=0$
. Blow-ups of
$\bar {\phi }(0)=0$
. Blow-ups of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
are in general not unique. The functions
$\bar {w}$
are in general not unique. The functions
![]() $(\phi _{\bar {w}})^{r}$
,
$(\phi _{\bar {w}})^{r}$
,
![]() $r>0$
, have the same intrinsic Lipschitz constant as
$r>0$
, have the same intrinsic Lipschitz constant as
![]() $\phi $
; in particular, every blow-up of
$\phi $
; in particular, every blow-up of
![]() $\phi $
is intrinsic Lipschitz continuous with intrinsic Lipschitz constant not greater than the one of
$\phi $
is intrinsic Lipschitz continuous with intrinsic Lipschitz constant not greater than the one of
![]() $\phi $
.
$\phi $
.
We say that
![]() $\psi :{\mathbb W}\to {\mathbb V}$
is intrinsic linear if its graph
$\psi :{\mathbb W}\to {\mathbb V}$
is intrinsic linear if its graph
![]() $\mathrm {gr}_{\psi }$
is a homogeneous subgroup of
$\mathrm {gr}_{\psi }$
is a homogeneous subgroup of
![]() ${\mathbb H}^{n}$
; in coordinates, this is equivalent to requiring that
${\mathbb H}^{n}$
; in coordinates, this is equivalent to requiring that
![]() $\mathrm {gr}_{\psi }$
is a vertical plane (recall Definition 3.2) of dimension
$\mathrm {gr}_{\psi }$
is a vertical plane (recall Definition 3.2) of dimension
![]() $2n+1-k$
. Another characterisation can be given as follows. For every
$2n+1-k$
. Another characterisation can be given as follows. For every
![]() $w\in {\mathbb W}$
define
$w\in {\mathbb W}$
define
![]() $w_{H}\in {\mathbb R}^{2n+1-k}$
as
$w_{H}\in {\mathbb R}^{2n+1-k}$
as
 $$ \begin{align} \begin{array}{ll} w_{H}:=(x_{k+1},\dots,y_{n})\qquad & \text{if }k<n\text{ and }w=(x_{k+1},\dots,y_{n},t)\\ w_{H}:=(y_{1},\dots,y_{n}) & \text{if }k=n\text{ and }w=(y_{1},\dots,y_{n},t)\text{.} \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ll} w_{H}:=(x_{k+1},\dots,y_{n})\qquad & \text{if }k<n\text{ and }w=(x_{k+1},\dots,y_{n},t)\\ w_{H}:=(y_{1},\dots,y_{n}) & \text{if }k=n\text{ and }w=(y_{1},\dots,y_{n},t)\text{.} \end{array} \end{align} $$
Then,
![]() $\psi $
is intrinsic linear if and only if there exists a
$\psi $
is intrinsic linear if and only if there exists a
![]() $k\times (2n-k)$
matrix M (here identified with a linear map
$k\times (2n-k)$
matrix M (here identified with a linear map
![]() $M:{\mathbb R}^{2n-k}\to {\mathbb R}^{k}\equiv {\mathbb V}$
) such that, for every
$M:{\mathbb R}^{2n-k}\to {\mathbb R}^{k}\equiv {\mathbb V}$
) such that, for every
![]() $w\in {\mathbb W}$
,
$w\in {\mathbb W}$
,
![]() $\psi (w)=M\,w_{H}$
.
$\psi (w)=M\,w_{H}$
.
We can now state the following definition.
Definition 4.9. Let
![]() $A\subset {\mathbb W}$
be open and
$A\subset {\mathbb W}$
be open and
![]() $\phi :A\to {\mathbb V}$
be given; we say that
$\phi :A\to {\mathbb V}$
be given; we say that
![]() $\phi $
is intrinsically differentiable at
$\phi $
is intrinsically differentiable at
![]() $\bar {w}\in A$
if there exists an intrinsic linear map
$\bar {w}\in A$
if there exists an intrinsic linear map
![]() $d\phi _{\bar {w}}:{\mathbb W}\to {\mathbb V}$
such that
$d\phi _{\bar {w}}:{\mathbb W}\to {\mathbb V}$
such that
 $$ \begin{align*} \lim_{s\to0}\left( \sup\left\{ \frac{d(\phi_{\bar{w}}(w),d\phi_{\bar{w}}(w))}{d(0,w)}:w\in{\mathbb W}\cap B(0,s)\right\}\right)=0. \end{align*} $$
$$ \begin{align*} \lim_{s\to0}\left( \sup\left\{ \frac{d(\phi_{\bar{w}}(w),d\phi_{\bar{w}}(w))}{d(0,w)}:w\in{\mathbb W}\cap B(0,s)\right\}\right)=0. \end{align*} $$
The map
![]() $d\phi _{\bar {w}}$
is called intrinsic differential of
$d\phi _{\bar {w}}$
is called intrinsic differential of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
; the intrinsic graph of
$\bar {w}$
; the intrinsic graph of
![]() $d\phi _{\bar {w}}$
is called tangent plane to
$d\phi _{\bar {w}}$
is called tangent plane to
![]() $\mathrm {gr}_{\phi }$
at
$\mathrm {gr}_{\phi }$
at
![]() $\Phi (\bar {w})$
and is denoted by
$\Phi (\bar {w})$
and is denoted by
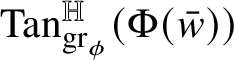 ${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}(\Phi (\bar {w}))$
.
${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}(\Phi (\bar {w}))$
.
The intrinsic gradient
![]() $\nabla ^{\phi }\phi (\bar {w}) $
is the unique
$\nabla ^{\phi }\phi (\bar {w}) $
is the unique
![]() $k\times (2n-k)$
matrix such that
$k\times (2n-k)$
matrix such that
![]() $d\phi _{\bar {w}}(w)=\nabla ^{\phi }\phi (\bar {w})\, w_{H}$
for every
$d\phi _{\bar {w}}(w)=\nabla ^{\phi }\phi (\bar {w})\, w_{H}$
for every
![]() $w\in {\mathbb W}$
. We also define the intrinsic Jacobian determinant
$w\in {\mathbb W}$
. We also define the intrinsic Jacobian determinant
![]() $J^{\phi }\phi (\bar {w})$
of
$J^{\phi }\phi (\bar {w})$
of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
as
$\bar {w}$
as
 $$ \begin{align*} J^{\phi}\phi(\bar{w}):=\left( 1+\sum_{M} (\det M)^{2} \right)^{1/2}, \end{align*} $$
$$ \begin{align*} J^{\phi}\phi(\bar{w}):=\left( 1+\sum_{M} (\det M)^{2} \right)^{1/2}, \end{align*} $$
where the sum ranges on all minors (of any size) of the matrix
![]() $\nabla ^{\phi }\phi $
.
$\nabla ^{\phi }\phi $
.
Remark 4.10. The notions introduced in Definition 4.9 (and, in particular, that of intrinsic Jacobian needed in Theorem 1.3) make sense also when the subgroups
![]() ${\mathbb W},{\mathbb V}$
are orthogonal; that is, when they are orthogonal as linear subspaces of
${\mathbb W},{\mathbb V}$
are orthogonal; that is, when they are orthogonal as linear subspaces of
![]() ${\mathbb H}^{n}\equiv {\mathbb R}^{2n+1}$
. In fact, as Remark 3.16 (see also [Reference Corni and Magnani33, §2.4]) in this case there exists an isometric
${\mathbb H}^{n}\equiv {\mathbb R}^{2n+1}$
. In fact, as Remark 3.16 (see also [Reference Corni and Magnani33, §2.4]) in this case there exists an isometric
![]() ${\mathbb H}$
-linear isomorphism sending
${\mathbb H}$
-linear isomorphism sending
![]() ${\mathbb W},{\mathbb V}$
to the subgroups defined in (4.3) and (4.2).
${\mathbb W},{\mathbb V}$
to the subgroups defined in (4.3) and (4.2).
Remark 4.11. It will be convenient to denote the components
![]() $(\nabla ^{\phi }\phi )_{ij}$
of the intrinsic gradient using indices that vary in the ranges
$(\nabla ^{\phi }\phi )_{ij}$
of the intrinsic gradient using indices that vary in the ranges
![]() $i=1,\dots , k$
and
$i=1,\dots , k$
and
![]() $j= k+1,\dots ,2n$
. This choice might seem a bit unusual for what concerns the index j, but it is somehow suggested by the definition of
$j= k+1,\dots ,2n$
. This choice might seem a bit unusual for what concerns the index j, but it is somehow suggested by the definition of
![]() $w_{H}$
. Further justification is provided in Subsection 4.5.
$w_{H}$
. Further justification is provided in Subsection 4.5.
In the following Proposition 4.12 we collect several statements that are equivalent to intrinsic differentiability: the equivalences among (a), (b) and (c) are straightforward, while for the equivalence with (d) we refer to [Reference Franchi, Serapioni and Serra Cassano52, Theorem 4.15].
Proposition 4.12. Consider an open set
![]() $A\subset {\mathbb W}$
, a map
$A\subset {\mathbb W}$
, a map
![]() $\phi :{\mathbb W}\to {\mathbb V}$
and a point
$\phi :{\mathbb W}\to {\mathbb V}$
and a point
![]() $\bar {w}\in A$
. Then the following statements are equivalent:
$\bar {w}\in A$
. Then the following statements are equivalent:
-
(a)
 $\phi $
is intrinsically differentiable at
$\phi $
is intrinsically differentiable at
 $\bar {w}$
;
$\bar {w}$
; -
(b) there exists an intrinsic linear map
 $\psi :{\mathbb W}\to {\mathbb V}$
such that
$\psi :{\mathbb W}\to {\mathbb V}$
such that
 $(\phi _{\bar {w}})^{r}\to \psi $
locally uniformly on
$(\phi _{\bar {w}})^{r}\to \psi $
locally uniformly on
 ${\mathbb W}$
as
${\mathbb W}$
as
 $r\to +\infty $
;
$r\to +\infty $
; -
(c) the blow-up of
 $\phi $
at
$\phi $
at
 $\bar {w}$
is unique and it is an intrinsic linear map;
$\bar {w}$
is unique and it is an intrinsic linear map; -
(d) there exists a
 $(2n+1-k)$
-dimensional vertical plane
$(2n+1-k)$
-dimensional vertical plane
 ${\mathscr P}$
that is complementary to
${\mathscr P}$
that is complementary to
 ${\mathbb V}$
and such that, as
${\mathbb V}$
and such that, as
 $r\to +\infty $
, the sets
$r\to +\infty $
, the sets
 $\delta _{r}(\Phi (\bar {w})^{-1}\mathrm {gr}_{\phi })$
converge to
$\delta _{r}(\Phi (\bar {w})^{-1}\mathrm {gr}_{\phi })$
converge to
 ${\mathscr P}$
with respect to the local Hausdorff convergence of sets; that is, (4.17)
${\mathscr P}$
with respect to the local Hausdorff convergence of sets; that is, (4.17) $$ \begin{align} \lim_{s\to 0^{+}} \left(\sup\left\{\frac{d(\Phi(\bar{w})^{-1}p,{\mathscr P})}{d(\Phi(\bar{w}),p)}: p\in\mathrm{gr}_{\phi}\cap B(\Phi(\bar{w}),s)\right\}\right)=0. \end{align} $$
$$ \begin{align} \lim_{s\to 0^{+}} \left(\sup\left\{\frac{d(\Phi(\bar{w})^{-1}p,{\mathscr P})}{d(\Phi(\bar{w}),p)}: p\in\mathrm{gr}_{\phi}\cap B(\Phi(\bar{w}),s)\right\}\right)=0. \end{align} $$
Moreover, the plane
![]() ${\mathscr P}$
in (d) coincides with
${\mathscr P}$
in (d) coincides with
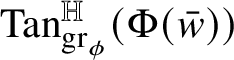 ${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}(\Phi (\bar {w}))$
.
${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}(\Phi (\bar {w}))$
.
It is worth observing that intrinsic graphs parametrising
![]() ${\mathbb H}$
-regular submanifolds are intrinsically differentiable; see Remark 4.18 for a precise statement.
${\mathbb H}$
-regular submanifolds are intrinsically differentiable; see Remark 4.18 for a precise statement.
As one can easily guess, intrinsic Lipschitz functions with small Lipschitz constant have small intrinsic gradient at differentiability points; the following lemma provides a quantitative version of this statement.
Lemma 4.13. Assume that
![]() ${\mathbb H}^{n}$
is endowed with the distance
${\mathbb H}^{n}$
is endowed with the distance
![]() $d=d_{\infty }$
introduced in (3.2). Let
$d=d_{\infty }$
introduced in (3.2). Let
![]() $\phi :A\to {\mathbb V}$
be an intrinsic Lipschitz function defined on an open set A of
$\phi :A\to {\mathbb V}$
be an intrinsic Lipschitz function defined on an open set A of
![]() ${\mathbb W}$
and let
${\mathbb W}$
and let
![]() $\alpha $
be the intrinsic Lipschitz constant of
$\alpha $
be the intrinsic Lipschitz constant of
![]() $\phi $
. Then for every point
$\phi $
. Then for every point
![]() $w\in A$
where
$w\in A$
where
![]() $\phi $
is intrinsically differentiable, we have
$\phi $
is intrinsically differentiable, we have
 $$ \begin{align} |(\nabla^{\phi}\phi(w))_{ij}|\leq\alpha\qquad\forall\: i=1,\dots,k,\ \forall\:j=k+1,\dots,2n. \end{align} $$
$$ \begin{align} |(\nabla^{\phi}\phi(w))_{ij}|\leq\alpha\qquad\forall\: i=1,\dots,k,\ \forall\:j=k+1,\dots,2n. \end{align} $$
Proof. By Remark 4.8, the intrinsic differential
![]() $d\phi _{w}$
is intrinsic Lipschitz with Lipschitz constant not greater than
$d\phi _{w}$
is intrinsic Lipschitz with Lipschitz constant not greater than
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $i,j$
be as in (4.18); then, by Remark 4.2, we have
$i,j$
be as in (4.18); then, by Remark 4.2, we have
 $$ \begin{align*} |(\nabla^{\phi}\phi(w))_{ij}| = |(d\phi_{w}(\exp(W_{j})))_{i}|\leq\alpha\|\exp(W_{j})\|_{\mathbb H}=\alpha\, d_{\infty}(0,\exp(W_{j}))=\alpha, \end{align*} $$
$$ \begin{align*} |(\nabla^{\phi}\phi(w))_{ij}| = |(d\phi_{w}(\exp(W_{j})))_{i}|\leq\alpha\|\exp(W_{j})\|_{\mathbb H}=\alpha\, d_{\infty}(0,\exp(W_{j}))=\alpha, \end{align*} $$
where
![]() $(d\phi _{w}(\exp (W_{j})))_{i}$
is the i-component of
$(d\phi _{w}(\exp (W_{j})))_{i}$
is the i-component of
![]() $d\phi _{w}(\exp (W_{j}))\in {\mathbb V}\equiv {\mathbb R}^{k}$
.
$d\phi _{w}(\exp (W_{j}))\in {\mathbb V}\equiv {\mathbb R}^{k}$
.
4.3 Blow-ups of intrinsic Lipschitz maps are almost always t-invariant
The aim of this section is the proof of the following Lemma 4.16, a very first step towards Theorem 1.1. Given
![]() $h\in {\mathbb R}$
, we write
$h\in {\mathbb R}$
, we write
 $\vec h:=\exp (hT)$
and we observe that, in coordinates,
$\vec h:=\exp (hT)$
and we observe that, in coordinates,
 $(x,y,t)\vec h=(x,y,t+h)$
.
$(x,y,t)\vec h=(x,y,t+h)$
.
We say that
![]() $\phi :{\mathbb W}\to {\mathbb V}$
is t-invariant if
$\phi :{\mathbb W}\to {\mathbb V}$
is t-invariant if
 $$ \begin{align*} \phi(w\vec h)=\phi(w)\qquad\text{for every }w\in{\mathbb W},\ h\in{\mathbb R}. \end{align*} $$
$$ \begin{align*} \phi(w\vec h)=\phi(w)\qquad\text{for every }w\in{\mathbb W},\ h\in{\mathbb R}. \end{align*} $$
With the notation introduced in (4.16),
![]() $\phi :{\mathbb W}\to {\mathbb V}$
is t-invariant if and only if there exists
$\phi :{\mathbb W}\to {\mathbb V}$
is t-invariant if and only if there exists
![]() $f_{\phi }:{\mathbb R}^{2n-k}\to {\mathbb R}^{k}\equiv {\mathbb V}$
such that
$f_{\phi }:{\mathbb R}^{2n-k}\to {\mathbb R}^{k}\equiv {\mathbb V}$
such that
Clearly, every intrinsic linear map
![]() $\psi :{\mathbb W}\to {\mathbb V}$
is t-invariant; a simple consequence of this fact is contained in the following observation.
$\psi :{\mathbb W}\to {\mathbb V}$
is t-invariant; a simple consequence of this fact is contained in the following observation.
Remark 4.14. If
![]() $\phi $
is intrinsically differentiable at
$\phi $
is intrinsically differentiable at
![]() $\bar {w}$
, then
$\bar {w}$
, then
 $$ \begin{align*} |\phi(\bar{w}\vec h)-\phi(\bar{w})|=o(|h|^{1/2})\qquad\text{as }h\to0. \end{align*} $$
$$ \begin{align*} |\phi(\bar{w}\vec h)-\phi(\bar{w})|=o(|h|^{1/2})\qquad\text{as }h\to0. \end{align*} $$
This is a simple consequence of the fact that, as
![]() $r\to +\infty $
,
$r\to +\infty $
,
![]() $(\phi _{\bar {w}})^{r}$
converges to an intrinsic linear (and then t-invariant) map.
$(\phi _{\bar {w}})^{r}$
converges to an intrinsic linear (and then t-invariant) map.
Let us collect some basic facts about intrinsic Lipschitz maps that are also t-invariant. Though very simple, they will be useful in the sequel.
Lemma 4.15. Let
![]() $\phi :{\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz continuous and t-invariant and let
$\phi :{\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz continuous and t-invariant and let
![]() $f_{\phi }$
be as in (4.19). Then
$f_{\phi }$
be as in (4.19). Then
-
(i)
 $f_{\phi }:{\mathbb R}^{2n-k}\to {\mathbb R}^{k}$
and
$f_{\phi }:{\mathbb R}^{2n-k}\to {\mathbb R}^{k}$
and
 $\phi :{\mathbb W}\equiv {\mathbb R}^{2n-k}\to {\mathbb V}\equiv {\mathbb R}^{k}$
are Euclidean Lipschitz continuous;
$\phi :{\mathbb W}\equiv {\mathbb R}^{2n-k}\to {\mathbb V}\equiv {\mathbb R}^{k}$
are Euclidean Lipschitz continuous; -
(ii) the intrinsic graph
 $\mathrm {gr}_{\phi }$
coincides with
$\mathrm {gr}_{\phi }$
coincides with  $$ \begin{align*} \{(f_{\phi}(w),w,t)\in{\mathbb R}^{k}\times{\mathbb R}^{2n-k}\times{\mathbb R}\equiv{\mathbb H}^{n}:w\in{\mathbb R}^{2n-k},t\in{\mathbb R}\}; \end{align*} $$
$$ \begin{align*} \{(f_{\phi}(w),w,t)\in{\mathbb R}^{k}\times{\mathbb R}^{2n-k}\times{\mathbb R}\equiv{\mathbb H}^{n}:w\in{\mathbb R}^{2n-k},t\in{\mathbb R}\}; \end{align*} $$
-
(iii)
 $\phi $
is Euclidean differentiable at
$\phi $
is Euclidean differentiable at
 $\bar {w}$
if and only if
$\bar {w}$
if and only if
 $f_{\phi }$
is Euclidean differentiable at
$f_{\phi }$
is Euclidean differentiable at
 $\bar {w}_{H}$
;
$\bar {w}_{H}$
; -
(iv)
 $\phi $
is intrinsically differentiable at
$\phi $
is intrinsically differentiable at
 $\bar {w}$
if and only if it is Euclidean differentiable at
$\bar {w}$
if and only if it is Euclidean differentiable at
 $\bar {w}$
. In this case,
$\bar {w}$
. In this case,
 $\nabla ^{\phi }\phi (\bar {w})=\nabla f_{\phi }(\bar {w}_{H})$
.
$\nabla ^{\phi }\phi (\bar {w})=\nabla f_{\phi }(\bar {w}_{H})$
.
Proof. The second part of statement (i) is a direct consequence of the first one, which we now prove only in case
![]() $k<n$
as the case
$k<n$
as the case
![]() $k=n$
requires only minor adjustment in the notation. For every
$k=n$
requires only minor adjustment in the notation. For every
![]() $u=(x_{k+1},\dots ,y_{n})\in {\mathbb R}^{2n-k}$
and
$u=(x_{k+1},\dots ,y_{n})\in {\mathbb R}^{2n-k}$
and
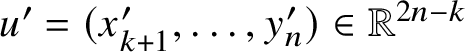 $u^{\prime }=(x_{k+1}^{\prime },\dots ,y_{n}^{\prime })\in {\mathbb R}^{2n-k}$
, consider
$u^{\prime }=(x_{k+1}^{\prime },\dots ,y_{n}^{\prime })\in {\mathbb R}^{2n-k}$
, consider
![]() $w:=(x_{k+1},\dots ,y_{n},0)\in {\mathbb W}$
and
$w:=(x_{k+1},\dots ,y_{n},0)\in {\mathbb W}$
and
![]() $w^{\prime }:=(x_{k+1}^{\prime },\dots ,y_{n}^{\prime },t^{\prime })\in {\mathbb W}$
, where
$w^{\prime }:=(x_{k+1}^{\prime },\dots ,y_{n}^{\prime },t^{\prime })\in {\mathbb W}$
, where
![]() $t^{\prime }=t^{\prime }(u,u^{\prime })$
is defined by
$t^{\prime }=t^{\prime }(u,u^{\prime })$
is defined by
 $$ \begin{align*} t^{\prime}:=\frac 12\sum_{j=k+1}^{n}(x_{j}y_{j}^{\prime}-x_{j}^{\prime}y_{j})-\sum_{j=1}^{k} (f_{\phi}(u^{\prime}))_{j}(y_{j}-y_{j}^{\prime}). \end{align*} $$
$$ \begin{align*} t^{\prime}:=\frac 12\sum_{j=k+1}^{n}(x_{j}y_{j}^{\prime}-x_{j}^{\prime}y_{j})-\sum_{j=1}^{k} (f_{\phi}(u^{\prime}))_{j}(y_{j}-y_{j}^{\prime}). \end{align*} $$
From (4.9) we deduce that for a suitable
![]() $\alpha>0$
and a positive C depending on the distance d,
$\alpha>0$
and a positive C depending on the distance d,
 $$ \begin{align*} |f_{\phi}(u) - f_{\phi}(u^{\prime}) | & = |\phi(w)-\phi(w^{\prime})|\\ &\leq \alpha \|(x_{k+1}-x_{k+1}^{\prime},\dots,y_{n}-y_{n}^{\prime},0) \|_{\mathbb H} \\ &\leq C\alpha d_{\infty}(0,(x_{k+1}-x_{k+1}^{\prime},\dots,y_{n}-y_{n}^{\prime},0))\\ &= C\alpha \|u-u^{\prime}\|_{{\mathbb R}^{2n-k}}. \end{align*} $$
$$ \begin{align*} |f_{\phi}(u) - f_{\phi}(u^{\prime}) | & = |\phi(w)-\phi(w^{\prime})|\\ &\leq \alpha \|(x_{k+1}-x_{k+1}^{\prime},\dots,y_{n}-y_{n}^{\prime},0) \|_{\mathbb H} \\ &\leq C\alpha d_{\infty}(0,(x_{k+1}-x_{k+1}^{\prime},\dots,y_{n}-y_{n}^{\prime},0))\\ &= C\alpha \|u-u^{\prime}\|_{{\mathbb R}^{2n-k}}. \end{align*} $$
This proves (i).
Statements (ii) and (iii) are trivial. Concerning (iv), if
![]() $f_{\phi }$
is Euclidean differentiable at
$f_{\phi }$
is Euclidean differentiable at
![]() $\bar {w}\in {\mathbb W}$
, one has
$\bar {w}\in {\mathbb W}$
, one has
 $$ \begin{align} \begin{aligned} \phi_{\bar{w}}(w)& = \phi(\bar{w})^{-1}\phi(\bar{w}\phi(\bar{w}) w \phi(\bar{w})^{-1}) = f_{\phi}((\bar{w}\phi(\bar{w}) w \phi(\bar{w})^{-1})_{H}) - f_{\phi}(\bar{w}_{H}) \\ &= f_{\phi}( \bar{w}_{H}+w_{H}) - f_{\phi}(\bar{w}_{H}) = \nabla f_{\phi}(\bar{w}) w_{H} + o(|w_{H}|) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \phi_{\bar{w}}(w)& = \phi(\bar{w})^{-1}\phi(\bar{w}\phi(\bar{w}) w \phi(\bar{w})^{-1}) = f_{\phi}((\bar{w}\phi(\bar{w}) w \phi(\bar{w})^{-1})_{H}) - f_{\phi}(\bar{w}_{H}) \\ &= f_{\phi}( \bar{w}_{H}+w_{H}) - f_{\phi}(\bar{w}_{H}) = \nabla f_{\phi}(\bar{w}) w_{H} + o(|w_{H}|) \end{aligned} \end{align} $$
and the intrinsic differentiability of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
follows because
$\bar {w}$
follows because
![]() $|w_{H}|\leq d_{\infty }(0,w)\leq C d(0,w)$
for a suitable
$|w_{H}|\leq d_{\infty }(0,w)\leq C d(0,w)$
for a suitable
![]() $C>0$
. Conversely, assume that
$C>0$
. Conversely, assume that
![]() $\phi $
is intrinsically differentiable at
$\phi $
is intrinsically differentiable at
![]() $\bar {w}$
; for every
$\bar {w}$
; for every
![]() $u\in {\mathbb R}^{2n-k}$
we define
$u\in {\mathbb R}^{2n-k}$
we define
![]() $w=(u,0)\in {\mathbb W}$
and, as in (4.20), we obtain
$w=(u,0)\in {\mathbb W}$
and, as in (4.20), we obtain
 $$ \begin{align*} f_{\phi}( \bar{w}_{H}+u) - f_{\phi}(\bar{w}_{H}) &= f_{\phi}( \bar{w}_{H}+w_{H}) - f_{\phi}(\bar{w}_{H})\\ & = \phi_{\bar{w}}(w) = d\phi_{\bar{w}}(w)+o(d_{\infty}(0,w))=\nabla^{\phi}\phi(\bar{w})w_{H} + o(|u|). \end{align*} $$
$$ \begin{align*} f_{\phi}( \bar{w}_{H}+u) - f_{\phi}(\bar{w}_{H}) &= f_{\phi}( \bar{w}_{H}+w_{H}) - f_{\phi}(\bar{w}_{H})\\ & = \phi_{\bar{w}}(w) = d\phi_{\bar{w}}(w)+o(d_{\infty}(0,w))=\nabla^{\phi}\phi(\bar{w})w_{H} + o(|u|). \end{align*} $$
This proves that
![]() $f_{\phi }$
is Euclidean differentiable at
$f_{\phi }$
is Euclidean differentiable at
![]() $\bar {w}_{H}$
and, by (iii), that
$\bar {w}_{H}$
and, by (iii), that
![]() $\phi $
is Euclidean differentiable at
$\phi $
is Euclidean differentiable at
![]() $w\in {\mathbb W}$
.
$w\in {\mathbb W}$
.
We now state and prove the following result, which will play a distinguished role in the proof of Theorem 1.1.
Lemma 4.16. Let
![]() $\phi :{\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz. Then there exists a
$\phi :{\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz. Then there exists a
![]() ${\mathscr L}^{2n+1-k}$
-negligible set
${\mathscr L}^{2n+1-k}$
-negligible set
![]() $E\subset {\mathbb W}$
such that, for every
$E\subset {\mathbb W}$
such that, for every
![]() $\bar {w}\in {\mathbb W}\setminus E$
and every blow-up
$\bar {w}\in {\mathbb W}\setminus E$
and every blow-up
![]() $\bar {\phi }:{\mathbb W}\to {\mathbb V}$
of
$\bar {\phi }:{\mathbb W}\to {\mathbb V}$
of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
,
$\bar {w}$
,
![]() $\bar {\phi }$
is t-invariant.
$\bar {\phi }$
is t-invariant.
Proof. We prove the statement assuming
![]() $k<n$
, the case
$k<n$
, the case
![]() $k=n$
requiring only straightforward modifications in the notation.
$k=n$
requiring only straightforward modifications in the notation.
We claim that
 $$ \begin{align} \text{for a.e. }\bar{w}\in{\mathbb W}\qquad|\phi(\bar{w}\vec h)-\phi(\bar{w})|=o(|h|^{1/2})\text{ as }h\to0. \end{align} $$
$$ \begin{align} \text{for a.e. }\bar{w}\in{\mathbb W}\qquad|\phi(\bar{w}\vec h)-\phi(\bar{w})|=o(|h|^{1/2})\text{ as }h\to0. \end{align} $$
To prove this, we write
![]() $\phi =(\phi _{1},\dots ,\phi _{k})\in {\mathbb V}\equiv {\mathbb R}^{k}$
and, for every fixed
$\phi =(\phi _{1},\dots ,\phi _{k})\in {\mathbb V}\equiv {\mathbb R}^{k}$
and, for every fixed
![]() $i\in \{1,\dots ,k\}$
and every fixed
$i\in \{1,\dots ,k\}$
and every fixed
![]() $(\bar {x}_{k+1},\dots , \bar {x}_{n},\bar {y}_{1},\dots ,\bar {y}_{i-1},\bar {y}_{i+1},\dots \bar {y}_{n})\in {\mathbb R}^{2n-k-1}$
, we consider the map
$(\bar {x}_{k+1},\dots , \bar {x}_{n},\bar {y}_{1},\dots ,\bar {y}_{i-1},\bar {y}_{i+1},\dots \bar {y}_{n})\in {\mathbb R}^{2n-k-1}$
, we consider the map
![]() $\psi _{i}:{\mathbb R}^{2}\to {\mathbb R}$
defined by
$\psi _{i}:{\mathbb R}^{2}\to {\mathbb R}$
defined by
Using (4.9) we obtain that for every
![]() $y,y^{\prime },t,t^{\prime }\in {\mathbb R}$
,
$y,y^{\prime },t,t^{\prime }\in {\mathbb R}$
,
where
![]() $\alpha $
is the intrinsic Lipschitz constant of
$\alpha $
is the intrinsic Lipschitz constant of
![]() $\phi $
. This ensures that
$\phi $
. This ensures that
![]() $\psi _{i}$
is intrinsic Lipschitz in
$\psi _{i}$
is intrinsic Lipschitz in
![]() ${\mathbb H}^{1}$
; that is, when seen as a map
${\mathbb H}^{1}$
; that is, when seen as a map
![]() $\psi _{i}:{\mathbb W}^{\prime }\to {\mathbb V}^{\prime }$
where
$\psi _{i}:{\mathbb W}^{\prime }\to {\mathbb V}^{\prime }$
where
![]() ${\mathbb W}^{\prime }:=\{(0,y,t):y,t\in {\mathbb R}\}$
and
${\mathbb W}^{\prime }:=\{(0,y,t):y,t\in {\mathbb R}\}$
and
![]() ${\mathbb V}^{\prime }:=\{(x,0,0):x\in {\mathbb R}\}$
. By Rademacher’s theorem for intrinsic Lipschitz graph of codimension 1 [Reference Franchi, Serapioni and Serra Cassano52],
${\mathbb V}^{\prime }:=\{(x,0,0):x\in {\mathbb R}\}$
. By Rademacher’s theorem for intrinsic Lipschitz graph of codimension 1 [Reference Franchi, Serapioni and Serra Cassano52],
![]() $\psi _{i}$
is intrinsically differentiable at
$\psi _{i}$
is intrinsically differentiable at
![]() ${\mathscr L}^{2}$
-a.e.
${\mathscr L}^{2}$
-a.e.
![]() $(y,t)\in {\mathbb W}^{\prime }$
and, by Remark 4.14, for every such
$(y,t)\in {\mathbb W}^{\prime }$
and, by Remark 4.14, for every such
![]() $(y,t)$
one has
$(y,t)$
one has
The claim (4.21) easily follows.
In order to prove the statement of the lemma, it suffices to prove that, for every fixed
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $E_{\varepsilon }\subset {\mathbb W}$
such that
$E_{\varepsilon }\subset {\mathbb W}$
such that
-
(a)
 ${\mathscr L}^{2n+1-k}(E_{\varepsilon })<\varepsilon $
and
${\mathscr L}^{2n+1-k}(E_{\varepsilon })<\varepsilon $
and -
(b) for every
 $\bar {w}\in {\mathbb W}\setminus E_{\varepsilon }$
and every blow-up
$\bar {w}\in {\mathbb W}\setminus E_{\varepsilon }$
and every blow-up
 $\bar {\phi }:{\mathbb W}\to {\mathbb V}$
of
$\bar {\phi }:{\mathbb W}\to {\mathbb V}$
of
 $\phi $
at
$\phi $
at
 $\bar {w}$
,
$\bar {w}$
,
 $\bar {\phi }$
is t-invariant.
$\bar {\phi }$
is t-invariant.
By (4.21) and the Severini–Egorov theorem, for every
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $E_{\varepsilon }\subset {\mathbb W}$
such that
$E_{\varepsilon }\subset {\mathbb W}$
such that
-
1.
 ${\mathscr L}^{2n+1-k}(E_{\varepsilon })<\varepsilon $
and
${\mathscr L}^{2n+1-k}(E_{\varepsilon })<\varepsilon $
and -
2. there exists a sequence
 $(\delta _{i})_{i}$
such that
$(\delta _{i})_{i}$
such that  $$ \begin{align*} |\phi(\bar{w}\vec h)-\phi(\bar{w})|<\frac{|h|^{1/2}}i \qquad\text{for every }\bar{w}\in{\mathbb W}\setminus E_{\varepsilon}\text{, }i\in\mathbb N\text{ and }h\in(-\delta_{i},\delta_{i}). \end{align*} $$
$$ \begin{align*} |\phi(\bar{w}\vec h)-\phi(\bar{w})|<\frac{|h|^{1/2}}i \qquad\text{for every }\bar{w}\in{\mathbb W}\setminus E_{\varepsilon}\text{, }i\in\mathbb N\text{ and }h\in(-\delta_{i},\delta_{i}). \end{align*} $$
By (4.6), the Lebesgue measure
![]() ${\mathscr L}^{2n+1-k}$
is doubling and the Lebesgue theorem holds in the metric measure space
${\mathscr L}^{2n+1-k}$
is doubling and the Lebesgue theorem holds in the metric measure space
![]() $({\mathbb W},d,{\mathscr L}^{2n+1-k})$
(see, e.g., [Reference Stein91, Chapter 1]). Therefore, up to modifying
$({\mathbb W},d,{\mathscr L}^{2n+1-k})$
(see, e.g., [Reference Stein91, Chapter 1]). Therefore, up to modifying
![]() $E_{\varepsilon }$
on a negligible set, we can also assume that
$E_{\varepsilon }$
on a negligible set, we can also assume that
-
(3) for every
 $\bar {w}\in {\mathbb W}\setminus E_{\varepsilon }$
$\bar {w}\in {\mathbb W}\setminus E_{\varepsilon }$
 $$ \begin{align*} \lim_{s\to 0}\frac{{\mathscr L}^{2n+1-k}(B(\bar{w},s)\cap{\mathbb W}\setminus E_{\varepsilon})}{{\mathscr L}^{2n+1-k}(B(\bar{w},s)\cap {\mathbb W})}=1. \end{align*} $$
$$ \begin{align*} \lim_{s\to 0}\frac{{\mathscr L}^{2n+1-k}(B(\bar{w},s)\cap{\mathbb W}\setminus E_{\varepsilon})}{{\mathscr L}^{2n+1-k}(B(\bar{w},s)\cap {\mathbb W})}=1. \end{align*} $$
By construction,
![]() $E_{\varepsilon }$
satisfies (a) above; we are going to prove it also satisfies (b), thus completing the proof.
$E_{\varepsilon }$
satisfies (a) above; we are going to prove it also satisfies (b), thus completing the proof.
Let then
![]() $\bar {w}\in {\mathbb W}\setminus E_{\varepsilon }$
and a blow-up
$\bar {w}\in {\mathbb W}\setminus E_{\varepsilon }$
and a blow-up
![]() $\bar {\phi }:{\mathbb W}\to {\mathbb V}$
of
$\bar {\phi }:{\mathbb W}\to {\mathbb V}$
of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
be fixed; up to a left-translation, we can assume without loss of generality that
$\bar {w}$
be fixed; up to a left-translation, we can assume without loss of generality that
![]() $\bar {w}=0$
. Let
$\bar {w}=0$
. Let
![]() $r_{j}\to +\infty $
be a sequence such that
$r_{j}\to +\infty $
be a sequence such that
 $$ \begin{align*} \lim_{j\to+\infty}\phi^{r_{j}}=\bar{\phi}\qquad\text{in }L^{\infty}_{loc}({\mathbb W}). \end{align*} $$
$$ \begin{align*} \lim_{j\to+\infty}\phi^{r_{j}}=\bar{\phi}\qquad\text{in }L^{\infty}_{loc}({\mathbb W}). \end{align*} $$
Let
![]() $R>0$
be fixed; we prove that
$R>0$
be fixed; we prove that
which would immediately give (b). In turn, it is enough to prove that for every
![]() $\eta>0$
there exists
$\eta>0$
there exists
![]() $\bar \jmath \in \mathbb N$
such that
$\bar \jmath \in \mathbb N$
such that
Observe that, by property (3), for j large enough the set
![]() $\delta _{r_{j}}({\mathbb W}\setminus E_{\varepsilon })$
is
$\delta _{r_{j}}({\mathbb W}\setminus E_{\varepsilon })$
is
![]() $\eta $
-dense in the box
$\eta $
-dense in the box
![]() $[-R,R]^{2n+1-k}$
; namely, for every
$[-R,R]^{2n+1-k}$
; namely, for every
![]() $w=( x_{k+1},\dots , y_{n}, t)\in [-R,R]^{2n+1-k}$
there exists
$w=( x_{k+1},\dots , y_{n}, t)\in [-R,R]^{2n+1-k}$
there exists
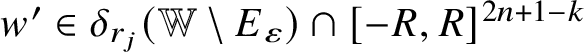 $w^{\prime }\in \delta _{r_{j}}({\mathbb W}\setminus E_{\varepsilon })\cap [-R,R]^{2n+1-k}$
such that
$w^{\prime }\in \delta _{r_{j}}({\mathbb W}\setminus E_{\varepsilon })\cap [-R,R]^{2n+1-k}$
such that
![]() $|w-w^{\prime }|<\eta $
. We write
$|w-w^{\prime }|<\eta $
. We write
![]() $w^{\prime }=( x_{k+1}^{\prime },\dots , y_{n}^{\prime }, t^{\prime })$
; setting
$w^{\prime }=( x_{k+1}^{\prime },\dots , y_{n}^{\prime }, t^{\prime })$
; setting
![]() $i:=\lfloor R^{1/2}/\eta \rfloor +1$
, for large enough j (and, namely, for
$i:=\lfloor R^{1/2}/\eta \rfloor +1$
, for large enough j (and, namely, for
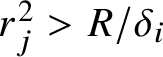 $r_{j}^{2}>R/\delta _{i}$
) we have
$r_{j}^{2}>R/\delta _{i}$
) we have
 $$ \begin{align*} &|\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime}, t^{\prime})-\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime}, 0)|\\ &\quad = r_{j}\left|\phi( \tfrac{x_{k+1}^{\prime}}{r_{j}},\dots, \tfrac{y_{n}^{\prime}}{r_{j}}, \tfrac{t^{\prime}}{r_{j}^{2}})- \phi( \tfrac{x_{k+1}^{\prime}}{r_{j}},\dots, \tfrac{y_{n}^{\prime}}{r_{j}}, 0)\right|\ \leq\ r_{j}\,\frac{|t^{\prime}|^{1/2}}{i\,r_{j}}\ \leq \frac{R^{1/2}}{i}\ <\ \eta, \end{align*} $$
$$ \begin{align*} &|\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime}, t^{\prime})-\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime}, 0)|\\ &\quad = r_{j}\left|\phi( \tfrac{x_{k+1}^{\prime}}{r_{j}},\dots, \tfrac{y_{n}^{\prime}}{r_{j}}, \tfrac{t^{\prime}}{r_{j}^{2}})- \phi( \tfrac{x_{k+1}^{\prime}}{r_{j}},\dots, \tfrac{y_{n}^{\prime}}{r_{j}}, 0)\right|\ \leq\ r_{j}\,\frac{|t^{\prime}|^{1/2}}{i\,r_{j}}\ \leq \frac{R^{1/2}}{i}\ <\ \eta, \end{align*} $$
where we used
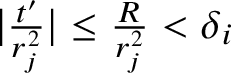 $|\tfrac {t^{\prime }}{r_{j}^{2}}|\leq \tfrac {R}{r_{j}^{2}}<\delta _{i}$
and the fact that
$|\tfrac {t^{\prime }}{r_{j}^{2}}|\leq \tfrac {R}{r_{j}^{2}}<\delta _{i}$
and the fact that
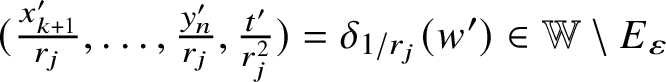 $( \tfrac {x_{k+1}^{\prime }}{r_{j}},\dots , \tfrac {y_{n}^{\prime }}{r_{j}}, \tfrac {t^{\prime }}{r_{j}^{2}})=\delta _{1/r_{j}}(w^{\prime })\in {\mathbb W}\setminus E_{\varepsilon }$
satisfies (2). By Remark 4.5 there exists
$( \tfrac {x_{k+1}^{\prime }}{r_{j}},\dots , \tfrac {y_{n}^{\prime }}{r_{j}}, \tfrac {t^{\prime }}{r_{j}^{2}})=\delta _{1/r_{j}}(w^{\prime })\in {\mathbb W}\setminus E_{\varepsilon }$
satisfies (2). By Remark 4.5 there exists
![]() $C>0$
(depending only on R and the Lipschitz constant of
$C>0$
(depending only on R and the Lipschitz constant of
![]() $\phi ^{r_{j}}$
, which is the same as the Lipschitz constant of
$\phi ^{r_{j}}$
, which is the same as the Lipschitz constant of
![]() $\phi $
and is thus independent of j) and we finally obtain for large enough j
$\phi $
and is thus independent of j) and we finally obtain for large enough j
 $$ \begin{align*} |\phi^{r_{j}}( x_{k+1},\dots, y_{n}, t)-\phi^{r_{j}}( x_{k+1},\dots, y_{n},0)| &\leq |\phi^{r_{j}}( x_{k+1},\dots, y_{n}, t)-\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime},t^{\prime})| \\ &\quad + |\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime}, t^{\prime})-\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime},0)| \\ &\quad + |\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime},0)-\phi^{r_{j}}( x_{k+1},\dots, y_{n},0)|\\ &\leq 2C|w-w^{\prime}|^{1/2} + \eta\\ &\leq 2C\eta^{1/2}+\eta. \end{align*} $$
$$ \begin{align*} |\phi^{r_{j}}( x_{k+1},\dots, y_{n}, t)-\phi^{r_{j}}( x_{k+1},\dots, y_{n},0)| &\leq |\phi^{r_{j}}( x_{k+1},\dots, y_{n}, t)-\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime},t^{\prime})| \\ &\quad + |\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime}, t^{\prime})-\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime},0)| \\ &\quad + |\phi^{r_{j}}( x_{k+1}^{\prime},\dots, y_{n}^{\prime},0)-\phi^{r_{j}}( x_{k+1},\dots, y_{n},0)|\\ &\leq 2C|w-w^{\prime}|^{1/2} + \eta\\ &\leq 2C\eta^{1/2}+\eta. \end{align*} $$
Since the requirements made on j depend on
![]() $\eta $
and R but not on
$\eta $
and R but not on
![]() $( x_{k+1},\dots , y_{n}, t)\in [-R,R]^{2n+1-k}$
, we have proved the existence of
$( x_{k+1},\dots , y_{n}, t)\in [-R,R]^{2n+1-k}$
, we have proved the existence of
![]() $\bar \jmath $
such that (4.22) holds. This concludes the proof.
$\bar \jmath $
such that (4.22) holds. This concludes the proof.
4.4
 ${\mathbb H}$
-regular submanifolds and
${\mathbb H}$
-regular submanifolds and
 ${\mathbb H}$
-rectifiable sets
${\mathbb H}$
-rectifiable sets
In this section we briefly introduce submanifolds with intrinsic
![]() $C^{1}$
regularity in Heisenberg groups together with the notion of
$C^{1}$
regularity in Heisenberg groups together with the notion of
![]() ${\mathbb H}$
-rectifiability. We refer to [Reference Franchi, Serapioni and Serra Cassano51] for a more comprehensive presentation.
${\mathbb H}$
-rectifiability. We refer to [Reference Franchi, Serapioni and Serra Cassano51] for a more comprehensive presentation.
Given an open set
![]() $U\subset {\mathbb H}^{n}$
, we say that
$U\subset {\mathbb H}^{n}$
, we say that
![]() $f:U\to {\mathbb R}$
is of class
$f:U\to {\mathbb R}$
is of class
![]() $C^{1}_{\mathbb H}$
if f is continuous and its horizontal derivatives
$C^{1}_{\mathbb H}$
if f is continuous and its horizontal derivatives
are represented by continuous functions on U. In this case, we write
 $f\in C^{1}_{\mathbb H}(U)$
. We agree that, for every
$f\in C^{1}_{\mathbb H}(U)$
. We agree that, for every
![]() $p\in U$
,
$p\in U$
,
![]() $\nabla _{\mathbb H} f(p)\in {\mathbb R}^{2k}$
is identified with the horizontal vector
$\nabla _{\mathbb H} f(p)\in {\mathbb R}^{2k}$
is identified with the horizontal vector
Definition 4.17. Let
![]() $k\in \{1,\dots ,n\}$
be fixed. We say that
$k\in \{1,\dots ,n\}$
be fixed. We say that
![]() $S\subset {\mathbb H}^{n}$
is an
$S\subset {\mathbb H}^{n}$
is an
![]() ${\mathbb H}$
-regular submanifold (or a
${\mathbb H}$
-regular submanifold (or a
![]() $C^{1}_{\mathbb H}$
-submanifold) of codimension k if, for every
$C^{1}_{\mathbb H}$
-submanifold) of codimension k if, for every
![]() $p\in S$
, there exist an open neighbourhood
$p\in S$
, there exist an open neighbourhood
![]() $U\subset {\mathbb H}^{n}$
of p and
$U\subset {\mathbb H}^{n}$
of p and
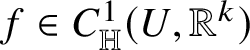 $f\in C^{1}_{\mathbb H}(U,{\mathbb R}^{k})$
such that
$f\in C^{1}_{\mathbb H}(U,{\mathbb R}^{k})$
such that
We also define the horizontal normal
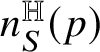 $n_{S}^{\mathbb H}(p)$
to S at p as the horizontal k-vector
$n_{S}^{\mathbb H}(p)$
to S at p as the horizontal k-vector
 $$ \begin{align*} n_{S}^{\mathbb H}(p):=\frac{\nabla_{\mathbb H} f_{1}(p)\wedge\dots\wedge\nabla_{\mathbb H} f_{k}(p)}{|\nabla_{\mathbb H} f_{1}(p)\wedge\dots\wedge\nabla_{\mathbb H} f_{k}(p)|}\in\Large\wedge_{k}{\mathfrak h}_{1} \end{align*} $$
$$ \begin{align*} n_{S}^{\mathbb H}(p):=\frac{\nabla_{\mathbb H} f_{1}(p)\wedge\dots\wedge\nabla_{\mathbb H} f_{k}(p)}{|\nabla_{\mathbb H} f_{1}(p)\wedge\dots\wedge\nabla_{\mathbb H} f_{k}(p)|}\in\Large\wedge_{k}{\mathfrak h}_{1} \end{align*} $$
and the (horizontal) tangent
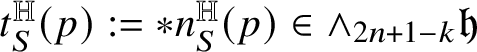 $t^{\mathbb H}_{S}(p):=*n_{S}^{\mathbb H}(p)\in \Large \wedge _{2n+1-k}{\mathfrak h}$
.
$t^{\mathbb H}_{S}(p):=*n_{S}^{\mathbb H}(p)\in \Large \wedge _{2n+1-k}{\mathfrak h}$
.
In the definition of the tangent multivector
![]() $t^{\mathbb H}_{S}$
, the symbol
$t^{\mathbb H}_{S}$
, the symbol
![]() $*$
denotes the Hodge operator. The latter, recalling the notation introduced in (3.4) and (3.5), can be defined as the linear isomorphism
$*$
denotes the Hodge operator. The latter, recalling the notation introduced in (3.4) and (3.5), can be defined as the linear isomorphism
![]() $\ast :\Large \wedge _{k}{\mathfrak h}\to \Large \wedge _{2n+1-k}{\mathfrak h}$
such that
$\ast :\Large \wedge _{k}{\mathfrak h}\to \Large \wedge _{2n+1-k}{\mathfrak h}$
such that
where
![]() $I^{\ast }:=\{1,\dots ,2n+1\}\setminus I$
and
$I^{\ast }:=\{1,\dots ,2n+1\}\setminus I$
and
![]() $\sigma (I)$
denotes the number of couples
$\sigma (I)$
denotes the number of couples
![]() $(i,i^{\ast })\in I\times I^{\ast }$
such that
$(i,i^{\ast })\in I\times I^{\ast }$
such that
![]() $i>i^{\ast }$
. Equivalently, the sign
$i>i^{\ast }$
. Equivalently, the sign
![]() $(-1)^{\sigma (I)}$
can be defined by requiring that
$(-1)^{\sigma (I)}$
can be defined by requiring that
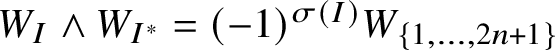 $W_{I}\wedge W_{I^{\ast }}=(-1)^{\sigma (I)}W_{\{1,\dots ,2n+1\}}$
and, all in all, this amounts to requiring that
$W_{I}\wedge W_{I^{\ast }}=(-1)^{\sigma (I)}W_{\{1,\dots ,2n+1\}}$
and, all in all, this amounts to requiring that
where the norm
![]() $|\cdot |$
is the one associated with the canonical scalar product on multivectors making the basis
$|\cdot |$
is the one associated with the canonical scalar product on multivectors making the basis
![]() $W_{I}$
orthonormal. Notice that, if
$W_{I}$
orthonormal. Notice that, if
![]() $v=v_{1}\wedge \dots \wedge v_{k}\in \Large \wedge _{k}{\mathfrak h}_{1}$
is a simple horizontal k-vector, then
$v=v_{1}\wedge \dots \wedge v_{k}\in \Large \wedge _{k}{\mathfrak h}_{1}$
is a simple horizontal k-vector, then
![]() $\ast v=w\wedge T$
for some
$\ast v=w\wedge T$
for some
![]() $w\in \Large \wedge _{2n-k}{\mathfrak h}_{1}$
. In particular, the horizontal tangent
$w\in \Large \wedge _{2n-k}{\mathfrak h}_{1}$
. In particular, the horizontal tangent
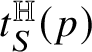 $t^{\mathbb H}_{S}(p)$
is in fact a vertical multivector; that is, it can be written as
$t^{\mathbb H}_{S}(p)$
is in fact a vertical multivector; that is, it can be written as
 $t^{\mathbb H}_{S}(p)=\tau ^{\mathbb H}_{S}(p)\wedge T$
for a unique unit vector in
$t^{\mathbb H}_{S}(p)=\tau ^{\mathbb H}_{S}(p)\wedge T$
for a unique unit vector in
 $\tau ^{\mathbb H}_{S}(p)\in \Large \wedge _{2n-k}{\mathfrak h}_{1}$
. Observe that, when S is of class
$\tau ^{\mathbb H}_{S}(p)\in \Large \wedge _{2n-k}{\mathfrak h}_{1}$
. Observe that, when S is of class
![]() $C^{1}$
, the definition of
$C^{1}$
, the definition of
![]() $\tau ^{\mathbb H}_{S}$
is consistent with (3.30).
$\tau ^{\mathbb H}_{S}$
is consistent with (3.30).
Both
![]() $n_{S}^{\mathbb H}$
and
$n_{S}^{\mathbb H}$
and
![]() $t_{S}^{\mathbb H}$
are unit simple vectors. Observe that they are well-defined (even though only up to a sign); that is, independent from the choice of the defining function f. One way of proving this fact is by considering the blow-up of S at p; indeed, one has
$t_{S}^{\mathbb H}$
are unit simple vectors. Observe that they are well-defined (even though only up to a sign); that is, independent from the choice of the defining function f. One way of proving this fact is by considering the blow-up of S at p; indeed, one has
 $$ \begin{align} \lim_{r\to0^{+}} \delta_{1/r}(p^{-1}S)={\mathrm{Tan}}^{\mathbb H}_{S}(p), \end{align} $$
$$ \begin{align} \lim_{r\to0^{+}} \delta_{1/r}(p^{-1}S)={\mathrm{Tan}}^{\mathbb H}_{S}(p), \end{align} $$
where the limit is taken with respect to the local Hausdorff convergence and
 ${\mathrm {Tan}}^{\mathbb H}_{S}(p):=\exp (\operatorname *{\mathrm {span}}\: t_{S}^{\mathbb H}(p))$
. See, for example, [Reference Franchi, Serapioni and Serra Cassano51]. The
${\mathrm {Tan}}^{\mathbb H}_{S}(p):=\exp (\operatorname *{\mathrm {span}}\: t_{S}^{\mathbb H}(p))$
. See, for example, [Reference Franchi, Serapioni and Serra Cassano51]. The
![]() $(2n+1-k)$
-plane
$(2n+1-k)$
-plane
 ${\mathrm {Tan}}^{\mathbb H}_{S}(p)$
is a vertical plane according to Definition 3.2 and it is called tangent plane to S at p. As a consequence of Theorem 4.19 (see also [Reference Julia, Nicolussi Golo and Vittone61, Lemma 3.4]), we have the weak convergence of measures
${\mathrm {Tan}}^{\mathbb H}_{S}(p)$
is a vertical plane according to Definition 3.2 and it is called tangent plane to S at p. As a consequence of Theorem 4.19 (see also [Reference Julia, Nicolussi Golo and Vittone61, Lemma 3.4]), we have the weak convergence of measures

Also, the vector
![]() $\tau ^{\mathbb H}_{S}$
is defined only up to a sign; its geometric meaning is provided by the equality
$\tau ^{\mathbb H}_{S}$
is defined only up to a sign; its geometric meaning is provided by the equality
 $$ \begin{align*} \exp(\operatorname*{\mathrm{span}}\: \tau^{\mathbb H}_{S}(p)) = {\mathrm{Tan}}^{\mathbb H}_{S}(p)\cap\exp({\mathfrak h}_{1}). \end{align*} $$
$$ \begin{align*} \exp(\operatorname*{\mathrm{span}}\: \tau^{\mathbb H}_{S}(p)) = {\mathrm{Tan}}^{\mathbb H}_{S}(p)\cap\exp({\mathfrak h}_{1}). \end{align*} $$
Remark 4.18. Proposition 4.12 implies that the notation
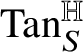 ${\mathrm {Tan}}^{\mathbb H}_{S}$
introduced in (4.23) is consistent with the notation
${\mathrm {Tan}}^{\mathbb H}_{S}$
introduced in (4.23) is consistent with the notation
 ${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}$
of Definition 4.9. As a consequence, if
${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}$
of Definition 4.9. As a consequence, if
![]() $A\subset {\mathbb W}$
is open and the function
$A\subset {\mathbb W}$
is open and the function
![]() $\phi :A\to {\mathbb V}$
parametrises an
$\phi :A\to {\mathbb V}$
parametrises an
![]() ${\mathbb H}$
-regular submanifold
${\mathbb H}$
-regular submanifold
![]() $S=\mathrm {gr}_{\phi }$
such that
$S=\mathrm {gr}_{\phi }$
such that
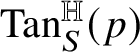 ${\mathrm {Tan}}^{\mathbb H}_{S}(p)$
is complementary to
${\mathrm {Tan}}^{\mathbb H}_{S}(p)$
is complementary to
![]() ${\mathbb V}$
for every
${\mathbb V}$
for every
![]() $p\in S$
, then
$p\in S$
, then
![]() $\phi $
is intrinsically differentiable at every point of A.
$\phi $
is intrinsically differentiable at every point of A.
It is well-known that
![]() ${\mathbb H}$
-regular submanifolds are locally intrinsic Lipschitz graphs and that an integral formula can be provided for their spherical Hausdorff measure
${\mathbb H}$
-regular submanifolds are locally intrinsic Lipschitz graphs and that an integral formula can be provided for their spherical Hausdorff measure
![]() ${\mathscr S}^{Q-k}$
. We resume these facts in the following statement, which summarises several results available in the (quite vast) literature and, in particular, [Reference Arena and Serapioni9, Theorem 4.2], [Reference Franchi, Serapioni and Serra Cassano51, Theorem 4.1] and [Reference Corni and Magnani33, formula (43)]; see also [Reference Ambrosio, Serra Cassano and Vittone4, Reference Bigolin and Serra Cassano17, Reference Bigolin and Serra Cassano18, Reference Citti and Manfredini29, Reference Corni32, Reference Di Donato36, Reference Di Donato35, Reference Julia, Nicolussi Golo and Vittone61, Reference Magnani70, Reference Monti and Vittone76]. It is worth recalling that the intrinsic Jacobian determinant
${\mathscr S}^{Q-k}$
. We resume these facts in the following statement, which summarises several results available in the (quite vast) literature and, in particular, [Reference Arena and Serapioni9, Theorem 4.2], [Reference Franchi, Serapioni and Serra Cassano51, Theorem 4.1] and [Reference Corni and Magnani33, formula (43)]; see also [Reference Ambrosio, Serra Cassano and Vittone4, Reference Bigolin and Serra Cassano17, Reference Bigolin and Serra Cassano18, Reference Citti and Manfredini29, Reference Corni32, Reference Di Donato36, Reference Di Donato35, Reference Julia, Nicolussi Golo and Vittone61, Reference Magnani70, Reference Monti and Vittone76]. It is worth recalling that the intrinsic Jacobian determinant
![]() $J^{\phi }\phi $
was introduced in Definition 4.9.
$J^{\phi }\phi $
was introduced in Definition 4.9.
Theorem 4.19. Let
![]() $S\subset {\mathbb H}^{n}$
be an
$S\subset {\mathbb H}^{n}$
be an
![]() ${\mathbb H}$
-regular submanifold of codimension
${\mathbb H}$
-regular submanifold of codimension
![]() $k\leq n$
. Then for every
$k\leq n$
. Then for every
![]() $p\in S$
there exist an open neighbourhood U of p, an open set
$p\in S$
there exist an open neighbourhood U of p, an open set
![]() $A\subset {\mathbb W}$
and an intrinsic Lipschitz
$A\subset {\mathbb W}$
and an intrinsic Lipschitz
![]() $\phi :A\to {\mathbb V}$
such that, up to an isometric
$\phi :A\to {\mathbb V}$
such that, up to an isometric
![]() ${\mathbb H}$
-linear isomorphism of
${\mathbb H}$
-linear isomorphism of
![]() ${\mathbb H}^{n}$
,
${\mathbb H}^{n}$
,
 $$ \begin{align*} & S\cap U=\mathrm{gr}_{\phi}\\ & \phi\text{ is intrinsically differentiable on }A\\ &\nabla^{\phi}\phi\text{ is continuous.} \end{align*} $$
$$ \begin{align*} & S\cap U=\mathrm{gr}_{\phi}\\ & \phi\text{ is intrinsically differentiable on }A\\ &\nabla^{\phi}\phi\text{ is continuous.} \end{align*} $$
Moreover,
 $$ \begin{align} {\mathscr S}^{Q-k}(E)=C_{n,k}\int_{\Phi^{-1}(E)} J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}\qquad\text{for every Borel set }E\subset S\cap U, \end{align} $$
$$ \begin{align} {\mathscr S}^{Q-k}(E)=C_{n,k}\int_{\Phi^{-1}(E)} J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}\qquad\text{for every Borel set }E\subset S\cap U, \end{align} $$
where
![]() $\Phi (w):=w\phi (w)$
and
$\Phi (w):=w\phi (w)$
and
![]() $C_{n,k}>0$
is the same constant as in Proposition 1.9.
$C_{n,k}>0$
is the same constant as in Proposition 1.9.
Remark 4.20. As pointed out in [Reference Corni and Magnani33], the area formula (4.25) holds more generally when
![]() ${\mathbb W},{\mathbb V}$
are orthogonal (recall Remark 4.10).
${\mathbb W},{\mathbb V}$
are orthogonal (recall Remark 4.10).
Remark 4.21. As explained in [Reference Magnani71] and [Reference Corni and Magnani33], the exact value of the constant
![]() $C_{n,k}$
(which, from the philological point of view, in the present article is introduced for the first time in Lemma 3.31) in Proposition 1.9 and Theorem 4.19 is
$C_{n,k}$
(which, from the philological point of view, in the present article is introduced for the first time in Lemma 3.31) in Proposition 1.9 and Theorem 4.19 is
 $$ \begin{align*} C_{n,k}=\Big( \sup\big\{ {\mathscr L}^{2n+1-k}({\mathbb W}\cap B(p,1)) : p\in B(0,1)\big\} \Big)^{-1}. \end{align*} $$
$$ \begin{align*} C_{n,k}=\Big( \sup\big\{ {\mathscr L}^{2n+1-k}({\mathbb W}\cap B(p,1)) : p\in B(0,1)\big\} \Big)^{-1}. \end{align*} $$
The rotational invariance of the distance d plays an important role; see [Reference Corni and Magnani33, Theorem 2.12].
We now introduce intrinsic rectifiable sets in Heisenberg groups.
Definition 4.22. Let
![]() $k\in \{1,\dots ,n\}$
; we say that
$k\in \{1,\dots ,n\}$
; we say that
![]() $R\subset {\mathbb H}^{n}$
is a
$R\subset {\mathbb H}^{n}$
is a
![]() ${\mathbb H}$
-rectifiable set of codimension k if
${\mathbb H}$
-rectifiable set of codimension k if
![]() ${\mathscr S}^{Q-k}(R)<\infty $
and there exists a finite or countable family
${\mathscr S}^{Q-k}(R)<\infty $
and there exists a finite or countable family
![]() $(S_{j})_{j}$
of
$(S_{j})_{j}$
of
![]() ${\mathbb H}$
-regular submanifolds of codimension k such that
${\mathbb H}$
-regular submanifolds of codimension k such that
 $$ \begin{align*} {\mathscr S}^{Q-k}\left(R\setminus\bigcup_{j} S_{j}\right)=0. \end{align*} $$
$$ \begin{align*} {\mathscr S}^{Q-k}\left(R\setminus\bigcup_{j} S_{j}\right)=0. \end{align*} $$
We say that
![]() $R\subset {\mathbb H}^{n}$
is a locally
$R\subset {\mathbb H}^{n}$
is a locally
![]() ${\mathbb H}$
-rectifiable set of codimension k if
${\mathbb H}$
-rectifiable set of codimension k if
![]() $R\cap B(0,r)$
is
$R\cap B(0,r)$
is
![]() ${\mathbb H}$
-rectifiable of codimension k for every
${\mathbb H}$
-rectifiable of codimension k for every
![]() $r>0$
.
$r>0$
.
Later we will use the well-known fact that sets that are rectifiable (see, e.g., [Reference Federer42]) in the Euclidean sense are also
![]() ${\mathbb H}$
-rectifiable. As a matter of terminology, we say that a set
${\mathbb H}$
-rectifiable. As a matter of terminology, we say that a set
![]() $R\subset {\mathbb H}^{n}\equiv {\mathbb R}^{2n+1}$
is locally Euclidean rectifiable of codimension k if
$R\subset {\mathbb H}^{n}\equiv {\mathbb R}^{2n+1}$
is locally Euclidean rectifiable of codimension k if
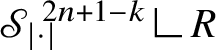 is a locally finite measure and there exists a finite or countable family
is a locally finite measure and there exists a finite or countable family
![]() $(S_{j})_{j}$
of Euclidean Lipschitz submanifolds of codimension k such that
$(S_{j})_{j}$
of Euclidean Lipschitz submanifolds of codimension k such that
 $$ \begin{align*} {{\mathscr S}_{|\cdot|}}^{\!\!\!2n+1-k}(R\setminus\bigcup_{j} S_{j})=0, \end{align*} $$
$$ \begin{align*} {{\mathscr S}_{|\cdot|}}^{\!\!\!2n+1-k}(R\setminus\bigcup_{j} S_{j})=0, \end{align*} $$
where
 ${{\mathscr S}_{|\cdot |}}^{\!\!\!2n+1-k}$
denotes the spherical Hausdorff measure with respect to the Euclidean distance on
${{\mathscr S}_{|\cdot |}}^{\!\!\!2n+1-k}$
denotes the spherical Hausdorff measure with respect to the Euclidean distance on
![]() ${\mathbb H}^{n}\equiv {\mathbb R}^{2n+1}$
. If
${\mathbb H}^{n}\equiv {\mathbb R}^{2n+1}$
. If
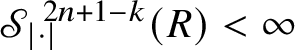 ${{\mathscr S}_{|\cdot |}}^{\!\!\!2n+1-k}(R)<\infty $
, we say that R is Euclidean rectifiable.
${{\mathscr S}_{|\cdot |}}^{\!\!\!2n+1-k}(R)<\infty $
, we say that R is Euclidean rectifiable.
Proposition 4.23. Let
![]() $R\subset {\mathbb H}^{2n+1}$
be locally Euclidean rectifiable of codimension k,
$R\subset {\mathbb H}^{2n+1}$
be locally Euclidean rectifiable of codimension k,
![]() $1\leq k\leq n$
. Then R is also locally
$1\leq k\leq n$
. Then R is also locally
![]() ${\mathbb H}$
-rectifiable of codimension k.
${\mathbb H}$
-rectifiable of codimension k.
A proof of Proposition 4.23 can be found, for instance, in [Reference Franchi, Serapioni and Serra Cassano51, Proposition 5.4].
We also recall that classical rectifiable sets of dimension m in
![]() ${\mathbb R}^{n}$
can be equivalently defined as those sets with finite
${\mathbb R}^{n}$
can be equivalently defined as those sets with finite
 ${\mathscr S}^{m}_{|\cdot |}$
-measure that can be covered, up to
${\mathscr S}^{m}_{|\cdot |}$
-measure that can be covered, up to
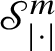 ${\mathscr S}^{m}_{|\cdot |}$
-negligible sets, by a countable family of (possibly rotated or translated) graphs of Lipschitz maps
${\mathscr S}^{m}_{|\cdot |}$
-negligible sets, by a countable family of (possibly rotated or translated) graphs of Lipschitz maps
![]() ${\mathbb R}^{m}\to {\mathbb R}^{n-m}$
. As we will prove later in Corollary 7.4, a similar statement holds in Heisenberg groups; namely,
${\mathbb R}^{m}\to {\mathbb R}^{n-m}$
. As we will prove later in Corollary 7.4, a similar statement holds in Heisenberg groups; namely,
![]() $R\subset {\mathbb H}^{n}$
is
$R\subset {\mathbb H}^{n}$
is
![]() ${\mathbb H}$
-rectifiable of codimension
${\mathbb H}$
-rectifiable of codimension
![]() $k\in \{1,\dots ,n\}$
if and only if
$k\in \{1,\dots ,n\}$
if and only if
![]() ${\mathscr S}^{Q-k}(R)<\infty $
and there exists a countable family
${\mathscr S}^{Q-k}(R)<\infty $
and there exists a countable family
![]() $(\phi _{j})_{j}$
of intrinsic Lipschitz maps
$(\phi _{j})_{j}$
of intrinsic Lipschitz maps
![]() $\phi _{j}:{\mathbb W}_{j}\to {\mathbb V}_{j}$
, where
$\phi _{j}:{\mathbb W}_{j}\to {\mathbb V}_{j}$
, where
![]() ${\mathbb W}_{j},{\mathbb V}_{j} $
are homogeneous complementary subgroups of
${\mathbb W}_{j},{\mathbb V}_{j} $
are homogeneous complementary subgroups of
![]() ${\mathbb H}^{n}$
with
${\mathbb H}^{n}$
with
![]() $\dim {\mathbb V}_{j}=k$
, such that
$\dim {\mathbb V}_{j}=k$
, such that
 $$ \begin{align*} {\mathscr S}^{Q-k}\left(R\setminus\bigcup_{j} \mathrm{gr}_{\phi_{j}}\right)=0. \end{align*} $$
$$ \begin{align*} {\mathscr S}^{Q-k}\left(R\setminus\bigcup_{j} \mathrm{gr}_{\phi_{j}}\right)=0. \end{align*} $$
Definition 4.24. If
![]() $R\subset {\mathbb H}^{n}$
is locally
$R\subset {\mathbb H}^{n}$
is locally
![]() ${\mathbb H}$
-rectifiable and
${\mathbb H}$
-rectifiable and
![]() $(S_{j})_{j}$
is a family of
$(S_{j})_{j}$
is a family of
![]() ${\mathbb H}$
-regular submanifolds as in Definition 4.22, we define the horizontal normal
${\mathbb H}$
-regular submanifolds as in Definition 4.22, we define the horizontal normal
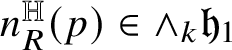 $n^{\mathbb H}_{R}(p)\in \Large \wedge _{k}{\mathfrak h}_{1}$
at
$n^{\mathbb H}_{R}(p)\in \Large \wedge _{k}{\mathfrak h}_{1}$
at
![]() $p\in R$
by
$p\in R$
by
 $$ \begin{align*} n^{\mathbb H}_{R}(p):=n^{\mathbb H}_{S_{j}}(p)\qquad\text{if }p\in R\cap S_{j}. \end{align*} $$
$$ \begin{align*} n^{\mathbb H}_{R}(p):=n^{\mathbb H}_{S_{j}}(p)\qquad\text{if }p\in R\cap S_{j}. \end{align*} $$
Accordingly, we set
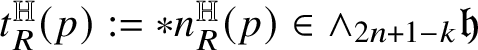 $t^{\mathbb H}_{R}(p):=*n_{R}^{\mathbb H}(p)\in \Large \wedge _{2n+1-k}{\mathfrak h}$
and
$t^{\mathbb H}_{R}(p):=*n_{R}^{\mathbb H}(p)\in \Large \wedge _{2n+1-k}{\mathfrak h}$
and
 ${\mathrm {Tan}}^{\mathbb H}_{R}(p):=\exp (\operatorname *{\mathrm {span}}(t^{\mathbb H}_{R}(p))$
. Eventually, we define
${\mathrm {Tan}}^{\mathbb H}_{R}(p):=\exp (\operatorname *{\mathrm {span}}(t^{\mathbb H}_{R}(p))$
. Eventually, we define
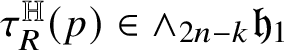 $\tau ^{\mathbb H}_{R}(p)\in \Large \wedge _{2n-k}{\mathfrak h}_{1}$
by requiring that
$\tau ^{\mathbb H}_{R}(p)\in \Large \wedge _{2n-k}{\mathfrak h}_{1}$
by requiring that
 $t^{\mathbb H}_{R}(p)=\tau ^{\mathbb H}_{R}(p)\wedge T$
.
$t^{\mathbb H}_{R}(p)=\tau ^{\mathbb H}_{R}(p)\wedge T$
.
The objects introduced in Definition 4.24 are well-defined
![]() ${\mathscr S}^{Q-k}$
-a.e. on R (as usual, up to a sign) because of the following well-known lemma, whose proof we sketch for the sake of completeness.
${\mathscr S}^{Q-k}$
-a.e. on R (as usual, up to a sign) because of the following well-known lemma, whose proof we sketch for the sake of completeness.
Lemma 4.25. Let
![]() $S_{1},S_{2}\subset {\mathbb H}^{n}$
be
$S_{1},S_{2}\subset {\mathbb H}^{n}$
be
![]() ${\mathbb H}$
-regular submanifolds of codimension
${\mathbb H}$
-regular submanifolds of codimension
![]() $k\in \{1,\dots ,n\}$
; then
$k\in \{1,\dots ,n\}$
; then
 $$ \begin{align*} {\mathscr S}^{Q-k}(\{p\in S_{1}\cap S_{2}:n^{\mathbb H}_{S_{1}}(p)\notin\{\pm n^{\mathbb H}_{S_{2}}(p)\}\})=0. \end{align*} $$
$$ \begin{align*} {\mathscr S}^{Q-k}(\{p\in S_{1}\cap S_{2}:n^{\mathbb H}_{S_{1}}(p)\notin\{\pm n^{\mathbb H}_{S_{2}}(p)\}\})=0. \end{align*} $$
Proof. Let
 $E:=\{p\in S_{1}\cap S_{2}:n^{\mathbb H}_{S_{1}}(p)\notin \{\pm n^{\mathbb H}_{S_{2}}(p)\}\}$
. For every
$E:=\{p\in S_{1}\cap S_{2}:n^{\mathbb H}_{S_{1}}(p)\notin \{\pm n^{\mathbb H}_{S_{2}}(p)\}\}$
. For every
![]() $p\in E$
, we have
$p\in E$
, we have
 $$ \begin{align*} \limsup_{r\to 0^{+}}\delta_{1/r}(p^{-1}E)\subset \limsup_{r\to 0^{+}}\delta_{1/r}(p^{-1}(S_{1}\cap S_{2}))\subset {\mathrm{Tan}}^{\mathbb H}_{S_{1}}(p)\cap {\mathrm{Tan}}^{\mathbb H}_{S_{2}}(p), \end{align*} $$
$$ \begin{align*} \limsup_{r\to 0^{+}}\delta_{1/r}(p^{-1}E)\subset \limsup_{r\to 0^{+}}\delta_{1/r}(p^{-1}(S_{1}\cap S_{2}))\subset {\mathrm{Tan}}^{\mathbb H}_{S_{1}}(p)\cap {\mathrm{Tan}}^{\mathbb H}_{S_{2}}(p), \end{align*} $$
where the
![]() $\limsup $
are taken with respect to the local Hausdorff topology. Since the right-hand side is a vertical plane of dimension at most
$\limsup $
are taken with respect to the local Hausdorff topology. Since the right-hand side is a vertical plane of dimension at most
![]() $2n-k$
, the statement now follows from [Reference Monti and Vittone77, Lemma B.3].
$2n-k$
, the statement now follows from [Reference Monti and Vittone77, Lemma B.3].
4.5 Currents induced by
 $C^{1}$
intrinsic graphs
$C^{1}$
intrinsic graphs
We now want to study currents induced by
![]() $C^{1}$
regular intrinsic graphs of codimension k in
$C^{1}$
regular intrinsic graphs of codimension k in
![]() ${\mathbb H}^{n}$
with
${\mathbb H}^{n}$
with
![]() $1\leq k\leq n$
. Assume that a
$1\leq k\leq n$
. Assume that a
![]() $C^{1}$
map
$C^{1}$
map
![]() $\phi :{\mathbb W}\to {\mathbb V}$
is fixed; we introduce the family
$\phi :{\mathbb W}\to {\mathbb V}$
is fixed; we introduce the family
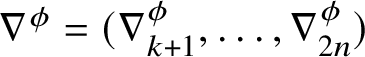 $\nabla ^{\phi }=(\nabla ^{\phi }_{k+1},\dots ,\nabla ^{\phi }_{2n})$
of vector fields on
$\nabla ^{\phi }=(\nabla ^{\phi }_{k+1},\dots ,\nabla ^{\phi }_{2n})$
of vector fields on
![]() ${\mathbb W}$
defined by
${\mathbb W}$
defined by
 $$ \begin{align} \nabla^{\phi}_{i}:=\begin{cases} X_{i} & \text{if }k+1\leq i\leq n\\ Y_{i-n}+\phi_{i-n}T=\partial_{y_{i-n}}+\phi_{i-n}\partial_{t}\quad& \text{if }n+1\leq i\leq n+k\\ Y_{i-n}& \text{if }n+k+1\leq i\leq 2n. \end{cases} \end{align} $$
$$ \begin{align} \nabla^{\phi}_{i}:=\begin{cases} X_{i} & \text{if }k+1\leq i\leq n\\ Y_{i-n}+\phi_{i-n}T=\partial_{y_{i-n}}+\phi_{i-n}\partial_{t}\quad& \text{if }n+1\leq i\leq n+k\\ Y_{i-n}& \text{if }n+k+1\leq i\leq 2n. \end{cases} \end{align} $$
The vectors
![]() $\nabla ^{\phi }_{i}$
are tangent to
$\nabla ^{\phi }_{i}$
are tangent to
![]() ${\mathbb W}$
because so are
${\mathbb W}$
because so are
![]() $X_{k+1},\dots ,Y_{n},T$
. The family
$X_{k+1},\dots ,Y_{n},T$
. The family
![]() $\nabla ^{\phi }$
was introduced in [Reference Ambrosio, Serra Cassano and Vittone4] in the case of codimension 1 and in [Reference Corni32, Reference Serra Cassano88] for codimension
$\nabla ^{\phi }$
was introduced in [Reference Ambrosio, Serra Cassano and Vittone4] in the case of codimension 1 and in [Reference Corni32, Reference Serra Cassano88] for codimension
![]() $k\leq n$
.
$k\leq n$
.
Remark 4.26. The notation introduced in (4.26) is consistent with the one in Definition 4.9; in fact (see, e.g., [Reference Corni32, Proposition 3.7]), when
![]() $\phi $
is of class
$\phi $
is of class
![]() $C^{1}$
, the components of the matrix
$C^{1}$
, the components of the matrix
![]() $\nabla ^{\phi }\phi (w)$
associated with the intrinsic differential
$\nabla ^{\phi }\phi (w)$
associated with the intrinsic differential
![]() $d\phi _{w}$
are precisely the derivatives
$d\phi _{w}$
are precisely the derivatives
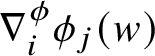 $\nabla ^{\phi }_{i}\phi _{j}(w)$
of
$\nabla ^{\phi }_{i}\phi _{j}(w)$
of
![]() $\phi =(\phi _{1},\dots ,\phi _{k})$
along the directions
$\phi =(\phi _{1},\dots ,\phi _{k})$
along the directions
![]() $\nabla ^{\phi }_{i}$
.
$\nabla ^{\phi }_{i}$
.
Recalling the notation
![]() $W_{i}$
and
$W_{i}$
and
![]() $\Phi $
introduced in (3.4) and (4.7), one can differentiate the graph map
$\Phi $
introduced in (3.4) and (4.7), one can differentiate the graph map
![]() $\Phi $
along the directions
$\Phi $
along the directions
![]() $\nabla ^{\phi }_{i}$
to obtain that, for every
$\nabla ^{\phi }_{i}$
to obtain that, for every
![]() $w\in {\mathbb W}$
, the vectors
$w\in {\mathbb W}$
, the vectors
 $$ \begin{align} \nabla^{\phi}_{i}\Phi(w)=\left(W_{i}+\sum_{h=1}^{k}\nabla^{\phi}_{i}\phi_{h}(w)X_{h}\right)(\Phi(w)),\qquad i=k+1,\dots,2n \end{align} $$
$$ \begin{align} \nabla^{\phi}_{i}\Phi(w)=\left(W_{i}+\sum_{h=1}^{k}\nabla^{\phi}_{i}\phi_{h}(w)X_{h}\right)(\Phi(w)),\qquad i=k+1,\dots,2n \end{align} $$
(which should be thought of as vectors in
![]() $\Phi (w)$
that are continuous with respect to w) are horizontal and tangent to the submanifold
$\Phi (w)$
that are continuous with respect to w) are horizontal and tangent to the submanifold
![]() $S:=\mathrm {gr}_{\phi }$
at the point
$S:=\mathrm {gr}_{\phi }$
at the point
![]() $\Phi (w)$
. The equality in (4.27) comes from a boring computation that we omit. Since the vectors
$\Phi (w)$
. The equality in (4.27) comes from a boring computation that we omit. Since the vectors
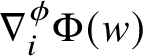 $\nabla ^{\phi }_{i}\Phi (w)$
,
$\nabla ^{\phi }_{i}\Phi (w)$
,
![]() $i=k+1,\dots ,2n$
, are also linearly independent, they generate the
$i=k+1,\dots ,2n$
, are also linearly independent, they generate the
![]() $(2n-k)$
-dimensional subspace
$(2n-k)$
-dimensional subspace
![]() $T_{\Phi (w)}S\cap {\mathfrak h}_{1}$
; hence, the multivector
$T_{\Phi (w)}S\cap {\mathfrak h}_{1}$
; hence, the multivector
 $$ \begin{align} \nabla^{\phi}\Phi(w):=\nabla^{\phi}_{k+1}\Phi(w)\wedge\dots\wedge\nabla^{\phi}_{2n}\Phi(w)\in\Large\wedge_{2n-k}{\mathfrak h}_{1} \end{align} $$
$$ \begin{align} \nabla^{\phi}\Phi(w):=\nabla^{\phi}_{k+1}\Phi(w)\wedge\dots\wedge\nabla^{\phi}_{2n}\Phi(w)\in\Large\wedge_{2n-k}{\mathfrak h}_{1} \end{align} $$
is a multiple of the unit multivector
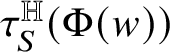 $\tau _{S}^{\mathbb H}(\Phi (w))$
defined in Subsection 3.5.
$\tau _{S}^{\mathbb H}(\Phi (w))$
defined in Subsection 3.5.
Remark 4.27. It is worth noticing that the intrinsic Jacobian determinant
![]() $J^{\phi }\phi (w)$
equals the norm
$J^{\phi }\phi (w)$
equals the norm
![]() $|\nabla ^{\phi }\Phi (w)|$
of the multivector
$|\nabla ^{\phi }\Phi (w)|$
of the multivector
![]() $\nabla ^{\phi }\Phi (w)$
. As usual, the norm on multivectors is the one induced by the left-invariant scalar product making
$\nabla ^{\phi }\Phi (w)$
. As usual, the norm on multivectors is the one induced by the left-invariant scalar product making
![]() $X_{1},\dots ,Y_{n},T$
orthonormal.
$X_{1},\dots ,Y_{n},T$
orthonormal.
We state for future reference the following result, which is essentially a restatement of Theorem 1.6.
Proposition 4.28. Let
![]() $A\subset {\mathbb W}$
and
$A\subset {\mathbb W}$
and
![]() $\phi :A\to {\mathbb V}$
be intrinsic Lipschitz. Then there exists a sequence
$\phi :A\to {\mathbb V}$
be intrinsic Lipschitz. Then there exists a sequence
![]() $(\phi _{i})_{i\in \mathbb N}$
of
$(\phi _{i})_{i\in \mathbb N}$
of
![]() $C^{\infty }$
smooth and uniformly intrinsic Lipschitz maps
$C^{\infty }$
smooth and uniformly intrinsic Lipschitz maps
![]() $\phi _{i}:{\mathbb W}\to {\mathbb V}$
such that
$\phi _{i}:{\mathbb W}\to {\mathbb V}$
such that
Moreover, there exists
![]() $C>0$
, depending only on the intrinsic Lipschitz constant of
$C>0$
, depending only on the intrinsic Lipschitz constant of
![]() $\phi $
and the distance d, such that
$\phi $
and the distance d, such that
where
![]() $\Phi _{i}$
is the graph map
$\Phi _{i}$
is the graph map
![]() ${\mathbb W}\ni w\mapsto w\phi _{i}(w)\in {\mathbb H}^{n}$
.
${\mathbb W}\ni w\mapsto w\phi _{i}(w)\in {\mathbb H}^{n}$
.
Proof. The first part of the statement is Theorem 1.6, while the second one is a consequence of Lemma 4.13, Remark 4.26 and (4.27).
Similar to (4.27), one gets
 $$ \begin{align} T\Phi(w)=\left(T+\sum_{h=1}^{k} T\phi_{h}(w)X_{h}\right)(\Phi(w)). \end{align} $$
$$ \begin{align} T\Phi(w)=\left(T+\sum_{h=1}^{k} T\phi_{h}(w)X_{h}\right)(\Phi(w)). \end{align} $$
The vector fields in (4.27) and (4.29) generate the tangent space to S at
![]() $\Phi (w)$
. We then fix the orientation of S is such a way that
$\Phi (w)$
. We then fix the orientation of S is such a way that
 $$ \begin{align} t_{S}(\Phi(w)):=\frac{\nabla^{\phi}\Phi\wedge T\Phi}{|\nabla^{\phi}\Phi\wedge T\Phi|}\quad\text{is positively oriented for every }w\in{\mathbb W}\text{.} \end{align} $$
$$ \begin{align} t_{S}(\Phi(w)):=\frac{\nabla^{\phi}\Phi\wedge T\Phi}{|\nabla^{\phi}\Phi\wedge T\Phi|}\quad\text{is positively oriented for every }w\in{\mathbb W}\text{.} \end{align} $$
Observe that
![]() $\langle t_{S},W_{k+1}\wedge \dots \wedge W_{2n}\wedge T\rangle \neq 0$
on S. Actually, our choice of the orientation for S corresponds to declaring that a unit tangent vector
$\langle t_{S},W_{k+1}\wedge \dots \wedge W_{2n}\wedge T\rangle \neq 0$
on S. Actually, our choice of the orientation for S corresponds to declaring that a unit tangent vector
![]() $t_{S}$
is positively oriented if and only if
$t_{S}$
is positively oriented if and only if
![]() $\langle t_{S},W_{k+1}\wedge \dots \wedge W_{2n}\wedge T\rangle>0$
on S.
$\langle t_{S},W_{k+1}\wedge \dots \wedge W_{2n}\wedge T\rangle>0$
on S.
Recalling the notation introduced in (3.29), we deduce from (4.27), (4.29) and (4.30) that
 $$ \begin{align*} \eta_{S}(\Phi(w))=\frac{\nabla^{\phi}\Phi(w)}{|\nabla^{\phi}\Phi(w)\wedge T\Phi(w)|}, \end{align*} $$
$$ \begin{align*} \eta_{S}(\Phi(w))=\frac{\nabla^{\phi}\Phi(w)}{|\nabla^{\phi}\Phi(w)\wedge T\Phi(w)|}, \end{align*} $$
which implies
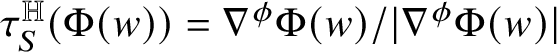 $\tau _{S}^{\mathbb H}(\Phi (w))={\nabla ^{\phi }\Phi (w)}/{|\nabla ^{\phi }\Phi (w)|}$
and, eventually,
$\tau _{S}^{\mathbb H}(\Phi (w))={\nabla ^{\phi }\Phi (w)}/{|\nabla ^{\phi }\Phi (w)|}$
and, eventually,
 $$ \begin{align} t_{S}^{\mathbb H}(\Phi(w))=\frac{\nabla^{\phi}\Phi(w)}{|\nabla^{\phi}\Phi(w)|}\wedge T. \end{align} $$
$$ \begin{align} t_{S}^{\mathbb H}(\Phi(w))=\frac{\nabla^{\phi}\Phi(w)}{|\nabla^{\phi}\Phi(w)|}\wedge T. \end{align} $$
The multivector
![]() $\nabla ^{\phi }\Phi $
also allows characterising the Heisenberg current associated with a
$\nabla ^{\phi }\Phi $
also allows characterising the Heisenberg current associated with a
![]() $C^{1}$
intrinsic graph. The following lemma is an important tool used in the proof of Theorem 1.1.
$C^{1}$
intrinsic graph. The following lemma is an important tool used in the proof of Theorem 1.1.
5 The constancy theorem for Heisenberg currents
The classical constancy theorem (see, e.g., [Reference Federer42, 4.1.7] or [Reference Simon90, Theorem 26.27]) states that, if
![]() ${\mathsf T}$
is an n-dimensional current in a connected open set
${\mathsf T}$
is an n-dimensional current in a connected open set
![]() $U\subset {\mathbb R}^{n}$
such that
$U\subset {\mathbb R}^{n}$
such that
![]() $\partial {\mathsf T}=0$
, then
$\partial {\mathsf T}=0$
, then
![]() ${\mathsf T}$
is constant; that is, there exists
${\mathsf T}$
is constant; that is, there exists
![]() $c\in {\mathbb R}$
such that
$c\in {\mathbb R}$
such that
 ${\mathsf T}(\omega )=c\int _{U}\omega $
for every smooth n-form
${\mathsf T}(\omega )=c\int _{U}\omega $
for every smooth n-form
![]() $\omega $
with compact support in U. The constancy theorem can be generalised (see, e.g., [Reference Krantz and Parks65, Proposition 7.3.5]) to currents supported on an m-dimensional plane
$\omega $
with compact support in U. The constancy theorem can be generalised (see, e.g., [Reference Krantz and Parks65, Proposition 7.3.5]) to currents supported on an m-dimensional plane
![]() ${\mathscr P}\subset {\mathbb R}^{n}$
: if
${\mathscr P}\subset {\mathbb R}^{n}$
: if
![]() ${\mathsf T}$
is an m-current with support in
${\mathsf T}$
is an m-current with support in
![]() ${\mathscr P}$
and such that
${\mathscr P}$
and such that
![]() $\partial {\mathsf T}=0$
, then there exists
$\partial {\mathsf T}=0$
, then there exists
![]() $c\in {\mathbb R}$
such that
$c\in {\mathbb R}$
such that
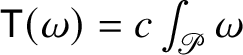 ${\mathsf T}(\omega )=c\int _{{\mathscr P}}\omega $
for every smooth m-form
${\mathsf T}(\omega )=c\int _{{\mathscr P}}\omega $
for every smooth m-form
![]() $\omega $
with compact support.
$\omega $
with compact support.
As mentioned in the Introduction, the version for planes of the constancy theorem implies the following fact (see [Reference Šilhavý89, Theorem 4.2]): if
![]() $R\subset {\mathbb R}^{n}$
is an m-rectifiable set and
$R\subset {\mathbb R}^{n}$
is an m-rectifiable set and
![]() ${\mathsf T}=\tau \mu $
is a normal m-current, where
${\mathsf T}=\tau \mu $
is a normal m-current, where
![]() $\mu $
is a Radon measure and
$\mu $
is a Radon measure and
![]() $\tau $
is a locally
$\tau $
is a locally
![]() $\mu $
-integrable m-vectorfield with
$\mu $
-integrable m-vectorfield with
![]() $\tau \neq 0 \ \mu $
-a.e., then
$\tau \neq 0 \ \mu $
-a.e., then
-
(i)
 is absolutely continuous with respect to the Hausdorff measure
is absolutely continuous with respect to the Hausdorff measure
 , and
, and -
(ii)
 $\tau $
is tangent to R at
$\tau $
is tangent to R at
 $\mu $
-almost every point of R.
$\mu $
-almost every point of R.
See also [Reference Federer42, 4.1.31] and [Reference Giaquinta, Modica and Souček57, Example 10 at page 146] for simpler cases and [Reference Alberti and Marchese1, §5] and [Reference Alberti, Massaccesi and Stepanov2] for similar-in-spirit results.
A similar program is developed in the present section for currents in Heisenberg groups. First, in Subsection 5.1 we prove Proposition 5.3, where a partial version of the Constancy Theorem 1.7 is proved. Proposition 5.3 can also be seen as a particular case of Theorem 1.8, but actually the proof of Theorem 1.8 follows from Proposition 5.3 by a blow-up argument. The proof of Theorem 1.8 is developed in Subsection 5.2: observe that we are not able to prove any ‘absolute continuity’ statement analogous to (i) above but only a ‘tangency’ statement corresponding to (ii). As we said in the Introduction, this is due to the absence of a good notion of projection on planes. The proof of the Constancy Theorem 1.7 for Heisenberg currents without boundary and supported on vertical planes is contained in Subsection 5.3. Observe that here we are able to prove not only the ‘tangency’ property (ii) but also the ‘absolute continuity’ one (i); in fact, by using group convolutions on vertical planes one can reduce to the case in which
![]() $\|{\mathsf T}\|$
is already absolutely continuous.
$\|{\mathsf T}\|$
is already absolutely continuous.
5.1 A partial version of Theorem 1.7
For the reader’s convenience, we recall some preliminary notation. First, given a Radon measure
![]() $\mu $
on
$\mu $
on
![]() ${\mathbb H}^{n}$
and a locally
${\mathbb H}^{n}$
and a locally
![]() $\mu $
-integrable function
$\mu $
-integrable function
![]() $\tau :{\mathbb H}^{n}\to {\mathcal J}_{2n+1-k}$
, we denote by
$\tau :{\mathbb H}^{n}\to {\mathcal J}_{2n+1-k}$
, we denote by
![]() $\tau \mu $
the Heisenberg
$\tau \mu $
the Heisenberg
![]() $(2n+1-k)$
-current defined by
$(2n+1-k)$
-current defined by
 $$ \begin{align*} \tau\mu(\omega):=\int_{{\mathbb H}^{n}} \langle\tau(p)\mid \omega(p)\rangle\:d\mu(p),\qquad \omega\in {\mathcal D}_{\mathbb H}^{2n+1-k}. \end{align*} $$
$$ \begin{align*} \tau\mu(\omega):=\int_{{\mathbb H}^{n}} \langle\tau(p)\mid \omega(p)\rangle\:d\mu(p),\qquad \omega\in {\mathcal D}_{\mathbb H}^{2n+1-k}. \end{align*} $$
Given natural numbers
![]() $a,b$
such that
$a,b$
such that
![]() $1\leq a+b\leq n$
, the
$1\leq a+b\leq n$
, the
![]() $(2a+b+1)$
-dimensional vertical plane
$(2a+b+1)$
-dimensional vertical plane
![]() ${{\mathscr P}_{a,b}}$
was introduced in (3.11) as
${{\mathscr P}_{a,b}}$
was introduced in (3.11) as
 $$ \begin{align} \begin{aligned} {{\mathscr P}_{a,b}}:=\:& \{(x,y,t)\in{\mathbb H}^{n}:x_{i}=y_{j}=0\text{ for all }a+b+1\leq i\leq n \text{ and }a+1\leq j\leq n\} \\ =\:& \begin{cases} \{(x_{1},\dots,x_{a+b},0,\dots,0,y_{1},\dots,y_{a},0,\dots,0,t)\}\quad & \text{if }a\geq 1\text{ and } a+b<n\\ \{(x_{1},\dots,x_{n},y_{1},\dots,y_{a},0,\dots,0,t)\}\quad & \text{if }a\geq 1\text{ and } a+b=n\\ \{(x_{1},\dots,x_{b},0,\dots,0,t)\}\quad & \text{if }a=0. \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {{\mathscr P}_{a,b}}:=\:& \{(x,y,t)\in{\mathbb H}^{n}:x_{i}=y_{j}=0\text{ for all }a+b+1\leq i\leq n \text{ and }a+1\leq j\leq n\} \\ =\:& \begin{cases} \{(x_{1},\dots,x_{a+b},0,\dots,0,y_{1},\dots,y_{a},0,\dots,0,t)\}\quad & \text{if }a\geq 1\text{ and } a+b<n\\ \{(x_{1},\dots,x_{n},y_{1},\dots,y_{a},0,\dots,0,t)\}\quad & \text{if }a\geq 1\text{ and } a+b=n\\ \{(x_{1},\dots,x_{b},0,\dots,0,t)\}\quad & \text{if }a=0. \end{cases} \end{aligned} \end{align} $$
We are interested in the case in which the codimension
![]() $2n-2a-b$
of
$2n-2a-b$
of
![]() ${{\mathscr P}_{a,b}}$
equals a given
${{\mathscr P}_{a,b}}$
equals a given
![]() $k\in \{1,\dots ,n\}$
; hence, we also assume that
$k\in \{1,\dots ,n\}$
; hence, we also assume that
![]() $n\leq 2a+b\leq 2n-1$
. Observe that, if
$n\leq 2a+b\leq 2n-1$
. Observe that, if
![]() $a=0$
, then necessarily
$a=0$
, then necessarily
![]() $b=n$
. A unit tangent vector to
$b=n$
. A unit tangent vector to
![]() ${{\mathscr P}_{a,b}}$
is
${{\mathscr P}_{a,b}}$
is
 $$ \begin{align*} t^{\mathbb H}_{{\mathscr P}_{a,b}}=X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\wedge T, \end{align*} $$
$$ \begin{align*} t^{\mathbb H}_{{\mathscr P}_{a,b}}=X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\wedge T, \end{align*} $$
and we agree that, when
![]() $a=0$
, this expression has to be read as
$a=0$
, this expression has to be read as
![]() $X_{1}\wedge \dots \wedge X_{n}\wedge T$
. We also notice that (5.1) induces a natural identification between the subgroup
$X_{1}\wedge \dots \wedge X_{n}\wedge T$
. We also notice that (5.1) induces a natural identification between the subgroup
![]() ${{\mathscr P}_{a,b}}$
and
${{\mathscr P}_{a,b}}$
and
![]() ${\mathbb R}^{2a+b+1}$
according to which the measures
${\mathbb R}^{2a+b+1}$
according to which the measures
![]() ${\mathscr S}^{2a+b+2}$
and
${\mathscr S}^{2a+b+2}$
and
![]() ${\mathscr L}^{2a+b+1}$
, being Haar measuresFootnote
9
on
${\mathscr L}^{2a+b+1}$
, being Haar measuresFootnote
9
on
![]() ${{\mathscr P}_{a,b}}$
, coincide up to a multiplicative constant.
${{\mathscr P}_{a,b}}$
, coincide up to a multiplicative constant.
Lemma 5.1 is stated in the setting of maximal codimension
![]() $k=n$
; however, it holds also for
$k=n$
; however, it holds also for
![]() $1\leq k\leq n-1$
, as shown later in Lemma 5.2. We use the following notation: given
$1\leq k\leq n-1$
, as shown later in Lemma 5.2. We use the following notation: given
![]() $i,j\in \{1,\dots ,n\}$
, by
$i,j\in \{1,\dots ,n\}$
, by
 $O(x_{i}),O(x_{i}^{2}),O(x_{i}x_{j})$
we denote smooth differential forms that can be written, respectively, as
$O(x_{i}),O(x_{i}^{2}),O(x_{i}x_{j})$
we denote smooth differential forms that can be written, respectively, as
 $x_{i}\alpha ,x_{i}^{2}\beta ,x_{i}x_{j}\gamma $
for suitable smooth differential forms
$x_{i}\alpha ,x_{i}^{2}\beta ,x_{i}x_{j}\gamma $
for suitable smooth differential forms
![]() $\alpha ,\beta ,\gamma $
. When applying exterior differentiation we will freely use straightforward formulae like
$\alpha ,\beta ,\gamma $
. When applying exterior differentiation we will freely use straightforward formulae like
 $d(O(x_{i}^{2}))=O(x_{i})$
,
$d(O(x_{i}^{2}))=O(x_{i})$
,
![]() $d(O(x_{i}x_{j}))=O(x_{i})+O(x_{j})$
and similar ones. Eventually, the equivalence class
$d(O(x_{i}x_{j}))=O(x_{i})+O(x_{j})$
and similar ones. Eventually, the equivalence class
![]() $[\,\cdot \,]_{{\mathcal J}}$
is as in Remark 3.4.
$[\,\cdot \,]_{{\mathcal J}}$
is as in Remark 3.4.
Lemma 5.1. Let
![]() $a,b$
be natural numbers such that
$a,b$
be natural numbers such that
![]() $2a+b=n$
and let
$2a+b=n$
and let
![]() ${{\mathscr P}_{a,b}}$
be the
${{\mathscr P}_{a,b}}$
be the
![]() $(n+1)$
-plane defined in (5.1). Assume there exists
$(n+1)$
-plane defined in (5.1). Assume there exists
![]() $\tau \in {\mathcal J}_{n+1}$
such that the Heisenberg
$\tau \in {\mathcal J}_{n+1}$
such that the Heisenberg
![]() $(n+1)$
-current
$(n+1)$
-current
![]() is such that
is such that
![]() $\partial {\mathsf T}=0$
. Then there exists
$\partial {\mathsf T}=0$
. Then there exists
![]() $\eta \in {\mathbb R}$
such that
$\eta \in {\mathbb R}$
such that
In particular,
![]() $\tau $
is a multiple of
$\tau $
is a multiple of
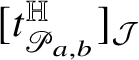 $[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
.
$[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
.
Proof. We assume that
![]() $a\geq 1$
; the case
$a\geq 1$
; the case
![]() $a=0$
requires only simple modifications at the level of notation.
$a=0$
requires only simple modifications at the level of notation.
We have to prove that there exists
![]() $\eta \in {\mathbb R}$
such that, for every
$\eta \in {\mathbb R}$
such that, for every
![]() $\lambda \in {\mathcal J}^{n+1}$
,
$\lambda \in {\mathcal J}^{n+1}$
,
Clearly, it is enough to check (5.2) for
![]() $\lambda $
ranging in the basis of
$\lambda $
ranging in the basis of
![]() ${\mathcal J}^{n+1}$
provided by Proposition 1.10 (with
${\mathcal J}^{n+1}$
provided by Proposition 1.10 (with
![]() $k:=n$
). Fix
$k:=n$
). Fix
![]() $I,J\subset \{1,\dots ,n\}$
and a standard Young tableau R such that
$I,J\subset \{1,\dots ,n\}$
and a standard Young tableau R such that
-
•
 $I\cap J=\emptyset $
and
$I\cap J=\emptyset $
and
 $|I|+|J|\leq n$
and
$|I|+|J|\leq n$
and -
• R is a
 $(2\times \frac {n-|I|-|J|}{2})$
-rectangular (recall Remark 3.25) tableau that contains the integers in the set
$(2\times \frac {n-|I|-|J|}{2})$
-rectangular (recall Remark 3.25) tableau that contains the integers in the set
 $\{1,\dots ,n\}\setminus (I\cup J)$
.
$\{1,\dots ,n\}\setminus (I\cup J)$
.
Testing
![]() $X_{1}\wedge \dots \wedge X_{a+b}\wedge Y_{1}\wedge \dots \wedge Y_{a}\wedge T$
against
$X_{1}\wedge \dots \wedge X_{a+b}\wedge Y_{1}\wedge \dots \wedge Y_{a}\wedge T$
against
![]() $\lambda =dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
, one realises that it is enough to show that
$\lambda =dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
, one realises that it is enough to show that

We are going to prove (5.3) first under some additional assumptions on
![]() $I,J$
or R; see the following Claims 1, 2 and 3. We fix an auxiliary function
$I,J$
or R; see the following Claims 1, 2 and 3. We fix an auxiliary function
![]() $\psi \in C^{\infty }_{c}({\mathbb H}^{n})$
such that
$\psi \in C^{\infty }_{c}({\mathbb H}^{n})$
such that
 $$ \begin{align*} \int_{{\mathscr P}_{a,b}} \psi\:d{\mathscr S}^{n+2}=1. \end{align*} $$
$$ \begin{align*} \int_{{\mathscr P}_{a,b}} \psi\:d{\mathscr S}^{n+2}=1. \end{align*} $$
Claim 1: If
![]() $I\cap \{a+b+1,\dots ,n\}\neq \emptyset $
, then
$I\cap \{a+b+1,\dots ,n\}\neq \emptyset $
, then
![]() $\langle \tau \mid dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \rangle =0$
.
$\langle \tau \mid dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \rangle =0$
.
Fix
![]() $\bar \imath \in I\cap \{a+b+1,\dots ,n\}$
and define
$\bar \imath \in I\cap \{a+b+1,\dots ,n\}$
and define
 $$ \begin{align*} \omega(x,y,t):=x_{\bar\imath}^{2} \;\psi(x,y,t)\: dx_{I\setminus\{\bar\imath\}}\wedge dy_{J\cup\{\bar\imath\}}\wedge\alpha_{R}. \end{align*} $$
$$ \begin{align*} \omega(x,y,t):=x_{\bar\imath}^{2} \;\psi(x,y,t)\: dx_{I\setminus\{\bar\imath\}}\wedge dy_{J\cup\{\bar\imath\}}\wedge\alpha_{R}. \end{align*} $$
By identifying
![]() $\omega \in C^{\infty }_{c}({\mathbb H}^{n},\Large \wedge ^{n} {\mathfrak h}_{1})$
with its equivalence class
$\omega \in C^{\infty }_{c}({\mathbb H}^{n},\Large \wedge ^{n} {\mathfrak h}_{1})$
with its equivalence class
![]() $[\omega ]$
according to the quotient in the right-hand side of (3.7), we have
$[\omega ]$
according to the quotient in the right-hand side of (3.7), we have
![]() $\omega \in {\mathcal D}_{\mathbb H}^{n}$
. One easily computes
$\omega \in {\mathcal D}_{\mathbb H}^{n}$
. One easily computes
 $$ \begin{align*} d\omega=\pm 2 x_{\bar\imath} \;\psi(x,y,t) \: dxy_{\bar\imath}\wedge dx_{I\setminus\{\bar\imath\}}\wedge dy_{J}\wedge\alpha_{R} + O(x_{\bar\imath}^{2}) \end{align*} $$
$$ \begin{align*} d\omega=\pm 2 x_{\bar\imath} \;\psi(x,y,t) \: dxy_{\bar\imath}\wedge dx_{I\setminus\{\bar\imath\}}\wedge dy_{J}\wedge\alpha_{R} + O(x_{\bar\imath}^{2}) \end{align*} $$
where the sign
![]() $\pm $
depends only on
$\pm $
depends only on
![]() $\bar \imath $
and I and, in the sequel, it can change from line to line. We obtain
$\bar \imath $
and I and, in the sequel, it can change from line to line. We obtain
 $$ \begin{align*} L^{-1}((d\omega)_{{\mathfrak h}_{1}} )=\pm 2 x_{\bar\imath} \;\psi(x,y,t) \: dx_{I\setminus\{\bar\imath\}}\wedge dy_{J}\wedge\alpha_{R} + O(x_{\bar\imath}^{2}) \end{align*} $$
$$ \begin{align*} L^{-1}((d\omega)_{{\mathfrak h}_{1}} )=\pm 2 x_{\bar\imath} \;\psi(x,y,t) \: dx_{I\setminus\{\bar\imath\}}\wedge dy_{J}\wedge\alpha_{R} + O(x_{\bar\imath}^{2}) \end{align*} $$
and, in turn,
 $$ \begin{align*} D\omega & = d\big(\omega+(-1)^{n} L^{-1}((d\omega)_{{\mathfrak h}_{1}})\wedge\theta\big)\\ & = \pm 2\;\psi(x,y,t) dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta + O(x_{\bar\imath}). \end{align*} $$
$$ \begin{align*} D\omega & = d\big(\omega+(-1)^{n} L^{-1}((d\omega)_{{\mathfrak h}_{1}})\wedge\theta\big)\\ & = \pm 2\;\psi(x,y,t) dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta + O(x_{\bar\imath}). \end{align*} $$
Since
![]() $O(x_{\bar \imath })=0$
on
$O(x_{\bar \imath })=0$
on
![]() ${{\mathscr P}_{a,b}}$
, we obtain
${{\mathscr P}_{a,b}}$
, we obtain
 $$ \begin{align*} 0&= \partial{\mathsf T} (\omega) = {\mathsf T}(D\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid D\omega\rangle d{\mathscr S}^{n+2}\\ &= \pm 2 \int_{{{\mathscr P}_{a,b}}} \psi\langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle d{\mathscr S}^{n+2}\\ &=\pm 2\langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
$$ \begin{align*} 0&= \partial{\mathsf T} (\omega) = {\mathsf T}(D\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid D\omega\rangle d{\mathscr S}^{n+2}\\ &= \pm 2 \int_{{{\mathscr P}_{a,b}}} \psi\langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle d{\mathscr S}^{n+2}\\ &=\pm 2\langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
and Claim 1 follows.
Claim 2: If
![]() $J\cap \{a+1,\dots ,n\}\neq \emptyset $
, then
$J\cap \{a+1,\dots ,n\}\neq \emptyset $
, then
![]() $\langle \tau \mid dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \rangle =0$
.
$\langle \tau \mid dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \rangle =0$
.
The proof is analogous to that of Claim 1. Fix
![]() $\bar \jmath \in J\cap \{a+1,\dots ,n\}$
and define
$\bar \jmath \in J\cap \{a+1,\dots ,n\}$
and define
![]() $\omega \in {\mathcal D}_{\mathbb H}^{n}$
by
$\omega \in {\mathcal D}_{\mathbb H}^{n}$
by
 $$ \begin{align*} \omega(x,y,t):=y_{\bar\jmath}^{2} \;\psi(x,y,t)\: dx_{I\cup\{\bar\jmath\}}\wedge dy_{J\setminus\{\bar\jmath\}}\wedge\alpha_{R}. \end{align*} $$
$$ \begin{align*} \omega(x,y,t):=y_{\bar\jmath}^{2} \;\psi(x,y,t)\: dx_{I\cup\{\bar\jmath\}}\wedge dy_{J\setminus\{\bar\jmath\}}\wedge\alpha_{R}. \end{align*} $$
A computation similar to the one in Claim 1 gives
and, again,
 $$ \begin{align*} 0= \partial{\mathsf T} (\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid D\omega\rangle d{\mathscr S}^{n+2} = \pm 2\langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
$$ \begin{align*} 0= \partial{\mathsf T} (\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid D\omega\rangle d{\mathscr S}^{n+2} = \pm 2\langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
allows us to conclude.
Claim 3: If the first row of R contains an element
![]() $\bar \imath $
such that
$\bar \imath $
such that
![]() $\bar \imath \geq a+1$
, then
$\bar \imath \geq a+1$
, then
![]() $\langle \tau \mid dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \rangle =0$
.
$\langle \tau \mid dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \rangle =0$
.
We observe that, since R is a standard Young tableau, the assumption of Claim 3 is equivalent to R containing a column made by two elements
![]() $\bar \imath ,\bar \jmath $
such that
$\bar \imath ,\bar \jmath $
such that
![]() $a+1\leq \bar \imath <\bar \jmath \leq n$
. Define
$a+1\leq \bar \imath <\bar \jmath \leq n$
. Define
![]() $\omega \in {\mathcal D}_{\mathbb H}^{n}$
by
$\omega \in {\mathcal D}_{\mathbb H}^{n}$
by
where Q is the standard Young tableau obtained by removing from R the column containing
![]() $\bar \imath ,\bar \jmath $
(for instance, Q is the empty tableau if R consists of the column
$\bar \imath ,\bar \jmath $
(for instance, Q is the empty tableau if R consists of the column
![]() $\bar \imath ,\bar \jmath $
only). One has
$\bar \imath ,\bar \jmath $
only). One has
 $$ \begin{align*} d\omega =\: & \psi(x,y,t)( y_{\bar\jmath}\,dy_{\bar\imath} + y_{\bar\imath}\,dy_{\bar\jmath}) \wedge dx_{I\cup\{\bar\imath,\bar\jmath\}}\wedge dy_{J}\wedge\alpha_{Q} + O(y_{\bar\imath}y_{\bar\jmath})\\ =\: & \psi(x,y,t) \big[(-1)^{c+1} y_{\bar\jmath}\,dxy_{\bar\imath}\wedge dx_{I\cup\{\bar\jmath\}} + (-1)^{d+2} y_{\bar\imath}\,dxy_{\bar\jmath}\wedge dx_{I\cup\{\bar\imath\}}\big] \wedge dy_{J}\wedge\alpha_{Q} + O(y_{\bar\imath}y_{\bar\jmath}) \end{align*} $$
$$ \begin{align*} d\omega =\: & \psi(x,y,t)( y_{\bar\jmath}\,dy_{\bar\imath} + y_{\bar\imath}\,dy_{\bar\jmath}) \wedge dx_{I\cup\{\bar\imath,\bar\jmath\}}\wedge dy_{J}\wedge\alpha_{Q} + O(y_{\bar\imath}y_{\bar\jmath})\\ =\: & \psi(x,y,t) \big[(-1)^{c+1} y_{\bar\jmath}\,dxy_{\bar\imath}\wedge dx_{I\cup\{\bar\jmath\}} + (-1)^{d+2} y_{\bar\imath}\,dxy_{\bar\jmath}\wedge dx_{I\cup\{\bar\imath\}}\big] \wedge dy_{J}\wedge\alpha_{Q} + O(y_{\bar\imath}y_{\bar\jmath}) \end{align*} $$
where
 $$ \begin{align*} & c:=|\{i\in I:i<\bar\imath\}|\\ &d:=|\{i\in I:i<\bar\jmath\}|=|\{i\in I\cup\{\bar\imath\}:i<\bar\jmath\}|-1. \end{align*} $$
$$ \begin{align*} & c:=|\{i\in I:i<\bar\imath\}|\\ &d:=|\{i\in I:i<\bar\jmath\}|=|\{i\in I\cup\{\bar\imath\}:i<\bar\jmath\}|-1. \end{align*} $$
Then
 $$ \begin{align*} L^{-1}((d\omega)_{{\mathfrak h}_{1}} )=- \psi(x,y,t)\big[(-1)^{c+1} y_{\bar\jmath}\,dx_{I\cup\{\bar\jmath\}} + (-1)^{d} y_{\bar\imath}\, dx_{I\cup\{\bar\imath\}}\big] \wedge dy_{J}\wedge\alpha_{Q} + O(y_{\bar\imath}y_{\bar\jmath}) \end{align*} $$
$$ \begin{align*} L^{-1}((d\omega)_{{\mathfrak h}_{1}} )=- \psi(x,y,t)\big[(-1)^{c+1} y_{\bar\jmath}\,dx_{I\cup\{\bar\jmath\}} + (-1)^{d} y_{\bar\imath}\, dx_{I\cup\{\bar\imath\}}\big] \wedge dy_{J}\wedge\alpha_{Q} + O(y_{\bar\imath}y_{\bar\jmath}) \end{align*} $$
and, in turn,
 $$ \begin{align*} D\omega =\: & d\big(\omega+(-1)^{n} L^{-1}((d\omega)_{{\mathfrak h}_{1}})\wedge\theta\big)\\ =\: & (-1)^{n+1} \;\psi(x,y,t)\big[ (-1)^{c+1} dy_{\bar\jmath}\wedge dx_{I\cup\{\bar\jmath\}} + (-1)^{d} dy_{\bar\imath}\wedge dx_{I\cup\{\bar\imath\}}\big]\wedge dy_{J}\wedge \alpha_{Q} \wedge\theta\\ & + O(y_{\bar\imath})+ O(y_{\bar\jmath})\\ =\: & (-1)^{n+1} \;\psi(x,y,t)\big[ (-1)^{c+d+2} dxy_{\bar\jmath}\wedge dx_{I} + (-1)^{c+d+1} dxy_{\bar\imath}\wedge dx_{I}\big]\wedge dy_{J}\wedge \alpha_{Q} \wedge\theta\\ & + O(y_{\bar\imath})+ O(y_{\bar\jmath})\\ =\: & \pm \;\psi(x,y,t)( dxy_{\bar\jmath}- dxy_{\bar\imath})\wedge dx_{I}\wedge dy_{J}\wedge \alpha_{Q}\wedge\theta + O(y_{\bar\imath})+ O(y_{\bar\jmath})\\ =\: & \mp \;\psi(x,y,t) dx_{I}\wedge dy_{J}\wedge \alpha_{R}\wedge\theta + O(x_{\bar\imath})+ O(x_{\bar\jmath}). \end{align*} $$
$$ \begin{align*} D\omega =\: & d\big(\omega+(-1)^{n} L^{-1}((d\omega)_{{\mathfrak h}_{1}})\wedge\theta\big)\\ =\: & (-1)^{n+1} \;\psi(x,y,t)\big[ (-1)^{c+1} dy_{\bar\jmath}\wedge dx_{I\cup\{\bar\jmath\}} + (-1)^{d} dy_{\bar\imath}\wedge dx_{I\cup\{\bar\imath\}}\big]\wedge dy_{J}\wedge \alpha_{Q} \wedge\theta\\ & + O(y_{\bar\imath})+ O(y_{\bar\jmath})\\ =\: & (-1)^{n+1} \;\psi(x,y,t)\big[ (-1)^{c+d+2} dxy_{\bar\jmath}\wedge dx_{I} + (-1)^{c+d+1} dxy_{\bar\imath}\wedge dx_{I}\big]\wedge dy_{J}\wedge \alpha_{Q} \wedge\theta\\ & + O(y_{\bar\imath})+ O(y_{\bar\jmath})\\ =\: & \pm \;\psi(x,y,t)( dxy_{\bar\jmath}- dxy_{\bar\imath})\wedge dx_{I}\wedge dy_{J}\wedge \alpha_{Q}\wedge\theta + O(y_{\bar\imath})+ O(y_{\bar\jmath})\\ =\: & \mp \;\psi(x,y,t) dx_{I}\wedge dy_{J}\wedge \alpha_{R}\wedge\theta + O(x_{\bar\imath})+ O(x_{\bar\jmath}). \end{align*} $$
As before, we obtain
 $$ \begin{align*} 0= \partial{\mathsf T} (\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid D\omega\rangle d{\mathscr S}^{n+2} = \mp\langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
$$ \begin{align*} 0= \partial{\mathsf T} (\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid D\omega\rangle d{\mathscr S}^{n+2} = \mp\langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
and the claim is proved.
Claim 4: (5.3) holds.
We already know that (5.3) holds in case
![]() $I,J,R$
satisfy any one of the assumptions in Claims 1, 2 and 3. We then assume that none of such assumptions hold; that is, that
$I,J,R$
satisfy any one of the assumptions in Claims 1, 2 and 3. We then assume that none of such assumptions hold; that is, that
 $$ \begin{align} \begin{aligned} & I\subset\{1,\dots,a+b\}\\ \text{and }& J\subset\{1,\dots,a\}\\ \text{and }& \text{the elements in the first row of }R\text{ are not greater than }\textit{a}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & I\subset\{1,\dots,a+b\}\\ \text{and }& J\subset\{1,\dots,a\}\\ \text{and }& \text{the elements in the first row of }R\text{ are not greater than }\textit{a}, \end{aligned} \end{align} $$
and we prove that necessarily

This would be enough to conclude.
The first two conditions in (5.4) imply that all of the
![]() $n-a-b=a$
integers
$n-a-b=a$
integers
![]() $a+b+1,\dots ,n$
appear in R. They all belong to the second row of R by the third condition in (5.4); hence, R has at least a columns. Therefore, the first row of R contains at least a elements, all of them not greater than a. It follows that the first row of R contains precisely
$a+b+1,\dots ,n$
appear in R. They all belong to the second row of R by the third condition in (5.4); hence, R has at least a columns. Therefore, the first row of R contains at least a elements, all of them not greater than a. It follows that the first row of R contains precisely
![]() $1,\dots ,a$
(displayed in this order) and that, in turn, the second row of R contains precisely
$1,\dots ,a$
(displayed in this order) and that, in turn, the second row of R contains precisely
![]() $a+b+1,\dots ,n$
(displayed in this order). In particular, R is the one displayed in (5.5). The remaining integers
$a+b+1,\dots ,n$
(displayed in this order). In particular, R is the one displayed in (5.5). The remaining integers
![]() $a+1,\dots ,a+b$
, not appearing in R, have to belong to either I or J; the second condition in (5.4) implies that they all belong to I, and the proof is concluded.
$a+1,\dots ,a+b$
, not appearing in R, have to belong to either I or J; the second condition in (5.4) implies that they all belong to I, and the proof is concluded.
Lemma 5.1 also holds for nonmaximal codimension
![]() $k<n$
, as we now prove. The reader will easily notice the similarity between the two proofs, the main difference lying in the use of the standard exterior differentiation d in place of Rumin’s operator D.
$k<n$
, as we now prove. The reader will easily notice the similarity between the two proofs, the main difference lying in the use of the standard exterior differentiation d in place of Rumin’s operator D.
Lemma 5.2. Let
![]() $a,b$
be natural numbers such that
$a,b$
be natural numbers such that
![]() $1\leq a+b\leq n$
and
$1\leq a+b\leq n$
and
![]() $n+1\leq 2a+b\leq 2n$
; let
$n+1\leq 2a+b\leq 2n$
; let
![]() ${{\mathscr P}_{a,b}}$
be the plane defined in (5.1). Assume there exists
${{\mathscr P}_{a,b}}$
be the plane defined in (5.1). Assume there exists
![]() $\tau \in {\mathcal J}_{2a+b+1}$
such that the Heisenberg
$\tau \in {\mathcal J}_{2a+b+1}$
such that the Heisenberg
![]() $(2a+b+1)$
-current
$(2a+b+1)$
-current
![]() is such that
is such that
![]() $\partial {\mathsf T}=0$
. Then there exists
$\partial {\mathsf T}=0$
. Then there exists
![]() $\eta \in {\mathbb R}$
such that
$\eta \in {\mathbb R}$
such that
In particular,
![]() $\tau $
is a multiple of
$\tau $
is a multiple of
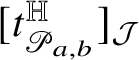 $[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
.
$[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
.
Proof. Observe that necessarily
![]() $a\geq 1$
. We assume also that
$a\geq 1$
. We assume also that
![]() $b\geq 1$
and omit the simple modifications one has to perform in order to treat the case
$b\geq 1$
and omit the simple modifications one has to perform in order to treat the case
![]() $b=0$
.
$b=0$
.
As in Lemma 5.1, we have to prove that (5.2) holds for every
![]() $\lambda $
in the basis of
$\lambda $
in the basis of
![]() ${\mathcal J}^{2a+b+1}$
provided by Proposition 1.10 (with
${\mathcal J}^{2a+b+1}$
provided by Proposition 1.10 (with
![]() $k:=2n-2a-b$
). To this aim, fix
$k:=2n-2a-b$
). To this aim, fix
![]() $I,J\subset \{1,\dots ,n\}$
and a standard Young tableau R such that
$I,J\subset \{1,\dots ,n\}$
and a standard Young tableau R such that
-
•
 $I\cap J=\emptyset $
and
$I\cap J=\emptyset $
and
 $|I|+|J|\leq 2n-2a-b$
;
$|I|+|J|\leq 2n-2a-b$
; -
• R contains the integers in the set
 $\{1,\dots ,n\}\setminus (I\cup J)$
;
$\{1,\dots ,n\}\setminus (I\cup J)$
; -
• the first row of R has length
 $\ell :=(2a+b-|I|-|J|)/2$
and the second one has length
$\ell :=(2a+b-|I|-|J|)/2$
and the second one has length
 $(2n-2a-b-|I|-|J|)/2$
.
$(2n-2a-b-|I|-|J|)/2$
.
Let us observe that the lengths of the two rows of R are never equal; actually, the difference between these lengths is fixed and equal to
![]() $2a+b-n\geq 1$
; see also Remark 3.25. In particular, the rightmost element in the first row of R belongs to a column of height 1 (there is no element in the second row ‘below it’).
$2a+b-n\geq 1$
; see also Remark 3.25. In particular, the rightmost element in the first row of R belongs to a column of height 1 (there is no element in the second row ‘below it’).
The proof will be accomplished if we prove that

In the following Claims 1, 2 and 3 we prove that (5.7) holds under some additional assumptions on
![]() $I,J$
or R; the argument will be completed later in Claim 4. We again fix an auxiliary function
$I,J$
or R; the argument will be completed later in Claim 4. We again fix an auxiliary function
![]() $\psi \in C^{\infty }_{c}({\mathbb H}^{n})$
such that
$\psi \in C^{\infty }_{c}({\mathbb H}^{n})$
such that
 $$ \begin{align*} \int_{{\mathscr P}_{a,b}} \psi\:d{\mathscr S}^{2a+b+2}=1. \end{align*} $$
$$ \begin{align*} \int_{{\mathscr P}_{a,b}} \psi\:d{\mathscr S}^{2a+b+2}=1. \end{align*} $$
Claim 1: If
![]() $I\cap \{a+b+1,\dots ,n\}\neq \emptyset $
, then (5.7) holds.
$I\cap \{a+b+1,\dots ,n\}\neq \emptyset $
, then (5.7) holds.
Fix
![]() $\bar \imath \in I\cap \{a+b+1,\dots ,n\}$
and define
$\bar \imath \in I\cap \{a+b+1,\dots ,n\}$
and define
 $\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
by
$\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
by
where Q is the Young tableau whose first row is equal to that of R and whose second row is made by the second row of R with the addition of the extra element
![]() $\bar \imath $
in the rightmost position. Namely, denoting by
$\bar \imath $
in the rightmost position. Namely, denoting by
![]() $\ell $
and r, with
$\ell $
and r, with
![]() $\ell>r$
, the lengths of the first and second rows of R, respectively, we have
$\ell>r$
, the lengths of the first and second rows of R, respectively, we have

The Young tableau Q is not necessarily a standard one; nonetheless,
 $\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
by Remark 3.26. One can compute
$\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
by Remark 3.26. One can compute
 $$ \begin{align*} d\omega &= \pm\:\psi(x,y,t)\:dx_{I}\wedge dy_{J}\wedge\alpha_{Q}\wedge\theta + O(x_{\bar\imath})\\ & = \pm\:\psi(x,y,t)\:dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta + O(x_{\bar\imath}), \end{align*} $$
$$ \begin{align*} d\omega &= \pm\:\psi(x,y,t)\:dx_{I}\wedge dy_{J}\wedge\alpha_{Q}\wedge\theta + O(x_{\bar\imath})\\ & = \pm\:\psi(x,y,t)\:dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta + O(x_{\bar\imath}), \end{align*} $$
where the second equality is justified by the fact that
![]() $dx_{I}\wedge \alpha _{Q}$
contains a factor
$dx_{I}\wedge \alpha _{Q}$
contains a factor
![]() $dx_{\bar \imath }\wedge (dxy_{h}- dxy_{\bar \imath })=dx_{\bar \imath }\wedge dxy_{h}$
for a suitable h (namely,
$dx_{\bar \imath }\wedge (dxy_{h}- dxy_{\bar \imath })=dx_{\bar \imath }\wedge dxy_{h}$
for a suitable h (namely,
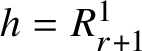 $h=R^{1}_{r+1}$
) appearing in the first row of R. Since
$h=R^{1}_{r+1}$
) appearing in the first row of R. Since
![]() $O(x_{\bar \imath })=0$
on
$O(x_{\bar \imath })=0$
on
![]() ${{\mathscr P}_{a,b}}$
, one gets
${{\mathscr P}_{a,b}}$
, one gets
 $$ \begin{align*} 0 & = \partial{\mathsf T} (\omega) = {\mathsf T}(d\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid d\omega\rangle d{\mathscr S}^{2a+b+2} =\pm \langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
$$ \begin{align*} 0 & = \partial{\mathsf T} (\omega) = {\mathsf T}(d\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid d\omega\rangle d{\mathscr S}^{2a+b+2} =\pm \langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
and Claim 1 follows.
Claim 2: If
![]() $J\cap \{a+1,\dots ,n\}\neq \emptyset $
, then (5.7) holds.
$J\cap \{a+1,\dots ,n\}\neq \emptyset $
, then (5.7) holds.
The proof is similar to that of Claim 1. Fix
![]() $\bar \jmath \in J\cap \{a+1,\dots ,n\}$
and define
$\bar \jmath \in J\cap \{a+1,\dots ,n\}$
and define
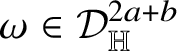 $\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
as
$\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
as
where Q is the Young tableau whose first row is equal to that of R and whose second row is made by the second row of R with the addition of the extra element
![]() $\bar \jmath $
in the rightmost position. Again,
$\bar \jmath $
in the rightmost position. Again,
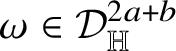 $\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
because of Remark 3.26. One can compute
$\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
because of Remark 3.26. One can compute
 $$ \begin{align*} d\omega &= \pm\:\psi(x,y,t)\:dx_{I}\wedge dy_{J}\wedge\alpha_{Q}\wedge\theta + O(y_{\bar\jmath}) \\ &= \pm\:\psi(x,y,t)\:dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta + O(y_{\bar\jmath}), \end{align*} $$
$$ \begin{align*} d\omega &= \pm\:\psi(x,y,t)\:dx_{I}\wedge dy_{J}\wedge\alpha_{Q}\wedge\theta + O(y_{\bar\jmath}) \\ &= \pm\:\psi(x,y,t)\:dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta + O(y_{\bar\jmath}), \end{align*} $$
where, as before, the second equality is justified by the fact that
![]() $dy_{J}\wedge \alpha _{Q}$
contains a factor
$dy_{J}\wedge \alpha _{Q}$
contains a factor
![]() $dy_{\bar \jmath }\wedge (dxy_{h}- dxy_{\bar \jmath })=dy_{\bar \jmath }\wedge dxy_{h}$
for a suitable h appearing in the first row of R. We deduce that
$dy_{\bar \jmath }\wedge (dxy_{h}- dxy_{\bar \jmath })=dy_{\bar \jmath }\wedge dxy_{h}$
for a suitable h appearing in the first row of R. We deduce that
 $$ \begin{align*} 0 & = \partial{\mathsf T} (\omega) = {\mathsf T}(d\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid d\omega\rangle d{\mathscr S}^{2a+b+2} =\pm \langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
$$ \begin{align*} 0 & = \partial{\mathsf T} (\omega) = {\mathsf T}(d\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid d\omega\rangle d{\mathscr S}^{2a+b+2} =\pm \langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
and Claim 2 follows.
Claim 3: If the first row of R contains an element
![]() $\bar \jmath $
such that
$\bar \jmath $
such that
![]() $\bar \jmath \geq a+1$
, then (5.7) holds.
$\bar \jmath \geq a+1$
, then (5.7) holds.
Since R is a standard Young tableau, the rightmost element in the first row of R is not smaller than
![]() $a+1$
; we can then assume that
$a+1$
; we can then assume that
![]() $\bar \jmath $
is precisely this element. As already noticed, there is no element in the second row of R ‘below’
$\bar \jmath $
is precisely this element. As already noticed, there is no element in the second row of R ‘below’
![]() $\bar \jmath $
. Consider the form
$\bar \jmath $
. Consider the form
 $\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
defined by
$\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
defined by
where Q is the (possibly empty) tableau obtained from R by removing the rightmost entry (i.e.,
![]() $\bar \jmath $
) of the first row. Since Q is a (possibly empty) standard Young tableau containing the same elements of R except for
$\bar \jmath $
) of the first row. Since Q is a (possibly empty) standard Young tableau containing the same elements of R except for
![]() $\bar \jmath $
, we have
$\bar \jmath $
, we have
![]() $\omega \wedge d\theta =0$
and, in particular,
$\omega \wedge d\theta =0$
and, in particular,
 $\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
. Since
$\omega \in {\mathcal D}_{\mathbb H}^{2a+b}$
. Since
 $$ \begin{align*} d\omega & =\psi(x,y,t) dy_{\bar\jmath}\wedge dx_{I\cup\{\bar\jmath\}}\wedge dy_{J}\wedge \alpha_{Q}\wedge \theta + O(y_{\bar\jmath}) \\ & = \pm\:\psi(x,y,t)\: dx_{I}\wedge dy_{J}\wedge\alpha_{Q}\wedge dxy_{\bar\jmath}\wedge \theta + O(y_{\bar\jmath}) \\ & = \pm\:\psi(x,y,t)\: dx_{I}\wedge dy_{J}\wedge \alpha_{R}\wedge \theta + O(y_{\bar\jmath}), \end{align*} $$
$$ \begin{align*} d\omega & =\psi(x,y,t) dy_{\bar\jmath}\wedge dx_{I\cup\{\bar\jmath\}}\wedge dy_{J}\wedge \alpha_{Q}\wedge \theta + O(y_{\bar\jmath}) \\ & = \pm\:\psi(x,y,t)\: dx_{I}\wedge dy_{J}\wedge\alpha_{Q}\wedge dxy_{\bar\jmath}\wedge \theta + O(y_{\bar\jmath}) \\ & = \pm\:\psi(x,y,t)\: dx_{I}\wedge dy_{J}\wedge \alpha_{R}\wedge \theta + O(y_{\bar\jmath}), \end{align*} $$
we deduce as before that
 $$ \begin{align*} 0 & = \partial{\mathsf T} (\omega) = {\mathsf T}(d\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid d\omega\rangle d{\mathscr S}^{2a+b+2} =\pm \langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
$$ \begin{align*} 0 & = \partial{\mathsf T} (\omega) = {\mathsf T}(d\omega) = \int_{{\mathscr P}_{a,b}}\langle\tau \mid d\omega\rangle d{\mathscr S}^{2a+b+2} =\pm \langle\tau \mid dx_{I}\wedge dy_{J}\wedge\alpha_{R}\wedge\theta\rangle \end{align*} $$
and Claim 3 follows.
Claim 4: At least one between (5.6) and (5.7) holds.
We know that (5.7) holds if
![]() $I,J,R$
satisfy any one of the assumptions of Claims 1, 2 and 3. We then assume that none of such assumptions holds; that is, that
$I,J,R$
satisfy any one of the assumptions of Claims 1, 2 and 3. We then assume that none of such assumptions holds; that is, that
 $$ \begin{align} \begin{aligned} & I\subset\{1,\dots,a+b\}\\ \text{and }& J\subset\{1,\dots,a\}\\ \text{and }& \text{the elements in the first row of }R\text{ are not greater than }\textit{a}\text{,} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & I\subset\{1,\dots,a+b\}\\ \text{and }& J\subset\{1,\dots,a\}\\ \text{and }& \text{the elements in the first row of }R\text{ are not greater than }\textit{a}\text{,} \end{aligned} \end{align} $$
and we prove that (5.6) holds.
By (5.8), all of the integers
![]() $a+b+1,\dots ,n$
appear in the second row of R. The length of such a row is then at least
$a+b+1,\dots ,n$
appear in the second row of R. The length of such a row is then at least
![]() $n-a-b$
. Since the difference between the lengths of the rows of R is equal to
$n-a-b$
. Since the difference between the lengths of the rows of R is equal to
![]() $2a+b-n$
, the length of the first row of R is at least a. By the third condition in (5.8), the first row of R contains at most a elements; hence, it contains precisely the a elements
$2a+b-n$
, the length of the first row of R is at least a. By the third condition in (5.8), the first row of R contains at most a elements; hence, it contains precisely the a elements
![]() $1,\dots ,a$
(in this order). In turn, the second row contains
$1,\dots ,a$
(in this order). In turn, the second row contains
![]() $n-a-b$
elements, which are forced to be the numbers
$n-a-b$
elements, which are forced to be the numbers
![]() $a+b+1,\dots ,n$
(in this order). In particular, R is the one displayed in (5.6). The remaining integers
$a+b+1,\dots ,n$
(in this order). In particular, R is the one displayed in (5.6). The remaining integers
![]() $a+1,\dots ,a+b$
, not appearing in R, have to belong to either I or J; the second condition in (5.8) implies that they all belong to I, and the proof is concluded.
$a+1,\dots ,a+b$
, not appearing in R, have to belong to either I or J; the second condition in (5.8) implies that they all belong to I, and the proof is concluded.
Proposition 3.13 allows extending Lemmata 5.1 and 5.2 to general vertical planes (Definition 3.2).
Proposition 5.3. Let
![]() $k\in \{1,\dots ,n\}$
,
$k\in \{1,\dots ,n\}$
,
![]() $\tau \in {\mathcal J}_{2n+1-k}$
and a vertical
$\tau \in {\mathcal J}_{2n+1-k}$
and a vertical
![]() $(2n+1-k)$
-plane
$(2n+1-k)$
-plane
![]() ${\mathscr P}\subset {\mathbb H}^{n}$
be fixed; assume that the current
${\mathscr P}\subset {\mathbb H}^{n}$
be fixed; assume that the current
![]() is such that
is such that
![]() $\partial {\mathsf T}=0$
. Then there exists
$\partial {\mathsf T}=0$
. Then there exists
![]() $\eta \in {\mathbb R}$
such that
$\eta \in {\mathbb R}$
such that
 $$ \begin{align*} \tau=\eta\:[t^{\mathbb H}_{{\mathscr P}}]_{{\mathcal J}}. \end{align*} $$
$$ \begin{align*} \tau=\eta\:[t^{\mathbb H}_{{\mathscr P}}]_{{\mathcal J}}. \end{align*} $$
Proof. By Proposition 3.13 there exists an
![]() ${\mathbb H}$
-linear isomorphism
${\mathbb H}$
-linear isomorphism
![]() ${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
such that
${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
such that
![]() ${\mathcal L}({\mathscr P})={{\mathscr P}_{a,b}}$
and
${\mathcal L}({\mathscr P})={{\mathscr P}_{a,b}}$
and
![]() ${\mathcal L}^{*}(d\theta )=d\theta $
. Consider the push-forward
${\mathcal L}^{*}(d\theta )=d\theta $
. Consider the push-forward
![]() ${\mathcal L}_\#{\mathsf T}$
of
${\mathcal L}_\#{\mathsf T}$
of
![]() ${\mathsf T}$
; that is, the Heisenberg
${\mathsf T}$
; that is, the Heisenberg
![]() $(2n+1-k)$
-current defined by
$(2n+1-k)$
-current defined by
 $$ \begin{align*} {\mathcal L}_\#{\mathsf T}(\omega):={\mathsf T}({\mathcal L}^{*}(\omega)),\qquad\omega\in{\mathcal D}_{\mathbb H}^{2n+1-k}. \end{align*} $$
$$ \begin{align*} {\mathcal L}_\#{\mathsf T}(\omega):={\mathsf T}({\mathcal L}^{*}(\omega)),\qquad\omega\in{\mathcal D}_{\mathbb H}^{2n+1-k}. \end{align*} $$
Also,
![]() ${\mathcal L}_\#{\mathsf T}$
has zero boundary by Corollary 3.12. The push-forward
${\mathcal L}_\#{\mathsf T}$
has zero boundary by Corollary 3.12. The push-forward
of the measure
, defined by
is a Haar measure on
![]() ${{\mathscr P}_{a,b}}$
and, in particular,
${{\mathscr P}_{a,b}}$
and, in particular,

for a suitable
![]() $\gamma>0$
. It follows that for every
$\gamma>0$
. It follows that for every
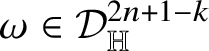 $\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
,
$\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
,
 $$ \begin{align*} {\mathcal L}_\#{\mathsf T}(\omega) = \int_{{\mathscr P}} \langle\tau \mid {\mathcal L}^{*}(\omega) \rangle \:d{\mathscr S}^{Q-k} = \int_{{\mathscr P}_{a,b}} \langle \gamma{\mathcal L}_{*}(\tau) \mid \omega \rangle \:d{\mathscr S}^{Q-k} \end{align*} $$
$$ \begin{align*} {\mathcal L}_\#{\mathsf T}(\omega) = \int_{{\mathscr P}} \langle\tau \mid {\mathcal L}^{*}(\omega) \rangle \:d{\mathscr S}^{Q-k} = \int_{{\mathscr P}_{a,b}} \langle \gamma{\mathcal L}_{*}(\tau) \mid \omega \rangle \:d{\mathscr S}^{Q-k} \end{align*} $$
where
![]() ${\mathcal L}_{*}:{\mathcal J}_{2n+1-k}\to {\mathcal J}_{2n+1-k}$
is the isomorphism defined by
${\mathcal L}_{*}:{\mathcal J}_{2n+1-k}\to {\mathcal J}_{2n+1-k}$
is the isomorphism defined by
Observe that we are implicitly using Proposition 3.11. By Corollary 3.12, the current
has zero boundary; therefore, Lemma 5.1 (if
![]() $k=n$
) or Lemma 5.2 (if
$k=n$
) or Lemma 5.2 (if
![]() $1\leq k< n$
) implies that there exists
$1\leq k< n$
) implies that there exists
![]() $\eta \in {\mathbb R}$
such that
$\eta \in {\mathbb R}$
such that
 $$ \begin{align*} \gamma\:{\mathcal L}_{*}(\tau) = \eta[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}} = \eta\, C\,[{\mathcal L}_{*}(t^{\mathbb H}_{{\mathscr P}})]_{{\mathcal J}} = \eta \,C\,{\mathcal L}_{*}[t^{\mathbb H}_{{\mathscr P}}]_{{\mathcal J}} \end{align*} $$
$$ \begin{align*} \gamma\:{\mathcal L}_{*}(\tau) = \eta[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}} = \eta\, C\,[{\mathcal L}_{*}(t^{\mathbb H}_{{\mathscr P}})]_{{\mathcal J}} = \eta \,C\,{\mathcal L}_{*}[t^{\mathbb H}_{{\mathscr P}}]_{{\mathcal J}} \end{align*} $$
for a suitable
![]() $C\neq 0$
depending on
$C\neq 0$
depending on
![]() ${\mathcal L}$
and
${\mathcal L}$
and
![]() ${\mathscr P}$
. Since
${\mathscr P}$
. Since
![]() ${\mathcal L}_{*}:{\mathcal J}_{2n+1-k}\to {\mathcal J}_{2n+1-k}$
is an isomorphism, we obtain that
${\mathcal L}_{*}:{\mathcal J}_{2n+1-k}\to {\mathcal J}_{2n+1-k}$
is an isomorphism, we obtain that
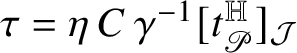 $\tau =\eta \,C\,\gamma ^{-1}[t^{\mathbb H}_{{\mathscr P}}]_{{\mathcal J}}$
and the proof is concluded.
$\tau =\eta \,C\,\gamma ^{-1}[t^{\mathbb H}_{{\mathscr P}}]_{{\mathcal J}}$
and the proof is concluded.
5.2 Proof of Theorem 1.8
We now prove Theorem 1.8. Recall once again that, for
![]() $k\in \{1,\dots ,n\}$
, the space
$k\in \{1,\dots ,n\}$
, the space
![]() ${\mathcal J}_{2n+1-k}$
was introduced as the dual space to
${\mathcal J}_{2n+1-k}$
was introduced as the dual space to
![]() ${\mathcal J}^{2n+1-k}$
. However, we need to also introduce the dual space to Rumin’s space
${\mathcal J}^{2n+1-k}$
. However, we need to also introduce the dual space to Rumin’s space
![]() ${\Large \wedge} ^{n}{\mathfrak h}/\mathcal I^{n}$
and, for convenience of notation, we will denote such dual space by
${\Large \wedge} ^{n}{\mathfrak h}/\mathcal I^{n}$
and, for convenience of notation, we will denote such dual space by
![]() ${\mathcal J}_{n}$
. The spaces
${\mathcal J}_{n}$
. The spaces
![]() ${\mathcal J}_{n}$
and
${\mathcal J}_{n}$
and
![]() ${\mathcal J}_{n+1},\dots ,{\mathcal J}_{2n}$
are endowed, respectively, with the operator norm
${\mathcal J}_{n+1},\dots ,{\mathcal J}_{2n}$
are endowed, respectively, with the operator norm
![]() $|\cdot |$
arising from either the norm on
$|\cdot |$
arising from either the norm on
![]() ${\Large \wedge}^{n}{\mathfrak h}/\mathcal I^{n}$
introduced in (3.28) or the standard norm on
${\Large \wedge}^{n}{\mathfrak h}/\mathcal I^{n}$
introduced in (3.28) or the standard norm on
![]() ${\mathcal J}^{2n+1-k}\subset \Large \wedge ^{2n+1-k}{\mathfrak h}$
,
${\mathcal J}^{2n+1-k}\subset \Large \wedge ^{2n+1-k}{\mathfrak h}$
,
![]() $k=1,\dots , n$
.
$k=1,\dots , n$
.
Proof of Theorem 1.8.
Without loss of generality, we can assume that R is a
![]() ${\mathbb H}$
-regular submanifold S. We have to prove that there exists
${\mathbb H}$
-regular submanifold S. We have to prove that there exists
![]() $\zeta :S\to {\mathbb R}$
such that
$\zeta :S\to {\mathbb R}$
such that
 $$ \begin{align} \!\vec{\,{\mathsf T}}(p)=\zeta(p)[t^{\mathbb H}_{S}(p)]_{{\mathcal J}}\qquad\text{for }\|{\mathsf T}\|_{a}\text{-a.e. }p\in S\text{.} \end{align} $$
$$ \begin{align} \!\vec{\,{\mathsf T}}(p)=\zeta(p)[t^{\mathbb H}_{S}(p)]_{{\mathcal J}}\qquad\text{for }\|{\mathsf T}\|_{a}\text{-a.e. }p\in S\text{.} \end{align} $$
Since
![]() is locally
is locally
![]() $(Q-k)$
-Ahlfors regular, we can differentiate the measure
$(Q-k)$
-Ahlfors regular, we can differentiate the measure
![]() $\|{\mathsf T}\|$
with respect to
$\|{\mathsf T}\|$
with respect to
![]() ; see, for example, [Reference Simon90, Theorem 4.7 and Remark 4.5]. In particular, we can write
; see, for example, [Reference Simon90, Theorem 4.7 and Remark 4.5]. In particular, we can write
![]() for a suitable
for a suitable
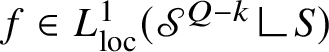 and, for
and, for
![]() ${\mathscr S}^{Q-k}$
-a.e.
${\mathscr S}^{Q-k}$
-a.e.
![]() $p\in S$
, one has
$p\in S$
, one has
 $$ \begin{align} \int_{S\cap B(p,r)} |f\!\vec{\,{\mathsf T}} -f(p)\!\vec{\,{\mathsf T}}(p)|\:d{\mathscr S}^{Q-k} = o\left( {\mathscr S}^{Q-k}(S\cap B(p,r))\right)=o(r^{Q-k}) \end{align} $$
$$ \begin{align} \int_{S\cap B(p,r)} |f\!\vec{\,{\mathsf T}} -f(p)\!\vec{\,{\mathsf T}}(p)|\:d{\mathscr S}^{Q-k} = o\left( {\mathscr S}^{Q-k}(S\cap B(p,r))\right)=o(r^{Q-k}) \end{align} $$
and
Statement (5.10) (and then Theorem 1.8) reduces to proving that there exists
![]() $\eta :S\to {\mathbb R}$
such that
$\eta :S\to {\mathbb R}$
such that
 $$ \begin{align} f(p)\!\vec{\,{\mathsf T}}(p)=\eta(p)[t^{\mathbb H}_{S}(p)]_{{\mathcal J}}\qquad\text{for }{\mathscr S}^{Q-k}\text{-a.e. }p\in S\text{.} \end{align} $$
$$ \begin{align} f(p)\!\vec{\,{\mathsf T}}(p)=\eta(p)[t^{\mathbb H}_{S}(p)]_{{\mathcal J}}\qquad\text{for }{\mathscr S}^{Q-k}\text{-a.e. }p\in S\text{.} \end{align} $$
Since
![]() $\partial {\mathsf T}$
also has locally finite mass, by Riesz’s theorem (recall also Remark 3.30) there exist a Radon measure
$\partial {\mathsf T}$
also has locally finite mass, by Riesz’s theorem (recall also Remark 3.30) there exist a Radon measure
![]() $\nu $
and a locally
$\nu $
and a locally
![]() $\nu $
-integrable function
$\nu $
-integrable function
![]() $\sigma :{\mathbb H}^{n}\to {\mathcal J}_{2n-k}$
such that
$\sigma :{\mathbb H}^{n}\to {\mathcal J}_{2n-k}$
such that
![]() $|\sigma |=1 \ \nu $
-a.e. and
$|\sigma |=1 \ \nu $
-a.e. and
![]() $\partial {\mathsf T}=\sigma \nu $
; that is,
$\partial {\mathsf T}=\sigma \nu $
; that is,
 $$ \begin{align*} \partial{\mathsf T}(\omega)=\int\langle\sigma\mid \omega\rangle\:d\nu,\qquad\omega\in{\mathcal D}_{\mathbb H}^{2n-k}. \end{align*} $$
$$ \begin{align*} \partial{\mathsf T}(\omega)=\int\langle\sigma\mid \omega\rangle\:d\nu,\qquad\omega\in{\mathcal D}_{\mathbb H}^{2n-k}. \end{align*} $$
Differentiating
![]() $\nu $
with respect to
$\nu $
with respect to
![]() , we obtain that for
, we obtain that for
![]() ${\mathscr S}^{Q-k}$
-a.e.
${\mathscr S}^{Q-k}$
-a.e.
![]() $p\in S$
,
$p\in S$
,
 $$ \begin{align} \nu(B(p,r)) = O\left( {\mathscr S}^{Q-k}(S\cap B(p,r))\right)=O(r^{Q-k}). \end{align} $$
$$ \begin{align} \nu(B(p,r)) = O\left( {\mathscr S}^{Q-k}(S\cap B(p,r))\right)=O(r^{Q-k}). \end{align} $$
We claim that (5.13) holds for those
![]() $p\in S$
for which (5.11), (5.12) and (5.14) hold. This would be enough to conclude.
$p\in S$
for which (5.11), (5.12) and (5.14) hold. This would be enough to conclude.
Let such a p be fixed. For
![]() $r>0$
, consider the map
$r>0$
, consider the map
![]() ${\mathcal L}_{p,r}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
defined by
${\mathcal L}_{p,r}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
defined by
![]() ${\mathcal L}_{p,r}(q):=\delta _{1/r}(p^{-1}q)$
and the push-forward
${\mathcal L}_{p,r}(q):=\delta _{1/r}(p^{-1}q)$
and the push-forward
![]() ${\mathsf T}_{p,r}:={{\mathcal L}_{p,r}}_\#{\mathsf T}$
; that is, the current
${\mathsf T}_{p,r}:={{\mathcal L}_{p,r}}_\#{\mathsf T}$
; that is, the current
 $$ \begin{align*} {\mathsf T}_{p,r}(\omega):={\mathsf T}({\mathcal L}_{p,r}^{*}\omega),\qquad \omega\in{\mathcal D}_{\mathbb H}^{2n+1-k}. \end{align*} $$
$$ \begin{align*} {\mathsf T}_{p,r}(\omega):={\mathsf T}({\mathcal L}_{p,r}^{*}\omega),\qquad \omega\in{\mathcal D}_{\mathbb H}^{2n+1-k}. \end{align*} $$
Observe that, by homogeneity and left-invariance, the equality
 ${\mathcal L}_{p,r}^{*}\omega = r^{-(Q-k)}(\omega \circ {\mathcal L}_{p,r} )$
holds for every
${\mathcal L}_{p,r}^{*}\omega = r^{-(Q-k)}(\omega \circ {\mathcal L}_{p,r} )$
holds for every
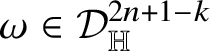 $\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
. If
$\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
. If
![]() $\bar r>0$
is such that
$\bar r>0$
is such that
![]() $\mathrm {spt}\:\omega \subset B(0,\bar r)$
, one gets
$\mathrm {spt}\:\omega \subset B(0,\bar r)$
, one gets
 $$ \begin{align*} \lim_{r\to 0^{+}}{\mathsf T}_{p,r}(\omega) & \stackrel{\phantom{(5.12)}}{=} \lim_{r\to 0^{+}} \frac{1}{r^{Q-k}}\int_{B(p,r\bar r)} \langle \!\vec{\,{\mathsf T}} \mid \omega\circ{\mathcal L}_{p,r} \rangle\: d\|{\mathsf T}\|\\ & \stackrel{(5.12)}{=} \lim_{r\to 0^{+}} \frac{1}{r^{Q-k}}\int_{S\cap B(p,r\bar r)} \langle f\!\vec{\,{\mathsf T}} \mid \omega\circ{\mathcal L}_{p,r} \rangle\: d{\mathscr S}^{Q-k}\\ & \stackrel{(5.11)}{=} \lim_{r\to 0^{+}} \frac{1}{r^{Q-k}}\int_{S\cap B(p,r\bar r)} \langle f(p)\!\vec{\,{\mathsf T}}(p) \mid \omega\circ{\mathcal L}_{p,r} \rangle\: d{\mathscr S}^{Q-k} \end{align*} $$
$$ \begin{align*} \lim_{r\to 0^{+}}{\mathsf T}_{p,r}(\omega) & \stackrel{\phantom{(5.12)}}{=} \lim_{r\to 0^{+}} \frac{1}{r^{Q-k}}\int_{B(p,r\bar r)} \langle \!\vec{\,{\mathsf T}} \mid \omega\circ{\mathcal L}_{p,r} \rangle\: d\|{\mathsf T}\|\\ & \stackrel{(5.12)}{=} \lim_{r\to 0^{+}} \frac{1}{r^{Q-k}}\int_{S\cap B(p,r\bar r)} \langle f\!\vec{\,{\mathsf T}} \mid \omega\circ{\mathcal L}_{p,r} \rangle\: d{\mathscr S}^{Q-k}\\ & \stackrel{(5.11)}{=} \lim_{r\to 0^{+}} \frac{1}{r^{Q-k}}\int_{S\cap B(p,r\bar r)} \langle f(p)\!\vec{\,{\mathsf T}}(p) \mid \omega\circ{\mathcal L}_{p,r} \rangle\: d{\mathscr S}^{Q-k} \end{align*} $$
and a change of variables gives
 $$ \begin{align*} \lim_{r\to 0^{+}}{\mathsf T}_{p,r}(\omega) & = \lim_{r\to 0^{+}} \int_{\delta_{1/r}(p^{-1}S)\cap B(0,\bar r)} \langle f(p)\!\vec{\,{\mathsf T}}(p) \mid \omega \rangle\: d{\mathscr S}^{Q-k}\\ & = \lim_{r\to 0^{+}} \int_{\delta_{1/r}(p^{-1}S)} \langle f(p)\!\vec{\,{\mathsf T}}(p) \mid \omega \rangle\: d{\mathscr S}^{Q-k}. \end{align*} $$
$$ \begin{align*} \lim_{r\to 0^{+}}{\mathsf T}_{p,r}(\omega) & = \lim_{r\to 0^{+}} \int_{\delta_{1/r}(p^{-1}S)\cap B(0,\bar r)} \langle f(p)\!\vec{\,{\mathsf T}}(p) \mid \omega \rangle\: d{\mathscr S}^{Q-k}\\ & = \lim_{r\to 0^{+}} \int_{\delta_{1/r}(p^{-1}S)} \langle f(p)\!\vec{\,{\mathsf T}}(p) \mid \omega \rangle\: d{\mathscr S}^{Q-k}. \end{align*} $$
By (4.24) we can define the limit current
![]() ${\mathsf T}_{\infty }$
as
${\mathsf T}_{\infty }$
as
 $$ \begin{align*} {\mathsf T}_{\infty}(\omega):=\lim_{r\to 0^{+}}{\mathsf T}_{p,r}(\omega) = \int_{{\mathrm{Tan}}^{\mathbb H}_{S}(p)} \langle f(p)\!\vec{\,{\mathsf T}}(p) \mid \omega \rangle\: d{\mathscr S}^{Q-k},\qquad \omega\in{\mathcal D}_{\mathbb H}^{2n+1-k}. \end{align*} $$
$$ \begin{align*} {\mathsf T}_{\infty}(\omega):=\lim_{r\to 0^{+}}{\mathsf T}_{p,r}(\omega) = \int_{{\mathrm{Tan}}^{\mathbb H}_{S}(p)} \langle f(p)\!\vec{\,{\mathsf T}}(p) \mid \omega \rangle\: d{\mathscr S}^{Q-k},\qquad \omega\in{\mathcal D}_{\mathbb H}^{2n+1-k}. \end{align*} $$
The current
![]() ${\mathsf T}_{\infty }$
is supported on the plane
${\mathsf T}_{\infty }$
is supported on the plane
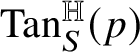 ${\mathrm {Tan}}^{\mathbb H}_{S}(p)$
. We now study its boundary and observe that for every
${\mathrm {Tan}}^{\mathbb H}_{S}(p)$
. We now study its boundary and observe that for every
 $\omega \in {\mathcal D}_{\mathbb H}^{2n-k}$
,
$\omega \in {\mathcal D}_{\mathbb H}^{2n-k}$
,
 $$ \begin{align*} \partial{\mathsf T}_{\infty}(\omega) &= {\mathsf T}_{\infty}(d_{C}\omega) = \lim_{r\to 0^{+}}{\mathsf T}_{p,r}(d_{C}\omega) =\lim_{r\to 0^{+}} {\mathsf T}({\mathcal L}_{p,r}^{*}d_{C}\omega) \end{align*} $$
$$ \begin{align*} \partial{\mathsf T}_{\infty}(\omega) &= {\mathsf T}_{\infty}(d_{C}\omega) = \lim_{r\to 0^{+}}{\mathsf T}_{p,r}(d_{C}\omega) =\lim_{r\to 0^{+}} {\mathsf T}({\mathcal L}_{p,r}^{*}d_{C}\omega) \end{align*} $$
and by Corollary 3.12
 $$ \begin{align*}, \partial{\mathsf T}_{\infty}(\omega) & = \lim_{r\to 0^{+}} {\mathsf T}(d_{C}{\mathcal L}_{p,r}^{*}\omega) = \lim_{r\to 0^{+}} \partial {\mathsf T}({\mathcal L}_{p,r}^{*}\omega) = \int_{{\mathbb H}^{n}} \langle\sigma \mid {\mathcal L}_{p,r}^{*}\omega\rangle\:d\nu. \end{align*} $$
$$ \begin{align*}, \partial{\mathsf T}_{\infty}(\omega) & = \lim_{r\to 0^{+}} {\mathsf T}(d_{C}{\mathcal L}_{p,r}^{*}\omega) = \lim_{r\to 0^{+}} \partial {\mathsf T}({\mathcal L}_{p,r}^{*}\omega) = \int_{{\mathbb H}^{n}} \langle\sigma \mid {\mathcal L}_{p,r}^{*}\omega\rangle\:d\nu. \end{align*} $$
By homogeneity, we have
 $ {\mathcal L}_{p,r}^{*}\omega =r^{-\Delta }(\omega \circ {\mathcal L}_{p,r})$
, where
$ {\mathcal L}_{p,r}^{*}\omega =r^{-\Delta }(\omega \circ {\mathcal L}_{p,r})$
, where
![]() $\Delta $
is the homogeneity degree of
$\Delta $
is the homogeneity degree of
![]() $\omega $
and
$\omega $
and
 $$ \begin{align*} &\Delta=Q-k-2=n& &\hspace{-2cm}\text{if }k=n\\ &\Delta=Q-k-1&&\hspace{-2cm}\text{if }1\leq k\leq n-1. \end{align*} $$
$$ \begin{align*} &\Delta=Q-k-2=n& &\hspace{-2cm}\text{if }k=n\\ &\Delta=Q-k-1&&\hspace{-2cm}\text{if }1\leq k\leq n-1. \end{align*} $$
We then obtain
 $$ \begin{align*} |\partial{\mathsf T}_{\infty}(\omega)| & = \lim_{r\to 0^{+}} {r^{-\Delta}}\left|\int_{{\mathbb H}^{n}} \langle\sigma \mid \omega\circ{\mathcal L}_{p,r}\rangle\:d\nu\right| \\ &\leq \lim_{r\to 0^{+}} r^{-\Delta+Q-k}\:\frac{\nu(B(p,r\bar r))}{r^{Q-k}}\:\sup|\omega|=0, \end{align*} $$
$$ \begin{align*} |\partial{\mathsf T}_{\infty}(\omega)| & = \lim_{r\to 0^{+}} {r^{-\Delta}}\left|\int_{{\mathbb H}^{n}} \langle\sigma \mid \omega\circ{\mathcal L}_{p,r}\rangle\:d\nu\right| \\ &\leq \lim_{r\to 0^{+}} r^{-\Delta+Q-k}\:\frac{\nu(B(p,r\bar r))}{r^{Q-k}}\:\sup|\omega|=0, \end{align*} $$
the last equality following from (5.14) and the inequality
![]() $\Delta < Q-k$
.
$\Delta < Q-k$
.
The current
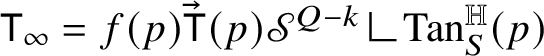 is such that
is such that
![]() $\partial {\mathsf T}_{\infty }=0$
. By Proposition 5.3 there exists
$\partial {\mathsf T}_{\infty }=0$
. By Proposition 5.3 there exists
![]() $\eta =\eta (p)\in {\mathbb R}$
such that
$\eta =\eta (p)\in {\mathbb R}$
such that
 $$ \begin{align*} f(p)\!\vec{\,{\mathsf T}}(p)=\eta[t^{\mathbb H}_{{\mathrm{Tan}}^{\mathbb H}_{S}(p)}]_{{\mathcal J}} =\eta [t^{\mathbb H}_{S}(p)]_{{\mathcal J}} \end{align*} $$
$$ \begin{align*} f(p)\!\vec{\,{\mathsf T}}(p)=\eta[t^{\mathbb H}_{{\mathrm{Tan}}^{\mathbb H}_{S}(p)}]_{{\mathcal J}} =\eta [t^{\mathbb H}_{S}(p)]_{{\mathcal J}} \end{align*} $$
and the proof is accomplished.
5.3 The constancy theorem in Heisenberg groups
In this section we prove Theorem 1.7. We start by establishing some standard facts inspired by classical results about mollification of distributions. Given
![]() $k\in \{1,\dots ,n\}$
, let
$k\in \{1,\dots ,n\}$
, let
![]() $a,b$
be fixed nonnegative integers such that
$a,b$
be fixed nonnegative integers such that
![]() $1\leq a+b\leq n$
and
$1\leq a+b\leq n$
and
![]() $2a+b=2n-k$
. Consider the vertical plane
$2a+b=2n-k$
. Consider the vertical plane
![]() ${{\mathscr P}_{a,b}}$
defined in (5.1); let us fix a mollification kernel
${{\mathscr P}_{a,b}}$
defined in (5.1); let us fix a mollification kernel
![]() $\varphi \in C^{\infty }_{c}({{\mathscr P}_{a,b}})$
such that
$\varphi \in C^{\infty }_{c}({{\mathscr P}_{a,b}})$
such that
 $$ \begin{align*} \int_{{\mathscr P}_{a,b}} \varphi\:d{\mathscr S}^{Q-k}=1\quad\text{and}\quad \mathrm{spt}\: \varphi\subset B(0,1)\cap {{\mathscr P}_{a,b}}. \end{align*} $$
$$ \begin{align*} \int_{{\mathscr P}_{a,b}} \varphi\:d{\mathscr S}^{Q-k}=1\quad\text{and}\quad \mathrm{spt}\: \varphi\subset B(0,1)\cap {{\mathscr P}_{a,b}}. \end{align*} $$
As usual, for every
![]() $\varepsilon>0$
we define the rescaled kernels
$\varepsilon>0$
we define the rescaled kernels
![]() $\varphi _{\varepsilon }:=\varepsilon ^{k-Q}(\varphi \circ \delta _{1/\varepsilon })$
and, given a Heisenberg
$\varphi _{\varepsilon }:=\varepsilon ^{k-Q}(\varphi \circ \delta _{1/\varepsilon })$
and, given a Heisenberg
![]() $(2n+1-k)$
-current
$(2n+1-k)$
-current
![]() ${\mathsf T}$
with support in
${\mathsf T}$
with support in
![]() ${{\mathscr P}_{a,b}}$
, we define the Heisenberg
${{\mathscr P}_{a,b}}$
, we define the Heisenberg
![]() $(2n+1-k)$
-current
$(2n+1-k)$
-current
![]() ${\mathsf T}_{\varepsilon }$
as
${\mathsf T}_{\varepsilon }$
as
 $$ \begin{align} {\mathsf T}_{\varepsilon}(\omega):=\int_{{\mathscr P}_{a,b}} \varphi_{\varepsilon}(p){\mathsf T}({\mathcal L}_{p}^{*} \omega)\:d{\mathscr S}^{Q-k}(p),\qquad\omega\in{\mathcal D}_{\mathbb H}^{2n+1-k} \end{align} $$
$$ \begin{align} {\mathsf T}_{\varepsilon}(\omega):=\int_{{\mathscr P}_{a,b}} \varphi_{\varepsilon}(p){\mathsf T}({\mathcal L}_{p}^{*} \omega)\:d{\mathscr S}^{Q-k}(p),\qquad\omega\in{\mathcal D}_{\mathbb H}^{2n+1-k} \end{align} $$
where
![]() ${\mathcal L}_{p}(q):=pq$
denotes left-translation by
${\mathcal L}_{p}(q):=pq$
denotes left-translation by
![]() $p\in {{\mathscr P}_{a,b}}$
.
$p\in {{\mathscr P}_{a,b}}$
.
Lemma 5.4. Let
![]() ${\mathsf T}$
be a Heisenberg
${\mathsf T}$
be a Heisenberg
![]() $(2n+1-k)$
-current with support in
$(2n+1-k)$
-current with support in
![]() ${{\mathscr P}_{a,b}}$
and with locally finite mass; for
${{\mathscr P}_{a,b}}$
and with locally finite mass; for
![]() $\varepsilon>0$
, consider
$\varepsilon>0$
, consider
![]() ${\mathsf T}_{\varepsilon }$
as in (5.15). Then the following statements hold:
${\mathsf T}_{\varepsilon }$
as in (5.15). Then the following statements hold:
-
(i)
 ${\mathsf T}_{\varepsilon }$
has support in
${\mathsf T}_{\varepsilon }$
has support in
 ${{\mathscr P}_{a,b}}$
;
${{\mathscr P}_{a,b}}$
; -
(ii)
 ${\mathsf T}_{\varepsilon }\rightharpoonup {\mathsf T}$
as
${\mathsf T}_{\varepsilon }\rightharpoonup {\mathsf T}$
as
 $\varepsilon \to 0^{+}$
; that is,
$\varepsilon \to 0^{+}$
; that is,
 ${\mathsf T}_{\varepsilon }(\omega )\to {\mathsf T}(\omega )$
for every
${\mathsf T}_{\varepsilon }(\omega )\to {\mathsf T}(\omega )$
for every
 $\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
;
$\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
; -
(iii) there exists a
 $C^{\infty }$
-smooth map
$C^{\infty }$
-smooth map
 $\tau _{\varepsilon }:{{\mathscr P}_{a,b}}\to {\mathcal J}_{2n+1-k}$
such that
$\tau _{\varepsilon }:{{\mathscr P}_{a,b}}\to {\mathcal J}_{2n+1-k}$
such that
 ;
; -
(iv) if
 $\partial {\mathsf T}=0$
, then
$\partial {\mathsf T}=0$
, then
 $\partial {\mathsf T}_{\varepsilon }=0$
.
$\partial {\mathsf T}_{\varepsilon }=0$
.
Proof. The statement in (i) is clear: in fact, if
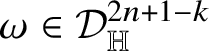 $\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
is such that
$\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
is such that
![]() $\mathrm {spt}\: \omega \cap {{\mathscr P}_{a,b}}=\emptyset $
, then
$\mathrm {spt}\: \omega \cap {{\mathscr P}_{a,b}}=\emptyset $
, then
![]() $\mathrm {spt}\:{\mathcal L}_{p}^{*}\omega \cap {{\mathscr P}_{a,b}}=\emptyset $
for every
$\mathrm {spt}\:{\mathcal L}_{p}^{*}\omega \cap {{\mathscr P}_{a,b}}=\emptyset $
for every
![]() $p\in {{\mathscr P}_{a,b}}$
and
$p\in {{\mathscr P}_{a,b}}$
and
![]() ${\mathsf T}_{\varepsilon }(\omega )=0$
.
${\mathsf T}_{\varepsilon }(\omega )=0$
.
Concerning (ii), let
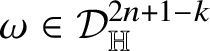 $\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
be fixed and let
$\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
be fixed and let
![]() $R>0$
be such that
$R>0$
be such that
![]() $\mathrm {spt}\:\omega \subset B(0,R)$
. Writing
$\mathrm {spt}\:\omega \subset B(0,R)$
. Writing
![]() ${\mathsf T}=\!\vec {\,{\mathsf T}}\|{\mathsf T}\|$
as in Remark 3.30, we estimate
${\mathsf T}=\!\vec {\,{\mathsf T}}\|{\mathsf T}\|$
as in Remark 3.30, we estimate
 $$ \begin{align*} |{\mathsf T}_{\varepsilon}(\omega)-{\mathsf T}(\omega)| & = \left| \int_{{\mathscr P}_{a,b}}\varphi_{\varepsilon}(p)\,{\mathsf T}({\mathcal L}_{p}^{*} \omega-\omega)\: d{\mathscr S}^{Q-k}(p)\right|\\ &\leq \sup_{p\in{{\mathscr P}_{a,b}}\cap B(0,\varepsilon)}\|{\mathcal L}_{p}^{*} \omega-\omega\|_{C^{0}(B(0,R+\varepsilon))}\|{\mathsf T}\|(B(0,R+\varepsilon)) \end{align*} $$
$$ \begin{align*} |{\mathsf T}_{\varepsilon}(\omega)-{\mathsf T}(\omega)| & = \left| \int_{{\mathscr P}_{a,b}}\varphi_{\varepsilon}(p)\,{\mathsf T}({\mathcal L}_{p}^{*} \omega-\omega)\: d{\mathscr S}^{Q-k}(p)\right|\\ &\leq \sup_{p\in{{\mathscr P}_{a,b}}\cap B(0,\varepsilon)}\|{\mathcal L}_{p}^{*} \omega-\omega\|_{C^{0}(B(0,R+\varepsilon))}\|{\mathsf T}\|(B(0,R+\varepsilon)) \end{align*} $$
and, in particular,
![]() ${\mathsf T}_{\varepsilon }(\omega )\to {\mathsf T}(\omega )$
as
${\mathsf T}_{\varepsilon }(\omega )\to {\mathsf T}(\omega )$
as
![]() $\varepsilon \to 0^{+}$
.
$\varepsilon \to 0^{+}$
.
Since
![]() ${\mathcal L}_{p}^{*} \omega (q)=\omega (pq)$
, statement (iii) follows from
${\mathcal L}_{p}^{*} \omega (q)=\omega (pq)$
, statement (iii) follows from
 $$ \begin{align*} {\mathsf T}_{\varepsilon}(\omega) &= \int_{{\mathscr P}_{a,b}}\int_{{\mathscr P}_{a,b}} \varphi_{\varepsilon}(p)\,\langle \!\vec{\,{\mathsf T}}(q)\mid \omega(pq)\rangle \,d\|{\mathsf T}\|(q)\:d{\mathscr S}^{Q-k} (p)\\ &= \int_{{\mathscr P}_{a,b}} \Big\langle \int_{{\mathscr P}_{a,b}} \varphi_{\varepsilon}(pq^{-1}) \!\vec{\,{\mathsf T}}(q)\,d\|{\mathsf T}\|(q)\: \Big|\:\omega(p) \Big\rangle\:d{\mathscr S}^{Q-k} (p). \end{align*} $$
$$ \begin{align*} {\mathsf T}_{\varepsilon}(\omega) &= \int_{{\mathscr P}_{a,b}}\int_{{\mathscr P}_{a,b}} \varphi_{\varepsilon}(p)\,\langle \!\vec{\,{\mathsf T}}(q)\mid \omega(pq)\rangle \,d\|{\mathsf T}\|(q)\:d{\mathscr S}^{Q-k} (p)\\ &= \int_{{\mathscr P}_{a,b}} \Big\langle \int_{{\mathscr P}_{a,b}} \varphi_{\varepsilon}(pq^{-1}) \!\vec{\,{\mathsf T}}(q)\,d\|{\mathsf T}\|(q)\: \Big|\:\omega(p) \Big\rangle\:d{\mathscr S}^{Q-k} (p). \end{align*} $$
Eventually, if
![]() $\partial {\mathsf T}=0$
one has
$\partial {\mathsf T}=0$
one has
 $$ \begin{align} \partial{\mathsf T}_{\varepsilon}(\omega)={\mathsf T}_{\varepsilon}(d_{C}\omega)=\int_{{\mathscr P}_{a,b}} \varphi_{\varepsilon}(p){\mathsf T}(d_{C}({\mathcal L}_{p}^{*} \omega))\:d{\mathscr S}^{Q-k}(p)=0, \end{align} $$
$$ \begin{align} \partial{\mathsf T}_{\varepsilon}(\omega)={\mathsf T}_{\varepsilon}(d_{C}\omega)=\int_{{\mathscr P}_{a,b}} \varphi_{\varepsilon}(p){\mathsf T}(d_{C}({\mathcal L}_{p}^{*} \omega))\:d{\mathscr S}^{Q-k}(p)=0, \end{align} $$
where we used Corollary 3.12.
Remark 5.5. One can more generally observe that, as in (5.16),
 $$ \begin{align*} \partial{\mathsf T}_{\varepsilon}(\omega)=\int_{{\mathscr P}_{a,b}} \varphi_{\varepsilon}(p)\: \partial{\mathsf T}({\mathcal L}_{p}^{*} \omega)\:d{\mathscr S}^{Q-k}(p); \end{align*} $$
$$ \begin{align*} \partial{\mathsf T}_{\varepsilon}(\omega)=\int_{{\mathscr P}_{a,b}} \varphi_{\varepsilon}(p)\: \partial{\mathsf T}({\mathcal L}_{p}^{*} \omega)\:d{\mathscr S}^{Q-k}(p); \end{align*} $$
that is,
![]() $\partial {\mathsf T}_{\varepsilon }=(\partial {\mathsf T})_{\varepsilon }$
.
$\partial {\mathsf T}_{\varepsilon }=(\partial {\mathsf T})_{\varepsilon }$
.
For the reader’s convenience, we separate the proof of Theorem 1.7 in the cases
![]() $k=n$
and
$k=n$
and
![]() $1\leq k\leq n-1$
; as one can expect, the former is computationally more demanding because of the use of the second-order operator D.
$1\leq k\leq n-1$
; as one can expect, the former is computationally more demanding because of the use of the second-order operator D.
It is convenient to fix some notation. If R is a Young tableau and the elements displayed in R are all different, by abuse of notation we write
![]() $\sum _{k\in R}$
to denote summation on all of the elements k displayed in R. Moreover, if R is rectangular and k is an element displayed in R, we denote by
$\sum _{k\in R}$
to denote summation on all of the elements k displayed in R. Moreover, if R is rectangular and k is an element displayed in R, we denote by
![]() $[R\!\setminus \! k]$
the (possibly empty) Young tableau obtained from R by removing the column containing k. For instance, if
$[R\!\setminus \! k]$
the (possibly empty) Young tableau obtained from R by removing the column containing k. For instance, if

then

Proof of Theorem 1.7, case
 $k=n$
.
$k=n$
.
Reasoning as in Proposition 5.3, by Proposition 3.13 one can assume without loss of generality that
![]() ${\mathscr P}={{\mathscr P}_{a,b}}$
for some nonnegative integers
${\mathscr P}={{\mathscr P}_{a,b}}$
for some nonnegative integers
![]() $a,b$
such that
$a,b$
such that
![]() $2a+b=n$
. Moreover, by Lemma 5.4 it is not restrictive to assume that
$2a+b=n$
. Moreover, by Lemma 5.4 it is not restrictive to assume that
![]() for a suitable
for a suitable
![]() $C^{\infty }$
-smooth
$C^{\infty }$
-smooth
![]() $\tau :{{\mathscr P}_{a,b}}\to {\mathcal J}_{n+1}$
. By Theorem 1.8,
$\tau :{{\mathscr P}_{a,b}}\to {\mathcal J}_{n+1}$
. By Theorem 1.8,
![]() $\tau $
can be written as
$\tau $
can be written as
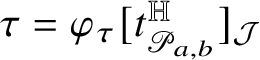 $\tau =\varphi _{\tau } [t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
for some
$\tau =\varphi _{\tau } [t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
for some
![]() $\varphi _{\tau }\in C^{\infty }({{\mathscr P}_{a,b}})$
; let us prove that
$\varphi _{\tau }\in C^{\infty }({{\mathscr P}_{a,b}})$
; let us prove that
![]() $\varphi _{\tau } $
is constant on
$\varphi _{\tau } $
is constant on
![]() ${{\mathscr P}_{a,b}}$
.
${{\mathscr P}_{a,b}}$
.
We are going to utilise test n-forms
![]() $\omega =f dx_{I}\wedge dy_{J}\wedge \alpha _{R}$
, where
$\omega =f dx_{I}\wedge dy_{J}\wedge \alpha _{R}$
, where
![]() $f\in C^{\infty }_{c}({\mathbb H}^{n})$
and the triple
$f\in C^{\infty }_{c}({\mathbb H}^{n})$
and the triple
![]() $(I,J,R)$
is as in Proposition 1.10 (with
$(I,J,R)$
is as in Proposition 1.10 (with
![]() $k=n$
); in particular, R is rectangular. As usual,
$k=n$
); in particular, R is rectangular. As usual,
![]() $\omega $
is a smooth section of
$\omega $
is a smooth section of
![]() $\Large \wedge ^{n}{\mathfrak h}_{1}$
, but we identify
$\Large \wedge ^{n}{\mathfrak h}_{1}$
, but we identify
![]() $\omega $
with an element in
$\omega $
with an element in
![]() ${\mathcal D}_{\mathbb H}^{n}$
as in (3.7). By (3.8) we have
${\mathcal D}_{\mathbb H}^{n}$
as in (3.7). By (3.8) we have
 $$ \begin{align} D\omega= (d\omega)_{\mathfrak v} + \theta\wedge d(L^{-1}((d\omega)_{{\mathfrak h}_{1}})). \end{align} $$
$$ \begin{align} D\omega= (d\omega)_{\mathfrak v} + \theta\wedge d(L^{-1}((d\omega)_{{\mathfrak h}_{1}})). \end{align} $$
Taking into account that
 $$ \begin{align*} d\omega =\: & \sum_{i\in I} (Y_{i}f) dy_{i}\wedge dx_{I}\wedge dy_{J}\wedge\alpha_{R} + \sum_{j\in J} (X_{j} f) dx_{j}\wedge dx_{I}\wedge dy_{J}\wedge\alpha_{R}\\ &+\sum_{k\in R} ((X_{k}f)dx_{k}+(Y_{k}f)dy_{k})\wedge dx_{I}\wedge dy_{J}\wedge\alpha_{R} + (Tf)\theta\wedge dx_{I}\wedge dy_{J}\wedge\alpha_{R}, \end{align*} $$
$$ \begin{align*} d\omega =\: & \sum_{i\in I} (Y_{i}f) dy_{i}\wedge dx_{I}\wedge dy_{J}\wedge\alpha_{R} + \sum_{j\in J} (X_{j} f) dx_{j}\wedge dx_{I}\wedge dy_{J}\wedge\alpha_{R}\\ &+\sum_{k\in R} ((X_{k}f)dx_{k}+(Y_{k}f)dy_{k})\wedge dx_{I}\wedge dy_{J}\wedge\alpha_{R} + (Tf)\theta\wedge dx_{I}\wedge dy_{J}\wedge\alpha_{R}, \end{align*} $$
we obtain
and
 $$ \begin{align} \begin{aligned} L^{-1}((d\omega)_{{\mathfrak h}_{1}}) =\: & \sum_{i\in I} \pm (Y_{i}f) dx_{I\setminus\{i\}}\wedge dy_{J}\wedge\alpha_{R} + \sum_{j\in J} \pm (X_{j} f) dx_{I}\wedge dy_{J\setminus\{j\}}\wedge\alpha_{R}\\ &+\sum_{k\in R} \left( \pm(X_{k}f) dx_{I\cup\{k\}}\wedge dy_{J} \pm(Y_{k}f) dx_{I}\wedge dy_{J\cup\{k\}}\right)\wedge\alpha_{[R\setminus k]}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} L^{-1}((d\omega)_{{\mathfrak h}_{1}}) =\: & \sum_{i\in I} \pm (Y_{i}f) dx_{I\setminus\{i\}}\wedge dy_{J}\wedge\alpha_{R} + \sum_{j\in J} \pm (X_{j} f) dx_{I}\wedge dy_{J\setminus\{j\}}\wedge\alpha_{R}\\ &+\sum_{k\in R} \left( \pm(X_{k}f) dx_{I\cup\{k\}}\wedge dy_{J} \pm(Y_{k}f) dx_{I}\wedge dy_{J\cup\{k\}}\right)\wedge\alpha_{[R\setminus k]}. \end{aligned} \end{align} $$
The signs
![]() $\pm $
appearing in (5.19) could be easily specified, but they are in fact irrelevant for our purposes.
$\pm $
appearing in (5.19) could be easily specified, but they are in fact irrelevant for our purposes.
Let us fix

If
![]() $a=0$
, then
$a=0$
, then
![]() $b=n$
,
$b=n$
,
![]() $\overline I=\{1,\dots ,n\}$
and
$\overline I=\{1,\dots ,n\}$
and
![]() $\overline R$
is the empty tableau. If
$\overline R$
is the empty tableau. If
![]() $b=0$
, then
$b=0$
, then
![]() $a=n/2$
and
$a=n/2$
and
![]() $\overline I=\emptyset $
.
$\overline I=\emptyset $
.
Assume
![]() $a\geq 1$
, fix a column of
$a\geq 1$
, fix a column of
![]() $\overline R$
and let
$\overline R$
and let
![]() $\alpha ,\gamma $
be its elements, with
$\alpha ,\gamma $
be its elements, with
![]() $\alpha <\gamma $
; in particular,
$\alpha <\gamma $
; in particular,
![]() $\gamma =\alpha +n-a$
. On choosing
$\gamma =\alpha +n-a$
. On choosing
 $$ \begin{align*} & I:=\overline I\cup\{\alpha\},\quad J:=\{\gamma\}\quad\text{and}\quad R:=[\overline R\!\setminus\! \alpha]\\ & f(x,y,t):=x_{\gamma}\: g(x,y,t)\quad\text{for an arbitrary }g\in C^{\infty}_{c}({\mathbb H}^{n}) \end{align*} $$
$$ \begin{align*} & I:=\overline I\cup\{\alpha\},\quad J:=\{\gamma\}\quad\text{and}\quad R:=[\overline R\!\setminus\! \alpha]\\ & f(x,y,t):=x_{\gamma}\: g(x,y,t)\quad\text{for an arbitrary }g\in C^{\infty}_{c}({\mathbb H}^{n}) \end{align*} $$
one gets from (5.18) and (5.19)
where we used the notation introduced before Lemma 5.1, and
 $$ \begin{align*} \theta\wedge d(L^{-1}((d\omega)_{{\mathfrak h}_{1}})) &= \pm (Y_{\alpha} X_{\gamma} f) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{ R}\wedge dxy_{\alpha}\wedge\theta + O(x_{\gamma}) + \sigma\\ &= \pm (Y_{\alpha} g) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{\overline R}\wedge\theta + O(x_{\gamma}) + \sigma \end{align*} $$
$$ \begin{align*} \theta\wedge d(L^{-1}((d\omega)_{{\mathfrak h}_{1}})) &= \pm (Y_{\alpha} X_{\gamma} f) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{ R}\wedge dxy_{\alpha}\wedge\theta + O(x_{\gamma}) + \sigma\\ &= \pm (Y_{\alpha} g) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{\overline R}\wedge\theta + O(x_{\gamma}) + \sigma \end{align*} $$
where, here and in the following,
![]() $\sigma $
denotes a form (which may vary from line to line) in the annihilator of
$\sigma $
denotes a form (which may vary from line to line) in the annihilator of
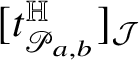 $[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
; equivalently,
$[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
; equivalently,
![]() $\langle X_{1}\wedge \dots \wedge X_{a+b}\wedge Y_{1}\wedge \dots \wedge Y_{a}\wedge T\mid \sigma \rangle =0$
. In particular,
$\langle X_{1}\wedge \dots \wedge X_{a+b}\wedge Y_{1}\wedge \dots \wedge Y_{a}\wedge T\mid \sigma \rangle =0$
. In particular,
![]() $\langle \tau \mid \sigma \rangle =0$
and from (5.17) we obtain
$\langle \tau \mid \sigma \rangle =0$
and from (5.17) we obtain
 $$ \begin{align} 0={\mathsf T}(D\omega)=\pm\int_{{\mathscr P}_{a,b}} \varphi_{\tau}(Y_{\alpha} g)\:d{\mathscr L}^{n+1} \quad\text{for every }g\in C^{\infty}_{c}({\mathbb H}^{n}). \end{align} $$
$$ \begin{align} 0={\mathsf T}(D\omega)=\pm\int_{{\mathscr P}_{a,b}} \varphi_{\tau}(Y_{\alpha} g)\:d{\mathscr L}^{n+1} \quad\text{for every }g\in C^{\infty}_{c}({\mathbb H}^{n}). \end{align} $$
In a similar way, on choosing
 $$ \begin{align*} & I:=\overline I\cup\{\gamma\},\quad J:=\{\alpha\}\quad\text{and}\quad R:=[\overline R\!\setminus\! \alpha]\\ & f(x,y,t):=y_{\gamma}\: g(x,y,t)\quad\text{for an arbitrary }g\in C^{\infty}_{c}({\mathbb H}^{n}) \end{align*} $$
$$ \begin{align*} & I:=\overline I\cup\{\gamma\},\quad J:=\{\alpha\}\quad\text{and}\quad R:=[\overline R\!\setminus\! \alpha]\\ & f(x,y,t):=y_{\gamma}\: g(x,y,t)\quad\text{for an arbitrary }g\in C^{\infty}_{c}({\mathbb H}^{n}) \end{align*} $$
one again gets
![]() $(d\omega )_{\mathfrak v}=O(y_{\gamma })=0$
on
$(d\omega )_{\mathfrak v}=O(y_{\gamma })=0$
on
![]() ${{\mathscr P}_{a,b}}$
and
${{\mathscr P}_{a,b}}$
and
 $$ \begin{align*} \theta\wedge d(L^{-1}((d\omega)_{{\mathfrak h}_{1}})) &= \pm (X_{\alpha} Y_{\gamma} f) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{ R}\wedge dxy_{\alpha}\wedge\theta + O(y_{\gamma}) + \sigma\\ &= \pm (X_{\alpha} g) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{\overline R}\wedge\theta + O(y_{\gamma}) + \sigma \end{align*} $$
$$ \begin{align*} \theta\wedge d(L^{-1}((d\omega)_{{\mathfrak h}_{1}})) &= \pm (X_{\alpha} Y_{\gamma} f) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{ R}\wedge dxy_{\alpha}\wedge\theta + O(y_{\gamma}) + \sigma\\ &= \pm (X_{\alpha} g) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{\overline R}\wedge\theta + O(y_{\gamma}) + \sigma \end{align*} $$
where
![]() $\sigma $
again denotes a form in the annihilator of
$\sigma $
again denotes a form in the annihilator of
 $[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
. From (5.17) we obtain
$[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
. From (5.17) we obtain
 $$ \begin{align*} 0={\mathsf T}(D\omega)=\pm\int_{{\mathscr P}_{a,b}} \varphi_{\tau}(X_{\alpha} g)\:d{\mathscr L}^{n+1} \quad\text{for every }g\in C^{\infty}_{c}({\mathbb H}^{n}), \end{align*} $$
$$ \begin{align*} 0={\mathsf T}(D\omega)=\pm\int_{{\mathscr P}_{a,b}} \varphi_{\tau}(X_{\alpha} g)\:d{\mathscr L}^{n+1} \quad\text{for every }g\in C^{\infty}_{c}({\mathbb H}^{n}), \end{align*} $$
which, together with (5.20), gives
 $$ \begin{align} \begin{aligned} & X_{\alpha} \varphi_{\tau} = Y_{\alpha} \varphi_{\tau} = 0\qquad\text{for every }\alpha=1,\dots,a\\ & T \varphi_{\tau} = X_{1} Y_{1} \varphi_{\tau} - Y_{1} X_{1} \varphi_{\tau}=0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & X_{\alpha} \varphi_{\tau} = Y_{\alpha} \varphi_{\tau} = 0\qquad\text{for every }\alpha=1,\dots,a\\ & T \varphi_{\tau} = X_{1} Y_{1} \varphi_{\tau} - Y_{1} X_{1} \varphi_{\tau}=0. \end{aligned} \end{align} $$
We recall once again that the equalities in (5.21) are proved only under the assumption
![]() $a\geq 1$
.
$a\geq 1$
.
If
![]() $b\geq 1$
, we fix
$b\geq 1$
, we fix
![]() $\beta \in \overline I$
and choose
$\beta \in \overline I$
and choose

The tableau R is obtained from
![]() $\overline R$
on replacing the entry
$\overline R$
on replacing the entry
![]() $a+b+1$
with
$a+b+1$
with
![]() $\beta $
. Then
$\beta $
. Then
and
 $$ \begin{align*} \theta\wedge d(L^{-1}((d\omega)_{{\mathfrak h}_{1}})) &= \pm (X_{\beta} Y_{a+b+1} f) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{R}\wedge \theta + O(y_{a+b+1}) + \sigma\\ &= \pm (X_{\beta} g) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{\overline R}\wedge\theta + O(y_{a+b+1}) + \sigma \end{align*} $$
$$ \begin{align*} \theta\wedge d(L^{-1}((d\omega)_{{\mathfrak h}_{1}})) &= \pm (X_{\beta} Y_{a+b+1} f) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{R}\wedge \theta + O(y_{a+b+1}) + \sigma\\ &= \pm (X_{\beta} g) dx_{\overline I}\wedge dy_{\overline J}\wedge\alpha_{\overline R}\wedge\theta + O(y_{a+b+1}) + \sigma \end{align*} $$
where
![]() $\sigma $
again denotes a form annihilating
$\sigma $
again denotes a form annihilating
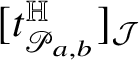 $[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
and we used the fact that
$[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
and we used the fact that
![]() $dx_{\overline I}\wedge dy_{\overline J}\wedge (\alpha _{R}-\alpha _{\overline R})$
annihilates
$dx_{\overline I}\wedge dy_{\overline J}\wedge (\alpha _{R}-\alpha _{\overline R})$
annihilates
 $[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
. From (5.17) we obtain
$[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
. From (5.17) we obtain
 $$ \begin{align*} 0={\mathsf T}(D\omega)=\pm\int_{{\mathscr P}_{a,b}} \varphi_{\tau}(X_{\beta} g)\:d{\mathscr L}^{n+1} \quad\text{for every }g\in C^{\infty}_{c}({\mathbb H}^{n}) \end{align*} $$
$$ \begin{align*} 0={\mathsf T}(D\omega)=\pm\int_{{\mathscr P}_{a,b}} \varphi_{\tau}(X_{\beta} g)\:d{\mathscr L}^{n+1} \quad\text{for every }g\in C^{\infty}_{c}({\mathbb H}^{n}) \end{align*} $$
so that
If
![]() $a\geq 1$
, (5.21) and (5.22) are enough to conclude that
$a\geq 1$
, (5.21) and (5.22) are enough to conclude that
![]() $\varphi _{\tau }$
is constant on
$\varphi _{\tau }$
is constant on
![]() ${{\mathscr P}_{a,b}}$
. If
${{\mathscr P}_{a,b}}$
. If
![]() $a=0$
, (5.22) still holds and we have only to prove that
$a=0$
, (5.22) still holds and we have only to prove that
We then choose
![]() $I=\overline I=\{1,\dots ,n\}$
,
$I=\overline I=\{1,\dots ,n\}$
,
![]() $J=\overline J=\emptyset $
,
$J=\overline J=\emptyset $
,
![]() $R=\overline R$
(in this case, the empty tableau) and we fix an arbitrary
$R=\overline R$
(in this case, the empty tableau) and we fix an arbitrary
![]() $f\in C^{\infty }_{c}({\mathbb H}^{n})$
. By (5.17), (5.18) and (5.19),
$f\in C^{\infty }_{c}({\mathbb H}^{n})$
. By (5.17), (5.18) and (5.19),
 $$ \begin{align*} D\omega &=\theta\wedge\left((Tf)dx_{\{1,\dots,n\}}+d\Big(\sum_{i=1}^{n} \pm(Y_{i}f)\,dx_{\{1,\dots,n\}\setminus\{i\}}\Big)\right)\\ & = \left(Tf+\sum_{i=1}^{n} \pm X_{i}Y_{i}f\right)\theta\wedge dx_{\{1,\dots,n\}} + \sigma \end{align*} $$
$$ \begin{align*} D\omega &=\theta\wedge\left((Tf)dx_{\{1,\dots,n\}}+d\Big(\sum_{i=1}^{n} \pm(Y_{i}f)\,dx_{\{1,\dots,n\}\setminus\{i\}}\Big)\right)\\ & = \left(Tf+\sum_{i=1}^{n} \pm X_{i}Y_{i}f\right)\theta\wedge dx_{\{1,\dots,n\}} + \sigma \end{align*} $$
for a suitable
![]() $\sigma $
in the annihilator of
$\sigma $
in the annihilator of
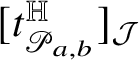 $[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
. This gives
$[t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
. This gives
 $$ \begin{align*} 0={\mathsf T}(D\omega)=\int_{{{\mathscr P}_{a,b}}} \left(Tf+\sum_{i=1}^{n} \pm X_{i}Y_{i}f\right)\varphi_{\tau}\:d{\mathscr L}^{n+1}\stackrel{(5.22)}{=}\int_{{{\mathscr P}_{a,b}}} (Tf)\varphi_{\tau}\:d{\mathscr L}^{n+1} \end{align*} $$
$$ \begin{align*} 0={\mathsf T}(D\omega)=\int_{{{\mathscr P}_{a,b}}} \left(Tf+\sum_{i=1}^{n} \pm X_{i}Y_{i}f\right)\varphi_{\tau}\:d{\mathscr L}^{n+1}\stackrel{(5.22)}{=}\int_{{{\mathscr P}_{a,b}}} (Tf)\varphi_{\tau}\:d{\mathscr L}^{n+1} \end{align*} $$
and (5.23) follows from the arbitrariness of f. This concludes the proof.
Proof of Theorem 1.7, case
 $1\leq k\leq n-1$
.
$1\leq k\leq n-1$
.
Reasoning as in Proposition 5.3, by Proposition 3.13 one can assume without loss of generality that
![]() ${\mathscr P}={{\mathscr P}_{a,b}}$
for some nonnegative integers
${\mathscr P}={{\mathscr P}_{a,b}}$
for some nonnegative integers
![]() $a,b$
such that
$a,b$
such that
![]() $1\leq a+b\leq n$
and
$1\leq a+b\leq n$
and
![]() $2a+b=2n-k$
. Observe that
$2a+b=2n-k$
. Observe that
![]() $a\geq 1$
. By Lemma 5.4 it is not restrictive to assume that
$a\geq 1$
. By Lemma 5.4 it is not restrictive to assume that
![]() for a suitable
for a suitable
![]() $C^{\infty }$
-smooth
$C^{\infty }$
-smooth
![]() $\tau :{{\mathscr P}_{a,b}}\to {\mathcal J}_{2n+1-k}$
. By Theorem 1.8,
$\tau :{{\mathscr P}_{a,b}}\to {\mathcal J}_{2n+1-k}$
. By Theorem 1.8,
![]() $\tau $
can be written as
$\tau $
can be written as
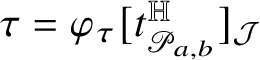 $\tau =\varphi _{\tau } [t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
for some
$\tau =\varphi _{\tau } [t^{\mathbb H}_{{\mathscr P}_{a,b}}]_{{\mathcal J}}$
for some
![]() $\varphi _{\tau }\in C^{\infty }({{\mathscr P}_{a,b}})$
; let us prove that
$\varphi _{\tau }\in C^{\infty }({{\mathscr P}_{a,b}})$
; let us prove that
![]() $\varphi _{\tau } $
is constant on
$\varphi _{\tau } $
is constant on
![]() ${{\mathscr P}_{a,b}}$
.
${{\mathscr P}_{a,b}}$
.
We are going to consider the Heisenberg
![]() $(2n-k)$
-form
$(2n-k)$
-form
![]() $\omega =f dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
, where
$\omega =f dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta $
, where
-
•
 $f\in C^{\infty }_{c}({\mathbb H}^{n})$
;
$f\in C^{\infty }_{c}({\mathbb H}^{n})$
; -
•
 $I\subset \{1,\dots ,n\}$
,
$I\subset \{1,\dots ,n\}$
,
 $J\subset \{1,\dots ,n\}$
,
$J\subset \{1,\dots ,n\}$
,
 $|I|+|J|\leq k+1$
and
$|I|+|J|\leq k+1$
and
 $I\cap J=\emptyset $
;
$I\cap J=\emptyset $
; -
• R is a (nonnecessarily standard) Young tableau that contains the elements of
 $\{1,\dots ,n\}\setminus (I\cup J)$
arranged in two rows of length, respectively,
$\{1,\dots ,n\}\setminus (I\cup J)$
arranged in two rows of length, respectively,
 $(2n-k-1-|I|-|J|)/2$
and
$(2n-k-1-|I|-|J|)/2$
and
 $(k+1-|I|-|J|)/2$
.
$(k+1-|I|-|J|)/2$
.
Observe that
 $\omega \in {\mathcal D}_{\mathbb H}^{2n-k}$
because of Remark 3.26. Then
$\omega \in {\mathcal D}_{\mathbb H}^{2n-k}$
because of Remark 3.26. Then
 $$ \begin{align} \begin{aligned} d\omega =& \sum_{i\in I}\pm (Y_{i}f)dx_{I\setminus\{i\}}\wedge dy_{J}\wedge\alpha_{R}\wedge dxy_{i}\wedge\theta \\ &+ \sum_{j\in J}\pm (X_{j}f)dx_{I}\wedge dy_{J\setminus\{j\}}\wedge\alpha_{R}\wedge dxy_{j}\wedge\theta\\ &+ \sum_{k\in R} \big( \pm (X_{k}f)dx_{I\cup\{k\}}\wedge dy_{J} \pm (Y_{k}f)dx_{I}\wedge dy_{J\cup\{k\}}\big)\wedge\alpha_{R}\wedge\theta \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} d\omega =& \sum_{i\in I}\pm (Y_{i}f)dx_{I\setminus\{i\}}\wedge dy_{J}\wedge\alpha_{R}\wedge dxy_{i}\wedge\theta \\ &+ \sum_{j\in J}\pm (X_{j}f)dx_{I}\wedge dy_{J\setminus\{j\}}\wedge\alpha_{R}\wedge dxy_{j}\wedge\theta\\ &+ \sum_{k\in R} \big( \pm (X_{k}f)dx_{I\cup\{k\}}\wedge dy_{J} \pm (Y_{k}f)dx_{I}\wedge dy_{J\cup\{k\}}\big)\wedge\alpha_{R}\wedge\theta \end{aligned} \end{align} $$
where, again, the signs
![]() $\pm $
will play no role.
$\pm $
will play no role.
We set

and fix
![]() $\alpha \in \{1,\dots , a\}$
. Observe that
$\alpha \in \{1,\dots , a\}$
. Observe that
![]() $\overline R$
is never rectangular, a fact that plays a role in the following construction. If
$\overline R$
is never rectangular, a fact that plays a role in the following construction. If
![]() $\alpha \geq n-a-b+1$
, we define R by removing
$\alpha \geq n-a-b+1$
, we define R by removing
![]() $\alpha $
from
$\alpha $
from
![]() $\overline R$
; that is,
$\overline R$
; that is,

otherwise, if
![]() $\alpha \leq n-a-b$
, we define a tableau R by removing from
$\alpha \leq n-a-b$
, we define a tableau R by removing from
![]() $\overline R$
the column containing
$\overline R$
the column containing
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha +a+b$
and placing
$\alpha +a+b$
and placing
![]() $\alpha +a+b$
as the rightmost element in the second row; that is,
$\alpha +a+b$
as the rightmost element in the second row; that is,

With this choice of R, we consider the Heisenberg form
 $\omega =f dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \in {\mathcal D}_{\mathbb H}^{2n-k}$
associated with
$\omega =f dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \in {\mathcal D}_{\mathbb H}^{2n-k}$
associated with
![]() $I:=\overline I$
and
$I:=\overline I$
and
![]() $J:=\{\alpha \}$
; by (5.24),
$J:=\{\alpha \}$
; by (5.24),
 $$ \begin{align*} d\omega&= \pm (X_{\alpha} f)\: dx_{\overline I}\wedge\alpha_{R}\wedge dxy_{\alpha}\wedge\theta + \sigma\\ &= \pm (X_{\alpha} f)\: dx_{\overline I}\wedge\alpha_{\overline R}\wedge\theta + \sigma, \end{align*} $$
$$ \begin{align*} d\omega&= \pm (X_{\alpha} f)\: dx_{\overline I}\wedge\alpha_{R}\wedge dxy_{\alpha}\wedge\theta + \sigma\\ &= \pm (X_{\alpha} f)\: dx_{\overline I}\wedge\alpha_{\overline R}\wedge\theta + \sigma, \end{align*} $$
where
![]() $\sigma $
is again a form annihilating
$\sigma $
is again a form annihilating
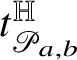 $t^{\mathbb H}_{{\mathscr P}_{a,b}}$
that can vary from line to line. This gives
$t^{\mathbb H}_{{\mathscr P}_{a,b}}$
that can vary from line to line. This gives
 $$ \begin{align*} 0={\mathsf T}(d\omega)=\pm\int_{{\mathscr P}_{a,b}}(X_{\alpha} f)\varphi_{\tau}\:d{\mathscr L}^{2a+b+1}\quad\text{for every }f\in C^{\infty}_{c}({\mathbb H}^{n}) \end{align*} $$
$$ \begin{align*} 0={\mathsf T}(d\omega)=\pm\int_{{\mathscr P}_{a,b}}(X_{\alpha} f)\varphi_{\tau}\:d{\mathscr L}^{2a+b+1}\quad\text{for every }f\in C^{\infty}_{c}({\mathbb H}^{n}) \end{align*} $$
and, in turn,
Using the same tableau R, but choosing
![]() $I:=\overline I\cup \{\alpha \}$
and
$I:=\overline I\cup \{\alpha \}$
and
![]() $J:=\emptyset $
, one gets for
$J:=\emptyset $
, one gets for
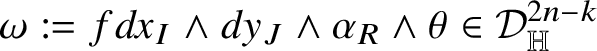 $\omega :=f dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \in {\mathcal D}_{\mathbb H}^{2n-k}$
that
$\omega :=f dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \in {\mathcal D}_{\mathbb H}^{2n-k}$
that
 $$ \begin{align*} d\omega&= \pm (Y_{\alpha} f)\: dx_{\overline I}\wedge\alpha_{R}\wedge dxy_{\alpha}\wedge\theta + \sigma\\ &= \pm (Y_{\alpha} f)\: dx_{\overline I}\wedge\alpha_{\overline R}\wedge\theta + \sigma, \end{align*} $$
$$ \begin{align*} d\omega&= \pm (Y_{\alpha} f)\: dx_{\overline I}\wedge\alpha_{R}\wedge dxy_{\alpha}\wedge\theta + \sigma\\ &= \pm (Y_{\alpha} f)\: dx_{\overline I}\wedge\alpha_{\overline R}\wedge\theta + \sigma, \end{align*} $$
for
![]() $\sigma $
annihilating
$\sigma $
annihilating
 $t^{\mathbb H}_{{\mathscr P}_{a,b}}$
. Similar to before, we deduce that
$t^{\mathbb H}_{{\mathscr P}_{a,b}}$
. Similar to before, we deduce that
which, together with (5.25) and the inequality
![]() $a\geq 1$
, implies
$a\geq 1$
, implies
If
![]() $b=0$
, (5.25), (5.26) and (5.27) imply that
$b=0$
, (5.25), (5.26) and (5.27) imply that
![]() $\varphi _{\tau }$
is constant on
$\varphi _{\tau }$
is constant on
![]() ${{\mathscr P}_{a,b}}$
. If
${{\mathscr P}_{a,b}}$
. If
![]() $b\geq 1$
, we have only to show that
$b\geq 1$
, we have only to show that
Let
![]() $\beta \in \{a+1,\dots ,a+b\}$
be fixed. We consider the test form
$\beta \in \{a+1,\dots ,a+b\}$
be fixed. We consider the test form
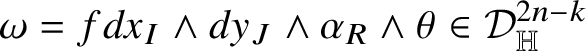 $\omega =f dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \in {\mathcal D}_{\mathbb H}^{2n-k}$
where
$\omega =f dx_{I}\wedge dy_{J}\wedge \alpha _{R}\wedge \theta \in {\mathcal D}_{\mathbb H}^{2n-k}$
where
![]() $I:=\overline I\setminus \{\beta \}$
,
$I:=\overline I\setminus \{\beta \}$
,
![]() $J:=\emptyset $
and R is the tableau obtained from R on placing an extra entry equal to
$J:=\emptyset $
and R is the tableau obtained from R on placing an extra entry equal to
![]() $\beta $
as the rightmost element in the second row, namely,
$\beta $
as the rightmost element in the second row, namely,

Then
 $$ \begin{align*} d\omega &=\pm(X_{\beta} f) dx_{I\cup\{\beta\}}\wedge\alpha_{R}\wedge\theta + \sigma\\ &=\pm(X_{\beta} f) dx_{\overline I}\wedge\alpha_{\overline R}\wedge\theta + \sigma \end{align*} $$
$$ \begin{align*} d\omega &=\pm(X_{\beta} f) dx_{I\cup\{\beta\}}\wedge\alpha_{R}\wedge\theta + \sigma\\ &=\pm(X_{\beta} f) dx_{\overline I}\wedge\alpha_{\overline R}\wedge\theta + \sigma \end{align*} $$
and, as before, the arbitrariness of f implies (5.28), as desired.
6 Proof of Rademacher’s Theorem 1.1
This section is devoted to the proof of our main result. We start with a boring (but necessary) preliminary observation.
Remark 6.1. Let
![]() ${\mathbb W},{\mathbb V}$
be homogeneous complementary subgroups of
${\mathbb W},{\mathbb V}$
be homogeneous complementary subgroups of
![]() ${\mathbb H}^{n}$
and let
${\mathbb H}^{n}$
and let
![]() $\phi :A\subset {\mathbb W}\to {\mathbb V}$
be fixed. By Remark 3.16 there exists an isometric
$\phi :A\subset {\mathbb W}\to {\mathbb V}$
be fixed. By Remark 3.16 there exists an isometric
![]() ${\mathbb H}$
-linear isomorphism
${\mathbb H}$
-linear isomorphism
![]() ${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
such that
${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
such that
![]() ${\mathcal L}({\mathbb V})={\mathbb V}_{0}:=\exp (\operatorname *{\mathrm {span}}\{X_{1},\dots , X_{k}\})$
. Let us write
${\mathcal L}({\mathbb V})={\mathbb V}_{0}:=\exp (\operatorname *{\mathrm {span}}\{X_{1},\dots , X_{k}\})$
. Let us write
![]() ${\mathbb W}_{1}:={\mathcal L}({\mathbb W})$
and
${\mathbb W}_{1}:={\mathcal L}({\mathbb W})$
and
![]() $A_{1}:={\mathcal L}(A)$
; then
$A_{1}:={\mathcal L}(A)$
; then
![]() ${\mathcal L}(\mathrm {gr}_{\phi })=\mathrm {gr}_{\phi _{1}}$
for
${\mathcal L}(\mathrm {gr}_{\phi })=\mathrm {gr}_{\phi _{1}}$
for
![]() $\phi _{1}:={\mathcal L}\circ \phi \circ {\mathcal L}^{-1}:A_{1}\to {\mathbb V}_{0}$
. Since also
$\phi _{1}:={\mathcal L}\circ \phi \circ {\mathcal L}^{-1}:A_{1}\to {\mathbb V}_{0}$
. Since also
![]() ${\mathbb W}_{0}:=\exp (\operatorname *{\mathrm {span}}\{X_{k+1},\dots ,Y_{n},T\})$
is complementary to
${\mathbb W}_{0}:=\exp (\operatorname *{\mathrm {span}}\{X_{k+1},\dots ,Y_{n},T\})$
is complementary to
![]() ${\mathbb V}_{0}$
, it follows from [Reference Franchi and Serapioni53, Proposition 3.1] (or, alternatively, from Theorem 1.4 of the present article) that
${\mathbb V}_{0}$
, it follows from [Reference Franchi and Serapioni53, Proposition 3.1] (or, alternatively, from Theorem 1.4 of the present article) that
![]() $\mathrm {gr}_{\phi _{1}}=\mathrm {gr}_{\phi _{0}}$
for some map
$\mathrm {gr}_{\phi _{1}}=\mathrm {gr}_{\phi _{0}}$
for some map
![]() $\phi _{0}:A_{0}\to {\mathbb V}_{0}$
defined on a suitable
$\phi _{0}:A_{0}\to {\mathbb V}_{0}$
defined on a suitable
![]() $A_{0}\subset {\mathbb W}_{0}$
.
$A_{0}\subset {\mathbb W}_{0}$
.
Let us check that, if
![]() $\phi $
is intrinsic Lipschitz, so is
$\phi $
is intrinsic Lipschitz, so is
![]() $\phi _{0}$
. Since
$\phi _{0}$
. Since
![]() ${\mathcal L}$
is an isometry,
${\mathcal L}$
is an isometry,
![]() $\phi _{1}$
is also intrinsic Lipschitz. Moreover,
$\phi _{1}$
is also intrinsic Lipschitz. Moreover,
![]() ${\mathbb W}_{1} $
is complementary to
${\mathbb W}_{1} $
is complementary to
![]() ${\mathbb V}_{0}$
; hence,
${\mathbb V}_{0}$
; hence,
![]() ${\mathbb W}_{1}=\mathrm {gr}_{L} $
for an intrinsic linear map
${\mathbb W}_{1}=\mathrm {gr}_{L} $
for an intrinsic linear map
![]() $L:{\mathbb W}_{0}\to {\mathbb V}_{0}$
; let
$L:{\mathbb W}_{0}\to {\mathbb V}_{0}$
; let
![]() $C>0 $
be such that
$C>0 $
be such that
![]() $\|L(w_{0})\|_{\mathbb H}\leq C\|w_{0}\|_{\mathbb H}$
for every
$\|L(w_{0})\|_{\mathbb H}\leq C\|w_{0}\|_{\mathbb H}$
for every
![]() $w_{0}\in {\mathbb W}_{0}$
. We prove that, for every
$w_{0}\in {\mathbb W}_{0}$
. We prove that, for every
![]() $\alpha>0$
, the inclusion
$\alpha>0$
, the inclusion
 $$ \begin{align*} &\{w_{0}v_{0}:w_{0}\in{\mathbb W}_{0},v_{0}\in{\mathbb V}_{0},\|v_{0}\|_{\mathbb H}\geq (\alpha C+\alpha+C)\|w_{0}\|_{\mathbb H}\}\\ &\quad \subset \{w_{1}v_{0}^{\prime}:w_{1}\in{\mathbb W}_{1},v_{0}^{\prime}\in{\mathbb V}_{0},\|v_{0}^{\prime}\|_{\mathbb H}\geq\alpha\|w_{1}\|_{\mathbb H}\} \end{align*} $$
$$ \begin{align*} &\{w_{0}v_{0}:w_{0}\in{\mathbb W}_{0},v_{0}\in{\mathbb V}_{0},\|v_{0}\|_{\mathbb H}\geq (\alpha C+\alpha+C)\|w_{0}\|_{\mathbb H}\}\\ &\quad \subset \{w_{1}v_{0}^{\prime}:w_{1}\in{\mathbb W}_{1},v_{0}^{\prime}\in{\mathbb V}_{0},\|v_{0}^{\prime}\|_{\mathbb H}\geq\alpha\|w_{1}\|_{\mathbb H}\} \end{align*} $$
holds. The intrinsic Lipschitz continuity of
![]() $\phi _{0}$
will then easily follow from the intrinsic Lipschitz continuity of
$\phi _{0}$
will then easily follow from the intrinsic Lipschitz continuity of
![]() $\phi _{1}$
. Let
$\phi _{1}$
. Let
![]() $w_{0}\in {\mathbb W}_{0}$
and
$w_{0}\in {\mathbb W}_{0}$
and
![]() $v_{0}\in {\mathbb V}_{0}$
be such that
$v_{0}\in {\mathbb V}_{0}$
be such that
![]() $\|v_{0}\|_{\mathbb H}\geq (\alpha C+\alpha +C)\|w_{0}\|_{\mathbb H}$
; then
$\|v_{0}\|_{\mathbb H}\geq (\alpha C+\alpha +C)\|w_{0}\|_{\mathbb H}$
; then
 $$ \begin{align*} & w_{0}v_{0}=w_{1} v_{0}^{\prime}\qquad\text{for }w_{1}:=w_{0}L(w_{0})\in{\mathbb W}_{1} \text{ and }v_{0}^{\prime}:=L(w_{0})^{-1}v_{0}\in{\mathbb V}_{0} \end{align*} $$
$$ \begin{align*} & w_{0}v_{0}=w_{1} v_{0}^{\prime}\qquad\text{for }w_{1}:=w_{0}L(w_{0})\in{\mathbb W}_{1} \text{ and }v_{0}^{\prime}:=L(w_{0})^{-1}v_{0}\in{\mathbb V}_{0} \end{align*} $$
and
as claimed.
Eventually, let us observe that
![]() $\phi _{0}$
is intrinsically differentiable a.e. if and only if
$\phi _{0}$
is intrinsically differentiable a.e. if and only if
![]() $\phi $
is intrinsically differentiable a.e. This follows from the geometric characterisation of intrinsic differentiability provided by Proposition 4.12 (d) and by Remark 4.6, which imply that
$\phi $
is intrinsically differentiable a.e. This follows from the geometric characterisation of intrinsic differentiability provided by Proposition 4.12 (d) and by Remark 4.6, which imply that
 $$ \begin{align*} & \phi_{0}\text{ is intrinsically differentiable a.e. on }{\mathbb W}_{0}\\ \Longleftrightarrow\ & \text{the blow-up of }\mathrm{gr}_{\phi_{0}}\text{ is a vertical plane at }{\mathscr S}^{Q-k}\text{-almost every point of }\mathrm{gr}_{\phi_{0}}\\ \Longleftrightarrow\ & \text{the blow-up of }\mathrm{gr}_{\phi}\text{ is a vertical plane at }{\mathscr S}^{Q-k}\text{-almost every point of }\mathrm{gr}_{\phi}\\ \Longleftrightarrow\ & \phi\text{ is intrinsically differentiable a.e. on }{\mathbb W}\text{.} \end{align*} $$
$$ \begin{align*} & \phi_{0}\text{ is intrinsically differentiable a.e. on }{\mathbb W}_{0}\\ \Longleftrightarrow\ & \text{the blow-up of }\mathrm{gr}_{\phi_{0}}\text{ is a vertical plane at }{\mathscr S}^{Q-k}\text{-almost every point of }\mathrm{gr}_{\phi_{0}}\\ \Longleftrightarrow\ & \text{the blow-up of }\mathrm{gr}_{\phi}\text{ is a vertical plane at }{\mathscr S}^{Q-k}\text{-almost every point of }\mathrm{gr}_{\phi}\\ \Longleftrightarrow\ & \phi\text{ is intrinsically differentiable a.e. on }{\mathbb W}\text{.} \end{align*} $$
This discussion shows that, in order to prove Theorem 1.1 for intrinsic Lipschitz graphs of codimension at most n, it is not restrictive to assume that
![]() ${\mathbb V}$
and
${\mathbb V}$
and
![]() ${\mathbb W}$
are those defined in (4.2) and (4.3).
${\mathbb W}$
are those defined in (4.2) and (4.3).
We can now prove our main result. For the reader’s convenience, the proof is divided into several steps.
Proof of Theorem 1.1.
As mentioned in the Introduction, thanks to [Reference Antonelli and Merlo8] we have to deal only with the case of intrinsic Lipschitz graphs of low codimension; in particular,
![]() ${\mathbb V}$
is an abelian horizontal subgroup of
${\mathbb V}$
is an abelian horizontal subgroup of
![]() ${\mathbb H}^{n}$
and
${\mathbb H}^{n}$
and
![]() $k:=\dim {\mathbb V}$
is at most n. By Remark 6.1, we can, without loss of generality, assume that
$k:=\dim {\mathbb V}$
is at most n. By Remark 6.1, we can, without loss of generality, assume that
![]() ${\mathbb V}=\exp (\operatorname *{\mathrm {span}}\{X_{1},\dots , X_{k}\})$
and
${\mathbb V}=\exp (\operatorname *{\mathrm {span}}\{X_{1},\dots , X_{k}\})$
and
![]() ${\mathbb W}=\exp (\operatorname *{\mathrm {span}}\{X_{k+1},\dots , Y_{n},T\})$
. By Theorem 1.5 we can also assume that
${\mathbb W}=\exp (\operatorname *{\mathrm {span}}\{X_{k+1},\dots , Y_{n},T\})$
. By Theorem 1.5 we can also assume that
![]() $\phi $
is defined on the whole
$\phi $
is defined on the whole
![]() ${\mathbb W}$
.
${\mathbb W}$
.
Step 1: Definition of a current
![]() ${\mathsf T}$
supported on
${\mathsf T}$
supported on
![]() $\mathrm {gr}_{\phi }$
. By Proposition 4.28 we can consider a sequence of smooth functions
$\mathrm {gr}_{\phi }$
. By Proposition 4.28 we can consider a sequence of smooth functions
![]() $\phi _{i}:{\mathbb W}\to {\mathbb V}$
such that
$\phi _{i}:{\mathbb W}\to {\mathbb V}$
such that
-
•
 $\phi _{i}\to \phi $
uniformly on
$\phi _{i}\to \phi $
uniformly on
 ${\mathbb W}$
and
${\mathbb W}$
and -
• there exists
 $C>0$
such that
$C>0$
such that
 $|\nabla ^{\phi _{i}}\Phi _{i}(w)|\leq C$
for all
$|\nabla ^{\phi _{i}}\Phi _{i}(w)|\leq C$
for all
 $w\in {\mathbb W}$
and all
$w\in {\mathbb W}$
and all
 $i\in \mathbb N$
,
$i\in \mathbb N$
,
where
![]() $\Phi _{i}$
is the graph map
$\Phi _{i}$
is the graph map
![]() $\Phi _{i}(w):=w\phi _{i}(w)$
and
$\Phi _{i}(w):=w\phi _{i}(w)$
and
![]() $\nabla ^{\phi _{i}}\Phi _{i}:{\mathbb W}\to \Large \wedge _{2n-k}{\mathfrak h}_{1}$
is defined as in (4.28). By Lemma 4.29, the Heisenberg
$\nabla ^{\phi _{i}}\Phi _{i}:{\mathbb W}\to \Large \wedge _{2n-k}{\mathfrak h}_{1}$
is defined as in (4.28). By Lemma 4.29, the Heisenberg
![]() $(2n+1-k)$
-current
$(2n+1-k)$
-current
associated with the intrinsic graph
![]() $S_{i}:=\mathrm {gr}_{\phi _{i}}$
can be written as
$S_{i}:=\mathrm {gr}_{\phi _{i}}$
can be written as

Possibly passing to a subsequence, we can assume that there exists
![]() $\zeta \in L^{\infty }({\mathbb W},{\mathcal J}_{2n+1-k})=(L^{1}({\mathbb W},{\mathcal J}^{2n+1-k}))^{*}$
such that
$\zeta \in L^{\infty }({\mathbb W},{\mathcal J}_{2n+1-k})=(L^{1}({\mathbb W},{\mathcal J}^{2n+1-k}))^{*}$
such that
 $$ \begin{align*} [\nabla^{\phi_{i}}\Phi_{i}\wedge T]_{{\mathcal J}}\ \stackrel{*}{\rightharpoonup} \ \zeta\quad\text{weakly-}*\text{ in }L^{\infty}({\mathbb W},{\mathcal J}_{2n+1-k}). \end{align*} $$
$$ \begin{align*} [\nabla^{\phi_{i}}\Phi_{i}\wedge T]_{{\mathcal J}}\ \stackrel{*}{\rightharpoonup} \ \zeta\quad\text{weakly-}*\text{ in }L^{\infty}({\mathbb W},{\mathcal J}_{2n+1-k}). \end{align*} $$
The uniform convergence
![]() $\Phi _{i}\to \Phi $
implies that for every
$\Phi _{i}\to \Phi $
implies that for every
 $\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
,
$\omega \in {\mathcal D}_{\mathbb H}^{2n+1-k}$
,

The Heisenberg current
![]() ${\mathsf T}$
is clearly supported on
${\mathsf T}$
is clearly supported on
![]() $\mathrm {gr}_{\phi }$
. The boundary
$\mathrm {gr}_{\phi }$
. The boundary
![]() $\partial {\mathsf T}$
of
$\partial {\mathsf T}$
of
![]() ${\mathsf T}$
is the null current; in fact,
${\mathsf T}$
is the null current; in fact,

where
![]() $d_{C}$
is as in Remark 3.7 and the last equality is due to Corollary 3.34. The equality
$d_{C}$
is as in Remark 3.7 and the last equality is due to Corollary 3.34. The equality
![]() $\partial {\mathsf T}=0$
is the key geometric information we will exploit.
$\partial {\mathsf T}=0$
is the key geometric information we will exploit.
Let us prove that
Let
![]() $\beta \in {\mathcal J}^{2n+1-k}$
be defined by
$\beta \in {\mathcal J}^{2n+1-k}$
be defined by
 $$ \begin{align*} &\beta:= dx_{k+1}\wedge\dots\wedge dx_{n}\wedge dy_{1}\wedge\dots\wedge dy_{n}\wedge\theta\hspace{-2cm}&&\text{if }k<n\\ &\beta:= dy_{1}\wedge\dots\wedge dy_{n}\wedge\theta&&\text{if }k=n. \end{align*} $$
$$ \begin{align*} &\beta:= dx_{k+1}\wedge\dots\wedge dx_{n}\wedge dy_{1}\wedge\dots\wedge dy_{n}\wedge\theta\hspace{-2cm}&&\text{if }k<n\\ &\beta:= dy_{1}\wedge\dots\wedge dy_{n}\wedge\theta&&\text{if }k=n. \end{align*} $$
Then, for every
![]() $\chi \in C^{\infty }_{c}({\mathbb W})$
we have
$\chi \in C^{\infty }_{c}({\mathbb W})$
we have
 $$ \begin{align*} \int_{{\mathbb W}} \chi(w) \langle\zeta(w)\mid \beta\rangle\,d{\mathscr L}^{2n+1-k}(w) =& \lim_{i\to\infty}\int_{{\mathbb W}} \chi(w) \underbrace{\langle \nabla^{\phi_{i}}\Phi_{i}(w)\wedge T \mid \beta\rangle}_{\equiv 1}\,d{\mathscr L}^{2n+1-k}(w)\\ =& \int_{{\mathbb W}} \chi(w)\,d{\mathscr L}^{2n+1-k}(w). \end{align*} $$
$$ \begin{align*} \int_{{\mathbb W}} \chi(w) \langle\zeta(w)\mid \beta\rangle\,d{\mathscr L}^{2n+1-k}(w) =& \lim_{i\to\infty}\int_{{\mathbb W}} \chi(w) \underbrace{\langle \nabla^{\phi_{i}}\Phi_{i}(w)\wedge T \mid \beta\rangle}_{\equiv 1}\,d{\mathscr L}^{2n+1-k}(w)\\ =& \int_{{\mathbb W}} \chi(w)\,d{\mathscr L}^{2n+1-k}(w). \end{align*} $$
This implies that
![]() $\langle \zeta (w)\mid \beta \rangle =1$
for
$\langle \zeta (w)\mid \beta \rangle =1$
for
![]() ${\mathscr L}^{2n+1-k}$
-a.e.
${\mathscr L}^{2n+1-k}$
-a.e.
![]() $w\in {\mathbb W}$
and (6.2) follows.
$w\in {\mathbb W}$
and (6.2) follows.
Step 2: Statement of sufficient conditions for differentiability. Since
 is
is
![]() $(Q-k)$
-Ahlfors regular (Remark 4.6), the Lebesgue differentiation theorem applies (see, e.g., [Reference Heinonen59, Theorem 1.8]) and we obtain for
$(Q-k)$
-Ahlfors regular (Remark 4.6), the Lebesgue differentiation theorem applies (see, e.g., [Reference Heinonen59, Theorem 1.8]) and we obtain for
![]() ${\mathscr S}^{Q-k}$
-a.e.
${\mathscr S}^{Q-k}$
-a.e.
![]() $\bar p\in \mathrm {gr}_{\phi }$
,
$\bar p\in \mathrm {gr}_{\phi }$
,
 $$ \begin{align} \begin{aligned} \int_{\mathrm{gr}_{\phi}\cap B(\bar p,r)} \left|\zeta(\Phi^{-1}(p))-\zeta(\Phi^{-1}(\bar p))\right| \:d{\mathscr S}^{Q-k}(p) &= o\left( {\mathscr S}^{Q-k}(\mathrm{gr}_{\phi}\cap B(\bar p,r))\right)\\ &=o(r^{Q-k})\qquad\text{as }r\to0^{+}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \int_{\mathrm{gr}_{\phi}\cap B(\bar p,r)} \left|\zeta(\Phi^{-1}(p))-\zeta(\Phi^{-1}(\bar p))\right| \:d{\mathscr S}^{Q-k}(p) &= o\left( {\mathscr S}^{Q-k}(\mathrm{gr}_{\phi}\cap B(\bar p,r))\right)\\ &=o(r^{Q-k})\qquad\text{as }r\to0^{+}. \end{aligned} \end{align} $$
By (6.2), (6.7) and Lemma 4.16, the following three properties
hold for
![]() ${\mathscr L}^{2n+1-k}$
-a.e.
${\mathscr L}^{2n+1-k}$
-a.e.
![]() $\bar {w}\in {\mathbb W}$
. We claim that
$\bar {w}\in {\mathbb W}$
. We claim that
![]() $\phi $
is intrinsically differentiable at every
$\phi $
is intrinsically differentiable at every
![]() $\bar {w}\in {\mathbb W}$
such that (6.4), (6.5) and (6.6) hold. This will be enough to conclude. Let such a
$\bar {w}\in {\mathbb W}$
such that (6.4), (6.5) and (6.6) hold. This will be enough to conclude. Let such a
![]() $\bar {w}$
be fixed.
$\bar {w}$
be fixed.
Step 3: Blow-up at
![]() $\bar {w}$
. Let
$\bar {w}$
. Let
![]() $\phi _{\infty }$
be one of the (possibly many) blow-ups of
$\phi _{\infty }$
be one of the (possibly many) blow-ups of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
. Namely, there exists a sequence
$\bar {w}$
. Namely, there exists a sequence
![]() $(r_{j})_{j}$
of positive numbers such that
$(r_{j})_{j}$
of positive numbers such that
![]() $r_{j}\to +\infty $
as
$r_{j}\to +\infty $
as
![]() $j\to +\infty $
and
$j\to +\infty $
and
 $$ \begin{align*} \lim_{j\to\infty} (\phi_{\bar{w}})^{r_{j}}=\phi_{\infty}\qquad\text{locally uniformly on }{\mathbb W}\text{,} \end{align*} $$
$$ \begin{align*} \lim_{j\to\infty} (\phi_{\bar{w}})^{r_{j}}=\phi_{\infty}\qquad\text{locally uniformly on }{\mathbb W}\text{,} \end{align*} $$
where
 $(\phi _{\bar {w}})^{r_{j}}(w)=\delta _{r_{j}}\big (\phi (\bar {w})^{-1}\phi (\bar {w}\phi (\bar {w})(\delta _{1/r_{j}} w)\phi (\bar {w})^{-1})\big )$
is as in Subsection 4.2. For
$(\phi _{\bar {w}})^{r_{j}}(w)=\delta _{r_{j}}\big (\phi (\bar {w})^{-1}\phi (\bar {w}\phi (\bar {w})(\delta _{1/r_{j}} w)\phi (\bar {w})^{-1})\big )$
is as in Subsection 4.2. For
![]() $r>0$
let us introduce the maps
$r>0$
let us introduce the maps
![]() ${\mathcal L}_{\bar {w},r}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
defined by
${\mathcal L}_{\bar {w},r}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
defined by
 $$ \begin{align*} {\mathcal L}_{\bar{w},r}(q):=\delta_{r}(\Phi(\bar{w})^{-1}q),\qquad r>0,\ q\in{\mathbb H}^{n}; \end{align*} $$
$$ \begin{align*} {\mathcal L}_{\bar{w},r}(q):=\delta_{r}(\Phi(\bar{w})^{-1}q),\qquad r>0,\ q\in{\mathbb H}^{n}; \end{align*} $$
![]() ${\mathcal L}_{\bar {w},r}$
is defined in such a way that
${\mathcal L}_{\bar {w},r}$
is defined in such a way that
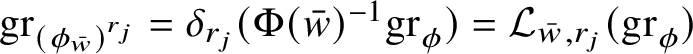 $\mathrm {gr}_{(\phi _{\bar {w}})^{r_{j}}}=\delta _{r_{j}}(\Phi (\bar {w})^{-1}\mathrm {gr}_{\phi })={\mathcal L}_{\bar {w},r_{j}}(\mathrm {gr}_{\phi })$
. Consider the push-forward
$\mathrm {gr}_{(\phi _{\bar {w}})^{r_{j}}}=\delta _{r_{j}}(\Phi (\bar {w})^{-1}\mathrm {gr}_{\phi })={\mathcal L}_{\bar {w},r_{j}}(\mathrm {gr}_{\phi })$
. Consider the push-forward
![]() ${\mathsf T}_{j}:=({\mathcal L}_{\bar {w},r_{j}})_\#{\mathsf T}$
; that is, the Heisenberg current defined by
${\mathsf T}_{j}:=({\mathcal L}_{\bar {w},r_{j}})_\#{\mathsf T}$
; that is, the Heisenberg current defined by
 $$ \begin{align*} {\mathsf T}_{j}(\omega):={\mathsf T}({\mathcal L}_{\bar{w},r_{j}}^{*}\omega)={\mathsf T}(r_{j}^{Q-k}\ \omega\circ {\mathcal L}_{\bar{w},r_{j}}),\qquad \omega\in{\mathcal D}_{\mathbb H}^{2n+1-k} \end{align*} $$
$$ \begin{align*} {\mathsf T}_{j}(\omega):={\mathsf T}({\mathcal L}_{\bar{w},r_{j}}^{*}\omega)={\mathsf T}(r_{j}^{Q-k}\ \omega\circ {\mathcal L}_{\bar{w},r_{j}}),\qquad \omega\in{\mathcal D}_{\mathbb H}^{2n+1-k} \end{align*} $$
where
 ${\mathcal L}_{\bar {w},r_{j}}^{*}$
denotes pullback of forms and the last equality comes from left-invariance and homogeneity. Observe that
${\mathcal L}_{\bar {w},r_{j}}^{*}$
denotes pullback of forms and the last equality comes from left-invariance and homogeneity. Observe that
![]() $\partial T_{j}=0$
for every j because
$\partial T_{j}=0$
for every j because
 $$ \begin{align*} {\mathsf T}_{j}(d_{C}\omega)={\mathsf T}({\mathcal L}_{\bar{w},r_{j}}^{*}(d_{C}\omega)) ={\mathsf T}(d_{C}({\mathcal L}_{\bar{w},r_{j}}^{*}\omega)) =\partial {\mathsf T}({\mathcal L}_{\bar{w},r_{j}}^{*}\omega)=0. \end{align*} $$
$$ \begin{align*} {\mathsf T}_{j}(d_{C}\omega)={\mathsf T}({\mathcal L}_{\bar{w},r_{j}}^{*}(d_{C}\omega)) ={\mathsf T}(d_{C}({\mathcal L}_{\bar{w},r_{j}}^{*}\omega)) =\partial {\mathsf T}({\mathcal L}_{\bar{w},r_{j}}^{*}\omega)=0. \end{align*} $$
By Remark 4.6 there exist a constant
![]() $C\geq 1$
, depending only on the intrinsic Lipschitz constant of
$C\geq 1$
, depending only on the intrinsic Lipschitz constant of
![]() $\phi $
, and a measurable function
$\phi $
, and a measurable function
![]() $J_{\phi }:{\mathbb W}\to {\mathbb R}$
such that
$J_{\phi }:{\mathbb W}\to {\mathbb R}$
such that

where
![]() $\Phi _\#$
denotes push-forward of measures. Using (6.1) and (6.7),
$\Phi _\#$
denotes push-forward of measures. Using (6.1) and (6.7),
 $$ \begin{align*} {\mathsf T}_{j}(\omega) &= C_{n,k}\: r_{j}^{Q-k}\int_{{\mathbb W}} \left\langle\zeta(w)\,\left|\, \frac{\omega(\delta_{r_{j}}(\Phi(\bar{w})^{-1}\Phi(w)))}{J_{\phi}(w)}\right. \right\rangle J_{\phi}(w)\:d{\mathscr L}^{2n+1-k}(w)\\ &= C_{n,k}\: r_{j}^{Q-k}\int_{\mathrm{gr}_{\phi}} \left\langle{\zeta(\Phi^{-1}(p))}\,\left|\, \frac{\omega(\delta_{r_{j}}(\Phi(\bar{w})^{-1}p))}{J_{\phi}(\Phi^{-1}(p))}\right. \right\rangle d{\mathscr S}^{Q-k}(p)\\ &= C_{n,k}\: r_{j}^{Q-k}\int_{\mathrm{gr}_{\phi}} \left[\left\langle{\zeta(\bar{w})}\,\left|\, \frac{\omega(\delta_{r_{j}}(\Phi(\bar{w})^{-1}p))}{J_{\phi}(\Phi^{-1}(p))}\right. \right\rangle d{\mathscr S}^{Q-k}(p) + o\big(r_{j}^{-(Q-k)}\big)\right]\\ &= C_{n,k}\: r_{j}^{Q-k}\int_{{\mathbb W}} \left[\left\langle {\zeta(\bar{w})}\mid \omega(\delta_{r_{j}}(\Phi(\bar{w})^{-1}\Phi(w))) \right\rangle \:d{\mathscr L}^{2n+1-k}(w) + o\big(r_{j}^{-(Q-k)}\big)\right], \end{align*} $$
$$ \begin{align*} {\mathsf T}_{j}(\omega) &= C_{n,k}\: r_{j}^{Q-k}\int_{{\mathbb W}} \left\langle\zeta(w)\,\left|\, \frac{\omega(\delta_{r_{j}}(\Phi(\bar{w})^{-1}\Phi(w)))}{J_{\phi}(w)}\right. \right\rangle J_{\phi}(w)\:d{\mathscr L}^{2n+1-k}(w)\\ &= C_{n,k}\: r_{j}^{Q-k}\int_{\mathrm{gr}_{\phi}} \left\langle{\zeta(\Phi^{-1}(p))}\,\left|\, \frac{\omega(\delta_{r_{j}}(\Phi(\bar{w})^{-1}p))}{J_{\phi}(\Phi^{-1}(p))}\right. \right\rangle d{\mathscr S}^{Q-k}(p)\\ &= C_{n,k}\: r_{j}^{Q-k}\int_{\mathrm{gr}_{\phi}} \left[\left\langle{\zeta(\bar{w})}\,\left|\, \frac{\omega(\delta_{r_{j}}(\Phi(\bar{w})^{-1}p))}{J_{\phi}(\Phi^{-1}(p))}\right. \right\rangle d{\mathscr S}^{Q-k}(p) + o\big(r_{j}^{-(Q-k)}\big)\right]\\ &= C_{n,k}\: r_{j}^{Q-k}\int_{{\mathbb W}} \left[\left\langle {\zeta(\bar{w})}\mid \omega(\delta_{r_{j}}(\Phi(\bar{w})^{-1}\Phi(w))) \right\rangle \:d{\mathscr L}^{2n+1-k}(w) + o\big(r_{j}^{-(Q-k)}\big)\right], \end{align*} $$
where, in the third equality, we used (6.4) and the fact that, if
![]() $\omega $
is supported in
$\omega $
is supported in
![]() $B(0,\bar r)$
, then
$B(0,\bar r)$
, then
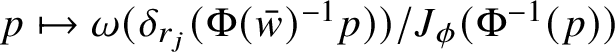 $p\mapsto \omega (\delta _{r_{j}}(\Phi (\bar {w})^{-1}p))/J_{\phi }(\Phi ^{-1}(p))$
is supported in
$p\mapsto \omega (\delta _{r_{j}}(\Phi (\bar {w})^{-1}p))/J_{\phi }(\Phi ^{-1}(p))$
is supported in
![]() $B(\Phi (\bar {w}),\bar r/r_{j})$
. Therefore,
$B(\Phi (\bar {w}),\bar r/r_{j})$
. Therefore,
 $$ \begin{align*} \lim_{j\to\infty}{\mathsf T}_{j}(\omega) & = C_{n,k} \lim_{j\to\infty} r_{j}^{Q-k}\int_{{\mathbb W}} \left\langle {\zeta(\bar{w})}\mid\omega(\delta_{r_{j}}(\Phi(\bar{w})^{-1}\Phi(w))) \right\rangle \:d{\mathscr L}^{2n+1-k}(w) \end{align*} $$
$$ \begin{align*} \lim_{j\to\infty}{\mathsf T}_{j}(\omega) & = C_{n,k} \lim_{j\to\infty} r_{j}^{Q-k}\int_{{\mathbb W}} \left\langle {\zeta(\bar{w})}\mid\omega(\delta_{r_{j}}(\Phi(\bar{w})^{-1}\Phi(w))) \right\rangle \:d{\mathscr L}^{2n+1-k}(w) \end{align*} $$
provided the limit in the right-hand side exists. We now perform the change of variable
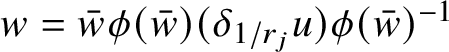 $w=\bar {w}\phi (\bar {w})(\delta _{1/r_{j}}u)\phi (\bar {w})^{-1}$
,
$w=\bar {w}\phi (\bar {w})(\delta _{1/r_{j}}u)\phi (\bar {w})^{-1}$
,
![]() $u\in {\mathbb W}$
, according to which
$u\in {\mathbb W}$
, according to which
 $$ \begin{align*} \delta_{r_{j}}(\Phi(\bar{w})^{-1}\Phi(w))=\Phi_{\bar{w}}^{r_{j}}(u),\qquad\text{where }\Phi_{\bar{w}}^{r_{j}}(u):=u\:( \phi_{\bar{w}})^{r_{j}}(u). \end{align*} $$
$$ \begin{align*} \delta_{r_{j}}(\Phi(\bar{w})^{-1}\Phi(w))=\Phi_{\bar{w}}^{r_{j}}(u),\qquad\text{where }\Phi_{\bar{w}}^{r_{j}}(u):=u\:( \phi_{\bar{w}})^{r_{j}}(u). \end{align*} $$
Therefore,
 $$ \begin{align*} \lim_{j\to\infty}{\mathsf T}_{j}(\omega) & = C_{n,k} \lim_{j\to\infty} \int_{{\mathbb W}} \left\langle {\zeta(\bar{w})}\mid \omega(\Phi^{r_{j}}_{\bar{w}}(u))\right\rangle \:d{\mathscr L}^{2n+1-k}(u) \\ & = C_{n,k} \int_{{\mathbb W}} \left\langle {\zeta(\bar{w})}\mid \omega(\Phi_{\infty}(u))\right\rangle \:d{\mathscr L}^{2n+1-k}(u) \end{align*} $$
$$ \begin{align*} \lim_{j\to\infty}{\mathsf T}_{j}(\omega) & = C_{n,k} \lim_{j\to\infty} \int_{{\mathbb W}} \left\langle {\zeta(\bar{w})}\mid \omega(\Phi^{r_{j}}_{\bar{w}}(u))\right\rangle \:d{\mathscr L}^{2n+1-k}(u) \\ & = C_{n,k} \int_{{\mathbb W}} \left\langle {\zeta(\bar{w})}\mid \omega(\Phi_{\infty}(u))\right\rangle \:d{\mathscr L}^{2n+1-k}(u) \end{align*} $$
due to the uniform convergence of
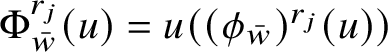 $\Phi ^{r_{j}}_{\bar {w}}(u) = u( (\phi _{\bar {w}})^{r_{j}}(u))$
to the graph map
$\Phi ^{r_{j}}_{\bar {w}}(u) = u( (\phi _{\bar {w}})^{r_{j}}(u))$
to the graph map
![]() $\Phi _{\infty }(u):= u\phi _{\infty } (u)$
.
$\Phi _{\infty }(u):= u\phi _{\infty } (u)$
.
We obtained that the Heisenberg
![]() $(2n+1-k)$
-current
$(2n+1-k)$
-current
![]() ${\mathsf T}_{\infty }$
defined by
${\mathsf T}_{\infty }$
defined by
 $$ \begin{align*} {\mathsf T}_{\infty}(\omega):=\lim_{j\to\infty}{\mathsf T}_{j}(\omega)= C_{n,k} \int_{{\mathbb W}} \left\langle {\zeta(\bar{w})}\mid \omega\circ\Phi_{\infty}\right\rangle \:d{\mathscr L}^{2n+1-k},\qquad\omega\in{\mathcal D}_{\mathbb H}^{2n+1-k} \end{align*} $$
$$ \begin{align*} {\mathsf T}_{\infty}(\omega):=\lim_{j\to\infty}{\mathsf T}_{j}(\omega)= C_{n,k} \int_{{\mathbb W}} \left\langle {\zeta(\bar{w})}\mid \omega\circ\Phi_{\infty}\right\rangle \:d{\mathscr L}^{2n+1-k},\qquad\omega\in{\mathcal D}_{\mathbb H}^{2n+1-k} \end{align*} $$
is supported on
![]() $\mathrm {gr}_{\phi _{\infty }}$
. Since
$\mathrm {gr}_{\phi _{\infty }}$
. Since
![]() $\partial {\mathsf T}_{j}=0$
for every j, then also
$\partial {\mathsf T}_{j}=0$
for every j, then also
![]() $\partial {\mathsf T}_{\infty }=0$
. Moreover,
$\partial {\mathsf T}_{\infty }=0$
. Moreover,
![]() $\phi _{\infty }$
is a uniform limit of uniformly intrinsic Lipschitz maps; hence, it is intrinsic Lipschitz and there exists a measurable function
$\phi _{\infty }$
is a uniform limit of uniformly intrinsic Lipschitz maps; hence, it is intrinsic Lipschitz and there exists a measurable function
![]() $J_{\phi _{\infty }}:{\mathbb W}\to {\mathbb R}$
such that
$J_{\phi _{\infty }}:{\mathbb W}\to {\mathbb R}$
such that

In particular,
 $$ \begin{align*} {\mathsf T}_{\infty}(\omega)= C_{n,k} \int_{\mathrm{gr}_{\phi_{\infty}}} \left\langle \left. \frac{\zeta(\bar{w})}{J_{\phi_{\infty}}({\Phi_{\infty}}^{-1}(p))} \,\right|\,\omega(p)\right\rangle \:d{\mathscr S}^{Q-k}(p),\qquad\omega\in{\mathcal D}_{\mathbb H}^{2n+1-k}; \end{align*} $$
$$ \begin{align*} {\mathsf T}_{\infty}(\omega)= C_{n,k} \int_{\mathrm{gr}_{\phi_{\infty}}} \left\langle \left. \frac{\zeta(\bar{w})}{J_{\phi_{\infty}}({\Phi_{\infty}}^{-1}(p))} \,\right|\,\omega(p)\right\rangle \:d{\mathscr S}^{Q-k}(p),\qquad\omega\in{\mathcal D}_{\mathbb H}^{2n+1-k}; \end{align*} $$
that is,

By (6.5), the intrinsic Lipschitz map
![]() $\phi _{\infty }$
is t-invariant: by Lemma 4.15 and Proposition 4.23,
$\phi _{\infty }$
is t-invariant: by Lemma 4.15 and Proposition 4.23,
![]() $\phi _{\infty }$
is Euclidean Lipschitz and
$\phi _{\infty }$
is Euclidean Lipschitz and
![]() $\mathrm {gr}_{\phi _{\infty }}$
is locally
$\mathrm {gr}_{\phi _{\infty }}$
is locally
![]() ${\mathbb H}$
-rectifiable of codimension k. By Theorem 1.8 and (6.6) we deduce that there exists
${\mathbb H}$
-rectifiable of codimension k. By Theorem 1.8 and (6.6) we deduce that there exists
![]() $\eta :\mathrm {gr}_{\phi _{\infty }}\to {\mathbb R}\setminus \{0\}$
such that
$\eta :\mathrm {gr}_{\phi _{\infty }}\to {\mathbb R}\setminus \{0\}$
such that
 $$ \begin{align} \zeta(\bar{w})=\eta(p)[t^{\mathbb H}_{\mathrm{gr}_{\phi_{\infty}}}(p)]_{{\mathcal J}}\qquad\text{for }{\mathscr S}^{Q-k}\text{-a.e.~}p\in\mathrm{gr}_{\phi_{\infty}}. \end{align} $$
$$ \begin{align} \zeta(\bar{w})=\eta(p)[t^{\mathbb H}_{\mathrm{gr}_{\phi_{\infty}}}(p)]_{{\mathcal J}}\qquad\text{for }{\mathscr S}^{Q-k}\text{-a.e.~}p\in\mathrm{gr}_{\phi_{\infty}}. \end{align} $$
Step 4: Every blow-up is linear. We claim that
![]() $\phi _{\infty }$
is intrinsic linear. Let
$\phi _{\infty }$
is intrinsic linear. Let
![]() $f_{\phi _{\infty }}:{\mathbb R}^{2n-k}\to {\mathbb R}^{k}$
be defined by
$f_{\phi _{\infty }}:{\mathbb R}^{2n-k}\to {\mathbb R}^{k}$
be defined by
![]() $\phi _{\infty }(w)=f_{\phi _{\infty }}(w_{H})$
for every
$\phi _{\infty }(w)=f_{\phi _{\infty }}(w_{H})$
for every
![]() $w\in {\mathbb W}$
, where the notation
$w\in {\mathbb W}$
, where the notation
![]() $w_{H}$
is the one introduced in (4.16);
$w_{H}$
is the one introduced in (4.16);
![]() $f_{\phi _{\infty }}$
is Euclidean Lipschitz continuous by Lemma 4.15 (i). By Lemma 4.15 (iv), the gradient
$f_{\phi _{\infty }}$
is Euclidean Lipschitz continuous by Lemma 4.15 (i). By Lemma 4.15 (iv), the gradient
![]() $\nabla f_{\phi _{\infty }}(w_{H})$
is defined for a.e.
$\nabla f_{\phi _{\infty }}(w_{H})$
is defined for a.e.
![]() $w\in {\mathbb W}$
and it uniquely determines
$w\in {\mathbb W}$
and it uniquely determines
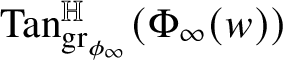 ${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi _{\infty }}}(\Phi _{\infty }(w))$
; since
${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi _{\infty }}}(\Phi _{\infty }(w))$
; since
![]() $\phi _{\infty }$
is intrinsic linear if and only if
$\phi _{\infty }$
is intrinsic linear if and only if
![]() $f_{\phi _{\infty }}$
is linear,
$f_{\phi _{\infty }}$
is linear,
![]() $\phi _{\infty }$
is intrinsic linear if and only if
$\phi _{\infty }$
is intrinsic linear if and only if
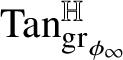 ${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi _{\infty }}}$
is constant on
${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi _{\infty }}}$
is constant on
![]() $\mathrm {gr}_{\phi _{\infty }}$
. Assume that
$\mathrm {gr}_{\phi _{\infty }}$
. Assume that
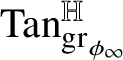 ${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi _{\infty }}}$
is not constant; then, by (6.8) and Proposition 3.38, there exist two vertical planes
${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi _{\infty }}}$
is not constant; then, by (6.8) and Proposition 3.38, there exist two vertical planes
![]() ${\mathscr P}_{1},{\mathscr P}_{2}$
that are not rank 1 connected and such that
${\mathscr P}_{1},{\mathscr P}_{2}$
that are not rank 1 connected and such that
 $$ \begin{align*} {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi_{\infty}}}(p)\in\{{\mathscr P}_{1},{\mathscr P}_{2}\}\text{ for }{\mathscr S}^{Q-k}\text{-a.e.~}p\in\mathrm{gr}_{\phi_{\infty}}\text{.} \end{align*} $$
$$ \begin{align*} {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi_{\infty}}}(p)\in\{{\mathscr P}_{1},{\mathscr P}_{2}\}\text{ for }{\mathscr S}^{Q-k}\text{-a.e.~}p\in\mathrm{gr}_{\phi_{\infty}}\text{.} \end{align*} $$
In particular, there exist two
![]() $k\times (2n-k)$
matrices
$k\times (2n-k)$
matrices
![]() $M_{1},M_{2}$
such that
$M_{1},M_{2}$
such that
![]() $\nabla f_{\phi _{\infty }}\in \{M_{1},M_{2}\}$
. By Lemma 4.15 (ii) and Remark 3.36, the rank of the matrix
$\nabla f_{\phi _{\infty }}\in \{M_{1},M_{2}\}$
. By Lemma 4.15 (ii) and Remark 3.36, the rank of the matrix
![]() $M_{1}-M_{2}$
is at least 2. However, a well-known result proved in [Reference Ball and James14, Proposition 1] (see also [Reference Müller78, Proposition 2.1]) states that, if a Lipschitz map has only two possible gradients
$M_{1}-M_{2}$
is at least 2. However, a well-known result proved in [Reference Ball and James14, Proposition 1] (see also [Reference Müller78, Proposition 2.1]) states that, if a Lipschitz map has only two possible gradients
![]() $M_{1},M_{2}$
and rank
$M_{1},M_{2}$
and rank
![]() $(M_{1}-M_{2})\geq 2$
, then the map is affine. This proves that
$(M_{1}-M_{2})\geq 2$
, then the map is affine. This proves that
![]() $f_{\phi _{\infty }}$
is linear and, actually, that
$f_{\phi _{\infty }}$
is linear and, actually, that
Step 5: Uniqueness of blow-ups. We have proved that every blow-up
![]() $\phi _{\infty }$
is intrinsic linear. We now prove that the blow-up of
$\phi _{\infty }$
is intrinsic linear. We now prove that the blow-up of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
is unique: by Proposition 4.12 (c), this is equivalent to the intrinsic differentiability of
$\bar {w}$
is unique: by Proposition 4.12 (c), this is equivalent to the intrinsic differentiability of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
. Assume, on the contrary, that there exist two different blow-ups
$\bar {w}$
. Assume, on the contrary, that there exist two different blow-ups
![]() $\phi _{\infty }^{1},\phi _{\infty }^{2}$
of
$\phi _{\infty }^{1},\phi _{\infty }^{2}$
of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
; observing that the matrices
$\bar {w}$
; observing that the matrices
![]() $M_{1},M_{2}$
introduced in Step 4 are uniquely determined by
$M_{1},M_{2}$
introduced in Step 4 are uniquely determined by
![]() $\zeta (\bar {w})$
(via the vertical planes
$\zeta (\bar {w})$
(via the vertical planes
![]() ${\mathscr P}_{1},{\mathscr P}_{2}$
provided by Proposition 3.38), we deduce from (6.9) that, possibly renaming
${\mathscr P}_{1},{\mathscr P}_{2}$
provided by Proposition 3.38), we deduce from (6.9) that, possibly renaming
![]() $M_{1}$
and
$M_{1}$
and
![]() $M_{2}$
,
$M_{2}$
,
Let
![]() $w\in {\mathbb W}$
be such that
$w\in {\mathbb W}$
be such that
![]() $\phi ^{1}_{\infty }(w)\neq \phi ^{2}_{\infty }(w)$
; that is,
$\phi ^{1}_{\infty }(w)\neq \phi ^{2}_{\infty }(w)$
; that is,
![]() $M_{1} w_{H}\neq M_{2} w_{H}$
. By definition of blow-up, there exist two diverging sequences
$M_{1} w_{H}\neq M_{2} w_{H}$
. By definition of blow-up, there exist two diverging sequences
 $(r_{j}^{1})_{j}$
,
$(r_{j}^{1})_{j}$
,
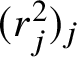 $(r_{j}^{2})_{j}$
such that
$(r_{j}^{2})_{j}$
such that
 $$ \begin{align*} (\phi_{\bar{w}})^{r_{j}^{1}}\to \phi^{1}_{\infty}\quad\text{and}\quad (\phi_{\bar{w}})^{r_{j}^{2}}\to \phi^{2}_{\infty} \end{align*} $$
$$ \begin{align*} (\phi_{\bar{w}})^{r_{j}^{1}}\to \phi^{1}_{\infty}\quad\text{and}\quad (\phi_{\bar{w}})^{r_{j}^{2}}\to \phi^{2}_{\infty} \end{align*} $$
and, up to passing to suitable subsequences, we can assume without loss of generality that
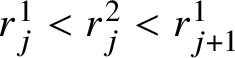 $r_{j}^{1}< r_{j}^{2} < r_{j+1}^{1}$
for every j. Let
$r_{j}^{1}< r_{j}^{2} < r_{j+1}^{1}$
for every j. Let
![]() $\delta :=d( \phi ^{1}_{\infty }(w),\phi ^{2}_{\infty }(w))>0$
; since the map
$\delta :=d( \phi ^{1}_{\infty }(w),\phi ^{2}_{\infty }(w))>0$
; since the map
![]() $r\mapsto (\phi _{\bar {w}})^{r}(w)$
is continuous and bounded (see Remark 4.5), for every large enough j we can find
$r\mapsto (\phi _{\bar {w}})^{r}(w)$
is continuous and bounded (see Remark 4.5), for every large enough j we can find
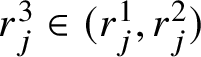 $r_{j}^{3}\in (r_{j}^{1},r_{j}^{2})$
such that
$r_{j}^{3}\in (r_{j}^{1},r_{j}^{2})$
such that
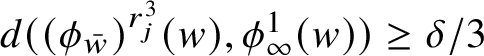 $d((\phi _{\bar {w}})^{r_{j}^{3}}(w),\phi ^{1}_{\infty }(w))\geq \delta /3$
and
$d((\phi _{\bar {w}})^{r_{j}^{3}}(w),\phi ^{1}_{\infty }(w))\geq \delta /3$
and
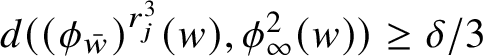 $d((\phi _{\bar {w}})^{r_{j}^{3}}(w),\phi ^{2}_{\infty }(w))\geq \delta /3$
. By Remark 4.5 and Ascoli–Arzelà’s theorem, up to passing to a subsequence we have that
$d((\phi _{\bar {w}})^{r_{j}^{3}}(w),\phi ^{2}_{\infty }(w))\geq \delta /3$
. By Remark 4.5 and Ascoli–Arzelà’s theorem, up to passing to a subsequence we have that
 $(\phi _{\bar {w}})^{r_{j}^{3}}\to \psi $
locally uniformly on
$(\phi _{\bar {w}})^{r_{j}^{3}}\to \psi $
locally uniformly on
![]() ${\mathbb W}$
for some
${\mathbb W}$
for some
![]() $\psi :{\mathbb W}\to {\mathbb V}$
. Observe that
$\psi :{\mathbb W}\to {\mathbb V}$
. Observe that
![]() $d(\psi (w),\phi ^{1}_{\infty }(w))\geq \delta /3$
and
$d(\psi (w),\phi ^{1}_{\infty }(w))\geq \delta /3$
and
![]() $d(\psi (w),\phi ^{2}_{\infty }(w))\geq \delta /3$
; thus,
$d(\psi (w),\phi ^{2}_{\infty }(w))\geq \delta /3$
; thus,
![]() $\psi $
is a blow-up of
$\psi $
is a blow-up of
![]() $\phi $
at
$\phi $
at
![]() $\bar {w}$
(in particular, it is t-invariant) that is different from both
$\bar {w}$
(in particular, it is t-invariant) that is different from both
![]() $\phi ^{1}_{\infty }$
and
$\phi ^{1}_{\infty }$
and
![]() $\phi ^{2}_{\infty }$
. This contradicts (6.9), and the proof is concluded.
$\phi ^{2}_{\infty }$
. This contradicts (6.9), and the proof is concluded.
We conclude this section with an observation. Let
![]() $\phi :A\subset {\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz. Theorem 1.1, together with Remark 4.6, implies that a tangentFootnote
10
plane
$\phi :A\subset {\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz. Theorem 1.1, together with Remark 4.6, implies that a tangentFootnote
10
plane
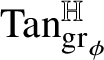 ${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}$
to
${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}$
to
![]() $\mathrm {gr}_{\phi }$
exists
$\mathrm {gr}_{\phi }$
exists
![]() ${\mathscr S}^{Q-k}$
-a.e. on
${\mathscr S}^{Q-k}$
-a.e. on
![]() $\mathrm {gr}_{\phi }$
: let us denote by
$\mathrm {gr}_{\phi }$
: let us denote by
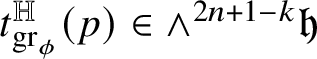 $t^{\mathbb H}_{\mathrm {gr}_{\phi }}(p)\in \Large \wedge ^{2n+1-k}{\mathfrak h}$
the unit tangent vector associated with
$t^{\mathbb H}_{\mathrm {gr}_{\phi }}(p)\in \Large \wedge ^{2n+1-k}{\mathfrak h}$
the unit tangent vector associated with
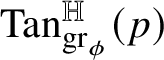 ${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}(p)$
at
${\mathrm {Tan}}^{\mathbb H}_{\mathrm {gr}_{\phi }}(p)$
at
![]() $p\in \mathrm {gr}_{\phi }$
. Again,
$p\in \mathrm {gr}_{\phi }$
. Again,
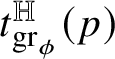 $t^{\mathbb H}_{\mathrm {gr}_{\phi }}(p)$
is defined only up to a sign; hence,
$t^{\mathbb H}_{\mathrm {gr}_{\phi }}(p)$
is defined only up to a sign; hence,
 $p\mapsto t^{\mathbb H}_{\mathrm {gr}_{\phi }}(p)$
could be not even measurable with respect to
$p\mapsto t^{\mathbb H}_{\mathrm {gr}_{\phi }}(p)$
could be not even measurable with respect to
 . As one can expect, there are, however, two canonical choices for the orientation: we present below one of the two, the other being of course the opposite one. See also [Reference Canarecci23] for some related issues. With this consistent choice of orientation for
. As one can expect, there are, however, two canonical choices for the orientation: we present below one of the two, the other being of course the opposite one. See also [Reference Canarecci23] for some related issues. With this consistent choice of orientation for
![]() $\mathrm {gr}_{\phi }$
, one will be allowed to define the
$\mathrm {gr}_{\phi }$
, one will be allowed to define the
![]() $(2n+1-k)$
-Heisenberg current
$(2n+1-k)$
-Heisenberg current
 canonically associated with
canonically associated with
![]() $\mathrm {gr}_{\phi }$
by
$\mathrm {gr}_{\phi }$
by

As a further property, we will prove in Proposition 7.5 that for entire graphs (
![]() $A={\mathbb W}$
) the equality
$A={\mathbb W}$
) the equality
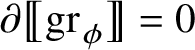 holds.
holds.
Let us fix our choice of
 $t^{\mathbb H}_{\mathrm {gr}_{\phi }}$
. As in Remark 6.1, up to an
$t^{\mathbb H}_{\mathrm {gr}_{\phi }}$
. As in Remark 6.1, up to an
![]() ${\mathbb H}$
-linear map
${\mathbb H}$
-linear map
![]() ${\mathcal L}$
we can assume that
${\mathcal L}$
we can assume that
![]() ${\mathbb W},{\mathbb V}$
are as in (4.2) and (4.3). In this case, our choice for the orientation of
${\mathbb W},{\mathbb V}$
are as in (4.2) and (4.3). In this case, our choice for the orientation of
![]() $\mathrm {gr}_{\phi }$
is (compare with (4.31))
$\mathrm {gr}_{\phi }$
is (compare with (4.31))
 $$ \begin{align*} t^{\mathbb H}_{\mathrm{gr}_{\phi}}(p):=\frac{\nabla^{\phi}\Phi(\Phi^{-1}(p))}{|\nabla^{\phi}\Phi(\Phi^{-1}(p))|}\wedge T \end{align*} $$
$$ \begin{align*} t^{\mathbb H}_{\mathrm{gr}_{\phi}}(p):=\frac{\nabla^{\phi}\Phi(\Phi^{-1}(p))}{|\nabla^{\phi}\Phi(\Phi^{-1}(p))|}\wedge T \end{align*} $$
where, remembering (4.27) and (4.28), we set
 $$ \begin{align*} \nabla^{\phi}\Phi(w):=\nabla^{\phi}_{k+1}\Phi(w)\wedge\dots\wedge\nabla^{\phi}_{2n}\Phi(w)\in\Large\wedge_{2n-k}{\mathfrak h}_{1} \end{align*} $$
$$ \begin{align*} \nabla^{\phi}\Phi(w):=\nabla^{\phi}_{k+1}\Phi(w)\wedge\dots\wedge\nabla^{\phi}_{2n}\Phi(w)\in\Large\wedge_{2n-k}{\mathfrak h}_{1} \end{align*} $$
and
 $$ \begin{align*} \nabla^{\phi}_{i}\Phi(w):=\left(W_{i}+\sum_{h=1}^{k}(\nabla^{\phi}\phi(w))_{hi}X_{h}\right)(\Phi(w)),\qquad i=k+1,\dots,2n. \end{align*} $$
$$ \begin{align*} \nabla^{\phi}_{i}\Phi(w):=\left(W_{i}+\sum_{h=1}^{k}(\nabla^{\phi}\phi(w))_{hi}X_{h}\right)(\Phi(w)),\qquad i=k+1,\dots,2n. \end{align*} $$
For general subgroups
![]() ${\mathbb W},{\mathbb V}$
, our choice corresponds to fixing a unit tangent vector
${\mathbb W},{\mathbb V}$
, our choice corresponds to fixing a unit tangent vector
![]() $t^{\mathbb H}_{{\mathbb W}}$
and declaring that
$t^{\mathbb H}_{{\mathbb W}}$
and declaring that
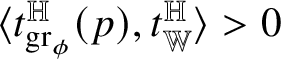 $\langle t^{\mathbb H}_{\mathrm {gr}_{\phi }}(p),t^{\mathbb H}_{{\mathbb W}}\rangle>0$
for
$\langle t^{\mathbb H}_{\mathrm {gr}_{\phi }}(p),t^{\mathbb H}_{{\mathbb W}}\rangle>0$
for
![]() ${\mathscr S}^{Q-k}$
-a.e.
${\mathscr S}^{Q-k}$
-a.e.
![]() $p\in \mathrm {gr}_{\phi }$
, where
$p\in \mathrm {gr}_{\phi }$
, where
![]() $\langle \cdot ,\cdot \rangle $
is the canonical scalar product on multivectors.
$\langle \cdot ,\cdot \rangle $
is the canonical scalar product on multivectors.
Let us point out that, when
![]() ${\mathbb W},{\mathbb V}$
are those in (4.2) and (4.3), as in Remark 4.27 we have
${\mathbb W},{\mathbb V}$
are those in (4.2) and (4.3), as in Remark 4.27 we have
![]() $J^{\phi }\phi =|\nabla ^{\phi }\Phi |$
; this equality and Theorem 1.3, which we will prove in Section 7, provide the alternative representation
$J^{\phi }\phi =|\nabla ^{\phi }\Phi |$
; this equality and Theorem 1.3, which we will prove in Section 7, provide the alternative representation

7 Applications
In this section we provide some consequences of Theorem 1.1. For computational reasons it is useful to fix a convenient distance on
![]() ${\mathbb H}^{n}$
; therefore, in the present section d denotes the distance
${\mathbb H}^{n}$
; therefore, in the present section d denotes the distance
![]() $d_{\infty }$
introduced in (3.2).
$d_{\infty }$
introduced in (3.2).
We need to fix some notation. When M is a matrix, we denote by
![]() $|M| $
its Hilbert–Schmidt norm. When
$|M| $
its Hilbert–Schmidt norm. When
![]() $M_{1},M_{2}$
are square matrices, inequalities of the form
$M_{1},M_{2}$
are square matrices, inequalities of the form
![]() $M_{1}\geq M_{2}$
are understood in the sense of bilinear forms; I denotes the identity matrix. Recall also the notation
$M_{1}\geq M_{2}$
are understood in the sense of bilinear forms; I denotes the identity matrix. Recall also the notation
![]() $W_{1},\dots ,W_{2n}$
introduced in (3.4) to denote horizontal left-invariant vector fields. Eventually, if A and B are given sets,
$W_{1},\dots ,W_{2n}$
introduced in (3.4) to denote horizontal left-invariant vector fields. Eventually, if A and B are given sets,
![]() $A\Delta B:=(A\setminus B)\cup (B\setminus A)$
denotes their symmetric difference.
$A\Delta B:=(A\setminus B)\cup (B\setminus A)$
denotes their symmetric difference.
The proof of the following lemma closely follows the one of the classical Whitney’s extension theorem; see, for example, [Reference Evans and Gariepy40, Theorem 6.10]. A version of Whitney’s extension theorem in
![]() ${\mathbb H}^{n}$
has been proved in [Reference Franchi, Serapioni and Serra Cassano48, Theorem 6.8]; see also [Reference Vittone92, Theorem 3.2.3].
${\mathbb H}^{n}$
has been proved in [Reference Franchi, Serapioni and Serra Cassano48, Theorem 6.8]; see also [Reference Vittone92, Theorem 3.2.3].
Lemma 7.1. For all integers
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $1\leq k\leq n$
there exist positive constants
$1\leq k\leq n$
there exist positive constants
![]() $\alpha _{0}=\alpha _{0}(n,k)$
and
$\alpha _{0}=\alpha _{0}(n,k)$
and
![]() $c_{0}=c_{0}(n,k)$
with the following property. For every
$c_{0}=c_{0}(n,k)$
with the following property. For every
![]() $\delta>0$
and every intrinsic Lipschitz map
$\delta>0$
and every intrinsic Lipschitz map
![]() $\phi :{\mathbb W}\to {\mathbb V}$
whose intrinsic Lipschitz constant
$\phi :{\mathbb W}\to {\mathbb V}$
whose intrinsic Lipschitz constant
![]() $\alpha $
is not greater than
$\alpha $
is not greater than
![]() $\alpha _{0}$
, there exists
$\alpha _{0}$
, there exists
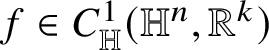 $f\in C^{1}_{\mathbb H}({\mathbb H}^{n},{\mathbb R}^{k})$
such that
$f\in C^{1}_{\mathbb H}({\mathbb H}^{n},{\mathbb R}^{k})$
such that
 $$ \begin{align} &\big|\mathrm{col}\big[X_{1}f(p)|\dots|X_{k} f(p)\big] - I\big|\leq c_{0}\alpha\quad\text{for every }p\in{\mathbb H}^{n} \hphantom{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\end{align} $$
$$ \begin{align} &\big|\mathrm{col}\big[X_{1}f(p)|\dots|X_{k} f(p)\big] - I\big|\leq c_{0}\alpha\quad\text{for every }p\in{\mathbb H}^{n} \hphantom{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\end{align} $$
 $$ \begin{align} & {\mathscr S}^{Q-k}((\mathrm{gr}_{\phi}\,\Delta\, S)\cup\{p\in\mathrm{gr}_{\phi}\cap S:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{S}(p)\})<\delta \hphantom{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\end{align} $$
$$ \begin{align} & {\mathscr S}^{Q-k}((\mathrm{gr}_{\phi}\,\Delta\, S)\cup\{p\in\mathrm{gr}_{\phi}\cap S:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{S}(p)\})<\delta \hphantom{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}\end{align} $$
Proof. As in Remark 6.1, it is not restrictive to assume that
![]() ${\mathbb W}$
and
${\mathbb W}$
and
![]() ${\mathbb V}$
are the subgroups defined in (4.2) and (4.3). Fix
${\mathbb V}$
are the subgroups defined in (4.2) and (4.3). Fix
![]() $\delta>0$
and an intrinsic Lipschitz function
$\delta>0$
and an intrinsic Lipschitz function
![]() $\phi :{\mathbb W}\to {\mathbb V}$
whose intrinsic Lipschitz constant
$\phi :{\mathbb W}\to {\mathbb V}$
whose intrinsic Lipschitz constant
![]() $\alpha $
is not greater than
$\alpha $
is not greater than
![]() $\alpha _{0}$
; the number
$\alpha _{0}$
; the number
![]() $\alpha _{0}>0$
will be chosen later. We organise the proof in several steps.
$\alpha _{0}>0$
will be chosen later. We organise the proof in several steps.
Step 0. We establish some notation and preliminary facts. By Theorem 1.1 there exists a measurable set
![]() $A\subset {\mathbb W}$
such that
$A\subset {\mathbb W}$
such that
![]() ${\mathscr L}^{2n+1-k}({\mathbb W}\setminus A)=0$
and
${\mathscr L}^{2n+1-k}({\mathbb W}\setminus A)=0$
and
![]() $\phi $
is intrinsically differentiable at every point of A. For every
$\phi $
is intrinsically differentiable at every point of A. For every
![]() $w\in A$
, let us introduce the homogeneous homomorphism
$w\in A$
, let us introduce the homogeneous homomorphism
![]() $L_{w}:{\mathbb H}^{n}\to {\mathbb R}^{k}$
,
$L_{w}:{\mathbb H}^{n}\to {\mathbb R}^{k}$
,
where
![]() $\nabla ^{\phi }\phi (w)$
is the intrinsic gradient (identified with a
$\nabla ^{\phi }\phi (w)$
is the intrinsic gradient (identified with a
![]() $k\times (2n-k)$
matrix) introduced in Definition 4.9. Notice that
$k\times (2n-k)$
matrix) introduced in Definition 4.9. Notice that
![]() $L_{w}$
is constructed in such a way that
$L_{w}$
is constructed in such a way that
 $$ \begin{align} {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(\Phi(w)) =\ker L_{w}. \end{align} $$
$$ \begin{align} {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(\Phi(w)) =\ker L_{w}. \end{align} $$
Moreover, for every
![]() $w\in A$
,
$w\in A$
,
 $$ \begin{align} \begin{aligned} & \mathrm{col}[X_{1} L_{w}|\dots|X_{k} L_{w}]=I\\ & |W_{j}(L_{w})_{i}|=|(\nabla^{\phi}\phi(w))_{ij}|\leq\alpha\qquad\forall\:i=1,\dots,k,\ \forall\:j=k+1,\dots,2n \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \mathrm{col}[X_{1} L_{w}|\dots|X_{k} L_{w}]=I\\ & |W_{j}(L_{w})_{i}|=|(\nabla^{\phi}\phi(w))_{ij}|\leq\alpha\qquad\forall\:i=1,\dots,k,\ \forall\:j=k+1,\dots,2n \end{aligned} \end{align} $$
where, as usual,
![]() $\Phi (w):=w\phi (w)$
is the graph map and, in the last formula, we used Lemma 4.13. By abuse of notation, in the sequel we will identify each
$\Phi (w):=w\phi (w)$
is the graph map and, in the last formula, we used Lemma 4.13. By abuse of notation, in the sequel we will identify each
![]() $L_{w}$
with the
$L_{w}$
with the
![]() $k\times 2n$
matrix
$k\times 2n$
matrix
![]() $\nabla _{\mathbb H} L_{w}=[\ I\ |\ -\nabla ^{\phi }\phi (w)\ ]$
, I being the
$\nabla _{\mathbb H} L_{w}=[\ I\ |\ -\nabla ^{\phi }\phi (w)\ ]$
, I being the
![]() $k\times k$
identity matrix. We also introduce the homogeneous homomorphism
$k\times k$
identity matrix. We also introduce the homogeneous homomorphism
![]() $\overline L:{\mathbb H}^{n}\to {\mathbb R}^{k}$
defined by
$\overline L:{\mathbb H}^{n}\to {\mathbb R}^{k}$
defined by
and we identify
![]() $\overline L$
and the
$\overline L$
and the
![]() $k\times 2n$
matrix
$k\times 2n$
matrix
![]() $[\, I\,|\,0\,]$
. We can estimate the Hilbert–Schmidt norm of
$[\, I\,|\,0\,]$
. We can estimate the Hilbert–Schmidt norm of
![]() $L_{w}-\overline L$
by
$L_{w}-\overline L$
by
 $$ \begin{align} |L_{w}-\overline L|\leq \sqrt{k(2n-k)}\,\alpha\qquad\text{for every }w\in A. \end{align} $$
$$ \begin{align} |L_{w}-\overline L|\leq \sqrt{k(2n-k)}\,\alpha\qquad\text{for every }w\in A. \end{align} $$
Let us observe that (7.8), the Lipschitz continuity of
![]() $L_{w}$
and Proposition 4.12 (and, in particular, (4.17)) imply that for every
$L_{w}$
and Proposition 4.12 (and, in particular, (4.17)) imply that for every
![]() $w\in A$
,
$w\in A$
,
 $$ \begin{align} \lim_{r\to 0^{+}} \left(\sup\left\{\frac{L_{w}(\Phi(w)^{-1}p)}{d(\Phi(w),p)}: p\in\mathrm{gr}_{\phi}\cap B(\Phi(w),r)\right\}\right)=0. \end{align} $$
$$ \begin{align} \lim_{r\to 0^{+}} \left(\sup\left\{\frac{L_{w}(\Phi(w)^{-1}p)}{d(\Phi(w),p)}: p\in\mathrm{gr}_{\phi}\cap B(\Phi(w),r)\right\}\right)=0. \end{align} $$
By Lusin’s theorem there exists a closed set
![]() $B\subset A$
such that
$B\subset A$
such that
![]() ${\mathscr L}^{2n+1-k}({\mathbb W}\setminus B)<\eta $
and
${\mathscr L}^{2n+1-k}({\mathbb W}\setminus B)<\eta $
and
![]() $\nabla ^{\phi }\phi |_{B}$
is continuous; the number
$\nabla ^{\phi }\phi |_{B}$
is continuous; the number
![]() $\eta $
will be chosen later in Step 8 depending on
$\eta $
will be chosen later in Step 8 depending on
![]() $\delta ,n$
and k. By the Severini–Egorov theorem, there exists a closed set
$\delta ,n$
and k. By the Severini–Egorov theorem, there exists a closed set
![]() $C\subset B$
such that
$C\subset B$
such that
![]() ${\mathscr L}^{2n+1-k}({\mathbb W}\setminus C)<\eta $
and the convergence in (7.11) is uniform on compact subsets of C.
${\mathscr L}^{2n+1-k}({\mathbb W}\setminus C)<\eta $
and the convergence in (7.11) is uniform on compact subsets of C.
Step 1. Define the closed set
![]() $F:=\Phi (C)$
and let U be the open set
$F:=\Phi (C)$
and let U be the open set
![]() $U:={\mathbb H}^{n}\setminus F$
; for every
$U:={\mathbb H}^{n}\setminus F$
; for every
![]() $p\in {\mathbb H}^{n}$
we set
$p\in {\mathbb H}^{n}$
we set
 $$ \begin{align*} r_{p}:=\frac1{20}d(p,F)=\frac1{20}\inf\{d(p,q):q\in F\}. \end{align*} $$
$$ \begin{align*} r_{p}:=\frac1{20}d(p,F)=\frac1{20}\inf\{d(p,q):q\in F\}. \end{align*} $$
We are going to use a variant of the classical
![]() $5r$
-covering argument (see, e.g., [Reference Heinonen59, Theorem 1.2]), which cannot be utilised here since the radii of the balls we use are not uniformly bounded. By Zorn’s lemma, there exists a maximal set
$5r$
-covering argument (see, e.g., [Reference Heinonen59, Theorem 1.2]), which cannot be utilised here since the radii of the balls we use are not uniformly bounded. By Zorn’s lemma, there exists a maximal set
![]() ${\mathscr C}\subset U$
such that the family of balls
${\mathscr C}\subset U$
such that the family of balls
![]() $\{B(p,r_{p}):p\in {\mathscr C}\}$
is pairwise disjoint; we claim that
$\{B(p,r_{p}):p\in {\mathscr C}\}$
is pairwise disjoint; we claim that
 $$ \begin{align*} U=\bigcup_{p\in {\mathscr C}} B(p,5r_{p}). \end{align*} $$
$$ \begin{align*} U=\bigcup_{p\in {\mathscr C}} B(p,5r_{p}). \end{align*} $$
The inclusion
![]() $\supset $
in the formula above is clear by the definition of
$\supset $
in the formula above is clear by the definition of
![]() $r_{p}$
; assume that the reverse inclusion does not hold; that is, that there exists
$r_{p}$
; assume that the reverse inclusion does not hold; that is, that there exists
![]() $q\in U\setminus \bigcup _{p\in {\mathscr C}} B(p,5r_{p})$
. By maximality of
$q\in U\setminus \bigcup _{p\in {\mathscr C}} B(p,5r_{p})$
. By maximality of
![]() ${\mathscr C}$
, there exists
${\mathscr C}$
, there exists
![]() $p\in {\mathscr C}$
and
$p\in {\mathscr C}$
and
![]() $ p^{\prime }\in U$
such that
$ p^{\prime }\in U$
such that
![]() $ p^{\prime }\in B(p,r_{p})\cap B(q,r_{q})$
and, in particular,
$ p^{\prime }\in B(p,r_{p})\cap B(q,r_{q})$
and, in particular,
It follows that
 $r_{q}\leq \frac {21}{19}r_{p}$
and, in turn,
$r_{q}\leq \frac {21}{19}r_{p}$
and, in turn,
 $$ \begin{align*} q\in B(q, r_{q})\subset B(p,r_{p}+r_{q})\subset B(p,\tfrac{40}{19}r_{p})\subset B(p,5r_{p}), \end{align*} $$
$$ \begin{align*} q\in B(q, r_{q})\subset B(p,r_{p}+r_{q})\subset B(p,\tfrac{40}{19}r_{p})\subset B(p,5r_{p}), \end{align*} $$
a contradiction.
Step 2. For every
![]() $q\in U$
we define
$q\in U$
we define
We claim that
![]() $\# {\mathscr C}_{q}\leq 129^{Q}$
and
$\# {\mathscr C}_{q}\leq 129^{Q}$
and
![]() $1/3\leq r_{q}/r_{p}\leq 3$
for every
$1/3\leq r_{q}/r_{p}\leq 3$
for every
![]() $p\in {\mathscr C}_{q}$
. In fact, if
$p\in {\mathscr C}_{q}$
. In fact, if
![]() $p\in {\mathscr C}_{q}$
, one has
$p\in {\mathscr C}_{q}$
, one has
 $$ \begin{align*} |r_{p}-r_{q}|\leq \frac{1}{20}d(p,q)\leq\frac{1}{20}(10r_{p}+10r_{q})=\frac{1}{2}(r_{p}+r_{q}). \end{align*} $$
$$ \begin{align*} |r_{p}-r_{q}|\leq \frac{1}{20}d(p,q)\leq\frac{1}{20}(10r_{p}+10r_{q})=\frac{1}{2}(r_{p}+r_{q}). \end{align*} $$
This implies that
![]() $r_{p}\leq 3r_{q}$
and
$r_{p}\leq 3r_{q}$
and
![]() $r_{q}\leq 3r_{p}$
, and the bounds on
$r_{q}\leq 3r_{p}$
, and the bounds on
![]() $r_{q}/r_{p}$
follow.
$r_{q}/r_{p}$
follow.
In addition, for every
![]() $p\in {\mathscr C}_{q}$
we have
$p\in {\mathscr C}_{q}$
we have
and, in particular,
![]() $B(p,r_{q}/3)\subset B(p,r_{p})\subset B(q,43r_{q})$
. The balls
$B(p,r_{q}/3)\subset B(p,r_{p})\subset B(q,43r_{q})$
. The balls
![]() $\{B(p,r_{q}/3):p\in {\mathscr C}_{q}\}$
are then pairwise disjoint and contained in
$\{B(p,r_{q}/3):p\in {\mathscr C}_{q}\}$
are then pairwise disjoint and contained in
![]() $B(q,43r_{q})$
; therefore,
$B(q,43r_{q})$
; therefore,
 $$ \begin{align*} \# {\mathscr C}_{q}\leq\frac{{\mathscr L}^{2n+1}(B(q,43r_{q}))}{{\mathscr L}^{2n+1}(B(0,r_{q}/3))}=129^{Q}, \end{align*} $$
$$ \begin{align*} \# {\mathscr C}_{q}\leq\frac{{\mathscr L}^{2n+1}(B(q,43r_{q}))}{{\mathscr L}^{2n+1}(B(0,r_{q}/3))}=129^{Q}, \end{align*} $$
as claimed.
Step 3. Now let
![]() $\mu :{\mathbb R}\to {\mathbb R}$
be a smooth nonincreasing function such that
$\mu :{\mathbb R}\to {\mathbb R}$
be a smooth nonincreasing function such that
For every
![]() $p\in {\mathscr C}$
define
$p\in {\mathscr C}$
define
 $$ \begin{align*} g_{p}(q):=\mu\left(\frac{d_{K}(p,q)}{5r_{p}}\right), \end{align*} $$
$$ \begin{align*} g_{p}(q):=\mu\left(\frac{d_{K}(p,q)}{5r_{p}}\right), \end{align*} $$
where, as in (3.3),
![]() $d_{K}$
is the homogeneous Korányi (or Cygan–Korányi) distance. Observe that
$d_{K}$
is the homogeneous Korányi (or Cygan–Korányi) distance. Observe that
![]() $d_{K}(p,\cdot )$
is smooth on
$d_{K}(p,\cdot )$
is smooth on
![]() ${\mathbb H}^{n}\setminus \{p\}$
. Being a homogeneous distance (see [Reference Cygan34]),
${\mathbb H}^{n}\setminus \{p\}$
. Being a homogeneous distance (see [Reference Cygan34]),
![]() $d_{K}$
is globally equivalent to d and, more precisely,
$d_{K}$
is globally equivalent to d and, more precisely,
It follows that
![]() $g_{p}\in {C}^{\infty }_{c}({\mathbb H}^{n})$
,
$g_{p}\in {C}^{\infty }_{c}({\mathbb H}^{n})$
,
![]() $0\leq g_{p}\leq 1$
and
$0\leq g_{p}\leq 1$
and
 $$ \begin{align} g_{p} &\equiv 1\quad\text{on }B(p,5r_{p})\nonumber\\ g_{p} &\equiv 0\quad\text{on }{\mathbb H}^{n}\setminus B(p,10r_{p}). \end{align} $$
$$ \begin{align} g_{p} &\equiv 1\quad\text{on }B(p,5r_{p})\nonumber\\ g_{p} &\equiv 0\quad\text{on }{\mathbb H}^{n}\setminus B(p,10r_{p}). \end{align} $$
Moreover, there is a constant
![]() $M=M(n)>0$
such that
$M=M(n)>0$
such that
![]() $|\nabla _{\mathbb H} g_{p}|\leq M/r_{p}$
; by Step 2,
$|\nabla _{\mathbb H} g_{p}|\leq M/r_{p}$
; by Step 2,
![]() $|\nabla _{\mathbb H} g_{p}(q)|\leq 3M/r_{q}$
whenever
$|\nabla _{\mathbb H} g_{p}(q)|\leq 3M/r_{q}$
whenever
![]() $p\in {\mathscr C}_{q}$
. Thanks to (7.12), one has
$p\in {\mathscr C}_{q}$
. Thanks to (7.12), one has
![]() $g_{p}(q)=0$
if
$g_{p}(q)=0$
if
![]() $p\in {\mathscr C}\setminus {\mathscr C}_{q}$
; hence,
$p\in {\mathscr C}\setminus {\mathscr C}_{q}$
; hence,
Define
![]() $\sigma (q):=\sum _{p\in {\mathscr C}} g_{p}(q)$
for every
$\sigma (q):=\sum _{p\in {\mathscr C}} g_{p}(q)$
for every
![]() $q\in {\mathbb H}^{n}$
. By (7.12) again, one obtains that
$q\in {\mathbb H}^{n}$
. By (7.12) again, one obtains that
![]() $g_{p}\equiv 0$
on
$g_{p}\equiv 0$
on
![]() $B(q,10r_{q})$
whenever
$B(q,10r_{q})$
whenever
![]() $p\notin {\mathscr C}_{q}$
, so
$p\notin {\mathscr C}_{q}$
, so
 $$ \begin{align*} \sigma(q^{\prime})=\sum_{p\in {\mathscr C}_{q}}g_{p}(q^{\prime})\qquad\text{for every }q\in U\text{ and }q^{\prime}\in B(q,10r_{q}). \end{align*} $$
$$ \begin{align*} \sigma(q^{\prime})=\sum_{p\in {\mathscr C}_{q}}g_{p}(q^{\prime})\qquad\text{for every }q\in U\text{ and }q^{\prime}\in B(q,10r_{q}). \end{align*} $$
Observe that
![]() $\sigma \geq 1$
on U; in fact, for every
$\sigma \geq 1$
on U; in fact, for every
![]() $q\in U$
there exists
$q\in U$
there exists
![]() $\tilde p$
such that
$\tilde p$
such that
![]() $q\in B(\tilde p,5r_{\tilde p})$
and, in particular,
$q\in B(\tilde p,5r_{\tilde p})$
and, in particular,
![]() $\sigma (q)\geq g_{\tilde p} (q)=1$
. Using (7.13) and the inequality
$\sigma (q)\geq g_{\tilde p} (q)=1$
. Using (7.13) and the inequality
![]() $\# {\mathscr C}_{q}<129^{Q}$
, we deduce that
$\# {\mathscr C}_{q}<129^{Q}$
, we deduce that
![]() $\sigma \in {C}^{\infty }(U)$
and there is a constant
$\sigma \in {C}^{\infty }(U)$
and there is a constant
![]() $M^{\prime }=M^{\prime }(n)>0$
such that
$M^{\prime }=M^{\prime }(n)>0$
such that
 $$ \begin{align*} |\nabla_{\mathbb H}\sigma(q)|\leq\frac{M^{\prime}}{r_{q}}\qquad\text{for all }q\in U. \end{align*} $$
$$ \begin{align*} |\nabla_{\mathbb H}\sigma(q)|\leq\frac{M^{\prime}}{r_{q}}\qquad\text{for all }q\in U. \end{align*} $$
Now we define a partition of the unity
![]() $\{v_{p}\}_{p\in {\mathscr C}}$
on U subordinate to the covering
$\{v_{p}\}_{p\in {\mathscr C}}$
on U subordinate to the covering
![]() $\{B(p,10r_{p}):p\in {\mathscr C})\}$
by setting
$\{B(p,10r_{p}):p\in {\mathscr C})\}$
by setting
 $$ \begin{align*}v_{p}(q):=\frac{g_{p}(q)}{\sigma(q)}.\end{align*} $$
$$ \begin{align*}v_{p}(q):=\frac{g_{p}(q)}{\sigma(q)}.\end{align*} $$
Notice that
![]() $v_{p}\in {C}^{\infty }_{c}(U)$
and
$v_{p}\in {C}^{\infty }_{c}(U)$
and
 $\nabla _{\mathbb H} v_{p}=\frac {\nabla _{\mathbb H} g_{p}}{\sigma }-\frac {g_{p}\,\nabla _{\mathbb H}\sigma }{\sigma ^{2}}$
; eventually, we deduce that for a suitable
$\nabla _{\mathbb H} v_{p}=\frac {\nabla _{\mathbb H} g_{p}}{\sigma }-\frac {g_{p}\,\nabla _{\mathbb H}\sigma }{\sigma ^{2}}$
; eventually, we deduce that for a suitable
![]() $M^{\prime \prime }=M^{\prime \prime }(n)>0$
,
$M^{\prime \prime }=M^{\prime \prime }(n)>0$
,
 $$ \begin{align} \sum_{p\in{\mathscr C}}v_{p}(q)=1,\qquad\sum_{p\in{\mathscr C}}\nabla_{\mathbb H} v_{p}(q)= 0\qquad\text{and}\qquad|\nabla_{\mathbb H} v_{p}(q)|\leq \frac{M^{\prime\prime}}{r_{q}} \end{align} $$
$$ \begin{align} \sum_{p\in{\mathscr C}}v_{p}(q)=1,\qquad\sum_{p\in{\mathscr C}}\nabla_{\mathbb H} v_{p}(q)= 0\qquad\text{and}\qquad|\nabla_{\mathbb H} v_{p}(q)|\leq \frac{M^{\prime\prime}}{r_{q}} \end{align} $$
for every
![]() $q\in U$
and every
$q\in U$
and every
![]() $p\in {\mathscr C}$
.
$p\in {\mathscr C}$
.
Step 4. For every
![]() $p\in {\mathscr C}$
, choose
$p\in {\mathscr C}$
, choose
![]() $\bar q_{p}\in F$
such that
$\bar q_{p}\in F$
such that
![]() $d(p,\bar q_{p})=d(p,F)$
; we then define
$d(p,\bar q_{p})=d(p,F)$
; we then define
![]() $ f:{\mathbb H}^{n}\to {\mathbb R}$
as
$ f:{\mathbb H}^{n}\to {\mathbb R}$
as
 $$ \begin{align*} f(q):=\left\{\begin{array}{ll} 0 & \text{if }q\in F \\ \displaystyle\sum_{p\in{\mathscr C}} v_{p}(q) L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q)=\sum_{p\in{\mathscr C}_{q}} v_{p}(q) L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q)\quad & \text{if }q\in U. \end{array}\right. \end{align*} $$
$$ \begin{align*} f(q):=\left\{\begin{array}{ll} 0 & \text{if }q\in F \\ \displaystyle\sum_{p\in{\mathscr C}} v_{p}(q) L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q)=\sum_{p\in{\mathscr C}_{q}} v_{p}(q) L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q)\quad & \text{if }q\in U. \end{array}\right. \end{align*} $$
Notice that
![]() $f\in {C}^{\infty }(U)$
and
$f\in {C}^{\infty }(U)$
and
 $$ \begin{align} \nabla_{\mathbb H} f(q)=\sum_{p\in{\mathscr C}_{q}}\Big[ L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q) \otimes \nabla_{\mathbb H} v_{p}(q) + v_{p}(q) L_{\Phi^{-1}(\bar q_{p})} \Big]\qquad\text{on }U\text{,} \end{align} $$
$$ \begin{align} \nabla_{\mathbb H} f(q)=\sum_{p\in{\mathscr C}_{q}}\Big[ L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q) \otimes \nabla_{\mathbb H} v_{p}(q) + v_{p}(q) L_{\Phi^{-1}(\bar q_{p})} \Big]\qquad\text{on }U\text{,} \end{align} $$
where we recall the identification between homogeneous homomorphisms
![]() $L_{w}$
and
$L_{w}$
and
![]() $k\times 2n$
matrices.
$k\times 2n$
matrices.
Step 5. We claim that
![]() $\nabla _{\mathbb H} f(q)=L_{\Phi ^{-1}(q)}$
for every
$\nabla _{\mathbb H} f(q)=L_{\Phi ^{-1}(q)}$
for every
![]() $q\in F$
. For every such q we define the compact set
$q\in F$
. For every such q we define the compact set
![]() $H:=F\cap \overline {B(q,1)}$
and, for
$H:=F\cap \overline {B(q,1)}$
and, for
![]() $\eta>0$
,
$\eta>0$
,
 $$ \begin{align*} \upsilon(\eta) &:=\sup\left\{ \left|\frac{L_{\Phi^{-1}(p)}(p^{-1}p^{\prime})}{d(p,p^{\prime})}\right|:p,p^{\prime}\in H,\ 0<d(p,p^{\prime})\leq\eta \right\}\\ &\quad + \sup\left\{|L_{\Phi^{-1}(p)}-L_{\Phi^{-1}(p^{\prime})}|:p,p^{\prime}\in H,\ d(p,p^{\prime})\leq\eta\right\}. \end{align*} $$
$$ \begin{align*} \upsilon(\eta) &:=\sup\left\{ \left|\frac{L_{\Phi^{-1}(p)}(p^{-1}p^{\prime})}{d(p,p^{\prime})}\right|:p,p^{\prime}\in H,\ 0<d(p,p^{\prime})\leq\eta \right\}\\ &\quad + \sup\left\{|L_{\Phi^{-1}(p)}-L_{\Phi^{-1}(p^{\prime})}|:p,p^{\prime}\in H,\ d(p,p^{\prime})\leq\eta\right\}. \end{align*} $$
The map
![]() $p\mapsto L_{\Phi ^{-1}(p)}$
is uniformly continuous on H; in fact,
$p\mapsto L_{\Phi ^{-1}(p)}$
is uniformly continuous on H; in fact,
![]() $\Phi ^{-1}:H\to C$
is uniformly continuous and, since
$\Phi ^{-1}:H\to C$
is uniformly continuous and, since
![]() $\nabla ^{\phi }\phi $
is continuous on C,
$\nabla ^{\phi }\phi $
is continuous on C,
![]() $w\mapsto L_{w}$
is also uniformly continuous on the compact set
$w\mapsto L_{w}$
is also uniformly continuous on the compact set
![]() $\Phi ^{-1}(H)$
. This, together with the fact that the convergence in (7.11) is uniform on compact subsets of C, implies that
$\Phi ^{-1}(H)$
. This, together with the fact that the convergence in (7.11) is uniform on compact subsets of C, implies that
 $$ \begin{align} \lim_{\eta\to 0^{+}}\upsilon(\eta)=0. \end{align} $$
$$ \begin{align} \lim_{\eta\to 0^{+}}\upsilon(\eta)=0. \end{align} $$
For every
![]() $q^{\prime }\in H$
, one has
$q^{\prime }\in H$
, one has
 $$ \begin{align} \left| f(q^{\prime})- f(q) - L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right| = \left| L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right|\leq \upsilon(d(q,q^{\prime}))\:d(q,q^{\prime}). \end{align} $$
$$ \begin{align} \left| f(q^{\prime})- f(q) - L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right| = \left| L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right|\leq \upsilon(d(q,q^{\prime}))\:d(q,q^{\prime}). \end{align} $$
Instead, for every
![]() $q^{\prime }\in U$
, one has
$q^{\prime }\in U$
, one has
 $$ \begin{align} \begin{aligned} &\left| f(q^{\prime})- f(q) - L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right|\\ &\quad = \left| f(q^{\prime})- L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right|\\ &\quad \leq \sum_{p\in{\mathscr C}_{q^{\prime}}} v_{p}(q^{\prime}) |L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q^{\prime}) - L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})|\\ &\quad \leq \sum_{p\in{\mathscr C}_{q^{\prime}}} v_{p}(q^{\prime})\Big[ |L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q^{\prime}) - L_{\Phi^{-1}(\bar q_{p})}(q^{-1}q^{\prime})|+|(L_{\Phi^{-1}(\bar q_{p})} - L_{\Phi^{-1}(q)})(q^{-1}q^{\prime})|\Big]\\ &\quad \leq \sum_{p\in{\mathscr C}_{q^{\prime}}} v_{p}(q^{\prime})\Big[ |L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q)|+|L_{\Phi^{-1}(\bar q_{p})}- L_{\Phi^{-1}(q)}|d(q,q^{\prime})\Big]. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\left| f(q^{\prime})- f(q) - L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right|\\ &\quad = \left| f(q^{\prime})- L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right|\\ &\quad \leq \sum_{p\in{\mathscr C}_{q^{\prime}}} v_{p}(q^{\prime}) |L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q^{\prime}) - L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})|\\ &\quad \leq \sum_{p\in{\mathscr C}_{q^{\prime}}} v_{p}(q^{\prime})\Big[ |L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q^{\prime}) - L_{\Phi^{-1}(\bar q_{p})}(q^{-1}q^{\prime})|+|(L_{\Phi^{-1}(\bar q_{p})} - L_{\Phi^{-1}(q)})(q^{-1}q^{\prime})|\Big]\\ &\quad \leq \sum_{p\in{\mathscr C}_{q^{\prime}}} v_{p}(q^{\prime})\Big[ |L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q)|+|L_{\Phi^{-1}(\bar q_{p})}- L_{\Phi^{-1}(q)}|d(q,q^{\prime})\Big]. \end{aligned} \end{align} $$
Since
![]() $20\,r_{q^{\prime }}\leq d(q,q^{\prime })$
, for every
$20\,r_{q^{\prime }}\leq d(q,q^{\prime })$
, for every
![]() $p\in {\mathscr C}_{q^{\prime }}$
we obtain
$p\in {\mathscr C}_{q^{\prime }}$
we obtain
 $$ \begin{align} \begin{aligned} d(q,\bar q_{p})&\leq d(q,p) + d(p,\bar q_{p}) \leq 2d(q,p) \leq 2(d(q,q^{\prime})+d(q^{\prime},p))\\ &\leq 2(d(q,q^{\prime})+10(r_{q^{\prime}}+r_{p})) \leq 2(d(q,q^{\prime})+40r_{q^{\prime}}) \leq 6\,d(q,q^{\prime}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} d(q,\bar q_{p})&\leq d(q,p) + d(p,\bar q_{p}) \leq 2d(q,p) \leq 2(d(q,q^{\prime})+d(q^{\prime},p))\\ &\leq 2(d(q,q^{\prime})+10(r_{q^{\prime}}+r_{p})) \leq 2(d(q,q^{\prime})+40r_{q^{\prime}}) \leq 6\,d(q,q^{\prime}). \end{aligned} \end{align} $$
Therefore, when
![]() $d(q,q^{\prime })\leq 1/6$
, we have
$d(q,q^{\prime })\leq 1/6$
, we have
![]() $\bar q_{p}\in H$
for every
$\bar q_{p}\in H$
for every
![]() $p\in {\mathscr C}_{q^{\prime }}$
; using (7.18) and Step 2 we then obtain
$p\in {\mathscr C}_{q^{\prime }}$
; using (7.18) and Step 2 we then obtain
 $$ \begin{align*} \left| f(q^{\prime})- f(q) - L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right| \leq 7\: \upsilon(6\,d(q,q^{\prime}))\:d(q,q^{\prime}). \end{align*} $$
$$ \begin{align*} \left| f(q^{\prime})- f(q) - L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right| \leq 7\: \upsilon(6\,d(q,q^{\prime}))\:d(q,q^{\prime}). \end{align*} $$
Recalling (7.16), this inequality and (7.17) eventually give
 $$ \begin{align*} \left|f(q^{\prime})- f(q) - L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right| = o(d(q,q^{\prime}))\qquad\text{as }q^{\prime}\to q \end{align*} $$
$$ \begin{align*} \left|f(q^{\prime})- f(q) - L_{\Phi^{-1}(q)}(q^{-1}q^{\prime})\right| = o(d(q,q^{\prime}))\qquad\text{as }q^{\prime}\to q \end{align*} $$
and the claim follows.
Step 6. Let us prove that
 $f\in {C}^{1}_{\mathbb H}({\mathbb H}^{n})$
; since
$f\in {C}^{1}_{\mathbb H}({\mathbb H}^{n})$
; since
![]() $f\in C^{\infty }(U)$
, it suffices to prove that
$f\in C^{\infty }(U)$
, it suffices to prove that
![]() $\nabla _{\mathbb H} f$
is continuous on F. We fix
$\nabla _{\mathbb H} f$
is continuous on F. We fix
![]() $q\in F$
and
$q\in F$
and
![]() $q^{\prime }\in {\mathbb H}^{n}$
with
$q^{\prime }\in {\mathbb H}^{n}$
with
![]() $d(q,q^{\prime })\leq 1/6$
and we define H and
$d(q,q^{\prime })\leq 1/6$
and we define H and
![]() $\upsilon $
as in Step 5. If
$\upsilon $
as in Step 5. If
![]() $q^{\prime }\in F$
, we have by Step 5
$q^{\prime }\in F$
, we have by Step 5
If
![]() $q^{\prime }\in U$
we choose
$q^{\prime }\in U$
we choose
![]() $\bar q\in F$
such that
$\bar q\in F$
such that
![]() $d(q^{\prime },\bar q)=d(q^{\prime },F)=20r_{q^{\prime }}$
to get
$d(q^{\prime },\bar q)=d(q^{\prime },F)=20r_{q^{\prime }}$
to get
 $$ \begin{align} \begin{aligned} |\nabla_{\mathbb H} f(q^{\prime})-\nabla_{\mathbb H} f(q)| &\leq |\nabla_{\mathbb H} f(q^{\prime})-L_{\Phi^{-1}(\bar q)}| + |L_{\Phi^{-1}(\bar q)}-L_{\Phi^{-1}( q)}|\\ &\leq|\nabla_{\mathbb H} f(q^{\prime})-L_{\Phi^{-1}(\bar q)}| + \upsilon(2d(q,q^{\prime})), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} |\nabla_{\mathbb H} f(q^{\prime})-\nabla_{\mathbb H} f(q)| &\leq |\nabla_{\mathbb H} f(q^{\prime})-L_{\Phi^{-1}(\bar q)}| + |L_{\Phi^{-1}(\bar q)}-L_{\Phi^{-1}( q)}|\\ &\leq|\nabla_{\mathbb H} f(q^{\prime})-L_{\Phi^{-1}(\bar q)}| + \upsilon(2d(q,q^{\prime})), \end{aligned} \end{align} $$
where in the last inequality we used the estimate
and, in particular, the fact that
![]() $\bar q\in H$
. Using (7.14) and (7.15), we estimate
$\bar q\in H$
. Using (7.14) and (7.15), we estimate
 $$ \begin{align} \begin{aligned} &|\nabla_{\mathbb H} f(q^{\prime})-L_{\Phi^{-1}(\bar q)}|\\ =\,& \bigg|\sum_{p\in{\mathscr C}_{q^{\prime}}}\Big[ L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q^{\prime}) \otimes \nabla_{\mathbb H} v_{p}(q^{\prime}) + v_{p}(q^{\prime}) L_{\Phi^{-1}(\bar q_{p})} \Big] - \sum_{p\in{\mathscr C}_{q^{\prime}}}v_{p}(q^{\prime})L_{\Phi^{-1}(\bar q)} \bigg|\\ \leq & \sum_{p\in{\mathscr C}_{q^{\prime}}}\big| L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}\bar q) \otimes \nabla_{\mathbb H} v_{p}(q^{\prime}) \big| +\sum_{p\in{\mathscr C}_{q^{\prime}}}\big| \big(L_{\Phi^{-1}(\bar q_{p}) }-L_{\Phi^{-1}(\bar q)}\big)({\bar q\,}^{-1}q^{\prime})\otimes \nabla_{\mathbb H} v_{p}(q^{\prime}) \big|\\ &+ \sum_{p\in{\mathscr C}_{q^{\prime}}}v_{p}(q^{\prime})|L_{\Phi^{-1}(\bar q_{p})}-L_{\Phi^{-1}(\bar q)} |\\ \leq & \frac{M^{\prime\prime}}{r_{q^{\prime}}}\sum_{p\in{\mathscr C}_{q^{\prime}}} \upsilon(d(\bar q,\bar q_{p}))d(\bar q,\bar q_{p}) + \frac{M^{\prime\prime}}{r_{q^{\prime}}}\sum_{p\in{\mathscr C}_{q^{\prime}}}\upsilon(d(\bar q,\bar q_{p}))d(q^{\prime},\bar q) +\sum_{p\in{\mathscr C}_{q^{\prime}}}\upsilon(d(\bar q,\bar q_{p})) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &|\nabla_{\mathbb H} f(q^{\prime})-L_{\Phi^{-1}(\bar q)}|\\ =\,& \bigg|\sum_{p\in{\mathscr C}_{q^{\prime}}}\Big[ L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q^{\prime}) \otimes \nabla_{\mathbb H} v_{p}(q^{\prime}) + v_{p}(q^{\prime}) L_{\Phi^{-1}(\bar q_{p})} \Big] - \sum_{p\in{\mathscr C}_{q^{\prime}}}v_{p}(q^{\prime})L_{\Phi^{-1}(\bar q)} \bigg|\\ \leq & \sum_{p\in{\mathscr C}_{q^{\prime}}}\big| L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}\bar q) \otimes \nabla_{\mathbb H} v_{p}(q^{\prime}) \big| +\sum_{p\in{\mathscr C}_{q^{\prime}}}\big| \big(L_{\Phi^{-1}(\bar q_{p}) }-L_{\Phi^{-1}(\bar q)}\big)({\bar q\,}^{-1}q^{\prime})\otimes \nabla_{\mathbb H} v_{p}(q^{\prime}) \big|\\ &+ \sum_{p\in{\mathscr C}_{q^{\prime}}}v_{p}(q^{\prime})|L_{\Phi^{-1}(\bar q_{p})}-L_{\Phi^{-1}(\bar q)} |\\ \leq & \frac{M^{\prime\prime}}{r_{q^{\prime}}}\sum_{p\in{\mathscr C}_{q^{\prime}}} \upsilon(d(\bar q,\bar q_{p}))d(\bar q,\bar q_{p}) + \frac{M^{\prime\prime}}{r_{q^{\prime}}}\sum_{p\in{\mathscr C}_{q^{\prime}}}\upsilon(d(\bar q,\bar q_{p}))d(q^{\prime},\bar q) +\sum_{p\in{\mathscr C}_{q^{\prime}}}\upsilon(d(\bar q,\bar q_{p})) \end{aligned} \end{align} $$
where, in the last inequality, we used the fact that, as in (7.19),
![]() $\bar q_{p}\in H$
. Recall that
$\bar q_{p}\in H$
. Recall that
![]() $r_{p}\leq 3 r_{q^{\prime }}$
for all
$r_{p}\leq 3 r_{q^{\prime }}$
for all
![]() $p\in {\mathscr C}_{q^{\prime }}$
; therefore, for every such p one can estimate
$p\in {\mathscr C}_{q^{\prime }}$
; therefore, for every such p one can estimate
and, in particular,
for every
![]() $p\in {\mathscr C}_{q^{\prime }}$
. Combining (7.21), (7.22) and (7.23) one finds
$p\in {\mathscr C}_{q^{\prime }}$
. Combining (7.21), (7.22) and (7.23) one finds
 $$ \begin{align*} |\nabla_{\mathbb H} f(q^{\prime})-L_{\Phi^{-1}(\bar q)}| \leq (120\,M^{\prime\prime}+20M^{\prime\prime} + 1)\sum_{p\in{\mathscr C}_{q^{\prime}}}\upsilon(d(\bar q,\bar q_{p}))\leq (140\,M^{\prime\prime} + 1)(129)^{Q}\upsilon(6d(q^{\prime},q)), \end{align*} $$
$$ \begin{align*} |\nabla_{\mathbb H} f(q^{\prime})-L_{\Phi^{-1}(\bar q)}| \leq (120\,M^{\prime\prime}+20M^{\prime\prime} + 1)\sum_{p\in{\mathscr C}_{q^{\prime}}}\upsilon(d(\bar q,\bar q_{p}))\leq (140\,M^{\prime\prime} + 1)(129)^{Q}\upsilon(6d(q^{\prime},q)), \end{align*} $$
which, together with (7.20), gives
as claimed.
Step 7. Let
![]() $\alpha _{1}:=\min \{1/2,\bar \alpha (1/2,n,k)\}$
, where
$\alpha _{1}:=\min \{1/2,\bar \alpha (1/2,n,k)\}$
, where
![]() $\bar \alpha (1/2,n,k)$
is the number provided by Remark 4.4. We claim that there exists
$\bar \alpha (1/2,n,k)$
is the number provided by Remark 4.4. We claim that there exists
![]() $c_{1}=c_{1}(n,k)>0$
such that, if
$c_{1}=c_{1}(n,k)>0$
such that, if
![]() $\alpha \leq \alpha _{1}$
, then
$\alpha \leq \alpha _{1}$
, then
We will later choose
![]() $\alpha _{0}$
and
$\alpha _{0}$
and
![]() $c_{0}$
in such a way that
$c_{0}$
in such a way that
![]() $\alpha _{0}\leq \alpha _{1}$
and
$\alpha _{0}\leq \alpha _{1}$
and
![]() $c_{0}\geq c_{1}$
; in this way, statements (7.1) and (7.2) are immediate consequences of (7.24).
$c_{0}\geq c_{1}$
; in this way, statements (7.1) and (7.2) are immediate consequences of (7.24).
If
![]() $q\in F$
, (7.24) follows from Step 5 and (7.10); hence, we can assume
$q\in F$
, (7.24) follows from Step 5 and (7.10); hence, we can assume
![]() $q\in U$
. By (7.15) and (7.14),
$q\in U$
. By (7.15) and (7.14),
 $$ \begin{align} \begin{aligned} \nabla_{\mathbb H} f(q) - \overline L =&\sum_{p\in{\mathscr C}_{q}} L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q) \otimes \nabla_{\mathbb H} v_{p}(q) + \sum_{p\in{\mathscr C}_{q}} v_{p}(q) (L_{\Phi^{-1}(\bar q_{p})}-\overline L)\\ =& \sum_{p\in{\mathscr C}_{q}} \Big( L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q)-(q_{{\mathbb V}}-\phi(q_{{\mathbb W}})) \Big) \otimes \nabla_{\mathbb H} v_{p}(q)\\ & + \sum_{p\in{\mathscr C}_{q}} v_{p}(q) (L_{\Phi^{-1}(\bar q_{p})}-\overline L), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \nabla_{\mathbb H} f(q) - \overline L =&\sum_{p\in{\mathscr C}_{q}} L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q) \otimes \nabla_{\mathbb H} v_{p}(q) + \sum_{p\in{\mathscr C}_{q}} v_{p}(q) (L_{\Phi^{-1}(\bar q_{p})}-\overline L)\\ =& \sum_{p\in{\mathscr C}_{q}} \Big( L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q)-(q_{{\mathbb V}}-\phi(q_{{\mathbb W}})) \Big) \otimes \nabla_{\mathbb H} v_{p}(q)\\ & + \sum_{p\in{\mathscr C}_{q}} v_{p}(q) (L_{\Phi^{-1}(\bar q_{p})}-\overline L), \end{aligned} \end{align} $$
where we recall that, for every
![]() $p\in {\mathbb H}^{n}$
, we write
$p\in {\mathbb H}^{n}$
, we write
![]() $p=p_{{\mathbb W}} p_{{\mathbb V}}$
for suitable (unique)
$p=p_{{\mathbb W}} p_{{\mathbb V}}$
for suitable (unique)
![]() $p_{{\mathbb W}}\in {\mathbb W}$
and
$p_{{\mathbb W}}\in {\mathbb W}$
and
![]() $p_{{\mathbb V}}\in {\mathbb V}$
. From (7.10) we obtain
$p_{{\mathbb V}}\in {\mathbb V}$
. From (7.10) we obtain
 $$ \begin{align} \bigg| \sum_{p\in{\mathscr C}_{q}} v_{p}(q) (L_{\Phi^{-1}(\bar q_{p})}-\overline L)\bigg| \leq \sqrt{k(2n-k)}\,\alpha. \end{align} $$
$$ \begin{align} \bigg| \sum_{p\in{\mathscr C}_{q}} v_{p}(q) (L_{\Phi^{-1}(\bar q_{p})}-\overline L)\bigg| \leq \sqrt{k(2n-k)}\,\alpha. \end{align} $$
We now estimate the first addend in the rightmost side of (7.25). First, we notice that for every
![]() $p\in {\mathscr C}_{q}$
,
$p\in {\mathscr C}_{q}$
,
 $$ \begin{align} \begin{aligned} |L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q) - \overline L({\bar q_{p}\!}^{-1}q)| & \leq |L_{\Phi^{-1}(\bar q_{p})} - \overline L| \:d(q, \bar q_{p})\\ &\leq \sqrt{k(2n-k)}\,\alpha\:(d(q,p)+d(p,\bar q_{p}))\\ & \leq \sqrt{k(2n-k)}\,\alpha\:(10(r_{p}+r_{q})+20 r_{p})\\ &\leq 100 \sqrt{k(2n-k)}\,\alpha\:r_{q}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} |L_{\Phi^{-1}(\bar q_{p})}({\bar q_{p}\!}^{-1}q) - \overline L({\bar q_{p}\!}^{-1}q)| & \leq |L_{\Phi^{-1}(\bar q_{p})} - \overline L| \:d(q, \bar q_{p})\\ &\leq \sqrt{k(2n-k)}\,\alpha\:(d(q,p)+d(p,\bar q_{p}))\\ & \leq \sqrt{k(2n-k)}\,\alpha\:(10(r_{p}+r_{q})+20 r_{p})\\ &\leq 100 \sqrt{k(2n-k)}\,\alpha\:r_{q}. \end{aligned} \end{align} $$
Noticing that
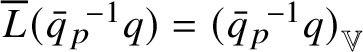 $\overline L({\bar q_{p}\!}^{-1}q)={({\bar q_{p}\!}^{-1}q)}_{{\mathbb V}}$
, we deduce that
$\overline L({\bar q_{p}\!}^{-1}q)={({\bar q_{p}\!}^{-1}q)}_{{\mathbb V}}$
, we deduce that
 $$ \begin{align*} | \overline L({\bar q_{p}\!}^{-1}q)- (q_{{\mathbb V}}-\phi(q_{{\mathbb W}}))| = |q_{{\mathbb V}}-(\bar q_{p})_{{\mathbb V}}+\phi(q_{{\mathbb W}})-q_{{\mathbb V}}| =|\phi(q_{{\mathbb W}})-(\bar q_{p})_{{\mathbb V}}| = |\phi(q_{{\mathbb W}})-\phi((\bar q_{p})_{{\mathbb W}})| \end{align*} $$
$$ \begin{align*} | \overline L({\bar q_{p}\!}^{-1}q)- (q_{{\mathbb V}}-\phi(q_{{\mathbb W}}))| = |q_{{\mathbb V}}-(\bar q_{p})_{{\mathbb V}}+\phi(q_{{\mathbb W}})-q_{{\mathbb V}}| =|\phi(q_{{\mathbb W}})-(\bar q_{p})_{{\mathbb V}}| = |\phi(q_{{\mathbb W}})-\phi((\bar q_{p})_{{\mathbb W}})| \end{align*} $$
and by Remark 4.3,
 $$ \begin{align*} \begin{aligned} | \overline L({\bar q_{p}\!}^{-1}q)- (q_{{\mathbb V}}-\phi(q_{{\mathbb W}}))| &\leq 2\alpha d(\bar q_{p},\Phi(q_{{\mathbb W}}))\\ &\leq 2\alpha(d(\bar q_{p},p)+d(p,q)+d(q,\Phi(q_{{\mathbb W}})))\\ &=2\alpha(d(\bar q_{p},p)+d(p,q)+|q_{{\mathbb V}}-\phi(q_{{\mathbb W}})|)\\ &\leq2\alpha(20 r_{p} + 10(r_{p}+r_{q}) + 2 d(q,\mathrm{gr}_{\phi}) ), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} | \overline L({\bar q_{p}\!}^{-1}q)- (q_{{\mathbb V}}-\phi(q_{{\mathbb W}}))| &\leq 2\alpha d(\bar q_{p},\Phi(q_{{\mathbb W}}))\\ &\leq 2\alpha(d(\bar q_{p},p)+d(p,q)+d(q,\Phi(q_{{\mathbb W}})))\\ &=2\alpha(d(\bar q_{p},p)+d(p,q)+|q_{{\mathbb V}}-\phi(q_{{\mathbb W}})|)\\ &\leq2\alpha(20 r_{p} + 10(r_{p}+r_{q}) + 2 d(q,\mathrm{gr}_{\phi}) ), \end{aligned} \end{align*} $$
where in the last inequality we used Remark 4.4 with
![]() $\varepsilon =1/2$
. Recalling that
$\varepsilon =1/2$
. Recalling that
![]() $r_{p}\leq 3r_{q}$
for every
$r_{p}\leq 3r_{q}$
for every
![]() $p\in {\mathscr C}_{q}$
, we deduce
$p\in {\mathscr C}_{q}$
, we deduce
 $$ \begin{align} | \overline L({\bar q_{p}\!}^{-1}q)- (q_{{\mathbb V}}-\phi(q_{{\mathbb W}}))|\leq 280\,\alpha\, r_{q} \end{align} $$
$$ \begin{align} | \overline L({\bar q_{p}\!}^{-1}q)- (q_{{\mathbb V}}-\phi(q_{{\mathbb W}}))|\leq 280\,\alpha\, r_{q} \end{align} $$
and the claim (7.24) is now a consequence of (7.25), (7.26), (7.27), (7.28) and the last statement in (7.14).
Step 8. Denote by
![]() $K>0$
a constant with the property (see, e.g., [Reference Garofalo and Nhieu56]) that
$K>0$
a constant with the property (see, e.g., [Reference Garofalo and Nhieu56]) that
 $$ \begin{align*} |g(p)-g(q)|\leq K \Big(\sup_{{\mathbb H}^{n}} |\nabla_{\mathbb H} g|\Big)d(p,q)\qquad\text{for every }g\in C^{1}_{\mathbb H}({\mathbb H}^{n},{\mathbb R}^{k})\text{ and }p,q\in{\mathbb H}^{n}. \end{align*} $$
$$ \begin{align*} |g(p)-g(q)|\leq K \Big(\sup_{{\mathbb H}^{n}} |\nabla_{\mathbb H} g|\Big)d(p,q)\qquad\text{for every }g\in C^{1}_{\mathbb H}({\mathbb H}^{n},{\mathbb R}^{k})\text{ and }p,q\in{\mathbb H}^{n}. \end{align*} $$
We now fix
![]() $c_{0}:=\max \{c_{1},2Kc_{1}\}$
and
$c_{0}:=\max \{c_{1},2Kc_{1}\}$
and
![]() $\alpha _{0}:=\min \{\alpha _{1},(2c_{1})^{-1}\}$
. The inequality (7.24) now implies that, if
$\alpha _{0}:=\min \{\alpha _{1},(2c_{1})^{-1}\}$
. The inequality (7.24) now implies that, if
![]() $\alpha \leq \alpha _{0}$
, then col
$\alpha \leq \alpha _{0}$
, then col
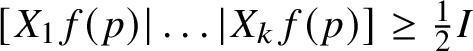 $[X_{1}f(p)|\dots |X_{k} f(p)]\geq \tfrac 12I$
; hence,
$[X_{1}f(p)|\dots |X_{k} f(p)]\geq \tfrac 12I$
; hence,
![]() $\nabla _{\mathbb H} f(p)$
has rank k for every
$\nabla _{\mathbb H} f(p)$
has rank k for every
![]() $p\in {\mathbb H}^{n}$
. In particular, the level set
$p\in {\mathbb H}^{n}$
. In particular, the level set
![]() $S=\{p\in {\mathbb H}^{n}:f(p)=0\}$
is a
$S=\{p\in {\mathbb H}^{n}:f(p)=0\}$
is a
![]() ${\mathbb H}$
-regular submanifold and statement (7.3) follows.
${\mathbb H}$
-regular submanifold and statement (7.3) follows.
Theorem 1.4 ensures that
![]() $S=\mathrm {gr}_{\psi }$
for an intrinsic Lipschitz
$S=\mathrm {gr}_{\psi }$
for an intrinsic Lipschitz
![]() $\psi :{\mathbb W}\to {\mathbb V}$
. We claim that the intrinsic Lipschitz constant of
$\psi :{\mathbb W}\to {\mathbb V}$
. We claim that the intrinsic Lipschitz constant of
![]() $\psi $
is at most
$\psi $
is at most
![]() $2Kc_{1}\alpha $
. To this aim, fix
$2Kc_{1}\alpha $
. To this aim, fix
![]() $w\in {\mathbb W}$
and
$w\in {\mathbb W}$
and
![]() $v\in {\mathbb V}\setminus \{0\}$
such that
$v\in {\mathbb V}\setminus \{0\}$
such that
![]() $\|w\|_{\mathbb H}< \|v\|_{\mathbb H}/(2Kc_{1}\alpha )$
, so that
$\|w\|_{\mathbb H}< \|v\|_{\mathbb H}/(2Kc_{1}\alpha )$
, so that
![]() $wv\in C_{\beta }$
for some
$wv\in C_{\beta }$
for some
![]() $\beta>2Kc_{1}\alpha $
. For every
$\beta>2Kc_{1}\alpha $
. For every
![]() $q\in {\mathbb H}^{n}$
we have
$q\in {\mathbb H}^{n}$
we have
![]() $\overline L(qw)=\overline L(q)$
and, in particular,
$\overline L(qw)=\overline L(q)$
and, in particular,
 $$ \begin{align*} |f(qw)-f(q)|&= |(f-\overline L)(qw)-(f-\overline L)(q)|\leq K\Big(\sup_{{\mathbb H}^{n}}|\nabla_{\mathbb H} f-\overline L|\Big)\|w\|_{\mathbb H}< \|v\|_{\mathbb H}/2, \end{align*} $$
$$ \begin{align*} |f(qw)-f(q)|&= |(f-\overline L)(qw)-(f-\overline L)(q)|\leq K\Big(\sup_{{\mathbb H}^{n}}|\nabla_{\mathbb H} f-\overline L|\Big)\|w\|_{\mathbb H}< \|v\|_{\mathbb H}/2, \end{align*} $$
the last inequality following from (7.24). Now, for every
![]() $p\in S=\mathrm {gr}_{\psi }$
we have
$p\in S=\mathrm {gr}_{\psi }$
we have
![]() $f(p)=0$
; hence,
$f(p)=0$
; hence,
 $$ \begin{align*} |f(pwv)| & =|f(pwv)-f(p)|\\ &\geq |f(pwv)-f(pw)|-|f(pw)-f(p)|\\ &> \left\langle f(pwv)-f(pw),\frac{v}{|v|}\right\rangle -\frac{\|v\|_{\mathbb H}}{2}\ \geq\ 0, \end{align*} $$
$$ \begin{align*} |f(pwv)| & =|f(pwv)-f(p)|\\ &\geq |f(pwv)-f(pw)|-|f(pw)-f(p)|\\ &> \left\langle f(pwv)-f(pw),\frac{v}{|v|}\right\rangle -\frac{\|v\|_{\mathbb H}}{2}\ \geq\ 0, \end{align*} $$
where we used Remark 2.7. This proves that
![]() $f(pwv)\neq 0$
; hence,
$f(pwv)\neq 0$
; hence,
![]() $\mathrm {gr}_{\psi }\cap pC_{\beta }=\{p\}$
for every
$\mathrm {gr}_{\psi }\cap pC_{\beta }=\{p\}$
for every
![]() $p\in \mathrm {gr}_{\psi }$
and all
$p\in \mathrm {gr}_{\psi }$
and all
![]() $\beta>2Kc_{1}\alpha $
. This implies that the intrinsic Lipschitz constant of
$\beta>2Kc_{1}\alpha $
. This implies that the intrinsic Lipschitz constant of
![]() $\psi $
is at most
$\psi $
is at most
![]() $2Kc_{1}\alpha $
and statement (7.4) follows because
$2Kc_{1}\alpha $
and statement (7.4) follows because
![]() $c_{0}\geq 2K c_{1}$
.
$c_{0}\geq 2K c_{1}$
.
Step 9. By construction, for every
![]() $w\in C$
we have
$w\in C$
we have
![]() $\Phi (w)\in F\subset \{f=0\}$
; hence,
$\Phi (w)\in F\subset \{f=0\}$
; hence,
![]() $\phi (w)=\psi (w)$
and
$\phi (w)=\psi (w)$
and
 $$ \begin{align*} {\mathrm{Tan}}^{\mathbb H}_{S}(\Phi(w))=\ker \nabla_{\mathbb H} f(\Phi(w))=\ker L_{w} \stackrel{(7.8)}{=}{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(\Phi(w)). \end{align*} $$
$$ \begin{align*} {\mathrm{Tan}}^{\mathbb H}_{S}(\Phi(w))=\ker \nabla_{\mathbb H} f(\Phi(w))=\ker L_{w} \stackrel{(7.8)}{=}{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(\Phi(w)). \end{align*} $$
In particular, the inclusion
holds, and (7.6) follows provided
![]() $\eta <\delta $
. The inclusion above also guarantees that
$\eta <\delta $
. The inclusion above also guarantees that
 $$ \begin{align} (\mathrm{gr}_{\phi}\,\Delta\, S)\cup\{p\in\mathrm{gr}_{\phi}\cap S:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{S}(p)\}\subset \Phi({\mathbb W}\setminus C)\cup \Psi({\mathbb W}\setminus C), \end{align} $$
$$ \begin{align} (\mathrm{gr}_{\phi}\,\Delta\, S)\cup\{p\in\mathrm{gr}_{\phi}\cap S:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{S}(p)\}\subset \Phi({\mathbb W}\setminus C)\cup \Psi({\mathbb W}\setminus C), \end{align} $$
where
![]() $\Psi $
is the graph map
$\Psi $
is the graph map
![]() $\Psi (w):=w\psi (w)$
. The intrinsic Lipschitz constants of
$\Psi (w):=w\psi (w)$
. The intrinsic Lipschitz constants of
![]() $\phi $
and
$\phi $
and
![]() $\psi $
are both bounded by
$\psi $
are both bounded by
![]() $\max \{\alpha _{0},c_{0}\alpha _{0}\}$
, which depends only on n and k; then, by Remark 4.6, there exists
$\max \{\alpha _{0},c_{0}\alpha _{0}\}$
, which depends only on n and k; then, by Remark 4.6, there exists
![]() $\kappa =\kappa (k,n)>0$
such that
$\kappa =\kappa (k,n)>0$
such that

Statements (7.29) and (7.30) imply that
 $$ \begin{align*} {\mathscr S}^{Q-k}((\mathrm{gr}_{\phi}\,\Delta\, S)\cup\{p\in\mathrm{gr}_{\phi}\cap S:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{S}(p)\})\leq 2\kappa\eta, \end{align*} $$
$$ \begin{align*} {\mathscr S}^{Q-k}((\mathrm{gr}_{\phi}\,\Delta\, S)\cup\{p\in\mathrm{gr}_{\phi}\cap S:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{S}(p)\})\leq 2\kappa\eta, \end{align*} $$
and (7.5) follows provided we also impose
![]() $\eta <(2\kappa )^{-1}\delta $
. This concludes the proof.
$\eta <(2\kappa )^{-1}\delta $
. This concludes the proof.
Theorem 7.2 is one of the main results of this section; recall that it implies Theorem 1.2.
Theorem 7.2. Let
![]() $A\subset {\mathbb W}$
be an open set and
$A\subset {\mathbb W}$
be an open set and
![]() $\phi :A\to {\mathbb V}$
an intrinsic Lipschitz function. Then, for every
$\phi :A\to {\mathbb V}$
an intrinsic Lipschitz function. Then, for every
![]() $\varepsilon>0$
there exists an intrinsic Lipschitz function
$\varepsilon>0$
there exists an intrinsic Lipschitz function
![]() $\psi :A\to {\mathbb V}$
such that
$\psi :A\to {\mathbb V}$
such that
![]() $\mathrm {gr}_{\psi }$
is an
$\mathrm {gr}_{\psi }$
is an
![]() ${\mathbb H}$
-regular submanifold and
${\mathbb H}$
-regular submanifold and
 $$ \begin{align} & {\mathscr S}^{Q-k}((\mathrm{gr}_{\phi}\,\Delta\, \mathrm{gr}_{\psi})\cup\{p\in\mathrm{gr}_{\phi}\cap \mathrm{gr}_{\psi}:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi}}(p)\})<\varepsilon \end{align} $$
$$ \begin{align} & {\mathscr S}^{Q-k}((\mathrm{gr}_{\phi}\,\Delta\, \mathrm{gr}_{\psi})\cup\{p\in\mathrm{gr}_{\phi}\cap \mathrm{gr}_{\psi}:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi}}(p)\})<\varepsilon \end{align} $$
Proof. As in Remark 6.1, it is not restrictive to assume that
![]() ${\mathbb W}$
and
${\mathbb W}$
and
![]() ${\mathbb V}$
are the subgroups defined in (4.2) and (4.3). By Theorem 1.5, without loss of generality, we can assume that
${\mathbb V}$
are the subgroups defined in (4.2) and (4.3). By Theorem 1.5, without loss of generality, we can assume that
![]() $A={\mathbb W}$
. Let
$A={\mathbb W}$
. Let
![]() $\alpha _{0},c_{0}$
be the constants provided by Lemma 7.1; up to reducing
$\alpha _{0},c_{0}$
be the constants provided by Lemma 7.1; up to reducing
![]() $\alpha _{0}$
, we can assume that
$\alpha _{0}$
, we can assume that
![]() $\alpha _{0}c_{0}\leq 1/2$
.
$\alpha _{0}c_{0}\leq 1/2$
.
Let
![]() $\alpha $
be the intrinsic Lipschitz constant of
$\alpha $
be the intrinsic Lipschitz constant of
![]() $\phi $
; if
$\phi $
; if
![]() $\alpha \leq \alpha _{0}$
, the statement directly follows from Lemma 7.1. We then assume
$\alpha \leq \alpha _{0}$
, the statement directly follows from Lemma 7.1. We then assume
![]() $\alpha>\alpha _{0}$
and define
$\alpha>\alpha _{0}$
and define
![]() $\lambda :=\alpha _{0}/\alpha <1$
. Let us consider the
$\lambda :=\alpha _{0}/\alpha <1$
. Let us consider the
![]() ${\mathbb H}$
-linear isomorphism
${\mathbb H}$
-linear isomorphism
![]() ${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
defined (if
${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
defined (if
![]() $k<n$
) by
$k<n$
) by
 $$ \begin{align*}{\mathcal L}(x^{\prime},x^{\prime\prime},y^{\prime},y^{\prime\prime},t):=\Big(\lambda x^{\prime},x^{\prime\prime},\frac{y^{\prime}}\lambda,y^{\prime\prime},t\Big) \end{align*} $$
$$ \begin{align*}{\mathcal L}(x^{\prime},x^{\prime\prime},y^{\prime},y^{\prime\prime},t):=\Big(\lambda x^{\prime},x^{\prime\prime},\frac{y^{\prime}}\lambda,y^{\prime\prime},t\Big) \end{align*} $$
for every
![]() $(x^{\prime },x^{\prime \prime },y^{\prime },y^{\prime \prime },t)\in {\mathbb R}^{k}\times {\mathbb R}^{n-k}\times {\mathbb R}^{k}\times {\mathbb R}^{n-k}\times {\mathbb R}\equiv {\mathbb H}^{n}$
, and (if
$(x^{\prime },x^{\prime \prime },y^{\prime },y^{\prime \prime },t)\in {\mathbb R}^{k}\times {\mathbb R}^{n-k}\times {\mathbb R}^{k}\times {\mathbb R}^{n-k}\times {\mathbb R}\equiv {\mathbb H}^{n}$
, and (if
![]() $k=n$
) by
$k=n$
) by
![]() ${\mathcal L}(x,y,t):=(\lambda x,y/\lambda ,t)$
for every
${\mathcal L}(x,y,t):=(\lambda x,y/\lambda ,t)$
for every
![]() $(x,y,t)\in {\mathbb R}^{n}\times {\mathbb R}^{n}\times {\mathbb R}\equiv {\mathbb H}^{n}$
. We discuss only the case
$(x,y,t)\in {\mathbb R}^{n}\times {\mathbb R}^{n}\times {\mathbb R}\equiv {\mathbb H}^{n}$
. We discuss only the case
![]() $k<n$
, as the case
$k<n$
, as the case
![]() $k=n$
can be treated with some modification in the notation only.
$k=n$
can be treated with some modification in the notation only.
We claim that
![]() $C_{\alpha _{0}}\subset {\mathcal L}(C_{\alpha })$
. To this aim, fix
$C_{\alpha _{0}}\subset {\mathcal L}(C_{\alpha })$
. To this aim, fix
![]() $w=(0,x^{\prime \prime },y^{\prime },y^{\prime \prime },t)\in {\mathbb W}$
and
$w=(0,x^{\prime \prime },y^{\prime },y^{\prime \prime },t)\in {\mathbb W}$
and
![]() $v=(x^{\prime },0,0,0,0)\in {\mathbb V}$
such that
$v=(x^{\prime },0,0,0,0)\in {\mathbb V}$
such that
![]() $wv\in C_{\alpha _{0}}$
; that is,
$wv\in C_{\alpha _{0}}$
; that is,
![]() $\|w\|_{\mathbb H}\leq \|v\|_{\mathbb H}/\alpha _{0}$
. Then
$\|w\|_{\mathbb H}\leq \|v\|_{\mathbb H}/\alpha _{0}$
. Then
 $$ \begin{align*} \|{\mathcal L}^{-1}(w)\|_{\mathbb H} &= \Big\|\Big(0,x^{\prime\prime},\lambda y^{\prime},y^{\prime\prime},t\Big)\Big\|_{\mathbb H} \leq \|(0,x^{\prime\prime},y^{\prime},y^{\prime\prime},t)\|_{\mathbb H} =\|w\|_{\mathbb H}\\ &\leq \frac{1}{\alpha_{0}}\|v\|_{\mathbb H} =\frac{1}{\alpha_{0}}\|(x^{\prime},0,0,0,0)\|_{\mathbb H}=\frac{\lambda}{\alpha_{0}}\Big\|\Big(\frac{x^{\prime}}{\lambda},0,0,0,0\Big)\Big\|_{\mathbb H} =\frac1\alpha\|{\mathcal L}^{-1}(v)\|_{\mathbb H}. \end{align*} $$
$$ \begin{align*} \|{\mathcal L}^{-1}(w)\|_{\mathbb H} &= \Big\|\Big(0,x^{\prime\prime},\lambda y^{\prime},y^{\prime\prime},t\Big)\Big\|_{\mathbb H} \leq \|(0,x^{\prime\prime},y^{\prime},y^{\prime\prime},t)\|_{\mathbb H} =\|w\|_{\mathbb H}\\ &\leq \frac{1}{\alpha_{0}}\|v\|_{\mathbb H} =\frac{1}{\alpha_{0}}\|(x^{\prime},0,0,0,0)\|_{\mathbb H}=\frac{\lambda}{\alpha_{0}}\Big\|\Big(\frac{x^{\prime}}{\lambda},0,0,0,0\Big)\Big\|_{\mathbb H} =\frac1\alpha\|{\mathcal L}^{-1}(v)\|_{\mathbb H}. \end{align*} $$
This proves that
![]() $wv\in {\mathcal L}(C_{\alpha })$
, as claimed.
$wv\in {\mathcal L}(C_{\alpha })$
, as claimed.
For every
![]() $p\in {\mathcal L}(\mathrm {gr}_{\phi })$
we have
$p\in {\mathcal L}(\mathrm {gr}_{\phi })$
we have
 $$ \begin{align*} {\mathcal L}(\mathrm{gr}_{\phi}) \cap pC_{\alpha_{0}}\subset {\mathcal L}(\mathrm{gr}_{\phi}) \cap p{\mathcal L}( C_{\alpha}) = {\mathcal L}(\mathrm{gr}_{\phi}\cap{\mathcal L}^{-1}(p) C_{\alpha}) ={\mathcal L}({\mathcal L}^{-1}(p))=p; \end{align*} $$
$$ \begin{align*} {\mathcal L}(\mathrm{gr}_{\phi}) \cap pC_{\alpha_{0}}\subset {\mathcal L}(\mathrm{gr}_{\phi}) \cap p{\mathcal L}( C_{\alpha}) = {\mathcal L}(\mathrm{gr}_{\phi}\cap{\mathcal L}^{-1}(p) C_{\alpha}) ={\mathcal L}({\mathcal L}^{-1}(p))=p; \end{align*} $$
hence (see Remark 2.3), the set
![]() ${\mathcal L}(\mathrm {gr}_{\phi })$
is the intrinsic Lipschitz graph of some function
${\mathcal L}(\mathrm {gr}_{\phi })$
is the intrinsic Lipschitz graph of some function
![]() $ \phi _{0}:{\mathbb W}\to {\mathbb V}$
with intrinsic Lipschitz constant at most
$ \phi _{0}:{\mathbb W}\to {\mathbb V}$
with intrinsic Lipschitz constant at most
![]() $\alpha _{0}$
. By Lemma 7.1, there exists
$\alpha _{0}$
. By Lemma 7.1, there exists
 $f_{0}\in C^{1}_{\mathbb H}({\mathbb H}^{n},{\mathbb R}^{k})$
such that
$f_{0}\in C^{1}_{\mathbb H}({\mathbb H}^{n},{\mathbb R}^{k})$
such that
 $$ \begin{align} &\mathrm{col}\Big[X_{1}f_{0}(p)|\dots|X_{k} f_{0}(p)\Big]\geq \frac12 I\quad\text{for every }p\in{\mathbb H}^{n} \end{align} $$
$$ \begin{align} &\mathrm{col}\Big[X_{1}f_{0}(p)|\dots|X_{k} f_{0}(p)\Big]\geq \frac12 I\quad\text{for every }p\in{\mathbb H}^{n} \end{align} $$
 $$ \begin{align} & \text{the level set }S_{0}:=\{p\in{\mathbb H}^{n}:f_{0}(p)=0\}\text{ is a }{\mathbb H}\text{-regular submanifold}\nonumber\\ &S_{0}=\mathrm{gr}_{\psi_{0}}\text{ for an intrinsic Lipschitz }\psi_{0}:{\mathbb W}\to{\mathbb V}\nonumber\\ & {\mathscr S}^{Q-k}((\mathrm{gr}_{\phi_{0}}\,\Delta\, S_{0})\cup\{p\in\mathrm{gr}_{\phi_{0}}\cap S_{0}:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi_{0}}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{S_{0}}(p)\})<\varepsilon/M^{Q-k} \end{align} $$
$$ \begin{align} & \text{the level set }S_{0}:=\{p\in{\mathbb H}^{n}:f_{0}(p)=0\}\text{ is a }{\mathbb H}\text{-regular submanifold}\nonumber\\ &S_{0}=\mathrm{gr}_{\psi_{0}}\text{ for an intrinsic Lipschitz }\psi_{0}:{\mathbb W}\to{\mathbb V}\nonumber\\ & {\mathscr S}^{Q-k}((\mathrm{gr}_{\phi_{0}}\,\Delta\, S_{0})\cup\{p\in\mathrm{gr}_{\phi_{0}}\cap S_{0}:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi_{0}}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{S_{0}}(p)\})<\varepsilon/M^{Q-k} \end{align} $$
where
![]() $M>0$
denotes the Lipschitz constant of
$M>0$
denotes the Lipschitz constant of
![]() ${\mathcal L}^{-1}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
. The function
${\mathcal L}^{-1}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
. The function
![]() $f:=f_{0}\circ {\mathcal L}$
is of class
$f:=f_{0}\circ {\mathcal L}$
is of class
 $C^{1}_{\mathbb H}({\mathbb H}^{n},{\mathbb R}^{k})$
and
$C^{1}_{\mathbb H}({\mathbb H}^{n},{\mathbb R}^{k})$
and
 $$ \begin{align*} & X_{i}f(p)=\lambda (X_{i} f_{0})({\mathcal L}(p))\quad\text{for every }i=1,\dots,k\\ & Y_{i}f(p)=\frac1\lambda (Y_{i} f_{0})({\mathcal L}(p))\quad\text{for every }i=1,\dots,k\\ & W_{i}f(p)=(W_{i} f_{0})({\mathcal L}(p))\quad\text{whenever }k+1\leq i\leq n\text{ or }n+k+1\leq i\leq 2n \end{align*} $$
$$ \begin{align*} & X_{i}f(p)=\lambda (X_{i} f_{0})({\mathcal L}(p))\quad\text{for every }i=1,\dots,k\\ & Y_{i}f(p)=\frac1\lambda (Y_{i} f_{0})({\mathcal L}(p))\quad\text{for every }i=1,\dots,k\\ & W_{i}f(p)=(W_{i} f_{0})({\mathcal L}(p))\quad\text{whenever }k+1\leq i\leq n\text{ or }n+k+1\leq i\leq 2n \end{align*} $$
so that, by (7.33) and (7.34),
 $$ \begin{align*} &|W_{i} f(p)|\leq \frac{1}{2\lambda}\quad\text{for every }p\in{\mathbb H}^{n}\text{ and }i=k+1,\dots,2n\\ &\mathrm{col}\Big[X_{1}f(p)|\dots|X_{k} f(p)\Big] \geq \frac\lambda 2 I\quad\text{for every }p\in{\mathbb H}^{n}. \end{align*} $$
$$ \begin{align*} &|W_{i} f(p)|\leq \frac{1}{2\lambda}\quad\text{for every }p\in{\mathbb H}^{n}\text{ and }i=k+1,\dots,2n\\ &\mathrm{col}\Big[X_{1}f(p)|\dots|X_{k} f(p)\Big] \geq \frac\lambda 2 I\quad\text{for every }p\in{\mathbb H}^{n}. \end{align*} $$
By Theorem 1.4 and Remarks 2.7 and 2.8, the level set
![]() $\{f=0\}$
, which is an
$\{f=0\}$
, which is an
![]() ${\mathbb H}$
-regular submanifold, is the intrinsic graph of an intrinsic Lipschitz function
${\mathbb H}$
-regular submanifold, is the intrinsic graph of an intrinsic Lipschitz function
![]() $\psi :{\mathbb W}\to {\mathbb V}$
whose Lipschitz constant can be estimated in terms of
$\psi :{\mathbb W}\to {\mathbb V}$
whose Lipschitz constant can be estimated in terms of
![]() $\lambda $
(i.e., of
$\lambda $
(i.e., of
![]() $\alpha $
) only; see Remark 2.9. Moreover, the equalities
$\alpha $
) only; see Remark 2.9. Moreover, the equalities
 $$ \begin{align*} &(\mathrm{gr}_{\phi}\,\Delta\, \mathrm{gr}_{\psi})\cup\{p\in\mathrm{gr}_{\phi}\cap \mathrm{gr}_{\psi}:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi}}(p)\} \\ &\quad ={\mathcal L}^{-1}\big( (\mathrm{gr}_{\phi_{0}}\,\Delta\, \mathrm{gr}_{\psi_{0}})\cup\{p\in\mathrm{gr}_{\phi_{0}}\cap \mathrm{gr}_{\psi_{0}}:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi_{0}}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi_{0}}}(p)\} \big) \end{align*} $$
$$ \begin{align*} &(\mathrm{gr}_{\phi}\,\Delta\, \mathrm{gr}_{\psi})\cup\{p\in\mathrm{gr}_{\phi}\cap \mathrm{gr}_{\psi}:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi}}(p)\} \\ &\quad ={\mathcal L}^{-1}\big( (\mathrm{gr}_{\phi_{0}}\,\Delta\, \mathrm{gr}_{\psi_{0}})\cup\{p\in\mathrm{gr}_{\phi_{0}}\cap \mathrm{gr}_{\psi_{0}}:{\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\phi_{0}}}(p)\neq {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi_{0}}}(p)\} \big) \end{align*} $$
and
 $$ \begin{align*} \{\phi=\psi\text{ and }\nabla^{\phi}\phi= \nabla^{\psi}\psi\} = {\mathcal L}^{-1}\big( \{\phi_{0}=\psi_{0}\text{ and }\nabla^{\phi_{0}}\phi_{0}= \nabla^{\psi_{0}}\psi_{0}\}\big) \end{align*} $$
$$ \begin{align*} \{\phi=\psi\text{ and }\nabla^{\phi}\phi= \nabla^{\psi}\psi\} = {\mathcal L}^{-1}\big( \{\phi_{0}=\psi_{0}\text{ and }\nabla^{\phi_{0}}\phi_{0}= \nabla^{\psi_{0}}\psi_{0}\}\big) \end{align*} $$
hold. Statements (7.31) and (7.32) now follow from (7.35) and (7.36), and the proof is accomplished.
Remark 7.3. Taking (7.4) into account, a further outcome of the proof of Theorem 7.2 is the existence of a function
![]() $u:(0,+\infty )\to (0,+\infty )$
such that, if A,
$u:(0,+\infty )\to (0,+\infty )$
such that, if A,
![]() $\phi $
and
$\phi $
and
![]() $\varepsilon $
are as in the statement of Theorem 7.2 and the intrinsic Lipschitz constant of
$\varepsilon $
are as in the statement of Theorem 7.2 and the intrinsic Lipschitz constant of
![]() $\phi $
is
$\phi $
is
![]() $\alpha>0$
, then the function
$\alpha>0$
, then the function
![]() $\psi $
provided by Theorem 7.2 has intrinsic Lipschitz constant at most
$\psi $
provided by Theorem 7.2 has intrinsic Lipschitz constant at most
![]() $u(\alpha )$
.
$u(\alpha )$
.
A first consequence of Theorem 7.2 is the equivalence between the two possible notions of
![]() ${\mathbb H}$
-rectifiability; this was already stated in Subsection 4.4.
${\mathbb H}$
-rectifiability; this was already stated in Subsection 4.4.
Corollary 7.4. Let
![]() $\phi :A\to {\mathbb V}$
be an intrinsic Lipschitz map defined on some subset
$\phi :A\to {\mathbb V}$
be an intrinsic Lipschitz map defined on some subset
![]() $A\subset {\mathbb W}$
; then
$A\subset {\mathbb W}$
; then
![]() $\mathrm {gr}_{\phi }$
is
$\mathrm {gr}_{\phi }$
is
![]() ${\mathbb H}$
-rectifiable.
${\mathbb H}$
-rectifiable.
In particular, a set
![]() $R\subset {\mathbb H}^{n}$
is
$R\subset {\mathbb H}^{n}$
is
![]() ${\mathbb H}$
-rectifiable of codimension k,
${\mathbb H}$
-rectifiable of codimension k,
![]() $k\in \{1,\dots ,n\}$
, if and only if
$k\in \{1,\dots ,n\}$
, if and only if
![]() ${\mathscr S}^{Q-k}(R)<\infty $
and there exists a countable family
${\mathscr S}^{Q-k}(R)<\infty $
and there exists a countable family
![]() $(\phi _{j})_{j}$
of intrinsic Lipschitz maps
$(\phi _{j})_{j}$
of intrinsic Lipschitz maps
![]() $\phi _{j}:{\mathbb W}_{j}\to {\mathbb V}_{j}$
where
$\phi _{j}:{\mathbb W}_{j}\to {\mathbb V}_{j}$
where
![]() ${\mathbb W}_{j},{\mathbb V}_{j} $
are homogeneous complementary subgroups of
${\mathbb W}_{j},{\mathbb V}_{j} $
are homogeneous complementary subgroups of
![]() ${\mathbb H}^{n}$
with
${\mathbb H}^{n}$
with
![]() $\dim {\mathbb V}_{j}=k$
and
$\dim {\mathbb V}_{j}=k$
and
 $$ \begin{align*} {\mathscr S}^{Q-k}\left(R\setminus\bigcup_{j} \mathrm{gr}_{\phi_{j}}\right)=0. \end{align*} $$
$$ \begin{align*} {\mathscr S}^{Q-k}\left(R\setminus\bigcup_{j} \mathrm{gr}_{\phi_{j}}\right)=0. \end{align*} $$
Proof. We can assume
![]() $A={\mathbb W}$
because of Theorem 1.5. By Theorem 7.2, for every
$A={\mathbb W}$
because of Theorem 1.5. By Theorem 7.2, for every
![]() $j\in \mathbb N$
there exists
$j\in \mathbb N$
there exists
![]() $\phi _{j}:{\mathbb W}\to {\mathbb V}$
such that
$\phi _{j}:{\mathbb W}\to {\mathbb V}$
such that
![]() $\mathrm {gr}_{\phi _{j}}$
is
$\mathrm {gr}_{\phi _{j}}$
is
![]() ${\mathbb H}$
-regular and
${\mathbb H}$
-regular and
 $$ \begin{align*} {\mathscr S}^{Q-k}(\mathrm{gr}_{\phi}\setminus \mathrm{gr}_{\phi_{j}})<1/j. \end{align*} $$
$$ \begin{align*} {\mathscr S}^{Q-k}(\mathrm{gr}_{\phi}\setminus \mathrm{gr}_{\phi_{j}})<1/j. \end{align*} $$
The first part of the statement follows as well as one implication of the second part of the statement. The other implication is a simple consequence of the fact that (Theorem 4.19)
![]() ${\mathbb H}$
-regular submanifolds are locally intrinsic Lipschitz graphs.
${\mathbb H}$
-regular submanifolds are locally intrinsic Lipschitz graphs.
A second consequence of Theorem 7.2 is the area formula of Theorem 1.3, which we now prove. Recall that the intrinsic Jacobian determinant
![]() $J^{\phi }\phi $
was introduced in Definition 4.9.
$J^{\phi }\phi $
was introduced in Definition 4.9.
Proof of Theorem 1.3.
Recalling Remark 4.10, it is not restrictive to assume that
![]() ${\mathbb W},{\mathbb V}$
are the subgroups in (4.3) and (4.2). By Theorem 1.5, one can assume that
${\mathbb W},{\mathbb V}$
are the subgroups in (4.3) and (4.2). By Theorem 1.5, one can assume that
![]() $A={\mathbb W}$
. Since every Borel nonnegative function h can be written as a series of characteristic functions of Borel subsets of
$A={\mathbb W}$
. Since every Borel nonnegative function h can be written as a series of characteristic functions of Borel subsets of
![]() $\mathrm {gr}_{\phi }$
, we can, without loss of generality, assume that
$\mathrm {gr}_{\phi }$
, we can, without loss of generality, assume that
![]() $h=\chi _{E}$
for some Borel subset
$h=\chi _{E}$
for some Borel subset
![]() $E\subset \mathrm {gr}_{\phi }$
, and we must prove that
$E\subset \mathrm {gr}_{\phi }$
, and we must prove that
 $$ \begin{align*} {\mathscr S}^{Q-k}(E)=C_{n,k}\int_{\Phi^{-1}(E)}J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}. \end{align*} $$
$$ \begin{align*} {\mathscr S}^{Q-k}(E)=C_{n,k}\int_{\Phi^{-1}(E)}J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}. \end{align*} $$
Let
![]() $\varepsilon>0$
be fixed; by Theorem 7.2 we can find an intrinsic Lipschitz map
$\varepsilon>0$
be fixed; by Theorem 7.2 we can find an intrinsic Lipschitz map
![]() $\psi :{\mathbb W}\to {\mathbb V}$
such that
$\psi :{\mathbb W}\to {\mathbb V}$
such that
![]() $\mathrm {gr}_{\psi }$
is an
$\mathrm {gr}_{\psi }$
is an
![]() ${\mathbb H}$
-regular submanifold and, defining the graph map
${\mathbb H}$
-regular submanifold and, defining the graph map
![]() $\Psi (w):=w\psi (w)$
and
$\Psi (w):=w\psi (w)$
and
![]() $D:=\{w\in {\mathbb W}:\phi (w)=\psi (w)\text { and }\nabla ^{\phi }\phi (w)=\nabla ^{\psi }\psi (w)\}$
, one has
$D:=\{w\in {\mathbb W}:\phi (w)=\psi (w)\text { and }\nabla ^{\phi }\phi (w)=\nabla ^{\psi }\psi (w)\}$
, one has
Using Theorem 4.19,
 $$ \begin{align*} {\mathscr S}^{Q-k}(E) & = {\mathscr S}^{Q-k}(E\cap \Psi(D))+{\mathscr S}^{Q-k}(E\setminus \Psi(D))\\ & = C_{n,k}\int_{\Psi^{-1}(E\cap \Psi(D))} J^{\psi}\psi\:d{\mathscr L}^{2n+1-k}+{\mathscr S}^{Q-k}(E\setminus \Psi(D))\\ & = C_{n,k}\int_{\Phi^{-1}(E)\cap D} J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}+{\mathscr S}^{Q-k}(E\setminus \Psi(D))\\ & = C_{n,k}\int_{\Phi^{-1}(E)} \!J^{\phi}\phi\:d{\mathscr L}^{2n+1-k} - C_{n,k}\int_{\Phi^{-1}(E)\setminus D} \!J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}+{\mathscr S}^{Q-k}(E\setminus \Psi(D)) \end{align*} $$
$$ \begin{align*} {\mathscr S}^{Q-k}(E) & = {\mathscr S}^{Q-k}(E\cap \Psi(D))+{\mathscr S}^{Q-k}(E\setminus \Psi(D))\\ & = C_{n,k}\int_{\Psi^{-1}(E\cap \Psi(D))} J^{\psi}\psi\:d{\mathscr L}^{2n+1-k}+{\mathscr S}^{Q-k}(E\setminus \Psi(D))\\ & = C_{n,k}\int_{\Phi^{-1}(E)\cap D} J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}+{\mathscr S}^{Q-k}(E\setminus \Psi(D))\\ & = C_{n,k}\int_{\Phi^{-1}(E)} \!J^{\phi}\phi\:d{\mathscr L}^{2n+1-k} - C_{n,k}\int_{\Phi^{-1}(E)\setminus D} \!J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}+{\mathscr S}^{Q-k}(E\setminus \Psi(D)) \end{align*} $$
so that
 $$ \begin{align*} \left| {\mathscr S}^{Q-k}(E)- C_{n,k}\int_{\Phi^{-1}(E)} J^{\phi}\phi\:d{\mathscr L}^{2n+1-k} \right| &\leq C_{n,k}\int_{{\mathbb W}\setminus D} J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}+{\mathscr S}^{Q-k}(E\setminus \Psi(D))\\ &\leq (C_{n,k}C+1)\varepsilon, \end{align*} $$
$$ \begin{align*} \left| {\mathscr S}^{Q-k}(E)- C_{n,k}\int_{\Phi^{-1}(E)} J^{\phi}\phi\:d{\mathscr L}^{2n+1-k} \right| &\leq C_{n,k}\int_{{\mathbb W}\setminus D} J^{\phi}\phi\:d{\mathscr L}^{2n+1-k}+{\mathscr S}^{Q-k}(E\setminus \Psi(D))\\ &\leq (C_{n,k}C+1)\varepsilon, \end{align*} $$
where, in the last inequality, we used (7.37) and the fact that, by Lemma 4.13,
![]() $J^{\phi }\phi \leq C$
for some positive C depending only on the intrinsic Lipschitz constant of
$J^{\phi }\phi \leq C$
for some positive C depending only on the intrinsic Lipschitz constant of
![]() $\phi $
. The arbitrariness of
$\phi $
. The arbitrariness of
![]() $\varepsilon $
concludes the proof.
$\varepsilon $
concludes the proof.
Eventually, as a further consequence of Theorem 7.2 we prove the fact that, as anticipated in Section 6, the canonical current associated with an entire intrinsic Lipschitz graph has zero boundary. We will use (6.11), whose validity is now guaranteed by Theorem 1.3.
Proposition 7.5. Let
![]() $\phi :{\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz. Then the
$\phi :{\mathbb W}\to {\mathbb V}$
be intrinsic Lipschitz. Then the
![]() $(2n+1-k)$
-Heisenberg current
$(2n+1-k)$
-Heisenberg current
 introduced in (6.10) is such that
introduced in (6.10) is such that
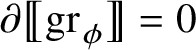 .
.
Proof. As in Remark 6.1 we can assume without loss of generality that the subgroups
![]() ${\mathbb W},{\mathbb V}$
are those defined in (4.3) and (4.2). Let
${\mathbb W},{\mathbb V}$
are those defined in (4.3) and (4.2). Let
![]() $\varepsilon>0$
be fixed and let
$\varepsilon>0$
be fixed and let
![]() $\psi :{\mathbb W}\to {\mathbb V}$
be the map provided by Theorem 7.2. It was shown in the proof of Theorem 7.2 that there exists
$\psi :{\mathbb W}\to {\mathbb V}$
be the map provided by Theorem 7.2. It was shown in the proof of Theorem 7.2 that there exists
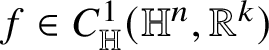 $f\in C^{1}_{\mathbb H}({\mathbb H}^{n},{\mathbb R}^{k})$
such that
$f\in C^{1}_{\mathbb H}({\mathbb H}^{n},{\mathbb R}^{k})$
such that
![]() $\mathrm {gr}_{\psi }=\{f=0\}$
; moreover, the construction performed in Lemma 7.1 ensures that
$\mathrm {gr}_{\psi }=\{f=0\}$
; moreover, the construction performed in Lemma 7.1 ensures that
![]() $f\in C^{\infty }({\mathbb H}^{n}\setminus \mathrm {gr}_{\psi })$
. As in the proof of Theorem 1.6, for every positive integer i there exists
$f\in C^{\infty }({\mathbb H}^{n}\setminus \mathrm {gr}_{\psi })$
. As in the proof of Theorem 1.6, for every positive integer i there exists
![]() $\psi _{i}\in C^{\infty }({\mathbb W},{\mathbb V}) $
such that
$\psi _{i}\in C^{\infty }({\mathbb W},{\mathbb V}) $
such that
Moreover, defining the graph maps
![]() $\Psi (w):=w\psi (w)$
and
$\Psi (w):=w\psi (w)$
and
![]() $\Psi _{i}(w):=w\psi _{i}(w)$
, as
$\Psi _{i}(w):=w\psi _{i}(w)$
, as
![]() $i\to +\infty $
, one has
$i\to +\infty $
, one has
The last convergence stated in (7.38) follows from the local uniform (with respect to
![]() $w\in {\mathbb W}$
) convergence
$w\in {\mathbb W}$
) convergence
 $$ \begin{align*} {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi_{i}}}(\Psi_{i}(w))=\ker\nabla_{\mathbb H} f(\Psi_{i}(w))\to \ker\nabla_{\mathbb H} f(\Psi(w))={\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi}}(\Psi(w)). \end{align*} $$
$$ \begin{align*} {\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi_{i}}}(\Psi_{i}(w))=\ker\nabla_{\mathbb H} f(\Psi_{i}(w))\to \ker\nabla_{\mathbb H} f(\Psi(w))={\mathrm{Tan}}^{\mathbb H}_{\mathrm{gr}_{\psi}}(\Psi(w)). \end{align*} $$
Using Proposition 1.9, Lemma 4.29 and formulae (7.38) and (6.11) we deduce that for every
 $\omega \in {\mathcal D}_{\mathbb H}^{2n-k}$
,
$\omega \in {\mathcal D}_{\mathbb H}^{2n-k}$
,

In particular,

The arbitrariness of
![]() $\varepsilon $
implies that
$\varepsilon $
implies that
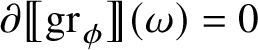
for every
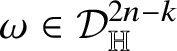 $\omega \in {\mathcal D}_{\mathbb H}^{2n-k}$
, as desired.
$\omega \in {\mathcal D}_{\mathbb H}^{2n-k}$
, as desired.
A Proof of Proposition 3.38
We provide here the proofs of Lemma 3.37 and Proposition 3.38 that were only stated in Subsection 3.6. The proof of Lemma 3.37 is quite simple.
Proof of Lemma 3.37.
Assume that (a) holds; then either
![]() $\dim {\mathscr P}_{1}\cap {\mathscr P}_{2}=m$
, in which case
$\dim {\mathscr P}_{1}\cap {\mathscr P}_{2}=m$
, in which case
![]() ${\mathscr P}_{1}={\mathscr P}_{2}$
and (b) trivially holds or
${\mathscr P}_{1}={\mathscr P}_{2}$
and (b) trivially holds or
![]() $\dim {\mathscr P}_{1}\cap {\mathscr P}_{2}=m-1$
. Let
$\dim {\mathscr P}_{1}\cap {\mathscr P}_{2}=m-1$
. Let
![]() $v_{1},\dots ,v_{m-1}$
be a basis of
$v_{1},\dots ,v_{m-1}$
be a basis of
![]() ${\mathscr P}_{1}\cap {\mathscr P}_{2}$
and choose
${\mathscr P}_{1}\cap {\mathscr P}_{2}$
and choose
![]() $w_{1}\in {\mathscr P}_{1}\setminus {\mathscr P}_{2}$
and
$w_{1}\in {\mathscr P}_{1}\setminus {\mathscr P}_{2}$
and
![]() $w_{2}\in {\mathscr P}_{2}\setminus {\mathscr P}_{1}$
; then, for every
$w_{2}\in {\mathscr P}_{2}\setminus {\mathscr P}_{1}$
; then, for every
![]() $t_{1},t_{2}$
as in statement (b) there exist
$t_{1},t_{2}$
as in statement (b) there exist
![]() $c_{1},c_{2}\in {\mathbb R}\setminus \{0\}$
such that
$c_{1},c_{2}\in {\mathbb R}\setminus \{0\}$
such that
 $$ \begin{align*} & t_{1} = c_{1}w_{1}\wedge v_{1}\wedge\dots\wedge v_{m-1} \\ & t_{2}=c_{2}w_{2}\wedge v_{1}\wedge\dots\wedge v_{m-1}. \end{align*} $$
$$ \begin{align*} & t_{1} = c_{1}w_{1}\wedge v_{1}\wedge\dots\wedge v_{m-1} \\ & t_{2}=c_{2}w_{2}\wedge v_{1}\wedge\dots\wedge v_{m-1}. \end{align*} $$
The difference
![]() $t_{1}-t_{2}$
is clearly a simple vector and (b) follows.
$t_{1}-t_{2}$
is clearly a simple vector and (b) follows.
Statement (b) implies (c); hence, we have only to show that (c) implies (a). Assume there exist
![]() $t_{1},t_{2}$
as in (c). Let
$t_{1},t_{2}$
as in (c). Let
![]() $h:=\dim {\mathscr P}_{1}\cap {\mathscr P}_{2}$
; we assume
$h:=\dim {\mathscr P}_{1}\cap {\mathscr P}_{2}$
; we assume
![]() $h\geq 1$
, but the following argument can be easily adapted to the case
$h\geq 1$
, but the following argument can be easily adapted to the case
![]() $ h=0$
. By assumption,
$ h=0$
. By assumption,
![]() $t:=t_{1}-t_{2}$
is simple; moreover, we have
$t:=t_{1}-t_{2}$
is simple; moreover, we have
![]() ${\mathscr P}_{1}\cap {\mathscr P}_{2}\subset \operatorname *{\mathrm {span}} t$
, because for every
${\mathscr P}_{1}\cap {\mathscr P}_{2}\subset \operatorname *{\mathrm {span}} t$
, because for every
![]() $v\in {\mathscr P}_{1}\cap {\mathscr P}_{2}$
we have
$v\in {\mathscr P}_{1}\cap {\mathscr P}_{2}$
we have
![]() $v\wedge t=v\wedge (t_{1}-t_{2})=0$
. In particular, after fixing a basis
$v\wedge t=v\wedge (t_{1}-t_{2})=0$
. In particular, after fixing a basis
![]() $v_{1},\dots , v_{h}$
of
$v_{1},\dots , v_{h}$
of
![]() ${\mathscr P}_{1}\cap {\mathscr P}_{2}$
, we can find
${\mathscr P}_{1}\cap {\mathscr P}_{2}$
, we can find
![]() $ v_{h+1},\dots , v_{m}\in \operatorname *{\mathrm {span}} t$
,
$ v_{h+1},\dots , v_{m}\in \operatorname *{\mathrm {span}} t$
,
![]() $e_{1},\dots ,e_{m-h}\in {\mathscr P}_{1}\setminus {\mathscr P}_{2}$
and
$e_{1},\dots ,e_{m-h}\in {\mathscr P}_{1}\setminus {\mathscr P}_{2}$
and
![]() $e_{m-h+1},\dots ,e_{2(m-h)}\in {\mathscr P}_{2}\setminus {\mathscr P}_{1}$
such that
$e_{m-h+1},\dots ,e_{2(m-h)}\in {\mathscr P}_{2}\setminus {\mathscr P}_{1}$
such that
 $$ \begin{align*} t &= v_{1}\wedge\dots \wedge v_{h}\wedge v_{h+1}\wedge\dots\wedge v_{m}\\ t_{1}&= v_{1}\wedge\dots \wedge v_{h}\wedge e_{1}\wedge\dots\wedge e_{m-h}\\ t_{2}&= v_{1}\wedge\dots \wedge v_{h}\wedge e_{m-h+1}\wedge\dots\wedge e_{2(m-h)}. \end{align*} $$
$$ \begin{align*} t &= v_{1}\wedge\dots \wedge v_{h}\wedge v_{h+1}\wedge\dots\wedge v_{m}\\ t_{1}&= v_{1}\wedge\dots \wedge v_{h}\wedge e_{1}\wedge\dots\wedge e_{m-h}\\ t_{2}&= v_{1}\wedge\dots \wedge v_{h}\wedge e_{m-h+1}\wedge\dots\wedge e_{2(m-h)}. \end{align*} $$
Then, on the one side,
![]() $t^{\prime }:= e_{1}\wedge \dots \wedge e_{m-h} - e_{m-h+1}\wedge \dots \wedge e_{2(m-h)}$
equals the simple vector
$t^{\prime }:= e_{1}\wedge \dots \wedge e_{m-h} - e_{m-h+1}\wedge \dots \wedge e_{2(m-h)}$
equals the simple vector
![]() $v_{h+1}\wedge \dots \wedge v_{m}$
; hence,
$v_{h+1}\wedge \dots \wedge v_{m}$
; hence,
![]() $\dim \operatorname *{\mathrm {span}} t^{\prime }=m-h$
. On the other side,
$\dim \operatorname *{\mathrm {span}} t^{\prime }=m-h$
. On the other side,
![]() $e_{1},\dots ,e_{2(m-h)}$
are linearly independent and one can easily check that, in case
$e_{1},\dots ,e_{2(m-h)}$
are linearly independent and one can easily check that, in case
![]() $m-h\geq 2$
, one would have
$m-h\geq 2$
, one would have
This implies that
![]() $h\geq m-1$
, which is statement (a).
$h\geq m-1$
, which is statement (a).
On the contrary, the proof of Proposition 3.38 is long and technical: there might well be a simpler one but the author was not able to find it. The proof provided here is based on Lemmata A.1 and A.3, where one essentially studies the model cases of the planes
![]() ${{\mathscr P}_{a,b}}$
introduced in (3.11). Proposition 3.38 will then follow by a quite standard use of Proposition 3.13.
${{\mathscr P}_{a,b}}$
introduced in (3.11). Proposition 3.38 will then follow by a quite standard use of Proposition 3.13.
Remark 3.27 will be utilised several times.
Lemma A.1. Let
![]() $a\geq 1$
be an integer such that
$a\geq 1$
be an integer such that
![]() $n\leq 2a\leq 2n-1$
; assume that
$n\leq 2a\leq 2n-1$
; assume that
![]() $\tau \in \Large \wedge _{2a}{\mathfrak h}_{1}$
is a simple
$\tau \in \Large \wedge _{2a}{\mathfrak h}_{1}$
is a simple
![]() $2a$
-vector such that
$2a$
-vector such that
Then the following statements hold:
-
(i) if
 $2a>n$
, then
$2a>n$
, then
 $\tau = X_{1}\wedge \dots \wedge X_{a}\wedge Y_{1}\wedge \dots \wedge Y_{a}$
;
$\tau = X_{1}\wedge \dots \wedge X_{a}\wedge Y_{1}\wedge \dots \wedge Y_{a}$
; -
(ii) if
 $2a=n$
, then either or
$2a=n$
, then either or $$ \begin{align*} \tau= X_{1}\wedge\dots\wedge X_{a}\wedge Y_{1}\wedge\dots\wedge Y_{a} \end{align*} $$
$$ \begin{align*} \tau= X_{1}\wedge\dots\wedge X_{a}\wedge Y_{1}\wedge\dots\wedge Y_{a} \end{align*} $$
 $$ \begin{align*} \tau=(-1)^{a}\,X_{a+1}\wedge\dots\wedge X_{2a}\wedge Y_{a+1}\wedge\dots\wedge Y_{2a}. \end{align*} $$
$$ \begin{align*} \tau=(-1)^{a}\,X_{a+1}\wedge\dots\wedge X_{2a}\wedge Y_{a+1}\wedge\dots\wedge Y_{2a}. \end{align*} $$
Remark A.2. When
![]() $2a=n$
one can use computations analogous to those in Remark 3.27 to check the action of
$2a=n$
one can use computations analogous to those in Remark 3.27 to check the action of
![]() $(-1)^{a}\,X_{a+1}\wedge \dots \wedge X_{2a}\wedge Y_{a+1}\wedge \dots \wedge Y_{2a}\wedge T$
in duality with elements of the basis of
$(-1)^{a}\,X_{a+1}\wedge \dots \wedge X_{2a}\wedge Y_{a+1}\wedge \dots \wedge Y_{2a}\wedge T$
in duality with elements of the basis of
![]() ${\mathcal J}^{2a+1}={\mathcal J}^{n+1}$
provided by Proposition 1.10. As a matter of fact, the equality
${\mathcal J}^{2a+1}={\mathcal J}^{n+1}$
provided by Proposition 1.10. As a matter of fact, the equality
does hold.
For instance, recalling Example 3.23. it can be easily checked that in
![]() ${\mathbb H}^{2}$
.
${\mathbb H}^{2}$
.
Proof of Lemma A.1.
Let us write
![]() $\tau =\tau ^{1}\wedge \dots \wedge \tau ^{2a}$
for suitable horizontal vectors
$\tau =\tau ^{1}\wedge \dots \wedge \tau ^{2a}$
for suitable horizontal vectors
![]() $\tau ^{i}\in {\mathfrak h}_{1}$
. Writing
$\tau ^{i}\in {\mathfrak h}_{1}$
. Writing
 $$ \begin{align*} \tau^{i}=\tau^{i}_{1}X_{1}+\dots+\tau^{i}_{2n}Y_{n},\qquad i=1,\dots,2a \end{align*} $$
$$ \begin{align*} \tau^{i}=\tau^{i}_{1}X_{1}+\dots+\tau^{i}_{2n}Y_{n},\qquad i=1,\dots,2a \end{align*} $$
we introduce the matrix
 $$ \begin{align*} M:=\text{col}\big[\:\tau^{1}\:|\cdots|\:\tau^{2a}\:\big] = \left[ \begin{array}{c|c|c} \tau^{1}_{1} &\dots & \tau^{2a}_{1}\\ \vdots& &\vdots\\ \tau^{1}_{2n} &\dots & \tau^{2a}_{2n} \end{array} \right] =\text{row} \left[ \begin{array}{c} M_{1}\\ \hline\vdots\\ \hline M_{2n} \end{array} \right] , \end{align*} $$
$$ \begin{align*} M:=\text{col}\big[\:\tau^{1}\:|\cdots|\:\tau^{2a}\:\big] = \left[ \begin{array}{c|c|c} \tau^{1}_{1} &\dots & \tau^{2a}_{1}\\ \vdots& &\vdots\\ \tau^{1}_{2n} &\dots & \tau^{2a}_{2n} \end{array} \right] =\text{row} \left[ \begin{array}{c} M_{1}\\ \hline\vdots\\ \hline M_{2n} \end{array} \right] , \end{align*} $$
where for every
![]() $i=1,\dots ,2n$
we denoted by
$i=1,\dots ,2n$
we denoted by
 $M_{i}=(\tau ^{1}_{i},\dots ,\tau ^{2a}_{i})\in {\mathbb R}^{2a}$
the ith row of M. It is worth noticing that for every
$M_{i}=(\tau ^{1}_{i},\dots ,\tau ^{2a}_{i})\in {\mathbb R}^{2a}$
the ith row of M. It is worth noticing that for every
![]() $I\subset \{1,\dots ,2n\}$
with
$I\subset \{1,\dots ,2n\}$
with
![]() $|I|=2a$
the equality
$|I|=2a$
the equality
holds, where we used notation (3.12) and denoted by
![]() $[M_{i}]_{i\in I}$
the
$[M_{i}]_{i\in I}$
the
![]() $2a\times 2a$
matrix formed by the rows
$2a\times 2a$
matrix formed by the rows
![]() $M_{i}$
,
$M_{i}$
,
![]() $i\in I$
, arranged in the natural order.
$i\in I$
, arranged in the natural order.
We now fix a subset
![]() $I\subset \{1,\dots ,2n\}$
of indices having maximal cardinality among all subsets
$I\subset \{1,\dots ,2n\}$
of indices having maximal cardinality among all subsets
![]() $\mathscr I\subset \{1,\dots ,2n\}$
satisfying the two properties
$\mathscr I\subset \{1,\dots ,2n\}$
satisfying the two properties
 $$ \begin{align} \begin{aligned} &\forall\ i,j\in\mathscr I\quad i\not\equiv j\mod n\\ & (M_{i})_{i\in\mathscr I}\text{ are linearly independent.} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\forall\ i,j\in\mathscr I\quad i\not\equiv j\mod n\\ & (M_{i})_{i\in\mathscr I}\text{ are linearly independent.} \end{aligned} \end{align} $$
We also define
 $$ \begin{align*} J & :=\{j\in\{1,\dots,2n\}:\exists\: i\in I\text{ such that }j\equiv i\text{ mod }n\}\setminus I\\ K & :=\{1,\dots,2n\}\setminus(I\cup J). \end{align*} $$
$$ \begin{align*} J & :=\{j\in\{1,\dots,2n\}:\exists\: i\in I\text{ such that }j\equiv i\text{ mod }n\}\setminus I\\ K & :=\{1,\dots,2n\}\setminus(I\cup J). \end{align*} $$
Clearly,
![]() $I\cap J=\emptyset $
.
$I\cap J=\emptyset $
.
Claim 1:
![]() $a\leq |I|\leq n$
and
$a\leq |I|\leq n$
and
![]() $|J|=|I|$
.
$|J|=|I|$
.
Let us prove the first claimed inequality. We have
![]() $\tau \neq 0$
, for otherwise we would obtain the contradiction
$\tau \neq 0$
, for otherwise we would obtain the contradiction
where

In particular, the rank of M is
![]() $2a$
and we can find distinct numbers
$2a$
and we can find distinct numbers
![]() $i_{1},\dots ,i_{2a}$
in
$i_{1},\dots ,i_{2a}$
in
![]() $\{1,\dots ,2n\}$
such that
$\{1,\dots ,2n\}$
such that
![]() $M_{i_{1}},\dots ,M_{i_{2a}}$
are linearly independent. It is then obvious that we can find a subset of
$M_{i_{1}},\dots ,M_{i_{2a}}$
are linearly independent. It is then obvious that we can find a subset of
![]() $\{i_{1},\dots ,i_{2a}\}$
made by at least a elements that are never congruent modulo n; this proves that
$\{i_{1},\dots ,i_{2a}\}$
made by at least a elements that are never congruent modulo n; this proves that
![]() $|I|\geq a$
.
$|I|\geq a$
.
The remaining part of the claim (
![]() $|I|\leq n$
and
$|I|\leq n$
and
![]() $|J|=|I|$
) is clear from the definitions of I and J.
$|J|=|I|$
) is clear from the definitions of I and J.
Claim 2: For every
![]() $k\in K$
,
$k\in K$
,
![]() $M_{k}\in \operatorname *{\mathrm {span}}\{M_{i}:i\in I\}$
.
$M_{k}\in \operatorname *{\mathrm {span}}\{M_{i}:i\in I\}$
.
Assume, on the contrary, that there exists
![]() $k\in K$
such that
$k\in K$
such that
![]() $(M_{i})_{i\in I\cup \{k\}}$
are linearly independent; then
$(M_{i})_{i\in I\cup \{k\}}$
are linearly independent; then
![]() $\mathscr I:=I\cup \{k\}$
would satisfy the two properties in (A.1) and this would contradict the maximality of I.
$\mathscr I:=I\cup \{k\}$
would satisfy the two properties in (A.1) and this would contradict the maximality of I.
Claim 3: There exists
![]() $J^{\prime }\subset J$
such that
$J^{\prime }\subset J$
such that
![]() $|J^{\prime }|=2a-|I|$
and
$|J^{\prime }|=2a-|I|$
and
![]() $(M_{i})_{i\in I\cup J^{\prime }}$
are linearly independent. In particular,
$(M_{i})_{i\in I\cup J^{\prime }}$
are linearly independent. In particular,
![]() $(M_{i})_{i\in I\cup J^{\prime }}$
form a basis of
$(M_{i})_{i\in I\cup J^{\prime }}$
form a basis of
![]() ${\mathbb R}^{2a}$
.
${\mathbb R}^{2a}$
.
We are going to implicitly use the facts that
![]() $I\cap J=\emptyset $
and
$I\cap J=\emptyset $
and
![]() $|I|=|J|$
. Let
$|I|=|J|$
. Let
![]() $j_{1},j_{2},\dots ,j_{|I|}$
be an enumeration of all of the elements of J; for
$j_{1},j_{2},\dots ,j_{|I|}$
be an enumeration of all of the elements of J; for
![]() $\ell =0,1,\dots ,|I|$
we inductively define
$\ell =0,1,\dots ,|I|$
we inductively define
![]() $J^{\prime }_{\ell }$
by
$J^{\prime }_{\ell }$
by
![]() $J^{\prime }_{0}:=\emptyset $
and
$J^{\prime }_{0}:=\emptyset $
and
 $$ \begin{align*} &\text{ if }M_{j_{\ell}}\notin\operatorname*{\mathrm{span}}\{M_{i}:i\in I\cup J^{\prime}_{\ell-1}\},\text{ then }J^{\prime}_{\ell}:=J^{\prime}_{\ell-1}\cup\{j_{\ell}\}\\ &\text{ if }M_{j_{\ell}}\in\operatorname*{\mathrm{span}}\{M_{i}:i\in I\cup J^{\prime}_{\ell-1}\},\text{ then }J^{\prime}_{\ell}:=J^{\prime}_{\ell-1}. \end{align*} $$
$$ \begin{align*} &\text{ if }M_{j_{\ell}}\notin\operatorname*{\mathrm{span}}\{M_{i}:i\in I\cup J^{\prime}_{\ell-1}\},\text{ then }J^{\prime}_{\ell}:=J^{\prime}_{\ell-1}\cup\{j_{\ell}\}\\ &\text{ if }M_{j_{\ell}}\in\operatorname*{\mathrm{span}}\{M_{i}:i\in I\cup J^{\prime}_{\ell-1}\},\text{ then }J^{\prime}_{\ell}:=J^{\prime}_{\ell-1}. \end{align*} $$
Setting
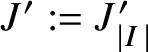 $J^{\prime }:=J^{\prime }_{|I|}$
, the elements
$J^{\prime }:=J^{\prime }_{|I|}$
, the elements
![]() $(M_{i})_{i\in J\cup J^{\prime }}$
are linearly independent by construction; let us prove that they span the whole
$(M_{i})_{i\in J\cup J^{\prime }}$
are linearly independent by construction; let us prove that they span the whole
![]() ${\mathbb R}^{2a}$
, which will also imply the equality
${\mathbb R}^{2a}$
, which will also imply the equality
![]() $|J^{\prime }|=2a-|I|$
. Assume, on the contrary, that the dimension of
$|J^{\prime }|=2a-|I|$
. Assume, on the contrary, that the dimension of
(the second equality holding by construction) is less than
![]() $2a$
; recalling Claim 2 and the fact that
$2a$
; recalling Claim 2 and the fact that
![]() $I\cup J\cup K=\{1,\dots ,2n\}$
, this would imply that
$I\cup J\cup K=\{1,\dots ,2n\}$
, this would imply that
and the rank of M would not be
![]() $2a$
. This is a contradiction, and Claim 3 is proved.
$2a$
. This is a contradiction, and Claim 3 is proved.
We now introduce
 $$ \begin{align*} & A:=\{i\in\{1,\dots,n\}:\{i,i+n\}\subset I\cup J^{\prime}\}\\ & B:=(I\cup J^{\prime})\setminus (A\cup(n+A))=I\setminus (A\cup(n+A))\\ & C:= K\cap\{1,\dots,n\}, \end{align*} $$
$$ \begin{align*} & A:=\{i\in\{1,\dots,n\}:\{i,i+n\}\subset I\cup J^{\prime}\}\\ & B:=(I\cup J^{\prime})\setminus (A\cup(n+A))=I\setminus (A\cup(n+A))\\ & C:= K\cap\{1,\dots,n\}, \end{align*} $$
where for
![]() $E\subset \{1,\dots ,n\}$
we write
$E\subset \{1,\dots ,n\}$
we write
![]() $n+E$
for
$n+E$
for
![]() $\{i\in \{n+1,\dots ,2n\}:i-n\in E\}$
. We notice the following properties:
$\{i\in \{n+1,\dots ,2n\}:i-n\in E\}$
. We notice the following properties:
-
(i) if
 $i\in A$
, then either (
$i\in A$
, then either (
 $i\in I$
and
$i\in I$
and
 $i+n\in J^{\prime }$
), or (
$i+n\in J^{\prime }$
), or (
 $i\in J^{\prime }$
and
$i\in J^{\prime }$
and
 $i+n\in I$
);
$i+n\in I$
); -
(ii)
 $|I|=|J|=|A|+| B|$
and
$|I|=|J|=|A|+| B|$
and
 $2|A|+|B|=|I|+|J^{\prime }|=2a$
;
$2|A|+|B|=|I|+|J^{\prime }|=2a$
; -
(iii)
 $K=C\cup (n+C)$
.
$K=C\cup (n+C)$
.
In particular,
 $$ \begin{align*} |A|-|C| = |A|-\tfrac12 |K| = |A|-\tfrac12 (2n-|I|-|J|) = 2|A|+|B| -n =2a-n\geq 0 \end{align*} $$
$$ \begin{align*} |A|-|C| = |A|-\tfrac12 |K| = |A|-\tfrac12 (2n-|I|-|J|) = 2|A|+|B| -n =2a-n\geq 0 \end{align*} $$
and we can define the (nonnecessarily standard) Young tableau

where
![]() $a_{1},\dots ,a_{|A|}$
is the increasing enumeration of the elements of A and
$a_{1},\dots ,a_{|A|}$
is the increasing enumeration of the elements of A and
![]() $c_{1},\dots ,c_{|C|}$
is the increasing enumeration of the elements of C; of course, when
$c_{1},\dots ,c_{|C|}$
is the increasing enumeration of the elements of C; of course, when
![]() $|A|=|C|$
(or, which is the same,
$|A|=|C|$
(or, which is the same,
![]() $2a=n$
) the tableau R is a
$2a=n$
) the tableau R is a
![]() $2\times |A|$
matrix.
$2\times |A|$
matrix.
We now consider the covector
![]() $\lambda :=dz_{B}\wedge \alpha _{R}$
; it can be easily checked that
$\lambda :=dz_{B}\wedge \alpha _{R}$
; it can be easily checked that
![]() $\lambda \wedge \theta \in {\mathcal J}^{2a+1}$
.
$\lambda \wedge \theta \in {\mathcal J}^{2a+1}$
.
Claim 4:
![]() $\langle \tau \mid \lambda \rangle \neq 0$
.
$\langle \tau \mid \lambda \rangle \neq 0$
.
It is enough to check that
in fact, if (A.3) were true one would get
as claimed. The signs
![]() $\pm $
in (A.4) are not relevant and depend on A and B only.
$\pm $
in (A.4) are not relevant and depend on A and B only.
Let us prove (A.3). By definition of
![]() $\alpha _{R}$
, the covector
$\alpha _{R}$
, the covector
![]() $\lambda $
can be written as
$\lambda $
can be written as
where
![]() $\tilde \lambda $
is a sum of covectors of the form
$\tilde \lambda $
is a sum of covectors of the form
![]() $\pm dz_{B}\wedge dxy_{A^{\prime }\cup C^{\prime }}$
, where
$\pm dz_{B}\wedge dxy_{A^{\prime }\cup C^{\prime }}$
, where
![]() $A^{\prime }\subset A$
and
$A^{\prime }\subset A$
and
![]() $C^{\prime }\subset C$
satisfy
$C^{\prime }\subset C$
satisfy
(in particular,
![]() $|A^{\prime }|<|A|$
). We have
$|A^{\prime }|<|A|$
). We have
and we claim that this determinant vanishes. Choose indeed
![]() $\bar a\in A\setminus A^{\prime }$
and let
$\bar a\in A\setminus A^{\prime }$
and let
![]() $\bar \jmath \in J^{\prime }$
be such that
$\bar \jmath \in J^{\prime }$
be such that
![]() $\bar \jmath \equiv \bar a$
mod n (recall property (i) above); by Claim 2 we obtain
$\bar \jmath \equiv \bar a$
mod n (recall property (i) above); by Claim 2 we obtain
 $$ \begin{align*} \operatorname*{\mathrm{span}}(M_{i})_{i\in B\cup A^{\prime}\cup C^{\prime}\cup(n+A^{\prime})\cup(n+C^{\prime})} \subset\: & \operatorname*{\mathrm{span}}(M_{i})_{i\in B\cup A^{\prime}\cup(n+A^{\prime})} + \operatorname*{\mathrm{span}}(M_{i})_{i\in C^{\prime}\cup(n+C^{\prime})}\\ \subset\: & \operatorname*{\mathrm{span}}(M_{i})_{i\in B\cup A^{\prime}\cup(n+A^{\prime})} + \operatorname*{\mathrm{span}}(M_{i})_{i\in I}\\ \subset\: & \operatorname*{\mathrm{span}}(M_{i})_{i\in I\cup J^{\prime}\setminus\{\bar\jmath\}}. \end{align*} $$
$$ \begin{align*} \operatorname*{\mathrm{span}}(M_{i})_{i\in B\cup A^{\prime}\cup C^{\prime}\cup(n+A^{\prime})\cup(n+C^{\prime})} \subset\: & \operatorname*{\mathrm{span}}(M_{i})_{i\in B\cup A^{\prime}\cup(n+A^{\prime})} + \operatorname*{\mathrm{span}}(M_{i})_{i\in C^{\prime}\cup(n+C^{\prime})}\\ \subset\: & \operatorname*{\mathrm{span}}(M_{i})_{i\in B\cup A^{\prime}\cup(n+A^{\prime})} + \operatorname*{\mathrm{span}}(M_{i})_{i\in I}\\ \subset\: & \operatorname*{\mathrm{span}}(M_{i})_{i\in I\cup J^{\prime}\setminus\{\bar\jmath\}}. \end{align*} $$
In particular,
![]() $\operatorname *{\mathrm {span}}(M_{i})_{i\in B\cup A^{\prime }\cup C^{\prime }\cup (n+A^{\prime })\cup (n+C^{\prime })}$
cannot be of maximal dimension
$\operatorname *{\mathrm {span}}(M_{i})_{i\in B\cup A^{\prime }\cup C^{\prime }\cup (n+A^{\prime })\cup (n+C^{\prime })}$
cannot be of maximal dimension
![]() $2a$
. This implies that the determinant in (A.5) is null, as claimed. The equality
$2a$
. This implies that the determinant in (A.5) is null, as claimed. The equality
![]() $\langle \tau \mid \tilde \lambda \rangle =0$
then immediately follows and, since
$\langle \tau \mid \tilde \lambda \rangle =0$
then immediately follows and, since
![]() $\langle \tau \mid \lambda \rangle = \langle \tau \mid dz_{B}\wedge dxy_{A}+\tilde \lambda \rangle $
, equality (A.3) follows.
$\langle \tau \mid \lambda \rangle = \langle \tau \mid dz_{B}\wedge dxy_{A}+\tilde \lambda \rangle $
, equality (A.3) follows.
Claim 5:
![]() $B=\emptyset $
.
$B=\emptyset $
.
By Remark 3.21, the covector
![]() $\alpha _{R}$
can be written as a finite linear combination
$\alpha _{R}$
can be written as a finite linear combination
![]() $\alpha _{R}=\sum _{\ell } c_{\ell } \alpha _{S_{\ell }}, c_{\ell }\in {\mathbb R},$
of covectors
$\alpha _{R}=\sum _{\ell } c_{\ell } \alpha _{S_{\ell }}, c_{\ell }\in {\mathbb R},$
of covectors
![]() $\alpha _{S_{\ell }}$
associated to standard Young tableaux
$\alpha _{S_{\ell }}$
associated to standard Young tableaux
![]() $S_{\ell }$
containing the elements of
$S_{\ell }$
containing the elements of
![]() $A\cup C$
. In particular, if
$A\cup C$
. In particular, if
![]() $B\neq \emptyset $
, one would have
$B\neq \emptyset $
, one would have
 $$ \begin{align*} \langle \tau\mid \lambda\rangle = \sum_{\ell} c_{\ell}\langle \tau\mid dz_{B}\wedge \alpha_{S_{\ell}}\rangle = \sum_{\ell} c_{\ell}\langle X_{1}\wedge\dots\wedge X_{a}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid dz_{B}\wedge \alpha_{S_{\ell}}\rangle=0, \end{align*} $$
$$ \begin{align*} \langle \tau\mid \lambda\rangle = \sum_{\ell} c_{\ell}\langle \tau\mid dz_{B}\wedge \alpha_{S_{\ell}}\rangle = \sum_{\ell} c_{\ell}\langle X_{1}\wedge\dots\wedge X_{a}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid dz_{B}\wedge \alpha_{S_{\ell}}\rangle=0, \end{align*} $$
the last equality due to Remark 3.27 (with
![]() $b:=0$
) and the fact that
$b:=0$
) and the fact that
![]() $dz_{B}$
contains no factors of the form
$dz_{B}$
contains no factors of the form
![]() $dx_{i}$
. This would contradict Claim 4; hence,
$dx_{i}$
. This would contradict Claim 4; hence,
![]() $B=\emptyset $
as claimed.
$B=\emptyset $
as claimed.
Claim 5 implies that
![]() $|A|=a$
and
$|A|=a$
and
Without loss of generality, we can assume that
![]() $I=A$
and
$I=A$
and
![]() $J=J^{\prime }=n+A$
.
$J=J^{\prime }=n+A$
.
Claim 6:
![]() $M_{k}=0$
for every
$M_{k}=0$
for every
![]() $k\notin A\cup (n+A)$
.
$k\notin A\cup (n+A)$
.
Assume that, on the contrary, there exists
![]() $k\notin A\cup (n+A)$
(i.e.,
$k\notin A\cup (n+A)$
(i.e.,
![]() $k\in K=C\cup (n+C)$
) such that
$k\in K=C\cup (n+C)$
) such that
![]() $M_{k}\neq 0$
. By Claim 3,
$M_{k}\neq 0$
. By Claim 3,
![]() $(M_{i})_{i\in A\cup (n+A)}$
form a basis of
$(M_{i})_{i\in A\cup (n+A)}$
form a basis of
![]() ${\mathbb R}^{2a}$
; hence,
${\mathbb R}^{2a}$
; hence,
which gives that
This would contradict the choice of I, because
![]() $\mathscr I:=A\cup \{k\}$
(in the first case) or
$\mathscr I:=A\cup \{k\}$
(in the first case) or
![]() $\mathscr I:=(n+A)\cup \{k\}$
(in the second one) would satisfy both conditions in (A.1), but
$\mathscr I:=(n+A)\cup \{k\}$
(in the second one) would satisfy both conditions in (A.1), but
![]() $|\mathscr I|>|I|$
.
$|\mathscr I|>|I|$
.
Claim 7:
![]() $\langle \tau \mid dxy_{D}\rangle =0$
for every
$\langle \tau \mid dxy_{D}\rangle =0$
for every
![]() $D\subset \{1,\dots ,n\}$
such that
$D\subset \{1,\dots ,n\}$
such that
![]() $|D|=|A|$
and
$|D|=|A|$
and
![]() $D\neq A$
.
$D\neq A$
.
This is an immediate consequence of the equality
![]() $\langle \tau \mid dxy_{D}\rangle = \pm \det [M_{i}]_{i\in D\cup (n+D)}$
together with Claim 6.
$\langle \tau \mid dxy_{D}\rangle = \pm \det [M_{i}]_{i\in D\cup (n+D)}$
together with Claim 6.
Claim 8:
![]() $\{n-a+1,n-a+2,\dots ,a\}\subset A$
.
$\{n-a+1,n-a+2,\dots ,a\}\subset A$
.
Here we are understanding that the claim is empty when
![]() $n=2a$
. Denoting by
$n=2a$
. Denoting by
![]() $\overline R$
the Young tableau defined in (A.2), one can easily check that the covector
$\overline R$
the Young tableau defined in (A.2), one can easily check that the covector
![]() $\alpha _{\overline R}$
can be written as a sum of elements of the form
$\alpha _{\overline R}$
can be written as a sum of elements of the form
![]() $\pm dxy_{D}$
where the subsets
$\pm dxy_{D}$
where the subsets
![]() $D\subset \{1,\dots ,n\}$
have cardinality
$D\subset \{1,\dots ,n\}$
have cardinality
![]() $|D|=|A|=a$
and all contain
$|D|=|A|=a$
and all contain
![]() $\{n-a+1,\dots ,a\}$
. If one had
$\{n-a+1,\dots ,a\}$
. If one had
![]() $\{n-a+1,\dots ,a\}\not \subset A$
, then one would get the contradiction
$\{n-a+1,\dots ,a\}\not \subset A$
, then one would get the contradiction
the last equality following from Claim 7.
Claim 9: If
![]() $2a>n$
, then
$2a>n$
, then
![]() $A=\{1,\dots ,a\}$
.
$A=\{1,\dots ,a\}$
.
The condition
![]() $2a>n$
implies that
$2a>n$
implies that
![]() $|C|=n-|A|=n-a<a=|A|$
. Let
$|C|=n-|A|=n-a<a=|A|$
. Let
![]() $a_{1}<a_{2}<\dots <a_{|A|}$
be the elements of A and
$a_{1}<a_{2}<\dots <a_{|A|}$
be the elements of A and
![]() $c_{1}<\dots <c_{|C|}$
those of C and define
$c_{1}<\dots <c_{|C|}$
those of C and define

The Young tableau
![]() $R_{1}$
is not necessarily a standard one, as it might happen that
$R_{1}$
is not necessarily a standard one, as it might happen that
![]() $a_{i}>c_{i}$
for some i; however, it can be easily seen that the tableau
$a_{i}>c_{i}$
for some i; however, it can be easily seen that the tableau

defined by setting
![]() $m_{i}:=\min \{a_{i},c_{i}\}, \mu _{i}:=\max \{a_{i},c_{i}\}$
(or, equivalently, by switching the positions of
$m_{i}:=\min \{a_{i},c_{i}\}, \mu _{i}:=\max \{a_{i},c_{i}\}$
(or, equivalently, by switching the positions of
![]() $a_{i}, c_{i}$
in case
$a_{i}, c_{i}$
in case
![]() $a_{i}>c_{i}$
) is a standard one. Notice that, since the ith column of
$a_{i}>c_{i}$
) is a standard one. Notice that, since the ith column of
![]() $R_{1}$
and the ith column of
$R_{1}$
and the ith column of
![]() $R_{2}$
contain the same elements
$R_{2}$
contain the same elements
![]() $a_{i},c_{i}$
, we have
$a_{i},c_{i}$
, we have
![]() $\alpha _{R_{2}}=\pm \alpha _{R_{1}}$
. Using Claim 7 we obtain
$\alpha _{R_{2}}=\pm \alpha _{R_{1}}$
. Using Claim 7 we obtain
 $$ \begin{align} \begin{aligned} \langle X_{1}\wedge\dots\wedge X_{a}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \alpha_{R_{2}}\rangle=& \langle\tau\mid \alpha_{R_{2}}\rangle=\pm \langle\tau\mid \alpha_{R_{1}}\rangle\\ =&\pm \langle\tau\mid dxy_{A}\rangle = \pm\det[M_{i}]_{i\in A\cup(n+A)}\neq 0, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle X_{1}\wedge\dots\wedge X_{a}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \alpha_{R_{2}}\rangle=& \langle\tau\mid \alpha_{R_{2}}\rangle=\pm \langle\tau\mid \alpha_{R_{1}}\rangle\\ =&\pm \langle\tau\mid dxy_{A}\rangle = \pm\det[M_{i}]_{i\in A\cup(n+A)}\neq 0, \end{aligned} \end{align} $$
which, by Remark 3.27, implies that
![]() $R_{2}=\overline R$
. Therefore, the rightmost entry in the first row of
$R_{2}=\overline R$
. Therefore, the rightmost entry in the first row of
![]() $R_{2}$
must be a, but this coincides with the rightmost entry in the first row of
$R_{2}$
must be a, but this coincides with the rightmost entry in the first row of
![]() $R_{1}$
; that is, with
$R_{1}$
; that is, with
![]() $\max A$
. Therefore,
$\max A$
. Therefore,
![]() $A\subset \{1,\dots ,n\}$
is such that
$A\subset \{1,\dots ,n\}$
is such that
![]() $|A|=a$
and
$|A|=a$
and
![]() $\max A=a$
, and the claim
$\max A=a$
, and the claim
![]() $A=\{1,\dots ,a\}$
follows.
$A=\{1,\dots ,a\}$
follows.
Claim 10: If
![]() $2a=n$
, then either
$2a=n$
, then either
![]() $A=\{1,\dots ,a\}$
or
$A=\{1,\dots ,a\}$
or
![]() $A=\{a+1,\dots ,2a\}$
.
$A=\{a+1,\dots ,2a\}$
.
The proof is similar to that of Claim 9. Notice that now
![]() $|C|=|A|=a$
; let
$|C|=|A|=a$
; let
![]() $a_{1}<a_{2}<\dots <a_{|A|}$
be the elements of A and
$a_{1}<a_{2}<\dots <a_{|A|}$
be the elements of A and
![]() $c_{1}<\dots <c_{|A|}$
those of C and define
$c_{1}<\dots <c_{|A|}$
those of C and define

as before. Again, let

be defined by
![]() $m_{i}:=\min \{a_{i},c_{i}\}, \mu _{i}:=\max \{a_{i},c_{i}\}$
;
$m_{i}:=\min \{a_{i},c_{i}\}, \mu _{i}:=\max \{a_{i},c_{i}\}$
;
![]() $R_{2}$
is a standard Young tableau,
$R_{2}$
is a standard Young tableau,
![]() $\alpha _{R_{2}}=\pm \alpha _{R_{1}}$
, and as in (A.6), we can conclude that
$\alpha _{R_{2}}=\pm \alpha _{R_{1}}$
, and as in (A.6), we can conclude that
![]() $R_{2}=\overline R$
. We now distinguish two cases:
$R_{2}=\overline R$
. We now distinguish two cases:
-
• if
 $1\in A$
, then
$1\in A$
, then
 $a_{1}=m_{1}=1$
and, since
$a_{1}=m_{1}=1$
and, since
 $R_{2}=\overline R$
, we have
$R_{2}=\overline R$
, we have
 $\mu _{1}=c_{1}=a+1$
. In particular,
$\mu _{1}=c_{1}=a+1$
. In particular,
 $C\subset \{1,\dots ,n\}=\{1,\dots ,2a\}$
is such that
$C\subset \{1,\dots ,n\}=\{1,\dots ,2a\}$
is such that
 $|C|=a$
and
$|C|=a$
and
 $\min C=a+1$
. This implies
$\min C=a+1$
. This implies
 $C=\{a+1,\dots ,n\}$
and in turn
$C=\{a+1,\dots ,n\}$
and in turn
 $A=\{1,\dots ,a\}$
;
$A=\{1,\dots ,a\}$
; -
• if
 $1\notin A$
, then
$1\notin A$
, then
 $1=m_{1}=c_{1}$
and
$1=m_{1}=c_{1}$
and
 $a+1=\mu _{1}=a_{1}$
. In particular,
$a+1=\mu _{1}=a_{1}$
. In particular,
 $A\subset \{1,\dots ,n\}=\{1,\dots ,2a\}$
is such that
$A\subset \{1,\dots ,n\}=\{1,\dots ,2a\}$
is such that
 $|A|=a$
and
$|A|=a$
and
 $\min A=a+1$
, which implies
$\min A=a+1$
, which implies
 $A=\{a+1,\dots ,n\}$
.
$A=\{a+1,\dots ,n\}$
.
The conclusion of the proof now follows easily. If
![]() $2a>n$
, by Claims 6 and 9 we have that
$2a>n$
, by Claims 6 and 9 we have that
![]() $M_{i}=0$
for every
$M_{i}=0$
for every
![]() $i\in \{a+1,\dots ,n, n+a+1,\dots ,2n\}$
. This implies that
$i\in \{a+1,\dots ,n, n+a+1,\dots ,2n\}$
. This implies that
![]() $\tau =tX_{1}\wedge \dots \wedge X_{a}\wedge Y_{1}\wedge \dots \wedge Y_{a}$
for some
$\tau =tX_{1}\wedge \dots \wedge X_{a}\wedge Y_{1}\wedge \dots \wedge Y_{a}$
for some
![]() $t\in {\mathbb R}$
, and t is forced to be 1 because
$t\in {\mathbb R}$
, and t is forced to be 1 because
![]() $\langle X_{1}\wedge \dots \wedge X_{a}\wedge Y_{1}\wedge \dots \wedge Y_{a}\mid \alpha _{R_{2}}\rangle \neq 0 $
and
$\langle X_{1}\wedge \dots \wedge X_{a}\wedge Y_{1}\wedge \dots \wedge Y_{a}\mid \alpha _{R_{2}}\rangle \neq 0 $
and
This concludes the proof in case
![]() $n>2a$
. The case
$n>2a$
. The case
![]() $n=2a$
follows analogously on considering Claims 6 and 10.
$n=2a$
follows analogously on considering Claims 6 and 10.
We now use Lemma A.1 to prove the following, more general, result, of which Lemma A.1 represents the case
![]() $b=0$
.
$b=0$
.
Lemma A.3. Let
![]() $a\geq 0$
and
$a\geq 0$
and
![]() $b\geq 1$
be integers such that
$b\geq 1$
be integers such that
![]() $n\leq 2a+b\leq 2n-1$
; assume that
$n\leq 2a+b\leq 2n-1$
; assume that
![]() $\tau \in \Large \wedge _{2a+b}{\mathfrak h}_{1}$
is a simple
$\tau \in \Large \wedge _{2a+b}{\mathfrak h}_{1}$
is a simple
![]() $(2a+b)$
-vector such that
$(2a+b)$
-vector such that
Then, the following statements hold:
-
(i) if
 $2a+b>n$
, then
$2a+b>n$
, then
 $\tau = X_{1}\wedge \dots \wedge X_{a+b}\wedge Y_{1}\wedge \dots \wedge Y_{a}$
;
$\tau = X_{1}\wedge \dots \wedge X_{a+b}\wedge Y_{1}\wedge \dots \wedge Y_{a}$
; -
(ii) if
 $2a+b=n$
, then either or
$2a+b=n$
, then either or $$ \begin{align*} \tau= X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a} \end{align*} $$
$$ \begin{align*} \tau= X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a} \end{align*} $$
 $$ \begin{align*} \tau=(-1)^{a(b+1)} \:X_{a+1}\wedge\dots\wedge X_{n}\wedge Y_{a+b+1}\wedge\dots\wedge Y_{n}. \end{align*} $$
$$ \begin{align*} \tau=(-1)^{a(b+1)} \:X_{a+1}\wedge\dots\wedge X_{n}\wedge Y_{a+b+1}\wedge\dots\wedge Y_{n}. \end{align*} $$
Remark A.4. As a matter of fact, if
![]() $2a+b=n$
, the equality
$2a+b=n$
, the equality
 $$ \begin{align*} [X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\wedge T]_{{\mathcal J}} = [(-1)^{a(b+1)} \:X_{a+1}\wedge\dots\wedge X_{n}\wedge Y_{a+b+1}\wedge\dots\wedge Y_{n}\wedge T]_{{\mathcal J}} \end{align*} $$
$$ \begin{align*} [X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\wedge T]_{{\mathcal J}} = [(-1)^{a(b+1)} \:X_{a+1}\wedge\dots\wedge X_{n}\wedge Y_{a+b+1}\wedge\dots\wedge Y_{n}\wedge T]_{{\mathcal J}} \end{align*} $$
holds. This can be proved by using Remark 3.27 and checking the action of
![]() $X_{a+1}\wedge \dots \wedge X_{n}\wedge Y_{a+b+1}\wedge \dots \wedge Y_{n}\wedge T$
in duality with elements of the basis of
$X_{a+1}\wedge \dots \wedge X_{n}\wedge Y_{a+b+1}\wedge \dots \wedge Y_{n}\wedge T$
in duality with elements of the basis of
![]() ${\mathcal J}^{2a+b+1}={\mathcal J}^{n+1}$
provided by Proposition 1.10.
${\mathcal J}^{2a+b+1}={\mathcal J}^{n+1}$
provided by Proposition 1.10.
For instance, in
![]() ${\mathbb H}^{3}$
one has the equality
${\mathbb H}^{3}$
one has the equality
![]() $[X_{1}\wedge X_{2}\wedge Y_{1}\wedge T]_{{\mathcal J}}=[X_{2}\wedge X_{3}\wedge Y_{3}\wedge T]_{{\mathcal J}}$
.
$[X_{1}\wedge X_{2}\wedge Y_{1}\wedge T]_{{\mathcal J}}=[X_{2}\wedge X_{3}\wedge Y_{3}\wedge T]_{{\mathcal J}}$
.
Proof of Lemma A.3.
Let us write
![]() $\tau =\tau ^{1}\wedge \dots \wedge \tau ^{2a+b}$
for suitable horizontal vectors
$\tau =\tau ^{1}\wedge \dots \wedge \tau ^{2a+b}$
for suitable horizontal vectors
![]() $\tau ^{i}\in {\mathfrak h}_{1}$
; writing
$\tau ^{i}\in {\mathfrak h}_{1}$
; writing
 $$ \begin{align*} \tau^{i}=\tau^{i}_{1}X_{1}+\dots+\tau^{i}_{2n}Y_{n},\qquad i=1,\dots,2a+b \end{align*} $$
$$ \begin{align*} \tau^{i}=\tau^{i}_{1}X_{1}+\dots+\tau^{i}_{2n}Y_{n},\qquad i=1,\dots,2a+b \end{align*} $$
we introduce the matrix
 $$ \begin{align*} M:=\text{col}\big[\:\tau^{1}\:|\cdots|\:\tau^{2a+b}\:\big] = \left[ \begin{array}{c|c|c} \tau^{1}_{1} &\dots & \tau^{2a+b}_{1}\\ \vdots& &\vdots\\ \tau^{1}_{2n} &\dots & \tau^{2a+b}_{2n} \end{array} \right] =\text{row} \left[ \begin{array}{c} M_{1}\\ \hline\vdots\\ \hline M_{2n} \end{array} \right] , \end{align*} $$
$$ \begin{align*} M:=\text{col}\big[\:\tau^{1}\:|\cdots|\:\tau^{2a+b}\:\big] = \left[ \begin{array}{c|c|c} \tau^{1}_{1} &\dots & \tau^{2a+b}_{1}\\ \vdots& &\vdots\\ \tau^{1}_{2n} &\dots & \tau^{2a+b}_{2n} \end{array} \right] =\text{row} \left[ \begin{array}{c} M_{1}\\ \hline\vdots\\ \hline M_{2n} \end{array} \right] , \end{align*} $$
where for every
![]() $i=1,\dots ,2n$
we denoted by
$i=1,\dots ,2n$
we denoted by
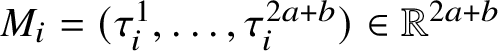 $M_{i}=(\tau ^{1}_{i},\dots ,\tau ^{2a+b}_{i})\in {\mathbb R}^{2a+b}$
the ith row of M. Again, for every
$M_{i}=(\tau ^{1}_{i},\dots ,\tau ^{2a+b}_{i})\in {\mathbb R}^{2a+b}$
the ith row of M. Again, for every
![]() $I\subset \{1,\dots ,2n\}$
with
$I\subset \{1,\dots ,2n\}$
with
![]() $|I|=2a+b$
the equality
$|I|=2a+b$
the equality
holds, where we used notation (3.12).
Claim 1:
![]() $M_{a+1},\dots ,M_{a+b}$
are linearly independent.
$M_{a+1},\dots ,M_{a+b}$
are linearly independent.
Assume not: then, for every
![]() $I\subset \{1,\dots ,2n\}$
with
$I\subset \{1,\dots ,2n\}$
with
![]() $|I|=2a$
we would get
$|I|=2a$
we would get
In particular,

which would provide a contradiction since
by assumption.
Claim 2: Up to a proper choice of
![]() $\tau ^{1},\dots ,\tau ^{2a+b}$
, the
$\tau ^{1},\dots ,\tau ^{2a+b}$
, the
![]() $b\times (2a+b)$
subblock
$b\times (2a+b)$
subblock
![]() $\widetilde M$
of M determined by the rows
$\widetilde M$
of M determined by the rows
![]() $M_{a+1},\dots , M_{a+b}$
satisfies
$M_{a+1},\dots , M_{a+b}$
satisfies
 $$ \begin{align*} \widetilde M=\left[ \begin{array}{c} M_{a+1}\\ \vdots\\ M_{a+b} \end{array} \right] = \left[ \begin{array}{c|c} &\\ 0_{b\times 2a} & I_{b}\\ & \end{array} \right] \end{align*} $$
$$ \begin{align*} \widetilde M=\left[ \begin{array}{c} M_{a+1}\\ \vdots\\ M_{a+b} \end{array} \right] = \left[ \begin{array}{c|c} &\\ 0_{b\times 2a} & I_{b}\\ & \end{array} \right] \end{align*} $$
where
![]() $0_{b\times 2a}$
denotes a
$0_{b\times 2a}$
denotes a
![]() $b\times 2a$
block with null entries and
$b\times 2a$
block with null entries and
![]() $I_{b}$
is the
$I_{b}$
is the
![]() $b\times b$
identity matrix.
$b\times b$
identity matrix.
By Claim 1, the matrix
![]() $\widetilde M$
has rank b; up to a permutation of
$\widetilde M$
has rank b; up to a permutation of
![]() $\tau ^{1},\dots ,\tau ^{2a+b}$
, we can assume that the rightmost
$\tau ^{1},\dots ,\tau ^{2a+b}$
, we can assume that the rightmost
![]() $b\times b$
minor of
$b\times b$
minor of
![]() $\widetilde M$
has nonzero determinant. Namely, calling
$\widetilde M$
has nonzero determinant. Namely, calling
 $\widetilde M^{j}=(\tau ^{j}_{a+1},\dots ,\tau ^{j}_{a+b})^{T}$
the jth column of
$\widetilde M^{j}=(\tau ^{j}_{a+1},\dots ,\tau ^{j}_{a+b})^{T}$
the jth column of
![]() $\tilde M$
(the superscript
$\tilde M$
(the superscript
![]() $^{T}$
denoting transposition), the rightmost minor
$^{T}$
denoting transposition), the rightmost minor
![]() $\overline {M}:=[\widetilde M^{2a+1}|\dots |\widetilde M^{2a+b}]$
of
$\overline {M}:=[\widetilde M^{2a+1}|\dots |\widetilde M^{2a+b}]$
of
![]() $\widetilde M$
satisfies
$\widetilde M$
satisfies
![]() $\det \overline {M}\neq 0$
. For
$\det \overline {M}\neq 0$
. For
![]() $i=2a+1,\dots ,2a+b$
we define
$i=2a+1,\dots ,2a+b$
we define
 $$ \begin{align*} \sigma^{i}:=\sum_{j=1}^{b} (\overline{M}^{-1})_{i}^{j}\:\tau^{2a+j} \end{align*} $$
$$ \begin{align*} \sigma^{i}:=\sum_{j=1}^{b} (\overline{M}^{-1})_{i}^{j}\:\tau^{2a+j} \end{align*} $$
and we notice that
![]() $\operatorname *{\mathrm {span}}\{\tau ^{1},\dots ,\tau ^{2a+b}\}=\operatorname *{\mathrm {span}}\{\tau ^{1},\dots ,\tau ^{2a},\sigma ^{2a+1},\dots ,\sigma ^{2a+b}\}$
, because of the equality
$\operatorname *{\mathrm {span}}\{\tau ^{1},\dots ,\tau ^{2a+b}\}=\operatorname *{\mathrm {span}}\{\tau ^{1},\dots ,\tau ^{2a},\sigma ^{2a+1},\dots ,\sigma ^{2a+b}\}$
, because of the equality
![]() $\operatorname *{\mathrm {span}}\{\tau ^{2a+1},\dots ,\tau ^{2a+b}\}=\operatorname *{\mathrm {span}}\{\sigma ^{2a+1},\dots ,\sigma ^{2a+b}\}$
. Notice that
$\operatorname *{\mathrm {span}}\{\tau ^{2a+1},\dots ,\tau ^{2a+b}\}=\operatorname *{\mathrm {span}}\{\sigma ^{2a+1},\dots ,\sigma ^{2a+b}\}$
. Notice that
 $$ \begin{align} \sigma^{2a+i}_{a+j}=\delta^{i}_{j}\qquad\text{for all }i,j\in\{1,\dots,b\}; \end{align} $$
$$ \begin{align} \sigma^{2a+i}_{a+j}=\delta^{i}_{j}\qquad\text{for all }i,j\in\{1,\dots,b\}; \end{align} $$
in particular, when in the matrix M the rightmost b columns
![]() $\tau ^{2a+1},\dots ,\tau ^{2a+b}$
are replaced by
$\tau ^{2a+1},\dots ,\tau ^{2a+b}$
are replaced by
![]() $\sigma ^{2a+1},\dots ,\sigma ^{2a+b}$
, the block
$\sigma ^{2a+1},\dots ,\sigma ^{2a+b}$
, the block
![]() $\widetilde M$
is replaced by a block of the form
$\widetilde M$
is replaced by a block of the form
 $$ \begin{align*} \left[ \begin{array}{c|c} &\\ *_{b\times 2a} & I_{b}\\ & \end{array} \right] \end{align*} $$
$$ \begin{align*} \left[ \begin{array}{c|c} &\\ *_{b\times 2a} & I_{b}\\ & \end{array} \right] \end{align*} $$
where
![]() $*_{b\times 2a}$
denotes a
$*_{b\times 2a}$
denotes a
![]() $b\times 2a$
matrix. Define
$b\times 2a$
matrix. Define
 $$ \begin{align*} \sigma^{i}:=\tau^{i}-\sum_{j=1}^{b} \tau^{i}_{a+j} \sigma^{2a+j},\qquad i=1,\dots,2a \end{align*} $$
$$ \begin{align*} \sigma^{i}:=\tau^{i}-\sum_{j=1}^{b} \tau^{i}_{a+j} \sigma^{2a+j},\qquad i=1,\dots,2a \end{align*} $$
so that
 $$ \begin{align} \sigma^{i}_{j}=0\qquad \text{for all }i=1,\dots,2a,j=a+1,\dots,a+b. \end{align} $$
$$ \begin{align} \sigma^{i}_{j}=0\qquad \text{for all }i=1,\dots,2a,j=a+1,\dots,a+b. \end{align} $$
It is easily seen that
![]() $\operatorname *{\mathrm {span}}\{\tau ^{1},\dots ,\tau ^{2a+b}\}=\operatorname *{\mathrm {span}}\{\sigma ^{1},\dots ,\sigma ^{2a+b}\}$
; in particular,
$\operatorname *{\mathrm {span}}\{\tau ^{1},\dots ,\tau ^{2a+b}\}=\operatorname *{\mathrm {span}}\{\sigma ^{1},\dots ,\sigma ^{2a+b}\}$
; in particular,
![]() $\sigma :=\sigma ^{1}\wedge \dots \wedge \sigma ^{2a+b}$
is a nonzero multiple of
$\sigma :=\sigma ^{1}\wedge \dots \wedge \sigma ^{2a+b}$
is a nonzero multiple of
![]() $\tau $
. Upon multiplying
$\tau $
. Upon multiplying
![]() $\sigma ^{1}$
by a nonzero factor, we can assume that
$\sigma ^{1}$
by a nonzero factor, we can assume that
![]() $\sigma =\tau $
. In this way, if one replaces
$\sigma =\tau $
. In this way, if one replaces
![]() $\tau ^{1},\dots ,\tau ^{2a+b}$
by
$\tau ^{1},\dots ,\tau ^{2a+b}$
by
![]() $\sigma ^{1},\dots ,\sigma ^{2a+b}$
, then the new matrix M is such that the block
$\sigma ^{1},\dots ,\sigma ^{2a+b}$
, then the new matrix M is such that the block
![]() $\widetilde M$
has the form
$\widetilde M$
has the form
 $$ \begin{align*} \left[ \begin{array}{c|c} &\\ 0_{b\times 2a} & I_{b}\\ & \end{array} \right] \end{align*} $$
$$ \begin{align*} \left[ \begin{array}{c|c} &\\ 0_{b\times 2a} & I_{b}\\ & \end{array} \right] \end{align*} $$
as wished.
In the following, we will keep on using the notation
![]() $\tau ^{1},\dots ,\tau ^{2a+b}$
for the new family
$\tau ^{1},\dots ,\tau ^{2a+b}$
for the new family
![]() $\sigma ^{1},\dots ,\sigma ^{2a+b}$
.
$\sigma ^{1},\dots ,\sigma ^{2a+b}$
.
Claim 3a: If
![]() $n>2a+b$
, then up to a proper choice of
$n>2a+b$
, then up to a proper choice of
![]() $\tau ^{1},\dots ,\tau ^{2a+b}$
, we can assume that the matrix M is of the form
$\tau ^{1},\dots ,\tau ^{2a+b}$
, we can assume that the matrix M is of the form

where
-
(i) the
 $2a+b$
columns of M have been arranged into three blocks of size, respectively, a, a and b;
$2a+b$
columns of M have been arranged into three blocks of size, respectively, a, a and b; -
(ii) the
 $2n$
rows of M have been arranged into six blocks of size, respectively, a, b,
$2n$
rows of M have been arranged into six blocks of size, respectively, a, b,
 $n-a-b$
, a, b and
$n-a-b$
, a, b and
 $n-a-b$
;
$n-a-b$
; -
(iii) 0 denotes null matrices of the proper size;
-
(iv)
 $I_{a},I_{b}$
denote identity matrices of size
$I_{a},I_{b}$
denote identity matrices of size
 $a,b$
;
$a,b$
; -
(v)
 $A_{1},A_{2},B,C_{1},C_{2},D_{1},D_{2}$
denote generic matrices of the proper size.
$A_{1},A_{2},B,C_{1},C_{2},D_{1},D_{2}$
denote generic matrices of the proper size.
Claim 3b: If
![]() $n=2a+b$
, then up to a proper choice of
$n=2a+b$
, then up to a proper choice of
![]() $\tau ^{1},\dots ,\tau ^{2a+b}$
, we can assume that
$\tau ^{1},\dots ,\tau ^{2a+b}$
, we can assume that

where the notation is similar to Claim 3a, (i)–(v).
We prove Claims 3a and 3b simultaneously; notice that there is nothing to prove in case
![]() $a=0$
. Using the block subdivision of M as in (A.10) and (A.11), we already know by Claim 2 that the second block of rows is of the form
$a=0$
. Using the block subdivision of M as in (A.10) and (A.11), we already know by Claim 2 that the second block of rows is of the form
![]() $[0|0|I_{b}]$
. Let us prove that we can choose
$[0|0|I_{b}]$
. Let us prove that we can choose
![]() $\tau ^{1},\dots ,\tau ^{2a+b}$
so that null and identity blocks
$\tau ^{1},\dots ,\tau ^{2a+b}$
so that null and identity blocks
![]() $0$
and
$0$
and
![]() $I_{a}$
appear where claimed in (A.10) and (A.11).
$I_{a}$
appear where claimed in (A.10) and (A.11).
We consider now a
![]() $(n-b)$
th Heisenberg group and we agree that all objects associated with it will be overlined; in particular, we denote by
$(n-b)$
th Heisenberg group and we agree that all objects associated with it will be overlined; in particular, we denote by
![]() $\overline X_{1},\dots ,\overline X_{n-b},\overline {Y}_{1},\dots ,\overline {Y}_{n-b},\overline T$
the standard basis of left-invariant vector fields in
$\overline X_{1},\dots ,\overline X_{n-b},\overline {Y}_{1},\dots ,\overline {Y}_{n-b},\overline T$
the standard basis of left-invariant vector fields in
![]() $\overline {{\mathbb H}}{}^{n-b}$
. Define
$\overline {{\mathbb H}}{}^{n-b}$
. Define
 $$ \begin{align*} \overline\tau^{i}:=\sum_{j=1}^{a} (\tau^{i}_{j}\overline X_{j}+\tau^{i}_{n+j}\overline Y_{j})+\sum_{j=a+1}^{n-b} (\tau^{i}_{b+j}\overline X_{j} + \tau^{i}_{n+b+j}\overline Y_{j}),\qquad i=1,\dots,2a. \end{align*} $$
$$ \begin{align*} \overline\tau^{i}:=\sum_{j=1}^{a} (\tau^{i}_{j}\overline X_{j}+\tau^{i}_{n+j}\overline Y_{j})+\sum_{j=a+1}^{n-b} (\tau^{i}_{b+j}\overline X_{j} + \tau^{i}_{n+b+j}\overline Y_{j}),\qquad i=1,\dots,2a. \end{align*} $$
Consider
![]() $\overline \tau :=\overline \tau ^{1}\wedge \dots \wedge \overline \tau ^{2a}$
; we prove that
$\overline \tau :=\overline \tau ^{1}\wedge \dots \wedge \overline \tau ^{2a}$
; we prove that
 $$ \begin{align} \langle\overline\tau\wedge\overline T \mid \overline\lambda\rangle = (-1)^{ab}\langle \overline X_{1}\wedge\dots\wedge \overline X_{a}\wedge \overline Y_{1}\wedge\dots\wedge \overline Y_{a}\wedge \overline T \mid \overline \lambda\rangle\qquad\text{for all }\overline \lambda\in\overline{{\mathcal J}}^{2a+1}, \end{align} $$
$$ \begin{align} \langle\overline\tau\wedge\overline T \mid \overline\lambda\rangle = (-1)^{ab}\langle \overline X_{1}\wedge\dots\wedge \overline X_{a}\wedge \overline Y_{1}\wedge\dots\wedge \overline Y_{a}\wedge \overline T \mid \overline \lambda\rangle\qquad\text{for all }\overline \lambda\in\overline{{\mathcal J}}^{2a+1}, \end{align} $$
where the symbol
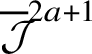 $\overline {{\mathcal J}}^{2a+1}$
stands for Rumin’s space of
$\overline {{\mathcal J}}^{2a+1}$
stands for Rumin’s space of
![]() $(2a+1)$
-covectors in
$(2a+1)$
-covectors in
![]() $\overline {{\mathbb H}}{}^{n-b}$
. Lemma A.1 then implies
$\overline {{\mathbb H}}{}^{n-b}$
. Lemma A.1 then implies
![]() $\overline \tau =\overline X_{1}\wedge \dots \wedge \overline X_{a}\wedge \overline Y_{1}\wedge \dots \wedge \overline Y_{a}$
(unless
$\overline \tau =\overline X_{1}\wedge \dots \wedge \overline X_{a}\wedge \overline Y_{1}\wedge \dots \wedge \overline Y_{a}$
(unless
![]() $2a+b=n$
, in which case we also have the possibility
$2a+b=n$
, in which case we also have the possibility
![]() $\overline \tau =(-1)^{a}\overline X_{a+1}\wedge \dots \wedge \overline X_{n-b}\wedge \overline Y_{a+1}\wedge \dots \wedge \overline Y_{n-b}$
) and this implies Claims 3a–3b up to some tedious arguments.
$\overline \tau =(-1)^{a}\overline X_{a+1}\wedge \dots \wedge \overline X_{n-b}\wedge \overline Y_{a+1}\wedge \dots \wedge \overline Y_{n-b}$
) and this implies Claims 3a–3b up to some tedious arguments.
Consider
![]() $\overline I\subset \{1,\dots ,2(n-b)\}$
such that
$\overline I\subset \{1,\dots ,2(n-b)\}$
such that
![]() $|\overline I|=2a$
; calling
$|\overline I|=2a$
; calling
![]() $\overline {M}$
the
$\overline {M}$
the
![]() $(2n-2b)\times 2a$
matrix whose columns are
$(2n-2b)\times 2a$
matrix whose columns are
![]() $\overline \tau ^{1},\dots ,\overline \tau ^{2a}$
and using for forms in
$\overline \tau ^{1},\dots ,\overline \tau ^{2a}$
and using for forms in
![]() $\overline {{\mathbb H}}{}^{n-b}$
the notation
$\overline {{\mathbb H}}{}^{n-b}$
the notation
![]() $d\overline z_{\overline I}$
analogous to that in (3.12), we have
$d\overline z_{\overline I}$
analogous to that in (3.12), we have
 $$ \begin{align*} \langle \overline\tau \mid d\overline z_{\overline I}\rangle = \det [\overline{M}_{i}]_{i\in\overline I}, \end{align*} $$
$$ \begin{align*} \langle \overline\tau \mid d\overline z_{\overline I}\rangle = \det [\overline{M}_{i}]_{i\in\overline I}, \end{align*} $$
where, of course,
![]() $\overline {M}_{i}$
is the ith row of
$\overline {M}_{i}$
is the ith row of
![]() $\overline {M}$
. Since
$\overline {M}$
. Since
![]() $\overline {M}$
is obtained from M by cancelling the third block of columns and the second and fifth blocks of rows (according to the arrangement in (A.10) and (A.11)) and since the second block of rows of M is
$\overline {M}$
is obtained from M by cancelling the third block of columns and the second and fifth blocks of rows (according to the arrangement in (A.10) and (A.11)) and since the second block of rows of M is
![]() $[0|0|I_{b}]$
, it is clear that
$[0|0|I_{b}]$
, it is clear that
 $$ \begin{align*} \langle \overline\tau \mid d\overline z_{\overline I}\rangle = & \det [\overline{M}_{i}]_{i\in\overline I} =(-1)^{ab}\det [M_{i}]_{\iota(\overline I)\cup \{a+1,\dots,a+b\}}\\ = & (-1)^{ab}\langle \tau\mid dz_{\iota(\overline I)\cup\{a+1,\dots,a+b\}}\rangle, \end{align*} $$
$$ \begin{align*} \langle \overline\tau \mid d\overline z_{\overline I}\rangle = & \det [\overline{M}_{i}]_{i\in\overline I} =(-1)^{ab}\det [M_{i}]_{\iota(\overline I)\cup \{a+1,\dots,a+b\}}\\ = & (-1)^{ab}\langle \tau\mid dz_{\iota(\overline I)\cup\{a+1,\dots,a+b\}}\rangle, \end{align*} $$
where
![]() $\iota :\{1,\dots ,2(n-b)\}\to \{1,\dots ,2n\}$
is defined by
$\iota :\{1,\dots ,2(n-b)\}\to \{1,\dots ,2n\}$
is defined by
 $$ \begin{align*} \iota(i):= \left\{ \begin{array}{ll} i & \text{if } 1\leq i\leq a\\ i+b & \text{if } a+1\leq i\leq n-b+a\\ i+2b\ & \text{if } n-b+a+1\leq i\leq 2n-2b. \end{array} \right. \end{align*} $$
$$ \begin{align*} \iota(i):= \left\{ \begin{array}{ll} i & \text{if } 1\leq i\leq a\\ i+b & \text{if } a+1\leq i\leq n-b+a\\ i+2b\ & \text{if } n-b+a+1\leq i\leq 2n-2b. \end{array} \right. \end{align*} $$
This implies that, for every disjoint subsets
![]() $\overline I,\overline J\subset \{1,\dots ,n-b\}$
and every standard Young tableau
$\overline I,\overline J\subset \{1,\dots ,n-b\}$
and every standard Young tableau
![]() $\overline R$
, with rows of the proper lengths
$\overline R$
, with rows of the proper lengths
 $\tfrac 12(2a-|\overline I|-|\overline J|)$
and
$\tfrac 12(2a-|\overline I|-|\overline J|)$
and
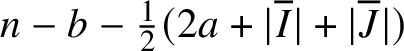 $n-b-\tfrac 12(2a+|\overline I|+|\overline J|)$
and whose entries are precisely the numbers in
$n-b-\tfrac 12(2a+|\overline I|+|\overline J|)$
and whose entries are precisely the numbers in
![]() $\{1,\dots ,n-b\}\setminus (\overline I\cup \overline J)$
, we have
$\{1,\dots ,n-b\}\setminus (\overline I\cup \overline J)$
, we have
 $$ \begin{align} \langle \overline\tau \mid d\overline x_{\overline I}\wedge d\overline y_{\overline J}\wedge\alpha_{\overline R}\rangle = (-1)^{ab} \langle \tau \mid d x_{\iota(\overline I)\cup\{a+1,\dots,a+b\}}\wedge dy_{\overline{J}}\wedge\alpha_{\iota(\overline R)}\rangle, \end{align} $$
$$ \begin{align} \langle \overline\tau \mid d\overline x_{\overline I}\wedge d\overline y_{\overline J}\wedge\alpha_{\overline R}\rangle = (-1)^{ab} \langle \tau \mid d x_{\iota(\overline I)\cup\{a+1,\dots,a+b\}}\wedge dy_{\overline{J}}\wedge\alpha_{\iota(\overline R)}\rangle, \end{align} $$
where
![]() $\iota (\overline R)$
denotes the tableau of the same form of R, obtained on replacing each entry, say i, of
$\iota (\overline R)$
denotes the tableau of the same form of R, obtained on replacing each entry, say i, of
![]() $\overline R$
with
$\overline R$
with
![]() $\iota (i)$
. Observe that
$\iota (i)$
. Observe that
![]() $\iota (R)$
is also a standard Young tableau because
$\iota (R)$
is also a standard Young tableau because
![]() $\iota $
is increasing. Taking Remark 3.27 and assumption (A.7) into account, equality (A.13) now implies (A.12).
$\iota $
is increasing. Taking Remark 3.27 and assumption (A.7) into account, equality (A.13) now implies (A.12).
From now on we assume that, if
![]() $n=2a+b$
, we are in the first case between the two displayed in (A.11); indeed, the following arguments can be easilyFootnote
11
generalised to the other possible case.
$n=2a+b$
, we are in the first case between the two displayed in (A.11); indeed, the following arguments can be easilyFootnote
11
generalised to the other possible case.
Claim 4: Up to a proper choice of
![]() $\tau ^{1},\dots ,\tau ^{2a+b}$
, we can assume that the blocks
$\tau ^{1},\dots ,\tau ^{2a+b}$
, we can assume that the blocks
![]() $A_{1},A_{2}$
in (A.10)–(A.11) are 0.
$A_{1},A_{2}$
in (A.10)–(A.11) are 0.
It is enough to replace
![]() $\tau ^{i}$
, for
$\tau ^{i}$
, for
![]() $i=2a+1,\dots ,2a+b$
, with
$i=2a+1,\dots ,2a+b$
, with
 $$ \begin{align*} \tau^{i} - \sum_{j=1}^{a} (\tau^{i}_{j} \tau^{j}+\tau^{i}_{n+j} \tau^{a+j}). \end{align*} $$
$$ \begin{align*} \tau^{i} - \sum_{j=1}^{a} (\tau^{i}_{j} \tau^{j}+\tau^{i}_{n+j} \tau^{a+j}). \end{align*} $$
We are using in a key way the two blocks of the form
![]() $I_{a}$
appearing in (A.10)–(A.11).
$I_{a}$
appearing in (A.10)–(A.11).
From now on the vectors
![]() $\tau $
are fixed; we are going to prove that the remaining blocks
$\tau $
are fixed; we are going to prove that the remaining blocks
![]() $B,C_{1},C_{2},D_{1},D_{2}$
in (A.10)–(A.11) are 0.
$B,C_{1},C_{2},D_{1},D_{2}$
in (A.10)–(A.11) are 0.
Claim 5: The blocks
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
in (A.10)–(A.11) are 0.
$B_{2}$
in (A.10)–(A.11) are 0.
We need to prove that
 $$ \begin{align*} \tau^{i}_{n+a+j}=0\qquad\text{for all }i=1,\dots,2a,\ j=1,\dots,b. \end{align*} $$
$$ \begin{align*} \tau^{i}_{n+a+j}=0\qquad\text{for all }i=1,\dots,2a,\ j=1,\dots,b. \end{align*} $$
Fix then such i and j. Let
![]() $\overline R$
be the standard Young tableau
$\overline R$
be the standard Young tableau

We define a new tableau Q in the following way:
-
• if
 $1\leq i\leq a$
, Q is the tableau obtained from
$1\leq i\leq a$
, Q is the tableau obtained from
 $\overline R$
on replacing, in the first row, the entry i with
$\overline R$
on replacing, in the first row, the entry i with
 $a+j$
;
$a+j$
; -
• if
 $a+1\leq i\leq 2a$
, Q is the tableau obtained from
$a+1\leq i\leq 2a$
, Q is the tableau obtained from
 $\overline R$
on replacing, in the first row, the entry
$\overline R$
on replacing, in the first row, the entry
 $i-a$
with
$i-a$
with
 $a+j$
.
$a+j$
.
Consider
 $$ \begin{align*} & \lambda:=dx_{\{a+1,\dots,a+b\}\setminus\{a+j\}}\wedge dy_{i}\wedge\alpha_{Q} && \text{if }1\leq i\leq a\\ & \lambda:=dx_{\{i-a\}\cup\{a+1,\dots,a+b\}\setminus\{a+j\}}\wedge\alpha_{Q} && \text{if }a+1\leq i\leq 2a. \end{align*} $$
$$ \begin{align*} & \lambda:=dx_{\{a+1,\dots,a+b\}\setminus\{a+j\}}\wedge dy_{i}\wedge\alpha_{Q} && \text{if }1\leq i\leq a\\ & \lambda:=dx_{\{i-a\}\cup\{a+1,\dots,a+b\}\setminus\{a+j\}}\wedge\alpha_{Q} && \text{if }a+1\leq i\leq 2a. \end{align*} $$
The tableau Q is not a standard Young one; nonetheless,
![]() $\lambda \wedge \theta \in {\mathcal J}^{2a+b+1}$
and, using Remark 3.21 and the assumption (A.7), we have
$\lambda \wedge \theta \in {\mathcal J}^{2a+b+1}$
and, using Remark 3.21 and the assumption (A.7), we have
Assume that
![]() $1\leq i\leq a$
; we can write
$1\leq i\leq a$
; we can write
 $$ \begin{align} \lambda=dx_{\{a+1,\dots,a+b\}\setminus\{a+j\}}\wedge dy_{i}\wedge\sum_{S}\sigma(S)\:dxy_{S} \end{align} $$
$$ \begin{align} \lambda=dx_{\{a+1,\dots,a+b\}\setminus\{a+j\}}\wedge dy_{i}\wedge\sum_{S}\sigma(S)\:dxy_{S} \end{align} $$
where
![]() $\sigma (S)\in \{1,-1\}$
is a suitable sign and the sum varies among the
$\sigma (S)\in \{1,-1\}$
is a suitable sign and the sum varies among the
![]() $2^{n-a-b}$
subsets
$2^{n-a-b}$
subsets
![]() $S\subset \{1,\dots ,a,a+j,a+b+1,\dots ,n\}\setminus \{i\}$
(i.e., S is a subset of the entries of Q) of cardinality a and containing exactly one element from each column of Q. For any such S we have
$S\subset \{1,\dots ,a,a+j,a+b+1,\dots ,n\}\setminus \{i\}$
(i.e., S is a subset of the entries of Q) of cardinality a and containing exactly one element from each column of Q. For any such S we have
 $$ \begin{align} \begin{aligned} \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j\}}\wedge dy_{i}\wedge dxy_{S} \rangle = & \det[M_{\ell}]_{\ell\in(\{a+1,\dots,a+b\}\setminus\{a+j\})\cup\{n+i\}\cup S\cup(n+S)}\\ = & \pm \det [N_{\ell}]_{\ell\in S\cup(n+S)\cup\{n+i\}}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j\}}\wedge dy_{i}\wedge dxy_{S} \rangle = & \det[M_{\ell}]_{\ell\in(\{a+1,\dots,a+b\}\setminus\{a+j\})\cup\{n+i\}\cup S\cup(n+S)}\\ = & \pm \det [N_{\ell}]_{\ell\in S\cup(n+S)\cup\{n+i\}}, \end{aligned} \end{align} $$
where
-
• the sign
 $\pm $
depends only on
$\pm $
depends only on
 $S,i,j$
,
$S,i,j$
, -
•
 $N_{\ell }:=(\tau ^{1}_{\ell },\dots ,\tau ^{2a}_{\ell },\tau ^{2a+j}_{\ell })$
is obtained from the
$N_{\ell }:=(\tau ^{1}_{\ell },\dots ,\tau ^{2a}_{\ell },\tau ^{2a+j}_{\ell })$
is obtained from the
 $\ell $
th row
$\ell $
th row
 $M_{\ell }$
of M on cancelling the last b components except for the
$M_{\ell }$
of M on cancelling the last b components except for the
 $(2a+j)$
th one,
$(2a+j)$
th one, -
• we used that the second block of rows in (A.10)-(A.11) is
 $[0|0|I_{b}]$
.
$[0|0|I_{b}]$
.
Using Claim 4, one finds
 $$ \begin{align} \text{if }S=\{1,\dots,a,a+j\}\setminus \{i\}\text{, then }\langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j\}}\wedge dy_{i}\wedge dxy_{S} \rangle = \pm\tau^{i}_{n+a+j}. \end{align} $$
$$ \begin{align} \text{if }S=\{1,\dots,a,a+j\}\setminus \{i\}\text{, then }\langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j\}}\wedge dy_{i}\wedge dxy_{S} \rangle = \pm\tau^{i}_{n+a+j}. \end{align} $$
Notice that the case
![]() $S=\{1,\dots ,a,a+j\}\setminus \{i\}$
correspods to S containing the elements in the first row of Q. Instead, if
$S=\{1,\dots ,a,a+j\}\setminus \{i\}$
correspods to S containing the elements in the first row of Q. Instead, if
![]() $S\neq \{1,\dots ,a,a+j\}\setminus \{i\}$
, then there exists an element
$S\neq \{1,\dots ,a,a+j\}\setminus \{i\}$
, then there exists an element
![]() $\bar \ell \in S$
belonging to the second row of Q; that is,
$\bar \ell \in S$
belonging to the second row of Q; that is,
![]() $\bar \ell \in S\cap \{a+b+1,\dots ,n\}$
. In this case,
$\bar \ell \in S\cap \{a+b+1,\dots ,n\}$
. In this case,
![]() $N_{\bar \ell }$
and
$N_{\bar \ell }$
and
![]() $N_{n+\bar \ell }$
are linearly dependent, because by Claim 3 all of their entries are null except (possibly) for the last one; in particular,
$N_{n+\bar \ell }$
are linearly dependent, because by Claim 3 all of their entries are null except (possibly) for the last one; in particular,
By (A.15), (A.16), (A.18) and (A.19) we obtain
 $$ \begin{align} 0 = \langle\tau \mid \lambda \rangle = \pm\tau^{i}_{n+a+j} \end{align} $$
$$ \begin{align} 0 = \langle\tau \mid \lambda \rangle = \pm\tau^{i}_{n+a+j} \end{align} $$
and the claim is proved in case
![]() $1\leq i\leq a$
. If
$1\leq i\leq a$
. If
![]() $a+1\leq i\leq 2a$
, (A.20) can be proved by a completely analogous argument that we omit. The claim is proved.
$a+1\leq i\leq 2a$
, (A.20) can be proved by a completely analogous argument that we omit. The claim is proved.
Claim 6: The block C in (A.10)–(A.11) is 0.
The block C is a square one, with size
![]() $b\times b$
; we start by proving that the elements on the diagonal of C are all null; that is, that
$b\times b$
; we start by proving that the elements on the diagonal of C are all null; that is, that
 $$ \begin{align} \tau^{2a+i}_{n+a+i}=0 \quad \text{ for any }i=1,\dots,b. \end{align} $$
$$ \begin{align} \tau^{2a+i}_{n+a+i}=0 \quad \text{ for any }i=1,\dots,b. \end{align} $$
Let then
![]() $i\in \{1,\dots ,b\}$
be fixed; consider
$i\in \{1,\dots ,b\}$
be fixed; consider
where
![]() $\overline R$
is as in (A.14). We can write
$\overline R$
is as in (A.14). We can write
 $$ \begin{align} \lambda=dx_{\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge dy_{a+i}\wedge\sum_{S}\sigma(S)\:dxy_{S} \end{align} $$
$$ \begin{align} \lambda=dx_{\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge dy_{a+i}\wedge\sum_{S}\sigma(S)\:dxy_{S} \end{align} $$
where
![]() $\sigma (S)\in \{1,-1\}$
is a suitable sign and the sum varies among the
$\sigma (S)\in \{1,-1\}$
is a suitable sign and the sum varies among the
![]() $2^{n-a-b}$
subsets
$2^{n-a-b}$
subsets
![]() $S\subset \{1,\dots ,a,a+b+1,\dots ,n\}$
of cardinality a and containing exactly one element from each column of
$S\subset \{1,\dots ,a,a+b+1,\dots ,n\}$
of cardinality a and containing exactly one element from each column of
![]() $\overline R$
. For any such S we have
$\overline R$
. For any such S we have
 $$ \begin{align} \begin{aligned} \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge dy_{a+i}\wedge dxy_{S} \rangle = & \det[M_{j}]_{j\in(\{a+1,\dots,a+b\}\setminus\{a+i\})\cup\{n+a+i\}\cup S\cup(n+S)}\\ = & \pm \det [N_{j}]_{j\in S\cup(n+S)\cup\{n+a+i\}}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge dy_{a+i}\wedge dxy_{S} \rangle = & \det[M_{j}]_{j\in(\{a+1,\dots,a+b\}\setminus\{a+i\})\cup\{n+a+i\}\cup S\cup(n+S)}\\ = & \pm \det [N_{j}]_{j\in S\cup(n+S)\cup\{n+a+i\}}, \end{aligned} \end{align} $$
where
-
• the sign
 $\pm $
depends only on S and i,
$\pm $
depends only on S and i, -
•
 $N_{j}:=(\tau ^{1}_{j},\dots ,\tau ^{2a}_{j},\tau ^{2a+i}_{j})$
is obtained from the jth row
$N_{j}:=(\tau ^{1}_{j},\dots ,\tau ^{2a}_{j},\tau ^{2a+i}_{j})$
is obtained from the jth row
 $M_{j}$
of M on cancelling the last b components except for the
$M_{j}$
of M on cancelling the last b components except for the
 $(2a+i)$
th one,
$(2a+i)$
th one, -
• we used that the second block of rows in (A.10)–(A.11) is
 $[0|0|I_{b}]$
.
$[0|0|I_{b}]$
.
Using Claims 4 and 5, one finds
 $$ \begin{align} \text{if }S=\{1,\dots,a\}\text{, then }\langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge dy_{a+i}\wedge dxy_{S} \rangle = \pm\tau^{2a+i}_{n+a+i}. \end{align} $$
$$ \begin{align} \text{if }S=\{1,\dots,a\}\text{, then }\langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge dy_{a+i}\wedge dxy_{S} \rangle = \pm\tau^{2a+i}_{n+a+i}. \end{align} $$
On the contrary, if
![]() $S\neq \{1,\dots ,a\}$
, then there exists an element
$S\neq \{1,\dots ,a\}$
, then there exists an element
![]() $\bar \ell \in S$
belonging to the second row of
$\bar \ell \in S$
belonging to the second row of
![]() $\overline R$
; that is,
$\overline R$
; that is,
![]() $\bar \ell \in S\cap \{a+b+1,\dots ,n\}$
. In this case,
$\bar \ell \in S\cap \{a+b+1,\dots ,n\}$
. In this case,
![]() $N_{\bar \ell }$
and
$N_{\bar \ell }$
and
![]() $N_{n+\bar \ell }$
are linearly dependent, because by Claim 3 all of their entries are null except (possibly) for the last one; in particular, (A.23) gives
$N_{n+\bar \ell }$
are linearly dependent, because by Claim 3 all of their entries are null except (possibly) for the last one; in particular, (A.23) gives
By (A.22), (A.24) and (A.25) we obtain
 $$ \begin{align*} 0=\langle X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \lambda\rangle = \langle\tau \mid \lambda \rangle = \pm\tau^{2a+i}_{n+a+i}, \end{align*} $$
$$ \begin{align*} 0=\langle X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \lambda\rangle = \langle\tau \mid \lambda \rangle = \pm\tau^{2a+i}_{n+a+i}, \end{align*} $$
and (A.21) is proved.
We now prove that the off-diagonal entries of C are null as well. We then fix
![]() $i,j\in \{1,\dots ,b\}$
with
$i,j\in \{1,\dots ,b\}$
with
![]() $j<i$
and prove that
$j<i$
and prove that
 $$ \begin{align} \tau^{2a+i}_{n+a+j}=\tau^{2a+j}_{n+a+i}=0. \end{align} $$
$$ \begin{align} \tau^{2a+i}_{n+a+j}=\tau^{2a+j}_{n+a+i}=0. \end{align} $$
Let us consider
 $$ \begin{align*} & \lambda_{1}:=dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dy_{\{n+a+j,n+a+i\}}\wedge\alpha_{\overline R}\\ & \lambda_{2}:=dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge \alpha_{Q} \end{align*} $$
$$ \begin{align*} & \lambda_{1}:=dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dy_{\{n+a+j,n+a+i\}}\wedge\alpha_{\overline R}\\ & \lambda_{2}:=dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge \alpha_{Q} \end{align*} $$
where
![]() $\overline R$
is as in (A.14) and Q is the tableau obtained by adding a column
$\overline R$
is as in (A.14) and Q is the tableau obtained by adding a column
![]() $(a+j,a+i)$
on the left of
$(a+j,a+i)$
on the left of
![]() $\overline R$
; that is,
$\overline R$
; that is,

Notice that Q is not a standard Young tableau; however,
![]() $\lambda _{1}\wedge \theta $
and
$\lambda _{1}\wedge \theta $
and
![]() $\lambda _{2}\wedge \theta $
belong to
$\lambda _{2}\wedge \theta $
belong to
![]() ${\mathcal J}^{2a+b+1}$
and, using Remark 3.21 and the assumption (A.7), one obtains
${\mathcal J}^{2a+b+1}$
and, using Remark 3.21 and the assumption (A.7), one obtains
 $$ \begin{align} \begin{aligned} & \langle\tau\mid \lambda_{1}\rangle = \langle X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \lambda_{1}\rangle = 0\\ & \langle\tau\mid \lambda_{2}\rangle = \langle X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \lambda_{2}\rangle = 0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \langle\tau\mid \lambda_{1}\rangle = \langle X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \lambda_{1}\rangle = 0\\ & \langle\tau\mid \lambda_{2}\rangle = \langle X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \lambda_{2}\rangle = 0. \end{aligned} \end{align} $$
The argument that follows is pretty much similar to the previous one as well as to that of Claim 5. We write
 $$ \begin{align} \begin{aligned} & \lambda_{1}=dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dy_{\{n+a+j,n+a+i\}}\wedge\sum_{S}\sigma(S)\:dxy_{S}\\ & \lambda_{2}=dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge\sum_{T}\sigma(T)\:dxy_{T} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \lambda_{1}=dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dy_{\{n+a+j,n+a+i\}}\wedge\sum_{S}\sigma(S)\:dxy_{S}\\ & \lambda_{2}=dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge\sum_{T}\sigma(T)\:dxy_{T} \end{aligned} \end{align} $$
where
![]() $\sigma (S),\sigma (T)\in \{1,-1\}$
are suitable signs and the sums vary among the subsets
$\sigma (S),\sigma (T)\in \{1,-1\}$
are suitable signs and the sums vary among the subsets
![]() $S,T$
of the sets of entries of
$S,T$
of the sets of entries of
![]() $\overline R,Q$
(respectively) with cardinality (respectively)
$\overline R,Q$
(respectively) with cardinality (respectively)
![]() $a,a+1$
and containing exactly one element from each column of (respectively)
$a,a+1$
and containing exactly one element from each column of (respectively)
![]() $\overline R,Q$
. For any such
$\overline R,Q$
. For any such
![]() $S,T$
we have
$S,T$
we have
 $$ \begin{align} \begin{aligned} & \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dy_{\{n+a+j,n+a+i\}}\wedge dxy_{S} \rangle\\ =\: & \det[M_{\ell}]_{\ell\in(\{a+1,\dots,a+b\}\setminus\{a+j,a+i\})\cup\{n+a+j,n+a+i\}\cup S\cup(n+S)}\\ =\: & \pm \det [O_{\ell}]_{\ell\in S\cup(n+S)\cup\{n+a+j,n+a+i\}}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dy_{\{n+a+j,n+a+i\}}\wedge dxy_{S} \rangle\\ =\: & \det[M_{\ell}]_{\ell\in(\{a+1,\dots,a+b\}\setminus\{a+j,a+i\})\cup\{n+a+j,n+a+i\}\cup S\cup(n+S)}\\ =\: & \pm \det [O_{\ell}]_{\ell\in S\cup(n+S)\cup\{n+a+j,n+a+i\}}, \end{aligned} \end{align} $$
and
 $$ \begin{align} \begin{aligned} \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dxy_{T} \rangle = & \det[M_{\ell}]_{\ell\in(\{a+1,\dots,a+b\}\setminus\{a+j,a+i\})\cup T\cup(n+T)}\\ = & \pm \det [O_{\ell}]_{\ell\in T\cup(n+T)}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dxy_{T} \rangle = & \det[M_{\ell}]_{\ell\in(\{a+1,\dots,a+b\}\setminus\{a+j,a+i\})\cup T\cup(n+T)}\\ = & \pm \det [O_{\ell}]_{\ell\in T\cup(n+T)}, \end{aligned} \end{align} $$
where
-
• the signs
 $\pm $
depend only on
$\pm $
depend only on
 $S,T,i$
and j,
$S,T,i$
and j, -
•
 $O_{\ell }:=(\tau ^{1}_{\ell },\dots ,\tau ^{2a}_{\ell },\tau ^{2a+j}_{\ell },\tau ^{2a+i}_{\ell })$
is obtained from the
$O_{\ell }:=(\tau ^{1}_{\ell },\dots ,\tau ^{2a}_{\ell },\tau ^{2a+j}_{\ell },\tau ^{2a+i}_{\ell })$
is obtained from the
 $\ell $
th row
$\ell $
th row
 $M_{\ell }$
of M on cancelling the last b components except for the
$M_{\ell }$
of M on cancelling the last b components except for the
 $(2a+j)$
th and
$(2a+j)$
th and
 $(2a+i)$
th ones,
$(2a+i)$
th ones, -
• we used that the second block of rows in (A.10)–(A.11) is
 $[0|0|I_{b}]$
.
$[0|0|I_{b}]$
.
Using Claims 4 and 5 and the fact that the diagonal of C is null, one finds that
-
(i) if
 $S=\{1,\dots ,a\}$
, then
$S=\{1,\dots ,a\}$
, then  $$ \begin{align*} &\langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dy_{n+a+j,n+a+i}\wedge dxy_{S} \rangle \\ =&\pm\det\left(\begin{array}{cc} \tau^{2a+j}_{n+a+j} & \tau^{2a+i}_{n+a+j}\\ \tau^{2a+j}_{n+a+i} & \tau^{2a+i}_{n+a+i} \end{array}\right) =\pm\det\left(\begin{array}{cc} 0 & \tau^{2a+i}_{n+a+j}\\ \tau^{2a+j}_{n+a+i} & 0 \end{array}\right) = \pm \tau^{2a+j}_{n+a+i}\tau^{2a+i}_{n+a+j}; \end{align*} $$
$$ \begin{align*} &\langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dy_{n+a+j,n+a+i}\wedge dxy_{S} \rangle \\ =&\pm\det\left(\begin{array}{cc} \tau^{2a+j}_{n+a+j} & \tau^{2a+i}_{n+a+j}\\ \tau^{2a+j}_{n+a+i} & \tau^{2a+i}_{n+a+i} \end{array}\right) =\pm\det\left(\begin{array}{cc} 0 & \tau^{2a+i}_{n+a+j}\\ \tau^{2a+j}_{n+a+i} & 0 \end{array}\right) = \pm \tau^{2a+j}_{n+a+i}\tau^{2a+i}_{n+a+j}; \end{align*} $$
-
(ii) if
 $T=\{1,\dots ,a,a+j\}$
, then
$T=\{1,\dots ,a,a+j\}$
, then  $$ \begin{align*} & \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dxy_{T} \rangle \\ =&\pm\det\left(\begin{array}{cc} \tau^{2a+j}_{a+j} & \tau^{2a+i}_{a+j}\\ \tau^{2a+j}_{n+a+j} & \tau^{2a+i}_{n+a+j} \end{array}\right) =\pm\det\left(\begin{array}{cc} 1 & 0\\ 0 & \tau^{2a+i}_{n+a+j} \end{array}\right) = \pm \tau^{2a+i}_{n+a+j}; \end{align*} $$
$$ \begin{align*} & \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dxy_{T} \rangle \\ =&\pm\det\left(\begin{array}{cc} \tau^{2a+j}_{a+j} & \tau^{2a+i}_{a+j}\\ \tau^{2a+j}_{n+a+j} & \tau^{2a+i}_{n+a+j} \end{array}\right) =\pm\det\left(\begin{array}{cc} 1 & 0\\ 0 & \tau^{2a+i}_{n+a+j} \end{array}\right) = \pm \tau^{2a+i}_{n+a+j}; \end{align*} $$
-
(iii) if
 $T=\{1,\dots ,a,a+i\}$
, then
$T=\{1,\dots ,a,a+i\}$
, then  $$ \begin{align*} &\langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dxy_{T} \rangle \\ =&\pm\det\left(\begin{array}{cc} \tau^{2a+j}_{a+i} & \tau^{2a+i}_{a+i}\\ \tau^{2a+j}_{n+a+i} & \tau^{2a+i}_{n+a+i} \end{array}\right) =\pm\det\left(\begin{array}{cc} 0 & 1\\ \tau^{2a+j}_{n+a+i} & 0 \end{array}\right) = \pm \tau^{2a+j}_{n+a+i}, \end{align*} $$
$$ \begin{align*} &\langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dxy_{T} \rangle \\ =&\pm\det\left(\begin{array}{cc} \tau^{2a+j}_{a+i} & \tau^{2a+i}_{a+i}\\ \tau^{2a+j}_{n+a+i} & \tau^{2a+i}_{n+a+i} \end{array}\right) =\pm\det\left(\begin{array}{cc} 0 & 1\\ \tau^{2a+j}_{n+a+i} & 0 \end{array}\right) = \pm \tau^{2a+j}_{n+a+i}, \end{align*} $$
where the
![]() $\pm $
signs will be irrelevant. If
$\pm $
signs will be irrelevant. If
![]() $S\neq \{1,\dots ,a\}$
, then there exists an element
$S\neq \{1,\dots ,a\}$
, then there exists an element
![]() $\bar \ell \in S\cap \{a+b+1,\dots ,n\}$
; it follows that
$\bar \ell \in S\cap \{a+b+1,\dots ,n\}$
; it follows that
![]() $O_{\bar \ell },O_{n+\bar \ell },O_{n+a+j},O_{n+a+i}$
are linearly dependent, because by Claims 3 and 5 all of their entries are null except (possibly) for the last two ones. In particular, (A.29) gives
$O_{\bar \ell },O_{n+\bar \ell },O_{n+a+j},O_{n+a+i}$
are linearly dependent, because by Claims 3 and 5 all of their entries are null except (possibly) for the last two ones. In particular, (A.29) gives
 $$ \begin{align} \begin{aligned} \text{if } &S\neq\{1,\dots,a\},\\ \text{then } & \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dy_{n+a+j,n+a+i}\wedge dxy_{S} \rangle = 0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \text{if } &S\neq\{1,\dots,a\},\\ \text{then } & \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dy_{n+a+j,n+a+i}\wedge dxy_{S} \rangle = 0. \end{aligned} \end{align} $$
If
![]() $T\neq \{1,\dots ,a,a+j\}$
and
$T\neq \{1,\dots ,a,a+j\}$
and
![]() $T\neq \{1,\dots ,a,a+i\}$
, then there exists an element
$T\neq \{1,\dots ,a,a+i\}$
, then there exists an element
![]() $\bar \ell \in T\cap \{a+b+1,\dots ,n\}$
; notice also that either
$\bar \ell \in T\cap \{a+b+1,\dots ,n\}$
; notice also that either
![]() $a+j\in T$
or
$a+j\in T$
or
![]() $a+i\in T$
. If
$a+i\in T$
. If
![]() $a+j\in T$
, then
$a+j\in T$
, then
![]() $O_{\bar \ell },O_{n+\bar \ell },O_{a+j},O_{n+a+j}$
are linearly dependent, again because by Claims 3 and 5 all of their entries are null except (possibly) for the last two. Similarly, when
$O_{\bar \ell },O_{n+\bar \ell },O_{a+j},O_{n+a+j}$
are linearly dependent, again because by Claims 3 and 5 all of their entries are null except (possibly) for the last two. Similarly, when
![]() $a+i\in T$
one has that
$a+i\in T$
one has that
![]() $O_{\bar \ell },O_{n+\bar \ell },O_{a+i},O_{n+a+i}$
are linearly dependent. We deduce by (A.30) that
$O_{\bar \ell },O_{n+\bar \ell },O_{a+i},O_{n+a+i}$
are linearly dependent. We deduce by (A.30) that
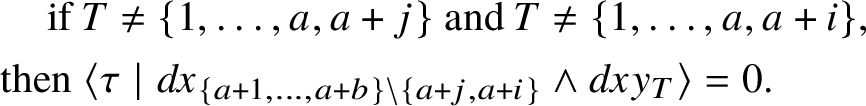 $$ \begin{align} \begin{aligned} \text{if } & T\neq\{1,\dots,a,a+j\}\text{ and }T\neq\{1,\dots,a,a+i\},\\ \text{ then } & \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dxy_{T} \rangle = 0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \text{if } & T\neq\{1,\dots,a,a+j\}\text{ and }T\neq\{1,\dots,a,a+i\},\\ \text{ then } & \langle\tau \mid dx_{\{a+1,\dots,a+b\}\setminus\{a+j,a+i\}}\wedge dxy_{T} \rangle = 0. \end{aligned} \end{align} $$
By (A.27), (A.28), (A.31) and (i)–(ii)–(iii) above we finally achieve
 $$ \begin{align*} \tau^{2a+j}_{n+a+i}\tau^{2a+i}_{n+a+j}=0\quad\text{and}\quad\pm \tau^{2a+j}_{n+a+i}\pm\tau^{2a+i}_{n+a+j}=0, \end{align*} $$
$$ \begin{align*} \tau^{2a+j}_{n+a+i}\tau^{2a+i}_{n+a+j}=0\quad\text{and}\quad\pm \tau^{2a+j}_{n+a+i}\pm\tau^{2a+i}_{n+a+j}=0, \end{align*} $$
and (A.26) is proved.
Claim 7: The blocks
![]() $D_{1}$
and
$D_{1}$
and
![]() $D_{2}$
in (A.10)–(A.11) are 0.
$D_{2}$
in (A.10)–(A.11) are 0.
The claim amounts to showing that
 $$ \begin{align} \tau^{2a+i}_{j}=0=\tau^{2a+i}_{n+j}\qquad\text{for any }1\leq i\leq b\text{ and }a+b+1\leq j\leq n. \end{align} $$
$$ \begin{align} \tau^{2a+i}_{j}=0=\tau^{2a+i}_{n+j}\qquad\text{for any }1\leq i\leq b\text{ and }a+b+1\leq j\leq n. \end{align} $$
Fix
![]() $i,j$
as in (A.33) and consider the Young tableau Q obtained from
$i,j$
as in (A.33) and consider the Young tableau Q obtained from
![]() $\overline R$
on replacing, in the second row, the entry j with
$\overline R$
on replacing, in the second row, the entry j with
![]() $a+i$
. Set
$a+i$
. Set
and write
 $$ \begin{align} \lambda=dx_{\{j\}\cup\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge\sum_{S}\sigma(S)\:dxy_{S} \end{align} $$
$$ \begin{align} \lambda=dx_{\{j\}\cup\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge\sum_{S}\sigma(S)\:dxy_{S} \end{align} $$
where
![]() $\sigma (S)\in \{1,-1\}$
is a suitable sign and the sum varies among the
$\sigma (S)\in \{1,-1\}$
is a suitable sign and the sum varies among the
![]() $2^{n-a-b}$
subsets
$2^{n-a-b}$
subsets
![]() $S\subset \{a+i\}\cup \{1,\dots ,a,a+b+1,\dots ,n\}\setminus \{j\}$
(i.e., S is a subset of the set of entries of Q) with cardinality a and containing exactly one element from each column of Q. For any such S we have
$S\subset \{a+i\}\cup \{1,\dots ,a,a+b+1,\dots ,n\}\setminus \{j\}$
(i.e., S is a subset of the set of entries of Q) with cardinality a and containing exactly one element from each column of Q. For any such S we have
 $$ \begin{align} \begin{aligned} \langle\tau \mid dx_{\{j\}\cup\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge dxy_{S} \rangle = & \det[M_{\ell}]_{\ell\in(\{j\}\cup\{a+1,\dots,a+b\}\setminus\{a+i\})\cup S\cup(n+S)}\\ = & \pm \det [N_{\ell}]_{\ell\in \{j\}\cup S\cup(n+S)}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle\tau \mid dx_{\{j\}\cup\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge dxy_{S} \rangle = & \det[M_{\ell}]_{\ell\in(\{j\}\cup\{a+1,\dots,a+b\}\setminus\{a+i\})\cup S\cup(n+S)}\\ = & \pm \det [N_{\ell}]_{\ell\in \{j\}\cup S\cup(n+S)}, \end{aligned} \end{align} $$
where
-
• the sign
 $\pm $
depends only on
$\pm $
depends only on
 $S,j$
and i,
$S,j$
and i, -
•
 $N_{\ell }:=(\tau ^{1}_{\ell },\dots ,\tau ^{2a}_{\ell },\tau ^{2a+i}_{\ell })$
is obtained from the
$N_{\ell }:=(\tau ^{1}_{\ell },\dots ,\tau ^{2a}_{\ell },\tau ^{2a+i}_{\ell })$
is obtained from the
 $\ell $
th row
$\ell $
th row
 $M_{\ell }$
of M on canceling the last b components except for the
$M_{\ell }$
of M on canceling the last b components except for the
 $(2a+i)$
th one,
$(2a+i)$
th one, -
• we used that the second block of rows in (A.10)–(A.11) is
 $[0|0|I_{b}]$
.
$[0|0|I_{b}]$
.
Using the previous claims, we obtain
 $$ \begin{align} \text{if }S=\{1,\dots,a\}\text{, then }\langle\tau \mid dx_{\{j\}\cup\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge dxy_{S} \rangle = \pm\tau^{2a+i}_{j}. \end{align} $$
$$ \begin{align} \text{if }S=\{1,\dots,a\}\text{, then }\langle\tau \mid dx_{\{j\}\cup\{a+1,\dots,a+b\}\setminus\{a+i\}}\wedge dxy_{S} \rangle = \pm\tau^{2a+i}_{j}. \end{align} $$
If
![]() $S\neq \{1,\dots ,a\}$
, then there exists an element
$S\neq \{1,\dots ,a\}$
, then there exists an element
![]() $\bar \ell \in S$
belonging to the second row of Q; that is,
$\bar \ell \in S$
belonging to the second row of Q; that is,
![]() $\bar \ell \in S\cap (\{a+i\}\cup \{a+b+1,\dots ,n\}\setminus \{j\})$
. In this case,
$\bar \ell \in S\cap (\{a+i\}\cup \{a+b+1,\dots ,n\}\setminus \{j\})$
. In this case,
![]() $N_{\bar \ell }$
and
$N_{\bar \ell }$
and
![]() $N_{n+\bar \ell }$
are linearly dependent, because by Claims 3, 4 and 5 all of their entries are null except (possibly) for the last one; in particular, (A.35) gives
$N_{n+\bar \ell }$
are linearly dependent, because by Claims 3, 4 and 5 all of their entries are null except (possibly) for the last one; in particular, (A.35) gives
By (A.34), (A.36), (A.37) and Remark 3.21 we obtain
 $$ \begin{align*} 0=\langle X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \lambda\rangle = \langle\tau \mid \lambda \rangle = \pm\tau^{2a+i}_{j} \end{align*} $$
$$ \begin{align*} 0=\langle X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\mid \lambda\rangle = \langle\tau \mid \lambda \rangle = \pm\tau^{2a+i}_{j} \end{align*} $$
and the first equality in (A.33) is proved.
We are left to show that also
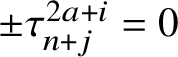 $\pm \tau ^{2a+i}_{n+j}=0$
for any
$\pm \tau ^{2a+i}_{n+j}=0$
for any
![]() $i,j$
as in (A.33); this can be done by considering (for the same Q above)
$i,j$
as in (A.33); this can be done by considering (for the same Q above)
and following a similar argument, which we omit. The proof of Claim 7 is then complete.
The proof of Lemma A.3 now follows from the equality
![]() $\tau =\tau ^{1}\wedge \dots \wedge \tau ^{2a+b}$
; the fact that the blocks
$\tau =\tau ^{1}\wedge \dots \wedge \tau ^{2a+b}$
; the fact that the blocks
![]() $A_{1},A_{2},B_{1},B_{2},C,D_{1},D_{2}$
in (A.10)–(A.11) are all null; and the equality
$A_{1},A_{2},B_{1},B_{2},C,D_{1},D_{2}$
in (A.10)–(A.11) are all null; and the equality
 $$ \begin{align*} &X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\\ = &(-1)^{ab}X_{1}\wedge\dots\wedge X_{a}\wedge Y_{1}\wedge\dots\wedge Y_{a}\wedge X_{a+1}\wedge\dots \wedge X_{a+b}. \\[-40pt] \end{align*} $$
$$ \begin{align*} &X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\\ = &(-1)^{ab}X_{1}\wedge\dots\wedge X_{a}\wedge Y_{1}\wedge\dots\wedge Y_{a}\wedge X_{a+1}\wedge\dots \wedge X_{a+b}. \\[-40pt] \end{align*} $$
Proof of Proposition 3.38.
Assume that there exists a
![]() $(2n+1-k)$
-dimensional vertical plane
$(2n+1-k)$
-dimensional vertical plane
![]() ${\mathscr P}_{1}$
whose unit tangent vector
${\mathscr P}_{1}$
whose unit tangent vector
![]() $t_{{\mathscr P}_{1}}^{\mathbb H}$
is such that
$t_{{\mathscr P}_{1}}^{\mathbb H}$
is such that
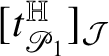 $[t_{{\mathscr P}_{1}}^{\mathbb H}]_{{\mathcal J}}$
is a multiple of
$[t_{{\mathscr P}_{1}}^{\mathbb H}]_{{\mathcal J}}$
is a multiple of
![]() $\zeta $
. By Proposition 3.13 there exist nonnegative integers a and b and an
$\zeta $
. By Proposition 3.13 there exist nonnegative integers a and b and an
![]() ${\mathbb H}$
-linear isomorphim
${\mathbb H}$
-linear isomorphim
![]() ${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
such that
${\mathcal L}:{\mathbb H}^{n}\to {\mathbb H}^{n}$
such that
![]() $a+b\leq n$
,
$a+b\leq n$
,
![]() $\dim {\mathscr P}_{1} =2a+b+1$
,
$\dim {\mathscr P}_{1} =2a+b+1$
,
![]() ${\mathcal L}^{*}(\theta )=\theta $
,
${\mathcal L}^{*}(\theta )=\theta $
,
![]() ${\mathcal L}^{*}(d\theta )=d\theta $
and
${\mathcal L}^{*}(d\theta )=d\theta $
and
where
![]() ${{\mathscr P}_{a,b}}$
is defined as in (3.11). Let us denote by
${{\mathscr P}_{a,b}}$
is defined as in (3.11). Let us denote by
![]() ${\mathcal L}_{*}:{\mathcal J}_{2n+1-k}\to {\mathcal J}_{2n+1-k}$
the isomorphism defined in (5.9). Clearly,
${\mathcal L}_{*}:{\mathcal J}_{2n+1-k}\to {\mathcal J}_{2n+1-k}$
the isomorphism defined in (5.9). Clearly,
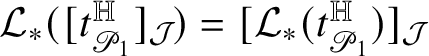 ${\mathcal L}_{*}([t^{\mathbb H}_{{\mathscr P}_{1}}]_{{\mathcal J}})=[{\mathcal L}_{*}(t^{\mathbb H}_{{\mathscr P}_{1}})]_{{\mathcal J}}$
is a multiple of
${\mathcal L}_{*}([t^{\mathbb H}_{{\mathscr P}_{1}}]_{{\mathcal J}})=[{\mathcal L}_{*}(t^{\mathbb H}_{{\mathscr P}_{1}})]_{{\mathcal J}}$
is a multiple of
 $$ \begin{align*} [t^{\mathbb H}_{{{\mathscr P}_{a,b}}}]_{{\mathcal J}} = [X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\wedge T]_{{\mathcal J}}; \end{align*} $$
$$ \begin{align*} [t^{\mathbb H}_{{{\mathscr P}_{a,b}}}]_{{\mathcal J}} = [X_{1}\wedge\dots\wedge X_{a+b}\wedge Y_{1}\wedge\dots\wedge Y_{a}\wedge T]_{{\mathcal J}}; \end{align*} $$
hence,
![]() ${\mathcal L}_{*}\zeta $
is a multiple of
${\mathcal L}_{*}\zeta $
is a multiple of
![]() $[X_{1}\wedge \dots \wedge X_{a+b}\wedge Y_{1}\wedge \dots \wedge Y_{a}\wedge T]_{{\mathcal J}}$
.
$[X_{1}\wedge \dots \wedge X_{a+b}\wedge Y_{1}\wedge \dots \wedge Y_{a}\wedge T]_{{\mathcal J}}$
.
Assume that
![]() ${\mathscr P}_{2}$
is another vertical
${\mathscr P}_{2}$
is another vertical
![]() $(2n+1-k)$
-plane in
$(2n+1-k)$
-plane in
![]() ${\mathbb H}^{n}$
such that
${\mathbb H}^{n}$
such that
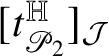 $[t^{\mathbb H}_{{\mathscr P}_{2}}]_{{\mathcal J}}$
is a multiple of
$[t^{\mathbb H}_{{\mathscr P}_{2}}]_{{\mathcal J}}$
is a multiple of
![]() $\zeta $
. The vertical plane
$\zeta $
. The vertical plane
![]() ${\mathscr P}_{3}:={\mathcal L}({\mathscr P}_{2})$
is such that
${\mathscr P}_{3}:={\mathcal L}({\mathscr P}_{2})$
is such that
![]() $t^{\mathbb H}_{{\mathscr P}_{3}}$
is a multiple of
$t^{\mathbb H}_{{\mathscr P}_{3}}$
is a multiple of
 ${\mathcal L}_{*}(t^{\mathbb H}_{{\mathscr P}_{2}})$
; hence,
${\mathcal L}_{*}(t^{\mathbb H}_{{\mathscr P}_{2}})$
; hence,
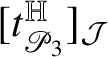 $[t^{\mathbb H}_{{\mathscr P}_{3}}]_{{\mathcal J}}$
is a multiple of
$[t^{\mathbb H}_{{\mathscr P}_{3}}]_{{\mathcal J}}$
is a multiple of
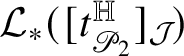 ${\mathcal L}_{*}([t^{\mathbb H}_{{\mathscr P}_{2}}]_{{\mathcal J}})$
; that is, of
${\mathcal L}_{*}([t^{\mathbb H}_{{\mathscr P}_{2}}]_{{\mathcal J}})$
; that is, of
![]() ${\mathcal L}_{*}\zeta $
and eventually of
${\mathcal L}_{*}\zeta $
and eventually of
![]() $[X_{1}\wedge \dots \wedge X_{a+b}\wedge Y_{1}\wedge \dots \wedge Y_{a}\wedge T]_{{\mathcal J}}$
. If
$[X_{1}\wedge \dots \wedge X_{a+b}\wedge Y_{1}\wedge \dots \wedge Y_{a}\wedge T]_{{\mathcal J}}$
. If
![]() $k<n$
, Lemma A.3 implies that
$k<n$
, Lemma A.3 implies that
![]() ${\mathscr P}_{3}={{\mathscr P}_{a,b}}$
; hence,
${\mathscr P}_{3}={{\mathscr P}_{a,b}}$
; hence,
![]() ${\mathscr P}_{2}={\mathscr P}_{1}$
. This proves part (i) of the statement.
${\mathscr P}_{2}={\mathscr P}_{1}$
. This proves part (i) of the statement.
If instead
![]() $k=n$
, Lemma A.3 implies that either
$k=n$
, Lemma A.3 implies that either
![]() ${\mathscr P}_{3}={{\mathscr P}_{a,b}}$
or
${\mathscr P}_{3}={{\mathscr P}_{a,b}}$
or
Observe that, if
![]() $a=0$
, then
$a=0$
, then
![]() ${\mathscr P}_{3}={{\mathscr P}_{a,b}}$
. On the contrary, if
${\mathscr P}_{3}={{\mathscr P}_{a,b}}$
. On the contrary, if
![]() $a\geq 1$
, then either
$a\geq 1$
, then either
![]() ${\mathscr P}_{3}={{\mathscr P}_{a,b}}$
or
${\mathscr P}_{3}={{\mathscr P}_{a,b}}$
or
![]() ${\mathscr P}_{3}$
and
${\mathscr P}_{3}$
and
![]() ${{\mathscr P}_{a,b}}$
are not rank 1 connected, because
${{\mathscr P}_{a,b}}$
are not rank 1 connected, because
All in all, we deduce that either
![]() ${\mathscr P}_{2}={\mathscr P}_{1}$
, or
${\mathscr P}_{2}={\mathscr P}_{1}$
, or
and
![]() ${\mathscr P}_{1}$
,
${\mathscr P}_{1}$
,
![]() ${\mathscr P}_{2}$
are not rank 1 connected. This concludes the proof.
${\mathscr P}_{2}$
are not rank 1 connected. This concludes the proof.
Acknowledgements
We are grateful to G. Alberti and A. Marchese for pointing out reference [Reference Šilhavý89] to us. The author thankd F. Boarotto, A. Julia and S. Nicolussi Golo for their patience and for providing a pleasant environment during the long preparation of this work.
Funding statement
This research was supported by the University of Padova, in particular through the STARS Project SUGGESTION, and by GNAMPA of INdAM (Italy).
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Conflicts of interest
None.