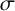1 Introduction
The distribution of the nontrivial zeros of Dirichlet L-functions is of great importance in analytic number theory. The generalised Riemann hypothesis claims that these zeros all lie on the line
![]() $\tfrac {1}{2}+i \mathbb {R}$
; however, it is possible that they could lie anywhere in the region
$\tfrac {1}{2}+i \mathbb {R}$
; however, it is possible that they could lie anywhere in the region
![]() $(0,1)+i \mathbb {R}$
. In practice, it often suffices to employ an unconditional result, known as a zero-density estimate, whose statement is not as strong as the generalised Riemann hypothesis. Let
$(0,1)+i \mathbb {R}$
. In practice, it often suffices to employ an unconditional result, known as a zero-density estimate, whose statement is not as strong as the generalised Riemann hypothesis. Let
![]() $\chi $
be a primitive Dirichlet character modulo q, and suppose that
$\chi $
be a primitive Dirichlet character modulo q, and suppose that
![]() $\sigma \in (\tfrac {1}{2},1)$
and
$\sigma \in (\tfrac {1}{2},1)$
and
![]() $T\in (2,\infty )$
. Define
$T\in (2,\infty )$
. Define
![]() $R(\sigma ,T)=[\sigma ,1]+i[-T,T]$
and let
$R(\sigma ,T)=[\sigma ,1]+i[-T,T]$
and let
![]() $L(s,\chi )$
be the L-function associated to the character
$L(s,\chi )$
be the L-function associated to the character
![]() $\chi $
. Zero-density estimates are concerned with the number
$\chi $
. Zero-density estimates are concerned with the number
or rather, the average of this number over a family
![]() $\mathcal {F}$
of characters. The families
$\mathcal {F}$
of characters. The families
![]() $\mathcal {F}=\mathcal {O}_r$
of primitive Dirichlet characters of order r will be the primary interest. We denote by
$\mathcal {F}=\mathcal {O}_r$
of primitive Dirichlet characters of order r will be the primary interest. We denote by
![]() $\mathcal {O}_r(Q)$
the set of
$\mathcal {O}_r(Q)$
the set of
![]() $\chi \in \mathcal {O}_r$
with conductor
$\chi \in \mathcal {O}_r$
with conductor
![]() $q\in (Q,2Q]$
. The generalised Riemann–von Mangoldt formula [Reference Davenport8, Reference Prachar18] gives the trivial bound
$q\in (Q,2Q]$
. The generalised Riemann–von Mangoldt formula [Reference Davenport8, Reference Prachar18] gives the trivial bound
![]() $N(\sigma ,T,\chi )\ll T\log qT$
for any primitive Dirichlet character
$N(\sigma ,T,\chi )\ll T\log qT$
for any primitive Dirichlet character
![]() $\chi $
, which is known to be sharp only for
$\chi $
, which is known to be sharp only for
![]() $\sigma =\tfrac {1}{2}$
(see [Reference Bohr and Landau3, Reference Selberg19]).
$\sigma =\tfrac {1}{2}$
(see [Reference Bohr and Landau3, Reference Selberg19]).
The earliest zero-density estimates to feature an average over a family of Dirichlet L-functions are due to Bombieri [Reference Bombieri4], Vinogradov [Reference Vinogradov20] and Montgomery [Reference Montgomery14, Reference Montgomery15]. Results containing averages over
![]() $\mathcal {O}_2(Q)$
were first given by Jutila [Reference Jutila12] and Heath-Brown [Reference Heath-Brown11], both of whom followed the method laid down by Montgomery to derive his results. Montgomery’s method reduces the problem to estimating mean values of the type
$\mathcal {O}_2(Q)$
were first given by Jutila [Reference Jutila12] and Heath-Brown [Reference Heath-Brown11], both of whom followed the method laid down by Montgomery to derive his results. Montgomery’s method reduces the problem to estimating mean values of the type
 $$ \begin{align*} \mathfrak{S}_k(Q,T)=\sum_{\chi\in{\mathcal{F}}(Q)}\int_{-T}^T\bigg|\mathop{\sum\nolimits^{{\prime}}}_{n\leqslant N}a_n\chi(n)n^{-it}\bigg|^{2k}\, dt \end{align*} $$
$$ \begin{align*} \mathfrak{S}_k(Q,T)=\sum_{\chi\in{\mathcal{F}}(Q)}\int_{-T}^T\bigg|\mathop{\sum\nolimits^{{\prime}}}_{n\leqslant N}a_n\chi(n)n^{-it}\bigg|^{2k}\, dt \end{align*} $$
and
 $$ \begin{align*} \mathfrak{L}_k(Q,T)=\sum_{\chi\in{\mathcal{F}}(Q)}\int_{-T}^T|L(\tfrac{1}{2}+it,\chi)|^{2k}\, dt, \end{align*} $$
$$ \begin{align*} \mathfrak{L}_k(Q,T)=\sum_{\chi\in{\mathcal{F}}(Q)}\int_{-T}^T|L(\tfrac{1}{2}+it,\chi)|^{2k}\, dt, \end{align*} $$
where
![]() $\mathcal {F}$
is the character family of interest and the prime (
$\mathcal {F}$
is the character family of interest and the prime (
![]() $'$
) denotes that the sum is to be taken over square-free n. A detailed outline of the method has been given in [Reference Corrigan5]. In particular, if
$'$
) denotes that the sum is to be taken over square-free n. A detailed outline of the method has been given in [Reference Corrigan5]. In particular, if
![]() $\mathcal {F}=\mathcal {O}_r$
for some
$\mathcal {F}=\mathcal {O}_r$
for some
![]() $r\geqslant 2$
, we can show that
$r\geqslant 2$
, we can show that
Indeed, (1.1) was proven for the case
![]() $r=2$
in [Reference Jutila13], for the cases
$r=2$
in [Reference Jutila13], for the cases
![]() $r=3,4,6$
in [Reference Corrigan6], and can be proven in the remaining cases using Theorem 1.6 of [Reference Balestrieri and Rome2]. The zero-density estimate of Jutila is derived using (1.1) and a suboptimal bound on
$r=3,4,6$
in [Reference Corrigan6], and can be proven in the remaining cases using Theorem 1.6 of [Reference Balestrieri and Rome2]. The zero-density estimate of Jutila is derived using (1.1) and a suboptimal bound on
![]() $\mathfrak {S}_1(Q,T)$
. In [Reference Corrigan5, Reference Corrigan and Zhao7], we used the large sieve for real characters of Heath-Brown [Reference Heath-Brown11] to derive an estimate for
$\mathfrak {S}_1(Q,T)$
. In [Reference Corrigan5, Reference Corrigan and Zhao7], we used the large sieve for real characters of Heath-Brown [Reference Heath-Brown11] to derive an estimate for
![]() $\mathfrak {S}_1(Q,T)$
sharper than those used by Jutila and Heath-Brown to derive their results, and consequently strengthened Jutila’s estimate to
$\mathfrak {S}_1(Q,T)$
sharper than those used by Jutila and Heath-Brown to derive their results, and consequently strengthened Jutila’s estimate to
 $$ \begin{align} \sum_{\chi\in\mathcal{O}_2(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon\min((QT)^{(4-4\sigma)/(3-2\sigma)},(Q^4T^3)^{1-\sigma}) \end{align} $$
$$ \begin{align} \sum_{\chi\in\mathcal{O}_2(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon\min((QT)^{(4-4\sigma)/(3-2\sigma)},(Q^4T^3)^{1-\sigma}) \end{align} $$
in [Reference Corrigan6]. Additionally, as analogues to (1.2), we showed for
![]() $T^5\gg Q$
that
$T^5\gg Q$
that
 $$ \begin{align} & \sum_{\chi\in{\mathcal{O}}_3(Q)}N(\sigma,T,\chi) \notag \\ &\quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(16-10\sigma)/9}T^{(4-4\sigma)/(3-2\sigma)},Q^{(16-16\sigma)/(9-6\sigma)}T^{(4-4\sigma)/(3-2\sigma)},(Q^4T^3)^{1-\sigma}) \end{align} $$
$$ \begin{align} & \sum_{\chi\in{\mathcal{O}}_3(Q)}N(\sigma,T,\chi) \notag \\ &\quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(16-10\sigma)/9}T^{(4-4\sigma)/(3-2\sigma)},Q^{(16-16\sigma)/(9-6\sigma)}T^{(4-4\sigma)/(3-2\sigma)},(Q^4T^3)^{1-\sigma}) \end{align} $$
and
 $$ \begin{align} & \sum_{\chi\in\mathcal{O}_4(Q)}N(\sigma,T,\chi) \notag \\ &\quad \mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon\min(Q^{(5-3\sigma)/3}T^{(4-4\sigma)/(3-2\sigma)},Q^{(5-5\sigma)/(3-2\sigma)}T^{(4-4\sigma)/(3-2\sigma)},(Q^4T^3)^{1-\sigma}). \end{align} $$
$$ \begin{align} & \sum_{\chi\in\mathcal{O}_4(Q)}N(\sigma,T,\chi) \notag \\ &\quad \mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon\min(Q^{(5-3\sigma)/3}T^{(4-4\sigma)/(3-2\sigma)},Q^{(5-5\sigma)/(3-2\sigma)}T^{(4-4\sigma)/(3-2\sigma)},(Q^4T^3)^{1-\sigma}). \end{align} $$
These results are derived using the large sieve for
![]() $\mathcal {O}_3$
and
$\mathcal {O}_3$
and
![]() $\mathcal {O}_4$
, respectively. Recently, Balestrieri and Rome [Reference Balestrieri and Rome2] generalised the work of Baier and Young [Reference Baier and Young1] and Gao and Zhao [Reference Gao and Zhao9] to derive a large sieve estimate for general
$\mathcal {O}_4$
, respectively. Recently, Balestrieri and Rome [Reference Balestrieri and Rome2] generalised the work of Baier and Young [Reference Baier and Young1] and Gao and Zhao [Reference Gao and Zhao9] to derive a large sieve estimate for general
![]() $\mathcal {O}_r$
where
$\mathcal {O}_r$
where
![]() $r\geqslant 2$
. Using (1.1) together with Theorem 1.6 of [Reference Balestrieri and Rome2], we can show along similar lines to (1.3) and (1.4) that, for
$r\geqslant 2$
. Using (1.1) together with Theorem 1.6 of [Reference Balestrieri and Rome2], we can show along similar lines to (1.3) and (1.4) that, for
![]() $T^{2r-1}\gg Q^{2r-5}$
,
$T^{2r-1}\gg Q^{2r-5}$
,
 $$ \begin{align} & \sum_{\chi\in\mathcal{O}_r(Q)}N(\sigma,T,\chi) \notag \\ &\quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(6-4\sigma)/3}T^{(4-4\sigma)/(3-2\sigma)},Q^{(6-6\sigma)/(3-2\sigma)}T^{(4-4\sigma)/(3-2\sigma)},(Q^4T^3)^{1-\sigma}). \end{align} $$
$$ \begin{align} & \sum_{\chi\in\mathcal{O}_r(Q)}N(\sigma,T,\chi) \notag \\ &\quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(6-4\sigma)/3}T^{(4-4\sigma)/(3-2\sigma)},Q^{(6-6\sigma)/(3-2\sigma)}T^{(4-4\sigma)/(3-2\sigma)},(Q^4T^3)^{1-\sigma}). \end{align} $$
If we could demonstrate that the estimate (1.1) still holds when
![]() $k=2$
, then we could unconditionally improve on these zero-density estimates. Following the method of Heath-Brown [Reference Heath-Brown11], we can at least show for
$k=2$
, then we could unconditionally improve on these zero-density estimates. Following the method of Heath-Brown [Reference Heath-Brown11], we can at least show for
![]() $\mathcal {F}=\mathcal {O}_r$
that
$\mathcal {F}=\mathcal {O}_r$
that
which is sharp in the Q-aspect, but unfortunately not in the T-aspect. Nonetheless, we can use (1.6) to improve on (1.2), (1.3), (1.4) and (1.5) in the Q-aspect. Indeed, in [Reference Corrigan5, Reference Corrigan and Zhao7] we used (1.6) to show that
 $$ \begin{align} \sum_{\chi\in\mathcal{O}_2(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon\min((Q^3T^4)^{(1-\sigma)/(2-\sigma)},(QT)^{(3-3\sigma)/\sigma}). \end{align} $$
$$ \begin{align} \sum_{\chi\in\mathcal{O}_2(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon\min((Q^3T^4)^{(1-\sigma)/(2-\sigma)},(QT)^{(3-3\sigma)/\sigma}). \end{align} $$
Our results in [Reference Corrigan5, Reference Corrigan and Zhao7] for
![]() $\mathcal {O}_3$
and
$\mathcal {O}_3$
and
![]() $\mathcal {O}_4$
can be improved by showing that Theorem 2.2 therein still holds under a weaker assumption on the relevant large sieve inequality, as in Lemma 3.1 below. Indeed, under this weaker assumption, we can strengthen the estimates in [Reference Corrigan and Zhao7] to
$\mathcal {O}_4$
can be improved by showing that Theorem 2.2 therein still holds under a weaker assumption on the relevant large sieve inequality, as in Lemma 3.1 below. Indeed, under this weaker assumption, we can strengthen the estimates in [Reference Corrigan and Zhao7] to
 $$ \begin{align} & \sum_{\chi\in\mathcal{O}_3(Q)}N(\sigma,T,\chi)\notag \\ & \quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(16-10\sigma)/9}T^{(4-4\sigma)/(2-\sigma)},Q^{(13-13\sigma)/(6-3\sigma)}T^{(4-4\sigma)/(2-\sigma)},(QT)^{(3-3\sigma)/\sigma}) \end{align} $$
$$ \begin{align} & \sum_{\chi\in\mathcal{O}_3(Q)}N(\sigma,T,\chi)\notag \\ & \quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(16-10\sigma)/9}T^{(4-4\sigma)/(2-\sigma)},Q^{(13-13\sigma)/(6-3\sigma)}T^{(4-4\sigma)/(2-\sigma)},(QT)^{(3-3\sigma)/\sigma}) \end{align} $$
for
![]() $T^3\gg Q^2$
, and
$T^3\gg Q^2$
, and
 $$ \begin{align} \sum_{\chi\in\mathcal{O}_4(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(5-3\sigma)/3}T^{(4-4\sigma)/(2-\sigma)},(QT)^{(4-4\sigma)/(2-\sigma)},(QT)^{(3-3\sigma)/\sigma}), \end{align} $$
$$ \begin{align} \sum_{\chi\in\mathcal{O}_4(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(5-3\sigma)/3}T^{(4-4\sigma)/(2-\sigma)},(QT)^{(4-4\sigma)/(2-\sigma)},(QT)^{(3-3\sigma)/\sigma}), \end{align} $$
for
![]() $T^2\gg Q$
. Again, using Theorem 1.6 of [Reference Balestrieri and Rome2], we can add to these the result
$T^2\gg Q$
. Again, using Theorem 1.6 of [Reference Balestrieri and Rome2], we can add to these the result
 $$ \begin{align} & \sum_{\chi\in\mathcal{O}_r(Q)}N(\sigma,T,\chi) \notag \\ &\quad \mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(6-4\sigma)/3}T^{(4-4\sigma)/(2-\sigma)},Q^{(5-5\sigma)/(2-\sigma)}T^{(4-4\sigma)/(2-\sigma)},(QT)^{(3-3\sigma)/\sigma}), \end{align} $$
$$ \begin{align} & \sum_{\chi\in\mathcal{O}_r(Q)}N(\sigma,T,\chi) \notag \\ &\quad \mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(6-4\sigma)/3}T^{(4-4\sigma)/(2-\sigma)},Q^{(5-5\sigma)/(2-\sigma)}T^{(4-4\sigma)/(2-\sigma)},(QT)^{(3-3\sigma)/\sigma}), \end{align} $$
which is valid for
![]() $T\gg Q$
. These estimates all improve in the Q-aspect on the corresponding estimates obtained using (1.1). In general, a sharp bound for
$T\gg Q$
. These estimates all improve in the Q-aspect on the corresponding estimates obtained using (1.1). In general, a sharp bound for
![]() $\mathfrak {L}_{k+1}(Q,T)$
will always lead to a stronger zero-density result than a sharp bound for
$\mathfrak {L}_{k+1}(Q,T)$
will always lead to a stronger zero-density result than a sharp bound for
![]() $\mathfrak {L}_k(Q,T)$
. To derive our main results, we consider bounds on
$\mathfrak {L}_k(Q,T)$
. To derive our main results, we consider bounds on
![]() $\mathfrak {L}_k(Q,T)$
when k is arbitrarily large.
$\mathfrak {L}_k(Q,T)$
when k is arbitrarily large.
2 Statement of results
Unfortunately, no sharp upper bounds have been established for
![]() $\mathfrak {L}_k(Q,T)$
when
$\mathfrak {L}_k(Q,T)$
when
![]() $k>2$
. In [Reference Corrigan6] we adapted the method of Heath-Brown [Reference Heath-Brown11] to show that
$k>2$
. In [Reference Corrigan6] we adapted the method of Heath-Brown [Reference Heath-Brown11] to show that
![]() $\mathfrak {L}_k(Q,T)\ll _\varepsilon (QT)^{k/2+\varepsilon }$
, though we can obtain a better result from a much more trivial approach. Indeed, Petrow and Young [Reference Petrow and Young16, Reference Petrow and Young17] showed that the Weyl bound
$\mathfrak {L}_k(Q,T)\ll _\varepsilon (QT)^{k/2+\varepsilon }$
, though we can obtain a better result from a much more trivial approach. Indeed, Petrow and Young [Reference Petrow and Young16, Reference Petrow and Young17] showed that the Weyl bound
holds for any Dirichlet character
![]() $\chi $
modulo q, from which we derive the trivial bound
$\chi $
modulo q, from which we derive the trivial bound
Using (2.2) to estimate
![]() $\mathfrak {L}_k(Q,T)$
for arbitrarily large k in the method of Montgomery, we derive the following result.
$\mathfrak {L}_k(Q,T)$
for arbitrarily large k in the method of Montgomery, we derive the following result.
Theorem 2.1. For any
![]() $Q,T\geqslant 2$
,
$Q,T\geqslant 2$
,
 $$ \begin{align*} \sum_{\chi\in\mathcal{O}_2(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon\min((QT)^{(8-8\sigma)/3},(Q^8T^5)^{(1-\sigma)/(6\sigma-3)}), \end{align*} $$
$$ \begin{align*} \sum_{\chi\in\mathcal{O}_2(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon\min((QT)^{(8-8\sigma)/3},(Q^8T^5)^{(1-\sigma)/(6\sigma-3)}), \end{align*} $$
where
![]() $\sigma \in (\tfrac {1}{2},1)$
.
$\sigma \in (\tfrac {1}{2},1)$
.
The above is stronger than (1.7) in the Q-aspect when
![]() $\sigma>\tfrac {7}{8}$
, and stronger in the T-aspect for all
$\sigma>\tfrac {7}{8}$
, and stronger in the T-aspect for all
![]() $\sigma>\tfrac {1}{2}$
. Additionally, it improves on (1.2) precisely when
$\sigma>\tfrac {1}{2}$
. Additionally, it improves on (1.2) precisely when
![]() $\sigma>\tfrac {3}{4}$
. Using the same method as is used to prove Theorem 2.1, we can show that the density conjecture
$\sigma>\tfrac {3}{4}$
. Using the same method as is used to prove Theorem 2.1, we can show that the density conjecture
 $$ \begin{align} \sum_{\chi\in\mathcal{O}_2(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(QT)^{2(1-\sigma)+\varepsilon} \end{align} $$
$$ \begin{align} \sum_{\chi\in\mathcal{O}_2(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(QT)^{2(1-\sigma)+\varepsilon} \end{align} $$
is a consequence of the Lindelöf hypothesis for L-functions with real characters.
For cubic characters, we have the following analogue of Theorem 2.1.
Theorem 2.2. For any
![]() $Q,T\geqslant 2$
,
$Q,T\geqslant 2$
,
 $$ \begin{align*} &\sum_{\chi\in\mathcal{O}_3(Q)} N(\sigma,T,\chi)\\ & \quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(22-16\sigma)/9}T^{(8-8\sigma)/3},Q^{4-4\sigma}T^{(8-8\sigma)/3},(Q^8T^5)^{(1-\sigma)/(6\sigma-3)}), \end{align*} $$
$$ \begin{align*} &\sum_{\chi\in\mathcal{O}_3(Q)} N(\sigma,T,\chi)\\ & \quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(22-16\sigma)/9}T^{(8-8\sigma)/3},Q^{4-4\sigma}T^{(8-8\sigma)/3},(Q^8T^5)^{(1-\sigma)/(6\sigma-3)}), \end{align*} $$
where
![]() $\sigma \in (\tfrac {1}{2},1)$
. Furthermore, this result holds if
$\sigma \in (\tfrac {1}{2},1)$
. Furthermore, this result holds if
![]() $\mathcal {O}_3$
is replaced by
$\mathcal {O}_3$
is replaced by
![]() $\mathcal {O}_6$
.
$\mathcal {O}_6$
.
The immediate advantage of the above result, as compared to (1.3) and (1.8), is that there is no restriction on the relation between Q and T. Additionally, Theorem 2.2 is stronger than (1.3) in the Q-aspect when
![]() $\sigma>\tfrac {5}{6}$
and in the T-aspect when
$\sigma>\tfrac {5}{6}$
and in the T-aspect when
![]() $\sigma>\tfrac {3}{4}$
, and stronger than (1.8) in the Q-aspect when
$\sigma>\tfrac {3}{4}$
, and stronger than (1.8) in the Q-aspect when
![]() $\sigma>\tfrac {9}{10}$
and in the T-aspect for all
$\sigma>\tfrac {9}{10}$
and in the T-aspect for all
![]() $\sigma>\tfrac {1}{2}$
. The fact that Theorem 2.2 holds for
$\sigma>\tfrac {1}{2}$
. The fact that Theorem 2.2 holds for
![]() $\mathcal {O}_6$
as well as
$\mathcal {O}_6$
as well as
![]() $\mathcal {O}_3$
is a direct result of Theorem 1.5 of [Reference Baier and Young1]. For
$\mathcal {O}_3$
is a direct result of Theorem 1.5 of [Reference Baier and Young1]. For
![]() $\mathcal {O}_4$
, we derive the following slightly stronger result.
$\mathcal {O}_4$
, we derive the following slightly stronger result.
Theorem 2.3. For any
![]() $Q,T\geqslant 2$
,
$Q,T\geqslant 2$
,
 $$ \begin{align*} &\sum_{\chi\in\mathcal{O}_4(Q)} N(\sigma,T,\chi) \\ &\quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(7-5\sigma)/3}T^{(8-8\sigma)/3},Q^{(11-11\sigma)/3}T^{(8-8\sigma)/3},(Q^8T^5)^{(1-\sigma)/(6\sigma-3)}), \end{align*} $$
$$ \begin{align*} &\sum_{\chi\in\mathcal{O}_4(Q)} N(\sigma,T,\chi) \\ &\quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(7-5\sigma)/3}T^{(8-8\sigma)/3},Q^{(11-11\sigma)/3}T^{(8-8\sigma)/3},(Q^8T^5)^{(1-\sigma)/(6\sigma-3)}), \end{align*} $$
where
![]() $\sigma \in (\tfrac {1}{2},1)$
.
$\sigma \in (\tfrac {1}{2},1)$
.
This improves the Q-aspect of (1.4) whenever
![]() $\sigma>\tfrac {9}{11}$
and (1.9) whenever
$\sigma>\tfrac {9}{11}$
and (1.9) whenever
![]() $\sigma>\tfrac {9}{10}$
. In the T-aspect, improvements are made in the same regions as with Theorems 2.1 and 2.2. Similarly, we have the following result.
$\sigma>\tfrac {9}{10}$
. In the T-aspect, improvements are made in the same regions as with Theorems 2.1 and 2.2. Similarly, we have the following result.
Theorem 2.4. For any
![]() $Q,T\geqslant 2$
and any integer
$Q,T\geqslant 2$
and any integer
![]() $r\geqslant 2$
,
$r\geqslant 2$
,
 $$ \begin{align*} &\sum_{\chi\in\mathcal{O}_r(Q)} N(\sigma,T,\chi) \\ &\quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(8-6\sigma)/3}T^{(8-8\sigma)/3},Q^{(14-14\sigma)/3}T^{(8-8\sigma)/3},(Q^8T^5)^{(1-\sigma)/(6\sigma-3)}), \end{align*} $$
$$ \begin{align*} &\sum_{\chi\in\mathcal{O}_r(Q)} N(\sigma,T,\chi) \\ &\quad\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon\min(Q^{(8-6\sigma)/3}T^{(8-8\sigma)/3},Q^{(14-14\sigma)/3}T^{(8-8\sigma)/3},(Q^8T^5)^{(1-\sigma)/(6\sigma-3)}), \end{align*} $$
where
![]() $\sigma \in (\tfrac {1}{2},1)$
.
$\sigma \in (\tfrac {1}{2},1)$
.
In the Q-aspect, this improves on (1.5) when
![]() $\sigma>\tfrac {5}{6}$
and on (1.10) when
$\sigma>\tfrac {5}{6}$
and on (1.10) when
![]() $\sigma>\tfrac {9}{10}$
.
$\sigma>\tfrac {9}{10}$
.
Remark 2.5. The reason for Theorem 2.1 containing the minimum of two quantities, as opposed to the minima of three quantities in Theorems 2.2, 2.3 and 2.4, essentially comes down to the fact that the available large sieve inequality for
![]() $\mathcal {O}_2$
is optimal, whereas this is not the case for
$\mathcal {O}_2$
is optimal, whereas this is not the case for
![]() $\mathcal {O}_r$
when
$\mathcal {O}_r$
when
![]() $r>2$
. The available large sieve inequalities for
$r>2$
. The available large sieve inequalities for
![]() $\mathcal {O}_r$
with
$\mathcal {O}_r$
with
![]() $r>2$
are given as minima of four quantities, two of which are used in the proofs of the last three theorems above. Note, however, that the last term in the minima of the above results is derived using the large-moduli approach of Montgomery (see [Reference Corrigan5, Theorem 3.1.3]), and as a result is independent of the large sieve inequalities (see (4.5) below).
$r>2$
are given as minima of four quantities, two of which are used in the proofs of the last three theorems above. Note, however, that the last term in the minima of the above results is derived using the large-moduli approach of Montgomery (see [Reference Corrigan5, Theorem 3.1.3]), and as a result is independent of the large sieve inequalities (see (4.5) below).
3 Lemmas
In this section we present the prerequisites in terms of an arbitrary family
![]() $\mathcal {F}$
of primitive Dirichlet characters. To estimate
$\mathcal {F}$
of primitive Dirichlet characters. To estimate
![]() $\mathfrak {S}_1(Q,T)$
, we consider the polynomials
$\mathfrak {S}_1(Q,T)$
, we consider the polynomials
![]() $\Delta (Q,T,N)$
such that
$\Delta (Q,T,N)$
such that
 $$ \begin{align*} \mathfrak{S}_1(Q,T)\mathop{\:\ll\:}_\varepsilon(QN)^\varepsilon\Delta(Q,T,N)\mathop{\sum\nolimits^{{\prime}}}_{n\leqslant N}|a_n|^2 \end{align*} $$
$$ \begin{align*} \mathfrak{S}_1(Q,T)\mathop{\:\ll\:}_\varepsilon(QN)^\varepsilon\Delta(Q,T,N)\mathop{\sum\nolimits^{{\prime}}}_{n\leqslant N}|a_n|^2 \end{align*} $$
for all
![]() $Q,T,N\geqslant 2$
and any sequence
$Q,T,N\geqslant 2$
and any sequence
![]() $(a_n)_{n\leqslant N}$
of complex numbers. In practice, a bound for
$(a_n)_{n\leqslant N}$
of complex numbers. In practice, a bound for
![]() $\Delta (Q,T,N)$
can easily be obtained from the corresponding large sieve estimate, as in [Reference Corrigan5]. The method of Montgomery can then be summarised in the following two results.
$\Delta (Q,T,N)$
can easily be obtained from the corresponding large sieve estimate, as in [Reference Corrigan5]. The method of Montgomery can then be summarised in the following two results.
Lemma 3.1. Suppose that
![]() $X,Y\geqslant 2$
are such that
$X,Y\geqslant 2$
are such that
![]() $X\ll Y\ll (QT)^A$
for some absolute constant A. Then
$X\ll Y\ll (QT)^A$
for some absolute constant A. Then
 $$ \begin{align*} & \sum_{\chi\in\mathcal{F}(Q)}N(\sigma,T,\chi) \\ &\quad\!\!\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon((\mathfrak{L}_k(Q,T)\Delta(Q,T,X)^kY^{k(1-2\sigma)})^{1/(k+1)}+\Delta(Q,T,X)X^{1-2\sigma}\kern1.3pt{+}\kern1.3pt\Delta(Q,T,Y)Y^{1-2\sigma}) \end{align*} $$
$$ \begin{align*} & \sum_{\chi\in\mathcal{F}(Q)}N(\sigma,T,\chi) \\ &\quad\!\!\mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon((\mathfrak{L}_k(Q,T)\Delta(Q,T,X)^kY^{k(1-2\sigma)})^{1/(k+1)}+\Delta(Q,T,X)X^{1-2\sigma}\kern1.3pt{+}\kern1.3pt\Delta(Q,T,Y)Y^{1-2\sigma}) \end{align*} $$
for any
![]() $k\geqslant 1$
, where the implied constant does not depend on k.
$k\geqslant 1$
, where the implied constant does not depend on k.
Proof. We demonstrated the case
![]() $k=1$
in [Reference Corrigan6]. The remaining cases follow similarly, by using Hölder’s inequality to derive the estimate
$k=1$
in [Reference Corrigan6]. The remaining cases follow similarly, by using Hölder’s inequality to derive the estimate
 $$ \begin{align*} &\#\mathcal{R}_2\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon Y^{k(1-2\sigma)/(k+1)}\\ &\quad\times\bigg(\sum_{(\varrho,\chi)\in\mathcal{R}_2}|M_X(\tfrac{1}{2}+it_\varrho,\chi)|^2\bigg)^{k/(k+1)} \bigg(\sum_{(\varrho,\chi)\in\mathcal{R}_2}|L(\tfrac{1}{2}+it_\varrho,\chi)|^{2k}\bigg)^{1/(k+1)}, \end{align*} $$
$$ \begin{align*} &\#\mathcal{R}_2\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon Y^{k(1-2\sigma)/(k+1)}\\ &\quad\times\bigg(\sum_{(\varrho,\chi)\in\mathcal{R}_2}|M_X(\tfrac{1}{2}+it_\varrho,\chi)|^2\bigg)^{k/(k+1)} \bigg(\sum_{(\varrho,\chi)\in\mathcal{R}_2}|L(\tfrac{1}{2}+it_\varrho,\chi)|^{2k}\bigg)^{1/(k+1)}, \end{align*} $$
where
![]() $\mathcal {R}_2$
is as defined in [Reference Corrigan6].
$\mathcal {R}_2$
is as defined in [Reference Corrigan6].
Lemma 3.2. For any
![]() $Q,T\geqslant 2$
,
$Q,T\geqslant 2$
,
 $$ \begin{align*} \sum_{\chi\in\mathcal{F}(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon((\mathfrak{L}_k(Q,T)^2Q^{2k}T^k)^{(1-\sigma)/(2-k+\sigma(2k-2))}+(Q^2T)^{(1-\sigma)/(2\sigma-1)}) \end{align*} $$
$$ \begin{align*} \sum_{\chi\in\mathcal{F}(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon((\mathfrak{L}_k(Q,T)^2Q^{2k}T^k)^{(1-\sigma)/(2-k+\sigma(2k-2))}+(Q^2T)^{(1-\sigma)/(2\sigma-1)}) \end{align*} $$
for any
![]() $k\geqslant 1$
, where the implied constant does not depend on k.
$k\geqslant 1$
, where the implied constant does not depend on k.
Proof. The case
![]() $k=1$
is shown in [Reference Corrigan6]. The remaining cases follow similarly using the estimate
$k=1$
is shown in [Reference Corrigan6]. The remaining cases follow similarly using the estimate
to derive a bound for
![]() $\#\mathcal {R}_2$
, where
$\#\mathcal {R}_2$
, where
![]() $\mathcal {R}_2$
is defined as in [Reference Corrigan6].
$\mathcal {R}_2$
is defined as in [Reference Corrigan6].
In this paper, we consider the case where k is taken arbitrarily large. The above lemmas are used to derive the following two results, from which our main results follow.
Lemma 3.3. Suppose that
![]() $\eta ,\vartheta \geqslant 0$
are constants such that the bound
$\eta ,\vartheta \geqslant 0$
are constants such that the bound
holds for all
![]() $\chi \in \mathcal {F}$
, where q is the conductor of
$\chi \in \mathcal {F}$
, where q is the conductor of
![]() $\chi $
. Then for any
$\chi $
. Then for any
![]() $Q,T\geqslant 2$
,
$Q,T\geqslant 2$
,
 $$ \begin{align*} &\sum_{\chi\in\mathcal{F}(Q)} N(\sigma,T,\chi) \\ &\quad \mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon(Q^{2\eta} T^{2\vartheta}\Delta(Q,T,X)Y^{1-2\sigma}+\Delta(Q,T,X)X^{1-2\sigma}+\Delta(Q,T,Y)Y^{1-2\sigma}), \end{align*} $$
$$ \begin{align*} &\sum_{\chi\in\mathcal{F}(Q)} N(\sigma,T,\chi) \\ &\quad \mathop{\:\ll\:}_\varepsilon (QT)^\varepsilon(Q^{2\eta} T^{2\vartheta}\Delta(Q,T,X)Y^{1-2\sigma}+\Delta(Q,T,X)X^{1-2\sigma}+\Delta(Q,T,Y)Y^{1-2\sigma}), \end{align*} $$
where
![]() $X,Y\geqslant 2$
are as in Lemma 3.1.
$X,Y\geqslant 2$
are as in Lemma 3.1.
Proof. Using the trivial bound
![]() $\#\mathcal {F}(Q)\ll Q^2$
and integrating trivially over
$\#\mathcal {F}(Q)\ll Q^2$
and integrating trivially over
![]() ${t\in [-T,T]}$
, the hypothesis gives
${t\in [-T,T]}$
, the hypothesis gives
for any integer
![]() $k\geqslant 1$
. Consequently,
$k\geqslant 1$
. Consequently,
 $$ \begin{align*} &\mathfrak{L}_k(Q,T)^{1/(k+1)} \Delta(Q,T,X)^{k/(k+1)} Y^{k(1-2\sigma)/(k+1)} \\ &\quad\mathop{\:\ll\:}_\varepsilon (QT)^{(A+2)/(k+1)+\varepsilon}Q^{2\eta} T^{2\vartheta}\Delta(Q,T,X)Y^{1-2\sigma}, \end{align*} $$
$$ \begin{align*} &\mathfrak{L}_k(Q,T)^{1/(k+1)} \Delta(Q,T,X)^{k/(k+1)} Y^{k(1-2\sigma)/(k+1)} \\ &\quad\mathop{\:\ll\:}_\varepsilon (QT)^{(A+2)/(k+1)+\varepsilon}Q^{2\eta} T^{2\vartheta}\Delta(Q,T,X)Y^{1-2\sigma}, \end{align*} $$
where A is as in Lemma 3.1. As the implied constant does not depend on k, we may take k to be sufficiently large that
![]() $(A+2)/(k+1)\leqslant \varepsilon $
. The result then follows by Lemma 3.1.
$(A+2)/(k+1)\leqslant \varepsilon $
. The result then follows by Lemma 3.1.
Lemma 3.4. Let
![]() $\eta ,\vartheta \geqslant 0$
be as in Lemma 3.3 and suppose that
$\eta ,\vartheta \geqslant 0$
be as in Lemma 3.3 and suppose that
![]() $Q,T\geqslant 2$
. Then
$Q,T\geqslant 2$
. Then
 $$ \begin{align*} \sum_{\chi\in\mathcal{F}(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(Q^{2+4\eta}T^{1+4\vartheta})^{(1-\sigma)/(2\sigma-1)+\varepsilon} \end{align*} $$
$$ \begin{align*} \sum_{\chi\in\mathcal{F}(Q)}N(\sigma,T,\chi)\mathop{\:\ll\:}_\varepsilon(Q^{2+4\eta}T^{1+4\vartheta})^{(1-\sigma)/(2\sigma-1)+\varepsilon} \end{align*} $$
whenever
![]() $\sigma \geqslant \tfrac {1}{2}+\varepsilon $
.
$\sigma \geqslant \tfrac {1}{2}+\varepsilon $
.
4 Proof of the main results
To derive our main results from the above lemmas, we will employ the Weyl bound (2.1). Note that the last term in the minima of the theorems follows by taking
![]() $(\eta ,\vartheta )=(\tfrac {1}{6},\tfrac {1}{6})$
in Lemma 3.4, and thus it suffices to use Lemma 3.3 to prove the remaining terms.
$(\eta ,\vartheta )=(\tfrac {1}{6},\tfrac {1}{6})$
in Lemma 3.4, and thus it suffices to use Lemma 3.3 to prove the remaining terms.
Proof of Theorem 2.1.
As in [Reference Corrigan6, Reference Corrigan and Zhao7], we can deduce by Corollary 1 of [Reference Heath-Brown11] that
For appropriate
![]() $\eta ,\vartheta \geqslant 0$
, Lemma 3.3 then gives
$\eta ,\vartheta \geqslant 0$
, Lemma 3.3 then gives
 $$ \begin{align} \sum_{\chi\in\mathcal{O}_2(Q)}N(\sigma,T,\chi)&\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon(Q^{2\eta} T^{2\vartheta}(QT+X)Y^{1-2\sigma}+QTX^{1-2\sigma}+Y^{2-2\sigma})\notag\\ &\mathop{\:\ll\:}_\varepsilon Q^{(2+4\eta)(1-\sigma)+\varepsilon}T^{(2+4\vartheta)(1-\sigma)+\varepsilon} \end{align} $$
$$ \begin{align} \sum_{\chi\in\mathcal{O}_2(Q)}N(\sigma,T,\chi)&\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon(Q^{2\eta} T^{2\vartheta}(QT+X)Y^{1-2\sigma}+QTX^{1-2\sigma}+Y^{2-2\sigma})\notag\\ &\mathop{\:\ll\:}_\varepsilon Q^{(2+4\eta)(1-\sigma)+\varepsilon}T^{(2+4\vartheta)(1-\sigma)+\varepsilon} \end{align} $$
on taking
![]() $X=QT$
and
$X=QT$
and
![]() $Y=Q^{1+2\eta }T^{1+2\vartheta }$
, from which the assertion follows on taking
$Y=Q^{1+2\eta }T^{1+2\vartheta }$
, from which the assertion follows on taking
![]() $(\eta ,\vartheta )=(\tfrac {1}{6},\tfrac {1}{6})$
.
$(\eta ,\vartheta )=(\tfrac {1}{6},\tfrac {1}{6})$
.
Proof of Theorem 2.2.
As in [Reference Corrigan6, Reference Corrigan and Zhao7], we can show using Theorem 1.4 of [Reference Baier and Young1] that
By Lemma 3.3, we see for appropriate
![]() $\eta ,\vartheta \geqslant 0$
that
$\eta ,\vartheta \geqslant 0$
that
 $$ \begin{align} \sum_{\chi\in\mathcal{O}_3(Q)}N(\sigma,T,\chi)&\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon(Q^{2\eta} T^{2\vartheta} \min(Q^{5/3}T+X,Q^{11/9}T+Q^{2/3}X)Y^{1-2\sigma} \notag \\ &\quad+\min(Q^{5/3}TX^{1-2\sigma}+Y^{2-2\sigma}, Q^{11/9}TX^{1-2\sigma}+Q^{2/3}Y^{2-2\sigma})) \notag\\ &\mathop{\:\ll\:}_\varepsilon\min(Q^{(10/3+4\eta)(1-\sigma)+\varepsilon},Q^{2/3+(10/9+4\eta)(1-\sigma)+\varepsilon})T^{(2+4\vartheta)(1-\sigma)+\varepsilon}, \end{align} $$
$$ \begin{align} \sum_{\chi\in\mathcal{O}_3(Q)}N(\sigma,T,\chi)&\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon(Q^{2\eta} T^{2\vartheta} \min(Q^{5/3}T+X,Q^{11/9}T+Q^{2/3}X)Y^{1-2\sigma} \notag \\ &\quad+\min(Q^{5/3}TX^{1-2\sigma}+Y^{2-2\sigma}, Q^{11/9}TX^{1-2\sigma}+Q^{2/3}Y^{2-2\sigma})) \notag\\ &\mathop{\:\ll\:}_\varepsilon\min(Q^{(10/3+4\eta)(1-\sigma)+\varepsilon},Q^{2/3+(10/9+4\eta)(1-\sigma)+\varepsilon})T^{(2+4\vartheta)(1-\sigma)+\varepsilon}, \end{align} $$
where in the first term of the minimum we have taken
and in the second we have taken
The desired result follows from taking
![]() $(\eta ,\vartheta )=(\tfrac {1}{6},\tfrac {1}{6})$
in (4.2).
$(\eta ,\vartheta )=(\tfrac {1}{6},\tfrac {1}{6})$
in (4.2).
Proof of Theorem 2.3.
As in [Reference Corrigan6, Reference Corrigan and Zhao7], Lemma 2.10 of [Reference Gao and Zhao9] can be used to show that
Then, by Lemma 3.3, for appropriate
![]() $\eta ,\vartheta \geqslant 0$
,
$\eta ,\vartheta \geqslant 0$
,
 $$ \begin{align} \sum_{\chi\in\mathcal{O}_4(Q)}N(\sigma,T,\chi)&\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon(Q^{2\eta} T^{2\vartheta} \min(Q^{3/2}T+X,Q^{7/6}T+Q^{2/3}X)Y^{1-2\sigma} \notag\\ &\quad +\min(Q^{3/2}TX^{1-2\sigma}+Y^{2-2\sigma}, Q^{7/6}TX^{1-2\sigma}+Q^{2/3}Y^{2-2\sigma}))\notag \\ &\mathop{\:\ll\:}_\varepsilon\min(Q^{(3+4\eta)(1-\sigma)+\varepsilon},Q^{2/3+(1+4\eta)(1-\sigma)+\varepsilon})T^{(2+4\vartheta)(1-\sigma)+\varepsilon}, \end{align} $$
$$ \begin{align} \sum_{\chi\in\mathcal{O}_4(Q)}N(\sigma,T,\chi)&\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon(Q^{2\eta} T^{2\vartheta} \min(Q^{3/2}T+X,Q^{7/6}T+Q^{2/3}X)Y^{1-2\sigma} \notag\\ &\quad +\min(Q^{3/2}TX^{1-2\sigma}+Y^{2-2\sigma}, Q^{7/6}TX^{1-2\sigma}+Q^{2/3}Y^{2-2\sigma}))\notag \\ &\mathop{\:\ll\:}_\varepsilon\min(Q^{(3+4\eta)(1-\sigma)+\varepsilon},Q^{2/3+(1+4\eta)(1-\sigma)+\varepsilon})T^{(2+4\vartheta)(1-\sigma)+\varepsilon}, \end{align} $$
where in the first term of the minimum we have taken
and in the second we have taken
The assertion then follows from taking
![]() $(\eta ,\vartheta )=(\tfrac {1}{6},\tfrac {1}{6})$
in (4.3).
$(\eta ,\vartheta )=(\tfrac {1}{6},\tfrac {1}{6})$
in (4.3).
Proof of Theorem 2.4.
It follows from Theorem 1.6 of [Reference Balestrieri and Rome2] that
Then, by Lemma 3.3, for appropriate
![]() $\eta ,\vartheta \geqslant 0$
,
$\eta ,\vartheta \geqslant 0$
,
 $$ \begin{align} \sum_{\chi\in\mathcal{O}_4(Q)}N(\sigma,T,\chi)&\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon(Q^{2\eta} T^{2\vartheta}\min(Q^2T+X,Q^{4/3}T+Q^{2/3}X)Y^{1-2\sigma} \notag\\ &\quad +\min(Q^2TX^{1-2\sigma}+Y^{2-2\sigma}, Q^{4/3}TX^{1-2\sigma}+Q^{2/3}Y^{2-2\sigma})) \notag\\ &\mathop{\:\ll\:}_\varepsilon\min(Q^{(4+4\eta)(1-\sigma)+\varepsilon},Q^{2/3+(4/3+4\eta)(1-\sigma)+\varepsilon})T^{(2+4\vartheta)(1-\sigma)+\varepsilon}, \end{align} $$
$$ \begin{align} \sum_{\chi\in\mathcal{O}_4(Q)}N(\sigma,T,\chi)&\mathop{\:\ll\:}_\varepsilon(QT)^\varepsilon(Q^{2\eta} T^{2\vartheta}\min(Q^2T+X,Q^{4/3}T+Q^{2/3}X)Y^{1-2\sigma} \notag\\ &\quad +\min(Q^2TX^{1-2\sigma}+Y^{2-2\sigma}, Q^{4/3}TX^{1-2\sigma}+Q^{2/3}Y^{2-2\sigma})) \notag\\ &\mathop{\:\ll\:}_\varepsilon\min(Q^{(4+4\eta)(1-\sigma)+\varepsilon},Q^{2/3+(4/3+4\eta)(1-\sigma)+\varepsilon})T^{(2+4\vartheta)(1-\sigma)+\varepsilon}, \end{align} $$
where in the first term of the minimum we have taken
and in the second we have taken
The proof is complete on taking
![]() $(\eta ,\vartheta )=(\tfrac {1}{6},\tfrac {1}{6})$
in (4.4).
$(\eta ,\vartheta )=(\tfrac {1}{6},\tfrac {1}{6})$
in (4.4).
It is clear from (4.1) how the density conjecture for real characters (2.3) follows from the Lindelöf hypothesis. However, an analogous result of the same strength cannot be established for
![]() $\mathcal {O}_3$
,
$\mathcal {O}_3$
,
![]() $\mathcal {O}_4$
or
$\mathcal {O}_4$
or
![]() $\mathcal {O}_r$
using (4.2), (4.3) or (4.4), respectively. Additionally, it is clear that the bound derived from Lemma 3.4 has no dependence on the character family
$\mathcal {O}_r$
using (4.2), (4.3) or (4.4), respectively. Additionally, it is clear that the bound derived from Lemma 3.4 has no dependence on the character family
![]() $\mathcal {F}$
. Indeed, using the above method, we can show that
$\mathcal {F}$
. Indeed, using the above method, we can show that
 $$ \begin{align} \sum_{q\leqslant Q}\mathop{\sum\nolimits^{*}}_{\chi\bmod{q}}N(\sigma,T,\chi)\ll(QT)^\varepsilon\min(Q^{(14-14\sigma)/3}T^{(8-8\sigma)/3},Q^{(8-8\sigma)/(6\sigma-3)}T^{(5-5\sigma)/(6\sigma-3)}), \end{align} $$
$$ \begin{align} \sum_{q\leqslant Q}\mathop{\sum\nolimits^{*}}_{\chi\bmod{q}}N(\sigma,T,\chi)\ll(QT)^\varepsilon\min(Q^{(14-14\sigma)/3}T^{(8-8\sigma)/3},Q^{(8-8\sigma)/(6\sigma-3)}T^{(5-5\sigma)/(6\sigma-3)}), \end{align} $$
which improves on Theorem 12.2 of [Reference Montgomery14], and confirms the density conjecture for
![]() $\sigma>\frac {11}{12}$
. Heath-Brown [Reference Heath-Brown10], however, was able to show that the density conjecture holds in the larger range
$\sigma>\frac {11}{12}$
. Heath-Brown [Reference Heath-Brown10], however, was able to show that the density conjecture holds in the larger range
![]() $\sigma>\tfrac {11}{14}$
.
$\sigma>\tfrac {11}{14}$
.
Acknowledgements
The author would like to thank the University of New South Wales for access to some of the resources that were necessary to complete this paper, as well as the Commonwealth of Australia for its support through an Australian Government Research Training Program Scholarship. Thanks are also given to Dr. Liangyi Zhao who brought the article [Reference Balestrieri and Rome2] to the author’s attention, and to the referee for the comprehensive review of the original draft.