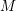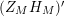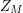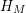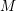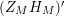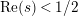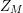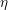Article
LOCAL COHOMOLOGY OF MULTI-REES ALGEBRAS, JOINT REDUCTION NUMBERS AND PRODUCT OF COMPLETE IDEALS
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2016, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
ON THE DISTRIBUTION OF ZEROS OF THE DERIVATIVE OF SELBERG’S ZETA FUNCTION ASSOCIATED TO FINITE VOLUME RIEMANN SURFACES
-
- Published online by Cambridge University Press:
- 14 December 2016, pp. 21-71
-
- Article
-
- You have access
- HTML
- Export citation
ON COMPONENTS OF STABLE AUSLANDER–REITEN QUIVERS THAT CONTAIN HELLER LATTICES: THE CASE OF TRUNCATED POLYNOMIAL RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2016, pp. 72-113
-
- Article
-
- You have access
- HTML
- Export citation
A VANISHING THEOREM FOR THE
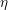 $\unicode[STIX]{x1D702}$-INVARIANT AND HURWITZ GROUPS
$\unicode[STIX]{x1D702}$-INVARIANT AND HURWITZ GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 20 October 2016, pp. 114-123
-
- Article
-
- You have access
- HTML
- Export citation
ELLIPTIC K3 SURFACES ASSOCIATED WITH THE PRODUCT OF TWO ELLIPTIC CURVES: MORDELL–WEIL LATTICES AND THEIR FIELDS OF DEFINITION
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2016, pp. 124-185
-
- Article
-
- You have access
- HTML
- Export citation
WEIGHT CHANGING OPERATORS FOR AUTOMORPHIC FORMS ON GRASSMANNIANS AND DIFFERENTIAL PROPERTIES OF CERTAIN THETA LIFTS
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2016, pp. 186-221
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
NMJ volume 228 Cover and Front matter
-
- Published online by Cambridge University Press:
- 08 November 2017, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
NMJ volume 228 Cover and Back matter
-
- Published online by Cambridge University Press:
- 08 November 2017, pp. b1-b3
-
- Article
-
- You have access
- Export citation