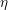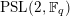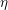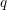1 Introduction
The
![]() $\unicode[STIX]{x1D702}$
-invariant of the signature operator for an oriented closed Riemannian
$\unicode[STIX]{x1D702}$
-invariant of the signature operator for an oriented closed Riemannian
![]() $3$
-manifold was introduced by Atiyah, Patodi and Singer in [Reference Atiyah, Patodi and Singer2]. It can be regarded as the correction term of the Hirzebruch signature theorem when one applies it to a
$3$
-manifold was introduced by Atiyah, Patodi and Singer in [Reference Atiyah, Patodi and Singer2]. It can be regarded as the correction term of the Hirzebruch signature theorem when one applies it to a
![]() $4$
-manifold with boundary. Namely the
$4$
-manifold with boundary. Namely the
![]() $\unicode[STIX]{x1D702}$
-invariant of a closed
$\unicode[STIX]{x1D702}$
-invariant of a closed
![]() $3$
-manifold is equal to the integral of the first Pontryagin form minus the signature of a bounding
$3$
-manifold is equal to the integral of the first Pontryagin form minus the signature of a bounding
![]() $4$
-manifold, which allows us to compute it without using analytic tools. For a homeomorphism
$4$
-manifold, which allows us to compute it without using analytic tools. For a homeomorphism
![]() $\unicode[STIX]{x1D711}$
of an oriented closed surface
$\unicode[STIX]{x1D711}$
of an oriented closed surface
![]() $\unicode[STIX]{x1D6F4}$
, we can construct the mapping torus
$\unicode[STIX]{x1D6F4}$
, we can construct the mapping torus
![]() $M_{\unicode[STIX]{x1D711}}=\unicode[STIX]{x1D6F4}\times [0,1]/(p,1)\sim (\unicode[STIX]{x1D711}(p),0)$
. In this paper we consider the case where
$M_{\unicode[STIX]{x1D711}}=\unicode[STIX]{x1D6F4}\times [0,1]/(p,1)\sim (\unicode[STIX]{x1D711}(p),0)$
. In this paper we consider the case where
![]() $\unicode[STIX]{x1D711}$
is of finite order and endow
$\unicode[STIX]{x1D711}$
is of finite order and endow
![]() $M_{\unicode[STIX]{x1D711}}$
with the metric which is induced from the standard metric of
$M_{\unicode[STIX]{x1D711}}$
with the metric which is induced from the standard metric of
![]() $S^{1}$
and
$S^{1}$
and
![]() $\unicode[STIX]{x1D711}$
-invariant metric of
$\unicode[STIX]{x1D711}$
-invariant metric of
![]() $\unicode[STIX]{x1D6F4}$
. An explicit formula of the
$\unicode[STIX]{x1D6F4}$
. An explicit formula of the
![]() $\unicode[STIX]{x1D702}$
-invariant of
$\unicode[STIX]{x1D702}$
-invariant of
![]() $M_{\unicode[STIX]{x1D711}}$
was first given by Meyerhoff–Ruberman in [Reference Meyerhoff and Ruberman13] using the Dedekind sum (see Section 2.1 for details). Another explicit formula using Meyer’s signature cocycle was given by the author in [Reference Morifuji14].
$M_{\unicode[STIX]{x1D711}}$
was first given by Meyerhoff–Ruberman in [Reference Meyerhoff and Ruberman13] using the Dedekind sum (see Section 2.1 for details). Another explicit formula using Meyer’s signature cocycle was given by the author in [Reference Morifuji14].
Let
![]() $X$
be a compact Riemann surface of genus
$X$
be a compact Riemann surface of genus
![]() $g\geqslant 2$
and
$g\geqslant 2$
and
![]() $G=\text{Aut}(X)$
the group of conformal automorphisms of
$G=\text{Aut}(X)$
the group of conformal automorphisms of
![]() $X$
. A theorem of Hurwitz states that
$X$
. A theorem of Hurwitz states that
![]() $|G|$
is bounded above by
$|G|$
is bounded above by
![]() $84(g-1)$
. The surface
$84(g-1)$
. The surface
![]() $X$
for which this bound is attained is called a Hurwitz surface and
$X$
for which this bound is attained is called a Hurwitz surface and
![]() $G$
is known as a Hurwitz group. It is also known that
$G$
is known as a Hurwitz group. It is also known that
![]() $G$
is a Hurwitz group if and only if there is a homomorphism from the
$G$
is a Hurwitz group if and only if there is a homomorphism from the
![]() $(2,3,7)$
triangle group onto
$(2,3,7)$
triangle group onto
![]() $G$
(see Conder [Reference Conder5] for details). There are infinitely many values of
$G$
(see Conder [Reference Conder5] for details). There are infinitely many values of
![]() $g$
for which one can find a Hurwitz group of order
$g$
for which one can find a Hurwitz group of order
![]() $84(g-1)$
and the first values for such
$84(g-1)$
and the first values for such
![]() $g$
are
$g$
are
![]() $3,7$
and
$3,7$
and
![]() $14$
. The smallest Hurwitz group is
$14$
. The smallest Hurwitz group is
![]() $\text{PSL}(2,\mathbb{F}_{7})$
of order
$\text{PSL}(2,\mathbb{F}_{7})$
of order
![]() $168$
which is the automorphism group of the Klein surface of genus
$168$
which is the automorphism group of the Klein surface of genus
![]() $3$
. The next one is
$3$
. The next one is
![]() $\text{PSL}(2,\mathbb{F}_{8})$
of order
$\text{PSL}(2,\mathbb{F}_{8})$
of order
![]() $504$
which corresponds to the Macbeath surface of genus
$504$
which corresponds to the Macbeath surface of genus
![]() $7$
(see Macbeath [Reference Macbeath9]). In the case of genus
$7$
(see Macbeath [Reference Macbeath9]). In the case of genus
![]() $14$
, it is known that there are three nonisomorphic Hurwitz surfaces and
$14$
, it is known that there are three nonisomorphic Hurwitz surfaces and
![]() $G$
is isomorphic to
$G$
is isomorphic to
![]() $\text{PSL}(2,\mathbb{F}_{13})$
of order
$\text{PSL}(2,\mathbb{F}_{13})$
of order
![]() $1092$
(see Macbeath [Reference Macbeath10]).
$1092$
(see Macbeath [Reference Macbeath10]).
In our previous papers [Reference Morifuji16, Reference Morifuji19], we showed that the reducibility (see Section 2.4 for the definition) of automorphisms of the above Hurwitz surfaces with genera
![]() $g=3,7$
and
$g=3,7$
and
![]() $14$
is characterized by vanishing of the
$14$
is characterized by vanishing of the
![]() $\unicode[STIX]{x1D702}$
-invariant of the corresponding mapping torus (see Proposition 2.5). The purpose of the present paper is to prove the following vanishing theorem for the
$\unicode[STIX]{x1D702}$
-invariant of the corresponding mapping torus (see Proposition 2.5). The purpose of the present paper is to prove the following vanishing theorem for the
![]() $\unicode[STIX]{x1D702}$
-invariant and Hurwitz groups, which is a natural generalization of these results.
$\unicode[STIX]{x1D702}$
-invariant and Hurwitz groups, which is a natural generalization of these results.
Theorem 1.1. Let
![]() $X$
be a Hurwitz surface with
$X$
be a Hurwitz surface with
![]() $\text{Aut}(X)=\text{PSL}(2,\mathbb{F}_{q})$
. If
$\text{Aut}(X)=\text{PSL}(2,\mathbb{F}_{q})$
. If
![]() $q$
is sufficiently large, then every
$q$
is sufficiently large, then every
![]() $\unicode[STIX]{x1D711}\in \text{PSL}(2,\mathbb{F}_{q})$
is reducible and
$\unicode[STIX]{x1D711}\in \text{PSL}(2,\mathbb{F}_{q})$
is reducible and
![]() $\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=0$
.
$\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=0$
.
This paper is organized as follows. In the next section, we quickly review several basic facts about the fixed point data, the
![]() $\unicode[STIX]{x1D702}$
-invariant of mapping tori with finite monodromies, conjugacy classes of
$\unicode[STIX]{x1D702}$
-invariant of mapping tori with finite monodromies, conjugacy classes of
![]() $\text{PSL}(2,\mathbb{F}_{q})$
and Hurwitz groups. The proof of Theorem 1.1 will be given in Section 3.
$\text{PSL}(2,\mathbb{F}_{q})$
and Hurwitz groups. The proof of Theorem 1.1 will be given in Section 3.
2 Preliminaries
In this section, we recall some basic notions which appeared in Theorem 1.1.
2.1 Fixed point data and the
 $\unicode[STIX]{x1D702}$
-invariant
$\unicode[STIX]{x1D702}$
-invariant
Let
![]() $\unicode[STIX]{x1D6F4}_{g}$
be an oriented closed surface of genus
$\unicode[STIX]{x1D6F4}_{g}$
be an oriented closed surface of genus
![]() $g$
and
$g$
and
![]() ${\mathcal{M}}_{g}$
the mapping class group of
${\mathcal{M}}_{g}$
the mapping class group of
![]() $\unicode[STIX]{x1D6F4}_{g}$
, the group of all isotopy classes of orientation preserving homeomorphisms of
$\unicode[STIX]{x1D6F4}_{g}$
, the group of all isotopy classes of orientation preserving homeomorphisms of
![]() $\unicode[STIX]{x1D6F4}_{g}$
. Let
$\unicode[STIX]{x1D6F4}_{g}$
. Let
![]() $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6F4}_{g}\rightarrow \unicode[STIX]{x1D6F4}_{g}$
be a homeomorphism of order
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6F4}_{g}\rightarrow \unicode[STIX]{x1D6F4}_{g}$
be a homeomorphism of order
![]() $m$
. We denote the set of points of
$m$
. We denote the set of points of
![]() $\unicode[STIX]{x1D6F4}_{g}$
at which
$\unicode[STIX]{x1D6F4}_{g}$
at which
![]() $\langle \unicode[STIX]{x1D711}\rangle \cong \mathbb{Z}/m$
does not act freely by
$\langle \unicode[STIX]{x1D711}\rangle \cong \mathbb{Z}/m$
does not act freely by
![]() $\text{Fix}\langle \unicode[STIX]{x1D711}\rangle$
. Let
$\text{Fix}\langle \unicode[STIX]{x1D711}\rangle$
. Let
![]() $\{x_{i}\}$
be a set of representatives of the orbits of
$\{x_{i}\}$
be a set of representatives of the orbits of
![]() $\text{Fix}\langle \unicode[STIX]{x1D711}\rangle$
under
$\text{Fix}\langle \unicode[STIX]{x1D711}\rangle$
under
![]() $\langle \unicode[STIX]{x1D711}\rangle$
and
$\langle \unicode[STIX]{x1D711}\rangle$
and
![]() $\unicode[STIX]{x1D6FC}_{i}=|\text{stab}_{\langle \unicode[STIX]{x1D711}\rangle }(x_{i})|$
, the order of the stabilizer at
$\unicode[STIX]{x1D6FC}_{i}=|\text{stab}_{\langle \unicode[STIX]{x1D711}\rangle }(x_{i})|$
, the order of the stabilizer at
![]() $x_{i}$
. Then
$x_{i}$
. Then
![]() $\unicode[STIX]{x1D711}^{m/\unicode[STIX]{x1D6FC}_{i}}$
generates
$\unicode[STIX]{x1D711}^{m/\unicode[STIX]{x1D6FC}_{i}}$
generates
![]() $\text{stab}_{\langle \unicode[STIX]{x1D711}\rangle }(x_{i})$
so it acts faithfully by rotation on the tangent space at
$\text{stab}_{\langle \unicode[STIX]{x1D711}\rangle }(x_{i})$
so it acts faithfully by rotation on the tangent space at
![]() $x_{i}$
. Let
$x_{i}$
. Let
![]() $\unicode[STIX]{x1D6FD}_{i}$
be an integer such that
$\unicode[STIX]{x1D6FD}_{i}$
be an integer such that
![]() $\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D6FD}_{i}m/\unicode[STIX]{x1D6FC}_{i}}$
acts by rotation through
$\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D6FD}_{i}m/\unicode[STIX]{x1D6FC}_{i}}$
acts by rotation through
![]() $2\unicode[STIX]{x1D70B}\sqrt{-1}/\unicode[STIX]{x1D6FC}_{i}$
. The integer
$2\unicode[STIX]{x1D70B}\sqrt{-1}/\unicode[STIX]{x1D6FC}_{i}$
. The integer
![]() $\unicode[STIX]{x1D6FD}_{i}$
is well-defined modulo
$\unicode[STIX]{x1D6FD}_{i}$
is well-defined modulo
![]() $\unicode[STIX]{x1D6FC}_{i}$
and
$\unicode[STIX]{x1D6FC}_{i}$
and
![]() $(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i})=1$
, so that
$(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i})=1$
, so that
![]() $\unicode[STIX]{x1D6FD}_{i}/\unicode[STIX]{x1D6FC}_{i}$
is uniquely determined as an element of
$\unicode[STIX]{x1D6FD}_{i}/\unicode[STIX]{x1D6FC}_{i}$
is uniquely determined as an element of
![]() $\mathbb{Q}/\mathbb{Z}$
. By the fixed point data of
$\mathbb{Q}/\mathbb{Z}$
. By the fixed point data of
![]() $\unicode[STIX]{x1D711}$
, we mean the collection
$\unicode[STIX]{x1D711}$
, we mean the collection
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D711})=\langle g,m~|~\unicode[STIX]{x1D6FD}_{1}/\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{r}/\unicode[STIX]{x1D6FC}_{r}\rangle ,$
where
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D711})=\langle g,m~|~\unicode[STIX]{x1D6FD}_{1}/\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{r}/\unicode[STIX]{x1D6FC}_{r}\rangle ,$
where
![]() $\unicode[STIX]{x1D6FD}_{i}/\unicode[STIX]{x1D6FC}_{i}\in \mathbb{Q}/\mathbb{Z}$
are not ordered. Moreover, the fixed point data satisfies the relation
$\unicode[STIX]{x1D6FD}_{i}/\unicode[STIX]{x1D6FC}_{i}\in \mathbb{Q}/\mathbb{Z}$
are not ordered. Moreover, the fixed point data satisfies the relation
Now, by using the fixed point data, the
![]() $\unicode[STIX]{x1D702}$
-invariant of the mapping torus
$\unicode[STIX]{x1D702}$
-invariant of the mapping torus
![]() $M_{\unicode[STIX]{x1D711}}$
equipped with the metric as in Introduction is given by
$M_{\unicode[STIX]{x1D711}}$
equipped with the metric as in Introduction is given by
where
![]() $s(\unicode[STIX]{x1D6FD}_{l},\unicode[STIX]{x1D6FC}_{l})$
denotes the Dedekind sum and is defined by the following formula:
$s(\unicode[STIX]{x1D6FD}_{l},\unicode[STIX]{x1D6FC}_{l})$
denotes the Dedekind sum and is defined by the following formula:
Here
![]() $((r))\in \mathbb{R}$
is defined to be
$((r))\in \mathbb{R}$
is defined to be
![]() $r-[r]-1/2$
if
$r-[r]-1/2$
if
![]() $r\not \in \mathbb{Z}$
and
$r\not \in \mathbb{Z}$
and
![]() $0$
if
$0$
if
![]() $r\in \mathbb{Z}$
, where
$r\in \mathbb{Z}$
, where
![]() $[r]$
is the greatest integer less than or equal to
$[r]$
is the greatest integer less than or equal to
![]() $r$
.
$r$
.
As a basic property of the
![]() $\unicode[STIX]{x1D702}$
-invariant, it is known that if two elements
$\unicode[STIX]{x1D702}$
-invariant, it is known that if two elements
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{M}}_{g}$
are conjugate, then
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{M}}_{g}$
are conjugate, then
![]() $\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D713}})$
holds. Moreover, for the inverse
$\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D713}})$
holds. Moreover, for the inverse
![]() $\unicode[STIX]{x1D711}^{-1}$
, we have
$\unicode[STIX]{x1D711}^{-1}$
, we have
![]() $\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}^{-1}})=-\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})$
.
$\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}^{-1}})=-\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})$
.
Remark 2.1. The formula (2.1) is due to Meyerhoff and Ruberman [Reference Meyerhoff and Ruberman13, Theorem 1.3]. On the other hand, another explicit formula of
![]() $\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})$
using Meyer’s signature cocycle [Reference Meyer12] was proved in [Reference Morifuji14, Main Theorem]. See also [Reference Morifuji18, Theorem 3.1] for a formula of the
$\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})$
using Meyer’s signature cocycle [Reference Meyer12] was proved in [Reference Morifuji14, Main Theorem]. See also [Reference Morifuji18, Theorem 3.1] for a formula of the
![]() $\unicode[STIX]{x1D702}$
-invariant in terms of Meyer’s function.
$\unicode[STIX]{x1D702}$
-invariant in terms of Meyer’s function.
2.2 Conjugacy classes of
 $\text{PSL}(2,\mathbb{F}_{q})$
$\text{PSL}(2,\mathbb{F}_{q})$
In this paper we use the same notations for conjugacy classes of
![]() $\text{PSL}(2,\mathbb{F}_{q})$
as in [Reference Adams1]. Let
$\text{PSL}(2,\mathbb{F}_{q})$
as in [Reference Adams1]. Let
![]() $\mathbb{F}_{q}$
be the finite field with
$\mathbb{F}_{q}$
be the finite field with
![]() $q=p^{n}$
elements where
$q=p^{n}$
elements where
![]() $p$
is a prime number and
$p$
is a prime number and
![]() $\text{GL}(2,\mathbb{F}_{q})$
the group of the
$\text{GL}(2,\mathbb{F}_{q})$
the group of the
![]() $2\times 2$
matrices over
$2\times 2$
matrices over
![]() $\mathbb{F}_{q}$
with nonzero determinant. Let
$\mathbb{F}_{q}$
with nonzero determinant. Let
![]() $Z$
be the center of
$Z$
be the center of
![]() $\text{GL}(2,\mathbb{F}_{q})$
, namely the subgroup consisting of all the scalar matrices in
$\text{GL}(2,\mathbb{F}_{q})$
, namely the subgroup consisting of all the scalar matrices in
![]() $\text{GL}(2,\mathbb{F}_{q})$
, and
$\text{GL}(2,\mathbb{F}_{q})$
, and
![]() $\text{SL}(2,\mathbb{F}_{q})=\{A\in \text{GL}(2,\mathbb{F}_{q})~|\det A=1\}$
. Then
$\text{SL}(2,\mathbb{F}_{q})=\{A\in \text{GL}(2,\mathbb{F}_{q})~|\det A=1\}$
. Then
![]() $\text{PSL}(2,\mathbb{F}_{q})$
is defined to be
$\text{PSL}(2,\mathbb{F}_{q})$
is defined to be
It is known that the order of
![]() $\text{GL}(2,\mathbb{F}_{q})$
is
$\text{GL}(2,\mathbb{F}_{q})$
is
![]() $(q+1)q(q-1)^{2}$
and
$(q+1)q(q-1)^{2}$
and
![]() $|\text{SL}(2,\mathbb{F}_{q})|=(q+1)q(q-1)$
. Moreover, the order of
$|\text{SL}(2,\mathbb{F}_{q})|=(q+1)q(q-1)$
. Moreover, the order of
![]() $\text{PSL}(2,\mathbb{F}_{q})$
is
$\text{PSL}(2,\mathbb{F}_{q})$
is
![]() $(q+1)q(q-1)/2$
if
$(q+1)q(q-1)/2$
if
![]() $q$
is odd and
$q$
is odd and
![]() $(q+1)q(q-1)$
if
$(q+1)q(q-1)$
if
![]() $q$
is even.
$q$
is even.
Table 1. Conjugacy classes of
![]() $\text{PSL}(2,\mathbb{F}_{q})$
for
$\text{PSL}(2,\mathbb{F}_{q})$
for
![]() $q\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}4$
.
$q\equiv 1\hspace{0.6em}{\rm mod}\hspace{0.2em}4$
.
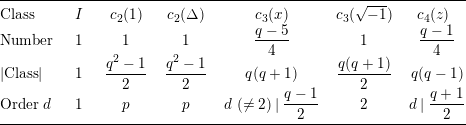
Table 2. Conjugacy classes of
![]() $\text{PSL}(2,\mathbb{F}_{q})$
for
$\text{PSL}(2,\mathbb{F}_{q})$
for
![]() $q\equiv -1\hspace{0.6em}{\rm mod}\hspace{0.2em}4$
.
$q\equiv -1\hspace{0.6em}{\rm mod}\hspace{0.2em}4$
.
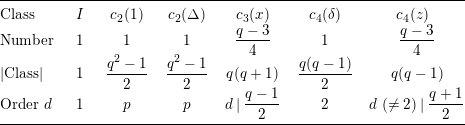
Let
![]() $\mathbb{E}$
be the unique quadratic extension of
$\mathbb{E}$
be the unique quadratic extension of
![]() $\mathbb{F}_{q}$
. If
$\mathbb{F}_{q}$
. If
![]() $q$
is odd, we choose
$q$
is odd, we choose
![]() $\unicode[STIX]{x1D6E5}\in \mathbb{F}_{q}^{\ast }-(\mathbb{F}_{q}^{\ast })^{2}$
and write
$\unicode[STIX]{x1D6E5}\in \mathbb{F}_{q}^{\ast }-(\mathbb{F}_{q}^{\ast })^{2}$
and write
![]() $\mathbb{E}=\mathbb{F}_{q}(\unicode[STIX]{x1D6FF})$
where
$\mathbb{E}=\mathbb{F}_{q}(\unicode[STIX]{x1D6FF})$
where
![]() $\unicode[STIX]{x1D6FF}=\sqrt{\unicode[STIX]{x1D6E5}}$
. For
$\unicode[STIX]{x1D6FF}=\sqrt{\unicode[STIX]{x1D6E5}}$
. For
![]() $z\in \mathbb{E}^{\ast }$
, let
$z\in \mathbb{E}^{\ast }$
, let
![]() $\overline{z}=z^{q}$
. This is the action of the nontrivial element of the Galois group of
$\overline{z}=z^{q}$
. This is the action of the nontrivial element of the Galois group of
![]() $\mathbb{E}$
over
$\mathbb{E}$
over
![]() $\mathbb{F}_{q}$
. The norm map
$\mathbb{F}_{q}$
. The norm map
![]() $N:\mathbb{E}^{\ast }\rightarrow \mathbb{F}_{q}^{\ast }$
is defined to be
$N:\mathbb{E}^{\ast }\rightarrow \mathbb{F}_{q}^{\ast }$
is defined to be
![]() $N(z)=z\overline{z}=z^{q+1}\in \mathbb{F}_{q}$
. Let
$N(z)=z\overline{z}=z^{q+1}\in \mathbb{F}_{q}$
. Let
![]() $\mathbb{E}^{1}$
be the kernel of the norm map, which has order
$\mathbb{E}^{1}$
be the kernel of the norm map, which has order
![]() $q+1$
.
$q+1$
.
Now we assume that
![]() $p$
is an odd prime number (namely
$p$
is an odd prime number (namely
![]() $q$
is odd). Then the conjugacy classes of
$q$
is odd). Then the conjugacy classes of
![]() $\text{PSL}(2,\mathbb{F}_{q})$
are described by using the following four types of matrices (see [Reference Adams1, Section 5] for details):
$\text{PSL}(2,\mathbb{F}_{q})$
are described by using the following four types of matrices (see [Reference Adams1, Section 5] for details):
- (i)
-
 $I=\left(\!\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}\!\right);$
$I=\left(\!\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix}\!\right);$
- (ii)
-
 $c_{2}(\unicode[STIX]{x1D6FE})=\left(\!\begin{smallmatrix}1 & \unicode[STIX]{x1D6FE}\\ 0 & 1\end{smallmatrix}\!\right)~(\unicode[STIX]{x1D6FE}\in \{1,\,\unicode[STIX]{x1D6E5}\});$
$c_{2}(\unicode[STIX]{x1D6FE})=\left(\!\begin{smallmatrix}1 & \unicode[STIX]{x1D6FE}\\ 0 & 1\end{smallmatrix}\!\right)~(\unicode[STIX]{x1D6FE}\in \{1,\,\unicode[STIX]{x1D6E5}\});$
- (iii)
-
 $c_{3}(x)=\left(\!\begin{smallmatrix}x & 0\\ 0 & x^{-1}\end{smallmatrix}\!\right)~(x\not =\pm 1),~c_{3}(x)=c_{3}(-x)=c_{3}(x^{-1})=c_{3}(-x^{-1});$
$c_{3}(x)=\left(\!\begin{smallmatrix}x & 0\\ 0 & x^{-1}\end{smallmatrix}\!\right)~(x\not =\pm 1),~c_{3}(x)=c_{3}(-x)=c_{3}(x^{-1})=c_{3}(-x^{-1});$
- (iv)
-
 $c_{4}(z)=\left(\!\!\begin{smallmatrix}x & \unicode[STIX]{x1D6E5}y\\ y & x\end{smallmatrix}\!\!\right)(z=x+\unicode[STIX]{x1D6FF}y\in \mathbb{E}^{1},~z\not =\pm 1),c_{4}(z)=c_{4}(\overline{z})=c_{4}(-z)=c_{4}(-\overline{z})$
.
$c_{4}(z)=\left(\!\!\begin{smallmatrix}x & \unicode[STIX]{x1D6E5}y\\ y & x\end{smallmatrix}\!\!\right)(z=x+\unicode[STIX]{x1D6FF}y\in \mathbb{E}^{1},~z\not =\pm 1),c_{4}(z)=c_{4}(\overline{z})=c_{4}(-z)=c_{4}(-\overline{z})$
.
Using these matrices, we have all the conjugacy classes of
![]() $\text{PSL}(2,\mathbb{F}_{q})$
as in Tables 1 and 2 above. In Table 2, ‘Number’ of the class
$\text{PSL}(2,\mathbb{F}_{q})$
as in Tables 1 and 2 above. In Table 2, ‘Number’ of the class
![]() $c_{4}(z)$
is different from the one in the table in [Reference Adams1, Section 6.4] (probably
$c_{4}(z)$
is different from the one in the table in [Reference Adams1, Section 6.4] (probably
![]() $(q-7)/4$
appeared there would be a typographic error). Here ‘Order
$(q-7)/4$
appeared there would be a typographic error). Here ‘Order
![]() $d$
’ in Tables 1 and 2 means the order of each representative in
$d$
’ in Tables 1 and 2 means the order of each representative in
![]() $\text{PSL}(2,\mathbb{F}_{q})$
. For example in Table 1,
$\text{PSL}(2,\mathbb{F}_{q})$
. For example in Table 1,
![]() $(c_{2}(1))^{p}=I$
and
$(c_{2}(1))^{p}=I$
and
![]() $(c_{3}(x))^{d}=I$
hold, where
$(c_{3}(x))^{d}=I$
hold, where
![]() $d~(\not =2)$
is a divisor of
$d~(\not =2)$
is a divisor of
![]() $(q-1)/2$
.
$(q-1)/2$
.
We easily see from Tables 1 and 2 that the maximum order
![]() $d_{0}$
of elements in
$d_{0}$
of elements in
![]() $\text{PSL}(2,\mathbb{F}_{q})$
is
$\text{PSL}(2,\mathbb{F}_{q})$
is
![]() $d_{0}=(q+1)/2$
if
$d_{0}=(q+1)/2$
if
![]() $q=p^{n}~(n>1)$
and
$q=p^{n}~(n>1)$
and
![]() $d_{0}=p$
if
$d_{0}=p$
if
![]() $q=p$
.
$q=p$
.
2.3 Hurwitz groups
In [Reference Macbeath10], Macbeath proved that the Hurwitz groups of type
![]() $\text{PSL}(2,\mathbb{F}_{q})$
satisfy the following conditions, where
$\text{PSL}(2,\mathbb{F}_{q})$
satisfy the following conditions, where
![]() $q=p^{n}$
(
$q=p^{n}$
(
![]() $p$
is a prime number).
$p$
is a prime number).
Proposition 2.2. (Macbeath [Reference Macbeath10])
The finite group
![]() $\text{PSL}(2,\mathbb{F}_{q})$
is a Hurwitz group if and only if either
$\text{PSL}(2,\mathbb{F}_{q})$
is a Hurwitz group if and only if either
-
(i)
 $q=7$
or
$q=7$
or -
(ii)
 $q=p\equiv \pm 1\hspace{0.6em}{\rm mod}\hspace{0.2em}7$
or
$q=p\equiv \pm 1\hspace{0.6em}{\rm mod}\hspace{0.2em}7$
or -
(iii)
 $q=p^{3}$
where
$q=p^{3}$
where
 $p\equiv \pm 2$
or
$p\equiv \pm 2$
or
 $\pm 3\hspace{0.6em}{\rm mod}\hspace{0.2em}7$
.
$\pm 3\hspace{0.6em}{\rm mod}\hspace{0.2em}7$
.
In cases (i) and (iii) there is only one Riemann surface on which
![]() $\text{PSL}(2,\mathbb{F}_{q})$
acts as a Hurwitz group. In case (ii) there are three Riemann surfaces for each
$\text{PSL}(2,\mathbb{F}_{q})$
acts as a Hurwitz group. In case (ii) there are three Riemann surfaces for each
![]() $q$
.
$q$
.
By Proposition 2.2, we see that there are infinitely many Riemann surfaces that admit Hurwitz groups as their automorphism groups. As mentioned in Introduction, first three Hurwitz groups are of the form
![]() $\text{PSL}(2,\mathbb{F}_{q})$
, namely
$\text{PSL}(2,\mathbb{F}_{q})$
, namely
![]() $q=7,8$
and
$q=7,8$
and
![]() $13$
which correspond to Riemann surfaces of genera
$13$
which correspond to Riemann surfaces of genera
![]() $g=3,7$
and
$g=3,7$
and
![]() $14$
. The next one is of order
$14$
. The next one is of order
![]() $1344$
which acts on a surface of genus
$1344$
which acts on a surface of genus
![]() $17$
, but in this case, it is known that
$17$
, but in this case, it is known that
![]() $G$
is isomorphic to an extension of the abelian group
$G$
is isomorphic to an extension of the abelian group
![]() $(\mathbb{Z}/2)^{3}$
by
$(\mathbb{Z}/2)^{3}$
by
![]() $\text{PSL}(2,\mathbb{F}_{7})$
. See Conder [Reference Conder4] for details.
$\text{PSL}(2,\mathbb{F}_{7})$
. See Conder [Reference Conder4] for details.
Next we consider the number of fixed points
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})=\#\text{Fix}\langle \unicode[STIX]{x1D711}\rangle$
for elements of Hurwitz groups
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})=\#\text{Fix}\langle \unicode[STIX]{x1D711}\rangle$
for elements of Hurwitz groups
![]() $\text{PSL}(2,\mathbb{F}_{q})$
. The following proposition is a special case of [Reference Macbeath11, Theorem 2].
$\text{PSL}(2,\mathbb{F}_{q})$
. The following proposition is a special case of [Reference Macbeath11, Theorem 2].
Proposition 2.3. (Macbeath [Reference Macbeath11])
Let
![]() $G=\text{PSL}(2,\mathbb{F}_{q})$
be one of the Hurwitz groups as in Proposition 2.2. If
$G=\text{PSL}(2,\mathbb{F}_{q})$
be one of the Hurwitz groups as in Proposition 2.2. If
![]() $\unicode[STIX]{x1D711}\in G$
has order
$\unicode[STIX]{x1D711}\in G$
has order
![]() $d>1$
and
$d>1$
and
![]() $q=p^{n}$
is odd, then
$q=p^{n}$
is odd, then
 $$\begin{eqnarray}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})=\left\{\begin{array}{@{}ll@{}}\displaystyle (q-1)\mathop{\sum }_{d\,|\,m_{i}}\frac{1}{m_{i}}\quad & \text{if}\quad \displaystyle d\,|\,\frac{q-1}{2};\\ \displaystyle (q+1)\mathop{\sum }_{d\,|\,m_{i}}\frac{1}{m_{i}}\quad & \text{if}\quad \displaystyle d\,|\,\frac{q+1}{2};\\ \displaystyle \frac{(n,2)}{2}p^{n-1}(p-1)\mathop{\sum }_{m_{i}\,=\,p}1\quad & \text{if}\quad d=p,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})=\left\{\begin{array}{@{}ll@{}}\displaystyle (q-1)\mathop{\sum }_{d\,|\,m_{i}}\frac{1}{m_{i}}\quad & \text{if}\quad \displaystyle d\,|\,\frac{q-1}{2};\\ \displaystyle (q+1)\mathop{\sum }_{d\,|\,m_{i}}\frac{1}{m_{i}}\quad & \text{if}\quad \displaystyle d\,|\,\frac{q+1}{2};\\ \displaystyle \frac{(n,2)}{2}p^{n-1}(p-1)\mathop{\sum }_{m_{i}\,=\,p}1\quad & \text{if}\quad d=p,\end{array}\right.\end{eqnarray}$$
where
![]() $(n,2)$
denotes the greatest common divisor of
$(n,2)$
denotes the greatest common divisor of
![]() $n$
and
$n$
and
![]() $2$
, and
$2$
, and
![]() $\{m_{1},m_{2},m_{3}\}=\{2,3,7\}$
.
$\{m_{1},m_{2},m_{3}\}=\{2,3,7\}$
.
Using Proposition 2.3, we can evaluate the number of fixed points explicitly. Moreover, we can easily see that an automorphism of order
![]() $d$
in
$d$
in
![]() $\text{PSL}(2,\mathbb{F}_{q})$
has no fixed point when
$\text{PSL}(2,\mathbb{F}_{q})$
has no fixed point when
![]() $d\not =2,3,7$
. This is a key fact for our purpose.
$d\not =2,3,7$
. This is a key fact for our purpose.
2.4 Some known results
An essential
![]() $1$
-submanifold of
$1$
-submanifold of
![]() $\unicode[STIX]{x1D6F4}_{g}$
is a disjoint union of simple closed curves in
$\unicode[STIX]{x1D6F4}_{g}$
is a disjoint union of simple closed curves in
![]() $\unicode[STIX]{x1D6F4}_{g}$
each component of which does not bound a
$\unicode[STIX]{x1D6F4}_{g}$
each component of which does not bound a
![]() $2$
-disk in
$2$
-disk in
![]() $\unicode[STIX]{x1D6F4}_{g}$
, and no two components of which are homotopic. A homeomorphism
$\unicode[STIX]{x1D6F4}_{g}$
, and no two components of which are homotopic. A homeomorphism
![]() $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6F4}_{g}\rightarrow \unicode[STIX]{x1D6F4}_{g}$
is reducible if it leaves some essential
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6F4}_{g}\rightarrow \unicode[STIX]{x1D6F4}_{g}$
is reducible if it leaves some essential
![]() $1$
-submanifold of
$1$
-submanifold of
![]() $\unicode[STIX]{x1D6F4}_{g}$
invariant. An irreducible homeomorphism is one which is not reducible.
$\unicode[STIX]{x1D6F4}_{g}$
invariant. An irreducible homeomorphism is one which is not reducible.
Remark 2.4. By the classification of surface homeomorphisms due to Nielsen and Thurston (see [Reference Casson and Bleiler3]), there are three types of mapping classes: (1) finite order, (2) reducible and (3) pseudo-Anosov. We easily see that (1) and (2) have some overlap, although (3) does not have any intersection with (1) nor (2). It is known that there are some characterizations of the reducibility of
![]() $\unicode[STIX]{x1D711}\in {\mathcal{M}}_{g}$
of finite order.
$\unicode[STIX]{x1D711}\in {\mathcal{M}}_{g}$
of finite order.
-
(i) Gilman shows in [Reference Gilman7, Theorem 3.1] that
 $\unicode[STIX]{x1D711}\in {\mathcal{M}}_{g}$
of finite order is irreducible if and only if the quotient orbifold
$\unicode[STIX]{x1D711}\in {\mathcal{M}}_{g}$
of finite order is irreducible if and only if the quotient orbifold
 $\unicode[STIX]{x1D6F4}_{g}/\langle \unicode[STIX]{x1D711}\rangle$
is homeomorphic to the
$\unicode[STIX]{x1D6F4}_{g}/\langle \unicode[STIX]{x1D711}\rangle$
is homeomorphic to the
 $2$
-sphere with three cone points.
$2$
-sphere with three cone points. -
(ii) Kasahara shows in [Reference Kasahara8, Theorem 4.1] that for
 $\unicode[STIX]{x1D711}\in {\mathcal{M}}_{g}$
of order
$\unicode[STIX]{x1D711}\in {\mathcal{M}}_{g}$
of order
 $m$
, if
$m$
, if
 $\unicode[STIX]{x1D711}$
is irreducible, then
$\unicode[STIX]{x1D711}$
is irreducible, then
 $m\geqslant 2g+1$
; and if
$m\geqslant 2g+1$
; and if
 $\unicode[STIX]{x1D711}$
is reducible, then
$\unicode[STIX]{x1D711}$
is reducible, then
 $m\leqslant 2g+2$
, moreover if the genus
$m\leqslant 2g+2$
, moreover if the genus
 $g$
is odd, then
$g$
is odd, then
 $m\leqslant 2g$
.
$m\leqslant 2g$
.
A characterization of reducible automorphisms of a Hurwitz surface by means of the
![]() $\unicode[STIX]{x1D702}$
-invariant first appeared in [Reference Morifuji16]. This result was generalized to the Hurwitz surfaces with genera
$\unicode[STIX]{x1D702}$
-invariant first appeared in [Reference Morifuji16]. This result was generalized to the Hurwitz surfaces with genera
![]() $7$
and
$7$
and
![]() $14$
in [Reference Morifuji19]. Namely we have:
$14$
in [Reference Morifuji19]. Namely we have:
Proposition 2.5. ([Reference Morifuji16, Theorem 1], [Reference Morifuji19, Theorem 1.1])
Let
![]() $X$
be the Klein surface of genus
$X$
be the Klein surface of genus
![]() $3$
or the Macbeath surface of genus
$3$
or the Macbeath surface of genus
![]() $7$
, or one of the three Hurwitz surfaces of genus
$7$
, or one of the three Hurwitz surfaces of genus
![]() $14$
. An automorphism
$14$
. An automorphism
![]() $\unicode[STIX]{x1D711}$
of
$\unicode[STIX]{x1D711}$
of
![]() $X$
is reducible if and only if the
$X$
is reducible if and only if the
![]() $\unicode[STIX]{x1D702}$
-invariant of the corresponding mapping torus
$\unicode[STIX]{x1D702}$
-invariant of the corresponding mapping torus
![]() $M_{\unicode[STIX]{x1D711}}$
vanishes.
$M_{\unicode[STIX]{x1D711}}$
vanishes.
Remark 2.6. For a surface with small genus, the same statement as in Proposition 2.5 holds (see [Reference Morifuji15, Theorem 4.1, Remark 4.2]).
However, this kind of theorem does not hold in general (see [Reference Morifuji17, Theorem 3.1] for instance). The next example was first pointed out by Toshiyuki Akita.
Example 2.7. For any odd prime number
![]() $p$
, there exists an automorphism
$p$
, there exists an automorphism
![]() $\unicode[STIX]{x1D711}$
of order
$\unicode[STIX]{x1D711}$
of order
![]() $p$
acting on a Riemann surface
$p$
acting on a Riemann surface
![]() $Y$
with the genus
$Y$
with the genus
![]() $g=p\overline{g}+(p-1)/2$
and
$g=p\overline{g}+(p-1)/2$
and
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})=3$
, where
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})=3$
, where
![]() $\overline{g}$
is the genus of
$\overline{g}$
is the genus of
![]() $Y/\langle \unicode[STIX]{x1D711}\rangle$
(see [Reference Farkas and Kra6, Chapter V]). Then we obtain
$Y/\langle \unicode[STIX]{x1D711}\rangle$
(see [Reference Farkas and Kra6, Chapter V]). Then we obtain
![]() $\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})\not =0$
. Actually
$\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})\not =0$
. Actually
![]() $\unicode[STIX]{x1D711}$
has the fixed point data
$\unicode[STIX]{x1D711}$
has the fixed point data
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D711})=\langle g,p~|~1/p,1/p,(p-2)/p\rangle$
and by the formula (2.1) in Section 2.1, the
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D711})=\langle g,p~|~1/p,1/p,(p-2)/p\rangle$
and by the formula (2.1) in Section 2.1, the
![]() $\unicode[STIX]{x1D702}$
-invariant of
$\unicode[STIX]{x1D702}$
-invariant of
![]() $M_{\unicode[STIX]{x1D711}}$
is given by
$M_{\unicode[STIX]{x1D711}}$
is given by
Here we have used the following property: if
![]() $\unicode[STIX]{x1D6FD}^{\prime }\equiv \pm \unicode[STIX]{x1D6FD}\hspace{0.6em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6FC}$
, then
$\unicode[STIX]{x1D6FD}^{\prime }\equiv \pm \unicode[STIX]{x1D6FD}\hspace{0.6em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6FC}$
, then
![]() $s(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6FC})=\pm s(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC})$
. Moreover, using the reciprocity law for the Dedekind sum:
$s(\unicode[STIX]{x1D6FD}^{\prime },\unicode[STIX]{x1D6FC})=\pm s(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC})$
. Moreover, using the reciprocity law for the Dedekind sum:
we have
because
![]() $s(p,1)=s(p,2)=0$
. Therefore, it follows that
$s(p,1)=s(p,2)=0$
. Therefore, it follows that
By Remark 2.4(i), we can see that
![]() $\unicode[STIX]{x1D711}$
is irreducible if
$\unicode[STIX]{x1D711}$
is irreducible if
![]() $\overline{g}=0$
and reducible if
$\overline{g}=0$
and reducible if
![]() $\overline{g}\not =0$
. Namely there exists a reducible automorphism
$\overline{g}\not =0$
. Namely there exists a reducible automorphism
![]() $\unicode[STIX]{x1D711}\in \text{Aut}(Y)$
such that
$\unicode[STIX]{x1D711}\in \text{Aut}(Y)$
such that
![]() $\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})\not =0$
.
$\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})\not =0$
.
3 Proof of Theorem 1.1
In this section we give a proof of Theorem 1.1. Let us assume that
![]() $q$
is odd (namely we assume that
$q$
is odd (namely we assume that
![]() $p\not =2$
). See [Reference Morifuji19, Theorem 1.1] for the case of
$p\not =2$
). See [Reference Morifuji19, Theorem 1.1] for the case of
![]() $q=2^{3}=8$
.
$q=2^{3}=8$
.
3.1 Reducibility
As pointed out at the end of Section 2.2, the maximum order
![]() $d_{0}$
of elements in
$d_{0}$
of elements in
![]() $\text{PSL}(2,\mathbb{F}_{q})$
is
$\text{PSL}(2,\mathbb{F}_{q})$
is
![]() $(q+1)/2$
if
$(q+1)/2$
if
![]() $q=p^{n}~(n>1)$
and
$q=p^{n}~(n>1)$
and
![]() $p$
if
$p$
if
![]() $q=p$
.
$q=p$
.
For a Hurwitz surface
![]() $X$
with genus
$X$
with genus
![]() $g$
and
$g$
and
![]() $\text{Aut}(X)=\text{PSL}(2,\mathbb{F}_{q})$
, we have
$\text{Aut}(X)=\text{PSL}(2,\mathbb{F}_{q})$
, we have
![]() $84(g-1)=(q+1)q(q-1)/2$
. If
$84(g-1)=(q+1)q(q-1)/2$
. If
![]() $d_{0}$
is less than
$d_{0}$
is less than
![]() $2g+1$
, then we see from Remark 2.4(ii) that every element in
$2g+1$
, then we see from Remark 2.4(ii) that every element in
![]() $\text{PSL}(2,\mathbb{F}_{q})$
is reducible. In fact, for
$\text{PSL}(2,\mathbb{F}_{q})$
is reducible. In fact, for
![]() $q=p^{3}$
as in Proposition 2.2(iii), we have
$q=p^{3}$
as in Proposition 2.2(iii), we have
because
![]() $q\geqslant 27$
. Similarly, for
$q\geqslant 27$
. Similarly, for
![]() $q=p$
as in Proposition 2.2(ii), we have
$q=p$
as in Proposition 2.2(ii), we have
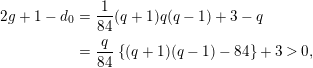 $$\begin{eqnarray}\displaystyle 2g+1-d_{0} & = & \displaystyle \frac{1}{84}(q+1)q(q-1)+3-q\nonumber\\ \displaystyle & = & \displaystyle \frac{q}{84}\left\{(q+1)(q-1)-84\right\}+3>0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2g+1-d_{0} & = & \displaystyle \frac{1}{84}(q+1)q(q-1)+3-q\nonumber\\ \displaystyle & = & \displaystyle \frac{q}{84}\left\{(q+1)(q-1)-84\right\}+3>0,\nonumber\end{eqnarray}$$
because
![]() $q\geqslant 13$
. When
$q\geqslant 13$
. When
![]() $q=7$
, a similar inequality does not hold. In fact, it is known that the Klein surface admits an irreducible automorphism of order
$q=7$
, a similar inequality does not hold. In fact, it is known that the Klein surface admits an irreducible automorphism of order
![]() $7$
(see [Reference Morifuji16] for example).
$7$
(see [Reference Morifuji16] for example).
Therefore, for a sufficiently large
![]() $q$
, we can conclude that every automorphism of a Hurwitz surface
$q$
, we can conclude that every automorphism of a Hurwitz surface
![]() $X$
with
$X$
with
![]() $\text{Aut}(X)=\text{PSL}(2,\mathbb{F}_{q})$
is reducible. This completes the proof of the first claim in Theorem 1.1.
$\text{Aut}(X)=\text{PSL}(2,\mathbb{F}_{q})$
is reducible. This completes the proof of the first claim in Theorem 1.1.
3.2 Vanishing of the
 $\unicode[STIX]{x1D702}$
-invariant
$\unicode[STIX]{x1D702}$
-invariant
It is enough to show that the
![]() $\unicode[STIX]{x1D702}$
-invariant of a mapping torus vanishes for each conjugacy class of
$\unicode[STIX]{x1D702}$
-invariant of a mapping torus vanishes for each conjugacy class of
![]() $\text{PSL}(2,\mathbb{F}_{q})$
because of the conjugacy invariance of
$\text{PSL}(2,\mathbb{F}_{q})$
because of the conjugacy invariance of
![]() $\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})$
.
$\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})$
.
Let
![]() $\unicode[STIX]{x1D711}\in \text{PSL}(2,\mathbb{F}_{q})$
be of order
$\unicode[STIX]{x1D711}\in \text{PSL}(2,\mathbb{F}_{q})$
be of order
![]() $d>1$
. As mentioned at the end of Section 2.3, if
$d>1$
. As mentioned at the end of Section 2.3, if
![]() $d\not =2,3,7$
, then by Proposition 2.3 we have
$d\not =2,3,7$
, then by Proposition 2.3 we have
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})=0$
. Since we are now assuming that
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711})=0$
. Since we are now assuming that
![]() $q$
is sufficiently large (hence
$q$
is sufficiently large (hence
![]() $p$
is also large), for elements of order
$p$
is also large), for elements of order
![]() $p$
we obtain
$p$
we obtain
![]() $\unicode[STIX]{x1D708}(c_{2}(1))=\unicode[STIX]{x1D708}(c_{2}(\unicode[STIX]{x1D6E5}))=0$
. Hence we can conclude that
$\unicode[STIX]{x1D708}(c_{2}(1))=\unicode[STIX]{x1D708}(c_{2}(\unicode[STIX]{x1D6E5}))=0$
. Hence we can conclude that
![]() $\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=0$
by the formula (2.1).
$\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=0$
by the formula (2.1).
Next for
![]() $\unicode[STIX]{x1D711}=c_{3}(\sqrt{-1})$
or
$\unicode[STIX]{x1D711}=c_{3}(\sqrt{-1})$
or
![]() $c_{4}(\unicode[STIX]{x1D6FF})$
, it is easy to see that
$c_{4}(\unicode[STIX]{x1D6FF})$
, it is easy to see that
![]() $\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=0$
holds because they are involutions (see [Reference Morifuji14, Example 3.2] for instance).
$\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=0$
holds because they are involutions (see [Reference Morifuji14, Example 3.2] for instance).
Finally let us consider the case where
![]() $\unicode[STIX]{x1D711}\in \text{PSL}(2,\mathbb{F}_{q})$
of order
$\unicode[STIX]{x1D711}\in \text{PSL}(2,\mathbb{F}_{q})$
of order
![]() $d$
is appeared as a subgroup of a cyclic group of order
$d$
is appeared as a subgroup of a cyclic group of order
![]() $(q-1)/2$
or
$(q-1)/2$
or
![]() $(q+1)/2$
. Namely we assume that
$(q+1)/2$
. Namely we assume that
![]() $\mathbb{Z}/d=\langle \unicode[STIX]{x1D711}\rangle$
is
$\mathbb{Z}/d=\langle \unicode[STIX]{x1D711}\rangle$
is
![]() $\langle c_{3}(x)\rangle$
or
$\langle c_{3}(x)\rangle$
or
![]() $\langle c_{4}(z)\rangle$
. However, in these cases, we can check that
$\langle c_{4}(z)\rangle$
. However, in these cases, we can check that
![]() $\unicode[STIX]{x1D711}$
is conjugate to
$\unicode[STIX]{x1D711}$
is conjugate to
![]() $\unicode[STIX]{x1D711}^{-1}$
(see Section 2.2(iii) and (iv)). Therefore, we have
$\unicode[STIX]{x1D711}^{-1}$
(see Section 2.2(iii) and (iv)). Therefore, we have
![]() $\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=0$
because
$\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=0$
because
![]() $\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}^{-1}})=-\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})$
holds. This completes the proof of Theorem 1.1.
$\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})=\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}^{-1}})=-\unicode[STIX]{x1D702}(M_{\unicode[STIX]{x1D711}})$
holds. This completes the proof of Theorem 1.1.
Acknowledgments
The author would like to thank Tomoyuki Wada for many useful comments. He would also like to thank the anonymous referee for helpful comments.