Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-18T13:45:50.809Z Has data issue: false hasContentIssue false
  • English
  • Français

A Probabilistic Extension of Action Language 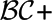${\cal BC}$+}$

Published online by Cambridge University Press:  10 August 2018

JOOHYUNG LEE  and
YI WANG
JOOHYUNG LEE
Affiliation:
School of Computing, Informatics and Decision Systems Engineering, Arizona State University, Tempe, USA (e-mails: [email protected]; [email protected])
YI WANG
Affiliation:
School of Computing, Informatics and Decision Systems Engineering, Arizona State University, Tempe, USA (e-mails: [email protected]; [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present a probabilistic extension of action language 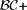${\cal BC}$+$. Just like 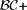${\cal BC}$+$ is defined as a high-level notation of answer set programs for describing transition systems, the proposed language, which we call p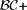${\cal BC}$+$, is defined as a high-level notation of LPMLN programs—a probabilistic extension of answer set programs. We show how probabilistic reasoning about transition systems, such as prediction, postdiction, and planning problems, as well as probabilistic diagnosis for dynamic domains, can be modeled in p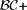${\cal BC}$+$ and computed using an implementation of LPMLN.

Type
Original Article
Information
Theory and Practice of Logic Programming , Volume 18 , Special Issue 3-4: 34th International Conference on Logic Programming , July 2018 , pp. 607 - 622
Copyright
Copyright © Cambridge University Press 2018 

References

Babb, J. and Lee, J. 2013. Cplus2ASP: Computing action language ${\cal C}+}$ in answer set programming. In Proceedings of International Conference on Logic Programming and Nonmonotonic Reasoning (LPNMR). 122–134.Google Scholar
Babb, J. and Lee, J. 2015. Action language ${$\cal BC$}+$. Journal of Logic and Computation, exv062.Google Scholar
Balduccini, M. and Gelfond, M. 2003. Diagnostic reasoning with A-Prolog. Theory and Practice of Logic Programming 3, 425–461.Google Scholar
Baral, C., Gelfond, M., and Rushton, N. 2004. Probabilistic reasoning with answer sets. In Logic Programming and Nonmonotonic Reasoning. Springer Berlin Heidelberg, Berlin, Heidelberg, 21–33.Google Scholar
Baral, C., Mcilraith, S., and Son, T. 2000. Formulating diagnostic problem solving using an action language with narratives and sensing.Google Scholar
Baral, C., Tran, N., and Tuan, L.-C. 2002. Reasoning about actions in a probabilistic setting. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI). 507–512.Google Scholar
D'Asaro, F. A., Bikakis, A., Dickens, L., and Miller, R. 2017. Foundations for a probabilistic event calculus. CoRR abs/1703.06815.Google Scholar
Eiter, T. and Lukasiewicz, T. 2003. Probabilistic reasoning about actions in nonmonotonic causal theories. In Proceedings Nineteenth Conference on Uncertainty in Artificial Intelligence (UAI-2003). Morgan Kaufmann Publishers, 192–199.Google Scholar
Gelfond, M. and Lifschitz, V. 1993. Representing action and change by logic programs. Journal of Logic Programming 17, 301–322.Google Scholar
Gelfond, M. and Lifschitz, V. 1998. Action languages5. Electronic Transactions on Artificial Intelligence 3, 195–210.Google Scholar
Giunchiglia, E., Lee, J., Lifschitz, V., McCain, N., and Turner, H. 2004. Nonmonotonic causal theories. Artificial Intelligence 153 (1–2), 49–104.Google Scholar
Giunchiglia, E. and Lifschitz, V. 1998. An action language based on causal explanation: Preliminary report. In Proceedings of National Conference on Artificial Intelligence (AAAI). AAAI Press, 623–630.Google Scholar
Iwan, G. 2002. History-based diagnosis templates in the framework of the situation calculus. AI Communications 15, 1, 31–45.Google Scholar
Lee, J., Lifschitz, V., and Yang, F. 2013. Action language ${$\cal BC$}$: Preliminary report. In Proceedings of International Joint Conference on Artificial Intelligence (IJCAI).Google Scholar
Lee, J. and Meng, Y. 2013. Answer set programming modulo theories and reasoning about continuous changes. In Proceedings of International Joint Conference on Artificial Intelligence (IJCAI).Google Scholar
Lee, J., Talsania, S., and Wang, Y. 2017. Computing LPMLN using ASP and MLN solvers. Theory and Practice of Logic Programming.Google Scholar
Lee, J. and Wang, Y. 2015. A probabilistic extension of the stable model semantics. In International Symposium on Logical Formalization of Commonsense Reasoning, AAAI 2015 Spring Symposium Series.Google Scholar
Lee, J. and Wang, Y. 2016. Weighted rules under the stable model semantics. In Proceedings of International Conference on Principles of Knowledge Representation and Reasoning (KR). 145–154.Google Scholar
Lee, J. and Wang, Y. 2018. Online appendix for the paper “A probabilistic extension of action language ${$\cal BC$}+$”.Google Scholar
Richardson, M. and Domingos, P. 2006. Markov logic networks. Machine Learning 62, 1–2, 107–136.Google Scholar
Skarlatidis, A., Paliouras, G., Vouros, G. A., and Artikis, A. 2011. Probabilistic event calculus based on markov logic networks. In Rule-Based Modeling and Computing on the Semantic Web. Springer, 155–170.Google Scholar
Younes, H. L. and Littman, M. L. 2004. PPDDL1. 0: An extension to PDDL for expressing planning domains with probabilistic effects.Google Scholar
Zhu, W. 2012. Plog: Its algorithms and applications. Ph.D. thesis, Texas Tech University.Google Scholar
Supplementary material: PDF

Lee and Wang supplementary material

Online Appendix

Download Lee and Wang supplementary material(PDF)
PDF 272 KB