Critical globalisation: Productive capacity and capital productivity in the United States, 1945–2020

Abstract

We study the dynamics of the profit rate of United States (US) non-financial resident firms between 1945 and 2020. The 1970s entailed the abandonment of industrial policy and the liberalisation and globalisation of markets. This left the US-resident productive sector at the mercy of an unstoppable growth of imports. These imports helped to contain inflation but cornered the US domestic market, which negatively affected the profit rate of non-financial resident firms. The increasing foreign competition forced US-resident firms to invest and increase their productive capacity. Such increasing productive capacity demanded higher market shares; however, US-resident firms continued to lose domestic and foreign markets. This explains the fall in the degree of productive capacity utilisation, capital productivity, and ultimately, the rate of profit since the 1980s.

Introduction

The recent evolution of the most advanced economies share a clear pattern: a downturn in economic growth rates and a growing process of tertiarisation compared to the so-called Golden Age period. Globalisation, which has been accentuated since the thrust of emerging economies, might explain this structural change in developed economies. The United States (US) is the most remarkable example of this process (Manera 2013).

A conjunction of downward phases in cycles of capitalism characterises depression. Every depression has come when the cycle in clusters of innovation has matured and become ‘saturated’; when world production and commodity prices enter a downward phase (inflation slows and even turns into deflation); when the cycle of construction and infrastructure investment has slumped; and above all, when the cycle of profitability is in a downward phase (Roberts 2022, 17). According to this definition of depression, the US has experienced depression since the 1980s, because since then the country has not recovered its previous trend rate of growth. Above all, it means that the profitability of the US domestic capitalist sectors has remained lower.

Another empirical regularity observed in developed economies is the decreasing trend of the profit rate over the last sixty years. Recent works, such as Basu et al (2022), Manera et al (2019b, 2022), and Lapavitsas (2013), assert that this decrease in the profit rate is mainly explained by the fall of the output-capital ratio (GDP/K), which we will refer to as capital productivity (Manera et al 2019a; Manera et al 2022b). However, which has been the leading cause of the decrease in capital productivity? Basu et al (2022) state that this fall is related to the increasing tertiarisation of the economy. We aim to contribute to the literature through the characterisation of four aspects of the US economy:

• The increase in competition between capitals due to the liberalisation and the increasing globalisation of markets (Pariboni 2016; Pérez-Montiel and Manera 2020) has been key to containing industrial prices. At the same time, it has led to higher competition. Higher competition has led US firms to maintain investment rates.

• The implementation of restrictive and anti-Keynesian monetary policies, at least until 2008, to control and reduce the high inflation rates of the 1970s (Blanchard et al 2012; Kim and Allmang 2021; Haluska 2022; Ghosh 2023).

• The service sector’s greater sophistication and diversification thanks to the new ICT technological revolution and the Knowledge Economy (Tridico and Pariboni 2018; Pariboni et al 2020)

• The dominance of the financial capital over the productive and industrial ones (Freeman 2010; Roberts 2016, 2022; Hellwig 2021).

We will argue that these four factors are causally interrelated and are critical to understanding the decreasing trend in capital productivity experienced by the United States in the last decades.

Our research aims to analyse the long-lasting switch experienced by the US economy since the 1970s (Borsato 2023). We argue that increasing globalisation has led to a progressive increase in imports and an increasing external deficit. This denotes a loss of the US resident firms’ foreign and domestic market shares. This is explained by the replacement of domestic production of high-end goods by products imported mainly from the European Union (e.g., automobiles and manufactured goods of prestigious brands) and low-priced consumer goods by products imported from China and other Asian countries. This, along with a more restrictive monetary policy, has made it possible to reduce the high inflation rates of the 1970s and 1980s; at the same time, significant growth in credit to families and companies has facilitated US mass consumption. On the other hand, increasing foreign competition has stimulated investment, which has led to an increasing productive capacity. This greater productive capacity, together with the loss of domestic and foreign market shares, has prevented US resident firms from maintaining their ‘normal’ degree of productive capacity utilisation. Finally, the decline in the degree of capacity utilisation explains the fall in capital productivity.

Our paper contributes to the debate on the declining trend in capacity utilisation in the United States economy (Bansak et al 2007; Pierce and Wisniewski 2018; Gahn 2020). Gahn (2023) tries to find an explanation for the declining trend in the degree of effective productive capacity utilisation (proxied by the output-capital ratio, which we call capital productivity) and concludes that: ‘There is a declining trend in effective capacity utilisation in the US and there is still no precise answer to this phenomenon’. Gahn finds that shocks to the level of production, distribution, productive technique, and inventories do not have persistent effects on the output-capital ratio. Therefore, our work offers a possible explanatory hypothesis for this enigma in the US.

On the other hand, our work offers an interpretation of the behaviour of the US rate of profit within a critical approach to neoliberal globalisation. In this sense, our paper can be read through the lens of Michael Roberts’ approach: in a context of falling returns on invested capital, the efforts to maintain the rate of profit lay on pressure on the labour force, with different manifestations: cuts in public spending, elimination of social rights, greater labour intensity, new labour-saving technologies, and privatisations. This might explain the increasing gap between growth in labour productivity and wages since the 1970s (Pensiero 2022). Thus, Roberts (2016) does not believe that Keynesian postulates would contribute to solving the problems of the US economy. He attributes the economic performance of the ‘glorious thirty years’ to the consequences of the Second World War when the United States put all its productive machinery to boost its economy. The solution to the main economic problems proposed by the author focuses on a way out that he qualifies as ‘socialist’: that governments take charge of the main sectors of the economy to produce for social needs instead of doing it for profit. The central derivative of it would be controlling investments and the ownership of the major banks and other large companies. This, for Roberts, is very different from Keynesian proposals. This argument also aligns with those who claim that industrial policy should be brought back to the front and play a key role in economic policy (Portella-Carbó and Dejuán 2019; Nieto et al 2020).

We organise the work as follows. Section two highlights the relationship between the degree of productive capacity utilisation, capital productivity, and the foreign sector. Section 3 empirically tests the relationship between the three mentioned variables, while Section 4 discusses the results. Finally, Section 5 concludes.

Degree of productive capacity utilisation, capital productivity, and the foreign sector

In this section, we demonstrate the dynamic relationship between the imports/GDP ratio ( ${\rm{m}}$ ), the degree of utilisation of productive capacity ( ${\rm{u}}$ ), and capital productivity ( ${\rm{\pi k}}$ ) in the United States between 1947 and 2020. Due to data availability, we use the data of the non-financial sector to construct capital productivity (GDP/K). On the other hand, we use the series of capacity utilisation corresponding to the manufacturing sector since available data for the series of the total industry starts in 1967. The remarkably high correlation between these two series, which reaches 99% (Graph 1), supports this choice.

Graph 1. Degree of productive capacity utilisation in the United States. Manufacturing sector and total industry, 1945–2020. Source: Own elaboration with Federal Reserve Bank of St. Louis data.

Graph 2 plots the series of ${\rm{u}}$ and ${\rm{\pi k}}$ of non-financial US firms: both series share a decreasing trend, although ${\rm{u}}$ shows more significant variability than ${\rm{\pi k}}$ . The Pearson correlation coefficient between them is 76.8%. We can see that between 1948 and 1968, the Keynesian regulation phase, the differences between the series remained relatively steady, with capital productivity being above capacity utilisation until the oil shock of 1973. The period 1950–1968 also experienced the full effects of the Treaty of Detroit (See Armstrong et al (1991a) and Noah (2012)), ¹ which generated a period of stability in the evolution of social inequalities and coincided with high growth rates (Manera et al 2022). Despite a fall of both ${\rm{u}}$ and ${\rm{\pi k}}$ in the 1950s due to the first saturation of the consumer goods market after World War II, the variables present a similar trajectory. From 1973 onwards, capital productivity has remained below capacity utilisation. Both series recovered during the great moderation phase, but without reaching the 50s and 60s values. We also see that in 1995 (when the World Trade Organization was created and international trade agreements were intensified), the positive trajectory of both series was reversed. Graph 2 also shows that from the middle 1990s onwards, the difference between the series has grown, i.e., the decreasing trend of capital productivity has become more pronounced than that of capacity utilisation. Between 2001–2008 capacity utilisation recovered in the context of increasing public expenditure and a housing bubble, but capital productivity continued its decreasing trajectory.

Graph 2. Degree of productive capacity utilisation and capital productivity in non-financial firms of the United States, 1952–2019. 1952=100.

Since capital productivity can be defined as the degree of capacity utilisation divided by the incremental capital-output ratio (icor) (Weisskopf 1979), the dynamics of the icor explain the differences between capital productivity and the degree of capacity utilisation. Thus, capital productivity has decreased more than capacity utilisation because the icor has increased. An increasing icor means increasing capital needed to increase a unit of total output. Thus, we posit that the constant productive reinvestments to face increasing globalisation and competition have incorporated productive capacity that requires greater market shares. These greater shares, however, have not materialised, which has caused a higher fall in capital productivity.

On the other hand, Graph 3 compares the propensity to import, which we use as a proxy of the market shares of the US economy, with the degree of capacity utilisation. The weight of imports over GDP remained stable at around 2.5% and 3% until the late sixties; however, by the end of the 1980s, it was already 8%, reaching 16% in 2009. The behaviour of exports (which, to a certain extent, can be considered autonomous (Girardi and Pariboni 2016; Pérez-Montiel and Manera 2022) is not sufficiently dynamic to offset the increase in imports; thus, since the end of the 1970s, the trade balance becomes negative.

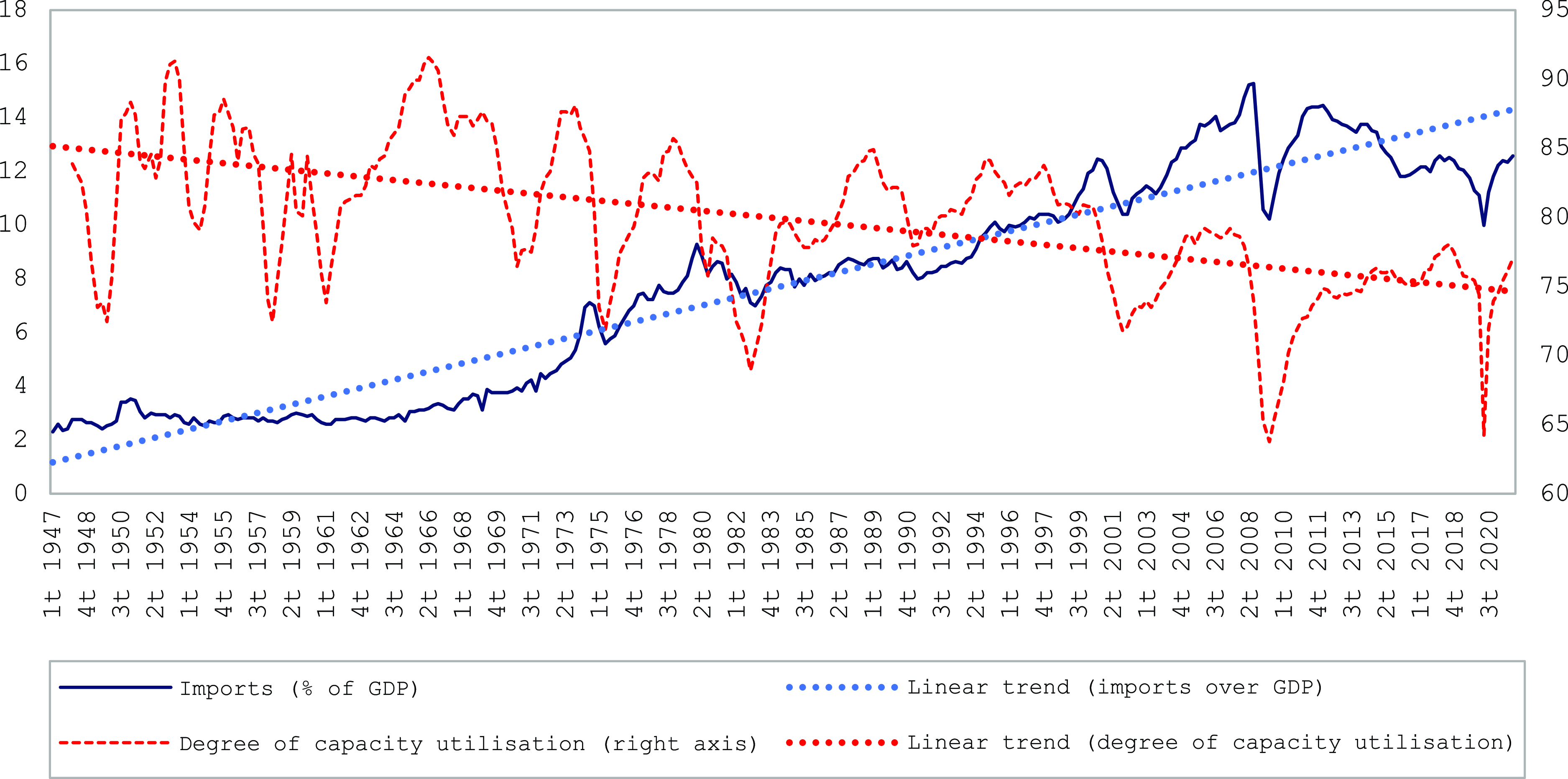
Graph 3. Weight of imports over GDP and degree of productive capacity utilisation in the United States (%), 1947–2020.

In the next section, we use quarterly US data to analyse the causal relationship between the propensity to import $({\rm{m}}$ ), the degree of productive capacity utilisation ( ${\rm{u}}$ ), and capital productivity ( ${\rm{\pi k}}$ ) between 1947 and 2019.

Empirical analysis

We study hysteresis and contemporaneous relationships between the propensity to import $({\rm{m}}$ ), the degree of productive capacity utilisation ( ${\rm{u}}$ ), and capital productivity ( ${\rm{\pi k}}$ ) between 1947 and 2019. We use time-varying impulse-response analysis and directed acyclic graphs (DAG) for this aim.

Time-varying impulse-response functions

The Lumsdaine-Papell and Bai-Perron’s unit root tests indicate that the variables under study have multiple and different structural breaks. Thus, instead of dividing the entire test into sub-periods, we use a time-varying parameter structural vector autoregressive (TVP-SVAR) model on the total sample. Unlike standard SVAR models, which impose the constraint that the coefficients are constant through time, the TVP-SVAR allows continuous smooth changes in the coefficients.

Following Sims (1980) and Sims et al (1990), who claim that a VAR in levels correctly estimates the dynamics of a system, ² we estimate a TVP-SVAR in levels, which is usual in the VAR literature (Elbourne 2008; Farzanegan and Markwardt 2009; Tang et al 2010; Iwayemi and Fowowe 2011; Alom et al 2013; Kohler and Stockhammer 2020, among others). The fact that some of the variables are I(1) is not a problem since the slope coefficients of the I(1) variables could be rewritten as differenced variable coefficients (Stockhammer et al 2019). Furthermore, using the variables in a VAR representation in levels ‘avoids the controversial question of which cointegration constraints impose in the estimate’ (Kilian and Lütkepohl 2017).

To order the variables in the SVAR model, we have used the DAG method, a data-driven method of ordering the data in a VAR model, thereby avoiding theoretical assumptions. To this aim, we use the PC algorithm of Spirtes et al (2000). Because simultaneity or instantaneous causality may appear due to omitted causal variables, Spirtes et al (2000) have developed methods for inferring the existence of omitted (latent) variables and working out their causal consequences (Hoover 2005: 74). The empirical literature considers the use of the PC algorithm as a valid tool to assign causal flows among variables based on observational data: Kalisch and Buhlmann (2007) show that the PC algorithm using statistical tests is computationally feasible and consistent even for very high-dimensional sparse DAGs; while Uhler et al (2013) show that additionally assuming a condition called strong faithfulness, the PC algorithm even yields uniform consistency. Finally, Demiralp and Hooverà (2003) study the PC algorithm with Monte Carlo simulations and show that the DAG is a valid statistical procedure to identify the contemporaneous causal order of a structural vector autoregression.

A directed acyclic graph analysis is a directed graph with no loop. It is composed of points representing variables and directed edges connecting these points. The DAG analysis uses graphs to represent the contemporaneous causal relationships between variables. In a directed acyclic graph, the direct edge between two points represents the contemporaneous causal relationship between two variables. The possibilities between two variables, A and B, are the following:

• A → B: represents that A contemporaneously causes B;

• A ← B: states that B contemporaneously causes A;

• A↔B: indicates that there is bidirectional contemporaneous causality between A and B;

• A–B: represents that there is a contemporaneous causality with uncertain direction between A and B;

• A B indicates that there is not any contemporaneous causality between A and B.

We use the PC algorithm by Spirtes et al (2000) to analyse the contemporaneous causal relationships between the variables. We built a full non-directed graph with three variables, each connected to the other two. Hereafter, we remove and direct the edges of the full non-directed graph. In the phase of removal, we first analyse the unconditional correlation coefficient and eliminate the edge connecting both variables when the correlation coefficient between them is 0. Once we have finished the correlation analysis, we analyse the first-order partial correlation coefficient (the correlation coefficient between two variables conditional on the third variable) on the remaining edges. The edge that connects both variables is removed when the first-order correlation coefficient between the two variables is 0. Likewise, after completing the first-order partial correlation coefficient analysis, the second-order partial correlation coefficient is analysed on the remaining edges, and subsequently, the third-order, …, until the N-2-order partial correlation coefficient. In our case, as N = 3, we only analyse the first-order partial correlation coefficient. To test whether the partial correlation coefficients are significantly different from 0, we use Fisher’s z-statistic.

Once we have ordered the variables, we estimate the TVP-SVAR model with two lags (based on the Bayesian information criteria of Schwarz (1978) and the Hannan-Quinn information criterion of Hannan and Quinn (1979)). We aim to capture the time-varying impacts that structural shocks on ${\rm{m\;}}$ ( ${\rm{u}}$ ) have on ${\rm{u}}$ ( ${\rm{\pi k}}$ ) without dividing our full sample into subsamples. Indeed, compared to the constant parameters SVAR model, the TVP-SVAR models allow the detection of the changes in the responses’ behaviour over time of the system to the identified structural shocks while conserving the full sample information specificity (Zhong et al 2023, 106708). The uncorrelatedness of the shocks allows us to identify impulse-response functions and rules out the presence of any omitted variables that enter multiple equations (Ghanem and Smith 2022).

The DAG analysis, whose results are presented in Figure 1, suggests ordering the variables in the TVP-SVAR as follows: ${\rm{m}}$ , ${\rm{u}}$ , ${\rm{\pi k}}$ . Once the restrictions are imposed, and the model is estimated, we compute time-varying impulse-response functions to assess the impact of an exogenous shock in ${\rm{m}}$ , ${\rm{u}}$ , and ${\rm{\pi k}}$ . We compute standard errors using the Monte Carlo method (1,000 repetitions) and report the IRFs with one-standard error band, namely a 68% confidence interval. ³ Figure 1 also shows the results of the impulse-response functions based on the TVP-SVAR model’s specification with the three variables in levels. It allows us to analyse the relationship between the variables under study on the entire sample interval. On the left-hand side of Figure 1, we can see the impulse-response paths of ${\rm{u}}\;$ to a positive shock in ${\rm{m}}$ . We found that an exogenous positive shock on the import share significantly negatively affects the degree of capacity utilisation. In contrast, a shock on ${\rm{u}}$ does not significantly affect ${\rm{m}}$ . We also observe that a positive shock on ${\rm{u}}$ has a positive and significant effect on ${\rm{\pi k}}$ . In contrast, an exogenous positive shock on ${\rm{\pi k}}$ does not significantly affect ${\rm{u}}$ .

Figure 1. Responses of m, u, and πk to time-varying shocks in m, u, and πk. Note: The vertical axis shows the value of the parameters, while the horizontal axis shows the time horizon (quarters). The shaded area is the 68% error band.

Contemporaneous causality

Since there are not only hysteresis relationships between macroeconomic variables, we also explore the existence of contemporaneous causal relationships. The loss of market share can contemporaneously affect aggregate demand, consequently affecting capacity utilisation and thus, capital productivity. The VAR approach does not allow the study of the contemporaneous relationships between variables, which remain hidden in the model’s error term and cannot be estimated. Therefore, we use the DAG analysis to study contemporaneous relationships between ${{\rm{m}}_{\rm{t}}}$ , ${{\rm{u}}_{\rm{t}}}$ , and ${\rm{\pi }}{{\rm{k}}_{\rm{t}}}$ . Following our hypothesis, we study the contemporaneous causal relationship between positive changes in m ( ${\rm{m}}_{\rm{t}}^ + $ ), negative changes in u ( ${\rm{u}}_{\rm{t}}^ - $ ), and negative changes in ${\rm{\pi k}}$ ( ${\rm{\pi k}}_{\rm{t}}^ - $ ). To build ${\rm{m}}_{\rm{t}}^ + $ , ${\rm{u}}_{\rm{t}}^ - $ , and ${\rm{\pi k}}_{\rm{t}}^ - $ , we use the partial sum decompositions of Hatemi-J (2012, 2014) and Hatemi-El-Khatib (2016). This enables us to study the causal relationship between positive (negative) changes in one variable and positive (negative) changes in another variable or any other combination (Hatemi-J et al 2017). Thus, this method allows us to study whether a negative change in the utilisation degree of productive capacity is contemporaneously caused by a positive change in the propensity to import. We can also study whether a decrease in the degree of capacity utilisation contemporaneously causes a negative change in capital productivity.

Let us assume that ${\rm{\pi }}{{\rm{k}}_{\rm{t}}}$ , ${{\rm{u}}_{\rm{t}}}$ , and ${{\rm{m}}_{\rm{t}}}$ have the same data generation process: ${\rm{\pi }}{{\rm{k}}_{\rm{t}}} \equiv {\rm{\pi }}{{\rm{k}}_{{\rm{t}} - 1}} + {{\rm{e}}_{1{\rm{t}}}} = {\rm{\pi }}{{\rm{k}}_0} + \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{T}} {{\rm{e}}_{1{\rm{i}}}}$ , ${{\rm{u}}_{\rm{t}}} \equiv {{\rm{u}}_{{\rm{t}} - 1}} + {{\rm{e}}_{2{\rm{t}}}} = {{\rm{u}}_0} + \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{T}} {{\rm{e}}_{2{\rm{i}}}}$ , and ${{\rm{m}}_{\rm{t}}} \equiv {{\rm{m}}_{{\rm{t}} - 1}} + {{\rm{e}}_{3{\rm{t}}}} = {{\rm{m}}_0} + \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{T}} {{\rm{e}}_{3{\rm{i}}}}$ , being ${\rm{\pi }}{{\rm{k}}_0}$ , ${{\rm{u}}_0}$ , and ${{\rm{m}}_0}$ the initial values of ${\rm{\pi }}{{\rm{k}}_{\rm{t}}}$ , ${{\rm{u}}_{\rm{t}}}$ , and ${{\rm{m}}_{\rm{t}}}$ respectively, while ${{\rm{e}}_{1{\rm{i}}}}$ , ${{\rm{e}}_{2{\rm{i}}}},{\rm{\;}}$ and ${{\rm{e}}_{3{\rm{i}}}}$ are i.i.d with ${\rm{\sigma }}_{{{\rm{e}}_1}}^2$ , ${\rm{\sigma }}_{{{\rm{e}}_2}}^2$ y ${\rm{\sigma }}_{{{\rm{e}}_3}}^2$ variance, respectively. Hatemi-J (2012, 2014) defines positive shocks as ${\rm{e}}_{1{\rm{t}}}^ + = {\rm{max}}\left( {{{\rm{e}}_{1{\rm{t}}}},0} \right)$ , ${\rm{e}}_{2{\rm{t}}}^ + = {\rm{max}}\left( {{{\rm{e}}_{2{\rm{t}}}},0} \right)$ and ${\rm{e}}_{3{\rm{t}}}^ + = {\rm{max}}\left( {{{\rm{e}}_{3{\rm{t}}}},0} \right);$ while he represents negative shocks as ${\rm{e}}_{1{\rm{t}}}^ - = {\rm{min}}\left( {{{\rm{e}}_{1{\rm{t}}}},0} \right),{\rm{\;e}}_{2{\rm{t}}}^ - = {\rm{min}}\left( {{{\rm{e}}_{2{\rm{t}}}},0} \right)$ and ${\rm{e}}_{3{\rm{t}}}^ - = {\rm{min}}\left( {{{\rm{e}}_{3{\rm{t}}}},0} \right)$ . Therefore, ${{\rm{e}}_{1{\rm{t}}}} = {\rm{e}}_{1{\rm{t}}}^ + + {\rm{e}}_{1{\rm{t}}}^ - $ , ${{\rm{e}}_{2{\rm{t}}}} = {\rm{e}}_{2{\rm{t}}}^ + + {\rm{e}}_{2{\rm{t}}}^ - $ , and ${{\rm{e}}_{3{\rm{t}}}} = {\rm{e}}_{3{\rm{t}}}^ + + {\rm{e}}_{3{\rm{t}}}^ - $ ; while ${\rm{\pi }}{{\rm{k}}_{\rm{t}}} = {\rm{\pi }}{{\rm{k}}_0} + \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{1{\rm{t}}}^ + + \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{1{\rm{t}}}^ - $ , ${{\rm{u}}_{\rm{t}}} = {{\rm{u}}_0} + \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{2{\rm{t}}}^ + + \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{2{\rm{t}}}^ - $ , and ${{\rm{m}}_{\rm{t}}} = {{\rm{m}}_0} + \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{3{\rm{t}}}^ + + \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{3{\rm{t}}}^ - $ . In this way, and following Granger and Yoon (2002), Hatemi-J (2012) defines accumulative positive and negative shocks as: ${\rm{\pi k}}_{\rm{t}}^ + = \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{1{\rm{t}}}^ + $ ; ${\rm{\pi k}}_{\rm{t}}^ - = \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{1{\rm{i}}}^ - $ ; ${\rm{u}}_{\rm{t}}^ + = \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{2{\rm{t}}}^ + $ ; ${\rm{u}}_{\rm{t}}^ - = \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{2{\rm{i}}}^ - $ ; ${\rm{m}}_{\rm{t}}^ + = \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{3{\rm{t}}}^ + $ ; and ${\rm{m}}_{\rm{t}}^ - = \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{t}} {\rm{e}}_{3{\rm{i}}}^ - $ .

Once we obtain ${\rm{m}}_{\rm{t}}^ + $ , ${\rm{u}}_{\rm{t}}^ - $ , and ${\rm{\pi k}}_{\rm{t}}^ - $ , the next step is building a non-directed full graph of ${\rm{m}}_{\rm{t}}^ + $ , ${\rm{u}}_{\rm{t}}^ - $ and ${\rm{\pi k}}_{\rm{t}}^ - $ . Next, we analyse the matrix of the remaining coefficients by the PC algorithm of the Tetrad software to obtain the contemporaneous causal relationships between ${\rm{m}}_{\rm{t}}^ + $ , ${\rm{u}}_{\rm{t}}^ - $ , and ${\rm{\pi k}}_{\rm{t}}^ - $ (Figure 2):

Figure 2. DAG analysis between m⁺, u-, and πk-. Note: Directed acyclic graphs between ${\rm{m}}_{\rm{t}}^ + $ , ${\rm{u}}_{\rm{t}}^ - $ , and ${\rm{\pi k}}_{\rm{t}}^ - $ . The asterisks *** denote statistical significance at the 1%.

As shown in Figure 2, ${\rm{u}}_{\rm{t}}^ - $ is a contemporaneous cause of ${\rm{\pi k}}_{\rm{t}}^ - $ , while ${\rm{m}}_{\rm{t}}^ + $ contemporaneously causes ${\rm{u}}_{\rm{t}}^ - $ . This indicates that the loss of market shares by the US resident productive sector contemporaneously reduces the utilisation degree of productive capacity of the United States, which in turn, contemporaneously causes a decrease in capital productivity.

Discussion

We have proposed an overall but consistent possible explanation of the loss of US industrial economic dynamism in the framework of increasing globalisation. Departing from the preposition that the adjustment of capacity to demand is slow in the US (Haluska et al 2023), we have hypothesised a causal relation between market loss (proxied by an increasing propensity to import) and a decrease of both productive capacity utilisation and capital productivity. What does this mean? The answer might seem only intuitive, but in our opinion, it is clear.

The 1970s crisis sponsored the abandonment of industrial policy and the liberalisation and globalisation of markets instead of triggering a resurgence of industrial-based technology policies. Thus, a profound change in economic policy priorities took place. Due to the shock in production costs caused by the energy crisis, the productive system was abandoned to its fate and had to face an unstoppable growth of imports. These imports helped to contain inflation, the main goal of the new neoliberal economic policy of the moment.

This economic policy prioritised monetary policy and abandoned previous full employment strategies of Keynesian inspiration (Armstrong et al 1991b). As a result, significant and strategic parts of US production were squandered and replaced by foreign production, often due to relocations promoted by US multinational companies. The central core of the US industrial productive system, which survived the deep crisis of the 1970s, had to contend with a new neoliberal economic policy paradigm, facing more international competition. This change hurt the rate of profit of non-financial resident firms through the decrease in capacity utilisation. In turn, increasing foreign competition led US resident firms to the renewal of the productive equipment. This demanded more production and market share to increase production per unit of capital invested. However, instead, what happened is that foreign productions, including those of US transnational capital, gained more and more domestic market share. This caused a further fall in the utilisation degree of productive equipment and a continued decrease in capital productivity and levels of profitability of productive capital.

In order to counteract the decreasing trend in the rate of profit, the resident productive sector took advantage of the new economic paradigm to contain wages (as argued by Basu et al (2022) and empirically demonstrated by Manera et al (2022) and Tippet et al (2022)). Simultaneously, the tax burden on capital income and corporate social contributions was reduced, with the consequent reduction of the Welfare State and increased social polarisation. The described process involves an increase in income inequality, resulting from the purpose of resident corporate capital to maintain its profits. In this sense, other researchers’ provided data align with our conclusion (Hacker and Pierson 2010; Saez and Zucman 2022). In fact, between 1980 and 2018, the US witnessed a slowdown in growth parallel to a greater concentration of incomes and wealth (Espinosa-Gracia and Sánchez-Chóliz 2023): the incomes of the top 0.1% of income earners have grown by 320% since 1980. At the same time, the top 0.01% increased its income by 430%, while the incomes of the 0.001% have grown by 600%. Simultaneously, the working class has yet to experience income increases in real terms (Austin 2013).

Conclusions

Capitalism is failing to develop productive forces globally and take humanity forward to a world of prosperity and the end of toil, poverty, and inequality (Roberts 2022, 18). A key measure of the productive forces’ development is capital productivity. In this paper, we argue that the decrease in capital productivity (proxied by the output/capital ratio) is the main cause of the decline in the profit rate in the United States.

So, what has been the main cause of the decrease of the output/capital ratio in the US? Why has the US capitalism, with its technological innovation capabilities, been unable to prevent its capital productivity from dropping? We argue that the 1970s entailed the abandonment of industrial policy and the liberalisation and globalisation of markets, which left the US productive sector at the mercy of the unstoppable growth of imports. These imports, which helped contain inflation, hoarded the US domestic market, which negatively affected the degree of productive capacity utilisation and the profit rate of the productive resident US firms. Increasing foreign competition demanded the renewal of productive equipment, and this new equipment demanded greater production volumes and more market shares to increase production per unit of invested capital. However, the domestic market share of US-resident companies declined in favour of non-resident firms. This explains the relentless fall in the utilisation degree of productive equipment and capital productivity since the 1980s.

Given the real wage, secular falls in capital productivity imply the reduction of the ex-post rate of profit. The decreasing profit rate’s most noticeable consequences are the firm sector’s political reaction to contain wages and the growing transfer of capital from the productive sector to the financial sector. In sum, from 1980 onwards, the change in the regulatory system of the US economy, which switched from Keynesian to neoliberal regulation, led to an increasing globalisation of the US economy. This has led to increasing tertiarisation, financialisation, property speculation, and inequality in the United States.