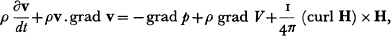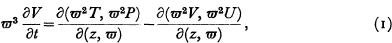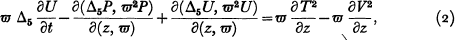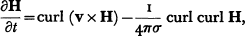Symposium - International Astronomical Union, Electromagnetic Phenomena in Cosmical Physics
- This volume was published under a former title. See this journal's title history.
Other
Preface
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. ix-xiii
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Opening address
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 1-2
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Part I: Magneto-Hydrodynamics
A. Theory
1. Magnetic fields in astrophysics
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 5-14
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
2. Magneto-hydrodynamic waves in compressible fluids by finite viscosity and heat conductivity
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 15-26
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
3. A fluid self-excited dynamo
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 27-32
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
4. Non-stable magneto-hydrodynamical processes in stars
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 33-45
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
5. The axisymmetric case in hydromagnetics
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 46-49
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
B. Experiments
6. Magneto-hydrodynamic experiments
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 50-60
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
7. Experimental work at the university of chicago on the onset of thermal instability in a layer of fluid heated from below
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 61-70
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
C. Ionized Gas in A Magnetic Field
8. Ionized gas in a magnetic field
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 71-80
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
9. Waves in a hot ionized gas in a magnetic field
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 81-86
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
10. Experimental study of plasmoids
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 87-98
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
11. A characteristic line current in a fully ionized gas
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 99-102
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Part II: Solar Electrodynamics
12. Solar electrodynamics
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 105-113
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
13. The processes in active regions on the sun and electromagnetics
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 114-122
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
14. The neutral point theory of solar flares
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 123-134
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
15. The neutral point discharge theory of solar flares. A reply to Cowling's criticism
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 135-140
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
16. Some effects of hydromagnetic waves in the solar atmosphere
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 141-149
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
17. Some considerations on thermal conduction and magnetic fields in prominences
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 150-157
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Part III: Stellar Magnetism
18. Stellar magnetic fields
-
- Published online by Cambridge University Press:
- 18 July 2016, pp. 161-165
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service

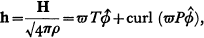
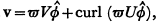
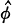 is a unit vector and
is a unit vector and