Symposium - International Astronomical Union, Advances In Hello- and Asteroseismology
- This volume was published under a former title. See this journal's title history.
Chapter 1: Observations of Solar Oscillations
Limb darkening oscillations: the discrepancy with Doppler data and the 160-minute period
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 87-88
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Chapter 2: Theory of Solar Oscillations
Sensitivity of solar p-modes to solar envelope structure
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 91-94
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
A solar model with turbulent diffusion mixing: surface abundances and oscillations
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 95-98
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The influence of a modified mixing-length theory and of an adopted description of the atmosphere on the solar five-minute oscillations
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 99-103
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Constraints on central solar conditions from helioseismology and neutrino counts
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 105-109
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Do solar models with weakly interacting massive particles reproduce the Stanford seismic data?
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 111-114
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The study of oscillations localized near a layer of density discontinuity in an example of solar model
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 115-116
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Inertial modes trapped in the solar convective envelope
-
- Published online by Cambridge University Press:
- 03 August 2017, p. 117
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Non-newtonian forces and the observed solar oscillation spectrum
-
- Published online by Cambridge University Press:
- 03 August 2017, p. 119
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Asymptotic properties of low degree gravity modes
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 121-124
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Stellar acoustic ray patterns
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 125-128
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
An optimal approach to the inverse problem
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 129-132
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Inverse problem: acoustic potential vs acoustic length
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 133-136
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
On the technique of the inversion of helioseismological data
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 137-140
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
An attempt to determine the structure of the solar core from observed g-mode frequencies
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 141-146
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Inversion of asymptotic gravity-mode frequencies and its application to the Sun
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 147-150
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
A search of the effects of magnetic field in the solar five-minute oscillations
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 151-154
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Magnetic perturbations to stellar oscillation eigenfrequencies
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 155-160
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Magnetic effects on solar p-modes
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 161-165
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
The effect of toroidal magnetic fields in the overshoot layer on the eigenfrequencies of stellar oscillations
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 167-170
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service

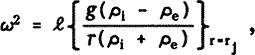
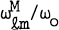 of high order acoustic modes due to the presence of a non-oblique axisymmetric magnetic field in the overshoot layer. We find that
of high order acoustic modes due to the presence of a non-oblique axisymmetric magnetic field in the overshoot layer. We find that