Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T04:36:20.531Z Has data issue: false hasContentIssue false
  • English
  • Français

A class of novel underactuated positioning systems for actuating/configuring the parallel manipulators

Published online by Cambridge University Press:  05 April 2022

Nan Ma Open the ORCID record for Nan Ma [Opens in a new window] ,
Xin Dong ,
Josue Camacho Arreguin ,
Christopher Bishop  and
Dragos Axinte
Nan Ma
Affiliation:
Department of Mechanical, Materials and Manufacturing Engineering, School of Engineering, University of Nottingham, Nottingham, UK
Xin Dong*
Affiliation:
Department of Mechanical, Materials and Manufacturing Engineering, School of Engineering, University of Nottingham, Nottingham, UK
Josue Camacho Arreguin
Affiliation:
Department of Mechanical, Materials and Manufacturing Engineering, School of Engineering, University of Nottingham, Nottingham, UK
Christopher Bishop
Affiliation:
Department of Mechanical, Materials and Manufacturing Engineering, School of Engineering, University of Nottingham, Nottingham, UK
Dragos Axinte
Affiliation:
Department of Mechanical, Materials and Manufacturing Engineering, School of Engineering, University of Nottingham, Nottingham, UK
*
*Corresponding author. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Parallel manipulators are increasingly utilized in extensive industrial applications due to their high accuracy, compact structure, and significant stiffness characteristics. However, most of the time, massive actuators are involved in constructing and controlling a parallel manipulator, which burdens the structure design and controller development. In this paper, a novel underactuated positioning system been built by different sets of linear motion units (defined as the positioning lines) is proposed, enabling to actuate the multiple degree-of-freedom manipulators with one motor. To achieve this, a smart shape memory alloy (SMA) clutch is presented to obtain the positioning function of each positioning line. Further, to get the decoupled motion regulation of the positioning lines, a new thermal kinematic model of the SMA clutch, which considers the heat dissipation influence on the metal components, was built and validated by the physical prototypes. The experimental results show that the constitutive model of the SMA clutch developed in this paper can be validated within the error of 5.3%. It can also be found that the heat dissipation of the metal component has a significant influence on the model accuracy of the SMA clutch (i.e., 2.6% of the model accuracy). The experiments on the underactuated positioning system produce the following results: the single positioning line can achieve high positioning (i.e., average error: 1.01%) and tracking (i.e., average error 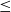$\leq$ 1 mm) abilities; the underactuated positioning system can perform decoupled motions in the three positioning lines with high accuracy (i.e., ±2 mm within the stroke of 180 mm).

Keywords

SMA clutchparallel mechanismlinear motionunderactuated manipulatorSMA modeling
Type
Research Article
Information
Robotica , Volume 40 , Issue 10 , October 2022 , pp. 3631 - 3650
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Jani, J. M., Leary, M., Subic, A. and Gibson, M. A., “A review of shape memory alloy research, applications and opportunities,” Mater. Des. 56(1–2), 1078–1113 (2014).CrossRefGoogle Scholar
Sun, L., Huang, W. M., Ding, Z., Zhao, Y. and Wang, C. C., “Stimulus-responsive shape memory materials: A review,” Mater. Des. 33(12), 577–640 (2012).CrossRefGoogle Scholar
Wang, L., Xu, H. and Guan, L., “Optimal design of a 3-PUU parallel mechanism with 2R1T DOFs,” Mech. Mach. Theory 114(4), 190–203 (2017).CrossRefGoogle Scholar
Wang, Y., Yu, J. and Pei, X., “Fast forward kinematics algorithm for real-time and high-precision control of the 3-RPS parallel mechanism,” Front. Mech. Eng. 13(3), 368–375 (2018).CrossRefGoogle Scholar
Yang, X., Wu, H., Li, Y. and Chen, B., “A dual quaternion solution to the forward kinematics of a class of six-DOF parallel robots with full or reductant actuation,” Mech. Mach. Theory 107(8), 27–36 (2017).CrossRefGoogle Scholar
Ma, N., Yu, J., Dong, X. and Axinte, D., “Design and stiffness analysis of a class of 2-DoF tendon driven parallel kinematics mechanism,” Mech. Mach. Theory 129(10), 202–217 (2018).CrossRefGoogle Scholar
Yu, J., Dong, X., Pei, X. and Kong, X., “Mobility and singularity analysis of a class of two degrees of freedom rotational parallel mechanisms using a visual graphic approach,” J. Mech. Robot. 4(4), 718 (2012).CrossRefGoogle Scholar
Ma, N., Dong, X., Palmer, D., Arreguin, J. C., Liao, Z., Wang, M. and Axinte, D., “Parametric vibration analysis and validation for a novel portable hexapod machine tool attached to surfaces with unequal stiffness,” J. Manuf. Process. 47(2), 192–201 (2019).CrossRefGoogle Scholar
Chablat, D. and Wenger, P., “Architecture optimization of a 3-DOF translational parallel mechanism for machining applications, the Orthoglide,” IEEE Trans. Robot. Autom. 19(3), 403–410 (2003).CrossRefGoogle Scholar
Tsai, M.-S., Shiau, T.-N., Tsai, Y.-J. and Chang, T. H., “Direct kinematic analysis of a 3-PRS parallel mechanism,” Mech. Mach. Theory 38(1), 71–83 (2003).CrossRefGoogle Scholar
Ma, N., Dong, X. and Axinte, D., “Modelling and experimental validation of a compliant under-actuated parallel kinematic manipulator,” IEEE/ASME Trans. Mechatron. 25(3), 1409–1421 (2020).CrossRefGoogle Scholar
Carricato, M. and Merlet, J.-P., “Stability analysis of underconstrained cable-driven parallel robots,” IEEE Trans. Robot. 29(1), 288–296 (2012).CrossRefGoogle Scholar
Wang, M., Palmer, D., Dong, X., Alatorre, D., Axinte, D. and Norton, A., “Design and development of a slender dual-structure continuum robot for in-situ aeroengine repair,” In: 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain (2018) (pp. 5648–5653).Google Scholar
Dong, X., Palmer, D., Axinte, D. and Kell, J., “In-situ repair/maintenance with a continuum robotic machine tool in confined space,” J. Manuf. Process. 38(8), 313–318 (2019).CrossRefGoogle Scholar
Palpacelli, M.-C., Carbonari, L., Palmieri, G. and Callegari, M., “Analysis and design of a reconfigurable 3-DoF parallel manipulator for multimodal tasks,” IEEE/ASME Trans. Mechatron. 20(4), 1975–1985 (2014).CrossRefGoogle Scholar
Tosi, D., Legnani, G., Pedrocchi, N., Righettini, P. and Giberti, H., “Cheope: A new reconfigurable redundant manipulator,” Mech. Mach. Theory 45(4), 611–626 (2010).CrossRefGoogle Scholar
Chen, C.-T., “Reconfiguration of a parallel kinematic manipulator for the maximum dynamic load-carrying capacity,” Mech. Mach. Theory 54, 62–75 (2012).CrossRefGoogle Scholar
Fukuda, T. and Nakagawa, S., “A dynamically reconfigurable robotic system (concept of a system and optimal configurations),” Int. Soc. Opt. Photonics (Abe Abramovich, ed.), vol. 856, (SPIE, USA, 1987) pp. 588–595. Google Scholar
Bi, Z. M. and Wang, L., “Optimal design of reconfigurable parallel machining systems,” Robot. Comput.-Integr. Manuf. 25(6), 951–961 (2009).CrossRefGoogle Scholar
Dash, A. K., Chen, I.-M., Yeo, S. H. and Yang, G., “Task-oriented configuration design for reconfigurable parallel manipulator systems,” Int. J. Comput. Integr. Manuf. 18(7), 615–634 (2005).CrossRefGoogle Scholar
Ma, N., Dong, X. and Arreguin, J. C.. A Novel Shape Memory Alloy (SMA) Wire-Based Clutch Design and Performance Test (Springer, 2020) pp. 369–376.Google Scholar
Hartl, D. J. and Lagoudas, D. C., “Aerospace applications of shape memory alloys,” Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 221(4), 535–552 (2007).CrossRefGoogle Scholar
Bil, C., Massey, K. and Abdullah, E. J., “Wing morphing control with shape memory alloy actuators,” J. Intell. Mater. Syst. Struct. 24(7), 879–898 (2013).CrossRefGoogle Scholar
Kolansky, J., Tarazaga, P. and Ohanian, O. J., “Experimental implementation of opposed shape memory alloy wires for actuator control,” J. Vib. Acoust. 137(1), 11007 (2015).CrossRefGoogle Scholar
Guo, Z., Pan, Y., Wee, L. B. and Yu, H., “Design and control of a novel compliant differential shape memory alloy actuator,” Sens. Actuator. A Phys. 225(1), 71–80 (2015).CrossRefGoogle Scholar
Ashrafiuon, H., Eshraghi, M. and Elahinia, M. H., “Position control of a three-link shape memory alloy actuated robot,” J. Intell. Mater. Syst. Struct. 17(5), 381–392 (2006).CrossRefGoogle Scholar
Villanueva, A., Smith, C. and Priya, S., “A biomimetic robotic jellyfish (Robojelly) actuated by shape memory alloy composite actuators,” Bioinspir. Biomim. 6(3), 36004 (2011).CrossRefGoogle ScholarPubMed
Lahouar, S., Ottaviano, E., Zeghoul, S., Romdhane, L. and Ceccarelli, M., “Collision free path-planning for cable-driven parallel robots,” Robot. Auton. Syst. 57(11), 1083–1093 (2009).CrossRefGoogle Scholar
Zhou, H. and Ma, N., “Modeling and experimental implementation of a flexible SMA wire-based gripper for confined space operation,” J. Intell. Mater. Syst. Struct., 1045389X–221077428X (2022).Google Scholar
Grosch, P., Di Gregorio, R., López, J. and Thomas, F., “Mo tion planning for a novel reconfigurable parallel manipulator with lockable revolute joints,” In: 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, (2010) (pp. 4697–4702).Google Scholar
Arghavani, J., Auricchio, F., Naghdabadi, R., Reali, A. and Sohrabpour, S., “A 3-D phenomenological constitutive model for shape memory alloys under multiaxial loadings,” Int. J. Plasticity 26(7), 976–991 (2010).CrossRefGoogle Scholar
Brinson, L. C., “One-dimensional constitutive behavior of shape memory alloys: thermomechanical derivation with non-constant material functions and redefined martensite internal variable,” J. Intell. Mater. Syst. Struct. 4(2), 229–242 (1993).CrossRefGoogle Scholar
Liang, C. and Rogers, C. A., “One-dimensional thermomechanical constitutive relations for shape memory materials,” J. Intell. Mater. Syst. Struct. 8(4), 285–302 (1997).CrossRefGoogle Scholar