In ‘The Foundations of Mathematics’, Frank Ramsey separates paradoxes into two groups, now taken to be the logical and the semantical. But he also revises the logical system developed in Whitehead and Russell’s Principia Mathematica, and in particular attempts to provide an alternate resolution of the semantical paradoxes. I reconstruct the logic that he develops for this purpose, and argue that it falls well short of his goals. I then argue that the two groups of paradoxes that Ramsey identifies are not properly thought of as the logical and semantical, and that in particular, the group normally taken to be the semantical paradoxes includes other paradoxes—the intensional paradoxes—which are not resolved by the standard metalinguistic approaches to the semantical paradoxes. It thus seems that if we are to take Ramsey’s interest in these problems seriously, then the intensional paradoxes deserve more widespread attention than they have historically received.

We show that if we interpret modal diamond as the derived set operator of a topological space, then the modal logic of Stone spaces is K4 and the modal logic of weakly scattered Stone spaces is K4G. As a corollary, we obtain that K4 is also the modal logic of compact Hausdorff spaces and K4G is the modal logic of weakly scattered compact Hausdorff spaces.

Sound and complete semantics for classical propositional logic can be obtained by interpreting sentences as sets. Replacing sets with commuting dense binary relations produces an interpretation that turns out to be sound but not complete for R. Adding transitivity yields sound and complete semantics for RM, because all normal Sugihara matrices are representable as algebras of binary relations.

This paper begins an axiomatic development of naive set theory—the consequences of a full comprehension principle—in a paraconsistent logic. Results divide into two sorts. There is classical recapture, where the main theorems of ordinal and Peano arithmetic are proved, showing that naive set theory can provide a foundation for standard mathematics. Then there are major extensions, including proofs of the famous paradoxes and the axiom of choice (in the form of the well-ordering principle). At the end I indicate how later developments of cardinal numbers will lead to Cantor’s theorem, the existence of large cardinals, and a counterexample to the continuum hypothesis.

Moritz Pasch (1843–1930) gave the first rigorous axiomatization of projective geometry in his Vorlesungen über neuere Geometrie (1882), in which he also clearly formulated the view that deductions must be independent from the meanings of the nonlogical terms involved. Pasch also presented in these lectures the main tenets of his philosophy of mathematics, which he continued to elaborate on throughout the rest of his life. This philosophy is quite unique in combining a deductivist methodology with a radically empiricist epistemology for mathematics. By taking into consideration publications from the entire span of Pasch’s career, the latter decades of which he devoted primarily to careful reflections on the nature of mathematics and of mathematical knowledge, Pasch’s highly original, but virtually unknown, philosophy of mathematics is presented.

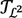Finitism is given an interpretation based on two ideas about strings (sequences of symbols): a replacement principle extracted from Hilbert’s work and a counting principle inspired by Tait. These principles are used to justify an equational arithmetic based on the algebra of lower elementary functions. The extension of this algebra to Grzegorczyk’s class 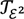ɛ2 can be justified by means of an additional finitistic choice principle, thus obtaining a second equational theory . It is unknown whether 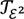is strictly stronger than since ɛ2 may coincide with the class of lower elementary functions.

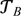If the objects of arithmetic are taken to be binary numerals instead of tally numerals, then it becomes possible to provide a finitistic justification for a theory that may be incomparable to 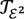(neither of the two includes the other). I conclude by suggesting that the equational theory of Kalmar elementary functions is a strict upper bound for finitistic arithmetic.

We study the logical structure of ‘real’ relations, and in particular the notion of occurrences of objects in a state. We start with formulating a number of principles for occurrences and defining corresponding mathematical models. These models are analyzed to get more insight in the formal properties of occurrences. In particular, we prove uniqueness results that tell us more about the possible logical structures relations might have.