Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T19:35:29.601Z Has data issue: false hasContentIssue false
  • English
  • Français

TWO (OR THREE) NOTIONS OF FINITISM

Published online by Cambridge University Press:  20 January 2010

MIHAI GANEA
MIHAI GANEA*
Affiliation:
Department of Philosophy, Boston University
*
*DEPARTMENT OF PHILOSOPHY, BOSTON UNIVERSITY, BOSTON, MA 02215. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Finitism is given an interpretation based on two ideas about strings (sequences of symbols): a replacement principle extracted from Hilbert’s work and a counting principle inspired by Tait. These principles are used to justify an equational arithmetic 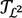based on the algebra of lower elementary functions. The extension of this algebra to Grzegorczyk’s class ɛ2 can be justified by means of an additional finitistic choice principle, thus obtaining a second equational theory 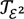. It is unknown whether 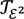is strictly stronger than 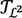since ɛ2 may coincide with the class of lower elementary functions.

If the objects of arithmetic are taken to be binary numerals instead of tally numerals, then it becomes possible to provide a finitistic justification for a theory 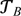that may be incomparable to 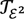(neither of the two includes the other). I conclude by suggesting that the equational theory of Kalmar elementary functions is a strict upper bound for finitistic arithmetic.

Type
Research Article
Information
The Review of Symbolic Logic , Volume 3 , Issue 1 , March 2010 , pp. 119 - 144
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Beeson, M. (1986). Proving programs and programming proofs. In Barcan Marcus, R., Dorn, G.J.W., and Weingartner, P., (eds.), Logic, Methodology and Philosophy of ScienceVII, proceedings of the International Congress, Salzburg, 1983, Amsterdam: North-Holland, pp. 51–81.Google Scholar
Berarducci, A., & Intrigila, B. (1991). Combinatorial principles in elementary number theory. Annals of Pure and Applied Logic, 55, 35–50.CrossRefGoogle Scholar
Bernays, P. (1923). Erwiderung auf die Note von Herrn Aloys Müller: Über Zahlen als Zeichen. Mathematische Annalen, 90, 159–63. English translation in Mancosu (1998), pp. 223–226.CrossRefGoogle Scholar
Bernays, P. (1930). Die Philosophie der Mathematik und die Hilbertsche Beweistheorie’. Blätter fur deutsche Philosophie, 4, 326–367. English translation in Mancosu (1998), pp. 234–265.Google Scholar
Buss, S. (1998). First order proof theory of arithmetic. In Buss, S., editor. Handbook of Proof Theory. Amsterdam: Elsevier Science BV, pp. 79–147.CrossRefGoogle Scholar
Clote, P. (1999). Computation models and function algebras. In Griffor, E. R., editor. Handbook of Computability Theory. Amsterdam: Elsevier, pp. 589–681.CrossRefGoogle Scholar
Cook, S. (1975). Feasible constructive proofs and the propositional calculus. In, Chandra, A. K., Meyer, A. R., Rounds, W. C., Stearns, R. E., Tarjan, R. E., Winograd, S., Young, P. R., (eds.) Proceedings of the 7th ACM Symposium on the Theory of Computation. New York: ACM (Association for computing machinery) pp. 83–97.Google Scholar
Cook, S., & Urquhart, A. (1993). Functional interpretations of feasibly constructive arithmetic. Annals of Pure and Applied Logic, 63, 103–200.CrossRefGoogle Scholar
Cornaros, C. (1995). On Grzegorczyk induction. Annals of Pure and Applied Logic, 74, l–21.CrossRefGoogle Scholar
Curry, H. (1941). A formalization of recursive arithmetic. American Journal of Mathematics, 63, 263–282.CrossRefGoogle Scholar
Detlefsen, M. (1986). Hilbert’s Program: An Essay on Mathematical Instrumentalism. Synthese Library 182. Boston, MA: Reidel/Kluwer Academic.CrossRefGoogle Scholar
Gandy, R. (1982). Limitations to mathematical knowledge. In van Dalen, D., Lascar, D., and Smiley, J., editors. Logic Colloquium ’80. Amsterdam: Elsevier, pp. 129–146.Google Scholar
Ganea, M. (2005). Arithmetic Without Numbers. Doctoral dissertation, Department of Philosophy, University of Illinois at Chicago.Google Scholar
George, A., & Velleman, D. J. (1998). Two conceptions of natural number. In Dales, H. G. and Oliveri, G., editors. Truth in Mathematics. New York: Oxford University Press, pp. 311–327.CrossRefGoogle Scholar
Girard, J. -Y. (1987). Proof Theory and Logical Complexity. Naples: Bibliopolis.Google Scholar
Gödel, K. (1931). Über formal unentscheibare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für Mathematik und Physik, 38, 173–198. English translation in Gödel (1986), pp. 144–195.CrossRefGoogle Scholar
Gödel, K. (1986). Collected Works I. Feferman, S., Dawson, J. W. Jr., Kleene, S. C., Moore, G. H., Solovay, R. M., van Heijenoort, J.Oxford: Oxford University Press.Google Scholar
Goodstein, R. (1954). Logic-free characterizations of recursive arithmetic. Mathematica Scandinavica, 2, 247–261.CrossRefGoogle Scholar
Goodstein, R. (1957). Recursive Number Theory—A Development of Recursive Arithmetic in a Logic-Free Equation Calculus. Studies in Logic and the Foundations of Mathematics. Amsterdam: North-Holland.Google Scholar
Hallett, M. (1995). Hilbert and logic. In Marion, M., and Cohen, R. S., editors. Quebec Studies in the Philosophy of Science I. Dordrecht: Kluwer Academic Publishers. pp. 135–187.Google Scholar
Hilbert, D. (1910). Elemente und Prinzipienfragen der Mathematik. Sommersemester 1910: Ausgearbeit von Richard Courant. Göttingen, Germany: Mathematisches Institut, Georg-August Universität. 163 pages, handwritten.Google Scholar
Hilbert, D. (1922). Neubegründung der Mathematik. Erste Mitteilung. Abhandlungen aus dem Mathematischen Seminar der Hamburgischen Universität, 1, 157–177. English translation in Mancosu (1998), pp. 198–214.CrossRefGoogle Scholar
Hilbert, D. (1925). Uber das Unendliche. Mathematische Annalen, 95, 161–190. Lecture given in Münster, 4 June 1925. English translation in van Heijenoort (1967), pp. 367–392.CrossRefGoogle Scholar
Hilbert, D. (1927). Die Grundlagen der Mathematik. Abhandlungen aus dem mathematischen Seminar der Hamburghischen Universität, 6 (1928), 65–85. English translation in van Heijenoort (1967), pp. 464–479.CrossRefGoogle Scholar
Hilbert, D., & Bernays, P. (1934). Grundlagen der Mathematik I. Berlin: Springer.Google Scholar
Hilbert, D., & Bernays, P. (1939). Grundlagen der Mathematik II. Berlin: Springer.Google Scholar
Ignjatovic, A. (1994). Hilbert’s program and the omega-rule. Journal of Symbolic Logic, 59(1), 322–343.CrossRefGoogle Scholar
Krajíček, J. (1995). Bounded Arithmetic, Propositional Logic, and Complexity Theory. Encyclopedia of Mathematics and Its Applications 60. New York: Cambridge University Press.CrossRefGoogle Scholar
Mancosu, P., editor. (1998). From Brouwer to Hilbert—The Debate on the Foundations of Mathematics in the 1920’s. New York: Oxford University Press.Google Scholar
Marion, M. (1995). Kronecker’s safe haven of real mathematics. In Marion, M., and Cohen, R. S., editors. pp. 189–215.Google Scholar
Nelson, E. (1986). Predicative Arithmetic. Mathematical Notes 32, Princeton: Princeton University Press.CrossRefGoogle Scholar
Parsons, C. (1980). Mathematical intuition. Proceedings of the Aristotelian Society, 80, 142–168.CrossRefGoogle Scholar
Parsons, C. (1986). Intuition in constructive mathematics. In Butterfield, J., editor. Language, Mind and Logic. New York: Cambridge University Press, pp. 211–229.Google Scholar
Parsons, C. (1994). Intuition and number. In George, A., editor. Mathematics and Mind. New York: Oxford University Press, pp. 141–157.CrossRefGoogle Scholar
Parsons, C. (1998). Finitism and intuitive knowledge. In Schirn, M., editor. Philosophy of Mathematics Today. New York: Clarendon Press, pp. 249–270.Google Scholar
Parsons, C. (2008). Mathematical Thought and Its Objects. New York: Cambridge University Press.Google Scholar
Rose, H. (1962). Ternary recursive arithmetic. Mathematica Scandinavica, 10, 201–216.CrossRefGoogle Scholar
Rose, H. (1984). Subrecursion—Functions and Hierarchies. Oxford, UK: Clarendon Press.Google Scholar
Sieg, W. (1999). Hilbert’s programs: 1917–1922. Bulletin of Symbolic Logic, 5(1), 1–44.CrossRefGoogle Scholar
Simpson, S. (1988). Partial realizations of Hilbert’s program. Journal of Symbolic Logic, 53(2), 349–363.CrossRefGoogle Scholar
Skolem, T. (1923). Begründung der elementaren Arithmetik durch die rekurriende Denkweise ohne Anwendung scheinbarer Verädnderlichen mit unendlichen Ausdenungsbereich. Videnskapsselskkapets skrifter, I. Matematisk-naturvidenskabelig klasse 6. English translation in van Heijenoort (1967), pp. 302–333.Google Scholar
Skolem, T. (1950). Some remarks on the foundation of set theory. In Proceedings of the International Congress of Mathematicians, Cambridge, Massachusetts, U.S.A., August 30 to September 6, 1950, American Mathematical Society, Providence 1952, vol. I, pp. 695–704; reprinted in Skolem, 1970, pp. 519–528.Google Scholar
Skolem, T. (1962). Proof of some theorems on recursively enumerable sets. Notre Dame Journal of Formal Logic, 3, 65–74.CrossRefGoogle Scholar
Skolem, T. (1970). Selected Works in Logic. Fenstad, J. E., editor. OsloUniversitetforlaget.Google Scholar
Smorýnski, C. (1977). The incompleteness theorems. In Barwise, J., editor. The Handbook of Mathematical Logic. New York: Elsevier. pp. 821–865.CrossRefGoogle Scholar
Tait, W. (1981). Finitism. Journal of Philosophy, 78, 524–546.CrossRefGoogle Scholar
Troelstra, A. S., & van Dalen, D. (1988). Constructivism in Mathematics I. Studies in Logic and the Foundations of Mathematics 121. New York: Elsevier.Google Scholar
van Heijenoort, J., editor. (1967). From Frege to Gödel. Cambridge, MA: Harvard University Press.Google Scholar
Weyl, H. (1921). Über die neuen Grundlagenkrise der Mathematik. Mathematische Zeitschrift, 10, 39–79. English translation in Mancosu (1998), pp. 86–118.CrossRefGoogle Scholar
Zach, R. (1998). Numbers and functions in Hilbert’s finitism. Taiwanese Journal for Philosophy and History of Science, 10, 33–60.Google Scholar
Zach, R. (2003). The practice of finitism: Epsilon calculus and consistency proofs in Hilbert’s program. Synthese, 137, 211–259.CrossRefGoogle Scholar
Zach, R. (2004). Hilbert’s “Verunglückter Beweis,” the first epsilon theorem and consistency proofs. History and Philosophy of Logic, 25, 79–94.CrossRefGoogle Scholar