Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T00:55:26.796Z Has data issue: false hasContentIssue false
  • English
  • Français

LOGIC IN THE TRACTATUS

Published online by Cambridge University Press:  12 January 2017

MAX WEISS
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

I present a reconstruction of the logical system of the Tractatus, which differs from classical logic in two ways. It includes an account of Wittgenstein’s “form-series” device, which suffices to express some effectively generated countably infinite disjunctions. And its attendant notion of structure is relativized to the fixed underlying universe of what is named.

There follow three results. First, the class of concepts definable in the system is closed under finitary induction. Second, if the universe of objects is countably infinite, then the property of being a tautology is 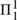$\Pi _1^1$-complete. But third, it is only granted the assumption of countability that the class of tautologies is 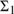${\Sigma _1}$-definable in set theory.

Wittgenstein famously urges that logical relationships must show themselves in the structure of signs. He also urges that the size of the universe cannot be prejudged. The results of this paper indicate that there is no single way in which logical relationships could be held to make themselves manifest in signs, which does not prejudge the number of objects.

Keywords

03A0503C8003C7003D7001A6003E4703D80logicinductionconsequenceWittgensteinFregeRussellTarski
Type
Research Article
Information
The Review of Symbolic Logic , Volume 10 , Issue 1 , March 2017 , pp. 1 - 50
Copyright
Copyright © Association for Symbolic Logic 2017 

References

BIBLIOGRAPHY

Ackermann, W. (1937). Die widerspruchsfreiheit der allgemeinen mengenlehre. Mathematische Annalen, 114, 305–315.Google Scholar
Avron, A. (2003). Transitive closure and the mechanization of mathematics. In Kamareddine, F. D. editor. Thirty five Years of Automating Mathematics. Dordrecht: Springer, pp. 149–171.Google Scholar
Barwise, J. (1975). Admissible Sets and Structures. Berlin: Springer-Verlag.Google Scholar
Barwise, J. (1977). On Moschovakis closure ordinals. Journal of Symbolic Logic, 42(2), 292–296.CrossRefGoogle Scholar
Bays, T. (2001). On Tarski on models. Journal of Symbolic Logic, 66(4), 1701–1726.CrossRefGoogle Scholar
Büchi, J. (1960). On a decision method in restricted second-order arithmetic. In Nagel, E., Suppes, P., and Tarski, A., editors. Proceedings of the International Congress for Logic, Methodology and Philosophy of Science. Stanford: Stanford University Press, pp. 1–11.Google Scholar
Fine, K. (2010). Towards a theory of part. Journal of Philosophy, 107(11), 559–589.CrossRefGoogle Scholar
Floyd, J. (2001). Number and ascriptions of number in Wittgenstein’s Tractatus . In Floyd, J. and Shieh, S., editors. Future Pasts. Cambridge, MA: Harvard University Press, pp. 145–193.Google Scholar
Fogelin, R. (1976). Wittgenstein. London: Routledge and Kegan Paul.Google Scholar
Frascolla, P. (1997). The “Tractatus” system of arithmetic. Synthese, 112(3), 353–378.Google Scholar
Frege, G. (1879). Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle: Louis Nebert.Google Scholar
Geach, P. (1981). Wittgenstein’s operator N. Analysis, 41(4), 178–181.Google Scholar
Goldfarb, W. (2012). Wittgenstein against logicism. Unpublished.Google Scholar
Heck, R. (2011). A logic for Frege’s theorem. In Frege’s Theorem. New York: Oxford University Press, pp. 267–296.Google Scholar
Henkin, L. (1950). Completeness in the theory of types. Journal of Symbolic Logic, 15(2), 81–91.Google Scholar
Hintikka, J. (1956). Identity, variables, and impredicative definitions. Journal of Symbolic Logic, 21(3), 225–245.Google Scholar
Jech, T. (2003). Set Theory (third edition). Berlin: Springer.Google Scholar
Kirby, L. (2009). Finitary set theory. Notre Dame Journal of Formal Logic, 50(3), 227–244.Google Scholar
Krivine, J.-L. (1998). Théorie des Ensembles. Paris: Cassini.Google Scholar
Lopez-Escobar, E. G. K. (1965). An interpolation theorem for denumerably long formulas. Fundamenta Mathematicae, LVII, 253–272.Google Scholar
Lopez-Escobar, E. G. K. (1966). On defining well-orderings. Fundamenta Mathematicae, 59(1), 13–21.CrossRefGoogle Scholar
Mancosu, P. (2010). Fixed- versus variable-domain interpretations of Tarski’s account of logical consequence. Philosophy Compass, 5(9), 745–759.Google Scholar
Martin-Löf, P. (1996). On the meanings of the logical constants and the justifications of the logical laws. Nordic Journal of Formal Logic, 1(1), 11–60.Google Scholar
Mirimanoff, D. (1917). Les antinomies des Russell et de Burali-Forti et le problème fondamentale de la théorie des ensembles. L’Enseignment Mathématique, 19, 37–52.Google Scholar
Potter, M. (2009). The logic of the Tractatus . In Gabbay, D. M. and Woods, J., editors. From Russell to Church, Volume 5 of Handbook of the History of Logic. Amsterdam: Elsevier, pp. 255–304.Google Scholar
Ricketts, T. (2012). Logical segmentation and generality in Wittgenstein’s Tractatus . In Potter, M. and Sullivan, P., editors. Wittgenstein’s Tractatus: History and Interpretation. Oxford: Oxford University Press, pp. 125–142.Google Scholar
Rogers, B. & Wehmeier, K. (2012). Tractarian first-order logic: Identity and the N-operator. Review of Symbolic Logic, 5(4), 538–573.Google Scholar
Rumfitt, I. (2006). ‘Yes’ and ‘no’. Mind, 109(436), 781–824.Google Scholar
Russell, B. (1903). The Principles of Mathematics. London: Allen and Unwin.Google Scholar
Russell, B. (1905). On denoting. Mind, 14(56), 479–493.CrossRefGoogle Scholar
Russell, B. (1918). The philosophy of logical atomism. In Marsh, R. C., editor. Logic and Knowledge. London: Allen and Unwin, pp. 177–281.Google Scholar
Shoenfield, J. (1967). Mathematical Logic. Natick, MA: A K Peters.Google Scholar
Smiley, T. (1996). Rejection. Analysis, 56, 1–9.Google Scholar
Soames, S. (1983). Generality, truth-functions, and expressive capacity in the Tractatus . Philosophical Review, 92(4), 573–589.Google Scholar
Sullivan, P. (2004). The general form of the proposition is a variable. Mind, 113(449), 43–56.Google Scholar
Sundholm, G. (1992). The general form of the operation in Wittgenstein’s Tractatus . Grazer Philosophische Studien, 42, 57–76.Google Scholar
Tarski, A. (1936). O pojeciu wynikania logicznego. Przeglad Filozoficzny, 39, 58–68.Google Scholar
Väänänen, J. (2001). Second order logic and foundations of mathematics. Bulletin of Symbolic Logic, 7(4), 504–520.Google Scholar
Wehmeier, K. (2004). Wittgensteinian predicate logic. Notre Dame Journal of Formal Logic, 45, 1–11.Google Scholar
Wehmeier, K. (2008). Wittgensteinian tableaux, identity, and codenotation. Erkenntnis, 69(3), 363–376.Google Scholar
Wehmeier, K. (2009). On Ramsey’s ‘silly delusion’ regarding Tractatus 5.53. In Primiero, G. and Rahman, S., editors. Acts of Knowledge – History, Philosophy and Logic. London: College Publications, pp. 353–368.Google Scholar
Whitehead, A. N. & Russell, B. (1910–1913). Principia Mathematica. Cambridge: Cambridge University Press.Google Scholar
Wittgenstein, L. (1921). Logische-philosophische abhandlung. Annalen der Naturphilosophie, XIV, 168–198.Google Scholar
Wittgenstein, L. (1922). Tractatus Logico-Philosophicus. London: Kegan Paul.Google Scholar
Wittgenstein, L. (1961). Tractatus Logico-Philosophicus. London: Routledge & Kegan Paul.Google Scholar
Wittgenstein, L. (1971). Prototractatus. London: Routledge & Kegan Paul.Google Scholar
Wittgenstein, L. (1979). Notebooks 1914–1916. Oxford: Blackwell.Google Scholar
Yablo, S. (1993). Paradox without self-reference. Analysis, 53(4), 252–252.Google Scholar