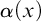1 Introduction
According to the traditional view, the semantics of a logical system specifies truth-conditions for the sentences in the language. This focus on truth restricts the scope of logic to a special kind of sentences, namely, statements, whose semantics can be adequately characterized in terms of truth-conditions. In recent years, a more general view of semantics has been developed, which goes under the name of inquisitive semantics (see [Reference Ciardelli, Groenendijk and Roelofsen4] for a language-oriented introduction and [Reference Ciardelli2] for a logic-oriented one). In this approach, the meaning of a sentence is laid out not by specifying when the sentence is true relative to a state of affairs, but rather by specifying when it is supported by a given state of information. This view allows us to interpret in a uniform way both statements and questions: for instance, the statement it rains will be supported by an information state s if the information available in s implies that it rains, while the question whether it rains will be supported by s if the information available in s determines whether or not it rains.
In its first-order version, referred to as InqBQ, inquisitive logic can be seen as a conservative extension of classical first-order logic with formulas expressing questions. Thus, in addition to standard first-order formulas like
![]() $Pa$
and
$Pa$
and
![]() $\forall x.Px$
, we also have formulas like
$\forall x.Px$
, we also have formulas like
![]() $?Pa$
(“does a have property P?”),
$?Pa$
(“does a have property P?”),
![]() $\overline{\exists}\, x.Px$
(“what is an instance of an individual having property P?”) and
$\overline{\exists}\, x.Px$
(“what is an instance of an individual having property P?”) and
![]() $\forall x.?Px$
(“which individuals have property P?”). A model for this logic is based on a set W of possible worlds, each representing a possible state of affairs, corresponding to a standard first-order structure. An information state is modeled as a subset
$\forall x.?Px$
(“which individuals have property P?”). A model for this logic is based on a set W of possible worlds, each representing a possible state of affairs, corresponding to a standard first-order structure. An information state is modeled as a subset
![]() $s\subseteq W$
. The idea, which goes back to the work of Hintikka [Reference Hintikka12], is that a set of worlds s stands for a body of information that is compatible with the actual world being one of the worlds
$s\subseteq W$
. The idea, which goes back to the work of Hintikka [Reference Hintikka12], is that a set of worlds s stands for a body of information that is compatible with the actual world being one of the worlds
![]() $w\in s$
and incompatible with it being one of the worlds
$w\in s$
and incompatible with it being one of the worlds
![]() $w\not \in s$
. The semantics of the language takes the form of a support relation holding between information states in a model and sentences of the language.
$w\not \in s$
. The semantics of the language takes the form of a support relation holding between information states in a model and sentences of the language.
From a mathematical point of view, a sentence of InqBQ expresses a property of a set s of first-order structures. The crucial difference between statements and questions is that statements express local properties of information states—which boil down to requirements on the individual worlds
![]() $w\in s$
—while questions express global requirements, having to do with the way the worlds in s are related to each other. Thus, for instance, the formula
$w\in s$
—while questions express global requirements, having to do with the way the worlds in s are related to each other. Thus, for instance, the formula
![]() $?Pa$
requires that the truth-value of
$?Pa$
requires that the truth-value of
![]() $Pa$
be the same in all worlds in s; the formula
$Pa$
be the same in all worlds in s; the formula
![]() $\overline{\exists}\, x.Px$
requires that there be an individual that has property P uniformly in all worlds in s; and the formula
$\overline{\exists}\, x.Px$
requires that there be an individual that has property P uniformly in all worlds in s; and the formula
![]() $\forall x.?Px$
requires that the extension of property P be the same across s. Global properties can also take the form of dependencies: thus, e.g.,
$\forall x.?Px$
requires that the extension of property P be the same across s. Global properties can also take the form of dependencies: thus, e.g.,
![]() $?Pa\to {?Qa}$
requires that the truth-value of
$?Pa\to {?Qa}$
requires that the truth-value of
![]() $Qa$
be functionally determined by the truth-value of
$Qa$
be functionally determined by the truth-value of
![]() $Pa$
in s, while
$Pa$
in s, while
![]() $\forall x.?Px\to \forall x.?Qx$
requires that the extension of property Q be functionally determined by the extension of property P in s. Thus, inquisitive first-order logic provides a language that can be used to talk about both local and global features of an information state.
$\forall x.?Px\to \forall x.?Qx$
requires that the extension of property Q be functionally determined by the extension of property P in s. Thus, inquisitive first-order logic provides a language that can be used to talk about both local and global features of an information state.
In contrast to inquisitive propositional logic, which has been thoroughly investigated (see, among others, [Reference Ciardelli1, Reference Ciardelli3, Reference Ciardelli and Roelofsen5, Reference Frittella, Greco, Palmigiano and Yang10, Reference Punčochář19, Reference Punčochář20, Reference Roelofsen22]), inquisitive first-order logic has received comparatively little attention [Reference Ciardelli2, Reference Grilletti11]. In particular, a detailed investigation of the expressive power of the logic has so far been missing. This paper makes a first, important step in this direction.
In the classical setting, a powerful tool to study the expressiveness of first-order logic is given by Ehrenfeucht–Fraïssé games (also known as EF games or back-and-forth games), introduced in 1967 by Ehrenfeucht [Reference Ehrenfeucht7], developing model-theoretic results presented by Fraïssé [Reference Fraïssé9]. These games provide a particularly perspicuous way of understanding what differences between models can be detected by means of first-order formulas of a certain quantifier rank. Reasoning about winning strategies in this game, one can prove that two first-order structures are elementarily equivalent, or one can find a formula telling them apart.
One of the main merits of EF games is that they allow for relatively easy proofs that certain properties of first-order structures are not first-order expressible. A classical application of this kind is the characterization of the cardinality quantifiers definable in classical first-order logic. This characterization says that the only cardinality quantifiers definable in classical first-order logic are those which, for some natural number m, are insensitive to the difference between any cardinals larger than m. This characterization yields a range of interesting undefinability results: for instance, it implies that the quantifiers an even number of individuals and infinitely many individuals are not first-order definable.
The basic idea of EF games has proven to be very flexible and adaptable to a wide range of logical settings, including fragments of first-order logic with finitely many variables [Reference Immerman14]; extensions of first-order logic with generalized quantifiers [Reference Kolaitis and Väänänen15]; monadic second order logic [Reference Fagin8]; modal logic [Reference van Benthem24]; and intuitionistic logic [Reference Połacik18, Reference Visser25]. In each case, the game provides an insightful characterization of the distinctions that can and cannot be made by means of formulas in the logic.
In this paper, we make two contributions to the study of inquisitive first-order logic. First, we introduce an EF-style game for InqBQ and show that this game provides a characterization of the expressive power of the logic. Second, we introduce a notion of inquisitive cardinality quantifier, and use the game to study which of these quantifiers are definable in InqBQ.
The notion of inquisitive cardinality quantifier is a natural generalization of the standard notion of cardinality quantifier: besides standard quantifers like infinitely many, which combine with a property to form a statement, we will now also have quantifers like how many, which combine with a property to form a question. Using the EF-game, we will be able to characterize exactly the range of cardinality quantifiers expressible in InqBQ. The characterization is similar to the one for classical first-order logic: the definable cardinality quantifiers are those that, for some finite threshold m, are incapable of distinguishing between cardinalities larger than m.
The result implies that many natural kinds of questions about cardinalities are not expressible in InqBQ. The prime example is the question how many individuals have property P, which is supported in a state s if the extension of P has the same cardinality in all the worlds in s. We show that this question is not expressible in InqBQ, even in restriction to finite models. This means that a logical treatment of how many questions in inquisitive logic requires a proper extension of InqBQ. Other examples of cardinality questions which we show not to be expressible in InqBQ are: whether the number of P is finite or infinite; whether it is even or odd; whether it is countable or uncountable.
From a meta-theoretical point of view, our characterization result is especially interesting in light of the fact that it is still an open question how the expressive power of InqBQ compares to those of first- and second-order logics. It is not known, e.g., whether InqBQ is compact and whether an entailment-preserving translation to first-order logic exists. Our result indicates that, at least with respect to the expression of cardinality properties, InqBQ is much more similar to first-order logic than to second-order logic, where quantifiers like ‘infinitely many’ and ‘an even number of’ can be expressed.
The paper is structured as follows: in Section 2 we provide some technical background on the logic InqBQ. In Section 3 we describe the game and show that it characterizes the distinguishing power of the logic. In Section 4 we characterize the cardinality quantifiers definable in InqBQ. In Section 5 we summarize our findings and mention some directions for future work.
2 Inquisitive first-order logic
In this section we provide a basic introduction to inquisitive first-order logic. For a more comprehensive introduction, the reader is referred to [Reference Ciardelli2].
Syntax
Let
![]() $\Sigma $
be a predicate logic signature. For simplicity, we first restrict to the case in which
$\Sigma $
be a predicate logic signature. For simplicity, we first restrict to the case in which
![]() $\Sigma $
is a relational signature, i.e., contains no function symbols. The extension to an arbitrary signature, which involves some subtleties familiar from the classical case [Reference Hodges13], is discussed in Section 3.4. The set
$\Sigma $
is a relational signature, i.e., contains no function symbols. The extension to an arbitrary signature, which involves some subtleties familiar from the classical case [Reference Hodges13], is discussed in Section 3.4. The set
![]() $\mathcal {L}$
of formulas of InqBQ over
$\mathcal {L}$
of formulas of InqBQ over
![]() $\Sigma $
is defined as follows, where
$\Sigma $
is defined as follows, where
![]() $R\in \Sigma $
is an n-ary relation symbol:
$R\in \Sigma $
is an n-ary relation symbol:
We will take negation to be a defined operator:
Formulas without occurrences of
and
![]() $\overline{\exists} $
are referred to as classical formulas and can be identified with standard
$\overline{\exists} $
are referred to as classical formulas and can be identified with standard
![]() $\textsf {FOL}$
-formulas, that is, first-order logic formulas. That is, the set
$\textsf {FOL}$
-formulas, that is, first-order logic formulas. That is, the set
![]() $\mathcal {L}_c$
of classical formulas is given by:
$\mathcal {L}_c$
of classical formulas is given by:
As usual, classical formulas may be viewed as formalizing statements, such as, for instance, ‘every object has property P’. In the following, the variables
![]() $\alpha ,\beta ,\gamma $
will range over classical formulas, while
$\alpha ,\beta ,\gamma $
will range over classical formulas, while
![]() $\varphi ,\psi ,\chi $
will range over arbitrary formulas. If
$\varphi ,\psi ,\chi $
will range over arbitrary formulas. If
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are classical formulas, then we can define: Footnote
1
$\beta $
are classical formulas, then we can define: Footnote
1
-
•
 $\alpha \lor \beta :=\neg (\neg \alpha \land \neg \beta )$
$\alpha \lor \beta :=\neg (\neg \alpha \land \neg \beta )$
-
•
 $\exists x.\alpha :=\neg \forall x.\neg \alpha $
$\exists x.\alpha :=\neg \forall x.\neg \alpha $
The connective
and the quantifier
![]() $\overline{\exists} $
, referred to respectively as inquisitive disjunction and inquisitive existential quantifier, allow us to form questions. For instance, if
$\overline{\exists} $
, referred to respectively as inquisitive disjunction and inquisitive existential quantifier, allow us to form questions. For instance, if
![]() $\alpha $
is a classical formula then the formula
$\alpha $
is a classical formula then the formula
represents the question whether
![]() $\alpha $
. We abbreviate this formula as
$\alpha $
. We abbreviate this formula as
![]() $?\alpha $
:
$?\alpha $
:
-
•

The formula
![]() $\overline{\exists}\, x.\alpha (x)$
represents the question what is an object satisfying
$\overline{\exists}\, x.\alpha (x)$
represents the question what is an object satisfying
![]() $\alpha (x)$
; and the formula
$\alpha (x)$
; and the formula
![]() $\forall x.?\alpha (x)$
represents the question which objects satisfy
$\forall x.?\alpha (x)$
represents the question which objects satisfy
![]() $\alpha (x)$
.
$\alpha (x)$
.
Semantics
A model for InqBQ consists of: a set W of worlds, representing possible states of affairs; a set D of individuals, the objects that the first-order variables range over; and an interpretation function I, which determines at each world the extension of all relation symbols, including identity.
Definition 2.1 (Models)
A model for the signature
![]() $\Sigma $
is a tuple
$\Sigma $
is a tuple
![]() $M=\langle W,D,I\rangle $
where W and D are sets and I is a function mapping each world
$M=\langle W,D,I\rangle $
where W and D are sets and I is a function mapping each world
![]() $w\in W$
and each n-ary relation symbol
$w\in W$
and each n-ary relation symbol
![]() $R\in \Sigma \cup \{=\}$
to a corresponding n-ary relation
$R\in \Sigma \cup \{=\}$
to a corresponding n-ary relation
![]() $I_w(R)\subseteq D^n$
—the extension of R at w. The interpretation of identity is subject to the following condition:
$I_w(R)\subseteq D^n$
—the extension of R at w. The interpretation of identity is subject to the following condition:
 $$ \begin{align*} &I_w (=) is \ a \text{ congruence }, i.e., \ an \ equivalence \ relation \sim_w \ such \ that, \ if \ R\in\Sigma \\ &and \ d_i\sim_w \ d_i' \ for \ i\le n, \ then \langle d_1,\dots,d_n\rangle\in \ I_w(R)\iff \langle \ d^{\prime}_1,\dots,d^{\prime}_n\rangle\in \ I_w(R). \end{align*} $$
$$ \begin{align*} &I_w (=) is \ a \text{ congruence }, i.e., \ an \ equivalence \ relation \sim_w \ such \ that, \ if \ R\in\Sigma \\ &and \ d_i\sim_w \ d_i' \ for \ i\le n, \ then \langle d_1,\dots,d_n\rangle\in \ I_w(R)\iff \langle \ d^{\prime}_1,\dots,d^{\prime}_n\rangle\in \ I_w(R). \end{align*} $$
As discussed in the introduction, in inquisitive logic the semantics of the language specifies when a formula is supported at an information state
![]() $s\subseteq W$
, rather than when a formula is true at a possible world
$s\subseteq W$
, rather than when a formula is true at a possible world
![]() $w\in W$
. As usual, to handle open formulas and quantification, the support relation is defined relative to an assignment, which is a function from variables to the set D of individuals; if g is an assignment and
$w\in W$
. As usual, to handle open formulas and quantification, the support relation is defined relative to an assignment, which is a function from variables to the set D of individuals; if g is an assignment and
![]() $d\in D$
, then
$d\in D$
, then
![]() $g[x\mapsto d]$
is the assignment which maps x to d and behaves like g on all other variables.
$g[x\mapsto d]$
is the assignment which maps x to d and behaves like g on all other variables.
Definition 2.2 (Support)
Let
![]() $M=\langle W,D,I\rangle $
be a model and let
$M=\langle W,D,I\rangle $
be a model and let
![]() $s\subseteq W$
.
$s\subseteq W$
.

As usual, if
![]() $\varphi (x_1,\dots ,x_n)$
is a formula whose free variables are among
$\varphi (x_1,\dots ,x_n)$
is a formula whose free variables are among
![]() $x_1,\dots ,x_n$
, then the value of g on variables other than
$x_1,\dots ,x_n$
, then the value of g on variables other than
![]() $x_1,\dots ,x_n$
is irrelevant. If
$x_1,\dots ,x_n$
is irrelevant. If
![]() $d_1,\dots ,d_n\in D$
, we can therefore write
$d_1,\dots ,d_n\in D$
, we can therefore write
![]() $M,s\models \varphi (d_1,\dots ,d_n)$
to mean that
$M,s\models \varphi (d_1,\dots ,d_n)$
to mean that
![]() $M,s\models _g\varphi $
holds with respect to an assignment g that maps
$M,s\models _g\varphi $
holds with respect to an assignment g that maps
![]() $x_i$
to
$x_i$
to
![]() $d_i$
. In particular, if
$d_i$
. In particular, if
![]() $\varphi $
is a sentence we can drop reference to g altogether. Moreover, we write
$\varphi $
is a sentence we can drop reference to g altogether. Moreover, we write
![]() $M\models \varphi $
as a shorthand for
$M\models \varphi $
as a shorthand for
![]() $M,W\models \varphi $
and we say that M supports
$M,W\models \varphi $
and we say that M supports
![]() $\varphi $
.
$\varphi $
.
It is easy to verify that the support relation has the following two basic features:
-
• Persistency: if
 $M,s\models _g\varphi $
and
$M,s\models _g\varphi $
and
 $t\subseteq s$
then
$t\subseteq s$
then
 $M,t\models _g\varphi $
;
$M,t\models _g\varphi $
; -
• Empty state property: if
 $M,\emptyset \models _g\varphi $
for all
$M,\emptyset \models _g\varphi $
for all
 $\varphi $
.
$\varphi $
.
Recovering classical logic
In restriction to classical formulas, the above definition of support gives a non-standard semantics for classical first-order logic. To see why, let us associate to each world
![]() $w\in M$
a corresponding relational structure
$w\in M$
a corresponding relational structure
![]() $\mathcal {M}_w$
, having as its domain the quotient
$\mathcal {M}_w$
, having as its domain the quotient
![]() $D/\!\sim _w$
and with the interpretation of relation symbols induced by
$D/\!\sim _w$
and with the interpretation of relation symbols induced by
![]() $I_w(R)$
. Then we have the following connection.
$I_w(R)$
. Then we have the following connection.
Proposition 2.3. For all classical formulas
![]() $\alpha \in \mathcal {L}_c$
, all models M, assignments g, and information states s:
$\alpha \in \mathcal {L}_c$
, all models M, assignments g, and information states s:
where
![]() $\overline g$
is the assignment mapping x to the
$\overline g$
is the assignment mapping x to the
![]() $\sim _w$
-equivalence class of
$\sim _w$
-equivalence class of
![]() $g(x)$
.
$g(x)$
.
Thus, as far as the standard fragment of the language is concerned, the relation of support is essentially a recursive definition of global truth with respect to a set of structures sharing the same domain. Notice that the standard definition of truth can be recovered as a special case of support by taking s to be a singleton. We will also write
![]() $M,w\models _g\alpha $
as an abbreviation for
$M,w\models _g\alpha $
as an abbreviation for
![]() $M,\{w\}\models _g\alpha $
.
$M,\{w\}\models _g\alpha $
.
Questions
As we just saw, evaluating a classical formula on an information state s amounts to evaluating it at each world in s and determining whether it is satisfied at each world. The same is not true for formulas that contain the operators
![]() and
and
![]() $\overline{\exists} $
; typically, such formulas allow us to express global requirements on a state, which cannot be reduced to requirements on the single worlds in the state. We will illustrate this point by means of some examples. First take a classical sentence
$\overline{\exists} $
; typically, such formulas allow us to express global requirements on a state, which cannot be reduced to requirements on the single worlds in the state. We will illustrate this point by means of some examples. First take a classical sentence
![]() $\alpha $
and consider the formula
$\alpha $
and consider the formula
![]() . We have:
. We have:
Thus, in order for s to support
![]() $?\alpha $
, all the worlds in s must agree on the truth-value of
$?\alpha $
, all the worlds in s must agree on the truth-value of
![]() $\alpha $
. In other words,
$\alpha $
. In other words,
![]() $?\alpha $
is supported at s only if the information available in s determines whether or not
$?\alpha $
is supported at s only if the information available in s determines whether or not
![]() $\alpha $
is true. Thus,
$\alpha $
is true. Thus,
![]() $?\alpha $
can be taken as a formal representation of the question “is
$?\alpha $
can be taken as a formal representation of the question “is
![]() $\alpha $
true?”
$\alpha $
true?”
Next take
![]() $\alpha (x)$
to be a classical formula having only the variable x free, and consider the formula
$\alpha (x)$
to be a classical formula having only the variable x free, and consider the formula
![]() $\overline{\exists}\, x.\alpha (x)$
. We have:
$\overline{\exists}\, x.\alpha (x)$
. We have:
Thus, in order for s to support
![]() $\overline{\exists}\, x.\alpha (x)$
there must be an individual d which satisfies
$\overline{\exists}\, x.\alpha (x)$
there must be an individual d which satisfies
![]() $\alpha (x)$
at all worlds in s. In other words,
$\alpha (x)$
at all worlds in s. In other words,
![]() $\overline{\exists}\, x.\alpha (x)$
is supported at s if the information available in s implies for some specific individual that it satisfies
$\overline{\exists}\, x.\alpha (x)$
is supported at s if the information available in s implies for some specific individual that it satisfies
![]() $\alpha (x)$
—i.e., gives us a specific witness for
$\alpha (x)$
—i.e., gives us a specific witness for
![]() $\alpha (x)$
. Thus,
$\alpha (x)$
. Thus,
![]() $\overline{\exists}\, x.\alpha (x)$
can be taken as a formal representation of the question “what is an object satisfying
$\overline{\exists}\, x.\alpha (x)$
can be taken as a formal representation of the question “what is an object satisfying
![]() $\alpha (x)$
?”
$\alpha (x)$
?”
Finally, let again
![]() $\alpha (x)$
be a classical formula having only x free, and let us denote by
$\alpha (x)$
be a classical formula having only x free, and let us denote by
![]() $I_w(\alpha )$
the set of objects which satisfy
$I_w(\alpha )$
the set of objects which satisfy
![]() $\alpha (x)$
at w, i.e.,
$\alpha (x)$
at w, i.e.,
![]() $I_w(\alpha ):=\{d\in D\mid M,w\models \alpha (d)\}$
. Consider the formula
$I_w(\alpha ):=\{d\in D\mid M,w\models \alpha (d)\}$
. Consider the formula
![]() . We have:
. We have:
Thus, in order for s to support
![]() $\forall x.?\alpha (x)$
, all the worlds in s must agree on which objects satisfy
$\forall x.?\alpha (x)$
, all the worlds in s must agree on which objects satisfy
![]() $\alpha (x)$
. In other words,
$\alpha (x)$
. In other words,
![]() $\forall x.?\alpha (x)$
is supported at s if the information available in s determines exactly which individuals satisfy
$\forall x.?\alpha (x)$
is supported at s if the information available in s determines exactly which individuals satisfy
![]() $\alpha (x)$
. Thus,
$\alpha (x)$
. Thus,
![]() $\forall x.?\alpha (x)$
can be taken as a formal representation of the question “which objects satisfy
$\forall x.?\alpha (x)$
can be taken as a formal representation of the question “which objects satisfy
![]() $\alpha (x)?$
”
$\alpha (x)?$
”
Identity and cardinalities
An aspect of InqBQ which is worth commenting on is the interpretation of identity. In InqBQ, the interpretation of identity may differ at different worlds. This allows us to deal with uncertainty about the identity relation: e.g., one may have information about two individuals, a and b (say, one knows
![]() $Pa$
and
$Pa$
and
![]() $Qb$
) and yet be uncertain whether a and b are distinct individuals, or the same. This also allows for uncertainty about how many individuals there are. Indeed, although a model is based on a fixed set D of epistemic individuals—objects to which information can be attributed—the domain of actual individuals at a world w is given by the equivalence classes modulo
$Qb$
) and yet be uncertain whether a and b are distinct individuals, or the same. This also allows for uncertainty about how many individuals there are. Indeed, although a model is based on a fixed set D of epistemic individuals—objects to which information can be attributed—the domain of actual individuals at a world w is given by the equivalence classes modulo
![]() $\sim _w$
; the number of actual individuals that exist at w is the number of such equivalence classes, i.e., the cardinality of the quotient
$\sim _w$
; the number of actual individuals that exist at w is the number of such equivalence classes, i.e., the cardinality of the quotient
![]() $D_w:=D/\!\!\sim _w$
. Similarly, if
$D_w:=D/\!\!\sim _w$
. Similarly, if
![]() $\alpha (x)$
is a classical formula having at most x free, then the number of individuals that satisfy
$\alpha (x)$
is a classical formula having at most x free, then the number of individuals that satisfy
![]() $\alpha (x)$
at w is given by the cardinality of the set
$\alpha (x)$
at w is given by the cardinality of the set
![]() $\alpha _w:=I_w(\alpha )/\!\!\sim _w$
.
$\alpha _w:=I_w(\alpha )/\!\!\sim _w$
.
Notice that, as a special case, we could take
![]() $\sim _w$
to be the actual relation of identity on D at each world. A model in which identity is treated in this way is called an id-model.
$\sim _w$
to be the actual relation of identity on D at each world. A model in which identity is treated in this way is called an id-model.
This section is only intended as a summary of the key definitions and features of InqBQ and as a quick illustration of how questions can be captured by formulas in this logic. With these basic notions in place, let us now turn to the first novel contribution of the paper: an Ehrenfeucht–Fraïssé game for InqBQ.
3 An Ehrenfeucht–Fraïssé game for InqBQ
The EF game for InqBQ is played by two players, S (Spoiler) and D (Duplicator), using two inquisitive models
![]() $M_0,M_1$
as a board. As in the classical case, the game proceeds in turns: at each turn, S picks an object from one of the two models and D must respond by picking a corresponding object from the other model. At the end of the game, a winner is decided by comparing the atomic formulae supported by the sub-structures built during the game.
$M_0,M_1$
as a board. As in the classical case, the game proceeds in turns: at each turn, S picks an object from one of the two models and D must respond by picking a corresponding object from the other model. At the end of the game, a winner is decided by comparing the atomic formulae supported by the sub-structures built during the game.
However, there are two crucial differences with the classical EF game. First, the objects that are picked during the game are not just individuals
![]() $d\in D_i$
, but also information states
$d\in D_i$
, but also information states
![]() $s\subseteq W_i$
. This is because the logical repertoire of InqBQ contains not only the operators
$s\subseteq W_i$
. This is because the logical repertoire of InqBQ contains not only the operators
![]() $\forall $
and
$\forall $
and
![]() $\overline{\exists} $
, which quantify over individuals, but also the operator
$\overline{\exists} $
, which quantify over individuals, but also the operator
![]() $\to $
, which quantifies over information states. Second, the roles of the two models in the game are not symmetric. This is connected to the absence of a classical negation in the language of
$\to $
, which quantifies over information states. Second, the roles of the two models in the game are not symmetric. This is connected to the absence of a classical negation in the language of
![]() $\textsf {InqBQ}$
; unlike in classical logic, it could be that a model
$\textsf {InqBQ}$
; unlike in classical logic, it could be that a model
![]() $M_0$
supports all the formulas supported by a model
$M_0$
supports all the formulas supported by a model
![]() $M_1$
, but not vice versa. This directionality is reflected by the game.
$M_1$
, but not vice versa. This directionality is reflected by the game.
3.1 The game
A position in an EF game for InqBQ is a tuple
where:
-
•
 $M_0=\left \langle W_0,D_0,I_0 \right \rangle $
and
$M_0=\left \langle W_0,D_0,I_0 \right \rangle $
and
 $M_1=\left \langle W_1,D_1,I_1 \right \rangle $
are models for InqBQ;
$M_1=\left \langle W_1,D_1,I_1 \right \rangle $
are models for InqBQ; -
•
 $s_0$
and
$s_0$
and
 $s_1$
are information states in the models
$s_1$
are information states in the models
 $M_0$
and
$M_0$
and
 $M_1$
respectively; and
$M_1$
respectively; and -
•
 $\overline a_0$
and
$\overline a_0$
and
 $\overline a_1$
are tuples of equal length of elements from
$\overline a_1$
are tuples of equal length of elements from
 $D_0$
and
$D_0$
and
 $D_1$
respectively.
$D_1$
respectively.
If not otherwise specified, a game between the models
![]() $M_0$
and
$M_0$
and
![]() $M_1$
starts from position
$M_1$
starts from position
![]() $\langle M_0,W_0,\varepsilon ;M_1,W_1,\varepsilon ; \rangle $
, where
$\langle M_0,W_0,\varepsilon ;M_1,W_1,\varepsilon ; \rangle $
, where
![]() $\varepsilon $
indicates the empty tuple.
$\varepsilon $
indicates the empty tuple.
Starting a round from a position
![]() $\langle M_0,s_0,\overline a_0; M_1,s_1,\overline a_1 \rangle $
, S can choose between the following possible moves:Footnote
2
$\langle M_0,s_0,\overline a_0; M_1,s_1,\overline a_1 \rangle $
, S can choose between the following possible moves:Footnote
2
-
•
 $\overline{\exists} $
-move: S picks an element
$\overline{\exists} $
-move: S picks an element
 $b_0\in D_0$
; D responds with an element
$b_0\in D_0$
; D responds with an element
 $b_1\in D_1$
; the game continues from the position
$b_1\in D_1$
; the game continues from the position
 $\left \langle M_0,s_0,\overline a_0b_0; M_1,s_1,\overline a_1b_1 \right \rangle $
;
$\left \langle M_0,s_0,\overline a_0b_0; M_1,s_1,\overline a_1b_1 \right \rangle $
; -
•
 $\forall $
-move: S picks an element
$\forall $
-move: S picks an element
 $b_1\in D_1$
; D responds with an element
$b_1\in D_1$
; D responds with an element
 $b_0\in D_0$
; the game continues from the position
$b_0\in D_0$
; the game continues from the position
 $\left \langle M_0,s_0,\overline a_0b_0; M_1,s_1,\overline a_1b_1 \right \rangle $
; and
$\left \langle M_0,s_0,\overline a_0b_0; M_1,s_1,\overline a_1b_1 \right \rangle $
; and -
•
 $\to $
-move: S picks a sub-state
$\to $
-move: S picks a sub-state
 $t_1\subseteq s_1$
; D responds with a sub-state
$t_1\subseteq s_1$
; D responds with a sub-state
 ${t_0\subseteq s_0}$
; S picks
${t_0\subseteq s_0}$
; S picks
 $i\in \{1,0\}$
. The game continues from
$i\in \{1,0\}$
. The game continues from
 $\left \langle M_i,t_i,\overline a_i; M_{1-i},t_{1-i},\overline {a}_{1-i} \right \rangle $
.
$\left \langle M_i,t_i,\overline a_i; M_{1-i},t_{1-i},\overline {a}_{1-i} \right \rangle $
.
Notice the asymmetry between the roles of the two models: by performing an
![]() $\to $
-move, S can pick an information state from
$\to $
-move, S can pick an information state from
![]() $M_1$
, but not a state in
$M_1$
, but not a state in
![]() $M_0$
.
$M_0$
.
With respect to termination condition, we consider different versions of the game. In the bounded version of the game, a pair of numbers
![]() $\left \langle i,q \right \rangle \in \mathbb {N}^2$
is fixed in advance. This number constrains the development of the game: in total, S can play only i implication moves and only q quantifier moves (i.e.,
$\left \langle i,q \right \rangle \in \mathbb {N}^2$
is fixed in advance. This number constrains the development of the game: in total, S can play only i implication moves and only q quantifier moves (i.e.,
![]() $\overline{\exists} $
-move or a
$\overline{\exists} $
-move or a
![]() $\forall $
-move). When there are no more moves available, the game ends. If
$\forall $
-move). When there are no more moves available, the game ends. If
![]() $\left \langle M_0,s_0,\overline a_0; M_1,s_1,\overline a_1 \right \rangle $
is the final position, the game is won by Player D if the following condition is satisfied, and by player S otherwise:
$\left \langle M_0,s_0,\overline a_0; M_1,s_1,\overline a_1 \right \rangle $
is the final position, the game is won by Player D if the following condition is satisfied, and by player S otherwise:
-
• Winning condition for D: for all atomic formulas
 $\alpha (x_1,\dots ,x_n)$
where n is the size of the tuples
$\alpha (x_1,\dots ,x_n)$
where n is the size of the tuples
 $\overline a_0$
and
$\overline a_0$
and
 $\overline a_1$
, we have: (1)
$\overline a_1$
, we have: (1) $$ \begin{align} M_0,s_0\models \alpha(\overline{a}_0)\; \implies\; M_1,s_1 \models\alpha(\overline{a}_1). \end{align} $$
$$ \begin{align} M_0,s_0\models \alpha(\overline{a}_0)\; \implies\; M_1,s_1 \models\alpha(\overline{a}_1). \end{align} $$
In the unbounded version of the game, no restriction is placed at the outset on the number of moves to be performed. Instead, player S has the option to declare the game over at the beginning of each round: in this case, the winner is determined as in the bounded version of the game. If the game never stops, then D is the winner.Footnote 3
Example 3.1. Take the signature
![]() $\Sigma = \{P\}$
, where P is a unary predicate symbol. Given the models
$\Sigma = \{P\}$
, where P is a unary predicate symbol. Given the models
![]() $M_0$
and
$M_0$
and
![]() $M_1$
in Figure 1, in the table we show a run of the bounded game with
$M_1$
in Figure 1, in the table we show a run of the bounded game with
![]() $\left \langle i,q \right \rangle = \left \langle 1,2 \right \rangle $
between
$\left \langle i,q \right \rangle = \left \langle 1,2 \right \rangle $
between
![]() $M_0$
and
$M_0$
and
![]() $M_1$
. At the end of the run, the position is
$M_1$
. At the end of the run, the position is
![]() $\left \langle M_1,\{v_1\},\left \langle e_2,e_1 \right \rangle ; M_0,\{w_0\},\left \langle d_1,d_2 \right \rangle \right \rangle $
. The winner is Spoiler, since
$\left \langle M_1,\{v_1\},\left \langle e_2,e_1 \right \rangle ; M_0,\{w_0\},\left \langle d_1,d_2 \right \rangle \right \rangle $
. The winner is Spoiler, since


Fig. 1 On the left, two inquisitive models in the signature
![]() $\Sigma = \{P\}$
. The top row represents the set of worlds of the models (e.g.,
$\Sigma = \{P\}$
. The top row represents the set of worlds of the models (e.g.,
![]() $\{w_0,w_1\}$
for the model
$\{w_0,w_1\}$
for the model
![]() $M_0$
) and the left column represents the domain (e.g.,
$M_0$
) and the left column represents the domain (e.g.,
![]() $\{d_1,d_2\}$
for
$\{d_1,d_2\}$
for
![]() $M_0$
);
$M_0$
);
![]() $I(P)$
is encoded by the entries of the table: a
$I(P)$
is encoded by the entries of the table: a
![]() $\bullet $
indicates that P holds, while a
$\bullet $
indicates that P holds, while a
![]() $\times $
indicates that P does not hold (e.g.,
$\times $
indicates that P does not hold (e.g.,
![]() $d_1 \in I_{w_0}(P)$
and
$d_1 \in I_{w_0}(P)$
and
![]() $d_2 \notin I_{w_0}(P)$
). On the right, a run of the Ehrenfeucht-Fraïssé game.
$d_2 \notin I_{w_0}(P)$
). On the right, a run of the Ehrenfeucht-Fraïssé game.
As usual, a winning strategy for a player is a strategy which guarantees victory to them, no matter what the opponent plays. If D has a winning strategy in the EF game of length
![]() $\left \langle i,q \right \rangle $
starting from position
$\left \langle i,q \right \rangle $
starting from position
![]() $\left \langle M_0,s_0,\overline {a}_0; M_1,s_1,\overline {a}_1 \right \rangle $
we write:
$\left \langle M_0,s_0,\overline {a}_0; M_1,s_1,\overline {a}_1 \right \rangle $
we write:
We write
![]() $\approx _{i,q}$
for the relation
$\approx _{i,q}$
for the relation
![]() $\preceq _{i,q} \cap \succeq _{i,q}$
. Notice that the game with bounds
$\preceq _{i,q} \cap \succeq _{i,q}$
. Notice that the game with bounds
![]() $i,q$
is finite (since the number of turns is bounded by
$i,q$
is finite (since the number of turns is bounded by
![]() $i+q$
), zero-sum (as can be seen from the winning condition) and has perfect information. Therefore, if
$i+q$
), zero-sum (as can be seen from the winning condition) and has perfect information. Therefore, if
![]() $(M_0,s_0,\overline {a}_0) \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
does not hold, then it follows from the Gale-Stewart Theorem that Spoiler has a winning strategy in the EF game of length
$(M_0,s_0,\overline {a}_0) \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
does not hold, then it follows from the Gale-Stewart Theorem that Spoiler has a winning strategy in the EF game of length
![]() $\langle i,q \rangle $
starting from the position
$\langle i,q \rangle $
starting from the position
![]() $\langle M_0,s_0,\overline {a}_0; M_1,s_1,\overline {a}_1 \rangle $
.
$\langle M_0,s_0,\overline {a}_0; M_1,s_1,\overline {a}_1 \rangle $
.
We write
![]() $M_0\preceq _{i,q} M_1$
as a shorthand for
$M_0\preceq _{i,q} M_1$
as a shorthand for
![]() $(M_0,W_0,\varepsilon ) \preceq _{i,q} (M_1,W_1,\varepsilon )$
.
$(M_0,W_0,\varepsilon ) \preceq _{i,q} (M_1,W_1,\varepsilon )$
.
The following two propositions follow easily from the definition of the game.
Proposition 3.2. If
![]() $(M_0,s_0,\overline {a}_0) \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
then for all
$(M_0,s_0,\overline {a}_0) \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
then for all
![]() $i'\le i$
and
$i'\le i$
and
![]() $q'\le q$
it holds
$q'\le q$
it holds
![]() $(M_0,s_0,\overline {a}_0) \preceq _{i',q'} (M_1,s_1,\overline {a}_1)$
.
$(M_0,s_0,\overline {a}_0) \preceq _{i',q'} (M_1,s_1,\overline {a}_1)$
.
Proof. We prove the result by contraposition. Suppose that Spoiler has a winning strategy in the game
![]() $ \operatorname {\mathrm {EF}}_{i',q'}(M_0,s_0,\overline {a}_0;M_1,s_1,\overline {a_1})$
for some
$ \operatorname {\mathrm {EF}}_{i',q'}(M_0,s_0,\overline {a}_0;M_1,s_1,\overline {a_1})$
for some
![]() $i'\leq i$
and
$i'\leq i$
and
![]() $q'\leq q$
. This means that, no matter which choices Duplicator makes during a run, Spoiler can perform
$q'\leq q$
. This means that, no matter which choices Duplicator makes during a run, Spoiler can perform
![]() $i'$
implication moves and
$i'$
implication moves and
![]() $q'$
quantifier move and force the game to end up in a position
$q'$
quantifier move and force the game to end up in a position
 $$ \begin{align*} &\left\langle M_0, t_0, \overline{a}_0\overline{b}_0 ;\; M_1, t_1, \overline{a}_1\overline{b}_1 \right\rangle &\text{(case 1)} \\ \text{or}\qquad &\left\langle M_1, t_1, \overline{a}_0\overline{b}_0 ;\; M_1, t_1, \overline{a}_1\overline{b}_1 \right\rangle &\text{(case 2)} \end{align*} $$
$$ \begin{align*} &\left\langle M_0, t_0, \overline{a}_0\overline{b}_0 ;\; M_1, t_1, \overline{a}_1\overline{b}_1 \right\rangle &\text{(case 1)} \\ \text{or}\qquad &\left\langle M_1, t_1, \overline{a}_0\overline{b}_0 ;\; M_1, t_1, \overline{a}_1\overline{b}_1 \right\rangle &\text{(case 2)} \end{align*} $$
for which there exists an atomic formula
![]() $\alpha (\overline {x},\overline {y})$
such that
$\alpha (\overline {x},\overline {y})$
such that
 $$ \begin{align*} &M_0, t_0 \models \alpha(\overline{a}_0,\overline{b}_0) \;\text{and}\; M_1, t_1 \nvDash \alpha(\overline{a}_1,\overline{b}_1) &&\text{in case 1} \\ \text{or}\qquad &M_1, t_1 \models \alpha(\overline{a}_1,\overline{b}_1) \;\text{and}\; M_0, t_0 \nvDash \alpha(\overline{a}_0,\overline{b}_0) &&\text{in case 2.} \end{align*} $$
$$ \begin{align*} &M_0, t_0 \models \alpha(\overline{a}_0,\overline{b}_0) \;\text{and}\; M_1, t_1 \nvDash \alpha(\overline{a}_1,\overline{b}_1) &&\text{in case 1} \\ \text{or}\qquad &M_1, t_1 \models \alpha(\overline{a}_1,\overline{b}_1) \;\text{and}\; M_0, t_0 \nvDash \alpha(\overline{a}_0,\overline{b}_0) &&\text{in case 2.} \end{align*} $$
We will show that, from this point on, Spoiler can still win the game after performing
![]() $i-i'$
additional implication moves and
$i-i'$
additional implication moves and
![]() $q-q'$
additional quantifier moves: This amounts to a winning strategy in the game
$q-q'$
additional quantifier moves: This amounts to a winning strategy in the game
![]() $ \operatorname {\mathrm {EF}}_{i,q}(M_0,s_0,\overline {a}_0;M_1,s_1,\overline {a_1})$
. We will focus here on case 1, since the other case is completely analogous.
$ \operatorname {\mathrm {EF}}_{i,q}(M_0,s_0,\overline {a}_0;M_1,s_1,\overline {a_1})$
. We will focus here on case 1, since the other case is completely analogous.
-
• Firstly, Spoiler performs
 $i-i'$
implication moves, always picking
$i-i'$
implication moves, always picking
 $t_1$
as the information state and choosing
$t_1$
as the information state and choosing
 $i := 0$
(that is, maintaining the order of the models). Since Duplicator can only choose substates of
$i := 0$
(that is, maintaining the order of the models). Since Duplicator can only choose substates of
 $t_0$
, the position of the game after these moves will be of the form: with
$t_0$
, the position of the game after these moves will be of the form: with $$ \begin{align*} \left\langle M_0, t^{\prime}_0, \overline{a}_0\overline{b}_0 ;\; M_1, t_1, \overline{a}_1\overline{b}_1 \right\rangle \end{align*} $$
$$ \begin{align*} \left\langle M_0, t^{\prime}_0, \overline{a}_0\overline{b}_0 ;\; M_1, t_1, \overline{a}_1\overline{b}_1 \right\rangle \end{align*} $$
 $t^{\prime }_0 \subseteq t_0$
.
$t^{\prime }_0 \subseteq t_0$
.
-
• Secondly, Spoiler performs
 $q-q'$
quantification moves in an arbitrary way; no matter what Duplicator responds, we end up in a position of the form: for
$q-q'$
quantification moves in an arbitrary way; no matter what Duplicator responds, we end up in a position of the form: for $$ \begin{align*} \left\langle M_0, t^{\prime}_0, \overline{a}_0\overline{b}_0\overline{c}_0 ;\; M_1, t_1, \overline{a}_1\overline{b}_1\overline{c}_1 \right\rangle \end{align*} $$
$$ \begin{align*} \left\langle M_0, t^{\prime}_0, \overline{a}_0\overline{b}_0\overline{c}_0 ;\; M_1, t_1, \overline{a}_1\overline{b}_1\overline{c}_1 \right\rangle \end{align*} $$
 $\overline {c}_0$
and
$\overline {c}_0$
and
 $\overline {c}_1$
of length
$\overline {c}_1$
of length
 $q-q'$
.
$q-q'$
.
This is indeed a winning position for Spoiler, since
 $$ \begin{align*} \left\{ \begin{array}{l@{\hspace{2em}}l} M_0, t^{\prime}_0 \models \alpha(\overline{a}_0,\overline{b}_0) &(\text{by persistency, since } t^{\prime}_0 \subseteq t_0) \\ M_1, t_1 \nvDash \alpha(\overline{a}_1,\overline{b}_1). \end{array} \right.\\[-37pt] \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{l@{\hspace{2em}}l} M_0, t^{\prime}_0 \models \alpha(\overline{a}_0,\overline{b}_0) &(\text{by persistency, since } t^{\prime}_0 \subseteq t_0) \\ M_1, t_1 \nvDash \alpha(\overline{a}_1,\overline{b}_1). \end{array} \right.\\[-37pt] \end{align*} $$
Proposition 3.3. Suppose
![]() $\left \langle i,q \right \rangle \neq \left \langle 0,0 \right \rangle $
.
$\left \langle i,q \right \rangle \neq \left \langle 0,0 \right \rangle $
.
![]() $(M_0,s_0,\overline {a}_0) \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
iff the following three conditions are satisfied:
$(M_0,s_0,\overline {a}_0) \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
iff the following three conditions are satisfied:
-
• If
 $\,i>0$
, then
$\,i>0$
, then
 $\forall t_1 \subseteq s_1\;\;\exists t_0 \subseteq s_0\;: (M_0,t_0,\overline {a}_0) \approx _{i-1,q} (M_1,t_1,\overline {a}_1)$
.
$\forall t_1 \subseteq s_1\;\;\exists t_0 \subseteq s_0\;: (M_0,t_0,\overline {a}_0) \approx _{i-1,q} (M_1,t_1,\overline {a}_1)$
. -
• If
 $q>0$
, then
$q>0$
, then
 $\forall b_0 \in D_0 \;\exists b_1 \in D_1: (M_0,s_0,\overline {a}_0b_0) \preceq _{i,q-1} (M_1,s_1,\overline {a}_1b_1)$
.
$\forall b_0 \in D_0 \;\exists b_1 \in D_1: (M_0,s_0,\overline {a}_0b_0) \preceq _{i,q-1} (M_1,s_1,\overline {a}_1b_1)$
. -
• If
 $q>0$
, then
$q>0$
, then
 $\forall b_1 \in D_1 \;\exists b_0 \in D_0: (M_0,s_0,\overline {a}_0b_0) \preceq _{i,q-1} (M_1,s_1,\overline {a}_1b_1)$
.
$\forall b_1 \in D_1 \;\exists b_0 \in D_0: (M_0,s_0,\overline {a}_0b_0) \preceq _{i,q-1} (M_1,s_1,\overline {a}_1b_1)$
.
Proof. The three conditions amount precisely to the fact that, for every move available to Spoiler, there is a corresponding move for Duplicator that leads to a sub-game in which Duplicator has a winning strategy. This is precisely what is needed for Duplicator to have a winning strategy in the original game.
3.2 IQ degree and types
We define the implication degree (
![]() $ \operatorname {\mathrm {Ideg}}$
) and quantification degree (
$ \operatorname {\mathrm {Ideg}}$
) and quantification degree (
![]() $ \operatorname {\mathrm {Qdeg}}$
) of a formula by the following inductive clauses, where p stands for an atomic formula:
$ \operatorname {\mathrm {Qdeg}}$
) of a formula by the following inductive clauses, where p stands for an atomic formula:

The combined degree of a formula is defined as
![]() $ \operatorname {\mathrm {IQdeg}}(\varphi ) = \left \langle \operatorname {\mathrm {Ideg}}(\varphi ), \operatorname {\mathrm {Qdeg}}(\varphi ) \right \rangle $
. We define a partial order
$ \operatorname {\mathrm {IQdeg}}(\varphi ) = \left \langle \operatorname {\mathrm {Ideg}}(\varphi ), \operatorname {\mathrm {Qdeg}}(\varphi ) \right \rangle $
. We define a partial order
![]() $\leq $
on such degrees by setting:
$\leq $
on such degrees by setting:
We denote by
![]() $\mathcal {L}_{i,q}^l$
the set of formulas
$\mathcal {L}_{i,q}^l$
the set of formulas
![]() $\varphi $
such that
$\varphi $
such that
![]() $ \operatorname {\mathrm {IQdeg}}(\varphi )\le \left \langle i,q \right \rangle $
and the set of free variables in
$ \operatorname {\mathrm {IQdeg}}(\varphi )\le \left \langle i,q \right \rangle $
and the set of free variables in
![]() $\varphi $
is included in
$\varphi $
is included in
![]() $\{x_1,\dots ,x_l\}$
. We can then define the key notion of
$\{x_1,\dots ,x_l\}$
. We can then define the key notion of
![]() $\left \langle i,q \right \rangle $
-type.
$\left \langle i,q \right \rangle $
-type.
Definition 3.4
 $\left \langle i,q \right \rangle $
-types
$\left \langle i,q \right \rangle $
-types
Let M be a model, s an information state, and
![]() $\overline {a}$
a tuple of elements in M of length l. The
$\overline {a}$
a tuple of elements in M of length l. The
![]() $\left \langle i,q \right \rangle $
-type of
$\left \langle i,q \right \rangle $
-type of
![]() $\left \langle M,s,\overline {a} \right \rangle $
is the set
$\left \langle M,s,\overline {a} \right \rangle $
is the set
We also define the following notation:
 $$ \begin{align*} &(M_0, s_0, \overline{a}_0) \sqsubseteq_{i,q} (M_1, s_1, \overline{a}_1) \overset{def}{\iff} \operatorname{\mathrm{tp}}_{i,q}(M_0,s_0,\overline{a}_0) \subseteq \operatorname{\mathrm{tp}}_{i,q}(M_1,s_1,\overline{a}_1) \\ &(M_0, s_0, \overline{a}_0) \equiv_{i,q} (M_1, s_1, \overline{a}_1) \overset{def}{\iff} \operatorname{\mathrm{tp}}_{i,q}(M_0,s_0,\overline{a}_0) = \operatorname{\mathrm{tp}}_{i,q}(M_1,s_1,\overline{a}_1) \end{align*} $$
$$ \begin{align*} &(M_0, s_0, \overline{a}_0) \sqsubseteq_{i,q} (M_1, s_1, \overline{a}_1) \overset{def}{\iff} \operatorname{\mathrm{tp}}_{i,q}(M_0,s_0,\overline{a}_0) \subseteq \operatorname{\mathrm{tp}}_{i,q}(M_1,s_1,\overline{a}_1) \\ &(M_0, s_0, \overline{a}_0) \equiv_{i,q} (M_1, s_1, \overline{a}_1) \overset{def}{\iff} \operatorname{\mathrm{tp}}_{i,q}(M_0,s_0,\overline{a}_0) = \operatorname{\mathrm{tp}}_{i,q}(M_1,s_1,\overline{a}_1) \end{align*} $$
Example 3.5. Consider the models
![]() $M_0$
,
$M_0$
,
![]() $M_1$
in Figure 1. Since
$M_1$
in Figure 1. Since
![]() $P(x)\in \mathcal {L}^{1}_{0,0}$
and
$P(x)\in \mathcal {L}^{1}_{0,0}$
and
![]() $M_1,\{v_0,v_1\}\models P(e_1)$
, we have
$M_1,\{v_0,v_1\}\models P(e_1)$
, we have
![]() $(M_1,\{v_0,v_1\},\left \langle e_1 \right \rangle ) \not \sqsubseteq _{0,0} (M_0,\{w_0,w_1\},\left \langle d_1 \right \rangle )$
; while
$(M_1,\{v_0,v_1\},\left \langle e_1 \right \rangle ) \not \sqsubseteq _{0,0} (M_0,\{w_0,w_1\},\left \langle d_1 \right \rangle )$
; while
![]() $M_0,\{w_0,w_1\}\not \models P(d_1)$
.
$M_0,\{w_0,w_1\}\not \models P(d_1)$
.
Notice that, if the signature is finite, there are only a finite number of non-equivalent formulas of combined degree at most
![]() $\left \langle i,q \right \rangle $
, and consequently only a finite number of
$\left \langle i,q \right \rangle $
, and consequently only a finite number of
![]() $\left \langle i,q \right \rangle $
-types. This can be shown inductively as follows:
$\left \langle i,q \right \rangle $
-types. This can be shown inductively as follows:
-
• The quotient
 ${\mathcal {L}^{l}_{0,0}/\!\equiv }\,$
is a distributive lattice under the operations
${\mathcal {L}^{l}_{0,0}/\!\equiv }\,$
is a distributive lattice under the operations
 $\land $
and
$\land $
and
 . Moreover, since we are working with a finite relational signature,
. Moreover, since we are working with a finite relational signature,
 $\mathcal {L}^{l}_{0,0}$
contains only finitely many atomic formulas, and the equivalence classes of these formulas generate the whole lattice. Since every finitely generated distributive lattice is finite,
$\mathcal {L}^{l}_{0,0}$
contains only finitely many atomic formulas, and the equivalence classes of these formulas generate the whole lattice. Since every finitely generated distributive lattice is finite,
 ${\mathcal {L}^{l}_{0,0}/\!\equiv }\,$
is finite, which means that
${\mathcal {L}^{l}_{0,0}/\!\equiv }\,$
is finite, which means that
 $\mathcal {L}^{l}_{0,0}$
contains only finitely many formulas up to logical equivalence.
$\mathcal {L}^{l}_{0,0}$
contains only finitely many formulas up to logical equivalence. -
• Formulas in
 $\mathcal {L}^{l}_{i,q}$
are equivalent to Boolean combinations of formulas in
$\mathcal {L}^{l}_{i,q}$
are equivalent to Boolean combinations of formulas in
 ${A \cup B}$
, for
${A \cup B}$
, for
 $A = \left \{ \varphi \to \psi \;\middle |\; \varphi , \psi \in \mathcal {L}^{l}_{i-1,q} \right \}$
and
$A = \left \{ \varphi \to \psi \;\middle |\; \varphi , \psi \in \mathcal {L}^{l}_{i-1,q} \right \}$
and
 $B = \left \{ \overline{\exists}\, x. \varphi , \forall x.\varphi \;\middle |\; \varphi \in \mathcal {L}^{l+1}_{i,q-1} \right \}$
—where we impose by definition
$B = \left \{ \overline{\exists}\, x. \varphi , \forall x.\varphi \;\middle |\; \varphi \in \mathcal {L}^{l+1}_{i,q-1} \right \}$
—where we impose by definition
 $\mathcal {L}^{l}_{i,q} = \emptyset $
if
$\mathcal {L}^{l}_{i,q} = \emptyset $
if
 $i<0$
or
$i<0$
or
 $q<0$
. By induction hypothesis, A and B contain only finitely many non-equivalent formulas.
$q<0$
. By induction hypothesis, A and B contain only finitely many non-equivalent formulas.
3.3 The EF theorem
What follows is the first main result of the paper: the relations
![]() $\preceq _{i,q}$
and
$\preceq _{i,q}$
and
![]() $\sqsubseteq _{i,q}$
coincide.
$\sqsubseteq _{i,q}$
coincide.
Theorem 3.6. Suppose the signature
![]() $\Sigma $
is finite. Then
$\Sigma $
is finite. Then
Proof. We will prove this by well-founded induction on
![]() $\left \langle i,q \right \rangle $
. For the basic case,
$\left \langle i,q \right \rangle $
. For the basic case,
![]() $\left \langle i,q \right \rangle = \left \langle 0,0 \right \rangle $
, we just have to verify that, if Condition (1) holds for all atomic formulas, then it holds for all formulas
$\left \langle i,q \right \rangle = \left \langle 0,0 \right \rangle $
, we just have to verify that, if Condition (1) holds for all atomic formulas, then it holds for all formulas
![]() $\varphi \in \mathcal {L}^{l}_{0,0}$
. This is straightforward. Next, suppose
$\varphi \in \mathcal {L}^{l}_{0,0}$
. This is straightforward. Next, suppose
![]() $\left \langle i,q \right \rangle> \left \langle 0,0 \right \rangle $
and suppose the claim holds for all
$\left \langle i,q \right \rangle> \left \langle 0,0 \right \rangle $
and suppose the claim holds for all
![]() $\left \langle i',q' \right \rangle <\left \langle i,q \right \rangle $
. For the left-to-right direction, proceed by contraposition. Suppose that for some
$\left \langle i',q' \right \rangle <\left \langle i,q \right \rangle $
. For the left-to-right direction, proceed by contraposition. Suppose that for some
![]() $\varphi \in \mathcal {L}_{i,q}^l$
the following conditions hold:
$\varphi \in \mathcal {L}_{i,q}^l$
the following conditions hold:
We proceed by induction on the structure of
![]() $\varphi $
; some cases are easy to consider:
$\varphi $
; some cases are easy to consider:
-
• If
 $\varphi $
is an atom, it follows
$\varphi $
is an atom, it follows
 $(M_0,s_0,\overline {a}_0) \not \preceq _{0,0} (M_1,s_1,\overline {a}_1)$
; so, by Proposition 3.2 also
$(M_0,s_0,\overline {a}_0) \not \preceq _{0,0} (M_1,s_1,\overline {a}_1)$
; so, by Proposition 3.2 also
 $(M_0,s_0,\overline {a}_0) \not \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
. Thus, in this case the conclusion follows.
$(M_0,s_0,\overline {a}_0) \not \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
. Thus, in this case the conclusion follows. -
• If
 $\varphi $
is a conjunction
$\varphi $
is a conjunction
 $\psi \land \chi $
then we have: So, either
$\psi \land \chi $
then we have: So, either $$ \begin{align*} \left\{ \begin{array}{l} M_0, s_0 \models \psi(\overline{a}_0) \land \chi(\overline{a}_0) \implies M_0, s_0 \models \psi(\overline{a}_0) \text{ and } M_0, s_0 \models \chi(\overline{a}_0) \\ M_1, s_1 \not\models \psi(\overline{a}_1) \land \chi(\overline{a}_1) \implies M_1, s_1 \not\models \psi(\overline{a}_1) \text{ or } M_1, s_1 \not\models \chi(\overline{a}_1). \\ \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{l} M_0, s_0 \models \psi(\overline{a}_0) \land \chi(\overline{a}_0) \implies M_0, s_0 \models \psi(\overline{a}_0) \text{ and } M_0, s_0 \models \chi(\overline{a}_0) \\ M_1, s_1 \not\models \psi(\overline{a}_1) \land \chi(\overline{a}_1) \implies M_1, s_1 \not\models \psi(\overline{a}_1) \text{ or } M_1, s_1 \not\models \chi(\overline{a}_1). \\ \end{array} \right. \end{align*} $$
 $\psi $
or
$\psi $
or
 $\chi $
is a less complex witness of
$\chi $
is a less complex witness of
 $(M_0,s_0,\overline {a}_0) \not \sqsubseteq _{i,q} (M_1,s_1,\overline {a}_1)$
.
$(M_0,s_0,\overline {a}_0) \not \sqsubseteq _{i,q} (M_1,s_1,\overline {a}_1)$
.
-
• If
 $\varphi $
is a disjunction
$\varphi $
is a disjunction
 , we can reach a conclusion analogous to the one we reached for conjunction.
, we can reach a conclusion analogous to the one we reached for conjunction.
The remaining cases are those in which
![]() $\varphi $
is of the form
$\varphi $
is of the form
![]() $\psi \to \chi $
,
$\psi \to \chi $
,
![]() $\forall x. \psi $
or
$\forall x. \psi $
or
![]() $\overline{\exists}\, x.\psi $
(cases
$\overline{\exists}\, x.\psi $
(cases
![]() $\Rightarrow ^{1}$
,
$\Rightarrow ^{1}$
,
![]() $\Rightarrow ^{2}$
,
$\Rightarrow ^{2}$
,
![]() $\Rightarrow ^{3}$
respectively). Let us consider the three cases separately.
$\Rightarrow ^{3}$
respectively). Let us consider the three cases separately.
Case
![]() $\Rightarrow ^{1}$
:
$\Rightarrow ^{1}$
:
![]() $\varphi $
is an implication
$\varphi $
is an implication
![]() $\psi \to \chi $
. In this case we have:
$\psi \to \chi $
. In this case we have:
 $$ \begin{align*} &M_1, s_1 \not\models \psi(\overline{a}_1) \to \chi(\overline{a}_1) \implies (\exists t_1 \subseteq s_1)\left[ M_1, t_1 \models \psi(\overline{a}_1) \text{ and } M_1, t_1 \not\models \chi(\overline{a}_1)\right], \\ &M_0, s_0 \models \psi(\overline{a}_0) \to \chi(\overline{a}_0) \implies (\nexists t_0 \subseteq s_0) \left[ M_0, t_0 \models \psi(\overline{a}_0) \text{ and } M_0, t_0 \not\models \chi(\overline{a}_0) \right]. \end{align*} $$
$$ \begin{align*} &M_1, s_1 \not\models \psi(\overline{a}_1) \to \chi(\overline{a}_1) \implies (\exists t_1 \subseteq s_1)\left[ M_1, t_1 \models \psi(\overline{a}_1) \text{ and } M_1, t_1 \not\models \chi(\overline{a}_1)\right], \\ &M_0, s_0 \models \psi(\overline{a}_0) \to \chi(\overline{a}_0) \implies (\nexists t_0 \subseteq s_0) \left[ M_0, t_0 \models \psi(\overline{a}_0) \text{ and } M_0, t_0 \not\models \chi(\overline{a}_0) \right]. \end{align*} $$
Thus there exists a state
![]() $t_1 \subseteq s_1$
with a different
$t_1 \subseteq s_1$
with a different
![]() $\langle i-1,q \rangle $
-type than every
$\langle i-1,q \rangle $
-type than every
![]() $t_0\subseteq s_0$
—either because it supports
$t_0\subseteq s_0$
—either because it supports
![]() $\psi $
or because it does not support
$\psi $
or because it does not support
![]() $\chi $
. So by induction hypothesis, if S performs a
$\chi $
. So by induction hypothesis, if S performs a
![]() $\to $
-move and chooses
$\to $
-move and chooses
![]() $t_1$
, for every choice
$t_1$
, for every choice
![]() $t_0$
of D we have
$t_0$
of D we have
![]() $(M_0,t_0,\overline {a}_0) \not \approx _{i-1,q} (M_1,t_1,\overline {a}_1)$
. It follows by Proposition 3.3 that
$(M_0,t_0,\overline {a}_0) \not \approx _{i-1,q} (M_1,t_1,\overline {a}_1)$
. It follows by Proposition 3.3 that
![]() $(M_0,s_0,\overline {a}_0) \not \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
as wanted.
$(M_0,s_0,\overline {a}_0) \not \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
as wanted.
Case
![]() $\Rightarrow ^{2}$
:
$\Rightarrow ^{2}$
:
![]() $\varphi $
is a universal
$\varphi $
is a universal
![]() $\forall x. \psi $
. In this case we have:
$\forall x. \psi $
. In this case we have:
 $$ \begin{align*} &M_1, s_1 \not\models \forall x. \psi(\overline{a}_1,x) \implies (\exists b_1 \in D_1)\; M_1, s_1 \not\models \psi(\overline{a}_1,b_1), \\ &M_0, s_0 \models \forall x. \psi(\overline{a}_0,x) \implies (\forall b_0 \in D_0)\; M_0, s_0 \models \psi(\overline{a}_0,b_0). \end{align*} $$
$$ \begin{align*} &M_1, s_1 \not\models \forall x. \psi(\overline{a}_1,x) \implies (\exists b_1 \in D_1)\; M_1, s_1 \not\models \psi(\overline{a}_1,b_1), \\ &M_0, s_0 \models \forall x. \psi(\overline{a}_0,x) \implies (\forall b_0 \in D_0)\; M_0, s_0 \models \psi(\overline{a}_0,b_0). \end{align*} $$
Thus if S performs a
![]() $\forall $
-move and chooses
$\forall $
-move and chooses
![]() $b_1$
, for every choice
$b_1$
, for every choice
![]() $b_0$
of D, by induction hypothesis we have
$b_0$
of D, by induction hypothesis we have
It follows by Proposition 3.3 that
![]() $(M_0,s_0,\overline {a}_0) \not \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
as wanted.
$(M_0,s_0,\overline {a}_0) \not \preceq _{i,q} (M_1,s_1,\overline {a}_1)$
as wanted.
Case
![]() $\Rightarrow ^{3}$
:
$\Rightarrow ^{3}$
:
![]() $\varphi $
is an inquisitive existential
$\varphi $
is an inquisitive existential
![]() $\overline{\exists}\, x. \psi $
. This case is similar to the previous one: S can perform an
$\overline{\exists}\, x. \psi $
. This case is similar to the previous one: S can perform an
![]() $\overline{\exists} $
-move and pick an element
$\overline{\exists} $
-move and pick an element
![]() $b_0$
in
$b_0$
in
![]() $ D_0$
with no counterpart in
$ D_0$
with no counterpart in
![]() $D_1$
, and by Proposition 3.3 we get the result.
$D_1$
, and by Proposition 3.3 we get the result.
This completes the proof of the left-to-right direction of the inductive step. Now consider the converse direction. Again, we proceed by contraposition. Suppose that S has a winning strategy in the EF game of length
![]() $\langle i,q\rangle $
starting from
$\langle i,q\rangle $
starting from
![]() $(M_0,s_0,\overline {a}_0;M_1,s_1,\overline {a}_1)$
. We consider again three cases, depending on the first move of the winning strategy (cases
$(M_0,s_0,\overline {a}_0;M_1,s_1,\overline {a}_1)$
. We consider again three cases, depending on the first move of the winning strategy (cases
![]() $\Leftarrow ^{1}$
,
$\Leftarrow ^{1}$
,
![]() $\Leftarrow ^{2}$
,
$\Leftarrow ^{2}$
,
![]() $\Leftarrow ^{3}$
respectively).
$\Leftarrow ^{3}$
respectively).
Case
![]() $\Leftarrow ^{1}$
: the first move is a
$\Leftarrow ^{1}$
: the first move is a
![]() $\to $
-move. Suppose S starts by choosing
$\to $
-move. Suppose S starts by choosing
![]() $t_1\subseteq s_1$
. As this is a winning strategy for S, for every choice
$t_1\subseteq s_1$
. As this is a winning strategy for S, for every choice
![]() $t_0\subseteq s_0$
of D we have
$t_0\subseteq s_0$
of D we have
By inductive hypothesis, this translates to
where
![]() $ \operatorname {\mathrm {tp}}(t_0) := \operatorname {\mathrm {tp}}_{i-1,q}(M_0,t_0,\overline {a}_0)$
and
$ \operatorname {\mathrm {tp}}(t_0) := \operatorname {\mathrm {tp}}_{i-1,q}(M_0,t_0,\overline {a}_0)$
and
![]() $ \operatorname {\mathrm {tp}}(t_1) := \operatorname {\mathrm {tp}}_{i-1,q}(M_1,t_1,\overline {a}_1)$
.
$ \operatorname {\mathrm {tp}}(t_1) := \operatorname {\mathrm {tp}}_{i-1,q}(M_1,t_1,\overline {a}_1)$
.
Given this, there exist two families
![]() $\{ \psi _{t_0}\mid t_0\subseteq s_0\}$
and
$\{ \psi _{t_0}\mid t_0\subseteq s_0\}$
and
![]() $\{\theta _{t_0}\mid t_0\subseteq s_0\}$
such that:
$\{\theta _{t_0}\mid t_0\subseteq s_0\}$
such that:
 $$ \begin{align*} \left\{ \begin{array}{ll} \psi_{t_0} \in \operatorname{\mathrm{tp}}(t_0) \setminus \operatorname{\mathrm{tp}}(t) &\text{if } \operatorname{\mathrm{tp}}(t_0)\setminus\operatorname{\mathrm{tp}}(t)\ne\emptyset \\ \psi_{t_0} := \bot &\text{otherwise} \end{array} \right. \\ \left\{ \begin{array}{ll} \theta_{t_0} \in \operatorname{\mathrm{tp}}(t) \setminus \operatorname{\mathrm{tp}}({t_0}) &\text{if } \operatorname{\mathrm{tp}}(t)\setminus\operatorname{\mathrm{tp}}({t_0})\ne\emptyset \\ \theta_{t_0} := \top &\text{otherwise.} \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{ll} \psi_{t_0} \in \operatorname{\mathrm{tp}}(t_0) \setminus \operatorname{\mathrm{tp}}(t) &\text{if } \operatorname{\mathrm{tp}}(t_0)\setminus\operatorname{\mathrm{tp}}(t)\ne\emptyset \\ \psi_{t_0} := \bot &\text{otherwise} \end{array} \right. \\ \left\{ \begin{array}{ll} \theta_{t_0} \in \operatorname{\mathrm{tp}}(t) \setminus \operatorname{\mathrm{tp}}({t_0}) &\text{if } \operatorname{\mathrm{tp}}(t)\setminus\operatorname{\mathrm{tp}}({t_0})\ne\emptyset \\ \theta_{t_0} := \top &\text{otherwise.} \end{array} \right. \end{align*} $$
Moreover, we can suppose the two families to be finite, as there are only a finite number of formulas of degree
![]() $\left \langle i-1,q \right \rangle $
up to logical equivalence (see Section 3.2). Define now the formula
$\left \langle i-1,q \right \rangle $
up to logical equivalence (see Section 3.2). Define now the formula
![]() $\varphi $
as follows:
$\varphi $
as follows:

We have: (i)
![]() $ \operatorname {\mathrm {IQdeg}}(\varphi ) \leq \left \langle i,q \right \rangle $
, (ii)
$ \operatorname {\mathrm {IQdeg}}(\varphi ) \leq \left \langle i,q \right \rangle $
, (ii)
![]() $\varphi \notin \operatorname {\mathrm {tp}}_{i,q}(M_0,s_0,\overline {a}_0)$
(since by construction
$\varphi \notin \operatorname {\mathrm {tp}}_{i,q}(M_0,s_0,\overline {a}_0)$
(since by construction
![]() $\varphi $
is falsified at
$\varphi $
is falsified at
![]() $t_1\subseteq s_1$
) and (iii)
$t_1\subseteq s_1$
) and (iii)
![]() $\varphi \in \operatorname {\mathrm {tp}}_{i,q}(M_1,s_1,\overline {a}_1)$
(since by construction
$\varphi \in \operatorname {\mathrm {tp}}_{i,q}(M_1,s_1,\overline {a}_1)$
(since by construction
![]() $\varphi $
holds at every state
$\varphi $
holds at every state
![]() $t_0\subseteq s_0$
). Thus we have
$t_0\subseteq s_0$
). Thus we have
![]() $(M_0,t_0,\overline {a}_0) \not \sqsubseteq _{i-1,q} (M_1,t_1,\overline {a}_1)$
, as we wanted.
$(M_0,t_0,\overline {a}_0) \not \sqsubseteq _{i-1,q} (M_1,t_1,\overline {a}_1)$
, as we wanted.
Case
![]() $\Leftarrow ^{2}$
: the first move is a
$\Leftarrow ^{2}$
: the first move is a
![]() $\forall $
-move. Suppose S starts by choosing
$\forall $
-move. Suppose S starts by choosing
![]() $b_1 \in D_1$
. As this is a winning strategy for S, for every choice
$b_1 \in D_1$
. As this is a winning strategy for S, for every choice
![]() $b_0\in D_0$
of D we have
$b_0\in D_0$
of D we have
By induction hypothesis, the above translates to
where
![]() $ \operatorname {\mathrm {tp}}(b_0):= \operatorname {\mathrm {tp}}_{i,q-1}(M_0,s_0,\overline {a}_0b_0)$
and
$ \operatorname {\mathrm {tp}}(b_0):= \operatorname {\mathrm {tp}}_{i,q-1}(M_0,s_0,\overline {a}_0b_0)$
and
![]() $ \operatorname {\mathrm {tp}}(b_1):= \operatorname {\mathrm {tp}}_{i,q-1}(M_1,s_1,\overline {a}_1b_1)$
.
$ \operatorname {\mathrm {tp}}(b_1):= \operatorname {\mathrm {tp}}_{i,q-1}(M_1,s_1,\overline {a}_1b_1)$
.
Now the formula
has IQ-degree at most
![]() $\left \langle i,q \right \rangle $
, and by construction we have
$\left \langle i,q \right \rangle $
, and by construction we have
![]() $\varphi \in \operatorname {\mathrm {tp}}_{i,q}(M_0,s_0,\overline {a}_0)$
and
$\varphi \in \operatorname {\mathrm {tp}}_{i,q}(M_0,s_0,\overline {a}_0)$
and
![]() $\varphi \notin \operatorname {\mathrm {tp}}_{i,q}(M_1,s_1,\overline {a}_1)$
. Thus, we have
$\varphi \notin \operatorname {\mathrm {tp}}_{i,q}(M_1,s_1,\overline {a}_1)$
. Thus, we have
![]() $(M_0,t_0,\overline {a}_0) \not \sqsubseteq _{i-1,q} (M_1,t_1,\overline {a}_1)$
.
$(M_0,t_0,\overline {a}_0) \not \sqsubseteq _{i-1,q} (M_1,t_1,\overline {a}_1)$
.
Case
![]() $\Leftarrow ^{3}$
: the first move is a
$\Leftarrow ^{3}$
: the first move is a
![]() $\overline{\exists} $
-move. Reasoning as in the previous case, we find that there exists a
$\overline{\exists} $
-move. Reasoning as in the previous case, we find that there exists a
![]() $b_0\in D_0$
—the element chosen by S—such that for every
$b_0\in D_0$
—the element chosen by S—such that for every
![]() $b_1\in D_1$
$b_1\in D_1$
In particular, it follows that the formula
is a formula of complexity at most
![]() $\left \langle i,q \right \rangle $
such that
$\left \langle i,q \right \rangle $
such that
![]() $\varphi \in \operatorname {\mathrm {tp}}_{i,q}(M_0,s_0,\overline {a}_0)$
and
$\varphi \in \operatorname {\mathrm {tp}}_{i,q}(M_0,s_0,\overline {a}_0)$
and
![]() $\varphi \notin \operatorname {\mathrm {tp}}_{i,q}(M_1,s_1,\overline {a_1})$
. Again, it follows that
$\varphi \notin \operatorname {\mathrm {tp}}_{i,q}(M_1,s_1,\overline {a_1})$
. Again, it follows that
![]() $(M_0,t_0,\overline {a}_0) \not \sqsubseteq _{i-1,q} (M_1,t_1,\overline {a}_1)$
.
$(M_0,t_0,\overline {a}_0) \not \sqsubseteq _{i-1,q} (M_1,t_1,\overline {a}_1)$
.
As a corollary, we also get a game-theoretic characterization of the distinguishing power of formulas in the
![]() $\langle i,q\rangle $
-fragment of InqBQ.
$\langle i,q\rangle $
-fragment of InqBQ.
Corollary 3.7. For a finite signature
![]() $\Sigma $
, we have:
$\Sigma $
, we have:
3.4 Extending the result to function symbols
The results we just obtained assume that the signature
![]() $\Sigma $
is relational. However, it is not hard to extend them to the case in which
$\Sigma $
is relational. However, it is not hard to extend them to the case in which
![]() $\Sigma $
contains function symbols (including nullary function symbols, i.e., constant symbols). In InqBQ, function symbols are interpreted rigidly: if
$\Sigma $
contains function symbols (including nullary function symbols, i.e., constant symbols). In InqBQ, function symbols are interpreted rigidly: if
![]() $f\in \Sigma $
is an n-ary function symbol, then the interpretation function I of a model M must assign to all worlds w in the model the same function
$f\in \Sigma $
is an n-ary function symbol, then the interpretation function I of a model M must assign to all worlds w in the model the same function
![]() $I_w(f):D^n\to D$
.Footnote
4
$I_w(f):D^n\to D$
.Footnote
4
As in the case of classical logic [Reference Hodges13] Section 3.3, the presence of function symbols requires some care in formulating the EF game. The reason is that allowing atomic formulas to contain arbitrary occurrences of function symbols allows us to generate with a finite number of choices in the game an infinite sub-structure of the model—which spoils the crucial locality feature of the game. Technically, a simple way to circumvent the problem this is to follow [Reference Hodges13] Section 3.3 and work with formulas which are unnested.
Definition 3.8 (Unnested formula)
An unnested atomic formula is a formula of one of the following forms:
An unnested formula is a formula that contains only unnested atoms.
Examples of nested formulas—i.e., non-unnested formulas—are
![]() $f(x) = g(y)$
,
$f(x) = g(y)$
,
![]() $R(f(x))$
and
$R(f(x))$
and
![]() $f(c) = x$
.
$f(c) = x$
.
We can now make the following amendments to the definition above: (i) the winning conditions for the game are determined by looking at whether Equation (1) is satisfied for all unnested atomic formulas, and (ii) the
![]() $\langle i,q\rangle $
-types are re-defined as sets of unnested formulas of degree at most
$\langle i,q\rangle $
-types are re-defined as sets of unnested formulas of degree at most
![]() $\langle i,q\rangle $
. Other than that, the statement of the result and the proof are the same as above.
$\langle i,q\rangle $
. Other than that, the statement of the result and the proof are the same as above.
Using identity we can turn an arbitrary formula into an equivalent unnested one (e.g., replacing
![]() $P(f(x))$
with
$P(f(x))$
with
![]() $\forall y.((y=f(x))\to Py)$
) so the restriction to unnested formula is not a limitation to the generality of the game-theoretic characterization; rather, it can be seen as an indirect way of assigning formulas containing function symbols with the appropriate
$\forall y.((y=f(x))\to Py)$
) so the restriction to unnested formula is not a limitation to the generality of the game-theoretic characterization; rather, it can be seen as an indirect way of assigning formulas containing function symbols with the appropriate
![]() $\langle i,q\rangle $
-degree—making explicit a quantification which is implicit in the presence of a function symbol.
$\langle i,q\rangle $
-degree—making explicit a quantification which is implicit in the presence of a function symbol.
3.5 A symmetric version of the game
As noticed before, a difference between the Ehrenfeucht–Fraïssé game for classical logic and the game introduced in Section 3 is that the latter is asymmetric—the two models under consideration do not play the same role. This allows us to study the relation
![]() $\sqsubseteq _{i,q}$
in addition to the relation
$\sqsubseteq _{i,q}$
in addition to the relation
![]() $\equiv _{i,q}$
. This contrast with the situation in classical first-order logic, where the relations
$\equiv _{i,q}$
. This contrast with the situation in classical first-order logic, where the relations
![]() $\sqsubseteq _q$
and
$\sqsubseteq _q$
and
![]() $\equiv _q$
coincide due to the semantics of negation. A natural question is whether we can define a symmetric version of the game which directly characterizes the relation
$\equiv _q$
coincide due to the semantics of negation. A natural question is whether we can define a symmetric version of the game which directly characterizes the relation
![]() $\equiv _{i,q}$
. In what follows we will consider a naïve modification of the game to obtain a symmetric version and study the induced equivalence relation between models. The symmetric way is just like the game introduced above, except that we replace the
$\equiv _{i,q}$
. In what follows we will consider a naïve modification of the game to obtain a symmetric version and study the induced equivalence relation between models. The symmetric way is just like the game introduced above, except that we replace the
![]() $\to $
-move and the winning condition as follows.
$\to $
-move and the winning condition as follows.
-
•
 $\to $
-move. S picks a sub-state
$\to $
-move. S picks a sub-state
 $t_i\subseteq s_i$
for
$t_i\subseteq s_i$
for
 $i=0$
or
$i=0$
or
 $1$
. D responds with a sub-state
$1$
. D responds with a sub-state
 $t_{1-i}\subseteq s_{1-i}$
. The game continues from
$t_{1-i}\subseteq s_{1-i}$
. The game continues from
 $\langle M_0,t_0,\overline {a}_0;M_1,t_1,\overline {a}_1 \rangle $
.
$\langle M_0,t_0,\overline {a}_0;M_1,t_1,\overline {a}_1 \rangle $
.Thus, in this version S is free to play a substate move in either model. This obviates the need for swapping roles of the two models.
-
• Winning condition for D: for all atomic formulas
 $\alpha (x_1,\dots ,x_n)$
where n is the size of the tuples
$\alpha (x_1,\dots ,x_n)$
where n is the size of the tuples
 $\overline a_0$
and
$\overline a_0$
and
 $\overline a_1$
, we have:
$\overline a_1$
, we have:  $$ \begin{align*} M_0,s_0\models \alpha(\overline{a}_0)\; \iff\; M_1,s_1 \models\alpha(\overline{a}_1). \end{align*} $$
$$ \begin{align*} M_0,s_0\models \alpha(\overline{a}_0)\; \iff\; M_1,s_1 \models\alpha(\overline{a}_1). \end{align*} $$
Notice that, compared to the original version, the implication has become a biconditional.
We will indicate with
![]() $M_0, s_0, \overline {a}_0 \approx ^{s}_{i,q} M_1, s_1 ,\overline {a}_1$
the existence of a winning strategy for Duplicator in the symmetric game from position
$M_0, s_0, \overline {a}_0 \approx ^{s}_{i,q} M_1, s_1 ,\overline {a}_1$
the existence of a winning strategy for Duplicator in the symmetric game from position
![]() $\left \langle M_0,s_0,\overline {a}_0; M_1,s_1,\overline {a}_1 \right \rangle $
with bounds
$\left \langle M_0,s_0,\overline {a}_0; M_1,s_1,\overline {a}_1 \right \rangle $
with bounds
![]() $\langle i,q\rangle $
; we indicate by
$\langle i,q\rangle $
; we indicate by
![]() $M_0, s_0, \overline {a}_0 \approx ^{s} M_1, s_1 ,\overline {a}_1$
the existence of a winning strategy for D in the unbounded version of the symmetric game. We will also use notational conventions analogous to the ones introduced for the original game. Notice that, as anticipated, the roles of the two models in the game are interchangeable:
$M_0, s_0, \overline {a}_0 \approx ^{s} M_1, s_1 ,\overline {a}_1$
the existence of a winning strategy for D in the unbounded version of the symmetric game. We will also use notational conventions analogous to the ones introduced for the original game. Notice that, as anticipated, the roles of the two models in the game are interchangeable:
Lemma 3.9.
![]() $\approx ^{s}_{i,q}$
and
$\approx ^{s}_{i,q}$
and
![]() $\approx ^{s}$
are symmetric relations.
$\approx ^{s}$
are symmetric relations.
Comparing this version with the original one, we clearly made Spoiler’s life much easier: now he can perform
![]() $\to $
-moves without any restrictions on the model from which he can choose the state; and the winning condition for Duplicator is more restrictive than the original one. So the following result should not come as a surprise:
$\to $
-moves without any restrictions on the model from which he can choose the state; and the winning condition for Duplicator is more restrictive than the original one. So the following result should not come as a surprise:
Lemma 3.10. If
![]() $M_0,s_0,\overline {a}_0 \approx ^s_{i,q} M_1,s_1,\overline {a}_1$
, then
$M_0,s_0,\overline {a}_0 \approx ^s_{i,q} M_1,s_1,\overline {a}_1$
, then
![]() $M_0,s_0,\overline {a}_0 \preceq _{i,q} M_1,s_1,\overline {a}_1$
.
$M_0,s_0,\overline {a}_0 \preceq _{i,q} M_1,s_1,\overline {a}_1$
.
Proof. The idea of the proof is simple: given a winning strategy for Duplicator in the game
![]() $ \operatorname {\mathrm {EF}}^s_{i,q}(M_0,s_0,\overline {a}_0;M_1,s_1,\overline {a}_1)$
, this is also a winning strategy in the game
$ \operatorname {\mathrm {EF}}^s_{i,q}(M_0,s_0,\overline {a}_0;M_1,s_1,\overline {a}_1)$
, this is also a winning strategy in the game
![]() $ \operatorname {\mathrm {EF}}_{i,q}(M_0,s_0,\overline {a}_0;M_1,s_1,\overline {a}_1)$
. The details are left to the reader.
$ \operatorname {\mathrm {EF}}_{i,q}(M_0,s_0,\overline {a}_0;M_1,s_1,\overline {a}_1)$
. The details are left to the reader.
As an immediate corollary we obtain the following result.
Corollary 3.11. Suppose the signature
![]() $\Sigma $
is finite. Then
$\Sigma $
is finite. Then
However, the converse of Corollary 3.11 does not hold in general.
Proposition 3.12.
Proof. Consider the models M and N in Figure 2a. We have:
-
•
 $M \preceq _{0,1} N$
: the winning strategy for Duplicator is described in Table 2b;
$M \preceq _{0,1} N$
: the winning strategy for Duplicator is described in Table 2b; -
•
 $M \succeq _{0,1} N$
: the winning strategy for Duplicator is described in Table 2c;
$M \succeq _{0,1} N$
: the winning strategy for Duplicator is described in Table 2c; -
•
 $M \not \approx ^s_{0,1} N$
: if Spoiler picks the element
$M \not \approx ^s_{0,1} N$
: if Spoiler picks the element
 $d_2$
, every move of Duplicator leads to Spoiler’s victory.
$d_2$
, every move of Duplicator leads to Spoiler’s victory.

Fig. 2
Thus, unlike the original version, the symmetric version of the game does not provide us with an exact characterization of the relation
![]() $\equiv _{i,q}$
determined by the logic. Nevertheless, the symmetric game is still useful: if we can show that Duplicator has a winning strategy in the symmetric game with bounds
$\equiv _{i,q}$
determined by the logic. Nevertheless, the symmetric game is still useful: if we can show that Duplicator has a winning strategy in the symmetric game with bounds
![]() $\langle i,q\rangle $
between two models, this suffices to show that these models are indistinguishable by formulae of degree
$\langle i,q\rangle $
between two models, this suffices to show that these models are indistinguishable by formulae of degree
![]() $\langle i,q \rangle $
. This is convenient, since strategies are often easier to describe in the symmetric game than in the original game, since we do not have to keep track of how the role of the models gets swapped in the course of the game. Indeed, we use this strategy in the proof of Theorem 4.5.
$\langle i,q \rangle $
. This is convenient, since strategies are often easier to describe in the symmetric game than in the original game, since we do not have to keep track of how the role of the models gets swapped in the course of the game. Indeed, we use this strategy in the proof of Theorem 4.5.
4 Characterizing the cardinality quantifiers definable in InqBQ
In this section we will use the EF-game for InqBQ to study in detail what InqBQ can express about the number of individuals satisfying a predicate P. The sentences we are concerned with include not only statements about the number of individuals satisfying P, like those in (1), but also questions about the number of individuals satisfying P, like those in (2).
-
(1)
-
a. There is no P.
-
b. There are at least three P.
-
c. The number of P is even.
-
d. There are infinitely many P.
-
-
(2)
-
a. Are there any P?
-
b. How many P are there?
-
c. Is the number of P even, or odd?
-
d. Are there infinitely many P?
-
Which among the statements in (1) and the questions in (2) can be expressed in InqBQ? Instead of pursuing a direct answer to this question, we will tackle the problem from a more general perspective. We will see that, in an inquisitive setting, all these sentences instantiate the form
![]() $Qx.Px$
, where Q is a quantifier which is sensitive only to the cardinality of its argument. Thus—interestingly—in the inquisitive setting, not only no and at least three, but also how many can be viewed as generalized quantifiers. We can then ask which cardinality quantifers are expressible in InqBQ. In this section, we will establish a simple answer to this question. From this answer, a verdict about the definability of the examples above, as well as many other similar examples, can be easily reached.
$Qx.Px$
, where Q is a quantifier which is sensitive only to the cardinality of its argument. Thus—interestingly—in the inquisitive setting, not only no and at least three, but also how many can be viewed as generalized quantifiers. We can then ask which cardinality quantifers are expressible in InqBQ. In this section, we will establish a simple answer to this question. From this answer, a verdict about the definability of the examples above, as well as many other similar examples, can be easily reached.
We will first look at cardinality quantifiers in the setting of standard first-order logic, FOL, and recall the characterization of cardinality quantifiers expressible in FOL; we will then present a generalization of the notion of a cardinality quantifier to
![]() $\textsf {InqBQ}$
, which encompasses also inquisitive quantifiers like how many; finally, we will use the Ehrenfeucht–Fraïssé game introduced in Section 3 to provide a characterization of the cardinality quantifiers expressible in
$\textsf {InqBQ}$
, which encompasses also inquisitive quantifiers like how many; finally, we will use the Ehrenfeucht–Fraïssé game introduced in Section 3 to provide a characterization of the cardinality quantifiers expressible in
![]() $\textsf {InqBQ}$
and use this characterization to show that, just like many interesting statements about cardinalities are not expressible in FOL, so many interesting questions about cardinalities are not expressible in InqBQ.
$\textsf {InqBQ}$
and use this characterization to show that, just like many interesting statements about cardinalities are not expressible in FOL, so many interesting questions about cardinalities are not expressible in InqBQ.
4.1 Cardinality quantifiers in classical first-order logic
In classical logic, a formula
![]() $\alpha (x)$
, with at most the variable x free, determines, relative to a model
$\alpha (x)$
, with at most the variable x free, determines, relative to a model
![]() $\mathcal {M}$
, a corresponding set of individuals:
$\mathcal {M}$
, a corresponding set of individuals:
Let K be a class of cardinals. This is an operator that can be added to classical first-order logic by stipulating that if
![]() $\alpha (x)$
is a classical formula with at most x free, then
$\alpha (x)$
is a classical formula with at most x free, then
![]() $Q_Kx.\alpha (x)$
is a formula, with the following semantics (
$Q_Kx.\alpha (x)$
is a formula, with the following semantics (
![]() $\#$
denotes the cardinality of a set):Footnote
5
$\#$
denotes the cardinality of a set):Footnote
5
By a cardinality quantifier we mean a quantifier which is of the form
![]() $Q_K$
for some class of cardinals K. Notice that the existential quantifier
$Q_K$
for some class of cardinals K. Notice that the existential quantifier
![]() $\exists $
is a cardinality quantifier, since
$\exists $
is a cardinality quantifier, since
![]() $\exists = Q_{\textsf {Card} \setminus \{0\}}$
, for
$\exists = Q_{\textsf {Card} \setminus \{0\}}$
, for
![]() $\textsf {Card}$
the class of all cardinals. By contrast, the universal quantifier
$\textsf {Card}$
the class of all cardinals. By contrast, the universal quantifier
![]() $\forall $
is not a cardinality quantifier, since the condition
$\forall $
is not a cardinality quantifier, since the condition
![]() $\mathcal {M} \models \forall x.P(x)$
, namely,
$\mathcal {M} \models \forall x.P(x)$
, namely,
![]() $P_{\mathcal {M}} = D$
, cannot be formulated solely in terms of
$P_{\mathcal {M}} = D$
, cannot be formulated solely in terms of
![]() $\# P_{\mathcal {M}}$
.Footnote
6
$\# P_{\mathcal {M}}$
.Footnote
6
Let
![]() $\chi _K[P]$
be a FOL-formula (thus, not containing
$\chi _K[P]$
be a FOL-formula (thus, not containing
![]() $Q_K$
). We say that
$Q_K$
). We say that
![]() $\chi _K[P]$
defines
$\chi _K[P]$
defines
![]() $Q_K$
if
$Q_K$
if
![]() $Q_Kx.Px\equiv \chi _K[P]$
. It is not hard to see that if this is the case, then for every formula
$Q_Kx.Px\equiv \chi _K[P]$
. It is not hard to see that if this is the case, then for every formula
![]() $\alpha (x)$
we have
$\alpha (x)$
we have
![]() $Q_Kx.\alpha (x)\equiv \chi _K[\alpha ]$
. We say that the quantifier
$Q_Kx.\alpha (x)\equiv \chi _K[\alpha ]$
. We say that the quantifier
![]() $Q_K$
is definable in FOL if there is a FOL-formula which defines it.
$Q_K$
is definable in FOL if there is a FOL-formula which defines it.
The statements in (1) can all be seen as having the form
![]() $Qx.Px$
, where Q is a cardinality quantifier. Indeed, we have the following characterizations, where
$Qx.Px$
, where Q is a cardinality quantifier. Indeed, we have the following characterizations, where
![]() $[3,\dots )$
is the class of cardinals
$[3,\dots )$
is the class of cardinals
![]() $\ge 3$
;
$\ge 3$
;
![]() $\textsf {Even}$
is the set of even natural numbers; Inf is the class of infinite cardinals.
$\textsf {Even}$
is the set of even natural numbers; Inf is the class of infinite cardinals.
-
(3)
 $$ \begin{align*} \hspace{-4pc} \begin{array}{llll} \\[-2.5pc] \text{a.} &\mathcal {M}\models (1.a) &\iff P_{\mathcal {M}}=\emptyset &\iff \# P_{\mathcal {M}}\in \{0\}\\ \text{b.} &\mathcal {M}\models (1.b) &\iff \#P_{\mathcal {M}}\ge 3 &\iff \#P_{\mathcal {M}}\in [3,\dots )\\ \text{c.} &\mathcal {M}\models (1.c) &\iff \#P_{\mathcal {M}}\text { is even} &\iff \#P_{\mathcal {M}}\in \textsf {Even}\\ \text{d.} &\mathcal {M}\models (1.d) & \iff \#P_{\mathcal {M}}\text { is infinite} &\iff \# P_{\mathcal {M}}\in \textsf {Inf.}\end{array} \end{align*} $$
$$ \begin{align*} \hspace{-4pc} \begin{array}{llll} \\[-2.5pc] \text{a.} &\mathcal {M}\models (1.a) &\iff P_{\mathcal {M}}=\emptyset &\iff \# P_{\mathcal {M}}\in \{0\}\\ \text{b.} &\mathcal {M}\models (1.b) &\iff \#P_{\mathcal {M}}\ge 3 &\iff \#P_{\mathcal {M}}\in [3,\dots )\\ \text{c.} &\mathcal {M}\models (1.c) &\iff \#P_{\mathcal {M}}\text { is even} &\iff \#P_{\mathcal {M}}\in \textsf {Even}\\ \text{d.} &\mathcal {M}\models (1.d) & \iff \#P_{\mathcal {M}}\text { is infinite} &\iff \# P_{\mathcal {M}}\in \textsf {Inf.}\end{array} \end{align*} $$
What cardinality quantifiers are definable in classical first-order logic? That is, for what classes K of cardinals is the quantifier
![]() $Q_K$
definable? The answer is given by the following theorem, which is an easy application of EF-games for FOL (and seems, to the best of our knowledge, to be folklore).
$Q_K$
definable? The answer is given by the following theorem, which is an easy application of EF-games for FOL (and seems, to the best of our knowledge, to be folklore).
Theorem 4.1. Let K be a class of cardinals. The quantifier
![]() $Q_K$
is definable in first-order logic if and only if there exists a natural number n such that K contains either all or none of the cardinals
$Q_K$
is definable in first-order logic if and only if there exists a natural number n such that K contains either all or none of the cardinals
![]() $\kappa \ge n$
.
$\kappa \ge n$
.
Consider again the statements in (1), repeated below for convenience with the corresponding classes of cardinals given on the right. It follows immediately from the characterization that the first two statements are expressible in classical first-order logic, while the third and fourth are not.
-
(4)
 $$ \begin{align*} \hspace{-9.4pc} \begin{array}{lll} \\[-2.5pc]\text{a.} &\textrm{There is no } P. &K=\{0\}\\ \text{b.} &\textrm{There are at least three } P. &K=[3,\dots )\\ \text{c.} &\textrm{The number of } P \textrm{ is even}. &K=\textsf {Even}\\ \text{d.} &\textrm{There are infinitely many } P. &K=\textsf {Inf}\end{array} \end{align*} $$
$$ \begin{align*} \hspace{-9.4pc} \begin{array}{lll} \\[-2.5pc]\text{a.} &\textrm{There is no } P. &K=\{0\}\\ \text{b.} &\textrm{There are at least three } P. &K=[3,\dots )\\ \text{c.} &\textrm{The number of } P \textrm{ is even}. &K=\textsf {Even}\\ \text{d.} &\textrm{There are infinitely many } P. &K=\textsf {Inf}\end{array} \end{align*} $$
4.2 Cardinality quantifiers in InqBQ
Let us now turn to the inquisitive case. A model M for inquisitive first-order logic represents a variety of states of affairs, one for each possible world w. At each world w, the state of affairs is represented by the first-order structure
![]() $\mathcal {M}_w$
, having as its domain the set
$\mathcal {M}_w$
, having as its domain the set
![]() $D_w:=D/\!\!\sim _w$
. Let
$D_w:=D/\!\!\sim _w$
. Let
![]() $\alpha (x)$
be a classical formula with at most the variable x free. Relative to each world w,
$\alpha (x)$
be a classical formula with at most the variable x free. Relative to each world w,
![]() $\alpha (x)$
determines an extension
$\alpha (x)$
determines an extension
![]() $\alpha _w$
, which is a set of individuals from
$\alpha _w$
, which is a set of individuals from
![]() $D_w$
:
$D_w$
:
Therefore, relative to an information state s, the formula
![]() $\alpha (x)$
determines a corresponding set of cardinals,
$\alpha (x)$
determines a corresponding set of cardinals,
![]() $\{\#\alpha _{w}\mid w\in s\}$
. We refer to this set of cardinals as the cardinality trace of
$\{\#\alpha _{w}\mid w\in s\}$
. We refer to this set of cardinals as the cardinality trace of
![]() $\alpha (x)$
in s.
$\alpha (x)$
in s.
Definition 4.2 (Cardinality trace)
Let M be a model, s an information state, and
![]() $\alpha (x)$
a classical formula where at most the variable x occurs free. The cardinality trace of
$\alpha (x)$
a classical formula where at most the variable x occurs free. The cardinality trace of
![]() $\alpha (x)$
in s is the set of cardinals:
$\alpha (x)$
in s is the set of cardinals:
A cardinal
![]() $\kappa $
is in
$\kappa $
is in
![]() $\mathrm {tr}_s(\alpha )$
if, according to the information available in s,
$\mathrm {tr}_s(\alpha )$
if, according to the information available in s,
![]() $\kappa $
might be the number of elements satisfying
$\kappa $
might be the number of elements satisfying
![]() $\alpha (x)$
; that is, if it might be the case that the extension of
$\alpha (x)$
; that is, if it might be the case that the extension of
![]() $\alpha (x)$
has cardinality
$\alpha (x)$
has cardinality
![]() $\kappa $
. Thus,
$\kappa $
. Thus,
![]() $\mathrm {tr}_s(\alpha )$
captures exactly the information available in s about the number of individuals satisfying
$\mathrm {tr}_s(\alpha )$
captures exactly the information available in s about the number of individuals satisfying
![]() $\alpha (x)$
.
$\alpha (x)$
.
Now let
![]() $\mathbb {K}$
be a class of sets of cardinals. We associate with
$\mathbb {K}$
be a class of sets of cardinals. We associate with
![]() $\mathbb {K}$
a corresponding quantifier
$\mathbb {K}$
a corresponding quantifier
![]() $Q_{\mathbb {K}}$
. We can add this quantifier to InqBQ by stipulating that if
$Q_{\mathbb {K}}$
. We can add this quantifier to InqBQ by stipulating that if
![]() $\alpha (x)$
is a classical formula with at most x free, then
$\alpha (x)$
is a classical formula with at most x free, then
![]() $Q_{\mathbb {K}} x.\alpha (x)$
is a formula, interpreted by the following clauseFootnote
7
:
$Q_{\mathbb {K}} x.\alpha (x)$
is a formula, interpreted by the following clauseFootnote
7
:
A cardinality quantifier is a quantifier which is of the form
![]() $Q_{\mathbb {K}}$
, where
$Q_{\mathbb {K}}$
, where
![]() $\mathbb {K}$
is a class of sets of cardinals.
$\mathbb {K}$
is a class of sets of cardinals.
Let
![]() $\chi _{\mathbb {K}}[P]$
be an InqBQ-formula (thus, without cardinality quantifiers). We say that
$\chi _{\mathbb {K}}[P]$
be an InqBQ-formula (thus, without cardinality quantifiers). We say that
![]() $\chi _{\mathbb {K}}[P]$
defines the quantifier
$\chi _{\mathbb {K}}[P]$
defines the quantifier
![]() $Q_{\mathbb {K}}$
if
$Q_{\mathbb {K}}$
if
![]() $Q_{\mathbb {K}} x.Px\equiv \chi _{\mathbb {K}}[P]$
. Again, it is not hard to see that if this holds, then for every classical formula
$Q_{\mathbb {K}} x.Px\equiv \chi _{\mathbb {K}}[P]$
. Again, it is not hard to see that if this holds, then for every classical formula
![]() $\alpha (x)$
we have
$\alpha (x)$
we have
![]() $Q_{\mathbb {K}} x.\alpha (x)\equiv \chi _{\mathbb {K}}[\alpha ]$
. We say that
$Q_{\mathbb {K}} x.\alpha (x)\equiv \chi _{\mathbb {K}}[\alpha ]$
. We say that
![]() $Q_{\mathbb {K}}$
is definable in InqBQ if there is an InqBQ-formula that defines it.
$Q_{\mathbb {K}}$
is definable in InqBQ if there is an InqBQ-formula that defines it.
In order to make the notion of a cardinality quantifier more concrete, let us see how the statements in (1) and the questions in (2) can be seen as instantiating the form
![]() $Qx.Px$
where Q is a cardinality quantifier in the sense of inquisitive logic.
$Qx.Px$
where Q is a cardinality quantifier in the sense of inquisitive logic.
Consider first the statements in (1). In general, in inquisitive semantics a statement
![]() $\alpha $
is supported by a state s iff the information available in s implies that
$\alpha $
is supported by a state s iff the information available in s implies that
![]() $\alpha $
is true. This means that
$\alpha $
is true. This means that
![]() $\alpha $
is true at all worlds
$\alpha $
is true at all worlds
![]() $w\in s$
. Keeping this in mind, we can see that the statements in (1) have the following semantics:
$w\in s$
. Keeping this in mind, we can see that the statements in (1) have the following semantics:
-
(5)
 $$ \begin{align*} \hspace{-0.2pc} \begin{array}{llll} \\[-2.5pc] \text{a.} &M,s\models (1.a) &\iff \forall w\in s: P_w=\emptyset &\iff \mathrm {tr}_s(P)\subseteq \{0\}\\ \text{b.} &M,s\models (1.b) &\iff \forall w\in s: \#P_w\ge 3 &\iff \mathrm {tr}_s(P)\subseteq [3,\dots )\\ \text{c.} &M,s\models (1.c) &\iff \forall w\in s: \#P_w\text { is even} &\iff \mathrm {tr}_s(P)\subseteq \textsf {Even}\\ \text{d.} &M,s\models (1.d) &\iff \forall w\in s: \#P_w\text { is infinite} &\iff \mathrm {tr}_s(P)\subseteq \textsf {Inf}\end{array} \end{align*} $$
$$ \begin{align*} \hspace{-0.2pc} \begin{array}{llll} \\[-2.5pc] \text{a.} &M,s\models (1.a) &\iff \forall w\in s: P_w=\emptyset &\iff \mathrm {tr}_s(P)\subseteq \{0\}\\ \text{b.} &M,s\models (1.b) &\iff \forall w\in s: \#P_w\ge 3 &\iff \mathrm {tr}_s(P)\subseteq [3,\dots )\\ \text{c.} &M,s\models (1.c) &\iff \forall w\in s: \#P_w\text { is even} &\iff \mathrm {tr}_s(P)\subseteq \textsf {Even}\\ \text{d.} &M,s\models (1.d) &\iff \forall w\in s: \#P_w\text { is infinite} &\iff \mathrm {tr}_s(P)\subseteq \textsf {Inf}\end{array} \end{align*} $$
Let us now check that all these statements correspond to statements of the form
![]() $Qx.Px$
for Q a cardinality quantifier. For this, we introduce a useful notation.
$Qx.Px$
for Q a cardinality quantifier. For this, we introduce a useful notation.
Definition 4.3 (Downward closure of a class)
Let K be a class. We denote by
![]() $K^{\downarrow }$
the class consisting of all sets X such that
$K^{\downarrow }$
the class consisting of all sets X such that
![]() $X\subseteq K$
.
$X\subseteq K$
.
Thus, if K is a set, then
![]() $K^{\downarrow }=\wp (K)$
. However, if K is a proper class, then
$K^{\downarrow }=\wp (K)$
. However, if K is a proper class, then
![]() $K^{\downarrow }$
will not be a set either; moreover,
$K^{\downarrow }$
will not be a set either; moreover,
![]() $K^{\downarrow }$
will not contain K, since K is not a set.
$K^{\downarrow }$
will not contain K, since K is not a set.
Now consider the cardinality quantifiers
![]() $Q_{1}$
–
$Q_{1}$
–
![]() $Q_4$
determined by the following classes:
$Q_4$
determined by the following classes:
We have:
 $$ \begin{align*} \begin{array}{l @{\;\iff\;} l @{\;\iff\;} l @{\;\iff\;} l} M,s\models Q_{1}x.Px &\mathrm{tr}_s(P)\in\mathbb{K}_{1} &\mathrm{tr}_s(P)\subseteq\{0\} &M,s\models (1.a)\\ M,s\models Q_{2}x.Px &\mathrm{tr}_s(P)\in\mathbb{K}_{2} &\mathrm{tr}_s(P)\subseteq[3,\dots) &M,s\models (1.b)\\ M,s\models Q_{3}x.Px &\mathrm{tr}_s(P)\!\in \mathbb{K}_{3} &\mathrm{tr}_s(P)\subseteq\textsf{Even} &M,s\models (1.c) \\ M,s\models Q_{4}x.Px &\mathrm{tr}_s(P)\in \mathbb{K}_{4} &\mathrm{tr}_s(P)\subseteq\textsf{Inf} &M,s\models (1.d) \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l @{\;\iff\;} l @{\;\iff\;} l @{\;\iff\;} l} M,s\models Q_{1}x.Px &\mathrm{tr}_s(P)\in\mathbb{K}_{1} &\mathrm{tr}_s(P)\subseteq\{0\} &M,s\models (1.a)\\ M,s\models Q_{2}x.Px &\mathrm{tr}_s(P)\in\mathbb{K}_{2} &\mathrm{tr}_s(P)\subseteq[3,\dots) &M,s\models (1.b)\\ M,s\models Q_{3}x.Px &\mathrm{tr}_s(P)\!\in \mathbb{K}_{3} &\mathrm{tr}_s(P)\subseteq\textsf{Even} &M,s\models (1.c) \\ M,s\models Q_{4}x.Px &\mathrm{tr}_s(P)\in \mathbb{K}_{4} &\mathrm{tr}_s(P)\subseteq\textsf{Inf} &M,s\models (1.d) \end{array} \end{align*} $$
Next, consider the questions in (2). Start with (2.a), the question whether there are any P. This question is settled in an information state s in case the information in s implies that there are no P, or it implies that there are some P. The former is the case if the extension of P is empty in all worlds
![]() $w\in s$
. The latter is the case if the extension of P is non-empty in all worlds
$w\in s$
. The latter is the case if the extension of P is non-empty in all worlds
![]() $w\in s$
. Thus, the semantics of (2.a) is as follows.
$w\in s$
. Thus, the semantics of (2.a) is as follows.
 $$ \begin{align*} M,s\models (2.a) &\iff (\forall w\in W: P_w=\emptyset)\text{ or }(\forall w\in W: P_w\neq\emptyset) \\ &\iff (\forall w\in W: \#P_w=0)\text{ or }(\forall w\in W: \#P_w\ge 1) \\ &\iff \mathrm{tr}_s(P)=\{0\}\text{ or }\mathrm{tr}_s(P)\subseteq [1,\dots). \end{align*} $$
$$ \begin{align*} M,s\models (2.a) &\iff (\forall w\in W: P_w=\emptyset)\text{ or }(\forall w\in W: P_w\neq\emptyset) \\ &\iff (\forall w\in W: \#P_w=0)\text{ or }(\forall w\in W: \#P_w\ge 1) \\ &\iff \mathrm{tr}_s(P)=\{0\}\text{ or }\mathrm{tr}_s(P)\subseteq [1,\dots). \end{align*} $$
Second, consider the question (2.b), how many individuals are P. This question is settled in an information state s if the information available in s determines exactly how many individuals are P. This is the case if there is a cardinal
![]() $\kappa $
such that at every world
$\kappa $
such that at every world
![]() $w\in s$
, the extension
$w\in s$
, the extension
![]() $P_w$
contains
$P_w$
contains
![]() $\kappa $
elements.Footnote
8
$\kappa $
elements.Footnote
8
 $$ \begin{align*} M,s\models (2.b) &\iff \exists\kappa\forall w\in W: \#P_w=\kappa \\ &\iff \mathrm{tr}_s(P) \;\text{contains at most one element} \\ &\iff \mathrm{tr}_s(P)\subseteq\{\kappa\} \;\text{for some cardinal}\; \kappa. \end{align*} $$
$$ \begin{align*} M,s\models (2.b) &\iff \exists\kappa\forall w\in W: \#P_w=\kappa \\ &\iff \mathrm{tr}_s(P) \;\text{contains at most one element} \\ &\iff \mathrm{tr}_s(P)\subseteq\{\kappa\} \;\text{for some cardinal}\; \kappa. \end{align*} $$
Next, consider (2.c), the question whether the number of P is even or odd. This is settled in an information state s in case the information available in s implies that the number of P is even, or that the number of P is odd.Footnote 9 The former holds if the extension of P is even at every world in s. The latter holds if the extension of P is odd al every world in s.
 $$ \begin{align*} M,s\models (2.c) &\iff (\forall w\in W: \#P_w\text{ is even})\text{ or }(\forall w\in W: \#P_w\text{ is odd}) \\ &\iff \mathrm{tr}_s(P)\subseteq\textsf{Even}\text{ or }\mathrm{tr}_s(P)\subseteq\textsf{Odd.} \end{align*} $$
$$ \begin{align*} M,s\models (2.c) &\iff (\forall w\in W: \#P_w\text{ is even})\text{ or }(\forall w\in W: \#P_w\text{ is odd}) \\ &\iff \mathrm{tr}_s(P)\subseteq\textsf{Even}\text{ or }\mathrm{tr}_s(P)\subseteq\textsf{Odd.} \end{align*} $$
Finally, consider (2.d), the question whether there are infinitely many P. This is settled in an information state s in case the information available in s implies that there are infinitely many P, or it implies that the aren’t infinitely many P. The former is the case if the extension of P is infinite at every world
![]() $w\in s$
, while the latter is the case if the extension of P is finite at every world
$w\in s$
, while the latter is the case if the extension of P is finite at every world
![]() $w\in s$
.
$w\in s$
.
 $$ \begin{align*} M,s\models (2.d) &\iff (\forall w\in s: \#P_w\text{ is finite})\text{ or }(\forall w\in s: \#P_w\text{ is infinite}) \\ &\iff \mathrm{tr}_s(P)\subseteq\textsf{Fin}\text{ or }\mathrm{tr}_s(P)\subseteq\textsf{Inf.} \end{align*} $$
$$ \begin{align*} M,s\models (2.d) &\iff (\forall w\in s: \#P_w\text{ is finite})\text{ or }(\forall w\in s: \#P_w\text{ is infinite}) \\ &\iff \mathrm{tr}_s(P)\subseteq\textsf{Fin}\text{ or }\mathrm{tr}_s(P)\subseteq\textsf{Inf.} \end{align*} $$
Now consider four cardinality quantifiers,
![]() $Q_{5}$
–
$Q_{5}$
–
![]() $Q_{8}$
, determined by the following classes:
$Q_{8}$
, determined by the following classes:
-
(6)
-
a.
 $\mathbb {K}_{5}=\{0\}^{\downarrow }\cup [1,\dots )^{\downarrow }$
$\mathbb {K}_{5}=\{0\}^{\downarrow }\cup [1,\dots )^{\downarrow }$
-
b.
 $\mathbb {K}_{6}=\bigcup \{\{\kappa \}^{\downarrow }\mid \kappa \text { a cardinal}\}$
$\mathbb {K}_{6}=\bigcup \{\{\kappa \}^{\downarrow }\mid \kappa \text { a cardinal}\}$
-
c.
 $\mathbb {K}_{7}=\textsf {Even}^{\downarrow }\cup \textsf {Odd}^{\downarrow }$
$\mathbb {K}_{7}=\textsf {Even}^{\downarrow }\cup \textsf {Odd}^{\downarrow }$
-
d.
 $\mathbb {K}_{8}=\textsf {Fin}^{\downarrow }\cup \textsf {Inf}^{\downarrow }$
$\mathbb {K}_{8}=\textsf {Fin}^{\downarrow }\cup \textsf {Inf}^{\downarrow }$
-
Then we have:
 $$ \begin{align*} \begin{array}{lll} M,s\models Q_{5}x.Px &\;\iff\; \mathrm{tr}_s(P)\in\mathbb{K}_{5} &\;\iff\; \mathrm{tr}_s(P)\subseteq\{0\}\text{ or }\mathrm{tr}_s(P)\subseteq[1,\dots) \\ &&\;\iff\; M,s\models (2.a) \\[.5em] M,s\models Q_{6}x.Px &\;\iff\; \mathrm{tr}_s(P)\in\mathbb{K}_{6} &\;\iff\; \mathrm{tr}_s(P)\subseteq\{\kappa\}\text{ for some }\kappa \\ &&\;\iff\; M,s\models (2.b) \\[.5em] M,s\models Q_{7}x.Px &\;\iff\; \mathrm{tr}_s(P)\in \mathbb{K}_{7} &\;\iff\; \mathrm{tr}_s(P)\subseteq\textsf{Even}\text{ or }\mathrm{tr}_s(P)\subseteq\textsf{Odd} \\ &&\;\iff\; M,s\models (2.c) \\[.5em] M,s\models Q_{8}x.Px &\;\iff\; \mathrm{tr}_s(P)\in \mathbb{K}_{8} &\;\iff\; \mathrm{tr}_s(P)\subseteq\textsf{Fin}\text{ or }\mathrm{tr}_s(P)\subseteq\textsf{Inf} \\ &&\;\iff\; M,s\models (2.d) \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lll} M,s\models Q_{5}x.Px &\;\iff\; \mathrm{tr}_s(P)\in\mathbb{K}_{5} &\;\iff\; \mathrm{tr}_s(P)\subseteq\{0\}\text{ or }\mathrm{tr}_s(P)\subseteq[1,\dots) \\ &&\;\iff\; M,s\models (2.a) \\[.5em] M,s\models Q_{6}x.Px &\;\iff\; \mathrm{tr}_s(P)\in\mathbb{K}_{6} &\;\iff\; \mathrm{tr}_s(P)\subseteq\{\kappa\}\text{ for some }\kappa \\ &&\;\iff\; M,s\models (2.b) \\[.5em] M,s\models Q_{7}x.Px &\;\iff\; \mathrm{tr}_s(P)\in \mathbb{K}_{7} &\;\iff\; \mathrm{tr}_s(P)\subseteq\textsf{Even}\text{ or }\mathrm{tr}_s(P)\subseteq\textsf{Odd} \\ &&\;\iff\; M,s\models (2.c) \\[.5em] M,s\models Q_{8}x.Px &\;\iff\; \mathrm{tr}_s(P)\in \mathbb{K}_{8} &\;\iff\; \mathrm{tr}_s(P)\subseteq\textsf{Fin}\text{ or }\mathrm{tr}_s(P)\subseteq\textsf{Inf} \\ &&\;\iff\; M,s\models (2.d) \end{array} \end{align*} $$
So, in the inquisitive setting, a new range of “inquisitive” cardinality quantifiers come into play, which combine with a property to yield questions like those exemplified in (2). In addition to standard cardinality quantifiers like ‘no’, ‘at least three’, ‘infinitely many’, we also have new, question-forming cardinality quantifiers like ‘how many’ and ‘whether finitely or infinitely many’.
4.3 Characterization
What cardinality quantifiers can be expressed in InqBQ? Given that, in the inquisitive setting, cardinality quantifiers are in one-to-one correspondence with classes of sets of cardinals, this question can be made precise as follows.
Question 4.4. For which classes of sets of cardinals
![]() $\mathbb {K}$
is the quantifier
$\mathbb {K}$
is the quantifier
![]() $Q_{\mathbb {K}}$
definable in
$Q_{\mathbb {K}}$
definable in
![]() $\textsf {InqBQ}$
?
$\textsf {InqBQ}$
?
The next theorem provides an answer to this question. In essence, what the theorem says is that the cardinality quantifiers definable in InqBQ are all and only the inquisitive disjunctions of cardinality quantifiers definable in classical first-order logic.Footnote 10 Before stating the Theorem, let us fix some useful notations. For any natural number n, we let:
-
•
 $[0,n] := \{m\in \textsf {Card}\mid m \leq n\}$
$[0,n] := \{m\in \textsf {Card}\mid m \leq n\}$
-
•
 $[n,\dots ) := \{ \kappa \in \textsf {Card} \,|\, \kappa \geq n \}$
$[n,\dots ) := \{ \kappa \in \textsf {Card} \,|\, \kappa \geq n \}$
Moreover, we introduce an equivalence relation
![]() $=_n$
that disregards differences between cardinals larger than n. More precisely, if
$=_n$
that disregards differences between cardinals larger than n. More precisely, if
![]() $\kappa $
and
$\kappa $
and
![]() $\kappa '$
are two cardinals:
$\kappa '$
are two cardinals:
If A and B are sets of cardinals, we write
![]() $A=_n B$
if A and B are the same set, modulo identifying all cardinals larger than n:
$A=_n B$
if A and B are the same set, modulo identifying all cardinals larger than n:
 $$ \begin{align*} A=_nB\iff &\forall \kappa\in A\exists\kappa'\in B \;\text{such that}\; \kappa=_n\kappa' \;\text{and}\\ &\forall \kappa'\in B\exists\kappa\in A \;\text{such that}\; \kappa=_n\kappa'. \end{align*} $$
$$ \begin{align*} A=_nB\iff &\forall \kappa\in A\exists\kappa'\in B \;\text{such that}\; \kappa=_n\kappa' \;\text{and}\\ &\forall \kappa'\in B\exists\kappa\in A \;\text{such that}\; \kappa=_n\kappa'. \end{align*} $$
Moreover, we say that a class of sets of cardinals
![]() $\mathbb {K}$
is:
$\mathbb {K}$
is:
-
•
 $=_n$
-invariant, if whenever
$=_n$
-invariant, if whenever
 $B\in \mathbb {K}$
and
$B\in \mathbb {K}$
and
 $A=_nB$
we have
$A=_nB$
we have
 $A\in \mathbb {K}$
and
$A\in \mathbb {K}$
and -
• downward-closed, if whenever
 $B\in \mathbb {K}$
and
$B\in \mathbb {K}$
and
 $A\subseteq B$
we have
$A\subseteq B$
we have
 $A\in \mathbb {K}$
.
$A\in \mathbb {K}$
.
We can now state our second main result.
Theorem 4.5 (Characterization of cardinality quantifiers definable in InqBQ)
Let
![]() $\mathbb {K}$
be a class of sets of cardinals. The following are equivalent:
$\mathbb {K}$
be a class of sets of cardinals. The following are equivalent:
-
1. The cardinality quantifier
 $Q_{\mathbb {K}}$
is definable in InqBQ.
$Q_{\mathbb {K}}$
is definable in InqBQ. -
2.
 $\mathbb {K}=K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
where for each
$\mathbb {K}=K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
where for each
 $K_i \subseteq \textsf {Card}$
there exists a natural number m such that
$K_i \subseteq \textsf {Card}$
there exists a natural number m such that
 $K_i$
contains either all or none of the cardinals
$K_i$
contains either all or none of the cardinals
 $\kappa \ge m$
.
$\kappa \ge m$
. -
3.
 $\mathbb {K}$
is downward closed and
$\mathbb {K}$
is downward closed and
 $=_m$
-invariant for some natural number m.
$=_m$
-invariant for some natural number m.
Proof. We show that
![]() $2\Rightarrow 1\Rightarrow 3\Rightarrow 2$
.
$2\Rightarrow 1\Rightarrow 3\Rightarrow 2$
.
![]() $\pmb {[2 \Rightarrow 1]}$
Suppose
$\pmb {[2 \Rightarrow 1]}$
Suppose
![]() $\mathbb {K}= K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
where for each
$\mathbb {K}= K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
where for each
![]() $K_i$
there exists a natural number m such that
$K_i$
there exists a natural number m such that
![]() $K_i$
contains either all or none of the cardinals
$K_i$
contains either all or none of the cardinals
![]() $\kappa \ge m$
. By Theorem 4.1, for each
$\kappa \ge m$
. By Theorem 4.1, for each
![]() $K_i$
we have a classical formula
$K_i$
we have a classical formula
![]() $\chi _{i}$
such that, in classical first-order logic:
$\chi _{i}$
such that, in classical first-order logic:
These formulas are also formulas of InqBQ, and it follows from Proposition 2.3 that we have:
 $$ \begin{align*} M,s\models\chi_i&\iff \forall w\in s: \mathcal{M}_w\models\chi_i\\ &\iff\forall w\in s: \#{P_{\mathcal{M}_w}} \in K_i\\ &\iff\mathrm{tr}_s(P)\subseteq K_i\\ &\iff\mathrm{tr}_s(P)\in K_i^{\downarrow}. \end{align*} $$
$$ \begin{align*} M,s\models\chi_i&\iff \forall w\in s: \mathcal{M}_w\models\chi_i\\ &\iff\forall w\in s: \#{P_{\mathcal{M}_w}} \in K_i\\ &\iff\mathrm{tr}_s(P)\subseteq K_i\\ &\iff\mathrm{tr}_s(P)\in K_i^{\downarrow}. \end{align*} $$
Now consider the inquisitive disjunction
. We have:

This shows that the InqBQ formula
defines the quantifier
![]() $Q_{\mathbb {K}}$
.
$Q_{\mathbb {K}}$
.
![]() $\pmb {[1 \Rightarrow 3]}$
Next, consider the implication from 1 to 3. Suppose
$\pmb {[1 \Rightarrow 3]}$
Next, consider the implication from 1 to 3. Suppose
![]() $Q_{\mathbb {K}}$
is definable in InqBQ by a formula
$Q_{\mathbb {K}}$
is definable in InqBQ by a formula
![]() $\varphi _{\mathbb {K}}$
. We need to show that
$\varphi _{\mathbb {K}}$
. We need to show that
![]() $\mathbb {K}$
is downward closed and
$\mathbb {K}$
is downward closed and
![]() $=_m$
invariant for some natural number m.
$=_m$
invariant for some natural number m.
We firstly show that
![]() $\mathbb {K}$
is downward closed. Suppose
$\mathbb {K}$
is downward closed. Suppose
![]() $A\subseteq B\in \mathbb {K}$
. This means that there exists a model M and an information state s such that
$A\subseteq B\in \mathbb {K}$
. This means that there exists a model M and an information state s such that
![]() $M,s\vDash \varphi _{\mathbb {K}}$
and
$M,s\vDash \varphi _{\mathbb {K}}$
and
![]() $\mathrm {tr}_s(P) = B$
. Consider now the state
$\mathrm {tr}_s(P) = B$
. Consider now the state
![]() $t := \{ w\in s \;|\; \#P_w \in A \} \subseteq s$
. By definition we have
$t := \{ w\in s \;|\; \#P_w \in A \} \subseteq s$
. By definition we have
![]() $\mathrm {tr}_t(P) = A$
; and by persistency
$\mathrm {tr}_t(P) = A$
; and by persistency
![]() $M, t \vDash \varphi _{\mathbb {K}}$
. Thus
$M, t \vDash \varphi _{\mathbb {K}}$
. Thus
![]() $A \in \mathbb {K}$
, as wanted.
$A \in \mathbb {K}$
, as wanted.
Next, we show that
![]() $\mathbb {K}$
is closed under
$\mathbb {K}$
is closed under
![]() $=_m$
for some m. We want to show that the condition above holds for
$=_m$
for some m. We want to show that the condition above holds for
![]() $m = q$
, where q is the quantifier degree of the defining formula
$m = q$
, where q is the quantifier degree of the defining formula
![]() $\varphi _{\mathbb {K}}$
. So, suppose
$\varphi _{\mathbb {K}}$
. So, suppose
![]() $A\in \mathbb {K}$
and
$A\in \mathbb {K}$
and
![]() $A=_{q} B$
. If we find two information models
$A=_{q} B$
. If we find two information models
![]() $M,N$
such that
$M,N$
such that
![]() $\mathrm {tr}_{W^M}(P) = A$
,
$\mathrm {tr}_{W^M}(P) = A$
,
![]() $\mathrm {tr}_{W^N}(P) = B$
and
$\mathrm {tr}_{W^N}(P) = B$
and
![]() $M \approx _{i,q} N$
then we are done, since in this case:
$M \approx _{i,q} N$
then we are done, since in this case:
Consider enumerations of the sets A and B:Footnote
11
![]() $A := \left \{ \kappa _{\alpha } \;\middle |\; \alpha < \lambda \right \}$
and
$A := \left \{ \kappa _{\alpha } \;\middle |\; \alpha < \lambda \right \}$
and
![]() $B := \left \{ \kappa ^{\prime }_{\alpha } \;\middle |\; \alpha < \lambda \right \}$
which both start with the same initial sequence
$B := \left \{ \kappa ^{\prime }_{\alpha } \;\middle |\; \alpha < \lambda \right \}$
which both start with the same initial sequence
![]() $\langle \kappa _1,\dots ,\kappa _l\rangle =\langle \kappa _1',\dots ,\kappa _l'\rangle $
enumerating
$\langle \kappa _1,\dots ,\kappa _l\rangle =\langle \kappa _1',\dots ,\kappa _l'\rangle $
enumerating
![]() $A \cap [0,q] = B \cap [0,q]$
. Let
$A \cap [0,q] = B \cap [0,q]$
. Let
![]() $M,N$
be the models defined by the following clauses:
$M,N$
be the models defined by the following clauses:
 $$ \begin{align*} \begin{array}{l@{\hspace{5em}}l} W^M := \left\{ w_{\alpha} \;\middle|\; \alpha < \lambda \right\} &W^N := \left\{ w_{\alpha} \;\middle|\; \alpha < \lambda \right\} = W^M \\[.8em] D^M := \left\{ d^\alpha_\beta \;\middle|\; \alpha<\lambda \;\&\; \beta<\kappa_{\alpha} \right\} &D^N := \left\{ e^\alpha_\beta \;\middle|\; \alpha<\lambda \;\&\; \beta<\kappa^{\prime}_{\alpha} \right\} \\[.8em] I^M_{w_\gamma}(P)\left(d^\alpha_\beta\right) \;\iff\; \alpha = \gamma &I^N_{w_\gamma}(P)\left(e^\alpha_\beta\right) \;\iff\; \alpha = \gamma \\[.8em] M \text{ is an } \textsf{id}\text{-model} &N \text{ is an } \textsf{id}\text{-model.} \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l@{\hspace{5em}}l} W^M := \left\{ w_{\alpha} \;\middle|\; \alpha < \lambda \right\} &W^N := \left\{ w_{\alpha} \;\middle|\; \alpha < \lambda \right\} = W^M \\[.8em] D^M := \left\{ d^\alpha_\beta \;\middle|\; \alpha<\lambda \;\&\; \beta<\kappa_{\alpha} \right\} &D^N := \left\{ e^\alpha_\beta \;\middle|\; \alpha<\lambda \;\&\; \beta<\kappa^{\prime}_{\alpha} \right\} \\[.8em] I^M_{w_\gamma}(P)\left(d^\alpha_\beta\right) \;\iff\; \alpha = \gamma &I^N_{w_\gamma}(P)\left(e^\alpha_\beta\right) \;\iff\; \alpha = \gamma \\[.8em] M \text{ is an } \textsf{id}\text{-model} &N \text{ is an } \textsf{id}\text{-model.} \end{array} \end{align*} $$
An example of these models is given in Figure 3. Notice that
![]() $\# I^M_{w_{\alpha }}(P) = \kappa _{\alpha }$
and
$\# I^M_{w_{\alpha }}(P) = \kappa _{\alpha }$
and
![]() $\# I^N_{w_{\alpha }}(P) = \kappa ^{\prime }_{\alpha }$
. In particular, it follows that
$\# I^N_{w_{\alpha }}(P) = \kappa ^{\prime }_{\alpha }$
. In particular, it follows that
![]() $\mathrm {tr}_{W^M}(P) = A$
and
$\mathrm {tr}_{W^M}(P) = A$
and
![]() $\mathrm {tr}_{W^N}(P) = B$
. So if we show that
$\mathrm {tr}_{W^N}(P) = B$
. So if we show that
![]() $M \approx _{i,q} N$
then we are done. In order to show this, we present here a winning strategy for Duplicator in the symmetric version of the EF-game between M and N (cf. Section 3.5):
$M \approx _{i,q} N$
then we are done. In order to show this, we present here a winning strategy for Duplicator in the symmetric version of the EF-game between M and N (cf. Section 3.5):
-
• If Spoiler plays an implication move and chooses an information state s from either of the models, then Duplicator responds by choosing the same state s from the other model (this is possible since
 $W^M = W^N$
).
$W^M = W^N$
). -
• If Spoiler plays a quantifier move and chooses an element
 $d^\alpha _\beta $
from the model M, we consider two separate cases:
$d^\alpha _\beta $
from the model M, we consider two separate cases:-
– If
 $d^\alpha _\beta = a_i$
for some i, that is, it has already been picked during the run—by either Spoiler or Duplicator—then Duplicator responds by choosing
$d^\alpha _\beta = a_i$
for some i, that is, it has already been picked during the run—by either Spoiler or Duplicator—then Duplicator responds by choosing
 $b_i$
.
$b_i$
. -
– If
 $d^\alpha _\beta $
has not been previously picked, then Duplicator chooses an element
$d^\alpha _\beta $
has not been previously picked, then Duplicator chooses an element
 $e^\alpha _\gamma $
(notice that the elements have the same superscript and possibly different subscripts) which has not been previously picked during the run. The fact that duplicator can find such an element is guaranteed by
$e^\alpha _\gamma $
(notice that the elements have the same superscript and possibly different subscripts) which has not been previously picked during the run. The fact that duplicator can find such an element is guaranteed by
 $A=_q B$
: this means that either
$A=_q B$
: this means that either
 $\kappa _{\alpha }=\kappa _{\alpha }'$
, or else
$\kappa _{\alpha }=\kappa _{\alpha }'$
, or else
 $\kappa _{\alpha },\kappa _{\alpha }'> q$
. In the former case the number of elements
$\kappa _{\alpha },\kappa _{\alpha }'> q$
. In the former case the number of elements
 $d^\alpha _\beta $
and
$d^\alpha _\beta $
and
 $e^\alpha _\gamma $
is exactly the same; in the latter case the number of elements
$e^\alpha _\gamma $
is exactly the same; in the latter case the number of elements
 $e^\alpha _\gamma $
is larger than the number of quantifier moves in the game.
$e^\alpha _\gamma $
is larger than the number of quantifier moves in the game.
-
-
• If Spoiler plays a quantifier move and chooses an element
 $e^\alpha _\beta $
from the model N, then Duplicator applies the same strategy as in the previous case, swapping the roles of the models M and N.
$e^\alpha _\beta $
from the model N, then Duplicator applies the same strategy as in the previous case, swapping the roles of the models M and N.

Fig. 3 Suppose
![]() $q=2$
, and consider the sets
$q=2$
, and consider the sets
![]() $A=\{2,3,5\}$
and
$A=\{2,3,5\}$
and
![]() $B=\{2,4\}$
. Notice that
$B=\{2,4\}$
. Notice that
![]() $A=_2B$
. We enumerate these sets as
$A=_2B$
. We enumerate these sets as
![]() $\langle 2,3,5\rangle $
and
$\langle 2,3,5\rangle $
and
![]() $\langle 2,4,4\rangle $
. The figure shows the models M and N derived from this enumeration. These models are indistinguishable in the EF-game with only 2 quantifier moves, regardless of the number of implication moves.
$\langle 2,4,4\rangle $
. The figure shows the models M and N derived from this enumeration. These models are indistinguishable in the EF-game with only 2 quantifier moves, regardless of the number of implication moves.
Notice that with this strategy Duplicator ensures that at the end of the run the final position:
-
1. has the same state s for both models;
-
2.
 $a_i = a_j$
if and only if
$a_i = a_j$
if and only if
 $b_i = b_j$
;
$b_i = b_j$
; -
3. corresponding elements
 $a_i,b_i$
in the two models have the same superscripts, that is,
$a_i,b_i$
in the two models have the same superscripts, that is,
 $a_i$
and
$a_i$
and
 $b_i$
are of the form
$b_i$
are of the form
 $d^\alpha _\beta $
and
$d^\alpha _\beta $
and
 $e^\alpha _\beta $
respectively.
$e^\alpha _\beta $
respectively.
This is indeed a winning strategy, since:
 $$ \begin{align*} M, s \models P(d^{\alpha}_{\beta}) \;\iff\; s \subseteq \{\alpha\} \;\iff\; N, s \models P(e^{\alpha}_{\gamma}) \\ M, s \models a_i = a_j \;\iff\; N, s \models b_i = b_j. \qquad \quad \end{align*} $$
$$ \begin{align*} M, s \models P(d^{\alpha}_{\beta}) \;\iff\; s \subseteq \{\alpha\} \;\iff\; N, s \models P(e^{\alpha}_{\gamma}) \\ M, s \models a_i = a_j \;\iff\; N, s \models b_i = b_j. \qquad \quad \end{align*} $$
![]() $\pmb {[3 \Rightarrow 2]}$
Suppose
$\pmb {[3 \Rightarrow 2]}$
Suppose
![]() $\mathbb {K}$
is downward closed and
$\mathbb {K}$
is downward closed and
![]() $=_m$
-invariant for some number m. Let
$=_m$
-invariant for some number m. Let
![]() $A_1,\dots ,A_n$
be the subsets of
$A_1,\dots ,A_n$
be the subsets of
![]() $[0,m+1]$
which are contained in
$[0,m+1]$
which are contained in
![]() $\mathbb {K}$
. Now define:
$\mathbb {K}$
. Now define:
 $$ \begin{align*} K_i = \left\{ \begin{array}{ll} A_i &\text{if}\; m+1\notin A_i \\ A_i \cup [m+1,\dots) &\text{if}\; m+1 \in A_i. \end{array} \right. \end{align*} $$
$$ \begin{align*} K_i = \left\{ \begin{array}{ll} A_i &\text{if}\; m+1\notin A_i \\ A_i \cup [m+1,\dots) &\text{if}\; m+1 \in A_i. \end{array} \right. \end{align*} $$
We claim that
![]() $\mathbb {K}=K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
. Start with the right-to-left inclusion. Let
$\mathbb {K}=K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
. Start with the right-to-left inclusion. Let
![]() $B\in K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
. This means that
$B\in K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
. This means that
![]() $B\subseteq K_i$
for some i. Now we distinguish two cases.
$B\subseteq K_i$
for some i. Now we distinguish two cases.
-
• Case 1:
 $K_i=A_i$
. Then
$K_i=A_i$
. Then
 $A_i\in \mathbb {K}$
by definition, and since
$A_i\in \mathbb {K}$
by definition, and since
 $\mathbb {K}$
is downward closed, also
$\mathbb {K}$
is downward closed, also
 $B\in \mathbb {K}$
.
$B\in \mathbb {K}$
. -
• Case 2:
 $K_i=A_i\cup [m+1,\dots )$
. We claim that in this case,
$K_i=A_i\cup [m+1,\dots )$
. We claim that in this case,
 $A_i=_m A_i\cup B$
: if so, since
$A_i=_m A_i\cup B$
: if so, since
 $A_i\in \mathbb {K}$
and
$A_i\in \mathbb {K}$
and
 $\mathbb {K}$
is
$\mathbb {K}$
is
 $=_m$
-invariant, we have
$=_m$
-invariant, we have
 $A_i\cup B\in \mathbb {K}$
, which in turn by downward closure yields
$A_i\cup B\in \mathbb {K}$
, which in turn by downward closure yields
 $B\in \mathbb {K}$
. To see that
$B\in \mathbb {K}$
. To see that
 $A_i=_nA_i\cup B$
, the only non-trivial step is to show that for all
$A_i=_nA_i\cup B$
, the only non-trivial step is to show that for all
 $\kappa \in B$
there exists some
$\kappa \in B$
there exists some
 $\kappa '\in A_i$
such that
$\kappa '\in A_i$
such that
 $\kappa '=_m\kappa $
. So, take
$\kappa '=_m\kappa $
. So, take
 $\kappa \in B$
: if
$\kappa \in B$
: if
 $\kappa \le m$
then
$\kappa \le m$
then
 $\kappa \in A_i$
(since
$\kappa \in A_i$
(since
 $B\subseteq K_i= A_i\cup [m+1,\dots )$
), so we can take
$B\subseteq K_i= A_i\cup [m+1,\dots )$
), so we can take
 $\kappa '=\kappa $
; if on the other hand
$\kappa '=\kappa $
; if on the other hand
 $\kappa> m$
, then
$\kappa> m$
, then
 $\kappa =_m m+1\in A_i$
.
$\kappa =_m m+1\in A_i$
.
Either way, we conclude
![]() $B\in \mathbb {K}$
, which gives the right-to-left inclusion.
$B\in \mathbb {K}$
, which gives the right-to-left inclusion.
For the converse inclusion, suppose
![]() $B\in \mathbb {K}$
. Again, we distinguish two cases.
$B\in \mathbb {K}$
. Again, we distinguish two cases.
-
• Case 1:
 $B\subseteq [0,m]$
. In this case,
$B\subseteq [0,m]$
. In this case,
 $B=A_i$
for some
$B=A_i$
for some
 $i\le n$
, and thus
$i\le n$
, and thus
 $B\in K_i^{\downarrow }$
.
$B\in K_i^{\downarrow }$
. -
• Case 2:
 $B\ni \kappa $
for some
$B\ni \kappa $
for some
 $\kappa>m$
. In this case,
$\kappa>m$
. In this case,
 $B=_m B\cup \{m+1\}$
, since
$B=_m B\cup \{m+1\}$
, since
 $\kappa =_m m+1$
. Since
$\kappa =_m m+1$
. Since
 $B\in \mathbb {K}$
and
$B\in \mathbb {K}$
and
 $\mathbb {K}$
is
$\mathbb {K}$
is
 $=_m$
-invariant, also
$=_m$
-invariant, also
 $B\cup \{m+1\}\in \mathbb {K}$
. Now take
$B\cup \{m+1\}\in \mathbb {K}$
. Now take
 $(B\cup \{m+1\})\cap [0,m+1]$
: by downward closure, this set is in
$(B\cup \{m+1\})\cap [0,m+1]$
: by downward closure, this set is in
 $\mathbb {K}$
, and since it is a subset of
$\mathbb {K}$
, and since it is a subset of
 $[0,m+1]$
, it coincides with
$[0,m+1]$
, it coincides with
 $A_i$
for some
$A_i$
for some
 $i\le n$
. Notice that
$i\le n$
. Notice that
 $m+1\in A_i$
, and thus,
$m+1\in A_i$
, and thus,
 $K_i=A_i\cup [m+1,\dots )$
. Therefore,
$K_i=A_i\cup [m+1,\dots )$
. Therefore,
 $B\subseteq K_i$
, which implies
$B\subseteq K_i$
, which implies
 $B\in K_i^{\downarrow }$
.
$B\in K_i^{\downarrow }$
.
In either case, we conclude that
![]() $B\in K_i$
for some
$B\in K_i$
for some
![]() $i\le n$
, which gives the left-to-right inclusion.□
$i\le n$
, which gives the left-to-right inclusion.□
Theorem 4.5 allows us to tell immediately which among the questions in (2) are expressible in InqBQ: (2.a), the question whether there is any P, is expressible, since it has the form
![]() $Q_{\mathbb {K}} x.Px$
for the class
$Q_{\mathbb {K}} x.Px$
for the class
![]() $\mathbb {K}_5=\{0\}^{\downarrow }\cup \,[1,\dots )^{\downarrow }$
, where both
$\mathbb {K}_5=\{0\}^{\downarrow }\cup \,[1,\dots )^{\downarrow }$
, where both
![]() $\{0\}$
and
$\{0\}$
and
![]() $[1,\dots )$
are definable in classical first-order logic. Indeed, the defining formula is simply
$[1,\dots )$
are definable in classical first-order logic. Indeed, the defining formula is simply
![]() $?\exists x.Px$
, which abbreviates
$?\exists x.Px$
, which abbreviates
![]() .
.
The remaining questions, (2.b), (2.c), and (2.d) are not expressible, since they have the form
![]() $Q_{\mathbb {K}} x.Px$
for the following classes
$Q_{\mathbb {K}} x.Px$
for the following classes
![]() $\mathbb {K}$
:
$\mathbb {K}$
:
Clearly, these classes are not the form
![]() $K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
for
$K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
for
![]() $K_1,\dots ,K_n$
definable in classical first-order logic. In a similar way, we can see that none of the following questions about the cardinality of P is expressible in InqBQ.
$K_1,\dots ,K_n$
definable in classical first-order logic. In a similar way, we can see that none of the following questions about the cardinality of P is expressible in InqBQ.
-
(7)
-
a. How many P are there, modulo k? (for
 $k\ge 2$
)
$k\ge 2$
) -
b. Is the number of P even, odd, or infinite?
-
c. Is the number of P a prime number, or a composite one?
-
d. Are there uncountably many P?
-
It is worth pausing to remark that, while InqBQ can express the question “what objects are P?” (by means of the formula
![]() $\forall x.?Px$
, see Section 2), it cannot express the corresponding cardinality question “how many object are P?” From the perspective of logical modeling of questions, this means that analyzing how many questions—an important class of questions—requires a proper extension of the logic InqBQ. Developing and investigating such an extension is an interesting prospect for future work.
$\forall x.?Px$
, see Section 2), it cannot express the corresponding cardinality question “how many object are P?” From the perspective of logical modeling of questions, this means that analyzing how many questions—an important class of questions—requires a proper extension of the logic InqBQ. Developing and investigating such an extension is an interesting prospect for future work.
Since the proof of Theorem 4.5 is quite flexible, the characterization result can be seen to hold also when we restrict to certain salient classes of models. For instance, since the proof uses only
![]() $\mathsf {id}$
-models, we obtain the following Corollary.
$\mathsf {id}$
-models, we obtain the following Corollary.
Corollary 4.6. The characterization given in Theorem 4.5 holds also when we restrict to the class of
![]() $\mathsf {id}$
-models.
$\mathsf {id}$
-models.
Moreover, it is an easy exercise to adapt the proof to show the following result, concerning the class of finite models and the class of finite
![]() $\mathsf {id}$
-models.
$\mathsf {id}$
-models.
Corollary 4.7. Let
![]() $\mathbb {K}$
be a set of sets of finite cardinals. The following are equivalent:
$\mathbb {K}$
be a set of sets of finite cardinals. The following are equivalent:
-
1. The cardinality quantifier
 $Q_{\mathbb {K}}$
is definable in InqBQ with respect to the class of finite models (resp. finite
$Q_{\mathbb {K}}$
is definable in InqBQ with respect to the class of finite models (resp. finite
 $\mathsf {id}$
-models). That is, there is a formula
$\mathsf {id}$
-models). That is, there is a formula
 $\chi _{\mathbb {K}}$
of InqBQ such that
$\chi _{\mathbb {K}}$
of InqBQ such that
 $Q_{\mathbb {K}} x.Px$
is equivalent to
$Q_{\mathbb {K}} x.Px$
is equivalent to
 $\chi _{\mathbb {K}}[P]$
in restriction to finite models (resp. finite
$\chi _{\mathbb {K}}[P]$
in restriction to finite models (resp. finite
 $\mathsf {id}$
-models).
$\mathsf {id}$
-models). -
2.
 $\mathbb {K}=K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
for some sets
$\mathbb {K}=K_1^{\downarrow }\cup \dots \cup K_n^{\downarrow }$
for some sets
 $K_1,\dots ,K_n\subseteq \mathbb {N}$
, where for each
$K_1,\dots ,K_n\subseteq \mathbb {N}$
, where for each
 $K_i$
there exists
$K_i$
there exists
 $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
 $K_i$
contains all or none of the numbers
$K_i$
contains all or none of the numbers
 $k\ge m$
.
$k\ge m$
.
5 Conclusion
EF games often provide an insightful perspective on a logic and a useful characterization of its expressive power. In this paper we have described an EF-game for inquisitive first-order logic, InqBQ, showing that it characterizes exactly the distinguishing power of the logic, and we used the game to study the expressive power of the logic with respect to certain cardinality properties.
In comparison to its classical counterpart, the game presents two novelties. Firstly, the roles of the two models on which the game is played are not symmetric: certain moves have to be performed mandatorily in one of the models. This feature reflects the fact that InqBQ lacks a classical negation and that the theory of a model—unlike in the classical case—can be properly included in that of another. Secondly, the objects that are picked in the course of the game are not just individuals
![]() $d\in D$
, but also information states, i.e., subsets
$d\in D$
, but also information states, i.e., subsets
![]() $s\subseteq W$
of the universe of possible worlds. This feature reflects the fact that InqBQ contains not only the quantifiers
$s\subseteq W$
of the universe of possible worlds. This feature reflects the fact that InqBQ contains not only the quantifiers
![]() $\forall ,\, \overline{\exists} $
over individuals, but also the implication
$\forall ,\, \overline{\exists} $
over individuals, but also the implication
![]() $\to $
, which allows for a restricted kind of quantification over information states.
$\to $
, which allows for a restricted kind of quantification over information states.
Moreover, we introduced the notion of a cardinality quantifier in InqBQ, that is, a quantifier which is sensitive only to the number of individuals which satisfy a given property. As we illustrated, the inquisitive setting provides a more general perspective on this notion: besides quantifers like infinitely many, which combine with a property to form a statement, we now also have quantifers like how many, which combine with a property to form a question.
Using the EF-game, we were able to characterize exactly the range of cardinality quantifiers expressible in InqBQ. The characterization is similar to the one for classical first-order logic: the definable quantifiers are those that, for some natural number n, do not make any distinctions between cardinals larger than n. As we anticipated in the introduction, this is particularly interesting as it sheds some light on the expressive power of InqBQ, which is still poorly understood. At present, we do not know exactly how InqBQ relates to standard first- and second-order predicate logic: we do not know, e.g., whether InqBQ is compact and whether an entailment-preserving translation to first-order logic exists. Our characterization result shows that, at least with respect to the expression of cardinality properties, InqBQ is very similar to first-order logic, sharing the same kind of expressive limitations, and very different from second-order logic.
We also saw that the characterization result yields a number of interesting examples of questions which are not expressible in InqBQ. Crucially, this includes the question how many individuals satisfy P, both in the general case and in restriction to finite models. This means that in order to capture how many questions in predicate logic, a proper extension of InqBQ is needed. Other interesting examples of questions which were proved not to be expressible are whether the number of P is even or odd (also in restriction to finite models) and whether the number of P is finite or infinite.
The work presented in this paper can be taken further in several directions. Firstly, in the context of classical logic, several variants of the EF game have been studied. For example, [Reference Väänänen23] presents a dynamic EF game, corresponding to a more fine-grained classification of classical structures. In the inquisitive case, an analogous refinement could lead to interesting insights into the structure of inquisitive models. Ehrenfeucht–Fraïssé games can also be used to compare different extensions of a fixed logic, as shown in [Reference Kolaitis and Väänänen15]. In this regard, the results presented in Section 4 already yield some interesting corollaries. For example, adding to InqBQ the quantifier how many (the operator
![]() $Q_5$
in Section 4.2) yields a logic which is strictly more expressive than
$Q_5$
in Section 4.2) yields a logic which is strictly more expressive than
![]() $\textsf {InqBQ}$
. More generally, the techniques introduced in this paper are likely to provide a useful tool for a systematic study of quantifiers in inquisitive logic.
$\textsf {InqBQ}$
. More generally, the techniques introduced in this paper are likely to provide a useful tool for a systematic study of quantifiers in inquisitive logic.
Second, as pointed out in Footnote 6, in this paper we only studied the simplest cardinality quantifiers, namely, those that operate on a single unary predicate. In further work, it would be natural to look at how our characterization result extends to the general case of cardinality quantifiers operating on several predicates, possibly of arities different from 1. This is not just a technical exercise: there are interesting cardinality questions involving multiple predicates, such as “are there more P or more Q?”.
Finally, one major goal for future work is to look beyond cardinality quantifiers and study generalized quantifiers in the inquisitive setting. The classical theory of generalized quantifiers is well-established [Reference Lindström16, Reference Mostowski17] and an important topic across logic, linguistics, and cognitive science. As illustrated in this paper and discussed in more detail in [Reference Ciardelli and Roelofsen6], the inquisitive perspective leads to a more general perspective on quantifiers. Among other things, this perspective allows us to bring interrogative words like who, which, and how many within the purview of generalized quantifier theory (on this enterprise, see also [Reference Rexach21]). How does the classical theory of generalized quantifiers scale up to this more general setting? What novelties arise? The Ehrenfeucht–Fraïssé game presented in this paper will likely prove to be a fundamental tool in answering these questions.
Acknowledgment
Financial support by the European Research Council under the EU’s Horizon 2020 research and innovation program (grant No. 680220) is gratefully acknowledged.