Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T20:27:49.323Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPLETE ADDITIVITY AND MODAL INCOMPLETENESS

Published online by Cambridge University Press:  04 July 2019

WESLEY H. HOLLIDAY  and
TADEUSZ LITAK
WESLEY H. HOLLIDAY*
Affiliation:
Department of Philosophy and Group in Logic and the Methodology of Science, University of California, Berkeley
TADEUSZ LITAK*
Affiliation:
Chair for Theoretical Computer Science (Informatik 8), FAU Erlangen-Nuremberg
*
*DEPARTMENT OF PHILOSOPHY AND GROUP IN LOGIC AND THE METHODOLOGY OF SCIENCE UNIVERSITY OF CALIFORNIA, BERKELEY BERKELEY, CA 94720, USA E-mail: [email protected]
†CHAIR FOR THEORETICAL COMPUTER SCIENCE (INFORMATIK 8) FAU ERLANGEN-NUREMBERG 91058 ERLANGEN, GERMANY E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we tell a story about incompleteness in modal logic. The story weaves together an article of van Benthem (1979), “Syntactic aspects of modal incompleteness theorems,” and a longstanding open question: whether every normal modal logic can be characterized by a class of completely additive modal algebras, or as we call them, 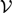${\cal V}$-baos. Using a first-order reformulation of the property of complete additivity, we prove that the modal logic that starred in van Benthem’s article resolves the open question in the negative. In addition, for the case of bimodal logic, we show that there is a naturally occurring logic that is incomplete with respect to 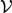${\cal V}$-baos, namely the provability logic 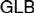$GLB$ (Japaridze, 1988; Boolos, 1993). We also show that even logics that are unsound with respect to such algebras do not have to be more complex than the classical propositional calculus. On the other hand, we observe that it is undecidable whether a syntactically defined logic is 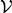${\cal V}$-complete. After these results, we generalize the Blok Dichotomy (Blok, 1978) to degrees of 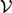${\cal V}$-incompleteness. In the end, we return to van Benthem’s theme of syntactic aspects of modal incompleteness.

Keywords

03B4506E2503F4503B4403B25modal logicBoolean algebras with operatorscompletely additive operatorsincompletenessprovability logicBlok Dichotomyconservativity
Type
Research Article
Information
The Review of Symbolic Logic , Volume 12 , Issue 3 , September 2019 , pp. 487 - 535
Copyright
Copyright © Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Andréka, H., Gyenis, Z., & Németi, I. (2016). Ultraproducts of continuous posets. Algebra Universalis, 76(2), 231–235.CrossRefGoogle Scholar
Andréka, H., Németi, I., & Sain, I. (2001). Algebraic logic. In Gabbay, D. M. and Guenthner, F., editors. Handbook of Philosophical Logic, second edition. Dordrecht: Kluwer, pp. 133–249.CrossRefGoogle Scholar
Beklemishev, L. (2011). Ordinal completeness of bimodal provability logic GLB. In Bezhanishvili, N., Löbner, S., Schwabe, K., & Spada, L., editors. Logic, Language, and Computation: 8th International Tbilisi Symposium on Logic, Language, and Computation, TbiLLC 2009, Bakuriani, Georgia, September 21–25, 2009. Revised Selected Papers. Heidelberg: Springer, pp. 1–15.Google Scholar
Beklemishev, L., Bezhanishvili, G., & Icard, T. (2010). On topological models of GLP. In Schindler, R., editor. Ways of Proof Theory. Ontos Mathematical Logic, Vol. 2. Heusenstamm: Ontos Verlag, pp. 135–155.Google Scholar
Beklemishev, L. & Gabelaia, D. (2014). Topological interpretations of provability logic. In Bezhanishvili, G., editor. Leo Esakia on Duality in Modal and Intuitionistic Logics. Outstanding Contributions to Logic, Vol. 4. Dordrecht: Springer, pp. 257–290.Google Scholar
van Benthem, J. (1978). Two simple incomplete modal logics. Theoria, 44(1), 25–37.CrossRefGoogle Scholar
van Benthem, J. (1979). Syntactic aspects of modal incompleteness theorems. Theoria, 45(2), 63–77.CrossRefGoogle Scholar
van Benthem, J. (1983). Modal Logic and Classical Logic. Milan: Bibliopolis.Google Scholar
van Benthem, J. (2001). Correspondence theory. In Gabbay, D. and Guenthner, F., editors. Handbook of Philosophical Logic, second edition, Vol. 3. Dordrecht: Springer, pp. 325–408.CrossRefGoogle Scholar
Bezhanishvili, G. & Holliday, W. H. (2019). A semantic hierarchy for intuitionistic logic. Indagationes Mathematicae, 30(3), 403–469.CrossRefGoogle Scholar
Bezhanishvili, N. & Ghilardi, S. (2014). The bounded proof property via step algebras and step frames. Annals of Pure Applied Logic, 165(12), 1832–1863.CrossRefGoogle Scholar
Bezhanishvili, N., & Kurz, A. (2007). Free modal algebras: A coalgebraic perspective. In Mossakowski, T., Montanari, U., and Haveraaen, M., editors. Algebra and Coalgebra in Computer Science. Lectures Notes in Computer Science, Vol. 4624. Berlin: Springer, pp. 143–157.CrossRefGoogle Scholar
Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal Logic. Cambridge Tracts in Theoretical Computer Science, Vol. 53. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Blok, W. J. (1978). On the degree of incompleteness of modal logic and the covering relation in the lattice of modal logics. Technical Report 78-07, University of Amsterdam.Google Scholar
Blok, W. J. & Köhler, P. (1983). Algebraic semantics for quasi-classical modal logics. The Journal of Symbolic Logic, 48(4), 941–964.CrossRefGoogle Scholar
Blok, W. J. & Pigozzi, D. (1989). Algebraizable Logics. Memoirs of the American Mathematical Society, no. 396. Providence, RI: American Mathematical Society.Google Scholar
Boolos, G. (1993). The Logic of Provability. Cambridge: Cambridge University Press.Google Scholar
Boolos, G. & Sambin, G. (1985). An incomplete systems of modal logic. Journal of Philosophical Logic, 14(4), 351–358.CrossRefGoogle Scholar
Buszkowski, W. (1986). Embedding Boolean structures into atomic Boolean algebras. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, 32, 227–228.CrossRefGoogle Scholar
Buszkowski, W. (2004). A representation theorem for co-diagonalizable algebras. Reports on Mathematical Logic, 38, 13–22.Google Scholar
ten Cate, B. & Litak, T. (2007). The importance of being discrete. Technical Report PP-2007-39, Institute for Logic, Language and Computation, University of Amsterdam.Google Scholar
Chagrov, A. V. (1990). Undecidable properties of extensions of a provability logic. II. Algebra and Logic, 29(5), 406–413.CrossRefGoogle Scholar
Chagrov, A. V. & Rybakov, M. N. (2003). How many variables does one need to prove PSPACE-hardness of modal logics? In Balbiani, P., Suzuki, N.-Y., Wolter, F., and Zakharyaschev, M., editors. Advances in Modal Logic, Vol. 4. London: King’s College Publications, pp. 71–82.Google Scholar
Chagrov, A. V. & Zakharyaschev, M. (1993). The undecidability of the disjunction property of propositional logics and other related problems. The Journal of Symbolic Logic, 58(3), 967–1002.CrossRefGoogle Scholar
Chagrov, A. V. & Zakharyaschev, M. (1997). Modal Logic. Oxford Logic Guides. Oxford: Clarendon Press.Google Scholar
Chagrova, L. A. (1998). On the degree of neighbourhood incompleteness of normal modal logics. In Kracht, M., de Rijke, M., Wansing, H., and Zakharyaschev, M., editors. Advances in Modal Logic, Vol. 1. Stanford: CSLI Publications, pp. 63–72.Google Scholar
Cirstea, C., Kurz, A., Pattinson, D., Schröder, L., & Venema, Y. (2011). Modal logics are coalgebraic. The Computer Journal, 54(1), 31–41.CrossRefGoogle Scholar
Conradie, W., Ghilardi, S., & Palmigiano, A. (2014). Unified correspondence. In Baltag, A. and Smets, S., editors. Johan van Benthem on Logic and Information Dynamics. Dordrecht: Springer, pp. 933–975.CrossRefGoogle Scholar
Conradie, W., Goranko, V., & Vakarelov, D. (2006). Algorithmic correspondence and completeness in modal logic. I. The core algorithm SQEMA. Logical Methods in Computer Science, 2(1), 1–26.CrossRefGoogle Scholar
Coumans, D. C. S. & van Gool, S. J. (2013). On generalizing free algebras for a functor. Journal of Logic and Computation, 23(3), 645–672.CrossRefGoogle Scholar
Cresswell, M. J. (1984). An incomplete decidable modal logic. The Journal of Symbolic Logic, 49(2), 520–527.CrossRefGoogle Scholar
Czelakowski, J. (2001). Protoalgebraic Logics. Trends in Logic. Dordrecht: Springer.CrossRefGoogle Scholar
Došen, K. (1989). Duality between modal algebras and neighborhood frames. Studia Logica, 48(2), 219–234.CrossRefGoogle Scholar
Dziobiak, W. (1978). A note on incompleteness of modal logics with respect to neighbourhood semantics. Bulletin of the Section of Logic, 7(4), 185–190.Google Scholar
Fine, K. (1974). An incomplete logic containing S4. Theoria, 40(1), 23–29.CrossRefGoogle Scholar
Fine, K. (1975, 04). Normal forms in modal logic. Notre Dame Journal of Formal Logic, 16(2), 229–237.CrossRefGoogle Scholar
Font, J. M. (2006). Beyond Rasiowa’s algebraic approach to non-classical logic. Studia Logica, 82(2), 179–209.CrossRefGoogle Scholar
Font, J. M., Jansana, R., & Pigozzi, D. (2003). A survey of abstract algebraic logic. Studia Logica, 74(1), 13–97.CrossRefGoogle Scholar
Font, J. M., Jansana, R., & Pigozzi, D. (2009). Update to “A survey of abstract algebraic logic”. Studia Logica, 91(1), 125–130.CrossRefGoogle Scholar
Gargov, G. & Goranko, V. (1993). Modal logic with names. Journal of Philosophical Logic, 22(6), 607–636.CrossRefGoogle Scholar
Ghilardi, S. (1995). An algebraic theory of normal forms. Annals of Pure and Applied Logic, 71(3), 189–245.CrossRefGoogle Scholar
Ghilardi, S. & Meloni, G. (1997). Constructive canonicity in non-classical logic. Annals of Pure and Applied Logic, 86(1), 1–32.CrossRefGoogle Scholar
Goldblatt, R. (2001). Persistence and atomic generation for varieties of Boolean algebras with operators. Studia Logica, 68(2), 155–171.CrossRefGoogle Scholar
Goldblatt, R. (2003). Mathematical modal logic: A view of its evolution. Journal of Applied Logic, 1(5–6), 309–392.CrossRefGoogle Scholar
Holliday, W. H. (2014). Partiality and adjointness in modal logic. In Goré, R., Kooi, B., and Kurucz, A., editors. Advances in Modal Logic, Vol. 10. London: College Publications, pp. 313–332.Google Scholar
Holliday, W. H. (2015). Possibility frames and forcing for modal logic. UC Berkeley Working Paper in Logic and the Methodology of Science. February 2018 version. Available at: https://escholarship.org/uc/item/0tm6b30q.Google Scholar
Holliday, W. H. & Litak, T. (2018). One modal logic to rule them all? In Bezhanishvili, G., D’Agostino, G., Metcalfe, G., and Studer, T., editors. Advances in Modal Logic, Vol. 12. London: College Publications, pp. 367–386.Google Scholar
Hopcroft, J. E., Motwani, R., & Ullman, J. D. (2003). Introduction to Automata Theory, Languages, and Computation (second edition). Boston: Addison-Wesley.Google Scholar
Humberstone, L. (2011). The Connectives. Cambridge, MA: MIT Press.CrossRefGoogle Scholar
Jansana, R. (2006). Willem Blok’s contribution to abstract algebraic logic. Studia Logica, 83(1), 31–48.CrossRefGoogle Scholar
Japaridze, G. K. (1988). The polymodal logic of provability. In Smirnov, V. A. and Bezhanishvili, M. N., editors. Intensional Logics and the Logical Structure of Theories: Proceedings of the Fourth Soviet-Finnish Symposium on Logic, Telavi, May 1985. Tbilisi: Metsniereba, pp. 16–48.Google Scholar
Jipsen, P. (1993). Discriminator varieties of Boolean algebras with residuated operators. In Algebraic Methods in Logic and in Computer Science. Banach Center Publications, Vol. 28. Warszawa: Institute of Mathematics, Polish Academy of Sciences, pp. 239–252.Google Scholar
Jónsson, B. & Tarski, A. (1951). Boolean algebras with operators. Part I. American Journal of Mathematics, 73(4), 891–939.CrossRefGoogle Scholar
Jónsson, B. & Tarski, A. (1952). Boolean algebras with operators. Part II. American Journal of Mathematics, 74(1), 127–162.CrossRefGoogle Scholar
Kracht, M. (1999). Tools and Techniques in Modal Logic. Studies in Logic and the Foundations of Mathematics, Vol. 142. Amsterdam: Elsevier.CrossRefGoogle Scholar
Kracht, M. & Wolter, F. (1991). Properties of independently axiomatizable bimodal logics. The Journal of Symbolic Logic, 56(4), 1469–1485.CrossRefGoogle Scholar
Kracht, M. & Wolter, F. (1997). Simulation and transfer results in modal logic: A survey. Studia Logica, 59(2), 149–177.CrossRefGoogle Scholar
Kracht, M. & Wolter, F. (1999). Normal monomodal logics can simulate all others. The Journal of Symbolic Logic, 64(1), 99–138.CrossRefGoogle Scholar
Kurz, A. & Rosický, J. (2012). Strongly complete logics for coalgebras. Logical Methods in Computer Science, 8(3:14), 1–32.CrossRefGoogle Scholar
Kuznetsov, A. V. (1975). On superintuitionistic logics. In Proceedings of the International Congress of Mathematicians (Vancouver, B. C., 1974), Vol. 1. Montreal, Quebec: Canadian Mathematical Congress, pp. 243–249.Google Scholar
Lemmon, E. J. & Scott, D. (1977). The “Lemmon Notes”: An Introduction to Modal Logic, ed. Segerberg, K.. Number 11 in American Philosophical Quarterly Monograph Series. Oxford: Basil Blackwell.Google Scholar
Lewis, D. (1974). Intensional logics without iterative axioms. Journal of Philosophical Logic, 3(4), 457–466.CrossRefGoogle Scholar
Litak, T. (2004). Modal incompleteness revisited. Studia Logica, 76(3), 329–342.CrossRefGoogle Scholar
Litak, T. (2005a). An Algebraic Approach to Incompleteness in Modal Logic. Ph.D. Thesis, Japan Advanced Institute of Science and Technology.Google Scholar
Litak, T. (2005b). On notions of completeness weaker than Kripke completeness. In Schmidt, R., Pratt-Hartmann, I., Reynolds, M., and Wansing, H., editors. Advances in Modal Logic, Vol. 5. London: College Publications, pp. 149–169.Google Scholar
Litak, T. (2006). Isomorphism via translation. In Governatori, G., Hodkinson, I. M., and Venema, Y., editors. Advances in Modal Logic, Vol. 6. London: College Publications, pp. 333–351.Google Scholar
Litak, T. (2008). Stability of the Blok theorem. Algebra Universalis, 58(4), 385–411.CrossRefGoogle Scholar
Litak, T., Pattinson, D., Sano, K., & Schröder, L. (2012). Coalgebraic predicate logic. In Czumaj, A., Mehlhorn, K., Pitts, A., and Wattenhofer, R., editors. Automata, Languages, and Programming: 39th International Colloquium (ICALP). Lecture Notes in Computer Science, Vol. 7392. Heidelberg: Springer, pp. 299–311.CrossRefGoogle Scholar
Litak, T., Pattinson, D., Sano, K., & Schröder, L. (2018). Model theory and proof theory of coalgebraic predicate logic. Logical Methods in Computer Science, 14(1:22), 1–52.Google Scholar
Litak, T. & Wolter, F. (2005). All finitely axiomatizable tense logics of linear time flows are coNP-complete. Studia Logica, 81(2), 153–165.CrossRefGoogle Scholar
Łukasiewicz, J. & Tarski, A. (1930). Untersuchungen über den Aussagenkalkül. Comptes Rendus des séances de la Societé des Sciences et des Lettres de Varsovie, 23, 30–50. English translation in Tarski 1956.Google Scholar
Makinson, D. (1971). Some embedding theorems for modal logic. Notre Dame Journal of Formal Logic, 12(2), 252–254.CrossRefGoogle Scholar
Moss, L. S. (2007). Finite models constructed from canonical formulas. Journal of Philosophical Logic, 36(6), 605–640.CrossRefGoogle Scholar
Pitts, A. M. (2013). Nominal Sets: Names and Symmetry in Computer Science. Cambridge Tracts in Theoretical Computer Science, Vol. 57. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Pitts, A. M. (2016). Nominal techniques. ACM SIGLOG News, 3(1), 57–72.Google Scholar
Rabin, M. O. (1969). Decidability of second-order theories and automata on infinite trees. Transactions of the American Mathematical Society, 141, 1–35.Google Scholar
Rasiowa, H. (1974). An Algebraic Approach to Non-classical Logics. Amsterdam: North-Holland.Google Scholar
Rautenberg, W., Wolter, F., & Zakharyaschev, M. (2006). Willem Blok and modal logic. Studia Logica, 83(1–3), 15–30. Special issue in memory of Willem Johannes Blok.CrossRefGoogle Scholar
Rice, H. G. (1953). Classes of recursively enumerable sets and their decision problems. Transactions of the American Mathematical Society, 74(2), 358–366.CrossRefGoogle Scholar
Schröder, L. (2008). Expressivity of coalgebraic modal logic: The limits and beyond. Theoretical Computer Science, 390(2–3), 230–247. Special issue on Foundations of Software Science and Computational Structures.CrossRefGoogle Scholar
Schröder, L. & Pattinson, D. (2010). Rank-1 modal logics are coalgebraic. Journal of Logic and Computation, 20(5), 1113–1147.CrossRefGoogle Scholar
Segerberg, K. (1971). An Essay in Classical Modal Logic. Filosofiska Studier, Vol. 13. Uppsala, Sweden: University of Uppsala.Google Scholar
Shapirovsky, I. (2008). PSPACE-decidability of Japaridze’s polymodal logic. In Areces, C. and Goldblatt, R., editors. Advances in Modal Logic, Vol. 7. London: College Publications, pp. 289–304.Google Scholar
Simpson, S. G. (2009). Subsystems of Second Order Arithmetic. Perspectives in Logic. New York: Association for Symbolic Logic, Cambridge University Press.CrossRefGoogle Scholar
Solovay, R. M. (1976). Provability interpretations of modal logic. Israel Journal of Mathematics, 25(3), 287–304.CrossRefGoogle Scholar
Surendonk, T. J. (2001). Canonicity for intensional logics with even axioms. The Journal of Symbolic Logic, 66(3), 1141–1156.CrossRefGoogle Scholar
Suzuki, T. (2010, 009). Canonicity results of substructural and lattice-based logics. The Review of Symbolic Logic, 4(1), 1–42.CrossRefGoogle Scholar
Tarski, A. (1956). Logic, Semantics, Metamathematics: Papers from 1923 to 1938. Oxford: Clarendon Press. Translated by J. H. Woodger.Google Scholar
Thomason, S. K. (1972). Semantic analysis of tense logics. The Journal of Symbolic Logic, 37(1), 150–158.CrossRefGoogle Scholar
Thomason, S. K. (1974a). An incompleteness theorem in modal logic. Theoria, 40(1), 30–34.CrossRefGoogle Scholar
Thomason, S. K. (1974b). Reduction of tense logic to modal logic. I. The Journal of Symbolic Logic, 39(3), 549–551.CrossRefGoogle Scholar
Thomason, S. K. (1974c). Reduction of tense logic to modal logic II. Theoria, 40(3), 154–169.CrossRefGoogle Scholar
Thomason, S. K. (1975a). Categories of frames for modal logic. The Journal of Symbolic Logic, 40(3), 439–442.CrossRefGoogle Scholar
Thomason, S. K. (1975b). Reduction of second-order logic to modal logic. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, 21(1), 107–114.CrossRefGoogle Scholar
Thomason, S. K. (1982). Undecidability of the completeness problem of modal logic. Banach Center Publications, 9(1), 341–345.CrossRefGoogle Scholar
Venema, Y. (2003). Atomless varieties. The Journal of Symbolic Logic, 68(2), 607–614.CrossRefGoogle Scholar
Venema, Y. (2007). Algebras and coalgebras. In Blackburn, P., van Benthem, J., and Wolter, F., editors. Handbook of Modal Logic. Amsterdam: Elsevier, pp. 331–426.CrossRefGoogle Scholar
Švejdar, V. (2003). The decision problem of provability logic with only one atom. Archive for Mathematical Logic, 42(8), 763–768.CrossRefGoogle Scholar
Wolter, F. (1993). Lattices of Modal Logics. Ph.D. Thesis, Fachbereich Mathematik, Freien Universität Berlin.Google Scholar
Wolter, F. (1996a). Properties of tense logics. Mathematical Logic Quarterly, 42(1), 481–500.CrossRefGoogle Scholar
Wolter, F. (1996b). Tense logic without tense operators. Mathematical Logic Quarterly, 42(1), 145–171.CrossRefGoogle Scholar
Wolter, F. & Zakharyaschev, M. (2006). Modal decision problems. In Blackburn, P., van Benthem, J., and Wolter, F., editors. Handbook of Modal Logic. Amsterdam: Elsevier, pp. 427–489.Google Scholar
Zakharyaschev, M., Wolter, F., & Chagrov, A. V. (2001). Advanced modal logic. In Gabbay, D. M. and Guenthner, F., editors. Handbook of Philosophical Logic, (second edition), Vol. 3. Dordrecht: Springer, pp. 83–266.CrossRefGoogle Scholar